| Issue |
A&A
Volume 667, November 2022
|
|
|---|---|---|
| Article Number | A12 | |
| Number of page(s) | 19 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202243310 | |
| Published online | 28 October 2022 | |
PRODIGE – envelope to disk with NOEMA
I. A 3000 au streamer feeding a Class I protostar★,★★
1
Max-Planck-Institut für extraterrestrische Physik,
Giessenbachstrasse 1,
85748
Garching, Germany
e-mail: mvaldivi@mpe.mpg.de
2
Department of Astronomy, The University of Texas at Austin,
2515 Speedway,
Austin, TX
78712, USA
3
Institut de Radioastronomie Millimétrique (IRAM),
300 rue de la Piscine,
38406
Saint-Martin d’Hères, France
4
IPAG, Université Grenoble Alpes, CNRS,
38000
Grenoble, France
5
Max-Planck-Institut für Astronomie,
Königstuhl 17,
69117
Heidelberg, Germany
6
Laboratoire d’Astrophysique de Bordeaux, Université de Bordeaux, CNRS,
B18N, Allée Geoffroy Saint-Hilaire,
33615
Pessac, France
7
Observatorio Astronómico Nacional (IGN),
Alfonso XII 3,
28014
Madrid, Spain
8
Centro de Astrobiología (CSIC-INTA),
Ctra. Ajalvir km 4, Torrejón de Ardoz,
28850
Madrid, Spain
9
Jesus College, University of Cambridge,
Jesus Lane,
Cambridge
CB5 8BL, UK
10
Institute of Astronomy, University of Cambridge,
Madingley Road,
Cambridge
CB3 0HA, UK
11
Department of Physics and Astronomy, McMaster University,
Hamilton, ON
L8S 4E8, Canada
Received:
11
February
2022
Accepted:
1
August
2022
Context. In the past few years, there has been a rise in the detection of streamers, asymmetric flows of material directed toward the protostellar disk with material from outside a star’s natal core. It is unclear how they affect the process of mass accretion, in particular beyond the Class 0 phase.
Aims. We investigate the gas kinematics around Per-emb-50, a Class I source in the crowded star-forming region NGC 1333. Our goal is to study how the mass infall proceeds from envelope to disk scales in this source.
Methods. We use new NOEMA 1.3 mm observations, including C18O, H2CO, and SO, in the context of the PRODIGE MPG – IRAM program, to probe the core and envelope structures toward Per-emb-50.
Results. We discover a streamer delivering material toward Per-emb-50 in H2CO and C18O emission. The streamer’s emission can be well described by the analytic solutions for an infalling parcel of gas along a streamline with conserved angular momentum, both in the image plane and along the line-of-sight velocities. The streamer has a mean infall rate of 1.3 × 10−6 M⊙ yr−1, five to ten times higher than the current accretion rate of the protostar. SO and SO2 emission reveal asymmetric infall motions in the inner envelope, additional to the streamer around Per-emb-50. Furthermore, the presence of SO2 could mark the impact zone of the infalling material.
Conclusions. The streamer delivers sufficient mass to sustain the protostellar accretion rate and might produce an accretion burst, which would explain the protostar’s high luminosity with respect to other Class I sources. Our results highlight the importance of late infall for protostellar evolution: streamers might provide a significant amount of mass for stellar accretion after the Class 0 phase.
Key words: ISM: kinematics and dynamics / ISM: individual objects: Per-emb-50 / ISM: structure / stars: protostars / stars: formation
The reduced datacubes is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/667/A12
© M. T. Valdivia-Mena et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model.
Open Access funding provided by Max Planck Society.
1 Introduction
The classical picture of star formation allows us to understand the collapse of a dense, individual core through simple physical assumptions, but does not fully explain the current observations of protostars and protoplanetary disks. In general, the classical models consist of a dense, mostly isolated core inside a molecular cloud that undergoes axisymmetric collapse and, due to the conservation of angular momentum, flattens and creates a disk around the central protostar (e.g., Shu 1977; Terebey et al. 1984). The first limitation of the classical models is that they depend on two assumptions: the spherical symmetry of the core collapse and its lack of interaction with material outside the protostar’s natal core. In reality, molecular clouds are asymmetric at all scales (André et al. 2014; Pineda et al. 2022), from the parsec-sized filaments (e.g., Hacar & Tafalla 2011; André et al. 2010), to asymmetric envelopes around protostars (Tobin et al. 2010). Numerical simulations of molecular clouds that follow the collapse of several cores, including turbulence and magnetic fields, can reproduce these observed filaments and asymmetric structures (e.g., Lebreuilly et al. 2021; Kuznetsova et al. 2019; Kuffmeier et al. 2017; Padoan et al. 2014).
A second problem with the standard model of inside-out, axisymmetric collapse of an isolated core is that it predicts a constant mass accretion rate ~ 10−5 M⊙ yr−1 (Stahler et al. 1980), but observed bolometric luminosities in embedded protostars imply accretion rates that are ten to 100 times lower than this value (Kenyon et al. 1990; Evans et al. 2009). This is known as the “luminosity problem”. Proposed solutions to this problem include an initial strong accretion phase followed by an accretion rate decay (Padoan et al. 2014), and strong bursts of accretion during the protostellar phase (Kuffmeier et al. 2018; Zhao et al. 2018; Vorobyov & Basu 2015). These solutions show that the accretion process is asymmetric both in space and time, which is incompatible with fully axisymmetric collapse. Therefore, even if the simple symmetric model allows for a comprehension of isolated sources, it does not capture all the phenomena that affect the star formation process.
Recently, numerical simulations have shown that the local environment surrounding the protostar has a deep impact on its evolution (Hennebelle et al. 2020; Kuffmeier et al. 2018, 2017; Padoan et al. 2014). In particular, simulations focusing on star and disk formation repeatedly find asymmetric flows toward the disk (e.g., Wurster et al. 2019; Kuznetsova et al. 2019; Kuffmeier et al. 2019, 2017). These long, thin inflows, called streamers, can deliver mass from outside the natal core to increase the available mass for the protostar (Pelkonen et al. 2021) and might have effects on the structure of protoplanetary disks (Kuffmeier et al. 2017). All these simulations show that the collapse from core to protostar is more complex than axisymmetric inside-out collapse.
In the last few years, observations have begun to find streamers from envelope to disk scales (see Pineda et al. 2022, and references within). Streamers are found from the highly embedded Class 0 phase (Pineda et al. 2020; Le Gouellec et al. 2019) through the less embedded Class I (Segura-Cox et al., in prep., Chou et al. 2016), all the way to Class II sources (e.g., Ginski et al. 2021; Garufi et al. 2022; Alves et al. 2020; Akiyama et al. 2019; Yen et al. 2019; Tang et al. 2012). They have also been found feeding not only single protostars, but also protostellar binaries, both funneling material toward the inner circumstellar disks (Phuong et al. 2020; Alves et al. 2019; Dutrey et al. 2014) and to the binary system as a whole (Pineda et al. 2020). These structures are observed in a diversity of molecules, such as 12CO (Alves et al. 2020) and HC3N (Pineda et al. 2020), and also in scattered light (Ginski et al. 2021; Akiyama et al. 2019). The first streamer to be characterized using only free-fall motion, and thus confirming it is infalling toward the protostar, is located toward the Class 0 source Per-emb-2 (Pineda et al. 2020). This streamer transports material from outside the dense core (>10 000 au) into the protoplanetary disk and protostar system. The infall rate of this streamer, which describes how much mass is deposited into disk-forming scales, is comparable to the accretion rate toward the protostar, implying that the streamer could change the future protostellar accretion rate by funneling extra material. This streamer was discovered with a carbon-chain species, HC3N, which traces the chemically evolved material better than it traces the more evolved protostellar core seen in N2H+ (Bergin & Tafalla 2007). These objects prove that the environment influences the star’s development and support the results from simulations that state the mass available to the protostar could be coming from further away than the natal core (Pelkonen et al. 2021).
Even though asymmetric infall is a ubiquitous feature in numerical simulations, to the best of our knowledge, only a few streamers have been found, and their infall properties quantified, using either average estimates of infalling material and/or free-fall motion models toward the disk and protostar system (e.g., Ginski et al. 2021; Pineda et al. 2020; Alves et al. 2019). This is where the MPG - IRAM observing program “PROtostars & DIsks: Global Evolution” (PRODIGE, CO-PIs: P. Caselli, Th. Henning) comes in; this program is designed as a coherent study of the physical and chemical properties of young protostellar systems, targeting 32 Class 0 and I sources, and eight Class II protoplanetary disks. One of its goals is to search for material flowing into Class 0 and I sources, and to investigate the mass budget during these phases. PRODIGE observations are done with the IRAM NOrthern Extended Millimeter Array (NOEMA), located at the Plateau de Bure in the French Alps. This program takes advantage of the PolyFix correlator to make an unbiased survey of molecular lines, thus allowing for the search of streamers in multiple chemical tracers.
In this paper, we present new NOEMA 1.3 mm (≈ 220 GHz) observations from the PRODIGE survey of five molecules (H2CO, C18O, 12CO, SO, and SO2) toward the Class I protostar Per-emb-50. Our aim is to characterize the core kinematics around this embedded protostar from approximately 300 au scales out to 3000 au from the source, to investigate how the mass infall proceeds from envelope to disk scales. The paper is divided as follows. Section 2 describes the NOEMA observations, data reduction, and imaging procedures. Section 3 shows the observed structures in each molecular tracer and how we separate the different kinematic components. We discuss how the structures found might affect the protostar and protostellar disk evolution in Per-emb-50, and how they fit in the general star formation paradigm in Sect. 4. We summarize our results in Sect. 5.
2 Observations and data reduction
2.1 Per-emb-50
Per-emb-50 is an embedded Class I protostar, according to its spectral energy distribution (SED) in the near- and mid-infrared (Evans et al. 2009; Enoch et al. 2009). It is located in the active star-forming region NGC 1333, at a distance of 293 pc (Ortiz-León et al. 2018; Zucker et al. 2018), in the Perseus giant molecular cloud. This protostar is approximately 10 times brighter than other Class I sources in the vicinity (Dunham et al. 2015; Enoch et al. 2009) and its protostellar accretion rate is estimated between (1.3–2.8) × 10−7 M⊙ yr−1, also around ten times larger than other Class I sources (Fiorellino et al. 2021). It has a clear outflow observed in 12CO (2-1) emission with an east-west orientation (Stephens et al. 2019).
VLA 8 mm continuum analysis shows a large dust disk in Per-emb-50, with a characteristic radius between 27-32 au (where there is a significant drop in the dust flux profile), and dust mass around 0.28–0.58 M⊙ (Segura-Cox et al. 2016). Radiative transfer models applied to millimeter observations suggest that grain growth has proceeded within the envelope, producing grains with sizes ~100 µm (Agurto-Gangas et al. 2019).
Properties of the protostar and its disk taken from the literature are summarized in Table 1.
2.2 NOEMA observations
The observations were obtained with NOEMA and are part of the MPG-IRAM Observing Program PRODIGE (Project ID L19MB). In this program, we used the Band 3 receiver and the new PolyFix correlator, tuned with a local-oscillator (LO) frequency of 226.5 GHz. PolyFix provides a full 16 GHz of bandwidth at coarse spectral resolution (2 MHz channel width) and is divided into four units (LSB Outer, LSB Inner, USB Inner and USB Outer). Simultaneously, we placed 39 high spectral resolution windows of 62.5 kHz channel resolution within the coarse resolution 16 GHz bandwidth.
Observations of Per-emb-50 were conducted in two separate periods for each antenna configuration. The C configuration data were observed on 29 December 2019 and 5 January 2021. The D configuration observations were taken on 6 August 2020, and on 7 and 8 September 2020. The maximum recoverable scale (MRS) for our data is 16.9″ at 220 GHz, approximately 5000 au at the distance of Per-emb-50.
We calibrated the data using the standard observatory pipeline in the Grenoble Image and Line Data Analysis Software (GILDAS) package Continuum and Line Interferometer Calibration (CLIC). We used 3C84 and 3C454.3 as bandpass calibrators. Phase and amplitude calibration sources were 0333+321 and 0322+222, and observations for these calibrators were taken every 20 min. LKHA101 and MWC349 were used as flux calibrators. The uncertainty in flux density was 10%. The continuum was bright enough to allow for self-calibration. Only for the continuum image used in this work, self-calibration was performed iteratively with solution intervals of 300 s, 135 s, and 45 s. The line observations were not done with self-calibrated data. The resulting continuum image, shown in Appendix A, was done with the lower inner (LI) continuum window and has a noise of 0.2 mJy beam−1.
Continuum subtraction and data imaging were done with the GILDAS package mapping using the uv_baseline and clean tasks. All line cubes were imaged using natural weight to minimize the rms, while the continuum maps were imaged with robust = 1, to improve the angular resolution. We imaged the continuum-subtracted cubes using the standard CLEAN algorithm and a manual mask for each channel. Once we converged to a final mask, we performed a final CLEAN down to the rms level using multiscale CLEAN algorithm implemented in mapping. This had an effect of reducing imaging artifacts (mainly negative emission bowls), thus improving the general image quality around bright sources.
Toward Per-emb-50, we detected 12CO(2–1), C18O(2–1), H2CO(30,3–20,2), SO(55–44) and SO2 (111,11-100,10) line emission. The 12CO(2–1) line is located in the coarse resolution bandwidth, whereas the rest of the lines are inside the highresolution windows. The final line cubes have a beam full width half maximum (FWHM) θ of approximately 1.2″, a primary beam FWHM of 22″ at 220 GHz, a field of view (FoV) of 45.8″ diameter, and a channel spacing of 0.08 km s−1. The effective spectral resolution is approximately 1.7 times the channel spacing. The average rms is around 13 mJy beam−1 or around 400 mK. The resulting properties of each line cube are reported in Table 2.
Properties of Per-emb-50 from the literature.
3 Results
3.1 Streamer in Per-emb-50
The integrated intensity images for H2CO (30,3-20,2) and SO (55–44) are shown in Fig. 1. The former unveils a large streamer in the southwest of the central star, whereas the latter shows extended emission surrounding the protostar. We refer to H2CO(30,3–20,2) as H2CO and SO(55–44) as SO in the rest of this paper. The integrated intensity maps were calculated between 5.5 and 9.5 km s−1 in the case of H2CO, and between −1 and 14 km s−1 in SO, which are the velocity ranges where all emissions over 3σ in each channel (see Table 2 for σ values) are present for each molecule.
The streamer stretches from the location of the protostar toward the southwest to the edge of the primary beam, with a total length of approximately 3000 au (22″) and a width of approximately 300 au (1″). As the width of the streamer is barely resolved, this width is considered an upper limit. Also, as the streamer reaches up to the primary beam FWHM, it is possible that it extends further, so the length is a lower limit as well. The peak integrated intensity in H2CO presents a signal-to-noise ratio (S/N) of 11. The streamer is detected with an S/N ≥ 6 along its 3000 au length.
This streamer is spatially unrelated to the outflow of Per-emb-50, since the emission does not spatially overlap with the outflow. The left panel of Fig. 1 shows the outflow observed in 12CO(2–1) emission, from the wide-band setup of our NOEMA observations. 12CO is integrated from VLSR = −4 to 4 km s−1 for the blueshifted emission and from 11 to 20 km s−1 for the red-shifted emission. The outflow, previously observed by Stephens et al. (2019), is in the east-west direction, whereas the H2CO streamer extends in the northeast-southwest direction.
Outside the primary beam and to the southwest of Per-emb-50, there is also enhanced H2CO and SO emission. It is difficult to characterize the nature of this structure because it is outside the primary beam, even after primary beam correction; emission in this region might be contaminated by emission from outside our FoV, leaking through the side-lobes of the antenna response pattern. In Sect. 4.1, we discuss the possibility that this emission consists of an extension of molecular emission further away from the protostar.
3.2 Streamer kinematics
We fit a Gaussian to the H2CO line emission without primary beam correction using pyspeckit (see Appendix B for details). The central velocity VLSR and velocity dispersion σv of the Gaussians that best fit the spectrum at each pixel with S/N > 4 are shown in Fig. 2.
H2CO line emission is characterized by mostly blueshifted emission with respect to Per-emb-50’s VLSR (7.5 km s−1, see Sect. 3.3). The velocity of the streamer further away from the protostar consists of mostly constant blueshifted velocities (with VLSR ≈ 7.2 km s−1) and low velocity dispersion of σv = 0.1–0.2 km s−1 Closer to the protostar, between positions 2 and 3 marked in Fig. 2, and shifted to the west with respect to the general direction of the streamer, there is a sudden increase in velocities, from 7.2 to 7.5 km s−1. We refer to this region as the “kink” in the rest of this paper, as it is a kink or bend in the overall shape of the emission and an abrupt break in the velocity distribution. It is improbable that the sudden redshift in velocities is caused by the outflow, as its west side consists of blueshifted emission, whereas the kink in the streamer is redshifted with respect to the rest of the streamer’s velocities. The kink is followed by a reversal back to blueshifted velocities approaching the protostar, in the inner 1000 au. There is a steep velocity (VLSR) gradient, a change of 7.1–6.5 km s−1 in ~750 au, and the velocity dispersion (σv) increases from 0.4 to 0.7 km s−1 in the same region. This gradient suggests that the gas follows infall motions dominated by the central gravitational force of the protostar, disk, and inner envelope.
Properties of the molecular line observations from NOEMA.
 |
Fig. 1 Integrated intensity images of H2CO (30.3–20.2) and SO(55–44), before primary beam correction, are shown on the left and right, respectively. Primary beam FWHM sizes are represented with filled dashed white circles in each image. The blue star represents the location of Per-emb-50. Beam sizes are represented by white ellipses in the bottom left corner of each image. Left: H2CO(30.3–20.2) integrated intensity between 5.5 and 9.5 km s−1. Red and blue contours correspond to the redshifted and blueshifted emisions coming from the outflow, respectively, traced in our wideband 12CO(2–1) emission. Contour levels are shown at 8, 16, and 24 K km s−1. The white contour represents the continuum emission at a 7 mJy beam−1 level (see Fig. A.1). Right: SO (55–44) integrated intensity between −1 and 14 km s−1. |
3.3 Protostellar mass and velocity
The integrated intensity image of C18O (2–1) is shown in the left panel of Fig. 3. We refer to C18O(2–1) as C18O in the rest of this paper, unless otherwise stated. The C18O observations show the most extended emission of our NOEMA observations and have a similar velocity range as SO, between −1 and 14 km s−1. This molecule’s emission closest to the protostar allowed us to determine the protostar’s velocity and mass.
We produced a position-velocity (PV) diagram for C18O along the major axis of the disk in Per-emb-50 found by Segura-Cox et al. (2016; 170° counter-clockwise from north, see Fig. 3). We used the astropy package pvextractor (Ginsburg et al. 2016) to obtain the PV diagram along a path centered on the protostar, spanning a total length of 2400 au and a total width of 1″. The resulting PV diagram in the right panel of Fig. 3 is consistent with rotation, with increasing velocity toward the protostar. The C18O emission might be tracing Keplerian rotation.
Our observations of C18O allowed us to constrain the mass of the protostar. We obtained a central protostellar velocity VLSR of 7.5 km s−1, and a central protostellar mass M* = 1.7 ± 0.2 M⊙ from the C18O PV diagram. For this, we first manually determined the velocity that minimizes the asymmetries in the PV diagram. This resulted in a VLSR = 7.5 km s−1, marked with a horizontal dotted line in Fig. 3. Afterward, we compared the PV diagram with the Keplerian rotation curves produced by the masses previously estimated for Per-emb-50 by Fiorellino et al. (2021) using IR spectroscopy; they obtain a range between 0.5 and 0.7 M⊙ for a star located at the birthline at the HR diagram (using the Palla & Stahler 1993 model) and 1.5–1.9 M⊙ for a 1 Myr old protostar. The Keplerian rotation curves were weighted according to the inclination angle as v = vkep sin(i), where i = 67° (see Table 1, Segura-Cox et al. 2016), with i = 0° corresponding to a face-on disk. The Keplerian rotation curves for a central protostar of 1 Myr present a good correlation with the 3σ contours (σ = 14 mJy beam−1, see Table 2) of the C18O PV diagram. We use the average between the 1 Myr mass upper and lower limits, 1.7 M⊙, and their difference as uncertainty (±0.2 M⊙), for the rest of this work.
 |
Fig. 2 Results of the Gaussian fit to the H2CO line emission toward Per-emb-50. Left: central velocity VLSR and velocity dispersion σv of the H2CO streamer are shown in the top and bottom panels, respectively. These are obtained from the Gaussian model for H2CO emission of each spectra with S/N > 4. The red star represents the central position of Per-emb-50. Black labeled crosses mark the positions where we extract spectra, shown to the right. Dashed black contours correspond to the continuum emission at a brightness level of 7 mJy beam−1 (see Fig. A.1). Dashed white lines represent the primary beam FWHM, centered at the location of Per-emb-50. The beam is drawn in the lower left corners of each image. Right: H2CO spectra at selected positions along the streamer, together with the Gaussian that best fits each spectrum. Blue lines indicate the H2CO spectra and the dashed black lines represent the best fit Gaussian function. The uncertainty in TMB is 0.3 K. The dotted gray line represents the protostar’s Vlsr = 7.5 km s−1. |
3.4 Streamline model
We modeled the kinematics of the streamer observed with H2CO emission to confirm that the velocity gradient observed in H2CO emission is consistent with infall motion, using the analytic solution for material falling from a rotating, finite-sized cloud toward a central object, dominated by the gravitational force of the latter. We used the analytic solutions of Mendoza et al. (2009), previously used by Pineda et al. (2020) on the Per-emb-2 streamer. The model returns the position xi = (x, y, z)i in au and velocity Vi = (vx, vy, vz)i in km s−1 (in Cartesian coordinates) of a parcel of mass along a streamline, where the z-axis is defined along the angular momentum vector of the disk and the x-y plane is the disk plane. The model’s input was the initial position and radial velocity of the parcel of mass within the cloud in spherical coordinates (initial radial distance r0, position angle ϑ0 with respect to the z-axis, inclination angle φ0 which marks the initial angle within the disk plane and radial velocity vr,0), and the initial angular velocity of the cloud Ω0. We also applied two rotations due to the inclination angle i and position angle PA of the disk, to obtain the position and velocity with respect to the observer’s point of view from the disk’s reference system.
The streamline model required as input the central mass that dominates the gravitation of the system. We used the sum of the masses of the protostar, disk, and envelope, Mtot = M* + Menv + Mdisk. We used M* = 1.7 ± 0.2 M⊙ (see Sect. 3.3) and Mdisk = 0.58 M⊙, the upper limit calculated in Segura-Cox et al. (2016). For the envelope mass, we used an upper limit of 0.39 M⊙ and a lower limit of 0.18 M⊙, obtained using the Bolocam 1.1 mm image from Enoch et al. (2006), taking the emission of Per-emb-50 with the disk component removed (see Appendix C for details).
We manually input the initial position (r0, ϑ0 and φ0), velocity vr,0, and inclinations i and PA to find the best parameters. We first assumed that the streamer’s rotation direction, given by i and PA, were the same as the dust disk i and PA from Segura-Cox et al. (2016) (see Table 1). The inclination angle i obtained from the dust disk was degenerate in three-dimensional space (it could be inclined in 67° or −67°). We used the rotation direction given by the C18O PV diagram in Sect. 3.3 and the outflow direction (see the left panel of Fig. 1) to determine that the angular velocity vector of the disk ω points toward the west (in the direction of the blueshifted outflow component) and is inclined toward the observer, thus i = −67°. Then, we attempted to find analytic solutions with other i and PA values. The i and PA from Segura-Cox et al. (2016), and our disambiguation gave the only rotation direction where we could find a solution for the velocity profile of the streamer.
Table 3 lists the parameters that resulted in the analytic solutions for an infalling mass that best reproduce the H2CO line profiles in the image plane and the structure of the velocity along the line of sight. Figure 4 shows the projected trajectory of the streamline model with the best parameters over the central velocity of the Gaussian fit to the H2CO emission, both in the image plane (left panel), and over the kernel density estimate (KDE) of the velocity and projected distance in the data (right panel). We used the KDE implementation in the python package SciPy (Virtanen et al. 2020) over the resulting central velocities obtained in Sect. 3.2. The streamline model is able to reproduce the general shape of the KDE and the acceleration toward the protostar in the inner 1000 au. The model is not able to reproduce the slight discontinuity seen in the KDE at ~1700 au, which is related to the kink feature (see Sect. 3.2). The difference between using the upper and lower limits of the envelope mass was negligible in both the image and velocity planes (red and blue curves in Fig. 4).
The centrifugal radius rc (called ru in Mendoza et al. 2009) given by the parameters in Table 3 is between rc = 238–258 au, using the upper or lower limit for the envelope mass, respectively, both of which are within the beam size. This radius is the limit where the streamer can be modeled as free-falling matter with constant angular momentum, so we interpret this radius as approximately where the streamer deposits its material. This implies that the streamer deposits its mass at a distance about 150 au from the gas disk’s edge, which we estimate has a radius of approximately 90 au using the SO line emission obtained in this work (see Sect. 3.8). We do not use the streamline model solutions for distances smaller than rc, as the model does not include motions within the gas and dust disk.
 |
Fig. 3 C18O integrated emission before primary beam correction alongside its PV diagram. Left: integrated intensity image of C18O between −1 and 14 km s−1. The semitransparent white line represents the position and width of the PV cut, built with the position angle of the disk from Segura-Cox et al. (2016). The white arrow represents the direction of positive offset of the PV cut. The primary beam FWHM size is represented with a dashed white circle. The beam size is represented by a white ellipse in the bottom left corner. Right: PV diagram of the C18O line emission along the indicated PV cut. The horizontal dotted line represents Per-emb-50’s VLSR = 7.5 km s−1. The vertical dotted line marks the central position of Per-emb-50. The PV diagram has an rms of 0.01 Jy beam−1. Intensity contours are placed at 5, 15, and 25 times the rms. The blue and black curves represent the Keplerian rotation curve for the minimum and maximum stellar mass, respectively, from Fiorellino et al. (2021): the solid lines represent masses calculated assuming the star is located at the birthline of the Palla & Stahler (1993) model (0.53–0.70 M⊙), whereas dashed lines represent the masses calculated for a 1 Myr protostar (1.52–1.90 M⊙). Velocities are weighted according to the inclination angle as v = vkep sin(i). The preferred Keplerian curve is the average between the dashed curves, with a mass of 1.7 M⊙. The scalebar in the top left represents a distance of 300 au, equivalent to the resolution of the NOEMA data. |
Parameters of the streamline model that reproduce best the H2CO observations.
 |
Fig. 4 Central velocity of the best fit for each spectra in the H2CO line emission, together with the streamline model for H2CO. The red and blue lines represent the best streamline model for an envelope mass of 0.18 M⊙ (total central mass of 2.47 M⊙) and 0.39 M⊙ (total mass of 2.68 M⊙), respectively. Left: central velocities with respect to position in the sky. The black polygon represents the region where velocities are sampled to build the kernel density estimation (KDE). The primary beam FWHM size is represented with a dashed white circle. The beam size is represented by a black ellipse in the bottom left corner. Right: central velocity KDE as a function of projected distance to Per-emb-50 is plotted in grayscale. The KDE levels are drawn from 0.5σ in steps of 0.5σ, where the σ level is equivalent to the standard deviation of a normalized bivariate normal distribution. The horizontal dashed line represents the central velocity of Per-emb-50 VLSR = 7.5 km s−1. The centrifugal radius resulting from each envelope mass are located below the curve. |
3.5 Streamer mass
We calculated the streamer’s mass and infall rate using the primary beam corrected C18O emission in the area where the streamer was detected in H2CO emission, as we could convert C18O emission to gas emission with simple assumptions. We used the primary beam corrected emission because we used the intensity of the C18O line, which we obtained by multiplying the map by the primary beam response, whereas in Sect. 3.2 we only needed the central velocity and velocity dispersion of each spectrum to characterize the streamer’s kinematics.
The C18O emission is the most extended of all the molecular transitions used in this work, as it traces not only the gas in the streamer, but also the extended gas in the inner envelope and the filament in which the protostar is embedded, which has a larger extension than the FoV. Nevertheless, the streamer is easily detected in C18O, with a S/N ≈ 10 at the streamer’s tail. The C18O emission shows a similar structure as in the H2CO map. We could not characterize the C18O extended emission and kinematics outside of the streamer as we lacked zero-spacing data, and we see some negative bowls in the image (see the black areas in the right panel of Fig. 3), indicating missing flux from larger scales. Therefore, for this work we use C18O emission to describe the protostar’s and the streamer’s masses only.
The C18O emission shows a similar central velocity as H2CO at the streamer’s tail but a different velocity distribution at the position of the protostar, as shown in Fig. 5. We used the same procedure for H2CO to obtain the best Gaussian that fits the spectrum of each pixel with S/N > 4, described in Appendix B. Where the emission is coincident with H2CO, C18O is well described with one Gaussian component that shares the same Vlsr and σv as the H2CO emission (a comparison can be made between Figs. 2 and 5). The kink in velocities observed in the middle of the streamer is also observed in C18O. Surrounding the protostar, outside of the area traced by the continuum, there is blueshifted emission toward the northwest and redshifted emission toward the east. These emissions probably trace a mixture of part of the inner envelope and disk rotation, and the inner section of the outflow, as it follows the same east-west direction as the 12CO outflow detected by Stephens et al. (2019). Therefore, it is safe to use C18O emission within the region used to characterize the streamer’s kinematics (black polygons in Figs. 2 and 5) to determine the streamer’s mass.
We obtained a mass lower limit for the streamer within the region drawn in Figs. 2 and 5. We detail the reasons why this is a lower limit in Sect. 4.1. We calculated the mass within the streamer assuming that C18O is optically thin, under local thermodynamic equilibrium (LTE), and that the streamer has a constant temperature Tex. We used the values in the vicinity of Per-emb-50 in Friesen et al. (2017) and Dhabal et al. (2019), which are between 10 and 20 K, and thus we assumed Tex = 15 ± 5 K. First, we obtained the column density of the C18O molecule, N(C18O), using the primary beam corrected C18O image. We explain the details of this procedure in Appendix D. The C18O column density is around 2.8 × 1015 cm−2 within 1000 au of the protostar, then it falls to ≈ 8.0 × 1014 cm−2 and in the outer 1500 au it reaches up to 3.6 × 1015 cm-2. Afterward, we transformed N(C18O) to molecular Hydrogen column density N(H2) using 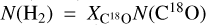 . We used the canonical ratio
. We used the canonical ratio 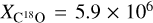 (Frerking et al. 1982). Finally, we obtained the gas mass in the streamer using:
(Frerking et al. 1982). Finally, we obtained the gas mass in the streamer using:
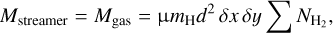 (1)
(1)
where 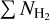 is the sum of
is the sum of 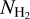 in the streamer in cm−2, d is the distance to the protostar in cm, δx δy is the size of the pixels in radians, µ = 2.7 is the molecular weight of the gas, considering the contribution from H2, He and heavy elements, and mH is the H atom mass. We used d = 293 ± 22 pc, the distance to NGC 1333 (Ortiz-León et al. 2018, see Table 1).
in the streamer in cm−2, d is the distance to the protostar in cm, δx δy is the size of the pixels in radians, µ = 2.7 is the molecular weight of the gas, considering the contribution from H2, He and heavy elements, and mH is the H atom mass. We used d = 293 ± 22 pc, the distance to NGC 1333 (Ortiz-León et al. 2018, see Table 1).
We obtained a lower limit for the total mass of the streamer Mstreamer = 1.2 × 102 M⊙, with an uncertainty of 15% due to uncertainties in flux calibration and in the distance to NGC 1333 (see Table 1).
 |
Fig. 5 Velocity VLSR and velocity dispersion σv of the best Gaussian fit for C18O emission. Gaussian fits are only done for spectra with S/N > 4. The primary beam FWHM size is represented with a white dashed circle. The beam size is represented in a white ellipse in the bottom left corner. Top: central velocity of the best fit Gaussian profile for each spectrum. The black contour shows the same region plotted in the right panel of Fig. 2, from where the mass is calculated. Bottom: velocity dispersion of the best fit Gaussian profile for each spectrum. |
3.6 Streamer infall rate
We calculated the mean infall rate and the infall rate along the streamer using the mass obtained in Sect. 3.5, and compared it to the protostellar accretion rate. In this work, there are two different rates: the infall rate 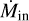 , which is the rate at which mass is deposited from the envelope to the disk scales; and accretion rate
, which is the rate at which mass is deposited from the envelope to the disk scales; and accretion rate 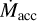 , which is the rate at which the protostar is accreting mass.
, which is the rate at which the protostar is accreting mass.
The free-fall timescale of the streamer, assuming the classic free-fall time equation,
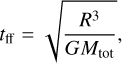 (2)
(2)
is 21.3 ± 0.8 kyr for an envelope mass of 0.18 M⊙ (Mtot = 2.47 M⊙), and 20.5 ± 0.7 kyr for Menv = 0.39 M⊙ (Mtot = 2.68 M⊙). In Eq. (2), Mtot is the total mass within a distance R = r0 = 3300 au from the protostar (obtained from the streamline model in Sect. 3.4), and G is the gravitational constant. We divided the total mass with the free-fall timescale to obtain an average 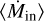 between (5.4–5.6) × 10−7 M⊙ yr−1. The upper limit is plotted as a dotted line in Fig. 6.
between (5.4–5.6) × 10−7 M⊙ yr−1. The upper limit is plotted as a dotted line in Fig. 6.
Since we constrained the streamer’s kinematics (see Sect. 3.4) and its column density at each position, we then derived the infall rate at every position of the streamer. We first calculated the free-fall timescale tff,model and average infall rate 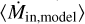 using the analytic solutions from Sect. 3.4 to compare it to the classical free-fall timescale
using the analytic solutions from Sect. 3.4 to compare it to the classical free-fall timescale 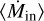 . For this, we calculated the travel time along the streamer by using the streamer’s trajectory and velocities from the streamline model, from r0 = 3300 au to the centrifugal radius, which we assumed is the landing point (we used rc = 238 au). We obtained a total free-fall time of 8.7 kyr for Menv = 0.18 M⊙ and 8.6 kyr for Menv = 0.39 M⊙, around two times lower than the times calculated previously, because the classic free-fall timescale (Eq. (2)) does not consider that the streamline already has an initial velocity toward the protostar at R. The resulting infall rate is
. For this, we calculated the travel time along the streamer by using the streamer’s trajectory and velocities from the streamline model, from r0 = 3300 au to the centrifugal radius, which we assumed is the landing point (we used rc = 238 au). We obtained a total free-fall time of 8.7 kyr for Menv = 0.18 M⊙ and 8.6 kyr for Menv = 0.39 M⊙, around two times lower than the times calculated previously, because the classic free-fall timescale (Eq. (2)) does not consider that the streamline already has an initial velocity toward the protostar at R. The resulting infall rate is 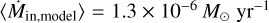 for both envelope masses. The average
for both envelope masses. The average 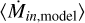 using the streamline model is plotted as a dashed line in Fig. 6. The mass and average infall rates found for the streamer are summarized in Table 4.
using the streamline model is plotted as a dashed line in Fig. 6. The mass and average infall rates found for the streamer are summarized in Table 4.
We also studied how the infall rate changes along the streamer, to determine if there are significant differences in the infall rate within the streamer. The left panel of Fig. 5 shows that molecular emission is clumpy on scales of the beam size, which suggests that there might be small-scale variations along the streamer. We separated the streamer into radial bins and obtained the mean three-dimensional distance to the protostar rbin, the total mass Mbin, the time taken to traverse the bin ∆tbin, and the infall rate 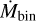 in each bin. The bins were 360 au wide (which is the major axis FWHM of the beam) and consisted of all pixels that were within a certain range of projected distances [r, r + 360] au from Per-emb-50. We sampled every 120 au (one-third of the major axis of the beam) from 200 au to 3300 au from the protostar, in projected distance. The resulting mass, crossing time, and infall rates for each bin are shown in Fig. 6.
in each bin. The bins were 360 au wide (which is the major axis FWHM of the beam) and consisted of all pixels that were within a certain range of projected distances [r, r + 360] au from Per-emb-50. We sampled every 120 au (one-third of the major axis of the beam) from 200 au to 3300 au from the protostar, in projected distance. The resulting mass, crossing time, and infall rates for each bin are shown in Fig. 6.
We calculated rbin as the distance of the streamline model point that is closest to the center of mass of the bin in the image plane. We used N(C18O) to find the center of mass within each bin and then find the point in the streamline model closest to it. Then, the distance rbin is the three-dimensional distance between that point and the protostar. We express this distance as the freefall timescale from rbin using:
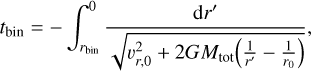 (3)
(3)
where vr,0 is the initial velocity (1.25 km s−1) at r0 (3300 au) from the streamline model toward the direction of the protostar. The integral is done numerically using the python package SciPy function integrate. The difference between the solution of Eq. (3) and the free-fall timescale given by the streamline model is less than 20 yr, which is negligible for the timescales we are working with.
We computed the infall rate of the streamer using the mass within each bin Mbin and the bin’s crossing time ∆tin. Mbin is calculated using Eq. (1), adding 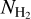 in all pixels that belonged to the bin. We then calculated ∆tbin the same way as the total free-fall timescale, but adding up the time obtained from the trajectory and velocities within the bin only. The infall rate for each bin is therefore
in all pixels that belonged to the bin. We then calculated ∆tbin the same way as the total free-fall timescale, but adding up the time obtained from the trajectory and velocities within the bin only. The infall rate for each bin is therefore 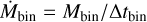 .
.
The infall rate along the streamer is consistently larger or equal to the accretion rate estimated for Per-emb-50, independent of the variations along the streamer. Figure 6 shows the resulting Mbin, Δtbin, and 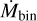 with respect to the distance to the protostar rbin, and compares the infall rates
with respect to the distance to the protostar rbin, and compares the infall rates 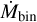 with the accretion rates
with the accretion rates 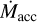 for Per-emb-50 estimated in Fiorellino et al. (2021). The average
for Per-emb-50 estimated in Fiorellino et al. (2021). The average 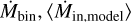 , estimated using the streamline model is between 5 and 10 times larger than the
, estimated using the streamline model is between 5 and 10 times larger than the 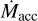 estimated for a 1 Myr protostar ((1.3–2.8) × 10−7 M⊙ yr−1), and just above the upper limit for the
estimated for a 1 Myr protostar ((1.3–2.8) × 10−7 M⊙ yr−1), and just above the upper limit for the 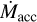 of Per-emb-50, assuming it is located at the birthline of the Palla & Stahler (1993) model (1.2 ×10−6 M⊙ yr−1). The protostellar mass calculated in Sect. 3.3 is consistent with a 1 Myr protostar, so likely the accretion rate is the former, resulting in
of Per-emb-50, assuming it is located at the birthline of the Palla & Stahler (1993) model (1.2 ×10−6 M⊙ yr−1). The protostellar mass calculated in Sect. 3.3 is consistent with a 1 Myr protostar, so likely the accretion rate is the former, resulting in 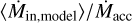 .
.
Therefore, the streamer is feeding more than enough mass to sustain the accretion rate of the protostar, and according to our total free-fall time, we can expect a similar infall rate for at least the next 8.7 kyr.
The mass per bin varies from 6 × 10−4 to 2 × 10−3 M⊙ from bin to bin. This variation drives the fluctuations observed in the infall rates, which are within a factor of three, with minima located at ~ 1000 and ~2000 au. Nevertheless, these variations are small and the streamer shows a consistently high infall rate along its full length, reflected in 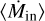 . The fluctuations are present in spatial scales larger than 300 au, so these are not affected by the resolution limit. The mass variations might be because the streamer is clumpy, with changes in scales smaller than our 300 au resolution. On the other hand, the MRS of the data is around 22″, but the data are already less sensitive to extended emission before reaching that distance, at around 4″. Thus, the apparent minima in the infall curve of Fig. 6 might be explained by a decreased sensitivity to extended sources.
. The fluctuations are present in spatial scales larger than 300 au, so these are not affected by the resolution limit. The mass variations might be because the streamer is clumpy, with changes in scales smaller than our 300 au resolution. On the other hand, the MRS of the data is around 22″, but the data are already less sensitive to extended emission before reaching that distance, at around 4″. Thus, the apparent minima in the infall curve of Fig. 6 might be explained by a decreased sensitivity to extended sources.
 |
Fig. 6 Mass, timescale, and infall rate with respect to the distance to the protostar along the streamline. Δtin is obtained from the model with Menv = 0.39 M⊙. The dotted line represents the mean infall rate obtained with the free-fall timescale from rest, |
3.7 Asymmetries in SO and SO2 emission
The right panel of Fig. 1 shows the SO integrated emission obtained with NOEMA. Unlike H2CO and C18O, SO emission in Per-emb-50 is brightest at about 150 au south of the protostar, and extended out to around 1000 au from it (see also Fig. B.1). The southern part of the SO emission overlaps with the brightest H2CO emission. It also presents emission at ≳3000 au from the protostar, but since this emission lies outside the primary beam, we will not describe it further in this work. SO is known to be a tracer of cold, dense gas (e.g., Swade 1989; Hacar & Tafalla 2011) and it is sublimated from dust grains by sufficient heating, for example, by accretion shocks around the centrifugal barrier (e.g., Sakai et al. 2014; van Gelder et al. 2021). SO is found in young, embedded sources, but it is harder to detect in T Tauri disks (Guilloteau et al. 2016; Dutrey et al. 2011), suggesting an increasing S depletion with disk age. This hints that SO traces the dense inner envelope and gas disk around the protostar.
We used SO2 (111,11–100,10) emission to aid in the interpretation of the SO emission. The SO2 integrated intensity image is shown in Fig. E.1, together with selected spectra. SO2 emission is compact and peaks at the south of Per-emb-50, close to where H2CO emission ends. Its peak is at the same location as the SO peak, but its emission is approximately five times weaker than SO. The SO2 molecule is a known shock tracer as it can trace warm areas in accretion shocks (van Gelder et al. 2021), in particular at the disk-envelope surface (e.g., Artur de la Villarmois et al. 2019). This suggests that the SO2 emission in the south of Per-emb-50 might trace shocked material, probably due to either the streamer impacting zone or another phenomena.
We generated the PV diagrams of SO and SO2 line emission along the same cut done for C18O in Sect. 3.3 to investigate the kinematics that these molecular lines trace. The resulting PV diagrams are shown in Fig. 7. The shapes of both PV diagrams differ from the C18O PV diagram (see Fig. 5), indicating that these molecules trace different kinematic components. SO has a skewed diamond-shaped emission, with both blueshifted and redshifted components at the north and south parts of the cut, which suggests a mixture of infall and rotation motions, whereas C18O has a bowtie shape consistent with motion dominated almost entirely by Keplerian rotation. Additionally, the brightest SO emission comes from redshifted velocities both toward the north and south of Per-emb-50, whereas blueshifted emission comes almost fully from the northern side of the inner envelope. Unlike SO, SO2 emission is only present around the peak, with no recognizable characteristic shape and it barely presents emission over 3σ at blueshifted velocities. Both diagrams peak at the same position, within the inner 300 au from the protostar toward the southeast, and in velocity, at approximately 9.5 km s−1. The shape of these two molecules’ emissions suggests that they follow motions that are asymmetric in the north-south direction.
We fit the “toy model” for infall and rotation motion from Sakai et al. (2014) to the SO PV diagram to investigate if the diamond shape is consistent with the rotation and infall kinematics of a flattened inner envelope. The free parameters in this model were the centrifugal radius of the material in the envelope rc,env (not to be confused with the centrifugal radius of the streamer, rc) and the mass of the central object Mtot. The best fit curves from this toy model are plotted in red and blue for the redshifted and blueshifted sides, respectively, overlaid on top of the SO PV diagram in Fig. 7. The model had to be divided in two parts to be able to reproduce the shape of the diagram: the redshifted and blueshifted side were best fitted with a different set of parameters. The redshifted side was best fitted with a toy model with Mtot,r = 4 M⊙ and rc,env,r = 130 au, whereas for the blueshifted side, Mtot,b = 2.9 M⊙ and rc,env,b = 100 au. Therefore, SO molecular emission traces asymmetric kinematics in the inner envelope consistent with infall and rotation, where the redshifted emission (which is brighter) possesses a different motion than the blueshifted side. The fact that the masses Mtot,r and Mtot,b are higher than the protostellar mass we determined kinematically (1.7 M⊙, see Sect. 3.3), plus the fact that they are different, suggests that the model does not capture all the kinematic phenomena in the envelope. These results lead us to investigate the SO emission in more detail.
 |
Fig. 7 Position-Velocity diagram of SO(55–44) (colored and black contours) and SO2(white contours) line emission along the position angle of the disk from Segura-Cox et al. (2016), plotted along the same offset scale as the right panel of Fig. 3. Negative offsets represent distances toward the north and positive offsets toward the south. The horizontal dotted line represents Per-emb-50’s VLSR = 7.48 km s−1. The vertical dotted line marks the central position of Per-emb-50. Both PV diagrams have an rms of 0.01 Jy beam−1. Intensity contours for SO are placed at 3, 5, 15, 25, 35, and 45 times the rms, whereas SO2 intensity contours are placed at 3, 5, and 10 times the rms. The red and blue solid curves show the model of rotation and infall that best match the SO for the redshifted and blueshifted velocities with respect to the protostar, respectively. The scalebar in the top left represents a distance of 300 au, equivalent to the resolution of the NOEMA data. |
3.8 Gaussian components of SO emission
The complex shape of the SO PV diagram, the strong peak at redshifted velocities, and the fact that it can be fitted with the Sakai et al. (2014) toy model with two different sets of parameters for the redshifted and blueshifted parts, suggest that there are at least three components being traced: rotation, infall, and a bright redshifted component. We separated the different kinematic components through Gaussian spectral fitting of SO to study them separately.
We fit one, two, and three Gaussians to the SO spectrum of each pixel with S/N > 4 using the same method for H2CO and C18O emission, described in Appendix B. Figure B.1 shows four spectra in different regions with their respective best fit curves. Most of the SO spectra required two Gaussians, or in some cases, three Gaussians to be reproduced. For each pixel, we evaluated how much improvement we obtained by adding a second and third Gaussian using the Akaike information criterion (AIC, see Appendix B for details). With the decomposed spectra, we investigated the separate physical components of SO emission that can be described using each Gaussian.
We find four signature components in SO emission: one consistent with inner envelope rotation, a compact feature around the protostar with a large velocity dispersion (σv > 2 km s−1), a third component consistent with the streamer’s kinematics from Sect. 3.1, and a fourth component completely redshifted with respect to Per-emb-50. We separated each of the components using the following steps. First, all Gaussian curves that had a velocity dispersion σv > 2 km s−1 correspond to the broad feature, which is consistent with marginally resolved disk rotation. Then, all Gaussians with σv < 2 km s−1 that had a central velocity VLSR > 8.1 km s−1 correspond to the bright, redshifted component. Third, the Gaussians left that had VLSR < 7.2 km s−1 and were located at a lower declination than +31°21′57.6″ are consistent with the streamer. Finally, all pixels left contain only one Gaussian curve, which had a central velocity map consistent with inner envelope rotation.
The central velocity VLSR of the four separated components are shown in Fig. 8. We show the best fit velocity dispersion for each component in Appendix F. Figure B.1 shows the components in selected SO spectra.
The inner envelope rotation component contributes to the diamond shape shown in the PV diagram in Fig. 7, with the blueshifted emission on the northern side and the redshifted emission on the southern side. This rotation component is resolved in our observations, extending by a factor of approximately 2 farther in radius than the continuum emission (see the top left panel in Fig. 8), so it does not correspond to disk rotation, and has the same rotation direction shown in our C18O data (see Fig. 3).
Within the continuum emission contour, the SO spectra present emission fitted with Gaussians with blueshifted and redshifted velocities with respect to Per-emb-50, and with σv > 2 km s−1 (see the top right panels in Fig. 8 and in Fig. F.1). The observed gradient in its central velocities is consistent with rotation kinematics, with the same rotation direction suggested by the C18O PV diagram (see Fig. 3) and the inner envelope rotation. However, as this component only emits within the continuum emission, we assume this gas belongs to the gas disk only, unlike C18O which also traces the flattened inner envelope rotation. Using the stellar mass obtained in Sect. 3.3 and the velocity dispersion from this SO component, we estimate the radius of this compact component assuming it traces Keplerian rotation and that at the disk edge the Keplerian velocity is vk ~ σv ≈ 4 km s−1. This estimate returns a disk radius of approximately 90 au. Therefore, this component is consistent with a gas disk around the protostar.
Toward the south of Per-emb-50, one of the fitted Gaussian components is consistent with the streamer structure found in H2CO, both in position in the sky and velocity (a comparison can be made between Fig. 2 and the bottom left panel in Fig. 8). This component is clearly separated from all other components in the south as it is blueshifted with respect to the protostar’s VLSR, whereas the other component close-by (inner envelope rotation) is redshifted (see Fig. 8 and the left panel in Fig. B.1). This component’s SO spectra shows the same central velocity as H2CO (see spectrum d in Fig. E.1) and acceleration toward blueshifted velocities found in the H2CO Gaussian fitting (see the bottom left panel in Fig. 8). SO traces only the inner 1000 au of the streamer, likely tracing its denser regions.
The fourth component found through Gaussian decomposition is strongly redshifted with respect to the protostar (see the bottom right panel in Fig. 8). This component has a larger velocity close to the center of the continuum emission (around 9.5 km s−1) and decreases radially (to approximately 8.0 km s−1). Its radial velocity gradient is not consistent with the direction of the outflow or the streamer. We propose that this component might trace another asymmetric infall, located along the line of sight. This infall is asymmetric as we do not see a strongly blueshifted counterpart (VLSR < 7 km s−1) covering a similar area, expected for an axisymmetric infall. The only strongly blueshifted component is very thin and located in the same area as the streamer. With the present observations, we do not have enough spatial resolution to characterize this infall further.
 |
Fig. 8 Best fit central velocity maps for the four signature components found in SO (55–44) emission in the inner 1000 au of Per-emb-50’s envelope. Examples of the individual spectra decomposition for each of these components are shown in Fig. B.1. Solid black contours represent the integrated intensity of H2CO emission at three and five times the rms of the integrated intensity map (0.25 K km s−1). Dashed black contours mark the continuum emission at a 7 mJy beam−1 level (see Fig. A.1). The red and blue arrows indicate the outflow direction determined by the redshifted and blueshifted CO (2–1) emissions, respectively, from Stephens et al. (2019). The clean beam is represented as a black ellipse in the bottom left corner of all of the images. It should be noted that the velocity ranges plotted in each figure are different, which is why the figures on the right have a different color scheme. Top left: inner envelope rotation. Top right: broad feature (σv > 2 km s−1). Bottom left: streamer. Bottom right: redshifted component. |
4 Discussion
4.1 Understanding why mass and infall rate are lower limits
The estimated mass of the streamer (see Sect. 3.5) is a lower limit because of observational limits in our data and the assumptions made in the mass calculation. We estimated the length of the streamer as 3300 au, using H2CO emission and the streamline model. This is possibly not the full length of the streamer for three reasons. First, the H2CO emission is cut off by the primary beam of the NOEMA observations (22″), and our observations are not sensitive to strong emission beyond this radius. Second, there is a strong offset emission toward the southwest of Per-emb-50, located just outside the primary beam at ~3000 au, seen in all of the molecular tracers used in this work (see Figs. 1 and 5). Moreover, there is significant C18O emission observed in the SMA MASSES program (Stephens et al. 2019) in the same location as the H2CO streamer, which extends to a bright emission located beyond the streamer’s observed extent in this work. Third, the streamline model requires an initial velocity vr,0 = 1.25 km s−1 in the direction of the protostar to fit the outer 1500 au of the streamer (see Table 3). The initial velocity might indicate that the streamer starts farther away and was already infalling by the time it reached r0.
Another observational limitation is the lack of zero-spacing data. C18O emission is extended and the observations have no sensitivity to scales larger than the MRS (22″), but our observations start losing sensitivity to scales larger than 4″ due to the coverage in u-v space. Therefore, we are not certain if the clumpiness observed in C18O is real or if it is influenced by missing flux due to lack of zero-spacings.
The main assumptions that we used in the streamer’s mass calculation were, first, a fixed ratio between column densities, which is suitable for an undepleted gas, 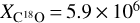 (Frerking et al. 1982), and second, a constant excitation temperature Tex. Most likely,
(Frerking et al. 1982), and second, a constant excitation temperature Tex. Most likely, 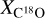 is not constant along the streamer. Within the dense core, it is more probable that there is a larger C18O depletion into grains due to an increase in density (see Bergin & Tafalla 2007, and references within). Where C18O is depleted,
is not constant along the streamer. Within the dense core, it is more probable that there is a larger C18O depletion into grains due to an increase in density (see Bergin & Tafalla 2007, and references within). Where C18O is depleted, 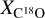 should be higher to estimate the mass correctly. Also, this conversion factor was calibrated using Taurus molecular clouds, and might differ in Perseus. Pineda et al. (2008) show that there is variation in the conversion factors of the C18O(1–0) line in different regions in Perseus. Furthermore, a constant Tex along the streamline is unlikely; the temperature might be higher closer to the protostar due to thermal heating. This is also suggested by the presence of SO2 emission toward the south of Per-emb-50. Unfortunately, we do not have a good estimation of the gas temperature in the vicinity of Per-emb-50. NH3 is a commonly used chemical thermometer, combining the (1,1) and (2,2) inversion transitions, both observed in NGC 1333 with Green Bank Telescope (GBT, Friesen et al. 2017). Although the NH3(1,1) line is present in Per-emb-50, the NH3(2,2) line is too faint to be detected around the protostar and provide a gas temperature estimation. Higher spatial resolution observations of both NH3 lines do not detect emission in this region (Dhabal et al. 2019). Instead, we used the values in the vicinity of Per-emb-50 in Friesen et al. (2017) and Dhabal et al. (2019), which are between 10 and 20 K. The variance in Tex adds less than 5% of the total uncertainty, and therefore it does not dominate the uncertainties.
should be higher to estimate the mass correctly. Also, this conversion factor was calibrated using Taurus molecular clouds, and might differ in Perseus. Pineda et al. (2008) show that there is variation in the conversion factors of the C18O(1–0) line in different regions in Perseus. Furthermore, a constant Tex along the streamline is unlikely; the temperature might be higher closer to the protostar due to thermal heating. This is also suggested by the presence of SO2 emission toward the south of Per-emb-50. Unfortunately, we do not have a good estimation of the gas temperature in the vicinity of Per-emb-50. NH3 is a commonly used chemical thermometer, combining the (1,1) and (2,2) inversion transitions, both observed in NGC 1333 with Green Bank Telescope (GBT, Friesen et al. 2017). Although the NH3(1,1) line is present in Per-emb-50, the NH3(2,2) line is too faint to be detected around the protostar and provide a gas temperature estimation. Higher spatial resolution observations of both NH3 lines do not detect emission in this region (Dhabal et al. 2019). Instead, we used the values in the vicinity of Per-emb-50 in Friesen et al. (2017) and Dhabal et al. (2019), which are between 10 and 20 K. The variance in Tex adds less than 5% of the total uncertainty, and therefore it does not dominate the uncertainties.
Given that the mass and mass infall rates we report are lower limits, the general results of this paper are strengthened: the streamer delivers more than enough mass toward the protostellar disk to sustain its high accretion rate in comparison with its neighbors (see Sects. 3.5 and 4.4). If the streamer masses or infall rates are actually higher, this streamer can deliver even more mass than what we report here.
4.2 Classical free-fall time versus the streamline model
For the first time, we calculated the infall timescales along a streamer using the streamline model based on the analytical solution from Mendoza et al. (2009). We show that in Per-emb-50, where the streamline model requires an initial radial velocity, the infall rate is underestimated by at least a factor of two when calculated with the classic – and initially static – free-fall timescale. The factor by which the timescale is underestimated depends on the initial velocity of the streamer: if the streamer presents an initial impulse at the starting radius r0, it will take less time to reach the protostellar disk than if the streamer started from rest. The streamline model allows us to estimate the initial radial velocity. This highlights the importance of the use of a streamline model to calculate the timescales involved in infall.
The calculation of the initial radial velocity (and consequently, the infall rate) relies on a streamer model that has good constraints both spatially in the image plane and kinematically in the velocity along the line of sight. If the streamer is fully contained along the line of sight, the velocity is correctly characterized, but we do not have information about the length of the streamer. On the other hand, if the streamer moves completely within the plane of the sky, there is information about the length and path of the streamer, but the velocity cannot be characterized. Fortunately, in the case of Per-emb-50, the streamer is mostly contained in the plane of the sky, with a small inclination at the start of the streamline (approximately 10° according to the streamline model in Sect. 3.4), and it becomes more inclined with respect to the line of sight where we see the acceleration closer to the disk. This allows us to sample both the distance (up to the primary beam edge) and the velocity, and therefore constrain the initial radial velocity.
4.3 Streamer is landing within disk scales
Our results indicate mass is infalling to disk scales (which corresponds to distances of ~ 100–200 au), both in the case of the streamer and the asymmetric infall seen in the redshifted component of SO emission (see Sect. 3.8). We can model the streamer down to ≈250 au from the edge of the gas disk (see Sect. 3.4) and the toy model in Sect. 3.7 has a centrifugal radius between 100 and 130 au, similar to the 90 au of the gas disk. It is possible that SO2 traces the impact zone where gas is infalling, either that of the streamer or the redshifted SO component. H2CO and SO emission that trace the streamer end within a beam size of the location of the SO2 peak emission (located at ~150 au, see Fig. E.1). This is compatible with the centrifugal radius of ≈250 au (see Sect. 3.4) obtained for the streamline model, as the emission is seen in projected distance and rc is a three-dimensional distance. According to the streamline model, the impact velocity component along the line of sight at the assumed impact location (rc) is 1.7 km s−1. The FWHM of the SO2 emission spectra at the location of the streamer’s end is similar to the estimated impact velocity, suggesting that the impact of the streamer is responsible for the SO2 velocity dispersion. However, SO2 peaks at the same velocity as the strong, redshifted component, which could be attributed to another asymmetric infall, and at the peak location, both have the same shape (see the top right panel of Fig. E.1). Therefore, it is unclear which infalling feature most influences the SO2 emission.
One interesting result is that the centrifugal radius of the streamer rc (~250 au, see Sect. 3.4) is about twice the centrifugal radii obtained for the rotating-infalling envelope, rc,env,r = 130 au and rc,env,b = 100 au (see Sect. 3.7). This suggests that the streamer and envelope have different origins and that the streamer might come from outside the dense core. The streamer component seen in the SO emission might indicate the entrance of the streamer to the inner envelope, where the latter is flattened and has a rotating and infalling motion of its own (represented by the redshifted component in Sect. 3.8). For the streamer material to reach the centrifugal radius of the inner envelope, which is slightly larger than the gas disk radius (90 au, see Sect. 3.8), and for its material to reach the gas disk, it must lose angular momentum, for example, through magnetic braking (Mestel & Spitzer 1956; Mouschovias & Paleologou 1980; Basu & Mouschovias 1994. Loss of angular momentum of material coming from > 10 000 au has been observed for Class 0 sources by Pineda et al. (2019) down to ~1000 au, becoming low enough to generate a rotationally supported disk in scales < 100 au. Future high-resolution observations can clarify the interaction between the streamer and the inner envelope for Class I sources.
4.4 Relation between streamers and accretion outbursts
The presence of streamers with a high infall rate, such as the one found toward Per-emb-50, are linked to accretion variability and luminosity outbursts. Simulations of turbulent molecular clouds suggest that infall from larger scales regulates the accretion toward the protostar, even in phases later than Class 0 (Padoan et al. 2014; Kuffmeier et al. 2018). In the case presented in this work, the relation between the streamer and an accretion burst (current or future), is supported by the high accretion rate and luminosity of Per-emb-50 in comparison with other Class I protostars, as well as other asymmetric structures found toward current (and past) outbursting sources.
The streamer feeding Per-emb-50 might explain the high accretion rate of this protostar in comparison to other Class I sources in NGC 1333. Its 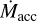 is ~10× higher than for other Class I sources in NGC 1333 (Fiorellino et al. 2021), and the infall rate provided by the streamer five to ten times larger than
is ~10× higher than for other Class I sources in NGC 1333 (Fiorellino et al. 2021), and the infall rate provided by the streamer five to ten times larger than 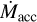 (see Sect. 3.6), more than enough to replenish the mass consumed by accretion. The luminosity (between 10 and 25 L⊙, Enoch et al. 2009; Dunham et al. 2015) and accretion rate are consistent with those of Class Is undergoing an accretion burst (Hsieh et al. 2019). However, Per-emb-50’s envelope mass is similar to those around other Class I objects (at 2.2 M⊙, Enoch et al. 2009; Agurto-Gangas et al. 2019), and the streamer might be the key ingredient to sustaining Per-emb-50’s high accretion rate.
(see Sect. 3.6), more than enough to replenish the mass consumed by accretion. The luminosity (between 10 and 25 L⊙, Enoch et al. 2009; Dunham et al. 2015) and accretion rate are consistent with those of Class Is undergoing an accretion burst (Hsieh et al. 2019). However, Per-emb-50’s envelope mass is similar to those around other Class I objects (at 2.2 M⊙, Enoch et al. 2009; Agurto-Gangas et al. 2019), and the streamer might be the key ingredient to sustaining Per-emb-50’s high accretion rate.
It is also possible that we are seeing the protostar in the onset of an accretion burst, as it is significantly brighter than other Class I protostars, or the streamer might produce one in the future. Since the streamer’s infall rate is five to ten times larger than the current accretion rate, it is possible that in the future 9000 yr the accretion rate could grow by one order of magnitude. This shows that streamers might provide a significant amount of mass for stellar accretion, and suggests that intense accretion events can take place during the Class I phase. Moreover, if more streamers in Class I protostars are found and their masses characterized (e.g., in this work and Yen et al. 2014), this also suggests that the main accretion phase of the protostar might extend beyond the Class 0 phase.
Recent observations toward young stellar objects find a correlation between accretion bursts and infall from larger scales. Asymmetric structures with a length of 1000 au have been associated with some FU Ori protostars (Liu et al. 2016). Other protostars with a known accretion burst in the past, such as Per-emb-2 (Pineda et al. 2020) and V883 Ori (White et al. 2019), also have asymmetric envelopes with an infall rate higher than their accretion rate. For these sources, it is suggested that the large-scale infall regulates the episodic accretion. This might be the case for Per-emb-50 as well, and we propose that the mass is delivered to the protostellar disk, which triggers a disk instability (similar to a gravitational instability, as suggested by Kuffmeier et al. 2018; Hennebelle et al. 2017), the mass is transported through the disk, and afterward is accreted by the protostar in a burst. This idea is supported by the disk’s mass in comparison to other disks: Per-emb-50’s dust disk has between 0.28 and 0.58 M⊙, around twice the mass seen in other Class I disks (Segura-Cox et al. 2016, 2018), which suggests that this disk might be accumulating mass coming from the streamer. Additionally, even if we are currently unable to resolve this disk, it has been suggested that gravitational instabilities produced by infalling material account for the spiral structures found in the disks of other protostars, for instance, in IRAS16293-2422 B (a Class 0 source, Zamponi et al. 2021), HH 111 VLA 1 (a Class I source, Lee et al. 2020), and Elias 2-27 (a Class II protostar, Paneque-Carreño et al. 2021). Higher-resolution observations of the gas disk around Per-emb-50 are required in order to study these possible instabilities.
4.5 Understanding where the streamer comes from
The streamer possibly connects to larger scale structures such as filaments and fibers. Within molecular clouds, simulations suggest that that up to 50% of the final protostellar mass comes from beyond their natal core (Pelkonen et al. 2021), and observations of other protostars show that gas can flow from beyond the protostar’s natal core, connecting the protostar with other structures (e.g., Chou et al. 2016). Our data, together with the observed environment where Per-emb-50 lives, suggest that this might be the case for this protostar as well.
First, as discussed previously (see Sect. 4.1), the H2CO and C18O emission are truncated by the NOEMA primary beam and there is significant C18O (2–1) emission observed in the SMA MASSES program (Stephens et al. 2019), located at the position of the offset emission outside the primary beam, directly in line with the streamer. Moreover, the MASSES emission is also cut short at its primary beam (48″, Stephens et al. 2019). The gas reservoir seen in MASSES C18O observations might be funneled by the streamer or might be part of it, implying that streamers might connect with larger structures in their natal molecular clump.
Zooming out, NGC 1333 consists of a complex association of filaments, revealed in dense gas observations (Chen et al. 2020; Dhabal et al. 2019; Friesen et al. 2017). At larger scales, the streamer points directly toward the crossing of two dense gas filaments observed in NH3 observations (filament b in Chen et al. 2020) and toward a bright extended emission source observed in C18O (see Fig. 9), located between Per-emb-50 and Per-emb-54. If the streamer continues outside the primary beam, it may connect both protostars, as observed with the protostar L1544-IRS1 and the starless core HRF40 by Chou et al. (2016). There are currently no observations at intermediate resolution (6–10″) with an appropriate tracer in NGC 1333 that connects the large-scale clumps and filaments surrounding Per-emb-50 to the core. Studies of filaments and fibers, such as those of Chen et al. (2020) and Dhabal et al. (2019), show an intricate connection between filaments and cores, but they are not sensitive enough to detect emission close to Per-emb-50, and the C18O(1–0) has too coarse a resolution (46″ beam, Hatchell et al. 2005). Nevertheless, the general direction of the streamer suggests that this streamer is connected to the larger-scale filaments.
4.6 Asymmetries in SO and SO2 emission
The SO and SO2 emission (see Fig. 7) are asymmetrical: they are both brighter toward the south and in redshifted velocities. SO shows that the kinematic properties of gas toward Per-emb-50 are complex and include both asymmetric infall and rotation. This is more evident in the Gaussian decomposition (see Sect. 3.8). These asymmetries show that the inner envelope of Per-emb-50 is not infalling monolithically, and thus does not follow the classical picture of core collapse (Terebey et al. 1984; Shu 1977).
Through Gaussian decomposition, we find that the red-shifted component that dominates the SO emission is centered around the protostar and has a central velocity of approximately 9.5 km s−1 (2 km s−1 redshifted with respect to Per-emb-50, see Sect. 3.8). We interpret this emission as another asymmetric infall completely contained within the line of sight. Given the velocity gradients seen in the bottom right panel of Fig. 8, this component might not be a streamer but rather a wider asymmetric infall, comprising one side of the envelope located between the observer and the protostar. Finding a possible second infall feature in Per-emb-50 shows that the envelope infall kinematics are complex and reaffirms the idea that mass accretion does not follow an inside-out, axisymetric fashion. The asymmetries might be related to the environment where Per-emb-50 is located, close to the intersection of two filaments in NGC 1333 (Chen et al. 2020) and close to several other protostars (Enoch et al. 2009; Dunham et al. 2015).
 |
Fig. 9 Integrated intensity map of C18O(1–0) emission of NGC 1333 from Hatchell et al. (2005), between 5 and 10 km s−1, centered at the location of Per-emb-50. White stars represent the location of close-by Class I protostars. Per-emb-50 and Per-emb-54 are indicated and labeled with white arrows. The white circle in the lower left corner represents the beam of the C18O(1–0) observations (46″). |
4.7 Comparison with other streamers
Streamers, defined as long (≳ 1000 au) and asymmetric accretion flows toward disk-forming scales (≲300 au, as in Pineda et al. 2020), are a relatively new phenomenon that are proving to be relevant in star formation, with new discoveries both in gas tracers (Alves et al. 2020; Segura-Cox et al., in prep.) and dust (Ginski et al. 2021). Per-emb-50’s streamer is the first Class I protostellar streamer with its infall rate characterized using a free-falling model. We illustrate the streamer and its relation with the various components found surrounding Per-emb-50 in Fig. 10.
Per-emb-50’s structure and kinematics are similar to other asymmetric features found in protostars in Perseus and other molecular clouds. The observed streamer size in this work is within the range of other observed streamers (between 1000 and 10 000 au), such as toward [BHB2007]11 (Alves et al. 2020), Per-emb-2 (Pineda et al. 2020), and SU Aur (Ginski et al. 2021; Akiyama et al. 2019). Similar infalling structures have been found at smaller scales (between roughly 200 to 1000 au), within inner envelopes of single systems (e.g., Garufi et al. 2022; Tang et al. 2012) and within the circumbinary disk and inner envelope of binary systems (e.g., Phuong et al. 2020; Takakuwa et al. 2014, 2017; Dutrey et al. 2014). The streamer in this work also shows a velocity gradient and a curved appearance in the image plane, similar to many of the streamers mentioned above (e.g., Pineda et al. 2020; Akiyama et al. 2019). We note that the infalling structures in smaller scales (200-1000 au) might be of a different nature, possibly driven by the tidal forces of the binary systems instead of pure free fall. However, these structures also play a role in feeding the circumstellar disks.
Our work uses the same analytical solution as in Pineda et al. (2020) for Per-emb-2, a Class 0 protostellar close binary (<20 au), the first streamer where mass and infall rate were obtained, but extends the method to include the analysis of infall rates along the streamer. In Per-emb-2, the streamer’s kinematics are consistent with a model with vr,0 = 0, so using the free-fall timescale does not severely underestimate the infall rate. Per-emb-50’s mean streamer infall rate 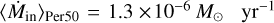 is similar to the infall rate in Per-emb-2,
is similar to the infall rate in Per-emb-2, 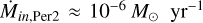 (Pineda et al. 2020). While the infall rate is similar in both sources, the mean ratio
(Pineda et al. 2020). While the infall rate is similar in both sources, the mean ratio 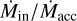 is higher for Per-emb-50 (5–10, in contrast with 1.4 for Per-emb-2). Nevertheless, both are >1, even assuming the highest accretion rate possible for Per-emb-50, (0.6-1.2) × 10−6 M⊙ yr−1 (blue area in Fig. 6). Per-emb-50 is unique in that it is the first streamer to definitively show, through the use of a free-fall model, that the infall rate can sustain the accretion rate. This implies that streamers can contribute important amounts of mass in later phases than Class 0, therefore suggesting that important accretion events can happen in the Class I phase, and in some cases, can occur in Class II sources (as suggested by Garufi et al. 2022; Alves et al. 2020; Tang et al. 2012).
is higher for Per-emb-50 (5–10, in contrast with 1.4 for Per-emb-2). Nevertheless, both are >1, even assuming the highest accretion rate possible for Per-emb-50, (0.6-1.2) × 10−6 M⊙ yr−1 (blue area in Fig. 6). Per-emb-50 is unique in that it is the first streamer to definitively show, through the use of a free-fall model, that the infall rate can sustain the accretion rate. This implies that streamers can contribute important amounts of mass in later phases than Class 0, therefore suggesting that important accretion events can happen in the Class I phase, and in some cases, can occur in Class II sources (as suggested by Garufi et al. 2022; Alves et al. 2020; Tang et al. 2012).
It is still uncertain if the lack of streamers found in observations is due to an observational bias, or if streamers are uncommon in the majority of star-forming systems. If streamers live as much as the estimated free-fall timescale of Per-emb-50 (tff ~ 9000 yr) and the protostar has only one streamer in their life, there is between a 2% and a 30% chance of observing one during the Class I phase, with the lower limit obtained by dividing tff by the estimated Class I phase duration (0.44. Myr, Evans et al. 2009) and the upper limit by dividing tff by itself plus the time between accretion bursts, estimated to occur once every few 10 000 yr (Frimann et al. 2017; Jørgensen et al. 2015). This is just an order of magnitude estimate, as the time between bursts is uncertain and has a wide range of values in different protostars (from a few thousand to a few tens of thousands of years, e.g., Hsieh et al. 2018; Frimann et al. 2017; Jørgensen et al. 2015), and previous works show this time might increase from Class 0 to Class I protostars (Hsieh et al. 2019; Audard et al. 2014). Nevertheless, asymmetric infall features are seen along the complete simulations of star formation within a molecular cloud (Kuznetsova et al. 2019; Kuffmeier et al. 2018).
As streamers are a new emerging phenomenon in observations, it is unclear which are the best molecules to trace them. Per-emb-50 shows the first streamer characterized with H2CO emission, whereas other streamers are observed in 12CO (e.g., Alves et al. 2020), HC3N (e.g., Pineda et al. 2020), and HCO+ (e.g., Yen et al. 2019). Upcoming NOEMA observations from the PRODIGE project can uncover more asymmetric infalls and streamers around Class 0 and Class I sources and, in the future, we might be able to make a statistical study of streamers in protostars and investigate which molecules are the best tracers of this phenomenon.
 |
Fig. 10 Schematic illustration of the different elements present around Per-emb-50. The streamer is represented as a thick light-blue line. The inner envelope is represented in light pink and the rotating gas disk is represented with a green ellipse. The inner envelope has a transparent gap inside to see the streamer behind it. The blue and red straight arrows show the outflow direction in the blueshifted and redshifted directions, respectively. The white circle shows the dust disk and the solid black ellipse marks its edge. The dashed circle represents the centrifugal radius. Curved arrows show the general direction of motion of each component: red and blue arrows show if the motions are seen as redshifted or blueshifted line emission, respectively. a: image plane view, where the right ascension increases toward the left and declination increases upward. b: line-of-sight view, where the observer is on the left and distance increases toward the right. |
5 Conclusions
In this work, we present new NOEMA observations of H2CO, C18O,12CO, SO, and SO2 molecular lines toward Per-emb-50, a Class I source in NGC 1333. We use these observations to characterize the kinematics from envelope to disk scales around the protostar. An illustration of our main findings is shown in Fig. 10. The main results are summarized as follows:
We find a streamer depositing material close to the edge of the gas disk around Per-emb-50. It presents an almost constant velocity in H2CO emission in the line of sight from roughly 1500 to 3000 au from the protostar. There is acceleration toward more blueshifted velocities closer to the protostar, up to around 1000 au;
The analytical solutions for infalling gas along a streamline can reproduce the observed kinematics of the H2CO emission. An initial velocity of 1.25 km s−1 at the initial position 3330 au away from the protostar is required to replicate the observed velocity along the line of sight. Taking the initial velocity into account, the free-fall timescale of the streamer is ~9000 yr;
The streamer delivers more than enough mass to sustain its protostellar accretion rate. We estimate a lower limit to the streamer’s mass at 1.2 × 10−2 M⊙, from which we obtain a mean infall rate of 1.3 × 10−6 M⊙ yr−1, with variations of up to a factor of three along the streamer. The infall rate is consistently about five to ten times larger than the estimated accretion rate of the protostar. This means that the streamer can deliver enough mass to sustain the high accretion rate of this protostar for at least the next 9000 yr;
We find signatures of asymmetry in SO and SO2 emission. The PV diagram of SO shows a diamond shape consistent with rotation and infall motions, but there is an asymmetry between the redshifted and blueshifted velocities. Through Gaussian decomposition, we find that SO traces mostly the inner envelope rotation and a redshifted asymmetric infall located along the line of sight. SO also traces the inner 1000 au of the streamer. SO2 emission hints at an impact zone toward the south of Per-emb-50, which is consistent with both the estimated landing site of the streamer and the peak of the redshifted asymmetric infall.
The description of the envelope around Per-emb-50 and each of its distinct kinematic components are limited by the resolution and primary beam of our observations, together with the lack of zero-spacing data. We emphasize that the streamer might extend further than the 3000 au we characterize in this work, as it is traced in C18O, which is observed outside of the primary beam of our observations, and points toward the crossing of two dense gas filaments. We also point out that the mass is a lower limit. Further observations with single dish antennas will allow the total flux (and therefore, mass) along the streamer to be obtained and its mass fluctuations to be confirmed. Intermediate resolution observations (≈ 6″) that cover an area larger than the NOEMA primary beam will allow us to investigate the connection of this streamer to the larger filament. Higher spatial resolution data of more than one SO and SO2 molecular transition will help determine the precise landing site of the streamer and allow us to characterize the redshifted infall better. Observations of other transitions of the same molecules observed in this work will allow the physical parameters (volume density and temperature) of the streamer and its landing site to be derived.
The presence of the streamer and the redshifted SO component highlight the importance of asymmetric infall for the growth and development of protostars at all evolutionary stages. The high infall rate of this source and the presence of streamers in Class I and II sources suggest that important accretion events of protostars can occur after the Class 0 phase.
Acknowledgements
The authors would like to thank the anonymous referee for their detailed suggestions, which helped improve the final version of this paper. The authors also thank the IRAM staff at the NOEMA observatory for their invaluable work making these observations possible. M.T.V. would like to thank L. Testi for his invaluable discussions and comments. M.T.V., J.E.P., P.C., D.S.-C., T.-H.H., and M.J.M. acknowledge the support by the Max Planck Society. D.S.-C. is supported by an NSF Astronomy and Astrophysics Postdoctoral Fellowship under award AST-2102405. A.L.-S. acknowledges funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program, for the Project “The Dawn of Organic Chemistry” (DOC), grant agreement No 741002, and from the European Union’s Horizon 2020 research and innovation programs under projects “Astro-Chemistry Origins” (ACO), Grant No 811312. D.S. acknowledges financial support by the Deutsche Forschungsgemeinschaft through SPP 1833: “Building a Habitable Earth” (SE 1962/6-1). A.F. thanks the Spanish MICIN for funding support from PID2019-106235GB-I00. T.H. acknowledges support from the European Research Council under the Horizon 2020 Framework Program via the ERC Advanced Grant Origins 83 24 28. A.D., S.G. and E.C. acknowledge support from the programs « Programme National de Physique Stellaire » (PNPS) and « Physique et Chimie du Milieu Interstellaire » (PCMI) of the CNRS/INSU with INC/INP co-funded by CEA and CNES. » I.J.-S. acknowledges support from grant No. PID2019-105552RB-C41 by the Spanish Ministry of Science and Innovation/State Agency of Research MCIN/AEI/10.13039/501100011033 and by “ERDF A way of making Europe”. N.C. acknowledges funding from the European Research Council (ERC) via the ERC Synergy Grant ECOGAL (grant 855130). M.T. acknowledges support from project PID2019-108765GB-I00 funded by MCIN/AEI/10.13039/501100011033. S.M. is supported by a Junior Research Fellowship from Jesus College, University of Cambridge. This work is based on observations carried out under project number L19MB with the IRAM NOEMA Interferometer. IRAM is supported by INSU/CNRS (France), MPG (Germany) and IGN (Spain). This research made use of Astropy (http://www.astropy.org), a community-developed core Python package for Astronomy (Astropy Collaboration 2013, 2018).
Appendix A Continuum at 220 GHz
Figure A.1 shows the continuum image at 1.3 mm (220 GHz) resulting from the LI continuum window of our dataset. The noise level of this image is 0.2 mJy beam−1.
 |
Fig. A.1 Continuum image at 220 GHz (1.3 mm) of Per-emb-50 obtained with NOEMA. The continuum is done only with the LI continuum window of the observations. The blue star represents the position of Per-emb-50. The white ellipse in the lower left corner represents the beam size. |
Appendix B Gaussian component fitting
We fit a single Gaussian component to all the spectra in the H2CO(30,3–20,2) and the C18O(2–1) cubes, using the Python PySpecKit library (Ginsburg & Mirocha 2011). We left out of the analysis all spectra with a peak signal-to-noise ratio lower than four. After fitting, we selected for further analysis the fitted spectra that met all of the following requirements:
the parameter uncertainties were all smaller than 50%,
the Gaussian component had a central velocity in the observed emission velocity range (between 5.5 and 9.5 km s−1 for H2CO and C18O), and
the fitted amplitude had a S/N > 4.
The results of the fit for H2CO(30,3–20,2) are shown in Fig. 2, and for C18O(2-1) the results are shown in Fig. 5.
We fit one, two, and three Gaussian components to the SO spectra near the protostar using the same criteria as above, similar to the multifit approach by Sokolov et al. (2019). After fitting, we kept the pixels where for each Gaussian, all of the above criteria were met, except for the central velocity, where the emission range changes from 5.5 – 9.5 km s−1 to −1.0 – 14.0 km s−1.
We used the Akaike information criterion (AIC) to decide whether one, two, or three Gaussian components reproduced best each SO spectra. This criterion uses the AIC value AIC to determine which model minimizes information loss:
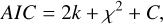 (B.1)
(B.1)
where k is related to the number of free parameters of the model (see below), χ2 is the classical chi-squared statistic, and C is a constant defined by the number of independent channels and the uncertainties (Choudhury et al. 2020). For k, each Gaussian component has three free parameters, so k = 3g, where g is the number of Gaussian components in each model. For C, we assumed that each channel in the spectra had a constant normal error, which corresponds to the rms of the SO cube, and we used the same data to test the three models. C was the same for all models and did not play a role in choosing the best model, so we set C = 0. The fit with the lowest AIC value was the preferred one for each spectrum.
We evaluated the probability that the model with the minimum information loss was a considerable improvement from the other two models for each spectrum. The difference between the minimum AIC, AICmin (which comes from the “best” model) and the AIC value of model i, AICi, is proportional to the probability that model i is as good as the minimum to minimize information loss as:
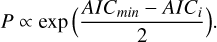 (B.2)
(B.2)
For SO(55 – 44), all of the fitted spectra have less than 5% probability that the competing models fit better the spectra than the model with minimum AIC. This means that, for those spectra that are well fitted by three Gaussians, the improvement from two Gaussians is significant. The same can be said for the improvement in those spectra that are best fitted with two Gaussians instead of only one. Therefore, we conclude that each spectra is well described by one, two, or three Gaussian components, depending on each case. Figure B.1 shows four spectra fitted with either one, two or three Gaussians.
 |
Fig. B.1 Sample spectra of SO in four selected locations in Per-emb-50’s inner envelope and disk region. Left and right: Beam averaged SO spectra (green line) at positions a to d. The black solid curve represents the best fit Gaussian function. The dashed-dotted lines represent the individual Gaussians that, added together, correspond to the best fit function. Each individual color in the dashed-dotted lines represents one of the kinematic components found in Sect. 3.8: blue corresponds to the inner envelope rotation, red matches the redshifted component, brown corresponds to the gas disk, and orange matches the streamer. Middle: Integrated intensity map of SO between −1 and 14 km s−1, as shown in Fig. 1, zoomed into the inner 1000 au closest to the protostar. Crosses (black and cyan) mark the locations of each spectrum, labeled a to d from highest to lowest, from right to left. |
Appendix C Envelope mass calculation
We obtained the envelope mass upper and lower limits using the flux in our continuum obtained with NOEMA (see Appendix A) and the Bolocam 1.1 mm image from Enoch et al. (2006). First, we obtained the flux in the Bolocam 1.1 mm continuum within a beam-sized aperture (θFWHM = 31″), centered at the location Per-emb-50, FBolocam = 324 ± 46 mJy, together with the peak value within this aperture IBolocam = 573 ± 55 mJy beam−1. Then, we obtained the total flux and peak value within the primary beam of the continuum obtained with NOEMA (22″), FNOEMA = 89 ± 2 mJy and INOEMA = 72.9 ± 1 mJy beam−1, respectively. We assumed that the NOEMA continuum contains disk emission only, as it does not contain zero-spacing information, whereas the Bolocam 1.1 mm image includes emission from the disk and envelope. We subtracted the flux in the NOEMA continuum from the flux obtained from Bolocam, thus obtaining the flux of the envelope only ∆S1 mm = SBolocam − SNOEMA, and used Equation 4 of Enoch et al. (2009) to calculate the envelope mass:
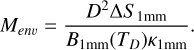 (C.1)
(C.1)
We assumed that the continuum at 1 mm consists of optically thin emission and used κ1mm = 0.0114 cm2 g−1, TD = 15 K as stated in Enoch et al. (2009), and a distance D = 293 pc (Ortiz-Leôn et al. 2018). Using the flux difference, we obtained an envelope mass of 0.18 M⊙. On the other hand, using the peak difference, we obtained 0.39 M⊙.
Appendix D Determination of column density
We first obtained the integrated intensity map of the primary beam corrected C18O(2–1) emission in the spatial region where the streamer is defined for the streamline model (see Fig. 5). We integrated the map between 5.5 and 9.5 km s−1. This velocity range covers the spectral emission of the streamer in C18O(2–1) completely. Then, we calculated the total column density of the C18O molecule using Equation 80 of Mangum & Shirley (2015) in each pixel of the integrated intensity map. We used a line strength  in relation to the dipole moment of the C18O molecule µ = 0.11079 Debye = 1.1079 × 10−19 esu cm, the rotor rotation constant for C18O B0 = 54891.420 MHz, the upper state energy for the C18O(2–1) transition Eu = 15.81 K, and the degeneracy of the C18O (2– 1) transition gJ = 2J + 1 = 5. We assumed a beam filling factor f = 1, as emission was resolved. The resulting equation for N(C18O) in cm−2, Tex in K and ∫TR dv in K km s−1 is
in relation to the dipole moment of the C18O molecule µ = 0.11079 Debye = 1.1079 × 10−19 esu cm, the rotor rotation constant for C18O B0 = 54891.420 MHz, the upper state energy for the C18O(2–1) transition Eu = 15.81 K, and the degeneracy of the C18O (2– 1) transition gJ = 2J + 1 = 5. We assumed a beam filling factor f = 1, as emission was resolved. The resulting equation for N(C18O) in cm−2, Tex in K and ∫TR dv in K km s−1 is
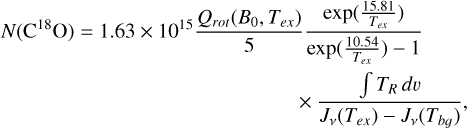 (D.1)
(D.1)
is the first order Taylor approximation of the partition function of a rigid-rotor diatomic molecule, and
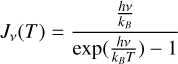 (D.3)
(D.3)
is the Rayleigh-Jeans equivalent temperature in K. We used Tbg = 2.7 K and v = 219.560 GHz (the frequency of the C18O(2–1) line). We used a constant Tex = 15 ± 5 K.
Appendix E SO2 spectra and image
Figure E.1 shows the integrated intensity map of SO2(111,11–100,10) between 5 and 12 km s−1, and to the left and right, spectra of SO, SO2, and H2CO in the same selected positions as in Fig. B.1
 |
Fig. E.1 Velocity integrated SO2(111,11 – 100,10) together with sample spectra of SO2, SO, and H2CO at positions a to d. Left and right: Beam averaged spectra at positions a to d. Each color represents the spectrum of a molecule: blue corresponds to H2CO, green to SO and red to SO2. The dotted vertical line marks the central velocity of the protostar VLSR = 7.5 km s−1. The dashed horizontal line represents the 0 K level. If a molecule does not appear at a panel, its because emission from that molecule has a S/N < 5. Middle: Velocity integrated image of the SO2(111,11 – 100,10) molecular transition. The crosses represent the places where each spectrum was extracted, labeled from a to d. The white contours represent the three and five times the rms of the integrated map contours of H2CO (0.25 K km s−1). The white ellipse in the bottom left corner represents the beam size. The blue star marks the position of Per-emb-50. |
Appendix F SO decomposition
Figure F.1 shows the velocity dispersion σv of each kinematic element found in Sect. 3.8 (see Fig. 8) through the Gaussian fitting described in Appendix B. It should be noted that all images have different colorscales.
 |
Fig. F.1 σv of the inner envelope rotation, disk, streamer and redshifted components in SO(55 – 44) found in Sect. 3.8. The dashed contour represents the 220 GHz continuum emission at the 7 mJy beam−1 level. The black ellipses in the lower left corners represent the beam size. |
References
- Agurto-Gangas, C., Pineda, J. E., Szucs, L., et al. 2019, A&A, 623, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Akiyama, E., Vorobyov, E. I., Baobabu Liu, H., et al. 2019, AJ, 157, 165 [Google Scholar]
- Alves, F. O., Caselli, P., Girart, J. M., et al. 2019, Science, 366, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Alves, F. O., Cleeves, L. I., Girart, J. M., et al. 2020, ApJ, 904, L6 [NASA ADS] [CrossRef] [Google Scholar]
- André, P., Men’shchikov, A., Bontemps, S., et al. 2010, A&A, 518, A102 [Google Scholar]
- André, P., Di Francesco, J., Ward-Thompson, D., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning, 27 [Google Scholar]
- Artur de la Villarmois, E., Jørgensen, J. K., Kristensen, L. E., et al. 2019, A&A, 626, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Audard, M., Ábrahám, P., Dunham, M. M., et al. 2014, in Protostars and Planets VI, ed. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning, 387 [Google Scholar]
- Basu, S., & Mouschovias, T. C. 1994, ApJ, 432, 720 [NASA ADS] [CrossRef] [Google Scholar]
- Bergin, E. A., & Tafalla, M. 2007, ARA&A, 45, 339 [Google Scholar]
- Chen, M. C.-Y., Di Francesco, J., Rosolowsky, E., et al. 2020, ApJ, 891, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Chou, H.-G., Yen, H.-W., Koch, P. M., & Guilloteau, S. 2016, ApJ, 823, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Choudhury, S., Pineda, J. E., Caselli, P., et al. 2020, A&A, 640, A6 [Google Scholar]
- Dhabal, A., Mundy, L. G., Chen, C.-Y., Teuben, P., & Storm, S. 2019, ApJ, 876, 108 [CrossRef] [Google Scholar]
- Dunham, M. M., Allen, L. E., Evans, I., Neal J., et al. 2015, ApJS, 220, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Dutrey, A., Wakelam, V., Boehler, Y., et al. 2011, A&A, 535, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dutrey, A., di Folco, E., Guilloteau, S., et al. 2014, Nature, 514, 600 [NASA ADS] [CrossRef] [Google Scholar]
- Endres, C. P., Schlemmer, S., Schilke, P., Stutzki, J., & Müller, H. S. 2016, J. Mol. Spectrosc., 327, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Enoch, M. L., Young, K. E., Glenn, J., et al. 2006, ApJ, 638, 293 [Google Scholar]
- Enoch, M. L., Evans, I., Neal, J., Sargent, A. I., & Glenn, J. 2009, ApJ, 692, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, I., Neal J., Dunham, M. M., Jørgensen, J. K., et al. 2009, ApJS, 181, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Fiorellino, E., Manara, C. F., Nisini, B., et al. 2021, A&A, 650, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frerking, M. A., Langer, W. D., & Wilson, R. W. 1982, ApJ, 262, 590 [Google Scholar]
- Friesen, R. K., Pineda, J. E., co-PIs, et al. 2017, ApJ, 843, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Frimann, S., Jørgensen, J. K., Dunham, M. M., et al. 2017, A&A, 602, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garufi, A., Podio, L., Codella, C., et al. 2022, A&A, 658, A104 [CrossRef] [EDP Sciences] [Google Scholar]
- Ginsburg, A., & Mirocha, J. 2011, PySpecKit: Python Spectroscopic Toolkit, Astrophysics Source Code Library, [record ascl:1109.001] [Google Scholar]
- Ginsburg, A., Robitaille, T., & Beaumont, C. 2016, Pvextractor: PositionVelocity Diagram Extractor, Astrophysics Source Code Library, [record ascl:1608.010] [Google Scholar]
- Ginski, C., Facchini, S., Huang, J., et al. 2021, ApJ, 908, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Guilloteau, S., Reboussin, L., Dutrey, A., et al. 2016, A&A, 592, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hacar, A., & Tafalla, M. 2011, A&A, 533, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hatchell, J., Richer, J. S., Fuller, G. A., et al. 2005, A&A, 440, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hennebelle, P., Lesur, G., & Fromang, S. 2017, A&A, 599, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hennebelle, P., Commerçon, B., Lee, Y.-N., & Charnoz, S. 2020, A&A, 635, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hsieh, T.-H., Murillo, N. M., Belloche, A., et al. 2018, ApJ, 854, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Hsieh, T.-H., Murillo, N. M., Belloche, A., et al. 2019, ApJ, 884, 149 [Google Scholar]
- Jørgensen, J. K., Visser, R., Williams, J. P., & Bergin, E. A. 2015, A&A, 579, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kenyon, S. J., Hartmann, L. W., Strom, K. M., & Strom, S. E. 1990, AJ, 99, 869 [Google Scholar]
- Kuffmeier, M., Haugbølle, T., & Nordlund, Å. 2017, ApJ, 846, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Kuffmeier, M., Frimann, S., Jensen, S. S., & Haugbølle, T. 2018, MNRAS, 475, 2642 [NASA ADS] [CrossRef] [Google Scholar]
- Kuffmeier, M., Calcutt, H., & Kristensen, L. E. 2019, A&A, 628, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuznetsova, A., Hartmann, L., & Heitsch, F. 2019, ApJ, 876, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Le Gouellec, V. J. M., Hull, C. L. H., Maury, A. J., et al. 2019, ApJ, 885, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Lebreuilly, U., Hennebelle, P., Colman, T., et al. 2021, ApJ, 917, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, C.-F., Li, Z.-Y., & Turner, N. J. 2020, Nat. Astron., 4, 142 [CrossRef] [Google Scholar]
- Liu, H. B., Takami, M., Kudo, T., et al. 2016, Sci. Adv., 2, e1500875 [Google Scholar]
- Mangum, J. G., & Shirley, Y. L. 2015, PASP, 127, 266 [Google Scholar]
- Mendoza, S., Tejeda, E., & Nagel, E. 2009, MNRAS, 393, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Mestel, L., & Spitzer, L. J. 1956, MNRAS, 116, 503 [NASA ADS] [CrossRef] [Google Scholar]
- Mouschovias, T. C., & Paleologou, E. V. 1980, ApJ, 237, 877 [NASA ADS] [CrossRef] [Google Scholar]
- Ortiz-León, G. N., Loinard, L., Dzib, S. A., et al. 2018, ApJ, 865, 73 [Google Scholar]
- Padoan, P., Haugbølle, T., & Nordlund, Å. 2014, ApJ, 797, 32 [Google Scholar]
- Palla, F., & Stahler, S. W. 1993, ApJ, 418, 414 [Google Scholar]
- Paneque-Carreño, T., Pérez, L. M., Benisty, M., et al. 2021, ApJ, 914, 88 [CrossRef] [Google Scholar]
- Pelkonen, V. M., Padoan, P., Haugbølle, T., & Nordlund, Å. 2021, MNRAS, 504, 1219 [NASA ADS] [CrossRef] [Google Scholar]
- Phuong, N. T., Dutrey, A., Diep, P. N., et al. 2020, A&A, 635, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pineda, J. E., Caselli, P., & Goodman, A. A. 2008, ApJ, 679, 481 [Google Scholar]
- Pineda, J. E., Zhao, B., Schmiedeke, A., et al. 2019, ApJ, 882, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Pineda, J. E., Segura-Cox, D., Caselli, P., et al. 2020, Nat. Astron., 4, 1158 [NASA ADS] [CrossRef] [Google Scholar]
- Pineda, J. E., Arzoumanian, D., André, P., et al. 2022, ArXiv e-prints, arXiv:2205.03935] [Google Scholar]
- Sakai, N., Sakai, T., Hirota, T., et al. 2014, Nature, 507, 78 [Google Scholar]
- Segura-Cox, D. M., Harris, R. J., Tobin, J. J., et al. 2016, ApJ, 817, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Segura-Cox, D. M., Looney, L. W., Tobin, J. J., et al. 2018, ApJ, 866, 161 [Google Scholar]
- Shu, F. H. 1977, ApJ, 214, 488 [Google Scholar]
- Sokolov, V., Wang, K., Pineda, J. E., et al. 2019, ApJ, 872, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Stahler, S. W., Shu, F. H., & Taam, R. E. 1980, ApJ, 241, 637 [NASA ADS] [CrossRef] [Google Scholar]
- Stephens, I. W., Bourke, T. L., Dunham, M. M., et al. 2019, ApJS, 245, 21 [CrossRef] [Google Scholar]
- Swade, D. A. 1989, ApJ, 345, 828 [NASA ADS] [CrossRef] [Google Scholar]
- Takakuwa, S., Saito, M., Saigo, K., et al. 2014, ApJ, 796, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Takakuwa, S., Saigo, K., Matsumoto, T., et al. 2017, ApJ, 837, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Tang, Y. W., Guilloteau, S., Piétu, V., et al. 2012, A&A, 547, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Terebey, S., Shu, F. H., & Cassen, P. 1984, ApJ, 286, 529 [Google Scholar]
- Tobin, J. J., Hartmann, L., Looney, L. W., & Chiang, H.-F. 2010, ApJ, 712, 1010 [CrossRef] [Google Scholar]
- van Gelder, M. L., Tabone, B., van Dishoeck, E. F., & Godard, B. 2021, A&A, 653, A159 [CrossRef] [EDP Sciences] [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
- Vorobyov, E. I., & Basu, S. 2015, ApJ, 805, 115 [NASA ADS] [CrossRef] [Google Scholar]
- White, J. A., Kóspál, Á., Rab, C., et al. 2019, ApJ, 877, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Wurster, J., Bate, M. R., & Price, D. J. 2019, MNRAS, 489, 1719 [NASA ADS] [CrossRef] [Google Scholar]
- Yen, H.-W., Takakuwa, S., Ohashi, N., et al. 2014, ApJ, 793, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Yen, H.-W., Gu, P.-G., Hirano, N., et al. 2019, ApJ, 880, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Zamponi, J., Maureira, M. J., Zhao, B., et al. 2021, MNRAS, 508, 2583 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, B., Caselli, P., Li, Z.-Y., & Krasnopolsky, R. 2018, MNRAS, 473, 4868 [Google Scholar]
- Zucker, C., Schlafly, E. F., Speagle, J. S., et al. 2018, ApJ, 869, 83 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Integrated intensity images of H2CO (30.3–20.2) and SO(55–44), before primary beam correction, are shown on the left and right, respectively. Primary beam FWHM sizes are represented with filled dashed white circles in each image. The blue star represents the location of Per-emb-50. Beam sizes are represented by white ellipses in the bottom left corner of each image. Left: H2CO(30.3–20.2) integrated intensity between 5.5 and 9.5 km s−1. Red and blue contours correspond to the redshifted and blueshifted emisions coming from the outflow, respectively, traced in our wideband 12CO(2–1) emission. Contour levels are shown at 8, 16, and 24 K km s−1. The white contour represents the continuum emission at a 7 mJy beam−1 level (see Fig. A.1). Right: SO (55–44) integrated intensity between −1 and 14 km s−1. |
| In the text | |
 |
Fig. 2 Results of the Gaussian fit to the H2CO line emission toward Per-emb-50. Left: central velocity VLSR and velocity dispersion σv of the H2CO streamer are shown in the top and bottom panels, respectively. These are obtained from the Gaussian model for H2CO emission of each spectra with S/N > 4. The red star represents the central position of Per-emb-50. Black labeled crosses mark the positions where we extract spectra, shown to the right. Dashed black contours correspond to the continuum emission at a brightness level of 7 mJy beam−1 (see Fig. A.1). Dashed white lines represent the primary beam FWHM, centered at the location of Per-emb-50. The beam is drawn in the lower left corners of each image. Right: H2CO spectra at selected positions along the streamer, together with the Gaussian that best fits each spectrum. Blue lines indicate the H2CO spectra and the dashed black lines represent the best fit Gaussian function. The uncertainty in TMB is 0.3 K. The dotted gray line represents the protostar’s Vlsr = 7.5 km s−1. |
| In the text | |
 |
Fig. 3 C18O integrated emission before primary beam correction alongside its PV diagram. Left: integrated intensity image of C18O between −1 and 14 km s−1. The semitransparent white line represents the position and width of the PV cut, built with the position angle of the disk from Segura-Cox et al. (2016). The white arrow represents the direction of positive offset of the PV cut. The primary beam FWHM size is represented with a dashed white circle. The beam size is represented by a white ellipse in the bottom left corner. Right: PV diagram of the C18O line emission along the indicated PV cut. The horizontal dotted line represents Per-emb-50’s VLSR = 7.5 km s−1. The vertical dotted line marks the central position of Per-emb-50. The PV diagram has an rms of 0.01 Jy beam−1. Intensity contours are placed at 5, 15, and 25 times the rms. The blue and black curves represent the Keplerian rotation curve for the minimum and maximum stellar mass, respectively, from Fiorellino et al. (2021): the solid lines represent masses calculated assuming the star is located at the birthline of the Palla & Stahler (1993) model (0.53–0.70 M⊙), whereas dashed lines represent the masses calculated for a 1 Myr protostar (1.52–1.90 M⊙). Velocities are weighted according to the inclination angle as v = vkep sin(i). The preferred Keplerian curve is the average between the dashed curves, with a mass of 1.7 M⊙. The scalebar in the top left represents a distance of 300 au, equivalent to the resolution of the NOEMA data. |
| In the text | |
 |
Fig. 4 Central velocity of the best fit for each spectra in the H2CO line emission, together with the streamline model for H2CO. The red and blue lines represent the best streamline model for an envelope mass of 0.18 M⊙ (total central mass of 2.47 M⊙) and 0.39 M⊙ (total mass of 2.68 M⊙), respectively. Left: central velocities with respect to position in the sky. The black polygon represents the region where velocities are sampled to build the kernel density estimation (KDE). The primary beam FWHM size is represented with a dashed white circle. The beam size is represented by a black ellipse in the bottom left corner. Right: central velocity KDE as a function of projected distance to Per-emb-50 is plotted in grayscale. The KDE levels are drawn from 0.5σ in steps of 0.5σ, where the σ level is equivalent to the standard deviation of a normalized bivariate normal distribution. The horizontal dashed line represents the central velocity of Per-emb-50 VLSR = 7.5 km s−1. The centrifugal radius resulting from each envelope mass are located below the curve. |
| In the text | |
 |
Fig. 5 Velocity VLSR and velocity dispersion σv of the best Gaussian fit for C18O emission. Gaussian fits are only done for spectra with S/N > 4. The primary beam FWHM size is represented with a white dashed circle. The beam size is represented in a white ellipse in the bottom left corner. Top: central velocity of the best fit Gaussian profile for each spectrum. The black contour shows the same region plotted in the right panel of Fig. 2, from where the mass is calculated. Bottom: velocity dispersion of the best fit Gaussian profile for each spectrum. |
| In the text | |
 |
Fig. 6 Mass, timescale, and infall rate with respect to the distance to the protostar along the streamline. Δtin is obtained from the model with Menv = 0.39 M⊙. The dotted line represents the mean infall rate obtained with the free-fall timescale from rest, |
| In the text | |
 |
Fig. 7 Position-Velocity diagram of SO(55–44) (colored and black contours) and SO2(white contours) line emission along the position angle of the disk from Segura-Cox et al. (2016), plotted along the same offset scale as the right panel of Fig. 3. Negative offsets represent distances toward the north and positive offsets toward the south. The horizontal dotted line represents Per-emb-50’s VLSR = 7.48 km s−1. The vertical dotted line marks the central position of Per-emb-50. Both PV diagrams have an rms of 0.01 Jy beam−1. Intensity contours for SO are placed at 3, 5, 15, 25, 35, and 45 times the rms, whereas SO2 intensity contours are placed at 3, 5, and 10 times the rms. The red and blue solid curves show the model of rotation and infall that best match the SO for the redshifted and blueshifted velocities with respect to the protostar, respectively. The scalebar in the top left represents a distance of 300 au, equivalent to the resolution of the NOEMA data. |
| In the text | |
 |
Fig. 8 Best fit central velocity maps for the four signature components found in SO (55–44) emission in the inner 1000 au of Per-emb-50’s envelope. Examples of the individual spectra decomposition for each of these components are shown in Fig. B.1. Solid black contours represent the integrated intensity of H2CO emission at three and five times the rms of the integrated intensity map (0.25 K km s−1). Dashed black contours mark the continuum emission at a 7 mJy beam−1 level (see Fig. A.1). The red and blue arrows indicate the outflow direction determined by the redshifted and blueshifted CO (2–1) emissions, respectively, from Stephens et al. (2019). The clean beam is represented as a black ellipse in the bottom left corner of all of the images. It should be noted that the velocity ranges plotted in each figure are different, which is why the figures on the right have a different color scheme. Top left: inner envelope rotation. Top right: broad feature (σv > 2 km s−1). Bottom left: streamer. Bottom right: redshifted component. |
| In the text | |
 |
Fig. 9 Integrated intensity map of C18O(1–0) emission of NGC 1333 from Hatchell et al. (2005), between 5 and 10 km s−1, centered at the location of Per-emb-50. White stars represent the location of close-by Class I protostars. Per-emb-50 and Per-emb-54 are indicated and labeled with white arrows. The white circle in the lower left corner represents the beam of the C18O(1–0) observations (46″). |
| In the text | |
 |
Fig. 10 Schematic illustration of the different elements present around Per-emb-50. The streamer is represented as a thick light-blue line. The inner envelope is represented in light pink and the rotating gas disk is represented with a green ellipse. The inner envelope has a transparent gap inside to see the streamer behind it. The blue and red straight arrows show the outflow direction in the blueshifted and redshifted directions, respectively. The white circle shows the dust disk and the solid black ellipse marks its edge. The dashed circle represents the centrifugal radius. Curved arrows show the general direction of motion of each component: red and blue arrows show if the motions are seen as redshifted or blueshifted line emission, respectively. a: image plane view, where the right ascension increases toward the left and declination increases upward. b: line-of-sight view, where the observer is on the left and distance increases toward the right. |
| In the text | |
 |
Fig. A.1 Continuum image at 220 GHz (1.3 mm) of Per-emb-50 obtained with NOEMA. The continuum is done only with the LI continuum window of the observations. The blue star represents the position of Per-emb-50. The white ellipse in the lower left corner represents the beam size. |
| In the text | |
 |
Fig. B.1 Sample spectra of SO in four selected locations in Per-emb-50’s inner envelope and disk region. Left and right: Beam averaged SO spectra (green line) at positions a to d. The black solid curve represents the best fit Gaussian function. The dashed-dotted lines represent the individual Gaussians that, added together, correspond to the best fit function. Each individual color in the dashed-dotted lines represents one of the kinematic components found in Sect. 3.8: blue corresponds to the inner envelope rotation, red matches the redshifted component, brown corresponds to the gas disk, and orange matches the streamer. Middle: Integrated intensity map of SO between −1 and 14 km s−1, as shown in Fig. 1, zoomed into the inner 1000 au closest to the protostar. Crosses (black and cyan) mark the locations of each spectrum, labeled a to d from highest to lowest, from right to left. |
| In the text | |
 |
Fig. E.1 Velocity integrated SO2(111,11 – 100,10) together with sample spectra of SO2, SO, and H2CO at positions a to d. Left and right: Beam averaged spectra at positions a to d. Each color represents the spectrum of a molecule: blue corresponds to H2CO, green to SO and red to SO2. The dotted vertical line marks the central velocity of the protostar VLSR = 7.5 km s−1. The dashed horizontal line represents the 0 K level. If a molecule does not appear at a panel, its because emission from that molecule has a S/N < 5. Middle: Velocity integrated image of the SO2(111,11 – 100,10) molecular transition. The crosses represent the places where each spectrum was extracted, labeled from a to d. The white contours represent the three and five times the rms of the integrated map contours of H2CO (0.25 K km s−1). The white ellipse in the bottom left corner represents the beam size. The blue star marks the position of Per-emb-50. |
| In the text | |
 |
Fig. F.1 σv of the inner envelope rotation, disk, streamer and redshifted components in SO(55 – 44) found in Sect. 3.8. The dashed contour represents the 220 GHz continuum emission at the 7 mJy beam−1 level. The black ellipses in the lower left corners represent the beam size. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.