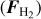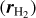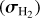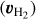| Issue |
A&A
Volume 664, August 2022
|
|
|---|---|---|
| Article Number | A97 | |
| Number of page(s) | 15 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202243228 | |
| Published online | 15 August 2022 | |
Regularized 3D spectroscopy with CubeFit: Method and application to the Galactic Center circumnuclear disk★,★★
1
LESIA, Observatoire de Paris, Université PSL, Sorbonne Université, Université Paris Cité, CNRS,
5 place Jules Janssen,
92195
Meudon, France
e-mail: thibaut.paumard@observatoiredeparis.psl.eu
2
Department of Physics and Astronomy, University of California Los Angeles,
430 Portola Plaza,
Los Angeles,
CA 90095,
USA
e-mail: ciurlo@astro.ucla.edu
Received:
31
January
2022
Accepted:
20
April
2022
Context. The Galactic Center black hole and the nuclear star cluster are surrounded by a clumpy ring of gas and dust, the circumnuclear disk (CND), that rotates about them at a standoff distance of ≃1.5 pc. The mass and density of individual clumps in the CND are disputed.
Aims. We seek to use H2 to characterize the clump size distribution and to investigate the morphology and dynamics of the interface between the ionized interior layer of the CND and the molecular reservoir lying farther out (corresponding to the inner rim of the CND, illuminated in ultraviolet light by the central star cluster).
Methods. We have observed two fields of approximately 20″ × 20″ in the CND at near-infrared wavelengths with the OSIRIS spectro-imager at the Keck Observatory. These two fields, located at the approaching and receding nodes of the CND, best display this interface. Our data cover two H2 lines as well as the Brγ line (tracing H II). We have developed the tool CubeFit, an original method for extracting maps of continuous physical parameters (such as the velocity field and velocity dispersion) from integral-field spectroscopy data, using regularization to largely preserve spatial resolution in regions of low signal-to-noise ratio.
Results. This original method enables us to isolate compact, bright features in the interstellar medium of the CND. Several clumps in the southwestern field assume the appearance of filaments, many of which are parallel to one another. We conclude that these clumps cannot be self-gravitating.
Key words: methods: data analysis / methods: numerical / techniques: high angular resolution / techniques: spectroscopic / ISM: individual objects: Sgr A West Circumnuclear Disk / Galaxy: center
Figures 4, 5, 8, 9 and B.1 to B.4 are also available in FITS format at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/664/A97
The data presented herein were obtained at the W. M. Keck Observatory, which is operated as a scientific partnership among the California Institute of Technology, the University of California and the National Aeronautics and Space Administration. The Observatory was made possible by the generous financial support of the W. M. Keck Foundation.
© T. Paumard et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1 Introduction
The circumnuclear disk (CND) is a well-defined ring of gas and dust orbiting the Galactic Center black hole and the nuclear cluster of massive young stars. It has an inner cavity of ≃1.5 pc radius, apparently evacuated by some combination of energetic outbursts caused by the black hole accretion flow and by supernovae from the central cluster of massive stars. The importance of the CND is that it is a reservoir of gas that will probably fuel future episodes of star formation and of copious accretion onto the central black hole; in a previous phase of its existence, it may have been responsible for forming the present cluster of massive young stars (Morris & Serabyn 1996; Morris et al. 1999; Lu et al. 2013). Consequently, in order to understand the activity of the central parsec of our Galaxy, especially including the role of the CND in star formation, it is important to elucidate the evolutionary path of the CND by understanding its structure and dynamics in as much detail as possible. Furthermore, because many galaxies with gas-rich nuclei apparently have nuclear disks surrounding their central supermassive black holes (e.g., Netzer 2015; Gravity Collaboration 2020; Vermot et al. 2021, and references therein), we can gather important but otherwise unattainable insights from the CND that are applicable to galactic nuclei in general and even to active galactic nuclei.
The CND is a warm (a few hundred K) molecular medium characterized by strong turbulence and “clumpiness” (Güsten et al. 1987; Genzel 1989; Marr et al. 1993; Jackson et al. 1993; Bradford et al. 2005; Oka et al. 2011; Martín et al. 2012; Requena-Torres et al. 2012; Mills et al. 2013; Tsuboi et al. 2018; Hsieh et al. 2021; Dinh et al. 2021). The very existence of clumps has led some authors to argue that either the clumps are tidally stable (Shukla et al. 2004; Christopher et al. 2005; Montero-Castaño et al. 2009) or that the CND is a transient feature with an age of less than a few dynamical times because the clumps have not yet had sufficient time to be tidally sheared out of existence (Güsten et al. 1987; Requena-Torres et al. 2012). However, the individual clumps can be transient features produced by instabilities or by large-scale disturbances to the disk (Blank et al. 2016; Dinh et al. 2021), even if the disk in which they are produced is itself a long-lived structure.
Tidal stability of the clumps requires densities that exceed ≃107 cm−3. Such a high density could only apply to a small fraction of the CND volume because the total mass is constrained by the optically thin far-infrared and submillimeter fluxes from the CND (Genzel et al. 2010; Etxaluze et al. 2011). Estimates of the total mass of the CND have varied over a wide range, depending on the densities and volumes inferred for the clumps. Density estimates, mostly based on the analysis of molecular rotational lines, range up to ≃106 cm−3 (Güsten et al. 1987; Oka et al. 2011; Requena-Torres et al. 2012; Lau et al. 2013; Mills et al. 2013; Smith & Wardle 2014; Tsuboi et al. 2018). Recently, Hsieh et al. (2021) reported CS observations of a large population of tiny clumps, many with inferred densities in the range 106 to 108 cm−3. However, almost all of the analyses based on molecular line observations have assumed that the molecular excitation is entirely collisional, although radiative excitation via the rotation-vibration lines is likely to contribute substantially to the excitation in this infrared-bright region (Mills et al. 2013). Consequently, the inferred densities in most treatments can be regarded as upper limits, and the question of whether any of the clumps in the CND are tidally stable remains open. The uncertainty in the density determinations and in the density distribution function (or the distribution of both clump sizes and clump densities) underlies the rather uncertain mass estimates, but the mass of the inner ring of the CND, from where most of the molecular lines and infrared continuum emission arise, probably lies in the range 2–10 × 104 M⊙.
The investigation reported here is therefore motivated in part by the need to elucidate the clump size distribution. Clump morphology is another key issue that we propose to investigate. To date, theoretical treatments of the clump characteristics have all assumed spherical clumps, but that assumption is valid only if the clumps are self-gravitating to the point of being tidally stable, which might apply only to a small fraction of the gas mass. If the clumps are not tidally stable, tidal shear will have pulled them into elongated streams. Indeed, the H2 morphologies sampled with the Hubble Space Telescope (HST) observations of Yusef-Zadeh et al. (2001) suggest that some fraction of the emission is organized into filamentary features. The detection of filamentary clumps on even smaller scales would imply an upper limit to their densities that is below the Roche density.
To address these questions, we observed two fields of the CND using the OH-Suppressing Infrared Integral Field Spectrograph (OSIRIS, Larkin et al. 2006) on the Keck II telescope. These fields – the northeastern (NE) and southwestern (SW) lobes in the nomenclature of Yusef-Zadeh et al. (2001) and Christopher et al. (2005) – lie at the two opposite nodes of the CND (Fig. 1).
In order to characterize the size and shape of the smallest clumps in this data set, we need to retain the full sampling-limited spatial resolution (at 0.1″ per pixel) while reconstructing maps of the brightness distribution, radial velocity, and radial velocity dispersion of the relatively low signal-to-noise ratio (S/N) interstellar emission lines contained in the spectral band. To this end, we have developed a new method to analyze spectro-imaging data. Inspired by deconvolution and interfero-metric image reconstruction, this method reconstructs optimal parameter maps (typically line flux, radial velocity, and velocity dispersion) under the two constraints that the model needs to be close to the data in the minimum χ2 sense and that the parameter maps must be smooth. This method was also used in another paper on infrared spectroscopy of the Galactic Center (Ciurlo et al. 2016). Here, we give additional details about the foundation of the method and provide more thorough testing and validation.
In Sect. 2, we describe our observations and data reduction procedure. Section 3 presents our technique for building parameter maps as well as first tests of the method using the strong OH lines present in the data. We apply this method to our data set and provide more ample validation in Sect. 4. We then discuss our findings in Sect. 5 and offer concluding remarks in Sect. 6.
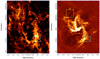 |
Fig. 1 Outline of the two mosaicked regions reported here superimposed on: the total intensity map of J = 4−3 CS emission from ALMA (left; Hsieh et al. 2021), and the 6-cm radio continuum image from the VLA (right; Zhao et al. 2016; Morris et al. 2017). The location of Sgr A* is indicated in each panel with a green cross. |
2 Observations and Data Reduction
We used the integral-field spectrograph OSIRIS (Larkin et al. 2006) at the W.M. Keck Observatory fed by the laser guide star adaptive optics system to observe two fields at the inner edge of the CND near the location of the two nodes of the CND orbit. The observations were carried out on May 13 and 19, 2010 (NE field, 14 frames) and July 24 and 25, 2011 (SW field, ten frames) and all consist of 900 s exposures taken in the Kn3 band (2.121–2.229 µm) with a 100 mas plate scale, giving a field-of-view for each frame of 4.8″ × 6.4″. The data have been reduced with the OSIRIS pipeline (Lockhart et al. 2019), which subtracts darks, assembles the cubes, corrects the sky lines and creates the final mosaics. The mosaics are photometrically calibrated using standard A stars observed the same night as the science observations. The procedure is described in Ciurlo et al. (2020). Furthermore, each mosaic is astrometrically calibrated using three stars whose absolute position is known through HST observations of the area (Hosek et al., in prep.). The uncertainty on the astrometric calibration is about 0.5″.
The final data products are two mosaics, one for the NE and one for the SW field. The NE field centered at J2000 coordinates (17:45:41.67,-28:59:48.8), near the receding node, is an approximately square field 20″ on each side with a small (<1″) horizontal gap ≃4″ south of its central point. The SW mosaic, centered at (17:45:38.17,-29:00:57.5), covers a rectangular area of 14″ × 14″ near the approaching node.
In the spectral band covered by our data, we detect two H2 lines (1–0 S(1) at 2.1217 µm and 1–0 S(0) at 2.2232 µm) and the Brγ line of the H I spectrum (2.1667 µm), tracing H II. The two H2 lines are several orders of magnitude stronger than any other H2 line in the band according to the high-resolution transmission molecular absorption (HITRAN) database (Gordon et al. 2017; Komasa et al. 2011; Wolniewicz et al. 1998).
The data are dominated by continuum flux from stars. We estimated this continuum emission for each spatial pixel as a spline function going through the average flux in 12–13 featureless regions (Tables 1 and 2) of the spectrum and subtracted it from the data. Unfortunately the H2 line at 2.12 µm is at the edge of the spectral bandpass so that we have no continuum estimate on the short wavelength side of this line and must resort to extrapolation there. The presence of the second line at 2.22 µm, to the extent that it can be considered as sharing the same radial velocity, alleviates this issue. The S/N per data point ranges from 0 to ≈35 for H2 from 0 to ≈18 for Brγ.
3 CubeFit: Data Modeling with Regularized Parameter Maps
Integral field spectroscopy is a powerful tool that allows the simultaneous spectroscopic observation of all pixels within a continuous field-of-view, sometimes with the goal of recording the individual spectra of many point sources and sometimes to study the spectral properties of diffuse emission. This paper focuses on the latter. Integral field spectroscopy data are 3D, with two spatial dimensions and one spectral dimension: D(l, m, λ) is some quantity related to the emitted intensity (e.g., flux density) originating from the direction (l, m) at wavelength λ, with uncertainties u(l, m, λ). D can be interpreted either as a collection of images recorded in many consecutive wavelength channels or as a collection of spectra (the “spaxels”) for each pixel of these images. Individual data points are called “voxels.” Observers typically want to interpret such data as a set of maps of physical parameters. Given a 1D spectral model S{ai}(λ) of n scalar physical parameters a0… an, one tries to construct a 2D map αi for each parameter so that the 3D model
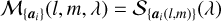 (1)
(1)
is a good match to the data, D, under a criterion that involves the uncertainties, u.
Wavelength ranges used for continuum estimation for the SW mosaic.
3.1 Traditional independent 1D fits
The most usual approach to this problem is to simply perform a spectral fit on each individual spaxel spectrum in the cube. In other terms, one determines ai(l, m) by minimizing for each point (l, m) in the field-of-view the following quantity:
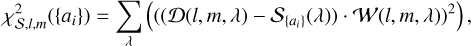 (2)
(2)
where W is the weight associated with each data point (usually, W = 1/u) note that minimizing the 1D χ2 term for each point (l, m) is equivalent to globally minimizing the 3D χ2:
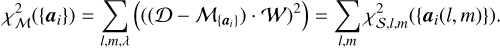 (3)
(3)
This method works very well and is sufficient as long as the S/N in the emission line is large (≳3–5) within the solid angle viewed by each spaxel. However, this condition of high S/N is quite restrictive. It means that this approach fails in low S/N areas of the field, inevitably ending up fitting independent noise spikes.
3.2 An Original Regularized 3D Fit
In order to avoid this problem, we propose adding to the χ2 term a penalty term that ensures that the parameter maps are regular, in the sense of the regularization approach detailed below: we want the maps of observable parameters to be as continuous as possible across adjacent pixels. The measured variations across the field should be representative of physical variations rather than noise, and any discontinuity should be smoothed by the imaging resolution of the instrument. This treatment is inspired by image deconvolution and interferometric image reconstruction, two problems that have strong similarities with the one that occupies us; in all these cases, the observer wants to interpret complex data as a set of regular high-resolution spatial maps. Our estimator takes the form
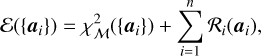 (4)
(4)
where each Ri is an appropriate penalty function that encodes prior knowledge on each parameter map. By globally minimizing such an estimator over an entire 3D data set, one ensures that the solution respects a compromise between proximity to the data and this prior knowledge. Quadratic-linear (or L2 – L1 for short) priors are often used to smooth small noise gradients while preserving the large gradients of edges as explained by Mugnier et al. (2004, and references therein). We used the norm from their Eq. (9):
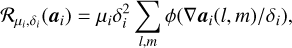 (5)
(5)
∇lai and ∇mai being the map finite-difference gradients along l and m, respectively. The two hyperparameters (per parameter map) µi and δi currently have to be set by hand. δi regulates the transition between the two regimes: small gradients (typical of noise) are penalized whereas strong gradients (more likely physical) are restored. The µi allows the various regularization terms in ℰ to be weighted.
We developed CubeFit1, a code that implements this method using the Yorick interpreted language2. We borrowed the L2– L1 regularization function from Yoda3 by Damien Gratadour, a Yorick port of the MISTRAL deconvolution software by Mugnier et al. (2004). The model-fitting engine is the conjugate gradient algorithm implemented in the Yorick package OptimPack4, version 1.3.2. A Python port of CubeFit is under development.
3.3 Test of the Method on OH Lines
The many strong OH lines present in the near-infrared spectral band give us the opportunity to test our method on high S/N data. In this section, we use CubeFit on versions of the two mosaics that are not sky-subtracted and compare the results with those obtained using a 1D approach. In the process, we determine field-variable corrections to the instrumental spectral resolution and wavelength calibration that we use in the later sections.
We used the eight OH lines between 2.12 and 2.23 µm in the list from Oliva & Origlia (1992). For the 1D spectral model S{ai}(λ), we used a Doppler-shifted, multiline Gaussian profile:
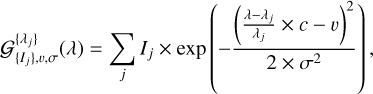 (8)
(8)
where c is the speed of light. The ten parameters are the intensities of the eight lines {Ij}, the common Gaussian width σ (in the radial velocity domain) and a common radial velocity υ. We fitted the data with this model using two methods: individual 1D fits on each spaxel (the maps have been σ-filtered to remove some bad fits) and with CubeFit.
Figure 2 shows the result of the 1D and 3D fits for the SW mosaic and their differences. The linewidth (which traces spectral resolution for those intrinsically very thin telluric lines) varies considerably across the mosaic. In each subfield, the resolution varies from ≃35 km s−1 in the southeastern corner to ≃60 km s−1 in the northwestern corner. These strong variations create sharp edges at the transition between subfields. In addition, the linewidth map shows some striping at a much smaller level than this overall gradient. The measured radial velocity map also shows a trend in the SE–NW direction on the order of a few kilometers per second. Because of the variations in the linewidth, it is better to express line strength in terms of flux (∝ intensity times width) rather than intensity. The corresponding map shows variations on the order of 5% within subfields. The differences between subfields are probably due to actual variations in the airglow spectrum during the night.
The maps produced by the two methods are very similar and exhibit the same features. As expected, the CubeFit 3D-fit parameter maps are slightly less noisy, but reproduce the sharpest features only partially (in particular the sharp edges between subfields and striping of the linewidth map), which explains the slight bias in the linewidth distribution (Fig. 2, bottom-left panel). Conversely, the CubeFit parameter maps do not need to be σ-filtered and some artifacts that can be seen in the 1D-fit parameter maps are very well corrected by the regulariza-tion of CubeFit. For instance, artifacts from two very bright stars can be seen in the 1D flux map at (dα, dδ) ≃ (−2″, −3″), and (−2″, −5″). Finally, striping can also be seen in the 3D-fit velocity map subfields and can hardly be seen in the 1D-fit parameter map due to the additional noise.
The same analysis on the NE mosaic yields very similar results. In the rest of this paper, we fit the intrinsic width and radial velocity of various lines. To do so, we corrected the model for variable spectral resolution and wavelength calibration residuals by adding, pixel by pixel, the OH linewidth, σOH(l, m) (in quadrature), and velocity offset, υOH(l, m), to the fitted linewidth and velocity:
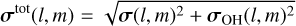 (9)
(9)
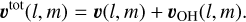 (10)
(10)
Since the S/N of the OH lines is so high, and in order to fully remove the sharp edges in the spectral resolution spatial variations, we used the results of the 1D fit for this purpose.
Further tests of the method are done in the next sections together with the analysis of the CND data and are summarized in Sect. 6.
 |
Fig. 2 Results of multiple OH line fits for the SW mosaic. Left column: linewidth (km s−1). Center column: radial velocity offset (km s−1). Right column: flux of the brightest line estimated as intensity times width normalized to the 1D fit median. Top row: median-filtered parameter maps from the 1D fit. Second row from top: regularized maps from the 3D fit. Third row from top: 3D parameter maps minus 3D fit (divided by 1D fit for flux). Bottom row: histograms of difference maps (black histograms) and Gaussian fits to those histograms (red curves). The moments of the Gaussian fits to the histograms are: median µ = −0.82 km s−1 and width σ = 1.38 km s−1 for the linewidth difference; µ = 0.10 km s−1 and σ = 0.95 km s−1 for the line velocity difference; and µ = −1.5% and σ = 2.0% for the relative flux estimate difference. |
4 Application to the CND Data
To apply CubeFit to the (sky-subtracted) CND data, we chose to use line flux as a parameter for the Gaussian profile rather than line amplitude. The amplitude I(l, m) at any point is linked to the flux F(l, m) and the total linewidth σtot (l, m) (Eq. (9)) by
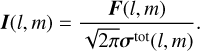 (11)
(11)
The reason for this choice is that line amplitude depends on the instrumental spectral resolution, which in our case varies across the field with sharp edges (Sect. 3.3). With our choice of parameters (line flux, intrinsic width, and velocity), we only fit astrophysical quantities, clean of instrumental signatures.
We also tried fitting the two H2 lines separately as well as together. In the regions where the two lines have sufficient S/N, the separate fits did not show a significant difference in radial velocity or linewidth, with difference histograms compatible with statistical uncertainties. We therefore chose to fit the two lines together. On the contrary, Brγ shows very different morphology and dynamics as demonstrated below and is fitted separately from H2. When fitting two lines together, the quantity of interest is the line ratio rather than each line flux separately. Dividing one flux map by the other causes several difficulties. Division by small factors with low S/N is a classical issue. In addition, the regularization in our method may lead to two maps with slightly different effective resolution, which would lead to artifacts in the division. We therefore use the ratio itself as a parameter rather than the two line fluxes.
On each mosaic, we finally performed two independent fits on the continuum-subtracted data: one on the Brγ line alone where the three parameters are line flux FBrγ, intrinsic width σBrγ, and intrinsic radial velocity shift υBrγ, and one on both H2 lines at once where the four parameters are H2 λ2.12 µm line flux 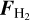 , flux ratio between the two lines
, flux ratio between the two lines 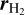 , common width
, common width 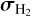 and common Doppler shift
and common Doppler shift 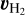 . The amplitude of the H2 λ2.12 µm line I2.12 is computed as per Eq. (11) and the amplitude of the H2 λ2.12 µm line is I2.22 = r × I2.12.
. The amplitude of the H2 λ2.12 µm line I2.12 is computed as per Eq. (11) and the amplitude of the H2 λ2.12 µm line is I2.22 = r × I2.12.
Finally, the 3D model functions MBrγ and 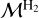 are expressed below using the multiline Gaussian function
are expressed below using the multiline Gaussian function 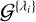 from Eq. (8):
from Eq. (8):
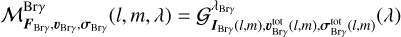 (12)
(12)
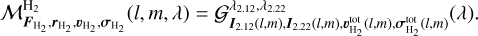 (13)
(13)
The H2 fit on the NE mosaic was performed in two passes. The first time, only 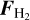 and
and 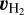 were fit.
were fit. 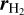 was set to 0.3 and
was set to 0.3 and 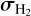 to 40 km s−1, both constant across the field. The Gaussian-smoothed and noise-added result of this fit was then used as the initial guess for a second fit where all parameters were free. A direct one-pass fit with constant maps as initial guess for all parameters had led to an erroneous local minimum. This two-pass treatment was not necessary for the SW mosaic. The Brγ fits were also done in two passes, where σ was fixed to 20 km s−1 during the first pass. Figure 3 shows the flux distribution of the three lines as recovered by CubeFit. The fixed values for the first pass were chosen as typical values as evaluated in previous tries in regions where the fit was of good quality.
to 40 km s−1, both constant across the field. The Gaussian-smoothed and noise-added result of this fit was then used as the initial guess for a second fit where all parameters were free. A direct one-pass fit with constant maps as initial guess for all parameters had led to an erroneous local minimum. This two-pass treatment was not necessary for the SW mosaic. The Brγ fits were also done in two passes, where σ was fixed to 20 km s−1 during the first pass. Figure 3 shows the flux distribution of the three lines as recovered by CubeFit. The fixed values for the first pass were chosen as typical values as evaluated in previous tries in regions where the fit was of good quality.
The resulting model cubes were interactively compared to the data cube using Cubeview for Yorick5 (Paumard 2003), which was extended for this purpose. This inspection revealed imperfect OH subtraction in very low S/N regions. OH lines very close to Brγ and to the H2 lines could bias our velocity and velocity width measurements. We therefore decided to cut the lowest S/N regions out of our final maps. This threshold is applied to the maximum intrinsic line flux per spectral channel:
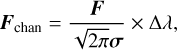 (14)
(14)
where Δλ is the bandwidth of a spectral channel. We consider a detection to be significant and parameters to be unbiased on spaxels with Fchan > Fchan,thresh where Fchan,thresh is twice the median over the field-of-view of the root-mean-square (RMS) of the residuals within each spaxel. In the absence of calibration residuals such as those caused by the OH lines, our method would not require a threshold to be set.
The regularization has the effect of smoothing noise without smoothing significant features in the various maps. It therefore serves our goal to increase S/N locally without degrading resolution. When data are missing altogether, the regularization term makes the fitting procedure act as an interpolation function: the output parameter maps therefore have fewer holes than the original data.
For estimating uncertainties, we followed the procedure described in Ciurlo et al. (2016), which makes use of this property: we generated four independent subsets of the original data by selecting every second row and every second column of spaxels. We then applied CubeFit to each subset independently. The RMS of the four independent estimates divided by 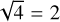 was taken to represent the statistical uncertainties of the original data.
was taken to represent the statistical uncertainties of the original data.
Table 3 lists statistical properties of the maps and their uncertainties: the flux per channel threshold (Fchan, thresh) for each map, and within the region where Fchan > Fchan, thresh, the minimum and maximum of F and the median of the uncertainties in the four parameters. As a comparison, the median uncertainties using a traditional 1D fitting method (directly estimated by the Yorick6 Levenberg-Marquardt-based fitting engine lmfit7) for the NE H2 data are 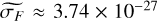 W m−2 arcsec−2,
W m−2 arcsec−2, 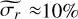 ,
,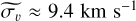 ,
, 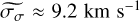 . The 1D-fit uncertainties can also be estimated by taking the RMS of each parameter map over four neighboring points, yielding median values of
. The 1D-fit uncertainties can also be estimated by taking the RMS of each parameter map over four neighboring points, yielding median values of 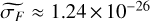 Wm−2 arcsec−2,
Wm−2 arcsec−2, 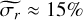 ,
, 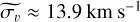 and
and 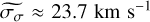 . The CubeFit uncertainties are therefore about ten times smaller than their 1D counterparts.
. The CubeFit uncertainties are therefore about ten times smaller than their 1D counterparts.
 |
Fig. 3 Composite line maps of the NE (left panel) and SW (right panel) mosaics. The flux of each of the three lines of interest has been assigned a color: red shows H2 (2.12 µm), green H2 (2.22 µm), and blue H II (traced by Brγ, 2.17 µm). Line flux is estimated by our fitting procedure. Regularization ensures that the maps are smooth and provides for extrapolation (in particular, there is no gap anymore between the two fields). It actually also provides some extrapolation, but we cut the field-of-view to the initial one (except for the gap). |
Statistical properties of the various fits.
4.1 NE Mosaic
The results for the NE mosaic are presented in Figs. 4 and 5 for H2 and Brγ, respectively. The Brγ line arises from neutral hydrogen but it traces the H II region. The corresponding uncertainty maps are in Figs. B.1 and B.2. The median uncertainties are listed in Table 3.
For both H2 and H II, the intrinsic linewidth map shows considerable structure with small, sharp features. The median of this width over the spaxels where H2 is reliably detected is 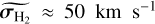 , and the minimum and maximum values are min
, and the minimum and maximum values are min 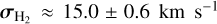 and
and 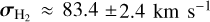 . Similarly, for
. Similarly, for 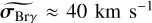 ,
, 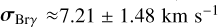 and
and 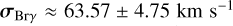 . Most interestingly, the linewidth maps appear anticorrelated with the line flux maps. This anticorrelation can be seen in Fig. 6, which displays line flux versus linewidth for the two species. It is reminiscent of the correlation seen by Ciurlo et al. (2019) between de-reddened line flux and extinction for H2 detected in the central cavity. Like them, we hypothesize that the more densely populated regions in the plot represent individual clumps for which a tight (anti)correlation exists, each being affected by a different amount of foreground extinction. For instance, the H2 width map shows sharp features in dark colors (i.e., small values) near (dα cos(δ), dδ) ≈ (6″, −3″) and (3″, 1″), where the flux map shows local maxima of matching shapes. Figure 7 shows a zoomed-in view of the two maps of this region. Since we are using an original method to measure line flux and width, we verify in Appendix A that this correlation is not an artifact of this new method.
. Most interestingly, the linewidth maps appear anticorrelated with the line flux maps. This anticorrelation can be seen in Fig. 6, which displays line flux versus linewidth for the two species. It is reminiscent of the correlation seen by Ciurlo et al. (2019) between de-reddened line flux and extinction for H2 detected in the central cavity. Like them, we hypothesize that the more densely populated regions in the plot represent individual clumps for which a tight (anti)correlation exists, each being affected by a different amount of foreground extinction. For instance, the H2 width map shows sharp features in dark colors (i.e., small values) near (dα cos(δ), dδ) ≈ (6″, −3″) and (3″, 1″), where the flux map shows local maxima of matching shapes. Figure 7 shows a zoomed-in view of the two maps of this region. Since we are using an original method to measure line flux and width, we verify in Appendix A that this correlation is not an artifact of this new method.
H2 is significantly detected almost everywhere in the field, whereas H II is concentrated along the southern and western edges of the field (i.e., on the area nearest to the central cavity). The various maps of the two species are very different from each other, so that H2 and H II presumably belong in distinct volumes of the interstellar medium (ISM). In particular the radial velocity map for H2 shows a rather smooth gradient from 0 km s−1 in the southeastern portion of the mosaic to 60 km s−1 in the northwestern area, while the velocity measured in H II is near 0 km s−1 in the northwestern area and approaches 40 km s−1 in the SW area. This variation does not appear as a smooth overall gradient. A plausible explanation is that H2 is dominated by the bulk orbital motion of the CND, while the ionized gas is more perturbed by its interactions with the nuclear cluster. The two line flux maps appear clumpy, with no clear spatial coherence.
4.2 SW Mosaic
The results for the SW mosaic are presented in Figs. 8 and 9 for H2 and Brγ, respectively. The corresponding uncertainty maps are in Figs. B.3 and B.4. The median uncertainties are listed in Table 3.
H2 is reliably detected almost over the entire field, except along the eastern edge. Brγ is also detected almost everywhere, except along the southern edge. In contrast to the NE field, the various maps show coherent structure in the form of elongated features presumably of filamentary nature. These elongated features can be seen consistently in all parameter maps (clearly in the linewidth, flux and velocity maps, less clearly in the flux ratio map).
As in the NE field, linewidth is anticorrelated with flux, at least locally (Figs. 10 and 11). However, the brightest H2 feature is not associated with a particularly strong local minimum in the width map. The filaments appear as deep valleys in the width map and ridges on the flux map. Two of the four such elongated features in the H2 maps, labeled A and B in Fig. 8, are oriented in the southeast–northwest direction and parallel to the four features labeled E to H on the Brγ maps (Fig. 9). The H2 and H II velocity maps also offer strong similarities: they can both be described as a plateau near υ ≈ −30 km s−1 occupying most of the field with the set of parallel filaments (A, B and E to H) at a significantly different velocity, near −80 km s−1. We also note that Brγ is brightest along the eastern edge of the field, precisely where H2 is not robustly detected.
In order to better probe the velocity field in the filaments, we extracted spectrograms (Figs. 12 and 13) along the four most prominent filaments of each map. The spectrograms extracted from the 3D cubes are similar to what would be achieved with a 0.3-arcsecond-wide long-slit spectrometer aligned on each filament. On slits A and B, the bulk of the emission has a velocity displacement of about −30 kms−1 with a drop to about −80 km s−1 on the eastern end (where the filamentary structures can be seen on the flux, linewidth and radial velocity maps). The (single-component) 3D fit yields a smooth transition between those two regions (white curve), especially for slit B. However, for both slits, another interpretation is also possible: that of two distinct, overlapping components (green, dash-dotted lines). The single component fit then gives a weighted average of the two actual components in the transition region. This interpretation is corroborated by looking at spectrogram D: Brγ emission is detected in this slit, but at ≃80 km s−1, which is not well matched by the white line delineating the H2 velocity. This indicates that H2 and H II are separated into two components along the line-of-sight. Similarly, H2 emission can be seen at slightly positive radial velocity on slits E to G (Fig. 13) where H II is again near −80 km s−1. Conversely, in slit H (which is located about 1″ north of slit B), both species are detected at compatible velocities (≃ − 80 km s−1).
 |
Fig. 4 Result of CubeFit on the NE mosaic for both H2 lines. A black curve on the flux map delineates the amplitude threshold (see text). This region is masked out in the other maps. The four maps are, from top left to bottom right: H2 λ2.12 µm line flux |
 |
Fig. 5 Result of CubeFit on the NE mosaic for the Brγ line. A black curve on the flux map delineates the amplitude threshold (see text). This region is masked out in the other maps. The three maps are, from left to right: line flux (FBrγ), intrinsic width (σBrγ), and intrinsic radial velocity shift (υBrγ)·features can be seen consistently in all parameter maps (clearly in the linewidth, flux and velocity maps, less clearly in the flux ratio map). |
 |
Fig. 6 Line flux vs. width density plot (arbitrary units) in the NE mosaic. Top: H2 (λ = 2.12 µm). Bottom: H II. The threshold imposed on intensity results in a tilted lower selection boundary on this plot. For both species, the two quantities are anticorrelated. Although remarkable, the overall anticorrelation is not very tight. Denser regions in the plot could be the trace of individual clumps in the CND with a tighter local anticorrelation, modulated by variable foreground extinction. |
5 Discussion
5.1 Comparison with Radio Maps
The two Brγ flux maps offer a striking resemblance to the Very Large Array (VLA) 6-centimeter continuum image (Fig. 1). This is most obvious for the SW mosaic where the Brγ emission occupies most of the field. The system of parallel elongated features seen in Fig. 9 (E to H) are seen very clearly in the VLA image as a detail in the Western Arc of the Minispiral. The fact that this system continues at larger distance from Sgr A* in H2 (features labeled A and В in Fig. 8) is a confirmation that the Western Arc is the ionized inner edge of the CND (Vollmer & Duschl 1999; Nitschai et al. 2020). The same similarity between Brγ and 6-centimeter continuum also exists in the field of the NE mosaic but is less obvious because both are much less luminous there than in the SW field. However, one can still clearly see that the Brγ and 6-centimeter emission are concentrated along the southern and western sides of the NE field (see also Fig. 3), and a small filament in the 6-centimeter continuum image in the southeastern corner of the NE field can be recognized in the Brγ image.
Likewise, the two H2 maps are very similar to the CS image from Fig. 1. The −80 km s−1 filamentary features seen in H2 emission in the SW mosaic are evident in the CS image. The main H2 features that can be seen in this mosaic are a thin filament running from the top center to the SW corner labeled С in Fig. 8, and a broad north-south ridge labeled D.
The fact that the morphology of many of the structures we identify in H2 and H II match those observed in the radio (CS and continuum, respectively) represents a very strong, independent proof of the robustness of CubeFit results, even at small scales.
 |
Fig. 7 Zoomed-in view of a feature in the NE H2 mosaic (λ = 2.12 µm) line flux and width maps. The bright S-shaped ridge in the flux maps corresponds to a similarly shaped valley in the width map. |
5.2 Bright Features are Compact
In both fields and in both species, we consistently see an anticorrelation between linewidth and flux, with large areas of low flux and broad linewidth contrasting with small regions of brighter flux and narrow linewidth. That can be explained in the following way. Hydrogen emission in HII regions is known to occur only (for H2) or primarily (for Brγ) at the surface of clumps because clumps are usually optically thick in the ultra-violet. The fact that we see broad lines means that several clumps are stacked along the line-of-sight, so that one sees the integral of a velocity gradient or a velocity dispersion among clumps. Then, we can interpret the narrow line areas in the field as individual compact clumps that are particularly bright and therefore dominate the integral over the line-of-sight. Those clumps can be presumed to be brighter as a consequence of a stronger ultraviolet field or a higher rate of collisional excitation. The particular H2 lines that we probe in this paper do not allow us to discriminate between the two excitation mechanisms, both of which are possible in this environment (Ciurlo et al. 2016).
In this context, the brightest feature in the H2 flux map for the SW field requires some attention as it is not associated with a strong local minimum of linewidth. Actually, this particular feature is at the intersection of the filaments labeled A and D. It is also at the transition between the −30 km s−1 plateau of the velocity map and the −80 km s−1 filaments. Therefore, this location is special. The appearance as the brightest flux maximum results from the overlap of several bright features. The velocity dispersion inside each of these individual features is small, as demonstrated by the width minima elsewhere in the A and D filaments, but the velocity dispersion among those individual features is large, which explains the overall large linewidth.
 |
Fig. 8 H2 in the SW mosaic; same panels as Fig. 4. Dash-dotted white lines indicate the locations of the virtual slits used in Fig. 12 and underline filamentary features. |
 |
Fig. 9 Brackett-γ emission in the SW mosaic; same panels as Fig. 5. Dash-dotted white lines indicate the location of the virtual slits used in Fig. 13 and underline filamentary features. |
5.3 The Filaments are Thin Clumps
Recognizing the Western Arc as the ionized inner edge of the CND raises the question of whether each clump is mostly molecular with an ionized surface, or whether some clumps are ionized and others neutral. In Figs. 8 and 9, filament A can be seen only in H2, E to G can be seen only in H II, but B and H, which are less than 1″ apart, are essentially detected in both species. There are two ways to interpret those two features. It is possible that ridges H (seen in H II) and B (seen in H2) trace two layers of different ionization states in a somewhat thick filament. Alternatively, it is also possible that they really are the trace of two distinct thin filaments, one of which is fully ionized and the other fully neutral. In this case, the fact that we also detect H II in slit B and H2 in slit H could be attributed to spatial resolution and slit width (0.3″). The fact that we see only one such transition between the two ionization states, and not one in each filament, supports the interpretation that they are separate thin filaments. For the filaments presented here, the apparent shape of the emission feature (be it Brγ or one of the two H2 lines) is a good representation of the actual shape of those clumps: rectilinear, thin (≲0.3″ thickness) and long (reaching ≳10″ length). This is in contrast with what has been seen in the central cavity (Ciurlo et al. 2019) where clumps appear to be only partially ionized. The observed elongation of the features we observe here is an argument against self-gravitating cloudlets.
 |
Fig. 10 Zoomed-in view of a feature in the SW mosaic: Brγ line flux and width maps. |
6 Conclusion
The regularized 3D fitting method that we propose in Sect. 3 proves to be a robust way of estimating maps of physical parameters such as line flux, velocity dispersion, and radial velocity, recovering those parameters in regions where the local average per-voxel S/N is as low as ≈l. The resulting maps have the desired properties of being smooth while retaining sharp features (see, e.g., the sharp local minima in the linewidth maps). The uncertainties, estimated by repeating the same process over four independent data subsets, are very small; they correspond to what could be obtained after smoothing the data with a radius of ≈5 pixels (0.5″), which would have severely degraded the spatial resolution of the parameter maps (Fig. A.l). We validated the results of CubeFit and the associated uncertainties by comparing them with a more classical spaxel-by-spaxel 1D fit in Sect. 4. We provide another validation in Appendix A, where we compare the results of CubeFit with a more classical 1D fit at a few locations. With this comparison, we also demonstrate that variations in linewidth across the field, as estimated by the 3D method, are robust. This method has also been applied to another data set in a companion paper, Ciurlo et al. (2016), where we detected H2 throughout the central cavity using the Spectrometer for Infrared Faint Field Imaging (SPIFFI) integral-field spectrometer at the European Southern Observatory (ESO) Very Large Telescope (VLT). Furthermore, in the application presented here we find small-scale features that corresponds to filaments and clumps observed in the radio and in other molecules. This provides a strong independent confirmation of the robustness of our findings with CubeFit.
We apply CubeFit to the Keck/OSIRIS data of the Galactic Center CND in Sect. 4. The linewidth map is a useful tool for identifying denser knots in the ISM, which appear as sharp local minima in the velocity dispersion. The ISM in the SW field is organized into two components: 1) a diffuse component near −30 km s−1 that contains only a few features, including two filaments oriented roughly in the north–south direction, and 2) a number of thin, compact, tidally sheared filaments, aligned along the orthoradial direction, with radial velocities near −80 km s−1. These two components contain both H II and H2, but each ortho-radial filament contains only one of the two species, with the most ionized closer to the center of the nuclear star cluster. Those filaments are aligned with the filaments that are evident in the radio continuum image (Fig. 1) and with the local direction of the magnetic field (Dowell et al., priv. comm.). In contrast, shear seems to play less of a role in shaping the emission in the NE field, and the Brγ and H2 emission seems to originate from distinct overlapping components. Here also, most of the surface is occupied by an optically thin medium emitting at low flux, with a few bright compact regions with presumably higher densities and optical depths.
Our observations therefore reveal a complex and clumpy environment, where low-density, high-filling factor material seems to coexist with higher-density, low-filling factor clumps that are tidally stretched and some of which are fully ionized. Those components have distinct kinematics, with radial velocities separated by ≃50 km s−1. This picture is very different from the assumption of spherical, self-gravitating clumps, which has sometimes been invoked in past studies.
Observing the rest of the CND in the three lines used here would help determine whether our conclusions hold generally.
 |
Fig. 11 Line flux vs. width density plot (arbitrary units) in the SW mosaic (see Fig. 6). The anticorrelation between line flux and width is quite remarkable in the lower panel (Brγ), where it takes the form of several narrow, densely populated streaks on the density plot. In the top panel (H2), the anticorrelation is weaker than in the bottom panel and the density distribution is more diffuse, but one can still identify linear features, showing that such a correlation exists locally. |
 |
Fig. 12 Slit-like spectrograms extracted from the SW mosaic data along the lines displayed in Fig. 8. The virtual slit has a width of 0.3 arcsec. Position–velocity images around each of the three spectral lines studied in this paper are displayed. The spectral axis is expressed as υLSR for each line. Overplotted in white is the H2 radial velocity derived with CubeFit at the same location, and the curve is the same in each subpanel. The dash-dotted green lines highlight the two-component solution described in the main text. |
 |
Fig. 13 Slit-like spectrograms extracted from the SW mosaic data along the lines displayed in Fig. 9. The virtual slit has a width of 0.3 arcsec. Position-velocity images around each of the three spectral lines studied in this paper are displayed. The spectral axis is expressed as υLSR for each line. Overplotted is the H II radial velocity derived with CubeFit at the same location, and the curve is the same in each subpanel. |
Acknowledgements
T.P. thanks Damien Gratadour for sharing the Yoda code and fruitful discussions concerning regularization. A.C., M.R.M., T.D. and A.M.G. acknowledge the support provided by the U.S. National Science Foundation (grants AST-1412615, AST-1518273), Jim and Lori Keir, the Gordon and Betty Moore Foundation, the Heising-Simons Foundation, the W.M. Keck Foundation, and Howard and Astrid Preston. The authors wish to recognize and acknowledge the very significant cultural role and reverence that the summit of Maunakea has always had within the indigenous Hawaiian community. We are most fortunate to have the opportunity to conduct observations from this mountain.
Appendix A Comparison with Classical 1D Method
In order to validate our method, we extracted a few spectra at typical places in the H2 field by averaging spaxels over a 0.5″ radius (a median on 78 spaxels per aperture) and performed a classical 1D Gaussian fit on the H2 λ 2.12 µm line in these spectra. The chosen location and spectra are displayed Fig. A.1. The average OH linewidth (weighted by  ) over the same aperture is then subtracted in quadrature and the uncertainty is propagated from the uncertainty estimated by the fit itself. The corresponding estimate from the 3D fit and its uncertainty are given by the average of
) over the same aperture is then subtracted in quadrature and the uncertainty is propagated from the uncertainty estimated by the fit itself. The corresponding estimate from the 3D fit and its uncertainty are given by the average of 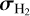 (Fig. 4) and σσ (Fig. B.1), also weighted by
(Fig. 4) and σσ (Fig. B.1), also weighted by 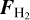 These 1D and 3D width measurements are listed in Table A.1 and agree very well. The classical 1D-fit approach corroborates the findings from CubeFit, confirming the intrinsic width variations over the field and confirming that the order of magnitude of our estimated uncertainties is correct.
These 1D and 3D width measurements are listed in Table A.1 and agree very well. The classical 1D-fit approach corroborates the findings from CubeFit, confirming the intrinsic width variations over the field and confirming that the order of magnitude of our estimated uncertainties is correct.
We also performed the 1D fit over the entire SW cube, once on the original non-smoothed cube and once on a smoothed version of the cube where every spaxel contains the average spectrum over a 0.5″ radius as above. We again subtracted the OH linewidth in quadrature. A close-up of the width map derived from these two fits and from CubeFit is displayed Fig. A.2. Results from the 1D fit on the non-smoothed data contain high-resolution features but are very noisy. Smoothing the cube enhances the S/N significantly, at the cost of erasing the small-scale features. CubeFit brings the best of the two worlds together, keeping the high-resolution features while removing most of the noise, thus enhancing those small-scale features. The sharp astrophysical features that we discuss in Sect. 5, very clear with our method, are difficult to make out from the non-smoothed 1D fit and are smoothed out in the smoothed 1D fit. Another advantage of our method is its resilience on bad data points. A few bad voxels in the cube result only in individual spikes in our method (some can be seen in the flux ratio map for the NE mosaic, Fig. 4) while smoothing smears them over large areas.
 |
Fig. A.1 Variation in |
 |
Fig. A.2 Close-up on three versions of the SW width map. Left: 1D fit on an original (non-smoothed) cube. Center: 3D fit with CubeFit. Right: 1D method fit on an aperture-smoothed cube. |
Appendix B Uncertainty Maps
Figures B.1, B.2, B.3, and B.4 show the uncertainty maps associated with the parameter maps in Figs. 4, 5, 8, and 9, respectively. Median values over the considered field-of-view for each mosaic and specie are listed in Table 3.
 |
Fig. B.1 Uncertainty maps corresponding to Fig. 4. Red lines delineate the same amplitude threshold as on the flux map. We display the flux-to-flux uncertainty ratio rather than the uncertainty itself. |
 |
Fig. B.2 Uncertainty maps corresponding to Fig. 5. Red lines delineate the same amplitude threshold as on the flux map. We display the flux-to-flux uncertainty ratio rather than the uncertainty itself. |
 |
Fig. B.3 Uncertainty maps corresponding to Fig. 8. Red lines delineate the same amplitude threshold as on the flux map. We display the flux-to-flux uncertainty ratio rather than the uncertainty itself. |
 |
Fig. B.4 Uncertainty maps corresponding to Fig. 9. Red lines delineate the same amplitude threshold as on the flux map. We display the flux-to-flux uncertainty ratio rather than the uncertainty itself. |
References
- Blank, M., Morris, M. R., Frank, A., Carroll-Nellenback, J. J., & Duschl, W. J. 2016, MNRAS, 459, 1721 [NASA ADS] [CrossRef] [Google Scholar]
- Bradford, C. M., Stacey, G. J., Nikola, T., et al. 2005, ApJ, 623, 866 [NASA ADS] [CrossRef] [Google Scholar]
- Christopher, M. H., Scoville, N. Z., Stolovy, S. R., & Yun, M. S. 2005, ApJ, 622, 346 [Google Scholar]
- Ciurlo, A., Paumard, T., Rouan, D., & Clénet, Y. 2016, A&A, 594, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ciurlo, A., Paumard, T., Rouan, D., & Clénet, Y. 2019, A&A, 621, A65 [EDP Sciences] [Google Scholar]
- Ciurlo, A., Campbell, R. D., Morris, M. R., et al. 2020, Nature, 577, 337 [Google Scholar]
- Dinh, C. K., Salas, J. M., Morris, M. R., & Naoz, S. 2021, ApJ, 920, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Etxaluze, M., Smith, H. A., Tolls, V., Stark, A. A., & González-Alfonso, E. 2011, AJ, 142, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Genzel, R. 1989, in IAU Symposium, The Center of the Galaxy, ed. M. Morris, 136, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Genzel, R., Eisenhauer, F., & Gillessen, S. 2010, Rev. Mod. Phys., 82, 3121 [Google Scholar]
- Gordon, I., Rothman, L., Hill, C., et al. 2017, J. Quant. Spectrosc. Radiat. Transf. Gravity Collaboration (Pfuhl, O., et al.) 2020, A&A, 634, A1 [Google Scholar]
- Güsten, R., Genzel, R., Wright, M. C. H., et al. 1987, ApJ, 318, 124 [CrossRef] [Google Scholar]
- Hsieh, P.-Y., Koch, P. M., Kim, W.-T., et al. 2021, ApJ, 913, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, J. M., Geis, N., Genzel, R., et al. 1993, ApJ, 402, 173 [CrossRef] [Google Scholar]
- Komasa, J., Piszczatowski, K., Lach, G., et al. 2011, J. Chem. Theory Comput., 7, 3105 [NASA ADS] [CrossRef] [Google Scholar]
- Larkin, J., Barczys, M., Krabbe, A., et al. 2006, SPIE Conf. Ser., 6269, 1 [Google Scholar]
- Lau, R. M., Herter, T. L., Morris, M. R., Becklin, E. E., & Adams, J. D. 2013, ApJ, 775, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Lockhart, K. E., Do, T., Larkin, J. E., et al. 2019, AJ, 157, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Lu, J. R., Do, T., Ghez, A. M., et al. 2013, ApJ, 764, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Marr, J. M., Wright, M. C. H., & Backer, D. C. 1993, ApJ, 411, 667 [NASA ADS] [CrossRef] [Google Scholar]
- Martín, S., Martín-Pintado, J., Montero-Castaño, M., Ho, P. T. P., & Blundell, R. 2012, A&A, 539, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mills, E. A. C., Güsten, R., Requena-Torres, M. A., & Morris, M. R. 2013, ApJ, 779, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Montero-Castaño, M., Herrnstein, R. M., & Ho, P. T. P. 2009, ApJ, 695, 1477 [CrossRef] [Google Scholar]
- Morris, M., & Serabyn, E. 1996, ARA&A, 34, 645 [Google Scholar]
- Morris, M., Ghez, A. M., & Becklin, E. E. 1999, Adv. Space Res., 23, 959 [NASA ADS] [CrossRef] [Google Scholar]
- Morris, M. R., Zhao, J.-H., & Goss, W. M. 2017, ApJ, 850, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Mugnier, L. M., Fusco, T., & Conan, J.-M. 2004, J. Opt. Soc. Am. A, 21, 1841 [Google Scholar]
- Netzer, H. 2015, ARA&A, 53, 365 [Google Scholar]
- Nitschai, M. S., Neumayer, N., & Feldmeier-Krause, A. 2020, ApJ, 896, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Oka, T., Nagai, M., Kamegai, K., & Tanaka, K. 2011, ApJ, 732, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Oliva, E., & Origlia, L. 1992, A&A, 254, 466 [NASA ADS] [Google Scholar]
- Paumard, T. 2003, PhD thesis, Institut d’astrophysique de Paris/Université Pierre & Marie Curie, France Requena-Torres, M. A., Güsten, R., Weiß, A., et al. 2012, A&A, 542, L21 [Google Scholar]
- Shukla, H., Yun, M. S., & Scoville, N. Z. 2004, ApJ, 616, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, I. L., & Wardle, M. 2014, MNRAS, 437, 3159 [NASA ADS] [CrossRef] [Google Scholar]
- Tsuboi, M., Kitamura, Y., Uehara, K., et al. 2018, PASJ, 70, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Vermot, P., Clénet, Y., Gratadour, D., et al. 2021, A&A, 652, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vollmer, B., & Duschl, W. J. 1999, in Astronomical Society of the Pacific Conference Series, The Central Parsecs of the Galaxy, eds. H. Falcke, A. Cotera, W. J. Duschl, F. Melia, & M. J. Rieke, 186, 265 [NASA ADS] [Google Scholar]
- Wolniewicz, L., Simbotin, I., & Dalgarno, A. 1998, ApJS, 115, 293 [CrossRef] [Google Scholar]
- Yusef-Zadeh, F., Stolovy, S. R., Burton, M., Wardle, M., & Ashley, M. C. B. 2001, ApJ, 560, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, J.-H., Morris, M. R., & Goss, W. M. 2016, ApJ, 817, 171 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Outline of the two mosaicked regions reported here superimposed on: the total intensity map of J = 4−3 CS emission from ALMA (left; Hsieh et al. 2021), and the 6-cm radio continuum image from the VLA (right; Zhao et al. 2016; Morris et al. 2017). The location of Sgr A* is indicated in each panel with a green cross. |
| In the text | |
 |
Fig. 2 Results of multiple OH line fits for the SW mosaic. Left column: linewidth (km s−1). Center column: radial velocity offset (km s−1). Right column: flux of the brightest line estimated as intensity times width normalized to the 1D fit median. Top row: median-filtered parameter maps from the 1D fit. Second row from top: regularized maps from the 3D fit. Third row from top: 3D parameter maps minus 3D fit (divided by 1D fit for flux). Bottom row: histograms of difference maps (black histograms) and Gaussian fits to those histograms (red curves). The moments of the Gaussian fits to the histograms are: median µ = −0.82 km s−1 and width σ = 1.38 km s−1 for the linewidth difference; µ = 0.10 km s−1 and σ = 0.95 km s−1 for the line velocity difference; and µ = −1.5% and σ = 2.0% for the relative flux estimate difference. |
| In the text | |
 |
Fig. 3 Composite line maps of the NE (left panel) and SW (right panel) mosaics. The flux of each of the three lines of interest has been assigned a color: red shows H2 (2.12 µm), green H2 (2.22 µm), and blue H II (traced by Brγ, 2.17 µm). Line flux is estimated by our fitting procedure. Regularization ensures that the maps are smooth and provides for extrapolation (in particular, there is no gap anymore between the two fields). It actually also provides some extrapolation, but we cut the field-of-view to the initial one (except for the gap). |
| In the text | |
 |
Fig. 4 Result of CubeFit on the NE mosaic for both H2 lines. A black curve on the flux map delineates the amplitude threshold (see text). This region is masked out in the other maps. The four maps are, from top left to bottom right: H2 λ2.12 µm line flux |
| In the text | |
 |
Fig. 5 Result of CubeFit on the NE mosaic for the Brγ line. A black curve on the flux map delineates the amplitude threshold (see text). This region is masked out in the other maps. The three maps are, from left to right: line flux (FBrγ), intrinsic width (σBrγ), and intrinsic radial velocity shift (υBrγ)·features can be seen consistently in all parameter maps (clearly in the linewidth, flux and velocity maps, less clearly in the flux ratio map). |
| In the text | |
 |
Fig. 6 Line flux vs. width density plot (arbitrary units) in the NE mosaic. Top: H2 (λ = 2.12 µm). Bottom: H II. The threshold imposed on intensity results in a tilted lower selection boundary on this plot. For both species, the two quantities are anticorrelated. Although remarkable, the overall anticorrelation is not very tight. Denser regions in the plot could be the trace of individual clumps in the CND with a tighter local anticorrelation, modulated by variable foreground extinction. |
| In the text | |
 |
Fig. 7 Zoomed-in view of a feature in the NE H2 mosaic (λ = 2.12 µm) line flux and width maps. The bright S-shaped ridge in the flux maps corresponds to a similarly shaped valley in the width map. |
| In the text | |
 |
Fig. 8 H2 in the SW mosaic; same panels as Fig. 4. Dash-dotted white lines indicate the locations of the virtual slits used in Fig. 12 and underline filamentary features. |
| In the text | |
 |
Fig. 9 Brackett-γ emission in the SW mosaic; same panels as Fig. 5. Dash-dotted white lines indicate the location of the virtual slits used in Fig. 13 and underline filamentary features. |
| In the text | |
 |
Fig. 10 Zoomed-in view of a feature in the SW mosaic: Brγ line flux and width maps. |
| In the text | |
 |
Fig. 11 Line flux vs. width density plot (arbitrary units) in the SW mosaic (see Fig. 6). The anticorrelation between line flux and width is quite remarkable in the lower panel (Brγ), where it takes the form of several narrow, densely populated streaks on the density plot. In the top panel (H2), the anticorrelation is weaker than in the bottom panel and the density distribution is more diffuse, but one can still identify linear features, showing that such a correlation exists locally. |
| In the text | |
 |
Fig. 12 Slit-like spectrograms extracted from the SW mosaic data along the lines displayed in Fig. 8. The virtual slit has a width of 0.3 arcsec. Position–velocity images around each of the three spectral lines studied in this paper are displayed. The spectral axis is expressed as υLSR for each line. Overplotted in white is the H2 radial velocity derived with CubeFit at the same location, and the curve is the same in each subpanel. The dash-dotted green lines highlight the two-component solution described in the main text. |
| In the text | |
 |
Fig. 13 Slit-like spectrograms extracted from the SW mosaic data along the lines displayed in Fig. 9. The virtual slit has a width of 0.3 arcsec. Position-velocity images around each of the three spectral lines studied in this paper are displayed. The spectral axis is expressed as υLSR for each line. Overplotted is the H II radial velocity derived with CubeFit at the same location, and the curve is the same in each subpanel. |
| In the text | |
 |
Fig. A.1 Variation in |
| In the text | |
 |
Fig. A.2 Close-up on three versions of the SW width map. Left: 1D fit on an original (non-smoothed) cube. Center: 3D fit with CubeFit. Right: 1D method fit on an aperture-smoothed cube. |
| In the text | |
 |
Fig. B.1 Uncertainty maps corresponding to Fig. 4. Red lines delineate the same amplitude threshold as on the flux map. We display the flux-to-flux uncertainty ratio rather than the uncertainty itself. |
| In the text | |
 |
Fig. B.2 Uncertainty maps corresponding to Fig. 5. Red lines delineate the same amplitude threshold as on the flux map. We display the flux-to-flux uncertainty ratio rather than the uncertainty itself. |
| In the text | |
 |
Fig. B.3 Uncertainty maps corresponding to Fig. 8. Red lines delineate the same amplitude threshold as on the flux map. We display the flux-to-flux uncertainty ratio rather than the uncertainty itself. |
| In the text | |
 |
Fig. B.4 Uncertainty maps corresponding to Fig. 9. Red lines delineate the same amplitude threshold as on the flux map. We display the flux-to-flux uncertainty ratio rather than the uncertainty itself. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




![$ \nabla {a_i}\left( {l,m} \right) = \,{\left[ {{\nabla _l}{a_i}{{\left( {l,m} \right)}^2} + {\nabla _m}{a_i}{{\left( {l,m} \right)}^2}} \right]^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}, $](/articles/aa/full_html/2022/08/aa43228-22/aa43228-22-eq7.png)