| Issue |
A&A
Volume 664, August 2022
|
|
|---|---|---|
| Article Number | A53 | |
| Number of page(s) | 13 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202142809 | |
| Published online | 09 August 2022 | |
A general stability-driven approach for the refinement of multi-planet systems★
Département d’Astronomie, Université de Genève,
Chemin Pegasi 51b,
1290
Versoix, Suisse
e-mail: manu.stalport@unige.ch
Received:
2
December
2021
Accepted:
16
May
2022
Context. Over recent years, the number of detected multi-planet systems has grown significantly. An important subclass of these are the compact configurations. Precise knowledge of this subclass is crucial for understanding the conditions in which planetary systems form and evolve. However, observations often leave these systems with large uncertainties, notably on the orbital eccentricities. This is especially prominent for systems with low-mass planets detected with radial velocities, and increasing numbers of these are being discovered in the exoplanet population. Refining these parameters with the help of orbital stability arguments is becoming a common approach.
Aims. Such dynamical techniques can be computationally expensive. In this work, we use an alternative procedure that is orders of magnitude faster than classical N-body integration approaches, and has the potential to narrow down parameter uncertainties.
Methods. We coupled a reliable exploration of the parameter space with the precision of the Numerical Analysis of Fundamental Frequencies (Laskar, J. 1990, Icarus, 88, 266) fast chaos indicator. We also propose a general procedure to calibrate the NAFF indicator on any multi-planet system without additional computational cost. This calibration strategy is illustrated using the compact multiplanet system HD 45364, in addition to yet-unpublished measurements obtained with the HARPS and CORALIE high-resolution spectrographs. We validate the calibration approach by a comparison with long integrations performed on HD 202696. We test the performances of this stability-driven approach on two systems with different architectures: first we study HD 37124, a three-planet system composed of planets in the Jovian regime; then, we analyse the stability constraints on HD 215152, a compact system of four low-mass planets.
Results. We revise the planetary parameters for HD 45364, HD 202696, HD 37124, and HD 215152, and provide a comprehensive view of the dynamical state these systems are in.
Conclusions. We demonstrate the potential of the NAFF stability-driven approach to refine the orbital parameters and planetary masses. We stress the importance of undertaking systematic global dynamical analyses on every new multi-planet system discovered.
Key words: planets and satellites: dynamical evolution and stability / methods: numerical / techniques: radial velocities / celestial mechanics
The new HARPS and CORALIE data of HD 45364 presented in Appendix A are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/664/A53
© M. Stalport et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1 Introduction
After the first detection of an exoplanet orbiting a main sequence star by Mayor & Queloz (1995), it did not take long to discover the first multi-planet system (Upsilon Andromedae, Butler et al. 1999). Since then, the number of discovered multi-planet systems has significantly increased1. Dedicated exoplanet missions such as Kepler and TESS or results from high-resolution spec-trographs such as HARPS boosted this number, and illustrated the large diversity of architectures observed. In the solar neighbourhood, the planetary orbits in multi-planet systems show very different shapes and levels of compactness. This observed diversity provides important constraints on planet formation and orbital evolution models. Indeed, the current planetary orbits act as tracers of their birth place and past orbital evolution under the influence of planet–disc and/or planet–planet gravitational interactions. Furthermore, direct comparison of the orbital configurations and properties of the planets within the same system provides indications in regards to formation processes (e.g. MacDonald et al. 2016; Hadden & Payne 2020; Leleu et al. 2021; Heising et al. 2021). Multi-planet systems therefore represent precious case studies that can help us to understand the formation of planetary systems as a whole. Among the most interesting multi-planet systems, compact architectures are particularly intriguing. With no equivalent in the Solar System, they are subject to strong dynamical constraints. Those systems therefore represent ideal candidates with which to test the role of planet–planet gravitational interactions in the formation and evolution of planetary systems (e.g. Hadden & Payne 2020). However, as those systems are often composed of small planets, they are also observationally challenging. As a result, such observations are likely to provide poor constraints on the orbital and planetary properties in these systems.
The study of dynamics, and in particular orbital stability, is a well-established tool with which to refine the orbital parameters of multi-planet systems. A common procedure is to build chaos maps, also sometimes referred to as stability maps, which explore the chaotic behaviour of two-dimensional sections of the parameter space (e.g. Goździewski et al. 2001; Correia et al. 2009; Couetdic et al. 2010; Lovis et al. 2011; Robertson et al. 2012; Satyal et al. 2014; Wittenmyer et al. 2014; Delisle et al. 2018; Hadden & Payne 2020; Leleu et al. 2021). They provide visual insights into the structure of the parameter space and help us to understand the dynamical state of the studied system. However, such a procedure has limitations, because it provides a partial view of the parameter space. Indeed, chaos maps explore the influence of only two parameters, while the whole parameter space of the multi-planet system can be of considerable size. In particular, chaos maps do not account for potential correlations between parameters. As such, they represent a restricted exploration of the parameter space, and caution must therefore be taken in their interpretation. In order to overcome this limitation, dynamical methods that include the stability information during the fitting procedure have been shown to be very efficient. Notably, a technique has been proposed that couples a genetic algorithm for exploration of the parameter space with the MEGNO fast chaos indicator that is used to discriminate the strongly chaotic solutions (Goździewski et al. 2003; Gozdziewski et al. 2008). This approach, named GAMP (for Genetic Algorithm with MEGNO Penalty), allows global exploration of the parameter space and efficient estimation of the orbital stability. The latter is based on heuristic arguments, coupling a level of chaos to a level of stability. This technique has been proven able to constrain the system when only a few radial velocity (RV) measurements are available.
A particularly well-indicated and well-established method for parameter space exploration is the Markov chain Monte Carlo (MCMC) algorithm, which consists in a random walk inside the parameter space influenced by some prior information and by constraints added by observational data. The resulting path of the walker defines a global posterior distribution of the same dimension as the parameter space. The projection of this global posterior onto each parameter serves as the baseline for their estimation: we often use the median of the distribution together with its 68.27% confidence interval. This technique is extensively used by the community to estimate model parameters from observational data. As a result of its popularity and efficiency, there is an interest to couple the MCMC exploration tool with the orbital stability constraint. This general approach is not new. To our knowledge, its first appearance dates back to 2006, when Ford (2006) proposed the use of N-body numerical simulations to remove all the solutions from the posterior distribution that turned unstable over the course of the integrations. This importance sampling based on orbital stability estimation is interpreted as another constraint on the system in addition to the observations. This strategy was applied by Veras & Ford (2010), who performed an exhaustive dynamical analysis of a set of five multi-planet systems. For each of them, the authors modelled the RV measurements and explored the parameter spaces of those models with MCMC. They performed N-body numerical simulations over 1 Myr on a sampled posterior for each system. In addition to close encounters, their stability criterion was set from the variations in the semi-major axes of the planets, which should not exceed a defined threshold. Similar approaches were employed later on, with the same aim of providing a rigorous revision of the orbital parameters (e.g. Joiner et al. 2014; Nelson et al. 2016; Trifonov et al. 2019; Quinn et al. 2019).
In this paper, we develop a technique coupling the efficiency of the MCMC to explore the parameter space with a significantly more rapid stability estimation in order to perform rejection sampling. This estimation is based on a heuristic approach, associating the physical stability (i.e. close encounter or escape) with a measurement of chaos. In particular, it makes use of the Numerical Analysis of Fundamental Frequencies (NAFF, Laskar 1990, 1993) fast chaos indicator. The latter quantifies the chaos of a planetary system by measuring the drift in the average mean motions of the planetary orbits over time. While in the secular theory, non-chaotic orbits do not display any drift in average mean motions, this is no longer true in chaotic trajectories. Furthermore, the larger the drifts, the more chaotic the orbits, and therefore the more unstable the planetary system. Nevertheless, a major drawback of this indicator in the context of this work is the lack of general calibration for the drift in the average mean motions. This issue is tackled here. This procedure – linking Bayesian techniques to explore the parameter space with the NAFF fast chaos indicator for the estimation of orbital stability – has been used in previous studies to refine the orbital elements and masses in multi-planet systems (Nielsen et al. 2020; Hara et al. 2020), but these latter did not make use of a universal NAFF calibration procedure. In this paper, we present the method and demonstrate its performance.
We first stress the link between orbital instability and chaos and introduce the NAFF indicator in Sect. 2.2. We propose a strategy to calibrate the drift in average mean motion that the NAFF measures (Sect. 3). The approach is illustrated with HD45364, a system of two massive planets in the 3:2 mean-motion resonance (MMR). We validate the calibration procedure on HD 202696, by comparing the results of the fast chaos estimation approach with brute-force long integrations. Subsequently, we apply the stability-driven refinement technique to HD 37124 in Sect. 4. The orbital dynamics of this three-planet system have already been studied, but so far no exhaustive revision of the parameters has been carried out. Our stability-driven refinement technique is also tested on a compact system of low-mass planets, namely HD 215152 (Delisle et al. 2018), which is one of the few compact configurations found with RV measurements only. The observations poorly constrain the orbital eccentricities, which leaves room for the refinement technique to play a significant role in updating the system parameters rigorously. We present this revision in Sect. 5. Finally, we discuss our results in Sect. 6.
2 Method
2.1 Strategy of the Present Refinement Technique
There are three general strategies with which stability information can be added to the results of the MCMC exploration. Firstly, stability information could be added as prior information for the MCMC based on either analytical arguments or trends in the observed multi-planet systems. However, so far the numerical integrations bring stronger constraints on the systems than any of these arguments. Secondly, stability constraints could be included during the MCMC exploration, as secondary likelihood information together with the observational data, but such a procedure requires some caution. Indeed, the number of steps a walker typically performs in a MCMC is on the order of 1 million or more, and therefore the orbital stability of as many solutions should be estimated. The use of analytic stability criteria is appropriate for that, because they require very small computing times. However, they are less reliable than the integration techniques, and are furthermore restricted to specific orbital architectures, which is not convenient for a general purpose. Recently, a fast stability estimation based on short integration times together with machine-learning pattern recognition has shown promising performances. Nevertheless, this tool, named SPOCK (Tamayo et al. 2020), is dependent on the training set for the machine learning algorithm. With an increasing diversity of system architectures used during the training phase, and provided an efficient computing cluster is available, this tool constitutes a very competitive alternative to the analytical criteria.
Finally, the orbital stability constraint could be added after the MCMC exploration. The orbital stability would be estimated on each solution composing the posterior sample. An unfavourable weight on the unstable configurations would reshape the posteriors. Such a strategy is analogous to importance sampling and is effective if enough stable samples remain in the distribution at the end of the process. As a result, the less constrained a system is, the larger the distribution should be in order to correctly explore the stable areas of the parameter space. Compared to the second strategy though, this latter necessitates the estimation of stability for far fewer system configurations, and can therefore be coupled with classical integration techniques. Furthermore, it allows us to highlight the impact of dynamical constraints on the system, by directly comparing the posteriors before and after the addition of the stability computation. Therefore, we opt for this third strategy in the present study. Our stability-driven approach therefore combines the posterior of global model parameter exploration with a decisional process for stability.
2.2 Choice of the Stability Criterion
In many studies that include stability information a posteriori of the MCMC, the stability proxy is simply the survival of the configuration of the system over the entire timespan of the integration (e.g. Trifonov et al. 2019; Quinn et al. 2019; Cloutier et al. 2019). Such a criterion is very reliable against the unstable behaviour of the configuration. However, it does not provide any information about the orbital stability after the integration ends. As such, somewhat large integration times are needed for the stability decision to make sense, that is, integration times that are not too small with regards to the age of the planetary system under study. This process is computationally expensive, but there exists alternative stability criteria. A convenient choice is to use chaos indicators, which have proven efficient in spotting orbital instabilities ahead of their appearance.
Chaos is a feature of the motion whereby a dynamical system harbours uneven, disordered evolution and with large variations in the trajectories. A consequence of these features is a hyper-sensitivity regarding the initial conditions from which the system is evolving. Many different chaos indicators have been built, of varying efficiency; for example, the well-established Lyapunov Characteristic Exponents (Benettin et al. 1980, for a review), the Numerical Analysis of Fundamental Frequencies NAFF (Laskar 1990, 1993), the Spectral Number SN (Michtchenko & Ferraz-Mello 1995; Michtchenko et al. 2002), the Conditional Entropy of Neary Orbits (Núñez et al. 1996), the Fast Lyapunov Indicator FLI (Froeschlé et al. 1997), the Mean Exponential Growth of Nearby Orbits MEGNO (Cincotta et al. 2003), the 0–1 test (Gottwald & Melbourne 2004), and the Shannon entropy (Giordano & Cincotta 2018; Cincotta et al. 2021). Their use is not restricted to planetary dynamics, and notably there have been applications to the stability of stellar orbits in galactic potentials (Udry & Pfenniger 1988). All of these indicators find their basic principle in the link between chaoticity and instability (e.g. Chambers et al. 1996; Murray & Holman 1997; Obertas et al. 2017; Rice et al. 2018; Hussain & Tamayo 2020). However, this observed link has limitations, as the information of one quantity does not always rely on the other, for instance when a dynamical system harbours what is called bounded chaos. In those systems, the topology of the parameter space is such that the chaotic area is spatially restricted, and the system can only diffuse between impervious boundaries. As a result, the dynamical system may harbour strong chaos but stable behaviour, because of the very limited impact on the variations of the orbital elements.
Aside from these particular cases, and although no explicit general relationship has been validated between chaoticity and instability time, it is nowadays generally accepted and empirically proven that the more chaotic the configuration of a system, the more unstable it will be, that is, the shorter its lifetime will be. Extensive numerical simulations of the chaotic behaviour of planetary systems furthermore showed that the stronger the chaos, the smaller the uncertainty on the survival time (Hussain & Tamayo 2020). This result implies that, due to intrinsic uncertainties coming from the chaotic nature of motion, it becomes highly doubtful to associate a moderately chaotic system with a certain survival time. Instead, in this work we focus on strong chaos, from which a following instability can be inferred. Our approach is designed to reach similar results to those of the ‘brute force’ long integration technique, with integration times that are shorter by orders of magnitude.
A subclass of chaos indicators is particularly well-suited, namely the fast chaos indicators. These converge rapidly to a stability answer, and thus do not necessitate long integration times. Among them, NAFF (Laskar 1990, 1993) has been widely used by the community. While most of the other chaos indicators mentioned estimate chaos from the differential evolution of two initially almost-identical system configurations – exploiting the hyper-sensitivity to initial conditions of chaotic orbits – the NAFF is based on a technique called frequency analysis. The latter was first presented by Laskar (1988) for the computation of the secular evolution of the solar system via a semi-analytical approach. It is a tool that estimates the main frequencies in a dynamical system with high precision, based on the hypothesis that the orbits are quasi-periodic. The NAFF indicator uses this tool in order to test the quasi-periodic hypothesis of the orbital motion.
Generically, in any coordinate system, each coordinate f of a quasi-periodic trajectory can be decomposed as:
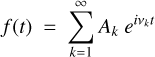 (1)
(1)
which is an infinite sum of harmonics, with frequency terms νk and amplitudes Ak, and with t being the time and i the imaginary unit. The aim of frequency analysis is to numerically approximate f by searching for the N highest-amplitude terms of the series with the help of numerical integration. Thus, we build a function f′ that numerically approaches f in order to get
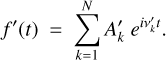 (2)
(2)
The procedure to get the approximative function f′ for the motion of a planet starts by integrating the whole system over time T. The planetary motion over that timespan is then split into its constituent frequencies with the help of a refined Fourier analysis. The frequency with the largest amplitude is removed, and a new spectrum is computed. This process is repeated N times in order to provide the N highest amplitude terms of the decomposition. This is an iterative process.
Frequency analysis is used to estimate the frequency associated with the mean longitude, which is the mean motion 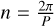 . That frequency appears always as the first term of the above decomposition because its amplitude is the highest. We therefore use the frequency analysis with N =1, and there is no confusion about the physical origin of that term. Furthermore, in the quasi-periodic hypothesis of motion, the mean motion does not harbour any secular variations or drifts; it is constant. The NAFF stability indicator precisely tests this hypothesis by searching for potential drifts in the value of the mean motion. Because the mean longitude is a quickly varying angle, this coordinate is sensitive to chaos on short timescales, which allows us to build a fast chaos indicator. The procedure employed by NAFF to do so is explained in Sect. 9 of Laskar (1990) and applied to exo-planet systems by Correia et al. (2005) for example. The idea is to split the total integration time into two halves and apply the frequency analysis technique to each half. This process will provide us with two very precise estimations of the fundamental frequency associated with the mean motion of the planet on its orbit. The comparison between these two frequencies is the basis of the chaos estimation. The smaller this difference, the closer the orbit is to real quasi-periodicity and thus the less chaotic the trajectory. However, if the difference is larger, the orbit displays stronger chaos and therefore the probability of instability increases.
. That frequency appears always as the first term of the above decomposition because its amplitude is the highest. We therefore use the frequency analysis with N =1, and there is no confusion about the physical origin of that term. Furthermore, in the quasi-periodic hypothesis of motion, the mean motion does not harbour any secular variations or drifts; it is constant. The NAFF stability indicator precisely tests this hypothesis by searching for potential drifts in the value of the mean motion. Because the mean longitude is a quickly varying angle, this coordinate is sensitive to chaos on short timescales, which allows us to build a fast chaos indicator. The procedure employed by NAFF to do so is explained in Sect. 9 of Laskar (1990) and applied to exo-planet systems by Correia et al. (2005) for example. The idea is to split the total integration time into two halves and apply the frequency analysis technique to each half. This process will provide us with two very precise estimations of the fundamental frequency associated with the mean motion of the planet on its orbit. The comparison between these two frequencies is the basis of the chaos estimation. The smaller this difference, the closer the orbit is to real quasi-periodicity and thus the less chaotic the trajectory. However, if the difference is larger, the orbit displays stronger chaos and therefore the probability of instability increases.
In this work, we compute the drift in mean motion of every planetary orbit. In order to compare that drift between planetary orbits of different scales, we normalise it with the initial mean motion of the planet under study. As such, we define our NAFF stability indicator as follows:
![$ \matrix{ {{\rm{NAFF}}} & { = \mathop {\max }\limits_j } & {\left[ {{{\log }_{10}}{{\left| {{n_{j,2}} - {n_{j,1}}} \right|} \over {{n_{j,0}}}}} \right]} \cr } , $](/articles/aa/full_html/2022/08/aa42809-21/aa42809-21-eq4.png) (3)
(3)
where nj,1 and nj,2 are the estimated mean motions over the first and second half of the integration, respectively, for every planet j in the system. nj,0 is the initial Keplerian mean motion of planet j. We retain the maximal drift value among all the planets as the proxy for the chaos in the system. The convergence of this chaos indicator is dictated by the precision in the estimation of the mean motion frequencies. The latter directly depends on the integration time, and usually reaches reliable results after ~104 revolutions of the outermost planet.
Let us note that we use the NAFF indicator as a binary decision maker concerning orbital stability. Therefore, we set up a NAFF threshold above which the variations of the estimated mean motions are considered too large for the system to be stable on long timescales. In Sect. 3, we propose a technique for finding an appropriate NAFF threshold according to the planetary system under study. This approach does not necessitate further numerical simulations. Another option for the use of NAFF would have been to assign a weight to each realisation of the MCMC posterior that is inversely proportional to the average mean motion drift. This weight would be added to the function informing us about the quality of the fit; for example, the χ2. However, we reiterate that we use NAFF to identify the strongly chaotic configurations, for which the drifts in mean motion are larger. A smooth weight function would therefore have its domain in the large NAFF values only, while all the small NAFF values would be assigned a weight of 1. We empirically noticed that such a function is well-approximated with a strict cut.
In Fig. 1, we illustrate this by comparing the results of the NAFF chaos indicator with the actual survival time of the system in the case of the MCMC posterior of the two-planet system HD 202696. The two massive planets reported in Trifonov et al. (2019) – with minimum masses of 1.99 and 1.92 mJup for planets b and c, respectively – orbit the star with a period ratio of ~ 1.81 (Pb ~ 528.2 days, Pc ~ 958 days). We fitted the 42 HIRES radial velocity data publicly available for this star (M = 1.91 M⊙). This was done using the Data and Analysis Center for Exoplanets (DACE) platform2: first via an iterative signal search in the peri-odogram of the RV time series, then modelling the significant periodicities with keplerians, and finally by computing the peri-odogram of the residuals to restart again until no significant peak is left. At the end of this process, we used a MCMC to efficiently explore the parameter space of the model. The implementation of this MCMC is described in Díaz et al. (2014), and is based on a Metropolis-Hastings algorithm. We removed the first 25% of the iterations as a burning phase, and sampled the posterior according to the correlation length of the chain. We then integrated every configuration of the resulting MCMC posterior distribution over 2 Myr, that is, twice the integration time used in the reference study by Trifonov et al. (2019). The numerical simulations were performed in the centre-of-mass inertial frame, and using the 15th-order adaptive time-step integrator IAS15 (Rein & Spiegel 2015). The latter is based on a Gauss-Radau quadrature and is implemented in the REBOUND Python package3 (Rein & Liu 2012). We also computed the NAFF chaos indicator on the first 31 250 yr only, that is, a 64th of the total integration time4. Of the 7813 system configurations making the MCMC posterior, 4688 reached the first 31 250 yr of integration and therefore received a NAFF estimation; the others became unstable (close encounter or escape) before that point in time. To proceed to the NAFF chaos computation, we recorded the mean longitudes of the planets at regular time-steps for a total of 20 000 output times. From these time series, we can decompose every planetary motion into its constituent frequencies and apply the frequency analysis technique. This serves to compute the average mean motion of every planet over each half of the integration, and derive the NAFF chaos indicator (Eq. (3)).
The numerical estimation of the frequencies obtained with the NAFF algorithm is affected by the output time-step δt as well as the total duration T of the integration. The precision on the frequencies is mainly limited by the total duration of the integration (Laskar 2003). On the other hand, the time-step δt has a weak impact on the precision of the frequencies but introduces alias issues. Indeed, one cannot distinguish between a frequency n and a frequency n + knNyquist, where k is an integer and nNyquist = π/δt is the Nyquist frequency. With our choice of sampling in the HD 202696 study, the resulting time step is found to be longer than the period of the outer planet, which means that the frequency we obtain with the NAFF algorithm is actually an alias of the mean motion. However, we are mainly interested in the difference in the mean motion between the two halves of the integration, which is given by: n2 − n1 = f2 − f1 + (k2 − k1)nNyquist, where f1 and f2 are the frequencies obtained through the NAFF algorithm. We then assume that the mean motion did not dramatically change and we select the value of k = k2 − k1 that minimises n2 − n1. This procedure works as long as the mean motion drift is small compared to the Nyquist frequency.
The scatter graph of Fig. 1 represents the 4688 configurations that benefit from a NAFF estimation after 31250 yr. Each of these is a dot in the space of NAFF versus the survival time of the system configurations, in log10 scale. Naturally, the maximum survival time that we can estimate is the total integration time, which is 2 Myr. As can be seen in the figure, a proportion of configurations reached that limit, and build up the horizontal series of points on the top. Despite some spread inherent to the chaotic nature of the systems, we observe a clear correlation in the strong chaos regime. Starting from NAFF ~ −2.5, the first configurations that survived the full integration appear, and this proportion increases with decreasing NAFF. In the figure, we also show the proportion of systems that survived the entire 2 Myr integration for consecutive NAFF ranges in orange. A value of 100% means that all the system configurations in a specific NAFF range are stable, in the sense that they survived the entire 2 Myr of integration (no escape, no close encounter), while a value of 0% indicates that none reached the end. This curve would represent our weight function. However, given its sharp increase in the more chaotic domain, we notice that a strict cut above a certain NAFF threshold is close to the weight function. Hence, we decide to use NAFF as a binary stability indicator, which considerably simplifies its use.
 |
Fig. 1 HD 202696. Black: scatter plot of the NAFF chaos indicator with respect to the actual survival time of the system configurations. Orange: proportion of stable systems (i.e. that survived the entire 2 Myr of integration) for consecutive ranges of NAFF. |
3 NAFF Calibration
The drift in the mean motions provides a relative measurement of chaos. Indeed, despite the normalisation performed in Eq. (3), it is not guaranteed that two different systems with the same maximal drift in the mean motions of the planetary orbits will have the same survival time. In other words, the NAFF indicator does not provide any information regarding the absolute chaos; the same NAFF value may correspond to different levels of orbital stability among various system architectures. However, in this work, we use NAFF as a binary stability decision maker. In order to set up a consistent stability threshold, a calibration of NAFF for every studied system becomes necessary.
To our knowledge, very few studies have attempted to calibrate the NAFF chaos indicator. At first, linear diffusion laws were hypothesised to extrapolate the evolution of the mean motion drifts (e.g. Robutel & Laskar 2001). Such an extrapolation could be used to predict the time after which the mean motions have varied by more than 100%; this time estimation could then be used in a similar fashion to the Lyapunov time. However, this process is approximative, as it relies on the hypothesis of linear growth in the mean motion drift. A more rigorous process of NAFF calibration was proposed by Couetdic et al. (2010), which consists in defining a grid of systems – similar to the grid used for chaos maps – and computing the NAFF chaos indicator (without normalisation in their case) for each system for two integration times T1 and T2 (T1 > T2). If a system is quasi-periodic, its NAFF estimation should get smaller over a longer integration timespan T1, because of the better numerical precision on the estimation of the fundamental frequencies. However, for chaotic systems, the chaotic diffusion would dominate and we would find that NAFF1 > NAFF2. To separate these two regimes, these latter authors select the NAFF threshold as the approximate value NAFF1 at which 99% of the systems harbour NAFF1 < NAFF2. This percentage was selected in order to minimise the amount of false positives and false negatives by comparison with long numerical integrations. This 99% value may not be convenient for significantly different system architectures. To verify this, one would need to perform additional long numerical integrations for any new system under study. In this section, we propose a general NAFF calibration technique that has the advantage that no additional numerical integration is required.
In the analysis of several multi-planet systems, it has been observed that adding new observations shifts the position of the derived solution of the system in the chaos maps towards zones of more regularity; for example GJ 876 (Correia et al. 2010), HD 45364 (Correia et al. 2009), HD 202206 (Couetdic et al. 2010), and HD 60532 (Laskar & Correia 2009). This is in agreement with the working hypothesis that observed planetary systems are stable. This hypothesis is justified by the rapidity with which orbital instabilities develop (e.g. Petit et al. 2020). Hence, unstable configurations would most probably have already been destroyed over the typical ~1 Gyr timescale of the lifetime of the system. Linking this with the previous observation, we come to the conclusion that every observed system should not be intrinsically strongly chaotic, and that the addition of observational constraints moves the systems deeper inside zones of regularity. When we model a system from observational data, the ensemble of the configurations that compose the posterior distribution often harbours two types of behaviour: some show weak chaos, others strong chaos. Taking all of the above into consideration, we hypothesise that as the constraining power of the data increases – either because of higher precision in the individual measurements or because of an increasing amount of data points – the weak-chaos subpopulation grows at the expense of the strong chaos one. We illustrate this point and exploit this observation to calibrate the NAFF chaos indicator.
3.1 Illustration with HD 45364
HD 45364 is composed of a pair of giant planets with orbital periods of Pb = 226.9 days and Pc = 342.9 days, and minimum masses of 0.19 and 0.66 mJup. The discovery was reported by Correia et al. (2009) using 58 HARPS spectra. These authors showed the system to lie in the 3:2 MMR, surrounded by a sea of strong chaos (cf. Fig. 4 in their article). Additional studies were subsequently led in order to infer the formation and migration history in a proto-planetary disc based on the resonant configuration (Rein et al. 2010; Correa-Otto et al. 2013; Delisle et al. 2015; Hadden & Payne 2020). In the present work, we analyse three datasets of different sizes, and compare them in terms of the chaoticity of their solutions. Firstly, we define the low-precision set (LPS) that contains only 33 RV measurements taken from the published RVs in Correia et al. (2009) with the last part of the time series removed. Secondly, we define the high-precision set (HPS) which consists of all 58 measurements used in the discovery paper. Finally, we introduce a third dataset composed of the 58 published RVs together with additional yet-unpublished RV measurements coming from both the CORALIE and HARPS spectrographs and taken between January 2001 and February 2021. Altogether, we add 57 measurements from HARPS and 68 from CORALIE, for a total of 183 RV measurements. The presentation of this new time series and its analysis with Lomb-Scargle periodograms is provided in Appendix A. This defines the high-precision set + (HPS+).
For each of these three datasets, we bin the RV measurements into nights of observation, fit the RV time series with a two-Keplerian model, and explore the parameter space of the latter with an MCMC algorithm; all of this using the DACE platform. Thus, for the LPS, HPS, and HPS+, we derive global posterior distributions for our model parameters, from which we construct subsamples of 6250 solutions. We then numerically integrate each solution over 50 kyr with the IAS15 integrator. The results of these integrations, when they reached the end (neither close-encounter nor escape), are used to compute the NAFF chaos indicator of the configurations. To do so, we output from each integration an evenly sampled series of 20 000 mean longitude values for each planetary orbit, on which we apply the frequency analysis technique.
Figure 2 shows the NAFF histograms for these three distributions: the LPS in orange, the HPS in green, and the HPS+ in blue. The histograms corresponding to the LPS and HPS datasets clearly show two different dynamical populations: the population of stronger chaos on the left, and the population of smaller mean motion drift and hence higher regularity on the right. The set of configurations obtained with less data (LPS) presents an asymmetry in favour of the more chaotic population, while the NAFF histogram of the HPS displays the opposite division. It is reasonable to expect that the addition of even more data would ultimately result in the total absence of the more chaotic configurations, and leave the MCMC posterior with only weakly chaotic dynamical behaviour. That is what is observed when we add the unpublished data: the MCMC posterior from the HPS+ set only contains system configurations in the regular weak chaos regime. This is why the new observations further constrain the system to lie in the stable 3:2 MMR island. As an illustrative counterpart, we also computed chaos maps around the 3:2 MMR in the subspace (ac,ec) for each of the RV datasets. These are presented in Fig. 3. For each map, 101 × 101 system configurations are generated and their future evolution is numerically computed over 50 kyr using the same setup. The NAFF indicator is estimated for each configuration that survived the entire integration, using the same strategy as explained above. Two main phenomena are observed in this suite of chaos maps: the estimation of the orbital eccentricity ec is converging towards small values, while the semi-major axis ac gets closer and closer to the 3:2 period commensurability. The crosses inform us about the area of the parameter space sampled by the MCMC. The addition of more data constrains this exploration to the stable resonant island. This explains the behaviour observed in Fig. 2. It is important to reiterate that while the other orbital parameters are fixed initially in each map, they vary from one map to another as they are updated with the addition of RV measurements. They also converge towards the stability island, explaining why its appearance becomes increasingly clear with the addition of RV data.
Based on this convergence towards a stable area of the parameter space and the disappearance of the more chaotic population from the posterior distribution, a convenient choice for the NAFF stability threshold is the NAFF value above which most of the solutions would disappear after the addition of more observational constraints. In other words, looking at Fig. 2 we choose this threshold as the bottom of the weakly chaotic population, that is, the bottom of the blue distribution. In the case of HD 45364, the limit value NAFF = –8.0 seems a convenient choice. However, there is some freedom in this decision. The important aspect to keep in mind though is to avoid rejecting configurations that are actually dynamically stable and thus constitute plausible solutions for the model of the system. This should motivate us to select slightly less constraining NAFF limits. It is clear that the stability information will not impact the HPS+ posterior distribution, which is already highly constrained by the large number of observations. In Table 1, we update the planetary parameters from the analysis of the HPS+ that contains both CORALIE and HARPS measurements.
 |
Fig. 2 HD 45364: comparison between the NAFF distributions of low-and high-precision sets of configurations (LPS, HPS, and HPS+, respectively). The HPS+ dataset adds yet-unpublished RV data from both CORALIE and HARPS spectrographs. |
3.2 Validation of the Calibration Strategy on HD 202696
In summary, we propose the following NAFF calibration process for any given multi-planet system.
Integrate a set of system configurations derived for example from an MCMC exploration algorithm. Compute the NAFF indicator for each configuration that survived the entire integration.
Based on the NAFF distribution, identify the value x that marks the start of the weakly chaotic distribution. Set up the stability threshold: NAFFthr = x. Any configuration with a NAFF smaller than this threshold is classified as stable.
It is important to note that the calibration strategy we introduce and illustrate here follows an exploratory approach. As a test of this calibration procedure and the stability-driven approach proposed in this work, we applied it to the two-planet system HD 202696 for which long 2 Myr integrations were performed. The NAFF chaos indicator in contrast was computed on the first 31 250 yr (cf. Fig. 1). We present the histogram of the NAFF values in Appendix B. It is composed of 4688 points, which is the number of system configurations that survived for at least 31 250 yr. This NAFF distribution harbours two closely spaced peaks at stronger chaos separated by a third peak in the weakly chaotic regime. As the middle peak could potentially be the expression of stable bounded chaos, we decide to not rule it out. As such, we set the NAFF stability threshold at the bottom of that peak, and choose NAFFthr = –4. A total of 2636 system configurations make it to the NAFF-stable sample.
In order to assess the performance of this fast stability estimation, we compared its results with long integrations. Figure 4 shows the parameter distributions obtained in three different ways. The original posteriors obtained from the set of RV measurements only and composed of 7813 solutions are shown in red. The subsets of truly stable configurations that survived the entire 2 Myr integrations (2630 solutions) are shown in black. Finally, the distributions of NAFF-stable configurations as derived after the first 31 250 yr of integration (2636 solutions) are shown in blue. Both the dynamically motivated black and blue distributions diverge from the original red distributions in the same way. Their high level of similarity confirms the equivalence of the stability-driven technique proposed in this work (blue distributions) with the ‘brute force’ long integrations (black distributions). Furthermore, the gain in computing time is significant, with nearly two orders of magnitude in the case of HD 202696. As a result, the parameters of the outermost planet are significantly refined with the stability-driven technique. Notably, its orbital eccentricity is damped. Consequently, we observe a simultaneous flattening in the distribution of its argument of periastron ωc, given the poorer definition of this parameter at smaller eccentricities. The parameters obtained from the NAFF-stable distributions are reported in Table 1.
In order to rigorously confirm this calibration technique, more highly constrained multi-planet systems of diverse architectures are needed, for which only the population of weakly chaotic configurations would remain in the posterior distribution after running a MCMC. Such systems remain elusive, but should grow in population little by little as more data are gathered and new precise instruments are built.
 |
Fig. 3 HD 45364: chaos maps around the 3:2 MMR in the subspace (ac,ec) for each set of RV measurements. The red crosses represent the 1σ dispersion around the median value of the MCMC posterior distribution for both ac and ec. The vertical dashed lines depict the location of the commensurability of the periods (Pc/Pb = 3/2), which changes from one map to another with different estimations of Pb. The colour code depicts the NAFF chaos level, while the squares are coloured white if the corresponding configurations did not reach the end of the simulation (either because of a close encounter or an escape). From left to right: LPS, HPS, and HPS+ datasets. |
HD 45364, HD 202696, HD 37124, and HD 215152: planetary masses and orbital elements revised with the stability-driven approach.
 |
Fig. 4 HD 202696: comparison between the posterior distributions generated from three different processes, for each planetary dynamical parameter. Red: posterior distributions as obtained from the observational data only. Black: subset of stable configurations as defined by the ‘brute force’ long integrations. Blue: NAFF-stable distributions. All configurations of the system are supposed co-planar, leading to undefined longitudes of the ascending nodes Ω. |
4 Application to a System of Jovian Planets: HD 37124
HD 37124 is currently known as a three-planet system. The planetary companions to this G4-type star (M = 0.83 M⊙) were successively published in Vogt et al. (2000, 2005) and Butler et al. (2003). In the latter, the authors used a set of 52 HIRES RV measurements to state the existence of three planets in the system. The model was still left unclear though, with a preference for three planets with orbital periods of 154.5, 844, and 2295 days, and all of them in the Jovian mass regime. Dynamical tests on this model showed significant planet–planet gravitational interactions, and a threshold of stability was set depending on the eccentricity of the outermost planet. However, the simulations did not exhaustively explore the parameter space, but a subspace of it (period and eccentricity). In this subsection, we aim to provide a revision of the orbital parameters for this system using the stability-driven approach introduced in Sect. 2.
We performed an iterative signal search in the periodogram on the same dataset as that used by Vogt et al. (2005), employing the DACE platform. We found three significant periods close to the ones indicated here above, and we modelled each of them with a Keplerian. We explored the parameters of this model with the MCMC described in Díaz et al. (2014) and implemented on DACE. Again, a burning phase of 25% was applied, and the posterior was further sampled according to the correlation length of the chain. We performed N-body simulations with IAS15 over 50 kyr on a sample of 10 000 solutions from the posterior. Of these 10 000 simulations, 4324 reached the end. More than half of the systems encountered an escape or close encounter between two bodies. For each of the 4324 configurations, we computed the NAFF chaos indicator based on 20000 evenly spaced mean longitude values for each planet. The NAFF distribution of these configurations is presented in Appendix B. Following the calibration procedure explained in Sect. 3, we set a stability threshold at NAFF = –2.5. As a result, the number of NAFF-stable configurations in our sample amounts to 2204.
We compare the distributions before and after the NAFF sorting. The main effects of the orbital stability constraint on HD 37124 are observed on the orbital eccentricities and planetary masses. These results are presented in Fig. 5. In this grid of graphs, the left column lists the distributions of the eccentricity for each of the three planets, both for the full distributions (solid red lines: 10000 system configurations) and the distributions of NAFF-stable configurations only (in blue: subsample of 2204 configurations). For planets b and c, we observe that the stability-driven approach slightly favours the low eccentricities. This result is generally expected. The same behaviour appears for the outermost planet, but is strongly stressed. Indeed, the large eccentricities allowed by the MCMC posterior bring the outermost planet sufficiently close to the middle one such that planet–planet interactions are strong enough to destroy the system. The stability-driven approach is therefore particularly sensitive to the orbital eccentricities. The right column presents the distributions for the planetary masses. While the mass estimation of the innermost planet is not significantly modified by the dynamical constraints, the same is not true for the two outer planets. Our stability-driven approach slightly increases the mass estimate of planet c, and concomitantly slightly decreases the mass estimate for planet d. The shift in the latter is the consequence of the correlation between ed and md as shaped by the observational data. The bottom plot of Fig. 5 shows the distributions projected on this 2D space. This plot highlights the positive correlation between ed and md. Provided the large eccentricity values are discarded, the domain of large masses is disfavoured as well. Table 1 provides the revised planetary parameters.
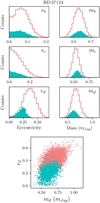 |
Fig. 5 HD 37124: distributions of the orbital eccentricities and planetary masses both before (in solid red) and after (in blue) the inclusion of the orbital stability information. |
5 Application to a Compact System of low-Mass Planets: HD215152
HD 215152 is a K3-type main sequence star (M = 0.77 M⊙) showing low levels of activity. A compact suite of four planets was discovered orbiting this star with the HARPS spectrograph (Delisle et al. 2018). With orbital periods of 5.76, 7.28, 10.86, and 25.2 days, the planets have estimated minimum masses of 2.0, 1.5, 2.7, and 3.5 M⊗, respectively. Such compact systems of low-mass planets are particularly challenging to find with RV measurements alone, and necessitate an extensive effort both in observations and data analysis. Nevertheless, given the small amplitudes of the RV variations that the planets apply on the star, some planetary parameters remain mostly unconstrained, notably the orbital eccentricities.
Delisle et al. (2018) explored the dynamics of the system with the computation of chaos maps. These maps showed that the two first planet pairs, involving the three innermost planets, lie outside (but close to) low-order mean motion resonances. Furthermore, these maps allowed the authors to place crude limits on the orbital eccentricity of the second planet ec for different inclinations of the co-planar system. An exhaustive exploration of the parameter space is necessary to provide rigorous dynamical constraints on the planetary parameters. We undertake this task in the present section. However, the orbital inclination and longitude of the ascending node are not constrained by the observations, and therefore we limit our study to the co-planar edge-on configuration.
We collected the posterior distribution of the eccentric model from Delisle et al. (2018), which is composed of 7501 solutions. We computed the orbital evolution of each solution over 5 kyr with the integrator IAS15. Again, on the simulations that reached the end (no close encounter or no escape), we computed the NAFF fast chaos indicator based on a time series of 20 000 equally spaced mean longitude measurements of each planet. Following the calibration procedure presented in Sect. 3, we set the stability threshold to NAFF = –1. At the end of this process, 140 solutions are classified as NAFF-stable and constitute the stable posterior distribution. This is too few to provide a reliable revision of the planetary parameters. This extreme proportion of unstable solutions is caused by the large exploration in the orbital eccentricities, mostly unconstrained by the RV measurements.
As such, we performed a new exploration of the four-planet model with tighter constraints on the orbital eccentricities. To proceed, we gathered the HARPS data published in Delisle et al. (2018) and applied a similar correlated noise model SPLEAF with a Matérn kernel function (Delisle et al. 2020). We recovered the four known planets through an iterative search in a periodogram. We modelled them with Keplerians, and explored the model parameters with a MCMC. The selected priors are mostly uninformative, except for the orbital eccentricities for which we imposed a Beta distribution with parameters a = 0.867 and b = 3.03 according to Kipping (2013). Furthermore, with the three innermost planets b, c, and d, which evolve in a tightly packed configuration, we cut those priors at 0.15, so as to constrain the eccentricities in [0,0.15]. This choice is in accordance with the chaos maps presented by Delisle et al. (2018, see their Fig. 6), which show high levels of chaos above ec ~ 0.05 in the plausible domain of orbital periods. The MCMC we employed is the adaptive Metropolis algorithm described by Delisle et al. (2018), which we use to ensure a derivation of the new posterior distribution equivalent to the one obtained by these authors. We performed 7M iterations and discarded the first 25% as burning phase. Consequently, 26 250 solutions compose the posterior distribution. We computed the orbital evolution of each of these solutions over 5k yr using the integrator IAS15. Of the 26 250 system configurations, 3938 reached the end of the simulation. The NAFF chaos indicator was estimated on each of them based on evenly sampled time series of the planetary mean longitudes. The NAFF distribution is presented in Appendix B. Two clear populations of systems appear: strongly and weakly chaotic. Following the NAFF calibration procedure, we set a stability threshold in between these two groups, at NAFF = –2.0. As a result, 3488 system configurations are flagged as stable and constitute the NAFF-stable posterior distribution. Exactly 450 solutions were discarded with our NAFF criterion. The other removed solutions from the posterior were therefore unstable during the N-body simulations, through either an encounter or escape of one of the planets.
In this tightly packed system, the impact of the orbital eccentricities on the overall stability of the system is significant. Despite the strong priors imposed on the distributions, the stability information further constrains the orbital eccentricities. Figure 6 presents the posterior distribution projected on the orbital eccentricities of the planets, both before the exclusion of NAFF-unstable systems (solid red lines: 26 250 solutions) and after (blue histograms: subgroup of 3488 configurations). These density plots show a clear preference for the lowest values of the eccentricity. This trend is less strong on the outermost planet, because of its larger separation to the three innermost planets. Because of its compactness, the system HD 215152 is located in a region of the parameter space that is densely populated with MMRs. Their overlap generates strong chaos, which causes the instability on short timescales of most of the system configurations among our MCMC posterior.
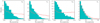 |
Fig. 6 HD 215152: posterior distribution projected on the orbital eccentricities (from left to right: innermost to outermost planet). The red line histograms represent the original posteriors, and are composed of 26 250 system configurations. The blue histograms are built up of the NAFF-stable solutions only, and consist in 3488 configurations. |
6 Conclusions
We developed a method to refine the planetary masses and orbital parameters in multi-planet systems via a global inclusion of dynamical constraints. Such an approach makes use of the NAFF fast chaos indicator, for which we propose a general calibration strategy. The latter needs to be iterated for each significantly different architecture (i.e. for each new multi-planet system under study), but does not necessitate additional computational cost. We illustrated our calibration strategy on HD 45364 and presented new RV measurements that further point towards the 3:2 MMR state for this system. Our calibration process was validated using HD 202696, by comparing the results of the approach with long 2 Myr numerical integrations. We then applied this technique to HD 37124, a system composed of three Jovian planets. We demonstrate the potential of the technique to refine the planetary parameters, and especially the orbital eccentricities and the planetary masses. Furthermore, given the global exploration of the parameter space that this technique uses, we are able to observe important correlations between parameters that explain the origin of some of the dynamical constraints. The stability-driven approach that we propose helps us to understand the dynamical state of the system. Finally, we applied the stability constraint to HD 215152, a four-planet system in a very compact configuration. Again, we observe a significant influence of the orbital eccentricities on the overall system stability, which allows us to put strong and rigorous constraints on their upper values. Such an impact on the orbital eccentricities is synthesised in Fig. 7. In that plot, the planets in HD 37124 and HD 215152 are presented in the (P,e) space together with their 68.27% confidence intervals on the eccentricity, both before (light red) and after (blue and grey) the update with the stability-driven refinement technique. The new views on these systems are in better agreement with the expected results from formation processes, which generally produce low-eccentricity orbits because of the damping effects in the proto-planetary disc. Those updates, when generalised to the exoplanet population level, can potentially bring useful constraints for formation and evolution models.
Overall, the stability-driven approach that we present in this work is faster than the brute force numerical integrations, and provides reliable constraints on the systems under study. Some caveats remain in the NAFF calibration procedure, and in particular the current lack of highly precise multi-planet systems. A growing number of them should help us to confirm the trend that we see in the systems’ posterior distributions regarding the proportion of strongly chaotic system configurations with respect to the precision of observational data, which is at the basis of our calibration strategy. Let us note that in this work, the impact of orbital inclination and in particular mutual inclination was not explored. The orbital inclinations of the planets in all the systems studied here were fixed at 90 degrees. The study of TOI-125 in Nielsen et al. (2020) explored the impact of mutual inclination on overall system stability based on our technique. An exhaustive presentation of this impact would prepare our approach for the inclined systems. While the very small mutual inclinations between the transiting planets should not have a strong dynamical influence, this is not the case for the exoplanets discovered via astrometry. Notably, the Gaia mission is expected to provide the community with numerous massive exoplanet detections on wide orbits, together with information about their orbital inclination. Concerning smaller non-transiting planets closer to their host star, the strong planet–planet interactions that some of them experience may unveil their orbital inclination as well. Indeed, the variations of the orbital elements could be measured in the radial velocity time series using dynamical fits, lifting the degeneracy between the mass and the orbital inclination. This has been achieved in a few cases, and requires high signal-to-noise-ratio RVs and long baselines of observations (e.g. Tan et al. 2013, with HD 82943).
Finally, we emphasise the importance of carrying out a systematic dynamical revision of newly discovered multi-planet systems, in particular for those in compact configurations, as the stability information can potentially be used to significantly refine planetary parameters. This is of considerable importance for selecting the best target candidates for future missions on the next-generation telescopes, such as the James Webb Space Telescope (JWST), PLATO, and the E-ELT.
 |
Fig. 7 HD 215152 and HD 37124 plotted in the period–eccentricity subspace together with the 68.27% confidence intervals on the eccentricities, both before applying the stability-driven approach (light red) and after (blue and grey). |
Acknowledgements
We thank the anonymous referee for his/her valuable comments and suggestions, which helped improve the quality of this manuscript. This work has been carried out in the frame of the National Centre for Competence in Research PlanetS supported by the Swiss National Science Foundation (SNSF). This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (project Spice Dune, grant agreement No 947634). This publication makes use of the Data & Analysis Center for Exoplanets (DACE), a platform of the Swiss National Centre of Competence in Research (NCCR) PlanetS, federating the Swiss expertise in Exoplanet research. Tools used: REBOUND (Rein & Liu 2012), SPLEAF (Delisle et al. 2020).
Appendix A Data Analysis of HD 45364
 |
Fig. A.1 HD 45364: Full RV time series containing the previously published HARPS data (in green), the additional HARPS data gathered after 2009 (HARPS03 and HARPS15), and the CORALIE data covering 20 years of observations (COR98, COR07 and COR14). Finally, the grey curve presents the bestfit of the two-Keplerian model. |
 |
Fig. A.2 HD 45364: Periodograms of the RV time series. The three horizontal lines correspond to different levels of false alarm probability (FAP) of 10%, 1%, and 0.1% from bottom to top. Top: Periodogram of the RV time series with no Keplerian in the model. The highest peak is very significant and corresponds to a signal of period 344.03 days. Middle : Periodogram of the residuals after subtraction of that signal, modelled with a Keplerian. Another highly significant signal is detected at a period = 227.69 days. Bottom: Periodogram of the residuals after subtraction of the two-keplerian model. |
We present a new and unpublished set of RV measurements of the star HD 45364, which consists in 57 measurements taken with HARPS between Sept 29, 2009 and Sept 18, 2017. Also included are 68 measurements taken with CORALIE between Jan 2, 2001 and Jan 24, 2021. These measurements are less precise than HARPS, but they have the advantage of increasing the baseline of observations. These two sets add to the already published HARPS measurements (Correia et al. 2009). The new HARPS and CORALIE data are further separated according to significant upgrades in the instruments, giving rise respectively to HARPS03 and HARPS15, and COR98, COR07, and COR14. The COR98 radial velocities show a strong correlation with the bissector span of the cross-correlation function (CCF). We corrected for this through a detrending with a Gaussian kernel. We then performed a periodic signal search in the Lomb-Scargle periodogram of the full dataset via the platform DACE, and fitted these periodicities with Keplerians. Two Keplerians corresponding to the known planets were included in the model, after which no significant signal remains in the residuals. We therefore see no hint of an additional planet in the system. In Fig. A.1, we present the updated RV time series together with the two-Keplerian model best fit. Figure A.2 traces back the elaboration of the two-Keplerian model via a successive signal search in the Lomb-Scargle periodogram.
Appendix B NAFF Distributions for HD 202696, HD 37124, and HD 215152
We present in this Appendix the posterior distributions of HD 202696, HD 37124, and HD 45364 projected onto the NAFF chaos indicator. These were obtained from an exploration of the parameter space of the model of each system, and dynamical simulations on each solution of the samples. Every single point composing the NAFF distributions therefore corresponds to a solution for the system that survived as well to the entire short-term N-body simulation in order to estimate its NAFF chaos level. The NAFF distributions of the systems HD 202696, HD 37124, and HD 215152 are displayed in Fig. B.1.
These distributions serve to assign the NAFF-stability threshold of each system. As they are the byproduct of the stability-driven approach, the NAFF calibration does not necessitate additional computational cost. The threshold separates the weakly chaotic population of solutions from those that are strongly chaotic (cf. Sect. 3). Hence, from the histograms above, we set stability thresholds to the following: for HD 202696 we set NAFF=–4.0, for HD 37124 we set NAFF=–2.5, and for HD 215152 we set NAFF=–2.0. These are spotted in Fig. B.1 with the vertical dotted lines.
 |
Fig. B.1 NAFF distributions for the posteriors of HD 202696, HD 37124, and HD 215152 (left, middle and right). These distributions are composed of 4 688, 4 324, and 3 938 system configurations, respectively. |
References
- Benettin, G., Galgani, L., Giorgilli, A., & Strelcyn, J. M. 1980, Meccanica, 15, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Butler, R. P., Marcy, G. W., Fischer, D. A., et al. 1999, ApJ, 526, 916 [NASA ADS] [CrossRef] [Google Scholar]
- Butler, R. P., Marcy, G. W., Vogt, S. S., et al. 2003, ApJ, 582, 455 [Google Scholar]
- Chambers, J. E., Wetherill, G. W., & Boss, A. P. 1996, Icarus, 119, 261 [Google Scholar]
- Cincotta, P. M., Giordano, C. M., & Simó, C. 2003, Phys. D Nonlinear Phenom., 182, 151 [Google Scholar]
- Cincotta, P. M., Giordano, C. M., Alves Silva, R., & Beaugé, C. 2021, Phys. D Nonlinear Phenom., 417, 132816 [NASA ADS] [CrossRef] [Google Scholar]
- Cloutier, R., Astudillo-Defru, N., Bonfils, X., et al. 2019, A&A, 629, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Correa-Otto, J. A., Michtchenko, T. A., & Beaugé, C. 2013, A&A, 560, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Correia, A. C. M., Udry, S., Mayor, M., et al. 2005, A&A, 440, 751 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Correia, A. C. M., Udry, S., Mayor, M., et al. 2009, A&A, 496, 521 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Correia, A. C. M., Couetdic, J., Laskar, J., et al. 2010, A&A, 511, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Couetdic, J., Laskar, J., Correia, A. C. M., Mayor, M., & Udry, S. 2010, A&A, 519, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delisle, J. B., Correia, A. C. M., & Laskar, J. 2015, A&A, 579, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delisle, J. B., Ségransan, D., Dumusque, X., et al. 2018, A&A, 614, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delisle, J. B., Hara, N., & Ségransan, D. 2020, A&A, 638, A95 [EDP Sciences] [Google Scholar]
- Díaz, R. F., Almenara, J. M., Santerne, A., et al. 2014, MNRAS, 441, 983 [Google Scholar]
- Ford, E. B. 2006, ApJ, 642, 505 [Google Scholar]
- Froeschlé, C., Gonczi, R., & Lega, E. 1997, Planet. Space Sci., 45, 881 [CrossRef] [Google Scholar]
- Giordano, C. M., & Cincotta, P. M. 2018, Celest. Mech. Dyn. Astron., 130, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Gottwald, G. A., & Melbourne, I. 2004, Proc. R. Soc. London Ser. A, 460, 603 [CrossRef] [Google Scholar]
- Goździewski, K., Bois, E., Maciejewski, A. J., & Kiseleva-Eggleton, L. 2001, A&A, 378, 569 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goździewski, K., Konacki, M., & Maciejewski, A. J. 2003, ApJ, 594, 1019 [CrossRef] [Google Scholar]
- Gozdziewski, K., Migaszewski, C., & Musielinski, A. 2008, ArXiv e-prints [arXiv:0802.0254] [Google Scholar]
- Hadden, S., & Payne, M. J. 2020, AJ, 160, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Hara, N. C., Bouchy, F., Stalport, M., et al. 2020, A&A, 636, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heising, M. Z., Sasselov, D. D., Hernquist, L., & Luisa Tió Humphrey, A. 2021, ApJ, 913, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Hussain, N., & Tamayo, D. 2020, MNRAS, 491, 5258 [NASA ADS] [CrossRef] [Google Scholar]
- Joiner, D. A., Sul, C., Dragomir, D., Kane, S. R., & Kress, M. E. 2014, ApJ, 788, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M. 2013, MNRAS, 434, L51 [Google Scholar]
- Laskar, J. 1988, A&A, 198, 341 [NASA ADS] [Google Scholar]
- Laskar, J. 1990, Icarus, 88, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Laskar, J. 1993, Physica D, 67, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Laskar, J. 2003, ArXiv Mathematics e-prints [arXiv:math/0305364] [Google Scholar]
- Laskar, J., & Correia, A. C. M. 2009, A&A, 496, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leleu, A., Alibert, Y., Hara, N. C., et al. 2021, A&A, 649, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lovis, C., Ségransan, D., Mayor, M., et al. 2011, A&A, 528, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- MacDonald, M. G., Ragozzine, D., Fabrycky, D. C., et al. 2016, AJ, 152, 105 [Google Scholar]
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [Google Scholar]
- Michtchenko, T. A., & Ferraz-Mello, S. 1995, A&A, 303, 945 [NASA ADS] [Google Scholar]
- Michtchenko, T. A., Lazzaro, D., Ferraz-Mello, S., & Roig, F. 2002, Icarus, 158, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Murray, N., & Holman, M. 1997, AJ, 114, 1246 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, B. E., Robertson, P. M., Payne, M. J., et al. 2016, MNRAS, 455, 2484 [NASA ADS] [CrossRef] [Google Scholar]
- Nielsen, L. D., Gandolfi, D., Armstrong, D. J., et al. 2020, MNRAS, 492, 5399 [NASA ADS] [CrossRef] [Google Scholar]
- Núñez, J. A., Cincotta, P. M., & Wachlin, F. C. 1996, Celest. Mech. Dyn. Astron., 64, 43 [CrossRef] [Google Scholar]
- Obertas, A., Van Laerhoven, C., & Tamayo, D. 2017, Icarus, 293, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Petit, A. C., Pichierri, G., Davies, M. B., & Johansen, A. 2020, A&A, 641, A176 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quinn, S. N., Becker, J. C., Rodriguez, J. E., et al. 2019, AJ, 158, 177 [Google Scholar]
- Rein, H., & Liu, S. F. 2012, A&A, 537, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rein, H., & Spiegel, D. S. 2015, MNRAS, 446, 1424 [Google Scholar]
- Rein, H., Papaloizou, J. C. B., & Kley, W. 2010, A&A, 510, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rice, D. R., Rasio, F. A., & Steffen, J. H. 2018, MNRAS, 481, 2205 [NASA ADS] [CrossRef] [Google Scholar]
- Robertson, P., Horner, J., Wittenmyer, R. A., et al. 2012, ApJ, 754, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Robutel, P., & Laskar, J. 2001, Icarus, 152, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Satyal, S., Hinse, T. C., Quarles, B., & Noyola, J. P. 2014, MNRAS, 443, 1310 [NASA ADS] [CrossRef] [Google Scholar]
- Tamayo, D., Cranmer, M., Hadden, S., et al. 2020, Proc. Natl. Acad. Sci., 117, 18194 [CrossRef] [Google Scholar]
- Tan, X., Payne, M. J., Lee, M. H., et al. 2013, ApJ, 777, 101 [Google Scholar]
- Trifonov, T., Stock, S., Henning, T., et al. 2019, AJ, 157, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Udry, S., & Pfenniger, D. 1988, A&A, 198, 135 [NASA ADS] [Google Scholar]
- Veras, D., & Ford, E. B. 2010, ApJ, 715, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Vogt, S. S., Marcy, G. W., Butler, R. P., & Apps, K. 2000, ApJ, 536, 902 [NASA ADS] [CrossRef] [Google Scholar]
- Vogt, S. S., Butler, R. P., Marcy, G. W., et al. 2005, ApJ, 632, 638 [Google Scholar]
- Wittenmyer, R. A., Tan, X., Lee, M. H., et al. 2014, ApJ, 780, 140 [Google Scholar]
823 multi-planet systems were known as of May 6, 2022 (from http://exoplanet.eu/catalog/).
The DACE platform is a facility of the National Center of Competence in Research PlanetS based at the University of Geneva dedicated to visualisation, exchange, and analysis of extrasolar planet data. It is available at https://dace.unige.ch
REBOUND is a package used to simulate the motion of particles under gravitational interactions with N -body. It harbours a wide variety of numerical integrators, and can be found at https://rebound.readthedocs.io/en/latest/
All Tables
HD 45364, HD 202696, HD 37124, and HD 215152: planetary masses and orbital elements revised with the stability-driven approach.
All Figures
 |
Fig. 1 HD 202696. Black: scatter plot of the NAFF chaos indicator with respect to the actual survival time of the system configurations. Orange: proportion of stable systems (i.e. that survived the entire 2 Myr of integration) for consecutive ranges of NAFF. |
| In the text | |
 |
Fig. 2 HD 45364: comparison between the NAFF distributions of low-and high-precision sets of configurations (LPS, HPS, and HPS+, respectively). The HPS+ dataset adds yet-unpublished RV data from both CORALIE and HARPS spectrographs. |
| In the text | |
 |
Fig. 3 HD 45364: chaos maps around the 3:2 MMR in the subspace (ac,ec) for each set of RV measurements. The red crosses represent the 1σ dispersion around the median value of the MCMC posterior distribution for both ac and ec. The vertical dashed lines depict the location of the commensurability of the periods (Pc/Pb = 3/2), which changes from one map to another with different estimations of Pb. The colour code depicts the NAFF chaos level, while the squares are coloured white if the corresponding configurations did not reach the end of the simulation (either because of a close encounter or an escape). From left to right: LPS, HPS, and HPS+ datasets. |
| In the text | |
 |
Fig. 4 HD 202696: comparison between the posterior distributions generated from three different processes, for each planetary dynamical parameter. Red: posterior distributions as obtained from the observational data only. Black: subset of stable configurations as defined by the ‘brute force’ long integrations. Blue: NAFF-stable distributions. All configurations of the system are supposed co-planar, leading to undefined longitudes of the ascending nodes Ω. |
| In the text | |
 |
Fig. 5 HD 37124: distributions of the orbital eccentricities and planetary masses both before (in solid red) and after (in blue) the inclusion of the orbital stability information. |
| In the text | |
 |
Fig. 6 HD 215152: posterior distribution projected on the orbital eccentricities (from left to right: innermost to outermost planet). The red line histograms represent the original posteriors, and are composed of 26 250 system configurations. The blue histograms are built up of the NAFF-stable solutions only, and consist in 3488 configurations. |
| In the text | |
 |
Fig. 7 HD 215152 and HD 37124 plotted in the period–eccentricity subspace together with the 68.27% confidence intervals on the eccentricities, both before applying the stability-driven approach (light red) and after (blue and grey). |
| In the text | |
 |
Fig. A.1 HD 45364: Full RV time series containing the previously published HARPS data (in green), the additional HARPS data gathered after 2009 (HARPS03 and HARPS15), and the CORALIE data covering 20 years of observations (COR98, COR07 and COR14). Finally, the grey curve presents the bestfit of the two-Keplerian model. |
| In the text | |
 |
Fig. A.2 HD 45364: Periodograms of the RV time series. The three horizontal lines correspond to different levels of false alarm probability (FAP) of 10%, 1%, and 0.1% from bottom to top. Top: Periodogram of the RV time series with no Keplerian in the model. The highest peak is very significant and corresponds to a signal of period 344.03 days. Middle : Periodogram of the residuals after subtraction of that signal, modelled with a Keplerian. Another highly significant signal is detected at a period = 227.69 days. Bottom: Periodogram of the residuals after subtraction of the two-keplerian model. |
| In the text | |
 |
Fig. B.1 NAFF distributions for the posteriors of HD 202696, HD 37124, and HD 215152 (left, middle and right). These distributions are composed of 4 688, 4 324, and 3 938 system configurations, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


