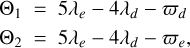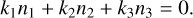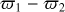| Issue |
A&A
Volume 667, November 2022
|
|
|---|---|---|
| Article Number | A128 | |
| Number of page(s) | 13 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202243971 | |
| Published online | 18 November 2022 | |
Global dynamics and architecture of the Kepler-444 system
Département d’Astronomie, Université de Genève,
Chemin Pegasi 51b,
1290
Versoix, Suisse, Switzerland
e-mail: manu.stalport@unige.ch
Received:
6
May
2022
Accepted:
13
September
2022
Context. S-type planets, which orbit one component of multiple-star systems, place strong constraints on planet formation and evolution models. A notable case study is Kepler-444, a triple-star system whose primary is orbited by five planets smaller than Venus in a compact configuration, and for which the stellar binary companion revolves around the primary on a highly eccentric orbit.
Aims. Several open questions remain about the formation and evolution of Kepler-444. Having access to the most precise up-to-date masses and orbital parameters is highly valuable when tackling those questions. We provide the first full dynamical exploration of this system, with the goal being to refine those parameters.
Methods. We apply orbital stability arguments to refine the system parameters on models with and without the stellar binary companion in order to understand the origin of the dynamical constraints. This approach makes use of the numerical analysis of fundamental frequencies fast chaos indicator. We also explore potential two- and three-planet mean-motion resonances (MMRs) in the system. Prior to investigating the dynamics of a model that includes the binary companion, we update its orbital parameters and mass using new observational constraints from both HIRES radial velocity and Gaia astrometric data, as well as archival imaging of the system.
Results. The planetary system does not appear in any of the low-order two- or three-planet MMRs. We provide the most precise up-to-date dynamical parameters for the planets and the stellar binary companion. The orbit of the latter is constrained by the new observations, and also by the stability analysis. This update further challenges the planets formation processes. We also test the dynamical plausibility of a sixth planet in the system, following hints found in HST data. We find that this putative planet could exist over a broad range of masses, and with an orbital period of between roughly 12 and 20 days.
Conclusions. We note the overall good agreement of the system with short-term orbital stability. This suggests that a diverse range of planetary system architectures could be found in multiple-star systems, potentially challenging the planet formation models further.
Key words: planets and satellites: dynamical evolution and stability / planets and satellites: individual: Kepler-444 / methods: data analysis / methods: numerical
© M. Stalport et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1 Introduction
Multiple-star systems represent about half of the K- to F-type stars of the Milky Way (e.g. Duquennoy & Mayor 1991; Offner et al. 2022), yet discovered planets in these systems constitute a small minority of the entire exoplanet population known to date. Nevertheless, constraints can be gleaned from this poorly studied planet population that are important for planet formation and orbital evolution processes. From the small sample available, it is therefore important to ensure the highest possible precision on the planetary orbital parameters and masses in order to add the strongest constraints to the models. In a previous paper, we introduced a technique to rigorously refine the planetary parameters in single-star systems through orbital stability arguments (Stalport et al. 2022). This technique is based on a global parameter space exploration via the Bayesian approach. The orbital stability is estimated on each realisation of the resulting posterior distribution with the numerical analysis of fundamental frequencies fast chaos indicator (NAFF, Laskar 1990, 1993), which we calibrate for each system studied. This approach proved efficient in refining the orbital eccentricities, which are particularly sensitive to the orbital stability. Furthermore, in some cases the planetary masses experience a significant update under the stability constraint.
The present paper extends the scope of the technique to multiple-star systems. In particular, we apply it to a notable triple-star planet-hosting system, Kepler-444 (Campante et al. 2015). In this system, a primary star (Kepler-444 A) is orbited by a tight binary star (Kepler-444 BC). The Kepler mission revealed the existence of five s-type planets smaller than Venus orbiting the primary. They orbit in a compact configuration, with orbital periods of between 3.5 and 10 days. The stellar doublet Kepler-444 BC orbits the primary in a highly eccentric orbit, which poses important questions as to its dynamical influence on the inner planetary system. The Kepler-444 system addresses many challenges to the formation and evolution models, which renders this system particularly interesting. Delivery of the most precise orbital parameters and masses would therefore be valuable for future studies.
Kepler-444 A is a bright (V = 8.86), K-type star of mass m* = 0.758 m⊙ and radius R* = 0.752 R⊙ (Campante et al. 2015). It displays significant pulsating signals, and thus constitutes a precious laboratory for asteroseismic models. Using such models, Buldgen et al. (2019) confirm the old age of the system (11 ± 0.8 Gyr), in accordance with previous kinematic and Ti abundance studies, which indicate that the system belongs to the Galactic thick disk (Campante et al. 2015). The stellar companions B and C have estimated masses of 0.29 m⊙ and 0.25 m⊙ according to Dupuy et al. (2016) who base their findings on mass-magnitude relationships. Furthermore, these objects orbit each other very tightly, with an estimated semi-major axis of 0.3 AU. The BC centre of mass performs a full revolution in the reference frame of the primary in about 200 yr, and on a highly eccentric orbit of ~0.86 according to this latter study. These results imply that the M-dwarfs pair periodically passes within 5 AU of the primary. Therefore, significant gravitational perturbations on the planetary orbits potentially take place. Furthermore, if primordial, the presence of this highly eccentric stellar doublet would have truncated the protoplanetary disk in which the planets formed to an estimated radius of ~2 AU (Dupuy et al. 2016), placing strong constraints on the planet-formation processes. Several scenarios could explain the current architecture of the triple-star system. Either the observed configuration is primordial, or it was built later on under the effect of gravitational interactions. However, Dupuy et al. (2016) analysed the orbit of the stellar binary BC with respect to the primary A and found a probability of 98% that this orbit lies in the same plane as the planetary orbits. The authors therefore conclude that the observed triple-star configuration is most likely primordial.
The Kepler-444 sub-Venus planets would then have formed in a truncated disk of Kepler-444 A, given the high probability of primordial orbital configuration of the BC stellar companions around the primary. The formation process of the planets in this disk and their orbital evolution remain open questions. Papaloizou (2016) investigated the smooth disk-driven migration of type I – given the small planetary masses – to explain the architecture of the current system. The authors were able to reproduce the current architecture under this process. However, for it to be effective, planet e has to be approximately three times more massive than planet d in order to bring this pair close to mean-motion resonance (MMR) while keeping the other pairs far from such a configuration. This condition is inconsistent with the transit timing variations (TTV) analyses of Mills & Fabrycky (2017), who find planetary masses and densities of 0.036 and 0.034 m⊕ and 1.27 and 1.08 g cm−3 for planets d and e, respectively. These authors suggest instead that either the migration was not smooth – for example because of the local disk properties or turbulences – or large perturbations arose in the system after the disk dispersal, significantly modifying the period ratios. Nevertheless, they also note that, given the low densities of planets d and e, it is unlikely that any collisional stripping process took place as this would have left planets on higher densities. Finally, the planets may also have formed in situ. Further insight into the atmospheric composition of the planets would help to refine the formation model for this distinctive system.
Given the small size of these planets and subsequently the shallowness of their transit signals, detecting features from the lower atmosphere via infrared transmission spectroscopy is out of reach with the current instruments. However, Bourrier et al. (2017), using the HST, discovered significant absorption of the stellar Lyman-alpha line at the times of transit of the outermost planets e and f. Two different scenarios could explain these features: the flux variations could come from strong and sudden activity variations of the star, or from the absorption of light by neutral hydrogen in the extended upper atmosphere of these planets. Pezzotti et al. (2021) showed that the match between the stellar models and the asteroseismic observations is incompatible with an active star, confirming previous results from Bourrier et al. (2017) that Kepler-444 should be a quiet old star without any transient features. Pezzotti et al. (2021) therefore favour the second scenario, in which neutral hydrogen escapes from the atmospheres of the outer planets. A possible origin for this hydrogen is steam photodissociated by stellar radiation in the upper planetary atmospheres, and sustained by water from the planet surface (Jura 2004). Given the age of the system, large primordial water mantles would be required for the planets to still show signatures of escape today (Bourrier et al. 2017). This scenario is consistent with the low mean densities measured by Mills & Fabrycky (2017) for planets d and e. If confirmed, the rich water content of these planets would invalidate an in situ formation scenario for the planetary system, given the rarity of water in the inner protoplanetary disk.
There remain many open questions about Kepler-444. Follow-up formation studies will certainly benefit from up-to-date orbital parameters of the system. Providing these revised parameters is the first goal of the present work. Furthermore, answering questions about the dynamical nature of this system could also provide insights into its formation process. How does the compactness of the planetary orbits impact their stability? In other words, how close does the planetary system lie from orbital instability? To what extent does the stellar binary companion perturb the inner system? This paper attempts to answer these open questions. Section 2 presents an analysis of the planetary system without the influence of the binary companion. We review the planetary parameters, paying particular attention to orbital stability, and investigate the MMR. In Sect. 3, we then review the orbit of the stellar binary companion Kepler-444 BC based on additional observations from Gaia and HIRES. We use those updated results in a dynamical model that includes the BC companion, and undertake a full revision of the planetary and BC companion parameters in Sect. 4. Furthermore, using HST data, Bourrier et al. (2017) found strong absorption of the stellar Lyman-alpha line uncorrelated with any of the planetary transits. The authors suggest that this feature may come from a yet-unknown sixth planet on a grazing orbit configuration, and with a large exosphere. We develop this line of investigation in Sect. 5 via exploration of the dynamical plausibility of a sixth-planet scenario. Finally, we summarise and discuss our results in Sect. 6.
2 Dynamical constraints on model 1: No binary companion BC
2.1 Stability-driven refinement technique
In Stalport et al. (2022), we presented an approach to refine the planetary masses and orbital parameters in multi-planet systems based on stability arguments. In particular, this technique determines the orbital stability based on heuristic arguments linking instability to dynamical chaos. So far, a formal relationship between these two concepts has not been discovered, yet they are empirically linked as many studies have emphasised (e.g. Chambers et al. 1996; Murray & Holman 1997; Obertas et al. 2017; Rice et al. 2018; Hussain & Tamayo 2020). For the stability estimation, we use the NAFF fast chaos indicator, together with a calibration procedure for the latter. The approach couples an efficient parameter space exploration with the fast stability estimation of NAFF in order to perform importance sampling on the distributions of solutions for the planetary systems.
The NAFF quantification of chaos is extensively described in Laskar (1990, 1993) and summarised in Stalport et al. (2022). NAFF exploits the finding from secular non-chaotic dynamics that the semi-major axes of the planetary orbits stay constant on average. This is no longer true in the presence of chaos. The NAFF chaos indicator uses the results of numerical integrations, and in particular we use even time series of the planetary mean longitudes. In the present work, we derive the planetary mean longitudes in Jacobi coordinates. From this time series, the frequency analysis technique is used to decompose the planetary motion into its constituent frequencies and estimate the mean motion over the time span of the time series. The mean motion is the frequency equivalent of the orbital period: n = 2π/P; it therefore benefits from precise computation in the frequency domain, and is equivalent to a measurement of the semi-major axis given Kepler’s third law. We split the total integration time into two halves, and employ frequency analysis over each part. The difference in mean motion between the two halves of the integration directly informs us about the level of chaos of the considered planetary orbit. Large differences are indicative of a significant drift in the mean motions, thus revealing chaos. We define the NAFF of the system as the difference between the mean motions normalised over the initial mean motion of the considered planetary orbit:
where nj,1 and nj,2 are the mean motions over the first and second half of the integration, respectively, for every planet j in the system. nj,0 is the initial Keplerian mean motion of planet j. The maximal drift among all the planetary orbits defines the chaos level of the whole system. The convergence of this chaos indicator is usually reached within ~ 104–105 orbital revolutions of the outermost body.
The NAFF chaos indicator is used to refine the planet parameters. Following a Bayesian framework, the system that we model is characterised by a posterior distribution which is at the basis of the parameter estimations. From this posterior, we select a sample of solutions from which we quantify the chaos via the NAFF computation. These numerical integrations first help in calibrating the NAFF indicator, and are then used to apply importance sampling. The calibration procedure is based on the hypothesis that the real system is stable. When modelling the latter, it is common to obtain two dynamically distinct populations of systems: a weakly chaotic population, and a population harbouring stronger chaos. This is illustrated by displaying the NAFF distribution of the sample. In Stalport et al. (2022), it was stressed that the strongly chaotic population is depleted in favour of the weak chaos when additional observations are added and thus when a better modelling of the system is available. Therefore, the calibration strategy consists in selecting the NAFF stability threshold at the bottom of the population of weak chaos, knowing that any stable solution should belong to this population. Naturally, the bottom of that distribution can be ill-defined, and we motivate our choice with a conservative approach, where the threshold value is selected so to limit the amount of systems falsely flagged unstable. This calibration strategy has the advantage of not necessitating additional numerical integrations in order to perform importance sampling. From the same posterior distribution, we then remove all the configurations of the system with NAFF larger than the defined threshold.
In this paper, when mentioning the stability-driven refinement technique, we refer to the process described above: on a sample of the posterior distribution, we proceed to the NAFF computation and calibration, and then undertake importance sampling in order to derive a stable posterior distribution. Let us note that the presence of the nearby doublet of M stars on a very eccentric orbit around the primary limits us in the choice of the integrator, preventing any symplectic scheme. We opt for IAS15 (Rein & Spiegel 2015), a fifteenth-order adaptive time-step integrator implemented in the REBOUND Python package1 (Rein & Liu 2012). In order to properly compare the results with and without the stellar binary in our model, we use the same integrator throughout this work, unless stated otherwise. A correction from general relativity was added in the numerical integrations following the formalism of Anderson et al. (1975), and implemented in the Python module REBOUNDx (Tamayo et al. 2020).
2.2 Global analysis
We first performed a stability analysis of the Kepler-444 system without the stellar binary in our dynamical model. This analysis serves as a reference to later explore the net effect of accounting for the binary, but also provides insight into the impact that dynamical constraints have on this compact system without additional perturbation.
To that aim, we downloaded the TTV posterior derived by Mills & Fabrycky (2017), which contains the planet parameters as constrained by the TTV analysis, and extracted a subsample of 28 000 system configurations. About 850 solutions are effectively mutually independent among this set, as noted by the authors of this latter. The reason for choosing a larger sample is to obtain statistically relevant results. Let us note that the eccentricity distributions are derived from the sum of two independent Gaussian distributions, for 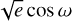 and
and 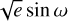 , respectively. The result favours low eccentricities, in accordance with other observed compact planetary systems and numerical simulations (Fabrycky et al. 2014; Pu & Wu 2015). Also, the longitudes of the ascending nodes of all the planets are fixed to zero.
, respectively. The result favours low eccentricities, in accordance with other observed compact planetary systems and numerical simulations (Fabrycky et al. 2014; Pu & Wu 2015). Also, the longitudes of the ascending nodes of all the planets are fixed to zero.
Each of the 28 000 solutions was numerically integrated with IAS15 over 10 kyr, meaning approximately 375 000 revolutions of the outer planet. We note the good precision of the integrations, with a relative total energy variation between 10-14 and 10-13. In every dynamical simulation, we record the mean longitudes of the planets at regular time steps for a total of 20 000 output times and use these time series to compute the NAFF chaos indicator on all the configurations that survived the entire integration (no close encounter, no escape). The criterion used for a close encounter, that is, for the minimal mutual distance acceptable between a planet pair, is common to all the planets: it corresponds to the initial Hill radius of the outermost planet. Such a criterion prevents our integrator from employing excessively small time steps. Furthermore, once this distance is reached, only a small amount of time passes before the collision occurs (Rice et al. 2018). Alternatively, we flag an escaped planet if its distance to the central star reaches five times the initial distance between the outermost planet and the star. In that case, we consider that the system architecture diverged too much from the initial configuration, and we stop the integration. The numerical simulations show a high level of stability. In Fig. 1 we plot the histogram of the NAFF distribution that we derive. This latter is composed of 27 890 values, which is the number of system configurations that survived the entire integration (no close encounter, no escape). Three families of systems are observed, at NAFF ~−1.7, −3.8, and −6.5, corresponding to increasing regularity in the motions. Following the calibration strategy described in Stalport et al. (2022), we expect that if we had more observations to further constrain the Kepler-444 planetary system, the peak in the distribution at NAFF ~−1.7 would be further depleted in favour of the peak at NAFF ~−6.5 in the new set of configurations.
The orbital stability of the systems population at NAFF ~−3.8 is unclear. To further investigate the dynamical behaviour of that population, we selected 100 system configurations inside the red vertical band represented in Fig. 1. The latter spans the peak, and is therefore representative of that intermediate population. We then computed the orbital evolution of each system over 10 Myr, that is, ~375 M of orbits of the outermost planet. For those long integrations, we employed the symplectic WHFAST integrator implemented in REBOUND (Rein & Tamayo 2015), together with a symplectic corrector of seventh order and a fixed time step of 1% of the innermost orbit. The integrations were stopped in case of a close encounter or escape using the same criteria as previously described. None of our integrations underwent a planet escape. Out of the 100 configurations, 26 made it to the end without instability. In the remaining 74 systems, there were 14 close encounters between planets b and c, none between planets c and d, 9 between planets d and e, and 51 between planets e and f. No close encounter between the central star and the innermost planet was recorded. Figure 2 illustrates those statistics. It is interesting to note that among the systems that suffer an instability, most of them involve the outermost planet pair e-f. This indicates that this pair is the most likely to suffer from instability. Most of the systems had a close encounter within 10 Myr. Among those that survived, a proportion could still experience instability on longer timescales. Therefore, it is reasonable to flag this intermediate population as unstable.
Returning to Fig. 1, we set the NAFF-stability threshold at the bottom of the stable population – that is, the rightmost peak – and opt for NAFF = −4.2. This means that any system is flagged as unstable if the relative variation in the mean motion of any planet is larger than about 0.006% over the two halves of the integration. Such an apparently small number is justified by the compactness of the planetary orbits. Out of the 28 000 system configurations, 26 988 survived the total integration time and were also flagged as NAFF-stable (NAFF < −4.2). Our NAFF stability criterion hence discarded an additional 902 system configurations, which is about nine times more than with the close-encounter criterion only. Overall, about 96% of the systems pass our stability criterion, which demonstrates that the posterior distribution obtained by Mills & Fabrycky (2017) is globally stable.
We compared their distribution with the new one, which is composed of NAFF-stable configurations only. As expected, there are no notable differences between the two given the overall stability of the original posterior. Notably, the planetary masses are not further refined by the orbital stability constraints. Additionally, despite the orbital compactness of the system, there is no clear impact of the stability constraint on the eccentricities. This is because the posterior distributions derived by Mills & Fabrycky (2017) are very much confined close to zero. Indeed, the 3σ upper limits on the eccentricity of each planet, from innermost to outermost, are 0.070, 0.066, 0.069, 0.051, and 0.064. This is small enough to ensure orbital stability as will be further illustrated in Sect. 2.3. As the posterior distributions are confined to low eccentricities, we do not expect the stability-driven approach to bring new constraints on the periastron directions, which are ill defined. Indeed, we do not observe any constraints on the NAFF-stable distributions for the arguments of periastron. The mean longitudes are not further constrained by the dynamics either. This is no surprise as the Kepler transit observations provide constraints on the orbital phases that are already relatively tight. Finally, the mutual inclinations between the different planetary orbits are not large enough to trigger orbital instability. Hence, we do not observe new constraints on the inclinations from the stability-driven approach.
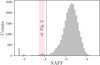 |
Fig. 1 NAFF distribution of the Kepler-444 planetary system based on the model posterior of Mills & Fabrycky (2017). The vertical dotted line indicates the position of our threshold of orbital stability. Any system configuration with a NAFF chaos estimation smaller than this threshold (right-hand side) is flagged as stable. |
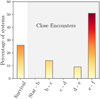 |
Fig. 2 Fate of 100 system configurations that belong to the population of intermediate chaos peaking at NAFF ~ −3.5 (cf. red vertical band of Fig. 1). This bar chart distinguishes the systems that survived the 10 Myr numerical integrations from those that encountered a close encounter, after which the simulation was stopped. Among the close encounters, we further differentiate between the bodies involved in the event. |
2.3 Resonant configuration
The planets pair d-e presents a period ratio very close to 5/4: Pe/Pd = 1.251. The potential for this pair to lie in the 5:4 MMR may have an impact on the overall stability of the system. Our objective is twofold. First, we aim to unveil the (non-)resonance nature of this d-e pair. Indeed, despite its proximity to the 5:4 MMR, the small planet-to-star mass ratios may induce resonance widths that are too small for the pair to be in resonance. Secondly, we aim to explore the impact that the proximity to the 5:4 MMR has on the overall stability of the planetary system.
Two resonant angles are associated with this first-order mean-motion resonance:
where λ is the mean longitude and  is the longitude of periastron. If the orbital periods are near commensurate –that is, if 5Pd ~4Pe – the resonant angles vary slowly, as does the difference between them
is the longitude of periastron. If the orbital periods are near commensurate –that is, if 5Pd ~4Pe – the resonant angles vary slowly, as does the difference between them 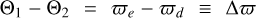 . Among the system configurations that survived our 10kyr integrations, we found different dynamical regimes. Figure 3 illustrates that by showing two examples. In one case, the periastra of the d-e pair stay aligned with some oscillation. In the other case, the periastra are misaligned and their difference is not confined to any value, but instead, it circulates. However, the apparent libration of
. Among the system configurations that survived our 10kyr integrations, we found different dynamical regimes. Figure 3 illustrates that by showing two examples. In one case, the periastra of the d-e pair stay aligned with some oscillation. In the other case, the periastra are misaligned and their difference is not confined to any value, but instead, it circulates. However, the apparent libration of 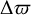 can be misleading, as it does not guarantee the resonance (e.g. Henrard & Lemaitre 1983).
can be misleading, as it does not guarantee the resonance (e.g. Henrard & Lemaitre 1983).
In order to further investigate the resonant behaviour of the d-e planet pair, we computed a chaoticity map, exploring the influence of the period ratio Pe/Pd on the x-axis and the eccentricity of planet e on the y-axis. Let us note that this choice of parameters for the map is somewhat arbitrary. However, in this subspace, we expect the first-order resonances between planets d and e to appear as clear V-shaped structures, making them easier to identify. All the other orbital parameters of the planets were initially fixed from the median of the posteriors given in Mills & Fabrycky (2017), except for the orbital inclinations that were all fixed at 90 deg. The masses of planets d and e were also fixed to values from this latter study. The masses of the other planets, unconstrained by TTVs, were estimated from the best radii estimations and with the mass-radius relation taken from Otegi et al. (2020): M = 0.9R3.45 for the rocky exoplanet population2. We initially varied only the eccentricity of planet e, ee, in [0,0.15], and the period of that same planet, Pe, such that Pe/Pd spans the interval [1.245,1.255]. As such, we created a grid of 151 × 151 system configurations, which we integrated using the same setup as described above. The NAFF results are this time used as a colour code, and not as a binary stability criterion. This confers a topology to the parameter space. The resulting map is presented in Fig. 4a.
The resonance appears clearly. It harbours a typical V-shape island of stability in the eccentricity-period subspace, and is surrounded by layers of usually strong chaos around the separatrix that delimit the resonance. However, the separatrix does not harbour strong instability in this case, or it is too thin to appear clearly on this map; its average level of chaos is globally less strong than our stability threshold of NAFF = −4.2 set in Sect. 2.2. It therefore seems that the proximity of the planets pair d-e to the resonance is not responsible for the overall instability of certain configurations of systems. Instead, the impact of large eccentricities plays a larger role in generating orbital instability. Furthermore, with the map displayed in Fig. 4a, it is still unclear whether the planet pair d-e actually lies inside or outside the topology of the 5:4 MMR. With the planetary parameters used to construct this map, the pair lies slightly outside of the resonance with reasonably low, non-zero eccentricities. The transit observations with Kepler provide strong constraints on the periods. For instance, the estimated period ratio of the d-e pair is represented by the vertical line. The uncertainty on the position of the latter along the x-axis is smaller than the width of a pixel. However, other planet parameters such as mass and orbital eccentricity have an impact on the resonance shape and are less well constrained. As a result, modifying the values of those parameters may place the d-e pair inside or outside of the 5:4 MMR. Figure 4b illustrates the impact that a change in the estimated masses of planets d and e would have on the dynamical state of the system. In this new map, the masses of these two planets were increased to their 1σ upper limit. This modification leads to an increase in the width of the MMR, meaning that the d-e planet pair could actually lie inside the resonance and with reasonably low orbital eccentricities. Therefore, we cannot conclude on the exact dynamical state of that pair, because several such states are compatible within the parameter uncertainties. Finally, we note that the eccentricity of planet e is very unlikely to be larger than 0.1, given the high level of chaos of those configurations. This is in agreement with the global study that we performed in Sect. 2.2, where the eccentricities never reached 0.1, which explains why the stability constraints did not have a significant impact.
We also investigated the possibility for the system to be trapped in a three-planet MMR. Resonances involving three bodies likely play a significant role during planet migration in the protoplanetary disk (Charalambous et al. 2018; Petit 2021). Additionally, they are crucial to understanding the development of orbital instability in tightly packed systems (Quillen 2011; Petit et al. 2020). Low-order three-planet MMRs are thinner but also populate the phase space more densely than two-planet MMRs. A triplet of planets is said to be in a three-body MMR if there exists integers k1, k2, and k3, such that
The resonance is further classified as order zero if k1 + k2+ k3 = 0, and order 1 if k1 + k2 + k3 = 1. Resonances of higher order are increasingly thin in the phase space. Their influence is therefore smaller and their detection is more difficult in practical terms. We searched for the closest three-planet MMR of order 0 and 1 based on the median planet parameters derived from the NAFF-stable distributions. We list the five closest MMRs in Table 1.
The b-c-d triplet of planets is the closest to a low-order three-body MMR. Therefore, we focused on this triplet to study the potential three-body resonant state in the planetary system. To this end, we studied the structure of the phase space in the plane of the period ratios P12 ≡ Pb/Pc and P23 ≡ Pc/Pd. In that plane, two-body MMRs appear as vertical or horizontal bands, while three-body MMRs are oblique lines. Figure 5 presents the 201 × 201 chaos map that we computed in this space, and the star marks the location of the Kepler-444 system. Here, we can see a web of two-planet MMRs. Notably, the thick horizontal band is associated with the 5:4 MMR between planets d and e. Once again, we notice that the d-e planet pair lies at the outskirts of that resonance. The three-body zeroth-order MMR that we identified at the first line of Table 1 is very thin, and is highlighted with a dotted line to guide the eye. This result shows that the b-c-d triplet is not in the considered three-body MMR. Given that this triplet is the closest to a three-body MMR, we conclude that none of the planetary triplets in the Kepler-444 system are in a three-body MMR.
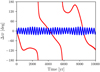 |
Fig. 3 Temporal evolution of the difference in the longitudes of periastron |
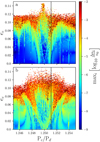 |
Fig. 4 Chaoticity maps of Kepler-444 near the 5:4 MMR of the d-e planets pair. The topology of the parameter subspace is revealed by a grid of 151 × 151 system configurations and a colour code given by the level of chaos in each configuration estimated via NAFF (cf. Sect. 2.1). The redder areas correspond to strongly chaotic configurations, as opposed to the blue ones. Finally, the boxes are coloured in white if the system turned unstable before the end of the integration (either ejection or close encounter). The vertical line indicates the position of the actual planet pair on this x-axis, as tightly constrained by the transits observations. The two grids differ from each other through the masses of planets d and e. Top a: planetary masses are fixed at the median of the TTV posterior obtained by Mills & Fabrycky (2017). Bottom b: masses of planets d and e are increased to their 1σ upper limits. |
Closest three-planet MMRs that satisfy k1n1 + k2n2 + k3n3 = 0 (k1, k2, k3 integers).
 |
Fig. 5 Chaoticity map of Kepler-444 in the space of the period ratios P12 and P23. The dotted line follows the expected location of the zeroth-order three-body MMR n1 − 2n2 + n3 = 0. The star depicts the position of the Kepler-444 b-c-d triplet in that space. The colour scale is different from that in Fig. 4 in order to optimise the visibility of the different MMRs. |
3 Revision of Kepler-444 BC orbit
In this section, we assess the constraints on the orbital parameters of the Kepler-444 A-BC binary orbit. The BC component is currently near the apastron of a high-eccentricity orbit, with Dupuy et al. (2016) finding e = 0.864 ± 0.023. These latter authors used the relative astrometry of A-BC, the radial velocity (RV) trend of the A component, and the relative RV (i.e. RVBC-RVA), and fixed the mass ratio (MB+MC)/MA to a value of 0.71.
There are three new sources of information that can potentially be used to further constrain the Kepler 444 A-BC orbit: (1) Additional radial velocities from Butler et al. (2017). While these significantly increase the density of RV points between 2012 and 2014, they do not extend the RV baseline relative to Dupuy et al. (2016). (2) The astrometric acceleration of the host star, as derived from a comparison between the HIPPARCOS and Gaia catalogue measurements of the stellar proper motion. Together, these two catalogues probe the astrometric acceleration of the star over a 25 yr baseline, which can be significant in constraining long-period orbits (see e.g. Snellen & Brown 2018; Dupuy et al. 2019). (3) The proper motion of the Kepler-444 BC companion, which is resolved from Kepler-444 A in the Gaia catalogue (Gaia Collaboration 2016, 2021). However, we find that this proper motion is not sufficiently reliable to be used in the orbital fit, as discussed in Sect. 3.2 below.
3.1 Orbital fit using the HIPPARCOS-Gaia Catalog of Accelerations and additional RV data
We fit a new orbit using only sources (1) and (2) of additional data, namely the new radial velocities and the astrometric acceleration of the host star; the companion proper motion is discussed in Sect. 3.2. The full set of data used for the orbital fit is as follows: Keck/HIRES RV values from Sozzetti et al. (2009), Dupuy et al. (2016), and Butler et al. (2017), Keck/NIRC2 relative astrometry and Keck/HIRES relative RV measurements from Dupuy et al. (2016), and absolute astrometry from the HIPPARCOS and Gaia measurements of Kepler-444 A. For the absolute astrometry, we used the EDR3 version of the HIPPARCOS-Gaia Catalog of Accelerations (HGCA; Brandt 2021), which gives locally calibrated positional and proper motion differences between the two epochs.
To fit the orbit, we used the orvara orbit fitting tool (Brandt et al. 2021a), an efficient orbit fitter designed to simultaneously fit host star radial velocities, relative astrometry, and absolute astrometry. We used the quoted measurements and errors from the works listed above, and an additional jitter term that was applied to all three RV instruments. We modified a branch of orvara such that it reads in a file listing relative RV measurements (i.e. RVBC-RVA), and calculates relative RV value(s) for each orbit model. The difference between the measured and calculated relative RV is incorporated into the orvara log-likelihood function, which is otherwise unchanged. This modified branch of the orvara code is available on github3.
Unlike Dupuy et al. (2016), we did not fix the mass ratio of ABC. Instead, we used the asteroseismologically determined mass of 0.76 ± 0.043 M⊙ for Kepler-444 A (see Campante et al. 2015), and a broad, uninformative prior for Kepler-444 BC, because the absolute astrometric information from the HGCA allows the mass of the secondary to be determined dynamically. We used the default priors as listed in Brandt et al. (2021a) for all other parameters. We ran 100 MCMC walkers for 50000 steps, and discarded the first 10 000 steps as burn-in. Among all the parameters, the largest autocorrelation time that we obtained is 2487, which means that the walker needs to perform 2487 iterations to obtain a new independent estimate.
The updated orbital parameters are given in Table 2, and the orbit is plotted in Fig. 6. We derive an eccentricity of 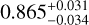 and an inclination of
and an inclination of 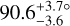 ; both of these values are in close agreement with the orbit presented in Dupuy et al. (2016), confirming that the binary is indeed near apastron of an edge-on, eccentric orbit, and is compatible with being aligned with the primary.
; both of these values are in close agreement with the orbit presented in Dupuy et al. (2016), confirming that the binary is indeed near apastron of an edge-on, eccentric orbit, and is compatible with being aligned with the primary.
Our approach yields a dynamically determined mass for the secondary of 0.633 ± 0.018 M⊙. This corresponds to a mass ratio of 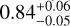 , which is slightly higher than the fixed ratio of 0.71 used by Dupuy et al. (2016), but remains consistent with photometry of the BC pair. We also find a marginally higher semi-major axis of
, which is slightly higher than the fixed ratio of 0.71 used by Dupuy et al. (2016), but remains consistent with photometry of the BC pair. We also find a marginally higher semi-major axis of 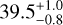 AU, and correspondingly a slightly longer period of
AU, and correspondingly a slightly longer period of 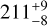 yr. The semi-major axis and period values are consistent to within 2.3σ and 1.1σ, respectively, with the values given in Dupuy et al. (2016).
yr. The semi-major axis and period values are consistent to within 2.3σ and 1.1σ, respectively, with the values given in Dupuy et al. (2016).
3.2 Kepler-444 BC proper motion
Kepler-444 BC is resolved from Kepler-444 A in the Gaia catalogue, meaning that there is a direct measurement of its proper motion. However, there is reason to be cautious of the Kepler-444 BC proper motion measurement: the Kepler-444BC binary is not only close (<2″) to its much brighter host star, but is also an unresolved binary. Indeed, the Gaia parallax of BC is inconsistent with the parallax of the A component at the 5σ level. The quoted parallax values for the two components indicate that BC is radially separated from A by 0.33 ± 0.07 pc, or 68 000 ± 15 000 au. This is clearly inconsistent with the orbit derived above, which has a semi-major axis of just ~40 au, and suggests an issue with the astrometric solution for BC. Further, Kepler-444 BC has a remarkably high ipd_frac_multi_peak value of 31 in the Gaia catalogue. This value represents the percentage of CCD transits where additional images were seen (see Fabricius et al. 2021), suggesting that either the BC pair is resolved in a subset of images, or a faint background star is confusing the images and biasing the astrometric solution. Together, these lines of evidence clearly indicate a system with an unreliable astrometric solution, and we therefore do not use the direct proper motion measurements of Kepler-444 BC when fitting its orbit.
This is in agreement with Pearce et al. (2020), who attempted to fit the orbit of Kepler-444 A-BC using only the Gaia DR2 direct measurements of Kepler-444 BC, and found that the astrometry of the companion was not sufficient to constrain its orbit. Their orbital fit for this companion is highly inconsistent with that of Dupuy et al. (2016), and they infer that the astrometric solution is biased, because Kepler-444 BC is an unresolved binary.
Revised orbital parameters for Kepler-444 A-BC.
4 Dynamical constraints on model 2: With the binary companion BC
We performed a global dynamical analysis with the stellar binary included in our model. For the sake of simplicity, we modelled the couple BC of M-type stars with a single body of mass equal to the sum of the masses of each component. The momentum induced by the separate components on the inner system is indeed expected to have very limited impact on the dynamics. This was further confirmed by Dupuy et al. (2016, see their Sect. 4.2) via numerical simulations. Furthermore, we apply a GR correction on the gravitational potential of the central star only, and the same formalism as the one used in Sect. 2 is employed. The stellar binary companion is indeed too far from the inner system for GR effects to play a significant role. The orbit of the binary companion was derived from our fit, which is described in Sect. 3. We built a global distribution of solutions combining the TTV posterior of Mills & Fabrycky (2017) for the planets with our posterior of orbit configurations for the stellar binary. Therefore, to each of the 28 000 planetary system configurations that we extracted in Sect. 2, we added a different solution for the orbit of the stellar binary. Every unique system configuration of the resulting global distribution was integrated over 100 kyr with IAS15. We then computed the NAFF chaos indicator on the configurations that survived the entire integration based on 20 000 evenly spaced records of the planetary mean longitudes. Again, most of the system configurations survive the entire numerical experiment; of the 28 000 systems, 27 311 make it to the end (no close-encounter, no escape). On the other hand, the NAFF distribution reveals a more contrasted picture. The left plot of Fig. 7 presents that distribution. The peak of the strongly chaotic population appears dramatically more significant compared to the model without a binary. Therefore, the inclusion of the stellar binary companion BC in the model leads to significant chaos in the inner planetary system.
From that NAFF distribution, we notice that the stability threshold is once again conveniently placed at NAFF = −4.2, and we keep only the systems for which their NAFF chaos estimate is smaller than this value. Removing the unstable systems, 19 660 configurations pass the stability criterion. This sample builds up the stable posterior. This new distribution brings additional constraints, which are unseen without the stability analysis and absent from the dynamical model without a stellar binary. As such, the masses of planets c and f encounter notable changes. The middle and right plots of Fig. 7 present their distributions before (black line histogram) and after (plain green) the sorting in NAFF. The stability constraint favours the lower end of the distribution for planet c, while the exact opposite is observed for planet f. Indeed, the gravitational perturbation that the latter encounters from the binary companion increases if the mass ratio decreases. As such, the smaller the planet mass with respect to the stellar binary, the stronger the perturbation and the more chaotic the system. In the case of planet c, the dominant effect is different. The planet is embedded in the planetary system, that is, it is surrounded by planetary companions. Therefore, the effect of the stellar binary is indirect. Instead, an increase in the mass of planet c directly results in stronger gravitational interactions with its planetary neighbours. This is particularly prominent in tightly packed configurations, which therefore develop increased chaos. As such, the lowest values for the mass of planet c are the most likely to provide stable system configurations.
Again, we note that the masses of close-to-MMR planets d and e are not further refined via the stability constraint. The best estimations remain those obtained via TTV analyses (Mills & Fabrycky 2017). This is in accordance with the dynamical studies of Tamayo et al. (2021) on Kepler-23, which showed the better ability of TTVs in refining the planetary masses compared to stability constraints. The other planetary dynamical parameters do not present significant updates with the stability constraint. We summarise the results and provide a review of the planetary parameters in Table A.1.
As noted above, the stellar binary companion Kepler-444 BC is responsible for increasing chaos in the planetary system. Therefore, we explored potential correlations between chaos in the planetary system and the exact orbit of the stellar binary. We find a dependency of both semi-major axis and orbital eccentricity on the chaos. This is illustrated in Fig. 8. The top left plot presents all the system configurations that survived the numerical simulation, and these are represented in terms of the NAFF chaos against the semi-major axis of the stellar binary aBC. The red area identifies the region of that space that is flagged unstable with our NAFF stability criterion. The stable configurations form an island, which further constrains the semi-major axis of the binary companion. The histogram on the bottom left further stresses this observation. It presents the aBC distribution for the stable (green) and the unstable (red) sub-populations of systems. These two populations significantly differ from each other. The stable distribution favours small aBC and is thinner than the unstable one. That latter effect is equivalent to a decrease in the orbit uncertainties. The same behaviour is observed for the orbital eccentricity of the stellar binary companion EccBC, with the difference that the stable distribution favours large values. This anti-correlation finds a natural explanation in the observations. The projected distance between A and BC is well constrained. The stellar companion is currently located around its apastron, at which the distance from the central star is given by a(1 + e). Therefore, measuring the distance between A and BC induces a degeneracy between the eccentricity and the semi-major axis of the BC companion, justifying the mirror effects between the two plots at the top of Fig. 8.
As a consequence of these opposite effects in the distributions of aBC and EccBC, the stellar binary companion BC passes even closer to the central star at periastron than originally estimated. Taking the median values of both distributions, we find that the periastron distance – that is, the distance of closest approach to the central star – of the stellar binary is 4.94 AU, which is within 5 AU. This result suggests the need for a careful study of the interactions between BC and the protoplanetary disk in which the planets formed, with the potential to refine the truncation radius and further constrain the expected planet compositions. This work is beyond the scope of the present study. We updated all the dynamical parameters of the binary companion BC, and present them below the planet parameters in Table A.1.
As a final note, we stress that about 70% of the system configurations pass our NAFF stability criterion. This percentage is large, indicative of a limited influence from the stellar companion on the inner planetary system. The planetary system is sufficiently embedded in the gravitational potential well of the primary star Kepler-444 A to avoid being decimated by the gravitational perturbation of the BC companion. This result suggests that the perturbative power of such companions with tight and eccentric orbits is limited, and we may expect to discover various planetary orbital architectures in multiple-star systems. Nevertheless, this proposition has to be contrasted, as we did not perform a detailed study of the dynamics on long timescales. Secular effects may play a significant role, and we briefly discuss this issue in Sect. 6.
 |
Fig. 6 Left: best-fit orbital solution (thick line) and 50 draws from the posterior distribution (thin, coloured lines) for the Kepler-444 A-BC system, presented in the plane of the sky. Blue points indicate the observed relative astrometry of Kepler-444 BC, while open circles indicate predicted on-sky locations of the companion between 1980 and 2080. Right: same orbital solutions, presented in a top-down view. The observed astrometry is also deprojected into this view, using the inclination of the best-fit orbit. An arrow indicates the direction of this orbit. The colour bar indicates the total mass of the secondary component (i.e. MB+MC), and applies to both panels. |
 |
Fig. 7 Left: NAFF distribution of the Kepler-444 system from the model posterior that includes the binary companion BC. The vertical dotted line represents our stability threshold. Any system configuration with a NAFF chaos estimation smaller than −4.2 (right-hand side) is flagged as stable. Middle: mass distributions of planet c, both presenting the full posterior distribution (black line) and the distribution of NAFF-stable configurations only (plain green). Right: same as middle but for planet f. |
 |
Fig. 8 Impact of the stability constraint on the orbit of the BC companion. Top left: NAFF chaos indicator with respect to the semi-major axis of the stellar binary companion aBC. The red zone depicts the area where the system configurations were flagged unstable. Bottom left: distributions of aBC for both the stable (in green) and the unstable (in red) populations of systems. These two populations are delimited by the threshold value NAFF = −4.2. Top and bottom right: same for the orbital eccentricity of the stellar binary companion EccBC. |
5 Dynamical insights for a sixth planet
During the observation campaign of Kepler-444 A with the HST, Bourrier et al. (2017) identified ~20% flux decreases in the stellar Ly-alpha line associated with the transits of planets e and f. In addition, these authors noticed an unexpected event: a strong ~40% flux decrease in the same spectral range, but at a time uncorrelated with any transit of the known planets. To explain this observation, they propose the existence of a sixth planet on a grazing configuration and with an extended, giant exosphere comparable in size to the one around GJ 436 b (Ehrenreich et al. 2015). With such a scenario, the authors were able to reproduce the observations. If the orbit of this hypothetical planet was co-planar with the average orbital plane of the other planets, its transit limit would lie at ~19 days of orbital period (~0.13 AU).
In this section, we explore the dynamical plausibility for a sixth outer planet in the Kepler-444 system. We do not aim to test an exhaustive six-planet dynamical model, but seek to assess the consistency of a putative planet g on the orbital stability of the whole system. To this end, we introduced a supplementary planet in the full dynamical model – consisting of the primary star, the planets, and the stellar binary BC – with null eccentricity and orbiting Kepler-444 A in the average orbital plane of the planets (i ~ 92 deg). For the other five planets, we supposed a null orbital eccentricity, while their orbital inclinations, transit times, and orbital periods were taken from the results presented in Table A.1. The masses of planets d and e were taken from the same table, while the masses of planets b, c, and f were inferred from the mass-radius relationship of Otegi et al. (2020), in the same way as for the computation of the map presented in Fig. 4. The BC parameters were taken from Table A.1. The orbital phase of the putative sixth planet in our simulations matches the observation of Bourrier et al. (2017). The authors indeed retrieved the expected inferior conjunction time of the hypothetical planet based on a comparison between their exospheric model and the flux-decrease observations of the Ly-α line. They also note that around a solar-like star, the limit above which the atmosphere of a giant planet would be stable is 0.15 AU (Koskinen et al. 2007), which also gives a crude estimate for the maximal semi-major axis of that hypothetical sixth planet at which the latter can still harbour a large exosphere. This translates into an orbital period of ~24.4 days. We computed a chaos map exploring the subspace mg versus Pg, where the mass of the supplementary planet was varied between 0.001 and 10.001 Earth masses, while its orbital period was explored in the range [10.5,23.0] days. This was done via a grid of 201 × 201 system configurations, each of them integrated over 100 kyr. The NAFF indicator was computed at the end of the integrations, and provides the basis for the colour coding that shows the level of chaos in the system configurations. The result is presented in Fig. 9.
First, this map shows that there is room for a sixth outermost planet without destabilising the whole system. The range of periods allowed is 12–20 days. Below 12 days, the compactness of the f–g planet pair results in close encounters between the two bodies. Above 20 days, the stellar binary companion BC periodically exchanges significant momentum with the outermost planet during the passage at periastron. Consequently, planet g undergoes regular upward pushes of its orbital eccentricity, leading ultimately to the orbit crossing with planet f and a close encounter. In between these limits, an additional sixth planet could harbour most of the tested orbital periods. These results therefore validate the dynamical plausibility of the hypothetical sixth planet introduced in Bourrier et al. (2017), and provide a range of possible orbital periods. In particular, a period window of between ~16 and 18 days shows low levels of chaos and corresponds to a planet g on a grazing orbit – supposing its orbit to be co-planar with the average orbital plane of the other planets – that would most likely have been missed in the Kepler observations. Furthermore, the mass of this planet has a very limited impact on the orbital stability. This leaves the possibility for a wide diversity of planets.
We stress that these simulations investigate the short-term chaos in the system. An exploration of the secular dynamics would be necessary to further study the orbital stability and refine the parameters of that potential sixth outer planet. This is beyond the scope of the present study.
 |
Fig. 9 201 × 201 chaoticity map of Kepler-444 using a model composed of six planets and the stellar binary companion (considered as a single body) orbiting the primary star. This map explores the plausibility of the existence of a putative sixth planet in the system via the exploration of overall system chaoticity in the 2D space mg vs. Pg. The level of chaos is provided by the NAFF indicator, and provides the basis for the colour coding. White boxes indicate that the corresponding system configurations did not survive the entire integration (close encounter or ejection). |
6 Conclusions
The 11Gyr-old triple-star system Kepler-444 constitutes a particularly challenging case study for the planet formation and evolution models. The binary Kepler-444 BC, which is on a highly eccentric orbit around Kepler-444 A, and the tightly packed succession of subVenus planets orbiting the primary, raise many questions in terms of dynamics. How close to global instability is this compact architecture? How much does the binary companion perturb the inner system? These questions are of importance in understanding the system evolution from the formation stage until now. In this work, we reviewed the architecture of Kepler-444 in light of orbital dynamics, and tackled the questions above.
We first investigated the dynamics of the inner system of Kepler-444, which is composed of the five planets and the primary star only. We inspected the orbital stability of the planets posterior distribution derived by Mills & Fabrycky (2017) via the strategy introduced in Stalport et al. (2022). We note a strong agreement with stability. Furthermore, we explored potential resonances in the planetary system. Notably, the planet pair d-e presents a period ratio close to 5/4. We reveal the 5:4 MMR in the phase space, but cannot come to any firm conclusion as to whether the pair is inside or outside that resonance; this strongly depends on the values used for the planet parameters. Additionally, we investigated the three-planet MMR of order zero and one. None of the planet triplets lie in such resonances. The formation process of compact systems is expected to place the planets in a resonant configuration via the disk-planet tidal interactions. This is not what is observed, which is consistent with the general results from the Kepler mission (Lissauer et al. 2011; Fabrycky et al. 2014). A potential explanation is the role of tidal dissipation with the star, which moves the planets away from the resonant configuration (Delisle & Laskar 2014; Millholland & Laughlin 2019). Investigations of the potential impact of tides on the system dynamics would provide better insights into the present-day architecture.
As a second step, we analysed new observations in order to update the orbit of the stellar binary companion Kepler-444 BC, in anticipation of its inclusion in our dynamical model. We used additional HIRES spectra, combined HIPPARCOS and Gaia measurements, to probe the astrometric acceleration of Kepler-444 A over 25 yr, and archival imaging of the system. With this revision, we were able to estimate the mass of the binary companion BC without any inference from mass-magnitude relationships. The new fits are consistent with the orbital configuration obtained by Dupuy et al. (2016).
We then applied the stability-driven refinement technique (Stalport et al. 2022) to the dynamical model including the stellar binary companion. We did not observe significant updates to the planet parameters besides a slight effect on the masses of planets c and f. As expected, the stability-driven approach does not allow further refinement of the masses where TTV analyses are able to estimate them, in this instance regarding planets d and e. However, we observe a strong dependency of the BC orbit on the stability of the planetary system. Thanks to this observation, we were able to further tighten the constraints on the BC orbit. A notable result is that the A-BC distance at periastron is estimated to 4.94 AU, with a 68.27% confidence interval of [3.84, 6.08] AU. Therefore, it is likely that the stellar binary companion passes within 5 AU of the central star. This new result has implications for our understanding of the conditions in which the planets formed, and suggests that further study of this topic would be useful. Notably, the truncation radius of the past protoplanetary disk under the influence of the BC companion can be revised in light of the present conclusion. Indirectly, this might have important consequences on the expected atmospheric composition of these planets, and will provide insights into the current scenarios. Additionally, the upcoming ESA PLATO mission will provide new valuable TTV measurements that will further constrain the masses of planets d and e, leading to deeper insights into the planet densities and their supposed composition. Furthermore, these new transit measurements could reveal TTV detections for (some of) the three other planets. The final, updated masses and orbital parameters of the planets and the stellar binary companion BC are presented in Table A.1. We encourage the use of those values in future studies of Kepler-444, as these are the most precise and up to date.
Finally, we also investigated the dynamical plausibility of a hypothetical sixth outer planet. Using the estimated conjunction time from Bourrier et al. (2017), we show that this putative body could exist within a certain range of orbital periods of between roughly 12 and 20 days. Additional targeted observations are needed to shed light on this potential planet. Notably, new measurements with HST in the appropriate temporal window would help to confirm or otherwise discard the existence of the sixth planet.
Acknowledgements
We thank the anonymous referee for insightful comments, which significantly improved the presentation of our work. This work has been carried out within the framework of the National Centre of Competence in Research PlanetS supported by the Swiss National Science Foundation under grants 51NF40_182901 and 51NF40_205606. The authors acknowledge the financial support of the SNSF. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (project SPICE DUNE, grant agreement No 947634). This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. The authors thank Trent Dupuy for helpful conversations. Tools used: REBOUND (Rein & Liu 2012), orvara (Brandt et al. 2021b).
Appendix A Updated parameters
Updated masses and orbital elements of the planets Kepler-444 Ab, c, d, e, and f, and the stellar binary companion Kepler-444 BC.
References
- Anderson, J. D., Esposito, P. B., Martin, W., Thornton, C. L., & Muhleman, D. O. 1975, ApJ, 200, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Bourrier, V., Ehrenreich, D., Allart, R., et al. 2017, A&A, 602, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brandt, T. D. 2021, ApJS, 254, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Brandt, T. D., Dupuy, T. J., Li, Y., et al. 2021a, AJ, 162, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Brandt, T. D., Dupuy, T. J., Li, Y., et al. 2021b, Astrophysics Source Code Library [record ascl:2105.012] [Google Scholar]
- Buldgen, G., Farnir, M., Pezzotti, C., et al. 2019, A&A, 630, A126 [EDP Sciences] [Google Scholar]
- Butler, R. P., Vogt, S. S., Laughlin, G., et al. 2017, AJ, 153, 208 [Google Scholar]
- Campante, T. L., Barclay, T., Swift, J. J., et al. 2015, ApJ, 799, 170 [Google Scholar]
- Chambers, J. E., Wetherill, G. W., & Boss, A. P. 1996, Icarus, 119, 261 [Google Scholar]
- Charalambous, C., Martí, J. G., Beaugé, C., & Ramos, X. S. 2018, MNRAS, 477, 1414Delisle, J. B., & Laskar, J. 2014, A&A, 570, L7 [Google Scholar]
- Dupuy, T. J., Kratter, K. M., Kraus, A. L., et al. 2016, ApJ, 817, 80 [Google Scholar]
- Dupuy, T. J., Brandt, T. D., Kratter, K. M., & Bowler, B. P. 2019, ApJ, 871, L4 [Google Scholar]
- Duquennoy, A., & Mayor, M. 1991, A&A, 248, 485 [NASA ADS] [Google Scholar]
- Ehrenreich, D., Bourrier, V., Wheatley, P. J., et al. 2015, Nature, 522, 459 [Google Scholar]
- Fabricius, C., Luri, X., Arenou, F., et al. 2021, A&A, 649, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabrycky, D. C., Lissauer, J. J., Ragozzine, D., et al. 2014, ApJ, 790, 146 [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A.G.A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Henrard, J., & Lemaitre, A. 1983, Celest. Mech., 30, 197 [Google Scholar]
- Hussain, N., & Tamayo, D. 2020, MNRAS, 491, 5258 [NASA ADS] [CrossRef] [Google Scholar]
- Jura, M. 2004, ApJ, 605, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Koskinen, T. T., Aylward, A. D., & Miller, S. 2007, Nature, 450, 845 [CrossRef] [Google Scholar]
- Laskar, J. 1990, Icarus, 88, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Laskar, J. 1993, Physica D, 67, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Lissauer, J. J., Ragozzine, D., Fabrycky, D. C., et al. 2011, ApJS, 197, 8 [Google Scholar]
- Millholland, S., & Laughlin, G. 2019, Nat. Astron., 3, 424 [Google Scholar]
- Mills, S. M., & Fabrycky, D. C. 2017, ApJ, 838, L11 [Google Scholar]
- Murray, N., & Holman, M. 1997, AJ, 114, 1246 [NASA ADS] [CrossRef] [Google Scholar]
- Obertas, A., Van Laerhoven, C., & Tamayo, D. 2017, Icarus, 293, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Offner, S. S. R., Moe, M., Kratter, K. M., et al. 2022, The Origin and Evolution of Multiple Star Systems [arXiv: 2203.10066] [Google Scholar]
- Otegi, J. F., Bouchy, F., & Helled, R. 2020, A&A, 634, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Papaloizou, J. C. B. 2016, Celest. Mech. Dyn. Astron., 126, 157 [Google Scholar]
- Pearce, L. A., Kraus, A. L., Dupuy, T. J., et al. 2020, ApJ, 894, 115 [CrossRef] [Google Scholar]
- Petit, A. C. 2021, Celest. Mech. Dyn. Astron., 133, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Petit, A. C., Pichierri, G., Davies, M. B., & Johansen, A. 2020, A&A, 641, A176 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pezzotti, C., Eggenberger, P., Buldgen, G., et al. 2021, A&A, 650, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pu, B., & Wu, Y. 2015, ApJ, 807, 44 [Google Scholar]
- Quillen, A. C. 2011, MNRAS, 418, 1043 [Google Scholar]
- Rein, H., & Liu, S. F. 2012, A&A, 537, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rein, H., & Spiegel, D. S. 2015, MNRAS, 446, 1424 [Google Scholar]
- Rein, H., & Tamayo, D. 2015, MNRAS, 452, 376 [Google Scholar]
- Rice, D. R., Rasio, F. A., & Steffen, J. H. 2018, MNRAS, 481, 2205 [NASA ADS] [CrossRef] [Google Scholar]
- Snellen, I. A. G., & Brown, A. G. A. 2018, Nat. Astron., 2, 883 [Google Scholar]
- Sozzetti, A., Torres, G., Latham, D. W., et al. 2009, ApJ, 697, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Stalport, M., Delisle, J. B., Udry, S., et al. 2022, A&A, 664, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tamayo, D., Rein, H., Shi, P., & Hernandez, D. M. 2020, MNRAS, 491, 2885 [NASA ADS] [CrossRef] [Google Scholar]
- Tamayo, D., Gilbertson, C., & Foreman-Mackey, D. 2021, MNRAS, 501, 4798 [NASA ADS] [CrossRef] [Google Scholar]
REBOUND is a package to compute the dynamical evolution of N-body systems. It can be found at https://rebound.readthedocs.io/en/latest/ and contains a large variety of numerical integrators.
All Tables
Closest three-planet MMRs that satisfy k1n1 + k2n2 + k3n3 = 0 (k1, k2, k3 integers).
Updated masses and orbital elements of the planets Kepler-444 Ab, c, d, e, and f, and the stellar binary companion Kepler-444 BC.
All Figures
 |
Fig. 1 NAFF distribution of the Kepler-444 planetary system based on the model posterior of Mills & Fabrycky (2017). The vertical dotted line indicates the position of our threshold of orbital stability. Any system configuration with a NAFF chaos estimation smaller than this threshold (right-hand side) is flagged as stable. |
| In the text | |
 |
Fig. 2 Fate of 100 system configurations that belong to the population of intermediate chaos peaking at NAFF ~ −3.5 (cf. red vertical band of Fig. 1). This bar chart distinguishes the systems that survived the 10 Myr numerical integrations from those that encountered a close encounter, after which the simulation was stopped. Among the close encounters, we further differentiate between the bodies involved in the event. |
| In the text | |
 |
Fig. 3 Temporal evolution of the difference in the longitudes of periastron |
| In the text | |
 |
Fig. 4 Chaoticity maps of Kepler-444 near the 5:4 MMR of the d-e planets pair. The topology of the parameter subspace is revealed by a grid of 151 × 151 system configurations and a colour code given by the level of chaos in each configuration estimated via NAFF (cf. Sect. 2.1). The redder areas correspond to strongly chaotic configurations, as opposed to the blue ones. Finally, the boxes are coloured in white if the system turned unstable before the end of the integration (either ejection or close encounter). The vertical line indicates the position of the actual planet pair on this x-axis, as tightly constrained by the transits observations. The two grids differ from each other through the masses of planets d and e. Top a: planetary masses are fixed at the median of the TTV posterior obtained by Mills & Fabrycky (2017). Bottom b: masses of planets d and e are increased to their 1σ upper limits. |
| In the text | |
 |
Fig. 5 Chaoticity map of Kepler-444 in the space of the period ratios P12 and P23. The dotted line follows the expected location of the zeroth-order three-body MMR n1 − 2n2 + n3 = 0. The star depicts the position of the Kepler-444 b-c-d triplet in that space. The colour scale is different from that in Fig. 4 in order to optimise the visibility of the different MMRs. |
| In the text | |
 |
Fig. 6 Left: best-fit orbital solution (thick line) and 50 draws from the posterior distribution (thin, coloured lines) for the Kepler-444 A-BC system, presented in the plane of the sky. Blue points indicate the observed relative astrometry of Kepler-444 BC, while open circles indicate predicted on-sky locations of the companion between 1980 and 2080. Right: same orbital solutions, presented in a top-down view. The observed astrometry is also deprojected into this view, using the inclination of the best-fit orbit. An arrow indicates the direction of this orbit. The colour bar indicates the total mass of the secondary component (i.e. MB+MC), and applies to both panels. |
| In the text | |
 |
Fig. 7 Left: NAFF distribution of the Kepler-444 system from the model posterior that includes the binary companion BC. The vertical dotted line represents our stability threshold. Any system configuration with a NAFF chaos estimation smaller than −4.2 (right-hand side) is flagged as stable. Middle: mass distributions of planet c, both presenting the full posterior distribution (black line) and the distribution of NAFF-stable configurations only (plain green). Right: same as middle but for planet f. |
| In the text | |
 |
Fig. 8 Impact of the stability constraint on the orbit of the BC companion. Top left: NAFF chaos indicator with respect to the semi-major axis of the stellar binary companion aBC. The red zone depicts the area where the system configurations were flagged unstable. Bottom left: distributions of aBC for both the stable (in green) and the unstable (in red) populations of systems. These two populations are delimited by the threshold value NAFF = −4.2. Top and bottom right: same for the orbital eccentricity of the stellar binary companion EccBC. |
| In the text | |
 |
Fig. 9 201 × 201 chaoticity map of Kepler-444 using a model composed of six planets and the stellar binary companion (considered as a single body) orbiting the primary star. This map explores the plausibility of the existence of a putative sixth planet in the system via the exploration of overall system chaoticity in the 2D space mg vs. Pg. The level of chaos is provided by the NAFF indicator, and provides the basis for the colour coding. White boxes indicate that the corresponding system configurations did not survive the entire integration (close encounter or ejection). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![${\rm{NAFF}} = \mathop {\max }\limits_j \left[ {{{\log }_{10}}{{\left| {{n_{j,2}} - {n_{j,1}}} \right|} \over {{n_{j,0}}}}} \right],$](/articles/aa/full_html/2022/11/aa43971-22/aa43971-22-eq1.png)