| Issue |
A&A
Volume 664, August 2022
|
|
|---|---|---|
| Article Number | A88 | |
| Number of page(s) | 21 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202142596 | |
| Published online | 12 August 2022 | |
Filamentary structures of ionized gas in Cygnus X★
1
National Radio Astronomy Observatory,
520 Edgemont Road,
Charlottesville,
VA 22903
USA
e-mail: kemig@nrao.edu
2
Leiden Observatory, Leiden University,
PO Box 9513
Leiden,
2300 RA
The Netherlands
3
Department of Physics and Astronomy, The Open University,
Walton Hall,
Milton Keynes,
MK7 6AA
UK
4
RAL Space, STFC Rutherford Appleton Laboratory,
Chilton, Didcot,
Oxfordshire,
OX11 0QX
UK
5
Green Bank Observatory,
PO Box 2
Green Bank,
WV 24944
USA
6
Department of Astronomy, University of Maryland,
College Park,
MD 20742
USA
7
Aix Marseille Univ, CNRS, CNES, LAM,
Marseille,
France
8
Institut Universitaire de France (IUF),
Paris,
France
9
Department of Astrophysics/IMAPP, Radboud University,
PO Box 9010
6500 GL
The Netherlands
10
Netherlands Institute for Radio Astronomy (ASTRON),
Postbus 2,
Dwingeloo,
7990 AA
The Netherlands
11
SURF/SURFsara,
Science Park 140,
Amsterdam,
1098 XG
The Netherlands
12
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69,
Bonn,
53121
Germany
Received:
5
November
2021
Accepted:
12
May
2022
Context. Ionized gas probes the influence of massive stars on their environment. The Cygnus X region (d ~ 1.5 kpc) is one of the most massive star-forming complexes in our Galaxy, within which the Cyg OB2 association (age of 3–5 Myr and stellar mass 2 × 104 M⊙) has a dominant influence.
Aims. We observe the Cygnus X region at 148 MHz using the Low Frequency Array (LOFAR) and take short-spacing information into account during image deconvolution into account. Together with data from the Canadian Galactic Plane Survey, we investigate the morphology, distribution, and physical conditions of low-density ionized gas in a 4° × 4° (~100 pc × 100 pc) region at a resolution of 2′ (0.9 pc).
Methods. The Galactic radio emission in the region analyzed is almost entirely thermal (free-free) at 148 MHz, with emission measures (EM) of 103 < EM [pc cm−6] < 106. As filamentary structure is a prominent feature of the emission, we use DisPerSE and Fil ChaP to identify filamentary ridges and characterize their radial (EM) profiles.
Results. The distribution of radial profiles has a characteristic width of 4.3 pc and a power-law distribution (β = −1.8 ± 0.1) in peak EM down to our completeness limit of 4200 pc cm−6. The electron densities of the filamentary structure range between 10 ≲ ne [cm−3] ≲ 400 with a median value of 35 cm−3, remarkably similar to [N II] surveys of ionized gas.
Conclusions. Cyg OB2 may ionize at most two-thirds of the total ionized gas and the ionized gas in filaments. More than half of the filamentary structures are likely photoevaporating surfaces flowing into a surrounding diffuse (~5 cm−3) medium. However, this is likely not the case for all ionized gas ridges. A characteristic width in the distribution of ionized gas indicates that the stellar winds of Cyg OB2 create a fraction of the ionized filaments through swept-up ionized gas or dissipated turbulence.
Key words: radio continuum: ISM / HII regions / ISM: general / open clusters and associations: individual: Cygnus OB2 / techniques: image processing
The reduced images are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/664/A88
© K. L. Emig et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1 Introduction
The intevironment has a profound impact on the evolution of galaxies (Hopkins et al. 2014, 2018) through the collective effects of protostellar outflows (Bally 2016), ionizing radiation (Matzner 2002), stellar winds, and supernovae (SNe; Yorke et al. 1989). One way to investigate their impact is through photoionized gas, in which stars of mass M✶ ≳ 7 M⊙, all O stars and stars earlier than B3 types, produce extreme ultraviolet (EUV) radiation of E > 13.6 eV, which is capable of photoionizing hydrogen in the surrounding medium. Ionized gas is an important component of the interstellar medium (ISM) that reflects feedback processes associated with: (i) ionizing radiation – through photoionized gas, radiation pressure, and photoevaporation – but ionized gas can also reflect feedback, (ii) stellar winds and SN processes – through shocks, turbulence, and gas phase changes, (iii) turbulent dissipation, and (iv) gas accretion onto galaxies.
Early in their lifetimes, massive stars dissociate and ionize their immediate environment. Dense H II regions form as pockets of ionized gas, increasing the thermal gas pressure within the molecular cloud by three orders of magnitude. The subsequent expansion of an H II region can mechanically unbind the parent cloud and induce turbulent motions (e.g., Walch et al. 2012) in the ISM. As an H II region expands, its volume density diminishes. Stellar winds and radiation pressure are also important contributors to the expansion of the ionized gas volume (e.g., Pabst et al. 2019, 2020; Olivier et al. 2021). As a result of peculiar motion and/or inhomogeneities in the medium, the star, its photons, and the gas it ionizes enter a surrounding low-density medium (ne ~ 0.1–100 cm−3) within a few megayears (e.g., Mezger 1978).
Within the plane of the Galaxy, photoionized gas is found in a variety of environments (and referred to with a variety of different names). Dense (ne > 103 cm−3) ionized gas pervades H II regions of a few parsecs in size. When stellar winds are influential in an H II region, the medium stratifies, with ionized gas at larger radii and hot gas filling the inner regions (Weaver et al. 1977; Churchwell et al. 2006). From leaky H II regions, ionizing photons escaping through porous material create (partially) ionized gas (1–100 cm−3) in the envelopes of H II regions. This diffuse ionized gas (1–100 cm−3) permeates to larger volumes in blister H II regions. Assisted by SN explosions, massive stars create large excavated regions or plasma tunnels that contain fully ionized gas (1–10 cm−3). Over-pressured – and thus denser, brighter, and more readily detected – photoevaporating ionized gas (of smaller path lengths) is frequently observed in a number of these scenarios as ionization fronts propagate into local neutral material. Ionizing photons that escape in these scenarios provide a surplus of the ionizing photon budget required to maintain (e.g., Reynolds 1984) the pervasive (volume filling factor ϕ ~ 0.25; Kulkarni & Heiles 1988) warm ionized medium (WIM) of the ISM, which resides in the Galactic plane (ne ~ 0.1 cm−3) and is characterized by large (z ~ 1 kpc) scale heights (for a review, see Haffner et al. 2009).
Blind surveys and large targeted samples with thermal radio continua (Mezger 1978; Murray & Rahman 2010), radio recombination line (RRL) emission (Shaver 1976; Lockman 1976; Anantharamaiah 1985, 1986; Roshi & Anantharamaiah 2000; Heiles et al. 1996; Alves et al. 2015), far-infrared (FIR) fine structure line emission from [N II] (Bennett et al. 1994; Goldsmith et al. 2015), and pulsar dispersion measures (Berkhuijsen et al. 2006, and references therein) have brought to light properties of low-density ionized gas within the Galactic plane. Mezger (1978) estimated that 84% of ionizing photons are emitted by O stars outside of compact H II regions, in gas characterized by densities of ne ≈ 5–10 cm−3 dubbed extended low-density (ELD) H II gas. However, a number of different conclusions have been reached regarding the dominant origin of this gas: (i) envelopes of H II regions (Shaver 1976; Anantharamaiah 1986; McKee & Williams 1997), (ii) a pervasive component (Heiles et al. 1996) that may be a continuation of the WIM (Bennett et al. 1994; Berkhuijsen et al. 2006), and (iii) just a handful of the most luminous star-forming regions in the Galaxy (Murray & Rahman 2010). Thus, the volume filling factor of gas with these densities is unclear. High-resolution pinhole surveys of FIR fine structure lines (Goldsmith et al. 2015; Pineda et al. 2019; Langer et al. 2021) trace somewhat denser gas (with mean values of ne ≈ 30–40 cm−3) and could plausibly be tied with these three possibilities.
The Cygnus X region is a massive star-forming complex that displays filament-like structure in low-density ionized gas (Wendker et al. 1991). “Cygnus X” refers to a ~10º wide region in the Galactic plane with enhanced radio emission (Piddington & Minnett 1952; for an overview of the region, see Reipurth & Schneider 2008). This coherent region of massive star formation lies at ~1.5 kpc (Schneider et al. 2006; Rygl et al. 2012) and dominates the observed emission, despite the view looking down a spiral arm in this direction. Open and massive OB associations are seen in this direction at a similar distance – Cyg OB1, OB2, OB6, and OB9 (Uyaniker et al. 2001). Yet, the region still retains a large reservoir (M > 106 M⊙) of molecular gas (Schneider et al. 2006, 2011). The presence of massive post-main-sequence stars indicates that star formation began in the region ~15 Myr ago (Comerón & Pasquali 2012; Comerón et al. 2016, 2020). Though the nature of the rarefied region is debated, it is consistent with the superbubble formalism (McKee & Ostriker 1977), indicating that stellar winds and/or SNe have contributed to excavating the parent cloud(s) (Bochkarev & Sitnik 1985; Ackermann et al. 2011).
Part of the region that is referred to as Cygnus X North (Schneider et al. 2006) harbors Cyg OB2 and other smaller clusters and associations, some of which are actively forming stars (Cong 1977; Odenwald et al. 1990; Comeron & Torra 1999; Comerón & Torra 2001; Le Duigou & Knodlseder 2002; Marston et al. 2004; Motte et al. 2007; Beerer et al. 2010; Panwar et al. 2020). The Cyg OB2 association strongly influences the medium, as characterized through pillars and globules (Wright et al. 2012; Schneider et al. 2016a; Deb et al. 2018). Cyg OB2 has a total stellar mass of 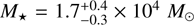 (Wright et al. 2015). It is not bound gravitationally and likely formed that way, in a relatively low-density environment given its mass (Wright et al. 2014), during bursts of star formation that occurred 3 and 5 Myr ago (Wright et al. 2010; Berlanas et al. 2020).
(Wright et al. 2015). It is not bound gravitationally and likely formed that way, in a relatively low-density environment given its mass (Wright et al. 2014), during bursts of star formation that occurred 3 and 5 Myr ago (Wright et al. 2010; Berlanas et al. 2020).
In this article we investigate low-density ionized gas in Cygnus X (North) with 148 MHz continuum observations using the Low Frequency Array (LOFAR; van Haarlem et al. 2013). We observe a region that encompasses 16 square degrees (~10 kpc2) within a single pointing near the Cyg OB2 association, as it contains a wide variety of evolutionary stages of star formation with low-density ionized gas. We aim to investigate the filamentary structure of ionized gas and characterize the influence of massive stars on their environment through ionization feedback.
We adopt a distance of d = 1.5 ± 0.1 kpc to the Cygnus X region and Cyg OB2 following Comerón et al. (2020, see their Sect. 2.2 for a detailed discussion). After an analysis of molecular line emission showed the region to be a coherent structure influenced by Cyg OB2 (Schneider et al. 2006, 2016a), the distance to the Cygnus X complex was determined as 1.40 ± 0.08 kpc through maser observations of massive stars (Rygl et al. 2012). A recent Gaia analysis (Berlanas et al. 2019) places a main subgroup of Cyg OB2 (80% of the OB population) at 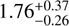 with a smaller subgroup at 1.35 ± 0.2 kpc. While a clear separation in distance distinguishes these two subgroups, Comerón et al. (2020) point out that a systematic offset in parallax may affect the distance determinations. At d = 1.5 kpc, the physical scale is 1′ ≈ 0.44 pc.
with a smaller subgroup at 1.35 ± 0.2 kpc. While a clear separation in distance distinguishes these two subgroups, Comerón et al. (2020) point out that a systematic offset in parallax may affect the distance determinations. At d = 1.5 kpc, the physical scale is 1′ ≈ 0.44 pc.
2 Data
2.1 LOFAR Observations and Data Processing
In this section we describe the data processing of LOFAR inter-ferometric observations of one pointing centered approximately on the massive star-forming region DR 21 at (αRA, δDec) = (309.5500°, +42.0708°) in J2000 coordinates. These data were obtained with the high band antennas (HBAs) covering 110– 190 MHz on July 19, 2013, under project LC0_032 (PI: G. White). Continuous frequency coverage was obtained between 126 and 165 MHz and which we make use of in this analysis. 23 stations of the full Dutch array recorded data during these observations, which have a maximum baseline of 120 km (4″) and minimum baseline lengths of 70 m corresponding to largest angular scales of 96′ (1.6°). The on-source integration time is 6 h and 50 min. A plot of the uυ coverage of this observation can be found in the appendix as Fig. A.1.
We recorded data throughout the observation also in the direction of Cygnus A (299.8682°, 40.7339°), a bright (~104 Jy), well-modeled source 7.4° away from the target center. The flexibility of digitally pointing the LOFAR beam allows HBA data to be recorded toward multiple phase centers within the station beam of ~20°. Because of the close proximity and simultaneous observation, we use Cygnus A as the primary calibrator source to derive flux, bandpass, and phase calibrations to transfer to the target pointing.
2.1.1 Calibrating the Visibilities
We describe the calibration of the visibility data in this section. We derive flux, bandpass, and phase calibrations of the primary calibrator pointing. We then apply these to the target pointing. Lastly, we mitigate side lobe contribution from Cygnus A to the target pointing by subtracting Cygnus A visibilities from the target visibilities; the trade-off to LOFAR’s large field of view is its susceptibility to strong side lobe contamination.
To begin processing of both the primary calibrator and target measurement sets (MSs), we flag the correlations between the two “ears” of each HBA core station (van Haarlem et al. 2013) and flag for radio frequency interference with AOFlagger (Offringa et al. 2012) at full time and frequency resolution (0.763 kHz channel) using the default HBA strategy (Offringa et al. 2012). We also flag station CS013 as its antennas were not properly phased up at the time of the observations. Then we average (by a factor of 64) the data to a channel resolution of 48.8 kHz1.
For the primary calibrator, we solved for the diagonal (XX and YY) gain, phase, and amplitude, at full frequency resolution with the Default Pipeline Processing Platform (DPPP; van Diepen & Dijkema 2018). We used a LOFAR model of Cygnus A at 150 MHz consisting of 33 000 components (courtesy J. McKean; McKean et al. 2016). The solutions have cleanly converged, and they also indicate the ionosphere was relatively mild. We apply only the phase solutions. Then, we solve again for the diagonal gain, phase and amplitude. Using the LOFAR Solutions Tool (LoSoTo; de Gasperin et al. 2019), we flag spurious jumps in the amplitude solutions of each channel – likely due to instrumental instabilities – as well as any residual RFI, which are identified as 7σ outliers averaged over a sliding window of 40 solution intervals in time.
For the target pointing, we use DPPP to apply the phase solutions of the first iteration of gain calibration of the primary calibrator and both the amplitude and phase solutions of the second iteration. The time steps of the visibility data that have flagged amplitude solutions will be flagged as the solutions are applied. Phase offsets due to asynchronized – on the order of O(10 nanoseconds) – station clocks of the remote stations (van Weeren et al. 2016) have been absorbed into the primary calibrator solutions. Furthermore, a calm ionosphere may be characterized by large patches of coherence in the total electron content (Intema et al. 2009), thus inducing similar phase errors (and Faraday rotation) toward the target and nearby primary calibrator. Phase (and amplitude) errors due to the ionosphere are absorbed into these solutions as well.
In the next step, we used DPPP to subtract Cygnus A from the target visibilities because of the close proximity of Cygnus A to our pointing center. We phase-shifted the target visibilities to the location of Cygnus A and then predicted the 33 000 source model of Cygnus A into the MODEL column. Next we smoothed our visibilities with a baseline-dependent averager (de Gasperin et al. 2019) and solved for the diagonal (XX and YY) gain at a 195.3 kHz frequency resolution and 1 min time resolution, attempting to smear the visibility structure of the target. We corrupted the MODEL column with the solutions. Then we subtracted the corrupted MODEL from the DATA. We phase-shifted these visibilities back to the target phase center of the observation. In this manner, we subtracted the off-axis signal of Cygnus A from the data. We find this approach produces more coherent solutions with a larger number of stations converging than with the standard “demixing” (van der Tol et al. 2007) capabilities of DPPP.
At this point, the target data are well calibrated against a source that has a peak flux 1000 times brighter than the apparent flux of any source in the target field. With our science aim to investigate extended diffuse emission that is well characterized with low-resolution (2′) imaging, self-calibration tests do not significantly improve our short baseline calibration.
2.1.2 Constructing a Short-spacing Map
The LOFAR data have excellent uv coverage to large-scale emission with baselines as short as 70 m providing sensitivity to a largest angular size of 96′. However, for observations near the Galactic plane, where large-scale emission surpasses tens of degrees, information on the smallest uυ scales is necessary to properly deconvolve and obtain the flux density of the extended O(1°) structures in the Cygnus X region.
We constructed a short-spacing map at 148 MHz and with 72′ resolution that is interpolated from multifrequency fits across 52, 408, 820, and 1420 MHz. To ensure that uυ coverage of the short-spacing map overlaps with the uυ coverage of the LOFAR observations, we targeted survey data with resolutions of approximately ~1° or less and which covered Galactic latitudes of |b| ≲ 7°.
We compiled the following data. We make use of 52.224 MHz survey data obtained with the Owens Valley Radio Observatory Long Wavelength Array (OVRO-LWA; Eastwood et al. 2018). It has a native resolution of 16.2′ × 15.0′, and inspection of the data in this region shows that the flux scale is calibrated to within ~20% as compared to lower-resolution surveys. We use the 408 MHz multi-instrument survey of Haslam et al. (1982) that has been de-striped (to <1 K) of large-scale striations (Remazeilles et al. 2015) and has a native resolution of 51′(Haslam et al. 1974). The 820 MHz survey with the Dwingeloo Telescope (Berkhuijsen 1972) has a native resolution of 72′, limiting the resolution of our frequency-interpolated map as it has the coarsest resolution of the data used. Lastly, the data used from the Stockert 25 m survey at 1420 MHz (Reich 1982) has a native resolution of 35′.
The procedure we employed first involves creating an image cutout of 12° × 12° centered on DR 21 from each survey. Then we smoothed the cutouts to the common resolution of 72′ and re-gridded the images using CASA (McMullin et al. 2007; Emonts et al. 2019) to a common pixel grid and pixel size of 4.7′. Next we converted the intensity scales from temperature brightness units to Jy beam−1, as the imager we used, wsclean (Offringa et al. 2014; Offringa & Smirnov 2017), currently only accepts Jy units. Pixel by pixel, we fit a power law2 to the “high-frequency” data points at 408, 820, and 1420 MHz, as previous studies have found this region largely consists of thermal, free-free emission down to 408 MHz (Landecker 1984; Xu et al. 2013). Then, to the 52 MHz data point, we fit for either a free-free turnover or a synchrotron component. We did this by extrapolating the high-frequency fit to 52 MHz. If the flux density at 52 MHz was less than the extrapolated value of the fit at that frequency, we fit for a free-free turnover,
![$ S\left( v \right) = {{{S_{0,{\rm{ff}}}}} \over {{\tau _0}}}{\left( {{v \over {{v_0}}}} \right)^2}\left( {1 - \exp \left[ { - {\tau _0}{{\left( {{v \over {{v_0}}}} \right)}^{\alpha - 2}}} \right]} \right), $](/articles/aa/full_html/2022/08/aa42596-21/aa42596-21-eq3.png) (1)
(1)
where α is the spectral index fit to high-frequency data, and v0 = 148 MHz such that S0,ff is the free-free component of the flux density at v0 in the optically thin (unabsorbed) regime and τ0, the only free parameter in this fit, is the optical depth at v0. Otherwise, if the flux density at 52 MHz was greater than the extrapolated value of the power-law fit, we added in a synchrotron component with spectral index −0.7 and fit,
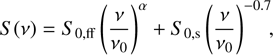 (2)
(2)
where S0,s is the synchrotron component of the flux density at v0 and the only free parameter in this fit. Synchrotron emission is present from SN remnants and/or from a diffuse Galactic component. Examples of pixel locations fit with a free-free turnover and with a synchrotron component are shown in Fig. 1. Although frequency-interpolation is performed at each pixel independently, point-to-point scatter is not introduced during this process. This is due to the coherence in intensity of neighboring pixels, which have been smoothed over by a Gaussian beam that is 235 square pixels in area.
The short-spacing map frequency-interpolated to 148 MHz is shown in Fig. 2 (center) for the region of sky falling within the 25% power of the LOFAR primary beam of the observation. We compare the frequency-interpolated short-spacing map at 148 MHz to an all-sky map at 150 MHz with 5° resolution (Landecker & Wielebinski 1970). The survey data in this region of the sky were originally observed at 178 MHz with 5° × 1.25° resolution (Turtle & Baldwin 1962) and then scaled to 150 MHz with a spectral index3 of β = −2.6. Since, the survey data have been re-calibrated to attain an 8 K zero-level calibration and a scaling error of 1% (Patra et al. 2015). We take a cutout from the survey data that covers our region of interest and convert the intensity units from temperature brightness to Jy beam−1. We convolve our short-spacing map to 5° resolution and re-grid it to match the 0.23° pixel scale. Taking the intensity ratio of the 150 MHz survey image over the convolved short-spacing map at 148 MHz results in intensity ratios that have a median value of 1.25. This is within sensible agreement as a 25% error falls within the uncertainty of our survey data.
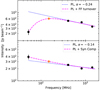 |
Fig. 1 Examples of the multifrequency fits (done on a pixel-by-pixel basis) to frequency-interpolate the “short-spacing” map – a low-resolution image with sensitivity to large angular scales – at 148 MHz. The black data points represent the survey data used in the fit. The orange data point represents the interpolated value at 148 MHz. The dotted blue line represents the power-law fit to the high-frequency data points at 408, 820, and 1420 MHz. The dashed magenta line represents the final SED fit – where either a free-free turnover (top) is fit (Eq. (1)) or a synchrotron component (bottom) is added (Eq. (2)) to match the low-frequency point at 52 MHz. |
2.1.3 Imaging
The final step in processing the LOFAR observations is imaging the data. We use the frequency-interpolated short-spacing map (Sect. 2.1.2) as a starting model during imaging in order to deconvolve the interferometric data with zero-level and total flux density information.
To prepare a template for the short-spacing map for wsclean (Offringa et al. 2014), we first ran wsclean with the image weight settings (see below) and one iteration so that the pixel grid and synthesized beam size were set. Next we converted the short-spacing map into intensity units of Jy pixel−1 according to the synthesized beam size of the wsclean image. This was done with the following routine. We re-gridded the short-spacing map to match the wsclean output pixel grid and size of 18″. Then we scaled its intensity by the ratio of the beam areas, (Awsclean/Ass), to convert units to Jy beam−1 with respect to the wsclean output synthesized beam. Next we converted the intensity to units of Jy pixel−1 by dividing by the beam area in units of pixels. At this point the short-spacing model is prepared for wsclean in true-sky flux density units, wsclean requires that we input two model images: one that is attenuated by the primary beam and one that is not. Therefore, we created a copy of our short-spacing model image, but we also applied the primary beam response. We set the primary beam model to zero outside of the first null as we do not image beyond that. With these steps4, the short-spacing map is prepared to be input to wsclean.
We ran wsclean using the -predict option to predict the short-spacing model image into the MODEL column of the MS. We then ran wsclean a second time, now with the -continue option to deconvolve the interferometric data. We imaged out to the first null of the primary beam over an area of 10° × 10°. We used Briggs image weighting with a robust parameter of −0.5 and a circular Gaussian taper of 1.5′, effectively smoothing out the long baselines. We CLEANed with multi-scale cleaning (Offringa & Smirnov 2017) on pixel scales of [0,18,36,72,144] and to a threshold of 4σ, where σ is scale dependent and internally calculated. We verified that color corrections do not need to be applied to LOFAR sub-bands, as is standard with LOFAR HBA continuum observations, making using of wsclean for imaging in order to obtain accurate monochromatic flux densities.
In Fig. 2 (right) we show the output short-spacing corrected image. In this paper, we analyze a 4° × 4° region covered by the LOFAR observations, which approximately encompasses the full-width half power of the primary beam. We smoothed the image to a circular beam of FWHM of 2′. The final image has a noise of 5 mJy beam−1 and effective frequency of 148.05 MHz.
For comparison, we also image the LOFAR data without the short-spacing map but using the same imaging parameters and show the results in Fig. 2 (left). Additionally, we checked our imaging results by convolving the final image to the 72′ resolution of the initial short-spacing map and verified that the total integrated fluxes are consistent. Lastly, we compare our imaging results by “feathering” (Stanimirovic 2002; Cotton 2017) the short-spacing map with the LOFAR data imaged without short spacings. Through feathering, images are combined in the domain of their Fourier transforms by a weighted average in order to extract the most appropriate spatial frequencies from each image. Taking the intensity ratio of the CASAfeather imaged divided by the wsclean created image, we find a mean and median value of 0.98 computed over the 4° × 4° region.
 |
Fig. 2 Imaging LOFAR 148 MHz observations of the Cygnus X region. The field of view displayed corresponds to 25% power of the primary beam. Left: deconvolved LOFAR image without short-spacing information. While these data are sensitive to emission on angular scales as large as 96′, negative (un-physical) emission induced by large-scale emission in the Galactic plane is present. Center: frequency-interpolated short-spacing map at 148 MHz (see Sect. 2.1.2) and 72′ resolution. Right: LOFAR data imaged with the short-spacing map as an initial model (see Sect. 2.1.3). |
2.2 Ancillary Data
We compared the LOFAR data with observations compiled through the Canadian Galactic Plane Survey (CGPS; Taylor et al. 2003) at 1420 MHz. These data were observed with the Synthesis Telescope at the Dominion Radio Astrophysical Observatory with short-spacing corrections using the Effelsberg Galactic Plane Survey (Reich et al. 1990) and the Stockert 25 m survey (Reich 1982). Since the effective resolution varies across the mosaic data products - the synthesized beam is declination dependent – we processed the mosaics to attain a common resolution of 2′. Then we stitch the smoothed mosaics together. The standard deviation in a relatively low emission region of the image is σ = 0.03 K (0.7 mJy beam−1).
 |
Fig. 3 Cygnus X star-forming region shown in CGPS 1.4 GHz continuum intensity (Taylor et al. 2003). The dashed white lines encompass the region of interest (4° × 4°, or ~100 pc × 100 pc) that we analyze with LOFAR 148 MHz observations. |
3 Continuum Emission
The Cygnus X star-forming complex encompasses an area of more than 30 square degrees as shown in Fig. 3. The region of interest analyzed with our LOFAR pointing, 4° × 4° (100 pc × 100 pc) is depicted with white dashed lines.
Figure 4 shows the continuum emission observed at 148 MHz with LOFAR and which is corrected for missing short-baseline information (Sect. 2.1). The 148 MHz emission in this region primarily traces thermal free-free emission from ionized gas with low density and small emission measure (EM; see Sect. 4 and, e.g., Wendker et al. 1991; Xu et al. 2013). Thermal radiation referred to as “free-free” emission is bremsstrahlung radiation emitted as the paths of free electrons are deflected in the presence of free ions.
The morphology of the 148 MHz emission includes extended (on degrees scales), resolved regions of photoionized gas in the vicinity of massive stars and star clusters. Filamentary structure is a prominent feature in bright emission regions and is also present, perhaps more fractal-like in faint emission regions. Shell-like regions also appear. An additional diffuse component surrounds much of the extended structures. Extragalactic radio galaxies with bright synchrotron emission at these frequencies appear as point-like sources at 2′ resolution. Analyzing the spectral energy distribution (SED; see Sect. 4) of unresolved objects is necessary to pull-out synchrotron dominated sources from the regions of active star formation embedded within a dense medium.
The locations of massive stars and star clusters in this region are shown in the top left panel of Fig. 5. We label the radio continuum features that were identified in Downes & Rinehart (1966) via 5 GHz observations at 10.8′ resolution − DR 7, 10, 11, 16, 18, 19, 20, 21, 22, and 23. Only DR 7 is not associated with the Cygnus X region; instead it is located more than 3.3 kpc distant in the Perseus Arm (Piepenbrink & Wendker 1988). The Cygnus X region has been extensively surveyed for massive stars and clusters (Le Duigou & Knodlseder 2002; Comerón & Pasquali 2012; Wright et al. 2015; Berlanas et al. 2018; Comerón et al. 2020). The stars that are members of the Cyg OB2 association are no longer individually embedded within dense ionized gas, while the stars in a number of the DR sources are in the process of dispersing their dense gas.
The 1.4 GHz continuum emission from the CGPS, also shown in Fig. 5, is strikingly similar to the LOFAR 148 MHz continuum emission. The morphologies and relative intensities of the extended, resolved emission (including filamentary structure) are comparable. The low-level, diffuse emission surrounding extended structures is relatively bright at lower frequencies. Similarities attest to the primarily thermal nature of the emission (Xu et al. 2013; Wendker et al. 1991). Differences in relative intensities arise in compact sources and are attributed to two effects. One, compact regions that appear relatively faint at 148 MHz have high EMs (EM > 106 pc cm−6) and large optical depths (τff > 10). Two, at 1.4 GHz the synchrotron emission from extragalactic sources is faint compared with the thermal component from Galactic regions.
Mid-infrared (MIR) emission at 3.6, 8.0, and 24 µm is compiled as a red-green-blue image in Fig. 5. Emission at 3.6 µm in blue and observed with the Spitzer Space Telescope5 shows the stellar population of young massive stars as point-like sources of emission (Beerer et al. 2010). 8 µm emission in green observed with the Midcourse Space Experiment (MSX; Price et al. 2001) and described by Schneider et al. (2006) especially with respect to CO, mainly traces UV heated polycyclic aromatic hydrocarbons (PAHs) in photodissociation regions (PDRs), thereby emphasizing interfaces between molecular clouds and intense UV fields from young massive stars. Spitzer 24 µm emission in red is predominantly produced by thermal emission from warm dust co-spatial with photoionized gas (Churchwell et al. 2006; Calzetti et al. 2007; Salgado et al. 2012). Emission that is bright primarily at 24 µm (red) corresponds well with the ionized gas traced by thermal, low-frequency radio emission. These two tracers correspond well in H II regions (partially) surrounded by PDR envelopes as well as for ionized regions without PDRs at their edges.
Molecular cloud emission as traced by 13CO(1−0) (Schneider et al. 2007) shows the cold gaseous reservoir in Fig. 5. 13CO is largely optically thin (e.g., unlike 12CO) in the region and traces gas with relatively low densities of ≳3000 cm−3. The full Cygnus X complex (see Fig. 3) contains 4.7 × 106 M⊙ of molecular gas (Schneider et al. 2006). High-contrast elongated filaments are observed as well as diffuse emission from higher-density clouds. Embedded regions such as DR21, DR15, and DR20 are sites of active star formation coincident with radio emission, whereas DR17, DR18, DR22, and DR23 are located at the edges of or separated from 13CO(1−0) emission. Several arc or shell-like structures are also visible in 13CO(1−0).
 |
Fig. 4 LOFAR 148 MHz continuum emission of the 4° × 4° (~100 pc × 100 pc) area in the Cygnus X region that we analyze at 2′ (0.9 pc) resolution. The emission in this region is primarily thermal, free-free emission from low-density photoionized gas. A number of extragalactic radio sources are present as bright point sources. The noise away from bright emission is σ = 5 mJy beairr−1. |
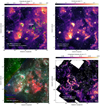 |
Fig. 5 Multi-wavelength emission in Cygnus X. Top left: location of massive stars and star clusters shown overlaid on LOFAR 148 MHz continuum emission. Small green stars represent massive OB stars of the Cyg OB2 association and within the field (Berlanas et al. 2018), and small blue stars mark the locations of supergiants (Comerón et al. 2020). The gray circle represents the core of Cyg OB2 as identified by Wright et al. (2015). Large green stars mark the location of (open) clusters in the region (Le Duigou & Knodlseder 2002). Numbers in black text denote the position of radio continuum sources as identified by Downes & Rinehart (1966), and filamentary structures identified by Wendker et al. (1991) are designated with their CXR number. Top right: 1.4 GHz continuum emission observed through the CGPS (Taylor et al. 2003) and smoothed to a common resolution of 2′. Contours from the LOFAR 148 MHz continuum are overlaid at [10−0,6,10−0,55,10−0.5…10°] Jy beairr−1. The morphology in the majority of extended features is consistent with thermal continuum from low-density ionized gas and where relative differences in the intensity of the emission indicate free-free optical depth effects. Bottom left: MIR emission. In blue we show Spitzer 3.6 µm emission tracing the stellar population, in green the MSX 8 µm emission primarily from PAHs heated by UV radiation from massive stars tracing the PDR surfaces, and in red Spitzer 24 µm emission of warm dust, corresponding well with the diffuse ionized gas observed at 148 MHz. Bottom right: 13CO (1−0) integrated intensity observed with FCRAO (Schneider et al. 2007) tracing the bulk of the molecular gas with densities ≳3000 cm−3. |
4 Ionized Gas Intensity Ratios
The flux density observed from optically thin, free-free emission is a function of frequency (e.g., Condon 1992; Emig et al. 2020),
 (3)
(3)
and is dependent on the electron temperature, Te, and the emission measure, EM+, of the ionized medium. The EM,
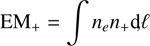 (4)
(4)
is defined by the electron density, ne, the ion density, n+, and the path-length integral of the emitting regions.
The optical depth of free-free emission is given by (Condon 1992; Emig et al. 2020)
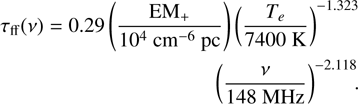 (5)
(5)
Self-absorbed, optically thick free-free emission follows a frequency dependence of S (v) = S0ν2(1 – exp(−τff(v))), as in Eq. (1). A power-law radio spectrum that is absorbed by a free-free component (along the line of sight) is given by S(v) = S0vα exp(−τff(v)).
The radio emission arising from the majority of extended, resolved features in the Cygnus X region is consistent with optically thin thermal, free-free emission at frequencies as low as 408 MHz (Wendker et al. 1991; Xu et al. 2013).
In Fig. 6 we show the intensity ratio of S(1.42 GHz) : S (148 MHz) where the intensities have units of Jy beam−1. In order to take this ratio, we re-gridded the CGPS 1.4 GHz image to the same pixel grid as the LOFAR image. An uncertainty of 25% in the intensity ratios encompasses systematic uncertainties present in the short-spacing map (see Sect. 2.1.2). A synchrotron spectrum following a power law with spectral index α = −0.7 has an intensity ratio of 0.21 between these two frequencies. Pointlike sources with the lowest intensity ratios are overwhelmingly background synchrotron-dominated galaxies. An optically thin free-free spectrum with α = −0.118 has a ratio of 0.77, and higher ratio values indicate free-free emission that is either self-absorbed or externally absorbed by another free-free component. These results show that the region is dominated by free-free emission at 148 MHz, in the smaller-scale structures as well as in much of the larger-scale diffuse emission. In a large portion of the image, 82% of pixels, the intensity ratio is >0.77 and appears to be dominated by free-free emission showing optical depth effects. The largest ratios are found in the compact sources of DR7, DR15, DR21, and DR22, for which optical depth effects are already important (e.g., τ > 0.1) at 1.4 GHz (Wendker et al. 1991).
We also conclude from Fig. 6 that two or more free-free components contribute to the observed continuum emission. This includes emission from the named regions and resolved structure, as well as large-scale emission. Specifically the emission outside of the resolved structure does not appear to be largely uniform in its intensity and physical properties.
To estimate its properties and check our flux scale, we determine the internal and external (line-of-sight) components estimated from the optically thin 1.42 GHz emission toward three sources. Using circular apertures with a 1′ radius, we extract flux from regions within DR23, CXR12, and DR17. The total flux densities at 1.42 GHz are measured to be St(1.42 GHz) = 3.3, 2.4, and 3.5 Jy, respectively. We determined external emission to be Se(1.42 GHz) = 0.7, 0.6, and 0.9 Jy in an uncontaminated region about 8′ away on average from each source. Subtracting the external emission, leaves internal emission to the sources of Si(1.42 GHz) = ST – Se = 2.6, 1.8 and 2.6 Jy. At the same locations in the 148 MHz continuum, we measure flux densities of St(148 MHz) = 2.1, 1.7, and 2.2 Jy, respectively.
If we were to fit for the free-free optical depth at 148 MHz, by comparing ST at the two frequencies, using Eq. (1), and assuming the emission only comes from a single component, the optical depths would be τ(148 MHz) = 1.7, 1.4, and 1.8 for regions in DR23, CXR12, and DR17, respectively. By using these values and combining Eqs. (3) and (5), we solve for the electron temperature and find 4400, 4100, and 4500 K. This is in contrast with a median temperature of T = 7400 K derived from RRL observations at 4.8 GHz and 2.6′ resolution (Piepenbrink & Wendker 1988). In other words, when we only fit one free-free component, the flux appears to be too low at 148 MHz and predicts too large of an optical depth.
Next, we consider two free-free components. One external line-of-sight component, which may have optical depth effects present and thus follows Se(v) = S0,ev2(1 – exp(−τe(v))), as in Eq. (1). A second, internal (to Cygnus X’s resolved structure) component that may have optical depth effects present, but in addition, could also be absorbed by optically thick free-free material along the line of sight, and follows Si(v) = S0,iv2(1 –exp exp(−τi(v))) exp(−τe(v)). The observed spectrum would be the summation of these two components ST = Se + Si. In this scenario, when plugging in the values for Se(l.A2 GHz) and Si(148 MHz) as we defined above and letting T = 7400 K, free-free optical depths are calculated to be τi = 0.8, 0.5, and 0.8, and τe = 0.5, 0.5, 0.5 for the regions DR23, CXR12, and DR17, respectively. And, we recover the expected flux at 148 MHz to within ten percent, ST,predicted(148 MHz) = 2.3, 1.8, and 2.3 Jy, respectively. This shows that the emission can be modeled as two free-free components and verifies the flux in our observations.
Unfortunately, the two point SED at 2′ resolution does not allow us to fit for multiple continuum components and free-free optical depth effects and perform this analysis in a systematic way for the whole map. We also tested whether additional (sub) images created across the HBA band – at 120.9, 137.2, 149.4, and 170.7 MHz – could be used to fit multiple SED components. For bright sources in the field, we do confirm a trend consistent with free-free emission within the LOFAR band. However, in the majority of the map, this subdivision did not provide reliable constraints on the contribution of additional continuum components. Instead in the next section, we focus only on the resolved filament-like components. We used FilChaP to subtract out external emission and isolate intrinsic emission, which is largely optically thin at 1.4 GHz and can thus be described by Eq. (3). In the future, LOFAR low band antenna (LBA) observations at 30–80 MHz will better constrain SED modeling, especially in the presence of multiple SED components.
 |
Fig. 6 Intensity ratio of continuum emission 5(1.42 GHz)/ S(148 MHz). A synchrotron α = −0.7 spectrum has an intensity ratio of 0.21 between these two frequencies. An optically thin free-free spectrum with α = −0.118 has a ratio of 0.77, and higher ratios indicate free-free emission that is either self-absorbed or externally absorbed by free-free emission. |
5 Analyzing Filamentary Structure
Filamentary structure is a prominent feature of the low-density (ne ≲ 100 cm−3) ionized gas in the Cygnus X region, as we point out in Sect. 3 and which is also seen over a larger area of the Cygnus X region in Fig. 3. We are motivated to derive properties of this filament-like emission to investigate how ionized gas and ionizing radiation interact with and shape their environment. To briefly summarize the contents of this section, Fig. 7 shows filament spines identified with the DisPerSE algorithm (Sousbie 2011). Figure 8 demonstrates the processing and fitting of the radial distribution of a filament profile using FilChaP (Suri et al. 2019). We plot the distributions of the peak EM fit to the radial profiles, the best-fit widths, and the inferred electron densities in Fig. 9. The peak EMs of the filament profiles follow a power law in their number distribution down to the estimated completeness limit. The widths of the filament profiles show a characteristic peak at a median value of 4.3 pc (noting that our beam resolution is 0.9 pc). The median electron density within filament profiles is ne = 35 cm−3, with densities spanning ne = 10–400 cm−3. Figures 10 and 11 compile and compare the peak EM, width and density.
 |
Fig. 7 Filaments identified with DisPerSE (in green). Purple data points mark the locations along the filament of the average radial profiles that contributed to the analysis. The gray-scale image is the EM, computed from the 1.4 GHz continuum intensity assuming optically thin thermal emission, and is the image on which the filaments are identified. Red (blue) boxes encompass select filaments identified with (without) a known massive star that locally contributes to ionization. |
5.1 Identifying Filamentary Structure
Using the Discrete Persistent Structures Extractor (DisPerSE; Sousbie 2011), we identify filamentary structure in the Cygnus X Region as shown in Fig. 7. DisPerSE uses discrete Morse theory to derive information on the topology of a given data set. Filaments are identified as the set of arcs joining maxima and saddle points. Persistence theory is used to filter out and identify filaments with significance. We refer the reader to Sousbie (2011) for a detailed description of the procedures. DisPerSE has been widely used to extract filamentary structures both in observational and simulated data sets (e.g., André et al. 2014, and references therein).
We applied the DisPerSE algorithm to a map of the EM derived from the CGPS 1.4 GHz intensity using Eq. (3). We filtered the filament identification output of DisPerSE using the –breakdown option to merge overlapping filament segments and with -trimBelow to remove arcs below a robust persistence6 of 5300 pc cm−6. The rms in low intensity regions of the EM map, interpreted as the offset value or background contribution, is 5300 pc cm−6 and the standard deviation, interpreted as the noise, is σ ~ 53 pc cm−6. Our input parameters to DisPerSE result in local maximum and saddle point peak EM intensities of ≳95OO pc cm−6 being identified. Filaments are output as lists of image coordinates sampled with points at each half pixel shift in direction.
We select an effective threshold of 9500 pc cm−6 because it qualitatively performed well in recovering structures expected by eye. When lowering the threshold, filament segments were found in the brightest regions, which did not seem to correlate well with locally bright extended segments of emission. However, a consequence of the high threshold is that we do not include some of the faintest filament-like structures that are clearly discernible by eye.
 |
Fig. 8 EM radial profile of a filament segment, shown with a solid black line. The radial profile has been baseline- and background-subtracted. Negative distances from the spine point toward the northeast and positive distances toward the southwest with respect to the filament. The dot-dashed blue line shows the best-fit Gaussian used to compute the filament profile properties. For comparison, the dashed red line shows the best-fit Plummer profile with a power-law index of p = 4. |
5.2 Fitting Profiles of Filamentary Structure
We characterized properties of filamentary structure using the python-based Filament Characterization Package (FilChaP; Suri et al. 2019), which was designed to work together with DisPerSE. Here we give a brief explanation of the procedures implemented in FilChaP and refer the reader to Suri et al. (2019) for more detailed descriptions. FilChaP takes as input a list of filament coordinates. At each sample point along the filament, a radial profile perpendicular to the filament spine is extracted. The radial profile extends to ±130 pixels, which we chose so that a baseline estimate includes true background emission at any location in the image7. The radial profiles extracted at four consecutive sample points of the filament are averaged together. This mean radial profile is baseline subtracted, effectively removing any background emission and baseline gradient. To the mean radial profile, FilChaP fits three line profiles – a Gaussian and two Plummer-like functions – and computes the second moment8 width. Plummer-like functions have been used to describe the column density of a filament with a dense and flat inner portion and a power-law decline at larger radii (e.g., Arzoumanian et al. 2011). The filament properties that we report are consistent with the four different types of fits and determinations. For simplicity, we use the properties derived from Gaussian fits to represent our results. We demonstrate a radial profile processed and fit with FilChaP in Fig. 8.
Through the line fitting process, 2141 mean radial profiles are attempted to be constructed. We removed fits that failed or had indications of being poor fits with Gaussian widths of less than 2 pixels. This left 1874 filament profiles which we analyzed.
5.3 Properties of Ffilamentary Structure
5.3.1 Peak EM of Filamentary Structure
FilChaP determines the peak of the EM radial profile (which has been background and baseline subtracted) from the best fit of a Gaussian profile to 1874 mean radial profiles extracted within filaments. In Fig. 9 we plot a histogram of the peak EMs. We find peak EMs ranging from 500 pc cm−6 to 105 pc cm−6, with a median value of 5.2 × 103 pc cm−6.
Regarding the completeness of the distribution, we expect that EMs in the range 4 × 103 < EM < 4 × 105 pc cm−6 are complete. From Eq. (5), we have that at 1.4 GHz a free-free optical depth of τff·(l.4 GHz) = 0.1 (1) corresponds to EM = 4 × 105 (106) pc cm−6. Thus, we expect to measure an upper limit of EM ≲ 4 × 105 pc cm−6. Since the rms in low intensity regions is equal to 5.3 × 103 pc cm−6, we expect an upper bound to fully sampled EMs of < 3.5 × 105 pc cm−6. Furthermore, we applied a cut to select filaments with a peak EM > 9.5 × 103 pc cm−6. Subtracting the “background” EM, which will be greater than or equal to 5.3 × 103 pc cm−6, results in an estimated completeness of 4.2 × 103 pc cm−6. Therefore, filamentary structure with a fitted peak EM below 4.2 × 103 pc cm−6 are not fully sampled.
We fit a power law to the number distribution of the peak EM for bins that we consider to be complete. This results in a best-fit power-law index of β = −2.0 + 0.2.
5.3.2 Widths of Filamentary Structure
In Fig. 9 we plot the best-fit full width at half maximum (FWHM) of each mean radial profile, converted into physical units assuming the average distance of d = 1.5 kpc to the complex. A peak in the width distribution arises at 4.3 pc, which is well separated from the beam resolution of 0.9 pc (2′). While the DisPerSE algorithm does not prevent large-scale features from being identified, there are regions of diffuse emission that could possibly be identified as “filaments” at lower resolution. For the EM we probe, we place a conservative upper completeness limit to the widths of filamentary structure of 8.6 pc, twice the median value.
In Fig. 10 we show the widths of filamentary structure with respect to their spatial location on the EM map. Bright compact regions of emission tend to have smaller widths (in blue). Also notable is the DR 23 region, which has somewhat wider filamentary structure (in orange, red) than average. While projection effects and variations in distances to the emission features could reasonably influence the apparent widths of the filaments, it is curious that a characteristic value of 4.3 pc is seen throughout the region.
 |
Fig. 9 Histograms of the properties of filamentary structure inferred from Gaussian fits to their EM radial profiles. Dashed black lines mark the median values. Dotted blue lines mark the estimated completeness limits in the EM and width plots. Left: peak EM of the best fit in units of pc cm−6. The median EM of the filamentary structure identified in this analysis is 5200 pc cm−6. The solid green line shows the power law, β = −2.0 ± 0.2, fit to the distribution for EM > 5200 pc cm−6. Center left: filament profile FWHM in units of pc. The median FWHM of the filamentary structure identified in this analysis is 4.3 pc. The resolution of the beam FWHM (2′ ~ 0.9 pc) is marked (with a dotted red line) as the lower completeness limit. Widths smaller than the beam resolution result from poor fits. Center right: average electron density of the filament profiles in units of cm−3, computed with the best-fit peak EM and width as |
5.3.3 Electron Densities of Filamentary Structure
We estimate the electron density of the filamentary structure from the best-fit peak EM and FWHM width of the line profile, as 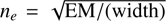 . This calculation assumes that the size of the gas cloud along the line of sight is equal to its projected dimension in the plane of the sky. Although this geometry is a good approximation for true filaments, a sheet-like morphology may be a more realistic approximation for the ionized surfaces of molecular clouds; we discuss this in more detail in Sect. 6.2.1. In this scenario, the path length along the line of sight may be longer, which would imply these densities are upper limits. Perusal of our map indicates that the density would be overestimated by at most a factor of three, and an approximate factor of two in uncertainty of the electron density is reasonable. Lastly, we acknowledge the gas may be clumpy or show substructure on scales smaller than the resolution of the observations; volume filling factors may be <1 for gas of various densities (e.g., Gao et al. 2015).
. This calculation assumes that the size of the gas cloud along the line of sight is equal to its projected dimension in the plane of the sky. Although this geometry is a good approximation for true filaments, a sheet-like morphology may be a more realistic approximation for the ionized surfaces of molecular clouds; we discuss this in more detail in Sect. 6.2.1. In this scenario, the path length along the line of sight may be longer, which would imply these densities are upper limits. Perusal of our map indicates that the density would be overestimated by at most a factor of three, and an approximate factor of two in uncertainty of the electron density is reasonable. Lastly, we acknowledge the gas may be clumpy or show substructure on scales smaller than the resolution of the observations; volume filling factors may be <1 for gas of various densities (e.g., Gao et al. 2015).
In Fig. 9 we plot the distribution in electron density of the mean radial profiles. Electron densities ranging from 10 cm−3 to 400 cm−3 are found, with a median value of 35 cm−3. In Fig. 10 we show the filamentary structure densities with respect to their spatial location on the EM map. We note that our census of electron densities may not be complete in the range of values we derive. For example, we find electron densities of ne = 20 cm−3 in some of the ionized ridges. At a size scale equal to our resolving beam, 0.9 pc, an EM of 360 pc cm−6 would result, and our analysis would not be sensitive to it.
5.3.4 Column Density of Ionized Gas
From the density and width we compute the column density of ionized gas. We assume the gas is completely ionized, with ne ~ nHII, and compute a column density of  . The ionized hydrogen column densities we derive range from about (1020–1021) cm−2 with a median value of 4.8 × 1020 cm−2. However, given how we derive the column density, we do not expect our census to be complete for this range of column densities.
. The ionized hydrogen column densities we derive range from about (1020–1021) cm−2 with a median value of 4.8 × 1020 cm−2. However, given how we derive the column density, we do not expect our census to be complete for this range of column densities.
5.3.5 Pressure of Ionized Gas
We calculate the electron pressure, as Pe/kB ~ Tene, from the ionized gas densities assuming Te = 7400 K. This is a typical temperature of fully ionized gas, and in fully ionized gas, the thermal pressure will equal approximately twice the electron pressure. We find electron pressures of 7.4 × 104 K cm−3 to 3.7 × 106 K cm−3 with a median value of Pe/kB ~ 2.8 × 105 K cm−3. We show these values along the upper axis of the electron density histogram in Fig. 9. In the majority of filamentary structures, comparing free-free emission with tracers at different frequencies, as shown in Fig. 5 for example, reveals that the gas is likely fully ionized. However, with such a rich diversity of activity, sweeping statements for the Cygnus X region do not tend to hold, and there may be a rare few of the fainter filamentary structures that are not fully ionized; there the electron temperature would be lower and the thermal pressure would not be equal to ≈ 2neTe.
Regions with 3 × 105 K cm−3 are over-pressured compared with typical values in the diffuse ISM, P/kB ~ 3.8 × 103 K cm−3 (Jenkins & Tripp 2001; Jenkins et al. 2011). Over-pressure compared to the general ISM is expected for a region where massive stars are interacting with their environment, as massive stars create regions of high pressure that will expand. Indeed the pressures we find do coincide with a small fraction (~0.05%) of nearly all gas surveyed by Jenkins et al. (2011) that has a large pressure (>3 × 105 K cm−3) and which is more prevalent at high velocities or for regions with enhanced starlight densities.
 |
Fig. 10 Spatial rendering of the derived properties of filamentary structure. Top: width of filaments’ mean radial profiles represented as colored data points and overplotted on the EM map. Compact bright regions tend to have smaller widths. Another notable region is DR 23, which has wider filamentary structure than average. Bottom: estimated density of each radial profile represented as colored data points and overplotted on the EM map. As expected, densities are highest in known star-forming regions. |
5.3.6 Correlation Between Properties of Filamentary Structure?
In Fig. 11 we plot the peak EM of the filament profiles as a function of the profile width, and we color the data points by the inferred electron density. Regions with the brightest EMs (likely associated with classic H II regions) tend to have smaller sizes and higher densities. Whereas, EMs of approximately EM ≲ 104 pc cm−6 (or electron densities ≲50 cm−3) are found with a wide range of widths. While the densities are approximate – likely accurate to within a factor of two – they do follow a general trend. The distribution in the plot is curious; a dearth of high intensity EM filamentary structure with large widths would physically be harder to maintain and may represent a true depopulated portion of this plot.
 |
Fig. 11 Peak EM of the best fit to the filament radial profile plotted with the best-fit FWHM. The shaded tan areas represent values that fall outside of our completeness limits. The colors of the data points represent the electron density inferred from the filament profile EM and width. |
6 Discussion
In this section we discuss the sources that maintain the ionization of the thermally emitting gas that we observe. We find Cyg OB2 may have a considerable influence, ionizing up to two-thirds of the emission in this region. We also discuss what is forming the filamentary structure – likely photoevaporating surfaces of neutral material, flowing into lower-density volume-filling ionized gas. While our calculations suggest that the stellar winds of Cyg OB2 may be dissipating turbulence in the form of transitory filaments, the filamentary structure densities correlate with incident radiation and thus suggest only a minority of filamentary structures are influenced by the stellar winds of Cyg OB2. Compression of the surrounding material may also help to form filaments (e.g., see Zavagno et al. 2020). We place our results in the context of ionized gas surveyed with [N II] FIR fine structure lines - finding remarkable agreement with properties - and we construct a framework in this region for ELD ionized gas and how it is maintained. Lastly, we inform on a bright future for LOFAR observations of diffuse emission in the Galactic plane.
6.1 Source of Ionization of the Filamentary Structure
6.1.1 Local Massive Stars
Signatures of the youngest, most dense regions of active star formation (e.g., DR21 and W75N) are not traced by free-free emission at the low frequency of 148 MHz because of large free-free opacities. Somewhat more evolved regions, which have begun dispersing their molecular material and bursting open, have lower gas densities and smaller EMs, as we see, leading to a more pronounced spatial separation between the star and warm gas that it ionizes. In these regions, local (d ≲ 10 pc for a single O3 star) sources supply ionizing photons. Examples of this include AFGL 2636, BD+43O 3654, DR16, DR20, DR22, and the complex environments of and between DR17 and DR23. The regions named have not just one but a small cluster of massive OB stars within them. These regions are generally found at larger distances (d ≳ 30 pc) from Cyg OB2, to the east in the image. Likewise (single) massive field stars, for example to the northeast and southeast regions of the image, shape local filamentary structure. In these regions, the ionized gas tends to be bounded on one side by cold, molecular gas; the low-density ionized gas does not often envelope cold gas and dust, only in select small pillar and globules.
 |
Fig. 12 The ionizing photon rate per unit area of Cyg OB2. Left: map of the ionizing photon (>13.6 eV) rate per unit area constructed from the observed OB stars of the Cyg OB2 association (for details, see Appendix B). Green contours are shown at log(Q0/area [photons s−1 cm−2]) = (9,9.25,9.5, …12.25). Right: ionizing photon rate per unit area as traced by thermal free-free emission. The green contours of the Cyg OB2 ionizing field are overlaid. |
6.1.2 Cyg OB2
To explore the role of Cyg OB2 in ionizing filamentary structure, we construct a map of the EUV (>13.6 eV) ionizing photon rate per unit area from Cyg OB2, as shown in Fig. 12, from catalogs of OB stars (Berlanas et al. 2018, and references therein). We describe how the map is created in detail in Appendix B, following the procedure of Tiwari et al. (2021). Two important features of the map are that it is a simple 2D projection and we do not attempt to account for any absorption or attenuation of ionizing photons. The total ionizing photon rate of the association from our model is 6 × 1050 EUV-photons s−1, which we note agrees with the expectation of a stellar population at zero age main sequence to 3 Myr old with stellar mass M⋆ ≈ 1.6 × 104 M⊙ (Starburst99; Leitherer et al. 1999).
In Fig. 12 we also show the ionizing photon flux estimated directly from the optically thin thermal radio continuum at 1.4 GHz, from the relation (e.g., Emig et al. 2020)
 (6)
(6)
The Cyg OB2 ionizing photon flux outshines a large portion of the inferred flux from the radio emission, and the radio structure generally avoids direct overlap with the locations of stars in Cyg OB2. We quantify how much of the low-density ionized gas can be maintained by the ionizing photons from Cyg OB2. We take the ratio of the two images that are shown in Fig. 12, which equates to the observed ionizing photon flux divided by Cyg OB2’s output ionizing photon flux. We compute that at 67% of the pixels in this region the ionizing photon flux from Cyg OB2 is sufficient to maintain the ionization.
We make a rough comparison of the influence of Cyg OB2’s ionizing radiation on filamentary structure. Starting from the mask of the filament spines, we extend the mask at each filament segment to a square region of 29 pixel sides centered on the segment. This results in about a third of the pixels in the image being attributed to a filament. Taking the ratio of the images and considering only the masked pixels, we again find that for 67% of the pixels the ionizing photon flux from Cyg OB2 is sufficient to provide the ionization.
We focus on some of the features and regions that appear to be influenced by Cyg OB2 in Fig. 13. These radio continuum features correlate well with 24 µm emission (see Fig. 5) and do not appear to be directly related to individual H II regions. In Table 1 we include estimated properties of identified filamentary structure. The widths, EMs, and densities have been computed with the filament analysis described in Sect. 5. The length has been estimated by eye using the furthest extent of a straight line along a filament, starting and ending where the emission reaches a local intensity of half maximum. In this manner, the length of the curved features such as CXR 9a,b are slightly underestimated. We also compute the ionizing photon flux and the ionizing photon rate. In these filamentary structures, the ionizing photon flux from Cyg OB2 at their projected distances is a factor of ten or more than required.
We also note that apart from coming from UV radiation, the presence of ionization in these structures (especially CXR 12; see Fig. 13) could come from electron collisions if shocks are present there. Bands containing shock tracers such as H and K in the near IR and 4.5 microns (Spitzer) show extended emission coincident with CXR 12. Future work exploring this as a possible physical mechanism would be worthwhile.
 |
Fig. 13 Zoomed-in view of filamentary structures whose properties we discuss in more detail (see Table 1 and Sects. 6.1 and 6.2). |
Properties of select filamentary structures that are likely influenced by Cyg OB2.
6.1.3 Internal B Stars?
The ionizing photon rates of the filamentary structure exemplified in Table 1 are ~2 × 1048 EUV-photons s−1, a rate that could be supplied by early type B stars local to the filamentary structure. Wendker et al. (1991) argued for the ridges being internally ionized by about three to ten stars of type B2 to B3. They give additional reasoning that filamentary structures ionized externally are typically smaller, strongly curved, and with shallower intensity gradients at the edges. However, searches for B stars in these (low extinction) regions have subsequently been made and can now rule out the presence of B stars with confidence (Comerón & Pasquali 2012; Comerón et al. 2020). Furthermore, in Sect. 5 we mention examples of externally illuminated ionized filamentary structure of similar length, width and curvature as those observed in the Cygnus X region, and in the next section (Sect. 6.2), we extensively discuss evidence for the (external) mechanisms responsible for the forming of filamentary structure.
6.2 Origin of the Filamentary Structure
6.2.1 Photoevaporation
When an ionized volume of gas is not in (pressure) equilibrium with neutral gas, an ionization front propagates into the neutral medium. With increasing distance from the ionizing source, an ionization front is preceded by a layer of swept up neutral gas and somewhat further away an H2 dissociation front (Elmegreen & Lada 1977). Since gas at the ionization front is over-pressured compared with the inner, low-density ionized gas, a flow occurs toward the ionizing source. The back-reaction created when the ionized gas pushes off the neutral material (the rocket effect) may eject even more mass and exert significant forces. Ionized gas with enhanced density (and intensity) is observed at this photoevaporating boundary. Photoevaporating surfaces are also referred to as ionized boundary layers and occur in champagne flows (Tenorio-Tagle 1979) and blister-like H II regions.
We sketched a rough portrait of the PDR-like transition from ionized gas, to atomic gas, and finally to molecular gas at a photoevaporating surface (see Hollenbach & Tielens 1999 and references therein). Here we derive the width of the neutral region of the interface in order to compare the distribution and morphology of the ionized gas (4.3 pc width) and the PAH emission. Assuming the gas in the filaments is fully ionized up to the ionization front, the median thermal pressure is P/kB = 2neTe ≈ 5.6 × 105 K cm−3. The temperature of neutral material is T ~ 100 K at an extinction of AV ~ 2 mag. Assuming the ionized gas at this ionization front is in pressure equilibrium with neutral material, the gas would have a density nPDR ~ 5600 cm−3. Adopting NPDR/Av = 2.1 × 1021 cm−2 mag−1 (Zhu et al. 2017), then NPDR/nPDR ≈ 0.2 pc. Thus, for these high pressures, we expect a relatively narrow region of approximately 0.2 pc (or 30″ for Cygnus X) of neutral gas bright in PAH emission between the ionized gas surface and the dissociation front. For less intense radiation or a less dense medium, the width of the neutral region extends further.
Photoevaporating boundaries are seen at the PDR interfaces traced by 8 µm emission in Fig. 5 in more compact regions of star formation that have local sources of intense radiation (e.g., filamentary structure associated with sources AFGL 2636, DR7, DR17, DR22, and DR23). Other possible examples are the filamentary structures that fall in the regions between DR16 and DR17 – where, in Fig. 5, emission is found surrounding massive stars but not overlapping with them.
For gas flowing away from the ionization front approximately at the sound speed, CH II ~ 10 km s−19, a filament-like structure of 4.3 pc would be visible for 0.4 Myr, but would continue eating away at the neutral clouds. An ionized mass of 940 M⊙, which is the mean value of the Table 1 entries, implies a mass loss rate of the neutral cloud of 2400 M⊙ Myr−1. Each photoevaporating surface with these approximate characteristics would evaporate 1.2 × 104 M⊙ of ionized gas over the lifetime, ~5 Myr, of Cyg OB2. This mass is comparable to the stellar mass of Cyg OB2 and about 10% of the mass of a typical molecular cloud of ~105 M⊙ (Tielens 2005).
The properties of the filamentary structure identified in Cygnus X are comparable with those of the California Nebula and the ionization front IC 434. The ionized filamentary structures of the California Nebula have EM = 2200 pc cm−6 and FWHM size of 1.1 pc, and they arise from a single, highvelocity O star passing by and illuminating a molecular cloud some 50 pc away (e.g., Bohnenstengel & Wendker 1976). The ionization front IC 434 arises from a photoevaporating flow at the surface of a molecular cloud, ionized by σ Ori with an EM of 2 × 104 pc cm−6 measured in Ha and about 0.2 pc wide (e.g., Ochsendorf et al. 2014). The densities computed for the California Nebula and IC 434 assuming  are ~44 and 47 cm−3, respectively.
are ~44 and 47 cm−3, respectively.
To determine if the filamentary structures show a relationship to ionizing radiation, we estimate the dimensionless ionization parameter, U, and plot it as a function of density in Fig. 14. The ionization parameter is equal to the ionizing photon flux, ϕ = Q0/(area) as in Eq. (6), divided by the density as well as the speed of light,
 (7)
(7)
The ionization parameter is a measure of the ionization rate over the recombination rate. The ionization parameter is indicative of the ratio between radiation and gas pressures. The electron density is expected to depend on U when its properties depend on the incident radiation field – also including when radiation pressure has influence. The ionization parameter has typical values of U ≳ (10−2–10−3) in H II regions while the WlM has U ~ 10−4 (e.g., Tielens 2005; Kewley et al. 2019). We compute U by plugging-in the EM of a given filament segment into Eq. (6) and dividing by the derived ne of the filament segment.
In Fig. 14 we also colored the data points, depending on whether a local massive star is known to the filament (and thus could be responsible for the ionization) shown in red, and regions without a clear ionization source in blue. Because there is a general trend of increasing U as the density increases in our data, irrespective of whether a local star is near the filamentary structure, this indicates that ionizing radiation influences the filament properties. This would argue against stellar winds compressing and regulating the ionized gas pressure and density (see Sect. 6.2.2).
We mention a caveat in these calculations. If the “filaments” are truly photoevaporating surfaces, then their emission is more likely to be distributed in sheets rather than filaments, and thus traversing a longer path length along the line of sight. The electron densities of the ionized gas measured in this way would be about two times smaller, if we assume that the path length along the line of sight is equal to the longest dimension of the filamentary structure (which seems to be at most a factor of four longer than the width).
Looking at this scenario from a different perspective, we also discuss whether filamentary structures that do not have or are significantly displaced from PAH or 13CO emission can plausibly be photoevaporating flows. The largest filamentary structures, which are far from individual star-forming regions and may be influenced by Cyg OB2, have significant offsets between the ionized ridge and neutral material (as traced by 13CO or 3.6,8 µm emission). Examples of this include CXR 12, CXR 11a,b, and the region just southeast of the Cyg OB2 core – all of which are shown in Fig. 13. Using CXR 11b as an example, the projected distance between the ionized ridge and the PAH emitting ridge is d ≈ 7′~ 3 pc. The large separation would imply that the neutral gas is rather diffuse; the estimated density is nPDR = NPDR/d ~ 450 cm−3, since Npdr ≈ 4.2 × 1021 cm−2. Pressure equilibrium, at T ≈ 100 K would thus be P/kB ~ 4.5 × 104 K cm−3. For a temperature of 7400 K, the ionized gas density is expected to be 6 cm−3. Even if we assume CXR 11b is a sheet rather than a filament and we let the path length along the line of sight equal the length along the plane of the sky, ℓ = 13.8 pc, the electron density is still a factor of three too large, 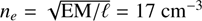 . We note that this is comparable to our error estimate for the density (Sect. 5.3.3). In conclusion, ionized filamentary structures that do not have neutral gas abutting the filament-like edge are likely not photoevaporating surfaces.
. We note that this is comparable to our error estimate for the density (Sect. 5.3.3). In conclusion, ionized filamentary structures that do not have neutral gas abutting the filament-like edge are likely not photoevaporating surfaces.
 |
Fig. 14 Dimensionless ionization parameter, U, estimated for each radial profile plotted against its electron density. The correlation between density and U indicates that the filament properties depend on the incident radiation field. No correlation as a function of density would indicate that other (feedback) processes influence the physical properties (density) of the filamentary structure. Red (blue) data points are those that fall within the red (blue) regions defined in Fig. 7 and correspond to the filament profiles in locations that have (do not have) a local massive star that likely contributes to ionization. Typical error bars are about 0.3 dex. |
6.2.2 Stellar Winds
Next, we turn our attention to the strong stellar winds of Cyg OB2. Multiple interactions of the winds from massive stars produce diffuse shock-heated X-ray gas10. A region of hot (T ≳106 K) plasma fills the volume surrounding the star(s) at small radii. Swept-up interstellar gas is compressed at larger radii (e.g., Weaver et al. 1977; Harper-Clark & Murray 2009; Lancaster et al. 2021a), forming a relatively dense shell of ionized gas and warm dust that is in pressure equilibrium with the hot gas and/or which may be fractal in structure (Lancaster et al. 2021b).
A Chandra X-ray survey centered on Cyg OB2 has revealed a R ≈ 4.1 pc cavity of hot (TX ≈ 5 × 106 K) and diffuse (nX ≈ 0.06 cm−3) gas (Albacete Colombo et al. 2018). In comparison, the core of Cyg OB2 (marked with a gray circle in Fig. 5) has a radius of r = 34′ ~ 15 pc. X-ray observations in the Cygnus X region are complicated by high levels of absorption (especially soft X-rays, which are dominated by wind-ISM interactions) in the Galactic plane; the total extent and intensity of the X-ray emission could reasonably be underestimated. Estimating the volume averaged thermal pressure from hot gas, we find PX/kB ≈ 2nXTX ~ 6 × 105 K cm−3, where nX and TX are the electron number density and temperature. This matches the median thermal pressure of the ionized filamentary structures, which is what would be expected for ionized gas in pressure equilibrium with hot shocked gas.
There are several radio filamentary structures abutting a cavity around the Cyg OB2 stars and where dense gas counterparts as traced through PAH or 2CO emission are not immediately obvious. The main region under consideration is shown in Fig. 13 (left); it stretches ~32 pc in projection, ending in the southwest with CXR 12. As seen most clearly in Fig. 5, the 24 µm emission (coincident with thermal radio emission) does not appear to be bordered by PAH emission at 8 µm. While 13CO avoids the regions of ionized gas (warm dust), 13CO is present in projection in some regions at larger radii. Another region to consider is CXR 9. While faint PAH emission and traces of 13CO emission are seen toward the south, in CXR 9b, dense gas does not seem to be related to CXR 9a. The regions in consideration are close to Cyg OB2 in projection, falling within about a 20 pc radius.
If the filamentary structures (which are not associated with neutral gas) are influenced by stellar winds, they may be shortlived turbulent features. A correlation between the luminosity of giant (r > 10 pc) H II regions (and their size) and the line-width has been established (e.g., Terlevich & Melnick 1981), though the origin of the supersonic turbulence may be gravity-driven or (wind)feedback-driven. We note the ionized gas line-widths in the (resolved) filamentary structures of Cygnus X are broader than the purely thermally broadened expectation. For example, the median ionized gas FWHM line-width of the zoom-in regions of Fig. 13, determined from H110a (4.8 GHz) observations, is Δυ = 27 km s−1 (Piepenbrink & Wendker 1988), whereas the Doppler-broadened thermal line-width11 is Δυth = 16 km s−1 (Brocklehurst & Seaton 1972). The rms turbulent velocity width is calculated as 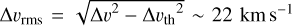 .
.
We determine the thermal energy in the hot gas as 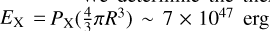 . Using Starburst99 (Leitherer et al. 1999), the energy output from stellar winds of an Μ⋆ = 2 × 104 M⊙ population of age 4 Myr is estimated at Ew ~ 3 × 1052 erg. Since the mechanical energy of the wind is more than four orders of magnitude larger than the hot gas energy and classic theory predicts it should be roughly half (Weaver et al. 1977), the hot gas may be venting into the medium and/or cooling at hot gas bubble interface may be extremely efficient (Harper-Clark & Murray 2009; Lancaster et al. 2021a). Judging also by the morphology of the gas, the hot gas does not appear to be entirely well contained.
. Using Starburst99 (Leitherer et al. 1999), the energy output from stellar winds of an Μ⋆ = 2 × 104 M⊙ population of age 4 Myr is estimated at Ew ~ 3 × 1052 erg. Since the mechanical energy of the wind is more than four orders of magnitude larger than the hot gas energy and classic theory predicts it should be roughly half (Weaver et al. 1977), the hot gas may be venting into the medium and/or cooling at hot gas bubble interface may be extremely efficient (Harper-Clark & Murray 2009; Lancaster et al. 2021a). Judging also by the morphology of the gas, the hot gas does not appear to be entirely well contained.
Averaging the mechanical energy of the wind over the 4 Myr lifetime of the association, the rate of energy injection by the winds is estimated at Ėw ~ 2 × 1038 erg s−1. We compare that with the calculated energy dissipation rate in the potentially turbulent-induced filament. The (kinetic) energy in the observed filamentary structure is 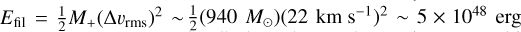 . Turbulent energy will be dissipated on a timescale comparable to the sound crossing timescale, t = width/Δυrms~ (3.6 pc/22 km s−1) ~ 0.2 Myr. We calculate the energy dissipation rate (potentially) provided by filaments by bringing the energy and timescales together, Ėfll ~ 8 × 1035 erg s−1. Hence, we conclude that only ~0.4% of the mechanical energy in the stellar winds of the Cyg OB2 association could be coupled to turbulent energy in the ionized gas.
. Turbulent energy will be dissipated on a timescale comparable to the sound crossing timescale, t = width/Δυrms~ (3.6 pc/22 km s−1) ~ 0.2 Myr. We calculate the energy dissipation rate (potentially) provided by filaments by bringing the energy and timescales together, Ėfll ~ 8 × 1035 erg s−1. Hence, we conclude that only ~0.4% of the mechanical energy in the stellar winds of the Cyg OB2 association could be coupled to turbulent energy in the ionized gas.
6.2.3 Envelopes of Cold Molecular Filaments
Filaments are ubiquitous in molecular clouds. Studies of the dust continuum from the Herschel Space Observatory suggest filaments have widths of 0.01–0.4 pc (e.g., Arzoumanian et al. 2011; Hacar et al. 2018). Furthermore, filamentary structure is also prevalent in the neutral ISM (Soler et al. 2020). However, we conclude that the ridges of low-density ionized gas could not be partially ionized envelopes surrounding cold-dust-and- molecular filaments. In the majority of the brightest ionized ridges, Fig. 5 shows no association with molecular emission. Even the fainter (likely lower-density) ridges of ionized emission do not overlap with molecular emission. There is a clear spatial offset, in which the ionized gas is typically found abutting one edge of the cold molecular material. Herschel column density maps have been created and their filaments analyzed in parts of the Cygnus region covered in this paper (Hennemann et al. 2012; Schneider et al. 2016b,a). Hennemann et al. (2012) examined the DR21 filaments, which are among the brightest filaments in the region, and they derived widths of ~0.3 pc, which may be partially affected by spatial resolution. We directly compare their FIR column density maps (see also Schneider et al. 2016b) with the ionized gas emission and the spines identified by DisPerSE, and that shows no spatial correlation.
6.2.4 On the Observed Width of the Ionized Emission
Although the filament-like structure is observed to have a characteristic width that is significantly larger than our spatial resolution, Panopoulou et al. (2022) and references therein showed how this may be an artifact due to extended and confusing emission and a fractal-like nature of the emission. Using FIR Herschel continuum images, Panopoulou et al. (2022) found filaments observed in the Herschel Gould Belt Survey to have a characteristic width of about four times the resolving beam; thus more distant sources appear to have larger widths, but this is apparently resolved to smaller scales in more nearby sources.
The median width we observe is about 5 times our beam size. Although we did not focus on the fainter emission in this analysis, it does show fractal-like structure – for example, the emission to the northeast of CXR12 – on scales smaller than the larger filament-like features we focused on. Our current analysis is limited in that we have not adequately probed smaller-scale emission, and more investigation is needed to understand if the ionized emission truly has a characteristic width. Given our findings in the previous subsections of Sect. 6, it will be interesting and necessary to extend this analysis to higher resolutions and deeper intensities.
6.3 Comparing Properties of Filamentary Structure with [NII] Findings
In Sect. 6.2 we noted that the filamentary-structure properties (EM, width, density) are consistent with those observed at photoevaporating surfaces of ionized boundary layers and stellar wind compressed ionized gas. Here we focus on a comparison of properties with ionized gas surveyed through [N II].
Ionized gas with electron densities distributed around 35 cm−3 appears to be consistent with ionized gas traced through the fine structure lines of [N II] at 122 and 205 µm with Herschel PACS (Goldsmith et al. 2015). Goldsmith et al. (2015) find a mean electron density of ne = 29 cm−3 over 96 lines of sight of 16″ each in the Galactic midplane. While [N II] fine structure lines provide a reliable probe of the density of gas in the range 10 < ne [cm−3] < 103, only densities as large as 100 cm−3 were detected in their lines of sight. Detections of [N II] that fall just outside, (ℓ, b) = (78.1132°, 0.0°), of the region we analyze resulted in an electron density of ne = (13.0 ± 1.7) cm−3 (Goldsmith et al. 2015). Furthermore, a lower limit of ne ≳ 30 cm−3 was derived from [N II] in the DR21 region (White et al. 2010). Additionally, Pineda et al. (2019) derive the electron densities of 21 discrete spectral components using [N II] 205 µm and RRLs. They find an average electron density of 41 cm−3 with values ranging from 8 to 170 cm−3. The electron densities we find are in remarkable agreement and indicate that what we observe in the Cygnus X region with low-frequency radio emission may point to the types of environments that are traced by these [N II] surveys.
This conclusion is also supported by the H II column densities that Goldsmith et al. (2015) derives. They find [N II] column densities of N(N+) = (1−20) × 1016 cm−3. Using their estimated nitrogen fractional abundance X(N+) = 2.9 × 10−4, their column densities would translate into ionized hydrogen column densities of N(H+) = (3–70) × 1019 cm−3. As shown in Fig. 9, the column densities of ionized gas found in the [N II] survey are consistent with the column densities of filamentary ionized gas in the Cygnus X region.
Langer et al. (2021) used a combination of [N II] 122 µm and 205 µm, RRLs, and 12CO to determine electron temperature and density of ionized gas and assess its proximity to star-forming regions. They concluded that this dense warm ionized gas is located in or near star-forming regions.
6.4 Connection to ELD Ionized Gas
Extended low-density ionized gas (Mezger 1978) has characteristic densities of ne = (5–10) cm−3 and path lengths of (50–200) pc. In the region we investigate, diffuse thermal emission of EM = 5300 pc cm−6 is seen across the O(100 pc) region. In addition to filling the Cygnus X region, emission may also arise along the line of sight, as we are looking down a spiral arm. Thus, considering path lengths of 0.1–1 kpc, the volume filling electron density is estimated at ne ≈ (2 – 7) cm−3. We take ne ≈ 5 cm−3 as a representative value, and note this is accurate to within a factor of two. The mass of ionized gas in the R ≈ 50 pc volume we analyze is then 6 × 104 M⊙ (or 2 × 105 M⊙ in a Strömgren volume). Ionized gas of density ne ~ 5 cm−3 and cloud size 100 pc are consistent with the properties of ELD ionized gas. Tying the volume-filling ionized gas in Cygnus X with ELD ionized gas is qualitatively consistent with previous results that connect ELD ionized gas to envelopes of H II regions (Shaver 1976; Anantharamaiah 1986; McKee & Williams 1997) and those that suggest ELD gas predominantly arises from (less than ~20 of) the most massive regions of star formation in our Galaxy - that have cleared much of their natal molecular cloud material but are still young enough to have considerable massive stars (Murray & Rahman 2010; Kado-Fong et al. 2020).
The thermal pressure felt by the volume filling warm ionized gas, for an electron temperature of Te ≈ 7400 K and a fully ionized medium, is P/kB = 2neTe ~ 7.4 × 104 K cm−3. While this pressure is a factor of ten lower than in the ionized filamentary structure (P/kB ~ 6 × 105 K cm−3) and the X-ray emitting plasma, it is still elevated compared with the diffuse ISM (P/kB ~ 4 × 103 K cm−3) (Jenkins et al. 2011). Over-pressurization is consistent even for the globally elevated ISM pressure expected in spiral arms and at small Galactic radii (Wolfire et al. 2003).
In the Cygnus X region, ELD ionized gas may be filled and replenished by photoevaporating regions (similar in properties to [N II] gas of Goldsmith et al. 2015; Pineda et al. 2019; Langer et al. 2021) eroding neutral clouds over the lifetime of the massive stars. As we calculated in Sect. 6.2.1, a characteristic filamentary structure in the region photoevaporates 1.2 × 104 M⊙of cloud mass over the lifetime of the massive stars. Five of the characteristic filamentary structures supply an equal mass of ionized gas in the region analyzed, and ten filamentary structures would replenish the full Strömgren volume.
6.5 Future LOFAR Observations
Our results have demonstrated new capabilities provided by LOFAR to characterize low-density ionized gas at low radio frequencies and high spatial resolution. Future investigations in conjunction with LOFAR’s LBA at 30–80 MHz will enable ionized gas (with typical ionized gas temperatures of 7000 K) to be characterized with free-free optical depths down to ~400 pc cm−6 (e.g., de Gasperin et al. 2021). With the LOFAR Two Meter Sky Survey (Shimwell et al. 2019, 2022), the Galactic Plane in the Northern Hemisphere will be covered to a spatial resolution of up to 6″. Our analysis builds on previous LOFAR analyses (e.g., Arias et al. 2019), which show the power of LOFAR to characterize continuum emission at low radio frequencies in the Galaxy.
7 Conclusions
Photoionized gas probes the influence of massive stars on their environment. The Cygnus X region (d ~ 1.5 kpc) is one of the most massive star-forming complexes in our Galaxy, and the Cyg OB2 association (age of 3–5 Myr and stellar mass of Μ⋆ ≈ 2 × 104 M⋆) has a dominant influence within this region. We observed the Cygnus X region at 148 MHz using LOFAR and corrected for missing short-spacing information during image deconvolution. Together with archival data from the CGPS, we investigated the morphology, distribution, and physical conditions of low-density ionized gas in a 4° × 4° (~ 100 pc × 100 pc) region at a resolution of 2′ (0.9 pc). As first discussed at radio frequencies by Wendker et al. (1991), the ionized gas in this region is characterized by filamentary structure. We used the DisPerSE and FilChaP packages to characterize the radial profiles of low-density ionized filaments. Our results are as follows:
We have demonstrated a procedure for correcting for a lack of short-spacing information in LOFAR observations. We compare our results with feathering and find them to be consistent within 6% (on average) across the region analyzed, thanks to LOFAR’s excellent sensitivity to large-scale emission. Future LOFAR HBA observations, especially together with the LOFAR LBA at 30–70 MHz, will characterize the low-density ISM to deep EMs and high spatial resolution.
Radio continuum emission in the region is largely consistent with free-free thermal emission down to our LOFAR observing frequency of 148 MHz. This agrees well with previously analyses down to 408 MHz (Wendker et al. 1991; Xu et al. 2013).
The low-density ionized gas traced by the radio continuum shows a strong correspondence with warm dust traced by 24 µm emission.
We characterize 1874 EM radial profiles from filaments. We find a power-law distribution in peak EM down to our completeness limit of 4200 pc cm−6. A characteristic width of 4.3 pc arises in the distribution, well separated from our spatial resolution of 0.9 pc. The median electron density within the filamentary structure is 35 cm−3 – quite similar to the ionized gas probed along the Galactic plane through [N II] (e.g., Goldsmith et al. 2015; Pineda et al. 2019). We derive thermal pressures within a median value of 6 × 105 K cm−3, which indicates that the filamentary structures are over-pressured compared with the neutral ISM.
We constructed an ionizing photon map of the Cyg OB2 association and compared it with the ionizing photon flux measured from the thermal radio continuum. We find that the ionizing photon flux from Cyg OB2 is sufficient to maintain ionization in 67% of the region and the filamentary structure.
We estimate that the (high-pressure) filamentary structures are likely photoevaporating surfaces flowing into volumefilling warm ionized gas that is relatively low in pressure (with density ne ~ 5 cm−3). We notice a trend between the ionization parameter, U, and electron density, which indicates that filamentary structures are primarily influenced by stellar radiation. We estimate that typical photoevaporating surfaces influenced by Cyg OB2 each convert ~2 × 104 Μ⊙of neutral material (or 10% of a typical ~105 M⊙ molecular cloud) into ionized gas over the lifetime of the association.
A minority of filamentary structures do not have or are significantly displaced from neutral gas (as traced by PAH and 13CO emission) and may not be photoevaporating surfaces. We estimated the influence of stellar winds from Cyg OB2 and find that ~0.4% of the mechanical energy in the winds may be coupled to turbulent energy in the ionized gas, in which case some of the ionized filamentary structures may be transitory features resulting from dissipated turbulence.
The volume-filling ionized gas in the Cygnus X region - M+ ~ 2 × 105 M⊙ with ne ~ 5 cm−3 and ~ 100 pc path length – is consistent with properties of ELD ionized gas (Mezger 1978) and previous findings that attribute ELD ionized gas to envelopes of H II regions and those that suggest the most massive star-forming regions likely dominate ELD emission. The ELD ionized gas that leaks from this largely inhomogeneous region can be replenished in mass by ~10 (typical) photoevaporating surfaces over the ~5 Myr lifetime of the OB stars.
While this study reports on interesting new properties, it also raises many intriguing questions. Future studies of ionized gas using RRLs (e.g., Anderson et al. 2021) would provide useful kinematic information. Identifying and analyzing filamentary and fractal-like structure on smaller scales and extending the structural analysis to larger scales could also differentiate between and constrain turbulent properties. Further investigation into shock tracers is warranted. Finally, high-resolution radio continuum observations in Cygnus X, for example with the Global View of Star Formation in the Milky Way survey (GLOSTAR) at 1″ (e.g., Ortiz-León et al. 2021), will reveal filamentary structure in unprecedented detail.
Acknowledgements
We thank Nicola Schneider for sharing data products, and Frits Sweijen and Alex Mechev for maintaining software on the grid infrastructure and in Leiden. K.L.E. thanks the Green Bank Observatory for hosting her as a (remote) guest during the completion of this work. The authors thank the anonymous referee for their time and efforts reviewing this manuscript. K.L.E., H.J.A.R. and A.G.G.M.T. acknowledge financial support from the Netherlands Organisation for Scientific Research (NWO) through TOP grant 614.001.351. G.J.W. gratefully acknowledges the support of an Emeritus Fellowship from the Leverhulme Trust. R.Jv.W. acknowledges support from the VIDI research program with project number 639.042.729, which is financed by NWO. A.G.G.M.T. acknowledges support through the Spinoza premier of the NWO. M.H. acknowledges funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement No 772663). This paper is based (in part) on results obtained with International LOFAR Telescope (ILT) equipment under project codes LC0_032. LOFAR (van Haarlem et al. 2013) is the Low Frequency Array designed and constructed by ASTRON. It has observing, data processing, and data storage facilities in several countries, that are owned by various parties (each with their own funding sources), and that are collectively operated by the ILT foundation under a joint scientific policy. The ILT resources have benefited from the following recent major funding sources: CNRS-INSU, Observatoire de Paris and Universite d’Orleans, France; BMBF, MIWF-NRW, MPG, Germany; Science Foundation Ireland (SFI), Department of Business, Enterprise and Innovation (DBEI), Ireland; NWO, the Netherlands; The Science and Technology Facilities Council, UK; Ministry of Science and Higher Education, Poland. The research presented in this paper has used data from the Canadian Galactic Plane Survey, a Canadian project with international partners, supported by the Natural Sciences and Engineering Research Council. Part of this work was carried out on the Dutch national e-infrastructure with the support of the SURF Cooperative through grant e-infra 160152.
Appendix A uυ Coverage
We show the uυ coverage of the LOFAR observation in Fig. A.1. At the 2′ resolution of our 148 MHz image, the observations encompass maximum baseline lengths of 4200 m (equivalent to the displayed range of the abscissa in the left hand plot). The figure shows LOFAR’s superb coverage to large-scale emission, up to 1.6°. We also show the zero-spacing information that is filled in by the 1.2° resolution short-spacing map.
 |
Fig. A.1 uv coverage. Left: Full LOFAR coverage used in this analysis. Colors depict baselines. Right: Zoomed-in view of the shortest baselines. The black circle encompasses the coverage provided with the 1.2° resolution short-spacing map. |
Appendix B Ionizing Photons from Cyg OB2
Using the procedure laid out in Tiwari et al. (2021), we estimate the ionizing photon rate per unit area from early-type Cyg OB2 cluster members by synthesizing a list of stars from catalogs by Wright et al. (2015) and Berlanas et al. (2018, 2020), who in part used the catalog of Comerón & Pasquali (2012). All stars from these catalogs have effective temperatures and luminosities assigned from spectroscopic analyses. We take the assigned parameters from Berlanas et al. (2018, 2020) if possible, then from Wright et al. (2015), and finally Comerón & Pasquali (2012) via Berlanas et al. (2018). With these effective temperatures and luminosities, we pick out models for each O or B star from the Potsdam Wolf-Rayet (PoWR) stellar atmosphere grids (Hamann & Gräfener 2004; Todt et al. 2015; Sander et al. 2015; Hainich et al. 2019). These models are gridded by effective temperature and gravity, so we first interpolate the gravity, log ɡ, from the grid’s associated temperature and luminosity values. From the synthetic spectra provided by the PoWR models, we integrate the total ionizing flux above 13.6 eV. We then use the stellar coordinates and the ionizing photon flux to estimate the ionizing photon rate per unit area at any location around the H II region using projected distances at 1.5 kpc and summing over the flux from all stars.
References
- Ackermann, M., Ajello, M., Allafort, A., et al. 2011, Science, 334, 1103 [NASA ADS] [CrossRef] [Google Scholar]
- Albacete Colombo, J.F., Drake, J.J., Flaccomio, E., et al. 2018, ApJSS accepted, [arXiv:1886.81231] [Google Scholar]
- Alves, M.I., Calabretta, M., Davies, R.D., et al. 2015, MNRAS, 450, 2025 [NASA ADS] [CrossRef] [Google Scholar]
- Anantharamaiah, K.R. 1985, J. Astrophys. Astron., 6, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Anantharamaiah, K.R. 1986, J. Astrophys. Astron., 7, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, L.D., Luisi, M., Liu, B., et al. 2021, ApJS, 254, 28 [NASA ADS] [CrossRef] [Google Scholar]
- André, P., Di Francesco, J., Ward-Thompson, D., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R.S. Klessen, C.P. Dullemond, & T. Henning (Tucson: University of Arizona Press), 27 [Google Scholar]
- Arias, M., Vink, J., Zhou, P., et al. 2019, AJ, 158, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Arzoumanian, D., André, P., Didelon, P., et al. 2011, A&A, 529, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bally, J. 2016, ARA&A, 54, 491 [Google Scholar]
- Beerer, I.M., Koenig, X.P., Hora, J.L., et al. 2010, AJ, 720, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, C.L., Fixsen, D.J., Hinshaw, G., et al. 1994, ApJ, 434, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Berkhuijsen, E.M. 1972, A&AS, 5, 263 [NASA ADS] [Google Scholar]
- Berkhuijsen, E.M., Mitra, D., & Müller, P. 2006, AN, 327, 82 [NASA ADS] [Google Scholar]
- Berlanas, S.R., Herrero, A., Comerón, F., et al. 2018, A&A, 612, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berlanas, S.R., Wright, N.J., Herrero, A., Drew, J.E., & Lennon, D.J. 2019, MNRAS, 484, 1838 [NASA ADS] [Google Scholar]
- Berlanas, S.R., Herrero, A., Comerón, F., et al. 2020, A&A, 642, A168 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bochkarev, N.G., & Sitnik, T.G. 1985, Ap&SS, 108, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Bohnenstengel, H.D., & Wendker, H.J. 1976, A&A, 52, 23 [NASA ADS] [Google Scholar]
- Brocklehurst, M., & Seaton, M.J. 1972, MNRAS, 157, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Kennicutt, R.C., Engelbracht, C.W., et al. 2007, ApJ, 666, 870 [NASA ADS] [CrossRef] [Google Scholar]
- Churchwell, E., Povich, M.S., Allen, D., et al. 2006, ApJ, 649, 759 [CrossRef] [Google Scholar]
- Comerón, F., & Pasquali, A. 2012, A&A, 543, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Comeron, F., & Torra, J. 1999, A&A, 349, 605 [NASA ADS] [Google Scholar]
- Comerón, F., & Torra, J. 2001, A&A, 375, 539 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Comerón, F., Djupvik, A.A., Schneider, N., & Pasquali, A. 2016, A&A, 586, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Comerón, F., Djupvik, A.A., Schneider, N., & Pasquali, A. 2020, A&A, 644, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Condon, J.J. 1992, ARA&A, 30, 575 [NASA ADS] [CrossRef] [Google Scholar]
- Cong, H.I.L. 1977, PhD thesis, Columbia University, USA [Google Scholar]
- Cotton, W.D. 2017, PASP, 129, 094501 [NASA ADS] [CrossRef] [Google Scholar]
- Deb, S., Kothes, R., & Rosolowsky, E. 2018, MNRAS, 481, 1862 [NASA ADS] [CrossRef] [Google Scholar]
- de Gasperin, F., Dijkema, T.J., Drabent, A., et al. 2019, A&A, 622, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Gasperin, F., Williams, W.L., Best, P., et al. 2021, A&A, 648, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Downes, D., & Rinehart, R. 1966, ApJ, 144, 937 [Google Scholar]
- Eastwood, M.W., Anderson, M.M., Monroe, R.M., et al. 2018, AJ, 156, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B.G., & Lada, C.J. 1977, ApJ, 214, 725 [NASA ADS] [CrossRef] [Google Scholar]
- Emig, K.L., Bolatto, A.D., Leroy, A.K., et al. 2020, ApJ, 903, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Emonts, B., Raba, R., Moellenbrock, G., et al. 2019, ASP Conf. Series, 527, 267 [NASA ADS] [Google Scholar]
- Gao, X.Y., Reich, W., Reich, P., Han, J.L., & Kothes, R. 2015, A&A, 578, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldsmith, P.F., Yildiz, U.A., Langer, W.D., & Pineda, J.L. 2015, ApJ, 814, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Hacar, A., Tafalla, M., Forbrich, J., et al. 2018, A&A, 610, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haffner, L.M., Dettmar, R.J., Beckman, J.E., et al. 2009, Rev. Mod. Phys., 81, 969 [CrossRef] [Google Scholar]
- Hainich, R., Ramachandran, V., Shenar, T., et al. 2019, A&A, 621, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hamann, W.-R., & Gräfener, G. 2004, A&A, 427, 697 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harper-Clark, E., & Murray, N. 2009, ApJ, 693, 1696 [Google Scholar]
- Haslam, C.G.T., Wilson, W.E., Graham, D.A., & Hunt, G.C. 1974, A&AS, 13, 359 [NASA ADS] [Google Scholar]
- Haslam, C.G.T., Salter, C.J., Stoffel, H., & Wilson, W.E. 1982, A&AS, 47, 1 [Google Scholar]
- Heiles, C., Reach, W.T., & Koo, B.-C. 1996, ApJ, 466, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Hennemann, M., Motte, F., Schneider, N., et al. 2012, A&A, 543, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hollenbach, D.J., & Tielens, A.G.G.M. 1999, Rev. Mod. Phys., 71, 173 [CrossRef] [Google Scholar]
- Hopkins, P.F., Keres, D., Onorbe, J., et al. 2014, MNRAS, 445, 581 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P.F., Wetzel, A., Keres, D., et al. 2018, MNRAS, 480, 800 [NASA ADS] [CrossRef] [Google Scholar]
- Intema, H.T., van der Tol, S., Cotton, W.D., et al. 2009, A&A, 501, 1185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jenkins, E.B., & Tripp, T.M. 2001, ApJS, 137, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, E.B., Tripp, T.M., Jenkins, E.B., & Tripp, T.M. 2011, ApJ, 734, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Kado-Fong, E., Kim, J.-G., Ostriker, E.C., & Kim, C.-G. 2020, ApJ, 897, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L.J., Nicholls, D.C., & Sutherland, R.S. 2019, ARA&A, 57, 511 [NASA ADS] [CrossRef] [Google Scholar]
- Kulkarni, S.R., & Heiles, C. 1988, in Galactic and Extragalactic Radio Astronomy, eds. G.A. Verschuur, & K.I. Kellermann (Berlin and New York: Springer-Verlag), 95 [CrossRef] [Google Scholar]
- Lancaster, L., Ostriker, E.C., Kim, J.-G., & Kim, C.-G. 2021a, ApJ, 914, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Lancaster, L., Ostriker, E.C., Kim, J.-G., & Kim, C.-G. 2021b, ApJ, 914, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Landecker, T.L. 1984, AJ, 89, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Landecker, T.L., & Wielebinski, R. 1970, Australian J. Phys. Astrophys. Suppl., 16, 1 [NASA ADS] [Google Scholar]
- Langer, W.D., Pineda, J.L., Goldsmith, P.F., et al. 2021, A&A, 651, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Duigou, J.-M., & Knodlseder, J. 2002, A&A, 392, 869 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leitherer, C., Schaerer, D., Goldader, J.D., et al. 1999, ApJS, 123, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Lockman, F.J. 1976, ApJ, 209, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Marston, A.P., Reach, W.T., Noriega-Crespo, A., et al. 2004, ApJS, 154, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Matzner, C.D. 2002, ApJ, 566, 302 [NASA ADS] [CrossRef] [Google Scholar]
- McKean, J.P., Godfrey, L.E.H., Vegetti, S., et al. 2016, MNRAS, 463, 3143 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C.F., & Ostriker, J.P. 1977, ApJ, 218, 148 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C.F., & Williams, J.P. 1997, ApJ, 476, 144 [CrossRef] [Google Scholar]
- McMullin, J.P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, ASP Conf. Ser., 376, 127 [NASA ADS] [Google Scholar]
- Mezger, P.O. 1978, A&A, 70, 565 [NASA ADS] [Google Scholar]
- Motte, F., Bontemps, S., Schilke, P., et al. 2007, A&A, 476, 1243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murray, N.W., & Rahman, M. 2010, ApJ, 709, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Ochsendorf, B.B., Cox, N.L.J., Krijt, S., et al. 2014, A&A, 563, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Odenwald, S.F., Campbell, M.F., Shivanandan, K., et al. 1990, AJ, 99, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Offringa, A.R., & Smirnov, O. 2017, MNRAS, 471, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Offringa, A.R., van de Gronde, J.J., & Roerdink, J.B.T.M. 2012, A&A, 539, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Offringa, A.R., McKinley, B., Hurley-Walker, N., et al. 2014, MNRAS, 444, 606 [NASA ADS] [CrossRef] [Google Scholar]
- Olivier, G.M., Lopez, L.A., Rosen, A.L., et al. 2021, ApJ, 908, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Ortiz-Leön, G.N., Menten, K.M., Brunthaler, A., et al. 2021, A&A, 651, A87 [CrossRef] [EDP Sciences] [Google Scholar]
- Pabst, C., Higgins, R., Goicoechea, J.R., et al. 2019, Natur, 565, 618 [NASA ADS] [CrossRef] [Google Scholar]
- Pabst, C.H.M., Goicoechea, J.R., Teyssier, D., et al. 2020, A&A, 639, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Panopoulou, G.V., Clark, S.E., Hacar, A., et al. 2022, A&A, 657, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Panwar, N., Sharma, S., Ojha, D.K., et al. 2020, ApJ, 905, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Patra, N., Subrahmanyan, R., Sethi, S., Shankar, N.U., & Raghunathan, A. 2015, ApJ, 801, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Piddington, J.H., & Minnett, H.C. 1952, Australian J. Sci. Res., 5, 17 [NASA ADS] [Google Scholar]
- Piepenbrink, A., & Wendker, H.J. 1988, A&A, 191, 313 [NASA ADS] [Google Scholar]
- Pineda, J.L., Horiuchi, S., Anderson, L.D., et al. 2019, ApJ, 866, 1 [NASA ADS] [Google Scholar]
- Price, S.D., Egan, M.P., Carey, S.J., Mizuno, D.R., & Kuchar, T.A. 2001, AJ, 121, 2819 [NASA ADS] [CrossRef] [Google Scholar]
- Reich, W. 1982, A&AS, 48, 219 [NASA ADS] [Google Scholar]
- Reich, W., Reich, P., & Fuerst, E. 1990, A&AS, 83, 539 [Google Scholar]
- Reipurth, B., & Schneider, N. 2008, ASP Monograph Pub., 4, 36 [Google Scholar]
- Remazeilles, M., Dickinson, C., Banday, A.J., et al. 2015, MNRAS, 451, 4311 [NASA ADS] [CrossRef] [Google Scholar]
- Reynolds, R.J. 1984, ApJ, 282, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Roshi, D.A., & Anantharamaiah, K.R. 2000, ApJ, 535, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Rygl, K.L.J., Brunthaler, A., Sanna, A., et al. 2012, A&A, 539, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salgado, F., Berne, O., Adams, J.D., et al. 2012, ApJ, 749, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Sander, A., Shenar, T., Hainich, R., et al. 2015, A&A, 577, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N., Bontemps, S., Simon, R., et al. 2006, A&A, 458, 855 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N., Simon, R., Bontemps, S., Comerön, F., & Motte, F. 2007, A&A, 474, 873 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N., Bontemps, S., Simon, R., et al. 2011, A&A, 529, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N., Bontemps, S., Motte, F., et al. 2016a, A&A, 591, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N., Bontemps, S., Motte, F., et al. 2016b, A&A, 587, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shaver, P.A. 1976, A&A, 49, 1 [NASA ADS] [Google Scholar]
- Shimwell, T.W., Tasse, C., Hardcastle, M.J., et al. 2019, A&A, 622, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shimwell, T.W., Hardcastle, M.J., Tasse, C., et al. 2022, A&A, 659, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soler, J.D., Beuther, H., Syed, J., et al. 2020, A&A, 642, A163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sousbie, T. 2011, MNRAS, 414, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Stanimirovic, S. 2002, ASP Conf. Ser., 278, 375 [NASA ADS] [Google Scholar]
- Suri, S.T., Sanchez-Monge, A., Schilke, P., et al. 2019, A&A, 623, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taylor, A.R., Gibson, S.J., Peracaula, M., et al. 2003, AJ, 125, 3145 [NASA ADS] [CrossRef] [Google Scholar]
- Tenorio-Tagle, G. 1979, A&A, 71, 59 [NASA ADS] [Google Scholar]
- Terlevich, R., & Melnick, J. 1981, MNRAS, 195, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Tielens, A.G.G.M. 2005, The Physics and Chemistry of the Interstellar Medium (Cambridge: Cambridge University Press) [CrossRef] [Google Scholar]
- Tiwari, M., Karim, R., Pound, M.W., et al. 2021, ApJ, 914, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Todt, H., Sander, A., Hainich, R., et al. 2015, A&A, 579, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Turtle, A.J., & Baldwin, J.E. 1962, MNRAS, 124, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Uyaniker, B., Fürst, E., Reich, W., Aschenbach, B., & Wielebinski, R. 2001, A&A, 371, 675 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Tol, S., Jeffs, B.D., & van der Veen, A.-J. 2007, IEEE, 55, 4497 [NASA ADS] [Google Scholar]
- van Diepen, G., & Dijkema, T.J. 2018, Astrophysics Source Code Library [record ascl:1884.883] [Google Scholar]
- van Haarlem, M.P., Wise, M.W., Gunst, A.W., et al. 2013, A&A, 556, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Weeren, R.J., Williams, W.L., Hardcastle, M.J., etal. 2016, ApJS, 223, 2 [CrossRef] [Google Scholar]
- Walch, S.K., Whitworth, A.P., Bisbas, T., Wünsch, R., & Hubber, D. 2012, MNRAS, 427, 625 [NASA ADS] [CrossRef] [Google Scholar]
- Weaver, R., Mccray, R., Castor, J., Shapiro, P., & Moore, R. 1977, ApJ, 218, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Wendker, H.J., Higgs, L.A., & Landecker, T.L. 1991, A&A, 241, 551 [NASA ADS] [Google Scholar]
- White, G.J., Abergel, A., Spencer, L., et al. 2010, A&A, 518, L114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wolfire, M.G., McKee, C.F., Hollenbach, D., & Tielens, A.G.G.M. 2003, ApJ, 587, 278 [CrossRef] [Google Scholar]
- Wright, N.J., Drake, J.J., Drew, J.E., & Vink, J.S. 2010, ApJ, 713, 871 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, N.J., Drake, J.J., Drew, J.E., et al. 2012, ApJ, 746, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, N.J., Parker, R.J., Goodwin, S.P., & Drake, J.J. 2014, MNRAS, 438, 639 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, N.J., Drew, J.E., & Mohr-Smith, M. 2015, MNRAS, 449, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, W.F., Gao, X.Y., Han, J.L., & Liu, F.S. 2013, A&A, 559, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yorke, H.W., Tenorio-Tagle, G., Bodenheimer, P., & Rozyczka, M. 1989, A&A, 216, 207 [NASA ADS] [Google Scholar]
- Zavagno, A., André, P., Schuller, F., et al. 2020, A&A, 638, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhu, H., Tian, W., Li, A., & Zhang, M. 2017, MNRAS, 471, 3494 [NASA ADS] [CrossRef] [Google Scholar]
We ran these steps using version 2.20_2 of the Default Pipeline Processing Platform (DPPP; van Diepen & Dijkema 2018). This version of DPPP outputs the data with minor updates to the metadata of the MS – as these data were recorded in Cycle 0 of LOFAR’s operation – that are necessary in order to use later versions of DPPP. In subsequent processing, we make use of the most recent DPPP versions.
We also verify the steps of our template preparation procedure with the CASA preparation procedure outlined by J. Kauffmann at https://sites.google.com/site/jenskauffmann/research-notes/adding-zero-spa
Spitzer data were acquired from the archive at https://irsa.ipac.caltech.edu/data/SPITZER/Cygnus-X/.
For the specific implementation, see http://www2.iap.fr/users/sousbie/web/html/index959e.html?post/definitions
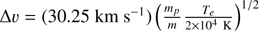 , where Δυ is the line FWHM, mp is the proton mass, and m is the nuclear mass (Brocklehurst & Seaton 1972).
, where Δυ is the line FWHM, mp is the proton mass, and m is the nuclear mass (Brocklehurst & Seaton 1972).
All Tables
Properties of select filamentary structures that are likely influenced by Cyg OB2.
All Figures
 |
Fig. 1 Examples of the multifrequency fits (done on a pixel-by-pixel basis) to frequency-interpolate the “short-spacing” map – a low-resolution image with sensitivity to large angular scales – at 148 MHz. The black data points represent the survey data used in the fit. The orange data point represents the interpolated value at 148 MHz. The dotted blue line represents the power-law fit to the high-frequency data points at 408, 820, and 1420 MHz. The dashed magenta line represents the final SED fit – where either a free-free turnover (top) is fit (Eq. (1)) or a synchrotron component (bottom) is added (Eq. (2)) to match the low-frequency point at 52 MHz. |
| In the text | |
 |
Fig. 2 Imaging LOFAR 148 MHz observations of the Cygnus X region. The field of view displayed corresponds to 25% power of the primary beam. Left: deconvolved LOFAR image without short-spacing information. While these data are sensitive to emission on angular scales as large as 96′, negative (un-physical) emission induced by large-scale emission in the Galactic plane is present. Center: frequency-interpolated short-spacing map at 148 MHz (see Sect. 2.1.2) and 72′ resolution. Right: LOFAR data imaged with the short-spacing map as an initial model (see Sect. 2.1.3). |
| In the text | |
 |
Fig. 3 Cygnus X star-forming region shown in CGPS 1.4 GHz continuum intensity (Taylor et al. 2003). The dashed white lines encompass the region of interest (4° × 4°, or ~100 pc × 100 pc) that we analyze with LOFAR 148 MHz observations. |
| In the text | |
 |
Fig. 4 LOFAR 148 MHz continuum emission of the 4° × 4° (~100 pc × 100 pc) area in the Cygnus X region that we analyze at 2′ (0.9 pc) resolution. The emission in this region is primarily thermal, free-free emission from low-density photoionized gas. A number of extragalactic radio sources are present as bright point sources. The noise away from bright emission is σ = 5 mJy beairr−1. |
| In the text | |
 |
Fig. 5 Multi-wavelength emission in Cygnus X. Top left: location of massive stars and star clusters shown overlaid on LOFAR 148 MHz continuum emission. Small green stars represent massive OB stars of the Cyg OB2 association and within the field (Berlanas et al. 2018), and small blue stars mark the locations of supergiants (Comerón et al. 2020). The gray circle represents the core of Cyg OB2 as identified by Wright et al. (2015). Large green stars mark the location of (open) clusters in the region (Le Duigou & Knodlseder 2002). Numbers in black text denote the position of radio continuum sources as identified by Downes & Rinehart (1966), and filamentary structures identified by Wendker et al. (1991) are designated with their CXR number. Top right: 1.4 GHz continuum emission observed through the CGPS (Taylor et al. 2003) and smoothed to a common resolution of 2′. Contours from the LOFAR 148 MHz continuum are overlaid at [10−0,6,10−0,55,10−0.5…10°] Jy beairr−1. The morphology in the majority of extended features is consistent with thermal continuum from low-density ionized gas and where relative differences in the intensity of the emission indicate free-free optical depth effects. Bottom left: MIR emission. In blue we show Spitzer 3.6 µm emission tracing the stellar population, in green the MSX 8 µm emission primarily from PAHs heated by UV radiation from massive stars tracing the PDR surfaces, and in red Spitzer 24 µm emission of warm dust, corresponding well with the diffuse ionized gas observed at 148 MHz. Bottom right: 13CO (1−0) integrated intensity observed with FCRAO (Schneider et al. 2007) tracing the bulk of the molecular gas with densities ≳3000 cm−3. |
| In the text | |
 |
Fig. 6 Intensity ratio of continuum emission 5(1.42 GHz)/ S(148 MHz). A synchrotron α = −0.7 spectrum has an intensity ratio of 0.21 between these two frequencies. An optically thin free-free spectrum with α = −0.118 has a ratio of 0.77, and higher ratios indicate free-free emission that is either self-absorbed or externally absorbed by free-free emission. |
| In the text | |
 |
Fig. 7 Filaments identified with DisPerSE (in green). Purple data points mark the locations along the filament of the average radial profiles that contributed to the analysis. The gray-scale image is the EM, computed from the 1.4 GHz continuum intensity assuming optically thin thermal emission, and is the image on which the filaments are identified. Red (blue) boxes encompass select filaments identified with (without) a known massive star that locally contributes to ionization. |
| In the text | |
 |
Fig. 8 EM radial profile of a filament segment, shown with a solid black line. The radial profile has been baseline- and background-subtracted. Negative distances from the spine point toward the northeast and positive distances toward the southwest with respect to the filament. The dot-dashed blue line shows the best-fit Gaussian used to compute the filament profile properties. For comparison, the dashed red line shows the best-fit Plummer profile with a power-law index of p = 4. |
| In the text | |
 |
Fig. 9 Histograms of the properties of filamentary structure inferred from Gaussian fits to their EM radial profiles. Dashed black lines mark the median values. Dotted blue lines mark the estimated completeness limits in the EM and width plots. Left: peak EM of the best fit in units of pc cm−6. The median EM of the filamentary structure identified in this analysis is 5200 pc cm−6. The solid green line shows the power law, β = −2.0 ± 0.2, fit to the distribution for EM > 5200 pc cm−6. Center left: filament profile FWHM in units of pc. The median FWHM of the filamentary structure identified in this analysis is 4.3 pc. The resolution of the beam FWHM (2′ ~ 0.9 pc) is marked (with a dotted red line) as the lower completeness limit. Widths smaller than the beam resolution result from poor fits. Center right: average electron density of the filament profiles in units of cm−3, computed with the best-fit peak EM and width as |
| In the text | |
 |
Fig. 10 Spatial rendering of the derived properties of filamentary structure. Top: width of filaments’ mean radial profiles represented as colored data points and overplotted on the EM map. Compact bright regions tend to have smaller widths. Another notable region is DR 23, which has wider filamentary structure than average. Bottom: estimated density of each radial profile represented as colored data points and overplotted on the EM map. As expected, densities are highest in known star-forming regions. |
| In the text | |
 |
Fig. 11 Peak EM of the best fit to the filament radial profile plotted with the best-fit FWHM. The shaded tan areas represent values that fall outside of our completeness limits. The colors of the data points represent the electron density inferred from the filament profile EM and width. |
| In the text | |
 |
Fig. 12 The ionizing photon rate per unit area of Cyg OB2. Left: map of the ionizing photon (>13.6 eV) rate per unit area constructed from the observed OB stars of the Cyg OB2 association (for details, see Appendix B). Green contours are shown at log(Q0/area [photons s−1 cm−2]) = (9,9.25,9.5, …12.25). Right: ionizing photon rate per unit area as traced by thermal free-free emission. The green contours of the Cyg OB2 ionizing field are overlaid. |
| In the text | |
 |
Fig. 13 Zoomed-in view of filamentary structures whose properties we discuss in more detail (see Table 1 and Sects. 6.1 and 6.2). |
| In the text | |
 |
Fig. 14 Dimensionless ionization parameter, U, estimated for each radial profile plotted against its electron density. The correlation between density and U indicates that the filament properties depend on the incident radiation field. No correlation as a function of density would indicate that other (feedback) processes influence the physical properties (density) of the filamentary structure. Red (blue) data points are those that fall within the red (blue) regions defined in Fig. 7 and correspond to the filament profiles in locations that have (do not have) a local massive star that likely contributes to ionization. Typical error bars are about 0.3 dex. |
| In the text | |
 |
Fig. A.1 uv coverage. Left: Full LOFAR coverage used in this analysis. Colors depict baselines. Right: Zoomed-in view of the shortest baselines. The black circle encompasses the coverage provided with the 1.2° resolution short-spacing map. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.