| Issue |
A&A
Volume 661, May 2022
|
|
|---|---|---|
| Article Number | A148 | |
| Number of page(s) | 11 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/202243086 | |
| Published online | 26 May 2022 | |
Short-term variability of DS Tucanae A observed with TESS
INAF - Osservatorio Astronomico di Palermo,
Piazza del Parlamento 1,
Palermo,
Italy
e-mail: salvatore.colombo@inaf.it
Received:
11
January
2022
Accepted:
24
February
2022
Context. Impulsive short-term variations occur in all kinds of solar-type stars and are the result of complex phenomena such as stellar magnetic field reconnection, low-level variability, or in some cases even star-planet interactions. The radiation arising from these events is often highly energetic and, in stars hosting planets, may interact with the planetary atmospheres. Studying the rate of these energetic phenomena is fundamental to understanding their role in modifying the chemical composition or, in some extreme cases, the disruption of the planetary atmospheres.
Aims. Here, we present a new procedure developed to identify the impulsive events in Transit Exoplanet Survey Satellite (TESS) light curves. Our goal is to produce a simple and effective tool with which to study the short-term activity of a star using only its light curve in order to derive the distribution and energy of short-term variations. As our first case, we studied the system DS Tuc.
Methods. Our technique consists of fitting the TESS light curves using iteratively Gaussian processes in order to remove all the longterm stellar activity contributions. We then identify the impulsive events and derive amplitudes, timescales, and the amount of energy emitted.
Results. We validate our procedure using the AU Mic TESS light curves, obtaining results consistent with those presented in the literature. We estimate the frequency distribution of energetic events for DS Tuc. In particular, we find that there are approximately two events per day with energy greater than 2 × 1032 erg. We find evidence for a favoured stellar phase for short-term activity on AU Mic, and also indications of short-term activity in phase with the planetary orbit. For DS Tuc, we find that the event distribution is not equally spaced in time but often grouped. The resulting distribution may be used to estimate the impact of short-term variability on planetary atmosphere chemical compositions.
Key words: stars: activity / planet-star interactions / stars: flare
© ESO 2022
1 Introduction
Solar-type stars show activity on several timescales, including those that are very short compared to planetary or stellar life timescales. The word ‘activity’ refers to several observed phenomena – including high-energy (extreme ultraviolet (EUV-X-ray) variable radiation – that may be responsible for changes in the chemistry and dynamics of planetary atmospheres.
The study of the effects of stellar activity on planets is of great importance for understanding the role of stars in defining the properties of planetary atmospheres and their chemical compositions. For example, flares generate a measurable increase in X-ray and UV fluxes. This radiation affects the planetary atmosphere in different ways: UV and EUV radiation is responsible for molecular dissociation and photo-ionisation in the upper layers, while X-rays induce secondary ionisation affecting deeper layers (Maloney et al. 1996; Cecchi-Pestellini et al. 2006; Locci et al. 2022). The interaction between radiation and planetary atmosphere results in a change in the chemical composition, an increase in temperature, and, in some extreme cases, atmospheric evaporation (Watson et al. 1981; Erkaev et al. 2007). These effects will change during the lifetime of a star because stellar activity evolves significantly, with the strongest effects occurring while the star is at a young age.
The frequency of energetic events, such as flares, has a direct effect on the chemical structure of the planetary atmosphere. Ionising radiation triggers changes in chemical composition with a timescale inversely proportional to the atmosphere density. If the time between two consecutive energetic events is smaller than the time needed from a specific species to go back to equilibrium, the emission produced by the subsequent event will trigger new chemistry in a highly non-linear path (Venot et al. 2016; Chen et al. 2021). In principle, to estimate the frequency of energetic events would require long and possibly contiguous observations at EUV-X-ray wavelengths. These are very difficult to obtain but we can take advantage of the fact that, in general, short-term events are observed in several bands and X-ray events are linked with short-term variability in the optical band. For example, in a recent XMM-Newton observation, DS Tuc A showed the occurrence of two twin X-ray flares also detected with the optical monitor (Pillitteri et al., in prep.). Therefore, as a rough assumption, we assume that short-term optical variability could be used as a tracer of short-term variability at higher energy (Flaccomio et al. 2018).
Moreover, finding periodicity in the short-term activity could reveal important information about the physical origin of these events. For example, they could be the result of a star-planet interaction (SPI): magnetospheric interactions between planetary and stellar magnetic fields can generate reconnection events and perturbations of the magnetic field topology. As a result, more flares could manifest in a system with a hot Jupiter than in one with a single star of the same age (Cohen et al. 2011). In other studies, Shkolnik et al. (2003, 2005, 2008) and Walker et al. (2008) reported evidence of chromospheric activity phased with the planetary orbital motion probed by Ca II H and K lines. Also, Pillitteri et al. (2015) claim to find evidence of flaring activity in X-rays in phase with the planetary period in the system HD 189733, although this finding was challenged by Route & Looney (2019). Furthermore, flaring activity could take place at specific active longitudes on the stellar surface; in that case, a periodicity based on stellar rotation is expected.
In this scenario, a high-precision time-series photometric mission allows us to study stellar activity with great detail. In particular, the Transiting Exoplanet Survey Satellite (TESS; Ricker et al. 2014) produces light curves with relatively short cadence (2 minutes) and duration of ≈25 days, which is sufficient to both observe the single events in detail and to estimate their rate. There are several techniques in the literature used to determine the short-term activity of stars. Most approaches are based on smoothing the light curve and detecting the spikes in the light curve above a chosen value (Davenport et al. 2014; Stelzer et al. 2016; Gilbert et al. 2022; Martioli et al. 2021). These techniques are usually easy to implement but often require user intervention. Another kind of approach uses deep learning methods (e.g. Vida et al. 2021), which, if well trained, are very powerful and do not require any user input. However, the training of neural networks is usually time-consuming.
In this work, we present a new automatic procedure to identify flares from any light curve and its application to the first case DS Tucanae A (DS Tuc A). Our approach includes the use of Gaussian processes to remove the stellar long-term contribution to the activity and then a procedure to identify and fit the shortterm energetic phenomena, determining their amplitude, decay time, and energy.
The paper is structured as follows: Sect. 2 describes the procedure used to remove the long- to medium-activity components in stellar light curves in order to identify and characterise the short-term phenomena. In Sect. 3, we present the results obtained from the analysis of DS Tuc A. In Sect. 4, we discuss the validation of our procedure and a comparison between DS Tuc A and AU Mic. Finally, in Sect. 5, we draw our conclusions.
2 Data analysis
In this section, we present our method to remove the long- to medium-activity components from stellar light curves in order to automatically identify the short-timescale energetic events. We analyse DS Tuc A, a relatively young (age around 40 Myr, Kraus et al. 2014; Bell et al. 2015; Crundall et al. 2019; Benatti et al. 2021) G6V star belonging to the physical binary system DS Tuc, with a light curve characterised by long-term photometric variations caused by a spot cycle (Benatti et al. 2021). DS Tuc A hosts an inflated Hot Jupiter (Benatti et al. 2021). The target is of particular interest because low-density atmospheres are very sensitive to high-energy-radiation-induced evaporation and photo-chemistry. We also analyse AU Microscopii (AU Mic), an M1 star with an age of 22 Myr (Mamajek & Bell 2014) that shows an edge-on debris disc and two Neptune-sized planets. AU Mic is known to be a magnetically active star with strong flaring activity (Robinson et al. 2001). Its activity is mainly dominated by star spots that produce a BY Draconis-type light curve with a quasi-periodic rotational modulation and a period of 4.863 ± 0.010 d (Plavchan et al. 2020). We use this system to validate our technique, comparing our findings with those of previous analyses already presented in the literature (e.g. Martioli et al. 2021; Gilbert et al. 2022).
We use all three two-minute-cadence TESS light curves available for the system DS Tuc A and the two analogous TESS light curves available for AU Mic1. We use the data corrected for time-correlated instrumentalsignatures (Jenkins et al. 2016)2. Moreover, TESS light-curve FITS files contain a flag that indicates the goodness of the data. For this analysis, we used only data flagged as non-polluted by any anomalies (i.e. FLAG= 0). Both DS Tuc A and AU Mic systems are known to host planets. Planetary transits are quite difficult to model correctly and an inaccurate model can result in false flares in the analysis. In order to avoid spurious effects due to transit, before proceeding with the analysis we remove the bins of the light curves corresponding to the transits of all the known planets for both systems from all the light curves used in this work (Benatti et al. 2021; Martioli et al. 2021). For the transit time duration, we consider the value defined in the literature. We removed the 10% additional transit duration (5% before and 5% after the transit) as a safety precaution to compensate for any uncertainties in transit or planetary period. To identify the flares, we performed a multistep procedure summarised in Fig. 1 and described in detail in the following.
2.1 Gaussian process regression
Data have been fitted with a Gaussian Processes (GP) model through the Python package celerite (Foreman-Mackey et al. 2017), combined to emcee (Foreman-Mackey et al. 2013) as sampler. The covariance is described in terms of a stochastically driven, damped harmonic oscillator called Simplified Harmonic Oscillator (SHO), of the following form
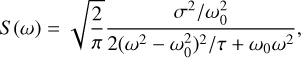 (1)
(1)
where S (ω) is the power spectrum density associated with the frequency ω, σ is the standard deviation of the process, τ is the timescale of the process, and ω0 is the non-damped frequency of the oscillator. An extra error term σJit is added to the data and included in the fitting procedure to account for unknown sources of error, and is added in quadrature to data errors.
Although it has been shown that this kernel function could give unreliable results for our specific sample, which is spot-dominated activity (Perger et al. 2021), with this fitting procedure, we aim to disentangle the long-timescale activity from the short-timescale signals, in which the flaring activity lives together with the noise, and we do not need to retrieve any physical information at this stage. Therefore, we do not need to run the chain to convergence and we set the chain to run for 10 K steps (using 32 walkers). To remove the low-probability points due to the initialisation of the random walkers, we set an initial burn-in of 50 000 steps.
Moreover, we excluded the short τ from the parameter space, which allows the fit to describe short-timescale variability. Consequently, we set the τ prior to cover only values greater than 103 days, which guarantees that only the long-term variability is described. Details of the imposed priors are presented in Table 1.
However, the presence of the Jitter in the fitting procedure allows the GP to describe a small fraction of the short-timescale signals. To avoid this, we iterate the GP fit removing the data over 3 sigmas from the residual curve at each step, which were obtained by the subtraction from data analysed at step n of the maximum a posteriori probability (hereafter MAP) GP prediction obtained in the nth iteration (see Fig. 1). This expedient removes the data around a peak, and the GP consequently smooths out the data, ignoring the short-timescale signals. The process is repeated until the number of data points over 3 sigmas is compatible with what we expected from the noise. An example of the procedure is presented in Fig. 2, in which data points are presented together with the GP prediction, at different iterations.
The subtraction from the initial data of the last MAP GP prediction gives us a final residual curve (RC) centred at zero, in which all the small-scale events (the points removed in the iterative process) are highlighted. This is presented in Fig. 3, where the DS Tuc A light curves and their resulting final residual curves are shown together with the identified events (red lines).
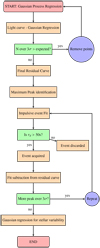 |
Fig. 1 Flow chart for the analysis procedure developed. |
Model priors.
 |
Fig. 2 Time vs. flux zoom showing the iterative GP procedure close to a short-term event. Each curve shows different steps of the fitting procedure. |
2.2 Event identification and characterisation
The next step in our analysis identifies and fits the short-term activity events from the RC (see Fig. 1). We identify the maximum between all the local curve maxima above 3σ. The code then fits the events using a function composed of an exponential increase and an exponential decay with the maximum being the event peak A located at t0 (the time coordinate of the peak):
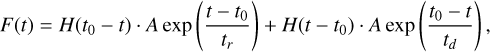 (2)
(2)
where we use H(t0−t) the Heaviside function (the value of which is zero for negative arguments and one for positive arguments) to switch from the rising part to the decaying part of the function. We then subtract the fit to the RC curve in order to highlight smaller energetic events occurring at the same time that will be identified through an iterative procedure. Figure 4 shows an example fit to the RC where multiple events are present. We stress that our goal is to describe the short-term variability, and not to derive the physics of each event; therefore, even a unique complex event will be described by multiple elementary events as in Eq. (2). The code fits all the events until there are no more local maxima over the 3 a threshold defined above. To avoid spurious points being considered as energetic events, the code only keeps an event if the associated decaying time is greater than 50 s; otherwise the event is discarded from further analysis.
 |
Fig. 3 First step of the analysis. Top panels a,b,c: three initial light curves (Sector 0, 27 and 28 respectively). Bottom panel d,e,f: final RCs after the GP analysis. The red crosses show the peaks of each event identified and the red lines the fits for each event. The dotted green line shows the 3a value and the blue line is the zero-line. |
2.3 Final products
After the analysis, for each light curve, we obtain the number of identified short-term events, their amplitudes and positions in time, their rising and decaying times, and their energies (see Sect. 3). After that, we remove the energetic impulsive events from the original light curve and run again a GP on the residual data (without the short-term events) in order to better constrain the stellar activity parameters, that is, the rotational period and the timescale of the active region lifetime.
For this task, we select a different kernel, namely the quasi-periodic kernel within the george Python package (Ambikasaran et al. 2014), which is expressed as follows:
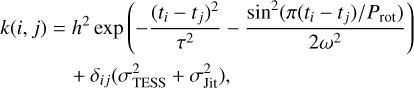 (3)
(3)
where k(i, j) is the ij element of the covariance matrix, ti and tj are two times of the light curve data set, n is the amplitude of the covariance, τ is the timescale of the exponential component (active region lifetime), ω is the weight of the periodic component (shape of the periodic component), Prot is the (rotational) period, δij is the Dirac delta function, σTESS are the data errors, and σJit is a white-noise term added to account for unknown sources of uncertainty. This kernel has been shown to give reliable results even in the case of stars with spot-dominated activity (Perger et al. 2021). For this task, we run the chain for 10000 steps after a burn-in phase of 50000 steps used to initialise the 32 random walkers. We decided to adopt a different kernel in this phase, because now our goal is to derive parameters linked to the physical properties of the medium-term variability of the star, while in the previous step our goal was simply a description of the shape of the stellar background. In that phase, we chose a less computationally expensive kernel, which is probably less representative of the physical origin of the variability, because of the shorter computation time and the need to proceed with an iterative procedure.
A re-binning procedure was performed on the light curves in order to reduce the computational cost. The bin step was set to 1 over 24 hours, over which we averaged both times and fluxes. We calculated each bin error as
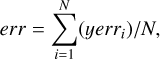 (4)
(4)
where yerri is a flux error and N is the data count that falls in the bin. We neglect the empty bins. The results of this analysis for the three sectors of DS Tuc A and the two sectors of AU Mic are summarised in Table 2.
Results of the GP for the long-term activity.
Observations data.
3 Light-curve analysis
TESS data of DS Tuc A cover about 70 days, divided into three different sets, all analysed in this work. Table 3 reports the dates of the relevant sectors. The procedure described in the previous section was applied separately to each sector. The Sector 1 light curve shows a low signal-to-noise ratio after 21 days of observations; in order to avoid spurious points being identified as flares we excluded this part of the curve (≈6 days) from the analysis. The light curves and the resulting RCs are reported in Fig. 3.
In particular, we identify 29, 63, and 56 events in the three sectors, respectively. Figure 5 shows the amplitude and decaying time distributions for the energetic events of DS Tuc.
We estimate the energy associated with each event by integrating the two fitted exponentials, which gives:
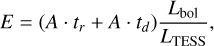 (5)
(5)
where A is the event peak, tr and td are the rising and decaying times estimated by the fit, Lbol = 0.725 L⨀ is the optical luminosity for DS Tuc A (Newton et al. 2019), and LTESS is the count in the TESS curve3. In order to associate an error to the energy, for each event we performed a bootstrap procedure with 1000 different fits, where the points on the light curves are taken randomly from a Gaussian, where a is equal to the error associated with the point. The relative error associated to the event energy is given by 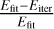 , where Efit is the value derived from the first fit and Eiter is the average of the energies estimated with the bootstrap procedure. However, with this procedure the associated errors are of the order of 0.1%. Figure 6 shows the rate of event energies for the three sectors of DS Tuc A and for the two sectors of AU Mic, which are discussed in the following section.
, where Efit is the value derived from the first fit and Eiter is the average of the energies estimated with the bootstrap procedure. However, with this procedure the associated errors are of the order of 0.1%. Figure 6 shows the rate of event energies for the three sectors of DS Tuc A and for the two sectors of AU Mic, which are discussed in the following section.
For DS Tuc, we find approximately two events per day with energy E > 2 × 1032 erg. However, it is clear from the cumulative curve in Fig. 6 that the sensitivity to events starts to increase at energies E > 2 × 1033. Figure 7 reports the amplitude as a function of decay time td of the identified events. The figure shows also the thresholds adopted to select the events (these depend on the specific sector) and the curves with constant energy. Our procedure is biased towards high-peak, short-decay-time events and tends to miss long events with a low amplitude of similar energy. Furthermore, at low energy, the peaks of faster events satisfy our criteria, that is, they are above the threshold that we set, whereas the peaks of longer events with the same energy are not high enough to be above this threshold.
As the star does not show significant differences between the three sectors, we can sum up the individual curves in Fig. 6 to obtain the cumulative energy frequency distribution of our target (Fig. 8). As discussed above, the break of the distributions in the region of weak events is a result of the biased procedure. From Figs. 7 and 8 we identified the break energy (where the identification of flares is considered complete) as Eb = 1034 erg for the cumulative curve of DS Tuc A. This choice is supported by Fig. 7 (and also by Fig. 9), which shows that most of the flares of DS Tuc have a time decay of shorter than 2000 s, which for our amplitude threshold corresponds approximately to our break energy (implying that we miss very few - if any - flares above our threshold). For AU Mic, the identification of the break energy is not straightforward, because, as suggested by Fig. 7, it shows flares with longer time decay and we likely miss several events even at high energies. For this reason, we present the results using two different break energies: 1033 erg and 3 × 1033 erg. As an independent check, we computed the slope of the curve as a function of the break energy. In the case of DS Tuc A, we find that the slope reaches a plateau for break energies between 1034 erg and 3 × 1034 erg: for higher break energies, the statistics are not sufficiently significant for the conclusions to be considered robust, and for lower energies, the curve is dominated by incompleteness. On the contrary, for the case of AU Mic, the slope does not reach a plateau in any range, confirming that the curve is incomplete throughout the entire high-statistic range.
In order to estimate the errors in the fitting parameters for both stars, taking into account the statistics, we perform a bootstrap procedure. From the set of N events for each star, we create 1000 new sets. Each of them is made extracting a random flare from the original set N times; it is worth noting that once a flare is extracted, it is again made available for the following extraction. This procedure takes into account the different frequencies of high- and low-energy flares. For each set, we calculate a cumulative curve and perform the fits using the function f = m • log(E) + q for the part of the curves at energy higher than Eb. In this way, for each star we obtain a distribution of m and q. The fit results are defined as the mean values for each distribution with the standard deviation as error. The cumulative functions with their fits are shown in Fig. 8. The parameters of the fits are reported in Table 4.
We investigated whether or not short-term events are enhanced in particular phases of the stellar rotation cycles or planetary period. Figure 10 shows the peaks of each energetic event in the light curve for all the sectors available, phase folded for both stellar and planetary periods (DS Tuc A b and AU Mic b). In all plots, phase = 0 is calculated at the first planetary transit.
We also plotted the histograms with the number of events and the total energy per phase bin both for stellar and planetary period. The histograms for both DS Tuc A and AU Mic are shown in Figs. 9 and 11. DS Tuc A shows two peaks in energy emitted, at stellar phases 0.3 and 0.5 (see Figs. 9a, b). At phase 0.3, the energy peak corresponds to a peak in the number of events (blue line in Fig. 9). It is clear from Fig. 10a that three out of the five events at phase 0.3 originate at the same stellar rotation cycle. Moreover, the second peak at phase 0.5 is generated by a single flare, as can be seen in Fig. 10a. The data suggest that there is not a favourite region where stellar activity is enhanced on Ds Tuc. During the planetary orbit, a bump both in the number of events and in the integrated energy is visible between phases 0.8 and 0.9 (see Figs. 9c, d). In the plot in Fig. 10b, it is clear that the bump in energy is due to only two events occurring in different planetary orbits. We conclude that there is no significant evidence of activity in DS Tuc A in phase with planetary period.
We performed an analogous analysis for AU Mic. In Figs. 11a, b, two peaks at phase 0.4 and 1 are present. The one at phase 1 is the result of a single energetic event and for this reason is not considered in the analysis. The other peak at phase 0.4 is the results of four major events occurring at different stellar rotations, each of them followed by a series of less energetic events in Sector 27 (see Fig. 10c). We claim that in AU Mic, there are hints of activity favoured at specific locations on the stellar surface. The behaviour of activity on Au Mic in phase with its rotation cycle may be a consequence of the fact that the distribution of the surface magnetic field in young stars is relatively stable for the timescale of the TESS observations (e.g. Folsom et al. 2013; Klein et al. 2021). These stars exhibit quite intense magnetic fields whose dynamo processes are not fully understood (e.g. Donati et al. 2014; Yu et al. 2019; Hill et al. 2019). As a result, there are regions on the stellar surface where magnetic reconnection phenomena are favoured and generate energetic events.
In histograms in Figs. 11c, d, two major peaks in energy are present: at phase ≈0.6 and ≈0.8. In Fig. 10d, it is clear that the peak at ≈0.8 is due to a series of events all generated at the same planetary period (same symbol and same colour in Fig. 10d). However, the peak at ≈0.6 is generated by events from four different planetary periods (from a total of six full planetary periods observed). We can conclude that for AU Mic we observe hints of SPI. This is not the first case of flare periodicity connected with the planetary orbit observed by TESS (Howard & Law 2021). Despite this and the numerous theoretical models that describe SPI (e.g. Lanza 2018, 2021, 2022), the case of AU Mic remains unexplained.
AU Mic b orbits at a relatively large distance from the star, and therefore we do not expect a strong interaction between stellar and planetary magnetic field (as in the kind described by Lanza 2018). The planet could also interact with the star through the gravitational potential. Tides generated by the planet could perturb the stellar magnetic internal configuration. The perturbations on the magnetic field could enhance the activity at some specific planetary orbital phases (Lanza 2022). However, this scenario requires a larger planetary mass and closer orbit than those of AU Mic b.
Energetic events are not evenly distributed during the observation as can be observed in Fig. 12. The plot in Fig. 12a shows the distribution of the energetic events over time. In particular, the deviation from the uniform distribution suggests that the events are likely to occur in groups. To explain this distribution, we envisage two possible explanations: (a) it could be the result of plasma sloshing in a pulse-heated loop (Reale 2016); each wave in the stellar loop generates an increase in the optical light curve and these are identified as energetic events (see Fig. 4); or (b) a large flare can trigger the occurrence of following new flares.
Figure 12b shows the same analysis but only with events with associated energy greater than 1034 erg. The distributions in time for the three sectors do not follow the expected distribution for equally spaced events, suggesting a link between consecutive energetic events, supporting hypothesis (b).
 |
Fig. 5 Histograms for events. Panel a: histogram for event amplitudes for DS Tuc A. Panel b: same as top panel but for decaying time. |
 |
Fig. 6 Cumulative events per day vs. energy for each set of observations of DS Tuc A and AU Mic. |
 |
Fig. 7 Amplitude vs. decay time for each identified event. The dotted horizontal coloured lines show the 3 a value used to discriminate the events from the noise. The dotted grey oblique lines are the iso-energy lines. |
 |
Fig. 8 Cumulative log frequency vs. log energy for the total set of observations. Error bars are given by the Poisson noise |
 |
Fig. 9 Phase histograms for the events. Top left panel a: Histogram for event energy (in orange) and number of events (in blue) per stellar phase for DS Tuc A. Top right panel b: same as left panel but for events with energy E > 1034 erg s−1. Bottom panels are as in top panels, but for planetary phase. |
 |
Fig. 10 Phase plots for the events. Top left panel a: event energy vs. event position phase-folded for the stellar rotation cycles for DS Tuc A. Top right panel b: same as the left panel but for the planetary period. Bottom panels are as in top panels but for AU Mic. Different symbols refer to different TESS sectors, while different colours represent different stellar or planetary periods. |
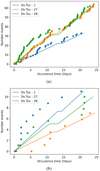 |
Fig. 12 Expected vs observed event distribution during the observed period for the three sectors of DS Tuc. The χ-axis shows the occurrence time of each energetic event, the y-axis shows the number of the events. The dots represent the real data, the solid lines represent an equally time-spaced distribution. Top panel a: all the events, bottom panel b: only events with associated energy greater than 1034 erg. |
4 Discussion
In order to validate our procedure we also analysed the two TESS observations (sectors 1 and 27) of the system AU Mic. We use AU Mic as a test to verify the robustness of our analysis and we compared our results with those present in the literature. We applied the procedure to AU Mic as described for DS Tuc A and the results are reported in Table 2, while the light curves and RCs are shown in Fig. 13.
In order to derive the energies of the identified events, we applied Eq. (5), adopting a value of Lbol = 0-09 L⨀ (Plavchan et al. 2009). According to our analysis, AU Mic shows approximately five energetic events per day with energies E > 5 × 1031 erg.
Martioli et al. (2021) performed an analogous analysis for AU Mic and claim a frequency of 6.35 flares per day, which is comparable to our results. We also compared our results with those of Gilbert et al. (2022), who used a technique based on Bayesian inference to detect flares in the AU Mic TESS light curves. Their cumulative curve (Fig. 5 in Gilbert et al. 2022) is comparable with those presented here in Fig. 6 for high energies. However, our technique reveals approximately twice as many low-energy events as those observed by Gilbert et al. (2022).
AU Mic shows, on average, less energetic events than DS Tuc. However, it is clear from the scatter plot in Fig. 7 that we are sensitive to lower amplitude (and therefore lower energy) events in AU Mic. This is likely due to the different bolometric magnitude of the two stars. Such a difference is also evident in the cumulative curves in Fig. 6 where the curves appear to be shifted by about one order of magnitude with good sensitivity to events with energy E > 1033 erg for AU Mic and E > 1034 erg for DS Tuc. As discussed in Sect. 3, this depends on the threshold used for defining the peaks of the energetic events, which is affected by the stellar background level when we derive the absolute energy and not relative variations. On the other side, the slope of the flare frequency of the two stars is similar. This implies that, even in different stellar spectral types, the physics of energetic phenomena is comparable.
The photosphere of DS Tuc A is also more variable than that of AU Mic. Indeed, Table 2 shows that the lifetimes of active regions for DS Tuc A (τ) are comparable to the rotation period. Thus, the stellar activity level is different for each period. On the contrary, AU Mic shows a lifetime of active regions which is roughly twice the period, which is also evident from comparison of the light curves in Figs. 13 and 3. In fact, DS Tuc A light curves are less regular than those of AU Mic.
5 Conclusions
Our procedure is able to identify and characterise the short-term variability in light curves, outlining the most important physical parameters of each short-term event. Moreover, beyond the short-term analysis, the procedure can also characterise the longterm stellar variability. We validate the procedure by comparing our results with those of Martioli et al. (2021) for AU Mic using other techniques, finding a rate of events of about five per day with energies Ef > 5 × 1031 (see Fig. 8).
In addition, we studied the system DS Tuc A and find a rate of energetic events of approximately two per day with energies greater than 2 × 1032 erg−s (see Fig. 6). The phase analysis of the events suggests that on DS Tuc A there are no preferred stellar or planetary phases for the events (see Fig. 10). However, the time distance between the events tends not to be constant; on the contrary, the events arise in groups (see Fig. 12).
The phase analysis of AU Mic shows that there may be a favourite region on the stellar surface where energetic events originate. In addition, there are some hints of SPI which are difficult to explain with current theoretical models.
The results of our analysis could be used as input for precise models of planetary atmosphere chemical evolution and moreover could be used as a tracer for X-ray flaring activity. The analysis of XMM-Newton observations that showed at least two relatively large, twin X-ray flares over a total exposure time of ~70 ks, with clear counterparts in the optical monitor (Benatti et al. 2021; Pillitteri et al., in prep.), suggests that optical flares can be used as a proxy for X-ray flares. Assuming that optical flares are a proxy for their X-ray counterparts, from the optical flare distribution we can estimate the X-ray flare distribution using the scaling law between optical and X-ray flare energy from Fig. 3 in Flaccomio et al. (2018). For X-ray flares in particular, from Fig. 8, we expect a frequency of two per day with energies Ex ≈ 2 × 1031 erg.
 |
Fig. 13 First step of the analysis of AU Mic. Top panels a,b show the three initial light curves (Sector 1 and 27 respectively). Bottom panels c,d show the final RCs after the GP analysis. The red crosses show the peaks of each event identified and the red lines the fits for each event. The dotted green line shows the 3a value and the blue line is the zero-line. |
Acknowledgements
We thank the anonymous referee for useful suggestions that have allowed us to improve the paper. We thank A.F. Lanza for fruitful discussion on SPI models. We acknowledge financial contribution from the agreement ASI-INAF No. 2018-16-HH.0 (THE StellaR PAth project). We acknowledge support from ASI-INAF agreement 2021-5-HH.0 Partecipazione alla fase B2/C della missione ARIEL (Atmospheric Remote-Sensing Infrared Exoplanet Large-survey). This paper includes data collected by the TESS mission. Funding for the TESS mission is provided by the NASA’s Science Mission Directorate.
References
- Ambikasaran, S., Foreman-Mackey, D., Greengard, L., Hogg, D. W., & O'Neil, M. 2014, IEEE Transactions on Pattern Analysis and Machine Intelligence, 38, 2 [Google Scholar]
- Bell, C. P. M., Mamajek, E. E., & Naylor, T. 2015, MNRAS, 454, 593 [Google Scholar]
- Benatti, S., Damasso, M., Borsa, F., et al 2021, A&A, 650, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cecchi-Pestellini, C., Ciaravella, A., & Micela, G. 2006, A&A, 458, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, H., Zhan, Z., Youngblood, A., et al 2021, Nat. Astron., 5, 298 [Google Scholar]
- Cohen, O., Kashyap, V. L., Drake, J. J., et al 2011, ApJ, 733, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Crundall, T. D., Ireland, M. J., Krumholz, M. R., et al 2019, MNRAS, 489, 3625 [Google Scholar]
- Davenport, J. R. A., Hawley, S. L., Hebb, L., et al 2014, ApJ, 797, 122 [Google Scholar]
- Donati, J. F., Hébrard, E., Hussain, G., et al 2014, MNRAS, 444, 3220 [NASA ADS] [CrossRef] [Google Scholar]
- Erkaev, N. V., Kulikov, Y. N., Lammer, H., et al 2007, A&A, 472, 329 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flaccomio, E., Micela, G., Sciortino, S., et al 2018, A&A, 620, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Folsom, C. P., Likuski, K., Wade, G. A., et al 2013, MNRAS, 431, 1513 [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Foreman-Mackey, D., Agol, E., Angus, R., & Ambikasaran, S. 2017, AJ, 154, 220 [NASA ADS] [CrossRef] [Google Scholar]
- Gilbert, E. A., Barclay, T., Quintana, E. V., et al 2022, AJ, 163, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, C. A., Folsom, C. P., Donati, J. F., et al 2019, MNRAS, 484, 5810 [NASA ADS] [CrossRef] [Google Scholar]
- Howard, W. S., & Law, N. M. 2021, ApJ, 920, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, J. M., Twicken, J. D., McCauliff, S., et al 2016, in Software and Cyberinfrastructure for Astronomy IV, SPIE Conf. Ser., 9913, 3E [Google Scholar]
- Klein, B., Donati, J.-F., Moutou, C., et al 2021, MNRAS, 502, 188 [Google Scholar]
- Kraus, A. L., Shkolnik, E. L., Allers, K. N., & Liu, M. C. 2014, AJ, 147, 146 [Google Scholar]
- Lanza, A. F. 2018, A&A, 610, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lanza, A. F. 2021, A&A, 653, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lanza, A. F. 2022, A&A, 658, A195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Locci, D., Petralia, A., Micela, G., et al 2022, Planet. Sci. J., 3, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Maloney, P. R., Hollenbach, D. J., & Tielens, A. G. G. M. 1996, ApJ, 466, 561 [Google Scholar]
- Mamajek, E. E., & Bell, C. P. M. 2014, MNRAS, 445, 2169 [Google Scholar]
- Martioli, E., Hébrard, G., Correia, A. C. M., Laskar, J., & Lecavelier des Etangs, A. 2021, A&A, 649, A177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Newton, E. R., Mann, A. W., Tofflemire, B. M., et al 2019, ApJ, 880, L17 [Google Scholar]
- Perger, M., Anglada-Escudé, G., Ribas, I., et al 2021, A&A, 645, A58 [EDP Sciences] [Google Scholar]
- Pillitteri, I., Maggio, A., Micela, G., et al 2015, ApJ, 805, 52 [Google Scholar]
- Plavchan, P., Werner, M. W., Chen, C. H., et al 2009, ApJ, 698, 1068 [Google Scholar]
- Plavchan, P., Barclay, T., Gagné, J., et al 2020, Nature, 582, 497 [Google Scholar]
- Reale, F. 2016, ApJ, 826, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al 2014, in Space Telescopes and Instrumentation 2014: Optical, Infrared, and Millimeter Wave, SPIE Conf. Ser., 9143, 20 [Google Scholar]
- Robinson, R. D., Linsky, J. L., Woodgate, B. E., & Timothy, J. G. 2001, ApJ, 554, 368 [Google Scholar]
- Route, M., & Looney, L. W. 2019, ApJ, 887, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Shkolnik, E., Walker, G. A. H., & Bohlender, D. A. 2003, ApJ, 597, 1092 [NASA ADS] [CrossRef] [Google Scholar]
- Shkolnik, E., Walker, G. A. H., Bohlender, D. A., Gu, P. G., & Kürster, M. 2005, ApJ, 622, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Shkolnik, E., Bohlender, D. A., Walker, G. A. H., & Collier Cameron, A. 2008, ApJ, 676, 628 [NASA ADS] [CrossRef] [Google Scholar]
- Stelzer, B., Damasso, M., Scholz, A., & Matt, S. P. 2016, MNRAS, 463, 1844 [NASA ADS] [CrossRef] [Google Scholar]
- Venot, O., Rocchetto, M., Carl, S., Roshni Hashim, A., & Decin, L. 2016, ApJ, 830, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Vida, K., Bódi, A., Szklenár, T., & Seli, B. 2021, A&A, 652, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walker, G. A. H., Croll, B., Matthews, J. M., et al 2008, A&A, 482, 691 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Watson, A. J., Donahue, T. M., & Walker, J. C. G. 1981, Icarus, 48, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, L., Donati, J. F., Grankin, K., et al 2019, MNRAS, 489, 5556 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Flow chart for the analysis procedure developed. |
| In the text | |
 |
Fig. 2 Time vs. flux zoom showing the iterative GP procedure close to a short-term event. Each curve shows different steps of the fitting procedure. |
| In the text | |
 |
Fig. 3 First step of the analysis. Top panels a,b,c: three initial light curves (Sector 0, 27 and 28 respectively). Bottom panel d,e,f: final RCs after the GP analysis. The red crosses show the peaks of each event identified and the red lines the fits for each event. The dotted green line shows the 3a value and the blue line is the zero-line. |
| In the text | |
 |
Fig. 4 Close-up view of one identified multiple event. Legend as in Fig. 3. |
| In the text | |
 |
Fig. 5 Histograms for events. Panel a: histogram for event amplitudes for DS Tuc A. Panel b: same as top panel but for decaying time. |
| In the text | |
 |
Fig. 6 Cumulative events per day vs. energy for each set of observations of DS Tuc A and AU Mic. |
| In the text | |
 |
Fig. 7 Amplitude vs. decay time for each identified event. The dotted horizontal coloured lines show the 3 a value used to discriminate the events from the noise. The dotted grey oblique lines are the iso-energy lines. |
| In the text | |
 |
Fig. 8 Cumulative log frequency vs. log energy for the total set of observations. Error bars are given by the Poisson noise |
| In the text | |
 |
Fig. 9 Phase histograms for the events. Top left panel a: Histogram for event energy (in orange) and number of events (in blue) per stellar phase for DS Tuc A. Top right panel b: same as left panel but for events with energy E > 1034 erg s−1. Bottom panels are as in top panels, but for planetary phase. |
| In the text | |
 |
Fig. 10 Phase plots for the events. Top left panel a: event energy vs. event position phase-folded for the stellar rotation cycles for DS Tuc A. Top right panel b: same as the left panel but for the planetary period. Bottom panels are as in top panels but for AU Mic. Different symbols refer to different TESS sectors, while different colours represent different stellar or planetary periods. |
| In the text | |
 |
Fig. 11 As in Fig. 9 but for AU Mic. |
| In the text | |
 |
Fig. 12 Expected vs observed event distribution during the observed period for the three sectors of DS Tuc. The χ-axis shows the occurrence time of each energetic event, the y-axis shows the number of the events. The dots represent the real data, the solid lines represent an equally time-spaced distribution. Top panel a: all the events, bottom panel b: only events with associated energy greater than 1034 erg. |
| In the text | |
 |
Fig. 13 First step of the analysis of AU Mic. Top panels a,b show the three initial light curves (Sector 1 and 27 respectively). Bottom panels c,d show the final RCs after the GP analysis. The red crosses show the peaks of each event identified and the red lines the fits for each event. The dotted green line shows the 3a value and the blue line is the zero-line. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.