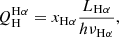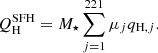| Issue |
A&A
Volume 661, May 2022
|
|
|---|---|---|
| Article Number | A99 | |
| Number of page(s) | 21 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202142812 | |
| Published online | 09 May 2022 | |
The miniJPAS survey: Identification and characterization of the emission line galaxies down to z < 0.35 in the AEGIS field
1
Instituto de Astrofísica de Andaluciá (CSIC), PO Box 3004
18080
Granada, Spain
e-mail: gimarso@iaa.es
2
Departamento de Física, Universidade Federal de Santa Catarina, PO Box 476, 88040-900 Florianópolis, SC, Brazil
3
Département de Physique, de Génie Physique et d’Optique, Université Laval, and Centre de Recherche en Astrophysique du Québec (CRAQ), Québec, QC G1V 0A6, Canada
4
Universidade de São Paulo, Instituto de Astronomia, Geofísica e Ciências Atmosféricas, R. do Matão 1226, 05508-090 São Paulo, Brazil
5
Department of Physics, Lancaster University, Lancaster LA1 4YB, UK
6
Donostia International Physics Center, Paseo Manuel de Lardizabal 4, 20018 Donostia-San Sebastian, Spain
7
Centro de Estudios de Física del Cosmos de Aragón (CEFCA), Plaza San Juan, 1, 44001 Teruel, Spain
8
Centro de Estudios de Física del Cosmos de Aragón (CEFCA), Unidad Asociada al CSIC, Plaza San Juan, 1, 44001 Teruel, Spain
9
Observatório do Valongo, Universidade Federal do Rio de Janeiro, 20080-090 Rio de Janeiro, RJ, Brazil
10
Ikerbasque, Basque Foundation for Science, 48013 Bilbao, Spain
11
Observatório Nacional, Rua General José Cristino, 77, São Cristóvão, 20921-400 Rio de Janeiro, Brazil
12
Department of Astronomy, University of Michigan, 311 West Hall, 1085 South University Ave., Ann Arbor, USA
13
Department of Physics and Astronomy, University of Alabama, Box 870324 Tuscaloosa, AL, USA
14
Instituto de Física, Universidade de São Paulo, Rua do Matão 1371, CEP 05508-090 São Paulo, Brazil
15
Departamento de Astronomia, Instituto de Astronomia, Geofísica e Ciências Atmosféricas da USP, Cidade Universitária, 05508-900 São Paulo, SP, Brazil
16
PPGCosmo & Departamento de Fśica, Universidade Federal do Espírito Santo, 29075-910 Vitória, ES, Brazil
17
INAF, Osservatorio Astronomico di Trieste, Via Tiepolo 11, 34131 Trieste, Italy
18
IFPU, Institute for Fundamental Physics of the Universe, Via Beirut 2, 34151 Trieste, Italy
19
Instruments4, 4121 Pembury Place, La Cañada-Flintridge, CA 91011, USA
20
Centro Brasileiro de Pesquisas Físicas, Rua Dr. Xavier Sigaud 150, CEP 22290-180 Rio de Janeiro, RJ, Brazil
Received:
2
December
2021
Accepted:
28
March
2022
The Javalambre-Physics of the Accelerating Universe Astrophysical Survey (J-PAS) is expected to map thousands of square degrees of the northern sky with 56 narrowband filters (spectral resolution of R ∼ 60) in the upcoming years. This resolution allows us to study emission line galaxies (ELGs) with a minimum equivalent width of 10 Å in the Hα emission line for a median signal-to-noise ratio (S/N) of 5. This will make J-PAS a very competitive and unbiased emission line survey compared to spectroscopic or narrowband surveys with fewer filters. The miniJPAS survey covered 1 deg2, and it used the same photometric system as J-PAS, but the observations were carried out with the pathfinder J-PAS camera. In this work, we identify and characterize the sample of ELGs from miniJPAS with a redshift lower than 0.35, which is the limit to which the Hα line can be observed with the J-PAS filter system. Using a method based on artificial neural networks, we detect the ELG population and measure the equivalent width and flux of the Hα, Hβ, [O III], and [N II] emission lines. We explore the ionization mechanism using the diagrams [OIII]/Hβ versus [NII]/Hα (BPT) and EW(Hα) versus [NII]/Hα (WHAN). We identify 1787 ELGs (83%) from the parent sample (2154 galaxies) in the AEGIS field. For the galaxies with reliable EW values that can be placed in the WHAN diagram (2000 galaxies in total), we obtained that 72.8 ± 0.4%, 17.7 ± 0.4%, and 9.4 ± 0.2% are star-forming (SF), active galactic nucleus (Seyfert), and quiescent galaxies, respectively. The distribution of EW(Hα) is well correlated with the bimodal color distribution of galaxies. Based on the rest-frame (u − r)–stellar mass diagram, 94% of the blue galaxies are SF galaxies, and 97% of the red galaxies are LINERs or passive galaxies. The nebular extinction and star formation rate (SFR) were computed from the Hα and Hβ fluxes. We find that the star formation main sequence is described as log SFR [M⊙ yr−1] = 0.90−0.02+0.02 log M⋆[M⊙]−8.85−0.20+0.19 and has an intrinsic scatter of 0.20−0.01+0.01. The cosmic evolution of the SFR density (ρSFR) is derived at three redshift bins: 0 < z ≤ 0.15, 0.15 < z ≤ 0.25, and 0.25 < z ≤ 0.35, which agrees with previous results that were based on measurements of the Hα emission line. However, we find an offset with respect to other estimates that were based on the star formation history obtained from fitting the spectral energy distribution of the stellar continuum. We discuss the origin of this discrepancy, which is probably a combination of several factors: the escape of ionizing photons, the SFR tracers, and dust attenuation, among others.
Key words: Galaxy: evolution / surveys / techniques: photometric / methods: data analysis
© ESO 2022
1. Introduction
The Hα emission line is an excellent tracer for estimating the current star formation rate (SFR) in galaxies because it is less affected by dust extinction than UV light (Kennicutt 1998; Garn et al. 2010; Oteo et al. 2015; Catalán-Torrecilla et al. 2015). The Hα line can be observed in the optical range up to z ∼ 0.4. Thus, it is very useful for the identification of emission line galaxies (ELGs) in spectroscopic and photometric surveys. The detection of other emission lines, such as [O III]λλ4959, 5007 Å and the [N II]λλ6548, 6584 Å doublets1, is crucial to determine the main ionization mechanism of ELGs (see, e.g., Cid Fernandes et al. 2011; Belfiore et al. 2016; Sánchez et al. 2018; Lacerda et al. 2020; Kalinova et al. 2021). Diagrams such as the WHAN (EW(Hα) vs. [NII]/Hα) (Cid Fernandes et al. 2011) or the BPT (Baldwin et al. 1981) (e.g., [OIII]/Hβ vs. [NII]/Hα) can differentiate galaxies in which the gas is ionized by young stars or by an active galactic nucleus (AGN), from low ionization nuclear emission regions (LINERs, Heckman 1980), or extended low-ionization emission lines (see, e.g., Lacerda et al. 2018), in which the ionization might be attributed to old and hot stars. Furthermore, the characterization of the galaxy populations through the SFR and its correlation with other galaxy properties, such as stellar mass, colors, ages, metallicity, and neutral gas content (Kewley et al. 2019; Förster Schreiber & Wuyts 2020), is essential to obtain insight into the formation and evolution of galaxies.
Galaxies grow in mass mainly through star formation, which is fed by gas accretion from the cosmic web. While massive galaxies undergo a larger fraction of their star formation at early times, less massive galaxies are still forming stars at a high rate today. The star formation main sequence (SFMS), a tight quasi-linear relation between stellar mass, (M⋆), and the SFR in log scale (Zahid et al. 2012; Renzini & Peng 2015; Cano-Díaz et al. 2016, 2019; Duarte Puertas et al. 2017; Belfiore et al. 2018; Boogaard et al. 2018; Sánchez et al. 2019; Shin et al. 2021; Vilella-Rojo et al. 2021), can reveal indications how this process takes place. Galaxies that are undergoing a starburst, for instance, lie above the SFMS, while galaxies that have already quenched their star formation lie below this relation.
The SFMS and its evolution with redshift are expected outcomes of hydrodynamical models. The currently best cosmological hydrodynamical simulations of galaxy formation such as Illustris (Sparre et al. 2015) or EAGLE (Furlong et al. 2015) predict a slope near unity. Semi-analytical models favor a sublinear slope that is generally higher than 0.8. For instance, Dutton et al. (2010) predicted a slope of 0.96 for galaxies with stellar masses between 109 and 1011 M⊙. However, Mitchell et al. (2014) used GALFORM and retrieved a slope of 0.87 at z = 0.1.
The slope of the SFMS in observations ranges from 0.6 to 1, depending on the data, the SFR tracer, and method used (see, e.g., the study of Speagle et al. 2014, and references therein). The discrepancies found by different studies are expected. On the one hand, spectroscopic surveys such as the Sloan Digital Sky Survey (SDSS, York et al. 2000) have aperture effects that can cause an underestimation of the total SFR within the galaxy (Duarte Puertas et al. 2017). On the other hand, the SFR derived from photometric surveys throughout Hα measurements needs to be corrected for the [N II] and dust extinction, which become the main sources of uncertainty.
The definition of the SFMS itself might also lead to significant differences between different works, even though they all trace the SFR through the Hα line. Some authors (e.g., Vilella-Rojo et al. 2021, z ≤ 0.017 or Shin et al. 2021, z ∼ 0.07 − 0.5) relied on color-color diagrams. Others selected star-forming (SF) galaxies based on the BPT diagrams with a cut in the equivalent width (EW) of Hα or Hβ. For example, Cano-Díaz et al. (2016, 0.005 ≤ z ≤ 0.03) imposed a minimum EW in Hα of 6 Å while Duarte Puertas et al. (2017, 0.005 ≤ z ≤ 0.22) used instead 3 Å and Zahid et al. (2012, z = 0.07, 0.8 and 2.26) adopted a EW of 4 Å in Hβ. In addition, the SFMS has also been defined as the ridge line in the M⋆–N–SFR-plane where N account for the number of galaxies in every M⋆–SFR bin (0.02 ≤ z ≤ 0.085, Renzini & Peng 2015).
In essence, there is no unique and homogeneous definition of the galaxies that belong to the SFMS. Furthermore, any dividing line between star-forming and quiescent galaxies affects the analysis of the SFMS because it includes or excludes some of the galaxies in the so-called ‘green valley’ (GV), that is, galaxies that are in transition and are interpreted as a crossroads in galaxy evolution (see, e.g., Mendez et al. 2011; Gonçalves et al. 2012; Schawinski et al. 2014; Díaz-García et al. 2019). Sánchez et al. (2019, 0.03 ≤ z ≤ 0.2) attributed the constancy of the SFMS slope across galaxy mass to the selection criterion (based on sSFR cut). There is no drop in the SFR at high masses. In the same vein, Belfiore et al. (2018, 0.03 ≤ z ≤ 0.15), who also used the Hα line as an SFR tracer, found that the flattening in the slope of the SFMS only occurs if galaxies with quiescent central regions (cLIERs) are included in the fit.
In addition, the detection limit and particularities of each study might lead to a specific bias in the selection criteria. For instance, a photometric survey that selects ELGs based on a minimum contrast would be limited to the minimum EW that can be measured and would therefore be biased toward highly actively SF galaxies. As a consequence, it produces an increase in normalization constant and a shallower slope (Khostovan et al. 2021). Finally, the minimization method employed in the fitting takes the uncertainties into account in different ways. It might therefore also have an impact on the shape of the SFMS.
Another important aspect that helps to understand how galaxies assemble their mass throughout cosmic time is estimating the intrinsic scatter of galaxies in the SFMS. It is expected that low-mass galaxies are more sensitive to stochastic events such as starbursts or feedback from supernovae. Theoretical simulations (Hopkins et al. 2014; Domínguez et al. 2015; Matthee & Schaye 2019) and observations (Salim et al. 2007; Emami et al. 2019; Boogaard et al. 2018; Santos et al. 2020) have both found an increase in scatter for low-mass galaxies (< 109 M⊙).
Other studies (Willett et al. 2015; Davies et al. 2019) found that the dispersion along the SFMS follows a U-shaped distribution, meaning that galaxies with high and low stellar masses scatter more from the SFMS. Interestingly, the U-shape depends on the way the SFMS is defined. While selecting SF galaxies based on u − r colors or morphology causes the SFMS to have higher scatter for galaxies at high mass, a selection based on a minimum sSFR, which is equivalent to a minimum EW in Hα, produces a decrease in scatter as the mass of the galaxy increases (see, e.g., Davies et al. 2019).
It has been proven by the analysis of stellar populations within galaxies through stellar continuum spectral energy distribution (SED) fitting that the SFMS holds true at high redshift with an increase in the global SFRs of galaxies (Daddi et al. 2004; Oliver et al. 2010; Karim et al. 2011; Ilbert et al. 2015; Schreiber et al. 2015; Tasca et al. 2015; Rodighiero et al. 2011). In terms of the SFR density (ρSFR), the Universe reached a peak at ∼3 Gyr after the Big Bang, and it has been decreasing ever since (Madau & Dickinson 2014; Driver et al. 2018; López Fernández et al. 2018; Sánchez et al. 2019; Leja et al. 2019; Bellstedt et al. 2020). Through Hα measurements, astronomers are also able to measure ρSFR both in the nearby Universe and at intermediate redshift, which has confirmed this trend (Gallego et al. 1995; Ly et al. 2007; Shioya et al. 2008; Dale et al. 2010; Westra et al. 2010; Drake et al. 2013; Sobral et al. 2013, 2015; Gunawardhana et al. 2013; Stroe & Sobral 2015; Van Sistine et al. 2016; Khostovan et al. 2020; Vilella-Rojo et al. 2021).
The incredible progress achieved in the past decades would not have been possible without the construction of large galaxy surveys. Multi-object spectroscopy (MOS) surveys such as the SDSS and the Galaxy And Mass Assembly (GAMA; Driver et al. 2011) or integral field unit (IFU) surveys such as the Calar Alto Legacy Integral Field Area (CALIFA; Sánchez et al. 2012, 2016; García-Benito et al. 2015) and the survey Mapping Nearby Galaxies at the Apache Point Observatory (MaNGA; Bundy et al. 2015; Law et al. 2015) provide a very detailed description of the optical SED of galaxies. However, they are partially biased through their preselection of samples, which is driven by some properties such as redshift, fluxes, or a galaxy size that is constrained to a particular range.
In contrast, narrowband photometric surveys such as HiZELS (Best et al. 2013; Sobral et al. 2013; Matthee et al. 2017), ALHAMBRA (Moles et al. 2008; Molino et al. 2014), DAWN (Coughlin et al. 2018), J-PLUS (Cenarro et al. 2019), S-PLUS (Mendes de Oliveira et al. 2019), the Deep and UDeep layers driven by the Subaru Strategic Program with the Hyper Suprime-Cam (HSC-SSP) (Hayashi et al. 2018, 2020), LAGER (Khostovan et al. 2020), or SHARDS (Pérez-González et al. 2013; Lumbreras-Calle et al. 2019), experience these effects to a lesser degree. In particular, narrowband photometric surveys are able to detect fainter objects than their spectroscopic counterpart at a fixed exposure time. Furthermore, they can fully observe galaxies whose light cannot be captured entirely by IFU-like surveys (see, e.g., Fig. 19 in Bonoli et al. 2021). However, their SED in the optical, infrared, or UV is limited by the number of filters and their width. More importantly, ELGs can only be detected in certain redshift intervals, which makes contamination from other sources more likely because the emission lines may be confused; for example, [O III] emitters may be detected as Hα emission line objects.
The special design of the Javalambre Physics of the Accelerating Universe Astrophysical Survey (J-PAS, Benitez et al. 2014) enables overcoming some of the caveats for spectroscopic and traditional photometric surveys. J-PAS will play a crucial role in the upcoming years, which will be very competitive compared to the new generations of spectroscopic surveys such as DESI (DESI Collaboration 2016), Euclid (Laureijs et al. 2011), or the WHT Enhanced Area Velocity Explorer-Stellar Population at intermediate redshift Survey (WEAVE-StePS; Costantin et al. 2019).
The unprecedented area that J-PAS will cover (∼8000 deg2 of the northern sky) is perhaps one of the main advantages compared to previous and current surveys. J-PAS will observe the sky with 56 bands: 54 narrowband filters in the optical range, plus two medium-band filters, one in the UV and another in the near-infrared. Separated by 100 Å, each narrowband filter has a width of ∼145 Å, which provides a resolving power of R ∼ 60 (J-spectrum hereafter). These unique characteristics make J-PAS an ideal survey for galaxy evolution studies (Bonoli et al. 2021), superseding the scientific impact achieved by other previous medium-band imaging surveys, such as ALHAMBRA (R ∼ 20). The narrowband setup of J-PAS allows the detection and measurement of galaxies with emission lines in a continuous range in redshift within a nonsegregated area (Martínez-Solaeche et al. 2021, hereafter MS21). J-PAS observations will be carried out with the 2.55 m telescope (T250) at the Observatorio Astrofísico de Javalambre, a facility developed and operated by the Centro the Estudios de Física del Cosmos de Aragón (CEFCA, in Teruel, Spain) using JPCam, a wide-field 14 CCD-mosaic camera with a pixel scale of 0.2267 arcsec pix−1 and an effective field of view (FoV) of ∼4.7 deg2 (Taylor et al. 2014; Marin-Franch et al. 2015; Bonoli et al. 2021).
The pathfinder camera of J-PAS started its observations using 60 optical bands in four fields of the sky that overlap with the All-wavelength Extended Groth Strip International survey (AEGIS; Davis et al. 2007), amounting to 1 deg2 with more than 60 000 objects2; hereafter, this is referred to as the miniJPAS survey (Bonoli et al. 2021). The pathfinder instrument used by the J-PAS collaboration is a single CCD direct imager (9.2k × 9.2k, 10 μm pixel) located at the center of the T250 FoV with a pixel scale of 0.23 arcsec pix−1, vignetted on its periphery. This provides an effective FoV of 0.27 deg2.
The goal of this paper is to identify the ELG population in the AEGIS field and characterize them through their SFR and the stellar population properties. This work shows the potential of J-PAS data in this regard. We apply a method based on artificial neural networks (ANN) developed in MS21 to obtain the EW of the main emission lines in the optical range: Hα, Hβ, [O III], and [N II]. Afterward, we analyze the main ionization mechanisms in galaxies through WHAN and BPT diagrams, and we compare the nebular properties of the gas with the properties of the stellar populations of their host galaxies derived in González Delgado et al. (2021). We characterize the SFR–M* relation derived from the flux of Hα, and we compute the cosmic evolution of ρSFR up to z = 0.35.
This paper is organized as follows. In Sect. 2 we present the galaxy sample taken from miniJPAS, which is the subject of this study. In Sect. 3 we summarize the method we employed, which is based on previous works of MS21 and González Delgado et al. (2021). In Sect. 4 we identify the ELG population by means of the EWs of the emission lines and their relations with the stellar population properties: stellar mass, intrinsic colors, luminosity-age, and so on. We derive the fraction of AGN, quiescent, and star-forming galaxies in miniJPAS. In Sect. 5 we characterize the star-forming galaxy population. We derive their SFR through Hα emission, and we fit the SFMS. In Sect. 6 we discuss the implications of our results in detail and compare them with previous works. We derive the ρSFR up to z = 0.35. Finally, we provide the outlook for J-PAS in Sect. 7, and we summarize in Sect. 8. Throughout this work, we adopt a ΛCDM cosmology with H0 = 70 km s−1 Mpc−1, ΩM = 0.3, and ΩΛ = 0.7. All magnitudes are presented in the AB system (Oke & Gunn 1983), and a Chabrier (2003) initial mass function (IMF) was employed.
2. Sample and data
The galaxy sample studied in this paper is a subsample of the galaxies analyzed in González Delgado et al. (2021, see Sect. 2.3). We selected all the objects detected in miniJPAS with a photometric redshift (photo-z) lower than 0.35, which is the highest redshift at which Hα can be observed in miniJPAS. The photo-z was estimated with the JPHOTOZ package developed by the photo-z team at CEFCA. This package is a customized version of the LePhare code (Arnouts & Ilbert 2011), which has a new set of stellar population synthesis galaxy templates that were optimized for the miniJPAS filter system (Hernán-Caballero et al. 2021). At the depth of miniJPAS (5σ limits between ∼21.5 and 22.5 mag for the narrowband filters and ∼24 mag for the broadband filters in a 3″ aperture), there are 17 500 galaxies per deg2 with valid photo-z estimates (rSDSS < 23), of which ∼4200 have |Δz|< 0.003. The typical error for rSDSS < 23 galaxies is σNMAD = 0.013 with an outlier rate of η = 0.39. The target photo-z accuracy σNMAD = 0.003 is achieved after imposing odds > 0.82 (see Hernán-Caballero et al. 2021, for details).
We imposed a maximum class-star probability of 0.1, as defined in SExtractor, in order to select only extended sources. We discarded galaxies with an S/N lower than 1.8 in the filters to capture the flux of the emission lines. The estimates of the EWs with the ANN for galaxies with a very low S/N yield large errors. Therefore, these errors indicate the limit to which galaxies can be analyzed. For this reason, we favor a more conservative approach by setting a very low constraint on the S/N of the filters with which the flux of the emission lines is captured. Thus, we can exclude galaxies a posteriori when their EW measurements are not reliable. The magnitude limit cut of the sources was set at 22.5 mag in the rSDSS band. This is the completeness limit for miniJPAS extended sources (Bonoli et al. 2021). Finally, the sample is composed of 2154 galaxies in total.
In Fig. 1 we show the relation between the apparent magnitude in the rSDSS band and the redshift for the galaxies in the parent sample. The color bar indicates the median S/N measured in the J-PAS narrowband filters. In this work, we made use of the MAG_AUTO photometry from the miniJPAS dual-mode catalog because it captures the entire light from the galaxy. Most of the galaxies in this sample (∼68%) are higher than 0.205 in redshift and have an S/N lower than 10.
 |
Fig. 1. Relation between the apparent magnitude in the rSDSS band and redshift for all galaxies in the parent sample. We used the MAG_AUTO photometry. Dots are color-coded according to the median S/N of the J-PAS narrowband filters. |
In Fig. 2 we show some examples of galaxies in this sample at different redshift and magnitude bins. Emission lines such as Hα or [O III] are clearly visible in most of them. Some lines are captured by more than one filter (see, e.g., 2241−6186). This is caused by the overlapping adjacent filters, whose separation (100 Å) is smaller that their width (∼145 Å).
 |
Fig. 2. J-spectra in magnitudes (MAG_AUTO photometry) for a set of galaxies within the AEGIS field observed by miniJPAS. Stars correspond to broadband filters (uJPAS, and SDSS g, r, and i). Black dots are the best fit obtained with BaySeAGal to the stellar continuum. Filters including the wavelength of Hα and [O III] emission lines within their bandpass are marked with dashed vertical lines. The images of these galaxies in the rSDSS band are attached in the lower left inset. The miniJPAS ID and the photo-z are shown in black in the left corner of each figure. |
3. Method
3.1. Artificial neural networks
The analysis of the emission lines was carried out with a machine-learning code based on ANN and described in MS21. Different ANNs were trained with the J-PAS synthetic photometry extracted from CALIFA, MaNGA, and SDSS galaxies after convolving the spectra with the J-PAS photometric system. The ANNs learned to perform different tasks. First, an ANN was trained to estimate the EW values for the main emission lines in the optical range: Hα, Hβ, [O III], and [N II]. This ANN is referred to as ANNR. As inputs, the ANNs used photometry colors measured with respect to the J-PAS filter, in which the Hα flux dominates. As outputs, the ANNs received the values of the EWs that were measured directly in the spectrum. We estimated the uncertainty in the EWs with a Monte Carlo approach. We considered the error in the photo-z and the error in photometric fluxes (see MS21 for further details). Second, another ANN was trained to distinguish galaxies with emission lines from those without them. This classifier (ANNC) also relies on the EWs, but it is independent of the prediction from the ANNR. Galaxies were previously classified as class 1 or class 2 depending on whether they exceeded a preselected EW threshold in any of the emission lines. Several ANNC with different thresholds (EWmin = 3, 5, 8, 11, and 14 Å) were trained in order to better study the regime of low emission, in which the ANNR is less sensitive.
As we discussed in MS21, there are many ways of combining the CALIFA, MaNGA, and SDSS surveys to build up a training set. Each survey has its own observational biases, and the emission lines were measured with different approaches. In this work, we made use of the CALMa training set for the ANNR, which performs better in unseen data (SDSS test sample). The CALMa training set employs both CALIFA and MaNGA spectra from spatially resolved regions over many diverse physical states, including AGN emission and SF regions. With the CALMa training set, we are able to fully reproduce the position of SF galaxies in the BPT diagram. We reached a precision of 0.092 and 0.078 dex for log ([N II]/Hα) and log ([O III]/Hβ), respectively, assuming an average S/N in the photometry of 10. We can measure an EW of 10 Å in the Hα, Hβ, [N II], and [O III] lines with a median S/N of 5, 1.5, 3.5, and 10, respectively.
For the ANNC classifier, we employed the CALIFA set, which is a subset of the CALMa set, but only includes CALIFA galaxies. The two training sets performed very similarly in the SDSS test sample. For the sake of simplicity, we therefore employed the CALIFA set.
3.2. Stellar population analysis
The stellar population properties of the galaxies in this sample were analyzed with BaySeAGal (Amorim et al., in prep.; González Delgado et al. 2021). This is a Bayesian parametric code that fits stellar metallicity (Z⋆), dust attenuation (τV), and the parameters related to the star formation history of galaxies. We assumed a delayed-τ model of the form
where t is the lookback-time, t0 is the starting point of star formation in lookback-time, τ is the SFR e-folding time, and ϕ is the normalization constant related to the total mass formed in stars. t0 and τ are sampled uniformly in logarithmic scale, which can vary between 1.4 and the maximum age at the redshift of the galaxy (13.7 Gyr at z = 0), and between 0.1 and 10 Gyr, respectively. For the present work, we chose the attenuation law proposed by Calzetti et al. (2000), which adds a unique foreground screen with a fixed ratio of RV = 4.05 (the average value for the Milky Way).
The code used the 2017 version of the Bruzual & Charlot (2003) stellar population (SSP) synthesis models (hereafter CB17). The SSP covers the metallicity range log Z⋆/Z⊙ = −2.3, −1.7, −0.7, −0.4, 0, and +0.4, and the ages span from 0 to 14 Gyr. The CB17 models follow the PARSEC evolutionary tracks (Marigo et al. 2013; Chen et al. 2015) and use the Miles (Sánchez-Blázquez et al. 2006; Falcón-Barroso et al. 2011; Prugniel et al. 2011) and IndoUS (Valdes et al. 2004; Sharma et al. 2016) stellar libraries in the spectral range observed by J-PAS.
It is important to emphasize that filters capturing the nebular emission lines are masked and were not used in the SED fitting. Therefore, the galaxy properties are only based on the stellar continuum, and it does not include the emission of nebular regions or the result of the AGN activity. The stellar continuum is derived from the ensemble of best fits and allows us to determine stellar masses (M*), metallicities (Z*), the amount of dust attenuation (AV), or the luminosity-weighted age (⟨log t⟩L) of galaxies. Furthermore, it is also used to extrapolate the photometry in the filters that lack a measurement or have a very low S/N (lower than 1.8). Because the ANN (as we designed it) cannot work with missing data, these extrapolations allow the ANN to access all the inputs needed (photometric fluxes). This does not apply to the filters containing emission lines at each redshift and the filters that are immediately next to them. For instance, the Hα emission line is captured by the J0660 filter for a galaxy in the local Universe (z = 0). Therefore, the fluxes in filters J0650, J0660, and J0670 are never extrapolated. When problems in the photometry with these filters occurred, we did not include the corresponding galaxies in our sample.
The use of alternative SED fitting codes to derive stellar population properties of miniJPAS galaxies does not affect the main results in this paper. González Delgado et al. (2021) analyzed in detail how the main properties derived for galaxies might change with different SED fitting approaches. The results are consistent between each other: nonparametric codes such as MUFFIT (Díaz-García et al. 2015), Alstar (the algebraic version of starlight Cid Fernandes et al. 2005), or TGASPEX (Magris et al. 2015) and BaySeAGal all obtained similar distributions of rest-frame (u − r) color, stellar mass, age, and metallicity up to z = 1.
A summary of the stellar population properties of the galaxies we analyzed is shown in Fig. 3. The distributions of the galaxy ages and the τ/t0 ratio are bimodal. BaySeAGal provides rest-frame colors and extinction-corrected colors. In particular, (u − r)int is very useful for distinguishing between red and blue galaxies. We followed the criterion of Díaz-García et al. (2019, hereafter the color criterion), in order to distinguish them. This criterion was adapted to match the miniJPAS photometric system (Díaz-García et al., in prep.). For a galaxy to be part of the red sequence, this criterion establishes a limit in (u − r)int from the galaxy stellar mass and redshift,
 |
Fig. 3. Distributions of mean stellar luminosity-weighted age (top left panel), galaxy stellar mass (lower right panel), extinction (lower left panel), and τ/t0 ratio (bottom right panel) obtained by BaySeAGal for the sample of galaxies described in Sect. 2. |
Galaxies with (u − r)int above 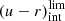 are classified as red galaxies, otherwise, they are considered to be blue. Furthermore, BaySeAGal provides the probability distribution function (PDF) for the model parameters. The uncertainty on the derived stellar population properties is defined as the standard deviation. As expected, the uncertainty depends on the S/N of the photometry. The median errors are lower in the red sequence than in the blue cloud. That is, ⟨σ(log M⋆)⟩ = 0.16 ± 0.03 dex, ⟨σ(⟨log t⟩L)⟩ = 0.19 ± 0.05 dex, ⟨σ(AV)⟩ = 0.19 ± 0.07 mag, and ⟨σ(τ/t0)⟩ = 0.10 ± 0.04 for galaxies in the red sequence, and ⟨σ(log M⋆)⟩ = 0.28 ± 0.04 dex, ⟨σ(⟨log t⟩L)⟩ = 0.25 ± 0.05 dex, ⟨σ(AV)⟩ = 0.33 ± 0.05 mag, and ⟨σ(τ/t0)⟩ = 0.5 ± 0.19 for those in the blue cloud.
are classified as red galaxies, otherwise, they are considered to be blue. Furthermore, BaySeAGal provides the probability distribution function (PDF) for the model parameters. The uncertainty on the derived stellar population properties is defined as the standard deviation. As expected, the uncertainty depends on the S/N of the photometry. The median errors are lower in the red sequence than in the blue cloud. That is, ⟨σ(log M⋆)⟩ = 0.16 ± 0.03 dex, ⟨σ(⟨log t⟩L)⟩ = 0.19 ± 0.05 dex, ⟨σ(AV)⟩ = 0.19 ± 0.07 mag, and ⟨σ(τ/t0)⟩ = 0.10 ± 0.04 for galaxies in the red sequence, and ⟨σ(log M⋆)⟩ = 0.28 ± 0.04 dex, ⟨σ(⟨log t⟩L)⟩ = 0.25 ± 0.05 dex, ⟨σ(AV)⟩ = 0.33 ± 0.05 mag, and ⟨σ(τ/t0)⟩ = 0.5 ± 0.19 for those in the blue cloud.
4. Identification of ELGs
In this section, we show the potential of our methods to identify ELG in the AEGIS field and determine their main ionization mechanism. The EW of Hα, Hβ, [O III], and [N II] and their relative strengths allow us to distinguish between different types of ELGs and derive the fraction of star-forming, Seyfert, and quiescent galaxies in miniJPAS.
4.1. Identification with ANNR: EW distributions
First, we show the EW distribution of the Hα, Hβ, [O III], and [N II] lines in Fig. 4 derived with the ANNR. We excluded from the histograms galaxies where the EWs are below zero. Even though the ANNR was not trained with absorption lines, certain configurations can indeed lead to negative values of the EWs. If the fluxes in the filters in which the emission lines are expected to appear are suppressed or are highly uncertain, or if they mimic the shape of an absorption line, the ANNR might predict EWs that are below zero. We find 20, 2, 299, and 23 galaxies with negative EWs in Hα, Hβ, [O III], and [N II], respectively. The median S/N in the EWs for these galaxies is below one, which indicates that these values are compatible with positive and null values.
 |
Fig. 4. Distribution of the EW of Hα and Hβ (left), [O III], and [N II] (right) in log scale as obtained with the ANNR. |
Generally, blue galaxies are star-forming galaxies, while red galaxies are quiescent. However, a galaxy might appear to be part of the red sequence due to the presence of dust, which absorbs a fraction of the total radiation more efficiently on the blue side of the spectrum. Therefore it is important to correct for dust extinction in order to distinguish between red and dust-reddened star-forming galaxies.
Figure 5 shows as expected that blue galaxies contain young populations of stars with high values of EW(Hα), while red galaxies are older and lack Hα emission or have very low values of EW(Hα). Between the red sequence and the blue cloud, we observe galaxies in the GV with intermediate ages and moderate values in the EWs of Hα.
 |
Fig. 5. Color–mass diagram for our sample of galaxies. The (u − r) color-corrected for dust extintion vs. stellar mass. Galaxies are color-coded with the EW of Hα (the luminosity-weighted stellar age) on the left side (right side). The intrinsic color, stellar mass, and luminosity-weighted age are obtained via BaySeAGal. Dashed black lines separate blue and red galaxies following Eq. (2), where we considered the median redshift of the sample (z = 0.25). Density contours are drawn in black at the top. |
4.2. Identification with the ANNC: Strong and weak ELGs
In addition to the color-criterion, we can also make use of the predictions of the ANNC to distinguish between galaxies above and below a certain threshold limit in the EW. The EW of Hα quantifies the relative intensity of the emission line flux with respect to the stellar continuum, and therefore it is a good indicator of the sSFR in the galaxy (Mármol-Queraltó et al. 2016; Khostovan et al. 2021). In Fig. 6 we plot the log EW(Hα) as a function of the stellar mass. In the left panel, we indicate in blue (red) the galaxies that belong to the blue cloud (red sequence) following the color criterion. On the right panel we show a similar scheme but galaxies are separated according to the class defined by the ANNC with EWmin = 3 Å. In other words, galaxies are considered strong ELs if any of the emission lines present an EW greater than 3 Å and weak ELs if all lines are below this limit. For a threshold of 0.1 in the ANNC probability, strong ELs represent 83% of the sample, while weak ELs are the remaining 17%. With the color criterion, 82% of the galaxies in the parent sample are classified as red and the remaining 18% are blue.
 |
Fig. 6. Equivalent width of Hα as a function of the stellar mass of the galaxy. Left panel: we used Eq. (2) to distinguish between red and blue galaxies. Right panel: we relied on the classification performed with a machine-learning code trained with strong EL and weak EL galaxies. Strong ELs were defined as those with EWs greater than 3 Å in any of the following emission lines: Hα, Hβ, [O III], or [N II], and weak ELs are all others. The dashed horizontal lines mark the 3 Å limit in the EW(Hα). Density contours are drawn in black at the top. |
The dashed line in Fig. 6 illustrates the EW(Hα) = 3 Å limit. As expected, most of the galaxies below this limit are classified as weak ELs. However, we detect a non-negligible number of weak ELs or red galaxies above this limit in both panels. We have to take into account that the ANNR is less accurate at low EWs and has a tendency to overestimate their values. Moreover, the relative errors in this regime are higher (see MS21). Therefore, it is not surprising to find a fraction of weak EL galaxies above this limit. Moreover, although Hα leads the ANNC classification, the algorithm includes other emission lines in addition to Hα, which might occasionally overcome this limit. At high EWs, the number of weak EL galaxies decreases significantly, and the discrepancy between the ANNR and the ANNC can be explained by the high uncertainty found in the photo-z or a low S/N in the photometric fluxes.
In two panels in Fig. 6, the two methods of classifying galaxies present a consistent picture. Most of the blue galaxies are strong ELs, and red galaxies are weak ELs. Nevertheless, we found some disagreement between the last two populations. While the ANNC is trained to separate galaxies as a function of the EW, Eq. (2) depends mainly on the global color and the mass of the galaxy. Thus, it is expected to find some galaxies with red intrinsic colors and a low level of star formation reflected on the nebular emission with EWs greater than 3 Å.
Finally, it is clear from these diagrams that galaxies are less efficient at forming new stars as the mass of the galaxy increases at z < 0.35. At some point around M* = 1011 M⊙, the EW of Hα falls sharply, with most galaxies above this mass showing red colors and low values in the EW(Hα), suggesting that the main sequence of star-forming galaxies has already ended.
4.3. Identification of star-forming galaxies and AGNs: BPT and WHAN diagrams
The BPT diagram (log[O III]/Hβ versus log[N II]/Hα) provides a means to unveil the main ionization mechanism of galaxies. It involves four emission lines, and galaxies are classified into four groups by three dividing lines: star-forming, composite, Seyfert, and LINERs. The Kauffmann et al. (2003, hereafter Ka03), curve is derived empirically using the SDSS galaxies and defines the region populated by SF galaxies. Usually referred to as the SF wing, galaxies evolve from high (low) to low (high) [O III]/Hβ ([N II]/Hα) ratios, increasing their mass (Maiolino & Mannucci 2019). The Kewley et al. (2001, hereafter Ke01), curve is determined using both stellar population synthesis models and photoionization. It defines the AGN wing that is dominated by AGN (including LINER or LINER-like emission, and shocks). Between these two lines lies the composite region, which might be populated by galaxies with a composite spectrum, that is, the ionization mechanism is a mix of star-formation processes and AGN activity or galaxies with very weak emission lines that are leaving the SFMS. Finally, the Schawinski et al. (2007, hereafter S07), line is an empirical division that distinguishes between Seyfert and LINER galaxies.
We show the BPT diagram for the galaxies in the parent sample with error lower than 0.2 dex in [O III]/Hβ and [N II]/Hα in the left panel of Fig. 7. In the right panel, we relax this threshold to 0.5 dex. These thresholds are arbitrary, and they have been chosen to show how the BPT diagram changes when galaxies with a high uncertainty in the measurement of the emission lines are included. However, they are not used for the final selection of SF galaxy sample. The stellar mass distribution of galaxies in the BPT is consistent with expectations: galaxies grow in mass while they evolve through the SF wing. However, as the error increases (right panel), some galaxies populate regions that are less likely to be occupied (the narrowest wedge at the top left within the composite region).
 |
Fig. 7. BPT diagram for the galaxies in the sample with an error of 0.2 dex (0.5 dex) in the [O III]/Hβ and [N II]/Hα ratios in the left (right) panel. The errors are not plotted in the right panel for clarity. The color bar indicates the stellar mass of the galaxy. The solid (Ka03), dashed (Ke01), and dotted lines (S07) define the regions for the four main spectral classes. The relative percentage of each galaxy type in each subsample is indicated in the figure. In each panel, the number of galaxies is specified in the lower left corner. The parent sample contains 2154 galaxies. |
Galaxies with very faint emission lines may be misclassified as LINERs from a BPT diagnostic. Sometimes called fake AGN (Cid Fernandes et al. 2011), one of the advantages of the WHAN (log EW(Hα) versus log ([N II])/Hα)) diagram is that it can identify these galaxies. Even more important is the fact that the WHAN diagram provides a simpler way of determining the main ionization mechanism of galaxies.
Figure 8 we show the WHAN diagram for the galaxies in the parent sample. The solid and dashed vertical lines represent the optimal projection of Ka03 and Ke01 onto the log EW(Hα) versus log ([N II])/Hα) space, that is, the dividing lines that better distinguish galaxy types in the WHAN diagram as they are defined in the BPT (Cid Fernandes et al. 2010, 2011). Similarly, the division between Seyferts and LINERs at EW(Hα) = 6 Å corresponds to the optimal projection of S07. Finally, the area below the dashed horizontal line at EW(Hα) = 3.16 Å is composed of galaxies with highly uncertain line measurements that are therefore compatible with quiescent galaxies. We did not distinguish between retired and passive galaxies as in Cid Fernandes et al. (2011) because our precision is not high enough to measure values of the EWs in the range of a few Å.
 |
Fig. 8. WHAN diagram for galaxies with an error smaller than 0.2 dex (0.5 dex) in both the EW(Hα) and the [N II]/Hα ratio in the left (right) panel. The errors are not shown in the right panel for clarity. The color bar indicates the stellar mass of the galaxy. The inset shows the relative percentage of each galaxy type in each subsample. Dashed and solid vertical lines define the optimal projections of the Ke01 and the Ka03 lines in the WHAN diagram (Cid Fernandes et al. 2010, 2011). Similarly, the dash-dotted horizontal line at EW(Hα) = 6 Å is the optimal transposition of the S07, and the dotted line at log EW(Hα) = 0.5 Å defines the limit of ELGs. In each panel, the galaxy counts are specified in the lower left corner. The parent sample contains 2154 galaxies. Density contours are drawn in black at the top. |
In the left panel of Fig. 8 we show galaxies with an error smaller than 0.2 dex in both the EW(Hα) and the [N II]/Hα ratio, while in the right panel, we relax this requirement to 0.5 dex. The percentage of each galaxy type is indicated in the legend. Galaxies with lower EW(Hα) have higher relative errors. Furthermore, many red galaxies do not appear in this diagram.
The color gradient in Fig. 8 indicates that galaxies are more massive as the EW(Hα) decreases and the [N II]/Hα ratio increases. Therefore, star-forming galaxies are on average less massive than Seyferts, while LINERs and passive galaxies are the most massive galaxies.
By comparing the position of each galaxy (i.e., their values with errors) in both diagrams, it is noticeable that the values of a given galaxy in the BPT convey more uncertainties than in their counterpart spot in WHAN. The reason is that the error in the y-axis of the BPT diagram stems from two sources: the error in the [O III] and Hβ emission lines. However, in the WHAN diagram, the only error source is the Hα emission line. As a consequence, with a maximum error of 0.2 dex, we can estimate the position of only 255 galaxies of the sample in the BPT and 753 galaxies in the WHAN. The median S/Ns of these subsamples in the narrowband filters are 10.7 and 11.4.
4.4. Fraction of galaxy types in miniJPAS
We identify 83% of the galaxies (1787) from the parent sample (2154 galaxies) in the AEGIS field as strong ELGs, and the remaining 17% (367 galaxies) are weak ELGs. In Table 1 we show the percentages of each galaxy type according to the WHAN diagram for all galaxies with an error smaller than 1 dex in the EW(Hα) and [N II]/Hα ratio. This criterion is fulfilled by 2000 galaxies, which leaves 154 galaxies from the parent sample unclassified. We eliminate the composite population, but we indicate the percentage of SF and Seyfert galaxies in the different separation curves: Ka03, Ke01, or Stasińska et al. (2008, hereafter S08). Although we showed in Fig. 8 the percentages for LINERs and passive galaxies, we grouped both classes together in this table. The emission lines for LINER galaxies are at the limit of what we can detect with the ANN given the S/N in the photometry. Hence, it is more challenging to distinguish them in the low S/N regime. We estimated the percentages and the errors of each galaxy type with a Monte Carlo (MC) method using the position of each galaxy in the diagram and its errors. Then, we computed the median and the standard deviation.
Percentage of each galaxy type according to the WHAN diagram.
Finally, we studied how the fractions of SF, Seyfert, and quiescent (passive or LINER) galaxies varied when we imposed brighter flux limit constraints. For this purpose, we generated new samples of galaxies that are below 20.5, 21.5, and 22.5 mag in the rSDSS band and computed the fraction of each galaxy type. The results are shown in Fig. 9. We do not observe a strong correlation with the rSDSS apparent magnitude. The fraction of each galaxy type is more uncertain when one or another of the separation curves is chosen.
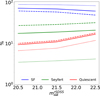 |
Fig. 9. Fraction of SF, Seyfert, and quiescent (passive or LINER) galaxies as a function of the maximum rSDSS apparent magnitude of each subsample. Solid, dashed, and dotted lines represent the fraction of each galaxy type according to the Ka03, Ke01, and S08 curves, respectively. |
5. Characterization of star-forming galaxies
In this section, we characterize the star-forming galaxy population in miniJPAS. We traced the SFR through the Hα emission line. First, we selected a suitable sample of star-forming galaxies with the identification tools we presented in the previous section. Then, we corrected the Hα flux from nebular extinction and derived the position of SF galaxies in the SFMS. We also analyzed the correlation between nebular and stellar extinction and the relation between the star formation history (SFH) of galaxies obtained with the SED fitting and their position in the SFMS.
5.1. Selection of star-forming galaxies
Our sample of star-forming galaxies was obtained from the parent sample (Sect. 2) by imposing different constraints. We relied on the WHAN diagram to exclude the galaxies in which the main ionization mechanism is not driven by star formation (AGN-like galaxies). We chose the Ka03 curve. In order to consider a galaxy as a member of the main sequence, we therefore imposed a maximum [N II]/Hα of 0.48. We also discarded galaxies with very low emission in the diagram (LINER and passive galaxies). Finally, galaxies must be classified as blue with the color criterion and the ANNC to be part of our sample. We found 1178 galaxies in total (SF sample hereafter).
In Fig. 10 we show the relation between the total stellar mass and the redshift for all galaxies in the parent sample. The solid black line indicates the limit at which galaxies cannot be observed in our flux-limited sample (see Sect. 2). In order to be complete in mass, we would need to discard a large fraction of galaxies and risk to loose statistical reliability. Furthermore, the mass dynamical range would be significantly reduced at high redshift. Therefore, we fit the SFMS in two cases: using the whole SF sample, or using only galaxies in the SF sample that are above the stellar mass detection limit (see Sect. 5.3). We will also study how stronger flux limit constraints affect the shape of the SFMS. As soon as J-PAS observes larger areas of the sky, we will be able to be more conservative in the mass limit of the selected sample.
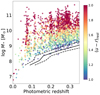 |
Fig. 10. Relation between galaxy stellar mass and redshift for all galaxies in the parent sample. The solid black line is the limit at which galaxies can no longer be observed with the criteria we used to select the sample (see Sect. 2). Dashed black lines represent the uncertainty limit (±σ). Galaxies are color-coded according to their (u − r) rest-frame color. |
5.2. Dust correction
In order to account for the extinction of dust, we followed the empirical extinction relation described in Calzetti et al. (1994). The intrinsic luminosity of galaxies (Lint) is attenuated by interstellar dust through the following equation:
where Lobs is the observed luminosity, Aλ is the extinction at wavelength λ, and k(λ) is the reddening curve. We considered the reddening curve of Calzetti et al. (2000) with RV = 4.05. The nebular color excess E(B − V) can be obtained from the Balmer decrement assuming regular gas conditions in star-forming galaxies (for a detailed description, see, e.g., Domínguez et al. 2013, and references therein) as follows:
where Hα and Hβ stand for the emission line fluxes. As the ANNR provides the values of the EWs, we used the stellar continuum derived from BaySeAGal at the Hα and Hβ wavelengths to compute the total flux of the emission lines.
In the left panel of Fig. 11 we show the distribution of the nebular (E(B − V)Hα/Hβ) and stellar (E(B − V)SED) color excess. A fraction of galaxies in the SF sample (∼15%) have a Balmer decrement below the theoretical value (2.86), but very close to it. Furthermore, its errors indicate that nebular extinction for these galaxies is compatible with null or very low values. Either way, we set the E(B − V)Hα/Hβ to zero for these galaxies. E(B − V)SED is 0.017 mag higher on average than E(B − V)Hα/Hβ with a dispersion of 0.072 mag. The median error on the E(B − V)Hα/Hβ and E(B − V)SED is 0.089 and 0.015, respectively. Some authors reported that E(B − V)Hα/Hβ is twice E(B − V)SED on average (Calzetti et al. 2000; Qin et al. 2019; Koyama et al. 2019). However, other studies found similar levels of nebular and stellar extinction (Kashino et al. 2013; Puglisi et al. 2016). In particular, we found agreement with the results of Kouroumpatzakis et al. (2021, see Fig. 8 and Table 1), who argued that nebular extinction is much more pronounced in the nuclear regions, affecting the relations found by single spectroscopic surveys such as the SDSS, which cannot capture the whole light produced in galaxies.
 |
Fig. 11. Distribution of the nebular (E(B − V)Hα/Hβ) and stellar (E(B − V)SED) color excess (left). Nebular extinction at the Hα wavelength as a function of stellar mass (right). Galaxies are color-coded with the EW of Hα and belong the SF sample described in Sect. 5.1. Black squares are the median obtained in the following stellar mass bins: 8 < log M* ≤ 9, 9 < log M* ≤ 9.5, 9.5 < log M* ≤ 10, 10 < log M* ≤ 10.5, and 10.5 < log M* ≤ 11. The error bars on the y-axis represent the standard deviation, gray contours represent the density of sources for 1σ, 2σ, and 3σ derived from SDSS galaxies in Duarte Puertas et al. (2017). Red stars are the values obtained by Sobral et al. (2016) by means of spectroscopy measurements in SF galaxies within the cluster CL 0939+4713 at z = 0.41. The dashed black line is the best polynomial fit obtained by Garn & Best (2010) in a sample of SDSS galaxies. |
The right panel of Fig. 11 shows the nebular extinction at the Hα wavelength (AHα) as a function of the galaxy stellar mass. We found a similar trend as in other studies. Red stars are the values obtained by Sobral et al. (2016) by means of spectroscopy measurements in SF galaxies within the cluster CL 0939+4713 at z = 0.41. Gray contours represent the density of sources for 1σ, 2σ, and 3σ derived from all SDSS SF galaxies in Duarte Puertas et al. (2017). Finally, the dashed black line is the best polynomial fit obtained by Garn & Best (2010) in a sample of SDSS galaxies. Applying aperture correction to the Hα/Hβ ratio as in Duarte Puertas et al. (2017) lowers the extinction 0.2 mag in average.
5.3. Fitting the star formation main sequence
The SFR was obtained from the Hα luminosity using the Kennicutt et al. (1994) relation converted to employ a Chabrier IMF (Chabrier 2003) and assuming case B recombination,
We used this relation to derive the SFR from the corrected Hα luminosity. Then, we fit the SFMS for the galaxies in the SF sample assuming a power-law relation between the stellar mass (M*) and the SFR,
We assumed that galaxies deviate from this relation with a scatter perpendicular to the line that we parameterized in terms of the scatter along the y-axis (σy), often called σint. We employed a Bayesian approach to derive the posterior distribution of σy, α, and β. We followed Robotham & Obreschkow (2015) in order to construct the likelihood function,
where 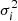 reads
reads
We assumed that the errors in the SFR and stellar mass of the galaxies are not correlated. This hypothesis is justified because both quantities are derived independently from each other. Although the flux of stellar continuum at Hα wavelength is used to estimate the total Hα flux, its error is negligible compared to the error in the EW. The errors are considered Gaussian and heteroscedastic, that is, each data point is drawn from a different Gaussian distribution. The last term in Eq. (7) ensures that the data are rotationally invariant. In other words, data have no defined predictor or response variable, and therefore we can predict the SFR from the stellar mass of the galaxy and vice versa.
The posterior distribution was sampled with the Markov chain Monte Carlo (MCMC) method, using the emcee Python implementation (Foreman-Mackey et al. 2013), with 250 walkers and 5000 steps per walker. We used a burn-in phase of 3500 steps.
Figure 12 shows the SFMS for the galaxies in the SF sample; in black we plot the ensemble of best fits obtained with the Bayesian routine. Galaxies are color-coded with the τ/t0 ratio, which is an indicator of the SFH (see Eq. (1)). High values of τ/t0 indicate an SFH with almost constant SFR throughout cosmic time, while low values are related to galaxies with a burst of star formation long ago with a decreasing SFR ever since.
 |
Fig. 12. SFR vs. stellar mass for the galaxy sample described in Sect. 5.1. Galaxies are color-coded with the τ/t0 ratio (see Sect. 3.2). Black lines are the best fits obtained with the Bayesian routine. The median posterior value and 1σ confidence interval are shown for each of the parameters. |
On the one hand, the color gradient observed in Fig. 12 suggests that galaxies with higher values of τ/t0 are more likely to be found above the SFMS and preferentially have stellar masses below 1010 M⊙. On the other hand, lower values of τ/t0 are associated with massive galaxies that lie below the SFMS.
We investigated how the parameters of the SFMS are affected when we included only the galaxies in the SF sample that lie above a certain flux limit. Additionally, we generated a new sample of galaxies that were selected from the SF sample with stellar masses above 109 M⊙ (SF0 sample). This is the stellar mass detection limit for the redshift between 0 and 0.35 (black line in Fig. 10). Subsequently, we studied again how the flux limit cut affects the parameters of the SFMS. The results are summarized in Table 2. We conclude that the selection function that depopulates the SFMS below mAB = 22.5 in the rSDSS band does not affect the shape of the SFMS. The results for the SF and SF0 sample are consistent (compatible within the errors).
Parameters of the SFMS with different selection cuts in the rSDSS band for the SF (SF0) sample at the top (bottom).
5.4. SFR at different redshift
The relation of the SFR and the stellar mass is expected to change as a function of the redshift due to changes in the cosmic gas accretion rates and the gas depletion timescales. Some authors modeled this relation with a power law (SFR ∝ (1 + z)a, Boogaard et al. 2018; Schreiber et al. 2015), others assumed that the evolution takes place in the zeropoint (log SFR ∝ βz, Shin et al. 2021). Another common approach is to split the sample into redshift bins and fit them independently (e.g., Davies et al. 2016; Thorne et al. 2021). Because the redshfit range of the SF sample is limited, we decided to employ the latter approach and fit the SFMS in three different redshift bins: 0 < z ≤ 0.15, 0.15 < z ≤ 0.25, and 0.25 < z ≤ 0.35. We removed all galaxies in each sample that lay below the stellar mass limiting value (solid black line in Fig. 10).
We show the results in Fig. 13. A small flattening of the relation is seen at intermediate redshifts, but it may not be significant. As expected due to the anticorrelation between the slope and the zeropoint, the latter becomes higher in the 0.15 < z ≤ 0.25 bin. Most likely, these discrepancies are caused by the effect of fitting the SFMS within a smaller dynamical range of mass and by the lower statistics. The intrinsic scatter of galaxies along the SFMS decreases at higher redshifts. This may be caused by a dependence on stellar mass rather than on redshift. Galaxies below 1.6 × 108 M⊙, 5 × 108 M⊙, and 109 M⊙ for 0 < z ≤ 0.15, 0.15 < z ≤ 0.25, and 0.25 < z ≤ 0.35, respectively, cannot be detected with fluxes brighter than 22.5 in the rSDSS band. We discuss the implication of this result in more detail in Sect. 6.1.2.
 |
Fig. 13. SFR vs. stellar mass for galaxies in different redshift bins color-coded with their the τ/t0 ratio (see Sect. 3.2). Black lines are the best fits obtained with the Bayesian routine. The median posterior value and 1σ confidence interval are shown for each of the parameters. The number of galaxies within each redshift bin is also indicated. |
5.5. Turnover mass hypothesis
Several studies have shown evidence that the relation between the SFR and the stellar mass turns over at a mass of M* ∼ 1010 M⊙ (Whitaker et al. 2014; Lee et al. 2015; Schreiber et al. 2015; Tomczak et al. 2016). In this section, we investigate this scenario by fitting a quadratic power law (Eq. (9)) and a broken power law (Eq. (10)) to the SF sample,
We obtained a turnover mass (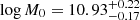 ) that is very close to the highest mass that we have in the SF sample (
) that is very close to the highest mass that we have in the SF sample (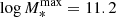 ). Furthermore, only 14 out of 1178 galaxies have a mass higher than M0. For the quadratic model, we obtained a quadratic term near zero (
). Furthermore, only 14 out of 1178 galaxies have a mass higher than M0. For the quadratic model, we obtained a quadratic term near zero (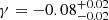 ). In Table A.1 (see next section) we show the best-fitting parameters for different separation curves. We employed the Bayesian information criterion (BIC) to determine the model that better describes the observed SMFS. The BIC is defined as BIC = nparamlnNgal − 2lnL, where nparam is the number of parameters in the model, Ngal is the number of galaxies, and L is the likelihood function. The linear model (Eq. (6)) obtained the lowest value. Therefore, it is the most likely model.
). In Table A.1 (see next section) we show the best-fitting parameters for different separation curves. We employed the Bayesian information criterion (BIC) to determine the model that better describes the observed SMFS. The BIC is defined as BIC = nparamlnNgal − 2lnL, where nparam is the number of parameters in the model, Ngal is the number of galaxies, and L is the likelihood function. The linear model (Eq. (6)) obtained the lowest value. Therefore, it is the most likely model.
5.6. AGN selection criteria
The exclusion of AGN-like galaxies from the SF sample is based on the [N II]/Hα ratio and the EW of Hα. We chose the curve of Ka03 to select SF galaxies, but we could have relied on other separation curves, such as Ke01 or S08. In this section we study how these choices can impact our result.
In Table A.1 we show the best-fit parameter values as a function of the separation curves, the redshift bin, and the fitting equation used to model the SFMS. The results are marginally consistent, meaning that the retrieved parameter does not change the main conclusion of the previous sections. Nevertheless, we observed a trend in the slope, the quadratic term, and in the turnover mass as we relaxed the maximum [N II]/Hα ratio allowed to be part of the SFMS. Galaxies at the border of the dividing lines populate the high-mass end. As a consequence, the quadratic terms and the turnover mass increase as the slope of the SFMS flattens. Nonetheless, the intrinsic scatter exhibits little variation, except for the highest redshift bin, where higher-mass galaxies increase the scatter. This exercise demonstrates that the SFMS can be affected by AGN contamination, which is only one ingredient in the definition of the SFMS. Other criteria based on color cuts or sSFR thresholds are also important and can have a non-negligible impact on the derived parameters of the SFMS (Belfiore et al. 2018; Sánchez et al. 2019; Khostovan et al. 2021).
6. Discussion
In the following sections, we compare the results of the SFMS with the literature. We derive the cosmic evolution of the star formation rate density up to z = 0.35, and we discuss the differences we found with respect to other studies that did not trace the SFR with Hα emission line.
6.1. SFMS: Comparison with the literature
We have modeled the SFMS in the mass range from 108 up to 1011 M⊙ in the redshift range 0 < z < 0.35. We employed a Bayesian approach (Sect. 5.3) that considers the intrinsic scatter of the SFMS and the heteroscedastic errors on the stellar masses and the SFRs. We derived the SFRs from the Hα emission line, and we corrected for dust extinction through the Balmer decrement. We relied on the [N II]/Hα ratio to remove from the sample galaxies hosting an AGN. The linear model explains the relation between the logSFR and log M* for the sample of SF galaxies better. Our selection criteria combine color-cut and emission line diagnostics and consequently favour a pure rather than a complete sample of SF galaxies. Most probably, we also excluded most of the GV population, and this might explain why the turnover-mass scenario is not compatible with our results. We compare our results with the literature below. We focus our attention on the slope of the SFMS and on the intrinsic scatter.
6.1.1. Slope
We find a result very similar to those of Sánchez et al. (2019) (MaNGA) and Cano-Díaz et al. (2016) (CALIFA), but our slope is steeper than those of Belfiore et al. (2018) and Cano-Díaz et al. (2019), who used MaNGA data. Our results are also consistent with the recent work of Vilella-Rojo et al. (2021), who studies the SFR of galaxies in the nearby Universe with J-PLUS data. SDSS galaxies have also been used to analyze the SFMS. The slopes found by Zahid et al. (2012) and Renzini & Peng (2015) are flatter than our results. Nevertheless, Duarte Puertas et al. (2017) applied aperture correction based on CALIFA data (Iglesias-Páramo et al. 2016) to recover the total flux from SDSS fiber spectroscopy and found a slope of 0.935, which is very close to our slope, which we obtained with the SF sample in the 0 < z ≤ 0.35 redshift range (see Fig. 14). Shin et al. (2021) obtained a flatter slope than we did based on galaxies from the Subaru Deep Field at intermediate redshift (0.1 < z ≤ 0.5). However, we recovered a slope that is marginally consistent with the one found by Boogaard et al. (2018), who used data from the Multi Unit Spectroscopic Explorer (MUSE) and employed the same method as we used to fit the SFMS.
 |
Fig. 14. Slope of the SFMS derived from the Hα emission line by different works as a function of the redshift. The bars on the x-axis represent the redshift range of the galaxies involved in each study. Our best fit of the SFMS is shown with large blue stars for the lowest redshift range (0 < z ≤ 0.15) and the SF sample (0 < z ≤ 0.35). The results of the literature are from Boogaard et al. (2018) (B18), Vilella-Rojo et al. (2021) (V21), Duarte Puertas et al. (2017) (D17), Renzini & Peng (2015) (R&P15), Zahid et al. (2012) (Z12), Shin et al. (2021) (S20), Belfiore et al. (2018) (Be18), Cano-Díaz et al. (2019) (C19), Sánchez et al. (2019) (S19), and Cano-Díaz et al. (2016) (C16). We also include the results derived by GALFROM (a semianalytical model) (Mitchell et al. 2014) (Mi15), and from hydrodynamical simulations, Sparre et al. (2015) (Sp15) and Furlong et al. (2015) (F15). |
6.1.2. Intrinsic scatter
The amount of intrinsic scatter is hard to constrain because the scatter caused by the measurements errors in both the stellar masses and the SFRs needs to be accounted for. As pointed out by Boogaard et al. (2018), this is one of the advantages of using the fitting model of Robotham & Obreschkow (2015). We obtained an intrinsic scatter of 0.20 dex for the SF sample (0 < z ≤ 0.35). This is consistent with previous works, which found values ranging from 0.15 up to 0.5 dex (see, e.g., Whitaker et al. 2012; Salmi et al. 2012; Speagle et al. 2014; Schreiber et al. 2015; Ilbert et al. 2015).
Many factors than can impact the amount of intrinsic scatter. First of all, different SFR indicators account for variations in the SFH on different timescales (see, e.g., Davies et al. 2016, and references therein). For instance, while Hα provides a direct measure of the current SFR in galaxies (< 10 − 20 Myr), UV-like tracers can detect changes in the SFH in only the last 100 Myr and are therefore less sensitive to recent episodes in the SFH that enhance or suppressed the star formation in the galaxy. Secondly, the selection criteria that defined the SFMS can boost or decrease artificially the scatter by excluding or including a fraction of galaxies that ‘belong’ or not to the SFMS.
The results obtained in each redshift bin show a decrease in intrinsic scatter for galaxies with higher redshift. The MC approach predicts σy to be compatible with zero in the last redshift bin. This might be the effect of the method. When we averaged over all galaxies in Eq. (8) and solved for σy, we found σy = 0.19, 0.09, and 0.17 dex for 0 < z ≤ 0.15, 0.15 < z ≤ 0.25, and 0.25 < z ≤ 0.35, respectively. However, we found a very similar value for the SF sample of galaxies (0.22 dex). As we pointed out in Sect. 5.4, the selection function in the SF sample together with the low statistics in each redshift bin might affect the results.
6.1.3. SFMS with BaySeAGal
The SED fitting performed by BaySeGal yields the SFH of galaxies, and therefore we can estimate the current SFR in each galaxy by summing all the mass that formed stars in the last 30 Myr. Since tau-delayed models cannot account for a bursty SFH, any value between 10 and 200 Myr provides essentially the same SFR. A comparison of the results of the SFMS derived from the flux of Hα with a different and independent technique provides valuable information about the potential inaccuracies and strengths of our method.
In Fig. 15 we show the SFMS for the same sample of galaxies described in Sect. 5.1 that is plotted in Fig. 12. The color code now represents the EW of Hα. As expected, galaxies with higher values in the EW of Hα are placed above the main sequence. This suggests that the two methods are consistent overall. Nevertheless, we obtained a zeropoint that is higher, meaning that the SFR derived from the analysis of the stellar populations gives higher values on average. This discrepancy later translates into the cosmic SFR density and the number of ionizing photons. In Sect. 6.3, we discuss the possible origin of this difference in detail.
 |
Fig. 15. SFR vs. stellar mass for the galaxy sample described in Sect. 5.1. SFRs are derived from BaySeGal. Galaxies are color-coded with the EW of Hα. Black lines are the best fits obtained with the Bayesian routine. The median posterior value and the 1σ confidence interval are shown for each of the parameters. |
We obtain a slope that is slightly flatter, but still closer to what we retrieved with Hα. The different assumptions made by each method mean that this difference is expected. While the Hα flux is very sensitive to recent changes in the star formation activity of a galaxy, the SFR derived from the SED fitting traces the SFR on longer timescales. As a consequence, recent episodes that enhance or suppress the SFR might result in a global change in slope with respect to an SFMS derived from the average SFR over the last 200 Myr.
6.2. Cosmic evolution of the star formation rate density
The star formation rate density of the universe has been estimated by different means. Galaxy redshift surveys found that ρSFR peaks at ∼3.5 Gyr after the Big Bang (z ∼ 2) and has decreased ever since (e.g., Gunawardhana et al. 2013; Sobral et al. 2013; Madau & Dickinson 2014; Driver et al. 2018). A similar trend was confirmed with galaxies in the nearby Universe using the so-called fossil record method (López Fernández et al. 2018; Sánchez et al. 2019; Bellstedt et al. 2020). Very recently, González Delgado et al. (2021) employed this method to derived the ρSFR from a subsample of galaxies in miniJPAS (0.05 ≤ z ≤ 0.15). The agreement with cosmological surveys is remarkable, even though different SED-fitting codes were used. In this section, we estimate the ρSFR from the SFR derived with the flux of Hα at the same redshift bins as described in Sect. 5.4.
The miniJPAS area comprises only 0.895 deg2 of the central regions of the AEGIS field. Therefore, our cosmological volume is somewhat limited, especially at low redshift. In this regard, a study of the ρSFR using miniJPAS data maybe affected by cosmic variance effects (Driver & Robotham 2010; Moster et al. 2011). The main source of uncertainty of ρSFR comes from this effect. We followed Eq. (4) in Driver & Robotham (2010) to quantify the cosmic variance of miniJPAS at different redshift bins,
where N is the number of fields observed by miniJPAS (simply one), A and B are the median transverse lengths, and C is the radial depth. We obtained a cosmic variance for the comoving number density of galaxies of 37% (0.16 dex), 27% (0.12 dex), and 21% (0.09 dex) for the volumes within 0 < z ≤ 0.15, 0.15 < z ≤ 0.25, and 0.25 < z ≤ 0.35, respectively. In the future, J-PAS will scan ∼8000 deg2 in the northen sky, and the effect of cosmic variance will be negligible (less than 1%).
In order to estimate ρSFR, we computed the total sum of the SFR for the galaxies in our sample and divided it by the volume contained in each redshift bin (Vint). We selected them from the parent sample with the same criteria as we used in Sect. 5.1 to generate the SF sample. However, we relied on the Ke01 curve to exclude AGNs. We found a total of 1361 galaxies. In this way, we ensured that we did not underestimate ρSFR by excluding objects that lie between the Ke01 and Ka03 lines, which might contribute much to the flux of Hα through ionized interstellar gas. In any case, the difference between selecting SF galaxies with the Ka03 or the Ke01 line is only 0.05 dex in log ρSFR.
The photometric depth of miniJPAS prevents us from detecting a fraction of galaxies below a certain mass limit. This effect becomes stronger for galaxies at higher redshift. Therefore, we have to apply volume corrections to reduce the impact of the lack of low-mass galaxies in the highest resdshift bins in this work. We used the classical Vint/Vmax technique described originally in Schmidt (1968) and Huchra & Sargent (1973), (see Appendix C in Vilella-Rojo et al. 2021, for a detailed discussion of this correction). This is formally expressed as:
where 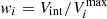 is the weight that each galaxy has in the total
is the weight that each galaxy has in the total 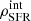 , and Vmax is the maximum volume occupied by a galaxy assuming that it cannot be observed at a magnitude fainter than 22.7. For galaxies with
, and Vmax is the maximum volume occupied by a galaxy assuming that it cannot be observed at a magnitude fainter than 22.7. For galaxies with 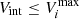 , the weight is simply one, but galaxies with
, the weight is simply one, but galaxies with 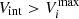 will contribute more.
will contribute more.
A direct comparison of ρSFR with the results obtained in González Delgado et al. (2021) also requires applying a correction to account for the galaxies that are detectable in the rSDSS band and are consequently fitted by the SED-fitting codes, but their emission lines cannot be measured because of the low S/N ratio. From the galaxies that belong to this group, we took those that were classified as blue by the color criterion and used their mass to place them in SFMS derived in Sect. 5.3. In this way, we can estimate their SFR with Eq. (6) and add their contribution to ρSFR. These corrections are indeed minor, as shown in Fig. 16 (red stars are the corrected values, and empty stars represent the uncorrected stars), but become slightly stronger at higher redshift.
 |
Fig. 16. Star formation rate density at z < 0.35. Red stars show the values obtained in this work from the luminosity of Hα. Empty stars are uncorrected values that do not take galaxies with undetectable nebular emission lines or with very low S/N (see text in Sect. 6.2) into account. Black circles are the values obtained by González Delgado et al. (2021) applying the fossil record method to a sample of miniJPAS galaxies in the range 0.05 < z ≤ 0.15. Squares are studies based on Hα (see references in Table 3). Solid lines represents the trends obtained by different studies based on the stellar continuum: Madau & Dickinson (2014, M&D14), López Fernández et al. (2018, LF18), and Bellstedt et al. (2020, B20). All values are scaled to the Chabrier (2003) IMF. |
In Fig. 16 we also show the values obtained by several studies that used the Hα flux to estimate the ρSFR at different redshift bins (squares, see references in Table 3). It is remarkable that most of them predict lower values of ρSFR than works that used the stellar continuum (solid line). Finally, black circles show the values obtained with the fossil record method by González Delgado et al. (2021) for miniJPAS galaxies in the range 0.05 < z ≤ 0.15.
Compilation of star formation rate densities derived from Hα.
Our results reproduce the ρSFR well that was found with other studies using Hα as a tracer to measure the SFR. Nevertheless, we found a non-negligible difference with respect to the results found by studies based on the stellar populations (Madau & Dickinson 2014; Driver et al. 2018; López Fernández et al. 2018; Sánchez et al. 2019; Leja et al. 2019; Bellstedt et al. 2020; González Delgado et al. 2021). Our estimation of ρSFR does not take the SFR into account that is ongoing in galaxies hosting an AGN.
6.3. Differences between the SFR derived through Hα and the SED fitting
The star formation rate density derived in this work is compatible with previous studies that used the Hα luminosity to determine its evolution with cosmic time in the nearby Universe. Nevertheless, our predictions are lower than those obtained with other methods based on the SED fitting of the stellar continuum. Even though ρSFR might be lower in the miniJPAS field, meaning we are affected by the large cosmic variance, our results differ from those derived with the analysis of the stellar populations in González Delgado et al. (2021).
In order to shed light on this difference, we compared the ionizing photon rates expected from Hα luminosity and from the SED fitting. When we assume that no photons escape from H II regions, the relation between the dust-corrected luminosity of Hα and the ionizing photon rates is
where xHα = 2.206 for case B hydrogen recombination.
In the case of the SED fitting, BaySeAGal provides the mass fraction (μj) of each SSP that better describes the observed spectrum. In other words, for each galaxy, we can reproduce the SFH. Therefore, we can retrieve the ionizing photon rates by weighting the number of H ionizing photons emitted per unit time and initial mass for the jth SSP (qH, j = qH(tj, Zj)),
We compare the two quantifies in Fig. 17. 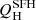 is 0.54 dex higher than
is 0.54 dex higher than 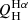 on average. We observe a clear trend with the nebular extinction (color bar) and the EW of Hα. Galaxies where we estimated low values of the nebular extinction lie farther away from the 1:1 line. On the same line, the differences between
on average. We observe a clear trend with the nebular extinction (color bar) and the EW of Hα. Galaxies where we estimated low values of the nebular extinction lie farther away from the 1:1 line. On the same line, the differences between 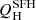 and
and  become smaller as the EW of Hα increases.
become smaller as the EW of Hα increases.
 |
Fig. 17. Comparison of the ionizing photon rates computed from Hα emission line and from the fit obtained with the analysis of the stellar populations with BaySeAGal (left; see text in Sect. 6.3). The dashed black line represents the 1:1 relation. μ and σ are the bias and the standard deviation. Right panel: difference between these quantities as a function of the EW of Hα. Density contours are drawn in black. In both cases, the galaxies are color-coded with the extinction of the interstellar gas calculated from the Balmer decrement. |
Interestingly, 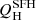 and
and 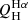 are closer at higher values. This trend has also been found in comparisons between the SFR derived from Hα and from the UV both in the integrated spectrum and in spatially resolved galaxies (Lee et al. 2009, 2016; Byun et al. 2021). Specifically, Byun et al. (2021) concluded that deficient Hα fluxes in the extended disks of galaxies are tightly correlated with recent starbursts, which are being rapidly suppressed over the last 10 Myr. This phenomenon can explain the difference found in the slope of the SFMS in Sect. 6.1.3. Because galaxies with a low Hα luminosity have higher SFRs according to the SED fitting, the slope becomes flatter.
are closer at higher values. This trend has also been found in comparisons between the SFR derived from Hα and from the UV both in the integrated spectrum and in spatially resolved galaxies (Lee et al. 2009, 2016; Byun et al. 2021). Specifically, Byun et al. (2021) concluded that deficient Hα fluxes in the extended disks of galaxies are tightly correlated with recent starbursts, which are being rapidly suppressed over the last 10 Myr. This phenomenon can explain the difference found in the slope of the SFMS in Sect. 6.1.3. Because galaxies with a low Hα luminosity have higher SFRs according to the SED fitting, the slope becomes flatter.
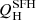 might also be overestimated if the mass fraction attributed to young stellar populations (YSP) were higher than it should be. This might happen if the SFH in the last 20 Myr were different from the global SFH that accounts for the formation and growth of mass in galaxies on scales of billion years and/or because our parametric code overestimated the fraction of mass that formed in recent epochs with respect to nonparametric codes that are more flexible to varying the fraction of the young stellar population on a shorter timescale. In order to determine how our result might be affected by different assumptions of the SFH, we used the SFH from ALSTAR and computed
might also be overestimated if the mass fraction attributed to young stellar populations (YSP) were higher than it should be. This might happen if the SFH in the last 20 Myr were different from the global SFH that accounts for the formation and growth of mass in galaxies on scales of billion years and/or because our parametric code overestimated the fraction of mass that formed in recent epochs with respect to nonparametric codes that are more flexible to varying the fraction of the young stellar population on a shorter timescale. In order to determine how our result might be affected by different assumptions of the SFH, we used the SFH from ALSTAR and computed 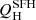 . We found that there is a bias of 0.81 dex, which is even higher than the results found with BaySeAGal.
. We found that there is a bias of 0.81 dex, which is even higher than the results found with BaySeAGal.
Studies that retrieved the stellar population properties of a sample of galaxies based on optical spectra (either form SDSS or CALIFA) and based on photometry from the GALEX survey showed that when the UV part of the spectrum is not included in the SED fitting, a brighter YSP contribution is found (López Fernández et al. 2016; Werle et al. 2019). However, this excess of light in the UV does not have a strong impact on the mass content of YSP because the mass is dominated by older stars.
BaySeAGal does not yet include a model of nebular emission lines. Therefore, the SED fitting only accounts for the emission of the stellar continuum and masks the filters in which the emission lines peak. We do not know how this might affect the shape of the SFH and the mass fraction attributed to the young stellar population. Moreover, a delta-delayed model might not be sufficient to describe SFHs with a recent burst of SFR. In the future, we expect to explore this aspect further.
Furthermore, other hypotheses need to be taken into account to explain this discrepancy. First, we should consider whether we underestimate the nebular extinction. Certainly, we would expect that galaxies with very low S/N show this effect more. When we rebuild Fig. 17 and include only galaxies with an error in Hα luminosity smaller than 0.25 dex, the bias decreases by 0.17 dex. Additionally, when we assume for the SF sample that the nebular extinction is underestimated by a factor of two, which would mean E(B − V)Hα/Hβ ∼ 2E(B − V)SED, as some studies reported (Qin et al. 2019; Koyama et al. 2019), the difference would only be reduced by 0.22 dex. In other words, it is plausible that we did not properly estimate the nebular extinction for a fraction of galaxies in the SF sample, but in the worst scenario, this effect alone cannot explain the difference between 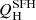 and
and 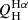 .
.
Another effect that might also contribute to this difference is the ionizing radiation that leaks from the H II regions. In this case, Eq. (13) would underestimate the Hα ionizing photon rates. Several studies have shown precisely that there is a fraction of ionizing photons that escapes, and they are therefore unable to ionize the interstellar gas (Giammanco et al. 2005; Otí-Floranes & Mas-Hesse 2010; Pellegrini et al. 2012; Anderson et al. 2015). Nevertheless, the average fraction is still debated and can vary from galaxy to galaxy and from region to region within the same galaxy. Unfortunately, there is no means to quantify this effect with the data employed in this work. Nonetheless, when we assume that 30% of the ionizing radiation leaks from H II regions, the difference could be reduced 0.16 dex.
Most probably, the difference that we observe between 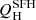 and
and 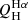 is a combination of all these factors. Certainly, fitting the SED of miniJPAS galaxies with information from the UV from GALEX or HST-UV observations and/or the IR from Spitzer would be very useful to unveil the origin of the discrepancy and test some of the previous hypotheses. However, this analysis is not the main goal of this work.
is a combination of all these factors. Certainly, fitting the SED of miniJPAS galaxies with information from the UV from GALEX or HST-UV observations and/or the IR from Spitzer would be very useful to unveil the origin of the discrepancy and test some of the previous hypotheses. However, this analysis is not the main goal of this work.
7. Outlook for J-PAS
The results presented in this paper prove that the main properties of ELGs can be studied with J-PAS data. The miniJPAS Pathfinder instrument allowed us to test and combine different methods of analysis to fully exploit the scientific potential of the data and draw the baseline for the prospect of J-PAS.
The vast amount of data to be collected by J-PAS will allow us to perform a more comprehensive research, exploring other aspects that remained elusive or were limited within the area covered by miniJPAS. For instance, we will be able to derive the properties of blue and SF galaxies in groups and clusters, the fraction of AGN, and their role in the quench of SF galaxies within dense and very low density environments.
For instance, if in 1 deg2 we were able to estimate the position of 255 galaxies in the BPT with an error smaller than 0.15 dex, the ionization mechanism of about two million galaxies in the Universe (z < 0.35) could be studied at the end of the J-PAS survey. With this amount of data, we will be able to determine the SFMS parameters better and place constraints on the evolution of ρSFR at least up to 0.35 in redshift. Thus, it will be possible to further explore the discrepancies found in Sect. 6.2.
The SFR coverage of J-PAS will be at least as competitive as that of the SDSS or GAMA surveys. In Fig. 18 we show the SFR as a function of the resdshift for our SF galaxy sample. The dotted blue line is the approximate SFR completeness limit assuming a flux limit of FHα = 10−18 W m−2 for GAMA and SDSS galaxies (Gunawardhana et al. 2013). The dotted black line represents the 95% completeness limit of miniJPAS for blue galaxies (Díaz-García et al., in prep.). We used the best fit obtained in Sect. 5.3 to transform the completeness limit in mass into SFR.
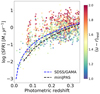 |
Fig. 18. Relation between the SFR derived from Hα and redshift for the galaxy sample described in Sect. 5.1. The blue dotted line is the approximate SFR completeness limit for GAMA and SDSS galaxies (Gunawardhana et al. 2013), and the dotted black line is the 95% completeness limit from blue galaxies in miniJPAS. Galaxies are color-coded with their (u − r) rest-frame color. |
Finally, in Fig. 19 we show the comoving number density of galaxies in miniJPAS as a function of redshift for the total galaxy population (black stars) for the star-forming galaxies (blue stars), for AGN-like galaxies (green stars), and for quiescent galaxies (red stars). Error bars represent the variation in the number density when a different division line in the WHAN diagram is considered, for example, k03, Ke01, or S08.
 |
Fig. 19. Comoving number density of galaxies in miniJPAS as a function of redshift. The total galaxy population (black star) is broken into star-forming (blue stars), AGN-like (green stars), and quiescent galaxies (red stars). We used the WHAN diagram with the Ka03 dividing line to separate AGN and SF galaxies. Quiescent galaxies include LINERs and passive galaxies. The uncertainty due to the cosmic variance is not included in the error budget. |
8. Summary and conclusion
We analyzed a subsample of galaxies (a total of 2154) from the AEGIS field observed by miniJPAS with redshift below 0.35 in detail. The method developed in MS21 used ANN trained with CALIFA and MaNGA in order to measure and detect the main emission lines in the J-spectrum: Hα, Hβ, [O III], and [N II].
We used a criterion based on the mass and color of the galaxy. We estimated that 83% and 17% in the sample are blue and red galaxies, respectively. With the ANN classifier, which is based on the EW of the emission lines, we found that 82% of the sample are strong ELs amd 18% are weak ELs.
We employed the BPT and WHAN diagrams to classify galaxies according to the main source of ionization and to select star-forming galaxies. We obtained that of the galaxies with reliable EW values (2000 galaxies in total), 72.8 ± 0.4%, 17.7 ± 0.4%, and 9.4 ± 0.2% are SF, Seyfert, and passive or LINER galaxies, respectively, using the WHAN diagram and the Ka03 separation line. One hundred and fifty-four galaxies from the parent sample remain unclassified because of high uncertainties in the measurement of the emission lines. Ninety-four percent of the SF galaxies and 97% of the LINER or passive galaxies are classified with the color criterion as blue and red, respectively.
The analyses of the properties of the stellar population performed in González Delgado et al. (2021) allowed us to compare and complement the information of the emission lines. For instance, we showed in color-mass diagrams that blue (red) galaxies are composed of a younger (older) stellar population, respectively, and present stronger (weaker) emission lines. This synergy between the properties of the gas and the stellar populations also appears in the BPT diagram, where galaxies become more massive as they evolve through the SF-wing.
We derived the SFR from the flux of Hα and relied on the Balmer decrement to correct for the extinction produced by interstellar dust. Subsequently, we fit the slope, zeropoint, and the intrinsic scatter of the SFMS, obtaining 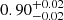 ,
, 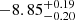 and,
and, 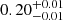 , respectively. We tested the turnover-mass hypothesis by fitting a quadratic and a broken power law. However, we did not observe a flattening of the slope at high mass. We argue that this is likely produced by our selection criteria of SF galaxies together with the limitation of the method to detect very weak emission lines in comparison with spectroscopic surveys. The results we obtained are compatible with those of other studies.
, respectively. We tested the turnover-mass hypothesis by fitting a quadratic and a broken power law. However, we did not observe a flattening of the slope at high mass. We argue that this is likely produced by our selection criteria of SF galaxies together with the limitation of the method to detect very weak emission lines in comparison with spectroscopic surveys. The results we obtained are compatible with those of other studies.
Finally, we computed the cosmic evolution of the ρSFR within three redshift bins: 0 < z ≤ 0.15, 0.15 < z ≤ 0.25, and 0.25 < z ≤ 0.35. We found agreement with previous measurements based on the Hα emission line. Nevertheless, we found an offset compared to the studies that derived ρSFR from the SED fitting of the stellar continuum. We discussed the origin of this discrepancy in detail, which is most probably a combination of several factors, such as the correction for dust attenuation, the SFR tracer, or the escape of ionizing photons.
The work presented in this paper builds the foundation upon which the analysis of ELGs in J-PAS will be conducted as soon as hundreds of squares degrees are mapped in the northern sky in the next years.
Acknowledgments
G.M.S., R.G.D., R.G.B., L.A.D.G., J.R.M., and E.P. acknowledge financial support from the State Agency for Research of the Spanish MCIU through the “Center of Excellence Severo Ochoa” award to the Instituto de Astrofísica de Andalucí a (SEV-2017-0709), and to the AYA2016-77846-P and PID2019-109067-GB100. S.D.P. is grateful to the Fonds de Recherche du Québec – Nature et Technologies. J.C.M. and S.B. acknowledge financial support from Spanish Ministry of Science, Innovation, and Universities through the project PGC2018-097585-B-C22. J.V.M. and S.D.P. acknowledge financial support from the Spanish Ministerio de Economía y Competitividad under grants AYA2016-79724-C4-4-P and PID2019-107408GB-C44, from Junta de Andalucía Excellence Project P18-FR-2664, and the funding of the “Center of Excellence Severo Ochoa” award to the Instituto de Astrofísica de Andalucía (SEV-2017-0709). A.E. and J.A.F.O. acknowledges the financial support from the Spanish Ministry of Science and Innovation and the European Union-NextGenerationEU through the Recovery and Resilience Facility project ICTS-MRR-2021-03-CEFCA. L.S.J. acknowledges support from CNPq (304819/2017-4) and FAPESP (2019/10923-5). R.A.D. acknowledges partial support support from CNPq grant 308105/2018-4. V.M. thanks CNPq (Brazil) for partial financial support. This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 888258. Based on observations made with the JST/T250 telescope and PathFinder camera for the miniJPAS project at the Observatorio Astrofísico de Javalambre (OAJ), in Teruel, owned, managed, and operated by the Centro de Estudios de Física del Cosmos de Aragón (CEFCA). We acknowledge the OAJ Data Processing and Archiving Unit (UPAD) for reducing and calibrating the OAJ data used in this work. Funding for OAJ, UPAD, and CEFCA has been provided by the Governments of Spain and Aragón through the Fondo de Inversiones de Teruel; the Aragón Government through the Research Groups E96, E103, and E16_17R; the Spanish Ministry of Science, Innovation and Universities (MCIU/AEI/FEDER, UE) with grant PGC2018-097585-B-C21; the Spanish Ministry of Economy and Competitiveness (MINECO/FEDER, UE) under AYA2015-66211-C2-1-P, AYA2015-66211-C2-2, AYA2012-30789, and ICTS-2009-14; European FEDER funding (FCDD10-4E-867, FCDD13-4E-2685); the Brazilian agencies FINEP, FAPESP, FAPERJ and by the National Observatory of Brazil. Additional funding was also provided by the Tartu Observatory and by the J-PAS Chinese Astronomical Consortium. The authors acknowledge the following people for providing valuable comments and suggestions on the first draft of this paper: Iris Breda, Ana Chies Santos, Maria Luiza Linhares Dantas, Alejando Lumbreras Calle, Elmo Tempel, José Eduardo Telles, and Rahna P. T. We also thank the anonymous referee for many useful comments and suggestions.
References
- Anderson, L. D., Deharveng, L., Zavagno, A., et al. 2015, ApJ, 800, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Arnouts, S., & Ilbert, O. 2011, Astrophysics Source Code Library [record ascl:1108.009] [Google Scholar]
- Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP, 93, 5 [Google Scholar]
- Belfiore, F., Maiolino, R., Maraston, C., et al. 2016, MNRAS, 461, 3111 [Google Scholar]
- Belfiore, F., Maiolino, R., Bundy, K., et al. 2018, MNRAS, 477, 3014 [Google Scholar]
- Bellstedt, S., Robotham, A. S. G., Driver, S. P., et al. 2020, MNRAS, 498, 5581 [NASA ADS] [CrossRef] [Google Scholar]
- Benitez, N., Dupke, R., Moles, M., et al. 2014, ArXiv e-prints [arXiv:1403.5237] [Google Scholar]
- Best, P., Smail, I., Sobral, D., et al. 2013, Thirty Years of Astronomical Discovery with UKIRT, 37, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Bonoli, S., Marín-Franch, A., Varela, J., et al. 2021, A&A, 653, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boogaard, L. A., Brinchmann, J., Bouché, N., et al. 2018, A&A, 619, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Bundy, K., Bershady, M. A., Law, D. R., et al. 2015, ApJ, 798, 7 [Google Scholar]
- Byun, W., Sheen, Y.-K., Seon, K.-I., et al. 2021, ApJ, 918, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Kinney, A. L., & Storchi-Bergmann, T. 1994, ApJ, 429, 582 [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Cano-Díaz, M., Sánchez, S. F., Zibetti, S., et al. 2016, ApJ, 821, L26 [Google Scholar]
- Cano-Díaz, M., Ávila-Reese, V., Sánchez, S. F., et al. 2019, MNRAS, 488, 3929 [Google Scholar]
- Catalán-Torrecilla, C., Gil de Paz, A., Castillo-Morales, A., et al. 2015, A&A, 584, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cenarro, A. J., Moles, M., Cristóbal-Hornillos, D., et al. 2019, A&A, 622, A176 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]
- Chen, Y., Bressan, A., Girardi, L., et al. 2015, MNRAS, 452, 1068 [Google Scholar]
- Cid Fernandes, R., Mateus, A., Sodré, L., Stasińska, G., & Gomes, J. M. 2005, MNRAS, 358, 363 [Google Scholar]
- Cid Fernandes, R., Stasińska, G., Schlickmann, M. S., et al. 2010, MNRAS, 403, 1036 [Google Scholar]
- Cid Fernandes, R., Stasińska, G., Mateus, A., & Vale Asari, N. 2011, MNRAS, 413, 1687 [Google Scholar]
- Costantin, L., Iovino, A., Zibetti, S., et al. 2019, A&A, 632, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coughlin, A., Rhoads, J. E., Malhotra, S., et al. 2018, ApJ, 858, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Cimatti, A., Renzini, A., et al. 2004, ApJ, 617, 746 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, D. A., Barlow, R. J., Cohen, S. A., et al. 2010, ApJ, 712, L189 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, L. J. M., Driver, S. P., Robotham, A. S. G., et al. 2016, MNRAS, 461, 458 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, L. J. M., Lagos, C. D. P., Katsianis, A., et al. 2019, MNRAS, 483, 1881 [Google Scholar]
- Davis, M., Guhathakurta, P., Konidaris, N. P., et al. 2007, ApJ, 660, L1 [NASA ADS] [CrossRef] [Google Scholar]
- DESI Collaboration (Aghamousa, A., et al.) 2016, ArXiv e-prints [arXiv:1611.00036] [Google Scholar]
- Díaz-García, L. A., Cenarro, A. J., López-Sanjuan, C., et al. 2015, A&A, 582, A14 [Google Scholar]
- Díaz-García, L. A., Cenarro, A. J., López-Sanjuan, C., et al. 2019, A&A, 631, A156 [Google Scholar]
- Domínguez, A., Siana, B., Henry, A. L., et al. 2013, ApJ, 763, 145 [CrossRef] [Google Scholar]
- Domínguez, A., Siana, B., Brooks, A. M., et al. 2015, MNRAS, 451, 839 [CrossRef] [Google Scholar]
- Drake, A. B., Simpson, C., Collins, C. A., et al. 2013, MNRAS, 433, 796 [NASA ADS] [CrossRef] [Google Scholar]
- Driver, S. P., & Robotham, A. S. G. 2010, MNRAS, 407, 2131 [Google Scholar]
- Driver, S. P., Hill, D. T., Kelvin, L. S., et al. 2011, MNRAS, 413, 971 [Google Scholar]
- Driver, S. P., Andrews, S. K., da Cunha, E., et al. 2018, MNRAS, 475, 2891 [Google Scholar]
- Duarte Puertas, S., Vilchez, J. M., Iglesias-Páramo, J., et al. 2017, A&A, 599, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dutton, A. A., van den Bosch, F. C., & Dekel, A. 2010, MNRAS, 405, 1690 [NASA ADS] [Google Scholar]
- Emami, N., Siana, B., Weisz, D. R., et al. 2019, ApJ, 881, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Falcón-Barroso, J., Sánchez-Blázquez, P., Vazdekis, A., et al. 2011, A&A, 532, A95 [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Förster Schreiber, N. M., & Wuyts, S. 2020, ARA&A, 58, 661 [Google Scholar]
- Furlong, M., Bower, R. G., Theuns, T., et al. 2015, MNRAS, 450, 4486 [Google Scholar]
- Gallego, J., Zamorano, J., Aragon-Salamanca, A., & Rego, M. 1995, ApJ, 455, L1 [Google Scholar]
- García-Benito, R., Zibetti, S., Sánchez, S. F., et al. 2015, A&A, 576, A135 [Google Scholar]
- Garn, T., & Best, P. N. 2010, MNRAS, 409, 421 [Google Scholar]
- Garn, T., Sobral, D., Best, P. N., et al. 2010, MNRAS, 402, 2017 [NASA ADS] [CrossRef] [Google Scholar]
- Giammanco, C., Beckman, J. E., & Cedrés, B. 2005, A&A, 438, 599 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gonçalves, T. S., Martin, D. C., Menéndez-Delmestre, K., Wyder, T. K., & Koekemoer, A. 2012, ApJ, 759, 67 [CrossRef] [Google Scholar]
- González Delgado, R. M., Díaz-García, L. A., de Amorim, A., et al. 2021, A&A, 649, A79 [Google Scholar]
- Gunawardhana, M. L. P., Hopkins, A. M., Bland-Hawthorn, J., et al. 2013, MNRAS, 433, 2764 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, M., Tanaka, M., Shimakawa, R., et al. 2018, PASJ, 70, S17 [NASA ADS] [Google Scholar]
- Hayashi, M., Shimakawa, R., Tanaka, M., et al. 2020, PASJ, 72, 86 [CrossRef] [Google Scholar]
- Heckman, T. M. 1980, A&A, 87, 152 [Google Scholar]
- Hernán-Caballero, A., Varela, J., López-Sanjuan, C., et al. 2021, A&A, 654, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hopkins, P. F., Kereš, D., Oñorbe, J., et al. 2014, MNRAS, 445, 581 [NASA ADS] [CrossRef] [Google Scholar]
- Huchra, J., & Sargent, W. L. W. 1973, ApJ, 186, 433 [Google Scholar]
- Iglesias-Páramo, J., Vílchez, J. M., Rosales-Ortega, F. F., et al. 2016, ApJ, 826, 71 [Google Scholar]
- Ilbert, O., Arnouts, S., Le Floc’h, E., et al. 2015, A&A, 579, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalinova, V., Colombo, D., Sánchez, S. F., et al. 2021, A&A, 648, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karim, A., Schinnerer, E., Martínez-Sansigre, A., et al. 2011, ApJ, 730, 61 [Google Scholar]
- Kashino, D., Silverman, J. D., Rodighiero, G., et al. 2013, ApJ, 777, L8 [Google Scholar]
- Kauffmann, G., Heckman, T. M., Tremonti, C., et al. 2003, MNRAS, 346, 1055 [Google Scholar]
- Kennicutt, R. C., Jr. 1998, ARA&A, 36, 189 [Google Scholar]
- Kennicutt, R. C., Jr., Tamblyn, P., & Congdon, C. E. 1994, ApJ, 435, 22 [Google Scholar]
- Kewley, L. J., Dopita, M. A., Sutherland, R. S., Heisler, C. A., & Trevena, J. 2001, ApJ, 556, 121 [Google Scholar]
- Kewley, L. J., Nicholls, D. C., & Sutherland, R. S. 2019, ARA&A, 57, 511 [Google Scholar]
- Khostovan, A. A., Malhotra, S., Rhoads, J. E., et al. 2020, MNRAS, 493, 3966 [NASA ADS] [CrossRef] [Google Scholar]
- Khostovan, A. A., Malhotra, S., Rhoads, J. E., et al. 2021, MNRAS, 503, 5115 [NASA ADS] [CrossRef] [Google Scholar]
- Kouroumpatzakis, K., Zezas, A., Maragkoudakis, A., et al. 2021, MNRAS, 506, 3079 [NASA ADS] [CrossRef] [Google Scholar]
- Koyama, Y., Shimakawa, R., Yamamura, I., Kodama, T., & Hayashi, M. 2019, PASJ, 71, 8 [NASA ADS] [Google Scholar]
- Lacerda, E. A. D., Cid Fernandes, R., Couto, G. S., et al. 2018, MNRAS, 474, 3727 [Google Scholar]
- Lacerda, E. A. D., Sánchez, S. F., Cid Fernandes, R., et al. 2020, MNRAS, 492, 3073 [Google Scholar]
- Laureijs, R., Amiaux, J., Arduini, S., et al. 2011, ArXiv e-prints [arXiv:1110.3193] [Google Scholar]
- Law, D. R., Yan, R., Bershady, M. A., et al. 2015, AJ, 150, 19 [CrossRef] [Google Scholar]
- Lee, J. C., Gil de Paz, A., Tremonti, C., et al. 2009, ApJ, 706, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, N., Sanders, D. B., Casey, C. M., et al. 2015, ApJ, 801, 80 [Google Scholar]
- Lee, J. C., Veilleux, S., McDonald, M., & Hilbert, B. 2016, ApJ, 817, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Leja, J., Carnall, A. C., Johnson, B. D., Conroy, C., & Speagle, J. S. 2019, ApJ, 876, 3 [Google Scholar]
- López Fernández, R., Cid Fernandes, R., González Delgado, R. M., et al. 2016, MNRAS, 458, 184 [CrossRef] [Google Scholar]
- López Fernández, R., González Delgado, R. M., Pérez, E., et al. 2018, A&A, 615, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lumbreras-Calle, A., Muñoz-Tuñón, C., Méndez-Abreu, J., et al. 2019, A&A, 621, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ly, C., Malkan, M. A., Kashikawa, N., et al. 2007, ApJ, 657, 738 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [Google Scholar]
- Magris, C. G., Mateu, P. J., Mateu, C., et al. 2015, PASP, 127, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Maiolino, R., & Mannucci, F. 2019, A&ARv, 27, 3 [Google Scholar]
- Marigo, P., Bressan, A., Nanni, A., Girardi, L., & Pumo, M. L. 2013, MNRAS, 434, 488 [Google Scholar]
- Marin-Franch, A., Taylor, K., Cenarro, J., Cristobal-Hornillos, D., & Moles, M. 2015, IAU Gen. Assem., 29, 2257381 [Google Scholar]
- Mármol-Queraltó, E., McLure, R. J., Cullen, F., et al. 2016, MNRAS, 460, 3587 [Google Scholar]
- Martínez-Solaeche, G., González Delgado, R. M., García-Benito, R., et al. 2021, A&A, 647, A158 [EDP Sciences] [Google Scholar]
- Matthee, J., & Schaye, J. 2019, MNRAS, 484, 915 [CrossRef] [Google Scholar]
- Matthee, J., Sobral, D., Best, P., et al. 2017, MNRAS, 471, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Mendes de Oliveira, C., Ribeiro, T., Schoenell, W., et al. 2019, MNRAS, 489, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Mendez, A. J., Coil, A. L., Lotz, J., et al. 2011, ApJ, 736, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Mitchell, P. D., Lacey, C. G., Cole, S., & Baugh, C. M. 2014, MNRAS, 444, 2637 [NASA ADS] [CrossRef] [Google Scholar]
- Moles, M., Benítez, N., Aguerri, J. A. L., et al. 2008, AJ, 136, 1325 [NASA ADS] [CrossRef] [Google Scholar]
- Molino, A., Benítez, N., Moles, M., et al. 2014, MNRAS, 441, 2891 [Google Scholar]
- Moster, B. P., Somerville, R. S., Newman, J. A., & Rix, H.-W. 2011, ApJ, 731, 113 [Google Scholar]
- Oke, J. B., & Gunn, J. E. 1983, ApJ, 266, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Oliver, S., Frost, M., Farrah, D., et al. 2010, MNRAS, 405, 2279 [NASA ADS] [Google Scholar]
- Oteo, I., Sobral, D., Ivison, R. J., et al. 2015, MNRAS, 452, 2018 [NASA ADS] [CrossRef] [Google Scholar]
- Otí-Floranes, H., & Mas-Hesse, J. M. 2010, A&A, 511, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pellegrini, E. W., Oey, M. S., Winkler, P. F., et al. 2012, ApJ, 755, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez-González, P. G., Cava, A., Barro, G., et al. 2013, ApJ, 762, 46 [Google Scholar]
- Prugniel, P., Vauglin, I., & Koleva, M. 2011, A&A, 531, A165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puglisi, A., Rodighiero, G., Franceschini, A., et al. 2016, A&A, 586, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Qin, J., Zheng, X. Z., Wuyts, S., Pan, Z., & Ren, J. 2019, ApJ, 886, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Renzini, A., & Peng, Y.-J. 2015, ApJ, 801, L29 [Google Scholar]
- Robotham, A. S. G., & Obreschkow, D. 2015, PASA, 32, e033 [Google Scholar]
- Rodighiero, G., Daddi, E., Baronchelli, I., et al. 2011, ApJ, 739, L40 [Google Scholar]
- Salim, S., Rich, R. M., Charlot, S., et al. 2007, ApJS, 173, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Salmi, F., Daddi, E., Elbaz, D., et al. 2012, ApJ, 754, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez, S. F., Kennicutt, R. C., Gil de Paz, A., et al. 2012, A&A, 538, A8 [Google Scholar]
- Sánchez, S. F., García-Benito, R., Zibetti, S., et al. 2016, A&A, 594, A36 [Google Scholar]
- Sánchez, S. F., Avila-Reese, V., Hernandez-Toledo, H., et al. 2018, Rev. Mex. Astron. Astrofis., 54, 217 [Google Scholar]
- Sánchez, S. F., Avila-Reese, V., Rodríguez-Puebla, A., et al. 2019, MNRAS, 482, 1557 [Google Scholar]
- Sánchez-Blázquez, P., Peletier, R. F., Jiménez-Vicente, J., et al. 2006, MNRAS, 371, 703 [Google Scholar]
- Santos, S., Sobral, D., Matthee, J., et al. 2020, MNRAS, 493, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Schawinski, K., Thomas, D., Sarzi, M., et al. 2007, MNRAS, 382, 1415 [Google Scholar]
- Schawinski, K., Urry, C. M., Simmons, B. D., et al. 2014, MNRAS, 440, 889 [Google Scholar]
- Schmidt, M. 1968, ApJ, 151, 393 [Google Scholar]
- Schreiber, C., Pannella, M., Elbaz, D., et al. 2015, A&A, 575, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sharma, K., Prugniel, P., & Singh, H. P. 2016, A&A, 585, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shin, K., Ly, C., Malkan, M. A., et al. 2021, MNRAS, 501, 2231 [NASA ADS] [CrossRef] [Google Scholar]
- Shioya, Y., Taniguchi, Y., Sasaki, S. S., et al. 2008, ApJS, 175, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Sobral, D., Smail, I., Best, P. N., et al. 2013, MNRAS, 428, 1128 [NASA ADS] [CrossRef] [Google Scholar]
- Sobral, D., Matthee, J., Best, P. N., et al. 2015, MNRAS, 451, 2303 [Google Scholar]
- Sobral, D., Stroe, A., Koyama, Y., et al. 2016, MNRAS, 458, 3443 [NASA ADS] [CrossRef] [Google Scholar]
- Sparre, M., Hayward, C. C., Springel, V., et al. 2015, MNRAS, 447, 3548 [Google Scholar]
- Speagle, J. S., Steinhardt, C. L., Capak, P. L., & Silverman, J. D. 2014, ApJS, 214, 15 [Google Scholar]
- Stasińska, G., Vale Asari, N., Cid Fernandes, R., et al. 2008, MNRAS, 391, L29 [NASA ADS] [Google Scholar]
- Stroe, A., & Sobral, D. 2015, MNRAS, 453, 242 [NASA ADS] [CrossRef] [Google Scholar]
- Tasca, L. A. M., Le Fèvre, O., Hathi, N. P., et al. 2015, A&A, 581, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taylor, K., Marín-Franch, A., Laporte, R., et al. 2014, J. Astron. Instrum., 3, 1350010 [Google Scholar]
- Thorne, J. E., Robotham, A. S. G., Davies, L. J. M., et al. 2021, MNRAS, 505, 540 [NASA ADS] [CrossRef] [Google Scholar]
- Tomczak, A. R., Quadri, R. F., Tran, K.-V. H., et al. 2016, ApJ, 817, 118 [Google Scholar]
- Valdes, F., Gupta, R., Rose, J. A., Singh, H. P., & Bell, D. J. 2004, ApJS, 152, 251 [Google Scholar]
- Van Sistine, A., Salzer, J. J., Sugden, A., et al. 2016, ApJ, 824, 25 [Google Scholar]
- Vilella-Rojo, G., Logroño-García, R., López-Sanjuan, C., et al. 2021, A&A, 650, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Werle, A., Cid Fernandes, R., Vale Asari, N., et al. 2019, MNRAS, 483, 2382 [Google Scholar]
- Westra, E., Geller, M. J., Kurtz, M. J., Fabricant, D. G., & Dell’Antonio, I. 2010, ApJ, 708, 534 [Google Scholar]
- Whitaker, K. E., van Dokkum, P. G., Brammer, G., & Franx, M. 2012, ApJ, 754, L29 [Google Scholar]
- Whitaker, K. E., Franx, M., Leja, J., et al. 2014, ApJ, 795, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Willett, K. W., Schawinski, K., Simmons, B. D., et al. 2015, MNRAS, 449, 820 [NASA ADS] [CrossRef] [Google Scholar]
- York, D. G., Adelman, J., Anderson, J. E., Jr., et al. 2000, AJ, 120, 1579 [NASA ADS] [CrossRef] [Google Scholar]
- Zahid, H. J., Dima, G. I., Kewley, L. J., Erb, D. K., & Davé, R. 2012, ApJ, 757, 54 [Google Scholar]
Appendix A: AGN selection criteria
In Table A.1 we show the best-fitting parameter as a function of the separation curves, the redshift bin, and the fitting equation we used to fit the SFMS. The results are discussed in the main text (Sect. 5.6)
Parameters of the SFMS derived in different redshift bins with the models described in Sects. 5.3 and 5.5 using different selection criteria (see Sect. 5.6).
All Tables
Parameters of the SFMS with different selection cuts in the rSDSS band for the SF (SF0) sample at the top (bottom).
Parameters of the SFMS derived in different redshift bins with the models described in Sects. 5.3 and 5.5 using different selection criteria (see Sect. 5.6).
All Figures
 |
Fig. 1. Relation between the apparent magnitude in the rSDSS band and redshift for all galaxies in the parent sample. We used the MAG_AUTO photometry. Dots are color-coded according to the median S/N of the J-PAS narrowband filters. |
| In the text | |
 |
Fig. 2. J-spectra in magnitudes (MAG_AUTO photometry) for a set of galaxies within the AEGIS field observed by miniJPAS. Stars correspond to broadband filters (uJPAS, and SDSS g, r, and i). Black dots are the best fit obtained with BaySeAGal to the stellar continuum. Filters including the wavelength of Hα and [O III] emission lines within their bandpass are marked with dashed vertical lines. The images of these galaxies in the rSDSS band are attached in the lower left inset. The miniJPAS ID and the photo-z are shown in black in the left corner of each figure. |
| In the text | |
 |
Fig. 3. Distributions of mean stellar luminosity-weighted age (top left panel), galaxy stellar mass (lower right panel), extinction (lower left panel), and τ/t0 ratio (bottom right panel) obtained by BaySeAGal for the sample of galaxies described in Sect. 2. |
| In the text | |
 |
Fig. 4. Distribution of the EW of Hα and Hβ (left), [O III], and [N II] (right) in log scale as obtained with the ANNR. |
| In the text | |
 |
Fig. 5. Color–mass diagram for our sample of galaxies. The (u − r) color-corrected for dust extintion vs. stellar mass. Galaxies are color-coded with the EW of Hα (the luminosity-weighted stellar age) on the left side (right side). The intrinsic color, stellar mass, and luminosity-weighted age are obtained via BaySeAGal. Dashed black lines separate blue and red galaxies following Eq. (2), where we considered the median redshift of the sample (z = 0.25). Density contours are drawn in black at the top. |
| In the text | |
 |
Fig. 6. Equivalent width of Hα as a function of the stellar mass of the galaxy. Left panel: we used Eq. (2) to distinguish between red and blue galaxies. Right panel: we relied on the classification performed with a machine-learning code trained with strong EL and weak EL galaxies. Strong ELs were defined as those with EWs greater than 3 Å in any of the following emission lines: Hα, Hβ, [O III], or [N II], and weak ELs are all others. The dashed horizontal lines mark the 3 Å limit in the EW(Hα). Density contours are drawn in black at the top. |
| In the text | |
 |
Fig. 7. BPT diagram for the galaxies in the sample with an error of 0.2 dex (0.5 dex) in the [O III]/Hβ and [N II]/Hα ratios in the left (right) panel. The errors are not plotted in the right panel for clarity. The color bar indicates the stellar mass of the galaxy. The solid (Ka03), dashed (Ke01), and dotted lines (S07) define the regions for the four main spectral classes. The relative percentage of each galaxy type in each subsample is indicated in the figure. In each panel, the number of galaxies is specified in the lower left corner. The parent sample contains 2154 galaxies. |
| In the text | |
 |
Fig. 8. WHAN diagram for galaxies with an error smaller than 0.2 dex (0.5 dex) in both the EW(Hα) and the [N II]/Hα ratio in the left (right) panel. The errors are not shown in the right panel for clarity. The color bar indicates the stellar mass of the galaxy. The inset shows the relative percentage of each galaxy type in each subsample. Dashed and solid vertical lines define the optimal projections of the Ke01 and the Ka03 lines in the WHAN diagram (Cid Fernandes et al. 2010, 2011). Similarly, the dash-dotted horizontal line at EW(Hα) = 6 Å is the optimal transposition of the S07, and the dotted line at log EW(Hα) = 0.5 Å defines the limit of ELGs. In each panel, the galaxy counts are specified in the lower left corner. The parent sample contains 2154 galaxies. Density contours are drawn in black at the top. |
| In the text | |
 |
Fig. 9. Fraction of SF, Seyfert, and quiescent (passive or LINER) galaxies as a function of the maximum rSDSS apparent magnitude of each subsample. Solid, dashed, and dotted lines represent the fraction of each galaxy type according to the Ka03, Ke01, and S08 curves, respectively. |
| In the text | |
 |
Fig. 10. Relation between galaxy stellar mass and redshift for all galaxies in the parent sample. The solid black line is the limit at which galaxies can no longer be observed with the criteria we used to select the sample (see Sect. 2). Dashed black lines represent the uncertainty limit (±σ). Galaxies are color-coded according to their (u − r) rest-frame color. |
| In the text | |
 |
Fig. 11. Distribution of the nebular (E(B − V)Hα/Hβ) and stellar (E(B − V)SED) color excess (left). Nebular extinction at the Hα wavelength as a function of stellar mass (right). Galaxies are color-coded with the EW of Hα and belong the SF sample described in Sect. 5.1. Black squares are the median obtained in the following stellar mass bins: 8 < log M* ≤ 9, 9 < log M* ≤ 9.5, 9.5 < log M* ≤ 10, 10 < log M* ≤ 10.5, and 10.5 < log M* ≤ 11. The error bars on the y-axis represent the standard deviation, gray contours represent the density of sources for 1σ, 2σ, and 3σ derived from SDSS galaxies in Duarte Puertas et al. (2017). Red stars are the values obtained by Sobral et al. (2016) by means of spectroscopy measurements in SF galaxies within the cluster CL 0939+4713 at z = 0.41. The dashed black line is the best polynomial fit obtained by Garn & Best (2010) in a sample of SDSS galaxies. |
| In the text | |
 |
Fig. 12. SFR vs. stellar mass for the galaxy sample described in Sect. 5.1. Galaxies are color-coded with the τ/t0 ratio (see Sect. 3.2). Black lines are the best fits obtained with the Bayesian routine. The median posterior value and 1σ confidence interval are shown for each of the parameters. |
| In the text | |
 |
Fig. 13. SFR vs. stellar mass for galaxies in different redshift bins color-coded with their the τ/t0 ratio (see Sect. 3.2). Black lines are the best fits obtained with the Bayesian routine. The median posterior value and 1σ confidence interval are shown for each of the parameters. The number of galaxies within each redshift bin is also indicated. |
| In the text | |
 |
Fig. 14. Slope of the SFMS derived from the Hα emission line by different works as a function of the redshift. The bars on the x-axis represent the redshift range of the galaxies involved in each study. Our best fit of the SFMS is shown with large blue stars for the lowest redshift range (0 < z ≤ 0.15) and the SF sample (0 < z ≤ 0.35). The results of the literature are from Boogaard et al. (2018) (B18), Vilella-Rojo et al. (2021) (V21), Duarte Puertas et al. (2017) (D17), Renzini & Peng (2015) (R&P15), Zahid et al. (2012) (Z12), Shin et al. (2021) (S20), Belfiore et al. (2018) (Be18), Cano-Díaz et al. (2019) (C19), Sánchez et al. (2019) (S19), and Cano-Díaz et al. (2016) (C16). We also include the results derived by GALFROM (a semianalytical model) (Mitchell et al. 2014) (Mi15), and from hydrodynamical simulations, Sparre et al. (2015) (Sp15) and Furlong et al. (2015) (F15). |
| In the text | |
 |
Fig. 15. SFR vs. stellar mass for the galaxy sample described in Sect. 5.1. SFRs are derived from BaySeGal. Galaxies are color-coded with the EW of Hα. Black lines are the best fits obtained with the Bayesian routine. The median posterior value and the 1σ confidence interval are shown for each of the parameters. |
| In the text | |
 |
Fig. 16. Star formation rate density at z < 0.35. Red stars show the values obtained in this work from the luminosity of Hα. Empty stars are uncorrected values that do not take galaxies with undetectable nebular emission lines or with very low S/N (see text in Sect. 6.2) into account. Black circles are the values obtained by González Delgado et al. (2021) applying the fossil record method to a sample of miniJPAS galaxies in the range 0.05 < z ≤ 0.15. Squares are studies based on Hα (see references in Table 3). Solid lines represents the trends obtained by different studies based on the stellar continuum: Madau & Dickinson (2014, M&D14), López Fernández et al. (2018, LF18), and Bellstedt et al. (2020, B20). All values are scaled to the Chabrier (2003) IMF. |
| In the text | |
 |
Fig. 17. Comparison of the ionizing photon rates computed from Hα emission line and from the fit obtained with the analysis of the stellar populations with BaySeAGal (left; see text in Sect. 6.3). The dashed black line represents the 1:1 relation. μ and σ are the bias and the standard deviation. Right panel: difference between these quantities as a function of the EW of Hα. Density contours are drawn in black. In both cases, the galaxies are color-coded with the extinction of the interstellar gas calculated from the Balmer decrement. |
| In the text | |
 |
Fig. 18. Relation between the SFR derived from Hα and redshift for the galaxy sample described in Sect. 5.1. The blue dotted line is the approximate SFR completeness limit for GAMA and SDSS galaxies (Gunawardhana et al. 2013), and the dotted black line is the 95% completeness limit from blue galaxies in miniJPAS. Galaxies are color-coded with their (u − r) rest-frame color. |
| In the text | |
 |
Fig. 19. Comoving number density of galaxies in miniJPAS as a function of redshift. The total galaxy population (black star) is broken into star-forming (blue stars), AGN-like (green stars), and quiescent galaxies (red stars). We used the WHAN diagram with the Ka03 dividing line to separate AGN and SF galaxies. Quiescent galaxies include LINERs and passive galaxies. The uncertainty due to the cosmic variance is not included in the error budget. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} \Psi (t) = \phi \frac{t_0-t}{\tau } \exp \left[-(t_0-t)/\tau \right], \end{aligned} $$](/articles/aa/full_html/2022/05/aa42812-21/aa42812-21-eq3.gif)
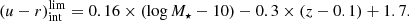
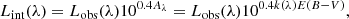
![$$ \begin{aligned} E(B{-}V) = 1.97 \log _{10} \left[\frac{(\mathrm{H}\alpha /\mathrm{H}\beta )_{\mathrm{obs} }}{2.86}\right], \end{aligned} $$](/articles/aa/full_html/2022/05/aa42812-21/aa42812-21-eq7.gif)
![$$ \begin{aligned} \mathrm{SFR} [M_\odot \,\mathrm{yr}^{-1}] = 4.9 \times 10^{-42}\,L_{\mathrm{H}\alpha } [\mathrm{erg/s}]. \end{aligned} $$](/articles/aa/full_html/2022/05/aa42812-21/aa42812-21-eq8.gif)
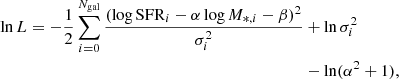
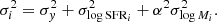
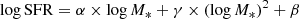
![$$ \begin{aligned}&\log \mathrm{SFR} = \beta - \log \left[1 + (M_*/M_0)^{-\alpha }\right]. \end{aligned} $$](/articles/aa/full_html/2022/05/aa42812-21/aa42812-21-eq32.gif)
![$$ \begin{aligned} \zeta _{\rm Cos.\,Var. } (\mathrm {per\,cent} ) =&[1.00 - 0.03 \sqrt{A/B -1}]\nonumber \\&\times [219.7 - 52.4 \log (AB \times 291.0 )]\nonumber \\&+ 3.21 \log (AB \times 291.0 )^2/\sqrt{NC/291.0}, \end{aligned} $$](/articles/aa/full_html/2022/05/aa42812-21/aa42812-21-eq36.gif)