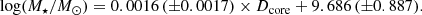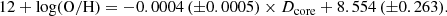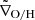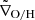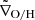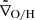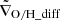| Issue |
A&A
Volume 660, April 2022
|
|
|---|---|---|
| Article Number | A105 | |
| Number of page(s) | 16 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202142790 | |
| Published online | 20 April 2022 | |
The Fornax3D project: The environmental impact on gas metallicity gradients in Fornax cluster galaxies
1
Armagh Observatory and Planetarium, College Hill, Armagh BT61 DG, UK
e-mail: Maritza.Lara-Lopez@armagh.ac.uk
2
Astrophysics Research Centre, School of Mathematics and Physics, Queen’s University Belfast, Belfast BT7 INN, UK
3
INAF-Osservatorio Astronomico di Capodimonte, Salita Moiariello 16, 80131 Napoli, Italy
4
European Southern Observatory, Karl-Schwarzschild-Straße 2, 85748 Garching bei München, Germany
5
Cardiff Hub for Astrophysics Research and Technology, School of Physics and Astronomy, Cardiff University, Queens Buildings, The Parade, Cardiff CF24 3AA, UK
6
Kapteyn Astronomical Institute, University of Groningen, PO Box 800, 9700 AV Groningen, The Netherlands
7
Dipartimento di Fisica e Astronomia ‘G. Galilei’, Università di Padova, Vicolo dell’Osservatorio 3, 35122 Padova, Italy
8
INAF-Osservatorio Astronomico di Padova, vicolo dell’Osservatorio 5, 35122 Padova, Italy
9
Sterrewacht Leiden, Leiden University, Postbus 9513, 2300 RA Leiden, The Netherlands
10
Max-Planck-Institut für Extraterrestrische Physik, Giessenbachstraße, 85741 Garching bei München, Germany
11
European Space Agency, European Space Exploration and Research Centre, Keplerlaan 1, 2201 AZ Noordwijk, The Netherlands
12
Instituto de Astrofísica de Canarias, Vía Láctea s/n, 38205 La Laguna, Tenerife, Spain
13
Depto. Astrofísica, Universidad de La Laguna, Calle Astrofísico Francisco Sánchez s/n, 38206 La Laguna, Tenerife, Spain
14
Department of Physics and Astronomy, Macquarie University, Sydney, NSW 2109, Australia
15
ARC Centre of Excellence for All Sky Astrophysics in 3 Dimensions (ASTRO 3D), Australia
16
Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
17
Instituto de Radioastronomía y Astrofísica, Universidad Nacional Autónoma de México, Apdo. Postal 72-3, 58089 Morelia, Mexico
18
Department of Astrophysics, University of Vienna, Türkenschanzstrasse 17, 1180 Vienna, Austria
19
Shanghai Astronomical Observatory, Chinese Academy of Sciences, 80 Nandan Road, Shanghai 200030, PR China
Received:
30
November
2021
Accepted:
8
February
2022
The role played by environment in galaxy evolution is a topic of ongoing debate among astronomers. There has been little success in elucidating the degree to which environment can alter, re-shape, or drive galaxy evolution, that is, using either observations or simulations. However, our knowledge of the effect of environment on gas metallicity gradients remains limited. Here we present our analysis of the gas metallicity gradients for a sample of ten Fornax cluster galaxies observed with MUSE as part of the Fornax3D project. We used detailed maps of emission lines to determine precise values of gas metallicity and metallicity gradients. The integrated gas metallicity of our Fornax cluster galaxies shows slightly higher metallicities (∼0.045 dex) in comparison to a control sample. In addition, we find signs of a mass and metallicity segregation from the center to the outskirts of the cluster. By comparing our Fornax cluster metallicity gradients with a control sample we find a general median offset of ∼0.04 dex/Re, with eight of our galaxies showing flatter or more positive gradients. The intermediate infallers in our Fornax sample show more positive gradients with respect to the control sample. We find no systematic difference between the gradients of recent and intermediate infallers when considering the projected distance of each galaxy to the cluster center. To identify the origin of the observed offset in the metallicity gradients, we performed a similar analysis with data from the TNG50 simulation. We identify 12 subhalos in Fornax-like clusters and compared their metallicity gradients with a control sample of field subhalos. This exercise also shows a flattening in the metallicity gradients for galaxies in Fornax-like halos, with a median offset of ∼0.05 dex/Re. We also analyzed the merger history, Mach numbers (ℳ), and ram pressure stripping of our TNG50 sample. We conclude that the observed flattening in metallicity gradients is likely due to a combination of galaxies traveling at supersonic velocities (ℳ > 1), which are experiencing high ram pressure stripping and flybys.
Key words: galaxies: abundances / galaxies: clusters: intracluster medium / galaxies: clusters: individual: Fornax cluster / galaxies: fundamental parameters / galaxies: spiral
© ESO 2022
1. Introduction
Gas metallicity is an important physical parameter in that it is directly linked to the star formation history of the host galaxy. Indeed, it provides important clues as to the physical properties of the interstellar medium (ISM), and the history, evolution, formation, and growth of galaxies.
For several decades, a great amount of effort was put into the analysis of scaling relations such as the mass–metallicity (M–Z) relation (e.g., Lequeux et al. 1979; Tremonti et al. 2004; Kewley & Ellison 2008; Lara-López et al. 2013). The M–Z relation provides essential insight into galaxy evolution (e.g., Savaglio et al. 2005; Erb et al. 2006; Lara-López et al. 2009a,b, 2010; Zahid et al. 2012; Sanders et al. 2021; Bellstedt et al. 2021), and is sensitive to metal loss due to stellar winds (Spitoni et al. 2010; Tremonti et al. 2004), supernovae (Brooks et al. 2007), active galactic nuclei (AGN) feedback (Lara-López et al. 2019), and environment (Mouhcine et al. 2007; Cooper et al. 2008; Ellison et al. 2009; Garduño et al. 2021).
With the advent of Integral Field Unit (IFU) spectroscopy, extensive analyses of the resolved physical conditions of the ISM within galaxies have been performed as part of large surveys, such as the Sydney-AAO Multi-object Integral-field unit survey (SAMI, Poetrodjojo et al. 2018), the Calar Alto Legacy Integral Field Area survey (CALIFA, Sánchez-Menguiano et al. 2016), and the Mapping Nearby Galaxies at APO (MANGA, Zhang et al. 2017); and surveys of nearby galaxies with high angular resolution, such as VIRUS-P Exploration of Nearby Galaxies (VENGA, Blanc et al. 2009; Kaplan et al. 2016), the Physics at High Angular resolution in Nearby Galaxies (PHANGS, Kreckel et al. 2019), and the MUSE Atlas of Disks (MAD, Erroz-Ferrer et al. 2019).
The spatial information provided by IFU surveys allows us to study resolved maps of gas metallicity for emission line galaxies in detail. Negative gas metallicity gradients are widely found in late-type galaxies in the local Universe (e.g., Zaritsky et al. 1994; Pilyugin et al. 2004, 2014; Moustakas et al. 2010; Rupke et al. 2010b; Ho et al. 2015; Sánchez-Menguiano et al. 2016, 2018; Belfiore et al. 2017). Such negative gradients are consistent with an inside-out growth scenario of the disks (e.g., White & Frenk 1991; Mo et al. 1998; Pérez et al. 2013).
Recently, a trend of the resolved metallicity gradient with the total stellar mass of a galaxy was observed by Belfiore et al. (2017) using a sample of 550 nearby galaxies from MANGA. These authors find that galaxies with log(M⋆/M⊙) < 9.5 show flatter gradients that steepen for more massive galaxies until log(M⋆/M⊙) ∼ 10.5, and then flatten slightly again for more massive systems. Similar results are found for SAMI galaxies (Poetrodjojo et al. 2021). However, so far simulations have been unable to reproduce this trend with stellar mass, with more work needed (e.g., Hemler et al. 2021).
Gas metallicity gradients have been shown to be sensitive to processes such as secular evolution and radial migration (e.g., Friedli et al. 1994; Vilchez & Esteban 1996; Marino et al. 2016). Morphological studies also claim that barred spirals exhibit flatter metallicity gradients than unbarred galaxies (e.g., Vila-Costas & Edmunds 1992; Zaritsky et al. 1994; Henry & Worthey 1999; Kreckel et al. 2019; Lara-López et al. 2021).
However, studies of the effect of environment on gas metallicity gradients have so far been rather limited, even though there is observational evidence that between 50% and 70% of the galaxy population is in groups and clusters (e.g., Eke et al. 2005). This naturally implies that processes taking place in the group environment can have a significant impact on the evolution of the galaxy population as a whole. Groups and clusters of galaxies have long been considered perfect laboratories to study the effect of feedback processes in galaxies and their role in (re)shaping galaxy properties and evolution. For instance, galaxy interactions and mergers can cause gas inflows, drive morphological transformations, trigger star formation, and even lead to activity in the galactic nucleus (e.g., Lambas et al. 2003; Nikolic et al. 2004; Woods & Geller 2007; Ellison et al. 2008, 2019; Davies et al. 2015; Gordon et al. 2018; Pan et al. 2019; Shah et al. 2020). However, the extent of the role played by the environment, also known as the nature versus nurture problem, has been a matter of debate for decades (e.g., Di Matteo et al. 2005; Hopkins et al. 2006; Lani et al. 2013; Paulino-Afonso et al. 2019; Tortora et al. 2020).
Galaxies in clusters tend to have higher metallicities than control samples by up to ∼0.04 dex (e.g., Ellison et al. 2009; Scudder et al. 2012; Lian et al. 2019). These higher metallicities can be explained by several scenarios. For instance, if galaxies undergo a burst of star formation as they enter the cluster environment, this may cause the increase of galaxy metallicity (e.g., Finlator & Davé 2008). In addition, strangulation/starvation may be at play, where the gas reservoir of a galaxy is stripped away or truncated due to interactions with the intra-cluster medium (ICM) or other galaxies. During this process, the cessation of pristine gas accretion on to the galaxy prevents the dilution of metals in the ISM (e.g., Larson et al. 1980; Bekki et al. 2002; Maier et al. 2022). Alternatively, cluster galaxies that experience inflows of pre-enriched gas, also known as “chemical pre-processing” would also explain higher metallicities (e.g., Peng et al. 2010; Gupta et al. 2018).
Recent studies find that environment might be responsible for flattening metallicity gradients. For instance, using galaxies from the GAs Stripping Phenomena in galaxies with MUSE (GASP survey, Poggianti et al. 2017) and MANGA, Franchetto et al. (2021) observed flatter gradients for galaxies in clusters. Also, Kewley et al. (2010) found that galaxies in pairs show flatter metallicity gradients. However, the physical explanation behind the observed flattening is still yet to be understood. Kewley et al. (2010) attributed this flattening to large inflows of gas induced by the tidal effects of galaxy interactions, whereas Franchetto et al. (2021) suggest that cluster galaxies with flatter gradients might have fallen into the cluster sooner and hence experienced environmental effects for a longer time.
In this paper, we aim to provide insights into the effects of the cluster environment on gas metallicity gradients by analyzing a sample of ten galaxies in the Fornax cluster observed with MUSE. Additionally, we use TNG50 simulations of Fornax-like subhalos to further investigate the impact of cluster environment on these galaxies. Specifically, we aim to elucidate particular cluster effects and to investigate their impact on gas metallicity gradients.
This paper is structured as follows. In Sect. 2 we present a description of the observations and our estimation of spectroscopic emission lines. In Sect. 3 we characterize the sample in terms of the M–Z relation and mass segregation. Our results are presented in Sect. 4, and our findings are discussed in Sect. 5. Finally, our conclusions are given in Sect. 6.
2. Observations
This paper is based on the Fornax3D survey (F3D, Sarzi et al. 2018), which observed galaxies brighter than mB ≤ 15 mag in the Fornax cluster within the viral radius with MUSE. The F3D sample consists of 33 galaxies selected from the catalog of the Fornax cluster members by Ferguson & Sandage (1989). This study focuses on the gas metallicity gradients and therefore we restrict our sample to emission line galaxies (ELGs), because these are needed to estimate gas metallicities. The final sample analyzed consists of ten late-type and dwarf irregular galaxies. Nine of the ELGs were observed with a single central pointing (providing the full coverage for seven of them, and partial coverage for FCC 285 and FCC 290), while FCC 312 was observed with three pointings (see Fig. A.1). For further details on the observations, we refer to Sarzi et al. (2018). In addition, the Fornax cluster galaxies included in this paper were classified as either recent or intermediate infallers by Iodice et al. (2019) following the prescription of Rhee et al. (2017). This classification was based on the position of the galaxies in the projected phase-space (PPS) diagram Rproj/Rvir versus Vlos/σlos, where Rproj and Rvir are the projected and viral radius, respectively, while Vlos and σlos are the line of sight radial velocity, and the cluster velocity dispersion, respectively.
The data reduction and calibration are described in Sarzi et al. (2018). Briefly, galaxies were observed with MUSE at ESO Very Large Telescope in Chile between July 2016 and December 2017 in Wide Field Mode (Bacon et al. 2010), with a 1 × 1 arcmin2 field coverage, a spatial sampling of 0.2 × 0.2 arcsec2, a wavelength range of 4650–9300 Å, and a spectral sampling of 1.25 Åper pixel. The measured spectral resolution was on average FWHMinst = 2.8 Å, with little variation (<0.2 Å) with wavelength and position over the field of view. The observations were made in good seeing conditions with a median FWHM = 0.88. The data were reduced with the MUSE pipeline version 1.6.2 (Weilbacher et al. 2016). Sky subtraction was performed by fitting and subtracting a sky model spectrum on each spaxel of the field of view, with an additional cleaning of the residual sky contamination achieved with the Zurich Atmospheric Purge algorithm (ZAP, Soto et al. 2016).
The emission lines were measured using the Gas and Absorption Line Fitting code (GandALF, Sarzi et al. 2006; Falcón-Barroso et al. 2006) in the wavelength range between 4800 and 6800 Å. The emission line fitting was performed spaxel by spaxel in order to provide high spatial resolution maps and abundances. For this study, we use the following emission lines: Hβ, [O III] λ5007, Hα, [N II] λ6584, and [S II] λλ6717, 31.
3. Sample characterization
We use the stellar masses and effective radii (Re) estimated by Raj et al. (2019) for our sample of ELGs. These parameters were estimated through a photometric analysis and isophotal fit following the methodology of Iodice et al. (2019). From the isophotal fit, the growth curve analysis was used to derive Re in several bands for all galaxies. The stellar mass of each galaxy was estimated through the integrated g − i color using the empirical relation from Taylor et al. (2011), which adopts a Chabrier initial mass function (IMF). The stellar masses and Re for our sample are listed in Table 1.
Properties of the Fornax ELGs.
For each galaxy, we selected only the star forming (SF) spaxels using the standard BPT diagram [N II]λ6584/Hα versus [O III] λ5007/Hβ (Baldwin et al. 1981) in conjunction with the discrimination of Kauffmann et al. (2003). The middle column of Fig. A.1 shows the map of BPT classification for each galaxy. Spaxels classified as composite, Seyfert, and low-ionization nuclear emission-line region (LINER) were selected following the prescription of Kewley et al. (2006), and are displayed in the same figure. With the exception of FCC 179 and FCC 290, the galaxies in our sample are mostly characterized by SF regions. FCC 179 shows Seyfert and LINER regions in the center and outskirts, with a ring of SF regions in between. The center of FCC 290 is full of LINER regions with composite regions scattered throughout the galaxy. It can therefore be classified as a central LINER, or cLIER (Belfiore et al. 2016).
From the plethora of available gas metallicity calibrations, we selected the one of Dopita et al. (2016), which is defined as:
Among its advantages, this calibration is independent of reddening, as all the emission lines involved are close in wavelength (within 20Å). We applied this calibration only to the SF spaxels in each galaxy. The obtained gas metallicity maps are shown in Figs. A.1–A.3.
3.1. The M–Z relation for Fornax galaxies
To locate our ELG sample in the context of the global M–Z relation, we integrated the emission line fluxes from the SF spaxels, and estimated the integrated gas metallicity through Eq. (1). The integrated gas metallicities of our sample are listed in Table 1. We then constructed the M–Z relation with the integrated values and total stellar masses, as shown in Fig. 1.
 |
Fig. 1. M–Z relation for SDSS (gray background) and Fornax cluster (red symbols) galaxies. The white solid line indicates the best fit to the SDSS data. Circles and triangles correspond to recent and intermediate infallers, respectively. The green squares correspond to the control sample. |
As a comparison, in the same figure we show the M–Z relation for a sample of ∼91 400 galaxies from the SDSS-DR7 (Abazajian et al. 2009). Emission-line fluxes of the SDSS galaxies were taken from the OSSY catalog1 (Oh et al. 2011). We selected only SF galaxies using the BPT diagram and the gas metallicities were estimated using the Dopita et al. (2016) calibration. According to Brinchmann et al. (2004), flux measurements become non-Gaussian below a signal-to-noise ratio (S/N) ∼2, and therefore we imposed a S/N > 3 for all the emission lines used. Additionally, the SDSS spectra suffer from an aperture bias due to the 3 diameter fiber used. As the integrated metallicities tend to be smaller than nuclear ones, it is possible that we overestimate the gas metallicities. To minimize the aperture bias, we selected only galaxies that have at least 20% of their total luminosity inside the SDSS fiber, which should approximate to the integrated value according to Kewley et al. (2005).
We fitted (using robust regression) the M–Z relation to the SDSS-SF sample and find the expression: 12 + log(O/H) = ax3 + bx2 + cx + d, with the coefficients a = − 0.0573 (±0.0007); b = 1.5478 (±0.0197); c = −13.5028 (±0.1786); and d = 46.2986 (±0.5375). In addition, we created a control sample by removing all SDSS galaxies in groups from the general SDSS-SF sample described above. We used the catalog of Tempel et al. (2012) for the SDSS-DR8, who used the friends-of-friends (FoF) method and identified groups based on their richness. For our purposes, we excluded from our SDSS-SF sample all galaxies with a richness greater than or equal to 2 in order to ensure that galaxy pairs are excluded as well as groups and clusters. Our final control sample comprises 60 947 field galaxies. From this sample, we selected galaxies within ±0.05 dex in log(M⋆/M⊙) of each Fornax galaxy, and estimated the median mass and metallicity, shown in green squares in Fig. 1. Finally, we estimated the difference (Fornax-control) in metallicity, and obtained a median difference of 0.045 dex for the whole sample.
Galaxies from the Fornax cluster follow the general M–Z relation for SDSS galaxies, and show a statistical 0.045 dex offset towards higher metallicities (see Fig. 1). The exception is FCC 312, which shows a low gas metallicity for its stellar mass. Previous works report slightly higher (∼0.05 dex) gas metallicities for SF galaxies in clusters (e.g., Ellison et al. 2009; Gupta et al. 2016), explained by the accretion of pre-enriched gas (e.g., Gupta et al. 2018). Even though our sample is small, our difference of 0.045 dex is consistent with these studies.
3.2. Stellar mass and metallicity segregation
Another distinctive feature in galaxy clusters is stellar mass segregation (Chandrasekhar 1943), or the tendency of more massive galaxies to be located closer to the center (e.g., De Lucia et al. 2004; Contini et al. 2012; Kim et al. 2020). Nonetheless, it is still controversial, with some authors finding observational and theoretical evidence for no segregation (e.g., Lares et al. 2004; Balogh et al. 2014; Roberts et al. 2015; Nascimento et al. 2017), or weak segregation (e.g., von der Linden et al. 2010; Ziparo et al. 2013; Vulcani et al. 2013; Joshi et al. 2017).
Recently, Kim et al. (2020) concluded that mass segregation is more visible in low-mass clusters simply as a result of the shorter dynamical friction time for more massive galaxies. As the Fornax cluster can be considered a low-mass cluster (Mvir ∼ 7 × 1013 M⊙, Drinkwater et al. 2001), we investigate whether or not mass segregation is present. Figure 2 shows the projected distance-versus-stellar-mass relation for our Fornax-ELG cluster sample. Although we find large scatter, with a Pearson correlation coefficient of −0.3 and a corresponding significance of p = 0.4 of its deviation from the null hypothesis, our data suggest a mild relation as described by Eq. (2).
 |
Fig. 2. Projected distance–stellar mass relation (left panel), and distance–gas metallicity relation (right panel) for Fornax ELGs. Circles and triangles correspond to recent and intermediate infallers, respectively. |
A mass segregation in clusters would naturally produce a similar effect in the galaxy metallicities due to the M–Z relation, and the gas metallicity would decrease as a function of projected clustercentric distance. We explore this in Fig. 2, and find a relation described by Eq. (3). Again, our data show a slight correlation, with a Pearson coefficient of −0.23 and a value p = 0.5.
Moreover, our sample shows a mild signature of both mass and metallicity segregation. Furthermore, using the early-type population of F3D galaxies, Spriggs et al. (2021) find signs of mass segregation.
4. Results
4.1. Gas metallicity gradients
In this section we explore the effect of cluster environment on the gas metallicity gradients of galaxies. We used the resolved gas metallicity estimations described in Sect. 3 for every MUSE spaxel. Metallicity gradients are presented in the literature either as a function of kpc scale, normalized as a function of R25, or Re. To compare our results with previous works in the literature and data from IllustrisTNG, we opted to use Re. All radial distances in the gradients are corrected for inclination and normalized to Re in r-band (Raj et al. 2019), and are given in Table 1. The resulting metallicity gradients for the whole of our Fornax ELG sample are shown in Fig. 3. All the linear fits were performed – over the full radial extent of each galaxy using all the spaxels – in the language and environment for statistical computing “R” with the package “HYPERFIT” (Robotham & Obreschkow 2015). We define the root-mean-square error (RMSE) as 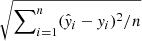 , where ŷi and yi are the predicted and observed values, respectively. The slope, intercept, and RMSE of the metallicity gradients are given in Table 2. To identify any systematic change due to the cluster environment, we proceeded to create a control sample as detailed in the following section.
, where ŷi and yi are the predicted and observed values, respectively. The slope, intercept, and RMSE of the metallicity gradients are given in Table 2. To identify any systematic change due to the cluster environment, we proceeded to create a control sample as detailed in the following section.
 |
Fig. 3. Linear fits of the gas metallicity radial profiles for Fornax-ELGs sample. |
Gas metallicity gradient coefficients and RMSE for our sample of Fornax ELGs.
4.2. Control sample
Previous papers looking for environmental effects used the stellar mass of galaxies as a baseline to create control samples, together with other properties such as color or morphology (e.g., Ellison et al. 2008, 2009; Scudder et al. 2012; Garduño et al. 2021; Sotillo-Ramos et al. 2021). Because of the limited number of ELGs with IFU data, we are focussing on the stellar mass as a reference, as it is one of the most fundamental galaxy properties, and scales with both star formation rate (SFR; e.g., Brinchmann et al. 2004; Noeske et al. 2007; Elbaz et al. 2007) and metallicity (e.g., Tremonti et al. 2004).
From the plethora of current IFU surveys, we used galaxies from the MAD survey (Erroz-Ferrer et al. 2019) that were also observed with MUSE, and therefore offer a direct comparison with our data. We selected the SF galaxies from their public database2 that are within ±0.2 dex of the stellar mass of each galaxy in our Fornax sample. The current public MAD data provide galaxies only with stellar masses higher than ∼108.4 M⋆/M⊙. Our final comparison sample from MAD is formed by 16 galaxies. We estimated metallicities using the same prescription used for Fornax ELGs, and normalized the metallicity gradients to their respective Re for a direct comparison. Each linear fit on the galaxies of the control sample was also performed with HYPERFIT.
The metallicity versus galactocentric distance relation for individual Fornax ELGs and their corresponding control sample from MAD is shown in Fig. 4. In each panel, the shaded regions show the dispersion of ±1σ in bins of 0.2 R/Re. The metallicity gradients for Fornax and MAD galaxies are shown in Fig. 5, where the vertical lines indicate the RMSE of the fit for both samples.
 |
Fig. 4. Gas metallicity radial profiles for our sample of Fornax ELGs. Each panel corresponds to a Fornax galaxy (gray dots) and its corresponding control sample from the MAD survey (color dots). The shaded areas around each gradient correspond to the 1σ dispersion in 0.2 dex of R/Re. The gradients of the control samples are colored according to the names inside each panel. The black vertical arrow in the panels of FCC 263, FCC 290, FCC 308, and FCC 312 shows the break radius from Raj et al. (2019). The red arrow in the panel of FCC 290 shows the drop in H2-to-dust ratio from Zabel et al. (2021). |
 |
Fig. 5. Gas metallicity gradients as a function of stellar mass. The black symbols show our Fornax ELGs sample, with circles and triangles corresponding to recent and intermediate infallers, respectively. The red symbols correspond to galaxies from the MAD survey. The small gray circles indicate galaxies from the SAMI survey. The cyan circles are galaxies from B19. For galaxies from Fornax, MAD, and B19, the vertical bars correspond to the RMSE. For SAMI galaxies, the bars indicate the 1σ error in the metallicity gradient. The green squares show the median values of |
We also take into account the metallicity gradients from the SAMI survey (Croom et al. 2012), as SAMI observed low-mass galaxies, which are difficult to find in other IFU surveys such as MANGA, CALIFA, and MAD. For SAMI galaxies, the gradients were taken from Poetrodjojo et al. (2021). From this paper, we selected the gradients estimated using the metallicity method of Dopita et al. (2016), and also normalized to Re. All the metallicity gradients from the SAMI sample are shown in Fig. 5 to illustrate the general trend with stellar mass.
To increase our control sample in the low-mass regime, we use a couple of galaxies from Bresolin (2019, hereafter B19). The gas metallicities were estimated following Dopita et al. (2016), and the corresponding gradients were normalized to Re. The obtained gradients are shown colored in cyan in Fig. 5.
In addition, we looked for any effect of the break radius on the metallicity gradient for Fornax late-type galaxies. Raj et al. (2019) estimated the break radius as the radius where the logarithmic surface brightness of a galaxy shows a discontinuity. We indicate the break radius for four of our galaxies as a vertical arrow in Fig. 4. The remaining members of our sample show either no break radius, or one that lies outside the area mapped by MUSE. Our data show no relation between the break radius and the metallicity gradient, suggesting that it might be more closely related to a break in star formation as suggested by Raj et al. (2019). In Fig. 4, the red arrow in the FCC 290 panel shows the drop in H2-to-dust ratio from Zabel et al. (2021). Interestingly, this drop suggests a change of the metallicity gradient towards a flatter or positive gradient.
4.3. Cluster-control comparison
Figure 5 shows the direct comparison between the Fornax metallicity gradients and control galaxies from MAD, SAMI, and B19. As described above, all the gradients were measured using the same metallicity method, and normalized to Re. The vertical bars show the RMSE of the fit for Fornax, MAD, and B19 galaxies, while for the SAMI galaxies they correspond to the 1σ error in the gradient.
To identify systematic changes in the metallicity gradients of Fornax ELGs, we combined all the control galaxies (from MAD, SAMI, and B19) and estimated the median value (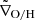 ) for all galaxies within ∼±0.2 dex in log(M⋆/M⊙) of each Fornax galaxy. The values
) for all galaxies within ∼±0.2 dex in log(M⋆/M⊙) of each Fornax galaxy. The values 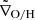 are indicated as green squares in Fig. 5.
are indicated as green squares in Fig. 5.
The bottom panel in the same figure shows the difference in metallicity gradient between each Fornax ELG and its corresponding 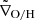 . With the exception of FCC 285 and FCC 312, our Fornax ELGs show more positive gradients with respect to those of the control sample, either flatter or positive (e.g., FCC 119 and FCC 306). FCC 119 also shows a positive stellar metallicity gradient, which is likely caused by the metal-poor nuclear star cluster in the center of FCC 119 (Fahrion et al. 2021). The vertical bars show the 1σ dispersion of the difference. The histogram of these differences (Fig. 9) shows a shift of ∼0.04 dex/Re towards flatter gradients for the Fornax sample. To quantify the probability of obtaining this difference by chance, we bootstrap the data by constructing samples with replacement 1000 times and find an error of ∼0.02% in our difference.
. With the exception of FCC 285 and FCC 312, our Fornax ELGs show more positive gradients with respect to those of the control sample, either flatter or positive (e.g., FCC 119 and FCC 306). FCC 119 also shows a positive stellar metallicity gradient, which is likely caused by the metal-poor nuclear star cluster in the center of FCC 119 (Fahrion et al. 2021). The vertical bars show the 1σ dispersion of the difference. The histogram of these differences (Fig. 9) shows a shift of ∼0.04 dex/Re towards flatter gradients for the Fornax sample. To quantify the probability of obtaining this difference by chance, we bootstrap the data by constructing samples with replacement 1000 times and find an error of ∼0.02% in our difference.
Considering the possibility that the observed flattening is related to the galaxy distance to the cluster center, we show in Fig. 6 the metallicity gradients of the Fornax ELGs as a function of the projected distance to the brightest cluster galaxy (BCG) NGC 1399. The lower panel in the same figure shows the difference with the control sample. No pattern emerges, indicating that the projected distance to the BCG does not play a significant role, although a larger sample is needed to confirm this result, and we do not discard that accurate 3D distances might change this outcome (Ryś et al. 2014).
 |
Fig. 6. Gas metallicity gradients as a function of the projected cluster-centric distance to the BCG. The bottom panel shows the difference in gas metallicity gradient between each Fornax galaxy and its corresponding |
4.4. TNG50 simulations from the IllustrisTNG Project
To further investigate the reliability of the suggested flattening from the observations, we performed a similar exercise using the high-resolution TNG50 data from the IllustrisTNG Project (Pillepich et al. 2019; Nelson et al. 2019a,b). First, we identified clusters with similar characteristics to the Fornax cluster. The virial mass of Fornax is Mvir ∼ 3–6 × 1013M⊙ from Drinkwater et al. (2001), but for the sake of increasing our statistics, we expanded the search of Fornax-like clusters to FoF groups in the range of ∼2–7 × 1013 M⊙ in virial mass. This gives a total of 12 Fornax-like clusters in TNG50.
For these 12 Fornax-like clusters, we proceeded to find simulated galaxies (or subhalos) with stellar masses similar to our Fornax-ELGs sample within the viral radius of each cluster at z = 0. Although stellar mass is our primary discriminator, we also restricted our sample to SFRs within a ±0.2 dex range. This retrieves a total of 15 subhalos. Because of the resolution of TNG50, we are unable to find subhalos with stellar masses lower than ∼ 108.0 M⊙.
Once our sample was constrained, we estimated gas metallicity gradients as done in Hemler et al. (2021) and Ma et al. (2017). First, the center of each galaxy was defined as the position of the particle (of any type) at the minimum potential, and we defined the origin of the coordinate system in this position. Gas cells with hydrogen number density nH < 0.13 cm−3 were excluded in order to avoid contributions from diffuse gas outside the galactic disk. Following Ma et al. (2017), we did not fit the inner quarter of the galaxy, as the gradient tends to be steeper or flatter in comparison with the outer star-forming region. Gas metallicities were estimated using the oxygen to hydrogen ratio 12 + log(NO/NH). These metallicities are systematically higher than the observational values we obtained following Dopita et al. (2016). However, the intrinsic differences between the TNG50 gradients should be indicative of any systematic difference.
In contrast with Hemler et al. (2021) and Ma et al. (2017), and for consistency with our observational data, our gas metallicity gradients are normalized to the Re of each subhalo. Individual inspection of each gradient shows that fitting data out to 2 Re results in reliable fits. Finally, only gradients with at least 16 gas cells were considered. This gives a final sample of 15 subhalos in Fornax-like clusters with reliable gradients. The galactocentric gradients were derived using “HYPERFIT”, and the results are shown in Fig. 7.
 |
Fig. 7. Gas metallicity gradients as a function of stellar mass for the subhalos from the TNG50 simulation. The black circles correspond to the subhalos in Fornax-like clusters, while the red circles indicate subhalos from our control sample (see text). The green squares show the median value |
We followed our observational methodology and defined a control sample of subhalos in TNG50. We define the equivalent of “field galaxies” in TNG50 as the subhalos that are alone within a radius of 5 × R200c, where R200c is the virial radius of the considered halo (e.g., Mistani et al. 2016). In this way, we guarantee that the central subhalos are isolated from other central subhalos. The control subhalos were then mass-matched, within a ±0.15 dex range, to each of the 15 Fornax-like subhalos described above. Measurement of the gas metallicity gradients was performed as described above, giving us a final control sample of 252 subhalos. The resulting gradients for Fornax-like and control subhalos are shown in Fig. 7, and its cluster-core distance relation in Fig. 8. Similarly to our observational methodology, we estimated the median value 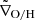 for the control sample of each Fornax-like subhalo. The median values are shown as green squares in the upper panel of Fig. 7, and the differences between the Fornax-like and control
for the control sample of each Fornax-like subhalo. The median values are shown as green squares in the upper panel of Fig. 7, and the differences between the Fornax-like and control 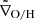 are shown in the lower panel of the same figure. The histogram of these differences is displayed in Fig. 9, showing a ∼0.05 dex/Re difference towards more positive gradients for Fornax-like subhalos. Although the difference is small, it is consistent and in the same direction as we find for our observational sample.
are shown in the lower panel of the same figure. The histogram of these differences is displayed in Fig. 9, showing a ∼0.05 dex/Re difference towards more positive gradients for Fornax-like subhalos. Although the difference is small, it is consistent and in the same direction as we find for our observational sample.
 |
Fig. 8. Gas metallicity gradients as a function of distance to cluster core for the subhalos from TNG50. The black circles correspond to the subhalos in Fornax-like clusters. Bottom panel: difference in metallicity gradient between each subhalo and the corresponding |
 |
Fig. 9. Histograms of the differences between the gas metallicity gradients and control samples for Fornax ELGs (left), and TNG50 (right). In both panels, the red vertical line shows the median value of the differences ( |
Different physical phenomena or mechanisms could explain a flattening in the gas metallicity gradient of cluster galaxies. For instance, minor mergers of chemically poor galaxies could potentially flatten the gradient of the most massive galaxy. Even though mergers are more likely to happen before the cluster is virialized, in order to assess or discard the possible role played by minor and major mergers in Fornax-like clusters, we analyzed the merger history of our TNG50 sample. To this aim, we used the merger tree history estimated by Rodriguez-Gomez et al. (2015) for each subhalo in our Fornax-like and control sample. Major mergers are defined as those occurring between subhalos with a mass ratio higher than 1:4, while minor mergers are those with a mass ratio in between 1:10 and 1:4. We considered the number of major and minor mergers of each subhalo up to redshift 2.
If recent mergers have had an influence in flattening the gas metallicity gradient, we would expect a relation between the gradient and the number of mergers for galaxies in clusters. However, in Fig. 10 we cannot see any evident trend for either minor or major mergers. The same result is found when we limit to different mass bins, and when we constrain the merger history to a more recent past (e.g., z ∼ 1). Hence, we can conclude that the merger history in Fornax-like cluster galaxies is not directly responsible for the flattening of the gas metallicity gradients.
 |
Fig. 10. Gas metallicity gradient as a function of the number of mergers up to redshift 2. Left and right panels: indicate major and minor mergers, respectively. Circles indicate subhalos from the control sample, while diamonds the subhalos in Fornax-like clusters. All the symbols are color coded according to their stellar mass. For the sake of clarity, all the subhalos in the control sample with a number of mergers between 0 and 2 were assigned random shifts (in the range ±0.25) around their actual value, while the subhalos in Fornax-like clusters are shifted to the right. |
Finally, we investigated the role played by ram pressure stripping (RPS) produced by the ICM. We followed Yun et al. (2019) and estimated the (mode of the) ram pressure acting on the galaxy based on the equation of Gunn et al. (1972): 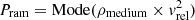 ), where ρmedium is the density of the medium gas cells, and vrel is the relative velocity of the gaseous component of a satellite with respect to its surrounding medium. The relative velocity is defined as vrel = Mode(vsatellite gas − Vmedium), where vsatellite gas is the velocity of the gas cells bounded to the satellite galaxy, and Vmedium is the typical velocity of the medium gas cells. Each medium gas cell is constrained to gas cells bound to the central subhalo within 20 times the stellar half mass radius around it.
), where ρmedium is the density of the medium gas cells, and vrel is the relative velocity of the gaseous component of a satellite with respect to its surrounding medium. The relative velocity is defined as vrel = Mode(vsatellite gas − Vmedium), where vsatellite gas is the velocity of the gas cells bounded to the satellite galaxy, and Vmedium is the typical velocity of the medium gas cells. Each medium gas cell is constrained to gas cells bound to the central subhalo within 20 times the stellar half mass radius around it.
We also estimated the Mach number (ℳ), defined as the speed at which an object moves relative to a fluid divided by the sound speed of the fluid: ℳ = vrel/ Mode(cs, medium). We were able to calculate the parameters for 14 subhalos in our Fornax-like sample. Figure 11 shows the Mach number versus ram pressure estimates, color coded by ∇O/H_diff and cluster-core distance, while the circle sizes correspond to the stellar mass of each subhalo. The distribution of our data shows a general agreement with those of Yun et al. (2019), where higher Mach numbers show larger ram pressures. A further interpretation of this figure is given in Sect. 5.
 |
Fig. 11. Ram pressure as a function of Mach number for the TNG50 subhalos in Fornax-like clusters. The small squares are color coded according to ∇O/H_diff, while the gray circles are color coded according to the cluster-core distance of each subhalo. The circle size corresponds to the stellar mass of each subhalo as indicated in the right bar. The vertical dotted line indicates the threshold between supersonic (ℳ > 1) and subsonic (ℳ < 1) velocities. |
5. Discussion
Late-type galaxies show, in general, negative metallicity gradients, likely as a result of an inside-out formation scenario (e.g., White & Frenk 1991; Pérez et al. 2013), where stars have been forming in their centers for longer, building up the metallicity there. Variations in the gas metallicity gradient can potentially indicate feedback processes due to cluster environment, either due to inflows or outflows of pristine or enriched gas that can alter the metallicity gradient, mergers, or tidal and flyby interactions, among others. However, the observational evidence of the effect of cluster environment on gas metallicity gradients is rather limited so far.
In this paper, we present our analysis of the gas metallicity gradients of ELGs in the Fornax cluster. Our gas metallicity gradients follow the general trend with stellar mass previously reported by Belfiore et al. (2017) and Poetrodjojo et al. (2021); see Fig. 5. As our sample of galaxies spans a stellar mass range between 107.4 and 1010.2M⊙, we are unable to comment about the observed flattening in the gradients for more massive galaxies.
By comparing Fornax-ELG gradients with those of galaxies from a control sample, we find that eight of our ELGs show more positive gradients, and a general median difference of ∼0.04 dex/Re is found for the whole sample. We did a similar exercise with data from the TNG50 simulation by selecting subhalos in Fornax-like clusters and comparing them with a sample of control subhalos. TNG50 data indicate a flattening (∼0.05 dex/Re ) for subhalos in Fornax-like clusters.
Our findings agree with previous results that report a flattening in the metallicity gradients in galaxy clusters (e.g., Lian et al. 2019; Franchetto et al. 2021), and in interacting galaxy pairs (Kewley et al. 2010; Rupke et al. 2010a,b). As galaxy interactions produce a flattening in the gas metallicity gradients, it is natural to expect this result in the very early stages of merger systems. However, according to simulations, the number of encounters within 10 kpc is about ten per galaxy in the Hubble time. Only about 0.1% of such encounters are expected to result in a merger, which gives a merger probability of 22–29% per halo (Gnedin 2003), although most mergers take place before the cluster virializes.
Our sample of ELGs is within the virial radius of the Fornax cluster, and hence the incidence of mergers is expected to be low (see also Joshi et al. 2020). In Sect. 4.4 we present our analysis of the merger history for our sample of Fornax-like subhalos. We find that in comparison with the control subhalos, the incidence of minor and major mergers is significantly lower up to z ∼ 2. Hence, it is highly unlikely that mergers are responsible for the observed flattening of the gas metallicity gradients.
Another explanation proposed by Franchetto et al. (2021) is that the cluster galaxies that show flatter gradients might have fallen into the cluster sooner and hence experienced environmental effects for longer. All the galaxies in our sample are infalling into the cluster, and were classified as recent and intermediate infallers by Iodice et al. (2019). As indicated in Fig. 5, eight of our ELGs, that is, four intermediate and four recent infallers, show flatter gradients with respect to the control sample, whereas the remaining two galaxies, recent infallers, show steeper gradients. On the other hand, all our four intermediate infallers show more positive gradients.
Tidal features (e.g., tail, arms, or streams) have been considered as possible proxies of merger systems (e.g., Oh et al. 2008; Hood et al. 2018). Even though galaxy mergers have been the focus of several investigations due to their ability to reshape galaxy properties such as morphology, the effect of smaller bodies such as orbiting satellites can produce observable perturbations too. In addition, tidal interactions are also responsible for the observed HI deficiency observed in several cluster galaxies (e.g., Gnedin 2003; Hughes et al. 2013).
In this paper, we examined two possible processes that could potentially cause a flattening in the gas metallicity gradients: flybys and ram pressure stripping. Flybys are rapid and transient events that occur when two independent galaxy halos interpenetrate but detach at a later time (e.g., Sinha & Holley-Bockelmann 2012; An et al. 2019). The importance of flybys in galaxy evolution was recently acknowledged, because multiple interactions with two or more neighbors are on average flyby-dominated. According to An et al. (2019), flybys substantially outnumber mergers (by a factor of five) toward z = 0. Hence the contribution of flybys to galactic evolution is stronger than previously thought. An extreme example of frequent high-speed galaxy encounters is known as galaxy harassment, and this is a likely mechanism for inducing a morphological transformation (Moore et al. 1996). Another possible process at play is RPS, which can create a lopsided pressure on the disk of gas in the galaxy, causing the lower metallicity gas at the outskirts to lose angular momentum and fall towards the center of the system, flattening the observed gradient. Whether the galaxy–galaxy (i.e., flybys) or cluster–galaxy (i.e., RPS) interactions dominate is yet to be understood.
To elucidate the impact these processes have on galaxies, we analyzed the Mach number and ram pressure in our sample of Fornax-like subhalos in TNG50 (Fig. 11). According to Yun et al. (2019), galaxies at supersonic velocities (ℳ > 1) will produce discontinuous features in the fluid such as shocks and contact discontinuities, whereas subsonic motions (ℳ < 1) would allow smooth changes. Our sample shows negative ∇O/H_diff for suhbalos with ℳ < 1, whereas those in the range 1 < ℳ < 2 show positive ∇O/H_diff, corresponding to flatter (or more positive) gradients with respect to their control sample. This indicates that supersonic velocities might be the main driving force producing flatter and positive metallicity gradients. As for subhalos with higher Mach numbers (ℳ > 2), Yun et al. (2019) suggest that they might be flybys. Our TNG50 sample shows five possible flybys, mostly located at large cluster-centric distances. However, their gas metallicity gradients show either positive or negative ∇O/H_diff. Therefore, our sample suggests that while flybys could produce flatter gradients, subhalos at supersonic velocities with 1 < ℳ < 2 are likely to have flatter or more positive gas metallicity gradients.
Returning to our observational sample, with the exception of FCC 179 and FCC 290, the galaxies in our sample show a disturbed morphology. It is difficult to address which kind of interactions have played a major role in defining such disruption. Although in some specific cases, the photometric images from Raj et al. (2019) provide some hints. For instance, a flyby might have happened in FCC308 and FCC312, where a thick disk is observed, while FCC 312 shows an extended warped tail. In addition, the gas metallicity gradient of FCC 290 (see Fig. 4) suggests an inflection at 0.74 R/Re to a flatter or positive gradient that corresponds to a drop in the H2-to-dust ratio. As indicated by Zabel et al. (2021), this drop means an outside-in stripping of the gas and dust disc, which results in a lower integrated H2-to-dust ratio. This is an example of how stripping of gas can produce flatter and positive gradients.
From our sample, FCC 308, FCC 263, and FCC 090 have been identified as having disturbed CO by Zabel et al. (2019). In addition, Fornax dwarf galaxies have been shown to have a molecular gas fraction about an order of magnitude smaller than expected, while several galaxies also show asymmetric gas distributions (Zabel et al. 2019). It is uncertain whether these effects are due to ram pressure stripping or flyby interactions, but in both cases, disturbing the gas could result in flatter gas metallicity gradients. Simulations show that strong perturbations can stir the gas and drive galactic-scale motion in the ISM, causing gas and metal redistribution on galactic scales (Ma et al. 2017).
Regarding the general properties of our sample, the integrated metallicity of our Fornax sample shows slightly higher metallicities (∼0.045 dex) than the galaxies of a control sample from the SDSS survey. Our result is in agreement with previous works that report slightly higher (∼0.05 dex) metallicities for late-type galaxies in clusters (Ellison et al. 2009; Scudder et al. 2012; Gupta et al. 2016; Lian et al. 2019; Coenda et al. 2020). In addition, our sample of ten ELGs is statistically small, and a larger sample is needed to properly quantify any difference in the integrated gas metallicity of Fornax-like clusters.
On the other hand, we detect signs of a mass and metallicity segregation, as described in Sect. 3. This is in agreement with models and numerical simulations that predict the segregation of galaxies by mass and the formation of a central BCG galaxy (e.g., De Lucia & Blaizot 2007). Our results agree with those of Gupta et al. (2016, 2017), who observed a negative metallicity gradient with clustercentric distance for part of their cluster sample. As indicated by Kim et al. (2020), the mass of the whole cluster may play an important role in defining the time-span of dynamical friction, and therefore mass segregation may only be detected in low-mass clusters.
Finally, a source of uncertainty in our study is related to the different spatial resolutions of the surveys we are using. While SAMI has a spatial resolution of 2.16, galaxies observed with MUSE have a spatial resolution of 0.2. According to Acharyya et al. (2020), the metallicity gradients are systematically shallower than the true value for surveys with a lower spatial resolution. This indicates that the true metallicity gradients for the SAMI sample could be steeper, and therefore the difference with our Fornax sample could be even larger.
A second caveat relates to the projected distance to the BCG shown in Fig. 6. Although the distances could change with more precise distance measurements such as those using planetary nebulae indicators (e.g., Spriggs et al. 2020, 2021, currently only available for some early-type galaxies in the Fornax cluster), it is uncertain whether or not a pattern would emerge based on the current results.
6. Conclusions
As part of the Fornax-3D project, we analyzed the gas metallicity gradients of ten ELGs in the Fornax cluster observed with MUSE. We used a control sample formed by galaxies from B19 and the MAD and SAMI surveys. Gas metallicities were estimated consistently for Fornax and control galaxies. A summary of our findings is listed below:
-
The integrated gas metallicity of Fornax ELGs follows the general M–Z relation for SDSS galaxies. In agreement with previous results, our Fornax sample shows slightly higher metallicities than the control sample, that is, higher by 0.045 dex.
-
Galaxies in the Fornax cluster show signs of mass and metallicity segregation, which is likely the result of dynamical friction having a stronger effect on medium-mass clusters.
-
Our data suggest ELGs in the Fornax cluster exhibit metallicity gradients that are flatter (or more positive) than our control sample by ∼0.04 dex/Re.
-
The derived metallicity gradients for Fornax galaxies as a function of stellar mass follows the general trend reported in previous works. That is, flatter gradients for low-mass galaxies that steepen for more massive galaxies, and then flatten slightly again for more massive galaxies (e.g., Belfiore et al. 2017; Poetrodjojo et al. 2021).
-
Our data suggest there is no relation between the flattening of the metallicity gradients and the projected distance to the BCG.
-
All our Fornax ELGs classified as intermediate infallers (although there are only four) show more positive metallicities gradients with respect to the control sample.
-
We identified 12 Fornax-like clusters in the TNG50 simulations, and selected a sample of 15 subhalos mass-matched with our Fornax sample. Similar to the observations, we identify a flattening of ∼0.05 dex/Re for subhalos in Fornax-like clusters. Additionally, no relation is found between flattening and distance to the cluster core.
-
We estimated the Mach number and ram pressure for our sample of TNG50 subhalos. The data indicate flatter or more positive gradients for subhalos with Mach numbers in the range 1 < ℳ < 2, likely due to supersonic velocities that also scale with larger RPS values. On the other hand, subhalos with ℳ > 2 are likely to be flybys and show either positive or negative ∇O/H_diff.
-
Most of the ELGs in our MUSE sample show disturbed morphologies, and therefore, as the simulations suggest, the observed flattening could be the result of either cluster–galaxy interactions (such as ram pressure stripping) or galaxy–galaxy interactions (such as flybys).
Acknowledgments
We acknowledge the careful examination by the referee. We thank Mark den Brok and Jarle Brinchmann for providing us extra information for the MAD galaxies. We thank Henry Poetrodjojo for kindly providing us the SAMI data needed for this work. G.v.d.V. acknowledges funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 724857 (Consolidator Grant ArcheoDyn). E.M.C. acknowledges support by Padua University grants DOR1935272/19, DOR2013080/20, and DOR2021 and by MIUR grant PRIN 2017 20173ML3WW-001. R.M.c.D. is the recipient of an Australian Research Council Future Fellowship (project number FT150100333). This research was supported by the Australian Research Council Centre of Excellence for All Sky Astrophysics in 3 Dimensions (ASTRO 3D), through project number CE170100013.
References
- Abazajian, K. N., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2009, ApJS, 182, 543 [Google Scholar]
- Acharyya, A., Krumholz, M. R., Federrath, C., et al. 2020, MNRAS, 495, 3819 [NASA ADS] [CrossRef] [Google Scholar]
- An, S.-H., Kim, J., Moon, J.-S., & Yoon, S.-J. 2019, ApJ, 887, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Bacon, R., Accardo, M., & Adjali, L. 2010, SPIE Conf. Ser., 7735, 773508 [NASA ADS] [Google Scholar]
- Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP, 93, 5 [Google Scholar]
- Balogh, M. L., McGee, S. L., Mok, A., et al. 2014, MNRAS, 443, 2679 [NASA ADS] [CrossRef] [Google Scholar]
- Bekki, K., Couch, W. J., & Shioya, Y. 2002, ApJ, 577, 651 [Google Scholar]
- Belfiore, F., Maiolino, R., Maraston, C., et al. 2016, MNRAS, 461, 3111 [Google Scholar]
- Belfiore, F., Maiolino, R., Tremonti, C., et al. 2017, MNRAS, 469, 151 [Google Scholar]
- Bellstedt, S., Robotham, A. S. G., Driver, S. P., et al. 2021, MNRAS, 503, 3309 [NASA ADS] [CrossRef] [Google Scholar]
- Blanc, G. A., Heiderman, A., Gebhardt, K., Evans, N. J., & Adams, J. 2009, ApJ, 704, 842 [NASA ADS] [CrossRef] [Google Scholar]
- Bresolin, F. 2019, MNRAS, 488, 3826 [NASA ADS] [Google Scholar]
- Brinchmann, J., Charlot, S., White, S. D. M., et al. 2004, MNRAS, 351, 1151 [Google Scholar]
- Brooks, A. M., Governato, F., Booth, C. M., et al. 2007, ApJ, 655, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Chandrasekhar, S. 1943, ApJ, 97, 255 [Google Scholar]
- Coenda, V., Mast, D., Muriel, H., & Martínez, H. J. 2020, A&A, 642, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Contini, E., De Lucia, G., & Borgani, S. 2012, MNRAS, 420, 2978 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, M. C., Tremonti, C. A., Newman, J. A., & Zabludoff, A. I. 2008, MNRAS, 390, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Croom, S. M., Lawrence, J. S., Bland-Hawthorn, J., et al. 2012, MNRAS, 421, 872 [NASA ADS] [Google Scholar]
- Davies, L. J. M., Robotham, A. S. G., Driver, S. P., et al. 2015, MNRAS, 452, 616 [NASA ADS] [CrossRef] [Google Scholar]
- De Lucia, G., & Blaizot, J. 2007, MNRAS, 375, 2 [Google Scholar]
- De Lucia, G., Kauffmann, G., & White, S. D. M. 2004, MNRAS, 349, 1101 [Google Scholar]
- Di Matteo, T., Springel, V., & Hernquist, L. 2005, Nature, 433, 604 [NASA ADS] [CrossRef] [Google Scholar]
- Dopita, M. A., Kewley, L. J., Sutherland, R. S., & Nicholls, D. C. 2016, Ap&SS, 361, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Drinkwater, M. J., Gregg, M. D., & Colless, M. 2001, ApJ, 548, L139 [Google Scholar]
- Eke, V. R., Baugh, C. M., Cole, S., et al. 2005, MNRAS, 362, 1233 [NASA ADS] [CrossRef] [Google Scholar]
- Elbaz, D., Daddi, E., Le Borgne, D., et al. 2007, A&A, 468, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ellison, S. L., Patton, D. R., Simard, L., & McConnachie, A. W. 2008, AJ, 135, 1877 [NASA ADS] [CrossRef] [Google Scholar]
- Ellison, S. L., Simard, L., Cowan, N. B., et al. 2009, MNRAS, 396, 1257 [NASA ADS] [CrossRef] [Google Scholar]
- Ellison, S. L., Viswanathan, A., Patton, D. R., et al. 2019, MNRAS, 487, 2491 [NASA ADS] [CrossRef] [Google Scholar]
- Erb, D. K., Shapley, A. E., Pettini, M., et al. 2006, ApJ, 644, 813 [NASA ADS] [CrossRef] [Google Scholar]
- Erroz-Ferrer, S., Carollo, C. M., den Brok, M., et al. 2019, MNRAS, 484, 5009 [Google Scholar]
- Fahrion, K., Lyubenova, M., van de Ven, G., et al. 2021, A&A, 650, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Falcón-Barroso, J., Bacon, R., Bureau, M., et al. 2006, MNRAS, 369, 529 [Google Scholar]
- Ferguson, H. C., & Sandage, A. 1989, ApJ, 346, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Finlator, K., & Davé, R. 2008, MNRAS, 385, 2181 [NASA ADS] [CrossRef] [Google Scholar]
- Franchetto, A., Mingozzi, M., & Poggianti, B. M. 2021, ApJ, 923, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Friedli, D., Benz, W., & Kennicutt, R. 1994, ApJ, 430, L105 [Google Scholar]
- Garduño, L. E., Lara-López, M. A., López-Cruz, O., et al. 2021, MNRAS, 501, 2969 [CrossRef] [Google Scholar]
- Gnedin, O. Y. 2003, ApJ, 582, 141 [Google Scholar]
- Gordon, Y. A., Pimbblet, K. A., Owers, M. S., et al. 2018, MNRAS, 475, 4223 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., Gott, J., & Richard, I. 1972, ApJ, 176, 1 [Google Scholar]
- Gupta, A., Yuan, T., Tran, K.-V. H., et al. 2016, ApJ, 831, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, A., Yuan, T., Martizzi, D., Tran, K.-V. H., & Kewley, L. J. 2017, ApJ, 842, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, A., Yuan, T., Torrey, P., et al. 2018, MNRAS, 477, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Hemler, Z. S., Torrey, P., Qi, J., et al. 2021, MNRAS, 506, 3024 [NASA ADS] [CrossRef] [Google Scholar]
- Henry, R. B. C., & Worthey, G. 1999, PASP, 111, 919 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, I. T., Kudritzki, R.-P., Kewley, L. J., et al. 2015, MNRAS, 448, 2030 [NASA ADS] [CrossRef] [Google Scholar]
- Hood, C. E., Kannappan, S. J., Stark, D. V., et al. 2018, ApJ, 857, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Hernquist, L., Cox, T. J., et al. 2006, ApJS, 163, 1 [Google Scholar]
- Hughes, T. M., Cortese, L., Boselli, A., Gavazzi, G., & Davies, J. I. 2013, A&A, 550, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iodice, E., Sarzi, M., Bittner, A., et al. 2019, A&A, 627, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Joshi, G. D., Wadsley, J., & Parker, L. C. 2017, MNRAS, 468, 4625 [NASA ADS] [CrossRef] [Google Scholar]
- Joshi, G. D., Pillepich, A., Nelson, D., et al. 2020, MNRAS, 496, 2673 [Google Scholar]
- Kaplan, K. F., Jogee, S., Kewley, L., et al. 2016, MNRAS, 462, 1642 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., Heckman, T. M., Tremonti, C., et al. 2003, MNRAS, 346, 1055 [Google Scholar]
- Kewley, L. J., & Ellison, S. L. 2008, ApJ, 681, 1183 [Google Scholar]
- Kewley, L. J., Jansen, R. A., & Geller, M. J. 2005, PASP, 117, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., Geller, M. J., & Barton, E. J. 2006, AJ, 131, 2004 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., Rupke, D., Zahid, H. J., Geller, M. J., & Barton, E. J. 2010, ApJ, 721, L48 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, S., Contini, E., Choi, H., et al. 2020, ApJ, 905, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Kreckel, K., Ho, I. T., Blanc, G. A., et al. 2019, ApJ, 887, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Lambas, D. G., Tissera, P. B., Alonso, M. S., & Coldwell, G. 2003, MNRAS, 346, 1189 [NASA ADS] [CrossRef] [Google Scholar]
- Lani, C., Almaini, O., Hartley, W. G., et al. 2013, MNRAS, 435, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Lara-López, M. A., Cepa, J., Bongiovanni, A., et al. 2009a, A&A, 493, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lara-López, M. A., Cepa, J., Bongiovanni, A., et al. 2009b, A&A, 505, 529 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lara-López, M. A., Bongiovanni, A., Cepa, J., et al. 2010, A&A, 519, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lara-López, M. A., Hopkins, A. M., López-Sánchez, A. R., et al. 2013, MNRAS, 434, 451 [Google Scholar]
- Lara-López, M. A., De Rossi, M. E., Pilyugin, L. S., et al. 2019, MNRAS, 490, 868 [CrossRef] [Google Scholar]
- Lara-López, M. A., Zinchenko, I. A., Pilyugin, L. S., et al. 2021, ApJ, 906, 42 [CrossRef] [Google Scholar]
- Lares, M., Lambas, D. G., & Sánchez, A. G. 2004, MNRAS, 352, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B., Tinsley, B. M., & Caldwell, C. N. 1980, ApJ, 237, 692 [Google Scholar]
- Lequeux, J., Peimbert, M., Rayo, J. F., Serrano, A., & Torres-Peimbert, S. 1979, A&A, 500, 145 [NASA ADS] [Google Scholar]
- Lian, J., Thomas, D., Li, C., et al. 2019, MNRAS, 489, 1436 [NASA ADS] [CrossRef] [Google Scholar]
- Ma, X., Hopkins, P. F., Feldmann, R., et al. 2017, MNRAS, 466, 4780 [Google Scholar]
- Maier, C., Haines, C. P., & Ziegler, B. L. 2022, A&A, 658, A190 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marino, R. A., Gil de Paz, A., & Sánchez, S. F. 2016, A&A, 585, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mistani, P. A., Sales, L. V., Pillepich, A., et al. 2016, MNRAS, 455, 2323 [NASA ADS] [CrossRef] [Google Scholar]
- Mo, H. J., Mao, S., & White, S. D. M. 1998, MNRAS, 295, 319 [Google Scholar]
- Moore, B., Katz, N., Lake, G., Dressler, A., & Oemler, A. 1996, Nature, 379, 613 [Google Scholar]
- Mouhcine, M., Baldry, I. K., & Bamford, S. P. 2007, MNRAS, 382, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Moustakas, J., Kennicutt, R. C., Jr., & Tremonti, C. A. 2010, ApJS, 190, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Nascimento, R. S., Ribeiro, A. L. B., & Lopes, P. A. A. 2017, MNRAS, 464, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, D., Springel, V., Pillepich, A., et al. 2019a, Comput. Astrophys. Cosmol., 6, 2 [Google Scholar]
- Nelson, D., Pillepich, A., Springel, V., et al. 2019b, MNRAS, 490, 3234 [Google Scholar]
- Nikolic, B., Cullen, H., & Alexander, P. 2004, MNRAS, 355, 874 [NASA ADS] [CrossRef] [Google Scholar]
- Noeske, K. G., Weiner, B. J., Faber, S. M., et al. 2007, ApJ, 660, L43 [CrossRef] [Google Scholar]
- Oh, S. H., Kim, W.-T., Lee, H. M., & Kim, J. 2008, ApJ, 683, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Oh, K., Sarzi, M., Schawinski, K., & Yi, S. K. 2011, ApJS, 195, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Pan, H.-A., Lin, L., Hsieh, B.-C., et al. 2019, ApJ, 881, 119 [NASA ADS] [Google Scholar]
- Paulino-Afonso, A., Sobral, D., Darvish, B., et al. 2019, A&A, 630, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peng, Y.-J., Lilly, S. J., Kovač, K., et al. 2010, ApJ, 721, 193 [Google Scholar]
- Pérez, E., Cid Fernandes, R., González Delgado, R. M., et al. 2013, ApJ, 764, L1 [Google Scholar]
- Pillepich, A., Nelson, D., Springel, V., et al. 2019, MNRAS, 490, 3196 [Google Scholar]
- Pilyugin, L. S., Vílchez, J. M., & Contini, T. 2004, A&A, 425, 849 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pilyugin, L. S., Grebel, E. K., & Kniazev, A. Y. 2014, AJ, 147, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Poetrodjojo, H., Groves, B., Kewley, L. J., et al. 2018, MNRAS, 479, 5235 [Google Scholar]
- Poetrodjojo, H., Groves, B., Kewley, L. J., et al. 2021, MNRAS, 502, 3357 [NASA ADS] [CrossRef] [Google Scholar]
- Poggianti, B. M., Moretti, A., Gullieuszik, M., et al. 2017, ApJ, 844, 48 [Google Scholar]
- Raj, M. A., Iodice, E., Napolitano, N. R., et al. 2019, A&A, 628, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rhee, J., Smith, R., Choi, H., et al. 2017, ApJ, 843, 128 [Google Scholar]
- Roberts, I. D., Parker, L. C., Joshi, G. D., & Evans, F. A. 2015, MNRAS, 448, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Robotham, A. S. G., & Obreschkow, D. 2015, PASA, 32, e033 [Google Scholar]
- Rodriguez-Gomez, V., Genel, S., Vogelsberger, M., et al. 2015, MNRAS, 449, 49 [Google Scholar]
- Rupke, D. S. N., Kewley, L. J., & Chien, L. H. 2010a, ApJ, 723, 1255 [NASA ADS] [CrossRef] [Google Scholar]
- Rupke, D. S. N., Kewley, L. J., & Barnes, J. E. 2010b, ApJ, 710, L156 [NASA ADS] [CrossRef] [Google Scholar]
- Ryś, A., van de Ven, G., & Falcón-Barroso, J. 2014, MNRAS, 439, 284 [CrossRef] [Google Scholar]
- Sánchez-Menguiano, L., Sánchez, S. F., Pérez, I., et al. 2016, A&A, 587, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez-Menguiano, L., Sánchez, S. F., Pérez, I., et al. 2018, A&A, 609, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sanders, R. L., Shapley, A. E., Jones, T., et al. 2021, ApJ, 914, 19 [CrossRef] [Google Scholar]
- Sarzi, M., Falcón-Barroso, J., Davies, R. L., et al. 2006, MNRAS, 366, 1151 [Google Scholar]
- Sarzi, M., Iodice, E., Coccato, L., et al. 2018, A&A, 616, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Savaglio, S., Glazebrook, K., Le Borgne, D., et al. 2005, ApJ, 635, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Scudder, J. M., Ellison, S. L., Torrey, P., Patton, D. R., & Mendel, J. T. 2012, MNRAS, 426, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Shah, E. A., Kartaltepe, J. S., Magagnoli, C. T., et al. 2020, ApJ, 904, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Sinha, M., & Holley-Bockelmann, K. 2012, ApJ, 751, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Sotillo-Ramos, D., Lara-López, M. A., Pérez-García, A. M., et al. 2021, MNRAS, 508, 1817 [NASA ADS] [CrossRef] [Google Scholar]
- Soto, K. T., Lilly, S. J., Bacon, R., Richard, J., & Conseil, S. 2016, MNRAS, 458, 3210 [Google Scholar]
- Spitoni, E., Calura, F., Matteucci, F., & Recchi, S. 2010, A&A, 514, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spriggs, T. W., Sarzi, M., Napiwotzki, R., et al. 2020, A&A, 637, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spriggs, T. W., Sarz, M., & Galán-de Anta, P. M. 2021, A&A, 653, A167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taylor, E. N., Hopkins, A. M., Baldry, I. K., et al. 2011, MNRAS, 418, 1587 [Google Scholar]
- Tempel, E., Tago, E., & Liivamägi, L. J. 2012, A&A, 540, A106 [CrossRef] [EDP Sciences] [Google Scholar]
- Tortora, C., Napolitano, N. R., Radovich, M., et al. 2020, A&A, 638, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [Google Scholar]
- Vila-Costas, M. B., & Edmunds, M. G. 1992, MNRAS, 259, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Vilchez, J. M., & Esteban, C. 1996, MNRAS, 280, 720 [NASA ADS] [CrossRef] [Google Scholar]
- von der Linden, A., Wild, V., Kauffmann, G., White, S. D. M., & Weinmann, S. 2010, MNRAS, 404, 1231 [Google Scholar]
- Vulcani, B., Poggianti, B. M., Oemler, A., et al. 2013, A&A, 550, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weilbacher, P. M., Streicher, O., & Palsa, R. 2016, Astrophysics Source Code Library [record ascl:1610.004] [Google Scholar]
- White, S. D. M., & Frenk, C. S. 1991, ApJ, 379, 52 [Google Scholar]
- Woods, D. F., & Geller, M. J. 2007, AJ, 134, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Yun, K., Pillepich, A., Zinger, E., et al. 2019, MNRAS, 483, 1042 [Google Scholar]
- Zabel, N., Davis, T. A., Smith, M. W. L., et al. 2019, MNRAS, 483, 2251 [Google Scholar]
- Zabel, N., Davis, T. A., Smith, M. W. L., et al. 2021, MNRAS, 502, 4723 [NASA ADS] [CrossRef] [Google Scholar]
- Zahid, H. J., Dima, G. I., Kewley, L. J., Erb, D. K., & Davé, R. 2012, ApJ, 757, 54 [Google Scholar]
- Zaritsky, D., Kennicutt, R. C., Jr., & Huchra, J. P. 1994, ApJ, 420, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, K., Yan, R., Bundy, K., et al. 2017, MNRAS, 466, 3217 [NASA ADS] [CrossRef] [Google Scholar]
- Ziparo, F., Popesso, P., Biviano, A., et al. 2013, MNRAS, 434, 3089 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Maps
In this section, we present the Hα flux, BPT class, and gas metallicity maps for each of the galaxies analyzed in this paper.
 |
Fig. A.1. From left to right, Hα flux, BPT classification, and gas metallicity maps for FCC 312, FCC 113, and FCC 179. The inset color bars show the Hα flux (left panel), gas metallicity (right panel), and the BPT classification (star forming, composite, Seyfert, and LINER, middle panel). |
All Tables
All Figures
 |
Fig. 1. M–Z relation for SDSS (gray background) and Fornax cluster (red symbols) galaxies. The white solid line indicates the best fit to the SDSS data. Circles and triangles correspond to recent and intermediate infallers, respectively. The green squares correspond to the control sample. |
| In the text | |
 |
Fig. 2. Projected distance–stellar mass relation (left panel), and distance–gas metallicity relation (right panel) for Fornax ELGs. Circles and triangles correspond to recent and intermediate infallers, respectively. |
| In the text | |
 |
Fig. 3. Linear fits of the gas metallicity radial profiles for Fornax-ELGs sample. |
| In the text | |
 |
Fig. 4. Gas metallicity radial profiles for our sample of Fornax ELGs. Each panel corresponds to a Fornax galaxy (gray dots) and its corresponding control sample from the MAD survey (color dots). The shaded areas around each gradient correspond to the 1σ dispersion in 0.2 dex of R/Re. The gradients of the control samples are colored according to the names inside each panel. The black vertical arrow in the panels of FCC 263, FCC 290, FCC 308, and FCC 312 shows the break radius from Raj et al. (2019). The red arrow in the panel of FCC 290 shows the drop in H2-to-dust ratio from Zabel et al. (2021). |
| In the text | |
 |
Fig. 5. Gas metallicity gradients as a function of stellar mass. The black symbols show our Fornax ELGs sample, with circles and triangles corresponding to recent and intermediate infallers, respectively. The red symbols correspond to galaxies from the MAD survey. The small gray circles indicate galaxies from the SAMI survey. The cyan circles are galaxies from B19. For galaxies from Fornax, MAD, and B19, the vertical bars correspond to the RMSE. For SAMI galaxies, the bars indicate the 1σ error in the metallicity gradient. The green squares show the median values of |
| In the text | |
 |
Fig. 6. Gas metallicity gradients as a function of the projected cluster-centric distance to the BCG. The bottom panel shows the difference in gas metallicity gradient between each Fornax galaxy and its corresponding |
| In the text | |
 |
Fig. 7. Gas metallicity gradients as a function of stellar mass for the subhalos from the TNG50 simulation. The black circles correspond to the subhalos in Fornax-like clusters, while the red circles indicate subhalos from our control sample (see text). The green squares show the median value |
| In the text | |
 |
Fig. 8. Gas metallicity gradients as a function of distance to cluster core for the subhalos from TNG50. The black circles correspond to the subhalos in Fornax-like clusters. Bottom panel: difference in metallicity gradient between each subhalo and the corresponding |
| In the text | |
 |
Fig. 9. Histograms of the differences between the gas metallicity gradients and control samples for Fornax ELGs (left), and TNG50 (right). In both panels, the red vertical line shows the median value of the differences ( |
| In the text | |
 |
Fig. 10. Gas metallicity gradient as a function of the number of mergers up to redshift 2. Left and right panels: indicate major and minor mergers, respectively. Circles indicate subhalos from the control sample, while diamonds the subhalos in Fornax-like clusters. All the symbols are color coded according to their stellar mass. For the sake of clarity, all the subhalos in the control sample with a number of mergers between 0 and 2 were assigned random shifts (in the range ±0.25) around their actual value, while the subhalos in Fornax-like clusters are shifted to the right. |
| In the text | |
 |
Fig. 11. Ram pressure as a function of Mach number for the TNG50 subhalos in Fornax-like clusters. The small squares are color coded according to ∇O/H_diff, while the gray circles are color coded according to the cluster-core distance of each subhalo. The circle size corresponds to the stellar mass of each subhalo as indicated in the right bar. The vertical dotted line indicates the threshold between supersonic (ℳ > 1) and subsonic (ℳ < 1) velocities. |
| In the text | |
 |
Fig. A.1. From left to right, Hα flux, BPT classification, and gas metallicity maps for FCC 312, FCC 113, and FCC 179. The inset color bars show the Hα flux (left panel), gas metallicity (right panel), and the BPT classification (star forming, composite, Seyfert, and LINER, middle panel). |
| In the text | |
 |
Fig. A.2. Similar to Fig. A.1 but for FCC 285, FCC 290, FCC 308, and FCC 306. |
| In the text | |
 |
Fig. A.3. Similar to Fig. A.1 but for FCC 119, FCC 090, and FCC 263. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned}&\mathrm{12 + log(O/H)} = 8.77 + { y}\nonumber \\&{ y} = \mathrm{log} ([\mathrm{N}\,{\small{\text{II}} }]/[\mathrm{S}\,{\small{\text{II}} }]) + 0.264 \times \mathrm{log} ([\mathrm{N}\,{\small{\text{II}}}]/\mathrm{H\alpha }). \end{aligned} $$](/articles/aa/full_html/2022/04/aa42790-21/aa42790-21-eq1.gif)