| Issue |
A&A
Volume 659, March 2022
|
|
|---|---|---|
| Article Number | A102 | |
| Number of page(s) | 20 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202141963 | |
| Published online | 11 March 2022 | |
Duality in spatially resolved star formation relations in local LIRGs
1
Centro de Astrobiología (CSIC/INTA), Ctra de Torrejón a Ajalvir, km 4, 28850 Torrejón de Ardoz, Madrid, Spain
e-mail: mariasg@cab.inta-csic.es
2
Observatorio Astronómico Nacional (OAN-IGN)-Observatorio de Madrid, Alfonso XII, 3, 28014 Madrid, Spain
3
Centro de Astrobiología (CAB, CSIC-INTA), ESAC Campus, 28692 Villanueva de la Cañada, Madrid, Spain
4
Department of Physics, General Studies, College of Engineering, Nihon University, 1 Nakagawara, Tokusada, Tamuramachi, Koriyama, Fukushima 963-8642, Japan
5
National Astronomical Observatory of Japan, 2-21-1 Osawa, Mitaka, Tokyo 181-8588, Japan
6
Department of Physics, University of Crete, 71003 Heraklion, Greece
7
Institute of Astrophysics, Foundation for Research and Technology-Hellas, Heraklion 70013, Greece
8
Instituto de Astrofísica de Andalucía (IAA-CSIC), Apdo. 3004, 18008 Granada, Spain
9
Telespazio UK for the European Space Agency (ESA), ESAC, Spain
Received:
5
August 2021
Accepted:
30
October 2021
We analyse the star formation (SF) relations in a sample of 16 nearby luminous infrared galaxies (LIRGs) with more than 2800 regions defined on scales of 90 to 500 pc. We used ALMA to map the distribution of the cold molecular gas traced by the J = 2–1 line of CO and archival Paα HST/NICMOS imaging to trace the recent SF. In four objects we find two different branches in the Kennicutt-Schmidt relation at 90 pc scales, suggesting the existence of a duality in this relation. The two branches correspond to two different dynamical environments within each galaxy. One branch, which corresponds to the central region of these galaxies (90% of the regions are located at radii < 0.85 kpc), shows higher gas and SF rate surface densities with higher velocity dispersion. The other branch, which shows lower molecular gas and SF rate surface densities, corresponds to the more external disk regions (r ∼ 1 kpc). Despite the scatter, the SF efficiency of the galaxies with dual behaviour increases with increasing boundedness as measured by the b parameter (b≡ ΣH2/σ2 ∝ αvir−1). At larger spatial scales (250 and 500 pc), the duality disappears. The rest of the sample does not show evidence of this dual behaviour at any scale.
Key words: galaxies: star formation / galaxies: ISM / infrared: galaxies
© ESO 2022
1. Introduction
The relationship between the rate at which stars form and the amount of gas contained in galaxies is commonly referred to as the star formation (SF) law or the Kennicutt-Schmidt (KS) relation (Schmidt 1959; Kennicutt 1998). This relation is expressed as
where ΣSFR and Σgas are the star formation rate (SFR) and the molecular gas surface densities, respectively, and N the power-law index. This relation was initially studied in spatially unresolved observations of galaxies, finding a power-law index of 1.4–1.5 (Kennicutt 1998; Yao et al. 2003). The physical processes that explain the observed power-law index are not clear yet. More recently, a duality has been found in the SF laws when normal and starburst galaxies are considered (Daddi et al. 2010; Genzel et al. 2010; García-Burillo et al. 2012). In these studies normal galaxies show depletion times (tdep = MH2/SFR) that are between 4 and 10 times longer than starburst. This duality introduces a discontinuity in the KS relation. In this case, when each galaxy population (normal and starburst) is treated independently, there is a linear relation (N ∼ 1).
Spatially resolved KS relation studies (≲1 kpc) (e.g. Leroy et al. 2008; Casasola et al. 2015; Pereira-Santaella et al. 2016a; Williams et al. 2018; Viaene et al. 2018) found a wide range of N values (N ≈ 0.6–3) with a considerable scatter in the relation (0.1–0.4 dex). These results suggest that there is a breakdown in the star formation law at sub-kiloparsec scales (sub-kpc; ≲300 pc), although the correlation is restored at larger spatial scales (Onodera et al. 2010; Schruba et al. 2010). This breakdown may be due to the different evolutionary states of individual giant molecular clouds within the galaxies when resolved at sub-kpc scales. In addition to the relation between ΣSFR and Σgas, other parameters, such as the velocity dispersion (σ) or boundedness of the gas (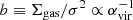 , where αvir is the virial parameter), have been studied to characterise the local dynamical state of the gas (e.g. Leroy et al. 2017; Sun et al. 2018). These studies suggest that the dynamical environment plays an important role in the ability to form stars within a galaxy.
, where αvir is the virial parameter), have been studied to characterise the local dynamical state of the gas (e.g. Leroy et al. 2017; Sun et al. 2018). These studies suggest that the dynamical environment plays an important role in the ability to form stars within a galaxy.
These previous sub-kpc studies focused on nearby normal and active galactic nuclei (AGN) galaxies. However, more intense local starburst galaxies (i.e. luminous and ultraluminous infrared galaxies; LIRGs and ULIRGs) have been barely studied at sub-kpc scales (e.g. Xu et al. 2015; Pereira-Santaella et al. 2016a; Paraficz et al. 2018; Saito et al. 2016). In this work, we present a detailed analysis of the SF relations at cloud scales (∼100 pc) in a sample of 16 local LIRGs.
2. The sample
We present new sub-kpc CO(2–1) observations obtained by the Atacama Large Millimeter Array (ALMA) of a representative sample of 16 local LIRGs. Our sample is drawn from the volume-limited sample of 34 local LIRGs (40 Mpc < D < 75 Mpc) defined by Alonso-Herrero et al. (2006) and contains 85% of their southern targets that can be observed with ALMA. Our sample contains six isolated galaxies, six pre-coalescence systems (interacting galaxies and pairs of galaxies), and four merger objects (Yuan et al. 2010; Rich et al. 2012; Bellocchi et al. 2013). Eight objects are classified as AGN in the optical and/or show evidence of AGN activity from mid-infrared diagnostics (Alonso-Herrero et al. 2012). In Table 1 we present the main properties of the individual galaxies in the sample.
Volume limited sample of local LIRGs.
3. Observations and data reduction
3.1. CO(2–1) ALMA data
We used ALMA Band 6 CO(2–1) observations carried out between August 2014 and August 2018 from several projects (see Table 2). The observations were obtained using a combination of extended and compact antenna array configurations, except in the case of the two galaxies that are part of 2017.1.00395.S which only used an extended antenna array configuration. The integration time of the sources ranges between ∼7 and ∼34 min. We calibrated the data using the standard ALMA reduction software CASA1 (McMullin et al. 2007). We subtracted the continuum emission in the uv plane using an order 0 baseline. For the cleaning we used the Briggs weighting with a robustness parameter of 0.5 (Briggs 1995), providing a spatial resolution of 48–106 pc (0.19″–0.37″). The maximum recoverable scale (MRS) for the compact plus extended configuration data ranges between ∼8″ and ∼11″ (1.7 and 2.3 kpc). In the case of the only extended configuration observations, the MRS is ∼3″ (1.1 kpc). In this paper we study spatial scales between 90 and 500 pc, which are 2 to 25 times smaller than the MRS, so we expect the missing flux due to the absence of short spacing to be low at these scales. In addition, for two of these systems with single-dish CO(2–1) observations, the integrated ALMA and single-dish fluxes agree within 15% (Pereira-Santaella et al. 2016a,b).
CO(2–1) observations of the sample.
The final data cubes have channels of 7.8 MHz (∼10 km s−1) for the sample, except ESO320-G030 and NGC 5135, which have channels of ∼4 MHz (∼5 km s−1) and ∼23 MHz (∼30 km s−1), respectively. The field of view (FoV) of the ALMA single pointing data has a diameter of ∼24″ (∼5–8 kpc). The three mosaics (MCG-02-33-098, NGC 3256, and NGC 7469) have a diameter between ∼38 and ∼48″ (∼11 and 17 kpc). We applied the primary beam correction to the data cubes. Further details on the observations for each galaxy are listed in Table 2.
A common spatial scale of about 70–90 pc was defined to have a homogeneous data set. We convolved to 80 pc the data cubes of the galaxies with spatial resolutions between 48 and 68 pc (ESO297-G011, NGC 1614, NGC 2369, NGC 3256, ESO320-G030, and NGC 7469). For the remaining objects we directly used cleaned data cubes with spatial resolutions between 72 and 89 pc. For NGC 7130 the original spatial resolution was ∼110 pc. We used this slightly larger spatial scale for the SF law in this galaxy. We obtained the CO(2–1) moment 0 and 2 maps in the following way. To identify the CO(2–1) emission in each channel of the data cube, we selected pixels with fluxes > 5σCO. We estimated the sensitivity σCO in a spectral channel without evident CO(2–1) emission and with no primary beam correction. In addition to the 5σCO criterion, and to ensure that the emission of data cubes does not include noise spikes, we did not consider spatial pixels that have emission from less than three spectral channels. Finally, for each pixel meeting the above criteria, we expanded the spectral range to include a channel before and after the emission to ensure that line profile wings below 5σCO are also considered. In addition to the nominal 90 pc resolution, we smoothed the data to 240 and 500 pc resolutions to study the effect of the spatial scale on the SF laws.
3.2. Ancillary HST/NICMOS data
We used the continuum subtracted near-infrared narrow-band Paα 1.87 μm images taken with the NICMOS instrument on board the Hubble Space Telescope (HST) to map the distribution of recent star formation in the galaxies in the sample (see Alonso-Herrero et al. 2006).
We downloaded the raw data from the Hubble Legacy Archive (HLA)2. The individual frames were combined using the PyDrizzle package with a final pixel size (0.03″) half of the original to improve the spatial sampling. The FoV of the images is approximately 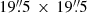 (∼4.2–7.4 kpc). To obtain the final images, we subtracted the background emission and corrected the astrometry using stars within the NICMOS FoV in the F110W (λeff = 1.13 μm) or F160W (λeff = 1.60 μm) filters and the Gaia DR2 catalogue3. Three objects (ESO297-G011, MCG-02-33-098 E/W, and IC4518 E) do not have Gaia stars in their NICMOS image FoV. In these cases we adjusted the astrometry using likely NICMOS counterparts of the regions detected in the ALMA continuum and CO(2–1) maps. After that, the images were rotated to have the standard north-up, east-left orientation. The Paα maps (spatial resolutions of 25–50 pc) were convolved with a Gaussian kernel to match the angular resolution of the ALMA maps.
(∼4.2–7.4 kpc). To obtain the final images, we subtracted the background emission and corrected the astrometry using stars within the NICMOS FoV in the F110W (λeff = 1.13 μm) or F160W (λeff = 1.60 μm) filters and the Gaia DR2 catalogue3. Three objects (ESO297-G011, MCG-02-33-098 E/W, and IC4518 E) do not have Gaia stars in their NICMOS image FoV. In these cases we adjusted the astrometry using likely NICMOS counterparts of the regions detected in the ALMA continuum and CO(2–1) maps. After that, the images were rotated to have the standard north-up, east-left orientation. The Paα maps (spatial resolutions of 25–50 pc) were convolved with a Gaussian kernel to match the angular resolution of the ALMA maps.
3.3. Region selection
We defined circular apertures centred on local maxima in the CO(2–1) moment 0 maps with a diameter of 90 pc, 240 pc, or 500 pc, depending on the spatial resolution of the maps. To do so, we first sorted the CO moment 0 pixel intensities. Then we defined circular regions using as centre the pixels in order of descending intensity to prevent any overlap between the regions. With this method we end up with independent non-overlapping regions centred on local emission maxima that cover all the CO emission in each galaxy. In total, we defined 4802 regions for the whole sample.
We estimated the cold molecular gas mass using the Galactic CO-to-H2 conversion factor, 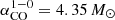 K−1(km s−1) pc−2 (Bolatto et al. 2013) and the CO(2–1)/CO(1–0) ratio (R21) of 0.7 obtained from the single-dish CO data of LIRG IC4687 (Albrecht et al. 2007). The R21 value used is within the range found by Garay et al. (1993) in infrared galaxies and is similar to the value found by Leroy et al. (2013) in nearby spiral galaxies. We explore the variation of the CO-to-H2 conversion factor in Sect. 3.5. We calculated the molecular gas mass surface density (ΣH2) taking into account the area of the selected regions.
K−1(km s−1) pc−2 (Bolatto et al. 2013) and the CO(2–1)/CO(1–0) ratio (R21) of 0.7 obtained from the single-dish CO data of LIRG IC4687 (Albrecht et al. 2007). The R21 value used is within the range found by Garay et al. (1993) in infrared galaxies and is similar to the value found by Leroy et al. (2013) in nearby spiral galaxies. We explore the variation of the CO-to-H2 conversion factor in Sect. 3.5. We calculated the molecular gas mass surface density (ΣH2) taking into account the area of the selected regions.
Once we had the regions in CO(2–1) emission maps, we selected the regions in the Paα maps. These regions are at the same spatial coordinates as the CO(2–1) regions. In this case we considered Paα detections when the line emission is above 3σPaα. The σPaα in these images corresponds to the background noise.
The regions that are below 3σ correspond to the upper limits. Paα emission is detected in 2783 regions (58% of the total). Then we estimated the SFR surface density (ΣSFR) of the regions. We used the HαKennicutt & Evans (2012) calibration, which assumes a Kroupa (2001) initial mass function, and a Hα/Paα ratio of 8.6 (case B at Te = 10.000 K and ne = 104 cm−3, Osterbrock & Ferland 2006). The variation in this ratio is ∼15% due to changes in the physical properties of the ionised gas (i.e. Te = 5–20 × 1000 K and ne = 102–106 cm−3). We took into account the area of the selected regions, obtaining the SFR surface density. All these ΣH2 and ΣSFR values are corrected for the inclination of each galaxy (see Table 1).
Both the SFR and the cold molecular gas surface density estimates are affected by flux calibration errors. We assume an uncertainty of about 10% in the ALMA data (see ALMA Technical Handbook4), and ∼15–20% in the NICMOS data (Alonso-Herrero et al. 2006; Böker et al. 1999).
3.4. Extinction correction
To correct the Paα emission for extinction, we used the Brδ and Brγ line maps observed at 240 pc scales with the SINFONI instrument on the Very Large Telescope (VLT) in eight objects from our sample (effective FoV between 8″ × 8″ and 12″ × 12″; Piqueras López et al. 2013) to derive AK (see Table 2). We calculated the Brδ/Brγ ratio in circular regions with a diameter of 240 pc. We assumed an intrinsic Brδ/Brγ ratio of 1.52 (Hummer & Storey 1987) and the Fitzpatrick (1999) extinction law. In each 240 pc region, we determined AK (AK = 0.11 × AV) and the column density from the CO(2–1) 240 pc maps (NH2).
The NH2 values were divided into five equally spaced ranges between log NH2/cm−2 = 22.55 and 23.88. For each range we estimated the mean and standard deviation of AK obtaining slightly increasing values with NH2 between 0.95 ± 0.6 and 1.98 ± 1.29 mag. To obtain an estimation of the extinction, we measured NH2 in the circular apertures with a diameter of 90 (110), 240, and 500 pc in our entire sample and assigned them the mean AK corresponding to their NH2 range. We assume that the galaxies without SINFONI data (half of the sample) follow the same trend found between AK and NH2 in the other eight galaxies.
3.5. Effects of the CO-to-H2 conversion factor
The obtained cold molecular gas masses depend on the conversion factor (αCO) used. In this paper we assume a Galactic αCO conversion factor to derive molecular gas masses. As argued in the following, we do not expect that a lower conversion factor, typical of ULIRGs (Papadopoulos et al. 2012) is appropriate for our targets.
Our sample does not contain strongly interacting objects or compact mergers like most local ULIRGs. The galaxies in our sample have a mean infrared luminosity of log(LIR/L⊙) = 11.30. In addition, galaxies in our sample show a mean effective radius of the molecular component (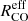 ) of 740 pc (Bellocchi et al., in prep.), while local ULIRGs show a mean value of
) of 740 pc (Bellocchi et al., in prep.), while local ULIRGs show a mean value of 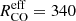 pc (Pereira-Santaella et al. 2021). Therefore, it is likely that the αCO of our sample differs from that of local ULIRGs.
pc (Pereira-Santaella et al. 2021). Therefore, it is likely that the αCO of our sample differs from that of local ULIRGs.
The CO-to-H2 conversion factor can be affected by the metallicity of the galaxies, showing higher values with decreasing metallicity (αCO = 4.35 (Z/Z⊙)−1.6 M⊙ pc−2(K km s−1)−1, Accurso et al. 2017). Rich et al. (2012) studied the metallicity in some local (U)LIRGs, showing a decrease in the abundance with increasing radius. In the case of the metallicity in local disks, Sánchez et al. (2014) observed a similar behaviour. Based on these works, the expected variation in the conversion factor due to metallicity gradients at r < 4 kpc is small, 20–30%.
4. Results and discussion
4.1. Star formation relation for individual galaxies
We studied the molecular KS relation for each LIRG at scales of 90 (110) pc. As an example, Fig. 1 shows the SFR surface density as a function of molecular gas surface density for NGC 7130 (similar figures for the rest of the sample are presented in Appendix A.1). The KS diagram suggests that the regions follow two different power laws. These two branches were identified using the Multivariate Adaptive Regression Splines (MARS) fit (Friedman 1991) in log ΣSFR and log ΣH2, which gives the position of the breaking points (cut points) for a linear regression with multiple slopes. We obtained the adjusted coefficient of determination, the cut points, and their errors using MARS fit in 100 realisations of the data based on the uncertainties in both axes.
 |
Fig. 1. Star formation relation and location of the regions considered in NGC 7130. Left panel: SFR surface density (ΣSFR) as a function of the molecular gas surface density (ΣH2) derived from CO(2–1) in NGC 7130 at 110 pc scale. The blue and black points show the two branches derived applying the MARS method with breaking points in the log ΣH2 axis. The black dashed lines mark constant depletion times (tdep = ΣH2/ΣSFR). The red and brown solid lines are the best fit for each branch. The Spearman’s rank correlation coefficients (ρs) and the power-law indices (N) of the derived best-fit KS relations are indicated. The pink dashed line is the best fit for whole points. The inverted triangles indicate upper limits. The error bars indicate the mean systematic uncertainties in ΣH2 of ±0.14 dex (horizontal) and the extinction correction in ΣSFR of ±0.21 dex (vertical). Right panel: Location of the regions on the CO(2–1) map (grey). The black and blue circles correspond to regions in each of the two branches. |
We consider that the MARS breaking point is significant when the adjusted coefficient of determination found by MARS (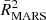 ) is larger than that of the linear fit (
) is larger than that of the linear fit (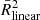 ). The adjusted coefficient of determination is used to compare the linear and MARS fits since it takes into account both the number of terms in the model and the number of data points. In this galaxy the break of a linear regression occurs at log ΣH2/(M⊙ yr−1 kpc−2) = 3.35 (for cut on ΣSFR, see Fig. A.1).
). The adjusted coefficient of determination is used to compare the linear and MARS fits since it takes into account both the number of terms in the model and the number of data points. In this galaxy the break of a linear regression occurs at log ΣH2/(M⊙ yr−1 kpc−2) = 3.35 (for cut on ΣSFR, see Fig. A.1).
We fit the two branches using the orthogonal distance regression (ODR) method. This fit gives power-law indices of N = 4.19 ± 0.46 and N = 0.68 ± 0.07. The right panel of Fig. 1 shows that the branch with higher gas and SFR densities (left panel) is located in the central region of the galaxy (at radii up to 0.85 kpc), while the other branch with lower gas and SFR densities is located in the more external disk regions. The duality is reinforced if we consider a factor αCO = 0.8 (Downes & Solomon 1998) typical of ULIRGs in the central regions of our galaxies.
We do not include in our analysis the upper limits. Pessa et al. (2021) studied the influence of the non-detections in several resolved scaling relations. In general, the non-detections could artificially flatten the relations at small spatial scales, resulting in a steepening when the analysis is carried out at larger spatial scales. This occurs because the pixels with signal are averaged with the non-detection pixels at larger scales. However, they found that ignoring the non-detections in the star formation relation has a small impact on the measured slope.
4.2. Star formation relation across the sample
We repeated the same analysis for the rest of the sample finding two different regimes (branches) in the KS relations in four galaxies (25% of the sample, hereafter referred to as dual galaxies; see Table 3 and Fig. A.2).
Statistical parameters for dual galaxies.
The remaining 12 galaxies (75% of the sample) can be modelled with a single power law (hereafter referred to as non-dual galaxies; see Table 4 and Fig. A.3) at 90 pc scales. For the four dual galaxies the cut points on both the ΣH2 and ΣSFR axes are similar (log ΣH2/(M⊙ pc−2) ≈ 3.25 and log ΣSFR/(M⊙ yr−1 kpc−2) ≈ 0.91).
Statistical parameters for the non-dual galaxies
Therefore, in the top left and top middle panels of Fig. 2 we combine all the regions of the dual galaxies with a cut on both axes obtained in each individual dual galaxy. We find that the power law for the regions above the cut points (hereafter referred to as high-N regions) is steeper than for the regions below them (hereafter referred to as low-N regions). The indices of the best power-law fits are N = 4.12 ± 0.22 (high-N regions) and N = 0.91 ± 0.04 (low-N regions) when using the ΣH2 cut point (Fig. 2 top left), and N = 1.89 ± 0.15 (high-N regions) and N = 0.89 ± 0.03 (low-N regions) when we consider the ΣSFR cut point (Fig. 2 top middle).
 |
Fig. 2. SFR surface density as a function of the molecular gas surface density using 90 (110) pc regions. Top left and top middle panels: the black and blue points correspond to the two different regimes (branches) identified in the four dual galaxies using the MARS method in each individual galaxy. Top right: the green circles correspond to the regions in the remaining 12 galaxies. Bottom row: the black and blue points correspond to the two branches identified using the MARS method in all the regions from the dual galaxies. The red, brown, and magenta solid lines indicate the best fit for each regime. The dashed lines indicate constant tdep. |
When we fit all the regions from the dual galaxies using the MARS method (Fig. 2 bottom row), we obtain a value of 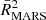 (0.67 ± 0.06 and 0.59 ± 0.03 on log10ΣH2 and log10ΣSFR, respectively) higher than
(0.67 ± 0.06 and 0.59 ± 0.03 on log10ΣH2 and log10ΣSFR, respectively) higher than 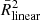 (0.55) and similar cut point values to those in the individual dual galaxies (log ΣH2/(M⊙ pc−2) = 3.27 ± 0.17 and log ΣSFR/(M⊙ yr−1 kpc−2) = 1.16 ± 0.19). At larger spatial scales (240 and 500 pc), the duality disappears and a standard single power-law KS relation is recovered (see Fig. 3).
(0.55) and similar cut point values to those in the individual dual galaxies (log ΣH2/(M⊙ pc−2) = 3.27 ± 0.17 and log ΣSFR/(M⊙ yr−1 kpc−2) = 1.16 ± 0.19). At larger spatial scales (240 and 500 pc), the duality disappears and a standard single power-law KS relation is recovered (see Fig. 3).
 |
Fig. 3. SFR surface density as a function of the molecular gas surface density using 240 (top row) and 500 (bottom row) pc regions. The blue and green circles correspond to the regions of the dual galaxies at 90 pc and the non-dual galaxies, respectively. The dark orange and magenta solid lines indicate the best fit. The dashed lines indicate constant tdep. |
For the 12 non-dual galaxies, we find a single linear power law with an index N = 1.15 ± 0.02 (Fig. 2 top right). The dual and non-dual behaviours are also present before applying the extinction correction in Fig. 4.
 |
Fig. 4. Comparison between the KS relation with and without extinction correction. Left panels: KS relation of galaxies with two branches, taking into account the extinction correction (top) and without this correction (bottom). Right panels: same, but for the non-dual galaxies. |
4.3. Radial distribution of the two regimes
To identify what causes the two branches in the SF laws for these four galaxies, we first investigate their spatial distribution. Figure 5 shows the cumulative distribution of the molecular gas mass of the regions, based on the ΣH2 cut selection, in the dual galaxies as a function of the radial distance. We find that the high-N regions are located in the central region of the galaxies, 50% (90%) at radii smaller than 0.50 kpc (0.85 kpc) from the centre. The molecular mass in the high-N regions follows the same radial distribution. The low-N regions are located at larger radii with a median radius of ∼1 kpc, and only ∼45% of the regions are at radii lower than 0.88 kpc. We find the same trends using the cut on ΣSFR.
 |
Fig. 5. Cumulative distribution of the molecular mass (left vertical axis and solid lines) of the 90 pc regions in the dual galaxies, selected applying a cut on ΣH2, as a function of the radial distance. The dashed lines (right vertical axis) show the cumulative distribution of the number of regions in each branch. Colours are as in Fig. 1. The dash-dotted lines correspond to the radii that include a percentage of regions. |
4.4. Self-gravity of the gas
We explored the dynamical state of molecular gas in the regions using the boundedness parameter (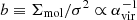 , where σ is the velocity dispersion and αvir the virial parameter). We obtained the velocity dispersion from the CO(2–1) moment 2. Figure 6 shows the cold molecular gas depletion time (tdep = ΣH2/ΣSFR) as a function of the boundedness parameter (b) at 90 pc scales. Despite the scatter (∼2.5 dex in tdep), at these scales there is a weak trend with decreasing tdep for increasing b in the dual galaxies (top left).
, where σ is the velocity dispersion and αvir the virial parameter). We obtained the velocity dispersion from the CO(2–1) moment 2. Figure 6 shows the cold molecular gas depletion time (tdep = ΣH2/ΣSFR) as a function of the boundedness parameter (b) at 90 pc scales. Despite the scatter (∼2.5 dex in tdep), at these scales there is a weak trend with decreasing tdep for increasing b in the dual galaxies (top left).
 |
Fig. 6. Cold molecular gas depletion time, tdep, as a function of the self-gravity of the regions (parameter b) at 90 pc scales for the dual (top left) and the non-dual galaxies (top right). The orange and magenta circles show the median tdep in bins of b. The points and error bars indicate the mean absolute deviation of the points in the bins. The values of these parameters estimated in M51 (Leroy+17) are shown in purple, and the open black rectangle represents the range of values in NGC 628 (Kreckel+18). The black and blue circles correspond to regions in the high- and low-N regimes, respectively, for the four dual objects (bottom row). The red and brown circles are the mean values of the regions in high- and low-N regimes, respectively. The error bars indicate the mean absolute deviation of the regions in high- and low-N regimes, respectively. |
When we consider the low- and high-N regions separately (bottom row), we find that the high-N regions in both cuts show a slightly better correlation between tdep and b, while for the low-N regions the trend disappears. The high-N regions show gas with larger b (with a mean b parameter of log b/M⊙ pc−2(km s−1)−2 ≈ 0.52) and have shorter tdep in both cuts than the low-N regions (with a mean b of log b/M⊙pc−2(km s−1)−2 ≈ 0.30). The non-dual galaxies do not show a clear relation. Table 5 summarises the correlations.
Spearman rank correlation coefficients.
Leroy et al. (2017) found, from the intensity weighted average on scales of 40 pc within regions of 370 pc, that gas with larger b (more bound) exhibits shorter tdep in the spiral galaxy M51. This means that when b increases the system is more gravitationally bounded. However, Kreckel et al. (2018) did not find any correlation between b and tdep in another spiral (NGC 628) at 50 pc scales within 500 pc regions, which is in agreement with our results for the non-dual galaxies and the low-N regions in dual galaxies. For the high-N regions in the dual galaxies, tdep seems to decrease for increasing b although the scatter is large. The depletion times in our sample are between four and eight times shorter than in these two spirals. This difference is consistent with what was found in previous works for starbursts (Daddi et al. 2010; Genzel et al. 2010; García-Burillo et al. 2012). However, for similar b, there is a factor of 10 in tdep. As a consequence, it is not clear if a universal relation between tdep and b exists.
4.5. Velocity dispersion of the gas
We explore the behaviour of the velocity dispersion in our sample. Figure 7 shows the SF efficiency of the cold molecular gas (SFE = ΣSFR/ΣH2) as a function of the velocity dispersion (σ). The velocity dispersion was obtained from the CO(2–1) moment 2. We find that the global mean values of the σ and SFE for the dual galaxies (log σ/km s−1 = 1.36 ± 0.16 and logSFE/Myr−1 = −2.56 ± 0.26) and for the non-dual galaxies (log σ/km s−1 = 1.41 ± 0.18 and logSFE/Myr−1 = −2.60 ± 0.31) are similar. However, when we consider the low- and high-N regions independently, the mean values are different. The high-N regions show higher mean values (log σ/km s−1 ∼ 1.56 for both cuts and logSFE/Myr−1 = −2.41 ± 0.44 for cut on ΣH2 and logSFE/Myr−1 = −2.10 ± 0.40 on ΣSFR) than the low-N regions (log σ/km s−1 ∼ 1.30 and log SFE/Myr−1 ∼ −2.62 for both cuts). In addition, for the high-N regions the SFE increases with increasing σ, though the scatter is large (∼2 dex).
 |
Fig. 7. SF efficiency of the molecular gas as a function of the velocity dispersion of the gas (σ) at 90 pc scales. Left and middle panels: cut on the ΣH2 and ΣSFR axis for each galaxy, respectively. Colours are as in previous figures. The red and brown points and error bars indicate the mean and mean absolute deviation for the regions in high- and low-N regimes, respectively. Right panel: similar to the left and middle panels, but for non-dual galaxies. The central regions (r < 0.50 kpc) are represented in green and the more external regions in grey. The black and blue points and error bars correspond to the mean and mean absolute deviation values of the central and external regions, respectively. The orange and magenta points and error bars are the mean and mean absolute deviation for all the regions in each panel. The inverted triangles indicate upper limits. |
The high-N regions are located in the central regions of the four dual objects, so we also investigate if the central regions of the non-dual galaxies have different SFE and/or σ. To do this, we consider the regions at radii < 500 pc, which is where most of the high-N regions are located in the dual galaxies (see Sect. 4.3). Unlike the dual galaxies, we find that for the non-dual galaxies, the internal (r < 500 pc) and external regions have similar mean SFE (logSFE/Myr−1 = −2.48 ± 0.34 and −2.66 ± 0.28 for the internal and external regions respectively) and just slightly higher σ (log σ/km s−1 = 1.53 ± 0.18 and 1.36 ± 0.16, respectively).
The large scatter at these scales may be due to the fact that we can resolve individual regions, obtaining information from the clouds in different evolutionary phases (Kruijssen & Longmore 2014). Several SF models suggest that the dynamical state of the cloud, and not only its density, affects its ability to collapse and form stars (e.g. Krumholz & McKee 2005; Hennebelle & Chabrier 2011; Federrath & Klessen 2013). These models focus on the properties of turbulent molecular clouds, proposing that the supersonic and compressive turbulence induces the formation of stars. In this case we would expect the SFE to increase with increasing gas velocity dispersion (Orkisz et al. 2017). This is consistent with our findings for the high-N regions in the dual galaxies. Cloud-cloud collisions could be enhanced near the location of the bar resonances in the central regions of these galaxies (Sánchez-García et al., in prep.). These collisions could result in an increased turbulence, which may induce a greater compression of the gas (increasing its density), and finally lead to an enhanced star formation. Moreover, the increase in gas density compensates for the high turbulence, causing, together, b to increase in these central.
5. Conclusions
We have presented a high-resolution study of the star formation relation in a sample of 16 local LIRGs on spatial scales of ∼90 pc. We have combined the SFR calculated from the HST/NICMOS Paα emission with cold molecular gas from ALMA CO(2–1) data to probe the star formation relations.
We find that four galaxies from our sample show dual behaviour in their KS relation at 90 pc scales. The regime with higher gas and SFR surface densities is characterised by a steeper power-law index in the central region of the galaxies (r < 0.85 kpc). The other regime, which shows lower values of gas and SFR surface densities, is located in the more external disk regions. This dual behaviour disappears at large spatial scales (240 and 500 pc).
The gas in the central region of the dual galaxies shows greater turbulence (higher σ) and slightly stronger self-gravity (higher b) than the external region. These dynamical conditions of the gas might lead to more efficient star formation in the central region. The rest of the galaxies do not show a clear trend between these two parameters. These variations within each galaxy and among the galaxies in the sample suggest that the local dynamical environment plays a role in the star formation process. The fraction of AGN and bars is similar for dual and non-dual galaxies, although a larger sample is needed to evaluate their impact on the SF law at 90 pc scale.
Acknowledgments
We thank the referee for the useful comments and suggestions. M.S.G. acknowledges support from the Spanish Ministerio de Economía y Competitividad through the grants BES-2016-078922, ESP2017-83197-P. L.C. and M.S.G. acknowledge support from the research project PID2019-106280GB-100. M.P.S. acknowledges support from the Comunidad de Madrid through the Atracción de Talento Investigador Grant 2018-T1/TIC-11035 and PID2019-105423GA-I00 (MCIU/AEI/FEDER,UE). A.A.-H. and S.G.-B. work was funded by grant PGC2018-094671-B-I00 funded by MCIN/AEI/ 10.13039/501100011033 and by ERDF A way of making Europe. S.G.B. acknowledges support from the research project PID2019-106027GA-C44 of the Spanish Ministerio de Ciencia e Innovación. J.P.L. acknowledges support from PID2019-105423GA-I00. E.B. acknowledges the support from Comunidad de Madrid through the Atracción de Talento grant 2017-T1/TIC-5213. S.C. acknowledges financial support from the State Agency for Research of the Spanish MCIU through the ‘Centre of Excellence Severo Ochoa’ award to the Instituto de Astrofísica de Andalucía (SEV-2017-0709). A.L. acknowledges the support from Comunidad de Madrid through the Atracción de Talento Investigador Grant 2017-T1/TIC-5213, and PID2019-106280GB-I00 (MCIU/AEI/FEDER,UE) This paper makes use of the following ALMA data: ADS/JAO.ALMA#2017.1.00255.S, ADS/JAO.ALMA#2013.1.00271.S, ADS/JAO.ALMA#2013.1.00243.S, ADS/JAO.ALMA#2015.1.00714.S and ADS/JAO.ALMA#2017.1.00395.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada) and NSC and ASIAA (Taiwan) and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc.
References
- Accurso, G., Saintonge, A., Catinella, B., et al. 2017, MNRAS, 470, 4750 [NASA ADS] [Google Scholar]
- Albrecht, M., Krügel, E., & Chini, R. 2007, A&A, 462, 575 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alonso-Herrero, A., Rieke, G. H., Rieke, M. J., et al. 2006, ApJ, 650, 835 [Google Scholar]
- Alonso-Herrero, A., García-Marín, M., Monreal-Ibero, A., et al. 2009, A&A, 506, 1541 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alonso-Herrero, A., Pereira-Santaella, M., Rieke, G. H., & Rigopoulou, D. 2012, ApJ, 744, 2 [Google Scholar]
- Bellocchi, E., Arribas, S., Colina, L., & Miralles-Caballero, D. 2013, A&A, 557, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Böker, T., Calzetti, D., Sparks, W., et al. 1999, ApJS, 124, 95 [CrossRef] [Google Scholar]
- Bolatto, A. D., Wolfire, M., & Leroy, A. K. 2013, ARA&A, 51, 207 [CrossRef] [Google Scholar]
- Briggs, D. S. 1995, Am. Astron. Soc. Meeting Abstracts, 187, 112.02 [Google Scholar]
- Casasola, V., Hunt, L., Combes, F., & García-Burillo, S. 2015, A&A, 577, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Corbett, E. A., Kewley, L., Appleton, P. N., et al. 2003, ApJ, 583, 670 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Elbaz, D., Walter, F., et al. 2010, ApJ, 714, L118 [NASA ADS] [CrossRef] [Google Scholar]
- Downes, D., & Solomon, P. M. 1998, ApJ, 507, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., & Klessen, R. S. 2013, ApJ, 763, 51 [Google Scholar]
- Fitzpatrick, E. L. 1999, PASP, 111, 63 [Google Scholar]
- Friedman, J. H. 1991, Ann. Stat., 19, 1 [NASA ADS] [Google Scholar]
- Garay, G., Mardones, D., & Mirabel, I. F. 1993, A&A, 277, 405 [NASA ADS] [Google Scholar]
- García-Burillo, S., Usero, A., Alonso-Herrero, A., et al. 2012, A&A, 539, A8 [Google Scholar]
- Genzel, R., Tacconi, L. J., Gracia-Carpio, J., et al. 2010, MNRAS, 407, 2091 [NASA ADS] [CrossRef] [Google Scholar]
- Hennebelle, P., & Chabrier, G. 2011, ApJ, 743, L29 [Google Scholar]
- Hummer, D. G., & Storey, P. J. 1987, MNRAS, 224, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., Jr 1998, ApJ, 498, 541 [Google Scholar]
- Kennicutt, R. C., & Evans, N. J. 2012, ARA&A, 50, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., Dopita, M. A., Sutherland, R. S., Heisler, C. A., & Trevena, J. 2001, ApJ, 556, 121 [Google Scholar]
- Kreckel, K., Faesi, C., Kruijssen, J. M. D., et al. 2018, ApJ, 863, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Kruijssen, J. M. D., & Longmore, S. N. 2014, MNRAS, 439, 3239 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., & McKee, C. F. 2005, ApJ, 630, 250 [Google Scholar]
- Leroy, A. K., Walter, F., Brinks, E., et al. 2008, AJ, 136, 2782 [Google Scholar]
- Leroy, A. K., Walter, F., Sandstrom, K., et al. 2013, AJ, 146, 19 [Google Scholar]
- Leroy, A. K., Schinnerer, E., Hughes, A., et al. 2017, ApJ, 846, 71 [Google Scholar]
- Lípari, S., Díaz, R., Taniguchi, Y., et al. 2000, AJ, 120, 645 [CrossRef] [Google Scholar]
- McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, in Astronomical Data Analysis Software and Systems XVI, eds. R. A. Shaw, F. Hill, & D. J. Bell, ASP Conf. Ser., 376, 127 [Google Scholar]
- Onodera, S., Kuno, N., Tosaki, T., et al. 2010, ApJ, 722, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Orkisz, J. H., Pety, J., Gerin, M., et al. 2017, A&A, 599, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Osterbrock, D. E., & Ferland, G. J. 2006, Astrophysics of Gaseous Nebulae and Active Galactic Nuclei [Google Scholar]
- Papadopoulos, P. P., van der Werf, P., Xilouris, E., Isaak, K. G., & Gao, Y. 2012, ApJ, 751, 10 [Google Scholar]
- Paraficz, D., Rybak, M., McKean, J. P., et al. 2018, A&A, 613, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pereira-Santaella, M., Diamond-Stanic, A. M., Alonso-Herrero, A., & Rieke, G. H. 2010, ApJ, 725, 2270 [Google Scholar]
- Pereira-Santaella, M., Alonso-Herrero, A., Santos-Lleo, M., et al. 2011, A&A, 535, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pereira-Santaella, M., Colina, L., García-Burillo, S., et al. 2016a, A&A, 587, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pereira-Santaella, M., Colina, L., García-Burillo, S., et al. 2016b, A&A, 594, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pereira-Santaella, M., Colina, L., García-Burillo, S., et al. 2021, A&A, 651, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pessa, I., Schinnerer, E., Belfiore, F., et al. 2021, A&A, 650, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petric, A. O., Armus, L., Howell, J., et al. 2011, ApJ, 730, 28 [Google Scholar]
- Piqueras López, J., Colina, L., Arribas, S., & Alonso-Herrero, A. 2013, A&A, 553, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rich, J. A., Torrey, P., Kewley, L. J., Dopita, M. A., & Rupke, D. S. N. 2012, ApJ, 753, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Saito, T., Iono, D., Xu, C. K., et al. 2016, PASJ, 68, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez, S. F., Rosales-Ortega, F. F., Iglesias-Páramo, J., et al. 2014, A&A, 563, A49 [CrossRef] [EDP Sciences] [Google Scholar]
- Sanders, D. B., Mazzarella, J. M., Kim, D. C., Surace, J. A., & Soifer, B. T. 2003, AJ, 126, 1607 [Google Scholar]
- Schmidt, M. 1959, ApJ, 129, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Schruba, A., Leroy, A. K., Walter, F., Sandstrom, K., & Rosolowsky, E. 2010, ApJ, 722, 1699 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, J., Leroy, A. K., Schruba, A., et al. 2018, ApJ, 860, 172 [NASA ADS] [CrossRef] [Google Scholar]
- van den Broek, A. C., van Driel, W., de Jong, T., et al. 1991, A&AS, 91, 61 [NASA ADS] [Google Scholar]
- Veilleux, S., Kim, D. C., Sanders, D. B., Mazzarella, J. M., & Soifer, B. T. 1995, ApJS, 98, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Viaene, S., Forbrich, J., & Fritz, J. 2018, MNRAS, 475, 5550 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, T. G., Gear, W. K., & Smith, M. W. L. 2018, MNRAS, 479, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, C. K., Cao, C., Lu, N., et al. 2015, ApJ, 799, 11 [Google Scholar]
- Yao, L., Seaquist, E. R., Kuno, N., & Dunne, L. 2003, ApJ, 597, 1271 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, T. T., Kewley, L. J., & Sanders, D. B. 2010, ApJ, 709, 884 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Figures
A.1. Star formation relation for individual galaxies and CO(2–1) maps and HST/NICMOS images
In this appendix we present the KS relations, the regions considered in this work, the ALMA CO(2–1) maps, and the HST/NICMOS Paα images for the whole sample.
 |
Fig. A.1. Star formation relation and emission line maps used to obtain the location of the regions considered in NGC7130. Top panels: Same as Fig. 1, but applying the MARS method to the log10ΣH2. Bottom panels: ALMA CO(2–1) (left) and HST/NICMOS Paα maps (right). This last map is smoothed to the ALMA resolution. The magenta filled ellipse (bottom left) represents the beam size (0″.36 × 0″.29 PA = 69°). |
 |
Fig. A.2. Same as Fig. 1, but applying the MARS method to the log10ΣH2 (top left and middle) and log10ΣSFR (bottom left and middle). Right panels: ALMA CO(2–1) (top) and HST/NICMOS Paα maps (bottom). This last map is smoothed to the ALMA resolution. The magenta filled ellipse represents the beam size. |
 |
Fig. A.2. continued. |
 |
Fig. A.2. continued. |
 |
Fig. A.3. Same as Fig. A.1. Top left panel: SFR surface density (ΣSFR) as a function of the molecular gas surface density (ΣH2) for the non-dual galaxies in the sample using 90 pc regions. The green circles indicate data points in each galaxy. The solid purple line indicates the best fit. The Spearman’s rank correlation coefficients (ρs) and the power-law index (N) of the derived best-fit KS relation are shown in the figure. The dashed lines indicate constant tdep values. Topright: Location of the regions on the CO(2–1) map (grey). Bottom panels: ALMA CO(2–1) (left) and HST/NICMOS Paα (right) maps. |
 |
Fig. A.3. continued. |
 |
Fig. A.3. continued. |
 |
Fig. A.3. continued. |
 |
Fig. A.3. continued. |
 |
Fig. A.3. continued. |
 |
Fig. A.3. continued. |
 |
Fig. A.3. continued. |
 |
Fig. A.3. continued. |
 |
Fig. A.3. continued. |
 |
Fig. A.3. continued. |
 |
Fig. A.3. continued. |
All Tables
All Figures
 |
Fig. 1. Star formation relation and location of the regions considered in NGC 7130. Left panel: SFR surface density (ΣSFR) as a function of the molecular gas surface density (ΣH2) derived from CO(2–1) in NGC 7130 at 110 pc scale. The blue and black points show the two branches derived applying the MARS method with breaking points in the log ΣH2 axis. The black dashed lines mark constant depletion times (tdep = ΣH2/ΣSFR). The red and brown solid lines are the best fit for each branch. The Spearman’s rank correlation coefficients (ρs) and the power-law indices (N) of the derived best-fit KS relations are indicated. The pink dashed line is the best fit for whole points. The inverted triangles indicate upper limits. The error bars indicate the mean systematic uncertainties in ΣH2 of ±0.14 dex (horizontal) and the extinction correction in ΣSFR of ±0.21 dex (vertical). Right panel: Location of the regions on the CO(2–1) map (grey). The black and blue circles correspond to regions in each of the two branches. |
| In the text | |
 |
Fig. 2. SFR surface density as a function of the molecular gas surface density using 90 (110) pc regions. Top left and top middle panels: the black and blue points correspond to the two different regimes (branches) identified in the four dual galaxies using the MARS method in each individual galaxy. Top right: the green circles correspond to the regions in the remaining 12 galaxies. Bottom row: the black and blue points correspond to the two branches identified using the MARS method in all the regions from the dual galaxies. The red, brown, and magenta solid lines indicate the best fit for each regime. The dashed lines indicate constant tdep. |
| In the text | |
 |
Fig. 3. SFR surface density as a function of the molecular gas surface density using 240 (top row) and 500 (bottom row) pc regions. The blue and green circles correspond to the regions of the dual galaxies at 90 pc and the non-dual galaxies, respectively. The dark orange and magenta solid lines indicate the best fit. The dashed lines indicate constant tdep. |
| In the text | |
 |
Fig. 4. Comparison between the KS relation with and without extinction correction. Left panels: KS relation of galaxies with two branches, taking into account the extinction correction (top) and without this correction (bottom). Right panels: same, but for the non-dual galaxies. |
| In the text | |
 |
Fig. 5. Cumulative distribution of the molecular mass (left vertical axis and solid lines) of the 90 pc regions in the dual galaxies, selected applying a cut on ΣH2, as a function of the radial distance. The dashed lines (right vertical axis) show the cumulative distribution of the number of regions in each branch. Colours are as in Fig. 1. The dash-dotted lines correspond to the radii that include a percentage of regions. |
| In the text | |
 |
Fig. 6. Cold molecular gas depletion time, tdep, as a function of the self-gravity of the regions (parameter b) at 90 pc scales for the dual (top left) and the non-dual galaxies (top right). The orange and magenta circles show the median tdep in bins of b. The points and error bars indicate the mean absolute deviation of the points in the bins. The values of these parameters estimated in M51 (Leroy+17) are shown in purple, and the open black rectangle represents the range of values in NGC 628 (Kreckel+18). The black and blue circles correspond to regions in the high- and low-N regimes, respectively, for the four dual objects (bottom row). The red and brown circles are the mean values of the regions in high- and low-N regimes, respectively. The error bars indicate the mean absolute deviation of the regions in high- and low-N regimes, respectively. |
| In the text | |
 |
Fig. 7. SF efficiency of the molecular gas as a function of the velocity dispersion of the gas (σ) at 90 pc scales. Left and middle panels: cut on the ΣH2 and ΣSFR axis for each galaxy, respectively. Colours are as in previous figures. The red and brown points and error bars indicate the mean and mean absolute deviation for the regions in high- and low-N regimes, respectively. Right panel: similar to the left and middle panels, but for non-dual galaxies. The central regions (r < 0.50 kpc) are represented in green and the more external regions in grey. The black and blue points and error bars correspond to the mean and mean absolute deviation values of the central and external regions, respectively. The orange and magenta points and error bars are the mean and mean absolute deviation for all the regions in each panel. The inverted triangles indicate upper limits. |
| In the text | |
 |
Fig. A.1. Star formation relation and emission line maps used to obtain the location of the regions considered in NGC7130. Top panels: Same as Fig. 1, but applying the MARS method to the log10ΣH2. Bottom panels: ALMA CO(2–1) (left) and HST/NICMOS Paα maps (right). This last map is smoothed to the ALMA resolution. The magenta filled ellipse (bottom left) represents the beam size (0″.36 × 0″.29 PA = 69°). |
| In the text | |
 |
Fig. A.2. Same as Fig. 1, but applying the MARS method to the log10ΣH2 (top left and middle) and log10ΣSFR (bottom left and middle). Right panels: ALMA CO(2–1) (top) and HST/NICMOS Paα maps (bottom). This last map is smoothed to the ALMA resolution. The magenta filled ellipse represents the beam size. |
| In the text | |
 |
Fig. A.2. continued. |
| In the text | |
 |
Fig. A.2. continued. |
| In the text | |
 |
Fig. A.3. Same as Fig. A.1. Top left panel: SFR surface density (ΣSFR) as a function of the molecular gas surface density (ΣH2) for the non-dual galaxies in the sample using 90 pc regions. The green circles indicate data points in each galaxy. The solid purple line indicates the best fit. The Spearman’s rank correlation coefficients (ρs) and the power-law index (N) of the derived best-fit KS relation are shown in the figure. The dashed lines indicate constant tdep values. Topright: Location of the regions on the CO(2–1) map (grey). Bottom panels: ALMA CO(2–1) (left) and HST/NICMOS Paα (right) maps. |
| In the text | |
 |
Fig. A.3. continued. |
| In the text | |
 |
Fig. A.3. continued. |
| In the text | |
 |
Fig. A.3. continued. |
| In the text | |
 |
Fig. A.3. continued. |
| In the text | |
 |
Fig. A.3. continued. |
| In the text | |
 |
Fig. A.3. continued. |
| In the text | |
 |
Fig. A.3. continued. |
| In the text | |
 |
Fig. A.3. continued. |
| In the text | |
 |
Fig. A.3. continued. |
| In the text | |
 |
Fig. A.3. continued. |
| In the text | |
 |
Fig. A.3. continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.