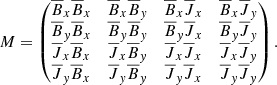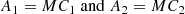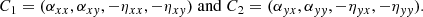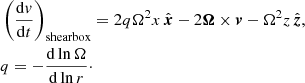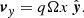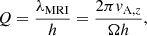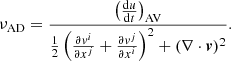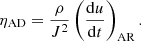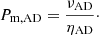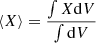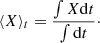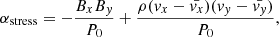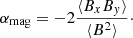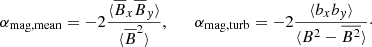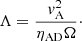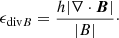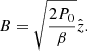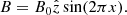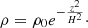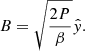| Issue |
A&A
Volume 659, March 2022
|
|
|---|---|---|
| Article Number | A91 | |
| Number of page(s) | 21 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/202141206 | |
| Published online | 10 March 2022 | |
Magnetorotational instability with smoothed particle hydrodynamics
Institute of Theoretical Astrophysics, University of Oslo, Postboks 1029, 0315 Oslo, Norway
e-mail: robertwi@astro.uio.no
Received:
28
April
2021
Accepted:
9
December
2021
The magnetorotational instability (MRI) is an important process in driving turbulence in sufficiently ionized accretion disks. It has been extensively studied using simulations with Eulerian grid codes, but remains fairly unexplored for meshless codes. Here, we present a thorough numerical study on the MRI using the smoothed particle magnetohydrodynamics method with the geometric density average force expression. We performed 37 shearing box simulations with different initial setups and a wide range of resolution and dissipation parameters. We show, for the first time, that MRI with sustained turbulence can be simulated successfully with smoothed-particle hydrodynamics (SPH), with results consistent with prior work with grid-based codes, including saturation properties such as magnetic and kinetic energies and their respective stresses. In particular, for the stratified boxes, our simulations reproduce the characteristic “butterfly” diagram of the MRI dynamo with saturated turbulence for at least 100 orbits. On the contrary, traditional SPH simulations suffer from runaway growth and develop unphysically large azimuthal fields, similar to the results from a recent study with meshless methods. We investigated the dependency of MRI turbulence on the numerical Prandtl number (Pm) in SPH, focusing on the unstratified, zero net-flux case. We found that turbulence can only be sustained with a Prandtl number larger than ∼2.5, similar to the critical values for the physical Prandtl number found in grid-code simulations. However, unlike grid-based codes, the numerical Prandtl number in SPH increases with resolution, and for a fixed Prandtl number, the resulting magnetic energy and stresses are independent of resolution. Mean-field analyses were performed on all simulations, and the resulting transport coefficients indicate no α-effect in the unstratified cases, but an active αω dynamo and a diamagnetic pumping effect in the stratified medium, which are generally in agreement with previous studies. There is no clear indication of a shear-current dynamo in our simulation, which is likely to be responsible for a weaker mean-field growth in the tall, unstratified, zero net-flux simulation.
Key words: methods: numerical / ISM: magnetic fields / magnetohydrodynamics (MHD)
© ESO 2022
1. Introduction
A popular mechanism for the generation of turbulence within accretion disks is the magnetorotational instability (MRI; Velikhov 1959; Chandrasekhar 1960; Fricke 1969; Balbus & Hawley 1991), which is a local linear instability that occurs for magnetic fields in Keplerian-like flows (e.g., accretion disks). The ensuing turbulence subsequently acts as a driver for angular momentum transport within the disk, allowing efficient mass accretion onto the central object (Shakura & Sunyaev 1973; Lynden-Bell & Pringle 1974). Due to its simple prerequisites of “activating” the instability (negative angular momentum gradient, weak magnetic field, and sufficiently ionized gas), the MRI is potentially a crucial component in many different astrophysical systems.
While the linear behavior of the MRI is well established (Balbus & Hawley 1991, 1992; Curry et al. 1994; Goodman & Xu 1994; Kersalé et al. 2004), the nonlinear phase is an active area of research. Modeling the full nonlinear behavior of the MRI requires numerical simulations, which for the past few decades have been readily applied to study the MRI in both global (Penna et al. 2010; Hawley et al. 2011, 2013; Parkin & Bicknell 2013; Deng et al. 2020) and local (Hawley et al. 1995) setups. While global simulations allow the inclusion of global properties such as winds, jets, and accretion, they require extensive computational resources to properly resolve the MRI growth rates. Sano et al. (2004) found that a minimum of six grid zones per MRI wavelength (λMRI) was required to model the linear phase. This criterion was further extended to the nonlinear regime by Noble et al. (2010), where an effective quality parameter (Q) was used to gauge the resolution requirement for correct MRI behavior. On the other hand, local setups allow higher resolution and remain simple and well-posed for investigating the nonlinearity and saturation of the MRI under specific initial conditions. In general, local setups apply a shearing box approximation (Goldreich & Lynden-Bell 1965; Hawley et al. 1995), which models either a small unstratified block of gas within the disk (neglecting gravity) or a slice of the disk with a vertically stratified density field (including the vertical gravity component). The initial configuration of the magnetic field is an important factor for the behavior and saturation of the MRI, and most studies apply either a constant mean magnetic field through the box (often referred to as the net flux case NF; Hawley et al. 1995; Sano et al. 2004; Guan et al. 2009; Simon et al. 2009) or an initial magnetic field which has a zero mean-field value (often referred to as the zero net flux case ZNF; Hawley et al. 1996; Fromang & Papaloizou 2007; Simon & Hawley 2009; Bodo et al. 2011). Both cases are idealized setups. In reality, the mean-field within local patches of the disk (with sizes around the scale height of disk) varies in time due to larger-scale current structures and nonideal magnetohydrodynamic (MHD) effects. In general, the initial mean-field within local setups is either along an azimuthal or vertical direction, as any radial mean-field leads to a constant increase in the azimuthal mean-field due to the shear.
The turbulence generated by the MRI is subcritical, which means that it requires a self-sustaining process to remain active (Rincon et al. 2007; Herault et al. 2011; Riols et al. 2013). A physical explanation for the turbulence saturation in the vertical net-flux case was proposed by Goodman & Xu (1994), Pessah & Goodman (2009), and Latter et al. (2009), in which saturation is driven by parasitic (secondary) instabilities that break down the so-called channel modes (axisymmetric radial streaming motions) generated by the primary (fastest-growing) MRI modes. These correspond to both Kelvin-Helmholtz instabilities which feed off the shear in the velocity field and tearing mode instabilities which feed off the current density. The secondary instabilities themselves eventually decay into small-scale turbulence which then, in combination with the vertical net-flux, regenerate the MRI modes, creating a self-sustaining loop. The mechanism for saturation becomes more difficult to pinpoint when there is no global mean-field in the box (ZNF), since both the magnetic field and turbulence are required to sustain each other. In addition, the unstratified ZNF case is statistically symmetric, which means that there are no net helicities within the flow, and this makes the generation of local mean-fields more difficult. However, dynamo cycles and coherent local mean-field growth have been observed in previous simulations of the unstratified ZNF case (Shi et al. 2016). The underlying process of growth still remains uncertain, but the two primary theories are the stochastic alpha effect (Vishniac & Brandenburg 1997; Silant’ev 2000; Heinemann et al. 2011) and the magnetic shear current effect (Rogachevskii & Kleeorin 2003, 2004; Squire & Bhattacharjee 2015a), which we examine in more detail in the upcoming sections.
Adding stratification to the shearing box represents a more realistic view of the accretions disk and brings forth new mechanisms that act on the behavior and saturation of the system. The stratified case enables buoyancy instabilities, which transports magnetic fields from the outer central region upward. Beyond |z|> 2H, the gas is magnetically dominated, less turbulent and buoyantly unstable (e.g., Shi et al. 2010; Guan & Gammie 2011). Meanwhile, the sign of the field flips within the mid-plane and this becomes a cyclical behavior that occurs around every 10 orbits (producing the characteristic butterfly diagram). This behavior of the magnetic field indicates an active mean-field dynamo (e.g., Brandenburg et al. 1995a; Stone et al. 1996; Hirose et al. 2006; Gressel 2010; Davis et al. 2010; Simon et al. 2011). The stratified disk dynamo is complicated, likely involving several mechanisms acting together; as such the cyclic behavior observed within these simulations still remains unclear. While the buoyancy instabilities dominate the regions beyond the scale height, the central region remain buoyantly stable, requiring an alternative mechanism in this region (Shi et al. 2010; Gressel 2010). One such mechanism is through the alpha-effect, or more explicitly the outward transport of small scale magnetic helicity flux (Vishniac & Cho 2001; Subramanian & Brandenburg 2004). Another mechanism that can advect magnetic fields is turbulent pumping which can expel magnetic field from high turbulent regions to lower turbulent regions (Gressel 2010). In addition, the dynamo mechanisms in the unstratified case likely plays a role here too, as the unstratified case represents an approximation of the mid-plane in the disk (Lesur & Ogilvie 2008; Käpylä & Korpi 2011).
The stratified shearing box is also dependent on the strength and geometry of the global magnetic mean-field, showing a wide range of different behaviors. For example, compared to an azimuthal mean-field, the presence of a vertical mean-field greatly enhances the stress within the fluid and exhibits powerful outflows which can increase the removal of angular momentum from the disk (Suzuki & Inutsuka 2009; Guan & Gammie 2011; Simon et al. 2011, 2013; Bai & Stone 2011).
Seminal work by Fromang et al. (2007) showed that for the ZNF unstratified case the saturated turbulence level decreased with higher resolution. This highlighted the importance of small-scale dissipation for the MRI. Further work has shown that more or less all MRI cases are sensitive to the small-scale dissipation, where kinematic viscosity (ν) and magnetic resistivity (η) play a major role. The ratio between the two, the so-called magnetic Prandtl number (Pm = ν/η), is shown to be fundamentally important in determining the MRI saturation and the stress, and in general the behavior of MHD turbulence in any system (Schekochihin et al. 2004a,b; Federrath et al. 2014; Federrath 2016). In nature, galaxies, galaxy clusters and molecular clouds have magnetic Prandtl numbers far greater than unity (Pm ≫ 1). For example, in molecular clouds Pm ≈ 1010 (Federrath 2016). On the opposite extreme, protostellar disks and stars usually have magnetic Prandtl numbers much smaller than unity (Pm ≪ 1) (Brandenburg & Subramanian 2005; Schekochihin et al. 2007). In MRI simulations, the Prandtl number can be either physical, where explicit dissipation is added to the system, or numerical, which is determined by the numerical dissipation of the numerical scheme. Higher Prandtl numbers generally increase the angular momentum transport (Fromang & Papaloizou 2007; Lesur & Longaretti 2007; Simon et al. 2009; Simon & Hawley 2009; Fromang et al. 2010). In the low Prandtl number limit, while the NF case still exhibits MRI turbulence and saturates at a low but finite value of angular momentum transport (Meheut et al. 2015), in the ZNF case turbulence cannot be sustained for Prandtl numbers below a certain critical value (Pm < 2 in Fromang et al. 2007)1. In addition, the convergence behavior of the MRI turbulence and the critical Prandtl number can also be sensitive to the vertical aspect ratio of the domain: while simulations with standard box (with vertical-over-radial aspect ratio, Lz/Lx = 1) exhibit decreased stress levels with increasing resolution, in the tall-box simulations (Lz/Lx > 2.5) the stress levels are converged. The stress saturation still depends on the Prandtl number in the tall boxes, albeit with a somewhat lower critical value and with longer lifetimes (Shi et al. 2016).
While a lot of the focus surrounding the Prandtl number has revolved around the physical Prandtl number, not many studies have been done on the numerical Prandtl number. Numerical dissipation acts differently compared to physical dissipation, depending heavily on the fluid flow and the resolution. How well the numerical Prandtl number relates to the observed dependency on the physical Prandtl number for MHD turbulence is still unclear, but a similar dependency is expected. The consequence of not knowing the numerical Prandtl number and its resolution dependency in MRI simulations is clear, as a low-order resistive scheme with a high-order viscosity scheme will eventually result in a low Pm value and can lead to misinterpretation in convergence studies. The numerical Prandtl number has been investigated in several grid codes (Fromang et al. 2007 [with ZEUS] Lesaffre & Balbus 2007 [with ZEUS3D] Simon et al. 2009 [with ATHENA] Federrath et al. 2011 [with FLASH]), which have found a Prandtl number of around Pm ∼ 2 with a very weak dependency on resolution. However, the true Pm value during nonlinear MRI simulation remains uncertain as the numerical dissipation is not readily available for grid codes and requires comparison to analytical work or analysis of Fourier transfer functions with certain assumptions and constraints. The estimates of the numerical Prandtl number in these papers are taken for subsonic flows and might significantly change for higher Mach flows. In this paper, we take a closer look at the numerical Prandtl number in SPH and see how it affects the turbulence within MRI simulations.
The vast majority of MRI simulations have been carried out with Eulerian grid-based codes. There have only been a handful of studies investigating the MRI with meshless methods in 2D (Gaburov & Nitadori 2011; Pakmor & Springel 2013; Hopkins & Raives 2016) and in 3D (Deng et al. 2019). The MRI is an especially difficult test for meshless codes due to the strong divergence-free constraint, which in Eulerian codes can be enforced to machine precision with the constrained transport method (Evans & Hawley 1988). However, improved divergence cleaning methods in recent years have been developed for meshless codes, which significantly reduce the divergence errors (Tricco & Price 2012; Tricco et al. 2016). A benefit of Lagrangian methods such as SPH is that they are always Galilean invariant and do not suffer from advection errors, which can otherwise be an issue for Eulerian codes in simulations with large bulk flows. In addition, SPH is naturally adaptive in resolution, making it ideal for simulations involving a wide range of spatial scales. Understanding the numerical aspects of the MRI in SPH is important, as SPH is widely used in astrophysical simulations where the MRI can be present.
In Deng et al. (2019) the authors investigated the MRI in 3D with the meshless finite mass (MFM) and the SPH methods for a wide array of different initial magnetic field configurations. For the unstratified NF case, it was shown that MFM and SPH showed similar behavior to Eulerian grid-based codes. However, for the unstratified ZNF case, both MFM and SPH showed rapid decay of the turbulence. This is likely related to the numerical dissipation schemes of the two methods, which we investigate for SPH in this paper. For the stratified azimuthal NF case, the MFM method could correctly produce the characteristic dynamo cycles for around 50 to 70 orbits before the turbulence eventually died out. SPH on the other hand could not develop sustained turbulence and instead developed unphysically strong azimuthal fields. This was attributed to a combination of discretization errors of the magnetic field in the radial component and divergence cleaning amplifying the vertical field component. In this paper, we further investigate this case with the newly developed geometric density SPH (GDSPH), which has been shown to improve the accuracy of SPH in problems involving large density gradients. Specifically, it allows grid-scale instabilities to grow that are suppressed in traditional SPH (Wadsley et al. 2017; Wissing & Shen 2020).
In this paper, we have performed MRI simulations of the unstratified NF case in the regular-sized box (Lz/Lx = 1) and the unstratified ZNF case in both regular and taller sized boxes (Lz/Lx = 4 as in Shi et al. 2016) with varying resolution and numerical dissipation parameters. We have investigated the numerical Prandtl number in SPH and its effect on the amplification and saturation of the MRI. We have also performed simulations on the stratified NF case with both the traditional SPH method (TSPH)2 and the GDSPH method to further investigate the unphysical growth in the azimuthal fields observed in Deng et al. (2019). For these simulations, we also vary the resolution and strength of the numerical dissipation. In addition, to all the simulations we also investigate the turbulent transport coefficients.
This paper is organized as follows. In Sect. 2, we go through the basics of dynamo theory, the simulation setup, and the post-process analysis. In Sect. 3, we present our result for the unstratified NF and ZNF cases and in Sect. 4 we present our result for the stratified case. In Sect. 5, we discuss our results and present some concluding remarks.
2. Theory
2.1. Dynamo theory
A magnetic dynamo describes the exponential growth and sustenance of magnetic fields due to being stretched, twisted, and folded by the underlying fluid motions. While specific velocity field configurations can lead to dynamo action (laminar dynamo), astrophysical fluids are usually highly turbulent, where motion is chaotic across a large range of spatial scales. Dynamo action can occur across all turbulent scales, but the magnetic field is stretched faster by the smaller scale motions than the larger-scale ones, leading to a faster growth on smaller scales (known as the small-scale dynamo) (Kulsrud & Anderson 1992; Kulsrud 1999). In ideal MHD, the growth rate is set primarily by the viscous scale of the fluid. However, for MHD with diffusion of the magnetic field (resistivity), this is no longer necessarily true, as the magnetic fields on small-scales can now be damped quickly. This makes the growth of the magnetic field more intricate, as it is determined by the relationship between the viscous scale lv and the resistive scale lη (Spitzer 1962). The ratio between these two, the magnetic Prandtl number 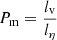 is thus very important in the resulting characteristic and saturation of the turbulent dynamo (Schekochihin et al. 2004a). For Pm > 1 the quickest twisting and folding of the magnetic field is driven at the viscous scale, where the underlying velocity field is smooth as there are no smaller velocity structures in the flow at this scale. The chaotic but smooth motion at this scale lends itself to dynamo action, which means that magnetic fields can efficiently be generated (Vaĭnshteĭn & Zel’dovich 1972; Zeldovich 1983; Zeldovich et al. 1990). The cut-off scale of magnetic fluctuations will still be set by the resistive scale, which allows for a buildup of power within the subviscous range. With higher Pm values than one, more of the subviscous scale becomes available for magnetic field amplification (Kulsrud & Anderson 1992; Schekochihin et al. 2004a).
is thus very important in the resulting characteristic and saturation of the turbulent dynamo (Schekochihin et al. 2004a). For Pm > 1 the quickest twisting and folding of the magnetic field is driven at the viscous scale, where the underlying velocity field is smooth as there are no smaller velocity structures in the flow at this scale. The chaotic but smooth motion at this scale lends itself to dynamo action, which means that magnetic fields can efficiently be generated (Vaĭnshteĭn & Zel’dovich 1972; Zeldovich 1983; Zeldovich et al. 1990). The cut-off scale of magnetic fluctuations will still be set by the resistive scale, which allows for a buildup of power within the subviscous range. With higher Pm values than one, more of the subviscous scale becomes available for magnetic field amplification (Kulsrud & Anderson 1992; Schekochihin et al. 2004a).
The small-scale dynamo has been shown to be a possible mechanism for amplifying the weak seed fields in the early universe to magnitudes observed in galaxies today (Boulares & Cox 1990; Beck et al. 1996; Kulsrud et al. 1997). However, magnetic fields in the universe exhibit a high degree of coherence at scales larger than the underlying turbulent motion (Beck et al. 2005; Beck 2015). Large-scale dynamo theory is an attempt to explain how these coherent large-scale magnetic field structures can be generated in highly turbulent environments. In essence, it investigates how the small-scale kinetic and magnetic fluctuations couple to the underlying large-scale field.
To figure out the effect of the small-scale field on the large-scale field, it is useful to introduce the formalism of mean-field theory (Moffatt 1978; Parker 1979; Krause & Raedler 1980; Ruzmaikin et al. 1988; Brandenburg & Subramanian 2005). Assuming a scale separation between the large-scale and small-scale, both the magnetic and velocity fields can be decomposed to a mean field component (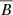 and
and 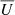 ) and a fluctuating component (b and u):
) and a fluctuating component (b and u):
Averaging the induction equation leads to the evolution equation for the magnetic mean-field:
Here U represents the large-scale velocity structure, η the magnetic diffusivity and ℰ is the electromotive force (EMF) produced by the fluctuating fields:
By studying how the fluctuating u and b fields reacts to an applied mean field, it can be shown that both u and b contain a component independent of the mean-field and an additional term which is linearly dependent on the applied mean-field:
Assuming the independent terms b0 and u0 are uncorrelated (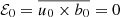 ) and the assumption of scale separation, we can expand ℰ in a Taylor series in
) and the assumption of scale separation, we can expand ℰ in a Taylor series in 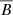 and
and 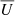 :
:
Here α, η and γ are the tensorial transport coefficients and  is the mean-field current density and
is the mean-field current density and 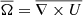 is the mean-field vorticity. The first term of Eq. (5) is the α-effect in which the small-scale turbulence generates an EMF which is proportional to the mean-field itself. This effect, coupled together with differential rotation, can develop the well-known αω dynamo. The alpha-effect depends crucially on the small-scale helcities within the turbulent flow, which require the system to break statistical symmetry either by stratification or through having a net helicity (Pouquet et al. 1976; Moffatt 1978; Brandenburg & Subramanian 2005). The second term in Eq. (5) generates an EMF in proportion to the mean-current and can act to either amplify or diffuse the mean-field. The last term of Eq. (5) is the Yoshizawa effect, which acts without the need for a large-scale magnetic field and can be seen as a turbulent battery mechanism (Yoshizawa & Yokoi 1993; Yokoi 2013). In addition to a mean vorticial velocity component, the effect requires small-scale cross-helicity between the turbulent fields (
is the mean-field vorticity. The first term of Eq. (5) is the α-effect in which the small-scale turbulence generates an EMF which is proportional to the mean-field itself. This effect, coupled together with differential rotation, can develop the well-known αω dynamo. The alpha-effect depends crucially on the small-scale helcities within the turbulent flow, which require the system to break statistical symmetry either by stratification or through having a net helicity (Pouquet et al. 1976; Moffatt 1978; Brandenburg & Subramanian 2005). The second term in Eq. (5) generates an EMF in proportion to the mean-current and can act to either amplify or diffuse the mean-field. The last term of Eq. (5) is the Yoshizawa effect, which acts without the need for a large-scale magnetic field and can be seen as a turbulent battery mechanism (Yoshizawa & Yokoi 1993; Yokoi 2013). In addition to a mean vorticial velocity component, the effect requires small-scale cross-helicity between the turbulent fields (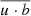 )3.
)3.
In this paper, we are interested in the dynamo action that arises within shearing boxes (see Sect. 2.2 for coordinate definitions and simulation setup). We define our mean-field by taking a horizontal average:
The turbulent field can then be calculated by removing the mean-field component from the total field (see Eq. (1)). For the velocity, the mean-field is determined from the shearing box approximation (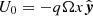 ). Here Ω is the angular velocity and q is the shearing parameter, which for Keplerian disks is q = 3/2. Since the horizontal average is only a function of z, Eq. (5) and subsequently Eq. (2) simplifies greatly (
). Here Ω is the angular velocity and q is the shearing parameter, which for Keplerian disks is q = 3/2. Since the horizontal average is only a function of z, Eq. (5) and subsequently Eq. (2) simplifies greatly (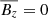 ,
, 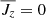 , and
, and 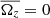 ):
):
The γ terms from Eq. (5) become zero as our only component of 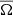 is in the z direction. The diagonal components αxx and αyy are the main driver of the alpha effect, generating a feedback loop between the radial and azimuthal fields. The sign of diagonal components will depend on Ω ⋅ g (here g is the gravitational acceleration) which will give us an odd symmetry around the midplane of our stratified box simulations. Depending on the gradient of the α parameter and structure of the magnetic field, it will either work in accordance or in discordance with the field. The antisymmetric components αxy and αyx can be related to the diamagnetic pumping term
is in the z direction. The diagonal components αxx and αyy are the main driver of the alpha effect, generating a feedback loop between the radial and azimuthal fields. The sign of diagonal components will depend on Ω ⋅ g (here g is the gravitational acceleration) which will give us an odd symmetry around the midplane of our stratified box simulations. Depending on the gradient of the α parameter and structure of the magnetic field, it will either work in accordance or in discordance with the field. The antisymmetric components αxy and αyx can be related to the diamagnetic pumping term 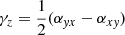 and describes the transport of mean-fields due to the turbulence. In a similar fashion, the diagonal components ηxx and ηyy describe the diffusion of the mean-field due to the turbulence. Finally, we have the off-diagonal components ηxy and ηyx that are responsible for the dynamo produced by the Ω × J effect (Rädler 1969) and the shear current effect (Rogachevskii & Kleeorin 2003). These equations provide a powerful tool to connect our simulation data to the mean-field theory. To calculate the transport coefficients we can fit Eqs. (7) and (8) to output data from our simulations. One starts by calculating
and describes the transport of mean-fields due to the turbulence. In a similar fashion, the diagonal components ηxx and ηyy describe the diffusion of the mean-field due to the turbulence. Finally, we have the off-diagonal components ηxy and ηyx that are responsible for the dynamo produced by the Ω × J effect (Rädler 1969) and the shear current effect (Rogachevskii & Kleeorin 2003). These equations provide a powerful tool to connect our simulation data to the mean-field theory. To calculate the transport coefficients we can fit Eqs. (7) and (8) to output data from our simulations. One starts by calculating
and
and the matrix
Then we solve the following matrix equations (using a least-square method):
for the transport coefficients:
Because the mean-field is not solely evolved by ℰ but also by the shearing and dissipation of the field, significant errors can arise in the transport coefficients from the correlation between different components. The main harmful error comes from correlations with 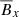 (due to the shear term). We can improve the signal and reduce the noise by minimizing the influence of
(due to the shear term). We can improve the signal and reduce the noise by minimizing the influence of 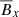 with the following two approximations. First, we set the diagonal transport coefficients to be equal (αxx = αyyηxx = ηyy), which have been shown to be an accurate approximation (Hubbard et al. 2009; Gressel 2010). The second approximation is to set αyx = 0, ηxy = 0 which is justified by the fact that
with the following two approximations. First, we set the diagonal transport coefficients to be equal (αxx = αyyηxx = ηyy), which have been shown to be an accurate approximation (Hubbard et al. 2009; Gressel 2010). The second approximation is to set αyx = 0, ηxy = 0 which is justified by the fact that 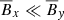 (Squire & Bhattacharjee 2015b). However, we have seen that including αyx, ηxy does not significantly change the result for the other transport coefficients. For comparison with previous studies, in the stratified case we allow a nonzero αyx and ηxy, and allow αxx and αyy to be different.
(Squire & Bhattacharjee 2015b). However, we have seen that including αyx, ηxy does not significantly change the result for the other transport coefficients. For comparison with previous studies, in the stratified case we allow a nonzero αyx and ηxy, and allow αxx and αyy to be different.
What causes the dynamo growth within shearing box simulations of the MRI remains uncertain and remains an active area of research. The unstratified shearing box simulations develop a so-called nonhelical shear dynamo which cannot be generated by the α-effect (in the traditional sense) as there is no net kinetic/magnetic helicity or density stratification within the flow. This implies that the mean of the α coefficients will tend toward zero. However, the α coefficients for a finite-sized system will fluctuate in time. If the fluctuations are sufficiently large, this has shown to enable dynamo growth. This has been called the incoherent-α dynamo, which could explain the dynamo mechanism in unstratified shearing boxes (Vishniac & Brandenburg 1997; Silant’ev 2000; Heinemann et al. 2011). However, a potential issue with the incoherent-α dynamo is that the mean fluctuations in α becomes smaller as the size of the box is increased, which decreases the growth rate of the dynamo. Another potential mechanism for the dynamo is the magnetic shear-current effect, which depends crucially on the off-diagonal turbulent resistivity coefficient ηyx (Rogachevskii & Kleeorin 2003; Squire & Bhattacharjee 2015a,b,c). The idea of the magnetic shear-current effect is that a bath of magnetic fluctuations under the influence of an azimuthal field produces an EMF that generates radial fields which subsequently act to amplify the azimuthal field resulting in a dynamo instability. The instability can be shown to happen if −ηyxΩz < 0 which means that dynamo action is possible from the shear-current effect if ηyx is negative. In this paper, we examine the shear-current effect and determine if it agrees well with previous results.
Furthermore, stratification adds several additional mechanisms that can affect the dynamo process. The α-effect can provide dynamo action and has been proposed to be a main driver of the dynamo together with the shear-current effect. Both of these effects can cause a phase-shift between the growing fields, explaining the cyclic nature of the radial and azimuthal fields seen in stratified shearing boxes. In addition, buoyancy instabilities expel the magnetic field outward.
2.2. Simulation setup
For all our simulations we use the MHD version of GASOLINE2 with the same default set of code parameters as in Wissing & Shen (2020). The simulations are set up using a shearing box approximation (Goldreich & Lynden-Bell 1965; Hawley et al. 1995), in which a corotating patch of disk with angular velocity Ω at a distance R is used as the computational domain. The patch is assumed small such that curvature can be neglected and we can employ a local cartesian coordinate system with x as the radial direction, y as the azimuthal direction and z as the vertical direction. The additional terms added to the equations of motion are:
Where the term 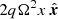 represents the tidal acceleration, 2Ω × v represents the Coriolis force and
represents the tidal acceleration, 2Ω × v represents the Coriolis force and 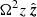 represents the vertical gravitational force from the central object. The equilibrium solution of Eq. (16) will be independent of time and follows a uniform shearing motion in the azimuthal direction
represents the vertical gravitational force from the central object. The equilibrium solution of Eq. (16) will be independent of time and follows a uniform shearing motion in the azimuthal direction
If any mean radial velocity exists, the simulation box will start to oscillate with an epicyclic frequency of 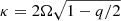 . This can be the case if set initially or if momentum is not tightly conserved. SPH conserves both momentum and energy very tightly and only suffers from nonconservation in the strong-field regime (β < 2) in the presence of large divergence errors. The shear parameter q is set to follow a Keplerian profile (q = 3/2) and the angular velocity is set to Ω = 1.0. For our periodic boundaries we do not employ explicit ghost or boundary particles, the particles across the boundary interact and exchange forces as regular. Position and velocities are relative to the central particle and neighbors across the boundaries receive a position offset of one domain length (Lx, Ly, Lz). We do not allow for a compact kernel radius that is larger than the smallest domain length of the box, as this would lead to the particle interacting with itself. This could in principle be allowed but would require additional code and some extra overhead. The boundary in the x-direction is shear periodic, which means that particles passing/interacting across the boundary receives an additional velocity offset of
. This can be the case if set initially or if momentum is not tightly conserved. SPH conserves both momentum and energy very tightly and only suffers from nonconservation in the strong-field regime (β < 2) in the presence of large divergence errors. The shear parameter q is set to follow a Keplerian profile (q = 3/2) and the angular velocity is set to Ω = 1.0. For our periodic boundaries we do not employ explicit ghost or boundary particles, the particles across the boundary interact and exchange forces as regular. Position and velocities are relative to the central particle and neighbors across the boundaries receive a position offset of one domain length (Lx, Ly, Lz). We do not allow for a compact kernel radius that is larger than the smallest domain length of the box, as this would lead to the particle interacting with itself. This could in principle be allowed but would require additional code and some extra overhead. The boundary in the x-direction is shear periodic, which means that particles passing/interacting across the boundary receives an additional velocity offset of 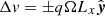 in which Lx is the length of the domain in the x direction. This is simpler than for grid codes, where shear periodic boundaries require careful reconstruction to retain conservative fluxes across the boundary. While retaining fluxes due to boundary conditions remain simple in SPH, there are other potential flux errors. The main one comes from the divergence error and, more precisely, the removal of the monopole current v(∇ ⋅ B) from the induction equation (Janhunen 2000; Dellar 2001; Price & Monaghan 2005). Removing this term from the induction equation ensures that the surface flux is conserved (which is crucial) and makes the magnetic field divergence become a passive scalar which is simply carried away with the flow. However, in doing this, it is no longer ensured that the volume integral of the magnetic field is conserved (the global mean-field). This issue is shared among the majority of numerical schemes and in this case the error will directly depend on the magnetic field divergence. The error is generally very small but can contaminate the solution, as MRI can be quite sensitive to any global radial mean-field. To avoid this we employ a correction to the flux, which ensures that no global radial mean-fields are generated. We do not employ this correction for simulations with outflow boundaries.
in which Lx is the length of the domain in the x direction. This is simpler than for grid codes, where shear periodic boundaries require careful reconstruction to retain conservative fluxes across the boundary. While retaining fluxes due to boundary conditions remain simple in SPH, there are other potential flux errors. The main one comes from the divergence error and, more precisely, the removal of the monopole current v(∇ ⋅ B) from the induction equation (Janhunen 2000; Dellar 2001; Price & Monaghan 2005). Removing this term from the induction equation ensures that the surface flux is conserved (which is crucial) and makes the magnetic field divergence become a passive scalar which is simply carried away with the flow. However, in doing this, it is no longer ensured that the volume integral of the magnetic field is conserved (the global mean-field). This issue is shared among the majority of numerical schemes and in this case the error will directly depend on the magnetic field divergence. The error is generally very small but can contaminate the solution, as MRI can be quite sensitive to any global radial mean-field. To avoid this we employ a correction to the flux, which ensures that no global radial mean-fields are generated. We do not employ this correction for simulations with outflow boundaries.
For the unstratified simulations, the last term of Eq. (16) is not included and the domain is periodic in both the y and z directions. For the stratified simulations, all terms are included and the domain is periodic in y and has outflow boundaries in z. The outflow boundary in z is set to remove any element with a smoothing length greater than h = 0.5 Lx to avoid the double-counting of elements across the computational domain. The stratified simulations acquire a density profile of ρ = e−zH with a scale height of H = cs/Ω where cs is the speed of sound. We use an isothermal equation of state (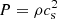 ), with cs = 1.0 set for all simulations. Before simulations are run, the initial particle distribution is relaxed to a glass distribution, then random velocity perturbations of around 5% of the sound speed are added to the shear flow to quickly initiate the MRI.
), with cs = 1.0 set for all simulations. Before simulations are run, the initial particle distribution is relaxed to a glass distribution, then random velocity perturbations of around 5% of the sound speed are added to the shear flow to quickly initiate the MRI.
To determine how well the MRI is resolved, we use the resolution metric developed by Noble et al. (2010) which defines an effective quality parameter (number of resolution elements per MRI wavelength):
where λMRI is the characteristic wavelength and is roughly equal to the fastest growing MRI mode, and vA, z is the vertical component of the Alfvén velocity, and h is the resolution length. We follow the example from Deng et al. (2019) where, instead of setting the resolution length to the smoothing length, it is based on the standard deviation of the smoothing kernel. For the Wendland C4 kernel, it gives an effective resolution element length heff = 0.9h. To properly resolve the linear MRI roughly only Q > 6 is required, however, the stress is highly resolution-dependent until a value of roughly Qz > 10 and Qy > 20 is reached (for the stratified NF case Hawley et al. 2011).
As mentioned in the introduction, the magnetic Prandtl number plays a large role in the growth of turbulent dynamos. To gauge the effective Prandtl number from a numerical scheme, the numerical dissipation needs to be determined and translated into an effective kinematic viscosity (ν) and physical resistivity (η). In Eulerian schemes, dissipation comes partly from advection of the fluid which introduces diffusion due to truncation errors in the flux reconstruction. This error will be proportional to both the resolution and the fluid velocity. For shear periodic boundary conditions this means that there will be uneven dissipation due to larger velocities near the edge than the center of domain. Moreover, additional dissipation is added to maintain numerical stability, this is often done through Riemann solvers in grid codes. Estimating the numerical diffusion in Eulerian schemes is not straightforward and often requires comparison to analytical solutions for an accurate estimate.
Compared to Eulerian grid codes, SPH does not suffer from these advection errors and artificial dissipation terms4 are added to handle flow discontinuities (e.g., shocks). These are primarily discretized from physical dissipation laws, but with diffusion parameters that depend on the resolution and potentially on flow properties. In Monaghan (1985) it was shown that the linear coefficient (αAV) in the artificial viscosity corresponds to a resolution-dependent physical viscosity in the continuum limit, which has been confirmed by several authors (Artymowicz & Lubow 1994; Lodato & Price 2010; Meru & Bate 2012). However, extrapolating to the continuum limit in this case underestimates the physical viscosity/resistivity. It becomes more difficult to estimate the physical dissipation when using particle-pair dependent signal velocities (as is done for our artificial resistivity). In this paper, we opt for another way to estimate the physical dissipation. By recording the energy lost due to artificial dissipation terms, we can directly estimate the parameters from the equivalent physical dissipation equations. From the Navier-Stokes equation we can estimate the shear viscosity with:
Here, we have assumed the fixed ratio between the bulk viscosity and the shear viscosity, which follows from the continuum limit derivation (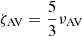 ) (Lodato & Price 2010). We estimate the physical resistivity from the Ohmic dissipation law:
) (Lodato & Price 2010). We estimate the physical resistivity from the Ohmic dissipation law:
Taking the ratio of the two equations then gives us the numerical Prandtl number:
For some of our simulations we force a certain average numerical Prandtl number 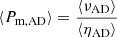 . This is done by adjusting either
. This is done by adjusting either 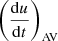 and
and 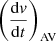 or
or 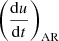 and
and 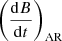 by a constant factor such that ⟨Pm, AD⟩ corresponds to the desired value. This is the same as changing the artificial dissipation coefficients (αB, αAV) by a constant factor at each time step.
by a constant factor such that ⟨Pm, AD⟩ corresponds to the desired value. This is the same as changing the artificial dissipation coefficients (αB, αAV) by a constant factor at each time step.
2.3. Post-process analysis
After the SPH simulations are done, the particle data is interpolated to uniform grid data for post-analysis. To obtain statistical properties of our simulations, we average our data in a few different ways. The first is the horizontal average given in Eq. (6). The second is the volume average:
and the final one is the time average:
All the averages are in general applied over the whole spatial/time domain of the simulation if not stated otherwise. To quantify the angular momentum transport and the saturation of the MRI, it is useful to calculate the stresses in the fluid. The total stress together with its magnetic and hydrodynamic component is given by:
where P0 is the initial pressure(in our case P0 = 1) and ρ is the density and here the first term in the equation represent the Maxwell stress (αMW) and the second term the Reynolds stress (αRey). A related quantity that we look at is the normalized magnetic stress:
In addition to looking at the effect of the total field, we also investigate the contributions from the mean-field (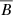 ) and turbulent component (b) in the magnetic energy and the stress. We define their respective normalized stress as in Shi et al. (2016):
) and turbulent component (b) in the magnetic energy and the stress. We define their respective normalized stress as in Shi et al. (2016):
Another useful quantity is the Elsasser number, which describes the relative strength of the magnetic dissipation term:
Here, vA is the Alfvén speed. For a Λ < 1 the linear properties of the MRI will change significantly and hinder saturation (Blaes & Balbus 1994; Wardle 1999; Balbus & Terquem 2001).
Finally, it is important to track the divergence error in numerical simulations to make sure it remains small and does not severely effect the results:
The mean of this quantity should preferably remain below 10−2 but higher values can still be acceptable (depending on the system).
3. Unstratified simulation results
3.1. Net-flux simulations
We setup our simulation with a shearing box of size L = (1.0, π, 1.0) with a resolution of [nx, ny, nz]=[48, 150, 48]. The magnetic field is initialized with a constant vertical component
With a plasma beta of β = 400 and pressure equal to P0 = 1.0. Using Eq. (18) we can see that we resolve λMRI with a vertical quality parameter of Qz = [22, 30, 45]. We carry out several simulations with various artificial resistivity coefficients αB = [0.25, 0.5, 1.0, 2.0, 4.0], where αB = 0.5 is the code default. The simulations are run for about 200 orbits or until the turbulence dies out. The results of the simulations are shown in Figs. 1–5.
 |
Fig. 1. Time evolution of several volume-averaged quantities over 200 orbits. Magnetic energy (top left), kinetic energy (top right), normalized Maxwell stress (bottom left) and the total stress (bottom right). The darkness of the curves is determined by the strength of the artificial resistivity parameter, αB = 0.25, 0.5, 1.0, 2.0, 4.0. Due to the high oscillatory nature of the simulation we have smoothed the curves using a Savitzky–Golay filter, the unsmoothed curves can still be seen as very transparent curves. The oscillations are related to the formation and destruction of channel modes. |
 |
Fig. 2. Time-averaged values of several quantities as a function of the artificial resistivity coefficient, for all our unstratified net-flux simulations. From the top left to bottom right: magnetic energy density, Maxwell stress, normalized Maxwell stress, ratio between Reynolds and Maxwell stresses, total stress, ratio between radial and total magnetic field energy. For some quantities we have plotted the total time average (shown in green), the time average of the turbulent component (shown in orange) and the time average of the mean-field component (shown in blue). |
 |
Fig. 3. Generation and break down of a channel mode during the unstratified net-flux run with αB = 0.5. The figure depicts a surface rendering of the radial velocity within the shearing box. The two-channel flow is clearly seen in the left picture which over an orbit is quickly broken down into turbulence, as seen in the right figure. The generation of the channel mode coincides with a peak in the magnetic energy and as the channel flow is destroyed the magnetic energy will decrease. The formation and destruction of these channel flows occur continuously throughout the simulation. |
 |
Fig. 4. Spacetime diagrams showing the azimuthal magnetic field at the top and the total stress at the bottom. The left figures shows the simulation with an artificial resistivity coefficient αB = 0.5 and the right figures show the simulation with αB = 4. The figures clearly show the peaks related to the continuous creation and destruction of channel modes. Increasing the resistivity leads to a suppression of small scale magnetic fluctuation, and this means that more of the stress will be generated by the mean-field component. |
 |
Fig. 5. Time-averaged turbulent transport coefficient from the unstratified net-flux cases. To minimize noise/bias we have set αxx = αyy, ηxx = ηyy, αyx = 0.0 and ηxy = 0.0. We can see that only the turbulent resistivity ηxx has a consistent value above 0.0, with a value of about 0.008. |
In Fig. 1 we can see that the turbulent dynamo in all the simulations reach a saturated state with a heavily fluctuating magnetic energy density, which is what we expect from the unstratified NF case (Hawley et al. 1995)5. From Fig. 2, we can see that as we decrease the resistivity, the magnetic energy and stress increases rapidly, where the total stress goes from αstress = 0.25 to 0.9. For the normalized magnetic stress (αmag), we can see that the average lies around 0.65 with only a weak dependency on the resistivity. The normalized magnetic stress is, in general, higher than what has been seen in previous Eulerian grid simulations, where αmag ≈ 0.4 to 0.6. The magnetic energy and Maxwell stress vary widely in the literature (αstress = 10−2 → 100) and our values are similar to the ones reported in Hawley et al. (1995) and Simon et al. (2009). From Fig. 2, the ratio between the Maxwell stress and Reynolds stress(αMW/αrey) shows a value of around 4.0 with an increasing trend for lower resistivity. This is also similar to values reported in Hawley et al. (1995) but somewhat lower than Simon et al. (2009) (αMW/αrey ≈ 7.6).
The higher αmag can likely be explained by the use of a smaller box size L = (1.0, π, 1.0) compared to most other studies, which use L = (1.0, 2π, 1.0). A smaller aspect ratio in the NF case does in general show stronger fluctuations in the turbulent state (Bodo et al. 2008; Lesaffre et al. 2009). The stronger fluctuations are a result of suppressing larger MRI modes that would otherwise participate in the nonlinear dynamics, which heavily effect the growth and decay of channel modes. In Fig. 3, we can see an example of the formation and destruction of such a channel mode; during this process the magnetic energy and stress will peak. In addition to being dependent on the aspect ratio of the box, the growth and destruction of these channel modes will depend on the dissipation. This can clearly be seen in Fig. 4 where we see the evolution of the horizontal averaged azimuthal field and stress over a period of thirty orbits for two different resistivities (αB = 0.5 and αB = 4). We can see that during this time channel modes are subsequently formed and destroyed, but with different frequency and behavior. In the high resistivity case, the magnetic energy peaks during channel mode formation but most of the small-scale magnetic fluctuations are quickly suppressed after channel mode breakdown. This means that less of the stress within this case comes from the turbulent component. This can also be seen in Fig. 2, where the mean-field component dominates over the turbulent component at αB = 4 while becoming almost equal at αB = 0.5. Interestingly, the normalized mean-field and turbulent magnetic stresses stays fairly constant αmag, mean ≈ 0.8 and αmag, turb ≈ 0.55.
The average divergence error remains either below or close to ϵdiv, err ≈ 10−2. For the simulations with αB = [0.25, 0.5, 1.0, 2.0, 4.0] the corresponding time-averaged Prandtl numbers is ⟨⟨Pm⟩⟩t = [1.95, 1.42, 0.96, 0.60, 0.35]. The standard default value of αB = 0.5 has a Pm ≈ 1.5. The Elsasser number remains far above 1 for all the cases and the average plasma beta rises linearly with αB with value between β ≈ 5 → 20.
Figure 5 shows the time-averaged values of the transport coefficients αxx, αxy, ηxx and ηyx for all the simulations. From the figure, we can see that both α coefficients have values very close to zero which is to be expected from the unstratified case. ηyx does also not have a significant value and remains close to zero. The only value that has a significant value above zero is the turbulent diffusivity which has a value of around ηxx ≈ 0.008.
3.2. Zero net-flux simulations
The setup follows from Deng et al. (2019), in which a shearing box together with a varying vertical magnetic field is initialized
Here, B0 is the initial magnetic field strength and is set such that the volume averaged plasma beta is β = 2P/B2 = 400. We run the simulations at three different resolutions [nx, ny, nz]=[48, 150, 48],[64, 200, 64],[96, 300, 96] with a standard box with length L = (1.0, π, 1.0). To test the effect of a taller box within SPH, we also run with a domain size of L = (1.0, π, 4.0) (same as in Shi et al. 2016), with a resolution of [nx, ny, nz]=[48, 150, 192]. Using Eq. (18), we can see that we resolve λMRI with an initial quality parameter of Qz = [22, 30, 45] in each respective resolution. We carry out several simulations at each resolution by varying the artificial resistivity coefficient αB = [0.25, 0.5, 1.0, 2.0, 4.0] (blue curves in Figs. 6 and 7), where αB = 0.5 is the default value. The corresponding time-averaged Prandtl numbers in the nx = 96 standard box is ⟨⟨Pm⟩⟩t = [2.54, 2.17, 1.35, 0.83, 0.54] and in the nx = 48 tall box ⟨⟨Pm⟩⟩t = [1.84, 1.47, 1.11, 0.67, 0.34]. In addition, we run four cases where we force a certain average numerical Prandtl number by adjusting either the artificial viscosity or the artifical resistivity (see Sect. 2.2). One case is run by adjusting the artificial resistivity, where we force the Prandtl number to be equal to Pm, AR = 3 (the red curve in Figs. 6 and 7). Two of the cases adjust the artificial viscosity with αB = 0.5, forcing a Prandtl number of Pm, AV = 3 and Pm, AV = 6 and one case adjust the artificial viscosity with αB = 0.25, forcing a Prandtl number of Pm, AV = 0.25 (green curves in Figs. 6 and 7). The simulations are run for about 200 orbits or until the turbulence dies out. The results of the simulations are shown in Figs. 6–13.
 |
Fig. 6. Time evolution of several volume-averaged quantities for the standard box, unstratified ZNF cases at as resolution of nx = 96: magnetic energy (top left), kinetic energy (top right), normalized Maxwell stress (bottom left) and the total stress (bottom right). The red line show the case of Pm, AR = 3.0 where we set the Prandtl number by altering the AR strength. The green lines show the case where we set the Prandtl number by altering the AV strength, the darkness of the curve is determined by the value of the set Prandtl number, Pm, AV = [0.25, 3.0, 6.0]. The blue curves represent the cases with a set AR coefficient without forcing the Prandtl number, where the darkness is determined by the strength of the artificial resistivity parameter, αB = [0.25, 0.5, 1.0, 2.0, 4.0]. Four of the nine cases reach a saturated state (αB = 0.25, Pm, AR = 3.0, Pm, AV = 3.0, Pm, AV = 6.0) The code default value of αB = 0.5 sustains turbulence for around 50 orbits before decaying. |
 |
Fig. 7. Time evolution of several volume-averaged quantities for the tall box, unstratified ZNF cases at a resolution of nx = 48: magnetic energy (top left), kinetic energy (top right), normalized Maxwell stress (bottom left) and the total stress (bottom right). The red line show the case of Pm, AR = 3.0 where we set the Prandtl number by altering the AR strength. The green lines show the case where we set the Prandtl number by altering the AV strength, the darkness of the curve is determined by the value of the set Prandtl number, Pm, AV = [0.25, 3.0, 6.0]. The blue curves represent the cases with a set AR coefficient without forcing the Prandtl number, where the darkness is determined by the strength of the artificial resistivity parameter, αB = [0.25, 0.5, 1.0, 2.0, 4.0]. Four of the nine cases reach a saturated state (αB = 0.25, Pm, AR = 3.0, Pm, AV = 3.0, Pm, AV = 6.0). The code default value of αB = 0.5 sustains turbulence for a long time but starts to decay after around 120 orbits. |
 |
Fig. 8. Time-averaged values of several quantities for all our unstratified, zero net-flux simulations with standard box size (L = [1.0, π, 4.0]) and resolution nx = 96. From the top left to bottom right: magnetic energy density, Maxwell stress, normalized Maxwell stress, ratio between Reynolds and Maxwell stresses, total stress, ratio between radial and total magnetic field energy. The x-axis shows the time-averaged effective Prandtl number of the simulation. For some quantities we have plotted the total time average (shown in green), the time average of the turbulent component (shown in orange) and the time average of the mean component (shown in blue). The circles represent the simulations where we have adjusted the strength of the artificial resistivity, while the star symbols represent the simulations where we have adjusted the artificial viscosity. |
 |
Fig. 9. Time-averaged values of several quantities for all our unstratified, zero net-flux simulations with tall box size (L = [1.0, π, 4.0]) and resolution nx = 48. From the top left to bottom right: magnetic energy density, Maxwell stress, normalized Maxwell stress, ratio between Reynolds and Maxwell stresses, total stress, ratio between radial and total magnetic field energy. The x-axis shows the time-averaged effective Prandtl number of the simulation. For some quantities we have plotted the total time average (shown in green), the time average of the turbulent component (shown in orange) and the time average of the mean component (shown in blue). The circles represent the simulations where we have adjusted the strength of the artificial resistivity, while the star symbols represent the simulations where we have adjusted the artificial viscosity. |
 |
Fig. 10. Spacetime diagrams showing the horizontal-averaged azimuthal magnetic field for the unstratified, zero net flux case (Pm, AV = 3). We can see that the tall box has larger structured mean-fields than the standard box. Compared to Shi et al. (2016) the rendered pattern of the mean-fields are similar, however, they produce much stronger mean-fields in their tall box simulations. |
 |
Fig. 11. Time-averaged values of several quantities for our resolution study of the unstratified, zero net-flux cases with Pm, AR = 3.0 and Pm, AV = 6.0, which includes tall box and standard box simulations. From the top left to bottom right: magnetic energy density, Maxwell stress, normalized Maxwell stress, ratio between Reynolds and Maxwell stresses, total stress, ratio between radial and total magnetic field energy. For some quantities we have plotted the total time average (shown in green), the time average of the turbulent component (shown in orange) and the time average of the mean component (shown in blue). The circles represent the simulations where we have adjusted the strength of the artificial resistivity, small circles represent standard box cases and large circles represent tall box. While the star (standard box size) and large stars (tall box size) represent the simulations where we have adjusted the artificial viscosity. |
 |
Fig. 12. Resolution dependence of the numerical Prandtl number for the unstratified, zero-flux cases on the left (Sect. 3.2) and for the stratified, net-flux cases to the right (Sect. 4). This shows cases with an AR coefficient set to αB = 0.5, which is our code default. We can see that we have an almost linear increase with higher resolution for both cases. |
 |
Fig. 13. Time-averaged turbulent transport coefficients from the unstratified, zero net-flux cases, with the standard box size cases (L = [1.0, π, 1.0], nx = 96) to the left and the tall box cases (L = [1.0, π, 4.0], nx = 48) to the right. The circles represent the simulations where we have adjusted the strength of the artificial resistivity, while the star symbols represent the simulations where we have adjusted the artificial viscosity. To minimize noise we have set αxx = αyy, ηxx = ηyy, αyx = 0.0 and ηxy = 0.0. We can see that the α coefficients have values of around zero as expected for the unstratified case and ηxx with a consistent positive value. For the standard box ηyx remain close to zero while for the tall box we see a consistent positive value which is contrary to what was seen by Shi et al. (2016). |
In Fig. 6 we show the time evolution of the magnetic energy, kinetic energy, normalized Maxwell stress, and the total stress for our high-resolution standard box cases with nx = 96. Only four of the nine cases reach a saturated state (αB = 0.25, Pm, AR = 3, Pm, AV = 3, Pm, AV = 6), which all have a Prandtl number of Pm > 2.5. The αB = 0.5 case sustain turbulence for about 50 orbits before decaying, and most of the other cases have their turbulence eliminated within the first 30 orbits, similar to what was seen in Deng et al. (2019), where the longest living case was about 20 orbits. An outlier is the evolution of Pm, AV = 0.25, where small stress oscillation can still be seen for a long time after the initial decay. This is simply caused by numerical noise, as we force a very low AV for this case together with a low AR coefficient αB = 0.25. In Fig. 7, we show the time evolution of the same quantities for the tall-box simulations with resolution nx = 48. We find that the same four cases reach a saturated state for the tall box (αB = 0.25, Pm, AR = 3, Pm, AV = 3, Pm, AV = 6). The αB = 0.5 case sustain turbulence for a longer time, decaying after around 120 orbits. Most of the other cases have their turbulence eliminated within the first 20 orbits.
In Figs. 8 and 9 we show the time-averaged quantities of the high-resolution (nx = 96), standard box runs and the lower resolution (nx = 48), tall box cases, respectively. For the tall box case, we only show the time averages of the saturated runs as all the other runs are killed after their initial turbulence die out. For the standard box, we can see that as we increase the Prandtl number the magnetic energy and stress increases rapidly until we reach a high enough Pm for saturation. The saturated cases reaches a total stress of around αstress = 0.01 and a normalized magnetic stress of αmag = 0.4, which is consistent with previous studies of the MRI (Hawley et al. 1995; Simon et al. 2009). From these figures, we can see that the total magnetic field energy and stresses are largely dominated by the turbulent component, with only a very weak mean-field component. The mean-field energy and stress do not change significantly as the Prandtl number is increased. We can also see that there is not a one to one correlation between energies and stresses for Pm, AR and Pm, AV simulations with the same Prandtl number. The resulting stress levels are higher when lowering the artificial resistivity compared to increasing the artificial viscosity. While saturation is mainly governed by the Prandtl number, stress levels will depend on both the Prandtl number and the strength of the resistivity (Simon & Hawley 2009). In addition, as shown in Fromang et al. (2007) the critical Prandtl number does have a dependence on the Reynolds number which also can have an effect on the amplitude of the saturated stress.
Comparing this to the time average results from the tall box shown in Fig. 9, we can see that similar to the standard box, magnetic energy and stress increases with Pm, reaching albeit higher values but with similar normalized magnetic stress values. From the magnetic energy density, it is clear that the turbulent part of the energy is dominant similar to the standard box case. This is quite different from the results presented in Shi et al. (2016) where the mean-field contributes most to the energy density.
In fact, they showed a rapid increase in mean-field energy density as the vertical aspect ratio of the domain was increased. We do see that the mean-field energy density of our tall box is larger than the standard box, however, it remains relatively weak. A visual comparison of the mean-fields can be seen in Fig. 10, where we see that the tall box has larger structured mean-fields than the standard box. The rendered pattern of the mean-fields are reminiscent of the result presented in Shi et al. (2016). The lack of significant mean-fields can be seen in the resulting stress levels of our simulations, which are only slightly larger than the ones from the standard box case and nowhere near the αstress = 10−1 presented in Shi et al. (2016).
We can see from Figs. 8 and 9 that, in general, there is a small increase in the ratio between Maxwell stress and Reynolds stress as Prandtl number is increased and seem to converge towards a value of roughly αMW/αrey ≈ 4.5 for the standard box and αMW/αrey ≈ 5 in the tall box. For the standard box, this is slightly higher than the typical values from Eulerian grid simulations, which report values of around αMW/αrey ≈ 3 ↔ 4 (Hawley et al. 1995, 1999; Abramowicz et al. 1996; Stone et al. 1996; Sano et al. 2004). However the tall box values are in accordance with those presented in Shi et al. (2016).
The average divergence error remains either below or close to ϵdiv, err ≈ 10−2. As expected, the divergence error is kept lower by increasing the artificial viscosity to reach a certain Prandtl number than by decreasing the resistivity. For the majority of cases, the Elsasser number remains far above 1, however, for the high resistivity cases (αB = 4, αB = 2) the number drops below one, which is likely why we see such a rapid decay of turbulence in these cases. We also show the relative radial energy ratio (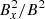 ), which shows a steep increase with Pm and for our saturated runs it reaches values around
), which shows a steep increase with Pm and for our saturated runs it reaches values around 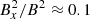 . This is similar to the values reported by Hawley et al. (1996) but is somewhat lower than the higher resolution simulation performed by Simon et al. (2009) and Shi et al. (2016), which reports values of around
. This is similar to the values reported by Hawley et al. (1996) but is somewhat lower than the higher resolution simulation performed by Simon et al. (2009) and Shi et al. (2016), which reports values of around 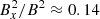 . Looking at Fig. 11, this is consistent with the increasing trend with resolution that we see. Increasing the vertical domain size slightly increases the value from about
. Looking at Fig. 11, this is consistent with the increasing trend with resolution that we see. Increasing the vertical domain size slightly increases the value from about 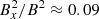 for the standard box to around
for the standard box to around 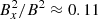 for the tall box. This is opposite to what is found in Shi et al. (2016), which see a consistent decrease in this value as the vertical domain size is increased, going from
for the tall box. This is opposite to what is found in Shi et al. (2016), which see a consistent decrease in this value as the vertical domain size is increased, going from 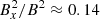 for the standard box to
for the standard box to 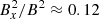 for the 4 times vertical ratio and
for the 4 times vertical ratio and 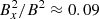 for the 8 times vertical ratio.
for the 8 times vertical ratio.
We also performed a resolution study on the standard box case to see how different time-averaged quantities change with resolution. We primarily look at the two cases where we set Pm, AV = 6 and Pm, AR = 3. From Fig. 11, we can see that for the saturated cases there is no strong resolution dependence on the total stress as reported by studies using Eulerian grid codes (Fromang et al. 2006). Instead, the stress saturates at around αstress = 0.01. This resolution independence is of course only for the cases where we force a certain numerical Prandtl number, as increasing the resolution for a fixed resistivity coefficient will alter the numerical Prandtl number. The resolution dependency of the numerical Prandtl number can be seen in Fig. 12, which shows that Pm has an almost linear increase with resolution. The normalized turbulent stress ratio remains fairly constant at around αmag ≈ 0.42 with a slight increase with resolution. The relative radial energy ratio (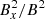 ) show a steady increase with resolution and have not converged for our highest resolution case. The divergence error is also reduced with increasing resolution, which is consistent with our cleaning scheme implementation.
) show a steady increase with resolution and have not converged for our highest resolution case. The divergence error is also reduced with increasing resolution, which is consistent with our cleaning scheme implementation.
Figure 13 shows the time-averaged values of the transport coefficients αxx, αxy, ηxx and ηyx for all the unstratified simulations. From the figures, we can see that both α coefficients have values very close to zero which is to be expected from the unstratified case. ηyx can be seen to have a slightly positive value for all cases exhibiting sustained turbulence, which is more significant in the tall box. The turbulent diffusivity can be seen to have a consistent positive value, which is around ηxx ≈ 0.006 for the standard box and ηxx ≈ 0.015 in the tall box. The nonnegative value in ηyx might explain why we do not see the generation of large mean-fields within our simulations as Shi et al. (2016) shows a consistent negative value for ηyx which as we explained in the introduction can act to generate local mean-fields through the shear-current effect. However, the lack of shear-current effect is consistent with other previous studies of the MRI (Brandenburg et al. 1995a; Brandenburg 2008; Gressel 2010).
4. Stratified simulation results
The stratified NF simulations represent a more realistic and complex situation than the unstratified case, as it includes the vertical tidal component (final term in Eq. (16)), which results in the following density stratification:
Here, H is the scale height and is set by H = cs/Ω = 1.0. As we adopt an isothermal equation of state we do not have to worry about the scale height changing during the simulation. In previous studies, the developed MRI turbulence shows a periodic dynamo cycle, where large-scale magnetic fields emanate from the central region and migrate outwards to the disk corona, growing in strength as they do so. This flips the sign of the field within the central region and the process is repeated. As we mentioned in the introduction, recently it has been shown that SPH develops unphysically strong azimuthal fields in simulations of the stratified shearing box (Deng et al. 2019). In this section, we further investigate this case with a larger array of different numerical dissipation parameters and resolutions. In addition, we compare the results from TSPH to the newly developed GDSPH, which has been shown to improve performance in cases involving large density gradients (Wissing & Shen 2020). We set up the simulation following Deng et al. (2019), in which they use a shearing box of length 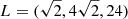 together with an azimuthal magnetic field:
together with an azimuthal magnetic field:
Here, the initial plasma beta is set to β = 25 throughout the box and, as the pressure will vary with density as 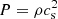 , we begin with a magnetic field that varies in the vertical direction. We run the simulations at four different resolutions [nx, N]=[46, 1.6 × 106],[58, 3.1 × 106],[73, 6.2 × 106],[93, 12.8 × 106], where the two lower resolution cases are the same as the ones run in Deng et al. (2019). As the resolution is adaptive, we have more resolution in the inner region of the disk (which is where the MRI turbulence is sustained) and less resolution outside in the disk corona. Using Eq. (18) we can see that we resolve λMRI with an average initial quality parameter of Qmid = [43, 55, 68, 90] in the midplane for each respective resolution. We carry out several simulation at a resolution of nx = 58, where we vary the artificial resistivity coefficient αB = [0.3, 0.5, 1.0, 2.0], where αB = 0.5 is the code default value. For all the simulation cases we run one with TSPH and one with GDSPH for comparison. Due to the outflow boundaries, there is mass loss from the simulation, which leads to a flattening of the density profile. This means that resolution will gradually be reduced as time goes on, which is why we at most run our simulation for about 100 orbits. The high-resolution cases are also very computationally costly and are stopped at a somewhat earlier time. The results of the simulations are shown in Figs. 14–21.
, we begin with a magnetic field that varies in the vertical direction. We run the simulations at four different resolutions [nx, N]=[46, 1.6 × 106],[58, 3.1 × 106],[73, 6.2 × 106],[93, 12.8 × 106], where the two lower resolution cases are the same as the ones run in Deng et al. (2019). As the resolution is adaptive, we have more resolution in the inner region of the disk (which is where the MRI turbulence is sustained) and less resolution outside in the disk corona. Using Eq. (18) we can see that we resolve λMRI with an average initial quality parameter of Qmid = [43, 55, 68, 90] in the midplane for each respective resolution. We carry out several simulation at a resolution of nx = 58, where we vary the artificial resistivity coefficient αB = [0.3, 0.5, 1.0, 2.0], where αB = 0.5 is the code default value. For all the simulation cases we run one with TSPH and one with GDSPH for comparison. Due to the outflow boundaries, there is mass loss from the simulation, which leads to a flattening of the density profile. This means that resolution will gradually be reduced as time goes on, which is why we at most run our simulation for about 100 orbits. The high-resolution cases are also very computationally costly and are stopped at a somewhat earlier time. The results of the simulations are shown in Figs. 14–21.
 |
Fig. 14. Time evolution of several volume-averaged quantities for the stratified net-flux simulations with varying artificial resistivity (αB = [0.3, 0.5, 1.0, 2.0]) at a resolution of nx = 58. Magnetic energy (top left), kinetic energy (top right), normalized Maxwell stress (bottom left) and the total stress (bottom right). The red lines show the simulations run with TSPH and blue lines show the runs with GDSPH where the darkness of the line represents the strength of the artificial resistivity. We have smoothed the curves using a Savitzky–Golay filter, the unsmoothed curves can still be seen as very transparent curves. |
 |
Fig. 15. Spacetime diagrams of the stratified net flux simulations, showing the evolution of the horizontal averaged radial (top) and azimuthal (bottom) fields for both GDSPH (left) and TSPH (right) in the case of αB = 0.3 with a resolution nx = 58. Both GDSPH and TSPH develop the characteristic butterfly diagram. However, the TSPH simulation quickly becomes unstable and exhibits a runaway growth in the magnetic field. |
 |
Fig. 16. Spacetime diagrams of the stratified net flux simulations, showing the evolution of the horizontal averaged radial (top) and azimuthal (bottom) fields for both GDSPH (left) and TSPH (right) in the case of αB = 1 with a resolution nx = 58. At this resistivity only GDSPH reproduce the butterfly diagram, where for TSPH a strong positive azimuthal field permeates the disk corona (|z|> 2). The azimuthal field is additionally amplified as the simulation goes on and starts to propagate into the central disk region. |
 |
Fig. 17. Stratified shearing box simulation with net-flux, shows the surface rendering of the azimuthal field (top) and the density (bottom). Left: case for GDSPH and right: case with TSPH. In the TSPH case we can see that there is excessive growth in the magnetic field in the outer part of the disk. |
 |
Fig. 18. Time-averaged values of several quantities for all our stratified net-flux simulations as a function of the artificial resistivity (αB) at a resolution of nx = 58. From the top left to bottom right: magnetic energy density, Maxwell stress, normalized Maxwell stress, ratio between Reynolds and Maxwell stresses, total stress, estimated numerical Prandtl number. For some quantities we have plotted the total time average (shown in green), the time average of the turbulent component (shown in orange) and the time average of the mean component (shown in blue). The circles represent the simulations run with GDSPH while the diamonds represent the simulations run with TSPH. |
 |
Fig. 19. Time evolution of several volume averaged quantities for the stratified net-flux simulations with varying resolution (nx = [48, 58, 74, 93]) and the artificial resistivity coefficient set to αB = 0.5. Magnetic energy (top left), kinetic energy (top right), normalized Maxwell stress (bottom left) and the total stress (bottom right). The green lines show the simulations run with TSPH and purple lines show the runs with GDSPH. The darkness of the line indicate the resolution, where the darkest line represents the highest resolution. |
 |
Fig. 20. Time-averaged values of several quantities for all our stratified net-flux simulations with artificial resistivity coefficient set to αB = 0.5, plotted over the resolution (particles along the x-axis). From the top left to bottom right: magnetic energy density, Maxwell stress, normalized Maxwell stress, ratio between Reynolds and Maxwell stresses, total stress, ratio between azimuthal and total magnetic field energy. For some quantities we have plotted the total time average (shown in green), the time average of the turbulent component (shown in orange) and the time average of the mean component (shown in blue). The circles represent the simulations run with GDSPH while the diamonds represent the simulations run with TSPH. |
 |
Fig. 21. Horizontal time-averaged turbulent transport coefficient in the z direction from the stratified net-flux cases. The darkness of the curves is determined by the strength of the artificial resistivity parameter, αB = 0.3, 0.5, 1.0, 2.0. We can see that we have a negative αyy effect that is negative (positive) in the top (bottom) half of the box. This enables the αω-dynamo to operate efficiently within the central region. αxx on the other hand has a positive gradient and will act against the shear term. Turbulent pumping advects magnetic fields outwards from the central region with velocity |
In Fig. 14 we can see the time evolution of the magnetic energy, kinetic energy, normalized Maxwell stress, and the total stress for a resolution with nx = 58. From this figure, we can see that all of the TSPH simulations exhibit an unphysical growth in the magnetic energy density, similar to what was seen in Deng et al. (2019). These simulations are stopped when they reach roughly an average plasma beta value of β = 1, which acts as a confirmation of erroneous growth. On the other hand, all the GDSPH simulations remain stable and those runs with moderate artificial resistivities all reach saturated magnetic energy and stress levels that are similar to what has been seen in the literature (Shi et al. 2010; Simon et al. 2011). To get a closer look at what is going on, we have in Fig. 15 plotted the time-space evolution of the horizontal averaged radial and azimuthal fields for both GDSPH and TSPH in the case of αB = 0.3 with a resolution nx = 58. Both GDSPH and TSPH develop the characteristic butterfly diagram, where the azimuthal fields are buoyantly transported outward and periodically flip signs in the central region. However, while the GDSPH case stably continues this behavior for over 100 orbits, the TSPH case quickly becomes unstable and exhibits a runaway growth. Increasing the resistivity to αB = 1.0 does not help stabilize the TSPH scheme, as can be seen in Fig. 16. The butterfly diagram is gone and instead, a strong positive azimuthal field permeates the disk corona (|z|> 2). The azimuthal field is additionally amplified as the simulation goes on and starts to propagate into the central disk region. The failure of buoyantly ejecting the positive fields in the disk corona is due to the magnetic field growing strong enough to stabilize the region (magnetic tension suppresses the bending of field lines). The time-space diagram of the TSPH case in Fig. 16 is reminiscent of the result presented in Deng et al. (2019) where a similar magnetic field growth was observed. The GDSPH case, on the other hand, still exhibits the butterfly diagram at higher resistivity, but with a longer periodic cycle for the flipping of the magnetic field (especially at early times). The TSPH case still has a very active and fluctuating radial field within the central region, and this is also reflected in the normalized Maxwell stresses in Fig. 14, where the values of the TSPH cases remain similar to the GDSPH runs with the same αB. This is further highlighted in Fig. 17, where we can see a rendering of the magnetic field and density within the box for both the TSPH and GDSPH cases. Both simulations exhibit a very similar central region, while the TSPH have significantly stronger azimuthal fields in the outskirts. As TSPH and GDSPH mainly differ at density gradients, it makes sense that the issue of the unphysical growth seems to lie in the outer region of the disk (beyond |z|> 1) where we have lower resolution and a significant density gradient.
Figure 18 shows time averages of different quantities. In general, as we decrease the resistivity, the magnetic energy and stress increases for both the TSPH and GDSPH runs. The total stress reaches a time-averaged value of around αstress ≈ 10−2 and a normalized Maxwell stress of around αmag = 0.3 for the low resistivity cases, similar to previous result from the literature (Shi et al. 2010; Simon et al. 2011). Looking at the mean and turbulent components of the magnetic energy density, we can see that the mean-field component is the dominant part, but with an increasing fraction from the turbulent field as we decrease the resistivity. The TSPH runs develop a much higher magnetic energy density than the GDSPH cases, with a highly dominating mean-field component, which comes mainly from the strong azimuthal fields in the corona. For the Maxwell stress, in our GDSPH simulations the turbulent and mean-field components contribute a similar amount to the total Maxwell stress. The normalized Maxwell stresses have similar values for both GDSPH and TSPH, with the turbulent component of around 0.45 and largely independent of the resistivity, but the mean-field component increases with decreasing resistivity.
From Fig. 18 we can also see that the ratio between the Maxwell stress and Reynolds stress show a value of around 5.0 for the GDSPH cases with an increasing trend for lower resistivity. For the TSPH runs, this ratio shoots up for the low resistivity cases to a value of around 8. The numerical Prandtl number has a steady increase as we decrease the resistivity. For GDSPH it goes from a value of around 0.7 for αB = 2.0 to a value of 1.6 for αB = 0.25. In TSPH the numerical Prandtl number is larger but not by much. The average divergence error for both GDSPH and TSPH remains close or below a value of ϵdiv, err ≈ 10−2.
To investigate the effect of resolution in the stratified simulations, we perform a resolution study with the following radial resolutions nx = [48, 58, 73, 93]. In these simulations, we use the code default artificial resistivity coefficient of αB = 0.5. The high-resolution cases (nx = 73, 93) are very costly, so we have only run them for about 60 orbits. In Fig. 19 we can see the time evolution of the magnetic energy, kinetic energy, normalized Maxwell stress, and the total stress for TSPH and GDSPH at different resolutions. From this figure, we can see that all the TSPH cases eventually become unstable, and the lowest resolution cases “survives” the longest. All of the GDSPH cases show a stable behavior, with only the lowest resolution case having a period of low stress before increasing to similar levels as the higher resolution cases. A significant early difference that can be seen between TSPH and GDSPH is shown in the magnetic energy density, where all the TSPH have a much larger initial “bump” than the GDSPH curves which flatten out after the initial increase. This larger initial bump correlates to stronger magnetic fields near the density contrast at around |z|≈1.
In Fig. 20 we can see that the values of magnetic energy density and stress remain fairly flat, with a slight initial increase with resolution but then a slight decrease for our highest resolution. It is not clear to why we see a decrease in the stress for the highest resolution. It could simply be a stochastic phenomena that would flatten out if we ran it for longer. However, both GDSPH and TSPH follow a similar curve, pointing towards a real effect. We can see that the turbulent component does become a more dominant part in both the energy density and in the stress as we increase resolution. The normalized Maxwell stress has a slight increase with resolution, going from around αmag = 0.2 to αmag = 0.3 and the total stress for GDSPH lies between αstress = 10−3 ↔ 10−2 which is in accordance to the values presented by Stone et al. (1996) and Shi et al. (2010). We can see that the ratio between the Maxwell stress and Reynolds stress is almost independent of resolution giving a value of 5.0 for the GDSPH cases and around 7.0 for TSPH. Similar to the unstratified case, we can in Fig. 12 see that we have a slow but linear increase in the numerical Prandtl number with resolution, going from around Pm = 1.3 to Pm = 1.5 for the GDSPH cases. The average divergence error slightly decreases with resolution for both TSPH and GDSPH with values around ϵdiv, err ≈ 10−2.
In Fig. 21 we show the horizontal time-averaged turbulent coefficients as a function of z. As we mentioned in the introduction, the dynamo action within stratified disks includes several mechanisms that can act in different sections of the disk. We find that the αxx, αyy, αxy and αyx all have a continuous gradient, with anti-symmetric behavior around the mid-plane. The behavior of αyy determines the effectiveness of the αω-dynamo, as it operates on the radial mean fields (see Eq. (9)). We can see that αyy has a negative gradient with negative values above the midplane, this is consistent with Brandenburg et al. (1995b), Brandenburg & Sokoloff (2002), Brandenburg (2008), Shi et al. (2016), and is indicative of an effective alpha effect for turbulent shear flows. The αxx has a positive gradient and will act against the shear term, however, the shear term is the dominant part of the induction equation for the toroidal mean field. The off diagonal terms of α is often interpreted as a turbulent/diamagnetic pumping term 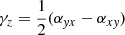 . For our case, γz is positive above the mid-plane and negative below, meaning that we have a net transport of mean-fields away from the mid-plane. The αxy and αyx coefficients have the opposite sign, which is similar to the results from Shi et al. (2016), but different from other works by Brandenburg (2008), Gressel (2010), where the two have the same sign. However, αxy and αyx usually have similar magnitude in earlier works which is not observed in our cases. The ηxx coefficient and ηyx are generally positive, which is similar to what was found by Brandenburg (2008), Gressel (2010) but contrary to Shi et al. (2016).
. For our case, γz is positive above the mid-plane and negative below, meaning that we have a net transport of mean-fields away from the mid-plane. The αxy and αyx coefficients have the opposite sign, which is similar to the results from Shi et al. (2016), but different from other works by Brandenburg (2008), Gressel (2010), where the two have the same sign. However, αxy and αyx usually have similar magnitude in earlier works which is not observed in our cases. The ηxx coefficient and ηyx are generally positive, which is similar to what was found by Brandenburg (2008), Gressel (2010) but contrary to Shi et al. (2016).
5. Discussion
In this paper, we performed 23 simulations of the unstratified shearing-box MRI and 14 simulations of the stratified shearing-box MRI using SPH. For the unstratified NF case, we reproduced the results from previous studies in the literature, albeit with slightly larger αmag values and in general larger mean-field stresses. We attribute this primarily to the use of a smaller box, which increases the amplitude and frequency of channel modes and causes large bursts of magnetic energy and stress levels.
We demonstrate that the saturation of the unstratified ZNF simulations is highly dependent on the numerical Prandtl number. Our simulations with a Prandtl number above 2.5 achieve saturation for at least 200 orbits. To further illustrate that the MRI saturation depends on the numerical Prandtl number, rather than simply on the resistivity, we ran a simulation with a forced Prandtl number of Pm, AV = 0.25 but with a low artificial resistivity coefficient αB = 0.25. This simulation does not saturate even though having a very low numerical resistivity. This confirms that the dependencies on the Prandtl numbers found in Fromang & Papaloizou (2007) still holds true for numerical Prandtl numbers within SPH. The saturation levels in energies and stresses are also mainly dependent on the Prandtl number. However, for saturated simulations with the same Prandtl number, the magnetic energy and stress are slightly higher in cases with varying artificial resistivity than the ones with varying artificial viscosity. This is also shown in Figs. 6 and 7: when comparing the Pm, AR = 3 case with Pm, AV = 3 run, the latter exhibit larger oscillations and lower saturation levels.
We do not observe a decrease in stress with increasing resolution as found in previous studies with Eulerian codes. Although the stresses are highly dependent on numerical Prandtl number, they have a weak dependency on the resolution at a fixed Prandtl number, either increasing or staying roughly at the same stress level with increasing resolution. A possible explanation is that the numerical Prandtl number in Eulerian codes is not independent of resolution. This is contrary to studies by Fromang et al. (2007) and Simon et al. (2009), where the authors found the numerical Prandtl number to be almost independent of resolution (Pm ≈ 1.6). These studies utilized Fourier transfer functions to compute the energy transfer between different scales. They found that an active MRI can exist in their simulations even though the numerical Prandtl number is lower than the critical value determined in studies with physical dissipation (Pm ∼ 2). Thus, it was concluded that numerical dissipation acts differently to physical dissipation. In this paper, we however find that active turbulence still requires similar critical Prandtl numbers found in studies using physical dissipation. It is likely that the numerical dissipation in SPH is more closely related to physical dissipation than in grid codes, as SPH does not suffer from advection errors. This difference seems to be the reason to why grid codes see a significant reduction in stress with resolution.
Ideally, one would like the numerical Prandtl number to remain independent of resolution, as this would ensure the correct dynamo behavior if one can resolve the turbulent medium. The Prandtl numbers in our simulations increase with resolution for a fixed artificial resistivity coefficient (αB = 0.5) ranging from ⟨Pm⟩∼1.5 for nx = 48 to ⟨Pm⟩∼2.1 at nx = 96. Although not independent, an increase of Pm with resolution ensures that it increases along with the other fluid parameters (e.g., Reynolds number and magnetic Reynolds number). This means that we have convergent results when modeling most astrophysical fluids. A worse result would have been if the Prandtl number decreased with resolution which could result in a lowering of stress with resolution and finally in the decay of the MRI. In addition, as mentioned in the introduction, the Prandtl number plays a major role in several dynamo mechanisms and is crucial for the saturation of the small-scale dynamo, which for example can be important for correctly simulating the growth and saturation of magnetic fields within galaxies. Our results highlight the importance of studying the numerical Prandtl number for all numerical schemes beyond MRI, for instance in turbulent boxes at different Mach numbers.
The main difference in our tall boxes compared to Shi et al. (2016) is the lack of significant mean-fields, which leads to stress levels that are only slightly larger than the ones in the standard box cases, but much smaller than αstress = 10−1 seen in Shi et al. (2016). Our simulations do develop similar large-scale patches in the toroidal field, but they are significantly weaker. The small-scale turbulent components are consistent with the Shi et al. (2016) results. The lack of mean-fields is likely due to the difference seen in ηyx, which was consistently negative for Shi et al. (2016) but for all our simulations are either zero or positive. This would effectively lead to less coherent mean-field growth within the box. However, the positive value of ηyx is consistent with previous studies with the quasi-kinematic approach (Brandenburg et al. 1995a; Brandenburg 2008; Gressel 2010). For future work, it is worth exploring higher resolutions and different aspect ratios for SPH, to see if higher mean-field growth can be observed.
We demonstrated, for the first time, that the new GDSPH can successfully sustain the turbulence in the stratified shearing boxes for at least 100 orbits without decaying, similar to the simulations using the GIZMO code with the meshless finite-mass (MFM) method (Deng et al. 2019). However, the TSPH runs remain unstable for all cases, which confirms the result from Deng et al. (2019). Isolating each MHD term and looking at the effect of the GDSPH weighing on each of them reveals that the unstable growth is governed by the TSPH induction and cleaning equation. The major effect comes from the TSPH induction equation, which always leads to larger growth rates at the outskirts of a disk (|z|> H) following the end of the linear phase. This leads to larger regions of the simulation being magnetically dominated, and consequently results in larger mass outflows and momentum oscillations within the box. The TSPH cleaning equations increases the oscillations of the magnetic energy in the outskirt, leading to quicker instability if paired together with the TSPH induction equation. The unphysical growth rate is possibly due to a magnetic flux error, as the energy is continuously increasing together with the magnetic field getting either more and more positive or negative. Global mean-field such as this can either be generated by the outflow boundaries or the monopole currents. Since outflow boundaries tend to expel flux roughly equally, the error is more likely to be caused by monopole currents, together with the gradient errors of TSPH near the density gradient. These fields eventually become so strong that they can no longer be buoyantly transported outward, because the critical wavelength is larger than the radial size of box. The negative radial fields in the outskirts will continue to increase the azimuthal field and subsequently the total magnetic energy. To be clear, this is not an intrinsic nonconservation of energy in the method (as seen in Lewis et al. 2015 due to an integrator bug), for either GDSPH or TSPH, both show excellent momentum and energy conservation for a wide range of tests shown in Wissing & Shen (2020). Kinetic energy will naturally transfer to magnetic energy due to the shear of net radial fields. In Deng et al. (2019) this unphysical increase of the azimuthal field was partly attributed to the divergence cleaning. While the divergence cleaning can increase the energy oscillations in the outskirt, the cleaning scheme is in itself guaranteed to decrease the overall magnetic energy and can not generate global mean-fields within the box. Because the hyperbolic divergence cleaning is conservative, which means that the spreading of the magnetic flux due to the cleaning is always symmetrical.
In addition, in our simulations the MRI turbulence is sustained longer than the MFM simulation presented in Deng et al. (2019), in which the turbulence decays around 40 orbits in their fiducial run. Our code has the ability to sustain long-term MRI turbulence similar to the Eulerian codes in previous MRI studies (Shi et al. 2010; Davis et al. 2010). However, as the simulations were terminated earlier in Deng et al. (2019), it is unclear if the MRI has actually fully died down in that work. We do also observe that the MRI can temporarily dip down to similar values before eventually being reenergized.
We also performed an analysis of the turbulent coefficients for all the simulations presented in this paper. We showed that no α-effect was present for the unstratified case as expected. For the stratified case, we have a negative αyy effect that is negative (positive) in the top (bottom) half of the box, which indicates an effective αω-dynamo. This is similar to what was found in Brandenburg (2008) and Shi et al. (2016). We find a turbulent pumping that transports the mean-fields away from the central region. However, we note that there is a significant uncertainty in the calculated αyx coefficients due to correlations with the shear term, as explained in Sect. 2.1. The turbulent resistivity ηxx and ηyx are found to be positive in all of our simulations, and are consistent with previous quasi-kinematic studies employing the test-field method (Brandenburg et al. 1995b; Brandenburg & Sokoloff 2002; Brandenburg 2008).
Using the constrained hyperbolic divergence cleaning scheme with variable cleaning speed from Tricco et al. (2016), we can keep the divergence error low in all cases. The mean normalized divergence error, ⟨ϵdivB⟩=⟨h|∇ ⋅ B|/|B|⟩, is typically of order 10−2.
In conclusion, we find that
-
SPH can effectively develop the MRI and reproduce many of the values and dependencies seen in previous studies with grid-based codes.
-
The geometric density SPH (GDSPH) successfully develops the characteristic “butterfly” diagram of the stratified MRI, showing saturated turbulence for at least 100 orbits. The results are similar to MRI simulations with the MFM method, and the turbulence is sustained longer.
-
The numerical dissipation in SPH is found to act in a similar fashion to physical dissipation. We find a critical Prandtl number of around Pm ≈ 2.5, which is similar to what grid codes find with physical dissipation.
-
The saturated stress for a certain numerical Prandtl number is found to be nearly independent of resolution, which is contrary to grid codes where stress is reduced with increased resolution. The results highlight the importance in determining the general behavior of the numerical Prandtl number in different turbulent flows, to ensure a more accurate saturation of the magnetic field.
-
A major difference can also be seen in the tall, unstratitified, zero net-flux case, where the mean-fíelds are much weaker than a previous study. From the mean-field analysis, we speculate that this might be due to a lack of shear-current effect our simulations. Nevertheless, we find that our transport coefficients are consistent with many previous studies that also do not find an effective shear-current effect.
By traditional SPH we mean the MHD equations that are derived directly from the Euler-Lagrange equations with the traditional SPH density estimate ρa = ∑bmbWab. See Price (2012) for more information.
A global magnetic field is probably required to create cross-helicity in a turbulent field. Cross-helicity is shown to occur when the mean-field is parallel to the direction of gravity in Rüdiger et al. (2011).
The artificial dissipation terms can be seen as approximate Riemann solvers as they functionally produce similar dissipation (Monaghan 1997).
Acknowledgments
We would like to thank the referee, Daniel Price, for helpful comments and suggestions which have improved the quality and clarity of the paper. The simulations were performed using the resources from the National Infrastructure for High Performance Computing and Data Storage in Norway, UNINETT Sigma2, allocated to Project NN9477K. We also acknowledge the support from the Research Council of Norway through NFR Young Research Talents Grant 276043.
References
- Abramowicz, M., Brandenburg, A., & Lasota, J.-P. 1996, MNRAS, 281, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Artymowicz, P., & Lubow, S. H. 1994, ApJ, 421, 651 [Google Scholar]
- Bai, X.-N., & Stone, J. M. 2011, ApJ, 736, 144 [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1991, ApJ, 376, 214 [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1992, ApJ, 400, 610 [CrossRef] [Google Scholar]
- Balbus, S. A., & Terquem, C. 2001, ApJ, 552, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, R. 2015, A&ARv, 24, 4 [Google Scholar]
- Beck, R., Brandenburg, A., Moss, D., Shukurov, A., & Sokoloff, D. 1996, ARA&A, 34, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, R., Fletcher, A., Shukurov, A., et al. 2005, A&A, 444, 739 [EDP Sciences] [Google Scholar]
- Blaes, O. M., & Balbus, S. A. 1994, ApJ, 421, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Bodo, G., Mignone, A., Cattaneo, F., Rossi, P., & Ferrari, A. 2008, A&A, 487, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bodo, G., Cattaneo, F., Ferrari, A., Mignone, A., & Rossi, P. 2011, ApJ, 739, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Boulares, A., & Cox, D. P. 1990, ApJ, 365, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A. 2008, Astron. Nachr., 329, 725 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., & Sokoloff, D. 2002, Geophys. Astrophys. Fluid Dyn., 96, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., & Subramanian, K. 2005, Phys. Rep., 417, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., Nordlund, A., Stein, R. F., & Torkelsson, U. 1995a, ApJ, 446, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., Nordlund, Å., Stein, R. F., & Torkelsson, U. 1995b, in Dynamo Generated Turbulence in Discs, eds. M. Meneguzzi, A. Pouquet, & P. L. Sulem, 462, 385 [NASA ADS] [Google Scholar]
- Chandrasekhar, S. 1960, Proc. Natl. Acad. Sci., 46, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Curry, C., Pudritz, R. E., & Sutherland, P. G. 1994, ApJ, 434, 206 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, S. W., Stone, J. M., & Pessah, M. E. 2010, ApJ, 713, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Dellar, P. J. 2001, J. Comput. Phys., 172, 392 [NASA ADS] [CrossRef] [Google Scholar]
- Deng, H., Mayer, L., Latter, H., Hopkins, P. F., & Bai, X.-N. 2019, ApJS, 241, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Deng, H., Mayer, L., & Latter, H. 2020, ApJ, 891, 154 [Google Scholar]
- Evans, C. R., & Hawley, J. F. 1988, ApJ, 332, 659 [Google Scholar]
- Federrath, C. 2016, J. Plasma Phys., 82, 535820601 [Google Scholar]
- Federrath, C., Chabrier, G., Schober, J., et al. 2011, Phys. Rev. Lett., 107, 114504 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., Schober, J., Bovino, S., & Schleicher, D. R. G. 2014, ApJ, 797, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Fricke, K. 1969, A&A, 1, 388 [NASA ADS] [Google Scholar]
- Fromang, S., & Papaloizou, J. 2007, A&A, 476, 1113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fromang, S., Hennebelle, P., & Teyssier, R. 2006, A&A, 457, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fromang, S., Papaloizou, J., Lesur, G., & Heinemann, T. 2007, A&A, 476, 1123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fromang, S., Papaloizou, J., Lesur, G., & Heinemann, T. 2010, in EAS Pub. Ser., eds. T. Montmerle, D. Ehrenreich, & A. M. Lagrange, 41, 167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaburov, E., & Nitadori, K. 2011, MNRAS, 414, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Lynden-Bell, D. 1965, MNRAS, 130, 125 [Google Scholar]
- Goodman, J., & Xu, G. 1994, ApJ, 432, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Gressel, O. 2010, MNRAS, 405, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Guan, X., & Gammie, C. F. 2011, ApJ, 728, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Guan, X., Gammie, C. F., Simon, J. B., & Johnson, B. M. 2009, ApJ, 694, 1010 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley, J. F., Gammie, C. F., & Balbus, S. A. 1995, ApJ, 440, 742 [Google Scholar]
- Hawley, J. F., Gammie, C. F., & Balbus, S. A. 1996, ApJ, 464, 690 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley, J. F., Balbus, S. A., & Winters, W. F. 1999, ApJ, 518, 394 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley, J. F., Guan, X., & Krolik, J. H. 2011, ApJ, 738, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley, J. F., Richers, S. A., Guan, X., & Krolik, J. H. 2013, ApJ, 772, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Heinemann, T., McWilliams, J. C., & Schekochihin, A. A. 2011, Phys. Rev. Lett., 107, 255004 [NASA ADS] [CrossRef] [Google Scholar]
- Herault, J., Rincon, F., Cossu, C., et al. 2011, Phys. Rev. E, 84, 036321 [NASA ADS] [CrossRef] [Google Scholar]
- Hirose, S., Krolik, J. H., & Stone, J. M. 2006, ApJ, 640, 901 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., & Raives, M. J. 2016, MNRAS, 455, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Hubbard, A., Del Sordo, F., Käpylä, P. J., & Brandenburg, A. 2009, MNRAS, 398, 1891 [NASA ADS] [CrossRef] [Google Scholar]
- Janhunen, P. 2000, J. Comput. Phys., 160, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Käpylä, P. J., & Korpi, M. J. 2011, MNRAS, 413, 901 [CrossRef] [Google Scholar]
- Kersalé, E., Hughes, D. W., Ogilvie, G. I., Tobias, S. M., & Weiss, N. O. 2004, ApJ, 602, 892 [CrossRef] [Google Scholar]
- Krause, F., & Raedler, K. H. 1980, Mean-field Magnetohydrodynamics and Dynamo Theory (Oxford: Pergamon Press) [Google Scholar]
- Kulsrud, R. M. 1999, ARA&A, 37, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Kulsrud, R. M., & Anderson, S. W. 1992, ApJ, 396, 606 [NASA ADS] [CrossRef] [Google Scholar]
- Kulsrud, R. M., Cen, R., Ostriker, J. P., & Ryu, D. 1997, ApJ, 480, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Latter, H. N., Lesaffre, P., & Balbus, S. A. 2009, MNRAS, 394, 715 [NASA ADS] [CrossRef] [Google Scholar]
- Lesaffre, P., & Balbus, S. A. 2007, MNRAS, 381, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Lesaffre, P., Balbus, S. A., & Latter, H. 2009, MNRAS, 396, 779 [NASA ADS] [CrossRef] [Google Scholar]
- Lesur, G., & Longaretti, P. Y. 2007, MNRAS, 378, 1471 [NASA ADS] [CrossRef] [Google Scholar]
- Lesur, G., & Ogilvie, G. I. 2008, A&A, 488, 451 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lewis, B. T., Bate, M. R., & Price, D. J. 2015, MNRAS, 451, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Lodato, G., & Price, D. J. 2010, MNRAS, 405, 1212 [NASA ADS] [Google Scholar]
- Lynden-Bell, D., & Pringle, J. E. 1974, MNRAS, 168, 603 [Google Scholar]
- Meheut, H., Fromang, S., Lesur, G., Joos, M., & Longaretti, P.-Y. 2015, A&A, 579, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meru, F., & Bate, M. R. 2012, MNRAS, 427, 2022 [NASA ADS] [CrossRef] [Google Scholar]
- Moffatt, H. K. 1978, Magnetic Field Generation in Electrically Conducting Fluids (Cambridge: Cambridge University Press) [Google Scholar]
- Monaghan, J. J. 1985, Comput. Phys. Rep., 3, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Monaghan, J. J. 1997, J. Comput. Phys., 136, 298 [NASA ADS] [CrossRef] [Google Scholar]
- Noble, S. C., Krolik, J. H., & Hawley, J. F. 2010, ApJ, 711, 959 [NASA ADS] [CrossRef] [Google Scholar]
- Pakmor, R., & Springel, V. 2013, MNRAS, 432, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1979, Cosmical Magnetic Fields. Their Origin and their Activity (New York: Oxford University Press) [Google Scholar]
- Parkin, E. R., & Bicknell, G. V. 2013, MNRAS, 435, 2281 [NASA ADS] [CrossRef] [Google Scholar]
- Penna, R. F., McKinney, J. C., Narayan, R., et al. 2010, MNRAS, 408, 752 [NASA ADS] [CrossRef] [Google Scholar]
- Pessah, M. E., & Goodman, J. 2009, ApJ, 698, L72 [NASA ADS] [CrossRef] [Google Scholar]
- Pouquet, A., Frisch, U., & Leorat, J. 1976, J. Fluid Mech., 77, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Price, D. J. 2012, J. Comput. Phys., 231, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Price, D. J., & Monaghan, J. J. 2005, MNRAS, 364, 384 [NASA ADS] [Google Scholar]
- Rädler, K. H. 1969, Monatsber. Deutsch. Akad Wissenschaftliche Berlin, 11, 194 [Google Scholar]
- Rincon, F., Ogilvie, G. I., & Proctor, M. R. E. 2007, Phys. Rev. Lett., 98, 254502 [NASA ADS] [CrossRef] [Google Scholar]
- Riols, A., Rincon, F., Cossu, C., et al. 2013, J. Fluid Mech., 731, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Rogachevskii, I., & Kleeorin, N. 2003, Phys. Rev. E, 68, 036301 [NASA ADS] [CrossRef] [Google Scholar]
- Rogachevskii, I., & Kleeorin, N. 2004, Phys. Rev. E, 70, 046310 [NASA ADS] [CrossRef] [Google Scholar]
- Rüdiger, G., Kitchatinov, L. L., & Brandenburg, A. 2011, Sol. Phys., 269, 3 [CrossRef] [Google Scholar]
- Ruzmaikin, A. A., Sokolov, D. D., & Shukurov, A. M. 1988, Magnetic Fields of Galaxies (Dordrecht: Kluwer Academic Publishers), 133 [Google Scholar]
- Sano, T., Inutsuka, S.-I., Turner, N. J., & Stone, J. M. 2004, ApJ, 605, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Schekochihin, A. A., Cowley, S. C., Taylor, S. F., Maron, J. L., & McWilliams, J. C. 2004a, ApJ, 612, 276 [NASA ADS] [CrossRef] [Google Scholar]
- Schekochihin, A. A., Cowley, S. C., Maron, J. L., & McWilliams, J. C. 2004b, Phys. Rev. Lett., 92, 054502 [NASA ADS] [CrossRef] [Google Scholar]
- Schekochihin, A. A., Iskakov, A. B., Cowley, S. C., et al. 2007, New J. Phys., 9, 300 [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 500, 33 [NASA ADS] [Google Scholar]
- Shi, J., Krolik, J. H., & Hirose, S. 2010, ApJ, 708, 1716 [NASA ADS] [CrossRef] [Google Scholar]
- Shi, J.-M., Stone, J. M., & Huang, C. X. 2016, MNRAS, 456, 2273 [NASA ADS] [CrossRef] [Google Scholar]
- Silant’ev, N. A. 2000, A&A, 364, 339 [Google Scholar]
- Simon, J. B., & Hawley, J. F. 2009, ApJ, 707, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, J. B., Hawley, J. F., & Beckwith, K. 2009, ApJ, 690, 974 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, J. B., Hawley, J. F., & Beckwith, K. 2011, ApJ, 730, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, J. B., Bai, X.-N., Stone, J. M., Armitage, P. J., & Beckwith, K. 2013, ApJ, 764, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Spitzer, L. 1962, Physics of Fully Ionized Gases (New York: Interscience Publishers) [Google Scholar]
- Squire, J., & Bhattacharjee, A. 2015a, Phys. Rev. Lett., 114, 085002 [NASA ADS] [CrossRef] [Google Scholar]
- Squire, J., & Bhattacharjee, A. 2015b, Phys. Rev. Lett., 115, 175003 [NASA ADS] [CrossRef] [Google Scholar]
- Squire, J., & Bhattacharjee, A. 2015c, Phys. Rev. E, 92, 053101 [NASA ADS] [CrossRef] [Google Scholar]
- Stone, J. M., Hawley, J. F., Gammie, C. F., & Balbus, S. A. 1996, ApJ, 463, 656 [NASA ADS] [CrossRef] [Google Scholar]
- Subramanian, K., & Brandenburg, A. 2004, Phys. Rev. Lett., 93, 205001 [NASA ADS] [CrossRef] [Google Scholar]
- Suzuki, T. K., & Inutsuka, S.-I. 2009, ApJ, 691, L49 [Google Scholar]
- Tricco, T. S., & Price, D. J. 2012, J. Comput. Phys., 231, 7214 [NASA ADS] [CrossRef] [Google Scholar]
- Tricco, T. S., Price, D. J., & Bate, M. R. 2016, J. Comput. Phys., 322, 326 [NASA ADS] [CrossRef] [Google Scholar]
- Vaĭnshteĭn, S. I., & Zel’dovich, Y. B. 1972, Sov. Phys. Usp., 15, 159 [CrossRef] [Google Scholar]
- Velikhov, E. 1959, Sov. Phys. JETP, 36, 995 [Google Scholar]
- Vishniac, E. T., & Brandenburg, A. 1997, ApJ, 475, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Vishniac, E. T., & Cho, J. 2001, ApJ, 550, 752 [NASA ADS] [CrossRef] [Google Scholar]
- Wadsley, J. W., Keller, B. W., & Quinn, T. R. 2017, MNRAS, 471, 2357 [NASA ADS] [CrossRef] [Google Scholar]
- Wardle, M. 1999, MNRAS, 307, 849 [NASA ADS] [CrossRef] [Google Scholar]
- Wissing, R., & Shen, S. 2020, A&A, 638, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yokoi, N. 2013, Geophys. Astrophys. Fluid Dyn., 107, 114 [Google Scholar]
- Yoshizawa, A., & Yokoi, N. 1993, ApJ, 407, 540 [NASA ADS] [CrossRef] [Google Scholar]
- Zeldovich, Y. B. 1983, Magnetic Fields in Astrophysics (Heidelrberg: Springer-Verlag) [Google Scholar]
- Zeldovich, Y. B., Ruzmaikin, A. A., & Sokoloff, D. D. 1990, The Almighty Chance (Singapore: World Scientific Publishing) [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1. Time evolution of several volume-averaged quantities over 200 orbits. Magnetic energy (top left), kinetic energy (top right), normalized Maxwell stress (bottom left) and the total stress (bottom right). The darkness of the curves is determined by the strength of the artificial resistivity parameter, αB = 0.25, 0.5, 1.0, 2.0, 4.0. Due to the high oscillatory nature of the simulation we have smoothed the curves using a Savitzky–Golay filter, the unsmoothed curves can still be seen as very transparent curves. The oscillations are related to the formation and destruction of channel modes. |
| In the text | |
 |
Fig. 2. Time-averaged values of several quantities as a function of the artificial resistivity coefficient, for all our unstratified net-flux simulations. From the top left to bottom right: magnetic energy density, Maxwell stress, normalized Maxwell stress, ratio between Reynolds and Maxwell stresses, total stress, ratio between radial and total magnetic field energy. For some quantities we have plotted the total time average (shown in green), the time average of the turbulent component (shown in orange) and the time average of the mean-field component (shown in blue). |
| In the text | |
 |
Fig. 3. Generation and break down of a channel mode during the unstratified net-flux run with αB = 0.5. The figure depicts a surface rendering of the radial velocity within the shearing box. The two-channel flow is clearly seen in the left picture which over an orbit is quickly broken down into turbulence, as seen in the right figure. The generation of the channel mode coincides with a peak in the magnetic energy and as the channel flow is destroyed the magnetic energy will decrease. The formation and destruction of these channel flows occur continuously throughout the simulation. |
| In the text | |
 |
Fig. 4. Spacetime diagrams showing the azimuthal magnetic field at the top and the total stress at the bottom. The left figures shows the simulation with an artificial resistivity coefficient αB = 0.5 and the right figures show the simulation with αB = 4. The figures clearly show the peaks related to the continuous creation and destruction of channel modes. Increasing the resistivity leads to a suppression of small scale magnetic fluctuation, and this means that more of the stress will be generated by the mean-field component. |
| In the text | |
 |
Fig. 5. Time-averaged turbulent transport coefficient from the unstratified net-flux cases. To minimize noise/bias we have set αxx = αyy, ηxx = ηyy, αyx = 0.0 and ηxy = 0.0. We can see that only the turbulent resistivity ηxx has a consistent value above 0.0, with a value of about 0.008. |
| In the text | |
 |
Fig. 6. Time evolution of several volume-averaged quantities for the standard box, unstratified ZNF cases at as resolution of nx = 96: magnetic energy (top left), kinetic energy (top right), normalized Maxwell stress (bottom left) and the total stress (bottom right). The red line show the case of Pm, AR = 3.0 where we set the Prandtl number by altering the AR strength. The green lines show the case where we set the Prandtl number by altering the AV strength, the darkness of the curve is determined by the value of the set Prandtl number, Pm, AV = [0.25, 3.0, 6.0]. The blue curves represent the cases with a set AR coefficient without forcing the Prandtl number, where the darkness is determined by the strength of the artificial resistivity parameter, αB = [0.25, 0.5, 1.0, 2.0, 4.0]. Four of the nine cases reach a saturated state (αB = 0.25, Pm, AR = 3.0, Pm, AV = 3.0, Pm, AV = 6.0) The code default value of αB = 0.5 sustains turbulence for around 50 orbits before decaying. |
| In the text | |
 |
Fig. 7. Time evolution of several volume-averaged quantities for the tall box, unstratified ZNF cases at a resolution of nx = 48: magnetic energy (top left), kinetic energy (top right), normalized Maxwell stress (bottom left) and the total stress (bottom right). The red line show the case of Pm, AR = 3.0 where we set the Prandtl number by altering the AR strength. The green lines show the case where we set the Prandtl number by altering the AV strength, the darkness of the curve is determined by the value of the set Prandtl number, Pm, AV = [0.25, 3.0, 6.0]. The blue curves represent the cases with a set AR coefficient without forcing the Prandtl number, where the darkness is determined by the strength of the artificial resistivity parameter, αB = [0.25, 0.5, 1.0, 2.0, 4.0]. Four of the nine cases reach a saturated state (αB = 0.25, Pm, AR = 3.0, Pm, AV = 3.0, Pm, AV = 6.0). The code default value of αB = 0.5 sustains turbulence for a long time but starts to decay after around 120 orbits. |
| In the text | |
 |
Fig. 8. Time-averaged values of several quantities for all our unstratified, zero net-flux simulations with standard box size (L = [1.0, π, 4.0]) and resolution nx = 96. From the top left to bottom right: magnetic energy density, Maxwell stress, normalized Maxwell stress, ratio between Reynolds and Maxwell stresses, total stress, ratio between radial and total magnetic field energy. The x-axis shows the time-averaged effective Prandtl number of the simulation. For some quantities we have plotted the total time average (shown in green), the time average of the turbulent component (shown in orange) and the time average of the mean component (shown in blue). The circles represent the simulations where we have adjusted the strength of the artificial resistivity, while the star symbols represent the simulations where we have adjusted the artificial viscosity. |
| In the text | |
 |
Fig. 9. Time-averaged values of several quantities for all our unstratified, zero net-flux simulations with tall box size (L = [1.0, π, 4.0]) and resolution nx = 48. From the top left to bottom right: magnetic energy density, Maxwell stress, normalized Maxwell stress, ratio between Reynolds and Maxwell stresses, total stress, ratio between radial and total magnetic field energy. The x-axis shows the time-averaged effective Prandtl number of the simulation. For some quantities we have plotted the total time average (shown in green), the time average of the turbulent component (shown in orange) and the time average of the mean component (shown in blue). The circles represent the simulations where we have adjusted the strength of the artificial resistivity, while the star symbols represent the simulations where we have adjusted the artificial viscosity. |
| In the text | |
 |
Fig. 10. Spacetime diagrams showing the horizontal-averaged azimuthal magnetic field for the unstratified, zero net flux case (Pm, AV = 3). We can see that the tall box has larger structured mean-fields than the standard box. Compared to Shi et al. (2016) the rendered pattern of the mean-fields are similar, however, they produce much stronger mean-fields in their tall box simulations. |
| In the text | |
 |
Fig. 11. Time-averaged values of several quantities for our resolution study of the unstratified, zero net-flux cases with Pm, AR = 3.0 and Pm, AV = 6.0, which includes tall box and standard box simulations. From the top left to bottom right: magnetic energy density, Maxwell stress, normalized Maxwell stress, ratio between Reynolds and Maxwell stresses, total stress, ratio between radial and total magnetic field energy. For some quantities we have plotted the total time average (shown in green), the time average of the turbulent component (shown in orange) and the time average of the mean component (shown in blue). The circles represent the simulations where we have adjusted the strength of the artificial resistivity, small circles represent standard box cases and large circles represent tall box. While the star (standard box size) and large stars (tall box size) represent the simulations where we have adjusted the artificial viscosity. |
| In the text | |
 |
Fig. 12. Resolution dependence of the numerical Prandtl number for the unstratified, zero-flux cases on the left (Sect. 3.2) and for the stratified, net-flux cases to the right (Sect. 4). This shows cases with an AR coefficient set to αB = 0.5, which is our code default. We can see that we have an almost linear increase with higher resolution for both cases. |
| In the text | |
 |
Fig. 13. Time-averaged turbulent transport coefficients from the unstratified, zero net-flux cases, with the standard box size cases (L = [1.0, π, 1.0], nx = 96) to the left and the tall box cases (L = [1.0, π, 4.0], nx = 48) to the right. The circles represent the simulations where we have adjusted the strength of the artificial resistivity, while the star symbols represent the simulations where we have adjusted the artificial viscosity. To minimize noise we have set αxx = αyy, ηxx = ηyy, αyx = 0.0 and ηxy = 0.0. We can see that the α coefficients have values of around zero as expected for the unstratified case and ηxx with a consistent positive value. For the standard box ηyx remain close to zero while for the tall box we see a consistent positive value which is contrary to what was seen by Shi et al. (2016). |
| In the text | |
 |
Fig. 14. Time evolution of several volume-averaged quantities for the stratified net-flux simulations with varying artificial resistivity (αB = [0.3, 0.5, 1.0, 2.0]) at a resolution of nx = 58. Magnetic energy (top left), kinetic energy (top right), normalized Maxwell stress (bottom left) and the total stress (bottom right). The red lines show the simulations run with TSPH and blue lines show the runs with GDSPH where the darkness of the line represents the strength of the artificial resistivity. We have smoothed the curves using a Savitzky–Golay filter, the unsmoothed curves can still be seen as very transparent curves. |
| In the text | |
 |
Fig. 15. Spacetime diagrams of the stratified net flux simulations, showing the evolution of the horizontal averaged radial (top) and azimuthal (bottom) fields for both GDSPH (left) and TSPH (right) in the case of αB = 0.3 with a resolution nx = 58. Both GDSPH and TSPH develop the characteristic butterfly diagram. However, the TSPH simulation quickly becomes unstable and exhibits a runaway growth in the magnetic field. |
| In the text | |
 |
Fig. 16. Spacetime diagrams of the stratified net flux simulations, showing the evolution of the horizontal averaged radial (top) and azimuthal (bottom) fields for both GDSPH (left) and TSPH (right) in the case of αB = 1 with a resolution nx = 58. At this resistivity only GDSPH reproduce the butterfly diagram, where for TSPH a strong positive azimuthal field permeates the disk corona (|z|> 2). The azimuthal field is additionally amplified as the simulation goes on and starts to propagate into the central disk region. |
| In the text | |
 |
Fig. 17. Stratified shearing box simulation with net-flux, shows the surface rendering of the azimuthal field (top) and the density (bottom). Left: case for GDSPH and right: case with TSPH. In the TSPH case we can see that there is excessive growth in the magnetic field in the outer part of the disk. |
| In the text | |
 |
Fig. 18. Time-averaged values of several quantities for all our stratified net-flux simulations as a function of the artificial resistivity (αB) at a resolution of nx = 58. From the top left to bottom right: magnetic energy density, Maxwell stress, normalized Maxwell stress, ratio between Reynolds and Maxwell stresses, total stress, estimated numerical Prandtl number. For some quantities we have plotted the total time average (shown in green), the time average of the turbulent component (shown in orange) and the time average of the mean component (shown in blue). The circles represent the simulations run with GDSPH while the diamonds represent the simulations run with TSPH. |
| In the text | |
 |
Fig. 19. Time evolution of several volume averaged quantities for the stratified net-flux simulations with varying resolution (nx = [48, 58, 74, 93]) and the artificial resistivity coefficient set to αB = 0.5. Magnetic energy (top left), kinetic energy (top right), normalized Maxwell stress (bottom left) and the total stress (bottom right). The green lines show the simulations run with TSPH and purple lines show the runs with GDSPH. The darkness of the line indicate the resolution, where the darkest line represents the highest resolution. |
| In the text | |
 |
Fig. 20. Time-averaged values of several quantities for all our stratified net-flux simulations with artificial resistivity coefficient set to αB = 0.5, plotted over the resolution (particles along the x-axis). From the top left to bottom right: magnetic energy density, Maxwell stress, normalized Maxwell stress, ratio between Reynolds and Maxwell stresses, total stress, ratio between azimuthal and total magnetic field energy. For some quantities we have plotted the total time average (shown in green), the time average of the turbulent component (shown in orange) and the time average of the mean component (shown in blue). The circles represent the simulations run with GDSPH while the diamonds represent the simulations run with TSPH. |
| In the text | |
 |
Fig. 21. Horizontal time-averaged turbulent transport coefficient in the z direction from the stratified net-flux cases. The darkness of the curves is determined by the strength of the artificial resistivity parameter, αB = 0.3, 0.5, 1.0, 2.0. We can see that we have a negative αyy effect that is negative (positive) in the top (bottom) half of the box. This enables the αω-dynamo to operate efficiently within the central region. αxx on the other hand has a positive gradient and will act against the shear term. Turbulent pumping advects magnetic fields outwards from the central region with velocity |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




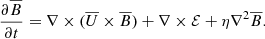
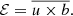

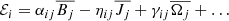
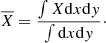
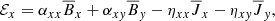
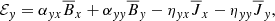
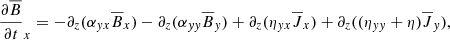
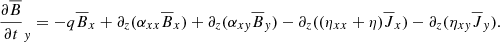
![$$ \begin{aligned} A_{1} = \left[\overline{B}_x\mathcal{E} _x, \overline{B}_{ y}\mathcal{E} _x,\overline{J}_x\mathcal{E} _x, \overline{J}_{ y}\mathcal{E} _x\right], \end{aligned} $$](/articles/aa/full_html/2022/03/aa41206-21/aa41206-21-eq26.gif)
![$$ \begin{aligned} A_{2} = \left[\overline{B}_x\mathcal{E} _{ y}, \overline{B}_{ y}\mathcal{E} _{ y},\overline{J}_x\mathcal{E} _{ y}, \overline{J}_{ y}\mathcal{E} _{ y} \right], \end{aligned} $$](/articles/aa/full_html/2022/03/aa41206-21/aa41206-21-eq27.gif)