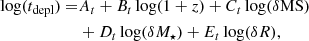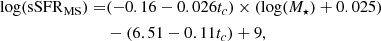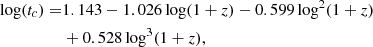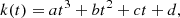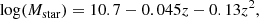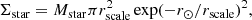| Issue |
A&A
Volume 659, March 2022
|
|
|---|---|---|
| Article Number | A64 | |
| Number of page(s) | 23 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/202039526 | |
| Published online | 07 March 2022 | |
Rapid early gas accretion for the inner Galactic disc
A case for a short accretion timescale
1
GEPI, Observatoire de Paris, PSL Research University, CNRS, 5 Place Jules Janssen, 92190 Meudon, France
e-mail: owain.snaith@obspm.fr
2
Sorbonne Université, CNRS UMR 7095, Institut d’Astrophysique de Paris, 98bis bd Arago, 75014 Paris, France
3
Leibniz-Institut für Astrophysik Potsdam (AIP), An der Sternwarte 16, 14482 Potsdam, Germany
4
Institute of Astronomy, Russian Academy of Sciences, 48 Pyatnitskya St., Moscow 119017, Russia
Received:
25
September
2020
Accepted:
26
November
2021
Context. Recent observations of the Milky Way and galaxies at high redshifts suggest that galaxy discs were already in place soon after the Big Bang. While the gas infall history of the Milky Way in the inner disc has long been assumed to be characterised by a short accretion timescale, this has not been directly constrained using observations.
Aims. Using data for the inner regions of the Milky Way recently produced by APOGEE and Gaia and of unprecedented quantity and quality, we aim to derive strong constraints on the infall history of the inner (< 6 kpc) Galaxy (with a focus on stars between 4 and 6 kpc, which we show is an appropriate proxy for the entire inner disc).
Methods. We implemented gas infall into a chemical evolution model of the Galaxy disc, and used a Schmidt–Kennicutt law to connect the infall to the star formation. We explore a number of models, and two different formulations of the infall law. In one formulation, the infall is non-parametric, and in the other the infall has an explicitly exponential form. We fit the model parameters to the time–[Si/Fe] distribution of solar vicinity stars, and the metallicity and [Si/Fe] distribution function of stars with a galactocentric radius of between 4 and 6 kpc from APOGEE.
Results. Our results point to a fast, early gas accretion, and an upper limit on the accretion timescale of around 2 Gyr in the inner disc of the Milky Way. This suggests that at least half the baryons were in place within 2−3 Gyr of the Big Bang, and that half the stars of the inner disc formed within the first 5 Gyr, during the thick disc formation phase. This implies that the stellar mass of the inner disc is dominated by the thick disc, supporting our previous work, and that the gas accretion onto the inner disc was rapid and early.
Key words: Galaxy: evolution / Galaxy: abundances / Galaxy: disk / methods: numerical
© O. Snaith et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
Understanding the history of the Milky Way requires a combination of observations (e.g. Ahumada et al. 2020; Hayden et al. 2015; Adibekyan et al. 2012; Queiroz et al. 2020), simulations (e.g. Guedes et al. 2011; Brook et al. 2012, 2020; Roškar et al. 2013; Buck 2020), models (e.g. Chiappini et al. 1997; Côté et al. 2017; Spitoni et al. 2019), and statistical analysis (Ness et al. 2019; Ciucă et al. 2021), because each approach offers different insights into its formation. The long timescale for many astrophysical processes means that we usually cannot see them taking place directly, and so must rely on models and simulations, which can then be compared to observations.
Recent surveys, such as Gaia (Gaia Collaboration 2016, 2018), APOGEE (Nidever et al. 2014; Majewski et al. 2017), GALAH (Buder et al. 2018), LAMOST (Cui et al. 2012), and local spectroscopic surveys such as the one carried out by Adibekyan et al. (2012), have provided detailed information about the properties of stars. Recently, accurate stellar ages (e.g. Haywood et al. 2013; Silva Aguirre et al. 2018; Mackereth et al. 2019) allowed us to constrain the star formation history (SFH) of the Galaxy (Snaith et al. 2014, 2015; Spitoni et al. 2019) to a degree which was previously impossible. This has resulted in evolution of our understanding of the transition from early to late star formation, and brought the timescale for the onset of the build-up of the thick and thin disc forward from very early times (e.g. Chiappini et al. 1997) to later times (e.g. Snaith et al. 2014; Spitoni et al. 2019, 2020).
Since we presented our model of the SFH of the Milky Way in Snaith et al. (2014, 2015), new observations from APOGEE (Nidever et al. 2014; Ahumada et al. 2020; Hayden et al. 2015) have been released, and have been studied in detail. These developments mean that our chemical evolution model must be compared to these newer data sets. However, since its first publication, our ‘closed-box’ model has remained highly robust to comparisons with data (e.g. Haywood et al. 2015, 2016a,b, 2018, 2019).
Solar vicinity data from Adibekyan et al. (2012), with precise ages from Haywood et al. (2013), offer insight into the makeup of the Milky Way. Many studies, such as Chiappini et al. (1997), up to more recent studies, such as Grisoni et al. (2018) and Spitoni et al. (2019), attempt to fit all the stars in the solar vicinity with a single chemical evolution. This evolution is tuned to account for both the high and low α sequence in the [Fe/H]–[α/Fe] distribution. The picture is made more complicated because stars do not remain at their place of origin, but move through the disc because of the action of various processes (e.g. Sellwood & Binney 2002; Sánchez-Blázquez et al. 2009; Schönrich & Binney 2009; Minchev et al. 2011; Radburn-Smith et al. 2012; Kubryk et al. 2015; Halle et al. 2018). Thus, any given region of the disc incorporates stars that evolved in a wide range of birth radii. This means they could potentially have formed in different environments, with different evolutions. The high α sequence is therefore associated with stars that formed in the inner region, which we consider to be an essentially ‘closed box’, after a period of rapid early infall. However, this was thought to be an approximation, because it is known from both observations and cosmological simulations that a degree of infall continues until the present day, despite the infall rate falling off with time (e.g. Dekel et al. 2009).
Other authors have found Milky Way-like parallel sequences in the [α/Fe]–[Fe/H] relation in simulations. For example, simulations by Brook et al. (2004, 2005) associated the dual sequences with high early star formation caused by mergers at early times. The simulations of Buck (2020) also produce a low-alpha sequence through mergers, while more recently Renaud et al. (2021) showed that α-enhanced stars may have formed during starburst episodes associated with mergers, while the low-alpha sequence may be the result of an in situ, more quiescent star formation. In these examples, interactions with other objects are used to build up the two sequences rather than purely stochastic processes. In our modelling, we are less interested in the origin of our accreted gas than its impact on the chemical evolution and overall accretion rate.
From spectroscopic survey data we can see that there is a split in the evolution of the [Fe/H]–[α/Fe] distribution into two sequences according to the distance from the Galactic centre (Bensby et al. 2011; Bovy et al. 2012; Haywood et al. 2013; Ahumada et al. 2020; Leung & Bovy 2019; Queiroz et al. 2020). The outer disc corresponds to the low alpha sequence, and may require dilution at later times in order to mimic observations (Snaith et al. 2015), while the inner regions correspond to the distinct high-alpha sequence.
APOGEE shows that the low-alpha sequence is increasingly dominant with increasing radius (Hayden et al. 2015; Leung & Bovy 2019; Queiroz et al. 2020; Anders et al. 2014). This implies that stars in the high- and low-alpha sequences in the solar vicinity have different origins, meaning that each sequence should be fitted using its own separate evolution. This is reinforced by results from dynamical simulations (e.g. Halle et al. 2015, 2018; Khoperskov et al. 2020a) that show that the outer Lindblad resonance (OLR) of the bar can suppress migration across it, although the OLR region itself is found to be quite broad. This effectively makes the regions inside and outside the OLR region separate environments by suppressing mixing. This may allow the inner and outer discs to have a different evolution, leading to the formation of two sequences in [Si/Fe]–[Fe/H]. Thus, the traditional galactic chemical evolution approach for the solar vicinity (Chiappini et al. 1997; Spitoni et al. 2019), which tries to fit both the high- and low-α sequences to a single evolution, is not the only, or necessarily the best way to approach modelling the solar vicinity.
There is increasing evidence that the thick disc is a massive component of the Milky Way (Haywood et al. 2013; Snaith et al. 2014, 2015) and that galaxy discs can build up rapidly at high redshift (Neeleman et al. 2020). For example, very low-metallicity stars (with [Fe/H] < −4) have been found on disc orbits, suggesting that disc assembly can begin very early (Sestito et al. 2019, 2020; Di Matteo et al. 2020). A detailed discussion of this scenario for the structure of the Milky Way can be found in Haywood et al. (2019), including an explanation of how infall in the outer regions of the disc produces the low-alpha sequence. Haywood et al. (2019) presented an analysis which shows that the Sun is an ‘outer disc’ star, with properties characteristic of the low-α sequence. The distribution of stars in abundance–metallicity space is thought to be built up through contributions from separate regions of the disc with distinct evolutions, as described in Snaith et al. (2015). The separate evolutions for the inner and outer discs are discussed in detail in Haywood et al. (2018, 2019) respectively.
There are a number of approximations used in our chemical evolution model (Snaith et al. 2014), which requires detailed testing. For the inner disc, we assume that metals can be diluted by all the gas which is eligible to form stars across cosmic time, i.e. a very large reservoir is in place from the beginning of the model run. This is implemented with the assumption that the total amount of gas present at t = 0 is equal to unity, and the integral of the SFH is also equal to one. The total stellar mass in these normalised units is around 0.7 because of gas released back into the interstellar medium (ISM) due to stellar evolution (and depends on the initial mass function (IMF), Snaith et al. 2015).
However, we argue that our model is a first-order approximation of where the majority of infall to the inner disc takes place early. The exact shape of the SFH is therefore assumed to be sculpted by other processes on top of the Schmidt–Kennicutt law (Kennicutt 1998) normally used in galactic chemical evolution models to convert gas into stars. This is in contradiction to the classical understanding of galaxy evolution, where the infall of gas is important for shaping galaxies (e.g. Dekel & Birnboim 2006). In this paper, we seek to open the box and allow explicit infall onto the galaxy in order to resolve the differences between our model with no infall and the results of observations, simulations, and models that provide evidence of explicit infall.
The data we use to tune our model is presented in Sect. 2. We briefly outline our chemical evolution model in Sect. 3. In Sect. 4 we explore various scenarios and parameter combinations using our model, and then present the key results from our preferred scenario. We discuss and contextualise our results in Sect. 5, and finally present our conclusions in Sect. 6.
2. Data
We make use of data from Delgado Mena et al. (2017), who provide highly precise spectroscopy for 1111 FGK stars from Adibekyan et al. (2012), and combine this with Gaia DR2 parallaxes. These data (with the exception of Gaia) were also used by Haywood et al. (2013) to derive the ages of stars using a Bayesian estimate for each star. The entire Delgado Mena et al. (2017) sample was pruned so that the age sample contained only robust estimates. These ages have a formal error of < 1 Gyr random error and 1 Gyr systematic error (i.e. there is a systematic change in the calculated ages if different stellar isochrones are used; Haywood et al. 2013). These data provide us with elemental abundance ratios for a range of elements including [Fe/H], [Mg/H], and [Si/H], as well as stellar ages for a total of 301 stars, after pruning.
From the chemistry of solar vicinity stars we can separate the stellar populations into those from the inner and outer discs (e.g. Haywood et al. 2019). This division is backed up by both observations (Queiroz et al. 2020) and dynamical simulations (Buck 2020). In addition to the split between inner and outer disc stars, the inner disc itself can be decomposed into the thick disc and an inner thin disc. Similarly to Snaith et al. (2015) and Haywood et al. (2013), the outer disc is defined according to the low-alpha sequence as those stars that obey
Our inner disc sample contains a total of 161 stars in the abundance–time distribution, with the remainder being assigned to the outer disc or discarded (see Fig. 1). Of the remaining stars, the thick disc and inner thin disc are separated by the knee of the age–[Si/Fe] distribution at around 8 Gyr ago. This is a logical place to subdivide the sample into different populations, because it marks a strong change in the behaviour of the chemical evolution (specifically the [Si/Fe], but this can also be seen in other elements such as Mg) of the stars.
 |
Fig. 1. Chemical and age distribution of stars from spectroscopic surveys. Top row and bottom left panel: decomposition of the chemistry–age distribution of stars from Delgado Mena et al. (2017) with ages by Haywood et al. (in prep.) Top row and bottom left panel: stars are coloured according to whether they are part of the inner or outer disc. Several young alpha-rich stars (Haywood et al. 2013) shown in blue are removed from the sample. Bottom right panel: distribution of inner disc stars taken from APOGEE, with the inner disc stars from Adibekyan et al. (2012) and Delgado Mena et al. (2017) plotted as white points. |
In addition to this solar vicinity data we also make use of data from APOGEE (e.g. Nidever et al. 2014; Majewski et al. 2017), specifically from SDSS DR16 (Ahumada et al. 2020) with distances taken from the Starhorse catalogue by Queiroz et al. (2020). We select data where 4 < Rgal < 6 kpc, where Rgal is the current distance of the star from the centre of the galaxy. This sample of 8871 stars is then used to calculate the metallicity and abundance distribution functions (MDF and αDF respectively). This provides us with a signature of the chemical evolution in the inner disc which samples the number of stars with a given metallicity and abundance. This encodes additional information, compared to the time–abundance distribution, which provides the locus of the regions of age–chemistry space sampled by stars. The distribution of stars we use to constrain the MDF and αDF of the inner disc are shown in the bottom right-hand panel of Fig. 1. We use the [Fe/H] and [Si/Fe] values drawn from the astronn VAC (Leung & Bovy 2019). However, we do not use stellar ages from APOGEE, instead relaying on the ages and abundances from Delgado Mena et al. (2017).
We seek to capture the average properties of stars in the inner disc using our one-zone model. Other works (e.g. Spitoni et al. 2019) make use of stars in the solar vicinity (approximately 8 kpc from the centre of the Galaxy), but because the solar vicinity appears to be a transition region between the inner and outer disc (separated by the OLR region, with a width of several kpc at around 9−10 kpc; Khoperskov et al. 2020a), stars close to the Sun are not specifically representative of the inner disc. Instead, we limit our range to less than 6 kpc to avoid contamination by outer-disc stars, and greater than 4 kpc to diminish contamination by the bulge and bar. We take the stars in this region to be representative of the entire inner disc. This is discussed in greater detail in Sect. 4.4.
The outer disc and young alpha-rich stars (Haywood et al. 2013) are removed from the sample, and we focus on the inner disc only. We also show a comparison between the stars in the Delgado Mena et al. (2017) sample and the stars selected from APOGEE in the bottom right panel of Fig. 1. One difference is that the Delgado Mena et al. (2017) data seem to be representative of the lower limit of the [Si/Fe]–[Fe/H] between [Fe/H] = −0.75 and [Fe/H] = 0. We also see two density peaks in the distribution, also seen by Queiroz et al. (2020), along the evolution of the upper sequence. It is interesting to note that the lower metallicity peak is very poorly sampled by our subsample of Delgado Mena et al. (2017) with robust ages. This may be due to the fact that the Delgado Mena et al. (2017) data do not extend far from the plane, while the velocity dispersion in the z-direction is large at lower metallicities. The fact that the Delgado Mena et al. (2017) data sample the lower edge of the APOGEE thick disc may be due to a small offset in the two catalogues, or due to the relatively small numbers of stars in that region of the plot.
2.1. Selection function
For careful comparison between the chemical evolution model and the MDF and αDF of APOGEE we must consider the selection function of the survey. Following the method of Fragkoudi et al. (2018), we make use of an N-body simulation containing 1 × 107 particles, and composed of three discs with different chemical distributions. The stars assigned to each of the three discs (thin disc, intermediate disc, and thick disc) are taken randomly from under a Gaussian distribution in [Fe/H] and [α/Fe], with a given centre and width. The chemical and morphological properties of these discs are given in Table 1 of Fragkoudi et al. (2018)1. This approach will allow us to explore the importance of the selection function, both in terms of the impact of the different pointings on the sky, and the distance effects due to the magnitude-limited nature of the survey.
We centre the simulated galaxy at the density peak of the disc, and place the Sun such that it lies at x = −8 kpc. We rescale the simulation such that the bar has a length of 4.5 kpc in order to match the Milky Way bar length found in Bland-Hawthorn & Gerhard (2016).
We assume that the inner disc has a flat metallicity gradient, which matches well with our one-zone chemical evolution model. We seek to identify the average SFH and chemical evolution of the inner region (or at least the region between 4−6 kpc) and so both the N-body model and GCE model are consistent in their assumptions. For more details about the simulation please see Sect. 2 of Fragkoudi et al. (2018), with further discussion in Khoperskov et al. (2020b).
We recover the direction and radius of each APOGEE pointing from the survey. In order to select the stars in the N-body model along each line of sight we convert the model into Galactic coordinates using Astropy (Astropy Collaboration 2013, 2018). We then select all stars in the simulation along each pointing using Balltree from sci-kit learn (Pedregosa et al. 2011). Thus, for each APOGEE pointing we have a corresponding field through the N-body simulation.
The N-body simulation produces far fewer star particles in the fields at high Galactic latitude and more at low Galactic latitude relative to the survey, and this is depicted in Fig. 2. Further, each star particle in the simulation consists of approximately 8 × 103 individual stars (assuming they have 1 solar mass). The low number of star particles at high latitude means that the stellar density field is poorly sampled, making it more difficult to study the selection function. In order to mitigate this effect, we re-bin the APOGEE pointings in order to find the selection function of a collection of pointings. We use a varying number of bins with Galactic latitude, following the gridding procedure from Duarte & Mamon (2014). The number of bins varies over latitude according to
 |
Fig. 2. Comparison between number of stars at a given Galactic latitude in different APOGEE pointings. Left: from the APOGEE survey. Right: from an N-body simulation. |
where δb is the range in latitude over the number of latitude bins. We set the number of latitude bins to 15 and 20 longitude bins at the equator.
In each bin, we identify the distance distribution from the APOGEE survey by generating a histogram of the stars, binned by distance, between 0 and 20 kpc. For each pointing we use these histograms to generate a cumulative probability function. We then assign each star from the N-body simulation a weighting by interpolating along this probability function and generate a random number between 0 and 1. We select the first star particle, ordered by distance, where its weighting exceeds the random number. We repeat this process, with replacement, until we have the same number of star particles as there are in the APOGEE survey pointings or bins.
There are differences between the overall N-body simulation MDF and the reconstructed MDF for individual pointings (Fragkoudi et al. 2018), but this seems to be less true as we sum all the various pointings because the model and reconstructed MDFs strongly converge.
In Fig. 3 we show the effect of the above selections on the N-body MDF and αDF between 4−6 kpc. Specifically, we show the original distribution functions (DFs) of the simulation, the DFs for all star particles along each APOGEE pointing or bin, and the result of the entire process, including matching the distance distribution function (DDF). The relatively small deviation of the final DFs from the original DFs suggests that convolving the APOGEE data with a complex selection function is unnecessary for our purposes. Given the uncertainties in comparing the observations, the simulation, the expected true distribution of stars, and the relatively small deviation between the different distributions in Fig. 3, we chose to use the MDF and αDF from the APOGEE sample without deconvolution.
 |
Fig. 3. MDF and αDF from an N-body simulation. Left panel: raw MDF, right: αDF. The blue line is the DFs of all star particles in the N-body model, the orange line shows the DFs of all particles along each APOGEE pointing, and the green line shows the DFs of the star particles along each pointing, with the same DDF as APOGEE. We show the MDF and αDF for stars with a galactocentric radius of 4−6 kpc. |
There are additional factors in the selection function which may influence the shape of the distribution functions. For example, we have not fully accounted for the three magnitude cohorts in APOGEE, where different pointings can reach different magnitude limits. The processing of APOGEE can give a greater weighting to stars in the brighter cohorts. This would impact our sample because there is a luminosity difference between metal-rich and metal-poor stars. This is because, at a given mass, metal-poor stars have a higher effective temperature and luminosity. Furthermore, thin-disc stars can be expected to suffer from higher extinction than thick-disc stars, because extinction is higher at lower Galactic latitudes. Majewski et al. (2017) show that extinction can cause the thick-disc population to extend to greater distances than the thin-disc stars. This can therefore be expected to impact the shape of the MDF, biasing it towards thick-disc stars. If this effect is considerable, the shape of the MDF and αDF can change, pushing infall and star formation to a different redshift. Thus, certain selection effects may remain in our data. A detailed calculation of the distribution functions is beyond the scope of this paper, but it must be noted that the results presented here, and the effects of the selection function, may not have been fully disentangled. Nevertheless, for this paper we assume these to be second-order effects.
An additional factor that may affect the results is the impact of radial migration. As there is no dynamical information in a chemical evolution model, we cannot hope to replicate the impact of churning (Sellwood & Binney 2002).
The astronn VAC from APOGEE gives us access to a guiding radius for the orbits. This has the advantage of reducing the effect of blurring, but requires various approximations in terms of the shape of the Milky Way potential. We discuss this in detail in Sect. 4.3.
3. Models
The model discussed in this paper makes use of the chemical yields and overall design of the model presented in Snaith et al. (2014, 2015). Our original model calculated the chemical evolution of the solar vicinity using a sample of stars similar to the one described in the previous section (and shown in the top row and bottom left panels of Fig. 1). The Snaith et al. (2015) chemical evolution model differs from the ‘traditional’ type of model in two ways: firstly it is designed to fit the high- and low-alpha sequences separately, rather than attempt to fit both with a single evolution, and secondly it decouples the amount of gas present in the system from the star formation rate. More explicitly, our previous model consisted of a gas reservoir that was used to form stars that then release gas and metals into the reservoir according to the chosen IMF and selected stellar yields. Inflows and outflows were treated implicitly; the gas reservoir was used only to dilute metals and form stars, and there is no explicit information as to whether the gas was in the hot, warm, or cold phase, and indeed could be in any form. We started the simulation with a total gas mass of unity, and constrained the system so that the integral of the SFH is also unity. This means that in normalised units, the stellar mass is always less than unity, because of the gas returned to the ISM by each stellar population, mainly from AGB stars and SNII (as discussed in Snaith et al. 2015).
However, we know from detailed studies of galaxy formation and evolution that gas falls into galaxies over time (e.g. Larson 1972; Dekel & Birnboim 2006). There is also a strong relationship between the cold gas density and the star formation rate (Schmidt 1959). In most chemical evolution models, it is assumed that the amount of gas in the cold phase follows a Schmidt–Kennicutt law (Schmidt 1959; Kennicutt 1998),
where Σg is the surface density of the star forming gas, ϵ is the normalisation constant we will call the star formation efficiency parameter, k is a constant usually assumed to be around k = 1.5 (Kennicutt 1998), and ΣSFR is the star formation rate surface density. Many models neglect gas that might be present in the warm or hot gas phases, and assume that all gas is potentially star forming.
Our model makes use of the instantaneous mixing approximation2, which is where we assume that the metals mix with all the gas present at the time of formation. For a detailed discussion of the model see Snaith et al. (2015)3. In this paper we elaborate on our previous model to include explicit infall and a Schmidt–Kennicutt relation between gas surface density, Σg, and star formation rate surface density, ΣSFR. The initial mass of the reservoir is zero, and pristine gas is added over time according to a given infall law. We assume pristine gas, following previous work, such as Troncoso et al. (2014). The exact mix of the infalling gas is unknown, and could be expected to be evolving. Thus, assuming pristine gas is a reasonable compromise to reduce the number of parameters. Various authors have discussed pre-enrichment of infalling gas, such as Tsujimoto et al. (2010). However, our assumption of pristine infall is a reasonable one, which is common in the literature considering the other uncertainties in the model (e.g. stellar yields or IMF, Romano et al. 2010; Snaith et al. 2015).
We use two different formalisms for the infall law. In one set of runs, the infall rate of pristine gas follows the traditional form (see e.g. Chiappini et al. 1997), and the gas infall rate declines exponentially, and is determined by,
where,
where n is the number of infall episodes, t is the time, tstart, i is the start of the infall episode, and τi is the timescale of the episode. Each era of the model run is able to have its own infall rate and constant, ϵi. For a given infall event, the total surface density after 14 Gyr is given by,
In each time-step we add pristine gas to the model with mass Ψbarydt. We set the model so that the final baryonic mass surface density of the disc is 60 M⊙ pc−2.
Alternatively, we add gas without an explicit functional form. We subdivide the evolution into 14 eras, each lasting 1 Gyr, with an infall rate given by the amplitude ‘A’. We make use of a modification of Eq. (5) and set τ = 1000 and stop infall after 1 Gyr, e.g.
This produces a series of essentially ‘top hat’ infall episodes, which sum together to form the overall infall history of the model galaxy.
We calculate the star formation in a given time-step according to Eq. (3), and the gas is removed from the ISM. We do not incorporate the frequently implemented star formation threshold of 7 M⊙ kpc−2 (e.g. Chiappini et al. 1997). We use k = 1.5, and ϵ is normalised by 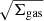 , or more formally, scaled by
, or more formally, scaled by 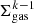 (e.g. Chiappini et al. 1997). This scales the star formation rate surface density with total baryon surface density, and means the star formation law is effectively scale-free. This means that our chosen total surface density (60 M⊙ pc−2) is irrelevant for choosing a chemical evolution and could be any value.
(e.g. Chiappini et al. 1997). This scales the star formation rate surface density with total baryon surface density, and means the star formation law is effectively scale-free. This means that our chosen total surface density (60 M⊙ pc−2) is irrelevant for choosing a chemical evolution and could be any value.
We then cycle back over all preceding time-steps to calculate the mass and abundances released from already formed stars. Over the 14 Gyr of the run, stars return approximately 30% of their mass back into the ISM, most within the first gigayear. In the infall model, a fraction of the gas is transformed into stars at each step according to Eq. (3). This is controlled by ϵ. In our exponential infall runs, each era can have a different ϵ value. While, in order to be able to use our fitting procedure, we fix the ϵ value at all times for the top hat runs.
In this paper we make use of the same yield tables used in the fiducial model in Snaith et al. (2014, 2015). We assume that the stellar yields overwrite the elements already present in the star when the gas is released back into the ISM. In particular we use Nomoto et al. (2006) for SNII, Karakas (2010) for AGB stars, and Iwamoto et al. (1999) for SNIa and an IMF from Kroupa (2001). We also set the initial values of the primordial gas to be 0.75 hydrogen and 0.25 helium. When calculating the [X/H] value for a given element, we use the average atomic mass in the Universe as an approximation for the specific mix of isotopes released from stars. Although these are not the most recent stellar yields in the literature, we use them in order to compare our result to our previous work (Snaith et al. 2014, 2015) and defer exploration of the impact of additional yield tables to a future study.
In order to mimic the observed MDF and αDF from APOGEE, we produce a histogram of the [Fe/H] and [Si/Fe] track weighted by the stellar mass distribution. However, for each time-step we add a random error drawn from a Gaussian distribution with σ = 0.02. We generate 30 histograms with different random errors and normalise the resulting histogram so that the sum of all bins is equal to unity. We use a fixed random number seed for each run so that our results are reproducible on different runs of the model (except when bootstrapping to calculate uncertainties).
The MDF and αDF are calculated by binning the points along the stellar evolution track (number of time-steps) by [Fe/H] or [α/Fe] and are given by,
where SFHj is the stellar mass in bin j, Mj(i) is the sum of all stars in the jth bin, and Mi, j is the sum over all stars in all bins.
As well as fitting the time–[Si/Fe] distribution, as we did in Snaith et al. (2014, 2015), we also fit the MDF and/or αDF according to,
where O[Si/Fe] is the value of the observed [Si/Fe] at a given age, M[Si/Fe] is the model value, OMDF, αDF − MMDF, αDF is the difference between the normalised observed and model MDFs (αDFs) in each bin, and ω is a tuning parameter which weights the difference of the distribution functions relative to the difference of abundances. Our choice for ω is discussed in the following section4. We also have the option to vary the ϵ parameter in Eq. (3).
In order to define a model with varying ϵ we make use of the results of Tacconi et al. (2018) to explore the evolution of the star formation efficiency (SFE) as the galaxy mass increases. In Tacconi et al. (2018), their Eq. (5) provides an evolution of the depletion time of the gas as a function of redshift and galaxy stellar mass, that is,
where At, Bt, Ct, Dt and Et are constants, z is the redshift, M⋆ is the stellar mass, δMS is given by δMS = sSFR/sSFRMS, where sSFRMS is given by
where tc is given by
δM⋆ = M⋆/5 × 1010, and δR is a function of the effective radius, which we ignore. From Table 3 of Tacconi et al. (2018) we use the best-fit parameters for the model with log(sSFRMS) taken from Eq. (12), originally defined by Speagle et al. (2014). We define a characteristic ϵ evolution using the star formation rate and stellar mass growth from the best fit to the ωMDF, αDF = 900 run for the flat infall initial conditions, which we discuss in the following section. We fit the resulting evolving ϵ with a third-order polynomial of the form
where (a, b, c, d) = (−0.0013, 0.0379, −0.3102, −0.0378), and k is the modifier on ϵ with time. In order to calculate the total stellar mass and star formation rate from the surface densities, we assume that the disc has an exponential profile with a radial scale length of 2.5 kpc (Porcel et al. 1998) and that the Sun is 8 kpc from the Galactic centre. We select the fixed value of 2.5 kpc to be illustrative of the range of possible values of the radial scale length. It is plausible that the different discs of the Milky Way have different scale lengths (e.g. Bovy et al. 2014), but we use a varying ϵ to be illustrative of a range of possible models rather than to obtain a precise fit because of the large number of additional parameters that would need to be taken into account. The impact of changing ϵ is similar to that of changing rd; changing one parameter is sufficient to explore a range of models.
Figure 4 shows the fitting algorithm and how it interacts with the galactic chemical evolution model. We start with an initial infall history, which produces a chemical evolution track over the 14 Gyr of the evolution of the galaxy. We can compare this to the observations using Eq. (10) in order to produce a single value out of the chemical evolution. We do this by comparing each star in the observations to the chemical evolution track according to their age. We also produce the MDF and αDF using the same bins as the MDF and αDF in the observations, following Eq. (8). We make use of the fitting algorithm to minimise Fij by changing the parameters that define the infall history and ϵ. We use the fmin_powell method from scipy (Virtanen et al. 2020) in Python.
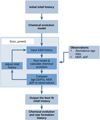 |
Fig. 4. Schematic of the galactic chemical evolution model, and the algorithm to identify the best fit infall history. |
4. An infall history for the milky way
Exponentially decaying infall is the most usual form of infall given in the literature (e.g. Chiappini et al. 1997; Spitoni et al. 2019), and so we first explore what exponential infall (as given by Eq. (5)) can tell us about the evolution of the Galaxy when fitted to the inner disc. We then explore the impact of adopting a more general formulation for infall (given by Eq. (7)) on the build-up of the disc.
4.1. Model with exponential infall
We first divide the history of the galaxy into four epochs, corresponding to the onset, the thick disc, the ‘quenching era’, and the thin-disc era. The first era, the onset, is the initial starburst and has a very rapid infall with a low τ and high ‘A’. This era acts to bring the [Si/Fe] down to the beginning of the data within the first gigayear. This is largely unconstrained, as we do not have data with ages greater than 13 Gyr while the model begins 14 Gyr ago. The second era is the second infall, which then builds up the stellar discs. The third era is the ‘quenching’ era we identified in Haywood et al. (2016b), and the fourth era corresponds to the thin-disc evolution. In correspondence to the Chiappini et al. (1997) GCE model, the first and second eras are the first and second infall in that model, and the third and fourth eras have no additional infall.
Each era has a full set of parameters, including A, the amplitude of the infall, tstart, the onset of the infall, τ, the timescale of the infall, and ϵ, the star formation efficiency parameter. However, Aonset, τonset, and ϵonset are fitted. Athick is set such that the final surface density of baryonic matter at z = 0 is 60 M⊙ pc−2, and τthick is varied from 2 to 10 Gyr (before fitting, and is one of the parameters fitted). However, there is still infall occurring during the quenching and thin-disc eras due to the exponential tail of the infall. ϵ in each era is set to a constant value relative to those of the other eras, although they can vary globally. The amplitude of infall during the quenching and thin-disc phases are set to a very low and a low value, respectively. Possible explanations for the quenching are discussed in Sect. 5. The quenching epoch was included to reproduce the strong change of gradient at around 8 Gyr in the [Si/Fe]–time distribution based on our experiences from Snaith et al. (2014, 2015) and Haywood et al. (2016b). In those works, without the hiatus, the transition is more gradual, and would not replicate this key feature of the chemical evolution. The initial conditions are fitted by eye, and then the overall model is fitted using f_min_powell. Although we included full quenching following previous work, we examine it in more detail in Appendix A. They were fitted to roughly match the time–[Si/Fe] distribution first, and then to remove the early low-[Fe/H] tail in the MDF. Removing this tail is mostly controlled by the parameters of the first infall era. The key parameters for the four eras are given in Table 1.
Initial parameters for the exponential runs.
Where ω > 0, we fit the model using the time–abundance distribution, MDF, and αDF. Where ωMDF = 900 and ωαDF = 900, the distribution functions are strongly dominant over the time–[Si/Fe] distribution when fitting the data, whereas for lower values of ωMDF and ωαDF (=0, 10) the time–[Si/Fe] distribution is dominant over the metallicity and alpha-distributions. The use of high values of ω, such as 900, is advantageous because ages are difficult to calculate and tend to have large uncertainties and other systematics (Leung & Bovy 2019), but confers the disadvantage that it requires surveys with well understood selection functions.
Figures 5 and 6 show a number of fitted chemical evolutions using the exponential infall model. Figure 5 shows the results fitted to the time–[Si/Fe] only (ωMDF and ωαDF = 0.0). The fitting function does not significantly change the resulting infall history, and has a small effect on the overall SFH. The different age–[Si/Fe] evolutions can be fitted with a range of ϵ values. However, as the initial infall time increases, the fit to the MDF becomes increasingly poor.
 |
Fig. 5. Fits of the exponential infall to the time–[Si/Fe] distribution (ωMDF, αDF = 0). Top row, from left to right: best-fit time–[Si/Fe] used to fit the data, the time–metallicity distribution, and the abundance–metallicity distribution. In each panel, the points show the data. Second row: MDF, αDF, and the recovered SFH. The grey histograms show the distribution functions for the inner disc in APOGEE. Third row: evolution of the baryonic mass, gas mass and stellar mass over time. Fourth row: infall rate, and the evolution of the SFE and ϵ. The different lines are for different initial conditions, and the dashed lines show the evolution of those unfitted initial states. |
 |
Fig. 6. Exponential infall model fitted to the MDF and αDF as well as the time–[Si/Fe] with ωMDF = 900 and ωαDF = 900. The panels are the same as in Fig. 5. |
However, when we set ωMDF, αDF = 900 we see different behaviour. We see a much stronger effect on the fitted infall history and SFH, as shown in Fig. 6. The fitted τ values are pulled to much shorter timescales overall. This can be seen in Table 2. The fitted timescales are drawn to more rapid formation times (which is the time taken to build half the baryonic mass). If τinitial > 2 then τfitted is close to 2. Only the τinitial = 1 has a shorter fitted timescale. The ‘short’ run shows a greater deviation from the abundance–time distribution than the other runs, presumably due to the lack of an onset era in the recovered SFH.
Best-fit values for the exponential runs.
The importance of the MDF in reproducing rapid infall regardless of the initial parameters is shown in Fig. 7. This figure shows that, as the weighting given to the MDF decreases, the infall timescale drifts to higher and higher formation times. The best-fit distribution is the one using τinitial = 2 Gyr for the high ω runs, with the MDF as the strongest constraint. Where the infall timescale is long, and the fit to the MDF and αDF is low or zero, the high-metallicity peak of the MDF builds up strongly until it is far in excess of the data. We see that adding a strong weighting to both DFs fits the MDF, but this has a weaker effect on the αDF. Indeed, a stronger fit to the MDF comes at the expense of the fit to the αDF. The dip in particular is not significantly better fit with ωMDF, αDF = 900 than with ωMDF, αDF = 0, except for the ‘long’ ICs. Thus, when using high ω values, the improvement to the fit is strongest for the MDF, but the αDF is not significantly improved.
 |
Fig. 7. Formation time and fitting parameters for the exponential infall runs with different ω values. From left to right, first panel: formation time for the different fitted runs. Second panel: values for the fitting parameter to the abundance–age relation. Third panel: fitting parameter to the αDF, and fourth panel: fitting parameter to the MDF. The triangular points show failed runs, where the end result is larger than the ICs. Left panel: triangles indicate cases where one or more of the fitting parameters is larger than a threshold. The vertical dashed lines show the values for the initial conditions. |
Overall, this suggests that the data (when fitted to abundances, αDF, and MDF) favour rapid early accretion in the inner disc, regardless of the initial timescale before fitting. Similarly, we see that the fit to the abundance–time distribution alone is degenerate. The model struggles in one particular respect: the dual peak distribution of the MDF is poorly recovered in many instances of the exponential model, even with the quenching epoch. The αDF also shows a third peak for the long infall run, suggesting that the fit is not perfect. This may be due to the small number of degrees of freedom, which prevents careful tailoring of the SFH to the data. This is because the parameters to be fitted were limited so that the parameter space was manageable.
Different combinations of infall and star formation efficiency (SFE) may exist that could fit the data better, but we did not find any. Our results are clearly indicative of a rapid infall, given that, where the evolution is strongly constrained, each run shows a very similar rapid evolution. The MDF is the stronger determinant, and harder for the model to closely fit. This could be due to the MDF being less responsive to the evolution of the system than the αDF. The αDF is more responsive to the instantaneous SFR because of the very short timescales of SNII. This was seen in Snaith et al. (2016) for example, where a strong local starburst can result in a strong peak in the [α/Fe] evolution. Meanwhile, the [Fe/H] evolution is a more complex function of the stellar yields for SNII or SNIa, the SNIa time delay function, the IMF, and so on. Thus, the tools we have available to control the evolution, the SFE, and the infall rate are not sufficient on their own to fully reproduce the MDF. In addition, the difference in the model and observed DFs could be influenced by the Milky Way bar. The relative absence of low-Fe, high-α stars in the model may be due to contamination by stars in the bar (which is 4.5−5 kpc in length). As we have no dynamical information in the model, this is cannot be taken into account. Similarly, we might expect the fraction of thin-disc, metal-rich, and kinematically cold stars to be higher at the edge of the bar.
4.2. Non-parametric infall model
Unlike in traditional infall models described by Eq. (5), we opt for the more flexible ‘top hat’ infall formulation given by Eq. (7). We break the 14 Gyr of the model evolution into 14 bins of 1 Gyr, with each era following Eq. (7). We fix ϵ for each infall episode and do not allow it to vary relative to that of the others, except where predetermined (e.g. using Eq. (13), or when quenched). The fitting function acts on the amplitude of the infall in each bin, and the global normalisation of ϵ. Thus, the global infall is the sum of the 14 independent infall eras. This allows us to be more flexible about the infall history than when we assumed the exponential functional form.
We run several scenarios to explore the influence of the specifics of the model and the initial conditions on the SFH and chemical evolution. We fit the model using the time–abundance distribution, and optionally the MDF and αDF. The five different types of run we use for the ‘top hat’ infall model involve different initial conditions and variations to ϵ. These include:
-
Flat – the infall in the initial conditions is constant across cosmic time before the fitting function is applied;
-
High ω – a run fitting the already fitted result of run 1 (with ωMDF, αDF = 900). This was done for later comparisons with other values of ωMDF, αDF;
-
Flat, vary ϵ – flat infall initial conditions but an ϵ that varies according to Eq. (13);
-
High ω, vary ϵ – a run fitting the already fitted result of run 1 but an ϵ that varies according to Eq. (13);
-
Quench – quenched star formation with infall ICs from the best-fit run of run 1. We apply quenching, such that the ϵ is almost zero for 3 Gyr around 8 Gyr ago.
This is summarised in Table 3. We allow ϵ to vary according to Eq. (13) in order to explore the importance of this parameter in the chemical evolution; it is expected to be most important at early times.
Description for the models for the non-parametric runs.
4.2.1. Constraining with the local data only
In this section, we discuss the free infall model fitted only to the abundance–time distribution (e.g. where ωMDF = 0. and ωαDF = 0.). This will allow us to assess the importance of including the distribution functions in our fit. Formerly, we fitted our closed box model to only the time–[Si/Fe] distribution, and found that the resulting SFH and chemical evolution fitted the MDF and αDF well. This was effectively a prediction of the model and was interpreted as a success for our derived SFH (Snaith et al. 2015).
Figure 8 shows that when fitting the time–[Si/Fe] distribution only, we are able to achieve an excellent fit without the need for explicit quenching. We also fit the [Fe/H]–time distribution adequately, although the flat initial condition run increases in [Fe/H] too rapidly at early times. However, these fits come at the expense of the fit to the MDF (which is an order of magnitude poorer than for the high-ω runs). Although we have a reasonable fit to the αDF, the fit to the MDF peaks very strongly at high metallicity. This implies that the model predicts too much star formation at later times. This can be seen in the SFH panel, where the star formation rate is higher at later times compared to the fits using the distribution functions. Table 4 shows that the median baryonic accretion timescales are longer than in the exponential models (with high ω) where ω = 0, ranging from 6.5 Gyr to 2.3 Gyr. As previously mentioned, the different responsiveness of the two DFs to the infall is due to the different origins of the α and Fe elements. This is one of the strengths of using the two types of elements in the first place, because their different origins and timescales provide access to different processes. The MDF responds less well to the current Φgas or SFE than to other details such as the IMF, yields, the SNIa time-delay function, the binary fraction, and so on.
 |
Fig. 8. Free-infall model fitted to the time–[Si/Fe] with ωMDF = 0 and ωαDF = 0. The panels are the same as Fig. 5. The different lines show different runs, where the model numbers are referenced in Table 3. |
The infall histories unconstrained by the distribution functions show secondary infall at later times assembling over 2−7 Gyr. The quenching era fully constrains the infall, bringing the assembly time in line with the high-sigma runs. This suggests that the inner disc is in place early and did not experience significant accretion at later times even though star formation was ongoing.
4.2.2. Adding the inner disc MDF and αDF
Figure 9 shows the best-fit infall, star formation, and chemical evolution for each of our five best-fit runs with ωαDF, MDF = 900. We used a higher initial ϵ normalisation value for the runs where we make use of Eq. (13) (scenarios 3 and 4) in order to improve convergence, because without the renormalisation, the function minimisation method struggles to fit the data. This change is to compensate for the decrement resulting from the application of Eq. (13) to the ϵ. The figure shows the best-fit chemical evolution history (top row) and the distribution functions (left and middle panels on the second row) for each of the four models, along with the corresponding SFH (right hand panel in the second row). The baryon, gas, and stellar surface density evolutions are shown in the third row, and the infall rate, the SFE, and ϵ are shown in the bottom row.
 |
Fig. 9. Free-infall model fitted to the MDF and αDF as well as the time–[Si/Fe] with ωMDF = 900 and ωαDF = 900. The panels are the same as in Fig. 5. The blue and green lines show the results of runs from the flat infall initial conditions but the runs shown in orange, red, and purple lines use the result shown by the blue line as their initial condition. |
Each of the models is a reasonably good fit to the MDF, αDF, and time–[Si/Fe], as expected, considering they were fitted to these distributions. They also match well with the time–[Fe/H] and [Fe/H]–[Si/Fe] distributions. However, it is noticeable that the plots without either explicit quenching or a strong change in ϵ do not show a strong gradient change at around 8 Gyr, as seen in the data, as well as in our work using the closed box model. We previously found (in Snaith et al. 2014, 2015; Haywood et al. 2019) that a break in star formation is able to produce the gradient change. We therefore included scenario 5 to reproduce this. The sharp gradient change is clear in scenario 5, although it may be that the quenching epoch is too long for an ideal match to the data. This long quenching era would lead to a gap in the age–abundance distribution around 8 Gyr, which is not obvious from the observations. However, the other evolutions show a change in gradient that appears to be too gradual to reproduce this key feature.
This implies that there may be additional physics shaping the chemical evolution of the Milky Way beyond the connection between infall and star formation rate. This is because in our model there is plenty of gas remaining in the system when the quenching occurs, meaning that the quenching cannot simply be the result of the ISM running out of material to fuel star formation (as is used in other GCE models such as Spitoni et al. 2019). We discuss possible scenarios for this in Sect. 5. Within the context of this model, the infall and star formation are not enough to fully reproduce the chemical evolution. Although the model can be expected to reasonably reproduce the properties of the Milky Way, we would need to include an alternative method of quenching.
Table 4 presents the value of the fitting parameter to the MDF, αDF, and abundance–time distributions for our best-fit runs, along with the predicted formation time of the disc (which is where half the final mass of the disc is in place). The uncertainties are calculated from best fits to 24 bootstrapped samples of the observational datasets and different random errors used to generate the distribution functions. The values are the medians of the bootstrapped runs, and the errors are their standard deviations. The best fits to the abundance–time distribution are the quenching runs, although the difference between the runs is small and well within the error associated with bootstrapping the data. The worst fit to the abundance–time distribution is the run with varying ϵ and flat initial infall, which is a significant outlier in terms of the baryon formation time. However, there is a corresponding increase in the model uncertainty, meaning that formally there is no meaningful difference in the fits from the time–abundance distribution. The large error does indicate that this model is the least successful. However, this run does show a good match to the αDF and MDF.
We also see that the recovered infall of the inner disc strongly favours the rapid early accretion of matter (within approximately the first 2 Gyr). In each run, the time taken for the galaxy to assemble half its baryonic mass is around 2 Gyr. This suggests that most of the inner disc is in place at early times. There is a pause in infall after around 10 Gyr in each run, except for scenario 3, and some subsequent infall, although only a small amount (< 10 M⊙ pc−2). Star formation occurs more slowly, with an assembly time of 4−5 Gyr (coincident with the thick disc formation era). This also matches well with the closed box model from our previous work, where the thick disc is a massive component of the Galaxy. The predicted formation times are very similar within the error, except for the run with varying ϵ with a flat initial infall, which has a longer timescale. This is likely due to the fitting procedure as the other runs agree well, and the error on this run is much larger.
We also note that the [Fe/H]–[Si/Fe] evolution of the different runs shows a similar evolution. The chemical evolution track between [Fe/H] = −0.5 and 0 lies above the Delgado Mena et al. (2017) data. However, the different evolutions very closely conform to the data selected from APOGEE. This should not come as a surprise as the models are most strongly constrained by the two distribution functions.
In order to understand the impact of ω on the resulting fits we explored a range of values. Figure 10 shows the impact of sigma on the formation time and fitting parameter to the different observables. We see that where the ωMDF is high, the formation time is very low, but where ωαDF is higher than ωMDF, there is a slight push to longer formation times. The figure also shows that the fitting parameter for the abundance–time distribution is strongly dependent on the values of ω, with the fitting parameter rapidly growing as the distribution functions make an increasing contribution to the overall fit. At higher weighting, each run – excluding scenario 3 – is very closely matched with rapid formation times. For the run with an initially flat infall, the SFE is very high, and the subsequent gas surface density at the present time is very low, suggesting that the flat ICs are too divergent from the final result to avoid unphysical local minima in parameter space. The other distributions have more reasonable surface densities for the gas and stars. Overall, when quenching is explicitly included, the infall is quite constrained, and tends towards shorter infall timescales and realistic gas fractions. As before, the fit to the dip in the αDF is not improved and is even made worse in the high ωMDF runs. This is the result of the improved fit to the MDF. This suggests that improvements should be made to the yields, IMF, SNIa delay time, and so on in order better fit both DFs at the same time. Even if the fit is relatively imprecise, the overall behaviour is clearly captured, suggesting that even if our fit is not perfect, it is at least identifying all the key features.
 |
Fig. 10. Formation time and fitting parameters for the free-infall runs with different ω values. From left to right: formation time for the different fitted runs, values for the fitting parameter to the abundance–age relation, fitting parameter to the αDF, and fitting parameter to the MDF. The triangular points show failed runs, where the end result is larger than the ICs. Left panel: triangles mark cases where one or more of the fitting parameters is larger than a threshold. |
Each run with high ω and many of the runs with ω = 0 (the flat infall run is the notable exception because of a very high value of ϵ) produce a similar accretion history, a local stellar surface density of around 50 M⊙ pc−2, and a gas density of 10−15 M⊙ pc−2, which is within the range of observations (Bovy & Rix 2013; Zhang et al. 2013), if a little gas-poor for the solar vicinity.
Figure 11 compares the results of our runs with the stellar mass growth for Milky Way-type galaxies by van Dokkum et al. (2013). These latter authors fit the stellar mass as a function of redshift for Milky Way-type galaxies with a best-fit polynomial,
 |
Fig. 11. Comparison between the models with the average stellar mass growth from van Dokkum et al. (2013). The models used here use free infall and high ω. We also show the median line of 24 runs where we bootstrapped the data. The variation from the minimum value to maximum value in each time-step is shown as the light coloured region around each line. ± the standard deviation is shown as the darker coloured region around each line. The black lines show how different values of the disc radial scale length –used to convert the stellar mass to the local stellar surface density– affect the van Dokkum et al. (2013) fit. The dotted line, dashed line and dot-dash line use Rscale = 2.1, 2.4, 1.8 kpc. These values are taken from Porcel et al. (1998). |
where Mstar is the stellar mass, and z is the redshift. We convert from stellar mass to the local stellar surface density via,
where r⊙ is the solar radius (8 kpc), and rscale is the disc scale length of 2.4 ± 0.3 kpc given by Porcel et al. (1998).
We also include the range of values recovered from the 24 bootstrapped samples of the observations. The stellar mass growth is similar to the van Dokkum et al. (2013) result, except slightly more rapid at early times. This is easily accounted for because the van Dokkum et al. (2013) result is an average of the growth of many galaxies, with a range of properties. In general, half the stellar mass is in place within 5 Gyr in both the van Dokkum et al. (2013) result and the different runs of the model, which confirms our results from Snaith et al. (2014, 2015).
The range of possible values of the radial scale length can strongly impact the growth rate of our model galaxy compared to the van Dokkum et al. (2013) result. Bland-Hawthorn & Gerhard (2016) report a range of radial scale lengths for the disc of 1.8−3 kpc for the thick and thin discs. Much of this range is captured in Fig. 11. On the other hand, Sharma et al. (2021) assume an evolving radial scale length, while the analysis of van Dokkum et al. (2013) presents a self-similar evolution for Milky Way-type galaxies. By exploring the evolution of the SFH of our model with a range of radial scale lengths, we can see the envelope of possible stellar mass growths. The effect of the different scale lengths is illustrative. We do not take into account the effect of a possible evolution of the scale length between the thick and thin discs, because the thin-disc scale length depends significantly on the metallicity of the stars used to measure its size; see the analysis of the scale-length of mono-abundance populations by Bovy et al. (2012, 2016). These latter authors find that the scale lengths can vary from less than 2 to more than 4 kpc depending on their abundance values.
4.3. Impact of the guiding radius
In the previous sections we concentrate on using the DFs from stars with a current galactocentric radius of 4−6 kpc based on the Starhorse distances. However, such results can be strongly influenced by radial motions, such as blurring. Leung & Bovy (2019) and Mackereth & Bovy (2018) calculate the orbits of stars in APOGEE using the galpy code (Bovy 2015, 2014) and the Galactic potential derived by Bovy (2015). This is an axisymmetrical potential and does not contain a bar. This highlights one of the potential issues with using the guiding centre: it necessitates assumptions about the shape of the Galactic potential, which remains fairly uncertain. Therefore, we chose to use the current distances from Starhorse for the majority of this study, which are similar to the radii calculated from Gaia data.
Nevertheless, we explore the consequences of using the guiding radii supplied in the astronn VAC for our result. We find that the αDF in particular remains fairly robust; see Fig. 12. This figure shows the MDFs (top) and αDFs (bottom) of the stars with a guiding or current (Starhorse) galactocentric radius between 4−6 kpc. The green region emphasises the difference between the DFs defined using the different radius estimations. We note that the MDFs show a significant difference, with a stronger high-metallicity peak using Starhorse radii. In fact, for the guiding radii the high-metallicity peak is so small that it is not readily apparent. On the other hand, there is a small increase in the size of the highest alpha peak in the αDF. These changes to the MDF and αDF are consistent, with early star formation being favoured over the later evolution when we make use of the guiding centre radius.
 |
Fig. 12. Different distribution functions using the Starhorse and guiding radii. The green area highlights the difference between the two distributions. |
This can be expected to have an effect on the star formation and infall history derived by our model. The shape of guiding radius DFs should bias the result towards early times, as the low-metallicity and high-alpha regions of the DFs are more strongly favoured. We also find that the population of stars between 4 and 6 kpc using the guiding radius is considerably larger. This is because, although the APOGEE survey tends to find more stars closer to the Sun because it is magnitude limited, those stars can have considerably different guiding radii from the solar circle. This means that some of the stars with current positions close to the Sun have guiding radii between 4 and 6 kpc because of the ellipticity of their orbits. Because the orbits of stars in the thick disc are more elliptical than in the thin disc, this will create a selection effect that will under-represent thin-disc stars in the DFs calculated using the guiding radius.
We use the exponential infall model from Sect. 4.1 to explore how the new DFs affect the mass assembly history. In Fig. 13 we show the outputs of the model fitted to the DFs with ωMDF, αDF = 900. We then compared this result to the best-fit ‘short’ run previously shown in Fig. 5. Using either radius will introduce selection effects, but without careful dynamical modelling, which is beyond the scope of this work, it would be difficult to take these effects fully into account.
 |
Fig. 13. Star formation, infall, and chemical evolution of models. These runs use ωMDF = 900 and ωαDF = 900. The DFs are defined using the Starhorse radii (green line) and the guiding radii (blue line). The run labelled ‘default’ represents the 4−6 kpc bin we have used in the previous sections. |
The resulting fits are reasonably similar to the previous results. The baryonic formation time is between 2 and 2.5 Gyr, and the stellar formation time is between 3.5 and 4 Gyr, which are very close to our the previous runs using the Starhorse radii. We find that the new best-fit result requires a lower SFH during the thin-disc phase, and a stronger initial infall relative to the result for the τini = 2 Gyr run. This means that the final stellar surface density has dropped from around 50 M⊙ pc−2 to 40 M⊙ pc−2. The baryonic and stellar formation times are largely unchanged at 2.5 Gyr and 3.9 Gyr respectively.
As previously discussed, the final shapes of the star formation and accretion history are relatively insensitive to the chosen initial conditions, and so we present the fits we have discovered, which are not necessarily the only solution. There is also a degree of inflexibility to the model, which prevents it from perfectly mimicking the observations.
One of the limitations of the present study is the absence of radial migration modelling. However, this is less of an issue when investigating the inner disc (R < 6 kpc) because of the smaller spread in metallicity of the thin disc. At larger radii (R > 7 kpc), the effect of radial mixing is a subject of considerable debate (see, for example, Sharma et al. 2021; Halle et al. 2015; Khoperskov et al. 2021, for some different perspectives on this discussion).
Changing the radii used to define the DFs does not significantly affect the results of the model in terms of the baryonic and stellar formation times, within the model constraints, and does not affect our conclusions. This suggests that our results are robust to the choice of stellar galactocentric radii used to define the distribution functions.
4.4. The radial evolution: changing behaviour with radius
We have chosen the region with a current galactocentric (Starhorse) radius of between 4 and 6 kpc for the majority of our studies. We chose this region to avoid the known transition from inner to outer discs around the solar circle (< 6 kpc), and to reduce the impact of the bar (> 4 kpc). Our model therefore reproduces the average behaviour of stars in this region. However, the 2 kpc width of this region offers the potential for varying behaviour with radius. In the previous sections, we study the entire region in order to gain insight into the average properties of star formation and infall in this region. In this section, we explore the radial effects.
We show our decomposition of the MDF and αDF by radius in Fig. 14. Although there is variation over the 4−6 kpc region, the overall 4−6 kpc MDF and αDF matches well with the smaller 5−5.5 kpc bin. For r < 5 kpc, the DFs favour the low metallicity, high-alpha peaks, and r > 5.5 very strongly favours the high-metallicity peak, without the bimodality seen at smaller radii. The αDF retains some bimodality outside of 5 kpc, but the high-alpha peak is much weaker.
 |
Fig. 14. MDF and αDF at different radii. Top row: DFs defined using the Starhorse radii with different radial cuts. Bottom row: DFs defined using the guiding radii with different radial cuts. Curves are smoothed using a Savitzky-Golay with a window of 5 and a polynomial order of 2. |
We include the MDF and αDF of all stars with galacto-centric radii < 6 kpc, which meets our definition of the entire inner disc. The properties of stars within 5 kpc is approximately uniform, but outside this region the behaviour begins to change. Similarly, comparing the MDF between 4 and 6 kpc with that of < 6 kpc we see only a slight deviation at high metallicity. Although the high-metallicity peak is smaller, there is a good match between the two distributions. This is also true for the αDF, where the late time star formation peaks are weaker for the < 6 kpc DFs.
We fit the model with the DFs shown in Fig. 14 (ωMDF, αDF = 900) using the ICs of the ‘medium’ value of τ (from Sect. 4.1) shown in Fig. 15. We find only a small variation in the recovered infall and star formation histories, although this can have a noticeable effect on the distribution functions. We find that in bins of increasing radius, the baryonic formation time is 1.43, 1.71, 2.60, 3.03 Gyr, meaning that there is a noticeable increase in the formation time with (Starhorse) radius. Similarly, the star formation time increases from 3.75 to 5.02 Gyr. The growth between the 2−4 kpc and 4−5 kpc bins increases the baryonic formation time by 0.3 Gyr, while from 5−5.5 kpc the growth in formation time is 0.9 Gyr and 0.4 Gyr from 5.5 to 6 kpc. The inner regions of the disc show less variation than the outer parts. The fitting parameter for the MDF shows similar values for the 4−6 kpc result (shown previously), the 5−5.5 kpc bin (which we noted is very similar to the 4−6 kpc DFs), and the 0−6 kpc cuts, with values of 0.0026, 0.0029, and 0.0025 respectively. Similarly, for the αDF, the values of the fitting parameter are 0.0033, 0.0037, and 0.0035. The poorest fits for both MDFs are for the 2−4 kpc bin, which was not included in the original modelling, and the 5.5−6 kpc bin, which shows the strong high-metallicity/low-alpha peak and a lack of bimodality. These have values for the MDF (αDF) of 0.0043 (0.0044) and 0.0040 (0.0056) respectively.
 |
Fig. 15. Best-fit infall and star formation histories for the different radial cuts (shown in kpc) for the exponential infall model. These runs use the τ = 5 initial conditions and ωMDF, αDF = 900. The different MDFs and αDFs in the different radial bins are shown in Fig. 15. The fitting values between the model and observations for the MDF and αDF are shown in the respective panels. |
This suggests that the 0−6 kpc disc can be captured by the model and that the baryonic and stellar formation times are 2.0 Gyr and 4.3 Gyr respectively. These values are slightly shorter than for the 4−6 kpc bin, but this only bolsters our conclusion that most gas infall occurred very early.
The APOGEE sight lines vary with galactocentric radius because of the geometry of the position of the Sun in the Galaxy. Thus, our conclusions in this section should be interpreted carefully in light of potential selection effects. For example, stellar populations are distributed differently in terms of radial and vertical scale length for different populations (see e.g. Bovy et al. 2012) and this may affect the DFs. This is one potential explanation (at least in part) for the changing behaviour of the DFs with radial scale length shown in Fig. 14. Nevertheless, our results demonstrate hints of the inside-out formation of the galaxy, where outer regions have larger star formation.
We see that the high-metallicity peak in the MDF is much stronger in the outer bins, as expected from the observations. This is due to the higher late-time star formation rate. This suggests that our baryonic and stellar formation times are an upper limit.
5. Discussion
The infall model presented in this paper fits the chemical evolution of the high-α sequence in solar vicinity data very well, but also the MDF and αDF of the inner disc. There is very little difference between how precisely the free infall model can match the data compared to the exponential infall, and in each case the models favour a rapid early infall. Each infall scenario predicts a baryonic formation time of between 1 and 2.5 Gyr.
In the infall model presented here, early infall is very rapid in each of the scenarios we explored. In the ‘top hat’ runs, we see that most of the gas falls in before 10 Gyr ago at most, while the exponential infall scenarios converge on a baryon formation time of around 2.5 Gyr. This means that in most of the models constrained using the abundance–time relation, αDF, and MDF, half the baryon mass of the inner disc was present by 11.5 Gyr ago, which is a good fit to the closed box approximation used in our previous works (Snaith et al. 2014, 2015; Haywood et al. 2016b). This shows that assuming an instantaneous accretion of all the gas was a good approximation.
Indeed, the closed box model, as shown in Haywood et al. (2016b), appears to reproduce the MDF even more effectively. This is due to a number of reasons. The SFH of the closed box model can be more carefully fitted to the data because we fitted the SFH directly, in approximately 0.5 Gyr bins, while in the infall model we have less direct control over the star formation rate as we only fit the infall and global ϵ. How closely the evolution ‘reacts’ to changes in infall is related to how much gas is present in the system, governed by ϵ.
However, the difficulty faced by the function optimisation code in fitting ϵ means that there may be other values of ϵ and infall parameters that are a closer fit, but are not identified. In order to improve this fit, we added explicit quenching into our runs, based on lessons learned from Snaith et al. (2014). This resulted in a better match with observations in runs fitted to the distribution functions. We still cannot distinguish between scenarios where the infall has a constant or varying ϵ, but our results suggest that some form of quenching is required at the transition between the thick and thin-disc eras in the ‘top hat’ runs, although the case for quenching in the exponential model is more ambiguous; see the appendix for more details.
However, at the time of quenching there are still considerable quantities of gas present in the system. Thus, there is a need to consider additional physics in order to quench the gas-rich galaxy. Haywood et al. (2016b) and Khoperskov et al. (2018) identify one possible explanation for this temporary suspension of star formation: bar quenching. This is a form of morphological quenching, where the formation of the bar can decrease the star formation rate by a factor of ten over a time-span of less than 1 Gyr, particularly in the inner regions of the disc. This could explain the prompt change in the star formation rate of the galaxy in both the infall and closed box models, even in the presence of significant quantities of gas. In this scenario, the turbulence in the ISM is increased, reducing the SFE, and this is supported by the observations of Consolandi (2016) who find that the inner regions of galaxies with bars are redder than in bar-less galaxies. Alternatively, a galaxy–galaxy interaction could have caused the quenching era, as it seems to coincide with the end of the thick disc and a major accretion event (e.g. Di Matteo et al. 2019).
In the inner regions of the disc, the bar can be expected to shape the SFH in ways not captured by our model. It is possible that the ability of the bar to suppress star formation could mean that, in the inner regions of the Milky Way, the star formation is prolonged relative to a simple Schmidt–Kennicutt law. This would allow the baryonic accretion of the inner regions to be even faster than estimated by our model (Khoperskov et al. 2018). It is also possible that the radial movements of the gas can redistribute matter prior to star formation, changing the infall history of the Milky Way in ways our model cannot capture. This is beyond the scope of this paper, but would provide for future research using hydrodynamical simulations.
To our knowledge, there is no model in the literature equivalent to that proposed here (with the exception of the closed-box model in Haywood et al. 2016b), because, traditionally, studies of chemical evolution models have not been designed to represent only the inner disc evolution. The only region in the Galaxy where the MDF can be said to be representative of the high-alpha sequence is in the inner disc (R < 6 kpc).
High-alpha-sequence stars are in the minority in the solar vicinity, with the sample being dominated by solar metallicity stars that are not on the high-alpha sequence. The model of Spitoni et al. (2019) is a recent representative of the class of models that tries to match the entire solar vicinity distribution. In their case, the amount of first infall episode is fixed according to the density of the thick disc in the solar vicinity, which we believe is not representative of the thick disc as a whole. Hence, the result of these latter authors is that the fraction of the stellar mass in the thick disc stars is just above 10% of the total surface density, while in our model it is around 50%. As mentioned in Haywood et al. (2019), while the age–chemistry relation of this population is probably an effect of the overall mixing that occurred at this time in a population of a few 1010 M⊙, the number density of this population in the solar vicinity is only a small percentage of the overall fraction of this population. Specifically, half of the stellar mass of the inner disc is in the thick-disc component formed more than 8 Gyr ago, while at the solar circle the thick disc stellar mass fraction is only 10%, because of the different radial scale lengths of the two components (Bovy et al. 2012).
Despite this, in our previous work (Snaith et al. 2014, 2015) we were able to make use of data in the solar vicinity to model the inner disc. However, in this case we first separated the high- and low-alpha sequences (as in Haywood et al. 2013) and fitted them separately. This is equivalent to our current decomposition based on distance from the Galactic centre. In addition, in our previous work we did not fit the DFs, only the region of age–[Si/Fe]–[Fe/H] space populated by those stars. It was in Haywood et al. (2016b) that the strong correspondence between the DFs produced by our model and the DFs of the inner disc was noted.
Although we pointed out that our fits to the data produce a stellar and gas surface density comparable with observations of the solar vicinity, this is not necessarily relevant, as the high-alpha sequence is expected to correspond to the entire inner disc. This means that global measurements from the solar vicinity are not particularly helpful. The model should be compared to the entire inner disc. Although we fixed the total baryon fraction at 60 M⊙ pc−2, this is not required, for these same reasons. We scale ϵ by  , and so the evolution is effectively scale free.
, and so the evolution is effectively scale free.
6. Conclusions
Here, we elaborate on our previous work (Snaith et al. 2014, 2015), and include explicit rather than implicit infall of gas in our chemical evolution model. We fitted our models to updated stellar ages based on Adibekyan et al. (2012) and Gaia, and made use of the MDF and αDF from APOGEE DR16 to refine our best-fit star formation histories. We expanded the closed-box model of the inner Galactic disc to include explicit infall and the Schmidt–Kennicutt law between gas surface density and star formation rate density.
Our free-infall, or ‘top hat’ infall model uses 14 infall episodes, each of 1 Gyr, to model the infall history of the Milky Way, whilst our exponential infall model includes four eras of star formation: the initial infall, the thick disc, the quenching, and the thin disc. The quenching epoch is inserted by hand in both sets of scenarios, and has a low (or zero) SFE.
Our main conclusions are summarised as:
-
The baryon formation time of the inner disc of the Milky Way was rapid, taking around 2 Gyr to assemble half its present-day baryonic (star + gas) mass. The stellar formation time, defined as the time taken for half the mass of stars to form, is longer, taking around 5 Gyr. This corresponds well with our prediction from Snaith et al. (2014) that the thick disc contains half the stellar mass of the inner regions of the Milky Way, and that the inner disc can be approximated with a closed box.
-
The MDF and αDF are essential for breaking the degeneracy of the different infall parameters, but the time–abundance distribution is also needed to capture the important features of the evolution.
-
The exact choice of galactocentric radius used to define the APOGEE subsample used to build the distribution functions can affect its overall shape. However, within the limitations of the model, this does not strongly impact our results.
-
Similarly, the selection function of APOGEE well represents the inner Galaxy, and does not strongly affect the results of our models.
-
The best-fit infall parameters we use produce a very similar chemical evolution track to the observations, because this infall model has most of the gas in place early on and is therefore similar to the closed box model overall.
-
A quenching epoch is used for recovering the key features in the chemical evolution and MDF in both the infall and closed box models, as first proposed in Haywood et al. (2016b). Without quenching, the characteristic sharp change in gradient in the age–[Si/Fe] distribution is not recovered by the ‘top hat’ infall model, and the MDF and αDF do not show the twin-peaked distribution seen in APOGEE. We discuss the quenching in the exponential infall model in more detail in the appendix. The precise shape of the dip is difficult to capture, even in runs with ωMDF, αDF = 900, because of the need to fit both the αDF and MDF at the same time.
-
A possible mechanism responsible for the break in star formation is bar quenching, which is different to the method proposed by Noguchi (2018). This is because there is considerable gas present in the ISM when the quenching is required, and so a lack of gas cannot be used to change the gradient of the [Si/Fe] evolution in the way we see in observations. Alternatively, the end of satellite accretion (e.g. Kruijssen et al. 2019) could have resulted in a change of conditions in the disc ultimately leading to quenching, or the emergence of the bar and the resulting redistribution of gas could have suppressed star formation.
-
All the models reproduce the massive thick disc we proposed in Snaith et al. (2014, 2015) for the inner regions of the Milky Way.
-
Additional physics beyond the Schimdt–Kennicutt star formation law is needed to fully understand the SFH of the Milky Way.
-
Our model is fully compatible with the infall paradigm for galaxy formation with a low SFE. This low efficiency can be assumed to be due to the gas reservoir into which we mix the metals being larger than the star forming ISM.
-
Our star formation histories compare favourably with the result of van Dokkum et al. (2013), implying that the Milky Way is representative of galaxies of the same type.
We can characterise the closed box model as an infall model with a low SFE and a rapid gas accretion rate at early times. In future we will expand our model to account for the outer disc. However, in order to model the outer disc we will need to make use of a multi-zone model, because, as proposed by Haywood et al. (2013), we believe that the outer disc initial condition is set by outflows from the inner disc and dilution by low-metallicity gas (Snaith et al. 2015; Haywood et al. 2018). This has recently been examined by Katz et al. (2021) using APOGEE DR16 data, but would benefit from modelling for further insight. Even in the infall model, the key components identified in Snaith et al. (2015) remain important, the high SFR in the thick disc, the low SFR in the thin disc, and (potentially) the quenching epoch are all important for shaping the chemical properties of the inner galaxy.
In Snaith et al. (2015) we incorrectly quote the parameters for the fit of stellar lifetimes by Raiteri et al. (1996) for a1 and a2 but they are used correctly in the code itself.
Acknowledgments
The authors thank the referee for their suggestions which enabled us to refine our arguments and our comparison with the observations. We thank Laura Boyle for identifying our error in quoting the equation of Raiteri et al. (1996) in Snaith et al. (2015). O.N.S. thanks the DIM ACAV+ for the funding that made this work possible. P.D.M. and M.H. thank the ANR (Agence Nationale de la Recherche) for its financial support through the MOD4Gaia project (ANR-15- CE31-0007, P.I.: P. Di Matteo). S.K. acknowledges the Russian Science Foundation (RSCF) grant 19-72-20089 for support in the preparation of the N-body models partially carried by using the equipment of the shared research facilities of HPC computing resources at Lomonosov Moscow State University (project RFMEFI62117X0011). This work was granted access to the HPC resources of CINES and TGCC-CEA under the allocation 2018-0410154 made by GENCI. Funding for the Sloan Digital Sky Survey IV has been provided by the Alfred P. Sloan Foundation, the US Department of Energy Office of Science, and the Participating Institutions. SDSS-IV acknowledges support and resources from the Center for High-Performance Computing at the University of Utah. The SDSS website is www.sdss.org. SDSS-IV is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS Collaboration including the Brazilian Participation Group, the Carnegie Institution for Science, Carnegie Mellon University, the Chilean Participation Group, the French Participation Group, Harvard-Smithsonian Center for Astrophysics, Instituto de Astrofísica de Canarias, The Johns Hopkins University, Kavli Institute for the Physics and Mathematics of the Universe (IPMU)/University of Tokyo, the Korean Participation Group, Lawrence Berkeley National Laboratory, Leibniz Institut für Astrophysik Potsdam (AIP), Max-Planck-Institut für Astronomie (MPIA Heidelberg), Max-Planck-Institut für Astrophysik (MPA Garching), Max-Planck-Institut für Extraterrestrische Physik (MPE), National Astronomical Observatories of China, New Mexico State University, New York University, University of Notre Dame, Observatário Nacional/MCTI, The Ohio State University, Pennsylvania State University, Shanghai Astronomical Observatory, United Kingdom Participation Group, Universidad Nacional Autónoma de México, University of Arizona, University of Colorado Boulder, University of Oxford, University of Portsmouth, University of Utah, University of Virginia, University of Washington, University of Wisconsin, Vanderbilt University, and Yale University. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. We have made use of numpy (Harris et al. 2020), scipy (Virtanen et al. 2020), matplotlib (Hunter 2007), F2PY (Peterson 2009) and pandas (The pandas development team 2020) libraries in the Python language as well as IPython (Perez & Granger 2007) and Jupyter notebook (Kluyver et al. 2016).
References
- Adibekyan, V. Z., Sousa, S. G., Santos, N. C., et al. 2012, A&A, 545, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ahumada, R., Prieto, C. A., Almeida, A., et al. 2020, ApJS, 249, 3 [Google Scholar]
- Anders, F., Chiappini, C., Santiago, B. X., et al. 2014, A&A, 564, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Bensby, T., Alves-Brito, A., Oey, M. S., Yong, D., & Meléndez, J. 2011, ApJ, 735, L46 [NASA ADS] [CrossRef] [Google Scholar]
- Bland-Hawthorn, J., & Gerhard, O. 2016, ARA&A, 54, 529 [Google Scholar]
- Bovy, J. 2014, Astrophysics Source Code Library [record ascl:1411.008] [Google Scholar]
- Bovy, J. 2015, ApJS, 216, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Bovy, J., & Rix, H.-W. 2013, ApJ, 779, 115 [Google Scholar]
- Bovy, J., Rix, H.-W., Liu, C., et al. 2012, ApJ, 753, 148 [Google Scholar]
- Bovy, J., Nidever, D. L., Rix, H.-W., et al. 2014, ApJ, 790, 127 [CrossRef] [Google Scholar]
- Bovy, J., Rix, H.-W., Schlafly, E. F., et al. 2016, ApJ, 823, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Brook, C. B., Kawata, D., Gibson, B. K., & Freeman, K. C. 2004, ApJ, 612, 894 [NASA ADS] [CrossRef] [Google Scholar]
- Brook, C. B., Gibson, B. K., Martel, H., & Kawata, D. 2005, ApJ, 630, 298 [NASA ADS] [CrossRef] [Google Scholar]
- Brook, C. B., Stinson, G. S., Gibson, B. K., et al. 2012, MNRAS, 426, 690 [Google Scholar]
- Brook, C. B., Kawata, D., Gibson, B. K., Gallart, C., & Vicente, A. 2020, MNRAS, 495, 2645 [NASA ADS] [CrossRef] [Google Scholar]
- Buck, T. 2020, MNRAS, 491, 5435 [NASA ADS] [CrossRef] [Google Scholar]
- Buder, S., Asplund, M., Duong, L., et al. 2018, MNRAS, 478, 4513 [Google Scholar]
- Chiappini, C., Matteucci, F., & Gratton, R. 1997, ApJ, 477, 765 [Google Scholar]
- Ciucă, I., Kawata, D., Miglio, A., Davies, G. R., & Grand, R. J. J. 2021, MNRAS, 503, 2814 [Google Scholar]
- Consolandi, G. 2016, A&A, 595, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Côté, B., O’Shea, B. W., Ritter, C., Herwig, F., & Venn, K. A. 2017, ApJ, 835, 128 [Google Scholar]
- Cui, X.-Q., Zhao, Y.-H., Chu, Y.-Q., et al. 2012, Res. Astron. Astrophys., 12, 1197 [Google Scholar]
- Dekel, A., & Birnboim, Y. 2006, MNRAS, 368, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Dekel, A., Birnboim, Y., Engel, G., et al. 2009, Nature, 457, 451 [Google Scholar]
- Delgado Mena, E., Tsantaki, M., Adibekyan, V. Z., et al. 2017, A&A, 606, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Matteo, P., Haywood, M., Lehnert, M. D., et al. 2019, A&A, 632, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Matteo, P., Spite, M., Haywood, M., et al. 2020, A&A, 636, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duarte, M., & Mamon, G. A. 2014, MNRAS, 440, 1763 [CrossRef] [Google Scholar]
- Fragkoudi, F., Di Matteo, P., Haywood, M., et al. 2018, A&A, 616, A180 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grisoni, V., Spitoni, E., & Matteucci, F. 2018, MNRAS, 481, 2570 [NASA ADS] [Google Scholar]
- Guedes, J., Callegari, S., Madau, P., & Mayer, L. 2011, ApJ, 742, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Halle, A., Di Matteo, P., Haywood, M., & Combes, F. 2015, A&A, 578, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Halle, A., Di Matteo, P., Haywood, M., & Combes, F. 2018, A&A, 616, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Hayden, M. R., Bovy, J., Holtzman, J. A., et al. 2015, ApJ, 808, 132 [Google Scholar]
- Haywood, M., Di Matteo, P., Lehnert, M. D., Katz, D., & Gómez, A. 2013, A&A, 560, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haywood, M., Di Matteo, P., Snaith, O., & Lehnert, M. D. 2015, A&A, 579, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haywood, M., Di Matteo, P., Snaith, O., & Calamida, A. 2016a, A&A, 593, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haywood, M., Lehnert, M. D., Di Matteo, P., et al. 2016b, A&A, 589, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haywood, M., Di Matteo, P., Lehnert, M., et al. 2018, A&A, 618, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haywood, M., Snaith, O., Lehnert, M. D., Di Matteo, P., & Khoperskov, S. 2019, A&A, 625, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Iwamoto, K., Brachwitz, F., Nomoto, K., et al. 1999, ApJS, 125, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Karakas, A. I. 2010, MNRAS, 403, 1413 [NASA ADS] [CrossRef] [Google Scholar]
- Katz, D., Gómez, A., Haywood, M., Snaith, O., & Di Matteo, P. 2021, A&A, 655, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kennicutt, R. C., Jr. 1998, ApJ, 498, 541 [Google Scholar]
- Khoperskov, S., Haywood, M., Di Matteo, P., Lehnert, M. D., & Combes, F. 2018, A&A, 609, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Khoperskov, S., Gerhard, O., Di Matteo, P., et al. 2020a, A&A, 634, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Khoperskov, S., Di Matteo, P., Haywood, M., Gómez, A., & Snaith, O. N. 2020b, A&A, 638, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Khoperskov, S., Haywood, M., Snaith, O., et al. 2021, MNRAS, 501, 5176 [NASA ADS] [CrossRef] [Google Scholar]
- Kluyver, T., Ragan-Kelley, B., Pérez, F., et al. 2016, in Positioning and Power in Academic Publishing: Players, Agents and Agendas, eds. F. Loizides, & B. Schmidt (IOS Press), 87 [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Kruijssen, J. M. D., Pfeffer, J. L., Reina-Campos, M., Crain, R. A., & Bastian, N. 2019, MNRAS, 486, 3180 [Google Scholar]
- Kubryk, M., Prantzos, N., & Athanassoula, E. 2015, A&A, 580, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Larson, R. B. 1972, Nat. Phys. Sci., 236, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Leung, H. W., & Bovy, J. 2019, MNRAS, 489, 2079 [CrossRef] [Google Scholar]
- Mackereth, J. T., & Bovy, J. 2018, PASP, 130, 114501 [Google Scholar]
- Mackereth, J. T., Bovy, J., Leung, H. W., et al. 2019, MNRAS, 489, 176 [Google Scholar]
- Majewski, S. R., Schiavon, R. P., Frinchaboy, P. M., et al. 2017, AJ, 154, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Minchev, I., Famaey, B., Combes, F., et al. 2011, A&A, 527, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neeleman, M., Prochaska, J. X., Kanekar, N., & Rafelski, M. 2020, Nature, 581, 269 [Google Scholar]
- Ness, M. K., Johnston, K. V., Blancato, K., et al. 2019, ApJ, 883, 177 [CrossRef] [Google Scholar]
- Nidever, D. L., Bovy, J., Bird, J. C., et al. 2014, ApJ, 796, 38 [Google Scholar]
- Noguchi, M. 2018, Nature, 559, 585 [Google Scholar]
- Nomoto, K., Tominaga, N., Umeda, H., Kobayashi, C., & Maeda, K. 2006, Nucl. Phys. A, 777, 424 [CrossRef] [Google Scholar]
- The pandas development team 2020, https://doi.org/10.5281/zenodo.3509134 [Google Scholar]
- Pedregosa, F., Varoquaux, G., Gramfort, A., et al. 2011, J. Mach. Learn. Res., 12, 2825 [Google Scholar]
- Perez, F., & Granger, B. E. 2007, Comput. Sci. Eng., 9, 21 [Google Scholar]
- Peterson, P. 2009, Int. J. Comput. Sci. Eng., 4, 296 [Google Scholar]
- Porcel, C., Garzon, F., Jimenez-Vicente, J., & Battaner, E. 1998, A&A, 330, 136 [NASA ADS] [Google Scholar]
- Queiroz, A. B. A., Anders, F., Chiappini, C., et al. 2020, A&A, 638, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Radburn-Smith, D. J., Roškar, R., Debattista, V. P., et al. 2012, ApJ, 753, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Raiteri, C. M., Villata, M., & Navarro, J. F. 1996, A&A, 315, 105 [NASA ADS] [Google Scholar]
- Renaud, F., Agertz, O., Read, J. I., et al. 2021, MNRAS, 503, 5846 [NASA ADS] [CrossRef] [Google Scholar]
- Romano, D., Karakas, A. I., Tosi, M., & Matteucci, F. 2010, A&A, 522, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roškar, R., Debattista, V. P., & Loebman, S. R. 2013, MNRAS, 433, 976 [CrossRef] [Google Scholar]
- Sánchez-Blázquez, P., Courty, S., Gibson, B. K., & Brook, C. B. 2009, MNRAS, 398, 591 [CrossRef] [Google Scholar]
- Schmidt, M. 1959, ApJ, 129, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Schönrich, R., & Binney, J. 2009, MNRAS, 396, 203 [Google Scholar]
- Sellwood, J. A., & Binney, J. J. 2002, MNRAS, 336, 785 [Google Scholar]
- Sestito, F., Longeard, N., Martin, N. F., et al. 2019, MNRAS, 484, 2166 [NASA ADS] [CrossRef] [Google Scholar]
- Sestito, F., Martin, N. F., Starkenburg, E., et al. 2020, MNRAS, 497, L7 [Google Scholar]
- Sharma, S., Hayden, M. R., & Bland-Hawthorn, J. 2021, MNRAS, 507, 5882 [NASA ADS] [CrossRef] [Google Scholar]
- Silva Aguirre, V., Bojsen-Hansen, M., Slumstrup, D., et al. 2018, MNRAS, 475, 5487 [NASA ADS] [Google Scholar]
- Snaith, O. N., Haywood, M., Di Matteo, P., et al. 2014, ApJ, 781, L31 [CrossRef] [Google Scholar]
- Snaith, O., Haywood, M., Di Matteo, P., et al. 2015, A&A, 578, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Snaith, O. N., Bailin, J., Gibson, B. K., et al. 2016, MNRAS, 456, 3119 [NASA ADS] [CrossRef] [Google Scholar]
- Speagle, J. S., Steinhardt, C. L., Capak, P. L., & Silverman, J. D. 2014, ApJS, 214, 15 [Google Scholar]
- Spitoni, E., Silva Aguirre, V., Matteucci, F., Calura, F., & Grisoni, V. 2019, A&A, 623, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spitoni, E., Verma, K., Silva Aguirre, V., & Calura, F. 2020, A&A, 635, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tacconi, L. J., Genzel, R., Saintonge, A., et al. 2018, ApJ, 853, 179 [Google Scholar]
- Troncoso, P., Maiolino, R., Sommariva, V., et al. 2014, A&A, 563, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tsujimoto, T., Bland-Hawthorn, J., & Freeman, K. C. 2010, PASJ, 62, 447 [CrossRef] [Google Scholar]
- van Dokkum, P. G., Leja, J., Nelson, E. J., et al. 2013, ApJ, 771, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Meth., 17, 261 [Google Scholar]
- Zhang, L., Rix, H.-W., van de Ven, G., et al. 2013, ApJ, 772, 108 [Google Scholar]
Appendix A: Quenching in the exponential infall model
We include an explicit quenching episode in our initial star formation histories for the exponential infall scenario. The decision to do this was driven by our result from Haywood et al. (2016b) and Snaith et al. (2014, 2015). However, in Fig. A.1 we see that the sharp transition between the thick- and thin-disc eras can be formed with a sharp change in ϵ rather than explicit quenching (the corresponding star formation histories are shown in Fig. A.2).
 |
Fig. A.1. Different star formation histories fitted using different initial star formation histories. The blue line shows the [Si/Fe]–time evolutions from Sect. 4.1. The orange lines show the [Si/Fe]–time evolution with the explicit quenching removed, and the green line shows the result when the late-time thin disc ϵ is set to be the same as the thick disc ϵ. |
In order to fit the data using the exponential infall model, it is not required that we include the quenching era where ϵ drops to zero, or close to zero, and is followed by a reignition of star formation. However, a sharp transition from high to low ϵ of around a factor of 3 is required to reproduce the sharp gradient change in the [Si/Fe] evolution. In Fig. A.1 the blue and orange lines are essentially indistinguishable. If we bootstrapped the data and made the fit multiple times, any different would be lost in the error. This result is replicated in the DFs, where the explicit quenching run (blue line), and the ϵ reduction run (orange line) are not significantly different. On the other hand, where there is no strong change in ϵ at around 8 Gyr ago, there is no sharp transition in the [Si/Fe]–time evolution, and the DFs do not reproduce the data as well.
At first sight, this result would appear to be in tension with our previous work in Snaith et al. (2014, 2015) which required an explicit quenching episode. However, the closed box model is able to much more effectively shape the SFH to the data, and so more carefully match the chemical evolution of the system. This is because the exponential infall model is more highly constrained than the closed box model, as it assumes: (1) that infall follows an exponential form, (2) the star formation rate is affected only by the amount of gas present and ϵ, (3) there are only three eras in which the infall parameters and ϵ can change, and (4) we control the amount of gas in the system not the star formation rate directly. In the closed box model there were twenty eight eras, each of which could change to shape the chemical evolution track. Thus, the closed box model is able to more precisely model the chemical evolution of the stars in our sample. Both models (exponential infall and closed box) show that the data outside the transition region can be matched by a star formation rate which is around three times lower in the thin disc phase than in the thick disc phase.
In Haywood et al. (2016b) the dearth of intermediate values in the αDF is used to argue for a quenching era in the Milky Way (more specifically the scenario where we have a high star formation rate followed by very low star formation rate for 1 Gyr and then a re-ignition of star formation at a lower rate). Our result here does not exclude this, because, as discussed, the closed box model better fits the [Si/Fe]–age data and the DFs, compared to the exponential infall model. In Figs. 5 and 6 we can see that although the exponential infall model correctly reproduces the key features of the αDF (the two peaks and the dip) the dip is not as broad. Such a broad dip was better reproduced using our closed box model, as shown in Fig. 4 of Haywood et al. (2016b).
All Tables
All Figures
 |
Fig. 1. Chemical and age distribution of stars from spectroscopic surveys. Top row and bottom left panel: decomposition of the chemistry–age distribution of stars from Delgado Mena et al. (2017) with ages by Haywood et al. (in prep.) Top row and bottom left panel: stars are coloured according to whether they are part of the inner or outer disc. Several young alpha-rich stars (Haywood et al. 2013) shown in blue are removed from the sample. Bottom right panel: distribution of inner disc stars taken from APOGEE, with the inner disc stars from Adibekyan et al. (2012) and Delgado Mena et al. (2017) plotted as white points. |
| In the text | |
 |
Fig. 2. Comparison between number of stars at a given Galactic latitude in different APOGEE pointings. Left: from the APOGEE survey. Right: from an N-body simulation. |
| In the text | |
 |
Fig. 3. MDF and αDF from an N-body simulation. Left panel: raw MDF, right: αDF. The blue line is the DFs of all star particles in the N-body model, the orange line shows the DFs of all particles along each APOGEE pointing, and the green line shows the DFs of the star particles along each pointing, with the same DDF as APOGEE. We show the MDF and αDF for stars with a galactocentric radius of 4−6 kpc. |
| In the text | |
 |
Fig. 4. Schematic of the galactic chemical evolution model, and the algorithm to identify the best fit infall history. |
| In the text | |
 |
Fig. 5. Fits of the exponential infall to the time–[Si/Fe] distribution (ωMDF, αDF = 0). Top row, from left to right: best-fit time–[Si/Fe] used to fit the data, the time–metallicity distribution, and the abundance–metallicity distribution. In each panel, the points show the data. Second row: MDF, αDF, and the recovered SFH. The grey histograms show the distribution functions for the inner disc in APOGEE. Third row: evolution of the baryonic mass, gas mass and stellar mass over time. Fourth row: infall rate, and the evolution of the SFE and ϵ. The different lines are for different initial conditions, and the dashed lines show the evolution of those unfitted initial states. |
| In the text | |
 |
Fig. 6. Exponential infall model fitted to the MDF and αDF as well as the time–[Si/Fe] with ωMDF = 900 and ωαDF = 900. The panels are the same as in Fig. 5. |
| In the text | |
 |
Fig. 7. Formation time and fitting parameters for the exponential infall runs with different ω values. From left to right, first panel: formation time for the different fitted runs. Second panel: values for the fitting parameter to the abundance–age relation. Third panel: fitting parameter to the αDF, and fourth panel: fitting parameter to the MDF. The triangular points show failed runs, where the end result is larger than the ICs. Left panel: triangles indicate cases where one or more of the fitting parameters is larger than a threshold. The vertical dashed lines show the values for the initial conditions. |
| In the text | |
 |
Fig. 8. Free-infall model fitted to the time–[Si/Fe] with ωMDF = 0 and ωαDF = 0. The panels are the same as Fig. 5. The different lines show different runs, where the model numbers are referenced in Table 3. |
| In the text | |
 |
Fig. 9. Free-infall model fitted to the MDF and αDF as well as the time–[Si/Fe] with ωMDF = 900 and ωαDF = 900. The panels are the same as in Fig. 5. The blue and green lines show the results of runs from the flat infall initial conditions but the runs shown in orange, red, and purple lines use the result shown by the blue line as their initial condition. |
| In the text | |
 |
Fig. 10. Formation time and fitting parameters for the free-infall runs with different ω values. From left to right: formation time for the different fitted runs, values for the fitting parameter to the abundance–age relation, fitting parameter to the αDF, and fitting parameter to the MDF. The triangular points show failed runs, where the end result is larger than the ICs. Left panel: triangles mark cases where one or more of the fitting parameters is larger than a threshold. |
| In the text | |
 |
Fig. 11. Comparison between the models with the average stellar mass growth from van Dokkum et al. (2013). The models used here use free infall and high ω. We also show the median line of 24 runs where we bootstrapped the data. The variation from the minimum value to maximum value in each time-step is shown as the light coloured region around each line. ± the standard deviation is shown as the darker coloured region around each line. The black lines show how different values of the disc radial scale length –used to convert the stellar mass to the local stellar surface density– affect the van Dokkum et al. (2013) fit. The dotted line, dashed line and dot-dash line use Rscale = 2.1, 2.4, 1.8 kpc. These values are taken from Porcel et al. (1998). |
| In the text | |
 |
Fig. 12. Different distribution functions using the Starhorse and guiding radii. The green area highlights the difference between the two distributions. |
| In the text | |
 |
Fig. 13. Star formation, infall, and chemical evolution of models. These runs use ωMDF = 900 and ωαDF = 900. The DFs are defined using the Starhorse radii (green line) and the guiding radii (blue line). The run labelled ‘default’ represents the 4−6 kpc bin we have used in the previous sections. |
| In the text | |
 |
Fig. 14. MDF and αDF at different radii. Top row: DFs defined using the Starhorse radii with different radial cuts. Bottom row: DFs defined using the guiding radii with different radial cuts. Curves are smoothed using a Savitzky-Golay with a window of 5 and a polynomial order of 2. |
| In the text | |
 |
Fig. 15. Best-fit infall and star formation histories for the different radial cuts (shown in kpc) for the exponential infall model. These runs use the τ = 5 initial conditions and ωMDF, αDF = 900. The different MDFs and αDFs in the different radial bins are shown in Fig. 15. The fitting values between the model and observations for the MDF and αDF are shown in the respective panels. |
| In the text | |
 |
Fig. A.1. Different star formation histories fitted using different initial star formation histories. The blue line shows the [Si/Fe]–time evolutions from Sect. 4.1. The orange lines show the [Si/Fe]–time evolution with the explicit quenching removed, and the green line shows the result when the late-time thin disc ϵ is set to be the same as the thick disc ϵ. |
| In the text | |
 |
Fig. A.2. Fitted star formation histories related to the chemical evolutions presented in Fig. A.1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} \begin{aligned}&\mathrm{[Si/Fe]} < -\mathrm{[Fe/H]}/6. + 1./15. \\&\mathrm{[Fe/H]} < -0.0. \end{aligned} \end{aligned} $$](/articles/aa/full_html/2022/03/aa39526-20/aa39526-20-eq1.gif)
![$$ \begin{aligned} B_{\rm l} = \cos [b_{\min } + (\delta b (i_{\rm lon} + 0.5))] \times 20 \times \frac{n_{\rm lon}}{n_{\rm lat}}, \end{aligned} $$](/articles/aa/full_html/2022/03/aa39526-20/aa39526-20-eq2.gif)
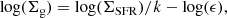
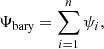
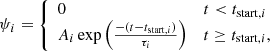
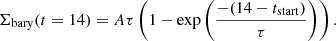
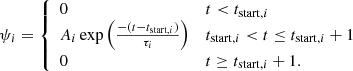
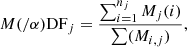
![$$ \begin{aligned} \begin{aligned} F_{ij} =&\sum _{i=1}^{n_{\rm star}}(O_{\rm [Si/Fe]}-M_{\rm [Si/Fe]})_i^2\\& +\omega _{\rm MDF} \sum _{j=1}^{n_{\rm bins}}(O_{\rm MDF}-M_{\rm MDF})_j^2 \\& +\omega _{\alpha \mathrm{DF}} \sum _{j=1}^{n_{\rm bins}}(O_{\alpha \mathrm{DF}}-M_{\alpha \mathrm{DF}})_j^2, \end{aligned} \end{aligned} $$](/articles/aa/full_html/2022/03/aa39526-20/aa39526-20-eq11.gif)