| Issue |
A&A
Volume 655, November 2021
|
|
|---|---|---|
| Article Number | A111 | |
| Number of page(s) | 18 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/202140453 | |
| Published online | 01 December 2021 | |
Radial structure and formation of the Milky Way disc
GEPI, Observatoire de Paris, Université PSL, CNRS, 5 place Jules Janssen, 92190 Meudon, France
e-mail: david.katz@obspm.fr
Received:
29
January
2021
Accepted:
14
July
2021
Context. The formation of the Galactic disc is an enthusiastically debated issue. Numerous studies and models seek to identify the dominant physical process(es) that shaped its observed properties; for example, satellite accretion, starburst, quenching, gas infall, and stellar radial migration.
Aims. Taking advantage of the improved coverage of the inner Milky Way provided by the SDSS DR16 APOGEE catalogue and of the ages published in the APOGEE-AstroNN Value Added Catalogue (VAC), we examined the radial evolution of the chemical and age properties of the Galactic stellar disc with the aim of better constraining its formation.
Methods. Using a sample of 199 307 giant stars with precise APOGEE abundances and APOGEE-AstroNN ages, selected in a ±2 kpc layer around the galactic plane, we assessed the dependency as a function of guiding radius of (i) the median metallicity, (ii) the ridge lines of the [Fe/H] − [Mg/Fe] and age–[Mg/Fe] distributions, and (iii) the age distribution function (ADF).
Results. The giant star sample allows us to probe the radial behaviour of the Galactic disc from Rg = 0 to 14−16 kpc. The thick disc [Fe/H] − [Mg/Fe] ridge lines follow closely grouped parallel paths, supporting the idea that the thick disc did form from a well-mixed medium. However, the ridge lines present a small drift in [Mg/Fe], which decreases with increasing guiding radius. At sub-solar metallicity, the intermediate and outer thin disc [Fe/H] − [Mg/Fe] ridge lines follow parallel sequences shifted to lower metallicity as the guiding radius increases. We interpret this pattern as the signature of a dilution of the interstellar medium from Rg ∼ 6 kpc to the outskirts of the disc, which occurred before the onset of the thin disc formation. The APOGEE-AstroNN VAC provides stellar ages for statistically significant samples of thin disc stars from the Galactic centre up to Rg ∼ 14 kpc. An important result provided by this dataset is that the thin disc presents evidence of an inside-out formation up to Rg ∼ 10 − 12 kpc. Moreover, about ∼7 Gyr ago, the [Mg/Fe] ratio in the outer thin disc (Rg > 10 kpc) was higher by about ∼0.03−0.05 dex than in the more internal regions of the thin disc. This could be the fossil record of a pollution of the outer disc gas reservoir by the thick disc during its starburst phase.
Key words: Galaxy: disk / Galaxy: evolution / Galaxy: abundances
© D. Katz et al. 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
The Milky Way stellar disc is a complex structure. Its formation and its evolution, together with the related physical and dynamical processes, are still fiercely debated. Recently, several surveys have provided very large statistical samples of stars with detailed chemical abundances; for example, RAVE (Steinmetz et al. 2020a,b), Gaia-ESO (Gilmore et al. 2012), APOGEE (Majewski et al. 2017; Ahumada et al. 2020; Jönsson et al. 2020), LAMOST (Cui et al. 2012; Zhao et al. 2012), or GALAH (De Silva et al. 2015; Buder et al. 2018, 2021). Combined with the very precise Gaia astrometry (Gaia Collaboration 2018, 2021; Lindegren et al. 2018, 2021a,b) they make it possible to examine the formation of the Galactic disc with an unprecedented level of detail. However, despite this amount of data the origin and the link between the two traditionally assumed components of the Milky Way disc, that is the thick and the thin discs, are not well established.
Spectroscopic studies of Solar neighbourhood stars showed that thick disc stars are generally older and have higher ratios of α-elements than thin disc stars (e.g., Fuhrmann 1998, 2004, 2008, 2011; Prochaska et al. 2000; Bensby et al. 2005, 2007; Haywood et al. 2013). The star distribution in the ([Fe/H], [α/Fe]) plane displays two sequences: a high-[α/Fe] sequence associated with the thick disc and a low-[α/Fe] sequence associated with the thin disc (Fuhrmann 1998; Haywood et al. 2013). Moreover, the velocity dispersions are larger in the thick disc than in the thin disc, and, as a whole, the thick disc rotates more slowly than the thin disc (e.g., Soubiran et al. 2003; Kordopatis et al. 2013; Robin et al. 2017). Although the two discs would appear to belong to different stellar populations, some studies suggested that these populations are composed of multiple sub-populations that smoothly span the observed range of properties (Norris 1987; Bovy et al. 2012, 2016; Mackereth et al. 2017).
Beyond the Solar vicinity, the thin and thick disc stars still appear as two distinct groups in the ([Fe/H], [α/Fe]) plane (e.g., Nidever et al. 2014; Hayden et al. 2015; Queiroz et al. 2020), but their pattern evolves with the Galactic location (R, |Z|)1. In the rest of the introduction, we use the term α-dichotomy to refer to the presence of two distinct high- and low-α sequences and the term α-bimodality to refer explicitly to the existence of two density peaks along a single sequence. The high-[α/Fe] sequence is observed up to R ∼ 10 − 12 kpc and gradually vanishes at larger radii, confirming that the thick disc has a shorter scale length than the thin disc (Bensby et al. 2011; Bovy et al. 2012; Cheng et al. 2012). The low-[α/Fe] sequence is present at all radii, but its morphology changes with the location in the Galaxy. In the inner disc (R ≤ 6 kpc), Hayden et al. (2015), Bovy et al. (2019), and Lian et al. (2020a,b) found the thick and thin disc stars to belong to a single sequence (i.e., α-bimodality), while Rojas-Arriagada et al. (2019) and Queiroz et al. (2020) observed two distinct sequences (i.e., α-dichotomy). Moreover, the observed metallicity gradient in the thin disc is flat in the inner disc in contrast with the gradient observed in the external regions (R > 6 kpc), suggesting different chemical evolutions of the two regions (Haywood et al. 2019).
Different approaches exist in the literature to explain the formation paths of the α-dichotomy and α-bimodality seen in the Galactic disc and the formation of the thick disc. Among the chemical evolution models, one of the first approaches seeking to explain first the metallicity-α-elements distribution in the solar vicinity (Chiappini et al. 1997, 2001) and then the α-dichotomy (e.g., Spitoni et al. 2019, 2020) is the two-infall model. The thick disc is formed at early times as the result of a collapse of primordial gas followed by a quiescent period where the star formation is quenched. After that, a new episode of fresh gas accretion takes place, the star formation resumes, and the thin disc is formed in an inside-out fashion. A recent approach that also consists of two phases of gas accretion was developed by Lian et al. (2020a,b,c,d) to reproduce the α-dichotomy and α-bimodality observed at different Galactic locations. The two gas accretion phases are associated with starbursts separated by a prolonged period of low-level star formation. According to Haywood et al. (2018, 2019), the thick disc forms from a turbulent gas-rich environment, which is followed by a low level of star formation. The inner thin disc is formed from the gas left by the thick disc formation, and there is no gas accretion. Snaith et al. (2015) showed that the inner and outer discs do not follow the same chemical evolution. The α-bimodality observed in the inner disc (R ≤ 6 kpc) is an effect of the inner disk evolution and comes from the quenching phase that occurred between the formation of the thick disc and the inner thin disc (Haywood et al. 2016). In the external disc, the low-α sequence is the result from the gas left over from the thick disk formation (which gave rise to the high-α sequence) combined with a radially dependent dilution (Haywood et al. 2019). In their scenario, the sequence itself cannot be reproduced by chemical evolution at a single radius, but it is the result of a radially dependent evolution.
Recently, Khoperskov et al. (2021) presented a set of chemo-dynamical Milky Way-type galaxy formation simulations. In these simulations, the high-[α/Fe] sequence is formed early from a burst of star formation in a turbulent, compact gaseous disc that forms a thick disc. The low-[α/Fe] sequence, in turn, is the result of a quiescent star formation supported by the slow accretion of enriched gas onto a radially extended thin disc. Stellar feedback-driven outflows during the formation of the thick disc are responsible for the enrichment of the surrounding gaseous halo, which subsequently feeds the disc on a longer timescale. Khoperskov et al. (2021) confirm the scheme presented in Haywood et al. (2019) by showing that the formation of the low-α sequence is a radially dependent process, which explains the α-dichotomy. These simulations do not include mergers, which therefore did not lead to the assembly of the α-dichotomy here.
Schönrich & Binney (2009a,b) developed a chemical evolution model that reproduced the α-dichotomy in the ([Fe/H] − [α/Fe]) plane observed in the Solar neighbourhood assuming a continuous star formation. The model includes, in particular, radial flow of gas and radial migration of stars as the main mechanisms making it possible to carry kinematically hot stars from the inner disc to the Solar vicinity and to create the thick disc. Recently, Sharma et al. (2021) confirmed the results of Schönrich & Binney (2009a,b) and extended them to different locations across the Galaxy.
Simulations of Milky Way mass galaxies with enough resolution have allowed to study the formation scenario of distinct discs self-consistently in a fully cosmological context (e.g., Calura & Menci 2009; Miranda et al. 2016). Such simulations predict that thin stellar discs form in an inside-out, upside-down fashion (e.g., Brook et al. 2012; Bird et al. 2013), but the formation mechanism of the α-dichotomy in the ([Fe/H] − [α/Fe]) plane is still under debate. Some authors (e.g., Brook et al. 2012; Grand et al. 2018; Noguchi 2018; Buck 2020; Agertz et al. 2021) have invoked gas-rich mergers as the main origin, but the formation channels of chemically distinct discs differ. For example, Grand et al. (2018) found two main paths to produce the α-dichotomy in different regions of the galaxies: an early centralised starburst mechanism that is relevant for the inner disc, and a shrinking disc mechanism that is relevant for the outer disc. For the centralised starburst pathway, an early and intense high-[α/Fe] star formation phase induced by gas-rich mergers is followed by a more quiescent low-[α/Fe] star formation. For the shrinking disc pathway, an early phase of high-[α/Fe] star formation is followed by a shrinking of the gas disc due to a temporarily lowered gas accretion rate, after which disc growth resumes. Otherwise, Clarke et al. (2019) claimed that the dichotomy arises from rapid star formation in high redshift clumps and that the two [α/Fe]-sequences form simultaneously early on in the evolution of the Milky Way, resulting in overlapping ages.
The time evolution of radial chemical abundance gradients (Anders et al. 2017) and of the [α/Fe] and [Fe/H] abundances (e.g., Haywood et al. 2013; Xiang et al. 2017; Silva Aguirre et al. 2018; Wu et al. 2019; Miglio et al. 2021; Ciucă et al. 2021) are crucial to exploring the formation history of the Galaxy. Age is not a directly observable quantity. Asteroseismology and high-resolution spectroscopic data allowed astronomers to measure precise masses of tens of thousands of red giants and then to derive stellar ages (Pinsonneault et al. 2014, 2018; Miglio et al. 2021). At present, thanks to the high-quality spectroscopic and astrometric measurements available, it becomes possible to estimate ages for a large sample of red-giants, making it possible to analyse larger volumes of the Galactic disc. Further estimations have been made available through the use of machine learning techniques. These techniques use stars with asteroseismic data as a training set (e.g., Ness et al. 2016; Mackereth et al. 2019a; Wu et al. 2019; Ciucă et al. 2021).
In the present study, we used the APOGEE atmospheric parameters and abundances (Jönsson et al. 2020) and the APOGEE-AstroNN distances, guiding radius, and ages (Bovy et al. 2019; Leung & Bovy 2019a; Mackereth et al. 2019a), contained in the 16 SDSS data release (Ahumada et al. 2020), to probe the radial structure of the Milky Way disc. The outline of the paper is as follows. In Sect. 2, we describe the data and the selection of the different samples. The chemical and age properties of the disc and in particular their evolution with guiding radius are examined in Sects. 3 and 4, respectively. In Sect. 5, we discuss the implications of the new observations for the structure and formation of the Milky Way disc. Finally, Sect. 6 summarises the main results.
2. Data
2.1. APOGEE and APOGEE-AstroNN
The present study relies on the APOGEE (Jönsson et al. 2020) and APOGEE-AstroNN data (Bovy et al. 2019) of the 16 SDSS data release (Ahumada et al. 2020). APOGEE DR16 contains 473 307 spectra of 437 445 stars observed from the Apache Point Observatory and from the Las Campanas Observatory. It is the first APOGEE release covering both hemispheres. The APOGEE data include radial velocities, atmospheric parameters (effective temperature, surface gravity, and metallicity), and individual abundances for 26 chemical species. Parameters and abundances were derived with the ASPCAP pipeline (García Pérez et al. 2016).
APOGEE-AstroNN is one of the six value-added catalogues (VAC) associated with APOGEE DR16. APOGEE-AstroNN contains atmospheric parameters, individual abundances for 20 chemical species, distances, ages, and kinematic and dynamic parameters. The atmospheric parameters and abundances were re-determined with a Bayesian multi-layer neural network (Leung & Bovy 2019b), trained on a subset of ∼33 000 SN > 200 APOGEE spectra and parameters from the main APOGEE catalogue. APOGEE-AstroNN provides two distance estimates (Leung & Bovy 2019a). The first one was obtained with a neural network designed to determine stellar luminosities from APOGEE spectra, while the second one (the use of which is recommended) is a weighted combination of the first estimate and of Gaia DR2 parallaxes (Gaia Collaboration 2018). The ages were determined with a third Bayesian neural network (Mackereth et al. 2019a), trained on APOKASC-2 (Pinsonneault et al. 2018) asteroseismic ages and APOGEE spectra. All three neural networks rely on the open-source Python package AstroNN (Leung & Bovy 2019b), from which the name of the VAC derives. Finally, APOGEE-AstroNN also includes orbital parameters calculated with the ‘fast’ method (Mackereth & Bovy 2018) using the MWPotential2014 gravitational potential from Bovy (2015).
In this study, we used the atmospheric parameters, abundances, and quality flags from APOGEE2. We complement them with additional information provided by APOGEE-AstroNN3; that is, distances, galactocentric cylindrical coordinates (current galactocentric radius R, azimuth ϕ, height Z), guiding radius (Rg), and, most importantly, ages.
2.2. Selection of the main sample
Several filters were applied to select the main sample. First, the highest signal-to-noise occurrences of the duplicated APOGEE identifiers were kept, and the others were discarded. This cut was made using the EXTRATARG flag. After this first step, the sample still contained a few thousand records with duplicated Gaia source identifiers. The first occurrence of each was kept and the others were removed. Then, the stars identified by the flags STARFLAG or ASPCAPFLAG has having (i) 40% or more bad pixels in their spectra, (ii) a neighbour more than 100 times brighter, (iii) broad lines, or (iv) the STAR_BAD bit set to true, were excluded. The stars with a missing or invalid metallicity, magnesium over iron ratio, guiding radius, or height were also discarded, as well as the stars with a signal-to-noise ratio lower than 50 or a metallicity- or magnesium-over-iron uncertainty larger or equal to 0.1 dex. The sample was then restricted to giant stars to avoid potential differential trends in the measure of the parameters of dwarfs and giants and in particular chemical abundances. The stars with effective temperatures and surface gravities, respectively in the ranges of [3200, 7500] K and [0.5, 3.5] dex, were selected as giants. The distances that were not at least five times greater than their uncertainties were considered as inaccurate, and the corresponding stars were suppressed. Finally, the sample was trimmed in guiding radius and height, respectively to [0, 18] kpc and [ − 2, 2] kpc. In this study, we preferentially used the guiding radius4 because it averages the effect of blurring and, in this respect, provides a better proxy for the birth radius than the galactic radius itself. Of course, this does not mitigate the effect of churning. Depending on its importance for the Milky Way (see e.g., Schönrich & Binney 2009a,b; Minchev et al. 2014; Sharma et al. 2021), it is possible that the guiding radii and the birth radii differ for a significant fraction of the stars. The vertical cut seeks to minimise the contamination of the sample by halo stars, without removing too many thick disc stars. After applying all of the above filters, the main sample contains 199 307 stars. Figure 1 shows their distribution in the (X, Y) and (X, Z) planes.
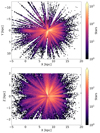 |
Fig. 1. Face-on (top) and edge-one (bottom) distributions of the stars of the main sample. X, Y, and Z are the Cartesian Galactic coordinates, with the Z axis positive in the northern Galactic hemisphere. The Galactic centre is located at X = Y = Z = 0 kpc and the Sun at X = 8.125 kpc (GRAVITY Collaboration 2018), Y = 0 kpc and Z = 20.8 pc (Bennett & Bovy 2019). In the top panel, the Galaxy rotates clockwise. |
2.3. Separating the thick and thin discs
In Sects. 3.2 and 4.1, we study the disc as a whole. In Sects. 3.1 and 4.2, we focus on the thin disc only. We use the star locations in the ([Fe/H], [Mg/Fe]) plane to assign them to the thick or to the thin disc. The boundaries used to separate the two groups are shown in Fig. 2 as black segments. The lower envelope of the thick disc and the upper envelope of the thin disc were chosen so as to ensure a separation of the high- and low-alpha sequences at all guiding radii (see Appendix A). The upper envelope of the thick disc and the lower envelope of the thin disc were used to reject outliers, and also for the latter, to further minimise the contamination by the accreted halo sequence (Mackereth et al. 2019b; Di Matteo et al. 2019). The stars attributed to the thick and thin disc are shown in Fig. 2, respectively as red and blue dots. The grey dots outside of the selection limits are associated with neither population. The white lines are stellar density iso-contours (see caption). The 199 307 main sample stars are distributed into 48 043 thick disc stars, 148 018 thin disc stars and 3246 ‘other’ stars. In Appendix A, we show the separation of the thick and thin disc stars as a function of guiding radius.
 |
Fig. 2. Distribution of the main sample in the ([Fe/H], [Mg/Fe]) plane. The black segments delineate the thick disc (red dots) and the thin disc (blue dots) selection boundaries. The grey dots are stars attributed to neither population. The white lines are stellar density iso-contours, that is, 90%, 70%, 50%, 30%, 20%, 10%, 7.5%, and 5% of the peak density. |
2.4. The age sample
Mackereth et al. (2019a) and Bovy et al. (2019) recommend restricting the usage of the APOGEE-AstroNN ages to the stars with metallicities [Fe/H] > −0.5 dex. Below this threshold, the APOKASC-2 catalogue (Pinsonneault et al. 2018) provides insufficient coverage to be efficient as a training sample for the neural network deriving the ages. When using the ages, we therefore further trim the main sample following the above recommendation. The age sample contains 173 374 stars, of which 31 345 are associated with the thick disc and 141 201 to the thin disc. Figure 3 overplots the main sample (grey dots) and the age sample (blue dots) in the ([Fe/H], [Mg/Fe]) plane. The metallicity cut truncates the metal-poor part of the high-alpha sequence. For this reason, and also because the oldest ages are affected by systematics (see below), we limited use of the ages when studying the high-alpha sequence. The metallicity cut also removes some stars in the low-alpha sequence. As presented in Appendix B, the percentage of thin disc stars discarded is lower than 5% up to Rg = 12 kpc, about 12.5% in the [12, 14] kpc interval, and exceeds 25% beyond Rg = 14 kpc. In Sect. 4, we restrict most of the analysis on the thin disc age to Rg < 14 kpc and consider the results obtained for the interval [12, 14] kpc with caution.
 |
Fig. 3. Distribution in the ([Fe/H], [Mg/Fe]) plane of the main sample stars without valid ages (grey dots) and of the age sample stars (blue dots). The white lines are stellar density iso-contours; that is, 90%, 70%, 50%, 30%, 20%, 10%, 7.5%, and 5% of the peak density. |
Mackereth et al. (2019a) and Bovy et al. (2019) quote an average precision on the estimates of the age of about 30%. Moreover, they report a trend in the estimate of the raw ages, the youngest being slightly overestimated, while the oldest are underestimated (slightly, at 6−8 Gyr, and as much as 3.5 Gyr at 10 Gyr). They explain the underestimation of the old ages by the loss of sensitivity to mass, in the low mass regime, of the carbon and nitrogen features. APOGEE-AstroNN provides three estimates of the age: the raw age determined by the neural network and two ages corrected with two different calibrations of the trend (Bovy et al. 2019). In this study, we used one of the two empirically corrected ages; that is, the AGE_LOWESS_CORRECT, following the recommendation expressed in the documentation.
Figure 4 shows the [Mg/Fe] ratio as a function of age of 1873 stars from the age sample located less than 500 pc from the Sun. It can be compared to previous studies of the evolution of the α-element abundances with age in the solar neighbourhood (e.g., Haywood et al. 2013; Bensby et al. 2014; Buder et al. 2019; Delgado Mena et al. 2019; Hayden et al. 2020). The overall behaviour is similar, with two regimes: a smooth increase of the alpha-elements-over-iron ratio in the young and intermediate age stars and a steeper increase in the oldest one. The transition is roughly at the same location, that is about 8 Gyr in Fig. 4 and in Haywood et al. (2013) and 8−9 Gyr in Bensby et al. (2014), Buder et al. (2019), and Delgado Mena et al. (2019). Looking more closely at the old star sequence in Fig. 4, one can see that it presents a steeper slope than derived in the previous studies and that the oldest ages ‘saturate’ around 11 Gyr. This is consistent with the underestimation of the oldest ages reported by Mackereth et al. (2019a) and Bovy et al. (2019).
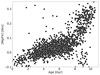 |
Fig. 4. Magnesium-over-iron ratio as a function of age of the 1873 age-sample stars located less than 500 pc from the Sun. |
3. Radial structure of the disc: Chemistry
In this section, we study how the chemical properties of the disc evolve with the guiding radius.
3.1. Thin disc radial metallicity trend
We first examine the radial metallicity trend. Figure 5 shows the median metallicity of the thin disc stars (see Sect. 2.3) as a function of the guiding radius. Beyond Rg ∼ 6 kpc, the thin disc exhibits a negative metallicity gradient, already known and characterised with several tracers: Cepheids (Luck et al. 2011; Lemasle et al. 2018), open clusters (Donor et al. 2020; Spina et al. 2021), and field stars (Grenon 1972; Anders et al. 2014, 2017; Hayden et al. 2015; Haywood et al. 2019). Looking closely at the outer disc, there is a suspicion of a ‘plateau’ for Rg ∈ [10, 11] kpc, which exhibits a slightly more pronounced contrast than the other oscillations along the negative slope. Considered in isolation, this is a relatively weak evidence of a discontinuity in the disc. Yet, we will see in Sect. 4 that there are other observables supporting a change in the properties of the disc around Rg ∼ 10 kpc. As reported by Hayden et al. (2015) and Haywood et al. (2019), inward of Rg ∼ 6 kpc, the slope of the metallicity gradient becomes much smoother and the trend becomes almost flat. These two studies, relying respectively on APOGEE DR 12 (Holtzman et al. 2015) and DR 14 (Abolfathi et al. 2018), were able to trace the quasi-plateau up to R ∼ 3.5 − 4 kpc. Thanks to the southern hemisphere observations, APOGEE DR16 now provides sufficient statistics to map the trend up to the Galactic centre. Around Rg ∼ 2.5 − 3 kpc, the gradient steepens again and reaches a second plateau in the inner 1−1.5 kpc, around [Fe/H] ∼ 0.3 dex. Using the APOGEE-AstroNN data, Bovy et al. (2019) mapped the mean metallicity of the Galactic disc up to the Galactic bar. Their map shows that the mean metallicity of the bar is lower than the one of the surrounding disc. As shown in Appendix C, the apparent differences in the behaviour between a lower metallicity bar and a median thin disc metallicity that rises at Rg < 3 kpc is due to the different way we select our respective samples, that is we only considered the thin disc stars (defined as the low-alpha stars), while Bovy et al. (2019) used both the high- and low-alpha stars.
 |
Fig. 5. Median metallicity of the thin disc stars as a function of the guiding radius. The median is calculated per bin of 250 pc. The shaded area delimits the ±1σ uncertainty on the estimate of the median. |
For comparison, in Appendix D, we measure the thin disc median metallicity as a function of radius instead of guiding radius. The overall shape of the metallicity trend is very similar to the one derived with the guiding radius: two plateaus, respectively at R < 2 kpc and R ∈ [4, 6] kpc, and two areas where the metallicity decreases with increasing radius, respectively at R ∈ [2, 4] kpc and R > 6 kpc. It could be noted that beyond 6 kpc, the metallicity gradient presents fewer oscillations as functions of radius than as a function of guiding radius. This could indicate a dynamical origin of these oscillations. For example, Khoperskov et al. (2020a) showed that the guiding radius space can reveal dynamical resonances, which, in direct space, are blurred and therefore more difficult to identify.
3.2. Patterns and ridge lines in the ([Fe/H], [Mg/Fe]) plane
We now turn our attention to the evolution of the metallicity versus alpha-element patterns in the Galactic disc. Figure 6 shows the distribution of the main-sample stars in the ([Fe/H], [Mg/Fe]) plane. Each thumbnail corresponds to an interval of 2 kpc in guiding radius, from Rg ∈ [0, 2] kpc (top left) to [16, 18] kpc (bottom right). In each one, iso-density contours are plotted at 5, 7.5, 10, 20, 30, 70, 90 (black lines), and 50% (blue line) of the maximum density (in the given thumbnail). The red lines are the lines of modes of the [Mg/Fe] distributions, hereafter referred to as the ‘ridge lines’. They are derived in 2 steps. First, in each Rg interval, the data are divided in metallicity slices of Δ[Fe/H] = 0.1 dex. Then, for each slice, the location of the mode of the [Mg/Fe] distribution (or the first two modes if the distribution is bimodal) is measured. The mode is not a good estimator for the ridge of a sequence that is too steep. For this reason, the steepest part of the high-alpha sequences has been excluded from the analysis. The mode was preferred over the median, because it allows us to describe the main tracks of multi-sequence data, without the need to separate these sequences first.
 |
Fig. 6. Evolution of the distribution of main sample stars in the ([Fe/H], [Mg/Fe]) plane as a function of guiding radius, from Rg ∈ [0, 2] kpc (top left) to [16, 18] kpc (bottom right). The iso-density contours are plotted at 5, 7.5, 10, 20, 30, 70, 90 (black lines) and 50% (blue line) of the maximum density. The ridge lines are plotted in red. |
Over the last decade, the radial and vertical dependences of the metallicity-alpha-element distribution have been studied in more and more detail with increasingly larger samples (e.g., Bensby et al. 2011; Anders et al. 2014; Nidever et al. 2014; Hayden et al. 2015; Queiroz et al. 2020). Figure 6 is mostly consistent with similar plots shown in the above papers. In the inner 10 kpc, it displays two over-densities, a high alpha-element (here [Mg/Fe]), and a low one. Between Rg = 6 and 10 kpc, the two over-densities define two different sequences. In Appendix E, we note that when the sample is restricted to a ±500 pc layer around the Galactic plane, two close but separated sequences are observed in the Rg ∈ [4, 6] kpc interval. Because of their scale height (Bovy et al. 2012), kinematics (Bensby et al. 2003), and age properties (Haywood et al. 2013), these two sequences are associated with the thick disc (high-alpha) and thin disc (low-alpha), respectively. Moving inward of Rg = 4 − 6 kpc, Fig. 6 shows that the two over-densities connect through a zone of lower density to form a single sequence. This is in agreement with the observations of Hayden et al. (2015), Bensby et al. (2017), Zasowski et al. (2019), Bovy et al. (2019), and Lian et al. (2020a,b), who also report a single sequence in the inner disc and/or in the bulge/bar area. Conversely, Rojas-Arriagada et al. (2019) and Queiroz et al. (2020) observe two sequences in the inner regions. In Appendix F, we compare the distributions of different APOGEE DR16 alpha elements in the ([Fe/H], [α/Fe]) plane (restricting the sample to the stars contained in the Rg ∈ [0, 2] kpc interval). The different elements produce different patterns: the global alpha-element abundance5 and oxygen show a double sequence, while magnesium, silicon, and calcium present a single sequence. This could explain, at least partly, why Queiroz et al. (2020), who use a combined α-element abundance, observe a double sequence, while we see a single one with magnesium. However, this does not explain the discrepancy with Rojas-Arriagada et al. (2019), who also used magnesium. Beyond Rg = 10 kpc, the high-alpha sequence gradually vanishes. This is in agreement with the finding that the thick disc has a shorter scale length than the thin disc (Bensby et al. 2011; Cheng et al. 2012; Bovy et al. 2012). It should be emphasised that in this paragraph the term ‘sequence’ is used in the geometrical sense. It does not presuppose the number of chemical tracks that form the sequence or sequences. In particular, based on Fig. 6, it can not be excluded that the single geometrical sequence observed in the inner disc be made of two chemical tracks, with the low-alpha one restricted to a narrow metallicity range. We discuss and propose an interpretation of the inner disc sequence in Sect. 5.
Although the detailed properties of the inner disc are still debated, the global behaviour of the disc is now rather well established. Here, we wish to address a specific issue: the evolution as a function of guiding radius of the location of the sequences in the ([Fe/H], [Mg/Fe]) plane. The sequences are broad and significantly overlap from one guiding radius annulus to the next. We therefore used the modes of the [Mg/Fe] profiles to describe the ridge line of the sequences. They are plotted separately per 2 kpc Rg annulus in Fig. 6 (as red lines) and together in Fig. 7, allowing us to compare their relative locations. In this last figure, we observe that the thick disc sequences are closely grouped. However, they present a small drift in [Mg/Fe] with guiding radius, the innermost sequence (Rg ∈ [0, 2] kpc) being located a few hundredths of a dex above the outermost sequence (Rg ∈ [8, 10] kpc). As shown in Appendix E, the drift remains essentially the same when the sample is sliced by interval of distance to the Galactic plane. The drift is observationally consistent with the measurements of Bensby et al. (2017), who noticed that the bulge stars coincide with the upper envelop of the local thick disc stars. Lian et al. (2020b) recently studied the median [Mg/Fe] versus metallicity trend6 in the bulge and compared the behaviours of on-bar and off-bar stars. They observed that the trends separate between [Fe/H] ∼ −0.3/−0.2 dex and solar metallicity, the on-bar one passing roughly 0.05−0.1 dex above the off-bar one. In Fig. 7, the thin disc sequences behave differently at sub-solar and super-solar metallicity. On the metal-rich side, the thin disc sequences between Rg = 2 and 12 kpc converge and overlap. Conversely, on the metal-poor side, the sequences between Rg = 6 and 16 kpc follow parallel paths, shifting to lower metallicity at larger guiding radius. This confirms the prediction for the outer disc of Haywood et al. (2019), who schematised a similar behaviour in the top panel of their Fig. 6. This is also in qualitative agreement with the trend observed by Ciucă et al. (2021) between the inner, local, and outer discs (see the left panel of their Fig. 9). These parallel paths are also reminiscent of the parallel chemical tracks in the model of Sharma et al. (2021) (see their Fig. 10). We discuss possible interpretations of this pattern in Sect. 5.1. For comparison, in Appendix G, we present the ridge lines derived per interval of Galactic radius.
 |
Fig. 7. Ridge lines of the ([Fe/H], [Mg/Fe]) sequences for different Rg annulus, from [0, 2] kpc (grey) to [14, 16] kpc (red). The shaded areas delimit the ±1σ uncertainties (derived by bootstrap) on the estimates of the modes. |
The ridge lines do not show where the cores of the star distributions are located along the sequences. To answer this question, Fig. 8 shows the ([Fe/H], [Mg/Fe]) iso-density contours at 70% of the maximum density, for the thin disc sample (as defined in Sect. 2.3), divided in 2 kpc guiding radius annulus, from Rg ∈ [0, 2] kpc (grey) to Rg ∈ [16, 18] kpc (dark red). The iso contours shift towards lower metallicity when the guiding radius increases, with a reduced shift between [2, 4] and [4, 6] kpc. This is, fortunately, consistent with the radial metallicity trend discussed in Sect. 3.1. In the inner disc, the contours present a weak negative [Mg/Fe] gradient with guiding radius, and they change sign at Rg ∈ [8, 10] kpc, becoming positive and steeper in the outer disc.
 |
Fig. 8. Iso-density contours in the ([Fe/H], [Mg/Fe]) plane at 70% of the maximum density, for the thin disc sample. Each contour corresponds to a 2 kpc guiding radius annulus, from Rg ∈ [0, 2] kpc (grey) to Rg ∈ [16, 18] kpc (dark red). |
4. Radial structure of the disc: Ages
We now use the ages of the APOGEE-AstroNN catalogue to study the evolution with guiding radius of the age–[Mg/Fe] distribution (Sect. 4.1) and of the age distribution function (Sect. 4.2).
4.1. Patterns and ridge lines in the (Age, [Mg/Fe]) plane
Figure 9 shows the distribution of the age-sample stars in the age–[Mg/Fe] plane. The sample is divided with the same bins in guiding radius as before. In each panel, the iso-density contours are plotted at 5, 10, 20, 30, 70, 90 (black), and 50% (blue) of the maximum density. As in Sect. 3.2, the ridge lines (in red) were derived using the mode of the [Mg/Fe] distributions per interval of Δage = 0.5 Gyr, from 0 to 8.5 Gyr. The ridge lines were not computed for older stars, because beyond ∼9 Gyr, the ages begin to be underestimated (see Sect. 2.4, Mackereth et al. 2019a; Bovy et al. 2019). The 380 stars contained in the outermost annulus, that is Rg ∈ [16, 18] kpc, were insufficient to derive its ridge line.
 |
Fig. 9. Distributions of the main sample stars in the age–[Mg/Fe] plane, from Rg ∈ [0, 2] kpc (top left) to [16, 18] kpc (bottom right). The iso-density contours are plotted at 5, 10, 20, 30, 70, 90 (black lines), and 50% (blue line) of the maximum density. The ridge lines, derived over the range [0, 8.5] Gyr, are plotted in red. |
As shown in Fig. 9, from Rg = 2 to 10 kpc, the distribution of the stars in the (age, [Mg/Fe]) plane presents two regimes. First, a low-[Mg/Fe] sequence made of young and intermediate-age stars and presenting a weak [Mg/Fe] gradient. Then, a high-[Mg/Fe] sequence exhibiting a steeper gradient. The transition between the two regimes occurs at around 8 Gyr. The separation into high- and low-[Mg/Fe] sequences allows us to associate the old-[Mg/Fe]-rich regime with the thick disc and the younger [Mg/Fe]-poor regime to the thin disc. The general pattern is similar to the one observed in the solar neighbourhood (Haywood et al. 2013; Bensby et al. 2014; Buder et al. 2019; Delgado Mena et al. 2019; Hayden et al. 2020) and at greater distances (Feuillet et al. 2019). The proportion of young stars decreases towards the Galactic centre. Within the innermost 2 kpc, most stars are older than 5 Gyr, so the thin disc appears more as an over-density than a fully fledged sequence. As discussed in Sect. 2.4, the under-estimation of the APOGEE-AstroNN ages of stars older than ∼9 Gyr most likely leads us to over-estimate the slope of the thick disc sequence, which nonetheless is steeper than the one of the thin disc (as shown in the solar neighbourhood by the above mentioned studies). Beyond Rg = 10 kpc, the gradual disappearance of the thick disc makes the sequence of the thin disc the main feature. The majority of its stars are younger than ∼8 Gyr.
Figure 10 shows the relative locations of the ridge lines of the age–[Mg/Fe] thin disc sequences, for different guiding radii. As already seen in the previous figure, the ridge lines present a gradient, the [Mg/Fe] ratio increasing with age. Here, we can see that they split in two main groups. The ridge lines beyond Rg = 10 kpc exhibit a stronger gradient than the ridge lines below. The two groups overlap below 2 Gyr and diverge at larger age, producing a gap which reaches Δ[Mg/Fe] ∼ 0.05 dex at 6 Gyr. In the inner group, the ridge lines from Rg ∈ [2, 4] to [8, 10] kpc are very tight. The outer group is more loose, that is the Rg ∈ [12, 16] kpc ridge lines appear to be slightly offset above the Rg ∈ [10, 12] kpc one. This global behaviour is broadly similar to the prediction of Haywood et al. (2019) (see their Fig. 6 bottom panel), as well as to the observations of Ciucă et al. (2021) (see their Fig. 9 right panel). Yet, we observe no offset between the inner and local discs, nor a smooth continuous radial trend, but rather a jump between Rg ∈ [8, 10] and [10, 12] kpc potentially followed by a weak outward gradient. For comparison, in Appendix H we present the ridge lines derived per interval of Galactic radius.
 |
Fig. 10. Ridge lines of the age–[Mg/Fe] thin disc sequences for different Rg annulus, from [0, 2] kpc (grey) to [14, 16] kpc (red). |
4.2. Radial trend of the thin disc age-distribution function
A key method to aid in understanding the assembly of the disc is to probe its star formation history. Figure 11 presents the age-distribution functions (ADFs) of the thin disc sample7. From the Galactic centre up to Rg ∈ [10, 12] kpc, the thin disc ADF shows a radial gradient, that is stars are older on average in the central regions, with the onset and conclusion of star formation occurring earlier towards the Galactic centre. The gradient provides a clear signature of the inside-out formation of the thin disc up to Rg ∼ 10 − 12 kpc. In contrast, the ADFs of the Rg ∈ [10, 12] and [12, 14] kpc intervals present very similar profiles, with no further sign of a drift towards younger ages between the two Rg bins. Another interesting feature is the change in the skewness of the profiles. For Rg < 8 kpc, the ADFs are skewed towards young ages, while for Rg > 10 kpc the ADFs are skewed towards old ages. It is interesting to note that Hayden et al. (2015) reported a similar evolution of the skewness of the metallicity-distribution function (MDF) of the disc stars contained in a ±500 pc layer around the Galactic plane, with the change of sign occurring around R = 10 kpc.
 |
Fig. 11. Age distribution functions of the thin disc sample divided in 2 kpc annulus, from Rg = [0, 2] (grey) to [14, 16] kpc (red). The number of stars in each annulus is given in the legend. |
The age sample is restricted to stars with [Fe/H] > −0.5 dex (see Sect. 2.4). As discussed in Appendix B, up to Rg = 12 kpc, this filter removes less than 5% of the thin disc stars. This should have a very limited impact on the observed drift of the ADFs with guiding radius as well as on their skewness. The situation is a bit different for the interval Rg ∈ [12, 14] kpc, where the percentage of stars discarded reaches 12.4%. The stars removed are by construction the most metal-poor thin disc stars in this range of guiding radius and presumably old stars, which would then preferentially populate the right wing of the profile. Another aspect that should be considered is that our sample is made of giant stars and is therefore not representative of the youngest generations of stars. The profiles of the ADFs, in particular in the first few Gyr, could be missing recently formed non-evolved stars and should be considered with caution.
Numerous models of formation of the disc assume or predict an inside-out formation (e.g., Chiappini et al. 1997; Brook et al. 2012; Bird et al. 2013; Minchev et al. 2014; Miranda et al. 2016; Grand et al. 2018; Vincenzo & Kobayashi 2020; Khoperskov et al. 2021; Spitoni et al. 2021). Figure 11 provides an observational confirmation of the inside-out formation of the thin disc up to Rg ∼ 10 − 12 kpc and suggests a coeval formation beyond that point.
5. Discussion
5.1. Formation of the Galactic disc: ‘Haywood et al.’ scenario
As presented in the introduction, numerous models have been developed to study the formation of the Milky Way disc, and its thick and thin components, by exploring different physical processes such as gas-rich mergers (Brook et al. 2012; Grand et al. 2018; Buck 2020; Agertz et al. 2021; Renaud et al. 2021a,b; Lian et al. 2020c,d), clumpy early galaxy (Bournaud et al. 2009; Clarke et al. 2019; Beraldo e Silva et al. 2021), radial migration (Schönrich & Binney 2009a,b; Loebman et al. 2011; Roškar et al. 2013; Feuillet et al. 2019; Sharma et al. 2021), double gas infall (Chiappini et al. 1997, 2001; Noguchi 2018; Spitoni et al. 2019, 2020, 2021; Palla et al. 2020), or multi-phase star formation history (Lian et al. 2020a,b). For several years, our team has been developing a scenario and a model of formation of the Galactic disc (Haywood et al. 2013, 2015, 2016, 2018, 2019; Snaith et al. 2014, 2015, 2021), which is hereafter referred to as the ‘Haywood et al.’ scenario. In this section, we summarise its main features. Figure 12 is intended to help in the presentation of the scenario. It presents the distribution of the main sample in the ([Fe/H], [Mg/Fe]) plane. The stars have been separated into three intervals of guiding radius: inner disc, Rg ∈ [0, 6] kpc (left); intermediate disc, Rg ∈ [6, 10] kpc (middle); and outer disc (right), Rg ∈ [10, 18] kpc. The numbered circles refer to the different stages of the formation of the disc along the chemical tracks, which are represented schematically by the red arrows: (1) formation of the thick disc, (2) quenching of the star formation, (3) dilution of the gas, and (4) formation of the thin disc.
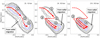 |
Fig. 12. Distribution of the stars of the main sample in the ([Fe/H], [Mg/Fe]) plane. The stars have been separated into three intervals of guiding radius: inner disc, Rg ∈ [0, 6] kpc (left); intermediate disc, Rg ∈ [6, 10] kpc; and outer disc, Rg ∈ [10, 18] kpc. The numbered circles refer to the different stages of the formation of the disc (see main text): (1) formation of the thick disc; (2) quenching of the star formation; (3) dilution of the gas in the intermediate and outer thin discs; and (4) formation of the thin disc. The red lines are schematic representations of the chemical tracks. The black arrows point to the locus populated by stars which have migrated from another section of the disc. |
In this scenario, the disc assembly starts with the thick disc. It forms from a gas-rich turbulent and well-mixed medium during a 3−4 Gyr starburst about 13 to 9 Gyr ago (Haywood et al. 2013, 2015; Snaith et al. 2014, 2015). During the thick disc phase, the star formation extends over an approximately 10 kpc radius, but the starburst is energetic enough to pollute the gas at larger distance (Haywood et al. 2019). The efficient mixing of the gas allows the thick disc to evolve along a single chemical track, with little dependence on the Galactic radius (label 1 in Fig. 12). About 8 Gyr ago, the star formation quenches (Haywood et al. 2013, 2016; Snaith et al. 2014, 2015). This marks the end of the thick disc formation and corresponds to an area of lower stellar density (label 2 in Fig. 12) in the ([Fe/H], [Mg/Fe]) plane. A possible origin8 of the quenching is the formation of the Milky Way bar, which by increasing the velocity dispersion of the gas could have reduced the star formation by up to a factor of 10 (Khoperskov et al. 2018). In the inner disc (R < 6 kpc), the star formation resumes from the gas enriched by the thick disc formation and therefore in the continuation of its sequence (Haywood et al. 2018), producing the low-alpha thin disc peak (label 4 in the left panel of Fig. 12). In the intermediate disc (R ∈ [6, 10] kpc), the metals are diluted by metal-poor gas that may have been in the outer disc for some time already at the time of dilution, but of which the exact origin is not known (see discussion in Haywood et al. 2019). The dilution does not affect the inner disc, which is possibly isolated from more external regions by the outer Lindblad resonance (OLR) of the ‘recently’ formed bar (Haywood et al. 2019). In the intermediate disc, the star formation resumes from the [Mg/Fe] ratio produced by the thick disc phase (magnesium and iron being diluted in similar proportions, the [Mg/Fe] abundance ratio is not significantly modified), but a lowered metallicity (label 3 Fig. 12). It proceeds at a lower rate than during the thick disc phase. The gas enrichment is dominated by thermonuclear supernovae (SNIa). As the chemical evolution proceeds, the iron content of the ISM increases and its [Mg/Fe] abundance ratio decreases, producing the low-alpha thin disc sequence (label 4 in the middle panel of Fig. 12). The gas dilution is stronger at greater distances from the Galactic centre, shifting the chemical tracks to lower metallicity in proportion to their Galactic radius (as schematically represented in Fig. 12 by the two parallel arrows). In the outer disc (R > 10 kpc), the chemical evolution is similar to the one in the intermediate disc. As the intensity of the dilution continues to increase with the Galactic radius, the outer disc starts to form its stars from a lower metallicity than the intermediate disc. It also starts from a higher [Mg/Fe] ratio. A possible explanation for this last point is that the outer disc would have been polluted by the thick disc mostly during the peak of the thick disc starburst phase, which is the period when the energy injected into the ISM reaches its maximum. Once past this peak, the thick disc would have continued its chemical evolution (increasing its metallicity and decreasing its [Mg/Fe] ratio) without significantly contaminating the outer disc any further (Haywood et al. 2019).
The thick and thin discs appear as two different over-densities in the ([Fe/H], [Mg/Fe]) plane. In the Haywood et al. scenario, different mechanisms are at work in the inner disc and in the intermediate disc to produce the α-bimodality9 and the α-dichotomy10, respectively. In the inner disc, the α-bimodality is produced by the quenching of the star formation, while in the intermediate disc the α-dichotomy is mainly driven by the dilution of the metals before the onset of the thin disc formation.
The Haywood et al. scenario is based on several theoretical works. Snaith et al. (2014, 2015) used a chemical model to constrain the star formation history (SFH) of the inner disc sequence and identified three main periods: an inital 3−4 Gyr starburst corresponding to the formation of the thick disc, a quenching of the SFR for about 1 Gyr, and a quiescent formation of the thin disc over the last 7−8 Gyr. Snaith et al. (2015) further showed that a dilution of the gas after the end of the thick disc phase made it possible to model the low-α sequence in the ([Si/Fe], [Fe/H]) plane. Recently, Snaith et al. (2021) reproduced the early, rapid, and efficient formation of the thick disc, originally seen with their closed-box model (Snaith et al. 2014, 2015), with an infall model. Khoperskov et al. (2020b) used a high-resolution N-body simulation of a Milky Way-type galaxy to investigate the effect of the bar on stellar migration. They showed that the slowing down of the bar could move outward stars formed in the inner disc. This mechanism can explain the presence of metal-rich stars ([Fe/H] > 0.2 − 0.3 dex; presumably born in the inner disc) in the intermediate and outer disc. Finally, the four chemo-dynamical simulations of Khoperskov et al. (2021) support several aspects of the Haywood et al. scenario: the high-α sequence forms early during a starburst episode, the low-α sequence forms later during a quiescent star formation phase, and, in one of the simulations, the low-α sequence results from the dilution of the ISM at the beginning of the formation of the thin disc.
5.2. Present work in the context of the Haywood et al. scenario
In this section, we discuss the observations of Sects. 3 and 4 in the context of the Haywood et al. scenario.
In this scenario, the thick disc is the first component of the disc to form. This is confirmed by Fig. 9, which shows that the thick disc stars are older than the thin disc stars throughout the disc. In the innermost guiding radius interval (Rg ∈ [0, 2] kpc), the age difference between the two populations appears small. We suspect that it is, at least partly, an effect of the underestimation of the older ages, which is shown in Sect. 2.4 to steepen the slope of the thick disc sequence in the solar neighbourhood and very likely has a similar effect here too. The ages used in the present study are not accurate enough in the old-stars regime to assess the period of formation of the thick disc precisely. Yet, Fig. 9 shows that the formation of the thick disc was completed about 8 Gyr ago.
The Haywood et al. scenario postulates that the thick disc formed from turbulent, well-mixed gas and evolved along a chemical track, which depends very little on the location in the disc. In Fig. 7, the thick disc ridge lines are indeed closely grouped. They exhibit a weak [Mg/Fe] trend, which decreases by about 0.05 dex in ∼10 kpc. This could be the signature of a weak star formation rate (SFR) gradient (stronger in the inner regions than in the outer ones) and/or a weak inside-out formation of the thick disc. Accurate old star ages would help to answer this question. Either way, the closeness, smoothness, and narrowness of the sequences continue to support the idea that the thick disc formed from a well-mixed medium.
As shown in Fig. 11, after the quenching, the star formation resumes first in the innermost regions of the disc, and then it gradually propagates outward. The thin disc forms inside-out up to Rg ∼ 10 − 12 kpc. This is a new ingredient for the Haywood et al. scenario, which has not addressed this question so far.
The thin disc ([Fe/H], [Mg/Fe]) ridge lines present two regimes (Fig. 7). On their metal-poor side and at Rg > 6 kpc, they present parallel sequences that are shifted in metallicity, while they overlap on their metal-rich side. The metal-poor side is also dominated by stars formed at large guiding radii, while the metal-rich side is mostly populated by inner disc stars (Fig. 8). Haywood et al. (2019) predicted such behaviour. At sub-solar metallicity, the parallel ridge lines, all the more metal-poor the further they are located in the disc, are interpreted as the consequence of the increase of the dilution of the gas with increasing radius. The dilution occurred during the quenching phase, setting the initial conditions for the formation of the thin disc, whose evolution then proceeded along parallel chemical tracks. At super-solar metallicity, the [Mg/Fe] ratio ridge lines increase and overlap with each other. In the scenario discussed here, these stars were born in the inner disc, and they did spread at larger radii. The super-solar metallicity stars represent a small fraction of the stars beyond Rg ∼ 6 − 8 kpc. Therefore, a moderate radial migration is enough to transport the appropriate number of stars in the intermediate and outer discs (Khoperskov et al. 2020b). Similarly, a small fraction of solar metallicity stars, born in the intermediate disc, migrate in the inner and outer discs.
Figure E.1 (top panel) shows that in the guiding radius interval Rg ∈ [4, 6] kpc, within ±500 pc of the Galactic plane, the thick and thin disc ridge lines are close but disjointed. There are two ways of interpreting this in the context of the scenario presented in Sect. 5.1. Some moderate dilution could have occurred inward of 6 kpc, and the thin disc ridge line would represent a chemical track. Alternatively, this ridge line could be produced by the contamination by low-alpha sub-solar metallicity stars born beyond Rg = 6 kpc. The bulk of the thin disc stars in that guiding radius interval have super-solar metallicities and are located in the continuation of the thick disc sequence. A moderate radial migration is enough to move the small number of sub-solar metallicity stars required by a couple of kpc from the intermediate to the inner disc. This favours the contamination hypothesis. It is also supported by the strong flattening of the thin disc median metallicity gradient around Rg = 6 kpc (see Fig. 5).
Figure 10 shows that the gas in the outer disc (Rg > 10 kpc) was enriched in [Mg/Fe] by about 0.03−0.05 dex, compared to the more internal regions of the disc, 7 Gyr ago. As presented in Sect. 5.1, the Haywood et al. scenario explains this offset by different enrichment mechanisms, that is in the inner and intermediate discs, the gas was enriched by the full thick disc formation, while in the outer disc it was polluted mostly during the peak of the thick disc starburst. In Fig. 10, the ridge lines are divided into two relatively narrow sets of lines, suggesting a relatively rapid change in the chemical composition of the gas, rather than a smooth evolution with radius. This is not the only property of the disc that changes around Rg ∼ 10 kpc. The inside-out formation of the disc seems to extend up to Rg ∼ 10 − 12 kpc (Fig. 11). The median metallicity trend presents a plateau in the Rg interval [10, 11] kpc (Fig. 5). It is also around Rg ∼ 8 − 10 kpc that the skewness of the ADF profiles changes sides (Fig. 11). Finally, Hayden et al. (2015) reported that the skewness of the MDF changes sign around R ∼ 10 kpc. One may wonder if the discontinuity observed in the formation of the Galactic disc between the intermediate and the outer disc could be related to dynamical processes in the disc. We notice that the OLR of the bar is placed in the region of transition of both discs. As shown by Halle et al. (2015) and confirmed by Khoperskov et al. (2020b), the OLR limits the exchange of angular momentum, separating the disc into two distinct parts with limited exchange.
5.3. Comparison with other models
In the Sharma et al. (2021) chemo-dynamical model, the disc [Fe/H] and [α/Fe] content evolve along ‘homologous’ chemical tracks, shifted with respect to each other in metallicity in proportion to the star birth radius, that is the more metal-rich tracks in the inner regions and the more metal-poor in the outer ones. The tracks are shown in their Fig. 10. The lower half of these tracks (i.e., below [α/Fe] ∼ 0.1 dex) is in qualitatively good agreement with the ([Fe/H], [Mg/Fe]) ridge lines of Fig. 7. It is in the high-alpha domain that we differ. The ‘knees’ of the Sharma et al. (2021) tracks, corresponding to the moment when the thermonuclear supernovae take over the core-collapse supernovae, are shifted to lower metallicities at larger radii and separate from each other. In Fig. 7, the thick disc ridge lines bend around the same metallicity of [Fe/H] ∼ −0.6 dex at all guiding radii and follow close paths up to [Fe/H] ∼ −0.2 dex. In the Sharma et al. (2021) model, the double thick-and-thin-disc sequence is produced by the radial migration. In the Haywood et al. scenario, it is the dilution, happening after the thick disc phase, that produces the parallel chemical tracks. This results in the double sequence (mostly visible in the intermediate disc), without the need for a strong radial migration. However, a moderate radial migration transports a small proportion of super-solar metallicity stars from the inner disc to the intermediate and outer discs, possibly caused by a slowing down of the bar pattern speed (see Khoperskov et al. 2020b).
In the Haywood et al. scenario, the inner and intermediate discs are assembled in two distinct star formation phases, separated by a quenching episode. Before the onset of the thin disc formation, the gas is diluted in the intermediate and outer discs. This double-phase process presents similarities with the double infall model, like in the recent work by Spitoni et al. (2019, 2020). Indeed, in their model, the second infall dilutes the gas. However, the dilution does not occur at the same stage of the chemical evolution. In their model, it occurs around solar [α/Fe] ratio (see Fig. 2 in Spitoni et al. 2019), while in the Haywood et al. scenario, the gas is diluted ‘earlier’, that is when it reaches [Mg/Fe] ∼ 0.1 − 0.15 dex. As discussed further in the next paragraph, another difference is that in the Haywood et al. scenario the gas is not diluted in the inner disc (R < 6 kpc), and a small proportion of the old super-solar metallicity stars formed there migrate to the intermediate and outer discs. The moment when the dilution occurs of course has an influence on the [Fe/H] − [Mg/Fe] and age–[Mg/Fe] tracks followed by the disc along its evolution. In the Spitoni et al. (2020) model, the [α/Fe] ratio reached a first minimum about 8 Gyr ago, then rises by about 0.1 dex over a brief period of ∼2 Gyr and then smoothly decreases up to the present day to slightly below solar (see e.g., their Fig. 6, middle panel). This behaviour is a little different from that observed in Fig. 10, where, for a given guiding radius, the [Mg/Fe] decreases quasi-linearly with decreasing age. As shown in Snaith et al. (2014), an earlier dilution combined with a quenching episode produces a smoother age–[α/Fe] trend, more in agreement with Fig. 10.
An important aspect of the Haywood et al. scenario is that the evolution of the thin disc would not have been monolithic, but would have followed different paths in the inner, intermediate, and outer regions. In a recent series of papers, Lian and collaborators also developed this idea11. They suggest that the outer disc (Lian et al. 2020d), the inner disc12 (Lian et al. 2020c), and the on-bar and off-bar bulges (Lian et al. 2020a,b) formed along different evolutionary channels: double infalls possibly fuelled by a gas-rich merger in the outer and inner discs and a rapid starburst, followed by a quenching episode and then a smooth, secular star formation in the bulge13. The Lian et al. (2020a,c,d) model presents many convergence points with the Haywood et al. scenario: a radial structuration, two different episodes of star formation separated by a quenching, and a dilution of the gas in the intermediate and outer discs. Yet, there are also some differences. As in the works of Spitoni et al. (2019, 2020, 2021), in their model the dilution produced by the second infall happens around slightly super-solar [Mg/Fe] (or even sub-solar values in some configurations), while in the Haywood et al. scenario, it happens earlier in the intermediate and outer disc (but not in the inner disc that forms old, super-solar metallicity stars, which for a small fraction will migrate outward – see below). The different timing for the dilution changes the way to ‘travel’ through the low-alpha sequence in the ([Fe/H], [Mg/Fe]) plane, that is once from metal-poor to metal-rich with the early dilution, and twice from metal-rich to metal-poor and then from metal-poor to metal-rich with the later dilution. The motivation for the later dilution in the Lian et al. (2020c,d) and in the Spitoni et al. (2019, 2020, 2021) studies is to model with a single chemical track the old super-solar metallicity stars with [Mg/Fe] ∈ [ − 0.1, 0.1] dex and the younger alpha-poor sub-solar metallicity stars. In the Haywood et al. scenario, the old super-solar metallicity stars with [Mg/Fe] ∈ [ − 0.1, 0.1] dex are formed in the inner disc along a different evolutionary path and have migrated to the intermediate and, for a small number, to the outer disc. The dilution can then happen at an earlier stage (i.e., at an higher [Mg/Fe] ratio), because the intermediate and outer disc tracks do not need to produce super-solar metallicity stars with [Mg/Fe] ∈ [ − 0.1, 0.1] dex.
6. Conclusions
Using a sample of 199 307 giant stars with precise APOGEE abundances and APOGEE-AstroNN ages, selected in a ±2 kpc layer around the Galactic plane, we assessed the radial evolution of the chemical and age properties of the Galactic stellar disc. The thick disc [Fe/H] − [Mg/Fe] ridge lines follow closely grouped parallel paths, supporting the idea that the thick disc did form from a well-mixed medium. However, the ridge lines present a small drift in [Mg/Fe], which decreases by about ∼0.05 dex from Rg ∈ [0, 2] to [8, 10] kpc. This suggests that the shift observed between the micro-lensed bulge stars and the local thick disc stars (Bensby et al. 2017) is not the result of a discrete transition between the disc and the bulge, but rather a smooth radial evolution of the thick disc.
The well-documented local and outer thin disc radial metallicity gradient flattens inward of Rg ∼ 6 kpc, confirming the findings by Hayden et al. (2015) and Haywood et al. (2019). APOGEE DR16 data allow us to trace the plateau to greater distances than were previously accessible. It extends up to Rg ∼ 2.5 − 3 kpc, at which point the metallicity raises again.
At sub-solar metallicity, the intermediate and outer thin disc [Fe/H] − [Mg/Fe] ridge lines follow parallel sequences shifted to lower metallicity as the guiding radius increases. We interpret this pattern as an indication of a dilution of the interstellar medium, which took place after the formation of the thick disc and before the onset of the thin disc formation. At super-solar metallicity, the ridge lines converge and overlap with those of the inner disc. This suggests that the small proportion of super-solar metallicity stars at Rg > 6 kpc were probably born in the inner disc and did move outward through radial migration.
The large APOGEE-AstroNN age sample allowed us to probe the distributions of stellar ages in the thin disc, as well as the evolution of the age–[Mg/Fe] patterns in the disc, from the Galactic centre to Rg ∼ 14 kpc. An important result provided by this dataset is that the thin disc presents evidence of an inside-out formation up to Rg ∼ 10 − 12 kpc. Moreover, about ∼7 Gyr ago, the outer thin disc (Rg > 10 kpc) was more [Mg/Fe] enriched than the more internal regions of the disc, by about ∼0.03 − 0.05 dex. This could be the fossil record of a pollution of the outer disc gas reservoir, by the thick disc during its starburst phase.
These results support earlier claims (e.g., Haywood et al. 2013, 2019; Snaith et al. 2015) that the thin disc did form following different chemical paths inward and outward of Rg ∼ 6 kpc. Several changes or discontinuities are also observed around Rg ∼ 10 − 11 kpc. Further work is required to assess their nature: chemical and/or dynamical. By comparison, the thick disc seems a rather homogeneous structure, from the Galactic centre up to Rg ∼ 10 kpc. However, ages for the old populations of similar quality to those available for the thin disc would provide precious constraints on the formation of the thick disc and, further, to the accreted and/or in situ halo.
The guiding radius is derived assuming the MWPotential2014 gravitational potential (Bovy 2015). This potential includes prescriptions for the bulge, the disc, and the dark matter halo and reproduces the overall behaviour of the Milky-Way rotation curve, including the steep decrease in the inner regions (see Fig. 8 in Bovy 2015). The potential is axi-symmetric and does not model the bar or spiral arms. In order to test how the axi-symmetric assumption influences the results, some of the analyses were repeated using the radius R. They are presented in Appendices D, G, and H.
Derived by a global fit of the full spectrum (Jönsson et al. 2020).
Selected as defined in Sect. 2.3.
Other quenching mechanisms have been proposed, such as a drastic drop of the gas accretion, caused by a switch from cold-flow mode to hot mode (Noguchi 2018); a massive merger heating the halo gas and inhibiting its accretion (Vincenzo et al. 2019); or a depletion of the circumgalactic medium (Kacprzak et al. 2020).
See also the recent study presented in Spitoni et al. (2021), which used the APOGEE DR16 and APOGEE-AstroNN data to constrain a multi-zone, double-infall chemical evolution model.
Bovy et al. (2019) used APOGEE-AstroNN metallicity, while we used ASPCAP metallicity. As can be seen from Fig. C.1, this has no effect on our conclusions.
Acknowledgments
The authors are grateful to the referee for his comments and suggestions, that improved the clarity and quality of the manuscript. This study used SDSS IV DR16 APOGEE and APOGEE-AstroNN data. Funding for the Sloan Digital Sky Survey IV has been provided by the Alfred P. Sloan Foundation, the US Department of Energy Office of Science, and the Participating Institutions. SDSS-IV acknowledges support and resources from the Center for High Performance Computing at the University of Utah. The SDSS website is https://www.sdss.org. SDSS-IV is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS Collaboration including the Brazilian Participation Group, the Carnegie Institution for Science, Carnegie Mellon University, Center for Astrophysics, Harvard & Smithsonian, the Chilean Participation Group, the French Participation Group, Instituto de Astrofísica de Canarias, The Johns Hopkins University, Kavli Institute for the Physics and Mathematics of the Universe (IPMU)/University of Tokyo, the Korean Participation Group, Lawrence Berkeley National Laboratory, Leibniz Institut für Astrophysik Potsdam (AIP), Max-Planck-Institut für Astronomie (MPIA Heidelberg), Max-Planck-Institut für Astrophysik (MPA Garching), Max-Planck-Institut für Extraterrestrische Physik (MPE), National Astronomical Observatories of China, New Mexico State University, New York University, University of Notre Dame, Observatário Nacional/MCTI, The Ohio State University, Pennsylvania State University, Shanghai Astronomical Observatory, United Kingdom Participation Group, Universidad Nacional Autónoma de México, University of Arizona, University of Colorado Boulder, University of Oxford, University of Portsmouth, University of Utah, University of Virginia, University of Washington, University of Wisconsin, Vanderbilt University, and Yale University. This research made use of the NASA’s Astrophysics Data System (ADS) bibliographic services, as well as of the open-source Python packages PANDAS (McKinney 2010), NUMPY (Harris et al. 2020), MATPLOTLIB (Hunter 2007) and Astropy (http://www.astropy.org) (Astropy Collaboration 2013, 2018). ONS thanks the DIM ACAV+ for founding during the preparation of this work.
References
- Abolfathi, B., Aguado, D. S., Aguilar, G., et al. 2018, ApJS, 235, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Agertz, O., Renaud, F., Feltzing, S., et al. 2021, MNRAS, 503, 5826 [NASA ADS] [CrossRef] [Google Scholar]
- Ahumada, R., Allende, Prieto C., Almeida, A., et al. 2020, ApJS, 249, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Anders, F., Chiappini, C., Santiago, B. X., et al. 2014, A&A, 564, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anders, F., Chiappini, C., Minchev, I., et al. 2017, A&A, 600, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Bennett, M., & Bovy, J. 2019, MNRAS, 482, 1417 [NASA ADS] [CrossRef] [Google Scholar]
- Bensby, T., Feltzing, S., & Lundström, I. 2003, A&A, 410, 527 [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Feltzing, S., Lundström, I., & Ilyin, I. 2005, A&A, 433, 185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Zenn, A. R., Oey, M. S., & Feltzing, S. 2007, ApJ, 663, L13 [CrossRef] [Google Scholar]
- Bensby, T., Alves-Brito, A., Oey, M. S., Yong, D., & Meléndez, J. 2011, ApJ, 735, L46 [NASA ADS] [CrossRef] [Google Scholar]
- Bensby, T., Feltzing, S., & Oey, M. S. 2014, A&A, 562, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Feltzing, S., Gould, A., et al. 2017, A&A, 605, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beraldo e Silva, L., Debattista, V. P., Nidever, D., Amarante, J. A. S., & Garver, B. 2021, MNRAS, 502, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Bird, J. C., Kazantzidis, S., Weinberg, D. H., et al. 2013, ApJ, 773, 43 [Google Scholar]
- Bournaud, F., Elmegreen, B. G., & Martig, M. 2009, ApJ, 707, L1 [Google Scholar]
- Bovy, J. 2015, ApJS, 216, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Bovy, J., Rix, H. W., Liu, C., et al. 2012, ApJ, 753, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Bovy, J., Rix, H. W., Schlafly, E. F., et al. 2016, ApJ, 823, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Bovy, J., Leung, H. W., Hunt, J. A. S., et al. 2019, MNRAS, 490, 4740 [Google Scholar]
- Brook, C. B., Stinson, G. S., Gibson, B. K., et al. 2012, MNRAS, 426, 690 [Google Scholar]
- Buck, T. 2020, MNRAS, 491, 5435 [NASA ADS] [CrossRef] [Google Scholar]
- Buder, S., Asplund, M., Duong, L., et al. 2018, MNRAS, 478, 4513 [Google Scholar]
- Buder, S., Lind, K., Ness, M. K., et al. 2019, A&A, 624, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buder, S., Sharma, S., Kos, J., et al. 2021, MNRAS, 506, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Calura, F., & Menci, N. 2009, MNRAS, 400, 1347 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, J. Y., Rockosi, C. M., & Morrison, H. L. 2012, in Galactic Archaeology: Near-Field Cosmology and the Formation of the Milky Way, eds. W. Aoki, M. Ishigaki, T. Suda, T. Tsujimoto, & N. Arimoto, ASP Conf. Ser., 458, 105 [NASA ADS] [Google Scholar]
- Chiappini, C., Matteucci, F., & Gratton, R. 1997, ApJ, 477, 765 [Google Scholar]
- Chiappini, C., Matteucci, F., & Romano, D. 2001, ApJ, 554, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Ciucă, I., Kawata, D., Miglio, A., Davies, G. R., & Grand, R. J. J. 2021, MNRAS, 503, 2814 [Google Scholar]
- Clarke, A. J., Debattista, V. P., Nidever, D. L., et al. 2019, MNRAS, 484, 3476 [NASA ADS] [CrossRef] [Google Scholar]
- Cui, X. Q., Zhao, Y. H., Chu, Y. Q., et al. 2012, Res. Astron. Astrophys., 12, 1197 [Google Scholar]
- De Silva, G. M., Freeman, K. C., Bland-Hawthorn, J., et al. 2015, MNRAS, 449, 2604 [NASA ADS] [CrossRef] [Google Scholar]
- Delgado Mena, E., Moya, A., Adibekyan, V., et al. 2019, A&A, 624, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Matteo, P., Haywood, M., Lehnert, M. D., et al. 2019, A&A, 632, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Donor, J., Frinchaboy, P. M., Cunha, K., et al. 2020, AJ, 159, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Feuillet, D. K., Frankel, N., Lind, K., et al. 2019, MNRAS, 489, 1742 [Google Scholar]
- Fuhrmann, K. 1998, A&A, 338, 161 [NASA ADS] [Google Scholar]
- Fuhrmann, K. 2004, Astron. Nachr., 325, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Fuhrmann, K. 2008, MNRAS, 384, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Fuhrmann, K. 2011, MNRAS, 414, 2893 [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García Pérez, A. E., Allende, Prieto C., Holtzman, J. A., et al. 2016, AJ, 151, 144 [CrossRef] [Google Scholar]
- Gilmore, G., Randich, S., Asplund, M., et al. 2012, The Messenger, 147, 25 [NASA ADS] [Google Scholar]
- Grand, R. J. J., Bustamante, S., Gómez, F. A., et al. 2018, MNRAS, 474, 3629 [NASA ADS] [CrossRef] [Google Scholar]
- GRAVITY Collaboration (Abuter, R., et al.) 2018, A&A, 615, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grenon, M. 1972, in IAU Colloq. 17: Age des Etoiles, eds. G. Cayrel de Strobel, & A. M. Delplace, 55 [Google Scholar]
- Halle, A., Di Matteo, P., Haywood, M., & Combes, F. 2015, A&A, 578, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Hayden, M. R., Bovy, J., Holtzman, J. A., et al. 2015, ApJ, 808, 132 [Google Scholar]
- Hayden, M. R., Sharma, S., Bland-Hawthorn, J., et al. 2020, MNRAS, submitted [arXiv:2011.13745] [Google Scholar]
- Haywood, M., Di Matteo, P., Lehnert, M. D., Katz, D., & Gómez, A. 2013, A&A, 560, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haywood, M., Di Matteo, P., Snaith, O., & Lehnert, M. D. 2015, A&A, 579, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haywood, M., Lehnert, M. D., Di Matteo, P., et al. 2016, A&A, 589, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haywood, M., Di Matteo, P., Lehnert, M., et al. 2018, A&A, 618, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haywood, M., Snaith, O., Lehnert, M. D., Di Matteo, P., & Khoperskov, S. 2019, A&A, 625, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holtzman, J. A., Shetrone, M., Johnson, J. A., et al. 2015, AJ, 150, 148 [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Jönsson, H., Holtzman, J. A., Prieto, C. A., et al. 2020, AJ, 160, 120 [CrossRef] [Google Scholar]
- Kacprzak, G. G., Nielsen, N. M., Nateghi, H., et al. 2020, MNRAS, 500, 2289 [NASA ADS] [CrossRef] [Google Scholar]
- Khoperskov, S., Haywood, M., Di Matteo, P., Lehnert, M. D., & Combes, F. 2018, A&A, 609, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Khoperskov, S., Gerhard, O., Di Matteo, P., et al. 2020a, A&A, 634, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Khoperskov, S., Di Matteo, P., Haywood, M., Gómez, A., & Snaith, O. N. 2020b, A&A, 638, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Khoperskov, S., Haywood, M., Snaith, O., et al. 2021, MNRAS, 501, 5176 [NASA ADS] [CrossRef] [Google Scholar]
- Kordopatis, G., Gilmore, G., Wyse, R. F. G., et al. 2013, MNRAS, 436, 3231 [CrossRef] [Google Scholar]
- Lemasle, B., Hajdu, G., Kovtyukh, V., et al. 2018, A&A, 618, A160 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leung, H. W., & Bovy, J. 2019a, MNRAS, 489, 2079 [CrossRef] [Google Scholar]
- Leung, H. W., & Bovy, J. 2019b, MNRAS, 483, 3255 [NASA ADS] [Google Scholar]
- Lian, J., Zasowski, G., Hasselquist, S., et al. 2020a, MNRAS, 497, 3557 [NASA ADS] [CrossRef] [Google Scholar]
- Lian, J., Zasowski, G., Hasselquist, S., et al. 2020b, MNRAS, 500, 282 [NASA ADS] [CrossRef] [Google Scholar]
- Lian, J., Thomas, D., Maraston, C., et al. 2020c, MNRAS, 497, 2371 [Google Scholar]
- Lian, J., Thomas, D., Maraston, C., et al. 2020d, MNRAS, 494, 2561 [NASA ADS] [CrossRef] [Google Scholar]
- Lindegren, L., Hernández, J., Bombrun, A., et al. 2018, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L., Klioner, S. A., Hernández, J., et al. 2021a, A&A, 649, A2 [EDP Sciences] [Google Scholar]
- Lindegren, L., Bastian, U., Biermann, M., et al. 2021b, A&A, 649, A4 [EDP Sciences] [Google Scholar]
- Loebman, S. R., Roškar, R., Debattista, V. P., et al. 2011, ApJ, 737, 8 [Google Scholar]
- Luck, R. E., Andrievsky, S. M., Kovtyukh, V. V., Gieren, W., & Graczyk, D. 2011, AJ, 142, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Mackereth, J. T., & Bovy, J. 2018, PASP, 130, 114501 [Google Scholar]
- Mackereth, J. T., Bovy, J., Schiavon, R. P., et al. 2017, MNRAS, 471, 3057 [Google Scholar]
- Mackereth, J. T., Bovy, J., Leung, H. W., et al. 2019a, MNRAS, 489, 176 [Google Scholar]
- Mackereth, J. T., Schiavon, R. P., Pfeffer, J., et al. 2019b, MNRAS, 482, 3426 [Google Scholar]
- Majewski, S. R., Schiavon, R. P., Frinchaboy, P. M., et al. 2017, AJ, 154, 94 [NASA ADS] [CrossRef] [Google Scholar]
- McKinney, W. 2010, in Proceedings of the 9th Python in Science Conference, eds. S. van der Walt, & J. Millman, 51 [Google Scholar]
- Miglio, A., Chiappini, C., Mackereth, J. T., et al. 2021, A&A, 645, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minchev, I., Chiappini, C., & Martig, M. 2014, A&A, 572, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miranda, M. S., Pilkington, K., Gibson, B. K., et al. 2016, A&A, 587, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ness, M., Hogg, D. W., Rix, H. W., et al. 2016, ApJ, 823, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Nidever, D. L., Bovy, J., Bird, J. C., et al. 2014, ApJ, 796, 38 [Google Scholar]
- Noguchi, M. 2018, Nature, 559, 585 [Google Scholar]
- Norris, J. 1987, ApJ, 314, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Palla, M., Matteucci, F., Spitoni, E., Vincenzo, F., & Grisoni, V. 2020, MNRAS, 498, 1710 [Google Scholar]
- Pinsonneault, M. H., Elsworth, Y., Epstein, C., et al. 2014, ApJS, 215, 19 [Google Scholar]
- Pinsonneault, M. H., Elsworth, Y. P., Tayar, J., et al. 2018, ApJS, 239, 32 [Google Scholar]
- Prochaska, J. X., Naumov, S. O., Carney, B. W., McWilliam, A., & Wolfe, A. M. 2000, AJ, 120, 2513 [Google Scholar]
- Queiroz, A. B. A., Anders, F., Chiappini, C., et al. 2020, A&A, 638, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Renaud, F., Agertz, O., Andersson, E. P., et al. 2021a, MNRAS, 503, 5868 [NASA ADS] [CrossRef] [Google Scholar]
- Renaud, F., Agertz, O., Read, J. I., et al. 2021b, MNRAS, 503, 5846 [NASA ADS] [CrossRef] [Google Scholar]
- Robin, A. C., Bienaymé, O., Fernández-Trincado, J. G., & Reylé, C. 2017, A&A, 605, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rojas-Arriagada, A., Zoccali, M., Schultheis, M., et al. 2019, A&A, 626, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roškar, R., Debattista, V. P., & Loebman, S. R. 2013, MNRAS, 433, 976 [CrossRef] [Google Scholar]
- Schönrich, R., & Binney, J. 2009a, MNRAS, 396, 203 [Google Scholar]
- Schönrich, R., & Binney, J. 2009b, MNRAS, 399, 1145 [Google Scholar]
- Sharma, S., Hayden, M. R., & Bland-Hawthorn, J. 2021, MNRAS, 507, 5882 [NASA ADS] [CrossRef] [Google Scholar]
- Silva Aguirre, V., Bojsen-Hansen, M., Slumstrup, D., et al. 2018, MNRAS, 475, 5487 [NASA ADS] [Google Scholar]
- Snaith, O. N., Haywood, M., Di Matteo, P., et al. 2014, ApJ, 781, L31 [CrossRef] [Google Scholar]
- Snaith, O., Haywood, M., Di Matteo, P., et al. 2015, A&A, 578, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Snaith, O., Haywood, M., Di Matteo, P., Lehnert, M. D., & Katz, D. 2021, A&A, submitted [Google Scholar]
- Soubiran, C., Bienaymé, O., & Siebert, A. 2003, A&A, 398, 141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spina, L., Ting, Y. S., De Silva, G. M., et al. 2021, MNRAS, 503, 3279 [CrossRef] [Google Scholar]
- Spitoni, E., Silva Aguirre, V., Matteucci, F., Calura, F., & Grisoni, V. 2019, A&A, 623, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spitoni, E., Verma, K., Silva Aguirre, V., & Calura, F. 2020, A&A, 635, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spitoni, E., Verma, K., Silva Aguirre, V., et al. 2021, A&A, 647, A73 [EDP Sciences] [Google Scholar]
- Steinmetz, M., Matijevič, G., Enke, H., et al. 2020a, AJ, 160, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Steinmetz, M., Guiglion, G., McMillan, P. J., et al. 2020b, AJ, 160, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Vincenzo, F., & Kobayashi, C. 2020, MNRAS, 496, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Vincenzo, F., Spitoni, E., Calura, F., et al. 2019, MNRAS, 487, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Y., Xiang, M., Zhao, G., et al. 2019, MNRAS, 484, 5315 [NASA ADS] [CrossRef] [Google Scholar]
- Xiang, M., Liu, X., Shi, J., et al. 2017, ApJS, 232, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Zasowski, G., Schultheis, M., Hasselquist, S., et al. 2019, ApJ, 870, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, G., Zhao, Y. H., Chu, Y. Q., Jing, Y. P., & Deng, L. C. 2012, Res. Astron. Astrophys., 12, 723 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Thick and thin disc separation versus guiding radius
As described in Sect. 2.3, the thick and thin disc stars were identified based on their location in the ([Fe/H], [Mg/Fe]) plane. The same criteria were applied for all stars, regardless of their location in the Galactic disc, which was done to avoid introducing a selection bias that would be a function of radius. However, as discussed in Sect. 3.2, the morphology of the high and low alpha sequences changes with guiding radius. The thick disc lower boundary and the thin disc upper boundary were chosen so as to separate the high- and low-alpha over-densities14 at all guiding radii. Similarly, the thick disc upper envelope and the thin disc lower envelope were defined so as to delineate the high- and low-alpha over-densities without truncating them in any of the guiding radius intervals. Figure A.1 illustrates the identification of the thick (red dots) and thin disc stars (blue dots) in nine successive guiding radius intervals, each 2 kpc wide. The black segments draw the selection limits.
 |
Fig. A.1. Distribution of the main sample stars in the ([Fe/H], [Mg/Fe]) plane for different intervals of guiding radius, from Rg ∈ [0, 2] kpc (top left) to [16, 18] kpc (bottom right). The black segments delineate the thick disc (red dots) and the thin disc (blue dots) boundaries. The grey dots are stars attributed to neither population. The white lines are stellar density iso-contours drawn at 90%, 70%, 50%, 30%, 20%, 10%, 7.5%, and 5% of the peak density. |
Appendix B: Age sample versus guiding radius
Figure B.1 shows the distributions of the stars of the age sample (blue dots) and of the main sample with invalid ages (grey dots) in the ([Fe/H], [Mg/Fe]) plane, for different intervals of guiding radius, from Rg ∈ [0, 2] kpc (top left) to [16, 18] kpc (bottom right). As the guiding radius increases, the low-alpha sequence gradually extends towards lower metallicity. As a consequence, the limit at [Fe/H] > −0.5 dex, defining the valid ages, gradually excludes a larger fraction of the low-alpha sequence. Table B.1 provides the percentage of the main sample thin disc stars without valid age as a function of guiding radius. Up to Rg = 12 kpc, the metallicity cut removes less than 5% of the thin disc stars and therefore should have a limited effect on the analysis of the ages presented in Sect. 4.2. We should be more cautious with the results obtained in the Rg ∈ [12, 14] kpc interval, in which the stars more metal-poor than −0.5 dex represent 12.4% of the main sample thin disc stars. Beyond Rg = 14 kpc, the thin disc sample was considered too significantly truncated by the metallicity filter. It was excluded from the analysis carried out in Sect. 4.2.
 |
Fig. B.1. Distribution of the main sample stars in the ([Fe/H], [Mg/Fe]) plane for different intervals of guiding radius, from Rg ∈ [0, 2] kpc (top left) to [16, 18] kpc (bottom right). The stars of the age sample are represented as blue dots, while the grey dots are stars from the main sample with invalid ages. The white lines are stellar density iso-contours drawn at 90%, 70%, 50%, 30%, 20%, 10%, 7.5%, and 5% of the peak density. |
Percentage of the main sample thin disc stars without valid age (cols. 2, 4, and 6) as a function of guiding radius (cols. 1, 3, and 5; expressed in kpc).
Appendix C: Inner-disc metallicity trend
In Sect. 3.1, we observe that the median metallicity at Rg < 2.5 − 3 kpc is higher than at larger guiding radius. This could seem in contradiction with the mean metallicity map of Bovy et al. (2019) (see their Fig. 5, middle panel), which shows a bar more metal-poor that the surrounding disc. Yet, to make a proper comparison, one should take into account the way the samples were selected. Our sample is made of thin disc stars (selected as low-alpha stars) contained in a ±2 kpc layer around the Galactic plane. Bovy et al. (2019) used all stars (with no filter on the alpha-element abundances) contained in a thinner layer of ±300 pc around the Galactic plane. In the top row of Fig. C.1, we measure the median metallicity as a function of guiding radius with different samples, gradually applying Bovy et al. (2019)’s selection criteria. The top left panel is a copy of Fig. 5, shown here to facilitate the comparison. The top middle panel shows the metallicity trend of the thin disc stars, restricted to the ±300 pc layer around the Galactic plane. As with the broader layer, the metallicity rises at Rg < 2.5 − 3 kpc. The top right panel shows the metallicity trend in the same thin ±300 pc layer, but including all disc stars. Consistently with the Bovy et al. (2019) map, when applying similar selection criteria, the median metallicity decreases from Rg = 3 − 4 kpc down to the Galactic centre.
 |
Fig. C.1. Top row: Median metallicity trend as a function of guiding radius for three different samples: the thin disc stars contained in the ±2 kpc layer around the Galactic plane (left), the thin disc stars in the ±300 pc layer (middle), and all the disc stars in the ±300 pc layer (right). The left plot is the same as Fig. 5, reproduced here to facilitate the comparison. The medians are calculated per bin of 250 pc. The shaded area delimits the ±1σ uncertainty on the estimate of the median. Bottom row: Median metallicity (X-Y) maps for the same three samples as on the top row: thin disc with Z ∈ [ − 2, 2] kpc (left), thin disc with Z ∈ [ − 300, 300] pc (middle), and full disc with Z ∈ [ − 300, 300] pc (right). X and Y are the Cartesian Galactic coordinates, with the Galactic centre located at X = Y = 0 kpc and the Sun at X = 8.125 kpc and Y = 0 kpc. The Galaxy rotates clockwise. The bar is schematically represented, as in Bovy et al. (2019), by a dashed ellipse with a semi-major axis of 5 kpc and an axis ratio of 0.4, inclined by 25° with respect to the Galactic centre-Sun direction. |
In order to better capture the 2D geometry of the disc metallicity behaviour, we plot the median metallicity maps of the disc in the bottom row of Fig. C.1 using the three same samples as in the top row. The left and middle bottom panels (mapping the thin disc stars, respectively, in the ±2 kpc and ±300 pc layers) both show a bar area, delineated by the dashed ellipse, that is more metal-rich than the surrounding disc. The right bottom panel is analogous15 to the middle panel of Bovy et al. (2019), Fig. 5, relying on similar selection criteria. Consistently, with their result it shows a bar area more metal-poor than its surroundings.
The apparent difference in the behaviour of our radial metallicity trend and Bovy et al. (2019) metallicity map simply reflects a different behaviour between the low-alpha stars and the whole bar-disc stars (high and low alpha together).
Appendix D: Metallicity trend versus radius
As explained in Sect. 2.2, we chose to conduct most of our analysis using the guiding radius, with the aim of mitigating the displacements of the stars caused by blurring. It is nonetheless interesting to repeat the analysis with the Galactic radius and to compare the results. Figure D.1 shows the median metallicity of the thin disc stars as a function of Galactic radius. The overall trend is very similar to the one observed in Fig. 5. In the innermost 2 kpc, the metallicity is roughly constant around [Fe/H] ∼ +0.3 dex. It then decreases up to R = 4 kpc, where it reaches the second plateau, which extends up to R = 6 kpc (as previously reported by Hayden et al. 2015; Haywood et al. 2019). Beyond this point, the well-studied disc radial metallicity gradient starts. Compared to Fig. 5, the two transitions at R = 2 and 4 kpc seem more abrupt and marked. Beyond 6 kpc, the gradient fluctuates less with respect to the Galactic radius than with respect to the guiding radius. The dynamical blurring is a plausible explanation for the smoother metallicity trend observed as a function of Galactic radius.
 |
Fig. D.1. Median metallicity of the thin disc stars as a function of the Galactic radius. The median is calculated per bin of 250 pc. The shaded area delimits the ±1σ uncertainty on the estimate of the median. |
Appendix E: Chemical patterns with different vertical cuts
For a given line of sight16, looking at a larger distance from the Sun also means looking further out of the Galactic plane. Our main sample is made of stars selected in a broad ±2 kpc layer around the Galactic plane. In order to verify that the [Fe/H] − [Mg/Fe] ridge line patterns were not resulting from a correlation in the selection function between the guiding radius Rg and the galactocentric vertical coordinate Z, we repeated the analysis conducted in Sect. 3.2 using narrower intervals of distance to the Galactic plane. Figures E.1 and E.2 reproduce, respectively, Figs. 6 and 7 for |Z|∈[0, 500] pc (top), |Z|∈[500, 1000] pc (middle), and |Z|∈[1000, 2000] pc (bottom).
 |
Fig. E.1. Same as Fig. 6, but for different intervals of distance to the Galactic plane: |Z|∈[0, 500] pc (top), |Z|∈[500, 1000] pc (middle), and |Z|∈[1000, 2000] pc (bottom). |
 |
Fig. E.2. Same as Fig. 7, but for different intervals of distance to the Galactic plane: |Z|∈[0, 500] pc (top), |Z|∈[500, 1000] pc (middle), and |Z|∈[1000, 2000] pc (bottom). |
In the three different vertical intervals, the pattern of the thick disc ridge lines is similar to the one shown in Fig. 7 for the main sample considered as a whole, that is the ridge lines are closely grouped and present a drift in [Mg/Fe]. In the closest interval to the plane (|Z|< 0.5 kpc), the thin disc behaviour is also globally similar to the one observed in Sect. 3.2, that is at sub-solar metallicity, the thin disc ridge lines follow parallel paths that converge and overlap at super-solar metallicity. However, in the top panel of Fig. E.1, in the guiding radius interval Rg ∈ [4, 6] kpc, the thin disc ridge line extends to lower metallicity than in Fig. 6 and is disjointed from the thick disc ridge line. It is most likely the smaller contribution of the thick disc close to the plane, which increases the contrast and visibility of the low-alpha sub-solar metallicity stars. At a greater distance from the plane, the proportion of thin disc stars decreases, and the shift between the ridge lines at sub-solar metallicity becomes less visible, especially in the farthest interval (1 < |Z|< 2 kpc).
Appendix F: Chemical patterns in the inner 2 kpc
There is not yet unanimity with regard to the morphology of the ([Fe/H], [α/Fe]) distribution in the inner regions of the Galaxy. Some studies report one sequence (Bensby et al. 2017; Zasowski et al. 2019; Bovy et al. 2019; Lian et al. 2020a,b, as well as this study) and others observe two (Rojas-Arriagada et al. 2019; Queiroz et al. 2020). The comparison is not always straightforward, as these results could be based on spectra collected with different instruments and/or on different alpha elements measured with different techniques. In this appendix, we compare different APOGEE DR16 abundance ratios. Figure F.1 presents the alpha-ratio versus metallicity distributions of the stars contained in the innermost guiding radius bin: Rg ∈ [0, 2] kpc. Five abundance ratios are shown: [α/M], [O/Fe], [Mg/Fe], [Si/Fe], and [Ca/Fe]. The first two, [α/M] and [O/Fe], present two sequences (connected by what could be the metal-poor tail of the low-alpha sequence). The other three, [Mg/Fe], [Si/Fe], and [Ca/Fe] show a single sequence. The processing and properties of the APOGEE SDSS DR16 data are described in Jönsson et al. (2020). The five abundance ratios discussed in this appendix were derived by the ASPCAP pipeline, but not with exactly the same method. The ‘abundance parameter’ [α/M] was derived by a global fitting of the full spectrum, while the individual abundances of O, Mg, Si, Ca, and Fe were measured using selected spectral windows and are expected to be more precise. In Fig. F.1, the double sequence shape of the [α/M] and [O/Fe] versus [Fe/H] distributions is enhanced by the ’finger’ feature around [Fe/H] ∼ 0.0 dex and [α/M]/[O/Fe] ∼ +0.2 dex. This feature is also visible in the full APOGEE catalogue and is discussed in Jönsson et al. (2020). It seems to be made of a small fraction of the cool (Teff < 4000 K) super-solar metallicity giants. The nature of this sub-group, processing artefact, or real physical feature, is not yet known, but Jönsson et al. (2020) recommend caution when using these stars.
 |
Fig. F.1. [α/M], [O/Fe], [Mg/Fe], [Si/Fe], and [Ca/Fe] versus [Fe/H] distributions of the stars in the guiding radius interval Rg ∈ [0, 2] kpc. The iso-density contours are plotted at 5, 7.5, 10, 20, 30, 70, 90 (black lines), and 50% (blue line) of the maximum density. |
The fact that different alpha elements behave differently raises the question of which one to use. In this study, we decided to use magnesium because it is described in Jönsson et al. (2020) as the most precise abundance (together with silicon) in DR16.
Appendix G: ([Fe/H], [Mg/Fe]) ridges versus radius
Figure G.1 shows the ridge lines of the ([Fe/H], [Mg/Fe]) sequences for different intervals of Galactic radius. Overall, it appears quite similar to Fig. 7, which displays the ridge lines as a function of guiding radius. The thick disc sequences are also slightly shifted to lower [Mg/Fe] here, proportionally to their radius. In the thin disc, at super-solar metallicity, the ridge lines defined by Galactic radius intervals are more scattered than those defined by guiding radius intervals. At sub-solar metallicity, the separations between the [6, 8], [8, 10], and [10, 12] kpc sequences are still well visible, but less so at a larger Galactic radius, where the dynamical blurring likely ‘hides’ the shifts between the sequences.
 |
Fig. G.1. Ridge lines of the ([Fe/H], [Mg/Fe]) sequences for different Galactic radius annulus, from [0, 2] kpc (grey) to [14, 16] kpc (red). The shaded areas delimit the ±1σ uncertainties (derived by bootstrap) on the estimates of the modes. |
Appendix H: (Age, [Mg/Fe]) ridges versus radius
Figure H.1 shows the relative locations of the ridge lines of the age-[Mg/Fe] thin disc sequences, for different interval in Galactic radius, from R ∈ [0, 2] kpc (grey) to [14, 16] kpc (red). The ridge lines are noisier than their counterpart calculated per interval of guiding radius (see Sect. 4.1), but the main features seen in Fig. 10 are still present. The ridge lines beyond R = 10 kpc present a steeper gradient than the ridge lines below. The difference of slope produces a gap between the two groups, beyond ∼2 − 3 Gyr.
 |
Fig. H.1. Ridge lines of the (Age, [Mg/Fe]) sequences for different Galactic radius annulus, from [0, 2] kpc (grey) to [14, 16] kpc (red). The shaded areas delimit the ±1σ uncertainties (derived by bootstrap) on the estimates of the modes. |
All Tables
Percentage of the main sample thin disc stars without valid age (cols. 2, 4, and 6) as a function of guiding radius (cols. 1, 3, and 5; expressed in kpc).
All Figures
 |
Fig. 1. Face-on (top) and edge-one (bottom) distributions of the stars of the main sample. X, Y, and Z are the Cartesian Galactic coordinates, with the Z axis positive in the northern Galactic hemisphere. The Galactic centre is located at X = Y = Z = 0 kpc and the Sun at X = 8.125 kpc (GRAVITY Collaboration 2018), Y = 0 kpc and Z = 20.8 pc (Bennett & Bovy 2019). In the top panel, the Galaxy rotates clockwise. |
| In the text | |
 |
Fig. 2. Distribution of the main sample in the ([Fe/H], [Mg/Fe]) plane. The black segments delineate the thick disc (red dots) and the thin disc (blue dots) selection boundaries. The grey dots are stars attributed to neither population. The white lines are stellar density iso-contours, that is, 90%, 70%, 50%, 30%, 20%, 10%, 7.5%, and 5% of the peak density. |
| In the text | |
 |
Fig. 3. Distribution in the ([Fe/H], [Mg/Fe]) plane of the main sample stars without valid ages (grey dots) and of the age sample stars (blue dots). The white lines are stellar density iso-contours; that is, 90%, 70%, 50%, 30%, 20%, 10%, 7.5%, and 5% of the peak density. |
| In the text | |
 |
Fig. 4. Magnesium-over-iron ratio as a function of age of the 1873 age-sample stars located less than 500 pc from the Sun. |
| In the text | |
 |
Fig. 5. Median metallicity of the thin disc stars as a function of the guiding radius. The median is calculated per bin of 250 pc. The shaded area delimits the ±1σ uncertainty on the estimate of the median. |
| In the text | |
 |
Fig. 6. Evolution of the distribution of main sample stars in the ([Fe/H], [Mg/Fe]) plane as a function of guiding radius, from Rg ∈ [0, 2] kpc (top left) to [16, 18] kpc (bottom right). The iso-density contours are plotted at 5, 7.5, 10, 20, 30, 70, 90 (black lines) and 50% (blue line) of the maximum density. The ridge lines are plotted in red. |
| In the text | |
 |
Fig. 7. Ridge lines of the ([Fe/H], [Mg/Fe]) sequences for different Rg annulus, from [0, 2] kpc (grey) to [14, 16] kpc (red). The shaded areas delimit the ±1σ uncertainties (derived by bootstrap) on the estimates of the modes. |
| In the text | |
 |
Fig. 8. Iso-density contours in the ([Fe/H], [Mg/Fe]) plane at 70% of the maximum density, for the thin disc sample. Each contour corresponds to a 2 kpc guiding radius annulus, from Rg ∈ [0, 2] kpc (grey) to Rg ∈ [16, 18] kpc (dark red). |
| In the text | |
 |
Fig. 9. Distributions of the main sample stars in the age–[Mg/Fe] plane, from Rg ∈ [0, 2] kpc (top left) to [16, 18] kpc (bottom right). The iso-density contours are plotted at 5, 10, 20, 30, 70, 90 (black lines), and 50% (blue line) of the maximum density. The ridge lines, derived over the range [0, 8.5] Gyr, are plotted in red. |
| In the text | |
 |
Fig. 10. Ridge lines of the age–[Mg/Fe] thin disc sequences for different Rg annulus, from [0, 2] kpc (grey) to [14, 16] kpc (red). |
| In the text | |
 |
Fig. 11. Age distribution functions of the thin disc sample divided in 2 kpc annulus, from Rg = [0, 2] (grey) to [14, 16] kpc (red). The number of stars in each annulus is given in the legend. |
| In the text | |
 |
Fig. 12. Distribution of the stars of the main sample in the ([Fe/H], [Mg/Fe]) plane. The stars have been separated into three intervals of guiding radius: inner disc, Rg ∈ [0, 6] kpc (left); intermediate disc, Rg ∈ [6, 10] kpc; and outer disc, Rg ∈ [10, 18] kpc. The numbered circles refer to the different stages of the formation of the disc (see main text): (1) formation of the thick disc; (2) quenching of the star formation; (3) dilution of the gas in the intermediate and outer thin discs; and (4) formation of the thin disc. The red lines are schematic representations of the chemical tracks. The black arrows point to the locus populated by stars which have migrated from another section of the disc. |
| In the text | |
 |
Fig. A.1. Distribution of the main sample stars in the ([Fe/H], [Mg/Fe]) plane for different intervals of guiding radius, from Rg ∈ [0, 2] kpc (top left) to [16, 18] kpc (bottom right). The black segments delineate the thick disc (red dots) and the thin disc (blue dots) boundaries. The grey dots are stars attributed to neither population. The white lines are stellar density iso-contours drawn at 90%, 70%, 50%, 30%, 20%, 10%, 7.5%, and 5% of the peak density. |
| In the text | |
 |
Fig. B.1. Distribution of the main sample stars in the ([Fe/H], [Mg/Fe]) plane for different intervals of guiding radius, from Rg ∈ [0, 2] kpc (top left) to [16, 18] kpc (bottom right). The stars of the age sample are represented as blue dots, while the grey dots are stars from the main sample with invalid ages. The white lines are stellar density iso-contours drawn at 90%, 70%, 50%, 30%, 20%, 10%, 7.5%, and 5% of the peak density. |
| In the text | |
 |
Fig. C.1. Top row: Median metallicity trend as a function of guiding radius for three different samples: the thin disc stars contained in the ±2 kpc layer around the Galactic plane (left), the thin disc stars in the ±300 pc layer (middle), and all the disc stars in the ±300 pc layer (right). The left plot is the same as Fig. 5, reproduced here to facilitate the comparison. The medians are calculated per bin of 250 pc. The shaded area delimits the ±1σ uncertainty on the estimate of the median. Bottom row: Median metallicity (X-Y) maps for the same three samples as on the top row: thin disc with Z ∈ [ − 2, 2] kpc (left), thin disc with Z ∈ [ − 300, 300] pc (middle), and full disc with Z ∈ [ − 300, 300] pc (right). X and Y are the Cartesian Galactic coordinates, with the Galactic centre located at X = Y = 0 kpc and the Sun at X = 8.125 kpc and Y = 0 kpc. The Galaxy rotates clockwise. The bar is schematically represented, as in Bovy et al. (2019), by a dashed ellipse with a semi-major axis of 5 kpc and an axis ratio of 0.4, inclined by 25° with respect to the Galactic centre-Sun direction. |
| In the text | |
 |
Fig. D.1. Median metallicity of the thin disc stars as a function of the Galactic radius. The median is calculated per bin of 250 pc. The shaded area delimits the ±1σ uncertainty on the estimate of the median. |
| In the text | |
 |
Fig. E.1. Same as Fig. 6, but for different intervals of distance to the Galactic plane: |Z|∈[0, 500] pc (top), |Z|∈[500, 1000] pc (middle), and |Z|∈[1000, 2000] pc (bottom). |
| In the text | |
 |
Fig. E.2. Same as Fig. 7, but for different intervals of distance to the Galactic plane: |Z|∈[0, 500] pc (top), |Z|∈[500, 1000] pc (middle), and |Z|∈[1000, 2000] pc (bottom). |
| In the text | |
 |
Fig. F.1. [α/M], [O/Fe], [Mg/Fe], [Si/Fe], and [Ca/Fe] versus [Fe/H] distributions of the stars in the guiding radius interval Rg ∈ [0, 2] kpc. The iso-density contours are plotted at 5, 7.5, 10, 20, 30, 70, 90 (black lines), and 50% (blue line) of the maximum density. |
| In the text | |
 |
Fig. G.1. Ridge lines of the ([Fe/H], [Mg/Fe]) sequences for different Galactic radius annulus, from [0, 2] kpc (grey) to [14, 16] kpc (red). The shaded areas delimit the ±1σ uncertainties (derived by bootstrap) on the estimates of the modes. |
| In the text | |
 |
Fig. H.1. Ridge lines of the (Age, [Mg/Fe]) sequences for different Galactic radius annulus, from [0, 2] kpc (grey) to [14, 16] kpc (red). The shaded areas delimit the ±1σ uncertainties (derived by bootstrap) on the estimates of the modes. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


