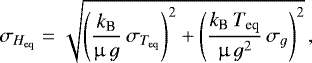EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 658 (February 2022) A&A, 658 (2022) A136 Full HTML
Free Access
Issue
A&A
Volume 658, February 2022
Article Number A136
Number of page(s) 14
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/202142336
Published online 10 February 2022

© ESO 2022

1 Introduction

Atmospheric escape, the process through which planetary atmospheres heat up, expand, and disperse into space, is a fundamental process that affects planetary atmospheric composition, structure, and evolution (e.g. Yelle 2004; García Muñoz 2007; Koskinen et al. 2010; Lopez & Fortney 2013; Shaikhislamov et al. 2014; Jin et al. 2014; Jin & Mordasini 2018; Owen & Wu 2017; Kubyshkina et al. 2018b; Modirrousta-Galian et al. 2020). For example, it is believed that atmospheric escape has profoundly shaped the evolution of the inner Solar System planets and that it has set the basic conditions for the development of a habitable Earth (e.g. Lammer et al. 2018, 2020; Airapetian et al. 2020).

Because of the low optical depth of the gas in upper planetary atmospheres, escape is typically studied observationally by employing transmission spectroscopy at ultraviolet (UV) wavelengths (e.g. Vidal-Madjar et al. 2003; Lecavelier des Etangs et al. 2012; Fossati et al. 2010; Linsky et al. 2010; Ehrenreich et al. 2015; Bourrier et al. 2018b; García Muñoz et al. 2021). However, most planet-hosting stars are dim in the UV and the background stellar light is spatially and temporally variable, particularly in the far-UV (FUV; e.g. Haswell et al. 2012; Llama & Shkolnik 2015, 2016). This often poses challenges to the interpretation of the observations, which have indeed led to controversial results (e.g. Vidal-Madjar et al. 2003, 2008; Ben-Jaffel 2007, 2008; Ben-Jaffel & Sona Hosseini 2010; Linsky et al. 2010; Ballester & Ben-Jaffel 2015).

Seager & Sasselov (2000) and Oklopčić & Hirata (2018) suggested that the metastable He I 23 S triplet at ≈10 830 Å may be an alternative to UV observations for probing upper atmospheres and escape. These features have the significant advantage of lying in a region of the near-infrared (nIR) relatively devoid of absorption lines from the Earth’s atmosphere and close to the peak of the spectral energy distribution (SED) of typical planet hosts. Early attempts at detecting these features at low spectral resolution from the ground were unsuccessful (Moutou et al. 2003), whereas absorption was detected for the warm giant WASP-107b at low resolution with the Hubble Space Telescope (HST; Spake et al. 2018). The He I triplet was then detected for a number of close-in gas giant planets, mostly via ground-based high-resolution transmission spectroscopy (e.g. Nortmann et al. 2018; Allart et al. 2018, 2019; Salz et al. 2018; Mansfield et al. 2018; Alonso-Floriano et al. 2019; Guilluy et al. 2020; Paragas et al. 2021).

The observational results of Nortmann et al. (2018) indicate that the presence and strength of the He I triplet in planetary transmission spectra depend strongly on stellar activity, and in particular on the high-energy stellar radiation: X-ray and extreme ultraviolet (EUV; together XUV). Oklopčić (2019) studied the formation of the triplet as a function of stellar SED finding that the formation and strength of the triplet does not depend exclusively on the XUV stellar emission but also on the near-UV (NUV) emission (i.e. ≲2600 Å), which is the radiation ionising He I in the metastable state (see also Lampón et al. 2020, 2021; Shaikhislamov et al. 2021; Khodachenko et al. 2021a). Therefore, the He I metastable lines are preferentially formed for planets with extended atmospheres orbiting stars with strong XUV and low NUV emission, that is, active K-type stars. The non-detection of the He I triplet for GJ436b (Nortmann et al. 2018), despite the heavily escaping atmosphere (e.g. Ehrenreich et al. 2015), demonstrates the importance of the shape of the stellar SED in the formation of these features.

Allart et al. (2019) applied a three-dimensional (3D) Monte Carlo code to WASP-107b to show that, through radiation pressure, the stellar nIR emission plays a significant role in shaping the He I planetary absorption. For this planet, Khodachenko et al. (2021a) and Wang & Dai (2020) derived a nearly solar helium abundance (He/H ≈ 0.1); however the latter authors disregarded radiation pressure, which led them to consider an extreme stellar wind of ten times solar to explain the observed ≈3 km s−1 blueshift of the planetary absorption features. Instead, Khodachenko et al. (2021a) were able to reproduce the observations considering a more moderate solar-like wind thanks to the self-consistent inclusion of the stellar radiation pressure acting on the metastable helium.

The detection and measurement of metastable He I provides a unique opportunity to constrain the atmospheric He abundance of exoplanets. Employing a one-dimensional (1D) aeronomy code based on the models developed by Salz et al. (2016) and Oklopčić & Hirata (2018), Ninan et al. (2020) and Palle et al. (2020) derived a He abundance five to ten times smaller than solar for the warm Neptune-like planet GJ3470b (i.e. He/H ≈ 0.01). This low He abundance was further confirmed by 3D multi-fluid self-consistent aeronomy simulations by Shaikhislamov et al. (2021, He/H ≈ 0.013), who further strengthened the importance of the stellar wind for modelling the observed He I transit absorption features. Using a 1D hydrodynamic (HD) code, Alonso-Floriano et al. (2019) and Lampón et al. (2020) also derived a similarly low He abundance for the hot Jupiter HD 209458b. Lampón et al. (2021) applied a 1D Parker-like solution fitted to the aeronomy simulationof Salz et al. (2016) to model the atmospheric outflow of HD 189733b, finally obtaining a rather low He abundance of He/H ≈ 0.008 (i.e. about ten times sub-solar). These results indicate that a non-solar He/H abundance ratio may be a common characteristic of hot Jupiters.

WASP-80b is a hot Jupiter orbiting a K-type star (Triaud et al. 2013, 2015; Mancini et al. 2014; Bonomo et al. 2017), which is rather active (e.g. Salz et al. 2016; King et al. 2018). Transmission spectroscopy of WASP-80b has been carried out in the optical from the ground and in the nIR with HST. The observations led to a tentative detection of the Na and K alkali lines (Sedaghati et al. 2017) and of water (Tsiaras et al. 2018; Fisher & Heng 2018), which is suggestive of low metallicity. Salz et al. (2016) computed 1D HD simulations of the upper atmosphere of WASP-80b, concluding that this is one of the most promising targets for the observational detection of atmospheric escape, particularly at FUV wavelengths. More recent estimates of the high-energy stellar emission by King et al. (2018) further strengthened the conclusion of Salz et al. (2016). Therefore, given that the planet orbits an active K-type star and that it is believed to host an extended atmosphere, WASP-80b appears to be an ideal candidate for the search and detection of metastable He I from the ground employing high-resolution transmission spectroscopy (Kirk et al. 2020).

We present here nIR transmission spectroscopy observations of WASP-80b, carried out with the GIANO-B high-resolution spectrograph (Claudi et al. 2017), covering the He I triplet. We also present 3D modelling of the planetary atmosphere attempting to reproduce the observational results with the final aim of constraining key parameters that characterise the planetary upper atmosphere.

This paper is organised as follows. Section 2 presents the observations and the data analysis, while in Sect. 3 we describe the results obtained from the observations. Section 4 shows the results obtained from 3D modelling of the upper atmosphere of WASP-80b, aimed at reproducing the observations. In Sect. 5 we summarise the work, discuss the observational and theoretical results, putting them in a wider context, and present our conclusions.

2 Observations and data analysis

2.1 Data reduction

We observed the WASP-80 system with the nIR echelle spectrograph GIANO-B installed on the 3.6 m Telescopio Nazionale Galileo (TNG) telescope (Oliva et al. 2006). The observations were carried out in GIARPS (GIANO-B + HARPS-N; Claudi et al. 2017) observing mode and were performed with the nodding acquisition mode, with the target observed at predefined A and B positions on the slit, following an ABAB pattern (Claudi et al. 2017). Therefore, the target and sky spectra were taken in pairs by using the two nodding positions along the slit (A and B); in this way, the slit looking at the sky provides an accurate reference for subtracting the thermal background and telluric emission lines.

GIANO-B achieves simultaneous coverage in the wavelength range 0.95–2.45 μm, split into 50 orders, at a spectral resolving power of R ~ 50 000. The dataset encompasses four primary transit events (UT 09 August 2019, UT 21 September 2019, UT 26 June 2020, and UT 17 September 2020) of WASP-80b that were observed within the context of the Global Architecture of Planetary Systems (GAPS) programme (Borsa et al. 2019; Guilluy et al. 2020; Giacobbe et al. 2021). Table 1 presents theobserving log by listing the number of collected spectra, exposure times, and achieved signal-to-noise ratio (S/N) in the spectral region of interest (10 825–10 845 Å), while Fig. 1 shows the variation in the S/N for each image (for spectral order 39). As Table 1 and Fig. 1 show, the data collected during the observed transit event on UT 17 September 2020 exhibit a lower S/N compared to the otherobservations, probably due to the presence of thin clouds. We thus discarded this transit from the analysis. The target was observed within an airmass range of 1.16–1.72 (see the left panel of Fig. 1).

The GIANO-B spectra were dark-subtracted, flat-field-corrected, and extracted (without applying the blaze function correction) with the GOFIO data reduction pipeline (Rainer et al. 2018), which also provides a preliminary wavelength calibration (defined in vacuum) using an U-Ne lamp spectrum as a template. The reduction process also includes bad pixels removal1. The resulting spectra are in the terrestrial rest frame. For the rest of the analysis, we focused on spectral order 39, where the helium triplet falls.

One spectrum (2 459 027.627261 BJDTDB, at phase 0.00475), collected during the night of UT 26 June 2020, exhibited an anomalous flux excess at λ ~ 10 832.74 Å and another at λ ~ 10 832.89 Å (pixel #688 and #689) probably due to a strong cosmic ray not perfectly corrected by the GOFIO pipeline. Thus, we also discarded this particular spectrum from the rest of the analysis.

The output of the GOFIO pipeline (wavelength solution and flux) required additional processing steps before we could proceedwith the data analysis. The mechanical instability of the instrument causes the wavelength solution to change during the observations, and, since the U-Ne lamp spectrum is only acquired at the end of the observations, the wavelength solution determined by GOFIO could not be particularly accurate. We corrected for this instability by following the recipe described by Brogi et al. (2018), Guilluy et al. (2019, 2020), and Giacobbe et al. (2021). In short, for each observation we aligned every spectrum to a common wavelength scale using spline interpolation based on the measured shift computed via cross-correlation with a time-averaged observed spectrum of the target used as a template. This means aligning the sequence to the reference frame of the Earth’s atmosphere, which is also assumed as the frame of the observer, neglecting any ~10 m s−1 differences due to winds. We successively used the atmospheric transmission spectrum generated via the ESO Sky Model Calculator2 to refine the standard GOFIO wavelength calibration.

thumbnail Fig. 1

Airmass (left panel) and S/N (right panel) measured during the GIARPS observations. The vertical dashed lines mark the t1, t2, t3, and t4 contact points (from left to right).
Table 1

WASP-80 b log of TNG-GIARPS observations.

2.2 Transmission spectroscopy

We performed transmission spectroscopy, applying the steps described below to each transit independently and considering the system parameters listed in Table 2. First, we corrected for contamination from the Earth’s atmosphere,which produces both absorption and emission lines in the spectral region around the helium triplet. We corrected for the Earth’s absorption lines by using the relation between airmass and the strength of the telluric lines (e.g. Snellen et al. 2008; Vidal-Madjar et al. 2010; Astudillo-Defru & Rojo 2013). To this end, we first shifted (via quadratic interpolation) each spectrum to the stellar rest frame by computing the stellar radial velocity, V⋆, in the telluric reference system. Assuming a circular orbit (see Table 2), this is given by (1)

where we accounted for the velocity of the observer induced by the rotation of the Earth and by the motion of the Earth around the Sun (i.e. the barycentric Earth radial velocity, Vbar), the stellar reflex motion induced by the planet (i.e. k⋆ sin[2π (ϕ(t))], where ϕ is the planet’s orbital phase and k⋆ is the stellarradial-velocity semi-amplitude), and the systemic velocity of the star-planet system with respect to the barycentre of the Solar System(Vsys). Then, we normalised each spectrum by dividing it by the average flux within two intervals on the immediate blue (10 826.0–10 828.0 Å) and red (10 838.5–10 839.5 Å) sides of the He I triplet, where telluric and stellar lines are absent.

Using the out-of-transit spectra alone, we created a telluric reference spectrum (T(λ)) by extracting the linear correlation that exists between the logarithm of the normalised flux and the airmass (e.g. Wyttenbach et al. 2015). Then, we divided all spectra by the reference telluric spectrum, which was rescaled such that each spectrum would have been acquired at the same airmass, namely the average airmass of the in-transit spectra (collected between the t1 and t4 contact points). In this way, we did not directly correct for telluric lines, but brought them to the same strength across all spectra so that they were automatically deleted when we created the transmission spectra. Since the shift of the telluric lines in the stellar rest frame due to the barycentric component in each analysed transit was much lower than the instrumental resolution, we performed the telluric removal in the stellar rest frame and not in the Earth’s one. In this way, we avoided spurious features in the telluric reference spectrum in correspondence of strong stellar lines because of the low S/N (see Borsa & Zannoni 2018). We remark that the final results do not depend on the rest frame of the telluric correction. Since during the transit on UT 26 June 2020 the telluric contamination was practically absent, we decided to not perform the telluric correction; this way we avoided correlated noise in the final spectra. Figure 2 shows the results of these preliminary reduction steps for each observing night. On the night of UT 21 September 2019, the strongest component of the helium triplet is blended with the water telluric absorption line at 10 835.1 Å (wavelength in the Earth’s rest frame). However, as the result we obtained from this observing night is in agreement with that obtained on the other two nights, we are confident that the applied telluric removal worked appropriately.

Ground-based observations are also contaminated by telluric emission lines. In particular, in the spectralregion of interest there are three OH emission lines that fall near the He I triplet (at ~10 832.1 Å, ~10 832.4 Å, and ~10 834.3 Å, where the wavelengths are in vacuum). However, since the observations were gathered with the nodding acquisition mode that allows for subtraction of the thermal background and emission lines (see Sect. 2.1), there was no need to perform an additional correction, in contrast to what has been done in other works (e.g. Nortmann et al. 2018; Salz et al. 2018; Allart et al. 2019).

For each night, we then built a master stellar spectrum, Smaster, from all out-of-transit spectra (i.e. with an orbital phase smaller than t1 or greater than t4) by computing the weighted mean, using w = 1/σ2 as the respective weights, where σ are the uncertainties associated with each wavelength bin. We then derived the transmission spectra, T, by dividing each spectrum bySmaster. Transmission spectra corrected for the telluric lines with the airmass relation can still present some correlations and telluric residuals caused by the variation in precipitable water vapour. We thus applied a second telluric correction following the approach of Wyttenbach et al. (2015). In short, for each observation we performed a linear fit between the telluric reference spectrum (previously calculated, i.e. (Tλ)) and the transmission spectrum. We then divided the transmission spectrum by the fit solution. All full in-transit transmission spectra (i.e. obtained between the t2 and t3 contact points) were finally averaged to create the transmission spectrum for each observed transit. The top panel of Fig. 3 shows the weighted-mean-averaged transmission spectrum for each night, while the bottom panel displays the averaged transmission spectrum over the three observed transits, Tave. We did not correct for the fringing pattern typical of GIANO-B spectra as the modulation caused by it is significantly smaller than the final error bars3. To remove possible linear trends in the continuum, we computed a robust linear fit of each T in the 10 815–10 850 Å range and divided it out. We avoided the region around the helium triplet (± 20 km s−1 centred at 1083.3 nm) when performing the linear fit. Then, we shifted via quadratic interpolation every T in the planetary reference frame by calculating the planet’s radial velocity in the stellar rest frame as (2)

where kP is the planet’s radial-velocity semi-amplitude. The 2D maps of the transmission spectra in the planet rest frame are shown in Fig. A.1.

Table 2

Stellar and planetary parameters adopted in this work.

thumbnail Fig. 2

Normalised spectra in the stellar rest frame of the three considered transits (grey dots), with the correspondent time-averaged spectrum overlaid. The spectra are plotted with vertical offsets for clarity. Vertical orange lines mark the position of the three components of the metastable He I triplet.
thumbnail Fig. 3

Transmission spectra in the region of the metastable He I triplet. Top: weighted-mean-averaged transmission spectrum for each observed transit. Bottom: weighted mean of the three observed transits. Vertical orange lines mark the position of the three components of the metastable He I triplet. Since the final error bars are calculated following error propagationby taking the square roots of the extracted spectra aligned in the telluric rest frame as initial errors, the final error bars correspond to one standard deviation.

3 Results

The presence of an extended and possibly escaping atmosphere containing a significant amount of metastable He would appear as absorption features in the transmission spectrum in the planet’s rest frame at the position of the stellar helium triplet. However, as Fig. 3 shows, this is not the case: we did not detect any significant absorption feature at the position of the He I triplet, neither when considering the single nights nor all transits combined together.

We thus estimated the upper limit, c (in Fin/Fout), of the He I absorption in the transmission spectrum of WASP-80b considering the standard deviation of Tave in a spectral region around the helium triplet (10 829–10 836 Å). We then translated it into an effective planetary radius, Reff, as 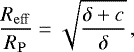(3)

where δ is the transit depth (i.e. 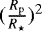), and c is the upper limit for the detection of a signal given the measured standard deviation of ~0.85% at the 95% confidence level. Finally, we estimated an upper limit for the effective radius of Reff   ~ 1.14 Rp at the 95% confidence level.

We refined this upper limit by performing an injection and retrieval analysis. The injected model consisted of a Gaussian function with a fixed full width at half maximum (FWHM; computed by convolving the instrumental resolution with the tidally locked planetary rotation), a fixed centre (the position of the reddest component of the He I (23S) triplet), and a variable amplitude. We changed the amplitude of the Gaussian function to mimic a planetary signal until the retrieved absorption had a statistical significance of 2σ compared to the continuum noise. In this way, we estimated a more accurate upper limit of c ~ 0.7% at the 95% confidence level, which translates into Reff ~1.11 Rp at the 95% confidence level.

4 Modelling

4.1 Stellar spectral energy distribution

The population of metastable He I in the upper planetary atmosphere is affected by the stellar XUV and UV flux, while the stellar nIR emission controls radiation pressure, driving the motion of the escaping He atoms (e.g. Oklopčić & Hirata 2018; Oklopčić 2019; Lampón et al. 2021; Khodachenko et al. 2021a). Therefore, to enable modelling of the planetary upper atmosphere and thus attempt to reproduce and explain the non-detection of metastable He I in WASP-80b, we estimated the stellar emission in the relevant bands as follows.

Except for the He I stellar absorption lines, the nIR stellar emission is purely photospheric. To model it, we employed MARCS models (Gustafsson et al. 2008), which account for both atomic and molecular opacities. We considered a stellar effective temperature (Teff) of 4150 ± 100 K and a surface gravity (log g) of 4.5 (Triaud et al. 2013, 2015; Gaia Collaboration 2018). The logg values derived for WASP-80 and listed in the literature are slightly higher than 4.5, namely 4.6–4.7, but log g has a negligible impact on the nIR emission. Instead, Teff, which has the largest impact on the nIR flux, is known with a rather large uncertainty of about 100 K. Also, the stellar radius listed in the literature spans between 0.571 and 0.606 R⊙ (Triaud et al. 2013, 2015; Bonomo et al. 2017; Gaia Collaboration 2018). For this reason, we estimated the minimum and maximum nIR flux in the region covered by the He I lines by combining the minimum and maximum Teff values (i.e. 4050 and 4250 K) and stellar radii, respectively. In this way, we obtained a minimum value for the nIR continuum flux around 10 830 Å at the distance of the planet (0.0344 AU; Triaud et al. 2015) of ≈5923 erg cm−2 s−1 Å−1 and a maximum flux of ≈7686 erg cm−2 s−1 Å−1. Therefore, as a consequence of the uncertainties on stellar radius and Teff, the nIR flux varies by at most a factor of ≈1.3.

The XUV emission of WASP-80 has been estimated by Salz et al. (2016) and King et al. (2018) on the basis of X-ray observations collected with ROSAT and XMM-Newton. Our starting point for estimating the stellar XUVflux is the result of King et al. (2018), who derived an XUV flux at the distance of the planet of 8900 ± 4300 erg cm−2 s−1 integrating over the 13.6 eV and 2.4 keV range (i.e. 5.2–912 Å). The uncertainty on the XUV emission given by King et al. (2018) is dominated mostly by the rather large uncertainty on the stellar distance of 60 ± 20 pc, which was based on a photometric parallax. In the meantime, the Gaia satellite provided a significantly more precise distance to the star of 49.73 ± 0.05 pc (Gaia Collaboration 2016, 2021). This enabled us to improve the precision of the measurement of the X-ray flux based on the XMM-Newton observations (LX = 4.85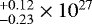 erg s−1) and thus also the accuracy of the XUV flux, which we estimated employing the scaling relations given by King et al. (2018) and the updated stellar X-ray luminosity. In this way, we obtained an XUV flux at the distance of the planet integrated over the 5.2–912 Å range of ≈6281 erg cm−2 s−1, which corresponds to a value of ≈7.5 erg cm−2 s−1 at the distance of 1 AU. This value is a factor of about three lower than that obtained using the scaling relation of Sreejith et al. (2020) and the measured 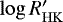value of about −4.04 (see below), which is within the uncertainties.

The UV (FUV and NUV) emission of WASP-80, particularly at wavelengths below 2600 Å, is not photospheric, and thus it cannot be estimated employing the MARCS model. Therefore, to estimate the UV flux at the distance of the planet we looked for a star as similar as possible to WASP-80 in terms of both atmospheric parameters and activity and with an observed UV spectrum. GJ832 is an early M dwarf with an effective temperature of about 3600 K (e.g. Kuznetsov et al. 2019) and a measured value of about −5.1 (Jenkins et al. 2006; Boro Saikia et al. 2018; Hojjatpanah et al. 2019; Sreejith et al. 2020), thus slightly cooler and less active than WASP-80 but with a measured UV flux and a modelled XUV flux that can be used as anchors (France et al. 2016). We estimated the UV spectral emission of WASP-80 by rescaling the stellar flux of GJ832 until the XUV flux matched that derived for WASP-80. In particular, to match the XUV flux of WASP-80, we had to multiply the XUV flux of GJ832 by a factor of 6.8, which is in line with the fact that WASP-80 is more active than GJ832, as indicated by the respective 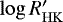values. The rescaled UV spectrum of GJ832 is shown in Fig. 4 in comparison to the MARCS model and the average XUV flux.

Given that WASP-80 is a rather active star, we looked for possible time variations in the high-energy stellar emission by looking at the CaII H&K line core emission. In particular, we summed up the HARPS-N spectra, obtained simultaneously to the GIANO data, from each night to obtain master spectra to increase the S/N. Figure 5 shows that the high-energy emission measured from the HARPS-N spectra is comparable among the three nights of our observations. We employed the master spectra to measure 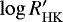(Noyes et al. 1984; Rutten 1984; Fossati et al. 2017), obtaining values ranging between −4.02 and −4.06. We also looked for variations inthe value within each night, determining that the variability lies within the uncertainties.

thumbnail Fig. 4

Photospheric emission of WASP-80 obtained from MARCS models (black line) and the MUSCLES SED of GJ832 (red line) rescaled in such a way as to reproduce the XUV emission of WASP-80 derived from the X-ray measurements and the scaling relations of King et al. (2018). The MARCS model has been convolved to a resolution comparable to that of the MUSCLES spectrum of GJ832 in the optical and infrared. The blue line shows the average XUV stellar emission at the distance of the planet. For reference, the vertical dashed lines indicate, from left to right, the position of the hydrogen ionisation threshold (≈912 Å), the position of the metastable He I ionisation threshold (≈2600 Å), and the approximate position of the He I features (≈10 830 Å).

4.2 3D hydrodynamic modelling

The 3D modelling results presented here are based on a multi-fluid self-consistent aeronomy model of the planetary wind and of its interaction with the stellar wind. The code has already been employed to model the upper atmosphere and reproduce the observations of the hot Jupiter HD 209458b (Shaikhislamov et al. 2020b), the warm Neptunes GJ436b (Khodachenko et al. 2019) and GJ3470b (Shaikhislamov et al. 2021), and the super-Earth π Men c (Shaikhislamov et al. 2020a). In particular, the works of Shaikhislamov et al. (2021) and Khodachenko et al. (2021a) focus on the modelling of metastable He I in the planetary atmospheres and on fitting the relative observations.

The code solves the continuity, momentum, and energy equations for all considered species, which are H, H+, H2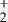, H, H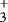, He, He+, and He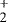. The metastable He I (23S) atoms are treated as a separate fluid with its own velocity and temperature, which are determined by those of the species from which they originate, namely He+ or He I (13S), depending on whether recombination or excitation from the ground state, respectively, generate the He I in the metastable state. Elastic collisions with other species also affect the macroscopic physical parameters of the He I (23S) fluid. All reactions, which populate and depopulate the He I (23S) component, are those listed by Oklopčić & Hirata (2018) and Shaikhislamov et al. (2021, their Table 1), while the details of the absorption calculations are described in Shaikhislamov et al. (2021).

We employed the UV flux derived as described in Sect. 4.1 to compute the photoionisation time of He I (23S) atoms, obtaining about 2.3 min at the planetary orbit. The XUV stellar flux ionises and heats upper atmospheres through the production of photoelectrons, finally leading to HD outflow. Different species interact via elastic, charge-exchange, and Coulomb collisions, which efficiently couple velocities and temperatures of atoms and ions in the region dominated by the planetary material (e.g. Debrecht et al. 2020). The 3D model also self-consistently calculates the stellar wind plasma over the whole star-planet system. Unless otherwise stated, for the simulations we considered a stellar wind velocity of 200 km s−1, a stellar wind temperature of 0.7 MK, and a stellar wind density of 103 cm−3 at the position of the planet. These values lead to a stellar mass-loss rate of 1011 g s−1, namely a sub-solar wind strength, but we test the impact of the stellar wind and present the results later in this section.

The model equations are solved on a spherical grid in the planet-centred reference frame with the polar-axis Z perpendicular to the orbital plane (see Shaikhislamov et al. 2020b). For all model runs, we set a temperature of 1000 K and a pressure of 0.05 bar at the base of the planetary atmosphere. The chosen lower boundary temperature is close to the planetary equilibrium temperature. The lower boundary pressure was chosen such that all XUV photons are absorbed within the simulation domain, that is, above the lower boundary (see Shaikhislamov et al. 2014, for more details). Each simulation was run continuously for 600 dimensionless times4, corresponding to about 18 planetary orbits, and we ensured convergence of the solution by checking the stability of the integral mass loss, which reaches a quasi-stationary level after about 200 dimensionless times (about six planetary orbits).

Figure 6 presents the structure of the expanding upper planetary atmosphere on the scale of the whole simulation domain obtained assuming a nearly solar He abundance (He/H = 0.05). It shows that the planetary atmosphere extends far from the planet and stretches both ahead and behind the planet along the orbit. From this model, we obtained a total mass-loss rate of 2.6 × 1010 g s−1. The simulation shown in Fig. 6 led to significant He I (23S) absorption of the order of 10%, in strong contrast with the observations. Figure 6 shows that most of the absorption takes place relatively close to the planet, within a spherical shell with a radius of about 3 Rp.

The left panel of Fig. 7 shows the density, velocity, and temperature profile of the planetary gas gathered from the simulation. As obtained by Salz et al. (2016), molecular hydrogen is dissociated very rapidly and the temperature rises steeply following H2 dissociation, reaching temperatures of about 104 K, a velocity of about 10 km s−1, and a mass-loss rate of 2.6 × 1010 g s−1. This is similar to what is found from simulations of classical hot Jupiters (e.g. Salz et al. 2016; Kubyshkina et al. 2018a; Shaikhislamov et al. 2020b). The right panel of Fig. 7 shows the reaction rates of kinetic processes populating and depopulating metastable He I. The recombination of He+ into He I (23S) is balanced by auto-ionisation collisions with H I at low altitudes (<1.2 Rp) and by electron collisional depopulation at higher altitudes. Photoionisation of metastable He I, instead, becomes relevant relatively far from the planet, at a distance at which the He I (23S) density is too low to affect the absorption during transit. Therefore, the stellar UV flux has relatively little impact on reproducing the observed non-detection. Similarly, we determine that radiation pressure accelerating the metastable He I atoms has a small impact on the absorption features.

Given the low photoionisation rate of the metastable He I, the only parameters affecting the absorption observed during transit are the stellar XUV flux, the He abundance, and possibly the stellar wind strength. Figure 8 shows the absorption profiles obtained by varying the stellar XUV flux and the He abundance in the planetary upper atmosphere. As expected, the absorption depth varies significantly when both XUV flux and atmospheric He abundance are varied. In particular, we varied the XUV flux by a factor of two, but this did not enable us to reproduce the observed non-detection. We remark that, as a result of the geometry of the model, the simulations take into account planetary rotation, which is assumed to be tidally locked with the planetary orbit around the host star. Therefore, we lowered the atmospheric He abundance until it matched the observations, obtaining that, for the estimated stellar XUV flux, the absorption depth falls below 0.7% for He/H values smaller than 5 × 10−3, which is about 16 times smaller than solar, thus putting a strong constraint on the He abundance in the planetary upper atmosphere. To strengthen this result, we computed an additional model increasing the stellar UV flux, and thus the metastable He I photoionisation rate, a hundredfold; however, in this case as well we obtained a significant He I absorption, in contrast to the observations.

A further parameter that may affect the He I absorption signal is the stellar wind, which can cause the planetary atmosphere to compress (e.g. Vidotto & Cleary 2020). Figure 9 shows how the stellar wind affects the He I absorption. Indeed, a stronger stellar wind compared to what was used for the simulations shown above reduces the He I absorption by a factor of about 1.5. This is the result of the stellar wind compressing the planetary atmospheric outflow with the bow shock moving to as close as 3.5 planetary radii. As a result, the atmospheric gas responsible for the absorption remains close to the planet, reducing the absorption signal. Figure 9 shows that an even stronger stellar wind with a mass-loss rate of 1013 g s−1 leads to the bow shock moving to about 2.2 planetary radii, further reducing the He I absorption signal. Therefore, we obtain that with the strongest stellar wind we consider, which is about four times stronger than solar and 16 times stronger than that derived for the K-type star HD 219134 (Vidotto et al. 2018), the He abundance leading to the fit of the non-detection is He/H ≲ 0.01, which is about a factor of ten smaller than solar.

Figure 9 also shows the effect that radiation pressure plays on the He I absorption. Artificially reducing the radiation pressure impinging on the metastable He I atoms by ten times shifts the absorption profile by about 2.5 km s−1 towards the red.

thumbnail Fig. 5

Comparison among the master HARPS spectra of the CaII K line obtained by combining the data collected on each night, convolved to a spectral resolution of 10 000 for visualisation purposes.
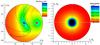thumbnail Fig. 6

Simulation results. Left: proton density distribution in the orbital plane of the whole simulated space comprising the WASP-80 system. The planet is at the centre of the coordinate system (0,0) and moves anti-clockwise relative to the starthat is located at (76,0). The red dots indicate the position and size of the star (right) and planet (centre). The black and red lines correspond to the proton fluid streamlines originated from the planet and the star, respectively. The axes are in units of planetary radii. Right: distribution of metastable He I local absorption (from 0, which is no absorption, to 1, which is full absorption) along the line of sight at mid-transit integrated over ±10 km s−1. The whole plotted circle corresponds to the stellar disk, while the lower boundary of the simulated planetary atmosphere is shown by the black circle.
thumbnail Fig. 7

Profiles along the planet-to-star direction. Left: temperature (black line) and velocity (grey line) of protons (in 104 K and km s−1, respectively; the scale for both is on the right axis) and density of major species labelled in the plot (left axis). Right: rates of the reactions responsible for the processes of population and depopulation of metastable He I listed in the legend. The black line shows the sum of reactions 1 and 2, while the blue line is the sum of reactions 7 and 8 (see legend). The x axes are in units of planetary radii.
thumbnail Fig. 8

Comparison between simulations and observations. Left: He I (23S) triplet absorption profiles obtained considering three different values of the stellar XUV flux (blue, red, and green lines) at a fixed He abundance of He/H = 0.05 (the fluxes in the legend are at 1 AU and in erg cm−2 s−1) and a 100 times higher value of the stellar NUV flux (grey line).Right: He I (23 S) triplet absorption profiles obtained considering different values of the He abundance. In both panels, the zero Doppler-shifted velocity on the x axis corresponds to a wavelength of 10 830.25 Å, the observed transmission spectrum is shown by black asterisks, and the horizontal dashed line marks the 2σ upper limit derived from the observations. The horizontal dotted line at 1.00 is for reference.
thumbnail Fig. 9

He I triplet absorption profiles obtained considering a fixed stellar XUV flux at the distance of 1 AU of 7.5 erg cm−2 s−1, a solar He abundance, and different stellar wind strengths expressed in terms of mass-loss rate in g s−1. Considering the strongest stellar wind taken into account, the observed non-detection is reached for He/H values smaller than ≈0.01. The long dashed red line shows the absorption obtained considering the same conditions taken for the solid red line except for a ten times weaker radiation pressure on the He I metastable atoms. The zero Doppler-shifted velocity on the x axis corresponds to a wavelength of 10 830.25 Å, the observed transmission spectrum is shown by black asterisks, and the horizontal dashed line marks the 2σ upper limit. The horizontal dotted line at 1.00 that we placed for reference is largely masked by the yellow line.

5 Discussion and conclusion

We employed the GIANO-B spectrograph to obtain the transmission spectrum of the hot Jupiter WASP-80b in the wavelength range covered by the triplet of metastable He I at 10 830 Å. In particular, we looked for He I absorption indicative of the presence of an extendedand possibly escaping atmosphere. As a matter of fact, HD modelling and considerations based on the planetary properties suggest that WASP-80b should be a prime target for the detection of metastable neutral He in the planetary upper atmosphere. However, the GIANO-B observations led to a non-detection, with an upper limit of 0.11 Rp (95% confidence level) on the size of the possible He I absorption signal.

We attempted to understand this unexpected result by employing a 3D aeronomy model that has proven to work well in reproducing the He I transmission spectroscopy observations of GJ3470b and WASP-107b (Shaikhislamov et al. 2021; Khodachenko et al. 2021a), as well as of HD 209458b and HD 189733b (Rumenskikh, in prep.). Even the presence of high-altitude clouds could not explain the non-detection. Indeed, considering a solar He abundance, the peak of the density of metastable He lies close to the layers that absorb most of the stellar XUV photons (Fig. 7), where no clouds can form because of photodissociation. Given the system properties, the most plausible solution suggested by the model for reproducing the non-detection is a low He abundance. In particular, we find He/H < 5×10−3 (about 16 times smaller than solar) for a stellar wind 25 times weaker than solar or He/H < 10−2 (about ten times smaller than solar) for a stellar wind four times stronger than solar. This is a remarkable result considering that for WASP-107b, which has physical properties similar to those of WASP-80b, the same model returns a solar He abundance. The major difference between the two planets is a factor of five higher mass of WASP-80b compared to WASP-107b, which leads to a more compact atmosphere for WASP-80b.

We attempted to understand the non-detection of He I in the upper atmosphere of WASP-80b by putting it in the wider context of published detections and non-detections. To this end, we collected the physical properties of the systems for which either measurements or non-detections of the He I metastable triplet have been reported (Table 3). We collected the system parameters from the literature, giving priority to more recent and/or homogeneous sources. The stellar XUV fluxes listed in Table 3have been either taken from the literature or, when unavailable, extracted employing the scaling relations of Sreejith et al. (2020). The XUV fluxes listed in Table 3 correspond to the amount of high-energy stellar radiation at wavelengths shorter than 912 Å irradiating the planet. This is not the most relevant wavelength range5 in relation to the production of metastable He I, but it is still representative of the high-energy stellar emission, it is the one typically reported in the literature, and it can be readily estimated on the basis of a variety of measurements obtained at X-ray, UV, and optical wavelengths (e.g. Sanz-Forcada et al. 2011; Chadney et al. 2015; King et al. 2018; Linsky et al. 2013, 2014; France et al. 2018; Sreejith et al. 2020).

So far, the search of the He I metastable triplet in the upper atmosphere of an exoplanet has been reported for 21 planets ranging from Earth-size rocky planets (e.g. Trappist-1b,e,f) to ultra-hot Jupiters (e.g. KELT-9b). However, for just seven of them have the observations led to a positive detection; in all other cases, only an upper limit could be derived. This suggests that the presence of metastable He is not ubiquitous in exoplanetary atmospheres, even when the atmosphere is clearly in an HD state (e.g. GJ436b). This is due to the fact that the shape of the stellar SED plays a central role in the production and destruction of metastable He (Oklopčić 2019), but other important factors may also play a significant role. To attempt to uncover them, we show in Fig. 10 the size of the measured He I absorption signal or upper limit (δRp), normalised to the atmospheric scale height (Heq), as a function of incident stellar XUV flux (see also Nortmann et al. 2018), with the planetary surface gravity (g) indicated by the symbol size (Fig. B.1 presents similar plots, showing δRp/Heq as a function of incident stellar XUV flux and planetary surface gravity, separately). We computed the atmospheric pressure scale height as (4)

and its uncertainty as (5)

where kB is the Boltzmann constant, Teq is the planetary equilibrium temperature listed in Table 3, g is the planetary gravity computed from the planetary mass and radius listed in Table 3, μ is the mean molecular weight (we assume a hydrogen-dominated atmosphere6 and hence a value of 1.3 times the mass of a hydrogen atom), and 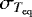and σg are the uncertainties on the planetary equilibrium temperature and gravity, respectively. To obtain a more homogeneous sample, we considered only planets with a radius larger than three Earth radii (i.e. we consider only planets that most certainly host a hydrogen-dominated atmosphere). Furthermore, we excluded WASP-12b and HAT-P-18b, whose measurements were conducted employing low-resolution observations and thus not compatible with the more sensitive high-resolution observations employed for the other reported measurements. Furthermore, following the typical uncertainties of scaling relations employed to convert X-ray, UV, or optical measurements into XUV flux (e.g. Linsky et al. 2013, 2014; France et al. 2018; Sreejith et al. 2020), we assigned an uncertainty to the stellar XUV flux of a factor of two.

Figure 10 does not indicate the presence of any clear correlation with any of the considered parameters (i.e. stellar spectral type, XUV irradiation, and planetary surface gravity), which are those believed to primarily drive the possible detection, or non-detection, of metastable He in planetary upper atmospheres. Although the number of planets for which the detection of the He I metastable triplet has been (successfully) attempted is still too small to draw clear conclusions, Fig. 10 suggests the presence of a problem in our understanding of the formation of the He I metastable triplet and/or the presence of further parameters that play a significant role in the formation of the triplet. Taking into account the main result obtained from our modelling of WASP-80b and previous results (GJ3470b, HD 209458b, HD 189733b; Ninan et al. 2020; Palle et al. 2020; Alonso-Floriano et al. 2019; Lampón et al. 2020, 2021), this parameter may be the He abundance and/or the stellar wind, though the stellar wind alone does not seem to be capable of sufficiently reducing the planetary absorption signal without a significantly sub-solar He/H abundance ratio, at least in the case of WASP-80b.

There are physical processes that have been identified as leading to a decrease in the He atmospheric abundance with respect to that of hydrogen. A mechanism possibly at work resulting in a reduction in the He abundance in the upper atmospheric layers is the phase separation of He and liquid metallic hydrogen, for which the former condenses and rains down towards the deeper atmosphericlayers (e.g. Stevenson & Salpeter 1977a,b; Guillot & Gautier 2015). This mechanism should be important for old planets less massive than Jupiter that remained far from the host star for a significant amount of time before migrating inwards (Fortney & Hubbard 2004). Also, magnetic fields may be responsible for the non-detection of He I absorption. This is because magnetic fields strongly affect the motion of the atmospheric gas, possibly in a way that makes the detection of metastable He I impossible with the data at hand (e.g. Adams 2011; Trammell et al. 2014; Khodachenko et al. 2015, 2021b).

Unfortunately, it is currently not possible to infer the He abundance of a planetary atmosphere from indicators other than the He I triplet. Similarly, it is very difficult to reliably constrain the wind strength of late-type stars in the absence of specific indicators such as a Lyα line amenable to reconstruction or the detection of radio emission (e.g. Wood et al. 2005; Fichtinger et al. 2017; Vidotto et al. 2018; Folsom et al. 2018, 2020). Therefore, it will be important to continue investigating this feature both theoretically and observationally. In particular, it is crucial that more in-depth modelling be carried out to identify the possible presence of additional physical factors controlling the formation and destruction of metastable He. Also, it is similarly important to attempt the observation of the triplet in other planets, though the focus should be on close-in giant planets that host a hydrogen-dominated envelope, to enable results to be compared within a larger yet homogeneous sample of planets. Along the same lines, more effort should be put into identifying and studying physical processes that could lead to the He abundance being altered with respect to that of hydrogen in giant planets. Finally, the non-detection of metastable He I presented here may possibly be the consequence of the presence of a magnetic field, which is why it is equally important to keep attempting to directly detect exoplanetary magnetic fields.

Table 3

Properties of the systems for which either measurements or non-detections of the He I metastable triplet have been published.

thumbnail Fig. 10

Size of the measured He I absorption signal, normalised to the atmospheric scale height computed considering the planetary parameters listed in Table 3 and a mean molecular weight of a pure hydrogen atmosphere, as a function of the incident stellar XUV flux (in logarithmic scale), with the symbol size indicating the planetary surface gravity. The uncertainties on the stellar XUV flux are set to be equal to a factor of two (see text). Downward arrows indicate upper limits.

Acknowledgements

We acknowledge financial contributions from PRIN INAF 2019 and from the agreement ASI-INAF number 2018-16-HH. I.F.S., M.L.K., M.A.E., M.S.R., I.B.M., and A.G.B. acknowledge the support of grant 075-15-2020-780 (GA No. 13.1902.21.0039) of the Russian Ministry of Education and Science. M.L.K. also acknowledges the projects I2939-N27 and S11606-N16 of the Austrian Science Fund (FWF). Parallel computing simulations have been performed at Computation Center of Novosibirsk State University and SB RAS Siberian Supercomputer Center. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. We thank J. Southworth for sharing with us published data relevant to the paper. We thank the anonymous referee for their insightful comments.

Appendix A Tomography of the He I transit measurements.

thumbnail Fig. A.1

Transmission spectra shown in tomography in the planetary rest frame for the three consideredtransits, as a function of wavelength and planetary orbital phase. The contact points t1, t2, t3, and t4 are marked with horizontal black lines. The feature at 1083.5 nm misaligned with theplanet rest frame present on the first and second night is a residual of a telluric H2O line.

Appendix B Measured He I absorption as a function of stellar XUV irradiation and planetary surface gravity

thumbnail Fig. B.1

Measured He I absorption signal as a function of stellar XUV flux and planetary gravity. Top: Size of the measured He I absorption signal, normalised to the atmospheric scale height computed considering the planetary parameters listed in Table 3 and a mean molecular weight of a pure hydrogen atmosphere, as a function of the incident stellar XUVflux (in logarithmic scale). Upper limits are marked by downward arrows. The symbol colour indicates the spectral type of the host as given by the legend. Bottom: Same as the upper panel, but as a function of planetary surface gravity.

References

  1. Adams, F. C. 2011, ApJ, 730, 27 [NASA ADS] [CrossRef] [Google Scholar]
  2. Airapetian, V. S., Barnes, R., Cohen, O., et al. 2020, Int. J. Astrobiol., 19, 136 [NASA ADS] [CrossRef] [Google Scholar]
  3. Allart, R., Bourrier, V., Lovis, C., et al. 2018, Science, 362, 1384 [Google Scholar]
  4. Allart, R., Bourrier, V., Lovis, C., et al. 2019, A&A, 623, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Alonso-Floriano, F. J., Snellen, I. A. G., Czesla, S., et al. 2019, A&A, 629, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Anderson, D. R., Collier Cameron, A., Delrez, L., et al. 2017, A&A, 604, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Astudillo-Defru, N., & Rojo, P. 2013, A&A, 557, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Bakos, G. Á., Torres, G., Pál, A., et al. 2010, ApJ, 710, 1724 [NASA ADS] [CrossRef] [Google Scholar]
  9. Ballester, G. E., & Ben-Jaffel, L. 2015, ApJ, 804, 116 [Google Scholar]
  10. Ben-Jaffel, L. 2007, ApJ, 671, L61 [NASA ADS] [CrossRef] [Google Scholar]
  11. Ben-Jaffel, L. 2008, ApJ, 688, 1352 [NASA ADS] [CrossRef] [Google Scholar]
  12. Ben-Jaffel, L., & Sona Hosseini, S. 2010, ApJ, 709, 1284 [Google Scholar]
  13. Bonfils, X., Gillon, M., Udry, S., et al. 2012, A&A, 546, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Bonomo, A. S., Desidera, S., Benatti, S., et al. 2017, A&A, 602, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Boro Saikia, S., Marvin, C. J., Jeffers, S. V., et al. 2018, A&A, 616, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Borsa, F., & Zannoni, A. 2018, A&A, 617, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Borsa, F., Rainer, M., Bonomo, A. S., et al. 2019, A&A, 631, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Bourrier, V., Lecavelier des Etangs, A., Ehrenreich, D., Tanaka, Y. A., & Vidotto, A. A. 2016, A&A, 591, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Bourrier, V., de Wit, J., Bolmont, E., et al. 2017, AJ, 154, 121 [NASA ADS] [CrossRef] [Google Scholar]
  20. Bourrier, V., Ehrenreich, D., Lecavelier des Etangs, A., et al. 2018a, A&A, 615, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Bourrier, V., Lecavelier des Etangs, A., Ehrenreich, D., et al. 2018b, A&A, 620, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Bourrier, V., Lovis, C., Beust, H., et al. 2018c, Nature, 553, 477 [NASA ADS] [CrossRef] [Google Scholar]
  23. Bourrier, V., Wheatley, P. J., Lecavelier des Etangs, A., et al. 2020, MNRAS, 493, 559 [Google Scholar]
  24. Bourrier, V., dos Santos, L. A., Sanz-Forcada, J., et al. 2021, A&A, 650, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Brogi, M., Giacobbe, P., Guilluy, G., et al. 2018, A&A, 615, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Carleo, I., Youngblood, A., Redfield, S., et al. 2021, AJ, 161, 136 [NASA ADS] [CrossRef] [Google Scholar]
  27. Casasayas-Barris, N., Orell-Miquel, J., Stangret, M., et al. 2021, A&A, 654, A163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Chadney, J. M., Galand, M., Unruh, Y. C., Koskinen, T. T., & Sanz-Forcada, J. 2015, Icarus, 250, 357 [Google Scholar]
  29. Claudi, R., Benatti, S., Carleo, I., et al. 2017, Eur. Phys. J. Plus, 132, 364 [NASA ADS] [CrossRef] [Google Scholar]
  30. Crossfield, I. J. M., Barman, T., Hansen, B., & Frewen, S. 2019, Res. Notes Am. Astron. Soc., 3, 24 [Google Scholar]
  31. Czesla, S., Lampón, M., Sanz-Forcada, J., et al. 2022, A&A, 657, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Debrecht, A., Carroll-Nellenback, J., Frank, A., et al. 2020, MNRAS, 493, 1292 [Google Scholar]
  33. Ehrenreich, D., Bourrier, V., Wheatley, P. J., et al. 2015, Nature, 522, 459 [Google Scholar]
  34. Ehrenreich, D., Lovis, C., Allart, R., et al. 2020, Nature, 580, 597 [Google Scholar]
  35. Fichtinger, B., Güdel, M., Mutel, R. L., et al. 2017, A&A, 599, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Figueira, P., Oshagh, M., Adibekyan, V. Z., & Santos, N. C. 2014, A&A, 572, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Fisher, C., & Heng, K. 2018, MNRAS, 481, 4698 [Google Scholar]
  38. Folsom, C. P., Fossati, L., Wood, B. E., et al. 2018, MNRAS, 481, 5286 [Google Scholar]
  39. Folsom, C. P., Ó Fionnagáin, D., Fossati, L., et al. 2020, A&A, 633, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Fortney, J. J.,& Hubbard, W. B. 2004, ApJ, 608, 1039 [NASA ADS] [CrossRef] [Google Scholar]
  41. Fossati, L., Haswell, C. A., Froning, C. S., et al. 2010, ApJ, 714, L222 [Google Scholar]
  42. Fossati, L., Marcelja, S. E., Staab, D., et al. 2017, A&A, 601, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Fossati, L., Koskinen, T., France, K., et al. 2018, AJ, 155, 113 [CrossRef] [Google Scholar]
  44. France, K., Loyd, R. O. P., Youngblood, A., et al. 2016, ApJ, 820, 89 [NASA ADS] [CrossRef] [Google Scholar]
  45. France, K., Arulanantham, N., Fossati, L., et al. 2018, ApJS, 239, 16 [Google Scholar]
  46. Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. García Muñoz A., 2007, Planet. Space Sci., 55, 1426 [Google Scholar]
  50. García Muñoz, A., Fossati, L., Youngblood, A., et al. 2021, ApJ, 907, L36 [Google Scholar]
  51. Giacobbe, P., Brogi, M., Gandhi, S., et al. 2021, Nature, 592, 205 [NASA ADS] [CrossRef] [Google Scholar]
  52. Gillon, M., Demory, B. O., Madhusudhan, N., et al. 2014, A&A, 563, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Gillon, M., Triaud, A. H. M. J., Demory, B.-O., et al. 2017, Nature, 542, 456 [NASA ADS] [CrossRef] [Google Scholar]
  54. Grimm, S. L., Demory, B.-O., Gillon, M., et al. 2018, A&A, 613, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Guillot, T., & Gautier, D. 2015, Treatise on Geophysics, Giant Planets, ed. G. Schubert (Amsterdam: Elsevier), 529 [CrossRef] [Google Scholar]
  56. Guilluy, G., Sozzetti, A., Brogi, M., et al. 2019, A&A, 625, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Guilluy, G., Andretta, V., Borsa, F., et al. 2020, A&A, 639, A49 [EDP Sciences] [Google Scholar]
  58. Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Harpsøe, K. B. W., Hardis, S., Hinse, T. C., et al. 2013, A&A, 549, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Hartman, J. D., Bakos, G. Á., Torres, G., et al. 2011, ApJ, 742, 59 [NASA ADS] [CrossRef] [Google Scholar]
  61. Haswell, C. A., Fossati, L., Ayres, T., et al. 2012, ApJ, 760, 79 [Google Scholar]
  62. Hojjatpanah, S., Figueira, P., Santos, N. C., et al. 2019, A&A, 629, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Jenkins, J. S., Jones, H. R. A., Tinney, C. G., et al. 2006, MNRAS, 372, 163 [Google Scholar]
  64. Jin, S., & Mordasini, C. 2018, ApJ, 853, 163 [Google Scholar]
  65. Jin, S., Mordasini, C., Parmentier, V., et al. 2014, ApJ, 795, 65 [Google Scholar]
  66. Khodachenko, M. L., Shaikhislamov, I. F., Lammer, H., & Prokopov, P. A. 2015, ApJ, 813, 50 [NASA ADS] [CrossRef] [Google Scholar]
  67. Khodachenko, M. L., Shaikhislamov, I. F., Lammer, H., et al. 2019, ApJ, 885, 67 [NASA ADS] [CrossRef] [Google Scholar]
  68. Khodachenko, M. L., Shaikhislamov, I. F., Fossati, L., et al. 2021a, MNRAS, 503, L23 [NASA ADS] [CrossRef] [Google Scholar]
  69. Khodachenko, M. L., Shaikhislamov, I. F., Lammer, H., et al. 2021b, MNRAS, 507, 3626 [NASA ADS] [CrossRef] [Google Scholar]
  70. King, G. W., Wheatley, P. J., Salz, M., et al. 2018, MNRAS, 478, 1193 [NASA ADS] [Google Scholar]
  71. Kirk, J., Alam, M. K., López-Morales, M., & Zeng, L. 2020, AJ, 159, 115 [Google Scholar]
  72. Kosiarek, M. R., Crossfield, I. J. M., Hardegree-Ullman, K. K., et al. 2019, AJ, 157, 97 [NASA ADS] [CrossRef] [Google Scholar]
  73. Koskinen, T. T., Yelle, R. V., Lavvas, P., & Lewis, N. K. 2010, ApJ, 723, 116 [CrossRef] [Google Scholar]
  74. Kreidberg, L., & Oklopčić, A. 2018, Res. Notes Am. Astron. Soc., 2, 44 [Google Scholar]
  75. Krishnamurthy, V., Hirano, T., Stefánsson, G., et al. 2021, AJ, 162, 82 [CrossRef] [Google Scholar]
  76. Kubyshkina, D., Fossati, L., Erkaev, N. V., et al. 2018a, A&A, 619, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Kubyshkina, D., Lendl, M., Fossati, L., et al. 2018b, A&A, 612, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  78. Kuznetsov, M. K., del Burgo, C., Pavlenko, Y. V., & Frith, J. 2019, ApJ, 878, 134 [Google Scholar]
  79. Lammer, H., Zerkle, A. L., Gebauer, S., et al. 2018, A&ARv, 26, 2 [Google Scholar]
  80. Lammer, H., Leitzinger, M., Scherf, M., et al. 2020, Icarus, 339, 113551 [Google Scholar]
  81. Lampón, M., López-Puertas, M., Lara, L. M., et al. 2020, A&A, 636, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  82. Lampón, M., López-Puertas, M., Sanz-Forcada, J., et al. 2021, A&A, 647, A129 [EDP Sciences] [Google Scholar]
  83. Lanotte, A. A., Gillon, M., Demory, B. O., et al. 2014, A&A, 572, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  84. Lecavelier des Etangs, A., Bourrier, V., Wheatley, P. J., et al. 2012, A&A, 543, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  85. Linsky, J. L., Yang, H., France, K., et al. 2010, ApJ, 717, 1291 [Google Scholar]
  86. Linsky, J. L., France, K., & Ayres, T. 2013, ApJ, 766, 69 [Google Scholar]
  87. Linsky, J. L., Fontenla, J., & France, K. 2014, ApJ, 780, 61 [Google Scholar]
  88. Llama, J., & Shkolnik, E. L. 2015, ApJ, 802, 41 [NASA ADS] [CrossRef] [Google Scholar]
  89. Llama, J., & Shkolnik, E. L. 2016, ApJ, 817, 81 [NASA ADS] [CrossRef] [Google Scholar]
  90. Lopez, E. D., & Fortney, J. J. 2013, ApJ, 776, 2 [Google Scholar]
  91. Mancini, L., Southworth, J., Ciceri, S., et al. 2014, A&A, 562, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  92. Mann, A. W., Johnson, M. C., Vanderburg, A., et al. 2020, AJ, 160, 179 [Google Scholar]
  93. Mansfield, M., Bean, J. L., Oklopčić, A., et al. 2018, ApJ, 868, L34 [Google Scholar]
  94. Modirrousta-Galian, D., Locci, D., Tinetti, G., & Micela, G. 2020, ApJ, 888, 87 [Google Scholar]
  95. Moutou, C., Coustenis, A., Schneider, J., Queloz, D., & Mayor, M. 2003, A&A, 405, 341 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  96. Ninan, J. P., Stefansson, G., Mahadevan, S., et al. 2020, ApJ, 894, 97 [Google Scholar]
  97. Nortmann, L., Pallé, E., Salz, M., et al. 2018, Science, 362, 1388 [Google Scholar]
  98. Noyes, R. W., Hartmann, L. W., Baliunas, S. L., Duncan, D. K., & Vaughan, A. H. 1984, ApJ, 279, 763 [Google Scholar]
  99. Oklopčić, A. 2019, ApJ, 881, 133 [Google Scholar]
  100. Oklopčić, A., & Hirata, C. M. 2018, ApJ, 855, L11 [Google Scholar]
  101. Oliva, E., Origlia, L., Baffa, C., et al. 2006, SPIE Conf. Ser., 6269, 626919 [Google Scholar]
  102. Owen, J. E., & Wu, Y. 2017, ApJ, 847, 29 [Google Scholar]
  103. Palle, E., Nortmann, L., Casasayas-Barris, N., et al. 2020, A&A, 638, A61 [EDP Sciences] [Google Scholar]
  104. Paragas, K., Vissapragada, S., Knutson, H. A., et al. 2021, ApJ, 909, L10 [NASA ADS] [CrossRef] [Google Scholar]
  105. Piaulet, C., Benneke, B., Rubenzahl, R. A., et al. 2021, AJ, 161, 70 [NASA ADS] [CrossRef] [Google Scholar]
  106. Rainer, M., Harutyunyan, A., Carleo, I., et al. 2018, SPIE Conf. Ser., 10702, 1070266 [Google Scholar]
  107. Rice, K., Malavolta, L., Mayo, A., et al. 2019, MNRAS, 484, 3731 [NASA ADS] [CrossRef] [Google Scholar]
  108. Rutten, R. G. M. 1984, A&A, 130, 353 [NASA ADS] [Google Scholar]
  109. Salz, M., Czesla, S., Schneider, P. C., & Schmitt, J. H. M. M. 2016, A&A, 586, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  110. Salz, M., Czesla, S., Schneider, P. C., et al. 2018, A&A, 620, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  111. Sanz-Forcada, J., Micela, G., Ribas, I., et al. 2011, A&A, 532, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  112. Seager, S., & Sasselov, D. D. 2000, ApJ, 537, 916 [Google Scholar]
  113. Sedaghati, E., Boffin, H. M. J., Delrez, L., et al. 2017, MNRAS, 468, 3123 [NASA ADS] [CrossRef] [Google Scholar]
  114. Shaikhislamov, I. F., Fossati, L., Khodachenko, M. L., et al. 2020a, A&A, 639, A109 [EDP Sciences] [Google Scholar]
  115. Shaikhislamov, I. F., Khodachenko, M. L., Lammer, H., et al. 2020b, MNRAS, 491, 3435 [NASA ADS] [Google Scholar]
  116. Shaikhislamov, I. F., Khodachenko, M. L., Sasunov, Y. L., et al. 2014, ApJ, 795, 132 [NASA ADS] [CrossRef] [Google Scholar]
  117. Shaikhislamov, I. F., Khodachenko, M. L., Lammer, H., et al. 2021, MNRAS, 500, 1404 [Google Scholar]
  118. Snellen, I. A. G., Albrecht, S., de Mooij, E. J. W., & Le Poole, R. S. 2008, A&A, 487, 357 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  119. Spake, J. J., Sing, D. K., Evans, T. M., et al. 2018, Nature, 557, 68 [Google Scholar]
  120. Sreejith, A. G., Fossati, L., Youngblood, A., France, K., & Ambily, S. 2020, A&A, 644, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  121. Stevenson, D. J., & Salpeter, E. E. 1977a, ApJS, 35, 239 [NASA ADS] [CrossRef] [Google Scholar]
  122. Stevenson, D. J., & Salpeter, E. E. 1977b, ApJS, 35, 221 [CrossRef] [Google Scholar]
  123. Tabernero, H. M., Zapatero Osorio, M. R., Allart, R., et al. 2021, A&A, 646, A158 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  124. Trammell, G. B., Li, Z.-Y., & Arras, P. 2014, ApJ, 788, 161 [NASA ADS] [CrossRef] [Google Scholar]
  125. Triaud, A. H. M. J., Anderson, D. R., Collier Cameron, A., et al. 2013, A&A, 551, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  126. Triaud, A. H. M. J., Gillon, M., Ehrenreich, D., et al. 2015, MNRAS, 450, 2279 [NASA ADS] [CrossRef] [Google Scholar]
  127. Tsiaras, A., Waldmann, I. P., Zingales, T., et al. 2018, AJ, 155, 156 [NASA ADS] [CrossRef] [Google Scholar]
  128. Vidal-Madjar, A., Lecavelier des Etangs, A., Désert, J. M., et al. 2003, Nature, 422, 143 [Google Scholar]
  129. Vidal-Madjar, A., Lecavelier des Etangs, A., Désert, J. M., et al. 2008, ApJ, 676, L57 [NASA ADS] [CrossRef] [Google Scholar]
  130. Vidal-Madjar, A., Arnold, L., Ehrenreich, D., et al. 2010, A&A, 523, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  131. Vidotto, A. A., & Cleary, A. 2020, MNRAS, 494, 2417 [Google Scholar]
  132. Vidotto, A. A., Lichtenegger, H., Fossati, L., et al. 2018, MNRAS, 481, 5296 [Google Scholar]
  133. von Braun, K., Boyajian, T. S., ten Brummelaar, T. A., et al. 2011, ApJ, 740, 49 [NASA ADS] [CrossRef] [Google Scholar]
  134. Wang, L., & Dai, F. 2020, ApJ, 914, 99 [Google Scholar]
  135. Wood, B. E., Müller, H. R., Zank, G. P., Linsky, J. L., & Redfield, S. 2005, ApJ, 628, L143 [NASA ADS] [CrossRef] [Google Scholar]
  136. Wyttenbach, A., Ehrenreich, D., Lovis, C., Udry, S., & Pepe, F. 2015, A&A, 577, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  137. Yee, S. W., Petigura, E. A., Fulton, B. J., et al. 2018, AJ, 155, 255 [NASA ADS] [CrossRef] [Google Scholar]
  138. Yelle, R. V. 2004, Icarus, 170, 167 [NASA ADS] [CrossRef] [Google Scholar]
  139. Zhang, M., Knutson, H. A., Wang, L., et al. 2021, AJ, 161, 181 [NASA ADS] [CrossRef] [Google Scholar]
  140. Zhang, M., Knutson, H. A., Wang, L., et al. 2022, AJ, 163, 68 [NASA ADS] [CrossRef] [Google Scholar]
  141. Zhao, M., O’Rourke, J. G., Wright, J. T., et al. 2014, ApJ, 796, 115 [NASA ADS] [CrossRef] [Google Scholar]
1

We updated the GOFIO bad-pixel mask to account for several bad pixels that contaminated the spectral region of interest.

3

We estimated the amplitude of any possible fringing pattern by fitting sinusoids to the transmission spectra and verified their amplitude to be less than 29% of the average error bar.

4

This is in units of Rp/V0, where V0 is the proton velocity at a temperature of 104 K (i.e. 9.07 km s−1).

5

The most relevant wavelength range would be that at wavelengths shorter than 500 Å.

6

We considered a hydrogen-dominated atmosphere, instead of a hydrogen-and-helium-dominated atmosphere, to reduce the uncertainties given by the unknown He abundance. This choice does not affect the possible detectability of a correlation between δRp/Heq and the system parameters.

All Tables

Table 1

WASP-80 b log of TNG-GIARPS observations.

In the text
Table 2

Stellar and planetary parameters adopted in this work.

In the text
Table 3

Properties of the systems for which either measurements or non-detections of the He I metastable triplet have been published.

In the text

All Figures

thumbnail Fig. 1

Airmass (left panel) and S/N (right panel) measured during the GIARPS observations. The vertical dashed lines mark the t1, t2, t3, and t4 contact points (from left to right).
In the text
thumbnail Fig. 2

Normalised spectra in the stellar rest frame of the three considered transits (grey dots), with the correspondent time-averaged spectrum overlaid. The spectra are plotted with vertical offsets for clarity. Vertical orange lines mark the position of the three components of the metastable He I triplet.
In the text
thumbnail Fig. 3

Transmission spectra in the region of the metastable He I triplet. Top: weighted-mean-averaged transmission spectrum for each observed transit. Bottom: weighted mean of the three observed transits. Vertical orange lines mark the position of the three components of the metastable He I triplet. Since the final error bars are calculated following error propagationby taking the square roots of the extracted spectra aligned in the telluric rest frame as initial errors, the final error bars correspond to one standard deviation.
In the text
thumbnail Fig. 4

Photospheric emission of WASP-80 obtained from MARCS models (black line) and the MUSCLES SED of GJ832 (red line) rescaled in such a way as to reproduce the XUV emission of WASP-80 derived from the X-ray measurements and the scaling relations of King et al. (2018). The MARCS model has been convolved to a resolution comparable to that of the MUSCLES spectrum of GJ832 in the optical and infrared. The blue line shows the average XUV stellar emission at the distance of the planet. For reference, the vertical dashed lines indicate, from left to right, the position of the hydrogen ionisation threshold (≈912 Å), the position of the metastable He I ionisation threshold (≈2600 Å), and the approximate position of the He I features (≈10 830 Å).
In the text
thumbnail Fig. 5

Comparison among the master HARPS spectra of the CaII K line obtained by combining the data collected on each night, convolved to a spectral resolution of 10 000 for visualisation purposes.
In the text
thumbnail Fig. 6

Simulation results. Left: proton density distribution in the orbital plane of the whole simulated space comprising the WASP-80 system. The planet is at the centre of the coordinate system (0,0) and moves anti-clockwise relative to the starthat is located at (76,0). The red dots indicate the position and size of the star (right) and planet (centre). The black and red lines correspond to the proton fluid streamlines originated from the planet and the star, respectively. The axes are in units of planetary radii. Right: distribution of metastable He I local absorption (from 0, which is no absorption, to 1, which is full absorption) along the line of sight at mid-transit integrated over ±10 km s−1. The whole plotted circle corresponds to the stellar disk, while the lower boundary of the simulated planetary atmosphere is shown by the black circle.
In the text
thumbnail Fig. 7

Profiles along the planet-to-star direction. Left: temperature (black line) and velocity (grey line) of protons (in 104 K and km s−1, respectively; the scale for both is on the right axis) and density of major species labelled in the plot (left axis). Right: rates of the reactions responsible for the processes of population and depopulation of metastable He I listed in the legend. The black line shows the sum of reactions 1 and 2, while the blue line is the sum of reactions 7 and 8 (see legend). The x axes are in units of planetary radii.
In the text
thumbnail Fig. 8

Comparison between simulations and observations. Left: He I (23S) triplet absorption profiles obtained considering three different values of the stellar XUV flux (blue, red, and green lines) at a fixed He abundance of He/H = 0.05 (the fluxes in the legend are at 1 AU and in erg cm−2 s−1) and a 100 times higher value of the stellar NUV flux (grey line).Right: He I (23 S) triplet absorption profiles obtained considering different values of the He abundance. In both panels, the zero Doppler-shifted velocity on the x axis corresponds to a wavelength of 10 830.25 Å, the observed transmission spectrum is shown by black asterisks, and the horizontal dashed line marks the 2σ upper limit derived from the observations. The horizontal dotted line at 1.00 is for reference.
In the text
thumbnail Fig. 9

He I triplet absorption profiles obtained considering a fixed stellar XUV flux at the distance of 1 AU of 7.5 erg cm−2 s−1, a solar He abundance, and different stellar wind strengths expressed in terms of mass-loss rate in g s−1. Considering the strongest stellar wind taken into account, the observed non-detection is reached for He/H values smaller than ≈0.01. The long dashed red line shows the absorption obtained considering the same conditions taken for the solid red line except for a ten times weaker radiation pressure on the He I metastable atoms. The zero Doppler-shifted velocity on the x axis corresponds to a wavelength of 10 830.25 Å, the observed transmission spectrum is shown by black asterisks, and the horizontal dashed line marks the 2σ upper limit. The horizontal dotted line at 1.00 that we placed for reference is largely masked by the yellow line.
In the text
thumbnail Fig. 10

Size of the measured He I absorption signal, normalised to the atmospheric scale height computed considering the planetary parameters listed in Table 3 and a mean molecular weight of a pure hydrogen atmosphere, as a function of the incident stellar XUV flux (in logarithmic scale), with the symbol size indicating the planetary surface gravity. The uncertainties on the stellar XUV flux are set to be equal to a factor of two (see text). Downward arrows indicate upper limits.
In the text
thumbnail Fig. A.1

Transmission spectra shown in tomography in the planetary rest frame for the three consideredtransits, as a function of wavelength and planetary orbital phase. The contact points t1, t2, t3, and t4 are marked with horizontal black lines. The feature at 1083.5 nm misaligned with theplanet rest frame present on the first and second night is a residual of a telluric H2O line.
In the text
thumbnail Fig. B.1

Measured He I absorption signal as a function of stellar XUV flux and planetary gravity. Top: Size of the measured He I absorption signal, normalised to the atmospheric scale height computed considering the planetary parameters listed in Table 3 and a mean molecular weight of a pure hydrogen atmosphere, as a function of the incident stellar XUVflux (in logarithmic scale). Upper limits are marked by downward arrows. The symbol colour indicates the spectral type of the host as given by the legend. Bottom: Same as the upper panel, but as a function of planetary surface gravity.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.