EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 682 (February 2024) A&A, 682 (2024) A115 Full HTML
Open Access
Issue
A&A
Volume 682, February 2024
Article Number A115
Number of page(s) 14
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/202347517
Published online 08 February 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

Absorption of high-energy stellar radiation in the upper atmosphere of close-in exoplanets can lead to the formation of hydrodynamic outflows and to the removal of a substantial portion of the atmosphere’s primordial light element envelope (Vidal-Madjar et al. 2003; Yelle 2004; Tian et al. 2005; Koskinen et al. 2014; Kubyshkina et al. 2018). Hydrodynamic escape is thought to play a significant role in shaping the observed properties of the Kepler planet population, likely contributing to carving the observed radius valley (Fulton et al. 2017) by stripping planets of their initial envelopes and turning them into rocky cores (Owen & Wu 2013, 2017).

Transit spectroscopy of light elements indeed provides evidence for evaporating atmospheres; hydrogen Lyα absorption signatures have been detected in a handful of transiting hot Jupiters and Neptunes (HD 209458b Vidal-Madjar et al. 2003; Ben-Jaffel 2007; HD 189733b Lecavelier Des Étangs et al. 2010; GJ 436b Kulow et al. 2014; Ehrenreich et al. 2015 and GJ 3470b Bourrier et al. 2018). We refer to Owen et al. (2023) for a comprehensive review. Reconstructing the atmospheric Lyα feature, however, is extremely challenging. Combined with the Earth’s geocoronal Lyα emission, interstellar scattering makes the core of the line (in the velocity range ±30 km s−1) practically inaccessible. Line detections are effectively limited to its Doppler wings, whose high velocities (typically blueshifted) likely probe regions far from the outflow thermal launching site, where the escaping material is bound to be accelerated by the stellar wind (Vidal-Madjar et al. 2003).

Seager & Sasselov (2000) first identified He I(23S) as an additional, promising absorption feature for exoplanet transmission spectroscopy. The feature arises from recombination of He II to the metastable1 2 3S triplet state, and subsequent radiative transitions to the 2 3P state (at 10 830.34, 10 830.25, and 10 829.09 Å, although the doublet at ~ 10 830 Å dominates the signal). More recently, Oklopčić & Hirata (2018) developed a 1D isothermal model for escaping hydrogen–helium atmospheres, where the equations for the neutral helium fraction are written separately for the singlet and triplet state. They apply this model to the specific case of GJ 436b and HD 209458b (both with detected, escaping Lyα), demonstrating the detectability of excess He I(2 3S) absorption during transits (at the 8 and 2% level, respectively). He I(23S) absorption is also relevant in the context of a recent development; the possibility to use this feature to infer planetary magnetic fields, either with spectropolarimetry (Oklopčić et al. 2020) or via line shifts (Schreyer et al. 2024).

Unlike Lyα, He I(2 3S) does not undergo massive interstellar absorption (as the metastable state is populated through helium ionization and subsequent recombination), and it is also observable from the ground. A dozen detections have been reported to date: WASP-107b (Spake et al. 2018); HAT-P-11b (Mansfield et al. 2018; Allart et al. 2018); WASP-69b (Nortmann et al. 2018); HD 189733b (Salz et al. 2018; Guilluy et al. 2020); HD 209458b (Alonso-Floriano et al. 2019); GJ 3470 b (Palle et al. 2020; Ninan et al. 2020); HAT-P-18 b (Paragas et al. 2021); TOI-560 b (Zhang et al. 2022). We refer to Bennett et al. (2023), and references therein, for a recent summary of the observational work pertaining to He I(2 3S) transit spectroscopy, including an ever-growing list of nondetections, for WASP-48b, GJ 436b (Nortmann et al. 2018); WASP-80b (Fossati et al. 2022); HD 97658b (Kasper et al. 2020); GJ 9827d (Kasper et al. 2020); GJ 1214b (Kasper et al. 2020; Orell-Miquel et al. 2022); WASP-12 b (Kreidberg & Oklopčić 2018); WASP-127 b (dos Santos et al. 2020); KELT-9 b (Sánchez-López et al. 2022); 55 Cnc e (Zhang et al. 2021); and the V1298 Tau system (Vissapragada et al. 2021). To this list Guilluy et al. (2023) recently added spectroscopic data for HAT-P-3b, HAT-P-33b, HAT-P-49b, HD89345b, K2-105b, Kepler-25c, Kepler-63b, Kepler-68b, and WASP-47d, none of which are detected.

As for Lyα, nondetections, particularly in young and active and/or highly irradiated planets, are especially important to understand. Poppenhaeger (2022) pointed out that most of the narrow band extreme ultraviolet (EUV) stellar flux that ionizes helium (the first step toward populating the metastable state) arises from individual emission lines, mostly by iron at coronal temperatures, and showed that the large scatter in the helium transit depth to stellar activity relation (Bennett et al. 2023) can be reduced by taking coronal iron abundance into account. Nevertheless, the nondetections of extreme systems, such as WASP-80b, remain puzzling.

Since hydrodynamic escape is driven primarily by EUV photons, the lack of observational data in this range severely hampers our ability to make accurate predictions for the atmospheric mass outflow rates and ionization properties. Broadband EUV observations that are virtually unaffected by absorption are only available for the Sun. In addition, EUV data are only available for a dozen stars of type F and later, from the Extreme UltraViolet Explorer (EUVE; Craig et al. 1997). Lacking system-specific data, stellar EUV spectra of planet hosts are either modeled by using the EUVE spectra of similar type stars or approximated on the basis of scaling relations with Lyα or X-rays (Chadney et al. 2015; Linsky et al. 2014; King et al. 2018). This is bound to yield substantial uncertainties.

An additional source of uncertainty is the helium abundance in the upper atmosphere. As an example, the 0.7% upper limit (at 2σ) for the hot Jupiter WASP-80b can be interpreted as being due to a highly subsolar He abundance (Fossati et al. 2022) or to low EUV irradiation by the host star (Fossati et al. 2023). When modeling observational data, the He abundance versus EUV flux degeneracy is often compounded by the choice of isothermal outflow models (or Parker winds; Parker 1958), where the atmospheric mass outflow rate and temperature are considered model parameters that can be tweaked to reproduce the observed transit spectroscopy feature (or lack thereof). An additional complication arises from the fact that hydrodynamic escape itself may enhance the atmospheric helium-to-hydrogen fraction (Malsky et al. 2023).

The primary goal of this work is to develop an efficient and reliable model that enables a systematic study of metastable helium transits over a broad parameter range, and where the hydrodynamic outflow solution (i.e., mass outflow rate and temperature) is calculated self-consistently with the He I(2 3S) density profile and expected transit absorption excess.

This is accomplished by modifying the public 1D photoionization hydrodynamic code ATES (Caldiroli et al. 2021) to solve the continuity equations separately for the neutral helium triplet and singlet (Sect. 2.1), and by developing a dedicated transmission spectroscopy module to calculate the expected line absorption depth during transits (Sect. 2.2). We use the new code and module to assess the impact of stellar host spectral type, planet gravity, and orbital distance on the expected He I(2 3S) transit signal (Sect. 3). By relaxing the isothermal outflow assumption, we can self-consistent model the outflow properties concurrently with the atmospheric absorption signal.

Throughout this paper we refer to photons in the range 4.8–13.6 eV (91202585 Å) as far-ultraviolet (FUV); photons in the range 13.6–124 eV (100–912 Å) are referred to as EUV radiation, whereas XUV indicates EUV plus X-ray photons, in excess of 124 eV (10–912 Å). We are bound to consider only planets with optical radii in excess of 1.5 R⊕ (or 0.134 RJ), which are likely to retain primordial (i.e., hydrogen-helium rich) atmospheres (Lopez & Fortney 2014).

2 Methodology

Our starting point is the 1D photoionization hydrodynamics code ATES (Caldiroli et al. 2021). Given the planetary system’s parameters (stellar irradiation spectrum2; planet mass, radius, and equilibrium temperature; orbital distance; stellar mass; and envelope H/He abundance), ATES computes the temperature, density, velocity, and ionization fraction profiles of the irradiated planetary atmosphere, along with the instantaneous steady-state mass-loss rate. The outflow extends from the planet optical radius, RP, to the system’s Hill radius, RH3. All the simulations discussed below are initialized with a total density of 1014 g cm−3 at the inner boundary; as discussed in section 3.6 of Salz et al. (2016a), this choice introduces a <50% error in the mass outflow rates. The outer boundary choice, on the other hand, has non-negligible effects on the expected He I(2 3S) transit absorption, particularly in comparison to isothermal models; we come back to this point in Sect. 4.

The code solves the 1D Euler, mass, and energy conservation equations in radial coordinates through a finite-volume scheme. The photoionization equilibrium solver includes cooling via bremsstrahlung and recombination, as well as collisional excitation and ionization. Ion advection is implemented in postprocessing. The (user-specified) He/H ratio is kept constant throughout a given simulation run. With the exception of the simulation in Sect. 3.3, all the simulations presented in this paper adopt a cosmological number density ratio: He/H = 0.083.

First, we extended the main code chemical network to include both the singlet and triplet states of He I, although cooling and heating terms due to triplet transitions were neglected since the density of the helium atoms in this state is five to seven orders of magnitude lower than for the singlet. Second, we developed a transmission probability module (TPM), which is an add-on routine that makes use of ATES solutions to compute the expected He I(2 3S) absorption signal during planetary transits. These are described in turn below.

Table 1

Best-fitting coefficients for the He I(23S) photoionization cross section.

2.1 Metastable helium triplet chemistry

Following Oklopčić & Hirata (2018), the stationary continuity equations for the neutral helium fraction are written separately for the singlet 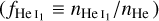and triplet 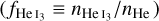states: (1)

where v is the flow velocity, Γ and α are the photoionization and recombination rate coefficients, A31 is the radiative transition rate between the metastable and the ground state, qij are the transition rates between level i and j (s refers to the transition to S-states and p to P-states) after collisions with free electrons of number density ne, and Qij is the transition rate after collisions with neutral hydrogen atoms of number density . Equations (1) are complemented by charge conservation; at variance with Oklopčić & Hirata (2018), we also include contributions to ne from .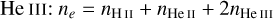

For the temperature-dependent reaction coefficients, we adopted the same notation and functional forms of Lampón et al. (2020); for the photoionization rates we adopted the formalism of Caldiroli et al. (2021, see their Eq. (6)). We approximated the photoionization cross section of He I(2 3S) by fitting a piece-wise power law to the experimental data of Norcross (1971); the best-fitting coefficients are listed in Table 1.

At each time step, the chemistry network determines the fractions of neutral helium in the singlet and triplet state by solving numerically the static limit (i.e., v = 0) of Eq. (1). The advec-tion terms are accounted for in post-processing (see Sect. 2.3 in Caldiroli et al. 2021).

We note that, under typical circumstances, the dominant mechanisms that populate and deplete the He I(2 3S) state are, respectively, recombinations from He II (set by α3) and electron collisions (set by q31s). Assuming (i) ionization equilibrium and (ii) fHeII≃1, the neutral helium fraction in the triplet state can be approximated as the ratio of the recombination coefficient to the collisional excitation rate: 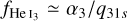. Figure 1 illustrates the temperature dependence of 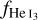. in the 2000–10 000 K range that is relevant to atmospheric outflows, we can expect the He I(2 3S) absorption feature to be a steeply decreasing function of the outflow temperature. As a consequence, any deviation from isothermal profiles will strongly affect the expected He I(2 3S) density, and the ensuing absorption signal.

thumbnail Fig. 1

Ratio of the He II to He I(2 3S) recombination coefficient [α3(T)] to the He I(23S) to He I(21S) collisional excitation rate [q31s(T`)], as a function of flow temperature.

2.2 Transmission probability module

Using as input the radial outflow properties calculated by ATES, the TPM computes the expected He I(2 3S) transit signal; in addition to the parameters needed for the main code, the TPM must be provided with the extent of the stellar radius, R⋆.

Assuming spherical symmetry, the transmission probability at wavelength λ, averaged over the extent of the stellar disk on the plane of the sky, can be written as 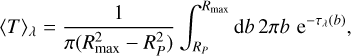(2)

where the integral extends from the planet optical radius to Rmax = min(RH, R⋆); τλ(b) is the He I(2 3S) optical depth along a line of sight (l.o.s.) with impact parameter b, measured from the planet center: 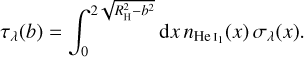(3)

For each triplet line, the (temperature and bulk velocity dependent) absorption cross section σ can be written as 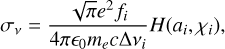(4)

where vi is the line center frequency; fi is the oscillator strength given by the NIST4 database; Δvi = vi vth/c, where the thermal velocity is 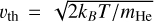; H(ai,χi) is the Voigt function, with ai = Ai/(4πΔvi) and χi = (v − vi) /Δvi; Ai is the Einstein coefficient of the transition, also from NIST. The Voigt function is computed as the real part of the Faddeeva function of argument 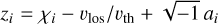, where vlos is the l.o.s. component of the outflow velocity.

Finally, the atmospheric transmission probability is normalized to the fraction of the stellar disk that is not covered by the atmosphere, while also accounting for the (100% opaque) planetary disk within RP: 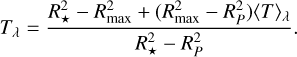(5)

We note that Eqs. (5) and (2) coincide if the atmosphere covers the entire stellar disk. The quantity (1 − Tλ), measured over the nominal, planet-frame absorption line(s) wavelengths, defines the absorption depth of the metastable helium transit. For all practical purposes, this is equivalent to the absorption depth in the 10 830.34+10 830.25 Å lines (i.e., the doublet absorption depth).

Instrumental line broadening and/or broadening due to the planet intrinsic rotation can also be accounted for by the TPM. The former is implemented via a simple convolution with a Gaussian of full width at half maximum 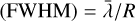, where 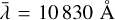Å and R is the instrument resolution. For the latter the TPM assumes that the planet is tidally locked, with orbital frequency ωp. The convolution is performed with a Gaussian of 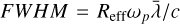, where the planet effective radius 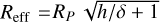is set by a combination of the line absorption depth, h, (possibly, but not necessarily, after the LSF convolution), and the optical transit depth, δ.

It should be noted that we do not include any instrumental or rotational line broadening in any of the simulations presented in the next sections.

3 Absorption depth as a function of star-planet parameters

We made use of the updated code, combined with the TPM, to assess how different stellar, planetary, and atmospheric parameters affect the physics and observability of metastable helium transits. We started by exploring different combinations of measurable system parameters, namely host stellar type, planet orbital distance, and (unlike previous studies) planet gravity.

The atmospheric outflow properties depend strongly on the planet gravitational potential, defined here as ϕP = GMP/RP, where MP and RP are the planet mass and radius. As first shown by Salz et al. (2016b), the evaporation efficiency plummets for planets with log(ϕP) ≳ 13 (in c.g.s. units). Caldiroli et al. (2022) demonstrated that this threshold is set by an energetic balance: for high-gravity planets, most of the stellar energy absorption occurs within a region where the average kinetic energy acquired by the ions through photo-electron collisions is insufficient for escape. As a result, only (mildly irradiated) low-gravity planets, with log(ϕP) ≲13, can exhibit energy-limited outflows, whereby all of the absorbed stellar radiation is used up to drive an outflow. This range encompasses super-Earths and mini-Neptunes, all the way to Neptune-sized planets.

These considerations led us to consider and/or simulate two known planets, representing a prototypical low-gravity and high-gravity case. As the low-gravity case we selected HAT-P-11b, a Neptune-sized planet with Mp = 0.081 ± 0.009 MJ and RP = 0.422 ± 0.014RJ (i.e., log(ϕP) = 12.54). HAT-P-11b is in a 4.88-day orbit (with semimajor axis 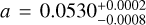AU) around a K4 V star with mass 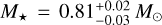and R⋆ = 0.75 ± 0.02R⊙ (Bakos et al. 2010). For the high-gravity case, we chose HD 189733b, a Jupiter-sized planet with Mp = 1.123 ± 0.045 MJ, RP = 1.138 ± 0.027RJ, yielding log(ϕp) = 13.25. HD 189733b is in a 2.2-day orbit ( 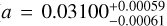AU; Bonomo et al. 2017) around a K2 V star with M⋆ = 0.806 ± 0.048 M⊙ and R⋆ = 0.756 ± 0.018 R⊙ (Paredes et al. 2021).

Input stellar spectra are drawn from the MUSCLES Treasury Surveys v22 (France et al. 2016; Youngblood et al. 2016; Loyd et al. 2016) for the following stars and spectral types: GJ 1214 (M4 V spectral type, Cloutier et al. 2021), GJ 832 (M1.5 V spectral type, Bailey et al. 2009), HD 85512 (K5 V spectral type, Pepe et al. 2011), HD 40307 (K2.5 V spectral type, Tuomi et al. 2013), and HD 97658 (K1 V spectral type, Ellis et al. 2021). For the purpose of modeling the EUV portion of the stellar spectra, MUSCLES makes use of empirical scaling relation based on Lyα fluxes (Linsky et al. 2014) and/or differential emission measure models (Duvvuri et al. 2021). The visible-IR spectra are from the PHOENIX atmosphere models (Husser et al. 2013; Allard 2016) In addition, we consider the Sun (G2 V spectral type), whose spectrum is taken from SORCE-LISIRD5; the 400–1150 Å interval is also based on the empirical relation with Lyα (Linsky et al. 2014).

Shown in Fig. 2 are the broadband spectra of the six chosen spectral types. Whereas H -ionizing photons are the main driver of the outflow thermodynamics, it is the He I ionizing photons that are mainly responsible for populating the He I(2 3S) state (via recombinations), while FUV photons deplete it, via photoionization (electron collisions also contribute to the depletion). As a result, the density profile of the metastable helium state is driven by a combination of the intensity of the HI ionizing flux at the planet’s surface, and the XUV to fUv hardness ratio, defined as HR = LXUV/LFUV (see Table 2 for a list of HR values for the chosen spectral types).

In addition, as we demonstrate below, the transit signal is very sensitive to the atmosphere’s physical extent compared to the stellar disk size. This ratio can be close to unity for planets orbiting M-type stars at moderate orbital distances.

3.1 Varying host spectral type

Here we present and discuss a suite of ATES simulations where the Neptune- and Jupiter-sized planets HAT-P-11b and HD 189733b, placed at their inferred orbital distances6, are exposed to the incident stellar spectra shown in Fig. 2. Throughout, the He-to-H abundance is set to the cosmological value 1/12.

3.1.1 Neptune-sized planets

Figure 3 illustrates the results for the case of the Neptune-sized planet HAT-P-11b. As expected, the host stars with higher XUV fluxes yield higher outflow mass density, temperature, and velocity (panels A, B, and C, respectively). The inferred, steady-state mass-loss rates (listed in Table 3) range between ≃109 g s−1 (for the M4 host) and ≃5 × 1010 g s−1 (K1 host). In all cases the outflow becomes supersonic within the simulation domain (i.e., within the Hill radius).

A key result (panel B) is that the outflow is not approximated well by an isothermal Parker wind. An isothermal profile is only acceptable for M-type spectra at very large distances from the planet surface (r ≳ 5 RP). The temperature profiles exhibit sharp inversions, as also shown by the pressure-temperature diagrams (panel D). The temperature profiles begin to rise very sharply starting from the height where the bulk of the stellar radiation is absorbed, at pressures in the range 10−7 –10−5 bar. This occurs at about 1.1 RP in the case of HAT-P-11b, which has a relatively high atmospheric density. The second temperature inversion occurs farther out, at pressures lower than 10−9 bar (and/or at heights above 1.5 RP); the location where the total cooling rate starts to decrease corresponds to the beginning of the temperature decline. Panels F and E show the radial profiles of the He I(23S) number density and triplet fraction; the ensuing He I(2 3S) transmission signals are shown in panel G. The main takeaway is that these profiles do not depend on the host spectral type in a straightforward way. He I(23 S) is mainly populated by He II recombinations, and is depleted by collisions with electrons and/or FUV photons. The lowest He I(23S) density profile is yielded by the M4-type and G2-type spectra, albeit for different reasons. in the former case this is caused by the low He I ionization rate, which in turn implies a low recombination rate. in the latter case the low density arises from intense FUV.

It is interesting to note in all cases, except for the Sun (G2 V), that the He I(23S) density profile exhibits a shallower decline compared to the total density profile, implying that the outermost regions of the atmosphere are responsible for a relatively large fraction of the absorption signal. This behavior is driven by the main mechanisms that populate or deplete the metastable state, and can be understood by inspecting the radial profiles of the reaction rates (see Fig. A.1). At large distances from the planet surface, the temperature decrease makes the balance between recombinations and electron collisions shift toward a relative overabundance of He I atoms in the metastable state. We also note that the He I(23 S) fraction values in the outermost part of the flow are in good agreement with the analytical estimate in Sect. 2 (i.e., He I(23S)/He~ 10−5). The sharp decline in the He I(23S) density profile for the case of the Sun occurs because of its intense He I(23S)-ionizing FUV flux, which efficiently depletes the metastable state via photoionization.

The resulting wavelength-dependent transmissions, Tλ, are shown in panel G. The transit absorption depths listed in Table 3 correspond to the value (1 − Tλ) at 10 830 Å. The most notable result is that M-type hosts yield the highest absorption depths, as high as ~35[/60]% for the case of a M1.5[/4] V host. This is in contrast with the results by Oklopčić (2019), which concluded that K-type hosts can be expected to have the strongest absorption signals. This discrepancy, we argue, is largely driven by the low outflow temperatures (2000–3000 K), which in turn implies much higher α3 rates (Fig. 1) than those given by the 7500 K chosen by Oklopčić (2019) for the M-type case (see their Fig. 7).

Additionally, we note that higher metastable state density profiles do not necessarily imply higher absorption depths. This is partly because the absorption depth depends on the ratio (Rmax/R⋆)2 (i.e., the fraction of the stellar disk that is actually eclipsed by the planet’s outflowing atmosphere). The small radii of M-type stars, combined with the large system Hill radii, tend to yield very deep absorption signals, up to ≃60% for the case of an M-type host (for this specific planet gravity and orbital distance). We caution, however, that the expected absorption depth depends somewhat counterintuitively on orbital distance; this is discussed further in Sect. 3.2.

Because of the larger stellar radii, K-type stars produce much shallower absorption depths, on the order of 7–10%. interestingly, the lowest absorption depth (among K-types) is expected for the hottest type (K1 V) because thermal and bulk motion-induced Doppler broadening cause the line to be broader, and hence shallower in the core. Finally, due to the large stellar radius and low He I(2 3S) density profiles, a Sun-like host is expected to yield very modest absorption features, ≲l.5%.

Table 2

Stellar parameters for the spectra shown in Fig. 2.

thumbnail Fig. 2

Broadband spectra of six prototypical planet-hosting stars considered in this work.
thumbnail Fig. 3

ATES simulations of the Neptune-sized planet HAT-P-11b, subject to varying stellar irradiation fields. The planet orbital distance is fixed to 0.053 AU. The different colors correspond to the host spectral types shown in Fig. 2. Shown are the radial profiles of the outflow total density (A); temperature (B); velocity (C), where a diamond symbol indicates where the outflow becomes supersonic; He fraction in the triplet state (E); and He I(23S) number density (F). All profiles extend from the planet surface to the system’s Hill radius. For the M4 V case, the Hill radius exceeds the size of the stellar disk (past which the outflow profile is shown as a dotted line in panel F). Panel D shows the outflow pressure-temperature diagram; the resulting He I(23S) transmission probability is shown in panel G.
Table 3

Simulated mass loss rate and He I(2 3S) transits.

3.1.2 Jupiter-sized planets

Figure 4 shows the results of varying the host spectral type for the case of the Jupiter-sized planet HD 189733b (at 0.031 AU). As expected, in spite of the smaller orbital distance, this gas giant yields much lower mass outflow rates, between ⋍108 g s−1 (Ml.5 V-type) and ≃5 × 109 g s¯1 (K1 V; see Table 3). The code fails to converge for the case of a M4 V spectral type, where the outflow likely approaches Jeans escape.

Lower 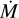values are driven by the lower density and velocity profiles (panels A and C) compared to the case of HAT-P-11b. The temperature profiles are also fairly insensitive to the stellar spectral type (panel B), and never resemble an isothermal wind. All temperature profiles start to increase right at the planet radius, reaching a peak value of T ≃ 10 000 K close to 2RP, and then fall off quite steeply toward T ≃ 1000–2000 K, at the Hill radius. We note in these cases that temperature values very close to the planet surface may be impacted by numerical accuracy; as a result, the P–T curves around ≃10−5bar may be nonphysical.

The He I(23 S) fraction and number density profiles (panels E and F) are qualitatively similar to those of HAT-P-11b, although the HD 189733b He I(23S) fraction profiles exhibit a “saddle” in the outer regions (except for the G2 V spectrum). As shown in Fig. A.2, this trend is caused by a sharp decline in the q31 transition rates, accompanied by the concurrent rise in the photoionization rate (owing to the steady decline in the photoionization rate, this does not happen in the case of a G2 V spectrum). Since the outflow velocities are always modest (below 10 km s−1), Doppler broadening is dominated by random thermal motion. Combined with the fact that the outflow temperatures (both peak and profile) are nearly independent of spectral type, this yields comparable line broadening for different spectral types. For K and G types, the absorption depth is driven by the He I(23S) density; M types stand out again thanks to the relatively small stellar disk size compared to the size of the atmosphere (see Table 3).

thumbnail Fig. 4

Same as Fig. 3, but for the gas giant HD 189733b at an orbital distance of 0.031 AU.

3.2 Varying orbital distance

Next, we vary the orbital distances of the two planets under scrutiny, using three host spectral types (M1.5 V, K1 V, and G2 V). The minimum distance is set to 0.01 for all cases; the maximum distance d is set by the code convergence requirements. Figures 5 and 6 show the results of this investigation for the Neptune- and Jupiter-sized planet, respectively7.

For a given host spectral type, orbital distance affects the metastable helium absorption signal in two main ways: first, a more intense flux triggers a denser outflow (and higher mass outflow rate); second, the location of the Hill radius (and thus the nominal extent of the atmosphere compared to the stellar disk’s) is affected by the orbital distance. The two effects act in opposite directions; the one that dominates depends on the specific case under consideration.

Starting with the Neptune-sized HAT-P-11b, irradiated by an Ml.5 V star (left column in Fig. 5), the first thing to note is that M increases with decreasing orbital distance, whereas the corresponding He I(23S) absorption depth falls from ⋍38 to ⋍3% for closer orbits. This somewhat counterintuitive effect is caused by the much reduced extension of the planet’s outflow compared to the stellar disk. It is worth noting that, at a distance of 0.01 AU, the expected absorption depth for this choice of parameters approaches its geometric maximum (i.e., 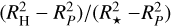). This, together with the apparent saturation in the line Doppler wings, indicates that the whole outflow is optically thick to He I(23 S), yielding a shallow optically thick absorption feature. The trends are qualitatively similar for the K1 V and G2 V spectral types; shallower optically thick absorption features can be expected at closer distances. Nevertheless, the larger radii of K types result in shallower absorption depths compared to G types.

The results are qualitatively different for the Jupiter-sized planet HD 189733b (see Fig. 6), mainly because of the much lower mass-loss rates. As for HAT-P-11b, irradiation by a Ml.5 V host at 0.01 AU produces an absorption feature that is close to its geometric maximum (though the profile is clearly still not saturated). However, larger orbital distances yield such low mass-loss rates (≲2 × 108 gs−1) that the resulting absorption depths are shallower in spite of the larger atmospheres. For Kl V and G2 V irradiation (middle and right columns in Fig. 6), at 0.01 AU and 0.03 AU we observe trends similar to those for HAT-P-11b (i.e., closer orbits lead to shallower absorption depths). At 0.05 AU, the trend is reversed owing to insufficient EUV irradiance.

To summarize, the extent of the atmosphere (i.e., the size of the Hill radius) is the dominating parameter in setting the expected He I(23S) absorption depth for a low-gravity Neptunesized planet such as HAT-P-11b. The feature becomes deeper for larger orbital distances (at least up to 0.05 AU). We caution that this result stems directly from the choice of the Hill radius as the integration limit; we come back to this point in Sect. 4.

For gas giants, such as the Jupiter-sized HD 189733b, the same trend is observed only for distances closer than 0.03 AU of a K1 V-type and/or G2 V-type host. Farther out, the absorption depth decreases with distances. For M1.5 V hosts the planet’s gravity wins, in the sense that the absorption depth decreases with increasing orbital distance in spite of any geometrical effects.

Once more, we note how the expected He I(23 S) densities (and corresponding transits) are highly sensitive to the outflow temperature profiles, and that an isothermal approximation is likely to fail by more than 1 order of magnitude (see Vissapragada et al. 2022 for a discussion of the applicability of Parker wind solutions, and Linssen et al. 2022 for how the Cloudy photoionization code can be used to resolve the temperature-mass-loss rate degeneracy that affects Parker wind models).

thumbnail Fig. 5

Simulated outflows from the Neptune-sized planet HAT-P-11b, orbiting a star of type M1.5 V (left column), K1 V (middle column), and G2 V (right column) at orbital distances in the range 0.01–0.1 AU. The top, second, and third row shows the outflow temperature, velocity, and He I(23S) density profiles, respectively. The dashed vertical line shown for the M1.5 V case indicates the extent of the stellar radius (only for this spectral type can the planet atmosphere be more extended than the actual host star). The diamond symbols in the velocity profiles indicates where the outflow becomes supersonic. The bottom row shows the resulting He I(23 S) transmission probability.

3.3 Varying XUV and He abundance

We investigate how the well-known uncertainties on the shape and intensity of the stellar XUV spectrum affect the physics and observability of the metastable helium feature. At variance with Oklopčić (2019), here we only vary the XUV portion of the spectrum, since (unlike the EUV) the stellar FUV flux can be directly measured. We verified that, as expected, progressively increasing the FUV flux decreases the metastable helium number density, and thus the expected absorption depth; the effects of varying the FUV portion of the spectrum on the mass-loss rates are negligible.

In an effort to minimize the number of variables, we simulate the case of HAT-P-11b irradiated by its actual host star (i.e., a K4 V type); we make use of the spectrum compiled by Ben-Jaffel et al. (2022), which uses HST and XMM-Newton data for the FUV and X-ray portion, respectively, and reconstruct the EUV spectrum with a coronal and transition region model. We then modify the HAT-P-11 spectrum by rescaling the XUV spectrum by a factor of 100,10,0.1, and 0.01.

As shown in the left column of Fig. 7, varying the XUV portion of the spectrum yields drastic changes in the metastable helium transits, as also found by Oklopčić (2019). Higher XUV fluxes naturally drive higher density outflows, as well as higher He I(23S) density profiles (panel C). The ×10 and ×100 XUV cases correspond to very high temperatures and velocities across the whole outflow (panels A and B); these give rise to very broad absorption features, characterized by deep absorption wings.

For the gas giant HD 189733b we adopted the spectrum of the K2 V star e Eri (from MUSCLES), which is routinely used in the literature as a proxy for the HD 189733 spectrum, and re-scale the XUV portion by a factor of 100, 10, and 0.1 (the outflow fails to converge for a factor 100 times lower XUV flux, owing to the high planet gravity). As shown in the right column of Fig. 7, the results are qualitatively different from those obtained for HAT-P-11b. In this case the temperature profiles are generally high enough to make the He I(2 3S) abundance fairly stable against temperature differences of a factor ≲2 (see Fig. 1). Combined with the relatively low outflow velocities (≲20 km s−1) this yields a modest dependence of the He I(2 3S) density profiles on the intensity of the ionizing radiation, particularly in the outer outflow regions, where He is singly or even doubly ionized. As a result, the absorption depths are fairly independent of the XUV intensity; only the 100×XUV case yields somewhat lower absorption, mainly because the feature becomes broader (and thus shallower) owing to the larger flow bulk velocity.

Finally, we examine the critical role of the chosen helium-to-hydrogen abundance. We repeated the same simulations as above, and varied the He/H number density ratio in the range 10−2–1. This is supposed to bracket the broad range of values that have been inferred from the literature to reproduce the observational data, particularly as it pertains to nondetections.

The resulting He I(2 3S) absorption depths are shown in Fig. 8. The expected transit depth varies between ≃1% for He/H = 0.01, up to ≃d6% for He/H = 1. However, this quantity is highly degenerate with the chosen stellar XUV intensity, such that the same He I(2 3S) absorption depth (e.g., ~10%) could be attained with 0.1×XUV and He/H = 0.5, baseline XUV and He/H = 0.2, or 10×XUV and He/H = 0.04.

Observations of HAT-P-11b with CARMENES (Allart et al. 2018) measured an absorption depth at 10830 Å of (1.08 ± 0.05)%. Based on our simulations, and also accounting for instrumental resolution and planet rotation, this level can be achieved with a baseline (i.e., 1×) XUV spectrum and He abundance of ~0.01, or with a 0.1× XUV spectrum and He abundance of ~0.03. Similar conclusions are reached by Allart et al. (2018) using a 3D model and a somewhat different input spectrum from Ben-Jaffel et al. (2022).

For the case of HD 189733b, different He I(2 3S) absorption depths have been reported in the literature: (0.88 ± 0.08)% with CARMENES (Salz et al. 2018), (0.75 0.03)% with GIANO-B (Guilluy et al. 2020), and (0.420 ± 0.013)% with Keck/NiRSPEC (Zhang et al. 2022), possibly indicative of variable absorption (Guilluy et al. 2020; Zhang et al. 2022; Pillitteri et al. 2022). Again, in order to match such low values, our simulations require a low XUV flux (10% of the nominal e Eri irradiation) combined with an extremely low He/H number ratio, ≲8 × 10−3. Qualitatively similar conclusions were drawn by Zhang et al. (2022) using TPCI (Salz et al. 2015).

thumbnail Fig. 6

Same as Fig. 5, but for the gas giant HD 189733 b. Owing to the planet’s strong gravity, the outflow fails to converge for an orbital separation larger than 0.05 AU, so only three separations are considered in this case.
thumbnail Fig. 7

Effects of different stellar XUV on HAT-P-11b and HD 189733b. Left column: HAT-P-11b, irradiated by the K4 V star HAT-P-11, with varying XUV intensity. Right column: HD 189733b, irradiated by the K2 V star є Eri, with varying XUV intensity. Temperature, velocity, and He I(23S) number density profiles are shown in panels A, B, and C, respectively. Panel D shows the resulting transmission.
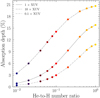thumbnail Fig. 8

Absorption depth as a function of the chosen He/H number density ratio for the case of HAT-P-11b, irradiated by HAT-P-11 (1×XUV), as well as an HAT-P-11-like spectrum with ten times lower and higher XUV irradiance.

4 Conclusions

We made use of the public 1D photoionization hydrodynamic code ATES (Caldiroli et al. 2021) to model atmospheric absorption by metastable helium during planetary transits. Since it is not affected by massive interstellar scattering, He I(23S) should provide a more direct probe of atmospheric escape compared to Lyα; unlike Lyα, it is observable from the ground.

In the first part of the paper we presented new modifications to the main code, aimed at solving the continuity equations separately for the neutral helium triplet and singlet; we then developed a new transmission module that calculates the expected line absorption depth during transits. We used the new version of the code and the TPM, which are both publicly available8, to study how known planetary parameters affect the expected depth of the metastable helium absorption feature. Our investigation features two main improvements with respect to the foundational work by Oklopčić (2019): (i) for a given system, the code calculates the outflow properties (temperature, pressure, ionization fraction, density, and velocity profiles, along with the steady-state mass-loss rate) concurrently with the He I(2 3S) absorption depth, as opposed to fixing or assuming suitable values for the temperature and mass outflow rate; (ii) in addition to the role of stellar irradiation (shape and intensity), the dependence of the He I(2 3S) absorption signal on planetary gravity is also explored (as shown by Caldiroli et al. 2022, the outflow efficiency depends strongly on this parameter, as does the mass outflow rate).

Point (i) is critical as it enables atmospheric escape to be modeled self-consistently, thus bypassing the well-known degeneracy between mass outflow rate and temperature (see, e.g., Linssen et al. 2022). Importantly, we show that the outflow is seldom isothermal; since the Hel(23S) density profile is extremely sensitive to temperature (Fig. 1), foregoing the isothermal assumption yields nonnegligible (qualitative and quantitative) changes in the expected transit depths.

At variance with Oklopčić (2019), who identified K-type stars as favorable hosts, we argue that nearby M dwarfs may be prime targets for metastable helium transmission spectroscopy. More specifically, the case of a Neptune-sized planet orbiting a late-type M dwarf at ~0.05–0.1 AU could yield intrinsic (i.e., before instrumental or other broadening) He I(2 3S) transit depths in excess of 30%. Such high values for the absorption depths are due to the combination of low outflow temperatures and low geometrical ratios between the planet atmosphere (which is assumed to extend up to the system’s Hill radius) and the stellar disk. We caution, however, that no such system is currently known. Moreover, such high absorption depths are only expected for the case of a primordial envelope with cosmological helium-to-hydrogen number density ratio. A further complication arises from strong stellar winds (which we entirely neglect): as shown by Vidotto & Cleary (2020), Carolan et al. (2021), and MacLeod & Oklopčić (2022), among others, the location where the stellar wind and atmospheric ram pressures reach equilibrium (relative to the sonic point and the Hill radius) likely determines the extent and geometry of the atmospheric outflow. In the most extreme case, where pressure balance is reached at a height (above RP) where the outflow is still subsonic, the outflow may be suppressed entirely.

Our analysis also demonstrates that the physics driving the strength of the atmospheric absorption signal during transits is far from straightforward. As an example, the He I(2 3S) transit depth is not always a decreasing function of orbital distance. This counter-intuitive trend is caused by the reduced (assumed) extension of the atmosphere compared to the stellar disk as the planet moves closer to the host star.

It is important to note that, while isothermal models can integrate the outflow out to arbitrary distances from the inner boundary, our model is inherently limited to the Hill radius, outside of which the outflow velocity is effectively unknown. However, any unbound material outside of the Hill radius is likely to form a permanent layer of absorbing gas that adds to the transiting exoplanet atmosphere. This extra absorption would be very difficult to isolate with standard setups for spectroscopic transit observations, which typically cover the transit itself plus a relatively short ingress and egress phase9. With this setup, any extra absorption due to a permanent screen of material is likely to be attributed to the star itself. Only in the case of a very long observation that spans the full planetary orbit would this extra absorption become apparent, as shown by the recent remarkable result by Zhang et al. (2023) on HAT-P-32 b, showing evidence of extra absorbing material extending out to ~50 times the planet radius.

Whereas metastable helium absorption is, in principle, a more viable and straightforward diagnostic of exoplanet atmospheric escape compared to Lyα, the growing body of observational evidence has proven hard to parse. We confirm the strong degeneracy between the He abundance and the intensity of the XUV radiation field. Generally speaking, low excess absorption (at the level of a few percent) can be easily reproduced with extremely low He abundances or a combination of low EUV irradiation and low He abundances. Similar conclusions have been drawn in the literature for several targets, and using different types of models, from Parker winds to sophisticated 3D models.

To date, observations of ~40 systems have yielded an even greater number of strict upper limits, below 3–4% (see, e.g., Bennett et al. 2023 and Guilluy et al. 2023). When compared against the spectroscopy data, our modeling, consistently with literature results, suggests that either a large fraction of the target systems may have helium depleted envelopes and/or that their EUV spectra are systematically overestimated.

In principle, a concurrent fit to the Hα and/or Lyα lines, along with the HeI(23S) triplet, could solve the degeneracy between He/H abundance and EUV flux, by constraining the former. An example of this kind of analysis is given by Yan et al. (2022) for WASP-52 b, where Hα and HeI(23S) absorption have been detected during transits. We note, however, that the steady state number density of neutral hydrogen in the n = 2 state is set mainly by Lyα excitation from the ground state. In turn, this depends on the intrinsic Lyα profile emitted by the star, and on the notoriously complex details of the Lyα radiative transfer, thus making this approach highly impractical.

As also suggested by Fossati et al. (2022), a viable mechanism for suppressing the helium-to-hydrogen ratio in the upper atmosphere is phase separation, a process whereby neutral helium separates from liquid metallic hydrogen and “rains” nto the planet interior (Fortney & Hubbard 2004, and references therein); it is worth noting that the timescale over which this process begins to operate is a strong function of planet mass, with smaller planets, on the order of 0.15 MJ, reaching He-to-H mass fractions of ~0.05, or number ratios of ~0.015. Since phase separation is only relevant for sub-Jovian planets beyond a few AU, it follows that, if confirmed, very low He abundances in the atmospheres of close-in gaseous planets would argue for the need of efficient migration. Observations of exoplanet host stars in the EUV band, for example with ESCAPE (France et al. 2022), will be critical to solving the ongoing debate around helium absorption measurements in exoplanet transits, and their implications for evolutionary models.

Acknowledgements

We are grateful to the anonymous reviewer for the insightful comments and suggestions.

Appendix A Reaction rates

thumbnail Fig. A.1

Reaction rates for the population and depopulation of the He I(23S) state for the simulations of HAT-P-11b shown in Figure 3 (both the q13 and advection rates are lower than 10−9 s−1).
thumbnail Fig. A.2

Same as Figure A.1, but for the simulations of HD 189733 b shown in Figure 4.

References

  1. Allard, F. 2016, in SF2A-2016: Proceedings of the Annual meeting of the French Society of Astronomy and Astrophysics, 223 [Google Scholar]
  2. Allart, R., Bourrier, V., Lovis, C., et al. 2018, Science, 362, 1384 [Google Scholar]
  3. Alonso-Floriano, F. J., Snellen, I. A. G., Czesla, S., et al. 2019, A&A, 629, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Bailey, J., Butler, R. P., Tinney, C. G., et al. 2009, ApJ, 690, 743 [Google Scholar]
  5. Bakos, G. Á., Torres, G., Pál, A., et al. 2010, ApJ, 710, 1724 [NASA ADS] [CrossRef] [Google Scholar]
  6. Ben-Jaffel, L. 2007, ApJ, 671, L61 [NASA ADS] [CrossRef] [Google Scholar]
  7. Ben-Jaffel, L., Ballester, G. E., Muñoz, A. G., et al. 2022, Nat. Astron., 6, 141 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bennett, K. A., Redfield, S., Oklopcic, A., et al. 2023, AJ, 165, 264 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bonomo, A. S., Desidera, S., Benatti, S., et al. 2017, A&A, 602, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Bourrier, V., Lecavelier des Étangs, A., Ehrenreich, D., et al. 2018, A&A, 620, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Caldiroli, A., Haardt, F., Gallo, E., et al. 2021, A&A, 655, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Caldiroli, A., Haardt, F., Gallo, E., et al. 2022, A&A, 663, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Carolan, S., Vidotto, A. A., Villarreal D'Angelo, C., & Hazra, G. 2021, MNRAS, 500, 3382 [Google Scholar]
  14. Chadney, J. M., Galand, M., Unruh, Y. C., Koskinen, T. T., & Sanz-Forcada, J. 2015, Icarus, 250, 357 [Google Scholar]
  15. Cloutier, R., Charbonneau, D., Deming, D., Bonfils, X., & Astudillo-Defru, N. 2021, AJ, 162, 174 [NASA ADS] [CrossRef] [Google Scholar]
  16. Craig, N., Abbott, M., Finley, D., et al. 1997, ApJS, 113, 131 [Google Scholar]
  17. dos Santos, L. A., Ehrenreich, D., Bourrier, V., et al. 2020, A&A, 640, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Drake, G. W. F. 1971, Phys. Rev. A, 3, 908 [NASA ADS] [CrossRef] [Google Scholar]
  19. Duvvuri, G. M., Sebastian Pineda, J., Berta-Thompson, Z. K., et al. 2021, ApJ, 913, 40 [NASA ADS] [CrossRef] [Google Scholar]
  20. Ehrenreich, D., Bourrier, V., Wheatley, P. J., et al. 2015, Nature, 522, 459 [Google Scholar]
  21. Ellis, T. G., Boyajian, T., von Braun, K., et al. 2021, AJ, 162, 118 [NASA ADS] [CrossRef] [Google Scholar]
  22. Fortney, J. J., & Hubbard, W. B. 2004, ApJ, 608, 1039 [NASA ADS] [CrossRef] [Google Scholar]
  23. Fossati, L., Guilluy, G., Shaikhislamov, I. F., et al. 2022, A&A, 658, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Fossati, L., Pillitteri, I., Shaikhislamov, I. F., et al. 2023, A&A, 673, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. France, K., Loyd, R. O. P., Youngblood, A., et al. 2016, ApJ, 820, 89 [NASA ADS] [CrossRef] [Google Scholar]
  26. France, K., Fleming, B., Youngblood, A., et al. 2022, J. Astron. Telesc. Instrum. Syst., 8, 014006 [NASA ADS] [CrossRef] [Google Scholar]
  27. Fulton, B. J., Petigura, E. A., Howard, A. W., et al. 2017, AJ, 154, 109 [Google Scholar]
  28. Guilluy, G., Andretta, V., Borsa, F., et al. 2020, A&A, 639, A49 [EDP Sciences] [Google Scholar]
  29. Guilluy, G., Bourrier, V., Jaziri, Y., et al. 2023, A&A, 676, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Husser, T. O., Wende-von Berg, S., Dreizler, S., et al. 2013, A&A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Kasper, D., Bean, J. L., Oklopcic, A., et al. 2020, AJ, 160, 258 [NASA ADS] [CrossRef] [Google Scholar]
  32. King, G. W., Wheatley, P. J., Salz, M., et al. 2018, MNRAS, 478, 1193 [NASA ADS] [Google Scholar]
  33. Koskinen, T. T., Lavvas, P., Harris, M. J., & Yelle, R. V. 2014, Phil. Trans. R. Soc. London Ser. A, 372, 20130089 [Google Scholar]
  34. Kreidberg, L., & Oklopcic, A. 2018, Res. Notes Am. Astron. Soc., 2, 44 [Google Scholar]
  35. Kubyshkina, D., Fossati, L., Erkaev, N. V., et al. 2018, ApJ, 866, L18 [NASA ADS] [CrossRef] [Google Scholar]
  36. Kulow, J. R., France, K., Linsky, J., & Loyd, R. O. P. 2014, ApJ, 786, 132 [Google Scholar]
  37. Lampón, M., López-Puertas, M., Lara, L. M., et al. 2020, A&A, 636, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Lecavelier Des Etangs, A., Ehrenreich, D., Vidal-Madjar, A., et al. 2010, A&A, 514, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Linsky, J. L., Fontenla, J., & France, K. 2014, ApJ, 780, 61 [Google Scholar]
  40. Linssen, D. C., Oklopcic, A., & MacLeod, M. 2022, A&A, 667, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Lopez, E. D., & Fortney, J. J. 2014, ApJ, 792, 1 [Google Scholar]
  42. Loyd, R. O. P., France, K., Youngblood, A., et al. 2016, ApJ, 824, 102 [NASA ADS] [CrossRef] [Google Scholar]
  43. MacLeod, M., & Oklopcic, A. 2022, ApJ, 926, 226 [NASA ADS] [CrossRef] [Google Scholar]
  44. Malsky, I., Rogers, L., Kempton, E. M. R., & Marounina, N. 2023, Nat. Astron., 7, 57 [Google Scholar]
  45. Mansfield, M., Bean, J. L., Oklopcic, A., et al. 2018, ApJ, 868, L34 [NASA ADS] [CrossRef] [Google Scholar]
  46. Ninan, J. P., Stefansson, G., Mahadevan, S., et al. 2020, ApJ, 894, 97 [Google Scholar]
  47. Norcross, D. W. 1971, J. Phys. B At. Mol. Phys., 4, 652 [NASA ADS] [CrossRef] [Google Scholar]
  48. Nortmann, L., Pallé, E., Salz, M., et al. 2018, Science, 362, 1388 [Google Scholar]
  49. Oklopčić, A. 2019, ApJ, 881, 133 [Google Scholar]
  50. Oklopčić, A. & Hirata, C. M. 2018, ApJ, 855, L11 [CrossRef] [Google Scholar]
  51. Oklopčić, A., Silva, M., Montero-Camacho, P., & Hirata, C. M. 2020, ApJ, 890, 88 [CrossRef] [Google Scholar]
  52. Orell-Miquel, J., Murgas, F., Palle, E., et al. 2022, A&A, 659, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Owen, J. E., & Wu, Y. 2013, ApJ, 775, 105 [Google Scholar]
  54. Owen, J. E., & Wu, Y. 2017, ApJ, 847, 29 [Google Scholar]
  55. Owen, J. E., Murray-Clay, R. A., Schreyer, E., et al. 2023, MNRAS, 518, 4357 [Google Scholar]
  56. Palle, E., Nortmann, L., Casasayas-Barris, N., et al. 2020, A&A, 638, A61 [EDP Sciences] [Google Scholar]
  57. Paragas, K., Vissapragada, S., Knutson, H. A., et al. 2021, ApJ, 909, L10 [NASA ADS] [CrossRef] [Google Scholar]
  58. Paredes, L. A., Henry, T. J., Quinn, S. N., et al. 2021, AJ, 162, 176 [NASA ADS] [CrossRef] [Google Scholar]
  59. Parker, E. N. 1958, ApJ, 128, 664 [Google Scholar]
  60. Pepe, F., Lovis, C., Ségransan, D., et al. 2011, A&A, 534, A58 [CrossRef] [EDP Sciences] [Google Scholar]
  61. Pillitteri, Micela, G., Maggio, A., Sciortino, S., & Lopez-Santiago, J. 2022, A&A, 660, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Poppenhaeger, K. 2022, MNRAS, 512, 1751 [CrossRef] [Google Scholar]
  63. Salz, M., Banerjee, R., Mignone, A., et al. 2015, A&A, 576, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Salz, M., Czesla, S., Schneider, P. C., & Schmitt, J. H. M. M. 2016a, A&A, 586, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Salz, M., Schneider, P., Czesla, S., & Schmitt, J. H. M. M. 2016b, A&A, 585, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. Salz, M., Czesla, S., Schneider, P. C., et al. 2018, A&A, 620, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Sánchez-López, A., Lin, L., Snellen, I. A. G., et al. 2022, A&A, 666, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  68. Schreyer, E., Owen, J. E., Spake, J. J., Bahroloom, Z., & Di Giampasquale, S. 2024, MNRAS, 527, 5117 [Google Scholar]
  69. Seager, S., & Sasselov, D. D. 2000, ApJ, 537, 916 [Google Scholar]
  70. Spake, J. J., Sing, D. K., Evans, T. M., et al. 2018, Nature, 557, 68 [Google Scholar]
  71. Stassun, K. G., Oelkers, R. J., Paegert, M., et al. 2019, AJ, 158, 138 [Google Scholar]
  72. Tian, F., Toon, O., Pavlov, A., & De Sterck, H. 2005, ApJ, 621, 1049 [NASA ADS] [CrossRef] [Google Scholar]
  73. Tuomi, M., Anglada-Escudé, G., Gerlach, E., et al. 2013, A&A, 549, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  74. Vidal-Madjar, A., Lecavelier des Étangs, A., Désert, J. M., et al. 2003, Nature, 422, 143 [NASA ADS] [CrossRef] [Google Scholar]
  75. Vidotto, A. A., & Cleary, A. 2020, MNRAS, 494, 2417 [Google Scholar]
  76. Vissapragada, S., Stefánsson, G., Greklek-McKeon, M., et al. 2021, AJ, 162, 222 [NASA ADS] [CrossRef] [Google Scholar]
  77. Vissapragada, S., Knutson, H. A., dos Santos, L. A., Wang, L., & Dai, F. 2022, ApJ, 927, 96 [NASA ADS] [CrossRef] [Google Scholar]
  78. Yan, D., Seon, K.-i., Guo, J., Chen, G., & Li, L. 2022, ApJ, 936, 177 [NASA ADS] [CrossRef] [Google Scholar]
  79. Yelle, R. V. 2004, Icarus, 170, 167 [NASA ADS] [CrossRef] [Google Scholar]
  80. Youngblood, A., France, K., Loyd, R. O. P., et al. 2016, ApJ, 824, 101 [Google Scholar]
  81. Zhang, M., Knutson, H. A., Wang, L., et al. 2021, AJ, 161, 181 [NASA ADS] [CrossRef] [Google Scholar]
  82. Zhang, M., Knutson, H. A., Wang, L., Dai, F., & Barragán, O. 2022, AJ, 163, 67 [NASA ADS] [CrossRef] [Google Scholar]
  83. Zhang, Z., Morley, C. V., Gully-Santiago, M., et al. 2023, Sci. Adv., 9, eadf8736 [Google Scholar]
1

Being radiatively decoupled from the ground (singlet) state, He I(23S) is metastable, with a lifetime of ≃2.18 h (Drake 1971).

2

ATES can either assume a power-law-like stellar spectrum or read in a binned numerical spectrum provided by the user.

3

The effective Roche lobe radius (RR ≃ 2/3RH) is occasionally used in the literature in place of the Hill radius (see, e.g., Guilluy et al. 2023). Using RR, and assuming a constant He I(23S) density profile, yields a ≈50% lower absorption depth.

6

As a result, in all cases HD 189733b’s irradiance is about three times as high as HAT-P-11b’s for the same choice of host star.

7

The results obtained for HAT-P-11b[HD 189733b] at an orbital distance of 0.05 [0.03] AU are essentially the same as discussed in the previous section since the planet’s orbital distance is 0.053[0.031] AU.

9

Whether this material settles along the orbital equator in a torus-like structure or takes on a cometary shape depends on the intensity of the stellar wind (see, e.g., Fig. 1 in MacLeod & Oklopčić 2022).

All Tables

Table 1

Best-fitting coefficients for the He I(23S) photoionization cross section.

In the text
Table 2

Stellar parameters for the spectra shown in Fig. 2.

In the text
Table 3

Simulated mass loss rate and He I(2 3S) transits.

In the text

All Figures

thumbnail Fig. 1

Ratio of the He II to He I(2 3S) recombination coefficient [α3(T)] to the He I(23S) to He I(21S) collisional excitation rate [q31s(T`)], as a function of flow temperature.
In the text
thumbnail Fig. 2

Broadband spectra of six prototypical planet-hosting stars considered in this work.
In the text
thumbnail Fig. 3

ATES simulations of the Neptune-sized planet HAT-P-11b, subject to varying stellar irradiation fields. The planet orbital distance is fixed to 0.053 AU. The different colors correspond to the host spectral types shown in Fig. 2. Shown are the radial profiles of the outflow total density (A); temperature (B); velocity (C), where a diamond symbol indicates where the outflow becomes supersonic; He fraction in the triplet state (E); and He I(23S) number density (F). All profiles extend from the planet surface to the system’s Hill radius. For the M4 V case, the Hill radius exceeds the size of the stellar disk (past which the outflow profile is shown as a dotted line in panel F). Panel D shows the outflow pressure-temperature diagram; the resulting He I(23S) transmission probability is shown in panel G.
In the text
thumbnail Fig. 4

Same as Fig. 3, but for the gas giant HD 189733b at an orbital distance of 0.031 AU.
In the text
thumbnail Fig. 5

Simulated outflows from the Neptune-sized planet HAT-P-11b, orbiting a star of type M1.5 V (left column), K1 V (middle column), and G2 V (right column) at orbital distances in the range 0.01–0.1 AU. The top, second, and third row shows the outflow temperature, velocity, and He I(23S) density profiles, respectively. The dashed vertical line shown for the M1.5 V case indicates the extent of the stellar radius (only for this spectral type can the planet atmosphere be more extended than the actual host star). The diamond symbols in the velocity profiles indicates where the outflow becomes supersonic. The bottom row shows the resulting He I(23 S) transmission probability.
In the text
thumbnail Fig. 6

Same as Fig. 5, but for the gas giant HD 189733 b. Owing to the planet’s strong gravity, the outflow fails to converge for an orbital separation larger than 0.05 AU, so only three separations are considered in this case.
In the text
thumbnail Fig. 7

Effects of different stellar XUV on HAT-P-11b and HD 189733b. Left column: HAT-P-11b, irradiated by the K4 V star HAT-P-11, with varying XUV intensity. Right column: HD 189733b, irradiated by the K2 V star є Eri, with varying XUV intensity. Temperature, velocity, and He I(23S) number density profiles are shown in panels A, B, and C, respectively. Panel D shows the resulting transmission.
In the text
thumbnail Fig. 8

Absorption depth as a function of the chosen He/H number density ratio for the case of HAT-P-11b, irradiated by HAT-P-11 (1×XUV), as well as an HAT-P-11-like spectrum with ten times lower and higher XUV irradiance.
In the text
thumbnail Fig. A.1

Reaction rates for the population and depopulation of the He I(23S) state for the simulations of HAT-P-11b shown in Figure 3 (both the q13 and advection rates are lower than 10−9 s−1).
In the text
thumbnail Fig. A.2

Same as Figure A.1, but for the simulations of HD 189733 b shown in Figure 4.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.