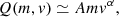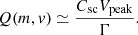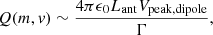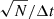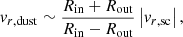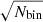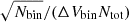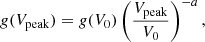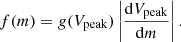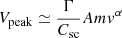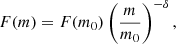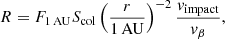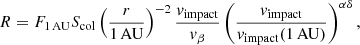| Issue |
A&A
Volume 656, December 2021
Solar Orbiter First Results (Cruise Phase)
|
|
|---|---|---|
| Article Number | A30 | |
| Number of page(s) | 13 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202140969 | |
| Published online | 14 December 2021 | |
First dust measurements with the Solar Orbiter Radio and Plasma Wave instrument
1
LESIA, Observatoire de Paris, Université PSL, CNRS, Sorbonne Université, Université de Paris, Paris, France
e-mail: arnaud.zaslavsky@obspm.fr
2
Institute of Physics and Technology, Arctic University of Norway, Tromsø, Norway
3
Institute of Atmospheric Physics of the Czech Academy of Sciences, Prague, Czech Republic
4
Space Research Center, Polish Academy of Sciences, Warsaw, Poland
5
Faculty of Mathematics and Physics, Charles University, Prague, Czech Republic
6
CNES, 18 Avenue Edouard Belin, 31400 Toulouse, France
7
Department of astronomy, Faculty of Mathematics, University of Belgrade, Serbia
8
Space Sciences Laboratory, University of California, Berkeley, CA, USA
9
Physics Department, University of California, Berkeley, CA, USA
10
Swedish Institute of Space Physics, Uppsala, Sweden
11
Radboud Radio Lab, Department of Astrophysics, Radboud University, Nijmegen, The Netherlands
12
LPP, CNRS, Ecole Polytechnique, Sorbonne Université, Observatoire de Paris, Université Paris-Saclay, Palaiseau, Paris, France
13
LPC2E, CNRS, 3A avenue de la Recherche Scientifique, Orléans, France
14
Université d’Orléans, Orléans, France
15
Technische Universität Dresden, Würzburger Str. 35, 01187 Dresden, Germany
16
Space Research Institute, Austrian Academy of Sciences, Graz, Austria
17
Astronomical Institute of the Czech Academy of Sciences, Prague, Czech Republic
18
Space and Plasma Physics, School of Electrical Engineering and Computer Science, Royal Institute of Technology, Stockholm, Sweden
Received:
31
March
2021
Accepted:
19
June
2021
Context. Impacts of dust grains on spacecraft are known to produce typical impulsive signals in the voltage waveform recorded at the terminals of electric antennas. Such signals (as may be expected) are routinely detected by the Time Domain Sampler (TDS) system of the Radio and Plasma Waves (RPW) instrument on board Solar Orbiter.
Aims. We investigate the capabilities of RPW in terms of interplanetary dust studies and present the first analysis of dust impacts recorded by this instrument. Our purpose is to characterize the dust population observed in terms of size, flux, and velocity.
Methods. We briefly discuss previously developed models of voltage pulse generation after a dust impact onto a spacecraft and present the relevant technical parameters for Solar Orbiter RPW as a dust detector. Then we present the statistical analysis of the dust impacts recorded by RPW/TDS from April 20, 2020 to February 27, 2021 between 0.5 AU and 1 AU.
Results. The study of the dust impact rate along Solar Orbiter’s orbit shows that the dust population studied presents a radial velocity component directed outward from the Sun. Its order of magnitude can be roughly estimated as vr, dust ≃ 50 km s−1, which is consistent with the flux of impactors being dominated by β-meteoroids. We estimate the cumulative flux of these grains at 1 AU to be roughly Fβ ≃ 8 × 10−5 m−2 s−1 for particles of a radius r ≳ 100 nm. The power law index δ of the cumulative mass flux of the impactors is evaluated by two differents methods, namely: direct observations of voltage pulses and indirect effect on the impact rate dependency on the impact speed. Both methods give the following result: δ ≃ 0.3 − 0.4.
Conclusions. Solar Orbiter RPW proves to be a suitable instrument for interplanetary dust studies, and the dust detection algorithm implemented in the TDS subsystem an efficient tool for fluxes estimation. These first results are promising for the continuation of the mission, in particular, for the in situ study of the inner Solar System dust cloud outside of the ecliptic plane, which Solar Orbiter will be the first spacecraft to explore.
Key words: instrumentation: detectors / methods: data analysis / meteorites, meteors, meteoroids / interplanetary medium
© A. Zaslavsky et al. 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
In recent decades, radio and plasma wave instruments have demonstrated the ability to probe dust in different space environments. Voyager’s plasma wave instrument (Gurnett et al. 1983) and planetary radio astronomy experiment (Aubier et al. 1983) both observed broadband signals that were interpreted as having been produced by dust impacts during the crossing of Saturn’s E ring by Voyager 1 and G ring by Voyager 2. The plasma wave instrument, operating in dipole mode with a roughly symmetrical configuration, observed smaller amplitude signals that the radio experiment, operated in monopole mode. The technique was used again along Voyager 2 orbit, with dust measurements at Uranus (Meyer-Vernet et al. 1986; Gurnett et al. 1987) and Neptune (Gurnett et al. 1991; Pedersen et al. 1991). Voyager measurements at the outer planets of the Solar System were followed up by others in space environments with an expected high dust flux, such as cometary trails with, for instance, VEGA 2’s plasma wave instrument at Halley’s comet (Oberc 1990).
From around the start of the year 2000, radio analyzers on board missions such as Wind (Bougeret et al. 1995), Cassini (Gurnett et al. 2004), or STEREO (Bougeret et al. 2008) recorded a large number of electric waveforms characteristic of dust impacts. The improvement in the technical performance of these radio detectors compared to the previous generation (the higher sampling frequency of the waveform analyzers in particular), along with the large number of examples available for study, has led to a better understanding of the mechanisms involved in the voltage pulse generation after a dust impact. Several recent studies have detailed the work of modeling and made comparisons to available data, such as works by Zaslavsky (2015) on STEREO, Meyer-Vernet et al. (2017), or Ye et al. (2019) on Cassini and Vaverka et al. (2019) on MMS. The paper by Mann et al. (2019) provides a complete summary of the works performed on various spacecraft, along with a prospect for the Parker Solar Probe and Solar Orbiter missions as well as a review of the voltage pulse mechanism in our present state of understanding. The paper by Lhotka et al. (2020) also presents a detailed analysis of spacecraft charging processes in various plasma environments and an application to dust impacts on MMS.
To summarize these models, voltage pulses result from the production of free electric charges by impact ionization after a grain of solid matter hits the spacecraft. These charges modify the spacecraft potential (and, depending on the impact location, the antennas) by way of two main effects: one being the perturbation of the electric current equilibrium between the spacecraft and the surrounding plasma due to the collection by the spacecraft of some of these free electric charges; the second being the perturbation of the spacecraft or the antenna potential by electrostatic influence from these free charges, that occurs when the impact plasma cloud is not neutral overall (which happens after some of the charges have been collected or have escaped from the vicinity of the spacecraft).
Over the years and thanks to these refinements in pulse modeling, radio analyzers have thus proven capable of providing robust estimates of dust fluxes in various mass ranges, varying from the nanometer to the micron. Examples of the successful use of this technique to derive dust fluxes include the detection of nanometer-sized dust with STEREO/WAVES (Meyer-Vernet et al. 2009b) and Cassini/RPWS (Meyer-Vernet et al. 2009a), measurements of the interstellar dust flux and direction at 1 AU by STEREO/WAVES (Zaslavsky et al. 2012) and Wind/WAVES (Malaspina et al. 2014), or measurements of the micron to ten microns sized dust density in the vicinity of Saturn by Cassini/RPWS (Ye et al. 2014, 2018).
The present paper, continuing on from these works, is devoted to the study of the dust impact data recorded by the Radio and Plasma Waves instrument and to the derivation of the interplanetary dust fluxes along Solar Orbiter’s orbit. This is of particular importance since in situ measurements of interplanetary dust in the inner heliosphere, which are necessary to constrain and validate dust production models, are limited. Notably there are only few data on the dust collision fragments that form in the inner solar system and then are ejected outward. Flux estimates for these dust grains, denoted as β-meteoroids, were made based on Helios observations (Zook & Berg 1975) and based on Ulysses observations (Wehry & Mann 1999). The dust collision evolution inside 1 AU were studied with model calculations having only few observational constrains (Mann et al. 2004).
Recently, the Parker Solar Probe (PSP) has been operating the FIELDS instrument (Bale et al. 2016), which provides observations of dust impacts. The PSP dust observations have been presented in a number of recent works (Page et al. 2020; Szalay et al. 2020; Malaspina et al. 2020). These observations provide a number of interesting results on dust fluxes in the close vicinity of the Sun. In the context of this paper, recent works on the second orbit of PSP with dust measurements between ca. 0.16 and 0.6 AU are of interest. Szalay et al. (2020) showed that the observations during the second solar encounter could be explained through particles that form as collision fragments near the Sun and then are ejected by the radiation pressure force. Mann & Czechowski (2021) showed that the same fluxes could be explained with a model that combines the collisional production of dust particles and their dynamics influenced by gravity, radiation pressure, and Lorentz force; the latter was found to have only a small effect on the particles that were observed with PSP during the second orbit.
In this paper, we first present and discuss the waveform data recorded by the instrument and the specificities of Solar Orbiter as a dust detector in Sect. 2. Then, in Sect. 3, we focus on the statistical study of the time repartition and of the voltage amplitudes of the hits recorded. Finally, in a last section, we build on this statistical study to determine the flux of the dust population observed we and compare our results to those obtained by other missions as well as to the theoretical predictions in the field.
2. Dust measurements with RPW
The RPW instrument on board Solar Orbiter (see a complete description in Maksimovic et al. (2020) is designed to measure and analyze the electric field fluctuations from near-DC to 16 MHz and magnetic fluctuations from several Hz to 0.5 MHz. In this article we are mainly interested by the electric waveforms provided by the time domain sampler (TDS) subsystem of RPW. In particular, TDS provides digitized snapshots of the voltage measured between the terminals of two of the spacecraft electric antennas (dipole mode) or between one the spacecraft electric antennas and the spacecraft ground (monopole mode). The waveforms used in this article were sampled at a rate of 262.1 kHz, after being processed by an analog high-pass filter with a cutoff around 100 Hz.
Figure 1 shows examples of impulsive signals recorded by TDS that we interpret as having been due to dust impacts. The examples shown here were selected from the so-called triggered snapshots that were flagged by the on-board detection algorithm as probable dust impacts (see Sect. 3.1 for the description of the algorithm).
 |
Fig. 1. Six examples of TDS snapshots showing impulsive signals interpreted as due to dust impacts onto the spacecraft. Signals recorded on the three different channels are represented in different colors. The left column shows signals recorded in monopole mode (SE1 mode), whereas the right column shows signals recorded in dipole in the two first channels and monopole in the third one (XLD1 mode). |
The left column shows events recorded in SE1 mode (for which TDS samples three monopoles: V1, V2, and V3), whereas the right column shows events recorded in XLD1 mode (two channels measure dipole voltages V1–V3 and V2–V1, and the third channel is linked to the monopole V2). Each channel (CH1, CH2, and CH3) represents voltage difference measured between individual antennas (V1, V2, and V3) for dipoles or between one antenna and the spacecraft body (SC) for monopoles. It should be noted that presented data are not corrected for transfer function (the existence of “overshoots” in these data is probably artificial). Examples shown on the lower panels of left column are typical of signals detected at the terminal of a monopole antenna by electron collection, similar to the one detected by STEREO/WAVES, for instance.
2.1. Voltage pulses and their link to mass and velocity of impacting dust grains
Before discussing these images, we recall the mechanism through which voltage pulses are thought to be produced. First, a dust grain impacts the spacecraft body and expels from it some material, part of which is ionized. The amount of free electric charge Q > 0 in the (overall neutral) cloud of expelled material is a function of the mass m of the impacting grain and of the relative velocity, v, of the impactor with respect to the target. The measurement of Q after an impact in a dedicated collector, together with an independent measurement of v in order to deduce the mass, m, of the impactor, is the general operating principle of dust impact ionization detectors (Auer 2001). Experiments show that the function Q(m, v) follows the general scaling:
where m is expressed in kg and v in km s−1. Since the parameters A and α quite strongly depends on the impacted material (Collette et al. 2014), it is of course preferable for the charge yield of the collector material as a function of m and v to be measured on ground. In the absence, for the moment, of such measurements for Solar Orbiter’s surface material, we have to use approximate values for A and α. Dietzel et al. (1973) as well as McBride & McDonnell (1999) suggest the use of A ∼ 1 and α ∼ 3.5, which is a rather high charge yield (we discuss this point when evaluating the size of the impactors in the last section of this article).
In the absence of a dedicated and well calibrated collector, but in the presence of electric antennas operated in monopole mode, we can still quite reliably deduce the amount of charge, Q, released during an impact thanks to the different dynamics of the electrons and the heavier positive charges in the expelled cloud of ionized matter. The dynamics of the light electrons quickly decouple from the one of the heavier positively charged matter (Pantellini et al. 2012). The electrons are quickly collected by (or repelled away from) the spacecraft, letting positive charges remain unscreened in the vicinity of the spacecraft. For a positively charged spacecraft, it can be shown that the combination of the effect of quick electron collection and ions getting repelled away from the spacecraft will produce a maximal change in the spacecraft ground potential equal, to a good approximation, to δφsc ≃ −Q/Csc (here Csc is the spacecraft’s body capacitance).
In monopole mode, the signal recorded is V(t) = Γ(φant(t)−φsc(t)), where φant is the monopole antenna potential and Γ a transfer function accounting for the (mostly capacitive) coupling between the antenna and the spacecraft body: Γ = Cant/(Cant + Cstray); in this formula, Cant is the antenna’s capacitance and Cstray accounts for the capacitive coupling through the preamplifier, the mechanical base of antenna, and various wires. If we assumes that φant is roughly constant during the process, then the charge, Q, produced by impact ionization is quite simply linked to the peak of the voltage pulse measured in monopole mode by:
Therefore, the use of formulas (1) and (2) makes it possible to link the properties of the impacting grain to those of the measured voltage signal.
We can see, in light of these explanations, why monopole measurements are favorable to dust detection. The main change induced by the impact occurs in the spacecraft ground potential, while antennas potentials stay roughly constant. Dipole measurements, which measure the variation of an antenna’s potential relative to another antenna, are therefore quite insensitive to this process. Still, signals are quite frequently observed in dipole mode, as can be seen on the right panels of Fig. 1.
For a signal to be observed in dipole mode, it must produce a pulse of substantially larger amplitude on a particular antenna than on the two others. An example of such a signal recorded on monopole mode can be seen on the top left panel of Fig. 1, with a peak amplitude on monopole V3 that is much larger than on V1 and V2. One interpretation for these signals is that the impact location may be close to a particular antenna, the potential of which would in turn undergo a much stronger variation under electrostatic influence from the positively charged cloud than the other monopoles. The derivation of the charge Q from dipole measurements is therefore more complicated, since the amplitude of the voltage pulse not only depends on Q but also on the position of the impact with respect to the monopoles. An order of magnitude of such a signal is (Meyer-Vernet et al. 2014) Vpeak ∼ ΓQ/(4πϵ0Lant), assuming only one arm of the dipole sees the whole unscreened charge Q, so that the charge in the cloud can be linked to the peak voltage in dipole mode by:
where Lant is the length of an antenna. Importantly, it should be noted that unlike the signal observed in monopole mode (for the at least two monopoles showing similar peak voltages), which is quite accurately linked to the released charge Q by Eq. (2) – in Eq. (3), only a rough order of magnitude is provided, since the voltage produced will, in fact, be very dependent on the location of the impact. An impact occurring at equidistance from two arms of the dipole, for instance, would produce a very small signal in dipole mode, even for an important release of charge; whereas an impact cloud expanding in the close vicinity of a particular dipole arm could produce a signal quite stronger than the estimation above.
On the right column of Fig. 1 (XLD1 mode), we show a few examples of events where the signal is mainly registered by a single antenna – hence, not mainly produced by the variation of the spacecraft potential, but rather by electrostatic influence on a particular antenna. The impact must be close to antenna V2 on cases shown on top and bottom right panels (which show identical pulses in channels CH2 and CH3) and to antenna V1 in the middle right panel (inverted pulses in channels CH1 and CH2).
2.2. Parameters for Solar Orbiter as a dust detector
Now that the main principles through which we interpret voltage pulses after a dust impact have been established, we describe in this part their application to the specific case of Solar Orbiter.
Solar Orbiter orbits the Sun along a series of roughly elliptical orbits, with a minimum perihelion of 0.28 AU and a maximum inclination with respect to the ecliptic above 30°. A description of the mission and its science objectives can be found in Müller et al. (2020).
The electric sensors of RPW are three stacer monopoles of a length, L = 6.5 m, and radius, a = 0.015 m, mounted on 1 m rigid booms to separate them from the spacecraft body, electrically biased in order to reduce variations of their potential with respect to the plasma at low frequencies (Maksimovic et al. 2020). They are in the same plane and make angles of roughly 120° with each other. The disposition of the antennas with respect to the spacecraft body is shown on Fig. 2. We note, in relation to the previous discussion on the generation of electric pulses after a dust impact, that the three monopoles are mounted on opposite sides of the spacecraft quite far away from each other (similarly to the case of spacecraft like WIND, MMS or Parker Solar Probe, but unlike the cases of Voyager, Cassini or STEREO), which implies that the effect of electrostatic influence can be very different from an antenna to the others and explains why signals are frequently observed in dipole mode.
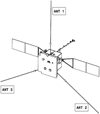 |
Fig. 2. Geometrical configuration of RPW’s electric sensors (labelled ANT1, 2, and 3), heat shield and deployed solar panels with respect to the spacecraft body. |
The capacitance associated with each monopole base has been measured on ground, with the values found as follows: Cb = 76.3 ± 4 pF for the monopole V1, Cb = 78.9 ± 3 pF for V2, and Cb = 76.2 ± 2.7 pF for V3. The stray capacitance is to a good approximation the sum of this base capacitance and of the preamplifier capacitance Camp, which, when both preamplifiers are ON, is Camp = 29 pF. Since the base capacitances are equal within measurement uncertainties, we shall use for the three monopoles the same value of the stray capacitance, Cstray ≃ 77 + 29 ≃ 108 pF.
Assuming the monopoles are in a vacuum and considering the spacecraft as an infinite ground plane, we find the capacitance of a monopole Cant = 2πϵ0L/(lnL/a − 1)≃71 pF. The presence of solar wind’s plasma, however, at the frequencies we are interested in (i.e., smaller than the local plasma frequency), decrease the capacitance to values Cant ∼ 2πϵ0L/(lnLD/a), where LD is the local Debye length (Meyer-Vernet & Perche 1989). With the Debye length varying in a range ∼3 − 10 m along the spacecraft’s orbit, we obtain Cant ∼ 55 − 70 pF (the capacitance increasing when going closer to the Sun). Using these values, the attenuation factor can be evaluated as Γ = Cant/(Cant + Cstray)≃0.34 − 0.39.
The isopotential surface of the spacecraft’s body has been evaluated from the Solar Orbiter numerical model. This value can be estimated from 25.11 m2, taking into account only the surface of the five satellite walls plus the heat shield, up to 31.43 m2 when we consider the envelope including the overall spacecraft. The backside of the solar panels (6 panels of 2.1 m × 1.2 m) are isopotential to the spacecraft body (unlike their frontside). The additional surface is then Spanels = 15.12 m2 (taking only one side into account). Therefore, we can evaluate the area of the interface between the plasma and the isopotential parts of the spacecraft to be Ssc ≃ Sbody + Spanels ≃ 43.4 ± 3.2 m2. The capacitance of a conductor of such a complex shape is difficult to estimate. An analytical order of magnitude estimation is given by the vacuum capacitance of the sphere of equivalent surface 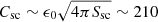 pF. A more refined modeling can be obtained through numerical simulations of the spacecraft charging. Such simulations have been recently performed for Solar Orbiter at ESA, and provided us with a value of the free space capacitance equal to Csc ≃ 355 pF (G. Déprez, priv. comm.). This is the value we adopt in this paper, although it is probably a bit of an underestimation since it does not take into account plasma sheath effects.
pF. A more refined modeling can be obtained through numerical simulations of the spacecraft charging. Such simulations have been recently performed for Solar Orbiter at ESA, and provided us with a value of the free space capacitance equal to Csc ≃ 355 pF (G. Déprez, priv. comm.). This is the value we adopt in this paper, although it is probably a bit of an underestimation since it does not take into account plasma sheath effects.
The surface, Ssc, discussed above would approximately correspond to the dust collecting area if the dust population velocity distribution was isotropic in the frame of the spacecraft. As we see in the following, it is probably not the case for the majority of the dust observed by Solar Orbiter, the velocity of which is mostly directed toward the heat shield. Therefore, the dust-collecting area to consider is strongly reduced compared to Ssc, and it is rather of the order of the heat shield’s surface Scol ≃ 2.5 m × 3.1 m ≃ 8 m2. We do not include the solar panels in the collecting surfaces, since their front side is electrically isolated from the rest of the spacecraft. Of course, an impact to a solar panel can produce a charge that could be collected by other conductive parts of the spacecraft. We neglect this effect in this study and recognize that our estimate of Scol is a low estimate of the actual collecting area.
Finally, we briefly discuss the relaxation time of perturbations of Solar Orbiter’s floating potential as follows. Linear theory gives τsc ≃ CscTph/Ie, where Ie = eneveSsc/4 is the electron current onto the spacecraft isopotential surface (e is the electron charge, ne the local electron density and 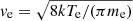 is the average electron velocity, with Te the local electron temperature, and me the electron mass). Tph ∼ 3 V is the temperature of the photoelectrons ejected from the spacecraft body expressed in electric potential unit. The assumption underlying this formula is that photoelectron current from the spacecraft is dominating over solar wind’s electron current, the spacecraft potential being as a consequence positive (assumption justified pretty much all along Solar Orbiter’s trajectory, setting apart short periods in the shadow of Venus). Assuming a typical variation of electron parameters in the solar wind (see e.g., Issautier et al. 1998; Stverak et al. 2015) one obtains for the relaxation time τsc ∼ 60 μs at 1 AU and ∼15 μs at 0.5 AU. These numbers are significant in that the estimation of the peak amplitude of the pulses observed in monopole mode Vpeak ∼ −Q/Csc is strictly valid only in the case were the rise time of the pulse τrise (controlled by the positive charges dynamics in the vicinity of the spacecraft) is not large compared to the relaxation time τsc of spacecraft electric potential perturbations. In the opposite case, where τsc is small compared to τrise, the amplitude of the signal is reduced by a factor of the order of τsc/τrise ≪ 1 (Zaslavsky 2015). This effect will not be taken into account in this article. A more precise study of the waveforms – which requires a very careful calibration – will be the subject of forthcoming studies and, among other things, will make it possible to quantify this effect.
is the average electron velocity, with Te the local electron temperature, and me the electron mass). Tph ∼ 3 V is the temperature of the photoelectrons ejected from the spacecraft body expressed in electric potential unit. The assumption underlying this formula is that photoelectron current from the spacecraft is dominating over solar wind’s electron current, the spacecraft potential being as a consequence positive (assumption justified pretty much all along Solar Orbiter’s trajectory, setting apart short periods in the shadow of Venus). Assuming a typical variation of electron parameters in the solar wind (see e.g., Issautier et al. 1998; Stverak et al. 2015) one obtains for the relaxation time τsc ∼ 60 μs at 1 AU and ∼15 μs at 0.5 AU. These numbers are significant in that the estimation of the peak amplitude of the pulses observed in monopole mode Vpeak ∼ −Q/Csc is strictly valid only in the case were the rise time of the pulse τrise (controlled by the positive charges dynamics in the vicinity of the spacecraft) is not large compared to the relaxation time τsc of spacecraft electric potential perturbations. In the opposite case, where τsc is small compared to τrise, the amplitude of the signal is reduced by a factor of the order of τsc/τrise ≪ 1 (Zaslavsky 2015). This effect will not be taken into account in this article. A more precise study of the waveforms – which requires a very careful calibration – will be the subject of forthcoming studies and, among other things, will make it possible to quantify this effect.
3. Statistical analysis of dust impacts
3.1. Impact rate and estimation of the impactors radial velocity
In this section, we present the results of the analysis of the impacts voltage pulses recorded along Solar Orbiter’s orbit from April 20, 2020 to February 27, 2021. For this purpose, we mainly use the data provided by the on-board analysis of TDS samples through an algorithm that flags a snapshot as being produced by a dust impact if it contains a signal that is sufficiently impulsive. This dust detection algorithm has been working with constant settings from April 20, 2020, hence the date at which we start our analysis.
The detection algorithm, described in detail by Soucek et al. (2021), works as follows: the instrument takes one waveform snapshot of 16384 samples every second. Each snapshot exceeding a minimum amplitude threshold is processed by the TDS on-board software to calculate the maximum and median amplitude and calculate the Fourier spectrum from the snapshot. From this spectrum, the software determines the frequency corresponding to the largest spectral peak and the FWHM (full width at half maximum) bandwidth of this peak. The algorithm then classifies the observed snapshots based on comparing the ratio R between the maximum and median absolute value in the snapshot and the spectral bandwidth to predefined thresholds. Specifically, snapshots with large R and large spectral bandwidth are identified as dust impacts. In this way, the algorithm allows us to identify even relatively small amplitude dust spikes.
The outcome of this detection is then used to select the “best” wave and dust snapshots to be transmitted to the ground and also to build statistical data products. The key data product used here is the number of detected dust impacts in a 16 second interval which is transmitted in short statistical data packet every 16 seconds. Due to the fact that the detection algorithm only examines one snapshot of 62 ms every second, the reported dust counts are much lower than the actual number of dust impacts, but the number of detected dust impacts can be considered directly proportional to the actual number of dust impacts.
Since some impulsive signals may be erroneously taken for dust (e.g., solitary waves, Vaverka et al. 2018, and various spacecraft generated effects), the dataset has been cleaned by removing all periods of fast sampling at 524 kHz, all measurements influenced by active sweeps performed by the BIAS subsystem of RPW and several days (in particular during commissioning), where TDS was configured to non-standard operation modes. We also removed the Venus flyby interval on December 27, 2020 when TDS detected numerous solitary waves and counted them as dust impacts.
We considered this TDS dust data product on a timescale of 1h, and computed the impact rate for each hour by dividing the number of snapshots flagged as dust by the total number of snapshots recorded during this hour multiplied by the duration of one snapshot (Δt = 62 ms): impact rate R = Nimpact/(NsnapshotsΔt).
Figure 3 shows the evolution of the impact rates with time. The upper panel shows the raw (i.e., not corrected for the duty cycle) cumulative impact number, showing that the total number of impacts detected by the algorithm during the period of our study is 2758. We can also notice several small data gaps corresponding to periods during which the instrument is switched off.
 |
Fig. 3. Impact rates recorded by RPW/TDS. Upper panel: raw cumulative dust count as a function of time since April 1, 2020. By raw, it is meant that it is the integer number of impacts provided by the detection algorithm, uncorrected for the instrument’s duty cycle. Middle panel: impact rate as a function of time since April 1, 2020. Each point corresponds to a two-day time interval. The error bars are computed from |
The middle panel shows the impact rate as a function of time, showing an increase in the flux with decreasing distance to the Sun, which is a general behavior that is in agreement with remote and in situ measurements from Helios (Leinert et al. 1981) or Parker Solar Probe (Szalay et al. 2020; Page et al. 2020).
Figure 4 illustrates the evolution of the impact rate with distance from the Sun. On the left panel of this figure, the impact rates measured when the spacecraft is going toward the Sun (spacecraft radial velocity vr, sc < 0) are separated from the ones measured when the spacecraft is going outward (vr, sc > 0). It can be seen that the impact rate is in average slightly larger when vr, sc < 0 than when vr, sc > 0. This is consistent with the dust population measured having a mean velocity directed outward from the Sun.
 |
Fig. 4. Estimation of the impactors radial velocity from the impact rates. Left panel: impact rate as a function of radial distance. The black points show fluxes recorded when the spacecraft is moving toward the Sun, the red points when moving outward from the Sun. Each point is computed by averaging the impact rate data on 50 distance intervals linearly spaced between 0.5 and 1 AU. Error bars show one standard deviation error on the computation of the mean. Middle panel: radial component of the dust velocity, Vr, dust, computed from Eq. (4). Error bars are computed by propagating errors on the impact rates shown on the left panel. Right panel: histogram of the obtained values of Vr, dust. |
One can use this difference in the impact rates to obtain a first estimation of the radial velocity vr, dust of the dust population: assuming that the velocity and fluxes are function of the distance to the Sun only (neglecting all time variability) and neglecting – for an order of magnitude estimation – the effect of tangential velocities, it can easily be shown that
where vr, sc is the radial velocity of the spacecraft, Rin the impact rate when the spacecraft is going toward the Sun, and Rout when going outward. The middle panel of Fig. 4 shows the result of applying formula (4) with the impact rates Rin and Rout shown on the left panel. The error bars are very large but the mean value obtained is reasonably constant with radial distance. The right panel shows a histogram of the values of vr, dust obtained, with a peak value at vr, dust = 30 km s−1 and an averaged value around 50 km s−1. The large error bars, the variations of the measured fluxes, and the use of a simple model let us only hope for an order of magnitude estimation of course, but this value is consistent with expectations for small particles on hyperbolic orbits and with the results from the numerical simulations of particles dynamics discussed in the last section of this paper.
Let us note that this estimate of a 50 km s−1 radial velocity of the impactor – a velocity comparable to the spacecraft orbital speed – implies that the impacts do not actually occur only on the heat shield (as was assumed in the previous section), but also on the sides of the spacecraft. The effective collecting area must then vary along the spacecraft trajectory. This effect, that may produce errors of the order of 10–20% on the fluxes estimations, will not be accounted for in the present paper. We will, as discussed in the previous section, keep in mind that the value of the collecting area Scol = 8 m2 used in this work is somehow underestimated. It should still provide a quite robust order of magnitude.
Figure 5 shows the distribution of the number of impacts recorded during time intervals of 6 hours, for three different values of the impact rate. The three intervals on which these number of occurrence distributions have been computed are highlighted in yellow on Fig. 3. They correspond to distances to the Sun ∼0.7 AU (left panel, mean impact rate ∼140 day−1), ∼1 AU (middle panel, mean impact rate ∼50 day−1), and ∼0.5 AU (right panel, mean impact rate ∼350 day−1). The comparison with Poisson distribution, over-plotted in red, shows a very good agreement consistent with the data being due to independent events at roughly constant rates, as expected for interplanetary dust impacts.
 |
Fig. 5. Distribution of number of impacts per time intervals of 6 hours, for three different periods of time corresponding to different mean impact rates. The red curve shows the Poisson distribution calculated from the mean impact rate observed in each of these periods of time. Errorbars on the histograms values are |
3.2. Peak voltages distribution and power-law index of the impactor’s cumulative mass flux
In order to further characterize the population of dust grains impacting Solar Orbiter, we look at the distribution of voltages measured in monopole mode. To this purpose we look at the snapshots dataset, which does not include all of the dust impacts detected by the onboard algorithm on which the results of the previous section are based. We assume that the subset of triggered snapshots is a random sample from the ensemble of all the recorded dust impact signals and, therefore, that both share the same statistical properties – or since this can’t be exactly true, we assume that selection bias are small and do not impact importantly the voltage amplitude statistics.
Measurements in monopole mode, as discussed in Sect. 2, are required in order to properly (as unambiguously as possible) link the peak amplitude of the pulse to the charge generated by impact ionization. Unfortunately, they are, for monopoles V1 and V3, only active during a small fraction of the mission time, that is, mainly during two periods: from May 30 to June 8 (185 dust snapshots telemetered) and from July 27 to August 13 (103 dust snapshots). Matters are different for monopole V2, which is quite routinely operated with 934 dust snapshots telemetered from April 1 to November 1 of 2020. Therefore, the particular focus is set on monopole V2 in the following.
Figure 6 shows the normalized distributions of peak voltage associated with dust impacts for different monopoles and different time periods. We can see that the peak voltage distribution has a power-law behavior. The left panel shows distributions computed on the whole period between April 1 - Nov. 31, with different colors corresponding to peak voltages at the terminals of different monopoles. We can see that voltage distributions are similar on all monopoles – which is to be expected since in average all monopoles should react in the same manner to dust impacts. The results of least-square fitting these histograms with power laws is presented in Table 1, where it can be seen that power-law exponents are, within the uncertainties, equal from a monopole to another, around −4/3.
 |
Fig. 6. Normalized density (i.e., number of dust detected per unit voltage interval) of voltage peaks in monopole mode. Left panel: distribution of the voltage peaks on all monopoles from April 1 to Nov. 30, 2020. Different colors accounts for different monopoles: V1 (blue), V2/SE1 (red), V3 (green), V2/XLD1 (black). Middle panel: distribution of peak amplitudes on monopole V2 during two different periods (highlighted in green in Fig. 3). Red points correspond to the high impact rate period close to the perihelion (May 13 – June 8), black points to the low impact rate period around the aphelion (Sep 17 – Nov 3). Right panel: result of the least square fitting of all the data recorded on monopole V2 from April 1 to Nov. 30, 2020. The slope of the red curve is −1.34 ± 0.07. In all these figures, error bars are computed from |
Power law indices of the peak voltage distributions.
The middle panel of Fig. 6 compares the peak amplitude recorded on monopole V2 at different distances from the Sun. The limited number of impacts on which such a comparison can be made imply quite important uncertainties on the slopes of the distribution. The two last lines of Table 1 show the results of linear fitting for these distributions, showing a slope that is a bit steeper at the perihelion than at the aphelion. This difference being within the uncertainties, it is hard to draw a conclusion based on this result and it is sensible to wait for more statistics to see whether this trend is confirmed.
The right panel of Fig. 6 shows the distributions of all impacts recorded on monopole V2 on the whole time of our voltage amplitude analysis, namely, from April 1 to November 31, 2020, along with the corresponding power-law least-square fit, with index −1.34 ± 0.07.
From these observations it seems reasonable to approximate the rate of observation of signals having peak voltages between Vpeak and Vpeak + dVpeak by dR = g(Vpeak)dVpeak, with
where a ≃ 1.34 and V0 an arbitrary voltage in the range where the power-law behavior applies.
An interesting result, of course, would be to deduce from these data information about the mass distribution of the impacting dust particles. We have seen in Sect. 2.1 that the released charge, Q, and, hence, the peak voltage, Vpeak, is linked to the mass, but also to the velocity of the impacting particle, and we do not have an independent measurement of the latter for each of the impacts. Therefore, we can only make inferences on the mass distribution by assuming the existence of a relationship, v(m), between the mass of the particle and its velocity with respect to the spacecraft. If such a relationship exists, then the function Vpeak(m, v) becomes a function of m only and – under the assumption that two different values of m cannot produce a peak voltage of the same amplitude; that is, the function Vpeak(m) is bijective on the observed mass interval – the mass distribution of the impactors f(m) can be directly linked to the measured distribution g(Vpeak) by:
For a first-order estimation, one could assume that the impact velocity is independent of the mass on the given mass range. Then, according to Eqs. (1) and (2):
is a linear function of m, and the mass distribution trivially has the same power-law shape than the distribution of voltage peaks. The cumulative mass flux of particles of mass larger than m onto the spacecraft (defined as 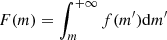 ) would then be given by:
) would then be given by:
where δ = a − 1 ≃ 0.34 and F(m0) is the cumulative flux of particles of mass larger than m0 (which may depend on the distance to the Sun).
Let us note that this estimation of the power-law index δ of the cumulative mass flux in the observed mass range must likely be an underestimation, since (if the velocity is an increasing function of m, which is probably the case in the observed mass range, see next section), f(m) will decrease with a steeper slope than g(Vpeak). This can easily be seen from Eq. (5), taking, for instance, Vpeak ∝ m1 + ε with ε > 0. We would then obtain for f(m) a power law index a + (a − 1)ε, which is always larger than a (if a > 1 which is the case here). Therefore, even without any precise knowledge of the function v(m), but under the assumption that this is an increasing function of m in the observed mass interval, it is possible to derive from these observations of peak voltages a lower bound for the power law index of the cumulative mass flux δ ≳ 0.34.
To conclude this section, we note that a more detailed derivation of the mass distribution of the particles could be obtained from these measurements by computing the function v(m) from numerical simulations, with proper assumptions for the initial conditions and dust β parameter. Since this function may depend on the distance from the Sun (which may explain the possible change of the power law index of the voltage distributions from perihelion to aphelion), this study may also require some time to accumulate more statistics and be able to construct not too noisy distributions of voltages at different distances from the Sun. Such a work is beyond the scope of these first results, but it offers an interesting perspective for a future study.
4. Estimation of the β-meteoroids flux and comparison to models and results from other missions
We now compare the observed impact rates to a dust flux model that bases on a number of assumptions. The existence of dust in the inner Solar System can be inferred from the brightness of the Zodiacal light and the F-corona which show that dust in the approximate 1–100 micrometer size range forms a cloud with overall cylindrical symmetry about an axis through the center of the Sun, perpendicular to the ecliptic (cf. Mann et al. 2014). The size distribution at 1 AU is estimated from a number of different in situ observations and described in the interplanetary dust flux model (Gruen et al. 1985). The majority of dust grains form by fragmentation from comets, asteroids and their fragment grains. The larger grains are in bound orbit about the sun; as a result of the Poynting-Robertson effect, they lose orbital energy and angular momentum and fall into the Sun after time scales of the order of 105 years. However, the majority of the Zodiacal dust is within shorter time fragmented by collision with other dust grains, the smaller fragments leave the inner Solar System and collision production from larger grains is needed to replenish the dust cloud (Mann et al. 2004). The dust with sizes that are smaller than roughly a micrometer experiences a larger radiation pressure force which is directed outward. If the radiation pressure to gravity ratio, often denoted as β is sufficiently high, the dust can be ejected outward. Those grains in hyperbolic orbits are often denoted as β-meteoroids, while those in in bound orbits are given as α-meteoroids (Zook & Berg 1975). Assuming that the larger dust grain that is fragmented moves in a circular orbit, its fragment attains a hyperbolic orbit if the radiation pressure to gravity ratio β exceeds 0.5. Based on light scattering models for different assumed dust compositions (Wilck & Mann 1996), this is the case for dust with sizes less than few 100 nm.
4.1. Mass of the impactors
The mass of the impactors can be estimated from the voltage observed, using Eq. (7) and spacecraft parameters from Sect. 2.2. For this, it is necessary to have an estimation of the velocity of the impactors and of the charge yield of the impacted material. For the particle velocity, we could have used the order of magnitude obtained from the observations of impact rates in direction forward and backward with respect to the Sun. However, as pointed out in Sect. 3.1 this is only a rough estimation and is associated with large uncertainties. Therefore, we chose to rely in this section on estimations of dust particles velocities from numerical simulations of dust dynamics in the interplanetary medium. The simulation we use takes into account gravitational and radiation pressure forces, but not the electromagnetic force (which should not be dominant for particles of sizes ≳40 nm). We chose the values of β based on the assumption that the majority of Zodiacal dust originate from comets and asteroids and remain in the interplanetary medium for long time. We used the β value for the asteroidal dust; those for the old cometary dust in the interplanetary medium are almost identical (see Wilck & Mann 1996) and assuming them would not change the results of our calculations.
The charge yield of the impacted material is another unknown of our study, which certainly plays an important role in determining the mass of the impactors. Figure 7 shows the impact velocities from the numerical simulations and the expected peak voltage for two examples of charge yield. The dark area on the right panel shows the region of expected voltage peaks as a function of the mass of the impactor for parameters A = 0.7 and α = 3.5 from McBride & McDonnell (1999). The red area is obtained for parameters A = 2.5 × 10−3 and α = 4.5, a quite lower charge yield, corresponding to materials like germanium-coated Kapton or solar cells and MLI (multi-layer thermal insulation) from STEREO’s spacecraft, the charge yield of which were measured on the ground and displayed in Table 1 of Collette et al. (2014).
 |
Fig. 7. Model for velocity and voltage peaks as a function of the impactor’s mass or size. Left panel: relative velocity with respect to Solar Orbiter as a function of particle mass. The solid line shows the average along the spacecraft trajectory, the upper dashed line shows the impact velocity at the perihelion and the lower dashed line the impact velocity at the aphelion. Right panel: expected peak voltage as a function of the mass of the impactor, calculated using values of impact velocities shown on the left panel. The solid line shows the peak voltage for the averaged velocity (solid line from left panel) and dashed lines for the perihelion and aphelion impact velocities. The black curves assume a high charge yield and the red curves a lower charge yield. The points show the values of the velocity/peak voltage obtained from four numerical simulations, corresponding to size ranges 40 − 75 nm, 75 − 100 nm, 100 − 140 nm, and 140 − 200 nm. The points are placed at the middle of the mass interval for each of the four simulated size ranges. The horizontal green line shows the detection threshold ∼5 mV. |
Figure 7 shows that particles in the size range 40 − 75 nm, regardless of the charge yield parameters used, are too small and not fast enough to produce measurable signals. Grains with sizes 75 − 100 nm (upper end) are expected to produce signals above the detection threshold in the high-charge yield case, but not in the low-charge yield one; grains with sizes ≳100 nm, finally, should produce measurable signals regardless of the precise charge yield. An estimation of the mass of the smallest particles detected (we consider a threshold voltage of 5 mV) from this figure gives m ≃ 0.8 × 10−17 kg (high charge yield) and m ≃ 1.3 × 10−17 kg (low charge yield), corresponding to sizes of (assuming, as in the whole of this paper, a mass density ρ = 2.5 g.cm−3 and grains of spherical shapes for size-mass conversions) r ≃ 92 nm and r ≃ 108 nm, respectively; we can quite confidently affirm that the smallest grains detected have sizes around 100 nm.
The curves for different charge yields diverge when masses are increased, and for signals of amplitude, such as 30 mV, we have sizes r ≃ 120 nm (high yield) and r ≃ 168 nm (low yield), indicating a larger mismatch, of course, and showing the necessity of ground measurement if we want to reach a better mass calibration on the whole voltage interval. That said, the power-law decrease in the peak voltage distribution shown in the previous section implies that the fluxes are dominated by impact from small grains, so that the determination of the mass of impactors producing high amplitudes peaks is less critical for our study.
This discussion of particles masses is based on the measurement of the voltage pulses in monopole mode, which, as was discussed previously, are the most reliable when it comes to estimating the charge released by impact ionization, and therefore the dust particles masses. However, the dust detection algorithm from which fluxes are computed works on a TDS channel that is operated in dipole mode most of the time – when the instrument is on XLD1 mode. The discussion above, and the curve presented in Fig. 7, remains relevant to this case as long as the signal produced is proportional to the charge released Q. According to the estimation given by Eq. (3) this should be the case for dipole measurements when considering a large enough number of hits. Assuming Vdipole = ΓQ/4πϵ0Lant, the smallest mass measured in dipole would be a factor 4πϵ0Lant/Csc ∼ 3 larger (and therefore the sizes a factor ∼1.4 larger). But the precise factor is complicated to evaluate, and could be closer to 1, on average, since observations of waveforms shows that differences in peak voltage from a monopole to another is often of the order of magnitude of the peak voltage itself. This provides a clear motivation for developing a quantitative theoretical modeling of the generation of signals generation in dipole mode, at least on a statistical basis.
4.2. Flux of β-meteoroids, comparison to predictions and measurements from other spacecraft
Figure 8 presents the impact rates averaged over two days (already presented on Fig. 3), together with impact rates computed for three models of the beta-meteoroid flux. The green line is the simplest model, with the impact rate given by:
 |
Fig. 8. Dust impact rate onto the spacecraft. Dots show the same data as the one presented in Fig. 3. The green curve shows the expected impact rate for beta meteoroids having a constant outward velocity vβ = 50 km s−1, and a flux density F1 AU = 8 × 10−5 m−2 s−1 at 1 AU. The red curve shows the flux from Eq. (10) with F1 AU = 8 × 10−5 m−2 s−1 and αδ = 1.3. The black curve shows the prediction from numerical simulation based on a model of production of dust by collisional fragmentation. The collecting area is assumed to be equal to the heat shield’s surface, Scol = 8 m2. |
where Scol = 8 m2 is the collection area (taken equal to the heat shield surface; cf. Sect. 2.2), vimpact = ||vβ−vsc|| is the relative speed between the spacecraft and the β-meteoroids, the velocity of which is taken radial and constant, vβ = 50 km s−1. Also, Fβ, 1 AU is the flux of particles in the detection range, which is to a good approximation equal to the cumulative flux of particles larger than ∼100 nm. The 1/r2 scaling of the β-meteoroids flux is a consequence of mass conservation (and of their production rate by fragmentation of larger particles being negligible at the distances from the Sun at which the spacecraft orbits). A fit of the data with Eq. (9) gives the following value for the cumulative flux: F1 AU ≃ 8 × 10−5 m−2 s−1.
This simple model provides, as can be seen on the figure, a fairly good agreement with the data, although it seems to systematically underestimate the high impact rate values around the perihelion. A reason for that can be seen from the left panel of Fig. 7: the mass of an impactor producing a given peak voltage will be smaller at the perihelion than at the aphelion (because the spacecraft’s velocity with in the Sun’s frame is larger at the perihelion that at the aphelion). Since smaller particles have higher fluxes, an increase in the rate of measurable signals is expected close to the Sun as compared to the previous simple model.
This effect of decrease in the dust particles mass measured when approaching the Sun can be quantified by assuming a cumulative mass flux varying in power law with an exponent δ, as written in the previous section, in Eq. (8). The impact rate is then found to be:
where F1 AU is (as previously) the cumulative flux of particles above the detection threshold at 1 AU and the factor (vimpact/vimpact(1 AU))αδ accounts for the variation of the mass of the detected impactors with the impact velocity.
We can fit Eq. (10) to the data in order to obtain the product αδ. The resulting curve is shown in red on Fig. 8. It shows a better agreement with data than the previous model and fits the high impact rates observed at the perihelion quite well. The value obtained is αδ = 1.3, which, considering values of α = 3.5 − 4.5, provides an estimation of the power-law index of the cumulative mass distribution of the impactors δ = 0.29 − 0.37. This value – obtained from a dataset with no voltage measurements but only impact counts per unit time – is similar to the one derived in the previous section by fitting peak voltage distributions, indicating that the estimation of δ in RPW’s detection range seems quite robust. Finally, we note that assuming the measurement of δ from voltage distributions to be reliable enough, we could use this estimation of αδ to independently estimate the power-law index α of the charge yield for Solar Orbiter material. We would then obtain α ≃ 1.3/0.34 ≃ 3.9.
The black curve on Fig. 8, finally, shows the prediction of impacts onto the spacecraft from a model of production of small dust grains by collisional fragmentation. This model assumes that the parent bodies move in Keplerian orbits within the circumsolar dust disk. Their mass distribution is a modified version of the interplanetary dust flux model (Gruen et al. 1985). The size distribution of the collision fragments are described based on models by Tielens et al. (1994) and Jones et al. (1996). It describes the fragmentation and partial vaporization of a target and projectile composed of a certain dust material. The vaporized and fragmented mass of the target are proportional to the projectile mass and to the velocity – and material-dependent coefficients. The mass distribution of fragments is of the form m−0.76, with the largest fragment mass specified as some (collision-velocity dependent) fraction of the target mass. A brief description of the collision model is given in Mann & Czechowski (2005), while the derivation of dust fluxes is described in Mann & Czechowski (2021). They are obtained from the dust trajectories under the influence of gravity and radiation pressure (since the Lorentz force does not have a strong influence for the considered dust sizes). The same trajectories were used to produce Fig. 7 of this article. The black curve shows the prediction from this model of the number of particles comprised between 100 nm and 200 nm impacting a surface Scol = 8 m2 per day. The curve obtained from the model considers a constant minimal size of detected dust at 100 nm all along the trajectory. It does not include the effect of variation of minimal mass detected discussed previously. It fits (without the need to vary any free parameter) the high impact rates at perihelion, but quite overestimates the low fluxes period. This would tend to indicate that the size of the particles detected is closer to 100 nm at the perihelion and probably a bit larger at aphelion.
Some effects that can play a role on the derivation of the particle flux from the observed impact rates have not been taken into account in this first study. They include a better model for the collection surface and its possible variation with distance to the Sun (the direction of the dust velocity in the spacecraft frame varying along the trajectory), although given the mostly cubic shape of the spacecraft, this effect is not expected to be very important. A possible difference in charge yield for an impact on the heat shield surface and one of the other five spacecraft walls could also be of some importance.
The result that we obtained for the β-meteoroid flux is similar to (although slightly higher than) the one derived using STEREO/WAVES by Zaslavsky et al. (2012), of Fβ ≃ 1 − 6 × 10−5 m−2 s−1 at 1 AU; it is also similar to the measurement with Solar Probe Plus FIELD instrument Fβ ≃ 3 − 7 × 10−5 m−2 s−1 interpolated at 1 AU (Szalay et al. 2020) and to the theoretical expectations, as shown in this paper.
In conclusion, we note that if the presented data can be described well with a flux of β-meteoroids, it is found to be lacking, in comparison to the observations from STEREO (Zaslavsky et al. 2012; Belheouane et al. 2012) or Wind (Malaspina et al. 2014), an observed flux of interstellar dust. The latter studies indeed showed a noticeable component of the impact rate modulated along the solar apex direction, which is not observed with Solar Orbiter RPW. This lack of an apparent interstellar dust component in the data is puzzling. It could be explained by a deflection of the interstellar dust grains in the solar magnetic field and the consequent depletion of their flux inside 1 AU, which is expected for grains of small size (Mann 2010). This is a point which deserves further study.
5. Conclusions
The analysis of the first data from Solar Orbiter Radio and Plasma Wave instrument shows this instrument to be a quite reliable dust detector for dust grains in the size range ≳100 nm. The fluxes of particles derived are consistent with previous observations in this size range and with theoretical prediction from models of dust production by collisional fragmentation.
The analysis of the difference in impact rates when the spacecraft’s velocity vector is directed sunward or anti-sunward is shown to be capable of providing a direct measurement on the order of magnitude of dust grains radial velocities, vr, dust ∼ 50 km s−1, which is consistent with theoretical predictions in the observed size range.
The analysis of voltage distribution in monopole mode, along with the analysis of the impact rates taking into account a variation of the mass of the smallest grains detected as a function of the impact velocity provide two independent methods for estimating the power law index δ of the cumulative mass flux of particles in our detection range. These two methods consistently provide a result of δ ≃ 1/3.
These first results are very promising overall. Still, a great deal of work remains to be done, in particular: a modeling of the signal generation mechanism in monopole mode that would include the effect of variation of the floating potential relaxation time with the local plasma parameters, as well as models of signal generation in dipole mode. Such works, together with a more precise modeling of grain’s velocity and additional statistics, could make it possible to derive more information on the dust cumulative mass flux from the peak voltage distributions.
Solar Orbiter will reach perihelion close to 0.3 AU in spring 2022. The impact rate is expected to be about three times (without taking the mass detection threshold effect) larger at this point than at the perihelion studied in this article. Solar Orbiter’s orbit will also reach increasingly higher latitudes in the years to come and will provide the first in situ exploration of the inner Solar System dust cloud out of the ecliptic. These perspectives are very promising and these first results show that RPW will have the capabilities to provide a scientific return from these opportunities.
Acknowledgments
Solar Orbiter is a mission of international cooperation between ESA and NASA, operated by ESA. The RPW instrument has been designed and funded by CNES, CNRS, the Paris Observatory, The Swedish National Space Agency, ESA-PRODEX and all the participating institutes. I. M. has been supported by the Research Council of Norway (grant no. 262941). J. V. was supported by the Czech Science Foundation under the project 20–13616Y. M. M. and Y. K. are supported by the Swedish National Space Agency grant 20/136. A. Z., I. M. and J. V. acknowledge discussions during the ISSI team on dust impacts at the International Space Science Institute in Bern, Switzerland.
References
- Aubier, M. G., Meyer-Vernet, N., & Pedersen, B. M. 1983, Geophys. Res. Lett., 10, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Auer, S. 2001, in Instrumentation, eds. E. Grün, B. S. Gustafson, S. Dermott, & H. Fechtig (Berlin, Heidelberg: Springer, Berlin Heidelberg), 385 [Google Scholar]
- Bale, S. D., Goetz, K., Harvey, P. R., et al. 2016, Space Sci. Rev., 204, 49 [Google Scholar]
- Belheouane, S., Zaslavsky, A., Meyer-Vernet, N., et al. 2012, Sol. Phys., 281, 501 [NASA ADS] [Google Scholar]
- Bougeret, J. L., Kaiser, M. L., Kellogg, P. J., et al. 1995, Space Sci. Rev., 71, 231 [CrossRef] [Google Scholar]
- Bougeret, J.-L., Goetz, K., Kaiser, M. L., et al. 2008, Space Sci. Rev., 136, 487 [CrossRef] [Google Scholar]
- Collette, A., Grün, E., Malaspina, D., & Sternovsky, Z. 2014, J. Geophys. Res.: Space Phys., 119, 6019 [NASA ADS] [CrossRef] [Google Scholar]
- Dietzel, H., Eichhorn, G., Fechtig, H., et al. 1973, J. Phys. E: Sci. Instrum., 6, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Gruen, E., Zook, H. A., Fechtig, H., & Giese, R. H. 1985, Icarus, 62, 244 [NASA ADS] [CrossRef] [Google Scholar]
- Gurnett, D. A., Grün, E., Gallagher, D., Kurth, W. S., & Scarf, F. L. 1983, Icarus, 53, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Gurnett, D. A., Kurth, W. S., Scarf, F. L., et al. 1987, J. Geophys. Res.: Space Phys., 92, 14959 [NASA ADS] [CrossRef] [Google Scholar]
- Gurnett, D. A., Kurth, W. S., Granroth, L. J., & Poynter, S. C. A. R. L. 1991, J. Geophys. Res., 96, 19,177 [Google Scholar]
- Gurnett, D. A., Kurth, W. S., Kirchner, D. L., et al. 2004, Space Sci. Rev., 114, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Issautier, K., Meyer-Vernet, N., Moncuquet, M., & Hoang, S. 1998, J. Geophys. Res., 103, 1969 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, A. P., Tielens, A. G. G. M., & Hollenbach, D. J. 1996, ApJ, 469, 740 [Google Scholar]
- Leinert, C., Richter, I., Pitz, E., & Planck, B. 1981, A&A, 103, 177 [NASA ADS] [Google Scholar]
- Lhotka, C., Rubab, N., Roberts, O. W., et al. 2020, Phys. Plasmas, 27, 103704 [CrossRef] [Google Scholar]
- Maksimovic, M., Bale, S. D., Chust, T., et al. 2020, A&A, 642, A12 [EDP Sciences] [Google Scholar]
- Malaspina, D. M., Horanyi, M., Zaslavsky, A., et al. 2014, Geophys. Res. Lett., 41, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Malaspina, D. M., Szalay, J. R., Pokorný, P., et al. 2020, ApJ, 892, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Mann, I. 2010, ARA&A, 48, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Mann, I., & Czechowski, A. 2005, ApJ, 621, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Mann, I., & Czechowski, A. 2021, A&A, 650, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mann, I., Kimura, H., Biesecker, D. A., et al. 2004, Space Sci. Rev., 110, 269 [Google Scholar]
- Mann, I., Meyer-Vernet, N., & Czechowski, A. 2014, Phys. Rep., 536, 1 [Google Scholar]
- Mann, I., Nouzák, L., Vaverka, J., et al. 2019, Ann. Geophys., 37, 1121 [NASA ADS] [CrossRef] [Google Scholar]
- McBride, N., & McDonnell, J. A. M. 1999, Planet. Space Sci., 47, 1005 [CrossRef] [Google Scholar]
- Meyer-Vernet, N., & Perche, C. 1989, J. Geophys. Res., 94, 2405 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer-Vernet, N., Aubier, M. G., & Pedersen, B. M. 1986, Geophys. Res. Lett., 13, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer-Vernet, N., Maksimovic, M., Czechowski, A., et al. 2009a, Sol. Phys., 256, 463 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer-Vernet, N., Lecacheux, A., Kaiser, M. L., & Gurnett, D. A. 2009b, Geophys. Rev. Lett., 36, L03103 [Google Scholar]
- Meyer-Vernet, N., Moncuquet, M., Issautier, K., & Lecacheux, A. 2014, Geophys. Rev. Lett., 41, 2716 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer-Vernet, N., Moncuquet, M., Issautier, K., & Schippers, P. 2017, J. Geophys. Res.: Space Phys., 122, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, D., St. Cyr, O. C., Zouganelis, I., et al. 2020, A&A, 642, A1 [Google Scholar]
- Oberc, P. 1990, Icarus, 86, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Page, B., Bale, S. D., Bonnell, J. W., et al. 2020, ApJS, 246, 51 [Google Scholar]
- Pantellini, F., Landi, S., Zaslavsky, A., & Meyer-Vernet, N. 2012, Plasma Phys. Controlled Fusion, 54 [Google Scholar]
- Pedersen, B. M., Meyer-Vernet, N., Aubier, M. G., & Zarka, P. 1991, J. Geophys. Res.: Space Phys., 96, 19187 [NASA ADS] [CrossRef] [Google Scholar]
- Soucek, J., Píša, D., Kolmasova, I., et al. 2021, A&A, 656, A26 (SO Cruise Phase SI) [CrossRef] [EDP Sciences] [Google Scholar]
- Stverak, S., Travnicek, P. M., & Hellinger, P. 2015, J. Geophys. Res.: Space Phys., 120, 8177 [NASA ADS] [CrossRef] [Google Scholar]
- Szalay, J. R., Pokorný, P., Bale, S. D., et al. 2020, ApJS, 246, 27 [Google Scholar]
- Tielens, A. G. G. M., McKee, C. F., Seab, C. G., & Hollenbach, D. J. 1994, ApJ, 431, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Vaverka, J., Nakamura, T., Kero, J., et al. 2018, J. Geophys. Res.: Space Phys., 123, 6119 [NASA ADS] [CrossRef] [Google Scholar]
- Vaverka, J., Pavlu, J., Nouzák, L., et al. 2019, J. Geophys. Res.: Space Phys., 124, 8179 [NASA ADS] [CrossRef] [Google Scholar]
- Wehry, A., & Mann, I. 1999, A&A, 341, 296 [NASA ADS] [Google Scholar]
- Wilck, M., & Mann, I. 1996, Planet. Space Sci., 44, 493 [Google Scholar]
- Ye, S.-Y., Gurnett, D. A., Kurth, W. S., et al. 2014, J. Geophys. Res.: Space Phys., 119, 6294 [NASA ADS] [CrossRef] [Google Scholar]
- Ye, S.-Y., Kurth, W. S., Hospodarsky, G. B., et al. 2018, Geophys. Res. Lett., 45, 10,101 [CrossRef] [Google Scholar]
- Ye, S.-Y., Vaverka, J., Nouzak, L., et al. 2019, Geophys. Res. Lett., 46, 10941 [NASA ADS] [CrossRef] [Google Scholar]
- Zaslavsky, A. 2015, J. Geophys. Res.: Space Phys., 120, 855 [NASA ADS] [CrossRef] [Google Scholar]
- Zaslavsky, A., Meyer-Vernet, N., Mann, I., et al. 2012, J. Geophys. Res., 117, A05102 [NASA ADS] [Google Scholar]
- Zook, H. A., & Berg, O. E. 1975, Planet. Space Sci., 23, 183 [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Six examples of TDS snapshots showing impulsive signals interpreted as due to dust impacts onto the spacecraft. Signals recorded on the three different channels are represented in different colors. The left column shows signals recorded in monopole mode (SE1 mode), whereas the right column shows signals recorded in dipole in the two first channels and monopole in the third one (XLD1 mode). |
| In the text | |
 |
Fig. 2. Geometrical configuration of RPW’s electric sensors (labelled ANT1, 2, and 3), heat shield and deployed solar panels with respect to the spacecraft body. |
| In the text | |
 |
Fig. 3. Impact rates recorded by RPW/TDS. Upper panel: raw cumulative dust count as a function of time since April 1, 2020. By raw, it is meant that it is the integer number of impacts provided by the detection algorithm, uncorrected for the instrument’s duty cycle. Middle panel: impact rate as a function of time since April 1, 2020. Each point corresponds to a two-day time interval. The error bars are computed from |
| In the text | |
 |
Fig. 4. Estimation of the impactors radial velocity from the impact rates. Left panel: impact rate as a function of radial distance. The black points show fluxes recorded when the spacecraft is moving toward the Sun, the red points when moving outward from the Sun. Each point is computed by averaging the impact rate data on 50 distance intervals linearly spaced between 0.5 and 1 AU. Error bars show one standard deviation error on the computation of the mean. Middle panel: radial component of the dust velocity, Vr, dust, computed from Eq. (4). Error bars are computed by propagating errors on the impact rates shown on the left panel. Right panel: histogram of the obtained values of Vr, dust. |
| In the text | |
 |
Fig. 5. Distribution of number of impacts per time intervals of 6 hours, for three different periods of time corresponding to different mean impact rates. The red curve shows the Poisson distribution calculated from the mean impact rate observed in each of these periods of time. Errorbars on the histograms values are |
| In the text | |
 |
Fig. 6. Normalized density (i.e., number of dust detected per unit voltage interval) of voltage peaks in monopole mode. Left panel: distribution of the voltage peaks on all monopoles from April 1 to Nov. 30, 2020. Different colors accounts for different monopoles: V1 (blue), V2/SE1 (red), V3 (green), V2/XLD1 (black). Middle panel: distribution of peak amplitudes on monopole V2 during two different periods (highlighted in green in Fig. 3). Red points correspond to the high impact rate period close to the perihelion (May 13 – June 8), black points to the low impact rate period around the aphelion (Sep 17 – Nov 3). Right panel: result of the least square fitting of all the data recorded on monopole V2 from April 1 to Nov. 30, 2020. The slope of the red curve is −1.34 ± 0.07. In all these figures, error bars are computed from |
| In the text | |
 |
Fig. 7. Model for velocity and voltage peaks as a function of the impactor’s mass or size. Left panel: relative velocity with respect to Solar Orbiter as a function of particle mass. The solid line shows the average along the spacecraft trajectory, the upper dashed line shows the impact velocity at the perihelion and the lower dashed line the impact velocity at the aphelion. Right panel: expected peak voltage as a function of the mass of the impactor, calculated using values of impact velocities shown on the left panel. The solid line shows the peak voltage for the averaged velocity (solid line from left panel) and dashed lines for the perihelion and aphelion impact velocities. The black curves assume a high charge yield and the red curves a lower charge yield. The points show the values of the velocity/peak voltage obtained from four numerical simulations, corresponding to size ranges 40 − 75 nm, 75 − 100 nm, 100 − 140 nm, and 140 − 200 nm. The points are placed at the middle of the mass interval for each of the four simulated size ranges. The horizontal green line shows the detection threshold ∼5 mV. |
| In the text | |
 |
Fig. 8. Dust impact rate onto the spacecraft. Dots show the same data as the one presented in Fig. 3. The green curve shows the expected impact rate for beta meteoroids having a constant outward velocity vβ = 50 km s−1, and a flux density F1 AU = 8 × 10−5 m−2 s−1 at 1 AU. The red curve shows the flux from Eq. (10) with F1 AU = 8 × 10−5 m−2 s−1 and αδ = 1.3. The black curve shows the prediction from numerical simulation based on a model of production of dust by collisional fragmentation. The collecting area is assumed to be equal to the heat shield’s surface, Scol = 8 m2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.