| Issue |
A&A
Volume 650, June 2021
|
|
|---|---|---|
| Article Number | A59 | |
| Number of page(s) | 15 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202040089 | |
| Published online | 04 June 2021 | |
Vortex-like kinematic signal, spirals, and beam smearing effect in the HD 142527 disk★
1
Univ. Grenoble Alpes, CNRS, IPAG,
38000
Grenoble,
France
e-mail: y04.boehler@gmail.com
2
Université Côte d’Azur, Observatoire de la Côte d’Azur, CNRS, Laboratoire Lagrange, Bd de l’Observatoire,
CS 34229,
06304
Nice Cedex 4,
France
3
Department of Physics and Astronomy, Rice University,
Main Street,
Houston,
TX
77005,
USA
4
Monash University,
Wellington Rd,
Clayton,
VIC
3800,
Australia
5
Univ. Lyon, Univ. Claude Bernard Lyon 1, ENS de Lyon, CNRS, Centre de Recherche Astrophysique de Lyon UMR5574,
69230
Saint-Genis-Laval,
France
6
Center for Astrophysics, Harvard & Smithsonian,
60 Garden Street,
Cambridge,
MA
02138,
USA
Received:
8
December
2020
Accepted:
12
March
2021
Vortices are one of the most promising mechanisms to locally concentrate millimeter dust grains and allow the formation of planetesimals through gravitational collapse. The outer disk around the binary system HD 142527 is known for its large horseshoe structure with azimuthal contrasts of ~3–5 in the gas surface density and of ~50 in the dust. Using 13CO and C18O J = 3–2 transition lines, we detect kinematic deviations to the Keplerian rotation, which are consistent with the presence of a large vortex around the dust crescent, as well as a few spirals in the outer regions of the disk. Comparisons with a vortex model suggest velocity deviations up to 350 m s−1 after deprojection compared to the background Keplerian rotation, as well as an extension of ±40 au radially and ~200° azimuthally, yielding an azimuthal-to-radial aspect ratio of ~5. Another alternative for explaining the vortex-like signal implies artificial velocity deviations generated by beam smearing in association with variations of the gas velocity due to gas pressure gradients at the inner and outer edges of the circumbinary disk. The two scenarios are currently difficult to differentiate and, for this purpose, would probably require the use of multiple lines at a higher spatial resolution. The beam smearing effect, due to the finite spatial resolution of the observations and gradients in the line emission, should be common in observations of protoplanetary disks and may lead to misinterpretations of the gas velocity, in particular around ring-like structures.
Key words: protoplanetary disks / submillimeter: planetary systems / stars: individual: HD 142527 / methods: observational
Reduced images and datacubes are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/650/A59
© Y. Boehler et al. 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
For a couple of years, observations with the Atacama Large Millimeter Array (ALMA) have detected numerous deviations to the Keplerian rotation in protoplanetary disks, most of which are consistent with the presence of embedded Jupiter-mass planets interacting with the disk (Teague et al. 2018a; Pinte et al. 2018; Casassus & Pérez 2019). The first detections were found in the multi-ringed disk around HD 163296. Using azimuthal averaging, Teague et al. (2018a) studied the gas kinematics which is sensitive to radial pressure gradients and therefore a direct probe for local variations of the gas surface density. With this method, they found gaps in the gas, possibly carved by embedded planets and colocated with gaps previously discovered in the dust. Pinte et al. (2018) found a local deviation, also called velocity kink, in the outer regions of the gaseous disk at ~260 au, which they interpreted as a perturbation due to a massive planet. Since then, numerous kinks, wiggles, and Doppler flips have been discovered in other protoplanetary disks (Pinte et al. 2019; Casassus & Pérez 2019; Pinte et al. 2020), suggesting the presence of numerous planets.
Regarding their formation, theories and simulations have long shown that large dust grains (i.e., ≥ 10–100 μm) must be trapped in local pressure maxima to avoid processes such as inward radial drift, bouncing, and grains fragmentation (Weidenschilling 1977; Birnstiel et al. 2010). When the dust-to-gas ratio in these traps reaches a value between 0.1 and 1 (with an initial value of 0.01), hydrodynamic instabilities such as the streaming instability can be triggered and potentially lead to the formation of planetesimals (Youdin & Goodman 2005; Johansen & Youdin 2007; Bai & Stone 2010; Raettig et al. 2015; Auffinger & Laibe 2018).
The process of dust trapping is likely common in protoplanetary disks. Comparisons of dust ring structures with gas emission suggest thatdust grains are trapped in radial gas pressure maxima in several disks (Dullemond et al. 2018; Rosotti et al. 2020). Evidence of both radial and azimuthal dust trapping has also been found in approximately ten protoplanetary disks so far. These dust concentrations can present large variations in magnitude, be single or multiple. They can be located in dust rings such as in V1247 Orionis (Kraus et al. 2017), MWC 758 (Boehler et al. 2018; Dong et al. 2018; Casassus et al. 2019), HD 143006 (Andrews et al. 2018), and HD 135344B (van der Marel et al. 2016; Cazzoletti et al. 2018), or they can be characterized by a large horseshoe structure such as in HD 142527 (Casassus et al. 2013; Muto et al. 2015; Boehler et al. 2017; Soon et al. 2019), IRS 48 (van der Marel et al. 2013; Calcino et al. 2019), AB Aur (Tang et al. 2012), and SZ91 (van der Marel et al. 2018).
Observations of these asymmetries at multiple wavelengths indicate that grains with a larger size a, proportional to λ/(2π), have a morecompact spatial distribution (van der Marel et al. 2015; Casassus et al. 2019). Indeed, the efficiency of the dust trapping depends on the Stokes number (i.e., the ratio of the dust stopping time to their orbital period), which is proportional to the grain size over gas density. The strongest effect of drag is expected for a Stokes number of ~ 1, while dust grains probed with ALMA have a Stokes number generally estimated around ~ 10−2–10−1. It is therefore likely that the dust trapping process is much more frequent than currently observed with ALMA. Its study will require longer wavelengths to probe grains with a Stokes number close to 1, even in dense gas areas (van der Marel et al. 2021), and to be less limited by the dust optical depth.
One of the main theories regarding the production of azimuthal dust concentrations invokes anticyclonic vortices (Barge & Sommeria 1995; Lyra & Lin 2013; Baruteau & Zhu 2016; Sierra et al. 2017), which can form via the Rossby wave instability (Lovelace et al. 1999; Li et al. 2000), for instance in a steep gradient in density (de Val-Borro et al. 2007; Zhu & Stone 2014b) or in viscosity (Varnière & Tagger 2006; Regály et al. 2012). The edge of a disk cavity or of a ring is thus a favorable site for vortex formation. However, these vortices also require a low viscosity to form, with a turbulent parameter α ≲ 10−3 (Shakura & Sunyaev 1973; Zhu & Stone 2014b).
More recently, numeric simulations have also shown that a companion with a mass ratio q ≥ 0.05 can create an eccentric cavity and trigger an azimuthal clump in the gas (Shi et al. 2012; Ragusa et al. 2017). For even larger mass ratios, the azimuthal gas contrast may reach a value between two and four in steady state, similar to what is observed in HD 142527 (Price et al. 2018; Ragusa et al. 2020). Performed with a relatively high turbulent viscosity (α ~ 5 × 10−3), these simulations did not produce vortices but were still able to trap dust particles in the gas clump, which is rotating at Keplerian velocity.
Apart from the presence of a massive companion, the main physical property that may favor one or the other scenario is thus the gas viscosity. With the level of turbulence in disks being poorly known (Flaherty et al. 2020), it is unclear whether vortices can actually develop. Only the detection of their kinematic signature will undoubtedly confirm their presence. The study of the gas kinematics is therefore the key element for understanding the origin of the dust concentrations in protoplanetary disks.
The binary system HD 142527 is located at 157 ± 2 pc, based on the stellar parallax (Gaia Collaboration 2018), and consists of a ~ 2.1 M⊙ Herbig star and of a ~ 0.3 M⊙ companion in an eccentric and non-coplanar orbit, currently at a distance of about 12 au from the central star (Biller et al. 2012; Claudi et al. 2019). It is surrounded by a bright circumbinary disk with an extremely large extent, from 100 au to 300 au in the dust emission and up to 800 au in the gas emission. Observations and models of the outer disk reveal a horseshoe morphology with an azimuthal contrast of ~ 3–5 in the gas surface density and of ~50 in the dust surface density (Muto et al. 2015; Boehler et al. 2017), leading to a gas-to-dust ratio of ~ 1 at the north of the disk (Yen & Gu 2020).
Moreover, Soon et al. (2019) found an azimuthal variation of the spectral index β, consistent with a dichotomy between small micron-size grains, coupled to the gas, and large millimeter grains strongly concentrated in the gas horseshoe structure, in very good agreement with the process of dust trapping in an azimuthal pressure maximum. The first piece ofevidence of non-Keplerian gas motions in the circumbinary disk was found by Yen & Gu (2020) using the C18O J = 1–0 transition line. This suggests a radial gas pressure bump in the north of the disk, similarly to what has been observed across the rings in the HD 163296 and AS 209 systems (Teague et al. 2018a,b). All these indications of dust trapping, as well as the large size and brightness of the circumbinary disk around HD 142527, make of this system the perfect target to look for the existence of a vortex in a protoplanetary disk.
Here, we present our data on the circumbinary disk around HD 142527 and perform a detailed analysis of the gas kinematics (Sect. 2). By comparison with models, we then show that the measured deviations are consistent with the presence of a large vortex (Sect. 3). In Sect. 4, we examine biases in the measurement of the gas velocity due to beam smearing and inspect how they may compare with the current observations around the horseshoe structure. In Sect. 5, we discuss the vortex scenario and develop strategies to distinguish true velocity signals from artifacts, both in HD 142527 and around kinks, spirals, and ring-like structures present in other disks. In Sect. 6, we summarize our findings.
2 Observations
2.1 Morphology of the dust and gas emission
This work is based on the analysis of the observations of the HD142527 disk obtained with ALMA (project 2012.1.00725.S), and already published in Boehler et al. (2017). We refer the reader to this paper for a description of the observational setup and data calibration. For the sake of completeness, we show in Fig. 1images of the dust continuum, as well as the spectrally integrated intensity (moment 0) maps of the 13CO and C18O J = 3–2 line emissionobtained in ALMA band 7 (~345 GHz). For each pixel in the integrated emission maps, we only kept the channels with a signal-to-noise higher than 5 σ. This procedure slightly underestimates the total emission but yields a better signal to noise, especially in the outer regions where line emission only comes from a few channels.
The major axis of the disk has a position angle (PA) of − 19° relative to celestial north. The disk is rotating in the clockwise direction and has an inclination of 27° (Fukagawa et al. 2013), with the far side toward the east (i.e., on the left in the figures). The azimuthal angle θ starts from the major axis (north side) and is counted positively counterclockwise. It is measured in the disk plane and therefore slightly differs, due to the disk inclination, from the usual PA measured in the image plane. A few azimuthal angles are indicated in Fig. 1, spaced by 45°.
The dust emission around the binary system HD 142527 has a horseshoe structure with a maximum in emission of 93 mJy beam−1, or 34.0 K in brightness temperature taking the inverse of the Planck function. It is located at θ = 52° and at a radius of ~ 166 au, taking a distance of 157 pc for the system. The dust emission is not azimuthally symmetric around the maximum of emission but features a secondary maximum in the clockwise direction at θ = −20° with a value of 71 mJy beam−1 (or 27.5 K). This double-peaked structure may trace a similar structure in dust surface density or may only come from a local decrease in temperature due to the shadow, seen in infrared thermal emission and scattered light (Verhoeff et al. 2011; Marino et al. 2015), cast by the inner disk surrounding the main star on the circumbinary disk.
Another tracer of the disk density is the gas through the 13CO and C18O emission lines. Both isotopologues are detected inside the disk cavity, and out to large radii, contrary to the millimeter dust emission that is concentrated in a smaller radial range due to radial drift and dust trapping (Muto et al. 2015; Boehler et al. 2017). The apparent depletion of the gas emission in the north of the disk, at about 200 au from the central star, does not imply a local decrease in the gas density and/or temperature, but is an artifact mainly produced by the continuum subtraction method. This process overestimates the amount of dust emission to remove as it does not take into account that dust emission can be absorbed at the molecular line frequency (Boehler et al. 2017; Weaver et al. 2018). The 13CO J = 3–2 and C18O optical depths are estimated to be about 10–15 and ~2–3 at the north side of the circumbinary disk. In our observations, the 13CO and C18O emission decrease in the horseshoe structure by about 50% and 60% at the center of the line after continuum subtraction.
Additionally, part of the 13CO and C18O emission from the back side of the disk can be absorbed by dust particles located in the midplane (Isella et al. 2018; Rab et al. 2020). This process can theoretically delete up to half of the emission if the line is optically thin and the dust highly optically thick. It can have a similar decrease for optically thick molecules if the emission from the front and back molecular layers consist of two different lines. This happens when the disk is sufficiently inclined, with gas emission layers at high altitude, such that two different radii, and then two different velocities, are probed along the line-of-sight (Teague et al. 2018b). The absorption of the line emission by the dust is, however, probably not the dominant process around the horseshoe structure, given the magnitude of the continuum subtraction effect, and the fact that the considered transition lines are optically thick and the disk faintly inclined.
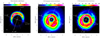 |
Fig. 1 From left to right: dust emission, 13CO and C18O J = 3–2 integrated line emission after continuum subtraction around the binary system HD 142527. The spatial resolution is indicated by the white ellipse at the bottom-left corner of the panels. Its value is 0.′′207 ×0.′′178 for the dust emission, obtained using super-uniform weighting, and 0.′′31 × 0.′′27 for the gas emission, obtained with the Briggs parameter fixed to 0.5. The rms noise is 90 μJy beam−1 for the dust emission, 5.9 mJy beam−1 per channel in 13CO and 7.8 mJy beam−1 in C18O. The integrated images for 13CO and C18O only take channels with a signal larger than 5 σ into account. |
2.2 Overview of the gas kinematics
The velocitymap from the 13CO J = 3–2 is shown on the left panel of Fig. 2. The velocity was obtained using the intensity weighted method, or moment 1 of the velocity in CASA (McMullin et al. 2007). This is the method we favored in the present work as the peak emission method appeared more sensitive to the rms noise within our data. A comparison of both methods is, however, given in Appendix B and visible in Fig. B.1. A careful study of the velocity can be performed by comparing the gas kinematics with the projected Keplerian velocity along the line-of-sight:
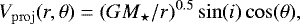 (1)
(1)
where G is the Newtonian gravitational constant, M⋆ the stellar mass, i the disk inclination, r the orbital radius, and θ the azimuthal angle. We discarded the inner 100 au of the system because our current spatial resolution prevent us to sample precisely the disk velocity in the inner region of the disk, but also to avoid known perturbations of the gas flow due to the binary (Casassus et al. 2015). We used a geometrically thin disk for the fit because we could not precisely constrain the gas scale height, while including it in the global fit did not change the value of the other parameters by more than 1σ. This is explained by the low inclination of the disk and the moderate spatial resolution of the data, but also by the intensity weighted method that probes both the front and back molecular layers of the disk. Teague et al. (2018b) also showed that assuming a gas scale height only created very small differences in the measured gas velocity for the disk around AS 209 due to its moderate inclination of 35°, even with the peak emission method, the 12CO molecule that emits at a high altitude, and a spatial resolution of 0.2′′.
The 2D map of the velocity deviations from the Keplerian profile is shown in the right panel of Fig. 2 while radial cuts for different azimuthal angles are presented in Fig. 3. We used the software Eddy described in Teague (2019) which is based on an MCMC method, and takes into account the signal-to-noise in each pixel of the image. We fixed the disk inclination to 27° and fit the mass of the binary, the systemic velocity of the system, the PA of the disk, and the center of rotation. Large discrepancies were found depending on the radial distance range considered. For R between 100 and 200 au, we obtain a binary mass of 2.53 ± 0.04M⊙, where for R > 200 au, we obtain a binary mass of 2.29 ± 0.07M⊙. These variations are due to the radial Doppler shifted structure denoted 1 at the north of the disk in the right panel of Fig. 2, covering a large area, and which presents super-Keplerian velocities at the inner side of its structure and sub-Keplerian velocities at the outer side.
Performing a fit throughout the circumbinary disk favors the regions at small radii due to a significantly higher signal-to-noise, yielding a binary mass of 2.48 ± 0.03M⊙. Therefore, to avoid biasing toward any specific radii, we proceeded in two steps. First, we used the MCMC code Eddy well outside from the cavity (i.e., R ≥ 150 au) to avoid any potential perturbations by the companion (Casassus et al. 2015) and kept the value of the center of rotation (x0, y0) = (15 h 56 min 41.872 s −42 day 19 min 23.694 s) located 40 mas south and 20 mas west of the phase center, and of the PA = 161.1° ± 0.4° of the disk. Second, we used a chi-square method along the minor and major axes of the disk to fit the mass and the systemic velocity Vlsr of the system between 100 and 400 au, without taking radial variations of the signal-to-noise ratio into account, and obtain a binary mass of 2.36 ± 0.07 M⊙, and a Vlsr of 3730 ± 20 m s−1.
Aside from the inner region that we cannot precisely sample and which displays non-Keplerian flows due to the presence of the binary, four kinematic features are shown in the right panel of Fig. 2. They are present independently of the exact fitting procedure used, and consist in (1) a large radial Doppler-shifted structure in the north of the disk with projected velocities up to 160 m s−1, roughly colocated with the dust crescent and possibly tracing an anticyclonic vortex (cf. Sect. 3), (2) a redshifted arc of ~ 180° in azimuth at the north of the disk, which may be related to the spiral S1 observed in near-IR scattered light, in 12CO and in 13CO by Fukagawa et al. (2013), Christiaens et al. (2014), and Garg et al. (2021), (3) a blueshifted arc of ~ 180° in azimuth at the east of the disk, which may be the dynamical counterpart of the spiral S4 recently observed by Garg et al. (2021), and (4) a smaller redshifted arc at the southwestern side of the disk. All these arcs and spirals have maximum projected velocity deviations on the order of 50 m s−1. This supports the idea that the outer region of the disk may present a radial succession of spiral and inter-spiral structures, each of them with deviations to the Keplerian rotation. Such spirals have also been recently observed at larger radii by Garg et al. (2021) using the 12CO J = 2–1 emission line.
 |
Fig. 2 Gas velocity of the circumbinary disk. Left: 13CO J = 3–2 velocity map performed using the intensity weighted method, and subtracted by the systemic velocity of 3.73 km s−1. Contours are displayed from −2.75 to 2.75 km s−1 and are spaced by 0.5 km s−1. Right: blue- and redshifted velocities (indicated by blue and red colors) along the line-of-sight compared to the Keplerian rotation, as expressed by Eq. (1). A polar ellipse represented by a black solid line denoted (1) indicates the potential presence of a anticyclonic vortex, and three spiral-like structures in black dotted-line denoted (2), (3), and (4) are superimposed. |
 |
Fig. 3 Radial profiles of the velocity measured in 13CO and C18O J = 3–2 subtracted by the systemic velocity displayed for various azimuthal angles θ, spaced by 45°. The dashed line represents the Keplerian prescription following Eq. (1) for a 2.36 M⊙ binary system. The two dotted lines in the top central panel indicate the Keplerian velocity for a binary mass of 2.86 M⊙ and 1.86 M⊙. |
3 A vortex-like kinematic signal around the dust concentration
3.1 Preliminary analysis
In this study, we focus on the radial Doppler-shifted feature, denoted (1) in the right panel of Fig. 2, and whose projected deviations to the Keplerian rotation reach 160 m s−1, compared to ~ 50 m s−1 along the spiral arcs. Radial cuts of the velocity deviations at different azimuthal angles are shown in Fig. 3. The velocities measured using the 13CO and C18O lines give very similar values, with differences no larger than 20–30 m s−1 between ~100 and ~350 au. This suggests that both isotopologues emit from a similar altitude and that the precision on the velocity measurement is only of a few tens of m s−1, well below the channel width of ~ 110 m s−1 in the observations.
The gas velocity is correctly matched by a Keplerian profile, represented by the black dashed line, on the Southern side of the disk. On the contrary, the gas velocity along the northern major axis presents a clear distinct S-profile that cannot be approximated by a single power law. The sensitivity to azimuthal motions is maximized along the major axis due to projection effects. On the contrary, we are blind to radial motions because they are perpendicular to the line-of-sight. We may also observe vertical motions as their projection along the line-of-sight is independent of the azimuthal angle. However, at first order, they can probably be neglected in the radial Doppler-shifted structure as 3D simulations have shown that vertical motions around vortices in steady state are negligible (Lin 2012; Richard et al. 2013) and while spirals can present vertical motions, their projected deviations are not higher than 50 m s−1 in the rest of the disk and with a different morphology.
Taking into account the clockwise rotation of the disk with the far side being in the east (i.e., on the left), the gas rotates at a super-Keplerian speed at radii between ~ 80 and 185 au, and at a sub-Keplerian speed at radii between ~185 and 300 au, confirming the deviations observed in Yen & Gu (2020). Projected velocities are of about ± 0.16 km s−1, or of 0.35 km s−1 after deprojection, about 10% of the background Keplerian rotation. The transition radius between these two regimes is at 185 au and corresponds to the distance at which the dust is radially concentrated in the horseshoe structure (Boehler et al. 2017; Soon et al. 2019; Yen & Gu 2020).
These azimuthal velocity deviations may only come from radial gas pressure gradients due to the outer ring-like structure (Teague et al. 2018a). It may also trace the azimuthal deviations coming from a vortex centered near this position (Huang et al. 2018; Robert et al. 2020). The vortex presence would imply radial deviations to the Keplerian rotation. At the adjacent angles θ = 45° and 315°, we are equally sensitive to radial and azimuthal motions. The interpretation of the projected velocities along the line-of-sight is therefore not as direct but the S-shape previously seen along the major axis is, however, still visible, suggesting that the azimuthal behavior of the gas described at θ = 0° is still present. In addition, velocities are slightly blueshifted at both angles indicating, at θ = 45°, that the gas is flowing inward in the radial direction while, at θ = 315°, gas is flowing radially outward. Finally, along the minor axis, we are only sensitive to radial velocity deviations. At the near side, outward gas motion is measured at R ~ 185 au while at the far side, at θ = 90°, the gas motion does not display any radial deviations.
The preliminary analysis of the velocity deviations in the north of the disk shows then that, at first glance, theyare compatible with the presence of a large vortex located at a radius of 185 au, centered between 315° and 45°, and extending azimuthally over about half of the circumbinary disk. A sketched view of this kinematic structure denoted (1) is shown in the right panel of Fig. 2. Alternatives to this scenario are also discussed in Sect. 4.
 |
Fig. 4 Sketch describing the vortex and its parameters. Such a vortex may be located on the northern side of the disk, at a similar localization than the polar ellipse denoted (1) and drawn in the right panel of Fig. 2. |
3.2 Vortex model
To better compare the deviations to the Keplerian rotation with the kinematic signature of a vortex, a model is required. Simulations by Huang et al. (2018) and Robert et al. (2020) have shown that the vortex size and its associated velocity can largely vary as a function of the process responsible for its origin (massive planet, binary, dead zones), the underlying gas surface density, or the disk viscosity. Our goal here is not to perform a full simulation able to reproduce the vortex-like kinematic signal but, on the contrary, to use a simple model to constrain the main parameters of a possible vortex, such as its position, size, aspect ratio, and velocity.
A sketch describing the vortex parameters is shown in Fig. 4. In the polar coordinates of the disk, the flow of the gas due to a vortex is often described with elliptic streamlines of constant velocity characterized by a central position (R0, θ0) and an aspect ratio χb∕a, with b the major axis in the azimuthal direction and a the minor axis in the radial direction (Kida 1981; Goodman et al. 1987; Chavanis 2000; Surville & Barge 2015). The flow of the gas is null at the vortex center (R0, θ0), then it increases with distance to that center, up the velocity Vmax before decreasing again to a null value. The exact vortex velocity profile cannot be measured from our current data, and we assume it has a Gaussian profile. Along the radial axis, we note Rv the distance from the vortex center at which the velocity reaches its maximum, Vmax, and wv the half-width of the Gaussian. Azimuthally, the maximum in velocity is reached at the distance of χRv from the vortex center.
For simplicity, we note in the following the distance to the vortex center in Cartesian coordinates (x, y) with x = R0× (θ −θ0) and y = r − R0. Along the radial axis, the absolute value of the vortex velocity is then:
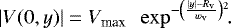 (2)
(2)
Thereafter, we can obtain the vortex velocity at any point (x, y) of the disk by finding the ellipse, of constant velocity, which crosses both this position (x, y) and the radial axis along the vortex eye. The elliptic streamlines of the vortex can be compared to circles inclined along the azimuthal axis. At the position (x, y) and angle ϕ of the vortex, we are at the position (x, χy) and at the angle ϕ′ of such a circle. ϕ′ is defined between the radial axis and the current position, and counted counterclockwise such that:
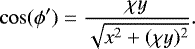 (3)
(3)
The ellipse going through the position (x, y) will then cross the radial axis of the vortex at the position y/ cos(ϕ′), with the absolute velocity:
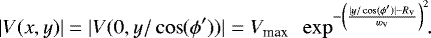 (4)
(4)
The final step is to calculate the velocity along the line-of-sight; the only observable quantity. This requires us to decompose the vortex velocity into its radial (Vr) and azimuthal (Vθ) components. Using the inclination i of the disk, the disk azimuthal angle θ, and the angle ϕ′ in the vortex reference frame, the projected velocity along the line-of-sight is given by:
![\begin{eqnarray*} V_{\mathrm{proj}} & = & \left[V_{\textrm{r}} ~ \sin(\theta) + V_{\theta} ~ \cos(\theta) \right] \sin(i), \nonumber \\ & = & |V| \left[{-} \sin(\phi^{\prime}) \sin(\theta) + \cos(\phi^{\prime}) \cos(\theta) \right] \sin(i), \nonumber \\ & = & |V| ~ \cos(\theta + \phi^{\prime}) ~ \sin(i). \end{eqnarray*}](/articles/aa/full_html/2021/06/aa40089-20/aa40089-20-eq5.png) (5)
(5)
3.3 Comparison of the observations with the vortex model
This comparison is focused in the circumbinary disk at a radius between 100 and 350 au, where the Doppler shifted structure denoted (1) in the right panel of Fig. 2 is present. In the polar 2D map (r, θ) shown in the top panel of Fig. 5, the observed kinematic feature consists in a redshifted clump located between − 50° to 50° and at radiibetween 180 and 300 au surrounded by a large blueshifted arc located at PA between − 100° and 100° and at radii between 120 and 200 au. This velocity structure has maximum projected kinematic deviations of ~ 150 m s−1 and is centered at ~185 au, at a radius similar to the dust and gas maximum surface densities inside the dust crescent (Muto et al. 2015; Boehler et al. 2017).
In the bottom panels of Fig. 5, we applied our vortex prescription to three different possibilities, whose parameters are given in Table 1. In models A and B, we made the hypothesis that the dust concentration is due to a single large vortex. Its size corresponds to the extension of the kinematic structure, with Rv = 42 au, Wv= 26 au, and an azimuthal-to-radial aspect ratio of ~5. The maximum velocity reached by the vortex is set to 350 m s−1, a value constrained by the deprojection of the observed velocity. This value is comparable to the local sound speed for a temperature of 30–40 K at the horseshoe position using the formula 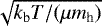 , with kb the Boltzmann constant, μ = 2.3 the mean molecular weight, and mh the hydrogen mass. The only difference between Models A and B is the azimuthal position with a vortex centered at the position of the dust emission maximum (r = 185 au, θ = 50°) in model A and at the position of the secondary maximum (r = 185 au, θ = −20°) in model B. We further tested a third model (Model C) where two smaller vortices are located at the two maxima in the dust emission.
, with kb the Boltzmann constant, μ = 2.3 the mean molecular weight, and mh the hydrogen mass. The only difference between Models A and B is the azimuthal position with a vortex centered at the position of the dust emission maximum (r = 185 au, θ = 50°) in model A and at the position of the secondary maximum (r = 185 au, θ = −20°) in model B. We further tested a third model (Model C) where two smaller vortices are located at the two maxima in the dust emission.
From these three models, it appears that our comparison favors the option of a large and single vortex, located near the secondary maximum in dust emission at PA = −20°. The model with two vortices, on the contrary, does not reproduce the morphology of the kinematic signal. Furthermore, the two vortices would have a small aspect ratio of ~2 to cover the extent of the kinematic deviations, and would therefore probably not withstand the elliptic instability (Lesur & Papaloizou 2009).
Parameters used in the three models to describe the vortex properties.
4 Other origins of kinematic deviations around the horseshoe structure
4.1 Velocity deviations are also observed in pure Keplerian disks
To probe the precision of the velocity measurements, we carried out a 3D model of the circumbinary disk around HD 142527, performed using the software RADMC3D (Dullemond et al. 2012) and based on the parameters previously determined in the studies of Boehler et al. (2017), Soon et al. (2019), and Yen & Gu (2020). A detailed description of the procedure is presented in Appendix Afigure A and images of the model are given in Fig. A.1. In this model, the disk is rotating in pure Keplerian rotation. The resulting signal is then convolved by a Gaussian of 0.1′′ and 0.3′′ in order to reproduce typical spatial resolutions of molecular lines in ALMA observations.
We show in the top-center and top-right panels of Fig. 6 that measurable deviations exist even in the case of ideal observations (i.e., without noise and at a velocity resolution of 25 m s−1). The velocity deviations are of a few percent and can be divided into two regions. At R ≤ 150–175 au, the velocity deviations appear sub-Keplerian, meaning redshifted in the north of the disk (at PA between − 90° and 90°) and blueshifted in the south of the disk. On the contrary, at R ≥ 150–175 au, the gas appears mainly super-Keplerian, with an inversion of the blueshifted and redshifted azimuthal locations. The only exception is the area near the north of the major axis, which will be detailed in Sect. 4.3.
In the top-left panel of Fig. 6, we present the velocity deviations measured in the observations. At a radius larger than 150 au, the observed kinematic signal is similar to the velocity pattern seen in the pure Keplerian model at 0.3′′, even if the velocity deviations reach a velocity of 150 m s−1 in our observations, instead of only 20–80 m s−1 in our models. We observe the rounded redshifted region at ~230 au, close to PA = 0°, surrounded by the blueshifted area at θ between −90° and 90°, and mainly a redshifted region in the south of the disk. The similarity of these characteristics can cast doubts about the correct physical interpretation of the kinematic deviations to the Keplerian rotation and might reveal a bias in the velocity measurements to start with. Inside the cavity, at R ≤ 100–150 au, the observed velocity deviations diverge from our models and probably trace perturbations of the Keplerian flow by the companion, as observed in Casassus et al. (2015).
 |
Fig. 5 Comparison of the velocity deviations measured in the HD 142527 system with vortex models. Top: Difference between the 13CO J = 3–2 velocity measured from our observations and the Keplerian prescription in a 2D-map (R, θ). Blue and red colors indicate blue- and redshifted velocities along the line-of-sight compared to the Keplerian rotation. θ = 0° represents the north of the major axis. Bottom: Three vortex prescriptions with their corresponding velocity amplitude in the planeof the disk (top), rotating clockwise around the vortex center on elliptical streamlines, and the projected velocity along the line-of-sight (bottom). Model A corresponds to a large vortex centered at the position of the continuum intensity maximum and Model B an equivalent vortex centered on the secondary maximum. Model C presents the kinematic signature for two smaller vortices at these positions. |
4.2 Line intensity gradients skew measured velocities through beam smearing
Observations are naturally limited by characteristics such as the rms noise, and the spatial and spectral resolutions. Each of them can bring systematic biases in the measurements. In the HD 142527 disk models, the two main regions in terms of velocity deviations are separated at a radius of about 150 au, corresponding to the distance at which the 13CO J = 3–2 emission peaks. This is visible in the middle line in Fig. 6 which shows the spatial distribution of the 13CO integrated emission. In the inner regions, as the 13CO flux increases with radius, we collect more emission from large radii than from small radii inside the synthesized beam, leading to a sub-Keplerian profile. The opposite effect happens in the outer regions where the gas emission mainly decreases with radius, leading to a super-Keplerian profile. The spurious velocity deviations in the models are then explained by the finite spatial resolution of the observations and the radial gradient of the molecular line emission. This effect, also called “beam smearing,” was discussed a first time in Keppler et al. (2019) for the kinematic analysis of the PDS 70s cavity (see the Appendix A.2).
A useful parameter to understand these artifacts in the velocity measurements is the radial variation of the line emission. For a given spatial resolution, this variation can be estimated by the emission ratio Iout∕Iin between the outer and inner edges of the synthesized beams. When this ratio is greater than 1, the measured velocity becomes sub-Keplerian, and vice versa. Starting from the initial non-convolved image, this ratio can be perfectly known in the models and is shown in the bottom-center and bottom-right panels of Fig. 6. As expected, the emission ratio Iout∕Iin is larger at 0.3′′ than at 0.1′′ and lead to stronger velocity biases. In real observations, the emission ratio can only be approached because the image received is already convolved by the observational beam. We show, however, in the bottom-left panel of Fig. 6 that the general tendency of the flux variations can be recovered, even if their magnitude is probably underestimated.
In general, we find in our models that the flux ratio Iout∕Iin is proportional to the beam size, with ratios at 0.3′′ about three times larger than at 0.1′′, which is an expected result when the spatial variation of the line emission is relatively smooth compared to the synthesized beam size. Furthermore, biases are also sensitive to the velocity range ΔV probed by the synthesized beam, which is proportional to the beam size, and increases at smaller distances from the star dueto the steeper gradient of the Keplerian velocity. This leads to velocity artifacts generally larger at 0.3′′ compared to 0.1′′ and particularly important in the inner regions of the disk. Along the northern major axis, as shown in the top panel of Fig. 7, the velocity deviations at 0.1′′ are about three times smaller thanat 0.3′′. Going to a higher spatial resolution will have then the double advantage of (i) reducing velocity biases and of (ii) allowing a better determination of the value and morphology of these biases, through a more precise knowledge of the disk structure.
 |
Fig. 6 Artificial velocity deviations measured in a perfectly Keplerian disk compared to the observations. Top: differences between the measured 13CO J = 3–2 velocity and the Keplerian prescription in a 2D-map (R, θ). Blue and red colors indicate blue- and redshifted velocities along the line-of-sight compared to the Keplerian rotation. Middle: 13CO integrated emission. Bottom: flux ratio Iout∕Iin of the emission at the outer and inner edges of the synthesized beam. The left panel is surrounded by a red rectangle because theflux ratio is only an approximation in observations, being measured after beam smoothing. Left column shows the observations. The central and the right columns are the models convolved at a spatial resolution of 0.3 and 0.1′′. The verticalblack bar on the top-left corner of the top panels is the averaged radial spatial resolution as a function of the azimuth. |
4.3 Dust also affects the measured gas velocity
The circumbinary disk around HD 142527 is not only made of gas but also contains a large concentration of dust particles at the north of the disk. The presence of this dust concentration, which is optically thick at 0.9 mm with τDust ~ 2–3 (Muto et al. 2015; Boehler et al. 2017), has an important impact on the measured gas velocity at the north of the disk, as shown in the top panel of Fig. 7. The four radial regions indicated in this figure are delimited by the radii at which the velocity shifts between a sub- and a super-Keplerian velocity at the spatial resolution of 0.3′′. Regions I and IV, which contain almost no millimeter dust emission, correspond to the two regions described previously in Sect. 4.2. The 13CO integrated emission uniformly increases for R ≤ 135 au and decreases for R ≥ 270 au, leading to the sub-Keplerian and to the super-Keplerian profiles.
The existence of the additional regions II and III, located between ~ 135 and ~ 270 au, is of main interest in our analysis as it corresponds to the location of the potential vortex signature in the observations, around the dust horseshoe position. As shown in the middle panel of Fig. 7, velocity biases in the models are related to the artificial and local cavity in the gas emission in the north of the disk, visible both in the models and in the observations in Fig. 1. The gas cavity is colocated with the presence of dust emission and mainly arises from the continuum subtraction process, which over-estimates the dust contribution to subtract (Boehler et al. 2017; Weaver et al. 2018), as already discussed in Sect. 2.1.
Independently of its origin, real or artificial, the top and bottom panels in Fig. 7 reveal that the measured velocity deviations are in good agreement with the flux variations measured after continuum-subtraction. We obtain a super-Keplerian profile in Region II (135 < R < 215 au), and a sub-Keplerian profile in Region III (215 < R < 270 au), matching the flux ratio smaller and greater than 1, reciprocally. The presence of dust has then an important impact on the measured velocity.
These deviations are not due to the continuum subtraction process, however. The measured velocity does not change before or after this process, as shown by Teague et al. (2018b) using the peak emission method, which can be performed indistinctly with or without continuum subtraction. Indeed, the emission that we subtract is the interpolation of the dust emission from adjacent line-free channels and is essentially a flat spectrum compared to the width of the line. For a typical protoplanetary disk located at a distance of ~ 150 pc, the 13CO J = 3–2 line has a spectral width of about 1–2 MHz at a spatial resolution of 0.1–0.3′′. At a line frequency ν of ~ 330 GHz, this gives a ratio Δν/ν of 6 × 10−6. Therefore, the dust thermal emission, with a spectral index between 2 and 3.7, only varies in amplitude by about 0.001% along the spectral width of the line and does not affect the measured velocity.
On the contrary, the fact that velocity biases follow flux variations after dust-subtraction indicates that the weight given to each regions inside the synthesized beam is not the absolute magnitude of the line but its excess over a “quasi-flat spectrum,” which can be zero-emission (if there is no dust) or the dust emission (if dust is present). When the gas emission becomes optically thick, the combined dust and gas emission at the line frequency is smaller than the sum of the two components taken separately, due to optical depth effects. The prominence of the line over the quasi-flat spectrum decreases and the weight given to the regions with more dust emission is then reduced for the measurement of the gas velocity.
To illustrate the artifacts in the velocity measurement due to dust concentrations, we present in the left panel of Fig. 8 a simple sketch of a disk where the gas surface density is slowly decreasing with radius and which contains a dust ring or horseshoe structure. If the gas emission is optically thick, this will create a local and sharp decrease in the gas emission when measured after continuum subtraction. Two synthesized beams are represented at the inner and outer rim location of the dust structure where flux variations, and then velocity biases, are maximum. The right panel of Fig. 8 shows qualitatively how the spectral profile of the emission line is modified at these two positions. Without the presence of the dust structure, the measured velocity profile is slightly super-Keplerian due to the slow decrease in the gas emission with radius. On the contrary, the steep gradient in the line emission at the rims position artificially creates strong deviations to the Keplerian rotation, with a super-Keplerian rotation at the inner rim and a sub-Keplerian rotation at the outer rim. We also note that the line profile is only modified by an offset after continuum subtraction, leaving the measured velocity unchanged.
A similar effect on the measured velocity will happen if the line emission coming from the back side of the disk is absorbed bydust particles lying on the midplane. The integrated emission at the ring position, and then the weight given to this location, will also be attenuated in the measurement of the gas velocity. This effect can, however, be mitigated if the front molecular layer of the disk, usually brighter, can be differentiated spectrally, as shown in 12CO for AS 209 (Teague et al. 2018b). Such an observation, however, will still be affected by the continuum subtraction effect if the molecular line is optically thick.
 |
Fig. 7 Velocity deviations due to the presence of dust along the north of the major axis. Top: velocity deviations measured in the pure Keplerian model at two different spatial resolutions. Middle: 13CO integrated emission and dust emission in the original non-convolved model. By definition, the integrated emission is always measured after continuum subtraction. The cavity between 150 au and 260 au is due to the continuum subtraction procedure. Bottom: flux ratio between the outer and inner edges of the synthesized beam. |
4.4 Beam smearing and gas pressure gradients may also explain the vortex-like kinematic feature
The main difficulty in identifying the origin of the radial Doppler-shifted structure at the north of the disk comes from the possible confusion with artifacts in the measurement of the velocity and other kinematic signals. We have shown in the top panel of Fig. 7 that beam smearing can produce along the north major axis a pattern similar in morphology to the azimuthal velocity deviations that a vortex would produce. However, these artifacts are of lower amplitude in our model, with velocities reaching 90 m s−1 on the inner side and 20 m s−1 on the outer side, while we measure about 150–160 m s−1 on both sides in the observations. Besides, the kinematic structure due to beam smearing is located at 215 au, at the outer edge of the artificial gas cavity due to continuum subtraction, while the radial Doppler-shift in the observations is centered at 185 au, at the radius where both dust and gas reach their maximum surface density. It is also more extended radially, from 85 to 300 au, compared to 135–270 au in the models.
It therefore appears unlikely that the beam smearing effect alone can produce the azimuthal velocity deviations. However, azimuthal kinematic deviations are also expected on the inner and outer sides of the circumbinary disk in HD 142527 due to radial gas pressure gradients (Teague et al. 2018a; Yen & Gu 2020). This process may produce super-Keplerian velocities at the inner edge of the horseshoe structure and sub-Keplerian velocities outward, as for an anticyclonic vortex. On the south side of the disk, possible deviations are up to 30 m s−1. With a gas surface density three to five times larger on the northern side of the disk, significant non-Keplerian motions may appear and add to the beam smearing effect to possibly produce the large velocity deviations that we observe.
Therefore, the presence of a vortex should be more easily constrained through radial motions to not be mistaken with azimuthal motions due to steep gas pressure gradients. At the northern side of the circumbinary disk, we observe a shift toward blueshifted emission on the order of 50 m s−1 at θ around ~ 45°–90° and ~ 270°–315°, as already mentioned in Sect. 3.1. This blueshifted emission is visible in Figs. 2, 3, and 5 and may correspond to inward motions of the gas at θ ~ 45°–90° and outward motions at θ ~ 270°–315°, similar to what would be expected for an anticyclonic vortex. However, as shown in Fig. 6, the beam smearing effect also predicts blueshifted emission at these angles due to a global decrease in the emission with radii. It is then currently very difficult to assess if the signal is due to a real vortex or is produced by beam smearing associated with gas pressure gradients.
In addition, we note that some uncertainties also exist in the comparison of the measured velocity with the Keplerian rotation. First, as shown by Yen & Gu (2020) in their appendix, uncertainties in the disk inclination of 2° may lead to errors in the measured velocity of about 25 m s−1 at intermediate angles. In our approach, the disk inclination was fixed but its uncertainty from previous measurements is on the order of 1° (Fukagawa et al. 2013; Yen & Gu 2020). Possible errors due to this process are then limited for our measurements and the general pattern predicted by Yen & Gu (2020) is not visible in the residuals of the velocity deviations. Actually, most of the uncertainties in the measurement of the Keplerian rotation in HD 142527 come from the complexity of the kinematic signal that presents large deviations from a pure Keplerian profile, in particular at the north of the disk, as shown in Fig. 7. Our fit was done using the same weight to each radii between 100 and 400 au. If we would have given more weight to the inner regionof the disk due to the higher local signal-to-noise, the blueshifted emission detected at PA around 45°–90° and 270°–315° would have been reduced. On the contrary, if velocity deviations due to gradients in the gas surface density or due to beam smearing are in fact larger on the inner side of the disk, as our model suggests, the true Keplerian rotation would be in reality slightly smaller and the blueshifted emission detected at these angles would then be more pronounced.
 |
Fig. 8 Velocity artifacts created by a ring or horseshoe dust structure. Left panel: sketch representing the integrated gas emission over the line width as a function of the disk radius. The black solid line is the gas emission without the dust ring, and the two red lines represent the emission in presence of the dust ring before and after continuum subtraction. The two ellipses indicate the position of two synthesized beams. Right panel: line emission profile (black solid line) in the simplified case where the line emission is the sum of the emission at the inner (blue dashed line) and outer (red dashed lines) edges of the synthesized beam. The velocity vc, represented by the dotted black vertical line, is the velocity at the center of the beam while vm, represented by the solid black line, is the intensity weighted velocity. |
5 Discussion
5.1 Observations and theories regarding the possible existence of a large vortex around HD 142527
Based on 13CO and C18O J = 3–2 data at a spatial resolution of0.3′′, current observations of the gas kinematics in the circumbinary disk around HD 142527 is consistent with the existence of a large vortex, even if complementary observations would be necessary to distinguish it from other possibilities. When compared with a model, the center of this anticyclonic vortex is located at 185 au from the star, at the estimated radius where both dust and gas surface densities reach their maximum (Boehler et al. 2017), with maximum velocity deviations of ~ 150–160 m s−1 in the azimuthal direction along the major axis, meaning ~ 350 m s−1 after deprojection. It is extended radially on each side on about two pressure scale heights, and azimuthally over ~ 200°, yielding an azimuthal-to-radial aspect ratio χ of ~ 5.
Using 12CO, 13CO, and C18O J = 2–1 emission lines, Garg et al. (2021) could estimate the morphology of the disk cavity and revealed a steep radial gradient in gas surface density at the inner edge of the circumbinary disk, making it a favorable site for vortex formation. Radially wide vortices (i.e., larger than a gas pressure scale height radially) have been predicted in simulations that include the displacement of the system barycenter due to the lopsided structure of the disk (Mittal & Chiang 2015; Baruteau & Zhu 2016). Such vortices should also be azimuthally extended, with ratio between 4 and 6, to withstand the elliptic instability (Lesur & Papaloizou 2009). Recently, Robert et al. (2020) performed numerical simulations in cavity-hosting disks with the formation of very extended vortices. For vertical aspect ratios H/R ≳ 0.13, with H the pressure scale height in the disk, they predict maximum velocity deviations projected along the line-of-sight of 150 m s−1 for a disk inclination similar to the one in HD 142527. This vertical aspect ratio, while slightly larger than usually considered in protoplanetary disks, may correspond to the vertical geometry of the circumbinary disk around HD 142527 as the inner rim is directly illuminated by the Herbig star. A large vortex in HD 142527, with a kinematic signal similar to the one observed around the horseshoe structure, is then theoretically possible.
Another interesting result of the simulations performed by Mittal & Chiang (2015) and Baruteau & Zhu (2016) is that dust grains can concentrate at a different azimuth than the vortex due to the indirect force exerted by the disk self-gravity. In brief, only small grains with a Stokes number ~ 0.01 concentrate in the eye of the vortex due to their strong coupling with the gas while larger grains will concentrate generally ahead of it, potentially with a difference of 90° in azimuth, and giving a double peak structure to the continuum emission. At first glance, it is tempting to connect thisscenario with the double-peaked structure observed in the dust emission in the circumbinary disk around HD 142527. Nevertheless, in the observations, the maximum in the dust emission is located at PA = 50°, 70° behind the azimuthal position of the vortex and of the secondary maximum in dust emission, both located at PA ~ −20°, contrary to the predictions in Mittal & Chiang (2015) and in Baruteau & Zhu (2016).
It is possible that the presence of the companion, not present in the previous simulations, plays an important role in the location of the large dust grains. Hammer et al. (2019, 2021) found that a large vortex characterized by a flat pressure bump would be sensitive to the overlapping of spiral density waves. Dust grains will then not concentrate in a small and centered area but in an elongated and complex structure, with a possible off-centered peak, a skewness around this peak, or even a double-peaked structure. While elongated, the double peaked structure in the continuum emission may, however, only be due to the shadow cast by the inner disk (Verhoeff et al. 2011; Marino et al. 2015). Recent modelings of the dust distribution using wavelengths between 0.9 and 3 mm, and the temperature given by optically thick molecules, suggest that dust grains are mainly concentrated near the major axis (Yen & Gu 2020), or even at the position of the secondary maximum (Soon et al. 2019), at approximately the vortex position. A solid understanding of the dust concentration process in the HD 142527 system will require a better mix of long wavelengths and high spatial resolution than the 0.30–0.43′′ currently available at λ > 1 mm.
5.2 Vortex versus binary
In an ALMA survey of disks presenting large central cavities, van der Marel et al. (2021) revealed that dust asymmetries were only present in disks with a sufficiently low gas surface density. This suggests that local gas pressuremaxima are actually common in such disks but that only dust grains with a Stokes number ≳ 102 are efficiently dragged into them. One possibility to create a local gas pressure is through a vortex, as already discussed in Sect. 5.1. While not mutually exclusive, another theory suggests that an azimuthal gas pressure maximum can be formed by the interaction between a binary, with a mass ratio q ≳ 0.05 with the main star, and the circumbinary disk. Numerical simulations have shown that the massive companion would create a large and eccentric cavity, leading to a gas asymmetry in the gas (Shi et al. 2012; D’Orazio et al. 2016; Ragusa et al. 2017; Price et al. 2018) rotating at Keplerian velocity and able to trap dust particles (Calcino et al. 2019; Ragusa et al. 2020).
These studies have been performed using a relatively high viscosity α = 5 × 10−3, and therefore did not produce vortices as they require α ≲ 10−3 (Zhu & Stone 2014b). It is, however, plausible that both processes can act together at a smaller viscosity. As shown by Price et al. (2018), the HD 142527 system is particularly well suited for the binary scenario with the only massive companion (q ~ 0.1–0.15) directly imaged in a large cavity (van der Marel et al. 2021). Other systems like AB Aur (Tang et al. 2012), IRS 48 (van der Marel et al. 2013), or HD 135344B (Cazzoletti et al. 2018) also present a large cavity with a horseshoe structure and may correspond to this scenario as well. On the contrary, asymmetries located across ring structures in the outer regions of the disks, like in MWC 758, HD 143006 and V1247 Orionis, probably require the presence of a vortex to form (Baruteau et al. 2019).
The main uncertainty about the formation and viability of vortices comes from the disk viscosity whose measurements are still scarce. To our knowledge, no estimation of the disk viscosity in the circumbinary disk around HD 142527 has been performed. Apart from the notable case of DM Tau where a turbulent viscosity α of ~ 0.08 has been measured in the upper layers of the disk using 12CO emission, only upper limits on the order of a few times 10−3 were found using the turbulent broadening property of the gas emission lines in HD 163296 (Flaherty et al. 2017), TW Hya (Flaherty et al. 2018; Teague et al. 2018a), MWC 480 and V4046 Sgr (Flaherty et al. 2020). Other methods, more indirect because integrating hypotheses on the grains properties, have generally suggested α values from a few 10−4 to a few 10−3 by estimating the dust settling degree in HL Tau (Pinte et al. 2016), or by using the radial dust dispersion across rings (Dullemond et al. 2018).
Simulations performed using a lower viscosity would help to constrain the complex dust concentration process in the HD 142527 disk. Further observations of the gas kinematics at a higher spatial resolution, for instance of 0.1′′ instead of 0.3′′, would allowvelocity biases due to beam smearing to diminish and a possible vortex signal to be more clearly distinguished from the background rotation. With a dust absorption coefficient β estimated to1.6 by Yen & Gu (2020) at the horseshoe position, it will also be judicious to choose a lower frequency, for example with the J = 2–1 transitions lines of the CO isotopologues, to significantly reduce the specific beam smearing effect around the dust crescent. Indeed, the dust optical depth would decrease by a factor of ~ 2, significantly diminishing the dust emission and the depth of the artificial gas cavity.
5.3 Beam smearing with kinks, spirals, and rings
During the analysis of the disk kinematics, we pointed out the beam smearing effect due to variations of the line emission inside of the synthesized beam and which may lead to a misinterpretation of kinematic signals. Indeed, local variations of a few tens to a few hundreds of m s−1 in the gas velocity have been used in the recent years to: (i) probe radial pressure gradients and then gaps in the gas surface density (Teague et al. 2018a,b), (ii) observe the kinematic signature of spirals (Teague et al. 2019) and (iii) to directly trace the presence of planets through the observation of Doppler flips or kinks (Pinte et al. 2018, 2019; Casassus & Pérez 2019; Pinte et al. 2020).
Velocityartifacts due to beam smearing present characteristics that may help in distinguishing them from real kinematic features. First, these artifacts should appear in regions where the line emission undergoes a steep spatial variation. This may be produced by a change in the gas surface density in the temperature, or processes such as photo-dissociation, freeze-out onto grains, chemical reactions, and optical depth effects around dust structures. Second, the artifacts will also increase in regions that present a strong gradient in the projected velocity. For a disk dominated by Keplerian motions, this will correspond to regions near the major axis with biases decreasing in azimuth with ~ cos(θ), and in regions close to the star with biases decreasing with the radius in ~ r−1.5. In addition, similarly to the projected Keplerian rotation, biases will increase with the disks inclination, in sin(i), and with the system mass, in 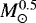 .
.
In comparison, kinks and Doppler flips are very localized features that do not reveal any preferential azimuthal locations (Pinte et al. 2018, 2019, 2020; Casassus & Pérez 2019). Nor do they seem to be linked with a specific point-like cavity or source of emission in the lines considered. Therefore, these kinematic signals do not correspond to the expected velocity artifacts due to beam smearing but better agree with the presence of a planet, located potentially at any azimuthal angle and perturbing the gas motion in the radial, vertical, or azimuthal direction (Pinte et al. 2019).
It is more difficult to directly interpret the gas kinematics around rings and spirals as both structures are generally accompanied by variations of the line emission, like around the horseshoe structure in HD 142527. The velocity artifacts created across dust rings have been shown in Fig. 8 and in Sect. 4.3. The possible decrease in the gas emission at the dust ring position, due to optical depth effects, will produce the measurement of a super-Keplerian and of a sub-Keplerian velocity at the inner and outer rims of the dust disk, respectively. This is similar to what is theoretically expected if dust grains are trapped in a radial pressure maximum (Kanagawa et al. 2015; Teague et al. 2018a). True kinematic signatures and artifacts being due to azimuthal motions, there will be both mostly visible around the major axis of the disk and their differentiation may require a careful analysis. Inversely, spirals would appear as maximum in the gas emission and the beam-smearing effect will artificially produce sub-Keplerian and super-Keplerian velocities on the inner and outer edges of these structures. However, compared to ring-like structures, spirals can be more easily distinguished by the variation of their kinematic signal as a function of the azimuth as significant non-azimuthal motions around spirals are also expected (Pinte et al. 2019).
6 Conclusion
We present a study focusing on the gas kinematics in the lopsided disk surrounding the binary system HD 142527 at a spatial resolution of 0.3′′ and at a wavelength of ~0.9 mm. Our major findings are:
- 1.
The main kinematic structure has a vortex-like morphology with potential azimuthal and radial motions. It is located at the north of the circumbinary disk, around the dust concentration, and has projected velocities up to 150 m s−1 compared to the Keplerian background. Three spiral-like kinematic features are also detected in the outer region of the circumbinary disk at R between 200 and 450 au. Two of them are probably related to the two most innermost spirals detected in this system (S1 and S4 following Garg et al. 2021).
- 2.
Using comparisons with a vortex model, the main kinematic feature is consistent with the existence of a large vortex located at R ~ 185 au, at the radius where dust and gas reach their maximum surface densities, and at a PA of ~−20°. Such a vortex may have formed through the Rossby-wave instability at the inner edge of the circumbinary disk, suggesting a relatively low turbulent viscosity α ≲ 10−3 (Zhu & Stone 2014b). Its very large size, of about ±40 au radially and ~200° azimuthally, suggests that the disk self-gravity plays an important role through the indirect force (Mittal & Chiang 2015; Baruteau & Zhu 2016). The relatively large velocities of approximately 350 m s−1 after deprojection, comparable to the local sound speed, have been predicted in simulations of vortices performed by Huang et al. (2018) and Robert et al. (2020).
- 3.
Velocity measurements are, however, subject to artifacts due to variations of the line emission at a sub-synthesized beam scale. If associated with non-Keplerian motions due to gas pressure gradients at the inner and outer edges of the circumbinary disk, the beam smearing effect may also create a kinematic signal similar to an anticyclonic vortex around the horseshoe structure. Our current observations, at a spatial resolution of 0.3′′, do not allow us to distinguish between these two possibilities.
- 4.
Velocity deviations due to beam smearing should be common in protoplanetary disks and may lead to the misinterpretations of kinematic signals, in particular around ring-like structures. The principal method to reduce them is to perform observations at a higher spatial resolution. This would also allow, through a better knowledge of the disk structure, to constrain much more precisely the amplitude and localization of such artifacts. In HD 142527, a spatial resolution of 0.1′′ is reachable in 2–3 hours of telescope time on target and would decrease by a factor of ~3 the current beam smearing effect along the major axis of the disk.
Acknowledgements
We thank the referee whose comments improved the quality of the manuscript, and G. Lesur for useful discussions about vortex properties. The authors acknowledge funding from ANR (Agence Nationale de la Recherche) of France under contract number ANR-16-CE31-0013 (Planet-Forming-Disks). JFG thanks the LABEX Lyon Institute of Origins (ANR-10-LABX-0066) of the Université de Lyon for its financial support within the programme ‘Investissements d’Avenir’ (ANR-11-IDEX-0007) of the French government operated by the ANR. This paper makes use of the following ALMA data: ADS/JAO.ALMA#2012.1.00725.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), MOST and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement.
Appendix A A 3D toy model for HD 142527
 |
Fig. A.1 From left to right: dust emission, 13CO J = 3–2 and C18O J = 3–2 integrated emission of the 3D toy model of HD 142527. The spatial resolution is 0.3′′. |
The model of the circumbinary disk around HD 142527 is built in a spherical framework (r, θ, ϕ) using cells of 1 au in radius,2° in azimuth and1° in elevation.The horseshoe structure in the dust and gas surface density is modeled using modified Gaussians along the radial and azimuthal directions following the formula:
![\begin{equation*} \begin{aligned} \Sigma(r, \theta) = {} & (\Sigma_{\textrm{max}}-\Sigma_{\textrm{min}})~\mathrm{exp}\left[-\left(\frac{r-R_0(\theta)}{w_{\textrm{in,out}}(\theta)} \right){}^2 \right]~\mathrm{exp}\left[-\left(\frac{\theta-\theta_{\textrm{max}}}{w_{\textrm{ctcl,cl}}} \right){}^2 \right] \\ & + \Sigma_{\textrm{min}}, \end{aligned}\end{equation*}](/articles/aa/full_html/2021/06/aa40089-20/aa40089-20-eq8.png) (A.1)
(A.1)
with Σmax the surface density at the position (R0(θmax), θmax), where the dust and gas surface densities aremaximum, and Σmin the surface density at the position (R0(θmin), θmin) for the azimuth where the gas and dust surface densities are minimum. The parameters win (θ) and wout(θ) are the radial half-widths of the Gaussian for r < R0 or for r > R0, and wctcl and wcl the azimuthal half-widths of the Gaussian in the counterclockwise and clockwise directions, starting from θmax.
To represent the eccentric aspect of the circumbinary disk, the parameters R0 (θ), and win,out(θ) vary as a function of the azimuth through the formula, for instance for R0(θ):
![\begin{equation*} \begin{aligned} R_0(\theta) = & ~ (R_0(\theta_{\textrm{max}})- R_0(\theta_{\textrm{min}})) ~ \mathrm{exp}\left[-\left(\frac{\theta-\theta_{\textrm{max}}} {w_{\textrm{ctcl, cl}}} \right){}^2 \right] + R_0(\theta_{\textrm{min}}).\end{aligned} \end{equation*}](/articles/aa/full_html/2021/06/aa40089-20/aa40089-20-eq9.png) (A.2)
(A.2)
The value of the parameters are given in Table A.1. They were inspired by the analysis in Boehler et al. (2017), using the same grain properties, but also by the studies performed by Soon et al. (2019) and Yen & Gu (2020), which took into account the azimuthal variation of the temperature, obtained using optically thick molecules, and then estimated that the gas surface density maximum was at θ ~ 15°. We then calculated the circumbinary disk temperature through radiative transfer by using RADMC-3D (Dullemond et al. 2012). No shadowing effect by the inner disk has been taken into account in this step. With the same code, we performed the ray-tracing in a square grid with a pixel size of 20 mas and a velocity resolution of 10 m s−1, about ten times smaller thanin our observations, to produce the final image before beam dilution. In this model, the gas is in pure Keplerian rotation around a single star of 2.36 M⊙ with v(r, z) = 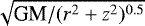 . We assume a disk inclination of 27° and a PA of − 19°. Images of the circumbinary disk model for the dust intensity, and the 13CO and C18O J = 3–2 integrated emission are given in Fig. A.1.
. We assume a disk inclination of 27° and a PA of − 19°. Images of the circumbinary disk model for the dust intensity, and the 13CO and C18O J = 3–2 integrated emission are given in Fig. A.1.
Density prescription for the Gaussians describing the dust and gas surface density on the northern and southern profiles.
Appendix B Comparison of the “peak” and “intensity weighted” methods
We have used in this study the intensity weighted method. Another popular method to estimate the gas velocity along the line-of-sight is the peak emission method. It consists in identifying for each pixel of the map the spectral position of the peak of the line emission. The precision of this method has recently been improved in Teague & Foreman-Mackey (2018) by performing a polynomial fit on the three channels around the maximum in emission. This method is especially useful when the front and back molecular layers can be disentangled spatially and spectrally (see also Appendix A.3 in Teague et al. 2018b). This allows the precise determination of the origin (r, θ, z) of the emission and the comparison of the front layer of the disk with the Keplerian velocity. However, such observations are still rare. Inour observations, the low inclination of the circumbinary disk around HD 142527, the choice of the 13CO and C18O transitions lines that emit at a lower altitude than 12CO, and the moderate spatial resolution of our observations, do not give us the ability to distinguish the two molecular layers.
 |
Fig. B.1 Radial profiles of the velocity for different PAs θ, spaced by 45°, where θ is the angle starting from the northern major axis and rotating counterclockwise. The red curve isthe velocity measured using the intensity weighted method (mom1 in CASA) with 13CO J = 3–2. The orange and blue curves correspond to the velocity measured using the peak emission method with the 13CO J = 3–2 and C18O J = 3–2 transition lines, respectively, with the procedure detailed in Teague & Foreman-Mackey (2018). |
We mainly privileged the intensity weighted method in our study because it appeared less affectedby the rms noise than the peak emission approach, in particular with the 13CO J = 3−2 transition line. This is probably due to the high optical depth of the line and to the moderate spatial resolution of our observations, which give to the peak of the emission a flattened aspect. Another reason for the better precision of the intensity weighted method within our data is the good signal-to-noise in the circumbinary disk where about 10 channels are involved in the measurement of the gas velocity.
We show in Fig. B.1 the velocity measured from the 13CO and C18O J = 3–2 transition lines using the intensity weighted and the peak emission methods. For the intensity weighted method, we only indicate the velocity measured in 13CO as both molecules show the same velocity (cf. Fig. 3). The results between both methods and molecules are in general agreement, with a Keplerian profile at the south of the disk and a super-Keplerian profile at the north for R ≲ 160–180 au and sub-Keplerian for R ≳ 160–180 au.
There are also slight differences between the methods and the lines involved, which is in itself not a surprising result. First, the two methods would only give the same results if the line profile was symmetric around the peak of emission, what may not be the case in practice. For instance, spectral profiles similar to the examples shown in the right panel of Fig. 8 would give very different values. Second, the two methods do not probe the same regions (r, θ, z) along the line-of-sight due to optical depth effects. In fact, the largest differences in the measured velocity in Fig. B.1 are found between the peak emission of the 13CO line, optically thick and only probing the front 13CO layer, and the two other measurements, which are the peak intensity method applied to the moderately optically thick C18O and the intensity weighted method, which probes all the line profile including optically thin wings, therefore also sensitive to the back molecular layer. Finally, the optical depth can also modify the surface brightness, and thus the velocity artifacts due to beam smearing, as the weight given to each region of the synthesized beam would change.
References
- Andrews, S. M., Huang, J., Pérez, L. M., et al. 2018, ApJ, 869, L41 [Google Scholar]
- Auffinger, J., & Laibe, G. 2018, MNRAS, 473, 796 [Google Scholar]
- Bai, X.-N., & Stone, J. M. 2010, ApJ, 722, 1437 [Google Scholar]
- Barge, P., & Sommeria, J. 1995, A&A, 295, L1 [NASA ADS] [Google Scholar]
- Baruteau, C., & Zhu, Z. 2016, MNRAS, 458, 3927 [NASA ADS] [CrossRef] [Google Scholar]
- Baruteau, C., Barraza, M., Pérez, S., et al. 2019, MNRAS, 486, 304 [Google Scholar]
- Biller, B., Lacour, S., Juhász, A., et al. 2012, ApJ, 753, L38 [Google Scholar]
- Birnstiel, T., Dullemond, C. P., & Brauer, F. 2010, A&A, 513, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boehler, Y., Weaver, E., Isella, A., et al. 2017, ApJ, 840, 60 [Google Scholar]
- Boehler, Y., Ricci, L., Weaver, E., et al. 2018, ApJ, 853, 162 [Google Scholar]
- Calcino, J., Price, D. J., Pinte, C., et al. 2019, MNRAS, 490, 2579 [Google Scholar]
- Casassus, S., & Pérez, S. 2019, ApJ, 883, L41 [CrossRef] [Google Scholar]
- Casassus, S., van der Plas, G., M, S. P., et al. 2013, Nature, 493, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Casassus, S., Marino, S., Pérez, S., et al. 2015, ApJ, 811, 92 [Google Scholar]
- Casassus, S., Marino, S., Lyra, W., et al. 2019, MNRAS, 483, 3278 [Google Scholar]
- Cazzoletti, P., van Dishoeck, E. F., Pinilla, P., et al. 2018, A&A, 619, A161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chavanis, P. H. 2000, A&A, 356, 1089 [NASA ADS] [Google Scholar]
- Christiaens, V., Casassus, S., Perez, S., et al. 2014, ApJ, 785, L12 [Google Scholar]
- Claudi, R., Maire, A.-L., Mesa, D., et al. 2019, A&A, 622, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Val-Borro, M., Artymowicz, P., D’Angelo, G., et al. 2007, A&A, 471, 1043 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dong, R., Liu, S.-y., Eisner, J., et al. 2018, ApJ, 860, 124 [NASA ADS] [CrossRef] [Google Scholar]
- D’Orazio, D. J., Haiman, Z., Duffell, P., MacFadyen, A., & Farris, B. 2016, MNRAS, 459, 2379 [Google Scholar]
- Dullemond, C. P., Juhasz, A., Pohl, A., et al. 2012, Astrophysics Source Code Library, [record ascl:1202.015] [Google Scholar]
- Dullemond, C. P., Birnstiel, T., Huang, J., et al. 2018, ApJ, 869, L46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flaherty, K. M., Hughes, A. M., Rose, S. C., et al. 2017, ApJ, 843, 150. [NASA ADS] [CrossRef] [Google Scholar]
- Flaherty, K. M., Hughes, A. M., Teague, R., et al. 2018, ApJ, 856, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Flaherty, K., Hughes, A. M., Simon, J. B., et al. 2020, ApJ, 895, 109 [Google Scholar]
- Fukagawa, M., Tsukagoshi, T., Momose, M., et al. 2013, PASJ, 65, L14 [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garg, H., Pinte, C., Christiaens, V., et al. 2021, MNRAS, 504, 782 [Google Scholar]
- Goodman, J., Narayan, R., & Goldreich, P. 1987, MNRAS, 225, 695 [Google Scholar]
- Hammer, M., Pinilla, P., Kratter, K. M., et al. 2019, MNRAS, 482, 3609 [Google Scholar]
- Hammer, M., Lin, M.-K., Kratter, K. M., et al. 2021 [arXiv:2104.02782] [Google Scholar]
- Huang, P., Isella, A., Li, H., et al. 2018, ApJ, 867, 3 [Google Scholar]
- Isella, A., Huang, J., Andrews, S. M., et al. 2018, ApJ, 869, L49 [Google Scholar]
- Johansen, A., & Youdin, A. 2007, ApJ, 662, 627 [Google Scholar]
- Kanagawa, K. D., Tanaka, H., Muto, T., et al. 2015, MNRAS, 448, 994 [NASA ADS] [CrossRef] [Google Scholar]
- Keppler, M., Teague, R., Bae, J., et al. 2019, A&A, 625, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kida, S. 1981, J. Phys. Soc. Japan, 50, 3517 [Google Scholar]
- Kraus, S., Kreplin, A., Fukugawa, M., et al. 2017, ApJ, 848, L11 [Google Scholar]
- Lesur, G., & Papaloizou, J. C. B. 2009, A&A, 498, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, H., Finn, J. M., Lovelace, R. V. E., et al. 2000, ApJ, 533, 1023 [Google Scholar]
- Lin, M.-K. 2012, MNRAS, 426, 3211 [Google Scholar]
- Liu, S.-F., Jin, S., Li, S., et al. 2018, ApJ, 857, 87 [Google Scholar]
- Lovelace, R. V. E., Li, H., Colgate, S. A., & Nelson, A. F. 1999, ApJ, 513, 805 [Google Scholar]
- Lyra, W., & Lin, M.-K. 2013, ApJ, 775, 17 [Google Scholar]
- Marino, S., Perez, S., & Casassus, S. 2015a, ApJ, 798, L44 [NASA ADS] [CrossRef] [Google Scholar]
- McMullin, J. P., Waters, B., Schiebel, D., et al. 2007, Astron. Data Anal. Softw. Syst. XVI, 376, 127 [Google Scholar]
- Mittal, T., & Chiang, E. 2015, ApJ, 798, L25 [Google Scholar]
- Muto, T., Tsukagoshi, T., Momose, M., et al. 2015, PASJ, 67, 122 [Google Scholar]
- Pinte, C., Dent, W. R. F., Ménard, F., et al. 2016, ApJ, 816, 25 [Google Scholar]
- Pinte, C., Price, D. J., Ménard, F., et al. 2018, ApJ, 860, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Pinte, C., van der Plas, G., Ménard, F., et al. 2019, Nat. Astron., 3, 1109 [Google Scholar]
- Pinte, C., Price, D. J., Ménard, F., et al. 2020, ApJ, 890, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Price, D. J., Cuello, N., Pinte, C., et al. 2018, MNRAS, 477, 1270 [Google Scholar]
- Rab, C., Kamp, I., Dominik, C., et al. 2020, A&A, 642, A165 [EDP Sciences] [Google Scholar]
- Raettig, N., Klahr, H., & Lyra, W. 2015, ApJ, 804, 35 [Google Scholar]
- Ragusa, E., Dipierro, G., Lodato, G., Laibe, G., & Price, D. J. 2017, MNRAS, 464, 1449 [NASA ADS] [CrossRef] [Google Scholar]
- Ragusa, E., Alexander, R., Calcino, J., et al. 2020, MNRAS, 499, 3362 [Google Scholar]
- Regály, Z., Juhász, A., Sándor, Z., & Dullemond, C. P. 2012, MNRAS, 419, 1701 [Google Scholar]
- Richard, S., Barge, P., & Le Dizès, S. 2013, A&A, 559, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robert, C. M. T., Méheut, H., & Ménard, F. 2020, A&A, 641, A128 [Google Scholar]
- Rosotti, G. P., Teague, R., Dullemond, C., et al. 2020, MNRAS, 495, 173 [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 500, 33 [NASA ADS] [Google Scholar]
- Shi, J.-M., Krolik, J. H., Lubow, S. H., & Hawley, J. F. 2012, ApJ, 749, 118 [Google Scholar]
- Sierra, A., Lizano, S., & Barge, P. 2017, ApJ, 850, 115 [Google Scholar]
- Soon, K.-L., Momose, M., Muto, T., et al. 2019, PASJ, 71, 124 [Google Scholar]
- Surville, C., & Barge, P. 2015, A&A, 579, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tang, Y.-W., Guilloteau, S., Piétu, V., et al. 2012, A&A, 547, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Teague, R. 2019, J. Open Source Softw., 4, 1220 [NASA ADS] [CrossRef] [Google Scholar]
- Teague, R., & Foreman-Mackey, D. 2018, Res. Notes Am. Astron. Soc., 2, 173 [Google Scholar]
- Teague, R., Bae, J., Bergin, E. A., Birnstiel, T., & Foreman-Mackey, D. 2018a, ApJ, 860, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Teague, R., Bae, J., Birnstiel, T., & Bergin, E. A. 2018b, ApJ, 868, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Teague, R., Bae, J., Huang, J., et al. 2019, ApJ, 884, L56 [Google Scholar]
- van der Marel, N., van Dishoeck, E. F., Bruderer, S., et al. 2013, Science, 340, 1199 [Google Scholar]
- van der Marel, N., Pinilla, P., Tobin, J., et al. 2015, ApJ, 810, L7 [Google Scholar]
- van der Marel, N., Cazzoletti, P., Pinilla, P., et al. 2016, ApJ, 832, 178 [Google Scholar]
- van der Marel, N., Williams, J. P., Ansdell, M., et al. 2018, ApJ, 854, 177 [Google Scholar]
- van der Marel, N., Birnstiel, T., Garufi, A., et al. 2021, AJ, 161, 33 [Google Scholar]
- Varnière, P., & Tagger, M. 2006, A&A, 446, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verhoeff, A. P., Min, M., Pantin, E., et al. 2011, A&A, 528, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weaver, E., Isella, A., & Boehler, Y. 2018, ApJ, 853, 113 [Google Scholar]
- Weidenschilling, S. J. 1977, MNRAS, 180, 57 [Google Scholar]
- Yen, H.-W., & Gu, P.-G. 2020, ApJ, 905, 89 [Google Scholar]
- Youdin, A. N., & Goodman, J. 2005, ApJ, 620, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, Z., & Stone, J. M. 2014, ApJ, 795, 53 [Google Scholar]
All Tables
Density prescription for the Gaussians describing the dust and gas surface density on the northern and southern profiles.
All Figures
 |
Fig. 1 From left to right: dust emission, 13CO and C18O J = 3–2 integrated line emission after continuum subtraction around the binary system HD 142527. The spatial resolution is indicated by the white ellipse at the bottom-left corner of the panels. Its value is 0.′′207 ×0.′′178 for the dust emission, obtained using super-uniform weighting, and 0.′′31 × 0.′′27 for the gas emission, obtained with the Briggs parameter fixed to 0.5. The rms noise is 90 μJy beam−1 for the dust emission, 5.9 mJy beam−1 per channel in 13CO and 7.8 mJy beam−1 in C18O. The integrated images for 13CO and C18O only take channels with a signal larger than 5 σ into account. |
| In the text | |
 |
Fig. 2 Gas velocity of the circumbinary disk. Left: 13CO J = 3–2 velocity map performed using the intensity weighted method, and subtracted by the systemic velocity of 3.73 km s−1. Contours are displayed from −2.75 to 2.75 km s−1 and are spaced by 0.5 km s−1. Right: blue- and redshifted velocities (indicated by blue and red colors) along the line-of-sight compared to the Keplerian rotation, as expressed by Eq. (1). A polar ellipse represented by a black solid line denoted (1) indicates the potential presence of a anticyclonic vortex, and three spiral-like structures in black dotted-line denoted (2), (3), and (4) are superimposed. |
| In the text | |
 |
Fig. 3 Radial profiles of the velocity measured in 13CO and C18O J = 3–2 subtracted by the systemic velocity displayed for various azimuthal angles θ, spaced by 45°. The dashed line represents the Keplerian prescription following Eq. (1) for a 2.36 M⊙ binary system. The two dotted lines in the top central panel indicate the Keplerian velocity for a binary mass of 2.86 M⊙ and 1.86 M⊙. |
| In the text | |
 |
Fig. 4 Sketch describing the vortex and its parameters. Such a vortex may be located on the northern side of the disk, at a similar localization than the polar ellipse denoted (1) and drawn in the right panel of Fig. 2. |
| In the text | |
 |
Fig. 5 Comparison of the velocity deviations measured in the HD 142527 system with vortex models. Top: Difference between the 13CO J = 3–2 velocity measured from our observations and the Keplerian prescription in a 2D-map (R, θ). Blue and red colors indicate blue- and redshifted velocities along the line-of-sight compared to the Keplerian rotation. θ = 0° represents the north of the major axis. Bottom: Three vortex prescriptions with their corresponding velocity amplitude in the planeof the disk (top), rotating clockwise around the vortex center on elliptical streamlines, and the projected velocity along the line-of-sight (bottom). Model A corresponds to a large vortex centered at the position of the continuum intensity maximum and Model B an equivalent vortex centered on the secondary maximum. Model C presents the kinematic signature for two smaller vortices at these positions. |
| In the text | |
 |
Fig. 6 Artificial velocity deviations measured in a perfectly Keplerian disk compared to the observations. Top: differences between the measured 13CO J = 3–2 velocity and the Keplerian prescription in a 2D-map (R, θ). Blue and red colors indicate blue- and redshifted velocities along the line-of-sight compared to the Keplerian rotation. Middle: 13CO integrated emission. Bottom: flux ratio Iout∕Iin of the emission at the outer and inner edges of the synthesized beam. The left panel is surrounded by a red rectangle because theflux ratio is only an approximation in observations, being measured after beam smoothing. Left column shows the observations. The central and the right columns are the models convolved at a spatial resolution of 0.3 and 0.1′′. The verticalblack bar on the top-left corner of the top panels is the averaged radial spatial resolution as a function of the azimuth. |
| In the text | |
 |
Fig. 7 Velocity deviations due to the presence of dust along the north of the major axis. Top: velocity deviations measured in the pure Keplerian model at two different spatial resolutions. Middle: 13CO integrated emission and dust emission in the original non-convolved model. By definition, the integrated emission is always measured after continuum subtraction. The cavity between 150 au and 260 au is due to the continuum subtraction procedure. Bottom: flux ratio between the outer and inner edges of the synthesized beam. |
| In the text | |
 |
Fig. 8 Velocity artifacts created by a ring or horseshoe dust structure. Left panel: sketch representing the integrated gas emission over the line width as a function of the disk radius. The black solid line is the gas emission without the dust ring, and the two red lines represent the emission in presence of the dust ring before and after continuum subtraction. The two ellipses indicate the position of two synthesized beams. Right panel: line emission profile (black solid line) in the simplified case where the line emission is the sum of the emission at the inner (blue dashed line) and outer (red dashed lines) edges of the synthesized beam. The velocity vc, represented by the dotted black vertical line, is the velocity at the center of the beam while vm, represented by the solid black line, is the intensity weighted velocity. |
| In the text | |
 |
Fig. A.1 From left to right: dust emission, 13CO J = 3–2 and C18O J = 3–2 integrated emission of the 3D toy model of HD 142527. The spatial resolution is 0.3′′. |
| In the text | |
 |
Fig. B.1 Radial profiles of the velocity for different PAs θ, spaced by 45°, where θ is the angle starting from the northern major axis and rotating counterclockwise. The red curve isthe velocity measured using the intensity weighted method (mom1 in CASA) with 13CO J = 3–2. The orange and blue curves correspond to the velocity measured using the peak emission method with the 13CO J = 3–2 and C18O J = 3–2 transition lines, respectively, with the procedure detailed in Teague & Foreman-Mackey (2018). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


