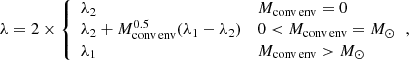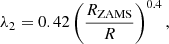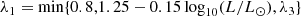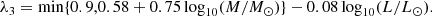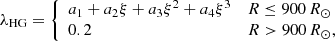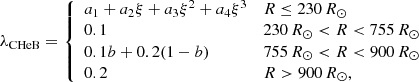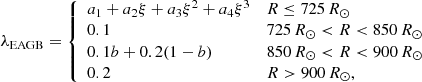| Issue |
A&A
Volume 650, June 2021
|
|
|---|---|---|
| Article Number | A107 | |
| Number of page(s) | 22 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202039992 | |
| Published online | 15 June 2021 | |
The role of mass transfer and common envelope evolution in the formation of merging binary black holes
1
Institute of Astrophysics, KU Leuven, Celestijnenlaan 200D, 3001 Leuven, Belgium
e-mail: pablo.marchant@kuleuven.be
2
Center for Interdisciplinary Exploration and Research in Astrophysics (CIERA), 1800 Sherman Ave, Evanston, IL 60201, USA
3
Laboratory of Nuclear Science, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
4
Department of Physics and Astronomy, Northwestern University, 2145 Sheridan Road, Evanston, IL 60208, USA
5
SUPA, School of Physics and Astronomy, University of Glasgow, Glasgow G12 8QQ, UK
6
Department of Physics, University of Oxford, Keble Rd, Oxford OX1 3RH, UK
7
Argelander-Institut für Astronomie der Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
Received:
25
November
2020
Accepted:
16
March
2021
As the number of merging binary black holes observed with ground-based gravitational-wave detectors grows, increasingly accurate theoretical models are required to compare them to the observed sample and disentangle contributions from multiple channels. In formation models involving isolated binary stars, important uncertainties remain regarding the stability of mass transfer and common-envelope evolution. To study some of these uncertainties, we have computed binary simulations using the MESA code consisting of a 30 M⊙ star in a low metallicity (Z⊙/10) environment with a black-hole companion. We have developed an updated prescription to compute mass transfer rates including the possibility of outflows from outer Lagrangian points, as well as a method to self-consistently determine the core-envelope boundary in cases where there is common-envelope evolution. We find that binaries survive common-envelope evolution only if unstable mass transfer happens after the formation of a deep convective envelope, resulting in a narrow range (0.2 dex) in period for successful envelope ejection. All cases where binary interaction is initiated with a radiative envelope have large binding energies (∼1050 erg), and they result in mergers during the common-envelope phase even under the assumption that all the internal and recombination energy of the envelope, as well as the energy from an inspiral, is used to eject the envelope. This is independent of whether or not helium is ignited in the core of the donor, conditions under which various rapid-population synthesis calculations assume a successful envelope ejection is possible. Moreover, we find that the critical mass ratio for instability is such that across a large range in initial orbital periods (∼1−1000 days), merging binary black holes can be formed via stable mass transfer. A large fraction of these systems undergo overflow of their L2 equipotential, in which case we find that stable mass transfer produces merging binary black holes even under extreme assumptions of mass and angular momentum outflows. Our conclusions are limited to the study of one donor mass at a single metallicity, but they suggest that population synthesis calculations overestimate the formation rate of merging binary black holes produced by common-envelope evolution and that stable mass transfer could dominate the formation rate from isolated binaries. This is in agreement with a few other recent studies. Further work is required to extend these results to different masses and metallicities as well as to understand how they can be incorporated into rapid population synthesis calculations.
Key words: binaries / close / stars: massive / stars: black holes / gravitational waves / X-rays: binaries
© ESO 2021
1. Introduction
In the last five years, the discoveries from ground-based gravitational wave (GW) detectors have driven a large effort to understand the origin of compact binary black holes (BHs). With 50 detections with a high significance (Abbott et al. 2019, 2020a), the majority of the observed GW sources correspond to binary BH mergers covering a large range of masses ∼5−100 M⊙. Important discoveries contained in the first Gravitational Wave Transient Catalog (Abbott et al. 2019) include the discovery of BHs more massive than those detected through electromagnetic observations in the Galaxy (Abbott et al. 2016) and the direct association of short gamma-ray bursts with binary neutron star mergers (Abbott et al. 2017). The increased size of the sample on the second Gravitational Wave Transient Catalog (Abbott et al. 2020a) points to additional features in the properties of merging binary BHs, indicative of the contribution of multiple formation channels (Abbott et al. 2021; Zevin et al. 2021). Accurate predictions from different formation channels are then necessary to understand their relative contributions.
A large number of formation scenarios have been proposed to form the merging binary BHs observed by ground-based detectors. Scenarios that involve binary systems include evolution through a common-envelope (CE) phase (e.g., Paczynski 1976; van den Heuvel 1976; Tutukov & Yungelson 1993; Belczynski et al. 2002; Dominik et al. 2012; Stevenson et al. 2017; Giacobbo & Mapelli 2018), chemically homogeneous evolution (Mandel & de Mink 2016; Marchant et al. 2016; de Mink & Mandel 2016; du Buisson et al. 2020; Riley et al. 2021), stable mass transfer (MT; van den Heuvel et al. 2017; Neijssel et al. 2019; Bavera et al. 2021) and Population III stars (Belczynski et al. 2004; Kinugawa et al. 2014; Inayoshi et al. 2017). Dynamical processes are also predicted to contribute to the observed sample, including isolated triple systems (Thompson 2011; Antonini et al. 2017; Vigna-Gómez et al. 2021) and interactions in globular (e.g., Kulkarni et al. 1993; Sigurdsson & Hernquist 1993; Portegies Zwart & McMillan 2000; Rodriguez et al. 2015; Di Carlo et al. 2019) and nuclear clusters (Antonini & Perets 2012). Additional formation scenarios include the pairing and growth of stellar mass BHs in the disks of active galactic nuclei (McKernan et al. 2014; Stone et al. 2017; Bartos et al. 2017), and primordial BH formation (Bird et al. 2016; Sasaki et al. 2018).
Our focus is on the formation of merging binary BHs through both CE evolution and stable MT. The majority of predicted binary BHs that formed through CE evolution or stable MT in an isolated binary involve an initial phase of stable MT. This removes the hydrogen envelope of the more massive star and leads to the formation of a wide single degenerate binary (Dominik et al. 2012; Langer et al. 2020). When the secondary evolves and thus fills its Roche lobe, depending on its response to mass loss and the mass ratio of the system, it can undergo a CE phase which ejects the envelope of the secondary at the cost of hardening the binary (cf. Belczynski et al. 2016). If the second phase of MT is stable, depending on the mass ratio of the system, a phase of nonconservative mass transfer can harden the binary without the need for CE evolution, as van den Heuvel et al. (2017) argue, thus potentially allowing for the formation of compact object binaries that can merge within a Hubble time. Recent studies have claimed that the contribution from stable mass transfer to the observed sample of merging binary BHs can be comparable or even larger than those that formed through CE evolution (Neijssel et al. 2019; Bavera et al. 2021).
However, binary evolution models have large uncertainties associated with the CE phase (see Ivanova et al. 2013 for a recent review). Important open issues include the unknown efficiency of CE evolution (Zorotovic et al. 2010; Davis et al. 2012; Toonen & Nelemans 2013), the mass boundary at which CE evolution terminates (the core-envelope boundary; Han et al. 1994; Dewi & Tauris 2000; Ivanova 2011), and the actual conditions for the onset of CE evolution (Hjellming & Webbink 1987; Soberman et al. 1997; Pavlovskii et al. 2017). Observational and theoretical constraints for the outcome of CE evolution in massive stars are also limited as the vast majority of observed post-CE systems as well as multidimensional hydrodynamical simulations of CE evolution correspond to low and intermediate-mass stars (see Iaconi & De Marco 2019 for a recent compilation of CE simulations and observed post-CE systems).
One uncertainty of CE evolution that is studied in population synthesis calculations is the impact of the evolutionary stage of the star at the onset of CE evolution. Belczynski et al. (2010) proposed that in low metallicity environments, a larger number of massive stars are expected to survive CE evolution, thus leading to an enhanced formation rate of merging binary BHs. This is argued as a consequence of halted expansion after core-hydrogen burning, with stellar models undergoing core-helium burning as blue supergiants and covering a larger range of radii after core-helium ignition. Belczynski et al. (2010) argued that interaction after core-helium ignition favors the ejection of the envelope as, at that point, a well defined core-envelope structure is formed. In various population synthesis codes, this argument is encoded in “pessimistic” and “optimistic” options for CE survival. In the pessimistic approach, all systems undergoing CE evolution before core-helium ignition are assumed to merge during CE evolution, while the optimistic approach allows for their survival. Recently, Klencki et al. (2020, 2021) have argued that this approach likely overestimates the number of merging binary BHs that formed as most of the systems predicted to survive CE in the optimistic scenario would initiate CE evolution with a radiative envelope that has a binding energy too large to eject through an inspiral.
The aim of this work is to study, in detail, how the evolutionary stage of the stellar progenitor of a BH affects MT stability and the outcomes of CE evolution. We do this by computing detailed models with the MESA code (Paxton et al. 2011, 2013, 2015, 2018, 2019) of a low metallicity massive star with a BH companion, meant to reproduce the evolution of a binary system after the formation of the first BH. Recent work on the formation of binary BHs using detailed binary evolution models (in contrast to rapid population synthesis calculations) has been presented by Eldridge & Stanway (2016) and Pavlovskii et al. (2017), covering a broad range of donor masses and metallicities. Our work, in contrast, focuses on a single donor mass of 30 M⊙ at a metallicity of Z⊙/10, but with a large resolution in the initial mass ratio and period. This allows us to study, in detail, how the stability of MT and the outcomes of CE evolution are affected by the evolutionary stage of the donor. For these calculations, we have made improvements to the commonly used MT prescription of Kolb & Ritter (1990, hereafter KR90) and implemented a method to model CE evolution which self-consistently determines the core-envelope boundary. Our methods are described in Sect. 2 and we present our results in Sect. 3. We conclude by discussing our results in Sect. 4. All input files necessary to reproduce our simulations as well as associated data products are available for download online1.
2. Methods
We performed our simulations using version 15140 of the MESA stellar evolution code. Our models consist of binary systems with a 30 M⊙ donor star and a BH companion. The objective of these simulations is to model a MT event happening after the formation of the first BH in the system, which is argued to be the most important MT phase where a CE can lead to the formation of a merging binary BH (cf. Dominik et al. 2012). Since we did not model the previous evolution of the system, we approximated the starting state of the donor star in the system as a zero-age main-sequence (ZAMS) star of its mass. Evolution was computed until either core carbon was depleted or until a merger between the donor star and the BH occurred.
Mass transfer rates were computed using the method described in Sect. 2.1, while the actual accretion rate into the BH was limited to its Eddington rate as described in Marchant et al. (2017). Our model for CE evolution is described in Sect. 2.2. Mass loss, either due to stellar winds from the donor or from mass ejected from the vicinity of the BH by MT above the Eddington limit, was assumed to take an amount of angular momentum corresponding to the specific orbital angular momentum of each component. We also accounted for the possibility of a star growing to the point that not only it overfilled its Roche lobe, but also overflowed its outer Lagrangian point. Whenever this happened, we accounted for the loss of mass and angular momentum as described in Sect. 2.1.5. Angular momentum loss from GW radiation was also included (Peters 1964), but it does not play a role in the timescales of evolution of our models which are of the order of millions of years. Our simulations do not take stellar rotation or spin-orbit coupling into account.
Our stellar models were computed at a low metallicity of Z = Z⊙/10, where we took the relative metal mass fractions from Grevesse & Sauval (1998) and the solar abundance to be Z⊙ = 0.0142 (Asplund et al. 2009). Opacities were computed using opacity tables from the OPAL project (Iglesias & Rogers 1996), together with the low temperature opacity tables of Ferguson et al. (2005). The equation of state used by MESA consists of a combination of OPAL (Rogers & Nayfonov 2002), HELM (Timmes & Swesty 2000), PC (Potekhin & Chabrier 2010), and SCVH (Saumon et al. 1995). Nuclear reaction rates were taken in order of preference from Cyburt et al. (2010) and Angulo et al. (1999).
Convection was modeled using the mixing length theory of Böhm-Vitense (1958) as described by Cox & Giuli (1968), using a mixing length parameter αMLT = 2. Convective regions were determined using the Ledoux criterion (Ledoux 1947). We included overshooting of the hydrogen burning convective core using a step-overshooting scheme, extending the size of the convective core by αov = 0.335 pressure scale heights following the calibration of Brott et al. (2011). Overshooting from other convective regions is not well understood, so for convective cores after the main-sequence, we included a small amount of exponential overshooting (Herwig 2000) given by a length scale for exponential decay of the mixing coefficient of f = 0.012. We also included semi-convective mixing (Langer et al. 1983) and thermohaline mixing (Kippenhahn et al. 1980). Following Schootemeijer et al. (2019), we adopted a large value for the efficiency parameter for semiconvection αsc = 100, while for thermohaline mixing we adopted an efficiency parameter of unity.
Stellar winds were accounted for using a combination of different mass loss rate prescriptions as described by Brott et al. (2011). This includes the line-driven mass loss rates derived by Vink et al. (2001) for stars with a hydrogen surface mass fraction of X > 0.7 and the Wolf–Rayet mass loss rate of Hamann et al. (1995) for X < 0.4, scaled by a factor of 10 to account for wind clumping (Yoon et al. 2010). For surface hydrogen mass fractions between X = 0.7 and X = 0.4, we interpolated between the rate of Vink et al. (2001) and Hamann et al. (1995) to provide a continuous transition. At temperatures below that of the bi-stability jump (as derived by Vink et al. 2001), we took the maximum between the rate of Nieuwenhuijzen & de Jager (1990) and the one resulting from the combination of the Vink et al. (2001) and Hamann et al. (1995) rates we just described. Additionally, we scaled the Nieuwenhuijzen & de Jager (1990) rate by the same factor (Z/Z⊙)0.85 predicted by Vink et al. (2001) for line-driven winds. This significantly lowers the mass loss rates of red-supergiants in low metallicity environments, although observations suggest there is only a weak dependence on metallicity (van Loon et al. 2005; Goldman et al. 2017). Nevertheless, we kept this scaling for the sake of comparison, as it is commonly used in population synthesis calculations.
2.1. Mass transfer
We modeled MT using an extension of the method developed by KR90, which accounts for MT from an extended atmosphere as described in Ritter (1988, hereafter R88) as well as the case where optically thick regions overflow the Roche lobe of the donor. In particular, this does not assume that the photosphere of the star operates as a hard rim, potentially leading to significant amounts of overflow during MT. Here we describe the method of KR90 in detail and our modifications to it, which include the possibility of outflows from the outer Lagrangian point of the donor. For the case of overflow from optically thick regions, we also discuss similarities between our method and that of Pavlovskii & Ivanova (2015).
2.1.1. The Roche potential
The computation of the MT rate depends on the Roche potential Φ, which is taken to be that of two point masses in a circular orbit:
where Md is the mass of the donor and the mass ratio is defined as q ≡ Ma/Md with Ma being the mass of the accretor. We used a coordinate system centered on the donor star (see Fig. 1), denoting distances normalized by the orbital separation a as 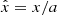 ;
; 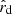 and
and 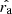 are the normalized distances of a point to the center of each star, and
are the normalized distances of a point to the center of each star, and 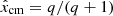 indicates the x-coordinate of the center of mass of the system. The x-coordinate of the first Lagrangian point is given by XL1. The x-coordinate of the outer Lagrangian point of the donor (which can be either L2 or L3 depending on the mass ratio) is given by XL out, which is defined as being negative. The Roche lobe radius of the system RRL is defined as the volume equivalent radius of the region below the equipotential at the first Lagrangian point ΦL1, and we used the fitting formula from Eggleton (1983) to approximate it:
indicates the x-coordinate of the center of mass of the system. The x-coordinate of the first Lagrangian point is given by XL1. The x-coordinate of the outer Lagrangian point of the donor (which can be either L2 or L3 depending on the mass ratio) is given by XL out, which is defined as being negative. The Roche lobe radius of the system RRL is defined as the volume equivalent radius of the region below the equipotential at the first Lagrangian point ΦL1, and we used the fitting formula from Eggleton (1983) to approximate it:
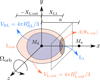 |
Fig. 1. Definition of the coordinate system and variables used in the calculation of MT. The coordinate system is centered in the donor star, with the x-axis defined as the line joining the donor and the accretor, with the accretor located at x = a where a is the orbital separation. The z-axis is oriented along the direction of the orbital angular momentum of the system, while the y-axis completes a standard right-handed oriented Cartesian set of coordinates. The Lagrangian point located behind the donor is either L3 or L2, depending on whether the donor is more or less massive than the accretor, respectively. |
Since we considered stars with significant overflow, potentially reaching the outer Lagrangian point of the donor, we also defined volume-equivalent radii beyond the equipotential of L1 by dividing space with a plane crossing L1, which is perpendicular to the line joining both stars, as depicted in Fig. 1. We refer to this plane as the L1 plane. The volume equivalent radius for an arbitrary value of Φ is then defined as V(Φ) = 4πR(Φ)3/3, where V(Φ) is the volume contained within the equipotential Φ and on the side of the L1 plane where the donor is located. In particular, we care about the radius associated with the equipotential of the outer Lagrangian point of the donor, for which we find that the following equation provides a fit with an error < 0.15% in the range of −10 < log10q < 103:
Figure 2 shows the value of RL out/RRL for different values of the mass ratio. In the limit of log10q → ±∞, we have that RL out/RRL → 1, while in the range of −1 < log10q < 1, which is typical of interacting binary stars, we find that RL out/RRL is between ∼1.2 and 1.3. Thus, a donor star growing beyond ∼20%−30% of its Roche lobe radius is expected to also fill its outer Lagrangian point.
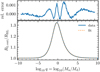 |
Fig. 2. Ratio between the volume equivalent radius associated with the outer Lagrangian point of the donor and its Roche lobe radius. Bottom panel: result from numerical integration of the Roche potential together with the fit given in Eq. (3). Top panel: relative error between the fit and the data, with the small variations being due to the finite precision of the volume calculation. |
2.1.2. Mass transfer through the L1 point
Restricting the discussion first to flows through the L1 point, the MT rate can be computed as an integral over the L1 plane,
where ρ and v are the density and velocity of the fluid in the L1 plane. The flow is assumed to be steady in which case the Bernoulli equation is satisfied,
where the integral is done along a streamline of the fluid with i and f denoting an initial and final point along a streamline. Following the work of Lubow & Shu (1975), the velocity near the Lagrangian point is expected to be equal to the sound speed. Depending on whether the photosphere of the star is inside the Roche lobe or has expanded beyond it, the flow is assumed to be isothermal (R88) or adiabatic (KR90), respectively. Combining either the adiabatic or isothermal approximation with Eq. (5) allows for the computation of ρ and v in the vicinity of the Lagrangian point as a function of the Roche potential Φ.
Either in the isothermal or adiabatic approximation, the surface integral in Eq. (4) can be expressed as an integral over the potential,
where A(Φ) is the area in the L1 plane below the equipotential Φ. Figure 1 illustrates the area A(ΦL out). The dA/dΦ term describes how the area enclosed by an equipotential in the L1 plane changes with Φ and encodes the properties of the Roche geometry. Along the L1 plane, given the symmetry of Φ and the L1 point being a local minimum, the Roche potential can be approximated as
where ΔΦ ≡ Φ − ΦL1. As shown in Appendix A, C3 = C5 = C4/2 and the value of dA/dΦ can be computed up to first order in ΔΦ as
Both R88 and KR90 approximate dA/dΦ as a constant, but as we want to consider the case where the star can significantly overfill its Roche lobe, we included the term of order ΔΦ when computing MT in the optically thick case. R88 and KR90 also rely on fits to the coefficients C1 and C2 as a function of the mass ratio. To avoid relying on fitting formulae with a limited range of validity, we directly computed the location of the L1 point, XL1, and computed all Ci coefficients explicitly from the Roche potential4. The variation of dA/dΦ with increasing overflow has also been taken into account for optically thick Roche lobe overflow (RLOF) by Pavlovskii & Ivanova (2015), but using tables with numerical integrations of the area in the L1 plane instead of a higher-order analytical approximation.
2.1.3. Optically thin mass transfer (Rph < RRL)
For the case of MT from a star with a photosphere radius Rph below its Roche lobe radius RRL, R88 considers the flow to have a constant temperature equal to Teff, in which case the relevant sound speed is the isothermal one,
where k is the Boltzmann constant, μ is the mean molecular weight, and mh is one atomic mass unit. This sound speed corresponds to the equation of an ideal gas plus radiation,
where arad is the radiation constant. We considered streamlines that start with negligible velocity from the photosphere of the star by taking vi = 0 and Φi = Φph in Eq. (5), where Φph is the value of the Roche potential at the photosphere. Combining Eqs. (5), (9), and (10), one can solve for the density of the flow at the L1 point,
where the ph and L1 subscripts indicate properties at the photosphere and the Lagrangian point.
Equation (11) can be evaluated in the vicinity of the L1 point to express the variation in density across the L1 plane as a function of the variation in Φ and v,
As for a steady flow, the L1 point operates as a nozzle, and acceleration perpendicular to the flow is expected to vanish on the L1 plane,
which combined with Eq. (12) results in dv = 0 (and thus v = vth) in the vicinity of L1.
These results can be used to evaluate the MT rate using Eq. (6). Transforming the integral into one over the density with Eq. (13) results in
As the density decays exponentially with the potential, see Eq. (11), only the regions in the very vicinity of L1 are expected to contribute to the MT rate, so we approximated dA/dΦ by its value at L1 to obtain
where M0, thin is the MT rate for a star just filling its Roche lobe,
The factor that is still required to compute the MT rate in an evolutionary code is the difference Φph − ΦL1. R88 opted to use the derivative of the potential with respect to volume equivalent radii rV covered by different equipotentials and approximated
Instead, we followed the method of Jackson et al. (2017) who developed an expansion of the Roche potential around the donor as a function of the equivalent radius rV,
with a1 and a2 given by
Using this, we computed ΦL1 with the Roche lobe radii from Eq. (2) and computed Φph using the photospheric radius of our stellar model.
In all our simulations, only a small fraction of the total MT comes from the contribution of this thin MT rate. However, it still operates as a physically motivated mechanism to smoothly turn on MT which helps prevent numerical instabilities in the calculations when a star initiates RLOF.
2.1.4. Optically thick mass transfer (Rph > RRL)
Following KR90, if layers of the star below the photosphere are overflowing the Roche lobe, then the MT rate is computed as
where Ṁthick is the contribution to the integral in Eq. (4) from the overflowing, optically thick regions,
To calculate the density and velocity of the flow at L1, we again made use of the Bernoulli equation, Eq. (5), by assuming the flow moves parallel to the equipotential surfaces and is adiabatic such that the pressure and sound speed are given along a streamline by
The constant k can be computed in terms of a reference pressure and density for each streamline, 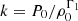 . This assumes that Γ1 is constant along the streamline; Pavlovskii & Ivanova (2015) considered the case of a variable Γ1 and found that the resulting MT rates are only modified by a few percent.
. This assumes that Γ1 is constant along the streamline; Pavlovskii & Ivanova (2015) considered the case of a variable Γ1 and found that the resulting MT rates are only modified by a few percent.
We assumed that along each equipotential surface, far from the Lagrangian point, the fluid is near hydrostatic equilibrium (dP0 ≃ −ρdΦ and v ≪ vs) and took the value of P0 and ρ0 there to compute k. Combining Eq. (22) with Eq. (5), and taking Φi = Φf, vi = 0 and vf = vs, one can compute the density of the flow in the L1 plane for a given value of ρ0,
Combining this density with Eq. (21) gives the contribution to the MT rate from the overflowing optically thick layers as
where
In our calculations, we considered P0 and ρ0 to be the density in the overflowing layers of our hydrostatic model, from which we also obtained Γ1. In this case, P(RRL) and P(Rph) are the pressure of the stellar model in the layer were R = RRL and R = Rph, respectively.
Equation (24) is exactly as derived by KR90, but in our calculations there are two important differences as to how we computed it. First, KR90 made the assumption of an ideal gas, replacing the P0/ρ0 ratio in Eq. (24) by kT/μmh. In layers dominated by radiation pressure, this underestimates the mass loss rate significantly, so we did not make this assumption and computed P0/ρ0 from our stellar model. The second difference is that we did not assume dA/dΦ to be constant, but instead evaluated it using Eq. (8), with ΔΦ being computed in the overflowing layers of the model as
2.1.5. Mass loss from the outer Lagrangian point of the donor
Models of interactive massive stars using the prescription of KR90 can exhibit radii much larger than their Roche lobe radii. In particular, in the simulations presented in this work involving a 30 M⊙ donor, we find cases where the outer Lagrangian point would overflow (R > RL out). For these cases, we need a model for the overflow from this outer Lagrangian point, which is L3 if Md > Ma and L2 otherwise.
The entire method described in Sects. 2.1.3 and 2.1.4 can be applied for an outflow through the outer Lagrangian point by replacing the Roche lobe radius with RL out using Eq. (3) and evaluating the dA/dΦ factor at the outer Lagrangian point instead of L1. However, an assumption needs to be made as to what happens to this outflow. We assume the material is ejected from the system carrying the specific angular momentum that corresponds to the outer Lagrangian point,
In order for this to be satisfied, the outflow needs to have a velocity much larger than the orbital velocity, otherwise tidal forces from the binary can modify the angular momentum content of ejected material. This has been studied in the case of overcontact binary systems that overflow the L2 point (Shu et al. 1979; Pejcha 2014; Pejcha et al. 2016) or have their stellar winds torqued as they accelerate (MacLeod & Loeb 2020). If the energy of the outflowing material is not sufficient to unbind it from the binary, it can also accumulate in a circumbinary disk.
Owing to these uncertainties, we also experimented with models where the specific angular momentum in Eq. (27) is increased by factors of 4 and 9, corresponding to points corotating with the orbit at 2 and 3 times the distance of Lout from the center of mass. However, any of our simulations that undergo stable MT while overflowing L2 or L3 should be considered with care, since this is an extreme regime where three-dimensional hydrodynamic effects become important.
2.1.6. Outflows from L2 when Ma/Md < 1
An alternative approach to the problem of large overflow in simulations was taken by Misra et al. (2020). Considering systems with neutron star accretors, they computed the equivalent radii associated with the full L2 equipotential (including both the donor and the accretor), and they assumed that whenever a stellar model exceeded this radius, then MT becomes unstable owing to the formation of an outflow with a high specific angular momentum. However, since for a compact object accretor there is not a hydrostatic structure within the Roche lobe of the accretor, the volume associated with the full L2 equipotential cannot be directly compared to the radii of a hydrostatic stellar model in order to assess overflow of the outer Lagrangian points.
Nevertheless, in cases where Md > Ma, some of the material streaming through L1 could potentially be ejected from the vicinity of L2 before the donor overflows L3. In this case, our simulations would underestimate angular momentum loss from the system, since the specific angular momentum associated with L2 can be up to 47% larger than that of L3, as is shown in Fig. 3. Figure 3 also indicates the volume equivalent radii for the donor associated with the L3 and L2 equipotentials when Ma/Md < 1, where for the donor’s L2 equivalent radius, we used the fit of Marchant et al. (2016),
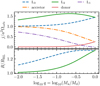 |
Fig. 3. Top: specific angular momentum in units of a2Ωorb for the donor, the accretor, and the first three Lagrangian points as a function of the mass ratio. Bottom: volume equivalent radii for the donor corresponding to the L2 and L3 equipotentials. Volume equivalent radius for L2 is taken from the fit of Marchant et al. (2016), which due to small errors in the fit results in a slightly larger value than the radius for the L3 equipotential at q = 1. |
Although for a broad range of mass ratios, the donor can expand significantly before filling out the L3 equipotential, much less expansion beyond the Roche lobe is required to fill out L2.
In order to assess potential uncertainties during phases of large overflow, where material streaming through L1 could be ejected from the vicinity of L2 when Ma/Md < 1, we also considered an alternate model. In this model, instead of accounting for overflows from the donor’s outer Lagrangian point, we assumed part of the mass streaming through L1 is ejected from L2. To do this, we computed an additional optically thin rate from Sect. 2.1.3 by replacing RRL with RL2 and evaluating dA/dΦ at L2 rather than L1. Whenever Rph > RL2, we considered the contribution to the optically thick mass transfer rate transferred through the L1 plane, but above the equipotential of L2, which is given by Eq. (24) with a modified lower interval for the integral:
Since this expression describes a flow through L1, dA/dΦ has to be evaluated at L1. We assumed both the optically thin component through L2 and the optically thick component going through L1 above the L2 equipotential are ejected from the system, taking the specific angular momentum that corresponds to the L2 point,
Similar to what was discussed in the previous section, material could be torqued or form a circumbinary disk before being ejected, so we also consider extreme cases where we increased the specific angular momentum removed by factors of 4 and 9.
The default setup of our simulations is the one described in Sect. 2.1.5, but we also performed simulations with this modified model with L2 outflows to test the robustness of our results. For simplicity, in the remainder of the manuscript we do not use the subscript 0 to refer to properties from our hydrostatic stellar models and refer to the photospheric radius of a star as R.
2.2. Common envelope evolution
Whenever our MT prescription gives a MT rate exceeding a given threshold Ṁhigh, we assume evolution proceeds through a CE phase. We treated CE evolution following the standard energy prescription (Tutukov & Yungelson 1979; Webbink 1984) which equates the binding energy of ejected layers to the difference in orbital energy product of an inspiral,
where αCE is a free parameter that represents the efficiency with which the orbital energy ejects the envelope. Using subscripts i and f to represent the pre- and post-CE properties of the system, the difference in orbital energy is
and we considered Md, f to be the core mass of the donor Mcore, while ignoring accretion into the accretor such that Ma, f = Ma, i. The binding energy depends on the value of Mcore and was computed by adding up the internal and gravitational potential energy of the removed layers at the onset of CE,
where u is the specific internal energy of the gas and we included an additional free parameter, αth, which was introduced by Han et al. (1995) to represent the efficiency with which thermal energy can be used to eject the envelope. In this work, we include the contribution of recombination energy from hydrogen and helium on u. For simplicity, we also assume αth = 1 throughout.
Computing the binding energy requires one to know Mcore, which is a nontrivial problem that can lead to large variations in the predicted binding energy (see for instance the discussion in Ivanova et al. 2013). Our goal is to determine Mcore self-consistently in our simulations by modeling the stripping of the stellar envelope. For this, at the onset of CE, we computed the value of Ebind for all choices of Mcore in the stellar model. The CE phase was then modeled by artificially removing mass from the star and computing, at each step, the binding energy one would have obtained from the pre-CE model if Mcore were assumed to be the current mass of the star. In this way, Eq. (32) can be used to determine the final orbital separation af as a function of Mcore, and the mass losing stellar model can be used to determine the point at which the star would contract inside its Roche lobe.
We did not simply force a rapid mass loss rate on our simulations until we found R < RRL, but instead softly turned off the mass loss rate as the star went inside its Roche lobe to determine the mass coordinate at which the star would be undergoing contraction in the absence of mass loss. In particular, we forced a mass loss rate from CE evolution of
where we interpolated between a high MT rate Ṁhigh, meant to reproduce a near adiabatic response, and a small MT rate, Ṁlow, which should be well below the thermal timescale of the envelope. In particular in our simulations, we chose Ṁhigh = 1 M⊙ yr−1, Ṁlow = 10−5 M⊙ yr−1, and δ = 0.02. Our choice of Ṁhigh was based on the thermal timescale of the envelope estimated as τth = Ebind/L and the associated MT rate Ṁth = M/τth. For the 30 M⊙ donor considered in this work evolved as a single star, and assuming a core-envelope boundary at the innermost point where X > 0.1 (Dewi & Tauris 2000), we find that Ṁth does not exceed 0.1 M⊙ yr−1. Similarly, our choice of Ṁlow is such that it is comparable to MT happening on a nuclear timescale. The dependence of our results on the free parameters Ṁhigh, Ṁlow, and δ is discussed in Appendix B, where we show how the outcome of some of our CE models are affected by these choices.
If the star contracts below R/RRL = 0.98, then we assumed the CE phase finished and proceeded with the evolution of the model in the standard way, applying our MT formalism described in the previous subsections. As pointed out by Ivanova (2011), a star can significantly contract during a phase of rapid mass loss, but re-expand by orders of magnitude on a few thermal timescales if mass loss is suddenly shut off. Because of this, they determined the core mass of a stellar model by performing rapid mass loss simulations and finding at which mass coordinate the resulting star would not re-expand after mass loss is shut off. In our simulations, we did find re-expansion after CE, which, according to Ivanova (2011), would indicate that the core boundary is at a deeper mass coordinate. However, but we find that the ensuing MT phase is stable when using our MT prescription.
This method is similar to the one presented by Deloye & Taam (2010) and Ge et al. (2010), who computed the adiabatic response of the stellar radii to rapid mass loss and compared it to the evolution of the Roche lobe radii in a binary to determine at which point a binary would detach. The main difference is that our method determines the mass coordinate at which detachment would happen without mass loss, capturing the nonadiabatic response of the star near the end of CE. Another similar method is the one presented by Eldridge et al. (2017), which was integrated into detailed binary evolution calculations but does not consider the contribution of thermal or recombination energy.
3. Results
In this work, we focus on the evolution of a 30 M⊙ star at a metallicity of Z⊙/10 in order to assess how some of the differences expected from evolution in low metallicity environments can affect the outcome of either MT or CE evolution. As we did not perform a broad analysis for different donor masses and metallicities, we cannot perform population synthesis to compute, for example, the resulting rates of binary BHs observable by ground-based detectors. However, this serves to assess if some of the assumptions commonly used in rapid population synthesis codes are justified. In particular, Belczynski et al. (2010) argued that for BH progenitors, ejection of the envelope during CE evolution is more likely to happen in low metallicity environments, as these systems are predicted to halt their expansion in the Hertzsprung gap (HG) before rising on the Hayashi line as red supergiants, spending a significant fraction of their core helium burning lifetime as blue supergiants. After core helium ignition, it is argued that a well defined core-envelope structure is formed, which allows for a successful envelope ejection. A halted expansion after the main sequence is a common feature in stellar evolution calculations at low metallicity (see Appendix C).
Before discussing grids of binary simulations, it is instructive to study how our 30 M⊙ donor evolves as a single star. The top panel of Fig. 4 shows the evolution in the Hertzsprung-Russell (HR) diagram for this star under the physical assumptions described in Sect. 2, for which we find that expansion is halted before becoming a red supergiant. Most of the helium-burning phase of this star would be spent as a blue supergiant with a convective envelope developing only near core helium depletion. This type of evolution is sensitive to physical assumptions in the model. In particular, Fig. 4 shows the effect of increasing overshooting during core hydrogen burning, as well as increasing wind strengths. With increased overshooting, the star undergoes rapid expansion after the main sequence and becomes a red supergiant before core helium ignition. The model with a higher mass loss rate slows down its expansion before becoming a red supergiant, but it expands to a larger radius during the HG than our default model. These variations are not captured in rapid population synthesis codes, in particular those reliant on the fits to single star evolution of Hurley et al. (2000) which are based on detailed stellar models without mass loss and with a fixed amount of overshooting. Stellar winds may be overestimated in our calculations (Björklund et al. 2021), while observations of massive stars suggest that our choice for overshooting from a convective hydrogen-burning core is underestimated for stars with masses > 15 M⊙ (Castro et al. 2014). Keeping in mind that due to uncertainties in stellar evolution, a halted expansion in the HG is uncertain, we can still study what would be the consequences in the evolution of a star if this effect is real.
 |
Fig. 4. Evolution of a 30 M⊙ single star with a metallicity of Z⊙/10, separated into different evolution phases. Dots indicate equal time intervals of 105 years. The Hertzsprung gap is defined as the evolutionary stage between the terminal-age main sequence and the moment where the ratio of the nuclear burning luminosity and the surface luminosity satisfies |log10(Lnuc/L)| < 0.001 for at least a thermal timescale estimated as GM2/RL, or the star develops a convective envelope > 1 M⊙. Top: evolution under our default set of physical inputs. Middle: evolution with core overshooting increased from 0.335 to 0.535 pressure scale heights. Bottom: evolution with wind mass loss rates tripled. |
Focusing only on our model that uses our default set of assumptions, we assessed if core helium ignition has a significant impact on the core-envelope structure of the star which could favor CE ejection. Figure 5 shows a Kippenhahn diagram for the 30 M⊙ model, indicating how the stellar radius and binding energy of the envelope evolve. Assuming that the core-envelope boundary is located at the points where the hydrogen mass fraction drops below either X = 0.1 or X = 0.3 (similar to Dewi & Tauris 2000), we find that the binding energy of the star remains at ∼1050 erg from terminal-age main sequence (TAMS) to the point where a convective envelope is developed. This happens despite a ∼30 fold increase in the stellar radius. This model experiences the formation and merger of multiple intermediate convection zones during the HG phase, so we performed convergence tests to verify that our results are not significantly affected by changes in temporal and spatial resolution during this phase (see Appendix D).
 |
Fig. 5. Kippenhahn diagram for our default 30 M⊙ model, separating different evolutionary stages as well as showing the evolution of the stellar radii. “He dep.” and “C dep.” stand for core helium and carbon depletion respectively. In addition, we show the result of computing Ebind under the assumption that the core–envelope boundary Mcore at which CE would finish is at the innermost mass coordinates where the hydrogen mass fraction is X = 0.1 or X = 0.3. We only show Ebind after the formation of the helium core, so no information is given on the main sequence. To provide a comparison point to rapid population synthesis codes, we also show the resulting Ebind from the fits of Claeys et al. (2014) and Xu & Li (2010). |
If one computes the binding energy using, for example, the fit provided by Claeys et al. (2014) rather than the structure of the model, the resulting binding energy is always underestimated, with more that an order of magnitude difference in late stages5. In particular, this fit to the binding energy is used in population synthesis calculations of GW sources, including the MOBSE (Giacobbo & Mapelli 2018) and COSMIC (Breivik et al. 2020) codes. Another parametrization of the binding energy that is used in published rapid population synthesis results is that of Xu & Li (2010), which is an option in the STARTRACK (Dominik et al. 2012) and COMPAS (Neijssel et al. 2019) codes6. In this case, we also find a consistent underestimation of the binding energy except for late stages near core-carbon burning where the envelope becomes almost fully convective. Both Claeys et al. (2014) and Xu & Li (2010) include internal energy in their fits, but not recombination energy. A systematic underestimation of the binding energy in population synthesis calculations implies an overestimation of post-CE orbital separations, or a prediction of successful envelope ejection in systems that would merge during CE. We also compared the binding energies of our models with different overshooting and wind strengths to the results obtained from the Claeys et al. (2014) and Xu & Li (2010) fits, and find that the fits consistently underestimate the binding energy of the envelope as well (see Fig. 6). Binding energies computed using the Xu & Li (2010) fit experience a jump when the star transitions out of the HG, which for the track with extra overshooting does not happen until the star begins to rise in the Hayashi line.
 |
Fig. 6. Binding energy of the envelope of a 30 M⊙ post main-sequence star as a function of radius. Tracks are shown for our default set of physical assumptions, as well as for a model with increased overshooting and one with increased mass loss rates. For each model, we also show the binding energy resulting from the fits of Xu & Li (2010) and Claeys et al. (2014). |
The constancy of the binding energy while the star expands with a radiative envelope is also illustrated by Fig. 7, which shows the full binding energy profiles at different evolutionary phases. In particular, between the end of the HG and the point where a deep convective envelope starts to develop, the radius of the star increases by more than an order of magnitude, but this expansion only happens in the outermost mass layers of the star. It is only after the formation of the convective envelope that a large fraction of the envelope mass is pushed to large radii with correspondingly low binding energies that would make envelope ejection during CE feasible. All of this points to the ignition of helium at the stellar core having no impact on the binding energy of the envelope, and also since the ignition of helium does not modify the mode of energy transport in the outer layers, the stability of MT should not be impacted in a fundamental way either.
 |
Fig. 7. Radius (top) and binding energy (bottom) profiles for a 30 M⊙ single star at different evolutionary stages. A profile near the end of core helium-burning (Yc = 0.08), but before the formation of a convective envelope, is included. Also, a profile is shown corresponding to the beginning of the formation of a deep convective envelope, taken as the first point in the evolution where the mass of the convective envelope Mconv env is larger than 1 M⊙. |
The near constancy and high value of the binding energy before the formation of a convective envelope has also been studied by Kruckow et al. (2016) and Klencki et al. (2021) comprehensively, covering a large range of masses and metallicities. However, the binding energies computed by Kruckow et al. (2016) and Klencki et al. (2021) as well as those shown in Fig. 5 rely on an assumed boundary for the core mass. By performing binary simulations using the method described in Sect. 2.2 to determine the core-envelope boundary self-consistently, we can verify if these computed binding energies with an assumed boundary are a good approximation.
3.1. Grid of simulations
Using our prescription for MT and our method to calculate the outcome of CE evolution, we computed a grid of models consisting of a 30 M⊙ donor with a BH accretor in a circular orbit. Our method for CE evolution still leaves the efficiency αCE as a free parameter, and we computed simulations with both αCE = 1, 0.4, 0.2, and 0.1. The grid spans a period range between −0.3 < log10(Pi/d) < 3.5 and initial mass ratios q = MBH/M1, i between 0.01 and 0.59. This includes BHs with masses as low as 0.3 M⊙ that are not expected to form through stellar evolution, but they were included to test the limits of MT stability. This allowed us to cover the entire parameter space where CE happens, as well as to cover systems from the boundary of RLOF at ZAMS, to effectively single star evolution at large periods. Owing to the small amount of radial expansion occurring in the phases where the star has a convective envelope, we adopted two different resolutions in the period for our grid. For log10(Pi/d) < 3.2, we used a spacing of Δlog10(Pi/d) = 0.1, while at higher initial orbital periods we increased the resolution in the period to Δlog10(Pi/d) = 0.01. The resolution in mass ratio of the grid is Δq = 0.02.
The final outcomes of our grid with αCE = 1 are shown in Fig. 8. As a simple approximation to determine if a simulation can produce a merging binary BH, for stars that reach core carbon depletion we assumed the donor star collapses directly to form a BH with a mass equal to its baryonic mass. Our 30 M⊙ donor produces final helium core masses ∼14 M⊙, for which the formation of a BH through direct collapse is indeed expected (Fryer 1999). From our simulations, we did not find any cases of successful envelope ejection from CE evolution for initial orbital periods below log10(Pi/d) < 3.2. Below this period range, the boundary between systems undergoing stable MT and those merging during CE evolution varies continuously with the period, going from q ∼ 0.5 for systems interacting close to ZAMS, down to q ∼ 0.15 for cases where interaction happens right before the formation of a deep convective envelope. The boundary is not sensitive to whether an interaction happens before or after the TAMS, or before or after the end of the HG. This is to be expected as the radial response to rapid mass loss is dependent on the mode of energy transport in the stellar envelope (Hjellming & Webbink 1987), and the envelope of the star across all these phases is radiative. Pavlovskii et al. (2017) also find stable MT between a star and a BH for such extreme mass ratios for different donor masses, but owing to their coarse mass ratio sampling (no more than three different mass ratios for each donor mass), they cannot describe in detail how the boundary for stability shifts with the initial orbital period.
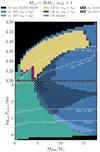 |
Fig. 8. Summary of final outcomes for simulations of circular binaries consisting of a BH and a 30 M⊙ star at a metallicity of Z⊙/10, and a CE efficiency parameter αCE = 1. Horizontal dotted lines indicate boundaries for an interaction before different evolutionary stages of the star. For systems that undergo stable MT, black horizontal lines indicate regions where the donor exceeded the L2 equipotential, while cross hatched regions mark regions where also the L3 equipotential is exceeded. Black rectangles indicate systems that do not interact or would result in a Roche lobe filling system at ZAMS. Systems that undergo stable MT or eject their envelope during CE evolution are denoted by “st. MT” and “CE ej.”, respectively, and they are separated into systems forming binary BHs that would merge in less or more than a Hubble time. Systems marked as “CE merger” merge during the CE phase. |
The lack of systems surviving CE evolution between the end of the HG and the formation of a deep convective envelope can be understood in terms of the binding energy of the envelope. As was discussed for the single 30 M⊙ model, the binding energy during this phase is ∼1050 erg. Considering evolution between the end of the HG and the formation of a convective envelope, we find that CE evolution only happens for BH masses ≲5 M⊙, and that stripping the hydrogen envelope of the 30 M⊙ star would result in a ∼14 M⊙ helium core. For these masses and assuming a fully efficient use of the orbital energy to eject the envelope, in order to release 1050 erg, the orbital separation needs to be reduced below 1.3 R⊙, an orbit for which a helium star of 14 M⊙ would overfill its Roche lobe. Population synthesis calculations that underestimate the binding energy during this phase and find successful CE ejection, for example, by using fits such as those of Claeys et al. (2014) or by assuming a fixed value of the λ parameter, potentially overestimate the rate of formation of merging binary BHs through CE evolution (Gallegos-Garcia et al., in prep.).
The boundary for unstable MT is also right at the place where it allows for a narrow band of systems undergoing stable MT that produce a binary BH merging in less than a Hubble time. In this case, the shrinkage of the orbit from stable MT is sufficient to produce a compact BH binary (van den Heuvel et al. 2017), and we find this outcome for a wide range of initial orbital periods ranging from 1 to 1000 days. Multiple systems undergoing stable MT fill their outer Lagrangian point during that process, but remain stable despite the increased angular momentum loss. For wider orbital periods, where MT occurs after the development of a deep convective envelope, the critical mass ratio for stability shifts upwards (up to q ∼ 0.5 for systems interacting after core helium depletion). The majority of our models with an assumed efficiency of αCE = 1 that manage to eject their envelopes during CE evolution result in wide BH binaries, for which GW radiation is insufficient to produce a merger in less than a Hubble time. Figure 9 shows the outcome of our simulations with CE efficiencies of αCE = 0.4, 0.2, and 0.1, in which case we find that most systems that produce wide binary BHs at αCE = 1 would merge during CE evolution rather than produce merging binary BHs at lower efficiencies.
One important concern in our simulations that form merging binary BHs through stable MT is that an important fraction of these undergo overflow of L2 or even L3. The methods we have developed to account for this are necessarily an approximation, as they rely on hydrostatic one-dimensional stellar models. Moreover, the simulations shown in Fig. 8 do not account for potential outflows through L2 when Ma < Md, which could remove significant mass and angular momentum from the system. Using the alternate method described in Sect. 2.1.6 for L2 outflows, we can test if the systems that form merging binary BHs through stable MT are sensitive to the potential presence of such outflows. Figure 10 shows simulations done using this method that cover the region where we find that stable MT leads to merging binary BHs, including cases where we assume that the specific angular momentum removed by material outflowing L2 is up to nine times the specific angular momentum of the L2 point. Compared to our simulations that only account for overflow of the outer Lagrangian point of the donor, we find that the boundary for instability is pushed to higher BH masses. However, we still find systems across a large range of periods that form merging binary BHs, as additional angular momentum losses lead to the formation of more compact binaries post-MT. Given this, the conclusion that stable MT can lead to the formation of merging binary BHs across a large range of periods appears to be robust.
 |
Fig. 10. Same as Fig. 8, but for a subset of models computed using the method described in Sect. 2.1.6 that considers outflows from L2 rather than L3 when Ma < Md. Each panel indicates simulations performed with different specific angular momentum assumed for the material outflowing through L2, which is considered to be jL2, 4jL2, or 9jL2. The purple dotted line indicates the boundary between stable MT and CE evolution as determined by our models that account only for outflows from the outer Lagrangian point of the donor. |
As our models do not include the evolution prior to the formation of the first BH, we cannot assess the relative likelihood of each of our individual simulations to occur in nature. However, if we make the simplistic assumption that after BH formation the orbital period is distributed flat in log10P and the mass ratio distribution is flat in q, our grid with αCE = 1 gives a ratio between the number of merging binary BHs that formed through CE evolution to those that formed via stable MT of 0.017. The actual outcome of our simulations for systems surviving CE evolution should be considered with care, since we approximated a complex three-dimensional phenomenon with one-dimensional hydrostatic models. However, even under the extreme case that all our systems that survive CE evolution would produce a binary BH that merges in less than a Hubble time, we find that the ratio between merging binary BHs that formed through CE evolution to those that formed via stable MT is 0.35. This resembles the results from population synthesis calculations of Neijssel et al. (2019), who find that depending on the metallicity distribution of the star formation history, most merging binary BHs that will be observed by current generation GW detectors at design sensitivity would have been formed through stable MT. Our results suggest that the yield of merging binary BHs from CE evolution is overestimated at low metallicities, which would further increase the relative contribution of stable MT relative to CE evolution in population synthesis calculations such as those of Neijssel et al. (2019).
3.2. Mass transfer and outer Lagrangian point overflow
We consider here two cases from our simulation grid that lead to the formation of a merging binary BH: a system interacting before the end of HG (MBH = 7.5 M⊙, Pi = 31.6 days) and one interacting after it (MBH = 4.5 M⊙, Pi = 1000 days). The short period system evolves without overflowing its outer Lagrangian point, while the long period one is expected to overflow it, so we can use it to study how the resulting outcome is modified when accounting for this on our MT prescription. To evaluate the impact of the changes we have made to the MT prescription of (KR90), we used four different setups for our simulations:
-
A full implementation of our MT prescription including overflows from the outer Lagrangian point as described in Sect. 2.1.5.
-
Same as 1, but without the assumption P/ρ = kT/μmH made in KR90 (see the discussion in Sect. 2.1.4)
-
Same as 1, but considering the area term dA/dΦ to be constant and ignoring the term linear in ΔΦ of Eq. (8).
-
Using the prescription of KR90 without modification and without outflows from the outer Lagrangian point.
Figure 11 shows the evolution in the HR diagram for both the Pi = 31.6 day and Pi = 1000 day system using our updated MT prescription. In both cases, MT first proceeds rapidly, stripping the majority of the hydrogen envelope in a few thousand years, followed by a longer phase (∼105 yr) driven by the evolution of the core during core-helium burning. In both cases, MT lowers the mass of the donor to ∼13 M⊙ and carbon is depleted while still undergoing RLOF. The 31.6 day system depletes carbon while still retaining hydrogen in its surface (surface mass fraction of Xs = 0.40), with a radius of 8.1 R⊙ and an orbital period of 1.8 days. After it first interacts, the 1000 day system always remains near or at RLOF, reaching carbon depletion with a surface hydrogen mass fraction Xs = 0.36, a radius of 7.5 R⊙, and an orbital period of 1.5 days. The resulting binary BHs have large delay times for a merger due to GW radiation, with the 31.6 day system being expected to merge after 6.4 Gyr and the 1000 day systems after 6.0 Gyr.
 |
Fig. 11. Evolution in the HR diagram for a 30 M⊙ donor star in two systems leading to the formation of a merging binary BH through stable MT. Dots in the tracks indicate intervals of 105 years, while thicker lines indicate periods of RLOF. |
Focusing on the 31.6 day system, which we do not predict to overflow its outer Lagrangian point, Fig. 12 shows the evolution of the MT rate and the Roche filling factor with the variations to the MT prescription described before. For our updated prescription, and in the absence of outflows from the outer Lagrangian point, the computed MT rate is expected to be higher than that of KR90. This is because dropping the assumption of P/ρ = kT/μmH of KR90 and accounting for the linear term in dA/dΦ increases the value of the integrand in Eq. (24). As shown in Fig. 12, we do find that both of these assumptions result in a lower MT rate and a higher amount of RLOF compared to our full MT scheme. This is very noticeable in the slower second MT phase, where our new MT prescription predicts a maximum Roche filling factor of R/RRL = 1.16, while the standard prescription from KR90 reaches R/RRL = 1.37 during this phase. For this example system, we find that the largest difference from the KR90 prescription comes from dropping the assumption that P/ρ = kT/μmH, while the contribution of the linear term in dA/dΦ has a much smaller impact. Without our updated MT prescription, the KR90 prescription predicts that the system overflows its outer Lagrangian point.
 |
Fig. 12. Evolution of the MT rate and overflow for a system with a 30 M⊙ donor star, a 7.5 M⊙ BH, and an initial orbital period of 31.6 days. Top: ratio of the computed MT rate under different assumptions, compared to the result from our full MT prescription. Middle: ratio of the stellar radius to the Roche lobe radius and to the volume equivalent radius of the L2 and L3 equipotentials (for the L2 equipotential, we only include the results of our default model for ease of visualization). Bottom: MT rate. |
The case for the 1000 day system, which undergoes overflow of its outer Lagrangian point in our model, is shown in Fig. 13. In this case, we also find that our updated prescription keeps the star significantly more compact, with the KR90 prescription reaching a Roche filling factor of R/RRL = 1.48, while our model reaches R/RRL = 1.34. With the updated MT scheme, the donor reaches an overflow of the outer Lagrangian point of R/RL out = 1.04, resulting in an outflow from L3 that at its maximum accounts for less than 9% of the total mass loss rate of the star. Since most mass is still transferred through L1, the additional angular momentum loss from mass loss through L3 only produces a small change in the final orbital separation, with the model using the prescription of KR90 resulting in a final orbital period of 1.6 days compared to the 1.5 day result when using our updated MT prescription. For this binary system, we find that during overflow of the outer Lagrangian point including the linear term in dA/dΦ has an effect comparable to that of assuming P/ρ = kT/μmH. As discussed in Appendix A, it is indeed expected that the linear term in dA/dΦ has a larger impact on mass outflows through L3 than from L1.
 |
Fig. 13. Same as Fig. 12, but for a system with a 30 M⊙ star with a 4.5 M⊙ BH companion at an initial orbital period of 1000 days. |
As the specific angular momentum that would be carried by material being ejected through the outer Lagrangian point is uncertain (we assume by default that it corresponds to the location of the Lagrangian point), we also repeated the 1000 day simulation but increased the angular momentum loss rate associated with this effect by factors of 4 and 9. In both cases, we still find the system to be stable, but they result in much shorter final periods of 1.2 day and 0.83 day. This corresponds to delay times of 3.6 Gyr and 1.2 Gyr, compared to the 6.0 Gyr delay time for our default model. This additional uncertainty could then allow for stable MT to produce systems with short delay times, where tidal spin-up can result in a high spin second formed BH (cf. Bavera et al. 2020). Another potential source of mass and angular momentum loss is the occurrence of L2 outflows when Ma < Md for which our default model does not account. For the 100 day system, we find that the donor slightly overfills the L2 equipotential, exceeding the L2 equivalent radius by 0.2%. This small amount of overflow is not expected to play a significant role, and indeed in our experiments with L2 outflows shown in Fig. 10, we do not see an important difference. For the 1000 day simulation, however, our default model overflows the L2 equivalent radius by 21%. Due to this, in the simulations with L2 outflows shown in Fig. 10, we find that the outcome is sensitive to potential outflows through L2, resulting in CE evolution and a merger if the specific angular momentum of material ejected through L2 is large.
In summary, we find that our modifications to the MT prescriptions of R88 and KR90 do not have a significant effect on the MT rate or the final masses after MT concludes. The changes, however, do affect the size of the donor through the MT phase, resulting in more compact stars with less overflow during MT. Systems where we predict overflow of the outer Lagrangian point result in smaller orbital periods than when using the prescriptions of R88 and KR90, but we do not find that the additional source of angular momentum loss has a significant impact on the stability of these systems.
3.3. Common envelope in donors with convective envelopes
To illustrate the result of our simulations that survive CE evolution, we consider a particular model that results in successful ejection in both our αCE = 1 and αCE = 0.1 grids, which has a 30 M⊙ star with a 14.1 M⊙ BH in an initial orbit of 2344 days. This model undergoes RLOF after core helium depletion and the evolution of their stellar and Roche lobe radii is shown in Fig. 14 for both CE efficiencies considered. Before the onset of RLOF, wind mass loss reduces the mass of the donor to 28.2 M⊙ and before hitting the threshold value of Ṁhigh = 1 M⊙ yr−1 at which we started modeling the system as a CE, the mass of the donor is reduced to 24.7 M⊙. The onset of CE happens after the star slightly overflows its outer Lagrangian point (R/RL out = 1.08), at which point our MT prescription predicts 53% of the mass to be lost by the star going through L3. During the CE calculation, we artificially removed the mass and adjusted the separation according to the binding energy of the removed layers, resulting in a sharper decrease in mass of the Roche lobe radius for the lower CE efficiency. The stellar radius remained larger than 103 R⊙ until the mass of the star was lowered below 15 M⊙, at which point the radius began to decrease sharply with the mass. The point at which we found detachment without any enforced mass loss from CE, see Eq. (34), varies with efficiency, with the αCE = 1 simulation detaching at a mass of 14.3 M⊙ and the αCE = 0.1 model detaching at 13.7 M⊙.
 |
Fig. 14. Evolution of the radius and Roche lobe radius for two models undergoing successful envelope ejection from CE evolution. Both models correspond to a simulation of a 30 M⊙ star with a 14.1 M⊙ BH with an initial orbital period of 2344 days, with the only difference between the simulations being the efficiency of CE, αCE = 1 or 0.1. The shaded blue region indicates pre-CE evolution which is identical for both cases. For each case, empty circles denote the moment our algorithm determines that CE evolution would end as the star contracts within its Roche lobe in the absence of mass loss from CE evolution. |
Figure 15 shows the binding energy profiles of the star at different phases of evolution. Between the beginning of RLOF and the onset of CE evolution, the donor loses ∼3 M⊙ of mass which modifies the binding energy of the convective envelope but not of the deeper layers. The binding energy of the ejected envelope changes significantly between the αCE = 1 and αCE = 0.1 simulations with Ebind = −3.9 × 1047 erg and Ebind = −4.3 × 1048 erg, respectively. For the fully efficient simulation, all ejected mass formed part of the convective envelope at the onset of CE. This factor of about 10 difference on the binding energy, coupled with the factor of 10 difference in CE efficiency leads to very different outcomes post-CE. The αCE = 1 simulation terminates CE evolution with an orbital separation of 570 R⊙, while the αCE = 0.1 simulation finishes CE with an orbital separation of 8.4 R⊙. As discussed by Deloye & Taam (2010), the core-envelope boundary is not uniquely defined, resulting in different values depending on the mass ratio and efficiency of the process. One caveat of our simulations is that the amount of mass loss previous to CE evolution is sensitive to our choice of Ṁhigh, which modifies the binding energy of the outer layers of the star (see Appendix B). This modifies the post-CE separation for systems we predict to remain wide, such as the α = 1 system discussed here. Accurate predictions for these wide post-CE models requires a better description of how the star transitions from stable MT to CE evolution.
 |
Fig. 15. Binding energy profiles of the donor in a system with an initial mass of 30 M⊙ and a BH companion of 14.1 M⊙ at an orbital period of 2344 days. Profiles are shown at RLOF, at the onset of CE evolution, and after detachment from CE for αCE = 1 and 0.1. Vertical lines indicate the final mass after CE evolution at the two efficiencies considered. |
After detachment, for both efficiencies we find that the donor undergoes a thermal pulse and re-expands, filling its Roche lobe but undergoing stable MT rather than developing a CE again. Figure 16 shows the evolution in the HR diagram both before and after CE evolution. For the case of fully efficient CE evolution, during this additional phase of MT the star would appear as an extended blue or yellow supergiant with a surface hydrogen mass fraction of Xs ∼ 0.4. The duration of this MT phase for the case of αCE = 1 is ∼2000 years, during which mass is transferred at a rate above the Eddington limit of the 14.1 M⊙ BH companion. For the αCE = 0.1 case, the donor star has a radius of just 2 R⊙ with a surface hydrogen mass fraction of Xs ∼ 0.3, and it transfers mass at super-Eddington rates for ∼800 years. Given that the Eddington luminosity of a 14.1 M⊙ BH is ∼2 × 1039 erg s−1, during this final MT phase the system can potentially appear as an ultra-luminous X-ray source (see Kaaret et al. 2017 for a recent review), but owing to the short time before core carbon depletion, the number of observable sources could be negligible compared to those that formed by other evolutionary pathways.
 |
Fig. 16. HR diagram showing the evolution of a system undergoing CE evolution composed of a 30 M⊙ donor with a 14.1 M⊙ BH companion at an initial period of 2344 days. Results are shown for two values of the efficiency of CE evolution, αCE = 1 and αCE = 0.1, with the evolution prior to CE being identical. |
Not all our simulations that survive CE evolution have short lifetimes as X-ray sources. For the system we have discussed so far, this is the case because CE evolution happens after core helium depletion. If we consider a system with a 7.5 M⊙ BH at an initial orbital period of 2000 days and αCE = 1, we find that the onset of CE happens when the donor has a central helium mass fraction of Yc = 0.02, and for the entirety of its post-CE lifetime until core carbon depletion (26 000 years), it is a Roche-lobe filling binary. This matches the results of Quast et al. (2019) who argue that post-CE systems can undergo MT on the nuclear timescale of the donor. We expect that in cases where the star does not halt its expansion in the HG, CE evolution is initiated with a much larger value of Yc, leading to a longer lifetime as an X-ray source post-CE.
The single model we considered with different values of αCE illustrates how the binding energy is dependent on the efficiency of CE evolution, but using the models from our grid we can see how the resulting binding energy of systems surviving CE evolution depends on the mass ratio as well. Figure 17 illustrates the binding energy as a function of the radius at RLOF resulting from models at three different initial mass ratios, αCE = 1, and varying initial orbital periods. For most of these simulations, we find that CE evolution terminates near or above the mass coordinate of the bottom of the convective envelope at RLOF, resulting in binding energies < 1048 erg. These low binding energies are below those predicted by the fits of Xu & Li (2010) and Claeys et al. (2014), although for a mass ratio of q = 0.17 we find binary models with binding energies between the value of these two fits. The q = 0.17 simulations with binding energies > 1048 erg behave similarly to the simulation with αCE = 0.1 shown in Fig. 15, where the binary only detaches after removing layers with a high binding energy that were radiative at the onset of CE evolution. This results in an order of magnitude variation of the binding energy with a varying mass ratio.
 |
Fig. 17. Binding energy of the envelope of a star with an initial mass of 30 M⊙ as a function of the radius at RLOF. Solid lines indicate the results from our αCE = 1 grid with three different mass ratios q = 0.17, 0.29, and 0.45. Dotted lines show the binding energy at a given radius deduced from a single star model, including the results obtained with the fit of Xu & Li (2010), the fit of Claeys et al. (2014), and assuming the bottom of the envelope to be at X = 0.1, X = 0.3, or to correspond to the bottom of the convective envelope. Symbols indicate whether the binary undergoes RLOF before or after core helium depletion. |
3.4. Common envelope in donors with radiative envelopes
As all of our simulations where CE evolution is triggered for a star with a radiative envelope are expected to merge during CE evolution, we cannot properly define a core-envelope boundary to compute the binding energy. However, we can artificially produce systems that eject their outer envelope by using artificially high values of αCE. Here, we consider systems consisting of a 30 M⊙ donor and a 3 M⊙ BH with initial orbital periods between 101 days and 103 days, and values of αCE of 10 and 20. The low mass of the BH, which would fall in the putative lower BH mass gap (Özel et al. 2010; Farr et al. 2011; Kreidberg et al. 2012; Abbott et al. 2020b), was chosen such that MT would be unstable across the range of chosen orbital periods.
All of these simulations managed to eject their envelopes during CE evolution, and Fig. 18 shows the resulting masses post-CE as well as the binding energy of the ejected layers. We find that CE terminates when the surface hydrogen mass fraction is relatively high (X ∼ 0.4−0.5) and that the binding energy of the envelope varies between 1.3 × 1050 erg and 6.6 × 1049 erg, a factor of 2 variation despite a change by a factor of 20 in radius at RLOF. Figure 18 also illustrates that whether RLOF occurs before or after the end of the HG has no impact on the binding energy. Estimating the binding energy using either the Claeys et al. (2014) or Xu & Li (2010) fits would underestimate the binding energy of the envelope for all these simulations. Since the binding energy just changes by a factor of 2 despite over an order of magnitude change in the radius of the star, population synthesis calculations that approximate Ebind using a fixed value of the dimensionless λ parameter cannot reproduce the variation of Ebind with radius, independent of the choice of λ.
 |
Fig. 18. Properties after CE evolution for the case of donor stars with a radiative envelope, with artificially high values of αCE = 10, 20 in order to allow for a successful CE ejection. Simulations correspond to binary systems composed of a star with a ZAMS mass of 30 M⊙ and a BH companion of 3 M⊙, with periods ranging from 101 days to 103 days. Results are shown as a function of the radius of the star when it fills its Roche lobe. Top panel: central helium mass fraction Yc at the onset of CE, showing RLOF before and after the end of the HG as a large drop in Yc. Second panel: surface hydrogen mass fraction after envelope ejection. Third panel: stellar mass after envelope ejection, also showing the mass of the helium core defined as the innermost mass coordinate with Y > 0.01. Bottom panel: binding energy of the ejected envelope, as well as the binding energy that would be predicted by the Claeys et al. (2014) and Xu & Li (2010) fits, and the one corresponding to λ = 1. |
4. Discussion
We have studied the outcomes from the interaction of low-metallicity massive stars with a companion BH using detailed binary evolution calculations performed with the MESA code. Our simulations, which consist of a 30 M⊙ low-metallicity donor with a companion BH, show several features relevant to understand the formation of merging binary BHs through both stable MT and CE evolution. For these simulations, we have also updated the MT prescription developed by KR90, including the possibility of overflow from an outer Lagrangian point, and we also implemented a method to self consistently determine the core-envelope boundary in cases of CE evolution. The main conclusions we derive from our simulations are as follows:
-
Stable MT after the formation of the first BH in a binary can produce merging binary BHs for a broad range of orbital periods. The boundary between stable and unstable MT is located at a point that allows for orbital hardening just from stable MT, without requiring a CE phase (van den Heuvel et al. 2017). This includes cases where MT between the star and the first formed BH is initiated during the main sequence. We also find cases where the low density envelope of the donor would overflow its outer Lagrangian point. Using our model to quantify this outflow, we find that binaries can remain stable despite the high specific angular momentum of this outflow, resulting in more compact binaries after MT than if the process is ignored.
-
We do not find any case of CE evolution initiated with a star with a radiative envelope where the envelope is successfully ejected. Between the TAMS and the start of the rise in the Hayashi line, the binding energy of the envelope remains at ∼1050 erg, varying by just a factor of two despite an increase of more than an order of magnitude in radius. Before the formation of a deep convective envelope, we find that the prescriptions of Xu & Li (2010), as developed by Dominik et al. (2012) for M > 20 M⊙, and Claeys et al. (2014) underestimate the binding energy of the envelope by up to an order of magnitude.
-
The parameter space where systems can survive CE is limited to a small range in the initial orbital period (∼0.2 dex) where RLOF happens after the formation of a deep convective envelope. Assuming that all internal and recombination energy as well as all the energy from inspiral during CE is used to eject the envelope, we find that the majority of these systems surviving CE would form binary BHs too wide to merge within a Hubble time.
-
As in Deloye & Taam (2010), we find that the core-envelope boundary is not uniquely defined, with different CE efficiencies (or similarly, different mass ratios) resulting in different binding energies for the envelope. In particular for the case discussed in Sect. 2.2, we computed binding energies that differ by over an order of magnitude depending on the efficiency of CE evolution. This is in contrast to the way binding energies are determined in population synthesis codes, where a star has a uniquely defined binding energy at each point of its evolution.
-
Under the simple assumption of a flat distribution in the mass ratio and a flat distribution in log P after the formation of the first BH, we find that stable MT would dominate the formation rate of merging binary BHs. If we consider CE efficiency to be 100%, the ratio of binaries surviving CE evolution (independent of whether they form a compact or wide binary BH) to those that form merging binary BHs from stable MT is 0.35. This is further reduced to 0.017 if we take only the CE simulations that produce merging binary BHs. This is in significant contradiction with rapid population synthesis calculations that predict the vast majority (> 90%) of BHs are formed via an initial phase of stable MT before the formation of the first BH, followed by a CE phase when the secondary fills its Roche lobe (cf. Table 4 of Dominik et al. 2012).
These results broadly agree with those of Klencki et al. (2020, 2021), who have used single star models with a fixed definition of the core-envelope boundary to propose that current population synthesis calculations may overestimate the production rate of merging binary BHs from CE evolution. Since our simulations are restricted to a 30 M⊙ donor at Z = Z⊙/10, it is necessary to further explore different masses and metallicities to understand how generally our conclusions apply (Gallegos-Garcia et al., in prep.). Recent investigations using rapid population synthesis codes have indicated that given current uncertainties in binary evolution such as the cosmic star formation rate (Neijssel et al. 2019) or the critical mass ratio for stable MT (Andrews et al. 2020), stable MT could be an important production channel for the merging binary BHs observed with gravitational waves. Our results indicate these rapid population synthesis calculations still significantly overestimate the number of systems surviving CE evolution at low metallicities, and accounting for this would further reduce the contribution from the CE evolution channel.
As we find that the boundary between stable and unstable MT is located right at a point that allows for the formation of merging binary BHs via stable MT, any uncertainties that can shift this boundary can have a large effect on the number and properties of expected GW sources. Among such uncertainties, we can point out that our simulations do not include stellar rotation or tidal coupling to the orbit. This additional sink of orbital angular momentum can potentially affect the stability of MT in our calculations. We have explicitly checked in our stable MT simulations that the moment of inertia of the star is too low to undergo the Darwin instability (Darwin 1879), which is the limit were tidal coupling leads to a runaway shrinkage of the orbit. Another important simplification is that we did not account for the effect of the companion in the momentum equation, which would make the adiabatic response of the star to mass loss dependent on the mass ratio of the system and its separation. It has also been argued that hydrodynamics need to be considered to assess the stability of MT for giant donors (Pavlovskii & Ivanova 2015), although a consistent treatment of hydrodynamics needs to consider the perturbation to the gravitational potential from the companion star as well. Additionally, a significant number of the systems we predict that form merging binary BHs also undergo overflow of the L2 and even the L3 equipotentials. Although for these large overflow cases, we have verified that merging binary BHs are formed even under extreme assumptions of mass and angular momentum outflows, three-dimensional hydrodynamic studies are required to accurately model outflows in such systems. All these uncertainties need to be studied in detail to determine if stable MT can indeed produce merging binary BHs.
Our simulations for the outcome of CE evolution also have important uncertainties. Although we do not have the core-envelope mass boundary as a free parameter, we still have the CE efficiency as an unknown variable. The efficiency can be reduced by radiative processes or also by a surplus of energy being removed as kinetic energy from the system (cf. Nandez & Ivanova 2016). Within the context of one-dimensional stellar models, it might be possible to constrain the efficiency of the CE process by means of simplified hydrodynamical simulations of the inspiral (Taam et al. 1978; Clayton et al. 2017; Fragos et al. 2019) or, ideally, with full three-dimensional simulations of CE evolution in massive stars (Taam & Sandquist 2000; Ricker et al. 2019; Law-Smith et al. 2020). Despite these uncertainties that significantly affect the outcome of systems that survive CE evolution, we consider our conclusion that massive stars would merge when undergoing CE prior to the formation of a convective envelope as much more certain. We find this result for the case of full efficiency for the CE process, including recombination energy. Our method to determine the core-envelope boundary can also be considered to produce a lower bound on the binding energies. If we were to consider the boundary deeper inside down at the point where thermal pulses would not happen post-CE (Ivanova 2011), we would find larger binding energies and less systems surviving CE evolution.
Our simulations do not exclude CE evolution as an efficient mechanism to form merging binary neutron stars. At lower masses, a larger fraction of the stellar expansion of a star during its lifetime happens after the formation of a deep convective envelope (Fig. 19). This results in a broader range of orbital periods where we expect the ejection of a CE to be possible, leading to binaries compact enough to merge from GW radiation. Following the work of Misra et al. (2020), the boundaries for stable MT between a star and a neutron star companion do not allow for stars massive enough to form a second neutron star in the system. This excludes stable MT as a formation channel for merging neutron stars. The case of MT and CE evolution in the case of neutron star companions will be studied in future work.
 |
Fig. 19. Radial evolution of single stars of various masses at a metallicity of Z⊙/10 modeled until core-carbon depletion. Numbers above each track indicate the mass of the model in solar masses, and symbols indicate different stages in the evolution of the star. The color of the tracks indicates the fraction of the hydrogen envelope that is part of an outer convective zone. |
In practice, since mixing length theory predicts no mixing at the edge of a convective region, overshooting in MESA is specified by a pair of variables f and f0, where f0 determines a distance in units of pressure scale heights into the convective region, from which the mixing coefficient from overshooting is computed. For step overshooting, we took f = 0.345 and f0 = 0.01, while for exponential overshooting we used f = 0.01 and f0 = 0.005.
To construct this fit, we numerically computed both RRL and RL out for a wide range of mass ratios, without using the Eggleton (1983) approximation as it has an error of ∼1% for some mass ratios. However, for consistency, when we evaluate RL out in the simulations in this work, we use Eq. (3) together with the fit of Eggleton (1983) to ensure that RL out > RRL.
R88 defines a function F(q) in their Eq. (A8), which contains the product C1C2, and provides a fit for this function. The expression provided by R88 has a typo which is corrected in Eq. (A3) of KR90. Despite this typographical error in R88, we have verified that the fit to F(q) provided in Eq. (A9) of R88 matches the correct expression.
Claeys et al. (2014) provide fits for the dimensionless λ parameter, which is defined as Ebind = G(M − Mcore)M/λR, where Mcore is the core mass that would remain after CE. We computed the corresponding binding energy by assuming that Mcore is the helium core mass of our model. A description of how we computed these λ fits from our stellar models is given in Appendix E.
The Xu & Li (2010) fits only cover masses up to 20 M⊙. For higher masses, Dominik et al. (2012) requested additional models and performed fits to these. Although the fitting formulae are not given in Dominik et al. (2012), they can be found on the publicly available source code of the COMPAS code at github.com/TeamCOMPAS/COMPAS/
Acknowledgments
We thank the referee for detailed feedback on our work. PM acknowledges support from the FWO junior postdoctoral fellowship No. 12ZY520N. M.G.-G. is grateful for the support from the Ford Foundation Predoctoral Fellowship. CPLB is supported by the CIERA Board of Visitors Professorship. VK is supported by a Senior CIERA Fellowship and by Northwestern University. PM thanks Alina Istrate for useful discussion.
References
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016, Phys. Rev. Lett., 116, 061102 [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2017, Phys. Rev. Lett., 119, 161101 [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2019, Phys. Rev. X, 9, 031040 [Google Scholar]
- Abbott, R., Abbott, T. D., Abraham, S., et al. 2020a, ArXiv e-prints [arXiv:2010.14527] [Google Scholar]
- Abbott, R., Abbott, T. D., Abraham, S., et al. 2020b, ApJ, 896, L44 [Google Scholar]
- Abbott, R., Abbott, T. D., Abraham, S., et al. 2021, ApJ, 913, L7 [CrossRef] [Google Scholar]
- Andrews, J. J., Cronin, J., Kalogera, V., Berry, C., & Zezas, A. 2020, AAS J., submitted [arXiv:2011.13918] [Google Scholar]
- Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [Google Scholar]
- Antonini, F., & Perets, H. B. 2012, ApJ, 757, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Antonini, F., Toonen, S., & Hamers, A. S. 2017, ApJ, 841, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Bartos, I., Kocsis, B., Haiman, Z., & Márka, S. 2017, ApJ, 835, 165 [CrossRef] [Google Scholar]
- Bavera, S. S., Fragos, T., Qin, Y., et al. 2020, A&A, 635, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bavera, S. S., Fragos, T., Zevin, M., et al. 2021, A&A, 647, A153 [CrossRef] [EDP Sciences] [Google Scholar]
- Belczynski, K., Kalogera, V., & Bulik, T. 2002, ApJ, 572, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Belczynski, K., Bulik, T., & Rudak, B. 2004, ApJ, 608, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Belczynski, K., Dominik, M., Bulik, T., et al. 2010, ApJ, 715, L138 [NASA ADS] [CrossRef] [Google Scholar]
- Belczynski, K., Holz, D. E., Bulik, T., & O’Shaughnessy, R. 2016, Nature, 534, 512 [Google Scholar]
- Bird, S., Cholis, I., Muñoz, J. B., et al. 2016, Phys. Rev. Lett., 116, 201301 [NASA ADS] [CrossRef] [Google Scholar]
- Björklund, R., Sundqvist, J. O., Puls, J., & Najarro, F. 2021, A&A, 648, A36 [EDP Sciences] [Google Scholar]
- Böhm-Vitense, E. 1958, Z. Astrophys., 46, 108 [Google Scholar]
- Breivik, K., Coughlin, S., Zevin, M., et al. 2020, ApJ, 898, 71 [CrossRef] [Google Scholar]
- Brott, I., de Mink, S. E., Cantiello, M., et al. 2011, A&A, 530, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castro, N., Fossati, L., Langer, N., et al. 2014, A&A, 570, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claeys, J. S. W., Pols, O. R., Izzard, R. G., Vink, J., & Verbunt, F. W. M. 2014, A&A, 563, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clayton, M., Podsiadlowski, P., Ivanova, N., & Justham, S. 2017, MNRAS, 470, 1788 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, J. P., & Giuli, R. T. 1968, Principles of Stellar Structure (New York: Gordon and Breach) [Google Scholar]
- Cyburt, R. H., Amthor, A. M., Ferguson, R., et al. 2010, ApJS, 189, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Darwin, G. H. 1879, Proc. R. Soc. Lond., 29, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, P. J., Kolb, U., & Knigge, C. 2012, MNRAS, 419, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Deloye, C. J., & Taam, R. E. 2010, ApJ, 719, L28 [CrossRef] [Google Scholar]
- de Mink, S. E., & Mandel, I. 2016, MNRAS, 460, 3545 [Google Scholar]
- Dewi, J. D. M., & Tauris, T. M. 2000, A&A, 360, 1043 [NASA ADS] [Google Scholar]
- Di Carlo, U. N., Giacobbo, N., Mapelli, M., et al. 2019, MNRAS, 487, 2947 [NASA ADS] [CrossRef] [Google Scholar]
- Dominik, M., Belczynski, K., Fryer, C., et al. 2012, ApJ, 759, 52 [NASA ADS] [CrossRef] [Google Scholar]
- du Buisson, L., Marchant, P., Podsiadlowski, P., et al. 2020, MNRAS, 499, 5941 [Google Scholar]
- Eggleton, P. P. 1983, ApJ, 268, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Eldridge, J. J., & Stanway, E. R. 2016, MNRAS, 462, 3302 [NASA ADS] [CrossRef] [Google Scholar]
- Eldridge, J. J., Stanway, E. R., Xiao, L., et al. 2017, PASA, 34, e058 [NASA ADS] [CrossRef] [Google Scholar]
- Farr, W. M., Sravan, N., Cantrell, A., et al. 2011, ApJ, 741, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [Google Scholar]
- Fragos, T., Andrews, J. J., Ramirez-Ruiz, E., et al. 2019, ApJ, 883, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Fryer, C. L. 1999, ApJ, 522, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Ge, H., Hjellming, M. S., Webbink, R. F., Chen, X., & Han, Z. 2010, ApJ, 717, 724 [NASA ADS] [CrossRef] [Google Scholar]
- Giacobbo, N., & Mapelli, M. 2018, MNRAS, 480, 2011 [NASA ADS] [CrossRef] [Google Scholar]
- Goldman, S. R., van Loon, J. T., Zijlstra, A. A., et al. 2017, MNRAS, 465, 403 [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [Google Scholar]
- Hamann, W.-R., Koesterke, L., & Wessolowski, U. 1995, A&A, 299, 151 [NASA ADS] [Google Scholar]
- Han, Z., Podsiadlowski, P., & Eggleton, P. P. 1994, MNRAS, 270, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z., Podsiadlowski, P., & Eggleton, P. P. 1995, MNRAS, 272, 800 [Google Scholar]
- Herwig, F. 2000, A&A, 360, 952 [NASA ADS] [Google Scholar]
- Hjellming, M. S., & Webbink, R. F. 1987, ApJ, 318, 794 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley, J. R., Pols, O. R., & Tout, C. A. 2000, MNRAS, 315, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley, J. R., Tout, C. A., & Pols, O. R. 2002, MNRAS, 329, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Iaconi, R., & De Marco, O. 2019, MNRAS, 490, 2550 [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Inayoshi, K., Hirai, R., Kinugawa, T., & Hotokezaka, K. 2017, MNRAS, 468, 5020 [NASA ADS] [CrossRef] [Google Scholar]
- Ivanova, N. 2011, ApJ, 730, 76 [Google Scholar]
- Ivanova, N., Justham, S., Chen, X., et al. 2013, A&ARv, 21, 59 [Google Scholar]
- Izzard, R. G. 2004, PhD Thesis, University of Cambridge [Google Scholar]
- Jackson, B., Arras, P., Penev, K., Peacock, S., & Marchant, P. 2017, ApJ, 835, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Kaaret, P., Feng, H., & Roberts, T. P. 2017, ARA&A, 55, 303 [Google Scholar]
- Kinugawa, T., Inayoshi, K., Hotokezaka, K., Nakauchi, D., & Nakamura, T. 2014, MNRAS, 442, 2963 [NASA ADS] [CrossRef] [Google Scholar]
- Kippenhahn, R., Ruschenplatt, G., & Thomas, H.-C. 1980, A&A, 91, 175 [NASA ADS] [Google Scholar]
- Klencki, J., Nelemans, G., Istrate, A. G., & Pols, O. 2020, A&A, 638, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klencki, J., Nelemans, G., Istrate, A. G., & Chruslinska, M. 2021, A&A, 645, A54 [EDP Sciences] [Google Scholar]
- Kolb, U., & Ritter, H. 1990, A&A, 236, 385 [NASA ADS] [Google Scholar]
- Kreidberg, L., Bailyn, C. D., Farr, W. M., & Kalogera, V. 2012, ApJ, 757, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Kruckow, M. U., Tauris, T. M., Langer, N., et al. 2016, A&A, 596, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kulkarni, S. R., Hut, P., & McMillan, S. 1993, Nature, 364, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, N., Fricke, K. J., & Sugimoto, D. 1983, A&A, 126, 207 [NASA ADS] [Google Scholar]
- Langer, N., Schürmann, C., Stoll, K., et al. 2020, A&A, 638, A39 [CrossRef] [EDP Sciences] [Google Scholar]
- Law-Smith, J. A. P., Everson, R. W., Ramirez-Ruiz, E., et al. 2020, AAS J., submitted [arXiv:2011.06630] [Google Scholar]
- Ledoux, P. 1947, ApJ, 105, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Lubow, S. H., & Shu, F. H. 1975, ApJ, 198, 385 [Google Scholar]
- MacLeod, M., & Loeb, A. 2020, ApJ, 902, 85 [CrossRef] [Google Scholar]
- Mandel, I., & de Mink, S. E. 2016, MNRAS, 458, 2634 [NASA ADS] [CrossRef] [Google Scholar]
- Marchant, P., Langer, N., Podsiadlowski, P., Tauris, T. M., & Moriya, T. J. 2016, A&A, 588, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marchant, P., Langer, N., Podsiadlowski, P., et al. 2017, A&A, 604, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McKernan, B., Ford, K. E. S., Kocsis, B., Lyra, W., & Winter, L. M. 2014, MNRAS, 441, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Meynet, G., Maeder, A., Schaller, G., Schaerer, D., & Charbonnel, C. 1994, A&AS, 103, 97 [Google Scholar]
- Misra, D., Fragos, T., Tauris, T. M., Zapartas, E., & Aguilera-Dena, D. R. 2020, A&A, 642, A174 [CrossRef] [EDP Sciences] [Google Scholar]
- Nandez, J. L. A., & Ivanova, N. 2016, MNRAS, 460, 3992 [Google Scholar]
- Neijssel, C. J., Vigna-Gómez, A., Stevenson, S., et al. 2019, MNRAS, 490, 3740 [NASA ADS] [CrossRef] [Google Scholar]
- Nieuwenhuijzen, H., & de Jager, C. 1990, A&A, 231, 134 [NASA ADS] [Google Scholar]
- Özel, F., Psaltis, D., Narayan, R., & McClintock, J. E. 2010, ApJ, 725, 1918 [NASA ADS] [CrossRef] [Google Scholar]
- Paczynski, B. 1976, in Structure and Evolution of Close Binary Systems, eds. P. Eggleton, S. Mitton, & J. Whelan, IAU Symp., 73, 75 [Google Scholar]
- Pavlovskii, K., & Ivanova, N. 2015, MNRAS, 449, 4415 [NASA ADS] [CrossRef] [Google Scholar]
- Pavlovskii, K., Ivanova, N., Belczynski, K., & Van, K. X. 2017, MNRAS, 465, 2092 [NASA ADS] [CrossRef] [Google Scholar]
- Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
- Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
- Paxton, B., Schwab, J., Bauer, E. B., et al. 2018, ApJS, 234, 34 [Google Scholar]
- Paxton, B., Smolec, R., Schwab, J., et al. 2019, ApJS, 243, 10 [Google Scholar]
- Pejcha, O. 2014, ApJ, 788, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Pejcha, O., Metzger, B. D., & Tomida, K. 2016, MNRAS, 455, 4351 [Google Scholar]
- Peters, P. C. 1964, Phys. Rev., 136, 1224 [Google Scholar]
- Pols, O. R., Schröder, K.-P., Hurley, J. R., Tout, C. A., & Eggleton, P. P. 1998, MNRAS, 298, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Portegies Zwart, S. F., & McMillan, S. L. W. 2000, ApJ, 528, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Potekhin, A. Y., & Chabrier, G. 2010, Contrib. Plasma Phys., 50, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Quast, M., Langer, N., & Tauris, T. M. 2019, A&A, 628, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ricker, P. M., Timmes, F. X., Taam, R. E., & Webbink, R. F. 2019, IAU Symp., 346, 449 [Google Scholar]
- Riley, J., Mandel, I., Marchant, P., et al. 2021, MNRAS, 505, 663 [CrossRef] [Google Scholar]
- Ritter, H. 1988, A&A, 202, 93 [NASA ADS] [Google Scholar]
- Rodriguez, C. L., Morscher, M., Pattabiraman, B., et al. 2015, Phys. Rev. Lett., 115, 051101 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, F. J., & Nayfonov, A. 2002, ApJ, 576, 1064 [Google Scholar]
- Sasaki, M., Suyama, T., Tanaka, T., & Yokoyama, S. 2018, Class. Quant. Grav., 35, 063001 [NASA ADS] [CrossRef] [Google Scholar]
- Saumon, D., Chabrier, G., & van Horn, H. M. 1995, ApJS, 99, 713 [Google Scholar]
- Schootemeijer, A., Langer, N., Grin, N. J., & Wang, C. 2019, A&A, 625, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shu, F. H., Lubow, S. H., & Anderson, L. 1979, ApJ, 229, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Sigurdsson, S., & Hernquist, L. 1993, Nature, 364, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Soberman, G. E., Phinney, E. S., & van den Heuvel, E. P. J. 1997, A&A, 327, 620 [NASA ADS] [Google Scholar]
- Stevenson, S., Vigna-Gómez, A., Mandel, I., et al. 2017, Nat. Commun., 8, 14906 [NASA ADS] [CrossRef] [Google Scholar]
- Stone, N. C., Metzger, B. D., & Haiman, Z. 2017, MNRAS, 464, 946 [NASA ADS] [CrossRef] [Google Scholar]
- Taam, R. E., & Sandquist, E. L. 2000, ARA&A, 38, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Taam, R. E., Bodenheimer, P., & Ostriker, J. P. 1978, ApJ, 222, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Tang, J., Bressan, A., Rosenfield, P., et al. 2014, MNRAS, 445, 4287 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, T. A. 2011, ApJ, 741, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Timmes, F. X., & Swesty, F. D. 2000, ApJS, 126, 501 [Google Scholar]
- Toonen, S., & Nelemans, G. 2013, A&A, 557, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tutukov, A., & Yungelson, L. 1979, in Mass Loss and Evolution of O-Type Stars, eds. P. S. Conti, & C. W. H. De Loore, 83, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Tutukov, A. V., & Yungelson, L. R. 1993, MNRAS, 260, 675 [NASA ADS] [CrossRef] [Google Scholar]
- van den Heuvel, E. P. J. 1976, in Structure and Evolution of Close Binary Systems, eds. P. Eggleton, S. Mitton, & J. Whelan, IAU Symp., 73, 35 [NASA ADS] [CrossRef] [Google Scholar]
- van den Heuvel, E. P. J., Portegies Zwart, S. F., & de Mink, S. E. 2017, MNRAS, 471, 4256 [NASA ADS] [CrossRef] [Google Scholar]
- van Loon, J. T., Cioni, M.-R. L., Zijlstra, A. A., & Loup, C. 2005, A&A, 438, 273 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vigna-Gómez, A., Toonen, S., Ramirez-Ruiz, E., et al. 2021, ApJ, 907, L19 [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Webbink, R. F. 1984, ApJ, 277, 355 [Google Scholar]
- Xu, X.-J., & Li, X.-D. 2010, ApJ, 716, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, S.-C., Woosley, S. E., & Langer, N. 2010, ApJ, 725, 940 [NASA ADS] [CrossRef] [Google Scholar]
- Zevin, M., Bavera, S. S., Berry, C. P. L., et al. 2021, ApJ, 910, 152 [Google Scholar]
- Zorotovic, M., Schreiber, M. R., Gänsicke, B. T., & Nebot Gómez-Morán, A. 2010, A&A, 520, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Computation of d A/dΦ
The coefficients of the quadratic terms in the Taylor expansion of Eq. (7) are given by
and the coefficients of the quartic terms are
When we consider outflows from the outer Lagrangian point of the donor, 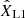 is switched by the normalized x-coordinate of the outer Lagrangian point,
is switched by the normalized x-coordinate of the outer Lagrangian point, 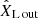 , which, with our definition, has a negative value.
, which, with our definition, has a negative value.
In order to estimate the area on the plane crossing L1 for a given ΔΦ, it is useful to use cylindrical coordinates y = ϖ sin θ, z = ϖ cos θ, in which case
where γ ≡ C1sin2θ + C2cos2θ. This can be integrated to obtain the area A(Φ),
which after differentiation by Φ gives Eq. (8).
The relative importance of the constant and linear terms for dA/dΦ shown in Eq. (8) can be assessed by using the ratio of dA/dΦ(ΔΦ = 0) and d2A/dΦ2(ΔΦ = 0). This essentially quantifies how large ΔΦ needs to be to produce a significant change in dA/dΦ, with smaller values indicating a higher sensitivity to ΔΦ, and thus a larger importance of the higher-order term. Figure A.1 shows this value at different mass ratios both for the L1 and Lout points of a star. This value is always positive, indicating that the inclusion of the higher-order term results in an increased value of the computed MT rate. We also see that the value of the ratio is much smaller for the outer Lagrangian point, and in the case where the donor is the more massive component in the binary, a variation of Φ on the order of 0.1 GMd/a can modify dA/dΦ significantly. This points out that the inclusion of the higher-order term has a larger impact on the computation of outflows from the outer Lagrangian point than from L1.
 |
Fig. A.1. Ratio of dA/dΦ to d2A/dΦ2 at L1 and at the outer Lagrangian point of a star expressed in units of GMd/a. |
Appendix B: Dependence on numerical parameters of CE algorithm
As our algorithm to model CE evolution has various numerical parameters, it is important to evaluate in detail how our results depend upon these. Here we modify the three parameters described in Sect. 2.2: Ṁhigh, Ṁlow, and δ, for which in our default model we used 1 M⊙ yr−1, 10−5 M⊙ yr−1, and 0.02, respectively. Here, we consider the difference in the outcome of the CE simulations shown in Sect. 3.3 for variations in these three parameters, with the properties of the system post-CE being shown in Table B.1. For all parameters, we find only ∼5% variations in the post-CE properties, except for variations of Ṁhigh when using an efficiency αCE = 1. Detachment in these systems happens in the proximity of the mass coordinate from the bottom of the convective envelope at the onset of CE. Variations in Ṁhigh modifies the mass of the star at the onset of CE, as is shown in Table B.1. This modifies the binding energy in the outermost layers, which is illustrated in Fig. B.1, making evolution sensitive to the exact point at which we switched between MT and CE evolution. This is not the case for the system with αCE = 0.1, as the core-envelope boundary is computed to be deeper in the star, in layers that are not affected by the exact point at which we switched between MT and CE evolution.
 |
Fig. B.1. Binding energy profiles of the donor in a system with an initial mass of 30 M⊙ and a BH companion of 14.1 M⊙ at an orbital period of 2344 days. Profiles are shown at RLOF and at the onset of CE evolution for different values of Ṁhigh. Symbols indicate the mass coordinate at which CE evolution terminates for each choice of Ṁhigh and for CE efficiencies of αCE = 1 and αCE = 0.1. |
Variation in the outcome of our CE simulations with respect to the numerical parameters of the model.
Appendix C: Comparison to other stellar evolution tracks
A comparison of our single metal-poor 30 M⊙ model to similar stellar evolution tracks that are publicly available is shown in Fig. C.1. These include tracks by Meynet et al. (1994), Pols et al. (1998), Tang et al. (2014), and Klencki et al. (2020). Out of these, the only ones that use the same stellar evolution code are our own models and those of Klencki et al. (2020). From the models of Meynet et al. (1994), we took the 25 M⊙ stellar track which is the closest one to 30 M⊙. The track taken from Pols et al. (1998) corresponds to their models with overshooting, and the one from Klencki et al. (2020) is from their set of nonrotating stellar tracks. All tracks experience a long-lived phase as blue supergiants, halting their rapid expansion in the HG phase at log10(Teff/K) ∼ 4.2 (except the lower mass one from Meynet et al. 1994 that does so at a higher Teff).
 |
Fig. C.1. Evolution of stars with a mass of ∼30 M⊙ and a metallicity of Z⊙/10 computed by different research groups and codes. Dots are plotted every 105 years. |
Appendix D: Single star resolution test
Given the formation of multiple intermediate convection zones in our models during the HG phase, we performed a resolution test to see if our results are significantly modified by increased spatial and temporal resolution. We made use of the mesh_delta_coeff and time_delta_coeff options that allow for an approximate scaling of all spatial and temporal resolution controls, and used models with approximately two, four, and eight times the resolution of our default setup. The resulting tracks in the HR diagram are shown in Fig. D.1. We see small variations with changes in resolution on the evolution during the HG phase, producing a variation of about 10% on the effective temperature at which the HG phase ends.
 |
Fig. D.1. Evolution in the HR diagram of a single 30 M⊙ model with a metallicity of Z⊙/10 computed with increasing spatial and temporal resolution. For each track, we indicate the average number of zones in the model as well as the steps taken in the simulation. The lowest resolution track shown corresponds to our default setup. |
In particular, for this work we are interested in how the binding energy of the envelope of a star compares to prescriptions present in the literature. Figure D.2 shows the binding energies obtained for models at increasing temporal and spatial resolution, as well as the results we obtain with the Xu & Li (2010) and Claeys et al. (2014) fits. Binding energies were computed from the stellar models taking the bottom of the envelope at the innermost mass coordinate where X > 0.1 and X > 0.3. Between the different models, we see variations in the computed binding energies at a given radius smaller than 12%. The larger variations happen at the end of the HG and are due to the slightly different radii achieved at the end of the HG. Ignoring the values between log10(R/R⊙) = 1.8−1.95, we find that the differences are smaller than 6%.
 |
Fig. D.2. Binding energy of the envelope of a post-main-sequence 30 M⊙ model with a metallicity of Z⊙/10 computed with increasing spatial and temporal resolution. For each track we indicate the average number of zones in the model as well as the steps taken in the simulation. The lowest resolution track shown corresponds to our default setup. For comparison, we include the binding energies obtained using our default resolution together with the fits of Xu & Li (2010) and Claeys et al. (2014). Before the formation of a convective envelope, the binding energies computed at X = 0.1 and X = 0.3 almost overlap. |
Appendix E: Application of λ fits to stellar models
The fits from Claeys et al. (2014) and Xu & Li (2010) depend on the mass of the star, its radius, and its evolutionary stage in terms of the star-types defined by Hurley et al. (2002). A model analogous to our 30 M⊙ model is assigned types “HG” during the HG, “CHeB” during core helium burning but before ascending the Hayashi line, and “EAGB” while on the Hayashi line. To distinguish between the CHeB and EAGB types in our models, we considered models with convective envelopes > 1 M⊙ to be of type EAGB, as we found this is close to the point where the star rises on the Hayashi line. As we are only concerned with these three assigned types, we only describe the fits associated with them.
E.1. Claeys et al. (2014)
The fits of Claeys et al. (2014) were first presented by Izzard (2004), who took them directly from the source code of the BSE code (Hurley et al. 2002). Claeys et al. (2014) do not specify the range of masses used to compute these fits. The fit for λ including internal but not recombination energy is
where
with RZAMS being the radius of the stellar model at the ZAMS. The value of λ1 is given by
with
This fixes a typo (0.9 instead of −0.9 in the minimum function) from Claeys et al. (2014) and Izzard (2004) that is inconsistent with the implementation in the BSE code from which the fit was taken. Claeys et al. (2014) also describe variations in the λ1 and λ3 values for stellar types that are not relevant for our 30 M⊙ model, so we do not describe those.
E.2. Xu & Li (2010)
The λ fits of Xu & Li (2010) cover up to a mass of 20 M⊙, while fits for higher masses were developed by Dominik et al. (2012). These fits are not published, but can be found in the source code of the COMPAS code. Fits are provided for the binding energy with and without thermal energy included, that is αth = 0 or 1 in Eq. (33). As we worked with αth = 1, we compared our results to the λ fit including thermal energy. Fits are provided individually for each of the HG, CHeB, and EAGB phases, and the ones that correspond to our 30 M⊙ model at Z⊙/10 are the Population II fits for masses 18 M⊙ < M < 35 M⊙. For HG stars λ is computed as
where ξ = R/R⊙ and the value of the fitting coefficients is given in Table E.1. For CHeB stars we have
Fitting coefficients for the λ fits of Xu & Li (2010) including thermal energy, as implemented by Dominik et al. (2012) for Population II stars with masses 18 M⊙ < M < 35 M⊙.
with the expression for the range 755 R⊙ < R < 900 R⊙ being a linear interpolation from 0.1 to 0.2 with b = (900 − ξ)/(900−755). For the case of EAGB stars the fit is given by
where b = (900 − ξ)/(900−850).
All resulting values are capped between 0.05 and 1.5. The interpolation in the range 755 R⊙ − 900 R⊙ for CHeB stars is missing in the implementation of Dominik et al. (2012), and it erroneously applies the fitting polynomial in this range resulting in negative values, producing a positive value only because the final result is capped to a minimum of 0.05. Not including this correction and having λ = 0.05 in this range of radii does not change our conclusions, as the binding energy is still underestimated compared to our own models.
All Tables
Variation in the outcome of our CE simulations with respect to the numerical parameters of the model.
Fitting coefficients for the λ fits of Xu & Li (2010) including thermal energy, as implemented by Dominik et al. (2012) for Population II stars with masses 18 M⊙ < M < 35 M⊙.
All Figures
 |
Fig. 1. Definition of the coordinate system and variables used in the calculation of MT. The coordinate system is centered in the donor star, with the x-axis defined as the line joining the donor and the accretor, with the accretor located at x = a where a is the orbital separation. The z-axis is oriented along the direction of the orbital angular momentum of the system, while the y-axis completes a standard right-handed oriented Cartesian set of coordinates. The Lagrangian point located behind the donor is either L3 or L2, depending on whether the donor is more or less massive than the accretor, respectively. |
| In the text | |
 |
Fig. 2. Ratio between the volume equivalent radius associated with the outer Lagrangian point of the donor and its Roche lobe radius. Bottom panel: result from numerical integration of the Roche potential together with the fit given in Eq. (3). Top panel: relative error between the fit and the data, with the small variations being due to the finite precision of the volume calculation. |
| In the text | |
 |
Fig. 3. Top: specific angular momentum in units of a2Ωorb for the donor, the accretor, and the first three Lagrangian points as a function of the mass ratio. Bottom: volume equivalent radii for the donor corresponding to the L2 and L3 equipotentials. Volume equivalent radius for L2 is taken from the fit of Marchant et al. (2016), which due to small errors in the fit results in a slightly larger value than the radius for the L3 equipotential at q = 1. |
| In the text | |
 |
Fig. 4. Evolution of a 30 M⊙ single star with a metallicity of Z⊙/10, separated into different evolution phases. Dots indicate equal time intervals of 105 years. The Hertzsprung gap is defined as the evolutionary stage between the terminal-age main sequence and the moment where the ratio of the nuclear burning luminosity and the surface luminosity satisfies |log10(Lnuc/L)| < 0.001 for at least a thermal timescale estimated as GM2/RL, or the star develops a convective envelope > 1 M⊙. Top: evolution under our default set of physical inputs. Middle: evolution with core overshooting increased from 0.335 to 0.535 pressure scale heights. Bottom: evolution with wind mass loss rates tripled. |
| In the text | |
 |
Fig. 5. Kippenhahn diagram for our default 30 M⊙ model, separating different evolutionary stages as well as showing the evolution of the stellar radii. “He dep.” and “C dep.” stand for core helium and carbon depletion respectively. In addition, we show the result of computing Ebind under the assumption that the core–envelope boundary Mcore at which CE would finish is at the innermost mass coordinates where the hydrogen mass fraction is X = 0.1 or X = 0.3. We only show Ebind after the formation of the helium core, so no information is given on the main sequence. To provide a comparison point to rapid population synthesis codes, we also show the resulting Ebind from the fits of Claeys et al. (2014) and Xu & Li (2010). |
| In the text | |
 |
Fig. 6. Binding energy of the envelope of a 30 M⊙ post main-sequence star as a function of radius. Tracks are shown for our default set of physical assumptions, as well as for a model with increased overshooting and one with increased mass loss rates. For each model, we also show the binding energy resulting from the fits of Xu & Li (2010) and Claeys et al. (2014). |
| In the text | |
 |
Fig. 7. Radius (top) and binding energy (bottom) profiles for a 30 M⊙ single star at different evolutionary stages. A profile near the end of core helium-burning (Yc = 0.08), but before the formation of a convective envelope, is included. Also, a profile is shown corresponding to the beginning of the formation of a deep convective envelope, taken as the first point in the evolution where the mass of the convective envelope Mconv env is larger than 1 M⊙. |
| In the text | |
 |
Fig. 8. Summary of final outcomes for simulations of circular binaries consisting of a BH and a 30 M⊙ star at a metallicity of Z⊙/10, and a CE efficiency parameter αCE = 1. Horizontal dotted lines indicate boundaries for an interaction before different evolutionary stages of the star. For systems that undergo stable MT, black horizontal lines indicate regions where the donor exceeded the L2 equipotential, while cross hatched regions mark regions where also the L3 equipotential is exceeded. Black rectangles indicate systems that do not interact or would result in a Roche lobe filling system at ZAMS. Systems that undergo stable MT or eject their envelope during CE evolution are denoted by “st. MT” and “CE ej.”, respectively, and they are separated into systems forming binary BHs that would merge in less or more than a Hubble time. Systems marked as “CE merger” merge during the CE phase. |
| In the text | |
 |
Fig. 9. Same as Fig. 8, but for CE efficiency parameters of αCE = 0.4, 0.2, and 0.1. |
| In the text | |
 |
Fig. 10. Same as Fig. 8, but for a subset of models computed using the method described in Sect. 2.1.6 that considers outflows from L2 rather than L3 when Ma < Md. Each panel indicates simulations performed with different specific angular momentum assumed for the material outflowing through L2, which is considered to be jL2, 4jL2, or 9jL2. The purple dotted line indicates the boundary between stable MT and CE evolution as determined by our models that account only for outflows from the outer Lagrangian point of the donor. |
| In the text | |
 |
Fig. 11. Evolution in the HR diagram for a 30 M⊙ donor star in two systems leading to the formation of a merging binary BH through stable MT. Dots in the tracks indicate intervals of 105 years, while thicker lines indicate periods of RLOF. |
| In the text | |
 |
Fig. 12. Evolution of the MT rate and overflow for a system with a 30 M⊙ donor star, a 7.5 M⊙ BH, and an initial orbital period of 31.6 days. Top: ratio of the computed MT rate under different assumptions, compared to the result from our full MT prescription. Middle: ratio of the stellar radius to the Roche lobe radius and to the volume equivalent radius of the L2 and L3 equipotentials (for the L2 equipotential, we only include the results of our default model for ease of visualization). Bottom: MT rate. |
| In the text | |
 |
Fig. 13. Same as Fig. 12, but for a system with a 30 M⊙ star with a 4.5 M⊙ BH companion at an initial orbital period of 1000 days. |
| In the text | |
 |
Fig. 14. Evolution of the radius and Roche lobe radius for two models undergoing successful envelope ejection from CE evolution. Both models correspond to a simulation of a 30 M⊙ star with a 14.1 M⊙ BH with an initial orbital period of 2344 days, with the only difference between the simulations being the efficiency of CE, αCE = 1 or 0.1. The shaded blue region indicates pre-CE evolution which is identical for both cases. For each case, empty circles denote the moment our algorithm determines that CE evolution would end as the star contracts within its Roche lobe in the absence of mass loss from CE evolution. |
| In the text | |
 |
Fig. 15. Binding energy profiles of the donor in a system with an initial mass of 30 M⊙ and a BH companion of 14.1 M⊙ at an orbital period of 2344 days. Profiles are shown at RLOF, at the onset of CE evolution, and after detachment from CE for αCE = 1 and 0.1. Vertical lines indicate the final mass after CE evolution at the two efficiencies considered. |
| In the text | |
 |
Fig. 16. HR diagram showing the evolution of a system undergoing CE evolution composed of a 30 M⊙ donor with a 14.1 M⊙ BH companion at an initial period of 2344 days. Results are shown for two values of the efficiency of CE evolution, αCE = 1 and αCE = 0.1, with the evolution prior to CE being identical. |
| In the text | |
 |
Fig. 17. Binding energy of the envelope of a star with an initial mass of 30 M⊙ as a function of the radius at RLOF. Solid lines indicate the results from our αCE = 1 grid with three different mass ratios q = 0.17, 0.29, and 0.45. Dotted lines show the binding energy at a given radius deduced from a single star model, including the results obtained with the fit of Xu & Li (2010), the fit of Claeys et al. (2014), and assuming the bottom of the envelope to be at X = 0.1, X = 0.3, or to correspond to the bottom of the convective envelope. Symbols indicate whether the binary undergoes RLOF before or after core helium depletion. |
| In the text | |
 |
Fig. 18. Properties after CE evolution for the case of donor stars with a radiative envelope, with artificially high values of αCE = 10, 20 in order to allow for a successful CE ejection. Simulations correspond to binary systems composed of a star with a ZAMS mass of 30 M⊙ and a BH companion of 3 M⊙, with periods ranging from 101 days to 103 days. Results are shown as a function of the radius of the star when it fills its Roche lobe. Top panel: central helium mass fraction Yc at the onset of CE, showing RLOF before and after the end of the HG as a large drop in Yc. Second panel: surface hydrogen mass fraction after envelope ejection. Third panel: stellar mass after envelope ejection, also showing the mass of the helium core defined as the innermost mass coordinate with Y > 0.01. Bottom panel: binding energy of the ejected envelope, as well as the binding energy that would be predicted by the Claeys et al. (2014) and Xu & Li (2010) fits, and the one corresponding to λ = 1. |
| In the text | |
 |
Fig. 19. Radial evolution of single stars of various masses at a metallicity of Z⊙/10 modeled until core-carbon depletion. Numbers above each track indicate the mass of the model in solar masses, and symbols indicate different stages in the evolution of the star. The color of the tracks indicates the fraction of the hydrogen envelope that is part of an outer convective zone. |
| In the text | |
 |
Fig. A.1. Ratio of dA/dΦ to d2A/dΦ2 at L1 and at the outer Lagrangian point of a star expressed in units of GMd/a. |
| In the text | |
 |
Fig. B.1. Binding energy profiles of the donor in a system with an initial mass of 30 M⊙ and a BH companion of 14.1 M⊙ at an orbital period of 2344 days. Profiles are shown at RLOF and at the onset of CE evolution for different values of Ṁhigh. Symbols indicate the mass coordinate at which CE evolution terminates for each choice of Ṁhigh and for CE efficiencies of αCE = 1 and αCE = 0.1. |
| In the text | |
 |
Fig. C.1. Evolution of stars with a mass of ∼30 M⊙ and a metallicity of Z⊙/10 computed by different research groups and codes. Dots are plotted every 105 years. |
| In the text | |
 |
Fig. D.1. Evolution in the HR diagram of a single 30 M⊙ model with a metallicity of Z⊙/10 computed with increasing spatial and temporal resolution. For each track, we indicate the average number of zones in the model as well as the steps taken in the simulation. The lowest resolution track shown corresponds to our default setup. |
| In the text | |
 |
Fig. D.2. Binding energy of the envelope of a post-main-sequence 30 M⊙ model with a metallicity of Z⊙/10 computed with increasing spatial and temporal resolution. For each track we indicate the average number of zones in the model as well as the steps taken in the simulation. The lowest resolution track shown corresponds to our default setup. For comparison, we include the binding energies obtained using our default resolution together with the fits of Xu & Li (2010) and Claeys et al. (2014). Before the formation of a convective envelope, the binding energies computed at X = 0.1 and X = 0.3 almost overlap. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} \Phi = \frac{G M_{\rm d}}{a}\left\{ -\frac{1}{\hat{r}_{\rm d}}-\frac{q}{\hat{r}_{\rm a}}-\frac{q+1}{2}\left[(\hat{x}-\hat{x}_{\rm cm})^2 + \hat{{ y}}^2\right]\right\} , \end{aligned} $$](/articles/aa/full_html/2021/06/aa39992-20/aa39992-20-eq1.gif)
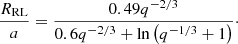
![$$ \begin{aligned}&\frac{R_{\rm L\,out}}{R_{\rm RL}}=1+\frac{2.74}{1+[(\ln q + 1.02)/\sigma ]^2}\times \frac{1}{7.13+q^{-0.386}}, \nonumber \\&\sigma = \frac{49.4}{12.2+q^{0.208}}\cdot \end{aligned} $$](/articles/aa/full_html/2021/06/aa39992-20/aa39992-20-eq7.gif)
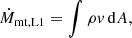
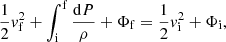
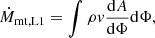
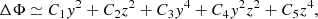
![$$ \begin{aligned} \frac{\mathrm{d}A}{\mathrm{d}\Phi } = \frac{\pi }{\sqrt{C_1C_2}}\left(1 - \frac{C_3(3C_1^2+2C_1C_2+3C_2^2)}{4C_1^2C_2^2}\Delta \Phi +\mathcal{O} \left[\left(\Delta \Phi \right)^2\right]\right). \end{aligned} $$](/articles/aa/full_html/2021/06/aa39992-20/aa39992-20-eq12.gif)
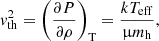
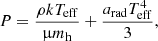
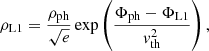
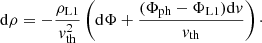
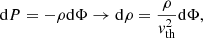
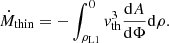
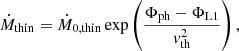
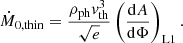
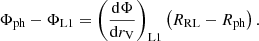
![$$ \begin{aligned} \Phi (r_{\rm V}) = &-\left(\frac{GM_{\rm a}}{a}+\frac{GM_{\rm a}}{2a(M_{\rm d}+M_{\rm a})}\right)\nonumber \\&-\frac{GM_{\rm d}}{r_{\rm V}}\left[1+a_1\left(\frac{r_{\rm V}}{a}\right)^3+a_2\left(\frac{r_{\rm V}}{a}\right)^6+\mathcal{O} \left(\frac{r_{\rm V}}{a}\right)^9\right], \end{aligned} $$](/articles/aa/full_html/2021/06/aa39992-20/aa39992-20-eq22.gif)
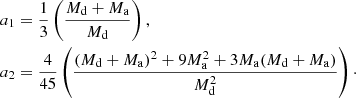
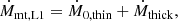
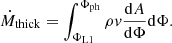
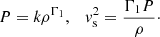
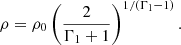
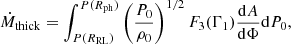
![$$ \begin{aligned} F_3(\Gamma _1) = \Gamma _1^{1/2}\left(\frac{2}{\Gamma _1+1}\right)^{{(\Gamma _1+1)}/[{2(\Gamma _1-1)}]}. \end{aligned} $$](/articles/aa/full_html/2021/06/aa39992-20/aa39992-20-eq30.gif)
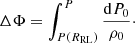
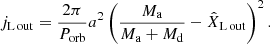
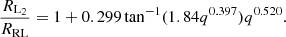
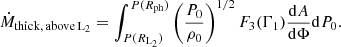
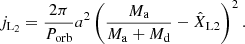
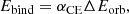
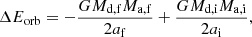
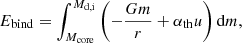
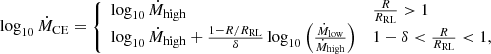
![$$ \begin{aligned} C_1&=\frac{1}{2}\left(\frac{\partial ^2 \Phi }{\partial { y}^2}\right)_{\mathrm{L}1}\\&=\frac{G M_{\rm d}}{2a^3}\left[\frac{1}{|\hat{X}_{\rm L1}|^3}+\frac{q}{|1-\hat{X}_{\rm L1}|^3}-(q+1)\right], \\ C_2&=\frac{1}{2}\left(\frac{\partial ^2 \Phi }{\partial z^2}\right)_{\mathrm{L}1}\\&=\frac{G M_{\rm d}}{2a^3}\left[\frac{1}{|\hat{X}_{\rm L1}|^3}+\frac{q}{|1-\hat{X}_{\rm L1}|^3}\right], \end{aligned} $$](/articles/aa/full_html/2021/06/aa39992-20/aa39992-20-eq40.gif)
![$$ \begin{aligned} C_3&=\frac{1}{24}\left(\frac{\partial ^4 \Phi }{\partial { y}^4}\right)_{\mathrm{L}1}\\&=-\frac{3G M_{\rm d}}{8 a^5}\left[\frac{1}{|\hat{X}_{\rm L1}|^5}+\frac{q}{|1-\hat{X}_{\rm L1}|^5}\right], \\ C_4&=\frac{1}{4}\left(\frac{\partial ^4 \Phi }{\partial { y}^2 z^2}\right)_{\mathrm{L}1}=2C_3 \\ C_5&=\frac{1}{24}\left(\frac{\partial ^4 \Phi }{\partial z^4}\right)_{\mathrm{L}1}=C_3. \end{aligned} $$](/articles/aa/full_html/2021/06/aa39992-20/aa39992-20-eq41.gif)
![$$ \begin{aligned} \varpi ^2=\frac{1}{\gamma }\Delta \Phi - \frac{C_3}{\gamma ^3}(\Delta \Phi )^2 +\mathcal{O} \left[(\Delta \Phi )^3\right], \end{aligned} $$](/articles/aa/full_html/2021/06/aa39992-20/aa39992-20-eq44.gif)