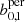| Issue |
A&A
Volume 648, April 2021
|
|
|---|---|---|
| Article Number | A74 | |
| Number of page(s) | 18 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202039048 | |
| Published online | 14 April 2021 | |
Persistent homology in cosmic shear: Constraining parameters with topological data analysis
1
Argelander-Institut für Astronomie, Auf dem Hügel 71, 53121 Bonn, Germany
e-mail: sven@astro.uni-bonn.de
2
University of Copenhagen, Department of Mathematical Sciences, Universitetsparken 5, 2100 Copenhagen, Denmark
3
Astrophysics Research Institute, Liverpool John Moores University, 146 Brownlow Hill, Liverpool L3 5RF, UK
4
Institute for Astronomy, University of Edinburgh, Royal Observatory, Blackford Hill, Edinburgh EH9 3HJ, UK
Received:
28
July
2020
Accepted:
8
December
2020
In recent years, cosmic shear has emerged as a powerful tool for studying the statistical distribution of matter in our Universe. Apart from the standard two-point correlation functions, several alternative methods such as peak count statistics offer competitive results. Here we show that persistent homology, a tool from topological data analysis, can extract more cosmological information than previous methods from the same data set. For this, we use persistent Betti numbers to efficiently summarise the full topological structure of weak lensing aperture mass maps. This method can be seen as an extension of the peak count statistics, in which we additionally capture information about the environment surrounding the maxima. We first demonstrate the performance in a mock analysis of the KiDS+VIKING-450 data: We extract the Betti functions from a suite of N-body simulations and use these to train a Gaussian process emulator that provides rapid model predictions; we next run a Markov chain Monte Carlo analysis on independent mock data to infer the cosmological parameters and their uncertainties. When comparing our results, we recover the input cosmology and achieve a constraining power on S8 ≡ σ8Ωm/0.3 that is 3% tighter than that on peak count statistics. Performing the same analysis on 100 deg2 of Euclid-like simulations, we are able to improve the constraints on S8 and Ωm by 19% and 12%, respectively, while breaking some of the degeneracy between S8 and the dark energy equation of state. To our knowledge, the methods presented here are the most powerful topological tools for constraining cosmological parameters with lensing data.
Key words: gravitational lensing: weak / cosmological parameters / methods: data analysis
© ESO 2021
1. Introduction
The Λ cold dark matter (ΛCDM) model is mostly regarded as the standard model of cosmology and has been incredibly successful in explaining and predicting a large variety of cosmological observations using only six free parameters. As of now, the tightest constraints on these cosmological parameters have been placed by observations of the cosmic microwave background (CMB, Planck Collaboration VI 2020). However, the next generation of surveys, such as the Rubin Observatory1 (Ivezic et al. 2008), Euclid2 (Laureijs et al. 2011) and the Nancy Grace Roman Space Telescope3 (RST, Spergel et al. 2013), promises to improve on these constraints and reduce parameter uncertainties to the sub-percent level. This is particularly interesting in light of tensions arising between observations of the early Universe (CMB) and the late Universe at a redshift of z ≲ 2. These tensions are most notable in the Hubble constant H0 (Riess et al. 2019) and the parameter 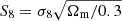 (Joudaki et al. 2020; Abbott et al. 2020), where Ωm is the matter density parameter and σ8 characterises the normalisation of the matter power spectrum. Future analyses will show whether these tensions are a statistical coincidence, the manifestation of unknown systematics or evidence for new physics.
(Joudaki et al. 2020; Abbott et al. 2020), where Ωm is the matter density parameter and σ8 characterises the normalisation of the matter power spectrum. Future analyses will show whether these tensions are a statistical coincidence, the manifestation of unknown systematics or evidence for new physics.
In the last decade, weak gravitational lensing has proven to be an excellent tool for studying the distribution of matter and constraining the cosmological parameters that describe our Universe. In particular, tomographic shear two-point correlation functions (Kaiser 1992) and derived quantities such as Complete Orthogonal Sets of E- and B-mode Integrals (COSEBIs, Schneider et al. 2010) and band powers (van Uitert et al. 2018) have been applied with great success to cosmic shear data (see Kilbinger et al. 2013; Heymans et al. 2013; Joudaki et al. 2017 for an analysis of CFHTLenS, Hildebrandt et al. 2020; Wright et al. 2020; Asgari et al. 2020 for the Kilo Degree Survey, Troxel et al. 2018 for the Dark Energy Survey and Hikage et al. 2019; Hamana et al. 2020 for the Hyper Suprime Camera Survey). However, while two-point statistics provide an excellent tool for capturing the information content of Gaussian random fields, the gravitational evolution of the matter distribution becomes non-linear in high-density regions, and additional methods are needed to extract the information residing in the non-Gaussian features that are formed therein. The demand for these new methods rises with the ever-increasing amount and quality of available data.
In addition to three-point correlation functions (Schneider & Lombardi 2003; Fu et al. 2014), which form a natural extension to two-point correlation functions, a variety of alternative statistics promise to improve cosmological parameter constraints (Zürcher et al. 2021), including peak statistics (Liu et al. 2015a,b; Kacprzak et al. 2016; Martinet et al. 2018, hereafter M+18), density split statistics (Gruen et al. 2018), convergence probability distribution functions (Liu & Madhavacheril 2019), shear clipping (Giblin et al. 2018), the scattering transform (Cheng et al. 2020), and Minkowski functionals (Petri et al. 2015; Marques et al. 2019; Parroni et al. 2020).
In this article, we demonstrate how ‘persistent homology’ can be used to analyse the data provided by weak gravitational lensing surveys. This non-linear statistic combines the information residing in Minkowski functionals and in peak statistics in a natural way, and supplements these by further capturing information about the environment surrounding the topological features. In the last two decades, persistent homology has been successfully applied in a large variety of fields involving topological data analysis: Among others, it has been used to analyse the spread of contagious diseases (Lo & Park 2018), to assess self-similarity in geometry (MacPherson & Schweinhart 2012) and to identify a new subgroup of breast cancer (Nicolau et al. 2011); for more examples, we refer to Otter et al. (2017) and references therein.
In cosmology, persistent homology has already been used to study the topology of the cosmic web (Sousbie 2011; van de Weygaert et al. 2013), of the interstellar magnetic fields (Makarenko et al. 2018) and the reionisation bubble network (Elbers & van de Weygaert 2019). Furthermore, it was shown to be an effective cosmic void finder (Xu et al. 2019). Additionally, a specific summary of the information contained in persistent homology, the ‘Betti numbers’, has emerged as a powerful tool to analyse both the cosmic web (Pranav et al. 2017) and Gaussian random fields (Pranav et al. 2019a, hereafter P+19). In the latter case, Betti numbers have been shown to provide a higher information content than both Euler characteristics and Minkowski functionals (Pranav et al. 2019b). In particular, they are very effective at detecting and quantifying non-Gaussian features in fields such as the CMB temperature map (compare P+19).
While several of the above-mentioned papers have shown that Betti numbers are sensitive to cosmological parameters, their results were only qualitative so far. To our knowledge, the current article is the first to quantify the power of Betti numbers for constraining cosmological parameters. Furthermore, our work differs from the previous ones in that we use ‘persistent’ Betti numbers, which further take into account the environment surrounding the topological features (for the definitions and further explanations, see Sect. 2.3). We show that this leads to a significant improvement in constraining power compared to the ‘non-persistent’ Betti numbers that have so far been used in cosmology.
In our analysis, we constrain cosmological parameters with a Markov chain Monte Carlo (MCMC) sampler, and therefore need to efficiently compute Betti functions over a broad range of values. Since we are not aware of a way to model Betti functions for non-Gaussian fields, we instead rely on Gaussian process regression (see e.g., Gelman et al. 2004), a machine learning tool that probabilistically predicts a given statistic when only small sets of training data are available. This procedure is not restricted to Betti functions and has been used in cosmology for a number of other statistical methods (Heitmann et al. 2014; Liu & Madhavacheril 2019; Burger et al. 2020; Mootoovaloo et al. 2020). Since persistent homology is particularly efficient in summarising and compressing the topological structure of large data sets, it is well suited for interacting with machine learning algorithms (Bresten & Jung 2019).
In this work, we train a Gaussian process regressor on a suite of KiDS+VIKING-450-like (Wright et al. 2019, hereafter KV450-like) N-body simulations to predict Betti functions for arbitrary cosmological parameters within a wide training range. All simulations are part of the w cold dark matter (wCDM) model of cosmology, meaning that they extend the standard model by allowing the equation of state of dark energy to vary. Calibrating our covariance matrix from a distinct ensemble of fully independent simulations, we then perform an MCMC analysis on mock data and recover the fiducial cosmological parameters of the simulation. We further show that persistent Betti functions are able to constrain cosmological parameters better than peak statistics, whose performance is similar to the one of tomographic cosmic shear (Kacprzak et al. 2016; M+18) and slightly better than that of Minkowski functionals (Zürcher et al. 2021).
We finally carry out a mock analysis based on Euclid-like simulations and find an even larger increase in constraining power in this setup. Thus, persistent Betti numbers promise to substantially improve the constraining power of weak gravitational lensing surveys, especially when they are used in combination with other probes.
This paper is organised as follows: In Sect. 2 we give a brief overview of the N-body simulations used in the signal calibration and in the estimation of the covariance matrix (Sect. 2.1), of the aperture mass maps reconstruction (Sect. 2.2), of the theory underlying persistent homology statistics (Sect. 2.3) and Gaussian process regression emulation (Sect. 2.4). An explanation of the peak count statistics can be found in Sect. 2.5. We present the results of our KV450-like and Euclid-like analyses in Sects. 3 and 4, respectively, and discuss them in Sect. 5.
2. Methods and numerical data products
Throughout this work, we assume the standard weak gravitational lensing formalism, a review of which can be found in Bartelmann & Schneider (2001).
2.1. Weak lensing simulations
So far, we cannot analytically compute the Betti functions that describe cosmic shear data due to their highly non-linear nature. Instead, we rely on numerical simulations4, namely the Scinet LIghtCone Simulations (SLICS, Harnois-Déraps et al. 2018; Harnois-Déraps & van Waerbeke 2015) and the cosmo-SLICS (Harnois-Déraps et al. 2019, hereafter H+19) for their evaluation. All simulations were performed in a flat wCDM framework, which we will assume throughout the scope of this paper.
First, we extracted the cosmology dependence with the cosmo-SLICS, a suite of cosmological N-body simulations in which the matter density Ωm, the parameter S8, the Hubble constant h and the parameter for the dark energy equation of state w0 are sampled at 26 points in a Latin hyper-cube (see Table A.1 for the exact list). At each cosmology, a pair of N-body simulations were evolved to redshift z = 0 with 15363 particles in a box of 505 h−1 Mpc, and subsequently ray-traced multiple times to yield 50 pseudo-independent light-cones that cover each 10 × 10 deg2. The initial conditions were chosen in order to suppress most of the sample variance when averaging a statistic over the pair. (For more details on the cosmo-SLICS, we refer the reader to H+19).
Second, we used the SLICS to estimate the covariance of the Betti functions. These consist of a set of 126 fully independent N-body simulations5 conducted with Ωm = 0.2905, Ωb = 0.0473, h = 0.6898, σ8 = 0.826 and ns = 0.969. These were also ray-traced into 10 × 10 deg2 light-cones, in a format otherwise identical to the cosmo-SLICS.
We took the KV450 data set (Wright et al. 2019) as an example of a current Stage-III weak lensing survey and created mock data sets with similar properties. Due to the box size of our simulations, the full KV450 survey footprint cannot be fitted onto a single light-cone. Instead we split the survey into 17 tiles following the setup presented in Appendix A.3 of Harnois-Déraps et al. (2018) and computed the (simulated) shear signal at the exact positions of the KV450 galaxies, repeating the process for ten light-cones (out of the 50 available) for each cosmo-SLICS pair and for the 126 SLICS realisations. We further used the observed ellipticities to simulate the shape noise, and the galaxy redshifts were randomly selected such that the cumulative redshift distribution follows the fiducial ‘direct calibration’ method (DIR) described in Hildebrandt et al. (2020). This way, any effect that the galaxy density, shape noise, and survey footprint may have on the Betti functions is infused in the simulations as well.
In Sect. 4 we further used a separate set of simulations in which the redshift distribution and galaxy number density has been modified to match that of future weak lensing experiments. These Euclid-like catalogues are also based on the SLICS and cosmo-SLICS, and we provide more details about them in that section. We note that in neither of the simulated surveys do we split the galaxy catalogues with redshift selection; we leave tomographic analysis for future work.
2.2. Maps of aperture mass
We performed our topological analysis on data obtained from weak gravitational lensing surveys, more precisely on maps of aperture mass (Schneider 1996), which reconstruct the lensing convergence κ inside an aperture filter and are hence directly related to the projected mass density contrast. There are several alternative ways to reconstruct convergence maps (see, e.g., Kaiser & Squires 1993; Seitz & Schneider 2001; Jeffrey et al. 2018, and references therein), however, these suffer from the so-called mass-sheet degeneracy: Even under ideal circumstances, κ can only be determined up to a constant. The introduction of a uniform mass sheet κ0 can change the extracted signal-to-noise ratio (S/N) in a way that does not reflect any physical meaning, hence we choose to perform our analysis on aperture mass maps, which are invariant under this effect.
2.2.1. Theoretical background
The aperture mass is obtained from a weak lensing catalogue as
where the filter function Q is computed via
and U is a compensated filter with ∫ dθ θU(θ) = 0 (Schneider 1996). The tangential shear at position θ′ with respect to θ, γt(θ′;θ), is calculated as
where γ(θ′) is the (complex) shear at position θ′. We note that both the shear γ and the angular position θ are interpreted as complex quantities in the above expression. In reality, we do not measure a shear field directly, but rather ellipticities ϵ of an ensemble of galaxies ngal, which are related to the shear and a measurement noise term ϵn as
where g = γ/(1 − κ) is the reduced shear and the last approximation holds in the weak shear limit (see e.g., Bartelmann & Schneider 2001). This transforms the integral of Eq. (1) into a sum
where ϵt(θi; θ) is the tangential ellipticity defined in analogy to Eq. (3).
Following M+18, we computed the noise in the aperture mass as
and calculated the S/N at a position θ as
Both numerator and denominator of Eq. (7) can be expressed as a convolution and can therefore be computed via a Fast Fourier-Transform (FFT), significantly decreasing the required computation time (Unruh et al. 2020). For our analysis, we used the following filter function (see Schirmer et al. 2007; M+18):
This function was designed to efficiently follow the mass profiles of dark matter haloes, which we model according to Navarro et al. (1997, hereafter NFW); since most of the matter is located within dark matter haloes, the function is well suited to detect peaks in the matter distribution. Here, θap is the aperture radius and xc represents the concentration index of the NFW profile. Following M+18, we set xc = 0.15, which is a good value for detection of galaxy clusters (Hetterscheidt et al. 2005).
2.2.2. Numerical implementation
The S/N defined in Eq. (7) is highly sensitive to the noise properties of the galaxy survey, and it is therefore critical to reproduce exactly the galaxy number density and the intrinsic shape noise of the data, as well as the overall survey footprint (see e.g., M+18). This motivates our use of KV450 mosaic simulations, which reproduce all of these quantities exactly. For each simulated galaxy in the catalogue, we randomly rotated the observed ellipticity of the corresponding real galaxy and added it to the simulated shear following the linear approximation in Eq. (4).
To calculate the aperture mass maps in a computationally inexpensive way, we distributed the galaxies on a grid of pixel size 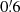 . For each pixel, we computed the sum of all respective galaxy ellipticities ∑iϵi as well as the sum of their squared absolute ellipticities ∑i|ϵi|2. The distribution of galaxies on a grid slightly shifts their positions, which introduces a small error in the computed quantity ϵt when the value |θi − θ| of Eq. (7) is comparable to the size of a pixel, but it enables a significantly faster computation6. Moreover, since the convolutions arising in both the numerator and denominator of Eq. (7) are linear in ϵ and |ϵ|2, respectively, computing Eq. (7) for individual galaxies or for whole pixels does not make a difference, and the latter is more efficient. Finally, we chose a filter radius of
. For each pixel, we computed the sum of all respective galaxy ellipticities ∑iϵi as well as the sum of their squared absolute ellipticities ∑i|ϵi|2. The distribution of galaxies on a grid slightly shifts their positions, which introduces a small error in the computed quantity ϵt when the value |θi − θ| of Eq. (7) is comparable to the size of a pixel, but it enables a significantly faster computation6. Moreover, since the convolutions arising in both the numerator and denominator of Eq. (7) are linear in ϵ and |ϵ|2, respectively, computing Eq. (7) for individual galaxies or for whole pixels does not make a difference, and the latter is more efficient. Finally, we chose a filter radius of 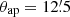 in this work, however the choice of this parameter could be revisited in order to optimise the cosmological constraints.
in this work, however the choice of this parameter could be revisited in order to optimise the cosmological constraints.
In addition to exhibiting an irregular shape, our KV450-like footprint is affected by internally masked regions, for example by the removal of bright foreground stars, saturated galaxies or satellite tracks. Each pixel that contains zero galaxies, which is true in particular for masked regions, was treated as masked. For the calculation of the aperture mass maps, these masked shear pixels were treated as having a shear of 0, and we subsequently masked pixels in the signal-to-noise maps for which at least 50% of the aperture was made of masked shear pixels; masked S/N pixels were assigned the value −∞. As our simulated data exactly traces the KV450 footprint, our cosmological parameter analysis is not affected by the masked regions.
2.3. Topological data analysis
This section describes the methods employed to conduct the topological analysis of the aperture mass maps detailed in Sect. 2.2.2, from the mathematical background to a full description of our numerical implementation.
Our analysis is based on the study of topological features in the S/N maps extracted from mock weak lensing data. More particularly, we are interested in studying how these relate to their environment in order to access non-Gaussian information contained in the correlation between different scales of the shear field. The idea of our approach is as follows: First, we take the survey area X and we remove from it all pixels that have S/N value above a threshold t. The result is a (topological) space that can be seen as a part of X (see Fig. 1). Next, we count the number of connected components7 and holes in this space. These are called the ‘Betti numbers’ β0 and β1. Lastly, we analyse how these numbers change as we vary the threshold t.
 |
Fig. 1. Visualisation of an excursion set. The original map (in this case a single peak) is depicted on the left. The middle plot depicts the same peak after a threshold is applied to the map, which cuts off the summit. The result seen from above is depicted on the right, which in this case has one hole (in white) and one connected component (in colour). Varying the threshold generates the full filtration. |
Figure 2 presents an example of a sequence of spaces obtained in this way. It shows the filtered aperture mass maps for nine values of t, obtained from a square-shaped zoom-in region of the full survey area X. Inspecting the panels from top-left to bottom-right, we see the gradual recovery of the full aperture mass map as the threshold t increases, starting from the lower values. One sees that a local minimum of the S/N map corresponds to a connected component appearing at some point and vanishing later on as it gets absorbed by an ‘older’ feature; a maximum corresponds to a hole that first appears and later gets filled in. Analysing how these features are created and vanish again allows us not only to count the corresponding extrema but to take into account their environment as well, thus obtaining information about the large-scale structure.
 |
Fig. 2. Excursion sets of a sample signal-to-noise map for a 3.3 × 3.3 deg2 field of SLICS for nine values t1, …, t9. The solid magenta ellipse highlights a connected component corresponding to a minimum of the signal-to-noise map; the solid orange and red ellipses each highlight a hole corresponding to a maximum. The dashed ellipses indicate the position of the features before their birth and after their death. The magenta feature is born at t2 and dies at t4 after being absorbed by older features that were born in t1. This lifeline is described by the interval [t2, t4) in Dgm(H0(𝕏)). Both the red and orange features are born at t5. The orange one dies at t7, while the red one, which corresponds to a sharper peak, persists longer and dies at t9. Hence, they give rise to intervals [t5, t7) and [t5, t9) in Dgm(H1(𝕏)). |
2.3.1. Homology of excursion sets and local extrema
Mathematically, the ideas described above can be expressed as follows: Let f : X → ℝ be a map from a topological space X to the reals. In our context, X will be the observed survey area, which we interpret as a subspace of the celestial sphere S2, and f will be the S/N of the aperture mass, f(θ) = S/N(θ), defined in Eq. (7). Taking sublevel sets of the map f (i.e. the portion of f with values less than some maximal value t) yields a sequence of subspaces of X: For t ∈ ℝ, define the ‘excursion set’ Xt = {x∈X∣f(x) ≤ t}.
To simplify notation, assume that f is bounded. If we choose t1 ≤ … ≤ tk > sup(f), we obtain a ‘filtration’ of the space X, which is defined as a sequence of subspaces with:
where we write Xi = Xti in the above expression to make the notation more compact. Our aim is to extract cosmological information8 from the distribution of aperture mass (represented by the map f) by studying topological invariants of the sequence 𝕏 = (Xi)i.
A ‘topological invariant’ of a space is a mathematical object (e.g., a number) that does not change if we continuously perturb it, for example by stretching or bending. The case that is relevant for us are the Betti numbers. As mentioned above, these count the number of connected components and holes of a space. If we compute the Betti numbers of our excursion sets Xi, we obtain information about the number of local extrema of the map f: The minima correspond to connected components appearing at some point of the filtration 𝕏 and vanishing later on; the maxima correspond to holes (see Fig. 2). The time it takes for the connected components or holes to vanish again is related to the relative height of the corresponding extremum, and therefore contains information about the environment.
From a more formal point of view, the nth Betti number βn(Y) of a space Y is computed from its nth homology group Hn(Y). Both homology groups and Betti numbers are important and well-studied invariants from algebraic topology. For an introduction to algebraic topology that is geared towards its applications in the sciences, see Ghrist (2014); a more rigorous introduction to this area of mathematics can also be found in Hatcher (2002). In our context, the homology group Hn(Y) is a vector space that we can associate with Y and βn(Y) is its dimension. The important point for us is that Betti numbers and homology groups translate the geometric (or rather topological) problem of counting connected components and holes into a question about linear algebra that can be efficiently solved by a computer (see Sect. 2.3.4).
We note that other topological invariants have been successfully used in cosmology, including the Euler characteristic9 χ(Y). Following Adler (1981), the Euler characteristic can be used to study real-valued random fields such as the CMB (Hamilton et al. 1986; Parroni et al. 2020). It is given by the alternating sum of the Betti numbers; in particular, if Y is a subset of ℝ2, we have χ(Y) = β0(Y)−β1(Y). Hence, one can compute the Euler characteristic from the Betti numbers, but the latter contain strictly more information (see also the discussion in Pranav et al. 2019b), motivating our choice for this current data analysis. Additionally, ‘persistent’ Betti numbers, which we describe in the next subsection, provide us with even more information. The information content extracted from different topological methods can be summarised as follows:

This is quantified in Sect. 3.2 (see in particular Fig. 5).
2.3.2. Persistent homology
As discussed in the last section, one approach to studying the topological properties of the sequence of excursion sets 𝕏 = (Xi)i is to analyse the sequence of Betti numbers βn(Xi), for n = 0, 1. Algebraically, this amounts to studying the sequence of vector spaces Hn(Xi) and computing each of their dimensions individually. However, one can do better: The inclusion maps Xi → Xi + 1 presented in Eq. (9) induce maps Hn(Xi)→Hn(Xi + 1), and these provide us with additional information. The sequence of all Hn(Xi) together with the connecting maps form what is called a ‘persistence module’ that we will write as Hn(𝕏), and which describes the persistent homology of 𝕏. For an introduction to persistent homology that focuses on its applications, we refer to Otter et al. (2017); a broader overview and further background material can be found in Oudot (2015).
The data of the persistence module Hn(𝕏) can be summarised in its persistence diagram Dgm(Hn(𝕏)). This is a collection of half-open intervals [ti, tj), where each interval10 can be interpreted as a feature11 that is ‘born at level’ ti and ‘dies’ at level tj. For example, an element in Dgm(H0(𝕏)) is an interval of the form [ti, tj) and it corresponds to a connected component that appears at level ti and merges with another component at level tj. Similarly, elements of Dgm(H1(𝕏)) correspond to holes that appear at ti and get filled at time tj. The filtration sequence presented in Fig. 2 exhibits such features, some of which we have highlighted in the panels: The magenta ellipses present a connected component corresponding to a minimum of the signal-to-noise map; the orange and red ellipses each highlight a hole corresponding to a maximum. As the sequence evolves, these features appear and disappear, giving rise to intervals.
To conduct our analysis, we study the nth persistent Betti number (or rank invariant) of 𝕏. This is defined as the number of features that are born before t and die after t′, and can be extracted from the persistence diagram Dgm(Hn(𝕏)) by
where, #{…} denotes the number of elements of the set {…}. We can consider these as functions from a subset of ℝ2 to ℝ; if we want to emphasise this point of view, we will also call them Betti functions. We note that when t′ = t we recover the non-persistent Betti numbers:
However, the persistent Betti numbers contain strictly more information than the sequence of regular Betti numbers. In particular, if one knows all values of βn𝕏, one can recover the entire persistence diagram Dgm(Hn(𝕏)), while this is not possible using the sequence (βn(Xi))i. Intuitively speaking, the persistent Betti functions do not only provide us with information about how many connected components or holes we have in each excursion set Xi, but they also tell us how long each such feature persists throughout the filtration. As explained above, the features correspond to local minima and maxima of the S/N map. Knowing about their lifetimes provides information about the relative height of these extrema and about their entanglement: Two completely separated peaks can be distinguished from two peaks sitting together on the summit of a region of high S/N.
2.3.3. Masks and relative homology
As explained in Sect. 2.1, our S/N maps contain masked regions where we do not have sufficient information about the aperture mass (and their pixel values are set to be constant −∞). In order to incorporate these in our analysis, we work with relative homology. The idea of using relative homology to study masked data was also used in P+19, where the authors give further interpretations of these groups. Other occurrences of relative homology in the persistent setting can be found in Pokorny et al. (2016) and Blaser & Brun (2019). Cf. also extended persistence and variants of it (Sect. 4 of Edelsbrunner & Harer 2008; de Silva et al. 2011).
Relative homology is a variant of ordinary homology, which generally speaking can be thought of as an algorithm that takes as an input a space X and a subspace M ⊆ X, and gives as an output for each n a vector space Hn(X, M) that describes the features of X that lie outside of M. In our setup, we consider the masked regions as the subspace M of our field X. As the signal-to-noise map takes the constant value −∞ on this subspace, we have M ⊆ Xi for all i and we get a sequence (Hn(Xi, M))i of relative homology groups that we want to understand.
Just as before, the inclusions Xi → Xi + 1 make this sequence into a persistence module Hn(𝕏, M). In analogy to Eq. (10), its Betti numbers are defined via:
Although the definition of these functions uses relative homology, they can be computed using only ordinary homology: From the long exact sequence for relative homology (Hatcher 2002, p. 117), one can deduce the following formula, which expresses these numbers in terms of the Betti numbers of 𝕏 and of M:
In our case, where X is a proper subspace of the two-sphere S2, the only non-zero terms of these invariants are:
These are the quantities that we want to compute, and the next section details how this is numerically done.
2.3.4. Computing persistent Homology: Grids and complexes
As explained in Sect. 2.1, we computed the signal-to-noise maps on a grid with square-shaped pixels. From a mathematical perspective, subdividing X in this way gives it the structure of a finite cubical complex, meaning a space that is obtained by glueing together cubes of maximal dimension (in this case squares) along lower-dimensional cubes (in this case edges and vertices). We obtain a function on this complex by assigning to each square the value of the map on the corresponding pixel and extending this using the lower-star filtration, meaning that an edge or a vertex gets assigned the minimal filtration value of a square it is adjacent to. By construction, the map takes a finite number of values t1 ≤ … ≤ tk on this complex, which define the filtration 𝕏. We compute the persistent Betti numbers of this filtered complex using the CUBICAL COMPLEXES module of GUDHI (Dlotko 2020)12. The masked regions form a subcomplex M of X and we compute 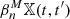 using Eq. (13). The number k of steps in the filtration we obtain is quite large, of the order of the number of pixels. GUDHI computes the persistent homology using all these filtration steps, however we evaluate the persistent Betti functions only at a few values (see Appendix B).
using Eq. (13). The number k of steps in the filtration we obtain is quite large, of the order of the number of pixels. GUDHI computes the persistent homology using all these filtration steps, however we evaluate the persistent Betti functions only at a few values (see Appendix B).
With X the full KV450-like footprint, the full corresponding complex is assembled from 17 tiles (see Sect. 2.1), which we label T1, …, T17. In the true KV450 survey, these tiles lie adjacent to each other, and large-scale structures extend across the boundaries. In the simulations however, each tile is constructed from a semi-independent realisation, with no tile-to-tile correlation. Therefore, we perform the calculation of aperture masses and the extraction of Betti numbers for each tile individually, making sure that the boundary of each tile is contained in the mask. This implies that the Betti functions 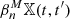 of the entire footprint can be computed as the sum
of the entire footprint can be computed as the sum
The reason for this is that in X, any two points lying in different tiles are separated by points in the mask. Intuitively speaking, this implies that any feature (e.g., a connected component or a hole) of X that lies outside the masked regions is entirely contained in one of the tiles Ti. Hence, counting the features in X is the same as counting them in each tile and summing them up13.
2.4. Predicting Betti numbers
As mentioned before, Betti numbers are a highly non-linear statistic, and we were unable to theoretically predict them for a given set of cosmological parameters. Due to the high computational cost of N-body simulations, it would also be completely impossible to perform a set of simulations for every point in our given parameter space. Therefore, we chose to emulate the Betti functions for a chosen set of filtration values by computing them in each simulation of cosmo-SLICS, and interpolating the results using the GAUSSIAN PROCESS REGRESSION (GP regression) of scikit-learn (Pedregosa et al. 2011)14.
Simply put, a GP regressor is a machine learning algorithm that takes a training data set 𝒟, which consists of n observations of a d-dimensional data vector yi, along with errors in the training data set σ2(y) and a list of the respective training nodes π. After training, the emulator provides predictions y* and their uncertainties σ2(y*) for arbitrary coordinates π*. In our case, the data vectors yi are the Betti functions extracted from the n = 26 different cosmo-SLICS cosmologies. We set the errors in the training data set σ2(y) as the variance measured between the different realisations of the light-cone, which varies with cosmology. Our training nodes π are the sets of cosmological parameters {Ωm, σ8, h, w0} in each cosmo-SLICS, listed in Table A.1. This method offers a model-independent, probabilistic interpolation of multi-dimensional data sets.
As our kernel, we chose the anisotropic Radial-basis function
where l is a vector with the same number of dimensions as the input values πi (in this case, division is defined element-wise) and A is a scalar. This kernel determines how similar two points πi, πj are to each other in order to then determine the weights for the individual data points in the interpolation. For each filtration value, we then determined the best hyper-parameters (A, l) by minimising the log-marginal-likelihood using a gradient descent from 400 different, randomly chosen initial values. For a detailed description of GP regression we refer the interested reader to Appendix A of H+19 and references therein.
2.5. Peak count statistics
As mentioned in the introduction, we assessed the performance of our topological data analysis by comparing its constraining power to that of the peak count statistics, which is another powerful method to capture information of the non-Gaussian part of the matter distribution. This statistic has been increasingly studied in the literature (e.g., M+18; Kacprzak et al. 2016; Shan et al. 2018; Liu et al. 2015a,b) and is relatively straightforward: It identifies and counts the maxima in the S/N maps, and bins the results as a function of the S/N value at the peak. Peaks of large S/N values convey the majority of the cosmological information (M+18) and correspond to the holes that appear at the latest stages in the filtration sequence presented before. They are typically associated with large galaxy clusters and are less affected by shape noise than peaks of lower S/N values, which however capture additional information from the large-scale structures. In addition to being easy to implement, their constraining power surpasses that of Minkowski functionals (Zürcher et al. 2021) and is competitive with two-point statistics (M+18), making them ideally suited for a performance comparison.
For consistency with the Betti function analysis, we ran our peak finder on the exact same S/N maps. For every simulated realisation of the KV450 survey, we counted the peaks on the 17 individual tiles and added the results afterwards. Following M+18, we binned the results in 12 S/N bins ranging from 0.0 to 4.0 and ignored the peaks outside this range. In the right-most panel of Fig. 3, we present the peak distribution relative to the mean measurement from the SLICS, colour-coded with the S8 value from the input cosmo-SLICS cosmology. The strong colour gradient illustrates the significant dependence of the signal on S8.
 |
Fig. 3. Difference of average Betti numbers b0 (left) and b1 (centre) and peak counts (right) between cosmo-SLICS and SLICS. Left and central panels: x-axis represents the respective filtration level t, which runs from the minimum to the maximum value of the S/N aperture map. The lines are colour-coded by the value of S8 in the respective cosmo-SLICS (see Table A.1). The lines shown here are averages over all mock realisations of the full survey footprint (10 for each cosmo-SLICS node, 126 for SLICS). |
As explained above, Betti functions are related to the numbers of peaks as well. However, the two methods do not yield completely equivalent information. First, Betti functions do not only take into account the local maxima, but also the minima. However, this has only a small effect on cosmological parameter constraints since most of the information resides in the peaks (M+18, see also Appendix B). Second, and more importantly, peak count statistics are very local in the sense that they decide about whether a pixel is counted as a peak by simply comparing it to the eight adjacent pixels.
Figure 4 illustrates this with a toy example, presenting three simple cases of reconstructed maps. The first two maps cannot be distinguished by peak counts as they both have four peaks with height 1, 2, 3, and 4. In contrast, Betti functions are able to identify structures at larger scales such as regions with high S/N values, and are able to differentiate between the first two panels in Fig. 4: In the first map, the excursion set X0 has four holes and these get filled one by one as the threshold t increases. We have
 |
Fig. 4. Three idealised S/N maps. Both peak count statistics and non-persistent Betti functions can distinguish the first from the third map. However, the peak counts of the first and the second map are identical, as are the non-persistent Betti functions of the second and the third. Persistent Betti functions can distinguish all three maps. For further explanations, see Sect. 2.5. |
This is different from the second map, where for all 0 ≤ t < 3, the excursion set Xt has only two holes (although the positions of the holes change),
However, while the peaks can differentiate between the second and the third map, the sequence of Betti numbers are the same. In the third map as well, we have two holes for all t between 0 and 3 and these get filled at t = 3 and t = 4. This illustrates that non-persistent Betti functions cannot distinguish very well between a small number of sharp peaks and a high number of peaks that only slightly protrude from their surroundings. (We ignore β0 here as for all t ≥ 0, all excursion sets have exactly one connected component). Persistent Betti functions can differentiate all three cases. They are able to detect that in the second map, the positions of the two holes at 0 ≤ t < 3 vary, while in the third map, the same two holes just get filled while t increases. The persistence diagrams Dgm(H1(𝕏)) associated with the three panels are:
As all these are different, so are the associated persistent Betti functions β1𝕏. This simple example illustrates how persistent Betti numbers combine the local information from peak count statistics with the non-local, large-scale information from non-persistent Betti functions.
3. Results
In this section, we present the results from our topological analysis based on the persistent Betti numbers. We gauge the performance of the technique from a comparison with an analysis based on their non-persistent alternatives, and additionally with a peak statistics analysis. We first present our measurements from the simulations, which serve to train the emulator and estimate the covariance matrices, then proceed with the parameter inference.
3.1. Calibrating the emulator and determining the covariances
For each light-cone of the cosmo-SLICS simulation suite, we measured the persistent Betti functions 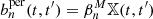 , and computed a non-persistent version bn by setting
, and computed a non-persistent version bn by setting 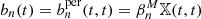 . We extracted the average values of b0, 1 and
. We extracted the average values of b0, 1 and 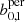 at a chosen set of values for each of the 26 different cosmologies from the mean over the ten light-cones.
at a chosen set of values for each of the 26 different cosmologies from the mean over the ten light-cones.
To demonstrate that Betti functions are indeed sensitive to the underlying cosmological parameters, we show the non-persistent Betti functions15 bn for different input cosmologies in Fig. 3, again colour-coded as a function of S8. As for the peak statistics, there is a strong colour gradient at every element of the data vector, both for b0 and b1, which indicates the sensitivity to that parameter.
In both the non-persistent and persistent settings, we obtained a data vector consisting of the function values at the chosen evaluation points (introduced in Sect. 2.3.4 and discussed in Appendix B), and further concatenated these values for b0 and b1 or  and
and  , respectively. We did not consider b2 and
, respectively. We did not consider b2 and 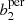 for our analysis as they only consist of a very small number of features, which mainly depend on the shape of the mask and contain very little cosmological information. We used these data vectors to train the hyperparameters of our GPR emulator, and were hereafter able to predict the Betti functions (at the chosen evaluation points) for arbitrary cosmological parameters enclosed within the training range. As a next step, we extracted the same Betti functions for each realisation of the SLICS and used these to determine a covariance matrix Cb for the data vector.
for our analysis as they only consist of a very small number of features, which mainly depend on the shape of the mask and contain very little cosmological information. We used these data vectors to train the hyperparameters of our GPR emulator, and were hereafter able to predict the Betti functions (at the chosen evaluation points) for arbitrary cosmological parameters enclosed within the training range. As a next step, we extracted the same Betti functions for each realisation of the SLICS and used these to determine a covariance matrix Cb for the data vector.
To assess the accuracy of the emulator, we performed a ‘leave-one-out cross-validation test’: We excluded one cosmology node and trained our emulator on the 25 remaining ones. We then let the emulator predict Betti functions for the previously excluded cosmology and compared it to the measured values; this process was repeated for each of the 26 cosmologies. The results are presented in Appendix C. As further discussed therein, this test demonstrates that we achieve an accuracy of a few percent on our predicted signal at most evaluation points. While a single outlier contains inaccuracies that are larger than the 1σ limit of the sample variance extracted from SLICS, the vast majority of cross-validation tests is contained within this limit.
For each set of cosmological parameters, the emulator not only provides a prediction for the Betti functions, but also an error estimate. We define the ‘covariance matrix’ of the emulator Ce as a diagonal matrix where the entries correspond to the uncertainty that is predicted by the GPR emulator. Combining with the sample variance Cb estimated from the SLICS, we subsequently set
as the covariance matrix for our cosmological parameter estimation. The emulator covariance Ce depends on the chosen cosmological parameters, therefore our covariance matrix C varies with cosmology. We note that it would also be possible to obtain an error estimate Ce from the cross-validation: For each evaluation point of the Betti functions, one can estimate the variance by
where xi, measured is the measured value of the Betti function at the ith training cosmology, whereas xi, predicted is the one predicted by the emulator when it is trained on all other cosmologies, leaving the ith one out. We verified that both the error estimates themselves and the posteriors on the cosmological parameters are consistent between the two methods.
We finally repeated this full machinery (GPR training and covariance estimation), this time on the peak count statistics measurements extracted from the same data sets and described in Sect. 2.5. We compare the respective performances in the next section.
3.2. Inference of cosmological parameters
Putting to use the covariance matrix and the prediction tools described in the last section, we performed a trial cosmological parameter inference using the mean of the SLICS measurements as our ‘observed data’ to test how well we can recover the fiducial values, and how the constraining power on the cosmological parameters compares with the peak count statistics described in Sect. 2.5. We sampled our cosmological parameter space using the MCMC sampler EMCEE (Foreman-Mackey et al. 2013), specifying a flat prior range that reflects the parameter space sampled by the cosmo-SLICS, namely: Ωm ∈ [0.1, 0.6], S8 ∈ [0.6, 1.0], h ∈ [0.5, 0.9], w0 ∈ [ − 1.8, −0.2]. Since our covariance matrix is extracted from a finite number of simulations, it is inherently noisy, which leads to a biased inverse covariance matrix (Hartlap et al. 2007). To mitigate this, we adopted a multivariate t-distribution (Sellentin & Heavens 2016) as our likelihood model. At each sampled point, we computed the log-likelihood as
where Ns is the number of simulations used to calibrate the covariance matrix (in our case 126), and χ2 was computed in the usual way via
Here, xmeasured are the respective Betti functions b0, 1 or 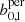 extracted from SLICS, while xpredicted are predicted by the emulator at the respective point in parameter space16.
extracted from SLICS, while xpredicted are predicted by the emulator at the respective point in parameter space16.
Following these steps, we performed an MCMC analysis both for the persistent and the non-persistent Betti functions, 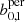 and b0, 1 and for the peak count statistics. The results are displayed in Fig. 5. As can be seen, all methods recover the fiducial simulation parameter within the 1σ limit. Furthermore, the persistent Betti functions bper offer slightly improved constraining power when compared to the non-persistent version b and to peak counts, and is notably the best at rejecting the low-Ωm and the high-σ8 regions of the parameter space. The 1σ contours are all smaller, yielding marginalised constraints on S8 of
and b0, 1 and for the peak count statistics. The results are displayed in Fig. 5. As can be seen, all methods recover the fiducial simulation parameter within the 1σ limit. Furthermore, the persistent Betti functions bper offer slightly improved constraining power when compared to the non-persistent version b and to peak counts, and is notably the best at rejecting the low-Ωm and the high-σ8 regions of the parameter space. The 1σ contours are all smaller, yielding marginalised constraints on S8 of 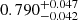 , compared to
, compared to 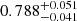 for non-persistent Betti numbers and
for non-persistent Betti numbers and 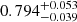 for peaks. Persistent homology therefore increases the constraining power on S8 by 3% compared to peak statistics, while the ‘figure of merit’ (i.e. one over the area of the 1σ contour) in the Ωm − σ8 plane is increased by 48%. This is not entirely surprising as b and peaks just counts features at each filtration step, whereas bper contains the entire information content of the persistence module, as discussed in Sect. 2.3.2.
for peaks. Persistent homology therefore increases the constraining power on S8 by 3% compared to peak statistics, while the ‘figure of merit’ (i.e. one over the area of the 1σ contour) in the Ωm − σ8 plane is increased by 48%. This is not entirely surprising as b and peaks just counts features at each filtration step, whereas bper contains the entire information content of the persistence module, as discussed in Sect. 2.3.2.
 |
Fig. 5. Results of an MCMC on the Betti numbers measured in the KV450-like SLICS. The contours represent the 1- and 2-σ posterior contours for an analysis with non-persistent (grey) and persistent (blue) Betti functions. For comparison, the red contours represent the posterior of an analysis with peak statistics, as done in M+18. The values on top of the diagonals represent the marginalised posterior for the persistent Betti functions bper. The fiducial parameters of SLICS are represented by the black lines. We conducted our analysis with Ωm, σ8, h and w0 as free parameters and employed flat priors with Ωm ∈ [0.1, 0.6], S8 ∈ [0.6, 1.0], h ∈ [0.5, 0.9], w0 ∈ [ − 1.8, −0.2]. The green lines correspond to the 1- and 2-σ posterior contours of a cosmological parameter analysis of the KiDS450-survey using tomographic two-point correlation functions, where the covariance matrix was extracted from SLICS and systematics were disregarded (see the ‘N-body’ setup in Table 4 of Hildebrandt et al. 2017). Since the setup of that analysis is very similar to ours, they can be used to compare the relative sizes (but not locations) of contours. We note that this parameter analysis was done in a ΛCDM-framework on KiDS data, whereas our analysis is done in a wCDM framework on mock data. |
For comparison, we also report in Fig. 5 the constraints from a two-point correlation function analysis (see the green curves). These were obtained from the actual measurements from the KiDS-450 data, which had a slightly different redshift distribution and number density than the KV450-like data used in this paper, but were derived with a covariance matrix extracted from the SLICS and ignored systematic uncertainty (see the N-body setup in Table 4 of Hildebrandt et al. 2017), in a setup otherwise very similar to ours. The contours are offset to lower S8 values as preferred by the KiDS-450 data, in contrast with the higher input SLICS cosmology. Due to the very similar analysis setup, the contours can be used to compare their size with the ones derived from our analysis. The increased constraining power with respect to peaks and homology is largely due to the tomographic analysis, which we reserve for future work.
It is worth noting that a part of the reported uncertainties for persistent Betti functions arise due to the inaccuracy of the emulator that is larger than for peaks; when these uncertainties are ignored, persistent Betti numbers achieve constraints of 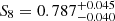 , an improvement of 8% with respect to peak statistics. This can potentially be realised in a future analysis involving a larger training set (we further discuss this in Appendix C). Although a gain of 3−8% in accuracy on S8 is small in comparison with the infrastructure work required, we show in the next section that the improvement is significantly increased once the weak lensing data better resolves the large-scale structure around the peaks.
, an improvement of 8% with respect to peak statistics. This can potentially be realised in a future analysis involving a larger training set (we further discuss this in Appendix C). Although a gain of 3−8% in accuracy on S8 is small in comparison with the infrastructure work required, we show in the next section that the improvement is significantly increased once the weak lensing data better resolves the large-scale structure around the peaks.
Before steering away from the KV450-like setup however, we finally investigate the systematic impact of two other survey parameters. Similarly to the shear peak count statistics, the Betti functions are extracted from the S/N of the aperture mass map. Therefore, their expectation value directly depends not only on the survey footprint but also on various terms influencing the noise, for example the effective number density of galaxies and their average internal ellipticity (see e.g., M+18). For the two-point correlation functions, these terms only influence the covariance matrix, at least to first order (Heydenreich et al. 2020), while here a 10% offset on the galaxy density or on the shape noise can bias the inferred parameters by 1−3σ. Full details of these tests are provided in Appendix D.
4. Outlook for Stage IV experiments
As discussed in Sect. 2.5, the gain of information from persistent Betti functions with respect to peak counting comes from the ability to extract information about the environment, for example by distinguishing whether peaks are isolated or clustered on a larger over-density. Consequently, we expect that resolving the large-scale structure with higher resolution, as will be made possible with upcoming Stage IV lensing experiments, should further increase this relative gain.
In this section, we explore this scenario by repeating the analysis presented previously on a set of simulations with Euclid-like source number densities. These are also constructed from the SLICS and cosmo-SLICS light-cones, but differ in a few key aspects: In contrast to the KV450-like mock data, the position of the galaxies are here placed at random on the 10 × 10 deg2 fields, and no masks are imposed on them. Our total survey area is therefore 100 deg2. The redshift distribution follows:
with z0 = 0.637, β = 1.5, and the overall proportionality constant is given by normalising the distribution to 30 gal arcmin−2.
In this analysis, we opted for an aggressive strategy in which we include peaks and features with S/N up to ten, which might end up being rejected in the future due to difficulties at modelling all systematic effects (e.g., baryons feedback) at the required level. We carried out a second analysis which cap the features at S/N of seven instead, and noticed only minor differences. In both cases, the peak statistics were binned such that a signal-to-noise range of one is covered by three bins.
One important aspect to note is that due to the much lower level of shape-noise in this Stage IV setup, the accuracy of the GPR emulator degrades in comparison to the KV450-like scenario, reaching ∼5% only for a few evaluation points. More details about the relative importance of the emulator accuracy are provided in Appendix C. Meanwhile, we have included the error associated with the emulator following Eqs. (20) and (21) in our analysis, hence our results should remain unbiased.
The results of our MCMC analysis are shown in Fig. 6, where we compare the performance of the persistent Betti numbers to peak counting. We find here again an increase in statistical power and the gain is amplified compared with the KV450-like analysis: Looking at the S8 constraints, we measure 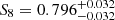 for peak statistics and
for peak statistics and 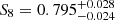 for persistent Betti numbers, an improvement of ∼19%. Contraints on Ωm are also improved, with a gain of ∼12% on the one-dimensional marginal error. Persistent Betti numbers are even able to set some constraints on the dark energy equation of state, measuring
for persistent Betti numbers, an improvement of ∼19%. Contraints on Ωm are also improved, with a gain of ∼12% on the one-dimensional marginal error. Persistent Betti numbers are even able to set some constraints on the dark energy equation of state, measuring 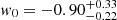 . This is an exciting new avenue that will be further investigated in future work involving tomographic decomposition of the source catalogues.
. This is an exciting new avenue that will be further investigated in future work involving tomographic decomposition of the source catalogues.
 |
Fig. 6. Results of an MCMC as described in Fig. 5, but here for 100 deg2 of Euclid-like lensing data. |
We emphasise that for the persistent Betti numbers, the emulator inaccuracy constitutes a part of the error budget. This uncertainty could be reduced by increasing the number of training nodes (see Appendix C). When disregarding the emulator uncertainty, we achieve constraints of 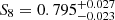 and
and 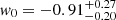 .
.
5. Discussion
Based on the topological analysis of an ensemble of realistic numerical simulations, we have demonstrated that persistent Betti functions are a highly competitive method to constrain cosmological parameters from weak lensing data. We carried out an MCMC sampling and found that persistent Betti functions improve the constraining power on S8 by ∼3−8% compared to peak count statistics, which themselves have a constraining power that is similar to the mainstream two-point statistics (M+18). Furthermore, this advantage over peak statistics is expected to exceed 20% in the upcoming Stage IV surveys. We included the effect of shape noise and of masking as they occur within the KV450 weak lensing survey, however, our methods can be directly adapted to other surveys. We believe that this gain in information over peak statistics is primarily caused by the sensitivity of Betti numbers to the large-scale structure. It would be interesting to see whether this sensitivity can be replicated using peak statistics when a set of different filter radii θap is used. However, we believe that persistent Betti numbers offer a simpler and numerically less expensive alternative to that.
Our results are obtained by estimating a covariance matrix from an ensemble of independent light cones, and by training a Gaussian Process Regression emulator on a suite of wCDM simulations. A non-negligible part of our error budget arises from inaccuracies in the emulator. These occur since we can only calibrate our model for 26 different cosmologies, which can certainly be improved in the future.
We investigated the influence of shape noise and number density on our analysis (see Appendix D). However, various other systematic effects inherent to weak lensing data analyses were not explored in this paper, including the uncertainty arising from photometric redshift errors, shape calibration, baryon feedback on the matter distribution or intrinsic alignments of galaxies. Before a full cosmological parameter analysis can be carried out from data, it is crucial to investigate and understand how to include these. Additionally, there are many internal parameters in our analysis pipeline that were chosen by hand, for example the aperture radius θap of the filter function or the points at which we evaluate the Betti functions. With careful optimisation, one would probably be able to extract an even higher amount of information from the persistent Betti numbers. In future work, it would be interesting to see if forward modelling techniques such as DELFI (Taylor et al. 2019) or BORG (Jasche & Lavaux 2019) can also be used in combination with Betti functions.
We also want to point out that persistent Betti numbers are just one way to compress the information of persistent homology. While they are certainly easy to understand and apply, they also suffer from some disadvantages, the most notable of which being that the difference between two Betti functions is always integer-valued, whereas we would prefer a real-valued distance function for a χ2-analysis. This problem can be mitigated by utilising different statistics of persistent homology (e.g., Reininghaus et al. 2015; Bubenik 2015); for an overview of further options, see also Oudot (2015, Chap. 8) and Pun et al. (2018).
Lastly, we note that topological data analysis is a promising avenue in cosmology that can find multiple applications well outside those presented in this paper. Other methods similar or complementary to persistent Betti functions can be used to detect and quantify structure in both continuous fields and point-clouds in arbitrary dimensions (see e.g., Otter et al. 2017, and references therein), which makes topological data analysis an incredibly versatile tool to study the distribution of matter in our Universe. While it has been used in cosmology before, for example to detect non-Gaussianities in the CMB (see P+19) or to find voids in the large-scale structure (Xu et al. 2019), its utilisation in modern astronomy is bound to grow in the near future.
All simulations products used in this paper can be made available upon request; see http://slics.roe.ac.uk
Such a collection of intervals is called a ‘diagram’ because it can be visualised as an actual diagram in the plane: For every interval [ti, tj), one can draw a point in ℝ2 with coordinates (ti, tj). An example of this can be found in Fig. B.1.
GUDHI is a well-established, open-source program (available in C++ with a python-interface) for topological data analysis. Among many other applications, it can calculate persistent Betti numbers of multi-dimensional fields. The program is publicly available at https://github.com/GUDHI/
Our algorithm was inspired by the GPR EMULATOR tool by Benjamin Giblin (https://github.com/benjamingiblin/GPR_Emulator).
Acknowledgments
We are grateful for useful hints from Fabian Lenzen and Vidit Nanda on persistent homology and from Pierre Burger and Peter Schneider on the data analysis. Furthermore we thank Shahab Joudaki, Konrad Kuijken, Frank Röttger, Sandra Unruh and the anonymous referee for helpful comments on previous versions of this article. Sven Heydenreich acknowledges support from the German Research Foundation (DFG SCHN 342/13), the International Max-Planck Research School (IMPRS) and the German Academic Scholarship Foundation. Benjamin Brück was supported by the Danish National Research Foundation through the Copenhagen Centre for Geometry and Topology (DNRF151). Joachim Harnois-Déraps acknowledges support from an STFC Ernest Rutherford Fellowship (project reference ST/S004858/1). Computations for the N-body simulations were enabled by Compute Ontario (www.computeontario.ca), Westgrid (www.westgrid.ca) and Compute Canada (www.computecanada.ca). The SLICS numerical simulations can be found at http://slics.roe.ac.uk/, while the cosmo-SLICS can be made available upon request. Author contributions. All authors contributed to the development and writing of this paper. SH led the data analysis, BB developed the necessary mathematical background, while JHD provided the suites of numerical simulation tailored to the measurement.
References
- Abbott, T. M. C., Aguena, M., Alarcon, A., et al. 2020, Phys. Rev. D, 102 [Google Scholar]
- Adler, R. J. 1981, The Geometry of Random Fields (Chichester: John Wiley& Sons, Ltd.) [Google Scholar]
- Angulo, R. E., Zennaro, M., Contreras, S., et al. 2020, ArXiv e-prints [arXiv:2004.06245] [Google Scholar]
- Asgari, M., Tröster, T., Heymans, C., et al. 2020, A&A, 634, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bartelmann, M., & Schneider, P. 2001, Phys. Rep., 340, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Blaser, N., & Brun, M. 2019, ArXiv e-prints [arXiv:1911.07484] [Google Scholar]
- Bresten, C., & Jung, J. H. 2019, ArXiv e-prints [arXiv:1910.08245] [Google Scholar]
- Bubenik, P. 2015, J. Mach. Learn. Res., 16, 77 [Google Scholar]
- Burger, P., Schneider, P., Demchenko, V., et al. 2020, A&A, 642, A161 [EDP Sciences] [Google Scholar]
- Cheng, S., Ting, Y.-S., Ménard, B., & Bruna, J. 2020, MNRAS, 499, 5902 [CrossRef] [Google Scholar]
- de Silva, V., Morozov, D., & Vejdemo-Johansson, M. 2011, Inverse Problems. An International Journal on the Theory and Practice of Inverse Problems, Inverse Methods and Computerized Inversion of Data, 27, 124003 [Google Scholar]
- Dlotko, P. 2020, GUDHI User and Reference Manual, 3.1.1 Edition (GUDHI Editorial Board) [Google Scholar]
- Edelsbrunner, H., & Harer, J. 2008, in Surveys on Discrete and Computational Geometry (Providence, RI: American Mathematical Society), Contemp. Math., 453, 257 [Google Scholar]
- Elbers, W., & van de Weygaert, R. 2019, MNRAS, 486, 1523 [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Fu, L., Kilbinger, M., Erben, T., et al. 2014, MNRAS, 441, 2725 [NASA ADS] [CrossRef] [Google Scholar]
- Gelman, A., Carlin, J. B., Stern, H. S., & Rubin, D. B. 2004, Bayesian Data Analysis, 2nd edn. (Chapman and Hall/CRC) [Google Scholar]
- Ghrist, R. 2014, Elementary Applied Topology, 1st edn. (Createspace) [Google Scholar]
- Giblin, B., Heymans, C., Harnois-Déraps, J., et al. 2018, MNRAS, 480, 5529 [Google Scholar]
- Gruen, D., Friedrich, O., Krause, E., et al. 2018, Phys. Rev. D, 98 [Google Scholar]
- Hamana, T., Shirasaki, M., Miyazaki, S., et al. 2020, PASJ, 72, 16 [CrossRef] [Google Scholar]
- Hamilton, A. J. S., Gott, J. R., III, & Weinberg, D. 1986, ApJ, 309, 1 [Google Scholar]
- Harnois-Déraps, J., & van Waerbeke, L. 2015, MNRAS, 450, 2857 [Google Scholar]
- Harnois-Déraps, J., Amon, A., Choi, A., et al. 2018, MNRAS, 481, 1337 [NASA ADS] [CrossRef] [Google Scholar]
- Harnois-Déraps, J., Giblin, B., & Joachimi, B. 2019, A&A, 631, A160 [CrossRef] [EDP Sciences] [Google Scholar]
- Hartlap, J., Simon, P., & Schneider, P. 2007, A&A, 464, 399 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hatcher, A. 2002, Algebraic Topology (Cambridge: Cambridge University Press) [Google Scholar]
- Heitmann, K., Lawrence, E., Kwan, J., Habib, S., & Higdon, D. 2014, ApJ, 780, 111 [Google Scholar]
- Hetterscheidt, M., Erben, T., Schneider, P., et al. 2005, A&A, 442, 43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heydenreich, S., Schneider, P., Hildebrandt, H., et al. 2020, A&A, 634, A104 [Google Scholar]
- Heymans, C., Grocutt, E., Heavens, A., et al. 2013, MNRAS, 432, 2433 [NASA ADS] [CrossRef] [Google Scholar]
- Hikage, C., Oguri, M., Hamana, T., et al. 2019, PASJ, 71, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Hildebrandt, H., Viola, M., Heymans, C., et al. 2017, MNRAS, 465, 1454 [Google Scholar]
- Hildebrandt, H., Köhlinger, F., van den Busch, J. L., et al. 2020, A&A, 633, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ivezic, Z., Axelrod, T., Brandt, W. N., et al. 2008, Serb. Astron. J., 176, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Jasche, J., & Lavaux, G. 2019, A&A, 625, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jeffrey, N., Abdalla, F. B., Lahav, O., et al. 2018, MNRAS, 479, 2871 [Google Scholar]
- Joudaki, S., Blake, C., Heymans, C., et al. 2017, MNRAS, 465, 2033 [NASA ADS] [CrossRef] [Google Scholar]
- Joudaki, S., Hildebrandt, H., Traykova, D., et al. 2020, A&A, 638, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Kacprzak, T., Kirk, D., Friedrich, O., et al. 2016, MNRAS, 463, 3653 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, N. 1992, ApJ, 388, 272 [Google Scholar]
- Kaiser, N., & Squires, G. 1993, ApJ, 404, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Kilbinger, M., Fu, L., Heymans, C., et al. 2013, MNRAS, 430, 2200 [NASA ADS] [CrossRef] [Google Scholar]
- Laureijs, R., Amiaux, J., Arduini, S., et al. 2011, ArXiv e-prints [arXiv:1110.3193] [Google Scholar]
- Liu, J., & Madhavacheril, M. S. 2019, Phys. Rev. D, 99 [Google Scholar]
- Liu, X., Pan, C., Li, R., et al. 2015a, MNRAS, 450, 2888 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, J., Petri, A., Haiman, Z., et al. 2015b, Phys. Rev. D, 91 [Google Scholar]
- Lo, D., & Park, B. 2018, PLoS One, 13 [Google Scholar]
- MacPherson, R., & Schweinhart, B. 2012, J. Math. Phys., 53 [Google Scholar]
- Makarenko, I., Shukurov, A., Henderson, R., et al. 2018, MNRAS, 475, 1843 [Google Scholar]
- Marques, G. A., Liu, J., Zorrilla Matilla, J. M., et al. 2019, JCAP, 2019, 019 [Google Scholar]
- Martinet, N., Schneider, P., Hildebrandt, H., et al. 2018, MNRAS, 474, 712 [NASA ADS] [CrossRef] [Google Scholar]
- Mootoovaloo, A., Heavens, A. F., Jaffe, A. H., & Leclercq, F. 2020, MNRAS, 497, 2213 [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Nicolau, M., Levine, A. J., & Carlsson, G. 2011, Proc. Natl. Acad. Sci., 108, 7265 [Google Scholar]
- Otter, N., Porter, M. A., Tillmann, U., Grindrod, P., & Harrington, H. A. 2017, EPJ Data Sci., 6, A17 [Google Scholar]
- Oudot, S. Y. 2015, in Persistence Theory: from Quiver Representations to Data Analysis (Providence, RI: American Mathematical Society), Math. Surv. Monogr., 209, 218 [Google Scholar]
- Parroni, C., Cardone, V. F., Maoli, R., & Scaramella, R. 2020, A&A, 633, A71 [CrossRef] [EDP Sciences] [Google Scholar]
- Pedregosa, F., Varoquaux, G., Gramfort, A., et al. 2011, J. Mach. Learn. Res., 12, 2825 [Google Scholar]
- Petri, A., Liu, J., Haiman, Z., et al. 2015, Phys. Rev. D, 91 [Google Scholar]
- Planck Collaboration VI. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pokorny, F. T., Goldberg, K., & Kragic, D. 2016, 2016 IEEE International Conference on Robotics and Automation (ICRA), 16 [Google Scholar]
- Pranav, P., Edelsbrunner, H., van de Weygaert, R., et al. 2017, MNRAS, 465, 4281 [Google Scholar]
- Pranav, P., Adler, R. J., Buchert, T., et al. 2019a, A&A, 627, A163 [EDP Sciences] [Google Scholar]
- Pranav, P., van de Weygaert, R., Vegter, G., et al. 2019b, MNRAS, 485, 4167 [Google Scholar]
- Pun, C. S., Xia, K., & Lee, S. X. 2018, ArXiv e-prints [arXiv:1811.00252] [Google Scholar]
- Reininghaus, J., Huber, S., Bauer, U., & Kwitt, R. 2015, Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 4741 [Google Scholar]
- Riess, A. G., Casertano, S., Yuan, W., Macri, L. M., & Scolnic, D. 2019, ApJ, 876, 85 [Google Scholar]
- Schirmer, M., Erben, T., Hetterscheidt, M., & Schneider, P. 2007, A&A, 462, 875 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, P. 1996, MNRAS, 283, 837 [Google Scholar]
- Schneider, P., & Lombardi, M. 2003, A&A, 397, 809 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, P., Eifler, T., & Krause, E. 2010, A&A, 520, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seitz, S., & Schneider, P. 2001, A&A, 374, 740 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sellentin, E., & Heavens, A. F. 2016, MNRAS, 456, L132 [Google Scholar]
- Shan, H., Liu, X., Hildebrandt, H., et al. 2018, MNRAS, 474, 1116 [Google Scholar]
- Sousbie, T. 2011, MNRAS, 414, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Spergel, D., Gehrels, N., Breckinridge, J., et al. 2013, ArXiv e-prints [arXiv:1305.5422] [Google Scholar]
- Taylor, P. L., Kitching, T. D., Alsing, J., et al. 2019, Phys. Rev. D, 100 [Google Scholar]
- Troxel, M. A., MacCrann, N., Zuntz, J., et al. 2018, Phys. Rev. D, 98 [Google Scholar]
- Unruh, S., Schneider, P., Hilbert, S., et al. 2020, A&A, 638, A96 [CrossRef] [EDP Sciences] [Google Scholar]
- van de Weygaert, R., Vegter, G., Edelsbrunner, H., et al. 2013, ArXiv e-prints [arXiv:1306.3640] [Google Scholar]
- van Uitert, E., Joachimi, B., Joudaki, S., et al. 2018, MNRAS, 476, 4662 [Google Scholar]
- Wright, A. H., Hildebrandt, H., Kuijken, K., et al. 2019, A&A, 632, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wright, A. H., Hildebrandt, H., van den Busch, J. L., et al. 2020, A&A, 640, L14 [CrossRef] [EDP Sciences] [Google Scholar]
- Xu, X., Cisewski-Kehe, J., Green, S. B., & Nagai, D. 2019, Astron. Comput., 27, 34 [Google Scholar]
- Zürcher, D., Fluri, J., Sgier, R., Kacprzak, T., & Refregier, A. 2021, JCAP, 2021, 028 [Google Scholar]
Appendix A: Additional information about the cosmo-SLICS simulations
For completeness, we list in Table A.1 the full suite of cosmological parameters that makes up the cosmo-SLICS series. Full details about this simulation suite can be found in H+19.
Cosmological parameters of the cosmo-SLICS wCDM simulations.
Appendix B: Choosing evaluation points for the Betti functions
While the domain of both persistent and non-persistent Betti functions is technically limited by the pixel-values of the signal-to-noise map, the raw data vector provided by GUDHI contains about 106 entries. As this level of refinement is neither practical nor necessary, we need to choose points at which to evaluate and compare the Betti functions. To help in this decision, we computed the persistent Betti numbers for SLICS and cosmo-SLICS on a dense grid. We then compared the mean squared differences between SLICS and cosmo-SLICS, weighted by the inverse variance of the respective Betti numbers within SLICS. This basically measures how well an evaluation point can distinguish different cosmologies. We rank the evaluation points according to this discrimination potential, starting with the ‘best evaluation point. We then recursively built our set of evaluation points in the following way.
Given a set of evaluation points, we extracted the mean of the persistent Betti numbers measured from SLICS, xSLICS, and the same data vector for each cosmology i of the cosmo-SLICS, xi. Furthermore, we extracted a covariance matrix C for this data vector from SLICS. Using these, we computed the quantity 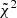 via:
via:
We then added the next evaluation point to our data vector and checked whether the new 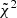 surpassed the old one by a certain threshold (in our case 0.2), while additionally demanding a minimum of 40 features per line-of-sight17. If those two criteria were fulfilled, we added this evaluation point to the data vector and repeated the process. If not, we checked the next-best evaluation point. This yields a total of 33 evaluation points for the KV450-like survey, and 46 evaluation points for the Euclid-like survey. We note that this method favours b1 over b0, consistent with the findings of M+18 that peaks have higher information content than troughs.
surpassed the old one by a certain threshold (in our case 0.2), while additionally demanding a minimum of 40 features per line-of-sight17. If those two criteria were fulfilled, we added this evaluation point to the data vector and repeated the process. If not, we checked the next-best evaluation point. This yields a total of 33 evaluation points for the KV450-like survey, and 46 evaluation points for the Euclid-like survey. We note that this method favours b1 over b0, consistent with the findings of M+18 that peaks have higher information content than troughs.
To visualise this, we plot all features of the persistence diagram as a scatter plot, where the x-coordinate of a point represents the filtration value at which the respective feature is born and the y-coordinate represents the filtration value of its death. In general, a persistent Betti function evaluated at (x, y) counts all features that lie towards the upper-left of the evaluation point (see Fig. B.1). Here, features that lie close to the diagonal arise more likely due to noise fluctuations, whereas features far away from the diagonal are statistically more significant. The final chosen evaluation points for the persistent Betti functions can be seen in Table B.1. Over the course of the analysis, we tested several methods of choosing evaluation points, including just setting them by hand. While different sets of evaluation points sometimes slightly change the size of the contours, they are all internally consistent and yield very similar results. In particular, completely disregarding b0 and 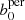 does not change the marginalised error on S8, but helps in constraining the most remote regions of the [Ωm − σ8] contours.
does not change the marginalised error on S8, but helps in constraining the most remote regions of the [Ωm − σ8] contours.
 |
Fig. B.1. Persistence diagram extracted from one tile Ti of the SLICS, in the KV450-like setup. The scattered points represent the features in Dgm(H0(𝕏)) (red) and Dgm(H1(𝕏)) (blue). For each feature, the x-value corresponds to the S/N-level at which that feature is born, whereas the y-value corresponds to the S/N-level at which it disappears again. The orange and green dots mark our evaluation points of the respective persistent Betti functions |
Chosen evaluation points for the Betti functions.
Appendix C: Evaluating the emulator accuracy
In this section, we further discuss the accuracy of the GPR emulator introduced in Sect. 2.4. As described therein, we evaluate the performance via a leave-one-out cross-validation test, and present our results in Fig. C.1 for the persistent Betti functions. As can be seen for the KV450-like case (upper panel), the emulator manages to predict most function values with a 5% accuracy. While some points are less precise, with inaccuracies ranging up to 15%, the mean inaccuracy (represented by the black line) stays well below 1%, meaning that the emulator neither systematically under- nor over-predicts any point of the Betti functions. We next assess the impact of the emulator uncertainty on the inferred cosmological parameters with an MCMC analysis in which we set the emulator covariance Ce to zero. As reported in Fig. C.2, this test confirms that the emulator covariance plays a non-negligible role at the moment since in that case the constraining power is increased for all parameters, and notably the constraints on S8 become tighter by ∼5%.
 |
Fig. C.1. Relative accuracy of the emulator for predicting the persistent Betti functions of a KV450-like (top) and a Euclid-like (bottom) survey. The thin-coloured lines represent the ratio between predicted and measured values for the 26 different cosmologies, estimated from a cross-validation test. The x-axis lists the points at which the functions are evaluated (see Table B.1 for their numerical values). The thick black line corresponds to the mean over all lines. The grey shaded area corresponds to the 1σ standard deviation of the covariance matrix extracted from SLICS. |
 |
Fig. C.2. Parameter constraints from the persistent Betti functions and the peak statistics as presented in Fig. 5 (blue and red, respectively), here compared to the case where the covariance of the emulator Ce is set to zero in the MCMC analyses (green and orange). We note that for the peaks, the emulator covariance plays a negligible role. |
We applied the same procedure to the Euclid-like simulations presented in Sect. 4 and show the cross-validation test in the bottom panel of Fig. C.1. Here, the emulator inaccuracies are significantly higher: While the mean fractional error in the cross-validation test still stays within a few percent, individual deviations often surpass 15%, some points even exceeding 50% fractional error. When compared with the fractional statistical error (the grey band in the figure), we observe that it is also larger compared to the KV450-like analysis. The resulting effect on the cosmological parameter analysis can be seen in Fig. C.3. While the peak statistics are only slightly affected in that case, the difference is significant for persistent Betti functions. In particular, the constraints on S8, Ωm, and w0 improve by 4, 9, and 15%, respectively.
 |
Fig. C.3. Same as Fig. C.2, here in the Euclid-like setup. We note that for the peaks, the emulator covariance plays a sub-dominant role. The results also indicate that, given a better emulator, persistent Betti numbers will be able to constrain the equation of state of dark energy without the need for tomographic analyses. |
The fact that a less noisy measurement yields a larger fractional statistical error might be counter-intuitive, but it can be understood in the following way: In contrast to other measurements, including two-point correlation functions, the presence of shape noise does not only lead to larger measurement errors, but it also changes the expectation value of the measurement itself. Due to the presence of noise, an additional number of features (or peaks) is added to each measurement. This number of pure noise peaks is, to leading order, independent of cosmology, and since adding a constant number to a series of measurements does not affect its variance, the total sampling variance σ is independent of the amount of noise features. When the shape noise is lowered in our Stage IV survey simulations, the variance stays approximately constant, but the amplitude of the data vector decreases, causing the fractional statistical error to increase, as seen by comparing the size of the grey bands in both panels of Fig. C.1. We carried out an extra test in which the intrinsic shape noise of every galaxy in the KV450-like setup was reduced by 90%, and saw the same trend: With lower noise levels, the fractional statistical error increased almost by a factor of two in that case.
This also explains why the emulator has more difficulties in maintaining a high level of accuracy: The constant noise contribution dilutes the relative variations due to cosmology, which makes the interpolation easier for the GPR. In the Euclid-like mocks, the emulator therefore accounts for a large fraction of the error budget. These emulator inaccuracies, and how to improve upon them, will be subject to further investigation.
While we are not yet able to reduce modelling uncertainties with the cosmo-SLICS, this will certainly be possible in the future. Figure A.2 of H+19 shows that for two-point correlation functions, the uncertainty of the emulator falls to the order of a percent when training it on a set of functions that has been modelled for 250 separate cosmologies. With larger projects like BACCO (Angulo et al. 2020), where simulations are conducted for 800 different cosmologies, this accuracy is definitely achievable if a ray-tracing is performed. In that case, it is interesting to investigate the impact of a better emulator on our analysis. This can be achieved simply by performing again a cosmological parameter analysis where we set Ce = 0, as shown in Figs. C.2 and C.3.
Appendix D: Treatment of biases by noise terms
To test the sensitivity to number density and shape noise, we created different galaxy catalogues of SLICS, where we both increased and reduced the shape noise of galaxies by 10%, and one where we reduced the number density by 10% by removing galaxies at random. We used these modified catalogues to extract the mean of the persistent Betti functions bper as well as their covariance matrix. We then performed a cosmological parameter inference as in Sect. 3, where in each case the xpredicted were provided by the emulator that has been trained on the unaltered cosmo-SLICS. As can be seen in Fig. D.1, a 10% change in these parameters roughly corresponds to a ∼1σ shift in the posterior distribution of S8. Additionally, the posterior distributions for both Ωm and σ8 are shifted by ∼3σ for the case of the lowered number density. It is therefore critical to reproduce these properties in the simulations in order to avoid very significant biases in the cosmological inference. In an actual cosmological data analysis, one should use mock data with a similar design to those used in this analysis, namely where galaxies have been distributed on the footprint exactly according to their positions in the data such as to reproduce number density, and additionally keeping their associate ellipticity.
 |
Fig. D.1. Effect on the inferred cosmological parameter in a KV450-like survey from varying shape noise by ±10% (left) and lowering the number density by 10% (right). The solid lines correspond to the fiducial values of SLICS. |
All Tables
All Figures
 |
Fig. 1. Visualisation of an excursion set. The original map (in this case a single peak) is depicted on the left. The middle plot depicts the same peak after a threshold is applied to the map, which cuts off the summit. The result seen from above is depicted on the right, which in this case has one hole (in white) and one connected component (in colour). Varying the threshold generates the full filtration. |
| In the text | |
 |
Fig. 2. Excursion sets of a sample signal-to-noise map for a 3.3 × 3.3 deg2 field of SLICS for nine values t1, …, t9. The solid magenta ellipse highlights a connected component corresponding to a minimum of the signal-to-noise map; the solid orange and red ellipses each highlight a hole corresponding to a maximum. The dashed ellipses indicate the position of the features before their birth and after their death. The magenta feature is born at t2 and dies at t4 after being absorbed by older features that were born in t1. This lifeline is described by the interval [t2, t4) in Dgm(H0(𝕏)). Both the red and orange features are born at t5. The orange one dies at t7, while the red one, which corresponds to a sharper peak, persists longer and dies at t9. Hence, they give rise to intervals [t5, t7) and [t5, t9) in Dgm(H1(𝕏)). |
| In the text | |
 |
Fig. 3. Difference of average Betti numbers b0 (left) and b1 (centre) and peak counts (right) between cosmo-SLICS and SLICS. Left and central panels: x-axis represents the respective filtration level t, which runs from the minimum to the maximum value of the S/N aperture map. The lines are colour-coded by the value of S8 in the respective cosmo-SLICS (see Table A.1). The lines shown here are averages over all mock realisations of the full survey footprint (10 for each cosmo-SLICS node, 126 for SLICS). |
| In the text | |
 |
Fig. 4. Three idealised S/N maps. Both peak count statistics and non-persistent Betti functions can distinguish the first from the third map. However, the peak counts of the first and the second map are identical, as are the non-persistent Betti functions of the second and the third. Persistent Betti functions can distinguish all three maps. For further explanations, see Sect. 2.5. |
| In the text | |
 |
Fig. 5. Results of an MCMC on the Betti numbers measured in the KV450-like SLICS. The contours represent the 1- and 2-σ posterior contours for an analysis with non-persistent (grey) and persistent (blue) Betti functions. For comparison, the red contours represent the posterior of an analysis with peak statistics, as done in M+18. The values on top of the diagonals represent the marginalised posterior for the persistent Betti functions bper. The fiducial parameters of SLICS are represented by the black lines. We conducted our analysis with Ωm, σ8, h and w0 as free parameters and employed flat priors with Ωm ∈ [0.1, 0.6], S8 ∈ [0.6, 1.0], h ∈ [0.5, 0.9], w0 ∈ [ − 1.8, −0.2]. The green lines correspond to the 1- and 2-σ posterior contours of a cosmological parameter analysis of the KiDS450-survey using tomographic two-point correlation functions, where the covariance matrix was extracted from SLICS and systematics were disregarded (see the ‘N-body’ setup in Table 4 of Hildebrandt et al. 2017). Since the setup of that analysis is very similar to ours, they can be used to compare the relative sizes (but not locations) of contours. We note that this parameter analysis was done in a ΛCDM-framework on KiDS data, whereas our analysis is done in a wCDM framework on mock data. |
| In the text | |
 |
Fig. 6. Results of an MCMC as described in Fig. 5, but here for 100 deg2 of Euclid-like lensing data. |
| In the text | |
 |
Fig. B.1. Persistence diagram extracted from one tile Ti of the SLICS, in the KV450-like setup. The scattered points represent the features in Dgm(H0(𝕏)) (red) and Dgm(H1(𝕏)) (blue). For each feature, the x-value corresponds to the S/N-level at which that feature is born, whereas the y-value corresponds to the S/N-level at which it disappears again. The orange and green dots mark our evaluation points of the respective persistent Betti functions |
| In the text | |
 |
Fig. C.1. Relative accuracy of the emulator for predicting the persistent Betti functions of a KV450-like (top) and a Euclid-like (bottom) survey. The thin-coloured lines represent the ratio between predicted and measured values for the 26 different cosmologies, estimated from a cross-validation test. The x-axis lists the points at which the functions are evaluated (see Table B.1 for their numerical values). The thick black line corresponds to the mean over all lines. The grey shaded area corresponds to the 1σ standard deviation of the covariance matrix extracted from SLICS. |
| In the text | |
 |
Fig. C.2. Parameter constraints from the persistent Betti functions and the peak statistics as presented in Fig. 5 (blue and red, respectively), here compared to the case where the covariance of the emulator Ce is set to zero in the MCMC analyses (green and orange). We note that for the peaks, the emulator covariance plays a negligible role. |
| In the text | |
 |
Fig. C.3. Same as Fig. C.2, here in the Euclid-like setup. We note that for the peaks, the emulator covariance plays a sub-dominant role. The results also indicate that, given a better emulator, persistent Betti numbers will be able to constrain the equation of state of dark energy without the need for tomographic analyses. |
| In the text | |
 |
Fig. D.1. Effect on the inferred cosmological parameter in a KV450-like survey from varying shape noise by ±10% (left) and lowering the number density by 10% (right). The solid lines correspond to the fiducial values of SLICS. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



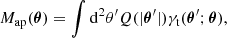
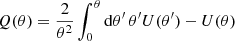
![$$ \begin{aligned} \gamma _{\rm t}(\boldsymbol{\theta }^\prime ;\boldsymbol{\theta }) = -\mathfrak{R} \left[\gamma (\boldsymbol{\theta }^\prime )\,\frac{(\boldsymbol{\theta }^{\prime *} -\boldsymbol{\theta }^{*})^2}{|\boldsymbol{\theta }\prime - \boldsymbol{\theta }|^2}\right], \end{aligned} $$](/articles/aa/full_html/2021/04/aa39048-20/aa39048-20-eq5.gif)
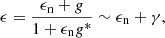
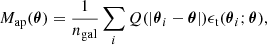
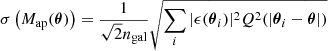
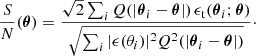
![$$ \begin{aligned} Q(\theta ) =&\left[1 + \exp \left(6 -150 \frac{\theta }{\theta _{\rm ap}}\right) + \exp \left(-47 +50 \frac{\theta }{\theta _{\rm ap}}\right)\right]^{-1} \nonumber \\& \times \left(\frac{\theta }{x_{\rm c}\theta _{\rm ap}}\right)^{-1} \tanh \left(\frac{\theta }{x_{\rm c}\theta _{\rm ap}}\right)\cdot \end{aligned} $$](/articles/aa/full_html/2021/04/aa39048-20/aa39048-20-eq10.gif)
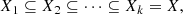
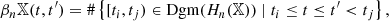
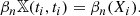
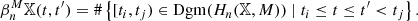
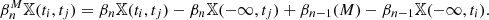
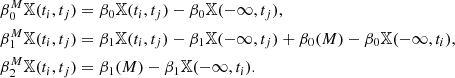
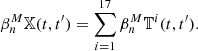
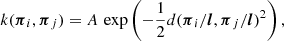
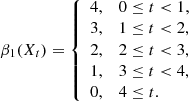
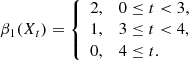
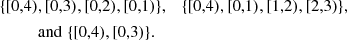
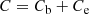
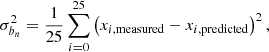
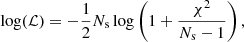
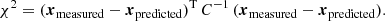
![$$ \begin{aligned} n(z) \propto z^{2} \mathrm{exp} \Bigg [-\Bigg (\frac{z}{z_0}\Bigg )^{\beta }\Bigg ], \end{aligned} $$](/articles/aa/full_html/2021/04/aa39048-20/aa39048-20-eq42.gif)
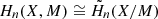
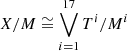
![$$ \begin{aligned} \tilde{\chi }^2 = \frac{1}{26} \sum _i\left[(\boldsymbol{x}_{\rm SLICS}-\boldsymbol{x}_i)^\mathrm{T}C^{-1}(\boldsymbol{x}_{\rm SLICS}-\boldsymbol{x}_i)\right]. \end{aligned} $$](/articles/aa/full_html/2021/04/aa39048-20/aa39048-20-eq51.gif)