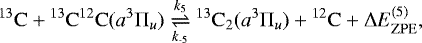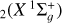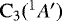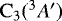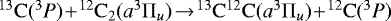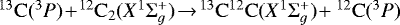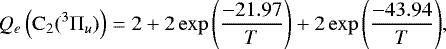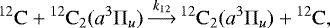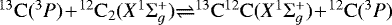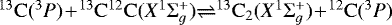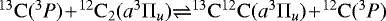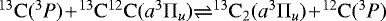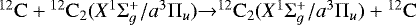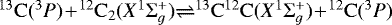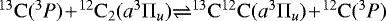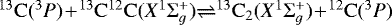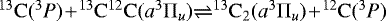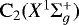EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 647 (March 2021) A&A, 647 (2021) A142 Full HTML
Free Access
Issue
A&A
Volume 647, March 2021
Article Number A142
Number of page(s) 12
Section Atomic, molecular, and nuclear data
DOI https://doi.org/10.1051/0004-6361/202040093
Published online 24 March 2021

© ESO 2021

1 Introduction

Observations of isotopic abundance ratios in interstellar molecules provide an avenue for tracking Galactic chemical evolution, from stellar nucleosynthesis to dense cloud formation and processing of the ejected material to new stars and planetary systems created therefrom (Wilson 1999). For example, the seemingly incompatible elemental [12C/13C] ratios found in the local interstellar medium (ISM; ~68 as inferred from CN: Milam et al. 2005, CO: Langer 1992, H2CO: Langer 1992 and CH+: Wilson 1999) and in the Solar System (~89) might be indicative of 13C enrichment of the ISM by asymptotic giant branch (AGB) stars since the formation of the Sun (Milam et al. 2005).

Apart from the intrinsic variations with galactocentric distance and time (Wilson 1999; Milam et al. 2005; Langer 1992), isotopic abundance ratios as measured in molecules are also important tracers of local environment effects. Interstellar species often show relative abundances of particular isotopologs that may significantly differ from those inherent in the gas owing to peculiarities in their chemistry (Furuya et al. 2011). In cold dense cloud cores, with typical temperatures (T) of ~10 K and visual extinctions (AV) of ~ 10 mag, this so-called isotopic fractionation (Langer et al. 1984; Terzieva & Herbst 2000; Furuya et al. 2011; Liszt & Ziurys 2012; Roueff et al. 2015; Furuya & Aikawa 2018; Loison et al. 2018, 2019, 2020; Colzi et al. 2020) has long been recognized and mainly attributed to gas-phase isotope-exchange reactions (Dalgarno & Black 1976; Watson et al. 1976). Given the very lowcollision energies in dense clouds, it becomes clear that the most efficient fractionation pathways therein must involve exothermic reactions for which the salient features of the potential energy surfaces (PESs; Rocha 2019) are basins rather than barriers (Henchman & Paulson 1989). Indeed, chemical fractionation via barrierless ion–molecule or neutral–neutral reactions is mostly driven by the small zero-point energy (ZPE) differences between reactants and products of isotopically distinct species (Mladenović & Roueff 2014, 2017); the role of isotope-selective gas–grain interactions and photodissociation in also altering fractionation ratios is discussed elsewhere (e.g., Furuya et al. 2011; Furuya & Aikawa 2018; Loison et al. 2018; Visser et al. 2009).

With regard to carbon isotopic fractionation, Watson et al. (1976) first pointed out the relevance of the reaction 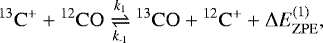\mathrm{^13C+}+\mathrm{^12CO}⇌k1k01 \mathrm{^13CO}+\mathrm{^12C+}+ΔEZPE(1),\begin{equation*}\mathrm{^{13}C^{+}}+\mathrm{^{12}CO}\underset{k_{\text{-}1}}{\stackrel{k_{1}}{\rightleftharpoons}} \mathrm{^{13}CO}+\mathrm{^{12}C^{+}}+\Delta E_{\mathrm{ZPE}}^{(1)} ,\end{equation*}(1)

which is particularly efficient at low T; k1 ∕k- 1 ≈ 33 at 10 K and 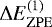ΔEZPE(1)$\Delta E_{\mathrm{ZPE}}^{(1)}$, the ZPE difference among 12CO and 13CO, is ≈ 35 K (Watson et al. 1976; Smith & Adams 1980; Langer et al. 1984). As first noted by Langer et al. (1984) reaction (1), on one hand, enhances the amount of 13C locked up in CO (and in species directly formed from it), and on the other hand makes 13 C+ less available to react with other C-bearing species, decreasing their 13C content. Because CO is by far the largest repository of gas-phase carbon (at least in oxygen-rich dense clouds Langer et al. 1984), the above scenario led to the suggestion that 12 C/13C values as measured from CO serve as a lower limit to the “true” elemental [12 C/13C] ratio gradient throughout the Galaxy, while those inferred from other species like H2 CO reflect an upper range (Wilson 1999; Langer 1992).

Ever since the postulation of reaction (1) as the main C fractionation route in strongly shielded regions (Watson et al. 1976), a notable contrast has emerged between the above general predictions (by chemistry models) of the strong 13 C depletion in C-containing molecules (Langer et al. 1984) and the general absence of this observable effect in surveys conducted, for example, in abundant species such as CS (Liszt & Ziurys 2012), CN (Milam et al. 2005), C2 (Hamano et al. 2019), CCS (Sakai et al. 2007), HNC (Liszt & Ziurys 2012), C3 (Giesen et al. 2020), and HC3N (Takano et al. 1998) that are not formed directly from CO and whose 12 C/13C ratios thus inferred are in agreement with (or even lower than) the gas elemental values. Such a conflict therefore opened up new avenues for the possibility of an overall 13C enrichment in species other than CO, and led to the proposition of alternative isotope-exchange reactions (e.g., 13 C(+)+CN: Langer 1992; Roueff et al. 2015, 13 CO+HCO+: Smith & Adams 1980; Mladenović & Roueff 2017, 13 C+C2: Roueff et al. 2015, and 13 C+C3: Giesen et al. 2020; Colzi et al. 2020; Loison et al. 2020) and novel formation pathways (Takano et al. 1998; Sakai et al. 2007; Furuya et al. 2011) deemed to contribute to the 13C fractionation chemistry. Despite previous assessments (Woods & Willacy 2009; Furuya et al. 2011; Roueff et al. 2015; Colzi et al. 2020; Loison et al. 2020), validation of this hypothesis is often hindered by a lack of accurate experimental and/or theoretical rate coefficients for some of these reactions (Furuya et al. 2011; Woods & Willacy 2009).

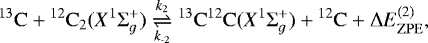In this work, we provide such values for the gas-phase reactions \mathrm{^13C}+\mathrm{^12C2}(X1Σg+)⇌k2k02\mathrm{^13C12C}(X1Σg+)+\mathrm{^12C}+ΔEZPE(2),\begin{equation*}\mathrm{^{13}C}+\mathrm{^{12}C_{2}}(X^{1}\Sigma_{g}^{+})\underset{k_{\text{-}2}}{\stackrel{k_{2}}{\rightleftharpoons}}\mathrm{^{13}C^{12}C}(X^{1}\Sigma_{g}^{+})+\mathrm{^{12}C}+\Delta E_{\mathrm{ZPE}}^{(2)}, \end{equation*}(2) \mathrm{^13C}+\mathrm{^13C12C}(X1Σg+)⇌k3k03\mathrm{^13C2}(X1Σg+)+\mathrm{^12C}+ΔEZPE(3),\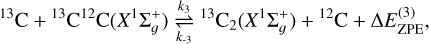begin{equation*}\mathrm{^{13}C}+\mathrm{^{13}C^{12}C}(X^{1}\Sigma_{g}^{+})\underset{k_{\text{-}3}}{\stackrel{k_{3}}{\rightleftharpoons}}\mathrm{^{13}C_{2}}(X^{1}\Sigma_{g}^{+})+\mathrm{^{12}C}+\Delta E_{\mathrm{ZPE}}^{(3)}, \end{equation*}(3) \mathrm{^13C}+\mathrm{^12C2}(a3Πu)⇌k4k04\mathrm{^13C12C}(a3Πu)+\mathrm{^12C}+ΔEZPE(4),\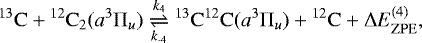begin{equation*}\mathrm{^{13}C}+\mathrm{^{12}C_{2}}(a^{3}\Pi_{u})\underset{k_{\text{-}4}}{\stackrel{k_{4}}{\rightleftharpoons}}\mathrm{^{13}C^{12}C}(a^{3}\Pi_{u})+\mathrm{^{12}C}+\Delta E_{\mathrm{ZPE}}^{(4)}, \end{equation*}(4)

and \mathrm{^13C}+\mathrm{^13C12C}(a3Πu)⇌k5k05\mathrm{^13C2}(a3Πu)+\mathrm{^12C}+ΔEZPE(5),\begin{equation*}\mathrm{^{13}C}+\mathrm{^{13}C^{12}C}(a^{3}\Pi_{u})\underset{k_{\text{-}5}}{\stackrel{k_{5}}{\rightleftharpoons}}\mathrm{^{13}C_{2}}(a^{3}\Pi_{u})+\mathrm{^{12}C}+\Delta E_{\mathrm{ZPE}}^{(5)}, \end{equation*}(5)

by means ofa theoretical approach (see below). The motivation here is primarily grounded in the prevalence of C2, the smallestpure carbon cluster, throughout the ISM; it has been detected (via its Phillips (A 1 Πu–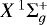X 1Σg+$X\,^{1}\Sigma_{g}^{+}$) and Swan (d 3 Πg–a 3Πu) bands) in a myriad of astronomical sources (Babb et al. 2019), including diffuse (Souza & Lutz 1977; Snow & McCall 2006), translucent (Hamano et al. 2019), and dense molecular clouds (Hobbs et al. 1983) and is known to be the primary reservoir of gas-phase carbon in oxygen-poor regions (Souza & Lutz 1977). Besides being key for probing the physical conditions of interstellar clouds (Snow & McCall 2006), C2, together with C(+), is thought to be the fundamental building block in the formation chemistry of larger hydrogen-deficient C-bearing species (Ehrenfreund & Charnley 2000; Kaiser 2002; Gu et al. 2006), and therefore plays an active role in their 13 C enrichment. From a top-down perspective, C2 radicals are also important units arising from the (photo)fragmentation of polycyclic aromatic hydrocarbons (PAHs) and fullerenes. In a number of experimental studies it was shown that PAHs, once fully dehydrogenated, fragment through sequential C2 -losses (see, e.g., Zhen et al. 2014). This is fully consistent with the general picture that some of the diffuse interstellar band (DIB) carriers, notably those responsible for the so-called C2 DIBs (Thorburn et al. 2003; Elyajouri et al. 2018), might be related to PAH cations and their derivatives upon photoprocessing.

As for the calculation of both forward and reverse rate coefficients of reactions (2)–(5), we herein employ the quasi-classical trajectory (QCT) method (Truhlar & Muckerman 1979; Peslherbe et al. 1999), with the previously obtained (nuclear-mass-independent) global PESs of 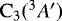C3(3A′)$\mathrm{C_{3}}(^{3}A')$ (Rocha & Varandas 2019) and 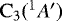C3(1A′)$\mathrm{C_{3}}(^{1}A')$ (Rocha & Varandas 2018) dictating the interactions between the involved nuclei (see Sect. 2). From the calculated rate coefficients as a function of T, equilibrium constants for these processes are also provided and their possible impact on the overall C isotopic fractionation chemistry is briefly discussed.

thumbnail Fig. 1

One-dimensional cuts of the nuclear-mass-independent PESs of C3 along the minimum-energy paths connecting reactants and products via C3 intermediates. The zero of energy is set relative to the infinitely separated C+C2(X 1Σg+)$_{2}(X\,^{1}\Sigma_{g}^{+})$ fragments. The reacting carbon atom is shown in yellow.

2 Methods

2.1 Potential energy surfaces

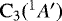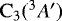The global adiabatic mass-independent PESs of ground-state C3(1A′)$\mathrm{C_{3}}(^{1}A')$ and C3(3A′)$\mathrm{C_{3}}(^{3}A')$ used here in the QCT calculations are depicted in Figs. 1 and 2. They were obtained by performing electronic structure calculations for a sufficient number of (fixed) nuclear configurations whose energies were then modeled by physically motivated many-body expansion forms (Rocha & Varandas 2018, 2019). To obtain a balanced and accurate description of both valence and long-range features of the potentials, ab initio calculations were carried out at the multireference configuration interaction [MRCI(+Q)] level of theory (Szalay et al. 2012), with the final total energies subsequently extrapolated to the complete (one-electron) basis set limit (Varandas 2018) prior to the fitting procedure. For the singlet PES, Rocha & Varandas (2018) improved the spectroscopy near its linear minima [ℓ-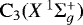C3(X 1Σg+)$\mathrm{C_{3}}(X\,^{1}\Sigma_{g}^{+})$] by morphing this global form with an accurate Taylor-series expansion taken from Schröder & Sebald (2016). In this spirit and to partially account for the incompleteness of the N$\mathcal{N}$-electron basis and other minor effects, both global PESs used in this work have their ab initio two-body terms replaced by the direct-fit, experimentally determined, diatomic curves (Rocha & Varandas 2019). The spectroscopic attributes of the isotopically substituted dissociation channels and of the C3 intermediates spanned by the trajectories are shown in Tables 1 and 2, respectively. Also listed in Table 3 are the corresponding ΔEZPE values of reactions (2)–(5) as predicted from the global PESs; their thermodynamic aspects are briefly summarized below.

As Fig. 1 shows, the underlying C exchange reactions proceed without activation barriers for collinear atom–diatom approaches. Along C∞v, the shape of the ground-state 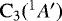C3(1A′)$\mathrm{C_{3}}(^{1}A')$ PES is characterized by a single, deep potential well; the stabilization energy of the ℓ-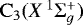C3(X 1Σg+)$\mathrm{C_{3}}(X\,^{1}\Sigma_{g}^{+})$ complex is 183 kcal mol-1 relative to the infinitely separated 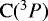C(3P)$\mathrm{C}(^{3}P)$+C2(a3Πu) fragments. In contrast, the minimum energy path (MEP) for the 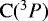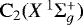C(3P)$\mathrm{C}(^{3}P)$+C2(X 1Σg+)$\mathrm{C_{2}}(X\,^{1}\Sigma_{g}^{+})$ insertion unravels the existence of two such wells; the shallower of the two with a well depth of − 125 kcal mol-1 characterizes the ℓ-C3(ã 3Πu) local minimum, while the deepest at − 158 kcal mol-1 defines the c-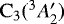C3(3A′2)$\mathrm{C_{3}}(^{3}A'_{2})$ equilateral triangular global minimum. The access from one basin to the other is granted via the C2v transition state (TS) ℓc-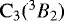C3(3B2)$\mathrm{C_{3}}(^{3}B_{2})$ with activation energy of 37 kcal mol-1 relative to ℓ-C3(ã 3Πu). We note that, due to the permutational nature of the PESs, three symmetry-equivalent and interconnected MEPs exist for rotations by ± 120° (see Fig. 2); this is expected to enhance the efficiency of the isotopic scrambling by long-lived C3 intermediates (Henchman & Paulson 1989). However, differently from the collinear insertions, Fig. 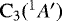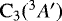2 unravels the presence of energy barriers along perpendicular approaches of the fragments; these are ≈ 9 and 2 kcal mol-1 for the C3(1A′)$\mathrm{C_{3}}(^{1}A')$ and C3(3A′)$\mathrm{C_{3}}(^{3}A')$ PESs, respectively, and therefore make reactive events arising from C2v atom–diatom encounters prohibitive at low T.

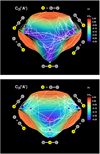thumbnail Fig. 2

Relaxed 3D plots in hyperspherical coordinates (Varandas 1987) of the nuclear-mass-independent PESs of ground-state (a) C3(1A′)$\mathrm{C_{3}}(^{1}A')$ and (b) C3(3A′)$\mathrm{C_{3}}(^{3}A')$. The zero of energy is set relative to the infinitely separated C+C2 fragments. Stationary points and minimum energy paths (solid yellow lines) as in Fig. 1. Solid white lines show the time evolution (in coordinate space) of sample reactive trajectories for the processes (a)\mathrm{^13C}(3P)​+​\mathrm{^12C2}(a3Πu)​→​\mathrm{^13C12C}(a3Πu)​+​\mathrm{^12C}(3P)$\mathrm{^{13}C}(^{3}P)\!+\!\mathrm{^{12}C_{2}}(a^{3}\Pi_{u})\!\rightarrow\!\mathrm{^{13}C^{12}C}(a^{3}\Pi_{u})\!+\!\mathrm{^{12}C}(^{3}P)$ and (b) \mathrm{^13C}(3P)​+​\mathrm{^12C2}(X1Σg+)​→​\mathrm{^13C12C}(X1Σg+)​+\mathrm{^12C}(3P)$\mathrm{^{13}C}(^{3}P)\!+\!\mathrm{^{12}C_{2}}(X^{1}\Sigma_{g}^{+})\!\rightarrow\!\mathrm{^{13}C^{12}C}(X^{1}\Sigma_{g}^{+})\!+\mathrm{^{12}C}(^{3}P)$. An isotopically distinct carbon atom is schematically represented in yellow.

2.2 Quasi-classical trajectory calculations

The quasi-classical trajectory (QCT) method employed in this work has been extensively described in the literature (Truhlar & Muckerman 1979; Peslherbe et al. 1999). Using a locally modified version of the VENUS96C code (Hase et al. 1996), batches of 104 trajectories were run for the ground adiabatic 1A′ and 3A′ PESs of C3 separately; non-adiabatic (Tully & Preston 1971; Voronin et al. 1998; Galvão et al. 2012) and spin-forbidden (Tachikawa et al. 1995; Galvão et al. 2013) transitions were not taken into account. Cross-sections and rate constants for the envisaged (forward and reverse) isotope-exchange reactions (Eqs. (2)–(5)) were obtained for fixed Ts by randomly sampling (Peslherbe et al. 1999) the orientation of the reactants; atom-diatom relative translational energy; the ro-vibrational state of the reactant dicarbon; and impact parameter (b). The integration of the Hamilton’s equations of motion employed a time-step of 0.1 fs such as to warrant conservation of the total energy to better than 10−4 hartree (Eh). Reactants were initially separated by 12 a0, with a maximum value of b (bmax) optimized by trial and error for each T and PES; see Tables A.1–A.3. Figure 2 shows sample reactive trajectories for reactions (2) and (4).

For a given T, (averaged) reaction cross-sections were then obtained as (Peslherbe et al. 1999) 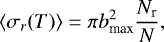〈σr(T)〉=πbmax2NrN,\begin{equation*}\langle \sigma_{r}(T) \rangle = \pi b_{\textrm{max}}^{2}\frac{N_{\textrm{r}}}{N}, \end{equation*}(6)

where Nr is the number of reactive trajectories out of a total of N that were run. To account in an approximate way for the deficiency of classical mechanics in conserving the quantum mechanical ZPE, we herein follow Nyman & Davidsson (1990) and Varandas (1993) and consider in the statistical analysis only trajectories that show enough vibrational energy to reach the ZPE of the products or the reformed reactants (Table 1); no ZPE constraints were a priori imposed on the C3 intermediate complexes (Table 2) (Truhlar 1979).

Assuming that the translational and internal degrees of freedom are at equilibrium, that is, the velocity distributions are Maxwellian and the reactants quantum numbers are determined from Boltzmann distributions, the thermal rate coefficients of reactions (2)–(5) were calculated as (Peslherbe et al. 1999) 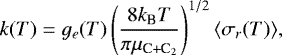k(T)=ge(T)(8kBTπμC+C2)1/2〈σr(T)〉,\begin{equation*}k(T)=g_{e}(T)\left(\frac{8k_{\textrm{B}}T}{\pi\mu_{\textrm{C+C}_{2}}}\right)^{1/2}\langle \sigma_{r}(T) \rangle, \end{equation*}(7)

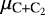with the estimated standard deviation (68.2% error) given by Δk(T)​=​k(T)[(N​−​Nr)/(NNr)]1/2$\Delta k(T)\!=\!k(T)[(N\!-\!N_{r})/(NN_{r})]^{1/2}$. In Eq. (7), kB is the Boltzmann constant, μC+C2$\mu_{\textrm{C+C}_{2}}$ is the reactants reduced mass and 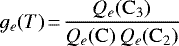ge(T)​=​Qe(C3)Qe(C) Qe(C2)\begin{equation*}g_{e}(T)\!=\!\frac{Q_{e}(\mathrm{C_{3}})}{Q_{e}(\mathrm{C})\,Q_{e}(\mathrm{C_{2}})} \end{equation*}(8)

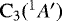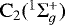is the electronic degeneracy factor that approximately accounts for fine structure effects (Truhlar 1972; Muckerman & Newton 1972; Graff & Wagner 1990; Zanchet et al. 2007, 2010); the Qe s are electronic partition functions. For C3(1A′)$\mathrm{C_{3}}(^{1}A')$ and C2(1Σg+)$\mathrm{C_{2}}(^{1}\Sigma^{+}_{g})$, they assume unit values, while 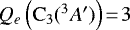Qe(C3(3A′))​=​3$Q_{e}\left(\mathrm{C_{3}}(^{3}A')\right)\!=\!3$. 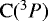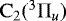For C(3P)$\mathrm{C}(^{3}P)$ and C2(3Πu)$\mathrm{C_{2}}(^{3}\Pi_{u})$, the Qes are: 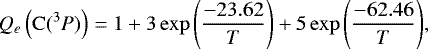Qe(C(3P))=1+3exp(−23.62T)+5exp(−62.46T),\begin{equation*}Q_{e}\left(\mathrm{C}(^{3}P)\right)=1+3\exp{\left(\frac{-23.62}{T}\right)}+5\exp{\left(\frac{-62.46}{T}\right)}, \end{equation*}(9)

and Qe(C2(3Πu))=2+2exp(−21.97T)+2exp(−43.94T),\begin{equation*}Q_{e}\left(\mathrm{C_{2}}(^{3}\Pi_{u})\right)=2+2\exp{\left(\frac{-21.97}{T}\right)}+2\exp{\left(\frac{-43.94}{T}\right)}, \end{equation*}(10)

where the first equation accounts for the populations of the 3 PJ=0, 3 PJ=1, and 3 PJ=2 spin-orbit terms of 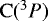C(3P)$\mathrm{C}(^{3}P)$ with energy gaps 23.62 and 62.46 K and degeneracy 2J+1 (Haris & Kramida 2017). The corresponding inverted multiplets 3ΠΩ = 2, 3 ΠΩ = 0, and 3 ΠΩ = 1 of 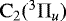C2(3Πu)$\mathrm{C_{2}}(^{3}\Pi_{u})$ are considered in Eq. (10); they are spaced by 21.97 and 43.94 K and are all doubly degenerate (Brooke et al. 2013; Ram et al. 2014). In deriving Eq. (8), it is assumed that the spin-orbit states of the reactants are thermally populated and that only specificfine-structure levels, that is, those that adiabatically correlate with the underlying PESs, may lead to reaction. For 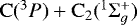C(3P)+C2(1Σg+)$\mathrm{C}(^{3}P)+\mathrm{C_{2}}(^{1}\Sigma^{+}_{g})$, we consider in Eq. (8) that of the nine spin-orbit states arising asymptotically (Eq. (9)) only the lowest three (correlating with the 3 A′ PES) are reactive, these being the 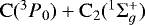C(3P0)+C2(1Σg+)$\mathrm{C}(^{3}P_{0})+\mathrm{C_{2}}(^{1}\Sigma^{+}_{g})$ and two of the three 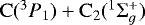C(3P1)+C2(1Σg+)$\mathrm{C}(^{3}P_{1})+\mathrm{C_{2}}(^{1}\Sigma^{+}_{g})$ states (Wilhelmsson & Nyman 1992; Russell & Manolopoulos 1999); for simplicity, no temperature dependence was a priori included into the corresponding partition function, that is, 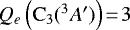Qe(C3(3A′))​=​3$Q_{e}\left(\mathrm{C_{3}}(^{3}A')\right)\!=\!3$ in Eq. (8) (Wilhelmsson & Nyman 1992). The remaining six states correlate with two other excited triplet PESs and are regarded as nonreactive. Such a scenario becomes even more intricate in the case of 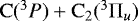C(3P)+C2(3Πu)$\mathrm{C}(^{3}P)+\mathrm{C_{2}}(^{3}\Pi_{u})$. Their asymptotic interaction gives rise to 18 (6 singlet, 6 triplet and 6 quintet) electronic states, correlating to a total of 54 spin-orbit levels (Eqs. (8)–(10)). This undoubtedly makes the determination of the appropriate adiabatic correlations, and hence 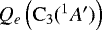Qe(C3(1A′))$Q_{e}\left(\mathrm{C_{3}}(^{1}A')\right)$ in Eq. (8), a nontrivial task. Due to lack of experimental and further theoretical evidence, we herein simply choose to correlate the ground-state PES of C3 to the lowest spin-obit states of its fragments (i.e. to the lowest A′ component of 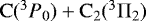C(3P0)+C2(3Π2)$\mathrm{C}(^{3}P_{0})+\mathrm{C_{2}}(^{3}\Pi_{2})$; Andersson et al. 2003; Abrahamsson et al. 2008), which means that this surface is the only one available for reaction among all 54 (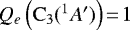Qe(C3(1A′))​=​1$Q_{e}\left(\mathrm{C_{3}}(^{1}A')\right)\!=\!1$ in Eq. (8)). We note that while the above surmises are the most appealing a priori, they may introduce, together with the single-surface ansatz (7) (Graff & Wagner 1990), additional approximations in the calculated rate coefficients; however, these can only be assessed once experimental kinetics data become available. In this respect, we note that the possible contributions of the other excited states to the overall dynamics (not considered here) cannot be grasped at the moment as these and their associated global PESs remain largely unexplored. We further note that we herein employ the same Qe s for both main and rare isotopologs, which is a reasonable approximation. 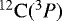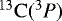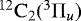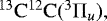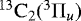For example, the energy differences between spin-orbit terms of \mathrm{^12C}(3P)$\mathrm{^{12}C}(^{3}P)$ and \mathrm{^13C}(3P)$\mathrm{^{13}C}(^{3}P)$ and of \mathrm{^12C2}(3Πu)$\mathrm{^{12}C_{2}}(^{3}\Pi_{u})$, \mathrm{^13C12C}(3Πu),$\mathrm{^{13}C^{12}C}(^{3}\Pi_{u}),$ and \mathrm{^13C2}(3Πu)$\mathrm{^{13}C_{2}}(^{3}\Pi_{u})$ are well below 0.01% (Haris & Kramida 2017; Brooke et al. 2013; Ram et al. 2014; Amiot 1983).

Table 1

Spectroscopic properties (in cm−1) of the reactant and product diatomics (of reactions (2)–(5)) correlating with the global singlet and triplet PESs of C3.

Table 2

Structural parameters (bond distances Re in a0 and angle α in degs), harmonic (ωi), fundamental (νi) frequencies and zero-point energies (in cm−1) of the 13 C singly and doubly substituted C3 minima of the PESs spanned by long-lived trajectories.

Table 3

Exothermicities (in cm−1 unless otherwise stated) of reactions (2)–(5) based on the data shown in Table 1.

3 Results and discussion

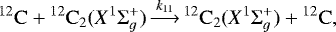Figure 3 shows the calculated forward and backward rate coefficients for the gas-phase isotope-exchange reactions (2)–(5) within the temperature range of 25 ≤ T∕K ≤ 500. Also shown for comparison are the corresponding QCT rates obtained for the \mathrm{^12C}+\mathrm{^12C2}(X1Σg+) →k11 \mathrm{^12C2}(X1Σg+)+\mathrm{^12C},\begin{equation*}\mathrm{^{12}C}+\mathrm{^{12}C_{2}}(X^{1}\Sigma_{g}^{+})\,{\stackrel{k_{11}}{\longrightarrow}}\,\mathrm{^{12}C_{2}}(X^{1}\Sigma_{g}^{+})+\mathrm{^{12}C}, \end{equation*}(11)

and \mathrm{^12C}+\mathrm{^12C2}(a3Πu) →k12 \mathrm{^12C2}(a3Πu)+\mathrm{^12C},\begin{equation*}\mathrm{^{12}C}+\mathrm{^{12}C_{2}}(a^{3}\Pi_{u})\,{\stackrel{k_{12}}{\longrightarrow}}\,\mathrm{^{12}C_{2}}(a^{3}\Pi_{u})+\mathrm{^{12}C}, \end{equation*}(12)

atom-exchange reactions and available results from the literature (Roueff et al. 2015; Colzi et al. 2020; Westley 1980); Tables A.1–A.3 gather all the numerical values. To further explore the temperature dependence of k, we have considered the popular Arrhenius-Kooij formula (Laidler 1984) 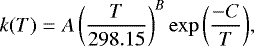k(T)=A(T298.15)Bexp(−CT),\begin{equation*}k(T)=A\left(\frac{T}{298.15}\right)^{B}\exp{\left(\frac{-C}{T}\right)}, \end{equation*}(13)

where A, B, and C are parameters to be adjusted to the QCT data; they are numerically defined in Table 4, with the final fitted forms also plotted in Fig. 3. We note that, in the least-squares fitting procedure, the nonlinear parameters C were allowed to float freely from their initial values, and therefore slightly deviate from the expected ΔEZPE values in Table 3. Physically, this is consistent with the presence of rotationally excited reactant and product C2 species (Mladenović & Roueff 2014). Suffice it to say that, due to the homonuclear nature of the 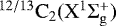\mathrm{^12/13C2(X1Σg+)}$\mathrm{^{12/13}C_{2}(X^{1}\Sigma_{g}^{+})}$ reactant molecules, only even rotational quantum numbers J were considered in the trajectory samplings; for the 13C12C species, the corresponding Boltzmann distributions include both odd and even J values.

As shown in Fig. 3, the calculated thermal rate constants for the C + C2 reactions increase as a function of temperature, revealing a positive T dependence.As previously noted (Sect. 2.1), this stems from the fact that, at higher T, not only are the (head-on collinear) MEPs sampled by the reactive trajectories but also other regions of the PESs become energetically accessible (e.g., bimolecular side-on encounters at high collision energies), increasing reaction probabilities. A similar temperature-dependent profile (k ∝ T0.6) was found experimentally for the barrierless N + C2 reaction (Loison et al. 2014). As expected, all these processes evolve via long-lived trajectories, with the strongly bound energized complexes spanning large sections of the molecular PESs; see Fig. 2. Figure 3 shows that the forward exothermic reactions (2)–(5) are fast with the calculated rate constants varying from 10−12 up to 10−10 cm3 molecule−1 s−1 within the temperature interval considered. At T = 10 K, Eq. (13) predicts k2, k3, k4, k5 to be 1.5 × 10−11, 7.6e− 12, 1.4 × 10−12, and 6.8 × 10−13 cm3 molecule−1 s−1, respectively; these values are typical of atom–radical reactions that are currently included in low-temperature astrochemical networks (Smith et al. 2004). Overall, the reactivity of 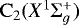C2(X1Σg+)$\mathrm{C_{2}}(X^{1}\Sigma_{g}^{+})$ with ground-state C atoms is about one order of magnitude higher than that of the first excited C2 (a3Πu) state. This is in general agreement with experimental results when the molecular partner is an unsaturatedhydrocarbon (Gu et al. 2006; Páramo et al. 2008). We further note that, except for T = 200 K (see Figs. 3a and b), the predicted rates of the isotope-exchange reactions (2) and (3) are in sharp contrast to the theoretically derived k via simple capture theory (CT; Roueff et al. 2015; Colzi et al. 2020), particularly at low T. Such discrepancies are large enough to suggest that, in addition to long-range interactions, the strongly bound (short-range) parts of the PESs considered here also influence the dynamics of all these reactive processes. One should bear in mind that, although an approximate treatment of the ZPE-leakage (Truhlar 1979) is warranted here (see Sect. 2.2), our QCT approach (like CT; Georgievskii & Klippenstein 2005) neglects, by its own nature, other quantum-mechanical (QM) effects such as tunneling; this is also justifiable on the large masses of the nuclei involved. While such an approximation may be less reliable in the low-temperature limit (Truhlar & Muckerman 1979; Peslherbe et al. 1999), accurate estimates of QM effects unavoidably require exact (nonadiabatic) quantum dynamics calculations which are even more demanding in the case of complex-forming reactions (Guo 2012), and hence are beyond the present scope of this work.

In contrast to the forward reactions, the backward processes in Eqs. (2)–(5) show temperature thresholds (Table 4); these latter are attributed to ZPE differences between reactant and product C2 isotopologs. Due to operation of statistical factors on the kinetics of (2) and (4) (i.e., 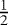12$\frac{1}{2}$ for backward and 1 for forward), we recognize from Figs. 3a and c that, in the high-T limit, the rate coefficients k- 2,- 4 are approximately half of k2,4 (Henchman et al. 1981). The contrary is the case for reactions (3) and (5) where statistical factors of 1 for backward and 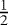12$\frac{1}{2}$ for the forward processes are operative (Henchman et al. 1981). Therefore, as shown in Figs. 3b and d, k- 3,- 5 ≈ 2k3,5 in the high-T limit. However, at lower temperatures, the manifestation of the statistical factors on all these rate coefficients is largely masked by the increased influence of such T thresholds (Henchman et al. 1981).

The (small) effects of the isotope substitution on the overall kinetics (i.e., the kinetic-isotope effect) can primarily be assessed from Figs. 3a and c. By comparing the thermoneutral reactions (11) and (12) with the forward ones in Eqs. (2) and (4), one can see that, given the lower ZPE content of the 13 C12C product species and the exothermic nature of these latter pair of reactions, abstraction by 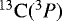\mathrm{^13C}(3P)$\mathrm{^{13}C}(^{3}P)$ is slightly faster than by 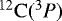\mathrm{^12C}(3P)$\mathrm{^{12}C}(^{3}P)$ at low T. Nevertheless, such an energy defect (ΔEZPE) becomes less significant in determining reactivity as long as higher internal and collision energies are accessible at higher T. We note that the calculated thermal rate coefficients of reaction (11) are about seven times greater than those reported by Westley (1980).

To quantify the possible impact of reactions (2)–(5) on the overall C fractionation chemistry, in Fig. 4 we plot their equilibrium constants (K) as a function of the temperature. These were obtained using both QCT data and the analytic forms in Eq. (13) as K(T)=kf(T)kr(T)≡\frac{[\mathrm{^12C}][\mathrm{^PC2}]}{[\mathrm{^13C}][\mathrm{^RC2}]},\begin{equation*}K(T)=\frac{k_{\textrm{f}}(T)}{k_{\textrm{r}}(T)}\equiv\frac{[\mathrm{^{12}C}][\mathrm{^{P}C_{2}}]}{[\mathrm{^{13}C}][\mathrm{^{R}C_{2}}]}, \end{equation*}(14)

where kf and kr are the forward and reverse rates, with R and P identifying the corresponding reactant and product C2 isotopolog. These K values are also compared with theoretical estimates based on statistical mechanics (Terzieva & Herbst 2000; Mladenović & Roueff 2014, 2017), 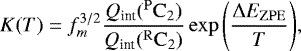K(T)=fm3/2\frac{Qint(\mathrm{^PC2})}{Qint(\mathrm{^RC2})}exp(ΔEZPET),\begin{equation*}K(T)=f_{m}^{3/2}\frac{Q_{\text{int}}(\mathrm{^{P}C_{2}})}{Q_{\text{int}}(\mathrm{^{R}C_{2}})}\exp{\left(\frac{\Delta E_{\mathrm{ZPE}}}{T}\right)}, \end{equation*}(15)

where the mass factor fm is given by 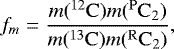fm=\frac{m(\mathrm{^12C})m(\mathrm{^PC2})}{m(\mathrm{^13C})m(\mathrm{^RC2})},\begin{equation*}f_{m}=\frac{m(\mathrm{^{12}C})m(\mathrm{^{P}C_{2}})}{m(\mathrm{^{13}C})m(\mathrm{^{R}C_{2}})}, \end{equation*}(16)

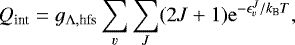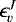with m(X) denoting the mass of the species X; ΔEZPE in Eq. (15) is in K. The internalpartition function, Qint, includes only the rovibrational degrees of freedom (no translation and electronic contributions) and is given by the standard expression, Qint=gΛ,hfs∑v∑J(2J+1)e−ϵvJ/kBT,\begin{equation*}Q_{\text{int}}=g_{\Lambda,\text{hfs}}\sum_{v}\sum_{J}(2J+1)\mathrm{e}^{-\epsilon^{J}_{v}/k_{\textrm{B}}T}, \end{equation*}(17)

where ϵvJ$\epsilon^{J}_{v}$ is the diatomic rovibrational energy (withtotal angular momentum J and vibrational quantum number v) measured relative to the corresponding ZPE; this is calculated from the experimentally derived two-body term of the associated C3 PES. In Eq. (17), gΛ,hfs accounts for the combined effects of Λ-doubling and nuclear spin (hyperfine) degeneracy and is defined in Irwin (1987, see Table 3 therein). For comparison, we also plot in Fig. 4 equilibrium constants for reactions (2) and (3) obtained via CT (Roueff et al. 2015; Colzi et al. 2020) and the experimental values of 13 C+ + 12CO⇌13CO + 12C+ taken from Liszt & Ziurys (2012).

The data presented in Fig. 4 clearly indicate that the C isotopic fractionation occurs most efficiently at low temperatures, notably in reactions (2) and (4). Under these conditions virtually all the available 13 C is in the form of 13 C12C, with only a small fraction being locked up in 13C2. Among 13C12C, ground-state 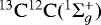\mathrm{^13C12C}(1Σg+)$\mathrm{^{13}C^{12}C}(^{1}\Sigma_{g}^{+})$ appears to be the dominant species owing to the higher exothermicity of reaction (2); see Table 4. Indeed, by extrapolating Eq. (13) in (14) to the typical temperature of dense clouds, T = 10 K, we obtain K2 ≈ 36, K4 ≈ 24, K3 ≈ 7, and K5 ≈ 5. These former values are quite close to the one predicted for the ion–molecule 13 C+ + 12CO reaction (Eq. (1)), K1 ≈ 33 (Langer et al. 1984). We note that, in the high-T limit, the equilibrium constants converge to well-defined values: 2 for the isotope-exchange reactions (2) and (4) and 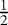12$\frac{1}{2}$ for (3) and (5). Such limits reflect the manifestation of the aforementioned statistical factors in the overall chemical kinetics and become equivalent to ‘symmetry’ (or probability) factors appearing in previous statistical thermodynamic considerations (Terzieva & Herbst 2000). In this regard, we note that the calculated Kvalues from Eq. (15) represent lower limits to the actual QCT data and are roughly consistent (as expected) with the ones predicted from CT (Roueff et al. 2015; Colzi et al. 2020). We reiterate that, similarly to Eq. (15), CT does not take into account all the details of the molecular PESs in estimating the macroscopic kinetic and thermodynamic attributes.

thumbnail Fig. 3

Forward and backward thermal rate coefficients and associated error bars for the reactions (a) \mathrm{^13C}(3P)​+​\mathrm{^12C2}(X1Σg+)⇌\mathrm{^13C12C}(X1Σg+)​+​\mathrm{^12C}(3P)$\mathrm{^{13}C}(^{3}P)\!+\!\mathrm{^{12}C_{2}}(X^{1}\Sigma_{g}^{+}){\rightleftharpoons}\mathrm{^{13}C^{12}C}(X^{1}\Sigma_{g}^{+})\!+\!\mathrm{^{12}C}(^{3}P)$ (Eq. (2), k2,- 2); (b) \mathrm{^13C}(3P)​+​\mathrm{^13C12C}(X1Σg+)⇌\mathrm{^13C2}(X1Σg+)​+​\mathrm{^12C}(3P)$\mathrm{^{13}C}(^{3}P)\!+\!\mathrm{^{13}C^{12}C}(X^{1}\Sigma_{g}^{+}){\rightleftharpoons}\mathrm{^{13}C_{2}}(X^{1}\Sigma_{g}^{+})\!+\!\mathrm{^{12}C}(^{3}P)$ (Eq. (3), k3,- 3); (c) \mathrm{^13C}(3P)​+​\mathrm{^12C2}(a3Πu)⇌\mathrm{^13C12C}(a3Πu)​+​\mathrm{^12C}(3P)$\mathrm{^{13}C}(^{3}P)\!+\!\mathrm{^{12}C_{2}}(a^{3}\Pi_{u}){\rightleftharpoons}\mathrm{^{13}C^{12}C}(a^{3}\Pi_{u})\!+\!\mathrm{^{12}C}(^{3}P)$ (Eq. (4), k4,- 4); (d) \mathrm{^13C}(3P)​+​\mathrm{^13C12C}(a3Πu)⇌\mathrm{^13C2}(a3Πu)​+​\mathrm{^12C}(3P)$\mathrm{^{13}C}(^{3}P)\!+\!\mathrm{^{13}C^{12}C}(a^{3}\Pi_{u}){\rightleftharpoons}\mathrm{^{13}C_{2}}(a^{3}\Pi_{u})\!+\!\mathrm{^{12}C}(^{3}P)$ (Eq. (5), k5,- 5) at temperatures up to 600 K. Also shown are the QCT values obtained for the \mathrm{^12C}+\mathrm{^12C2}(X1Σg+/a3Πu)→\mathrm{^12C2}(X1Σg+/a3Πu)+\mathrm{^12C}$\mathrm{^{12}C}+\mathrm{^{12}C_{2}}(X^{1}\Sigma_{g}^{+}/a^{3}\Pi_{u}){\rightarrow}\mathrm{^{12}C_{2}}(X^{1}\Sigma_{g}^{+}/a^{3}\Pi_{u})+\mathrm{^{12}C}$ atom-exchange reactions (Eqs. (11) and (12)) and available results from the literature (Roueff et al. 2015; Colzi et al. 2020; Westley 1980); CT stands for capture theory (Georgievskii & Klippenstein 2005). Solid thick lines show the predicted QCT thermally averaged rates using the Arrhenius-Kooij formula of Eq. (13).
Table 4

Parameters of Eq. (13) for the forward and reverse rate coefficients of reactions (2)–(5), (11), and (12).

thumbnail Fig. 4

Equilibrium constants and associated error bars for the reactions (a) \mathrm{^13C}(3P)​+​\mathrm{^12C2}(X1Σg+)⇌\mathrm{^13C12C}(X1Σg+)​+​\mathrm{^12C}(3P)$\mathrm{^{13}C}(^{3}P)\!+\!\mathrm{^{12}C_{2}}(X^{1}\Sigma_{g}^{+}){\rightleftharpoons}\mathrm{^{13}C^{12}C}(X^{1}\Sigma_{g}^{+})\!+\!\mathrm{^{12}C}(^{3}P)$ (Eq. (2), K2 = k2∕k-2) and \mathrm{^13C}(3P)​+​\mathrm{^12C2}(a3Πu)⇌\mathrm{^13C12C}(a3Πu)​+​\mathrm{^12C}(3P)$\mathrm{^{13}C}(^{3}P)\!+\!\mathrm{^{12}C_{2}}(a^{3}\Pi_{u}){\rightleftharpoons}\mathrm{^{13}C^{12}C}(a^{3}\Pi_{u})\!+\!\mathrm{^{12}C}(^{3}P)$ (Eq. (4), K4 = k4∕k-4); (b) \mathrm{^13C}(3P)​+​\mathrm{^13C12C}(X1Σg+)⇌\mathrm{^13C2}(X1Σg+)​+​\mathrm{^12C}(3P)$\mathrm{^{13}C}(^{3}P)\!+\!\mathrm{^{13}C^{12}C}(X^{1}\Sigma_{g}^{+}){\rightleftharpoons}\mathrm{^{13}C_{2}}(X^{1}\Sigma_{g}^{+})\!+\!\mathrm{^{12}C}(^{3}P)$ (Eq. (3), K3 = k3∕k-3) and \mathrm{^13C}(3P)​+​\mathrm{^13C12C}(a3Πu)⇌\mathrm{^13C2}(a3Πu)​+​\mathrm{^12C}(3P)$\mathrm{^{13}C}(^{3}P)\!+\!\mathrm{^{13}C^{12}C}(a^{3}\Pi_{u}){\rightleftharpoons}\mathrm{^{13}C_{2}}(a^{3}\Pi_{u})\!+\!\mathrm{^{12}C}(^{3}P)$ (Eq. (5), K5 = k5∕k-5) at temperatures up to 600 K. Points and solid thick lines are obtained from Eq. (14) using the QCT thermally averaged rates and their analytic forms in Eq. (13), respectively, while dashed thick lines represent theoretical estimates based on statistical mechanics (Eq. (15)). Also shown are the corresponding values predicted via capture theory (Roueff et al. 2015; Colzi et al. 2020) for reactions (2) and (3) and experimental data (exp) for 13 C+ +12CO⇌13CO + 12C+ (Eq. (1), K1 = k1∕k-1) as taken from Liszt & Ziurys (2012). For clarity, the K values for the thermoneutral reactions (11) and (12) are also indicated. High-temperature limits are represented by gray solid lines.
thumbnail Fig. 5

Variation of the 12C/13C isotope ratios derived from C2(X1Σg+)$\mathrm{C_{2}}(X^{1}\Sigma_{g}^{+})$ and C2 (a3Πu) (by means of reactions (2) and (4), respectively) as a function of the gas kinetic temperature (Tkin). Solid (blue and red) lines represent the theoretical values calculated from Eq. (18) assuming chemical equilibrium conditions, while the corresponding (pink and back) dashed lines show their behavior as obtained from a reduced kinetic model with fixed integration time of 1.6 × 105 yr (see text). Also shown by the gray points (with error bars) are the corresponding values obtained from observational surveys conducted by Hamano et al. (2019) and Bakker & Lambert (1998) towards Cyg OB2 No. 12 and HD 56126, respectively, as well as those reported by Colzi et al. (2020) for 10 K using a gas-grain chemical model in three different simulation timescales. The horizontal dashed line (also in the inset) highlights the elemental [12C/13C] Solar System abundance ratio.

4 Astrophysical implications

To further (qualitatively) assess the extent to which the most relevant reactions (2) and (4) influence the net 13 C chemical enrichment in diverse astronomical environments and their possible effects on observational data, we plot in Fig. 5 the expected theoretical 12 C/13C atomic carbon ratios versus kinetic temperature (Tkin) as possibly measured from C2 (e.g., via its Phillips (A 1 Πu–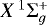X 1Σg+$X\,^{1}\Sigma_{g}^{+}$) and Swan (d 3 Πg–a 3Πu) bands). Following Smith & Adams (1980), the calculated ratios were obtained from Eq. (14), that is, assuming chemical equilibrium conditions \frac{^12C}{^13C}(T)=2 × \frac{[\mathrm{^12C}]}{[\mathrm{^13C}]} × 1K(T)≡2 × [12C2][13C12C](T),\begin{equation*}\frac{^{12}\mathrm{C}}{^{13}\mathrm{C}}(T)=2\,{\times}\,\frac{[\mathrm{^{12}C}]}{[\mathrm{^{13}C}]}\,{\times}\,\frac{1}{K(T)}\equiv 2\,{\times}\, \frac{[^{12}\mathrm{C}_{2}]}{[^{13}\mathrm{C}^{12}\mathrm{C}]}(T), \end{equation*}(18)

where K(T) are the corresponding equilibrium constants (K2 and K4 for the 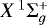X 1Σg+$X\,^{1}\Sigma_{g}^{+}$ and a 3 Πu states, respectively, see, e.g., Fig. 4a) and [12C]∕[13C] is the elemental (reservoir) carbon abundance ratio taken to be equal to the Solar System value of 89; the factor of 2 appears due to statistical considerations; see, e.g., Bakker & Lambert (1998). For comparison, we also show the corresponding values obtained from observational surveys on C2 isotopologs conducted by Hamano et al. (2019) in the context of translucent clouds (i.e., in the line of sight of Cyg OB2 No. 12) and Bakker & Lambert (1998) towards the circumstellar envelope of the post-AGB star HD 56126. As emphasized by Hamano et al. (2019), their work reports the first marginal detection of 13 C 12C in the ISM. 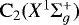Due to the lack of observational data on [12C2]/[13C12C]$[^{12}\mathrm{C}_{2}]/[^{13}\mathrm{C}^{12}\mathrm{C}]$ in molecular clouds, we resort to the 12 C/13C ratios derived from C2(X1Σg+)$\mathrm{C_{2}}(X^{1}\Sigma_{g}^{+})$ by Colzi et al. (2020) using a time-dependent gas-grain chemical model; the model results are also plotted in Fig. 5 for three different simulation timescales. Figure 5 shows that, although the calculated 12 C-to-13C ratios depict slightly varying degrees of fractionation depending on whether they are inherited from 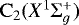C2(X1Σg+)$\mathrm{C_{2}}(X^{1}\Sigma_{g}^{+})$ or C2 (a3Πu), the general profiles are both consistent with a 13C-enhancement at the lower temperatures of interstellar clouds. However, we note that, at even lower Tkin, all 12 C/13C ratios drop to very small values; this is not necessary true in reality given that interstellar chemistry may unavoidably deviate from thermodynamic equilibrium. To gauge the impact of such a departure from equilibrium on the calculated ratios, we follow Smith & Adams (1980) and impose time dependence on 12 C/13C by integrating analytically the corresponding kinetic differential (continuity) equations for 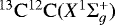\mathrm{^13C12C}(X1Σg+)$\mathrm{^{13}C^{12}C}(X^{1}\Sigma_{g}^{+})$ (Eq. (2)) and 13C12C(a3Πu) (Eq. (4)); for brevity, the final formulas are not be given here, and we refer the reader to Eqs. (12) and (13) of Smith & Adams (1980) for details. The theoretical 12 C/13C ratios obtained in this way are shown by the dashed lines in Fig. 5. We note that in solving the corresponding rate equations, we assume [12C]∕[13C] as terrestrial (as in Eq. (18)) and consider a fixed integration time of 1.6 × 105 yr with a 12 C fractional abundance of 1 × 10−5 ; these latter parameters are both consistent with an early cloud chemistry (Colzi et al. 2020). On the basis of these assumptions, Fig. 5 reveals a clear mismatch between the calculated early chemistry and equilibrium 12 C-to-13C ratios for Tkin ≾ 30 K. However, for larger temperatures, reactive equilibrium appears to be promptly reached; see Fig. 5. Moreover, the plotted data from Colzi et al. (2020) indicate that the predicted ratios from chemical kinetics also converge (as expected) to those at equilibrium for longer simulation times. Yet, at 10 K, our theoretical 12 C/13C ratio derived from 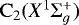C2(X1Σg+)$\mathrm{C_{2}}(X^{1}\Sigma_{g}^{+})$ agrees quite well with the value reported by Colzi et al. (2020) within the 1.6 × 105 yr timescale. As for the observational data, the calculated 12 C/13C ratios show fairly good correlations with those given by Bakker & Lambert (1998) and Hamano et al. (2019). The larger deviations observed towards Cyg OB2 No. 12 (see Fig. 5) provide further evidence that, besides 13 C+C2 chemical fractionation, other competing photo-induced processes and/or secondary reactions are at work in translucent clouds; reportedly, one should also take into account the large uncertainties in the measurements by Hamano et al. (2019). As highlighted by these latter authors, future observations of 12 C13C using higher quality spectra will provide a clear picture on the C2 carbon isotope ratios in the ISM. Meanwhile, the determination of accurate laboratory and theoretical reaction rate coefficients for the most efficient fractionation pathways like 13 C+C2 and 13 C+C3 (Giesen et al. 2020; Colzi et al. 2020) would be useful for the interpretation of interstellar C fractionation chemistry via astrochemical models (Roueff et al. 2015; Colzi et al. 2020; Loison et al. 2020).

5 Summary

In the present work, we provide accurate theoretical rate coefficients as a function of the temperature for all possible isotope-exchange reactions of C with 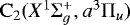C2(X1Σg+,a3Πu)$\mathrm{C_{2}}(X^{1}\Sigma_{g}^{+},a^{3}\Pi_{u})$. To this end, we used the quasi-classical trajectory method, with the previously obtained (mass-independent) PESs of 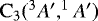C3(3A′,1A′)$\mathrm{C_{3}}(^{3}A',^{1}A')$ providing the required forces between the colliding partners. The calculated rate coefficients within the range of 25 ≤ T∕K ≤ 500 exhibit a positive temperature dependence and our results show a behavior that clearly differs from previous theoretical estimates based on simple capture theory (Roueff et al. 2015; Colzi et al. 2020). This suggests that, in addition to long-range interactions, the strongly bound (short-range) parts of the underlying PESs also influence the dynamics of the reactive processes. For each reaction considered, analytic three-parameter Arrhenius-Kooij formulas are derived that readily interpolate and extrapolate the associated forward and reverse rates. To quantify their possible impact on the interstellar C isotopic chemistry, equilibrium constants of all such processes are evaluated from the calculated kinetics data, unraveling their increased efficiency into 13 C incorporation at low T. For the most relevant reactions and assuming both equilibrium and time-dependent conditions, theoretical 12 C/13C atomic carbon ratios as a function of the gas kinetic temperature are also reported and compared with available model chemistry and observational data on C2. Despite some previous claims (Bakker & Lambert 1998), the present theoretical results strongly support the suggestion made by other authors (Roueff et al. 2015; Colzi et al. 2020) that the C + C2 reactions (particularly (2) and (4)) may act as important routes in the overall C-fractionation chemistry, notably in low-temperature C-rich environments. Besides providing key input data for astrochemical models of cold dense clouds (Furuya et al. 2011; Roueff et al. 2015; Colzi et al. 2020; Loison et al. 2020), the calculated rate constants over such a broad T range may also fulfill the needs of models of photo-dissociation regions (Röllig & Ossenkopf 2013), translucent clouds (Hamano et al. 2019), protoplanetary disks (Woods & Willacy 2009), and circumstellar envelopes of evolved C-stars (Bakker & Lambert 1998). Apart from its astrophysical implications, this work is expected to provide safe grounds on which to base future methodological developments toward the calculation of theoretical rate constants ofastrochemically relevant isotope-exchange reactions without resorting to (and avoid the burden of) quantum dynamics, while still recovering all intrinsic details of the interacting potentials between the colliding particles.

Acknowledgements

This work has received funding from the European Union’s Horizon 2020 research and innovation program under the Marie Sklodowska-Curie grant agreement No 894321.

Appendix A Additional tables

Table A.1

Maximum impact parameters, and thermal rate and equilibrium constants as a function of the temperature of the isotope-exchange reactions (2) and (4).

Table A.2

Maximum impact parameters, and thermal rate and equilibrium constants as a function of the temperature of the isotope-exchange reactions (3) and (5).

Table A.3

Maximum impact parameters and thermal rate constants as a function of the temperature for the atom-exchange reactions (11) and (12).

References

  1. Abrahamsson, E., Andersson, S., Marković, N., & Nyman, G. 2008, Phys. Chem. Chem. Phys., 10, 4400 [Google Scholar]
  2. Amiot, C. 1983, ApJS, 52, 329 [NASA ADS] [CrossRef] [Google Scholar]
  3. Andersson, S., Marković, N., & Nyman, G. 2003, J. Phys. Chem. A, 107, 5439 [CrossRef] [Google Scholar]
  4. Babb, J. F., Smyth, R. T., & McLaughlin, B. M. 2019, ApJ, 876, 38 [Google Scholar]
  5. Bakker, E. J., & Lambert, D. L. 1998, ApJ, 508, 387 [NASA ADS] [CrossRef] [Google Scholar]
  6. Breier, A. A., Büchling, T., Schnierer, R., et al. 2016, J. Chem. Phys., 145, 234302 [NASA ADS] [CrossRef] [Google Scholar]
  7. Brooke, J. S., Bernath, P. F., Schmidt, T. W., & Bacskay, G. B. 2013, J. Quant. Spectr. Rad. Transf., 124, 11 [NASA ADS] [CrossRef] [Google Scholar]
  8. Chen, W., Kawaguchi, K., Bernath, P. F., & Tang, J. 2015, J. Chem. Phys., 142, 064317 [Google Scholar]
  9. Colzi, L., Sipilä, O., Roueff, E., Caselli, P., & Fontani, F. 2020, A&A, 640, A51 [CrossRef] [EDP Sciences] [Google Scholar]
  10. Dalgarno, A., & Black, J. H. 1976, Rep. Prog. Phys., 39, 573 [Google Scholar]
  11. Ehrenfreund, P., & Charnley, S. B. 2000, ARA&A, 38, 427 [Google Scholar]
  12. Elyajouri, M., Lallement, R., Cox, N. L. J., et al. 2018, A&A, 616, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Furuya, K., & Aikawa, Y. 2018, ApJ, 857, 105 [NASA ADS] [CrossRef] [Google Scholar]
  14. Furuya, K., Aikawa, Y., Sakai, N., & Yamamoto, S. 2011, ApJ, 731, 38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Galvão, B. R. L., Caridade, P. J. S. B., & Varandas, A. J. C. 2012, J. Chem. Phys., 137, 22A515 [Google Scholar]
  16. Galvão, B. R. L., Varandas, A. J. C., Braga, J. P., & Belchior, J. C. 2013, J. Phys. Chem. Lett., 4, 2292 [CrossRef] [Google Scholar]
  17. Georgievskii, Y., & Klippenstein, S. J. 2005, J. Chem. Phys., 122, 194103 [NASA ADS] [CrossRef] [Google Scholar]
  18. Giesen, T. F., Mookerjea, B., Fuchs, G. W., et al. 2020, A&A, 633, A120 [CrossRef] [EDP Sciences] [Google Scholar]
  19. Graff, M. M., & Wagner, A. F. 1990, J. Chem. Phys., 92, 2423 [NASA ADS] [CrossRef] [Google Scholar]
  20. Gu, X., Guo, Y., Zhang, F., Mebel, A. M., & Kaiser, R. I. 2006, Faraday Discuss., 245 [Google Scholar]
  21. Guo, H. 2012, Int. Rev. Phys. Chem., 31, 1 [CrossRef] [Google Scholar]
  22. Hamano, S., Kawakita, H., Kobayashi, N., et al. 2019, ApJ, 881, 143 [Google Scholar]
  23. Haris, K., & Kramida, A. 2017, ApJS, 233, 16 [NASA ADS] [CrossRef] [Google Scholar]
  24. Hase, W. L., Duchovic, R. J., Hu, X., et al. 1996, QCPE Bull., 16, 43 [Google Scholar]
  25. Henchman, M., & Paulson, J. F. 1989, J. Chem. Soc., Faraday Trans. 2, 85, 1673 [Google Scholar]
  26. Henchman, M. J., Adams, N. G., & Smith, D. 1981, J. Chem. Phys., 75, 1201 [Google Scholar]
  27. Hobbs, L. M., Black, J. H., & van Dishoeck, E. F. 1983, ApJ, 271, L95 [Google Scholar]
  28. Irwin, A. W. 1987, A&A, 182, 348 [NASA ADS] [Google Scholar]
  29. Kaiser, R. I. 2002, Chem. Rev., 102, 1309 [Google Scholar]
  30. Krieg, J., Lutter, V., Endres, C. P., et al. 2013, J. Phys. Chem. A, 117, 3332 [CrossRef] [Google Scholar]
  31. Laidler, K. J. 1984, J. Chem. Edu., 61, 494 [Google Scholar]
  32. Langer, W. D. 1992, IAU Symp., 150, 193 [Google Scholar]
  33. Langer, W. D., Graedel, T. E., Frerking, M. A., & Armentrout, P. B. 1984, ApJ, 277, 581 [NASA ADS] [CrossRef] [Google Scholar]
  34. Liszt, H. S., & Ziurys, L. M. 2012, ApJ, 747, 55 [Google Scholar]
  35. Loison, J.-C., Hu, X., Han, S., et al. 2014, Phys. Chem. Chem. Phys., 16, 14212 [Google Scholar]
  36. Loison, J.-C., Wakelam, V., Gratier, P., & Hickson, K. M. 2018, MNRAS, 484, 2747 [Google Scholar]
  37. Loison, J.-C., Wakelam, V., Gratier, P., et al. 2019, MNRAS, 485, 5777 [NASA ADS] [CrossRef] [Google Scholar]
  38. Loison, J.-C., Wakelam, V., Gratier, P., & Hickson, K. M. 2020, MNRAS, 498, 4663 [Google Scholar]
  39. Milam, S. N., Savage, C., Brewster, M. A., Ziurys, L. M., & Wyckoff, S. 2005, ApJ, 634, 1126 [NASA ADS] [CrossRef] [Google Scholar]
  40. Mladenović, M., & Roueff, E. 2014, A&A, 566, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Mladenović, M., & Roueff, E. 2017, A&A, 605, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Muckerman, J. T., & Newton, M. D. 1972, J. Chem. Phys., 56, 3191 [Google Scholar]
  43. Nyman, G., & Davidsson, J. 1990, J. Chem. Phys., 92, 2415 [Google Scholar]
  44. Peslherbe, G. H., Wang, H., & Hase, W. L. 1999, Monte Carlo Sampling for Classical Trajectory Simulations (Wiley-Blackwell), 171 [Google Scholar]
  45. Páramo, A., Canosa, A., Le Picard, S. D., & Sims, I. R. 2008, J. Phys. Chem. A, 112, 9591 [CrossRef] [Google Scholar]
  46. Ram, R. S., Brooke, J. S. A., Bernath, P. F., Sneden, C., & Lucatello, S. 2014, ApJS, 211, 5 [Google Scholar]
  47. Rocha, C. M. R. 2019, Proc. Int. Astron. Union, 15, 61 [Google Scholar]
  48. Rocha, C. M. R., & Varandas, A. J. C. 2018, Chem. Phys. Lett., 700, 36 [Google Scholar]
  49. Rocha, C. M. R., & Varandas, A. J. C. 2019, J. Phys. Chem. A, 123, 8154 [Google Scholar]
  50. Röllig, M., & Ossenkopf, V. 2013, A&A, 550, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Roueff, E., Loison, J. C., & Hickson, K. M. 2015, A&A, 576, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Russell, C. L.,& Manolopoulos, D. E. 1999, J. Chem. Phys., 110, 177 [Google Scholar]
  53. Sakai, N., Ikeda, M., Morita, M., et al. 2007, ApJ, 663, 1174 [NASA ADS] [CrossRef] [Google Scholar]
  54. Schröder, B., & Sebald, P. 2016, J. Chem. Phys., 144, 044307 [NASA ADS] [CrossRef] [Google Scholar]
  55. Smith, D., & Adams, N. G. 1980, ApJ, 242, 424 [NASA ADS] [CrossRef] [Google Scholar]
  56. Smith, I. W. M., Herbst, E., & Chang, Q. 2004, MNRAS, 350, 323 [NASA ADS] [CrossRef] [Google Scholar]
  57. Snow, T. P., & McCall, B. J. 2006, ARA&A, 44, 367 [NASA ADS] [CrossRef] [Google Scholar]
  58. Souza, S. P., & Lutz, B. L. 1977, ApJ, 216, L49 [NASA ADS] [CrossRef] [Google Scholar]
  59. Szalay, P. G., Müller, T., Gidofalvi, G., Lischka, H., & Shepard, R. 2012, Chem. Rev., 112, 108 [Google Scholar]
  60. Tachikawa, H., Hamabayashi, T., & Yoshida, H. 1995, J. Phys. Chem., 99, 16630 [Google Scholar]
  61. Takano, S., Masuda, A., Hirahara, Y., et al. 1998, A&A, 329, 1156 [NASA ADS] [Google Scholar]
  62. Terzieva, R., & Herbst, E. 2000, MNRAS, 317, 563 [NASA ADS] [CrossRef] [Google Scholar]
  63. Thorburn, J. A., Hobbs, L. M., McCall, B. J., et al. 2003, ApJ, 584, 339 [NASA ADS] [CrossRef] [Google Scholar]
  64. Tokaryk, D. W., & Civiš, S. 1995, J. Chem. Phys., 103, 3928 [Google Scholar]
  65. Truhlar, D. G. 1972, J. Chem. Phys., 56, 3189 [Google Scholar]
  66. Truhlar, D. G. 1979, J. Phys. Chem., 83, 188 [Google Scholar]
  67. Truhlar, D. G., & Muckerman, J. T. 1979, Reactive Scattering Cross Sections III: Quasiclassical and Semiclassical Methods (Boston, MA: Springer), 505 [Google Scholar]
  68. Tully, J. C., & Preston, R. K. 1971, J. Chem. Phys., 55, 562 [CrossRef] [Google Scholar]
  69. Varandas, A. J. C. 1987, Chem. Phys. Lett., 138, 455 [CrossRef] [Google Scholar]
  70. Varandas, A. J. C. 1993, J. Chem. Phys., 99, 1076 [Google Scholar]
  71. Varandas, A. J. C. 2018, Annu. Rev. Chem., 69, 177 [Google Scholar]
  72. Visser, R., van Dishoeck, E. F., & Black, J. H. 2009, A&A, 503, 323 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Voronin, A. I., Marques, J. M. C., & Varandas, A. J. C. 1998, J. Phys. Chem. A, 102, 6057 [Google Scholar]
  74. Watson, W. D., Anicich, V. G., & Huntress, W. T., J. 1976, ApJ, 205, L165 [NASA ADS] [CrossRef] [Google Scholar]
  75. Westley, F. 1980, Table of Recommended Rate Constants for Chemical Reactions Occurring in Combustion (Washington: National Standard Reference Data System) [Google Scholar]
  76. Wilhelmsson, U., & Nyman, G. 1992, J. Chem. Phys., 96, 1886 [Google Scholar]
  77. Wilson, T. L. 1999, Rep. Prog. Phys., 62, 143 [Google Scholar]
  78. Woods, P. M., & Willacy, K. 2009, ApJ, 693, 1360 [NASA ADS] [CrossRef] [Google Scholar]
  79. Zanchet, A., Halvick, P., Rayez, J.-C., Bussery-Honvault, B., & Honvault, P. 2007, J. Chem. Phys., 126, 184308 [NASA ADS] [CrossRef] [Google Scholar]
  80. Zanchet, A., González-Lezana, T., Aguado, A., Gómez-Carrasco, S., & Roncero, O. 2010, J. Phys. Chem. A, 114, 9733 [CrossRef] [PubMed] [Google Scholar]
  81. Zhen, J., Castellanos, P., Paardekooper, D. M., Linnartz, H., & Tielens, A. G. G. M. 2014, ApJ, 797, L30 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Spectroscopic properties (in cm−1) of the reactant and product diatomics (of reactions (2)–(5)) correlating with the global singlet and triplet PESs of C3.

In the text
Table 2

Structural parameters (bond distances Re in a0 and angle α in degs), harmonic (ωi), fundamental (νi) frequencies and zero-point energies (in cm−1) of the 13 C singly and doubly substituted C3 minima of the PESs spanned by long-lived trajectories.

In the text
Table 3

Exothermicities (in cm−1 unless otherwise stated) of reactions (2)–(5) based on the data shown in Table 1.

In the text
Table 4

Parameters of Eq. (13) for the forward and reverse rate coefficients of reactions (2)–(5), (11), and (12).

In the text
Table A.1

Maximum impact parameters, and thermal rate and equilibrium constants as a function of the temperature of the isotope-exchange reactions (2) and (4).

In the text
Table A.2

Maximum impact parameters, and thermal rate and equilibrium constants as a function of the temperature of the isotope-exchange reactions (3) and (5).

In the text
Table A.3

Maximum impact parameters and thermal rate constants as a function of the temperature for the atom-exchange reactions (11) and (12).

In the text

All Figures

thumbnail Fig. 1

One-dimensional cuts of the nuclear-mass-independent PESs of C3 along the minimum-energy paths connecting reactants and products via C3 intermediates. The zero of energy is set relative to the infinitely separated C+C2(X 1Σg+)$_{2}(X\,^{1}\Sigma_{g}^{+})$ fragments. The reacting carbon atom is shown in yellow.
In the text
thumbnail Fig. 2

Relaxed 3D plots in hyperspherical coordinates (Varandas 1987) of the nuclear-mass-independent PESs of ground-state (a) C3(1A′)$\mathrm{C_{3}}(^{1}A')$ and (b) C3(3A′)$\mathrm{C_{3}}(^{3}A')$. The zero of energy is set relative to the infinitely separated C+C2 fragments. Stationary points and minimum energy paths (solid yellow lines) as in Fig. 1. Solid white lines show the time evolution (in coordinate space) of sample reactive trajectories for the processes (a)\mathrm{^13C}(3P)​+​\mathrm{^12C2}(a3Πu)​→​\mathrm{^13C12C}(a3Πu)​+​\mathrm{^12C}(3P)$\mathrm{^{13}C}(^{3}P)\!+\!\mathrm{^{12}C_{2}}(a^{3}\Pi_{u})\!\rightarrow\!\mathrm{^{13}C^{12}C}(a^{3}\Pi_{u})\!+\!\mathrm{^{12}C}(^{3}P)$ and (b) \mathrm{^13C}(3P)​+​\mathrm{^12C2}(X1Σg+)​→​\mathrm{^13C12C}(X1Σg+)​+\mathrm{^12C}(3P)$\mathrm{^{13}C}(^{3}P)\!+\!\mathrm{^{12}C_{2}}(X^{1}\Sigma_{g}^{+})\!\rightarrow\!\mathrm{^{13}C^{12}C}(X^{1}\Sigma_{g}^{+})\!+\mathrm{^{12}C}(^{3}P)$. An isotopically distinct carbon atom is schematically represented in yellow.
In the text
thumbnail Fig. 3

Forward and backward thermal rate coefficients and associated error bars for the reactions (a) \mathrm{^13C}(3P)​+​\mathrm{^12C2}(X1Σg+)⇌\mathrm{^13C12C}(X1Σg+)​+​\mathrm{^12C}(3P)$\mathrm{^{13}C}(^{3}P)\!+\!\mathrm{^{12}C_{2}}(X^{1}\Sigma_{g}^{+}){\rightleftharpoons}\mathrm{^{13}C^{12}C}(X^{1}\Sigma_{g}^{+})\!+\!\mathrm{^{12}C}(^{3}P)$ (Eq. (2), k2,- 2); (b) \mathrm{^13C}(3P)​+​\mathrm{^13C12C}(X1Σg+)⇌\mathrm{^13C2}(X1Σg+)​+​\mathrm{^12C}(3P)$\mathrm{^{13}C}(^{3}P)\!+\!\mathrm{^{13}C^{12}C}(X^{1}\Sigma_{g}^{+}){\rightleftharpoons}\mathrm{^{13}C_{2}}(X^{1}\Sigma_{g}^{+})\!+\!\mathrm{^{12}C}(^{3}P)$ (Eq. (3), k3,- 3); (c) \mathrm{^13C}(3P)​+​\mathrm{^12C2}(a3Πu)⇌\mathrm{^13C12C}(a3Πu)​+​\mathrm{^12C}(3P)$\mathrm{^{13}C}(^{3}P)\!+\!\mathrm{^{12}C_{2}}(a^{3}\Pi_{u}){\rightleftharpoons}\mathrm{^{13}C^{12}C}(a^{3}\Pi_{u})\!+\!\mathrm{^{12}C}(^{3}P)$ (Eq. (4), k4,- 4); (d) \mathrm{^13C}(3P)​+​\mathrm{^13C12C}(a3Πu)⇌\mathrm{^13C2}(a3Πu)​+​\mathrm{^12C}(3P)$\mathrm{^{13}C}(^{3}P)\!+\!\mathrm{^{13}C^{12}C}(a^{3}\Pi_{u}){\rightleftharpoons}\mathrm{^{13}C_{2}}(a^{3}\Pi_{u})\!+\!\mathrm{^{12}C}(^{3}P)$ (Eq. (5), k5,- 5) at temperatures up to 600 K. Also shown are the QCT values obtained for the \mathrm{^12C}+\mathrm{^12C2}(X1Σg+/a3Πu)→\mathrm{^12C2}(X1Σg+/a3Πu)+\mathrm{^12C}$\mathrm{^{12}C}+\mathrm{^{12}C_{2}}(X^{1}\Sigma_{g}^{+}/a^{3}\Pi_{u}){\rightarrow}\mathrm{^{12}C_{2}}(X^{1}\Sigma_{g}^{+}/a^{3}\Pi_{u})+\mathrm{^{12}C}$ atom-exchange reactions (Eqs. (11) and (12)) and available results from the literature (Roueff et al. 2015; Colzi et al. 2020; Westley 1980); CT stands for capture theory (Georgievskii & Klippenstein 2005). Solid thick lines show the predicted QCT thermally averaged rates using the Arrhenius-Kooij formula of Eq. (13).
In the text
thumbnail Fig. 4

Equilibrium constants and associated error bars for the reactions (a) \mathrm{^13C}(3P)​+​\mathrm{^12C2}(X1Σg+)⇌\mathrm{^13C12C}(X1Σg+)​+​\mathrm{^12C}(3P)$\mathrm{^{13}C}(^{3}P)\!+\!\mathrm{^{12}C_{2}}(X^{1}\Sigma_{g}^{+}){\rightleftharpoons}\mathrm{^{13}C^{12}C}(X^{1}\Sigma_{g}^{+})\!+\!\mathrm{^{12}C}(^{3}P)$ (Eq. (2), K2 = k2∕k-2) and \mathrm{^13C}(3P)​+​\mathrm{^12C2}(a3Πu)⇌\mathrm{^13C12C}(a3Πu)​+​\mathrm{^12C}(3P)$\mathrm{^{13}C}(^{3}P)\!+\!\mathrm{^{12}C_{2}}(a^{3}\Pi_{u}){\rightleftharpoons}\mathrm{^{13}C^{12}C}(a^{3}\Pi_{u})\!+\!\mathrm{^{12}C}(^{3}P)$ (Eq. (4), K4 = k4∕k-4); (b) \mathrm{^13C}(3P)​+​\mathrm{^13C12C}(X1Σg+)⇌\mathrm{^13C2}(X1Σg+)​+​\mathrm{^12C}(3P)$\mathrm{^{13}C}(^{3}P)\!+\!\mathrm{^{13}C^{12}C}(X^{1}\Sigma_{g}^{+}){\rightleftharpoons}\mathrm{^{13}C_{2}}(X^{1}\Sigma_{g}^{+})\!+\!\mathrm{^{12}C}(^{3}P)$ (Eq. (3), K3 = k3∕k-3) and \mathrm{^13C}(3P)​+​\mathrm{^13C12C}(a3Πu)⇌\mathrm{^13C2}(a3Πu)​+​\mathrm{^12C}(3P)$\mathrm{^{13}C}(^{3}P)\!+\!\mathrm{^{13}C^{12}C}(a^{3}\Pi_{u}){\rightleftharpoons}\mathrm{^{13}C_{2}}(a^{3}\Pi_{u})\!+\!\mathrm{^{12}C}(^{3}P)$ (Eq. (5), K5 = k5∕k-5) at temperatures up to 600 K. Points and solid thick lines are obtained from Eq. (14) using the QCT thermally averaged rates and their analytic forms in Eq. (13), respectively, while dashed thick lines represent theoretical estimates based on statistical mechanics (Eq. (15)). Also shown are the corresponding values predicted via capture theory (Roueff et al. 2015; Colzi et al. 2020) for reactions (2) and (3) and experimental data (exp) for 13 C+ +12CO⇌13CO + 12C+ (Eq. (1), K1 = k1∕k-1) as taken from Liszt & Ziurys (2012). For clarity, the K values for the thermoneutral reactions (11) and (12) are also indicated. High-temperature limits are represented by gray solid lines.
In the text
thumbnail Fig. 5

Variation of the 12C/13C isotope ratios derived from C2(X1Σg+)$\mathrm{C_{2}}(X^{1}\Sigma_{g}^{+})$ and C2 (a3Πu) (by means of reactions (2) and (4), respectively) as a function of the gas kinetic temperature (Tkin). Solid (blue and red) lines represent the theoretical values calculated from Eq. (18) assuming chemical equilibrium conditions, while the corresponding (pink and back) dashed lines show their behavior as obtained from a reduced kinetic model with fixed integration time of 1.6 × 105 yr (see text). Also shown by the gray points (with error bars) are the corresponding values obtained from observational surveys conducted by Hamano et al. (2019) and Bakker & Lambert (1998) towards Cyg OB2 No. 12 and HD 56126, respectively, as well as those reported by Colzi et al. (2020) for 10 K using a gas-grain chemical model in three different simulation timescales. The horizontal dashed line (also in the inset) highlights the elemental [12C/13C] Solar System abundance ratio.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.