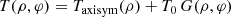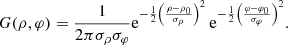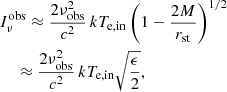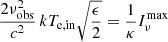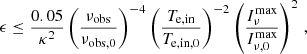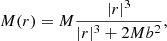| Issue |
A&A
Volume 646, February 2021
|
|
|---|---|---|
| Article Number | A37 | |
| Number of page(s) | 20 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202037787 | |
| Published online | 02 February 2021 | |
Geometric modeling of M87* as a Kerr black hole or a non-Kerr compact object
1
LESIA, Observatoire de Paris, Université PSL, CNRS, Sorbonne Universités, UPMC Univ. Paris 06, Univ. de Paris, Sorbonne Paris Cité, 5 place Jules Janssen, 92195 Meudon, France
e-mail: frederic.vincent@obspm.fr
2
Black Hole Initiative at Harvard University, 20 Garden St., Cambridge, MA 02138, USA
e-mail: maciek.wielgus@gmail.com
3
Center for Astrophysics | Harvard & Smithsonian, 60 Garden Street, Cambridge, MA 02138, USA
4
Nicolaus Copernicus Astronomical Center, Polish Academy of Sciences, Bartycka 18, 00-716 Warszawa, Poland
5
Physics Department, University of Gothenburg, 412-96 Göteborg, Sweden
6
Institute of Physics, Silesian University in Opava, Opava, Czech Republic
7
Laboratoire Univers et Théories, Observatoire de Paris, Université PSL, CNRS, Université de Paris, 92190 Meudon, France
8
Institut d’Astrophysique de Paris, CNRS et Sorbonne Université, UMR 7095, 98bis Bd Arago, 75014 Paris, France
Received:
21
February
2020
Accepted:
25
October
2020
Context. The Event Horizon Telescope (EHT) collaboration recently obtained the first images of the surroundings of the supermassive compact object M87* at the center of the galaxy M87. This provides a fascinating probe of the properties of matter and radiation in strong gravitational fields. It is important to determine from the analysis of these results what can and cannot be inferred about the nature of spacetime around M87*
Aims. We want to develop a simple analytic disk model for the accretion flow of M87*. Compared to general-relativistic magnetohydrodynamic models, this new approach has the advantage that it is independent of the turbulent character of the flow and is controlled by only a few easy-to-interpret, physically meaningful parameters. We want to use this model to predict the image of M87*, assuming that it is either a Kerr black hole or an alternative compact object.
Methods. We computed the synchrotron emission from the disk model and propagate the resulting light rays to the far-away observer by means of relativistic ray tracing. Such computations were performed assuming different spacetimes, such as Kerr, Minkowski, nonrotating ultracompact star, rotating boson star, or Lamy spinning wormhole. We performed numerical fits of these models to the EHT data.
Results. We discuss the highly lensed features of Kerr images and show that they are intrinsically linked to the accretion-flow properties and not only to gravitation. This fact is illustrated by the notion of the secondary ring, which we introduce. Our model of a spinning Kerr black hole predicts mass and orientation consistent with the EHT interpretation. The non-Kerr images result in a similar quality of numerical fits and may appear very similar to Kerr images, once blurred to the EHT resolution. This implies that a strong test of the Kerr spacetime may be out of reach with the current data. We note that future developments of the EHT could alter this situation.
Conclusions. Our results show the importance of studying alternatives to the Kerr spacetime to be able to test the Kerr paradigm unambiguously. More sophisticated treatments of non-Kerr spacetimes and more advanced observations are needed to proceed further in this direction.
Key words: black hole physics / accretion / accretion disks / relativistic processes / galaxies: individual: M87
© F. H. Vincent et al. 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
The galaxy Messier 87 (M87) is a giant elliptical galaxy located in the Virgo cluster, first observed by the French astronomer Charles Messier in 1781. In the past century it has been known to give rise to a kiloparsec-scale radio jet (Curtis 1918). The central engine of this jet is likely a supermassive black hole, M87*. It is, like our Galactic center, a low-luminosity galactic nucleus, displaying a hot, optically thin and most likely geometrically thick accretion and ejection flow (Yuan & Narayan 2014). The distance to M87 is on the order of the mean distance to the Virgo cluster, that is, 16.5 Mpc (Mei et al. 2007). The mass of M87* has been assessed to be 3.5 × 109 M⊙ by means of gas-dynamics fitting (Walsh et al. 2013) and to 6.6 × 109 M⊙ by means of stellar-dynamics study (Gebhardt et al. 2011).
The Event Horizon Telescope (EHT) collaboration has recently published the first reconstructed millimeter images of the close vicinity of M87* (EHT L1). The images show a circular crescent feature with a diameter of ≈40 μas, with a non-isotropic flux distribution, surrounding a central fainter region. These features are in good agreement with what is known from theoretical imaging of black holes (Bardeen 1973; Luminet 1979; Marck 1996; Chan et al. 2015; Cunha & Herdeiro 2018). The crescent morphology of the source was constrained by “free-form” imaging (EHT L4), simple geometric models, and direct fitting to general-relativistic magnetohydrodynamic (GRMHD) simulations (EHT L6). The large collection of GRMHD simulations created a framework for the physical interpretation of the EHT results (EHT L5, Porth et al. 2019). This analysis allowed us to interpret the 40 μas circular feature as a lensed accretion and ejection flow within a few M from the black hole. The non-isotropy can be linked to a relativistic beaming effect. The central fainter region is consistent with being the shadow of the black hole (Falcke et al. 2000). Within this framework, the mass of M87* was estimated to be 6.5 ± 0.7 × 109 M⊙, assuming a distance of 16.8 ± 0.8 Mpc (EHT L1), which is in agreement with the independent stellar dynamics measurement. For the images shown in this article, we use the consistent values of 6.2 × 109 M⊙ for the mass and 16.9 Mpc for the distance, following the choice made in EHT L5.
The assumptions of the GRMHD-based analysis and interpretation have given rise to theoretical investigations regarding the nature of the features seen in the EHT images (Gralla et al. 2019; Johnson et al. 2020; Narayan et al. 2019; Gralla & Lupsasca 2020). The main question is to what extent these features can be directly linked to gravitation and how much are they influenced by the highly model-dependent astrophysics of the emission. There are at least several effects to consider in this context, corresponding to particular choices and simplifications made in the GRMHD simulations library of the EHT (Porth et al. 2019, and references therein). Those include, but are not limited to utilizing a prescription for electron temperature, ignoring the dynamical feedback of radiation, viscosity, resistivity, and the presence of nonthermal electrons (EHT L5). Apart from that, the turbulent character of the flow adds time dependence to the model, and the possibly strongly resolution–dependent relationship between the simulations and the real variability of the source is poorly understood (see, e.g., White et al. 2019). Given all those uncertainties, it is both interesting and important to interpret the EHT measurements in the framework of simple physically motivated geometric models. So far, such models have not been extensively discussed in the context of the M87* image interpretation. Only Nalewajko et al. (2020) have recently adopted a geometric model, but with a simple power-law prescription for the emission, and no absorption.
Models for M87* environment have been published using both analytical or GRMHD descriptions of the flow. Analytical models used disk-dominated radiatively inefficient accretion flows (RIAF) or RIAF+jet models (Yuan 2000; Di Matteo et al. 2003; Broderick & Loeb 2009). The GRMHD models describe the disk+jet environment of M87* (Dexter et al. 2012; Mościbrodzka et al. 2016; Davelaar et al. 2019).
The aim of this paper is to contribute to the physical interpretation of the EHT images using a simple analytical geometric model that is able of capturing the most prominent features of a more realistic setup, avoiding the uncertain astrophysics embedded in the latter. For simplicity, we restrict ourselves to a pure disk model and do not take into account any ejection feature. We stress that the origin of the photons forming the EHT image might be the base of the M87 jet or the disk. This point was investigated in EHT L5 with the library of state-of-the-art GRMHD simulations. Among a variety of models, only the so-called SANE (Standard And Normal Evolution) models, which have a particularly high Rhigh parameter (Mościbrodzka et al. 2016), were found to be dominated by the jet emission at that scale. For most of the models, including all the so-called MAD (Magnetically Arrested Disk) models, the emission observed by the EHT is actually dominated by the disk component. This setup can describe, e.g., a magnetically arrested state of accretion, where the innermost disk emission dominates over the jet emission contribution We consider thermal synchrotron emission and absorption in this disk. Our geometric model of the plasma surrounding the black hole is as simple as possible. This simplicity allows us to limit the sensitivity, as much as possible, to the uncertainties that affect more elaborate models.
We believe that such a framework is well adapted for testing the impact of the gravitation on the observables of the central compact object. Our goals are to, first, discuss the prominent Kerr image features obtained within this context with a particular emphasis on the accretion-model dependence of highly lensed regions and, second, to try to answer the question whether the EHT images, analyzed independently of a broader astrophysical context and external constraints, can deliver a test of the Kerr-spacetime paradigm. For that purpose we compare the accretion disk images computed for several different models of spacetime. While certain non-Kerr spacetimes were briefly discussed in EHT L1 and EHT L5, all quantitative considerations by the EHT consortium were performed within the framework of the Kerr spacetime paradigm. We aim to fill this gap with the current paper. We highlight that throughout this article, we always consider that gravitation is described by general relativity. While we consider different spacetimes that may require exotic forms of the stress-energy tensor, Einstein’s theory of gravitation is never modified.
This paper is organized as follows: Sect. 2 considers that M87* is a Kerr black hole. After introducing our disk model in Sect. 2.1, we present millimeterwave Kerr images in Sect. 2.2, in which we discuss the origins of these images main features, related to the properties of highly bent null geodesics. Section 2.3 briefly discusses the modification in the image generated by non-axisymmetric structures. Section 3 is dedicated to studying how the M87* image changes when the spacetime is different from Kerr. We consider the Minkowski spacetime (Sect. 3.1), the spacetime of a static ultracompact star with an emitting surface (Sect. 3.2), a rotating boson–star spacetime (Sect. 3.3), and a Lamy wormhole spacetime (Sect. 3.4). In Sect. 4, we discuss fits to the EHT data of our Kerr and non-Kerr models. Section 5 gives conclusions and perspectives.
2. Emission from a thick disk in a Kerr spacetime
In this section, the Kerr spacetime is labeled by means of the Boyer-Lindquist spherical coordinates (t, r, θ, φ). We work in units where the gravitational constant and the speed of light are equal to 1, G = c = 1. Radii are thus expressed in units of the black hole mass M.
2.1. Disk model and emission
We consider a geometrically thick, optically thin accretion disk in a setup illustrated in Fig. 1.
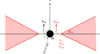 |
Fig. 1. Geometrically thick disk model (in red) surrounding a compact object (black disk) of mass M. The disk has an inner radius rin, where the electron number density and temperature are ne, in and Te, in. The number density scales as r−2 and the temperature as r−1. All quantities are independent of the height z. The opening angle of the disk is called θop. Here and throughout the article, the compact object and accretion disk spins (black and red arrows, respectively) are assumed to be aligned. The inclination angle i between the spin axis and the line of sight is shown in green. |
For simplicity, we parametrize the geometry of the accretion disk by only two parameters: its inner radius rin and opening angle θop. We do not prescribe any outer radius for the disk. This outer radius is effectively imposed by selecting a field of view for computing the images and by the radially decaying profiles of temperature and density. The disk is assumed to be axisymmetric with respect to the z axis that lies along the black hole spin. The compact object and accretion-disk spins are assumed to be aligned, as is the case for the entire EHT GRMHD library. Throughout this article we fix the opening angle to θop = 30°, so the disk is moderately geometrically thick. This choice places our considerations between the limit cases of geometrically thin model considered by Gralla et al. (2019) and spherical accretion considered by Narayan et al. (2019), and within the thickness range expected for a real accretion flow in M87* (Yuan & Narayan 2014).
We model the emission by thermal synchrotron radiation. This is also a simplification because shocks and turbulence in the accretion flow are likely to generate nonthermal emission. However, we chose to neglect this additional complexity. This is again primarily for the sake of simplicity, but also because the broad features of the image are unlikely to be extremely sensitive to the details of the emission process, and because nonthermal emission modeling would necessarily imply somewhat arbitrary extra assumptions anyway. Thermal synchrotron emission is modeled following the formulas derived by Pandya et al. (2016). Both the emission and absorption coefficients are self-consistently taken into account in our computation. These coefficients depend on the electron number density and temperature and on the magnetic field strength. The parameters of our model are the density and temperature at the inner disk radius, ne, in and Te, in. We assume simple power laws for their scaling, ne, in ∝ r−2 for the density, and Te, in ∝ r−1 for the temperature, following the description of Vincent et al. (2019).
We do not consider any vertical variation of the accretion flow properties. As for the magnetic field prescription, we simply impose the magnetization σ = B2/(4π)/(mpc2ne), equal to the ratio of the magnetic to particle energy densities, where B is the magnetic field magnitude, mp the proton mass, and c the velocity of light (kept here for clarity). This quantity is always set to σ = 0.1 in this article. This is an arbitrary choice, which has little impact on our results given that we do not discuss a mixed disk+jet model, in which case the magnetization should typically differ in the disk and in the jet. We note that our choice of power laws for the electron density, temperature, and the magnetic field are that of the standard model of Blandford & Königl (1979). This also agrees with the inner evolution of these quantities in GRMHD simulations of M87* (see, e.g., Davelaar et al. 2019). We stress that only the inner few tens of M of the flow matters for the images that we discuss. We thus parametrize the radial dependence of the disk quantities to capture the relevant properties of this region.
For all the images shown in this article, we assume the observing frequency of νobs, 0 = 230 GHz, corresponding to the observing frequency of the EHT. The orientation of the model is determined by the assumption that the jet aligns with the black hole and disk spin axis and by the observed jet position angle on the sky. We fix the inclination (angle between the black hole spin and the line of sight) to i = 160° (Walker et al. 2018), meaning that the black hole and disk spin vectors are directed “into the page” for all images presented in this work (EHT L5) (see Fig. 1). This nearly face-on inclination may be in general unfavorable for considering deviations in the image geometry, when compared to near-edge-on views (Bardeen 1973). The position angle of the approaching jet (angle east of north of the black hole spin projection onto the screen plane of the observer) is fixed to PA = 290 ° ≡ − 70° (Kim et al. 2018). The field of view of the presented images is fixed to f = 160 μas and the number of pixels to 200 × 200 (unless otherwise noted).
One extra crucial assumption has to be made: the choice of the dynamics of the accretion flow. We always consider Keplerian rotation outside of the innermost stable circular orbit (ISCO), irrespective of the height z with respect to the equatorial plane. If the inner radius is smaller than rISCO, the emitting matter four-velocity below ISCO is given as
where uZAMO is the four-velocity of the zero-angular-momentum observer (ZAMO) and V is the accretion flow velocity as measured by the ZAMO. It can be written as
so that (Vr)2 + (Vφ)2 = V2 = (Γ2 − 1)/Γ2. This velocity is parametrized by choosing V ∈ [0, 1] and vφ ≡ Vφ/V ∈ [0, 1]. In the following, we always fix V to its value at the ISCO. For the two spin-parameter values considered, a = 0 and a = 0.8M, this gives V = 0.5 and V = 0.61, respectively. We can then chose vφ to simulate a limit case corresponding either to a flow with purely circular velocity (if vφ = 1) or a radially plunging flow (if vφ = 0). We note that the emitter velocity is always independent of the height z, defined using Boyer-Lindquist coordinates by z = r cos θ.
We ensure that the observed flux is on the order of 0.5 − 1 Jy, in agreement with the state of M87* at the time of the 2017 EHT campaign. The flux is primarily impacted by the choice of the electron number density and temperature at the inner radius. Given that these two quantities are degenerate because we are fitting a single flux value (rather than the full spectrum), we decided to fix the electron number density at r = 2M to ne, 2M = 5 × 105 cm−3, which is in reasonable agreement with the results published in the literature by various authors (Broderick & Loeb 2009; Davelaar et al. 2019, EHT L5). The number density at the chosen value of rin is thus fixed by the assumed r−2 density scaling. The inner temperature Te, in is then chosen to obtain a reasonable value of the observed flux. We find that the choice of Te, in = 8 × 1010 K (or kTe, in/mec2 = 13.5 in units of the electron rest mass) leads to reasonable flux values for all setups considered in this work.
The final step of our simulation is to perform general-relativistic ray tracing, either in the Kerr spacetime or in other geometries, to obtain theoretical images. This is done using the open-source ray tracing code GYOTO (see Vincent et al. 2011, 2012)1 to compute null geodesics backward in time, from a distant observer located at the distance of D = 16.9 Mpc away from the disk. We summarize the fixed properties of the model and images in Table 1.
Fixed properties of the M87* models and images assumed throughout this paper.
2.2. Main features of the images
Figures 2 and 3 show the Kerr-spacetime disk images obtained for two different values of the spin parameter. In this section, we discuss the main features of these images, focusing on the impact of the flow geometry and dynamics, as well as on the highly lensed flux portion of the image, generally called the “photon ring”.
 |
Fig. 2. Images of a thick disk surrounding a nonrotating (a = 0) black hole. The top row shows the simulated ray-traced image and the bottom row consists of the upper row images blurred to the EHT resolution (about 20 μas). The dashed blue circle shown in the lower row images has a diameter of 40 μas, consistent with the estimated diameter of the ring feature in the M87* image, reported by the EHT. This diameter translates to 11.05M in mass units of distance. The blue arrow shows the projected direction of the jet. The disk inner radius is 6M for the left panel (corresponding to the ISCO) and 2M for the two other panels (corresponding to the event horizon). The azimuthal velocity below ISCO is paramterized by vφ = 1 (purely azimuthal velocity) for the middle panel and vφ = 0 (purely radial plunge) for the right panel. The inner electron number density is equal to 5 × 105 cm−3 when rin = 2M and 5.5 × 104 cm−3 when rin = 6M (see text for details on how these numbers are chosen). |
 |
Fig. 3. Same as Fig. 2 with a spin parameter of a = 0.8M. The inner density is of 2.4 × 105 cm−3 when rin = 2.91M, and 7.8 × 105 cm−3 when rin = 1.6M. |
Figure 2 shows the resulting image for a spin parameter a = 0 and three different choices for the accretion disk properties. We note that such nonrotating configurations are unlikely to account for the powerful large-scale jet of M87 (EHT L5). These configurations are still of interest for a comparison with the rotating ones. The top left panel shows a Keplerian flow with an inner radius at the Schwarzschild spacetime ISCO, rISCO = 6M. The top middle panel has an inner radius going down to the event horizon at rH = 2M, with a purely azimuthal velocity below the ISCO (vφ = 1). The top-right panel is the same as the middle panel, but with vφ = 0 (pure radial inflow). The bottom panels show the same images, convolved with a Gaussian kernel with full width at half maximum of 20 μas, which is approximately the EHT angular resolution (EHT L4). In this and the following images, we indicate the approximate position of the crescent feature reported by the EHT, 40 μas, with a dashed circle. For the compact object mass and distance assumed in this paper, this translates into 11.05M diameter. Figure 3 shows the same setup for a spin of a = 0.8M, where rISCO = 2.91M and rH = 1.6M.
The unblurred images presented in Figs. 2 and 3 all show thick annular areas with the addition of a very thin bright ring. The thick annular area is due to the emission from the inner parts of the disk, with a feeble lensing effect on the null geodesics. It is generally referred to as the primary image of the disk and is composed of geodesics that cross the equatorial plane at most once (Luminet 1979). The polar radius of the primary image clearly varies with the assumed rin. The brightness distribution with azimuthal angle in the primary image is a consequence of the special-relativistic beaming effect: parts of the flow coming toward the observer are boosted. This effect is clearly visible in the left and central top panels of Fig. 2 where the flow is in circular rotation and coming toward the observer in the south direction. The top right panel of the same figure is obtained when the inner radius is set at the event horizon and the flow velocity is chosen to be purely radial below the ISCO. In this case, the flux distribution is less dependent on the azimuth than for the circularly rotating cases. We have however checked that, when taking into account special-relativistic effects only, the image becomes boosted in the west direction where the flow approaches the observer. The blurred image of this radial-inflow case (bottom right panels of Fig. 2) is thus very isotropic, which is not consistent with the observed EHT image. This elementary discussion shows that the size of the primary image and its flux distribution with azimuthal angle are directly linked to the choice of the inner radius and to the dynamics of the gas in the inner disk regions. This result agrees with that obtained by Nalewajko et al. (2020) with a simpler model.
The very thin bright ring, also present in the unblurred images, is often loosely referred to as the photon ring, and is considered to be the image on sky of the unstable Kerr equatorial prograde photon orbit. However, the set of orbits that actually matters in order to form this highly lensed feature is the set of spherical Kerr photon orbits first analyzed by Teo (2003), along with numerous recent developments (see, e.g., Cunha et al. 2017a; Johnson et al. 2020). These are bound unstable photon orbits evolving at constant Boyer-Lindquist radii, with periodical excursion in the θ direction (the span of this excursion, θmin < θ < θmax, depends on the angular momentum of the photon). The orbits are not periodic in φ and are either prograde or retrograde, depending on the sign of the conserved angular momentum of the photon. These orbits exist within a radial range rph, pro < r < rph, retro, where rph, pro and rph, retro are the usual Kerr equatorial prograde and retrograde photon orbit radii. In particular, for the Schwarzschild spacetime, in which only one photon orbit exists at rph = 3M, the set of spherical photon orbits is simply the sphere r = 3M. The thin bright ring in Kerr images is thus due to light rays that approach a spherical Kerr photon orbit before reaching the far-away observer.
As stated above, the spherical Kerr photon orbits are periodic in θ. The complete θ excursion from θmin to θmax (or the other way round) can be covered by a null geodesic an arbitrary number of times n, corresponding to n crossings of the equatorial plane, before leaving the orbit and reaching the faraway observer (remember that these orbits are unstable). As n increases, the Boyer-Lindquist radius of such an orbit becomes very close to that of a spherical photon orbit and the impact point on sky tends to the critical curve. Thus, the thin bright ring is actually the sum of an exponentially converging sequence of subrings lying at smaller and smaller polar radii on sky, and labeled by the number n of crossings of the black hole equatorial plane (see Fig. 5). This fact was first noted by Luminet (1979) for the Schwarzschild case. The resolution of the image truncates this sequence at a finite number of subrings; see, for example, the bottom right panel of Fig. 6 in which the outermost subring is clearly seen, the subsequent subring is only barely visible, and the following subrings are lost owing to finite resolution. We note that for the M87* image, the complete set of subrings of the thin bright ring lies within ≲1 μas on sky so that a very high resolution would be needed to resolve some of its components. Gralla et al. (2019) use the term lensing ring for the outermost such subring (corresponding to the set of geodesics that cross the equatorial plane exactly twice), while these authors keep the terminology photon ring for the sum of all subsequent subrings (corresponding to the set of geodesics that cross the equatorial plane more than twice).
Johnson et al. (2020) give an analytic expression for the limiting curve on sky, toward which the series of subrings converge in the limit of n → ∞. Gralla et al. (2019) named this limiting curve the critical curve and we kept this name. Introducing ξ – the polar radius on the observer’s screen in units of M, and ϕ – the polar angle on the observer’s screen, the critical curve is written as
where
In this equation, r is the Boyer-Lindquist radius of the Kerr spherical photon orbit followed by the photon on its way to the observer. One counterintuitive property of this critical curve, already discussed by Johnson et al. (2020), is the fact that one Kerr spherical photon orbit (one value of r) is mapped to two values of the polar angle, ϕ and 2π − ϕ. This is due to the arccos definition of ϕ. As a consequence, the critical curve should be seen as the image on the sky of the set of Kerr spherical orbits, with each spherical orbit being mapped to two points along the curve. We note that actually only a subset of the full set of Kerr spherical photon orbits (rph, pro < r < rph, retro) is imaged on the sky, depending on the value of the inclination i. The full set only gets imaged on the sky for i = 90° (see Fig. 2 of Johnson et al. 2020).
In this article, we are interested in the full sequence of highly lensed subrings on the sky, which incorporates the notions of the lensing ring, photon ring, and critical curve introduced above. However, it is crucial to realize that a pixel on the observer’s camera belonging to one of these subrings does not always contain a detectable amount of flux. Its flux content, and hence its ability to be considered as a highly lensed region on sky, depends on the corresponding null geodesic interaction with the accretion flow. As a consequence, the full set of highly lensed subrings should be seen as a mathematical, theoretical locus on sky, the flux content of which fully depends on the accretion flow properties. We thus introduce the observation-oriented notion of the secondary ring (as opposed to the primary image) to refer to the region on the observer’s sky where the received null geodesics have approached a Kerr spherical photon orbit within δr ≲ M in terms of the radial Boyer-Lindquist coordinate r, and have visited the regions of the accretion flow emitting most of the radiation. In this definition, δr can be of order M for lensing-ring photons, while δr ≪ M for photon-ring photons (see the bottom panels of Fig. 4). The regions of the flow emitting most of the radiation, in our framework, coincide with the inner regions close to r = rin, where all physical quantities are maximal. We note that this definition implicitly depends on the orientation of the observer with respect to the flow. Indeed, the projection on sky of the regions of the flow emitting most of the radiation depends on the inclination and position angle.
 |
Fig. 4. Top panels: zoom on the central 80 μas field of the image of a thick disk surrounding a Schwarzschild black hole (left) or a Kerr black hole with spin parameter a = 0.8M (right). Bottom panels: three geodesics are plotted on the (ρ, z) plane of height vs. cylindrical radius (in units of M). The arrows show the direction of backward-ray-tracing integration in GYOTO. The observer is located at 16.9 Mpc toward the bottom right of the panels. These geodesics correspond to the pixels labeled by the red, green, and blue arrows of the top panels, which are, respectively, part of the photon ring (3 crossings of the equatorial plane), lensing ring (2 crossings), and primary image (1 crossing) in the terminology of Gralla et al. (2019). The half disk filled in black corresponds to the event horizon. The black solid half circle of the left panel corresponds to the Schwarzschild photon sphere at r = 3M. The black-line delineated white crescent of the right panel corresponds to the locus of spherical Kerr orbits for a = 0.8M, with the locations of the prograde and retrograde equatorial photon orbits denoted by black dots. The dashed thick black line within the crescent corresponds to the spherical orbit at the inner Boyer-Lindquist radius of the red geodesic. The thick disk corresponds to the pale red region. In the Schwarzschild case (left panel), the red geodesic approaches the photon sphere. In the Kerr case (right panel), the red geodesic approaches a spherical orbit at its minimum Boyer-Lindquist radius. Both the red and green geodesics belong to the secondary ring. |
Our definition is based on more than just the number of crossings of the equatorial plane by null geodesics. As discussed in the Appendix A, a definition based only on the number of crossings of the equatorial plane is not adequate as geodesics can cross this plane at very large radii, and such crossings are not relevant for the definition of the secondary ring. Moreover, and most importantly, the secondary ring definition must be linked to the particular accretion flow model used and its emission law. This crucial point is illustrated in Fig. 4, which shows the link between the Kerr spherical orbits, accretion flow geometry, and secondary ring of the image.
This figure first shows that highly lensed geodesics (with more than two crossings of the equatorial plane close to the black hole) approach a Kerr spherical orbit in the vicinity of the black hole. Most importantly, this figure also shows that not all geodesics that approach Kerr spherical orbits correspond to bright pixels of the image. A secondary-ring geodesic is not only highly bent, but it is also selected by the fact that it should visit the inner parts of the accretion flow in order to transport enough flux. The red geodesic of the bottom right panel of Fig. 4 is a good example: its spherical-orbit radius is exactly equal to the radius of the bright inner edge of the disk, allowing us to transport a lot of flux. Consequently, both the polar radius on sky and the azimuthal flux distribution of the secondary ring depend on the properties of the accretion flow; they are not simply dictated by gravitation. Should the inner radius of the disk of the bottom right panel of Fig. 4 be moved down to the event horizon, the red geodesic would transport a much smaller amount of flux, and would thus not be considered as belonging to the secondary ring. The geodesic optical path within the flow would be longer, but this increase scales as r, while the decrease in density scales as r2, so that the resulting flux would be smaller. Gralla & Lupsasca (2020) have recently shown that the dependence of the lensing-ring polar radius on the accretion flow geometry can reach tens of percent (see their Fig. 5). We note that this result, obtained for a geometrically thin disk, should be considered as a lower limit in a geometrically thick disk context. Figure 5 illustrates the notion of secondary ring and highlights its dependence on the properties of the plasma surrounding the black hole.
 |
Fig. 5. Example of a secondary ring. Top: two null geodesics, in Schwarzschild spacetime, that are part of the n = 2 (blue) and n = 3 (red) photon subrings (see text), n being the number of crossings of the equatorial plane. The black disk represents the black hole event horizon, and the thin black circle shows the location of the unstable spherical photon orbit. Bottom: the plane of the sky of the distant observer. The various concentric rings depict the photon subrings (see text) corresponding to the different values of the number n of crossings of the equatorial plane of the black hole. The lensing ring and critical curve (see text) are explicitly labeled. If only one blob of emitting matter (in green in the top panel) is present close to the black hole and interesects the red geodesic only, and not the blue geodesic, then only the n = 3 subring will be illuminated on sky, and the others will remain dark. The secondary ring will then coincide with the n = 3 subring. This would not be so should the blob of emitting matter be situated elsewhere. The spacing between the subrings on the observer’s sky is of course very exaggerated and lies within ≲1 μas for M87*. |
Four important notions have been introduced so far: lensing, photon rings, secondary rings, and the critical curve. Some of these concepts have nontrivial definitions. Figure 6 gives a pedagogical illustration of these notions. We insist that the only new word that we introduce in this work, that is, the notion of secondary ring, is really needed. This concept conveys the crucial idea that highly lensed features in the image plane intrinsically depend on the astrophysical accretion model, which does not appear clearly in the definition of other notions (lensing, photon rings).
 |
Fig. 6. Left sketch: black hole surroundings. The black hole event horizon is represented by a black disk, and the geometrically thick accretion disk is represented by the shaded red region (only one half of the disk is shown to save space). The sketch is rotated to have the same orientation of the black hole spin vector (black arrow) as in the central panel. The dashed red and blue circles around the black hole are the location of two Kerr spherical photon orbits (not to scale), the radii of which are given below. Central panel: plot of the critical curve on the observer’s sky as defined by the polar Eq. (3), for a black hole spin of a = 0.8M and an inclination angle of i = 160°. The critical curve is rotated to account for the position angle of M87* (PA = −70° as labeled on the panel, or 290° east of north). The projection of the black hole spin vector is shown by the black arrow (opposite to the approaching jet projection depicted by the blue arrow in Fig. 2). Three pairs of points are shown in red, green, and blue along the curve and are the images of the Kerr spherical orbits with radii r = 2.31M, 2.7M, and 3.05M, respectively. The Kerr equatorial prograde and retrograde photon orbits for a = 0.8M are rph, pro = 1.82M and rph, retro = 3.81M. The gray bent arrow at the left of the critical curve shows the direction of increase of the Kerr spherical orbit radius that the photon is following on its way to the observer (same evolution on the right side of the critical curve). Two null geodesics connecting the red and blue Kerr spherical orbits to the corresponding points on the critical curve are illustrated between the left drawing and the central panel. Right panel: ray-traced image of the model with the same field of view as in the middle panel. This image is a zoom on the central 45 μas of the top left panel of Fig. 3. The 4 important notions introduced in the text, lensing, photon, secondary rings, and critical curve, are labeled. The zoom on the region of the right panel surrounded by the dashed red rectangle is shown in the bottom right insert. This allows us to better see the difference between the lensing and photon rings. The critical curve is extremely close in angular radius to the photon ring (they are impossible to distinguish with the naked eye when comparing the central and right panels). However, the two notions are different mathematically. In the limit of an infinite resolution, the photon ring of the right panel would decompose into a sequence of rings converging to the critical curve. |
We now discuss more quantitatively our Kerr images. We note that in Figs. 2 and 3, the angular size of the dark central region depends a lot on the inner radius of the accretion flow. This is in agreement with the simple model of Gralla et al. (2019). In particular, the secondary ring is not the outer boundary of this central dark region when the flow extends to the horizon. On the other hand, Narayan et al. (2019) recently showed that a spherical optically thin flow in a Schwarzschild spacetime results in a central dark region the angular size of which is independent of the location of the inner edge of the emitting region. This discrepancy once again highlights the importance of the careful modeling of the accretion flow for the interpretation of EHT images.
It is also interesting to determine the brightness ratio of the secondary ring to the primary image. We checked that in the nonrotating case, the secondary ring weight is of 5% when rin = rISCO, 20% when rin = rH with azimuthal flow velocity, and 15% when rin = rH with radial flow velocity. For the a = 0.8M case, the secondary ring weight is of 30% when rin = rISCO, 25% when rin = rH with azimuthal flow velocity, and 20% when rin = rH with radial flow velocity. These numbers are obtained following the methodology presented in Appendix A. As explained there, they should be considered as slightly overestimated. For comparison, Johnson et al. (2020) characterize the secondary ring to be responsible for ∼10% of the total flux seen in ray-traced GRMHD simulations, with specifically a weight of 20% reported for their Fig. 1. Our results are thus in good agreement with the more sophisticated GRMHD simulations.
2.3. Non-axisymetric emission
The flux distribution seen in Figs. 2 and 3, in which the region in the south of the image is brighter than the part to the north, is primarily due to the beaming effect. This occurs because the emission is assumed to be axisymmetric. However, non-axisymmetric flux distribution is necessarily present in realistic turbulent flows. It is thus a natural question to ask what should be the condition on the non-axisymmetry of the emission such that the flux repartition would be substantially altered. To investigate this point, we study a very simple non-axisymmetric feature in our disk model. We consider that some region of the disk, centered at a cylindrical radius (defined in Boyer-Lindquist coordinates by ρ = r sin θ) of ρ = ρ0 and azimuth φ = φ0, with typical extensions σρ and σφ, is hotter than the rest by some increment ΔT. Specifically, we consider that the temperature around (ρ0, φ0) reads
where Taxisym(ρ) is the axisymmetric temperature defined in the previous section, ΔT = T0 G(ρ, φ), T0 is a chosen parameter, and the function G(ρ, φ) is the following product of Gaussians:
To enhance the difference with respect to the axisymmetric case, we choose (ρ0, φ0) such that this region is located toward the north on the sky, that is, opposed to the beamed region. The parameters σρ and σφ are chosen such that the hotter region has a comparable extension on the sky as compared to the beamed region of the axisymmetric images.
Figure 7 shows the images obtained when T0 is varied. The images indicate that the temperature has to increase by a factor of around 8 for the non-axisymmetric structure to overcome the beaming effect. Seeing such an unusually hot coherent component in the GRMHD simulations is rather uncommon. This can be seen in Fig. 9 of EHT L5, where a collection of GRMHD snapshots fitted to the EHT data create a distribution centered around an expected brightness maximum position angle of ≈200° (about 90° clockwise from position angle of the approaching jet projection) with turbulence related scatter of σ ≈ 60°. Nevertheless, there is a non-zero probability for a very different fitted orientation. It is not entirely clear how accurate GRMHD models are at reproducing the intrinsic turbulence-induced structural variability of a realistic accretion flow in the vicinity of a black hole, as EHT is the first instrument to deliver observational data that could be used to test this.
 |
Fig. 7. Non-axisymmetric disk compared to axisymmetric case for spin a = 0.8 M. Only blurred images are shown. The second, third, and fourth panel from the left are obtained by considering a hotter region in the disk defined by a temperature increment of T0/Tinner = 2, 4, or 8, respectively. This comparison shows that the non-axisymmetry of the flow must be substantial (approximately an order of magnitude contrast) to overcome the beaming effect. |
3. Emission from a geometrically thick disk in non-Kerr spacetimes
In this section, we present millimeter images of a geometrically thick disk surrounding compact objects that are different from the standard Kerr black hole. We first focus on the nonrotating Minkowski and ultracompact star spacetimes (see Sects. 3.1 and 3.2) and then on the rotating boson star and Lamy wormhole spacetimes (see Sects. 3.3 and 3.4). Our goal is to determine whether or not the current EHT data can exclude non-Kerr spacetimes based on arguments independent of the geometric structure of the accretion flow. This section presents theoretical images, while the fits to EHT data are discussed in Sect. 4.
3.1. Minkowski spacetime
We start by considering the most extreme non-Kerr case of a flat spacetime described by Minkowski geometry. While there may be little physical motivation to consider such an object as a viable alternative to a Kerr black hole, with this exercise we investigate whether any spacetime curvature is absolutely necessary to explain the EHT images. This means that we only consider the laws of special relativity and discard all general relativistic effects. This describes what could be thought of as a Michell-Laplace relativistic black hole (Michell 1784; Laplace 1796). It is a “relativistic” black hole because of the important addition of special relativity as compared to the original object. We want to compare this “flat-spacetime black hole” to a Schwarzschild black hole. In both cases, an accretion disk is assumed to lie in the equatorial plane of the object, with the same inner radius rin = 6M. There is of course no physical motivation to terminate the accretion disk at this radius for our Michell-Laplace relativistic black hole. Our choice is dictated by the comparison to the Schwarzschild spacetime. The angular velocity of the emitting matter of the Michell-Laplace relativistic black hole is assumed to follow the Newtonian law Ω ∝ r−3/2.
Figure 8 shows a comparison between these two cases.
 |
Fig. 8. Images of a geometrically thick accretion disk with inner radius rin = 6M in a Schwarzschild spacetime (left column) or in Minkowski spacetime (right column). As in all figures, the bottom row corresponds to the top row images blurred to the EHT resolution (20 μas), the dashed blue circle has a diameter of 40 μas (size of the ring feature reported by the EHT), and the blue arrow shows the projected direction of the approaching jet. |
The high-resolution images can be immediately distinguished by the absence of a secondary ring in the Minkowski spacetime. We return to that aspect in Sect. 5.2, discussing future observational perspectives. Nevertheless, the extreme similarity between the images observed with the EHT resolution (bottom row of Fig. 8) is a good illustration that reasoning based exclusively on the image morphology can tell little about the nature of the central object.
3.2. Nonrotating ultracompact star
We compute the image of M87* assuming that the central compact object is not a black hole but rather an ultracompact nonrotating star with a surface slightly above the radius of its event horizon. While we refer to this hypothetical object as a star, its only assumed property is the presence of a surface, as we do not consider any internal physics of the object.
Birkhoff’s theorem ensures that the metric at the exterior of this object is the Schwarzschild metric, provided the ultracompact star is spherically symmetric. We note that should the star rotate its exterior metric is not in general that of Kerr, so that the generalization to a rotating spacetime is not straightforward.
Our ultracompact-star spacetime is defined as follows. The star surface is modeled as a spherical surface of Boyer-Lindquist radial coordinate rst = (2 + ϵ)M with ϵ ≪ 1 in a Schwarzschild spacetime. The surface of the star is assumed to be fully optically thick so that its interior, which is not properly modeled in our setup, is never visited by any photon.
The surface of the star is assumed to emit blackbody radiation at the temperature of the inner accretion flow, Te, in, here assumed to be Te, in, 0 = 8 × 1010 K. This is of course a very strong assumption. It is likely, however, that this surface should be thermalized given that null geodesics are highly curved when emitted at the surface of the star and thus efficiently couple different parts of the surface (Broderick et al. 2009). Moreover, the considerations presented in this work are not qualitatively affected if the surface temperature is not exactly equal to the inner accretion flow temperature.
We now discuss more quantitatively the radiation emitted at the surface of the star. The observing frequency νobs is fixed in the whole article to the EHT observing frequency, νobs, 0 = 230 GHz. The emitted frequency at the surface of the star is simply related to that by νem = νobs/g, where g = (1 − 2M/rst)1/2 is the redshift factor, which decreases to 0 as rst approaches the Schwarzschild event horizon. The Planck function Bν(ν, Te, in) peaks at a very high frequency of νmax ≈ 5 × 1021 Hz. The emitted frequency reaches this value for (rst − 2M)/M = ϵ ≈ 10−17. In the following we thus safely assume that the Planck function is in its Rayleigh-Jeans regime. Using the frame-invariance of Iν/ν3, we can thus express the observed specific intensity as
where k is the Boltzmann constant, c is kept explicitly for clarity, and we have used the assumption that ϵ ≪ 1. We want this observed specific intensity, corresponding to the interior of the secondary ring in the ray-traced images of Fig. 9, to be equal to some fraction 1/κ of the maximum observed specific intensity from the accretion disk, 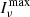 . We thus write
. We thus write
 |
Fig. 9. Images of a geometrically thick accretion disk with inner radius rin = 6M in a Schwarzschild spacetime (left column); in the spacetime of an ultracompact star with surface radius rst = 2.05M, emitting blackbody radiation at the inner temperature of the accretion flow Te, in = 8 × 1010 K (middle column); or in the same spacetime as the middle column, but with rst = 2.0005M (right column). As in all figures, the bottom row corresponds to the top row images blurred to the EHT resolution of 20 μas; the dashed blue circle has a diameter of 40 μas (size of the ring feature reported by the EHT) and the blue arrow shows the projected direction of the approaching jet. |
and
When considering a Schwarzschild black hole surrounded by a thick disk with rin = 6M (see Fig. 2, top left panel), the maximum observed specific intensity from the accretion disk is on the order of 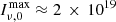 Jy ⋅ srad−1. Fixing κ = 10 (the stellar surface emission is negligible), corresponding to the dynamic range of the EHT images (EHT L4), we derive ϵ = 0.0005, and for κ = 1 (the stellar surface dominates) we find ϵ = 0.05. The following equation gives a practical expression for ϵ
Jy ⋅ srad−1. Fixing κ = 10 (the stellar surface emission is negligible), corresponding to the dynamic range of the EHT images (EHT L4), we derive ϵ = 0.0005, and for κ = 1 (the stellar surface dominates) we find ϵ = 0.05. The following equation gives a practical expression for ϵ
which can be understood as a joint constraint on ϵ and the surface temperature. Figure 9 shows the image of an accretion disk with rin = 6M surrounding a Schwarzschild black hole (left panel), and an ultracompact star with surface radius defined by ϵ = 0.05 (middle panel) or ϵ = 0.0005 (right panel). Provided that ϵ is small enough, there is no noticeable difference between the Schwarzschild and ultracompact-star cases. We bring up future perspectives of constraining ϵ in Sect. 5.3.
Although we do not discuss gravastars (Mazur & Mottola 2004) in this article, we note that nonrotating gravastars would lead to similar images as our Fig. 9, because in both cases a near-horizon surface is present and the external spacetime is Schwarzschild.
3.3. Rotating boson star
In this section, we consider the spacetime of a rotating boson star, as computed by Grandclément et al. (2014). We are modeling what is known as a mini boson star, in the sense that we do not consider any self-interaction between the bosons. Boson stars are composed of an assembly of spin-0 bosons constituting a macroscopic quantum body that evades collapse to a black hole by means of Heisenberg uncertainty relation (Liebling & Palenzuela 2017). Boson stars have no hard surface, no event horizon, and no central singularity. As such they are extremely different from black holes and are a good testbed for horizonless spacetimes (Vincent et al. 2016).
A boson star is defined by two parameters, k ∈ ℕ and 0 ≤ ω ≤ 1; we note that ω is in units of mbc2/ℏ, where mb is the mass of the boson (see Grandclément et al. 2014, for details). The angular momentum of a boson star is quantized and proportional to the integer k because of the quantum nature of the object. The parameter ω is related to the compactness of the star, with compactness increasing when ω approaches 0. In this work, we consider a boson star defined by (k = 1, ω = 0.77), which has already been discussed in Vincent et al. (2016). For k = 1 boson stars may or may not have photon orbits depending on the value of ω (Grandclément 2017). If photon orbits exist, there must be at least two of them, one of which is stable, leading to a questionable stability of the spacetime. This statement is actually much more general and applies to any axisymmetric, stationary solution of the Einstein field equations with a matter content obeying the null energy condition (Cunha et al. 2017b). The (k = 1, ω = 0.77) boson star spacetime is interesting because there is no known reason to question its stability. In particular, it has neither a stable photon orbit nor an ergoregion. Its parameters translate to a spin of a = 0.8M, the same as the Kerr black hole discussed in Sect. 2.
Figure 10 shows a comparison between the image of a geometrically thick accretion disk surrounding a Kerr black hole and the rotating boson star discussed above.
 |
Fig. 10. Images of a geometrically thick accretion disk with inner radius rin = 2.91M in a Kerr spacetime with spin parameter a = 0.8M (left column). Same image, but with a disk inner radius at rin = 3.5M, in a rotating boson star spacetime defined by (k = 1, ω = 0.77), which corresponds to the same value of the spin parameter (middle column). Same boson-star spacetime with rin = 2.09M, corresponding to the ICO of that spacetime (right column). As in all figures, the bottom row corresponds to the top row images blurred to the EHT resolution of 20 μas; the dashed blue circle has a diameter of 40 μas (size of the ring feature reported by the EHT) and the blue arrow shows the projected direction of the approaching jet. |
For the Kerr spacetime, the inner radius of the accretion disk is fixed at the ISCO, rin, Kerr = 2.91M. For the boson-star spacetime, using the same inner radius leads to an image that is slightly too small on sky. We thus increased it to rin, BS = 3.5M in order to match the Kerr image as closely as possible. The inner number density is chosen accordingly, following our r−2 power law. Choosing a different inner radius for the two spacetimes is not an issue; our goal is only to determine whether a boson-star spacetime can mimic a Kerr spacetime. The emitting matter of the boson-star spacetime follows circular timelike geodesics of the boson-star metric, the equation of which can be found in Grandclément et al. (2014). These authors analyzed the stability of time-like circular geodesics for boson stars. They show that all circular timelike geodesics are stable for boson stars, so that it is sufficient to speak of the innermost circular orbit (ICO). Our (k = 1, ω = 0.77) boson star has an ICO at rICO = 2.09M. Our choice of rin, BS = 3.5M means that the inner disk radius is at ≈1.7 times the ICO radius for the boson-star spacetime. For comparison, we also show the image corresponding to a choice of rin, BS = rICO in the right column of Fig. 10.
The boson-star case with a larger inner radius of the accretion flow leads to a blurred image very similar to Kerr, given that the thin secondary ring of the Kerr image is washed out by the limited resolution of the observations. On the other hand, setting the inner radius at the ICO leads to a much smaller image on sky (assuming the same mass), which results in a blurred image that is very different from Kerr. This shows that the accretion flow properties matter when comparing a boson star to a Kerr black hole. Modifying the spacetime geometry alone is not sufficient to independently produce an observationally different image on the accretion flow geometry. This demonstrates that more sophisticated simulations, connecting general relativity and the accretion flow magnetohydrodynamics, may be necessary to convincingly discuss the observable differences between black holes and other compact objects.
Recently, Olivares et al. (2020) published the first GRMHD simulation of an accretion flow surrounding a nonrotating boson star. These authors computed the associated 230 GHz image, taking into account physical parameters typical of the Sgr A* environment, concluding that it is possible to distinguish a boson star from a black hole by comparing the nonrotating boson-star image to a Schwarzschild and a = 0.937M Kerr images. They reported the boson-star image to be more compact and symmetric, similar to the results we present in the last column of Fig. 10, as a consequence of a gas accumulation at small radii. However, this picture may be different for a fast-spinning boson star; we note that there are no slow-rotating boson stars. Answering this question requires further GRMHD studies, which might in particular be able to discuss the jet power delivered by a boson star.
3.4. Lamy spinning wormhole
In this section we consider the rotating wormhole solution first described in Lamy et al. (2018), which we hereafter refer to as Lamy wormhole. This solution was found by generalizing the spherically symmetric regular (i.e., singularity-free) black hole solution of Hayward (2006) to the rotating case. This metric takes the same form as the Kerr metric expressed in Boyer-Lindquist coordinates, but with the constant M replaced by the function
where b is a charge homogeneous to a length and is expressed in M units with our conventions. In the original Hayward metric, b is interpreted as a scale at which quantum gravity effects would act and regularize the classical singularity. It should therefore typically take extremely small values. However, this parameter has been reinterpreted by Fan & Wang (2016) as the magnetic charge associated with a magnetic monopole in a nonlinear electrodynamics theory that sources the Hayward metric. In this context, b can take macroscopic values.
We consider only one pair of values for the spin parameter and charge, a = 0.8M and b = M. This choice fully specifies the metric. It can be shown that this spacetime corresponds to a rotating wormhole (Lamy et al. 2018). In particular, it has no event horizon and of course no curvature singularity. The topology of this spacetime corresponds to two asymptotically flat regions: one with r > 0 and one with r < 0, connected by a throat at r = 0. The energy conditions are violated in the full region r < 0, however the stress-energy tensor decreases quickly to zero when |r| increases so that the exotic matter is concentrated near the throat. This spacetime is very exotic, however, quickly converges to Kerr away from r = 0. Typically, for r ≳ 10M, the metric is Kerr; the relative difference of gtt for instance is less than 0.05% in the equatorial plane for r > 10M. Thus, a Lamy wormhole can be seen as an interesting testbed for the wormhole-like non-Kerrness of spacetime. The final important property of this spacetime (as well as all Lamy spacetimes) is that it admits spherical photon orbits similar to Kerr’s. The locus of these orbits depends of course on the values of a and b. These orbits are analyzed in Lamy (2018).
Figure 11 shows three images of a thick disk surrounding our Lamy wormhole compared to a Kerr image. The bottom left panel helps explain the highly lensed central part of the image, as it is not confused with the primary image.
 |
Fig. 11. Two top panels and bottom left panel show three images with a field of view of 80 μas of a thick disk surrounding a Lamy wormhole with spin a = 0.8M and charge b = M. The inner disk radius is at rin = 1.6M (ISCO radius of the Lamy spacetime, top left panel), 2.91M (ISCO radius of the Kerr spacetime with spin a = 0.8M, top right panel), or 6M (bottom left panel). The bottom right panel shows the image of a thick disk with inner radius rin = 6M, computed with the same field of view, surrounding a Kerr black hole with spin a = 0.8M. In these panels, the image resolution is 300 × 300 pixels. |
The striking feature of the highly lensed part of this panel is the existence of two rings and of a crescent in between the rings. These features are also noticeable in the top right panel, although less clear as they overlap with the primary image. These features are due to extreme light bending in the central regions of the Lamy spacetime because of the existence of spherical photon orbits. They are absent in the boson-star image in Fig. 10, as the k = 1, ω = 0.77 boson star has no photon orbits.
To go one step further in the analysis of the impact of photon orbits on the image, we considered a more compact boson-star spacetime, where k = 1 and ω = 0.70, which has been already studied in Vincent et al. (2016). This spacetime has photon spherical orbits. Figure 12 shows null geodesics corresponding to one of the bright pixels of the inner crescent feature of the bottom left panel of Fig. 11 computed in Lamy, Kerr, and the two different boson-star spacetimes. This figure highlights the close similarity of the geodesics corresponding to the two horizonless spacetimes with photon orbits (Lamy in red and boson star with k = 1, ω = 0.70 in black). Both of these spacetimes lead to a very big change of the Boyer-Lindquist θ coordinate of the null geodesic before and after approaching the compact object. On the contrary, the horizonless spacetime with no photon orbit (boson star with k = 1, ω = 0.77, in green) leads to a very different geodesic with a much smaller change of θ when approaching the compact object. Appendix B shows that the similarity between the boson star (k = 1, ω = 0.70) and Lamy spacetimes is not restricted to the particular geodesic represented in Fig. 12. The complete images are extremely similar and possess a comparable inner crescent feature (see Appendix B).
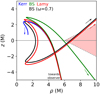 |
Fig. 12. Four geodesics corresponding to the same screen pixel for a Kerr (blue; integration stopped when approaching the event horizon), boson star (green for the k = 1, ω = 0.77 boson star considered in this paper; black for a more compact k = 1, ω = 0.7 boson star), or Lamy (red) spacetime. The selected pixel is one of that forming the crescent-shape highly lensed feature visible on the bottom left panel of Fig. 11. The arrows represent the direction of backward-in-time ray-tracing integration. The observer is thus at a large negative value of z. The disk inner radius in all cases is at rin = 6M. |
We note that such a crescent feature was also noticed for edge-on views in these two spacetimes by Vincent et al. (2016) and Lamy et al. (2018). It is thus plausible that such features are characteristic of a large class of horizonless spacetimes with photon orbits (Wielgus et al. 2020).
Figure 13 compares the EHT-like images obtained for Kerr and Lamy spacetimes. It shows that the complex features of the Lamy spacetime are partially lost when blurred at the EHT resolution. Still, there is a clear excess of flux in the central fainter region as compared to Kerr. Given that the non-Kerrness of Lamy spacetime depends directly on the charge b, it would be possible to derive a constraint on this parameter by performing fits of various Lamy spacetimes with different values of the charge. Such a constraint goes beyond our current analysis.
 |
Fig. 13. Images of a geometrically thick accretion disk with inner radius rin = 2.91M in a Kerr spacetime with spin a = 0.8M (left column), or in a Lamy wormhole spacetime with spin a = 0.8M and charge b = M. The inner disk radius is at rin = 2.91M for the left and right panels, and at rin = 1.6M for the central panel. As in all figures, the bottom row corresponds to the top row images blurred to the EHT resolution of 20 μas, the dashed blue circle has a diameter of 40 μas (size of the ring feature reported by the EHT), and the blue arrow shows the projected direction of the approaching jet. |
4. Fitting models to the EHT data
Up to this point we only discussed the differences between Kerr and non-Kerr images based on qualitative image-domain comparison. It is important to notice that we did not consider the sparsity-related limitations of the EHT image reconstruction capabilities (EHT L4). Effectively, our images represented the actual view of the model at the assumed resolution without any reconstruction-related distortions. In contrast, this section is devoted to comparing models of different compact objects directly to the M87* observational Fourier domain data.
The total intensity data from 2017 EHT observations of M87* have been publicly released2. The data consist of four independent days of observations in two independently recorded and processed frequency bands (HI and LO, EHT L3). We performed fitting of the models presented in Sects. 2 and 3 to all eight released EHT datasets. As is the case in very long baseline interferometry (VLBI), data correspond to the sparsely sampled Fourier transform of the images on the sky (Thompson et al. 2017). Because of the sparsity limitations, sophisticated postprocessing is required to reconstruct the corresponding image EHT L4. While Fourier domain (referred to as visibility domain in this context) data offer well understood error budget, reconstructed images may suffer from difficulty to assess systematic uncertainties. This is why all quantitative model fitting should take place in the visibility domain. In our case we are sampling the ideal (unblurred) model images using a synthetic model of the EHT array, utilizing the exact coverage of the M87* observations in the 2017 EHT campaign, and the expected magnitude of uncertainties. That part of the work was performed in the framework of the eht-imaging library3 (Chael et al. 2016, 2019). For the crude fitting procedure that we utilize in this paper, we consider scaling, rotation, and blurring of the model images, minimizing the reduced χ2 errors calculated against robust interferometric closure quantities (closure phases and log closure amplitudes; Blackburn et al. 2020). In each iteration of the error minimization procedure, the updated model is sampled and compared with the observed closure data. The procedure of selecting the linearly independent set of closure data products and defining the exact form of the minimized error functions follows that described in EHT L4 and EHT L6. From the estimated scaling parameter, we recover the mass M of the model best fitting the data. The rotation parameter allows us to calculate the position angle of the bright feature found in the best-fitting model. We note that both scale and orientation of the image were fixed in the discussions in previous sections to the values given in Table 1. The results of the fitting procedure are summarized in Fig. 14. All models individually give very consistent mass estimates for all days and bands, indicating that the errors are not of random statistical character, but rather are dominated by the systematic model uncertainties. Zero-spin models consistently result in much lower estimated mass, roughly consistent with the competing M87* mass measurement based on gas dynamics (Walsh et al. 2013). This is most likely a consequence of the choice of rin = rISCO = 6M, resulting in a larger image for the fixed object mass than in the case of a smaller rin. The GRMHD simulations suggest that the ISCO has little importance for hot optically thin flows (Yuan & Narayan 2014), hence such a choice of rin may be seen as inconsistent with the additional astrophysical or magnetohydrodynamical constraints. The models with spin a = 0.8 yield object mass consistent with the EHT and with the stellar dynamics measurement (Gebhardt et al. 2011). All models localize the maximum of the emission in the south of the image (see Fig. 14, right panel). The position angle of 200°, which approximates the expected orientation, given the observed position of the jet on the sky (jet position angle in the observer’s plane minus 90°; EHT L5), is indicated with a dashed horizontal line. We also see indication of counterclockwise rotation between first and last day of the observations, consistently with results reported in EHT L4 and EHT L6. None of the fits are of very high quality, as expected from very simple models with little number of degrees of freedom (see Fig. 15) and there is no clear indication of any of the models outperforming others. Some models, such as the ultracompact star with a surface located at 2.05M (Fig. 9, middle column, fitting results not shown in this section) are in dramatic disagreement with the data, resulting in reduced χ2 errors larger than 100 for each of the EHT data sets. Similarly, the model of a boson star shown in the last column of Fig. 10, being rather symmetric in appearance, fits data poorly with reduced χ2 > 30 for all EHT data sets. The fitting errors reported in Fig. 15 are of similar magnitude as the average errors resulting from fitting individual snapshots from GRMHD simulations to the EHT data (EHT L5). This supports the notion that geometric models could effectively represent mean properties of the more complicated simulations.
 |
Fig. 14. Results of fitting the models of Sect. 3 to the EHT data sets. Gray bands denote previous measurements of mass and orientation of the M87*. Left: masses of the best-fit models. Different models with spin a = 0.8 give mass measurement consistent with that reported by the EHT. Models with zero spin give systematically inconsistent mass estimate. Right: position angles (east of north) of the brightest region in the best-fit models. All models constrain the brightness maximum to be located in the south of the source image, consistent with the EHT results. |
 |
Fig. 15. Quality of the fits measured by the reduced χ2 errors resulting from fitting to the interferometric closure quantities in the EHT data sets. |
5. Conclusions and perspectives
In this article we develop a simple geometric model for the inner accretion flow of M87*, the supermassive black hole at the center of the galaxy M87. We use this model to obtain predictions of the millimeter image of the close surroundings of M87* and compare them to the EHT findings. We focused mainly on two questions.
First, we tried to develop on the recent studies devoted to improving our understanding of the sharp highly lensed features of strong-field images (Gralla et al. 2019; Johnson et al. 2020). Our findings regarding this issue are summarized in Sect. 5.1 below.
Secondly, we investigated whether objects alternative to Kerr black holes (be they physically justified or not) could produce observational signatures similar to those seen by the EHT. We show that interpreting EHT data sets with geometric flow models results in the image-domain morphology being consistent with the EHT findings (see also Figs. C.1 and C.2), and several non-Kerr spacetimes fitting the EHT data similarly well as their Kerr counterparts.
We show that without an imposed assumption on the compact object mass, no spacetime curvature effects are needed to explain the current EHT results (see Michell-Laplace black hole). Even if a mass prior from stellar dynamics is assumed, exotic objects such as boson stars or Lamy wormholes can provide images consistent with the EHT observations of M87* with a favorable geometric configuration of the accretion flow. Hence, we conclude that the published EHT observations, while consistent with the Kerr paradigm, do not provide a strong and unambiguous test of its validity. Our results agree also with the general point made earlier by Abramowicz et al. (2002). Although, as stated by these authors, there cannot be any direct electromagnetic proof of the existence of an event horizon, there is a hope for a robust detection of a secondary ring by a more developed future version of the EHT. This would be of great importance, showing the existence of null spherical orbits, which is however still very different from showing that the object is a Kerr black hole. On the other hand, resolving sharp, strongly lensed image features inconsistent with the ring geometry, such as what is seen for horizonless spacetimes with photon orbits (see Appendix B), would make a very strong argument against the Kerr paradigm. Sections 5.2 and 5.3 below give our main conclusions regarding these topics. Finally, Sect. 5.4 gives some future research perspectives.
5.1. Definition of the secondary ring
Although the set of Kerr spherical orbits plays a crucial role in defining the thin bright ring region on the sky due to highly lensed photons (Teo 2003), the properties of this feature also depend strongly on the proprieties of the accretion flow.
That is why we defined in Sect. 2.2 the secondary ring as the region on the observer’s sky where the received null geodesics, first, have approached a Kerr spherical photon orbit within δr ≲ M in term of the radial Boyer-Lindquist coordinate r and, second, have visited the regions of the accretion flow emitting most of the radiation.
It is clear from this definition that the secondary ring is not only dictated by gravitation. The astrophysics of the emitting gas has a role in determining both the polar radius and azimuthal distribution of flux in the ring. This dependence is of course at an extremely minute scale (≈μas) and does not matter as far as the current EHT data are concerned. However, it will matter with future, higher-resolution space VLBI data.
5.2. Detecting the secondary ring
Johnson et al. (2020) proposed that VLBI observations with extremely long baselines could allow for measurement of the secondary ring properties to constrain the spin of M87*. This idea is based on the simple observation that the Fourier amplitudes of sharp image features decay slower with the spatial frequency than those of extended features, and therefore should dominate the signal on extremely long baselines. As an illustration, the top panel of Fig. 16 presents visibility amplitudes of images4 of Schwarzschild black hole and Minkowski spacetime Michell-Laplace object (what is shown exactly is the horizontal slice through the amplitudes of the Fourier transforms of the two images). In this example, the contribution from a sharp ring feature clearly dominates the signal on baselines longer than 40 Gλ, and at 100 Gλ the contribution of the sharp feature is one order of magnitude stronger than that of the primary image. Simply detecting an excess of power at very high spatial frequencies would therefore indicate the presence of a sharp feature. However, determining the exact character of the feature, for example, photon ring, sharp edge, or Lamy wormhole’s inner crescent, would likely require a more sophisticated modeling approach. This can be seen in the bottom panel of Fig. 16, where a very similar spectral-power fall-off characterizes both the Kerr spacetime, where a secondary ring is present, and the boson-star spacetime, where that feature is missing. However, the two cases clearly differ in detailed structure. Detecting the presence of a sharp secondary ring feature would exclude solutions such as our Michell-Laplace relativistic black hole or a boson star without photon orbits, as that discussed in Sect. 3. Given the limitation of the Earth’s size and atmospheric stability, space VLBI observations would be required to achieve this feat. Missions potentially capable of performing such a measurement are already being proposed (see, e.g., Kardashev et al. 2014; Pesce et al. 2019).
 |
Fig. 16. Fourier transform of the data. Top: one dimensional horizontal slice from a 2D Fourier transform of the images presented in Fig. 8. For the Schwarzschild metric, the image was decomposed into the primary image (smooth ring, dashed blue) and sharp secondary ring (dashed red). For very long baselines (large spatial frequencies) the secondary ring dominates the total emission. Bottom: similar, but for the images shown in Fig. 10. While the boson-star image does not exhibit a secondary ring, the amplitude falloff is similar to that of the Kerr spacetime. |
5.3. Constraining the ultracompact star surface location
The constraints put on ϵ by the EHT images depend on the dynamic range of the images, that is, on the ratio of the brightest image part to the least bright part, which can be reliably distinguished from the noise. Since the dynamic range of EHT images is on the order of few tens, only an upper limit for the contrast κ between the brightest and faintest parts of the image was given by EHT L1, κ ≥ 10. Simulations show that the expansion of the EHT array planned for the 2020s should improve the dynamic range by an order of magnitude (Blackburn et al. 2019), tightening the constraints on ϵ by two orders of magnitude (see Eq. (10)). These constraints are ultimately limited by the jet emission from the region between the black hole and the observer, for example, from the wall of the jet.
5.4. Future perspectives
In this paper we focused on comparisons between Kerr and non-Kerr spacetime models of M87*. Hence, we did not present extensive studies of the influence of the model parameters on the image and its interpretation. As an example, we often fixed the radius rin at the ISCO of the spacetime. While the ISCO plays an important role in analytic models of relativistic geometrically thin accretion as the inner disk radius (Novikov & Thorne 1973), its relevance for at least some realistic accretion scenarios is expected to be less prominent (Abramowicz et al. 1978, 2010). Since the ISCO radius strongly depends on spin, so does the size of the primary image of a disk model terminated at the ISCO; this would result in a spin-dependent diameter-mass calibration of the EHT results, contrary to the GRMHD predictions (EHT L5, EHT L6). In the future, it will be interesting to discuss the influence of the geometric model parameters on the obtained results, as well as to compare geometric models and GRMHD simulations and their relevance for the interpretation of the M87* images.
We also plan to discuss the impact of an ejection flow on the observables to be able to discuss all the possible states of M87* (disk- or jet-dominated). Our goal is to highlight the usefulness of the geometric models to facilitate the understanding of the constraints that can be placed on the physical parameters of the accretion flow and the compact object.
See also http://gyoto.obspm.fr
Acknowledgments
We thank C. Gammie, R. Narayan, S. Doeleman, H. Olivares, and L. Rezzolla for helpful comments and discussions. This work was supported by the Black Hole Initiative at Harvard University, which is funded by grants the John Templeton Foundation and the Gordon and Betty Moore Foundation to Harvard University. J. P. L. was supported by a grant from the French Space Agency CNES. E. G. acknowledges support from the CNRS program 80 PRIME TNENGRAV. M. A. A. acknowledges the Czech Science Foundation grant No. 17-16287S. F. H. V. acknowledges financial support from the Action Fédératrice PhyFOG of the Scientific Council of Observatoire de Paris.
References
- Abramowicz, M., Jaroszynski, M., & Sikora, M. 1978, A&A, 63, 221 [NASA ADS] [Google Scholar]
- Abramowicz, M. A., Kluźniak, W., & Lasota, J. P. 2002, A&A, 396, L31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Abramowicz, M. A., Jaroszyński, M., Kato, S., et al. 2010, A&A, 521, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bardeen, J. M. 1973, Black Holes (Les Astres Occlus), 215 [Google Scholar]
- Blackburn, L., Doeleman, S., Dexter, J., et al. 2019, ArXiv e-prints [arXiv:1909.01411] [Google Scholar]
- Blackburn, L., Pesce, D. W., Johnson, M. D., et al. 2020, ApJ, 894, 31 [CrossRef] [Google Scholar]
- Blandford, R. D., & Königl, A. 1979, ApJ, 232, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Broderick, A. E., & Loeb, A. 2009, ApJ, 697, 1164 [NASA ADS] [CrossRef] [Google Scholar]
- Broderick, A. E., Loeb, A., & Narayan, R. 2009, ApJ, 701, 1357 [NASA ADS] [CrossRef] [Google Scholar]
- Chael, A. A., Johnson, M. D., Narayan, R., et al. 2016, ApJ, 829, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Chael, A. A., Bouman, K. L., Johnson, M. D., et al. 2019, ehtim: Imaging, analysis, and simulation software for radio interferometry (Astrophysics Source Code Library) [Google Scholar]
- Chan, C.-K., Psaltis, D., Özel, F., Narayan, R., & Sadowski, A. 2015, ApJ, 799, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Cunha, P. V. P., Grover, J., Herdeiro, C., et al. 2016, Phys. Rev. D, 94, 104023 [CrossRef] [Google Scholar]
- Cunha, P. V. P., Berti, E., & Herdeiro, C. A. R. 2017a, Phys. Rev. Lett., 119, 251102 [CrossRef] [Google Scholar]
- Cunha, P. V. P., Herdeiro, C. A. R., & Radu, E. 2017b, Phys. Rev. D, 96, 024039 [CrossRef] [Google Scholar]
- Cunha, P. V. P., & Herdeiro, C. A. R. 2018, Gen. Relativ. Gravit., 50, 42 [CrossRef] [Google Scholar]
- Curtis, H. D. 1918, Publ. Lick Obs., 13, 9 [NASA ADS] [Google Scholar]
- Davelaar, J., Olivares, H., Porth, O., et al. 2019, A&A, 632, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dexter, J., McKinney, J. C., & Agol, E. 2012, MNRAS, 421, 1517 [NASA ADS] [CrossRef] [Google Scholar]
- Di Matteo, T., Allen, S. W., Fabian, A. C., Wilson, A. S., & Young, A. J. 2003, ApJ, 582, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2019a, ApJ, 875, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2019b, ApJ, 875, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2019c, ApJ, 875, L6 [Google Scholar]
- Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2019d, ApJ, 875, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2019e, ApJ, 875, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Falcke, H., Melia, F., & Agol, E. 2000, ApJ, 528, L13 [Google Scholar]
- Fan, Z.-Y., & Wang, X. 2016, Phys. Rev. D, 94, 124027 [CrossRef] [Google Scholar]
- Gebhardt, K., Adams, J., Richstone, D., et al. 2011, ApJ, 729, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Gralla, S. E., & Lupsasca, A. 2020, Phys. Rev. D, 101, 044031 [CrossRef] [Google Scholar]
- Gralla, S. E., Holz, D. E., & Wald, R. M. 2019, Phys. Rev. D, 100, 024018 [Google Scholar]
- Grandclément, P. 2017, Phys. Rev. D, 95, 084011 [CrossRef] [Google Scholar]
- Grandclément, P., Somé, C., & Gourgoulhon, E. 2014, Phys. Rev. D, 90, 024068 [NASA ADS] [CrossRef] [Google Scholar]
- Hayward, S. A. 2006, Phys. Rev. Lett., 96, 031103 [CrossRef] [PubMed] [Google Scholar]
- Johnson, M. D., Lupsasca, A., Strominger, A., et al. 2020, Sci. Adv., 6, eaaz1310 [CrossRef] [Google Scholar]
- Kardashev, N. S., Novikov, I. D., Lukash, V. N., et al. 2014, Phys. Usp., 57, 1199 [CrossRef] [Google Scholar]
- Kim, J. Y., Krichbaum, T. P., Lu, R. S., et al. 2018, A&A, 616, A188 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lamy, F. 2018, Theses, Université Sorbonne Paris Cité - Université Paris Diderot (Paris 7) [Google Scholar]
- Lamy, F., Gourgoulhon, E., Paumard, T., & Vincent, F. H. 2018, CQG, 35, 115009 [NASA ADS] [CrossRef] [Google Scholar]
- Laplace, P. S. 1796, Exposition du Système du Monde (Imprimerie du Cercle-Social (Paris)) [Google Scholar]
- Liebling, S. L., & Palenzuela, C. 2017, Liv. Rev. Relativ., 20, 5 [CrossRef] [Google Scholar]
- Luminet, J. P. 1979, A&A, 75, 228 [Google Scholar]
- Marck, J.-A. 1996, CQG, 13, 393 [CrossRef] [Google Scholar]
- Mazur, P. O., & Mottola, E. 2004, Proc. Nat. Acad. Sci., 101, 9545 [NASA ADS] [CrossRef] [Google Scholar]
- Mei, S., Blakeslee, J. P., Côté, P., et al. 2007, ApJ, 655, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Michell, J. 1784, Philos. Trans. R. Soc., 74, [Google Scholar]
- Mościbrodzka, M., Falcke, H., & Shiokawa, H. 2016, A&A, 586, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nalewajko, K., Sikora, M., & Różańska, A. 2020, A&A, 634, A38 [CrossRef] [EDP Sciences] [Google Scholar]
- Narayan, R., Johnson, M. D., & Gammie, C. F. 2019, ApJ, 885, L33 [Google Scholar]
- Novikov, I. D., & Thorne, K. S. 1973, Black Holes (Les Astres Occlus) (N.Y.: Gordon and Breach), 343 [Google Scholar]
- Olivares, H., Younsi, Z., Fromm, C. M., et al. 2020, MNRAS, 497, 521 [CrossRef] [Google Scholar]
- Pandya, A., Zhang, Z., Chandra, M., & Gammie, C. F. 2016, ApJ, 822, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Pesce, D. W., Haworth, K., Melnick, G. J., et al. 2019, BAAS, 51, 176 [Google Scholar]
- Porth, O., Chatterjee, K., Narayan, R., et al. 2019, ApJS, 243, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Teo, E. 2003, Gen. Relativ. Gravit., 35, 1909 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, A. R., Moran, J. M., & Swenson, G. W. 2017, Interferometry and Synthesis in Radio Astronomy, 3rd Edn. [Google Scholar]
- Vincent, F. H., Paumard, T., Gourgoulhon, E., & Perrin, G. 2011, CQG, 28, 225011 [NASA ADS] [CrossRef] [Google Scholar]
- Vincent, F. H., Gourgoulhon, E., & Novak, J. 2012, CQG, 29, 245005 [CrossRef] [Google Scholar]
- Vincent, F. H., Meliani, Z., Grandclément, P., Gourgoulhon, E., & Straub, O. 2016, CQG, 33, 105015 [NASA ADS] [CrossRef] [Google Scholar]
- Vincent, F. H., Abramowicz, M. A., Zdziarski, A. A., et al. 2019, A&A, 624, A52 [CrossRef] [EDP Sciences] [Google Scholar]
- Walker, R. C., Hardee, P. E., Davies, F. B., Ly, C., & Junor, W. 2018, ApJ, 855, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Walsh, J. L., Barth, A. J., Ho, L. C., & Sarzi, M. 2013, ApJ, 770, 86 [NASA ADS] [CrossRef] [Google Scholar]
- White, C. J., Stone, J. M., & Quataert, E. 2019, ApJ, 874, 168 [CrossRef] [Google Scholar]
- Wielgus, M., Horák, J., Vincent, F., & Abramowicz, M. 2020, Phys. Rev. D, 102, 084044 [CrossRef] [Google Scholar]
- Yuan, F. 2000, MNRAS, 319, 1178 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, F., & Narayan, R. 2014, ARA&A, 52, 529 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Practical computation of the flux measured in the secondary ring
The lensing and photon rings, as defined by Gralla et al. (2019), are found by tracking the number of crossings of the equatorial plane of null geodesics. In the realistic astrophysical context that we are dealing with here, such a definition is not sufficient. Indeed, a geodesic can cross the equatorial plane at a large radius, long after visiting the innermost regions of spacetime (for an example see the blue geodesic of the bottom panel of Fig. A.2, which crosses the equatorial plane at r ≈ 30M). Still, keeping track of the equatorial plane crossings of geodesics is a very practical and easy-to-implement way of dealing with highly lensed geodesics, while the general definition introduced in Sect. 2.2 is not very practical to implement. To determine the flux measured in the secondary ring of the image, we thus keep track of the null geodesics that cross the equatorial plane more than once within a Boyer-Lindquist coordinate sphere r < 10M. This value is chosen rather arbitrarily, after considering many highly bent geodesics as those illustrated in Fig. 4. This criterion is very easy to implement in the context of our backward-ray-tracing code.
Figure A.1 shows two images, with the secondary ring present or removed by applying this recipe.
 |
Fig. A.1. Left: image of the central 80 μas of a thick disk surrounding a Kerr black hole with spin parameter a = 0.8M, shown in logarithmic color scale. Right: same image, putting to zero all pixels corresponding to geodesics that cross more than once the equatorial plane within the coordinate sphere r = 10M. |
The cut seems by eye somewhat too large from this figure. The high-flux pixels of the bright ring seem less extended than our mask. This is due to the fact already highlighted above that the flux distribution in the secondary ring depends a lot on the properties of the accretion flow. Figure A.2 illustrates this by following two geodesics, one of which (in red) belongs to the high-flux secondary ring, while the other (in blue) lies just outside. This figure shows that the red and blue geodesics are extremely similar and cannot be simply distinguished based on pure gravitational arguments such as number of crossings of the equatorial plane, number of θ turning points, or sharpness of these turning points. The red geodesic transports a lot of flux only because it visits the innermost disk region, which is not the case for its blue counterpart. This figure makes it clear that simple definitions of the secondary ring flux, such as the one that we adopt, are not enough to select the sharp high-flux region of the image. Thegeometry of the accretion flow should also be taken into account, as discussed in Sect. 2.2, which makes a proper definition quite cumbersome. We note that it is not sufficient to record the number of crossings of the thick disk, given that the blue geodesic crosses it one more time than the red geodesic. In this case, we restricted ourselves to the simple definition mentioned above, which allows us to obtain reasonably accurate estimates of the weight of the secondary ring flux. However, this value is somewhat overestimated because of the rather large angular thickness of the mask as compared to the thin secondary ring.
 |
Fig. A.2. Similar figure to Fig. 4 to which we refer for the details of the bottom panel. The top panel is shown in logarithmic scale. The red and blue geodesics of the bottom panel correspond to the pixels labeled by the red and blue arrows in the top panel. the red geodesic is within the secondary ring while the blue geodesic lies just outside. The red geodesic asymptotically approaches the event horizon when ray traced back in time. |
Appendix B: Comparison between horizonless spacetimes with photon orbits
Section 3.4, and Fig. 12 in particular, highlight the similarity between our Lamy spacetime and a boson-star spacetime with k = 1 and ω = 0.7. This comparison was made on only one highly bent null geodesic, which is extremely similar for the two horizonless spacetimes. Figure B.1 shows a comparison of the full 80 μas field image between these two spacetimes. The two images are strikingly similar.
 |
Fig. B.1. Images on a field of view of 80 μas of a thick disk with inner radius rin = 6M surrounding a Lamy wormhole (left) or a boson-star spacetime with k = 1 and ω = 0.7 (right). The compact object spin parameter is approximately the same for both panels. The two spacetimes, although extremely different at a theoretical level, are both horizonless and possess photon orbits. |
In contrast, the (k = 1, ω = 0.77) boson-star image is very different (see top middle panel of Fig. 10, computed with a field of view of 160 μas). The important difference between the two boson-star spacetimes is the fact that for (k = 1, ω = 0.77), there is no photon orbits, while for (k = 1, ω = 0.7), photon orbits exist (they appear at ω = 0.75; Cunha et al. 2016). This is a good illustration that the main features of highly lensed images are dictated by photon orbits; that is, not only planar photon orbits, but the general set of fundamental photon orbits that generalize Kerr spherical photon orbits (see Cunha et al. 2017a). Even for spacetimes that have nothing in common at a theoretical level (like a Lamy wormhole and a boson star), images are very similar as soon as similar photon orbits exist. Lamy photon orbits have been studied in detail by Lamy (2018). Rotating-boson-star photon orbits have been studied by Cunha et al. (2016) and Grandclément (2017). These works give the radius of the unstable equatorial photon orbit, which lies at rph = 4.2M for the boson-star spacetime and rph ≈ 2.2M for the Lamy spacetime. We give an approximate value for the second quantity because Lamy (2018) studies a spacetime with a = 0.9M and b = M, thus slightly different from our case.
The small difference of scales in the two panels of Fig. B.1 are likely due to this difference of location of the equatorial photon orbit. A more detailed comparison would be necessary to analyze further the similarity between these images and link them to the properties of fundamental photon orbits. It is likely that a large class of horizonless spacetimes with photon orbits will lead to images similar to what we present in this work for two particular spacetimes, indicating sharp features that could be potentially resolved by the future VLBI arrays.
Appendix C: Best-fitting images
Figures C.1 and C.2 present the results of the procedure of fitting models to the visibility domain data released by the EHT. In these examples we only show best fits to the data observed on April 11, 2017 in HI band for several models that allowed us to obtain fit quality similar as the Kerr spacetime examples. The best-fitting jet position angle and object mass are given for the each type of object.
 |
Fig. C.1. Images best-fitting EHT data from April 11, 2017, HI band, corresponding to a geometrically thick accretion disk with inner radius rin = 6M in a Schwarzschild spacetime (left column), in the spacetime of an ultracompact star with surface radius rst = 2.0005M emitting blackbody radiation at the inner temperature of the accretion flow Te, in = 8 × 1010 K (middle column), or in a Minkowski spacetime (right column). As in all figures, the bottom row corresponds to the top row images blurred to the EHT resolution of 20 μas; the dashed blue circle has a diameter of 40 μas (size of the ring feature reported by the EHT) and the blue arrow shows the projected direction of the approaching jet. The best-fitting compact-object mass and jet position angle east of north are specified in each bottom panel. |
 |
Fig. C.2. Images best-fitting EHT data from April 11, 2017, HI band, corresponding to a geometrically thick accretion disk in a Kerr spacetime with spin a = 0.8M (left column), in a boson-star spacetime of the same spin with k = 1 and ω = 0.77 (middle column), or in a Lamy spacetime of the same spin with b = M (right column). The disk inner radius is of rin = 2.91M for the left and right panels, and rin = 3.5M for the central panel. As in all figures, the bottom row corresponds to the top row images blurred to the EHT resolution of 20 μas; the dashed blue circle has a diameter of 40 μas (the size of the ring feature reported by the EHT) and the blue arrow shows the projected direction of the approaching jet. The best-fitting compact-object mass and jet position angle east of north are specified in each bottom panel. |
All Tables
All Figures
 |
Fig. 1. Geometrically thick disk model (in red) surrounding a compact object (black disk) of mass M. The disk has an inner radius rin, where the electron number density and temperature are ne, in and Te, in. The number density scales as r−2 and the temperature as r−1. All quantities are independent of the height z. The opening angle of the disk is called θop. Here and throughout the article, the compact object and accretion disk spins (black and red arrows, respectively) are assumed to be aligned. The inclination angle i between the spin axis and the line of sight is shown in green. |
| In the text | |
 |
Fig. 2. Images of a thick disk surrounding a nonrotating (a = 0) black hole. The top row shows the simulated ray-traced image and the bottom row consists of the upper row images blurred to the EHT resolution (about 20 μas). The dashed blue circle shown in the lower row images has a diameter of 40 μas, consistent with the estimated diameter of the ring feature in the M87* image, reported by the EHT. This diameter translates to 11.05M in mass units of distance. The blue arrow shows the projected direction of the jet. The disk inner radius is 6M for the left panel (corresponding to the ISCO) and 2M for the two other panels (corresponding to the event horizon). The azimuthal velocity below ISCO is paramterized by vφ = 1 (purely azimuthal velocity) for the middle panel and vφ = 0 (purely radial plunge) for the right panel. The inner electron number density is equal to 5 × 105 cm−3 when rin = 2M and 5.5 × 104 cm−3 when rin = 6M (see text for details on how these numbers are chosen). |
| In the text | |
 |
Fig. 3. Same as Fig. 2 with a spin parameter of a = 0.8M. The inner density is of 2.4 × 105 cm−3 when rin = 2.91M, and 7.8 × 105 cm−3 when rin = 1.6M. |
| In the text | |
 |
Fig. 4. Top panels: zoom on the central 80 μas field of the image of a thick disk surrounding a Schwarzschild black hole (left) or a Kerr black hole with spin parameter a = 0.8M (right). Bottom panels: three geodesics are plotted on the (ρ, z) plane of height vs. cylindrical radius (in units of M). The arrows show the direction of backward-ray-tracing integration in GYOTO. The observer is located at 16.9 Mpc toward the bottom right of the panels. These geodesics correspond to the pixels labeled by the red, green, and blue arrows of the top panels, which are, respectively, part of the photon ring (3 crossings of the equatorial plane), lensing ring (2 crossings), and primary image (1 crossing) in the terminology of Gralla et al. (2019). The half disk filled in black corresponds to the event horizon. The black solid half circle of the left panel corresponds to the Schwarzschild photon sphere at r = 3M. The black-line delineated white crescent of the right panel corresponds to the locus of spherical Kerr orbits for a = 0.8M, with the locations of the prograde and retrograde equatorial photon orbits denoted by black dots. The dashed thick black line within the crescent corresponds to the spherical orbit at the inner Boyer-Lindquist radius of the red geodesic. The thick disk corresponds to the pale red region. In the Schwarzschild case (left panel), the red geodesic approaches the photon sphere. In the Kerr case (right panel), the red geodesic approaches a spherical orbit at its minimum Boyer-Lindquist radius. Both the red and green geodesics belong to the secondary ring. |
| In the text | |
 |
Fig. 5. Example of a secondary ring. Top: two null geodesics, in Schwarzschild spacetime, that are part of the n = 2 (blue) and n = 3 (red) photon subrings (see text), n being the number of crossings of the equatorial plane. The black disk represents the black hole event horizon, and the thin black circle shows the location of the unstable spherical photon orbit. Bottom: the plane of the sky of the distant observer. The various concentric rings depict the photon subrings (see text) corresponding to the different values of the number n of crossings of the equatorial plane of the black hole. The lensing ring and critical curve (see text) are explicitly labeled. If only one blob of emitting matter (in green in the top panel) is present close to the black hole and interesects the red geodesic only, and not the blue geodesic, then only the n = 3 subring will be illuminated on sky, and the others will remain dark. The secondary ring will then coincide with the n = 3 subring. This would not be so should the blob of emitting matter be situated elsewhere. The spacing between the subrings on the observer’s sky is of course very exaggerated and lies within ≲1 μas for M87*. |
| In the text | |
 |
Fig. 6. Left sketch: black hole surroundings. The black hole event horizon is represented by a black disk, and the geometrically thick accretion disk is represented by the shaded red region (only one half of the disk is shown to save space). The sketch is rotated to have the same orientation of the black hole spin vector (black arrow) as in the central panel. The dashed red and blue circles around the black hole are the location of two Kerr spherical photon orbits (not to scale), the radii of which are given below. Central panel: plot of the critical curve on the observer’s sky as defined by the polar Eq. (3), for a black hole spin of a = 0.8M and an inclination angle of i = 160°. The critical curve is rotated to account for the position angle of M87* (PA = −70° as labeled on the panel, or 290° east of north). The projection of the black hole spin vector is shown by the black arrow (opposite to the approaching jet projection depicted by the blue arrow in Fig. 2). Three pairs of points are shown in red, green, and blue along the curve and are the images of the Kerr spherical orbits with radii r = 2.31M, 2.7M, and 3.05M, respectively. The Kerr equatorial prograde and retrograde photon orbits for a = 0.8M are rph, pro = 1.82M and rph, retro = 3.81M. The gray bent arrow at the left of the critical curve shows the direction of increase of the Kerr spherical orbit radius that the photon is following on its way to the observer (same evolution on the right side of the critical curve). Two null geodesics connecting the red and blue Kerr spherical orbits to the corresponding points on the critical curve are illustrated between the left drawing and the central panel. Right panel: ray-traced image of the model with the same field of view as in the middle panel. This image is a zoom on the central 45 μas of the top left panel of Fig. 3. The 4 important notions introduced in the text, lensing, photon, secondary rings, and critical curve, are labeled. The zoom on the region of the right panel surrounded by the dashed red rectangle is shown in the bottom right insert. This allows us to better see the difference between the lensing and photon rings. The critical curve is extremely close in angular radius to the photon ring (they are impossible to distinguish with the naked eye when comparing the central and right panels). However, the two notions are different mathematically. In the limit of an infinite resolution, the photon ring of the right panel would decompose into a sequence of rings converging to the critical curve. |
| In the text | |
 |
Fig. 7. Non-axisymmetric disk compared to axisymmetric case for spin a = 0.8 M. Only blurred images are shown. The second, third, and fourth panel from the left are obtained by considering a hotter region in the disk defined by a temperature increment of T0/Tinner = 2, 4, or 8, respectively. This comparison shows that the non-axisymmetry of the flow must be substantial (approximately an order of magnitude contrast) to overcome the beaming effect. |
| In the text | |
 |
Fig. 8. Images of a geometrically thick accretion disk with inner radius rin = 6M in a Schwarzschild spacetime (left column) or in Minkowski spacetime (right column). As in all figures, the bottom row corresponds to the top row images blurred to the EHT resolution (20 μas), the dashed blue circle has a diameter of 40 μas (size of the ring feature reported by the EHT), and the blue arrow shows the projected direction of the approaching jet. |
| In the text | |
 |
Fig. 9. Images of a geometrically thick accretion disk with inner radius rin = 6M in a Schwarzschild spacetime (left column); in the spacetime of an ultracompact star with surface radius rst = 2.05M, emitting blackbody radiation at the inner temperature of the accretion flow Te, in = 8 × 1010 K (middle column); or in the same spacetime as the middle column, but with rst = 2.0005M (right column). As in all figures, the bottom row corresponds to the top row images blurred to the EHT resolution of 20 μas; the dashed blue circle has a diameter of 40 μas (size of the ring feature reported by the EHT) and the blue arrow shows the projected direction of the approaching jet. |
| In the text | |
 |
Fig. 10. Images of a geometrically thick accretion disk with inner radius rin = 2.91M in a Kerr spacetime with spin parameter a = 0.8M (left column). Same image, but with a disk inner radius at rin = 3.5M, in a rotating boson star spacetime defined by (k = 1, ω = 0.77), which corresponds to the same value of the spin parameter (middle column). Same boson-star spacetime with rin = 2.09M, corresponding to the ICO of that spacetime (right column). As in all figures, the bottom row corresponds to the top row images blurred to the EHT resolution of 20 μas; the dashed blue circle has a diameter of 40 μas (size of the ring feature reported by the EHT) and the blue arrow shows the projected direction of the approaching jet. |
| In the text | |
 |
Fig. 11. Two top panels and bottom left panel show three images with a field of view of 80 μas of a thick disk surrounding a Lamy wormhole with spin a = 0.8M and charge b = M. The inner disk radius is at rin = 1.6M (ISCO radius of the Lamy spacetime, top left panel), 2.91M (ISCO radius of the Kerr spacetime with spin a = 0.8M, top right panel), or 6M (bottom left panel). The bottom right panel shows the image of a thick disk with inner radius rin = 6M, computed with the same field of view, surrounding a Kerr black hole with spin a = 0.8M. In these panels, the image resolution is 300 × 300 pixels. |
| In the text | |
 |
Fig. 12. Four geodesics corresponding to the same screen pixel for a Kerr (blue; integration stopped when approaching the event horizon), boson star (green for the k = 1, ω = 0.77 boson star considered in this paper; black for a more compact k = 1, ω = 0.7 boson star), or Lamy (red) spacetime. The selected pixel is one of that forming the crescent-shape highly lensed feature visible on the bottom left panel of Fig. 11. The arrows represent the direction of backward-in-time ray-tracing integration. The observer is thus at a large negative value of z. The disk inner radius in all cases is at rin = 6M. |
| In the text | |
 |
Fig. 13. Images of a geometrically thick accretion disk with inner radius rin = 2.91M in a Kerr spacetime with spin a = 0.8M (left column), or in a Lamy wormhole spacetime with spin a = 0.8M and charge b = M. The inner disk radius is at rin = 2.91M for the left and right panels, and at rin = 1.6M for the central panel. As in all figures, the bottom row corresponds to the top row images blurred to the EHT resolution of 20 μas, the dashed blue circle has a diameter of 40 μas (size of the ring feature reported by the EHT), and the blue arrow shows the projected direction of the approaching jet. |
| In the text | |
 |
Fig. 14. Results of fitting the models of Sect. 3 to the EHT data sets. Gray bands denote previous measurements of mass and orientation of the M87*. Left: masses of the best-fit models. Different models with spin a = 0.8 give mass measurement consistent with that reported by the EHT. Models with zero spin give systematically inconsistent mass estimate. Right: position angles (east of north) of the brightest region in the best-fit models. All models constrain the brightness maximum to be located in the south of the source image, consistent with the EHT results. |
| In the text | |
 |
Fig. 15. Quality of the fits measured by the reduced χ2 errors resulting from fitting to the interferometric closure quantities in the EHT data sets. |
| In the text | |
 |
Fig. 16. Fourier transform of the data. Top: one dimensional horizontal slice from a 2D Fourier transform of the images presented in Fig. 8. For the Schwarzschild metric, the image was decomposed into the primary image (smooth ring, dashed blue) and sharp secondary ring (dashed red). For very long baselines (large spatial frequencies) the secondary ring dominates the total emission. Bottom: similar, but for the images shown in Fig. 10. While the boson-star image does not exhibit a secondary ring, the amplitude falloff is similar to that of the Kerr spacetime. |
| In the text | |
 |
Fig. A.1. Left: image of the central 80 μas of a thick disk surrounding a Kerr black hole with spin parameter a = 0.8M, shown in logarithmic color scale. Right: same image, putting to zero all pixels corresponding to geodesics that cross more than once the equatorial plane within the coordinate sphere r = 10M. |
| In the text | |
 |
Fig. A.2. Similar figure to Fig. 4 to which we refer for the details of the bottom panel. The top panel is shown in logarithmic scale. The red and blue geodesics of the bottom panel correspond to the pixels labeled by the red and blue arrows in the top panel. the red geodesic is within the secondary ring while the blue geodesic lies just outside. The red geodesic asymptotically approaches the event horizon when ray traced back in time. |
| In the text | |
 |
Fig. B.1. Images on a field of view of 80 μas of a thick disk with inner radius rin = 6M surrounding a Lamy wormhole (left) or a boson-star spacetime with k = 1 and ω = 0.7 (right). The compact object spin parameter is approximately the same for both panels. The two spacetimes, although extremely different at a theoretical level, are both horizonless and possess photon orbits. |
| In the text | |
 |
Fig. C.1. Images best-fitting EHT data from April 11, 2017, HI band, corresponding to a geometrically thick accretion disk with inner radius rin = 6M in a Schwarzschild spacetime (left column), in the spacetime of an ultracompact star with surface radius rst = 2.0005M emitting blackbody radiation at the inner temperature of the accretion flow Te, in = 8 × 1010 K (middle column), or in a Minkowski spacetime (right column). As in all figures, the bottom row corresponds to the top row images blurred to the EHT resolution of 20 μas; the dashed blue circle has a diameter of 40 μas (size of the ring feature reported by the EHT) and the blue arrow shows the projected direction of the approaching jet. The best-fitting compact-object mass and jet position angle east of north are specified in each bottom panel. |
| In the text | |
 |
Fig. C.2. Images best-fitting EHT data from April 11, 2017, HI band, corresponding to a geometrically thick accretion disk in a Kerr spacetime with spin a = 0.8M (left column), in a boson-star spacetime of the same spin with k = 1 and ω = 0.77 (middle column), or in a Lamy spacetime of the same spin with b = M (right column). The disk inner radius is of rin = 2.91M for the left and right panels, and rin = 3.5M for the central panel. As in all figures, the bottom row corresponds to the top row images blurred to the EHT resolution of 20 μas; the dashed blue circle has a diameter of 40 μas (the size of the ring feature reported by the EHT) and the blue arrow shows the projected direction of the approaching jet. The best-fitting compact-object mass and jet position angle east of north are specified in each bottom panel. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



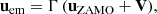
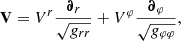
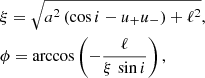
![$$ \begin{aligned}&u_{\pm } = \frac{r}{a^2 (r-M)^2} \left[-r^3 + 3M^2r - 2a^2 M \right. .\\&\quad ~~ \left. \pm 2\sqrt{M (r^2 - 2Mr + a^2) (2r^3 - 3Mr^2 + a^2 M) } \right], \nonumber \\&\ell = \frac{M(r^2 - a^2) - r (r^2 - 2Mr + a^2)}{a (r-M)}. \nonumber \end{aligned} $$](/articles/aa/full_html/2021/02/aa37787-20/aa37787-20-eq4.gif)