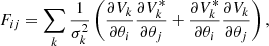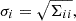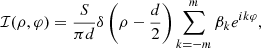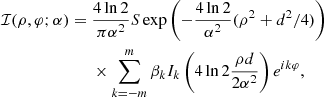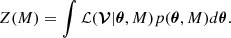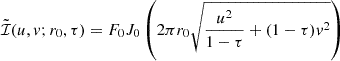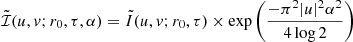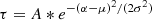| Issue |
A&A
Volume 699, July 2025
|
|
|---|---|---|
| Article Number | A279 | |
| Number of page(s) | 18 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202555235 | |
| Published online | 10 July 2025 | |
Origin of the ring ellipticity in the black hole images of M87*
1
Instituto de Astrofísica de Andalucía-CSIC, Glorieta de la Astronomía s/n, E-18008 Granada, Spain
2
Korea Astronomy and Space Science Institute, Daedeok-daero 776, Yuseong-gu, Daejeon 34055, Republic of Korea
3
Department of Astronomy, Yonsei University, Yonsei-ro 50, Seodaemun-gu, 03722 Seoul, Republic of Korea
4
Mizusawa VLBI Observatory, National Astronomical Observatory of Japan, 2-12 Hoshigaoka, Mizusawa, Oshu, Iwate 023-0861, Japan
5
Tuorla Observatory, Department of Physics and Astronomy, University of Turku, FI-20014 Turun Yliopisto, Finland
6
Finnish Centre for Astronomy with ESO, University of Turku, FI-20014 Turun Yliopisto, Finland
7
Aalto University Metsähovi Radio Observatory, Metsähovintie 114, FI-02540 Kylmälä, Finland
8
Center for Astrophysics | Harvard & Smithsonian, 60 Garden Street, Cambridge, MA 02138, USA
9
Black Hole Initiative at Harvard University, 20 Garden Street, Cambridge, MA 02138, USA
10
Steward Observatory and Department of Astronomy, University of Arizona, 933 N. Cherry Ave., Tucson, AZ 85721, USA
11
Data Science Institute, University of Arizona, 1230 N. Cherry Ave., Tucson, AZ 85721, USA
12
Program in Applied Mathematics, University of Arizona, 617 N. Santa Rita, Tucson, AZ 85721, USA
13
Institute for Mathematics and Interdisciplinary Center for Scientific Computing, Heidelberg University, Im Neuenheimer Feld 205, Heidelberg 69120, Germany
14
Institut für Theoretische Physik, Universität Heidelberg, Philosophenweg 16, 69120 Heidelberg, Germany
15
CP3-Origins, University of Southern Denmark, Campusvej 55, DK-5230 Odense, Denmark
16
Institute of Astronomy and Astrophysics, Academia Sinica, 11F of Astronomy-Mathematics Building, AS/NTU No. 1, Sec. 4, Roosevelt Rd., Taipei 106216, Taiwan, ROC
17
Department of Physics, National Taiwan Normal University, No. 88, Sec. 4, Tingzhou Rd., Taipei 116, Taiwan, ROC
18
Center of Astronomy and Gravitation, National Taiwan Normal University, No. 88, Sec. 4, Tingzhou Road, Taipei 116, Taiwan, ROC
19
Department of Physics, University of Illinois, 1110 West Green Street, Urbana, IL 61801, USA
20
Instituto de Astronomía, Universidad Nacional Autónoma de México (UNAM), Apdo Postal 70-264, Ciudad de México, Mexico
21
Institut für Theoretische Physik, Goethe-Universität Frankfurt, Max-von-Laue-Straße 1, D-60438 Frankfurt am Main, Germany
22
Perimeter Institute for Theoretical Physics, 31 Caroline Street North, Waterloo, ON N2L 2Y5, Canada
23
Department of Physics and Astronomy, University of Waterloo, 200 University Avenue West, Waterloo, ON N2L 3G1, Canada
24
Waterloo Centre for Astrophysics, University of Waterloo, Waterloo, ON N2L 3G1, Canada
25
Anton Pannekoek Institute for Astronomy, University of Amsterdam, Science Park 904, 1098 XH Amsterdam, The Netherlands
26
Institute for Research in Electronics and Applied Physics, University of Maryland, 8279 Paint Branch Drive, College Park, MD 20742, USA
27
Massachusetts Institute of Technology Haystack Observatory, 99 Millstone Road, Westford, MA 01886, USA
28
National Astronomical Observatory of Japan, 2-21-1 Osawa, Mitaka, Tokyo 181-8588, Japan
29
Departament d’Astronomia i Astrofísica, Universitat de València, C. Dr. Moliner 50, E-46100 Burjassot, València, Spain
30
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, D-53121 Bonn, Germany
31
Department of Physics, Faculty of Science, Universiti Malaya, 50603 Kuala Lumpur, Malaysia
32
Department of Physics & Astronomy, The University of Texas at San Antonio, One UTSA Circle, San Antonio, TX 78249, USA
33
Physics & Astronomy Department, Rice University, Houston, TX 77005-1827, USA
34
Observatori Astronòmic, Universitat de València, C. Catedrático José Beltrán 2, E-46980 Paterna, València, Spain
35
Department of Space, Earth and Environment, Chalmers University of Technology, Onsala Space Observatory, SE-43992 Onsala, Sweden
36
Yale Center for Astronomy & Astrophysics, Yale University, 52 Hillhouse Avenue, New Haven, CT 06511, USA
37
Astronomy Department, Universidad de Concepción, Casilla 160-C, Concepción, Chile
38
Fermi National Accelerator Laboratory, MS209, P.O. Box 500, Batavia, IL 60510, USA
39
Department of Astronomy and Astrophysics, University of Chicago, 5640 South Ellis Avenue, Chicago, IL 60637, USA
40
East Asian Observatory, 660 N. A’ohoku Place, Hilo, HI 96720, USA
41
James Clerk Maxwell Telescope (JCMT), 660 N. A’ohoku Place, Hilo, HI 96720, USA
42
California Institute of Technology, 1200 East California Boulevard, Pasadena, CA 91125, USA
43
Institute of Astronomy and Astrophysics, Academia Sinica, 645 N. A’ohoku Place, Hilo, HI 96720, USA
44
Department of Physics and Astronomy, University of Hawaii at Manoa, 2505 Correa Road, Honolulu, HI 96822, USA
45
Institut de Radioastronomie Millimétrique (IRAM), 300 Rue de la Piscine, F-38406 Saint Martin d’Hères, France
46
Department of Astrophysics, Institute for Mathematics, Astrophysics and Particle Physics (IMAPP), Radboud University, P.O. Box 9010, 6500 GL Nijmegen, The Netherlands
47
Department of Astronomy, University of Massachusetts, Amherst, MA 01003, USA
48
Instituto de Astronomia, Geofísica e Ciências Atmosféricas da Universidade de São Paulo, Brazil
49
Kavli Institute for Cosmological Physics, University of Chicago, 5640 South Ellis Avenue, Chicago, IL 60637, USA
50
Department of Physics, University of Chicago, 5720 South Ellis Avenue, Chicago, IL 60637, USA
51
Enrico Fermi Institute, University of Chicago, 5640 South Ellis Avenue, Chicago, IL 60637, USA
52
Princeton Gravity Initiative, Jadwin Hall, Princeton University, Princeton, NJ 08544, USA
53
Cornell Center for Astrophysics and Planetary Science, Cornell University, Ithaca, NY 14853, USA
54
Institute of Astronomy and Astrophysics, Academia Sinica, 645 N. A’ohoku Place, Hilo, HI 96720, USA
55
Shanghai Astronomical Observatory, Chinese Academy of Sciences, 80 Nandan Road, Shanghai 200030, PR China
56
Key Laboratory of Radio Astronomy and Technology, Chinese Academy of Sciences, A20 Datun Road, Chaoyang District, Beijing 100101, PR China
57
WattTime, 490 43rd Street, Unit 221, Oakland, CA 94609, USA
58
Department of Astronomy, University of Illinois at Urbana-Champaign, 1002 West Green Street, Urbana, IL 61801, USA
59
Research Center for Astronomical Computing, Zhejiang Laboratory, Hangzhou 311100, PR China
60
Tsung-Dao Lee Institute, Shanghai Jiao Tong University, Shengrong Road 520, Shanghai 201210, PR China
61
Department of Astrophysical Sciences, Peyton Hall, Princeton University, Princeton, NJ 08544, USA
62
Dipartimento di Fisica “E. Pancini”, Università di Napoli “Federico II”, Compl. Univ. di Monte S. Angelo, Edificio G, Via Cinthia, I-80126 Napoli, Italy
63
INFN Sez. di Napoli, Compl. Univ. di Monte S. Angelo, Edificio G, Via Cinthia, I-80126 Napoli, Italy
64
Wits Centre for Astrophysics, University of the Witwatersrand, 1 Jan Smuts Avenue, Braamfontein, Johannesburg 2050, South Africa
65
Department of Physics, University of Pretoria, Hatfield, Pretoria 0028, South Africa
66
Centre for Radio Astronomy Techniques and Technologies, Department of Physics and Electronics, Rhodes University, Makhanda 6140, South Africa
67
ASTRON, Oude Hoogeveensedijk 4, 7991 PD Dwingeloo, The Netherlands
68
LESIA, Observatoire de Paris, Université PSL, CNRS, Sorbonne Université, Université de Paris, 5 Place Jules Janssen, F-92195 Meudon, France
69
JILA and Department of Astrophysical and Planetary Sciences, University of Colorado, Boulder, CO 80309, USA
70
National Astronomical Observatories, Chinese Academy of Sciences, 20A Datun Road, Chaoyang District, Beijing 100101, PR China
71
Las Cumbres Observatory, 6740 Cortona Drive, Suite 102, Goleta, CA 93117-5575, USA
72
Department of Physics, University of California, Santa Barbara, CA 93106-9530, USA
73
National Radio Astronomy Observatory, 520 Edgemont Road, Charlottesville, VA 22903, USA
74
Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, 32-D476, 77 Massachusetts Ave., Cambridge, MA 02142, USA
75
Google Research, 355 Main St., Cambridge, MA 02142, USA
76
Institut für Theoretische Physik und Astrophysik, Julius-Maximilian-Universität Würzburg, Emil-Fischer-Straße 31, 97074 Würzburg, Germany
77
Department of History of Science, Harvard University, Cambridge, MA 02138, USA
78
Department of Physics, Harvard University, Cambridge, MA 02138, USA
79
NCSA, University of Illinois, 1205 W. Clark St., Urbana, IL 61801, USA
80
Royal Netherlands Meteorological Institute, Utrechtseweg 297, 3731 GA De Bilt, The Netherlands
81
Instituto de Astronomia, Geofísica e Ciências Atmosféricas, Universidade de São Paulo, R. do Matão, 1226, São Paulo, SP 05508-090, Brazil
82
Dipartimento di Fisica, Università degli Studi di Cagliari, SP Monserrato-Sestu km 0.7, I-09042 Monserrato, (CA), Italy
83
INAF – Osservatorio Astronomico di Cagliari, Via della Scienza 5, I-09047 Selargius, (CA), Italy
84
INFN, Sezione di Cagliari, I-09042 Monserrato, (CA), Italy
85
Instituto Nacional de Astrofísica, Óptica y Electrónica, Apartado Postal 51 y 216, 72000 Puebla Pue., Mexico
86
Consejo Nacional de Humanidades, Ciencia y Tecnología, Av. Insurgentes Sur 1582, 03940 Ciudad de México, Mexico
87
Key Laboratory for Research in Galaxies and Cosmology, Chinese Academy of Sciences, Shanghai 200030, PR China
88
Graduate School of Science, Nagoya City University, Yamanohata 1, Mizuho-cho, Mizuho-ku, Nagoya 467-8501, Aichi, Japan
89
Department of Physics, McGill University, 3600 Rue University, Montréal, QC H3A 2T8, Canada
90
Trottier Space Institute at McGill, 3550 Rue University, Montréal, QC H3A 2A7, Canada
91
NOVA Sub-mm Instrumentation Group, Kapteyn Astronomical Institute, University of Groningen, Landleven 12, 9747 AD Groningen, The Netherlands
92
Department of Astronomy, School of Physics, Peking University, Beijing 100871, PR China
93
Kavli Institute for Astronomy and Astrophysics, Peking University, Beijing 100871, PR China
94
Department of Astronomical Science, The Graduate University for Advanced Studies (SOKENDAI), 2-21-1 Osawa, Mitaka, Tokyo 181-8588, Japan
95
Department of Astronomy, Graduate School of Science, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo 113-0033, Japan
96
The Institute of Statistical Mathematics, 10-3 Midori-cho, Tachikawa, Tokyo 190-8562, Japan
97
Department of Statistical Science, The Graduate University for Advanced Studies (SOKENDAI), 10-3 Midori-cho, Tachikawa, Tokyo 190-8562, Japan
98
Kavli Institute for the Physics and Mathematics of the Universe, The University of Tokyo, 5-1-5 Kashiwanoha, Kashiwa 277-8583, Japan
99
Leiden Observatory, Leiden University, Postbus 2300, 9513 RA Leiden, The Netherlands
100
ASTRAVEO LLC, PO Box 1668, Gloucester, MA 01931, USA
101
Applied Materials Inc., 35 Dory Road, Gloucester, MA 01930, USA
102
Institute for Astrophysical Research, Boston University, 725 Commonwealth Ave., Boston, MA 02215, USA
103
University of Science and Technology, Gajeong-ro 217, Yuseong-gu, Daejeon 34113, Republic of Korea
104
Institute for Cosmic Ray Research, The University of Tokyo, 5-1-5 Kashiwanoha, Kashiwa, Chiba 277-8582, Japan
105
Joint Institute for VLBI ERIC (JIVE), Oude Hoogeveensedijk 4, 7991 PD Dwingeloo, The Netherlands
106
CSIRO, Space and Astronomy, PO Box 76, Epping, NSW 1710, Australia
107
Department of Physics, Ulsan National Institute of Science and Technology (UNIST), Ulsan 44919, Republic of Korea
108
Department of Physics, Korea Advanced Institute of Science and Technology (KAIST), 291 Daehak-ro, Yuseong-gu, Daejeon 34141, Republic of Korea
109
Kogakuin University of Technology & Engineering, Academic Support Center, 2665-1 Nakano, Hachioji, Tokyo 192-0015, Japan
110
Graduate School of Science and Technology, Niigata University, 8050 Ikarashi 2-no-cho, Nishi-ku, Niigata 950-2181, Japan
111
Physics Department, National Sun Yat-Sen University, No. 70, Lien-Hai Road, Kaosiung City 80424, Taiwan, ROC
112
School of Astronomy and Space Science, Nanjing University, Nanjing 210023, PR China
113
Key Laboratory of Modern Astronomy and Astrophysics, Nanjing University, Nanjing 210023, PR China
114
INAF-Istituto di Radioastronomia, Via P. Gobetti 101, I-40129 Bologna, Italy
115
Common Crawl Foundation, 9663 Santa Monica Blvd. 425, Beverly Hills, CA 90210, USA
116
Instituto de Física, Pontificia Universidad Católica de Valparaíso, Casilla 4059, Valparaíso, Chile
117
INAF-Istituto di Radioastronomia & Italian ALMA Regional Centre, Via P. Gobetti 101, I-40129 Bologna, Italy
118
Department of Physics, National Taiwan University, No. 1, Sec. 4, Roosevelt Rd., Taipei 106216, Taiwan, ROC
119
Instituto de Radioastronomía y Astrofísica, Universidad Nacional Autónoma de México, Morelia 58089, Mexico
120
David Rockefeller Center for Latin American Studies, Harvard University, 1730 Cambridge Street, Cambridge, MA 02138, USA
121
Yunnan Observatories, Chinese Academy of Sciences, 650011 Kunming, Yunnan Province, PR China
122
Center for Astronomical Mega-Science, Chinese Academy of Sciences, 20A Datun Road, Chaoyang District, Beijing 100012, PR China
123
Key Laboratory for the Structure and Evolution of Celestial Objects, Chinese Academy of Sciences, 650011 Kunming, PR China
124
Gravitation and Astroparticle Physics Amsterdam (GRAPPA) Institute, University of Amsterdam, Science Park 904, 1098 XH Amsterdam, The Netherlands
125
School of Physics and Astronomy, Shanghai Jiao Tong University, 800 Dongchuan Road, Shanghai 200240, People's Republic of China
126
Institut de Radioastronomie Millimétrique (IRAM), Avenida Divina Pastora 7, Local 20, E-18012 Granada, Spain
127
National Institute of Technology, Hachinohe College, 16-1 Uwanotai, Tamonoki, Hachinohe City, Aomori 039-1192, Japan
128
Research Center for Astronomy, Academy of Athens, Soranou Efessiou 4, 115 27 Athens, Greece
129
Department of Physics, Villanova University, 800 Lancaster Avenue, Villanova, PA 19085, USA
130
Physics Department, Washington University, CB 1105, St. Louis, MO 63130, USA
131
Departamento de Matemática da Universidade de Aveiro and Centre for Research and Development in Mathematics and Applications (CIDMA), Campus de Santiago, 3810-193 Aveiro, Portugal
132
School of Physics, Georgia Institute of Technology, 837 State St NW, Atlanta, GA 30332, USA
133
School of Space Research, Kyung Hee University, 1732, Deogyeong-daero, Giheung-gu, Yongin-si, Gyeonggi-do 17104, Republic of Korea
134
Canadian Institute for Theoretical Astrophysics, University of Toronto, 60 St. George Street, Toronto, ON M5S 3H8, Canada
135
Dunlap Institute for Astronomy and Astrophysics, University of Toronto, 50 St. George Street, Toronto, ON M5S 3H4, Canada
136
Canadian Institute for Advanced Research, 180 Dundas St West, Toronto, ON M5G 1Z8, Canada
137
Dipartimento di Fisica, Università di Trieste, I-34127 Trieste, Italy
138
INFN Sez. di Trieste, I-34127 Trieste, Italy
139
Gemini Observatory/NSF NOIRLab, 670 N. A’ohōkū Place, Hilo, HI 96720, USA
140
Frankfurt Institute for Advanced Studies, Ruth-Moufang-Strasse 1, D-60438 Frankfurt, Germany
141
School of Mathematics, Trinity College, Dublin 2, Ireland
142
Department of Physics, University of Toronto, 60 St. George Street, Toronto, ON M5S 1A7, Canada
143
Department of Physics, Tokyo Institute of Technology, 2-12-1 Ookayama, Meguro-ku, Tokyo 152-8551, Japan
144
Hiroshima Astrophysical Science Center, Hiroshima University, 1-3-1 Kagamiyama, Higashi-Hiroshima, Hiroshima 739-8526, Japan
145
Aalto University Department of Electronics and Nanoengineering, PL 15500, FI-00076 Aalto, Finland
146
Institut de Radioastronomie Millimétrique (IRAM), 300 rue de la Piscine, F-38406 Saint Martin d’Hères, France
147
Jeremiah Horrocks Institute, University of Central Lancashire, Preston PR1 2HE, UK
148
National Biomedical Imaging Center, Peking University, Beijing 100871, PR China
149
College of Future Technology, Peking University, Beijing 100871, PR China
150
Tokyo Electron Technology Solutions Limited, 52 Matsunagane, Iwayado, Esashi, Oshu, Iwate 023-1101, Japan
151
Department of Physics and Astronomy, University of Lethbridge, Lethbridge, Alberta T1K 3M4, Canada
152
Netherlands Organisation for Scientific Research (NWO), Postbus 93138, 2509 AC Den Haag, The Netherlands
153
Frontier Research Institute for Interdisciplinary Sciences, Tohoku University, Sendai 980-8578, Japan
154
Astronomical Institute, Tohoku University, Sendai 980-8578, Japan
155
Department of Physics and Astronomy, Seoul National University, Gwanak-gu, Seoul 08826, Republic of Korea
156
University of New Mexico, Department of Physics and Astronomy, Albuquerque, NM 87131, USA
157
Physics Department, Brandeis University, 415 South Street, Waltham, MA 02453, USA
158
Radboud Excellence Fellow of Radboud University, Nijmegen, The Netherlands
159
School of Natural Sciences, Institute for Advanced Study, 1 Einstein Drive, Princeton, NJ 08540, USA
160
School of Physics, Huazhong University of Science and Technology, Wuhan, Hubei 430074, PR China
161
Mullard Space Science Laboratory, University College London, Holmbury St. Mary, Dorking, Surrey RH5 6NT, UK
162
Center for Astronomy and Astrophysics and Department of Physics, Fudan University, Shanghai 200438, PR China
163
Astronomy Department, University of Science and Technology of China, Hefei 230026, PR China
164
Department of Physics and Astronomy, Michigan State University, 567 Wilson Rd, East Lansing, MI 48824, USA
⋆ Corresponding author: astrorohandahale@gmail.com
Received:
21
April
2025
Accepted:
14
May
2025
We investigate the origin of the elliptical ring structure observed in the images of the supermassive black hole M87*, aiming to disentangle contributions from gravitational, astrophysical, and imaging effects. Leveraging the enhanced capabilities of the Event Horizon Telescope (EHT)'s 2018 array, including improved (u,v)-coverage from the Greenland Telescope, we measured the ring's ellipticity using five independent imaging methods, obtaining a consistent average value of τ = 0.08−0.02+0.03 with a position angle of ξ = 50.1−7.6+6.2 degrees. To interpret this measurement, we compared it to general relativistic magnetohydrodynamic (GRMHD) simulations spanning a wide range of physical parameters including the thermal or nonthermal electron distribution function, spins, and ion-to-electron temperature ratios in both low- and high-density regions. We find no statistically significant correlation between spin and ellipticity in GRMHD images. Instead, we identify a correlation between ellipticity and the fraction of non-ring emission, particularly in nonthermal models and models with higher jet emission. These results indicate that the ellipticity measured from the M87* emission structure is consistent with that expected from simulations of turbulent accretion flows around black holes, where it is dominated by astrophysical effects rather than gravitational ones. Future high-resolution imaging, including space very long baseline interferometry and long-term monitoring, will be essential to isolate gravitational signatures from astrophysical effects.
Key words: accretion, accretion disks / black hole physics / gravitation / galaxies: active
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The Event Horizon Telescope (EHT) collaboration published the first image of a black hole shadow of the supermassive black hole (SMBH) at the center of the giant elliptical galaxy M87, featuring a distinctive ring-like structure (Event Horizon Telescope Collaboration 2019a, b, c, d, e, f). In the context of general relativity (GR), the standard usage of the term “black hole shadow” is defined as the appearance of a black hole illuminated from all directions, including from behind the observer (e.g., Falcke et al. 2000), corresponding to the interior of the so-called critical curve formed by photon trajectories asymptotically approaching bound photon orbits (Gralla et al. 2019). The ring-like structure in EHT images is primarily a “direct image” (n=0 emission, where n is the number of half-orbits) that consists of photons from the accretion flow that are strongly lensed by the black hole's gravity but complete zero half-orbits around it before reaching the observer (e.g., Gralla et al. 2019; Johnson et al. 2020). The “photon ring” is an infinite series of self-similar subrings of light from photons that complete one or more half-orbits (n≥1) around the black hole before reaching the observer (Johnson et al. 2020). GR predicts that the critical curve is nearly circular for low inclination angles, such as the ∼17° inclination estimated for the M87 black hole, M87* (Mertens et al. 2016). Because the black hole spin introduces asymmetry in the shape of the critical curve, if the EHT can provide observational access to the critical curve then the measurement of its shape is a pathway to spin measurement. In this paper, we use “gravitational ellipticity” to refer to the shape distortion of the critical curve. For M87*, spin-induced shadow ellipticity is expected to reach up to ∼0.02 for a spin parameter a∼0.94 and inclination i=17° (e.g., Fig. 7, Johnson et al. 2020). Moreover, gravitational effects such as the displacement of the inner shadow relative to the photon ring, which are dependent on black hole spin and inclination, can also contribute to observed asymmetries (e.g., Gralla et al. 2019; Chael et al. 2021). Some exotic spacetimes could produce even larger distortions (e.g., Johannsen-Psaltis Metric in Fig. 5 of Younsi et al. 2023).
However, very long baseline interferometry (VLBI) observations do not directly resolve the shadow itself, but rather an observed emission structure that appears ring-like due to synchrotron radiation from plasma near the photon orbit (e.g., Event Horizon Telescope Collaboration 2019e, hereafter M87* 2017 V). This observed shape, which we refer to as the “emission ellipticity”, can deviate from circularity due to asymmetric plasma distributions. For instance, emission from turbulent flows can introduce ring ellipticity (e.g., Tiede et al. 2022a; Tiede & Broderick 2024). Finally, we note that limited (u,v)-coverage, noise, and algorithmic choices can introduce asymmetries or artifacts in the reconstructed image, even if the source is circular. In this study, we aim to disentangle the contributions to ellipticity by systematically comparing these two sources: gravitational ellipticity and emission ellipticity. Our goal is to assess the degree to which the observed ellipticity in M87* EHT images is a result of fundamental spacetime properties, astrophysical factors, or artifacts introduced by imaging algorithms.
In the EHT 2017 results of M87*, the observed ring-like structure appeared with approximately zero ellipticity, with a diameter of 42±3 μas. While ellipticity was measured in the reconstructed images (∼0.05−0.06), no interpretation or calibration was performed (see Figure 18 in Event Horizon Telescope Collaboration 2019f). A subsequent analysis by Tiede et al. (2022a) demonstrated that images reconstructed using the best set of imaging parameter combinations, the so-called Top Set of eht-imaging, could not reliably recover ellipticity, often favoring circular rings and yielding an upper limit of ellipticity of ∼0.3. This limitation was primarily due to sparse (u,v)-coverage, particularly in the north-south direction, as well as the Top Set imaging parameter combinations that were not fully optimized for elliptical models. Later, Tiede & Broderick (2024) reported an M87* ring ellipticity of 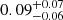 using THEMIS, a Bayesian imaging approach that was consistent with general relativistic magnetohydrodynamic (GRMHD) simulations. These results raised important questions about the origins of the ellipticity in the M87* images and the effectiveness of different imaging methods in accurately recovering it.
using THEMIS, a Bayesian imaging approach that was consistent with general relativistic magnetohydrodynamic (GRMHD) simulations. These results raised important questions about the origins of the ellipticity in the M87* images and the effectiveness of different imaging methods in accurately recovering it.
The 2018 observations confirmed the persistent structure of the M87* black hole shadow with a consistent ring diameter of 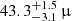 as, consistent with the 2017 results Event Horizon Telescope Collaboration (2024, hereafter M87* 2018 I). However, annual changes in brightness asymmetry were observed with the position angle shifting from about 180° in 2017 to 210° in 2018 which may be attributed to turbulence in the accretion flow. Changes in the brightness asymmetry were previously reported by Wielgus et al. (2020). The addition of the Greenland Telescope (GLT; Inoue et al. 2014) in 2018 substantially improved (u,v)-coverage (Fig. 1), particularly in the north-south direction, leading to improved image fidelity. We note that the EHT 2018 observations included four frequency bands: two at lower frequencies (band 1 and 2 at 213.1 GHz and 215.1 GHz) and two at higher frequencies (band 3 and 4 at 227.1 GHz and 229.1 GHz). The GLT participated only in bands 3 and 4, so we focused on data from the higher frequency bands in this study. Among the four observing days, we used data from April 21, which had the highest number of participating stations.
as, consistent with the 2017 results Event Horizon Telescope Collaboration (2024, hereafter M87* 2018 I). However, annual changes in brightness asymmetry were observed with the position angle shifting from about 180° in 2017 to 210° in 2018 which may be attributed to turbulence in the accretion flow. Changes in the brightness asymmetry were previously reported by Wielgus et al. (2020). The addition of the Greenland Telescope (GLT; Inoue et al. 2014) in 2018 substantially improved (u,v)-coverage (Fig. 1), particularly in the north-south direction, leading to improved image fidelity. We note that the EHT 2018 observations included four frequency bands: two at lower frequencies (band 1 and 2 at 213.1 GHz and 215.1 GHz) and two at higher frequencies (band 3 and 4 at 227.1 GHz and 229.1 GHz). The GLT participated only in bands 3 and 4, so we focused on data from the higher frequency bands in this study. Among the four observing days, we used data from April 21, which had the highest number of participating stations.
 |
Fig. 1. EHT 2017 and 2018 (u,v)-coverage. The plot shows observations from April 10, 2017 (gray) and April 21, 2018 (blue and orange). Both are at 229.1 GHz, which corresponds to the hi-band and band 4 in EHT 2017 and 2018, respectively. Orange points highlight the GLT baselines. Red circles show the coverage gaps in 2017, and dashed circles mark the 25 and 50 μas resolution. |
In this study, we followed the formalism based on Tiede & Broderick (2024) to measure the ellipticity of the ring-like emission structure in M87* using the 2018 EHT observations. We begin by evaluating the precision of ellipticity measurements using a Fisher information analysis in Sect. 2. Next, in Sect. 3, we refine the Top Set imaging parameter combinations for the regularized maximum likelihood (RML) and deconvolution imaging methods from M87* 2018 I using elliptical crescent models. Additionally, we tested a broader range of elliptical crescent models with various ellipticities and ellipticity position angles to assess any biases in the imaging methods using the data with the new 2018 (u,v)-coverage. In Sect. 4, we apply the same imaging pipelines (and parameter combinations) to the EHT 2018 M87* data to measure the ellipticity of the M87* emission ring. We then compare these results with those obtained from GRMHD model reconstructions. Finally, in Sect. 5, we investigate the origin of the observed ellipticity by comparing our results with theoretical models; we provide a summary and conclusions in Sect. 6.
2. Fisher information analysis
The Fisher information matrix quantifies the amount of information that observed data carry about certain model parameters θ. The Fisher information matrix is given by
where ℒ(θ) is the likelihood function of the data conditioned on the parameters θ. The terms θi and θj are elements of the parameter vector θ. The expectation 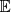 is taken with respect to the probability distribution of the data. For independent Gaussian-distributed data with variance σ2, the Fisher matrix simplifies to
is taken with respect to the probability distribution of the data. For independent Gaussian-distributed data with variance σ2, the Fisher matrix simplifies to
where Vk represents the observed complex visibilities. The inverse of the Fisher information matrix gives the covariance matrix of the parameter estimates. Hence, Σ=F−1, where Σij represents the covariance between parameters θi and θj. We assumed a Gaussian posterior distribution for the parameters, where the standard deviations are given by the square root of the diagonal elements of the covariance matrix,
which represents the uncertainty in the estimation of each parameter θi.
Given the improved EHT array in 2018, as shown in Fig. 1, we estimated the precision with which the EHT can measure ellipticity using Fisher information analysis.
For this analysis, we used an extension of the m-ring model from Johnson et al. (2020). This model has a simple analytic form in both the image and visibility domains, with analytic gradients. This model was also used for the feature extraction done in Event Horizon Telescope Collaboration (2019d, hereafter M87* 2017 IV) and M87∗ 2018 I, making it useful for physical interpretation. The m-ring model consists of a thin ring with nonuniform brightness in azimuthal directions given by a Fourier series. In polar coordinates (ρ,φ), it is defined as
where S is the total flux density of the ring, d is the diameter of the ring, δ is the Dirac delta function. The coefficients satisfy 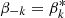 for a real image, and we set β0=1 to ensure that S>0. The parameter m represents the azimuthal order of the m-ring. A finite-width m-ring is obtained by convolving Eq. (4) with a Gaussian of FWHM α. This blurred m-ring is given by
for a real image, and we set β0=1 to ensure that S>0. The parameter m represents the azimuthal order of the m-ring. A finite-width m-ring is obtained by convolving Eq. (4) with a Gaussian of FWHM α. This blurred m-ring is given by
where Ik denotes the k-th modified Bessel function of the first kind (Roelofs et al. 2023). A stretched m-ring with ellipticity τ, rotated by an ellipticity position angle ξ and width α is given by ℐ(1−τcos(2(φ−ξ))ρ,φ;α).
We used a first-order (i.e., m=1) stretched m-ring model as shown in Fig. 2, as it is the simplest case (e.g., Tiede et al. 2022a; Tiede & Broderick 2024). The ellipticity parameter τ is defined as τ=1−b/a, where a and b are the major and minor axes of the ellipse, respectively. The ellipticity position angle ξ represents the angle of the major axis a, measured counterclockwise from the north (east of north), as shown in Fig. 2. For this analysis, we kept the brightness position angle (PA), η, aligned with the ellipticity PA, ξ. Hence, we define ξ over the full range of 0 to 360°. We estimate the precision with which the parameters of this model, fit to data on April 21, 2018 at band 4, can be recovered. We employed the above Fisher information approach implemented within the ngEHTforecast package1. This method does not explicitly fit the m-ring model to the data. Instead, it performs a second-order expansion of the logarithmic probability density around the best-fit location, providing an estimate of the uncertainty of each of fitted parameter. The parameter precision estimates assume that the fitting process utilizes complex visibilities as input data, with broad priors imposed on the station gain amplitudes and phases for each scan (Pesce et al. 2022).
 |
Fig. 2. Definition of parameters τ, ξ for m-ring model, along with respective marginalized uncertainties using Fisher information analysis. Left: A visualization of a stretched m-ring model with parameters τ=0.1, ξ=45°, a brightness asymmetry of 0.23, and a diameter of d=46 μas, blurred with a Gaussian kernel with a full width at half maximum of 10 μas. The brightness position angle, η=45°, is aligned with ξ. Right: Maps of marginalized uncertainties in the parameters τ (top row) and ξ (bottom row) for m-ring models with various values of τ and ξ, derived using Fisher information analysis on M87* band 4 data. |
For this analysis, we tested m-ring models with τ ranging from 0 to 0.3 and ξ ranging from 0 to 360°. The diameter of the thin elliptical m-rings is 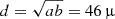 as, which is then blurred by a 10 μas circular Gaussian (Tiede et al. 2022a). We assume a brightness asymmetry β1=0.23 for the m-ring (see Table 7 in M87∗ 2018 I). Figure 2 shows the marginalized uncertainties στ and σξ, calculated using Eq. (3), for the parameters τ and ξ, respectively. We computed στ and σξ for data with and without GLT to assess its relevance in (u,v)-coverage. As seen in Fig. 2, στ and σξ are approximately three to five times larger for the data without GLT. This demonstrates that the additional (u,v)-coverage provided by GLT baselines enhances the precision in constraining τ and ξ. Furthermore, στ and σξ are nearly three times larger for the models with north-south alignment (i.e., ξ=0° or 180°). For models with the same ξ but different τ, στ and σξ remain approximately constant. During the 2017 and 2018 EHT campaigns, the James Clerk Maxwell Telescope (JCMT) only recorded a single polarization feed, which could have contributed to systematic polarization leakage in 2018. To evaluate this issue, we performed a similar analysis for data without JCMT. As shown in Fig. 2, removing JCMT has a minimal effect (<10%) on the marginalized uncertainties of τ and ξ. Therefore, JCMT data are retained for the remainder of the analysis.
as, which is then blurred by a 10 μas circular Gaussian (Tiede et al. 2022a). We assume a brightness asymmetry β1=0.23 for the m-ring (see Table 7 in M87∗ 2018 I). Figure 2 shows the marginalized uncertainties στ and σξ, calculated using Eq. (3), for the parameters τ and ξ, respectively. We computed στ and σξ for data with and without GLT to assess its relevance in (u,v)-coverage. As seen in Fig. 2, στ and σξ are approximately three to five times larger for the data without GLT. This demonstrates that the additional (u,v)-coverage provided by GLT baselines enhances the precision in constraining τ and ξ. Furthermore, στ and σξ are nearly three times larger for the models with north-south alignment (i.e., ξ=0° or 180°). For models with the same ξ but different τ, στ and σξ remain approximately constant. During the 2017 and 2018 EHT campaigns, the James Clerk Maxwell Telescope (JCMT) only recorded a single polarization feed, which could have contributed to systematic polarization leakage in 2018. To evaluate this issue, we performed a similar analysis for data without JCMT. As shown in Fig. 2, removing JCMT has a minimal effect (<10%) on the marginalized uncertainties of τ and ξ. Therefore, JCMT data are retained for the remainder of the analysis.
3. Geometric tests
Before analyzing the M87* data, two sets of tests with geometric models were conducted to evaluate the accuracy of the imaging and feature extraction methods in recovering the true values and assessing potential biases in the imaging methods. We used geometric models with various ellipticity, τ, and the position angle of the ellipse's major axis, ξ (north to east), to check potential biases depending on (u,v)-coverage. The first test selects the Top Set imaging parameter combinations of the RML and CLEAN methods using four elliptical crescent models (m=1) of τ=0.187 and ξ=[0°,45°,90°,315°]. The values of τ and ξ are chosen to be consistent with Tiede et al. (2022a). The second test evaluates the ellipticity feature extraction using 42 elliptical crescent models (m=1) with τ=[0.0,0.05,0.1,0.15,0.2,0.25,0.3] and ξ=[0°,60°,120°,180°,240°,300°]. We used eht-imaging to generate synthetic data using the geometric models listed above. Before generating the synthetic data, we also added a milliarcsec-scale Gaussian to these geometric models. This Gaussian mimics jet emission on scales of milliarcseconds to arcseconds, to which short intra-site baselines of the EHT are sensitive (M87∗ 2017 IV). We added station gain corruptions derived from M87* and thermal noise to mimic the real observational data (M87∗ 2018 I). Synthetic data with random gain corruptions are also tested using Bayesian imaging, where the posterior distribution of the gain parameters is estimated.
Imaging was performed using both forward and inverse modeling techniques. The forward modeling consists of RML and Bayesian methods, while the inverse modeling employs a CLEAN-based deconvolution method. For RML imaging, we used eht-imaging (Chael et al. 2016, 2018, 2019) and SMILI (Akiyama et al. 2017a, b, 2019). For Bayesian imaging, we used Comrade (Tiede 2022) and THEMIS (Broderick et al. 2020a, b). For CLEAN-based deconvolution, we used DIFMAP (Shepherd 1997, 2011). A more detailed explanation of each imaging method is provided in M87∗ 2017 IV and M87∗ 2018 I (see Appendix A for updates to the Bayesian imaging methods). We note that while M87∗ 2018 I has employed both imaging methods and visibility domain model fitting, we focused on the imaging methods in this study.
3.1. Imaging parameter selection with the elliptical crescent models
The dataset for the first test is used to sub-select the Top Set imaging parameter combinations for the RML and CLEAN methods. Bayesian methods do not require a parameter survey, and thus the geometric models used in this step were not tested. Imaging results from the RML and CLEAN methods depend on a set of parameters determined by various imaging assumptions, including hyperparameters and optimization choices. Each combination of parameters can yield slightly different image morphology and fit quality for the data. Therefore, it is necessary to survey different parameter combinations and select those that provide the best fit to the data and most closely reproduce the groundtruth image (if from synthetic data), referred to as the Top Set. For eht-imaging, SMILI, and DIFMAP, the Top Set was previously selected in M87∗ 2018 I based on four geometric models (cres180, dblsrc, disk, ring), using data from M87*. The number of Top Set parameter combinations varies across methods due to differences in their parameter space. Additionally, variations between bands arise from different (systematic) uncertainties inherent to each dataset (see M87∗ 2018 I). However, we did not test whether the Top Set parameters are valid for different elliptical structures. To investigate this, we selected a new Top Set by imaging four additional geometric models of elliptical crescents: ecres000, ecres045, ecres090, and ecres315 (Fig. 3, top). The imaging survey is performed over the original Top Set from M87∗ 2018 I, meaning the new Top Set corresponds to a subset of the original.
 |
Fig. 3. Elliptical crescent models with different ellipse position angles. From left to right, ecres000, ecres045, ecres090, and ecres315. From top to bottom, groundtruth images and fiducial images from eht-imaging, SMILI, and DIFMAP for band 4. DIFMAP images are presented with a beam convolution of a 20 μas circular Gaussian (M87∗ 2018 I). |
The Top Set selection is based on two metrics: (i) the normalized cross-correlation (ρNX) between the reconstructed and groundtruth images for synthetic data and (ii) the reduced χ2 on the real M87* data. Since the latter was already satisfied in the original Top Set (i.e., χ2<2), the new Top Set is selected based solely on the ρNX of the elliptical crescent geometric models. The ρNX cutoff was determined in the same manner as described in M87∗ 2017 IV and M87∗ 2018 I, by convolving the groundtruth image with the effective resolution from the longest baseline (∼24 μas; see Fig. 1). Then, the cutoff value was determined as 0.75 for both band 3 and band 4, with no variations across the models.
As a result, several parameter combinations passed the thresholds, demonstrating their ability to reconstruct the elliptical crescent structure while distinguishing the structural position angle. Table 1 summarizes the number of new Top Set parameter combinations for each pipeline and band compared to the original Top Set. The images reconstructed using the fiducial parameters are shown in Fig. 3.
Number of new Top Set parameter combinations.
3.2. Evaluation with the elliptical crescent models
After selecting the new Top Set parameters for the RML (eht-imaging and SMILI) and CLEAN (DIFMAP) methods, we performed additional imaging of the geometric models using all methods for performance evaluation. The Bayesian methods, THEMIS and Comrade, do not require a Top Set selection since their only hyperparameters are the field of view and the number of pixels. Therefore, we directly performed the geometric tests with these two methods. For these models, ξ coincides with the position angle of the brightest spot (see Appendix B for tests with different alignments). This approach aims to identify specific cases where ellipticity or position angle models are not well recovered due to (u,v)-coverage limitations. To measure ellipticity and the ellipticity position angle, we used a stretched m-ring template from VIDA (Tiede et al. 2022b). For all feature extraction in this work, we used a m-ring of order four in azimuth and order one in width, following Tiede et al. (2022a).
Figure 4 presents a subset of the measured τ−ξ distributions from the respective geometric model reconstructions for different imaging pipelines. The results indicate that ξ is less constrained at 0° and 180° due to relatively poorer (u,v) coverage in these directions, as expected from the Fisher information analysis (Sect. 2). The measured ellipticity is still influenced by the underlying angular resolution. For instance, convolving the images and models with a 5 μas circular Gaussian reduces the ellipticity measurement of 0.1 by ∼3% (see Appendix C for more discussions about the resolution effect on measured ring features). In our results, the resolution limit of DIFMAP is given as ∼20 μas (M87∗ 2018 I), while the forward modeling results from RML methods including Bayesian approaches can achieve super-resolution. Therefore, measured ellipticities from reconstructed images that are up to ∼30% lower than the true value are considered acceptable (gray shaded, vertical area in Fig. 4; see also Fig. C.1). As a result, all imaging methods successfully recovered the true τ and ξ values within their own resolution limit. However, it is worth noting that, ignoring the resolution effects, the RML and deconvolution imaging methods tend to underestimate the ellipticity for models with extreme ellipticities in all 42 tests.
 |
Fig. 4. Subset ellipticity measurements for geometric models (6 out of 42) for all imaging methods. From left to right: groundtruth image of a given geometric model, τ−ξ distribution using Comrade, THEMIS, eht-imaging, SMILI, and DIFMAP for band 4 synthetic data. Each row corresponds to a different geometric model, with the true model shown in the leftmost column. The vertical and horizontal dashed lines in each panel of τ−ξ distribution indicate the true values. The contours denote 68% and 95% confidence intervals. The vertical dashed line shows τ measured with VIDA for the groundtruth model. The gray shaded region spans the range of τ values for the groundtruth model, from the unconvolved case to the convolution of a circular Gaussian of 20 μas FWHM. |
4. Ring ellipticity of M87* and its comparison with GRMHD simulation snapshots
4.1. Ring ellipticity of M87*
Following the geometric tests that validated the imaging pipelines and their parameter combinations for ellipticity measurement, they were applied to the M87* data2 (see Fig. 5). The imaging results correspond to a subset of images in M87∗ 2018 I for RML and CLEAN methods (Table 1), while remaining consistent for Bayesian methods. Ring features were extracted from the images using VIDA3, as summarized in Table 2. The measured ellipticities are consistent across all imaging approaches and at both frequency bands, 3 and 4, yielding an average ellipticity of 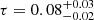 . The average position angle of the ellipse is
. The average position angle of the ellipse is 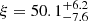 degrees, consistent across different imaging methods within 2σ. The average across all methods and bands is computed by taking weighted median and 1σ error. Given the relatively better performance of Bayesian imaging methods, as described in Sect. 3 and shown in Fig. 4, we computed the average
degrees, consistent across different imaging methods within 2σ. The average across all methods and bands is computed by taking weighted median and 1σ error. Given the relatively better performance of Bayesian imaging methods, as described in Sect. 3 and shown in Fig. 4, we computed the average 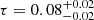 and
and 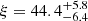 only from these methods. These averages are in good agreement with the values obtained by averaging over all methods. Notably, the direction of ξ is approximately aligned with the angle of brightest spot on the ring, ∼200−230° (M87∗ 2018 I).
only from these methods. These averages are in good agreement with the values obtained by averaging over all methods. Notably, the direction of ξ is approximately aligned with the angle of brightest spot on the ring, ∼200−230° (M87∗ 2018 I).
 |
Fig. 5. EHT 2018 M87* images and ellipticity (τ) and ellipticity position angle (ξ) distributions. (left to right) Images from each imaging method (Comrade, THEMIS, eht-imaging, SMILI, and DIFMAP). For Comrade and THEMIS, mean posterior images are shown. Fiducial images from the respective Top Sets are shown for the other methods. The two right panels show the distributions of τ and ξ for each method. Top and bottom rows show results for band 3 and band 4, respectively. Colors correspond to each method (see legend). |
Measured ellipticity and position angle for EHT 2018 M87*images.
The measured τ is also consistent with results of Tiede et al. (2022a), which reported τ=0−0.3 and inferred accretion turbulence as the dominant source of the measured ellipticity, and with those of Tiede & Broderick (2024) which reported 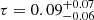 . We note that while this work used 2018 EHT observations, the above comparisons are made with the works that used 2017 EHT observations. The uncertainties in our results are lesser than those of previous studies from the 2017 EHT data, owing to the improved (u,v)-coverage in the 2018 EHT.
. We note that while this work used 2018 EHT observations, the above comparisons are made with the works that used 2017 EHT observations. The uncertainties in our results are lesser than those of previous studies from the 2017 EHT data, owing to the improved (u,v)-coverage in the 2018 EHT.
4.2. Comparison with GRMHD simulations
With the results, we applied the same imaging and feature extraction methods to GRMHD models with different physical parameters to investigate the underlying physical dependencies. For this purpose, we used two GRMHD libraries of KHARMA (Prather et al. 2021) and BHAC (Porth et al. 2017). Thermal electron distribution (Maxwell-Jüttner distribution) models were drawn from KHARMA, while nonthermal electron distribution (kappa distribution) models were sourced from BHAC (Fromm et al. 2022; Cruz-Osorio et al. 2022). Out of the 299 GRMHD models that were considered in M87∗ 2018 II, we selected 218 models with an outflow power exceeding 1042 erg/s (M87∗ 2017 I, M87∗ 2017 V, M87∗ 2018 II). After the outflow threshold was applied, we selected 100 models for imaging and feature extraction, of which roughly 75% were thermal models and the remainder nonthermal. There were 18 models for each spin value of −0.94, −0.5, +0.5, and +0.94 from the KHARMA thermal models, resulting in 72 thermal models in total. The remaining 28 models were chosen from the BHAC nonthermal models that met the threshold; we selected seven models for each spin. Since black hole spin and inclination determine a displacement of the inner shadow that can manifest as non-circularity (e.g., Tiede et al. 2022a), this sample can investigate the potential correlation between spin and ellipticity. Among the 100 selected GRMHD models, 83 are strongly magnetized, magnetically arrested disk (MAD) models, and 17 are weakly magnetized standard and normal evolution (SANE) models. Random snapshots were taken from each model and scaled to the best-fit mass based on snapshot scoring implemented in M87∗ 2018 II. The scaling factor is a ratio of observed-to-simulated mass-to-distance ratios.
The scaled snapshots were then used to generate synthetic data following the same procedure described in Sect. 3. The synthetic data were imaged using eht-imaging and Comrade, as representatives of RML and Bayesian methods, respectively. As presented in Fig. 6, the images were consistent with the groundtruth. We then extracted the ellipticities from these images using VIDA and compared them with the true ellipticity. The groundtruth GRMHD snapshot images were convolved with a 12 μas circular Gaussian to take resolution effect into account. The 12 μas size corresponds to the obtained super-resolution from Comrade and eht-imaging, which is estimated by comparing ρNX of the original and blurred groundtruth images with different sizes of circular Gaussian kernel. This is an average from results for all 100 GRMHD models and is consistent between Comrade and eht-imaging. Figure 7 shows the differences of τ and ξ between reconstructed images (from eht-imaging and Comrade) and the true values that are centered at zero in both parameters. This suggests that the observed ellipticity and its angle are real and not an artifact of the imaging process or instrumental limitations. The broader spread in ξ is due to models with low ellipticity, where the orientation angle is naturally more difficult to constrain.
 |
Fig. 6. Subset of GRMHD images (10 out of 100 models) from KHARMA and BHAC libraries: (from top to bottom) ground truth, reconstructed images by Comrade (mean image) and eht-imaging (one random from Top Set) for band 4. Thermal models from KHARMA are marked in orange and nonthermal models are marked in blue. The ground truths are shown after blurring with a 12 μas circular Gaussian. |
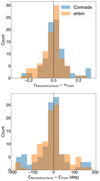 |
Fig. 7. Histograms of differences in τ (top) and ξ (bottom) between reconstructed and true GRMHD values. Results from Comrade (blue) and eht-imaging (orange) are shown, both centered around zero for each parameter. |
5. Origin of the M87* ring ellipticity
As introduced in Sect. 1, observed ellipticity in EHT images can arise from two main sources: (i) gravitational ellipticity due to spacetime curvature and (ii) emission ellipticity from astrophysical structure. In this section, we focus on disentangling the contributions using GRMHD simulations with varying physical parameters. We utilized all 299 GRMHD models described in Sect. 4.2, which span a wide range of parameters, including black hole spin, electron distribution function (eDF) (thermal and nonthermal), magnetic field states (SANE and MAD), and ion-to-electron temperature ratios in both low- and high-density regions (Rlow and Rhigh, respectively; see Mościbrodzka et al. 2016 for definitions). For each model, we measured the image ellipticity from the corresponding groundtruth GRMHD snapshot, scaled to the best-fit mass and blurred with a 12 μas Gaussian, as described in Sect. 4.2. Figure 8 shows that the observed M87* ellipticity is consistent with the distribution of all 299 GRMHD models, falling within their median and 68% confidence intervals.
 |
Fig. 8. Ellipticity of truth GRMHD models (blurred with 12 μas Gaussian) for different GRMHD parameters. All 299 models are shown in blue, and the models that pass the jet power criteria are shown in orange (note that while plotting we combined the nonthermal models with the same parameters but different nonthermal emission fraction (ϵ)). The over-plotting on the histograms shows the median value and the 68% confidence interval. The ellipticity of M87 is shown as a dashed green line, with its error range shown in the shaded green region. In the top rightmost panel, the ellipticity of the critical curve for a Kerr black hole (see Figure 7, Johnson et al. 2020) for different spins (inclination = 17°) is plotted to compare it with the histograms of the respective spins. The spin = 0.5 case is shown by dashed black line; the spin = +0.94 is represented by a solid black line and the spin = +0.999 case is given by a dotted black line. |
General relativistic magnetohydrodynamic simulations are uniquely suited to probing both gravitational ellipticity and emission ellipticity. The gravitational ellipticity arises from the curvature of spacetime near the event horizon and is directly influenced by black hole spin. For instance, a Kerr black hole with spin of a=0.94−0.999 and viewed at an inclination of 17° can produce a gravitational ellipticity of ∼0.02 (see Fig. 8, top right). This level of distortion cannot explain the measured ellipticity of M87*. Even if we consider a 3° uncertainty (Mertens et al. 2016) on the inclination of M87*, with 20° inclination and spin a=0.999, the maximum ellipticity reaches only ∼0.03 (Johnson et al. 2020). Moreover, as shown in Table 3 and Fig. 8, there is no statistically significant correlation between the spin and the measured ellipticity in full GRMHD images. This indicates that while spin contributes to the gravitational ellipticity, it does not dominate the total observed ellipticity in the images. Table 3 also shows no significant correlation between ellipticity and magnetic field state (SANE and MAD), implying that the global magnetic field structure does not have a strong influence on ellipticity. In contrast, Fig. 8 and Table 3 suggest that nonthermal models and simulations with higher values of Rhigh are correlated with larger emission ellipticity. Nonthermal models tend to generate more extended or diffuse emission, and increasing Rhigh shifts emission from the disk to the jet region; both effects increase the ellipticity of the ring in the image.
Spearman correlation for ellipticity of GRMHD truth models and their physical parameters.
To quantify the role of asymmetric non-ring emission, we defined a “non-ring flux fraction” by subtracting the best-fit circular Gaussian ring (using VIDA) from each GRMHD image and setting negative residuals to zero. The ratio of the remaining positive flux to the total flux defines the non-ring flux fraction. We computed Spearman correlation coefficients between this quantity and the measured image ellipticity, using a bootstrapping method to account for sample variance (e.g., Curran 2014; Cheng et al. 2023). Figure 9 reveals a positive correlation between the non-ring flux fraction and ellipticity. We note that upon visual inspection, it does not seem that the outliers appear from transient flux eruption events. This supports the conclusion that emission ellipticity, driven by turbulent accretion structures outside the ring, is the dominant contributor to ellipticity in GRMHD images. These results suggest that the observed ellipticity in the M87* image is naturally explained by emission ellipticity arising from astrophysical effects such as turbulent accretion flow.
 |
Fig. 9. Ellipticity of all 299 GRMHD truths (convolved with 12 μas Gaussian) compared with the non-ring flux fraction. The left and right panels are the same, but the colors are different for (non)thermal models (left) and Rhigh values (right). The ellipticity of M87 is shown by a dashed black line, with its error range shown in the shaded gray region. The median τ for each case is shown in the legend. |
6. Summary and conclusions
In this study, we measured the ellipticity of the emission ring in the black hole images of M87* using the EHT 2018 observations. Fisher information analysis was employed to first assess the feasibility of ellipticity measurements, after the addition of the GLT, which filled gaps in the north-south (u,v)-coverage. This analysis shows that the inclusion of the GLT improves the precision in constraining ellipticity parameters by ∼3−5 times. With the improved (u,v)-coverage compared to the EHT 2017, we then managed to extract the ellipticity successfully from five different methods that cross-compare the results. This is the first method-wide confirmation of the ellipticity measurement.
For imaging with the RML and deconvolution methods, the imaging parameter combinations were sub-selected from the original ones in M87∗ 2018 I, based on imaging results for four elliptical geometric models. This step is not required for Bayesian imaging methods such as Comrade and THEMIS. All imaging methods (and parameters) were then evaluated using various geometric elliptical ring models with differing position angles and ellipticities, and they successfully recovered the groundtruth values in most cases.
Applying these approaches to the M87 data, we measured the ellipticity to be 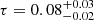 on average, with consistency across all imaging methods and previous findings from EHT 2017 (Tiede & Broderick 2024). In addition, the position angle of the ellipse is measured as
on average, with consistency across all imaging methods and previous findings from EHT 2017 (Tiede & Broderick 2024). In addition, the position angle of the ellipse is measured as 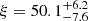 degrees, indicating that the ring structure is slightly elongated along an axis that is roughly aligned with the brightest spot on the ring, ∼200−230° (M87∗ 2018 I). We also note that while Kim et al. (2025) reported τ=0.06±0.04 for the image of M87 at 86 GHz, which is consistent with our measurements at 230 GHz, this is an astrophysical effect at 86 GHz. Comparison with GRMHD simulations first confirms that the measured ellipticity is real, but no strong constraints on the parameters including the spin are yet found. However, the parameters providing more non-ring flux (that is, nonthermal emission and higher Rhigh) tend to reproduce larger ellipticity. This is confirmed by comparison with the non-ring flux fraction to the measured ellipticity. In line with this, to explain the measured ellipticity of M87, the astrophysical effects such as turbulent accretion flow are required. It is worth noting that the additional non-circularity by the inclined black hole (e.g., tilted accretion disk) or exotic spacetime are not completely ruled out.
degrees, indicating that the ring structure is slightly elongated along an axis that is roughly aligned with the brightest spot on the ring, ∼200−230° (M87∗ 2018 I). We also note that while Kim et al. (2025) reported τ=0.06±0.04 for the image of M87 at 86 GHz, which is consistent with our measurements at 230 GHz, this is an astrophysical effect at 86 GHz. Comparison with GRMHD simulations first confirms that the measured ellipticity is real, but no strong constraints on the parameters including the spin are yet found. However, the parameters providing more non-ring flux (that is, nonthermal emission and higher Rhigh) tend to reproduce larger ellipticity. This is confirmed by comparison with the non-ring flux fraction to the measured ellipticity. In line with this, to explain the measured ellipticity of M87, the astrophysical effects such as turbulent accretion flow are required. It is worth noting that the additional non-circularity by the inclined black hole (e.g., tilted accretion disk) or exotic spacetime are not completely ruled out.
With the current ground-based array, our ability to precisely measure the ellipticity of the emission ring is constrained by the dominance of turbulent astrophysical effects associated with the direct image (Gralla & Lupsasca 2020; Johnson et al. 2020). In the case of M87*, detecting the gravitational influence on ellipticity, and hence measuring the spin, requires us to overcome these limitations through one of two approaches. The first approach involves continued long-term monitoring of M87*, allowing for temporal averaging of the turbulent effects, thereby enabling the underlying gravitational signature to emerge more clearly. For instance, in Fig. 10, we present the measured ellipticities of 1000 snapshots spanning ∼370 days for one of the GRMHD models, along with the ellipticity of the time-averaged image in the right panel. The average image clearly reveals the photon ring, while the turbulent accretion flow is averaged out. This example illustrates that future observations could detect ellipticity arising from gravitational effects, as highlighted by the red line in the left panel.
 |
Fig. 10. Ellipticities of 1000 snapshots spanning ∼370 days for a GRMHD model with the following parameters: magnetic field configuration = MAD; thermal eDF; black hole spin = −0.5; Rhigh=160, Rlow=1; and inclination angle = 17°. The ellipticity of each snapshot is measured after blurring with a 12 μas Gaussian (blue). The median and 68% confidence interval of the time series are shown with a solid green line and shaded region, respectively. The ellipticity of the time-averaged image (right) is shown with a red line. |
The second approach entails space VLBI observations, which would provide the necessary angular resolution to detect the photon ring (Gralla et al. 2019; Johnson et al. 2020). Unlike the direct image, the photon ring is expected to be less affected by astrophysical turbulence, making it a more direct probe of the underlying spacetime structure and gravitational effects near the black hole. We also note that the direct image is more elliptical than the photon ring (see Figure 6 in Gralla & Lupsasca 2020). To better distinguish the relative effects on the ellipticity from different potential origins, higher precision measurements of ellipticities from better angular resolution are necessary. Looking ahead, future observations with higher angular resolution, such as those from the next-generation EHT (ngEHT; Johnson et al. 2023; Doeleman et al. 2023), the Event Horizon Imager (EHI; Roelofs et al. 2019), the Terahertz Exploration and Zooming-in for Astrophysics (THEZA; Gurvits et al. 2022), and the Black Hole Explorer (BHEX; Johnson et al. 2024; Akiyama et al. 2024), will offer further constraints by resolving finer photon ring structures. As demonstrated by the addition of the GLT to the EHT array, the inclusion of future sites in the EHT and ngEHT arrays will improve the precision of measurements of the ring ellipticity of M87*.
Acknowledgments
R.D. acknowledges that the project that gave rise to these results received the support of a fellowship from “la Caixa” Foundation (ID 100010434), with the fellowship code LCF/BQ/DI22/11940030. I.C. is supported by the KASI-Yonsei Postdoctoral Fellowship. The Event Horizon Telescope Collaboration thanks the following organizations and programs: the Academia Sinica; the Academy of Finland (projects 274477, 284495, 312496, 315721); the Agencia Nacional de Investigación y Desarrollo (ANID), Chile via NCN19_058 (TITANs), Fondecyt 1221421 and BASAL FB210003; the Alexander von Humboldt Stiftung; an Alfred P. Sloan Research Fellowship; Allegro, the European ALMA Regional Centre node in the Netherlands, the NL astronomy research network NOVA and the astronomy institutes of the University of Amsterdam, Leiden University, and Radboud University; the ALMA North America Development Fund; the Astrophysics and High Energy Physics programme by MCIN (with funding from European Union NextGenerationEU, PRTR-C17I1); the Black Hole Initiative, which is funded by grants from the John Templeton Foundation (60477, 61497, 62286) and the Gordon and Betty Moore Foundation (Grant GBMF-8273) – although the opinions expressed in this work are those of the author and do not necessarily reflect the views of these Foundations; the Brinson Foundation; the Canada Research Chairs (CRC) program; Chandra DD7-18089X and TM6-17006X; the China Scholarship Council; the China Postdoctoral Science Foundation fellowships (2020M671266, 2022M712084); ANID through Fondecyt Postdoctorado (project 3250762); Conicyt through Fondecyt Postdoctorado (project 3220195); Consejo Nacional de Humanidades, Ciencia y Tecnología (CONAHCYT, Mexico, projects U0004-246083, U0004-259839, F0003-272050, M0037-279006, F0003-281692, 104497, 275201, 263356, CBF2023-2024-1102, 257435); the Colfuturo Scholarship; the Consejo Superior de Investigaciones Científicas (grant 2019AEP112); the Delaney Family via the Delaney Family John A. Wheeler Chair at Perimeter Institute; Dirección General de Asuntos del Personal Académico-Universidad Nacional Autónoma de México (DGAPA-UNAM, projects IN112820 and IN108324); the Dutch Research Council (NWO) for the VICI award (grant 639.043.513), the grant OCENW.KLEIN.113, and the Dutch Black Hole Consortium (with project No. NWA 1292.19.202) of the research programme the National Science Agenda; the Dutch National Supercomputers, Cartesius and Snellius (NWO grant 2021.013); the EACOA Fellowship awarded by the East Asia Core Observatories Association, which consists of the Academia Sinica Institute of Astronomy and Astrophysics, the National Astronomical Observatory of Japan, Center for Astronomical Mega-Science, Chinese Academy of Sciences, and the Korea Astronomy and Space Science Institute; the European Research Council (ERC) Synergy Grant “BlackHoleCam: Imaging the Event Horizon of Black Holes” (grant 610058) and Synergy Grant “BlackHolistic: Colour Movies of Black Holes: Understanding Black Hole Astrophysics from the Event Horizon to Galactic Scales” (grant 10107164); the European Union Horizon 2020 research and innovation programme under grant agreements RadioNet (No. 730562), M2FINDERS (No. 101018682) and FunFiCO (No. 777740); the European Research Council for advanced grant “JETSET: Launching, propagation and emission of relativistic jets from binary mergers and across mass scales” (grant No. 884631); the European Horizon Europe staff exchange (SE) programme HORIZON-MSCA-2021-SE-01 grant NewFunFiCO (No. 10108625); the Horizon ERC Grants 2021 programme under grant agreement No. 101040021; the FAPESP (Fundação de Amparo á Pesquisa do Estado de São Paulo) under grant 2021/01183-8; the Fondes de Recherche Nature et Technologies (FRQNT); the Fondo CAS-ANID folio CAS220010; the Generalitat Valenciana (grants APOSTD/2018/177 and ASFAE/2022/018) and GenT Program (project CIDEGENT/2018/021); the Gordon and Betty Moore Foundation (GBMF-3561, GBMF-5278, GBMF-10423); the Institute for Advanced Study; the ICSC – Centro Nazionale di Ricerca in High Performance Computing, Big Data and Quantum Computing, funded by European Union – NextGenerationEU; the Istituto Nazionale di Fisica Nucleare (INFN) sezione di Napoli, iniziative specifiche TEONGRAV; the International Max Planck Research School for Astronomy and Astrophysics at the Universities of Bonn and Cologne; the Italian Ministry of University and Research (MUR) – Project CUP F53D23001260001, funded by the European Union – NextGenerationEU; DFG research grant “Jet physics on horizon scales and beyond” (grant No. 443220636); Joint Columbia/Flatiron Postdoctoral Fellowship (research at the Flatiron Institute is supported by the Simons Foundation); the Japan Ministry of Education, Culture, Sports, Science and Technology (MEXT; grant JPMXP1020200109); the Japan Society for the Promotion of Science (JSPS) Grant-in-Aid for JSPS Research Fellowship (JP17J08829); the Joint Institute for Computational Fundamental Science, Japan; the Key Research Program of Frontier Sciences, Chinese Academy of Sciences (CAS, grants QYZDJ-SSW-SLH057, QYZDJSSW-SYS008, ZDBS-LY-SLH011); the Leverhulme Trust Early Career Research Fellowship; the Max-Planck-Gesellschaft (MPG); the Max Planck Partner Group of the MPG and the CAS; the MEXT/JSPS KAKENHI (grants 18KK0090, JP21H01137, JP18H03721, JP18K13594, 18K03709, JP19K14761, 18H01245, 25120007, 19H01943, 21H01137, 21H04488, 22H00157, 23K03453); the MICINN Research Projects PID2019-108995GB-C22, PID2022-140888NB-C22; the MIT International Science and Technology Initiatives (MISTI) Funds; the Ministry of Science and Technology (MOST) of Taiwan (103-2119-M-001-010-MY2, 105-2112-M-001-025-MY3, 105-2119-M-001-042, 106-2112-M-001-011, 106-2119-M-001-013, 106-2119-M-001-027, 106-2923-M-001-005, 107-2119-M-001-017, 107-2119-M-001-020, 107-2119-M-001-041, 107-2119-M-110-005, 107-2923-M-001-009, 108-2112-M-001-048, 108-2112-M-001-051, 108-2923-M-001-002, 109-2112-M-001-025, 109-2124-M-001-005, 109-2923-M-001-001, 110-2112-M-001-033, 110-2124-M-001-007 and 110-2923-M-001-001); the National Science and Technology Council (NSTC) of Taiwan (111-2124-M-001-005, 112-2124-M-001-014 and 112-2112-M-003-010-MY3); the Ministry of Education (MoE) of Taiwan Yushan Young Scholar Program; the Physics Division, National Center for Theoretical Sciences of Taiwan; the National Aeronautics and Space Administration (NASA, Fermi Guest Investigator grant 80NSSC23K1508, NASA Astrophysics Theory Program grant 80NSSC20K0527, NASA NuSTAR award 80NSSC20K0645); NASA Hubble Fellowship Program Einstein Fellowship; NASA Hubble Fellowship grants HST-HF2-51431.001-A, HST-HF2-51482.001-A, HST-HF2-51539.001-A, HST-HF2-51552.001A awarded by the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., for NASA, under contract NAS5-26555; the National Institute of Natural Sciences (NINS) of Japan; the National Key Research and Development Program of China (grant 2016YFA0400704, 2017YFA0402703, 2016YFA0400702); the National Science and Technology Council (NSTC, grants NSTC 111-2112-M-001 -041, NSTC 111-2124-M-001-005, NSTC 112-2124-M-001-014); the US National Science Foundation (NSF, grants AST-0096454, AST-0352953, AST-0521233, AST-0705062, AST-0905844, AST-0922984, AST-1126433, OIA-1126433, AST-1140030, DGE-1144085, AST-1207704, AST-1207730, AST-1207752, MRI-1228509, OPP-1248097, AST-1310896, AST-1440254, AST-1555365, AST-1614868, AST-1615796, AST-1715061, AST-1716327, AST-1726637, OISE-1743747, AST-1743747, AST-1816420, AST-1935980, AST-1952099, AST-2034306, AST-2205908, AST-2307887); NSF Astronomy and Astrophysics Postdoctoral Fellowship (AST-1903847); the Natural Science Foundation of China (grants 11650110427, 10625314, 11721303, 11725312, 11873028, 11933007, 11991052, 11991053, 12192220, 12192223, 12273022, 12325302, 12303021); the Natural Sciences and Engineering Research Council of Canada (NSERC); the National Research Foundation of Korea (the Global PhD Fellowship Grant: grants NRF-2015H1A2A1033752; the Korea Research Fellowship Program: NRF-2015H1D3A1066561; Brain Pool Program: RS-2024-00407499; Basic Research Support Grant 2019R1F1A1059721, 2021R1A6A3A01086420, 2022R1C1C1005255, 2022R1F1A1075115); Netherlands Research School for Astronomy (NOVA) Virtual Institute of Accretion (VIA) postdoctoral fellowships; NOIRLab, which is managed by the Association of Universities for Research in Astronomy (AURA) under a cooperative agreement with the National Science Foundation; Onsala Space Observatory (OSO) national infrastructure, for the provisioning of its facilities/observational support (OSO receives funding through the Swedish Research Council under grant 2017-00648); the Perimeter Institute for Theoretical Physics (research at Perimeter Institute is supported by the Government of Canada through the Department of Innovation, Science and Economic Development and by the Province of Ontario through the Ministry of Research, Innovation and Science); the Portuguese Foundation for Science and Technology (FCT) grants (Individual CEEC program – 5th edition, https://doi.org/10.54499/UIDB/04106/2020, https://doi.org/10.54499/UIDP/04106/2020, PTDC/FIS-AST/3041/2020, CERN/FIS-PAR/0024/2021, 2022.04560.PTDC); the Princeton Gravity Initiative; the Spanish Ministerio de Ciencia, Innovación y Universidades (grants PID2022-140888NB-C21, PID2022-140888NB-C22, PID2023-147883NB-C21, RYC2023-042988-I); the Severo Ochoa grant CEX2021-001131-S funded by MICIU/AEI/10.13039/501100011033; The European Union's Horizon Europe research and innovation program under grant agreement No. 101093934 (RADIOBLOCKS); The European Union “NextGenerationEU”, the Recovery, Transformation and Resilience Plan, the CUII of the Andalusian Regional Government and the Spanish CSIC through grant AST22_00001_Subproject_10; “la Caixa” Foundation (ID 100010434) through fellowship codes LCF/BQ/DI22/11940027 and LCF/BQ/DI22/11940030; the University of Pretoria for financial aid in the provision of the new Cluster Server nodes and SuperMicro (USA) for a SEEDING GRANT approved toward these nodes in 2020; the Shanghai Municipality orientation program of basic research for international scientists (grant no. 22JC1410600); the Shanghai Pilot Program for Basic Research, Chinese Academy of Science, Shanghai Branch (JCYJ-SHFY-2021-013); the Simons Foundation (grant 00001470); the Spanish Ministry for Science and Innovation grant CEX2021-001131-S funded by MCIN/AEI/10.13039/501100011033; the Spinoza Prize SPI 78-409; the South African Research Chairs Initiative, through the South African Radio Astronomy Observatory (SARAO, grant ID 77948), which is a facility of the National Research Foundation (NRF), an agency of the Department of Science and Innovation (DSI) of South Africa; the Swedish Research Council (VR); the Taplin Fellowship; the Toray Science Foundation; the UK Science and Technology Facilities Council (grant no. ST/X508329/1); the US Department of Energy (USDOE) through the Los Alamos National Laboratory (operated by Triad National Security, LLC, for the National Nuclear Security Administration of the USDOE, contract 89233218CNA000001); and the YCAA Prize Postdoctoral Fellowship. This work was also supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (RS-2024-00449206). We acknowledge support from the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) of Brazil through PROEX grant number 88887.845378/2023-00. We acknowledge financial support from Millenium Nucleus NCN23_002 (TITANs) and Comité Mixto ESO-Chile. We thank the staff at the participating observatories, correlation centers, and institutions for their enthusiastic support. This paper makes use of the following ALMA data: ADS/JAO.ALMA#2017.1.00841.V and ADS/JAO.ALMA#2016.1.01154.V. ALMA is a partnership of the European Southern Observatory (ESO; Europe, representing its member states), NSF, and National Institutes of Natural Sciences of Japan, together with National Research Council (Canada), Ministry of Science and Technology (MOST; Taiwan), Academia Sinica Institute of Astronomy and Astrophysics (ASIAA; Taiwan), and Korea Astronomy and Space Science Institute (KASI; Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, Associated Universities, Inc. (AUI)/NRAO, and the National Astronomical Observatory of Japan (NAOJ). The NRAO is a facility of the NSF operated under cooperative agreement by AUI. This research used resources of the Oak Ridge Leadership Computing Facility at the Oak Ridge National Laboratory, which is supported by the Office of Science of the U.S. Department of Energy under contract No. DE-AC05-00OR22725; the ASTROVIVES FEDER infrastructure, with project code IDIFEDER-2021-086; the computing cluster of Shanghai VLBI correlator supported by the Special Fund for Astronomy from the Ministry of Finance in China; We also thank the Center for Computational Astrophysics, National Astronomical Observatory of Japan. This work was supported by FAPESP (Fundacao de Amparo a Pesquisa do Estado de Sao Paulo) under grant 2021/01183-8. APEX is a collaboration between the Max-Planck-Institut für Radioastronomie (Germany), ESO, and the Onsala Space Observatory (Sweden). The SMA is a joint project between the SAO and ASIAA and is funded by the Smithsonian Institution and the Academia Sinica. The JCMT is operated by the East Asian Observatory on behalf of the NAOJ, ASIAA, and KASI, as well as the Ministry of Finance of China, Chinese Academy of Sciences, and the National Key Research and Development Program (No. 2017YFA0402700) of China and Natural Science Foundation of China grant 11873028. Additional funding support for the JCMT is provided by the Science and Technologies Facility Council (UK) and participating universities in the UK and Canada. The LMT is a project operated by the Instituto Nacional de Astrófisica, Óptica, y Electrónica (Mexico) and the University of Massachusetts at Amherst (USA). The IRAM 30-m telescope on Pico Veleta, Spain is operated by IRAM and supported by CNRS (Centre National de la Recherche Scientifique, France), MPG (Max-Planck-Gesellschaft, Germany), and IGN (Instituto Geográfico Nacional, Spain). The SMT is operated by the Arizona Radio Observatory, a part of the Steward Observatory of the University of Arizona, with financial support of operations from the State of Arizona and financial support for instrumentation development from the NSF. Support for SPT participation in the EHT is provided by the National Science Foundation through award OPP-1852617 to the University of Chicago. Partial support is also provided by the Kavli Institute of Cosmological Physics at the University of Chicago. The SPT hydrogen maser was provided on loan from the GLT, courtesy of ASIAA. This work used the Extreme Science and Engineering Discovery Environment (XSEDE), supported by NSF grant ACI-1548562, and CyVerse, supported by NSF grants DBI-0735191, DBI-1265383, and DBI-1743442. XSEDE Stampede2 resource at TACC was allocated through TG-AST170024 and TG-AST080026N. XSEDE JetStream resource at PTI and TACC was allocated through AST170028. This research is part of the Frontera computing project at the Texas Advanced Computing Center through the Frontera Large-Scale Community Partnerships allocation AST20023. Frontera is made possible by National Science Foundation award OAC-1818253. This research was done using services provided by the OSG Consortium (Pordes et al. 2007; Sfiligoi et al. 2009), which is supported by the National Science Foundation award Nos. 2030508 and 1836650. Additional work used ABACUS2.0, which is part of the eScience center at Southern Denmark University, and the Kultrun Astronomy Hybrid Cluster (projects Conicyt Programa de Astronomia Fondo Quimal QUIMAL170001, Conicyt PIA ACT172033, Fondecyt Iniciacion 11170268, Quimal 220002). Simulations were also performed on the SuperMUC cluster at the LRZ in Garching, on the LOEWE cluster in CSC in Frankfurt, on the HazelHen cluster at the HLRS in Stuttgart, and on the Pi2.0 and Siyuan Mark-I at Shanghai Jiao Tong University. The computer resources of the Finnish IT Center for Science (CSC) and the Finnish Computing Competence Infrastructure (FCCI) project are acknowledged. This research was enabled in part by support provided by Compute Ontario (http://computeontario.ca), Calcul Quebec (http://www.calculquebec.ca), and the Digital Research Alliance of Canada (https://alliancecan.ca/en). The EHTC has received generous donations of FPGA chips from Xilinx Inc., under the Xilinx University Program. The EHTC has benefited from technology shared under open-source license by the Collaboration for Astronomy Signal Processing and Electronics Research (CASPER). The EHT project is grateful to T4Science and Microsemi for their assistance with hydrogen masers. This research has made use of NASA's Astrophysics Data System. We gratefully acknowledge the support provided by the extended staff of the ALMA, from the inception of the ALMA Phasing Project through the observational campaigns of 2017 and 2018. We would like to thank A. Deller and W. Brisken for EHT-specific support with the use of DiFX. We thank Martin Shepherd for the addition of extra features in the Difmap software that were used for the CLEAN imaging results presented in this paper. We acknowledge the significance that Maunakea, where the SMA and JCMT EHT stations are located, has for the indigenous Hawaiian people.
https://github.com/aeb/ngEHTforecast, accessed with the git commit 115bf73.
A m-ring model of first-order in width and fourth-order in azimuth template was used, consistent with the template used in the geometric tests (see also, Tiede et al. 2022a).
References
- Akiyama, K., Kuramochi, K., Ikeda, S., et al. 2017a, ApJ, 838, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Akiyama, K., Ikeda, S., Pleau, M., et al. 2017b, AJ, 153, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Akiyama, K., Tazaki, F., Moriyama, K., et al. 2019, https://doi.org/10.5281/zenodo.2616725 [Google Scholar]
- Akiyama, K., Niinuma, K., Hada, K., et al. 2024, in Space Telescopes and Instrumentation 2024: Optical, Infrared, and Millimeter Wave, eds. L. E. Coyle, M. D. Perrin, & S. Matsuura (SPIE), 91 [Google Scholar]
- Broderick, A. E., Gold, R., Karami, M., et al. 2020a, ApJ, 897, 139 [Google Scholar]
- Broderick, A. E., Pesce, D. W., Tiede, P., Pu, H. -Y., & Gold, R. 2020b, ApJ, 898, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Chael, A. A., Johnson, M. D., Narayan, R., et al. 2016, ApJ, 829, 11 [Google Scholar]
- Chael, A. A., Johnson, M. D., Bouman, K. L., et al. 2018, ApJ, 857, 23 [Google Scholar]
- Chael, A., Bouman, K., Johnson, M., et al. 2019, https://doi.org/10.5281/zenodo.2614016 [Google Scholar]
- Chael, A., Johnson, M. D., & Lupsasca, A. 2021, ApJ, 918, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, X., Cho, I., Kawashima, T., et al. 2023, Galaxies, 11, 46 [Google Scholar]
- Cruz-Osorio, A., Fromm, C. M., Mizuno, Y., et al. 2022, Nat. Astron., 6, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Curran, P. A. 2014, ArXiv e-prints [arXiv:1411.3816] [Google Scholar]
- Doeleman, S. S., Barrett, J., Blackburn, L., et al. 2023, Galaxies, 11, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Event Horizon Telescope Collaboration 2019a, ApJ, 875, L1 (M87* 2017 I) [Google Scholar]
- Event Horizon Telescope Collaboration 2019b, ApJ, 875, L2 (M87* 2017 II) [Google Scholar]
- Event Horizon Telescope Collaboration 2019c, ApJ, 875, L3 (M87* 2017 III) [Google Scholar]
- Event Horizon Telescope Collaboration 2019d, ApJ, 875, L4 (M87* 2017 IV) [CrossRef] [Google Scholar]
- Event Horizon Telescope Collaboration 2019e, ApJ, 875, L5 (M87* 2017 V) [NASA ADS] [CrossRef] [Google Scholar]
- Event Horizon Telescope Collaboration 2019f, ApJ, 875, L6 (M87* 2017 VI) [NASA ADS] [CrossRef] [Google Scholar]
- Event Horizon Telescope Collaboration 2024, A&A, 681, A79 (M87* 2018 I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Event Horizon Telescope Collaboration 2025, A&A, 693, A265 (M87* 2018 II) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Falcke, H., Melia, F., & Agol, E. 2000, ApJ, 528, L13 [Google Scholar]
- Fromm, C. M., Cruz-Osorio, A., Mizuno, Y., et al. 2022, A&A, 660, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gralla, S. E., & Lupsasca, A. 2020, Phys. Rev. D, 101, 044031 [NASA ADS] [CrossRef] [Google Scholar]
- Gralla, S. E., Holz, D. E., & Wald, R. M. 2019, Phys. Rev. D, 100, 024018 [Google Scholar]
- Gurvits, L. I., Paragi, Z., Amils, R. I., et al. 2022, Acta Astronautica, 196, 314 [Google Scholar]
- Hoffman, M. D., & Gelman, A. 2014, J. Mach. Learn. Res., 15, 1593 [Google Scholar]
- Inoue, M., Algaba-Marcos, J. C., Asada, K., et al. 2014, Radio Sci., 49, 564 [Google Scholar]
- Johnson, M. D., Lupsasca, A., Strominger, A., et al. 2020, Sci. Adv., 6, eaaz1310 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, M. D., Akiyama, K., Blackburn, L., et al. 2023, Galaxies, 11, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, M. D., Akiyama, K., Baturin, R., et al. 2024, SPIE Conf. Ser., 13092, 130922D [Google Scholar]
- Kim, J. -S., Müller, H., Nikonov, A. S., et al. 2025, A&A, 696, A169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lartillot, N., & Philippe, H. 2006, Syst. Biol., 55, 195 [Google Scholar]
- Mertens, F., Lobanov, A. P., Walker, R. C., & Hardee, P. E. 2016, A&A, 595, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mościbrodzka, M., Falcke, H., & Shiokawa, H. 2016, A&A, 586, A38 [Google Scholar]
- Pesce, D. W., Palumbo, D. C. M., Ricarte, A., et al. 2022, Galaxies, 10, 109 [Google Scholar]
- Pordes, R., Petravick, D., Kramer, B., et al. 2007, J. Phys. Conf. Ser., 78, 012057 [NASA ADS] [CrossRef] [Google Scholar]
- Porth, O., Olivares, H., Mizuno, Y., et al. 2017, Comput. Astrophys. Cosmol., 4, 1 [Google Scholar]
- Prather, B., Wong, G., Dhruv, V., et al. 2021, J. Open Source Softw., 6, 3336 [Google Scholar]
- Roelofs, F., Falcke, H., Brinkerink, C., et al. 2019, A&A, 625, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roelofs, F., Johnson, M. D., Chael, A., et al. 2023, ApJ, 957, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Sfiligoi, I., Bradley, D. C., Holzman, B., et al. 2009, 2009 WRI World Congress on Computer Science and Information Engineering, 2, 428 [CrossRef] [Google Scholar]
- Shepherd, M. C. 1997, ASP Conf. Ser., 125, 77 [Google Scholar]
- Shepherd, M. 2011, Astrophysics Source Code Library, [record ascl:1103.001] [Google Scholar]
- Syed, S., Bouchard-Côté, A., Deligiannidis, G., & Doucet, A. 2021, J. Roy. Stat. Soc. Ser. B: Stat. Methodol., 84, 321 [Google Scholar]
- Tiede, P. 2022, J. Open Source Softw., 7, 4457 [NASA ADS] [CrossRef] [Google Scholar]
- Tiede, P., & Broderick, A. E. 2024, ApJ, 971, 172 [Google Scholar]
- Tiede, P., Broderick, A. E., Palumbo, D. C. M., & Chael, A. 2022a, ApJ, 940, 182 [NASA ADS] [CrossRef] [Google Scholar]
- Tiede, P., Broderick, A. E., & Palumbo, D. C. M. 2022b, ApJ, 925, 122 [CrossRef] [Google Scholar]
- Wielgus, M., Akiyama, K., Blackburn, L., et al. 2020, ApJ, 901, 67 [Google Scholar]
- Younsi, Z., Psaltis, D., & Özel, F. 2023, ApJ, 942, 47 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Bayesian imaging methods
In M87∗ 2018 I, THEMIS used a 5×5 pixel grid (raster) as it was used in M87∗ 2017 IV. Since this size, may not be suitable for the 2018 EHT coverage or elliptical rings, similar to Tiede & Broderick (2024), we performed a small survey of different imaging models, changing the number of pixels and computing the Bayesian evidence to find the optimal raster size. The Bayesian evidence (Z) of a model M with parameters θ is given by,
where ℒ is the log-likelihood, and 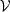 is the observed data. In a Bayesian setting, the optimal model corresponds to the one with the highest evidence. The Bayesian evidence was computed using thermodynamic integration (Lartillot & Philippe 2006), utilizing the parallel tempering scheme from Syed et al. (2021). Given the computational complexity of running a survey for each set of data, we instead focused on one of the geometric elliptical ring synthetic datasets in Sect. 3. Specifically, we considered the elliptical ring with τ=0.1 and ξ=120°. The evidence for this survey is given in Tab A.1. According to these values, 6×6 raster has the highest evidence. Furthermore, Fig. A.1, which shows how the true value of τ=0.1 and ξ=120° is recovered correctly by the 6×6 raster. Hence, throughout the analysis in this paper, we used the 6×6 raster for THEMIS.
is the observed data. In a Bayesian setting, the optimal model corresponds to the one with the highest evidence. The Bayesian evidence was computed using thermodynamic integration (Lartillot & Philippe 2006), utilizing the parallel tempering scheme from Syed et al. (2021). Given the computational complexity of running a survey for each set of data, we instead focused on one of the geometric elliptical ring synthetic datasets in Sect. 3. Specifically, we considered the elliptical ring with τ=0.1 and ξ=120°. The evidence for this survey is given in Tab A.1. According to these values, 6×6 raster has the highest evidence. Furthermore, Fig. A.1, which shows how the true value of τ=0.1 and ξ=120° is recovered correctly by the 6×6 raster. Hence, throughout the analysis in this paper, we used the 6×6 raster for THEMIS.
 |
Fig. A.1. Evaluation of different rasters of THEMIS through synthetic data tests. The true m-ring model with τ=0.1 and ξ=120° is shown on the top. The posterior mean images from THEMIS for 5×5, 6×6, and 7×7 rasters are shown in the middle. τ and ξ - ξTruth posteriors are shown at the bottom. The contours are shown for 68% and 95% confidence intervals. The dashed line marks the truth values. |
Evidence of different raster sizes.
In M87∗ 2018 I, Comrade imaging used closure phases and visibility amplitudes as the data products, and fit only for gain amplitudes. The prior used for the raster assumed that the pixels are independently distributed (Dirichlet prior). There have been several developments in Comrade since then. In this paper, we used complex visibilities as the data products and fit for both amplitude and phase gains (with reference to one station). The image model is a 64×64 raster with a field of view of 200 μas. An extended Gaussian component was used to model the emission on milliarcsecond scales. The location, position angle, and fractional flux are the model parameters, while the size is fixed as 1000 μas. The total flux of the image plus the Gaussian component was fixed to 1.1 Jy as assumed in network calibration for the M87* data. For the raster, we use a first-order Gaussian Markov random field (GMRF) prior on the log-ratio transformed pixel intensities. Hence, the pixels are spatially correlated. The GMRF is added to a mean image which is a 40 μas Gaussian (size of the Gaussian does not drastically change the reconstructed images). The variance and correlation length of the random field are the hyperparameters. The variance and the correlation length are included as parameters in the model. The amplitude gain priors are the same as used in M87∗ 2018 I. We allow gains to vary every scan. For the gain phases, the gain phase for ALMA is set to be zero. In the case when ALMA is not present in the scan, we select the next reference station alphabetically. For rest of the gain phase priors, we use von Mises prior with zero mean and a concentration parameter π−2 (which is essentially a uniform prior on the interval [−π,π]). Sampling is performed using Hoffman & Gelman (2014), in the Julia sampling package AdvancedHMC.jl4, in the same way as done in M87∗ 2018 I.
Appendix B: Additional geometric tests
In Sect. 3, we performed the tests with geometric models where the ellipticity position angle ξ was aligned with the brightness position angle η. In order to be certain that an offset between position angles, will not introduce any additional biases in measuring ellipticity, we performed this additional test shown in Fig. B.1. We chose the η to be perpendicular to ξ to test the extreme case. This test was performed with Comrade for all τ and ξ but Fig. B.1 shows only the two cases when ξ=0° and ξ=120°. In all cases, Comrade recovers the true τ correctly. For ξ, we see the same pattern as seen in Fig. 4 and as mentioned in Sec. 3. Even in these tests, we found that true ξ can be recovered with narrow posteriors for all cases, except when ξ is aligned North-South, for which we get broad posteriors.
 |
Fig. B.1. Geometric tests for the cases when brightness PA η is perpendicular to ξ. The leftmost column shows the ground truth for the cases τ=0.1, ξ=0°, η=90° (top) and ξ=120° (bottom). Mean images from Comrade posteriors are shown in the middle. The rightmost column shows measured τ and ξ posteriors (68% and 95% confidence contours) compared with true values in dashed lines. The gray shaded region marks the region between τ of the groundtruth model without any convolution and with convolution of a Gaussian up to 20 μas size. |
Appendix C: The effect of resolution on the measured ellipticity
VIDA stretched m-ring template models the ellipticity of a m-ring by stretching a symmetric m-ring template in x-direction and compressing it in y-direction. Assuming this definition of measured ellipticity, we want to solve for an analytical equation that relates τ with a Gaussian blurring kernel. To do so, consider a zero-order symmetric m-ring with flux F0 and radius r0,  , which has a Fourier transform given by, F0J0(2πr0|u|). J0 is a zeroth-order Bessel function of the first kind and u,v are the spatial coordinates in the Fourier domain. Stretching the m-ring in the u-direction by β and compressing in the v-direction by β, we get:
, which has a Fourier transform given by, F0J0(2πr0|u|). J0 is a zeroth-order Bessel function of the first kind and u,v are the spatial coordinates in the Fourier domain. Stretching the m-ring in the u-direction by β and compressing in the v-direction by β, we get:
where 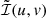 is the intensity profile in the Fourier domain (or the amplitude visibilities at u,v), τ=1−b/a=1−(2r0β)/(2r0/β)=1−β2. If we blur this stretched m-ring with a circular Gaussian of full-width at half maximum (FWHM) α, we get,
is the intensity profile in the Fourier domain (or the amplitude visibilities at u,v), τ=1−b/a=1−(2r0β)/(2r0/β)=1−β2. If we blur this stretched m-ring with a circular Gaussian of full-width at half maximum (FWHM) α, we get,
From Eq. C.2, it is not possible to get a τ−α relation without the u and v dependence. Instead, we used geometric elliptical m-ring models with ξ=120° and τ0=[0.05,0.1,0.15,0.2,0.25,0.3] and measured the ellipticity with VIDA by blurring the models with different circular Gaussian FWHM (α). We then fitted a Gaussian to each measured τ−α data (see Eq. C.3) for all different τ0−ξ models.
When Eq. C.3 is fit to different τ−α data for the τ0 cases, we get μ=0 and A=τ0 for all the cases as shown in Eq. C.4.
where σ was measured as 21.5±0.5 μas for all the cases. We note that we have data only up to one σ of the fitted Gaussians. The drop in τ is high when τ0 is high, as shown in Fig. C.1 (top). The maximum change is seen in the τ0=0.3 case, when it is blurred by α=20 μas, τ goes from 0.3 to ∼0.225. When 0.05<τ0<1.0, given the nominal resolution of ∼20 μas, the change in true ellipticity Δτ is 0.017≲Δτ≲0.034. While the diameter of the m-ring drops by a maximum of ∼4 μas, the width increases by a maximum of ∼13 μas, after blurring with α=20 μas as shown in Fig. C.1 (bottom).
 |
Fig. C.1. The effect of blurring with different Gaussian FWHM (α) on the ring parameters measured by VIDA. (Top) Ellipticity of a stretched m-ring with true ξ=120° and τ0=[0.05,0.1,0.15,0.2,0.25,0.3]. The black dashed line marks the fitted curves. (Bottom) Diameter (circle) and width (diamond) of a stretched m-ring with the same true ξ and τ0 as on the top. |
All Tables
Spearman correlation for ellipticity of GRMHD truth models and their physical parameters.
All Figures
 |
Fig. 1. EHT 2017 and 2018 (u,v)-coverage. The plot shows observations from April 10, 2017 (gray) and April 21, 2018 (blue and orange). Both are at 229.1 GHz, which corresponds to the hi-band and band 4 in EHT 2017 and 2018, respectively. Orange points highlight the GLT baselines. Red circles show the coverage gaps in 2017, and dashed circles mark the 25 and 50 μas resolution. |
| In the text | |
 |
Fig. 2. Definition of parameters τ, ξ for m-ring model, along with respective marginalized uncertainties using Fisher information analysis. Left: A visualization of a stretched m-ring model with parameters τ=0.1, ξ=45°, a brightness asymmetry of 0.23, and a diameter of d=46 μas, blurred with a Gaussian kernel with a full width at half maximum of 10 μas. The brightness position angle, η=45°, is aligned with ξ. Right: Maps of marginalized uncertainties in the parameters τ (top row) and ξ (bottom row) for m-ring models with various values of τ and ξ, derived using Fisher information analysis on M87* band 4 data. |
| In the text | |
 |
Fig. 3. Elliptical crescent models with different ellipse position angles. From left to right, ecres000, ecres045, ecres090, and ecres315. From top to bottom, groundtruth images and fiducial images from eht-imaging, SMILI, and DIFMAP for band 4. DIFMAP images are presented with a beam convolution of a 20 μas circular Gaussian (M87∗ 2018 I). |
| In the text | |
 |
Fig. 4. Subset ellipticity measurements for geometric models (6 out of 42) for all imaging methods. From left to right: groundtruth image of a given geometric model, τ−ξ distribution using Comrade, THEMIS, eht-imaging, SMILI, and DIFMAP for band 4 synthetic data. Each row corresponds to a different geometric model, with the true model shown in the leftmost column. The vertical and horizontal dashed lines in each panel of τ−ξ distribution indicate the true values. The contours denote 68% and 95% confidence intervals. The vertical dashed line shows τ measured with VIDA for the groundtruth model. The gray shaded region spans the range of τ values for the groundtruth model, from the unconvolved case to the convolution of a circular Gaussian of 20 μas FWHM. |
| In the text | |
 |
Fig. 5. EHT 2018 M87* images and ellipticity (τ) and ellipticity position angle (ξ) distributions. (left to right) Images from each imaging method (Comrade, THEMIS, eht-imaging, SMILI, and DIFMAP). For Comrade and THEMIS, mean posterior images are shown. Fiducial images from the respective Top Sets are shown for the other methods. The two right panels show the distributions of τ and ξ for each method. Top and bottom rows show results for band 3 and band 4, respectively. Colors correspond to each method (see legend). |
| In the text | |
 |
Fig. 6. Subset of GRMHD images (10 out of 100 models) from KHARMA and BHAC libraries: (from top to bottom) ground truth, reconstructed images by Comrade (mean image) and eht-imaging (one random from Top Set) for band 4. Thermal models from KHARMA are marked in orange and nonthermal models are marked in blue. The ground truths are shown after blurring with a 12 μas circular Gaussian. |
| In the text | |
 |
Fig. 7. Histograms of differences in τ (top) and ξ (bottom) between reconstructed and true GRMHD values. Results from Comrade (blue) and eht-imaging (orange) are shown, both centered around zero for each parameter. |
| In the text | |
 |
Fig. 8. Ellipticity of truth GRMHD models (blurred with 12 μas Gaussian) for different GRMHD parameters. All 299 models are shown in blue, and the models that pass the jet power criteria are shown in orange (note that while plotting we combined the nonthermal models with the same parameters but different nonthermal emission fraction (ϵ)). The over-plotting on the histograms shows the median value and the 68% confidence interval. The ellipticity of M87 is shown as a dashed green line, with its error range shown in the shaded green region. In the top rightmost panel, the ellipticity of the critical curve for a Kerr black hole (see Figure 7, Johnson et al. 2020) for different spins (inclination = 17°) is plotted to compare it with the histograms of the respective spins. The spin = 0.5 case is shown by dashed black line; the spin = +0.94 is represented by a solid black line and the spin = +0.999 case is given by a dotted black line. |
| In the text | |
 |
Fig. 9. Ellipticity of all 299 GRMHD truths (convolved with 12 μas Gaussian) compared with the non-ring flux fraction. The left and right panels are the same, but the colors are different for (non)thermal models (left) and Rhigh values (right). The ellipticity of M87 is shown by a dashed black line, with its error range shown in the shaded gray region. The median τ for each case is shown in the legend. |
| In the text | |
 |
Fig. 10. Ellipticities of 1000 snapshots spanning ∼370 days for a GRMHD model with the following parameters: magnetic field configuration = MAD; thermal eDF; black hole spin = −0.5; Rhigh=160, Rlow=1; and inclination angle = 17°. The ellipticity of each snapshot is measured after blurring with a 12 μas Gaussian (blue). The median and 68% confidence interval of the time series are shown with a solid green line and shaded region, respectively. The ellipticity of the time-averaged image (right) is shown with a red line. |
| In the text | |
 |
Fig. A.1. Evaluation of different rasters of THEMIS through synthetic data tests. The true m-ring model with τ=0.1 and ξ=120° is shown on the top. The posterior mean images from THEMIS for 5×5, 6×6, and 7×7 rasters are shown in the middle. τ and ξ - ξTruth posteriors are shown at the bottom. The contours are shown for 68% and 95% confidence intervals. The dashed line marks the truth values. |
| In the text | |
 |
Fig. B.1. Geometric tests for the cases when brightness PA η is perpendicular to ξ. The leftmost column shows the ground truth for the cases τ=0.1, ξ=0°, η=90° (top) and ξ=120° (bottom). Mean images from Comrade posteriors are shown in the middle. The rightmost column shows measured τ and ξ posteriors (68% and 95% confidence contours) compared with true values in dashed lines. The gray shaded region marks the region between τ of the groundtruth model without any convolution and with convolution of a Gaussian up to 20 μas size. |
| In the text | |
 |
Fig. C.1. The effect of blurring with different Gaussian FWHM (α) on the ring parameters measured by VIDA. (Top) Ellipticity of a stretched m-ring with true ξ=120° and τ0=[0.05,0.1,0.15,0.2,0.25,0.3]. The black dashed line marks the fitted curves. (Bottom) Diameter (circle) and width (diamond) of a stretched m-ring with the same true ξ and τ0 as on the top. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ F_{ij} = {\mathbb {E}} \left [\frac {\partial \ln {\cal {{L}}}(\theta )}{\partial \theta _i} \frac {\partial \ln {\cal {{L}}}(\theta )}{\partial \theta _j}\right ], $$](/articles/aa/full_html/2025/07/aa55235-25/aa55235-25-eq5.gif)