| Issue |
A&A
Volume 645, January 2021
|
|
|---|---|---|
| Article Number | A14 | |
| Number of page(s) | 17 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202039736 | |
| Published online | 24 December 2020 | |
The diffuse interstellar band around 8620 Å
I. Methods and application to the GIBS data set★
1
University Côte d’Azur, Observatory of the Côte d’Azur, CNRS, Lagrange Laboratory, Observatory Bd, CS 34229,
06304
Nice Cedex 4,
France
e-mail: he.zhao@oca.eu; mathias.schultheis@oca.eu
2
Instituto de Astrofísica, Facultad de Física, Pontificia, Universidad Católica de Chile, Av. Vicuña Mackenna 4860,
Santiago, Chile
3
Millennium Institute of Astrophysics,
Av. Vicuña Mackenna 4860,
782–0436
Macul,
Santiago, Chile
4
Departamento de Astrofísica, Universidad de La Laguna,
38205
La Laguna Tenerife, Spain
5
European Southern Observatory,
Karl Schwarschild-Straße 2,
85748
Garching bei München, Germany
6
Excellence Cluster ORIGINS,
Boltzmann-Straße 2,
85748
Garching bei München, Germany
Received:
21
October
2020
Accepted:
13
November
2020
Context. Diffuse interstellar bands (DIBs) are interstellar absorption features that widely exist in the optical and near-infrared wavelength range. DIBs play an important role in the lifecycle of the interstellar medium and can also be used to trace the Galactic structure.
Aims. We developed a set of procedures to automatically detect and measure the DIB around 8620 Å (the Gaia DIB) for a wide range of temperatures. The method was tested on ~5000 spectra from the Giraffe Inner Bulge Survey (GIBS) that has a spectral window similar to that of the Gaia–RVS spectra. Based on this sample, we studied the correlation between the equivalent width (EW) of the Gaia DIB and the interstellar reddening E(J − KS) toward the inner Galaxy, as well as the DIB intrinsic properties.
Methods. Our procedure automatically checks and eliminates invalid cases, and then applies a specific local normalization. The DIB profile is fit with a Gaussian function. Specifically, the DIB feature is extracted from the spectra of late-type stars by subtracting the corresponding synthetic spectra. For early-type stars we applied a specific model based on the Gaussian process that needs no prior knowledge of the stellar parameters. In addition, we provide the errors contributed by the synthetic spectra and from the random noise.
Results. After validation, we obtained 4194 reasonable fitting results from the GIBS database. An EW versus E(J − KS) relation is derived as E(J − KS) = 1.875 (±0.152) × EW − 0.011 (±0.048), according to E(B − V)∕EW = 2.721, which is highly consistent with previous results toward similar sightlines. After a correction based on the Vista Variables in the Via Lactea (VVV) database for both EW and reddening, the coefficient derived from individual GIBS fields, E(J − KS)∕EW = 1.884 ± 0.225, is also in perfect agreement with literature values. Based on a subsample of 1015 stars toward the Galactic center within − 3° < b < 3° and − 6° < l < 3°, we determined a rest-frame wavelength of the Gaia DIB as 8620.55 Å.
Conclusions. The procedures for automatic detection and measurement of the Gaia DIB are successfully developed and have been applied to the GIBS spectra. A Gaussian profile is proved to be a proper and stable assumption for the Gaia DIB as no intrinsic asymmetry is found. A tight linearity of its correlation with the reddening is derived toward the inner Milky Way, which is consistent with previous results.
Key words: ISM: lines and bands / dust, extinction / Galaxy: bulge
The catalog is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/645/A14
© H. Zhao et al. 2020
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Diffuse interstellar bands (DIBs) are a set of absorption features that were first discovered in 1919 (Heger 1922). These features originate in the interstellar medium (ISM; Merrill 1934, 1936) and usually contain broader widths than typical atomic lines (Herbig 1975; Hobbs et al. 2008). Herbig (1975) was the first to systematically discuss the behavior of 39 DIBs in the region of 4400–6850 Å. An extended search was made by Sanner et al. (1978) from 6500 to 8900 Å. Jenniskens & Desert (1994) made a systematic search for the DIBs on the spectra of four reddened early-type stars and presented a catalog containing 229 DIBs, of which 133 were newly detected. The total number of the DIBs increases with the quality and wavelength coverage of the spectra. The recently released Apache Point Observatory Catalog contains more than 500 DIBs covering optical and near-infrared (NIR) bands (Fan et al. 2019). More than 100 yr have passed since the first discovery of DIBs, but we still know very little about their carriers. The correlation between the strength of the DIBs and interstellar extinction is a general property for many strong DIBs (Sanner et al. 1978; Lan et al. 2015). However, the lack of a linear polarization in strong DIBs (Cox et al. 2007) and their missing link to far-ultraviolet extinction (Desert et al. 1995; Xiang et al. 2017) result in the thought that large carbonaceous molecules in the gas phase rather than small dust grains are the carriers of the DIBs, for example, polycyclic aromatic hydrocarbons (PAHs, Leger & D’Hendecourt 1985; van der Zwet & Allamandola 1985; Salama et al. 1999; Cox & Spaans 2006) and fullerenes (Kroto 1988; Campbell et al. 2015). The Buckminsterfullerene,  , is the first and only identified DIB carrier for four DIBs λ9365, λ9428, λ9577, and λ9632, according tothe match of the band wavelengths and the strength ratios between observational and laboratory data (Campbell et al. 2015; Campbell & Maier 2018; Lallement et al. 2018; Cordiner et al. 2019).
, is the first and only identified DIB carrier for four DIBs λ9365, λ9428, λ9577, and λ9632, according tothe match of the band wavelengths and the strength ratios between observational and laboratory data (Campbell et al. 2015; Campbell & Maier 2018; Lallement et al. 2018; Cordiner et al. 2019).
Because DIBs are weak and easily blended with stellar lines (Kos et al. 2013), early works preferred high-quality early-type stars with only several to a few hundred observations at best. During the past ten years, the upcoming large spectroscopic surveys opened a new era in the DIB research, with a considerable number of spectra that allowed constructing a three-dimensional (3D) map of the DIBs and unveiling kinematic information and statistical properties of their carriers. Using the spectra from the Gaia–ESO Spectroscopic Survey (Gilmore et al. 2012), Chen et al. (2013) and Puspitarini et al. (2015) first detected the DIBs in the spectra of late-type stars with automated techniques by fitting the observed spectrum with a combination of a synthetic stellar spectrum, a synthetic telluric transmission, and empirical DIB profiles. In addition to the use of synthetic spectra, Kos et al. (2013) developed a method for detecting interstellar DIBs on cool-star spectra using artificial templates constructed from real spectra at high latitudes that are morphologically similar to the target spectrum. This method requires no prior knowledge of stellar parameters but can only be applied with large databases. Kos and collaborators applied the method to study the DIB around 8620 Å with ~500 000 spectra from the Radial Velocity Experiment (RAVE; Steinmetz et al. 2006) and built a pseudo-3D map of the DIB strength covering about 3 kpc from the Sun with a spatial resolution between 0.075 and 0.8 kpc (Kos et al. 2014). Yuan & Liu (2012) also reported the detection of two optical DIBs λ5780 and λ6283 in about 2000 low-resolution spectra (R ~ 2000) from the Sloan Digital Sky Survey (SDSS; Eisenstein et al. 2011). By stacking thousands of SDSS spectra of stars, galaxies, and quasars, Lan et al. (2015) successfully created an intensity map of 20 DIBs covering ~5000 deg2 and measured their correlations with various ISM tracers (atomic, molecule, and dust). The tight correlation between the strength of the DIBs and interstellar extinction was confirmed toward substantial sightlines. The strong DIB at λ = 1.527 μm (i.e., APOGEE DIB) was thoroughly studied using data from the Apache Point Observatory Galactic Evolution Experiment (APOGEE; Majewski et al. 2016) by Zasowski et al. (2015), Elyajouri et al. (2016), and Elyajouri & Lallement (2019). In addition to the common correlation between its strength and extinction, various properties were investigated based on the large number of APOGEE spectra: Zasowski et al. (2015) derived the velocity curve of the DIB carrier and estimated the rest-frame wavelength of the APOGEE DIB; Elyajouri & Lallement (2019) revealed the depletion of the DIB carrier in dense clouds.
Based on large sky survey projects and new techniques, strong DIBs are identified to be a powerful tool for ISM tomography and consequently can probe the Galactic structure, although the carriers are unknown. The forthcoming third data release of the ESA Gaia mission that will contain the parameterization of several million spectra will be a leap forward in the sky coverage and spatial resolution of the DIB intensity map. These spectra are observed with the Gaia Radial Velocity Spectrometer (RVS; Recio-Blanco et al. 2016; Gaia Collaboration 2018; Katz et al. 2019) for stars as faint as G ~ 15.5 mag, with a spectral window from 847 to 871 nm at a resolution of ~11 200. DIB λ8620 is also the strongest DIB covered by the Gaia–RVS spectra, known as the “Gaia DIB”. It was first reported by Geary (1975) and has been widely studied for its correlation with interstellar extinction (Sanner et al. 1978; Munari 2000; Wallerstein et al. 2007; Munari et al. 2008; Kos et al. 2013; Damineli et al. 2016). Its carrier is not associated with dust grains (Cox et al. 2011) and is still not identified.
In this paper, we describe our automatic procedure for the detection and measurement of the Gaia DIB, which can be applied for large spectroscopic surveys such as the forthcoming Gaia DR3 release. We applied this method to nearly 5000 spectra from the Giraffe Inner Bulge Survey (GIBS; Zoccali et al. 2014) located in highly extincted regions. The full procedures of the DIB measurements, as well as the error analysis, are presented in Sect. 2. The GIBS data are introduced in Sect. 3. Section 4 shows the fitting results and the related discussions. Our main conclusions are summarized in Sect. 5.
2 Procedures of the DIB measurement
Most of the DIB studies have focused either on late-type stars (e.g., Kos et al. 2013) or on early-type stars (e.g., Munari et al. 2008)with a reasonable number of spectra to treat (several tens of thousands of stars). The challenge of this work is to implement aprocedure that is valid for a wide temperature range and applicable to very large spectral surveys such as that of Gaia RVS. This requires a set of automatic procedures that has to be fast in terms of computing time and also reliable. Figure 1 shows the flowchart of our full procedures, and we describe our automatic procedures in detail below.
2.1 Inputs and spectral check
The global inputs of our procedure are the observed spectra corrected for their radial velocities together with their best-fit synthetic spectrum and the corresponding stellar parameters. We used these stellar parameters together with the corresponding synthetic spectra for stars with temperatures from 3500 K to 7000 K, which we call cool stars. We chose this limit in order to ensure that we did not encounter problems with the synthetic spectra at the border of their grid. For stars above 7000 K, which are called hot stars, we used a specific technique based on the Gaussian process that does not require synthetic spectra, as described in Kos (2017).
The input spectra and parameters (effective temperature Teff, signal-to-noise ratio S/N, radial velocity of the target star RVstar, and its uncertainty σ(RVstar)) were checked before further processes to eliminate invalid cases. Cool-star spectra should have nonzero flux for both observed and synthetic spectra, while for hot-star spectra, only a nonzero observed flux is required. Stars with Teff < 3500 K were discarded because those spectra are mainly dominated by molecular lines that cannot easily be reproduced well by synthetic spectra. In addition, in order to avoid fitting random-noise profiles instead of the true DIB profiles, we restricted our analysis to stars with S∕N > 50. We describein Sect. 2.6.1 the effect of the S/N on the error in the DIB measurement. RVstar was used to convert the central wavelength measured in the stellar rest frame into the heliocentric frame. Targets with large radial velocity errors (σ(RVstar) > 5 km s−1) were discarded as well.
2.2 Interstellar spectra and renormalization
The interstellar spectra were derived by dividing the observed spectra by the corresponding synthetic spectra for cool stars. For hot stars, the Gaia DIB is usually not blended with stellar lines and can be directly measured on the observed spectra, while for cool stars, the stellar lines first need to be removed by using the synthetic spectra. We refer here to the cool interstellar spectra and to the hot interstellar spectra as CIS and HIS, respectively.
We analyzed and measured the Gaia DIB in a 35 Å wide region around its central wavelength (Jenniskens & Desert 1994; Galazutdinov et al. 2000; Munari et al. 2008), that is, 8605–8640 Å. Although the input spectra should be normalized, the interstellar spectra usually do not have uniform continua. Especially for hot-star spectra, heavily uneven continua can be found with the strong hydrogen Paschen 14 line (see Fig. 2 or the examples shown in Munari et al. 2008). Therefore, a specific renormalization technique was applied to the local spectra within the 8605–8640 Å spectral window. For HIS, the local spectrum was first fit by a second-order polynomial, where the differences of the flux of each pixel to the fitting curve were calculated, as well as their standard deviation. Pixels far away from the fitting curve were replaced by the corresponding points on the fitting curve. Specifically, for the pixels above the polynomial, they were replaced when their distances were larger than five times the standard deviation. When the pixel was below the fitting curve, the threshold was 0.5 times the standard deviation. Different rejected thresholds were set to ensure that the fitted continuum can access the real continuum and is not lowered by the stellar and/or DIB features. The remaining pixels, together with the points replacing outliers, were fit again by a second-order polynomial. After 20 iterations, the final fitted polynomial was used as the continuum to renormalize the original local spectrum. Figure 2 illustrates the local renormalization with five RAVE spectra of hot stars. The spectra and their atmospheric parameters were taken from RAVE–DR6 (Steinmetz et al. 2020a,b). The curvatures caused by the Paschen 14 line are alleviated, but the DIB and stellar features are kept.
The same technique was also applied to the cool-star spectrum, but using a linear form. The local renormalization and the derivation of CIS were made simultaneously following these steps:
- 1.
Derive a rough interstellar spectrum, Rrough = Fλ∕Sλ, where Fλ is the observed spectrum and Sλ is the synthetic spectrum. Fλ and Sλ have the same spectral samplings.
- 2.
Renormalize Rrough and extract its continuum, Fcont.
- 3.
Renormalize the observed spectrum, Fnorm = Fλ∕Fcont.
- 4.
Derive the final interstellar spectrum: Rλ = Fnorm∕Sλ.
A renormalized CIS is shown in Fig. 3 with the corresponding fit of the DIB feature on it. The spectrum and stellar parameters come from RAVE–DR6 as well.
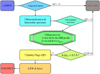 |
Fig. 1 Flowchart compiling our full procedures of the detection and measurement of the Gaia DIB. |
2.3 Preliminary detection
In order to process a large number of spectra, the fitting of the DIB profile was completely automated without any visual inspection. We therefore made a preliminary detection of the DIB profile to produce initial guesses for the fitting and eliminated cases whose noise is at the level of or exceeds the depth of the DIB feature. The detection was made within the wavelength range between 8614.3 and 8625.7 Å according to a radial velocity of ± 200 km s−1 of the DIB carrier at the stellar frame. This is a reasonable assumption if the DIB carrier mainly traces the local ISM at several kiloparsecs from the Sun. When the largest depth of the spectrum in this region is larger than 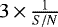 , we considered this DIB as a true detection, and the considered spectrum entered the main process of the DIB profile fitting (see Fig. 1), where the depth and its according position were used as the initial conditions of D and λC in the DIB fitting. Otherwise, the case was discarded.
, we considered this DIB as a true detection, and the considered spectrum entered the main process of the DIB profile fitting (see Fig. 1), where the depth and its according position were used as the initial conditions of D and λC in the DIB fitting. Otherwise, the case was discarded.
2.4 Mainprocess: fitting the DIB profile
The observed profile of the Gaia DIB along the line of sight could be the superposition of several features with different widths but at almost the same wavelength (Jenniskens & Desert 1994), which can be described by a Gaussian profile (Kos et al. 2013). We decided to fit the DIB feature on the spectra with a Gaussian profile because (1) previous studies revealed no intrinsic asymmetry of the Gaia DIB (Munari et al. 2008; Kos et al. 2013; Puspitarini et al. 2015), (2) the departures from a Gaussian profile caused by the multiple cloud superposition is smaller than other sources of uncertainty (Elyajouri et al. 2016), and (3) a Gaussian fit is easier, more stable, and faster in terms of computing time than the asymmetric Gaussian fit.
 |
Fig. 2 Examples of the local renormalization for five RAVE spectra (R = 7500) of hot stars. The black lines are the original spectra, and the orange lines indicate the renormalized spectra. The black arrows indicate the Gaia DIB. The names and atmospheric parameters are also indicated. The strong stellar feature near the DIB profile seen on HD 150850 and HD 166167 is the N I line. |
2.4.1 Models for the cool and hot Interstellar spectra
The DIB profiles on CIS and HIS were fit by different techniques that are described below. CIS was modeled using a Gaussian function that describes the DIB profile and a constant that accounts for the continuum,
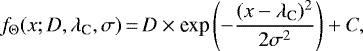 (1)
(1)
where D and σ are the depth and width of the DIB profile, λC is the measured central wavelength, C is the constant continuum, and x is the spectral wavelength.
However, a simple Gaussian model is not suitable for HIS because they are usually distorted by the strong Paschen 13 and 14 lines and sometimes contain a strong N I line around 8629 Å (see, e.g., HD 150850 and HD 167745 in Fig. 2). To fit the DIB profile together with the distorted continuum and possible stellar lines, we applied a similar method as in Kos (2017) using the Gaussian process (GP) described in detail below.
The GP is defined as a collection of random variables, any finite number of which have a joint multivariate Gaussian distribution (Schulz et al. 2018). Formally, let the input space be 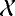 , and f denotes a function mapping the input space to reals:
, and f denotes a function mapping the input space to reals: 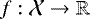 . Then, f is a GP if for any vector of inputs
. Then, f is a GP if for any vector of inputs ![$\vec{x} \,{=}\, [x_1,x_2, \ldots,x_n]^{T}$](/articles/aa/full_html/2021/01/aa39736-20/aa39736-20-eq6.png) such that
such that  for all i, the outputs
for all i, the outputs ![$f(\vec{x}) \,{=}\, [f(x_1),f(x_2), \ldots,f(x_n)]^T$](/articles/aa/full_html/2021/01/aa39736-20/aa39736-20-eq8.png) is Gaussian distributed. GP is specified by a mean function m(x) reflecting the expected function value at input x, and a kernel (also called covariance function) k(x, x′) models the dependence between the output values at different input points (Schulz et al. 2018). GP can be used as a supervised learning technique for classification and regression.
is Gaussian distributed. GP is specified by a mean function m(x) reflecting the expected function value at input x, and a kernel (also called covariance function) k(x, x′) models the dependence between the output values at different input points (Schulz et al. 2018). GP can be used as a supervised learning technique for classification and regression.
Gaussian process regression (GPR) is a nonparametric Bayesian approach to regression problems (Gershman & Blei 2012). The output y of a function f at input x can be written as
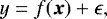 (2)
(2)
where 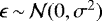 represents the observational error.
represents the observational error. 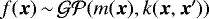 is distributed as a GP (Schulz et al. 2018). GPR can capture many different relations between inputs and outputs by using a theoretically infinite number of parameters (Williams 1998).
is distributed as a GP (Schulz et al. 2018). GPR can capture many different relations between inputs and outputs by using a theoretically infinite number of parameters (Williams 1998).
For HIS, our goal is to apply GPR to fit the DIB profile and the remaining spectrum simultaneously. The prior mean function is often set to m(x) = 0 in order to avoid expensive posterior computations. Because we wish to extract the information of the DIB feature, however, a Gaussian mean function (Eq. (1)) is applied with C ≡ 1. For the kernels, we followed the strategy of Kos (2017): the exponential-squared kernel models the stellar absorption lines,
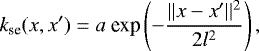 (3)
(3)
and a Matérn 3/2 kernel models the correlated noise,
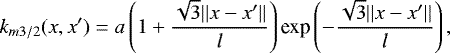 (4)
(4)
where a scales the kernels, and l is the characteristic width of each kernel.
In principle, the fitting technique based on GP can be applied to spectra of both hot and cool stars. Because it is computationally expensive, however, we only applied it to hot-star spectra, which take only a small fraction of the substantial spectra in large spectroscopic surveys such as Gaia RVS. Nevertheless, as an illustration of this method, we applied it to GIBS data (see Sect. 3).
2.4.2 Parameter optimization and MCMC fit
Maximum likelihood estimation was used to optimize the parameters in the Gaussian model for CIS, that is, Θ = {D, λC, σ, C}. Given the spectrum 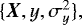 where X is the wavelength, y is the flux, and
where X is the wavelength, y is the flux, and 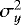 is the observational uncertainties (if
is the observational uncertainties (if 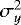 is not accessible, it was fixed to 0.001), the log marginal likelihood is
is not accessible, it was fixed to 0.001), the log marginal likelihood is
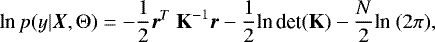 (5)
(5)
where r = y − fΘ(X) is the residual vector and fΘ is the Gaussian model. N is the pixel size of the spectrum. K is the covariance matrix,
 (6)
(6)
To implement GPR for HIS, we optimized five parameters, three for the DIB profile (D, λC, σ), and two for the kernels (lse and lm3∕2). The scaling factor a of the kernel can be estimated as the variance of the noise and does not need to be fit. We used the square of the inverse of the S/N to approximate it. The optimal parameters were estimated by maximizing the type II maximum likelihood (Rasmussen & Williams 2006). Its log marginal likelihood is almost the same as Eq. (5), but the covariance matrix becomes nondiagonal,
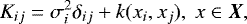 (7)
(7)
where σi is the observational error, δij is the Kronecker delta, and k(xi, xj) is the element of the specified kernel.
A Markov chain Monte Carlo (MCMC) procedure (Foreman-Mackey et al. 2013) was performed to implement the parameter estimates for the Gaussian fit and GPR. The initial conditions are perturbed by a normal distribution around the initial guess with a standard deviation of 0.01. Different walkers of the MCMC can therefore start with different conditions. One hundred walkers were progressed for 50 steps to complete the burn-in stage. The best fits were then used as the initial conditions to sample the posterior with 100 walkers and 200 steps. The best estimate and its statistical uncertainty were taken in terms of the 50th, 16th, and 84th percentiles of the posterior distribution.
The initial conditions of D and λC were measured by the preliminary detection (see Sect. 2.3). The initial values of lse and lm3∕2 were set to 0.3 and 0.15 for all the cases. C has an initial guess of 1.0 assuming a well-normalized CIS. The initial guess of σ is hard to determine. Based on the GIBS results (see Sect. 4), σ0 = 1.2 is a proper guess. Strong DIB profiles are not sensitive to the initial guess, while weak profiles in general show a good fitting behavior with this value. Examples of the DIB fittings for CIS and HIS are shown in Figs. 3 and 4, respectively. We indicate the first initial fit and a second fit for the error analysis (see Sect. 2.6.2). The final selected fits are marked as solid lines.
2.4.3 Priors
As a Bayesian approach, priors can be used to prevent unphysical or unreasonable fittings. For the Gaussian fit applied to the CIS, we adopted flat priors,
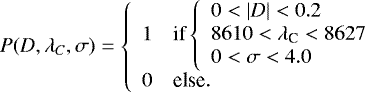 (8)
(8)
More rigorous priors are needed for HIS to avoid treating the DIB profile as the correlated noise and fit by the kernels of GP. The priors of lse and lm3∕2 provided by Kos (2017) were taken. 0.22 Å was assumed as the boundary of the characteristic widths of stellar feature and the random noise, and therefore it is the lower limit of lse and the upper limit of lm3∕2. lm3∕2 has a lower limit of 0.08 Å. lse is flat at high values and gradually decreases to −∞ at the value of the DIB width. D has a flat prior the same as for CIS. The priors of λC and σ are the Gaussian priors centered at their initial conditions with a width of 0.5 Å, which are simpler than those of Kos (2017) because they lack the preliminary fit of the DIB profile. The prior of λC is stricter than that of σ because its initial guess can be determined by the preliminary detection. Some examples of the priors of lse, lm3∕2, λC, and σ are presented in Fig. 5.
 |
Fig. 3 Gaussian model for CIS of the star HD 149349 observed by the RAVE survey (R = 7500). Upper panel: black and blue lines show the observed and synthetic spectra, respectively. The atmospheric parameters from RAVE–DR6 are also indicated. Lower panel: renormalized interstellar spectrum represented by the black line. The dashed and solid red lines represent the profiles from the first and second (finally selected) fits, respectively. The blue shades indicate the masked regions discussed in Sect. 2.6.2. |
2.5 Quality flags
To select reliable DIB profiles, Elyajouri et al. (2016) applied a series of tests to the fit parameters (D, λC, σ) and generated different quality flags (QF). We follow their main principles. The flowchart of QF is schematically shown in Fig. 6, and below we describe in detail our procedure to determine QF ranging from QF = 5 (highest quality) to QF = 0 (lowest quality). Cases with negative QF were notfit, that is, QF = −1 was rejected by the preliminary detection, and QF = −2 means invalid spectra.
- 1.
Global test: the first test gives the upper limit of the depth D and the realistic range of the measured central wavelength λC. Here λC is converted from the stellar frame into the heliocentric frame using RVstar. The cases with D > 0.15 (the deepest absorption detected on GIBS spectra) was eliminated (arrow (a) in Fig. 6). These are spurious features generated mainly by the mismatch between the observed and synthetic spectra. We also eliminated the fittings with λC outside the range 8614.3–8625.7 Å, which is the same interval as we applied in the preliminary detection.
- 2.
Test of the DIB depth: when the first test was passed successfully (arrow (b)), we compared their depth with the standarddeviation of the fitting residuals, R = std (data–model). R was calculated for two regions: RA is for the global spectrum [8605–8640] Å, and RB is in a region close to the DIB feature [λC − 3σ, λC + 3σ]Å. When D was larger than the maximum of RA and RB (arrow (d)), then the test on the width was directly applied. When the interstellar spectrum is globally too noisy to detect the DIB or the DIB is too shallow (arrow (c)), we only compared D with the local standard deviation RB. This step allowed us to recover the DIB on the spectra that are noisy in some regions far from the DIB, but have good quality near the DIB. The cases passing this test (arrow (e)) were subjected to the same test on width as the previous ones (arrow (d)). Failed cases (arrow (g)) were examined differently.
- 3.
Test of the DIB width: in the final test, we defined some limits to select DIBs with reasonable widths. The profiles that exceed the global or local noise level (arrows (d) and (e)) gain high QF with 1.2 ≤ σ ≤ 3.2Å or low QF with 0.6 ≤ σ ≤ 1.2Å. The shallow DIBs (arrow (g)) were directly tested within the range of 0.6–1.2 Å. Any case with σ < 0.6Å was discarded (arrow (h)) and marked as QF = 0. Both the lower (0.6 Å) and upper (3.2 Å) limits were derived from the GIBS results (see Sect. 4.2.3). Profiles with σ < 0.6Å were likely to come from random noise. Extremely broad profiles (σ > 3.2Å) are due to unphysical features originating from the data processing or the fitting process. We set 1.2 Å as the boundary of the two ranges of σ to (1) select narrow DIBs through arrow (f) and (2) eliminate the flat and elongated features of uncertain origin (Elyajouri et al. 2016) for shallow DIBs (arrow (g)).
We created six QFs based on the tests to evaluate the fit quality. QF = 5 represents the best fits and the detected DIBs with proper parameters {D, λC, σ}. Recovered DIBs with QF = 4 are locally detected. Narrow DIBs with 0.6 ≤ σ ≤ 1.2Å are flagged as 3 or 2 because they exceed the global or local noise level. QF = 1 corresponds to spectra with very low S/N or shallow DIBs. A failed detection is marked as QF = 0.
 |
Fig. 4 Fitting by GPR for HIS of the star HD 166167 observed by the RAVE survey (R = 7500). Top: locally renormalized observed spectrum (black line), and the completed fit by GPR (blue curve). The atmospheric parameters from RAVE–DR6 are also indicated. Middle: decomposition of the blue curve in the top panel. The red line represents the Gaussian DIB profile, and the orange line given by the kernels of GP describes the remainder of the spectrum. Bottom: reshaped spectrum based on the first fit (black line; see Sect. 2.6.2). The solid and dashed DIB profiles are from the first (finally selected) and second fits, respectively. |
 |
Fig. 5 Examples of priors for lse, lm3∕2, σ, and λC. The priors have an original guess of σ0 = 2.0Å and λC = 8620Å. This means that P(lse) starts at 2.0 Å to drop to −∞. P(σ) and P(λC) are centeredat 2.0 and 8620 with a width of 0.5 Å. |
2.6 Equivalent width and error analysis
The equivalent width (EW) is proportional to the column density of the DIB carriers and reflects the relative oscillator strength (Jenniskens & Desert 1994). With the Gaussian profile, the EW is calculated by the depth D and width σ,
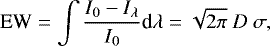 (9)
(9)
where I0 and Iλ are fluxes of the continuum and spectrum, respectively. For CIS, the calculated EW was further scaled by C because the fit C is usually not unit. There are two main sources of the EW errors, σEW, one associated with the random noise (σnoise), and the other (σspect) contributed by the continuum (HIS) or the mismatches between observed and synthetic spectra (CIS). The total error is considered as
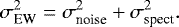 (10)
(10)
We estimated σnoise for different DIB profiles by a random-noise simulation. σspect was accessed through a second fit for each interstellar spectrum. In the following, the estimation of these two errors is explained in detail.
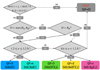 |
Fig. 6 Flowchart of our criteria to generate QF. The flag numbers and the corresponding classification paths are listed in the bottom box. Detailed explanations are given in Sect. 2.5. |
2.6.1 Random-noise simulation
The randomnoise discussed in this section mainly refers to the observational uncertainty, which is Gaussian and independent. The random-noise level of a spectrum is usually characterized by its S/N. The uncertainty introduced during the data reduction and interstellar spectra derivation is discussed and estimated in Sect. 2.6.2. Although the random noise is assumed to be Gaussian, the local noise might still distort the DIB profile and affect the fit parameters and consequently the physical quantities such as EW and radial velocity. To account for the error of EW contributed by the random noise, Elyajouri et al. (2017) made a conservative estimation: 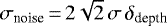 , where σ is the fit width of the DIB profile, and δdepth is the uncertainty of the DIB depth. Puspitarini et al. (2015) applied a similar formula with a scaling factor
, where σ is the fit width of the DIB profile, and δdepth is the uncertainty of the DIB depth. Puspitarini et al. (2015) applied a similar formula with a scaling factor 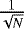 , where N is the number of pixels covering the DIB width. Their formulas were derived from a series of simulations with varying Gaussian noise and can quickly approximateσnoise. The use of σ in their formulas might lead to a strong overestimation for large DIB profiles, however.
, where N is the number of pixels covering the DIB width. Their formulas were derived from a series of simulations with varying Gaussian noise and can quickly approximateσnoise. The use of σ in their formulas might lead to a strong overestimation for large DIB profiles, however.
For a more comprehensive study and more accurate estimate of the effect of the random noise on the DIB fitting, we performed a series of random-noise simulation in the wavelength range between 8605 and 8640 Å with a pixel size of 0.1 Å, containing different Gaussian DIB profiles ({D0, μ0, σ0}) and constant continua (C0 ≡ 1). Then for every spectrum, a Gaussian noise (ɛ) was added according to an assigned S/N, that is, 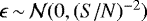 . The parameter grids were constructed as D0 ranges from 0.01 to 0.20 with a step of 0.01, μ0 ≡ 8620.0Å, and σ0 ranges from 0.05 to 5.0 Å with a step of 0.05 Å. For 20 ≤ S∕N ≤ 100, the step size is 1. For an S/N within 100–300, the step size 5. Higher S/N (300–1000) were assigned a step size of 50. Finally, the sample contains 270 000 pseudo-spectra in total with different DIB profiles and S/N. These spectra were fit by a Gaussian model with the Levenberg-Marquardt method, and the fit parameters {Df, μf, σf, Cf} were used to study the effect of the random noise. The true (EW0) and fit (EWf) EWs were calculated with Eq. (9).
. The parameter grids were constructed as D0 ranges from 0.01 to 0.20 with a step of 0.01, μ0 ≡ 8620.0Å, and σ0 ranges from 0.05 to 5.0 Å with a step of 0.05 Å. For 20 ≤ S∕N ≤ 100, the step size is 1. For an S/N within 100–300, the step size 5. Higher S/N (300–1000) were assigned a step size of 50. Finally, the sample contains 270 000 pseudo-spectra in total with different DIB profiles and S/N. These spectra were fit by a Gaussian model with the Levenberg-Marquardt method, and the fit parameters {Df, μf, σf, Cf} were used to study the effect of the random noise. The true (EW0) and fit (EWf) EWs were calculated with Eq. (9).
Figure 7 shows the distribution of the fractional error between EW0 and EWf (|EW0 −EWf|∕EW0) in the D0 − σ0 plane for some specific S/N, overlapped with some contours of EW0 calculated by the according D0 and σ0. The change in fractional errors is rough because we only fit each spectrum once. The shown σ0 is limited to 3.2, the same as the largest valid width detected on GIBS spectra. Generally, the fractional error decreases with the increase in S/N and EW0. For S∕N > 200, the fractional errors are smaller than 10% (white regions in subpanels in Fig. 7) for most of the fitting results, but for S∕N = 100, EW0 has to be as large as 0.4 Å to ensure that most of the fractional errors are within 10%. Nevertheless, some shallow profiles could still gain large errors up to 20%. If the spectra have S∕N ≈ 50, the random noise can cause fractional errors as large as 20% even for EW0 > 0.5Å, which is stronger than most of the Gaia DIBs detected in previous works (Sanner et al. 1978; Munari et al. 2008; Puspitarini et al. 2015). Therefore we only regard sources with S/N higher than 50. Moreover, for a given EW0, shallow DIBprofiles tend to gain larger errors than narrow ones because the shallow profiles cover more pixels. If σ0 is approximate to the pixel size of the spectra, the fractional error maintains a high level and does not significantly decrease with S/N. This also occurs when D0 is approximateto 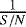 . This implies the detection limits for the width and depth of DIB. The effects of the random noise on D0 and σ0 are similar to that on EW, while the error of μ0 is more sensitive to D0 than σ0. The random noise has almost no effect on the continuum C0 for well-normalized spectra.
. This implies the detection limits for the width and depth of DIB. The effects of the random noise on D0 and σ0 are similar to that on EW, while the error of μ0 is more sensitive to D0 than σ0. The random noise has almost no effect on the continuum C0 for well-normalized spectra.
Based on the random-noise simulation, the effect of random noise on the DIB fitting was studied in detail. Estimating of σnoise is not straightforward, however, because in practice we can only access the fit parameters and not their true values. That is to say, we have to use {D, μ, σ} instead of {D0, μ0, σ0} to estimate the error of EWf contributed by the random noise, that is, σnoise. We try to build a model based on the random forest regression, which is an ensemble machine-learning method combining a large number of decision trees (Breiman 2001). The model returns σnoise when given {D, σ, S/N}. μ and C were not used because in our simulation μ0 and C0 were fixed. A quarter of the simulation results that were uniformly selected with EW0 constituted the training set, and the test set consisted of the remaining part. The regression was completed by the Python scikit-learn package (Pedregosa et al. 2011). We used 100 trees in the forest (n_estimators = 100) and followed the default values of other main parameters. The differences between the true and estimated σnoise are mainly within 0.05 Å for the training set and 0.1 Å for the test set, and they do not significantly change with EW0. The uncertainty for S∕N < 50 could be up to 0.2 Å and higher. The performance of the model is limited by the fact that the features we used {D, σ, S/N} in the algorithm are not enough to fully access the true σnoise. The estimate of σnoise is accurate for large DIB or high-quality spectra, but it is less reliable for small DIB or low-S/N spectra.
 |
Fig. 7 Distribution of the fractional error (|EW0 −EWf|∕EW0 × 100) in the D0 − σ0 plane, overlapped with the contours of EW0. In each subpanel, the fitting results are from the pseudo-spectra with the same S/N but various profiles. The colorbar is shown within 100%, while the fractional error may exceed it in some very small EW0 regions. |
2.6.2 Spectral contribution
To obtain σspect, each spectrum was fit twice. The first fit is detailed in Sect. 2.4. The second fit considered the effect of the observed–synthetic mismatch for CIS and continuum for HIS. The difference of EWs between these two fits was used to estimate σspect.
For CIS, the second fit is still a Gaussian fit, but with five masked regions centered at 8611.8, 8616.3, 8621.6, 8626.2, and 8634.1 Å, with a width of 1 Å for each of them. These regions correspond to some strong stellar lines, for instance, the Fe I lines at 8610.602, 8611.804, 8613.935, 8616.276, 8621.601, and 8632.412 Å; the Ca I line at 8633.933 Å; and the Ti I line at 8618.425 Å (the strength of these stellar lines would vary with the stellar types and metallicities), that may be poorly modeled by the synthetic spectra. Figure 3 shows that the mismatches in the masked regions are higher than average. Consequently, a large σspect is obtained. Although this method is incomplete because we cannot mask all of the abundant stellar lines in the DIB analysis interval, it is still a good estimate of σspect for strong DIBs, as discussed by Puspitarini et al. (2015).
Although the local renormalization corrects for the curved continuum of HIS, some curvatures could still remain and lead to an underestimated EW. After extracting the fitted DIB profile, we therefore applied polynomials from first to sixth order to fit the remaining HIS to approximate the possible curved continuum. Then the best fit was used to renormalize HIS again, and we refit the DIB profile with the Gaussian model (Eq. (1)).
To ensure that the second fit is reasonable, the new DIB profile was preferred only if it was stronger and deeper than the first. Otherwise, we retained the results from the first fit. For example, the second fit was accepted for star HD 149349 (Fig. 3), while it was rejected for star HD 166167 (Fig. 4). Furthermore, we obtained an EW of 0.234 ± 0.039Å for star HD 166167, which is consistent with the value of 0.217 Å reported by Munari et al. (2008), who applied a sixth-order polynomial to fit the continuum and then calculated the EW by integration. Additionally, the cases with large differences between the measured central wavelength of the two fits were eliminated, that is, ΔλC > 0.5Å (the sixth step in Fig. 1). These cases were also marked QF = 0.
2.7 Outputs and summary
The final output of each fitting was included in the fit parameters ({D, λC, σ, C} for CIS, {D, λC, σ, lse, lm3∕2} for HIS), calculated EW and its errors (σEW, σnoise, σspect), and QF. For discarded cases, all the parameters were set as –1.
3 Application to the GIBS dataset
3.1 GIBS spectra
The GIBS is a survey of red clump (RC) stars selected from the Vista Variables in the Via Lactea (VVV) catalogs (Minniti et al. 2010)in the Milky Way bulge (Zoccali et al. 2014). We used 4797 low-resolution spectra from 20 observational fields in the GIBS survey (see Fig. 8). The GIBS spectra analyzed here are from the GIRAFFE LR8 setup at the resolution R = 6500 with the spectral coverage of 8206 Å < λ < 9400 Å. For the analysis, we selected a smaller range of 8450–8950 Å because beyond the shorter interval adopted for the analysis, many skylines affect the spectra and we are interested in the region around the calcium triplet lines where the Gaia DIB is located. We calculated the S/N of each spectra between 8850 and 8858.5 Å, where no strong stellar lines are present. We also used the templates of RCs to subtract stellar components from the DIB measurement. The synthetic spectra used in this work were generated by the Turbospectrum code (Alvarez & Plez 1998), the MARCS atmosphere model (Gustafsson et al. 2008), and the line list of the Gaia–ESO survey (Heiter et al., in prep.) with Teff = 4500 K, log g = 2.5 and the particular metallicity of each star. As the residuals in the interstellar spectra are too high because of the mismatch between observed and synthetic spectra, we did not apply the CIS method to the GIBS data set.
 |
Fig. 8 Locations of 20 fields (blue and white circles) in the GIBS survey, overplotted on an extinction map derived by Gonzalez et al. (2012). The locations of all the 31 fields of the GIBS survey can be found in Fig. 1 of Zoccali et al. (2014). |
3.2 Extinction
Based on the VVV survey, Gonzalez et al. (2011, 2012) built the first complete bulge extinction map (G12 henceforth) with a differential method. They first derived the mean (J − KS) color of the RC stars in 1835 subfields and then compared it to the color of RCs in a referred region with known extinction, that is, Baade’s Window. The extinction calculated with the BEAM calculator1 is shown in Fig. 8. The resolution varies from 2′ to 6′. With a newly developed JKS photometry catalog of the VVV survey based on point spread funciton (PSF) fitting (Surot et al. 2019), Surot et al. (2020) calculated the mean (J − KS) of RC+RGB (red giant branch) stars in finer bins. A calibration was then made by comparison with G12 in areas with |b| > 3° to derive the absolute extinction values. The improved extinction map (S20 henceforth) has a higher resolution that can reach subarcmin in low-latitude regions.
We derived the extinctions of the GIBS targets from S20 according to their spatial positions. Neither S20 nor G12 were able to resolve the extinction of individual GIBS targets for |b| > 3° because the spatial resolution of these maps decrease with increasing latitudes.
3.3 Specific model for GIBS spectra
We used the GIBS spectra to validate our procedures of the DIB detection and measurement presented in Sect. 2 and also test the fitting technique based on GPR. We applied the GPR method to fit the DIB profile on the derived interstellar spectra from GIBS because (1) the data size is small, therefore the computational time is acceptable, and (2) the templates with constant Teff and log g cause considerable mismatch and correlated noise that prevent fitting the simple Gaussian model. The simple Gaussianmodel has been widely used to fit various DIB profiles on a substantial number of spectra, for example, Kos et al. (2013), Lan et al. (2015), Zasowski et al. (2015), and Elyajouri et al. (2017). We therefore did not select a specific sample to test the Gaussian fit used for cool-star spectra. An illustration is shown in Fig. 3.
Furthermore, we applied both Gaussian and asymmetric Gaussian models to the GIBS spectra to study the amplitude and the effect of the asymmetry caused by the velocity dispersion of DIB carriers along different sightlines. We chose a simple method presented in Kos (2017) to implement the asymmetry, which was introduced by making the width a function of the wavelength,
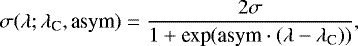 (11)
(11)
where asym is the amplitude of the asymmetry, and it is limited within ± 0.75 in the fittings.
4 Results and discussions
In this section, we study the correlation between EW and reddening, as well as the properties of the Gaia DIB based on the fitting results. In general, the Gaussian fit and the asymmetric Gaussian fit yielded similar profiles (see Sect. 4.2.1). We therefore base our results and discussions on the Gaussian fit alone.
Because of the applied synthetic spectra, the local renormalization for the GIBS spectra could lead to nonunit continua and cause an overestimation of the EW. We therefore performed a calibration to the EW according to the residual spectra (data–model). The fit profiles were shifted according to the mean flux of the residual spectra where the EW were recalculated as well. Most of the mean flux is within 0.95–1.0, implying an overestimation of the EW. For 378 cases the local continua areabove 1.0. After visual inspection, they were eliminated because the fit profiles were not physical or too noisy. The cases that did not pass the preliminary detection were also discarded. Finally, we obtained 4194 valid GIBS spectra for our DIB analysis. As the average S/N of GIBS spectra is about 80 per pixel, the fit parameters (D, λC, σ) and EW arenoise dominated, especially for small DIBs.
4.1 Linear correlation between EW and reddening
Several studies have revealed a linear correlation between EW and reddening in the optical bands for the Gaia DIB, usually taking the form of E(B − V) = a × EW. Some early estimates of a are based on several dozen hot stars, for example, 2.85 (Sanner et al. 1978) (the coefficient was calculated by Kos et al. 2013), 2.69 (Munari 2000), 4.61 (Wallerstein et al. 2007), and 2.72 (Munari et al. 2008). The measurement of E(B − V) in Wallerstein et al. (2007) is doubtful, as discussed in Munari et al. (2008). By merging several thousand RAVE cool-star spectra, Kos et al. (2013) derived a = 2.49 with an offset of 0.028. Kos et al. (2013) also studied 114 RAVE hot stars (including 31 objects from Munari et al. 2008), which yielded a highly consistent value of 2.48. Puspitarini et al. (2015) also derived a linear relation between EW of the Gaia DIB and A0 (extinction at λ = 5500Å) toward the Galactic anticenter based on 64 cool stars from Gaia–ESO, but no coefficient was given. From Fig. 7 in Puspitarini et al. (2015), we estimate a coefficient of A0 ∕EW 8620 = 2.3∕0.35 = 6.57. Applying the CCM89 model (Cardelli et al. 1989), we have E(B − V)∕EW = 2.12 (RV = 3.1), a value significantly lower than others. While Damineli et al. (2016) reported a quadratic relation between 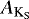 and EW based on ~100 hot stars in and around the stellar cluster Westerlund 1. Their relation is close to Munari et al. (2008) for EW < 0.5Å. As discussed below, we derived a linear correlation between EW and E(J − KS) for our GIBS sample by averaging over different reddening bins (Sect. 4.1.1) or individual fields (Sect. 4.1.2).
and EW based on ~100 hot stars in and around the stellar cluster Westerlund 1. Their relation is close to Munari et al. (2008) for EW < 0.5Å. As discussed below, we derived a linear correlation between EW and E(J − KS) for our GIBS sample by averaging over different reddening bins (Sect. 4.1.1) or individual fields (Sect. 4.1.2).
 |
Fig. 9 Correlation between the EW of the Gaia DIB and the reddening E(J − KS). The black points are the measurements from individual targets. The white and red dots are the median values taken from different reddening bins. The red error bars present the standard deviations in each bins. The red line is fit to the white and red dots. The white squares are the results from Munari et al. (2008). |
4.1.1 EW versus E(J −KS) relation
The correlation between the EW of the Gaia DIB and the reddening E(J − KS) from S20 for individual GIBS targets is shown in Fig. 9, overlapped with the measurements from Munari et al. (2008). We derived the linear relation over the GIBS targets by taking the median values from different reddening bins, ranging from E(J − KS) = 0.2 to 0.9 with a bin size of 0.1 mag (the white and red dots in Fig. 9). The linear fitting for these median points yields E(J − KS) = 1.875 (±0.152) × EW − 0.011 (±0.048). The coefficients and their standard errors were derived with the Python package statsmodels (Seabold & Perktold 2010).
The median points in bins with E(J − KS) < 0.2 mag were not used because they deviate significantly from the linear relation. This is because (a) spectra containing very small DIBs (EW < 0.05Å before calibration) did not pass the preliminary detection because of their low S/N. Therefore the median value of EW is higher than expected. (b) Most of the small DIBs are noise dominated and might be overestimated by the local increase of noise. It is not possible to select and discard the overestimated cases even by visual inspection. Reliable fittings with EW ≈ 0.1–0.2 Å can also be found in low-extinction regions, however.
In the absence of optical photometry and in order to compare our results with previous works, a conversion between E(J − KS) and E(B − V) is needed. For the NIR bands, we applied the extinction law derived by Nishiyama et al. (2009) toward the Galactic center: 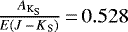 , which is widely used for Galactic Bulge studies, while for the optical–NIR conversion, we still used the CCM89 model with RV = 3.1 and the corresponding ratio
, which is widely used for Galactic Bulge studies, while for the optical–NIR conversion, we still used the CCM89 model with RV = 3.1 and the corresponding ratio 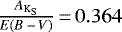 because (1) Gonzalez et al. (2011, 2012) used the same ratio to calculate E(J − KS) for RC stars, which has been used by Surot et al. (2020) to calibrate their extinction map. Therefore E(J − KS) used in this work already implies a specific ratio between
because (1) Gonzalez et al. (2011, 2012) used the same ratio to calculate E(J − KS) for RC stars, which has been used by Surot et al. (2020) to calibrate their extinction map. Therefore E(J − KS) used in this work already implies a specific ratio between 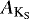 and E(B − V). (2) Although many works have pointed out that the extinction law toward the inner Milky Way deviates from the CCM89 model with RV = 3.1 (e.g., Indebetouw et al. 2005; Nishiyama et al. 2006, 2009; Nataf et al. 2016; Damineli et al. 2016), the optical–NIR relation is not studied as well as for NIR bands, and the ratio of
and E(B − V). (2) Although many works have pointed out that the extinction law toward the inner Milky Way deviates from the CCM89 model with RV = 3.1 (e.g., Indebetouw et al. 2005; Nishiyama et al. 2006, 2009; Nataf et al. 2016; Damineli et al. 2016), the optical–NIR relation is not studied as well as for NIR bands, and the ratio of 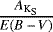 toward the Galactic Bulge is still only poorly determined (Nataf et al. (2016) did not cover E(B − V) and Damineli et al. (2016) mainly studied Westerlund 1). With the translation (
toward the Galactic Bulge is still only poorly determined (Nataf et al. (2016) did not cover E(B − V) and Damineli et al. (2016) mainly studied Westerlund 1). With the translation (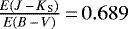 ), we obtain
), we obtain 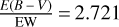 , which is highly consistent with the result of Munari et al. (2008) (see the red line and white squares in Fig. 9). The comparison with other works is shown in Fig. 10, and the coefficients for the linear relation in the NIR bands are listed in Table 1.
, which is highly consistent with the result of Munari et al. (2008) (see the red line and white squares in Fig. 9). The comparison with other works is shown in Fig. 10, and the coefficients for the linear relation in the NIR bands are listed in Table 1.
The choice of extinction law significantly affects the comparison. Assuming the CCM89 model in NIR bands (RV = 3.1), 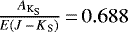 , we have
, we have 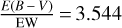 . With the extinction laws derived by Damineli et al. (2016) from optics to NIR,
. With the extinction laws derived by Damineli et al. (2016) from optics to NIR, 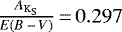 and
and 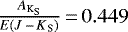 , we obtain a ratio of
, we obtain a ratio of 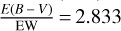 . Although without the optical photometry for GIBS targets, the high consistency between optical and NIR relations against the Gaia DIB still needs to be confirmed by more studies, our comparison and the consistency found in this work and Damineli et al. (2016) imply that the correlations of EW with optical and NIR extinctions are at least not very far away from each other. However, the relations between EW 8620 and extinction in different bands and the extinction law have been studied very little. On the other hand, the correlation between EW and extinction is also related to the dust properties along the line of sight. Ramírez-Tannus et al. (2018) reported a linear correlation between extinction-normalized EW, EW ∕AV, and
. Although without the optical photometry for GIBS targets, the high consistency between optical and NIR relations against the Gaia DIB still needs to be confirmed by more studies, our comparison and the consistency found in this work and Damineli et al. (2016) imply that the correlations of EW with optical and NIR extinctions are at least not very far away from each other. However, the relations between EW 8620 and extinction in different bands and the extinction law have been studied very little. On the other hand, the correlation between EW and extinction is also related to the dust properties along the line of sight. Ramírez-Tannus et al. (2018) reported a linear correlation between extinction-normalized EW, EW ∕AV, and 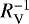 for 14 DIBs in M17. They derived a relation between EW and E(B − V). Li et al. (2019) used E(B − V) to normalize the EW and reported no relation with
for 14 DIBs in M17. They derived a relation between EW and E(B − V). Li et al. (2019) used E(B − V) to normalize the EW and reported no relation with 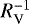 . They suggested that the hydrogen column density, NH, is a more appropriate normalization than extinction and reddening. Theoretically, small dust grains would present a steep extinction curve with small RV, and very large grains experience a flat curve with RV → ∞ (Draine 2003). This means that different RV values should indicate different correlations between EW and extinction, especially in the ultraviolet and optical bands. Although the variation in RV in a single region is always smaller than the uncertainty in EW and extinction, we could investigate it from different sightlines: the linear coefficient between EW and E(J − KS) toward the Galactic Bulge (this work and Munari 2000; Munari et al. 2008) is apparently larger than the value toward the Galactic anticenter (Puspitarini et al. 2015), although this difference might also be caused by the dependence of the extinction laws on different lines of sight. Kos et al. (2013) derived a mediate value from a substantial number of sightlines. Nevertheless, our studies are also affected by the method of extinction calculation and DIB measurement, which undermines the credibility of the variation of EW–extinction correlation for different sightlines. On the other hand, the environmental dependence of the DIB carriers complicates this question as well. For example, the deviation from linear relation in high-extinction regions (AV ≈ 10 mag) may be caused by the carrier depletion in dense cores (Elyajouri & Lallement 2019). The forthcoming Gaia–RVS spectra are expected to bring new insights into the DIB properties. Its large spatial coverage and uniform DIB and extinction measurements will give us an opportunity to unveil the relation between the DIB strength and the corresponding dust properties.
. They suggested that the hydrogen column density, NH, is a more appropriate normalization than extinction and reddening. Theoretically, small dust grains would present a steep extinction curve with small RV, and very large grains experience a flat curve with RV → ∞ (Draine 2003). This means that different RV values should indicate different correlations between EW and extinction, especially in the ultraviolet and optical bands. Although the variation in RV in a single region is always smaller than the uncertainty in EW and extinction, we could investigate it from different sightlines: the linear coefficient between EW and E(J − KS) toward the Galactic Bulge (this work and Munari 2000; Munari et al. 2008) is apparently larger than the value toward the Galactic anticenter (Puspitarini et al. 2015), although this difference might also be caused by the dependence of the extinction laws on different lines of sight. Kos et al. (2013) derived a mediate value from a substantial number of sightlines. Nevertheless, our studies are also affected by the method of extinction calculation and DIB measurement, which undermines the credibility of the variation of EW–extinction correlation for different sightlines. On the other hand, the environmental dependence of the DIB carriers complicates this question as well. For example, the deviation from linear relation in high-extinction regions (AV ≈ 10 mag) may be caused by the carrier depletion in dense cores (Elyajouri & Lallement 2019). The forthcoming Gaia–RVS spectra are expected to bring new insights into the DIB properties. Its large spatial coverage and uniform DIB and extinction measurements will give us an opportunity to unveil the relation between the DIB strength and the corresponding dust properties.
 |
Fig. 10 Comparison between the EW–E(J − KS) linear relations derived from different works. Relations derived in optical bands are translated into the extinction laws applied in Sect. 4.1.1. The lines of this work (red) and Munari et al. (2008; black) overlap. |
Coefficients and their uncertainties of the linear relations between the Gaia DIB EW and reddenings given in the literature and this work.
 |
Fig. 11 Correlation between the EW of the Gaia DIB and the reddening E(J − KS) derived from individual GIBS fields before (left panel) and after (right panel) the correction. The red lines are fit to the red dots in each panel, and white dots are discarded. The dot-dashed black lines present the relation derived by Munari et al. (2008). The dot-dashed green lines indicate E(J − KS) = 0.10 and 0.25 mag in left and right panels, respectively. Four fields are indicated in each panel for comparison, and a detailed discussion ispresented in Sect. 4.1.2 and Appendix A. |
4.1.2 EW versus E(J − KS) relation from individual GIBS fields
We decreased the EW dispersion by averaging the measurements by calculating the median values of the EW and E(J − KS) for each GIBS field individually. The correlation between EW and E(J − KS) derived from the 20 GIBS fields is shown in Fig. 11 (left panel). After discarding fields with E(J − KS) < 0.1 (indicated by the dot-dashed green line), we gain a linear relation of E(J − KS) = 1.802 (±0.258) × EW + 0.004 (±0.065), corresponding to 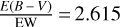 , which is slightly smaller than the value derived before (2.721). The EW dispersion in each field does not notably decrease compared to that in the reddening bins. A possible reason is that the low spatial resolution of E(J − KS) obscures the environmental variation in each GIBS field, which is traced by the Gaia DIB, leading to large dispersion of EW but small dispersion of E(J − KS) (the dispersion of E(J − KS) is usually smaller thanits uncertainty of individual targets). This cannot account for the large dispersion in the fields with large EW, however, especially for the field (l, b) = (8, −2) (indicated by “F1” in Fig. 11).
, which is slightly smaller than the value derived before (2.721). The EW dispersion in each field does not notably decrease compared to that in the reddening bins. A possible reason is that the low spatial resolution of E(J − KS) obscures the environmental variation in each GIBS field, which is traced by the Gaia DIB, leading to large dispersion of EW but small dispersion of E(J − KS) (the dispersion of E(J − KS) is usually smaller thanits uncertainty of individual targets). This cannot account for the large dispersion in the fields with large EW, however, especially for the field (l, b) = (8, −2) (indicated by “F1” in Fig. 11).
The problem may come from the contamination of stars in the GIBS target selection that are not RC stars. The RC stars in the GIBS survey are selected based on the J versus (J − KS) color-magnitude diagram (CMD) witha limit in the J magnitude and a lower cut of J − KS, while J − KS is not stringently constrained at the red end (see Fig. 3 in Zoccali et al. 2014). Therefore the RC sample might be contaminated by highly reddened dwarfs and/or RGB stars. The spectra of the contaminators that might be very different from the RC template may give rise to pseudo-features on the interstellar spectra, causing incorrect fittings and calculations of EW. Although E(J − KS) we used for the targets come from S20, which is not sensitive to stellar type, their map was calibrated by Gonzalez et al. (2012), which was based on RC stars. This means that contaminators far away from the peak color (J − KS) will also gain incorrect E(J − KS) values.
We therefore performed the correction for both reddening and EW based on VVV–DR2 catalog2 (Minniti et al. 2017). We constructed a purer sample of RC stars by applying an additional color cut. For each field, RC candidates were first selected from the VVV catalog in a circular region located at the field center with a radius of 0.5°. Then we fit the (J − KS) colors within the range of the J magnitudes given by the GIBS targets (see the dashed orange lines in Fig. A.1) with a Gaussian function to obtain the peak color as well as the 1σ width. This criterion ensures that our RC sample is as pure as possible, with the disadvantage that we loose stars. The percentage of the rejected stars differs for different fields. In total, we obtained 2437 targets in the purer sample, compared to 4194 in original sample. This means that about 42% stars are discarded. Assuming an intrinsic color of the RC stars of 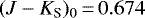 (Gonzalez et al. 2011), we obtain an average E(J − KS) for each GIBS field where the standard deviation of J − KS is treated as the uncertainty of E(J − KS), ΔE(J − KS), including not only the error of E(J − KS) calculated by RC stars, but also the dispersion of E(J − KS) in each field. For low-reddening fields, ΔE(J − KS) are similar to the mean errors of E(J − KS) given by S20. The average value of ΔE(J − KS), 0.066, is also close to the resultant error of RC stars when a photometric error of 0.03 for the J and KS bands and a spread of
(Gonzalez et al. 2011), we obtain an average E(J − KS) for each GIBS field where the standard deviation of J − KS is treated as the uncertainty of E(J − KS), ΔE(J − KS), including not only the error of E(J − KS) calculated by RC stars, but also the dispersion of E(J − KS) in each field. For low-reddening fields, ΔE(J − KS) are similar to the mean errors of E(J − KS) given by S20. The average value of ΔE(J − KS), 0.066, is also close to the resultant error of RC stars when a photometric error of 0.03 for the J and KS bands and a spread of 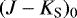 of 0.03 is assumed. The increase in ΔE(J − KS) in highly extincted fields is caused by the J-magnitude range applied for GIBS targets. A wider J-magnitude range covers a wider range of extinction and results in a larger dispersion of E(J − KS). ΔE(J − KS) is consequently dominated by the dispersion and can reach values above 0.1 mag.
of 0.03 is assumed. The increase in ΔE(J − KS) in highly extincted fields is caused by the J-magnitude range applied for GIBS targets. A wider J-magnitude range covers a wider range of extinction and results in a larger dispersion of E(J − KS). ΔE(J − KS) is consequently dominated by the dispersion and can reach values above 0.1 mag.
Furthermore, the median EW of each field was recalculated by only considering the targets with J − KS within the 1σ region (dashed green lines in Fig. A.1). The correlation between EW and E(J − KS) for individual fields after correction is presented in the right panel in Fig. 11. The dispersion of EW in each field markedly decreases and now is comparable to the uncertainty of E(J − KS). A tighter linearity of the correlation was also derived by considering fields with E(J − KS) > 0.25 with a Pearson correlation coefficient of 0.95, compared to the value 0.88 before the correction. The coefficient of the linear relation is E(J − KS) = 1.884 (±0.225) × EW − 0.012 (±0.072), corresponding to 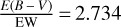 , which is highly consistent with Munari et al. (2008) as well. Using our new purer sample (see Fig. A.2), we obtain a similar relation (as discussed in detail in Appendix A). The relative strength (EW∕AV ≈ 0.1Åmag−1) and the tight correlation with reddening confirm that Gaia DIB is a powerful tracer of ISM species, independent of the foreground extinction, as suggested by Kos et al. (2013).
, which is highly consistent with Munari et al. (2008) as well. Using our new purer sample (see Fig. A.2), we obtain a similar relation (as discussed in detail in Appendix A). The relative strength (EW∕AV ≈ 0.1Åmag−1) and the tight correlation with reddening confirm that Gaia DIB is a powerful tracer of ISM species, independent of the foreground extinction, as suggested by Kos et al. (2013).
Four fields were selected to demonstrate the correction effect: F1 (l, b) = (8, −2), F2 (l, b) = (0, −1), F3 (l, b) = (−5, −2), and F4 (l, b) = (−4, −6). They are indicated in Fig. 11. The applied correction performs very well for highly extincted regions. However, it intensifiesthe deviation of the fields with low extinctions because (a) the S/N of the GIBS target limits the detection of small DIBS (see also Fig. 7), and (b) at high latitudes where extinction is lower, J − KS is not very sensitive to small-scale variation in the reddening. Optical data such as B − V would be more sensitive.
 |
Fig. 12 Comparison between the EWs of Gaussian and asymmetric Gaussian fits. The color represents the number density. The dashed black line traces the one-to-one correspondence. |
4.2 Properties of the Gaia DIB
4.2.1 Asymmetry of the DIB profile
Different DIBs have diverse profiles, from single profiles (Sarre et al. 1995) to resolved substructures (Galazutdinov et al. 2002). Asymmetric shapes originate from the distortion of unresolved substructures or blended DIBs (Kos 2017). The Gaia DIB is suggested to be blended by two DIBs (Jenniskens & Desert 1994), while no intrinsic asymmetry has been unveiled by previous works. For most of the GIBS results, the difference between Gaussian and asymmetric Gaussian EW is comparable to their uncertainties (Fig. 12). As shown in Fig. 13, large asymmetries only occur in small DIBs, which probably originate in noise. No signature of intrinsic asymmetry of the Gaia DIB is revealed by Figs. 12 and 13 for large or small EWs.
4.2.2 Rest-frame wavelength
The rest-frame wavelength of the Gaia DIB is reported as 8620.8 Å by Galazutdinov et al. (2000) from one single star, and 8621.2 Å by Jenniskens & Desert (1994) from four hot stars, and 8620.4 Å by Munari (2000) and Munari et al. (2008) from dozens of RAVE hot stars. The determination of Munari et al. (2008) was based on the assumption that the average velocity of their carriers, which are close to the Galactic center, is essentially zero, after adopting the ISM radial velocity map of Brand & Blitz (1993). Therefore the average central wavelength λC represents the rest-frame wavelength.
We followed this method and selected spectra from the GIBS fields with − 3° < b < 3° and − 6° < l < 3°. Finally, we obtained 1015 spectra. Theobserved λC is in the stellar frame, and it has to be converted into the heliocentric frame based on the stellar radial velocity. The converted λC presents a Gaussian distribution (Fig. 14, middle panel, green histograms) with a mean value of 8620.55 Å and a standard deviation of 0.55 Å. Our derived rest-frame wavelength is close to the result of Munari et al. (2008), but the large uncertainty makes it still not sufficiently definite. A more accurate method is investigating measurements toward the Galactic anticenter, as illustrated in Zasowski et al. (2015), which we intend to apply to the Gaia–RVS spectra.
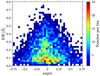 |
Fig. 13 EW as a function of the asymmetry (asym). The color shows the number of stars in each calculated bin. |
4.2.3 Parameter distributions
Figure 14 shows the distributions of the measured DIB parameters from the GIBS spectra: depth D versus EW, line center λC, and width σ. Unreasonable results with very small or large measurements were eliminated. Small EWs increase with depth, while the relation deviates from linearity when EW > 0.2Å. Profiles with D > 0.15 come from spectra without proper normalization and were discarded. The limit of D in the QF test (Sect. 2.5) was therefore set as 0.15.
The peak value of λC for all the GIBS targets is the same as that of the subsample for deriving the rest-frame wavelength. The distribution of the subsample can be well fit by a Gaussian function. However, the λC distribution of all the GIBS targets apparently deviates from the Gaussian profile and contains a bump around 8624 Å. The origin of this second bump is not clear and will be studied in a forthcoming paper.
The valid widths are within 0.6–3.2 Å, with a peak value of 1.74 Å. This value is close to the peak value of the APOGEE DIB λ1.5273 derived by Zasowski et al. (2015). These two DIBs also have a similar relative strength. An abrupt decrease in σ occurs at ~ 1.4 Å; it is larger than that of the APOGEE DIB but consistent with APOGEE measurements for sightlines with l < 40°. As the inner Galaxy generally contains broader features than the outer Galaxy (Zasowski et al. 2015), we set a lower value σ = 1.2 for the QF test to distinguish narrow and shallow DIBs. We did not find any DIB width larger than 3.2 Å but a steep decrease from 2 to 3. However, Zasowski et al. (2015) revealed that the APOGEE DIB can be as broad as 6 Å toward the Galactic center. The upper limit of σ in the QF test could change if we were to find physical DIB profiles with larger width in further studies.
 |
Fig. 14 Distributions of the DIB parameters. Left panel: depth D vs. EW. The color represents the number density. Middle panel: measured line center λC in the heliocentric frame. The upper axis shows the corresponding radial velocities of the DIB carriers. The green histograms present the subsample selected to determine the rest-frame wavelength (see Sect. 4.2.2). Right panel: histograms of the width σ. |
5 Conclusions
The main goal of this work was to develop a procedure for the automatic detection and measurement of the Gaia DIB (λ ≈ 8620Å). A preliminary detection was applied to exclude low-S/N spectra and/or DIBs below the detection limit. The DIB feature was extracted from the cool-star spectra using synthetic spectra, while for hot stars, we applied a specific model based on GP (Kos 2017) to directly measure the DIB feature on the observed spectra without any stellar templates. The DIB profile was fit by a Gaussian function, and the EW was also calculated. A simulation based on pseudo-spectra with different S/N illustrated the effect of the random noise on the DIB fitting, as well as the EW calculation. Based on these simulations, a minimum S/N of 50 is required to detect DIBs. The error contributed by the synthetic spectra for cool stars and local continua forhot stars was also considered through a second fit. Furthermore, some tests on fitted parameters, {D, λC, σ}, similar to Elyajouri et al. (2016), were used to assess their qualities.
These procedures and techniques were applied on a sample of 4979 GIBS spectra. The main results are summarized below.
By taking the median values from different reddening bins, we derived a linear relation between the EW of the Gaia DIB and the reddening: E(J − KS) = 1.875 (±0.152) × EW − 0.011 (±0.048). Applying the CCM89 model and the NIR extinction laws toward Galactic center from Nishiyama et al. (2009), we find E(B − V)∕EW = 2.721, which is highly consistent with the results of Munari (2000) (2.69) and Munari et al. (2008) (2.72). Additionally, the difference of the coefficient between our result and other studies with different sightlines implies a possible variation in the relation for different ISM conditions.
The median measurements from individual GIBS fields presented a relation with a coefficient of E(J − KS)∕EW = 1.802 ± 0.258, with a relatively large dispersion of the EW in each field due to the contamination of non-RC stars in the GIBS sample. We eliminated them by using an additional color cut. This led to a smaller dispersion and improved the linearity of the EW–E(J − KS) correlation for individual fields. The corrected relation, E(J − KS) = 1.884 (±0.225) × EW − 0.012 (±0.072), also compares well with other results.
Assuming that the average radial velocity of the DIB carrier is zero when they are distributed close to the Galacticcenter (Brand & Blitz 1993), we determined the rest-frame wavelength of the Gaia DIB as λ0 = 8620.55 ± 0.55Å.
We also fit the GIBS spectra with an asymmetric Gaussian model. The results are in general consistent with those from the Gaussian model. No intrinsic asymmetry is found. This shows that the Gaussian profile is a proper assumption for the Gaia DIB and can be applied to the spectra from other spectroscopic surveys.
Acknowledgements
We thank the anonymous referee for very helpful suggestions and constructive comments. We would like to thank Dr. Janez Kos for his help with the Gaussian process technique and his useful suggestions. This work made use of the data from the sky surveys of GIBS and VVV. Funding for RAVE has been provided by: the Leibniz Institute for Astrophysics Potsdam (AIP); the Australian Astronomical Observatory; the Australian National University; the Australian Research Council; the French National Research Agency; the German Research Foundation (SPP 1177 and SFB 881); the European Research Council (ERC-StG 240271 Galactica); the Istituto Nazionale di Astrofisica at Padova; The Johns Hopkins University; the National Science Foundation of the USA (AST-0908326); the W. M. Keck foundation; the Macquarie University; the Netherlands Research School for Astronomy; the Natural Sciences and Engineering Research Council of Canada; the Slovenian Research Agency; the Swiss National Science Foundation; the Science & Technology FacilitiesCouncil of the UK; Opticon; Strasbourg Observatory; and the Universities of Basel, Groningen, Heidelberg and Sydney. E.V. acknowledges the Excellence Cluster ORIGINS Funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy – EXC – 2094 –390783311. H.Z. is funded by the China Scholarship Council (No.201806040200).
Appendix A Correction for individual fields
As a standard candle (Paczyński & Stanek 1998), RC stars are widely used to trace interstellar extinction (Indebetouw et al. 2005; Gao et al. 2009; Wang & Chen 2019) and nebular distance (Güver et al. 2010; Shan et al. 2018; Wang et al. 2020; Chen et al. 2020). RC candidates are usually selected from (J − KS, KS) CMD with empirical borders defined by naked eyes (e.g., Wang et al. 2020; Chen et al. 2020). To exclude the contamination of other types of stars, peak colors are determined in different KS bins to form the track of RC toward a given line of sight. With a similar method, we corrected for E(J − KS) and EW for individual GIBS fields (Sect. 4.1.2).
Figure A.1 presents the (J − KS, J) CMD for four selected fields (see Sect. 4.1.2 and Fig. 11) to illustrate the tightening caused by the correction in the linearity correlation between EW and E(J − KS). F1 shows that many stars are found to be to the right of the peak color out of the 1σ region, which might be highly reddened non-RC stars, leading to a much higher average E(J − KS) of F1, as shown in Fig. 11. The corrected reddening becomes significantly lower and fits the linear relation much better with the corrected EW. On theother hand, F2 contains some foreground stars (possible dwarf stars) located at the blue side of the peak color. After correction, E(J − KS) and EW slightly increase and are highly consistent with the linear relation derived by Munari et al. (2008). The largely increased uncertainty of E(J − KS) is due to the wide range of J magnitudes (≈1.2 mag). A trend can be found toward the lower right of the peak color (the brightest part in F2 CMD in Fig. A.1). This means that the RC stars, which all lie at the bulge distance, spread in the CMD following the reddening vector because of the differential reddening over the selected region. Therefore the dispersion of EW in F2 is not only caused by the uncertainties, but implies the trace of environmental variation, which is hardly unveiled by the 2D extinction maps.
F3 have contaminators on both sides. The corrected E(J − KS) slightly increases, but the EW is nearly unchanged, while the dispersion of EW becomes apparently smaller after the contaminators are eliminated. This is the case in nearly all the fields. The correction can alleviate the EW dispersion. The correction also causes the increase in the median EW for the fields with E(J − KS) < 0.2 mag. F4 is typical of these fields. Its reddening decreases by about 0.05 mag, while its EW increases by about 0.05 mag, so that it becomes more like an outlier. The reasons for the overestimation of EW could be that (1) small DIBs cannot be detected because of the low spectral S/N, thus the median values increase, (2) the reduction in RC density at high latitudes makes it harder to accurately estimate the reddening for these fields, and (3) dwarfs with high reddening could have J − KS very close to the peak colors and can hardly be excluded. Consequently, some of the detected DIBs may be pseudo-features caused by the mismatches between the spectra of the dwarfs and the template for RC stars. Their EWs increase the median EW of the field. This means that our correction does not perform well for low-reddening fields at high latitudes.
We derived the purer RC sample with targets in each field within 1σ width of (J − KS). Finally, we obtained 2437 cases. The EW–E(J − KS) relation derived by the purer RC sample is shown in Fig. A.2. We still derive median values of EW and E(J − KS) with E(J − KS) within 0.2–0.9 mag with a step of 0.1 mag. The linear relation is E(J − KS) = 1.825 (±0.123) × EW + 0.002 (±0.039). The coefficient is consistent (although slightly smaller) with previous derived values, and the intercept is much closer to zero. We can also find that (1) almost no cases with E(J − KS) > 1.0. High reddening, especially in F1, is excluded by the correction, and (2) large EW still exist, implying that they are true features. They trace the variation in the ISM, while E(J − KS) failed because of the low resolution of the extinction map.
 |
Fig. A.1 (J − KS, J) CMD for four selected GIBS fields. The gray-scale image shows the number density of the stars selected from VVV–DR2 catalog. The red dots are the GIBS targets in each field. JKS photometry of GIBS targets are provided by the PSF photometry catalog developed by Surot et al. (2019). The dashed green lines indicate the 1σ extent widths around the RC peak densities for the regions defined by the range of J magnitudes of GIBS targets in each field (dashed orange lines). The name and coordinates of each field are indicated at the upper left corner in each panel. |
References
- Alvarez, R., & Plez, B. 1998, A&A, 330, 1109 [NASA ADS] [Google Scholar]
- Brand, J., & Blitz, L. 1993, A&A, 275, 67 [NASA ADS] [Google Scholar]
- Breiman, L. 2001, Mach. Learn., 45, 5 [CrossRef] [Google Scholar]
- Campbell, E. K., & Maier, J. P. 2018, ApJ, 858, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Campbell, E. K., Holz, M., Gerlich, D., & Maier, J. P. 2015, Nature, 523, 322 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, H. C., Lallement, R., Babusiaux, C., et al. 2013, A&A, 550, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, B., Wang, S., Hou, L., et al. 2020, MNRAS, 496, 4637 [NASA ADS] [CrossRef] [Google Scholar]
- Cordiner, M. A., Linnartz, H., Cox, N. L. J., et al. 2019, ApJ, 875, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, N. L. J., & Spaans, M. 2006, A&A, 451, 973 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cox, N. L. J., Boudin, N., Foing, B. H., et al. 2007, A&A, 465, 899 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cox, N. L. J., Ehrenfreund, P., Foing, B. H., et al. 2011, A&A, 531, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Damineli, A., Almeida, L. A., Blum, R. D., et al. 2016, MNRAS, 463, 2653 [NASA ADS] [CrossRef] [Google Scholar]
- Desert, F. X., Jenniskens, P., & Dennefeld, M. 1995, A&A, 303, 223 [Google Scholar]
- Draine, B. T. 2003, ARA&A, 41, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenstein, D. J., Weinberg, D. H., Agol, E., et al. 2011, AJ, 142, 72 [Google Scholar]
- Elyajouri, M., & Lallement, R. 2019, A&A, 628, A67 [CrossRef] [EDP Sciences] [Google Scholar]
- Elyajouri, M., Monreal-Ibero, A., Remy, Q., & Lallement, R. 2016, ApJS, 225, 19 [Google Scholar]
- Elyajouri, M., Lallement, R., Monreal-Ibero, A., Capitanio, L., & Cox, N. L. J. 2017, A&A, 600, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fan, H., Hobbs, L. M., Dahlstrom, J. A., et al. 2019, ApJ, 878, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galazutdinov, G. A., Musaev, F. A., Krełowski, J., & Walker, G. A. H. 2000, PASP, 112, 648 [NASA ADS] [CrossRef] [Google Scholar]
- Galazutdinov, G., Moutou, C., Musaev, F., & Krełowski, J. 2002, A&A, 384, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gao, J., Jiang, B. W., & Li, A. 2009, ApJ, 707, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Geary, J. C. 1975, PhD thesis, The University of Arizona, USA [Google Scholar]
- Gershman, S. J., & Blei, D. M. 2012, J. Math. Psychol., 56, 1 [CrossRef] [Google Scholar]
- Gilmore, G., Randich, S., Asplund, M., et al. 2012, The Messenger, 147, 25 [NASA ADS] [Google Scholar]
- Gonzalez, O. A., Rejkuba, M., Zoccali, M., Valenti, E., & Minniti, D. 2011, A&A, 534, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gonzalez, O. A., Rejkuba, M., Zoccali, M., et al. 2012, A&A, 543, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Güver, T., Özel, F., Cabrera-Lavers, A., & Wroblewski, P. 2010, ApJ, 712, 964 [NASA ADS] [CrossRef] [Google Scholar]
- Heger, M. L. 1922, Lick Observ. Bull., 10, 146 [Google Scholar]
- Herbig, G. H. 1975, ApJ, 196, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Hobbs, L. M., York, D. G., Snow, T. P., et al. 2008, ApJ, 680, 1256 [NASA ADS] [CrossRef] [Google Scholar]
- Indebetouw, R., Mathis, J. S., Babler, B. L., et al. 2005, ApJ, 619, 931 [NASA ADS] [CrossRef] [Google Scholar]
- Jenniskens, P.,& Desert, F. X. 1994, A&AS, 106, 39 [Google Scholar]
- Katz, D., Sartoretti, P., Cropper, M., et al. 2019, A&A, 622, A205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kos, J. 2017, MNRAS, 468, 4255 [NASA ADS] [CrossRef] [Google Scholar]
- Kos, J., Zwitter, T., Grebel, E. K., et al. 2013, ApJ, 778, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Kos, J., Zwitter, T., Wyse, R., et al. 2014, Science, 345, 791 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kroto, H. 1988, Science, 242, 1139 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lallement, R., Cox, N. L. J., Cami, J., et al. 2018, A&A, 614, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lan, T.-W., Ménard, B., & Zhu, G. 2015, MNRAS, 452, 3629 [Google Scholar]
- Leger, A., & D’Hendecourt, L. 1985, A&A, 146, 81 [Google Scholar]
- Li, K., Li, A., & Xiang, F. Y. 2019, MNRAS, 489, 708 [CrossRef] [Google Scholar]
- Majewski, S. R., APOGEE Team, & APOGEE-2 Team. 2016, Astron. Nachr., 337, 863 [NASA ADS] [CrossRef] [Google Scholar]
- Merrill, P. W. 1934, PASP, 46, 206 [NASA ADS] [CrossRef] [Google Scholar]
- Merrill, P. W. 1936, ApJ, 83, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Minniti, D., Lucas, P. W., Emerson, J. P., et al. 2010, New Astron., 15, 433 [Google Scholar]
- Minniti, D., Lucas, P., & VVV Team. 2017, VizieR Online Data Catalog: II/348 [Google Scholar]
- Munari, U. 2000, Molecules in Space and in the Laboratory, eds. I. Porceddu, & S. Aiello, 67, 179 [Google Scholar]
- Munari, U., Tomasella, L., Fiorucci, M., et al. 2008, A&A, 488, 969 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nataf, D. M., Gonzalez, O. A., Casagrande, L., et al. 2016, MNRAS, 456, 2692 [NASA ADS] [CrossRef] [Google Scholar]
- Nishiyama, S., Nagata, T., Kusakabe, N., et al. 2006, ApJ, 638, 839 [Google Scholar]
- Nishiyama, S., Tamura, M., Hatano, H., et al. 2009, ApJ, 696, 1407 [NASA ADS] [CrossRef] [Google Scholar]
- Paczyński, B., & Stanek, K. Z. 1998, ApJ, 494, L219 [NASA ADS] [CrossRef] [Google Scholar]
- Pedregosa, F., Varoquaux, G., Gramfort, A., et al. 2011, J. Mach. Learn. Res., 12, 2825 [Google Scholar]
- Puspitarini, L., Lallement, R., Babusiaux, C., et al. 2015, A&A, 573, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramírez-Tannus, M. C., Cox, N. L. J., Kaper, L., & de Koter A. 2018, A&A, 620, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rasmussen, C. E., & Williams, C. K. 2006, Gaussian Process for Machine Learning (The MIT Press) [Google Scholar]
- Recio-Blanco, A., de Laverny, P., Allende Prieto, C., et al. 2016, A&A, 585, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salama, F., Galazutdinov, G. A., Krełowski, J., Allamand ola, L. J., & Musaev, F. A. 1999, ApJ, 526, 265 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Sanner, F., Snell, R., & vanden Bout P. 1978, ApJ, 226, 460 [NASA ADS] [CrossRef] [Google Scholar]
- Sarre, P. J., Miles, J. R., Kerr, T. H., et al. 1995, MNRAS, 277, L41 [NASA ADS] [Google Scholar]
- Schulz, E., Speekenbrink, M., & Krause, A. 2018, J. Math. Psychol., 85, 1 [CrossRef] [Google Scholar]
- Seabold, S., & Perktold, J. 2010, in 9th Python Science Conference [Google Scholar]
- Shan, S. S., Zhu, H., Tian, W. W., et al. 2018, ApJS, 238, 35 [CrossRef] [Google Scholar]
- Steinmetz, M., Zwitter, T., Siebert, A., et al. 2006, AJ, 132, 1645 [Google Scholar]
- Steinmetz, M., Guiglion, G., McMillan, P. J., et al. 2020a, AJ, 160, 83 [CrossRef] [Google Scholar]
- Steinmetz, M., Matijevič, G., Enke, H., et al. 2020b, AJ, 160, 82 [CrossRef] [Google Scholar]
- Surot, F., Valenti, E., Hidalgo, S. L., et al. 2019, A&A, 629, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Surot, F., Valenti, E., Gonzalez, O. A., et al. 2020, A&A, 644, A140 [CrossRef] [EDP Sciences] [Google Scholar]
- van der Zwet, G. P., & Allamandola, L. J. 1985, A&A, 146, 76 [NASA ADS] [Google Scholar]
- Wallerstein, G., Sandstrom, K., & Gredel, R. 2007, PASP, 119, 1268 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, S., & Chen, X. 2019, ApJ, 877, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, S., Zhang, C., Jiang, B., et al. 2020, A&A, 639, A72 [CrossRef] [EDP Sciences] [Google Scholar]
- Williams, C. K. 1998, Learning in Graphical Models Berlin: (Springer), 599 [CrossRef] [Google Scholar]
- Xiang, F. Y., Li, A., & Zhong, J. X. 2017, ApJ, 835, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, H. B., & Liu, X. W. 2012, MNRAS, 425, 1763 [NASA ADS] [CrossRef] [Google Scholar]
- Zasowski, G., Ménard, B., Bizyaev, D., et al. 2015, ApJ, 798, 35 [Google Scholar]
- Zoccali, M., Gonzalez, O. A., Vasquez, S., et al. 2014, A&A, 562, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
We accessed the data by SIMBAD/VizieR-II/348, https://vizier.u-strasbg.fr/viz-bin/VizieR-3?-source=II/348/vvv2
All Tables
Coefficients and their uncertainties of the linear relations between the Gaia DIB EW and reddenings given in the literature and this work.
All Figures
 |
Fig. 1 Flowchart compiling our full procedures of the detection and measurement of the Gaia DIB. |
| In the text | |
 |
Fig. 2 Examples of the local renormalization for five RAVE spectra (R = 7500) of hot stars. The black lines are the original spectra, and the orange lines indicate the renormalized spectra. The black arrows indicate the Gaia DIB. The names and atmospheric parameters are also indicated. The strong stellar feature near the DIB profile seen on HD 150850 and HD 166167 is the N I line. |
| In the text | |
 |
Fig. 3 Gaussian model for CIS of the star HD 149349 observed by the RAVE survey (R = 7500). Upper panel: black and blue lines show the observed and synthetic spectra, respectively. The atmospheric parameters from RAVE–DR6 are also indicated. Lower panel: renormalized interstellar spectrum represented by the black line. The dashed and solid red lines represent the profiles from the first and second (finally selected) fits, respectively. The blue shades indicate the masked regions discussed in Sect. 2.6.2. |
| In the text | |
 |
Fig. 4 Fitting by GPR for HIS of the star HD 166167 observed by the RAVE survey (R = 7500). Top: locally renormalized observed spectrum (black line), and the completed fit by GPR (blue curve). The atmospheric parameters from RAVE–DR6 are also indicated. Middle: decomposition of the blue curve in the top panel. The red line represents the Gaussian DIB profile, and the orange line given by the kernels of GP describes the remainder of the spectrum. Bottom: reshaped spectrum based on the first fit (black line; see Sect. 2.6.2). The solid and dashed DIB profiles are from the first (finally selected) and second fits, respectively. |
| In the text | |
 |
Fig. 5 Examples of priors for lse, lm3∕2, σ, and λC. The priors have an original guess of σ0 = 2.0Å and λC = 8620Å. This means that P(lse) starts at 2.0 Å to drop to −∞. P(σ) and P(λC) are centeredat 2.0 and 8620 with a width of 0.5 Å. |
| In the text | |
 |
Fig. 6 Flowchart of our criteria to generate QF. The flag numbers and the corresponding classification paths are listed in the bottom box. Detailed explanations are given in Sect. 2.5. |
| In the text | |
 |
Fig. 7 Distribution of the fractional error (|EW0 −EWf|∕EW0 × 100) in the D0 − σ0 plane, overlapped with the contours of EW0. In each subpanel, the fitting results are from the pseudo-spectra with the same S/N but various profiles. The colorbar is shown within 100%, while the fractional error may exceed it in some very small EW0 regions. |
| In the text | |
 |
Fig. 8 Locations of 20 fields (blue and white circles) in the GIBS survey, overplotted on an extinction map derived by Gonzalez et al. (2012). The locations of all the 31 fields of the GIBS survey can be found in Fig. 1 of Zoccali et al. (2014). |
| In the text | |
 |
Fig. 9 Correlation between the EW of the Gaia DIB and the reddening E(J − KS). The black points are the measurements from individual targets. The white and red dots are the median values taken from different reddening bins. The red error bars present the standard deviations in each bins. The red line is fit to the white and red dots. The white squares are the results from Munari et al. (2008). |
| In the text | |
 |
Fig. 10 Comparison between the EW–E(J − KS) linear relations derived from different works. Relations derived in optical bands are translated into the extinction laws applied in Sect. 4.1.1. The lines of this work (red) and Munari et al. (2008; black) overlap. |
| In the text | |
 |
Fig. 11 Correlation between the EW of the Gaia DIB and the reddening E(J − KS) derived from individual GIBS fields before (left panel) and after (right panel) the correction. The red lines are fit to the red dots in each panel, and white dots are discarded. The dot-dashed black lines present the relation derived by Munari et al. (2008). The dot-dashed green lines indicate E(J − KS) = 0.10 and 0.25 mag in left and right panels, respectively. Four fields are indicated in each panel for comparison, and a detailed discussion ispresented in Sect. 4.1.2 and Appendix A. |
| In the text | |
 |
Fig. 12 Comparison between the EWs of Gaussian and asymmetric Gaussian fits. The color represents the number density. The dashed black line traces the one-to-one correspondence. |
| In the text | |
 |
Fig. 13 EW as a function of the asymmetry (asym). The color shows the number of stars in each calculated bin. |
| In the text | |
 |
Fig. 14 Distributions of the DIB parameters. Left panel: depth D vs. EW. The color represents the number density. Middle panel: measured line center λC in the heliocentric frame. The upper axis shows the corresponding radial velocities of the DIB carriers. The green histograms present the subsample selected to determine the rest-frame wavelength (see Sect. 4.2.2). Right panel: histograms of the width σ. |
| In the text | |
 |
Fig. A.1 (J − KS, J) CMD for four selected GIBS fields. The gray-scale image shows the number density of the stars selected from VVV–DR2 catalog. The red dots are the GIBS targets in each field. JKS photometry of GIBS targets are provided by the PSF photometry catalog developed by Surot et al. (2019). The dashed green lines indicate the 1σ extent widths around the RC peak densities for the regions defined by the range of J magnitudes of GIBS targets in each field (dashed orange lines). The name and coordinates of each field are indicated at the upper left corner in each panel. |
| In the text | |
 |
Fig. A.2 Same as Fig. 9, but with a purer RC sample. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


