EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 654 (October 2021) A&A, 654 (2021) A116 Full HTML
Open Access
Issue
A&A
Volume 654, October 2021
Article Number A116
Number of page(s) 12
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/202141128
Published online 22 October 2021

© H. Zhao et al. 2021

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1 Introduction

Diffuse interstellar bands (DIBs) are a set of absorption features that can be observed nearly everywhere in the spectra from optical to infrared wavelengths. DIBs were first observed in 1919 (Heger 1922) and then named and definitively determined as interstellar features in the 1930s (Merrill & Wilson 1938). Strong optical DIBs, such as the famous λ5780 and λ5797 (Heger 1922) and λ6284 and λ6614 (Merrill 1930), were discovered and studied first. Then, with the increase of spectral resolution, more and more DIBs, especially weak features, were reported. An example mentioned in Krełowski (2018), a recent review, was that in the spectral window 5700–5860 Å, Heger (1922) mentioned two DIBs, Herbig (1975) mentioned five, and after, with Hobbs et al. (2009), the number increased to 30. In the latest published catalog (Fan et al. 2019), this range contained 51 DIBs. Of course, most of them are very weak features that can only be detected in high-resolution, high signal-to-noise (S/N) spectra. DIBs were also discovered at infrared bands (e.g., Cox et al. 2014; Hamano et al. 2015; Galazutdinov et al. 2017a) and in distant galaxies (Monreal-Ibero et al. 2015, 2018).

The most important topic with regard to the DIBs is the identification of their carriers, which is usually described as “the longest-standing unsolved mystery in astronomical spectroscopy” (see Zack & Maier 2014; Tielens 2014; Geballe 2016, and Krełowski 2018 for recent reviews). Today, carbon-bearing molecules, such as carbon chains (Maier et al. 2004), polycyclic aromatic hydrocarbons (PAHs, Omont et al. 2019), and fullerenes (Omont 2016), are thought to be the most likely candidates for the DIB carriers. As the direct comparison between the observations and the laboratory predictions is very difficult, buckminsterfullerene (C60+)$(C_{60}^{+})$ is the first and only identified DIB carrier for five near-infrared (NIR) DIBs (Campbell et al. 2015, 2016a,b; Walker et al. 2016, 2017; Cordiner et al. 2017, 2019; Campbell & Maier 2018; Lallement et al. 2018; Linnartz et al. 2020), although some debates still exist (e.g., Galazutdinov et al. 2017b, 2021). Besides the laboratory investigations, modern spectroscopy also provides observational clues for the carrier research. Mutual correlations between different DIBs (e.g., McCall et al. 2010; Friedman et al. 2011; Elyajouri et al. 2017) facilitate the estimation of a single carrier for a set of DIBs, although it is still too early to conclude the same origin for any pair because of the variation of their strength ratio (Krełowski et al. 2016). Elyajouri et al. (2018) reported a tight correlation between the strength of the so-called C2 -DIBs (Thorburn et al. 2003) and the C2 column density, which is very different from other non-C2 DIBs. They also discovered substructures for at least 14 C2-DIBs, which may reveal information about the rotational branches of the carriers. It should be noted that although dust grain lost its qualificationas the carrier candidate (see e.g., Cox et al. 2007, 2011; Xiang et al. 2017), the tight correlation between the DIB strength and interstellar extinction for many strong DIBs (e.g., Lan et al. 2015) means that the DIB carriers are well mixed with the interstellar dust grains.

The studies related to the DIB carriers focus on their physical identifications, while very few works pay attention to the kinematics and distances of the DIB carriers. As the statistical research was not available during the early studies, which usually made use of only a few to tens of spectra, the unresolved carriers alleviate the importance and necessity of the kinematic study. However, kinematic research benefits from the large spectroscopic surveys and can reveal the rotation curve of the DIB carriers, such as the longitude–velocity diagram built for the NIR DIB λ15273 (Zasowski et al. 2015) based on the APOGEE spectra (Eisenstein et al. 2011). The three-dimensional (3D) distribution of the DIB carrier is revealed by modern spectroscopic surveys (e.g., Kos et al. 2014; Zasowski et al. 2015). Furthermore, DIBs are also proven to be good tracers of Galactic arms (Puspitarini et al. 2015; Puspitarini & Lallement 2019). In this work, we aim to establish a kinematic study of the DIB λ8620 (although the rest-frame wavelength, λ0, for this DIB is larger than 8620 Å, we still call it DIB λ8620 for brevity) and estimate the kinematic distance of its carrier.

The DIB λ8620 was first observed in the spectrum of the star HD 183143 (Geary 1975) and then confirmed as an interstellar band by Sanner et al. (1978), who further reported λ0 = 8620.7 ± 0.3Å and derived a linear correlation between the DIB strength and E(B − V). Later on, various λ0 were measured by different works: 8620.75 Å (Herbig & Leka 1991), 8621.2 Å (Jenniskens & Desert 1994), 8620.8 Å (Galazutdinov et al. 2000), and 8620.18 Å (Fan et al. 2019). In the new century, DIB λ8620 attracts more attention because it is within the spectral window of the RAdial Velocity Experiment (RAVE) survey (Steinmetz et al. 2006). A tight correlation with E(B − V) was confirmed by Munari et al. (2008) using 68 hot stars from RAVE, and λ0 = 8620.4 ± 0.1Å was suggested. Moreover, Kos et al. (2013, 2014) built the first pseudo-3D intensity map for DIB λ8620 using ~500 000 RAVE spectra. The correlation between the DIB strength and interstellar extinction was also studied by Wallerstein et al. (2007), Puspitarini et al. (2015), and Damineli et al. (2016). Nearly all the linear coefficients derived by different works are slightly different from each other, but most of them still correspond with each other considering the uncertainties. Zhao et al. (2021, hereafter Paper I) developed a set of procedures for automatic detection and measurement of the DIB λ8620 in a spectral window between 8605 and 8640 Å. The DIB quantities, depth, width, central wavelength (λC), and equivalent width (EW), can be measured from the Gaussian profile, together with their uncertainties and the quality flag (QF), whichevaluates the reliability of the fit. The procedures were tested with 4797 low-resolution spectra from the Giraffe Inner Bulge Survey (GIBS; Zoccali et al. 2014), a survey of red clump (RC) stars in the Galactic bulge. We derived the EW–E(J − KS) linear relation in three ways by the median quantities in reddening bins, in observational fields, and with a pure RC sample (see Table 1 and Sect. 4.1 in Paper I for details). The recommended result was E(J − KS) = 1.884 (± 0.225) × EW − 0.012 (± 0.072), which was a medium value in comparison with other results and closest to Munari et al. (2008), under the conversion with a specific extinction law.

In this paper, we continue to study the kinematics and distance of the carrier of DIB λ8620, with high-quality results from the GIBS samples used in Paper I and new samples from the Gaia–ESO Spectroscopic Survey (GES; Gilmore et al. 2012). In Sect. 2, we describe the spectra used in this work and define the fields for further analysis. The linear relation between EW and extinction is derived and discussed in Sect. 3. Section 4 presents the kinematic studies of the DIB carriers. The estimation of the carrier distance is introduced and discussed in Sect. 5. In Sect. 6, a rough comparison between DIB λ8620 and DIB λ15273 is made to study their possible correlation. The main conclusions are summarized in Sect. 7.

2 Samples and fields

Giraffe Inner Bulge Survey (GIBS) is a dedicated survey to study the kinematics and chemistry of RC stars in the Galactic bulge (Zoccali et al. 2014). In Paper I, we constructed a pure RC sample applying an additional criterion where we consider stars only to be on the RC if their J − KS colors lie within 1σ width of the peak of the RC J − KS (see Paper I, Appendix A for more details). This guarantees, as discussed in Paper I, a pure RC sample, and avoids contamination by foreground dwarfs and/or red giant branch (RGB) stars. In addition, we applied a cut of S∕N > 50 to ensure high-quality measurements. Finally, our working sample consists of 1780 DIBs distributed in 20 GIBS fields in total. The DIB measurements of the first ten GIBS targets are shown in Table 1.

Gaia–ESO (GES) is a public spectroscopic survey targeting all the major components of the Milky Way with the purpose of characterizing the chemistry and the kinematics of these populations. A detailed description of the data processing and general characterization of the data set can be found in Gilmore et al. (2012). For this paper, we used the official public data release DR41 and the high-resolution grating HR21 centered at 8757Å with a spectral resolution of R ~ 16 200 on the GIRAFFE spectrograph. We restricted our sample within |b| ≤ 10° and S∕N > 50, which gives a total of 4117 spectra.

The stellar parameters of the GES stars were estimated by applying the MATISSE (Recio-Blanco et al. 2006, 2016) parameterization algorithm to the corresponding spectra, refining the results thanks to the GAUGUIN procedure (Bijaoui 2012; Recio-Blanco et al. 2016). On one hand, MATISSE is a projection method for which the full input spectra are projected into a set of vectors derived during a learning phase, based on the noise-free reference grids. These vectors are a linear combinationof reference spectra and could be viewed roughly as the derivatives of these spectra with respect to the different stellar parameters. MATISSE is thus a local multi-linear regression method. On the other hand, GAUGUIN is a classical local optimization method implementing a Gauss–Newton algorithm. It is based on a local linearization around a given set of parameters that are associated with a reference synthetic spectrum (via linear interpolation of the derivatives). A few iterations are carried out through linearization around the new solutions, until the algorithm converges toward the minimum distance. In this application, GAUGUIN is initialized by the MATISSE parameters solution.

Both parameterization algorithms together with the DIB measurement rely on a grid of synthetic spectra specifically computed for FGKM-type stars analyzed by GES. This grid contains high-resolution synthetic spectra over the spectral range 845–895 nm. It covers metallicities from [M/H] = −5.0 to +1.0 dex and variations in [α∕Fe] (five values for each metallicity). The grid computation adopted the same methodology as the grid computed for the AMBRE project (de Laverny et al. 2013) and is described in de Laverny et al. (2012). We remind the reader that it is based on the MARCS model atmospheres (Gustafsson et al. 2008) and the Turbospectrum code for radiative transfer (Plez 2012). For the present application, we adopted the GES atomic and molecular line lists (Heiter et al. 2021) and a microturbulence velocity that varies with the atmospheric parameter values (empirical relation adopted within GES, Bergemann 2021, in prep).

The DIBs in GES spectra were detected and measured by the procedures developed in Paper I. We were able to recover l 760 DIBs in tota with QF > 0. The fit results for the first ten GES targets are shown in Table 1, and the full catalog can be accessed online. A fit example is shown in Fig. 1. Due to the DIBs’ sparse sampling, we manually defined 18 GES fields with at least ten stars in each field (see Fig. 2).

In total, our combined GIBS and GES sample consists of 20 GIBS fields and 18 GES fields. Figure 2 shows the spatial distribution of the fields, overplotted with the extinction map of Schlegel et al. (1998, hereafter SFD), calibrated by Schlafly & Finkbeiner (2011). Table 2 lists the central coordinates and radii of each field, together with the number of DIBs in them.

Table 1

Fitresults of DIB λ8620 in the GIBS and GES data sets, as well as extinction, distance, and radial velocity of the background stars.

3 Equivalent width and extinction

The tight linear correlation between EW and interstellar extinction for DIB λ8620 has been reported in many works (e.g., Wallerstein et al. 2007; Munari et al. 2008; Kos et al. 2013; Puspitarini et al. 2015) and also plays an important role in the study of the property of the DIB carrier. In Paper I, we derived a linear relation of E(J − KS) = 1.884 (± 0.225) × EW − 0.012 (± 0.072) with a pureRC sample, where EW was the median value in each GIBS field and E(J − KS) in each field was derived based on the peak color estimated by the VVV–DR2 catalog (Minniti et al. 2017) and intrinsic color given by Gonzalez et al. (2011). In this section, we briefly describe our measurements of the EW and the E(J − KS) for the GES targets, while we use the results from Paper I for GIBS targets.

thumbnail Fig. 1

Fit of the DIB λ8620 in the spectrum of the GES target 06440722–0055038. Upper panel: black and blue lines show the observed and synthetic spectra, respectively. Lower panel: black line is the renormalized interstellar spectrum. The red line represents the fitted Gaussian profile. The measured EW, central wavelength (λC), and width (σ) are also indicated.

3.1 EW measurement

As the DIB profile is fitted by a Gaussian function in our procedures, the EW can be calculated by the fitted depth (D) and width (σ), EW = 2π D σ$\textrm{EW}\,{=}\,\sqrt{2 \pi}\,\textit{D}\,\sigma$. The error of EW is estimated using the same method as described in Paper I, considering the contribution of both the random noise (i.e., S/N) and the error based on the discrepancy between theobserved and the synthetic spectrum. Puspitarini et al. (2015) also analyzed the DIB λ8620 in 162 GES spectra. Due to the low S/N of these spectra, only 43 passed our quality-flag criteria (QF > 0). Figure 3 shows the comparison of the EW for these 43 stars where Puspitarini et al. (2015) systematically obtained slightly larger EW than the result in this work, with a mean difference of 0.031 Å and a standard deviation of 0.022 Å. The mean difference is similar to the average error of EW in this work (0.020 Å) and in that of Puspitarini et al. (2015, 0.045 Å). The systematic difference might be caused by the use of different synthetic spectra in Puspitarini et al. (2015) and this work. Specifically, the synthetic model used in Puspitarini et al. (2015) was based on an the ATLAS 9 model atmosphere and the SYNTHE suite (Kurucz 2005; Sbordone et al. 2004; Sbordone 2005), which is different from the MARCS model atmospheres (Gustafsson et al. 2008) used in this work. The different fit methods also contribute to the discrepancy in EW, that is we applied a Gaussian fit to the DIB profile, while Puspitarini et al. (2015) fitted the DIB feature with an empirical model averaging the profiles detected in several spectra based on the data analysis reported by Chen et al. (2013).

3.2 Extinction

The distances to and the individual reddenings of the GES stars were calculated by the spectro-photometric method described in Rojas-Arriagada et al. (2017, hereafter R17), using the stellar parameters (Teff, log g, [Fe/H]) with the corresponding errors together with the PARSEC isochrones (Marigo et al. 2017). The extinction of our GIBS sample was derived by the high-resolution extinction map from Surot et al. (2020, hereafter S20) using RGB+RC stars from the VVV survey (Minniti et al. 2010). We refer the reader to Paper I for a more detailed description. Figure 4 shows the comparison between E(J − KS) calculated by R17 and S20 for 1626 GES sample stars with |ℓ| ≤ 10°. The derived 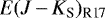EJKsR17$\EJKs_{\textrm{R17}}$ is systematically larger than that of EJKsS20$\EJKs_{\textrm{S20}}$ with a mean difference (R17 − S20) of 0.056 mag and a standard deviation of 0.082 mag. As this difference between R17 and S20 is smaller than the variation of E(J − KS) in each field, we did not attempt to correct for this.

3.3 Correlation between EW and extinction

Figure 5 shows the correlation between EW and E(J − KS) for the individual GES targets (left panel) and the median values for each field (right panel). Although a large dispersion is found for individual measurements, the median EW and E(J − KS) for each field present a tight correlation with a Pearson correlation coefficient (rp) of 0.91. The linear relation is derived as E(J − KS) = 1.842 (± 0.203) × EW − 0.005 (± 0.023), which is highly consistent with the relation recommended by Paper I for the GIBS fields (the dashed green line in Fig. 5), even when taking into account the different resolutions between the GES (R ~ 16 200) and GIBS (R = 6500) spectra and the difference between 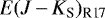EJKsR17$\EJKs_{\textrm{R17}}$ and EJKsS20$\EJKs_{\textrm{S20}}$. For the latter, the reasons are 1) the recommended relation in Paper I was derived using an RC-based E(J − KS) (which is not from the S20 map), although EJKsS20$\EJKs_{\textrm{S20}}$ was used for GIBS individual targets. We emphasize here again that in Paper I we derived the relation in three ways, two of them were based on the median EJKsS20$\EJKs_{\textrm{S20}}$ in each field, but the preferred one used theRC-based E(J − KS); and 2) we applied a cut of E(J − KS) > 0.25 mag as described in Paper I, and the typical EJKsR17$\EJKs_{\textrm{R17}}$ of GES fields are within 0.3 mag as they are located at higher Galactic latitudes (see Fig. 2). Thus, the two relations were derived in different E(J − KS) ranges. Their consistency might indicate a decrease of the difference between R17 and S20 for higher E(J − KS). For the further analysis, we use as in Paper I the median quantities for each GES field rather than the individual measurements.

Additionally, we also find a linear relation (rp = 0.88) between EW and AV derived from the SFD map with a calibration by Schlafly & Finkbeiner (2011), except for the GIBS field #7 located at (ℓ, b) = (8.5°, −1.9°), where the corresponding AV is clearly overestimated (see Fig. 6). This outlier is due to the fact that at low galactic latitudes, the SFD map may not be reliable. Indeed, a comparison with S20 reveals much lower extinction values for this field (AV ~ 4 mag). The linear fit yields a coefficient of AV∕EW = 10.733 ± 0.972. With the relation in NIR band E(J − KS)∕EW = 1.884, we obtain E(J − KS)∕AV = 0.176, slightly higher than the ratio of 0.170 predicted by the CCM model (Cardelli et al. 1989) with RV = 3.1. On the other hand, the tight correlation with extinction makes DIB λ8620 a powerful tracer of any possible extinction law variation for different lines of sight. However, Krełowski (2018) argued the variation of the EW ∕E(B − V) ratio for DIB λ8620 by two stars HD 204827 and HD 219287 which have similar E(B − V) but very different DIB profiles (see Fig. 11 in his paper).

thumbnail Fig. 2

Locations of 20 GIBS observational fields (red dots) and 18 GES selected fields (blue dots), overplotted on the extinction map of Schlegel et al. (1998) calibrated by Schlafly & Finkbeiner (2011).
Table 2

Selected GIBS and GES fields.

thumbnail Fig. 3

Comparison of the EW computed in this work with the one from Puspitarini et al. (2015) for 43 common targets. The dashed green line traces the one-to-one correspondence.
thumbnail Fig. 4

Left panel: comparison between E(J − KS) derived by R17 and S20. The dashed green line traces the one-to-one correspondence. The color represents the number density. Right panel: distribution of the differences between R17 and S20. The red line represents a Gaussian fit.

4 Kinematics of the DIB carrier

4.1 Rest-frame wavelength

As the most important observational parameter, the precise DIB rest-frame wavelength (λ0) is required for inferring the kinematic information of the DIB carrier. Although without a physical identification of the carrier, λ0 can be determined with the empirical assumption that the radial velocity toward the Galactic center or the Galactic anti-center (see Zasowski et al. 2015) is essentially null. Similarly to Paper I, 603 DIBs with − 3° < b < 3° and − 6° < ℓ < 3° are selected from our pure GIBS sample which includes only the most reliable measurements (i.e., the error in EW is small). We obtained a median central wavelength in the heliocentric frame of 8620.52 ± 0.36Å, close to the results of Paper I and Munari et al. (2008).

However, both of the previous works did not consider the effect of the solar motion toward the Galactic center. Therefore, the rest-frame wavelength in the Local Standard of Rest (LSR) should be derived as λ0 = cc−U⊙⋅Cobs,$\lambda_0\,{=}\,\frac{c}{c-U_{\odot}} \cdot C_{\textrm{obs,}}$ where c is the speed of light, Cobs the measured central wavelength in the heliocentric frame, and U⊙ the solar motion toward the Galactic center. In this work, we assume U⊙ = 10.6 ± 1.2 km s−1 (Reid et al. 2019, Model A5) which gives a λ0 = 8620.83Å that is in good agreement with the value of 8620.79 Å in Galazutdinov et al. (2000). However, the solar motion U⊙ can vary between 10.1 ± 1.0 km s−1 (Mróz et al. 2019), 10.3 km s−1 (Bovy et al. 2012), 10.6 ± 1.2 km s−1 (Reid et al. 2019), 10.7 ± 1.8 km s−1 (Reid et al. 2014), and 11.1 km s−1 (Reid & Brunthaler 2004; Schönrich et al. 2010). For an exhaustive summary of the measurements of the solar motion, we refer the reader to Wang et al. (2021). We note that a difference of ΔU⊙ = 1 km s−1 causes an error of ~0.03 Å in λ0, while the typical error of Cobs in the fit is about 0.36 Å.

4.2 Distribution of the carrier velocities

We investigate here the radial velocity of the DIB carrier with respect to the LSR, VLSR = VHC +V⊙ ⋅ A, where V⊙ = (10.6, 10.7, 7.6) km s−1 is the solar motion fitted by Model A5 of Reid et al. (2019), and A = (cos(b)cos(ℓ), cos(b)sin(ℓ), sin(b)) is the directional array of the DIB carrier. Figure 7 presents VLSR as a function of Galactic longitude for the GIBS (red circles) and GES (blue circles) fields, respectively, where we show the median VLSR in each field. The error bars show the standard error of the mean (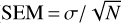SEM = σ/N$\textrm{SEM}\,{=}\,\sigma/\sqrt{N}$, N is the sample size) in each field. Indicated are Galactic rotation curves computed by Model A5 in Reid et al. (2019) with different galactocentric radii (RGC).

Limited by the available sightlines, we cannot find a clear Galactic rotation from the GIBS∕GES fields as seen in Zasowski et al. (2015, Fig. 8). Moreover, fields with |ℓ| ≤ 10° present a large velocity dispersion caused by both the fitting errors (an error of 0.36 Å in Cobs amounts to ΔVLSR ~ 10 km s−1) and the velocity crowding (Wenger et al. 2018). In Sect. 5, we apply two Galactic rotation models in order to derive kinematic distance for the DIB carrier.

4.3 Galactocentric velocity and velocity dispersion

One of the known kinematic characteristics of the Galactic boxy/peanut bulge is its cylindrical rotation, which has already been investigated in many studies (see e.g., Ness et al. 2013; Zoccali et al. 2014; Rojas-Arriagada et al. 2020). This rotation curve is steeper in the bulge than for the Galactic disk (see e.g., Howard et al. 2009; Shen et al. 2010; Zoccali et al. 2014). In contrast, the velocity dispersion in the bulge is higher with respect to the Galactic disk (by a factor of two or more), indicating more isotropic kinematics. Using these kinematic properties, we can determine if the DIB carriers are associated with the background stars or in the foreground disk. Here, we investigate the validity of this assumption. We use the APOGEE DR16 data set (Majewski et al. 2017) as a comparison sample, and in particular the Galactic bulge sample from Rojas-Arriagada et al. (2020) with |ℓ| ≤ 11°, for three different Galactic latitude bins |b| = 1°, 4°, 8°. As shown by Rojas-Arriagada et al. (2020), a simple cut at RGC ≤ 3.5 kpc ensures a reliable bulge sample, which we applied.

Furthermore, we define a typical “Galactic disk” sample of APOGEE within the same longitude and latitude range as the bulge sample but with line-of-sight distances within 3 kpc. The distances of our APOGEE stars were calculated by the same method used in Rojas-Arriagada et al. (2020) using the spectro-photometric distances together with PARSEC isochrones (Rojas-Arriagada et al. 2017). VHC has been transformed to Galactocentric velocities (VGC) using the following formula (e.g., Ness et al. 2013; Zoccali et al. 2014), where (ℓ, b) are the galactic coordinates: VGC=VHC+220 sin(l) cos(b)+16.5[sin(b) sin(25)+cos(b) cos(25) cos(l−53)]. \begin{equation*}\begin{split} V_{\textrm{GC}} = &V_{\textrm{HC}} + 220\,\textrm{sin}(\ell)\,\textrm{cos}(b) \\ & + 16.5[\textrm{sin}(b)\,\textrm{sin(25)} + \textrm{cos}(b)\,\textrm{cos}(25)\,\textrm{cos}(\ell-53)]. \end{split} \end{equation*}(1)

Figure 8 shows the rotation curves and velocity dispersion for the APOGEE sample (dashed lines) as well as our DIB measurements (solid lines). The APOGEE stars at different latitudes are further separated into eight equal longitude bins, where the median VGC in each bin is used. Our full sample (GES and GIBS) has been divided into three groups with |b| < 3°, 3° < |b| < 7° and 7° < |b| < 10°. The right panel of Fig. 8 shows the comparison between the bulge sample of APOGEE stars and our DIB samples. It is evident that in terms of rotation and velocity dispersion, our DIB measurements do not follow the general bulge characteristics of the stars. This is most striking in the velocity dispersion where the DIBs show more than a factor of two smaller velocity dispersion with respect to the bulge stars. In the left panel of Fig. 8, we see, on the other hand, a much better agreement, with the disk sample from APOGEE showing similar velocity dispersion and rotation velocities. We therefore conclude that the DIB carriers located inside the Galactic disk (4 < RGC < 11 kpc) could be far away from the background stars and much closer to us.

thumbnail Fig. 5

Correlation between EW and E(J − KS) derived from GES individual targets (left) and fields (right). The dots with the same color are from the same field, and their median value shown in right panel is colored in the same way. The dashed green line in the right panel shows the relation derived by Paper I. The error bars indicate the standard deviation in each field. The red lines in both panels are fit to the dots in the right panel. The Pearson correlation coefficient (rp) is also indicated.
thumbnail Fig. 6

Correlation between EW and AV (SFD) for the median values in each GIBS (red) and GES (blue) field. The green line represents the linear fit, excluding the field with AV > 8 mag (the red square). The Pearson correlation coefficient (rp) is also indicated.
thumbnail Fig. 7

Longitude–velocity (ℓ − VLSR) diagram for the GIBS (red) and GES (blue) fields, respectively. The circles indicate the median VLSR and standard error of the mean for each field. Velocity curves calculated by Model A5 in Reid et al. (2019) for different galactocentric distances (RGC) are overplotted.
thumbnail Fig. 8

Median galactocentric radial velocity (top) and velocity dispersion (bottom) calculated in GIBS fields (circles), GES fields (squares), and APOGEE bins (triangles), as a function of Galactic longitude, for different latitudes marked with different colors. The APOGEE stars used in the left panels are in the disk with line-of-sight distances smaller than 3 kpc. Bulge stars (RGC ≤ 3 kpc) are used in right panels.

5 Distance of the DIB carrier

As an interstellar feature, the DIB profile measured in the spectrum of a background star is the result of an integration of the DIB carrier between the observer and the star. The distance of the background star is then an upper limit on the typical distance of the DIB carrier along the sight line (Zasowski et al. 2015). Based on hundreds of thousands spectra, Kos et al. (2014) and Zasowski et al. (2015) built 3D intensity maps for DIB λ8620 and DIB λ15273, respectively,using stellar distances and tracing the cumulation and variation of the DIB carriers along substantial sight lines. Their pioneering works encourage the following studies with large spectroscopic surveys, while in this work we attempt to estimate thedistance of the DIB carrier more “directly” by the carrier radial velocity and Galactic rotation model; that is, the kinematic distance.

5.1 Kinematic distance

We calculated the kinematic distance of the DIB carrier using the median VLSR in each field together with two different Galactic rotation models. One is a two-parameter “universal” rotation model (Model A5 in Reid et al. 2019), the other is a linear rotation model (Model 2 in Mróz et al. 2019). For Model A5 in Reid et al. (2019), the kinematic distance is computed with a Monte Carlo method introduced by Wenger et al. (2018), using their python package kd2 and considering the error of VLSR as well as the parameter uncertainty of the rotation model. For Model 2 in Mróz et al. (2019), only the error of VLSR is considered. Figure 9 shows the comparison between the estimated galactocentric distances RGC derived by the two models for our sample, which give consistent results with slightly larger distances for Mróz et al. (2019) within 4 < RGC < 6 kpc, while these are smaller for RGC > 9 kpc. As both Reid et al. (2019) and Mróz et al. (2019) fit the models mainly within the 4–15 kpc range, kinematic distances in the inner Galaxy with RGC < 4 kpc are not reliable and should not be used. In addition, in the inner Galaxy the orbits of the stars are highly eccentric (see e.g., Rojas-Arriagada et al. 2020), causing large errors for the kinematic distances.

We also calculated the line-of-sight distance: dlos=R⊙⋅cos(l)±RGC2−R⊙2⋅sin2(l),\begin{equation*}d_{\textrm{los}} = R_{\odot} \cdot {\textrm{cos}}(\ell) \pm \sqrt{R_{\textrm{GC}}^2 - R_{\odot}^2 \cdot {\textrm{sin}^2}(\ell)}, \end{equation*}(2)

where R⊙ = 8.15 kpc (Reid et al. 2019), ℓ is the median Galactic latitude of each field, and for RGC we use the results from the model of Reid et al. (2019). The calculation was also completed by the kd package. For the inner Galaxy, Eq. (2) gives two possible solutions, of which we always chose the closest one. In case where the solution is negative or has no rational solution, the result has been dropped.

Finally, we obtained RGC > 4 kpc for 14 GIBS and 14 GES fields. Nine GIBS and ten GES fields had valid dlos. These measurements, together with their uncertainties, are listed in Table 2. A face-on view of the distribution of the fields with valid dlos is shown in Fig. 10. The fields within |ℓ| < 10° experience large uncertainties than the fields outside. Seven fields are located within or beyond the Scutum–Centaurus Arm, while 11 other fields are around the Sagittarius Arm and the Orion Spur. The only field toward the Galactic anti-center at (ℓ, b) = (−147.2°, −2.0°) almost reaches the edge of the Perseus Arm.

thumbnail Fig. 9

Comparison between kinematic distances derived by Model 2 in Mróz et al. (2019) and Model A5 in Reid et al. (2019). The red and blue dots indicate the GIBS and GES fields, respectively. The dashed green line traces the one-to-one correspondence. The dashed black lines indicate RGC = 4 kpc.

5.2 Comparison with stellar distances

The distances to the background stars are the upper limit on the carrier distances and can be used to test the reliability of our distance measurements. As the targets in the GIBS sample are RC stars, we can calculate their distance assuming MK_S = −1.61 mag (Ruiz-Dern et al. 2018)and 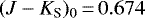(J−KS)0 = 0.674$(J-K_{\textrm{S}})_0\,{=}\,0.674$ mag (Gonzalez et al. 2012). For the GES sample, we used spectro-photometric distances (see Sect. 2). For each field, we calculated the median distance together with its standard deviation. The results are shown in Table 2 for field medians and Table 1 for individual stars (some examples; full catalog can be accessed online). For a test, we also cross-matched the GES sample with the catalog of Gaia–EDR3 (Gaia Collaboration 2021) within 1′′ and used the photogeometric distances estimated by Bailer-Jones et al. (2021) from the Gaia parallaxes. The resulting median distances for each field are consistent with our calculations within the distance uncertainties.

Figure 11 displays the comparison between the median stellar distances and the kinematic distance of the DIB carrier for nine GIBS and ten GES fields with valid dlos. All of the points lie below the identity line (dashed green), indicating all the estimated carrier distances are smaller than the stellar distances. This is not very surprising for GIBS as the RC stars in GIBS fields are mainly distributed in the Galactic bulge, and we required the nearer solution for dlos. It is more interesting for GES fields, of which the median distances are much closer to the Sun, meaning that the kinematic distance of the DIB carrier is still smaller than the stellar distance. This confirms the reliability of the derived kinematic distance to some extent. While we still need to emphasize that kinematic distances are of high uncertainty in the direction of the Galactic center and the Galactic anti-center (see e.g., Balser et al. 2015; Wenger et al. 2018) and need to be carefully used.

The comparison in Fig. 11 also demonstrates that the DIB carrier can be located much closer to the observer than the background stars. So, when we make use of DIBs as a tool to trace the ISM environments and Galactic structure, such as local ISM medium (Piecka & Paunzen 2020), Galactic arms (Puspitarini & Lallement 2019), and Galactic warp (Istiqomah et al. 2020), target stars at distant zones and/or high latitudes require more attention.

thumbnail Fig. 10

Face-on view of the spatial distribution of nine GIBS and ten GES fields with valid dlos ; i.e., the kinematic distance of the DIB carrier calculated by the field-median radial velocity and model A5 in Reid et al. (2019), overplotted with the Milky Way sketch created by Robert Hurt and Robert Benjamin (Churchwell et al. 2009). The Galactic center is located at (−8, 0). Red and blue dots indicate the GIBS and GES fields, respectively.

6 Comparison with the NIR DIB λ15273

The correlation between different DIBs is one of the most important methods to study the relations of their carriers and to find the commoncarrier for a set of DIBs (see Elyajouri et al. 2017, 2018; Sonnentrucker et al. 2018; Galazutdinov et al. 2020 and Bondar 2020 for some recent studies). The tightest correlation is between DIB λ6196 and DIB λ6614 (McCall et al. 2010), although the conclusion of their common origin still encounters some problems (Krełowski et al. 2016). Elyajouri et al. (2017) reported tight correlations between the strong NIR DIB at 1.5273 μm and the weak DIBs in its vicinity (λ15617, λ15653, and λ15673), as well as some strong optical DIBs, proposing DIB λ15273 as a good tracer of the interstellar environments.

In this section, we make a simple comparison between DIB λ8620 measured in this work and DIB λ15273 in the APOGEE spectra measured by Zasowski et al. (2015). We accessed the full APOGEE DIB catalog with 49,474 entries3, but cross-matched them with our GIBS∕GES sample within 1′′, where only 16 common targets were found (GES). This is due to the fact that APOGEE and GIBS∕GES trace different stellar populations in their target selection; that is GIBS trace RC stars, while APOGEE traces brighter and cooler giants on the RGB. Therefore, we selected the APOGEE DIBs based on the same fields with respect to GIBS and GES and compared their median EW in each field. In total, we find six GES and three GIBS fields matching the APOGEE footprint. Figure 12 shows the comparison between the EW of the two DIBs where a linear relation between the two carriers can be found (rp = 0.90). Clearly, more observationsof these two DIB carriers spanning a larger EW range are needed in order to draw firmer conclusions. A linear fit to all the fields yields a ratio of EW λ15273∕EW λ8620 = 1.411 ± 0.242, demonstrating that the DIB λ15273 is stronger than DIB λ8620.

It should be noted that Elyajouri & Lallement (2019) reported measurements4 of DIB λ15273 that were systematically weaker than those in Zasowski et al. (2015) due to the use of different stellar models. With their results, DIB λ8620 would, on the contrary, be larger than the DIB λ15273, with a ratio of EW λ15273∕EW λ8620 = 0.670 ± 0.132 (rp = 0.75, see triangles in Fig. 12; the fields are selected with the same method for Zasowski et al. 2015). However, this correlation was built only with the median values in very few common fields. Thus, the present result is still a rough one, and further investigations with bigger data sets are expected. The correlation between DIB λ8620 and DIB λ15273, as well as other optical and infrared DIBs, will benefit from forthcoming new large spectroscopic data. The DIB λ8620 shows a promising diagnostic of the interstellar conditions and a tracer of the Galactic structure.

We derived a linear correlation between EW and AV with EW λ8620∕AV = 0.093 Å mag−1 for our GIBS∕GES fields (Sect. 3.3). Compared to EW λ15273∕AV = 0.102Åmag−1 from Zasowski et al. (2015), we can obtain a ratio of 1.097 for EW λ15273∕EW λ8620, which is about 22% lower than the value from the direct EW comparison with Zasowski et al. (2015). This difference could be caused by the different extinction sources used in Zasowski et al. (2015) and this work; Zasowski et al. (2015) applied the RJCE method (Majewski et al. 2011) for their extinction values, while we used the AV from the SFD map with a calibration of Schlafly & Finkbeiner (2011).

Zasowski et al. (2015) roughly estimated the carrier abundance relative to hydrogen for DIB λ15273 as NDIB∕NH ~ 2.3 × 10−11∕f with its relationship to AV, λ0 = 15272.42Å, and a mean hydrogen-to-extinction relation of NH∕AV = 2 × 1021 cm−2 mag−1 (Dickey & Lockman 1990), where f is the transition oscillator strength (e.g., Spitzer 1978). With our derived relation EW λ8620∕AV = 0.093Åmag−1 and λ0 = 8620.83Å, the carrier abundance for DIB λ8620 is estimated as 1.4 × 10−11∕f, slightly lower than the value of the DIB λ15273.

thumbnail Fig. 11

Comparison between stellar distance and the kinematic distance of the DIB carrier for nine GIBS (red dots) and ten GES fields (blue dots). The dashed green line traces the one-to-one correspondence.
thumbnail Fig. 12

Median EW comparison between DIB λ8620 and DIB λ15273 for GIBS (red) and GES (blue) fields. Filled circles indicate the DIB λ15273 measured by Zasowski et al. (2015) and triangles by Elyajouri & Lallement (2019). The dashed red line is the fit between the GIBS∕GES sample and the Zasowski et al. (2015) sample, and the dashed orange line between GIBS∕GES and Elyajouri & Lallement (2019). The error bars represent the standard deviation in each field. The Pearson correlation coefficients (rp) are also indicated.

7 Conclusions and summary

In this work,we successfully detected the DIB λ8620 in 760 GES spectra with |b| ≤ 10° and S∕N > 50. Their EW, as well as depth, central wavelength, and width, were measured with a Gaussian profile. Our EWs were slightly smaller than those measured in Puspitarini et al. (2015), with a mean difference of 0.031 Å for 43 common targets. The linear relation between EW and E(J − KS) (rp = 0.91) derived from field median values is highly consistent with the recommended correlation derived in Paper I.

Combined with a pure GIBS sample from Paper I, we confirmed a linear relation between EW and AV (SFD) with rp = 0.88, using 2540 DIBs distributed in 38 fields. We obtained E(J − KS)∕AV = 0.176 from their linear fit with EW, which was slightly higher than the ratio of 0.170 predicted by the CCM model (Cardelli et al. 1989). Furthermore, the rest-frame wavelength of DIB λ8620 was redetermined as λ0 = 8620.83 ± 0.36Å after the consideration of the solar motion.

We also studied the kinematics of the DIB carriers based on the median radial velocities in each field. Most of our fields distributed close to the Galactic center (|ℓ| ≤ 10°), thus they were crowded in the ℓ − VLSR diagram with large scatters. The ℓ − VGC diagram showed that the DIB carriers mainly occupied in the local Galactic disk as traced by a sample of APOGEE stars.

Applying the Galactic rotation models (Reid et al. 2019; Mróz et al. 2019), we calculated the kinematic distances of the DIB carriers for each field and got valid line-of-sight distances (dlos) for nine GIBS and ten GES fields. All derived dlos are smaller than the median distances to background stars in each field. It demonstrates that the DIB carriers can be located much closer to us than the background stars. Therefore, when we make use of target stars to build the integrated DIB map, we have to be careful with the distant- and/or high-latitude zones, as well as the region where stars are not well sampled.

For the first time, we roughly investigated the mutual correlation between DIB λ8620 measured in this work and DIB λ15273 in Zasowski et al. (2015) and Elyajouri & Lallement (2019), respectively, with three GIBS fields and six GES fields, resulting in a liner coefficient of EW λ15273∕EW λ8620 = 1.411 ± 0.242 for the measurements from Zasowski et al. (2015) and 0.670 ± 0.132 for Elyajouri & Lallement (2019). The Pearson correlation coefficients are 0.90 and 0.75, respectively. The difference was caused by the use of different stellar templates for APOGEE spectra. The linear correlation suggested that DIB λ8620 may also correlate with other optical and infrared DIBs such as DIB λ15273, which can be used to trace the interstellar environments and Galactic structure with the measurements in large spectroscopic surveys.

Acknowledgements

H.Z. is funded by the China Scholarship Council (No. 201806040200). M.S. acknowledges the Programme National de Cosmologie et Galaxies (PNCG) of CNRS/INSU, France, for financial support. A.R.A. acknowledges support from FONDECYT through grant 3180203. The synthetic spectra grid calculations for GES targets have been performed with the high-performance computing facility SIGAMM, hosted by OCA.

References

  1. Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Demleitner, M., & Andrae, R. 2021, AJ, 161, 147 [Google Scholar]
  2. Balser, D. S., Wenger, T. V., Anderson, L. D., & Bania, T. M. 2015, ApJ, 806, 199 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bijaoui, A. 2012, in Seventh Conference on Astronomical Data Analysis, eds. J.-L. Starck, & C. Surace, 2 [Google Scholar]
  4. Bondar, A. 2020, MNRAS, 496, 2231 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bovy, J., Allende Prieto, C., Beers, T. C., et al. 2012, ApJ, 759, 131 [NASA ADS] [CrossRef] [Google Scholar]
  6. Campbell, E. K., & Maier, J. P. 2018, ApJ, 858, 36 [NASA ADS] [CrossRef] [Google Scholar]
  7. Campbell, E. K., Holz, M., Gerlich, D., & Maier, J. P. 2015, Nature, 523, 322 [NASA ADS] [CrossRef] [Google Scholar]
  8. Campbell, E. K., Holz, M., & Maier, J. P. 2016a, ApJ, 826, L4 [NASA ADS] [CrossRef] [Google Scholar]
  9. Campbell, E. K., Holz, M., Maier, J. P., et al. 2016b, ApJ, 822, 17 [Google Scholar]
  10. Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [Google Scholar]
  11. Chen, H. C., Lallement, R., Babusiaux, C., et al. 2013, A&A, 550, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Churchwell, E., Babler, B. L., Meade, M. R., et al. 2009, PASP, 121, 213 [Google Scholar]
  13. Cordiner, M. A., Cox, N. L. J., Lallement, R., et al. 2017, ApJ, 843, L2 [NASA ADS] [CrossRef] [Google Scholar]
  14. Cordiner, M. A., Linnartz, H., Cox, N. L. J., et al. 2019, ApJ, 875, L28 [NASA ADS] [CrossRef] [Google Scholar]
  15. Cox, N. L. J., Boudin, N., Foing, B. H., et al. 2007, A&A, 465, 899 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Cox, N. L. J., Ehrenfreund, P., Foing, B. H., et al. 2011, A&A, 531, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Cox, N. L. J., Cami, J., Kaper, L., et al. 2014, A&A, 569, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Damineli, A., Almeida, L. A., Blum, R. D., et al. 2016, MNRAS, 463, 2653 [NASA ADS] [CrossRef] [Google Scholar]
  19. de Laverny, P., Recio-Blanco, A., Worley, C. C., & Plez, B. 2012, A&A, 544, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. de Laverny, P., Recio-Blanco, A., Worley, C. C., et al. 2013, The Messenger, 153, 18 [NASA ADS] [Google Scholar]
  21. Dickey, J. M.,& Lockman, F. J. 1990, ARA&A, 28, 215 [NASA ADS] [CrossRef] [Google Scholar]
  22. Eisenstein, D. J., Weinberg, D. H., Agol, E., et al. 2011, AJ, 142, 72 [Google Scholar]
  23. Elyajouri, M., & Lallement, R. 2019, A&A, 628, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Elyajouri, M., Lallement, R., Monreal-Ibero, A., Capitanio, L., & Cox, N. L. J. 2017, A&A, 600, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Elyajouri, M., Lallement, R., Cox, N. L. J., et al. 2018, A&A, 616, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Fan, H., Hobbs, L. M., Dahlstrom, J. A., et al. 2019, ApJ, 878, 151 [NASA ADS] [CrossRef] [Google Scholar]
  27. Friedman, S. D., York, D. G., McCall, B. J., et al. 2011, ApJ, 727, 33 [NASA ADS] [CrossRef] [Google Scholar]
  28. Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Galazutdinov, G. A., Musaev, F. A., Krełowski, J., & Walker, G. A. H. 2000, PASP, 112, 648 [NASA ADS] [CrossRef] [Google Scholar]
  30. Galazutdinov, G. A., Lee, J.-J., Han, I., et al. 2017a, MNRAS, 467, 3099 [NASA ADS] [CrossRef] [Google Scholar]
  31. Galazutdinov, G. A., Shimansky, V. V., Bondar, A., Valyavin, G., & Krełowski, J. 2017b, MNRAS, 465, 3956 [NASA ADS] [CrossRef] [Google Scholar]
  32. Galazutdinov, G., Bondar, A., Lee, B.-C., et al. 2020, AJ, 159, 113 [CrossRef] [Google Scholar]
  33. Galazutdinov, G. A., Valyavin, G., Ikhsanov, N. R., & Krełowski, J. 2021, AJ, 161, 127 [NASA ADS] [CrossRef] [Google Scholar]
  34. Geary, J. C. 1975, PhD thesis, The University of Arizona, USA [Google Scholar]
  35. Geballe, T. R. 2016, J. Phys. Conf. Ser., 728, 062005 [NASA ADS] [CrossRef] [Google Scholar]
  36. Gilmore, G., Randich, S., Asplund, M., et al. 2012, The Messenger, 147, 25 [NASA ADS] [Google Scholar]
  37. Gonzalez, O. A., Rejkuba, M., Zoccali, M., Valenti, E., & Minniti, D. 2011, A&A, 534, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Gonzalez, O. A., Rejkuba, M., Zoccali, M., et al. 2012, A&A, 543, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Hamano, S., Kobayashi, N., Kondo, S., et al. 2015, ApJ, 800, 137 [NASA ADS] [CrossRef] [Google Scholar]
  41. Heger, M. L. 1922, Lick Observ. Bull., 10, 146 [Google Scholar]
  42. Heiter, U., Lind, K., Bergemann, M., et al. 2021, A&A, 645, A106 [EDP Sciences] [Google Scholar]
  43. Herbig, G. H. 1975, ApJ, 196, 129 [NASA ADS] [CrossRef] [Google Scholar]
  44. Herbig, G. H., & Leka, K. D. 1991, ApJ, 382, 193 [NASA ADS] [CrossRef] [Google Scholar]
  45. Hobbs, L. M., York, D. G., Thorburn, J. A., et al. 2009, ApJ, 705, 32 [Google Scholar]
  46. Howard, C. D., Rich, R. M., Clarkson, W., et al. 2009, ApJ, 702, L153 [NASA ADS] [CrossRef] [Google Scholar]
  47. Istiqomah, A. N., Puspitarini, L., & Arifyanto, M. I. 2020, J. Phys. Conf. Ser., 1523, 012009 [NASA ADS] [CrossRef] [Google Scholar]
  48. Jenniskens, P., & Desert, F. X. 1994, A&AS, 106, 39 [NASA ADS] [Google Scholar]
  49. Kos, J., Zwitter, T., Grebel, E. K., et al. 2013, ApJ, 778, 86 [NASA ADS] [CrossRef] [Google Scholar]
  50. Kos, J., Zwitter, T., Wyse, R., et al. 2014, Science, 345, 791 [NASA ADS] [CrossRef] [Google Scholar]
  51. Krełowski, J. 2018, PASP, 130, 071001 [CrossRef] [Google Scholar]
  52. Krełowski, J., Galazutdinov, G. A., Mulas, G., et al. 2016, Acta Astron., 66, 391 [Google Scholar]
  53. Kurucz, R. L. 2005, Mem. Soc. Astron. It. Suppl., 8, 14 [Google Scholar]
  54. Lallement, R., Cox, N. L. J., Cami, J., et al. 2018, A&A, 614, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Lan, T.-W., Ménard, B., & Zhu, G. 2015, MNRAS, 452, 3629 [Google Scholar]
  56. Linnartz, H., Cami, J., Cordiner, M., et al. 2020, J. Mol. Spectr., 367, 111243 [NASA ADS] [CrossRef] [Google Scholar]
  57. Maier, J. P., Walker, G. A. H., & Bohlender, D. A. 2004, ApJ, 602, 286 [CrossRef] [Google Scholar]
  58. Majewski, S. R., Zasowski, G., & Nidever, D. L. 2011, ApJ, 739, 25 [Google Scholar]
  59. Majewski, S. R., Schiavon, R. P., Frinchaboy, P. M., et al. 2017, AJ, 154, 94 [NASA ADS] [CrossRef] [Google Scholar]
  60. Marigo, P., Girardi, L., Bressan, A., et al. 2017, ApJ, 835, 77 [Google Scholar]
  61. McCall, B. J., Drosback, M. M., Thorburn, J. A., et al. 2010, ApJ, 708, 1628 [NASA ADS] [CrossRef] [Google Scholar]
  62. Merrill, P. W. 1930, ApJ, 72, 98 [NASA ADS] [CrossRef] [Google Scholar]
  63. Merrill, P. W., & Wilson, O. C. 1938, ApJ, 87, 9 [NASA ADS] [CrossRef] [Google Scholar]
  64. Minniti, D., Lucas, P. W., Emerson, J. P., et al. 2010, New Astron., 15, 433 [Google Scholar]
  65. Minniti, D., Lucas, P., & VVV Team 2017, VizieR Online Data Catalog: II/348 [Google Scholar]
  66. Monreal-Ibero, A., Weilbacher, P. M., Wendt, M., et al. 2015, A&A, 576, L3 [EDP Sciences] [Google Scholar]
  67. Monreal-Ibero, A., Weilbacher, P. M., & Wendt, M. 2018, A&A, 615, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  68. Mróz, P., Udalski, A., Skowron, D. M., et al. 2019, ApJ, 870, L10 [Google Scholar]
  69. Munari, U., Tomasella, L., Fiorucci, M., et al. 2008, A&A, 488, 969 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Ness, M., Freeman, K., Athanassoula, E., et al. 2013, MNRAS, 432, 2092 [NASA ADS] [CrossRef] [Google Scholar]
  71. Omont, A. 2016, A&A, 590, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Omont, A., Bettinger, H. F., & Tönshoff, C. 2019, A&A, 625, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Piecka, M., & Paunzen, E. 2020, MNRAS, 495, 2035 [NASA ADS] [CrossRef] [Google Scholar]
  74. Plez, B. 2012, Astrophysics Source Code Library [record ascl:1205.004] [Google Scholar]
  75. Puspitarini, L., & Lallement, R. 2019, J. Phys. Conf. Ser., 1245, 1245 [NASA ADS] [Google Scholar]
  76. Puspitarini, L., Lallement, R., Babusiaux, C., et al. 2015, A&A, 573, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Recio-Blanco, A., Bijaoui, A., & de Laverny, P. 2006, MNRAS, 370, 141 [Google Scholar]
  78. Recio-Blanco, A., de Laverny, P., Allende Prieto, C., et al. 2016, A&A, 585, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  79. Reid, M. J., & Brunthaler, A. 2004, ApJ, 616, 872 [Google Scholar]
  80. Reid, M. J., Menten, K. M., Brunthaler, A., et al. 2014, ApJ, 783, 130 [Google Scholar]
  81. Reid, M. J., Menten, K. M., Brunthaler, A., et al. 2019, ApJ, 885, 131 [Google Scholar]
  82. Rojas-Arriagada, A., Recio-Blanco, A., de Laverny, P., et al. 2017, A&A, 601, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  83. Rojas-Arriagada, A., Zasowski, G., Schultheis, M., et al. 2020, MNRAS, 499, 1037 [Google Scholar]
  84. Ruiz-Dern, L., Babusiaux, C., Arenou, F., Turon, C., & Lallement, R. 2018, A&A, 609, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  85. Sanner, F., Snell, R., & vanden Bout, P. 1978, ApJ, 226, 460 [NASA ADS] [CrossRef] [Google Scholar]
  86. Sbordone, L. 2005, Mem. Soc. Astron. It. Suppl., 8, 61 [Google Scholar]
  87. Sbordone, L., Bonifacio, P., Castelli, F., & Kurucz, R. L. 2004, Mem. Soc. Astron. It. Suppl., 5, 93 [Google Scholar]
  88. Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [Google Scholar]
  89. Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [Google Scholar]
  90. Schönrich, R., Binney, J., & Dehnen, W. 2010, MNRAS, 403, 1829 [CrossRef] [Google Scholar]
  91. Shen, J., Rich,R. M., Kormendy, J., et al. 2010, ApJ, 720, L72 [NASA ADS] [CrossRef] [Google Scholar]
  92. Sonnentrucker, P., York, B., Hobbs, L. M., et al. 2018, ApJS, 237, 40 [NASA ADS] [CrossRef] [Google Scholar]
  93. Spitzer, L. 1978, Physical Processes in the Interstellar Medium (Hoboken: Wiley) [Google Scholar]
  94. Steinmetz, M., Zwitter, T., Siebert, A., et al. 2006, AJ, 132, 1645 [Google Scholar]
  95. Surot, F., Valenti, E., Gonzalez, O. A., et al. 2020, A&A, 644, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  96. Thorburn, J. A., Hobbs, L. M., McCall, B. J., et al. 2003, ApJ, 584, 339 [Google Scholar]
  97. Tielens, A. G. G. M. 2014, in The Diffuse Interstellar Bands, eds. J. Cami, & N. L. J. Cox (Bristol: IOP Publishing), 297, 399 [NASA ADS] [Google Scholar]
  98. Walker, G. A. H., Campbell, E. K., Maier, J. P., Bohlender, D., & Malo, L. 2016, ApJ, 831, 130 [CrossRef] [Google Scholar]
  99. Walker, G. A. H., Campbell, E. K., Maier, J. P., & Bohlender, D. 2017, ApJ, 843, 56 [NASA ADS] [CrossRef] [Google Scholar]
  100. Wallerstein, G., Sandstrom, K., & Gredel, R. 2007, PASP, 119, 1268 [NASA ADS] [CrossRef] [Google Scholar]
  101. Wang, F., Zhang, H. W., Huang, Y., et al. 2021, MNRAS, 504, 199 [NASA ADS] [CrossRef] [Google Scholar]
  102. Wenger, T. V., Balser, D. S., Anderson, L. D., & Bania, T. M. 2018, ApJ, 856, 52 [Google Scholar]
  103. Xiang, F. Y., Li, A., & Zhong, J. X. 2017, ApJ, 835, 107 [NASA ADS] [CrossRef] [Google Scholar]
  104. Zack, L. N., & Maier, J. P. 2014, in The Diffuse Interstellar Bands, eds. J. Cami, & N. L. J. Cox (IOP Publishing: Bristol), 297, 237 [NASA ADS] [Google Scholar]
  105. Zasowski, G., Ménard, B., Bizyaev, D., et al. 2015, ApJ, 798, 35 [Google Scholar]
  106. Zhao, H., Schultheis, M., Recio-Blanco, A., et al. 2021, A&A, 645, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  107. Zoccali, M., Gonzalez, O. A., Vasquez, S., et al. 2014, A&A, 562, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

All Tables

Table 1

Fitresults of DIB λ8620 in the GIBS and GES data sets, as well as extinction, distance, and radial velocity of the background stars.

In the text
Table 2

Selected GIBS and GES fields.

In the text

All Figures

thumbnail Fig. 1

Fit of the DIB λ8620 in the spectrum of the GES target 06440722–0055038. Upper panel: black and blue lines show the observed and synthetic spectra, respectively. Lower panel: black line is the renormalized interstellar spectrum. The red line represents the fitted Gaussian profile. The measured EW, central wavelength (λC), and width (σ) are also indicated.
In the text
thumbnail Fig. 2

Locations of 20 GIBS observational fields (red dots) and 18 GES selected fields (blue dots), overplotted on the extinction map of Schlegel et al. (1998) calibrated by Schlafly & Finkbeiner (2011).
In the text
thumbnail Fig. 3

Comparison of the EW computed in this work with the one from Puspitarini et al. (2015) for 43 common targets. The dashed green line traces the one-to-one correspondence.
In the text
thumbnail Fig. 4

Left panel: comparison between E(J − KS) derived by R17 and S20. The dashed green line traces the one-to-one correspondence. The color represents the number density. Right panel: distribution of the differences between R17 and S20. The red line represents a Gaussian fit.
In the text
thumbnail Fig. 5

Correlation between EW and E(J − KS) derived from GES individual targets (left) and fields (right). The dots with the same color are from the same field, and their median value shown in right panel is colored in the same way. The dashed green line in the right panel shows the relation derived by Paper I. The error bars indicate the standard deviation in each field. The red lines in both panels are fit to the dots in the right panel. The Pearson correlation coefficient (rp) is also indicated.
In the text
thumbnail Fig. 6

Correlation between EW and AV (SFD) for the median values in each GIBS (red) and GES (blue) field. The green line represents the linear fit, excluding the field with AV > 8 mag (the red square). The Pearson correlation coefficient (rp) is also indicated.
In the text
thumbnail Fig. 7

Longitude–velocity (ℓ − VLSR) diagram for the GIBS (red) and GES (blue) fields, respectively. The circles indicate the median VLSR and standard error of the mean for each field. Velocity curves calculated by Model A5 in Reid et al. (2019) for different galactocentric distances (RGC) are overplotted.
In the text
thumbnail Fig. 8

Median galactocentric radial velocity (top) and velocity dispersion (bottom) calculated in GIBS fields (circles), GES fields (squares), and APOGEE bins (triangles), as a function of Galactic longitude, for different latitudes marked with different colors. The APOGEE stars used in the left panels are in the disk with line-of-sight distances smaller than 3 kpc. Bulge stars (RGC ≤ 3 kpc) are used in right panels.
In the text
thumbnail Fig. 9

Comparison between kinematic distances derived by Model 2 in Mróz et al. (2019) and Model A5 in Reid et al. (2019). The red and blue dots indicate the GIBS and GES fields, respectively. The dashed green line traces the one-to-one correspondence. The dashed black lines indicate RGC = 4 kpc.
In the text
thumbnail Fig. 10

Face-on view of the spatial distribution of nine GIBS and ten GES fields with valid dlos ; i.e., the kinematic distance of the DIB carrier calculated by the field-median radial velocity and model A5 in Reid et al. (2019), overplotted with the Milky Way sketch created by Robert Hurt and Robert Benjamin (Churchwell et al. 2009). The Galactic center is located at (−8, 0). Red and blue dots indicate the GIBS and GES fields, respectively.
In the text
thumbnail Fig. 11

Comparison between stellar distance and the kinematic distance of the DIB carrier for nine GIBS (red dots) and ten GES fields (blue dots). The dashed green line traces the one-to-one correspondence.
In the text
thumbnail Fig. 12

Median EW comparison between DIB λ8620 and DIB λ15273 for GIBS (red) and GES (blue) fields. Filled circles indicate the DIB λ15273 measured by Zasowski et al. (2015) and triangles by Elyajouri & Lallement (2019). The dashed red line is the fit between the GIBS∕GES sample and the Zasowski et al. (2015) sample, and the dashed orange line between GIBS∕GES and Elyajouri & Lallement (2019). The error bars represent the standard deviation in each field. The Pearson correlation coefficients (rp) are also indicated.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.