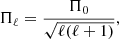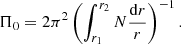EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 643 (November 2020) A&A, 643 (2020) A162 Full HTML
Free Access
Issue
A&A
Volume 643, November 2020
Article Number A162
Number of page(s) 24
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/202038989
Published online 19 November 2020

© ESO 2020

1. Introduction

The reputation of eclipsing binaries in providing the “royal road to success” (Russell 1948) in stellar astrophysics is well-deserved: The combined analysis of the timeseries of spectroscopic and photometric data enables the determination of the masses and radii of the individual components to a precision of 1% or better (Torres et al. 2010). These so-called dynamical parameters add to the already powerful prescriptions of identical initial chemical composition and equivalent ages of the individual components provided by binarity, the combination of which provides strong constraints for the calibration of stellar structural and evolutionary models (e.g. Ribas et al. 2000; Torres et al. 2010, 2014; Tkachenko et al. 2014a,b, 2020; Stancliffe et al. 2015; Claret & Torres 2018; Constantino & Baraffe 2018; Johnston et al. 2019a,b).

One of the principal aspects of the evolutionary models that is being calibrated in these studies (at present) is the morphology of the chemical mixing profiles within the stellar structures, particularly in the boundary regions of stars with convective cores (e.g. Pols et al. 1995; Schneider et al. 2014; Higl & Weiss 2017; Tkachenko et al. 2020). It has been postulated that the longstanding binary mass-discrepancy problem, the discrepancy between dynamical masses and those derived from evolutionary models (first presented by Ribas et al. 2000), is a result of insufficient core-boundary mixing in the evolutionary models: Studies such as Higl & Weiss (2017) and Tkachenko et al. (2020) have shown that the inclusion of a properly calibrated core-boundary mixing profile in the evolutionary models significantly decreases the observed magnitudes of binary mass discrepancy for stars that have convective cores.

Another method through which one can calibrate internal mixing profiles is asteroseismology (Aerts et al. 2010), particularly the study of low-frequency gravity-mode (g-mode) pulsations (e.g. Pedersen et al. 2018; Michielsen et al. 2019). These modes are typically exhibited by intermediate-mass main-sequence stars above ∼1.2 M⊙ that are born with convective cores and are excited by either the flux-blocking mechanism at the base of the small (< 10% of the stellar radius) convective region of the outer envelope (Guzik et al. 2000; Dupret et al. 2005) or the κ-mechanism (Dziembowski et al. 1993) for stars with purely radiative envelopes. Due to the largely radiative (and therefore stably stratified) nature of the envelopes of intermediate-mass stars, these g modes are able to propagate all the way from the near-core region to the surface, unlike in lower-mass stars (cf. Figs. 1.7 and 1.8 of Aerts et al. 2010). It is this propensity that makes g-mode pulsations particularly sensitive to near-core mixing phenomena and chemical stratification (Miglio et al. 2008).

It was theoretically predicted by Tassoul (1980) that in non-rotating, chemically homogeneous stars with a convective core and a radiative envelope, g modes of high radial order (n ≫ ℓ, where ℓ is the spherical harmonic degree of the mode) are equally spaced in period. The expression for this so-called asymptotic period spacing is:

(1)

where,

(2)

In these equations, r is the distance from the stellar centre, N is the Brunt-Väisälä frequency and r1 and r2 are the radial boundaries of the g-mode propagation cavity in the star. These equations demonstrate that the asymptotic period spacing is indeed sensitive to the local conditions in the regions in which these modes propagate. Miglio et al. (2008) further expanded upon the theoretical predictions of Tassoul (1980), showing that periodic dips (i.e. intermittent decreases in the period spacing between modes of consecutive radial orders) in the pattern occur when chemical gradients are present in the stellar interior, with the radial location of the gradient affecting the periodicity and the magnitude of the gradient affecting the magnitude of each dip. Bouabid et al. (2013) then included the effects of diffusive mixing and rotation on the period-spacing pattern using the framework of the traditional approximation of rotation (Townsend 2003a,b). Their conclusions were that (1) mixing reduces the steepness of the chemical gradients in the stellar interior, and therefore reduces the depth of the dips in the g-mode period spacing pattern; and that (2) rotation introduces a slope into the pattern by shifting the periods based on the azimuthal order (m) of the mode.

The full interior-probing potential of g-mode period-spacing patterns was only unlocked after the advent of high-precision, high duty cycle, space-based photometric data such as those provided by CoRoT (Auvergne et al. 2009), Kepler (Borucki et al. 2010), K2 (Howell et al. 2014), BRITE (Weiss et al. 2014) and TESS (Ricker et al. 2015). These data do not suffer from the aliasing and low duty cycle of ground-based data, enabling the unambiguous identification and characterisation of pulsational frequencies extracted from the photometric data. Following the first detection of period-spacing patterns in the CoRoT photometry by Degroote et al. (2010), a whole host of studies involving the detection and modelling of period-spacing patterns have been published, from individual case studies (e.g. Chapellier et al. 2012; Pápics et al. 2012, 2014, 2015; Kurtz et al. 2014; Saio et al. 2015; Murphy et al. 2016; Kallinger & Weiss 2017; Zwintz et al. 2017) to ensembles of a handful to hundreds of stars (e.g. Bedding et al. 2015; Van Reeth et al. 2015a,b, 2016; Ouazzani et al. 2017; Pápics et al. 2017; Mombarg et al. 2019; Li et al. 2019a,b, 2020a). These studies reveal a large range of observed radial orders for dipole g modes, covering ng ∈ [10, 100] (see Aerts 2019 for a review).

One of the weaknesses of the period-spacing pattern as a diagnostic is the degeneracy between the free parameters (e.g. mass, age, metallicity, chemical composition, interior mixing profiles) used in the evolutionary models (e.g. Valle et al. 2017) from which the theoretical patterns are derived (e.g. Moravveji et al. 2015). This means that evolutionary models with different input parameters may result in very similar theoretical period-spacing patterns. While it is possible to alleviate some of these degeneracies through a proper statistical treatment (e.g. Aerts et al. 2018), ideally the inclusion of independent constraints on the various free parameters should be considered. In the single-star case, this can take the form of spectroscopic constraints on the effective temperature, surface gravity and metallicity, as well as luminosity constraints from the astrometric data provided by the Gaia space mission (Gaia Collaboration 2016, see Pedersen et al. 2020 for details on the proper treatment of Gaia luminosities). However, as mentioned, far more stringent constraints are afforded by binarity, specifically in the form of the highly precise dynamical parameters that can be extracted from detached eclipsing binaries with main-sequence components. Johnston et al. (2019b) have shown how the inclusion of binary information significantly improves the constraining of stellar models when combined with asteroseismic information.

The complementary nature of binarity and g-mode asteroseismology is well-known, with a number of individual case studies on particular stars (e.g. Maceroni et al. 2009, 2013; Welsh et al. 2011; Chapellier & Mathias 2013; Debosscher et al. 2013; Hambleton et al. 2013; Keen et al. 2015; Schmid et al. 2015; Schmid & Aerts 2016; Matson et al. 2016; Lee & Park 2018; Zhang et al. 2018, 2020; Guo & Li 2019; Guo et al. 2017a,b, 2019, 2020). However, these case studies tend to be either (1) purely observational, (2) feature only tidally excited g modes (e.g. Guo et al. 2017a), (3) involve non-eclipsing binaries (e.g. Schmid et al. 2015), or (4) do not report the detection of period-spacing patterns (e.g. Debosscher et al. 2013). Also, of these studies only Schmid & Aerts (2016), Zhang et al. (2018, 2020), and Guo & Li (2019) include detailed asteroseismic modelling, with Schmid & Aerts (2016) presenting the most detailed modelling effort of the three as they used theoretical period-spacing patterns, derived from evolutionary models, to match their observed period-spacing patterns. This provides stronger constraints on the stellar structure when compared to, for example, fitting for Π0 (Ouazzani et al. 2019; Mombarg et al. 2020).

Overall, there is a lack of studies that combine detailed asteroseismic modelling with eclipsing binary analysis. This would enable two independent calibrations of the amount of core-boundary mixing that would have to be included in the evolutionary models in order to match either the dynamical parameters or the observed g-mode period-spacing patterns, enabling simultaneous confrontation of dynamical, evolutionary and asteroseismic parameters. In addition, there has thus far only been one ensemble study of eclipsing binaries with g-mode period-spacing patterns (Li et al. 2020a), which is a rather curious phenomenon considering that hundreds of stars with g-mode period-spacing patterns have been discovered (Li et al. 2020b).

Gaulme & Guzik (2019) performed a systematic search for pulsators in Kepler eclipsing binary systems, reporting a total of 115 g-mode pulsators (γ Doradus). They did not investigate the asteroseismic viability of said stars or perform any sort of asteroseismic or statistical analysis of their g-mode pulsator sample. In this paper, we present a sample of detached eclipsing binaries with excellent g-mode asteroseismic potential, which we define as the detection of g-mode period-spacing patterns that span six radial orders or more without any gaps in the pattern, as short period-spacing patterns and those with gaps result in additional degeneracy during asteroseismic modelling. These stars are identified through an independent systematic search of the Kepler Eclipsing Binary Catalogue (KEBC, Prša et al. 2011; Slawson et al. 2011; Kirk et al. 2016; Abdul-Masih et al. 2016).

In addition, we present the observational spectroscopic, photometric and asteroseismic analysis of the pulsating eclipsing binary KIC9850387 as a case study of the most promising candidate for future evolutionary and asteroseismic modelling. Section 2 details the sample selection process and an introduction to KIC9850387, Sect. 3 details our spectroscopic follow-up and analysis, and Sect. 4 details the photometric analysis of the system. The asteroseismic analysis of the hosted pulsating star is presented in Sect. 5 and we present a discussion of our results and conclusions in Sect. 6.

2. Identifying optimal targets

To identify optimal targets for asteroseismic analysis, we first selected all eclipsing binaries observed by Kepler during its nominal mission in the KEBC. We selected all stars with Kepler Input Catalogue (KIC, Brown et al. 2011) effective temperatures between 6000 and 10 000 K that had morphology parameter values below 0.5. The morphology parameter in the KEBC indicates the degree of “detachedness” of an eclipsing system (Matijevič et al. 2012). This parameter is calculated by an automated classification algorithm and takes values between 0 and 1, with overcontact systems being assigned a value of 1 and completely detached systems being assigned a value of 0. Matijevič et al. (2012) had compared their morphology parameter results with a manual classification and concluded that those systems that scored below 0.5 can be considered to be predominantly detached, and as such we restricted our analysis to those systems to ensure that any pulsational signature detected could be disentangled from binary evolutionary effects such as mass transfer (e.g. Niemczura et al. 2017).

We then performed a pulsational screening of the sample using the following steps: (1) Prewhiten the long-cadence light curves with the first 1000 orbital harmonics, using the detrended simple aperture photometry (SAP) fluxes and the orbital frequencies provided by the KEBC; (2) Manually inspect the residual periodograms for high-amplitude low-frequency peaks that correspond to g-mode pulsations; (3) Visually identify periodograms that contain dense clusters (six or more) of g-mode frequency peaks, which increases the likelihood of finding period-spacing patterns; (4) Perform a manual period-spacing search in the orbital-harmonic-removed frequency spectra of the best candidates.

2.1. Sample characterisation

Based on our selection criteria, we performed pulsational screening on a total of 296 eclipsing binaries listed in the KEBC. After step 2 of our pulsational screening, we identified g-mode pulsations in 93 of those systems. Of these systems, 24 exhibited dense clusters of g-mode frequencies in the Fourier domain. Eleven out of these 24 systems also showed prominent pressure (p) modes. After performing the period-spacing search (step 4), we identified candidate period-spacing patterns in seven out of the 24 systems, with only two displaying continuous patterns of longer than six radial orders. We have therefore assembled a sample of pulsators in eclipsing binary systems displaying a variety of pulsational attributes that are of asteroseismic interest, but whose analysis is outside the scope of this paper. Our goal was to identify targets that were clearly strong in terms of g-mode asteroseismic potential, and based on that criterion, we selected only the two out of the 296 targets displaying period-spacing patterns that fulfilled our criteria.

In addition to the pulsational screening, we also characterised the sub-sample of 93 eclipsing binary systems with g-mode pulsating components in terms of its pulsational properties and binary and atmospheric properties, to determine if there were any correlations between the two types of properties. The pulsational characterisation we performed comprised: (1) determining the frequency of highest amplitude (fmax) in the g-mode regime (defined to be the region below 5 d−1), and (2) calculating the number of independent frequencies (Nind) in said g-mode regime (see Sect. 5 for a detailed description our methodology for the identification of independent frequencies).

At present, the KEBC does not provide additional binary orbital information outside of the orbital period (Porb), morphology (Morph), and the timestamp of the first superior conjunction. However, one can derive estimates of the eccentricity (e) and the argument of periastron (ω) directly from the photometry itself, as ecosω is proportional to the phase separation of the eclipses (Δϕ) and e sin ω is proportional to the ratio of the primary (p) and secondary (s) eclipse widths according to (wp − ws)/(wp + ws) in the phase domain (see e.g. Prša 2018 for more information). Prša et al. (in prep.) devised an approximation of the morphology of an eclipse through a combination of linear and quadratic functions, and fitted this functional combination to the eclipse regions of all doubly eclipsing (i.e. displaying both a primary and a secondary eclipse) systems in the KEBC with sufficiently high signal-to-noise ratios (S/N) to determine the ingresses, egresses and midpoints of each eclipse. This provided the inputs to obtain Δϕ and (wp − ws)/(wp + ws), and therefore e and ω. We were therefore able to obtain e and ω for 81 out of 93 of the selected eclipsing binary systems with g-mode pulsating components that fulfilled the criteria of Prša et al. A full description of the methodology will be presented in Prša et al. (in prep.).

Table A.1 displays the KIC IDs, pulsational (Nind and fmax) and binary/atmospheric (log Porb, Morph, Teff, e, and ω) parameters1 of the 93 eclipsing binary systems with g-mode pulsating components in our sample, as well as whether p-mode frequencies were also observed in their frequency spectra. We also include a selection of eight phase-folded light curves of the systems in our sample in Fig. A.1 to showcase the variety of morphologies exhibited by the light curves of our sample. 32 of the stars identified during our analysis have been previously reported in the study of Gaulme & Guzik (2019). In addition, 13 other systems, not listed in Gaulme & Guzik (2019), have also been previously studied in an asteroseismic context. For these cases, we also include in Table A.1 all of the references to the studies that refer to the discovery or analysis of g modes. The 45 systems without a reference in Table A.1 are therefore eclipsing binary systems whose g-mode pulsational characteristics were discovered during this study.

Li et al. (2020a) performed a study of 35 Kepler eclipsing and spectroscopic binaries in which they identified clear period-spacing patterns, with the majority of those selected from the catalogue of Gaulme & Guzik (2019). 11 of those are also in our sample as part of the 24 systems whose periodograms contain dense clusters of g-mode frequencies. Of these 11 systems, we only found period-spacing patterns in seven of them (as mentioned earlier in this section). We suspect that the reason that they found more period-spacing patterns than we did is due to a difference in methodology: Li et al. had used a S/N cutoff of 3.5 while we used the more-conservative S/N = 4 (Breger et al. 1993), and they subtracted binned and phase-folded light curves from the original timeseries, while we prewhitened the orbital harmonics to remove the binary signature. Our approach would necessarily result in a lower number of extracted frequencies per star (due to the higher S/N cutoff) and a potential reduction in pulsational amplitude and therefore S/N (due to the orbital-harmonic prewhitening) when compared to the approach of Li et al.

The stars that are in their sample, but not ours, have one or more of the following characteristics: (1) Non-eclipsing; (2) Not clearly detached (Morph >  0.5); (3) Undefined morphology (i.e. Morph = −1); (4) Undefined KIC temperatures (Teff = −1); (5) Higher-order eclipsing system (the quintuple system KIC4150611). We posit that our catalogue and that of Li et al. (2020a) are complementary, as we include all g-mode (and hybrid p- and g-mode) pulsators independently identified in detached eclipsing binaries, with both pulsational and orbital characterisation.

Figure 1 shows various distributions of pulsational parameters (Nind and fmax) versus the binary and atmospheric (log Porb, Teff, e) parameters. We did not include the distributions with respect to Morph and ω as our sample consists only of detached binaries. Given that ω is simply a spatial orientation parameter, any potential correlation would simply be pure coincidence. We also calculated the Spearman’s rank correlation (ρ) to test if there were any correlations between the pulsational parameters and binary and atmospheric parameters (other than ω). We obtained |ρ| values below 0.3 for all combinations of pulsational parameters and binary and atmospheric parameters parameters, with p-values of the null hypothesis (that the parameters are uncorrelated) larger than 0.1 except for fmax/Teff, Nind/Teff and fmax/e, where the p-values are larger than 0.01. These values indicate that at best, there is only a weak correlation between any of the g-mode pulsational parameters and binary and atmospheric parameters, as expected for detached main-sequence binaries.

thumbnail Fig. 1.

Pulsational versus binary/atmospheric properties of the eclipsing binaries with g-modes. The plots in the left column show the distributions of Nind and those in the right column show the distributions of fmax. The first row is a display of stacked histograms of Nind and fmax, with the vertical axis representing the number of systems (N*). For the first row of plots, systems where only g modes were detected are represented in blue, and systems where both p and g modes were detected are represented in orange. The 2nd, 3rd and 4th rows are displays of the variation of fmax and Nind with respect to log Porb (2nd row), Teff (3rd row) and e (4th row). For the 2nd, 3rd and 4th rows of plots, stars where only g modes were detected are represented by blue circles, and stars where both p and g modes were detected are represented by orange triangles.

2.2. KIC9850387: An eclipsing binary with multimodal period-spacing patterns

Of the two systems that we considered to be our best candidates, KIC9850387 was very obviously the better one: our preliminary analysis revealed two g-mode period-spacing patterns of more than eight radial orders each (the longest in our sample) corresponding to different ℓ values in its frequency spectrum, as well as a few high-amplitude p modes. According to the KEBC, KIC9850387 has a period of 2.74 d and a morphology value of 0.47 with evenly spaced eclipses of near-equal widths, indicative of a circular or near-circular orbit. The KIC parameters for this system are as follows: Kmag = 13.549, Teff = 6808 K, log g = 4.028, R = 1.818 R⊙, and [Fe/H] = −0.291 (Brown et al. 2011). It should be noted that since these parameters were derived from photometric colours, they are likely inaccurate in general, and are probably even worse for binary systems. However, we list them here for completeness. KIC9850387 was first studied by Zhang et al. (2020), who claimed that the system was a pre-main-sequence SB1 eclipsing system containing a hybrid p- and g-mode pulsator, and reported the detection of an ℓ = 1 period-spacing pattern with a mean period spacing of 2756.2 ± 0.8 s. This system was also studied by Li et al. (2020a), who had reported a ℓ = 1, m = 1 and a ℓ = 2, m = 2 period-spacing pattern, with Π0 = 3894 ± 7 s and a core-rotation rate frot, core = 0.0053 d−1.

3. High-resolution spectroscopy

We embarked on a dedicated spectroscopic follow-up campaign of KIC9850387 using the HERMES spectrograph (Raskin et al. 2011) attached to the 1.2 m Mercator telescope at the Roque de los Muchachos observatory on La Palma, Spain. Due to the relative faintness of the star (Kmag = 13.549) and the 1.2 m diameter of the Mercator, it was difficult to obtain spectra with a S/N above 20, with short-enough exposure times to prevent excessive line smearing due to the low orbital period (P = 2.74 d).

However, through the use of techniques such as least-squares deconvolution (LSD, as described in Tkachenko et al. 2013a) and spectral disentangling (see Sect. 3.2), we were confident of being able to, at the very least, obtain precise radial velocities from the spectra, if not atmospheric parameters. The principle assumption of the LSD technique is that the observed spectrum is a convolution of a mean line profile with a predetermined line mask (Donati et al. 1997), which is a template of delta functions with wavelengths and line depths corresponding to a synthetic spectrum. LSD is the solution of the inverse problem, which is the determination of the mean line profile given an observed spectrum and a line mask.

This LSD profile has a significantly increased S/N when compared to any single spectral line, scaling with the square root of the number of spectral lines used in the mask that are also in the observed spectrum, therefore enabling more precise determinations of radial velocities. Tests with LSD profiles determined from synthetic spectra with white noise added to resemble spectra with S/N = 20 resulted in radial velocity precisions of the order of 0.4 km s−1. These precisions are acceptable for stars with low orbital periods because they tend to have high radial velocity semi-amplitudes of the order of 100 km s−1.

We obtained a total of 18 spectra between April and September 2019 with the HERMES spectrograph, and generated LSD profiles from the normalised spectra using the line mask of a dwarf star with Teff = 7000 K, which is reasonably close to the KIC Teff = 6808 K. This line mask comprises more than 3000 lines, and was calculated using the GSSP software package (described in Sect. 3.3). Unfortunately, we were only able to clearly visually discern the signature of the primary in each profile. The eclipse depth ratios indicated that the secondary should be a G-type dwarf, assuming that the primary is an F-type dwarf as indicated by the KIC Teff and log g. As such it would be much fainter than the primary and therefore have a low light contribution, which when combined with the low S/N, results in the signature of the secondary being indistinguishable from the noise.

Since Zhang et al. (2020) claimed that the system was a SB1, based on only six low-resolution (R ∼ 1800) LAMOST spectra (De Cat et al. 2015), we decided to check their claims. To that end, we obtained between October and November 2019 an additional eight spectra with a S/N ∼ 50 from the HIRES spectrograph (Vogt et al. 1994) attached to the 10 m Keck Telescope at the Mauna Kea Observatories in Hawai’i, USA. Once again, we calculated the LSD profiles for these new spectra, and signatures of both components were visually discernible, although those of the secondary were clearly less distinct (see Fig. 2 for a comparison of the HERMES and HIRES LSD profiles at similar orbital phases). It is therefore conclusive that KIC9850387 is an eclipsing, double-lined spectroscopic binary (SB2) system.

thumbnail Fig. 2.

Comparison of the LSD profiles generated from a HERMES (left panel) and a HIRES (right panel) spectrum of KIC9850387 taken at an orbital phase of ∼ − 0.45. Synthetic LSD profiles in black are fitted to the observed LSD profiles in blue in order to determine the radial velocities of the primary (indicated by the vertical orange dashed lines) and the secondary (indicated by the vertical red dashed line) component.

3.1. Spectroscopic orbital elements

We obtained the radial velocities for each component by fitting synthetic LSD profiles to the observed HERMES and HIRES LSD profiles. We fitted the 18 HERMES LSD profiles as if the system was a SB1 (as we are unable to discern the secondary) and the eight HIRES LSD profiles as a SB2. We used a grid of synthetic LSD profiles to fit our observed profiles, calculated from synthetic spectra with Teff = 7000 K, log g = 4.0 dex and [M/H] = 0.0. We allowed for the v sin i as a proxy of rotational broadening to vary as a free parameter to account for the effects of line-profile variations in the primary star, and included a scaling factor for the depth of each profile to account for the light contribution of each component to the total flux. The best-fitting v sin i values for the primary star ranged between 9 and 11 km s−1, showing temporal variations of line-broadening consistent with non-radial pulsations (Aerts et al. 2014). In total, we obtained 24 and eight radial velocities for the primary and the secondary components, respectively. Due to the lower light contribution of the secondary, its velocities are less precisely determined than those of the primary.

A preliminary Keplerian orbital fit was then performed using the Markov chain Monte Carlo (MCMC) routine emcee (Foreman-Mackey et al. 2013) to optimise the orbital elements. We chose to fix the orbital period at the value obtained from the KEBC due to the much longer timebase and the much finer sampling of the Kepler data, and similarly, we assumed a circular orbit as indicated by the photometry. This preliminary fit, while not as robust as our final combined fit with both radial velocities and Kepler photometry (see Sect. 4.1), was still relatively good and is a necessary step as it provides constraints for the process of spectral disentangling, particularly the radial velocity semi-amplitudes of the individual components (K1 and K2).

3.2. Spectral disentangling

The SB2 nature of KIC9850387 requires additional consideration during the determination of atmospheric parameters of the individual components: Each observed spectrum is a sum of the spectra of the individual components that have been (1) Doppler shifted by the radial velocities of the individual components at the time of observation, and (2) scaled by the wavelength-dependent light contribution of the individual components to the total flux, which depends on the spectral energy distribution of the individual components.

One of the ways in which binary stellar spectra can be analysed is by separating them into their individual components, which can be accomplished using the technique known as spectral disentangling (Simon & Sturm 1994; Hadrava 1995). Spectral disentangling involves the modelling of the Doppler shift of spectral lines at each orbital phase, enabling the simultaneous determination of both orbital elements and the mean spectrum of each component of the system. This technique has been widely applied to separation of a variety of multiple systems, from single- to multiple-lined systems (Hensberge et al. 2000; Pavlovski & Hensberge 2005, 2010). While there are a number of different ways in which spectral disentangling can be performed (see Pavlovski & Hensberge 2010 for a summary of different methodologies), we adopted a Fourier domain-based disentangling procedure implemented in the code FDBinary (Ilijic et al. 2004).

Due to the possibility of additional systematic effects (such as instrumental wavelength-dependent line-depth variations) on the final result, which are difficult to properly account for when combining the HERMES and HIRES spectra, we performed spectral disentangling on the 18 HERMES spectra and the eight HIRES spectra separately, enabling us to compare and contrast the results from each dataset. We initially attempted to optimise the orbital parameters in the spectral disentangling procedure for both types of spectra. However, we obtained wildly varying values for K2 depending on the wavelength region that was being disentangled: This is likely due to the low S/N for the HERMES spectra, and the poor orbital phase coverage for the HIRES spectra, resulting in an inability to properly disentangle the signal of the secondary (which has a low light contribution) from the primary.

As such, we chose to fix the orbital parameters during disentangling at the values obtained from our radial velocity fit. Even though the disentangled component spectra had a significantly higher S/N (∼50 for the HERMES and 120 for the HIRES) compared to any single observed spectrum, scaling with square root of the number of observations, only the disentangled primary component spectrum of the each dataset was of sufficiently high S/N for atmospheric parameter determination. The line depths of the disentangled secondary component spectrum of the higher-quality Keck dataset were unfortunately still too low for proper atmospheric parameter determination. However, the eclipsing nature of KIC9850387 means that several secondary atmospheric parameters could be instead determined through the subsequent eclipse modelling process (see Sect. 4.1), and the disentangled spectrum of the secondary can still be used for a qualitative consistency check for these parameters.

3.3. Atmospheric parameter determination

The atmospheric parameters of the primary star were determined by fitting synthetic spectra to our disentangled primary component HERMES and HIRES spectra using the Grid Search in Stellar Parameters (GSSP) software package (Tkachenko 2015). As the name suggests, GSSP is able to fit a grid of synthetic spectra that are generated on-the-fly using the SYNTHV radiative transfer code (Tsymbal 1996) combined with a grid of atmospheric models from the LLMODELS code (Shulyak et al. 2004). The best-fitting values and error estimates of the atmospheric parameters Teff, log g, microturbulent velocity (vmicro), macroturbulent velocity (vmacro), projected rotational velocity (vrot sin i), the global metallicity ([M/H]), and the light contribution of primary component to the total flux Lp, can then be determined from the distribution of χ2 values of the fit of each synthetic spectrum to the observed spectrum.

The HERMES spectra that we obtained had significantly higher S/N (∼20) in the redder parts of the visual spectrum (∼5000−7000 Å), and consequently the disentangled primary component spectrum also displayed such behaviour. We therefore chose to fit the disentangled primary component HERMES spectrum in region between 5000 and 6650 Å to minimise the effect of spectral normalisation errors as a result of low S/N, as well as improve the precision of the fit overall. This region also contains the Hα line that is essential for the constraining of Teff. To enable a consistent comparison with the HERMES spectra, we also fit the same wavelength region for the HIRES spectra (whose wavelength range unfortunately does not cover the Hβ region). We also chose not to include the Hγ region as the normalised continuum level drops below unity for AF-type stars in this region, resulting in increased spectral normalisation errors that would inevitably propagate into the disentangled component spectra.

Even though the disentangled primary component HERMES spectrum had significantly improved S/N when compared to the individual observed spectra, it was still too noisy to properly disentangle the various types of velocity broadening (microturbulent, macroturbulent and rotational). Therefore, we chose to fix vmicro at 2.0 km s−1 and vmacro at 0 km s−1 (as per Tkachenko et al. 2013a), allowing only vrot sin i to vary in the fit for both the HERMES and HIRES component spectra. This was done in order to obtain a similar basis for the comparison of the HERMES and HIRES results. In addition, [M/H] and Lp are largely degenerate parameters: [M/H] affects the basic thermodynamical properties of the star and therefore also affects metal-line depths, and Lp is a global line-depth scaling factor. This degeneracy is further compounded by the fact that log g is not well-constrained in the spectroscopic analysis of F-type stars, as the Balmer lines are largely insensitive to log g in this temperature range.

To break this degeneracy, constraints would have to be placed on [M/H] and Lp parameter (and ideally log gp), and since we are able to determine Lp and log gp with high precision from eclipse modelling, we employ an iterative methodology using both types of spectra to determine the atmospheric parameters: (1) Perform an initial fit in GSSP with unconstrained prior ranges for [M/H] and Lp to obtain an estimate for the primary effective temperature (Teff, p); (2) Perform eclipse modelling (described in Sect. 4.1) using the Teff, p estimate to obtain estimates for Lp and log g; (3) Fix the Lp and log gp estimates in GSSP and perform another iteration of atmospheric parameter determination to obtain [M/H] and Teff, p; (4) Iterate between atmospheric analysis and eclipse modelling until the differences in Teff, p, Lp and log gp between consecutive iterations is less than 1%.

Using this methodology, we were able to obtain well-constrained spectroscopic determinations of Teff, p, [M/H] and the projected rotational velocity of the primary component vrot, p sin i, which are the only parameters that we are unable to determine directly from eclipse modelling. It was found within a few iterations that the results were consistent between the HERMES and HIRES component spectra. We therefore decided to perform further iterations only with the higher S/N HIRES spectra, as the results were far more precise. In addition, the different types of velocity broadening were able to be disentangled, and we were able to determine vmicro, p as well. Including vmicro, p as a free parameter as opposed to fixing it at 2.0 km s−1 had a minimal effect on the other atmospheric parameters: The maximum-likelihood estimates of these parameters were slightly shifted within the error bars, although the error bars themselves were slightly smaller when including vmicro, p.

It should be noted that we did not attempt to fit for vmacro: It is well known that in F-type stars, vmacro and vrot, p sin i are degenerate (see Fossati et al. 2011 for a detailed discussion). Even though this degeneracy is lifted for slow rotators, and a significant improvement in the fit can be obtained upon inclusion of macroturbulence, the poor phase coverage of the HIRES spectra means that a significant amount of pulsational distortion (from the high-amplitude g modes) is present in the disentangled primary component HIRES spectrum2. This pulsational distortion manifests as asymmetric line-profile variations, which were already noted in the wings of the primary component in the HIRES LSD profiles (see the right panel of Fig. 2), and the inclusion of vmacro in the fit attempts to correct for that. Figure 3 shows the effects of including vmacro in the fit (resulting in the broader wings of the synthetic spectral line with the inclusion of vmacro). Aerts et al. (2014) have shown that macroturbulent broadening is able to mimic the effects of pulsational broadening, and that a timeseries of high-resolution spectra would be required to properly disentangle these two types of broadening due to the temporal nature of pulsations. As such, due to the limitations of our dataset, we chose to ignore macroturbulence.

thumbnail Fig. 3.

Comparison of synthetic spectral fits with (dashed black) and without (solid black) including vmacro, compared to a Mg I line of the disentangled primary component HIRES spectrum (in blue).

In addition to the atmospheric parameters of the star, we were also able to determine the abundances for 11 different chemical elements from the disentangled primary component spectrum. GSSP can be used to fit for individual chemical abundances once [M/H] is known. After completing the atmospheric parameter determination, we fixed their values at the maximum-likelihood estimates and varied only the individual chemical abundances. The maximum-likelihood estimates and 68% confidence intervals of these abundances (relative to the solar values taken from Asplund et al. 2009) are listed in Table 1. The relative abundances obtained are largely consistent with [M/H] = −0.109 except for yttrium (Y), which was found to be overabundant by ∼0.1 dex.

Table 1.

Relative chemical abundances derived from the disentangled primary component HIRES spectrum of KIC9850387.

Table 2 lists the maximum-likelihood estimates and 68% confidence intervals of Teff, p, [M/H], vmicro, p and vrot, p sin i, along with the parameters derived from eclipse modelling (see Sect. 4.1). The 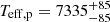K that we obtained is systematically higher than that used by Zhang et al. (2020) (Teff, p = 6947 ± 152 K; Frasca et al. 2016) in their analysis, and we posit that this is due to a combination of the following factors: (1) the lower resolution of the LAMOST spectra from which the spectroscopic parameters were derived; (2) the difference in methodology used (Frasca et al. 2016 use a grid of low-resolution spectra of real stars to determine their parameters); and (3) fitting the observed spectrum as if the system was a single star and not a binary. The best-fitting synthetic spectrum with respect to a metal-line and the Hα region of the disentangled primary component HIRES spectrum is displayed in Fig. 4. We have also plotted a synthetic spectrum generated with input parameters derived from eclipse modelling and the disentangled secondary component HIRES spectrum for the metal-line region, showing that the derived Teff, s, log gs and Ls values are, at the very least, qualitatively consistent with the morphology of the secondary spectrum.

thumbnail Fig. 4.

Best-fitting synthetic spectrum (in black), generated by GSSP, to the disentangled primary component HIRES spectrum (in blue). The disentangled secondary component HIRES spectrum (in red) is also plotted, with a synthetic spectrum generated with input parameters derived from eclipse modelling (listed in Table 2). The left panel is a metal-line region and the Hα region in displayed in the right panel.

Table 2.

Systemic, primary, and secondary parameters of KIC9850387, derived through a combination of atmospheric (see Sect. 3.3) and eclipse modelling (see Sect. 4.1).

4. Kepler photometry

KIC9850387 is one of the “module-3 stars” in the Kepler catalogue: One of the 21 CCD modules of the Kepler space telescope failed less than a year after launch in January 2010, which means that those stars that happened to fall on the part of the field-of-view covered by the module were not observed. Kepler performed 90° rotations every ∼93 d, which meant that different stars were within the field-of-view of that module in any given quarter. The overall result is that 20% of all stars in the nominal Kepler mission have additional3 yearly 93 day gaps in their light curves after the failure of the module.

For KIC9850387, this means that the dataset is missing three (Q7, Q11 and Q15) out of the 18 quarters (from Q0 to Q17) worth of data compiled during the nominal Kepler mission from May 2009 to May 2013. While this result has minimal consequence for the purposes of eclipse modelling, the consequences in the context of pulsational analysis and interpretation are significant, and we discuss that in detail in Sect. 5.

Instead of utilising the detrended SAP fluxes that we used in our preliminary analysis, we chose to extract the light curves of KIC9850387 directly from the pixel data files provided by the MAST (Mikulski Archive for Space Telescopes). In addition, we utilise a custom mask as defined in Pápics et al. (2013): This mask includes a larger number of pixels than the standard mask, reducing the effects of systematic instrumental trends in the extracted fluxes. Consequently, the amount of detrending that has to be applied to the extracted fluxes is significantly reduced, thereby reducing the potential impact of said detrending in the low-frequency regime and therefore, on the g modes themselves. The remaining systematic trends in each quarter were then corrected by applying a second-order polynomial to the extracted fluxes (as performed in e.g. Tkachenko et al. 2013b; Debosscher et al. 2013; Schmid et al. 2015).

4.1. Eclipse modelling setup

The dominant source of variability in the light curve of KIC9850387 is its prominent eclipses, enabling the extraction of the fundamental properties of each component when combined with spectroscopic data. To accurately model these eclipses, we utilised a genetic algorithm written in python (Abdul-Masih et al., in prep.; based on Charbonneau 1995) wrapped around the state-of-the-art PHOEBE2.0 code (version 2.1.15, Prša et al. 2016; Horvat et al. 2018) in order to generate and fit a binary model to our observations. PHOEBE2.0 includes a whole suite of improved physics including (1) a triangular discretisation of stellar surfaces; (2) a robust treatment of reflection and heat redistribution through the inclusion of Lambertian scattering (see Prša et al. 2016 for more details); and (3) an improved treatment of limb darkening by interpolating emergent intensities directly from a grid of Castelli & Kurucz (2004) atmospheric models, rather than the standard practice of assuming a parametric limb-darkening function and interpolating coefficients from tables of coefficients (e.g. from Claret & Bloemen 2011).

Most importantly, PHOEBE2.0 provides model outputs in the form of both photometric fluxes and radial velocities, and hence its inclusion in our framework allows for the simultaneous fitting of the Kepler photometric fluxes as well as the radial velocities. Due to the extensive computation time required for each synthetic data point (whether fluxes or velocities), computing synthetic fluxes corresponding to each of the 52 757 observed fluxes (∼420 orbital cycles) of the Kepler light curve would be impractical. Each PHOEBE2.0 eclipse model is therefore constructed by first computing 140 fluxes across a single orbital phase, and then interpolating through these 140 synthetic fluxes to obtain the 52 757 model fluxes corresponding to each observed flux value of the phase-folded light curve. Simultaneously, synthetic radial velocities were computed to match each of the 24 observed radial velocities, and we fit them independent of our previous spectroscopic orbital analysis described in Sect. 3.1. The efficiency of the genetic algorithm was of critical importance as we utilised 17 free parameters in our PHOEBE2.0 models. Through these 17 fit parameters, we are able to derive a total of 21 characteristic systemic, primary and secondary parameters of KIC9850387 (see Table 2).

Parameter and error estimation is then performed in the vein of Abdul-Masih et al. (2019) by converting the χ2 values of each model output from the genetic algorithm into a probability, using the following methodology (Tramper et al. 2011): (1) Normalise the χ2 values according to the following equation: 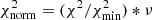, where 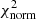is the normalised χ2, 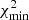is the minimum χ2 value and v is the number of degrees of freedom. This makes it such that normalised reduced χ2, 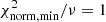. The implicit assumption being made is that the best-fitting model provides a good fit to the data (Tramper et al. 2011), which is not necessarily true in general as this depends on our initial parameter space. This is mitigated to a large extent by our iterative approach (described in Sect. 4.2), enabling the optimisation of the parameter space between iterations; (2) Convert the 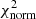values into probabilities using an incomplete gamma function as follows: 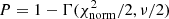; (3) Construct 68% confidence intervals for each parameter by considering all models with P >  0.32.

4.2. Obtaining a robust binary model

The presence of large-amplitude pulsational variability complicates the eclipse modelling process: Debosscher et al. (2013) had noted that both types of variability would have to be disentangled in order to produce a robust binary model. Furthermore, large-amplitude ellipsoidal variation can be observed in the light curve, necessitating the use of a higher order binary-model physics such as gravitational distortion and irradiation to reproduce the observations. Subtracting a model composed of polynomials (e.g. the polyfit models described in Prša et al. 2011) or a binned model of the light curve (e.g. Li et al. 2020a) may inadvertently result in the removal of pulsational variation, and as such we chose not to adopt such techniques.

We therefore adopt the iterative approach in the vein of studies such as Maceroni et al. (2013) and Debosscher et al. (2013). This methodology is coupled with the iterative methodology for the determination of spectroscopic parameters detailed in Sect. 3.3: (1) Generate a pulsational model by iteratively prewhitening (see Degroote et al. 2009 for a detailed description of the method) the light curve (up to the Nyquist frequency of 24.47 d−1) after clipping the eclipses and interpolating through the gaps with cubic splines. We prewhiten the light curve in decreasing order of amplitude of the frequencies in the Lomb-Scargle periodogram (Scargle 1982) until the standard deviation in the residual light curve decreases by less than 0.05% between subsequent prewhitening iterations; (2) Remove the pulsational model from the unaltered light curve, and derive the best-fitting PHOEBE2.0 model for the residual light curve, fixing the Teff, p at the spectroscopic estimate. Our genetic algorithm setup uses a population of 256 models and is run for 1000 generations, resulting in a total of 256 000 model computations in each iteration; (3) Remove the best-fitting PHOEBE2.0 model from the unaltered light curve, and generate a new pulsational model; (4) Perform iterations of eclipse model and pulsational model determination until the difference in the χ2 value of the best-fitting PHOEBE2.0 model between consecutive iterations changes by less than 1%. Once this point is reached, we retain the eclipse-modelling parameters of the final iteration, and calculate a final pulsational model after removing the best-fitting eclipse model from the unaltered light curve.

While the oft-quoted procedure in the literature in terms of frequency extraction is to prewhiten the light curve until a frequency is extracted below a S/N cutoff of 4 (Breger et al. 1993), this cutoff is highly dependent on the manner in which the S/N is calculated. One of the ways in which the S/N is calculated is based on a frequency window around each extracted frequency (e.g. Tkachenko et al. 2013b) and therefore varies with the density of peaks in that frequency region, as well as with the number of frequencies that have been prewhitened up to that point. Therefore, depending on the star and the adopted S/N calculation methodology, anything from tens to thousands of frequencies would be required before that level is reached. For example, Debosscher et al. (2013) prewhitened over 6000 frequencies, and Tkachenko et al. (2013b) had to reduce their S/N criterion for several of their stars as they found significant residual variation. It was also noted by Li et al. (2019a) that adopting the S/N cutoff of 3 instead of 4 resulted in the extraction of additional frequencies that formed parts of their identified period-spacing patterns.

Another issue that arises when considering the prewhitening cutoff is that some binary parameters are not well-constrained if there is significant residual variation in the light curve (as noted by Debosscher et al. 2013): we discovered that adopting the S/N cutoff of 4, where the noise level was determined from a 1 d−1 window around each peak (as we did for our sample characterisation in Sect. 2), resulted the gravity darkening exponent (β) being poorly constrained during eclipse modelling. We therefore adopted an iteration-to-iteration relative standard deviation reduction (inspired by the approaches in Pápics et al. 2012) of 0.05% as our prewhitening cutoff. We found that this represented a good compromise between removing pulsational variation from the light curve for eclipse modelling while resulting in the extraction of a conservatively high number of frequencies (∼500) in each iteration, making it likely that all frequencies of asteroseismic potential were extracted.

As noted by Balona (2014), excessive prewhitening of a light curve results in the extraction of spurious frequencies, and therefore the interpretation of the extracted frequencies must be performed with caution. Only a handful to several tens of frequencies have significant asteroseismic value, and a fraction of the frequencies extracted from the light curves of heat-driven pulsators are combination frequencies (see Pápics 2012; Kurtz et al. 2015a for detailed discussions of the origins and interpretations of combination frequencies). While these combination frequencies are ideal for the studying of non-linear effects in pulsations, their interpretation is outside of the scope of this paper. Figure 5 shows the percentage decrease in standard deviation of the light curve with the number of extracted frequencies (up to 1000). A 15 day section of the original light curve and the light curve after removing 478 frequencies in our final iteration is shown in Fig. 6.

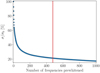thumbnail Fig. 5.

Percentage decrease in standard deviation of the light curve of KIC9850387 with the number of prewhitened frequencies. The vertical red line represents the number of frequencies after which the prewhitening was stopped, based on an iteration-to-iteration relative standard deviation reduction.

thumbnail Fig. 6.

15-day section of the light curve of KIC9850387, showing the original light curve (in blue) and after 478 pulsational frequencies have been removed (in orange).

It was discovered after a few iterations that there was significant out-of-eclipse variability in the residual light curve after eclipse-model removal in the positive half-phase of the orbit (i.e. after each primary eclipse and before each secondary eclipse). Although this could be a result of spot modulation, the asynchronous nature of the binary with respect to the primary star (i.e. the surface rotation rate of the primary star frot, surf(p) = 0.122 d−1 is close to 1/3 of the orbital frequency forb = 0.364 d−1) makes this scenario unlikely. We therefore concluded that Doppler boosting (see e.g. Bloemen et al. 2012) is the likely mechanism behind this phenomenon, and we included in our models for subsequent iterations. The clear asymmetry between each half-phase of the out-of-eclipse light curve (with the pulsations removed) is shown in Fig. 7, and the fit of our models was substantially improved.

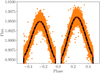thumbnail Fig. 7.

Observed asymmetry in the out-of-eclipse light curve with the pulsations removed (in orange), compared to our PHOEBE2.0 models with Doppler boosting included (in black). The red points correspond to the synthetic fluxes that were interpolated through to create the complete eclipse model.

Our iterative process allowed for the simultaneous optimisation of the eclipse model and dynamical parameters, as well as of the pulsational frequencies that are analysed in Sect. 5. The maximum-likelihood estimates and 68% confidence intervals of our parameters from eclipse modelling are listed in Table 2, along with the spectroscopic parameters (see Sect. 3.3). There are significant differences between our parameters and those derived by Zhang et al. (2020), which is unsurprising considering that they only used the radial velocities of the primary star (with fewer measurements), a different effective temperature of the primary star, and fixed Porb at the KEBC value and e = 0. However, their orbital inclination (i = 82.25 ± 0.03), and their log g values for the primary (3.98 ± 0.03) and secondary (4.34 ± 0.03) star are in good agreement with those that we derived.

It can be seen that Irefl is completely degenerate for both components, implying that the effect of reflection is rather weak. However, β was found to be well-constrained for the primary star, and its value of 0.460 is in between the classical theoretical values derived for fully radiative envelopes (1.0; von Zeipel 1924), and fully convective envelopes (0.32; Lucy 1967). However, according to Espinosa Lara & Rieutord (2012), β is theoretically expected to vary with the amount of ellipsoidal variation of the star, decreasing from 1.0 to 0.8 with increasing degrees of ellipsoidal variation regardless of the type of stellar envelope. They posit that low values of β that have been reported (e.g. in Djurašević et al. 2003, 2006) are the result of physical effects such as irradiation and asychronous rotation weakening the correlation between Teff and g. Based on these arguments, we can only conclude that there is a weak correlation between Teff and g and posit that this may be due to the asynchronous rotation of the star and residual pulsational variation in the modelled light curve.

Our best-fitting eclipse model and Keplerian orbital fit from PHOEBE2.0 is displayed in Fig. 8, and we find also good agreement between the K1 and K2 values derived from our preliminary spectroscopic orbital fit (see Sect. 3.1) and those derived through this analysis. However, there is increased variation in the in-eclipse phases of the residuals (particularly around the primary eclipse) compared to the out-of-eclipse phases, and this phenomenon manifests in the Lomb-Scargle periodogram, as described in Sect. 5.

thumbnail Fig. 8.

Best-fitting PHOEBE2.0 model to our observational data. Top left panel: best-fitting eclipse model (in black) to the unaltered light curve (in blue) and the light curve with the pulsations removed (in orange). The red points correspond to the synthetic fluxes that were interpolated through to create the complete eclipse model. Top right panel: best-fitting Keplerian orbital fit to the primary (in blue) and secondary (in red) radial velocities. The residuals of the fit of the eclipse model and the radial velocities are displayed in the bottom left and bottom right panels respectively, with the same colour-coding as the top panels.

Figure 9 shows the positions of the components of KIC9850387 on the log Teff − log g (or Kiel) diagram, along with the best-fitting isochrone cloud4 at an age of 1.27 Gyr (Johnston et al. 2019b), generated from single-star evolutionary tracks output from the stellar evolutionary code MESA (revision 10348; Paxton et al. 2011, 2018) at an initial metallicity (Zini) of 0.010, to the dynamical parameters. One can clearly see that the dynamical parameters of the secondary component are in good agreement with those predicted by evolutionary theory (the black data points) but the primary is not. It was noted by Tkachenko et al. (2020) that the enforcement of binary co-evolution resulted in increased mass discrepancy for several of their stars, and while relaxing the equivalent-age criterion reduces the discrepancy in the primary mass, it does not eliminate it entirely (these parameters only agree within 2-σ of the dynamical mass). However, if we also consider evolutionary models calculated at initial metallicities that fall within the spectroscopic errors (i.e. 0.008 ≲ Zini ≲ 0.012), this discrepancy disappears. Overall, our results disagree with the claim of Zhang et al. (2020) that the components are pre-main-sequence stars and strongly support a main-sequence binary evolutionary stage. A full description of our isochrone-cloud fitting methodology, asteroseismic modelling and comparisons of dynamical, evolutionary and asteroseismic parameters will be presented in our companion paper, Sekaran et al. (in prep.).

thumbnail Fig. 9.

Positions of the components of KIC9850387 on the log Teff − log g diagram. The red regions corresponds to the best-fitting isochrone cloud (Johnston et al. 2019b) to the dynamical parameters of both components. The black regions on the isochrone-cloud represent the log Teff − log g values corresponding to the dynamical masses of the individual components. The grey curves are MESA evolutionary tracks with different amounts of core-boundary mixing (solid and dashed), with their corresponding masses (in units of M⊙) indicated at the base of each track. The inset plots are magnified regions around the position of the primary (top) and secondary (bottom) component.

5. Asteroseismic analysis

The first step in the asteroseismic analysis is to remove frequencies that are within a certain resolution criterion of another higher-amplitude frequency. As mentioned in Sect. 4, we extracted more than the standard (as per the Breger et al. 1993 criterion) amount of frequencies to optimise the binary model, and as such we would need to identify the independent pulsational frequencies. The standard practice in these instances is to remove any frequency that is within a multiple (1 or 1.5 times) of the Rayleigh resolution (R = 1/Δτ) of another (Degroote et al. 2010), where Δτ is the length of the dataset. This results in a frequency resolution of R = 0.00068 d−1. Due to the additional gaps in the light curve mentioned in Sect. 4, each frequency peak in the Lomb-Scargle periodogram is split into a multiplet with each peak separated by the Kepler orbital frequency of 1/372.5 = 0.00268 d−1 (see Murphy 2014; Bowman et al. 2016 for more details). This phenomenon is displayed in Fig. 10, which shows the low-frequency region of the periodogram where clear series of peaks that could form period-spacing patterns are visible. The inset plot is the spectral window for the periodogram, clearly showing this multiplet phenomenon.

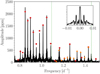thumbnail Fig. 10.

Low-frequency region of the Lomb-Scargle periodogram of KIC9850387, with the peaks that form the ℓ = 1 and ℓ = 2 period-spacing patterns indicated by red circles and orange triangles, respectively. The vertical green dashed lines represent the orbital harmonics, and the inset plot shows the spectral window.

The spectral window shows one prominent peak to either side of the main pulsation frequency separated by the Kepler orbital frequency, as well as less-prominent peaks at twice the Kepler orbital frequency. We therefore adopted a more conservative resolution criterion of twice the Kepler orbital frequency (i.e. R = 0.00536 d−1) such that both the first- and second-order side-peaks are considered when removing frequencies5. In addition, we also removed frequencies below 0.01 d−1 as they were likely a consequence of residual ellipsoidal variation in the out-of-eclipse light curve (a phenomenon also noted in Maceroni et al. 2013).

In addition, frequency multiplets were observed around each orbital harmonic (see Fig. 11). It can be seen from the inset plot that these are not exactly at each orbital harmonic but around each orbital harmonic, and the peaks disappear if the light curve was clipped and interpolated between the eclipse regions. We therefore conclude that these peaks are a result of residual variation from incomplete eclipse removal (as mentioned in Sect. 4.1) and not tidally induced or perturbed pulsational peaks as displayed by pulsating binaries such as U Gru (Bowman et al. 2019) and V453 Cyg (Southworth et al. 2020). As such, we also removed any peaks that were within the adopted resolution criterion (R = 0.00536 d−1) of any orbital harmonic. A total of 193 frequencies remained for further analysis after frequency removal.

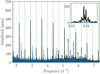thumbnail Fig. 11.

Residual peaks around orbital harmonics (vertical green dashed lines) in the Lomb-Scargle periodogram of KIC9850387. The periodogram of the original light curve is shown in black, and the periodogram of the light curve after the eclipse regions were clipped and interpolated through with cubic splines is shown in blue. The inset plot shows a magnified region of the frequency multiplet with the highest amplitude.

The second step in the asteroseismic analysis of any heat-driven pulsator is the identification of combination frequencies. As mentioned in Sect. 4.2, many of the frequencies extracted are potentially mathematical combinations of other frequencies. As discussed in detail in Pápics (2012), some of these frequencies are a result of non-linear interaction between two or more “parent” frequencies and have a physical interpretation (see e.g. Bowman 2016), while others are simply mathematical artefacts caused by interpreting pulsational frequencies in terms of harmonic functions. Nevertheless, these two types of combinations can be distinguished from each other by considering the phase behaviour of the combination frequencies (Degroote et al. 2009) and therefore have to be identified.

We performed our combination frequency search by adopting the methodology of Pápics (2012): we allow for combinations up to the combination order 𝒪 = 2, and consider combinations with frequencies up to the second harmonic. This means that we allow for combinations up to, for example, 2f1 ± 2f2, where f1 and f2 are two extracted frequencies. We also include the orbital frequency (forb) in the list of frequencies that we derive combinations of. We consider a frequency to be combination of two other frequencies if (1) it is of lower amplitude than both of the “parent” frequencies, and (2) if it is within our adopted frequency resolution criterion (i.e. within 0.00536 d−1) of the mathematical combination. All of the frequencies (f) that were left after removing those that failed our resolution criteria (the first step), and their corresponding errors (σf) are listed in Table B.1, along with their corresponding amplitudes (A) and amplitude errors (σA), phases ϕ and phase errors (σϕ), S/N values, and the combination frequency associated with each (if any). The S/N values that we quote here are computed from the Lomb-Scargle periodogram of the residual light curve after frequency extraction, where the noise level is determined from the mean amplitude of the periodogram in a 1 d−1 window centred on each extracted frequency. For the asteroseismic analysis, we retain all independent frequencies with S/N >  4 along with S/N >  3 frequencies that comprise part of a period-spacing pattern.

Both p-mode and g-mode frequencies were extracted from the light curve of KIC9850387. Due to the low mass of the secondary (Ms = 1.0476 M⊙), it is highly unlikely that any of the frequencies extracted are due to the pulsations of the secondary star. Stars in the mass-vicinity of 1.0 M⊙ tend to pulsate stochastically at very high frequencies well above 3000 μHz or 250 d−1 (García & Ballot 2019), which is also well above the Nyquist frequency of 24.47 d−1. We therefore conclude that all of the frequencies extracted are a result of pulsations originating in the more-massive primary star.

5.1. p modes

The p-mode regime of the Lomb-Scargle periodogram of KIC9850387 (see Fig. 12) is rather sparse, containing just a few independent p modes. No frequency splittings or other characteristic spacing was observed from these frequencies, although the frequency difference (Δf) between adjacent p-mode frequencies decreases as the frequency increases. The surface rotational frequency of frot, surf(p) = 0.122 d−1 is very similar to that found by Schmid et al. (2015) for their slowly-rotating F-type pulsating binary KIC10080943, but unfortunately there is no rotational signature in the p modes for this star.

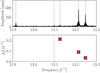thumbnail Fig. 12.

Independent p-mode frequencies (vertical red dashed lines) in the Lomb-Scargle periodogram (in black) of KIC9850387 (top panel). The frequency difference (Δf) between consecutive p-mode frequencies are represented by red “x” markers (bottom panel). The orbital harmonics in both panels are indicated by vertical green dashed lines.

5.2. g-mode period-spacing patterns

The Lomb-Scargle periodogram of KIC9850387 features numerous g-mode peaks, and we were able to construct two different period-spacing patterns of ℓ = 1 and ℓ = 2 modes. Due to the fact that KIC9850387 is a slow rotator, the mean period-spacing values for these modes should be approximately equal to the asymptotic period-spacing values. Based on this assumption, we obtained Π1 ≈ 2754 ± 16 s and Π2 ≈ 1568 ± 12 s and confirmed that these were indeed an ℓ = 1 and an ℓ = 2 pattern, from the distributions of Πℓ values published by Van Reeth et al. (2016). Using Eqs. (1) and (2), we also calculated Π0 for each mode pattern, obtaining Π0, ℓ = 1 = 3842 ± 29 s and Π0, ℓ = 2 = 3896 ± 22 s, which are within 2σ of each other and indicating that both patterns originate from the same star. These values are also consistent with the Π0 = 3898 ± 1 obtained by Zhang et al. (2020) for their ℓ = 1 pattern, and the Π0 = 3894 ± 7 s obtained by Li et al. (2020a).

These patterns comprise at least ten radial orders for each mode, a remarkable discovery in the context of eclipsing binary pulsators, allowing for stringent constraints of stellar structure during asteroseismic modelling (as detailed in Schmid & Aerts 2016). The patterns that we have obtained are longer than those reported by Li et al. (2020a). Figure 13 shows the period-spacing patterns that were constructed from the g-mode frequencies of KIC9850387.

thumbnail Fig. 13.

Period-spacing patterns of KIC9850387. Bottom panel: ℓ = 1 (red circles) and ℓ = 2 (orange triangles) period-spacing patterns, with the period-spacing on the vertical axis and the period on the horizontal axis. Top panel: corresponding periods that were selected to form the pattern, with the Lomb-Scargle periodogram (in black). The orbital harmonics are indicated by vertical green dashed lines in both panels.

6. Discussion and conclusions

In this paper, we detailed the identification and characterisation of a sample of detached eclipsing binaries with excellent g-mode asteroseismic potential by performing pulsational screening of all eclipsing binaries in the KEBC between 6000 K and 10 000 K that were considered to be predominantly detached according to Matijevič et al. (2012). We identified a total of 93 eclipsing binary systems with g-mode pulsating components, of which 11 systems contained hybrid p- and g-mode pulsators. We found clear period-spacing patterns in a total of seven stars, of which two featured continuous patterns longer than six radial orders. We also characterised the pulsations of these 93 eclipsing binary systems with g-mode pulsating components by calculating the frequency of highest amplitude (fmax) in the g-mode regime, and the number of independent frequencies (Nind) in said g-mode regime, and compared these parameters with the binary/orbital parameters log Porb, Morph, Teff, e, and ω using the Spearman’s rank correlation (ρ). The low |ρ| and moderate-to-high p-values indicate that the g-mode pulsational parameters and binary and atmospheric parameters are weakly correlated at best, as expected for detached main-sequence binaries.

In addition, we presented the observational spectroscopic, photometric and asteroseismic analysis of the pulsating eclipsing binary KIC9850387. First classified as a γ Doradus pulsator by Gaulme & Guzik (2019), this star was identified during our sample selection and characterisation process as the most promising candidate in our sample for future evolutionary and asteroseismic modelling due to the discovery of multimodal period-spacing patterns in its frequency spectra. We then proceeded with spectroscopic follow-up, compiling a total of 18 HERMES (Raskin et al. 2011) and eight HIRES (Vogt et al. 1994) spectra. Radial velocities were extracted from these spectra and used to determine the spectroscopic orbital elements, and these elements were then used to perform spectral disentangling. We were able to determine the atmospheric parameters and chemical abundances for the primary star by fitting synthetic spectra. However, due to the low S/N of the disentangled secondary component spectrum, we were only able to obtain qualitative agreement between the disentangled component spectrum and the parameters extracted from the subsequent eclipse modelling process.

We employed an iterative methodology in the vein of studies such as Maceroni et al. (2013) and Debosscher et al. (2013) to simultaneously optimise the pulsational and eclipse models, enabling the extraction of a whole host of parameters including the component masses, radii and the effective temperature of the secondary. We obtained 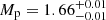M⊙ and 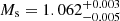M⊙, and 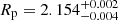R⊙ and 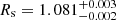R⊙, implying precisions well below the 1% level. We also obtaine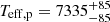d K and 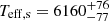K by iterating between atmospheric and eclipse modelling. We also noted that there is no mass discrepancy for either component, and that the models with the greatest agreement with the observed Teff and log g tended to have low amounts of core-boundary mixing. As detailed in Sects. 3 and 4, our results are in general disagreement with those of Zhang et al. (2020). We found that the system is a SB2 comprising two main-sequence components. The latter results contradict their claims that the system is a SB1 comprising two pre-main-sequence components. We posited that this disagreement is a result of the different quantity and quality of spectra used: We used numerous high-resolution HERMES and HIRES spectra, while Zhang et al. (2020) used only a few lower-resolution LAMOST spectra. Therefore, they were unable to properly characterise the secondary component and subsequently performed eclipse modelling based on insufficient spectroscopic information.

After performing a combination frequency search, we analysed the independent p modes and g modes of the star. The p-mode frequency spectrum was sparse with only four independent p modes observed and no frequency splittings or characteristic spacing. Analysis of the rich frequency spectrum of g modes revealed ℓ = 1 and ℓ = 2 period-spacing patterns that were longer than ten radial orders each. Li et al. (2020a) had reported a core rotation rate of 0.0053 d−1 from their fitting of the slopes of the ℓ = 1 and ℓ = 2 period-spacing patterns. This is below our adopted resolution criterion of 0.00536 d−1 and would render any frequency splitting in the g-mode regime indistinguishable from effects of the spectral window of the star (see Fig. 10). In contrast with our spectroscopic and photometric analysis, our asteroseismic analysis results agree with the conclusion of Zhang et al. (2020) that KIC9850387 is a γ Doradus-δ Scuti hybrid pulsator.

The period-spacing series obtained for this star allow for constraints on the interior mixing profile inferred from evolutionary modelling. As such, we coupled this observational analysis with an evolutionary and asteroseismic modelling-based analysis for the purposes of comparing the observationally and theoretically derived parameters of this star. This theoretical analysis and parameter comparison will be presented in the companion paper Sekaran et al. (in prep.).

1

log Porb, Morph, Teff are taken from the KEBC, and e and ω are determined by Prša et al. (in prep.).

2

Spectral disentangling interprets radial velocity variation in the spectral lines as originating completely from orbital motion, and therefore completely ignores pulsational variation.

3

All Kepler light curves have monthly gaps of several days coinciding with the downlinking of science data from the satellite towards the earth, during which there is a disruption of data collection.

4

An isochrone cloud is a collection of isochrones with different initial input physics (in this case, different core-boundary and envelope mixing values). See Johnston et al. (2019b) for a detailed description and applications of the isochrone-cloud methodology.

5

It was noted by Murphy (2014) that prewhitening the central frequency of a multiplet does not remove the entire multiplet, and as such justifies our approach.

Acknowledgments

The authors would like to thank the anonymous referee who helped us improve the presentation of our results. The research leading to these results has received funding from the Fonds Wetenschappelijk Onderzoek – Vlaanderen (FWO) under the grant agreements G0H5416N (ERC Opvangproject) and G0A2917N (BlackGEM), and from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement no. 670519: MAMSIE). MA acknowledges support from the FWO-Odysseus program under project G0F8H6N. DH acknowledges support from the Alfred P. Sloan Foundation and the National Aeronautics and Space Administration (80NSSC19K0597). The authors wish to recognize and acknowledge the very significant cultural role and reverence that the summit of Mauna Kea has always had within the indigenous Hawai’ian community. We are most fortunate to have the opportunity to conduct observations from this mountain. The authors would also like to thank the Leuven MAMSIE team for useful discussions.

References

  1. Abdul-Masih, M., Prša, A., Conroy, K., et al. 2016, AJ, 151, 101 [CrossRef] [Google Scholar]
  2. Abdul-Masih, M., Sana, H., Sundqvist, J., et al. 2019, ApJ, 880, 115 [NASA ADS] [CrossRef] [Google Scholar]
  3. Aerts, C. 2019, Rev. Mod. Phys., submitted [arXiv:1912.12300] [Google Scholar]
  4. Aerts, C., Christensen-Dalsgaard, J., & Kurtz, D. W. 2010, Asteroseismology (Springer Science+Business Media B.V.) [Google Scholar]
  5. Aerts, C., Simón-Díaz, S., Groot, P. J., & Degroote, P. 2014, A&A, 569, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Aerts, C., Molenberghs, G., Michielsen, M., et al. 2018, ApJS, 237, 15 [NASA ADS] [CrossRef] [Google Scholar]
  7. Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
  8. Auvergne, M., Bodin, P., Boisnard, L., et al. 2009, A&A, 506, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Balona, L. A. 2014, MNRAS, 439, 3453 [NASA ADS] [CrossRef] [Google Scholar]
  10. Bedding, T. R., Murphy, S. J., Colman, I. L., & Kurtz, D. W. 2015, Eur. Phys. J. Web Conf., 101, 01005 [CrossRef] [EDP Sciences] [Google Scholar]
  11. Bloemen, S., Marsh, T. R., Degroote, P., et al. 2012, MNRAS, 422, 2600 [Google Scholar]
  12. Borkovits, T., Derekas, A., Fuller, J., et al. 2014, MNRAS, 443, 3068 [NASA ADS] [CrossRef] [Google Scholar]
  13. Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  14. Bouabid, M. P., Dupret, M. A., Salmon, S., et al. 2013, MNRAS, 429, 2500 [NASA ADS] [CrossRef] [Google Scholar]
  15. Bowman, D. M. 2016, PhD Thesis, Jeremiah Horrocks Institute, University of Central Lancashire, Preston, UK [Google Scholar]
  16. Bowman, D. M., Kurtz, D. W., Breger, M., Murphy, S. J., & Holdsworth, D. L. 2016, MNRAS, 460, 1970 [NASA ADS] [CrossRef] [Google Scholar]
  17. Bowman, D. M., Johnston, C., Tkachenko, A., et al. 2019, ApJS, 883, L26 [NASA ADS] [CrossRef] [Google Scholar]
  18. Bradley, P. A., Guzik, J. A., Miles, L. F., et al. 2015, AJ, 149, 68 [NASA ADS] [CrossRef] [Google Scholar]
  19. Breger, M., Stich, J., Garrido, R., et al. 1993, A&A, 271, 482 [NASA ADS] [Google Scholar]
  20. Brown, T. M., Latham, D. W., Everett, M. E., & Esquerdo, G. A. 2011, AJ, 142, 112 [NASA ADS] [CrossRef] [Google Scholar]
  21. Castelli, F., & Kurucz, R. L. 2004, A&A, 419, 725 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Chapellier, E., & Mathias, P. 2013, A&A, 556, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Chapellier, E., Mathias, P., Weiss, W. W., Le Contel, D., & Debosscher, J. 2012, A&A, 540, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Charbonneau, P. 1995, ApJS, 101, 309 [NASA ADS] [CrossRef] [Google Scholar]
  25. Claret, A., & Bloemen, S. 2011, A&A, 529, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Claret, A., & Torres, G. 2018, ApJ, 859, 100 [NASA ADS] [CrossRef] [Google Scholar]
  27. Constantino, T., & Baraffe, I. 2018, A&A, 618, A177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Debosscher, J., Blomme, J., Aerts, C., & De Ridder, J. 2011, A&A, 529, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Debosscher, J., Aerts, C., Tkachenko, A., et al. 2013, A&A, 556, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. De Cat, P., Fu, J. N., Ren, A. B., et al. 2015, ApJS, 220, 19 [NASA ADS] [CrossRef] [Google Scholar]
  31. Degroote, P., Briquet, M., Catala, C., et al. 2009, A&A, 506, 111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Degroote, P., Aerts, C., Baglin, A., et al. 2010, Nature, 464, 259 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  33. Djurašević, G., Rovithis-Livaniou, H., Rovithis, P., et al. 2003, A&A, 402, 667 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Djurašević, G., Rovithis-Livaniou, H., Rovithis, P., et al. 2006, A&A, 445, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Donati, J. F., Semel, M., Carter, B. D., Rees, D. E., & Collier Cameron, A. 1997, MNRAS, 291, 658 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  36. Dupret, M. A., Grigahcène, A., Garrido, R., Gabriel, M., & Scuflaire, R. 2005, A&A, 435, 927 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Dziembowski, W. A., Moskalik, P., & Pamyatnykh, A. A. 1993, MNRAS, 265, 588 [NASA ADS] [Google Scholar]
  38. Espinosa Lara, F., & Rieutord, M. 2012, A&A, 547, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
  40. Fossati, L., Ryabchikova, T., Shulyak, D. V., et al. 2011, MNRAS, 417, 495 [NASA ADS] [CrossRef] [Google Scholar]
  41. Frasca, A., Molenda-Żakowicz, J., De Cat, P., et al. 2016, A&A, 594, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. García, R. A., & Ballot, J. 2019, Liv. Rev. Sol. Phys., 16, 4 [Google Scholar]
  44. Gaulme, P., & Guzik, J. A. 2019, A&A, 630, A106 [CrossRef] [EDP Sciences] [Google Scholar]
  45. Guo, Z., & Li, G. 2019, ApJS, 882, L5 [CrossRef] [Google Scholar]
  46. Guo, Z., Gies, D. R., & Fuller, J. 2017a, ApJ, 834, 59 [NASA ADS] [CrossRef] [Google Scholar]
  47. Guo, Z., Gies, D. R., & Matson, R. A. 2017b, ApJ, 851, 39 [NASA ADS] [CrossRef] [Google Scholar]
  48. Guo, Z., Fuller, J., Shporer, A., et al. 2019, ApJ, 885, 46 [NASA ADS] [CrossRef] [Google Scholar]
  49. Guo, Z., Shporer, A., Hambleton, K., & Isaacson, H. 2020, ApJ, 888, 95 [CrossRef] [Google Scholar]
  50. Guzik, J. A., Kaye, A. B., Bradley, P. A., Cox, A. N., & Neuforge, C. 2000, ApJS, 542, L57 [NASA ADS] [CrossRef] [Google Scholar]
  51. Hadrava, P. 1995, A&AS, 114, 393 [NASA ADS] [Google Scholar]
  52. Hambleton, K. M., Kurtz, D. W., Prša, A., et al. 2013, MNRAS, 434, 925 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  53. Hełminiak, K. G., Konacki, M., Maehara, H., et al. 2019, MNRAS, 484, 451 [CrossRef] [Google Scholar]
  54. Hensberge, H., Pavlovski, K., & Verschueren, W. 2000, A&A, 358, 553 [NASA ADS] [Google Scholar]
  55. Higl, J., & Weiss, A. 2017, A&A, 608, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Horvat, M., Conroy, K. E., Pablo, H., et al. 2018, ApJS, 237, 26 [NASA ADS] [CrossRef] [Google Scholar]
  57. Howell, S. B., Sobeck, C., Haas, M., et al. 2014, PASP, 126, 398 [NASA ADS] [CrossRef] [Google Scholar]
  58. Ilijic, S., Hensberge, H., Pavlovski, K., & Freyhammer, L. M. 2004, in Spectroscopically and Spatially Resolving the Components of the Close Binary Stars, eds. R. W. Hilditch, H. Hensberge, & K. Pavlovski, ASP Conf. Ser., 318, 111 [Google Scholar]
  59. Johnston, C., Pavlovski, K., & Tkachenko, A. 2019a, A&A, 628, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Johnston, C., Tkachenko, A., Aerts, C., et al. 2019b, MNRAS, 482, 1231 [NASA ADS] [CrossRef] [Google Scholar]
  61. Kahraman Aliçavus, F., & Soydugan, E. 2014, in Precision Asteroseismology, eds. J. A. Guzik, W. J. Chaplin, G. Handler, & A. Pigulski, IAU Symp., 301, 433 [Google Scholar]
  62. Kallinger, T., & Weiss, W. W. 2017, in Second BRITE-Constellation Science Conference: Small Satellites – Big Science, eds. K. Zwintz, & E. Poretti, 5, 113 [Google Scholar]
  63. Keen, M. A., Bedding, T. R., Murphy, S. J., et al. 2015, MNRAS, 454, 1792 [NASA ADS] [CrossRef] [Google Scholar]
  64. Kirk, B., Conroy, K., Prša, A., et al. 2016, AJ, 151, 68 [NASA ADS] [CrossRef] [Google Scholar]
  65. Kjurkchieva, D., & Atanasova, T. 2017, Serb. Astron. J., 195, 33 [CrossRef] [Google Scholar]
  66. Kjurkchieva, D. P., & Vasileva, D. L. 2018, Ap&SS, 363, 19 [CrossRef] [Google Scholar]
  67. Kjurkchieva, D., Vasileva, D., & Dimitrov, D. 2016, AJ, 152, 189 [NASA ADS] [CrossRef] [Google Scholar]
  68. Kurtz, D. W., Saio, H., Takata, M., et al. 2014, MNRAS, 444, 102 [NASA ADS] [CrossRef] [Google Scholar]
  69. Kurtz, D. W., Shibahashi, H., Murphy, S. J., Bedding, T. R., & Bowman, D. M. 2015a, MNRAS, 450, 3015 [NASA ADS] [CrossRef] [Google Scholar]
  70. Kurtz, D. W., Hambleton, K. M., Shibahashi, H., Murphy, S. J., & Prša, A. 2015b, MNRAS, 446, 1223 [NASA ADS] [CrossRef] [Google Scholar]
  71. Lee, J. W., & Park, J.-H. 2018, MNRAS, 480, 4693 [CrossRef] [Google Scholar]
  72. Li, G., Bedding, T. R., Murphy, S. J., et al. 2019a, MNRAS, 482, 1757 [NASA ADS] [CrossRef] [Google Scholar]
  73. Li, G., Van Reeth, T., Bedding, T. R., Murphy, S. J., & Antoci, V. 2019b, MNRAS, 487, 782 [Google Scholar]
  74. Li, G., Guo, Z., Fuller, J., et al. 2020a, MNRAS, 497, 4363 [CrossRef] [Google Scholar]
  75. Li, G., Van Reeth, T., Bedding, T. R., et al. 2020b, MNRAS, 491, 3586 [NASA ADS] [CrossRef] [Google Scholar]
  76. Lucy, L. B. 1967, ZAp, 65, 89 [NASA ADS] [Google Scholar]
  77. Lurie, J. C., Vyhmeister, K., Hawley, S. L., et al. 2017, AJ, 154, 250 [NASA ADS] [CrossRef] [Google Scholar]
  78. Maceroni, C., Montalbán, J., Michel, E., et al. 2009, A&A, 508, 1375 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  79. Maceroni, C., Montalbán, J., Gandolfi, D., Pavlovski, K., & Rainer, M. 2013, A&A, 552, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  80. Matijevič, G., Prša, A., Orosz, J. A., et al. 2012, AJ, 143, 123 [NASA ADS] [CrossRef] [Google Scholar]
  81. Matson, R. A., Gies, D. R., Guo, Z., & Orosz, J. A. 2016, AJ, 151, 139 [NASA ADS] [CrossRef] [Google Scholar]
  82. Michielsen, M., Pedersen, M. G., Augustson, K. C., Mathis, S., & Aerts, C. 2019, A&A, 628, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  83. Miglio, A., Montalbán, J., Noels, A., & Eggenberger, P. 2008, MNRAS, 386, 1487 [NASA ADS] [CrossRef] [Google Scholar]
  84. Mombarg, J. S. G., Van Reeth, T., Pedersen, M. G., et al. 2019, MNRAS, 485, 3248 [NASA ADS] [CrossRef] [Google Scholar]
  85. Mombarg, J. S. G., Dotter, A., Van Reeth, T., et al. 2020, ApJ, 895, 51 [CrossRef] [Google Scholar]
  86. Moravveji, E., Aerts, C., Pápics, P. I., Triana, S. A., & Vandoren, B. 2015, A&A, 580, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  87. Murphy, S. J. 2014, PhD Thesis, Jeremiah Horrocks Institute, University of Central Lancashire, Preston, UK [Google Scholar]
  88. Murphy, S. J., Fossati, L., Bedding, T. R., et al. 2016, MNRAS, 459, 1201 [NASA ADS] [CrossRef] [Google Scholar]
  89. Niemczura, E., Hümmerich, S., Castelli, F., et al. 2017, Sci. Rep., 7, 5906 [NASA ADS] [CrossRef] [Google Scholar]
  90. Ouazzani, R.-M., Salmon, S. J. A. J., Antoci, V., et al. 2017, MNRAS, 465, 2294 [NASA ADS] [CrossRef] [Google Scholar]
  91. Ouazzani, R. M., Marques, J. P., Goupil, M. J., et al. 2019, A&A, 626, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  92. Pápics, P. I. 2012, Astron. Nachr., 333, 1053 [NASA ADS] [CrossRef] [Google Scholar]
  93. Pápics, P. I., Briquet, M., Baglin, A., et al. 2012, A&A, 542, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  94. Pápics, P. I., Tkachenko, A., Aerts, C., et al. 2013, A&A, 553, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  95. Pápics, P. I., Moravveji, E., Aerts, C., et al. 2014, A&A, 570, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  96. Pápics, P. I., Tkachenko, A., Aerts, C., et al. 2015, ApJS, 803, L25 [NASA ADS] [CrossRef] [Google Scholar]
  97. Pápics, P. I., Tkachenko, A., Van Reeth, T., et al. 2017, A&A, 598, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  98. Pavlovski, K., & Hensberge, H. 2005, A&A, 439, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  99. Pavlovski, K., & Hensberge, H. 2010, in Binaries – Key to Comprehension of the Universe, eds. A. Prša, & M. Zejda, ASP Conf. Ser., 435, 207 [Google Scholar]
  100. Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
  101. Paxton, B., Schwab, J., Bauer, E. B., et al. 2018, ApJS, 234, 34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  102. Pedersen, M. G., Aerts, C., Pápics, P. I., & Rogers, T. M. 2018, A&A, 614, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  103. Pedersen, M. G., Escorza, A., Pápics, P. I., & Aerts, C. 2020, MNRAS, 495, 2738 [CrossRef] [Google Scholar]
  104. Pols, O. R., Tout, C. A., Eggleton, P. P., & Han, Z. 1995, MNRAS, 274, 964 [NASA ADS] [CrossRef] [Google Scholar]
  105. Prša, A. 2018, Modeling and Analysis of Eclipsing Binary Stars (IOP Publishing) [Google Scholar]
  106. Prša, A., Batalha, N., Slawson, R. W., et al. 2011, AJ, 141, 83 [NASA ADS] [CrossRef] [Google Scholar]
  107. Prša, A., Conroy, K. E., Horvat, M., et al. 2016, ApJS, 227, 29 [NASA ADS] [CrossRef] [Google Scholar]
  108. Raskin, G., van Winckel, H., Hensberge, H., et al. 2011, A&A, 526, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  109. Ribas, I., Jordi, C., & Giménez, Á. 2000, MNRAS, 318, L55 [Google Scholar]
  110. Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [Google Scholar]
  111. Rowe, J. F., Borucki, W. J., Koch, D., et al. 2010, ApJS, 713, L150 [Google Scholar]
  112. Russell, H. N. 1948, The Royal Road of Eclipses (Cambridge, MA: Harvard Observatory), 7, 181 [Google Scholar]
  113. Saio, H., Kurtz, D. W., Takata, M., et al. 2015, MNRAS, 447, 3264 [Google Scholar]
  114. Scargle, J. D. 1982, ApJ, 263, 835 [Google Scholar]
  115. Schmid, V. S., & Aerts, C. 2016, A&A, 592, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  116. Schmid, V. S., Tkachenko, A., Aerts, C., et al. 2015, A&A, 584, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  117. Schneider, F. R. N., Langer, N., de Koter, A., et al. 2014, A&A, 570, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  118. Shulyak, D., Tsymbal, V., Ryabchikova, T., Stütz, C., & Weiss, W. W. 2004, A&A, 428, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  119. Simon, K. P., & Sturm, E. 1994, A&A, 281, 286 [NASA ADS] [Google Scholar]
  120. Slawson, R. W., Prša, A., Welsh, W. F., et al. 2011, AJ, 142, 160 [Google Scholar]
  121. Southworth, J., Bowman, D. M., Tkachenko, A., & Pavlovski, K. 2020, MNRAS, 497, L19 [Google Scholar]
  122. Sowicka, P., Handler, G., Dębski, B., et al. 2017, MNRAS, 467, 4663 [Google Scholar]
  123. Stancliffe, R. J., Fossati, L., Passy, J. C., & Schneider, F. R. N. 2015, A&A, 575, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  124. Tassoul, M. 1980, ApJS, 43, 469 [Google Scholar]
  125. Tkachenko, A. 2015, A&A, 581, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  126. Tkachenko, A., Van Reeth, T., Tsymbal, V., et al. 2013a, A&A, 560, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  127. Tkachenko, A., Aerts, C., Yakushechkin, A., et al. 2013b, A&A, 556, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  128. Tkachenko, A., Aerts, C., Pavlovski, K., et al. 2014a, MNRAS, 442, 616 [Google Scholar]
  129. Tkachenko, A., Degroote, P., Aerts, C., et al. 2014b, MNRAS, 438, 3093 [Google Scholar]
  130. Tkachenko, A., Pavlovski, K., Johnston, C., et al. 2020, A&A, 637, A60 [CrossRef] [EDP Sciences] [Google Scholar]
  131. Torres, G., Andersen, J., & Giménez, A. 2010, A&ARv, 18, 67 [Google Scholar]
  132. Torres, G., Vaz, L. P. R., Sandberg Lacy, C. H., & Claret, A. 2014, AJ, 147, 36 [Google Scholar]
  133. Townsend, R. H. D. 2003a, MNRAS, 343, 125 [Google Scholar]
  134. Townsend, R. H. D. 2003b, MNRAS, 340, 1020 [Google Scholar]
  135. Tramper, F., Sana, H., de Koter, A., & Kaper, L. 2011, ApJS, 741, L8 [Google Scholar]
  136. Tsymbal, V. 1996, in M.A.S.S., Model Atmospheres and Spectrum Synthesis, eds. S. J. Adelman, F. Kupka, & W. W. Weiss, ASP Conf. Ser., 108, 198 [Google Scholar]
  137. Uytterhoeven, K., Moya, A., Grigahcène, A., et al. 2011, A&A, 534, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  138. Valle, G., Dell’Omodarme, M., Prada Moroni, P. G., & Degl’Innocenti, S. 2017, A&A, 600, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  139. Van Reeth, T., Tkachenko, A., Aerts, C., et al. 2015a, A&A, 574, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  140. Van Reeth, T., Tkachenko, A., Aerts, C., et al. 2015b, ApJS, 218, 27 [Google Scholar]
  141. Van Reeth, T., Tkachenko, A., & Aerts, C. 2016, A&A, 593, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  142. Vogt, S. S., Allen, S. L., Bigelow, B. C., et al. 1994, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, eds. D. L. Crawford, & E. R. Craine, Proc. SPIE, 2198, 362 [Google Scholar]
  143. von Zeipel, H. 1924, MNRAS, 84, 702 [Google Scholar]
  144. Weiss, W. W., Rucinski, S. M., Moffat, A. F. J., et al. 2014, PASP, 126, 573 [Google Scholar]
  145. Welsh, W. F., Orosz, J. A., Aerts, C., et al. 2011, ApJS, 197, 4 [Google Scholar]
  146. Zhang, X. B., Fu, J. N., Luo, C. Q., Ren, A. B., & Yan, Z. Z. 2018, ApJ, 865, 115 [Google Scholar]
  147. Zhang, X., Chen, X., Zhang, H., Fu, J., & Li, Y. 2020, ApJ, 895, 124 [Google Scholar]
  148. Zwintz, K., Van Reeth, T., Tkachenko, A., et al. 2017, A&A, 608, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

Appendix A: Sample of eclipsing binary systems with g-mode pulsating components

thumbnail Fig. A.1.

Phase-folded light curves of eclipsing binary systems with g-mode pulsating components. Selection of phase-folded light curves of eclipsing binary systems with g-mode pulsating components, showing the plethora of variation in the visual morphologies of these systems.

Table A.1.

KIC IDs, pulsational (Nind and fmax) parameters, and binary and atmospheric (log Porb, Morph, Teff, e, and ω) parameters of the 93 detached eclipsing binary systems with g-mode pulsating components identified during our study.

Appendix B: List of frequencies of KIC9850387

Table B.1.

Full list of frequencies extracted from the light curve of KIC9850387 after the eclipses were removed, with their corresponding amplitudes, phases, and respective errors.

All Tables

Table 1.

Relative chemical abundances derived from the disentangled primary component HIRES spectrum of KIC9850387.

In the text
Table 2.

Systemic, primary, and secondary parameters of KIC9850387, derived through a combination of atmospheric (see Sect. 3.3) and eclipse modelling (see Sect. 4.1).

In the text
Table A.1.

KIC IDs, pulsational (Nind and fmax) parameters, and binary and atmospheric (log Porb, Morph, Teff, e, and ω) parameters of the 93 detached eclipsing binary systems with g-mode pulsating components identified during our study.

In the text
Table B.1.

Full list of frequencies extracted from the light curve of KIC9850387 after the eclipses were removed, with their corresponding amplitudes, phases, and respective errors.

In the text

All Figures

thumbnail Fig. 1.

Pulsational versus binary/atmospheric properties of the eclipsing binaries with g-modes. The plots in the left column show the distributions of Nind and those in the right column show the distributions of fmax. The first row is a display of stacked histograms of Nind and fmax, with the vertical axis representing the number of systems (N*). For the first row of plots, systems where only g modes were detected are represented in blue, and systems where both p and g modes were detected are represented in orange. The 2nd, 3rd and 4th rows are displays of the variation of fmax and Nind with respect to log Porb (2nd row), Teff (3rd row) and e (4th row). For the 2nd, 3rd and 4th rows of plots, stars where only g modes were detected are represented by blue circles, and stars where both p and g modes were detected are represented by orange triangles.
In the text
thumbnail Fig. 2.

Comparison of the LSD profiles generated from a HERMES (left panel) and a HIRES (right panel) spectrum of KIC9850387 taken at an orbital phase of ∼ − 0.45. Synthetic LSD profiles in black are fitted to the observed LSD profiles in blue in order to determine the radial velocities of the primary (indicated by the vertical orange dashed lines) and the secondary (indicated by the vertical red dashed line) component.
In the text
thumbnail Fig. 3.

Comparison of synthetic spectral fits with (dashed black) and without (solid black) including vmacro, compared to a Mg I line of the disentangled primary component HIRES spectrum (in blue).
In the text
thumbnail Fig. 4.

Best-fitting synthetic spectrum (in black), generated by GSSP, to the disentangled primary component HIRES spectrum (in blue). The disentangled secondary component HIRES spectrum (in red) is also plotted, with a synthetic spectrum generated with input parameters derived from eclipse modelling (listed in Table 2). The left panel is a metal-line region and the Hα region in displayed in the right panel.
In the text
thumbnail Fig. 5.

Percentage decrease in standard deviation of the light curve of KIC9850387 with the number of prewhitened frequencies. The vertical red line represents the number of frequencies after which the prewhitening was stopped, based on an iteration-to-iteration relative standard deviation reduction.
In the text
thumbnail Fig. 6.

15-day section of the light curve of KIC9850387, showing the original light curve (in blue) and after 478 pulsational frequencies have been removed (in orange).
In the text
thumbnail Fig. 7.

Observed asymmetry in the out-of-eclipse light curve with the pulsations removed (in orange), compared to our PHOEBE2.0 models with Doppler boosting included (in black). The red points correspond to the synthetic fluxes that were interpolated through to create the complete eclipse model.
In the text
thumbnail Fig. 8.

Best-fitting PHOEBE2.0 model to our observational data. Top left panel: best-fitting eclipse model (in black) to the unaltered light curve (in blue) and the light curve with the pulsations removed (in orange). The red points correspond to the synthetic fluxes that were interpolated through to create the complete eclipse model. Top right panel: best-fitting Keplerian orbital fit to the primary (in blue) and secondary (in red) radial velocities. The residuals of the fit of the eclipse model and the radial velocities are displayed in the bottom left and bottom right panels respectively, with the same colour-coding as the top panels.
In the text
thumbnail Fig. 9.

Positions of the components of KIC9850387 on the log Teff − log g diagram. The red regions corresponds to the best-fitting isochrone cloud (Johnston et al. 2019b) to the dynamical parameters of both components. The black regions on the isochrone-cloud represent the log Teff − log g values corresponding to the dynamical masses of the individual components. The grey curves are MESA evolutionary tracks with different amounts of core-boundary mixing (solid and dashed), with their corresponding masses (in units of M⊙) indicated at the base of each track. The inset plots are magnified regions around the position of the primary (top) and secondary (bottom) component.
In the text
thumbnail Fig. 10.

Low-frequency region of the Lomb-Scargle periodogram of KIC9850387, with the peaks that form the ℓ = 1 and ℓ = 2 period-spacing patterns indicated by red circles and orange triangles, respectively. The vertical green dashed lines represent the orbital harmonics, and the inset plot shows the spectral window.
In the text
thumbnail Fig. 11.

Residual peaks around orbital harmonics (vertical green dashed lines) in the Lomb-Scargle periodogram of KIC9850387. The periodogram of the original light curve is shown in black, and the periodogram of the light curve after the eclipse regions were clipped and interpolated through with cubic splines is shown in blue. The inset plot shows a magnified region of the frequency multiplet with the highest amplitude.
In the text
thumbnail Fig. 12.

Independent p-mode frequencies (vertical red dashed lines) in the Lomb-Scargle periodogram (in black) of KIC9850387 (top panel). The frequency difference (Δf) between consecutive p-mode frequencies are represented by red “x” markers (bottom panel). The orbital harmonics in both panels are indicated by vertical green dashed lines.
In the text
thumbnail Fig. 13.

Period-spacing patterns of KIC9850387. Bottom panel: ℓ = 1 (red circles) and ℓ = 2 (orange triangles) period-spacing patterns, with the period-spacing on the vertical axis and the period on the horizontal axis. Top panel: corresponding periods that were selected to form the pattern, with the Lomb-Scargle periodogram (in black). The orbital harmonics are indicated by vertical green dashed lines in both panels.
In the text
thumbnail Fig. A.1.

Phase-folded light curves of eclipsing binary systems with g-mode pulsating components. Selection of phase-folded light curves of eclipsing binary systems with g-mode pulsating components, showing the plethora of variation in the visual morphologies of these systems.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.