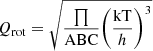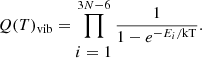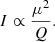EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 642 (October 2020) A&A, 642 (2020) A206 Full HTML
Open Access
Issue
A&A
Volume 642, October 2020
Article Number A206
Number of page(s) 11
Section Atomic, molecular, and nuclear data
DOI https://doi.org/10.1051/0004-6361/202038230
Published online 20 October 2020

© L. Margulès et al. 2020

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1. Introduction

Some 23 sulfur-containing molecules have been discovered in the interstellar medium (ISM)1 (McGuire 2018). The majority of these are analogs of oxygen-containing compounds, and hence can be extremely useful in exploring the chemistry of the ISM through comparison of reaction pathways and relative abundances. Sulfur-containing compounds are also of interest, because significantly lower sulfur levels are found in dense regions of the ISM than in diffuse regions (Martín-Doménech et al. 2016). There has been substantial interest in understanding the origin of this “missing sulfur problem;” one approach is to search for as-yet undetected molecular sulfur reservoir(s) in dense regions (see Laas & Caselli 2019 and references therein for an overview).

Propynal was first detected in the ISM in 1988 (Irvine et al. 1988) and it has since been observed in several sources (Loison et al. 2016). Propynethial, the sulfur analog of propynal is thus a molecule of interest in exploring the chemistry of the ISM, and sulfur-bearing species in particular. Propynethial is a transient species when generated via flash pyrolysis of dipropargyl sulfide under laboratory conditions. To date, only four spectroscopic studies have been performed in the gas phase, while one study has been carried out using matrix isolation. Brown et al. (1982) first recorded the microwave spectrum (8.5–40 GHz) of propynethial and determined spectroscopic constants of both the major isotopic species and the 34S isotopologue. In a second study, Wong (2016) recorded and analyzed the high-resolution infrared spectrum of propynethial at the Australian Synchrotron Facility, attempting to improve the accuracy of the ground state rotational and centrifugal distortion constants by analyzing the ν5 band at 1100 cm−1. However, this work has yet to be published due to possible perturbations associated with the ground state. Recent work by Crabtree et al. (2016) found propynethial present during a microwave spectroscopic analysis of the products formed from the electric discharge of CS2 and C2H2 in Ne. The photoelectron spectrum was also investigated (Nefedov et al. 1992). In a matrix, Kargamanov et al. (1987) recorded the spectrum from 3500–400 cm−1 and assigned the spectrum by comparing it with that of the oxygen analog propynal (Kargamanov et al. 1987).

Propynethial is a planar molecule with Cs symmetry that has 12 fundamental vibrations, which have either a/b-hydrid or c-type rovibrational band structure. The limited amount of available data makes it difficult to accurately assign rotational transitions from propynethial to allow its detection in the ISM. The aim of the current study is to analyze the submillimeter-wave spectrum of propynethial and improve the spectroscopic constants of the ground state in order to provide an accurate prediction in this domain. In this work, a number of new lines of propynethial were measured and fit together with those from previous works.

2. Experimental methods

2.1. Synthesis

The synthesis of propynethial was performed by flash vacuum thermolysis of 3,3′-thiobis-1-propyne (dipropargyl sulfide) (Gal & Choi 1988), following the approach used by Brown et al. (1982). With an oven heated to 600°C and a pressure of 0.1 mbar, a stoichiometric mixture of propynethial and allene (a compound without a permanent dipolar moment) was obtained and the gaseous flow was directly introduced into the 1.2 m length pyrex cell of the spectrometer.

2.2. Measurements

The absorption measurements of the propynethial between 150 and 630 GHz use the fast-scan terahertz spectrometer in Lille. The details of the spectrometer (except for the fast-scan feature) are described in Zakharenko et al. (2015). As a radiation source in the spectrometer, we used a commercially available VDI frequency multiplication chain driven by a home-made fast sweep frequency synthesizer. The fast sweep system is based on the up-conversion of an AD9915 direct digital synthesizer (DDS) operating between 320 and 420 MHz into the Ku band (12.5–18.25 GHz) and mixing the signals from the AD9915 and an Agilent E8257 synthesizer with subsequent sideband filtering. The DDS provides rapid frequency scanning with up to 50 ms per-point frequency switching rate. In order to obtain an optimum signal-to-noise ratio, the spectrum was scanned with a slower rate of 1 ms per point and with four scans co-averaged. The sample pressure during measurements was about 15 Pa at room temperature. Estimated uncertainties for measured line frequencies are 30 kHz and 50 kHz depending on the observed S/N and the frequency range.

3. Analysis of the spectra

Propynethial, like its oxygen analog propynal, is a near prolate symmetric top with the A rotational constant being significantly larger than the B and C constants. It has nonzero dipole components along the a- (μa = 1.763(1) D) and b-axis (μb = 0.661(1) D) as determined by Brown et al. (1982). In addition, like propynal, propynethial has several fundamental vibrational modes below 600 cm−1 that have substantial populations at room temperature and are responsible for the bulk of weaker lines that appear between the strong K-stacks of the ground state. To start the analysis, the spectroscopic parameters from the work by Brown et al. (1982) were used to simulate the spectrum of the ground state. The most intense transitions, the aR ones, were firstly analyzed and fit up to 330 GHz. They were found only a few MHz from initial predictions. Subsequently bR and bQ lines were re-predicted, searched for, and included in the fit up to 330 GHz. The rest of the analysis was done using the same scheme up to 630 GHz. We employed ASFIT (Kisiel 2001) for fitting, and predictions were made with SPCAT (Pickett 1991). The molecule is close to the prolate limit case (κ = −0.982), and so we used Watson’s S-reduced Hamiltonian. The global fit included the microwave transitions from Brown et al. (1982), Crabtree et al. (2016), and 3288 new lines from this work. The maximum quantum numbers included in the fit were J = 107 and Ka = 24. The root mean-square error considering the full dataset is 26.6 kHz, using 26 parameters. The resultant effective parameters are shown in Table 1. Part of the new measurements are in Table 2. The complete version of the global fit Table (S1) is supplied at the CDS. The fitting files useable with SPFIT, namely .lin (S2) and .par (S3), which contain the measured lines and the spectroscopic parameters, respectively, and the prediction .cat (S4) are also available at the CDS.

Table 1.

Spectroscopic parameters of propynethial in MHz – S reduction.

Table 2.

Measured frequencies of propynethial and residuals from the fit.

In Sect. 5, we present an observational search for propynal in the same sources in which we search for propynethial. The predicted spectrum of propynal in its ground vibrational state was made using the centimeter and millimeter-wave data available in the literature (Howe & Goldstein 1955; Costain & Morton 1959; Winnewisser 1973), as well as recent FIR spectra from The AILES beamline of SOLEIL (Barros et al. 2015).

4. Partition function

When low-energy, vibrationally excited states exist, the vibrational part of the partition function should be taken into account to derive column densities. For example at a relatively low temperature (150 K), with glycoaldehyde Widicus Weaver et al. (2005) showed that the states of glycolaldehyde up to 313 cm−1 are adequately populated. Like propynal, propynethial has several fundamental vibrational modes below 600 cm−1, some of which have not yet been experimentally observed. As such, we carried out computational chemistry calculations at a B3LYP level of theory using a 6-311+G(d) basis set using the Gaussian16 (Frisch et al. 2016) to derive the complete set. Table 3 lists the fundamental vibrations of propynethial, their symmetry and mode description in addition to their predicted and experimental band centers. In order to determine the accuracy of the predictions, additional calculations were also carried out on the oxygen analog, propynal, and the predictions were compared to the experimental values (see Table 4). As can be seen from the calculations on propynal, the anharmonic calculations are significantly different to those observed experimentally. The best methodology therefore is to scale the B3LYP fundamental harmonic frequencies by using the appropriate scaling factor2 and not using the anharmonic values in estimating the band centers. This methodology was applied to the computational chemistry calculations carried out on propynethial.

Table 3.

Comparison of the band positions (cm−1) for propynethial from ab initio and density functional theory methods using a 6-311+G(d) basis set.

Table 4.

Comparison of the band positions (cm−1) for propynal from ab initio and density functional theory methods using a 6-311+G(d) basis set.

The tabulated values for the partition function are given in Table 5, with Qtot(T) = Qvib(T)Qrot(T). We considered various temperatures. Qrot is approximated as

Q rot = ∏ ABC ( kT h ) 3 $$ \begin{aligned} {Q_{{\rm{rot}}}} = \sqrt {\frac{\prod }{{{\rm{ABC}}}}{{\left( {\frac{{{\rm{kT}}}}{h}} \right)}^3}} \end{aligned} $$(1)

Table 5.

Rotational, vibrational, and total partition functions at various temperatures.

The vibrational partition function was calculated with respect to the zero-point level using the following expression:

Q ( T ) vib = ∏ i = 1 3 N − 6 1 1 − e − E i / kT . $$ \begin{aligned} Q(T)_{\rm vib}=\prod \limits _{\begin{matrix} i=1 \end{matrix}}^{3N-6} \frac{1}{1-e^{-E_i/\mathrm{kT}}} .\end{aligned} $$(2)

The experimental rotational constants in this calculation come from our analysis. The experimental vibrational states frequencies are those from Kargamanov et al. (1987) corrected for the matrix effect, except for the two lowest states not experimentally observed where we used the calculated scaled harmonic frequencies.

The seven lowest vibrational excited state levels were considered. The remaining ones above 900 cm−1 (1295 K) were found to have no influence on the partition function calculations.

5. Radioastronomical observations

We searched for both propynethial and its oxygen-substituted counterpart propynal in a number of astronomically observed datasets, most of which are publicly available and all of which have previously been published elsewhere. These include ALMA observations of the high-mass star-forming region NGC 6334I (Brogan et al. 2018; McGuire et al. 2018a, 2017), observations of the Sgr B2N high-mass star-forming region using the Green Bank Telescope (GBT) from the Prebiotic Interstellar Molecule Survey (PRIMOS) project (Neill et al. 2012), as well as the datasets from the Astrochemical Surveys at IRAM (ASAI) Large Program, which was conducted with the IRAM 30 m telescope. The ASAI spectra cover a range of source types, from cold, dark clouds to class 0/1 protostars and shocked outflows, with observational details available in Lefloch et al. (2018). We note that the frequency coverage of the ASAI observations varies from source to source (Fig. A.1). As a result, some favorable transitions of our target species are not covered.

The observational details of these sources are described elsewhere; here, we focus only on the salient physical parameters necessary to derive column densities. In the case of propynethial, because these are non-detections, we had to make assumptions about the physical conditions in which the molecules might be found. For sources with detections of propynal (Sgr B2N, TMC-1, and L1527), we used the physical parameters derived for that molecule to estimate the upper limits to the column density and the abundance of propynethial in that source. For the other sources, we used the parameters from the literature. These parameters and the literature sources they were obtained from are provided in the respective tables.

5.1. Upper-limit analysis and results

We find no evidence of propynethial in any of our studied sources (Fig. 1). Propynal is known in TMC-1, Sgr B2(N), and Barnard 1 from prior work (Irvine et al. 1988; Turner 1991; Loison et al. 2016), and we report a detection in L1527, which, to the best of our knowledge, has not been previously seen in these data. All upper limits to propynethial and propynal are derived using the formalisms outlined in Turner (1991) that assume the molecules are well described by a single excitation temperature and include corrections for optical depth. In this case, all transitions considered for both propynal and propynethial are extremely optically thin (τ ≪ 1) in all sources. Frequencies, energy levels, degeneracies, and line strengths were obtained from the laboratory spectroscopy described in this work. The partition function for each molecule, which includes a correction for the lowest torsional vibrational mode of the molecule, is given in Tables B.1 and 6. Both species possess some low-lying vibrational modes that might contribute non-trivially to the partition function. For propynal, the experimentally determined vibrational energies in Table 4 were used; the scaled harmonic frequencies presented in Table 3 were used for propynethial.

thumbnail Fig. 1.

Transitions of propynethial used to calculate the upper limits given in Table 6. In each panel, the red trace shows the transition simulated using the derived upper-limit column density and the physical parameters assumed for that source. The frequency of the transition is given in the top right of each panel, and the quantum numbers for each transition in the top left. The source name is given above each panel. Due to the large variances between observations, the intensity and velocity axes are not uniform between each panel.

Table 6.

Upper limits to propynethial and the line parameters used to calculate them in each of the sets of observations.

For each source, we simulated a spectrum of each molecule using the physical conditions for the source (including any effects of beam dilution) and the line parameters measured in this work. Then, the 1σ upper limit to the column density was derived using the line that gave the most rigorous constraint (i.e., the line that would be the highest signal to noise in the event of a detection). These lines are provided in Tables B.1 and 6 along with the resulting upper limits. We note that in some cases, multiple transitions of a species contribute to single line due to close frequency spacings.

5.2. Propynal detections and comparison to propynethial

5.2.1. Sgr B2N

A detection of propynal in Sgr B2(N) was reported by Turner (1991) in his 1989 survey data obtained with the NRAO 12-m telescope (the telescope diameter was actually 11 m for much of the work and was only resurfaced to 12 m for the final portions). From that study, we utilized the excitation temperature and linewidth of 49.7 K and 10.75 km s−1, respectively. To the best of our knowledge, the source was assumed to fill the beam, which varied from 60–80″ between the highest and lowest-frequency transitions observed (83.8 and 113.8 GHz).

As far as we know, the data from the Turner (1989) survey is not currently available in electronic format, precluding a detailed analysis. A cursory look at the spectra presented in that survey via the article figures showed no indication of any transitions of propynethial above the reported noise limits in any passband.

We were able to perform a more complete search in this source using the data available from the GBT PRIMOS program. The most prominent transitions predicted in these data were between 45 and 50 GHz. The GBT beam at 48 GHz where the upper limit was derived is 16″. If both propynethial and propynal did indeed fill the larger 12-m beam, then there would be no mismatch from the observations, and we would derive an abundance ratio of [propynethial]/[propynal] of < 1.5.

However, Hollis et al. (2007) derived a 5″ source size for warm, compact emission from complex molecules. This more compact size for warmer molecular emission has been seen in numerous other studies in the recent literature (see, e.g., Belloche et al. 2014 and Bonfand et al. 2017). If we adopted this source size instead, we would derive an upper limit of propynethial of < 6.7 × 1014 cm−2 from the PRIMOS observations. If we adopted an average 70″ beam size for the Turner (1991) analysis, the column density of propynal would increase to 7.3  ×  1015, resulting in a [propynethial]/[propynal] ratio of < 0.1.

5.2.2. L1527

The ASAI data toward L1527 contain several spectral lines of propynal with a sufficiently high S/N to derive a column density and excitation temperature. The resolution of the ASAI observations (195 kHz; 0.3–0.8 km s−1) do not provide sufficient resolution elements across these weak lines (ΔV = 1.2 km s−1). As a result, the parameters derived from Gaussian fits to these lines have large statistical uncertainties (Table B.2). We used these values and the associated uncertainties to construct a rotation diagram (Goldsmith & Langer 1999) of propynal in L1527 and derive a column density and excitation temperature, assuming the source fills the beam (Fig. 2). The spectrum of propynal simulated using our derived best fit parameters is shown in Fig. B.1 compared to the observational data for all transitions with S/N > 3. These are the same transitions used to generate the rotation diagram. To our knowledge, propynal has not previously been reported in this source. Combined with our propynethial upper limit (derived using the values of Tex and ΔV determined for propynal), we derive an abundance ratio of [propynethial]/[propynal] of < 7.

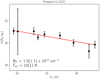thumbnail Fig. 2.

Rotation diagram of propynal detection in L1527, using the lines and parameters reported in Table B.2. The reported errors in column density and temperature are the 1σ statistical errors from the least squares fit to the data, while the error bars for the data points are derived from the 1σ statistical errors in intensity and velocity width from the Gaussian fits to the lines.

5.2.3. TMC-1

The first reported detection of propynal in the ISM was by Irvine et al. (1988) in the Nobeyama 45-m observations of TMC-1. The beam size of the Nobeyama 45 m varied from 90 to 45″ between the two measured transitions at 18.7 and 37.3 GHz, respectively. The IRAM 30-m beam is 16″ at 156.6 GHz, where the propynethial upper limit was derived. Especially for small molecules, the size of the emitting region is assumed to be much larger than any of these (Kaifu et al. 2004), thus we assume the beam size mismatch is not likely to be an issue in the comparison. We used the Tex from that work of 10 K to derive the upper limit to propynethial in our work. The resulting abundance ratio of [propynethial]/[propynal] is < 1.7 in TMC-1. We note that Loison et al. (2016) also reported a detection of propynal in TMC-1. Their reported column density of 8.0 × 1011 cm−2 falls slightly outside the uncertainty of the measurement of Irvine et al. (1988). However, because Loison et al. (2016) do not appear to have provided an uncertainty on their measurement, we cannot comment more on any potential disagreement between the values.

5.2.4. L1544

Jimenez-Serra et al. (2016) reported a single-line (90, 9 − 80, 8) detection of propynal in L1544 using the IRAM 30-m telescope, deriving a column density of 1.8 − 6.3 × 1011 cm−2 over a range of assumed Tex = 5 − 10 K toward the dust-continuum peak in L1544 (corresponding to the same pointing location as the ASAI data). While Fig. 1 of Jimenez-Serra et al. (2016) does appear to show a reasonable S/N corresponding to the 90, 9 − 80, 8, we do not see any emission in the ASAI data at this frequency. Our derived upper limit of 6.4 × 1010 cm−2 is outside the range of column densities derived by Jimenez-Serra et al. (2016) if we assume Tex = 10 K, as we do here. If we were instead to assume Tex = 5 K and use the 90, 9 − 80, 8 transition as our fiducial, we would derive a column density of 2.9 × 1011 cm−2, in agreement with Jimenez-Serra et al. (2016). Figure 3 shows simulations of the 90, 9 − 80, 8 from our derived upper limits compared to the observations, with a shaded curve representing the range of line profiles that would result from the values derived in Jimenez-Serra et al. (2016). Based on the ASAI observations, and the lack of emission in any other transition of propynal covered by these observations, we conclude that the ASAI data do not support a detection of propynal in L1544, and set an upper limit of 6.4 × 1010 cm−2 based on these results.

thumbnail Fig. 3.

Simulation of the 90, 9 − 80, 8 transition of propynal toward L1544 using our derived upper-limit parameters in red over the ASAI observations in black. The shaded blue curve represents the range of potential line profiles for this transition based on the values reported in Jimenez-Serra et al. (2016).

5.3. Barnard 1

Loison et al. (2016) report a single-line (90, 9 − 80, 8) detection of propynal in Barnard 1, deriving a column density of 7.9 × 1011 cm−2. This is ∼5× higher than our 1σ upper limit. Indeed, the 90, 9 − 80, 8 transition of propynal is covered by the ASAI data, and no emission is seen. We attempted to reconcile the differences, before making a comparison to propynethial. The salient parameters are presented in Table 7.

Table 7.

Comparison of observational and source parameters for Barnard 1 in this work and in that of Loison et al. (2016).

For comparison, we simulated the spectra of propynal using the 0.6 km s−1 linewidth from Loison et al. (2016) using both their derived column density and our upper limit. We used our value for the partition function (Q[10 K] = 142) for both simulations. The resulting spectra for the 90, 9 − 80, 8 observed in Loison et al. (2016) as well as the 110, 11 − 100, 10 transitions we used to set our upper limit are shown in Fig. 4. While the Loison et al. (2016) column density is consistent within the ∼3σ noise level of the ASAI observations for the 90, 9 − 80, 8, it overproduces the observations for the 110, 11 − 100, 10 transition we use to set our upper limit. Further complicating matters, Loison et al. (2016) do not appear to have provided an estimate of the uncertainty in their derived column density.

thumbnail Fig. 4.

Simulations of propynal emission in the 90, 9 − 80, 8 and 110, 11 − 100, 10 transitions overlaid on the ASAI observations of Barnard 1. The bold, blue trace represents the expected emission profile given the column density and linewidth reported in Loison et al. (2016), although using our partition function. The thinner red trace is the upper limit presented from our work, simulated using the linewidth from Loison et al. (2016).

Nevertheless, visually, the detection of the 90, 9 − 80, 8 presented in Fig. 1 of Loison et al. (2016) appears significant. Thus, while the ASAI observations cannot confirm that detection, and there are discrepancies we are unable to resolve, we feel it is worthwhile to report a ratio to our propynethial upper limit here. Depending on whether a linewidth of 0.6 or 0.8 km s−1 is used, our derived upper limit varies between 5.8–9.1 × 1011 cm−2 for propynethial. Taking the propynal column of 7.9  ×  1011 cm−2 from Loison et al. (2016), the resulting abundance ratio of [propynethial]/[propynal] is < 0.7 − 1.5 in Barnard 1.

6. Discussion

The measurements of the submillimeter-wave spectrum of propynethial reported here have allowed accurate predictions of line positions and intensities through ∼700 GHz. These new measurements have enabled us to search for this species in a number of datasets at millimeter and submillimeter wavelengths, and set upper limits to the abundance of propynethial with confidence. The non-detection of propynethial in the 11 different astronomical sources searched here adds to a growing list of sulfur analogs to known interstellar species that have not yet been found in the ISM. Recent examples include thioacetaldehyde (CH3CHS; Margulès et al. 2020), thioketene (H2CCS; McGuire et al. 2019), ethynethiol (HCCSH; McGuire et al. 2019), and thioacetamide (CH3C(S)NH2; Remijan et al., in prep.).

The [propynethial]/[propynal] abundance ratios reported here are relatively large (< 0.1–17) compared to the solar sulfur-to-oxygen ratio of ∼0.02 (Cameron 1973). The largest factor contributing to the non-detection is certainly the abundance of propynethial and the associated formation and destruction chemistry. A detailed analysis of the molecular reaction network and modeling is beyond the scope of this work, but would be a useful related study.

Aside from abundance, there are two major factors that contribute to the difficulty of detecting propynethial relative to propynal: its partition function (Q) and permanent dipole moment components (μa and μb). Assuming the transitions are described by a single excitation temperature in the optically thin limit, the intensity of an observed transition (I) is proportional to the square of the dipole moment and the inverse of the partition function (cf., Eq. (1) of Hollis et al. 2004):

I ∝ μ 2 Q . $$ \begin{aligned} I \propto \frac{\mu ^2}{Q}. \end{aligned} $$(3)

Carvajal et al. (2019) recently reviewed the importance and impact of partition functions in the derivation of abundances of interstellar molecules. In this case, the vibrational contributions to both species are quite similar. However, the increased mass of sulfur in propynethial results in rotational constants ∼33% smaller than propynal. As shown in Eq. (1), this has the effect of increasing the rotational contribution to the partition function for propynethial by a factor of 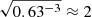0 . 63 − 3 ≈ 2 $ \sqrt{0.63^{-3}} \approx 2 $. This in turn reduces the intensity of propynethial transitions relative to propynal by the same amount (cf., Eq. (3)).

The dipole moment components of propynal were reported in Brown et al. (1982) to be μa = 2.4 and μb = 1.468. The components for propynethial are smaller by factors of 0.75 and 0.45, respectively. Because the strength of the transitions relies on μ2, propynethial transitions are weaker than the corresponding propynal transitions by factors of ∼1.8 and ∼4.9 for a- and b-type transitions.

These two factors combine to make propynethial ∼3.6–9.8 times more difficult to detect than propynal, explaining the comparatively high relative abundance limits that we were able to set here. Given that the most rigorous constraints were those set in Sgr B2(N) and Barnard 1 of 0.1–1.5, depending on source size assumptions, these sources are likely the best to conduct follow-up targeted searches for propynethial. Using the source and molecule parameters assumed here, the best limits might be set by observations with the Next Generation Very Large Array (ngVLA; Selina et al. 2018) near ∼80 GHz.

7. Conclusions

We recorded the submillimeter-wave spectrum of propynethial up to 630 GHz. In total, 3288 new transitions were measured and assigned to the ground state, which permits accurate predictions up to 700 GHz. The four lowest vibrational states, ν5 = 1, ν9 = 1, ν12 = 1, ν9 = 2, and ν8 = 1, are all strong enough in our spectrum to be assigned, and an analysis of these states together with the ground state is in progress. A search for propynethial and propynal was conducted in a number of astrophysical environments. Propynethial was not detected in any source, and upper limits were derived. Propynal was detected for the first time in L1527.

Acknowledgments

The present investigations were supported by the CNES and the CNRS program “Physique et Chimie du Milieu Interstellaire” (PCMI). J. C. G. thanks the Centre National d’Etudes Spatiales (CNES) for a grant. Support for B. A. M. was provided by NASA through Hubble Fellowship grant #HST-HF2-51396 awarded by the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., for NASA, under contract NAS5-26555. The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc.

References

  1. Araki, M., Takano, S., Sakai, N., et al. 2017, ApJ, 847, 51 [NASA ADS] [CrossRef] [Google Scholar]
  2. Barros, J., Appadoo, D., McNaughton, D., et al. 2015, J. Mol. Spectr., 307, 44 [NASA ADS] [CrossRef] [Google Scholar]
  3. Belloche, A., Garrod, R. T., Müller, H. S. P., & Menten, K. M. 2014, Science, 345, 1584 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  4. Bonfand, M., Belloche, A., Menten, K. M., Garrod, R. T., & Müller, H. S. P. 2017, A&A, 604, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Brand, J., Callomon, J., & Watson, J. 1963, Discuss. Faraday Soc., 35, 175 [CrossRef] [Google Scholar]
  6. Brogan, C. L., Hunter, T. R., Cyganowski, C. J., et al. 2018, ApJ, 866, 87 [NASA ADS] [CrossRef] [Google Scholar]
  7. Brown, R. D., Godfrey, P. D., Champion, R., & Woodruff, M. 1982, Aust. J. Chem., 35, 1747 [CrossRef] [Google Scholar]
  8. Cameron, A. G. W. 1973, Space Sci. Rev., 15, 121 [NASA ADS] [CrossRef] [Google Scholar]
  9. Carvajal, M., Favre, C., Kleiner, I., et al. 2019, A&A, 627, A65 [CrossRef] [EDP Sciences] [Google Scholar]
  10. Cernicharo, J., Marcelino, N., Roueff, E., et al. 2012, ApJ, 759, L43 [NASA ADS] [CrossRef] [Google Scholar]
  11. Cernicharo, J., Lefloch, B., Agúndez, M., et al. 2018, ApJ, 853, L22 [NASA ADS] [CrossRef] [Google Scholar]
  12. Chen, X., Launhardt, R., & Henning, T. 2009, ApJ, 691, 1729 [NASA ADS] [CrossRef] [Google Scholar]
  13. Costain, C. C., & Morton, J. R. 1959, J. Chem. Phys., 31, 389 [NASA ADS] [CrossRef] [Google Scholar]
  14. Crabtree, K. N., Martin-Drumel, M.-A., Brown, G. G., et al. 2016, J. Chem. Phys., 144, 124201 [CrossRef] [Google Scholar]
  15. Crapsi, A., Caselli, P., Walmsley, C. M., et al. 2005, ApJ, 619, 379 [Google Scholar]
  16. Crockett, N. R., Bergin, E. A., Neill, J. L., et al. 2014, ApJ, 787, 112 [NASA ADS] [CrossRef] [Google Scholar]
  17. Frisch, M., Trucks, G., Schlegel, H., et al. 2016, Gaussian 16 (Wallingford, CT: Gaussian, Inc.) [Google Scholar]
  18. Gal, Y.-S., & Choi, S.-K. 1988, J. Polym. Sci. Part C: Polym. Lett., 26, 115 [CrossRef] [Google Scholar]
  19. Goldsmith, P. F., & Langer, W. D. 1999, ApJ, 517, 209 [NASA ADS] [CrossRef] [Google Scholar]
  20. Gratier, P., Majumdar, L., Ohishi, M., et al. 2016, ApJS, 225, 1 [NASA ADS] [CrossRef] [Google Scholar]
  21. Higuchi, A. E., Sakai, N., Watanabe, Y., et al. 2018, ApJS, 236 [Google Scholar]
  22. Hily-Blant, P., Faure, A., Vastel, C., et al. 2018, MNRAS, 480, 1174 [NASA ADS] [CrossRef] [Google Scholar]
  23. Hollis, J. M., Jewell, P. R., Lovas, F. J., & Remijan, A. 2004, ApJ, 613, L45 [NASA ADS] [CrossRef] [Google Scholar]
  24. Hollis, J. M., Jewell, P. R., Remijan, A. J., & Lovas, F. J. 2007, ApJ, 660, L125 [NASA ADS] [CrossRef] [Google Scholar]
  25. Howe, J. A., & Goldstein, J. H. 1955, J. Chem. Phys., 23, 1223 [CrossRef] [Google Scholar]
  26. Irvine, W. M., Brown, R., Cragg, D., et al. 1988, ApJ, 335, L89 [NASA ADS] [CrossRef] [Google Scholar]
  27. Jimenez-Serra, I., Vasyunin, A. I., Caselli, P., et al. 2016, ApJ, 830, 1 [Google Scholar]
  28. Jørgensen, J. K., Schöier, F. L., & van Dishoeck, E. F. 2002, A&A, 389, 908 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Kaifu, N., Ohishi, M., Kawaguchi, K., et al. 2004, PASJ, 56, 69 [NASA ADS] [CrossRef] [Google Scholar]
  30. Kargamanov, N. D., Korolev, V. A., & Mal’tsev, A. K. 1987, Russian. Chem. Bull., 36, 2152 [CrossRef] [Google Scholar]
  31. Kisiel, Z. 2001, Spectroscopy from Space (Springer), 91 [CrossRef] [Google Scholar]
  32. Laas, J. C., & Caselli, P. 2019, A&A, 624, A108 [CrossRef] [EDP Sciences] [Google Scholar]
  33. Lefloch, B., Bachiller, R., Ceccarelli, C., et al. 2018, MNRAS, 477, 4792 [NASA ADS] [CrossRef] [Google Scholar]
  34. Lis, D. C., & Goldsmith, P. F. 1990, ApJ, 356, 195 [NASA ADS] [CrossRef] [Google Scholar]
  35. Loison, J.-C., Agúndez, M., Marcelino, N., et al. 2016, MNRAS, 456, 4101 [Google Scholar]
  36. Margulès, L., Ilyushin, V. V., McGuire, B. A., et al. 2020, J. Mol. Spectr., 371, 111304 [CrossRef] [Google Scholar]
  37. Martín-Doménech, R., Jiménez-Serra, I., Caro, G. M., et al. 2016, A&A, 585, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. McGuire, B. A. 2018, ApJS, 239, 17 [Google Scholar]
  39. McGuire, B. A., Carroll, P. B., Dollhopf, N. M., et al. 2015, ApJ, 812, 1 [NASA ADS] [CrossRef] [Google Scholar]
  40. McGuire, B. A., Carroll, P. B., Loomis, R. A., et al. 2016, Science, 352, 1449 [NASA ADS] [CrossRef] [Google Scholar]
  41. McGuire, B. A., Shingledecker, C. N., Willis, E. R., et al. 2017, ApJ, 851, L46 [NASA ADS] [CrossRef] [Google Scholar]
  42. McGuire, B. A., Brogan, C. L., Hunter, T. R., et al. 2018a, ApJ, 863, L35 [NASA ADS] [CrossRef] [Google Scholar]
  43. McGuire, B. A., Burkhardt, A. M., Kalenskii, S. V., et al. 2018b, Science, 359, 202 [NASA ADS] [CrossRef] [Google Scholar]
  44. McGuire, B. A., Shingledecker, C. N., Willis, E. R., et al. 2019, ApJ, 883, 201 [CrossRef] [Google Scholar]
  45. Melosso, M., Melli, A., Puzzarini, C., et al. 2018, A&A, 609, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Nefedov, O. M., Korolev, V. A., Zanathy, L., Soloukie, B., & Bock, H. 1992, Mendeleev Commun., 2, 67 [CrossRef] [Google Scholar]
  47. Neill, J. L., Muckle, M. T., Zaleski, D. P., et al. 2012, ApJ, 755, 153 [NASA ADS] [CrossRef] [Google Scholar]
  48. Pickett, H. M. 1991, J. Mol. Spectr., 148, 371 [NASA ADS] [CrossRef] [Google Scholar]
  49. Remijan, A. J., Hollis, J. M., Lovas, F. J., et al. 2008, ApJ, 675, L85 [NASA ADS] [CrossRef] [Google Scholar]
  50. Selina, R. J., Murphy, E. J., McKinnon, M., et al. 2018, ed. E.Murphy, Science with a Next Generation Very Large Array, 15 [Google Scholar]
  51. Turner, B. E. 1989, ApJS, 70, 539 [NASA ADS] [CrossRef] [Google Scholar]
  52. Turner, B. E. 1991, ApJS, 76, 617 [NASA ADS] [CrossRef] [Google Scholar]
  53. Vastel, C., Ceccarelli, C., Lefloch, B., & Bachiller, R. 2014, ApJ, 795, L2 [Google Scholar]
  54. Widicus Weaver, S., Butler, R., Drouin, B., et al. 2005, ApJS, 158, 188 [NASA ADS] [CrossRef] [Google Scholar]
  55. Winnewisser, G. 1973, J. Mol. Spectr., 46, 16 [NASA ADS] [CrossRef] [Google Scholar]
  56. Wong, A. 2016, PhD Thesis, Monash University, Australia [Google Scholar]
  57. Zakharenko, O., Motiyenko, R. A., Margulès, L., & Huet, T. R. 2015, J. Mol. Spectr., 317, 41 [Google Scholar]

Appendix A: Observational source parameters

Table A.1.

Source parameters assumed for propynethial in each of the sets of observations, and for propynal in those observations that resulted in a non-detection.

thumbnail Fig. A.1.

Global overview of the frequency coverage of the ASAI data toward each source.

Appendix B: Propynal analysis

Table B.1.

Propynal column densities and upper limits, with associated line parameters.

Table B.2.

Frequencies, quantum numbers, fit brightness temperatures and linewidths, and transition properties for lines used to derive the column density and excitation temperature of propynal in L1527.

thumbnail Fig. B.1.

Transitions of propynal identified in the ASAI data toward L1527 with an S/N ratio of ≥3. Transition parameters are given in Table B.2. The observational data are shown in black. A simulation of propynal using the derived best fit column density and temperature is shown in red using a noise-weighted average linewidth derived from our Gaussian fits to the individual lines (1.2 km s−1) and simulated at the same resolution and frequency sampling as the observations.

All Tables

Table 1.

Spectroscopic parameters of propynethial in MHz – S reduction.

In the text
Table 2.

Measured frequencies of propynethial and residuals from the fit.

In the text
Table 3.

Comparison of the band positions (cm−1) for propynethial from ab initio and density functional theory methods using a 6-311+G(d) basis set.

In the text
Table 4.

Comparison of the band positions (cm−1) for propynal from ab initio and density functional theory methods using a 6-311+G(d) basis set.

In the text
Table 5.

Rotational, vibrational, and total partition functions at various temperatures.

In the text
Table 6.

Upper limits to propynethial and the line parameters used to calculate them in each of the sets of observations.

In the text
Table 7.

Comparison of observational and source parameters for Barnard 1 in this work and in that of Loison et al. (2016).

In the text
Table A.1.

Source parameters assumed for propynethial in each of the sets of observations, and for propynal in those observations that resulted in a non-detection.

In the text
Table B.1.

Propynal column densities and upper limits, with associated line parameters.

In the text
Table B.2.

Frequencies, quantum numbers, fit brightness temperatures and linewidths, and transition properties for lines used to derive the column density and excitation temperature of propynal in L1527.

In the text

All Figures

thumbnail Fig. 1.

Transitions of propynethial used to calculate the upper limits given in Table 6. In each panel, the red trace shows the transition simulated using the derived upper-limit column density and the physical parameters assumed for that source. The frequency of the transition is given in the top right of each panel, and the quantum numbers for each transition in the top left. The source name is given above each panel. Due to the large variances between observations, the intensity and velocity axes are not uniform between each panel.
In the text
thumbnail Fig. 2.

Rotation diagram of propynal detection in L1527, using the lines and parameters reported in Table B.2. The reported errors in column density and temperature are the 1σ statistical errors from the least squares fit to the data, while the error bars for the data points are derived from the 1σ statistical errors in intensity and velocity width from the Gaussian fits to the lines.
In the text
thumbnail Fig. 3.

Simulation of the 90, 9 − 80, 8 transition of propynal toward L1544 using our derived upper-limit parameters in red over the ASAI observations in black. The shaded blue curve represents the range of potential line profiles for this transition based on the values reported in Jimenez-Serra et al. (2016).
In the text
thumbnail Fig. 4.

Simulations of propynal emission in the 90, 9 − 80, 8 and 110, 11 − 100, 10 transitions overlaid on the ASAI observations of Barnard 1. The bold, blue trace represents the expected emission profile given the column density and linewidth reported in Loison et al. (2016), although using our partition function. The thinner red trace is the upper limit presented from our work, simulated using the linewidth from Loison et al. (2016).
In the text
thumbnail Fig. A.1.

Global overview of the frequency coverage of the ASAI data toward each source.
In the text
thumbnail Fig. B.1.

Transitions of propynal identified in the ASAI data toward L1527 with an S/N ratio of ≥3. Transition parameters are given in Table B.2. The observational data are shown in black. A simulation of propynal using the derived best fit column density and temperature is shown in red using a noise-weighted average linewidth derived from our Gaussian fits to the individual lines (1.2 km s−1) and simulated at the same resolution and frequency sampling as the observations.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.