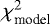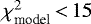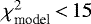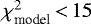EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 642 (October 2020) A&A, 642 (2020) A142 Full HTML
Free Access
Issue
A&A
Volume 642, October 2020
Article Number A142
Number of page(s) 15
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/202038029
Published online 13 October 2020

© ESO 2020

1 Introduction

The asymptotic giant branch (AGB) is a late evolutionary stage of low- and intermediate-mass stars (i.e. with initial masses from 0.8 M⊙ to 8 M⊙), just before they evolve into planetary nebulae (PNe) and white dwarfs (see Habing 1996; Habing & Olofsson 2003; Höfner & Olofsson 2018, for reviews). Due to strong stellar winds and low surface gravities, AGB stars have high mass-loss rates (MLRs) and are surrounded by circumstellar envelopes (CSEs), inside which molecules and dust grains form. The dust is formed within a few (up to 10) stellar radii, R⋆, from the stellar surface (with R⋆ ~ 0.5 au to a few au). Radiation pressure on dust continuously pushes it outwards. Drag between dust and gas drives the CSE gas outwards as well, forming an outflow of material from the star whose content enriches the interstellar medium.

Dust is an important ingredient of CSEs; however, the mechanisms governing dust formation and outflows are not well understood yet. For example, there exists much evidence that many AGB stars have companions (Jorissen 2003; Maercker et al. 2012; Lagadec & Chesneau 2015; Kervella et al. 2016; Jorissen et al. 2018) that are massive enough to induce discs and spirals in CSEs. Subsequently, these can significantly affect outflows (Theuns & Jorissen 1993; Mastrodemos & Morris 1999) and, finally, the morphologies of PNe (Jones & Boffin 2017). However, spherically symmetric distributions are usually adopted by default when modelling CSEs of stars lacking detailed information on their CSE geometry. These models, which include dust radiative transfer, are used to compute spectral energy distributions (SEDs; Elitzur & Ivezić 2001) so that dust parameters can be constrained (e.g. dust species and grain size distributions). The knowledge of the dust parameters is essential, as they control a wide range of physical processes, for example, dust formation (e.g. Höfner & Olofsson 2018, and references therein), surface chemistry that can occur on dust grains in gas-rich environments (e.g. Herbst et al. 2005), and radiation pressure on the dust grains controlling the outflows (e.g. Höfner & Olofsson 2018; Bladh et al. 2019).

Interferometric observations now make it possible to reach the necessary milliarcsecond (mas) scales that are required to resolve CSE details such as spirals. For an AGB star at a distance of ≲ 1 kpc, 1 mas corresponds to sub-au distances, that is to say sizes of the order of the radius of an AGB star. The Atacama Large Millimeter Array (ALMA) can reach some 20–40 mas and the Very Large Telescope Interferometer (VLTI) can reach, at best, 2 mas. Hence it is possible to directly observe the details of the morphology of a CSE (Maercker et al. 2012; Kervella et al. 2014; Lykou et al. 2015; Paladini et al. 2017; Homan et al. 2018).

Analyses of the impact of the dust-cloud morphology on the SED have been done previously in the case of PNe and post-AGBs. For example, using direct imaging, Ueta et al. (2001a) found a toroidal structure for the post-AGB star HD 235858 (proto-PN IRAS 22272+5435). SED modelling of the central source indicated that dust grains with different sizes reside in the AGB and post-AGB shells. Similarly, Murakawa et al. (2008) observed the post-AGB star IRAS 09371+1212 (“Frosty Leo”), and used non-spherical two-dimensional simulations to estimate the total CSE mass and MLR. They were able to reproduce the data with two dust species at different locations in the nebula. Oppenheimer et al. (2005) published observations and radiative-transfer simulations of the dust in three proto-PNe (IRAS 17441-2411, IRAS 08005-2356, and IRAS 04296+3429). The first two are narrow-waist bipolar proto-PNe, and this extreme two-lobe structure is likely caused by a binary companion (Soker & Rappaport 2000). However, these studies combined SED fitting and image reproduction of data where the CSE morphology was resolved.

The impact of geometry on the dusty SEDs of post-AGB stars has been known for decades (Van Winckel 2003). In general, in post-AGB systems surrounded by a circumbinary disc (e.g. Oomen et al. 2018; Kamath & Van Winckel 2019; Ertel et al. 2019), the CSE contains warm dust with the infrared (IR) excess starting at shorter wavelengths, typically from 1 to 3 μm.

In the case of AGB stars, Jeffers et al. (2014) directly observe, for the first time, an equatorial density enhancement around an AGB star, namely IRC +10216 (CW Leo). They interpret this as either a torus or a ring, and simulated the radiative transfer with these geometries. The resulting SEDs, however, appear as good as identical for both geometries. Cernicharo et al. (2015) and Decin et al. (2015) detect spherical shells in the CSE of CW Leo, which are confirmed by Guélin et al. (2018). These shells can be explained by a companion.

Blum et al. (2014) analysed Spitzer/MIPS (Rieke et al. 2004) spectra of a large number of Large Magellanic Cloud AGB stars. Among these stars they find that HV 915 exhibits a disc-like signature in its spectrum, visible as CO band head emission. Normally this is found in spectra of young stellar objects and is attributed to dense and hot gas in discs. However, a specific study on the impact of morphology on the dust SEDs of AGB stars has, to the best of our knowledge, not been done yet.

The questions we address in this paper are whether it is possible to identify features in dusty SEDs that are caused by specific dust-cloud morphologies, and whether these signatures are unique to specific morphologies. We also investigate the possibility of the opposite case where different morphologies with different dust masses possibly give rise to the same SED. With this, we want to evaluate by how much CSE dust masses may be mis-estimated when adopting an incorrect dust morphology. To investigate these questions, we used the AGB star EP Aqr as a benchmark. Its CSE has been the subject of several detailed observations (Tuyet Nhung et al. 2019; Homan et al. 2018; Hoai et al. 2019; Tuan-Anh et al. 2019) which point at spiral arms embedded in a disc-like geometry, as seen nearly face-on.

This paper has the following structure. We summarise the stellar properties of EP Aqr in Sect. 2; the dust, spatial grid, and grain properties in Sect. 3, and the simulations and statistical tools in Sect. 4. In Sect. 5 we present our results which are discussed in Sect. 6 and summarised in Sect. 7.

2 Properties of EP Aqr

2.1 Properties and recent observations

EP Aquarii (EP Aqr, HD 207076, HIP 107516, Gaia DR2 2673831344664664320) is an oxygen-rich star on the AGB. Table 1 summarises its properties. There have been several recent investigations of the CSE around EP Aqr (Nhung et al. 2015; Homan et al. 2018; Tuyet Nhung et al. 2019; Hoai et al. 2019; Tuan-Anh et al. 2019), most of them of the CO lines with ALMA.

Tuan-Anh et al. (2019) find jets extending from 25 to 1000 au. In the CO emission, Homan et al. (2018) find a vertically confined spiral extending up to ~ 10′′ (~1000 au) from EP Aqr. The one armed-spiral is visible between 1′′ and 5′′ from the star where it exhibits two revolutions. This spiral is both flat and seen nearly face-on (with an inclination between 4° and 18°). At 0′′⋅5 from the star, a local void is observed in SiO emission and a bridge of gas between the central star and the void in CO emission, both indicating the presence of a (substellar) companion with an upper mass limit of 0.1 M⊙. The existence of a spiral around this star makes it a good candidate for our tests exploring spectral features in SEDs specifically due to spirals or discs.

Nhung et al. (2015) measure a MLR for EP Aqr of ~1.2 × 10−7 M⊙ yr−1 and a terminal outflow velocity of 10–11 km s−1 (see their Fig. 12), in agreement with more recent values from Hoai et al. (2019). These authors find a MLR of (1.6 ± 0.4) × 10−7 M⊙ yr−1, an outflow velocity of 10–11 km s−1 from the stellar poles, and an outflow velocity of 2 km s−1 at the stellar equator.

2.2 Observed SED and model SED

We used the MARCS1 grid of stellar model atmospheres (Gustafsson et al. 2008) to extract the photospheric spectrum that we used as input for RADMC-3D2, a three-dimensional radiative-transfer code to model the SED under various geometries (Dullemond 2012, and Sect. 4). RADMC-3D is written in Fortran and handles arbitrary dust spatial distributions, with any dust species, with any number of stars, and with the possibility of adding molecular lines. The input MARCS synthetic spectrum covers a wavelength range up to 20 μm, after which we extrapolated the spectrum with a black body (BB).

We searched the MARCS grid for models with solar metallicity, an effective temperature Teff of 3200 K, and with current stellar masses of 1 or 2 M⊙, which are close to the temperature and mass of EP Aqr, namely 3236 K and 1.7 M⊙, respectively (Dumm & Schild 1998). The properties of the adopted MARCS model are listed in Table 1 together with observed properties. We chose a model with a mass of 1 M⊙ since such models better fit the observed photometry in the visual and ultraviolet (V-UV) domains, that is the domains which we normalised the MARCS model SED to, as listed in Table 2. For comparison we plotted the photometry on top of this MARCS model in the last frame of Fig. 2. Not listed in Table 2, but included in this study, are spectra from the Infrared Space Observatory Short Wavelength Spectrograph (ISO-SWS) as extracted by Sloan et al. (2003)3 and previously analysed by Heras & Hony (2005), and Herschel-PACS (Pilbratt et al. 2010; Poglitsch et al. 2010) spectra from Nicolaes et al. (2018).

We mention here a few caveats concerning stellar variability and reddening with how this stellar SED model was implemented in RADMC-3D. Both V-UV, and the IR to far-infrared (FIR) wavelength regimes are simultaneously sensitive to the surrounding dust (from reddening or dust emission, respectively) and variability of the star itself. However, the IR and FIR is more sensitive to dust emission than to variability. We did not take variability into account here since we focussed on the effects from the dust itself for a pulsation-averaged EP Aqr. However, to consider variability we would need to re-simulate all dust morphologies for a set of stellar SEDsthat correspond to different phases of the star’s variability. This would not in any case be feasible since such a set of models would be static, and not take time-dependent propagation of variable radiation fields into account.

Reddening becomes an issue when the dust envelope is optically thick. Our input stellar SED model was normalised to the observed flux densities at V-UV wavelengths. Thus we initially did not take reddening into account when we searched for a stellar SED model. Furthermore, Heras & Hony (2005) found that the real dust envelope of EP Aqr is optically thin, which is also evident later in this study where we compare simulated dust SEDs with observed data. However, it is also shown later in this study that effects from reddening is significant for the more massive dust envelopes. If we were to search for correct dust envelope models, that fit the data, we would take reddening into account when we search for stellar SED models. However, our focus in this study is to better understand the effects of dust emission by comparing SEDs from different dust morphologies and with different total dust masses, including the more massive and optically thick dust envelopes. As such we used one stellar SED model and focussed on the effects on the SEDs in the IR and FIR regimes by varying the dust models only. It is also worth noting that the interstellar reddening computed from Gontcharov (2012) map is considered to be negligible (Table 1).

Table 1

EP Aqr observed and adopted properties.

Table 2

Photometry of EP Aqr.

3 Description of dust properties

3.1 Dust composition and optical properties

In Table 3 we summarise the dust properties used for our simulations. Since EP Aqr is an O-rich AGB star, we opt to include common dust species for such stars. Two of the most common Si-bearing species are fosterite (Mg2SiO4) and enstatite (MgSiO3; Höfner & Olofsson 2018), and these are often found in combination with alumina (Al2 O3) and fayalite (Fe2 SiO4, which forms further out from the star; Gobrecht et al. 2016; Millar 2016). We opted to primarily include 99% amorphous Mg2 SiO4 and 1% crystalline Fe2 SiO4. This was chosen for simplicity, due to the clear silicate features in the ISO-SWS spectrum, and for example Jones et al. (2014) show that, for O-rich AGB stars in the Large Magellanic Cloud, dust consists primarily of amorphous Si species. However, in our comparison with observational data, we also used another composition mixture containing 9% amorphous Al2 O3 dust, plus 90% Mg2 SiO4 and 1% Fe2 SiO4. This composition was estimated from the flux density ratio at the 10 μm silicate feature and at the 13 μm Al-feature in the ISO-SWS spectrum. It is consistent with the abundance of Al2 O3 in the AGB stars observed by Jones et al. (2014) which have MLR similar to EP Aqr. For a study of the actual dust content of EP Aqr, we refer to the analysis of ISO-SWS spectra of AGB stars by Heras & Hony (2005). They fitted five different dust species to the spectrum and, in their Fig. 2, a good match was obtained with ~ 9% Al2 O3, ~ 80% of a mixture of silicates, and ≲10% of iron-rich dust.

We extracted the refractive indices of the considered dust species from the Databases of Dust Optical Properties from the Astrophysical Laboratory Group of the AIU Jena4. The originalreferences for these optical properties are, for fosterite Jäger et al. (2003), for fayalite Fabian et al. (2001), and for alumina Begemann et al. (1997). These were used to compute the mass-absorption and scattering coefficients for input into RADMC-3D. A version of the Bohren & Huffman (1983) Mie code, originally written in Fortran, and rewritten in Python by C. Dullemond in 2017 for inclusion in RADMC-3D, was used for this. This code assumes spherical grains with a Gaussian grain size distribution and a logarithmic size spread. The Gaussian spread reduces artefacts caused by a too-narrow, unrealistic size range of spherical grains, such as resonances and sharp features in the spectra. Recent results (Norris et al. 2012; Ohnaka et al. 2016, 2017, and summarised in the review by Höfner & Olofsson 2018) state that grains of sizes 0.1–0.5 μm are detectedin the vicinity of AGB stars. We thus adopted relatively small and compact grains with a size distribution centred on 0.2 μm (in effect 11 different grain sizes between 0.15 and 0.27 μm in logarithmic bins). For simplicity we kept the grain size constant with distance to the star so that we had the same extinction coefficients throughout the dust distribution. We note that Mg2 SiO4 and Fe2 SiO4 grains of these sizes have albedos close to one at wavelengths around 0.7 μm (see Table 3). This will result in very strong contributions from scattered light to the dust SED in the full optical range, as wediscuss later (Sect. 5).

The RADMC-3D code includes several methods for simulating scattering. Since the Bohren & Huffman Mie code computes scattering angles, we compared results with no scattering, isotropic scattering, and anisotropic Henyey-Greenstein approximated scattering (Henyey & Greenstein 1941). Simulations with no scattering are obviously faster, but also unrealistic since most of the scattering occurs at short wavelengths where most of the heating of the dust also happens (through absorption). For example, with Rayleigh scattering, we may assume that most scattering occurs at wavelengths shorter than 10 μm for grains with the size of 0.2 μm. There were only insignificant differences in the SED when comparing the two different scattering modes. The computational time was comparable and even shorter with anisotropic scattering. Thus we chose to use anisotropic Henyey-Greenstein scattering in our simulations. Because of heavy computational effort for the densest geometries, we reduced the scattering tolerance in the simulations. By default RADMC-3D destroys scattered photons when the optical thickness reaches 30 and we reduced this limit to five as recommended by the author of RADMC-3D in situations of computationally heavy simulations. We also compared SEDs of both settings and found no noticeable differences.

The choice of the grain mass density of 3 g cm−3 was based on findings that interplanetary dust particles in the solar system have densities ranging between 1 and 3 g cm−3 depending on their origin and population (Moro-Martín 2013). Since we are interested in the impact on the SED of the CSE morphology, we kept the grain density constant for all models.

Table 3

Simulation parameters.

3.2 Dust morphology and spatial grid description

Our focus in this study is the spiral-shaped morphology, however, we included a disc for comparisons. As such we limited the simulations to four CSE morphologies: a sphere, a spiral, a disc, and a combined sphere-spiral envelope. With these we include the extremes with no spherical component, and intermediate cases of a spiral embedded in a sphere.

The gas spiral that Homan et al. (2018) find around EP Aqr is the basis for the spiral models. This spiral is observed between the radial distances ~ 1′′ and 5′′ from the central star and follows an Archimedean spiral with 2 to 2.5 revolutions. At the distance of EP Aqr, the observed spiral thus covers the region extending from 100 to 500 au from the star. The extension of our spiral model goes from 5 to 5000 au with a radial inter-arm distance of 250 au (corresponding to 2 revolutions within 500 au, as observed). The inner radius of 5 au corresponds to ~ 10 R⋆, which is approximately the inner limit for iron-rich dust formation (e.g. Fe2 MgSiO4, see e.g. Höfner & Olofsson 2018). Because of numerical constraints, we set this as the inner limit for all dust species. However, we must note that we miss some hot dust emission by not including dust within ~ 2 to 10 R⋆, with the effect that we predict a marginally colder dust SED than if this dust had been included. On the other hand, we use this radial limit for all models so the comparisons between them are valid. The outer limit of 5000 au for all dust species is based on Herschel-PACS images of EP Aqr, revealing that the dust shell extends out to about 0.04 pc (or ~ 8250 au) at both 70 and 160 μm (see Fig. 1 of Cox et al. 2012). 5000 au is again a compromise since it is numerically difficult to simulate three-dimensional models of larger sizes. However, this is an acceptable compromise since the dust emission from such a large distance from the star has only marginal effects on the resulting SED.

An Archimedean spiral is described as 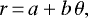(1)

where r is the distance to the centre of thestar, θ is the running azimuthal angle, a is the radiusat θ = 0, and b controls the width between each revolution of the spiral (see Fig. 1 for a schematic overview of these parameters).

To simply implement spirals in an octree refined cubic grid we chose to keep the vertical extent equal to each arm’s horizontal width. We limited the vertical extent to 90% of the radius of the empty region close to the star (defined by Rin), that is 4.5 au. These choices were based on limitations of a cubic grid and the assumption that the spiral of EP Aqr is confined to a plane, as seen by Homan et al. (2018).

An octree grid is a cubic grid where each refinement level equally divides grid-cells of a higher level grid. In three-dimensions, this means that a grid-cell is divided into eight refined cells for each level of refinement. As we will further discuss below, we applied four levels of refinement in the area around the spiral arms, inside the disc, or in the area around the inner edge of the sphere, in the case of spherical distributions. The side of the base cell (i.e. 32 au) is thus 16 times larger than that of the finest, fourth-level grid cell.

In the spiral model, we increasingly refined the spatial grid around the centre of the spiral, with the first refinement being one base cube size from the centre of the spiral. All maximally refined cells of the spirals were assigned dust densities computed from a pre-defined total dust mass and the radial power law ρ ∝ r−2 (Table 3). The finest grid cells of 2.0 au were chosen as a compromise between best grid resolution at the inner radius Rin and reasonable computing time. Because we implemented a cubic grid we also obtained a square-shaped cross section through the spiral arm.

In the disc model, we applied a coarser grid than in the spiral model due to computational constraints. Since the grid directly affects the dust envelope morphology, the thickness of the disc is 9 au only when r < 128 au (as stated in Table 3). The disc thickness then increases to 13 au within 128 ≤ r < 256 au, 17 au within 256 ≤ r < 512 au, and finally to 25 au outside 512 au. The emission at wavelengths larger than 100 μm from the dust located farther away than 1000 au in these thick discs represents less than 10% of the emission from thinner discs. We then conclude that this way of modelling discs is an acceptable compromise between accuracy and computational convenience.

The grid for the spherical models was maximally refined in the area around the inner radius of the sphere, but could generally be coarser than what we used for spirals and discs. The grid cells are of the same sizes as for the other morphologies and the refinement steps are instead located at 10, 19, 35, and 67 au.

The combined sphere-spiral models included the same spiral as described above inside a spherical dust model. The spiral component of the spatial grid was thus combined with the spherical dust model spatial grid. From the literature we estimated that an Archimedean spiral with our constraints should be around 1% of the total dust mass of the envelope. For example, Kim et al. (2019) suggest that spirals are ~ 2 times the density of the inter-arm regions, while Guélin et al. (2018) find shells in the envelope of CW Leo that have ~ 3 times the density of the intershell regions, which, with our spiral model, gives a spiral mass that is ~ 0.3 to 0.6% of the total dust mass. A more massive spiral-example can be seen in Figs. 5 and 9 of Chen et al. (2020) where we see that the densities of their spirals are around ~102 to ~ 103 (and even as high as 104) times that of the inter-arm regions. This would give a spiral mass of ~10 to ~50% of the total dust mass in our model. Evidently there exist a wide range of possible ratios. However, in general the ratio is small so we limit our masses to the lower values 0.5 and 5% in the spiral component, and 99.5 and 95% in the spherical component, respectively.

The discs and spirals were primarily simulated at face-on (0°) and edge-on (90°) inclinations. The inclination can have a particularly important impact on optically thick cases, as will be discussed in Sect. 6.3 where we also include simulations at inclinations of 25°, 50°, 60°, 70°, 80°, 85°, and 90°. For example, Ueta et al. (2001b) stressed the importance of the inclination angle in the case of modelling emission of PNe and how different morphologies are hard to disentangle under certain inclinations.

All geometrical models follow the same radial density power law ρ  ∝   r−2, where a density normalisation factor was used to obtain the input total dust masses. For each geometry, we used five different total dust masses in logarithmic steps, from 10−8 to 10−4 M⊙. To make the comparison with other studies easier, we estimated the total MLRs corresponding to these dust masses. For this, we assumed a gas-to-dust ratio of 100, which is a value commonly derived from observationsin various environments. For example, Meixner et al. (2004) found a ratio of 75 in the proto-PN HD 56126, and Danilovich et al. (2015) find ratios close to 100 for several AGB stars (see their Table 5 where h is a function of the gas-to-dust ratio).

A radial density power law proportional to r−2 and a constant outflow velocity v(r) = v∞ imply a constant MLR. We assumed v(r) = 11 km s−1, which is the terminal outflow velocity as found by Nhung et al. (2015) for EP Aqr. The total (gas and dust) mass density of a spherical CSE is then given by the law of mass conservation, (2)

Since we assumed a constant MLR and a constant terminal velocity, we can simply calculate the amount of mass distributed between 5 and 5000 au. Including a gas-to-dust ratio of 100 one obtains (3)

where v∞[au yr−1] ≈ 2.32.

With the above assumed terminal velocity and spherical CSE geometry, the dust mass to total MLR correspondence is 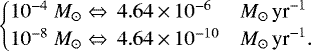(4)

Thus we can state that the observed EP Aqr MLR of 1.2 × 10−7 M⊙ yr−1 (Nhung et al. 2015) corresponds to ~ 2.6 × 10−6 M⊙ of dust within 5 to 5000 au.

thumbnail Fig. 1

Schematic overview of spiral parameters. The inner radius for the dust is indicated by Rin at 5 au, while the outer radius Rout is beyond the limits of this image. The same radii are adopted as limits for the disc and spherical geometries. The parameters θ and b are defined in Eq. (1).

4 Simulations and statistics

We used RADMC-3D version 0.41 (Dullemond 2012) to simulate SEDs for the CSE geometries described in Sect. 3.2. We primarily ran five simulations for each geometry, one for each dust mass given in Sect. 3.2. All the other parameters are listed in Table 3. The total simulation time using 20 to 30 cores for each SED is about ~ 12 h for those models with the highest densities.

The output data of RADMC-3D can be either in the form of SEDs over the whole input wavelengths grid, images at arbritrarily chosen wavelengths within the wavelength grid, or spectra at certain wavelength-sub-ranges. We mainly used the SED outputs for this study. It is possible to retrieve the SED as it would be seen by an observer,or the SED resulting from the dust component. Whenever we only plot the dust SED output from RADMC-3D, we denote it as the dust SED. To more easily distinguish differences in the dust emission, we use the dust SED in much of the analysis here, but we also note when these differences would be detectable for an observer. We approximated a general gauge for this purpose from the average error of ISO-SWS spectra which is σISO ≈ 3.6 Jy.

To gauge the differences, or similarities, between different simulated SEDs we used (5)

which is a reduced Pearson-χ2 test (N is the number of wavelength bins). In the above relation, Sν (model) is the predicted flux density.

For each geometry and inclination, we searched for the model best fitting the observed SED of EP Aqr. This gave us actual examples of how different the MLRs may be, depending on the adopted geometry. The best fit was found by searching for the 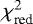minimum, with 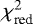defined as (6)

where Sν (obs) are EP Aqr observed flux densities, either derived for the photometric passbands listed in Table 2, or from ISO-SWS and Herschel-PACS spectra (Sloan et al. 2003; Nicolaes et al. 2018, respectively). The σν parameter is the corresponding error bar at frequency ν of the observed SED. The reduced χ2 has N − 1 degrees of freedom, where N is the number of wavelength bins, since we constrained the total dust mass from this minimisation process. We convolved our simulated SEDs with photometric filters downloaded from the SVO Filter Profile Service5 (Rodrigo et al. 2012; Rodrigo & Solano 2013) when comparing with observed photometry.

5 Results

In Fig. 2 we show the modelled SEDs with the EP Aqr SED model, with only face-on inclinations for the spiral and disc models (i.e. spiral or disc lies in the plane of the sky, i = 0°). Here we cansee significant differences in the simulated spectra, particularly the strong silicate features at 10 and 18 μm for the spheres. The most massive sphere has an absorption feature at 10 μm, while the less massive spheres have emission features at 10 and 18 μm instead, andthe most massive spirals and discs have no spectral features at these wavelengths. We also see that the most massive models differ significantly from the EP Aqr SED model at wavelengths shorter than 1 μm. This is expected since these models contain much more dust than the real CSE of EP Aqr actually contains. This is also not a problem since we are using this star with a known spiral as a test object for our models, and some models will of course differ.

We see that discs are associated with SEDs peaking at shorter wavelengths than the spheres, even though they have the same inner radius. Also for post-AGB stars is a warmer SED temperature indicative of a disc caused by a binary central star (Van Winckel 2003). This is not conclusive, however, since also a sphere with a smaller inner radius will have a warmer SED temperaturethan our models.

In Table 4 we list the radii along the line-of-sight (LOS) within which the dust cloud optical thickness is larger than unity at any considered wavelength, assuming edge-on geometry for spirals and discs (i.e. inclination angle of 90°). Maximum optical thickness is obtained with our extinction coefficients at λ = 0.38 μm. It is, in effect, a measure of approximately how deep we see into each geometry. It can be seen that only spherical dust shells with masses less than 10−6 M⊙ and dusty discs with 10−8 M⊙ are (marginally) optically thin. Thus for a given dust mass, dusty spheres are optically thinner than discs and spirals, which is easily understandable since in the disc and spiral cases, the same amount of dust occupies a smaller volume.

This difference in optical depth impacts the emission or absorption nature of the silicate features. The effects of optical thickness are more apparent in Fig. 3 where we only show the dust contribution to the SED (for both face-on and edge-onmodels) without the stellar SED. Here we see that silicate features in spherical models change from emission to absorption going from optically thin to optically thick dust distributions. Similarly, in the face-on spirals and discs, the silicate features change from emission to absorption, and even become featureless. Because of the smaller absorption, stars with face-on spirals and discs appear more luminous than those with only spherical envelopes.

The optically thick spirals and discs seen edge-on exhibit a very strong silicate absorption feature at 10 μm. Furthermore, the more massive edge-on discs appear as cold BBs but they are also primarily shaped by the very strong silicate absorption. In the most massive edge-on cases we only receive emission from the outer parts of the dust distribution. This results in both apparently colder and fainter SEDs. In Sect. 6.3, we investigate in a more quantitative manner the impact of inclination.

Inclination and optical thickness also result in non-intuitive effects for the scattered light portion of the dust SED. As mentioned in Sect. 3.1, our dust has high albedo and this results in significant contributions of scattered light in all face-on or optically thin cases. The scattered light is visible as a peak at wavelengths around 0.3–5 μm in Fig. 3. In the optically thin cases of 10−7 M⊙ and 10−8 M⊙, the flux density of the scattered peak does not change much when observed face-on or edge-on, as may be seen in Fig. 3 from the comparison of the “Disc 0°” and “Disc 90°” cases. However, in the optically thick spirals and discs (with higher dust masses) seen edge-on, the scattered light is significantly reduced, while it remains strong in the face-on situations in agreement with the fact that the scattering angle parameter g is close to one, which corresponds to mostly forward scattering. Moreover, in the edge-on situations with large dust masses, the central parts of the discs and spirals are masked behind significant amounts of optically thick dust along the LOS. The optically thick nature of these situations is revealed by the fact that the SED now closely resembles a BB. In those cases, we only observe the outer rim of the dust distribution (see Table 4) whereas in the face-on cases, the colder outer dust, the warmer inner dust, and the light scattered on the inner dust grains all contribute to the observed light.

We discuss the differences between the model SEDs in more detail in Sect. 6.1, and mention a few details here. If we use the error bar of the ISO-SWS spectrum (on average σISO ≈ 3.6 Jy) and assumethat dust contribution is detectable when its excess is more than 3 σISO above the stellar SED, we find that spirals and discs of masses ≳ 10−7 M⊙ and spheres of masses > 10−6 M⊙ are detectable. These masses of 100% spirals or discs (i.e. no spherical dust distribution included) correspond to MLRs of 4.6 × 10−9 and 4.6 × 10−8 M⊙ yr−1, respectively. It is worth noting that we are considering mas scales and would need interferometers to resolve the spiral (since a spiral width of ~9 au is 90 mas at ~100 pc). However, an outer radius of 5000 au is large enough to be resolved in many observations (some 44′′ at 114 pc). The highest angular resolutions of ALMA are some 20 to 40 mas and, as an example in the optical, the VLTI can reach some 2 mas.

thumbnail Fig. 2

All face-on, 5–5000 au simulated SEDs, and the stellar SED MARCS model (in black). The dust masses are 10−4 (blue), 10−5 (green), 10−6 (red), 10−7 (cyan), and 10−8 M⊙ (magenta). Top row: SEDs from CSE with 100% sphere, spiral and disc, respectively. Second row: combined sphere-spiral model SEDsand a comparison between the photometry listed in Table 2 (orange data points) and the MARCS model.
Table 4

Radii outside which the dust distributions are optically thin for all considered wavelengths.

thumbnail Fig. 3

All 5–5000 au simulated dust SEDs – without the stellar SED model – of dust masses 10−4 (blue), 10−5 (green), 10−6 (red), 10−7 (cyan), and 10−8 M⊙ (magenta). The dust cloud morphology and inclination are indicated in the top right courner of each panel. The long wavelength portion of the SEDs (> 2 μm) are primarily dust heat emission while the short wavelength portion (<2 μm) are scattered light on dust from the star.

6 Discussion

Here we first discuss the possibility of deducing the CSE geometry from the dusty SED (Sect. 6.1). Then in Sect. 6.2, we show how to estimate the amount of dust mass missed by assuming a spherical geometry and build a mass-correction term to approximately correct for this error. Third in Sect. 6.3, we compare SEDs of different inclinations for the most massive distributions where the strongest impact is expected. Finally in Sect. 6.4, we use best-fits of each model to the observed data of EP Aqr to test the mass correction term of Sect. 6.2.

6.1 Simulated spectral features

The dust SEDs are shown in Fig. 3, and dust emission at 10 and 50 μm from 100% spirals and discs is compared with spheres in Fig. 4 to visualise differences and similarities between SEDs. Since the more massive edge-on discs are optically thick, and appear as featureless SEDs with colder black-body temperatures and less flux at wavelengths shorter than ~ 50 μm, their SEDs are more akin to less massive spheres with larger radii. This is most visible in Fig. 4 for SEDs from edge-on discs of masses 10−4 and 10−5 M⊙, which decrease in flux density to undetectable levels at these wavelengths (below the 3 σISO ≈ 10.8 Jy), since the emission peak is at longer wavelengths.

Disc SEDs with a dust mass of 10−8 M⊙ exhibit only negligible differences when compared to SEDs of spheres with dust masses < 10−6 M⊙. However, this dust excess is less than 3 σISO above the stellar SED and would be difficult to detect in observations (compare with the horizontal dotted line in Fig. 4). Also, the strong absorption at 10 μm of the edge-on disc with a dust mass of 10−4 M⊙, visible in Fig. 3, would not be detectable in reality since it would be overwhelmed by the stellar SED.

All geometrical models have the same spectral appearance when they are optically thin with silicate features at 10 and 18 μm. For the optically thick cases, all spherical geometries exhibit a strong absorption at 10 μm (for dust masses larger than 10−5 M⊙), while the other geometries, as mentioned above, rather show a black-body-like spectral shape when optically thick. Therefore, the lack of silicate features at 10 and/or 18 μm could be an indication of non-spherical dust cloud geometries since these have higher optical thickness than corresponding spherical geometries with the same dust mass (see Table 4).

To demonstrate these effects, we fitted BB SEDs to the simulated dust SEDs’ thermal emission at wavelengths > 2 μm (only dust emission without stellar SED, and excluding the combined sphere-spiral geometry). Since our simulated and observed data are expressed as flux density per unit frequency and as a function of wavelength, we use the Planck function as expressed per unit frequency, (7)

where λ  =  c∕ν, h is the Planck’s constant, kB is Boltzmann’s constant, c is the speed of light in vacuum, and Tdust is the dust temperature. For this reason, the maximum flux density per unit frequency as a function of wavelength, as listed in Table 5, follows the frequency dependant Wien’s displacement law.

To compute BB-radii (Rdust), we refer to Lamers & Cassinelli (1999) who stated that 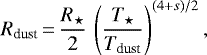(8)

where s = 1 for optically thin dust. The Rdust then gives the edge of the dust condensation region, which we take to be the distance between star and dust. The stellar properties (radius R⋆ and effective temperatureT⋆) are those listed in Table 1. This way we obtain BB temperatures that correspond to the thermal emission of the dust and can more easily see how the thermal emission, as seen edge-on, moves to longer wavelengths when the dust is optically thick (more massive dust envelopes).

In Table 5, we list the fitted dust BB-radii of spheres and edge-on geometries, and in Table 4we list radii along the LOS where the dust envelope becomes optically thick as seen edge-on. The sphere BB-temperatures are generally close to 290 K, while the edge-on geometries have significantly colder dust BB-temperatures and appear as optically thin at much larger distances from the star. For example, the optically thin SEDs peak at wavelengths around 10–20 μm, while the more massive edge-on spirals and discs SEDs peak at wavelengths around 50–100 μm. A general conclusion could be that SEDs with no discernable features and peaking at longer wavelengths can originate from disc-like distributions that are optically thick and observed close to edge-on. However, we find that SEDs that are peaking at shorter wavelengths can also originate from disc-like geometries as seen more face-on rather than edge-on, as also concluded by Van Winckel (2003). Furthermore, inclusion of larger grains is also known to result in colder emission due to differences in the absorption coefficients as compared to small grains (see e.g. Miyake & Nakagawa 1993; Wolf & Hillenbrand 2003; Krivov et al. 2008).

thumbnail Fig. 4

Comparisons of dust flux densities from Fig. 3 at 10 μm (top panel) and 50 μm (bottom panel) for spheres (black with dots), spirals (red with circles) and discs (green with squares) without a spherical component, and as seen face-on (solid lines) or edge-on (dashed lines). The horizontal black dotted line shows the flux density threshold of 3 σISO ≈ 10.8 Jy.
Table 5

Fitted dust BB-temperatures and wavelengths, λBB, that correspond to the frequency of the peak of the BB-function Bν(λ, Tdust) for spherical models, and edge-on spirals and discs.

Table 6

Mass corrections for spirals, discs, and sphere-spiral combinations, corresponding sphere masses, mass corrections, and numbers, as given by Eq. (5), for all models that fulfils .

6.2 Morphology-mass correction term

To compensate for the ignorance of the dust morphology, we constructed a dust mass correction term by searching for similar SEDs from different morphologies. We did this by using Eq. (5) and retaining those SEDs that fall within the 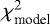-limit of 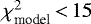when compared to SEDs of the purely spherical morphology. This is a large range since we have SEDs from a wideand sparse dust mass range, rather than a narrow and well-filled dust mass range. The 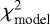-limit was chosen as a compromise between the number of similar SEDs (for each set of models) and the quality of the similarities.

The mass corrections CM for the different geometries are defined as 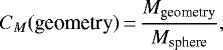(9)

where the subscript geometry can be exchanged to any dust geometry. With this correction factor, an observed dust mass, deduced from a SED under the assumption of spherical geometry, can be transformed into a corresponding spiral, sphere-spiral, or disc dust mass through multiplication by the CM factor.

We list spiral and disc masses, corresponding sphere masses, and subsequent CM factors (i.e. mass corrections) for each SED that fulfil 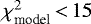in Table 6. In Fig. 5, we show examples of two spherical SEDs compared with face-on oriented disc and spiral SEDs. This figure showcases the bluntness of our 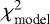-limit and the meaning of “quality” of the similarities. For example, in the case of face-on 100% spirals, we see that the SEDs with the highest allowed 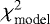exhibit no silicate features at 10 and 18 μm due to optical thickness, in constrast to the other models with the highest allowed 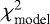. It should be noted that our 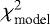-limit was partly chosen so that it would include 100% spiral SEDs that exhibit these silicate features, and along a range of dust masses until the silicate features are no longer visible. Thus, we included additional SEDs here for the CM factor of the 100% spirals, than for the other envelope morphologies.

We obtain, in the face-on cases, regular trends for the CM factor with growing sphere dust mass, while for most edge-on cases we obtain CM factors over a wide range. To better understand the differences of the CM factors from the edge-on geometries, we plot the bolometric dust IR luminosity (λ > 2 μm) for each dust geometry in Fig. 6 (based on SEDs shown in Fig. 3). For the spheres, the IR luminosity increases linearly (in a log-log plot) with mass, which is expected for mostly optically thin distributions (Hildebrand 1983). For face-on geometries, the IR luminosity first increases and then flattens out. However, for edge-on geometries, the IR luminosity increases and then decreases with increasing mass. This is also visible in the shape and flux densities of the higher-massed edge-on SEDs in Fig. 3. The effect is that edge-on spirals and discs, that are optically thick, have fainter SEDs that also appear akin to cold BBs (see comparison with BBs in Sect. 6.1). This peculiar behaviour is caused by the fact that only the colder outer dust is observed in optically thick edge-on geometries. This complicates the 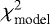-comparison with edge-on geometries. For these, the CM factors span an extended range even though the 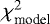values remain low for an extended mass range (as seen in Table 6), making it difficult to constrain the CM factor.

For the face-on geometries, the entire radial extent of the distributions are visible for observers, regardless of optical thickness, and thus the emission temperature changes much less when we compare different total dust masses. Therefore, we focus here on the CM factors of the face-on geometries and plot these in Fig. 7. A caveat to keep in mind is the lack of silicate features for the included highest masses of the 100% spirals, as shown in Figs. 3 and 5. This issue is connected to the aforementioned higher optical thickness for the spirals when compared to discs and spheres with the same dust mass.

In Fig. 7 we plot the face-on spiral and disc masses versus their corresponding sphere masses given in Table 6 with 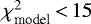. For the face-on spirals without a spherical component we find an average CM (spiral) = 0.011 ± 0.003, while for the discs we find an average CM (disc) = 0.047 ± 0.009, where the errors are one standard deviation of the included corrections in Table 6. We use these as the lower and higher limit when formulating the common correction, CM (combined) ≈ 0.03 ± 0.02, which is shown as black dashed and dotted lines in Fig. 7. For the spiral-sphere combinations we find the corrections CM (5% spiral) = 0.093 ± 0.009 and CM (0.5% spiral) = 0.5 ± 0.0. As expected, decreasing the spiral components’ mass fraction increases the correction term and brings it closer to unity. The yellow line in Fig. 7 shows where CM = 1, meaning thelimit where the dust envelopes become purely spherical. These numbers show that by deducing a dust mass from an SED with an assumed spherical geometry, the real dust mass may be as low as 3% of the deduced mass if the real geometry is a vertically flat spiral or disc.

We must stress the low number of data points here, and the large number of parameters that govern the distributions. For example, the mass corrections are only found within a small range of spherical-model dust masses, namely 1 × 10−7–2 × 10−5 M⊙ for the 100% spirals and discs, and we are not able to find SEDs similar enough to higher masses of spherical SEDs. All of these corrections are not generally applicable for a wider range of observed (dust sphere) masses.

thumbnail Fig. 5

Comparisons of different “worst” cases of , for face-on spirals and discs, as listed in Table 6. Top panel: dust SEDs corresponding to the spherical dust mass of 1 × 10−5 M⊙ (black dashed line), i.e. face-on 100% spiral of mass 2 × 10−7 M⊙ and a few additional SEDs down to 1 × 10−8 M⊙ (red lines), and a face-on 5% spiral with the dust mass 8 × 10−7 M⊙ (cyan line). Bottom panel: dust SEDs corresponding to the spherical dust mass of 2 × 10−5 M⊙ (black dashed line), i.e. a face-on disc with the dust mass 8 × 10−7 M⊙ (green line), and a face-on 0.5% spiral with the dust mass 1 × 10−5 M⊙ (magenta line). The vertical yellow dotted line marks the wavelength limit of 2 μm.
thumbnail Fig. 6

Dust IR luminosities for spherical distributions (black), and spirals (red dots) and discs (green squares) without a spherical component. Solid lines are face-on distributions and dashed lines are edge-on distributions.
thumbnail Fig. 7

Masses of face-on distributions of spirals and discs on the y-axis, compared with corresponding spherical masses on the x-axis, from modelsTable 6, i.e. SEDs of spirals and discs that are similar to sphere-SEDs according to the limit , and their corresponding masses. The black dashed line is a common mass correction for the non-spherical geometries, CM (combined) ≈ 0.03 ± 0.02, with the black dotted lines being the uncertainties. Mass corrections found with best fits to the EP Aqr observed data (see Sect. 6.4 for details) are included as a green cross (disc), red plus (100% spiral), cyan Y (5% spiral), and magenta inverted Y (0.5% spiral). A diagonal yellow line is included to show where CM = 1.

6.3 Impact of inclination

We have so far compared geometries corresponding to face-on and edge-on inclination angles. For these cases we note that optically thick discs and spirals have significantly different SEDs when observed at the two different inclinations, mostly due to differences in optical thickness along the LOS. However, also the radiating surface is very different; the face-on surface is 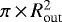, where Rout is the outer radius, while the edge-on surface is of the order of 2 Rout × h, where h is the distribution’s vertical width. The emission flux density ratio between face-on and edge-on orientations is then proportional to the ratio of the surface areas, that is ∝ Rout∕h, which for a disc is as small as ~0.003. From Fig. 4 we see that at 50 μm the flux density ratio is 0.01, which is consistent with this estimate (while at 10 μm we obtain a deep absorption).

Here we now compare the effects of different inclination angles. The spiral Homan et al. (2018) observe around EP Aqr has an inclination between 4° and 18°. We used the most massive (10−4 M⊙) spiral and disc models, with no spherical component, since these are the most optically thick and hence will have the most significant differences when comparing inclinations. We simulated SEDs at inclinations of 0°, 25°, 50°, 60°, 70°, 80°, and between 85° and 90° with increments of 1°. Since we see significant impacts on the features at 10 and 18 μm, we compared the flux densities at 10 and 18 μm, and around the minima between these features, at 13 μm.

In Table 7 we list the different flux ratios obtained from dust-only SEDs at the wavelengths 10, 13, and 18 μm, and in Fig. 8 we plot the corresponding dust SEDs without the stellar SED. Here we can see that, with our choice of morphologies with limited scale heights, we do not obtain any significant impact for inclinations i < 85 °. For the dust disc, we find the most extreme cases of absorption features in the range 85°–90°, similar to what was found earlier. This connects to the choice of scale height and the lower optical thickness of the disc when compared to the spiral (see Table 4), since a higher optical thickness extinguishes spectral lines. In any case, these resultsshow that with our limited choice of spirals and disc geometries, they emit SEDs similar to those seen face-on for most inclinations.

Table 7

Flux ratios at wavelengths 10, 13, and 18 μm as a function of inclinations i.

6.4 Comparison with observed photometry

To test the mass correction factor estimated in Sect. 6.2, we also compared our models with the photometry of EP Aqr presented in Table 2, and with the ISO-SWS and Herschel-PACS spectra listed in Sect. 2. Our goal here is not to reproduce the observed dust emission to a high degree of accuracy, but to test the similarities and differences of these simulated SEDs to a realistic case. For studies that reproduce the dust emission, we refer to earlier publications, for example Heras & Hony (2005) who used one-dimensional radiative transfer for that purpose.

We used the IR and FIR data, that is wavelengths longer than 2 μm where the relevant dust emission appear, and iterated through the different models to find the best-fitting one for each dust geometry with the help of Eq. (6). The best fits are shown in Fig. 9 and their corresponding dust masses and 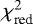values are listed in Table 8. The large 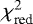values are due to the offset between the ISO-SWS spectrum and the Herschel-PACS spectra.

In Fig. 9 we also include an additional panel with the same geometrical dust distributions, but with another dust composition: 90% Mg2 SiO4, 9% Al2 O3, and 1% Fe2 SiO4. We see here that the aluminium feature at ~ 13 μm dominates the spectrum. However, we see a similar trend as with the previous dust composition: namely that the pure spiral, without a spherical component, has flatter and more featureless spectra than the other morphologies. The sphere and face-on disc spectra are most similar. When comparing the simulated spectra with the ISO-SWS spectrum, we can see that Al2 O3 is not a significant ingredient of the dust of EP Aqr.

When comparing the spectra in the two top panels in Fig. 9 (distributions of two-species), we find that the face-on disc and the sphere-spiral distributions exhibit spectral features that correspond well to the ISO-SWS spectra, and the silicate features at 10 and 18 μm. However, the discs and 5% spiral underestimate the Herschel-PACS flux densities which indicate that they lack cold dust emission. For the edge-on discs and spirals it is not possible to find better fits since higher dust masses shiftthe SED-peak to longer wavelengths. In addition, models which are optically thick along the LOS do not fit the data either. However, this is consistent with Heras & Hony (2005) who found that the dust around EP Aqr is optically thin. The best-fitting spherical model also exhibits the expected features at 10 and 18 μm; however, it underestimates the flux density at 10 μm and marginally overestimates the Herschel-PACS flux densities.

The two combined sphere-spiral geometries, when observed face-on, reproduce the features at 10 and 18 μm. The 0.5% spiral also reproduces the FIR Herschel spectrum whereas the 5% spiral underestimates this spectrum. Not so surprising is the fact that the best-fit total dust masses of the sphere-spiral models are higher than for the 100% spiral and disc, resulting in higher CM values than for those without a spherical component, as already seen in Fig. 7. Additionally, the 100% spiral model gives featureless SEDs at both inclination angles. This results in the face-on spiral fitting the photometry well but not the ISO-SWS spectrum.

To connect to the mass correction term CM, we see in Table 8 that the 100% face-on spiral and the disc result in CM = 0.03 and 0.04, respectively, meaning that our spiral and disc masses, and the subsequent MLRs, are more than one order of magnitude smaller than that of the corresponding spherical distribution. These correspond well to what was found in Sect. 6.2, that is CM (combined) = 0.01 to 0.05. These are also plotted in Fig. 7 as cross and plus signs, respectively, for the spiral and disc. For the 5 and 0.5% sphere-spiral combinations, we find higher CM values than for the 100% face-on spiral since these are similar to the spherical distribution, whereas the 0.5% spiral has an order of magnitude larger CM value of 0.4. The sphere-spiral combined distributions are indicated in Fig. 7 as magenta and cyan Y symbols.

Our CM estimates from Sect. 6.2 are quite conservative. This is due to the combination of the large error in the mass correction, the many parameters (e.g. spiral and disc thickness, inter-arm distance, dust composition, stellar SED, sphere-spiral mass ratio), and the few data points we used to find CM. However, we have shown that an observed SED may lead, when interpreted with a spherical model, to a total dust mass in a range that may be more than one order of magnitude larger than if the dust were distributed in a spiral or a disc. However, in the case of a realistic mass ratio between a dust spiral and the surrounding dust sphere (i.e. 5% of the total dust mass residing in a spiral), the correction factor is ~ 0.5 instead. Depending on the ratio between the mass of the dust spiral and sphere, there should exist a range of correction factors between ~ 0.01 to 1, that is up to no difference at all.

Table 8

Best-fit dust models with two dust species (Mg2SiO4 and Fe2 SiO4) and their 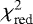values for EP Aqr.

thumbnail Fig. 8

Simulated dust SEDs from spirals and discs without spherical components, and without including the stellar SED, at different inclinations. The green dashed lines are inclinations between 85° and 90°, where we show 89° for the spiraland 87°, 88°, and 89° for the disc.
thumbnail Fig. 9

Comparison between best-fit models, photometry and IR spectra for EP Aqr. Top and mid panels: dust with 99% Mg2SiO4 and 1% Fe2SiO4. Top panel: SEDs from face-on geometry only. Mid panel: SEDs from edge-on geometry only. Bottom panel: compares the same dust masses and morphologies with these dust species; 90% Mg2SiO4, 9% Al2O3, and 1% Fe2SiO4. The different morphologies are indicated by different colours and symbols as annotated in the panels. The black dashed curve is the stellar photospheric SED model. The yellow spectrum is from ISO-SWS (Sloan et al. 2003). The blue and red spectra are from Herschel-PACS (Nicolaes et al. 2018). The photometry (Table 2) is shown as black dots (the error bars were smaller than the symbols and are not shown here).

7 Conclusions

In this pilot study we used RADMC-3D to simulate SEDs for spherical, spiral, and disc-shaped dust distributions. The dust was distributed within the radial extensions of 5–5000 au around the O-rich AGB star EP Aqr. We found significant differences when comparing SEDs from the more massive dust envelopes.

We found that the spirals and discs become partially optically thick at lower total dust masses than the equivalent sphere due to the higher local densities of the former. This was especially true when no sphericalcomponent was included. This caused differences in spectral features, mainly at the 10 and 18 μm silicate features. Optically thick discs and spirals, when seen face-on, had almost no strong spectral features and appeared more akin to black bodies. More massive edge-on discs exhibited an absorption at 10 μm which was overwhelmed by the stellar SED. The edge-on, non-spherical, high-mass geometries (10−4 and 10−5 M⊙) appeared as black bodies at longer wavelengths. This was the opposite of how face-on distributions appeared, since for edge-on distributions only the outer, colder dust was visible along the line-of-sight, while with face-on and optically thick distributions, the warmer inner dust emission was still visible.

General conclusions from the spectral features were that (i) if observations of an O-rich AGB star show significant warm dust emission, but no detectable silicate features, it would be prudent to consider non-spherical models; (ii) if observations of an AGB star show colder CSE dust than expected, the cause could be an edge-on spiral or disc. However, the same effect may have other causes, for example larger dust grains.

We compared differences in dust masses of similar SEDs from spheres, face-on spirals and discs. We formulated a correction term which is the ratio between the mass of two different distributions with similar SEDs. This correction term may be used to estimate themass of a spiral or a disc even though a spherical model has been used to model the observed SED. In the extreme cases of spirals and discs with no spherical component, we found that the correction term was between 0.01 and 0.05 times that of the mass of an assumed spherical distribution. This term was larger if a sphere was included around the spiral. For example, when the spiral consisted of 5% of the total dust mass, the mass correction was a factor of 0.09, and when the spiral was 0.5%, the mass correction was 0.5.

These estimates were based on many assumptions (e.g. the disc and spiral morphologies), however, they were consistent with the masses of our dust geometries when they were compared with the observed far-IR photometric and spectroscopic data of EP Aqr. The difference in mass of dust geometries that exhibited comparable SEDs may correspond to up to one to two orders of magnitude differences in estimated MLRs for an AGB star. However, additional comparisons of additional variations of dust morphology with additional known spiral-hosting AGB stars is required to constrain observable differences better. For example, it would be useful to study how a range of mass ratios between the spherical and spiral components of dust envelopes affects the correction term we formulated in Sect. 6.2.

Acknowledgements

This research has been funded by the Belgian Science Policy Office under contract BR/143/A2/STARLAB. L.D. acknowledges support from ERC consolidator grant 646758 AEROSOL. We would like to thank the members of Team L.E.E.N. at KU Leuven for their interesting discussions, and general support for this project. We also want to thank Daniel Wiegert for his technical support with significant computational time at his private cluster. This work has made use of the SIMBAD database, operated at CDS, Strasbourg, France, the SVO Filter Profile Service supported from the Spanish MINECO through grant AYA2017-84089, and data from Herschel-PACS. PACS has been developed by a consortium of institutes led by MPE (Germany) and including UVIE (Austria); KU Leuven, CSL, IMEC (Belgium); CEA, LAM (France); MPIA (Germany); INAF-IFSI/OAA/OAP/OAT, LENS, SISSA (Italy); IAC (Spain). This development has been supported by the funding agencies BMVIT (Austria), ESA-PRODEX (Belgium), CEA/CNES (France), DLR (Germany), ASI/INAF (Italy), and CICYT/MCYT (Spain). This work has also made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement.

References

  1. Begemann, B., Dorschner, J., Henning, T., et al. 1997, ApJ, 476, 199 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bladh, S., Liljegren, S., Höfner, S., Aringer, B., & Marigo, P. 2019, A&A, 626, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Blum, R. D., Srinivasan, S., Kemper, F., Ling, B., & Volk, K. 2014, AJ, 148, 86 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bohren, C. F., & Huffman, D. R. 1983, Absorption and Scattering of Light by Small Particles (Weinheim: Wiley-VCH) [Google Scholar]
  5. Cernicharo, J., Marcelino, N., Agúndez, M., & Guélin, M. 2015, A&A, 575, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Chen, Z., Ivanova, N., & Carroll-Nellenback, J. 2020, ApJ, 892, 110 [NASA ADS] [CrossRef] [Google Scholar]
  7. Cox, N. L. J., Kerschbaum, F., van Marle, A. J., et al. 2012, A&A, 537, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog: II/246 [Google Scholar]
  9. Danilovich, T., Teyssier, D., Justtanont, K., et al. 2015, A&A, 581, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Decin, L., Richards, A. M. S., Neufeld, D., et al. 2015, A&A, 574, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Drimmel, R., Bucciarelli, B., & Inno, L. 2019, Res. Notes Amer. Astron. Soc., 3, 79 [Google Scholar]
  12. Dullemond, C. P. 2012, Astrophysics Source Code Library [record ascl:1202.015] [Google Scholar]
  13. Dumm, T., & Schild, H. 1998, New Astron., 3, 137 [NASA ADS] [CrossRef] [Google Scholar]
  14. Elitzur, M., & Ivezić, Ž. 2001, MNRAS, 327, 403 [NASA ADS] [CrossRef] [Google Scholar]
  15. Ertel, S., Kamath, D., Hillen, M., et al. 2019, AJ, 157, 110 [CrossRef] [Google Scholar]
  16. Fabian, D., Henning, T., Jäger, C., et al. 2001, A&A, 378, 228 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
  17. Fouque, P., Le Bertre, T., Epchtein, N., Guglielmo, F., & Kerschbaum, F. 1992, A&AS, 93, 151 [NASA ADS] [Google Scholar]
  18. Gaia Collaboration 2018, VizieR Online Data Catalog: I/345 [Google Scholar]
  19. Gobrecht, D., Cherchneff, I., Sarangi, A., Plane, J. M. C., & Bromley, S. T. 2016, A&A, 585, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Gontcharov, G. A. 2012, Astron. Lett., 38, 87 [NASA ADS] [CrossRef] [Google Scholar]
  21. Guélin, M., Patel, N. A., Bremer, M., et al. 2018, A&A, 610, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Habing, H. J. 1996, A&ARv, 7, 97 [NASA ADS] [CrossRef] [Google Scholar]
  24. Habing, H. J.,& Olofsson, H., eds. 2003, Asymptotic Giant Branch Stars (New York: Springer) [Google Scholar]
  25. Henyey, L. G., & Greenstein, J. L. 1941, ApJ, 93, 70 [Google Scholar]
  26. Heras, A. M., & Hony, S. 2005, A&A, 439, 171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Herbst, E., Chang, Q., & Cuppen, H. M. 2005, J. Phys. Conf. Ser., 6, 18 [NASA ADS] [CrossRef] [Google Scholar]
  28. Hildebrand, R. H. 1983, QJRAS, 24, 267 [NASA ADS] [Google Scholar]
  29. Hoai, D. T., Nhung, P. T., Tuan-Anh, P., et al. 2019, MNRAS, 484, 1865 [NASA ADS] [CrossRef] [Google Scholar]
  30. Höfner, S., & Olofsson, H. 2018, A&ARv, 26, 1 [NASA ADS] [CrossRef] [Google Scholar]
  31. Homan, W., Richards, A., Decin, L., de Koter, A., & Kervella, P. 2018, A&A, 616, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Jäger, C., Dorschner, J., Mutschke, H., Posch, T., & Henning, T. 2003, A&A, 408, 193 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Jeffers, S. V., Min, M., Waters, L. B. F. M., et al. 2014, A&A, 572, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Jones, D., & Boffin, H. M. J. 2017, Nat. Astron., 1, 0117 [CrossRef] [Google Scholar]
  35. Jones, O. C., Kemper, F., Srinivasan, S., et al. 2014, MNRAS, 440, 631 [NASA ADS] [CrossRef] [Google Scholar]
  36. Jorissen, A. 2003, Asymptotic Giant Branch Stars, eds. H. Habing, & H. Olofsson (New York: Springer Verlag), 461 [Google Scholar]
  37. Jorissen, A., Van Eck, S., Merle, T., & Van Winckel, H. 2018, Why Galaxies Care About AGB Stars, poster presented at IAU Symp. 343 [Google Scholar]
  38. Kamath, D., & Van Winckel, H. 2019, MNRAS, 486, 3524 [NASA ADS] [CrossRef] [Google Scholar]
  39. Keenan, P. C., & McNeil, R. C. 1989, ApJS, 71, 245 [NASA ADS] [CrossRef] [Google Scholar]
  40. Kervella, P., Montargès, M., Ridgway, S. T., et al. 2014, A&A, 564, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Kervella, P., Homan, W., Richards, A. M. S., et al. 2016, A&A, 596, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Kim, H., Liu, S.-Y., & Taam, R. E. 2019, ApJS, 243, 35 [NASA ADS] [CrossRef] [Google Scholar]
  43. Krivov, A. V., Müller, S., Löhne, T., & Mutschke, H. 2008, ApJ, 687, 608 [NASA ADS] [CrossRef] [Google Scholar]
  44. Lagadec, E., & Chesneau, O. 2015, ASP Conf. Ser., 497, 145 [Google Scholar]
  45. Lamers, H. J. G. L. M., & Cassinelli, J. P. 1999, Introduction to Stellar Winds (Cambridge: Cambridge University Press) [CrossRef] [Google Scholar]
  46. Lindegren, L., Hernández, J., Bombrun, A., et al. 2018, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Lykou, F., Klotz, D., Paladini, C., et al. 2015, A&A, 576, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Maercker, M., Mohamed, S., Vlemmings, W. H. T., et al. 2012, Nature, 490, 232 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  49. Mastrodemos, N., & Morris, M. 1999, ApJ, 523, 357 [NASA ADS] [CrossRef] [Google Scholar]
  50. McDonald, I., Zijlstra, A. A., & Watson, R. A. 2017, MNRAS, 471, 770 [NASA ADS] [CrossRef] [Google Scholar]
  51. Meixner, M., Zalucha, A., Ueta, T., Fong, D., & Justtanont, K. 2004, ApJ, 614, 371 [NASA ADS] [CrossRef] [Google Scholar]
  52. Millar, T. J. 2016, J. Phys. Conf. Ser., 728, 052001 [CrossRef] [Google Scholar]
  53. Miyake, K., & Nakagawa, Y. 1993, Icarus, 106, 20 [NASA ADS] [CrossRef] [Google Scholar]
  54. Moro-Martín, A. 2013, Dusty Planetary Systems (Netherlands: Springer Netherlands), 431 [Google Scholar]
  55. Murakawa, K., Ohnaka, K., Driebe, T., et al. 2008, A&A, 489, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Nhung, P. T., Hoai, D. T., Winters, J. M., et al. 2015, A&A, 583, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Nicolaes, D., Groenewegen, M. A. T., Royer, P., et al. 2018, A&A, 618, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Norris, B. R. M., Tuthill, P. G., Ireland, M. J., et al. 2012, Nature, 484, 220 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  59. Ohnaka, K., Weigelt, G., & Hofmann, K. H. 2016, A&A, 589, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Ohnaka, K., Weigelt, G., & Hofmann, K. H. 2017, A&A, 597, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Oomen, G.-M., Van Winckel, H., Pols, O., et al. 2018, A&A, 620, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Oppenheimer, B. D., Bieging, J. H., Schmidt, G. D., et al. 2005, ApJ, 624, 957 [NASA ADS] [CrossRef] [Google Scholar]
  63. Paladini, C., Klotz, D., Sacuto, S., et al. 2017, A&A, 600, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
  65. Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. Ramos-Medina, J., Sánchez Contreras, C., García-Lario, P., et al. 2018, A&A, 611, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Rieke, G. H., Young, E. T., Engelbracht, C. W., et al. 2004, ApJS, 154, 25 [NASA ADS] [CrossRef] [Google Scholar]
  68. Rodrigo, C., & Solano, E. 2013, Filter Profile Service Access Protocol Version 1.0, Tech. rep. [Google Scholar]
  69. Rodrigo, C., Solano, E., & Bayo, A. 2012, SVO Filter Profile Service Version 1.0, Tech. rep. [CrossRef] [Google Scholar]
  70. Sloan, G. C., Kraemer, K. E., Price, S. D., & Shipman, R. F. 2003, ApJS, 147, 379 [NASA ADS] [CrossRef] [Google Scholar]
  71. Soker, N., & Rappaport, S. 2000, ApJ, 538, 241 [NASA ADS] [CrossRef] [Google Scholar]
  72. Theuns, T., & Jorissen, A. 1993, MNRAS, 265, 946 [NASA ADS] [CrossRef] [Google Scholar]
  73. Tuan-Anh, P., Hoai, D. T., Nhung, P. T., et al. 2019, MNRAS, 487, 622 [NASA ADS] [CrossRef] [Google Scholar]
  74. Tuyet Nhung, P. T., Hoai, D. T., Tuan-Anh, P., et al. 2019, Res. Astron. Astrophys., 19, 043 [NASA ADS] [CrossRef] [Google Scholar]
  75. Ueta, T., Meixner, M., Hinz, P. M., et al. 2001a, ApJ, 557, 831 [NASA ADS] [CrossRef] [Google Scholar]
  76. Ueta, T., Meixner, M., Dayal, A., et al. 2001b, ApJ, 548, 1020 [NASA ADS] [CrossRef] [Google Scholar]
  77. van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  78. Van Winckel, H. 2003, ARAA, 41, 391 [Google Scholar]
  79. Winters, J. M., Le Bertre, T., Jeong, K. S., Nyman, L.-Å., & Epchtein, N. 2003, A&A, 409, 715 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  80. Winters, J. M., Le Bertre, T., Pety, J., & Neri, R. 2007, A&A, 475, 559 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  81. Wolf, S., & Hillenbrand, L. A. 2003, ApJ, 596, 603 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

EP Aqr observed and adopted properties.

In the text
Table 2

Photometry of EP Aqr.

In the text
Table 3

Simulation parameters.

In the text
Table 4

Radii outside which the dust distributions are optically thin for all considered wavelengths.

In the text
Table 5

Fitted dust BB-temperatures and wavelengths, λBB, that correspond to the frequency of the peak of the BB-function Bν(λ, Tdust) for spherical models, and edge-on spirals and discs.

In the text
Table 6

Mass corrections for spirals, discs, and sphere-spiral combinations, corresponding sphere masses, mass corrections, and numbers, as given by Eq. (5), for all models that fulfils .

In the text
Table 7

Flux ratios at wavelengths 10, 13, and 18 μm as a function of inclinations i.

In the text
Table 8

Best-fit dust models with two dust species (Mg2SiO4 and Fe2 SiO4) and their 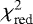values for EP Aqr.

In the text

All Figures

thumbnail Fig. 1

Schematic overview of spiral parameters. The inner radius for the dust is indicated by Rin at 5 au, while the outer radius Rout is beyond the limits of this image. The same radii are adopted as limits for the disc and spherical geometries. The parameters θ and b are defined in Eq. (1).
In the text
thumbnail Fig. 2

All face-on, 5–5000 au simulated SEDs, and the stellar SED MARCS model (in black). The dust masses are 10−4 (blue), 10−5 (green), 10−6 (red), 10−7 (cyan), and 10−8 M⊙ (magenta). Top row: SEDs from CSE with 100% sphere, spiral and disc, respectively. Second row: combined sphere-spiral model SEDsand a comparison between the photometry listed in Table 2 (orange data points) and the MARCS model.
In the text
thumbnail Fig. 3

All 5–5000 au simulated dust SEDs – without the stellar SED model – of dust masses 10−4 (blue), 10−5 (green), 10−6 (red), 10−7 (cyan), and 10−8 M⊙ (magenta). The dust cloud morphology and inclination are indicated in the top right courner of each panel. The long wavelength portion of the SEDs (> 2 μm) are primarily dust heat emission while the short wavelength portion (<2 μm) are scattered light on dust from the star.
In the text
thumbnail Fig. 4

Comparisons of dust flux densities from Fig. 3 at 10 μm (top panel) and 50 μm (bottom panel) for spheres (black with dots), spirals (red with circles) and discs (green with squares) without a spherical component, and as seen face-on (solid lines) or edge-on (dashed lines). The horizontal black dotted line shows the flux density threshold of 3 σISO ≈ 10.8 Jy.
In the text
thumbnail Fig. 5

Comparisons of different “worst” cases of , for face-on spirals and discs, as listed in Table 6. Top panel: dust SEDs corresponding to the spherical dust mass of 1 × 10−5 M⊙ (black dashed line), i.e. face-on 100% spiral of mass 2 × 10−7 M⊙ and a few additional SEDs down to 1 × 10−8 M⊙ (red lines), and a face-on 5% spiral with the dust mass 8 × 10−7 M⊙ (cyan line). Bottom panel: dust SEDs corresponding to the spherical dust mass of 2 × 10−5 M⊙ (black dashed line), i.e. a face-on disc with the dust mass 8 × 10−7 M⊙ (green line), and a face-on 0.5% spiral with the dust mass 1 × 10−5 M⊙ (magenta line). The vertical yellow dotted line marks the wavelength limit of 2 μm.
In the text
thumbnail Fig. 6

Dust IR luminosities for spherical distributions (black), and spirals (red dots) and discs (green squares) without a spherical component. Solid lines are face-on distributions and dashed lines are edge-on distributions.
In the text
thumbnail Fig. 7

Masses of face-on distributions of spirals and discs on the y-axis, compared with corresponding spherical masses on the x-axis, from modelsTable 6, i.e. SEDs of spirals and discs that are similar to sphere-SEDs according to the limit , and their corresponding masses. The black dashed line is a common mass correction for the non-spherical geometries, CM (combined) ≈ 0.03 ± 0.02, with the black dotted lines being the uncertainties. Mass corrections found with best fits to the EP Aqr observed data (see Sect. 6.4 for details) are included as a green cross (disc), red plus (100% spiral), cyan Y (5% spiral), and magenta inverted Y (0.5% spiral). A diagonal yellow line is included to show where CM = 1.
In the text
thumbnail Fig. 8

Simulated dust SEDs from spirals and discs without spherical components, and without including the stellar SED, at different inclinations. The green dashed lines are inclinations between 85° and 90°, where we show 89° for the spiraland 87°, 88°, and 89° for the disc.
In the text
thumbnail Fig. 9

Comparison between best-fit models, photometry and IR spectra for EP Aqr. Top and mid panels: dust with 99% Mg2SiO4 and 1% Fe2SiO4. Top panel: SEDs from face-on geometry only. Mid panel: SEDs from edge-on geometry only. Bottom panel: compares the same dust masses and morphologies with these dust species; 90% Mg2SiO4, 9% Al2O3, and 1% Fe2SiO4. The different morphologies are indicated by different colours and symbols as annotated in the panels. The black dashed curve is the stellar photospheric SED model. The yellow spectrum is from ISO-SWS (Sloan et al. 2003). The blue and red spectra are from Herschel-PACS (Nicolaes et al. 2018). The photometry (Table 2) is shown as black dots (the error bars were smaller than the symbols and are not shown here).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.