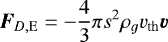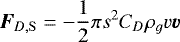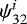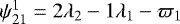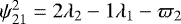| Issue |
A&A
Volume 641, September 2020
|
|
|---|---|---|
| Article Number | A125 | |
| Number of page(s) | 12 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202038297 | |
| Published online | 18 September 2020 | |
Dust distribution around low-mass planets on converging orbits
1
Department of Physics and Astronomy, University of Padova,
via Marzolo 8,
35131
Padova,
Italy
e-mail: Francesco.Marzari@pd.infn.it
2
Theoretical Division, Los Alamos National Laboratory,
Los Alamos,
NM
87545,
USA
e-mail: gennaro@lanl.gov
Received:
29
April
2020
Accepted:
8
July
2020
Context. Super-Earths can form at large orbital radii and migrate inward due to tidal interactions with the circumstellar disk. In this scenario, convergent migration may occur and lead to the formation of resonant pairs of planets.
Aims. We explore the conditions under which convergent migration and resonance capture take place, and what dynamical consequences can be expected on the dust distribution surrounding the resonant pair.
Methods. We combine hydrodynamic planet–disk interaction models with dust evolution calculations to investigate the signatures produced in the dust distribution by a pair of planets in mean-motion resonances.
Results. We find that convergent migration takes place when the outer planet is the more massive. However, convergent migration also depends on the local properties of the disk, and divergent migration may result as well. For similar disk parameters, the capture in low degree resonances (e.g., 2:1 or 3:2) is preferred close to the star where the resonance strength can more easily overcome the tidal torques exerted by the gaseous disk. Farther away from the star, convergent migration may result in capture in high degree resonances. The dust distribution shows potentially observable features typically when the planets are trapped in a 2:1 resonance. In other cases, with higher degree resonances (e.g., 5:4 or 6:5) dust features may not be sufficiently pronounced to be easily observable.
Conclusions. The degree of resonance established by a pair of super-Earths may be indicative of the location in the disk where capture occurred. There can be significant differences in the dust distribution around a single super-Earth and a pair of super-Earths in resonance.
Key words: planet–disk interactions / zodiacal dust
© ESO 2020
1 Introduction
In multi-planet systems close to their final formation stages, the convergent migration of two planets with adjacent orbits may occur due to tidal interactions with the surrounding circumstellar gas. Convergent migration is an important aspect of the dynamical evolution in a multi-planet system since it can lead to resonant orbital configurations. If the resonant forcing generated by gravitational interactions between two neighboring planets overcomes the tidal forcing, the resonant configuration can outlast the presence of the gaseous disk. Otherwise, the orbits can become so compact that they produce collision or scattering events (Marzari et al. 2010; Lega et al. 2013). In the long term, dispersal of the disk may also destabilize a resonant configuration.
In the case of two giant planets, the typical scenario for resonant capture is that of a more massive planet orbiting closer to the star than a less massive one. For a pair of planets like Jupiter and Saturn, for example, the exterior Saturn-mass body may not open a deep gap in the gas and its inward migration would be faster than that of the inner Jupiter-size planet, which is typically able to carve a deeper gap, and therefore drifts inward at a slower rate. Once the planets are close enough to each other, they end up in a mean-motion resonance, which depends on the disk parameters (Masset & Snellgrove 2001; Lee & Peale 2002; Moorhead & Adams 2005; Thommes 2005; Beaugé et al. 2006; Crida et al. 2008; D’Angelo & Marzari 2012). The pair may then form and maintain a common gap, which can also significantly affect the surrounding distribution of dust (Marzari et al. 2019).
The migration of small planets, typically unable to open a gap in the gas, is solely affected by type I torques, driven at corotation and Lindblad resonances (e.g., Tanaka et al. 2002; Paardekooper et al. 2010, 2011, and references therein). Inward convergent migration, in these cases, requires a more massive planet orbiting exterior to a less massive planet, since the type I migration rate is linearly dependent on the mass of the body (e.g., Tanaka et al. 2002, and references therein). In this study we want to explore the evolution of two planets in the super-Earth to Uranus mass range in order to test whether convergent migration leads to resonance trapping, which mean-motion resonances are involved, and under what conditions they can occur.
Hands et al. (2014) explored the simultaneous migration of multiple planets forming at large orbital radii and migrating inward. They found that a large number of systems end up in resonance, as expected according to Szuszkiewicz & Podlewska-Gaca (2012). They adopt an N-body model with artificial damping terms mimicking the torques due to tidal interactions with the gaseous disk. This approach, similar to that exploited by Lee & Peale (2002), Beaugé et al. (2006), and Rein & Liu (2012), works reasonably well for massive planets in a type II-like migration regime. It is also well suited for statistical studies of smaller planets because it relieves the computational overhead with respect to more sophisticated methods. However, in the case of a small planet, it is not straightforward to assume that two planets embedded in a circumstellar disk migrate at the same rate as they would have in isolation. The perturbations induced by a second body can have non-trivial effects. The wakes produced at the Lindblad resonances by one planet may interfere with those of the other planet, leading to a dynamical evolution for double planets that is different from that of a single planet, possibly significantly different. If the pair orbits in a compact configuration, even corotation torques may be affected by changes in the horseshoe dynamics of the gas in the proximity of each planet, due to the gravitational perturbations of the other planet. As a consequence, the total torque on each planet may change depending on the orbits of the planets and on the characteristics of the disk. An example of wake superposition in the disk is shown in Fig. 1 and is discussed in more detail in the following sections.
In order to perform a detailed exploration of convergent migration of low-mass planets, we adopt here an approach based on hydrodynamics simulations. This approach is more computationally expensive, but also more accurate as it allows direct computations of the tidal torques acting on the planets. A similar approach was used by Papaloizou & Szuszkiewicz (2005) while exploring the convergent migration of Earth-mass planets. Differently from what is done in the present work, they considered high-mass disks, ranging from 0.5 to 4 times the mass of the “minimum mass solar nebula” with a piece-wise gas surface density, a local isothermal equation of state, and inviscid gas. In this paper, we use an energy equation for the gas that accounts for heating and cooling and for lower gas densities, as are expected toward the final stages of formation. We also use a viscous gas, and apply different prescriptions for the viscosity. Contrary to Papaloizou & Szuszkiewicz (2005), we find that convergent migration is not always attained when the outer planet is more massive than the inner one, and that the type of resonance in which the planets are locked generally depends on the disk properties and planet location. Furthermore, this computational method also allows us to compute the evolution of dust particles populating the protoplanetary disk and to search for signatures that the two planets may leave in the dust distribution as a result of their resonant configuration. This modeling effort is particularly relevant in light of the complex morphology of circumstellar disks observed by ALMA.
In Sect. 2, we describe the numerical algorithm adopted here to model the evolution of the disk, planets, and dust grains. The dynamics of a pair of planets that approach each other close to the star and are trapped in low degree resonances (e.g., 2:1 and 3:2) is discussed in Sect. 3. In Sect. 4 we model planets starting resonances, and encountering them, farther away from the star, and in which we find trapping in higher-degree resonances, such as 5:4 and 6:5. We also show cases of divergent migration with similar initial conditions, but occurring at high disk densities. Section 5 is dedicated to the exploration of the dust features in the proximity of two resonant planets. Finally, in Sect. 6, we summarize and discuss the implications of our results.
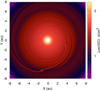 |
Fig. 1 Gas density distribution after 10 Kyr from the beginning of a simulation with an initial surface density Σ0 = 50 g cm−2 at 1 au. The position of the planets corresponds to the locations of the two gas “overdense” regions. |
2 Numerical model
The evolution of the gaseous disk, of the two planets, and of dust particles is computed with the 2D FARGO code (Masset 2000), as modified by Picogna et al. (2018) to include the particle dynamics. We performed simulations in which the energy equation contains viscous heating and radiative cooling through the disk surface:
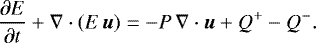 (1)
(1)
Here E and P are the total energy (surface) density and pressure, respectively, and u is the gas velocity field. The quantity Q+ is the viscous dissipation term computed from the components of the viscosity stress tensor (Mihalas & Weibel Mihalas 1999; D’Angelo et al. 2003). The term 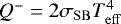 represents the local radiative cooling (σSB is the Stefan–Boltzmann constant) in which the effective temperature Teff depends on the vertical optical thickness of the disk and is computed by exploiting the Rosseland mean opacity κ (Bell & Lin 1994), as in D’Angelo et al. (2003).
represents the local radiative cooling (σSB is the Stefan–Boltzmann constant) in which the effective temperature Teff depends on the vertical optical thickness of the disk and is computed by exploiting the Rosseland mean opacity κ (Bell & Lin 1994), as in D’Angelo et al. (2003).
In the simulations, we model the evolution of 4 × 105 dust particles with radii 10 μm, 100 μm, 1 mm, and 1 cm. Their trajectories are integrated taking into account the gas and the planetary perturbations. We adopted these sizes since they are important in determining peculiar features of circumstellar disks that can be potentially detected, for example by ALMA in the (sub)mm band.
The aerodynamic forces acting on the dust particles are computed as in Picogna & Kley (2015). We briefly summarize the main forces determining the dynamical behavior of the dust grains. The drag force acting on a spherical dust particle of radius s, moving with a velocity v relative to the gas is written as
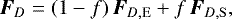 (2)
(2)
are the drag forces in the Epstein and Stokes regimes, respectively. In Eq. (3), 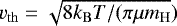 is the mean thermal velocity of the gas molecules, T the local temperature of the gas, ρg the gas volume density, mH the hydrogen atom mass, and μ the mean molecular weight of the gas.
is the mean thermal velocity of the gas molecules, T the local temperature of the gas, ρg the gas volume density, mH the hydrogen atom mass, and μ the mean molecular weight of the gas.
The drag force in the Stokes regime is proportional to the drag coefficient CD, whose value is taken from Weidenschilling (1977) and depends on the Reynolds number. The transition between the two drag forces is determined by the coefficient f, given by
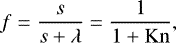 (5)
(5)
where λ is the mean free path of the gas molecules and Kn = λ∕s is the Knudsen number. Comparing the expressions for FD,E and FD,S, it can be shown that they are equal when Kn = 4∕9 for Reynoldsnumbers < 1 (see Weidenschilling 1977).
Due to drag forces, particles experience a radial drift relative to the gas; in particular, they respond to density and velocity gradients in the gas. The drift velocity (relative to the gas), in conditions of a stationary gas surface density, can be approximated as (Birnstiel et al. 2010; Pinilla et al. 2012)
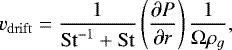 (6)
(6)
where Ω = Ω(r) is the disk’s Keplerian frequency. Indicating with ms the mass of a particle, St = msvΩ∕FD represents the Stokes number (sometimes referred to as non-dimensional stopping time) and Ω the Keplerian frequency of the disk. Since vdrift depends on the radial derivative of the gas pressure P, any local pressure maximum in the disk (with a significant azimuthal extent) will collect and trap grains, both orbiting in the vicinity of the maximum and those drifting inward from farther disk regions.
The dust particles are initially distributed with a surface density that is constant in azimuth around the star and declines as the inverse of the orbital distance, σ(t = 0) ∝ 1∕r. This density distribution can be re-normalized to a different value at a reference radius (e.g., at 1 au) since the particles do not interact among themselves and there is no back-reaction of the dust on the gas. Therefore, the particles can be thought of as tracers of the dynamical evolution of the dust population. The particles that cross the inner border of the disk grid are re-initialized at the outer border.
 |
Fig. 2 Evolution of the radial profiles of the disks. Left: average gas surface density of the unperturbed disks after 12 Kyr (solid lines) compared to the initial distributions (thinner dashed lines) for various model setups, as indicated in the legend. The higher density and warmer models have constant kinematic viscosity ν (see text). Right: average gas temperature for the same models as in the left panel. |
2.1 Disk initial setup
In modeling the circumstellar disk with FARGO, we adopt a polar grid (r, ϕ), typically with 682 × 512 elements uniformly covering the disk, which extends from r = 0.5 au to 12 au from the star and 2π in azimuth. The initial surface gas density scales as
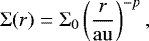 (7)
(7)
with the power law index fixed to p = 0.5. We adopt different values for Σ0, smaller than those predicted for the minimum mass solar nebula (Weidenschilling 1977; Hayashi 1981). We focus our study on the migration of super-Earths under the hypothesis that they formed at orbital radii of a few astronomical units or beyond, and are close to their final mass. The disk is therefore expected to be old and to have partially dissipated via viscous evolution and photo-evaporation (and winds in general). We consider values of Σ0 ranging from 50 to 1000 g cm−2.
The diskaspect ratio is initialized to h = H∕r = 0.036, and two different prescriptions for the kinematic viscosity ν are applied. We adopt either a constant α-viscosity parameter, with values ranging from 0.001 to 0.01, or a constant value ν = 10−5 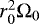 (Ω0 is Ω at r0 = 1 au). These two viscosity prescriptions can produce non-trivial differences in the evolution of the gaseous disk. The former prescription leads to a kinematic viscosity
(Ω0 is Ω at r0 = 1 au). These two viscosity prescriptions can produce non-trivial differences in the evolution of the gaseous disk. The former prescription leads to a kinematic viscosity 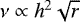 , an increasing function of the radius if h is constant in radius or the disk is flared. The latter prescription corresponds instead to a variable α situation, with α ~ 0.01 at 1 au for h in the range 0.02–0.04.
, an increasing function of the radius if h is constant in radius or the disk is flared. The latter prescription corresponds instead to a variable α situation, with α ~ 0.01 at 1 au for h in the range 0.02–0.04.
Figure 2 shows the unperturbed surface density (averaged in azimuth around the star) of some disk models on the left, after they settle in a steady state (solid curves), along with the initial profiles (dashed curves). The corresponding temperatures are shown on the right. The results indicate that there is only marginal evolution of Σ inside a few au, where the density profile tends to steepen somewhat. Otherwise, the surface density power index remains nearly constant at p ≈ 0.5 during the evolution. Other unperturbed models were also calculated and behave similarly.
The temperature profile of the disk is an important quantity in type I migration since it affects the torque experienced by the planet (see, e.g., Kley & Nelson 2012, and references therein). Neglecting the planetary perturbations, when the disk reaches a near-steady state and is vertically optically thick, heating and cooling are in equilibrium at a temperature such that
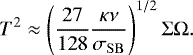 (8)
(8)
In the range of temperature between ≈ 200 K and several hundred K, Bell & Lin’s opacity does not very much. Therefore, in the models with constant ν we expect T ∝ 1∕r (where p ≈ 0.5). At T ≈ 100 K and below, κ ∝ T2 and the gas temperature is expected to be approximately proportional to 1∕r2. We note that κ ∝ T2 at low temperatures when micron-sized ice grains dominate the opacity (see Pollack et al. 1985.) If the disk is vertically optically thin (e.g., κΣ ≪ 1), then at equilibrium
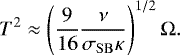 (9)
(9)
In the α-viscosity models, the kinematic viscosity is ν ∝ αT∕Ω, hence T ∝ r−3∕10 for T ≪ 100 K. These approximate scaling behaviors are in agreement with the curves in the right panel of Fig. 2, in the appropriate temperature ranges.
For practical purposes, quasi-steady states of density and of temperature are attained at much earlier times than those displayed in Fig. 2. In all simulations that include planets, we run the numerical models for 300 orbital periods of the inner planet, by keeping the planets’ orbits fixed, allowing the system to relax. We then release both planets, whose orbits can evolve from then onward under the influence of the disk’s gravitational torques. In the plots presented here, only the free evolution of the planets (i.e., from the time of release) is shown.
2.2 Initial planetary configurations
We consider two different initial configurations for the planets. In the first, Model 1, the inner planet, whose mass is m1 = 5 M⊕, initially moves on a circular orbit at a1 = 2 au, while the outer planet of mass m2 = 15 M⊕, is placed on a circular orbit at a2 = 3.3 au. In the second configuration, Model 2, the mass of the planets is the same as in Model 1, but we start with m1 at a1 = 4 au and m2 at a2= 6.5 au. In both setups,the two planets begin their orbital evolution outside of the 2:1 mean-motion resonance.
In the two models, we expect a different balance between the resonance strength and the torque exerted by the gaseous disk. Following the strength criterion adopted by Murray & Dermott (1999) to describe the power relation between spin–orbit resonances and tidal torques on a satellite, we can compare the scaling of the mean motion resonance (hereinafter MMR) strength with that of the disk torque on the planets. The former, according to Murray & Dermott (1999), in a simplified three-body problem scales as the mean motion squared (i.e., as r−3). Consequently, while approaching the star the resonance forcing acting on the planets increases. The torque term due to the gaseous diskscales as
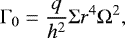 (10)
(10)
where q is the planet-to-star mass ratio. If the disk’s aspect ratio is nearly independent of (or weakly dependent on) the radial distance, the torque Γ0 scales as r1∕2 (since Σ ∝ r−1∕2) and it increases outward. As a consequence, the balance between the resonance strength and the tidal torque sways in favor of the former (and hence of low degree MMR locking of the orbits) as the planets move closer to the star. Higher degree (i.e., more compact) resonant configurations are expected at larger orbital distances. We note that the same outcome would be expected if Γ0 were nearly independent of r, for example if the disk had a typical flaring index d lnh∕d lnr ≈ 2∕7 (e.g., Chiang & Youdin 2010).
 |
Fig. 3 Capture in the 2:1 (black and blue solid line) and 3:2 (magenta solid line) MMRs of the two planets resulting from converging migration in Model 1. At the resonance, the ratio a2 ∕a1 becomes constant. The initial surface density of the gas is Σ0 = 50 and 400 g cm−2 for the capture in the 2:1 MMR and Σ0 = 800 g cm−2 for the capture in the 3:2 MMR (see legend). The turbulence viscosity parameter in these cases is α = 0.01. |
3 Model 1: low degree resonances
In Model 1, for low values of the surface densities, Σ0 = 50 and 400 g cm−2, and for a turbulence viscosity corresponding to α = 0.01, the two planets become trapped in the 2:1 MMR. The torque exerted on the planets by the gaseous disk is not strong enough to overcome the resonant forcing once the planets reach this resonance, and their orbits are therefore locked. For a higher density, Σ0 = 800 g cm−2, the planets cross the 2:1 MMR and are permanently captured in the 3:2 MMR. After capture, the planets migrate inward at the same speed. This is illustrated in Fig. 3, where we show the evolution in time of the ratio between the semi-major axis of the outer planet a2 and that of the inner planet a1.
A noteworthy behavior is that of the case ending with the capture in the 3:2 MMR. In Fig. 4, we display the evolution of the semi-major axis, eccentricity, and critical arguments of the system. As expected, the outer and more massive planet migrates faster than the inner one until it approaches the resonance location. During the evolution, the pair is temporarily trapped in 2:1 resonance (see Fig. 3), an event marked by a large jump in the orbital eccentricity of both planets (and especially of the inner one). The 2:1 MMR is eventually crossed. Once the planets become trapped in the 3:2 MMR, they begin to migrate at the same speed, which is intermediate between their migration velocities prior to resonance capture. While in resonance the orbital eccentricity of both planets rapidly grows and remains high for an extended period of time during which the two critical arguments of the resonance librate:

We note that λi is the true longitude of the planet, whereas ϖi is the longitude of pericenter, for i = 1 (the inner planet) and 2 (the outer planet). The critical angles are slightly shifted with respect to the predicted values of 0 and π because of dissipative effects driven by the gas, but they show the symmetric apsidal corotation predicted by Beaugé et al. (2006). When the inner planet approaches ≈1.3 au, there is a change in the dynamical evolution of the pair, possibly due to the increase in the surface density gradient of the gas distribution (see Fig. 2). The migration speed slows down, as expected in a disk with slope p ≈ 1∕2, and the eccentricity is damped to small values.
 |
Fig. 4 Capture and evolution of two planets in 3:2 resonance. The panels show the time evolution of the semi-major axis (top), the orbital eccentricity (middle), and the critical arguments of the resonance
|
4 Model 2: high degree resonances
In Model 2, where the planets begin to migrate when they are farther away from the star, the behavior is significantly different. As anticipated above, for similar disk conditions the pair is expected (in general, but not always) to establish more compact orbital configurations prior to capture. When a viscosity α = 0.01 is applied for the low density value Σ0 = 50 g cm−2, we find again capture in the 2:1 MMR. Already at a density as low as Σ0 = 100 g cm−2, the gravitational torques exerted by the gas can drive the planets across the 2:1 MMR, and they become trapped in 3:2 resonance (see Fig. 5). In Model 1 this outcome is found for a significantly higher density, Σ0 = 800 g cm−2 (see Fig. 3), while for Σ0 = 400 g cm−2 capture in the 2:1 MMR is still the likely outcome.
As argued in Sect. 2, the different dynamical behavior of Model 2 with respect to Model 1 is due to the different balance between the tidal torques acting on the planets and the resonant forcing. The strength of the gas perturbations is expected to be greater in the orbital configuration realized by Model 2 (based on the torque strength corresponding to the applied Σ), and this is further confirmed by the larger offset of the resonance libration centers with respect to 0 and π. This is shown in Fig. 6, where the two critical arguments of the resonance are shown. At the beginning of the simulation it appears that 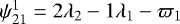 is already librating around 0, but this is only due to the sampling interval as the output interval of the calculation is not short enough. In reality, the critical argument circulates with
is already librating around 0, but this is only due to the sampling interval as the output interval of the calculation is not short enough. In reality, the critical argument circulates with 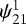 varying rapidly between 0 and π. This behavior is not caught in the plot.
varying rapidly between 0 and π. This behavior is not caught in the plot.
When the surface density of the disk is progressively increased above Σ0 = 100 g cm−2 for the same value of viscosity (α = 0.01), convergent migration no longer occurs. As shown in Fig. 7, when the density is Σ0 = 400 g cm−2 and higher, the planets’ migration paths diverge. This may be due either to the onset of outward migration of the outer planet (middle panel of Fig. 7) or to the outer planet slowing down its inward migration (bottom panel of Fig. 7). This outcome may occur for various reasons related to the balance between the Lindblad and corotation torques, which may also be altered by density perturbations due to gravitational interactions between the two planets. We do not investigate the physical and orbital conditions under which divergent migration may occur, but we note that (under the conditions investigated here) convergent migration is not guaranteed even if the outer planet is more massive than the inner one.
To restore conditions conducive to convergent migration and resonance capture it was necessary either to reduce the viscosity parameter α to a value of 0.001 or to apply a constant kinematic viscosity on the order of 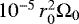 (therefore altering the disk structure). Under these conditions, convergent migration resumes, but the high density and strong torques prevent the planets from being captured in low degree resonances (e.g., 2:1 and 3:2), and instead the system ends up in stable high degree mean-motion resonances (e.g., 5:4 or 6:5). This behavior is illustrated in Fig. 8, where four cases with different initial density and viscosity parameters lead to trapping in high degree resonances. It is noteworthy that in the case with α = 0.001 and Σ0 = 400 g∕cm2 the planets are temporarily captured in 4:3 resonance; however, it is broken on a short timescale by the strong torques exerted by the gas. Theeccentricity evolution of the two planets is shown in Fig. 9 where at each resonance crossing a sudden jump in eccentricity is observed for both planets, as also discussed for some previous cases. When trapped in the 5:4 MMR, after an initial rapid growth, the orbital eccentricity begins to decrease to low values, as in Fig. 4. This may possibly be due to the inner planet approaching a steep density gradient of the disk’s gas while moving closer to the star. The damping of eccentricity suggests that this resonance may be stable over long timescales, even in the presence of the dissipative force due to the disk torques. A similar behavior is observed for the 6:5 resonance, and we tested with N-body calculations (aimed at mimicking the behavior after disk dispersal) that both resonances are stable at least over a timescale of 1 Gyr. We note that, in order to achieve capture in 6:5 resonance, we initialized the planets on more compact orbits compared to the other cases, just outside the 4:3 MMR. In this way the 5:4 MMR is approached when the planets are farther from the sun and the balance between the resonance strength and the tidal force inducing migration is tipped in favor of the disk torque (compared to the other cases), allowing the exterior planet to cross this resonance and attain the 6:5 MMR.
(therefore altering the disk structure). Under these conditions, convergent migration resumes, but the high density and strong torques prevent the planets from being captured in low degree resonances (e.g., 2:1 and 3:2), and instead the system ends up in stable high degree mean-motion resonances (e.g., 5:4 or 6:5). This behavior is illustrated in Fig. 8, where four cases with different initial density and viscosity parameters lead to trapping in high degree resonances. It is noteworthy that in the case with α = 0.001 and Σ0 = 400 g∕cm2 the planets are temporarily captured in 4:3 resonance; however, it is broken on a short timescale by the strong torques exerted by the gas. Theeccentricity evolution of the two planets is shown in Fig. 9 where at each resonance crossing a sudden jump in eccentricity is observed for both planets, as also discussed for some previous cases. When trapped in the 5:4 MMR, after an initial rapid growth, the orbital eccentricity begins to decrease to low values, as in Fig. 4. This may possibly be due to the inner planet approaching a steep density gradient of the disk’s gas while moving closer to the star. The damping of eccentricity suggests that this resonance may be stable over long timescales, even in the presence of the dissipative force due to the disk torques. A similar behavior is observed for the 6:5 resonance, and we tested with N-body calculations (aimed at mimicking the behavior after disk dispersal) that both resonances are stable at least over a timescale of 1 Gyr. We note that, in order to achieve capture in 6:5 resonance, we initialized the planets on more compact orbits compared to the other cases, just outside the 4:3 MMR. In this way the 5:4 MMR is approached when the planets are farther from the sun and the balance between the resonance strength and the tidal force inducing migration is tipped in favor of the disk torque (compared to the other cases), allowing the exterior planet to cross this resonance and attain the 6:5 MMR.
The simulations performed with Model 1 and Model 2 show that resonant capture in low degree resonances occurs preferentially when the pair reaches the resonance in the inner disk within a few au of the star, even for high values of gas density, because only then can the resonance forcing typically overcome the tidal forcing exerted by the gas. High-degree MMRs (i.e., compact orbital configurations above the 3:2 MMR) are instead easier to attain when the pair of planets crosses the resonances in the outer disk, beyond several au from the star where tidal forces can more easily overcome the resonant forcing. Since the orbital migration of the pair after capture generally leads them inward, compact MMRs can also be observed close to the star. Therefore, the degree of resonant configuration observed at present may provide some indication of the disk location at which capture occurred, and of the extent of the coupled inward migration. For example, a compact orbital configuration (e.g., 4:3 or 5:4 MMR) observed close to the star, around or inside 1 au, may indicate that it was established farther out in the disk, and that the pair underwent a long-range orbital migration.
 |
Fig. 5 Capture in the 2:1 (black solid line) and 3:2 (green dashed line) MMRs of the two planets, resulting from converging migration in Model 2. The initial surface density of the gas is Σ0 = 50 g cm−2 for the capture in the 2:1 MMR and Σ0 = 100 g cm−2 for the capture in the 3:2 MMR. The turbulence viscosity parameter in these cases is α = 0.01. |
 |
Fig. 6 Critical arguments of the 2:1 MMR as a function of time ( |
 |
Fig. 7 Divergent migration of two planets resulting from surface density values Σ0 = 400, 800, 1200 g cm−2 and viscosity α = 0.01 (top panel). In the middle panel the evolution of the outer planet is shown for the cases with Σ0 = 400 and 800 g cm−2, as indicated. In both cases, after an initial phase of inward migration, the planet drifts outward (but the longer-term behavior was not investigated). In the bottom panel the divergent migration is instead due to the outer planet slowing down. In all cases, the inner planet keeps migrating inward. |
 |
Fig. 8 Capture in 5:4 resonance in three different configurations. The first has Σ0 = 400 g cm−2 and viscosity corresponding to α = 0.001, the second Σ0 = 500 g cm−2 and constantkinematic viscosity ν = 10−5, and the third Σ0 = 1000 g cm−2 and ν = 10−5. The bottom curve shows capture in 6:5 resonance with Σ0 = 400 g cm−2 and viscosity equal to α = 0.001. In this last case, however, the planets start on close orbits, just exterior to the 4:3 MMR. |
 |
Fig. 9 Eccentricity evolution of the two planets in the case with Σ0 = 400 g cm−2 and viscosity α = 0.001. Before capture each resonance crossing is characterized by a large jump in orbital eccentricity. |
5 Dust evolution near the resonant planets
To model the dynamical features that two planets locked in resonance produce in the dust distribution around them, we integrated the trajectories of 400 000 dust grains. We started the integration when the planets begin to migrate, and considered both Model 1 and Model 2. We integrated the trajectories of particles four different sizes: 10 μm, 100 μm, 0.1 cm, and 1 cm. The Stokes numbers of the particles in these models, evaluated at about 5 au from the star, are ≲ 3 × 10−3 when the gas surface density of the disk at 5 au is Σ0 = 1000 g cm−2. In the models with the lowest density, Σ0 = 50 g cm−2, the Stokes numbers have values ≲7 × 10−2.
We first consider the case when the pair is locked in 2:1 resonance in Model 2, because the greater distance from the star allows a better characterization of the dust features. In Fig. 10, we show the distribution of 10 μm and 1 cm dust particles in the case with Σ0 = 50 g cm−2 (Model 2) after 10 Kyr from the beginning of the planet migration (top panel) and after 70 Kyr (bottom panel). Prior to resonance capture, two independent gaps in the dust distribution start to develop around the two planets, where the distribution appears slight denser at the outer edge of each gap (compared to the density at their inner edge, see top panel of Fig. 10). When the resonance is established, the migration rate of the inner planet increases due to the tidal forcing exerted on the exterior planet (see discussion in Sect. 3), and its gap slowly vanishes (see Fig. 10, bottom panel).
Meanwhile, the gap around the outer planet is not replenished and the region behind the planet becomes depleted of dust. This effect may be associated with the faster inward velocity of the planet compared to that of the particles caused by gas drag. Observations of wide gaps in the dusty disks, like the one in the bottom panel of Fig. 10, would be difficult to interpret since they may be produced by a migrating low-mass planet or by a non-migrating massive planet. A significant enhancement in the dust surface density is also observed at the inner border of the outer planet’s gap, where dust is pushed inward. This dust feature is caused by the radial gradient of the perturbed pressure that prevents dust from approaching the planet (by altering the local rotation rate of the gas). The fact that solids can be collected ahead of the planet as it migrates inward is another indication that the drag-induced drift of the dust is slower than the migration velocity of the planet.
To examine in some more detail the density distribution of the dust, we divided the radial range into a series of discrete radial bins so that, by counting the number of particles in each bin, the evolution of the surface density of dust (σ) can be monitored in an average sense. In Fig. 11, the value of σ is shown after t = 70 Kyr in each radial bin, normalized to the corresponding value at t = 0. The main gap, extending beyond the orbit of the outer planet, is approximately 1.5 au wide and its depth is on average about 1% of the initial dust density. The highest density feature, a dust ring around 6.1 au, peaks at a value more than ten times higher than the local initial density of the dust. This feature is maintained by the 6:5 mean motion resonance with the outer planet, following the planet during its inward migration, and is populated by solids that filter through the planet’s orbit from the inner disk regions. Farther out, the region of enhanced density, located at about 7.2 au, is instead a remnant of the dust orbiting at the outer border of the initial gap produced by the planet, where dust was collected during the early phases of evolution of the system. It does not follow the planet during its orbital evolution because the inward drift of the dust due to gas drag is slower than the planet migration speed and it is temporary in nature since the density slowly declines with time (toward the average value of the surrounding distribution). The wider dust density peak at about 5 au is instead clearly due to the sweeping effect operated by gas drag, in response to the perturbed radial gradient of the gas pressure, and the perturbation moves inward along with the planet. There are only minor differences among the distributions of the different particle species (see Fig. 11). This is likely because the dynamical evolution is dominated by drag effects on solids well coupled to the gas (Stokes numbers are generally ≪ 1, as mentioned above) and by the gravitational perturbations of the planets. A similar outcome was already noted in the simulations of Marzari et al. (2019).
From observations, the wide gap that develops around the pair of planets in resonance could be incorrectly interpreted as due to a single more massive planet. The similarity of the large-scale dust distributions for these cases is illustrated in Fig. 12, where the normalized surface density of the dust due to two planets orbiting in 2:1 resonance (those in Fig. 11) is compared to that of a single planet with mass equal to 100, 200, and 300 M⊕. The physical properties of the gas disk are the same in all simulations. There are significant differences in the morphology of the gap (and of other small-scale features) in the dust formed by the two planets compared to what a single and more massive planet would produce. However, given the scale of these features, they would be difficult to detect with current instruments. For the cases with a single planet, the outer edge of the dust gap becomes wider as the planet mass increases, a behavior reflecting the formation of a wider gap in the gas as tidal perturbations increase. Overall, the width of the dust gap produced by a single 200 M⊕ planet is comparable to that generated by the two planets in resonance. The amount of dust depletion over the region is also comparable. This is further confirmed by the two smooth density maps shown in Fig. 13, where the case with two planets (in a 2:1 resonance) is compared to that with a single planet with m = 200 M⊕. In the first case (top panel), the inner border of the gap is denser due to sweeping and trapping of dust during the inward migration of the outer planet. In both cases, particles remain trapped in horseshoe orbits, although the density of solids appears higher in the case with two planets. This is probably caused because the two smaller planets in resonance migrate a substantial distance and can collect solids filtering from the interior toward the exterior of the orbits. The single more massive planet clears a gap much more rapidly and is more effective at depleting the horseshoe region of dust. This effect is somewhat artificial since we do not model the growth of the planet which, if slow enough, would help increase the dust density in the region. It is clear from the previous plots that when interpreting large-scale features observed in dust distributions around stars, particular care is necessary before reaching conclusions based on perturbations effects in single-planet models.
The behavior of the dust appears different, but with some similarities, in the case with low density (Σ0 = 50 g cm−2) in Model 1 (see Fig. 14). The two planets, once trapped in 2:1 resonance, experience an extended period of stalled migration during which their semi-major axes are nearly stationary (see bottom panel of Fig. 14). The exterior border of the outer planet’s gas gap acts as a barrier to dust particles migrating inward, and they accumulate at that location (see top and middle panels of Fig. 10). Between the two planets, between 2.5 and 3 au, the dust density is significantly reduced (to ~0.1% of the initialvalue) likely due to the barrier effect operated by the outer planet, which prevents dust grains from crossing inside the planet’s orbit.
Concurrently, dust drifting inward is halted exterior to the inner planet’s orbit (again due to the perturbed pressure’s radial gradient) where grains collect and form a mild density excess, approximately a factor of five as large as the local initial density. In this case to a wide gap may be detected by observations whose dynamical origin, however, is somewhat different from that illustrated in Fig. 10 (exterior to the outer planet, see bottom panel). In that case, the migration speed of the planets is probably responsible for the widening of the gap (see also Fig. 14, where the migration of the pair is nearly stalled). In the case shown in Fig. 10 only two high-density dust rings are produced; instead, in the case shown in Fig. 14 there are three: one trailing the inner planet and two around the outer planet. In both configurations the density peaks trailing the outer planet may be the most significant features (from an observational standpoint) in the dust distributions, exceeding the surrounding density levels by factors ≳ 10 (see histograms in Figs. 11 and 14). In the other simulations based on Model 1, with capture in resonance, the planets rapidly move too close to the star because of the high values of Σ0. These configurations do not appear to show features amenable to observations (over the timescales of our simulations).
In the Model 2 case with capture in 3:2 resonance, the inward drift of the planets is faster compared to the case with capture in the 2:1 MMR since the disk density is higher and the features in the dust distribution are more complex (see Fig. 15). In this case the inner planet forms only a very shallow gap in the surrounding dust since the inward migration prevents the formation of large radial gradients in gas distribution. Contrary to the case shown in Fig. 10, the outer planet does not develop a deep and extended gap in the dust, but it does show significant density enhancements in the dust interior and exterior of the planet’s orbit: the density σ at these peaks ranges from 10 to 30 times above the local initial values. Beyond the outer planet, at greater radial distances, there appear to be low-density regions, where the sigma value is about 20% less than the initial values. In this case, the dust signatures induced by the planets in resonance are less pronounced (with respect to the previous cases) and may be more difficult to detect.
When the planets are trapped in higher-degree resonances (e.g., 5:4 and 6:5), the signatures in the surrounding dust distributions are relatively minor, as illustrated in Fig. 16. In these models the absence of gaps in the dust is probably related to the fast migration velocity because, in Model 2, the capture in such compact orbital configurations occurs when the disk surface density is high (Σ0 ≥ 400 g cm−2). Consequently, the gravitational perturbations of the planets are less effective at perturbing the pressure gradient of the gas and the efficiency in collecting dust is significantly diminished. In the case of the 5:4 MMR (top panel of Fig. 16) a common gap is formed, but its depth is only about a factor of 3 smaller than the local initial dust density, a difference that is likely difficult to detect by observations.
In summary, our simulations indicate that only wide resonant configurations, like the 2:1 MMR, may induce significant features in the surrounding dust distribution that can be more likely probed by observations. When the planets are locked in higher-degree resonances and migrate fast, they are more inefficient at perturbing the dust.
An additional noteworthy feature of the dust distributions is the enhanced dust density at the borders of the gap carved by the planets locked in 2:1 and 3:2 resonances. At these locations the concentration of millimeter- to centimeter-sized solids may increase tenfold relative to the initial dust distribution, potentially triggering streaming instability events. In turn, these events may lead to the formation of a significant population of planetesimals. This phenomenon was recently modeled with numerical simulations by Eriksson et al. (2020).
 |
Fig. 10 Dust distribution around the planets trapped in 2:1 resonance at t = 10 Kyr (top panel) and t = 70 Kyr (bottom panel) in Model 2. The black circles give the planets’ positions. Only dust particles 10 μm and 1 cm in size are shown to avoid overcrowding the plot. |
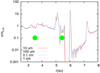 |
Fig. 11 Histogram of the dust surface density, normalized to that at t = 0, around a pair of planets trapped in 2:1 resonance The plot refers to the same case as in Fig. 10, at time t = 70 Kyr (see bottom panel of that figure). The green filled circles give the positions of the planets. The different line colors correspond to different grain sizes, from 10 μm to 1 cm. Only minor differences are observed among the various sizes because all grains are well coupled to the gas. |
 |
Fig. 12 Comparison between the dust gap (normalized surface density) produced by two planets in 2:1 resonance for 10 μm particles (see Fig. 11) and those carved by a single massive planet. The red line shows the gap for the two-planet case, the green dashed line that for a single planet of mass 100 M⊕, the blue dashed line that for a 200 M⊕ planet, and the black dotted line that for a 300 M⊕ planet. |
 |
Fig. 13 Smoothed maps of the dust distribution in the proximity of the planets. The top panel shows the density distribution, normalized to the total number of dust particles in the model, around two planets in 2:1 resonance (Figs. 10 and 11). The color bar range is in units of 10−3 ; the azimuthal resolution is 0.2 rad while the radial resolution is 0.15 au. The bottom panel illustrates the dust distribution for a single planet with mass m = 200 M⊕. As smoothing function, we applied a simple bell-shaped function (Lucy 1977). |
 |
Fig. 14 Top panel: dust distribution around planets locked in 2:1 resonance at t = 40 Kyr in a Model 1 with Σ0 = 50 g cm−2. The black circles give the planets’ positions. Middle panel: histogram of the dust surface density where the planets’ orbital radius is given by a green filled circle. Bottom panel: semi-major axis evolution with time of the outer planet showing a period of stalled migration when the pair of planets are trapped in resonance. |
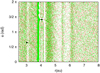 |
Fig. 15 Dust distribution at t = 100 Kyr for the two planets locked in 3:2 resonance (Model 2). |
6 Summary and discussion
We performed hydrodynamic simulations of planet–disk interactions in multi-planet systems. We considered a pair of super-Earths embedded in disks of various gas densities and viscosities, where the exterior planet is the more massive. This configuration should favor convergent migration because the disk’s thermo-dynamical state is such that a stronger tidal torque is exerted on the outer planet than is on the inner one. By adding dust particles to the simulations, we also computed their trajectories in the proximity of the planets in order to test the influence of the resonant configurations on the dust distributions. We considered two different setups, where we changed the initial distance of the planets from the star. In Model 1, the inner planet is initially located at 2 au, while in Model 2 the inner planet starts from 4 au. These two models provide a different balance between the resonance strength and the tidal forcing (by the gas) at the locations of resonance capture.
We find that resonance trapping always occurs in first-order resonances, even of high degree, for different values of the initial gas density and viscosity. However, convergent migration may be inhibited either by a temporary outward migration of the outer planet or by a slowdown of its inward migration compared to that of the inner planet. We did not investigate these configurations in detail, but it appears that either of these two outcomes may be due to mutual perturbations between the planets. In Model 2, divergent migration tends to occur for high values of the gas density and of the α-viscosity parameter. A reduction of the viscosity parameter or the use of a constant kinematic viscosity ν allows convergent migration to resume.
Close to the star, the capture in low degree resonances (e.g., 2:1 or 3:2) is favored because resonant interactions scale as Ω2, whereas the tidal forcing in these calculations is ∝ r1∕2. In Model 2, where the distance from the star is greater, trapping in high degree resonances (5:4 or 6:5) can occur. N-body calculations indicate that these compact resonances are dynamically stable, once the gas dissipates, over timescales on the order of several billion years. This behavior suggests that low degree MMRs presently detected among super-Earths may have occurred when the planets were on converging orbits and became trapped relatively close to the star. Therefore, their formation sites might have been within a few to several au from the star. Instead, high degree resonances are generally expected to occur far from the star, at several au, suggesting formation at larger radii. The degree of the resonance may thus provide some indication about the formation distance from the star of the pair.
In the range of planetary masses adopted in our models, a gap in the dust is expected to form on a short timescale if a single non-migrating planet is considered. The situation may be different when considering a system of two planets that are allowed to migrate. If the orbits of the pair converge, they can be trapped in resonance and the surrounding dust distribution can be significantly affected. Once in resonance, the inner planet may be forced to migrate at a faster rate (than it does prior to capture in the MMR), due to the gravitational push by the outer more massive planet. Consequently, the dust gap around the inner planet may be progressively erased. This outcome is shown in simulations where the planets become trapped in the 2:1 MMR. In this scenario, the presence of the inner planet cannot be detected by looking for dust gaps through observations of disks. At larger radial distances, the gap around the exterior and more massive planet steadily widens because of two distinct and mutually exclusive mechanisms. In the first case (see Fig. 10), the pair of planets migrate quickly and the dust does not drift inward fast enough to replace the dust swept aheadof the planet, which leads to the formation of a wide gap extending beyond the exterior planet. In the second case (see Fig. 14), once trapped in resonance the planets undergo a period of stalled migration and the outer planet acts as a barrier to the dust grains drifting inward. In this latter case, a large gap in the dust develops between the two planets since the local dust has drifted toward the inner planet. In both cases the large gap developing around the planets’ orbits might be mistaken for that produced by a single giant planet.
Higher-degree resonances appear to have less impact on the dust distribution. The 3:2 resonance leads to the formation of a region of enhanced density of dust grains in front of the outer planet and of a depleted region behind it, likely a remnant of the early migration phases of the pair. The 5:4 and 6:5 resonances are even less effective in sculpting the dust distribution, possibly because to achieve these resonant configurations the planets need to migrate inward quite rapidly. In the long term, if the migration of the pair locked in resonance reduces or stalls, it is likely that the planets will open a single wide gap in the dust distribution because of the close proximity of their orbits.
Due to the large computational overhead of hydrodynamic simulations, we only sampled a limited number of disk parameters, planetary masses, and initial orbits. Different density slopes d ln Σ∕d lnr of the gas, different values of kinematicviscosity ν, and disk thermal states may change the migration pattern of the planets. The occurrence of convergent or divergent migration is significantly affected by these parameters, and the convergent migration may occur at different locations in the disk depending on the parameter choice. The migration speed is another important aspect influencing the type of resonance that is established and the dynamical response of the dust distribution around the pair of planets. However, the partial disappearance of the gap around the inner planet, the formation of a wide gap around the outer planet for the 2:1 MMR, and the less conspicuous features that appear in the dust for higher-degree resonances are robust results.
 |
Fig. 16 Dust distributions around two planets trapped in 5:4 resonance (Σ0 = 400 g cm−2, α = 0.001) at t = 60 Kyr (top panel) and around two planets trapped in 6:5 (Σ0 = 400 g cm−2, α = 0.001) at t = 48 Kyr (bottom panel). |
Acknowledgments
We would like to thank the referee, Alexander Mustill, for his comments and suggestions. G.D. acknowledges support from NASA’s Research Opportunities in Space and Earth Science (ROSES) through NASA’s Exoplanets Research Program (proposal 80HQTR19T0086). Computational resources supporting this work were provided by the NASA High-End Computing (HEC) Program through the NASA Advanced Supercomputing (NAS) Division at Ames Research Center.
Appendix A Effects of stellar irradiation
Irradiation from the central star affects the thermal structure of a circumstellar disk and essentially determines its temperature beyond some distance from the star. The lower the disk’s density Σ and the smaller the kinematic viscosity ν, the shorter the radial distance at which heating by stellar radiation can significantly impact the thermal balance of the gas. In order to asses possible effects of irradiation in the disk models discussed above, the right-hand side of Eq. (1) is modified to include a stellar heating term Qirr, as in Eq. (10) of D’Angelo & Marzari (2012, where the term Q− is also modified accordingly; see discussion).
 |
Fig. A.1 Average gas density (left) and temperature (right) of the unperturbed disks after 12 Kyr. The solid curves represent the models shown in Fig. 2 (see legend); the dashed curves refer to the corresponding models that include stellar irradiation, as outlined in the text. As expected, beyond some distance from the star, gastemperature is determined by the stellar irradiation temperature. |
In the 2D (r, ϕ) geometry, irradiation cannot be accurately taken into account due to the lack of the disk’s vertical structure, which is needed to estimate energy deposition in a vertical column of gas at a given radial distance (see, e.g., Bitsch et al. 2013, and references therein). Our implementation is therefore approximate and follows an approach often applied in prior studies (e.g., Dubus et al. 1999; Menou & Goodman 2004, and references therein), with some simplifications outlined in Hueso & Guillot (2005). We assume that the stellar effective temperature and radius are equal to 4300 K and 2.6 R⊙, respectively.
Stellar irradiation is expected to affect a wider range of distances, extending inward, as gas density and kinematic viscosity decrease. Fig. A.1 includes some results of Fig. 2 (solid lines, see legend) and equivalent models that account for irradiation (dashed lines). As anticipated above, gas temperatureis determined by the stellar irradiation temperature beyond a radial distance where viscous heating Q+ ≪ Qirr. The disk structure in our models with Σ0 ≳ 500 g cm−2 is not significantly affected by stellar irradiation over the range of radial distances considered here.
Referring to Fig. A.1, in the highest density model (green curves) Σ is essentially unaffected by irradiation (out to 12 au) and T starts deviating from the no-irradiation model at r > 6 au. Since, in Model 2, the outer planet starts its evolution at 6.5 au, differences in the orbital evolution of the pair might not be large. The situation is expected to be different for the lower density configurations, since the difference in temperature is significant even at short orbital distances from the star. The higher temperature produces a higher aspect ratio h, which wouldcontribute to a slower migration velocity (possibly of both planets). This reduction may be partly offset by the somewhat larger Σ at small r (compare orange and blue solid and dashed curves in the left panel of Fig. A.1). However, the configuration with Σ0 = 50 g cm−2 results in capture in the 2:1 MMR in the model without irradiation and is therefore expected to produce the same resonant orbits in the model with irradiation. The configuration with Σ0 = 100 g cm−2, which produces a 3:2 MMR in the no-irradiation model, may in principle result in a less compact MMR in the model with irradiation. We performed a calculation of this particular configuration and show the results in Fig. A.2. Despite the changes in the radial distribution of temperature and of Σ, the evolution of the pair results again in the capture in the 3:2 MMR. The plot indicates that the exterior planet is briefly caught in the 2:1 MMR with the interior planet, before skipping the resonance and continuing to migrate inward. During the temporary capture in the 2:1 MMR, the orbital eccentricity of the two planets remains low (< 0.01). Since resonance breaking is not aided by an increase in eccentricity, the temporary capture can be considered stochastic in nature.
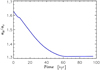 |
Fig. A.2 Ratio of the semi-major axes of a pair of planets using the disk configuration with Σ0 = 100 g cm−2, turbulence viscosity corresponding to α = 0.01, and including stellar irradiation. The planets are initiated according to the setup in Model 2. The outer planet transits the 2:1 MMR with the inner planet and becomes trapped in the 3:2 MMR, as in the model that does not account for irradiation (see Sect. 4). |
Clearly, there may be additional and more subtle effects brought about by the warmer gas, although in general it is expected that disk regions farther from the star are affected more than are the inner disk regions (e.g., as in our Model 1). We plan to investigate in greater detail the effects of irradiation in low-density low-viscosity disks, including resonance capture of a pair of planets and dust evolution, in subsequent work.
References
- Beaugé, C., Michtchenko, T. A., & Ferraz-Mello, S. 2006, MNRAS, 365, 1160 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, K. R., & Lin, D. N. C. 1994, ApJ, 427, 987 [NASA ADS] [CrossRef] [Google Scholar]
- Birnstiel, T., Dullemond, C. P., & Brauer, F. 2010, A&A, 513, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Crida, A., Morbidelli, A., Kley, W., & Dobbs-Dixon, I. 2013, A&A, 549, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiang, E., & Youdin, A. N. 2010, Ann. Rev. Earth Planet Sci., 38, 493 [Google Scholar]
- Crida, A., Sándor, Z., & Kley, W. 2008, A&A, 483, 325 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Angelo, G., & Marzari, F. 2012, ApJ, 757, 50 [NASA ADS] [CrossRef] [Google Scholar]
- D’Angelo, G., Henning, T., & Kley, W. 2003, ApJ, 599, 548 [NASA ADS] [CrossRef] [Google Scholar]
- Dubus, G., Lasota, J.-P., Hameury, J.-M., & Charles, P. 1999, MNRAS, 303, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Eriksson, L. E. J., Johansen, A., & Liu, B. 2020, A&A, 635, A110 [CrossRef] [EDP Sciences] [Google Scholar]
- Hands, T. O., Alexander, R. D., & Dehnen, W. 2014, MNRAS, 445, 749 [CrossRef] [Google Scholar]
- Hayashi, C. 1981, Prog. Theor. Phys. Supp., 70, 35 [CrossRef] [Google Scholar]
- Hueso, R., & Guillot, T. 2005, A&A, 442, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kley, W., & Nelson, R. P. 2012, ARA&A, 50, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, M. H., & Peale, S. J. 2002, ApJ, 567, 596 [NASA ADS] [CrossRef] [Google Scholar]
- Lega, E., Morbidelli, A., & Nesvorný, D. 2013, MNRAS, 431, 3494 [NASA ADS] [CrossRef] [Google Scholar]
- Lucy, L. B. 1977, AJ, 82, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Marzari, F., Baruteau, C., & Scholl, H. 2010, A&A, 514, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marzari, F., D’Angelo, G., & Picogna, G. 2019, AJ, 157, 45 [CrossRef] [Google Scholar]
- Masset, F. 2000, A&AS, 141, 165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masset, F., & Snellgrove, M. 2001, MNRAS, 320, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Menou, K., & Goodman, J. 2004, ApJ, 606, 520 [NASA ADS] [CrossRef] [Google Scholar]
- Mihalas, D., & Weibel Mihalas B. 1999, Foundations of radiation hydrodynamics (New York: Dover, 1999) [Google Scholar]
- Moorhead, A. V., & Adams, F. C. 2005, Icarus, 178, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Murray, C. D., & Dermott, S. F. 1999, Solar System Dynamics (Cambridge University Press) [Google Scholar]
- Paardekooper,S. J., Baruteau, C., Crida, A., & Kley, W. 2010, MNRAS, 401, 1950 [NASA ADS] [CrossRef] [Google Scholar]
- Paardekooper,S. J., Baruteau, C., & Kley, W. 2011, MNRAS, 410, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Papaloizou, J. C. B., & Szuszkiewicz, E. 2005, MNRAS, 363, 153 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Picogna, G., & Kley, W. 2015, A&A, 584, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Picogna, G., Stoll, M. H. R., & Kley, W. 2018, A&A, 616, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinilla, P., Birnstiel, T., Ricci, L., et al. 2012, A&A, 538, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pollack, J. B., McKay, C. P., & Christofferson, B. M. 1985, Icarus, 64, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Rein, H., & Liu, S. F. 2012, A&A, 537, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Szuszkiewicz, E., & Podlewska-Gaca, E. 2012, Orig. Life. Evol. Biosph., 42, 113 [CrossRef] [Google Scholar]
- Tanaka, H., Takeuchi, T., & Ward, W. R. 2002, ApJ, 565, 1257 [NASA ADS] [CrossRef] [Google Scholar]
- Thommes, E. W. 2005, ApJ, 626, 1033 [NASA ADS] [CrossRef] [Google Scholar]
- Weidenschilling, S. J. 1977, MNRAS, 180, 57 [Google Scholar]
All Figures
 |
Fig. 1 Gas density distribution after 10 Kyr from the beginning of a simulation with an initial surface density Σ0 = 50 g cm−2 at 1 au. The position of the planets corresponds to the locations of the two gas “overdense” regions. |
| In the text | |
 |
Fig. 2 Evolution of the radial profiles of the disks. Left: average gas surface density of the unperturbed disks after 12 Kyr (solid lines) compared to the initial distributions (thinner dashed lines) for various model setups, as indicated in the legend. The higher density and warmer models have constant kinematic viscosity ν (see text). Right: average gas temperature for the same models as in the left panel. |
| In the text | |
 |
Fig. 3 Capture in the 2:1 (black and blue solid line) and 3:2 (magenta solid line) MMRs of the two planets resulting from converging migration in Model 1. At the resonance, the ratio a2 ∕a1 becomes constant. The initial surface density of the gas is Σ0 = 50 and 400 g cm−2 for the capture in the 2:1 MMR and Σ0 = 800 g cm−2 for the capture in the 3:2 MMR (see legend). The turbulence viscosity parameter in these cases is α = 0.01. |
| In the text | |
 |
Fig. 4 Capture and evolution of two planets in 3:2 resonance. The panels show the time evolution of the semi-major axis (top), the orbital eccentricity (middle), and the critical arguments of the resonance
|
| In the text | |
 |
Fig. 5 Capture in the 2:1 (black solid line) and 3:2 (green dashed line) MMRs of the two planets, resulting from converging migration in Model 2. The initial surface density of the gas is Σ0 = 50 g cm−2 for the capture in the 2:1 MMR and Σ0 = 100 g cm−2 for the capture in the 3:2 MMR. The turbulence viscosity parameter in these cases is α = 0.01. |
| In the text | |
 |
Fig. 6 Critical arguments of the 2:1 MMR as a function of time ( |
| In the text | |
 |
Fig. 7 Divergent migration of two planets resulting from surface density values Σ0 = 400, 800, 1200 g cm−2 and viscosity α = 0.01 (top panel). In the middle panel the evolution of the outer planet is shown for the cases with Σ0 = 400 and 800 g cm−2, as indicated. In both cases, after an initial phase of inward migration, the planet drifts outward (but the longer-term behavior was not investigated). In the bottom panel the divergent migration is instead due to the outer planet slowing down. In all cases, the inner planet keeps migrating inward. |
| In the text | |
 |
Fig. 8 Capture in 5:4 resonance in three different configurations. The first has Σ0 = 400 g cm−2 and viscosity corresponding to α = 0.001, the second Σ0 = 500 g cm−2 and constantkinematic viscosity ν = 10−5, and the third Σ0 = 1000 g cm−2 and ν = 10−5. The bottom curve shows capture in 6:5 resonance with Σ0 = 400 g cm−2 and viscosity equal to α = 0.001. In this last case, however, the planets start on close orbits, just exterior to the 4:3 MMR. |
| In the text | |
 |
Fig. 9 Eccentricity evolution of the two planets in the case with Σ0 = 400 g cm−2 and viscosity α = 0.001. Before capture each resonance crossing is characterized by a large jump in orbital eccentricity. |
| In the text | |
 |
Fig. 10 Dust distribution around the planets trapped in 2:1 resonance at t = 10 Kyr (top panel) and t = 70 Kyr (bottom panel) in Model 2. The black circles give the planets’ positions. Only dust particles 10 μm and 1 cm in size are shown to avoid overcrowding the plot. |
| In the text | |
 |
Fig. 11 Histogram of the dust surface density, normalized to that at t = 0, around a pair of planets trapped in 2:1 resonance The plot refers to the same case as in Fig. 10, at time t = 70 Kyr (see bottom panel of that figure). The green filled circles give the positions of the planets. The different line colors correspond to different grain sizes, from 10 μm to 1 cm. Only minor differences are observed among the various sizes because all grains are well coupled to the gas. |
| In the text | |
 |
Fig. 12 Comparison between the dust gap (normalized surface density) produced by two planets in 2:1 resonance for 10 μm particles (see Fig. 11) and those carved by a single massive planet. The red line shows the gap for the two-planet case, the green dashed line that for a single planet of mass 100 M⊕, the blue dashed line that for a 200 M⊕ planet, and the black dotted line that for a 300 M⊕ planet. |
| In the text | |
 |
Fig. 13 Smoothed maps of the dust distribution in the proximity of the planets. The top panel shows the density distribution, normalized to the total number of dust particles in the model, around two planets in 2:1 resonance (Figs. 10 and 11). The color bar range is in units of 10−3 ; the azimuthal resolution is 0.2 rad while the radial resolution is 0.15 au. The bottom panel illustrates the dust distribution for a single planet with mass m = 200 M⊕. As smoothing function, we applied a simple bell-shaped function (Lucy 1977). |
| In the text | |
 |
Fig. 14 Top panel: dust distribution around planets locked in 2:1 resonance at t = 40 Kyr in a Model 1 with Σ0 = 50 g cm−2. The black circles give the planets’ positions. Middle panel: histogram of the dust surface density where the planets’ orbital radius is given by a green filled circle. Bottom panel: semi-major axis evolution with time of the outer planet showing a period of stalled migration when the pair of planets are trapped in resonance. |
| In the text | |
 |
Fig. 15 Dust distribution at t = 100 Kyr for the two planets locked in 3:2 resonance (Model 2). |
| In the text | |
 |
Fig. 16 Dust distributions around two planets trapped in 5:4 resonance (Σ0 = 400 g cm−2, α = 0.001) at t = 60 Kyr (top panel) and around two planets trapped in 6:5 (Σ0 = 400 g cm−2, α = 0.001) at t = 48 Kyr (bottom panel). |
| In the text | |
 |
Fig. A.1 Average gas density (left) and temperature (right) of the unperturbed disks after 12 Kyr. The solid curves represent the models shown in Fig. 2 (see legend); the dashed curves refer to the corresponding models that include stellar irradiation, as outlined in the text. As expected, beyond some distance from the star, gastemperature is determined by the stellar irradiation temperature. |
| In the text | |
 |
Fig. A.2 Ratio of the semi-major axes of a pair of planets using the disk configuration with Σ0 = 100 g cm−2, turbulence viscosity corresponding to α = 0.01, and including stellar irradiation. The planets are initiated according to the setup in Model 2. The outer planet transits the 2:1 MMR with the inner planet and becomes trapped in the 3:2 MMR, as in the model that does not account for irradiation (see Sect. 4). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.