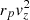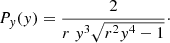| Issue |
A&A
Volume 641, September 2020
|
|
|---|---|---|
| Article Number | A115 | |
| Number of page(s) | 10 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202037940 | |
| Published online | 18 September 2020 | |
Statistical deprojection of intervelocities, interdistances, and masses in the Isolated Galaxy Pair Catalog
1
LUTH, UMR CNRS 8102, Paris Observatory, 92195 Meudon Cedex, France
e-mail: laurent.nottale@obspm.fr
2
GEPI, UMR CNRS 8111, Paris Observatory, 92195 Meudon Cedex, France
e-mail: pierre.chamaraux@obspm.fr
Received:
12
March
2020
Accepted:
1
July
2020
Aims. In order to study the internal dynamics of actual galaxy pairs, we need to derive the probability distribution function (PDF) of true 3D, orbital intervelocities and interdistances between pair members from their observed projected values along with the pair masses from Kepler’s third law. For this research, we used 13 114 pairs from the Isolated Galaxy Pair Catalog (IGPC).
Methods. The algorithms of statistical deprojection previously elaborated were applied to these observational data. We derived the orbital velocity PDFs for the whole catalog and for several selected subsamples. The interdistance PDF is deprojected and compared to the analytical profiles expected from semi-theoretical arguments.
Results. The PDF of deprojected pair orbital velocities is characterized by the existence of a main probability peak around ≈150 km s−1 for all subsamples of the IGPC as well as for the Uppsala Galaxy Pair Catalog. The interdistance PDFs of both the projected and deprojected data are described at large distances by the same power law with exponent ≈ − 2. The whole distributions, including their cores, are fairly fitted by King profiles. The mass deprojection yields a mass/luminosity ratio for the pairs of M/L = (30 ± 5) in solar units.
Conclusions. The orbital velocity probability peak is observed at the same value, ≈150 km s−1, as the main exoplanet velocity peak, which points toward a possible universality of Keplerian structures, whatever the scale. The pair M/L ratio is just seven times the standard ratio for luminous matter, which does not require the existence of nonbaryonic dark matter in these systems.
Key words: catalogs / galaxies: groups: general / galaxies: statistics
© L. Nottale and P. Chamaraux 2020
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
In a recent paper (Nottale & Chamaraux 2018a), we provided new methods for statistical deprojection of the velocity differences and interdistances between the members of galaxy pairs and we validated these values by numerical simulations. In the present work, we perform the deprojection of intervelocity and interdistance probability distribution functions (PDFs) in real pairs catalogs.
The isolated galaxy pairs that are gravitationally bound represent the simplest galaxy systems, of which the orbital motions can be analytically described. From the statistical study of those motions using large pair samples, we could in principle find out the mass distribution of those systems and information about their formation processes. Several studies have been devoted to such motion analyses (e.g., Peterson 1979a,b; Chengalur et al. 1996) and references therein.
More recently, interest has focused on close pairs, with projected interdistances between members rp < 25 h−1 kpc; members of those pairs are subject to strong gravitational interactions and it has been found that those lead to a significant enhancement of star formation compared to that observed in isolated galaxies (Lambas et al. 2003). Moreover, in these systems dwarf satellite galaxies have been merged, also leading to an enhanced star formation in the past (Lambas et al. 2012; Rodriguez 2020) and references therein.
We are mainly interested by the dynamics within isolated galaxy pairs to derive important statistical physical properties, such as distributions of intervelocities and interdistances between their members and mass distribution of the pairs; these properties can provide information about the formation history of these isolated galaxy pairs.
We constructed two new pair catalogs using well-defined criteria and improved observational data in order to understand the true 3D dynamics of galaxy pairs using our deprojection methods. The first is the UGC Galaxy Pair Catalog (UGPC), a catalog of ≈1000 pairs with high accuracy radial velocities (Chamaraux & Nottale 2016) extracted from Nilson’s Uppsala Galaxy Catalog (UGC; Nilson 1973), which has the advantage to be complete in apparent diameter. The second is the Isolated Galaxy Pair Catalog (IGPC), a catalog of more than 13 000 pairs (Nottale & Chamaraux 2018b) with galaxy members brighter than absolute magnitude −18.5. This catalog was built using the HyperLEDA database (HyperLEDA; Makarov et al. 2014) to identify galaxy pairs and extract their parameters from the large surveys, mainly the Sloan Digital Sky Survey (SDSS; Alam et al. 2015).
We intend to obtain statistical information on the true (3D) physical characteristics of those pairs. In particular, we investigate the orbital velocities of the pair galaxies (3D velocity of one member with respect to the other) and their interdistance, the pair masses and M/L ratios through luminosity and Kepler’s third law, and possibly their orbital elements, semimajor axes and eccentricities, which will be studied in a subsequent paper.
We have at our disposal only one component of the velocity difference (along the line of sight) and two components of the interdistance (projection on the sky plane). Moreover, contrary to the star-planet or double star Kepler motion, the galaxy pair problem encounters an additional difficulty since we only have access to instantaneous data for one effective point on each orbit (at the timescale of our observations compared to the orbital period).
Therefore we devised new statistical methods to obtain the PDF of those 3D quantities from the projected quantities (Nottale & Chamaraux 2018a). It has been pointed out, in particular by Faber & Gallagher (1979), that the previous methods of analysis of pair dynamics, which did not have the 3D PDFs at their disposal, were highly unsatisfactory. We show in the present paper that, once our deprojection methods are applied to real galaxy pair catalogs, these methods solve the problem of a reliable derivation of the statistics of pair dynamical parameters.
In Sect. 2 we give the results of the deprojection method applied to PDFs of velocity differences between pair members, for several subsamples of the IGPC, involving different isolation criteria, different accuracies of velocity measurements, and different deprojection methods. We complete these results by applying the deprojection to the UGPC. The obtained distributions show varying maxima and minima of probability density, but all of these are characterized by the existence of a dominant probability peak around the same orbital velocity of ≈150 km s−1. In Sect. 3 we perform a statistical deprojection of the distances between members of the galaxy pairs. Then we compare the obtained PDF to the projected PDF and we fit these with simple functions (power laws at large distances). This allows for an analytical deprojection that is found to be in agreement with the numerical deprojection. Section 4 is devoted to the derivation of the pair mass PDF from a deprojection of Kepler’s third law and to its comparison with the luminosity PDF, allowing us to derive a mean M/L ratio for these pairs. Section 5 is devoted to a discussion of these results, in particular to a comparison between the orbital velocity distribution of pair galaxies and exoplanets, and our conclusions are delineated in Sect. 6.
2. Deprojection of pair intervelocities
In Fig. 1 we give the distribution of intervelocity uncertainties in the IGPC. This distribution allows us to define a subsample of 6026 pairs with highly accurate intervelocities (δV < 20 km s−1) and a larger subsample of 11 259 pairs including less precise values (δV < 70 km s−1). We use these subsamples in the data analysis to check the influence of the velocity accuracy on our results.
 |
Fig. 1. Histogram of the uncertainties on the intervelocities between members of galaxy pairs in the IGP Catalog (13 114 pairs). The bin width is 4 km s−1. The observed distribution shows two populations, one with accurate velocity errors < 20 km s−1 and a probability peak between 4 and 8 km s−1 (6026 pairs), and the other with less accurate values having errors peaked around 55 km s−1. |
The statistical deprojection of intervelocities is performed from the initial PDF of radial velocity differences between pair members. This PDF is given by the histogram of V = |Vz2 − Vz1|. Thus, the first step in the deprojection consists in the choice of the bin width. The Vz PDF has to be strictly monotonous, that is, decreasing with increasing velocity with possible plateaux on limited zones, corresponding to hollows in the true (3D) velocity PDF. A bin width that is too small involves fluctuations that may break the expected monotony. Let Ni be the number of points contained in a bin of mean velocity Vi and Ni + 1 in the bin of mean velocity Vi + 1, where Vi + 1 > Vi. If Ni + 1 > Ni, the computed number of pairs with true intervelocities (Vi + Vi + 1)/2 are negative, which is obviously excluded.
An example of such a monotonous histogram of projected intervelocities for observational data from the IGPC is given in Fig. 2. The large number of pairs (> ≈ 10 000 in the IGPC) allows us to use bins of width 22 km s−1, while for smaller catalogs such as the UGPC (≈1000 pairs), the minimal bin width is around 30 km s−1.
 |
Fig. 2. Histogram of the projected intervelocities between members of galaxy pairs in the IGP Catalog, for the subsample of 11 259 pairs having errors < 70 km s−1. The bin is 22 km s−1. The observed distribution agrees with the expected monotony of the projected PDF. |
The IGPC has the advantage of providing information about the degree of isolation of the pairs. We defined a variable ρ as the ratio ρ = r3/rp of the projected distance r3 of the galaxy with ΔV < 500 km s−1 that is closest to the pair center over the pair member interdistance rp. The catalog contains all pairs with ρ > 2.5, but it is therefore easy to select subsamples of “fairly isolated pairs” (ρ > 5; 7449 pairs) or “highly isolated pairs” (ρ > 10; 4268 pairs), for which specific studies are carried out.
2.1. Deprojection of highly isolated pair intervelocities
The subsample of highly isolated pairs (ρ > 10) is worth of a specific study, since they can be considered as true two-body Keplerian systems free of external gravitational perturbations. The result of their statistical deprojection, which provides us with the PDF of their true orbital velocities, is shown in Fig. 4 for the whole subcatalog and for the subsample of pairs that has accurate velocities as well (mean error 6.4 km s−1).
We used the two-bin difference method and estimated its uncertainty by varying the bin width (Fig. 3). We also use the moving bin method for which we estimated the error with a numerical simulation. We performed this simulation by randomly projecting 50 times the obtained real 3D distribution, then deprojecting again with the same method each of the projected distributions. This results in the cloud of points shown in Fig. 3, which corresponds to a 2σ uncertainty.
 |
Fig. 3. Upper panel: probability distribution function of the 3D true intervelocities between members of galaxy pairs (i.e., orbital velocities of the galaxies in the pairs) in the IGP Catalog, deprojected from the radial velocity differences, for the subsample of 4268 highly isolated pairs ρ > 10 (see text). The deprojection method used here is the two-bin difference, with bins of 28, 30, 32, and 34 km s−1. Whatever the bin width, probability peaks at ≈150 km s−1 and ≈360 km s−1 appear in a stable way. Lower panel: deprojected PDF of the 3D true intervelocities between members of galaxy pairs in the IGP Catalog, for the subsample of highly isolated pairs ρ > 10, where an additional selection has accurate velocities (errors < 20 km s−1, 1859 pairs). The deprojection uses the moving bin method; the numbers are the density in effective bins of 1 km s−1. The error is estimated from 50 numerical simulations (see text). The upper and lower panels agree on the existence of the main peak at 150 km s−1 and possibly another lower one at ≈360 km s−1. |
Comparing with the fairly isolated sample, we confirmed the existence of a main probability peak at ≈150 km s−1. We found a possible secondary peak around 360 km s−1 for the highly isolated pairs, which is not seen in the subsample ρ > 5. The PDF shows a fast decrease around 380 km s−1, in agreement with the limit we derived from an analysis of the “false” cosmological pair contamination (Chamaraux & Nottale 2016; Nottale & Chamaraux 2018b).
2.2. Deprojection of fairly isolated pair intervelocities
Let us first apply the two-bin deprojection method to the subcatalog, where ρ > 5.
The deprojection formula reads (Nottale & Chamaraux 2018a):
The simplest way to implement Eq. (1) consists of (1) constructing the histogram 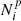 of radial (projected) velocities Vr in bins [Vi − 1, Vi] of given width δV; (2) computing the differences
of radial (projected) velocities Vr in bins [Vi − 1, Vi] of given width δV; (2) computing the differences 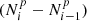 between the numbers in successive bins; and (3) multiplying by the rank i = Vi/δV of the bin.
between the numbers in successive bins; and (3) multiplying by the rank i = Vi/δV of the bin.
This method, in which the difference is taken between two adjacent bins, is not optimized and it can therefore be improved. It is more efficient (as in finite difference methods) to take the differences between two intervals separated by one bin, 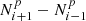 . This improvement is based on the fact that
. This improvement is based on the fact that 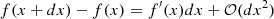 , while
, while 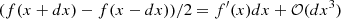 .
.
The uncertainties of this deprojection method can be estimated from numerical simulation. We previously found (Nottale & Chamaraux 2018a) that these uncertainties are half those obtained with the adjacent-bin method), thus we achieved a significant improvement. The result of this deprojection is given in Fig. 4.
 |
Fig. 4. Probability distribution function of the 3D true intervelocities between members of galaxy pairs in the IGP Catalog (deprojected from radial velocity differences) for the subsample of 7449 fairly isolated pairs ρ > 5 (see text). Upper panel: deprojection method used here is the two-bin difference, with bins of 26, 28 and 30 km s−1. Lower panel: two-bin difference deprojection method, for a bin width 30 km s−1, accompanied by the estimated uncertainties derived from numerical simulations (±1 σ, gray curves). The uncertainties derived from the simulation clearly agree with the fluctuations observed for different bins in the left panel. No matter which bin width and method are used, a probability peak at ≈150 km s−1 appears to be stable. |
2.3. Deprojection of all pair intervelocities
Finally, we performed the deprojection of the whole catalog, containing all pairs having an isolation parameter ρ > 2.5. We excluded the 1855 pairs with inaccurate intervelocities δV > 70 km s−1. We give in the upper panel of Fig. 5 the result of this deprojection for the 11 259 remaining pairs and in the lower panel of Fig. 5 the deprojection of the subsample of 6026 pairs with accurate intervelocities (δV < 20 km s−1).
 |
Fig. 5. Deprojected PDF of the 3D true intervelocities between members of galaxy pairs in the IGP Catalog (all ρ > 2.5 values). The blue curves are obtained by the deprojection method using two-bin differences (bin of 30 km s−1). The red curves indicate the result of deprojection by moving bins (see text and Nottale & Chamaraux 2018a). The ±1σ uncertainty curves (gray lines) are obtained from simulation of the deprojection process. Both methods agree within error bars. Upper panel: subsample of 11 259 pairs with errors < 70 km s−1. The projected distribution of these pairs is given in Fig. 2. Lower panel: subsample of 6026 pairs having accurate velocities with errors < 20 km s−1. Both subsamples confirm the existence of a large probability peak around ≈150 km s−1, in agreement with the PDFs of fairly (Fig. 4) and highly isolated pair (Fig. 3) intervelocities. |
The existence of a main probability peak of orbital velocities around 150 km s−1, detected in fairly and highly isolated pairs, is confirmed for the whole catalog. However this peak is somewhat wider for all ρs than for the more isolated pairs ρ > 5 and ρ > 10. This result is not unexpected, since the highly isolated pairs can be considered as true two-body Keplerian systems. The fairly isolated pairs can be slightly perturbed by a third body, while the perturbation may be larger for 2.5 < ρ < 5. The unperturbed pairs exhibit a clear energy structure at 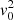 , where v0 ≈ 150 km s−1 and “line width” ≈ ± 50 km s−1. No matter the origin of this structure, we expect this structure to be subjected to a broadening effect in the perturbed pairs, which are no longer strictly two-body systems.
, where v0 ≈ 150 km s−1 and “line width” ≈ ± 50 km s−1. No matter the origin of this structure, we expect this structure to be subjected to a broadening effect in the perturbed pairs, which are no longer strictly two-body systems.
Moreover, possible secondary peaks are suspected in the highly isolated subsample, in particular around ≈360 km s−1. However this peak is not as stable as the 150 km s−1 peak, since it is absent in the fairly isolated subsample and marginally present in the whole sample. The reason for these fluctuations may be a combination of the effect of perturbations of the pair by other bodies, radial velocity errors, and because the projected probability density has a lower value for higher velocities and is therefore subjected to higher relative uncertainties.
2.4. Deprojection of pair intervelocities in the UGC pair catalog
Finally, the results obtained in the IGP catalog are confirmed with the UGC Galaxy Pair Catalog (UGCP). The deprojection of the projected intervelocity PDF for these pairs with highly accurate velocities once again yields a clear main peak at 150 km s−1 and a possible secondary peak at ≈350 km s−1 (see Fig. 6).
 |
Fig. 6. Upper panel: histogram of the projected (i.e., radial) velocity differences between members of galaxy pairs in the UGC pair catalog for a bin width of 40 km s−1. Lower panel: deprojected PDF of the 3D true intervelocities between members of galaxy pairs in the UGC pair Catalog, for the unbiased subsample with blue major axes < 1.2 arcmin. The red continuous curve is obtained by the deprojection method using a moving bin. The dashed black curve represents the result of deprojection by constant bins of width 30 km s−1. Both methods yield a main peak at ≈150 km s−1 and a possible secondary peak at ≈350 km s−1, in agreement with the results from the IGP catalog. |
3. Deprojection of pair interdistances
3.1. Statistical deprojection
In Nottale & Chamaraux (2018a) we gave the normalized probability density of rp values projected from a given r value as follows:
we note the correction of a misprint in Eq. (7) of Nottale & Chamaraux (2018a) in which the r in the denominator, which allows the normalization, was lacking. Therefore the probability density of projected distances Prp(rp) is given from that of true 3D distances Pr(r) by the integral
Since it does not seem possible to invert this expression in the general case, we constructed an algorithm to perform this inversion numerically (Nottale & Chamaraux 2018a). The deprojected distribution is recovered from the matrix product
where the column vector 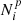 gives the projected number of pairs lying in the bin of rank i, the column vector
gives the projected number of pairs lying in the bin of rank i, the column vector 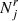 gives the deprojected number of pairs lying in the bin of rank j, and the matrix Pji is the transpose of
gives the deprojected number of pairs lying in the bin of rank j, and the matrix Pji is the transpose of
for i ≤ j.
We give in Fig. 7 the observed distribution of the projected interdistances for the full IGP Catalog of 13 114 pairs obtained with a bin width of 0.01 Mpc (100 bins between 0 and 1 Mpc). We deprojected this PDF using the above matrix method applied to 40 bins of 0.025 Mpc in width.
 |
Fig. 7. Probability density distributions of the interdistances between members of galaxy pairs in the IGP Catalog. The black curve indicates the observed (projected) PDF. The red curve represents the bias correct, deprojected PDF (see text about the deprojection method). Both curves are normalized to an effective bin of 0.01 Mpc. |
There is a small bias in this method since the vectors giving the projected and deprojected numbers are defined in the same range 0 − 1 Mpc, while some projected pairs with rp < 1 Mpc may actually come from true interdistances r > 1 Mpc. This artificially slightly increases the deprojected PDF for r > ≈0.8 Mpc. We corrected this bias by adding four bins beyond 1 Mpc in the projected PDF extrapolated from its power-law fit (see hereafter). This results in the expected continuously decreasing distribution shown in Fig. 7, where the bias has disappeared for r < 1 Mpc. The respective projected and unprojected probability densities are found to be remarkably identical, except for small interdistances r and rp < ≈0.1 Mpc.
3.2. Relation between projected and 3D interdistance PDFs
This similitude between the projected and deprojected PDFs can be easily understood because the true 3D PDF is very well fitted by a power law (except at very small scales), as can be seen in Figs. 7, 9, and 11.
Indeed, assuming a pure power law for the true interdistance between the pair members (strictly valid at large scales),
the projected interdistances PDF is given by Nottale & Chamaraux (2018a)
where the function Γ is the continuous generalization of the factorial function. Therefore, this theoretical argument confirms that if the deprojected PDF is a power law, the projected PDF is also given by a power law (both at large scales), with the same exponent (and reciprocally).
This is supported by the observed distributions. We can see in Fig. 7 that the projected and deprojected PDFs are indistinguishable for distances r and rp > ≈0.15 Mpc; moreover, the fit of the two distributions yields a similar exponent g ≈ 1 (see Figs. 8–11).
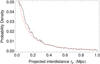 |
Fig. 8. Fit of the observed PDF of the projected interdistances between pair members of the IGPC by a one parameter Hubble profile ∝(1 + rp/ap)−2 (see Sect. 3.3 for a justification of this law). The PDF is obtained from a normalized histogram with a bin of 0.01 Mpc. The fitted parameter is ap = (0.17 ± 0.01) Mpc. |
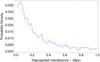 |
Fig. 9. Fit of the PDF of the deprojected interdistances between pair members of the IGPC by a one parameter Hubble profile ∝(1 + r/a)−2 (see Sect. 3.3). The statistical deprojection was performed from a rp histogram with 40 intervals (bin of 0.025 Mpc), but the normalized PDF is given with an effective bin of 0.01 Mpc for comparison with the projected PDF. The fitted parameter is larger than for projected data (see Fig. 8), namely, a = (0.28 ± 0.02) Mpc. |
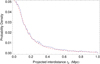 |
Fig. 10. Fit of the PDF of the projected interdistances between pair members of the IGPC by a two-parameter King profile |
 |
Fig. 11. Fit of the PDF of the deprojected interdistances between pair members of the IGPC by a two-parameter King profile |
We note that the IGP Catalog is limited to projected interdistances rp ≤ 1 Mpc while some pairs with r > 1 Mpc may be projected to rp ≤ 1 Mpc. This explains why the upper limit of the above integral is taken to be infinity. We corrected this bias in the Sect. 3.1.
However, a power law is no longer physical at small scales owing to its divergence at r → 0. We therefore consider two improved models that remain a power law at large scales but include a cutoff at small scales. The first is a law long ago proposed by Hubble (1930) for luminosity profiles of elliptical galaxies, that is,
The second law considered including a core radius is the King profile (King 1966), that is,
where P0 is a normalization constant, which is given by
where 2F1 is the hypergeometric function. It is well approximated in the relevant range of the variables (to better than ≈5%) by P0 ≈ 1 + 0.55g/rc.
This PDF of true interdistances can be integrated to yield the PDF of projected interdistances
It is remarkable that we recover the basic power law (rp/rc)−2g, now corrected by an hypergeometric function. We can show that this exact solution is well approximated by another King profile with the same exponent g = gp, but with a different core radius rc (except when r → 0, where the King profile has a zero slope).
This result is supported by the observed, projected, and deprojected distributions (Figs. 10 and 11). A least-square fit yields rcp = 0.13 and gp = 0.97 ± 0.03, which lies within 1σ of gp = 1. The deprojected distribution is well represented by a King profile with the same fixed exponent g = 1, but with a core radius rc = 0.19 (see Fig. 11); a least-squares fit of this distribution more precisely yields g = 0.87 ± 0.08 and rc = 0.17 ± 0.02, which are compatible with these values.
3.3. Theoretical expectation for the interdistance PDF
This asymptotically power-law shape of the interdistance PDF can be derived from a simple (partly theoretical) argument based on the observed pair masses (derived from their luminosities) and intervelocity PDFs.
From Kepler third law GM = r v2, we expect r ∝ M/v2. The luminosity PDF of pairs in the IGPC is found to be well fitted by a pure exponential law PL(L)∝exp(−L/L0) except for small luminosities. Such a law is not incompatible with a standard Schechter law (Schechter 1976) for the most luminous pairs, as can be seen in Fig. 1 of Nottale & Chamaraux (2018b). The same behavior is true for masses assuming a mean constant M/L ratio (see Fig. 12). We have seen that the intervelocity PDF is systematically dominated by a probability density peak lying around 150 km s−1. It can therefore be approximated by a Gaussian law ![$ P_v(v)\propto \exp[-\frac{1}{2}(v-v_0)^2/\sigma_v^2] $](/articles/aa/full_html/2020/09/aa37940-20/aa37940-20-eq22.gif) , with v0 ≈ 150 km s−1 and σv ≈ 85 km s−1.
, with v0 ≈ 150 km s−1 and σv ≈ 85 km s−1.
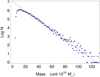 |
Fig. 12. Fit by an exponential law of the PDF of pair masses derived from total pair luminosities and a mean M/L ratio of 30 as found from the mass deprojection performed in Sect. 4. |
The PDF of M/v2 can be derived from the individual PDFs of M and v provided they are independent. We find, for an exponential PDF of mass,
meaning that the interdistance PDF is the Laplace transform of the function 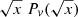 , where x has the dimension of the square of a velocity. For a Gaussian velocity PDF Pv, we find that this expression is fairly approximated by a function ∝xexp(−x/w2) (with w ≈ 200 km s−1 for v0 ≈ 160 km s−1 and σv ≈ 85 km s−1), the Laplace transform of which is well known to be a generalized power law,
, where x has the dimension of the square of a velocity. For a Gaussian velocity PDF Pv, we find that this expression is fairly approximated by a function ∝xexp(−x/w2) (with w ≈ 200 km s−1 for v0 ≈ 160 km s−1 and σv ≈ 85 km s−1), the Laplace transform of which is well known to be a generalized power law,
which is similar to a Hubble luminosity profile.
This is supported by a direct analytical integration of Eq. (12) whose result is shown in Fig. 13. Depending on the choice of the peak value and width of the Gaussian velocity PDF, we find excellent agreement of this analytical function with Hubble profiles that have exponents in the range 1.9 − 2.2 (except at small distances r < 0.1 Mpc). A similar result is obtained for more elaborated velocity PDFs made of a sum of normal distributions fitting the observed deprojected PDF.
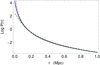 |
Fig. 13. Analytical integration of the PDF of interdistances from an exponential mass PDF and a Gaussian intervelocity PDF, compared to various expectations. Blue curve: the exact integral; red dashed curve: pure power law with exponent −1.9; the black dashed curve: precise fit of deprojected data; and green dashed curve: Hubble profile P(r)∝(1 + r/a)−2.1 with a = 0.05. As expected, the analytical integral is no longer valid at very small distances r < 0.1 Mpc. |
We also may support the obtention of a King profile by a similar argument. In Fig. 14, the three functions ![$ v \exp[-\frac{1}{2}(v-v_0)^2/\sigma_v^2] $](/articles/aa/full_html/2020/09/aa37940-20/aa37940-20-eq26.gif) , ∝v2exp(−v2/w2) and ∝sin(v2/u2) are very close in the velocity range [0 − 230] km s−1, dominated by the main velocity peak around 150 km s−1; these functions are plotted directly in terms of velocity v instead of the variable, which comes in the Laplace transform x = v2. Now the Laplace transform of the function sin(βx) is just the King profile β/(β2 + r2) with exponent g = 1.
, ∝v2exp(−v2/w2) and ∝sin(v2/u2) are very close in the velocity range [0 − 230] km s−1, dominated by the main velocity peak around 150 km s−1; these functions are plotted directly in terms of velocity v instead of the variable, which comes in the Laplace transform x = v2. Now the Laplace transform of the function sin(βx) is just the King profile β/(β2 + r2) with exponent g = 1.
 |
Fig. 14. Comparison between the function v Pv(v) (blue curve), which occurs in the derivation of the PDF Pr(r) of pair members interdistances through a Laplace transform (see text), and two close functions whose Laplace transforms yield a Hubble interdistance profile (red curve) and a King interdistance profile (yellow curve), respectively. |
Our results for the projected and deprojected PDFs of IGPC pairs, which have been shown to have the same asymptotic exponents, support this expectation of an exponent 2g ≈ −2 (see Figs. 8 and 9). The fits by Hubble profiles (which are one-parameter functions) are, as expected, of lower quality than those by the two-parameter King profiles, but they remain fair knowing that they are derived from a simple theoretical argument.
4. Pair masses and M/L ratio
The mass M of a galaxy pair is given from Kepler’s third law by GM = aV2, where a is the orbital semimajor axis of one body around the other and V = 2πa/T, T being the orbital period. In the circular case, r = a = cst and v = V = const., so that the mass PDF can be derived from a deprojection of the product of observables 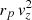 into r v2. We discussed the noncircular case in Nottale & Chamaraux (2018a); we can show that the effect of eccentricities that are not too large remains small on the mass determination (see Fig. 15).
into r v2. We discussed the noncircular case in Nottale & Chamaraux (2018a); we can show that the effect of eccentricities that are not too large remains small on the mass determination (see Fig. 15).
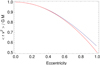 |
Fig. 15. Effect of eccentricity on the mass deprojection from Kepler’s third law (see text). |
We gave an original deprojection method of 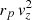 in Nottale & Chamaraux (2018a), which uses a deprojection matrix that has been confirmed by numerical simulations. We summarize this matrix method in this section. For a given value of r and v (one pair), the expected distribution of the product
in Nottale & Chamaraux (2018a), which uses a deprojection matrix that has been confirmed by numerical simulations. We summarize this matrix method in this section. For a given value of r and v (one pair), the expected distribution of the product 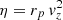 is given by
is given by
For a population of pairs, having divided the η range into N bins, the projection matrix is written as
where j = 1 to N, i = 1 to N + 1 − j and Aji = 0 for the remaining coefficients. Finally the histogram of the deprojected product is given from the histogram of the projected product by the matrix relation 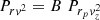 , where the deprojection matrix is written as
, where the deprojection matrix is written as
We applied this deprojection method to the IGP Catalog using a 20 × 20 matrix on the subsample of 11 259 pairs with intervelocity errors < 70 km s−1. The result is given in Fig. 16 (black points and dashed lines), where the deprojected mass PDF has been converted into a luminosity PDF through the application of a constant M/L ratio. The global shape obtained is compatible with the observed PDF of pair luminosities (a decreasing exponential) and they can therefore be fitted to one another. This fit determines a M/L ratio of μ = M/L = 30 ± 5.
 |
Fig. 16. Deprojection of the product |
The statistical agreement between the deprojected and observed PDFs is established from a simulation achieved in the following way: From the deprojections of projected intervelocities and interdistances, we constructed analytical models of the true velocities PDF (Gaussian or sum of Gaussian laws) and distances PDF (power law). We then performed several random projections of vz and rp from these PDFs, which provided us with a sample of 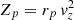 values. Finally, we applied our deprojection method to these values. The average and standard errors calculated in this way (red and gray lines in Fig. 16) include within ±1 sigma for M/L = 30 both the observed luminosity PDF and the deprojected
values. Finally, we applied our deprojection method to these values. The average and standard errors calculated in this way (red and gray lines in Fig. 16) include within ±1 sigma for M/L = 30 both the observed luminosity PDF and the deprojected 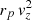 for the real pairs in the IGPC; this agreement is very satisfying despite the known difficulty of a reliable determination of pair masses (Faber & Gallagher 1979). The error bar ±5 on the M/L ratio is estimated from varying the M/L ratio and requiring that all deprojected points remain in agreement with the simulation (and therefore with the observed luminosity PDF).
for the real pairs in the IGPC; this agreement is very satisfying despite the known difficulty of a reliable determination of pair masses (Faber & Gallagher 1979). The error bar ±5 on the M/L ratio is estimated from varying the M/L ratio and requiring that all deprojected points remain in agreement with the simulation (and therefore with the observed luminosity PDF).
In this first method, we directly derived the mass from the relation M = rv2 through the deprojection of 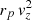 . A second method consists of writing this relation under the form v = (M/r)1/2 = (μL/r)1/2 and to compare the observed deprojected velocity PDF with the deprojection of the PDF of (L/rp)1/2. The M/L ratio μ can then be derived from this comparison, provided these two PDFs are found to be similar. This is the case within uncertainties, as shown in Fig. 17.
. A second method consists of writing this relation under the form v = (M/r)1/2 = (μL/r)1/2 and to compare the observed deprojected velocity PDF with the deprojection of the PDF of (L/rp)1/2. The M/L ratio μ can then be derived from this comparison, provided these two PDFs are found to be similar. This is the case within uncertainties, as shown in Fig. 17.
 |
Fig. 17. Comparison between the PDF of the orbital velocity (6026 pairs with accurate radial velocities, blue curve with its error bars) and the PDF of (GM/rp)1/2, where the pair masses M are obtained from their luminosity L through a constant M/L ratio, M = μL (red curve). An excellent agreement between the two curves (everywhere within ±1 sigma) is obtained by fitting the M/L ratio to the value μ = 33 ± 7. The uncertainty was estimated by varying the value of μ (orange curves, μ = 26 and 40). |
The problem of finding the behavior of the PDF of (M/rp)1/2 is equivalent to finding the PDF of 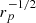 provided there is no correlation between mass and interdistance. The PDF of
provided there is no correlation between mass and interdistance. The PDF of 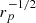 shows a very narrow peak at rp = r (see Fig. 18), thus implying a small projection effect. This is supported both by a numerical simulation and by the analytical expectation. We find that the theoretically expected normalized PDF of this variable
shows a very narrow peak at rp = r (see Fig. 18), thus implying a small projection effect. This is supported both by a numerical simulation and by the analytical expectation. We find that the theoretically expected normalized PDF of this variable 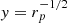 for a given value of the 3D interdistance r is written as
for a given value of the 3D interdistance r is written as
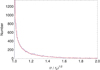 |
Fig. 18. Numerical simulation of the PDF of (r/rp)1/2 compared with its theoretical expression (Eq. (17)). |
We can also show that the effect of eccentricity on (GM/r)1/2 is weak and in the opposite way of its projection effect. This allows us to compare the velocity PDF directly with the PDF of (GM/rp)1/2 in Fig. 17, since it is very close to the deprojected PDF of (GM/r)1/2 (a fact that we explicitly checked). The M/L ratio obtained by this second method, μ = 33 ± 7 fairly confirms the value of the first method (direct deprojection of mass through 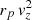 ), μ = 30 ± 5.
), μ = 30 ± 5.
5. Discussion
One of the main results of the present paper is the evidence of a systematic probability peak at ≈150 km s−1 in the PDF of pair galaxy orbital (deprojected) velocities. Now these isolated pairs achieve one of the simplest possible Keplerian systems, the two-body problem, at extragalactic scales of (0.01 − 1) Mpc. Expressed in terms of reduced mass, this becomes equivalent to a central mass problem with m < M.
It is therefore interesting to compare these systems to the archetype of Keplerian systems, that is, to the numerous star-planet couples now found in exoplanet searches. It is already remarkable that, despite the 1011 − 1012 factor between their interdistances (from ≈ AU to Mpc), the magnitude of their orbital velocities is very similar, on the order of ≈100 km s−1. This can be understood from the equivalence principle, according to which the inertial mass disappears from the equation of purely gravitational dynamics. If there are structures, we therefore expect these to occur in an universal way in velocity-space (energy structures become E/m ∼ v2 and momentum structures become p/m = v), while those in position-space are derived through the intervention of mass. We recover the above interdistance factor as being nothing else than the mass factor 1011 − 1012 (for our sample) between galaxy masses and typical star masses (≈ solar masses).
But we can improve on this result: not only is the orbital velocity magnitude the same, but exoplanets, as galaxy pairs, show a probability peak at just the same velocity value (i.e., around 150 km s−1). In Fig. 19 we plotted the distribution of orbital velocities of exoplanets (2019 data) having masses > 0.05 Jupiter mass. This distribution shows two main peaks: one at velocities ≈20 − 50 km s−1, which are typical of the inner solar system and the other at ≈150 km s−1. It is remarkable that this value is just the velocity of the first exoplanet discovered around a solar-type star, 51 Peg (Mayor & Queloz 1995) and that it has been predicted from a planetary formation model fitted to the inner solar system structure, before the actual discovery of exoplanets (Nottale 1993, Chapt. 7). Since then, a large number of exoplanets continued to contribute to this probability peak (see Fig. 19), which can be shown to be robust against the various biases affecting exoplanet data.
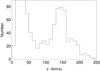 |
Fig. 19. Observed distribution of orbital velocities of 1183 exoplanets having masses > 0.05 Jupiter mass, extracted from the NASA Exoplanet Archive (2019) (June 2019 data containing 4104 confirmed planets). This PDF exhibits a large probability peak at a velocity of ≈150 km s−1, which is the same value as the main orbital velocity peak of galaxies in pairs. |
This result points toward a possible universality of Keplerian structures in velocity space, no matter which the interdistance scale or the mass scale are used (Nottale 1993, 1996, 2011; Nottale et al. 2000).
As regards our determination of pair masses, we found a ratio M/L = 30 ± 5, which corresponds to a normal value for galaxies and their halos. Such a value is in fair agreement with M/L = 48 ± 18 obtained by Peterson (1979b) from a very careful analysis of a sample of 39 galaxy pairs (mainly spiral- spiral) having accurate velocities and photometric measurements; of course uncertainties are much larger than ours because of the very limited size of the pairs sample. Whatever it may be, the accuracy of our result compared to previous estimates of pair masses mainly comes from our fit of the whole deprojected PDF, instead of using only averages (which revealed to be highly biased because of the strong non-Gaussianity of the distribution). Now the mean ratio of luminous + HI gas mass over luminosity is, for spiral and S0 galaxies, M/L = 4.2 ± 0.5 when taking H0 = 70 km s−1 Mpc−1. We note that the majority of the galaxies in the IGP Catalog are spiral galaxies. Thus the dark matter contribution we obtain is between six and eight times that of luminous and gaseous matter, which is likely to be mainly due to the presence of large interpenetrating halos around each pair member. On the other hand, such a value means that a nonbaryonic contribution is not necessarily needed at the scale of galaxy pairs.
6. Conclusions
This paper is mainly devoted to the statistical deprojection of intervelocities, interdistances, and masses (through Kepler’s third law) in two galaxy pair catalogs, the Isolated Galaxy Pair Catalog (IGPC) containing more than 13000 pairs, completed by the UGC pair catalog (≈1000 pairs).
The deprojected PDF of pair intervelocities is found to be systematically dominated by a probability peak at ≈150 km s−1. This result is obtained for both catalogs and all selected subsamples. The fact that there exists a probability peak at the same orbital velocity for exoplanets suggests a possible universality of Keplerian structures no matter which spatial and mass scales are used.
The deprojected PDF of galaxy interdistances in pairs is found to be fairly described by a power law of exponent −2 with a cutoff at small distances, well fitted by a King profile. This behavior allows the projected PDF to be described by a very similar King law. Moreover, this power law can be analytically derived through a Laplace transform from the observed PDF of pair luminosities (and therefore of pair masses for a constant M/L ratio), which we find to be accurately given by a decreasing exponential, and from the obtained PDF of deprojected (orbital) velocities.
We obtained the deprojected mass PDF from velocities and distances through Kepler’s third law by two different and complementary methods and we find this mass PDF to fairly agree with the shape of the observed luminosity PDF. This result allowed us to calculate an accurate mass/luminosity ratio M/L = 30 ± 5 by fitting the two distributions with each other.
The present paper focuses on the deprojection of observational data and analysis of the deprojected data on galaxy pairs. The physical implications of our results will be considered in a forthcoming work. We also intend to extend the statistical deprojection methods to other orbital elements, in particular to eccentricities and semimajor axes.
Acknowledgments
We acknowledge very useful remarks from an unknown referee. This research has made use of the NASA Exoplanet Archive, which is operated by the California Institute of Technology, under contract with the National Aeronautics and Space Administration under the Exoplanet Exploration Program.
References
- Alam, S., Albareti, F. D., Prieto, C. A., et al. 2015, ApJS, 219, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Chamaraux, P., & Nottale, L. 2016, Astrophy. Bull., 71, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Chengalur, J. N., Salpeter, E. E., & Terzian, Y. 1996, ApJ, 461, 546 [NASA ADS] [CrossRef] [Google Scholar]
- Faber, S. M., & Gallagher, J. S. 1979, ARA&A, 17, 135 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Hubble, E. P. 1930, ApJ, 71, 231 [NASA ADS] [CrossRef] [Google Scholar]
- HyperLEDA Database http://leda.univ-lyon1.fr [Google Scholar]
- King, I. 1966, AJ, 71, 64 [Google Scholar]
- Lambas, D. G., Tissera, P. B., Alonso, M. S., & Coldwell, G. 2003, MNRAS, 346, 1189 [NASA ADS] [CrossRef] [Google Scholar]
- Lambas, D. G., Alonso, S., Mesa, V., & O’Mill, A. L. 2012, A&A, 539, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Makarov, D., Prugniel, P., Terekhova, N., Courtois, H., & Vauglin, I. 2014, A&A, 570, A13 [CrossRef] [EDP Sciences] [Google Scholar]
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [Google Scholar]
- NASA Exoplanet Archive 2019, https://exoplanetarchive.ipac.caltech.edu/ [Google Scholar]
- Nilson, P. N. 1973, Uppsala General Catalogue of Galaxies (Uppsala Obs. Ann.), 6 [Google Scholar]
- Nottale, L. 1993, Fractal Space-Time and Microphysics: Towards a Theory of Scale Relativity (London: World Scientific) [CrossRef] [Google Scholar]
- Nottale, L. 1996, A&A, 315, L9 [Google Scholar]
- Nottale, L. 2011, Scale Relativity and Fractal Space-Time: A New Approach to Unifying Relativity and Quantum Mechanics (London: Imperial College Press) [CrossRef] [Google Scholar]
- Nottale, L., & Chamaraux, P. 2018a, A&A, 614, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nottale, L., & Chamaraux, P. 2018b, Astrophys. Bull., 73, 310 [NASA ADS] [CrossRef] [Google Scholar]
- Nottale, L., Schumacher, G., & Lefèvre, E. T. 2000, A&A, 361, 379 [NASA ADS] [Google Scholar]
- Peterson, S. D. 1979a, ApJS, 40, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, S. D. 1979b, ApJ, 232, 20 [CrossRef] [Google Scholar]
- Rodriguez, F., Gonzalez, E. J., O’Mill, A. L., et al. 2020, A&A, 634, A123 [CrossRef] [EDP Sciences] [Google Scholar]
- Schechter, P. 1976, ApJ, 203, 297 [Google Scholar]
All Figures
 |
Fig. 1. Histogram of the uncertainties on the intervelocities between members of galaxy pairs in the IGP Catalog (13 114 pairs). The bin width is 4 km s−1. The observed distribution shows two populations, one with accurate velocity errors < 20 km s−1 and a probability peak between 4 and 8 km s−1 (6026 pairs), and the other with less accurate values having errors peaked around 55 km s−1. |
| In the text | |
 |
Fig. 2. Histogram of the projected intervelocities between members of galaxy pairs in the IGP Catalog, for the subsample of 11 259 pairs having errors < 70 km s−1. The bin is 22 km s−1. The observed distribution agrees with the expected monotony of the projected PDF. |
| In the text | |
 |
Fig. 3. Upper panel: probability distribution function of the 3D true intervelocities between members of galaxy pairs (i.e., orbital velocities of the galaxies in the pairs) in the IGP Catalog, deprojected from the radial velocity differences, for the subsample of 4268 highly isolated pairs ρ > 10 (see text). The deprojection method used here is the two-bin difference, with bins of 28, 30, 32, and 34 km s−1. Whatever the bin width, probability peaks at ≈150 km s−1 and ≈360 km s−1 appear in a stable way. Lower panel: deprojected PDF of the 3D true intervelocities between members of galaxy pairs in the IGP Catalog, for the subsample of highly isolated pairs ρ > 10, where an additional selection has accurate velocities (errors < 20 km s−1, 1859 pairs). The deprojection uses the moving bin method; the numbers are the density in effective bins of 1 km s−1. The error is estimated from 50 numerical simulations (see text). The upper and lower panels agree on the existence of the main peak at 150 km s−1 and possibly another lower one at ≈360 km s−1. |
| In the text | |
 |
Fig. 4. Probability distribution function of the 3D true intervelocities between members of galaxy pairs in the IGP Catalog (deprojected from radial velocity differences) for the subsample of 7449 fairly isolated pairs ρ > 5 (see text). Upper panel: deprojection method used here is the two-bin difference, with bins of 26, 28 and 30 km s−1. Lower panel: two-bin difference deprojection method, for a bin width 30 km s−1, accompanied by the estimated uncertainties derived from numerical simulations (±1 σ, gray curves). The uncertainties derived from the simulation clearly agree with the fluctuations observed for different bins in the left panel. No matter which bin width and method are used, a probability peak at ≈150 km s−1 appears to be stable. |
| In the text | |
 |
Fig. 5. Deprojected PDF of the 3D true intervelocities between members of galaxy pairs in the IGP Catalog (all ρ > 2.5 values). The blue curves are obtained by the deprojection method using two-bin differences (bin of 30 km s−1). The red curves indicate the result of deprojection by moving bins (see text and Nottale & Chamaraux 2018a). The ±1σ uncertainty curves (gray lines) are obtained from simulation of the deprojection process. Both methods agree within error bars. Upper panel: subsample of 11 259 pairs with errors < 70 km s−1. The projected distribution of these pairs is given in Fig. 2. Lower panel: subsample of 6026 pairs having accurate velocities with errors < 20 km s−1. Both subsamples confirm the existence of a large probability peak around ≈150 km s−1, in agreement with the PDFs of fairly (Fig. 4) and highly isolated pair (Fig. 3) intervelocities. |
| In the text | |
 |
Fig. 6. Upper panel: histogram of the projected (i.e., radial) velocity differences between members of galaxy pairs in the UGC pair catalog for a bin width of 40 km s−1. Lower panel: deprojected PDF of the 3D true intervelocities between members of galaxy pairs in the UGC pair Catalog, for the unbiased subsample with blue major axes < 1.2 arcmin. The red continuous curve is obtained by the deprojection method using a moving bin. The dashed black curve represents the result of deprojection by constant bins of width 30 km s−1. Both methods yield a main peak at ≈150 km s−1 and a possible secondary peak at ≈350 km s−1, in agreement with the results from the IGP catalog. |
| In the text | |
 |
Fig. 7. Probability density distributions of the interdistances between members of galaxy pairs in the IGP Catalog. The black curve indicates the observed (projected) PDF. The red curve represents the bias correct, deprojected PDF (see text about the deprojection method). Both curves are normalized to an effective bin of 0.01 Mpc. |
| In the text | |
 |
Fig. 8. Fit of the observed PDF of the projected interdistances between pair members of the IGPC by a one parameter Hubble profile ∝(1 + rp/ap)−2 (see Sect. 3.3 for a justification of this law). The PDF is obtained from a normalized histogram with a bin of 0.01 Mpc. The fitted parameter is ap = (0.17 ± 0.01) Mpc. |
| In the text | |
 |
Fig. 9. Fit of the PDF of the deprojected interdistances between pair members of the IGPC by a one parameter Hubble profile ∝(1 + r/a)−2 (see Sect. 3.3). The statistical deprojection was performed from a rp histogram with 40 intervals (bin of 0.025 Mpc), but the normalized PDF is given with an effective bin of 0.01 Mpc for comparison with the projected PDF. The fitted parameter is larger than for projected data (see Fig. 8), namely, a = (0.28 ± 0.02) Mpc. |
| In the text | |
 |
Fig. 10. Fit of the PDF of the projected interdistances between pair members of the IGPC by a two-parameter King profile |
| In the text | |
 |
Fig. 11. Fit of the PDF of the deprojected interdistances between pair members of the IGPC by a two-parameter King profile |
| In the text | |
 |
Fig. 12. Fit by an exponential law of the PDF of pair masses derived from total pair luminosities and a mean M/L ratio of 30 as found from the mass deprojection performed in Sect. 4. |
| In the text | |
 |
Fig. 13. Analytical integration of the PDF of interdistances from an exponential mass PDF and a Gaussian intervelocity PDF, compared to various expectations. Blue curve: the exact integral; red dashed curve: pure power law with exponent −1.9; the black dashed curve: precise fit of deprojected data; and green dashed curve: Hubble profile P(r)∝(1 + r/a)−2.1 with a = 0.05. As expected, the analytical integral is no longer valid at very small distances r < 0.1 Mpc. |
| In the text | |
 |
Fig. 14. Comparison between the function v Pv(v) (blue curve), which occurs in the derivation of the PDF Pr(r) of pair members interdistances through a Laplace transform (see text), and two close functions whose Laplace transforms yield a Hubble interdistance profile (red curve) and a King interdistance profile (yellow curve), respectively. |
| In the text | |
 |
Fig. 15. Effect of eccentricity on the mass deprojection from Kepler’s third law (see text). |
| In the text | |
 |
Fig. 16. Deprojection of the product |
| In the text | |
 |
Fig. 17. Comparison between the PDF of the orbital velocity (6026 pairs with accurate radial velocities, blue curve with its error bars) and the PDF of (GM/rp)1/2, where the pair masses M are obtained from their luminosity L through a constant M/L ratio, M = μL (red curve). An excellent agreement between the two curves (everywhere within ±1 sigma) is obtained by fitting the M/L ratio to the value μ = 33 ± 7. The uncertainty was estimated by varying the value of μ (orange curves, μ = 26 and 40). |
| In the text | |
 |
Fig. 18. Numerical simulation of the PDF of (r/rp)1/2 compared with its theoretical expression (Eq. (17)). |
| In the text | |
 |
Fig. 19. Observed distribution of orbital velocities of 1183 exoplanets having masses > 0.05 Jupiter mass, extracted from the NASA Exoplanet Archive (2019) (June 2019 data containing 4104 confirmed planets). This PDF exhibits a large probability peak at a velocity of ≈150 km s−1, which is the same value as the main orbital velocity peak of galaxies in pairs. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} P_v(v)= -v \left[ \frac{d P_{v_z} (v_z)}{dv_z} \right]_v. \end{aligned} $$](/articles/aa/full_html/2020/09/aa37940-20/aa37940-20-eq1.gif)
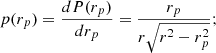
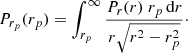
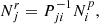
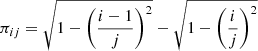
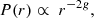
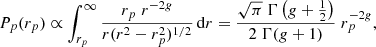
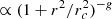
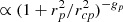
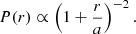
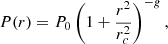
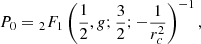
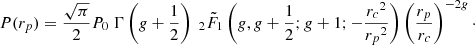
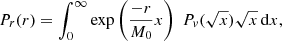
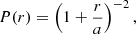
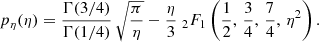
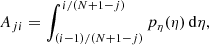
![$$ \begin{aligned} B= \mathrm{Reverse[Inverse[Transpose[A]]}. \end{aligned} $$](/articles/aa/full_html/2020/09/aa37940-20/aa37940-20-eq33.gif)