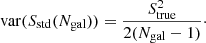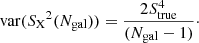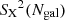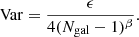| Issue |
A&A
Volume 641, September 2020
|
|
|---|---|---|
| Article Number | A41 | |
| Number of page(s) | 17 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201834837 | |
| Published online | 04 September 2020 | |
Biases in galaxy cluster velocity dispersion and mass estimates in the small Ngal regime
1
Instituto de Astrofísica de Canarias (IAC), C/ Vía Láctea s/n, 38205 La Laguna, Tenerife, Spain
e-mail: ferragamo_ext@iac.es
2
Universidad de La Laguna, Departamento de Astrofísica, C/ Astrofísico Francisco Sánchez s/n, 38206 La Laguna, Tenerife, Spain
3
Dipartimento di Fisica, Sezione di Astronomia, Università di Trieste, Via Tiepolo 11, 34143 Trieste, Italy
4
INAF/Osservatorio Astronomico di Trieste, Via Tiepolo 11, 34143 Trieste, Italy
Received:
12
December
2018
Accepted:
9
June
2020
Aims. We present a study of the statistical properties of three velocity dispersion and mass estimators: biweight, gapper, and standard deviation for a small number of galaxies (Ngal ≤ 75).
Methods. Using a set of 73 numerically simulated galaxy clusters, we first characterised the statistical bias and the variance for each one of the three estimators (biweight, gapper, and standard deviation) in the determination of the velocity dispersion and the dynamical mass of the clusters through the σ–M relation. These results were used to define a new set of unbiased estimators that are able to correct for these statistical biases with a minimum increase in associated variance. We also used the same set of numerical simulations to characterise two other physical biases that affect the estimates: the effect of velocity segregation on the selection of cluster members, and the effect of using cluster members within different physical radii from the cluster centre.
Results. The standard deviation (and its unbiased counterpart) is the estimator with the lowest variance estimator after the biweight and gapper. The effect of velocity segregation in the selection of galaxies within the sub-sample of the most massive galaxies in the cluster introduces a bias of 2% in the velocity dispersion estimate when it is calculated using a quarter of the most massive cluster members. We also find a dependence of the velocity dispersion estimate on the aperture radius as a fraction of R200. This is consistent with previous results in the literature.
Conclusions. The proposed set of unbiased estimators effectively provides a correction of the velocity dispersion and mass estimates from the statistical and physical effects discussed above for small numbers of cluster members. When these new estimators are applied to a subset of simulated observations, they can retrieve bias-corrected values for the mean velocity dispersion and the mean mass; the standard deviation has the lowest variance. Although for a single galaxy cluster the statistical and physical effects discussed here are comparable to or slightly smaller than the bias introduced by interlopers, they are relevant when ensemble properties and scaling relations for large number of clusters are studied.
Key words: large-scale structure of Universe / galaxies: clusters: general / cosmology: observations
© ESO 2020
1. Introduction
Galaxy clusters (GCs) are tracers of the evolution of structures throughout the history of the Universe. Cosmological parameters, such as the matter density Ωm and the amplitude of matter fluctuation σ8, are very sensitive to the abundance of GCs per unit of mass over time (e.g. Voit 2005; Allen et al. 2011; Planck Collaboration XX 2014; Planck Collaboration XXIV 2016).
Because it is not possible to weigh GCs directly, we need to use mass proxies based on other mass-related observables through scaling relations (e.g. Stanek et al. 2010; Kravtsov & Borgani 2012). Several of these observational proxies that are used to obtain the total cluster mass are available today: X-ray intracluster emission, weak-lensing models, and very recently, the Sunyaev–Zel’dovich (SZ) effect (Sunyaev & Zeldovich 1970). In this last method, ground-based telescopes and instruments such as the Atacama Cosmology Telescope (ACT; Hincks et al. 2010), the South Pole Telescope (SPT; Chang et al. 2009), or the NIKA2 instrument at IRAM (Macias-Perez et al. 2017), and space missions such as the ESA Planck satellite (Planck Collaboration XX 2014; Planck Collaboration XXII 2016), are opening new windows for the detection of GCs through their SZ effect.
The integrated amplitude of the inverse Compton parameter along the line of sight, Y, is a good proxy for retrieving the mass of hot intra-cluster gas (e.g. Arnaud et al. 2010; Planck Collaboration XX 2014; Planck Collaboration XXIV 2016; Ruel et al. 2014; Sifón et al. 2016). Moreover, the mass can be estimated using the GC luminosity in the X-ray that is provided by surveys performed by the XMM satellite. Finally, in the visible range, it is possible to infer the GC mass by studying the deformation of background galaxy shapes due to weak lensing (e.g. Zitrin et al. 2015; Umetsu et al. 2014), computing their richness (e.g. Popesso et al. 2007; Rozo et al. 2009), or by estimating the GC velocity dispersion by measuring the radial velocity of galaxy members (e.g. Biviano et al. 2006). Unfortunately, each of these observables suffers from biases that lead to inaccurate estimates of the mass. A precise characterisation of these biases has become of special importance in recent years because of the recent Planck results on cluster counts (Planck Collaboration XX 2014; Planck Collaboration XXIV 2016), showing that some cosmological parameters, especially σ8, inferred from X-ray observations and SZ mass estimates, are are slightly inconsistent with those deduced from the study of the primordial anisotropies of the cosmic microwave background (CMB).
Several authors have used the velocity dispersion mass proxy to study and characterise scaling relations between the dynamical and the SZ mass (Ruel et al. 2014; Sifón et al. 2016; Amodeo et al. 2017). In this type of study, it is necessary to quantify the velocity dispersion of a large number of clusters, so that observational programs with limited telescope time are forced to obtain radial velocities for a few members for each cluster target. Several techniques have been proposed to minimise the effect of the low number of cluster members in determining an accurate velocity dispersion. Beers et al. (1990) have studied the behaviour of different locations and scale estimators in the presence of deviation from Gaussianity and a reduced sample of galaxies. They focused their work on the robustness and in particular, on the efficiency, of these statistical tools. In particular the biweight (Tukey 1958) became the standard for estimating the velocity dispersion of galaxy samples of almost all sizes because of its robustness and high efficiency. In the past decade, the development of N-body and hydro-dynamical simulations has given us the possibility of testing velocity dispersion estimators directly on samples that mimic observations of GCs.
The correct choice of an appropriate scale estimator can prevent the occurrence of strong deviation from the actual velocity dispersion even when GCs are sampled with only a few galaxy members. Unfortunately, these poor galaxy samples often contain only bright galaxies owing to observational limitations. There are several studies that take velocity segregation of galaxies due to their luminosity and spectral type into account (e.g. Biviano et al. 1992; Goto 2005; Barsanti et al. 2016; Bayliss et al. 2017). Dynamical friction (Chandrasekhar 1943) may be one of the reasons that the velocity dispersion is underestimated (e.g. Merritt 1985; Boylan-Kolchin et al. 2008; Wetzel & White 2010). We present an analysis of three different velocity dispersion estimators: biweight (Tukey 1958), gapper (Wainer & Thissen 1976), and standard deviation. Using 73 simulated GCs, we test their statistical properties when they are applied to samples made up of a few galaxy members or are contaminated by interlopers. We pay particular attention to the case of samples that only contain massive GC members.
This work is organised as follows. In Sect. 2 we give a brief description of the simulations used in this paper. In Sect. 3 we present the recipe for unbiased estimates of GC velocity dispersion and mass. In Sect. 4 we present a comparison of the bias and variance for three scale estimators, biweight, gapper, and standard deviation, as a function of the number of galaxy members considered. In Sect. 5 we test the robustness of the three estimators when galaxy samples contain interlopers. In Sect. 6 we quantify the effect induced on the velocity dispersion estimate by sampling galaxy members in only a fraction of visible objects and within apertures different from R200. In Sects. 7.1 and 7.2 we describe how the mass can be biased even in presence of an unbiased velocity dispersion. In Sect. 8 we apply the correction to a set of simulated observations based on the Planck PSZ1 optical follow-up (Planck Collaboration Int. XXXVI 2016; Barrena et al. 2018), and we give the recipe to correct for the biases in velocity dispersion and mass estimates. Finally, we present our conclusions in Sect. 9.
Throughout this paper, we define R200 as the radius within which the mean cluster density is 200 times the critical density of the Universe at redshift z. The mass 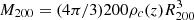 is the total mass within R200. Other quantities with the subscript 200 have to be considered as evaluated at or lying within R200.
is the total mass within R200. Other quantities with the subscript 200 have to be considered as evaluated at or lying within R200.
2. Simulations
In order to carry out the proposed analyses, we used a sample of 73 simulated massive clusters selected from the simulations described in Munari et al. (2013). The original full sample contains about 300 cluster-sized or group-sized structures with masses M200 > 1013 M⊙. Here, our selected sample corresponds to all clusters located at five redshifts (z = 0.12, 0.36, 0.46, 0.6, and 0.82), and with masses M200 > 2 × 1014 M⊙.
The simulations were generated in 29 Lagrangian regions, centred around the massive haloes identified in a large-volume parent simulation box of 1 h−1 Gpc a side, and then re-simulated with higher resolution. The simulation starts in the initial conditions described in Bonafede et al. (2011), and was carried out in two subsequent steps at different resolutions. The entire simulation was performed using the hydro-dynamical GADGET-3 code (Springel et al. 2001). Gravitational forces were simulated using the TreeePM method, in which the Plummer-equivalent softening length ϵ = 5 h−1 kpc is assumed in physical units for z < 2 and fixed in comoving units for z > 2. This simulation follows the evolution of 10243 dark matter (DM) particles with mass mDM = 8.47 × 108 h−1M⊙ and the same number of gas particles with initial mass mgas = 1.53 × 108M⊙, assuming the Λ-CDM cosmological model with ΩDM = 0.24, Ωb = 0.04, ΩΛ = 0.72, H0 = 72 km s−1 Mpc−1, σ8 = 0.8, and nS = 0.96.
For the simulation model, we used the AGN simulation set described in Munari et al. (2013). This is a set of radiative simulations that account for the effect of star formation and the feedback triggered by both supernova explosions (SNe) and active galactic nuclei (AGN). Radiative cooling rates were computed following Wiersma et al. (2009). The prescription by Tornatore et al. (2007) was used to include metal enrichment of the intra-cluster medium (ICM) due to SNe (both type II and Ia) and asymptotic giant branch (AGB) stars, taking also into account the Chabrier (2003) initial mass function (IMF) for the stellar population. For a more accurate description of the simulations and the different prescriptions, see Munari et al. (2013) and Rasia et al. (2015).
The bounded structures were identified first through a friend-of-friend (FoF) algorithm. Then, the identifications were refined using the SUBFIND algorithm (Springel et al. 2001; Dolag et al. 2009). The DM sub-haloes identified in this way that contain stellar structure were considered galaxies. In analogy with Munari et al. (2013), we considered only galaxies that contain a bounded stellar mass 3 × 109 M⊙. This choice guarantees that we retained all sub-haloes more massive than ∼1011 M⊙. In total, there are 105, 196 galaxies in our sample of 73 clusters, 17 433 of which lie within the R200 radius. On average, we thus have 1440 galaxies per cluster, 239 of which are inside R200.
3. Recipe for bias-corrected velocity dispersion and mass estimators in galaxy clusters
Using DM only or hydro-dynamical cosmological simulations, Evrard et al. (2008), Munari et al. (2013), and Saro et al. (2013) characterised scaling relations between GCs velocity dispersion of tracers, that is, DM particles, sub-haloes, and galaxies, and M200:
where 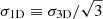 , and the 3D velocity dispersion, σ3D, is calculated using all the DM particles or galaxies within a sphere of radius R200, using the biweight estimator (Beers et al. 1990). However, DM particles, sub-haloes and galaxies lead to different values of the parameters A and α (Munari et al. 2013). Moreover, owing to the triaxiality of GCs and to the non-virialised state of some clusters, all the constraints for α are slightly different from the value α = 1/3 derived from the virial theorem.
, and the 3D velocity dispersion, σ3D, is calculated using all the DM particles or galaxies within a sphere of radius R200, using the biweight estimator (Beers et al. 1990). However, DM particles, sub-haloes and galaxies lead to different values of the parameters A and α (Munari et al. 2013). Moreover, owing to the triaxiality of GCs and to the non-virialised state of some clusters, all the constraints for α are slightly different from the value α = 1/3 derived from the virial theorem.
In order to use GCs for cosmological studies, it is crucial to obtain an accurate, precise, and unbiased estimate for the velocity dispersion and consequently, for the cluster masses. Among other possibilities, this goal can be achieved through spectroscopic follow-ups (e.g. Allen et al. 2011). Nevertheless, owing to observational limits, it is very expensive to measure the line-of-sight velocity of all cluster members in real GC observations. In the new era of large galaxy cluster samples, where we often find a galaxy cluster with a limited number of spectroscopic members (Ngal ≲ 30), it is important to characterise whether this limited number of galaxies might lead to biased estimates of the velocity dispersion and/or the cluster mass.
The aim of this work is to characterise the statistical and physical biases for velocity dispersion and mass estimates in the regime of only a few galaxies, and to provide a recipe to correct for them. The four basic steps of our proposed recipe are listed below and are explained in the following sections.
i. Evaluate the velocity dispersion of the cluster using an unbiased estimator.
ii. Estimate the aperture radius and the mass fraction of the cluster members and correct for these sampling effects.
iii. Estimate the fraction of interlopers that might contaminate the cluster members sample and correct the velocity dispersion.
iv. Calculate the GC mass and correct for statistical biases introduced by the σ–M relation.
In the following sections we demonstrate that these four steps are a good way to estimate actual velocity dispersion and mass with samples that contain only a few galaxy members.
4. Statistical bias and variance for velocity dispersion estimators
4.1. Velocity dispersion estimators and notation
Beers et al. (1990) presented a set of mean and scale estimators, and studied their efficiency in the presence of deviations from a Gaussian distribution. We here decided to focus our attention on three of these estimators: the standard deviation, the biweight, and the gapper. The standard deviation,
is defined as the lowest variance scale estimator for a Gaussian distribution. However, its dependence on μ (the mean of the distribution) makes it not a robust estimator.
The biweight scale estimator is a function of the sample median (Tukey 1958), and it is defined as
where the ui quantities are given by
with a = 9.0, and MAD = median (|xi − M|) are the tuning constant and the median absolute deviation, respectively. Finally, the gapper is a robust estimator (Wainer & Thissen 1976) based on the gaps of an order statistics, xi, xi + 1, …, xn. It is defined as a weighted average of gaps:
where the gaps are given by
and the (approximately Gaussian) weights are given by
For a more detailed description of these estimators, see Beers et al. (1990). With the notation introduced in Eqs. (2), (3) and (5), we refer in a generic way to any of the three scale estimators as SX(Ngal) throughout, where X= “std”, “bwt”, or “gap”, for each one of the three cases.
4.2. Statistical bias and variance for the three estimators
Our aim in this work is to characterise the statistical behaviour of the three methods as a function of the number of galaxies by quantifying the possible bias of each technique specifically for small numbers of galaxies. As explained in Sect. 2, we used a set of 73 simulated GCs with redshifts 0.12 ≤ z ≤ 0.82 and masses 2 ≤ M200/(1014 M⊙) ≤ 20. Following the definition in Munari et al. (2013), we considered as galaxies only those DM subhaloes that contain a bounded stellar structure with a mass ≥3 × 109 M⊙.
We first characterise the distribution of velocities in our set of simulations. Figure 1 shows the histogram of the radial velocities for the 73 GCs along the three main projection axes of all cluster members contained in a cylinder of projected radius R200 along each selected axis. Even though these global distributions are apparently close to a Gaussian, each one of the 73 individual GC distribution is not because substructures are present. A quantitative analysis shows that the overall distributions are far from Gaussianity. In particular, we estimated the following dimensionless parameter:
 |
Fig. 1. Histograms showing the distribution of individual line-of-sight velocities of all cluster members contained in a cylinder of projected radius R200 along each selected axis for all the 73 simulated clusters, and for three possible orientations of the simulation box along the line of sight (x-, y-, and z-axes). The red line corresponds to a Gaussian profile with the same mean and variance as the full sample. |
which is related to the fourth moment of the distribution. We would expect c = 2 for a perfect Gaussian sample. However, when the factor c is evaluated for each of the 73 clusters, we find a mean value c = 1.6 ± 0.4 that implies a departure from a Gaussian of the simulated GC velocity distributions. As expected for relaxed clusters, the mean value of the c parameter is found to be lower than 2. The quoted error of 0.4 corresponds to the scatter of the c parameter over the 73 simulated clusters. As the statistical error in the determination of the c parameter is significantly smaller than this value (on average, the number of galaxies within R200 for each cluster is 239, therefore we might naively expect a statistical error of about 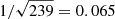 for one cluster, and less than 0.01 for the ensemble of 73 clusters), this large scatter reflects the intrinsic variety of cluster properties in our simulations. We use this c parameter below when we estimate the variance of the three estimators.
for one cluster, and less than 0.01 for the ensemble of 73 clusters), this large scatter reflects the intrinsic variety of cluster properties in our simulations. We use this c parameter below when we estimate the variance of the three estimators.
We now evaluate the bias and the variance of the three scale estimators SX(Ngal). To do this, we explored 20 different values for Ngal between Ngal = 7 and Ngal = 75, logarithmically spaced to better analyse the low-Ngal tail. We generated 2250 configurations by randomly selecting galaxies that are projected in a circle of radius R200, 750 times for each main axis as line of sight and avoiding galaxy repetition. For each configuration, we estimated SX(Ngal) by repeating this procedure for each Ngal and for each galaxy cluster. The average values for SX(Ngal) were obtained by averaging the 73 × 2250 velocity dispersions normalised with respect to Sstd(< R200), which represents the velocity dispersion of all the galaxies in the simulation within a circle of projected radius R200, and calculated using the standard deviation estimator. For completeness, we present in Table 1 the ratio of this relative bias when it is calculated with different estimators.
Ratio of the relative bias SX(< R200)/SY(< R200) between two estimators X and Y, obtained with all the galaxies in the simulation within a circle of projected radius R200.
In the left panel of Fig. 2 we show that each estimator is able to recover the velocity dispersion when compared to the standard deviation of the full sample Sstd(< R200). By construction, for high Ngal (i.e. when all galaxies in the simulation within R200 are used), the standard deviation estimator Sstd(Ngal)/Sstd(< R200) tends to one, while the other two estimators recover the asymptotic value given in Table 1.
 |
Fig. 2. Mean velocity dispersion SX/Sstd(< R200) as a function of the number of galaxies Ngal (left panel) and its variance (right panel) for our sample of 73 simulated galaxy clusters. The dispersion SX(Ngal) is calculated for the standard deviation (green line), biweight (blue line), and gapper (red line) estimators. |
In the low-Ngal regime, all estimators are biased. The gapper (red line) returns an almost constant estimate of the velocity dispersion at any Ngal, but that average value is slightly biased with respect to the true variance (1.008 ± 0.010, as shown in Table 1). The biweight shows a stronger dependence on the number of elements that are used for the estimation, especially in the low-Ngal regime. For Ngal smaller than 30, it underestimates the true dispersion by up to 4 % at Ngal = 10. A very similar behaviour is shown by the standard deviation estimator. We note that in this latter case, the dependence on Ngal can be theoretically predicted, as shown in Appendix A, giving the analytic form 1 − 1/(4(Ngal − 1)). Based on this dependence on Ngal, we obtained a numerical fit to these curves in the left panel of Fig. 2 using the following parametric equation:
Table 2 shows the best-fit values for the parameters D, β, and B, for each one of the three estimators (biweight, gapper, and standard deviation).
Another crucial aspect for choosing a σv estimator is its variance. We would expect the standard deviation to be the lowest variance estimator for a Gaussian distribution. We illustrate this in Appendix B, where we also show the behaviour of all three estimators in the same limit of Gaussian velocity distributions. For the more realistic case given by our set of numerical simulations, we confirm that this also holds. The right panel of Fig. 2 shows the variance of the three estimators, Var(SX(Ngal)), and it shows that the standard deviation still has the lowest variance. Moreover, we can compare this measured variance with the optimal one expected for the theoretical behaviour for a homogeneous population given by1
where the parameter c was defined in Eq. (8). We find that the variance of the standard deviation is indeed very close to the optimal one, as well as the variance of the gapper. For low Ngal values (≲20), the variance of the biweight estimator is significantly worse. Numerical fits to the dependence of the variance as a function of Ngal are given in Appendix C.
Using either the parametric fitting given in Eq. (9) or the numerical values from the left panel of Fig. 2, we can now construct unbiased velocity dispersion estimators by explicitly correcting for that statistical bias. We use the primed notation S′X(Ngal) when we refer to these corrected estimators, which are given by
and where the approximation in the second line uses the fact that the correction term is small compared to unity.
Figure 3 is equivalent to the Fig. 2, but now computed for the set of corrected estimators defined in Eq. (11). By construction, the new S′X(Ngal) estimators are now unbiased (left panel), and their variance (right panel) has increased by only a small amount. As for the case of unprimed estimators, the corrected standard deviation is still the minimum variance estimator, although the three of them present very similar values for Ngal ≳ 30. For this reason, we decided to use S′std(Ngal) as the reference estimator in the following sections, although we could have used any of the three estimators.
 |
Fig. 3. Mean (left panel) and variance (right panel) of the corrected estimators S′X(Ngal)/S′std(< R200) as a function of the number of galaxies Ngal in our sample of 73 simulated galaxy clusters for the standard deviation (green line), biweight (blue line), and gapper (red line). |
5. Bias from interloper contamination
Galaxy clusters are not isolated structures in the Universe. This fact, together with the inevitable confusion associated with redshift-space measurements, implies that any spectroscopic sample of potential cluster members might be contaminated. This population of pseudo-cluster members, called “interlopers”, modifies the velocity distribution and therefore affects the estimation of the velocity dispersion (e.g. Wojtak et al. 2007, 2018; Pratt et al. 2019). Using numerical simulations of the entire visual cone, Mamon et al. (2010) showed that the fraction of galaxies outside the virial sphere that appear on sky projected within the virial radius could reach up to ∼27%, making the interlopers a potentially important source of error for an unbiased determination of the underlying velocity distribution. As shown below, the overall error due to interlopers is indeed similar to or slightly larger than the statistical and physical biases discussed in this paper.
According to the definition of interlopers given in Pratt et al. (2019), it is useful to consider this population as the sum of two different types of objects: (i) galaxies that are gravitationally bounded to the clusters that are far from the cluster centre, but because of projection effects appear within a projected circle of a smaller radius (hereafter type 1 interlopers); and (ii) background or foreground galaxies with similar redshifts to that of the cluster, but belonging to the large-scale structure that surrounds the cluster itself (hereafter type 2 interlopers). In our particular case of zoomed simulations, they only include type 1 interlopers.
It is not possible to provide a general recipe to correct the velocity dispersion bias of a given estimator due to the presence of interlopers because the fraction of these objects in general depends not only on Ngal, but also on the particular criteria adopted for assigning cluster membership to galaxies observed in the cluster field, as well as the type of interlopers. Moreover, there are multiple methods in the literature for identifying interlopers, usually linked to specific cluster mass reconstruction methods. A very complete list can be found in Wojtak et al. (2018) and references therein. Unfortunately, none of these methods are capable of completely removing all contaminants (Wojtak et al. 2018), and moreover, these techniques have good results when applied to large galaxy samples (hundreds of members), but they are usually less effective when applied to smaller samples (dozens of members), as in the case of the caustic method (Diaferio 1999).
Here we limit our discussion to one particular member selection method, called the sigma clipping, and we illustrate the procedure to carry out the correction of the velocity estimation for the two types of interlopers. We emphasise that in a general case, specific simulations are required to quantify the bias associated with each particular method. The sigma clipping (Yahil & Vidal 1977) is one of the most frequently used techniques for removing interlopers. This method clips galaxies whose radial velocity is above a certain threshold, which is particularly effective in the external regions of the clusters.
5.1. Type 1 interlopers
We first estimate the effect of type 1 interlopers in our simulations. It is important to emphasise here that all our velocity dispersion quantities were computed using the galaxies contained in a cylinder of projected radius R200. By construction, they are therefore affected by type 1 interlopers. In order to transform them into a velocity dispersion computed within a sphere of radius R200, and therefore, free of type 1 interlopers, the average conversion factors that we find in our simulated sample are 0.990, 0.981, and 0.985 for the biweight, gapper, and standard deviation estimators, respectively. In summary, as a consequence of the presence of (type 1) interlopers, the velocity dispersion is overestimated between 1% and 2%. This bias is relatively small and comparable to the statistical biases discussed in the previous sections. In principle, it has to be corrected in the corresponding S′X estimators when transforming from velocity dispersion into masses, but only if the adopted σ–M scaling relation from simulations already accounted for the effect of type 1 interlopers.
We further explore the possible correction of this bias using the sigma clipping method. Although this method might be effective in removing interlopers, cutting the tail of a distribution will necessarily introduce a bias in the estimation of the velocity dispersion. To quantify this effect, we tested four grades of clipping (no clip, 3σ, 2.7σ, and 2.5σ) in Fig. 4 for one of the estimators. As expected, the higher the clip, the lower the variance recovered by the estimator. However, it is interesting to note that this new bias partially alleviates the effect introduced by the type 1 interloper contamination. As in Mamon et al. (2010), we also find that both effects are compensated for at around 2.7σ when we used the gapper to estimate the dispersion. However, we note that when the other two estimators are used, the clipping that compensates for the effect of the interlopers is different. We find that a 2.5σ clipping for the biweight, and a 3σ clipping for the standard deviation compensates for the effect of type 1 interlopers.
 |
Fig. 4. Effect of type 1 interlopers on the velocity estimates as a function of the number of galaxies for the gapper estimator. The velocity dispersion Sgap(Ngal) is computed first using the full galaxy sample (solid black line, equivalent to the red line in Fig. 2), and then it is compared to the estimates after clipping the galaxy sample at 3, 2.7, and 2.5 sigma in the velocity space. |
5.2. Type 2 interlopers
As explained above, we used zoomed hydrodynamical simulations from a parent one, where the region of clusters was re-simulated at higher resolution. Although this technique is very useful to explore the appropriate mass range in which stars and galaxies form, it has the disadvantage of re-simulating only a finite region around the centre of the cluster (in the case of study, ∼5 R200). Thus, all galaxies in our simulated catalogues are bounded to the cluster, and following our definition, they correspond to type 1 interlopers only.
To understand the effect introduced by type 2 interlopers, we repeated the procedure described in the previous sub-section, but this time replaced some galaxies from the actual cluster distribution with random velocity values drawn from a uniform distribution in the velocity interval [ − 2.7, 2.7]×Sstd(< R200). This uniform distribution was intended to mimic a field of background and foreground galaxies in the extreme case of a velocity distribution that is completely different from that of the galaxies. Figure 5 presents the results obtained for five different fractions of interlopers: 5%, 10%, 15%, 20%, and 30%. As expected, the inclusion of these type 2 interlopers produces a positive bias in the velocity dispersion, which at first order is found to be directly proportional to the relative fraction of interlopers. It is also noteworthy that all the three estimators are similarly affected by this type 2 interloper contamination.
Although Fig. 5 shows a broad range of values for the fraction of type 2 interlopers, in real objects we would expect this number to be in the range of 5–10% within a virial radius (Saro et al. 2013), because the fraction of type 1 objects is significantly larger. If this is the case, then the effect of type 2 interlopers in the extreme case considered here will be at most 10% . This is consistent with other results in the literature, which indeed present lower values. For example, Mamon et al. (2010) showed that the total fraction of interlopers in their simulations (including types 1 and 2) is ∼27%, while their effect on the velocity estimation at R200 is about 2%. Moreover, this effect is basically cancelled out in their final estimation of the velocity dispersion within R200 when the 2.7σ clipping was used, which suggests that the fraction of type 2 interlopers with a very different velocity distribution to the one of the true members is rather small. On the other hand, in our simulated cluster sample we find a median fraction of type 1 interlopers of ∼29%, which is consistent with the value of Mamon et al. (2010).
It is also important to note the strong dependence of type 2 interlopers on the sample aperture (Mamon et al. 2010; Saro et al. 2013), which rapidly increases beyond R200. In practice, this means that the interloper contamination is the most damaging effect when an unbiased velocity estimation for a single cluster for radii much larger than R200 is to be obtained.
Finally, we note that in real observations, the fraction of interlopers, and particularly type 2, depends closely on the observational strategy and the particular algorithms and procedures used for member selection. Therefore the effective number of contaminants cannot be estimated precisely with a general recipe. Studies such as Mamon et al. (2010), Saro et al. (2013) are necessary to statistically quantify their abundance in each particular observing strategy. We focused here on providing a general recipe for correcting the statistical and/or physical bias associated with the velocity estimators, therefore we do not discuss this effect further. We emphasise, however, that for a reliable velocity estimation, the bias due to interlopers has to be taken into account and corrected for specifically for each particular survey.
6. Physical biases on velocity dispersion estimators
In the ideal case in which we can choose a uniformly selected sample of true cluster members inside R200, the corrected set of scale estimators presented above will provide an unbiased estimation of the velocity dispersion of the cluster. However, observational strategies and technical limitations prevent us from reaching the ideal case. In this section we study two possible ways in which a particular selection of cluster members might produce biased velocity dispersion estimates.
6.1. Effects due to the selected fraction of massive galaxies
For a fixed integration time, the telescope aperture limits the detection magnitude and prevents us from detecting faint objects. In other cases, the technical requirements of spectrographs make it impossible to sample the cluster members adequately for arbitrary low brightness values. In practice, line-of-sight velocity samples therefore contain only a fraction of GC members, generally the brightest objects in the GC, which are also the most massive. This fraction of objects is particularly small for high-redshift GCs. In this subsection, we investigate whether there is an induced bias due to this mass segregation.
In order to simulate this effect, we mimicked observational conditions by selecting three percentages of all visible galaxies in the simulation, that is, 50%, 33%, and 25%, by sorting the cluster members by mass and dividing the sample into two, three, and four mass bins, starting from the most massive object. For each case, as explained in Sect. 4, we averaged 2250 configurations (750 for each axis, x, y, and z), considering numbers of galaxies between 8 and 75, avoiding galaxy repetition and evaluating the dispersion with the biweight, gapper, and standard deviation methods.
Figure 6 (left panel) shows S′std(Ngal)/Sstd(< R200) as a function of Ngal calculated with the corrected standard deviation estimator, and using galaxies picked up from 100%, 1/2, 1/3, and 1/4 of the complete cluster member samples. A bias appears, with a non-linear dependence on the fraction of massive galaxies considered in each case, but almost insensitive to the Ngal parameter. This means that the velocity dispersion is sensitive to the fraction of massive galaxies used to estimate it. In particular, when only the most massive galaxies of the clusters (1/4 of the sample) are taken into account, we would find a velocity dispersion that might be underestimated by up to 2%. We can interpret this velocity bias in terms of a physical mechanism, the dynamical friction (Chandrasekhar 1943), that mostly affects the most massive galaxies, so that the velocity dispersion is lower than that obtained when objects are used that are randomly selected from the complete galaxy sample. Table 3 shows the average bias of the primed estimators S′X, calculated with respect to the full set of cluster members within R200 (i.e. Sstd(< R200)) for each fraction that we examinated and for the three estimators (biweight, gapper, and standard deviation). As this physical bias is almost independent of Ngal, we might use these values directly to produce a new corrected (unbiased) estimator.
 |
Fig. 5. Combined effect of type 1 and 2 interlopers on S′X(Ngal)/Sstd(< R200) as a function of the number of galaxies. The velocity dispersion, S′X(Ngal), is first computed using the full galaxy sample (equivalent to the three colour lines shown in the left panel of Fig. 3). We also evaluated the response of biweight (blue), standard deviation (green), and gapper (red lines) using samples contaminated by a certain fraction of type 2 interlopers, as described in the text. By construction, our simulations also include the type 1 interlopers because the velocity dispersion is estimated in the cylinder. |
 |
Fig. 6. Left panel: mean (bias) of S′std(Ngal)/Sstd(< R200) as a function of the number of galaxies Ngal, calculated by choosing galaxies within 100% (solid black line), 1/2 (solid blue line), 1/3 (solid red line), and 1/4 (solid green line) of the complete cluster member samples. Right panel: variance of S′std(Ngal)/Sstd(< R200) as a function of the number of galaxies Ngal. The dashed line represents the theoretical expectation for the variance of the dispersion according to Eq. (10). |
Relative bias of the primed estimators due to the selected fraction of massive galaxies.
In the right panel of Fig. 6 we show the variance of S′std(Ngal)/Sstd(< R200). The fraction of massive galaxies does not significantly affect the dispersion estimator variance.
6.2. Effect of aperture sub-sampling
All the analyses presented above include galaxies from the complete sample of cluster members, or a fraction of them, but the sample was always selected within R200. However, there is already evidence in the literature that the velocity dispersion estimate needs to be corrected when galaxies are not sampled out to the virial cluster radius (e.g. Mamon et al. 2010; Sifón et al. 2016). In this subsection, we determine how the selection region affects the σv estimate in our simulations by characterising the physical bias that is introduced when the velocity dispersion is evaluated enclosed in a radius r from the galaxy cluster centre. In particular, we compute the velocity dispersion using all the galaxies inside a cylinder of variable radius 0.2 ≤ r/R200 ≤ 1.5. In addition, we average over all 73 simulated GCs and construct the ⟨S′X(< r)/Sstd(< R200)⟩ as a function of the r/R200 profile (Fig. 7). The corresponding numerical values are given in Table 4. The velocity dispersion is (on average) overestimated where the region explored by the spectroscopic sample is smaller than R200. The results are consistent with those obtained by Sifón et al. (2016) when the biweight estimator is used for both S′X(< r) and S′X(< R200) (see Fig. 4 and Table 3 in that paper).
 |
Fig. 7. Average velocity dispersion profile within a given enclosed radius r, ⟨S′std(< r)/Sstd(< R200)⟩, normalised to R200. The red line represents the mean at each radius of the individual 73 simulated GC profiles (grey lines). The numerical values are given in Table 4. The dashed blue line represents the Sifón et al. (2016) profile, which is almost coincident with our derived profile. |
Average velocity dispersion profile within a given enclosed radius r, ⟨S′std(< r)/Sstd(< R200)⟩, normalised to R200.
We finally evaluate the combined effect of this aperture sub-sampling and the selection effect of a fraction of massive galaxies discussed in the previous subsection. We performed the same analysis described above for eight fractions of R200, r/R200 = 0.2, 0.3, 0.4, 0.5, 0.8, 1.0, 1.2 and 1.5, and also considered different fractions of massive members. Unfortunately, we were unable to calculate the dispersion for the smaller fractions for radii smaller than half R200 for our simulation set because not all the simulated clusters contain at least seven galaxies in these inner regions. For larger radii (r ≳ R200), however, we find that the bias caused by the fraction of massive galaxies we used remains almost constant at all radii. Therefore we can apply the correction factors presented in Table 3 in combination with the radial correction profile shown in Fig. 7 and in Table 4 to correct simultaneously for both effects.
7. Bias in the mass estimation
7.1. Statistical bias in the estimation of M200
In the previous sections we have studied how velocity dispersion estimators can be affected by different statistical and physical factors, and we have quantified the expected bias in these cases. In this section, we now show that mass estimators are also affected by the same effects.
The mass of a GC is not a direct observable. When we estimate the cluster mass using velocity dispersion estimates, we basically apply a function M–σ1D that has previously been calibrated either in simulations or using observations. Any non-linear transformation of σ1D introduces a bias similar to the one that we have discussed for the SX estimators, which will be more significant in the low-Ngal regime.
Following Eq. (1), when we have obtained an estimate of the velocity dispersion (SX), the mass of the cluster can be computed as
with parameters A = 1177.0 km s−1 and α = 0.364 constrained by Munari et al. (2013) using the biweight as velocity dispersion estimator.
However, and in analogy to what we described in Sect. 4, even when we use an unbiased estimator for the velocity dispersion, and because that Eq. (12) contains a non-linear function of the variance, we expect a statistical bias with some dependence at low Ngal. Using the results from Appendix A, as the transformation to obtain the mass is of the type f(v)∝v1/(2α) with 1/α ∼ 3, we can predict the amount of bias.
As for the study of the dispersion estimators, in the case of mass estimators we also select as the reference velocity dispersion the dispersion that is estimated with the standard deviation using all the galaxies within R200. In the top row of Fig. 8 we show the results of the bias (left panel) and associated variance (right panel) of the mass estimator based on Eq. (12) using SX(Ngal) as the velocity estimator. This case is noted as ⟨M(SX)/M(Sstd(< R200))⟩, and M(Sstd(< R200)) represents the mass obtained using Eq. (12) for the input value of Sstd(< R200).
 |
Fig. 8. Mean (left panels) and variance (right panels) of M(SX(Ngal))/M(Sstd(< R200)) and M(S′x(Ngal))/M(S′std(< R200)), which represent the standard mass estimator, Eq. (12), applied to normal and unbiased velocity dispersion estimators, standard deviation (green), gapper (red), and biweight (blue). The theoretical expectation for M(Sstd(Ngal))/M(Sstd(< R200)) is represented with the black dashed line. |
This mass estimator M(Sstd) is positively biased by a factor
as predicted by Eq. (A.5). In a similar way, the M(Sbwt) and M(Sgap) mass estimators are also positively biased.
For comparison, the bottom row of Fig. 8 shows the equivalent results of the bias (left panel) and associated variance (right panel) of the mass estimator, but now using S′X(Ngal) as the input velocity estimation. These quantities are represented as ⟨M(S′X)/M(Sstd(< R200))⟩. As anticipated, even when we use an unbiased velocity dispersion estimator, the non-linearity of the mass–velocity dispersion relation results in a biased mass estimate. It is interesting to note that the velocity dispersion bias is propagated into the mass bias, as seen by comparing the top and bottom panels of this figure. On one hand, as the Sgap is independent from Ngal, in the transformation from the normal estimator to the bias-corrected one, the only change is the normalisation (i.e. a constant factor, and therefore the variance does not increase). On the other hand, the mass bias of Sstd (top panel) is mitigated by the fact that the normal standard deviation tends to underestimate the velocity dispersion at low Ngal. This effect is absent from the M(S′std) profile (bottom panel) because S′std is by construction unbiased. Focusing our attention on the variance of these mass estimators, shown in the right panels of Fig. 8, we see that for M(SX) (top panel), the standard deviation has the lowest variance, whereas the gapper and biweight show almost the same behaviour as functions of Ngal. Instead, in the bottom panel, the three Var(M(S′X)) functions show a behaviour similar to what we see for the dispersion estimators. The gapper variance remains almost untouched, and the standard deviation behaves like the gapper, whereas the biweight has the higher variance.
As in Sect. 4, we propose a parametric description of the bias as a function of Ngal, based on the analytic form of the bias for the standard deviation case. We also use here three parameters (E,F and γ) in order to apply it to the gapper- and biweight-based mass estimators:
The best-fit parameters describing the bias for the unprimed M(SX) and primed M(S′X) mass estimators are listed in Tables 5 and 6, respectively.
After we have fitted for this bias, we can propose bias-corrected mass estimators for these two cases by defining
Following the same convention for the notation as we adopted in previous sections, hereafter these bias-corrected estimators are represented with a prime, that is, M′(SX(Ngal)) and M′(S′X(Ngal)).
Figure 9 shows the bias and variance of M′(SX) (top panel) and M′(S′X) (bottom panel). Both estimators are unbiased by construction. Concerning their variance, as expected, the biweight has the largest variance, whereas the standard deviation behaves similarly to the gapper but sill remains the lowest variance estimator. Analytical fits to the dependence of the variance as a function of Ngal are given in Appendix C.
 |
Fig. 9. Mean (left panels) and variance (right panels) of the unbiased mass estimators M′(SX)/M′(Sstd(< R200)) (top row) and M′(S′X)/M′(S′std(< R200)) (bottom row). In all panels, we show the results for the standard deviation (green), gapper (red), and biweight (blue) estimators. |
7.2. Physical biases in the M200 estimation
In Sect. 6 we explained how biases in velocity dispersion estimation could appear when only the more massive cluster members of the cluster are taken into account, or when a fraction of the virial radius R200 is sampled. These biases due to the physics of galaxy clusters are also propagated to the mass estimation.
In the top panels of Fig. 10 we show that choosing galaxies from the subset of the most massive galaxies also introduces a bias in the mass estimation. For illustration purposes, we only show the effect on the M′(SX) estimator, but a similar figure can be generated for M′(S′X). We find that the mass could be underestimated by up to 5 % when 1/4 of the sample is used that contains the most massive galaxies. Tthe small biases in the velocity estimation are now clearly amplified, especially at low Ngal.
 |
Fig. 10. Mean and variance of the M′(SX)/M′(Sstd(< R200)) mass estimator as a function of the number of galaxies Ngal (top panels) and as a function of the aperture radius r (bottom panels). In black, blue, green, and red are represented the fractions that include 100%, 1/2, 1/3, and 1/4 of the most massive galaxies, respectively. |
The aperture effect on the mass estimators is also shown in the bottom panel of Fig. 10. All the biases are stronger here as well, as in the case of the velocity dispersion with a profile that prevents steeper sampling at greater apertures. From the variance point of view, it increases in the core of the cluster and remains almost untouched for r ≥ R200.
It is evident that owing to the high variance of the mass estimation, the combination of these effects may be considered negligible for a single cluster mass determination, but in order to determine the mean bias of a scale relation, it is very important to obtain the most accurate mass estimation possible.
8. Applying corrections to a realistic case
In this section, we show how well we can retrieve a bias-corrected velocity dispersion and mass estimation for a simulated sample of galaxy clusters under realistic observing conditions, but where only type 1 interlopers are considered. We follow the method outlined in Sect. 3 and discussed in the previous sections. The basic steps are listed below.
i. Use the unbiased estimator S′X, defined in Eq. (11), to estimate the cluster velocity dispersion.
ii. Correct this velocity dispersion for the two physical effects (mass fraction and sampling aperture) described in the text, using Table 3 (or Fig. 6) and Table 4 (or Fig. 7), respectively. The second correction requires a first-order estimation of R200, which can be obtained from the S′X value from the previous step and the σ200–M200 relation in Eq. (1).
iii. Estimate the percentage of contaminants (interlopers) of the cluster member sample and correct, if needed, the velocity dispersion using the curves in Fig. 5. This provides the final velocity dispersion estimate, corrected for all effects described in the paper.
iv. Compute the galaxy cluster mass using the unbiased mass estimator M′(S′X) defined in Eq. (16), and use the corrected S′X value from the previous step as input.
To perform this test, we decided to mimic the observational strategy that we adopted in our Planck PSZ1 follow-up program carried out during a two-year international time project (ITP13B/15A; Planck Collaboration Int. XXXVI 2016; Barrena et al. 2018). This observational program has the aim of validating and characterising the unknown Planck SZ sources of the PSZ1 catalogue in the northern hemisphere. To do this, we used the DOLORES and OSIRIS spectrographs at the 3.5 m Telescopio Nazionale Galileo (TNG) and the 10.4 m Gran Telescopio Canarias (GTC), respectively, both located at Roque de los Muchachos Observatory (La Palma, Spain).
These facilities allow multi-object spectroscopy (MOS) observations that fit our aim very well. However, the high number of clusters to be observed (about 200) and the need to obtain spectroscopy of very faint objects, ′rmag > 22, did not allow us to use more than one MOS mask or some long slits per cluster. For this reason, we were only able to obtain a reduced number of cluster members, Ngal < 40. Our observational strategy started with the photometric redshift estimation. When the zphot was determined, we divided the GC sample into two redshift bins, z ≤ 0.4 and z > 0.4, in order to observe them at the TNG and the GTC, respectively. Here, we mimic the galaxy selection procedure and the resulting galaxy catalogues. Owing to the different fields of view (FOV) of the two instruments and the differences in the two-mask designer software, we decided to implement both configurations following the same prescription as described above. In Fig. 11 we show two examples of a TNG and GTC mask scheme. There are some differences in the two configurations: (i) TNG masks are always centred on the GC centre, while GTC masks, owing to the gap between the two CCD, are shifted ∼100″ to the left; (ii) the GTC mask designer tool is more precise than that of the TNG. For this reason, the minimum distance between galaxies is 5.4″ and 8″ for GTC and TNG masks, respectively.
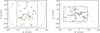 |
Fig. 11. Left panel: example of DOLORES/TNG simulated mask. Right panel: example of OSIRIS/GTC simulated mask. See text for details. Black and green dots represent cluster members outside or inside the telescope field of view, respectively. Black rectangles are the slitlets, and the red points the line-of-sight velocity measurements (the symbol size is proportional to the mass of each galaxy with respect to the most massive galaxy in the mask). The circle in the dotted line represents the projected R200 radius. |
In order to simulate a cluster observation, we selected each cluster at a random orientation and fraction of visible galaxies. To mimic observational issues such as spectral contamination or incorrect mask centring, we set a random number of slits as the effective catalogue of measured radial velocities. We repeated this procedure to obtain 100 mock samples out of the 73 GC objects simulated in this study. For each of these samples we calculated the mean ratio between the estimated and the reference cluster velocity dispersion. Because the parameters of the scaling relation between σ200–M200, Eq. (1), were constrained using the biweight estimation of the velocity dispersion, Sbwt(< R200), we decided to use it as a reference velocity dispersion for this analysis. For each of these samples we calculated the mean ratio between the estimated and the reference velocity dispersion of each cluster. Averaging over all the mock samples, we obtained
Using the estimators S′X defined in Eq. (11) with the parameters in Table 2, we corrected the bias due to the number of galaxies. To correct the biases due to the GC physics, the first step is to identify in which fraction of massive galaxies the detected cluster members reside. The second step is to calculate the aperture radius, which is the sampling radius. To do this, first we needed to estimate R200. Based on a first estimate of the cluster mass using SX(Ngal), we can derive a first-order approximation to that radius, noted as 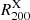 . This value was used to apply the aperture correction shown in the right panel of Fig. 7 to S′X. In our case, each velocity dispersion was corrected individually after averaging over all the clusters, and then averaging over all the 100 configurations to obtain
. This value was used to apply the aperture correction shown in the right panel of Fig. 7 to S′X. In our case, each velocity dispersion was corrected individually after averaging over all the clusters, and then averaging over all the 100 configurations to obtain
which represent bias-corrected estimates of the velocity dispersion. We note that these quantities are referred to the velocity dispersion computed in the cylinder Sbwt(< R200), and thus they include type 1 interlopers, as described in Sect. 5.1. If we wish to correct these values for this effect, we have to multiply these values by the corrections factors quoted in that subsection, that is, 0.990, 0.981, and 0.985 for the biweight, gapper, and standard deviation estimators, respectively.
Using these velocity dispersion, we can now calculate the cluster masses, M(S′X), and obtain
As shown above, these masses are overestimated, and in order to correct for this bias, we have to use the primed mass estimator, M′, as explained in Sect. 7.1. In this case, we obtain
It is also interesting to compare these mass estimates with the true mass, M200, that is directly estimated from the simulation as the mass of all particles within R200. These values were used to constrain the parameters in Eq. (1) (Munari et al. 2013). The direct estimation of the velocity dispersion using SX leads to a biased estimation of M200:
If the dispersion estimator is the corrected one, S′X, we now retrieve a mass that is almost unbiased:
Finally, M′ provides the final unbiased estimate of M200:
Again, for this example these quantities are referred to a true mass computed from the velocity dispersion computed in the cylinder Sbwt(< R200). If we wish to isolate the effect of type 1 interlopers, then the true M200 has to be computed using the velocity dispersion in a sphere of radius R200, and the primed velocity dispersion estimates also have to be corrected for the same bias.
These numbers show that in this realistic situation, the proposed set of corrected estimators is also able to recover an unbiased estimate for the velocity dispersion and mass of the galaxy clusters.
9. Conclusions
We have used 73 simulated GCs from hydrodynamic simulations with AGN feedback and star formation. We took three different estimators into account: the biweight, the gapper, and the standard deviation. We focused on the limit of a low number of galaxy members (Ngal < 75), and studied the bias and error (variance) of each estimator.
This study presents a detailed study of three techniques to estimate the velocity dispersion by quantifying possible biases brought about by their definition and observational limits. In a future paper, we will apply the optimal technique with the corresponding corrections to a real sample of GCs in order to estimate bias-corrected dynamical masses and compare them with those evaluated using different proxies.
We proposed a recipe with the aim of estimating reliable velocity dispersion and mass estimators with the lowest bias and variance possible in the low-Ngal regime. We constructed unbiased estimators based on the standard deviation, biweight, and gapper while correcting for their Ngal dependence, S′X. In this case, we focused our attention on the variance of these estimators. Although asymptotically, the three estimators have the same variance, in the range of a number of galaxies in which we are interested, Ngal < 40, the corrected biweight has an even higher variance than the normal biweight, and consequently, higher than the other two estimators. After the bias correction, the variance of the standard deviation and gapper were compatible for Ngal ≥ 20, whereas for Ngal < 20, the corrected standard deviation was the lowest variance estimator.
We also tested the robustness of the three S′X estimators when the galaxy sample is contaminated by interlopers, considering both gravitationally bound interlopers (type 1) and background or foregrounds galaxies (type 2). For type 1 interlopers, the bias in the velocity dispersion estimator is found to be ∼2%, comparable to the other statistical biases discussed above, and consistent with the results obtained by other authors, who also included type 2 interlopers in their analysis (e.g. Mamon et al. 2010). This bias can be corrected using a 2.7σ clipping technique (Yahil & Vidal 1977). For type 2 interlopers, we explored the conservative approach of assigning them a uniform velocity distribution, which is completely different from the true distribution of cluster members. Our results show that the three estimators are similarly affected, and that at first order, the bias in S′X is roughly proportional to the percentage of type 2 interlopers in our approach. Although comparable to the other effects discussed in this paper, the contribution of type 2 interlopers could provide the main bias in the velocity dispersion estimation, especially for radii beyond R200, if their fraction is as large as 10% (e.g. Saro et al. 2013). Finally, this fraction of type 2 contaminants depends on the particular GCs member selection procedure and can therefore vary from survey to survey. Thus, a general formula based only on Ngal cannot be provided.
We also studied how observational limitations affect the estimation of the velocity dispersion in GCs. We recognised the most likely sources of bias in (i) the selection effect due to the luminosity of GC members observed and hence in the fraction of massive galaxies used to estimate the velocity dispersion; and (ii) the aperture radius of the observation, and hence the fraction of the viral radius explored. We saw that the bias increased for a smaller fraction of massive galaxies. This bias was estimated to be around the 2% when only 1/4 of the more massive galaxies was considered.
For the effect produced by the sampling aperture, we found that the maximum deviation was produced for an aperture radius of 0.3–0.4 R200. This agrees with the results of Sifón et al. (2016).
We also tested the mass estimators defined by Eq. (1) with the parameters of Munari et al. (2013). In this case, we observed that all three estimators depended on the number of galaxies and overestimated the reference mass at low-Ngal. The standard deviation profile can be analytically derived by taking into account the fact that the mass is a non-linear function of the variance, as explained in Appendix A. In this case, we also defined a new set of mass estimators, M(SX) and M′(S′X), and corrected the mass estimator that we applied to the biweight, gapper, and standard deviation, or to their corrected counterparts, respectively. We constructed these estimators to be unbiased over the entire range of Ngal and found that the mass estimator based on the standard deviation, whether corrected or not, was that of the lowest variance.
The ultimate aim of this paper is not only to correct the velocity dispersion and mass estimates of a single cluster, but also to develop a method to obtain bias-corrected mean mass estimates in order to constrain the parameter of mass-scaling relations. For this reason, we also applied these techniques to a set of mock observations to retrieve the bias-corrected mean velocity dispersion and masses. These types of analyses are relevant for precision cosmology analyses with large samples of galaxy clusters in the light of forthcoming results from space missions such as eROSITA or Euclid.
Acknowledgments
We thank Andrea Biviano for useful discussions and for the comments on the draft. We also thank the anonymous referee for useful suggestions related to the discussion of interlopers. We are greatly indebted to Volker Springel for providing us with the non-public version of GADGET-3. Simulations have been carried out in CINECA (Bologna), with CPU time allocated through the Italian SuperComputing Resource Allocation (ISCRA) and through an agreement between CINECA and the University of Trieste. AF, RB, JB and JARM acknowledge financial support from the Spanish Ministry of Economy and Competitiveness (MINECO) under the projects ESP2013-48362-C2-1-P, AYA2014-60438-P and AYA2017-84185-P.
References
- Allen, S. W., Evrard, A. E., & Mantz, A. B. 2011, ARA&A, 49, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Amodeo, S., Mei, S., Stanford, S. A., et al. 2017, ApJ, 844, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaud, M., Pratt, G. W., Piffaretti, R., et al. 2010, A&A, 517, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barrena, R., Streblyanska, A., Ferragamo, A., et al. 2018, A&A, 616, A42 [CrossRef] [EDP Sciences] [Google Scholar]
- Barsanti, S., Girardi, M., Biviano, A., et al. 2016, A&A, 595, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bayliss, M. B., Zengo, K., Ruel, J., et al. 2017, ApJ, 837, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Beers, T. C., Flynn, K., & Gebhardt, K. 1990, AJ, 100, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Biviano, A., Girardi, M., Giuricin, G., Mardirossian, F., & Mezzetti, M. 1992, ApJ, 396, 35 [CrossRef] [Google Scholar]
- Biviano, A., Murante, G., Borgani, S., et al. 2006, A&A, 456, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonafede, A., Dolag, K., Stasyszyn, F., Murante, G., & Borgani, S. 2011, MNRAS, 418, 2234 [NASA ADS] [CrossRef] [Google Scholar]
- Boylan-Kolchin, M., Ma, C.-P., & Quataert, E. 2008, MNRAS, 383, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]
- Chandrasekhar, S. 1943, ApJ, 97, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Chang, C. L., Ade, P. A. R., & Aird, K. A. 2009, American Institute of Physics Conference Series, eds. B. Young, B. Cabrera, & A. Miller, Am. Inst. Phys. Conf. Ser., 1185, 475 [NASA ADS] [Google Scholar]
- Diaferio, A. 1999, MNRAS, 309, 610 [NASA ADS] [CrossRef] [Google Scholar]
- Dolag, K., Borgani, S., Murante, G., & Springel, V. 2009, MNRAS, 399, 497 [Google Scholar]
- Evrard, A. E., Bialek, J., Busha, M., et al. 2008, ApJ, 672, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Goto, T. 2005, MNRAS, 359, 1415 [NASA ADS] [CrossRef] [Google Scholar]
- Hincks, A. D., Acquaviva, V., Ade, P. A. R., et al. 2010, ApJS, 191, 423 [Google Scholar]
- Kravtsov, A. V., & Borgani, S. 2012, ARA&A, 50, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Macias-Perez, J. F., Adam, R., Ade, P., et al. 2017, Proceedings of the European Physical Society Conference on High Energy Physics. 5-12 July, 2017 Venice, Italy (EPS-HEP2017), Online at http://pos.sissa.it/cgi-bin/reader/conf.cgi?confid=314, 42 [Google Scholar]
- Mamon, G. A., Biviano, A., & Murante, G. 2010, A&A, 520, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Merritt, D. 1985, ApJ, 289, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Munari, E., Biviano, A., Borgani, S., Murante, G., & Fabjan, D. 2013, MNRAS, 430, 2638 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XX. 2014, A&A, 571, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXII. 2016, A&A, 594, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIV. 2016, A&A, 594, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XXXVI. 2016, A&A, 586, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popesso, P., Biviano, A., Böhringer, H., & Romaniello, M. 2007, A&A, 464, 451 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pratt, G. W., Arnaud, M., Biviano, A., et al. 2019, Space Sci. Rev., 215, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Rasia, E., Borgani, S., Murante, G., et al. 2015, ApJ, 813, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Rozo, E., Rykoff, E. S., Evrard, A., et al. 2009, ApJ, 699, 768 [NASA ADS] [CrossRef] [Google Scholar]
- Ruel, J., Bazin, G., Bayliss, M., et al. 2014, ApJ, 792, 45 [Google Scholar]
- Saro, A., Mohr, J. J., Bazin, G., & Dolag, K. 2013, ApJ, 772, 47 [CrossRef] [Google Scholar]
- Sifón, C., Battaglia, N., Hasselfield, M., et al. 2016, MNRAS, 461, 248 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., Yoshida, N., & White, S. D. M. 2001, New A, 6, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Stanek, R., Rasia, E., Evrard, A. E., Pearce, F., & Gazzola, L. 2010, ApJ, 715, 1508 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R. A., & Zeldovich, Y. B. 1970, Comments Astrophys. Space Phys., 2, 66 [NASA ADS] [Google Scholar]
- Tornatore, L., Borgani, S., Dolag, K., & Matteucci, F. 2007, MNRAS, 382, 1050 [NASA ADS] [CrossRef] [Google Scholar]
- Tukey, J. W. 1958, Ann. Math. Stat., 29, 614 [CrossRef] [Google Scholar]
- Umetsu, K., Medezinski, E., Nonino, M., et al. 2014, ApJ, 795, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Voit, G. M. 2005, Rev. Mod. Phys., 77, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Wainer, H., & Thissen, D. 1976, Psychometrika, 41, 9 [CrossRef] [Google Scholar]
- Wetzel, A. R., & White, M. 2010, MNRAS, 403, 1072 [NASA ADS] [CrossRef] [Google Scholar]
- Wiersma, R. P. C., Schaye, J., & Smith, B. D. 2009, MNRAS, 393, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Wojtak, R., Łokas, E. L., Mamon, G. A., et al. 2007, A&A, 466, 437 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wojtak, R., Old, L., Mamon, G. A., et al. 2018, MNRAS, 481, 324 [NASA ADS] [CrossRef] [Google Scholar]
- Yahil, A., & Vidal, N. V. 1977, ApJ, 214, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Zitrin, A., Fabris, A., Merten, J., et al. 2015, ApJ, 801, 44 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Bias in the estimation of the non-linear function of variance g(v)
When we assume a random variable x with probability pi, we can estimate any ordinary moment as
The moment of second order is the variance, ![$ E[{\rm{Var}}(x)] = E[v] = {\langle {x^2}\rangle _n} - \langle x\rangle _n^2 $](/articles/aa/full_html/2020/09/aa34837-18/aa34837-18-eq43.gif) , which is unbiased for any number of data, N.
, which is unbiased for any number of data, N.
In this appendix we explain how a bias is induced when a quantity is calculated as a non-linear function of variance, m = g(v). We evaluate E[g(v)], which is the estimate of the function g(v). We can use as the estimator of m the function g applied at the estimated value of E[v],
The estimator g(E[v]) is only unbiased if the function g(v) is linear. When m is a non-linear function of the variance, for instance, standard deviation and mass, we can write the mean of g(E[v]) as
When the variable v is unbiased, we can assume that ⟨ΔE[v]⟩ = 0 and
which implies that the unbiased estimate of g(v) is
When the standard deviation σ = v1/2, we have
which is the unbiased standard deviation estimator.
Appendix B: Statistical bias and variance for velocity dispersion and mass estimators in the limit of a Gaussian distribution
In analogy to the cases discussed in the main text, in this appendix we show how the velocity dispersion and mass estimators presented above behave in the limit of a perfectly Gaussian velocity distribution. To this end, we generated 73 Gaussian distributions fixing the mean (μ = 0), and the dispersion σ = Strue, where Strue is the dispersion corresponding to M200 through Eq. (1) for each cluster in this new simulated sample.
As in the main text, we explored 20 different values for Ngal between Ngal = 7 and Ngal = 75. We used 50 000 different configurations for each Ngal and each cluster, thus using 73 × 50 000 velocity dispersion estimates normalised with respect to Strue. We note that by fixing the width of the Gaussian distribution, we avoided selecting a reference estimator, and we can therefore investigate the absolute bias of each estimator with respect to the same Strue value.
Velocity dispersion estimators
Figure B.1 illustrates the behaviour of the (uncorrected) velocity estimators. We note that the gapper and the standard deviation recover the true velocity dispersion, asymptotically, for high Ngal. However, this is not the case for the biweight estimator, which presents a small asymptotic bias. For small numbers of galaxies, the behaviour of the three estimators is very similar to the one showed in Fig. 2. The standard deviation follows the exact analytic profile derived in Appendix A, as expected, whereas the gapper is shown to be an almost unbiased estimator for any value of Ngal. Table B.1 presents the best-fit values of the parameters D, β, and B in Eq. (9), obtained now for this case of Gaussian velocity distributions.
 |
Fig. B.1. Mean (left panel) and variance (right panel) of SX(Ngal) as a function of the number of galaxies Ngal for the case of Gaussian-distributed random velocities. Green, red, and blue lines represent the behaviour of the standard deviation, gapper, and biweight estimators, respectively. |
Best-fit parameters for the functions describing SX(Ngal) in the case of Gaussian velocity distributions.
Concerning the variance, from a theoretical point of view we would expect the standard deviation to be the lowest variance estimator for a Gaussian distribution. This is confirmed in Fig. B.1, which shows that as expected, the standard deviation follows the theoretical prescription given by
In this case of Gaussian velocity distributions, it is also interesting to test the response of the square of these three estimators 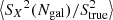 , which in the case of the standard deviation corresponds to the variance. From a theoretical point of view, the variance is one of the ordinary moments of a distribution, and is not biased. Figure B.2 presents the results, confirming this well-known behaviour for the standard deviation, and showing that the other two estimators are clearly biased in this low Ngal regime. Moreover, the variance of the variance follows the expected analytic dependence for the standard deviation,
, which in the case of the standard deviation corresponds to the variance. From a theoretical point of view, the variance is one of the ordinary moments of a distribution, and is not biased. Figure B.2 presents the results, confirming this well-known behaviour for the standard deviation, and showing that the other two estimators are clearly biased in this low Ngal regime. Moreover, the variance of the variance follows the expected analytic dependence for the standard deviation,
We note that the gapper and biweight have a similar dependence of the variance on Ngal. The biweight estimator presents a higher variance.
 |
Fig. B.2. Mean (left) and variance (right) of |
Following the method applied in Sect. 4, we can construct the unbiased scale estimators S′X. We verified that this new set of corrected estimators S′X, defined as in Eq. (11) and using the parameters listed in Table B.1, provides unbiased estimates for the velocity dispersion.
Mass estimators
We now discuss the behaviour of the mass estimators in the case of Gaussian velocity distributions. Here, the reference true mass, M(Strue), is calculated applying Eq. (1), using the parameters A = 1177.0 km s−1 and α = 0.364 from Munari et al. (2013). Figure B.3 illustrates the bias for the uncorrected mass estimator M(Sstd(Ngal))/M(Strue). In general, the dependence on Ngal for all mass estimators is very similar to that in Fig. 8. In particular, the standard deviation mass estimator follows the theoretical analytic form presented in Eq. (A.5). The right panel in the same figure shows the variance of M(SX(Ngal))/M(Strue). Although we note a slightly higher variance at low Ngal, the shapes of the variance profiles are similar to those presented in Fig. 8 for the real cluster simulations.
 |
Fig. B.3. Mean (left) and variance (right) of M(SX(Ngal))/M(Strue) as a function of Ngal for the case of Gaussian random velocities. The dashed line in the left panel represents the expected analytic formula for the dependence of F(Sstd) on Ngal for the standard deviation described in Appendix A. Green, red, and blue lines represent the behaviour of the standard deviation, gapper, and biweight estimators, respectively. |
Bias-corrected mass estimators for Gaussian distributions, based on the plain estimators SX, or their unbiased counterparts S′X, can be obtained using Eq. (15) with the parameters listed in Tables B.2 and B.3, respectively. Similarly to the case of true velocity distributions, in this case of Gaussian velocities, the biweight also has the largest variance, whereas the standard deviation has the lowest, with almost the same behaviour as the gapper.
Best-fit parameters of the functions ⟨M(SX(Ngal))/M(Strue)⟩ for Gaussian velocity distributions.
Best-fit parameters of the functions ⟨M(S′X(Ngal))/M(Strue)⟩ for Gaussian velocity distributions.
Appendix C: Analytical fit to the variance of the different estimators
Section 4.1 and Eqs. (11), (15), and (16) present the definitions of different estimators for the velocity dispersion and the mass for galaxy clusters. For all these cases, Figs. 2, 3, 8, and 9 show the mean and variance ofs the three estimators as a function of Ngal. Analytical expressions for the corrected estimators were given in the main text.
In some applications, it is useful to also have an analytical fit to the variance of these estimators. Here we provide this fit using a common expression for all cases with only two free parameters:
Table C.1 contains the best-fit values for the ϵ and β parameters for all these estimators. In general, the standard deviation estimator has the lowest variance in all cases, and the variance of the gapper is also very close but slightly larger. The biweight estimator has a stronger dependence on Ngal, especially in the low-Ngal regime.
Coefficient of the numerical fit to the dependence of the variance as a function of Ngal for different estimators.
All Tables
Ratio of the relative bias SX(< R200)/SY(< R200) between two estimators X and Y, obtained with all the galaxies in the simulation within a circle of projected radius R200.
Relative bias of the primed estimators due to the selected fraction of massive galaxies.
Average velocity dispersion profile within a given enclosed radius r, ⟨S′std(< r)/Sstd(< R200)⟩, normalised to R200.
Best-fit parameters for the functions describing SX(Ngal) in the case of Gaussian velocity distributions.
Best-fit parameters of the functions ⟨M(SX(Ngal))/M(Strue)⟩ for Gaussian velocity distributions.
Best-fit parameters of the functions ⟨M(S′X(Ngal))/M(Strue)⟩ for Gaussian velocity distributions.
Coefficient of the numerical fit to the dependence of the variance as a function of Ngal for different estimators.
All Figures
 |
Fig. 1. Histograms showing the distribution of individual line-of-sight velocities of all cluster members contained in a cylinder of projected radius R200 along each selected axis for all the 73 simulated clusters, and for three possible orientations of the simulation box along the line of sight (x-, y-, and z-axes). The red line corresponds to a Gaussian profile with the same mean and variance as the full sample. |
| In the text | |
 |
Fig. 2. Mean velocity dispersion SX/Sstd(< R200) as a function of the number of galaxies Ngal (left panel) and its variance (right panel) for our sample of 73 simulated galaxy clusters. The dispersion SX(Ngal) is calculated for the standard deviation (green line), biweight (blue line), and gapper (red line) estimators. |
| In the text | |
 |
Fig. 3. Mean (left panel) and variance (right panel) of the corrected estimators S′X(Ngal)/S′std(< R200) as a function of the number of galaxies Ngal in our sample of 73 simulated galaxy clusters for the standard deviation (green line), biweight (blue line), and gapper (red line). |
| In the text | |
 |
Fig. 4. Effect of type 1 interlopers on the velocity estimates as a function of the number of galaxies for the gapper estimator. The velocity dispersion Sgap(Ngal) is computed first using the full galaxy sample (solid black line, equivalent to the red line in Fig. 2), and then it is compared to the estimates after clipping the galaxy sample at 3, 2.7, and 2.5 sigma in the velocity space. |
| In the text | |
 |
Fig. 5. Combined effect of type 1 and 2 interlopers on S′X(Ngal)/Sstd(< R200) as a function of the number of galaxies. The velocity dispersion, S′X(Ngal), is first computed using the full galaxy sample (equivalent to the three colour lines shown in the left panel of Fig. 3). We also evaluated the response of biweight (blue), standard deviation (green), and gapper (red lines) using samples contaminated by a certain fraction of type 2 interlopers, as described in the text. By construction, our simulations also include the type 1 interlopers because the velocity dispersion is estimated in the cylinder. |
| In the text | |
 |
Fig. 6. Left panel: mean (bias) of S′std(Ngal)/Sstd(< R200) as a function of the number of galaxies Ngal, calculated by choosing galaxies within 100% (solid black line), 1/2 (solid blue line), 1/3 (solid red line), and 1/4 (solid green line) of the complete cluster member samples. Right panel: variance of S′std(Ngal)/Sstd(< R200) as a function of the number of galaxies Ngal. The dashed line represents the theoretical expectation for the variance of the dispersion according to Eq. (10). |
| In the text | |
 |
Fig. 7. Average velocity dispersion profile within a given enclosed radius r, ⟨S′std(< r)/Sstd(< R200)⟩, normalised to R200. The red line represents the mean at each radius of the individual 73 simulated GC profiles (grey lines). The numerical values are given in Table 4. The dashed blue line represents the Sifón et al. (2016) profile, which is almost coincident with our derived profile. |
| In the text | |
 |
Fig. 8. Mean (left panels) and variance (right panels) of M(SX(Ngal))/M(Sstd(< R200)) and M(S′x(Ngal))/M(S′std(< R200)), which represent the standard mass estimator, Eq. (12), applied to normal and unbiased velocity dispersion estimators, standard deviation (green), gapper (red), and biweight (blue). The theoretical expectation for M(Sstd(Ngal))/M(Sstd(< R200)) is represented with the black dashed line. |
| In the text | |
 |
Fig. 9. Mean (left panels) and variance (right panels) of the unbiased mass estimators M′(SX)/M′(Sstd(< R200)) (top row) and M′(S′X)/M′(S′std(< R200)) (bottom row). In all panels, we show the results for the standard deviation (green), gapper (red), and biweight (blue) estimators. |
| In the text | |
 |
Fig. 10. Mean and variance of the M′(SX)/M′(Sstd(< R200)) mass estimator as a function of the number of galaxies Ngal (top panels) and as a function of the aperture radius r (bottom panels). In black, blue, green, and red are represented the fractions that include 100%, 1/2, 1/3, and 1/4 of the most massive galaxies, respectively. |
| In the text | |
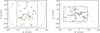 |
Fig. 11. Left panel: example of DOLORES/TNG simulated mask. Right panel: example of OSIRIS/GTC simulated mask. See text for details. Black and green dots represent cluster members outside or inside the telescope field of view, respectively. Black rectangles are the slitlets, and the red points the line-of-sight velocity measurements (the symbol size is proportional to the mass of each galaxy with respect to the most massive galaxy in the mask). The circle in the dotted line represents the projected R200 radius. |
| In the text | |
 |
Fig. B.1. Mean (left panel) and variance (right panel) of SX(Ngal) as a function of the number of galaxies Ngal for the case of Gaussian-distributed random velocities. Green, red, and blue lines represent the behaviour of the standard deviation, gapper, and biweight estimators, respectively. |
| In the text | |
 |
Fig. B.2. Mean (left) and variance (right) of |
| In the text | |
 |
Fig. B.3. Mean (left) and variance (right) of M(SX(Ngal))/M(Strue) as a function of Ngal for the case of Gaussian random velocities. The dashed line in the left panel represents the expected analytic formula for the dependence of F(Sstd) on Ngal for the standard deviation described in Appendix A. Green, red, and blue lines represent the behaviour of the standard deviation, gapper, and biweight estimators, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} \frac{\sigma _{\rm 1D}}{\mathrm{km\,s}^{-1}} = A\left[\frac{h(z)\ M_{200}}{10^{15}\,{M}_{\odot }}\right]^{\alpha }, \end{aligned} $$](/articles/aa/full_html/2020/09/aa34837-18/aa34837-18-eq2.gif)
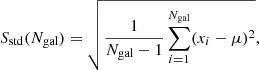
![$$ \begin{aligned} S_{\rm bwt}({N_{\rm gal}}) = \left(\frac{{N_{\rm gal}}^2}{{N_{\rm gal}}-1}\right)^{1/2}\frac{\left[\Sigma _{|u_i|<1}\,(x_i-M)^2\, (1-u_i^2)^4\right]^{1/2}}{\left| \Sigma _{|u_i|<1}\, (1-u_i^2)\, (1-5u_i^2) \right|}, \end{aligned} $$](/articles/aa/full_html/2020/09/aa34837-18/aa34837-18-eq5.gif)
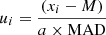
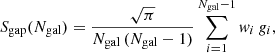
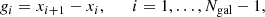
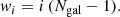
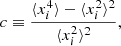
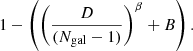
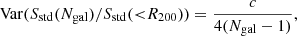
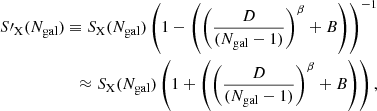
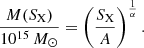
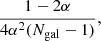
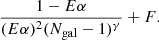
![$$ \begin{aligned}&M\prime \left( {S_{\rm X}}({N_{\rm gal}})\right) = M\left({S_{\rm X}}({N_{\rm gal}}) \right)\left[\frac{1-E\alpha }{(E\alpha )^2(N_{\rm gal}-1)^\gamma }+F\right]^{-1}\end{aligned} $$](/articles/aa/full_html/2020/09/aa34837-18/aa34837-18-eq18.gif)
![$$ \begin{aligned}&M\prime \left( {S\prime }_{\rm X}({N_{\rm gal}}) \right) = M\left({S\prime }_{\rm X}({N_{\rm gal}}) \right)\left[\frac{1-E\prime \alpha }{(E\prime \alpha )^2(N_{\rm gal}-1)^{\gamma ^\prime }}+F\prime \right]^{-1}. \end{aligned} $$](/articles/aa/full_html/2020/09/aa34837-18/aa34837-18-eq19.gif)
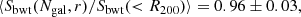
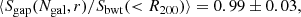
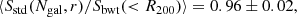
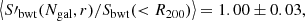
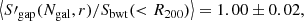
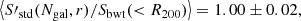
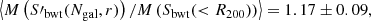
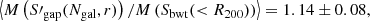
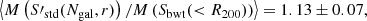
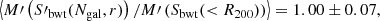
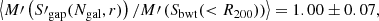
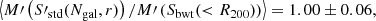
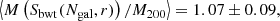
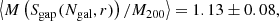
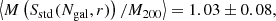
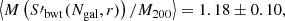
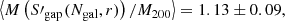
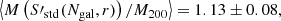
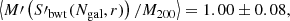
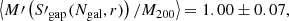
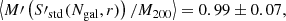
![$$ \begin{aligned} E[x^j]=\sum _{i=1}^Nx_i^j p_i. \end{aligned} $$](/articles/aa/full_html/2020/09/aa34837-18/aa34837-18-eq42.gif)
![$$ \begin{aligned} E[g(v)]=g(E[v]). \end{aligned} $$](/articles/aa/full_html/2020/09/aa34837-18/aa34837-18-eq44.gif)
![$$ \begin{aligned} \langle g(E[v])\rangle \simeq g(v) +g^\prime (v) \langle \Delta E[v]\rangle +\frac{1}{2}g^{\prime \prime }(v) \langle (\Delta E(v))^2\rangle . \end{aligned} $$](/articles/aa/full_html/2020/09/aa34837-18/aa34837-18-eq45.gif)
![$$ \begin{aligned} \left\langle (\Delta E[v])^2\right\rangle =\mathrm{var}(E[v])=\frac{2v^2}{N}, \end{aligned} $$](/articles/aa/full_html/2020/09/aa34837-18/aa34837-18-eq46.gif)
![$$ \begin{aligned} E[g(v)]= g(v) -\frac{1}{2}g^{\prime \prime }(v) \frac{2v^2}{N}\cdot \end{aligned} $$](/articles/aa/full_html/2020/09/aa34837-18/aa34837-18-eq47.gif)
![$$ \begin{aligned} E[\sigma ]=\sigma +\frac{1}{4}\frac{\sigma }{n}, \end{aligned} $$](/articles/aa/full_html/2020/09/aa34837-18/aa34837-18-eq48.gif)