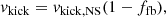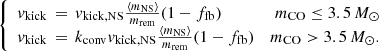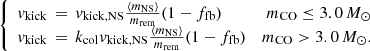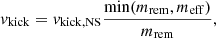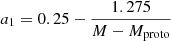| Issue |
A&A
Volume 639, July 2020
|
|
|---|---|---|
| Article Number | A41 | |
| Number of page(s) | 22 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201935332 | |
| Published online | 07 July 2020 | |
BSE versus StarTrack: Implementations of new wind, remnant-formation, and natal-kick schemes in NBODY7 and their astrophysical consequences
1
Helmholtz-Instituts für Strahlen- und Kernphysik, Nussallee 14-16, 53115 Bonn, Germany
2
Argelander-Institut für Astronomie, Auf dem Hügel 71, 53121 Bonn, Germany
e-mail: sambaran@astro.uni-bonn.de
3
Nicolaus Copernicus Astronomical Centre of the Polish Academy of Sciences, ul. Bartycka 18, 00-716 Warszawa, Poland
4
Center for Theoretical Astrophysics, Los Alamos National Laboratory, PO Box 1663, Los Alamos, NM 87545, USA
5
National Astronomical Observatories and Key Laboratory of Computational Astrophysics, Chinese Academy of Sciences, 20A Datun Rd., Chaoyang District, Beijing 100101, PR China
6
Astronomisches Rechen-Institut am Zentrum für Astronomie der Universität Heidelberg, Mönchhofstraße 12-14, 69120 Heidelberg, Germany
7
Main Astronomical Observatory, National Academy of Sciences of Ukraine, 27 Akademika Zabolotnoho St., 03143 Kyiv, Ukraine
8
Swinburne University of Technology, Hawthorn, VIC 3122, Australia
9
Kavli Institute for Astronomy and Astrophysics, Peking University, 5 Yi He Yuan Road, Haidian District, Beijing 100871, PR China
10
Department of Astronomy, School of Science, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo 113-0033, Japan
11
RIKEN Center for Computational Science, 7-1-26 Minatojima-minami-machi, Chuo-ku, Kobe, Hyogo 650-0047, Japan
Received:
21
February
2019
Accepted:
6
April
2020
Context. As a result of their formation via massive single and binary stellar evolution, the masses of stellar-remnant black holes (BH) are subjects of great interest in this era of gravitational-wave detection from binary black hole (BBH) and binary neutron star merger events.
Aims. In this work, we present new developments in the stellar-remnant formation and related schemes of the current N-body evolution program NBODY7. We demonstrate that the newly implemented stellar-wind and remnant-formation schemes in the stellar-evolutionary sector or BSE of the NBODY7 code, such as the “rapid” and the “delayed” supernova (SN) schemes along with an implementation of pulsational-pair-instability and pair-instability supernova (PPSN/PSN), now produce neutron star (NS) and BH masses that agree nearly perfectly, over large ranges of zero-age-main-sequence (ZAMS) mass and metallicity, with those from the widely recognised StarTrack population-synthesis program. We also demonstrate the new, recipe-based implementations of various widely debated mechanisms of natal kicks on NSs and BHs, such as “convection-asymmetry-driven”, “collapse-asymmetry-driven”, and “neutrino-emission-driven” kicks, in addition to a fully consistent implementation of the standard, fallback-dependent, momentum-conserving natal kick.
Methods. All the above newly implemented schemes are also shared with the standalone versions of SSE and BSE. All these demonstrations are performed with both the updated standalone BSE and the updated NBODY7/BSE.
Results. When convolved with stellar and primordial-binary populations as observed in young massive clusters, such remnant-formation and natal-kick mechanisms crucially determine the accumulated number, mass, and mass distribution of the BHs retained in young massive, open, and globular clusters (GCs); these BHs would eventually become available for long-term dynamical processing.
Conclusions. Among other conclusions, we find that although the newer, delayed SN remnant formation model gives birth to the largest number (mass) of BHs, the older remnant-formation schemes cause the largest number (mass) of BHs to survive in clusters, when incorporating SN material fallback onto the BHs. The SN material fallback also causes the convection-asymmetry-driven SN kick to effectively retain similar numbers and masses of BHs in clusters as for the standard, momentum-conserving kick. The collapse-asymmetry-driven SN kick would cause nearly all BHs to be retained in clusters irrespective of their mass, remnant-formation model, and metallicity, whereas the inference of a large population of BHs in GCs would potentially rule out the neutrino-driven SN kick mechanism. Pre-SN mergers of massive primordial binaries would potentially cause BH masses to deviate from the theoretical, single-star ZAMS to mass-remnant mass relation unless a substantial of the total merging stellar mass of up to ≈40% is lost during a merger process. In particular, such mergers, at low metallicities, have the potential to produce low-spinning BHs within the PSN mass gap that can be retained in a stellar cluster and be available for subsequent dynamical interactions. As recent studies indicate, the new remnant-formation modelling reassures us that young massive and open clusters would potentially contribute to the dynamical BBH merger detection rate to a similar extent as their more massive GC counterparts.
Key words: stars: black holes / stars: massive / stars: mass-loss / stars: kinematics and dynamics / supernovae: general / methods: numerical
© ESO 2020
1. Introduction
The formation mechanisms of double compact object binaries undergoing general-relativistic (hereafter GR) inspiral and their occurrence rates has always been a topic of diverse interest (e.g. Abadie et al. 2010). Naturally, this has become a focus of concern since the first direct detection of gravitational waves (hereafter GW) from a binary-black hole (BBH) inspiral and merger of stellar origin by the Laser Interferometer Gravitational-wave Observatory (LIGO; Abbott et al. 2016a). Among the most important ingredients in theoretical modelling and population synthesis of BBH mergers are the natal masses and kicks of stellar-remnant black holes (hereafter BH); this also applies to neutron stars (hereafter NS) while modelling NS-containing binaries. The importance of realistic BH mass estimates became clear right after the very first LIGO detection of ≈30 M⊙ BHs (Abbott et al. 2016b; Belczynski et al. 2016a).
As long as the proto-remnant mass, mproto, in a supernova (hereafter SN) explosion and the amount of material fallback during the SN depend on the carbon-oxygen (CO) core mass and on the pre-SN stellar mass (Fryer 1999; Hurley et al. 2000; Fryer & Kalogera 2001; Fryer et al. 2012), the final remnant mass would depend on the entire life cycle of the progenitor star. In such cases, starting from a given zero-age main-sequence (ZAMS) mass, the sequentially dependent evolutions of the radius, luminosity, mass loss of the star via wind, and total mass would determine the final remnant mass. This is typically the case for the formation of relatively heavier (≳1.4 M⊙) NSs and BHs. For example, by applying “alternative”, theoretical and semi-empirical wind recipes in the main sequence and evolved stages of O- and B-type progenitors, Belczynski et al. (2010a) demonstrated that ≳30 M⊙ BHs, as observed by the LIGO-Virgo (Abbott et al. 2016a, 2017a,b), can easily form from progenitors that have dwarf galaxy- and globular cluster (hereafter GC)-like metallicities, whose masses are impossible to achieve with the “standard” Hurley et al. (2000) wind prescription even at a very low metallicity.
The formation of compact binaries through both field binary evolution (e.g. Belczynski et al. 2002, 2010b, 2016a; Voss & Tauris 2003; Stevenson et al. 2017; Mapelli et al. 2017; Giacobbo et al. 2018) and dynamical interactions in stellar clusters (e.g. Banerjee et al. 2010; Ziosi et al. 2014; Morscher et al. 2015; Rodriguez et al. 2016, 2018; Mapelli 2016; Wang et al. 2016; Askar et al. 2017, 2018; Banerjee 2017, 2018a,b; Park et al. 2017) is now widely studied. In both formation channels, stellar wind, BH masses, and natal kicks play a role. A few widely visible stellar and binary population synthesis programs such as StarTrack (Belczynski et al. 2008, hereafter B08) and MOBSE (Giacobbo et al. 2018; Di Carlo et al. 2019) have now adopted latest stellar-wind and remnant-formation prescriptions (Belczynski et al. 2010a, 2016b, 2020; Fryer et al. 2012). On the other hand, much simpler and crude prescriptions are often used in works that explore the dynamical-formation channel, especially those using the publicly available and widely used direct N-body codes NBODY6 (Aarseth 2003; Nitadori & Aarseth 2012), NBODY7 (Aarseth 2012), and NBODY6++GPU (Wang et al. 2015). We note that such studies of the dynamical-formation channel, nevertheless incorporate adequate or near-adequate treatment of stellar content, Newtonian dynamical interactions, and their GR counterparts; this is the case given that both the field-population-synthesis and dynamical codes presently resort to similar, parametrised recipes for treating the internal evolution of tidally interacting and mass-transferring binaries (Hurley et al. 2002). This, in turn, often makes model ingredients such as BH retention and mass distribution, which critically influence the evolution and compact-binary formation of a cluster, questionable in an otherwise realistic simulation. We note, in particular, that the BH population that is retained in a cluster following the birth of BHs and then becomes available for dynamical processing, influences the formation of both BH- and NS-containing compact binaries (Banerjee 2018a), alongside governing the cluster’s long-term evolution (Chatterjee et al. 2017; Banerjee 2017; Arca Sedda et al. 2018).
This work, for the first time, introduces three major upgrades to the widely used direct N-body evolutionary program NBODY7 (Aarseth 2012), which is a direct descendant of NBODY6 (Aarseth 2003; Nitadori & Aarseth 2012): (a) the semi-empirical stellar wind prescriptions as in Belczynski et al. (2010a, hereafter B10); (b) remnant formation and material fallback according to the “rapid” and the “delayed” SN models of Fryer et al. (2012, hereafter F12), incorporating the occurrences of pair-instability supernova (PSN) and pulsation pair-instability supernova (PPSN) according to the conditions of Belczynski et al. (2016b, hereafter B16); and (c) an explicit modulation of BH and NS natal kicks based on the fallback fraction during their formation. The stellar- and binary-evolution drivers of NBODY6/7 (as well of the Monte Carlo-based star cluster-evolution codes MOCCA; Hypki & Giersz 2013; Giersz et al. 2013 and CMC; Joshi et al. 2000) are the well-known, fitting formulae and recipe-based (as also for e.g. StarTrack) SSE (Hurley et al. 2000) and BSE (Hurley et al. 2002) programs1. After the introduction of the above updates (a), (b), and (c), BSE and NBODY7 are as rich and diverse in essentially all stellar- and binary-evolutionary aspects as modern population-synthesis codes such as StarTrack and MOBSE. This would not only enable the NBODY6/7 community to do more realistic computations but also allow for direct, cross-community comparisons of results.
We note that the above-mentioned upgrades (a) and (c) are partly available in the current public version of NBODY7, but the implementations do not produce outcomes that are fully consistent with StarTrack (see e.g. Banerjee 2017); these implementations should produce consistent outcomes since BSE and StarTrack utilize the same underlying fitting formulae for the stellar-structural parameters (Hurley et al. 2000). In particular, the “maximum BH mass effect” (Belczynski et al. 2010a) is absent in that implementation.
In this work, we validate the above new updates of BSE by comparing its outcomes, for wide ranges of ZAMS mass and metallicity, with those from StarTrack. We note that detailed comparisons among several binary-population-synthesis codes, in the context of the formation of white dwarfs (hereafter WDs) containing binaries, have recently been conducted by Toonen et al. (2014). In this work, however, we focus mostly on NS and BH outcomes since the above upgrades mostly affect SN outcomes.
In Sects. 2, 2.1, and 2.2, we describe our new updates to BSE. In Sect. 2.3, we make detailed comparisons of the remnant outcomes of the updated BSE with those from StarTrack. In Sects. 3, 3.1, and 3.2, we describe how the updated BSE is adapted to the direct N-body integration code NBODY7, the new implementation of the explicit use of SN fallback fraction in determining SN natal kicks, and the new implementations of alternative natal kick models. In Sect. 4, we discuss how the single-stellar, initial mass–final mass relations are affected by the presence of an observationally motivated population of massive primordial binaries in a dynamically active environment such as young massive and open clusters. In Sect. 5, we make a preliminary comparison between (isolated) massive binary evolutions from the updated BSE and StarTrack. In Sect. 6, we summarise our results and indicate forthcoming studies along this line.
2. Updated BSE: Stellar-wind and remnant-formation schemes
In the following, the new implementations in the standalone BSE are described and the outcomes are compared with those of StarTrack.
2.1. Stellar-wind prescription
The recipe for stellar wind follows the semi-empirical prescriptions of B10, which is currently considered the most updated wind model. In the subroutine MLWIND, these prescriptions are implemented in such a way that they are activated individually when the star is evolved until the second asymptotic giant branch (AGB) (BSE stellar type KW ≤ 6; Hurley et al. 2000), in the following sequence of priority: (1) metallicity (Z)-independent luminous blue variable (LBV) wind (Eq. (8) of B10; Humphreys & Davidson 1994), (2) Z-dependent Vink et al. (2001) winds (Eqs. (6) and (7) of B10), (3) Z-dependent Nieuwenhuijzen & de Jager (1990) wind (Eq. (3) of B10), and (4) the Hurley et al. (2000) treatments for lower-mass or colder stars (Kudritzki & Reimers 1978 wind for the giant branch and beyond and Vassiliadis & Wood 1993 wind for the AGB; Eqs. (1) and (2) of B10, respectively). For naked-helium and more evolved stars (KW > 6), only the Z-dependent Wolf-Rayet (WR) wind (Eq. (9) of B10; Hamann & Koesterke 1998; Vink & de Koter 2005) is applied. The conditions for activating the various winds remain the same as in B10. The key difference between this new MLWIND function and that of the original BSE (or of the current public version of NBODY7) is that in the original (older) codes the Nieuwenhuijzen & de Jager (1990) and the Kudritzki & Reimers (1978) winds are applied for low-mass and high-mass stars. In new MLWIND, for massive, hot stars, Vink et al. (2001) winds are applied instead. As it turns out, this makes a substantial difference in the resultant wind mass loss and hence in the remnant mass, especially for sub-solar metallicities.
2.2. Remnant-mass prescriptions
The remnant-mass model is a very important ingredient of stellar-evolution modelling in NBODY7 and BSE, which determines the masses of the NSs and BHs formed as the final product of stellar (and binary; see Sect. 4) evolution. In other words, this prescription together with the underlying stellar structure model and mass-loss recipes (see Hurley et al. 2000 and Sects. 1 and 2.1) determines the “initial–final” relation of stellar evolution. Although the final remnant mass can be expected to be an overall increasing function of the initial ZAMS mass, such initial-final curves often possess intricate excursions depending on the details of the remnant-mass prescription, wind mass-loss prescription, and underlying stellar structure (see e.g. B10, F12; below).
The subroutine HRDIAG in NBODY7 is also directly ported into the standalone BSE after omitting the 100 M⊙ limit from BSE/star. This subroutine derives the remnant mass from the CO core mass in the AGB or naked-helium phases (in addition to dealing with the earlier evolutionary phases) and adequately incorporates the older remnant-mass prescriptions provided by Belczynski et al. (2002), B08, and Eldridge & Tout (2004). The subroutine is now enhanced by incorporating the remnant-mass prescriptions of F12 for the rapid and delayed SN (Eqs. (15)–(17) and (18)–(20) of F12, respectively)2. Moreover, the PPSN and PSN conditions, as described in B16 (see references therein), are implemented in the HRDIAG routine. In the present version of the routine, any of the five remnant-mass schemes can be chosen with a switch (nsflag = 1, 2, 3, 4, 5 for Belczynski et al. 2002, B08, F12-rapid, F12-delayed, and Eldridge & Tout 2004 recipes, respectively) and the PPSN/PSN mass cut-off can be (de)activated independently (psflag = 0 or 1). The fallback amount and fraction onto a BH, mfb, and ffb, respectively, are calculated for each case according to their definitions in F12. As in previous studies, a 10% neutrino mass loss is assumed to obtain the gravitational mass of the remnant from its baryonic mass (=mproto + mfb) in the case of a BH formation and Eq. (13) of F12 (Lattimer & Yahil 1989; Timmes et al. 1996) to account for the neutrino loss during the formation of a NS. The available electron-capture-supernova (ECS; Podsiadlowski et al. 2004) NS formation scheme in NBODY7/HRDIAG, which is analogous to the scheme in B08 producing the characteristic mECS, NS = 1.26 M⊙ NSs, is kept intact (activated with ecflag = 1). Hereafter in this text, “NS” implies a regular NS produced through core-collapse SN and an ECS product is denoted by “ECS-NS”. Both the new MLWIND and HRDIAG routines, as described above, are now shared between the standalone BSE and NBODY7.
In Appendix A, we elaborate on all the amendments in the standalone BSE code to implement the new ingredients as described above and also in Sects. 3.1 and 3.2. We note that this updated BSE, which is used in the rest of this work, retains the same binary-interaction physics (i.e. treatments of tidal evolution, mass transfer, common envelope (CE) evolution, and mergers) as described in Hurley et al. (2002) along with its subsequent amendments as available in the public version of BSE.
2.3. Comparison with StarTrack
Figure 1 demonstrates the agreement in the ZAMS mass-remnant mass relation between the updated BSE and StarTrack for the B083, F12-delayed, and F12-rapid remnant-mass models without PPSN/PSN and for Z = 0.0002, 0.006, and 0.02. Figure 2 demonstrates similar agreements for the F12-rapid case and the metallicities indicated therein, including the PPSN/PSN recipes of B16. The middle panel of Fig. 2 shows the PSN “mass gap” from BSE for Z = 0.0001 and the resuming of BH formation beyond this gap (≳260 M⊙ along the ZAMS axis).
 |
Fig. 1. Comparisons of the ZAMS mass-remnant mass relation between the updated BSE (Sects. 2.1 and 2.2) and StarTrack. The comparison is done for the cases of B08, F12-delayed, and F12-rapid remnant-mass models and for the metallicities Z = 0.0002, 0.006, and 0.02, as indicated in the legends. In all cases in this figure, PPSN/PSN is disabled. In all panels, the black dashed line is the outcome from the new BSE and the blue solid line is the corresponding StarTrack result. The mass gap between NSs and BHs, which is characteristic of the F12-rapid remnant mass model, is also indicated in the corresponding panels (the grey, horizontal lines at ≈2.0 M⊙ and ≈5.0 M⊙ in the F12-rapid panels). |
 |
Fig. 2. Comparisons of the ZAMS mass-remnant mass relation between the updated BSE and StarTrack including PPSN/PSN (F12-rapid SN model) for Z = 0.0001 and 0.002. The line legends are the same as in Fig. 1. Middle panel: PSN mass gap, as obtained from the current BSE for Z = 0.0001, by extending the ZAMS mass beyond 300 M⊙. Bottom panel: between the ZAMS mass-remnant mass relations as obtained from the updated BSE (thick dashed lines) and StarTrack (thin solid lines) up to very large ZAMS masses, extending beyond the PSN mass gap (the black horizontal lines at 40.5 M⊙ and 121.5 M⊙), for a wide range of metallicities. The lower mass gap between NSs and BHs, which is characteristic of the F12-rapid remnant mass model, is also indicated in this panel (the grey, horizontal lines at ≈2.0 M⊙ and ≈5.0 M⊙). |
The bottom panel of Fig. 2 shows such ZAMS mass-remnant mass relations (for the F12-rapid remnant mass model, including B16-PPSN/PSN) up to very large ZAMS masses, beyond the PSN mass gap, for a wide range of Z (colour coding). This panel also demonstrates the excellent agreement between BSE and StarTrack ZAMS mass-remnant mass curves for such large ZAMS masses. For each Z, the extent of the PSN mass gap is also in agreement; that is both the ZAMS mass, at which PSN commences, and the ZAMS mass BH mass point, at which BH formation resumes. We note that with increasing Z, the PSN mass gap diminishes. The BH formation resumes whenever the mass of the He core in the evolved phase (AGB and beyond) of the parent star, exceeds 135 M⊙ (see B16; Woosley 2017). However, a portion of the H-envelope is retained (i.e. the star is of AGB type) at low Z depending on the total wind mass loss; this suggests that the least massive pre-SN star beyond the PSN mass gap, which would directly collapse into a BH, may well exceed 135 M⊙ (see also B16). For a pre-SN star with such a large mass, the direct collapse condition is satisfied irrespective of the remnant-mass model. For solar-like Z, the much stronger winds eliminate the H-envelope nearly completely (i.e. the pre-remnant star is of naked helium type). This means that the pre-SN (pre-collapse) star, just beyond the PSN mass gap, has ≈135 M⊙; given the 10% neutrino mass loss (see B16; Sect. 2.2), this results in a BH of ≈120 M⊙. Hence, the overall PSN BH mass gap, as obtained from BSE/StarTrack, ranges between ≈40 M⊙ and ≈120 M⊙. The limits of this mass gap closely agree with those of Woosley (2017).
Figure 3 shows the close agreements between the BSE and StarTrack ZAMS mass-remnant mass curves, until 300 M⊙ ZAMS mass, for the F12-rapid remnant mass model without and with PPSN/PSN and for Z = 0.02, 0.002, and 0.0002. The clipping of the BH mass at 40.5 M⊙ from the PPSN is apparent in the Z = 0.0002 column. It is also worth considering such comparisons between initial mass-final mass relations for lower ZAMS masses which are WD progenitors. Figure 4 demonstrates the agreement between the initial mass-final mass relations from BSE and StarTrack over the ZAMS mass range of 1 M⊙ − 20 M⊙. It is evident that the outcomes from BSE and StarTrack agree nearly perfectly beginning from low-mass WDs to massive NSs.
 |
Fig. 3. Comparisons of the ZAMS mass-remnant mass relation between the updated BSE and StarTrack up to ≈300 M⊙ ZAMS mass, excluding (top panels) and including (bottom panels) PPSN/PSN (F12-rapid SN model) for Z = 0.0002, 0.002, 0.02. The line legends are the same as in Fig. 1. The significant “clipping” of the BH mass (at ≈40 M⊙) for ZAMS masses ≳100 M⊙ at very low metallicities such as Z = 0.0002, when PPSN/PSN is included (see also B16 and Sect. 2.2), is apparent. |
 |
Fig. 4. Comparisons of the ZAMS mass-remnant mass relation between the updated BSE (thin, black line) and StarTrack (thick, blue line) for lower ZAMS masses (1 M⊙ − 20 M⊙) for F12-rapid remnant mass model. Over this mass range, the switching from WD formation to NS formation is evident (NS formation from the first drop of the curve to 1.26 M⊙). The comparison is shown for the two metallicities Z = 0.02 and 0.0017. |
2.4. Time-step parameters in BSE
We note that such near-perfect agreement of remnant masses between BSE and StarTrack depends on the choice of the stellar-evolutionary time-step parameters pts1, pts2, and pts3 (Hurley et al. 2000) for the main-sequence (MS) and evolved phases, respectively. These BSE input parameters (pts1, pts2, and pts3 respectively) are essentially fractions of stellar lifetimes in the MS, sub-giant, and more evolved phases, which are taken as stellar-evolutionary time-steps in the respective evolutionary stages. For a given underlying stellar structure (Hurley et al. 2000), the accuracy and hence the convergence of the stellar-evolutionary calculation by BSE would be compromised if the time-step parameters are chosen to be too large. On the other hand, choosing values that are too small would result in impractically long computing time and numerical difficulties.
This is demonstrated in Fig. 5, where the B08 remnant-formation scheme (already available in the to-date-public NBODY7/HRDIAG) is applied. As can be seen, the spurious spikes in the BSE ZAMS mass-remnant mass curves, which appear in the maximum-mass part of the curves (see B10) especially at low Z, decline with decreasing time-step parameters. In particular, pts1 = 0.05, pts2 = 0.01, pts3 = 0.02, as defaulted in BSE, still produce considerable spikes for the lower Zs. The combination of pts1 = 0.001, pts2 = 0.01, pts3 = 0.02 is found to be optimal between speed and convergence over a wide range of Z (third row, right panel of Fig. 5), which is what is chosen in the BSE and NBODY7 computations in Figs. 1–3 and the remaining figures in this work. The final panel of Fig. 5 demonstrates that despite taking very small time-step parameters, the current public version of NBODY7/MLWIND produces ZAMS mass-remnant mass relations that overshoot their StarTrack counterparts significantly, especially for low Z and ≳100 M⊙ ZAMS masses. In particular, the saturation effect in BH mass is completely absent unlike the cases with the new MLWIND (with the same implementation of the B08 remnant scheme in HRDIAG) and StarTrack whose outcomes agree nearly perfectly, as demonstrated above.
 |
Fig. 5. Panels 1–6: comparisons of the ZAMS mass-remnant mass relation between the updated BSE (thin lines) and StarTrack (thick lines) for the B08 remnant-formation scheme and for Z = 0.0002, 0.006, 0.02, for different choices of the stellar-evolutionary time-step parameters pts1, pts2, and pts3. The values of these time-step parameters are indicated in the corresponding panels; only one value is indicated when pts1 = pts2 = pts3, otherwise the respective values are indicated. Panel 7: same comparison with pts1 = pts2 = pts3 = 0.001 when the default, to-date-public version of HRDIAG/MLWIND is utilized (see Sect. 2.4 for the details). The StarTrack data in these panels are from B10. |
3. Adoption of the updated BSE in NBODY7: Remnant natal kicks
Although the new MLWIND and HRDIAG routines can be readily shared between the standalone BSE and NBODY7, the main stellar- and binary-evolution engines in the two codes are implemented in different ways, which may produce different remnant masses. Figure 6 demonstrates good agreements between the ZAMS mass-remnant mass relations, over a range of Z and remnant-mass prescriptions, when the new MLWIND and HRDIAG are adopted in NBODY7. The NBODY7 data in Fig. 6 are obtained whilst evolving model clusters of initial mass Mcl(0) ≈ 5.0 × 104 M⊙ (N(0) ≈ 85 K), initially-Plummer (1911) profile with half-mass radius rh(0) ≈ 2 pc, having the standard stellar initial mass function (IMF; Kroupa 2001), where all stars are initially single. With the choices of the BSE time-step parameters suggested in Sect. 2.4, these runs practically do not slow down during the evolution of the most massive remnant progenitors (the first ≈20 Myr) since the primary bottleneck on computing time (up to a given physical time) still comes from the direct N-body integration. These BSE time-step parameters (pts1 = 0.001, pts2 = 0.01) need to be set in the routine trdot in NBODY7 as opposed to specifying them as input parameters in the standalone BSE.
 |
Fig. 6. Comparisons of the ZAMS mass-remnant mass relation between the updated BSE from within NBODY7 and StarTrack, for different Z and remnant-formation prescriptions. For Z = 0.002 and Z = 0.02, PPSN/PSN do not affect the ZAMS mass-remnant mass relation since the He-core mass never reaches the PPSN/PSN threshold (see B16). The mass gap between the NSs and BHs for the F12-rapid cases is indicated with the grey horizontal lines, as in the previous figures. |
3.1. Retention of black holes in stellar clusters: Standard, fallback-controlled natal kicks
In the present context, the retention of stellar remnants, especially of BHs, in stellar clusters (young massive clusters, open clusters, and GCs) after their birth is widely debated. How many and which masses of BHs remain gravitationally bound to their parent cluster after their birth through a core-collapse SN, depending on their natal kicks, is instrumental in determining their long-term population evolution in the cluster, their impact on the structural and internal kinematic evolution of the cluster (e.g.; Kremer et al. 2018; Askar et al. 2018), and the nature of their dynamical pairing and GR merger (e.g.; Banerjee 2017; Farr et al. 2017; Rodriguez et al. 2018; Samsing 2018). The BH natal kicks are also very important for the formation of BBHs and BH-star systems and their coalescences through field binary evolution (e.g. Belczynski et al. 2016a; Stevenson et al. 2017). However, BH natal kicks are, to date, poorly constrained and understood from both observational and theoretical point of view (Willems et al. 2005; Fragos et al. 2009; Repetto et al. 2012, 2017; Repetto & Nelemans 2015; Mandel 2016; Belczynski et al. 2016c). The single Galactic-field NSs (the vast majority of which would be the products of core-collapse SN), on the other hand, are observationally inferred to have large natal kick magnitudes, distributed according to a Maxwellian with one-dimensional dispersion σNS ≈ 265 km s−1 (average speed of ≈420 km s−1; Hobbs et al. 2005).
A common model (as in e.g. Belczynski et al. 2008; Giacobbo et al. 2018) for core-collapse-SN natal kick magnitude, vkick, assumes NS-like kicks for BHs as well (see e.g. Repetto et al. 2012; Janka 2013; Repetto & Nelemans 2015), but which are scaled down linearly with an increasing material-fallback fraction, ffb (see Sect. 2.2); this means that for ffb = 1 (i.e. a failed SN or direct collapse) the natal kick is necessarily zero as follows:
where vkick, NS is chosen randomly from a Maxwellian of σNS = 265 km s−1. For the model computations presented in this subsection, both BHs and NSs are treated with this kick scheme, except for the ECS-NSs, which are given zero or ∼few km s−1 natal kicks (Podsiadlowski et al. 2004; Gessner & Janka 2018).
The vkick, according to Eq. (1), is applied in NBODY7 by transporting the ffb, as computed in HRDIAG (see Sect. 2.2), to the standard version of the subroutine KICK of NBODY7 via a dedicated common block. The KICK routine already includes an elaborate algorithm for generating an isotropic distribution of velocity vectors with their magnitudes, vkicks, chosen from a Maxwellian distribution of a specified dispersion. As in the original NBODY7/KICK routine, the ECS-NSs are distinguished based on their mECS, NS = 1.26 M⊙, which are subjected to lowered dispersion or zero vkicks and are exempted from the above fallback treatment (the ECS engine is assumed to produce a full explosion). Keeping in mind that the newly planted remnant-formation schemes in HRDIAG, such as F12-rapid (Sect. 2.2), produce non-monotonic ZAMS mass-NS mass relations and in particular sub-Chandrasekhar NSs (see e.g. Fig. 10), a very narrow mass window around mECS, NS = 1.26 M⊙ is allowed for the ECS-NS treatment. This is unlike the default NBODY7/KICK, in which the ECS-NS treatment was invoked for mNS ≤ 1.28 M⊙ because the ECS-NSs were the least massive NSs produced according to the Belczynski et al. (2002) and B08 prescriptions. Analogous updates are now also implemented in the standalone BSE kick treatment, which would then accordingly modify the response of a binary to a SN.
Figure 7 shows the early (up to 20 Myr) evolution of the total mass (MBH, bound) and number (NBH, bound) of the BHs bound within the Mcl(0) = 5.0 × 104 M⊙ (initially all single stars) model cluster (see Sect. 3) for the various remnant-formation schemes (i.e. B08, F12-delayed, F12-rapid, F12-rapid+B16-PPSN/PSN; see Sect. 2.2) for this standard, fallback-controlled kick prescription, as given by Eq. (1), when adopted in NBODY7 as above (Z = 0.0001 assumed)4. The differences in the NBH, bound − t curves between the remnant-formation cases arise owing to the differences in ffb whose quantity determines the vkick of the BH (or NS). The differences in the MBH, bound − t curves additionally arise because of the differences in the masses of the BHs (for a given ZAMS mass and Z) between the various remnant-formation cases. We note that in all of the remnant-formation prescriptions considered in this work, all BHs and the heaviest NSs form with a nonzero ffb. In the F12-rapid/delayed schemes, all NSs form with a small amount of fallback (fallback mass, Mfb > 0.2 M⊙; see F12). However, for all NSs, ffb is small (≲10−2) and the corresponding vkick is typically large enough (but see Sect. 3.2) to eject them from a young massive, open, or GC. The only NSs that would be retained in clusters following their birth would be the ECS-NSs that receive small natal kicks (see above) in the present (and the following; Sect. 3.2) kick scheme(s).
 |
Fig. 7. Early (up to 20 Myr) evolution of the total mass, MBH, bound (top left), and number, NBH, bound (bottom left) of the BHs bound within the Mcl(0) = 5.0 × 104 M⊙ (initially all single stars) model cluster (see Sect. 3) for the various remnant-formation schemes (legend), for the standard, fallback-controlled kick model as given by Eq. (1) (Z = 0.0001 is assumed). The corresponding evolutions of the half-mass radius of the cluster’s BH subsystem, rh, BH, bound (top right), and that of only the luminous members, rh, * (bottom right), are also shown. |
As can be seen, in terms of retained BHs (but see below), the B08 remnant-mass model produces more BHs (in both mass and number) than any other remnant model. This is because of the wider “direct-collapse hump” in its ZAMS mass-remnant mass relations for lower ZAMS masses (∼20 − 40 M⊙; see Fig. 1 and B10). The higher BH retention expands a cluster more; the expansion beyond ∼50 Myr is driven mainly by the centrally segregated BH subsystem. For the F12-rapid case, having PPSN/PSN or not makes little difference in practice as long as bulk properties are concerned, since there are only a few stars undergoing PPSN/PSN given the standard IMF in the model cluster. However, the PPSN truncation has important implications for interpreting BBH merger masses (see e.g. B16, Mandel & Farmer 2017). The dips in the MBH, bound − t and NBH, bound − t curves for the F12-rapid cases (top-left and bottom-left panels of Fig. 7) are due to a significant number of BHs receiving partial fallback. This partial fallback occurs in the dip between the two direct-collapse humps of the corresponding ZAMS-remnant curves (see Fig. 6), which escape marginally, and takes time. For massive GCs and nuclear clusters, whose escape speeds (vesc) are much higher (vesc ≳ 100 km s−1), this feature would vanish. The BH subsystems, for all cases, nevertheless sink and concentrate similarly for all the remnant-formation cases (top-right panel of Fig. 7).
Figure 8 shows the BH mass distributions for the four remnant-formation scenarios as indicated in the legends in the panels, for Z = 0.0001. Each panel shows both the mass distribution with which the BHs are born (steel blue histogram) and the mass distribution of the BHs retaining at t ≈ 20 Myr in the Mcl(0) = 5.0 × 104 M⊙ cluster comprised of standard IMF and initially single-only stars. At a time such as t ≈ 20 Myr, which is well after the completion of the BH formation, where the last BH forms at ≈11 Myr, all the unbound BHs (due to vkick > vesc) have escaped through the tidal radius. But the remaining, bound BHs are still in the midst of segregating towards the centre of the cluster (Fig. 7, top right panel) and their dynamical processing has yet to begin. Therefore, the blue histograms fairly represent the mass distributions of the BHs, which become available for long-term dynamical processing, for the various remnant-formation schemes; these schemes correspond to Mcl(0) ≈ 5.0 × 104 M⊙ with vesc ≈ 40 km s−1, standard IMF, Z = 0.0001.
 |
Fig. 8. Mass distributions of BHs obtained in the Mcl(0) = 5.0 × 104 M⊙ model clusters (initially all single stars; Sect. 3) for four remnant-formation scenarios as indicated in the legends (Z = 0.0001 taken). On each panel, both the natal mass distribution of the BHs and the distribution at t ≈ 20 Myr cluster-evolutionary time are shown (the steel-blue and blue histograms, respectively). The latter distribution represents well the mass spectrum of those BHs, which remain gravitationally bound to a medium-mass (young massive or open; in this case taken to be of ≈5 × 104 M⊙) cluster after their birth and which are, therefore, available for long-term dynamical processing in the parent cluster (see Sect. 3.1). The retained BH mass distributions (blue histograms), in these panels, are the outcomes of the standard, fallback-controlled natal kick model (Eq. (1)). |
As shown in Fig. 8, the F12-delayed case inherently produces the largest number of BHs from stellar evolution, as opposed to the resulting retained BHs in which B08 is most successful, as mentioned above. The F12-delayed case is inherently successful because this case has the largest proto-remnant core + fallback masses (see F12), resulting in the lowest BH- and NS-formation threshold with respect to the core-collapsing progenitor mass. But this case also produces the largest number of escapees owing to its smallest direct-collapse hump, ultimately resulting in the smallest number of retainers (see Fig. 7). The F12-rapid cases produce fewer escapees (more direct- and near direct-collapse BHs) owing to the “double hump” (see Fig. 6). The BH distribution is truncated at ≈40 M⊙, as expected, when PPSN/PSN is included.
The discrepancy between the natal and retained mass distribution, as in Fig. 8, gives the number and the mass retention fraction of BHs in a cluster, given the Z and remnant-formation model. Table 1 provides such BH retention fractions, corresponding to the standard, fallback-controlled natal kicks (Eq. (1)), for the various remnant-formation models and Zs considered in this work.
Formation and retention of stellar-remnant BHs in a Mcl(0) ≈ 5.0 × 104 M⊙ model cluster (Sect. 3) as a function of metallicity (Col. 1) and SN–remnant-formation scheme (Col. 2; Sect. 2.2; “+MB” implies the cluster model includes a population of massive primordial binaries as described in Sect. 4).
3.2. Retention of black holes in stellar clusters: Alternative natal-kick prescriptions
While the fallback-modulated natal kick prescription has some observational and theoretical motivation (see Sect. 3.1 and references therein) and is often applied in N-body and population-synthesis studies, it is far from any robust constraint on observational or theoretical grounds, especially for BHs. Therefore, there exists ample room for alternatives of such prescriptions, in particular, for translating the NSs-like kicks to BHs that comprise a much wider remnant-mass range (see e.g. Fig. 8). From the theoretical perspective, a key uncertainty lies in identifying the mechanism(s) that generate spatial and directional asymmetries in the SNs’ ejected (baryonic) material, which, in turn, momentum-propel the remnant. On the other hand, the asymmetry in the neutrino flux during an SN could alone be enough to kick an NS with the typical observed speed (Hobbs et al. 2005). If we assume one dominant SN-kick mechanism and take the observed NS natal kicks as the constraint, then we are already left with several possibilities as formulated below.
3.2.1. Convection-asymmetry-driven natal kick
The convection-asymmetry-driven kick mechanism assumes that the natal kicks are produced by asymmetries in the convection within the collapsing SN core (Scheck et al. 2004, 2008; Fryer & Young 2007). This is similar to the standard kick prescription, but a more accurate prescription would be to boost the kick for systems with longer convection durations: a lower-mode convection produces stronger kicks and it develops with time, so the longer it takes to explode the stronger is the kick. In that case,
In this equation, ⟨mNS⟩ is a typical NS mass, mrem is the remnant (NS or BH) mass, mCO is the CO core mass, and kconv is an efficiency factor (somewhere between 2 and 10) with the theory that we are more likely to get a low-mode convection in explosions that take longer to develop, i.e. those with larger mCO.
3.2.2. Collapse-asymmetry-driven natal kick
Another alternative ejecta kick mechanism would be that produced when asymmetries in the pre-collapse silicon and oxygen shells produce asymmetric explosions (Burrows & Hayes 1996; Fryer 2004; Meakin & Arnett 2006, 2007). In contrast to the convection-asymmetry mechanism (see above), this mechanism would produce stronger kicks for shorter convective durations (smaller mCO) since the asymmetries would be washed out by long periods of convection, that is
In this equation, kcol ≈ 0.1 is the suppression factor for larger mCOs.
3.2.3. Neutrino-driven natal kick
The neutrino mechanism (Fuller et al. 2003; Fryer & Kusenko 2006) would produce the kick through asymmetric neutrino emission. In that case, a formulation would be
where, meff (5 M⊙ ≲ meff ≲ 10 M⊙) is the effective remnant mass beyond which the neutrino emission would not increase significantly with increasing mass of the SN core. Unlike the baryonic material, neutrinos do not fall back onto the remnant to return a part (or whole) of the ejecta momentum, despite the occurrence of such a fallback (or of a failed SN). Hence the omission of the (1 − ffb) term in Eq. (4).
3.2.4. Dependence of BH retention on natal-kick mechanism
It would be interesting to study the impact of these different natal-kick prescriptions on the retention of BHs and NSs in a cluster and, potentially, formulate signatures to observationally distinguish between such cases. For this purpose, we continue to utilize the Mcl(0) ≈ 5.0 × 104 M⊙, rh(0) ≈ 2 pc model cluster (initially single-only stars; Sect. 3) in this work, which facilitates comparisons. To be definite, kconv = 5.0 (Eq. (2)), meff = 7.0 M⊙ (Eq. (4)), and ⟨mNS⟩ = 1.4 M⊙ are used.
Figure 9 shows the early time evolution of MBH, bound, NBH, bound, and NNS, bound in the cluster for the different natal-kick prescriptions formulated in Sects. 3.1, 3.2.1–3.2.3, as obtained from NBODY7 computations (Z = 0.0001). To implement the alternative kick recipes in NBODY7/KICK and BSE/KICK, which can be selected with a switch (KMECH) in the KICK routines, the corresponding mCO is also transported from HRDIAG to KICK via the dedicated common block (see Sect. 3.1).
 |
Fig. 9. Early evolution of the total mass, MBH, bound (top panel), and number, NBH, bound (middle), of the BHs and the number, NNS, bound (bottom), of the NSs bound within the Mcl(0) = 5.0 × 104 M⊙ (initially all single stars) model cluster (see Sect. 3) for the various natal-kick engines (legends; see Sects. 3.1 and 3.2), for the F12-rapid+B16-PPSN/PSN remnant-mass model (Sect. 2.2; Z = 0.0001 is assumed). The collapse-asymmetry-driven kick engine produces relatively low kicks also for some NSs which marginally escape the cluster, taking time, resulting in their build-up at ≈20 Myr followed by a slow decline (bottom panel). After ≈55 Myr when the ECS-NSs begin to form, the latter’s population build up solely for all the kick-mechanism cases. |
As seen, the standard and convection-asymmetry-driven cases collect a very similar number and mass of BHs within the cluster, while the collapse-asymmetry-driven case collects more BHs. This is expected since the latter kick model imparts much lower kicks (cf., Eqs. (1)–(3)) onto the BHs and also onto the relatively massive NSs. The neutrino mechanism behaves the worst in this regard with no BHs retained in the cluster: if the observed high NS kicks are indeed due to asymmetric neutrino emission alone then, provided that the BH natal kick mechanism is the same as for NSs, all BHs would get substantially higher kicks despite significant fallback; the emitted neutrinos would not return any momentum since they do not participate in fallback (see Sect. 3.2.3). If there is indeed, depending on dynamical age, a significant number (∼100) of stellar-mass BHs retaining and comprising a BH subsystem in several Galactic GCs (e.g. Askar et al. 2018; Kremer et al. 2018, 2019), then the neutrino-driven kick mechanism is disfavoured.
The NNS, bound converges to a few after ≈50 Myr after which ECS-NSs start to build up as a consequence of their slow/zero vkick dispersion (see Sect. 3.1). However, there are a significant number of slow-escaping, NSs built up around 10−20 Myr (see Fig. 9, bottom panel). This build-up is unique for the case of the collapse-asymmetry-driven kick, which may be interesting for radio observations in young massive clusters and for supporting or ruling out such a kick scenario. We note that the model clusters utilized in these NBODY7 runs have vesc ≈ 40 km s−1, which is one-half to one-third of typical vescs in massive GCs. Thus we would potentially retain some BHs in massive, compact GCs in all the kick-mechanism cases anyway, although the overall trends would be similar as in Fig. 9. A survey of such GC models exploring the various natal-kick mechanisms, based on the Monte Carlo cluster evolution program MOCCA, is underway (Leveque et al., in prep.).
Figure 10 compares, analogously to Fig. 8 (see Sect. 3.1), the mass spectra of the BHs retained in the parent cluster (at t ≈ 20 Myr) for the different natal-kick prescriptions considered in this work (Z = 0.0001 is assumed). As above, the standard and convection-asymmetry-driven mechanisms produce similar retained BH mass spectra and nearly same BH retention in terms of number and mass. The BHs ≲10 M⊙ escape the cluster at or shortly after birth. In contrast, the collapse-symmetry-driven mechanism produces low natal kicks for all BHs (see also Fig. 11) so that all of them are retained in the cluster, following their natal mass spectrum. We note that such complete retention of BHs for the collapse-asymmetry-driven kick mechanism is due to the low kicks for mCO > 3 M⊙ (Eq. (3)), which is below the BH-formation threshold. Therefore, this is a generic feature and holds true for all remnant-mass schemes and metallicities. In particular, as shown in Fig. 10 (left panel), ≲10 M⊙ BHs would also be retained in GCs and open clusters; this particular feature is unique to the collapse-asymmetry-driven kick mechanism, which can therefore be used to support or rule out such a kick scenario. We note, in this context, that the BH identified in the GC NGC 3201 through radial-velocity measurements has a minimum mass of 4 M⊙ (Giesers et al. 2018).
 |
Fig. 10. Left: comparison between the retained mass distribution of the BHs (inside a Mcl(0) ≈ 5 × 104 M⊙, rh(0) ≈ 2 pc, initially single-only stars model cluster; see also Fig. 8) for the various natal-kick prescriptions considered in this work (legends; see Sects. 3.1 and 3.2). The F12-rapid+B16-PPSN/PSN remnant-mass model (Sect. 2.2) and Z = 0.0001 is assumed. The dashed histogram represents the natal mass distribution of the BHs for these remnant-mass model and Z. No BHs are retained in such clusters in the neutrino-driven-kick case (Sect. 3.2.3; Fig. 9). In contrast, nearly all BHs are retained if the kicks are collapse asymmetry driven. Right: natal mass distribution of NSs for the F12-rapid(+B16-PPSN/PSN) remnant-mass model (black histogram). The retained mass distributions of the NSs for the collapse-asymmetry-driven kick model at t ≈ 20 Myr and 60 Myr are also shown (grey and blue histograms, respectively). The marginally escaping NSs at 20 Myr (Sect. 3.2.4; Fig. 9, bottom panel) are all depleted by 60 Myr when only the low-/zero-kicked ECS-NSs retain in the cluster. |
The natal mass distribution of the NSs is also shown in Fig. 10. The prominent sub-Chandrasekhar peak is a feature of the F12-rapid scheme applied, convolved with the standard IMF of the cluster; these NSs are just the (1 M⊙ proto-remnant +0.2 M⊙ fallback) × 0.9 NSs (see F12). As mentioned before (Sect. 3.1), only the ECS-NSs are retained in the cluster for a longer term, which is demonstrated in Fig. 10 (right panel, blue histogram). For massive GCs, some of the slow-escaping NSs would additionally be retained in the collapse-asymmetry-driven-kick case (see above; Fig. 10, right panel, gray histogram).
Figure 11 shows the vkicks generated by NBODY7, as a function of mCO (left panel) and mrem (right panel), for the different natal-kick recipes considered in this work; because of the logarithmic vertical axis, direct-collapse BHs with ffb = 1 and vkick = 0 are not shown in these panels. In comparison with the typical vesc of the present model clusters, these panels clarify that for such clusters the standard and convection-asymmetry-driven kick models would yield similar BH retention, the collapse-asymmetry-driven case would retain all BHs, whereas the neutrino-driven case would eject nearly all BHs. The 1.26 M⊙ ECS-NSs (see Sect. 3.1), which are given vkicks from a Maxwellian distribution of much lowered dispersion (one-dimensional dispersion of σECSNS ≈ 3 km s−1; see e.g. Gessner & Janka 2018), make up the vertical stripe along the mrem axis (Fig. 11, right panel). Most of these ECS-NSs are retained in these model clusters owing to their low natal kicks. From Fig. 11, it is also apparent that such conclusions concerning the retention of BHs and NSs in clusters remain nearly unaltered for 10 km s−1 ≲ vesc ≲ 100 km s−1, that is for young massive clusters, moderately massive open clusters, and typical GCs. The mass gap between NSs and BHs (Fig. 11, right panel) is a characteristic of the F12-rapid remnant scheme adopted in this example.
 |
Fig. 11. Natal kicks, vkick, as generated by NBODY7, as a function of mCO (left panel) and mrem (right panel), for the different natal-kick recipes considered in this work. The F12-rapid+B16-PPSN/PSN remnant-mass model (Sect. 2.2) and Z = 0.0001 is assumed. Because of the logarithmic vertical axis, direct-collapse BHs with ffb = 1 and vkick = 0 are not shown in these panels; the sharp drop in vkick with increasing mCO or mrem is the approach towards direct collapse. The typical vesc for the Mcl(0) ≈ 5.0 × 104 M⊙, rh(0) ≈ 2 pc clusters considered in this study (blue, solid line) and the Hobbs et al. (2005)σNS ≈ 265 km s−1, whose value in all the kick models are scaled (see Sects. 3.1 and 3.2; black, solid line), are indicated. |
4. Effect of massive primordial binaries
Until now, model clusters initially comprising only single stars are considered in this work. It would be worth looking at the case in which a population of primordial binaries is present in the model, especially among the BH-progenitor stars. The merger among the members of a massive-stellar binary, especially during their advanced (non-remnant) stellar-evolutionary stages, can lead to a stellar structure (the relative masses of the CO-core, He-core, and H-envelope) that is not achievable through the evolution of a single star or even of a ZAMS mass that is equal to the sum of the ZAMS masses of the members (see below, Fig. 13); hence this merger can produce a (single) BH that deviates significantly from the corresponding single-star ZAMS mass-remnant mass relation (see e.g. Marchant et al. 2016; Kruckow et al. 2018; Spera et al. 2019). Such merger events would therefore modify the natal and the retained BH mass spectra, which would in turn modify the BH-driven, long-term cluster evolution and the dynamical GR-merger events involving BHs. We note that in the dynamically active environment of a dense stellar cluster, massive-stellar mergers can happen not only in the course of a massive-binary evolution (leading to Roche lobe overflow and CE phases; see e.g. Ivanova et al. 2013) but also during close binary-single and binary-binary interactions (e.g. in-orbit stellar collisions during Kozai oscillations in a dynamically formed hierarchical triple or during a resonant triple-interaction; see e.g. Banerjee et al. 2012; Leigh & Geller 2013). Even the outcomes of the massive-binary evolution channel can get significantly altered via close dynamical encounters that would alter the orbital parameters of the binaries. In principle, in such an environment, a given massive star can undergo multiple mergers until a BH is formed (e.g. Fujii & Portegies Zwart 2013; Wang et al. 2020) or even a BH non-progenitor can grow in mass to become a BH progenitor. Finally, we note that BH masses can get altered by not only such star-star mergers but also by other stellar-hydrodynamical processes such as envelope ejection during a CE phase and enhanced stellar wind in a tidally interacting binary; such processes can either be an outcome of massive-binary evolution or triggered dynamically (or both).
A detailed study of the influence of dynamical interactions on massive-binary evolution is beyond the scope of the present work. To find out to what extent BH masses can get altered because their progenitors are binary members, we evolved with NBODY7Mcl(0) ≈ 5.0 × 105 M⊙, rh(0) ≈ 2 pc model clusters as before but with all stars (also sampled from a standard IMF) of ZAMS mass ≳16 M⊙ initially paired in binaries among themselves. A high fraction of massive-stellar (O star) binaries (fObin(0) = 100% initially in these models) are indeed consistent with observations of young massive clusters (Sana & Evans 2011; Sana et al. 2013). Motivated by such observations, these O-type stellar binaries initially follow the orbital-period distribution of Sana & Evans (2011) and a uniform mass-ratio distribution. In this distribution, an O star is paired only with another O star as typically observed, and the pairing among the lower-mass stars is obtained separately (see below). The orbital periods of the primordial binaries that are not O stars (≲16 M⊙ ZAMS) follow a Duquennoy & Mayor (1991) distribution that represents a dynamically processed binary population (Kroupa 1995) and their mass-ratio distribution is also uniform. The initial binary fraction among the non-O-type stars is small; fbin(0) ≈ 5%. The initial eccentricities of the O-type stellar binaries follow the Sana & Evans (2011) eccentricity distribution and those for the rest of the binaries are drawn from the thermal eccentricity distribution (Spitzer 1987)5. As explained in Banerjee (2018a), such a scheme for including primordial binaries provides a reasonable compromise between the economy of computing and consistencies with observations.
The filled, black squares in Fig. 12 (top row) show the remnant mass versus ZAMS mass for the above model cluster with massive primordial binaries, when evolved with NBODY7 that includes the updated BSE (Sect. 2). For the BH progenitors that have undergone a star-star merger before the BH formation, the ZAMS mass of the primary, which is the more massive of the members participating in the star-star merger at the time of the merger, is plotted in the abscissa. Owing to BH progenitors undergoing mergers in their evolved phases and/or because of other stellar-hydrodynamical processes before the BH formation (see above)6, the resulting BH masses deviate significantly from the ZAMS mass-remnant mass relations (for single ZAMS stars by definition) for the assumed remnant-formation scheme (F12-rapid with and without PPSN/PSN) and metallicity (Z = 0.0001). The majority of the BHs are over-massive, showing broader natal and retained BH mass distributions as contrasted with those from single stars only, for models with and without PPSN/PSN physics included; the standard, fallback-controlled natal kick is assumed in Fig. 12. Also, because of the formation of more massive BHs, the total mass of the BHs formed/retained in the cluster is similar to that of the initially-single-star-only model clusters (Fig. 12, third row) despite the BHs forming and retaining in a smaller number (due to the mergers; Fig. 12, fourth row). These dependences, as demonstrated in Fig. 12, suggest that BH retention in a cluster and the retained mass spectrum of BHs both depend on the binary properties of the progenitor stars of BHs. Table 1 demonstrates the somewhat increased mass and number retention fractions of BHs, at Z = 0.0001, in the presence of a massive primordial-binary population as adopted in this work (cf. top and bottom sections of the table). We note that although complex, dynamical-interaction-mediated channels leading to star-star mergers (see above) among members from different binaries can and do occur in these models, most of these mergers are between the members of the same O-star primordial binary occurring from Roche lobe overflow. The overflow itself can, of course, be triggered via dynamical perturbation of the orbit of the binary7.
 |
Fig. 12. Remnant production and retention in the NBODY7-computed, Mcl(0) ≈ 5.0 × 104 M⊙, rh(0) ≈ 2 pc model cluster with all BH-progenitor stars paired in primordial binaries (see Sect. 4). In all the panels, “+MB” indicates the presence of such a population of massive primordial binaries; the absence of this symbol in a legend implies the case in which all stars are initially single. The F12-rapid remnant-formation prescription and Z = 0.0001 is assumed without (left column) and with (right column) PPSN/PSN. Top row: ZAMS mass vs. remnant mass (black filled squares) compared with the corresponding StarTrack outcomes from pure single-star evolution (blue solid lines; cf. Fig. 6). For the BH progenitors that have undergone a star-star merger before the BH formation, the ZAMS mass of the primary (the more massive of the members participating in the star-star merger, at the time of the merger) is plotted in the abscissa. For reference, the ZAMS mass-remnant mass points (orange empty squares) from an identical model cluster but with initially only single stars (as in Sect. 3; cf. Fig. 6) are also shown. Second row: natal and retained mass distributions of the BHs (steel blue and blue filled histograms, respectively; assuming the standard, fallback-controlled natal kicks). These are compared with the corresponding BH natal mass distribution without any massive primordial binaries (dashed empty histogram, cf. Fig. 8). Third row: cumulative time development of the total BH mass, MBH, as they are born (steel blue solid line) and the total BH mass, MBH, bound, that is bound to the cluster as a function of time (solid blue line). The MBH(t) corresponding to initially only single stars is also shown (black, dashed line). Fourth row: same as the third row but for the BH numbers NBH and NBH, bound. |
The BH masses in Fig. 12 should, however, be taken with caution. The BH masses depend on how the evolved stars are “mixed” at their merger to compose the stellar collision product. This is rather simplistic in BSE, where a complete mixing is assumed to compute the stellar-evolutionary age and hence the CO-core and He-core masses of the merged star. A simple recipe for the dynamical mass loss during the merger process is assumed, which results in a mass loss of ≲15% of the total available mass budget per merger (e.g. Glebbeek et al. 2009)8. In reality, a star-star merger is likely to be a much more complex process whose study is beyond the scope of the present work. Nevertheless, this study suggests that the natal or retained BH mass function in clusters can potentially be substantially modified and broadened, despite PPSN/PSN, provided that the clusters contain a high fraction of massive primordial binaries at their young age, as observed in young massive and open clusters.
This is because of the unusual structure obtained in merger products, which contain a much more massive H-envelope when the He-core is below the PPSN threshold of 45 M⊙ (that see B16), compared to that of a single-stellar-evolution product of the same He-core mass. The substantial H-envelope in the merger products results in BHs (formed via direct collapse) well exceeding 50 M⊙ despite the sub-PPSN He core. We note that the BH mass surpasses the mBH = 40.5 M⊙ PPSN cut-off; this mass would result from the collapse of a 45 M⊙ He-core after subtracting for the 10% neutrino mass loss. This is also the case for a ZAMS mass that approaches ≈100 M⊙ from below, resulting in the He-core approaching the PPSN threshold of 45 M⊙, and for pure single-star evolution as well, but in this case only by a few M⊙ (see Figs. 2 and 6). As a consequence of much more massive H-envelope for similar He-core masses, this surpassing happens to a much larger extent for the BHs obtained from merger products that result from the observationally motivated massive binary population, as adopted in this work, in a dynamically active environment. However, this still retains the notion that BBH mergers comprising one or both of the members with mBH ≳ 40 M⊙ (the single-stellar PPSN cut-off limit) are necessarily of dynamical origin (see e.g. Rodriguez et al. 2018). This is because after being formed from a star-star merger product, a BH can continue to interact with stellar members and remnants and participate in a GR merger only in a dynamically active environment. However, the occurrence of BBH mergers within the PSN mass gap in this way would not require low natal spins of (first-generation) BHs. On the other hand, if stellar progenitors indeed produce very low spin BHs irrespective of their own spin, internal structure, and chemical composition (Spruit 2002; Fuller et al. 2019), then, again, in contrast to the widely conceived notion of second-generation BHs with high spins, these mass-gap BBH mergers would exhibit a low effective spin parameter, provided the first-generation, mass-gap BH has merged with another first-generation BH (see also Spera et al. 2019 in this context).
On the other hand, when the He-core mass exceeds the PPSN threshold of 45 M⊙ and until the end of the PSN gap is reached (He-core mass of 135 M⊙; see Sect. 2.3), the outcome becomes independent of the mass of the H-envelope around it. Namely, when the He-core mass lies between 45 M⊙ and 65 M⊙ (the PPSN range) a BH of 40.5 M⊙ is born via direct collapse as a result of PPSN and for He-core between 65 M⊙ and 135 M⊙ no remnant is left due to PSN; the BH formation is resumed and the BH mass again depends on the H-envelope mass if the He-core exceeds 135 M⊙ (see Sect. 2.3 and Fig. 2). We note that in the present BSE scheme a stellar object is always treated in the same, single-star way (see Sect. 2.2) irrespective of whether it is a merger product or not. Hence, even for a merger product with an unusually massive H-envelope, a 40.5 M⊙ BH (no BH) is formed whenever the PPSN (PSN) condition is reached; these conditions and the corresponding outcomes are dependent solely on the He-core mass. This is why in Fig. 12 there are only 40.5 M⊙ or no BHs beyond the start of the horizontal, single-star PPSN line (at ZAMS mass ≈100 M⊙ for Z = 0.0001) even in the presence of massive primordial binaries. A merger which typically leads to a similar or more massive He-core, depending on the mass ratio and epochs of the merger members, exclusively satisfies either the PPSN or PSN condition when a star of ZAMS mass ≳100 M⊙ is involved. In this example, all but one of the PPSN derived BHs and PSN points, beyond 100 M⊙ ZAMS, come from star-star merger products. For reference, Fig. 13 re-plots the top row of Fig. 12 with the sum of the ZAMS masses of the members of the star-star mergers along the abscissa, for the primordial-binary model. Of course, the deviations from the single-star ZAMS mass-remnant mass relations are less dramatic in this figure, especially for large combined ZAMS masses, and not all BHs beyond ≳100 M⊙ combined ZAMS are formed via PPSN.
 |
Fig. 13. Same as in the top row of Fig. 12 except that for the model cluster with massive primordial binaries (see Sect. 4), the ZAMS mass of the primary plus the ZAMS mass of the secondary of the pre-remnant-formation, star-star mergers are plotted along the abscissa. The legends are the same as in Fig. 12. |
We note that when a much more massive H-envelope, compared to what would be available from single stellar evolution, is present owing to, for example a merger as considered in this work, a PPSN may shed only a part of the envelope resulting in a BH that is significantly more massive than what the collapse of the He-core alone (i.e. if the envelope is entirely expelled) would give. The PPSN/PSN recipe of B16 (see above and Sect. 2.2), as implemented in the current StarTrack and in the new BSE introduced in this work and which is also applied for star-star merger products, assumes complete stripping of the H-envelope, always resulting in a 40.5 M⊙ BH. This agrees with the hydrodynamic study of PPSN/PSN in single massive stars by Woosley (2017), in which a small remaining H-envelope results in BHs up to ≈52 M⊙ as outcomes of PPSN in low-Z, massive stars. More massive BHs would potentially result from merger products where the PPSN is triggered in the presence of a substantially more massive H-rich envelope. This would, in turn, diminish the PSN mass gap (see Sect. 2.3 and references therein, Fig. 2). Also, owing to the enhanced pressure from such an envelope, PPSN may be triggered prematurely when the He-core is of ≲45 M⊙, resulting in a longer PPSN phase with a larger number of mass-loss episodes. At present, such stellar models are unavailable. Although beyond the scope of the present study, a more elaborate study of this regime will be presented elsewhere.
Of course, the extent of the exceeding of the single-star PPSN cut-off depends on the amount of dynamical mass loss during the star-star merger process. The physical process of merger among stars and the associated mass loss is poorly understood; this is especially the case for massive stars beyond the MS. At present, the mass loss from star-star mergers in NBODY7/BSE is at most moderate, ranging from ≈15% (energetic, equal-mass MS-MS mergers) to zero (non-MS or low-K.E. mergers; see above); the MS-MS merger mass loss is consistent with basic hydrodynamic (e.g. Lombardi et al. 2002) and the “sticky-star” (e.g. Gaburov et al. 2008) treatments of the process. However, if the mass loss per merger is much higher, that is comparable to the mass of the secondary in all mergers, then the H-envelope in the merger products would be similarly massive as in single-stellar evolution. In such a case, the remnant mass–ZAMS mass relations and the PSN mass gaps would be much less affected by massive-stellar mergers from primordial binaries.
Figure 14 demonstrates this for the case of F12-rapid remnant-formation including PPSN/PSN and low metallicity (Z = 0.0001). The panels in Fig. 14 show the remnant mass–ZAMS mass outcomes from different calculations of the primordial-binary model with increasing fraction, fmrg, of the secondary’s (the less massive merger participant’s) mass lost during a merger: from fmrg = 0.3 in energetic MS-MS mergers only (NBODY7/BSE default) through fmrg = 0.5 in all star-star mergers, to fmrg = 0.8 in all star-star mergers9,10. Figure 14 suggests that despite mergers of massive primordial binaries, fmrg = 0.5 (≲25% loss of the total primary + secondary mass at the time of the merger; see de Mink et al. 2013 in this context) already restores the PPSN/PSN plateauing of BH mass as obtained from the latest core-collapse calculations (maximum BH mass of ≈52 M⊙; Woosley 2017) and fmrg = 0.8 (≲40% loss of the total available mass budget) nearly restores the entire single-star remnant mass–ZAMS mass relation. In other words, if the single-star remnant mass–ZAMS mass relation is to be unaffected by massive primordial-binary mergers, then substantial mass loss of up to ≈40% would be necessary in such mergers.
 |
Fig. 14. Remnant production and retention in the NBODY7-computed, Mcl(0) ≈ 5.0 × 104 M⊙, rh(0) ≈ 2 pc model cluster with all BH-progenitor stars paired in primordial binaries (see Sect. 4). The legends are the same as in the top panels of Fig. 12. The panels show different computations that adopt different extents of mass loss during a star-star merger process: the left panel shows the case that has defaulted in NBODY7/BSE, namely, mass-loss fraction of fmrg = 0.3 from the secondary for energetic MS-MS collisions only (see text) and zero otherwise (the data in this panel are identical to those in the top right panel of Fig. 12), the middle panel shows the NBODY7 computation where a mass-loss fraction of fmrg = 0.5 from the secondary is implemented for all star-star mergers, and the right panel shows the computation where a mass-loss fraction of fmrg = 0.8 from the secondary is implemented for all star-star mergers. With increasing extent of mass loss in mergers (left to right panel), the single-star ZAMS mass-remnant mass relation (orange, empty squares) gets affected by massive-stellar mergers (black, filled squares) to a diminishing extent. The F12-rapid remnant-formation prescription, including PPSN/PSN, and Z = 0.0001, is assumed in this demonstration. |
5. Comparison with StarTrack binary evolution
In Sect. 2.3, the comparison between the remnant outcomes of StarTrack and BSE were limited to single stellar evolution. In the present context, it would be worth comparing between the outcomes of binary evolution with StarTrack and the updated BSE. Such a comparison (as such, between any two binary-evolution programs) is a more complex affair than comparing single-stellar evolution due to the differences in the treatments of binary-interaction physics, namely tidal interaction, mass transfer, CE evolution, as well as in the treatments of star-star and star-remnant merger products. The difficulty of such a comparison exercise is augmented by the fact that these binary-interaction processes are themselves poorly understood (Ivanova et al. 2013).
At the moment, it is formidable to do a BSE–StarTrack comparison while integrated within NBODY7 as done above for BSE alone. Integration of StarTrack within NBODY7 is far from straightforward partly because of the difference in programming languages (C in StarTrack versus Fortran in NBODY7 and BSE) and partly because of the rather rigid structure of the subroutines of NBODY7 that connect BSE to its N-body integration engine. A foreseeable solution would be to use a bridging framework such as AMUSE (Portegies Zwart & McMillan 2018) but, currently, neither NBODY7 nor StarTrack is adequately adapted for use in AMUSE.
Therefore, to preliminarily assess the differences in the outcomes of BSE and StarTrack in the context of remnant formation, which is the focus in this work, we evolve 12 selected massive binaries with updated BSE and StarTrack. The individual binary parameters and the corresponding remnant outcomes with BSE and StarTrack are summarised in Table 2. For both BSE and StarTrack evolutions, metallicity Z = 0.0001, CE efficiency parameter αCE = 1.0, F12-rapid+B16-PPSN/PSN remnant model, and star-star and star-BH merger mass-loss fraction of fmrg = 0.5 of the secondary (less massive) member are applied. The mass transfer is set to be Eddington limited (Eddington limiting factor = 1.0).
Remnant outcomes of selected massive binaries when evolved with StarTrack (Col. 5) and updated BSE (Col. 6).
The main difference between these BSE and StarTrack outcomes is that StarTrack leads to more star-star mergers (especially during CE) than BSE, leading to a single BH remnant. As evident from Table 2, all but one of the binaries yield just one remnant in StarTrack (including one no-remnant outcome due to PSN). In contrast, through BSE evolution, 8 out of the 12 binaries lead to double remnants, 3 of which are BBHs and 2 of these merge within a short delay time.
The main cause of differences in binary-evolutionary outcomes between BSE and StarTrack, in these examples is a result of the differences in the treatment of tidal energy loss among the interacting binary members. In particular, as described in Belczynski et al. (2008), StarTrack employs 50 times stronger tidal energy loss than BSE (Hurley et al. 2002) for convective stellar envelopes and the energy dissipation is weaker for radiative envelopes owing to the use of tidal constants of Claret (2007). These differences cause the initial, post-SN, and post-CE-ejection detached (and eccentric) binaries to shrink (and circularise) at different rates, leading to subsequent binary interactions at different stellar-evolutionary ages. In particular, the more efficient tidal dissipation for convective envelopes would lead to faster orbit shrinking (during spin-orbit synchronisation), leading to Roche lobe filling at a younger age when the member stars have smaller radii, thus leading to mergers in more of the systems. At the same time, for radiative envelopes, the reduced tidal efficiency leads to mergers by slowing down the orbital circularisation, enabling Roche lobe overflow near the periastron at a younger age when the stars have swelled less.
Interestingly, if we only consider the most massive remnant produced from each binary evolution, their masses agree reasonably well among BSE and StarTrack and very closely for 7 out of the 12 binaries. This is demonstrated in Fig. 15; see also Table 2. The differences between StarTrack and BSE remnant masses are less visible in this way since, for most of the evolutions, the mass of the heavier among the two remnants or of the single remnant is determined mainly by the PPSN mass ceiling and star-star and star-BH merger mass loss, which are taken to be identical for BSE and StarTrack in this exercise.
 |
Fig. 15. Remnant outcomes of 12 massive binaries, with initial parameters as given in Table 2, when evolved with updated BSE (black filled squares) and StarTrack (magenta filled squares). Plotted along the X-axis are the binaries’ primary (the more massive member) ZAMS masses and the masses of the single remnant or of the heavier of the two remnants of the binary evolutions are plotted along the Y-axis. Because of the adopted NS upper mass limit, a remnant of > 2.5 M⊙ (≤2.5 M⊙) is a BH (NS). These BSE and StarTrack evolutionary calculations are done for the F12-rapid+B16-PPSN/PSN remnant-mass model with the same choices of evolutionary parameters; the values of the most relevant parameters are Z = 0.0001, αCE = 1.0, and fmrg = 0.5. |
The difference in treatments of tidal interaction and also in implementations and numerical approaches would lead to differences in outcomes of low-mass interacting binaries as well. Such a study is beyond the present scope; see Toonen et al. (2014) in this context.
6. Summary and outlook
The work presented above is summarised below, in which motivations for the next steps are also described. A re-implementation of the B10 wind model (Sect. 2.1) and the adoption of newer remnant-mass prescriptions such as F12-rapid and F12-delayed, including the PPSN/PSN conditions of B16 (Sect. 2.2) in the widely used population synthesis program BSE, reproduces the ZAMS mass-remnant mass relations of StarTrack nearly perfectly over a wide range of ZAMS mass, remnant-formation scheme, and metallicity. (Sect. 2.3, Figs. 1–3). Such agreements however require smaller stellar-evolutionary time-step parameters (the pts1, pts2, and pts3 parameters) than their default values while running BSE (Sect. 2.4, Fig. 5), which slightly slows down the program. The new BSE, therefore, now incorporates remnant-mass and stellar-wind prescriptions, in terms of detail, flexibility and the outcomes, at par with current and up-to-date population-synthesis programs such as StarTrack and MOBSE.
These new developments in BSE naturally get ported into the direct N-body code NBODY7 since the latter adopts BSE as its stellar-evolution and remnant-formation driver. The adoption of the new BSE routines (the functions MLWIND and HRDIAG) in NBODY7 yields a similar quality of reproduction of the StarTrack ZAMS mass-remnant mass relations, for NSs and BHs formed from single stars within model star clusters (Sect. 3, Fig. 6).
To deal with the retention of NSs and BHs in such model clusters at their birth, an explicit fallback modulation is implemented in the natal-kick generator of NBODY7, which can be directly ported into the corresponding implementation in the standalone BSE program (their KICK routines; Sect. 3.1). In addition to this standard, fallback-controlled natal kick prescription, its variants describing convection-asymmetry-driven and collapse-asymmetry-driven natal kicks are prescribed along with a neutrino-driven kick model (Sect. 3.2, Fig. 11).
The above implementations have now been tested to work very stably in an extensive set of long-term NBODY7 runs (Banerjee, in prep.). These new stellar-evolutionary ingredients and natal-kick models have now as well been ported to NBODY6++GPU and tested to perform as stably (in prep.).
The various remnant and natal-kick prescriptions in the routines HRDIAG and KICK can, at present, be selected based on switches built in these routines (for NBODY7, also the stellar-evolutionary time-step parameters), requiring recompilation of BSE and NBODY7. In the near future, arrangements will be made to provide these switches in the inputs, to make the options more accessible. Such a tested version of standalone BSE, with all the newly implemented prescriptions described in this work, can be obtained freely from GitHub11.
For a given cluster (and given IMF), the amount of BHs retained (i.e. remaining gravitationally bound to the cluster) due to sufficiently low natal kicks that become available for long-term dynamical processing depends on the remnant-formation mechanism (Fig. 7), the natal-kick mechanism (Fig. 9), and metallicity (Table 1). For all remnant-formation and natal-kick schemes (except for the collapse-asymmetry-driven case; see below), the retained BHs are generally top heavier in mass spectrum compared to their birth mass spectrum (Figs. 8 and 10) as a consequence of the preferential escape of lower-mass BHs as a result of their higher natal kicks (or smaller fallback mass; Fig. 11). The F12-delayed remnant-formation model gives birth to the largest number of BHs (as opposed to the resulting retained BHs where B08 maximises), but it also produces the largest number of escapees ultimately resulting in the smallest number of retainers.
Table 1 gives the BH mass and number retention fractions in a moderately massive stellar cluster as a function of remnant-formation scheme and metallicity for the standard, fallback-controlled natal kick. The convection-asymmetry-driven kick mechanism would result in nearly the same retention fractions, the collapse-asymmetry-driven mechanism would lead to all retention fractions ≈1.0, and the neutrino-driven mechanism would lead to all retention fractions ≈0.0 (Figs. 9 and 11). Hence, if ∼100 BHs still are retained in some present-day GCs as inferred when their observed photometric and internal-kinematic structures are compared with model computations (e.g. Askar et al. 2018; Kremer et al. 2018, 2019), then the neutrino-driven mechanism can possibly be ruled out. If forthcoming observations suggest the presence of ≲10 M⊙ BHs in GCs and/or open clusters and/or young massive clusters, then this would provide support to the collapse-asymmetry mechanism (Sect. 3.2.4, Fig. 10). For the case of the latter kick mechanism, a population of slow-escaping core-collapse NSs can also be expected in the field of view of ∼10 − 20 Myr-aged young clusters (Sect. 3.2.4, Fig. 9), which may be identified in the future through radio observations. The BH retention fractions in Table 1 represent those in a moderate-escape-velocity system, essentially due to direct collapse or a substantial amount of material fallback alone. For massive GCs, their higher escape velocity would additionally aid retention, potentially resulting in somewhat higher retention fractions in all cases. These inferences encourage future, more elaborate studies of discriminatory signatures of natal-kick mechanisms in stellar clusters, especially in more massive systems (Leveque et al., in prep.).
If BH-progenitor stars exist in high primordial-binary fractions, as observed in young massive and open clusters, then, depending on the mass loss during star-star merger process, the natal and cluster-retained mass spectra of the BHs would become wider; at low metallicities, the BH mass can exceed well beyond 40 M⊙ even in the presence of PPSN, forming BHs bound to a stellar cluster well within the PSN mass gap (Sect. 4, Fig. 12). Since such BHs are still direct derivatives of stellar progenitors, they would potentially have very low spins (unless the star-star merger happens late in the evolution of both stars). A high primordial-binary fraction among BH progenitors would also lead to a moderately higher BH-retention fraction in both mass and number (Table 1), although the total number of BHs produced, under such circumstance, would be somewhat smaller owing to the mergers (Fig. 12). The BH masses get altered because of pre-BH-formation stellar mergers and/or other stellar-hydrodynamical processes (e.g. CE envelope ejection, tidally-enhanced stellar wind). In this work, these modified BH masses are the outcomes of the simplistic treatment of these complex physical processes in the binary-evolution engine of BSE along with the single-star-like treatment while forming remnant masses from stellar-merger products that would have altered stellar structure, which is why their values should be taken with caution.
The above effect, if real, would still preserve the (potentially future) LIGO-detected BBH mergers comprising ≳40 M⊙ members as signatures of dynamically triggered BBH mergers in clusters, except that such inferences no longer need to depend on low natal spins of BHs (see e.g. Rodriguez et al. 2018). If stellar progenitors indeed produce low-spinning BHs irrespective of their own spin (Belczynski et al. 2020), internal structure, and chemical composition, then such mass-gap BBH mergers could potentially exhibit low effective spin parameter. In a separate study we will investigate whether a dynamically active environment such as that inside a stellar cluster aid in inducing star-star mergers that lead to low-spin, PSN-mass-gap BHs. If the single-star remnant mass–ZAMS mass relation is to be unaffected by massive primordial-binary mergers, then a substantial mass loss of up to ≈40% would be necessary in such mergers (Sect. 4, Fig. 14). In this context, it would be worth bearing in mind that the PPSN cut-off mass is not strictly constrained (see B16). In particular, the recent measurement of a ≈50 M⊙ primary in the BBH merger event GW170729 (Abbott et al. 2019a,b; but see Fishbach et al. 2020) may call for a moderate revision of the PPSN BH mass limit in population-synthesis codes to increase it by ≈10 M⊙, as was already proposed in Belczynski et al. (2020, see their Fig. 3). Considering the full mass spectrum of BBHs detected to date by LIGO-Virgo (Abbott et al. 2019a), GW170729 is statistically consistent with being a first-generation merger (Chatziioannou et al. 2019; Kimball et al. 2020). Also, a more elaborate study of the influence of a dynamically active environment on massive-binary evolution will commence in the near future.
The ZAMS mass-remnant mass relations for the B08 case correspond to those of B10, which adopts the B08 remnant-mass model along with the newer wind recipes as described in Sect. 2.1 of this paper. This same wind model accompanies all the remnant-mass models considered in this work.
Hereafter, the subscript “bound” indicates quantities measured within the cluster’s tidal radius, Rt ≈ 90 pc, as is customary. Most of the BHs within Rt are indeed gravitationally bound to the cluster but, at a given time, a few of these may be about to escape the cluster. The number of the latter depends on the vkick of the BHs and the escape speed from the cluster (vesc ≈ 40 km s−1 here).
We note the recent work by Geller et al. (2019) questioning the validity of the assumption of an initial thermal eccentricity distribution of the primordial binaries. The sub-population of primordial binaries that directly influences the present results is the O-star-binary population for which the adopted (sub-thermal) initial Sana & Evans (2011) eccentricity distribution is motivated by observations.
The BH masses are printed right at their formation by arranging a special output in the new KICK routine (Sects. 3.1 and 3.2), as also for the NBODY7 data points in Fig. 6. Hence, any merger(s) or stellar-hydrodynamical process(es), influencing an NBODY7 BH mass in Fig. 12, must have happened before the BH formation. Otherwise, the BH mass necessarily lie on the ZAMS mass-remnant mass relation as in Fig. 6. In particular, the post-formation mass gain of a BH (due to e.g. mass transfer, BH-star collision) is not captured in Fig. 12.
In the version of BSE adopted in NBODY7, a 30% mass loss from the secondary (the less massive merger participant) is assumed when the kinetic energy of approach of the merging non-compact stars exceeds the internal binding energy of the secondary, provided the stars geometrically overlap at the merger and provided they are in the MS. Merger among more evolved stars and grazing encounters are even poorly understood/studied and no mass loss is associated with such mergers in NBODY7/BSE. If one of the merging members is a NS or a BH, an unstable Thorne-Żytkow object is formed. In such a case, the entire secondary is assumed to be dissipated in the case of an NS core and half of the secondary mass is retained onto the BH in the case of a BH core.
The filled black points are not all mapped across the panels in Fig. 14 since varying fmrg alters the local gravitational potential and hence the dynamical interactions, so that a particular merger does not necessarily re-occur in the different N-body computations and the sequence of the mergers is also altered over the different runs.
Acknowledgments
We thank the anonymous referee for their useful comments and suggestions which have improved the manuscript. SB acknowledges the support from the Deutsche Forschungsgemeinschaft (DFG; German Research Foundation) through the individual research grant “The dynamics of stellar-mass black holes in dense stellar systems and their role in gravitational-wave generation” (BA 4281/6-1; PI: S. Banerjee). SB acknowledges the pleasant hospitality of the Nicolaus Copernicus Astronomical Centre of the Polish Academy of Sciences (CAMK) where this work was initiated. SB acknowledges the generous support and efficient system maintenance of the computing teams at the Argelander-Institut für Astronomie (AIfA) and the CAMK where the computations have been performed. KB acknowledges support from the Polish National Science Center (NCN) grant Maestro (2018/30/A/ST9/00050). The work of CF was done at Los Alamos National Laboratory under project number 20190021DR. This work was supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Project-ID 138713538 – SFB 881 (“The Milky Way System”, subproject A06) and by the Volkswagen Foundation under the Trilateral Partnerships grants No. 90411 and 97778. The special GPU accelerated supercomputer Laohu at NAOC has been used and we thank the Center of Information and Computing of NAOC for support. This work has been benefited from support by the International Space Science Institute, Bern, Switzerland, through its International Team program ref. no. 393 “The Evolution of Rich Stellar Populations and BH Binaries” (2017–18). The work of PB was also partially supported under the special program of the NAS of Ukraine “Support for the development of priority fields of scientific research” (CPCEL 6541230). RS and PB acknowledge support through the Silk Road Project at the National Astronomical Observatories (NAOC), Chinese Academy of Sciences, through the National Natural Science Foundation of China (NSFC, grant No. 11673032), and through the Strategic Priority Research Program (Pilot B) “Multi-wavelength gravitational wave universe” of the Chinese Academy of Sciences (No. XDB23040100). Visits of SB and KB have been supported by the Silk Road Project at NAOC. JH has been supported by the Kavli Visitor Program of Kavli Institute for Astronomy and Astrophysics, Peking University. LW acknowledges the support from Alexander von Humboldt Foundation and JSPS International Research Fellow (School of Science, The university of Tokyo). We thank Mirek Giersz and Diogo Belloni for pointing out an issue with white dwarf formation and white dwarf masses under our newly implemented schemes which has helped us to locate and fix an important bug in one of the routines in the updated BSE code presented in this work. The “time step issue” in BSE (Sect. 2.4) was hinted by Mirek Giersz during a lunch at CAMK.
References
- Aarseth, S. J. 2003, Gravitational N-Body Simulations (Cambridge, UK: Cambridge University Press), 430 [Google Scholar]
- Aarseth, S. J. 2012, MNRAS, 422, 841 [NASA ADS] [CrossRef] [Google Scholar]
- Abadie, J., Abbott, B. P., Abbott, R., et al. 2010, Classical Quantum Gravity, 27, 173001 [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016a, Phys. Rev. Lett., 116, 061102 [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016b, ApJ, 818, L22 [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2017a, Phys. Rev. Lett., 118, 221101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2017b, Phys. Rev. Lett., 119, 141101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2019a, Phys. Rev. X, 9, 031040 [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2019b, ApJ, 882, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Arca Sedda, M., Askar, A., & Giersz, M. 2018, MNRAS, 479, 4652 [NASA ADS] [CrossRef] [Google Scholar]
- Askar, A., Szkudlarek, M., Gondek-Rosińska, D., Giersz, M., & Bulik, T. 2017, MNRAS, 464, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Askar, A., Arca Sedda, M., & Giersz, M. 2018, MNRAS, 478, 1844 [NASA ADS] [CrossRef] [Google Scholar]
- Banerjee, S. 2017, MNRAS, 467, 524 [NASA ADS] [Google Scholar]
- Banerjee, S. 2018a, MNRAS, 473, 909 [NASA ADS] [CrossRef] [Google Scholar]
- Banerjee, S. 2018b, MNRAS, 481, 5123 [CrossRef] [Google Scholar]
- Banerjee, S., Baumgardt, H., & Kroupa, P. 2010, MNRAS, 402, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Banerjee, S., Kroupa, P., & Oh, S. 2012, MNRAS, 426, 1416 [NASA ADS] [CrossRef] [Google Scholar]
- Belczynski, K., Kalogera, V., & Bulik, T. 2002, ApJ, 572, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Belczynski, K., Kalogera, V., Rasio, F. A., et al. 2008, ApJS, 174, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Belczynski, K., Bulik, T., Fryer, C. L., et al. 2010a, ApJ, 714, 1217 [NASA ADS] [CrossRef] [Google Scholar]
- Belczynski, K., Benacquista, M., & Bulik, T. 2010b, ApJ, 725, 816 [NASA ADS] [CrossRef] [Google Scholar]
- Belczynski, K., Holz, D. E., Bulik, T., & O’Shaughnessy, R. 2016a, Nature, 534, 512 [NASA ADS] [CrossRef] [Google Scholar]
- Belczynski, K., Heger, A., Gladysz, W., et al. 2016b, A&A, 594, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belczynski, K., Repetto, S., Holz, D. E., et al. 2016c, ApJ, 819, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Belczynski, K., Klencki, J., Fields, C. E., et al. 2020, A&A, 636, A104 [CrossRef] [EDP Sciences] [Google Scholar]
- Burrows, A., & Hayes, J. 1996, Phys. Rev. Lett., 76, 352 [NASA ADS] [CrossRef] [Google Scholar]
- Chatterjee, S., Rodriguez, C. L., & Rasio, F. A. 2017, ApJ, 834, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Chatziioannou, K., Cotesta, R., Ghonge, S., et al. 2019, Phys. Rev. D, 100, 104015 [CrossRef] [Google Scholar]
- Claret, A. 2007, A&A, 467, 1389 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Mink, S. E., Langer, N., Izzard, R. G., Sana, H., & de Koter, A. 2013, ApJ, 764, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Di Carlo, U. N., Giacobbo, N., Mapelli, M., et al. 2019, MNRAS, 487, 2947 [NASA ADS] [CrossRef] [Google Scholar]
- Duquennoy, A., & Mayor, M. 1991, A&A, 248, 485 [NASA ADS] [Google Scholar]
- Eldridge, J. J., & Tout, C. A. 2004, MNRAS, 353, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Farr, W. M., Stevenson, S., Miller, M. C., et al. 2017, Nature, 548, 426 [NASA ADS] [CrossRef] [Google Scholar]
- Fishbach, M., Farr, W. M., & Holz, D. E. 2020, ApJ, 891, L31 [CrossRef] [Google Scholar]
- Fragos, T., Willems, B., Kalogera, V., et al. 2009, ApJ, 697, 1057 [NASA ADS] [CrossRef] [Google Scholar]
- Fryer, C. L. 1999, ApJ, 522, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Fryer, C. L. 2004, ApJ, 601, L175 [NASA ADS] [CrossRef] [Google Scholar]
- Fryer, C. L., & Kalogera, V. 2001, ApJ, 554, 548 [NASA ADS] [CrossRef] [Google Scholar]
- Fryer, C. L., & Kusenko, A. 2006, ApJS, 163, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Fryer, C. L., & Young, P. A. 2007, ApJ, 659, 1438 [NASA ADS] [CrossRef] [Google Scholar]
- Fryer, C. L., Belczynski, K., Wiktorowicz, G., et al. 2012, ApJ, 749, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Fujii, M. S., & Portegies Zwart, S. 2013, MNRAS, 430, 1018 [Google Scholar]
- Fuller, G. M., Kusenko, A., Mocioiu, I., & Pascoli, S. 2003, Phys. Rev. D, 68, 103002 [NASA ADS] [CrossRef] [Google Scholar]
- Fuller, J., Piro, A. L., & Jermyn, A. S. 2019, MNRAS, 485, 3661 [NASA ADS] [Google Scholar]
- Gaburov, E., Lombardi, J. C., & Portegies Zwart, S. 2008, MNRAS, 383, L5 [NASA ADS] [Google Scholar]
- Geller, A. M., Leigh, N. W. C., Giersz, M., Kremer, K., & Rasio, F. A. 2019, ApJ, 872, 165 [CrossRef] [Google Scholar]
- Gessner, A., & Janka, H.-T. 2018, ApJ, 865, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Giacobbo, N., Mapelli, M., & Spera, M. 2018, MNRAS, 474, 2959 [NASA ADS] [CrossRef] [Google Scholar]
- Giersz, M., Heggie, D. C., Hurley, J. R., & Hypki, A. 2013, MNRAS, 431, 2184 [NASA ADS] [CrossRef] [Google Scholar]
- Giesers, B., Dreizler, S., Husser, T.-O., et al. 2018, MNRAS, 475, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Glebbeek, E., Gaburov, E., de Mink, S. E., Pols, O. R., & Portegies Zwart, S. F. 2009, A&A, 497, 255 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hamann, W.-R., & Koesterke, L. 1998, A&A, 335, 1003 [NASA ADS] [Google Scholar]
- Hobbs, G., Lorimer, D. R., Lyne, A. G., & Kramer, M. 2005, MNRAS, 360, 974 [NASA ADS] [CrossRef] [Google Scholar]
- Humphreys, R. M., & Davidson, K. 1994, PASP, 106, 1025 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley, J. R., Pols, O. R., & Tout, C. A. 2000, MNRAS, 315, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley, J. R., Tout, C. A., & Pols, O. R. 2002, MNRAS, 329, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Hypki, A., & Giersz, M. 2013, MNRAS, 429, 1221 [NASA ADS] [CrossRef] [Google Scholar]
- Ivanova, N., Justham, S., Chen, X., et al. 2013, A&ARv, 21, 59 [Google Scholar]
- Janka, H.-T. 2013, MNRAS, 434, 1355 [Google Scholar]
- Joshi, K. J., Rasio, F. A., & Portegies Zwart, S. 2000, ApJ, 540, 969 [NASA ADS] [CrossRef] [Google Scholar]
- Kimball, C., Berry, C., & Kalogera, V. 2020, Res. Notes Am. Astron. Soc., 4, 2 [CrossRef] [Google Scholar]
- Kremer, K., Ye, C. S., Chatterjee, S., Rodriguez, C. L., & Rasio, F. A. 2018, ApJ, 855, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Kremer, K., Chatterjee, S., Ye, C. S., Rodriguez, C. L., & Rasio, F. A. 2019, ApJ, 871, 38 [CrossRef] [Google Scholar]
- Kroupa, P. 1995, MNRAS, 277, 1491 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Kruckow, M. U., Tauris, T. M., Langer, N., Kramer, M., & Izzard, R. G. 2018, MNRAS, 481, 1908 [NASA ADS] [CrossRef] [Google Scholar]
- Kudritzki, R. P., & Reimers, D. 1978, A&A, 70, 227 [Google Scholar]
- Lattimer, J. M., & Yahil, A. 1989, ApJ, 340, 426 [NASA ADS] [CrossRef] [Google Scholar]
- Leigh, N. W. C., & Geller, A. M. 2013, MNRAS, 432, 2474 [NASA ADS] [CrossRef] [Google Scholar]
- Lombardi, J. C., Jr., Warren, J. S., Rasio, F. A., Sills, A., & Warren, A. R. 2002, ApJ, 568, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Mandel, I. 2016, MNRAS, 456, 578 [NASA ADS] [CrossRef] [Google Scholar]
- Mandel, I., & Farmer, A. 2017, Nature, 547, 284 [CrossRef] [Google Scholar]
- Mapelli, M. 2016, MNRAS, 459, 3432 [NASA ADS] [CrossRef] [Google Scholar]
- Mapelli, M., Giacobbo, N., Ripamonti, E., & Spera, M. 2017, MNRAS, 472, 2422 [NASA ADS] [CrossRef] [Google Scholar]
- Marchant, P., Langer, N., Podsiadlowski, P., Tauris, T. M., & Moriya, T. J. 2016, A&A, 588, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meakin, C. A., & Arnett, D. 2006, ApJ, 637, L53 [CrossRef] [Google Scholar]
- Meakin, C. A., & Arnett, D. 2007, ApJ, 665, 690 [NASA ADS] [CrossRef] [Google Scholar]
- Morscher, M., Pattabiraman, B., Rodriguez, C., Rasio, F. A., & Umbreit, S. 2015, ApJ, 800, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Nieuwenhuijzen, H., & de Jager, C. 1990, A&A, 231, 134 [NASA ADS] [Google Scholar]
- Nitadori, K., & Aarseth, S. J. 2012, MNRAS, 424, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Park, D., Kim, C., Lee, H. M., Bae, Y.-B., & Belczynski, K. 2017, MNRAS, 469, 4665 [NASA ADS] [CrossRef] [Google Scholar]
- Plummer, H. C. 1911, MNRAS, 71, 460 [CrossRef] [Google Scholar]
- Podsiadlowski, P., Langer, N., Poelarends, A. J. T., et al. 2004, ApJ, 612, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Portegies Zwart, S., & McMillan, S. 2018, Astrophysical Recipes; The Art of AMUSE (Bristol, UK: IOP Publishing) [CrossRef] [Google Scholar]
- Repetto, S., & Nelemans, G. 2015, MNRAS, 453, 3341 [NASA ADS] [CrossRef] [Google Scholar]
- Repetto, S., Davies, M. B., & Sigurdsson, S. 2012, MNRAS, 425, 2799 [NASA ADS] [CrossRef] [Google Scholar]
- Repetto, S., Igoshev, A. P., & Nelemans, G. 2017, MNRAS, 467, 298 [Google Scholar]
- Rodriguez, C. L., Chatterjee, S., & Rasio, F. A. 2016, Phys. Rev. D, 93, 084029 [NASA ADS] [CrossRef] [Google Scholar]
- Rodriguez, C. L., Amaro-Seoane, P., Chatterjee, S., & Rasio, F. A. 2018, Phys. Rev. Lett., 120, 151101 [NASA ADS] [CrossRef] [Google Scholar]
- Samsing, J. 2018, Phys. Rev. D, 97, 103014 [NASA ADS] [CrossRef] [Google Scholar]
- Sana, H., & Evans, C. J. 2011, IAU Symp., 272, 474 [NASA ADS] [CrossRef] [Google Scholar]
- Sana, H., de Koter, A., de Mink, S. E., et al. 2013, A&A, 550, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scheck, L., Plewa, T., Janka, H. T., Kifonidis, K., & Müller, E. 2004, Phys. Rev. Lett., 92, 011103 [NASA ADS] [CrossRef] [Google Scholar]
- Scheck, L., Janka, H. T., Foglizzo, T., & Kifonidis, K. 2008, A&A, 477, 931 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spera, M., Mapelli, M., Giacobbo, N., et al. 2019, MNRAS, 485, 889 [NASA ADS] [CrossRef] [Google Scholar]
- Spitzer, L. 1987, Dynamical Evolution of Globular Clusters (Princeton, NJ: Princeton University Press), 191 [Google Scholar]
- Spruit, H. C. 2002, A&A, 381, 923 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stevenson, S., Vigna-Gómez, A., Mandel, I., et al. 2017, Nat. Commun., 8, 14906 [NASA ADS] [CrossRef] [Google Scholar]
- Timmes, F. X., Woosley, S. E., & Weaver, T. A. 1996, ApJ, 457, 834 [NASA ADS] [CrossRef] [Google Scholar]
- Toonen, S., Claeys, J. S. W., Mennekens, N., & Ruiter, A. J. 2014, A&A, 562, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vassiliadis, E., & Wood, P. R. 1993, ApJ, 413, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Vink, J. S., & de Koter, A. 2005, A&A, 442, 587 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Voss, R., & Tauris, T. M. 2003, MNRAS, 342, 1169 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, L., Spurzem, R., Aarseth, S., et al. 2015, MNRAS, 450, 4070 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, L., Spurzem, R., Aarseth, S., et al. 2016, MNRAS, 458, 1450 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, L., Kroupa, P., Takahashi, K., & Jerabkova, T. 2020, MNRAS, 491, 440 [CrossRef] [Google Scholar]
- Willems, B., Henninger, M., Levin, T., et al. 2005, ApJ, 625, 324 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E. 2017, ApJ, 836, 244 [NASA ADS] [CrossRef] [Google Scholar]
- Ziosi, B. M., Mapelli, M., Branchesi, M., & Tormen, G. 2014, MNRAS, 441, 3703 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Summary of the changes implemented in the updated BSE code
Below, we summarise the changes in the various subroutines of the updated BSE described in this work with respect to the current publicly available version of this program.
mlwind.f
Significant reorganisation of the original mlwind function is done to implement the B10 wind recipe correctly; see Sect. 2.1 for the details. The original Hurley et al. (2000) wind and various variants of both B10 and Hurley et al. (2000) wind recipes can be activated by appropriate choice of the mdflag flag variable. mdflag = 3 selects the B10 wind which option is now recommended.
hrdiag.f
In the subroutine hrdiag, the rapid and delayed remnant-mass prescriptions of F12 are implemented utilizing the relevant analytical formulae; see Sect. 2.2 for the details. These formulae are inserted in the same parts of the code in which the final baryonic remnant mass is evaluated from the older prescriptions. All the older remnant prescriptions are preserved and can be selected via choices of the input flag variable nsflag: currently nsflag = 3 (4) selects the F12-rapid (delayed) prescriptions.
The decision for undergoing PSN (giving a remnant of zero mass) or PPSN truncation according to the criteria in B16 is taken before the baryonic remnant mass evaluation and is implemented as an extension of the existing conditional statement that handles the cases of no remnant formation. PSN/PPSN can be enabled (disabled) with the choice of the input flag variable psflag = 1 (0).
Care is taken that these extensions are analogously coded in both the hydrogen rich-star and helium-star sections of hrdiag, as for the other remnant prescriptions.
Apart from these, two additional COMMON BLOCKs are introduced. One is
COMMON /FBACK/ FBFAC,FBTOT,MCO,ECS,
which enables the transport of the fallback fraction, fallback mass, CO core mass, and an indicator for the occurrence of an ECS to other subroutines where they would be useful such as kick (see below). The other is
COMMON /FLAGS2/ psflag,kmech,ecflag
to port relevant new input flags (ecflag for enabling ECS is now read from input just for symmetry and convenience).
We note that the ECS indicator, which is set to unity directly in the conditional statement in hrdiag that assigns the ECS-NS mass, is implemented to override the default approach of sensing ECS events (outside hrdiag) via 1.26 M⊙ NSs. This is an arrangement to address the fact that in the newly implemented F12-rapid scheme, the core-collapse NSs’ mass can go down to ≈1.1 M⊙ so that a 1.26 M⊙ NS can also be a core-collapse NS.
kick.f
The analytical formulae for modelling the various core-collapse SN natal kick mechanisms, as explored in this work (see Sects. 3.1 and 3.2), are all implemented in the subroutine kick. To evaluate the kick-velocity magnitude, the SN fallback fraction and the CO core mass are needed which are supplied by the subroutine hrdiag through the FBACK common block (see above). The kick subroutine also uses the FLAGS2 common block to receive the value of the input flag variable kmech that toggles among the kick models.
We note that unlike mlwind and hrdiag, the kick subroutine is structurally quite different in NBODY7, which also has to keep track of the identities of the members receiving the kick. The natal kick formulae have been analogously implemented in the NBODY7 version of kick. This NBODY7 subroutine is currently private and will be made public elsewhere.
star.f
The subroutine star differs slightly from its public BSE version and is now identical with star.f that is supplied with the public version of NBODY7.
sse.f
An extra READ statement is added in this main routine to read in the choices of the input flags psflag, kmech, and ecflag (see above).
bse.f
The same as in sse.f.
const_bse.h
In this header file, the common block
COMMON /FLAGS2/ psflag,kmech,ecflag
is added to carry the user-input values of psflag, kmech, and ecflag to other subroutines.
README_NEW
The descriptions of the new ingredients, including references, are elaborated in this companion manual. The functionalities of the new input flags (see above) and the amended formats of the runtime input files are also described here.
Stellar mass limit
Apart from the changes described above, the imposed 100 M⊙ stellar mass limit is, by default, commented out in star.f, hrdiag.f, mix.f, and evolv2.f. This facilitates the user to explore the very-massive-star regime where PPSN and PSN would occur and also the outcome of massive stellar mergers. However, it should be borne in mind that extending beyond 100 M⊙ is a rather large extrapolation of the underlying stellar structure employed in BSE.
The stellar-mass ceiling is by default suppressed in the public NBODY7.
All Tables
Formation and retention of stellar-remnant BHs in a Mcl(0) ≈ 5.0 × 104 M⊙ model cluster (Sect. 3) as a function of metallicity (Col. 1) and SN–remnant-formation scheme (Col. 2; Sect. 2.2; “+MB” implies the cluster model includes a population of massive primordial binaries as described in Sect. 4).
Remnant outcomes of selected massive binaries when evolved with StarTrack (Col. 5) and updated BSE (Col. 6).
All Figures
 |
Fig. 1. Comparisons of the ZAMS mass-remnant mass relation between the updated BSE (Sects. 2.1 and 2.2) and StarTrack. The comparison is done for the cases of B08, F12-delayed, and F12-rapid remnant-mass models and for the metallicities Z = 0.0002, 0.006, and 0.02, as indicated in the legends. In all cases in this figure, PPSN/PSN is disabled. In all panels, the black dashed line is the outcome from the new BSE and the blue solid line is the corresponding StarTrack result. The mass gap between NSs and BHs, which is characteristic of the F12-rapid remnant mass model, is also indicated in the corresponding panels (the grey, horizontal lines at ≈2.0 M⊙ and ≈5.0 M⊙ in the F12-rapid panels). |
| In the text | |
 |
Fig. 2. Comparisons of the ZAMS mass-remnant mass relation between the updated BSE and StarTrack including PPSN/PSN (F12-rapid SN model) for Z = 0.0001 and 0.002. The line legends are the same as in Fig. 1. Middle panel: PSN mass gap, as obtained from the current BSE for Z = 0.0001, by extending the ZAMS mass beyond 300 M⊙. Bottom panel: between the ZAMS mass-remnant mass relations as obtained from the updated BSE (thick dashed lines) and StarTrack (thin solid lines) up to very large ZAMS masses, extending beyond the PSN mass gap (the black horizontal lines at 40.5 M⊙ and 121.5 M⊙), for a wide range of metallicities. The lower mass gap between NSs and BHs, which is characteristic of the F12-rapid remnant mass model, is also indicated in this panel (the grey, horizontal lines at ≈2.0 M⊙ and ≈5.0 M⊙). |
| In the text | |
 |
Fig. 3. Comparisons of the ZAMS mass-remnant mass relation between the updated BSE and StarTrack up to ≈300 M⊙ ZAMS mass, excluding (top panels) and including (bottom panels) PPSN/PSN (F12-rapid SN model) for Z = 0.0002, 0.002, 0.02. The line legends are the same as in Fig. 1. The significant “clipping” of the BH mass (at ≈40 M⊙) for ZAMS masses ≳100 M⊙ at very low metallicities such as Z = 0.0002, when PPSN/PSN is included (see also B16 and Sect. 2.2), is apparent. |
| In the text | |
 |
Fig. 4. Comparisons of the ZAMS mass-remnant mass relation between the updated BSE (thin, black line) and StarTrack (thick, blue line) for lower ZAMS masses (1 M⊙ − 20 M⊙) for F12-rapid remnant mass model. Over this mass range, the switching from WD formation to NS formation is evident (NS formation from the first drop of the curve to 1.26 M⊙). The comparison is shown for the two metallicities Z = 0.02 and 0.0017. |
| In the text | |
 |
Fig. 5. Panels 1–6: comparisons of the ZAMS mass-remnant mass relation between the updated BSE (thin lines) and StarTrack (thick lines) for the B08 remnant-formation scheme and for Z = 0.0002, 0.006, 0.02, for different choices of the stellar-evolutionary time-step parameters pts1, pts2, and pts3. The values of these time-step parameters are indicated in the corresponding panels; only one value is indicated when pts1 = pts2 = pts3, otherwise the respective values are indicated. Panel 7: same comparison with pts1 = pts2 = pts3 = 0.001 when the default, to-date-public version of HRDIAG/MLWIND is utilized (see Sect. 2.4 for the details). The StarTrack data in these panels are from B10. |
| In the text | |
 |
Fig. 6. Comparisons of the ZAMS mass-remnant mass relation between the updated BSE from within NBODY7 and StarTrack, for different Z and remnant-formation prescriptions. For Z = 0.002 and Z = 0.02, PPSN/PSN do not affect the ZAMS mass-remnant mass relation since the He-core mass never reaches the PPSN/PSN threshold (see B16). The mass gap between the NSs and BHs for the F12-rapid cases is indicated with the grey horizontal lines, as in the previous figures. |
| In the text | |
 |
Fig. 7. Early (up to 20 Myr) evolution of the total mass, MBH, bound (top left), and number, NBH, bound (bottom left) of the BHs bound within the Mcl(0) = 5.0 × 104 M⊙ (initially all single stars) model cluster (see Sect. 3) for the various remnant-formation schemes (legend), for the standard, fallback-controlled kick model as given by Eq. (1) (Z = 0.0001 is assumed). The corresponding evolutions of the half-mass radius of the cluster’s BH subsystem, rh, BH, bound (top right), and that of only the luminous members, rh, * (bottom right), are also shown. |
| In the text | |
 |
Fig. 8. Mass distributions of BHs obtained in the Mcl(0) = 5.0 × 104 M⊙ model clusters (initially all single stars; Sect. 3) for four remnant-formation scenarios as indicated in the legends (Z = 0.0001 taken). On each panel, both the natal mass distribution of the BHs and the distribution at t ≈ 20 Myr cluster-evolutionary time are shown (the steel-blue and blue histograms, respectively). The latter distribution represents well the mass spectrum of those BHs, which remain gravitationally bound to a medium-mass (young massive or open; in this case taken to be of ≈5 × 104 M⊙) cluster after their birth and which are, therefore, available for long-term dynamical processing in the parent cluster (see Sect. 3.1). The retained BH mass distributions (blue histograms), in these panels, are the outcomes of the standard, fallback-controlled natal kick model (Eq. (1)). |
| In the text | |
 |
Fig. 9. Early evolution of the total mass, MBH, bound (top panel), and number, NBH, bound (middle), of the BHs and the number, NNS, bound (bottom), of the NSs bound within the Mcl(0) = 5.0 × 104 M⊙ (initially all single stars) model cluster (see Sect. 3) for the various natal-kick engines (legends; see Sects. 3.1 and 3.2), for the F12-rapid+B16-PPSN/PSN remnant-mass model (Sect. 2.2; Z = 0.0001 is assumed). The collapse-asymmetry-driven kick engine produces relatively low kicks also for some NSs which marginally escape the cluster, taking time, resulting in their build-up at ≈20 Myr followed by a slow decline (bottom panel). After ≈55 Myr when the ECS-NSs begin to form, the latter’s population build up solely for all the kick-mechanism cases. |
| In the text | |
 |
Fig. 10. Left: comparison between the retained mass distribution of the BHs (inside a Mcl(0) ≈ 5 × 104 M⊙, rh(0) ≈ 2 pc, initially single-only stars model cluster; see also Fig. 8) for the various natal-kick prescriptions considered in this work (legends; see Sects. 3.1 and 3.2). The F12-rapid+B16-PPSN/PSN remnant-mass model (Sect. 2.2) and Z = 0.0001 is assumed. The dashed histogram represents the natal mass distribution of the BHs for these remnant-mass model and Z. No BHs are retained in such clusters in the neutrino-driven-kick case (Sect. 3.2.3; Fig. 9). In contrast, nearly all BHs are retained if the kicks are collapse asymmetry driven. Right: natal mass distribution of NSs for the F12-rapid(+B16-PPSN/PSN) remnant-mass model (black histogram). The retained mass distributions of the NSs for the collapse-asymmetry-driven kick model at t ≈ 20 Myr and 60 Myr are also shown (grey and blue histograms, respectively). The marginally escaping NSs at 20 Myr (Sect. 3.2.4; Fig. 9, bottom panel) are all depleted by 60 Myr when only the low-/zero-kicked ECS-NSs retain in the cluster. |
| In the text | |
 |
Fig. 11. Natal kicks, vkick, as generated by NBODY7, as a function of mCO (left panel) and mrem (right panel), for the different natal-kick recipes considered in this work. The F12-rapid+B16-PPSN/PSN remnant-mass model (Sect. 2.2) and Z = 0.0001 is assumed. Because of the logarithmic vertical axis, direct-collapse BHs with ffb = 1 and vkick = 0 are not shown in these panels; the sharp drop in vkick with increasing mCO or mrem is the approach towards direct collapse. The typical vesc for the Mcl(0) ≈ 5.0 × 104 M⊙, rh(0) ≈ 2 pc clusters considered in this study (blue, solid line) and the Hobbs et al. (2005)σNS ≈ 265 km s−1, whose value in all the kick models are scaled (see Sects. 3.1 and 3.2; black, solid line), are indicated. |
| In the text | |
 |
Fig. 12. Remnant production and retention in the NBODY7-computed, Mcl(0) ≈ 5.0 × 104 M⊙, rh(0) ≈ 2 pc model cluster with all BH-progenitor stars paired in primordial binaries (see Sect. 4). In all the panels, “+MB” indicates the presence of such a population of massive primordial binaries; the absence of this symbol in a legend implies the case in which all stars are initially single. The F12-rapid remnant-formation prescription and Z = 0.0001 is assumed without (left column) and with (right column) PPSN/PSN. Top row: ZAMS mass vs. remnant mass (black filled squares) compared with the corresponding StarTrack outcomes from pure single-star evolution (blue solid lines; cf. Fig. 6). For the BH progenitors that have undergone a star-star merger before the BH formation, the ZAMS mass of the primary (the more massive of the members participating in the star-star merger, at the time of the merger) is plotted in the abscissa. For reference, the ZAMS mass-remnant mass points (orange empty squares) from an identical model cluster but with initially only single stars (as in Sect. 3; cf. Fig. 6) are also shown. Second row: natal and retained mass distributions of the BHs (steel blue and blue filled histograms, respectively; assuming the standard, fallback-controlled natal kicks). These are compared with the corresponding BH natal mass distribution without any massive primordial binaries (dashed empty histogram, cf. Fig. 8). Third row: cumulative time development of the total BH mass, MBH, as they are born (steel blue solid line) and the total BH mass, MBH, bound, that is bound to the cluster as a function of time (solid blue line). The MBH(t) corresponding to initially only single stars is also shown (black, dashed line). Fourth row: same as the third row but for the BH numbers NBH and NBH, bound. |
| In the text | |
 |
Fig. 13. Same as in the top row of Fig. 12 except that for the model cluster with massive primordial binaries (see Sect. 4), the ZAMS mass of the primary plus the ZAMS mass of the secondary of the pre-remnant-formation, star-star mergers are plotted along the abscissa. The legends are the same as in Fig. 12. |
| In the text | |
 |
Fig. 14. Remnant production and retention in the NBODY7-computed, Mcl(0) ≈ 5.0 × 104 M⊙, rh(0) ≈ 2 pc model cluster with all BH-progenitor stars paired in primordial binaries (see Sect. 4). The legends are the same as in the top panels of Fig. 12. The panels show different computations that adopt different extents of mass loss during a star-star merger process: the left panel shows the case that has defaulted in NBODY7/BSE, namely, mass-loss fraction of fmrg = 0.3 from the secondary for energetic MS-MS collisions only (see text) and zero otherwise (the data in this panel are identical to those in the top right panel of Fig. 12), the middle panel shows the NBODY7 computation where a mass-loss fraction of fmrg = 0.5 from the secondary is implemented for all star-star mergers, and the right panel shows the computation where a mass-loss fraction of fmrg = 0.8 from the secondary is implemented for all star-star mergers. With increasing extent of mass loss in mergers (left to right panel), the single-star ZAMS mass-remnant mass relation (orange, empty squares) gets affected by massive-stellar mergers (black, filled squares) to a diminishing extent. The F12-rapid remnant-formation prescription, including PPSN/PSN, and Z = 0.0001, is assumed in this demonstration. |
| In the text | |
 |
Fig. 15. Remnant outcomes of 12 massive binaries, with initial parameters as given in Table 2, when evolved with updated BSE (black filled squares) and StarTrack (magenta filled squares). Plotted along the X-axis are the binaries’ primary (the more massive member) ZAMS masses and the masses of the single remnant or of the heavier of the two remnants of the binary evolutions are plotted along the Y-axis. Because of the adopted NS upper mass limit, a remnant of > 2.5 M⊙ (≤2.5 M⊙) is a BH (NS). These BSE and StarTrack evolutionary calculations are done for the F12-rapid+B16-PPSN/PSN remnant-mass model with the same choices of evolutionary parameters; the values of the most relevant parameters are Z = 0.0001, αCE = 1.0, and fmrg = 0.5. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.