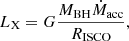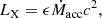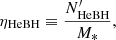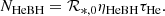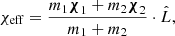EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 696 (April 2025) A&A, 696 (2025) A54 Full HTML
Open Access
Issue
A&A
Volume 696, April 2025
Article Number A54
Number of page(s) 9
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/202553829
Published online 03 April 2025

© The Authors 2025

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Black hole (BH) spin is a rapidly evolving field of study (e.g. Reynolds 2021; Genzel et al. 2024). In particular, there is an apparent dichotomy between the spins of stellar-mass BHs found in X-ray binaries and gravitational wave (GW) mergers (Orosz et al. 2009, 2011; Abbott et al. 2016, 2019, 2023; Roulet et al. 2021; Miller-Jones et al. 2021; Draghis et al. 2024): the BHs in X-ray binaries are estimated to be more rapidly spinning than those in GW mergers (see, however, Zdziarski et al. 2024; Belczynski et al. 2024). While BHs in low-mass X-ray binaries can be spun up by accretion (Podsiadlowski et al. 2003; O’Shaughnessy et al. 2005; Fragos & McClintock 2015), theoretical studies imply that BHs in high-mass X-ray binaries and GW mergers can form distinct populations and/or there exist observational selection effects (Fishbach & Kalogera 2022; Liotine et al. 2023; Misra et al. 2023; Romero-Shaw et al. 2023). As such, these systems are an excellent testbed for stellar evolution theory (for a recent review, see Mandel 2024, and references therein).

While most GW merger events have been detected with low effective spins, χeff1 (χeff  ∼ 0.05; Roulet & Zaldarriaga 2019; Abbott et al. 2023), and thus provide evidence of efficient angular momentum coupling between the core and envelope of the BH progenitors (Spruit 2002; Fuller & Ma 2019, see also Skoutnev & Beloborodov 2024a,b), there exists a tail in the spin distribution where values go as high as unity. The origin of this long tail has not been determined and may be model-dependent (e.g. see Zevin et al. 2021; Callister et al. 2022). Recent literature suggests that a high-spin tail implies a contribution from the isolated binary evolution channel with tidally spun-up second-born BH (Bavera et al. 2020; Olejak & Belczynski 2021) or dynamically induced multiple mergers, for example in globular clusters or active galactic nucleus disks (Mapelli 2020; Banerjee 2021; Mandel & Broekgaarden 2022; Santini et al. 2023; Kıroğlu et al. 2025; Delfavero et al. 2024; Li et al. 2025). An asymmetric distribution of effective spins (Roulet et al. 2021) implies that a substantial contribution originates from isolated binary evolution.

In the isolated binary evolution channel, binary black holes (BBHs) that merge within a Hubble time can form via one or more phases of stable mass transfer (SMT; van den Heuvel et al. 2017; Gallegos-Garcia et al. 2021; Bavera et al. 2021a; Olejak et al. 2021; van Son et al. 2022; Shao & Li 2022; Briel et al. 2023; Picco et al. 2024; Dorozsmai & Toonen 2024) or involve a common envelope (CE) phase (Tutukov & Yungelson 1993; Giacobbo et al. 2018; Kruckow et al. 2018; Spera et al. 2019; Ginat et al. 2020; Belczynski et al. 2020; Renzo et al. 2021; Gallegos-Garcia et al. 2023; Boesky et al. 2024; Romagnolo et al. 2025). In both of the above sub-channels, the BBH phase is typically preceded by a helium star–BH (He+BH) phase during which the He+BH binary has an orbital period of less than ∼1 d (Korb et al. 2025). It has been suggested that He stars in short-period binaries can be spun up by tides so much so that the Kerr parameter of the second-formed BH can reach close to unity (Detmers et al. 2008; Kushnir et al. 2016; Qin et al. 2018; Belczynski et al. 2020; Bavera et al. 2021b; Olejak & Belczynski 2021; Fuller & Lu 2022; Ma & Fuller 2023).

Although the stellar wind from stripped helium stars is expected to be very fast (e.g. see Sander et al. 2012), the short periods imply that the Bondi accretion radius of the BH (Bondi & Hoyle 1944; Shakura 1973) can subtend a solid angle large enough to capture a substantial amount of wind mass lost from the He stars. As such, observable X-ray emission can be produced from the shortest-period He+BH binaries, which would also potentially contribute to the tail of the BH spin distribution in GW merger data due to efficient tidal spin-up of the second-formed BH’s progenitor He star. Previous studies have largely focused on X-ray emission from He+neutron star binaries (Shao & Li 2015; Shao et al. 2019; Mondal et al. 2020; Chen et al. 2023; Misra et al. 2024; Li et al. 2024), BHs with non-degenerate star companions (Vanbeveren et al. 2020; Sen et al. 2021; Shao & Li 2019; Liotine et al. 2023; Misra et al. 2023; Romero-Shaw et al. 2023; Kruckow et al. 2024; Xing et al. 2025), or ultra-compact BH binaries, where X-rays are produced from mass accretion due to Roche-lobe overflow (Shao & Li 2020; Wang et al. 2021; Qin et al. 2024).

Recent studies have shown that observable X-ray emission can be produced from stellar-mass BHs even at low mass accretion rates (Xie & Yuan 2012; Sen et al. 2024). In this work, we study the production and observability of X-ray emission from short-period He+BH binaries and its correlation with the tidal spin-up of He stars and the spins of their remnant BHs. Our work is particularly relevant for ongoing Chandra surveys of the Large Magellanic Cloud (LMC; ∼Z⊙/2, Choudhury et al. 2021) and Sextans A (∼Z⊙/10; Kaufer et al. 2004; Lorenzo 2024), which are slated to detect X-ray point-sources down to ∼1032 erg s−1 (Antoniou 2022) and ∼1035 erg s−1 (Antoniou 2023), respectively. Soon, proposed missions such as AXIS (Mushotzky 2018), HEX-P (Madsen et al. 2018; Lehmer et al. 2023), and STROBE-X (Ray et al. 2019) may provide further observational constraints for our model predictions.

The paper is organised as follows. Section 2 discusses the rapid binary evolution models and the X-ray prescription used to model the He+BH phase. We present the distribution of X-ray luminosities and predictions from our population synthesis calculations in Sect. 3. We give our take-home messages in Sect. 4.

2. Methods

We synthesised populations of BBH mergers and their He+BH progenitors utilising the fast binary evolution codes BSE (Hurley et al. 2000, 2002) and StarTrack (Belczynski et al. 2008, 2020). We chose the initial stellar binary distribution according to Sana et al. (2012), namely, orbital periods within 0.15 ≤ log10(P/d) ≤ 3.5 following the distribution f(log10P)∝(log10P/d)−0.55 and eccentricities following f(e)∝e−0.45. The initial binary components are zero-age main sequence (ZAMS) stars, distributed according to the Salpeter mass function (Salpeter 1955), f(m)∝(m/M⊙)−2.35, over the range 5 M⊙ to 150 M⊙, and are paired with each other randomly. We evolved 106 binaries for each of the four metallicity values Z= Z⊙, 0.5 Z⊙, 0.1 Z⊙, and 0.01 Z⊙ (here, Z⊙ = 0.02), which correspond to a total stellar mass (integrated over all masses) of ∼9.6 × 107 M⊙ (for a binarity fraction of 100%).

2.1. BSE models

We used an updated version of BSE, as described in Banerjee & Olejak (2024), derived from the original version of SSE/BSE (Hurley et al. 2000, 2002). The updated BSE contains several extensions regarding stellar wind, stellar remnant mass, binary mass transfer physics, and the natal spin of BHs, described in detail in Banerjee & Olejak (2024).

During a mass transfer episode, the mass transfer and accretion rates are limited by the thermal timescales of the donor and the accretor or the dynamical timescale (Hurley et al. 2002). Apart from this limit, BSE assumes a β = 100% mass accretion efficiency onto a non-degenerate accretor. As for accretion onto a degenerate or compact member (a white dwarf, neutron star, or BH), the mass accretion rate is capped by the Eddington limit. Any mass that is not accreted onto the recipient is assumed to be lost from the system altogether, and this mass loss extracts orbital angular momentum from the system. For mass transfer onto a non-degenerate companion, we assumed that the lost material carries with it the specific angular momentum of the donor, as defaulted in BSE (the ‘γ = −1’ option). For super-Eddington-rate mass transfer onto a degenerate or compact companion, the released material carries the specific angular momentum of the accretor (as if it is a wind from the accretor).

We derived the birth masses of neutron stars (NSs) and BHs according to the ‘delayed’ remnant mass model of Fryer et al. (2012), incorporating the pair-instability supernova (PSN) and pulsational PSN models of Belczynski et al. (2016). The remnant masses are also influenced by the stellar wind mass loss that incorporates, among other ingredients (see Hurley et al. 2000; Banerjee et al. 2020), the Vink et al. (2001) bi-stability-jump wind model for O-type stars and the wind Eddington factor from Gräfener et al. (2011, as implemented in Giacobbo et al. 2018). The remnant natal kicks are drawn from a Maxwellian velocity distribution of σ = 265 km s−1 (Hobbs et al. 2005), which are then reduced based on the supernova (SN) fallback fraction (Fryer et al. 2012).

In these calculations, BHs are, in general, born with a low spin magnitude (Kerr parameter, aBH, i = |χi|; i = 1 or 2) as obtained by the fast-rotating MESA massive-star models of Belczynski et al. (2020). Here, owing to efficient angular momentum transport from the stellar core driven by the Tayler-Spruit dynamo (Spruit 2002), BHs are born with 0.05 ≲ aBH, i ≲ 0.15. However, when a ‘second-born’ BH is formed from a tidally spun-up He star in a close He+BH binary (orbital period < 1.0 day), the BH is born with a potentially higher spin, aBH, 2 ≤ 1.0, based on the BH spin-up model of Bavera et al. (2020); Bavera et al. (2021b).

The default model of the maximum donor-to-recipient mass ratio for a binary to undergo stable mass transfer, qcrit (Hurley et al. 2002), produces BBH mergers predominantly (> 90%) via the CE channel (see e.g. Giacobbo et al. 2018; Olejak et al. 2020; Banerjee 2022). In one set of binary-evolutionary models, we adopted this default qcrit model (which allows Hertzsprung-gap donors to undergo a CE) and designated the resulting BBH-merger population and its progenitor population as ‘CE-dominated’. In a second set of population synthesis runs, we used a constant, high qcrit = 8, as in Banerjee & Olejak (2024), that instead results in BBH mergers predominantly (> 85%) via the SMT channel (see e.g. Gallegos-Garcia et al. 2021; Olejak et al. 2021; Marchant et al. 2021; Picco et al. 2024). We designate the latter type of population as ‘SMT-dominated’.

2.2. StarTrack models

For a second model of the population of He+BH systems (later BBH mergers), we used the StarTrack rapid population synthesis code (Belczynski et al. 2008, 2020), in particular, the default model described in Olejak et al. (2024). This model incorporates updated mass transfer stability criteria (Pavlovskii et al. 2017; Olejak et al. 2021), leading to BBH mergers predominantly formed via the SMT scenario.

During mass transfer onto a non-degenerate accretor, we assumed a fixed accretion efficiency of β = 50%, where β represents the fraction of transferred mass that is accreted by the companion star (Vinciguerra et al. 2020). Any non-accreted mass is expelled from the system, carrying away the specific angular momentum of the binary (Podsiadlowski 1992). For mass transfer onto a BH, we adopted the analytical approximations provided by King et al. (2001), as implemented by Mondal et al. (2020). This results in highly non-conservative mass transfer, where the accretion rate onto the BH is capped at the Eddington limit (see e.g. King et al. 2023). In this scenario, the non-accreted mass is lost with the specific angular momentum of the accretor.

We employed the rapid SN engine model with a mixing parameter fmix = 2.5, consistent with the convection-enhanced SN engines proposed by Fryer et al. (2022). BH formation in our model is accompanied by natal kicks drawn from a Maxwellian velocity distribution with a dispersion σ = 265 kms−1 (Hobbs et al. 2005). However, the kick magnitudes are reduced by the amount of fallback, following the prescriptions of Fryer et al. (2012) and Belczynski et al. (2012), which makes significant natal kicks for massive BHs unlikely.

To account for observed massive BH-BH mergers (with MBH≥ 50 M⊙), we adopted a high threshold for PSNe, assuming that stars with helium core masses exceeding MHe > 90 M⊙ are disrupted (Belczynski 2020). For natal BH spins, we assumed low but non-zero values in the range aBH, 1 ≈ 0.05 − 0.15 (Belczynski et al. 2020), based on the assumption of efficient angular momentum transport in massive stars (Spruit 2002). Additionally, we included efficient tidal spin-up of stripped helium cores in close BH-helium core systems with orbital periods shorter than 1.1 days, following the prescriptions outlined in Belczynski et al. (2020). To estimate the natal spin of the second-born BH, we used Eq. (15) of Belczynski et al. (2022).

2.3. X-ray luminosity

To determine the X-ray luminosity from the vicinity of the BH, we followed the analysis of Sen et al. (2024), who investigated the X-ray emission from BHs with main sequence OB star companions. We adopted their assumptions as applicable for hot stripped helium star companions, outlined below.

X-rays can be emitted from an accretion disk around the BH when the wind matter from the companion star carries enough angular momentum to circularise into an orbit greater than the innermost stable circular orbit of the BH (Iben & Tutukov 1996; Frank 2002; Sen et al. 2021). The X-ray luminosity LX from the accretion disk is estimated by Eq. (21) of Sen et al. (2024):

L X = G M BH M ˙ acc R ISCO , $$ \begin{aligned} L_{\rm X} = G \frac{M_{\rm BH} \dot{M}_{\rm acc}}{R_{\rm ISCO}} ,\end{aligned} $$(2)

where G is the gravitational constant, MBH is the mass of the first-formed BH, and Ṁacc and RISCO are the mass accretion rate onto the BH and the radius of the innermost stable circular orbit of the BH given by Eqs. (22) and (29) from Sen et al. (2024), respectively.

When an accretion disk cannot form, X-rays can be emitted from the BH corona via synchrotron emission, given by Eq. (31) of Sen et al. (2024):

L X = ϵ M ˙ acc c 2 , $$ \begin{aligned} L_{\rm X} = \epsilon \dot{M}_{\rm acc} c^2 ,\end{aligned} $$(3)

where ϵ is the radiative efficiency. The radiative efficiency of X-ray emission without an accretion disk in turn depends on the mass accretion rate and the electron heating efficiency within the advection-dominated accretion flow (Narayan & Yi 1995; Xie & Yuan 2012). Typically, the X-ray luminosity from an accretion disk is a few orders of magnitude greater than in the absence of an accretion disk.

The wind velocity of the companion plays a crucial role in determining the formation of an accretion disk (Eq. (18) of Sen et al. 2021), with the typical wind speeds from O-type stars being too high to form a disk (see also Hirai & Mandel 2021). The higher the wind speed, the more difficult it is for a disk to form. It has recently been shown (Sander et al. 2023) that the terminal wind velocity from stripped hydrogen-free stars does not follow the simple scaling relation of the well-known Castor-Abbott-Klein theory (Castor et al. 1975). Hence, to make a conservative estimate of the number of He+BH binaries that can form an accretion disk, we set an upper limit on the terminal wind velocities for our stripped helium stars, using the empirically determined terminal wind velocities of Galactic WC stars analysed by Sander et al. (2012).

For models that have stripped stars with a radius of less or more than 1 R⊙, we set the terminal wind velocity to 5000 km s−1 or 3000 km s−1, respectively (Table 4 of Sander et al. 2012). Our assumption ensures that an accretion disk forms in the rarest of cases. As such, the predicted X-ray luminosities should be lower limits. To derive the X-ray luminosity from synchrotron emission, we took the electron heating efficiency to be 0.1% (Xie & Yuan 2012; Sen et al. 2024). This ensures a lower limit on the X-ray luminosity in the absence of an accretion disk. For higher electron heating efficiencies (10–50%), the radiative efficiency and X-ray luminosity can be up to two orders of magnitude higher (Xie & Yuan 2012; Sen et al. 2024).

3. Results

We investigated the correlation between (I) the spin-up of the He star during the He+BH phase and (II) the natal spin of the second-born BH with the X-ray luminosity from the vicinity of the first-born BH during the He+BH phase. Our analysis only focuses on those He+BH systems that form BH-BH and NS-BH mergers within a Hubble time.

3.1. Evolution during the helium star+black hole phase

We investigated the X-ray properties of the He+BH binaries that will produce a BH-BH or BH-NS merger within a Hubble time. Figure 1 shows the evolution of the spin period of the He star with the estimated X-ray luminosity of the first-born BH during the He+BH phase for different sets of binary evolutionary models. In all four panels, there is a population of fast-spinning (Pspin < 1 d) He stars with a BH companion that is expected to have X-ray luminosities above 1035 erg s−1. The shortest period He+BH binaries are the most likely to experience strong enough tides to spin up the He star (Ma & Fuller 2023) and simultaneously favour the formation of an accretion disk from which copious amounts of X-rays can be emitted (Sen et al. 2021). X-ray luminosities above 1037 erg s−1 are found to arise from He+BH binaries where an accretion disk can form around the BH.

thumbnail Fig. 1.

For the BSE models: distribution of the estimated X-ray luminosity, LX, with the spin period of the stripped He star during the He+BH phase (sampled every 0.02 Myr), for metallicities Z = 0.01 Z⊙, and Z⊙ and two criteria for the mass transfer stability (see text). All He+BH systems with orbital periods greater than 1 d that merge within a Hubble time end up in yellow (see the colour bar).

At low metallicity (here 0.01 Z⊙; see also Fig. A.1), for the CE-dominated set of models (left panel), there is also a population of models that have spin periods ≥1000 d and X-ray luminosities above 1037 erg s−1. This population, absent in the SMT-dominated channel, arises from the fact that the orbital separation at the onset of the CE phase was reduced in one timestep to a very short orbital period (< 1 d). The CE phase is expected to proceed on a dynamical timescale with a duration of a few thousand years or less (Ivanova et al. 2013, for more recent works, see Hirai & Mandel 2022; Di Stefano et al. 2023; Gagnier & Pejcha 2023; Wei et al. 2024; Vetter et al. 2024; Nie et al. 2025). The CE phase is too short for tides to increase the spin velocities of the He cores significantly. In such cases, stars temporarily retain the spin associated with their pre-CE orbit. Once a binary evolves through the He+BH phase, the He star can be tidally spun up to much higher values. While the CE phase dramatically shrinks the orbital period (from 103 days to about 1 day), BBH mergers progenitors in the SMT channel typically reduce separation during Roche-lobe overflow (specifically, the one from which the He+BH system emerges) less significantly and more gradually.

We find that at Z = 0.01 Z⊙, 0.1 Z⊙, 0.5 Z⊙ and Z⊙, the lifetime-weighted fraction of He+BH binaries that have X-ray luminosities higher than 1035 erg s−1 is 0.457, 0.412, 0.506, and 0.202 for the CE-dominated channel and 0.346, 0.410, 0.298, and 0.147 for the SMT-dominated channel, respectively. This implies that a large fraction of short-period (< 1 d; e.g. Ma & Fuller 2023) He+BH binaries that are expected to spin up due to efficient tides, should also show bright, observable X-ray emission at the four investigated metallicities.

Few Wolf-Rayet stars have been identified as non-coronal X-ray emitters (Freund et al. 2024) in the recently released eROSITA catalogue (Merloni et al. 2024). The X-rays in such systems (e.g. HD 50896, HD 92740, and HD 113904) may be produced from the accretion of the stellar wind of the Wolf-Rayet star onto a compact companion. As such, these are interesting targets for follow-up multi-epoch spectroscopy. These objects may also be relevant in the context of long-duration gamma-ray burst progenitors via the collapsar scenario (Blandford & Znajek 1977; MacFadyen & Woosley 1999; Yoon & Langer 2005; Fryer et al. 2022; Gottlieb et al. 2024).

3.2. Spin of the second-formed black hole

We determined the correlation between the X-ray luminosity from He+BH binaries that will produce a BH-BH merger and the birth spin of the second-formed BH. Figure 2 shows the predicted X-ray luminosity at the last timestep of the He+BH phase and the natal spin of the second formed BH. We show the results for two separate rapid binary population synthesis codes, BSE (left panels) and StarTrack (right panels). This is to improve the robustness of our conclusions to uncertainties in stellar and binary evolution physics and its implementation (Belczynski et al. 2022; Agrawal et al. 2022), while acknowledging that accounting for the differences are beyond the scope of this work.

thumbnail Fig. 2.

Distribution of the estimated X-ray luminosity, LX, with the predicted spin of the second-born BH, aBH, 2, at the end of the He+BH phase from BSE (left) and StarTrack (right), for metallicities Z = 0.01 Z⊙ (top) and Z⊙ (bottom) and the SMT-dominated case.

The contribution of the classical CE channel to the population of BBH merger progenitors has been challenged by recent literature after revisiting mass transfer stability during Roche-lobe overflow (Pavlovskii et al. 2017; Gallegos-Garcia et al. 2021; Shao & Li 2021; Ge et al. 2023) and the expected strict conditions for successful CE ejection (Klencki et al. 2020; Romagnolo et al. 2025). Moreover, some studies indicate that the SMT channel can reproduce the distribution of BH spins of GW population (Olejak & Belczynski 2021) as well as the reported anti-correlation between the χeff and mass ratio of GW sources (Callister et al. 2021; Olejak et al. 2024; Banerjee & Olejak 2024). Therefore, we focused on the results for the SMT-dominated channel, which adopts revised conditions for stability of mass transfer, limiting the contribution of the CE channel.

For both BSE and StarTrack, there is a population of rapidly spinning second-born BHs (aBH, 2 > 0.6) with LX > 1037 erg s−1, originating from He+BH binaries that had an accretion disk around the first-born BH. These He+BH systems, where an accretion disk can form, show no correlation between their X-ray luminosity and the spin of the second-born BH. At low X-ray luminosities (see also Fig. A.2), we find a correlation between the natal spin of the second-born BH and the X-ray luminosity from the first-born BH at the end of the He+BH phase over 1030 erg s−1 < LX < 1036 erg s−1, although the exact nature of the correlation is unique for each of the two rapid population synthesis codes and metallicity. The StarTrack models produce much fewer He+BH binaries where an accretion disk can form with LX > 1037 erg s−1. However, the mass accretion rates are high enough to produce bright X-ray emission from advection-dominated accretion flows near the BH corona without an optically thick, geometrically thin disk.

For both codes, there is a significant decrease in the number of BBH progenitors at Z⊙ compared to 0.01 Z⊙. Strong stellar winds remove most of the mass of initially massive stars and tend to widen the systems such that a BBH merger cannot occur within a Hubble time. There is, however, a difference between the sub-populations from BSE and StarTrack at high metallicity. In particular, the BSE population is dominated by low-spinning BBH merger progenitors (aBH, 2 ≤ 0.4), while the StarTrack population amply reaches higher BH spins (aBH, 2 ≤ 0.6). BSE and StarTrack adopts different prescriptions for the final spin of tidally locked He stars. In particular, BSE adopts Bavera et al. (2021b) that introduces a dependence on the He star mass, whereas StarTrack uses a simpler, mass-independent prescription described in Belczynski et al. (2020). As a result, the Bavera et al. (2021b) prescription limits the possible spin-up of low-mass BH progenitors (MHe ≲ 10 M⊙), which are dominant in the high metallicity environment.

Moreover, BSE derives the spin of second-born BH by considering the widening of the binary orbit during the He+BH phase. As a result, tidally locked systems can leave tidal locking during the He+BH phase and end up with low natal BH spins. The simplified StarTrack approach derives the second-born BH spin based on the initial orbital period of the He+BH phase, neglecting the eventual widening of the orbit during the He+BH phase. A combination of the above two effects leads to contrasting spins of predicted populations of BBH mergers at high metallicity for two codes, with StarTrack likely overestimating the efficiency of tidal spin-up.

3.3. Number of observable He+BH systems

The formation efficiency, ηHeBH, of He+BH systems that end up as binary compact object mergers is

η HeBH ≡ N HeBH ′ M ∗ , $$ \begin{aligned} {\eta _{\rm HeBH}}\equiv \frac{{N^{\prime }_{\rm HeBH}}}{M_*}, \end{aligned} $$(4)

where M* is the total simulated stellar mass, after corrections for the initial mass function truncation and binary fraction, corresponding to a particular set of evolved binaries. The quantity 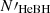N ′ HeBH $ {N\prime_{\mathrm{HeBH}}} $ is the total number of He+BH systems evolving into a double-compact-object merger within a Hubble time that the set has produced (for given metallicity and input physical assumptions; see Sect. 2). For a set of 106 binaries as evolved here (Sect. 2), M* ≈ 9.6 × 107 M⊙, assuming that stars form with a Kroupa (2001) initial mass function over the entire ZAMS stellar-mass range, 0.08 M⊙ − 150.0 M⊙, and with a 100% binary fraction over the simulated ZAMS mass range, 5.0 M⊙ − 150.0 M⊙. Figure 3 (left panel) shows the resulting ηHeBH as a function of metallicity and case, for our computed sets.

thumbnail Fig. 3.

Left panel: Formation efficiency, ηHeBH, of He+BH binaries as a function of metallicity, Z, as obtained from the different binary-evolutionary models computed in this study (see the legend). Note that, here, ηHeBH comprises only the population of He+BH binaries that evolve into BBH or NS+BH mergers within a Hubble time. Right panel: Estimated galaxy-wide counts, NHeBH, obs, of bright, observable X-ray sources (with LX > 1035  ergs−1) corresponding to the Local Group galaxies (and their individual star formation rates; see the text) named along the upper X-axis. Number estimates from StarTrack are not shown, as only evolutionary data for the first and last time steps of the He+BH phase are available.

We assumed that the present-day (i.e. at redshift zero) galaxy-wide star formation rate (hereafter SFR), ℛ*,0, remains constant over the mean lifetime, τHe ≲ 1 Myr, of such an He+BH phase. The present-day, galaxy-wide count of such He+BH binaries is then

N HeBH = R ∗ , 0 η HeBH τ He . $$ \begin{aligned} {N_{\rm HeBH}} = {\mathcal{R} }_{*,0}{\eta _{\rm HeBH}}{\tau _{\rm He}}. \end{aligned} $$(5)

We estimated the count of bright or observable X-ray sources as NHeBH, obs = fXNHeBH, where fX is the fractional He+BH lifetime with predicted LX > 1035  erg s−1 as obtained from the X-ray luminosities of our evolutionary He+BH binary models.

We estimated the NHeBH, obs for Milky Way (MW) and other widely observed Local Group galaxies. We adopted the observationally determined ℛ*,0 values of 2.0 M⊙ yr−1 for the MW (Elia et al. 2022), 0.2 M⊙ yr−1 for the LMC (Harris & Zaritsky 2009), 0.05 M⊙ yr−1 for the Small Magellanic Cloud (SMC; Schootemeijer et al. 2021), and 0.006 M⊙ yr−1 for Sextans A (Plummer & Hunter 1995). Since our computed binary populations are at discrete metallicities, we matched a galaxy with the population that has its metallicity closet to the galaxy’s observed metallicity. Based on the observed average metallicities of the above-considered galaxies (Davies et al. 2015; Choudhury et al. 2016; Lorenzo 2024), we matched MW, LMC, SMC, and Sextans A with the Z⊙, 0.5 Z⊙, 0.1 Z⊙, and 0.1 Z⊙ populations, respectively, assuming Z⊙ = 0.02 as in BSE and StarTrack. The resulting NHeBH, obs values for these galaxies are shown in Fig. 3 (right panel). Notably, the trend of NHeBH, obs with Z is opposite to that of ηHeBH with Z. For the chosen set of galaxies, the decline of ℛ*,0 with decreasing Z dominates over the increasing trend of ηHeBH. As such, this simplistic calculation only considers the galaxies’ mean metallicities, ignoring their internal metallicity dispersions.

We calculate that NHeBH, obs ∼ 2 for the MW and ∼1 for the LMC, as demonstrated in Fig. 3 (right panel). There is only one observed high-mass X-ray binary in the MW harbouring a Wolf-Rayet star (Cyg X-3; Giacconi et al. 1967; Zdziarski et al. 2013) and none observed in the LMC. Our results may imply that the accretion efficiency of BHs in orbit with He stars is much lower than assumed in our work or that very short-period He+BH systems are rarer than predicted by the current binary population synthesis calculations. If the latter is true, the tidal spin-up during the He+BH phase is likely not responsible for the high-spin tail of GW mergers.

Although our predicted number of observable He+BH binaries in the local neighbourhood is low, our results are sensitive to adopted assumptions on several uncertain processes, for example the mass transfer physics (Gallegos-Garcia et al. 2021; Olejak et al. 2021; Sen et al. 2022; Willcox et al. 2023; Picco et al. 2024), stripped-star winds (Detmers et al. 2008; Sander 2023; Shenar 2024) and core-collapse SNe (Aguilera-Dena et al. 2022, 2023; Fryer et al. 2022; Janka & Kresse 2024). There are also significant limitations in predicting detailed properties of the structure and radius of helium cores using rapid codes (e.g. Laplace et al. 2020, 2021; Wang et al. 2024; Hovis-Afflerbach et al. 2024), which may affect our results.

4. Conclusions

In the isolated binary evolution channel, the immediate progenitors of BBH binaries that can merge within a Hubble time are expected to be short-period He+BH systems (see Korb et al. 2025, and references therein). With sufficiently short periods (< 1 d), it has been proposed that the He star companion to the BH can be tidally spun up such that the resultant BH formed from the collapse of the He star has a high Kerr parameter (e.g. Detmers et al. 2008; Qin et al. 2018; Fuller & Lu 2022; Ma & Fuller 2023). Such an evolutionary channel has been invoked to explain the high effective spin parameters of a few BBH mergers observed by LIGO/Virgo (Belczynski et al. 2020; Olejak & Belczynski 2021). However, detections of highly spinning He stars in short-period binaries with BHs have not been unambiguously confirmed, and so the existence of this formation channel has not yet been proven.

We investigated the possibility of using X-ray emission from very short-period He+BH binaries as an observational constraint to determine the detectability and formation efficiencies of the progenitors of BBH mergers. We used recently published prescriptions (Sen et al. 2021, 2024) to estimate lower limits on the X-ray luminosity from the vicinity of the BH in short-period He+BH binaries. We post-processed the X-ray recipe into two rapid population synthesis codes, BSE and StarTrack, to study populations of such binaries at four metallicities, Z = Z⊙, 0.5 Z⊙, 0.1 Z⊙, and 0.01Z⊙.

Our population synthesis calculations from both BSE and StarTrack predict that a significant fraction (10–50%) of GW-merger-producing He+BH binaries should produce X-ray luminosities in excess of 1035 erg s−1 (i.e. luminosities observable with current X-ray telescopes) at all metallicities. The intrinsic formation efficiencies of such observable He+BH systems increase with a decrease in metallicity. Because evolutionary selection effects favour the formation of BBH merger progenitors at low metallicities (see also van Son et al. 2025) and observational selection effects only allow the detection of the brightest X-ray sources, our models predict that ∼2 and ∼1 He+BH binaries in the MW and the LMC are detectable in X-rays. However, our work only investigates the observability in X-rays of He+BH binaries that will produce a GW merger within a Hubble time. As such, our predictions are lower limits since the He+BH binaries that do not evolve to form merging GW binaries could still produce observable X-rays during their He+BH phase.

Upcoming X-ray surveys of the LMC (Antoniou 2022) and Sextans A (Antoniou 2023), and the ongoing X-ray surveys of the MW that have identified Wolf-Rayet stars with atypical coronal emission (Freund et al. 2024), may provide the observational leads needed to identify the population of X-ray-emitting short-period He+BH binaries. Combined with follow-up optical studies of Sextans A (Lorenzo 2024), empirical constraints on the efficiency of the tidal spin-up of He stars during the He+BH phase as a possible channel to explain the highly effective spin parameters of some BBH mergers may be possible. They could also be interesting systems as progenitors of long-duration gamma-ray bursts (Blandford & Znajek 1977; MacFadyen & Woosley 1999; Yoon & Langer 2005; Fryer et al. 2022; Gottlieb et al. 2024).

1

Defined as (Racine 2008; Santamaría et al. 2010; Ajith et al. 2011)

χ eff = m 1 χ 1 + m 2 χ 2 m 1 + m 2 · L ̂ , $$ \begin{aligned} \chi _{\rm eff} = \frac{m_{\rm 1}\boldsymbol{\chi }_{\rm 1} + m_{\rm 2}\boldsymbol{\chi }_{\rm 2}}{m_{\rm 1}+m_{\rm 2}} \cdot \hat{L} ,\end{aligned} $$(1)

where m1, m2, χ1, and χ2 are the masses and spin vectors of the component BHs, and 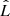L ̂ $ \hat{L} $ is the unit vector of the Newtonian angular momentum of the binary.

Acknowledgments

We thank the anonymous referee, Mathieu Renzo and Norbert Langer for insightful comments that improved the manuscript. KS is funded by the National Science Center (NCN), Poland, under grant number OPUS 2021/41/B/ST9/00757. AO acknowledges funding from the Netherlands Organisation for Scientific Research (NWO), as part of the Vidi research program BinWaves (project number 639.042.728, PI: de Mink). SB acknowledges funding for this work by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) through the project “The dynamics of stellar-mass black holes in dense stellar systems and their role in gravitational wave generation” (project number 405620641; PI: S. Banerjee). Part of the computations presented here have been performed on the Marvin HPC facility of the University of Bonn. SB acknowledges the generous support and efficient system maintenance of the computing teams at the AIfA, HISKP, and the University of Bonn.

References

  1. Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016, Phys. Rev. X, 6, 041015 [Google Scholar]
  2. Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2019, Phys. Rev. X, 9, 031040 [Google Scholar]
  3. Abbott, R., Abbott, T. D., Acernese, F., et al. 2023, Phys. Rev. X, 13, 041039 [Google Scholar]
  4. Agrawal, P., Szécsi, D., Stevenson, S., Eldridge, J. J., & Hurley, J. 2022, MNRAS, 512, 5717 [NASA ADS] [CrossRef] [Google Scholar]
  5. Aguilera-Dena, D. R., Langer, N., Antoniadis, J., et al. 2022, A&A, 661, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Aguilera-Dena, D. R., Müller, B., Antoniadis, J., et al. 2023, A&A, 671, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Ajith, P., Hannam, M., Husa, S., et al. 2011, Phys. Rev. Lett., 106, 241101 [NASA ADS] [CrossRef] [Google Scholar]
  8. Antoniou, V. 2022, Using the LMC to Understand X-ray Binary Evolution: Mind the Metallicity Gap, Chandra Proposal ID 24400340 [Google Scholar]
  9. Antoniou, V. 2023, Insight into the early Universe using very metal-poor massive X-ray binaries, Chandra Proposal ID 25620223 [Google Scholar]
  10. Banerjee, S. 2021, MNRAS, 500, 3002 [Google Scholar]
  11. Banerjee, S. 2022, Phys. Rev. D, 105, 023004 [NASA ADS] [CrossRef] [Google Scholar]
  12. Banerjee, S., & Olejak, A. 2024, A&A, submitted [arXiv:2411.15112] [Google Scholar]
  13. Banerjee, S., Belczynski, K., Fryer, C. L., et al. 2020, A&A, 639, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Bavera, S. S., Fragos, T., Qin, Y., et al. 2020, A&A, 635, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Bavera, S. S., Fragos, T., Zevin, M., et al. 2021a, A&A, 647, A153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Bavera, S. S., Zevin, M., & Fragos, T. 2021b, Res. Notes Am. Astron. Soc., 5, 127 [Google Scholar]
  17. Belczynski, K. 2020, ApJ, 905, L15 [Google Scholar]
  18. Belczynski, K., Kalogera, V., Rasio, F. A., et al. 2008, ApJS, 174, 223 [Google Scholar]
  19. Belczynski, K., Wiktorowicz, G., Fryer, C. L., Holz, D. E., & Kalogera, V. 2012, ApJ, 757, 91 [NASA ADS] [CrossRef] [Google Scholar]
  20. Belczynski, K., Heger, A., Gladysz, W., et al. 2016, A&A, 594, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Belczynski, K., Klencki, J., Fields, C. E., et al. 2020, A&A, 636, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Belczynski, K., Romagnolo, A., Olejak, A., et al. 2022, ApJ, 925, 69 [NASA ADS] [CrossRef] [Google Scholar]
  23. Belczynski, K., Done, C., Hagen, S., Lasota, J.-P., & Sen, K. 2024, A&A, 690, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Blandford, R. D., & Znajek, R. L. 1977, MNRAS, 179, 433 [NASA ADS] [CrossRef] [Google Scholar]
  25. Boesky, A. P., Broekgaarden, F. S., & Berger, E. 2024, ApJ, 976, 24 [NASA ADS] [Google Scholar]
  26. Bondi, H., & Hoyle, F. 1944, MNRAS, 104, 273 [Google Scholar]
  27. Briel, M. M., Stevance, H. F., & Eldridge, J. J. 2023, MNRAS, 520, 5724 [Google Scholar]
  28. Callister, T. A., Haster, C.-J., Ng, K. K. Y., Vitale, S., & Farr, W. M. 2021, ApJ, 922, L5 [NASA ADS] [CrossRef] [Google Scholar]
  29. Callister, T. A., Miller, S. J., Chatziioannou, K., & Farr, W. M. 2022, ApJ, 937, L13 [NASA ADS] [CrossRef] [Google Scholar]
  30. Castor, J. I., Abbott, D. C., & Klein, R. I. 1975, ApJ, 195, 157 [Google Scholar]
  31. Chen, H.-L., Tauris, T. M., Chen, X., & Han, Z. 2023, ApJ, 951, 91 [NASA ADS] [CrossRef] [Google Scholar]
  32. Choudhury, S., Subramaniam, A., & Cole, A. A. 2016, MNRAS, 455, 1855 [NASA ADS] [CrossRef] [Google Scholar]
  33. Choudhury, S., de Grijs, R., Bekki, K., et al. 2021, MNRAS, 507, 4752 [CrossRef] [Google Scholar]
  34. Davies, B., Kudritzki, R.-P., Gazak, Z., et al. 2015, ApJ, 806, 21 [NASA ADS] [CrossRef] [Google Scholar]
  35. Delfavero, V., Ford, K. E. S., McKernan, B., et al. 2024, ArXiv e-prints [arXiv:2410.18815] [Google Scholar]
  36. Detmers, R. G., Langer, N., Podsiadlowski, P., & Izzard, R. G. 2008, A&A, 484, 831 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Di Stefano, R., Kruckow, M. U., Gao, Y., Neunteufel, P. G., & Kobayashi, C. 2023, ApJ, 944, 87 [NASA ADS] [CrossRef] [Google Scholar]
  38. Dorozsmai, A., & Toonen, S. 2024, MNRAS, 530, 3706 [NASA ADS] [CrossRef] [Google Scholar]
  39. Draghis, P. A., Miller, J. M., Costantini, E., et al. 2024, ApJ, 969, 40 [NASA ADS] [CrossRef] [Google Scholar]
  40. Elia, D., Molinari, S., Schisano, E., et al. 2022, ApJ, 941, 162 [NASA ADS] [CrossRef] [Google Scholar]
  41. Fishbach, M., & Kalogera, V. 2022, ApJ, 929, L26 [NASA ADS] [CrossRef] [Google Scholar]
  42. Fragos, T., & McClintock, J. E. 2015, ApJ, 800, 17 [Google Scholar]
  43. Frank, J., King, A., & Raine, D. J. 2002, Accretion Power in Astrophysics, Third Edition [Google Scholar]
  44. Freund, S., Czesla, S., Predehl, P., et al. 2024, A&A, 684, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Fryer, C. L., Belczynski, K., Wiktorowicz, G., et al. 2012, ApJ, 749, 91 [Google Scholar]
  46. Fryer, C. L., Olejak, A., & Belczynski, K. 2022, ApJ, 931, 94 [NASA ADS] [CrossRef] [Google Scholar]
  47. Fuller, J., & Lu, W. 2022, MNRAS, 511, 3951 [NASA ADS] [CrossRef] [Google Scholar]
  48. Fuller, J., & Ma, L. 2019, ApJ, 881, L1 [Google Scholar]
  49. Gagnier, D., & Pejcha, O. 2023, A&A, 674, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Gallegos-Garcia, M., Berry, C. P. L., Marchant, P., & Kalogera, V. 2021, ApJ, 922, 110 [NASA ADS] [CrossRef] [Google Scholar]
  51. Gallegos-Garcia, M., Berry, C. P. L., & Kalogera, V. 2023, ApJ, 955, 133 [NASA ADS] [CrossRef] [Google Scholar]
  52. Ge, H., Tout, C. A., Chen, X., et al. 2023, ApJ, 945, 7 [NASA ADS] [CrossRef] [Google Scholar]
  53. Genzel, R., Eisenhauer, F., & Gillessen, S. 2024, A&ARv, 32, 3 [NASA ADS] [Google Scholar]
  54. Giacconi, R., Gorenstein, P., Gursky, H., & Waters, J. R. 1967, ApJ, 148, L119 [NASA ADS] [CrossRef] [Google Scholar]
  55. Giacobbo, N., Mapelli, M., & Spera, M. 2018, MNRAS, 474, 2959 [Google Scholar]
  56. Ginat, Y. B., Glanz, H., Perets, H. B., Grishin, E., & Desjacques, V. 2020, MNRAS, 493, 4861 [CrossRef] [Google Scholar]
  57. Gottlieb, O., Renzo, M., Metzger, B. D., Goldberg, J. A., & Cantiello, M. 2024, ApJ, 976, L13 [NASA ADS] [Google Scholar]
  58. Gräfener, G., Vink, J. S., de Koter, A., & Langer, N. 2011, A&A, 535, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Harris, J., & Zaritsky, D. 2009, AJ, 138, 1243 [NASA ADS] [CrossRef] [Google Scholar]
  60. Hirai, R., & Mandel, I. 2021, PASA, 38, e056 [NASA ADS] [CrossRef] [Google Scholar]
  61. Hirai, R., & Mandel, I. 2022, ApJ, 937, L42 [NASA ADS] [CrossRef] [Google Scholar]
  62. Hobbs, G., Lorimer, D. R., Lyne, A. G., & Kramer, M. 2005, MNRAS, 360, 974 [Google Scholar]
  63. Hovis-Afflerbach, B., Götberg, Y., Schootemeijer, A., et al. 2024, A&A, submitted [arXiv:2412.05356] [Google Scholar]
  64. Hurley, J. R., Pols, O. R., & Tout, C. A. 2000, MNRAS, 315, 543 [Google Scholar]
  65. Hurley, J. R., Tout, C. A., & Pols, O. R. 2002, MNRAS, 329, 897 [Google Scholar]
  66. Iben, I. J., & Tutukov, A. V. 1996, ApJS, 105, 145 [NASA ADS] [CrossRef] [Google Scholar]
  67. Ivanova, N., Justham, S., Chen, X., et al. 2013, A&ARv, 21, 59 [Google Scholar]
  68. Janka, H.-T., & Kresse, D. 2024, Ap&SS, 369, 80 [NASA ADS] [CrossRef] [Google Scholar]
  69. Kaufer, A., Venn, K. A., Tolstoy, E., Pinte, C., & Kudritzki, R.-P. 2004, AJ, 127, 2723 [NASA ADS] [CrossRef] [Google Scholar]
  70. King, A. R., Davies, M. B., Ward, M. J., Fabbiano, G., & Elvis, M. 2001, ApJ, 552, L109 [NASA ADS] [CrossRef] [Google Scholar]
  71. King, A., Lasota, J.-P., & Middleton, M. 2023, New Astron. Rev., 96, 101672 [CrossRef] [Google Scholar]
  72. Kıroğlu, F., Kremer, K., Biscoveanu, S., González Prieto, E., & Rasio, F. A. 2025, ApJ, 979, 237 [Google Scholar]
  73. Klencki, J., Nelemans, G., Istrate, A. G., & Pols, O. 2020, A&A, 638, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  74. Korb, E., Mapelli, M., Iorio, G., & Costa, G. 2025, A&A, 695, A199 [Google Scholar]
  75. Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
  76. Kruckow, M. U., Tauris, T. M., Langer, N., Kramer, M., & Izzard, R. G. 2018, MNRAS, 481, 1908 [CrossRef] [Google Scholar]
  77. Kruckow, M. U., Andrews, J. J., Fragos, T., et al. 2024, A&A, 692, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  78. Kushnir, D., Zaldarriaga, M., Kollmeier, J. A., & Waldman, R. 2016, MNRAS, 462, 844 [NASA ADS] [CrossRef] [Google Scholar]
  79. Laplace, E., Götberg, Y., de Mink, S. E., Justham, S., & Farmer, R. 2020, A&A, 637, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  80. Laplace, E., Justham, S., Renzo, M., et al. 2021, A&A, 656, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  81. Lehmer, B. D., Garofali, K., Binder, B. A., et al. 2023, Front. Astron. Space Sci., 10, 1293918 [NASA ADS] [Google Scholar]
  82. Li, L., Wang, B., Liu, D., et al. 2024, MNRAS, 534, 3400 [NASA ADS] [CrossRef] [Google Scholar]
  83. Li, Y. J., Wang, Y. Z., Tang, S. P., Chen, T., & Fan, Y. Z. 2025, ArXiv e-prints [arXiv:2501.09495] [Google Scholar]
  84. Liotine, C., Zevin, M., Berry, C. P. L., Doctor, Z., & Kalogera, V. 2023, ApJ, 946, 4 [NASA ADS] [CrossRef] [Google Scholar]
  85. Lorenzo, M., Garcia, M., & Najarro, F. 2024, in One step closer to the First Stars: +150 OB stars in the metal-poor galaxy Sextans A, eds. J. Mackey, J. S. Vink, & N. St-Louis, IAU Symp., 361, 52 [Google Scholar]
  86. Ma, L., & Fuller, J. 2023, ApJ, 952, 53 [CrossRef] [Google Scholar]
  87. MacFadyen, A. I., & Woosley, S. E. 1999, ApJ, 524, 262 [NASA ADS] [CrossRef] [Google Scholar]
  88. Madsen, K. K., Harrison, F., Broadway, D., et al. 2018, in Space Telescopes and Instrumentation 2018: Ultraviolet to Gamma Ray, eds. J. W. A. den Herder, S. Nikzad, & K. Nakazawa, SPIE Conf. Ser., 10699, 106996M [NASA ADS] [Google Scholar]
  89. Mandel, I. 2024, Bull. Soc. Roy. Sci. Liege, 93, 302 [Google Scholar]
  90. Mandel, I., & Broekgaarden, F. S. 2022, Liv. Rev. Relativity, 25, 1 [NASA ADS] [CrossRef] [Google Scholar]
  91. Mapelli, M. 2020, Front. Astron. Space Sci., 7, 38 [NASA ADS] [CrossRef] [Google Scholar]
  92. Marchant, P., Pappas, K. M. W., Gallegos-Garcia, M., et al. 2021, A&A, 650, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  93. Merloni, A., Lamer, G., Liu, T., et al. 2024, A&A, 682, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  94. Miller-Jones, J. C. A., Bahramian, A., Orosz, J. A., et al. 2021, Science, 371, 1046 [Google Scholar]
  95. Misra, D., Kovlakas, K., Fragos, T., et al. 2023, A&A, 672, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  96. Misra, D., Kovlakas, K., Fragos, T., et al. 2024, A&A, 682, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  97. Mondal, S., Belczyński, K., Wiktorowicz, G., Lasota, J.-P., & King, A. R. 2020, MNRAS, 491, 2747 [Google Scholar]
  98. Mushotzky, R. 2018, in Space Telescopes and Instrumentation 2018: Ultraviolet to Gamma Ray, eds. J. W. A. den Herder, S. Nikzad, & K. Nakazawa, SPIE Conf. Ser., 10699, 1069929 [NASA ADS] [Google Scholar]
  99. Narayan, R., & Yi, I. 1995, ApJ, 452, 710 [NASA ADS] [CrossRef] [Google Scholar]
  100. Nie, Y.-D., Shao, Y., He, J.-G., et al. 2025, ApJ, 979, 112 [NASA ADS] [Google Scholar]
  101. Olejak, A., & Belczynski, K. 2021, ApJ, 921, L2 [NASA ADS] [CrossRef] [Google Scholar]
  102. Olejak, A., Belczynski, K., Bulik, T., & Sobolewska, M. 2020, A&A, 638, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  103. Olejak, A., Belczynski, K., & Ivanova, N. 2021, A&A, 651, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  104. Olejak, A., Klencki, J., Xu, X.-T., et al. 2024, A&A, 689, A305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  105. Orosz, J. A., Steeghs, D., McClintock, J. E., et al. 2009, ApJ, 697, 573 [NASA ADS] [CrossRef] [Google Scholar]
  106. Orosz, J. A., McClintock, J. E., Aufdenberg, J. P., et al. 2011, ApJ, 742, 84 [NASA ADS] [CrossRef] [Google Scholar]
  107. O’Shaughnessy, R., Kaplan, J., Kalogera, V., & Belczynski, K. 2005, ApJ, 632, 1035 [Google Scholar]
  108. Pavlovskii, K., Ivanova, N., Belczynski, K., & Van, K. X. 2017, MNRAS, 465, 2092 [Google Scholar]
  109. Picco, A., Marchant, P., Sana, H., & Nelemans, G. 2024, A&A, 681, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  110. Plummer, J. D., & Hunter, D. A. 1995, Am. Astron. Soc. Meeting Abstr., 187, 1105 [NASA ADS] [Google Scholar]
  111. Podsiadlowski, P. 1992, PASP, 104, 717 [CrossRef] [Google Scholar]
  112. Podsiadlowski, P., Rappaport, S., & Han, Z. 2003, MNRAS, 341, 385 [NASA ADS] [CrossRef] [Google Scholar]
  113. Qin, Y., Fragos, T., Meynet, G., et al. 2018, A&A, 616, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  114. Qin, K., Xu, K., Liu, D.-D., et al. 2024, ApJ, 961, 110 [NASA ADS] [Google Scholar]
  115. Racine, E. 2008, Phys. Rev. D, 78, 044021 [Google Scholar]
  116. Ray, P., Arzoumanian, Z., Ballantyne, D., et al. 2019, Bull. Am. Astron. Soc., 51, 231 [Google Scholar]
  117. Renzo, M., Callister, T., Chatziioannou, K., et al. 2021, ApJ, 919, 128 [NASA ADS] [CrossRef] [Google Scholar]
  118. Reynolds, C. S. 2021, ARA&A, 59, 117 [NASA ADS] [CrossRef] [Google Scholar]
  119. Romagnolo, A., Klencki, J., Vigna-Gómez, A., & Belczynski, K. 2025, A&A, 693, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  120. Romero-Shaw, I., Hirai, R., Bahramian, A., Willcox, R., & Mandel, I. 2023, MNRAS, 524, 245 [NASA ADS] [CrossRef] [Google Scholar]
  121. Roulet, J., & Zaldarriaga, M. 2019, MNRAS, 484, 4216 [NASA ADS] [CrossRef] [Google Scholar]
  122. Roulet, J., Chia, H. S., Olsen, S., et al. 2021, Phys. Rev. D, 104, 083010 [NASA ADS] [CrossRef] [Google Scholar]
  123. Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
  124. Sana, H., de Mink, S. E., de Koter, A., et al. 2012, Science, 337, 444 [Google Scholar]
  125. Sander, A. A. C. 2023, in Winds of Stars and Exoplanets, eds. A. A. Vidotto, L. Fossati, & J. S. Vink, IAU Symp., 370, 130 [NASA ADS] [Google Scholar]
  126. Sander, A., Hamann, W. R., & Todt, H. 2012, A&A, 540, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  127. Sander, A. A. C., Lefever, R. R., Poniatowski, L. G., et al. 2023, A&A, 670, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  128. Santamaría, L., Ohme, F., Ajith, P., et al. 2010, Phys. Rev. D, 82, 064016 [CrossRef] [Google Scholar]
  129. Santini, A., Gerosa, D., Cotesta, R., & Berti, E. 2023, Phys. Rev. D, 108, 083033 [CrossRef] [Google Scholar]
  130. Schootemeijer, A., Langer, N., Lennon, D., et al. 2021, A&A, 646, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  131. Sen, K., Xu, X. T., Langer, N., et al. 2021, A&A, 652, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  132. Sen, K., Langer, N., Marchant, P., et al. 2022, A&A, 659, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  133. Sen, K., El Mellah, I., Langer, N., et al. 2024, A&A, 690, A256 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  134. Shakura, N. I. 1973, Sov. Ast., 16, 756 [NASA ADS] [Google Scholar]
  135. Shao, Y., & Li, X.-D. 2015, ApJ, 802, 131 [Google Scholar]
  136. Shao, Y., & Li, X.-D. 2019, ApJ, 885, 151 [NASA ADS] [CrossRef] [Google Scholar]
  137. Shao, Y., & Li, X.-D. 2020, ApJ, 898, 143 [NASA ADS] [CrossRef] [Google Scholar]
  138. Shao, Y., & Li, X.-D. 2021, ApJ, 920, 81 [NASA ADS] [CrossRef] [Google Scholar]
  139. Shao, Y., & Li, X.-D. 2022, ApJ, 930, 26 [NASA ADS] [CrossRef] [Google Scholar]
  140. Shao, Y., Li, X.-D., & Dai, Z.-G. 2019, ApJ, 886, 118 [Google Scholar]
  141. Shenar, T. 2024, ArXiv e-prints [arXiv:2410.04436] [Google Scholar]
  142. Skoutnev, V. A., & Beloborodov, A. M. 2024a, ApJ, 974, 290 [NASA ADS] [CrossRef] [Google Scholar]
  143. Skoutnev, V. A., & Beloborodov, A. M. 2024b, ArXiv e-prints [arXiv:2411.08492] [Google Scholar]
  144. Spera, M., Mapelli, M., Giacobbo, N., et al. 2019, MNRAS, 485, 889 [Google Scholar]
  145. Spruit, H. C. 2002, A&A, 381, 923 [CrossRef] [EDP Sciences] [Google Scholar]
  146. Tutukov, A. V., & Yungelson, L. R. 1993, MNRAS, 260, 675 [Google Scholar]
  147. van den Heuvel, E. P. J., Portegies Zwart, S. F., & de Mink, S. E. 2017, MNRAS, 471, 4256 [Google Scholar]
  148. van Son, L. A. C., de Mink, S. E., Callister, T., et al. 2022, ApJ, 931, 17 [NASA ADS] [CrossRef] [Google Scholar]
  149. van Son, L. A. C., Roy, S. K., Mandel, I., et al. 2025, ApJ, 979, 209 [Google Scholar]
  150. Vanbeveren, D., Mennekens, N., van den Heuvel, E. P. J., & Van Bever, J. 2020, A&A, 636, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  151. Vetter, M., Röpke, F. K., Schneider, F. R. N., et al. 2024, A&A, 691, A244 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  152. Vinciguerra, S., Neijssel, C. J., Vigna-Gómez, A., et al. 2020, MNRAS, 498, 4705 [NASA ADS] [CrossRef] [Google Scholar]
  153. Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  154. Wang, B., Chen, W.-C., Liu, D.-D., et al. 2021, MNRAS, 506, 4654 [NASA ADS] [CrossRef] [Google Scholar]
  155. Wang, C., Bodensteiner, J., Xu, X.-T., et al. 2024, ApJ, 975, L20 [NASA ADS] [Google Scholar]
  156. Wei, D., Schneider, F. R. N., Podsiadlowski, P., et al. 2024, A&A, 688, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  157. Willcox, R., MacLeod, M., Mandel, I., & Hirai, R. 2023, ApJ, 958, 138 [NASA ADS] [CrossRef] [Google Scholar]
  158. Xie, F.-G., & Yuan, F. 2012, MNRAS, 427, 1580 [NASA ADS] [CrossRef] [Google Scholar]
  159. Xing, Z., Fragos, T., Zapartas, E., et al. 2025, A&A, 693, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  160. Yoon, S. C., & Langer, N. 2005, A&A, 443, 643 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  161. Zdziarski, A. A., Mikolajewska, J., & Belczynski, K. 2013, MNRAS, 429, L104 [Google Scholar]
  162. Zdziarski, A. A., Banerjee, S., Chand, S., et al. 2024, ApJ, 962, 101 [NASA ADS] [CrossRef] [Google Scholar]
  163. Zevin, M., Bavera, S. S., Berry, C. P. L., et al. 2021, ApJ, 910, 152 [Google Scholar]

Appendix A: Supplementary plots

thumbnail Fig. A.1.

Same as Fig. 1 but for Z = 0.1 Z⊙ and 0.5 Z⊙.

thumbnail Fig. A.2.

Same as Fig. 2 but for Z = 0.1 Z⊙ and 0.5 Z⊙.

All Figures

thumbnail Fig. 1.

For the BSE models: distribution of the estimated X-ray luminosity, LX, with the spin period of the stripped He star during the He+BH phase (sampled every 0.02 Myr), for metallicities Z = 0.01 Z⊙, and Z⊙ and two criteria for the mass transfer stability (see text). All He+BH systems with orbital periods greater than 1 d that merge within a Hubble time end up in yellow (see the colour bar).
In the text
thumbnail Fig. 2.

Distribution of the estimated X-ray luminosity, LX, with the predicted spin of the second-born BH, aBH, 2, at the end of the He+BH phase from BSE (left) and StarTrack (right), for metallicities Z = 0.01 Z⊙ (top) and Z⊙ (bottom) and the SMT-dominated case.
In the text
thumbnail Fig. 3.

Left panel: Formation efficiency, ηHeBH, of He+BH binaries as a function of metallicity, Z, as obtained from the different binary-evolutionary models computed in this study (see the legend). Note that, here, ηHeBH comprises only the population of He+BH binaries that evolve into BBH or NS+BH mergers within a Hubble time. Right panel: Estimated galaxy-wide counts, NHeBH, obs, of bright, observable X-ray sources (with LX > 1035  ergs−1) corresponding to the Local Group galaxies (and their individual star formation rates; see the text) named along the upper X-axis. Number estimates from StarTrack are not shown, as only evolutionary data for the first and last time steps of the He+BH phase are available.
In the text
thumbnail Fig. A.1.

Same as Fig. 1 but for Z = 0.1 Z⊙ and 0.5 Z⊙.
In the text
thumbnail Fig. A.2.

Same as Fig. 2 but for Z = 0.1 Z⊙ and 0.5 Z⊙.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.