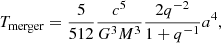EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 671 (March 2023) A&A, 671 (2023) A62 Full HTML
Open Access
Issue
A&A
Volume 671, March 2023
Article Number A62
Number of page(s) 15
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/202244712
Published online 06 March 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

The LIGO-Virgo-KAGRA (LVK) Collaboration has released the Gravitational Wave Transient Catalog 3 (GWTC-3; The LIGO Scientific Collaboration 2021b), consisting of 69 confident binary black hole (BBH) merger events and whose detection threshold to count events has a false alarm rate of less than 1 yr−1. The LVK Collaboration has also inferred the intrinsic properties of the targeted sample of BBHs in the GWTC-3 (e.g., merger rates, masses, and effective inspiral spins), among which the effective inspiral spin χeff1 has been widely considered as a probe to distinguish the formation channels of merging BBH events (Abbott et al. 2016b; Farr et al. 2017, 2018; The LIGO Scientific Collaboration 2021c; Roulet et al. 2021). The majority of the BBHs reported by the LVK Collaboration have a low χeff, while several BBH mergers show a clearly high positive χeff, for example, 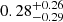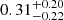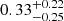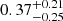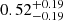0 . 28 − 0.29 + 0.26 $ 0.28_{-0.29}^{+0.26} $, 0 . 31 − 0.22 + 0.20 $ 0.31_{-0.22}^{+0.20} $, 0 . 33 − 0.25 + 0.22 $ 0.33_{-0.25}^{+0.22} $, 0 . 37 − 0.25 + 0.21 $ 0.37_{-0.25}^{+0.21} $, 0 . 52 − 0.19 + 0.19 $ 0.52_{-0.19}^{+0.19} $ for GW190706, GW190519, GW190620, GW170729, GW190517, respectively (Abbott et al. 2021). GW190403 and GW190805 with high χeff were reported from deeper searches in GWTC-2.1 (The LIGO Scientific Collaboration 2021a) but with a low-significance false alarm rate threshold of two per day. We also note that these high values of χeff are under heavy debate (see e.g., Callister et al. 2022; Vitale et al. 2022 references therein).

Substantial progress in understanding the origin of BBHs has been made in the field over the last seven years since the discovery of the first gravitational wave (GW) event: GW150914 (Abbott et al. 2016a). However, the formation process of BBH merger events remains an open scientific question. Leading models of BBH formation include isolated binary evolution via either common envelope (CE; e.g., Phinney 1991; Tutukov & Yungelson 1973; Belczynski et al. 2007, 2016; Ivanova et al. 2013; Postnov & Yungelson 2014; Vigna-Gómez et al. 2018; Qin et al. 2018; Bavera et al. 2020, 2022; Hu et al. 2022, 2023), stable Roche-lobe overflow (RLOF; e.g., van den Heuvel et al. 2017; Inayoshi et al. 2017; Bavera et al. 2021; Olejak et al. 2021; Olejak & Belczynski 2021; Gallegos-Garcia et al. 2021; Marchant et al. 2021; Tanikawa et al. 2022; Shao & Li 2022; van Son et al. 2022a,b), or chemical mixing (Marchant et al. 2016; Mandel & de Mink 2016; de Mink & Mandel 2016; Song et al. 2016; du Buisson et al. 2020; Riley et al. 2021; Qin et al. 2022b), as well as dynamical assembly in globular clusters and galactic nuclear clusters (e.g., Rodriguez et al. 2015; Antonini et al. 2016; Safarzadeh et al. 2020; Mapelli et al. 2021; Fragione et al. 2022) or efficient migration assisted in active galactic nuclei (AGN) disks (Secunda et al. 2019; McKernan et al. 2020; Tagawa et al. 2020; Saavik Ford & McKernan 2022). Alternatively, two BHs can be the outcome of hierarchical stellar-mass BH mergers (Doctor et al. 2020; Kimball et al. 2020, 2021; Gerosa & Fishbach 2021).

Zevin et al. (2021) recently investigated multiple formation pathways (isolated binary evolution channels and dynamical assembly channels) and found that neither channel can contribute more than approximately 70% of the BBHs reported in the GWTC-2. Moreover, Mandel & Farmer (2022; see also Mapelli 2020; Mandel & Broekgaarden 2022) pointed out that the merger rates for BBHs can vary by orders of magnitude for different formation scenarios. So far, quantitatively predicting the properties of merging BBHs is a challenge due to uncertain physics involved in single and/or binary evolution (Abadie et al. 2010; Dominik et al. 2015; de Mink & Belczynski 2015; Giacobbo & Mapelli 2018; Tang et al. 2020; Broekgaarden et al. 2022; Belczynski et al. 2022; Peng et al. 2022).

Merging BBHs could be formed through the process of double-core evolution. This scenario involving the CE phase has been recently investigated, focusing on low-mass He-rich stars leading to form double neutron stars (NSs; Dewi et al. 2006; Hwang & Lombardi 2015; Vigna-Gómez et al. 2018). More massive stars with a mass-ratio close to one at low metallicities evolving from zero age main sequence (ZAMS) in close binaries can undergo several stable mass transfer phases during core hydrogen burning (Case A mass transfer phase) and thus form double He-rich stars as potential progenitors of BBHs (see Fig. 3 in Marchant et al. 2016). However, two massive stars could first evolve to form a close binary system composed of a He-star and a main-sequence companion star after the first mass transfer. Subsequently, the second mass transfer from the main-sequence or giant star to the He-star would lead to the formation of massive He-rich binary stars in a short orbit.

For now most BBH systems reported by the LVK Collaboration are still consistent with zero BH spins. Recently, by employing a variety of complementary methods to measure the distribution of spin magnitudes and orientations for BBH mergers, Callister et al. (2022) found that the existence of a subpopulation of BHs with vanishing spins is not required by current data. The fact that, at the moment, no event necessarily requires a high spin of course does not mean that among the events already detected, there are not any that may present a high spin. High BH spins may indicate that the inefficient angular momentum (AM) transport mechanism within the BH progenitor is preferred (Qin et al. 2019a,b, 2022c). This conclusion can be reached with the assumption that BBHs are formed through the classical isolated binary evolution channel involving the CE phase, before which the initially more massive star collapses to form the first-born BH. According to this evolution channel, the progenitor of the first-born BH is in a wide orbit in which the tides from its companion are too weak to change the spin AM of both components. Therefore, the resultant BH spin inherited from the AM content of its progenitor is exclusively determined by the AM transport efficiency within the progenitor star during post main sequence expansion. In the case of an efficient transport, any removal of the outer layers (at the time of the CE phase) slows the whole star, even its core. If there is a less efficient coupling, the core spins faster than the envelope, and removing the envelope will result in a core that rotates faster than in the case of the efficient AM transport.

Alternatively, as Olejak & Belczynski (2021) have shown, fast-spinning BHs in merging BBHs can be formed by tidal spin-up through either a stable mass transfer phase, leading to the mass ratio reversal, or the CE phase, forming equal-mass BH components. For the case of stable mass transfer (see Fig. 1 in Olejak & Belczynski 2021), the initially more massive star evolves first to become a BH, and then its companion obtains enough mass via the first RLOF to become a massive He-rich star due to losing its hydrogen envelope to the first-born BH in the second RLOF. The He-rich star subsequently evolves to become a fast-spinning BH by the tides (Qin et al. 2018). As for the CE phase case (see Fig. 2 in Olejak & Belczynski 2021), the two stars with initially equal mass instead form twin-mass He-rich stars following the RLOF mass transfer and subsequent CE phase. Two fast-spinning BHs are then formed via Wolf-Rayet tides. More recently, employing the assumption of the Eddington-limited accretion for the BHs and efficient AM transport within massive stars, Zevin & Bavera (2022) investigated the isolated binary evolution regarding the formation of highly spinning BHs and concluded that it is difficult to form systems with moderate or high spins in the primary BH component. However, the BH can be efficiently spun up by highly super-Eddington accretion (Bavera et al. 2021; van Son et al. 2020; Qin et al. 2022a; Shao & Li 2022).

The Tayler-Spruit (TS) dynamo (Spruit 2002), produced by differential rotation in the radiative layers, is considered to be one of potential mechanisms responsible for the efficient transport of AM between the stellar core and its radiative envelope. In brief, the TS dynamo starts for a small radial magnetic field component (its precise initial value has no importance since it is rapidly enhanced by the dynamo mechanism). This component is wound up per differential rotation, and an azimuthal component field is formed. An azimuthal field is unstable due to Tayler instability (i.e., a non-axisymmetric pinch-type instability). The Tayler instability also has the effect of amplifying both the azimuthal and the radial fields. Then, a new radial component is wound up, and the instability starts again. This amplification mechanism lasts until the growth timescale of the magnetic field is equal to its damping timescale. Assuming that a stationary situation is reached at every time step and that the length over which the instability can develop is small enough to allow the excess energy in the differential rotation to overcome the stabilizing entropy gradient but large enough for the magnetic field to not decay too fast, it is possible to deduce the diffusion and viscosity coeffiecients. The revised TS dynamo (Fuller et al. 2019) is based on the fact that the damping timescale can be much longer than the one assumed in the original TS dynamo. In the case of the revised dynamo, larger magnetic fields can be reached and stronger coupling can be achieved (see the discussion in Eggenberger et al. 2022).

Stellar models with the original TS dynamo can reproduce the rotation rates for the Sun (Eggenberger et al. 2005), white dwarfs, and NSs (Heger et al. 2005; Suijs et al. 2008). However, the TS dynamo has been challenged for how it explains the slow rotation rates of cores in red giants (Eggenberger et al. 2012; Cantiello et al. 2014). Recently, the revised TS dynamo (Fuller et al. 2019), which was proposed to better match lower core rotation rates for subgiant and red giant stars and obtain better agreement with observed values, has also faced difficulty in reproducing the observational constraints on asteroseismic data of evolved stars (Eggenberger et al. 2019; den Hartogh et al. 2020). Compared to the original TS dynamo, lower BH spins are predicted when applying the revised TS dynamo to massive He-rich stars in close binary systems (Fuller & Lu 2022). More recently, Eggenberger et al. (2022) derived a new calibrated version of the original TS dynamo to better account for the evolution of the core rotation rates along the red giant branch stars, compared to the revised TS dynamo. There was a theoretical debate on the existence of the dynamo (Zahn et al. 2007). Ji et al. (2022) recently performed three-dimensional magnetohydrodynamic simulations of the Tayler instability in rotating stellar interiors and claimed to observe dynamo action via the amplification of the poloidal magnetic field, indicating that Tayler instability could be important for magnetic field generation and AM transport in the radiative regions of evolving stars. Detailed comparisons between the different versions of TS dynamo are beyond the scope of this work. Therefore, we have focused on the impact of the original TS dynamo within massive He-rich stars on the spin of resultant BHs and what occurs when the TS dynamo is not included.

In this paper, we systematically investigate an alternative evolutionary scenario to form BBHs from double He-rich stars: the double-core evolution scenario first proposed by Brown (1995), who studied the formation of double NSs. In Sect. 2, we introduce the main methods used in the stellar and binary evolution models. We present our detailed results in Sect. 3. The conclusions and discussion are summarized in Sect. 4.

2. Methods

We used release 15140 of MESA stellar evolution code (Paxton et al. 2011, 2013, 2015, 2018, 2019) to perform all of the binary evolution calculations in this work. We adopted three different kinds of metallicities, Z = Z⊙, 0.1 Z⊙, 0.01 Z⊙, where the solar metallicity is Z⊙ = 0.0142 (Asplund et al. 2009). We created He-rich stars at zero age helium main sequence (ZAHeMS) following the same method as in Qin et al. (2018), Bavera et al. (2020), Hu et al. (2022), Fragos et al. (2023), and we then relaxed the created He-rich stars to reach the thermal equilibrium when the ratio of the He-burning luminosity to the total luminosity was greater than or equal to 99%. We modeled convection using the standard mixing-length theory (Böhm-Vitense 1958), with a parameter of α = 1.5, and semiconvection according to Langer et al. (1983), with an efficiency parameter of αsc = 1.0. We adopted Ledoux convection criterion to treat the boundaries of the convective zones and considered the step overshooting as an extension given by αp = 0.1Hp, where Hp is the pressure scale height at the Ledoux boundary limit. The network of approx12.net was adopted for nucleosynthesis.

We treated rotational mixing and AM transport as diffusive processes (Heger & Langer 2000), including the effects of Eddington-Sweet circulations and the Goldreich-Schubert-Fricke instability as well as the secular and dynamical shear mixing. We included diffusive element mixing from these processes with an efficiency parameter of fc = 1/30 (Chaboyer & Zahn 1992; Heger & Langer 2000). We used the standard efficient AM transport mechanism (e.g., Spruit 1999, 2002). Stellar winds of He-rich stars were modeled with the standard “Dutch” scheme and multiplied with a scaling factor of 2/3 to match the recently updated modeling of helium star winds (Higgins et al. 2021).

He-rich stars were modeled to reach carbon exhaustion in their center. The baryonic remnant mass was calculated following the “delayed” supernova prescription, as in Fryer et al. (2012). In order to calculate the mass and spin of the BH, we followed the framework in Batta & Ramirez-Ruiz (2019), which has also been implemented in other recent works (Bavera et al. 2020; Hu et al. 2022). We took into account neutrino loss, as was done in Zevin et al. (2020). We adopted 2.5 M⊙ as the maximum NS mass. For comparison (see Appendix A), we also considered BHs formed through direct core collapse without receiving any mass loss or natal kicks (Fryer 1999; Belczynski et al. 2008). Very recently, it was reported on VFTS 243 that an X-ray quiet BH was born with a negligible kick in a massive binary within the Large Magellanic Cloud (Shenar et al. 2022).

Tidal interaction in close binary systems plays a critical role in the evolution of the orbit and the internal AM of the two stellar components. In this work, we used the dynamical tides model (Zahn 1975; Hut 1981) to calculate the synchronization timescale (Tsync), which is dependent on the tidal coefficient E2. The two He-rich stars were assumed to be non-rotating at ZAHeMS. The main reason is that He-rich stars can be quickly spun up in close orbits. For both He-rich (also H-rich) stars, Qin et al. (2018) recently updated an approximate expression of E2, mainly depending the convective core radius and the star’s radius for a wide range of initial masses and evolutionary stages at different metallicities.

In this study, we focused on detailed investigations of a parameter space study with various initial conditions of close double He-rich stars. We included initial masses of He-rich stars from 5–65 M⊙ with initial orbital periods in a range of 0.1–6 days. Assuming two different AM transport mechanisms, we evolved two He-rich stars with equal mass at different initial metallicities.

3. Results

3.1. Hertzsprung-Russell diagrams of single He-rich stars

In this section, we present the Hertzsprung-Russell (HR) diagram of single He-rich stars from the onset of core helium burning (i.e., ZAHeMS) to the exhaustion of the stars’ central carbon. All of the He-rich stars were assumed to be non-rotating with different metallicities (1.0 Z⊙, 0.1 Z⊙,  and 1.0 Z⊙) and in the mass range of 5–60 M⊙ at a step of 5 M⊙. In Fig. 1, the core helium burning phase begins at the right ends of the different curves labeled by the core He mass. Evolution then brings the stars to the left of the HR diagram as the effective temperature increases. The evolution of the luminosity was different depending on the initial metallicity, rapidly decreasing in the beginning at 1.0 Z⊙ in the high mass range and increasing at 0.01 Z⊙ in this same mass domain. This is an effect of the different mass-loss rates at different metallicities. At high metallicities, the strong mass-loss rate rapidly decreased the luminosity. At a low metallicity, the mass was much less decreased, and the main effect came from the fact that the mean molecular weight increased, which in turn increased the luminosity and overcame the effect of weak mass loss. These low-metallicity stars evolved toward bluer regions of the HR diagram, which is similar to H-rich stars evolving chemically homogeneously on the main sequence. The main difference, however, is that for more massive He-rich stars, their mass decreases and consequently their radius shrinks.

thumbnail Fig. 1.

Hertzsprung-Russell diagram of various single non-rotating He-rich stars with different initial metallicities (Left panel: 1.0 Z⊙. Middle panel: 0.1 Z⊙. Right panel: 0.01 Z⊙.) evolving from ZAHeMS to central helium exhaustion. The blue dashed lines refer to contours of constant radii.

3.2. Spin of BHs formed from double-core evolution

3.2.1. Impact of TS dynamo on BH spins

In this section, we first show how different efficiencies of AM transport within He-rich stars change their rotation frequency at different evolutionary stages and thus the resulting spin parameters of BHs. As a case study, we evolved a binary system of two equal-mass He-rich stars with initial mass MZamsHe = 39.80 M⊙ at the initial orbital period Pinit. = 0.63 days until the end of each star’s central carbon depletion.

We show in Fig. 2 that the AM of the star and its core increases rapidly at the beginning of the evolution due to the tidal interaction that spun up the star. Under the assumption that the lost wind mass carries the specific AM of the mass-losing star (Jeans mass loss), the He-rich star and its inner core will thus slow down. This situation, however, can be reversed for He-rich stars in a close binary system in which tides are efficient in spinning up the outer layers of the stars and their cores through strong coupling within the stars. We present the impact of the TS dynamo on the evolution of the internal rotation frequency of He-rich stars at different evolutionary stages in the top two panels of Fig. 2. In the top-left panel, we present the models with the TS dynamo included (hereafter, “TS on”) at solar metallicity. We leave the discussion of a lower-metallicity model for the next section. With TS on, the model in the top-left panel shows a flat distribution of a constant rotation frequency for the He-rich star in the middle of core helium burning. This distribution is because the star evolves like a solid body during the core He burning phase with TS on. The whole star then gets spun up by the tidal interaction from its companion as it evolves past the core helium burning phase, after which the rotation frequency of the star’s outer layers slightly decreases toward the surface due to increasing chemical gradient in the late evolutionary stage. The rotation frequency of the star continues to increase after the middle of the core helium burning, which is due to the tidal spin-up from its companion. Similar models that do not include the TS dynamo (hereafter, “TS off”) show clear differences (see top-right panel in Fig. 2). The first difference caused by less efficient coupling (i.e., TS off) is that the whole star between the outer layers and the stellar core is not a solid body from the early evolutionary stage (i.e., middle of core helium burning) to the late stages. Additionally, the star model with TS off has a much larger rotational frequency throughout the whole evolutionary phase when compared with the TS-on models. This is because inefficient coupling (TS off) between the outer layers and the stellar core allows the star to retain more AM, enabling it to be spun up if tides are strong.

thumbnail Fig. 2.

Angular velocity profiles of He-rich stars at three evolutionary stages: middle of core helium burning (blue), central carbon ignition (yellow), and central carbon depletion (red). The initial mass of the He-rich star is MZamsHe = 39.80 M⊙ and the initial orbital period is Pinit. = 0.63 days. Different efficiencies of AM transport mechanism and metallicities were assumed. Left column: TS on. Right column: TS off. Top row: 1.0 Z⊙. Bottom row: 0.01 Z⊙.

In this section, we discuss the impact of the TS dynamo on the evolution of the AM of the He-rich stars and their inner cores at different evolutionary stages. We show in Fig. 3 two binary evolutionary sequences of the same initial orbital period, Pinit. = 0.63 days, and different initial masses, MZamsHe = 10.00 M⊙ (top row) and MZamsHe = 39.80 M⊙ (bottom row), with TS on and TS off. In our discussion, we focus only on the solar metallicity models. In the top-left panel, there are clear differences in the total AM of He-rich stars with TS on and TS off starting before the middle of the core helium burning stage. For the model with TS on, during the core He burning phase, the total AM of the star slowly decreases and then reaches the lower limit at the central He depletion. Additionally, the total AM remains almost constant during the whole carbon burning phase. Nevertheless, the model with the TS off shows that the star’s total AM slightly decreases from the core He burning phase and then remains constant until depletion of the central carbon. The AM of the carbon-oxygen core of the He-rich star shows a similar trend but with a shallow decay after igniting its central carbon. The resulting BHs calculated using the prescription in Batta & Ramirez-Ruiz (2019) show the spins as 0.08 (TS on) and 0.29 (TS off). The bottom-left panel of Fig. 3 presents a similar finding for more massive He-rich binaries (MZamsHe = 39.80 M⊙) but with a much higher difference in the BH spin values: 0.07 (TS on) and 0.49 (TS off). There are two main reasons for this difference. Firstly, He-rich stars in a very close binary are synchronized with their orbit due to strong tides, which allows a more massive star to carry more AM when given the same initial orbit as that of binary systems with fewer components. Additionally, more massive He-rich stars are expected to have a shorter lifetime before core collapse, resulting in more AM content within the progenitors and thus high resultant BH spins.

thumbnail Fig. 3.

AM of He-rich stars and their carbon-oxygen cores (black lines: Jtotal, blue lines: JCO) as a function of model number for two binary sequences (Top row: two equal-mass He-rich stars with initial helium star mass MZamsHe = 10.0 M⊙, initial orbital period Pinit. = 0.63 days. Bottom row: MZamsHe = 39.8 M⊙, Pinit. = 0.63 days). Similar to Fig. 2, we assume two different efficiencies of AM transport mechanism, i.e., solid lines: TS on, dashed lines: TS off. Left column: 1.0 Z⊙. Middle column: 0.1 Z⊙. Right column: 0.01 Z⊙. The three evolutionary stages are marked with different symbols: Square: middle of core helium burning. Circle: central helium depletion. Filled circle: central carbon ignition. The spin parameters of BHs formed from He-rich stars are presented.

3.2.2. Impact of metallicity on BH spins

As shown in the previous section, the TS dynamo has a significant impact on the evolution of the AM of He-rich stars and their cores at later evolutionary stages, which further determines the spin values of the BH at birth. In the following paragraphs, we describe how the initial metallicity of He-rich stars can play a role in determining the spins of resulting BHs.

It is well known that stellar winds are strongly dependent on the metallicity of mass-losing He-rich stars (Vink et al. 2001; Vink & de Koter 2005; Eldridge & Vink 2006; Sander et al. 2020). At central carbon depletion, He-rich stars have a much larger mass (around 37.5 M⊙) at 0.01 Z⊙ when compared with stars at solar metallicity (around 20 M⊙). We show in the two bottom panels of Fig. 2 that the He-rich star and its inner core have a similar and higher rotation rate at different evolutionary stages when compared with corresponding TS-on models at Z⊙. Additionally, the bottom-right panel shows that the He-rich star evolves deviating from a solid body, slightly decreasing rotation rate from the stellar core to its outer layers. At solar metallicity, the TS-off models retain more AM, but the difference is much less marked than at subsolar metallicity (e.g., 0.01 Z⊙; see two bottom panels in Fig. 2). This difference is caused by the effect of the metallicity-dependent wind mass loss, which plays a critical role in determining the final AM content of the progenitor star.

Figure 3 shows that at 0.1 Z⊙, both He-rich stars and their cores have a higher AM at different evolutionary stages when compared with those at 1.0 Z⊙ (see the top-left panel in Fig. 3). We note that the TS dynamo plays a small role in determining the evolution of the AM of He-rich stars and their cores at low metallicities (see the top-middle and right panel). This is expected, as the wind carrying the specific AM of the mass-losing He-rich star is weaker at lower metallicities, which weakens the effect of AM transport within stars. Therefore, the spin values of resultant BHs formed at lower metallicities are accordingly higher: 0.1 Z⊙ and 0.14 at 0.01 Z⊙ for TS on and 0.43 Z⊙ and 0.49 at 0.01 Z⊙ for TS off.

3.2.3. Parameter space analysis

We show in the top-left panel of Fig. 4 BH masses as a function of the He-rich initial mass and initial orbital period at solar metallicity. The binary systems either start to overflow their Roche lobes at the first model for Pinit. ∼ 0.1 days (0.2 days for MZamsHe ∼ 30 M⊙) or undergo the second Lagrangian point (L2), overflowing for MZamsHe ∼ 38 M⊙ and Pinit. ∼ 0.1 days. Given the “delayed” supernova prescription (Fryer et al. 2012), the lower mass limit of the He-rich star that can collapse to form a BH (assuming solar metallicity) is around 12 M⊙; below this, an NS is formed instead (the study of NS formation is not considered in this work). A He-rich star can form a BH with a maximum mass of around 26 M⊙. We note that at 0.1 Z⊙ (see top-middle panel), a BH with a maximum mass of around 40 M⊙ can be formed. Notably, the initial orbital period starts to have an impact on the mass of the resulting BH when its immediate progenitor (He-rich star) has an initial mass ≳40 M⊙. This is because He-rich stars tend to lose more mass at higher rotation rates when in a closer binary system, which is due to the rotationally enhanced mass loss (Langer 1997; Maeder & Meynet 2000). It is clearly shown at 0.01 Z⊙ that more massive BHs (> 55 M⊙; see top-right panel) can be formed. It is worth noting that the efficient AM transport within He-rich stars plays a negligible role in determining the BH mass.

thumbnail Fig. 4.

BH mass (filled circles) as a function of a He-rich star’s initial mass and the initial orbital period. The squares represent NSs forming from the He-rich stars. Left column: 1.0 Z⊙. Middle column: 0.1 Z⊙. Right column: 0.01 Z⊙. Top row: TS on. Bottom row: TS off. The cross symbols represent the systems overflowing their Roche lobes at their initial models, while the plus symbols refer to the systems overflowing the second Legrangian point (L2) at the initial models.

In Fig. 5, we present the spin parameters a* of BHs formed from collapsing He-rich stars in close binaries with various conditions and assumed AM transport processes. We first focus on the impact of the different efficiencies of the AM transport within He-rich stars on the resultant spins of BHs.. We note that the tides start to play a role in the resultant spins when the initial orbital period Pinit. is not longer than 1.0 day for all metallicities. As demonstrated in recent studies (Qin et al. 2018; Fuller & Lu 2022), the interplay between the tides and wind mass loss of He-rich stars determines the AM of resultant BHs at birth and thus their spin magnitudes. At solar metallicity, the formed BHs are found to have low spin values (i.e., a* ≲ 0.4, see top-left panel). This is because the wind mass loss of He-rich stars at a high metallicity is dominant over the tides. The spin magnitudes of BHs formed at lower metal poor environments are shown in the middle (0.1 Z⊙) and right panel (0.01 Z⊙). Therefore, at a given initial orbital period (Pinit. ≲ 1.0 day), high BH spins can be reached for models at 0.1 and 0.01 Z⊙. At 0.01 Z⊙, as can be seen in the top-right panel of Fig. 5, the spin magnitudes continue to increase with the initial orbital period for all the different initial masses of He-rich stars. This is because the progenitor of the BH has very weak winds at 0.01 Z⊙ and thus loses negligible mass and AM. Furthermore, it is clear that the spins of BHs originating from He-rich stars with an initial mass ≲20 M⊙ slightly increase with initial mass. This is because the wind of low-mass He-rich stars at very low metallicity (0.01 Z⊙) is significantly weak. Accordingly, for He-rich stars with an initially higher mass, more infalling mass with its corresponding AM can be accreted to the newly formed BHs (Batta & Ramirez-Ruiz 2019), resulting in higher final BH spins.

thumbnail Fig. 5.

As in Fig. 4 but colors denote the BH spin parameter a⋆.

We show the spins of resultant BHs assuming inefficient AM transport within He-rich stars in the second row of Fig. 5. As shown clearly in the bottom left-panel, high BH spins (> 0.9) can be reached at solar metallicity. Additionally, the spin covers the whole range (i.e., from minimum to maximum). For initial orbital periods Pinit. ≲ 1.0 day, we note that the BH spin gradually decreases with the increasing initial mass of He-rich stars, which is because massive He-rich stars are prone to be slowed down by their strong winds at high metallicity. This is in contrast to the results of models at very low metallicity (see the top-right panel of Fig. 5), where the wind mass loss of He-rich stars is significantly weak at 0.01 Z⊙. Notably, the figure shows that He-rich stars tend to form higher spinning BHs at lower metallicities that correspond to weaker wind mass loss (see bottom-right panel).

3.3. Merging timescales and comparisons with observed merging BBHs

After two BHs form from the core collapse of He-rich stars, GW emission shrinks the separation by removing the orbital AM and eventually leads to the merger of the compact objects. The timescale for two point masses to spiral in through GW emission from an initial eccentricity of zero (circular orbit) is given by Peters (1964)

T merger = 5 512 c 5 G 3 M 3 2 q − 2 1 + q − 1 a 4 , $$ \begin{aligned} T_{\mathrm{merger} } = \frac{5}{512}\frac{c^{5}}{G^{3}M^{3}}\frac{2 q^{-2}}{1+q^{-1}}a^{4}, \end{aligned} $$(1)

where M is the BH mass, q is the mass ratio of the two BHs (q = 1 for our case), and a is the orbital separation.

The color bar in Fig. 6 corresponds to Tmerger of merging BBHs due to GW emission. Comparing the two rows of different AM transport mechanisms in Fig. 6 shows negligible impact on the merging timescale. This is because significant differences are expected only for the AM content of the BH progenitors and not for the properties (two component masses and the final separation) of the binary system just after the birth of two BHs. The parameter space of systems that are able to merge within a Hubble time is extended in lower metallicities. This is because BH progenitors at a higher metallicity tend to lose more mass, and the BBHs at birth thus have larger separations (Tmerger ∝ a4). Given a specific initial orbital period and metallcity, BBHs with initially higher mass have shorter merging timescales (Tmerger ∝ M−3).

thumbnail Fig. 6.

As in Fig. 5 but colors represent merger time Tmerger. Black dots represent the systems whose merger times are longer than a Hubble time.

Figure 7 shows merging timescales Tmerger as a function of the effective inspiral spin χeff and the chirp mass Mchirp given different efficiencies of AM transport and various initial conditions. For comparison with each panel, the 69 high-confidence BBH events (false alarm rate of less than one per year) officially reported from the LVK are also shown. We assumed that the formed BHs have spin components perfectly aligned to the direction of the orbital AM. In the following, we describe some main findings from this figure. First of all, we note that initial metallicity plays an important role in forming systems with the observable properties (χeff and Mchirp). For example, lower metallicities correspond to formed systems with higher χeff and larger Mchirp. More specifically, the Mchirp can be reached around 26 M⊙ at solar metallicity (40 and 58 M⊙ at 0.1 and 0.01 Z⊙, respectively). Furthermore, the magnitude of χeff can vary from 0.0 (Pinit. = 1.0 day) to 1.0 (Pinit. = 0.2 days). We note that so far no BBHs with χeff = 1 have been reported by the LVK collaboration. Third, the AM transport mechanism in these observable properties of BBHs starts to play a more important role at higher metallicities (solar metallicity, see the two left panels in Fig. 7). Additionally, under the assumption of inefficient AM transport, double He-rich stars can form observable BBHs with χeff > 0.80 (< 0.5 with TS on) with initially Pinit. = 0.4 days and χeff > 0.5(< 0.25 with TS on) with initially Pinit. = 0.6 days. It is also clearly shown in the left panels of Fig. 7 that a greater number of BBHs formed from double He-rich stars at solar metallicity will not be merged within a Hubble time when compared with low-metallicity models. We note the trend that the observed BBHs with higher values of both χeff and Mchirp can be better explained in our modeling at lower metallicites. In particular, the percentage of the BBHs that have an χeff higher than that of GW190517 (which has the highest χeff reported in the LVK) is 8.9% at 1.0 Z⊙, 20.3% at 0.1 Z⊙, and 26.9% at 0.01 Z⊙ (for TS off: 18.1% at 1.0 Z⊙, 23.2% at 0.1 Z⊙, and 28.7% at 0.01 Z⊙). According to the LVK, GW190521 was reported to have the highest Mchirp (Abbott et al. 2020), which might be a straddling binary using a population informed prior (Fishbach & Holz 2020). This event is an outlier in our models, as the upper limit of the BH mass in this study is assumed not to be higher than approximately 65 M⊙, due to (pulsational) pair-instability supernovae (see discussion in the next section). Additionally, GW190517−055101 has the largest χeff reported in the GWTC-2 (Abbott et al. 2021), which can be explained with our models at lower metallicities (see the second and third rows in Fig. 7), regardless of the assumed efficiencies of AM transport. Therefore, the BBH progenitor of this event might have gone through the double-core evolution at low metallicities (e.g., Z < 0.1 Z⊙.)

thumbnail Fig. 7.

Tmerger (colored dots) as a function of χeff and Mchirp. The three panels in first row correspond to different initial metallicities (left panel: 1.0 Z⊙; middle panel: 0.1 Z⊙; right panel: 0.01 Z⊙) of He-rich stars. The second row refers to the models including inefficient AM transport mechanism (TS off). The dotted lines refer to the specific initial orbital periods and are marked with numbers in units of days. The observed high-confidence BBH events (69 BBHs with false alarm rate of less than one per year) reported from the LVK are shown with the error bars at 90% credibility in each panel. Black triangles represent BBHs whose Tmerger is longer than a Hubble time. Two BBH events are highlighted: GW190517 (square) and GW190521 (star).

4. Conclusions and discussion

In this work, we first presented the HR diagram of single non-rotating He-rich stars in a mass range of 5–60 M⊙ at different metallicities and evolving from ZAHeMS to central helium exhaustion. We then systematically studied an alternative formation scenario of BBHs (i.e., the double-core evolution) by modeling double He-rich stars in various parameter spaces (metallicity and initial mass of He-rich stars as well as the orbital period). Later, we also investigated the impact of the different AM transport mechanisms on the evolution of He-rich stars in different evolutionary stages, the properties of resulting BBHs at birth, and the merging timescale.

We calculated the baryonic remnant mass following the “delayed” supernova prescription shown in Fryer et al. (2012) and by taking into account the impact of accretion feedback onto the newly formed BHs. The upper limit of the BH mass we obtained in this work is around 26, 40, and 58 M⊙ at 1.0 Z⊙, 0.1 Z⊙ and 0.01 Z⊙, respectively. We found that tides for double He-rich stars can only be important when the initial orbital periods are less than 1.0 day, which is similar to findings of previous studies of a He-rich star accompanied by a BH or NS (Qin et al. 2018; Bavera et al. 2020; Fuller & Lu 2022). We note that the initial metallicity of He-rich stars should be high for the efficient AM transport to play a significant role in determining the spin magnitude of the newly formed BHs since their progenitors (massive He-rich stars) are more inclined to be slowed down by stronger wind mass-loss, especially when rotating like a solid body. The χeff for BBHs formed through the double-core evolution is not always high, but it can cover the whole range of BH spin, that is, from minimum (0.0) to maximum (1.0), depending on the initial orbital period of the binary systems. The chirp mass Mchirp of the BBH is strongly dependent on the initial metallicity of He-rich stars (e.g., Belczynski et al. 2010; Stevenson et al. 2017, 2019). More specifically, the chirp mass Mchirp of the BBH from double-core evolution at 1.0 Z⊙ cannot be larger than 26 M⊙, regardless of the efficiency of the AM transport within He-rich stars.

After detailed investigations of the double-core evolution, we would expect this channel to be able to predict a certain fraction of BBH populations with high χeff and Mchirp. More events with the above features are expected to be captured by the LVK in the upcoming fourth observing run due to its improved sensitivity. The quantitative merger rate from this channel is beyond the scope of the current work. Therefore, we plan to investigate the quantitative contribution of this channel to the intrinsic BBH population with the population synthesis study as well as the impact of different physical processes on the outcomes in the near future.

The formation of massive He-rich binary stars might not involve the CE phase, but the criteria for its occurrence are still under development. Recent investigations suggest that the merger rate of BBHs from the CE channel might be overestimated in rapid population synthesis studies (e.g., Pavlovskii et al. 2017; Marchant et al. 2021; Klencki et al. 2021; Gallegos-Garcia et al. 2021; Olejak et al. 2021). Their studies indicate that the stable mass transfer channel could be the dominant channel for the formation of merging BBHs (e.g., Shao & Li 2022; Briel et al. 2023). van Son et al. (2022a) recently found that the stable mass transfer channel preferentially forms BBH systems with more massive component BH masses. Furthermore, by varying the metallicity dependent cosmic star formation history, van Son et al. (2022b) found the variations affect the slope of the high mass end of the BBH mass distribution but also have a slight impact on the CE channel. In addition, massive He-rich binary stars could be formed through the CHE channel. In this channel, the two massive stars initially evolve in a close orbit and thus have strong chemical mixing due to strong tides.

In this final paragraph, we briefly summarize some main uncertainties in our binary modeling. First, stellar wind mass loss is one of the key uncertain physical processes in the evolution of massive stars, and it can have a significant impact on the mass and the spin of resultant BHs. Second, it is unclear whether supernova kicks (natal kicks) are imparted onto BHs during the core collapse process. The BHs formed from direct core collapse of massive stars were considered to receive no natal kick (Belczynski et al. 2008). Nevertheless, we note a recent work by Farr et al. (2011), Tauris (2022) argued that rather than dynamical formation, isolated binary evolution can still explain the observed BBHs if BHs have their spin axis tossed by the supernova kicks during their formation process in the core collapse of massive stars. The stellar evolution theory predicts a “mass gap” in the BH birth function caused by the (pulsational) pair instability supernovae (Fowler & Hoyle 1964; Rakavy & Shaviv 1967; Barkat et al. 1967; Fraley 1968; Heger et al. 2003), which is still uncertain and thus plays a critical role in determining the upper limit of the BH mass below the gap (see Woosley & Heger 2021, and references therein). The constraints from current observations of BBHs reported from the LVK are still weak due to a statistically small sample. We expect the sample of BBH events with higher χeff and Mchirp will be significantly expanded in the upcoming fourth run, which will be used to make stronger constraints on the supernova kicks during the formation process of BHs from massive stars.

1

χeff = (M1χ1z + M2χ2z)/(M1 + M2), where M1 and M2 are the component masses of the two BHs; χ1z and χ2z are dimensionless BH spin magnitudes aligned to the direction of the orbital angular momentum.

Acknowledgments

We would like to thank the anonymous referee for the helpful comments and suggestions. Y.Q. acknowledges the support from the Doctoral research start-up funding of Anhui Normal University and from Key Laboratory for Relativistic Astrophysics in Guangxi University. This work was supported by the National Natural Science Foundation of China (Grant Nos. 12003002, 12192220, 12192221, 11863003, 12173010) and the Natural Science Foundation of Universities in Anhui Province (Grant No. KJ2021A0106). G.M. has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant agreement No 833925, project STAREX). All figures were made with the free Python module Matplotlib (Hunter 2007).

References

  1. Abadie, J., Abbott, B. P., Abbott, R., et al. 2010, CQG, 27, 173001 [NASA ADS] [CrossRef] [Google Scholar]
  2. Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016a, ApJ, 818, L22 [Google Scholar]
  3. Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016b, Phys. Rev. Lett., 116, 061102 [Google Scholar]
  4. Abbott, R., Abbott, T. D., Abraham, S., et al. 2020, Phys. Rev. Lett., 125, 101102 [Google Scholar]
  5. Abbott, R., Abbott, T. D., Abraham, S., et al. 2021, Phys. Rev. X, 11, 021053 [Google Scholar]
  6. Antonini, F., Chatterjee, S., Rodriguez, C. L., et al. 2016, ApJ, 816, 65 [NASA ADS] [CrossRef] [Google Scholar]
  7. Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
  8. Barkat, Z., Rakavy, G., & Sack, N. 1967, Phys. Rev. Lett., 18, 379 [Google Scholar]
  9. Batta, A., & Ramirez-Ruiz, E. 2019, ArXiv e-prints [arXiv:1904.04835] [Google Scholar]
  10. Bavera, S. S., Fragos, T., Qin, Y., et al. 2020, A&A, 635, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Bavera, S. S., Fragos, T., Zevin, M., et al. 2021, A&A, 647, A153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Bavera, S. S., Fragos, T., Zapartas, E., et al. 2022, A&A, 657, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Belczynski, K., Taam, R. E., Kalogera, V., Rasio, F. A., & Bulik, T. 2007, ApJ, 662, 504 [Google Scholar]
  14. Belczynski, K., Taam, R. E., Rantsiou, E., & van der Sluys, M. 2008, ApJ, 682, 474 [NASA ADS] [CrossRef] [Google Scholar]
  15. Belczynski, K., Dominik, M., Bulik, T., et al. 2010, ApJ, 715, L138 [Google Scholar]
  16. Belczynski, K., Holz, D. E., Bulik, T., & O’Shaughnessy, R. 2016, Nature, 534, 512 [NASA ADS] [CrossRef] [Google Scholar]
  17. Belczynski, K., Romagnolo, A., Olejak, A., et al. 2022, ApJ, 925, 69 [NASA ADS] [CrossRef] [Google Scholar]
  18. Böhm-Vitense, E. 1958, ZAp, 46, 108 [NASA ADS] [Google Scholar]
  19. Briel, M. M., Stevance, H. F., & Eldridge, J. J. 2023, MNRAS, stad399 [Google Scholar]
  20. Broekgaarden, F. S., Berger, E., Stevenson, S., et al. 2022, MNRAS, 516, 5737 [NASA ADS] [CrossRef] [Google Scholar]
  21. Brown, G. E. 1995, ApJ, 440, 270 [NASA ADS] [CrossRef] [Google Scholar]
  22. Callister, T. A., Miller, S. J., Chatziioannou, K., & Farr, W. M. 2022, ApJ, 937, L13 [NASA ADS] [CrossRef] [Google Scholar]
  23. Cantiello, M., Mankovich, C., Bildsten, L., Christensen-Dalsgaard, J., & Paxton, B. 2014, ApJ, 788, 93 [Google Scholar]
  24. Chaboyer, B., & Zahn, J. P. 1992, A&A, 253, 173 [NASA ADS] [Google Scholar]
  25. de Mink, S. E., & Belczynski, K. 2015, ApJ, 814, 58 [Google Scholar]
  26. de Mink, S. E., & Mandel, I. 2016, MNRAS, 460, 3545 [NASA ADS] [CrossRef] [Google Scholar]
  27. den Hartogh, J. W., Eggenberger, P., & Deheuvels, S. 2020, A&A, 634, L16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Dewi, J. D. M., Podsiadlowski, P., & Sena, A. 2006, MNRAS, 368, 1742 [NASA ADS] [CrossRef] [Google Scholar]
  29. Doctor, Z., Wysocki, D., O’Shaughnessy, R., Holz, D. E., & Farr, B. 2020, ApJ, 893, 35 [NASA ADS] [CrossRef] [Google Scholar]
  30. Dominik, M., Berti, E., O’Shaughnessy, R., et al. 2015, ApJ, 806, 263 [Google Scholar]
  31. du Buisson, L., Marchant, P., Podsiadlowski, P., et al. 2020, MNRAS, 499, 5941 [Google Scholar]
  32. Eggenberger, P., Maeder, A., & Meynet, G. 2005, A&A, 440, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Eggenberger, P., Montalbán, J., & Miglio, A. 2012, A&A, 544, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Eggenberger, P., den Hartogh, J. W., Buldgen, G., et al. 2019, A&A, 631, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Eggenberger, P., Moyano, F. D., & den Hartogh, J. W. 2022, A&A, 664, L16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Eldridge, J. J., & Vink, J. S. 2006, A&A, 452, 295 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Farr, W. M., Kremer, K., Lyutikov, M., & Kalogera, V. 2011, ApJ, 742, 81 [NASA ADS] [CrossRef] [Google Scholar]
  38. Farr, W. M., Stevenson, S., Miller, M. C., et al. 2017, Nature, 548, 426 [NASA ADS] [CrossRef] [Google Scholar]
  39. Farr, B., Holz, D. E., & Farr, W. M. 2018, ApJ, 854, L9 [NASA ADS] [CrossRef] [Google Scholar]
  40. Fishbach, M., & Holz, D. E. 2020, ApJ, 904, L26 [Google Scholar]
  41. Fowler, W. A., & Hoyle, F. 1964, ApJS, 9, 201 [Google Scholar]
  42. Fragione, G., Kocsis, B., Rasio, F. A., & Silk, J. 2022, ApJ, 927, 231 [NASA ADS] [CrossRef] [Google Scholar]
  43. Fragos, T., Andrews, J. J., Bavera, S. S., et al. 2023, ApJS, 264, 45 [NASA ADS] [CrossRef] [Google Scholar]
  44. Fraley, G. S. 1968, Ap&SS, 2, 96 [NASA ADS] [CrossRef] [Google Scholar]
  45. Fryer, C. L. 1999, ApJ, 522, 413 [NASA ADS] [CrossRef] [Google Scholar]
  46. Fryer, C. L., Belczynski, K., Wiktorowicz, G., et al. 2012, ApJ, 749, 91 [Google Scholar]
  47. Fuller, J., & Lu, W. 2022, MNRAS, 511, 3951 [NASA ADS] [CrossRef] [Google Scholar]
  48. Fuller, J., Piro, A. L., & Jermyn, A. S. 2019, MNRAS, 485, 3661 [NASA ADS] [Google Scholar]
  49. Gallegos-Garcia, M., Berry, C. P. L., Marchant, P., & Kalogera, V. 2021, ApJ, 922, 110 [NASA ADS] [CrossRef] [Google Scholar]
  50. Gerosa, D., & Fishbach, M. 2021, Nat. Astron., 5, 749 [NASA ADS] [CrossRef] [Google Scholar]
  51. Giacobbo, N., & Mapelli, M. 2018, MNRAS, 480, 2011 [Google Scholar]
  52. Heger, A., & Langer, N. 2000, ApJ, 544, 1016 [CrossRef] [Google Scholar]
  53. Heger, A., Fryer, C. L., Woosley, S. E., Langer, N., & Hartmann, D. H. 2003, ApJ, 591, 288 [CrossRef] [Google Scholar]
  54. Heger, A., Woosley, S. E., & Spruit, H. C. 2005, ApJ, 626, 350 [Google Scholar]
  55. Higgins, E. R., Sander, A. A. C., Vink, J. S., & Hirschi, R. 2021, MNRAS, 505, 4874 [NASA ADS] [CrossRef] [Google Scholar]
  56. Hu, R.-C., Zhu, J.-P., Qin, Y., et al. 2022, ApJ, 928, 163 [NASA ADS] [CrossRef] [Google Scholar]
  57. Hu, R. C., Zhu, J. P., Qin, Y., et al. 2023, ArXiv e-prints [arXiv:2301.06402] [Google Scholar]
  58. Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
  59. Hut, P. 1981, A&A, 99, 126 [NASA ADS] [Google Scholar]
  60. Hwang, J., Lombardi, J. C., Jr., Rasio, F. A., & Kalogera, V., 2015, ApJ, 806, 135 [NASA ADS] [CrossRef] [Google Scholar]
  61. Inayoshi, K., Hirai, R., Kinugawa, T., & Hotokezaka, K. 2017, MNRAS, 468, 5020 [Google Scholar]
  62. Ivanova, N., Justham, S., Chen, X., et al. 2013, A&ARv, 21, 59 [Google Scholar]
  63. Ji, S., Fuller, J., & Lecoanet, D. 2022, MNRAS, submitted, [arXiv:2209.08104] [Google Scholar]
  64. Kimball, C., Talbot, C., Berry, C. P. L., et al. 2020, ApJ, 900, 177 [NASA ADS] [CrossRef] [Google Scholar]
  65. Kimball, C., Talbot, C., Berry, C. P. L., et al. 2021, ApJ, 915, L35 [CrossRef] [Google Scholar]
  66. Klencki, J., Nelemans, G., Istrate, A. G., & Chruslinska, M. 2021, A&A, 645, A54 [EDP Sciences] [Google Scholar]
  67. Langer, N. 1997, ASP Conf. Ser., 120, 83 [Google Scholar]
  68. Langer, N., Fricke, K. J., & Sugimoto, D. 1983, A&A, 126, 207 [NASA ADS] [Google Scholar]
  69. Maeder, A., & Meynet, G. 2000, A&A, 361, 159 [NASA ADS] [Google Scholar]
  70. Mandel, I., & Broekgaarden, F. S. 2022, Liv. Rev. Rel., 25, 1 [CrossRef] [Google Scholar]
  71. Mandel, I., & de Mink, S. E. 2016, MNRAS, 458, 2634 [NASA ADS] [CrossRef] [Google Scholar]
  72. Mandel, I., & Farmer, A. 2022, Phys. Rep., 955, 1 [NASA ADS] [CrossRef] [Google Scholar]
  73. Mapelli, M. 2020, Front. Astron. Space Sci., 7, 38 [NASA ADS] [CrossRef] [Google Scholar]
  74. Mapelli, M., Dall’Amico, M., Bouffanais, Y., et al. 2021, MNRAS, 505, 339 [CrossRef] [Google Scholar]
  75. Marchant, P., Langer, N., Podsiadlowski, P., Tauris, T. M., & Moriya, T. J. 2016, A&A, 588, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  76. Marchant, P., Pappas, K. M. W., Gallegos-Garcia, M., et al. 2021, A&A, 650, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. McKernan, B., Ford, K. E. S., & O’Shaughnessy, R. 2020, MNRAS, 498, 4088 [CrossRef] [Google Scholar]
  78. Olejak, A., & Belczynski, K. 2021, ApJ, 921, L2 [NASA ADS] [CrossRef] [Google Scholar]
  79. Olejak, A., Belczynski, K., & Ivanova, N. 2021, A&A, 651, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  80. Pavlovskii, K., Ivanova, N., Belczynski, K., & Van, K. X. 2017, MNRAS, 465, 2092 [Google Scholar]
  81. Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
  82. Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [Google Scholar]
  83. Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
  84. Paxton, B., Schwab, J., Bauer, E. B., et al. 2018, ApJS, 234, 34 [NASA ADS] [CrossRef] [Google Scholar]
  85. Paxton, B., Smolec, R., Schwab, J., et al. 2019, ApJS, 243, 10 [Google Scholar]
  86. Peng, W., Song, H., Meynet, G., et al. 2022, A&A, 657, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  87. Peters, P. C. 1964, Phys. Rev., 136, 1224 [Google Scholar]
  88. Phinney, E. S. 1991, ApJ, 380, L17 [NASA ADS] [CrossRef] [Google Scholar]
  89. Postnov, K. A., & Yungelson, L. R. 2014, Liv. Rev. Rel., 17, 3 [NASA ADS] [CrossRef] [Google Scholar]
  90. Qin, Y., Fragos, T., Meynet, G., et al. 2018, A&A, 616, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  91. Qin, Y., Fragos, T., Meynet, G., et al. 2019a, IAU Symp., 346, 426 [NASA ADS] [Google Scholar]
  92. Qin, Y., Marchant, P., Fragos, T., Meynet, G., & Kalogera, V. 2019b, ApJ, 870, L18 [Google Scholar]
  93. Qin, Y., Wang, Y.-Z., Bavera, S. S., et al. 2022a, ApJ, 941, 179 [NASA ADS] [CrossRef] [Google Scholar]
  94. Qin, Y., Wang, Y.-Z., Wu, D.-H., Meynet, G., & Song, H. 2022b, ApJ, 924, 129 [NASA ADS] [CrossRef] [Google Scholar]
  95. Qin, Y., Shu, X., Yi, S., & Wang, Y.-Z. 2022c, Res. Astron. Astrophys., 22, 035023 [Google Scholar]
  96. Rakavy, G., & Shaviv, G. 1967, ApJ, 148, 803 [Google Scholar]
  97. Riley, J., Mandel, I., Marchant, P., et al. 2021, MNRAS, 505, 663 [Google Scholar]
  98. Rodriguez, C. L., Morscher, M., Pattabiraman, B., et al. 2015, Phys. Rev. Lett., 115, 051101 [Google Scholar]
  99. Roulet, J., Chia, H. S., Olsen, S., et al. 2021, Phys. Rev. D, 104, 083010 [NASA ADS] [CrossRef] [Google Scholar]
  100. Saavik Ford, K. E., & McKernan, B. 2022, MNRAS, 517, 5827 [NASA ADS] [CrossRef] [Google Scholar]
  101. Safarzadeh, M., Hamers, A. S., Loeb, A., & Berger, E. 2020, ApJ, 888, L3 [Google Scholar]
  102. Sander, A. A. C., Vink, J. S., & Hamann, W. R. 2020, MNRAS, 491, 4406 [Google Scholar]
  103. Secunda, A., Bellovary, J., Mac Low, M.-M., et al. 2019, ApJ, 878, 85 [NASA ADS] [CrossRef] [Google Scholar]
  104. Shao, Y., & Li, X.-D. 2022, ApJ, 930, 26 [NASA ADS] [CrossRef] [Google Scholar]
  105. Shenar, T., Sana, H., Mahy, L., et al. 2022, Nat. Astron., 6, 1085 [NASA ADS] [CrossRef] [Google Scholar]
  106. Song, H. F., Meynet, G., Maeder, A., Ekström, S., & Eggenberger, P. 2016, A&A, 585, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  107. Spruit, H. C. 1999, A&A, 349, 189 [NASA ADS] [Google Scholar]
  108. Spruit, H. C. 2002, A&A, 381, 923 [CrossRef] [EDP Sciences] [Google Scholar]
  109. Stevenson, S., Vigna-Gómez, A., Mandel, I., et al. 2017, Nat. Commun., 8, 14906 [Google Scholar]
  110. Stevenson, S., Sampson, M., Powell, J., et al. 2019, ApJ, 882, 121 [Google Scholar]
  111. Suijs, M. P. L., Langer, N., Poelarends, A. J., et al. 2008, A&A, 481, L87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  112. Tagawa, H., Haiman, Z., & Kocsis, B. 2020, ApJ, 898, 25 [NASA ADS] [CrossRef] [Google Scholar]
  113. Tang, P. N., Eldridge, J. J., Stanway, E. R., & Bray, J. C. 2020, MNRAS, 493, L6 [Google Scholar]
  114. Tanikawa, A., Yoshida, T., Kinugawa, T., et al. 2022, ApJ, 926, 83 [NASA ADS] [CrossRef] [Google Scholar]
  115. Tauris, T. M. 2022, ApJ, 938, 66 [NASA ADS] [CrossRef] [Google Scholar]
  116. The LIGO Scientific Collaboration, the Virgo Collaboration, the KAGRA Collaboration (Abbott, R., et al.) 2021a, ArXiv e-prints [arXiv:2111.03606] [Google Scholar]
  117. The LIGO Scientific Collaboration, the Virgo Collaboration, the KAGRA Collaboration (Abbott, R., et al.) 2021b, ArXiv e-prints [arXiv:2111.03634] [Google Scholar]
  118. The LIGO Scientific Collaboration, the Virgo Collaboration (Abbott, R., et al.) 2021c, ArXiv e-prints [arXiv:2108.01045] [Google Scholar]
  119. Tutukov, A., & Yungelson, L. 1973, Nauchnye Informatsii, 27, 70 [NASA ADS] [Google Scholar]
  120. van den Heuvel, E. P. J., Portegies Zwart, S. F., & de Mink, S. E. 2017, MNRAS, 471, 4256 [Google Scholar]
  121. van Son, L. A. C., De Mink, S. E., Broekgaarden, F. S., et al. 2020, ApJ, 897, 100 [Google Scholar]
  122. van Son, L. A. C., de Mink, S. E., Callister, T., et al. 2022a, ApJ, 931, 17 [NASA ADS] [CrossRef] [Google Scholar]
  123. van Son, L. A. C., de Mink, S. E., Chruslinska, M., et al. 2022b, ApJ, submitted, [arXiv:2209.03385] [Google Scholar]
  124. Vigna-Gómez, A., Neijssel, C. J., Stevenson, S., et al. 2018, MNRAS, 481, 4009 [Google Scholar]
  125. Vink, J. S., & de Koter, A. 2005, A&A, 442, 587 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  126. Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  127. Vitale, S., Biscoveanu, S., & Talbot, C. 2022, A&A, 668, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  128. Woosley, S. E., & Heger, A. 2021, ApJ, 912, L31 [NASA ADS] [CrossRef] [Google Scholar]
  129. Zahn, J. P. 1975, A&A, 41, 329 [NASA ADS] [Google Scholar]
  130. Zahn, J. P., Brun, A. S., & Mathis, S. 2007, A&A, 474, 145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  131. Zevin, M., & Bavera, S. S. 2022, ApJ, 933, 86 [NASA ADS] [CrossRef] [Google Scholar]
  132. Zevin, M., Spera, M., Berry, C. P. L., & Kalogera, V. 2020, ApJ, 899, L1 [Google Scholar]
  133. Zevin, M., Bavera, S. S., Berry, C. P. L., et al. 2021, ApJ, 910, 152 [Google Scholar]

Appendix A: Direct core collapse with mass and angular momentum conserved

In this section, we present the results of BBH formation through the double-core evolution channel, assuming that the mass and AM are conserved during the formation process in the core collapse of He-rich stars. As shown earlier in the main text, tides can only be important for tidal interaction of double He-rich stars if the initial orbital periods are less than one day. We show in Fig. A.1 the evolution of three cases (MZamsHe = 12, 20, and 40 M⊙ for the same Pinit. = 0.6 days) from the beginning of core helium burning to carbon depletion in their center. We adopted efficient (TS on) and inefficient (TS off) AM transport within He-rich stars and three initial metallicities (1.0 Z⊙, 0.1 Z⊙, and 0.01 Z⊙).

thumbnail Fig. A.1.

Evolution of the spin parameter a⋆ as a function of the orbital period and mass of He-rich stars at different metallicities and AM transport mechanisms. Top-left panel: TS on and 1.0 Z⊙. Middle-left panel: TS on and 0.1 Z⊙. Bottom-left panel: TS on and 0.01 Z⊙. Top-right panel: TS off and 1.0 Z⊙. Middle-right panel: TS off and 0.1 Z⊙. Bottom-right panel: TS off and 0.01 Z⊙. The spin a⋆ at different evolutionary stages are marked with symbols. Star: Beginning of core He burning. Square: Middle of core He burning. Triangle: Central He depletion. Circle: Central carbon depletion.

We show in the top-left panel of Fig. A.1 the evolution of BH spin as a function of the He-rich star mass and its orbital period, under the assumption that He-rich stars can at any time directly collapse to form BHs without losing mass and corresponding AM. To illustrate this process, we describe the case of a 40 M⊙ double He-rich star. The star was efficiently spun up and thus formed a fast-spinning BH at the beginning of core helium burning. The orbital separation then slightly expanded during the core helium burning and made the BH spin (approximately 0.4 at the middle of core helium burning) gradually decrease and end up being close to zero at the central helium depletion. We note that there is a negligible discrepancy of BH spin calculated at the point between the central helium depletion and the central carbon depletion. The other two cases of less massive He-rich stars could form lower-mass binary BHs that slowly rotate in closer binaries due to weaker wind mass loss. At lower metallcities, the same binaries form faster spinning BHs in shorter orbits (see middle-left panel for 0.1 Z⊙ and bottom-left panel for 0.01 Z⊙). When the inefficient AM transport (TS off) is adopted, the formed BBHs can have higher spins than the ones of BBH (TS on) at the same initial metallicity.

With the same parameter space, we also computed the evolution of the BH spin under different metallicities and efficiencies of AM transport for each binary system. We present first the results assuming efficient AM transport. As shown in Fig. A.2, all He-rich stars with an initial mass of less than 12 M⊙ at 1.0 Z⊙ form NSs. The He-rich stars with an initial orbital period longer than 1.0 day ended up being non-spinning BHs. We find that BHs can have moderate spin magnitudes with Pinit. in a range of 0.3 - 1.0 days, below which fast-spinning BHs are formed. Similar to Fig. A.2, we can see for lower metallicities (see Fig. A.2 and Fig. A.3) that the spins of the formed BHs decrease as the orbit slowly expands. We show the results with different metallicities of the inefficient AM transport in Fig. A.5, Fig. A.6, and Fig. A.7. The mass and spin of the newly formed BHs calculated using direct core collapse with mass and AM conserved are slightly larger compared to those that take into account the accretion feedback during core collapse modeling (see details in Batta & Ramirez-Ruiz 2019).

thumbnail Fig. A.2.

Evolution of the spin parameter a⋆ (the color bar) as a function of the orbital period and mass of He-rich stars with TS included at solar metallicity. The colored lines linking the two symbols show the evolution of the binary. The color along the line represents BH spins a⋆ along the evolution from the ZAHeMS to the central carbon depletion, assuming that the He-rich star progenitors directly collapse to form BHs with mass and AM conserved.

thumbnail Fig. A.3.

As in Fig. A.2 but for metallicity Z = 0.1 Z⊙.

thumbnail Fig. A.4.

As in Fig. A.2 but for metallicity Z = 0.01 Z⊙.

thumbnail Fig. A.5.

As in Fig. A.2 but without TS included.

thumbnail Fig. A.6.

As in Fig. A.5 but for metallicity Z = 0.1 Z⊙.

thumbnail Fig. A.7.

As in Fig. A.5 but for metallicity Z = 0.01 Z⊙.

All Figures

thumbnail Fig. 1.

Hertzsprung-Russell diagram of various single non-rotating He-rich stars with different initial metallicities (Left panel: 1.0 Z⊙. Middle panel: 0.1 Z⊙. Right panel: 0.01 Z⊙.) evolving from ZAHeMS to central helium exhaustion. The blue dashed lines refer to contours of constant radii.
In the text
thumbnail Fig. 2.

Angular velocity profiles of He-rich stars at three evolutionary stages: middle of core helium burning (blue), central carbon ignition (yellow), and central carbon depletion (red). The initial mass of the He-rich star is MZamsHe = 39.80 M⊙ and the initial orbital period is Pinit. = 0.63 days. Different efficiencies of AM transport mechanism and metallicities were assumed. Left column: TS on. Right column: TS off. Top row: 1.0 Z⊙. Bottom row: 0.01 Z⊙.
In the text
thumbnail Fig. 3.

AM of He-rich stars and their carbon-oxygen cores (black lines: Jtotal, blue lines: JCO) as a function of model number for two binary sequences (Top row: two equal-mass He-rich stars with initial helium star mass MZamsHe = 10.0 M⊙, initial orbital period Pinit. = 0.63 days. Bottom row: MZamsHe = 39.8 M⊙, Pinit. = 0.63 days). Similar to Fig. 2, we assume two different efficiencies of AM transport mechanism, i.e., solid lines: TS on, dashed lines: TS off. Left column: 1.0 Z⊙. Middle column: 0.1 Z⊙. Right column: 0.01 Z⊙. The three evolutionary stages are marked with different symbols: Square: middle of core helium burning. Circle: central helium depletion. Filled circle: central carbon ignition. The spin parameters of BHs formed from He-rich stars are presented.
In the text
thumbnail Fig. 4.

BH mass (filled circles) as a function of a He-rich star’s initial mass and the initial orbital period. The squares represent NSs forming from the He-rich stars. Left column: 1.0 Z⊙. Middle column: 0.1 Z⊙. Right column: 0.01 Z⊙. Top row: TS on. Bottom row: TS off. The cross symbols represent the systems overflowing their Roche lobes at their initial models, while the plus symbols refer to the systems overflowing the second Legrangian point (L2) at the initial models.
In the text
thumbnail Fig. 5.

As in Fig. 4 but colors denote the BH spin parameter a⋆.
In the text
thumbnail Fig. 6.

As in Fig. 5 but colors represent merger time Tmerger. Black dots represent the systems whose merger times are longer than a Hubble time.
In the text
thumbnail Fig. 7.

Tmerger (colored dots) as a function of χeff and Mchirp. The three panels in first row correspond to different initial metallicities (left panel: 1.0 Z⊙; middle panel: 0.1 Z⊙; right panel: 0.01 Z⊙) of He-rich stars. The second row refers to the models including inefficient AM transport mechanism (TS off). The dotted lines refer to the specific initial orbital periods and are marked with numbers in units of days. The observed high-confidence BBH events (69 BBHs with false alarm rate of less than one per year) reported from the LVK are shown with the error bars at 90% credibility in each panel. Black triangles represent BBHs whose Tmerger is longer than a Hubble time. Two BBH events are highlighted: GW190517 (square) and GW190521 (star).
In the text
thumbnail Fig. A.1.

Evolution of the spin parameter a⋆ as a function of the orbital period and mass of He-rich stars at different metallicities and AM transport mechanisms. Top-left panel: TS on and 1.0 Z⊙. Middle-left panel: TS on and 0.1 Z⊙. Bottom-left panel: TS on and 0.01 Z⊙. Top-right panel: TS off and 1.0 Z⊙. Middle-right panel: TS off and 0.1 Z⊙. Bottom-right panel: TS off and 0.01 Z⊙. The spin a⋆ at different evolutionary stages are marked with symbols. Star: Beginning of core He burning. Square: Middle of core He burning. Triangle: Central He depletion. Circle: Central carbon depletion.
In the text
thumbnail Fig. A.2.

Evolution of the spin parameter a⋆ (the color bar) as a function of the orbital period and mass of He-rich stars with TS included at solar metallicity. The colored lines linking the two symbols show the evolution of the binary. The color along the line represents BH spins a⋆ along the evolution from the ZAHeMS to the central carbon depletion, assuming that the He-rich star progenitors directly collapse to form BHs with mass and AM conserved.
In the text
thumbnail Fig. A.3.

As in Fig. A.2 but for metallicity Z = 0.1 Z⊙.
In the text
thumbnail Fig. A.4.

As in Fig. A.2 but for metallicity Z = 0.01 Z⊙.
In the text
thumbnail Fig. A.5.

As in Fig. A.2 but without TS included.
In the text
thumbnail Fig. A.6.

As in Fig. A.5 but for metallicity Z = 0.1 Z⊙.
In the text
thumbnail Fig. A.7.

As in Fig. A.5 but for metallicity Z = 0.01 Z⊙.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.