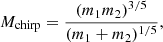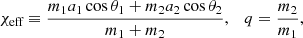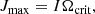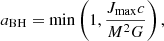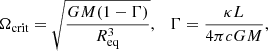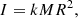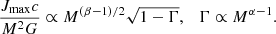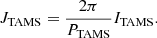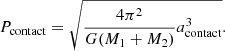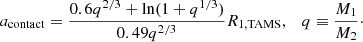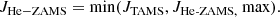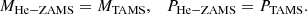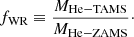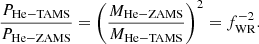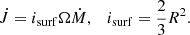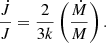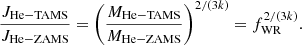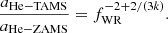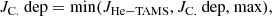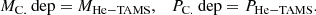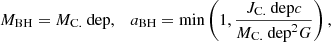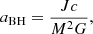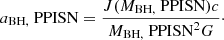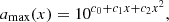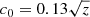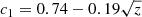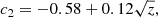EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 691 (November 2024) A&A, 691 (2024) A339 Full HTML
Open Access
Issue
A&A
Volume 691, November 2024
Article Number A339
Number of page(s) 13
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/202348190
Published online 25 November 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Ever since the first observation of a merging binary black hole (BBH; Abbott et al. 2016), continuous improvements to ground-based interferometers have resulted in weekly discoveries when current-generation detectors are online. As detector biases are well understood, with close to 100 detected sources (Abbott et al. 2019, 2021, 2023a; Nitz et al. 2023) it has become possible to place constraints on the intrinsic distribution of merging BBH masses and spins at redshifts near zero (Abbott et al. 2023b). Since the number of sources is still limited, the inference of intrinsic distributions mostly relies on parameterized models, including features such as a bump or cutoff in the mass distribution, which are expected from pulsational pair-instability supernovae (PPISNe; Belczynski et al. 2014; Marchant et al. 2016; Belczynski et al. 2016; Woosley 2017; Fishbach & Holz 2017; Talbot & Thrane 2018; Marchant et al. 2019; Farmer et al. 2019). Different parameterized distributions can, however, lead to physically different interpretations. The model used by the LIGO/Virgo/KAGRA (LVK) collaboration for the distribution of black hole (BH) spins indicated counter-aligned BH spins (Abbott et al. 2023b), while Roulet et al. (2021), Galaudage et al. (2021), Callister et al. (2021), and Hoy et al. (2022) argued that this conclusion is dependent on the model distribution used.

With an increasing number of measurements, it is also becoming possible to determine correlations between different BBH properties and place constraints on their joint distributions. For low-mass binaries, the best constrained intrinsic property is the chirp mass,

M chirp = ( m 1 m 2 ) 3 / 5 ( m 1 + m 2 ) 1 / 5 , $$ \begin{aligned} M_\mathrm{chirp} =\frac{(m_1 m_2)^{3/5}}{(m_1+m_2)^{1/5}}, \end{aligned} $$(1)

where m1 and m2 are the individual component masses. Useful constraints are also placed on both the effective spin, χeff, and the mass ratio, q, defined as

χ eff ≡ m 1 a 1 cos θ 1 + m 2 a 2 cos θ 2 m 1 + m 2 , q = m 2 m 1 , $$ \begin{aligned} \chi _\text{eff}\equiv \frac{m_1 a_1\cos \theta _1 + m_2 a_2\cos \theta _2}{m_1+m_2},\quad q=\frac{m_2}{m_1} ,\end{aligned} $$(2)

where a1 and a2 are the dimensionless spin parameters of each BH, and θ1 and θ2 are the angles between the individual spin vectors and the orbital angular momentum. Despite there being a significant correlated uncertainty between χeff and q for individual detections (e.g., Hannam et al. 2013; Mandel & Smith 2021), current observations already suggest the presence of an intrinsic (anti)correlation between these two properties, as well as a nontrivial dependence of the χeff distribution as a function of Mchirp (Safarzadeh et al. 2020; Callister et al. 2021; Abbott et al. 2023b; Franciolini & Pani 2022; Adamcewicz et al. 2023). Our understanding of these distributions will rapidly evolve, as the currently ongoing O4 observing run is expected to significantly increase the number of observed BBH mergers (Abbott et al. 2020).

The precise distribution of spins is critical for differentiating between various formation scenarios of merging BBHs. Dynamical processes in dense environments can result in an isotropic distribution of angles between the orbital plane and the spins of each BH, in contrast to near-aligned spins in binary formation channels (Mandel & O’Shaughnessy 2010; Rodriguez et al. 2016). High BH spins can also be indicative of hierarchical BH mergers, as a generic outcome from the merger of two similar-mass, slowly spinning BHs is the formation of a BH with a dimensionless spin of ∼0.7 (Pretorius 2005; Berti & Volonteri 2008; Gerosa & Berti 2017; Rodriguez et al. 2019; Tagawa et al. 2021; Gerosa & Fishbach 2021). In isolated binary systems it has been predicted that envelope stripping coupled with efficient angular momentum transport between the stellar core and the outer layers should lead to small aligned BH spins (Belczynski et al. 2020).

Merging BBHs with high spins (χeff > 0.5) could also arise in binary systems, either through tidal coupling in a short-period post-common-envelope binary (Qin et al. 2018; Zaldarriaga et al. 2018; Bavera et al. 2020, 2021; Fuller & Lu 2022; Ma & Fuller 2023) or through chemically homogeneous evolution (CHE). Large-scale flows are predicted to mix the hydrogen burning core with the envelope in rapidly rotating massive stars, preventing radial expansion in the CHE channel (Maeder 1987). de Mink et al. (2009) argued that this process operates in short-period binaries (periods on the order of one day), where rapid rotation arises from tidal synchronization. If both components of a massive binary undergo CHE, it is then possible for a merging BBH to form without an additional process that hardens the binary (Mandel & de Mink 2016; Marchant et al. 2016; de Mink & Mandel 2016; du Buisson et al. 2020; Riley et al. 2021; Stevenson & Clarke 2022). BBHs formed through CHE can then produce pairs of high-spin BHs (Marchant et al. 2016; Fuller & Ma 2019), although the final spin is sensitive to mass loss after the main sequence.

Various attempts have been made to constrain the individual contributions of different formation channels to the observed sample of merging compact objects. One possible approach to this is the use of individual predicted distributions from different channels, which can then be scaled to attempt to reproduce the observed distribution coupled with its observation biases (Zevin et al. 2017; Bouffanais et al. 2019; Safarzadeh et al. 2020; Wong et al. 2021; Zevin et al. 2021; Périgois et al. 2023). Alternatively, predicted distributions from each channel can be used to individually infer the likelihood that a single source is produced by a specific formation scenario (e.g., Qin et al. 2022; Antonelli et al. 2023). However, conclusions from model comparison can be severely affected if one lacks knowledge of some formation channels (Cheng et al. 2023), and predicted distributions have large uncertainties, with different codes predicting drastically different outcomes even for individual binary systems (e.g., Belczynski et al. 2022). It is thus critical to identify the qualitative features that arise from specific formation channels both in masses and spins, independent of the large uncertainties in population modeling (e.g., van Son et al. 2022).

In this work we study the limit set by the critical rotation rate of a BH progenitor on its resulting spin. Based on nonrotating models of stripped stars, we provide estimates of this spin limit and discuss its dependence on mass and metallicity in Sect. 2. In Sect. 3 we connect this limit with evolutionary processes that form merging BBHs, by developing a simple semi-analytical model that describes the evolution of CHE binaries. In Sect. 4 we then compare our results to the detailed population synthesis calculations of du Buisson et al. (2020, hereafter dB20), which include rotating models and have been reanalyzed to include predictions on the spins of BBHs produced via CHE. We conclude our work and discuss its broader implications in Sect. 5.

2. Stellar critical rotation and black hole spins

In the past two decades, various results have pointed to the need of efficient angular momentum transport in stellar interiors. This includes asteroseismic measurements of the rotation rates of the cores of evolved stars (see Aerts et al. 2019 for a recent review) as well as the angular momentum content of white dwarfs and young neutron stars (Suijs et al. 2008). One potential mechanism that allows for efficient angular momentum transport throughout the life of a star is the Tayler-Spruit (TS) dynamo (Spruit 2002). This dynamo process amplifies seed magnetic fields through differential rotation in radiative layers, leading to a stronger coupling of the stellar core and its outer layers. Fuller et al. (2019) further developed the model for the TS dynamo, and argued this process is more efficient than previously thought (we refer to this model as the TSF dynamo). The model by Fuller et al. (2019) provides a better fit to asteroseismic measurements of red giant and red clump stars, and to the rotation rates of white dwarfs. It also leads to near solid-body rotation of the hydrogen depleted cores.

The TSF dynamo reduces significantly the final rotation rates of massive stripped stars, as it couples the outer mass-losing layers to the core that remains until core-collapse (Fuller & Ma 2019). If angular momentum transport is efficient enough to make a stripped star remain near solid-body rotation until late burning phases, the critical rotational frequency Ωcrit sets a limit on the maximum angular momentum of the star,

J max = I Ω crit , $$ \begin{aligned} J_\mathrm{max} = I \Omega _\mathrm{crit} , \end{aligned} $$(3)

where I is the moment of inertia. The critical rotation rate Ωcrit represents the limit at which centrifugal, radiation and gravitational forces are perfectly balanced at the stellar equator. If the star collapses directly into a BH, then its dimensionless BH spin is limited to

a BH = min ( 1 , J max c M 2 G ) , $$ \begin{aligned} a_\mathrm{BH} = \min \left(1,\frac{J_\mathrm{max} c}{M^2G}\right), \end{aligned} $$(4)

where M is the stellar mass. In practice, as the BH is assembled, if some layers have enough angular momentum to support a disk at the innermost stable circular orbit then outflows may need to remove the surplus angular momentum before accretion, which would ensure the formation of a subcritical BH (e.g., Batta & Ramirez-Ruiz 2019; Murguia-Berthier et al. 2020).

Owing to the large luminosities of massive stars, one needs to account for the impact of radiation on the critical rotation rate. Ignoring gravity darkening, the critical rate depends on the Eddington factor Γ and the equatorial radius Req as (Langer 1997)

Ω crit = G M ( 1 − Γ ) R eq 3 , Γ = κ L 4 π c G M , $$ \begin{aligned} \Omega _\text{crit}=\sqrt{\frac{GM(1-\Gamma )}{R_\mathrm{eq} ^3}},\quad \Gamma =\frac{\kappa L}{4\pi c G M}, \end{aligned} $$(5)

with κ and L being the surface opacity and luminosity, respectively. The critical rotation rate including radiation is commonly referred to as the Γ − Ω limit. In this section we aim to provide a qualitative estimate of the impact of the Γ − Ω limit on BH spins. We used nonrotating stellar models to estimate aBH. Even if we were to use rotationally deformed stellar models, the expression for the critical rotation rate of Langer (1997) is only approximate as it ignores the impact of gravity darkening (Maeder & Meynet 2000; Sanyal et al. 2015; Fabry et al. 2022). Darkening is expected to increase the critical rotation frequency, allowing for higher final spins. Although assessing the impact of gravity darkening is beyond the scope of this paper, in Sect. 4 we study the spin limit within the context of population synthesis calculations that include rotational deformation.

The dependence of the limiting aBH on mass can be understood by expressing the moment of inertia as

I = k M R 2 , $$ \begin{aligned} I = kMR^2, \end{aligned} $$(6)

where k is the square of the ratio between the gyration radius and the stellar radius. Here we ignored rotational deformation and used Req = R. If we take k to be independent of mass at a given evolutionary stage (which is the case for polytropic models with the same polytropic index), and consider mass-radius and mass-luminosity relationships of the form R ∝ Mβ and L ∝ Mα, respectively, we get

J max c M 2 G ∝ M ( β − 1 ) / 2 1 − Γ , Γ ∝ M α − 1 . $$ \begin{aligned} \frac{J_\mathrm{max} c}{M^2G} \propto M^{(\beta -1)/2}\sqrt{1-\Gamma },\quad \Gamma \propto M^{\alpha -1}. \end{aligned} $$(7)

Power law relationships are not valid across all stellar masses, so the power law exponents are normally also taken to be functions of mass. In particular, the mass-luminosity exponent for main sequence stars is α > 1, while it approaches unity at very high masses (e.g., Köhler et al. 2015). This leads to Γ → 1 as mass increases, which pushes down the spin limit in Eq. (7). Similarly, both stellar models and homology relationships show that main sequence massive stars have β < 1 (Kippenhahn et al. 2013), which is also found from observations of eclipsing binaries (e.g., Torres et al. 2010, Eker et al. 2018). Having β < 1 indicates that the spin limit in Eq. (7) is reduced with mass. As more massive stars approach the Eddington limit near their surface they might experience inflation, where a small amount of mass expands to large radii (e.g., Sanyal et al. 2015). In this case β > 1 but also the approximation that k is independent of mass is not valid. If we want to understand in detail how the critical rotation limit on spins works at various evolutionary stages and masses, we need to rely on numerical calculations.

To make quantitative estimates, we computed mock models of stripped stars using version 23.05.1 of the MESA stellar evolution code1 (Paxton et al. 2011, 2013, 2015, 2018, 2019; Jermyn et al. 2023). Details about input microphysics are described in Appendix A. We also used these models to discuss the spins produced by CHE stars, so evolution is initiated at the zero-age main sequence (ZAMS). We considered nonrotating models without mass loss that are forced to evolve homogeneously until core helium depletion by enforcing a large diffusion mixing coefficient throughout the entire star. Initial masses are sampled logarithmically between log10M/M⊙ = 0.8 (6.3 M⊙) and log10M/M⊙ = 2.4 (251 M⊙) and kept fixed during the evolution. Three metallicities are sampled, Z⊙/10, Z⊙/50 and Z⊙/250 where the solar metallicity Z⊙ = 0.0142 and the relative metal fractions are adopted from Asplund et al. (2009). All simulations are run until core carbon depletion. Although we did not include rotation in these simulations, the results were then compared to the population synthesis calculations of dB20, which did include rotating binary models.

As we did not include mass loss, the resulting models are not meant to represent the evolution of a single star, but to be indicative of the structure of a star with a given mass at a specific evolutionary stage. Since CHE stars in binaries contract and tidally decouple after the main sequence, stellar winds can efficiently spin them down and we do not expect them to remain homogeneous. However, a stellar model evolved without mass loss will produce a composition discontinuity between the CO core and the remaining helium envelope, which is not present in mass-losing models. It is for this reason that we kept our models homogeneous through helium burning, to better represent the structure of a model at each evolutionary stage and metallicity.

The position in the Hertzsprung-Russell diagram for the mock CHE models at different evolutionary stages is illustrated in Fig. 1. As the stars evolve, they continuously increase their luminosity and (except for some of the most massive models) continuously contract. At each of these stages we can consider the maximum angular momentum that the star can contain under solid-body rotation, Jmax, and compute the resulting upper limit on the BH spin amax = Jmaxc/GM2 were the star to collapse at that stage. As shown in Fig. 2, we find that for all metallicities and masses amax decreases as the star evolves. In particular, at core-carbon depletion, stars with masses above 25 M⊙ would not be able to produce a maximally spinning BH. Barring the assumption of solid-body rotation, which we discuss later, this is a feature that should be common not only to CHE but to any formation scenario that involves the formation of BHs through stripped envelope stars. This also includes stripped stars that are tidally spun up by their companion (e.g., Qin et al. 2018). With increasing metallicity, increased opacity yields larger radii and higher Eddington factors at carbon depletion, and thus a lower limit on the spin (see Eq. 5). A fit to amax at core carbon depletion is provided in Appendix B.

thumbnail Fig. 1.

Mock CHE models described in Sect. 2 on the Hertzsprung-Russell diagram. Colors indicate different evolutionary stages, including the ZAMS, TAMS, helium ZAMS and TAMS, and core carbon depletion (C dep.). Simulations cover the mass range 6.3–251 M⊙ and were performed without mass loss. Different line styles indicate different metallicity values. Two evolutionary tracks with a metallicity of Z⊙/50 and masses of 10 M⊙ and 100 M⊙ are shown in gray for reference.

thumbnail Fig. 2.

Dimensionless spins, amax, corresponding to the angular momentum and mass of a critically rotating star undergoing CHE at different evolutionary stages. At a fixed mass and metallicity, this value monotonically reduces with each successive evolutionary stage. Values are estimated from the nonrotating models described in Sect. 2.

The limit we find on BH spins is consistent with current measured values in X-ray binaries. The most massive BH with a dynamical mass estimate and a constrained spin is Cyg X-1, with a mass of 21.2 ± 2.2 M⊙ and a > 0.9985 (Miller-Jones et al. 2021). It might be possible in the near future to identify more massive BHs in X-ray binaries, which would allow our predicted spin limit to be tested using electromagnetic observations. On the other hand, merging binary BHs with masses > 20 M⊙ are now frequently detected, possibly allowing a direct test. Even if critical rotation sets a limit on the spins of BHs formed from stripped stars, for this spin limit to appear in gravitational wave (GW) observations there must be an evolutionary process that forms merging binary BHs from stars that critically rotate close to core-collapse. In the context of long gamma-ray burst (lGRB) formation via the collapsar model (Woosley 1993), tidal spin-up of stripped stars by degenerate companions has been suggested as a mechanism to form a rapidly spinning BH (Podsiadlowski et al. 2004; Izzard et al. 2004). If such systems also result in a compact object merger, then the second formed compact object would dominate the effective spin of the system (Qin et al. 2018; Bavera et al. 2020, 2021). Another mechanism to form high-spin merging binary BHs is the CHE scenario (Mandel & de Mink 2016; de Mink & Mandel 2016; Marchant et al. 2016). In the next section we consider the CHE scenario, by means of a simple semi-analytical model that lets us understand what limits the masses and spins that can be produced by this channel.

3. Semi-analytical model for chemically homogeneous evolution

To explore the possible parameter space in chirp mass and effective spin covered by CHE, we constructed a simple semi-analytical model. This model relies on a few physical quantities obtained from stellar evolution models described in Sect. 2 and provides clear insight into the physics that determine the boundaries in BBH properties produced by CHE. For simplicity, we considered only equal-mass binaries and assume solid-body rotation. Even if we were to relax the assumption of equal mass ratios, Fig. 3 shows that the q = 1 case represents an upper limit for the effective spin at a given chirp mass, which does not change significantly for q close to 1. Through multiple evolutionary stages we needed to account for the evolution of the angular momentum of each component, as well as their masses and orbital periods. Our model and its assumptions are described next, and are also summarized in Table 1.

  1. Terminal-age main sequence (TAMS): We ignored evolution during core hydrogen burning and assumed as a starting point that both stars have evolved chemically homogeneous and have reached the TAMS while remaining tidally synchronized. The parameters that describe this stage are the orbital period PTAMS and the mass of each star MTAMS. Given the assumption of synchronicity the angular momentum of each star at this stage is equal to

    J TAMS = 2 π P TAMS I TAMS . $$ \begin{aligned} J_\mathrm{TAMS} = \frac{2\pi }{P_\mathrm{TAMS} }I_\mathrm{TAMS} . \end{aligned} $$(8)

    The orbital period at TAMS cannot be arbitrarily small. We considered as a limit the period at which the stars would be in contact2. For a star of mass M1 with a companion of mass M2, this period can be computed from Kepler’s third law and the separation at contact,

    P contact = 4 π 2 G ( M 1 + M 2 ) a contact 3 . $$ \begin{aligned} P_\mathrm{contact} =\sqrt{\frac{4\pi ^2}{G(M_1+M_2)}a_\mathrm{contact} ^3}. \end{aligned} $$(9)

    The separation at contact is determined using the fit for the Roche lobe size of Eggleton (1983) and the stellar radius of the CHE star at TAMS,

    a contact = 0.6 q 2 / 3 + ln ( 1 + q 1 / 3 ) 0.49 q 2 / 3 R 1 , TAMS , q ≡ M 1 M 2 · $$ \begin{aligned} a_\mathrm{contact} =\frac{0.6q^{2/3}+\ln (1+q^{1/3})}{0.49q^{2/3}}R_\mathrm{1,TAMS} ,\quad q\equiv \frac{M_1}{M_2}\cdot \end{aligned} $$(10)

  2. Helium ZAMS (He-ZAMS): After the main sequence, a CHE star will contract until it reaches thermal equilibrium at the beginning of core-helium burning, the He-ZAMS. We assumed tidal synchronization stops during this short contraction phase and that the angular frequency of the star evolves by conserving the angular momentum at TAMS. If contraction is homologous, meaning the radial position of each mass element contracts by the same fraction α, then the angular frequency of the star increases as Ω ∝ α−2. In contrast, ignoring changes in surface opacity or luminosity, the critical rotation rate increases as Ωcrit ∝ α−3/2. The contracting star is then expected to evolve closer to critical rotation (Ω/Ωcrit ∝ α−1/2). In practice contraction is not exactly homologous, and the critical rotation rate will be modified as the luminosity and surface opacity change, but this illustrates that during contraction after TAMS stars can evolve toward critical rotation. To determine the angular momentum at the He-ZAMS, we needed to account for the maximum angular momentum, JHe − ZAMS, max, that the star can possibly have while rotating at its critical speed. We simply limited the angular momentum at this stage to

    J He − ZAMS = min ( J TAMS , J He-ZAMS, max ) . $$ \begin{aligned} J_\mathrm{He-ZAMS} = \min (J_\mathrm{TAMS} , J_\text{He-ZAMS,} \text{ max}). \end{aligned} $$(11)

    The loss of excess angular momentum needs to be accompanied by mass loss. However, if ejection happens through the formation of a decretion disk (similar to Be-stars; e.g., Rivinius et al. 2013) then significant amounts of angular momentum can be removed with a small amount of mass ejected. We ignored the uncertain mass loss and orbital period evolution during the contraction from TAMS to He-ZAMS,

    M He − ZAMS = M TAMS , P He − ZAMS = P TAMS . $$ \begin{aligned} M_\mathrm{He-ZAMS} =M_\mathrm{TAMS} ,\quad P_\mathrm{He-ZAMS} =P_\mathrm{TAMS} . \end{aligned} $$(12)

  3. Core helium burning: During the post-MS evolution the components will undergo mass loss, possibly as Wolf-Rayet (WR) stars. We parameterized the total fraction of mass lost by a free parameter, fWR, defined as

    f WR ≡ M He − TAMS M He − ZAMS · $$ \begin{aligned} f_\mathrm{WR} \equiv \frac{M_\mathrm{He-TAMS} }{M_\mathrm{He-ZAMS} }\cdot \end{aligned} $$(13)

    This is such that fWR = 1 represents no mass loss, while fWR = 0 would indicate that the entire stellar mass is removed. As mass is lost the orbital period of the binary will also change. Under the approximation where the stellar winds remove orbital angular momentum equal to the specific orbital angular momentum of the corresponding component, the orbital period satisfies

    P He − TAMS P He − ZAMS = ( M He − ZAMS M He − TAMS ) 2 = f WR − 2 . $$ \begin{aligned} \frac{P_\mathrm{He-TAMS} }{P_\mathrm{He-ZAMS} }=\left(\frac{M_\mathrm{He-ZAMS} }{M_\mathrm{He-TAMS} }\right)^2= f_\mathrm{WR} ^{-2}. \end{aligned} $$(14)

    Since 0 < fWR < 1, mass loss will lead to orbital expansion. To determine the evolution of each star’s angular momentum in connection to mass loss, we assumed mass loss removes spin angular momentum equal to that of spherical shells of the stellar radius rotating at the surface angular frequency,

    J ˙ = i surf Ω M ˙ , i surf = 2 3 R 2 . $$ \begin{aligned} \dot{J}=i_\mathrm{surf} \Omega \dot{M}, \quad i_\mathrm{surf} =\frac{2}{3}R^2. \end{aligned} $$(15)

    Writing the moment of inertia of the star in terms of k (which is the squared ratio between the gyration radius and the stellar radius), we obtain

    J ˙ J = 2 3 k ( M ˙ M ) . $$ \begin{aligned} \frac{\dot{J}}{J} = \frac{2}{3k}\left(\frac{\dot{M}}{M}\right). \end{aligned} $$(16)

    Our simulations indicate that during core helium burning k covers the range ∼0.08–0.1. Ignoring the time dependence of k, the previous equation can be integrated to provide the angular momentum of the star at the helium TAMS (He-TAMS),

    J He − TAMS J He − ZAMS = ( M He − TAMS M He − ZAMS ) 2 / ( 3 k ) = f WR 2 / ( 3 k ) . $$ \begin{aligned} \frac{J_\mathrm{He-TAMS} }{J_\mathrm{He-ZAMS} }=\left(\frac{M_\mathrm{He-TAMS} }{M_\mathrm{He-ZAMS} }\right)^{2/(3k)}= f_\mathrm{WR} ^{2/(3k)}. \end{aligned} $$(17)

    This can be related to the dimensionless spin of the star, that is, the spin of a BH that a star would produce through direct collapse, a = Jc/M2G. In terms of fWR we have

    a He − TAMS a He − ZAMS = f WR − 2 + 2 / ( 3 k ) . $$ \begin{aligned} \frac{a_\mathrm{He-TAMS} }{a_\mathrm{He-ZAMS} } = f_\mathrm{WR} ^{-2+2/(3k)}. \end{aligned} $$(18)

    This equation indicates that the final compact object spin is reduced under our assumption of solid-body rotation as long as k < 1/3. Owing to the central concentration of mass in stars, this is generally the case.

  4. Carbon depletion and BBH formation: Similar to the evolution from TAMS to He-ZAMS, we limited the angular momentum of a star to its maximum value at critical rotation,

    J C. dep = min ( J He − TAMS , J C. dep, max ) , $$ \begin{aligned} J_\text{C.} \text{ dep}=\min (J_\mathrm{He-TAMS} , J_\text{C.} \text{ dep,} \text{ max}), \end{aligned} $$(19)

    and we kept the mass and orbital period from the He-TAMS,

    M C. dep = M He − TAMS , P C. dep = P He − TAMS . $$ \begin{aligned} M_\text{C.} \text{ dep}=M_\mathrm{He-TAMS} ,\quad P_\text{C.} \text{ dep}=P_\mathrm{He-TAMS} . \end{aligned} $$(20)

    We assumed direct collapse to a BH, ignoring any loss of mass or angular momentum at stages beyond carbon depletion. For the mass range we are concerned with, this is supported both by theory (e.g., Fryer 1999) and observations of BH binaries with massive companions such as Cyg X-1 (Mirabel & Rodrigues 2003) and VFTS-243 (Shenar et al. 2022). The resulting mass and spin of the BHs was finally computed as

    M BH = M C. dep , a BH = min ( 1 , J C. dep c M C. dep 2 G ) , $$ \begin{aligned} M_\mathrm{BH} =M_\text{C.} \text{ dep},\quad a_\mathrm{BH} =\min \left(1,\frac{J_\text{C.} \text{ dep}c}{M_\text{C.} \text{ dep}^2G}\right), \end{aligned} $$(21)

    while the orbital period of the BBH is taken to be that at carbon depletion. The delay time until BBH merger is then computed from the results of Peters (1964) for the case of a circular orbit. As a simple model for the impact of (P)PISNe, we ignored any BH that would form within the predicted PISN gap, taking the lower limit of the gap to be MBH = 43.94 M⊙ from Marchant et al. (2019).

thumbnail Fig. 3.

Resulting effective spin for orbit-aligned BBHs as a function of mass ratio and chirp mass, under the assumption that both BHs have the maximum spin allowed by the critical rotation limit of their progenitors. Results are shown for a metallicity of Z ≃ Z⊙/50, and the truncation of the q = 0.25 line is due to the limited range of masses modeled.

Table 1.

Overview of the steps in the semi-analytic model presented in Sect. 3.

Our model then relies on three input parameters: the component masses at TAMS, the orbital period at TAMS, and the fraction of mass lost after the main sequence (MTAMS, PTAMS, and (1-fWR), respectively). The model is semi-analytical as it does require results from detailed calculations of stellar evolution. Specifically, we required, as a function of mass: the radius and moment of inertia at TAMS (RTAMS and ITAMS), the maximum angular momenta at He-ZAMS and carbon depletion (JHe-ZAMS, max and JC. dep, max), and the squared ratio between the gyration and surface radius, k. All of these quantities, which are determined by MESA calculations in our work, are metallicity dependent.

We focused on predictions at the metallicity Z = Z⊙/50 to describe the qualitative results. Results from the other computed metallicities (Z⊙/10 and Z⊙/250) are qualitatively similar. As we find that k covers values between ∼0.08 and 0.1 during core helium burning, we adopted k = 0.09. By considering different values for MTAMS and PTAMS we can explore what sets the highest and lowest spins produced for different BH masses. This is done in Fig. 4, where for each choice of MTAMS and PTAMS we continuously vary fWR between unity and zero. The right-most point of each curve represents the case of no mass loss (fWR = 1). The most apparent feature in Fig. 4 is an exclusion region for high spins and high BH masses. This limit is set by critical rotation at carbon depletion (i.e., the Γ − Ω limit; see Sect. 2), and determines the final BH spin as a function of BH mass, independent of the initial orbital period, when WR mass loss is negligible. The Γ − Ω limit is not restricted to CHE evolution, but should be a common feature of evolutionary channels where BHs are formed from helium stars.

thumbnail Fig. 4.

Resulting BH masses and spins of CHE stars using a semi-analytical model (see Sect. 3). The model assumes a mass ratio of unity, so two BHs with identical properties are produced. We consider the outcome for three masses at TAMS (25 M⊙, 40 M⊙, and 60 M⊙) and three orbital periods at TAMS scaled from the period at which the binary would be in contact. Each line represents the results for a fixed MTAMS and PTAMS with a variable fWR (where MBH = fWRMTAMS). Cases where the resulting BBH would be too wide to merge within the age of the Universe are marked with a dotted line. Note that for fWR close to unity, lines with different values of PTAMS converge to the same spins at any given mass. The effect of (P)PISNe is ignored in this figure. Precise boundaries depend on the metallicity used to determine stellar properties in the semi-analytical model used, which in this case were taken from calculations at Z⊙/50.

Subtler are the conditions that define the minimum spins that can be achieved at any given mass from CHE. There are two ways in which angular momentum could be reduced: the stars either reach the TAMS at a higher orbital period (leading to slower rotation due to synchronization) or lose mass to remove angular momentum after TAMS. Since we still need the resulting BBH to merge, we can question which of these two options results in a smaller final spin. Is it better to start at contact at TAMS and then lose as much mass as possible before the orbit widens too much? Or can lower spins be achieved by starting with an orbit at TAMS as wide as possible to yield a merging BBH without any additional mass loss? Figure 4 shows that the former is the case. For each MTAMS considered, the lowest spin achievable while still resulting in a merging BBH comes from binaries that are at contact in TAMS. An important caveat is that our choice of fWR is arbitrary, while in practice the fraction of mass lost will be determined by the metallicity and mass at the He-ZAMS.

The upper and lower bounds on the spins discussed so far are illustrated in Fig. 5 for Z = Z⊙/50 (see Appendix C for a version with all metallicities). Two additional bounds are included, one accounting for the (P)PISNe gap following the results of Marchant et al. (2019) and another one coming from the limits of CHE evolution. CHE is expected to be a process favored at higher masses (Maeder 1987), and so we cannot have an arbitrarily low MTAMS. In Fig. 5 we illustrate this by drawing an exclusion region that corresponds to MTAMS ≤ 30 M⊙. These boundaries can be compared to the results of detailed simulations to see if this simple model can reproduce the predicted features, which we do in the following section. We point out, however, that various physical effects are not included in this model. In particular, mass loss is expected to increase at higher masses and metallicities. This also implies that at the high metallicities where we would expect significant post-MS mass loss, mass loss will have potentially widened the orbit of the stars during the MS itself. This restricts the minimum period at TAMS and thus the lower limit on the final spins. Despite this, even in detailed models the impact of mass loss on the orbital period is approximate, and orbital widening can be reduced or even inverted by tidal coupling of the wind (Brookshaw & Tavani 1993; MacLeod & Loeb 2020; Schrøder et al. 2021).

thumbnail Fig. 5.

Physical processes setting the boundaries for BH masses and spins for the CHE formation scenario. The four colored areas indicate excluded regions due to four different physical processes. The MTAMS and tmerge limits apply only to CHE, while the Γ − Ω and (P)PISNe boundaries apply in general to all field formation scenarios. In this figure an assumed limit for the MTAMS of CHE stars is set at 30 M⊙, which sets the boundary at the left of the figure. Precise boundaries depend on the metallicity used to determine stellar properties in the semi-analytical model used, which in this case were taken from calculations at Z⊙/50.

4. Comparison to population synthesis results

The semi-analytical model presented in the previous section provides an overall idea of the limits of CHE in terms of masses and effective spins. However, as we varied multiple parameters without accounting for their possible correlation (such as the fraction of mass lost after the MS and the period at TAMS), it is instructive to compare our results with detailed population synthesis calculations. In this section we reanalyze the population synthesis results of dB20 by including information on stellar spins and compare them against our results.

4.1. The population synthesis simulations of dB20

The work of dB20 already provided predictions for the rates and the mass distribution of merging BBHs formed through CHE. These results were based on a large grid of MESA models, exploring the parameter space of initial masses, orbital periods and metallicity. For computational reasons the simulations of dB20 were restricted to a mass ratio of q = 1, which was taken to be representative of the evolution of binaries in the range q = 0.8–1. In order to provide rate predictions this grid of detailed binary simulations was combined with the theoretical predictions of Taylor & Kobayashi (2015) for the cosmic star formation history, accounting in particular for the distribution of formed stars at different metallicities. The results of dB20 are provided in the form of a comoving box simulation, indicating the formation redshift of all BBHs formed within it through CHE.

Consistent with the results of Marchant et al. (2016), for any given metallicity the MESA simulations of dB20 show a tight correlation between the final orbital period and mass of a binary. This is a consequence of wind mass loss, which at high metallicities lowers the total mass and, under the assumption of Jeans’ mode mass loss (stellar winds removing orbital angular momentum equal to that of each component), result in orbital widening. At a fixed metallicity and chirp mass, the small spread in orbital periods is connected to the narrow range in initial orbital periods that are expected to lead to CHE (Mandel & de Mink 2016; Marchant et al. 2016; Song et al. 2016; Riley et al. 2021). For BH formation through direct collapse, this leads to a similar relationship between the period and the chirp mass of the binary BH (see the top panel of Fig. 6).

thumbnail Fig. 6.

Final chirp masses and orbital periods in the MESA simulations of dB20. Top: Final properties assuming direct collapse into a BH (with its mass at carbon depletion) and ignoring mass loss due to (P)PISNe. Each dot indicates the final result of one CHE simulation. Systems above the dashed gray line have merger times longer than the age of the Universe and are marked with a lighter color. Results are shown for their grids with metallicities of log10Z = −2.375, −2.5, −2.75, −3, −3.5, −4, and −5, with the labels indicating their approximate values in terms of the solar metallicity (taken here to be Z⊙ = 0.017 as in Grevesse et al. 1996 for consistency with the definition used in dB20). Bottom: Same as the top panel but after including the impact of (P)PISNe as described in Marchant et al. (2019).

Including the effect of (P)PISNe produces a more complex relationship between the chirp mass and the orbital period of BBHs formed through CHE. Mass loss due to PPISNe was included in the results of dB20 by interpolating the pre-PPISN to BH mass relationship of Marchant et al. (2019). The change in orbital properties was determined by assuming mass loss was instantaneous, followed by circularization of the orbit at constant orbital angular momentum prior to BH formation. The bottom panel of Fig. 6 shows the resulting final orbital periods and chirp masses after the inclusion of mass loss due to PPISNe. As the relationship between pre-PPISNe mass and BH mass is non-monotonic, the simple relationship between Mchirp and the final orbital period does not hold anymore. Owing to the occurrence of (P)PISNe, no BHs are produced between 44 M⊙ and 123 M⊙, which constitutes the PISN mass gap according to Marchant et al. (2019).

The resulting spins of BBHs formed through CHE were not discussed by dB20. In all simulations that are unaffected by (P)PISNe we assumed that all angular momentum and mass collapse into the BH, resulting in a BH spin of

a BH = Jc M 2 G , $$ \begin{aligned} a_\text{BH}=\frac{Jc}{M^2G}, \end{aligned} $$(22)

where J and M are the final pre-collapse spin angular momentum and mass. Measurements of individual spins in merging binary BHs have large errors, but the effective spin is much better constrained. As dB20 only consider equal-mass binaries with aligned spins, χeff is equal to aBH in their simulations. For cases undergoing PPISNe, we used the angular momentum profile of the star at the endpoint of the calculation, which in dB20 corresponds to either core-carbon depletion or the onset of collapse due to pair-instability. Taking the final expected BH mass MBH from Marchant et al. (2019) we consider only the angular momentum J(MBH) contained within the corresponding mass coordinate. The final spin is then computed as

a BH, PPISN = J ( M BH, PPISN ) c M BH, PPISN 2 G · $$ \begin{aligned} a_\text{BH,} \text{ PPISN}=\frac{J(M_\text{BH,} \text{ PPISN})c}{M_\text{BH,} \text{ PPISN}^2G}\cdot \end{aligned} $$(23)

This assumes the mass ejection from PPISN is instantaneous. One caveat of this approach is that the resulting BH spin can exceed unity, indicating the potential formation of a GRB through the collapsar model (Woosley 1993; MacFadyen & Woosley 1999). For simplicity we simply cap the dimensionless spin at unity. More detailed models to relate the angular momentum distribution of a stellar model to the final mass and spin of the BH are available (e.g., Batta & Ramirez-Ruiz 2019), which consistently produce subcritical spins.

The resulting chirp masses and effective spins from the MESA models of dB20 are shown in Fig. 7. Without the inclusion of (P)PISNe, these two quantities follow clear relationships at each metallicity, with higher chirp masses resulting in lower spins. This is a consequence of wind mass loss after TAMS, lowering the spin of the star before BH formation. At each metallicity the lowest spins produced for merging BBHs correspond to the point where the resulting delay time is equal to the age of the Universe, an effect we explained in Sect. 3. Compared to our nonrotating simulations, we see that the models from dB20 exceed the critical rotation limit estimated from the single star nonrotating models. This is in part due to significant differential rotation, with some of the Z⊙/50 models having twice the rotational frequency near their cores relative to their surface at carbon depletion. But additional differences are expected, as the models of dB20 also include centrifugal support and exhibit a different composition profile at carbon depletion compared to our single star simulations.

thumbnail Fig. 7.

Same as Fig. 6 but showing the resulting chirp masses and effective spins of BBHs formed through CHE in the MESA simulations of dB20.

At very low metallicities (≤Z⊙/200) the MESA simulations produce low spins that break from the general trend. We have identified that in these cases, owing to a smaller relative difference between the size of the stars at TAMS and the He-ZAMS, stars remain synchronous after the end of the main sequence. This leads to angular momentum being removed from each component by tides on the He main sequence, as stars spin up during the contraction phase after core-hydrogen depletion. This effect is potentially spurious, as the model used for tidal evolution is based on the dynamical tide process of Zahn (1977) using precomputed properties of main-sequence stars (see Paxton et al. 2015 for details). Recently Ma & Fuller (2023) have shown that tidal synchronization likely only operates in stripped stars for very short orbital periods, which are forbidden in CHE evolution as the orbit needs to be wide enough to fit the stars during their main sequence evolution.

For this work we also recomputed the detection probabilities from dB20 using updated noise curves. We used noise curves corresponding to the O3 measured sensitivity, and the O4 and O5/A+ expected sensitivities as described in Abbott et al. (2020). In particular, for O3 we used the measured noise curve based on three months of data from the LIGO-Hanford detector, while for O4 we used the pessimistic noise curve estimate with a range for binary neutron star detection of 160 Mpc3. We also included the effect of spins on detectability by using the IMPRPhenomB waveform model with non-precessing spins from Ajith et al. (2011).

4.2. Rates of high-spin mergers from chemically homogeneous evolution

Using the insight developed from the semi-analytical model presented in Sect. 3, we reanalyzed the rate predictions of dB20 for CHE evolution while considering the predicted spins for these models. Before discussing rates for specific detector sensitivities, we first compare the properties of our semi-analytical model with the results of dB20 for a detector with infinite sensitivity (which we refer to as “cosmological” rates). Figure 8 illustrates how the cosmological BBH mergers are distributed in effective spins and chirp masses. As PPISNe produce a pileup of systems near the PISN gap (Belczynski et al. 2016), we see that the distribution in Fig. 8 peaks at Mchirp ∼ 38 M⊙. An additional pileup is seen at the top of the distribution (for Mchirp between 30 M⊙ and 40 M⊙ and χeff > 0.6), coming from the spins of BHs being limited by the critical rotation of their progenitor stars. For comparison, we also considered the predicted region for CHE evolution shown in Fig. 5. Although the semi-analytical model qualitatively reproduces various features of the detailed simulations, it is shifted significantly toward lower effective spins. The mergers with χeff ≲ 0.2 and 30 ≲ Mchirp ≲ 40 correspond to the very metal poor systems that undergo tidal synchronization after TAMS. As discussed in Sect. 4.1 the low spins in these very metal-poor simulations could be spurious.

thumbnail Fig. 8.

Distribution of the rate of merging BBHs formed through CHE per unit chirp mass and unit effective spin that is observable from Earth with a detector with infinite sensitivity, derived from the simulations of dB20. We refer to these rates as “cosmological”. Numbers are normalized to the maximum value of the differential rate dR/dMchirp/dχeff. The two panels highlight predicted systems below and above the PISN gap. The dashed white contour corresponds to the predicted region below the PISN gap that arises from CHE, computed with the semi-analytical model shown in Fig. 5.

One of the reasons why the simulations of dB20 and our semi-analytical model make a different prediction for the minimum spins produced by CHE was discussed in Sect. 3. The lowest spins predicted arise from binaries that are at contact at TAMS and lose a significant amount of mass during the post-MS. But systems that would undergo significant post-MS mass loss would also be expected to be widened by mass loss before TAMS, so the two free parameters in the semi-analytical model are not really independent. However, another source of discrepancy comes from angular momentum coupling and how close to solid-body rotation the MESA simulations of dB20 are. Differential rotation also modifies how the Γ − Ω limit translates into an upper limit on BH spins, as it allows for a larger angular momentum budget in the stellar core without exceeding critical rotation at the surface.

To test the impact of angular momentum transport in our results, we recomputed a simulation from dB20, replacing the TS dynamo with the modified version from Fuller et al. (2019), as implemented by Fuller & Lu (2022). We also computed a model with an artificially high angular momentum diffusivity in order to enforce solid-body rotation throughout. The simulation chosen corresponds to the merging BBH with the lowest chirp mass produced in the MESA grids of dB20, with Mchirp = 16 M⊙ and χeff = 0.44. The resulting BH spin from these simulations is shown in Fig. 9. Throughout most of the evolution of the binary, all three simulations match closely, indicating the original calculation was near solid-body rotation. However, the simulations diverge during core-helium burning, with the original calculation from dB20 resulting in a much higher BH spin. The simulation using the modified TS dynamo of Fuller et al. (2019) remains almost identical to the one where solid-body rotation is enforced, producing a BBH with χeff = 0.25. A similar experiment for a simulation that produces a merging BBH with Mchirp = 28.5 M⊙ and χeff = 0.31 in dB20 gives instead a value of χeff = 0.18 when using the modified TS dynamo.

thumbnail Fig. 9.

Mass of each component versus instantaneous dimensionless spin during the evolution of an equal-mass binary undergoing CHE. Shown are the original simulation from dB20 using the TS dynamo (normal TS), one recomputed using the modified version of the TS dynamo from Fuller et al. (2019, TSF), and one where solid-body rotation is enforced. These simulations were computed with the same setup and MESA version (11701) used by dB20.

Keeping in mind that the results of dB20 might overestimate the spins of the resulting merging BBHs, we analyzed the range of spins covered by their simulations of CHE. To dissect how different systems contribute, we distinguished the rate between regions of low mass (Mchirp < 30 M⊙), high mass up to the PISN gap4 (30 M⊙ < Mchirp < 38.3 M⊙), and systems above the PISN gap (Mchirp > 107 M⊙). Similarly, we distinguished between systems with low (χeff < 0.5) and high (χeff > 0.5) effective spins. The resulting merger rates are given in Table 2. Restricted to systems below the PISN gap the cosmological rate is predicted to be 6800 yr−1, for which the dominant contribution (41%) comes from the high-spin and low Mchirp regime, with high-spin systems constituting the majority (60%). This matches the general view that CHE produces mostly high-spin BHs.

Table 2.

Predicted detection rates (per year of detector time) for BBH mergers produced from CHE, derived from the simulations of dB20.

Most high-spin systems come from low metallicity (Z ≲ Z⊙/10) environments that experience little mass loss and have short merger times (see Figs. 6 and 7). One way to visualize this is by considering the evolution of the comoving merger rate as a function of redshift, which is done in Fig. 10. We can see that at redshift zero the predicted volumetric rate is dominated by low-spin systems below the PISN gap, accounting for 84% of the local rate. It is only above redshift 1.5 that high-spin systems constitute the majority of the comoving rate. Observations done with current detectors are not sensitive beyond a redshift of z ∼ 1, so we expect significant differences between the rate of high-spin mergers in the observable Universe, against those actually observed with current detectors. Another important feature of Fig. 10 is that systems predicted above the PISN gap become dominant at redshift ≃5. Predictions above the PISN gap are one of the most uncertain features of the model, as they require the formation of binary stars in excess of 100 M⊙ for each component (Heger & Woosley 2002). However, this makes mergers above the gap an interesting target for third-generation detectors, which will be sensitive to such massive mergers at redshifts beyond 10 (Hall & Evans 2019).

thumbnail Fig. 10.

Evolution of the BBH merger rate and of different populations of merger events predicted by dB20 for CHE. Top: Fraction of the total rate for specific constraints on the chirp mass and effective spins of BBH mergers. Bottom: Comoving merger rate corresponding to the same constraints in chirp mass and effective spins. The dotted line indicates the cosmological rate resulting from the addition of all others.

As current ground based GW detectors are not sensitive to high redshift mergers, we expect the observed population of BBHs formed through CHE to be dominated by low-spin systems. Figure 11 shows the detectable rate distribution produced by CHE as a function of Mchirp and χeff with the measured sensitivity for O3 as well as projected sensitivities for O4 and O5 (which is planned to include the A+ upgrade). Owing to the lack of sensitivity at redshifts above unity, both for O3 and O4 we find that the majority of observed BBHs would populate a narrow band going from Mchirp ≃ 18 M⊙ and χeff ≃ 0.45 down to Mchirp ≃ 38 and χeff ≃ 0.25. This corresponds to the limit for which, at any given metallicity, BBHs that are too wide to merge in the age of the Universe are produced. Compared to the currently observed population we find that this band lies at higher χeff than the majority of observed sources. As shown in Table 2, for the sensitivity of O3 we would expect 30% of observed sources produced by CHE below the PISN gap to have χeff > 0.5, while only a single source has been detected with both median component masses below 60 M⊙ and a median effective spin above 0.5 (GW200308_173609). The predicted χeff band of observable CHE mergers would be lowered by about a half if we assumed the enhanced TS dynamo of Fuller et al. (2019).

thumbnail Fig. 11.

Observable rate of BBH mergers formed through CHE considering the detector sensitivity of O3, O4, and O5 for the LIGO detectors. The distribution of the rate is shown as a function of Mchirp and χeff. Data points indicate all observations made so far as reported in the current GW transient catalogs (GWTC-1, GWTC-2, and GWTC-3). For each observation, the median values of Mchirp and χeff are shown together with their 90% credible intervals.

As the sensitivity of detectors increases in the future, the contribution from mergers with high BH spins produced through CHE should become more important in observations. As shown in Fig. 11 and Table 2, high-spin (χeff > 0.5) and low-spin (χeff > 0.5) CHE BBHs are predicted make similar contributions to observations during the fifth observing run, with 52% of mergers detected below the PISN gap corresponding to the high-spin population. This indicates that direct constraints on the evolution of the merger rate as a function of redshift (including subpopulations of merging BBHs) will be possible before the onset of third-generation detections. For instance, current observations show an indication that the distribution of χeff broadens with redshift (Biscoveanu et al. 2022).

Our predicted observable rates for merging BHs formed by CHE would require that almost all GW sources observed to date are a consequence of CHE (see also Stevenson & Clarke 2022). Predicted rates are also in direct contradiction for mergers with both components above the PISN gap, which have not been observed so far. The third observing run of the LVK collaboration, for which detections are described in GWTC-2 and GWTC-3 (Abbott et al. 2021, 2023a), accumulated a total of 275 days of observations with at least two detectors. According to our results for O3, this would translate into 5.5 detections of mergers above the gap. The lack of such detections could point to weaknesses in the CHE model, but also in our understanding of mass loss rates at very low metallicities and of the distribution of orbital properties of very massive binaries. However, we do find that BHs formed above the gap should have spins a < 0.25, owing to the limit set on their progenitors by critical rotation. This should be the case for any BH formed above the gap from a stripped-envelope star (not just through CHE) and should serve to clearly distinguish them from objects formed through hierarchical mergers, which are expected to have spins a ≳ 0.7 (Pretorius 2005; Berti & Volonteri 2008; Gerosa & Berti 2017).

5. Conclusions

In this work we describe an upper limit on the spins of merging BBHs formed through binary evolution. This limit arises from the critical rotation rate of stripped star progenitors before their collapse, preventing the formation of BHs with spins near unity for BH masses ≳25 M⊙. To study how this limit arises through binary evolution, we considered BBH formation through CHE, a process that allows for the formation of rapidly rotating BH progenitors. We analyzed the BH spins produced by CHE with a semi-analytical model, as well as by reanalyzing the population synthesis results of dB20 by including information on BH spins formed through CHE. We compared our results to current observations and provide predictions for upcoming observing runs of ground-based GW detectors.

Based on our semi-analytical model, we identified three different processes (in addition to the PISN gap) that restrict the range of masses and effective spins that can be achieved through CHE (see Fig. 5). The lowest achievable spins come from CHE binaries with delay times close to the age of the Universe, making this population favored in current observations as they merge at low redshifts. Another restriction is set by the minimum mass for CHE to operate, resulting in a boundary with increasing χeff as a function of Mchirp. Finally, we find that CHE binaries that experience little mass loss after the main sequence have spins determined by the critical rotation rate of their progenitors, which is determined by a combination of gravity and radiation pressure for massive, luminous stars. Identifying any of these features in GW observations would provide important insight into stellar evolution processes that remain poorly constrained. Although we studied only the evolution of BBH progenitors through CHE, the spin limit due to critically rotating BH progenitors should be shared by any formation channel for BBHs that involves the collapse of stars without a hydrogen envelope. The same physical restriction applies to hydrogen-rich progenitors, but translating this into BH spins is significantly more difficult owing to uncertainties on remnant masses, coupling between the hydrogen-rich envelope and the core, and the diversity of stellar endpoints depending on the relative mass of the envelope and the core.

Comparing our analytical models with the simulations of dB20 we find that, although qualitatively the expected boundaries in Mchirp and χeff are present, the final spins are higher in the detailed binary simulations. We attribute this in part to angular momentum transport, as simulations that include more efficient coupling between cores and outer layers can lower the final spins by a factor of ∼2. Coupling is expected to impact both the lower and upper limits of spins that can be produced by CHE, with stronger coupling resulting in lower final spins owing to increased loss of angular momentum through stellar winds. The simulations of dB20 predict that during the ongoing O4 run (and also previous observing runs) the majority of detected BBHs formed through CHE would have effective spins lower than 0.5. Only in future science runs will the high-spin population (which merges promptly at high redshifts) become dominant. Based on two of the dB20 simulations that we recomputed using efficient angular momentum coupling, we also suggest that the spins computed in dB20 can be reduced significantly, although a more comprehensive study is needed to verify this.

The upper limit on BH spins we have identified also has consequences for the formation of gamma-ray bursts from collapsing stars through the collapsar model (Woosley 1993; MacFadyen & Woosley 1999). If BHs with spins near unity are required to produce a highly relativistic jet through the Blanford-Znajek process (Blandford & Znajek 1977; McKinney 2005), then the progenitors of lGRBs formed by stripped stars would be limited to pre-collapse masses ≲20 M⊙. Only broad-lined Ic supernovae have been associated with lGRB events from massive star collapses (Galama et al. 1998), possibly indicating that only stripped stars are their progenitors. The precise limits on progenitor masses are sensitive to angular momentum coupling, and future GW observations can help identify it. Constraining which stellar progenitors can produce lGRBs is also critical for linking observations of high-spin merging BBHs with the observed rates of lGRBs (Bavera et al. 2022).

Finally, a detection with both BHs unambiguously above the PISN gap is still missing and in contradiction with the results of dB20. This could be related to our lack of knowledge of the distribution of binary properties at both very high masses and low metallicities. Perhaps the stellar binaries we predict to form merging BBHs above the gap do not exist in nature. Another big uncertainty concerns the location of the PISN mass gap, which depends strongly on the value of the 12C(α, γ)16O reaction rate (Takahashi 2018; Farmer et al. 2019). Recent calculations using updated values for this rate (Mehta et al. 2022; Farag et al. 2022) have pushed the mass gap to the range ∼60–140 M⊙ in BH masses, shifting both boundaries upward by ∼20 M⊙. This can further lower predicted rates for BBHs above the PISN gap, with a corresponding increase in the amount of detections below it. In any case, we expect the spins of BHs formed above the gap to be significantly restricted by the limit of critical rotation on their progenitors, with spins below 0.25, providing a clear distinction from BHs formed through hierarchical mergers.

1

Input files to reproduce our simulations together with our data are available at https://zenodo.org/doi/10.5281/zenodo.10199794

2

As a less restrictive constraint one could consider the limit at which a contact binary at TAMS would be just below the limit of L2 overflow.

3

These noise curves are available at https://dcc.ligo.org/LIGO-T2000012/public

4

These limits correspond to the PISN gap for equal-mass binaries from Marchant et al. (2019).

Acknowledgments

PM acknowledges support from the FWO junior fellowship number 12ZY520N and the FWO senior fellowship number 12ZY523N. IM is a recipient of the Australian Research Council Future Fellowship FT190100574. Analysis of results relied on the Julia programming language (Bezanson et al. 2017) and the Makie plotting package (Danisch & Krumbiegel 2021).

References

  1. Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016, Phys. Rev. Lett., 116, 061102 [Google Scholar]
  2. Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2019, Phys. Rev. X, 9, 031040 [Google Scholar]
  3. Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2020, Liv. Rev. Relat., 23, 3 [NASA ADS] [Google Scholar]
  4. Abbott, R., Abbott, T. D., Abraham, S., et al. 2021, Phys. Rev. X, 11, 021053 [Google Scholar]
  5. Abbott, R., Abbott, T. D., Acernese, F., et al. 2023a, Phys. Rev. X, 13, 041039 [Google Scholar]
  6. Abbott, R., Abbott, T. D., Acernese, F., et al. 2023b, Phys. Rev. X, 13, 011048 [NASA ADS] [Google Scholar]
  7. Adamcewicz, C., Lasky, P. D., & Thrane, E. 2023, ApJ, 958, 13 [NASA ADS] [CrossRef] [Google Scholar]
  8. Aerts, C., Mathis, S., & Rogers, T. M. 2019, ARA&A, 57, 35 [Google Scholar]
  9. Ajith, P., Hannam, M., Husa, S., et al. 2011, Phys. Rev. Lett., 106, 241101 [NASA ADS] [CrossRef] [Google Scholar]
  10. Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [Google Scholar]
  11. Antonelli, A., Kritos, K., Ng, K. K. Y., Cotesta, R., & Berti, E. 2023, Phys. Rev. D, 108, 084044 [NASA ADS] [CrossRef] [Google Scholar]
  12. Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
  13. Batta, A., & Ramirez-Ruiz, E. 2019, ArXiv e-prints [arXiv:1904.04835] [Google Scholar]
  14. Bavera, S. S., Fragos, T., Qin, Y., et al. 2020, A&A, 635, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Bavera, S. S., Fragos, T., Zevin, M., et al. 2021, A&A, 647, A153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Bavera, S. S., Fragos, T., Zapartas, E., et al. 2022, A&A, 657, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Belczynski, K., Buonanno, A., Cantiello, M., et al. 2014, ApJ, 789, 120 [NASA ADS] [CrossRef] [Google Scholar]
  18. Belczynski, K., Heger, A., Gladysz, W., et al. 2016, A&A, 594, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Belczynski, K., Klencki, J., Fields, C. E., et al. 2020, A&A, 636, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Belczynski, K., Romagnolo, A., Olejak, A., et al. 2022, ApJ, 925, 69 [NASA ADS] [CrossRef] [Google Scholar]
  21. Berti, E., & Volonteri, M. 2008, ApJ, 684, 822 [NASA ADS] [CrossRef] [Google Scholar]
  22. Bezanson, J., Edelman, A., Karpinski, S., & Shah, V. B. 2017, SIAM Rev., 59, 65 [Google Scholar]
  23. Biscoveanu, S., Callister, T. A., Haster, C.-J., et al. 2022, ApJ, 932, L19 [NASA ADS] [CrossRef] [Google Scholar]
  24. Blandford, R. D., & Znajek, R. L. 1977, MNRAS, 179, 433 [NASA ADS] [CrossRef] [Google Scholar]
  25. Bouffanais, Y., Mapelli, M., Gerosa, D., et al. 2019, ApJ, 886, 25 [NASA ADS] [CrossRef] [Google Scholar]
  26. Brookshaw, L., & Tavani, M. 1993, ApJ, 410, 719 [NASA ADS] [CrossRef] [Google Scholar]
  27. Callister, T. A., Haster, C.-J., Ng, K. K. Y., Vitale, S., & Farr, W. M. 2021, ApJ, 922, L5 [NASA ADS] [CrossRef] [Google Scholar]
  28. Cheng, A. Q., Zevin, M., & Vitale, S. 2023, ApJ, 955, 127 [NASA ADS] [CrossRef] [Google Scholar]
  29. Chugunov, A. I., Dewitt, H. E., & Yakovlev, D. G. 2007, Phys. Rev. D, 76, 025028 [NASA ADS] [CrossRef] [Google Scholar]
  30. Cyburt, R. H., Amthor, A. M., Ferguson, R., et al. 2010, ApJS, 189, 240 [NASA ADS] [CrossRef] [Google Scholar]
  31. Danisch, S., & Krumbiegel, J. 2021, J. Open Source Softw., 6, 3349 [NASA ADS] [CrossRef] [Google Scholar]
  32. de Mink, S. E., & Mandel, I. 2016, MNRAS, 460, 3545 [NASA ADS] [CrossRef] [Google Scholar]
  33. de Mink, S. E., Cantiello, M., Langer, N., et al. 2009, A&A, 497, 243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. du Buisson, L., Marchant, P., Podsiadlowski, P., et al. 2020, MNRAS, 499, 5941 [Google Scholar]
  35. Eggleton, P. P. 1983, ApJ, 268, 368 [Google Scholar]
  36. Eker, Z., Bakış, V., Bilir, S., et al. 2018, MNRAS, 479, 5491 [NASA ADS] [CrossRef] [Google Scholar]
  37. Fabry, M., Marchant, P., & Sana, H. 2022, A&A, 661, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Farag, E., Renzo, M., Farmer, R., Chidester, M. T., & Timmes, F. X. 2022, ApJ, 937, 112 [NASA ADS] [CrossRef] [Google Scholar]
  39. Farmer, R., Renzo, M., de Mink, S. E., Marchant, P., & Justham, S. 2019, ApJ, 887, 53 [Google Scholar]
  40. Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [Google Scholar]
  41. Fishbach, M., & Holz, D. E. 2017, ApJ, 851, L25 [NASA ADS] [CrossRef] [Google Scholar]
  42. Franciolini, G., & Pani, P. 2022, Phys. Rev. D, 105, 123024 [NASA ADS] [CrossRef] [Google Scholar]
  43. Fryer, C. L. 1999, ApJ, 522, 413 [NASA ADS] [CrossRef] [Google Scholar]
  44. Fuller, J., & Lu, W. 2022, MNRAS, 511, 3951 [NASA ADS] [CrossRef] [Google Scholar]
  45. Fuller, J., & Ma, L. 2019, ApJ, 881, L1 [Google Scholar]
  46. Fuller, J., Piro, A. L., & Jermyn, A. S. 2019, MNRAS, 485, 3661 [NASA ADS] [Google Scholar]
  47. Galama, T. J., Vreeswijk, P. M., van Paradijs, J., et al. 1998, Nature, 395, 670 [Google Scholar]
  48. Galaudage, S., Talbot, C., Nagar, T., et al. 2021, ApJ, 921, L15 [NASA ADS] [CrossRef] [Google Scholar]
  49. Gerosa, D., & Berti, E. 2017, Phys. Rev. D, 95, 124046 [NASA ADS] [CrossRef] [Google Scholar]
  50. Gerosa, D., & Fishbach, M. 2021, Nat. Astron., 5, 749 [NASA ADS] [CrossRef] [Google Scholar]
  51. Grevesse, N., Noels, A., & Sauval, A. J. 1996, ASP Conf. Ser., 99, 117 [Google Scholar]
  52. Hall, E. D., & Evans, M. 2019, Class. Quant. Grav., 36, 225002 [NASA ADS] [CrossRef] [Google Scholar]
  53. Hannam, M., Brown, D. A., Fairhurst, S., Fryer, C. L., & Harry, I. W. 2013, ApJ, 766, L14 [Google Scholar]
  54. Heger, A., & Woosley, S. E. 2002, ApJ, 567, 532 [Google Scholar]
  55. Hoy, C., Mills, C., & Fairhurst, S. 2022, Phys. Rev. D, 106, 023019 [NASA ADS] [CrossRef] [Google Scholar]
  56. Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
  57. Irwin, A. W. 2012, Astrophysics Source Code Library [record ascl:1211.002] [Google Scholar]
  58. Itoh, N., Hayashi, H., Nishikawa, A., & Kohyama, Y. 1996, ApJS, 102, 411 [NASA ADS] [CrossRef] [Google Scholar]
  59. Izzard, R. G., Ramirez-Ruiz, E., & Tout, C. A. 2004, MNRAS, 348, 1215 [NASA ADS] [CrossRef] [Google Scholar]
  60. Jermyn, A. S., Schwab, J., Bauer, E., Timmes, F. X., & Potekhin, A. Y. 2021, ApJ, 913, 72 [NASA ADS] [CrossRef] [Google Scholar]
  61. Jermyn, A. S., Bauer, E. B., Schwab, J., et al. 2023, ApJS, 265, 15 [NASA ADS] [CrossRef] [Google Scholar]
  62. Kippenhahn, R., Weigert, A., & Weiss, A. 2013, Stellar Structure and Evolution (Berlin, Heidelberg: Springer) [Google Scholar]
  63. Köhler, K., Langer, N., de Koter, A., et al. 2015, A&A, 573, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Langer, N. 1997, ASP Conf. Ser., 120, 83 [Google Scholar]
  65. Ma, L., & Fuller, J. 2023, ApJ, 952, 53 [CrossRef] [Google Scholar]
  66. MacFadyen, A. I., & Woosley, S. E. 1999, ApJ, 524, 262 [NASA ADS] [CrossRef] [Google Scholar]
  67. MacLeod, M., & Loeb, A. 2020, ApJ, 902, 85 [NASA ADS] [CrossRef] [Google Scholar]
  68. Maeder, A. 1987, A&A, 178, 159 [NASA ADS] [Google Scholar]
  69. Maeder, A., & Meynet, G. 2000, A&A, 361, 159 [NASA ADS] [Google Scholar]
  70. Mandel, I., & de Mink, S. E. 2016, MNRAS, 458, 2634 [NASA ADS] [CrossRef] [Google Scholar]
  71. Mandel, I., & O’Shaughnessy, R. 2010, Class. Quant. Grav., 27, 114007 [NASA ADS] [CrossRef] [Google Scholar]
  72. Mandel, I., & Smith, R. J. E. 2021, ApJ, 922, L14 [NASA ADS] [CrossRef] [Google Scholar]
  73. Marchant, P., Langer, N., Podsiadlowski, P., Tauris, T. M., & Moriya, T. J. 2016, A&A, 588, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  74. Marchant, P., Renzo, M., Farmer, R., et al. 2019, ApJ, 882, 36 [Google Scholar]
  75. McKinney, J. C. 2005, ApJ, 630, L5 [NASA ADS] [CrossRef] [Google Scholar]
  76. Mehta, A. K., Buonanno, A., Gair, J., et al. 2022, ApJ, 924, 39 [CrossRef] [Google Scholar]
  77. Miller-Jones, J. C. A., Bahramian, A., Orosz, J. A., et al. 2021, Science, 371, 1046 [Google Scholar]
  78. Mirabel, I. F., & Rodrigues, I. 2003, Science, 300, 1119 [Google Scholar]
  79. Murguia-Berthier, A., Batta, A., Janiuk, A., et al. 2020, ApJ, 901, L24 [NASA ADS] [CrossRef] [Google Scholar]
  80. Nitz, A. H., Kumar, S., Wang, Y.-F., et al. 2023, ApJ, 946, 59 [NASA ADS] [CrossRef] [Google Scholar]
  81. Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
  82. Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [Google Scholar]
  83. Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
  84. Paxton, B., Schwab, J., Bauer, E. B., et al. 2018, ApJS, 234, 34 [NASA ADS] [CrossRef] [Google Scholar]
  85. Paxton, B., Smolec, R., Schwab, J., et al. 2019, ApJS, 243, 10 [Google Scholar]
  86. Périgois, C., Mapelli, M., Santoliquido, F., Bouffanais, Y., & Rufolo, R. 2023, Universe, 9, 507 [CrossRef] [Google Scholar]
  87. Peters, P. C. 1964, Phys. Rev., 136, 1224 [Google Scholar]
  88. Podsiadlowski, P., Mazzali, P. A., Nomoto, K., Lazzati, D., & Cappellaro, E. 2004, ApJ, 607, L17 [NASA ADS] [CrossRef] [Google Scholar]
  89. Poniatowski, L. G., Sundqvist, J. O., Kee, N. D., et al. 2021, A&A, 647, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  90. Potekhin, A. Y., & Chabrier, G. 2010, Contrib. Plasma Phys., 50, 82 [NASA ADS] [CrossRef] [Google Scholar]
  91. Poutanen, J. 2017, ApJ, 835, 119 [NASA ADS] [CrossRef] [Google Scholar]
  92. Pretorius, F. 2005, Phys. Rev. Lett., 95, 121101 [NASA ADS] [CrossRef] [Google Scholar]
  93. Qin, Y., Fragos, T., Meynet, G., et al. 2018, A&A, 616, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  94. Qin, Y., Wang, Y.-Z., Bavera, S. S., et al. 2022, ApJ, 941, 179 [NASA ADS] [CrossRef] [Google Scholar]
  95. Riley, J., Mandel, I., Marchant, P., et al. 2021, MNRAS, 505, 663 [Google Scholar]
  96. Rivinius, T., Carciofi, A. C., & Martayan, C. 2013, A&ARv, 21, 69 [Google Scholar]
  97. Rodriguez, C. L., Zevin, M., Pankow, C., Kalogera, V., & Rasio, F. A. 2016, ApJ, 832, L2 [NASA ADS] [CrossRef] [Google Scholar]
  98. Rodriguez, C. L., Zevin, M., Amaro-Seoane, P., et al. 2019, Phys. Rev. D, 100, 043027 [Google Scholar]
  99. Rogers, F. J., & Nayfonov, A. 2002, ApJ, 576, 1064 [Google Scholar]
  100. Roulet, J., Chia, H. S., Olsen, S., et al. 2021, Phys. Rev. D, 104, 083010 [NASA ADS] [CrossRef] [Google Scholar]
  101. Safarzadeh, M., Farr, W. M., & Ramirez-Ruiz, E. 2020, ApJ, 894, 129 [NASA ADS] [CrossRef] [Google Scholar]
  102. Sanyal, D., Grassitelli, L., Langer, N., & Bestenlehner, J. M. 2015, A&A, 580, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  103. Saumon, D., Chabrier, G., & van Horn, H. M. 1995, ApJS, 99, 713 [NASA ADS] [CrossRef] [Google Scholar]
  104. Schrøder, S. L., MacLeod, M., Ramirez-Ruiz, E., et al. 2021, ArXiv e-prints [arXiv:2107.09675] [Google Scholar]
  105. Shenar, T., Sana, H., Mahy, L., et al. 2022, Nat. Astron., 6, 1085 [NASA ADS] [CrossRef] [Google Scholar]
  106. Song, H. F., Meynet, G., Maeder, A., Ekström, S., & Eggenberger, P. 2016, A&A, 585, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  107. Spruit, H. C. 2002, A&A, 381, 923 [CrossRef] [EDP Sciences] [Google Scholar]
  108. Stevenson, S., & Clarke, T. A. 2022, MNRAS, 517, 4034 [Google Scholar]
  109. Suijs, M. P. L., Langer, N., Poelarends, A. J., et al. 2008, A&A, 481, L87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  110. Tagawa, H., Haiman, Z., Bartos, I., Kocsis, B., & Omukai, K. 2021, MNRAS, 507, 3362 [NASA ADS] [CrossRef] [Google Scholar]
  111. Takahashi, K. 2018, ApJ, 863, 153 [Google Scholar]
  112. Talbot, C., & Thrane, E. 2018, ApJ, 856, 173 [NASA ADS] [CrossRef] [Google Scholar]
  113. Taylor, P., & Kobayashi, C. 2015, MNRAS, 452, L59 [NASA ADS] [CrossRef] [Google Scholar]
  114. Timmes, F. X., Hoffman, R. D., & Woosley, S. E. 2000, ApJS, 129, 377 [NASA ADS] [CrossRef] [Google Scholar]
  115. Torres, G., Andersen, J., & Giménez, A. 2010, A&ARv, 18, 67 [Google Scholar]
  116. van Son, L. A. C., de Mink, S. E., Renzo, M., et al. 2022, ApJ, 940, 184 [NASA ADS] [CrossRef] [Google Scholar]
  117. Wong, K. W. K., Breivik, K., Kremer, K., & Callister, T. 2021, Phys. Rev. D, 103, 083021 [Google Scholar]
  118. Woosley, S. E. 1993, ApJ, 405, 273 [Google Scholar]
  119. Woosley, S. E. 2017, ApJ, 836, 244 [Google Scholar]
  120. Zahn, J.-P. 1977, A&A, 57, 383 [NASA ADS] [Google Scholar]
  121. Zaldarriaga, M., Kushnir, D., & Kollmeier, J. A. 2018, MNRAS, 473, 4174 [Google Scholar]
  122. Zevin, M., Pankow, C., Rodriguez, C. L., et al. 2017, ApJ, 846, 82 [NASA ADS] [CrossRef] [Google Scholar]
  123. Zevin, M., Bavera, S. S., Berry, C. P. L., et al. 2021, ApJ, 910, 152 [Google Scholar]

Appendix A: Details on microphysical inputs of MESA simulations

Our MESA calculations rely on various inputs regarding microphysical processes, which we list here. Opacities for various temperature and density regimes are taken from OPAL (Iglesias & Rogers 1996), low-temperature opacities from Ferguson et al. (2005) and Compton-scattering opacities from Poutanen (2017). The equation of state is determined from a combination of Rogers & Nayfonov (2002), Irwin (2012), Saumon et al. (1995), Timmes et al. (2000), Potekhin & Chabrier (2010), and Jermyn et al. (2021), with different equations of state used at different conditions for temperature, density and composition (see Jermyn et al. 2023 for details on how these are patched together). Nuclear reaction rates are taken from Angulo et al. (1999) and Cyburt et al. (2010), with screening accounted for as in Chugunov et al. (2007). Thermal neutrino emission is determined as in Itoh et al. (1996).

Appendix B: Fit to maximum BH spin

The values of the maximum dimensionless spin derived from our simulation are given in Table B.1. These correspond to the value of amax at carbon depletion in Fig. 2. For convenience, we provide the following fit to our results:

a max ( x ) = 10 c 0 + c 1 x + c 2 x 2 , $$ \begin{aligned} a_\mathrm{max} (x) = 10^{c_0 + c_1x+c_2 x^2}, \end{aligned} $$(B.1)

Table B.1.

Maximum BH dimensionless spin, amax, as a function of BH mass and progenitor metallicity.

where x = log10(MBH/M⊙). The dependence on metallicity is included through c0, c1, and c2,

c 0 = 0.13 z c 1 = 0.74 − 0.19 z c 2 = − 0.58 + 0.12 z , $$ \begin{aligned} c_0&= 0.13\sqrt{z} \end{aligned} $$(B.2)

c 0 = 0.13 z c 1 = 0.74 − 0.19 z c 2 = − 0.58 + 0.12 z , $$ \begin{aligned} c_1&= 0.74-0.19\sqrt{z} \end{aligned} $$(B.3)

c 0 = 0.13 z c 1 = 0.74 − 0.19 z c 2 = − 0.58 + 0.12 z , $$ \begin{aligned} c_2&= -0.58 + 0.12 \sqrt{z}, \end{aligned} $$(B.4)

with z = log10(0.1 Z⊙/Z). This fit has not been tested beyond the range of masses and metallicities explored in Sect. 2. It is also important to point out that these predictions rely on an understanding of the radii of very massive helium stars near the Eddington limit. Our results have been computed using hydrostatic stellar evolution models, but an accurate prediction of the stellar radius in this regime requires the inclusion of hydrodynamics (e.g., Poniatowski et al. 2021).

Appendix C: Estimated Mchirp − χeff boundaries at different metallicities

As the discussion on the semi-analytical model presented in Sect. 3 focused on the Z⊙/50 models, we briefly discuss here the results when considering the other two metallicities studied. Figure C.1. As we adopted the results of Marchant et al. (2019) for the bounds of the PISN gap, this band remains fixed at the different metallicities. Both the MTAMS and tmerge bounds exhibit only a weak dependence with metallicity, although this ignores important effects that are not part of our semianalytical model (see the discussion at the end of Sect. 3). The most clear variation is seen in the Γ − Ω limit, which follows the trend already visible in Fig. 2.

thumbnail Fig. C.1.

Same as Fig. 5 but showing the boundaries at different metallicities.

All Tables

Table 1.

Overview of the steps in the semi-analytic model presented in Sect. 3.

In the text
Table 2.

Predicted detection rates (per year of detector time) for BBH mergers produced from CHE, derived from the simulations of dB20.

In the text
Table B.1.

Maximum BH dimensionless spin, amax, as a function of BH mass and progenitor metallicity.

In the text

All Figures

thumbnail Fig. 1.

Mock CHE models described in Sect. 2 on the Hertzsprung-Russell diagram. Colors indicate different evolutionary stages, including the ZAMS, TAMS, helium ZAMS and TAMS, and core carbon depletion (C dep.). Simulations cover the mass range 6.3–251 M⊙ and were performed without mass loss. Different line styles indicate different metallicity values. Two evolutionary tracks with a metallicity of Z⊙/50 and masses of 10 M⊙ and 100 M⊙ are shown in gray for reference.
In the text
thumbnail Fig. 2.

Dimensionless spins, amax, corresponding to the angular momentum and mass of a critically rotating star undergoing CHE at different evolutionary stages. At a fixed mass and metallicity, this value monotonically reduces with each successive evolutionary stage. Values are estimated from the nonrotating models described in Sect. 2.
In the text
thumbnail Fig. 3.

Resulting effective spin for orbit-aligned BBHs as a function of mass ratio and chirp mass, under the assumption that both BHs have the maximum spin allowed by the critical rotation limit of their progenitors. Results are shown for a metallicity of Z ≃ Z⊙/50, and the truncation of the q = 0.25 line is due to the limited range of masses modeled.
In the text
thumbnail Fig. 4.

Resulting BH masses and spins of CHE stars using a semi-analytical model (see Sect. 3). The model assumes a mass ratio of unity, so two BHs with identical properties are produced. We consider the outcome for three masses at TAMS (25 M⊙, 40 M⊙, and 60 M⊙) and three orbital periods at TAMS scaled from the period at which the binary would be in contact. Each line represents the results for a fixed MTAMS and PTAMS with a variable fWR (where MBH = fWRMTAMS). Cases where the resulting BBH would be too wide to merge within the age of the Universe are marked with a dotted line. Note that for fWR close to unity, lines with different values of PTAMS converge to the same spins at any given mass. The effect of (P)PISNe is ignored in this figure. Precise boundaries depend on the metallicity used to determine stellar properties in the semi-analytical model used, which in this case were taken from calculations at Z⊙/50.
In the text
thumbnail Fig. 5.

Physical processes setting the boundaries for BH masses and spins for the CHE formation scenario. The four colored areas indicate excluded regions due to four different physical processes. The MTAMS and tmerge limits apply only to CHE, while the Γ − Ω and (P)PISNe boundaries apply in general to all field formation scenarios. In this figure an assumed limit for the MTAMS of CHE stars is set at 30 M⊙, which sets the boundary at the left of the figure. Precise boundaries depend on the metallicity used to determine stellar properties in the semi-analytical model used, which in this case were taken from calculations at Z⊙/50.
In the text
thumbnail Fig. 6.

Final chirp masses and orbital periods in the MESA simulations of dB20. Top: Final properties assuming direct collapse into a BH (with its mass at carbon depletion) and ignoring mass loss due to (P)PISNe. Each dot indicates the final result of one CHE simulation. Systems above the dashed gray line have merger times longer than the age of the Universe and are marked with a lighter color. Results are shown for their grids with metallicities of log10Z = −2.375, −2.5, −2.75, −3, −3.5, −4, and −5, with the labels indicating their approximate values in terms of the solar metallicity (taken here to be Z⊙ = 0.017 as in Grevesse et al. 1996 for consistency with the definition used in dB20). Bottom: Same as the top panel but after including the impact of (P)PISNe as described in Marchant et al. (2019).
In the text
thumbnail Fig. 7.

Same as Fig. 6 but showing the resulting chirp masses and effective spins of BBHs formed through CHE in the MESA simulations of dB20.
In the text
thumbnail Fig. 8.

Distribution of the rate of merging BBHs formed through CHE per unit chirp mass and unit effective spin that is observable from Earth with a detector with infinite sensitivity, derived from the simulations of dB20. We refer to these rates as “cosmological”. Numbers are normalized to the maximum value of the differential rate dR/dMchirp/dχeff. The two panels highlight predicted systems below and above the PISN gap. The dashed white contour corresponds to the predicted region below the PISN gap that arises from CHE, computed with the semi-analytical model shown in Fig. 5.
In the text
thumbnail Fig. 9.

Mass of each component versus instantaneous dimensionless spin during the evolution of an equal-mass binary undergoing CHE. Shown are the original simulation from dB20 using the TS dynamo (normal TS), one recomputed using the modified version of the TS dynamo from Fuller et al. (2019, TSF), and one where solid-body rotation is enforced. These simulations were computed with the same setup and MESA version (11701) used by dB20.
In the text
thumbnail Fig. 10.

Evolution of the BBH merger rate and of different populations of merger events predicted by dB20 for CHE. Top: Fraction of the total rate for specific constraints on the chirp mass and effective spins of BBH mergers. Bottom: Comoving merger rate corresponding to the same constraints in chirp mass and effective spins. The dotted line indicates the cosmological rate resulting from the addition of all others.
In the text
thumbnail Fig. 11.

Observable rate of BBH mergers formed through CHE considering the detector sensitivity of O3, O4, and O5 for the LIGO detectors. The distribution of the rate is shown as a function of Mchirp and χeff. Data points indicate all observations made so far as reported in the current GW transient catalogs (GWTC-1, GWTC-2, and GWTC-3). For each observation, the median values of Mchirp and χeff are shown together with their 90% credible intervals.
In the text
thumbnail Fig. C.1.

Same as Fig. 5 but showing the boundaries at different metallicities.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.