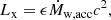| Issue |
A&A
Volume 693, January 2025
|
|
|---|---|---|
| Article Number | A27 | |
| Number of page(s) | 13 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202451275 | |
| Published online | 23 December 2024 | |
Formation of wind-fed black hole high-mass X-ray binaries: The role of Roche-lobe-overflow post black hole formation
1
Département d’Astronomie, Université de Genève, Chemin Pegasi 51, CH-1290 Versoix, Switzerland
2
Gravitational Wave Science Center (GWSC), Université de Genève, CH1211 Geneva, Switzerland
3
Institute of Astrophysics, FORTH, N. Plastira 100, Heraklion 70013, Greece
4
Department of Physics, The University of Hong Kong, Pokfulam Road, Hong Kong
5
School of Physics and Astronomy, Monash University, Clayton, VIC 3800, Australia
6
OzGrav: The Australian Research Council Centre of Excellence for Gravitational Wave Discovery, Clayton, VIC 3800, Australia
7
Department of Physics, University of Florida, 2001 Museum Rd, Gainesville, FL 32611, USA
8
Center for Interdisciplinary Exploration and Research in Astrophysics (CIERA), Northwestern University, 1800 Sherman Ave, Evanston, IL 60201, USA
9
Department of Physics & Astronomy, Northwestern University, 2145 Sheridan Road, Evanston, IL 60208, USA
10
Electrical and Computer Engineering, Northwestern University, 2145 Sheridan Road, Evanston, IL 60208, USA
11
Institute of Space Sciences (ICE, CSIC), Campus UAB, Carrer de Magrans, 08193 Barcelona, Spain
12
Institut d’Estudis Espacials de Catalunya (IEEC), Carrer Gran Capità, 08034 Barcelona, Spain
⋆ Corresponding author; Zepei.Xing@unige.ch
Received:
27
June
2024
Accepted:
27
October
2024
The three dynamically confirmed wind-fed black hole high-mass X-ray binaries (BH-HMXBs) are suggested to all contain a highly spinning black hole (BH). However, based on the theories of efficient angular momentum transport inside the stars, we expect that the first-born BHs in binary systems should have low spins, which is consistent with gravitational-wave observations. As a result, the origin of the high BH spins measured in wind-fed BH-HMXBs remains a mystery. In this paper, we conduct a binary population synthesis study on wind-fed BH-HMXBs at solar metallicity with the use of the newly developed code POSYDON, considering three scenarios for BH accretion: Eddington-limited, moderately super-Eddington, and fully conservative accretion. Taking into account the conditions for accretion-disk formation, we find that regardless of the accretion model, these systems are more likely to have already experienced a phase of Roche-lobe overflow after the BH formation. To account for the extreme BH spins, highly conservative accretion onto BHs is required, when assuming the accreted material carries the specific angular momentum at the innermost stable orbit. Besides, in our simulations we found that the systems with donor stars within the mass range of 10 − 20 M⊙ are prevalent, posing a challenge in explaining simultaneously all observed properties of the BH-HMXB in our Galaxy, Cygnus X-1, and potentially hinting that the accretion efficiency onto non-degenerate stars, before the formation of the BH, is also more conservative than assumed in our simulations.
Key words: stars: black holes / stars: evolution / X-rays: binaries
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Black hole (BH) X-ray binaries contain a BH accreting material from a companion star generating X-ray emission. Depending on the donor star mass and accretion processes, BH X-ray binaries can be classified as low-mass X-ray binaries (BH-LMXBs) and high-mass X-ray binaries (BH-HMXBs). The BH-LMXBs consist of a low-mass donor star (∼2 M⊙) that transfers mass through Roche-lobe overflow (RLO) onto the BH. The BH-HMXBs typically involve a massive (≳10 M⊙) OB-type donor star and a BH that accretes a fraction of the companion’s stellar wind. Only three wind-fed BH-HMXBs have been dynamically confirmed: Cygnus X-1, LMC X-1, and M33 X-7 (we list their properties in Table 1). All of them have been observed to contain a BH with a high spin and a donor star that is still on its main sequence (MS), almost filling its Roche lobe. Nevertheless, there are several candidate BH-HMXBs, including SS433 (Seifina & Titarchuk 2010), Cygnus X-3 (Zdziarski et al. 2013), HD96670 (Gomez & Grindlay 2021), IC10 X-1 (Prestwich et al. 2007; Laycock et al. 2015), and NGC300 X-1 (Crowther et al. 2010), whose nature remains debated.
Properties of wind-fed BH-HMXBs.
To explain why BH-HMXBs are much less numerous than Wolf-Rayet + O star binaries in our Galaxy – the latter being thought to be the progenitor of the former – it has been proposed that the binaries are detectable as BH-HMXBs only when the stellar winds carry sufficient angular momentum (AM) to form an accretion disk (e.g., Illarionov & Sunyaev 1975; Vanbeveren et al. 2020; Sen et al. 2021). More recently, Hirai & Mandel (2021), through semi-analytical modeling of the steady-state equations for asymmetric winds, found that an accretion disk is formed when the MS donor’s Roche-lobe filling factor, fRL, defined as the ratio between the stellar radius and its Roche lobe radius, is ≳0.8 − 0.9, providing an explanation for the high fRL of all three known systems.
Intriguingly, based on either the disk continuum fitting or the reflection line fitting methods, the BHs in these systems are almost maximally spinning (see, e.g., McClintock et al. 2014; Reynolds 2014, 2021, and references therein). However, these methods are subject to potential uncertainties, which we discuss in Sect. 4.1. The binary BH (BBH) population from gravitational-wave observations indicates low aligned spins for BHs (e.g., Abbott et al. 2019, 2023; Miller et al. 2020; Roulet et al. 2021). Arguments have been made that BH-HMXBs and BBHs originate from two distinct binary populations, (Fishbach & Kalogera 2022) and due to selection effects, it is natural that these two populations show different properties (Liotine et al. 2023). Binary population synthesis (BPS) studies have shown that only a small fraction of BH-HMXBs result in BBH mergers (Neijssel et al. 2021; Gallegos-Garcia et al. 2022; Romero-Shaw et al. 2023).
However, the question of where the extreme spins come from has not yet been answered. Prescriptions of efficient AM transport within stellar interiors, such as the Tayler-Spruit (TS) dynamo (Spruit 2002), the revised prescription by Fuller et al. (2019), and the calibrated TS dynamo presented in Eggenberger et al. (2022), can explain the rotation profile of the Sun (Eggenberger et al. 2005) and the core-rotation rate of low-mass red giants and subgiants from asteroseismic measurements (Beck et al. 2012; Mosser et al. 2012; Deheuvels et al. 2014; Gehan et al. 2018). These theories predict low natal BH spins in general (Fuller & Ma 2019) but especially for the first-born BHs in binary systems (Fragos & McClintock 2015). The second-born BHs can obtain spins through tidal interactions between their progenitors and the first-born BHs, which usually occur in tight orbits following common-envelope events. In the framework of efficient AM transport, the effective inspiral spin distribution of BBHs can be reproduced in the isolated binary evolution channel (Qin et al. 2018; Bavera et al. 2020, 2021; Belczynski et al. 2020; Olejak & Belczynski 2021).
Looking at BH-HMXBs, Qin et al. (2019) investigated two possible scenarios that can produce spinning BHs, namely the case A mass transfer (MT) channel and the chemical homogeneous evolution channel, and concluded that only if the internal AM transport is inefficient during the late evolution of the progenitor stars can high-spin BHs be produced. The scenario is not yet supported by any other observational evidence or theoretical arguments. Another way for BHs to acquire significant spins is through super-Eddington accretion (Moreno Méndez 2011). The observed isotropic-equivalent X-ray luminosity of ultraluminous X-ray sources (e.g., Winter et al. 2006; Kovlakas et al. 2020) can exceed the Eddington limit by a few orders of magnitude. However, the possible geometrical beaming of the X-ray emission means that the actual accretion rate onto the BH does not have to be significantly super Eddington (King et al. 2001; Poutanen et al. 2007; Kovlakas et al. 2022). Qin et al. (2022) explored the possibility of highly super-Eddington accretion and its impact on BH spin in the context of BH-HMXBs. This study, however, was limited in that they only considered one specific binary configuration, they did not model the evolution of the binary prior to the BH formation, and they neglected the fact that observed BH-HMXBs, such as Cygnus X-1, are currently detached.
In this work, we use the newly developed BPS code POSYDON (Fragos et al. 2023), which incorporates extensive grids of detailed stellar structure and binary evolution models, to investigate the population of wind-fed BH-HMXBs. Among other advantages, detailed binary evolution simulations can accurately model the case A MT. The case A MT phase after BH formation is of great importance for the formation of wind-fed BH-HMXBs, but it is often treated poorly in rapid BPS codes due to the lack of information about the internal structure of stars (Dorozsmai & Toonen 2024).
The paper is organized as follows. In Sect. 2, we briefly introduce the new binary-star model grids and the details of our BPS study. In Sect. 3, we present the results of our binary models and population properties. We discuss the implications of this work on wind-fed BH-HMXBs in Sect. 4 and summarize the conclusions of this paper in Sect. 5.
2. Method
For all the computations presented in this paper, we used the publicly available BPS code POSYDON1, which incorporates single- and binary-star model grids at solar metallicity simulated with the stellar evolution code Modules for Experiments in Stellar Astrophysics (MESA, Paxton et al. 2011, 2013, 2015, 2018, 2019; Jermyn et al. 2023). The specific details of the stellar and binary physics employed in the production of pre-calculated grids are outlined in Fragos et al. (2023). Here we highlight the wind prescriptions and the assumptions for mass accretion onto non-degenerate stars adopted in our models. We utilized the Dutch scheme in MESA for stars with an initial mass exceeding 8 M⊙. Specifically, we applied the wind-loss prescription of de Jager et al. (1988) for cool stars with effective temperatures below 10000 K and the Vink et al. (2001) scheme for hot stars with effective temperatures above 11 000 K. For temperatures between these two thresholds, we implemented a linear interpolation of the wind-loss rates. Additionally, for hot stars with a surface hydrogen fraction below 0.4, we adopted the Wolf-Rayet wind prescription proposed by Nugis & Lamers (2000). For accretion onto a non-degenerate star, we accounted for the rotation of the accretor. The transferred material, carrying AM, spins up the outer layers of the accretor, differentiating between ballistic and Keplerian disk MT scenarios (de Mink et al. 2013). As the accretor’s rotational velocity increases, the accretion rate is reduced by the enhancement of the stellar winds (Langer 1998). Crucially, accretion halts when the accretor approaches critical rotation, with its stellar winds intensifying as needed to maintain sub-critical rotation.
By default, in POSYDON, accretion onto BHs is assumed to be Eddington limited. As part of this work, beyond the publicly available grids, we computed two additional binary-star model grids of binaries consisting of a compact object and a hydrogen-rich MS star (CO-HMS grids), where we varied the accretion efficiency onto BHs. The two additional grids share the same initial parameters and input physics with the original grid. In the first new grid, we consider the limiting case of the fully conservative accretion onto the BH, while in the second one, the accretion efficiency η was established based on general relativistic radiation magnetohydrodynamic (GRRMHD) simulations (Kwan et al., in prep.). In that study, the authors carried out a series of simulations of super-Eddington disks in the magnetically arrested disk (MAD) state following the setup in Dai et al. (2018) and Thomsen et al. (2022) but around stellar-mass BHs. They varied the BH mass, spin and accretion rate Ṁacc achieved in equilibrium states across different simulations to explore how these parameters affect the energy output and outflow properties. Based on the simulation results, they obtained an averaged fit for the relation between η and the MT rate Ṁtr (which is assumed to equal the sum of the mass accretion rate and the outflow rate obtained in the GRRMHD simulation):
for ṁ ≥ 10, where ṁ is the MT rate in units of the Eddington accretion rate ṀEdd. In cases where 0 < ṁ < 10, we adopted an accretion rate of min(Ṁtr,10ṀEddη(10)). Generally, η ranges within 10% and 30% and is inversely correlated with Ṁtr.
For our synthetic HMXB population models, we simulated 500 000 binaries for each accretion model, starting from two stars at zero-age MS. The primary star masses range within 10 and 120 M⊙, with the distribution determined by the initial mass function from Kroupa (2001). The secondary masses fall within the interval of 7 and 120 M⊙, following a flat distribution from the minimum to the primary star mass. The initial orbital period distribution follows Sana et al. (2013) from 1 d to 6000 d, with an extension down to 0.75 d, being uniform in logarithmic space. We identified wind-fed BH-HMXBs by searching for detached binaries containing a BH and a companion star with a Roche-lobe filling factor, fRL, falling between 0.9 ≲ fRL < 1, which is valid across most of the parameter variations explored by Hirai & Mandel (2021). We set a minimal mass of 10 M⊙ for the companion star during the wind-fed phase. In all presented population models, we used the nearest-neighbor scheme for the interpolation between models in a grid (see Sect. 7 in Fragos et al. 2023).
To determine the explodability of the pre-supernova core and the BH mass from the core properties, we adopted the Patton & Sukhbold (2020) prescription and supernova engine from Sukhbold et al. (2016). We assumed the supernova kick velocities of the BHs from core-collapse supernova follow a Maxwellian distribution with a velocity dispersion of σCCSN = 265 km s−1 (Hobbs et al. 2005), rescaled by a factor of 1.4 M⊙/MBH. The natal spin of a BH is calculated based on the internal rotational profile of the BH progenitor star, right before core collapse (see Sect. 8.3.4 in Fragos et al. 2023). The further evolution of the BH spin parameter χBH is calculated by assuming the accreted material carries the specific AM at the innermost stable circular orbit (ISCO). After the accretion of an infinitesimal mass, the dimensionless BH spin parameter χBH, f can be calculated as (Bardeen 1970):
where Mi and Mf are the BH masses before and after accretion, respectively – with (Mf−Mi) ≪ Mf – and rISCO, i is the initial normalized ISCO radius that can be calculated as rISCO, i = 3 + Z2 − [(3 − Z1)(3 + Z1 + 2Z2)]1/2, with ![$ Z_{1} = 1 + (1-\chi_\mathrm{{BH,i}}^{2})^{1/3}[(1+\chi_\mathrm{{BH,i}})^{1/3}+(1-\chi_\mathrm{{BH,i}})^{1/3}] $](/articles/aa/full_html/2025/01/aa51275-24/aa51275-24-eq8.gif) and
and 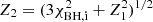 . The BH spin is updated at every timestep for the binary-star models in the CO-HMS grid.
. The BH spin is updated at every timestep for the binary-star models in the CO-HMS grid.
To estimate the X-ray luminosity of the wind-fed BH-HMXBs, we calculated the wind mass accretion rate Ṁw,acc onto the BHs based on the results of Hirai & Mandel (2021), who integrated the mass flux through the accretion radius in their simulations. The mass accretion fraction, defined as the ratio of the mass accretion rate to the total mass-loss rate from the donor star, exhibits a similar trend as the Bondi–Hoyle accretion (Bondi & Hoyle 1944), although it is subject to large model uncertainties related to wind acceleration parameters and Eddington factors (Hirai & Mandel 2021). As a rough estimate, we adopted the values of the mass accretion fraction at fRL → 1 from Hirai & Mandel (2021) based on their reference parameter configuration, and subsequently interpolated or extrapolated across various mass ratios. Thus, the X-ray luminosity is given as
where ϵ = 0.1 is the radiative efficiency of accretion.
3. Results
3.1. Individual wind-fed BH-HMXBs
We first illustrate a reference binary-star evolutionary model that at some point in its evolution appears as a bright wind-fed BH-HMXB system. The reference binary initially consists of a primary star of 34.9 M⊙ and a secondary star of 28.7 M⊙ with an orbital period of 10.4 d. The binary went through a case A MT phase and subsequently a case B MT phase. The primary star formed a BH of 12.2 M⊙ with an initial spin of 0.047. The secondary lost mass due to stellar winds but gained ≈0.8 M⊙ from accretion. In Figure 1, we show the evolution of the binary from ≈ 0.3 Myr before it entered the wind-fed HMXB phase until the stage when the donor star undergoes significant contraction during its helium-burning phase. One can see that as the donor star evolves, it keeps expanding until it fills its Roche lobe. It stays at the wind-fed HMXB phase for a short period of ≈ 0.1 Myr before the RLO phase. After a fast RLO phase, the donor star loses nearly half of the envelope mass, and its surface helium mass fraction increases by approximately a factor of two. This is consistent with the observations of Cygnus X-1, where the donor star’s surface helium abundance is enhanced by more than a factor of two (Shimanskii et al. 2012). The donor star’s center helium mass fraction increased to 0.9, indicating that the star is approaching the end of its MS. At this stage, the change in the hydrogen and helium abundance profiles of the partially stripped star leads to changes in the mass-radius relation during the MS (see, e.g., Quast et al. 2019; Farrell et al. 2022). The donor star contracts due to the mass loss, and the binary becomes detached again. Then, the donor star stays very close to the Roche lobe radius, and the binary appears as a wind-fed HMXB for a longer period of ≈ 0.3 − 0.5 Myr. Under the assumption of Eddington-limited accretion, the BH barely accretes any mass during the fast MT phase. Alternatively, the BH accretes ≃2 M⊙ and spins up to χBH ≈ 0.45, assuming the moderately super-Eddington accretion scenario, while it reaches a nearly maximum spin with fully conservative accretion. Because the transferred material that is not accreted by the BH leaves the system and carries away the BH’s specific orbital AM, the Eddington-limited accretion leads to the largest binary orbital shrinkage due to MT. Moreover, Eddington-limited accretion results in the most significant stripping of the envelope, which subsequently leads to the quickest introduction of the Wolf-Rayet wind. Consequently, the duration of the second wind-fed phase is the shortest for the Eddington-limited accretion scenario. In the scenario of fully conservative accretion, the donor star experiences the least stripping and continues expanding after the fast RLO. As a result, following a long wind-fed phase, the binary enters a second slow RLO phase during the late MS stage of the donor star. Regardless of the differences, for all three accretion scenarios, the binary spends more time as an observable wind-fed HMXB after the RLO phase, rather than before.
 |
Fig. 1. Evolution of an example binary through the wind-fed HMXB phase under three BH accretion scenarios. The top panels show the evolution of the donor star radius (black solid line), Roche lobe radius (orange dashed line), 0.9 times the Roche lobe radius (orange dotted line), and orbital period (gray solid line). The green and blue areas indicate the duration of the wind-fed BH-HMXB phase before and after MT via RLO, respectively. The plus symbol denotes the end of the MS for the donor star. The bottom panels show the evolution of the BH mass (black solid line), donor star mass (orange solid line), donor star convective core mass (orange dotted line), and BH spin (gray solid line). |
3.2. Population of wind-fed BH-HMXBs
The individual binary models described in Sect. 3.1 provided us with some insights into the formation of wind-fed BH-HMXBs. However, it is a population study that can reveal whether the features identified in the evolution of a few individual binary models are representative of the whole population and would allow us to evaluate their significance. Binaries that remain in a bright wind-fed BH-HMXB phase over a longer period of time are more likely to be detected. Consequently, we present distributions of the population properties for wind-fed BH-HMXBs in our simulations, weighted by the duration of the wind-fed HMXB phase for each binary.
While in Sect. 3.1 we describe the evolutionary history of one reference binary, several variations of evolutionary pathways are present in our BH-HMXB population models. For the moderately super-Eddington accretion model, for example, we found that prior to BH formation, 48.3% of binaries went through both case A and case B MT, 21.6% only experienced case A MT, 11.9% avoided any MT, 11.6% underwent case B MT, and 6.5% entered a contact phase. The contact phase involves two MS stars in a close orbit and remains stable during MT. In POSYDON, we treated it using the contact MT scheme within MESA, following Marchant et al. (2016). The first two channels dominate the population, characterized by similar initial conditions. The binaries that avoided MT contain a relatively massive primary star above ≈60 M⊙ (Bavera et al. 2023). However, due to strong stellar winds, the BHs originating from these massive stars do not exhibit a significantly different mass distribution. Among these channels, the case B MT channel is the only one showing a longer pre-RLO duration. These binaries tend to have wide orbits before RLO and more evolved secondary stars, resulting in a shorter post-RLO wind-fed phase. We display the fractions of the evolutionary pathways for all three accretion scenarios in Table A.1 in Appendix A.
Figure 2 shows the expected distributions of orbital periods, component masses, BH spins, and X-ray luminosity for an observable wind-fed BH-HMXB population under the moderately super-Eddington accretion model. The figure distinguishes wind-fed BH-HMXBs that are observable before and after an RLO phase, respectively shown with orange and blue colors. Notably, there is a higher probability of observing a wind-fed BH-HMXB after the occurrence of MT via RLO, constituting 63% of the total duration. Romero-Shaw et al. (2023) also mention that in their BPS models, some binaries engage in a second wind-fed BH-HMXB phase after MT via RLO when the mass ratio is close to unity. Our detailed binary models show that when weighted by duration, the binaries that are in the post-RLO wind-fed BH-HMXB phase are predominant, which are characterized by a broader range of mass ratios. This can be seen in the subplot of Md versus MBH in Figure 2, where the mass ratio can reach approximately two. Compared to rapid BPS codes, which typically move across single stellar tracks during MT phases, POSYDON models the readjustment of mass-losing stars. Consequently, the partially stripped MS donor stars can shrink more substantially than rapid BPS codes generally predict, leading to a higher contribution from the post-RLO wind-fed BH-HMXB phase. The wind-fed BH-HMXB phase following RLO onto the BH constitutes an even higher fraction (almost 80% by duration) of bright BH-HMXBs, with X-ray luminosities above 1037 erg s−1 (see Appendix D).
 |
Fig. 2. Corner plot showing the time-weighted distributions of the properties of wind-fed BH-HMXBs from the moderately super-Eddington accretion scenario. The dark and light blue contours represent the 68% and 95% confidence regions, respectively, for the orbital period, donor star mass, BH mass, BH spin, and X-ray luminosity of systems after RLO. Similarly, the dark and light orange contours are for systems before RLO. The black dot, square, and triangle with error bars indicate the positions of Cygnus X-1, LMC X-1, and M33 X-7, respectively. |
As the MS donor stars should be in close orbits, nearly filling the Roche lobes, the majority of the binaries exhibit orbital periods of ∼ 1 − 20 d, which is anticipated. The binaries that are in wide orbits extending to thousands of days in period contain post-MS donor stars. Those supergiant donor stars evolve much faster than MS stars, resulting in small contributions to the whole population. A smaller fraction of stripped stars, fitting in close orbits with orbital periods less than 1 d, meet the requirement after experiencing common envelope evolution. Overall, MS donor stars account for ≈90% of the whole population. However, it is important to note that Hirai & Mandel (2021) focused on line-driven winds from MS stars, and their conclusions about disk formation are only applicable to massive MS stars. Post-MS stars may have less stringent conditions for disk formation. Nevertheless, our population results indicate that post-MS donor stars are unlikely to make significant contributions due to their short evolutionary timescales.
Regarding the donor star masses, there is a clear difference between the observations and the simulation samples. The three observed binaries contain donor stars above ≈30 M⊙, while majority of donor stars are below ≈20 M⊙ in our simulations. The three observed BH-HMXBs have different metallicities. As a result, direct comparison of donor star masses is not robust, as the simulations were conducted at solar metallicity. The implications of the distribution of the donor star masses are discussed in Sect. 4. The donor stars are mostly close to the terminal-age MS. We have included the distributions of the central and surface helium abundance of the donor stars in Appendix B.
The BH masses in the wind-fed BH-HMXB population are mostly within the range of ∼8 − 17 M⊙, and moderately super-Eddington accretion has increased the BH masses by a few solar masses compared to their birth values. For the BH spins, a bimodal distribution is evident, with the two peaks corresponding to the population before and after RLO. Finally, we show a rough estimate of the X-ray luminosity, acknowledging the model uncertainties associated with the accretion fraction calculated in Hirai & Mandel (2021). We find that on average the post-RLO sub-population exhibits higher X-ray luminosities compared with the pre-RLO one. This is a result of the fact that on average the post-RLO sub-population has stronger stellar winds and higher mass ratios (q = MBH/Md) compared to the pre-RLO one.
The HMXB population properties resulting from the other two accretion models can be found in Appendix C. The most notable distinctions caused by accretion are evident in BH masses and spins. In Figure 3, the top panels show the time-weighted probability distributions of the BH mass and spin for the three accretion scenarios, distinguishing between the wind-fed phases before and after MT via RLO. In the pre-RLO HMXB sub-populations, the distributions are the same, as expected. Most of the BH masses are below ≈15 M⊙, and the spins are below ≈0.2. In the case of Eddington-limited accretion, the BH mass and spin ranges remain nearly unchanged after the RLO, but the mean of the BH mass shifts toward higher values. The higher normalization of the distribution denotes that on average the duration of the post-RLO wind-fed HMXB phase is longer, and that the probability of observing a wind-fed BH-HMXB after it has experienced an RLO phase is higher. Moderately super-Eddington accretion slightly increases the BH masses and spins up the BHs to a range of χBH ∼ 0.2 − 0.6. For fully conservative accretion, a bimodal distribution of BH masses emerges, as the BHs could accrete a substantial amount of mass through RLO to be in the range of ∼15 − 25 M⊙. After accretion, BH spins become extremely high, exceeding ≈0.9 for a majority of them. In the bottom panels of Figure 3, we present the probability distributions of the donor star mass and the orbital period in which the three scenarios exhibit no significant differences. The fully conservative scenario leads to more stable MT, resulting in the disappearance of stripped stars coming from common envelope evolution. Regardless of the accretion scenarios, the total duration of the wind-fed BH-HMXB phase following MT via RLO is always longer than that before MT. The fraction of post-RLO duration relative to the total duration is greater than 60% for all three accretion scenarios.
 |
Fig. 3. Time-weighted probability distributions of the BH mass (top left), BH spin (top right), donor star mass (bottom left), and orbital period (bottom right) in wind-fed BH-HMXBs. The blue and orange colors indicate post-RLO and pre-RLO sub-populations, respectively. The unfilled bins, hashed bins, and filled bins represent the Eddington-limited, moderately super-Eddington, and fully conservative accretion scenarios, respectively. The black dot, square, and triangle with error bars, placed at arbitrary probability values, respectively indicate the properties of Cygnus X-1, LMC X-1, and M33 X-7. |
4. Discussion
4.1. Black hole spins
Our study has shown that, assuming efficient AM transport inside stars, the BHs in wind-fed BH-HMXBs are born with spins ≲0.2. Eddington-limited accretion does not lead to significant changes in the spins. The moderately super-Eddington accretion model can produce BHs with spins of χBH ∼ 0.3 − 0.6, whereas the fully conservative MT can spin up most of the BHs to extreme spins if the accreted material carries the specific AM at ISCO. It is evident that explaining the observed BH spins in BH-HMXBs poses a challenge in the absence of substantial accretion onto the BHs. Even when considering the impact of supernova processes on the natal BH spins, such as those arising from slow ejecta (Schrøder et al. 2018) or shock instability (Moreno Méndez & Cantiello 2016), the attainment of extreme spins remains elusive. Batta et al. (2017) found that BHs with high spins of ∼0.8 can be produced, but only if the fallback material reaches the position of the companion star and extracts AM from the orbit.
The moderately super-Eddington accretion model is also insufficient to reproduce the extreme BH spins in BH-HMXBs. In the GRRMHD simulations used to estimate the BH accretion efficiency for our moderately super-Eddington model, ordered magnetic fields are shown to thread the super-Eddington disks. These disks eventually enter the MAD state, where the AM carried by the transferred material near the BH is less than the AM at the ISCO (e.g., Lowell et al. 2024). Therefore, the increase in BH spins in our simulations should be considered as an upper limit. Additionally, BHs fed by MADs launch powerful jets that can effectively spin down the BHs when the spin is very large (Tchekhovskoy et al. 2012); Lowell.2024. If the disks around the BHs in HMXBs easily reach the MAD state, it naturally excludes the possibility that the AM of the BH is obtained through gas accretion. However, if the disk does not contain enough magnetic flux to enter a MAD state, the accretion process can spin up the BH to a very high equilibrium spin value (Gammie et al. 2004). Such a disk does not have significant magnetic pressure to power magnetic outflow, and it is expected that BHs accrete a higher fraction of the disk gas from the non-MAD state super-Eddington disks, which leads to higher accretion efficiency and thus higher BH spins. In the fully conservative accretion model, we find that a large fraction of BHs accreted more material than their initial masses, indicating that the accretion is more than adequate to produce extreme spins.
It is essential to note that the two primary methods for measuring BH spins in HMXBs may be susceptible to systematic uncertainties (Taylor & Reynolds 2018; Salvesen & Miller 2021; Falanga et al. 2021) and model dependency (Belczynski et al. 2024; Zdziarski et al. 2024a). For example, Zdziarski et al. (2024b) argue that when considering a warm, optically thick, thermal Comptonizing layer on top of the disk, the spin of Cygnus X-1 is measured to be low, χBH ≲ 0.3. Yet, if the extreme measured spins are real, explaining them in the context of super-Eddington accretion requires that mass and AM accretion efficiencies higher than those predicted by GRRMHD simulations of MAD-state super-Eddington disks be considered.
If both the mass accretion and AM transport to BHs are efficient enough to produce highly spinning BHs, the properties of coalescing BBH populations would also likely be influenced. During the evolution of merging BBHs, RLO accretion onto the first-born BH is anticipated. The BHs can undergo spin-up due to efficient accretion. In this case, we would not expect the first-born BHs to exhibit nearly zero spins in BBH mergers. Shao & Li (2022) employed mildly super-Eddington accretion of case A MT onto BHs, highlighting its capability to account for the observed highly spinning BHs in BBH mergers. Bavera et al. (2021) found that highly conservative accretion onto BHs effectively reduces the contribution from the stable MT channel for BBH mergers, as the binaries do not shrink sufficiently during MT to coalesce due to gravitational waves within the Hubble time. However, most rapid BPS codes, such as COSMIC, which was utilized by Bavera et al. (2021) to model the MT phase, are recognized for their inadequate treatment of case A MT (Dorozsmai & Toonen 2024). In contrast, BPS codes that utilize detailed binary models and assume fully conservative accretion onto BHs (e.g., Briel et al. 2023) indicate that the stable MT channel remains viable. However, a direct comparison between the models presented in these studies should be done with caution, as they also differ in several other key physics assumptions. The specific properties of BBHs, the distribution of effective inspiral spins, and their formation channels under efficient BH accretion scenarios should be investigated in future studies.
4.2. Donor star masses
The three observed wind-fed BH-HMXBs exhibit donor stars with masses ≳30 M⊙. In our population studies, we found that donor stars within ∼10 − 20 M⊙ are expected to be prevalent in wind-fed BH-HMXBs at solar metallicity. One caveat in comparing our population models to the observed properties of the three known wind-fed BH-HMXBs is that our population models assume solar metallicity, while the observed systems have varied metallicities. Specifically, M33 X-7 has been suggested to have a metallicity between 0.1 Z⊙ (Orosz et al. 2007) and 0.5 Z⊙ (Ramachandran et al. 2022). Similarly, LMC X-1 is expected to have sub-solar metallicity, consistent with the Large Magellanic Cloud metallicity. For these two systems, comparisons with our simulations are not straightforward, as lower metallicities can lead to the formation and survival of more massive stars. For Cygnus X-1, however, a solar or even a supersolar metallicity (Shimanskii et al. 2012) is suggested, making its 40 M⊙ donor star hard to reconcile with our simulations (but see discussion in Neijssel et al. (2021)).
The prevalence of ∼10 − 20 M⊙ stars in our simulations can be explained as follows. Firstly, the accretion onto non-degenerate stars in POSYDON is regulated by stellar rotation, typically leading to low accretion efficiency (Fragos et al. 2023). Consequently, the secondary stars generally do not gain substantial mass before the BH formation. Such inefficient accretion has been suggested to prevent the formation of merging NS–BH with first-born NSs (Xing et al. 2024) and potentially contributes to discrepancies between the predicted and observed Be X-ray binary donor mass distributions (Vinciguerra et al. 2020; Akira Rocha et al. 2024). In the case of wind-fed BH-HMXBs, if the mass accretion efficiency is higher during earlier evolutionary stages, the donor star could have accreted more mass before BH formation, potentially alleviating the tension between our simulations and the observations. Certainly, increased mass accretion efficiency could also lead to a wider orbit, with less material removing orbital AM, which potentially influences the subsequent evolution of the binary and thus the properties of the HMXB. However, AM loss during MT between non-degenerate stars remains highly uncertain (e.g., MacLeod & Loeb 2020) and different treatments can alter the orbital evolution (e.g., Sen et al. 2022) and MT stability (Willcox et al. 2023). Whether the ejected material forms a circumbinary disk (e.g., Wei et al. 2024; Valli et al. 2024) also affects the orbital evolution. A comprehensive study combining mass accretion and AM loss is needed in order to fully understand the effects of MT on the donor star’s mass. Such studies are currently limited with POSYDON, as computing multiple grids of detailed binary evolution models is expensive. Using rapid BPS codes with parametric methods provides a simpler way to explore the trends arising from these variations (Romero-Shaw et al. 2023; Willcox et al. 2023).
Secondly, at solar metallicity, when the primary star becomes a BH, the secondary star should have lost a significant fraction of its mass through stellar winds if it was initially a massive star ≳40 M⊙. Moreover, many BH-HMXBs should be in the second wind-fed phase after the donor stars have transferred mass to the BHs through RLO. Romero-Shaw et al. (2023) produced wind-fed BH-HMXBs with donor stars that can reach ∼70 M⊙ at solar metallicity. In our simulations, when the BH forms, the massive donor star has lost a substantial amount of mass due to stellar winds and MT, reducing its mass to below ≈50 M⊙. A major difference arises from the modeling of stellar winds of massive stars at the MS stage. We found that massive stars ≳80 M⊙ at solar metallicity have strong winds that can deplete the hydrogen envelope and induce Wolf–Rayet winds during their MS stage (Bavera et al. 2023). As a result, the maximum donor star mass in our simulations is below 50 M⊙.
Moreover, according to the initial mass function, the number of low-mass stars surpasses the number of high-mass stars. With a flat distribution of the initial mass ratio and without any selection effect on the donor stars, it is natural to expect a prevalence of ∼10 − 20 M⊙ donor stars as they are more common and have longer lifetimes compared with a ∼40 M⊙ star.
The differences between modeled and observed donor star masses might indicate that certain physical assumptions or treatments in our stellar and binary evolution are not robust. Wind prescriptions, mass accretion efficiency for non-degenerate stars, and AM loss from non-conservative MT, as suggested in Romero-Shaw et al. (2023), could all impact the population properties. Therefore, it is imperative to investigate them further with the goal of seeking a consistent model that can be applied to diverse binary systems.
Another avenue worth exploring involves investigating the selection effects that favor massive donor stars. Our estimation of X-ray luminosity is too rough to be quantitatively analyzed, as we only adopted one set of parameters to estimate the accretion efficiency for all binaries from Hirai & Mandel (2021) and interpolated or extrapolated among different mass ratios. Moreover, the mass accretion rate obtained in Hirai & Mandel (2021) is an upper limit because not all mass passing through the accretion radius is guaranteed to be accreted. In our simulations, most donor stars with masses within ∼10 − 20 M⊙ can produce an X-ray luminosity over 1037 erg s−1. However, if we apply the low-end efficiency in Hirai & Mandel (2021) to all binaries, those with an X-ray luminosity above 1037 erg s−1 account for ≈21% of the total population, and ≈56% of them contain a donor star greater than 20 M⊙. A corner plot showing the property distributions for these X-ray bright binaries can be found in Appendix D.
5. Conclusions
The three observed wind-fed BH-HMXBs demonstrate high BH spins, the origin of which remains an open question. We used the new-generation BPS code POSYDON to investigate the population properties of wind-fed BH-HMXBs, adopting three CO-HMS grids with different assumed accretion efficiencies onto BHs. We summarize the key conclusions as follows:
-
Wind-fed BH-HMXBs at solar metallicity are more likely to have already been though a fast RLO phase after the BH formation. Regardless of the mass-accretion models, in our simulations, the total duration of wind-fed BH-HMXBs in a post-RLO phase is higher than that in a pre-RLO phase. After MT via RLO, the partially stripped donor star contracts due to the changes in its hydrogen and helium abundance profile, remaining close to its Roche lobe. At this stage, the binary stays detached for a long period, appearing as a wind-fed BH-HMXB. We highlight the importance of employing detailed modeling in BPS studies, which includes a self-consistent treatment of MT and subsequent readjustment of stars experiencing mass loss or gain.
-
An accretion efficiency prescription inspired by GRRMHD simulations can produce BHs with moderate spins in the range of ∼0.3 − 0.6, while fully conservative MT can spin up BHs to near-maximal spins, when assuming that the accreted material carries the specific AM at the ISCO. To explain the high spins observed in the three wind-fed BH-HMXBs by super-Eddington accretion, mass and AM accretion efficiency onto BHs higher than that predicted by GRRMHD simulation of super-Eddington disks in the MAD state is required.
-
In our simulations, MS donor stars with masses in the range of ∼10 − 20 M⊙ dominate the wind-fed BH-HMXB population at solar metallicity. This is in tension with the fact that the only confirmed wind-fed BH-HMXB in our Galaxy, Cygnus X-1, contains a donor star of ≈40 M⊙. Assuming the mass measurements are reliable, observational selection effects that favor massive donor stars need to be further explored and an accretion model onto non-degenerate stars that leads to more conservative MT needs to be considered.
We emphasize the critical role of detailed binary modeling, informed by insights from GRRMHD simulations, in advancing our understanding of the formation of wind-fed BH-HMXBs and their observed properties. Future efforts should focus on refining BH accretion models with improved GRRMHD predictions and re-evaluating observations and potential selection effects to reconcile the discrepancies between theoretical predictions and observed systems.
We utilized the version of the POSYDON code identified by the commit hash 8602bc3, available at https://github.com/POSYDON-code/POSYDON/, along with the POSYDON v1.0 dataset published at https://zenodo.org/records/14205146 and the dataset assuming super-Eddington accretion published at https://zenodo.org/records/14216817.
Acknowledgments
The POSYDON project is supported primarily by two sources: the Swiss National Science Foundation (PI Fragos, project numbers PP00P2_211006 and CRSII5_213497) and the Gordon and Betty Moore Foundation (PI Kalogera, grant award GBMF8477). This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie RISE action, grant agreement No 873089 (ASTROSTAT- II). Z.X. acknowledges support from the China Scholarship Council (CSC). E.Z. acknowledges funding support from the Hellenic Foundation for Research and Innovation (H.F.R.I.) under the “3rd Call for H.F.R.I. Research Projects to support Post-Doctoral Researchers” (Project No: 7933). S.S.B., T.F., and Z.X. were supported by the project number PP00P2_211006. T.K. and L.D. acknowledge the support from the National Natural Science Foundation of China and the Hong Kong Research Grants Council (12122309, N_HKU782/23, 17305523, 17314822). S.S.B. was also supported by the project number CRSII5_213497. M.B. ackowledges support from the Boninchi Foundation. K.A.R. and M.S. are supported by the Gordon and Betty Moore Foundation (PI Kalogera, grant award GBMF8477) K.A.R. is also supported by the Riedel Family Fellowship. K.A.R. also thanks the LSSTC Data Science Fellowship Program, which is funded by LSSTC, NSF Cybertraining Grant No. 1829740, the Brinson Foundation, and the Moore Foundation; their participation in the program has benefited this work. K.K. acknowledges support from the Spanish State Research Agency, through the María de Maeztu Program for Centers and Units of Excellence in R&D, No. CEX2020-001058-M. J.J.A. acknowledges support for Program number (JWST-AR-04369.001-A) provided through a grant from the STScI under NASA contract NAS5-03127. I.M. acknowledges support from the Australian Research Council Centre of Excellence for Gravitational Wave Discovery (OzGrav), through project number CE230100016.
References
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2019, ApJ, 882, L24 [Google Scholar]
- Abbott, R., Abbott, T. D., Acernese, F., et al. 2023, Phys. Rev. X, 13, 011048 [NASA ADS] [Google Scholar]
- Akira Rocha, K., Kalogera, V., Doctor, Z., et al. 2024, arXiv e-prints [arXiv:2403.07172] [Google Scholar]
- Bardeen, J. M. 1970, Nature, 226, 64 [Google Scholar]
- Batta, A., Ramirez-Ruiz, E., & Fryer, C. 2017, ApJ, 846, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Bavera, S. S., Fragos, T., Qin, Y., et al. 2020, A&A, 635, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bavera, S. S., Fragos, T., Zevin, M., et al. 2021, A&A, 647, A153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bavera, S. S., Fragos, T., Zapartas, E., et al. 2023, Nat. Astron., 7, 1090 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, P. G., Montalban, J., Kallinger, T., et al. 2012, Nature, 481, 55 [Google Scholar]
- Belczynski, K., Klencki, J., Fields, C. E., et al. 2020, A&A, 636, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belczynski, K., Done, C., Hagen, S., Lasota, J.-P., & Sen, K. 2024, A&A, 690, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bondi, H., & Hoyle, F. 1944, MNRAS, 104, 273 [Google Scholar]
- Briel, M. M., Stevance, H. F., & Eldridge, J. J. 2023, MNRAS, 520, 5724 [Google Scholar]
- Crowther, P. A., Barnard, R., Carpano, S., et al. 2010, MNRAS, 403, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Dai, L., McKinney, J. C., Roth, N., Ramirez-Ruiz, E., & Miller, M. C. 2018, ApJ, 859, L20 [Google Scholar]
- de Jager, C., Nieuwenhuijzen, H., & van der Hucht, K. A. 1988, A&AS, 72, 259 [NASA ADS] [Google Scholar]
- de Mink, S. E., Langer, N., Izzard, R. G., Sana, H., & de Koter, A. 2013, ApJ, 764, 166 [Google Scholar]
- Deheuvels, S., Doğan, G., Goupil, M. J., et al. 2014, A&A, 564, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dorozsmai, A., & Toonen, S. 2024, MNRAS [arXiv:2207.08837] [Google Scholar]
- Draghis, P. A., Miller, J. M., Costantini, E., et al. 2024, ApJ, 969, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Eggenberger, P., Maeder, A., & Meynet, G. 2005, A&A, 440, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eggenberger, P., Moyano, F. D., & den Hartogh, J. W. 2022, A&A, 664, L16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Falanga, M., Bakala, P., La Placa, R., et al. 2021, MNRAS, 504, 3424 [Google Scholar]
- Farrell, E., Groh, J. H., Meynet, G., & Eldridge, J. J. 2022, MNRAS, 512, 4116 [NASA ADS] [CrossRef] [Google Scholar]
- Fishbach, M., & Kalogera, V. 2022, ApJ, 929, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Fragos, T., & McClintock, J. E. 2015, ApJ, 800, 17 [Google Scholar]
- Fragos, T., Andrews, J. J., Bavera, S. S., et al. 2023, ApJS, 264, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Fuller, J., & Ma, L. 2019, ApJ, 881, L1 [Google Scholar]
- Fuller, J., Piro, A. L., & Jermyn, A. S. 2019, MNRAS, 485, 3661 [NASA ADS] [Google Scholar]
- Gallegos-Garcia, M., Fishbach, M., Kalogera, V., L Berry, C. P., & Doctor, Z. 2022, ApJ, 938, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Gammie, C. F., Shapiro, S. L., & McKinney, J. C. 2004, ApJ, 602, 312 [NASA ADS] [CrossRef] [Google Scholar]
- Gehan, C., Mosser, B., Michel, E., Samadi, R., & Kallinger, T. 2018, A&A, 616, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gomez, S., & Grindlay, J. E. 2021, ApJ, 913, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Hirai, R., & Mandel, I. 2021, PASA, 38, e056a [Google Scholar]
- Hobbs, G., Lorimer, D. R., Lyne, A. G., & Kramer, M. 2005, MNRAS, 360, 974 [Google Scholar]
- Illarionov, A. F., & Sunyaev, R. A. 1975, A&A, 39, 185 [NASA ADS] [Google Scholar]
- Jermyn, A. S., Bauer, E. B., Schwab, J., et al. 2023, ApJS, 265, 15 [NASA ADS] [CrossRef] [Google Scholar]
- King, A. R., Davies, M. B., Ward, M. J., Fabbiano, G., & Elvis, M. 2001, ApJ, 552, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Kovlakas, K., Zezas, A., Andrews, J. J., et al. 2020, MNRAS, 498, 4790 [Google Scholar]
- Kovlakas, K., Fragos, T., Schaerer, D., & Mesinger, A. 2022, A&A, 665, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, N. 1998, A&A, 329, 551 [NASA ADS] [Google Scholar]
- Laycock, S. G. T., Maccarone, T. J., & Christodoulou, D. M. 2015, MNRAS, 452, L31 [Google Scholar]
- Liotine, C., Zevin, M., Berry, C. P. L., Doctor, Z., & Kalogera, V. 2023, ApJ, 946, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, J., McClintock, J. E., Narayan, R., Davis, S. W., & Orosz, J. A. 2008, ApJ, 679, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, J., McClintock, J. E., Narayan, R., Davis, S. W., & Orosz, J. A. 2010, ApJ, 719, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Lowell, B., Jacquemin-Ide, J., Tchekhovskoy, A., & Duncan, A. 2024, ApJ, 960, 82 [CrossRef] [Google Scholar]
- MacLeod, M., & Loeb, A. 2020, ApJ, 895, 29 [Google Scholar]
- Marchant, P., Langer, N., Podsiadlowski, P., Tauris, T. M., & Moriya, T. J. 2016, A&A, 588, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McClintock, J. E., Narayan, R., & Steiner, J. F. 2014, Space Sci. Rev., 183, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, S., Callister, T. A., & Farr, W. M. 2020, ApJ, 895, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Miller-Jones, J. C. A., Bahramian, A., Orosz, J. A., et al. 2021, Science, 371, 1046 [Google Scholar]
- Moreno Méndez, E. 2011, MNRAS, 413, 183 [Google Scholar]
- Moreno Méndez, E., & Cantiello, M. 2016, New Astron., 44, 58 [Google Scholar]
- Mosser, B., Goupil, M. J., Belkacem, K., et al. 2012, A&A, 548, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neijssel, C. J., Vinciguerra, S., Vigna-Gómez, A., et al. 2021, ApJ, 908, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Nugis, T., & Lamers, H. J. G. L. M. 2000, A&A, 360, 227 [NASA ADS] [Google Scholar]
- Olejak, A., & Belczynski, K. 2021, ApJ, 921, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Orosz, J. A., McClintock, J. E., Narayan, R., et al. 2007, Nature, 449, 872 [NASA ADS] [CrossRef] [Google Scholar]
- Orosz, J. A., Steeghs, D., McClintock, J. E., et al. 2009, ApJ, 697, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Orosz, J. A., McClintock, J. E., Aufdenberg, J. P., et al. 2011, ApJ, 742, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Patton, R. A., & Sukhbold, T. 2020, MNRAS, 499, 2803 [NASA ADS] [CrossRef] [Google Scholar]
- Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
- Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [Google Scholar]
- Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
- Paxton, B., Schwab, J., Bauer, E. B., et al. 2018, ApJS, 234, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Paxton, B., Smolec, R., Schwab, J., et al. 2019, ApJS, 243, 10 [Google Scholar]
- Pietsch, W., Haberl, F., Sasaki, M., et al. 2006, ApJ, 646, 420 [NASA ADS] [CrossRef] [Google Scholar]
- Poutanen, J., Lipunova, G., Fabrika, S., Butkevich, A. G., & Abolmasov, P. 2007, MNRAS, 377, 1187 [NASA ADS] [CrossRef] [Google Scholar]
- Prestwich, A. H., Kilgard, R., Crowther, P. A., et al. 2007, ApJ, 669, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Qin, Y., Fragos, T., Meynet, G., et al. 2018, A&A, 616, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Qin, Y., Marchant, P., Fragos, T., Meynet, G., & Kalogera, V. 2019, ApJ, 870, L18 [Google Scholar]
- Qin, Y., Shu, X., Yi, S., & Wang, Y.-Z. 2022, RAA, 22, 035023 [Google Scholar]
- Quast, M., Langer, N., & Tauris, T. M. 2019, A&A, 628, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramachandran, V., Oskinova, L. M., Hamann, W. R., et al. 2022, A&A, 667, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reynolds, C. S. 2014, Space Sci. Rev., 183, 277 [Google Scholar]
- Reynolds, C. S. 2021, ARA&A, 59, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Romero-Shaw, I., Hirai, R., Bahramian, A., Willcox, R., & Mandel, I. 2023, MNRAS, 524, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Roulet, J., Chia, H. S., Olsen, S., et al. 2021, Phys. Rev. D, 104, 083010 [NASA ADS] [CrossRef] [Google Scholar]
- Salvesen, G., & Miller, J. M. 2021, MNRAS, 500, 3640 [Google Scholar]
- Sana, H., de Koter, A., de Mink, S. E., et al. 2013, A&A, 550, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schrøder, S. L., Batta, A., & Ramirez-Ruiz, E. 2018, ApJ, 862, L3 [CrossRef] [Google Scholar]
- Seifina, E., & Titarchuk, L. 2010, ApJ, 722, 586 [NASA ADS] [CrossRef] [Google Scholar]
- Sen, K., Xu, X. T., Langer, N., et al. 2021, A&A, 652, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sen, K., Langer, N., Marchant, P., et al. 2022, A&A, 659, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shao, Y., & Li, X.-D. 2022, ApJ, 930, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Shimanskii, V. V., Karitskaya, E. A., Bochkarev, N. G., et al. 2012, Astron. Rep., 56, 741 [CrossRef] [Google Scholar]
- Spruit, H. C. 2002, A&A, 381, 923 [CrossRef] [EDP Sciences] [Google Scholar]
- Sukhbold, T., Ertl, T., Woosley, S. E., Brown, J. M., & Janka, H. T. 2016, ApJ, 821, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, C., & Reynolds, C. S. 2018, ApJ, 855, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Tchekhovskoy, A., McKinney, J. C., & Narayan, R. 2012, J. Phys. Conf. Ser., 372, 012040 [NASA ADS] [CrossRef] [Google Scholar]
- Thomsen, L. L., Kwan, T. M., Dai, L., et al. 2022, ApJ, 937, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Valli, R., Tiede, C., Vigna-Gómez, A., et al. 2024, A&A, 688, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vanbeveren, D., Mennekens, N., van den Heuvel, E. P. J., & Van Bever, J. 2020, A&A, 636, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vinciguerra, S., Neijssel, C. J., Vigna-Gómez, A., et al. 2020, MNRAS, 498, 4705 [NASA ADS] [CrossRef] [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wei, D., Schneider, F. R. N., Podsiadlowski, P., et al. 2024, A&A, 688, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Willcox, R., MacLeod, M., Mandel, I., & Hirai, R. 2023, ApJ, 958, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Winter, L. M., Mushotzky, R. F., & Reynolds, C. S. 2006, ApJ, 649, 730 [NASA ADS] [CrossRef] [Google Scholar]
- Xing, Z., Bavera, S. S., Fragos, T., et al. 2024, A&A, 683, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zdziarski, A. A., Mikolajewska, J., & Belczynski, K. 2013, MNRAS, 429, L104 [Google Scholar]
- Zdziarski, A. A., Banerjee, S., Chand, S., et al. 2024a, ApJ, 962, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Zdziarski, A. A., Chand, S., Banerjee, S., et al. 2024b, ApJ, 967, L9 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Formation channels of wind-fed BH-HMXBs
Here we present the fractions of evolutionary pathways prior to BH formation for wind-fed BH-HMXBs in Table A.1 across the three BH accretion scenarios. All scenarios exhibit similar fractions.
Fractions of evolutionary pathways of wind-fed BH-HMXBs
Appendix B: Surface and center helium abundance
In this section, we present the population property distributions, in the form of a corner plot, that includes center helium abundance Ycenter and surface helium abundance Ysurf of the donor star under the moderately super-Eddington accretion scenario. In Figure B.1, we show the time-weighted distribution of orbital period, donor star mass, BH spin, donor star’s center helium abundance, and surface helium abundance. For both pre-RLO and post-RLO systems, the majority of the donor stars have Ycenter above ≈0.8, which means that they are approaching the terminal-age MS. As a consequence of RLO, the outer layer of the envelope of the donor stars is stripped, leading to an evident increase in Ysurf.
Appendix C: Population property distributions for Eddington-limited and fully conservative BH accretion
Here we display population property distributions, in the form of corner plots, for the population properties of wind-fed BH-HMXBs under the model assumptions of Eddington-limited and fully conservative BH accretion. Figure C.1 shows the same distributions as Figure 2 but for the Eddington-limited accretion model. The BH spins are ≲0.3, with no significant BH spin-up observed to distinguish the populations before and after MT via RLO. Figure C.2 shows the case of fully conservative BH accretion. Bimodal distributions can be seen for BH masses and spins due to accretion. Most of the BHs can be spun up to have spins above 0.8 after MT via RLO and the binaries remain at this stage longer. The distributions of orbital periods and donor star masses appear similar across different BH accretion models.
Appendix D: Population property distributions for X-ray bright sources
When adopting the low-end wind accretion efficiency from Hirai & Mandel (2021), a large fraction of the binaries with donor stars below 20 M⊙ exhibit X-ray luminosities below 1037 erg s−1. To illustrate the characteristics of X-ray bright systems, we display a corner plot of the binaries with X-ray luminosity exceeding 1037 erg s−1 in Figure D.1. About 79% of them are post-RLO systems. The donor stars exhibit a relatively flat distribution from 10 to 30 M⊙, extending up to ≈40 M⊙. The X-ray bright systems are characterized by a higher proportion of massive donor stars because of their strong winds. In Figure D.2, we show the distribution of mass ratio q = Md/MBH versus orbital period for wind-fed BH-HMXBs under the moderately super-Eddington accretion model for both the entire population and the X-ray bright systems. For the entire population, the post-RLO systems have mass ratios mostly ranging from approximately 0.8 to 1.6, with a small fraction reaching around 2. For the X-ray bright systems, their mass ratios show a flatter distribution from approximately 0.8 to 2.4.
 |
Fig. D.1. Same as Figure 2 but for binaries with X-ray luminosity exceeding 1037 erg s−1, following the application of low wind accretion efficiency. |
 |
Fig. D.2. Distribution of mass ratio versus orbital period for wind-fed BH-HMXBs. The left panel shows the distribution for the entire population and the right panel shows the distribution for systems with X-ray luminosity exceeding 1037 erg s−1, assuming low wind accretion efficiency. |
All Tables
All Figures
 |
Fig. 1. Evolution of an example binary through the wind-fed HMXB phase under three BH accretion scenarios. The top panels show the evolution of the donor star radius (black solid line), Roche lobe radius (orange dashed line), 0.9 times the Roche lobe radius (orange dotted line), and orbital period (gray solid line). The green and blue areas indicate the duration of the wind-fed BH-HMXB phase before and after MT via RLO, respectively. The plus symbol denotes the end of the MS for the donor star. The bottom panels show the evolution of the BH mass (black solid line), donor star mass (orange solid line), donor star convective core mass (orange dotted line), and BH spin (gray solid line). |
| In the text | |
 |
Fig. 2. Corner plot showing the time-weighted distributions of the properties of wind-fed BH-HMXBs from the moderately super-Eddington accretion scenario. The dark and light blue contours represent the 68% and 95% confidence regions, respectively, for the orbital period, donor star mass, BH mass, BH spin, and X-ray luminosity of systems after RLO. Similarly, the dark and light orange contours are for systems before RLO. The black dot, square, and triangle with error bars indicate the positions of Cygnus X-1, LMC X-1, and M33 X-7, respectively. |
| In the text | |
 |
Fig. 3. Time-weighted probability distributions of the BH mass (top left), BH spin (top right), donor star mass (bottom left), and orbital period (bottom right) in wind-fed BH-HMXBs. The blue and orange colors indicate post-RLO and pre-RLO sub-populations, respectively. The unfilled bins, hashed bins, and filled bins represent the Eddington-limited, moderately super-Eddington, and fully conservative accretion scenarios, respectively. The black dot, square, and triangle with error bars, placed at arbitrary probability values, respectively indicate the properties of Cygnus X-1, LMC X-1, and M33 X-7. |
| In the text | |
 |
Fig. B.1. Corner plot similar to Figure 2 including the surface and center helium abundance. |
| In the text | |
 |
Fig. C.1. Same as Figure 2 but for Eddington-limited BH accretion. |
| In the text | |
 |
Fig. C.2. Same as Figure 2 but for fully conservative BH accretion. |
| In the text | |
 |
Fig. D.1. Same as Figure 2 but for binaries with X-ray luminosity exceeding 1037 erg s−1, following the application of low wind accretion efficiency. |
| In the text | |
 |
Fig. D.2. Distribution of mass ratio versus orbital period for wind-fed BH-HMXBs. The left panel shows the distribution for the entire population and the right panel shows the distribution for systems with X-ray luminosity exceeding 1037 erg s−1, assuming low wind accretion efficiency. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



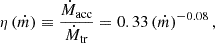
![$$ \begin{aligned} \chi _{\rm BH,f} = \frac{r_{\mathrm{ISCO,i} }^{1/2}}{3} \frac{M_{\mathrm{i} }}{M_{\mathrm{f} }}\biggl \{4-\left[3\, r_{\mathrm{ISCO,i} }\left(\frac{M_{\mathrm{i} }}{M_{\mathrm{f} }}\right)^2-2\right]^{1/2} \biggl \}, \end{aligned} $$](/articles/aa/full_html/2025/01/aa51275-24/aa51275-24-eq7.gif)