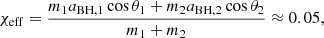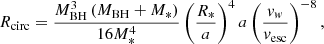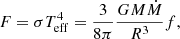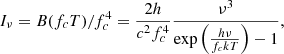EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 690 (October 2024) A&A, 690 (2024) A21 Full HTML
Open Access
Issue
A&A
Volume 690, October 2024
Article Number A21
Number of page(s) 10
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/202450229
Published online 27 September 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

LIGO/Virgo/KAGRA (LVK) interferometers have detected gravitational waves from ∼70 double black hole (BH-BH) mergers (The LIGO Scientific Collaboration 2023). These merging black holes (BHs) have masses in the range ∼3–100 M⊙, with many primary (the more massive) BHs having masses of ∼10 M⊙ and ∼35 M⊙(Callister & Farr 2024). The most massive LVK event (GW190521) showed two merging BHs with estimated mass of ∼95 M⊙ and ∼69 M⊙. The majority of these mergers have low positive effective spin parameters, with the distribution peaking at

χ eff = m 1 a BH , 1 cos θ 1 + m 2 a BH , 2 cos θ 2 m 1 + m 2 ≈ 0.05 , $$ \begin{aligned} \chi _{\rm eff}= \frac{m_1 a_{\rm BH,1} \cos \theta _1+m_2 a_{\rm BH,2} \cos \theta _2}{m_1 + m_2} \approx 0.05, \end{aligned} $$(1)

where mi denotes BH masses, aBH, i = cJi/Gmi2 are the BH spin magnitudes (Ji: BH angular momentum, with c as the speed of light and G as the gravitational constant), while θi refers to the angles between the system’s angular momentum and BH spins. Out of these 70 mergers, 6 of them show high positive effective spins χeff > 0.3 (mean), while none show a high negative spin χeff < −0.3. However, there are three events with moderate negative spin estimates: −0.3 < χeff < −0.1. Low values of the effective spin parameter may result from small individual BH spin magnitudes (Belczynski et al. 2020b). This is supported by LVK data, which shows that BH individual spin magnitudes in BH-BH mergers peak at aBH ∼ 0.1–0.2; however, the distribution has a long tail that extends to large values (The LIGO Scientific Collaboration 2023; see Callister & Farr 2024 for slightly different results).

Electromagnetic observations have revealed a population of BHs hosted in binary star systems1. Out of several known binary configurations hosting BHs, only high-mass X-ray binaries (HMXBs) can potentially lead to BH-BH mergers, as BH companion stars are massive enough to form a BH. There are only three HMXBs known to have such massive (≳20 M⊙) companions and they have moderate-mass BHs: LMC X-1 with a ∼30 M⊙ star and a 10.9 M⊙ BH (Orosz et al. 2009); Cyg X-1 with a ∼40 M⊙ star and a 21.2 M⊙ BH (Miller-Jones et al. 2021); and M33 X-7 with a ∼38 M⊙ star and a 11.4 M⊙ BH (Ramachandran et al. 2022; revised down from the previous estimates of a 70 M⊙ donor and 15.6 M⊙ BH in Orosz et al. 2007). We note that the binary LMC X-3 is not a HMBXB since its stellar companion is less massive (3.63 M⊙) than the BH (6.98 M⊙) Orosz et al. (2014) and will not form a BH anyway. The spins of BHs in HMXBs were obtained with two methods, namely: disc continuum fitting, and reflection spectroscopy. Reflection spectroscopy is complex for soft state spectra (e.g. Tomsick et al. 2018), so here we focus on spin values from a disc continuum fitting. These are typically very high2:

Since masses and spins of LVK BHs and HMXB BHs appear to be different, it might seem that these two groups of systems belong to populations with different formation scenarios. Here, we show that all these BHs may instead form a single population. The difference in BH mass arises naturally from the diverse formation environments: all known HMXB-BH systems reside in Local Group galaxies with relatively high metallicity, so they have strong stellar winds before the core collapse. This results in lower black hole masses compared to those forming in low metallicity galaxies, which are within the sensitivity range of LVK. We demonstrate the difference in expected black hole masses explicitly using a population synthesis model. This model also reproduces the spin values in the LVK BHs, for models where high spins are produced only by tidal spin-ups in extremely close binaries. The known HMXB-BH systems are in binary systems that are not close enough for tidal spin-up. Hence, the population synthesis models predict they should not have high spins, which conflicts with the reported high values. However, the disc continuum method relies on the emission thermalising. If, instead, the disc is covered by a warm, optically thick skin, whereby the emission is Comptonised, the spin values are all consistent with aBH ∼ 0.1 (Belczynski et al. 2021; Zdziarski et al. 2024a,b; this paper). With this interpretation, the LVK BH-BH mergers and the HMXBs can be considered as members of the same binary star population.

2. BH masses

To demonstrate the unicity of the BH population, we use the population synthesis code StarTrack (Belczynski et al. 2002, 2008) and employ the delayed core-collapse supernova (SN) engine for neutron star/BH mass calculation (Fryer et al. 2012) that does not produce a lower mass gap between NSs and BHs. We used a model in which the pair-instability (upper) mass gap is calculated with non-standard fusion reaction rates and heavy mixing for massive stars; this allows for BHs to form up to 90 M⊙ (Farmer et al. 2020; Costa et al. 2021). This type of model had already been developed by Belczynski (2020) in the context of the MBH = 90 M⊙ detected at the low-metallicity GW190521 LVK merger, at distance of ∼4 Gpc (Abbott et al. 2020).

In Fig. 1, we show the dependence of the helium core mass on metallicity for single stars obtained with the stellar wind treatment presented in Belczynski et al. (2010a). The helium core mass is a good approximation of the BH mass since binary interactions (Roche Lobe overflow or common envelope evolution) tend to remove the H-rich envelope from stars in close binaries (progenitors of BH-BH mergers if these form through isolated binary evolution). The lower the metallicity, the lower the opacity in stellar atmospheres, and the lower the wind mass loss, which produces progressively higher mass BHs with decreasing metallicity.

thumbnail Fig. 1.

Helium core mass is a function of the initial star mass for various metallicities. The helium core is a good approximation of the black hole mass for stars in close binaries that form BH-BH mergers (binary interactions remove H-rich envelope). Black arrows show the current stellar metallicity range of LVK (low-redshift Universe: z < 0.7) and for HMXBs that are limited to the local group of galaxies. LVK is bound to probe more massive BHs than electromagnetic HMXB observations.

Cyg X-1 is located in the Milky Way disc, which hosts stars that have metallicity values that are close to solar (Z = 0.014, Asplund et al. 2009). For such values, we obtain a maximum BH mass of MBH ∼ 20 M⊙, which is consistent with the highest mass stellar-origin BH known in the Milky Way for the same Cyg X-1 (MBH = 21 M⊙, Miller-Jones et al. 2021). LMC X-1 is located in the Large Magellanic Cloud (Z ≈ 0.005) and M33 X-7 in M33 galaxy (Z = 0.01). In this metallicity range, BHs are not expected to be more massive than MBH ∼ 35 M⊙.

LVK BH-BH mergers have already been detected (O3) to significant redshifts of z ≲ 0.7. The detected BH-BH mergers may have formed even at much larger redshifts due to non-zero delay times between star formation and BH-BH mergers (Dominik et al. 2012; Fishbach & Kalogera 2021). Therefore, galaxies and stars that can produce BH-BH mergers cover a wide range of metallicities. It is even claimed that Population III (metal-free) stars (Z = 0) may contribute to LVK detections (Kinugawa et al. 2014). Assuming a metallicity range Z = 0.0001–0.02 for LVK we obtain a broad range of BH mass: ∼3–90 M⊙. This range is consistent with the LVK BH mass estimates in BH-BH mergers. The recent discovery of a MBH ≈ 33 M⊙ BH in the binary Gaia BH3 (Gaia Collaboration 2024) strongly supports a scenario in which metal-poor massive stars are progenitors of the high-mass BHs observed by LVK (see e.g. Olejak et al. 2020). In conclusion, the same model of stellar evolution produces correct mass ranges for the three discussed HMXB BHs (narrow) and LVK BHs (wide).

3. BH spins: Stellar evolution

Population synthesis models are also used to predict the BH spin distribution. In most cases, they produce low-spinning BHs (aBH ∼ 0.1) from non-interacting stars and slow-to-rapidly-spinning BHs (aBH = 0.1–1.0) for Wolf-Rayet (WR) stars that were subject to tidal spin-up in close binaries (Belczynski et al. 2020b; Bavera et al. 2020). Such models can explain the low and high effective spins of LVK BH-BH mergers (Olejak & Belczynski 2021).

The low BH spins obtained by population synthesis models are the consequence of the assumed efficient angular momentum transport from stellar cores to envelopes, an effect that has been now aptly confirmed by observations (Aerts et al. 2019; Langer 2012) consistent with the action of the magnetic Tayler (1973) instability (Spruit 2002; Fuller et al. 2019; Eggenberger et al. 2022; Petitdemange et al. 2024). The heuristic Spruit (2002) version of the mechanism used in population synthesis codes was recently confirmed by numerical calculations of Petitdemange et al. (2024).

Therefore, unless their progenitors in HMXBs belong to a special category of stars with uncoupled cores and envelopes, the BHs in these systems would have been formed with low spins (aBH ∼ 0.1). The known HMXB orbital periods are too long for tidal interactions to spin up the stars before they form BHs (the size of the present BH companion would not fit into a < 1.3 days orbit of the tidal locking regime; see e.g. Belczynski et al. 2020a); thus, if their spins are really large, they must have have gained angular momentum by accretion. To spin-up a BH from aBH ∼ 0.1–0.9 it is necessary to roughly to double its mass (Bardeen 1970). For Cyg X-1, this would require accreting ∼10 M⊙ in less than 4 Myr (Miller-Jones et al. 2021), namely, with an accretion rate of > 2.5 × 10−6 M⊙ yr−1 ; this rate would be higher by factor of 100 if the accretion lifetime of Cyg X-1 was only a few tens of thousands of years (Miller-Jones et al. 2021). This gives an accretion rate of > 6 ṀEdd, where ṀEdd = LEdd/ηc2 is the Eddington accretion rate with an assumed efficiency of ∼0.1. Contrary to the still expressed opinion (see e.g. Miller-Jones et al. 2021), the Eddington rate is not a maximum theoretical limit (Begelman 1979) and black holes can accrete from discs at rates of up to (at least) a few tens of ṀEdd (Kitaki et al. 2021; Yoshioka et al. 2022, but see Hu et al. 2022); thus, an accretion rate ≳ 12.5 ṀEdd in Cyg X-1 would not be, from this point of view, extravagant. The problem is to find an evolutionary path that would take a high-mass binary through such a super-Eddington phase and produce the observed Cyg X-1, whose O supergiant donor star has yet to fill its Roche lobe. This is unlikely to happen with respect to accretion from wind, even when it is L1-focused (Wiktorowicz et al. 2021). Therefore, according to the best stellar physics available BH spins in the known HMXBs should be low, with a ≲ 0.4 – consistent with LVK BH spins (Fishbach & Kalogera 2022) and estimates of BH spin in HMXBs by Belczynski et al. (2021); Zdziarski et al. (2024a,b); however, this is clearly incompatible with the generally accepted high spin values in these systems (Miller & Miller 2015). These high spin values have been obtained by assuming the presence of a standard disc in the system (see Sect. 7 for the standard-disc definition), which can be justified only if the system is in a soft spectral state. In the following, we argue that since Cyg X-1 has never been observed in such a state, the high black hole spin from disc continuum fitting is not a firm requirement.

4. BH spins from disc spectral fitting: HMXBs

The main tracer of BH spin in electromagnetic systems is the radius of the innermost stable circular orbit (RISCO). This sets the inner radius of the accretion disc in the standard Shakura-Sunyaev (Shakura & Sunyaev 1973 and its relativistic extension: Novikov-Thorne; Novikov & Thorne 1973) models. Measuring the inner edge of the disc gives an estimate of BH spin, with RISCO decreasing from 6–1.0Rg (with Rg being the gravitational radius) as aBH increases from 0–1.0. For the Thorne (1974) limit aBH = 0.998, RISCO = 1.24Rg, but one should keep in mind that this limit is valid only for sub–Eddington flows (Abramowicz & Lasota 1980; Sądowski et al. 2011). The most direct way to measure the RISCO uses the luminosity emitted by the accretion disc itself.

Standard accretion disc models balance gravitational heating from viscous torques with blackbody cooling, resulting in an optically thick, geometrically thin structure with effective temperature at each radius, Teff4(R)∝(L/R2)(RISCO/R). This gives a total spectrum, which is a sum of all radii of blackbody spectra of different temperatures. The emissivity peaks around R ∼ RISCO, so the peak temperature is ∝(L/RISCO2)1/4 K, namely, it is a factor 2.2 × higher for the same disc luminosity at high spin than at low spin.

In all X-ray binaries, we can observe cycles during which the brightness and spectral hardness form a characteristic ‘tortoise-head’ pattern. In general, the spectrum contains both thermal disc emission, together with a power law tail extending to much higher energies, clearly showing that there is an additional non-disc component to the accretion flow. Most transients show a phase in this cycle where the spectrum is sufficiently soft to be termed ‘disc-dominated’, where the accretion disc assumption is likely to be reliable. The problem is that not all X-ray sources complete the full cycle. As we show below, this is the case for Cyg X-1.

Indeed, there is clear evidence that in Cyg X-1, the accretion flow has not formed a standard blackbody disc. The blue points in Fig. 2 show the hardness-intensity diagram of the LMXB GX339-4. This source picks out a well-defined track, transitioning from low and hard (bottom-right) to disc-dominated (upper left, hardness ratio below ∼0.2), with fast transitions (horizontal) between the two states. The red points compare data from Cyg X-1 (both data taken from Belloni 2010). The mass and distance of GX339-4 are not well known, so we have scaled the relative count rate (brightness) between the two systems to match the lower transition luminosity. We can see how GX339-4 transitions from low/hard state (hardness ratio > 1; the ratio is defined as the ratio of counts in the energy bands 6.3–10.5 and 3.8–6.3 keV) to high/soft state (hardness ratio of < 0.1). In contrast, Cyg X-1 never reaches as far to the left as seen in the GX339-4 disc-dominated states.

thumbnail Fig. 2.

The spectral hardness versus intensity diagram for all the RXTE data to 2005 from GX339-4 (blue) and Cyg X-1 (red), shifted in intensity so that the transition from soft to hard overlapped. Hardness ratio is defined as the ratio of counts in the energy bands 6.3–10.5 and 3.8–6.3 keV. (Data from Belloni 2010.) The Cyg X-1 Suzaku data used here is shown as the magenta star.

Hence, Cyg X-1 always has a strong tail of emission to higher energies (e.g. Gierliński et al. 1999; Gou et al. 2009; Walton et al. 2016), keeping it stuck in the more complex intermediate states where there is no reason to believe that the accretion flow forms a standard accretion disc. Instead, the soft component in intermediate state spectra is often better fit by optically thick, warm (few keV) Comptonisation (see e.g. transition spectra from LMXB-BH MAXI J1820+070 in Fig. 2 of Kawamura et al. 2023).

Cyg X-1 has a higher mass BH (21.2 M⊙; Miller-Jones et al. 2021) than GX339-4 (∼2–10 M⊙; Heida et al. 2017), but this should make its disc spectra softer rather than harder since the ISCO is farther out for more massive BHs, making the disc temperature lower. A hotter disc temperature could instead result if Cyg X-1 has a substantially larger spin than GX339-4, but the reflection and reverberation spin estimates for GX339-4 are both extremely high. Therefore, there is no evidence that a standard disc forms in the whole available set of observations of Cyg X-1, making this system’s standard disc-fitting method of BH spin determination inapplicable.

Instead, the strong soft component need not be emitted by a simple blackbody disc, where the energy is dissipated mainly on the midplane but can have heating further up into the photosphere. This forms a warm layer on the top of the disc, making it appear hotter and giving a higher spin when fit with standard disc models. Such a warm layer on the disc is sometimes required in the black hole binaries (e.g. in very high and intermediate type spectra: Kubota et al. 2001; Remillard & McClintock 2006) and is generic in active galactic nuclei (Porquet et al. 2019; Gierliński & Done 2004b; Petrucci et al. 2018). On the other hand, it is well known that the simplistic assumption of dissipation that is concentrated at the disc midplane (usually in the form of dissipation proportional to pressure) is in contradiction with both observations (see e.g. Hubeny & Long 2021) and numerical simulations (Blaes 2014).

Thus, there is no physical reason to assume that a standard accretion disc emits the observed X-ray spectrum of Cyg X-1. In fact, there are good reasons to think that such an assumption is inappropriate for this system. There is no ‘canonical’ model describing the inner disc structure in X-ray binaries – no model correctly describes the ‘tortoise-head’ cycle. Hence, we can test various options that would reproduce the observed spectrum and check whether the deduced spin value is model-dependent; if it is, we consider which model corresponds best to the value obtained from stellar evolution. A similar approach was adopted by Zdziarski et al. (2024a,b).

5. Cyg X-1 spin from the soft component

We confronted two models of Cyg X-1 emission. We used data from the softest state ever seen (observed by Suzaku in 2013; magenta star in Fig. 2), when the soft component is at its most dominant, and, thus, uncertainties from modelling the high energy coronal tail are smallest (observation B4 from Kawano et al. 2017, see this paper for details of the data). We fit these data using the XSPEC spectral fitting package and all the models below include absorption along the line of sight using TBABS with column density as a free parameter (see Appendix A for the details). We show results from a series of model fits in Fig. 3, where the original (absorbed) X-ray Suzaku data is grey, with the reconstructed (corrected for absorption) spectrum shown with orange points. We assume here the standard mass and distance, and we fix the disc inclination to the binary inclination of i = 30°.

thumbnail Fig. 3.

Cyg X-1 spectra for for: Left: Standard accretion disc (red), modeled with KERRBB, and a hot Comptonising plasma (blue) giving the high energy emission – as sketched in the top right corner; model (a). Middle: Standard accretion disc entirely covered by a warm Comptonising plasma (green), and then an inner hot Comptonising plasma (blue); model (b). Right: Same as middle panel, but with the spin fixed at aBH = 0.1. Note: the low BH spin is fully consistent with the X-ray spectral data.

We first fit the standard disc model to these data. The results are shown in the left panel of Fig. 3. This includes all special and general relativistic ray tracing effects, as well as allowing a correction to the blackbody temperatures to account for the incomplete thermalisation expected from full models of the vertical disc structure (colour temperature correction, fixed to 1.7). We allowed for a fraction of these disc spectra to be Compton upscattered to form the power law tail, modelled using the standard formalism, which assumes the electron energy is typically higher than 100 keV. We recovered the usual, very high black hole spin (aBH = 0.96) seen in all standard-disc fits to the soft component (Zhao et al. 2021a; Zdziarski et al. 2024a,b).

The middle panel of Fig. 3 shows what happens when we additionally allow a warm skin on the top of the disc. We model this using another Compton upscattering model, which allows the electron temperature to remain as a free parameter, as well as the scattered fraction (set by the optical depth of the skin). This is formally a much better fit to the data, even accounting for the two additional free parameters: optical depth and temperature of the warm disc skin. A simple F-test gives a probability of the improvement being random as p = 3.7 × 10−7. This is well below the generally accepted limit of p < 0.05 for a result to be significant. More importantly, the best fit reduces BH spin to aBH = 0.77. The BH spin here is extremely poorly constrained as the soft component shape in this model is set more by the electron temperature of the skin than by the temperature of the disc at the ISCO. We illustrate this in the right panel of Fig. 3, where we show a fit with almost the same χν2 but for aBH = 0.1, as predicted by standard stellar evolution.

This demonstrates that formal solutions for BH spin from spectra with their reported extremely small error bars or very definitive values (e.g. aBH > 0.9985 at 3σ level, Zhao et al. 2021b) are model-dependent and are not the only solution (see also Zdziarski et al. 2024a,b who arrive at the same conclusion).

5.1. Considering whether a disc can form in Cyg X-1 for a low BH spin

The modelling of the disc continuum spectra assumes that an accretion disc can form around the BH for any value of the BH spin and/or any orientation of the accretion disc with respect to the spin of the BH. In a binary system, a disc will form only if the circularisation radius of the transferred matter is larger than the radius of the accreting body. In other words, a disc can form if the angular momentum of the accreting matter is large enough to allow it to circle around the accretor. For wind accretion (Bondi-Hoyle; Bondi 1952), the condition is (Frank et al. 2002):

R circ = M BH 3 ( M BH + M ∗ ) 16 M ∗ 4 ( R ∗ a ) 4 a ( v w v esc ) − 8 , $$ \begin{aligned} R_{\rm circ}=\frac{M_{\rm BH}^3\left(M_{\rm BH}+ M_*\right)}{16M_{*}^4}\left(\frac{R_*}{a}\right)^4 a \left(\frac{v_w}{v_{\rm esc}}\right)^{-8}, \end{aligned} $$(2)

where M* is the mass of the donor star, a the orbital separation, vw the wind velocity, and vesc the escape velocity from the donor. For the parameters of Cyg X-1, when aBH = 0, RISCO ≈ 1.1 × 107 cm but Rcirc ≈ 1.9 × 1010(vw/vesc)−8 cm, so that, for instance, for vw/vesc > 2.2 no disc can form. Sen et al. (2021) analysed the problem in great detail and showed that for the observed binary and stellar parameters of Cyg X-1 (Miller-Jones et al. 2021), a maximally spinning BH may be required to form an accretion disc in the prograde orientation when the BH accretes from a wind.

However, we note that the O star companion in Cyg X-1 is nearly filling its Roche lobe (Roche-lobe filling factor is greater than 0.9, Miller-Jones et al. 2021), where the formation of a focused accretion stream is expected (Blondin et al. 1991; Hadrava & Čechura 2012; El Mellah et al. 2019). In Cyg X-1, the existence of a focused accretion stream has also been observationally verified (Miller et al. 2005; Poutanen et al. 2008; Hanke et al. 2009). A high Roche lobe filling factor has been found for LMC X-1 (Orosz et al. 2009) and the O donor in M33 X-7 effectively fills its Roche lobe (although not in a standard way; see Ramachandran et al. 2022).

In such a configuration, spherically symmetric Bondi-Hoyle accretion is not accurate. The tidal and gravitational effects of the BH distort the shape of the O star and wind streamlines from the O star, respectively (El Mellah et al. 2019; Hirai & Mandel 2021). Hirai & Mandel (2021) showed that for Cyg X-1, the effects of rotation and gravity darkening can lead to the formation of a prograde accretion disc around a non-rotating BH when the Roche lobe filling factor of the O star is greater than ∼0.8.

Hence, the criterion of the formation of an accretion disc in Cyg X-1 does not rule out any assumptions on the spin of the BH. The high Roche lobe filling factor of the O star enables the formation of a focused wind with sufficient angular momentum to make a prograde accretion disc. In such cases, the circularisation radius for the bulk of the accretion flow is of the order of the solar radius (see e.g. Frank et al. 2002), orders of magnitude larger than the ISCO radius. The above arguments, together with our modelling of the disc continuum spectra, imply that the observations of Cyg X-1 are consistent with the notion that its BH could also be slowly spinning.

6. M33 X-7 BH spin from the soft component

The source X-7 in the nearby galaxy M33 is an eclipsing HMBH on a quasi-circular, 3.45 day orbit. In this system, according to phase-resolved simultaneous HST and XMM-Newton observations by Ramachandran et al. (2022), an ≈11.4 M⊙ BH accretes matter lost from its O9II, metal-poor, ≈38 M⊙ supergiant companion. The previous mass estimate by Orosz et al. (2007) had a higher BH mass of ≈15.6 M⊙ (and ≈70 M⊙ companion).

Assuming the older BH mass, Liu et al. (2008) used the continuum fitting method to get a BH spin aBH = 0.84. We have used the standard continuum method to determine the M33 X-7 spin value for the new BH mass and obtained aBH = 0.7 (see Appendix B), as expected. With this new spin value, the M33 X-7 BH is no longer in the very-rapidly rotating class, to which Cyg X-1 with aBH ∼ 0.9985 and LMC X-1 with aBH > 0.9 belong. Nevertheless, since we have concluded that the spin determination in Cyg X-1 is strongly model-dependent, supported by the findings of Zdziarski et al. (2023); Zdziarski et al. (2024b), who arrived to same conclusion regarding LMC X-1, we thought it useful to check if the same applies to M33 X-7. Similarly to these sources, when a warm-skin Comptonising model is used, the black hole spin is completely unconstrained, with acceptable values ranging from −1 to ∼0.9 at 90% confidence level (see Appendix B). Below, we discuss the possible reason for this common property of the only three HMBXs that are potential progenitors of BHBH binary systems.

7. Discussion

We have shown that the X-ray spectra of Cyg X-1 and M33 X-7 can be fitted with both standard disc and warm Comptonised disc models (see also Zdziarski et al. 2024a,b for the same conclusion about Cyg X-1 and LMC X-1). We have also noticed that even in its softest state, the spectrum of Cyg X-1 is not soft enough to justify a standard-disc model fit, so there are very good reasons to consider alternatives.

In order to avoid ambiguities and misunderstandings, one has to define precisely what is understood by fitting spectra with a ‘standard disc’ model. This model describes an axially symmetric, stationary, geometrically thin Keplerian accretion flow. It is assumed that the angular momentum transport is provided by a ‘viscous’ (noting that in astrophysical discs, the viscosity must be ‘anomalous’) torque and that the local dissipation of the same torque is the source of the energy radiated away from the disc surface. Then, from the mass and angular momentum conservation equations for the vertically averaged disc parameters, assuming thermal equilibrium, we obtain

F = σ T eff 4 = 3 8 π G M M ˙ R 3 f , $$ \begin{aligned} F=\sigma T_{\mathrm{eff} }^4 = \frac{3}{8 \pi } \frac{G M \dot{M}}{R^3}f, \end{aligned} $$(3)

where Teff is the effective temperature and f contains information about the boundary conditions. This is the equation that provides the flux – or effective temperature profile, Teff(R) – for a Keplerian stationary disc. It does not say that the disc emits radiation like a blackbody. It contains no information about the vertical energy transport in the disc and is independent of the angular momentum and dissipation mechanism; in fact, it only assumes the existence of such mechanism (independently of the value of the viscosity parameter, α, and does not even assume the existence of such a parameter). Equation (3) is the basis of the ‘standard’ disc X-ray spectrum model. There, it is assumed that the colour temperature is close to the effective temperature; namely, the disc, locally radiates approximately as a blackbody would. Since the accretor is a BH, one adds to the model general-relativistic effects, including radiation back-falling onto the disc, and appropriate inner boundary conditions (usually zero torque at ISCO). Since the observed spectra are not strictly a sum of blackbodies, the disc annulus emission is represented by a colour-corrected (or diluted) blackbody:

I ν = B ( f c T ) / f c 4 = 2 h c 2 f c 4 ν 3 exp ( h ν f c k T ) − 1 , $$ \begin{aligned} I_\nu =B(f_cT)/f_c^4 = \frac{2 h}{c^2 f_c^4} \frac{\nu ^3}{\exp \left(\frac{h \nu }{f_c k T}\right)-1}, \end{aligned} $$(4)

where Iν is the intensity, Bν is the Planck spectrum, h the Planck constant, ν the radiation frequency, and fc is a colour temperature correction factor representing the extent to which electron scattering through the disc vertical structure is expected to affect the emergent spectrum. This can be calculated by solving the disc vertical radiative transfer equations using a code such as TLUSTY (see Davis & El-Abd 2019; Davis et al. 2005 and references therein). However, contrary to stellar atmospheres, accretion discs are not in radiative equilibrium, namely, the divergence of the radiative flux is not equal to zero, but to the (viscous) heating rate per unit volume. Hence, the calculations requires the viscous-dissipation vertical structure as input. In a simplistic application of the α-model of Shakura & Sunyaev (1973), it is assumed that this dissipation profile is identical to that of the total pressure. Instead, for the disc emission calculations, the dissipation is assumed to follow the density profile in TLUSTY (Done & Davis 2008). Both these prescriptions have maximal dissipation at the mid-plane, whereas MRI simulations often show maximum dissipation closer to the disc surface (see e.g. Blaes 2014). Some versions of TLUSTY (Hubeny & Hubeny 1998) use a step-wise power-law dependence of viscosity that allows for a chosen fraction of the dissipation to occur in the surface layers. Such a dissipation profile is needed to reproduce disc spectra of cataclysmic variables Hubeny & Long (2021) and when applied to BH X-ray emitting disc, such dissipation stratification produces disc coronas (Davis & El-Abd 2019), as suggested by Svensson & Zdziarski (1994).

In this regard, the real, physical dissipation profiles are still unknown since numerical simulations cannot yet produce realistic vertical structures of geometrically thin accretion discs. That is why disc models with warm surface layers are as physically legitimate as the presumed ‘standard’ model, especially when there is strong evidence as in Cyg X-1 that the structure is not a standard disc.

It is also useful to point out that the α-disc model cannot explain the brightness-hardness ratio tortoise-head hysteresis observed in transient X-ray sources. The physical reason for this variability is still unknown. Observations (e.g. Done et al. 2007; Basak & Zdziarski 2016; Basak et al. 2017) and models (e.g. Dubus et al. 2001) suggests that accretion discs in BH X-ray binaries are truncated, but the physical mechanism of this excision is still a mystery.

This does not mean that the α-disc model on which the ‘standard’ spectral model is based is to be rejected. This model has found many successful applications. The soft state spectra in transients show peak disk temperature and total luminosity changing together with L ∝ T4, indicating a constant inner radius for the disc and constant fc (Done et al. 2007). The radial dependence of the disc temperature shows the predicted T ∝ R−3/4 behaviour in eclipsing cataclysmic variables in their disk (outbursting) states (Horne & Cook 1985), as well as showing the very different radial profile expected from non-equilibrium discs in quiescent dwarf-novae; (Lasota 2001).

None of the known HMBHs exhibit a convincing L ∝ T4 soft state relation that characterises a standard disc (see Sect. 4). Cyg X-1 is never in a soft state, while in LMC X-1 Gierliński & Done (2004a) discovered that the disc luminosity follows instead a L ∝ T−1 track. Zdziarski et al. (2024a) found that such a anti-correlation between luminosity and temperature can be naturally explained as an effect of the warm Comptonisation layer on top of a standard disc. The luminosity variations in M33 X-7 are not large enough to determine whether a L(T) relation is present3.

The three BHHMBXs, Cyg X-1, LMC X-1, and M33 X-7, whose spectra are well fitted by a model of a disc covered with warm comptonising layer have one feature in common: they accrete not only from a focused stream, but also capture some matter from the strong wind of the BH companion. It is natural to speculate that this is the source of the warm layer, making it a ubiquitous feature of the HMBH spectra.

8. Conclusion

The difference between HMXB and LVK BH masses has already been noticed after the first gravitational wave detection and attributed to metallicity effect (Abbott et al. 2016), as anticipated by Belczynski et al. (2010b). Taking into account that interferometric detectors of gravitational waves sample a volume that is a few hundred thousand times larger than the X-ray telescopes (for HMXB BH mass determination), the difference in BH masses between LVK and HMXBs is not surprising as it implies a huge difference in the metallicity range sampled (see Fig. 1).

Although assessing the problem of BH mass differences between HMXB and gravitational–wave sources is rather straightforward, the task of addressing the apparent conflicting spin values is more complicated. At face value, the spin values attributed to the BH in the HMXBs that are massive enough to form LVK sources (Cyg X-1, LMC X-1, M33 X-7) seem to require two distinct populations: slowly spinning (LVK) and rapidly spinning (HMXBs) BHs.

Since the majority of LVK BHs are slowly spinning (aBH ∼ 0.1–0.2), we argue, under the assumption that they are stellar-origin BHs (i.e. they are not primordial BHs: Hawking 1971, but see Mroz et al. 2024), that this must indicate that massive stars are subject to efficient angular momentum transport (Spruit 2002; Fuller et al. 2019; Eggenberger et al. 2022; Petitdemange et al. 2024). This leads to good agreement of predicted BH spins in BH-BH mergers with LVK data (Belczynski et al. 2020b; Bavera et al. 2020). These slowly spinning BHs can form in isolated binary evolution and various dense (open, globular, nuclear) cluster environments. A small fraction of LVK BHs may be moderately or even rapidly spinning (see the long tail of BH spins with aBH ≳ 0.4: left panel of Fig. 15 in The LIGO Scientific Collaboration 2023). These moderately and rapidly spinning BHs can also be explained in the framework of efficient angular momentum transport. Although the star rotation slows down during its evolution towards the formation of a BH, the tidal spin-up of a WR star (BH progenitor) in close BH+WR binary systems (BH-BH progenitors) can easily result in a moderately or rapidly spinning BH (Olejak & Belczynski 2021). In dense clusters, dynamical interactions may lead to the formation of BH-BH mergers with components that are second- or even third-generation BHs (formed by earlier BH-BH mergers) that naturally exhibit significant spins (Rodriguez et al. 2019).

Under the natural assumption that BHs in HMXBs are formed directly from massive stars and within the paradigm of efficient angular momentum transport, these BHs also must have low spins (aBH ∼ 0.1; e.g. Belczynski et al. 2020b). We have demonstrated that this conclusion is fully consistent with BH spin estimate based on a fitting of the disc spectra in HMXBs with models where the disc is covered by a warm Comptonised layer. In particular, we show that with this model, the X-ray spectra of the softest (but still pretty hard) state of Cyg X-1 is consistent with a slowly spinning BH, as confirmed by Zdziarski et al. (2024b) for another set of data. The same is true of X-7 in M33, whose BH spin is completely unconstrained when its soft X-ray spectra are fitted with the warm-skin model. The same warm-skin solutions also give a low spin for LMC X-1 (Zdziarski et al. 2024a. We have shown that the warm-skin solution is as physically plausible as the so–called standard solution, especially in the case of systems that are not in a generic soft X-ray spectral state. We speculate that this warm skin is ubiquitous in the HMXB-BH due to the presence of additional accretion from lower angular momentum material in the stellar wind as well as Roche Lobe overflow.

Thus, we conclude that the LVK and HMXB BHs are consistent with having the same origin, that is, both classes of BHs form directly from stars with efficient angular momentum transport.

1

E.g. see https://universeathome.pl/universe/blackholes.php and references therein.

2

The spins attributed through various methods to LMXB BH vary from very low to very high values, sometimes for the same system (e.g. Reynolds 2021). However, on the one hand these binary systems are not BHBH binary progenitors, on the other, their evolutionary history is still a puzzle (Wiktorowicz et al. 2014).

3

Liu et al. (2008) present a variability in counts (not in counts per second) which reflects mostly the variability of the exposure time.

Acknowledgments

Unfortunately, Chris Belczyski died while working on the re-submission of the present paper. We will miss his deep knowledge, inexhaustible enthusiasm, and kindness. We thank Jerome Orosz, Henric Krawczynski, Andrew King, Aleksandra Olejak and Andrzej Zdziarski for very useful comments on this study. This research has made use of data obtained from the Chandra Data Archive and the Chandra Source Catalog. We are grateful to the anonymous referee for very helpful suggestions and comments. KB was supported by the Polish National Science Center (NCN) grant Maestro (2018/30/A/ST9/00050). CD acknowledges support from STFC through grant ST/P000541/1. SH acknowledges support from STFC through the studentship grant ST/V506643/1. KS is funded by the National Science Center (NCN), Poland, under grant number OPUS 2021/41/B/ST9/00757.

References

  1. Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016, ApJ, 818, L22 [Google Scholar]
  2. Abbott, R., Abbott, T. D., Abraham, S., et al. 2020, Phys. Rev. Lett., 125, 101102 [Google Scholar]
  3. Abramowicz, M. A., & Lasota, J. P. 1980, Acta Astron., 30, 35 [NASA ADS] [Google Scholar]
  4. Aerts, C., Mathis, S., & Rogers, T. M. 2019, ARA&A, 57, 35 [Google Scholar]
  5. Arnaud, K. A. 1996, ASP Conf. Ser., 101, 17 [Google Scholar]
  6. Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bardeen, J. M. 1970, Nature, 226, 64 [Google Scholar]
  8. Basak, R., & Zdziarski, A. A. 2016, MNRAS, 458, 2199 [NASA ADS] [CrossRef] [Google Scholar]
  9. Basak, R., Zdziarski, A. A., Parker, M., & Islam, N. 2017, MNRAS, 472, 4220 [NASA ADS] [CrossRef] [Google Scholar]
  10. Bavera, S. S., Fragos, T., Qin, Y., et al. 2020, A&A, 635, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Begelman, M. C. 1979, MNRAS, 187, 237 [NASA ADS] [Google Scholar]
  12. Belczynski, K. 2020, ApJ, 905, L15 [Google Scholar]
  13. Belczynski, K., Kalogera, V., & Bulik, T. 2002, ApJ, 572, 407 [NASA ADS] [CrossRef] [Google Scholar]
  14. Belczynski, K., Kalogera, V., Rasio, F. A., et al. 2008, ApJS, 174, 223 [Google Scholar]
  15. Belczynski, K., Bulik, T., Fryer, C. L., et al. 2010a, ApJ, 714, 1217 [NASA ADS] [CrossRef] [Google Scholar]
  16. Belczynski, K., Dominik, M., Bulik, T., et al. 2010b, ApJ, 715, L138 [Google Scholar]
  17. Belczynski, K., Hirschi, R., Kaiser, E. A., et al. 2020a, ApJ, 890, 113 [NASA ADS] [CrossRef] [Google Scholar]
  18. Belczynski, K., Klencki, J., Fields, C. E., et al. 2020b, A&A, 636, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Belczynski, K., Done, C., Hagen, S., Lasota, J. P., Sen, K., et al. 2021, ArXiv e-prints, [arXiv:2111.09401v2] [Google Scholar]
  20. Belloni, T. M. 2010, Lect. Notes Phys., 794, 53 [NASA ADS] [CrossRef] [Google Scholar]
  21. Blaes, O. 2014, Space Sci. Rev., 183, 21 [NASA ADS] [CrossRef] [Google Scholar]
  22. Blondin, J. M., Stevens, I. R., & Kallman, T. R. 1991, ApJ, 371, 684 [NASA ADS] [CrossRef] [Google Scholar]
  23. Bondi, H. 1952, MNRAS, 112, 195 [Google Scholar]
  24. Callister, T. A., & Farr, W. M. 2024, Phys. Rev. X, 14, 021005 [NASA ADS] [Google Scholar]
  25. Costa, G., Bressan, A., Mapelli, M., et al. 2021, MNRAS, 501, 4514 [NASA ADS] [CrossRef] [Google Scholar]
  26. Davis, S. W., & El-Abd, S. 2019, ApJ, 874, 23 [NASA ADS] [CrossRef] [Google Scholar]
  27. Davis, S. W., Blaes, O. M., Hubeny, I., & Turner, N. J. 2005, ApJ, 621, 372 [CrossRef] [Google Scholar]
  28. Dominik, M., Belczynski, K., Fryer, C., et al. 2012, ApJ, 759, 52 [Google Scholar]
  29. Done, C., & Davis, S. W. 2008, ApJ, 683, 389 [CrossRef] [Google Scholar]
  30. Done, C., Gierliński, M., & Kubota, A. 2007, A&ARv, 15, 1 [Google Scholar]
  31. Dubus, G., Hameury, J. M., & Lasota, J. P. 2001, A&A, 373, 251 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Eggenberger, P., Moyano, F. D., & den Hartogh, J. W. 2022, A&A, 664, L16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. El Mellah, I., Sander, A. A. C., Sundqvist, J. O., & Keppens, R. 2019, A&A, 622, A189 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Farmer, R., Renzo, M., de Mink, S., Fishbach, M., & Justham, S. 2020, ApJ, 902, L36 [CrossRef] [Google Scholar]
  35. Fishbach, M., & Kalogera, V. 2021, ApJ, 914, L30 [CrossRef] [Google Scholar]
  36. Fishbach, M., & Kalogera, V. 2022, ApJ, 929, L26 [NASA ADS] [CrossRef] [Google Scholar]
  37. Frank, J., King, A., & Raine, D. J. 2002, Accretion Power in Astrophysics: Third Edition (CUP) [Google Scholar]
  38. Fryer, C. L., Belczynski, K., Wiktorowicz, G., et al. 2012, ApJ, 749, 91 [Google Scholar]
  39. Fuller, J., Piro, A. L., & Jermyn, A. S. 2019, MNRAS, 485, 3661 [NASA ADS] [Google Scholar]
  40. Gaia Collaboration (Panuzzo, P., et al.) 2024, A&A, 686, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Gierliński, M., & Done, C. 2004a, MNRAS, 347, 885 [Google Scholar]
  42. Gierliński, M., & Done, C. 2004b, MNRAS, 349, L7 [Google Scholar]
  43. Gierliński, M., Zdziarski, A. A., Poutanen, J., et al. 1999, MNRAS, 309, 496 [CrossRef] [Google Scholar]
  44. Gou, L., McClintock, J. E., Liu, J., et al. 2009, ApJ, 701, 1076 [NASA ADS] [CrossRef] [Google Scholar]
  45. Gou, L., McClintock, J. E., Remillard, R. A., et al. 2014, ApJ, 790, 29 [NASA ADS] [CrossRef] [Google Scholar]
  46. Hadrava, P., & Čechura, J. 2012, A&A, 542, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Hanke, M., Wilms, J., Nowak, M. A., et al. 2009, ApJ, 690, 330 [NASA ADS] [CrossRef] [Google Scholar]
  48. Hawking, S. 1971, MNRAS, 152, 75 [Google Scholar]
  49. Heida, M., Jonker, P. G., Torres, M. A. P., & Chiavassa, A. 2017, ApJ, 846, 132 [Google Scholar]
  50. Hirai, R., & Mandel, I. 2021, PASA, 38 [CrossRef] [Google Scholar]
  51. Horne, K., & Cook, M. C. 1985, MNRAS, 214, 307 [NASA ADS] [Google Scholar]
  52. Hu, H., Inayoshi, K., Haiman, Z., et al. 2022, ApJ, 935, 140 [NASA ADS] [CrossRef] [Google Scholar]
  53. Hubeny, I., & Hubeny, V. 1998, ApJ, 505, 558 [NASA ADS] [CrossRef] [Google Scholar]
  54. Hubeny, I., & Long, K. S. 2021, MNRAS, 503, 5534 [CrossRef] [Google Scholar]
  55. Kawamura, T., Done, C., Axelsson, M., & Takahashi, T. 2023, MNRAS, 519, 4434 [NASA ADS] [CrossRef] [Google Scholar]
  56. Kawano, T., Done, C., Yamada, S., et al. 2017, PASJ, 69, 36 [NASA ADS] [CrossRef] [Google Scholar]
  57. Kinugawa, T., Inayoshi, K., Hotokezaka, K., Nakauchi, D., & Nakamura, T. 2014, MNRAS, 442, 2963 [NASA ADS] [CrossRef] [Google Scholar]
  58. Kitaki, T., Mineshige, S., Ohsuga, K., & Kawashima, T. 2021, PASJ, 73, 450 [NASA ADS] [CrossRef] [Google Scholar]
  59. Kubota, A., Makishima, K., & Ebisawa, K. 2001, ApJ, 560, L147 [NASA ADS] [CrossRef] [Google Scholar]
  60. Langer, N. 2012, ARA&A, 50, 107 [CrossRef] [Google Scholar]
  61. Lasota, J.-P. 2001, New Astron. Rev., 45, 449 [Google Scholar]
  62. Li, L.-X., Zimmerman, E. R., Narayan, R., & McClintock, J. E. 2005, ApJS, 157, 335 [NASA ADS] [CrossRef] [Google Scholar]
  63. Liu, J., McClintock, J. E., Narayan, R., Davis, S. W., & Orosz, J. A. 2008, ApJ, 679, L37 [NASA ADS] [CrossRef] [Google Scholar]
  64. Liu, J., McClintock, J. E., Narayan, R., Davis, S. W., & Orosz, J. A. 2010, ApJ, 719, L109 [NASA ADS] [CrossRef] [Google Scholar]
  65. Miller, M. C., & Miller, J. M. 2015, Phys. Rep., 548, 1 [NASA ADS] [CrossRef] [Google Scholar]
  66. Miller, J. M., Wojdowski, P., Schulz, N. S., et al. 2005, ApJ, 620, 398 [NASA ADS] [CrossRef] [Google Scholar]
  67. Miller-Jones, J. C. A., Bahramian, A., Orosz, J. A., et al. 2021, Science, 371, 1046 [Google Scholar]
  68. Mroz, P., Udalski, A., Szymanski, M. K., et al. 2024, Nature, 632, 749 [CrossRef] [Google Scholar]
  69. Novikov, I. D., & Thorne, K. S. 1973, Black Holes (Les Astres Occlus) [Google Scholar]
  70. Olejak, A., & Belczynski, K. 2021, ApJ, 921, L2 [NASA ADS] [CrossRef] [Google Scholar]
  71. Olejak, A., Belczynski, K., Bulik, T., & Sobolewska, M. 2020, A&A, 638, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Orosz, J. A., McClintock, J. E., Narayan, R., et al. 2007, Nature, 449, 872 [NASA ADS] [CrossRef] [Google Scholar]
  73. Orosz, J. A., Steeghs, D., McClintock, J. E., et al. 2009, ApJ, 697, 573 [NASA ADS] [CrossRef] [Google Scholar]
  74. Orosz, J. A., Steiner, J. F., McClintock, J. E., et al. 2014, ApJ, 794, 154 [NASA ADS] [CrossRef] [Google Scholar]
  75. Petitdemange, L., Marcotte, F., Gissinger, C., & Daniel, F. 2024, A&A, 681, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  76. Petrucci, P. O., Ursini, F., De Rosa, A., et al. 2018, A&A, 611, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Porquet, D., Done, C., Reeves, J. N., et al. 2019, A&A, 623, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  78. Poutanen, J., Zdziarski, A. A., & Ibragimov, A. 2008, MNRAS, 389, 1427 [Google Scholar]
  79. Ramachandran, V., Oskinova, L. M., Hamann, W. R., et al. 2022, A&A, 667, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  80. Remillard, R. A., & McClintock, J. E. 2006, ARA&A, 44, 49 [Google Scholar]
  81. Reynolds, C. S. 2021, ARA&A, 59, 117 [NASA ADS] [CrossRef] [Google Scholar]
  82. Rodriguez, C. L., Zevin, M., Amaro-Seoane, P., et al. 2019, Phys. Rev. D, 100, 043027 [Google Scholar]
  83. Sądowski, A., Bursa, M., Abramowicz, M., et al. 2011, A&A, 532, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  84. Sen, K., Xu, X. T., Langer, N., et al. 2021, A&A, 652, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  85. Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
  86. Spruit, H. C. 2002, A&A, 381, 923 [CrossRef] [EDP Sciences] [Google Scholar]
  87. Steiner, J. F., Narayan, R., McClintock, J. E., & Ebisawa, K. 2009, PASP, 121, 1279 [Google Scholar]
  88. Svensson, R., & Zdziarski, A. A. 1994, ApJ, 436, 599 [NASA ADS] [CrossRef] [Google Scholar]
  89. Tayler, R. J. 1973, MNRAS, 161, 365 [CrossRef] [Google Scholar]
  90. The LIGO Scientific Collaboration, the Virgo Collaboration, the KAGRA Collaboration, et al. 2023, Phys. Rev. X, 13, 011048 [NASA ADS] [Google Scholar]
  91. Thorne, K. S. 1974, ApJ, 191, 507 [Google Scholar]
  92. Tomsick, J. A., Parker, M. L., García, J. A., et al. 2018, ApJ, 855, 3 [NASA ADS] [CrossRef] [Google Scholar]
  93. Tripathi, A., Zhou, M., Abdikamalov, A. B., et al. 2020, ApJ, 897, 84 [CrossRef] [Google Scholar]
  94. Walton, D. J., Tomsick, J. A., Madsen, K. K., et al. 2016, ApJ, 826, 87 [NASA ADS] [CrossRef] [Google Scholar]
  95. Wiktorowicz, G., Belczynski, K., & Maccarone, T. 2014, Binary Syst Env. Evol., 37 [Google Scholar]
  96. Wiktorowicz, G., Lasota, J.-P., Belczynski, K., et al. 2021, ApJ, 918, 60 [CrossRef] [Google Scholar]
  97. Yoshioka, S., Mineshige, S., Ohsuga, K., Kawashima, T., & Kitaki, T. 2022, PASJ, 74, 1378 [NASA ADS] [CrossRef] [Google Scholar]
  98. Zdziarski, A. A., Johnson, W. N., & Magdziarz, P. 1996, MNRAS, 283, 193 [NASA ADS] [CrossRef] [Google Scholar]
  99. Zdziarski, A. A., Szanecki, M., Poutanen, J., Gierliński, M., & Biernacki, P. 2020, MNRAS, 492, 5234 [NASA ADS] [CrossRef] [Google Scholar]
  100. Zdziarski, A. A., Veledina, A., Szanecki, M., et al. 2023, ApJ, 951, L45 [NASA ADS] [CrossRef] [Google Scholar]
  101. Zdziarski, A. A., Banerjee, S., Chand, S., et al. 2024a, ApJ, 962, 101 [NASA ADS] [CrossRef] [Google Scholar]
  102. Zdziarski, A. A., Chand, S., Banerjee, S., et al. 2024b, ApJ, 967, L9 [NASA ADS] [CrossRef] [Google Scholar]
  103. Zhao, X., Gou, L., Dong, Y., et al. 2021a, ApJ, 916, 108 [NASA ADS] [CrossRef] [Google Scholar]
  104. Zhao, X., Gou, L., Dong, Y., et al. 2021b, ApJ, 908, 117 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Fitting Cyg X-1 spectra

We fit Cyg X-1 using two models: 1) considering a standard disc and 2) where the disc is covered by some warm optically thick material (models a and b, respectively). In both cases we model the spectra using XSPEC v.12.13.0 (Arnaud 1996).

For the standard disc we use the XSPEC model KERRBB (Li et al. 2005). This considers multi-colour blackbody emission originating from a disc structure, assuming Novikov & Thorne (1973) emissivity. All relativistic effects are taken into account, including ray-tracing from the disc to the observer. Additionally, this model always assumes that the disc extends to the ISCO.

However, Cyg X-1 always shows a high energy tail that cannot be disc emission. This is generally understood as originating from a hot optically thin inner corona, which Compton up-scatters incident disc photons to higher energies. To model this we convolve our disc emission, KERRBB, with SIMPL (Steiner et al. 2009). This takes an input seed spectrum (in this case KERRBB) and scatters a fraction of the seed photons into a power-law component (hence emulating a Comptonised spectrum). In XSPEC syntax, the model is SIMPL*KERRBB.

For model b we also have the addition of a warm optically thick skin covering the disc. This will also Compton up-scatter the disc photon to higher energies, but not sufficiently so to give a high energy tail. Instead this will give a spectrum that looks similar to a disc, but with the peak shifted to slightly higher energies and a shallower drop-off than the usual Wien tail. We model this using the convolution model THCOMP (Zdziarski et al. 1996, 2020). This takes an input seed spectrum and Compton scatters to higher energies, similar to SIMPL, however unlike SIMPL THCOMP takes the electron temperature of the Comptonising plasma as an input argument, setting the high energy turn over. Additionally, for this optically thick skin we assume that all input seed photons are Compton scattered, unlike the case for the high-energy tail where only a fraction are scattered. In XSPEC syntax the model is now CSIMPL*THCOMP*KERRBB.

The line of sight absorption to Cyg X-1 is complex and variable. Hence we need to include an absorption component in both our models, for which we use TBABS. Due to the variable nature of the absorber in Cyg X-1 we leave the column-density in TBABS as a free parameter throughout. We note that in Fig. 3 we show the spectrum corrected for absorption in colour and the original uncorrected spectrum in grey.

As the data originate from two different instruments, XIS (soft-xrays) and HXD (hard-xrays), while both onboard Suzaku, we included a cross-calibration constant in all our models. Throughout, this was fixed to 1.15, that is: increasing the model flux in the hard band by a factor 1.15. Finally, the total XSPEC models are: CONST*TBABS*CSIMPL*KERRBB for model a, and CONST*TBABS*CSIMPL*THCOMP*KERRBB for model b.

Appendix B: Revisiting M33-X7

Here we revisit the black hole spin estimate of M33-X7, performed by Liu et al. (2008), using the same methodology as for Cyg X-1. We extract the four Chandra ACIS spectra, referred to as the ’gold’ spectra in Liu et al. (2008). An initial inspection of the data show strongly disc dominated spectra, with no clear non-thermal high energy tail within the observed energy range. Hence, we used a slightly simpler model than with Cyg X-1, modelling the continuum as either a pure disc (using KERRBB, Li et al. (2005)) or a disc with a warm Comptonising medium above it (using THCOMP*KERRBB, Zdziarski et al. 1996, 2020). We also include the effects of absorption along our line of sight, which will affect the low energy emission, using TBABS. Hence the total XSPEC models are: TBABS*KERRBB for the pure disc case, and TBABS*THCOMP*KERRBB for the warm Comptonised case.

We note that since the analysis of Liu et al. (2008) the black hole mass of M33 X-7 has been updated from 15.65  M⊙ (Orosz et al. 2007) to 11.4  M⊙ (Ramachandran et al. 2022). The main effect of this will be to lower the black hole spin estimate in the case of a pure disc, as a lower black hole mass will shift the peak of the spectrum to higher energies, much in the same way as an increase in black hole spin will do. For completeness we fit the data using both the new and previous mass estimates, to highlight that our conclusions are not sensitive to this change.

Figure B.1 shows the four ACIS spectra along with their respective model fits, for the pure disc (left) and warm Comptonised medium (right). The data show a change in normalisation between some of the spectra, corresponding to a ∼10 % change in the mass-accretion rate (see e.g the difference between the green-black data model and the magenta-orange data model in Fig. B.1). Hence, during the spectral fitting we allow the mass-accretion rate to vary between the datasets, but then tie all other parameters as these should not vary between observations. The spectra were grouped such that each energy bin contained a minimum of 20 counts, allowing for the use of χ2 statistics.

thumbnail Fig. B.1.

Chandra ACIS spectra of M33-X7, re-binned for clarity. We have used the four ’gold’ spectra from Liu et al. (2008), corresponding to obs IDs: acisf1730 (black), acisf6382 (orange), acisf6387 (green), and acisf6376 (magenta). The solid lines show the best fitting model to each spectrum, where we have used a standard disc (KERRBB) on the left, and a disc covered by a warm Comptonising medium (THCOMP*KERRBB) on the right. The magenta line corresponds to the mass 15.65  M⊙ (Orosz et al. 2007, the green line to the mass fixed to 11.4  M⊙, derived in Ramachandran et al. (2022). We note that every spectrum has been de-absorbed using the best fit model. For each model the spectra were fit simultaneously, with only the mass accretion rate, Ṁ, allowed to vary between them.

Figure B.2 shows the change in χ2 as we step the fit through the possible values for black hole spin, with a standard disc on the left and a disc covered by a warm Comptonising material on the right. The standard disc clearly gives a strongly constrained value for the black hole spin, and in fact for the old mass estimate we recover the value derived in Liu et al. (2008) of ∼0.84. However, it is clear that a change in mass will affect this result, with the new mass estimate reducing the black hole spin to ∼0.70. However, the accretion flow is not necessarily characterised by a standard disc. Instead it is likely that it could be covered in a warm Comptonising material, as discussed previously for Cyg X-1 and in LMC X-1 (Zdziarski et al. 2024a,b). Unlike the case of a pure disc, this gives completely unconstrained black hole spin, with acceptable values ranging from -1 to ∼0.9 at 90 % confidence. As with both Cyg X-1 and LMC X-1, this demonstrates the strongly model dependent nature of black hole spin estimates.

thumbnail Fig. B.2.

Δχ2 curves with black hole spin as the interesting parameter for our spectral fits to M33-X7. The left panel shows the case for a standard accretion disc model (KERRBB), while the right panel shows the case where there is a warm Comptonising material above the disc (THCOMP*KERRBB). We have included both the previous mass estimate of 15.65  M⊙ (Orosz et al. 2007, magenta line) and the updated estimate of 11.4  M⊙ (Ramachandran et al. 2022, green line). The dashed black horizontal line shows Δχ2 = 2.7, indicating 90 % confidence for one interesting parameter.

All Figures

thumbnail Fig. 1.

Helium core mass is a function of the initial star mass for various metallicities. The helium core is a good approximation of the black hole mass for stars in close binaries that form BH-BH mergers (binary interactions remove H-rich envelope). Black arrows show the current stellar metallicity range of LVK (low-redshift Universe: z < 0.7) and for HMXBs that are limited to the local group of galaxies. LVK is bound to probe more massive BHs than electromagnetic HMXB observations.
In the text
thumbnail Fig. 2.

The spectral hardness versus intensity diagram for all the RXTE data to 2005 from GX339-4 (blue) and Cyg X-1 (red), shifted in intensity so that the transition from soft to hard overlapped. Hardness ratio is defined as the ratio of counts in the energy bands 6.3–10.5 and 3.8–6.3 keV. (Data from Belloni 2010.) The Cyg X-1 Suzaku data used here is shown as the magenta star.
In the text
thumbnail Fig. 3.

Cyg X-1 spectra for for: Left: Standard accretion disc (red), modeled with KERRBB, and a hot Comptonising plasma (blue) giving the high energy emission – as sketched in the top right corner; model (a). Middle: Standard accretion disc entirely covered by a warm Comptonising plasma (green), and then an inner hot Comptonising plasma (blue); model (b). Right: Same as middle panel, but with the spin fixed at aBH = 0.1. Note: the low BH spin is fully consistent with the X-ray spectral data.
In the text
thumbnail Fig. B.1.

Chandra ACIS spectra of M33-X7, re-binned for clarity. We have used the four ’gold’ spectra from Liu et al. (2008), corresponding to obs IDs: acisf1730 (black), acisf6382 (orange), acisf6387 (green), and acisf6376 (magenta). The solid lines show the best fitting model to each spectrum, where we have used a standard disc (KERRBB) on the left, and a disc covered by a warm Comptonising medium (THCOMP*KERRBB) on the right. The magenta line corresponds to the mass 15.65  M⊙ (Orosz et al. 2007, the green line to the mass fixed to 11.4  M⊙, derived in Ramachandran et al. (2022). We note that every spectrum has been de-absorbed using the best fit model. For each model the spectra were fit simultaneously, with only the mass accretion rate, Ṁ, allowed to vary between them.
In the text
thumbnail Fig. B.2.

Δχ2 curves with black hole spin as the interesting parameter for our spectral fits to M33-X7. The left panel shows the case for a standard accretion disc model (KERRBB), while the right panel shows the case where there is a warm Comptonising material above the disc (THCOMP*KERRBB). We have included both the previous mass estimate of 15.65  M⊙ (Orosz et al. 2007, magenta line) and the updated estimate of 11.4  M⊙ (Ramachandran et al. 2022, green line). The dashed black horizontal line shows Δχ2 = 2.7, indicating 90 % confidence for one interesting parameter.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.