| Issue |
A&A
Volume 690, October 2024
|
|
|---|---|---|
| Article Number | A256 | |
| Number of page(s) | 18 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202450940 | |
| Published online | 15 October 2024 | |
Whispering in the dark
Faint X-ray emission from black holes with OB star companions
1
Institute of Astronomy, Faculty of Physics, Astronomy and Informatics, Nicolaus Copernicus University, Grudziadzka 5, 87-100 Torun, Poland
2
Departamento de Física, Universidad de Santiago de Chile, Av. Victor Jara, 3659 Santiago, Chile
3
Center for Interdisciplinary Research in Astrophysics and Space Exploration (CIRAS), USACH, Santiago, Chile
4
Argelander-Institut für Astronomie, Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
5
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
6
Institut für Physik, Otto-von-Guericke Universität, Universitätsplatz 2, 39106 Magdeburg, Germany
7
Institut für Physik und Astronomie, Universität Potsdam, Karl-Liebknecht-Str. 24/25, 14476 Potsdam, Germany
Received:
31
May
2024
Accepted:
27
July
2024
Context. Recently, astrometric and spectroscopic surveys of OB stars revealed a few stellar-mass black holes (BHs) with orbital periods of as low as 10 days. Contrary to wind-fed BH high-mass X-ray binaries (HMXBs), no X-ray counterpart was detected, probably because of the absence of a radiatively efficient accretion disc around the BH. Nevertheless, dissipative processes in the hot, dilute, and strongly magnetised plasma around the BH (so-called BH corona) can still lead to non-thermal X-ray emission (e.g. synchrotron).
Aims. We determine the X-ray luminosity distribution from BH+OB star binaries up to orbital periods of a few thousand days.
Methods. We used detailed binary evolution models computed with MESA for initial primary masses of 10–90 M⊙ and orbital periods of 1–3000 d. We computed the X-ray luminosity for a broad range of radiative efficiencies that depend on the mass accretion rate and flow geometry.
Results. For typical conditions around stellar-mass BHs, we show that particle acceleration through magnetic reconnection can heat the BH corona. A substantial fraction of the gravitational potential energy from the accreted plasma is converted into non-thermal X-ray emission. Our population synthesis analysis predicts that at least 28 (up to 72) BH+OB star binaries in the Large Magellanic Cloud (LMC) produce X-ray luminosities of above 1031 erg s−1, which are observable with focused Chandra observations. We identify a population of SB1 systems in the LMC and HD96670 in the Milky Way comprising O stars with unseen companions of masses of above 2.3 M⊙, which aligns well with our predictions and may be interesting sources for follow-up observations. The predicted luminosities of the OB companions to these X-ray-emitting BHs are 104.5 − 5.5 L⊙.
Conclusions. These findings advocate for prolonged X-ray observations of the stellar-mass black hole candidates identified in the vicinity of OB stars. Such long exposures could reveal the underlying population of X-ray-faint BHs and provide constraints for the evolution from single to double degenerate binaries and identify the progenitors of gravitational wave mergers.
Key words: stars: black holes / stars: evolution / stars: massive / X-rays: binaries
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The detection of merging stellar-mass black holes (BHs) and neutron stars (Abbott et al. 2016, 2019) has triggered a thrilling quest to discover their progenitors. Co-evolution of massive binary stars (i.e. hydrogen burning starts at the same instant of time in both binary components) is a possible formation channel of merging compact objects (Belczynski et al. 2008; Marchant et al. 2016, 2021; Kruckow et al. 2018; Spera et al. 2019; Vigna-Gómez et al. 2019; Mapelli 2020; Bavera et al. 2021; Jiang et al. 2023). The stable mass-transfer channel has been shown to significantly contribute to double compact object mergers (van den Heuvel et al. 2017; Gallegos-Garcia et al. 2021; van Son et al. 2022; Shao & Li 2022; Briel et al. 2023; Picco et al. 2024; Dorozsmai & Toonen 2024; Olejak et al. 2024). However, many unconstrained assumptions (such as mass and angular momentum loss, internal mixing, and stellar winds) used in the modelling of binary evolution cripple our capacity to make reliable predictions regarding the rates and properties of double compact object mergers (Broekgaarden et al. 2022; Mandel & Broekgaarden 2022; Marchant & Bodensteiner 2024).
In the co-evolutionary scenario, high-mass X-ray binaries (HMXBs) represent an ephemeral albeit decisive phase before the formation of double compact objects from massive binaries. HMXBs contain a massive star in orbit with an X-ray-bright compact object (Walter et al. 2015; Kretschmar et al. 2019; Motta et al. 2021; Chaty 2022; Fortin et al. 2023). A few of them were found to host stellar-mass BHs accreting stellar material from mass transfer via Roche lobe overflow and/or the capture of a fraction of the stellar wind (e.g. Cygnus X-1 Orosz et al. 2011, and LMC X-1 Orosz et al. 2009). Beyond their role in explaining mergers, these systems are excellent test beds for theories of stellar evolution (Belczynski et al. 2008; Fishbach & Kalogera 2022), gravity and magnetism in the strong field regime (Narayan & Yi 1995; Bozzo et al. 2008; Karino et al. 2019), stellar winds, and X-ray irradiation (Krtička et al. 2018; Vilhu et al. 2021).
The plasma surrounding accreting stellar-mass BHs is a source of X-rays whose intensity and spectral properties depend on the flow geometry (disc or sphere-like) and on the mass-accretion rate (Shakura 1973; Narayan & Yi 1995; Frank et al. 2002). At high mass-accretion rates, a geometrically thin and optically thick accretion disc can form that is radiatively efficient and X-ray bright. However, at lower mass-accretion rates (Sharma et al. 2007; Xie & Yuan 2012) and/or when the flow is not centrifugally supported (Narayan & Yi 1994), an accretion disc seldom forms and the radiative efficiency of the plasma drops. In very sub-Eddington accretion flows, most of the kinetic energy of the electrons is not radiated away but is advected into the BH event horizon (ADAF; Ichimaru 1977; Narayan & Yi 1994; Narayan et al. 1998; Yuan 2001). Also, a significant fraction of the material captured by the gravitational potential of the BH may not eventually accrete onto the BH, instead being lost in strong winds (ADIOS – Blandford & Begelman 1999; Yuan et al. 2012, 2015). As a result, the X-ray luminosity of most stellar-mass BHs might be below the detectability threshold of all-sky instruments (∼1035 erg s−1, taken from Vanbeveren et al. 2020), while remaining detectable during outbursts.
Population synthesis models predict thousands of BHs in orbit with a main sequence, giant, or supergiant companion in the Milky Way (Shao & Li 2019, 2020). Nevertheless, most BHs in a binary with a main sequence OB star are expected to be X-ray faint due to the inability to form a radiatively efficient accretion disc around the BH (Sen et al. 2021; Hirai & Mandel 2021). In the absence of an accretion disc, X-rays are dominated by non-thermal emission from electrons accelerated in the hot, dilute, magnetised and spherical (i.e. non-centrifugally maintained) region around the BH, called the BH ‘corona’ (Bisnovatyi-Kogan & Lovelace 1997; Quataert & Narayan 1999). This radiative model has been corroborated by observations of supermassive BHs like Sagittarius A* (Baganoff et al. 2003), M 87* (Event Horizon Telescope Collaboration 2019), and NGC 3115 (Wong et al. 2011). In this work, we use the above model to investigate the properties of X-ray emission from stellar-mass BHs in orbit with a main OB star.
The sample of detected stellar-mass BHs is likely very incomplete. The Milky Way and Magellanic Clouds are predicted to harbour millions and hundreds of stellar-mass BHs, respectively (Timmes et al. 1996; Breivik et al. 2017; Langer et al. 2020; Chawla et al. 2022; Jayasinghe et al. 2023). Nevertheless, only a few tens of these objects have been confirmed through X-ray detection (Walter et al. 2015; Corral-Santana et al. 2016), with a further handful recently confirmed through monitoring of the stellar companion (Giesers et al. 2018; Thompson et al. 2019; Liu et al. 2019; Rivinius et al. 2020; Masuda & Hirano 2021; Jayasinghe et al. 2021; Gomez & Grindlay 2021; Saracino et al. 2022; Shenar et al. 2022a; Tanikawa et al. 2023; El-Badry et al. 2023a,b; Chakrabarti et al. 2023; Gaia Collaboration 2024). Most of the approximately 60 stellar-mass BHs detected through X-ray emission are transients, with periodicities of the order of years to decades (McClintock & Remillard 2006; Corral-Santana et al. 2016). In contrast, their X-ray luminosity during quiescence is several orders of magnitude lower than 1035 erg s−1.
The Large Magellanic Cloud (LMC) represents an ideal laboratory in which to hunt for stellar mass BHs with the above techniques owing to its homogeneous sample of well-characterised massive stars and low interstellar extinction compared to the Milky Way (Evans et al. 2011, 2015; Sana et al. 2013; Villaseñor et al. 2021; Mahy et al. 2020b; Shenar et al. 2022b). Several single-lined spectroscopic (SB1) binaries have been identified (Villaseñor et al. 2021; Shenar et al. 2022b). The Chandra T-ReX programme (Crowther et al. 2022) has shown that faint X-ray sources down to 1031 erg s−1 can be detected, but the statistics regarding X-ray-faint (1031–1035 erg s−1) BHs are still unclear. Here, we present a population synthesis study to predict the X-ray luminosity function of BH+OB binaries in the LMC with specific attention to the faint end of the distribution. We discuss the possibility of confirming the presence of a candidate BH through targeted X-ray searches with Chandra (Evans & Civano 2018) and SRG/eROSITA (Predehl et al. 2021; Sunyaev et al. 2021).
In Section 2, we present an investigation of the radiative mechanisms around BHs accreting at low mass-accretion rates. In Section 3, we describe the detailed binary evolution models and the assumptions we make when estimating the X-ray luminosity during the BH+OB star phase from the models. We describe our results in Sect. 4 and compare our model predictions with observations in Sect. 5. We discuss relevant uncertainties and observational challenges in Sect. 6. Section 7 summarises the takeaway messages from our work and future directions.
2. Radiative efficiency
When a black hole accretes plasma at a rate Ṁnet (in M⊙ yr−1, measured within a few times the event horizon’s radius), the release of gravitational potential energy is susceptible to produce X-rays with a luminosity 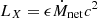 , with ϵ the radiative efficiency and c is the speed of light in vacuum. The radiative efficiency of this plasma (and, in turn, the spectral properties of the emission) depends on the flow geometry and the mass accretion rate (Liu & Qiao 2022). If the plasma is supplied by a Roche lobe overflowing stellar companion, a disc unavoidably forms (Savonije 1978). If the companion to the BH is not Roche-lobe filling, the flow geometry is set by the specific angular momentum l of the accreted plasma from the stellar wind of the companion (Sect. 3.2).
, with ϵ the radiative efficiency and c is the speed of light in vacuum. The radiative efficiency of this plasma (and, in turn, the spectral properties of the emission) depends on the flow geometry and the mass accretion rate (Liu & Qiao 2022). If the plasma is supplied by a Roche lobe overflowing stellar companion, a disc unavoidably forms (Savonije 1978). If the companion to the BH is not Roche-lobe filling, the flow geometry is set by the specific angular momentum l of the accreted plasma from the stellar wind of the companion (Sect. 3.2).
The accretion regime is determined by the ratio Ṁnet/ṀEdd, where ṀEdd is the Eddington mass accretion rate. ṀEdd is set as the mass accretion rate at which the BH radiates at the Eddington luminosity if the radiative efficiency is ϵ = 10%. The Eddington luminosity is given by
with G the gravitational constant, MBH is the mass of the BH, and κ is the opacity. A typical value for the case of Thomson scattering of free electrons is 0.4 cm2 g−1. This gives
In massive systems where the stellar companion to the BH fills its Roche lobe, the high mass transfer rate may lead to a super-Eddington accretion (Ṁnet/ṀEdd > 1) and the formation of ultraluminous X-ray binaries (e.g. Quast et al. 2019). When the stellar companion to the BH does not fill its Roche lobe, the BH can accrete mass from the stellar wind of the companion. In this case, an accretion disc can form if the specific angular momentum of the accreted stellar wind matter is sufficient to orbit around the BH beyond its event horizon.
2.1. Sub-Eddington accretion regime
When an accretion disc forms around a BH with a stellar companion that does not fill its Roche lobe, the mass accretion rate typically lies between 0.1% and 100% of the Eddington mass accretion rate (e.g. see Fig. A.1 of Sen et al. 2021). Accretion is mediated by a geometrically thin and optically thick accretion disc. The radiative efficiency lies ϵ between 6% and 43%, depending on the black hole spin and the misalignment between the disc and the black hole spin (Novikov & Thorne 1973).
A decrease in the mass accretion rate without a change in the accretion flow geometry is possible, for instance, if the density of the OB star wind drops without changes in the wind velocity. In this case, the plasma might no longer be dense enough to cool radiatively at a rate which balances viscous heating. The disc thickens and becomes a ‘slim-disc’, as the relative contribution of the thermal support increases. A large fraction of the gravitational potential energy released might be advected into the black hole’s event horizon, as described by the ADAF (Ichimaru 1977; Narayan & Yi 1994). Therefore, the radiative efficiency ϵ drops. It might be the reason for the transition between the high/soft and the low/hard states we observe in black hole hosting X-ray binaries (Belloni 2010). It could also explain the low X-ray luminosity of the BH candidate around the O-type main-sequence star HD96670, in spite of its short orbital period (Gomez & Grindlay 2021).
Alternatively, if the flow is magnetised, it can also transit to a magnetically arrested disc (MAD, Begelman et al. 2022) where accretion proceeds through episodic ejection of magnetic bubbles via the interchange instability (Porth et al. 2021) and through a reconnecting current sheet between the inner edge of the disc and the black hole event horizon (Ripperda et al. 2022). On the other hand, if the mass supply rate decreases due to an increase in wind speed and/or orbital separation, it is accompanied by a drop in specific angular momentum and the disc vanishes.
Owing to the scale-invariant properties of black holes, emission from supermassive black holes can provide fruitful insights to model X-ray faint stellar-mass black holes. Sagittarius A* is thought to be fed by the winds from orbiting nearby Wolf-Rayet stars (Russell et al. 2017; Ressler et al. 2023). Only a fraction of the mass supplied at the Bondi radius reaches the black hole event horizon though: Faraday rotation (Bower et al. 2003; Marrone et al. 2007; Wang et al. 2013) and extrapolation of magneto-hydrodynamic simulations (Ressler et al. 2018) lead to 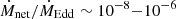 in the immediate vicinity of the BH, but the presence of a disc is unclear. In spite of its status of active galactic nucleus, M87* also accretes at a low rate, with
in the immediate vicinity of the BH, but the presence of a disc is unclear. In spite of its status of active galactic nucleus, M87* also accretes at a low rate, with 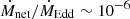 (Prieto et al. 2016), orders of magnitude below the geometrically thin, optically thick disc regime.
(Prieto et al. 2016), orders of magnitude below the geometrically thin, optically thick disc regime.
It was found from polarimetry that the emission from these objects originates in a dilute and highly magnetised corona populated with hot synchrotron-emitting electrons (Bower et al. 2018). Similar conclusions were drawn for stellar-mass black holes accreting at a rate below 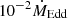 (e.g. Cygnus X-1 in the low/hard state, Cangemi et al. 2021). The range of mass accretion rates onto stellar mass BHs from the stellar wind of its companion is also expected to be the range
(e.g. Cygnus X-1 in the low/hard state, Cangemi et al. 2021). The range of mass accretion rates onto stellar mass BHs from the stellar wind of its companion is also expected to be the range 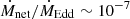 –10−2 (Fig. A.1 of Sen et al. 2021). In both stellar-mass and supermassive BHs, coronal heating is ensured by particle acceleration processes at play once the plasma becomes dilute enough to be collisionless (Gruzinov 1998).
–10−2 (Fig. A.1 of Sen et al. 2021). In both stellar-mass and supermassive BHs, coronal heating is ensured by particle acceleration processes at play once the plasma becomes dilute enough to be collisionless (Gruzinov 1998).
2.2. Particle acceleration
In collisionless environments, particles are susceptible to being accelerated up to relativistic speeds by shocks, turbulence, and magnetic reconnection (Gruzinov 1998).
2.2.1. Shocks and turbulence
The surroundings of an accreting black hole are prone to magnetised relativistic shocks due to the accretion-ejection dynamics. They are expected in black hole’s jets (Malzac 2013) and collimated disc outflows (Jacquemin-Ide et al. 2021). At shocks, particles can bounce back and forth across the shock and gain each time a certain amount of kinetic energy (see review by Pelletier et al. 2017). This process called diffusive shock acceleration (i.e. first-order Fermi process), can accelerate particles up to relativistic speeds (Ellison et al. 1990). Furthermore, black holes’ corona may show strong Alfvénic turbulence (Sandoval et al. 2024; Grošelj et al. 2024) where particles undergo stochastic acceleration (i.e. second-order Fermi process) through multiple magnetic mirroring episodes which provide them with a net amount of kinetic energy (Fermi 1949). Both processes accelerate ions and electrons into a non-thermal power-law energy distribution (Comisso & Sironi 2022). It has been shown to be a process susceptible to contributing to the heating of black holes’ coronae (Chandran et al. 2018; Hankla et al. 2022).
2.2.2. Magnetic reconnection
Particles can also be accelerated via magnetic reconnection which occurs in current sheets formed at the interface between magnetic field lines of opposite polarity. In these sheets, a very high non-ideal electric field appears at the X-points when magnetic field lines reconnect (Asenjo & Comisso 2019). It accelerates particles which gather into magnetic islands, called plasmoids, formed in the current sheet by the tearing instability (Zenitani & Hoshino 2007). The rate at which electromagnetic energy is dissipated and converted into particle kinetic energy (the reconnection rate) depends on the cold magnetisation parameter σ of the plasma, defined as the ratio of the magnetic to the inertial mass energy of the particles (for a recent review, see Kagan et al. 2015):
with B the magnitude of the magnetic field, n the plasma number density, ΓL the bulk Lorentz factor and me the mass of the electron. Estimates for stellar-mass black holes indicate that the magnetic field in which the electrons are embedded can be strong enough to accelerate them up to relativistic Lorentz factors via magnetic reconnection in the corona (Poutanen & Vurm 2009). The efficiency of this mechanism is hardly affected by the presence or not of a disc, as shown by the spherically symmetric simulations ran by Galishnikova et al. (2023) where reconnecting current sheets spontaneously form as the highly magnetised plasma is accreted. Furthermore, the reconnection rate is enhanced by turbulence (Lazarian & Vishniac 1999; Lazarian et al. 2012) and turbulence-driven magnetic reconnection has been shown to be an efficient acceleration mechanism at the basis of the black hole’s jet (Singh et al. 2015).
2.2.3. Relative contribution
The relative contribution of the above mechanisms to particle acceleration depends on the magnetisation parameter σ. For instance, particle acceleration at relativistic shocks is significantly quenched when σ is above 10−2 (Lemoine & Pelletier 2010; Sironi et al. 2013; Plotnikov et al. 2018), while the magnetic reconnection rate plateaus at 10% when σ is above a few 10 (Werner et al. 2018).
We now evaluate the magnetisation parameter in the BH vicinity assuming that the stellar magnetic flux is advected inward by the accreted material. We work in the wind accretion regime, where the wind speed υw≫ aΩ the orbital speed (Ω is the orbital angular speed) and the accretion radius Racc ≪ a the orbital separation. At the bow shock, formed upstream of the black hole by the gravitational beaming of the stellar wind, the density can be approximated by:
where Ṁw is the stellar mass loss rate. Similarly, if the stellar magnetic field is dominated by its radial component (ud-Doula & Owocki 2002), the magnetic field at the bow shock is:
where R* is the stellar radius and B* is the magnetic field at the stellar surface. Within the shock, we assume spherical Bondi accretion and get the mass density and magnetic field profiles (Cunningham et al. 2012):
where we introduced the parameter s to represent the decrease of the accretion rate as we get closer to the BH due to outflows (Xie & Yuan 2012). Hereafter, in Sect. 3.2, we introduce the accretion radius which stands for the gravitational cross-section of the BH. As the stellar wind is beamed toward the BH, it forms a bow shock of size comparable to the accretion radius. Within this region, we assume that the plasma flowing onto the BH is spherically symmetric. Then, using Eq. (3) and the expression the accretion radius in Eq. (19), we deduce the magnetisation parameter σ of the electrons at 10rg, where rg = GMBH/c2 is the gravitational radius from the BH, to be:
where we assumed that n = ρ/mp since the ions’ mass dominates and ΓL = 1. We consider a fiducial value of s = 0.4 to account for the outflows within the shocked region around the BH (Xie & Yuan 2012). In these conditions, lower limits on σ can be obtained by setting υw to the terminal wind speed of an O star (typically ∼2000 km s−1). We take the following standard values: a stellar mass loss rate typical of an LMC O-type star 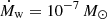 yr−1 (Brands et al. 2022), a stellar magnetic field of B* = 30 G (30 G is below the detection sensitivity of ∼80% of the stars observed in the MiMeS survey, Wade et al. 2016; Grunhut et al. 2017; Petit et al. 2019), and a stellar radius of R* = 20 R⊙. Then, for orbital separations ranging between 3 R* and 100 R*, σ is at least 103 − 106. The magnetisation parameter can also be estimated from observations interpreted via radiative models. For instance, in the BH-hosting HMXB Cygnus X-1, the analysis of the polarised synchrotron emission (Cangemi et al. 2021) indicates that σ = 103 − 106 in the innermost regions, which is coherent with the values obtained for a magnetic field near equipartition with the ion energy density (Malzac & Belmont 2009). This agrees with the values we derived from our toy model of stellar magnetic flux compression.
yr−1 (Brands et al. 2022), a stellar magnetic field of B* = 30 G (30 G is below the detection sensitivity of ∼80% of the stars observed in the MiMeS survey, Wade et al. 2016; Grunhut et al. 2017; Petit et al. 2019), and a stellar radius of R* = 20 R⊙. Then, for orbital separations ranging between 3 R* and 100 R*, σ is at least 103 − 106. The magnetisation parameter can also be estimated from observations interpreted via radiative models. For instance, in the BH-hosting HMXB Cygnus X-1, the analysis of the polarised synchrotron emission (Cangemi et al. 2021) indicates that σ = 103 − 106 in the innermost regions, which is coherent with the values obtained for a magnetic field near equipartition with the ion energy density (Malzac & Belmont 2009). This agrees with the values we derived from our toy model of stellar magnetic flux compression.
Given the high magnetisation parameters we can expect around stellar-mass BHs fed by the wind from an OB stellar companion, it is safe to assume that the main particle acceleration mechanism in the corona is magnetic reconnection in the relativistic regime (i.e. σ higher than a few 10), where the reconnection rate is ∼10% (or even higher if reconnection is turbulence-driven). In the MAD regime, the approximate equipartition between accretion and magnetic energy density implies that a large fraction of 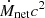 could serve to accelerate the electrons via magnetic reconnection. This is in agreement with observations of supermassive BHs where fits from detailed radiative models indicate that the electron heating parameter δ, that is, the fraction of the viscously dissipated energy that heats the electrons, is high, with values ranging between 0.1 and 0.5 (Yuan et al. 2003; Yu et al. 2011; Liu & Wu 2013).
could serve to accelerate the electrons via magnetic reconnection. This is in agreement with observations of supermassive BHs where fits from detailed radiative models indicate that the electron heating parameter δ, that is, the fraction of the viscously dissipated energy that heats the electrons, is high, with values ranging between 0.1 and 0.5 (Yuan et al. 2003; Yu et al. 2011; Liu & Wu 2013).
2.3. Non-thermalised emission
In classic radiatively inefficient accretion flows, be it because of the lack of accretion disc or of the low Ṁnet/ṀEdd, the ions and the electrons are no longer coupled through Coulomb interactions due to the low plasma density (Mościbrodzka et al. 2016). The temperatures of the ions and electrons differ and the electron distribution can develop a significant non-thermal component through particle acceleration. Indeed, Coulomb collisions between electrons become negligible for 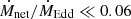 (Sharma et al. 2007), and therefore the presence of a non-thermal population is needed to account for the spectrum of Cygnus X-1 in the low/hard state for instance (Cangemi et al. 2021). We show in Sect. 2.2 that the energy reservoir contained in the magnetised accretion flow can be efficiently tapped through magnetic reconnection in the very sub-Eddington regime
(Sharma et al. 2007), and therefore the presence of a non-thermal population is needed to account for the spectrum of Cygnus X-1 in the low/hard state for instance (Cangemi et al. 2021). We show in Sect. 2.2 that the energy reservoir contained in the magnetised accretion flow can be efficiently tapped through magnetic reconnection in the very sub-Eddington regime 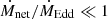 (see also Sharma et al. 2007). The electrons accelerated through this process will emit non-thermal radiation through synchrotron, bremsstrahlung, and inverse Compton scattering. Hereafter, we focus on the collisionless regime and estimate the synchrotron luminosity from the purely non-thermal population of electrons which should dominate at low mass accretion rate.
(see also Sharma et al. 2007). The electrons accelerated through this process will emit non-thermal radiation through synchrotron, bremsstrahlung, and inverse Compton scattering. Hereafter, we focus on the collisionless regime and estimate the synchrotron luminosity from the purely non-thermal population of electrons which should dominate at low mass accretion rate.
2.3.1. Synchrotron
As charged particles spiral around magnetic field lines, they emit synchrotron radiation. The radiative energy emission rate from a single electron of charge −e (with e > 0) and Lorentz factor γ in an ambient magnetic field B is:
where σT is the electron cross-section for Thomson scattering. The total synchrotron luminosity Lsync produced by the electrons contained in a fiducial uniform sphere of radius 10rg around the BH is:
where n is the number density of electrons and rg = GMBH/c2. We obtain a synchrotron luminosity:
where we used the ambient magnetic field and electron number density values in the denominator found by Cangemi et al. (2021) in the vicinity of the ∼20M⊙ BH in Cygnus X-1 (Miller-Jones et al. 2021), from the analysis of the polarised emission.
This idealised one-zone model does not account for the non-uniform density and magnetic field, nor the shape of the underlying distribution of electron energy. In the relativistic regime, the maximum Lorentz factor reachable by an electron accelerated by magnetic reconnection over a length scale rg in an ambient magnetic field B is:
where K is the plasma multiplicity. Even at low mass accretion rates and for a maximally rotating BH (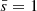 ), we expect K > 1 (El Mellah et al. 2022), so γmax > 103 in the magnetised plasma surrounding stellar-mass BHs capturing the wind from an OB companion.
), we expect K > 1 (El Mellah et al. 2022), so γmax > 103 in the magnetised plasma surrounding stellar-mass BHs capturing the wind from an OB companion.
Acceleration through magnetic reconnection is typically described by a power law distribution N(γ)∝γ−p with an exponent p ∼ 0.9 − 1.2 (Werner et al. 2016; El Mellah et al. 2022). Hence, the contribution of the highest energy electrons dominate the emission. However, this simplified estimate of the synchrotron power with γ = 100 shows that, provided electrons are accelerated to significant Lorentz factors and embedded in a high magnetic field, they can produce a significant amount of non-thermal synchrotron emission. For stellar-mass BHs without an accretion disc, the peak of this emission is expected at a photon energy of 17 keV (with the values above of Lorentz factor and magnetic field), in hard X-rays.
2.3.2. Bremsstrahlung
In the absence of magnetic fields, particles free fall directly in the BH such that energy transfer and cooling are negligible. In this case, the X-ray emission is bremsstrahlung dominated and the process can be treated adiabatically. From the mass continuity equation 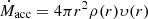 , we can write
, we can write
where r is the distance to the BH. Assuming 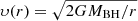 as the free-fall velocity, we get
as the free-fall velocity, we get
For an adiabatic process, T ∝ ρ2/3, the temperature profile of the free-falling particles become
where T0 and ρ0 are assumed to match the ambient wind temperature and density of the OB star companion, far away from the BH. The energy per unit time emitted by the gas into a 4π solid angle from a volume dV is given by (Frank et al. 2002)
where ne(r) and np(r) are electron and proton number densities respectively and T(r) is the temperature stratification. Assuming the infalling wind matter is fully ionised, spherically symmetric, and composed of hydrogen and helium, Eq. (16) can be integrated from the Schwarzschild radius Rsch to the accretion radius Racc using the temperature and density dependencies above.
For a stellar-mass BH accreting mass from the interstellar medium, it has been shown that the resulting luminosity is extremely low, orders of magnitude below observable limits (see discussion in Sect. 7.8, following Eq. (7.16) of Frank et al. 2002). For BHs accreting material from the wind of an OB star companion, the mass accretion rate is largely set by the wind mass loss rate of the OB star and the binary orbital period. The radiative luminosity in the X-ray band is at most ∼1030 erg s−1 at orbital period of 10 d and falls steeply with the mass accretion rate, such that at orbital periods of 100 d the luminosity is less than ∼1027 erg s−1 (Quast et al., in prep.). Hence, thermal bremsstrahlung is not expected to contribute to observable X-ray emission.
X-ray line emissivity due to bound-bound transitions can be significantly higher than the thermal bremsstrahlung emission if the temperature of ions drops below 106 K. However, this temperature regime should not be relevant near the BH since the ion temperature is much higher than the electron temperature in the magnetised plasma, and electron temperature is typically above 106 K.
2.3.3. Inverse Compton scattering
Relativistic electrons upscatter soft X-ray photons through Inverse Compton in optically thin and hot accretion flow. The seed photons can come from the multi-colour black body emission from an underlying thin disc (at high mass and angular momentum accretion rates), or the synchrotron emission. In the latter case, it could shift the peak of synchrotron emission up to hard X-rays (Sridhar et al. 2021), although Comptonisation is expected to be subdominant when 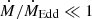 (Esin et al. 1997).
(Esin et al. 1997).
3. Methods
We discuss the grid of binary evolution models utilised for this work in Sect. 3.1. We discuss the criterion for forming an accretion disc around the BH in BH+OB star binaries in Sect. 3.2. We outline the procedure to calculate the X-ray luminosity from a BH+OB star binary in the presence and absence of a geometrically thin, optically thick accretion disc in Sects. 3.3 and 3.4, respectively. In Sect. 3.5, we define the distribution functions that are used to predict the observable stellar parameters from our binary models during the BH+OB star phase.
3.1. Stellar evolution models
We use the detailed binary evolution models computed by Marchant (2017) and Pauli et al. (2022) using the 1D stellarevolution code MESA1 (Modules for Experiments in Stellar Astrophysics, Paxton et al. 2011, 2013, 2015, 2018, 2019), version 8845 and 10398 respectively2. A detailed description of all stellar and binary physics assumptions can be found in Marchant (2017), Langer et al. (2020), Sen et al. (2022), Pauli et al. (2022) and Sen et al. (2023). We outline below the necessary details required to follow our work.
The initial mass of the primary star M1, i (initially more massive and forms the compact object) ranges from ∼10–90 M⊙ in steps of log (M1, i/M⊙) = 0.05. The initial orbital periods Pi and mass ratios qi (initial mass of the secondary star M2, i divided by the initial mass of the primary star M1, i) range from 1.4–3162 d (in steps of log (Pi/d = 0.05) and 0.25–0.95 (in steps of 0.05), respectively. Models with initial primary masses 10–40 M⊙ are taken from the work of Marchant (2017), and the models with initial primary masses 40–90 M⊙ are taken from the work of Pauli et al. (2022). Both sets of models assume a metallicity suitable for the LMC.
The models start from the onset of core hydrogen burning of the primary, and both components are assumed to start core hydrogen burning simultaneously. When the initially more massive star fills its Roche lobe, mass transfer via Roche-lobe Overflow is modelled using the “contact” scheme in MESA (Marchant et al. 2016). Mass transfer is assumed to be conservative until the accretor spins up to critical rotation (Packet 1981). Any further mass transferred from a Roche-lobe filling donor to a critically rotating stellar companion is removed from the star through enhanced stellar wind mass and momentum loss (Langer et al. 2003; Petrovic et al. 2005). When the combined luminosity of both binary components is insufficient to drive this excess mass loss, we assume the binary model will merge and terminate the evolution.
If both binary components fill its Roche lobe during a mass transfer phase, the evolution of the binary model in such a contact configuration is calculated until one of the stars overflows the L2 Lagrangian point of the binary model. Otherwise, the evolution of both stars is followed until the end of the core carbon burning of the primary. The details of the mass transfer model and the ensuing mass transfer efficiency during different mass transfer phases are studied in detail in Sen et al. (2022). In the models, mass transfer is conservative until orbital periods of 5 d, where tides (Detmers et al. 2008; Zahn 1977) can halt the spin-up of the mass-gaining star. For longer orbital periods, the overall mass transfer efficiency of the binary models is ∼5–10%.
Upon core carbon depletion of the primary, we assume that if the helium core mass of the primary is larger than 6.6 M⊙, the helium core of the primary directly collapses into a BH without a natal kick and the mass of the BH formed equals the helium core mass of the primary (Ertl et al. 2016; Müller et al. 2016; Sukhbold et al. 2018; Langer et al. 2020). The BH kick depends on the neutrino energy available and the asymmetry of the fall-back material (Belczynski et al. 2012; Janka 2013). Empirical evidence towards the magnitude of BH kicks remains inconclusive (e.g. Farr et al. 2011), with some studies positing the need for a low kick (Wong et al. 2012), while others requiring a significantly high kick (Repetto et al. 2012). It has been recently shown that a BH kick is not necessary to explain the lack of observed wind-fed BH HMXBs in the Milky Way compared to the number of Wolf-Rayet+O star binaries (Sen et al. 2021). When the first BH forms, the secondary (hereafter called the OB star companion to the BH) still burns hydrogen in its core. This marks the onset of the BH+OB star phase studied in this work.
The further evolution of the OB star companion in the BH+OB binary is modelled as a single star. The mass and angular momentum loss determine the orbital period evolution during the BH+OB star phase via the stellar wind of the OB star companion (Quast et al. 2019; El Mellah et al. 2020). For the typical mass ratios of the BH to the OB star companion, and the fraction of the OB stellar wind accreted by the BH (Sen et al. 2021), we can assume that the orbital period remains constant during the BH+OB star phase (El Mellah et al. 2020, Fig. 10). Hence, we assume the orbital period during the BH+OB star phase is equal to the orbital period of the binary model at the formation of the BH. The above simple assumptions result in a strict lower limit to the BH mass, and a constant orbital period during the BH+OB star phase. This leads to a small modelling uncertainty (at most a factor of 2, El Mellah et al. 2020) in the calculated mass accretion rate Ṁacc (Eq. (22)).
As the models undergo mass transfer before the BH+OB star phase and there is no kick velocity, we assume the orbit during the BH+OB star phase will remain circular. Lastly, we assume that the BHs formed from the collapse of the primary have negligible spins (Kerr parameter χ = 0, Qin et al. 2018; Ma & Fuller 2023). The BH+OB star phase ends when the OB star companion completes core hydrogen burning or fills its Roche lobe while on the main sequence.
3.2. Disc-formation criterion
To determine whether a disc forms, the specific angular momentum of the infalling matter onto the BH must be compared to the specific angular momentum lISCO of a test particle at the ISCO of the BH. For a spinning black hole, it is entirely set by the black hole mass MBH and its dimensionless spin ![$ \bar{s}\in [0,1] $](/articles/aa/full_html/2024/10/aa50940-24/aa50940-24-eq30.gif) , with
, with 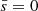 for a non-spinning black hole and
for a non-spinning black hole and 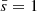 for a maximally spinning black hole:
for a maximally spinning black hole:
where 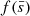 a dimensionless function of
a dimensionless function of 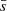 only. Efficient angular momentum transport predicts that the first-born BH in a massive binary system will be slowly spinning (Qin et al. 2018; Ma & Fuller 2023; Marchant et al. 2023).
only. Efficient angular momentum transport predicts that the first-born BH in a massive binary system will be slowly spinning (Qin et al. 2018; Ma & Fuller 2023; Marchant et al. 2023).
If accretion proceeds through stellar wind capture (instead of Roche lobe overflow), a bow shock forms around the black hole (El Mellah & Casse 2015). Within the shocked region, matter flattens into a disc, that is, a centrifugally maintained structure, provided its specific angular momentum is higher than lISCO. When the BH accretes matter from the OB star wind, and the wind speed at the orbital separation υw is larger than the orbital speed aΩ, we have (cf. Eq. (10) of Sen et al. 2021, where the criterion is expressed in terms of the ratio of the circularisation radius of a Keplerian accretion disc to the innermost stable circular orbit of the BH)
where a is the orbital separation, Ω is the orbital angular speed, q = MOB/MBH is the mass ratio, MOB is the mass of the OB star and η is the specific angular momentum of the accreted material in units of Racc2Ω/2 (Shapiro & Lightman 1976), with Racc the accretion radius which is given by, in the wind accretion regime
Equation (18) shows that accretion discs form preferentially in systems where the wind speed is low compared to the orbital speed. We can express the condition for disc formation as
where P is the orbital period. Hydrodynamical simulations of accretion onto stellar-mass BHs suggest that η ∼ 1/3 (Livio et al. 1986; Ruffert 1999). For a Schwarzschild BH, 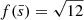 (Carroll 2019). In the Newtonian approximation,
(Carroll 2019). In the Newtonian approximation, 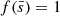 for a non-spinning BH. In Sect. 4, we show the results for
for a non-spinning BH. In Sect. 4, we show the results for 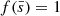 to be consistent with the accretion disc formation criterion in Sen et al. (2021), but also discuss the statistics for
to be consistent with the accretion disc formation criterion in Sen et al. (2021), but also discuss the statistics for 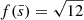 in Sect. 6.4.
in Sect. 6.4.
3.3. X-ray luminosity from a Keplerian accretion disc
If an accretion disc can form, the X-ray luminosity LX from the accretion disc is calculated as
where G is the Gravitational constant, RISCO is the radius of the innermost stable circular orbit of the BH, MBH is the mass of the BH, Ṁacc is the mass accretion rate at the accretion radius Racc given by the Bondi-Hoyle accretion rate (Bondi & Hoyle 1944), along with a self-limiting effect from the Eddington luminosity (Davidson & Ostriker 1973; Vanbeveren et al. 2020)
where Ṁw is the wind loss rate of the OB star, a is the orbital separation, Racc is the accretion radius of the BH, υw is the wind velocity of the O star, υrel is the relative velocity of the BH with respect to the wind velocity (see Eqs. (1)–(8) of Sen et al. 2021), and ηEdd represents the self-limiting effect of the Eddington luminosity,
Here, LEdd, BH is the Eddington luminosity of the BH given by
where X is the hydrogen mass fraction of the accreted material and κe = 0.2(1 + X) cm2 g−1 is the electron scattering opacity. Combining the above equations,
where α depends on the Eddington accretion rate 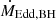 ,
,
with
and
where MO, RO, and Γe are the mass, radius, and Eddington factor of the OB star companion.
3.4. X-ray luminosity without an accretion disc
When the specific angular momentum carried by the OB star wind matter is insufficient to form a Keplerian accretion disc around the BH, the wind matter can spiral into the BH following the magnetic field lines. During this in-fall, we show in Sect. 2.2.3 that electrons can receive a portion of the viscously dissipated energy of the in-falling matter, and emit radiation in the X-ray band. The X-ray luminosity LX is
where ϵ is the radiative efficiency and Ṁnet is the net mass-accretion rate at the radius of the ISCO of the BH.
Recent simulations of hot accretion flows have revealed the presence of outflows in ADAFs, such that the mass inflow rate of the accreting gas decreases as the material approaches the event horizon of the BH (Stone et al. 1999; Yuan & Bu 2010). We assume the mass-accretion rate scales with the radius from the BH by a power-law (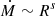 , Stone et al. 1999; Igumenshchev et al. 2000; Stone & Pringle 2001; Yuan & Bu 2010). Hence, the relation between the net mass-accretion rate at the radius of the innermost stable circular orbit Ṁnet and the mass-accretion rate at the accretion radius Ṁacc is given by
, Stone et al. 1999; Igumenshchev et al. 2000; Stone & Pringle 2001; Yuan & Bu 2010). Hence, the relation between the net mass-accretion rate at the radius of the innermost stable circular orbit Ṁnet and the mass-accretion rate at the accretion radius Ṁacc is given by
In consistency with Sect. 2.2.3, we assume s ≈ 0.4 (Xie & Yuan 2012). We assume this parameter to be constant during the BH+OB star phase in all our models.
Xie & Yuan (2012, Fig. 1) studied the radiative efficiency ϵ of hot accretion flows around a stellar-mass BH orbiting an OB star companion. They derive ϵ as a function of the net mass-accretion rate Ṁnet (i.e. ϵ = ϵ(δ,Ṁnet)), for three different values of the viscous dissipation parameter δ (defined in Sect. 2.2.3). From their Figure 1, we extract the values of the radiative efficiency as a function of the net mass-accretion rate to calculate the X-ray luminosity during the BH+OB star phase in our models for viscous dissipation parameter δ = 0.001, 0.1, 0.5. While we show in Sect. 2 that viscous heating of electrons can be efficient even in the case of stellar mass BHs with OB star companions, we present our results for all three values above to derive a lower limit on the number of faint X-ray sources from BH+OB star binaries for the most inefficient case of viscous heating.
3.5. Histogram distribution functions
The distribution function of an observable parameter Xobs is constructed by weighing the values of Xobs at each timestep during the BH+OB star phase with the initial mass function (Salpeter 1955) and binary distribution functions (Sana et al. 2013) of the progenitor binary model ‘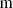 ’, then summing over all models and normalising to unity. The number fraction hobs in a given histogram bin [X1,X2] of the observable Xobs is given by
’, then summing over all models and normalising to unity. The number fraction hobs in a given histogram bin [X1,X2] of the observable Xobs is given by
where N is the total number of binary models that go through the BH+OB star phase, Δt[X1, X2],m is the amount of time the value of the observable Xobs lies between X1 and X2 for a given model m, ΔtBH + O, m is the total duration of the BH+OB star phase of the model m. Lastly, Wm is the birth weight of each model given by
Using the above definitions, we derive the distributions of observable properties during the BH+OB phase of our models. As such, the histograms show the distribution of observables in an unbiased, ideal and complete sample of BH+OB star binaries. Finally, to compare the X-ray luminosity arising from shocks in the OB star wind (LX, wind) to the X-ray luminosity arising from the vicinity of the BH, we take LX, wind as 10−7 times the bolometric luminosity of the OB star (Feldmeier et al. 1997; Huenemoerder et al. 2012; Crowther et al. 2022; Bernini-Peron et al. 2023).
4. Results
4.1. Mass-accretion rate
Figure 1 shows the distribution of the mass-accretion rate at the accretion radius (left panel) and the net mass-accretion rate near the event horizon of the BH (right panel). Higher mass-accretion rates are reached for shorter orbital period systems (Eq. (22), expressed in terms of orbital separation). The peak in the mass-accretion rate distribution is 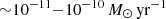 and
and 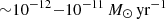 for 1.4–10 d and 10–100 d initial orbital periods respectively. The shortest-period systems can also form an accretion disc around the BH (Sen et al. 2021), denoted by the black hatching. We note however that there is a significant contribution from the 10–100 d binaries to the population of BH+OB star systems that can form an accretion disc (see Sect. 4.3).
for 1.4–10 d and 10–100 d initial orbital periods respectively. The shortest-period systems can also form an accretion disc around the BH (Sen et al. 2021), denoted by the black hatching. We note however that there is a significant contribution from the 10–100 d binaries to the population of BH+OB star systems that can form an accretion disc (see Sect. 4.3).
 |
Fig. 1. Distribution of the mass-accretion rate at the accretion radius (Eq. (22), left panel) and the mass-accretion rate at the event horizon of the BH (Eq. (32), right panel), during the BH+OB star phase. The three colours denote the contributions from different initial orbital period ranges. The coloured histograms are stacked on each other, and the sum of the ordinate values equals unity. The black hatching shows the contribution from the BH+OB star binaries where a Keplerian accretion disc can form. |
The highest mass-accretion rates (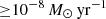 ) is mostly from models in the 10–100 d initial orbital period range. The shortest initial orbital period models (< 2 d) enter a contact phase and merge on the main sequence (Menon et al. 2021). Many of the short-period binary models (2–10 d) in our grid do not survive their prior Case A and Case AB mass transfer phase (Fig. 1 of Sen et al. 2022, Appendix C of Pauli et al. 2022) to reach the BH+OB star phase.
) is mostly from models in the 10–100 d initial orbital period range. The shortest initial orbital period models (< 2 d) enter a contact phase and merge on the main sequence (Menon et al. 2021). Many of the short-period binary models (2–10 d) in our grid do not survive their prior Case A and Case AB mass transfer phase (Fig. 1 of Sen et al. 2022, Appendix C of Pauli et al. 2022) to reach the BH+OB star phase.
The total number of short-period (1.4–10 d) binary models contributing to the distribution of mass-accretion rate is much smaller than the number of models with longer initial orbital periods (10–100 d). Correspondingly, the peak in the distribution of mass-accretion rate does not occur at the highest mass-accretion rates but at lower mass-accretion rates where more models contribute to the histogram function (Eq. (33)), despite our assumed intrinsic period distribution favouring short-period binaries (Eq. (34)).
The mass-accretion rate typically decreases for models with longer orbital periods (Eq. (22)). The drop in the number of systems with mass-accretion rates below 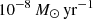 is produced by our assumption that longer-period binaries are less likely to be born (Eq. (34)). Hence, the peak in the distribution of mass-accretion rates arises at ∼10−12–10−11 M⊙ yr−1, from BH+OB star binaries with intermediate orbital periods.
is produced by our assumption that longer-period binaries are less likely to be born (Eq. (34)). Hence, the peak in the distribution of mass-accretion rates arises at ∼10−12–10−11 M⊙ yr−1, from BH+OB star binaries with intermediate orbital periods.
We assume that mass outflows reduce the mass-accretion rate from the accretion radius to the BH event horizon (Eq. (32)). The right panel shows that the peak in the distribution of the net mass-accretion rate near the event horizon of the BH is ∼2 orders of magnitude lower than that at the accretion radius. This reduction in mass-accretion rate results in a proportionate decrease in X-ray luminosity (Eq. (31)) predicted from ADAFs around BHs in the BH+OB star binaries. We note that observations have confirmed the presence of outflows in Sgr A* (Hawley & Balbus 2002; Yuan et al. 2003; Igumenshchev et al. 2003). In case the same may not true for accretion onto stellar-mass BHs (e.g. see Fender & Gallo 2014), our predictions for the X-ray luminosity will be ∼2 orders of magnitude higher than presented in the next section.
4.2. X-ray luminosity
Figure 2 shows the X-ray luminosity distribution from BH+OB star binaries according to our binary evolution models due to accretion onto the BH (coloured histograms) and shocks in the wind of the OB star companion (black step histogram). In all the panels, the X-ray luminosity in the range 1035 − 1038 erg s−1 originate solely from a Keplerian accretion disc (Shakura 1973) around the BHs (Eq. (25)). These strong X-ray sources comprise 7.85% of the entire population of BH+OB star binaries in our grid. The orbital period distribution (see Figure 6 of Langer et al. 2020) of the BH+OB star binaries peaks above ∼100 d, where the strong wind velocity of the OB star companion disfavours the formation of an accretion disc (Sen et al. 2021). Hence, most BH+OB star binaries in our model grid do not form an accretion disc. We call the BH+OB star binaries with X-ray luminosity above 1035 erg s−1 ‘X-ray-bright’.
 |
Fig. 2. Distribution of X-ray luminosity from BH+OB star binaries for three values of the viscous dissipation parameter δ = 0.001 (top panel), 0.1 (middle panel), 0.5 (bottom panel). Light blue, dark blue, and red colours denote the contributions from binary models with different initial donor mass ranges of 10–20 M⊙, 20–40 M⊙, and 40–90 M⊙, respectively. The coloured histograms are stacked on each other, and the sum of their ordinate values equals unity (see Eq. (33)). The black step histogram shows the distribution of X-ray luminosity arising from the shocks in the winds of the OB star companion and is separately normalised to unity. |
We find that the contribution from binary models in the 40–90 M⊙ range to the population of X-ray-bright BH+OB star binaries is negligible. We identify two reasons. Firstly, the IMF strongly disfavours the most massive binaries in the population. Secondly, the most massive models enter a contact phase up to an initial orbital period of ∼3 d (Figures C1–C3 of Pauli et al. 2022). Hence, the shortest-period models, likely to form an accretion disc during a BH+OB phase, do not reach their BH+OB star phase.
The X-ray luminosity distribution shows a second, broader peak at luminosities in the range from 1025 − 1035 erg s−1 which is associated with systems having ADAFs (Narayan & Yi 1995) around BHs that do not have Keplerian accretion disc around them (Sect. 3.4). The largest contribution comes from the binaries with initial primary masses of 20–40 M⊙. A large fraction of the primaries in the initial mass range of 10–20 M⊙ have helium core mass smaller than 6.6 M⊙ such that they are not expected to collapse into BHs while the contribution from the 40–90 M⊙ range is suppressed by the IMF and comparatively shorter lifetimes of more massive O-star companions.
For the case of the most inefficient viscous coupling δ = 0.001 (top panel), our models predict that 20.55% of the BH+OB star binaries in the LMC to have X-ray luminosities between 1031–1033 erg s−1. We take the lower cut-off of observable X-ray luminosity to be 1031 erg s−1 based on X-ray detection from O and B stars in the LMC with the Chandra Visionary programme T-ReX (see Figure 3 of Crowther et al. 2022). Our results imply that for the one X-ray-bright BH+OB binary (LMC X-1, Orosz et al. 2009) found in the LMC, we expect ∼2.6 faint X-ray sources observable with Chandra, for the least efficient viscous heating (see also, Sect. 4.5). We call the BH+OB star binaries with X-ray luminosity between 1031–1035 erg s−1 ‘X-ray-faint’.
Xie & Yuan (2012, Figure 1) found that the radiative efficiency increases by ∼one order of magnitude each time when the efficiency of viscous coupling is increased from δ = 0.001 to 0.1 to 0.5. This is reflected in the distribution of X-ray luminosity from the middle and bottom panels in the 1025 − 1035 erg s−1 range. The maximum value of X-ray luminosity reaches 1034 erg s−1 and 1035 erg s−1 for δ = 0.1 and 0.5, respectively. This increases the number of observable BH+OB star binaries in X-rays. For efficient viscous heating parameters of δ = 0.1 and δ = 0.5, our models predict ∼4.1 and ∼6.8 X-ray-faint BH+OB star binaries in the LMC, respectively.
The bolometric luminosity of the OB star companions during the BH+OB star phase is in the range log L/L⊙ = 4…6. The X-ray luminosity that arises from shocks embedded in the wind of the OB star companion (LX, wind) ranges from 1030 − 1033 erg s−1 in our models. Hence, the wind X-ray luminosity from the OB star is in the same range as our predictions of the X-ray luminosity from advection-dominated accretion flows around the BH. However, the X-ray emission originating from shocks in the OB star wind is thermalised, while the X-ray emission from the surrounding of the BH will be non-thermal in the case of advection-dominated accretion (Ichimaru 1977; Narayan et al. 1998). We discuss the possibility of disentangling the two contributions to the total X-ray luminosity in Sect. 6.1.
The X-ray luminosity of observed Be X-ray binaries is higher than 1034 erg s−1, even for the faint persistent sources (Cheng et al. 2014). For inefficient viscous heating of electrons, the X-ray luminosity predicted from the BH+O star binaries remain below the lower limit of the X-ray luminosity from Be X-ray binaries (top and middle panels). For δ = 0.5 (bottom panel), only 2% of the BH+O star binaries may have X-ray luminosity between 1034 − 1035 erg s−1, which is lower than the fraction of BH+O star binaries predicted to have a Keplerian accretion disc around the BH. We discuss this in more detail in Sect. 6.2.
Confirmed and plausible BH+OB star binaries in the LMC.
4.3. X-ray-bright systems
The left panel of Fig. 3 shows the distribution of the Roche lobe filling factor of the OB star companion when an accretion disc can form during the BH+OB star phase of the binary models. We find a distinct bimodal distribution, partly as a natural consequence of the binary orbital periods (1.4 d–10d vs. 10–100 d) that contribute to the different peaks (0.3 vs. 0.9). The filling factors of models arising from 1.4–10 d models peak at ∼0.9. The orbital periods are short enough that the accretion disc can form only towards the end of the main sequence of the O star companions when the stellar radius increases and the wind speed decreases. On the other hand, the contribution from 10–100 d binary models comes primarily from BHs with B star companions, where the terminal velocity of the B star wind is a factor of two lower than O stars. Moreover, many binary models with small initial mass ratios merge on the main sequence at the 1.4–10 d orbital period range (e.g. Figure 1 and Figure F1 of Sen et al. 2022).
 |
Fig. 3. Observable properties of X-ray-bright systems. Left panel: Distribution of the Roche lobe filling factor of BH+OB star binaries where an accretion disc can form (Sect. 3.2). Light blue, dark blue, and red colours denote the contributions from binary models with different initial orbital period ranges of 1.4–10 d, 10–100 d, and 100–3162 d, respectively. The coloured histograms are stacked on each other, and the sum of their ordinate values is equal to 0.0785 (the fraction of X-ray-bright systems predicted from our entire population of BH+OB star binaries). Right panel: Disc-formation thresholds (Eq. (10) of Sen et al. 2021) shown by slanted solid, dashed, and dotted lines for three BH masses corresponding to the three observed wind-fed BH HMXBs (Orosz et al. 2007, 2009; Miller-Jones et al. 2021; Ramachandran et al. 2022). The black slanted line shows the disc-formation threshold of the maximum BH mass from our binary model grid. An accretion disc can form below the slanted lines and vice versa. The three circles correspond to the observed orbital period and calculated OB star wind speed at the position of the BH (assuming a β-law for the wind velocity profile, with β = 1, Eq. (1) of Sen et al. 2021) of the three BH-hosting wind-fed HMXBs. The horizontal solid lines correspond to the range of wind speed by varying β from 0.5 (upper-speed limit) to 2 (lower limit). The arrows indicate the new position of the square markers if the BH’s orbital period was twice as long. The grey region is where the wind-accretion approximation υw > aΩ is no longer valid. The heatmap shows the distribution of the orbital period of the binary models and wind speed of the OB star companions during the BH+OB star phase when an accretion disc can form. The colour bar gives the predicted fraction of BH HMXBs in each pixel. The sum of the pixels is equal to unity. |
The right panel of Fig. 3 shows the distribution of the X-ray-bright BH+OB models on the orbital period-wind speed plane, where they occupy two separate regions. The binaries with orbital periods of 1–20 d during the BH+OB star phase have companions that have wind speeds above 1000 km s−1. The companions in these binaries are mostly O stars originating from initial orbital periods of 1.4–10 d, and have high Roche-lobe filling factors (cf. left panel). On the contrary, the peak at orbital period ∼30 d and wind speed ∼600 km s−1 comes from BHs with less massive, B-star companions. These models have initial orbital periods ∼10–100 d and initial mass ratios between 0.6–0.3. We also note the absence of predicted wind-fed HMXBs at short orbital periods and low wind speeds, because our short-period models with low initial mass ratios generally merge on the main sequence.
4.4. X-ray-faint systems
Figure 4 shows the orbital period and OB star luminosity of the BH+OB star binaries that are predicted to emit X-ray emission above 1031 erg s−1, the observational threshold of current X-ray telescopes/surveys (Crowther et al. 2022). For δ = 0.001, the predicted distribution of orbital periods peak near ∼10 d. The mass-accretion rate falls inversely with the square of the orbital separation (Eq. (22)), thereby making higher orbital period binaries less likely to overcome the X-ray luminosity threshold in the LMC. At the shortest orbital periods, all our binary models do not survive the mass transfer phases before the BH+OB star phase (Sect. 4.1), due to which the probability distribution decreases below 10 d.
 |
Fig. 4. Distribution of orbital period and luminosity of the OB star companion from BH+OB star binaries that can produce X-ray luminosity 1031–1035 erg/s through wind accretion, for two values of the viscous heating parameter δ = 0.001 (left panel) and 0.5 (right panel). The colour bar gives the predicted fraction of X-ray-faint BH+OB star binaries in each pixel. The sum of the pixels in each panel is equal to unity. VFTS 243 (Shenar et al. 2022b) is shown by a black star. Two more potential BH+OB star binaries are marked with thin and thick diamonds (Shenar et al. 2022b). A further six SB1 systems with unseen companions (having mass above 2.35 M⊙) are marked by white circles (Table 1; data from Shenar et al. 2022b). |
The wind-mass-loss rate of the OB stars increases with luminosity (see e.g. Kudritzki & Puls 2000; Puls et al. 2008) and mass (Vink et al. 2001). BHs in orbit with more massive (luminous) stars at the same orbital period have a greater mass-accretion rate than less massive (luminous) stars (Eq. (22)), as the mass accretion rate is proportional to the wind mass-loss rate. Consequently, the luminosity of the OB star has to be higher at long orbital periods to keep the mass-accretion rate onto the BH high enough to produce observable X-ray emission. As such, we see that the distribution of observable BH+OB star binaries extends towards higher luminosities at higher orbital periods.
For δ = 0.5 (right panel of Fig. 4), the radiative efficiency ϵ increases by ∼ 2 orders of magnitude compared to δ = 0.001, which leads to higher X-ray luminosity produced from the same mass-accretion rate. We see a larger contribution from longer-period binaries to the distribution of BH+OB star binaries with observable X-ray emission. The increased radiative efficiency compensates for the lower mass-accretion rate at longer periods. For high efficiencies of viscous dissipation, a significant number of our BH+OB star models with orbital periods ∼100 d can produce observable X-rays in the LMC (see also Fig. A.1, for δ = 0.1).
4.5. Absolute number of X-ray-faint BH+OB star binaries in the LMC
Langer et al. (2020) studied the distribution of BH+OB star binaries arising from the initial primary mass range of 10–40 M⊙. Assuming constant star formation, they estimated ∼120 BH+OB star binaries from the above parameter space in the LMC. The relative contributions from the 10–40 M⊙ and 40–90 M⊙ range to the total population of BH+OB star binaries in our study is ∼88% and ∼12%, respectively (Fig. 2). This implies an additional ∼16 BH+OB star binaries from the 40–90 M⊙ range of initial primary masses.
Our models predict that 7.85% of the total population of BH+OB star binaries from the 10–90 M⊙ are have X-ray luminosity above 1035 erg s−1 (Fig. 2). This implies that our models predict ∼10 X-ray-bright BH+OB star binaries in the LMC. Yet, only one wind-fed BH HMXB has been observed in the LMC (LMC X-1, Orosz et al. 2009). We discuss this discrepancy in the number of observed to predicted wind-fed BH HMXBs in Sect. 6.4.
Of the ∼126 BH+OB star binaries that are not expected to form an accretion disc around the BH, the number of X-ray-faint BH+OB star binaries depend on the efficiency of viscous heating adopted in our models. The predicted numbers range among 28...44...72 for δ = 0.001...0.1...0.5, respectively. Thus, a significant handful of BH+OB star binaries in the LMC are expected to produce faint yet observable X-ray emission, even for the most inefficient case of viscous heating. Moreover, if accretion disc formation is inhibited in some of the BH+OB binaries that are predicted to be X-ray-bright in this work, the high mass-accretion rates predicted in the X-ray-bright systems will make them observable as X-ray-faint sources. Hence, the number of X-ray-faint BH+OB star binaries will increase for more stringent constraints on the accretion disc formation criterion (Sect. 6.4).
5. Comparison with observations
Table 1 lists confirmed and tentative BH+OB star binaries observed in the LMC. LMC X-1 is a long-studied system with continuous X-ray emission produced from a Keplerian accretion disc (see, e.g. Pakull & Angebault 1986; Orosz et al. 2009). VFTS 243 is a recently discovered X-ray inactive BH+O star binary in the Tarantula Nebula (Shenar et al. 2022a). Shenar et al. (2022b) identified two more systems, VFTS 514 and 779, as strong candidates to host BHs that do not show strong X-ray emission. The remaining systems are SB1 binaries with unseen companions of mass above 2.35 M⊙3 (Table 2 of Shenar et al. 2022b).
5.1. X-ray-bright systems
In the right panel of Fig. 3, we use the criterion for the formation of an accretion disc to show the domains where a disc is expected or not (with 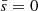 and η = 1/3), for black hole masses corresponding to three high-mass X-ray binaries: LMC X-1 (Orosz et al. 2009), Cygnus X-1 (Orosz et al. 2011) and M33 X-7 (Orosz et al. 2007; Valsecchi et al. 2010; Ramachandran et al. 2022). The wind speed of the main sequence companion to the BH is computed at the orbital separation with a β-law (Eq. (1) of Sen et al. 2021). Each coloured circle marker lies below its respective threshold for accretion disc formation. This shows that even if the OB star companion does not fill its Roche lobe, an accretion disc can form through wind capture in these three systems, from where copious amounts of X-rays can be emitted. In the grey region, the wind launching is quenched and mass accretion onto the BH can only proceed through Roche lobe overflow.
and η = 1/3), for black hole masses corresponding to three high-mass X-ray binaries: LMC X-1 (Orosz et al. 2009), Cygnus X-1 (Orosz et al. 2011) and M33 X-7 (Orosz et al. 2007; Valsecchi et al. 2010; Ramachandran et al. 2022). The wind speed of the main sequence companion to the BH is computed at the orbital separation with a β-law (Eq. (1) of Sen et al. 2021). Each coloured circle marker lies below its respective threshold for accretion disc formation. This shows that even if the OB star companion does not fill its Roche lobe, an accretion disc can form through wind capture in these three systems, from where copious amounts of X-rays can be emitted. In the grey region, the wind launching is quenched and mass accretion onto the BH can only proceed through Roche lobe overflow.
We see that the binary models cannot reproduce the position of LMC X-1 in the orbital period-wind speed plane. The mass of the BH and the O star companion is 10.91 ± 1.41 M⊙ and 31.79 ± 3.48 M⊙ respectively. However, our models at the relevant initial mass (30–50 M⊙, which can form a ∼10 M⊙ BH), and initial orbital period (1–3 d) range merge on the main sequence after a contact phase. This may indicate the short period may detach after a brief contact phase. Investigating the physics of the contact phase is beyond the scope of this work (see, e.g. Fabry et al. 2022, 2023). Alternatively, at an orbital period of 3.9 d the black hole in LMC X-1 is deeply engulfed in the wind acceleration region of the 31.8 M⊙ O star. X-rays from the BH can ionise the stellar wind decreasing its speed (Krtička & Kubát 2009). This effect is not taken into account in our simple analysis. We assume that the O star companion has a radiatively driven wind which follows the β-law (as in Orosz et al. 2007).
On the other hand, our models predict a subpopulation of X-ray-bright BH+OB star binaries above 15 d with wind speeds below 800 km s−1. The OB star companions in this population also have a low filling factor. There are no observed wind-fed HMXBs in this region. Despite the low-number statistics, this may imply two possibilities. First, binaries may not undergo stable mass transfer at low initial mass ratios and long orbital periods (see however, Schürmann & Langer 2024, where the criterion for unstable mass transfer is more relaxed). On the other hand, our criterion to determine the formation of an accretion disc may be inadequate to filter out BH+OB models where the OB star has low filling factors. We discuss this further in Sect. 6.4.
5.2. X-ray-faint systems
5.2.1. HD 96670
HD 96670 is a single-line spectroscopic binary in the Carina OB2 association, tentatively hosting a BH of mass 6.2 M⊙ in orbit with an O star of mass ∼22.7 M⊙ and radius ∼ 17.1 R⊙. The orbital period of the binary is 5.28 d (Gomez & Grindlay 2021). The orbital separation of the binary is ∼39.2 R⊙, and the Roche-lobe filling factor of the O star is ∼0.885. Assuming the effective temperature of the O star to be 38 000 K (Hohle et al. 2010), we estimate its luminosity to be log(L/L⊙) ∼ 5.75.
We assume the ratio of the terminal velocity to the escape velocity for O stars to be 2.6 (Vink et al. 2001; Kudritzki & Puls 2000), β = 1 in the wind velocity law, and the Eddington factor at the surface of the O star to be ∼0.2 (see Eqs. (1–8) of Sen et al. 2021). Then, the estimated wind velocity υw of the O star at the position of the BH to be ∼932.3 km s−1. The orbital velocity is ∼375.4 km s−1. For the fiducial value of accretion efficiency (η = 1/3) and a non-spinning BH, we find that an accretion disc does not form (Eq. (10) of Sen et al. 2021). This is consistent with the lack of bright X-ray emission from this system.
We estimate the wind mass-loss rate to be one-third of the mass-loss rate derived from Eq. (24) of Vink et al. (2001), Ṁw ∼10−5.71 M⊙ yr−1. The accretion radius, mass-accretion rate at the accretion radius Ṁacc, net mass-accretion rate near the BH event horizon Ṁnet and Eddington mass-accretion rate of the BH ṀEdd can be estimated to be 2.36 R⊙, 2.85 × 10−9 M⊙ yr−1, 4.85 × 10−11 M⊙ yr−1 and 1.33 × 10−7 M⊙ yr−1, respectively. For Ṁnet/ṀEdd = 0.00036, the radiative efficiency is ∼0.003 (Figure 1 of Xie & Yuan 2012). The above quantities lead to an estimated X-ray luminosity of 8 × 1033 erg s−1 from ADAF. The observed X-ray flux from this system ranges from 2.2 × 1032 erg s−1 (NuSTAR, Gomez & Grindlay 2021) to 2.4 × 1034 erg s−1 (XMM-Newton, Saxton et al. 2008). Our results are in the right ballpark, although further study may be required to accurately constrain the X-ray variability and/or photometric properties of the system (e.g. see Wang & Grindlay 2022).
5.2.2. VFTS 243
The constrained stellar and binary parameters of VFTS 243 enable us to estimate the X-ray luminosity from ADAF around its ∼10 M⊙ BH. The mass, radius and luminosity of the O star companion is ∼25 M⊙, ∼10.3 R⊙ and ∼105.2 L⊙ respectively. The wind mass loss rate, with a clumping factor of 10, is ∼1.5 × 10−7 M⊙ yr−1. For the adopted terminal wind velocity of 2100 km s−1, we estimate the net mass-accretion rate near the event horizon ∼1.6 × 10−13 M⊙ yr−1. The Eddington mass-accretion rate of a non-spinning 10 M⊙ BH is ∼2.2 × 10−7 M⊙ yr−1, leading to a ratio 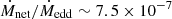 . The radiative efficiency of an ADAF at the above ratio of Ṁnet/ṀEdd is ∼0.0001, ∼0.001 and ∼0.01 (extrapolated from Fig. 1 of Xie & Yuan 2012) for δ = 0.001, 0.1 and 0.5 respectively. The resulting X-ray luminosity is ∼1029, 1030 and 1031 erg s−1 respectively. Hence, VFTS 243 is not expected to be observable even in faint X-rays. The Chandra T-ReX programme (Crowther et al. 2022) constrained the X-ray luminosity of this system log(LX/erg s−1) < 32.15, which is within our above estimates.
. The radiative efficiency of an ADAF at the above ratio of Ṁnet/ṀEdd is ∼0.0001, ∼0.001 and ∼0.01 (extrapolated from Fig. 1 of Xie & Yuan 2012) for δ = 0.001, 0.1 and 0.5 respectively. The resulting X-ray luminosity is ∼1029, 1030 and 1031 erg s−1 respectively. Hence, VFTS 243 is not expected to be observable even in faint X-rays. The Chandra T-ReX programme (Crowther et al. 2022) constrained the X-ray luminosity of this system log(LX/erg s−1) < 32.15, which is within our above estimates.
We note however that even though VFTS 243 may lie within the parameter space of Fig. 4, our detailed calculation above shows it will not be observable in faint X-rays. This is because the parameter space for BH+OB star binaries showing observable faint X-ray emission is degenerate with the parameter space for BH+OB star binaries that do not show faint X-ray emission (cf. Fig. 4 and Fig. 6 of Langer et al. 2020). We note however that the orbital period distribution of all BH+OB star binaries peak above ∼100 d, while the ones that may be identifiable via faint X-rays peak around ∼10 d.
5.2.3. VFTS 399
The VLT Flames survey in the Tarantula nebula (Evans et al. 2011) identified an SB1 system, VFTS 399, which has a O9 IIIn star with a compact object companion (Clark et al. 2015). Clark et al. (2015) reported an X-ray luminosity of 5 × 1034 erg s−1 while an orbital solution could not be obtained. An orbital solution was neither presented in the recent work of Villaseñor et al. (2021) for this object. The system also has a very low dispersion velocity σ ≈ 10 km s−1 relative to its environment (Sana et al. 2013). Clark et al. (2015) also note that for the empirical lower bound on the orbital period distribution of ∼20 d of Be X-ray binaries (Cheng et al. 2014; Haberl et al. 2022), the mass of the compact object companion in VFTS 399 has to be greater than 2.5 M⊙, based on their radial velocity measurements. For higher orbital periods, the mass of the compact object companion is still higher, hinting at the possibility of a BH, although apparently excluded by the detection of X-ray pulsations.
5.2.4. Other systems
Figure 4 shows that both for δ = 0.001 (left panel) and δ = 0.5 (right panel), the orbital period of VFTS 514 is longer than the predicted distribution of X-ray-faint BH+OB star binaries from our grid. The position of VFTS 779 shows that it may be observable in faint Xrays for δ= 0.5. Five of the six SB1 systems are near the peak of the predicted distribution of X-ray-faint BH+OB binaries. We note that there is a lack of X-ray observations of SB1 systems having B-type stars with log(L/L⊙) ≲ 5 (Crowther et al. 2022). Unambiguous identification of the presence of a BH in these systems and a targeted X-ray observation programme on these systems may provide empirical evidence to constrain the strength of viscous coupling in hot accretion flows around stellar-mass BH binaries. For example, Villaseñor et al. (2021) identified 16 SB1 systems with B-type stars having a high probability of hosting compact object companions.
6. Discussion
6.1. Disentangling thermal from non-thermal X-ray emission
Figure 5 shows the distribution of X-ray luminosity from ADAF and OB star luminosity for the BH+O star binaries that do not form a Keplerian accretion disc. For inefficient viscous heating (left panel), the peak of the distribution lies below the canonical wind X-ray emission LX, w = 10−7Lbol relation (Crowther et al. 2022, solid black line). For efficient viscous heating (right panel), the peak of the distribution is nearly an order of magnitude above the typical wind X-ray luminosity expected from the main sequence companion to the BH. We suggest that targeted X-ray observations on the B stars in the SB1 sample of Shenar et al. (2022b) (see Table 1) provide a suitable opportunity to investigate the presence of BHs, and study accretion physics around stellar mass BHs. We identify two B stars, VFTS 186 and VFTS 640, in the T-ReX catalogue that show LX, w/Lbol > 10−6. However, we note that Evans et al. (2015) categorises them as single stars based on radial velocity measurements. We identify two more O stars with LX, w/Lbol > 10−6.5 in the T-ReX catalogue of Crowther et al. (2022, see their Table A2, T-ReX label cc4651, c7552) showing an X-ray excess, above the canonical wind X-ray luminosity. The X-ray excess could be ascribed to accretion onto an orbiting BH, a possibility which deserves follow-up observations. Finally, we notice that the non-detection of X-rays from the black hole candidate VFTS 243 sets an upper limit to the X-ray emission of ∼2 × 10−7Lbol, marginally above the expected emission from the wind (Shenar et al. 2022a).
 |
Fig. 5. Distribution of X-ray luminosity produced from ADAFs around BHs without Keplerian accretion discs and the bolometric luminosity of the OB star companion, for two values of the viscous dissipation parameter δ = 0.001 (left panel) and 0.5 (right panel). The colour bar gives the predicted number of BH+OB star binaries in each pixel. The sum of the pixels in each panel is equal to unity. The solid black line shows the LX, w = 10−7LOB relation, with the dotted line and the dot-dashed line showing the ±1 dex range. The black and grey downward arrow denotes the upper limit to the X-ray luminosity from VFTS 827 and VFTS 243. |
Even in systems where the X-ray luminosity due to accretion is lower than the X-ray intrinsic emission from the stellar wind, detecting the former is not beyond reach. Indeed, their spectral properties are fundamentally different (e.g. Gierliński et al. 1999). In the radiatively inefficient regime, the X-ray luminosity from the low-density plasma near the BH is non-thermal (see Sect. 2.3.1). For instance, synchrotron emission from relativistic electrons accelerated by magnetic reconnection would yield a power-law of spectral index of 0 (El Mellah et al. 2022) to −0.7 (Ponti et al. 2017), depending on the efficiency of radiative cooling. In the case of a strong magnetic field, this emission could peak in hard X-rays, beyond the maxima from wind X-ray emission. This spectral disentangling between the thermal emission of the stellar wind and the non-thermal emission from the dilute accretion flow was used by Munar-Adrover et al. (2014) to measure an X-ray luminosity of from the X-ray faint system MWC 656, later refined to LX ∼ 4 × 10−8Lbol (Ribó et al. 2017). Even if the presence of the BH in this system has been challenged in a recent work (Janssens et al. 2023), it is a promising precedent which illustrates that non-thermal emission can be detected below the thermal wind X-ray luminosity level.
6.2. Be X-ray binaries and BH+OBe binaries
The typical X-ray luminosity of Be X-ray binaries is higher than that expected from advection-dominated accretion in the BH+OB star binaries. The predicted and the observed distribution of the outburst X-ray luminosity ranges from 1034 − 1039 erg s−1 (Cheng et al. 2014 and Fig. 4 of Liu et al. 2024). Hence, the X-ray luminosity of the majority of X-ray-faint BH+OB star binaries predicted in this work are not expected to overlap with the X-ray luminosity from the population of fairly brighter Be X-ray binaries or the BH+OB star binaries having a Keplerian accretion disc around the BH. We also note that all the known Be X-ray binaries are found to host a neutron star, not a BH (Ziolkowski 2014; Brown et al. 2018).
We show in Fig. C.1 that more than 80% of our BH+OB star systems will host an OB star that rotates at more than 80% of its critical rotational velocity. As such, we expect the majority of the predicted X-ray-faint BHs to have an OBe companion. In absolute numbers, our models predict ∼109 BH+OBe systems in the LMC, amongst the ∼4500 photometrically detected OBe stars in the LMC (Schootemeijer et al. 2022). BH+OBe systems have rarely been observed (with one candidate being AS386, Khokhlov et al. 2018). Our results provide an alternative way to search for these elusive BH+OBe systems.
Smoothed Particle Hydrodynamics simulations done by Brown et al. (2018) show that for an eccentricity of 0, the average X-ray luminosity due to mass accretion onto the BH from the decretion disc of the OBe star in a BH+OBe system is around 1031 erg s−1 (see their Figures 6 and 7). We also note that Brown et al. (2018) assume a radiative efficiency of 0.1 in their X-ray luminosity estimates (see their Eq. (4)), which may overestimate their X-ray luminosity prediction. Moreover, Zhang et al. (2004) propose that the decretion disc can get significantly truncated in the presence of a BH. Based on the above studies, the X-ray luminosity, due to mass accretion onto the BH from the decretion disc around the OBe star of a BH+OBe star binary, may not be strong enough to overlap with our predictions for X-ray luminosity from ADAF around the BH.
6.3. BH spin
Qin et al. (2018), Fuller & Ma (2019) showed that the black hole formed from the initially more massive star in a binary has a negligible spin parameter (see also Marchant et al. 2023). Moreover, a BH needs to accumulate mass equal to its mass to significantly increase its natal spin parameter (King & Kolb 1999; Wong et al. 2012), which is not feasible from sub-Eddington mass accretion (Fig. 1) over a timescale of a few Myrs. This is reflected in our assumption that the spin of the BH during the BH+OB star phase is zero. Sen et al. (2021) showed that the formation of an accretion disc is favoured in the case of more rapidly spinning black holes, as the innermost circular orbit radius of the black hole decreases with increasing BH spin. Hence, the predicted number of X-ray-bright BH+OB star binaries will increase for spinning black holes.
Previous studies of X-ray-bright BH+OB star binaries such as Cyg X-1 (Gou et al. 2011; Miller-Jones et al. 2021; Zhao et al. 2021) and LMC X-1 (Gou et al. 2009; Mudambi et al. 2020) have inferred that the black holes in these systems are maximally spinning (aBH > 0.90). On the other hand, recent simulations have found that deduced spins of wind-fed BH HMXBs may be model-dependent (Belczynski et al. 2021; Zdziarski et al. 2024). The X-ray spectral energy distribution can be statistically well-fitted with the assumption of a slowly spinning black hole and a Comptonised layer above the Keplerian accretion disc. Our population synthesis results, based on the accretion disc formation criteria of Sen et al. (2021), show that ∼10 non-spinning BHs in BH+OB star binaries can form accretion discs around them in the LMC, relaxing the necessity for maximally spinning black holes to form wind-fed BH HMXBs. Furthermore, Batta et al. (2017) showed that a failed supernova explosion with sufficient fallback accretion can produce rapidly spinning BHs with a spin parameter > 0.8, while the expected spin parameter from direct collapse is < 0.3.
6.4. Accretion disc formation criterion
Our criterion with 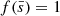 overpredicts the number of observable wind-fed BH HMXBs in the LMC by an order of magnitude. For
overpredicts the number of observable wind-fed BH HMXBs in the LMC by an order of magnitude. For 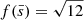 , Eq. (20) predicts ∼1.5% of the BH+OB binaries are expected to form an accretion disc. This leads to only ∼2 predicted X-ray-bright BH+OB star binaries in the LMC, consistent with one observed wind-fed BH HMXB, LMC X-1. Furthermore, for
, Eq. (20) predicts ∼1.5% of the BH+OB binaries are expected to form an accretion disc. This leads to only ∼2 predicted X-ray-bright BH+OB star binaries in the LMC, consistent with one observed wind-fed BH HMXB, LMC X-1. Furthermore, for 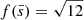 , the number of X-ray-faint BHs are 35…51…80 for δ = 0.001, 0.1 & 0.5.
, the number of X-ray-faint BHs are 35…51…80 for δ = 0.001, 0.1 & 0.5.
Recent rapid binary population synthesis simulations by Romero-Shaw et al. (2023) showed that an accretion disc formation criterion that solely relies on the Roche lobe filling factor (Hirai & Mandel 2021) of the OB star companion may explain the scarcity of wind-fed BH HMXB in the Milky Way. However, their criterion was derived from a specific set of binary parameters, especially a mass ratio of 2 (MOB/MBH) and orbital periods up to ∼20 d. At lower mass ratios, we find that the wind speed of an OB star companion to the BH may be low enough to form an accretion disc even at orbital periods of 10s of days (Fig. 3).
If we additionally constrain our accretion disc formation criterion such that the OB companion must have a Roche lobe filling factor above 0.85 (see Fig. 3, we find that our models predict ∼2.5 X-ray-bright BH+OB star systems in the LMC. However, we do not see any physical reason to discount the BH+OB star binaries at long orbital periods that may also be observable as wind-fed BH HMXBs. We also note that the Roche lobe filling factor of the O star in HD96670 is > 0.85, but no bright X-ray emission (> 1035 erg s−1) has been detected. A further investigation into the accretion disc formation may be useful, but beyond the scope of this work.
7. Conclusion
Understanding the production of X-rays from BH+OB star binaries is essential in order to explain the observed population of BH high-mass X-ray binaries (Fornasini et al. 2023; Zhang et al. 2024). In the present work, we study the population of BH+OB star binaries that are not expected to have a Keplerian accretion disc around the BH (Langer et al. 2020; Sen et al. 2021). These binaries are expected to be the higher mass counterparts of the population of Be X-ray binaries (Vinciguerra et al. 2020; Liu et al. 2024), but without copious X-ray emission (Sharma et al. 2007; Xie & Yuan 2012). Moreover, these X-ray-faint BH+OB star binaries are the tentative progenitors of the binary BHs that can merge within a Hubble time (Belczynski et al. 2008; Romero-Shaw et al. 2023) from the isolated binary evolution channel.
We use approximately 20 000 detailed binary evolution models that include differential rotation, time-dependent tidal interactions, and angular momentum transport during the mass-transfer phases. Only ∼8% of the total population of BH+OB star binaries in our grid are expected to form wind-fed BH HMXB systems like LMC X-1. Our models predict at least approximately 28 BH+OB star binaries to be observable in the LMC with current X-ray telescopes like Chandra and the upcoming SRG/eROSITA (LX = 1031–1035 erg s−1).
We show in Sect. 2 that viscous heating imparted to electrons can be high in the presence of magnetic fields of ∼30 G, regardless of whether the flow is collisional (Xie & Yuan 2012) or not (Sharma et al. 2007). For efficient viscous heating, our models predict that a significant fraction of BH+OB star binaries without accretion discs can produce X-ray luminosity of 1031–1035 erg s−1 (Sect. 4.5). Up to about 72 X-ray-faint BH+OB star binaries in the LMC may be observable due to high viscous heating efficiency in ADAFs around stellar mass black holes.
Recent photometric and spectroscopic observations into the massive star content of the LMC provide an excellent testbed for our model predictions (Evans et al. 2011, 2015; Almeida et al. 2017; Mahy et al. 2020b,a). Identifying a population of X-ray-faint BH+OB star binaries from recent observational samples of SB1 binaries (Villaseñor et al. 2021; Shenar et al. 2022b; Mahy et al. 2022; Banyard et al. 2023) will provide crucial constraints on the contribution of the isolated binary evolution channel to the population of double BH mergers.
Our study of faint X-ray emission from BH+OB star binaries advocate for prolonged X-ray exposure of the stellar-mass BH candidates identified in the vicinity of OB stars without an X-ray-bright counterpart. Our method may also be applied to isolated BHs in order to produce complementary predictions in the X-ray band. This may be useful for future all-sky multi-wavelength surveys with high sensitivity to hunt for the large unidentified population of BHs in the Milky Way (Scarcella et al. 2021).
Inlists can be found at website.
The most massive neutron star discovered is ∼2.35 M⊙ (Romani et al. 2022).
Acknowledgments
KS is funded by the National Science Center (NCN), Poland, under grant number OPUS 2021/41/B/ST9/00757. The authors thank Feng Yuan, Ying Qin and the referee Yong Shao for their valuable comments. The authors also acknowledge Pablo Marchant, whose models were used in this work.
References
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016, Phys. Rev. X, 6, 041015 [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2019, Phys. Rev. X, 9, 031040 [Google Scholar]
- Almeida, L. A., Sana, H., Taylor, W., et al. 2017, A&A, 598, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asenjo, F. A., & Comisso, L. 2019, Phys. Rev. D, 99, 063017 [NASA ADS] [CrossRef] [Google Scholar]
- Baganoff, F. K., Maeda, Y., Morris, M., et al. 2003, ApJ, 591, 891 [Google Scholar]
- Banyard, G., Mahy, L., Sana, H., et al. 2023, A&A, 674, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Batta, A., Ramirez-Ruiz, E., & Fryer, C. 2017, ApJ, 846, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Bavera, S. S., Fragos, T., Zevin, M., et al. 2021, A&A, 647, A153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Begelman, M. C., Scepi, N., & Dexter, J. 2022, MNRAS, 511, 2040 [NASA ADS] [CrossRef] [Google Scholar]
- Belczynski, K., Kalogera, V., Rasio, F. A., et al. 2008, ApJS, 174, 223 [Google Scholar]
- Belczynski, K., Wiktorowicz, G., Fryer, C. L., Holz, D. E., & Kalogera, V. 2012, ApJ, 757, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Belczynski, K., Done, C., Hagen, S., Lasota, J. P., & Sen, K. 2021, ArXiv e-prints [arXiv:2111.09401] [Google Scholar]
- Belloni, T. M. 2010, Lecture Notes Phys., 794, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Bernini-Peron, M., Marcolino, W. L. F., Sander, A. A. C., et al. 2023, A&A, 677, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bisnovatyi-Kogan, G. S., & Lovelace, R. V. E. 1997, ApJ, 486, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & Begelman, M. C. 1999, MNRAS, 303, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Bondi, H., & Hoyle, F. 1944, MNRAS, 104, 273 [Google Scholar]
- Bower, G. C., Wright, M. C. H., Falcke, H., & Backer, D. C. 2003, ApJ, 588, 331 [Google Scholar]
- Bower, G. C., Broderick, A., Dexter, J., et al. 2018, ApJ, 868, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Bozzo, E., Falanga, M., & Stella, L. 2008, ApJ, 683, 1031 [Google Scholar]
- Brands, S. A., de Koter, A., Bestenlehner, J. M., et al. 2022, A&A, 663, A36 [Google Scholar]
- Breivik, K., Chatterjee, S., & Larson, S. L. 2017, ApJ, 850, L13 [CrossRef] [Google Scholar]
- Briel, M. M., Stevance, H. F., & Eldridge, J. J. 2023, MNRAS, 520, 5724 [Google Scholar]
- Broekgaarden, F. S., Berger, E., Stevenson, S., et al. 2022, MNRAS, 516, 5737 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, R. O., Ho, W. C. G., Coe, M. J., & Okazaki, A. T. 2018, MNRAS, 477, 4810 [Google Scholar]
- Cangemi, F., Beuchert, T., Siegert, T., et al. 2021, A&A, 650, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carroll, S. M. 2019, Spacetime and Geometry: An Introduction to General Relativity [Google Scholar]
- Chakrabarti, S., Simon, J. D., Craig, P. A., et al. 2023, AJ, 166, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Chandran, B. D. G., Foucart, F., & Tchekhovskoy, A. 2018, J. Plasma Phys., 84, 905840310 [NASA ADS] [CrossRef] [Google Scholar]
- Chaty, S. 2022, Accreting Binaries, Nature, Formation, and Evolution [CrossRef] [Google Scholar]
- Chawla, C., Chatterjee, S., Breivik, K., et al. 2022, ApJ, 931, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, Z. Q., Shao, Y., & Li, X. D. 2014, ApJ, 786, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, J. S., Bartlett, E. S., Broos, P. S., et al. 2015, A&A, 579, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Comisso, L., & Sironi, L. 2022, ApJ, 936, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Corral-Santana, J. M., Casares, J., Muñoz-Darias, T., et al. 2016, A&A, 587, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crowther, P. A., Broos, P. S., Townsley, L. K., et al. 2022, MNRAS, 515, 4130 [NASA ADS] [CrossRef] [Google Scholar]
- Cunningham, A. J., McKee, C. F., Klein, R. I., Krumholz, M. R., & Teyssier, R. 2012, ApJ, 744, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Davidson, K., & Ostriker, J. P. 1973, ApJ, 179, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Detmers, R. G., Langer, N., Podsiadlowski, P., & Izzard, R. G. 2008, A&A, 484, 831 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dorozsmai, A., & Toonen, S. 2024, MNRAS, 530, 3706 [NASA ADS] [CrossRef] [Google Scholar]
- El-Badry, K., Rix, H.-W., Cendes, Y., et al. 2023a, MNRAS, 521, 4323 [NASA ADS] [CrossRef] [Google Scholar]
- El-Badry, K., Rix, H.-W., Quataert, E., et al. 2023b, MNRAS, 518, 1057 [Google Scholar]
- El Mellah, I., & Casse, F. 2015, MNRAS, 454, 2657 [NASA ADS] [CrossRef] [Google Scholar]
- El Mellah, I., Bolte, J., Decin, L., Homan, W., & Keppens, R. 2020, A&A, 637, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- El Mellah, I., Cerutti, B., Crinquand, B., & Parfrey, K. 2022, A&A, 663, A169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ellison, D. C., Jones, F. C., & Reynolds, S. P. 1990, ApJ, 360, 702 [NASA ADS] [CrossRef] [Google Scholar]
- Ertl, T., Janka, H. T., Woosley, S. E., Sukhbold, T., & Ugliano, M. 2016, ApJ, 818, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Esin, A. A., McClintock, J. E., & Narayan, R. 1997, ApJ, 489, 865 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, I. N., & Civano, F. 2018, Astron. Geophys., 59, 2.17 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, C. J., Taylor, W. D., Hénault-Brunet, V., et al. 2011, A&A, 530, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, C. J., Kennedy, M. B., Dufton, P. L., et al. 2015, A&A, 574, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2019, ApJ, 875, L1 [Google Scholar]
- Fabry, M., Marchant, P., & Sana, H. 2022, A&A, 661, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabry, M., Marchant, P., Langer, N., & Sana, H. 2023, A&A, 672, A175 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Farr, W. M., Sravan, N., Cantrell, A., et al. 2011, ApJ, 741, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Feldmeier, A., Puls, J., & Pauldrach, A. W. A. 1997, A&A, 322, 878 [NASA ADS] [Google Scholar]
- Fender, R., & Gallo, E. 2014, Space Sci. Rev., 183, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Fermi, E. 1949, Phys. Rev., 75, 1169 [NASA ADS] [CrossRef] [Google Scholar]
- Fishbach, M., & Kalogera, V. 2022, ApJ, 929, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Fornasini, F. M., Antoniou, V., & Dubus, G. 2023, ArXiv e-prints [arXiv:2308.02645] [Google Scholar]
- Fortin, F., García, F., Simaz Bunzel, A., & Chaty, S. 2023, A&A, 671, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frank, J., King, A., & Raine, D. J. 2002, Accretion Power in Astrophysics: Third Edition [Google Scholar]
- Fuller, J., & Ma, L. 2019, ApJ, 881, L1 [Google Scholar]
- Gaia Collaboration (Panuzzo, P., et al.) 2024, A&A, 686, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galishnikova, A., Philippov, A., Quataert, E., et al. 2023, Phys. Rev. Lett., 130, 115201 [NASA ADS] [CrossRef] [Google Scholar]
- Gallegos-Garcia, M., Berry, C. P. L., Marchant, P., & Kalogera, V. 2021, ApJ, 922, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Gierliński, M., Zdziarski, A. A., Poutanen, J., et al. 1999, MNRAS, 309, 496 [CrossRef] [Google Scholar]
- Giesers, B., Dreizler, S., Husser, T.-O., et al. 2018, MNRAS, 475, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Gomez, S., & Grindlay, J. E. 2021, ApJ, 913, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Gou, L., McClintock, J. E., Liu, J., et al. 2009, ApJ, 701, 1076 [NASA ADS] [CrossRef] [Google Scholar]
- Gou, L., McClintock, J. E., Reid, M. J., et al. 2011, ApJ, 742, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Grošelj, D., Hakobyan, H., Beloborodov, A. M., Sironi, L., & Philippov, A. 2024, Phys. Rev. Lett., 132, 085202 [CrossRef] [Google Scholar]
- Grunhut, J. H., Wade, G. A., Neiner, C., et al. 2017, MNRAS, 465, 2432 [NASA ADS] [CrossRef] [Google Scholar]
- Gruzinov, A. V. 1998, ApJ, 501, 787 [NASA ADS] [CrossRef] [Google Scholar]
- Haberl, F., Maitra, C., Vasilopoulos, G., et al. 2022, A&A, 662, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hankla, A. M., Zhdankin, V., Werner, G. R., Uzdensky, D. A., & Begelman, M. C. 2022, MNRAS, 509, 3826 [Google Scholar]
- Hawley, J. F., & Balbus, S. A. 2002, ApJ, 573, 738 [NASA ADS] [CrossRef] [Google Scholar]
- Hirai, R., & Mandel, I. 2021, PASA, 38, e056 [NASA ADS] [CrossRef] [Google Scholar]
- Hohle, M. M., Neuhäuser, R., & Schutz, B. F. 2010, Astron. Nachr., 331, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Huenemoerder, D. P., Oskinova, L. M., Ignace, R., et al. 2012, ApJ, 756, L34 [Google Scholar]
- Ichimaru, S. 1977, ApJ, 214, 840 [NASA ADS] [CrossRef] [Google Scholar]
- Igumenshchev, I. V., Abramowicz, M. A., & Narayan, R. 2000, ApJ, 537, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Igumenshchev, I. V., Narayan, R., & Abramowicz, M. A. 2003, ApJ, 592, 1042 [Google Scholar]
- Jacquemin-Ide, J., Lesur, G., & Ferreira, J. 2021, A&A, 647, A192 [EDP Sciences] [Google Scholar]
- Janka, H.-T. 2013, MNRAS, 434, 1355 [Google Scholar]
- Janssens, S., Shenar, T., Degenaar, N., et al. 2023, A&A, 677, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jayasinghe, T., Stanek, K. Z., Thompson, T. A., et al. 2021, MNRAS, 504, 2577 [NASA ADS] [CrossRef] [Google Scholar]
- Jayasinghe, T., Rowan, D. M., Thompson, T. A., Kochanek, C. S., & Stanek, K. Z. 2023, MNRAS, 521, 5927 [CrossRef] [Google Scholar]
- Jiang, L., Chen, W.-C., Tauris, T. M., Müller, B., & Li, X.-D. 2023, ApJ, 945, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Kagan, D., Sironi, L., Cerutti, B., & Giannios, D. 2015, Space Sci. Rev., 191, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Karino, S., Nakamura, K., & Taani, A. 2019, PASJ, 71, 58 [Google Scholar]
- Khokhlov, S. A., Miroshnichenko, A. S., Zharikov, S. V., et al. 2018, ApJ, 856, 158 [NASA ADS] [CrossRef] [Google Scholar]
- King, A. R., & Kolb, U. 1999, MNRAS, 305, 654 [NASA ADS] [CrossRef] [Google Scholar]
- Kretschmar, P., Fürst, F., Sidoli, L., et al. 2019, New Astron. Rev., 86 [Google Scholar]
- Krtička, J., & Kubát, J. 2009, MNRAS, 394, 2065 [Google Scholar]
- Krtička, J., Kubát, J., & Krtičková, I. 2018, A&A, 620, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kruckow, M. U., Tauris, T. M., Langer, N., Kramer, M., & Izzard, R. G. 2018, MNRAS, 481, 1908 [CrossRef] [Google Scholar]
- Kudritzki, R.-P., & Puls, J. 2000, ARA&A, 38, 613 [Google Scholar]
- Langer, N., Wellstein, S., & Petrovic, J. 2003, IAU Symp., 212, 275 [Google Scholar]
- Langer, N., Schürmann, C., Stoll, K., et al. 2020, A&A, 638, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lazarian, A., & Vishniac, E. T. 1999, ApJ, 517, 700 [Google Scholar]
- Lazarian, A., Vlahos, L., Kowal, G., et al. 2012, Space Sci. Rev., 173, 557 [Google Scholar]
- Lemoine, M., & Pelletier, G. 2010, MNRAS, 402, 321 [Google Scholar]
- Liu, B. F., & Qiao, E. 2022, iScience, 25, 103544 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, H., & Wu, Q. 2013, ApJ, 764, 17 [Google Scholar]
- Liu, J., Zhang, H., Howard, A. W., et al. 2019, Nature, 575, 618 [Google Scholar]
- Liu, B., Sartorio, N. S., Izzard, R. G., & Fialkov, A. 2024, MNRAS, 527, 5023 [Google Scholar]
- Livio, M., Soker, N., de Kool, M., & Savonije, G. J. 1986, MNRAS, 222, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Ma, L., & Fuller, J. 2023, ApJ, 952, 53 [CrossRef] [Google Scholar]
- Mahy, L., Almeida, L. A., Sana, H., et al. 2020a, A&A, 634, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mahy, L., Sana, H., Abdul-Masih, M., et al. 2020b, A&A, 634, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mahy, L., Sana, H., Shenar, T., et al. 2022, A&A, 664, A159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Malzac, J. 2013, MNRAS, 429, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Malzac, J., & Belmont, R. 2009, MNRAS, 392, 570 [CrossRef] [Google Scholar]
- Mandel, I., & Broekgaarden, F. S. 2022, Liv. Rev. Relativ., 25, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Mapelli, M. 2020, Front. Astron. Space Sci., 7, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Marchant, P. 2017, Ph.D. Thesis, University of Bonn, Germany [Google Scholar]
- Marchant, P., & Bodensteiner, J. 2024, ARA&A, 62, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Marchant, P., Langer, N., Podsiadlowski, P., Tauris, T. M., & Moriya, T. J. 2016, A&A, 588, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marchant, P., Pappas, K. M. W., Gallegos-Garcia, M., et al. 2021, A&A, 650, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marchant, P., Podsiadlowski, P., & Mandel, I. 2023, ArXiv e-prints [arXiv:2311.14041] [Google Scholar]
- Marrone, D. P., Moran, J. M., Zhao, J.-H., & Rao, R. 2007, ApJ, 654, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Masuda, K., & Hirano, T. 2021, ApJ, 910, L17 [NASA ADS] [CrossRef] [Google Scholar]
- McClintock, J. E., & Remillard, R. A. 2006, Compact stellar X-ray sources, 39, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Menon, A., Langer, N., de Mink, S. E., et al. 2021, MNRAS, 507, 5013 [NASA ADS] [CrossRef] [Google Scholar]
- Miller-Jones, J. C. A., Bahramian, A., Orosz, J. A., et al. 2021, Science, 371, 1046 [Google Scholar]
- Mościbrodzka, M., Falcke, H., & Shiokawa, H. 2016, A&A, 586, A38 [Google Scholar]
- Motta, S. E., Rodriguez, J., Jourdain, E., et al. 2021, New Astron. Rev., 93, 101618 [CrossRef] [Google Scholar]
- Mudambi, S. P., Rao, A., Gudennavar, S. B., Misra, R., & Bubbly, S. G. 2020, MNRAS, 498, 4404 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, B., Heger, A., Liptai, D., & Cameron, J. B. 2016, MNRAS, 460, 742 [Google Scholar]
- Munar-Adrover, P., Paredes, J. M., Ribó, M., et al. 2014, ApJ, 786, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Narayan, R., Mahadevan, R., & Quataert, E. 1998, in Theory of Black Hole Accretion Disks, eds. M. A. Abramowicz, G. Björnsson, & J. E. Pringle, 182 [Google Scholar]
- Narayan, R., & Yi, I. 1994, ApJ, 428, L13 [Google Scholar]
- Narayan, R., & Yi, I. 1995, ApJ, 452, 710 [NASA ADS] [CrossRef] [Google Scholar]
- Novikov, I. D., & Thorne, K. S. 1973, in Black Holes (Les Astres Occlus), 343 [Google Scholar]
- Olejak, A., Klencki, J., Xu, X.-T., et al. 2024, ArXiv e-prints [arXiv:2404.12426] [Google Scholar]
- Orosz, J. A., McClintock, J. E., Narayan, R., et al. 2007, Nature, 449, 872 [NASA ADS] [CrossRef] [Google Scholar]
- Orosz, J. A., Steeghs, D., McClintock, J. E., et al. 2009, ApJ, 697, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Orosz, J. A., McClintock, J. E., Aufdenberg, J. P., et al. 2011, ApJ, 742, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Packet, W. 1981, A&A, 102, 17 [NASA ADS] [Google Scholar]
- Pakull, M. W., & Angebault, L. P. 1986, Nature, 322, 511 [NASA ADS] [CrossRef] [Google Scholar]
- Pauli, D., Langer, N., Aguilera-Dena, D. R., Wang, C., & Marchant, P. 2022, A&A, 667, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
- Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [Google Scholar]
- Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
- Paxton, B., Schwab, J., Bauer, E. B., et al. 2018, ApJS, 234, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Paxton, B., Smolec, R., Schwab, J., et al. 2019, ApJS, 243, 10 [Google Scholar]
- Pelletier, G., Bykov, A., Ellison, D., & Lemoine, M. 2017, Space Sci. Rev., 207, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Petit, V., Wade, G. A., Schneider, F. R. N., et al. 2019, MNRAS, 489, 5669 [NASA ADS] [CrossRef] [Google Scholar]
- Petrovic, J., Langer, N., & van der Hucht, K. A. 2005, A&A, 435, 1013 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Picco, A., Marchant, P., Sana, H., & Nelemans, G. 2024, A&A, 681, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plotnikov, I., Grassi, A., & Grech, M. 2018, MNRAS, 477, 5238 [Google Scholar]
- Ponti, G., George, E., Scaringi, S., et al. 2017, MNRAS, 468, 2447 [NASA ADS] [CrossRef] [Google Scholar]
- Porth, O., Mizuno, Y., Younsi, Z., & Fromm, C. M. 2021, MNRAS, 502, 2023 [NASA ADS] [CrossRef] [Google Scholar]
- Poutanen, J., & Vurm, I. 2009, ApJ, 690, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Predehl, P., Andritschke, R., Arefiev, V., et al. 2021, A&A, 647, A1 [EDP Sciences] [Google Scholar]
- Prieto, M. A., Fernández-Ontiveros, J. A., Markoff, S., Espada, D., & González-Martín, O. 2016, MNRAS, 457, 3801 [NASA ADS] [CrossRef] [Google Scholar]
- Puls, J., Vink, J. S., & Najarro, F. 2008, A&ARv, 16, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Qin, Y., Fragos, T., Meynet, G., et al. 2018, A&A, 616, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quast, M., Langer, N., & Tauris, T. M. 2019, A&A, 628, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quataert, E., & Narayan, R. 1999, ApJ, 520, 298 [Google Scholar]
- Ramachandran, V., Oskinova, L. M., Hamann, W. R., et al. 2022, A&A, 667, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Repetto, S., Davies, M. B., & Sigurdsson, S. 2012, MNRAS, 425, 2799 [Google Scholar]
- Ressler, S. M., Quataert, E., & Stone, J. M. 2018, MNRAS, 478, 3544 [NASA ADS] [CrossRef] [Google Scholar]
- Ressler, S. M., White, C. J., & Quataert, E. 2023, MNRAS, 521, 4277 [CrossRef] [Google Scholar]
- Ribó, M., Munar-Adrover, P., Paredes, J. M., et al. 2017, ApJ, 835, L33 [Google Scholar]
- Ripperda, B., Liska, M., Chatterjee, K., et al. 2022, ApJ, 924, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Rivinius, T., Baade, D., Hadrava, P., Heida, M., & Klement, R. 2020, A&A, 637, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Romani, R. W., Kandel, D., Filippenko, A. V., Brink, T. G., & Zheng, W. 2022, ApJ, 934, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Romero-Shaw, I., Hirai, R., Bahramian, A., Willcox, R., & Mandel, I. 2023, MNRAS, 524, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Ruffert, M. 1999, A&A, 346, 861 [NASA ADS] [Google Scholar]
- Russell, C. M. P., Wang, Q. D., & Cuadra, J. 2017, MNRAS, 464, 4958 [CrossRef] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Sana, H., de Koter, A., de Mink, S. E., et al. 2013, A&A, 550, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sandoval, A., Riquelme, M., Spitkovsky, A., & Bacchini, F. 2024, MNRAS, 530, 1866 [NASA ADS] [CrossRef] [Google Scholar]
- Saracino, S., Kamann, S., Guarcello, M. G., et al. 2022, MNRAS, 511, 2914 [NASA ADS] [CrossRef] [Google Scholar]
- Savonije, G. J. 1978, A&A, 62, 317 [NASA ADS] [Google Scholar]
- Saxton, R. D., Read, A. M., Esquej, P., et al. 2008, A&A, 480, 611 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scarcella, F., Gaggero, D., Connors, R., et al. 2021, MNRAS, 505, 4036 [NASA ADS] [CrossRef] [Google Scholar]
- Schootemeijer, A., Lennon, D. J., Garcia, M., et al. 2022, A&A, 667, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schürmann, C., & Langer, N. 2024, ArXiv e-prints [arXiv:2404.08615] [Google Scholar]
- Sen, K., Xu, X. T., Langer, N., et al. 2021, A&A, 652, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sen, K., Langer, N., Marchant, P., et al. 2022, A&A, 659, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sen, K., Langer, N., Pauli, D., et al. 2023, A&A, 672, A198 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shakura, N. I. 1973, Sov. Ast., 16, 756 [NASA ADS] [Google Scholar]
- Shao, Y., & Li, X.-D. 2014, ApJ, 796, 37 [Google Scholar]
- Shao, Y., & Li, X.-D. 2019, ApJ, 885, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Shao, Y., & Li, X.-D. 2020, ApJ, 898, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Shao, Y., & Li, X.-D. 2022, ApJ, 930, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Shapiro, S. L., & Lightman, A. P. 1976, ApJ, 204, 555 [NASA ADS] [CrossRef] [Google Scholar]
- Sharma, P., Quataert, E., Hammett, G. W., & Stone, J. M. 2007, ApJ, 667, 714 [NASA ADS] [CrossRef] [Google Scholar]
- Shenar, T., Sana, H., Mahy, L., et al. 2022a, Nat. Astron., 6, 1085 [NASA ADS] [CrossRef] [Google Scholar]
- Shenar, T., Sana, H., Mahy, L., et al. 2022b, A&A, 665, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Singh, C. B., de Gouveia Dal Pino, E. M., & Kadowaki, L. H. S. 2015, ApJ, 799, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Sironi, L., Spitkovsky, A., & Arons, J. 2013, ApJ, 771, 54 [Google Scholar]
- Spera, M., Mapelli, M., Giacobbo, N., et al. 2019, MNRAS, 485, 889 [Google Scholar]
- Sridhar, N., Sironi, L., & Beloborodov, A. M. 2021, MNRAS, 507, 5625 [NASA ADS] [CrossRef] [Google Scholar]
- Stone, J. M., & Pringle, J. E. 2001, MNRAS, 322, 461 [CrossRef] [Google Scholar]
- Stone, J. M., Pringle, J. E., & Begelman, M. C. 1999, MNRAS, 310, 1002 [Google Scholar]
- Sukhbold, T., Woosley, S. E., & Heger, A. 2018, ApJ, 860, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R., Arefiev, V., Babyshkin, V., et al. 2021, A&A, 656, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tanikawa, A., Hattori, K., Kawanaka, N., et al. 2023, ApJ, 946, 79 [CrossRef] [Google Scholar]
- Thompson, T. A., Kochanek, C. S., Stanek, K. Z., et al. 2019, Science, 366, 637 [NASA ADS] [CrossRef] [Google Scholar]
- Timmes, F. X., Woosley, S. E., & Weaver, T. A. 1996, ApJ, 457, 834 [NASA ADS] [CrossRef] [Google Scholar]
- ud-Doula, A., & Owocki, S. P. 2002, ApJ, 576, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Valsecchi, F., Glebbeek, E., Farr, W. M., et al. 2010, Nature, 468, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Vanbeveren, D., Mennekens, N., van den Heuvel, E. P. J., & Van Bever, J. 2020, A&A, 636, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van den Heuvel, E. P. J., Portegies Zwart, S. F., & de Mink, S. E. 2017, MNRAS, 471, 4256 [Google Scholar]
- van Son, L. A. C., de Mink, S. E., Callister, T., et al. 2022, ApJ, 931, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Vigna-Gómez, A., Justham, S., Mandel, I., de Mink, S. E., & Podsiadlowski, P. 2019, ApJ, 876, L29 [CrossRef] [Google Scholar]
- Vilhu, O., Kallman, T. R., Koljonen, K. I. I., & Hannikainen, D. C. 2021, A&A, 649, A176 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Villaseñor, J. I., Taylor, W. D., Evans, C. J., et al. 2021, MNRAS, 507, 5348 [CrossRef] [Google Scholar]
- Vinciguerra, S., Neijssel, C. J., Vigna-Gómez, A., et al. 2020, MNRAS, 498, 4705 [NASA ADS] [CrossRef] [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wade, G. A., Neiner, C., Alecian, E., et al. 2016, MNRAS, 456, 2 [Google Scholar]
- Walter, R., Lutovinov, A. A., Bozzo, E., & Tsygankov, S. S. 2015, A&ARv, 23, 2 [Google Scholar]
- Wang, H., & Grindlay, J. 2022, Am. Astron. Soc. Meeting Abstracts, 240, 205.12 [NASA ADS] [Google Scholar]
- Wang, Q. D., Nowak, M. A., Markoff, S. B., et al. 2013, Science, 341, 981 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, G. R., Uzdensky, D. A., Cerutti, B., Nalewajko, K., & Begelman, M. C. 2016, ApJ, 816, L8 [Google Scholar]
- Werner, G. R., Uzdensky, D. A., Begelman, M. C., Cerutti, B., & Nalewajko, K. 2018, MNRAS, 473, 4840 [Google Scholar]
- Wong, K.-W., Irwin, J. A., Yukita, M., et al. 2011, ApJ, 736, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Wong, T.-W., Valsecchi, F., Fragos, T., & Kalogera, V. 2012, ApJ, 747, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Xie, F.-G., & Yuan, F. 2012, MNRAS, 427, 1580 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, Z., Yuan, F., & Ho, L. C. 2011, ApJ, 726, 87 [Google Scholar]
- Yuan, F. 2001, MNRAS, 324, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, F., & Bu, D.-F. 2010, MNRAS, 408, 1051 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, F., Quataert, E., & Narayan, R. 2003, ApJ, 598, 301 [Google Scholar]
- Yuan, F., Bu, D., & Wu, M. 2012, ApJ, 761, 130 [Google Scholar]
- Yuan, F., Gan, Z., Narayan, R., et al. 2015, ApJ, 804, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Zahn, J. P. 1977, A&A, 57, 383 [Google Scholar]
- Zdziarski, A. A., Banerjee, S., Chand, S., et al. 2024, ApJ, 962, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Zenitani, S., & Hoshino, M. 2007, ApJ, 670, 702 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, F., Li, X. D., & Wang, Z. R. 2004, ApJ, 603, 663 [Google Scholar]
- Zhang, S., Liu, B., & Bromm, V. 2024, MNRAS, 528, 180 [CrossRef] [Google Scholar]
- Zhao, X., Gou, L., Dong, Y., et al. 2021, ApJ, 908, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Ziolkowski, J. 2014, Multifrequency Behaviour of High Energy Cosmic Sources, 175 [Google Scholar]
Appendix A: Predictions for δ = 0.1
Appendix B: Observable parameter distribution for X-ray-bright systems
 |
Fig. B.1. Same as Fig. 4 but showing the distribution of BH+OB star binaries that can produce X-ray luminosity above 1035 erg/s. The black markers show the position of the three observed wind-fed BH HMXBs. |
Appendix C: Rotational velocity distribution of the OB companions
Figure C.1 shows the distribution of the ratio of the rotational velocity to the critical velocity of the OB star companions to the black hole during the BH+OB phase. In our models, about ∼72.5% and ∼80.8% of the OB stars during the BH+OB phase are rotating above 95% and 80% of their critical rotational velocity, respectively. As such, they may be observable as OBe stars (e.g. Shao & Li 2014; Schootemeijer et al. 2022).
 |
Fig. C.1. The ratio of the rotational velocity to the critical rotational velocity of the OB star companion during the BH+OB phase for all our binary models. The three colours denote the contributions from different initial orbital period ranges. The histograms are stacked on top of each other and the sum of ordinate values equals unity. |
All Tables
All Figures
 |
Fig. 1. Distribution of the mass-accretion rate at the accretion radius (Eq. (22), left panel) and the mass-accretion rate at the event horizon of the BH (Eq. (32), right panel), during the BH+OB star phase. The three colours denote the contributions from different initial orbital period ranges. The coloured histograms are stacked on each other, and the sum of the ordinate values equals unity. The black hatching shows the contribution from the BH+OB star binaries where a Keplerian accretion disc can form. |
| In the text | |
 |
Fig. 2. Distribution of X-ray luminosity from BH+OB star binaries for three values of the viscous dissipation parameter δ = 0.001 (top panel), 0.1 (middle panel), 0.5 (bottom panel). Light blue, dark blue, and red colours denote the contributions from binary models with different initial donor mass ranges of 10–20 M⊙, 20–40 M⊙, and 40–90 M⊙, respectively. The coloured histograms are stacked on each other, and the sum of their ordinate values equals unity (see Eq. (33)). The black step histogram shows the distribution of X-ray luminosity arising from the shocks in the winds of the OB star companion and is separately normalised to unity. |
| In the text | |
 |
Fig. 3. Observable properties of X-ray-bright systems. Left panel: Distribution of the Roche lobe filling factor of BH+OB star binaries where an accretion disc can form (Sect. 3.2). Light blue, dark blue, and red colours denote the contributions from binary models with different initial orbital period ranges of 1.4–10 d, 10–100 d, and 100–3162 d, respectively. The coloured histograms are stacked on each other, and the sum of their ordinate values is equal to 0.0785 (the fraction of X-ray-bright systems predicted from our entire population of BH+OB star binaries). Right panel: Disc-formation thresholds (Eq. (10) of Sen et al. 2021) shown by slanted solid, dashed, and dotted lines for three BH masses corresponding to the three observed wind-fed BH HMXBs (Orosz et al. 2007, 2009; Miller-Jones et al. 2021; Ramachandran et al. 2022). The black slanted line shows the disc-formation threshold of the maximum BH mass from our binary model grid. An accretion disc can form below the slanted lines and vice versa. The three circles correspond to the observed orbital period and calculated OB star wind speed at the position of the BH (assuming a β-law for the wind velocity profile, with β = 1, Eq. (1) of Sen et al. 2021) of the three BH-hosting wind-fed HMXBs. The horizontal solid lines correspond to the range of wind speed by varying β from 0.5 (upper-speed limit) to 2 (lower limit). The arrows indicate the new position of the square markers if the BH’s orbital period was twice as long. The grey region is where the wind-accretion approximation υw > aΩ is no longer valid. The heatmap shows the distribution of the orbital period of the binary models and wind speed of the OB star companions during the BH+OB star phase when an accretion disc can form. The colour bar gives the predicted fraction of BH HMXBs in each pixel. The sum of the pixels is equal to unity. |
| In the text | |
 |
Fig. 4. Distribution of orbital period and luminosity of the OB star companion from BH+OB star binaries that can produce X-ray luminosity 1031–1035 erg/s through wind accretion, for two values of the viscous heating parameter δ = 0.001 (left panel) and 0.5 (right panel). The colour bar gives the predicted fraction of X-ray-faint BH+OB star binaries in each pixel. The sum of the pixels in each panel is equal to unity. VFTS 243 (Shenar et al. 2022b) is shown by a black star. Two more potential BH+OB star binaries are marked with thin and thick diamonds (Shenar et al. 2022b). A further six SB1 systems with unseen companions (having mass above 2.35 M⊙) are marked by white circles (Table 1; data from Shenar et al. 2022b). |
| In the text | |
 |
Fig. 5. Distribution of X-ray luminosity produced from ADAFs around BHs without Keplerian accretion discs and the bolometric luminosity of the OB star companion, for two values of the viscous dissipation parameter δ = 0.001 (left panel) and 0.5 (right panel). The colour bar gives the predicted number of BH+OB star binaries in each pixel. The sum of the pixels in each panel is equal to unity. The solid black line shows the LX, w = 10−7LOB relation, with the dotted line and the dot-dashed line showing the ±1 dex range. The black and grey downward arrow denotes the upper limit to the X-ray luminosity from VFTS 827 and VFTS 243. |
| In the text | |
 |
Fig. A.1. Same as Fig. 4 but for δ = 0.1. |
| In the text | |
 |
Fig. A.2. Same as Fig. 5 but for δ = 0.1. |
| In the text | |
 |
Fig. B.1. Same as Fig. 4 but showing the distribution of BH+OB star binaries that can produce X-ray luminosity above 1035 erg/s. The black markers show the position of the three observed wind-fed BH HMXBs. |
| In the text | |
 |
Fig. C.1. The ratio of the rotational velocity to the critical rotational velocity of the OB star companion during the BH+OB phase for all our binary models. The three colours denote the contributions from different initial orbital period ranges. The histograms are stacked on top of each other and the sum of ordinate values equals unity. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



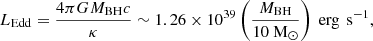
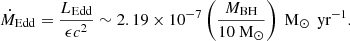
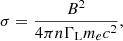
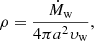
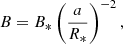
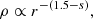
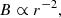
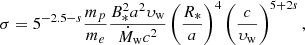
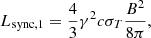
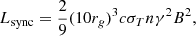
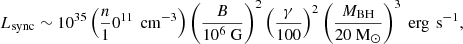
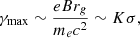
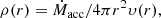
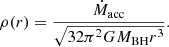
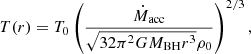
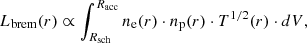
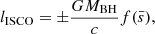
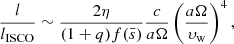
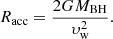
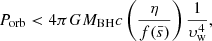
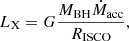
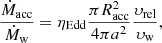
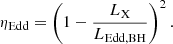
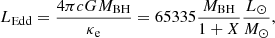
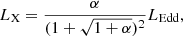
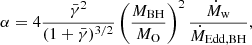
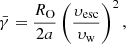
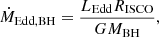
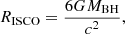
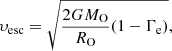
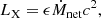
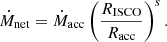
![$$ \begin{aligned} h_{\rm obs} \, ( X_{\rm 1} < X_{\rm obs} < X_{\rm 2} ) = \frac{\sum _{\rm m = 1}^\mathrm{N} \,W_{\rm m} \, \Delta t_{\rm [X_{\rm 1},X_{\rm 2}],m}}{\sum _{\rm m = 1}^\mathrm{N} \, W_{\rm m} \, \Delta t_{\rm BH+O,m}}\,, \end{aligned} $$](/articles/aa/full_html/2024/10/aa50940-24/aa50940-24-eq58.gif)