| Issue |
A&A
Volume 635, March 2020
|
|
|---|---|---|
| Article Number | A22 | |
| Number of page(s) | 11 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201935977 | |
| Published online | 02 March 2020 | |
Expected performances of the Characterising Exoplanet Satellite (CHEOPS)
I. Photometric performances from ground-based calibration
1
Department of Astronomy, University of Geneva, Chemin des Maillettes 51, 1290 Versoix, Switzerland
e-mail: adrien.deline@unige.ch
2
Cavendish Laboratory, University of Cambridge, J J Thomson Avenue, Cambridge CB3 0HE, UK
3
Centre for Space and Habitability, University of Bern, Gesellschaftsstrasse 6, 3012 Bern, Switzerland
Received:
29
May
2019
Accepted:
5
August
2019
Context. The characterisation of Earth-size exoplanets through transit photometry has stimulated new generations of high-precision instruments. In that respect, the Characterising Exoplanet Satellite (CHEOPS) is designed to perform photometric observations of bright stars to obtain precise radii measurements of transiting planets. The CHEOPS instrument will have the capability to follow up bright hosts provided by radial-velocity facilities. With the recent launch of the Transiting Exoplanet Survey Satellite (TESS), CHEOPS may also be able to confirm some of the long-period TESS candidates and to improve the radii precision of confirmed exoplanets.
Aims. The high-precision photometry of CHEOPS relies on careful on-ground calibration of its payload. For that purpose, intensive pre-launch campaigns of measurements were carried out to calibrate the instrument and characterise its photometric performances. This work reports on the main results of these campaigns. It provides a complete analysis of data sets and estimates in-flight photometric performance by means of an end-to-end simulation. Instrumental systematics were measured by carrying out long-term calibration sequences. Using an end-to end model, we simulated transit observations to evaluate the impact of in-orbit behaviour of the satellite and to determine the achievable precision on the planetary radii measurement.
Methods. After introducing key results from the payload calibration, we focussed on the data analysis of a series of long-term measurements of uniformly illuminated images. The recorded frames were corrected for instrumental effects and a mean photometric signal was computed on each image. The resulting light curve was corrected for systematics related to laboratory temperature fluctuations. Transit observations were simulated, considering the payload performance parameters. The data were corrected using calibration results and estimates of the background level and position of the stellar image. The light curve was extracted using aperture photometry and analysed with a transit model using a Markov chain Monte Carlo algorithm.
Results. In our analysis, we show that the calibration test set-up induces thermally correlated features in the data that can be corrected in post-processing to improve the quality of the light curves. We find that on-ground photometric performances of the instrument measured after this correction is of the order of 15 parts per million over five hours. Using our end-to-end simulation, we determine that measurements of planet-to-star radii ratio with a precision of 2% for a Neptune-size planet transiting a K-dwarf star and 5% for an Earth-size planet orbiting a Sun-like star are possible with CHEOPS. These values correspond to transit depths obtained with signal-to-noise ratios of 25 and 10, respectively, allowing the characterisation and detection of these planets. The pre-launch CHEOPS performances are shown to be compliant with the mission requirements.
Key words: planets and satellites: detection / techniques: photometric / space vehicles: instruments / instrumentation: photometers
© ESO 2020
1. Introduction
After the first observations of a transiting exoplanet in 1999 (Charbonneau et al. 2000; Henry et al. 2000), the number of planets identified to pass in front of their host stars kept increasing. Following the early successes of wide-field surveys such as the Wide Angle Search for Planets (WASP; Pollacco et al. 2006), the launch in 2009 of Kepler, a dedicated transit search satellite (Koch et al. 1998; Borucki et al. 2010), produced a continuous stream of transiting planet candidates. At the end of its nominal duration, the Kepler mission identified more than 4700 candidates, including over 2300 confirmed extrasolar planets in transit. The radii of these objects, derived from the in-transit light curve (Winn 2010), span a large range from Mars-size up to Jupiter-size planets. Unfortunately, the vast majority of stars with transit planets identified by Kepler are too faint to be easily followed up from the ground, making the determination of the planetary masses by precise Doppler measurements challenging. Combining masses and radii measurements of exoplanets is essential to obtain an estimate of their bulk densities and to retrieve information about their physical structures and possibly their formation processes. The Transiting Exoplanet Survey Satellite (TESS; Ricker et al. 2015) was launched in April 2018 with the purpose of performing a whole-sky transit search survey on brighter stars. A dozen confirmed transiting exoplanets have already been found (Gandolfi et al. 2018; Wang et al. 2019; Trifonov et al. 2019). The typical duration of observation sequence for each field observed by TESS is 27 days. During this time, a transiting planet with period longer than ten days would best transit once or twice, limiting the precision of planetary radius measurement for these systems. In this context, the Characterising Exoplanet Satellite (CHEOPS; Broeg et al. 2013; Fortier et al. 2014) has been designed to perform pointed follow-up observations of bright stars with the goal to reach a photometric precision similar to Kepler. When combined with TESS survey potential, CHEOPS will have the capability to confirm candidates and to improve some of these radii measurements.
The CHEOPS spacecraft will be launched on a circular Sun-synchronous orbit at an altitude of 700 km and a local time of ascending node of 6AM. This configuration corresponds to a nearly polar orbit (inclination of 98°) with a period of almost 100 min. The CHEOPS telescope will be able to point target up to 60° off the ecliptic plane corresponding to an overall sky coverage of 70%. The cadence of the observations will be better than 1 min. The nominal mission duration is 3.5 years with a goal of 5 years. The launch date is planned between mid-October and mid-November 2019.
The spacecraft is made of two main modules: the platform and the payload. The platform maintains the thermal stability of the payload, ensures the powering of the instrument, and operates the data down-link to Earth. The performance of the payload attitude and control system (AOCS) is designed to maintain tracking on target with better than 4 arcsec (rms). The payload includes the telescope, a Ritchey-Chrétien design with a primary mirror of 32 cm in diameter, and an efficient stray-light suppression system made of a baffle and a field stop. The payload detector is a 1024 × 1024-pixel frame-transfer, back-illuminated, charge-coupled device (CCD) from the CCD47-20 family of sensors manufactured by the company e2v. The CCD and the front-end electronics are both thermally stabilised at the precision of 10 mK and have operating temperatures of −40 °C and −10 °C, respectively, to limit the noise contributions of the dark current and electronic gain variability. The pixel scale on the detector corresponds to 1 arcsec on the sky.
The point spread function (PSF) of the target image on the detector has a radius of 12 pixels (distance from the PSF centre at which 90% of the energy is encircled), to ensure the illumination of enough pixels to minimise the photometric effect of satellite tracking residuals. To maximise science data down-link and to achieve a 1 min sample rate, a circular sub-frame of 200 × 200 pixels centred on the target is downloaded. This represents a field of view of 3.3 arcmin in diameter. The photometric spectral domain of CHEOPS covers a range from 330 nm to 1100 nm (see Fig. 1), similar to the space mission Gaia (Gaia Collaboration 2016). During the course of its orbit around the Earth, the spacecraft keeps rolling to maintain its cold plate radiators opposite to the Earth direction. As a result, the field of view rotates around the pointing line of sight defined by the target location on the detector. This creates a circular motion of the background stars at a rate of one rotation per orbital period (100 min).
 |
Fig. 1. Normalised spectral transmissions (in units of energy) of CHEOPS (blue) and other space missions: Kepler in green (Van Cleve & Caldwell 2016), Gaia in orange (G passband; Maíz Apellániz & Weiler 2018), and TESS in brown (Ricker et al. 2015). |
The CHEOPS mission has been designed with two science requirements in mind. First the instrument has the capability to detect an Earth-size planet with a period of 50 days transiting a G5 star (R* = 0.9 R⊙) with V-magnitude of 9. This corresponds to a light curve with a typical noise of 20 parts per million (ppm) when six hours of data are combined. Second, the instrument is able to measure a transit light curve with signal-to-noise ratio (S/N) of 30 on a K-type star (R* = 0.7 R⊙) from a transiting Neptune-size planet with a period of 13 days. This corresponds to reaching a photometric precision of 85 ppm on the light curve in three hours.
This work is based on results obtained during ground calibration campaigns to assess the photometric precision of CHEOPS satellite. A brief description of equipment used is mentioned in Sect. 2 where relevant references are provided for more details. The main calibration products required for the data analysis of this study are described in Sect. 3. We then develop two approaches to assess CHEOPS performances. The first is based on the analysis of long-term data set obtained during the calibration campaign (Sect. 4). In the second, we develop an end-to-end data simulation with transit observations (Sect. 5).
This paper is part of a mini-series entitled Expected performances of the Characterising Exoplanet Satellite (CHEOPS), which includes two other publications. One describes the software CHEOPSim developed for the CHEOPS mission to simulate scientific data (Futyan et al. 2020). The CHEOPSim software is briefly introduced in Sect. 5.1.1. The other publication details the data reduction pipeline (DRP) that will be used during the mission to extract the photometry from the raw data and provide light curves of planetary systems (Hoyer et al. 2020).
2. Calibration test set-up
A set-up was specifically developed and integrated to perform the calibration of the CHEOPS payload, including the flying CCD (Wildi et al. 2015a). The system is based on a “super-stable (light) source” (SSS) capable of reaching a stability of 3 ppm over 1 min (Wildi et al. 2015b) and covering the whole passband of CHEOPS. The SSS system could also be used to modify the source spectrum by inserting optical filters or by directing the light through a monochromator. The stabilised flux was then injected in an optical fibre and guided to the focal plane module (FPM) of the set-up, located on an optical table. The FPM was able to switch between two different modes: a point-source mode simulating a single-star field and an extended-source mode illuminating uniformly (better than 99.5% uniformity) the whole CHEOPS CCD. The diverging beam coming from the FPM was collimated by an off-axis parabolic mirror before being directed towards the payload by a tip-tilt folding flat mirror. For performance tests, the payload was located inside a thermal-vacuum chamber (TVC) with a window allowing the pupil of the telescope to be fully illuminated by the stabilised beam (see Fig. 2). The purpose of the TVC was to reproduce the space conditions in which the satellite will have to operate in orbit. In that respect, the test set-up provides the possibility to vary some of the payload parameters allowing us to explore the ranges within which we expect CHEOPS to evolve while in space.
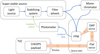 |
Fig. 2. Functional diagram of the CHEOPS calibration bench. The blue arrows represent the optical fibres used to guide the light through the calibration bench. The SSS is equipped with a system that can send the light in the monochromator or bypass it. The light beam (orange) emitted by the FPM first hits the off-axis parabolic (OAP) mirror before being folded by a flat tip-tilt mirror. After exiting the bench, the light goes through a window into the TVC and enters the payload telescope. In the FPM, part of the source flux is picked up and sent to a feedback photometer that is used to control the stabilising system of the SSS. |
During the calibration campaign, technical limitations and lack of time prevented us to perform long and systematic series of precise photometric measurements with star-like point-source images. This mode was only used to measure the shape of the PSF on the detector, which is essential to produce a realistic end-to-end modelling. We conducted our series of photometric measurements using the extended-source mode and all results presented in this work were obtained with uniformly illuminated images. During the course of this work, we found out that the light source stabilisation was correlated with the laboratory temperature. The optical fibre used by the feedback loop has a refractive index sensitive to thermal changes (Moraleda et al. 2013; Wang et al. 2014). This means that the flux measured by the photometer to drive the lamp stabilisation mechanism is inaccurate. This leads to erroneous feedback stabilisation commands. Unfortunately, time pressure to deliver the payload for integration on the platform prevented us to elaborate a solution to fix the feedback loop. We decided to operate the whole system in open loop, keeping the photometer only as a flux sensor, and to perform post-processing correction of this effect on the recorded data.
3. Instrument calibration products
In this section, we essentially focus on calibration measurements relevant for high-precision photometry, assuming nominal operations. We briefly present calibration results and stability performances of electronic bias offset, detector dark current and read-out electronic system gain. The process to measure the photo-response non-uniformity of the detector is presented. The precision of flat-field correction is finally assessed.
3.1. Bias offset, dark current, gain, and instrument stability
The bias level was computed with an average precision of 0.2 ADU pixel−1. The read-out noise (RON) is 14 e− and 7 e− for read-out frequencies of 230 kHz and 100 kHz, respectively. When operated at nominal temperature, the CCD dark current measured over the whole detector frame has an average value of 0.028 e− s−1 (value of the mode of the intensity histogram). We identified two hot pixels (>10 e− s−1) and five warm pixels (>5 e− s−1) on the detector.
The read-out electronic system gain and the non-linearity are two quantities describing the conversion of the number of electrons recorded by the CCD to digital units stored by the computer. The scaling conversion is the gain, that is a multiplicative factor expressed in ADU/e−. This value depends mainly on the temperature and power voltages operating the detector. The non-linearity term quantifies the deviation from the gain conversion above and mostly depends on the CCD read-out frequency. The value of the gain in nominal conditions was measured with a precision of 0.6%. The gain variations during changes of CCD temperature and power operating voltages were measured and modelled during the characterisation phases of the detector (Deline et al. 2017). Measured gain sensitivities are typically of the order of 30 ppm mV−1 and 1 ppm mK−1 for the voltages and temperature respectively. Using a simple thermal model (a second-order spline curve) deviations are found smaller than 0.1% rms. During our measurements, we stayed within dynamical range of our detector defined when the non-linearity is less than 3%. This corresponds to an upper value of 121 ke−.
A long series of measurements, over hours, have shown bias level and read-out noise to be very stable with variations smaller than 30 milli-ADU per day and 1 milli-ADU per day, respectively. During these sequences the stability of the bias voltages powering the detector was of the order of tens of μV, whereas the temperatures were varying on a milli-Kelvin scale. When combining these numbers with the gain sensitivities, we find that for nominal operations the effect of the gain variations is of the order of 1 ppm and have a negligible contribution to our noise budget.
3.2. Flat fields
Owing to the manufacturing process, the CCD have small spatial variations in thickness, pixel sizes, well depths, and substrate material. These imperfections generate pixel-to-pixel non-uniformity of the detector photo-response. If not accurately measured, when combined with the expected guiding errors of a few arcseconds, this non-uniformity creates photometric errors. An accurate characterisation of pixel photo-response non-uniformity, or flat field, is an essential step to obtain precise photometry.
3.2.1. Measurements
Photons are absorbed by the CCD at different depths depending on their wavelengths. This colour dependency has to be accounted for to measure the detector flat-field responses accurately since the spectral distribution of the stellar flux depends on the nature of the star considered. To characterise in detail the detector response over the CHEOPS passband, we measured flat fields on restricted wavelength domain using 23 different narrow-band filters (Δλ = 30 nm) from 442.5 nm to 734.3 nm and 4 broadband Johnson/Bessel filters (U, B, R, I) (see Fig. 3). Flat-field images are calibrated, converted into photoelectrons, and normalised to their mean. The average rms precision per pixel for each flat field is 6 10−4. Different spatial features are visible for each range of wavelength, such as the typical diamond pattern visible in the blue. The measurements were repeated a week later and we could not detect any variation in the flat-field images, suggesting flat fields are stable on timescales of days.
 |
Fig. 3. Flat fields measured with the narrow-band filters at 442.5 nm (upper left), 580.3 nm (upper right), and 734.3 nm (lower left) and the broadband Johnson/Bessel I filter (lower right). The colour scale is not linear and has been optimised to highlight small variations using histogram equalisation. The four dark corners on all images are not dead pixels but are caused by a stray-light suppression component of the payload called field stop. |
3.2.2. Flat-field synthesis
Our ability to establish an overall flat-field response from chunks of flat fields is essential to correct it accurately for a large range of stellar types. To demonstrate we could produce “à la carte” flat-field synthesis, we uniformly illuminated the CCD with a Tungsten lamp (2500 K) and we measured its corresponding flat field. To account for the transformation of the source emission spectrum into photoelectrons by the payload (optical telescope and CCD), we computed the spectral distributions of the Tungsten and calibration flat fields in electrons. We then established the best linear combination of our series of filter spectral distributions (discarding the U broadband filter) to reproduce the observed tungsten spectral shape (see Fig. 4). We used these coefficients to compute the linear sum of the filter flat fields and normalised this sum. We compared our synthetic flat field with the measured flat field. We found a dispersion of residuals of 7 10−4 rms (see Fig. 5) corresponding to the average rms precision per pixel for each flat field. We also noticed a spatial structure in the residuals with an amplitude of about 0.06%, whose shape seemed to indicate a slight under correction in the infrared.
 |
Fig. 4. Weighted spectral distributions of the U, B, R, I (Johnson/Bessel filters) and narrow-band filters used to fit the Tungsten lamp profile (black). The weighted sum of the distributions is the “best-fit curve” (green). The spectral transmission of the top-hat filter (yellow dashed line) has been added for information (see Sect. 4.1). |
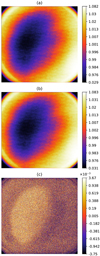 |
Fig. 5. Results of the flat-field synthesis. Panel a: target flat field measured with the Tungsten lamp. Panel b: synthesised flat field. Panel c: residual image with a dispersion of 0.073% rms, slightly greater than the noise-limited precision (0.058%). The image colour scales are expressed in normalised number of photoelectrons. These scales are not linear and have been optimised to highlight small variations using histogram equalisation. |
The light source used in this validation test reproduces the spectrum of a very cool star. For hotter stars, the fine sampling available at short wavelengths guarantees an even better synthetic flat field.
4. Photometric performances
This section reports on the analyses and results from a long-term series of measurements obtained during the calibration campaign with the purpose of assessing the photometric performances of CHEOPS.
4.1. Measurement
During 27.35 h, we collected an uninterrupted series of data, with an exposure time of 3 s, simulating an observation equivalent to the duration of 16 CHEOPS orbits. During this long sequence, the payload was operated in nominal science conditions (R-channel read-out, CCD at −40 °C, nominal bias voltages, and read-out frequency of 230 kHz). The front-end electronics was stabilised at −5 °C, 5 °C warmer than its nominal value, without consequences on operation performances. The detector of the instrument was uniformly illuminated using the extended-source mode of the FPM and the light source was operated in open-loop mode. To avoid photometric variations due to intensity variation of strong emission lines, we used a top-hat filter to select a continuous wavelength range, between 500 nm and 800 nm (see Fig. 4), where the source spectrum is free from such features. A total of 12243 images were recorded and analysed.
4.2. Data processing
4.2.1. Raw light curve
Each frame was corrected for its bias level, converted to electrons, and corrected from non-linearity effects and dark current. We σ-clipped each image to correct cosmic hits and bad pixels (two iterations with a 4σ threshold). Finally, we computed the mean flux on the whole image and used this value as our photometry measurement. The photometric sequence (or light curve equivalent) is visible on Fig. 6. The effects of open-loop operations, without feedback regulation of the lamp, are obvious in this figure.
 |
Fig. 6. Raw light curve (top panel) extracted from the images with a sampling time of 8.04 s. Light source variations (bottom panel) measured by the feedback photometer at a sampling frequency of about 12 Hz. |
4.2.2. Correcting the data from the light source variability
The constant monitoring of the source flux by the photometer provided a light curve sampled at about 12 Hz (see bottom panel of Fig. 6). We used this high-frequency data to correct the CCD light curve from the source variability.
During the measurements, the two data sets were not synchronised in time. We estimated the timing mismatch by cross correlation, assuming these data sets have similar patterns and we measured a time delay of 13.24 s. We shifted and resampled the photometer data accordingly to match the CCD acquisition rate with duration corresponding to CCD exposure time (3 s) and sampling time of (8.04 s). Finally, we normalised the photometer data by its average voltage by which we divided the CCD curve. The corrected curve is shown on top panel of Fig. 7. Variable features at 1% level visible on the light curve before correction are removed. The corrected light curve shows peak-to-valley amplitude variability of less than 200 ppm.
 |
Fig. 7. Light curve corrected for the source variability (top panel). Temperature of the optical table (middle panel). Residuals after correction of temperature correlation (bottom panel). The black points represent the 10-min data binned. |
4.2.3. Residual temperature correlation
The thermal sensitivity of the lamp regulation feedback (mostly due to the feedback fibre) affects the values measured by the photometer in such a way that they do not accurately reflect the flux received by the CCD. We expect a correlation with the laboratory temperature change. A PT100 thermal sensor is attached on the optical table and records its temperature for each CCD exposure with a resolution and precision of 0.01° C. When we bin the data of the temperature sensor over 10 min, a gentle drift with time is visible and obviously anti-correlated with the corrected light curve (see the two top panels of Fig. 7).
No time delay between the light and temperature curves was detected. With the goal to decorrelate the light curve variations using the measurement of the optical table temperature, we calculated the coefficient of linearity between the two data sequences. We noticed that this coefficient depended on the time sampling resolution of the thermal sensor considered as expected by its limited resolution. We found that when the temperature measurement is averaged over 10-min durations the error due to the limited resolution of the PT100 cancelled out and the linear coefficient converges to −347 e−/°C (see Fig. 8). To decorrelate the flux from the measured temperature variations, we used this correlation parameter and correct each photometric data point with its instantaneous temperature measurement. The corrected and de-trended light curve is shown on Fig. 7.
 |
Fig. 8. Temperature-flux scatter plot (left panel), with the raw data in grey and the 10-min binned data overplotted in green. The respective linear fits are indicated by the grey and red solid lines. Linear-fit parameters (slope and value at T = 0°C) versus time-length considered for binning (right panels). |
4.3. Photometric precision
The Allan variance analysis of the corrected and de-trended light curve is shown in Fig. 9. The visible deviation from the expected white noise regime suggests a noise floor and an additional correlated noise structure is present in the data. If one discards data points taken during the abrupt variations of the lamp, corresponding to measurement taken at t > 1320 min, the variation of the data Allan variance may be modelled using a white noise model and a noise floor of 15 ppm. It is realistic to believe that during these extremes variations of the lamp, second-order effects may not be properly accounted and corrected by a simple flux normalisation. Unfortunately, strict deadlines to deliver the payload on time did not allow us to repeat the measurements to confirm this assumption.
 |
Fig. 9. Noise curve of corrected and de-trended light curve (orange) with the estimated errors represented by the shaded areas. The blue curve shows the result after discarding the points taken during abrupt variations of the lamp (t > 1320 min). The noise values are not computed for time bins greater than 5 h to ensure at least four points in the binned data. The brown dashed curve is the quadratic sum of the white noise slope (oblique black dashed line) and an arbitrary threshold at 15 ppm (horizontal red dashed line). |
So far, in our analysis, the whole image area of the CCD has been considered. Practically, to be compared with a photometric extraction with a circular aperture of 33 pixels in radius as will be done during target observations (Hoyer et al. 2020), we need to consider the case of a limited number of pixels. In that case, the S/N of a light curve can be computed according to the number of pixels considered with the following equation: 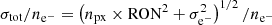 and σe− are the number of pixels, number of photoelectrons, and photoelectron shot noise, respectively. In addition, the number of photoelectrons in the photometric aperture is limited by the fact that the flux is adjusted such as the value of strongest peak of the PSF in a pixel never reaches the saturation of the detector. According to the shape of the CHEOPS PSF, we know that the value of the flux contained in a single pixel represents at maximum 2% of the integrated flux in the PSF. With this constraint, a PSF peak value equal to 70% of the CCD dynamical range (typical to prevent saturation) gives a total number of electrons in the whole circular aperture (33 pixels in radius) that corresponds to a relative noise of 522 ppm. Using the same equation in the case of uniformly illuminated images and a flux of 49 600 e− pixel−1, we find 74 pixels would generate similar S/N level.
and σe− are the number of pixels, number of photoelectrons, and photoelectron shot noise, respectively. In addition, the number of photoelectrons in the photometric aperture is limited by the fact that the flux is adjusted such as the value of strongest peak of the PSF in a pixel never reaches the saturation of the detector. According to the shape of the CHEOPS PSF, we know that the value of the flux contained in a single pixel represents at maximum 2% of the integrated flux in the PSF. With this constraint, a PSF peak value equal to 70% of the CCD dynamical range (typical to prevent saturation) gives a total number of electrons in the whole circular aperture (33 pixels in radius) that corresponds to a relative noise of 522 ppm. Using the same equation in the case of uniformly illuminated images and a flux of 49 600 e− pixel−1, we find 74 pixels would generate similar S/N level.
We then repeated our photometric analysis, extracting only 8×8-pixel regions of our CCD. This would correspond to a PSF with a maximum value of 75 ke− (62% of the dynamical range). Five light curves were computed selecting different areas of the CCD. The overall analysis of the data is identical to that applied previously and described in sections above. Figure 10 shows the result of the Allan analysis of the first 22 h of the five light curves. In all cases, the noise follows the white noise regime and reach 20 ppm in 5 h, in accordance with mission design requirements.
 |
Fig. 10. Noise curves of the flux extracted from five 8×8-pixel windows located at different positions on the detector (as indicated by the legend). The oblique black dashed line indicates the theoretical white noise slope while the horizontal line illustrates the 20 ppm level. |
5. Photometric performances from simulated observations
In this section, we investigate the expected in-flight performances by conducting an end-to-end simulation based on a realistic payload simulator (CHEOPSim) and results from the calibration campaign. Two sequences of observations were simulated. Each sequence can be related to a core science requirement of the mission. In the next section, we describe how the data have been produced, in the following section the data processing is detailed and finally the results are presented in terms of residual noise and precision on determination of the planet-to-star radii ratio.
5.1. Simulated observations
5.1.1. Characterising Exoplanet Satellite simulator
The CHEOPSim software, developed for the CHEOPS mission, simulates the scientific data produced by the CHEOPS payload (Futyan et al. 2020). This simulator produces a series of CCD images in a format similar to the one that will be available for science analysis on the ground. It includes the following features: the modelling of the stars (limb darkening, granulation, activity), the modelling of the transits, the modelling of the background (stray light, zodiacal light, cosmic rays), the modelling of the satellite (orbit, pointing jitters, field of view rotation, South Atlantic Anomaly, Earth occultation), the modelling of the telescope optics (optical transmission, PSF), and the modelling of the detector (bias offset, read-out noise, dark current, gain, non-linearity, flat field, quantum efficiency, bad pixels, saturation, frame transfer, smearing trails, charge-transfer inefficiency). Time series produced are discontinued with interruptions corresponding to South Atlantic Anomaly crossings (when data are not down-linked to ground in order to save telemetry) and when the target line of sight is occulted (by Earth) or too close to the stray-light limit (minimum angle separation to the sunlit limb of the Earth).
All features included in the modelling of the detector are based on performance measurements done during payload calibration. The CHEOPSim software uses PSF measured on the ground during the calibration campaign (see Fig. 11). We note that PSF shape is likely to be slightly different in space because of the absence of gravity (for more details on CHEOPSim, see Futyan et al. 2020).
 |
Fig. 11. Simulation image computed by CHEOPSim. The central target star has a V-band magnitude of 12, while the background field is that of BD-082823. The colour scale is the flux corrected for all instrumental and background signals, and normalised to the highest peak of the central PSF. The red circle represents a typical photometric aperture with a radius of 33 pixels. |
5.1.2. Description of the data sets
We simulated data sets of two series of observations representative of the mission requirements introduced in Sect. 1, with the purpose of validating the capability of CHEOPS in fulfilling its scientific goals. The first series of data simulates a sequence of two consecutive transit observations of an Earth-size planet orbiting a Sun-like star (G2V) with a period of 50 days. The second series simulates a single transit of a Neptune-size planet orbiting a K5V star with a period of 13 days. See Table 1 for more details about simulation parameters. In both cases, the planetary orbits are circular and the transit geometry has an impact parameter b = 0. Stellar photosphere effects, such as spots or granulation, were not considered but the three-dimensional nature of the atmospheres has been taken into account (limb-darkening effect).
Parameters of the simulated data sets.
The star field used in the background is the actual real stellar background that would have been found when pointing the star BD-082823, corresponding to a galactic longitude and latitude of 248.4966° and +34.7560°, respectively. It represents a field crowding configuration typical of most of CHEOPS observations (see Fig. 11).
The focus of this work is to evaluate the impact of the combination of satellite jitter, detector features, PSF shape, and stellar background on scientific results. To simplify the analysis, the cosmic rays and smearing trails were not included in our simulation. This assumption is equivalent to consider that the correction is efficient enough for the cosmic rays to have a marginal impact on the data and the smearing model is good enough to correct this effect in the case of very short exposure times (not the case considered in our simulations).
5.2. Data analysis
We developed a photometric extraction package to analyse CHEOPSim data. Our software computes photometry of the target from the raw images generated by the simulator. When executed on the whole series of data, it produces a light curve of the target star. This software is independent from the CHEOPS automatic DRP operated by the Science Operation Centre to reduce CHEOPS observations (Hoyer et al. 2020). We would like to point out that our software development also served the purpose to provide us with a validation tool independent from the DRP during review phases.
The electronic bias offset is estimated from the overscan regions and subtracted uniformly from the image. The image is converted from ADU to electrons with the gain and the non-linearity established during the calibration. Similar to the bias level, the dark current is computed from active CCD pixels not exposed to the sky and removed from the image. We synthesised the flat field corresponding to the spectrum of the target (see Sect. 3.2.2) and corrected the photo-response non-uniformity of the detector.
To estimate the background level, we select CCD pixels located on a ring centred on the target star. The size of the ring inner radius is 50 pixels to exclude most of the flux from the target including its halo. The size of the outer radius is 90 pixels to keep the ring in the image when satellite pointing jitter (4″ rms) is considered. To compute a robust background value, we build the intensity histogram of pixels in the ring and we model it by a normal distribution (𝒩(μ, σ2)). The best-fit parameter μ corresponds to the mean background value. The PSF position is computed on the background-subtracted image by a classical iterative centroid measurement method. For each iteration, we weight the image with a two-dimensional Gaussian function, and we calculate the new centre. This new position is used for the next iteration. The cycle stops when the centre remains within 10−4 pixels or after 30 iterations. As the background and the PSF centre depend on each other, our algorithm first assumes a PSF position at the image centre, estimates the background level, computes the PSF location, and then repeats the last two steps from the new PSF centre.
The photometric extraction is done by counting the number of electrons recorded on the CCD within a radius of 33 pixels centred on the target. The size of this radius is found to maximise the S/N of the light curve. To maintain a constant number of pixels in the aperture, the intersection area of each pixel and the aperture disc is computed analytically and used to weight the pixel value located on the edge of the extraction zone.
The errors on individual photometric data points of the light curve are computed from photon noise combined with the quadratic sum of all other measured uncertainties from calibration mostly dominated by gain and flat-field uncertainties (typically 0.6% each). By comparison the precision on the bias level, dark current background are of the order of a few electrons.
The light curve obtained from the photometric extraction is adjusted by a transit model implemented in batman (Kreidberg 2015) with a quadratic limb-darkening model1. We use the emcee (Foreman-Mackey et al. 2013) implementation of the Markov chain Monte Carlo (MCMC) algorithm to look for the best solution. The corner algorithm (Foreman-Mackey 2016) is used to visualise the multidimensional posterior distributions of the transit parameters from the MCMC outputs.
The eccentricity is by definition fixed to zero. The out-of-transit flux F0 and the planet-to-star radii ratio Rp/R* have uniform priors. The orbital period P and the mid-transit time t0 have Gaussian priors with typical uncertainties of 12 h and 60 h, respectively, for the first case (Earth size, bright star), and both parameters have uncertainties of 30 min for case 2 (Neptune size, faint star). To take into account the correlation between t0 and P, the prior of t0 is centred one orbital period before the observed transit. The prior of the semi-major axis a/R* is also Gaussian-shaped assuming 5% uncertainty on the stellar mass and 10% on the stellar radius. The impact parameter b is uniformly constrained in the interval ensuring the planetary transit (b < 1 + Rp/R*). The uniform priors of the limb-darkening coefficients restrain their values to realistic ranges, as detailed by Kipping (2013).
5.3. Results
The phase-folded light curves and the results of our analyses are shown in Figs. 12 and 13. The gaps visible in the sequences are caused by regular observation interruptions each time the satellite crosses the South Atlantic Anomaly or when the target is occulted by the Earth. With the first case (Earth transits), we compute a rms of 10.2 ppm when the residuals of the fit are averaged on the transit durations. Similarly a value of 51.7 ppm is measured for the second case (Neptune transit). These values should be compared with the expected photon noise level (computed from the square root of the flux) of 8.3 ppm (6 h of data) and 43 ppm (3 h of data). The small differences are the contributions of other terms from the error budget (gain, jitter, flat field, etc.) considered by the end-to-end simulations.
 |
Fig. 12. Light curves of the stellar flux (top) extracted from the simulated images of two transits of an Earth-size planet in front of a Sun-like star (case 1). The two transits are phase-folded. The black points are the 60-min binned data and the red curve corresponds to the best-fit model. The regular data gaps visible in the series are related to pointing visibility limits of CHEOPS during its orbit. Time is expressed from mid-transit. Phase-folded residuals (bottom). |
 |
Fig. 13. Light curve of the stellar flux (top) extracted from the simulated images of a Neptune-size planet transiting a K5 dwarf star (case 2). The black points represent 30-min binned data and the red curve corresponds to the best-fit model. Time is expressed from mid-transit. Residuals of the best fit (bottom). |
From corner plots of the MCMC outputs, we display five parameters showing interesting features: t0, P, Rp/R*, a/R* and b (see Fig. 14). We note that correlations for the simulation of the Neptune planet (case 2) are stronger than for the Earth planet (case 1), possibly due to the higher S/N of the transit, especially the definition of the ingress and egress phases (see Figs. 12 and 13). The strong correlation between t0 and P is explained by the fact that an overestimation of the orbital period tends to increase the duration between two transits and hence moves the mid-transit time backwards in time. The effect of the impact parameter is visible by its correlation with the planetary radius and the semi-major axis. Indeed, when b gets different from zero, the decrease of the duration and depth of the transit is balanced by a smaller a/R* (longer transit) and a larger Rp/R* (deeper transit).
 |
Fig. 14. Corner plots of the posterior distributions of the transit parameters t0, P, Rp/R*, a/R*, and b obtained for case 1 (Earth – left graph) and case 2 (Neptune – right graph). The red dashed lines represents the prior distributions. The blue vertical dashed lines highlight the mean value and 68% confidence interval of the marginalised distributions. |
The corner plots indicate the marginalised distributions of the parameters along with a representation of the corresponding priors (red dashed lines on Fig. 14). This allows us to see if the data constrain the parameters or if their values are only defined by the priors we initially set. Contrary to case 1, the absence of a second transit in case 2 prevents the parameters t0 and P to be constrained by the data and their prior and posterior distributions are almost identical. In both cases, the transit duration can be set by either a/R* or b, creating a degeneracy between these two parameters and explaining the prior-shaped posterior of the semi-major axis. We note that the impact parameter is also constrained by the transit ingress and egress. A better coverage of these phases could potentially help lift the degeneracy.
The uncertainties on the parameter values are estimated for both cases by computing the 68% confidence intervals on the marginalised distributions (see Table 2). In the case of the Earth-size planet, we obtain an uncertainty for the planet-to-star radii ratio of the order of 5%, which corresponds to a precision on the transit depth of about 10%, or a transit S/N of 10. With a transit depth of 100 ppm, a S/N of 10 corresponds to 10 ppm uncertainty on the transit depth. Our residual value on the light curve fit is consistent with this number (10.2 ppm). For the Neptune-size planet, we obtain a precision of 2% on Rp/R* (or 4% on (Rp/R*)2), equivalent to a transit S/N of 25. The residuals of the fit (51.7 ppm rms) and the transit depth of 2550 ppm suggest a transit S/N of 49, twice higher, potentially leading to 1% accuracy on Rp/R*. In that case, the transit S/N does not provide a good estimate of the expected precision on the radius. The correlation with the impact parameter and orbit interruptions tends to increase the uncertainty on Rp/R* measurement. A better prior knowledge of b could potentially lead to an improvement of the results.
Transit parameters for the two cases, derived from the posterior distributions.
We took advantage of this work to compare the performances of our tool and the version 10.1 of the DRP of CHEOPS. The same analysis was performed with the light curves obtained with the DRP and we found residual noise levels of 9.1 ppm for the Earth transit and 51.6 ppm for the Neptune transit. We also compared the depths of the transits and found identical parameter values and uncertainties.
6. Discussion and conclusions
In this work, we first reported on CHEOPS performances measured during the payload calibration campaign. We focussed on key features and correction of instrumental effects to achieve ultra-high precision photometry. For instance, we showed that the characterisation of the photo-response non-uniformity of the detector allows us to perform flat-field correction for any given stellar spectrum with a precision of about 0.07%. Then, we used the calibration products to carry out an end-to-end simulation. We analysed the simulated data and assessed mission performances to obtain precise stellar radius.
The photometric precision of CHEOPS was measured by using long-term series of uniformly illuminated images acquired during the calibration campaign. After correction of instrumental effects, we extracted the average photometric signal of each exposure and corrected from calibration bench variations. Our analysis demonstrated that CHEOPS photometric performances when operated in a nominal condition are within requirements (20 ppm over 6 h).
The data produced by CHEOPSim were analysed using an aperture photometry package developed specifically for this work. The results were compared with the mission requirements. In the case of an Earth-size planet transiting a Sun-like star, we achieved a residual noise level of 10.2 ppm over 6 h, which is better than the results measured during the calibration campaign. The analysis of the transit fit suggests we can measure the planet-to-star radii ratio with a precision of 5%, which corresponds to a S/N of 10 on the transit depth, that is compliant with the science objective of the mission. It is interesting to notice that, despite the interruption gaps, a very high S/N is reached, suggesting the detection may be possible with a single transit only. In the case of the Neptune-size planet in front of a K-dwarf star, we reached a residual noise of 51.7 ppm over 3 h, which is better than the photometric precision requirement of 85 ppm. The precision on the planetary radius we obtained is 2%, equivalent to a S/N of 25 on the transit depth. The corresponding S/N requirement is technically of 30 but does not account for interruptions in the light curves, which obviously reduces the number of data points and the overall precision. The correlation between the planetary radius and the impact parameter partially contribute to the increase of uncertainties.
The results presented are based on measurements from the payload calibration and hence cover all the effects related to the instrument. This takes into account the chromatic transmission and the PSF induced by the optical telescope, along with the various effects linked to the detector and its read-out electronic chain (bias offset, dark current, gain, and overall stability in time). Other aspects present once in space, such as the PSF shape in absence of gravity, the spatial distribution of the stray light, or the variations of the telescope temperature along the orbit of CHEOPS, are expected to have a marginal impact on the global photometric error budget. Overall, all elements and measurements we collected during the pre-launch calibration activities suggest that CHEOPS is meeting all its requirements and demonstrates outstanding photometric performances of the system.
Acknowledgments
This work has been carried out within the framework of the National Centre for Competence in Research PlanetS supported by the Swiss National Science Foundation. The authors acknowledge the financial support of the SNSF. The CHEOPS instrument and science simulator, CHEOPSim, is developed under the responsibility of the CHEOPS Mission Consortium. CHEOPSim is implemented by D. Futyan as part of the Science Operation Centre located at the University of Geneva. We would also like to thank the referee for the contribution to this work.
References
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Broeg, C., Fortier, A., Ehrenreich, D., et al. 2013, Eur. Phys. J. Web Conf., 47, 03005 [CrossRef] [EDP Sciences] [Google Scholar]
- Charbonneau, D., Brown, T. M., Latham, D. W., & Mayor, M. 2000, ApJ, 529, L45 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Deline, A., Sordet, M., Wildi, F., & Chazelas, B. 2017, SPIE Conf. Ser., 10562, 105624E [Google Scholar]
- Foreman-Mackey, D. 2016, J. Open Source Softw., 24 [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Fortier, A., Beck, T., Benz, W., et al. 2014, in Space Telescopes and Instrumentation 2014: Optical, Infrared, and Millimeter Wave, 9143, 91432J [Google Scholar]
- Futyan, D., Fortier, A., Beck, M., et al. 2020, A&A, 635, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gandolfi, D., Barragán, O., Livingston, J. H., et al. 2018, A&A, 619, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Henry, G. W., Marcy, G. W., Butler, R. P., & Vogt, S. S. 2000, ApJ, 529, L41 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hoyer, S., Guterman, P., Demangeon, O., et al. 2020, A&A, 635, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kipping, D. M. 2013, MNRAS, 435, 2152 [Google Scholar]
- Koch, D. G., Borucki, W., Webster, L., et al. 1998, in Space Telescopes and Instruments V, eds. P. Y. Bely, & J. B. Breckinridge, 3356, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Kreidberg, L. 2015, PASP, 127, 1161 [NASA ADS] [CrossRef] [Google Scholar]
- Maíz Apellániz, J., & Weiler, M. 2018, A&A, 619, A180 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moraleda, A. T., García, C. V., Zaballa, J. Z., & Arrue, J. 2013, Sensors (Basel), 13, 13076 [CrossRef] [Google Scholar]
- Pollacco, D. L., Skillen, I., Collier Cameron, A., et al. 2006, PASP, 118, 1407 [NASA ADS] [CrossRef] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Tel. Instrum. Syst., 1, 014003 [Google Scholar]
- Trifonov, T., Rybizki, J., & Kürster, M. 2019, A&A, 622, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Cleve, J. E., & Caldwell, D. A. 2016, Kepler Instrument Handbook, Tech. Rep. [Google Scholar]
- Wang, Z.-Y., Qiu, Q., & Shi, S.-J. 2014, Chin. Phys. B, 23, 034201 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, S., Jones, M., Shporer, A., et al. 2019, AJ, 157, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Wildi, F. P., Chazelas, B., Deline, A., Sordet, M., & Sarajlic, M. 2015a, in Techniques and Instrumentation for Detection of Exoplanets VII, 9605, 96051B [CrossRef] [Google Scholar]
- Wildi, F. P., Deline, A., & Chazelas, B. 2015b, in Techniques and Instrumentation for Detection of Exoplanets VII, 9605, 96051T [CrossRef] [Google Scholar]
- Winn, J. N. 2010, in Exoplanet Transits and Occultations, ed. S. Seager, 55 [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Normalised spectral transmissions (in units of energy) of CHEOPS (blue) and other space missions: Kepler in green (Van Cleve & Caldwell 2016), Gaia in orange (G passband; Maíz Apellániz & Weiler 2018), and TESS in brown (Ricker et al. 2015). |
| In the text | |
 |
Fig. 2. Functional diagram of the CHEOPS calibration bench. The blue arrows represent the optical fibres used to guide the light through the calibration bench. The SSS is equipped with a system that can send the light in the monochromator or bypass it. The light beam (orange) emitted by the FPM first hits the off-axis parabolic (OAP) mirror before being folded by a flat tip-tilt mirror. After exiting the bench, the light goes through a window into the TVC and enters the payload telescope. In the FPM, part of the source flux is picked up and sent to a feedback photometer that is used to control the stabilising system of the SSS. |
| In the text | |
 |
Fig. 3. Flat fields measured with the narrow-band filters at 442.5 nm (upper left), 580.3 nm (upper right), and 734.3 nm (lower left) and the broadband Johnson/Bessel I filter (lower right). The colour scale is not linear and has been optimised to highlight small variations using histogram equalisation. The four dark corners on all images are not dead pixels but are caused by a stray-light suppression component of the payload called field stop. |
| In the text | |
 |
Fig. 4. Weighted spectral distributions of the U, B, R, I (Johnson/Bessel filters) and narrow-band filters used to fit the Tungsten lamp profile (black). The weighted sum of the distributions is the “best-fit curve” (green). The spectral transmission of the top-hat filter (yellow dashed line) has been added for information (see Sect. 4.1). |
| In the text | |
 |
Fig. 5. Results of the flat-field synthesis. Panel a: target flat field measured with the Tungsten lamp. Panel b: synthesised flat field. Panel c: residual image with a dispersion of 0.073% rms, slightly greater than the noise-limited precision (0.058%). The image colour scales are expressed in normalised number of photoelectrons. These scales are not linear and have been optimised to highlight small variations using histogram equalisation. |
| In the text | |
 |
Fig. 6. Raw light curve (top panel) extracted from the images with a sampling time of 8.04 s. Light source variations (bottom panel) measured by the feedback photometer at a sampling frequency of about 12 Hz. |
| In the text | |
 |
Fig. 7. Light curve corrected for the source variability (top panel). Temperature of the optical table (middle panel). Residuals after correction of temperature correlation (bottom panel). The black points represent the 10-min data binned. |
| In the text | |
 |
Fig. 8. Temperature-flux scatter plot (left panel), with the raw data in grey and the 10-min binned data overplotted in green. The respective linear fits are indicated by the grey and red solid lines. Linear-fit parameters (slope and value at T = 0°C) versus time-length considered for binning (right panels). |
| In the text | |
 |
Fig. 9. Noise curve of corrected and de-trended light curve (orange) with the estimated errors represented by the shaded areas. The blue curve shows the result after discarding the points taken during abrupt variations of the lamp (t > 1320 min). The noise values are not computed for time bins greater than 5 h to ensure at least four points in the binned data. The brown dashed curve is the quadratic sum of the white noise slope (oblique black dashed line) and an arbitrary threshold at 15 ppm (horizontal red dashed line). |
| In the text | |
 |
Fig. 10. Noise curves of the flux extracted from five 8×8-pixel windows located at different positions on the detector (as indicated by the legend). The oblique black dashed line indicates the theoretical white noise slope while the horizontal line illustrates the 20 ppm level. |
| In the text | |
 |
Fig. 11. Simulation image computed by CHEOPSim. The central target star has a V-band magnitude of 12, while the background field is that of BD-082823. The colour scale is the flux corrected for all instrumental and background signals, and normalised to the highest peak of the central PSF. The red circle represents a typical photometric aperture with a radius of 33 pixels. |
| In the text | |
 |
Fig. 12. Light curves of the stellar flux (top) extracted from the simulated images of two transits of an Earth-size planet in front of a Sun-like star (case 1). The two transits are phase-folded. The black points are the 60-min binned data and the red curve corresponds to the best-fit model. The regular data gaps visible in the series are related to pointing visibility limits of CHEOPS during its orbit. Time is expressed from mid-transit. Phase-folded residuals (bottom). |
| In the text | |
 |
Fig. 13. Light curve of the stellar flux (top) extracted from the simulated images of a Neptune-size planet transiting a K5 dwarf star (case 2). The black points represent 30-min binned data and the red curve corresponds to the best-fit model. Time is expressed from mid-transit. Residuals of the best fit (bottom). |
| In the text | |
 |
Fig. 14. Corner plots of the posterior distributions of the transit parameters t0, P, Rp/R*, a/R*, and b obtained for case 1 (Earth – left graph) and case 2 (Neptune – right graph). The red dashed lines represents the prior distributions. The blue vertical dashed lines highlight the mean value and 68% confidence interval of the marginalised distributions. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.