| Issue |
A&A
Volume 632, December 2019
|
|
|---|---|---|
| Article Number | A1 | |
| Number of page(s) | 13 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201935875 | |
| Published online | 21 November 2019 | |
Beam-deconvolved Planck LFI maps
1
University of Helsinki, Department of Physics, PO Box 64, 00014 Helsinki, Finland
e-mail: elina.keihanen@helsinki.fi
2
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85741 Garching, Germany
3
European Space Agency, ESAC, Planck Science Office, Camino bajo del Castillo, s/n, Urbanización Villafranca del Castillo, Villanueva de la Cañada, Madrid, Spain
4
INAF – Osservatorio Astronomico di Trieste, Via G.B. Tiepolo 11, Trieste, Italy
5
INAF – OAS Bologna, Istituto Nazionale di Astrofisica – Osservatorio di Astrofisica e Scienza dello Spazio di Bologna, Area della Ricerca del CNR, Via Gobetti 101, 40129 Bologna, Italy
Received:
13
May
2019
Accepted:
19
September
2019
The Planck Collaboration made its final data release in 2018. In this paper we describe beam-deconvolution map products made from Planck Low Frequency Instrument (LFI) data using the artDeco deconvolution code to symmetrize the effective beam. The deconvolution results are auxiliary data products, available through the Planck Legacy Archive. Analysis of these deconvolved survey difference maps reveals signs of residual signal in the 30 GHz and 44 GHz frequency channels. We produce low-resolution maps and corresponding noise covariance matrices (NCVMs). The NCVMs agree reasonably well with the half-ring noise estimates except for 44 GHz, where we observe an asymmetry between EE and BB noise spectra, possibly a sign of further unresolved systematic error. In contrast to the official Planck LFI maps, the beam-deconvolution maps have not been corrected for bandpass mismatch, and the residual noise is not well approximated by white noise.
Key words: cosmic background radiation / methods: data analysis
© ESO 2019
1. Introduction
In 2018, the Planck1 collaboration made its third major data release, PR3 (Planck Collaboration I 2019), based on the entire mission, which covers 48 months for the Low Frequency Instrument (LFI) and 29 months for the High Frequency Instrument (HFI). The release comprises an extensive set of maps, including frequency maps for the full mission, partial maps for 12- and 6-month periods, and maps of various detector combinations. Descriptions of the data processing pipelines from time-ordered data to final map products are given in Planck Collaboration II (2019) and Planck Collaboration III (2019).
The PR3 maps are not corrected for beam shape; each data sample is assigned entirely to the pixel where the centre of the beam falls. The beam properties of Planck LFI are described in Planck Collaboration IV (2016). Beam shapes affect the maps in several ways. An effect immediately visible by eye is that the image of a point source is not symmetric, but is deformed according to the shape of the detector beam. More importantly, from a cosmology point of view, the usual map-making procedure produces maps with an effective beam that varies across the sky. The FEBeCop code (Mitra et al. 2011) constructs an effective beam, which describes the local deformation taking into account the detector beam shape and the local distribution of measurements. The effective beam is different for every sky pixel, and also depends on the survey and detector combination.
Beam asymmetries complicate the analysis of survey difference maps and other null maps, which play an important role in data validation. Two maps made of the same local sky region at different times are not identical, since the pattern of beam orientations is different due to the scanning strategy. Furthermore, beam shape mismatch is a source of leakage of temperature signals to polarization. Detectors with different beam shapes collect different signals from the same point on the sky. The difference is then falsely interpreted as a polarization signature by the usual map-making methods. The LFI applies horn-uniform weighting (Planck Collaboration II 2019) to alleviate the problem. With horn-uniform weighting, the leakage depends mainly on the mismatch between beams within a horn, which is usually smaller than the mismatch between horns.
At the power spectrum level, the average beam smearing is described by a beam window function. A conventional beam window does not correct for leakage effects, but a more sophisticated matrix window formalism (Planck Collaboration IV 2016) provides a tool for the correction of the latter effect as well.
In this work we perform beam deconvolution on LFI data. We use the artDeco deconvolution code (Keihänen & Reinecke 2012) to correct for the asymmetric smearing produced by the beams of the detectors. We take as our starting point the calibrated and destriped timelines for LFI detectors, now publicly available through the Planck Legacy Archive (PLA)2. The input data are thus already calibrated, and cleaned of correlated noise, as far as possible.
ArtDeco operates in harmonic space, and yields a harmonic representation of the sky signal without beam smoothing. This can be converted into a conventional sky map, but because the harmonic representation is limited up to a cut-off ℓmax that depends on the beam width, we must smooth the maps with a Gaussian window to eliminate ringing artefacts. A point source in a deconvolved map is thus not reduced to a point, but into a symmetric Gaussian shape of finite width.
Deconvolution products offer several benefits over the usual un-deconvolved maps. Deconvolution map-making produces a map with a symmetric effective beam with the same shape at every point on the sky, regardless of detector or survey combination. In our case the effective beam has a simple Gaussian form, which is easy to handle in further processing steps. In harmonic space the situation is simpler still, since there is no smoothing involved. As potential use cases that could benefit from deconvolved inputs, we mention component separation and analysis of point sources.
Deconvolution map-making eliminates the leakage of temperature signal to polarization via beam shape mismatch. Another source of leakage is the mismatch in frequency response between detectors. This is not affected by deconvolution, and thus it is still present in the deconvolved maps. With beam effects out of the way, we can perform a more robust analysis of survey difference maps, possibly revealing residual systematics that were previously hidden by beam effects.
In cosmological analysis it is useful to analyse the lowest multipoles of the cosmic microwave background (CMB) anisotropy spectrum separately. Deconvolution offers a natural way of extracting the low-multipole signal, as it operates primarily in harmonic space. With this in mind, we construct pixelized low-resolution maps and corresponding noise covariance matrices (NCVMs). To validate the NCVMs, we compare them to half-ring noise estimates.
It is outside the scope of this paper to perform full-scale analysis of the deconvolved maps up to power spectra and cosmological parameters. However, the deconvolved maps and related NCVM are available through PLA for the community to study.
Beam symmetrization does not come without a price. Deconvolution alters the residual noise in a non-trivial way. In the PR3 maps, the residual noise at high multipoles is approximatively white. In the deconvolved maps this is no longer true, since the deconvolution process creates noise correlations between neighbouring pixels. At low multipoles, the effects are captured in the NCVMs. At high multipoles we rely on half-ring noise estimates.
This paper is organised as follows. In Sect. 2 we review the deconvolution process. In Sect. 3 we describe the deconvolved high-resolution Planck LFI maps, and highlight differences with respect to the PR3 maps. We also analyse survey-difference maps and search for signs of residual systematics. In Sect. 4 we describe the production of deconvolved low-resolution maps and their NCVMs. We validate the NCVM products both in harmonic and pixel space. Finally, we give some conclusions in Sect. 5.
2. Deconvolution of Planck LFI data
2.1. ArtDeco
The artDeco beam deconvolver takes as input the time-ordered information (TOI) and detector pointings for one or several detectors, and their beam shapes. The code produces as output a set of harmonic coefficients asℓm of the sky, up to some maximum value ℓmax. The algorithm is described in Keihänen & Reinecke (2012).
The beam shapes are given in the form of the harmonic expansion of the beam shape, bsℓk, where s = 0, ±2. Index s = 0 corresponds to the temperature signal, while s = ±2 components are related to polarization. Parameter kmax defines the maximum absolute value of index k, and controls the level of beam asymmetry taken into account in the analysis. In this analysis we account for beam asymmetry up to kmax = 6. The simulations carried out in Keihänen & Reinecke (2012) show that this is sufficient in the case of elliptic beams. The real Planck beams have more complex structure, although the true ellipticities are smaller than those assumed in the earlier simulations. In another context (Keihänen et al. 2017) we have used the realistic LFI beams for a power spectrum analysis involving beam deconvolution, and demonstrated that the kmax = 6 limit captures well the structure of the realistic LFI beams.
From the harmonic coefficients asℓm, one can further construct a beam-deconvolved sky map, through a spherical harmonic transform. The harmonic coefficients must be smoothed before the transform. The smoothing serves two purposes: it eliminates ringing artefacts that arise from the sharp cut-off of the spectrum at ℓmax; and it suppresses the small-scale noise, which deconvolution tends to amplify. The smoothing width that fulfills these two requirements is comparable to or slightly larger than the width of the actual detector beam.
2.2. Input TOI
The artDeco deconvolver operates under the assumption that noise in the input data is uncorrelated between samples. The raw Planck LFI TOI do not fulfill this requirement, since the data stream is contaminated by correlated 1/f noise. The Planck LFI pipeline uses the Madam destriper (Keihänen et al. 2010) for noise removal and mapmaking. Pre-whitened TOIs are available in the form of ring objects, where samples on the same pointing period and with the same position are coadded to make one ring element. The input data are thus already calibrated and cleaned of correlated noise. We use these ring objects as inputs for the deconvolution operation. These ring objects are available through the PLA.
Even after destriping, a small amount of residual correlated noise is still present; this adds to the signal power in the lowest multipoles. The properties of residual noise and its effect on deconvolution are addressed in Keihänen et al. (2016). Deconvolution amplifies the noise in the high-multipole regime of the angular power spectrum, and creates correlation between neighbouring pixels. At low multipoles, the main effect is the rescaling of the signal (including noise) in compensation for the missing beam power.
When deconvolving partial data sets, for instance single-year data or detector subsets, there is some freedom in combining the destriping and deconvolution steps. One option is to use the full frequency data set for destriping, to maximally utilise all data available and to remove the correlated noise as accurately as possible, and then use a subset of the cleaned TOI for deconvolution. This is referred to as the full destriping option. Another option is to use the same data subset for both the destriping and the deconvolution steps, which is called independent destriping. The latter option leaves considerably more residual noise, but offers the benefit that the residual noise is uncorrelated between data sets.
The input ring objects available through the PLA are produced by destriping the full frequency data set. Since we take these objects as inputs, we are automatically using the full destriping option. We thus have for each frequency one set of ring objects, which serves as input in all deconvolution runs for that frequency.
2.3. Beams
Planck LFI beams consist of three components (Planck Collaboration IV 2016). The main beam is defined as extending to 1°.9, 1°.3, and 0°.9 from the beam boresight at 30, 44, and 70 GHz, respectively. The near sidelobes cover the region between the main beam and 5°. The remaining part is defined as far sidelobes. An estimate of the sidelobe contribution to the signal is already removed as part of the calibration step (Planck Collaboration II 2016). We consider in the deconvolution process the main and near sidelobe beam components.
We use the radiometer scanning beams as described in Planck Collaboration IV (2016). The scanning beams include the effective beam elongation caused by the satellite motion. These must be distinguished from the effective beams that take into account the scanning strategy and are a superposition of different beam orientations. The effective beam is different for every survey and detector combination. Characteristics of both beam types for LFI, together with plots of the beam shapes, can be found in Planck Collaboration IV (2014) and in Planck Collaboration IV (2016).
Effective beams are a combination of intrinsic detector beam shape and pixel shape. They are typically less asymmetric (measured by fitted ellipticity) than the scanning beams, due to the averaging over beam orientations. The difference is particularly striking at 44 GHz; the ellipticities of radiometer scanning beams vary between 1.188 (LFI25S) and 1.388 (LFI24M) (Planck Collaboration IV 2016) while the ellipticity of the combined effective beam for the whole mission is only 1.035. Effective beams and scanning beams reflect different aspects of the same beam. For instance, the image of a point source in an un-deconvolved map resembles the image of the effective beam. On the other hand, temperature leakage to polarization via beam mismatch is dependent on the mismatch between scanning beams, since the polarization signal is obtained effectively by differencing the timelines of two radiometers.
2.4. Deconvolution products
We have produced deconvolved maps for all LFI frequencies, single horns, and for horn pairs with complementary polarization directions. For each horn combination, we produce a full mission map, single year maps, and individual single survey maps. A single survey refers to a period of approximately six months; exact definitions of the surveys can be found in Planck Collaboration II (2016). Deconvolution parameters for different detector combinations are listed in Table 1. The same parameters apply to all survey combinations.
Deconvolution parameters by horn combination, deconvolution parameters ℓmax and kmax, polarization (T/F), and FWHM width of the smoothing kernel.
For each survey and detector combination, we release both the harmonic coefficients, which are the primary deconvolution output, and a pixelized HEALPix3 map (Górski et al. 2005) constructed from them.
The pixelized maps have resolution Nside = 1024, corresponding to 3′.4 × 3′.4 pixels. We apply smoothing by a symmetric Gaussian beam of full-width half-maximum (FWHM) width 40′ (30 GHz), 30′ (44 GHz) or 20′ (70 GHz). These widths were chosen to suppress the angular power of the map below a fraction of 10−6 of the unsuppressed value at the cut-off ℓmax. This is sufficient to safely remove all visible ringing around the strongest sources.
The smoothing window is
where the σ parameter of the Gaussian function is related to the FWHM through 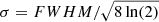 , that is σ = 16′.9864, 12′.7398, 8′.4932 for FWHM = 40′, 30′, 20′, respectively. The effective beam in pixel space is thus a Gaussian, with width as given above. Since we release the deconvolved harmonic coefficients along with the maps, an interested user can easily produce alternative maps with any desired smoothing width.
, that is σ = 16′.9864, 12′.7398, 8′.4932 for FWHM = 40′, 30′, 20′, respectively. The effective beam in pixel space is thus a Gaussian, with width as given above. Since we release the deconvolved harmonic coefficients along with the maps, an interested user can easily produce alternative maps with any desired smoothing width.
3. High-resolution maps
3.1. Full-mission temperature maps
We examine first the deconvolved, full-mission temperature maps for 30, 44, and 70 GHz. Deconvolved maps and the PR3 products are shown side by side in Fig. 1. The two sets of maps are visually very similar. Variations become more visible when we look at the difference map (deconvolved−PR3), shown in the third column.
 |
Fig. 1. From left to right: deconvolved temperature maps for 30, 44, and 70 GHz, corresponding PR3 maps, and differences between the two. The data include four years of observations for all radiometers of the respective frequency channel. The deconvolved maps are smoothed with a Gaussian beam of FWHM = 40′ (30 GHz), 30′ (44 GHz), or 20′ (70 GHz). We subtracted from the deconvolved maps the same monopole that had been subtracted from the PR3 map. The difference maps are dominated by white noise, which is suppressed in the deconvolved maps. The temperature scales of the maps are ±300 μK for temperature and ±100 μK for the difference. |
The difference outside the Galactic region is dominated by noise. The smoothing applied to deconvolution maps effectively suppresses noise at small scales. The unsuppressed noise in the PR3 map is clearly visible in the difference map.
Another effect is the rescaling of the signal due to beam efficiency. The signal collected by the far sidelobe component of the beam is removed as part of the calibration process, and it is effectively lost. The lost power is accounted for in the beam model. The beam efficiencies for LFI radiometer beams are given in Planck Collaboration IV (2016). The combined efficiency of main and near sidelobe beam components varies in the range 98.99–99.14% for 30 GHz, in 99.75–99.79% for 44 GHz, and in 98.94–99.34% for 70 GHz. The deconvolution process effectively scales the signal up by a corresponding factor, compensating for the missing power. As a consequence, we see a faint copy of the galaxy image in the difference map.
A zoom into a point source reveals the symmetrization of the effective beam. As illustration, we show in Fig. 2 the Crab Nebula, as seen in the deconvolved 30 GHz temperature map and in the corresponding undeconvolved map. In this figure, one can also see the effect deconvolution has on residual noise. The weak striping visible in the upper left corner of the deconvolved map is noise, which becomes correlated in the direction orthogonal to the direction of beam elongation.
 |
Fig. 2. A 10° patch around the Crab Nebula in the 30 GHz temperature map. Left: deconvolved. Right: PR3 30 GHz LFI map. |
3.2. Survey difference
As a first validation test we produce temperature cross-spectra from PR3 and deconvolved half-ring maps at 70 GHz. We first smooth the PR3 map by a Gaussian FWHM = 16′ window to match the final smoothing of the deconvolution map. We perform no component separation, but we apply a mask with 88.4% sky coverage to exclude regions of strong foreground emission. We use POLSPICE (Chon et al. 2004) to correct for the mode-coupling caused by the masking. We divide the PR3 spectrum by the effective window function that is released with the instrument model, and by the 16′ smoothing window. The deconvolution spectrum is divided by the Gaussian 20′ smoothing window, and by the pixel window. In the case of the PR3 map we do not correct for the pixel window, since it is already included in the effective beam window. The test shows a good agreement between the spectra, as shown in Fig. 3.
 |
Fig. 3. Half-ring cross-spectra in TT, from masked PR3 and deconvolution maps at 70 GHz, after correction for mask and beam window. |
As we see above, the difference between deconvolved and PR3 full mission maps arises largely from effects not directly related to beam asymmetry. To see the effects of actual beam symmetrization more clearly, we now proceed to look at survey difference maps. A survey in this context refers to a period of six months, during which the scan axis of Planck rotates by 180°, and detectors scan almost the complete sky. During the subsequent 6 months the sky is scanned again, this time with effectively inverted beam orientation. When we take the difference between odd and even single survey maps, most of the sky signal cancels out, apart from a residual that arises from beam shape mismatch.
Beam deconvolution is expected to remove the beam residuals, leaving only noise in the survey difference maps, since the deconvolved maps have identical effective beams. With beam residuals out of the way, remaining signal residuals provide valuable information on other systematic artefacts in the data.
Single surveys do not provide complete sky coverage. The coverage varies between 79% and 98%, depending on survey and frequency (Planck Collaboration VI 2016). The artDeco deconvolver operates with harmonic coefficients, which necessarily represent the entire sky. If data are not available for the full sky, the correct sky signal is well recovered in the region covered by the measurements. In the missing region (and close to its boundary), we obtain a solution that is based on extrapolation of the recovered signal.
We construct an odd-even difference map from the first four surveys as combination S1 + S3 − S2 − S4. We leave out the last four surveys, which have lower sky coverage (Planck Collaboration II 2019). To suppress noise and to bring out the beam residuals more clearly, we build the maps at 1° resolution (FWHM). We apply smoothing with a Gaussian beam, the width of which is chosen to make the combined width of the smoothing kernel and the average detector beam equal to 1°. The required additional smoothing is 50′.63, 53′.58, and 58′.53 for 30, 44, and 70 GHz, respectively.
The masked odd-even survey difference T maps are shown in Fig. 4. The pixels outside the mask are covered in all four surveys. For each frequency, we show the deconvolved version on the left, and the corresponding PR3 map on the right. We note that the PR3 maps are destriped with the independent destriping option, as discussed in Sect. 2.2, while the deconvolved maps are destriped with the full destriping option. This follows from the fact that the destriped ring objects, which are the input to deconvolution, are only available from full-mission runs. The deconvolved maps thus contain less correlated noise to begin with.
 |
Fig. 4. Survey difference T maps S1 + S3 − S2 − S4. The maps are smoothed to 1° resolution. Deconvolution reduces beam shape residuals, revealing other signal residuals. |
In the Galactic region, the PR3 30 GHz maps show signal residuals with typical beam residual characteristics, the signal varying between positive and negative values. Point sources give rise to “butterfly” shapes. Deconvolution reduces the residuals significantly, but does not remove them completely. It is likely that there are other systematic effects than beam at play here. As described in Planck Collaboration II (2019), a possible cause is the incomplete convergence in the calibration iterative approach.
The effect of deconvolution is clearest for 44 GHz: PR3 maps show strong beam residuals, arising from beam shape mismatch between the two survey combinations. Deconvolution symmetrizes the effective beam, and removes the residuals almost perfectly. At 70 GHz, the residuals are small to start with and no signal residuals are visible in either map.
3.3. Polarization maps
Beam-shape mismatch is a source of leakage of temperature signal into polarization. When the same point on the sky is observed twice by the same detector, but in different beam orientations, the two measurements collect slightly different temperature signals. The usual map binning operation interprets the difference as a polarization signal. Because the temperature signal is much stronger than the polarization signal, the leakage can affect the polarization measurements significantly. According to Planck Collaboration IV (2016), beam leakage can contribute as much as 15% of the polarization signal at 70 GHz.
Simulations show that beam deconvolution can drastically reduce temperature leakage (Keihänen & Reinecke 2012). In real Planck measurements, however, beam mismatch is not the only effect. Another, and often more significant, source of temperature leakage is bandpass mismatch, coming from the fact that different radiometers have slightly different frequency responses. Two radiometers record different foreground temperature signals, and the difference is interpreted incorrectly as a polarization signal. This affects deconvolved and un-deconvolved maps alike, and partially hides the beam correction.
Figure 5 shows the Q and U polarization component maps for LFI frequencies. We compare deconvolved and PR3 LFI maps, and plot their difference in the third column. Since we are interested in the effect of beam deconvolution, we use in this comparison PR3 maps that are not corrected for bandpass leakage. The maps are smoothed to 1° resolution to suppress the noise. The smoothing procedure is the same as the one applied to single survey maps in Sect. 3.2. The difference map is plotted over a 2 μK scale to bring out the structure above the Galactic plane.
 |
Fig. 5. Deconvolved (left) and PR3 (middle) polarization maps for LFI channels, and their differences (right). From top down: 30 GHz; 44 GHz; and 70 GHz. These maps are smoothed to 1° resolution (FWHM) to suppress noise. The maps are not corrected for bandpass leakage. |
We expect the difference maps to include the temperature leakage through beam shape mismatch, but this is difficult to verify, since the difference maps are dominated by other effects. As in the case with temperature maps, deconvolution scales the map up to compensate for the missing power absorbed by the far sidelobe beam component. Since the missing power is slightly different for different radiometers, this also changes the relative weighting of radiometers, and hence the bandpass leakage pattern. As a result, the difference map between deconvolved and PR3 LFI polarization maps is a combination of beam leakage and changes in scaling and in the bandpass leakage pattern.
Although the temperature-to-polarization leakage is dominated by bandpass mismatch, it still makes sense to remove the component that comes from beam asymmetry. Bandpass leakage is relatively well understood and can be corrected for more easily than beam leakage. The bandpass correction for the 2018 release is described in Planck Collaboration II (2019). Furthermore, bandpass leakage only affects foreground emission, while beam leakage distorts both foregrounds and the CMB.
We do not show survey difference maps in polarization, since the beam effects are obscured by effects of bandpass mismatch. The hit count distribution per radiometer varies between surveys, and so does the bandpass leakage pattern.
3.4. IQUSS deconvolution
As an alternative to the usual deconvolution procedure, we have applied a procedure similar to the “IQUSS” mapmaking presented in Planck Collaboration II (2019). We split the harmonic temperature coefficients aTℓm further into a component that represents the average temperature signal, and components that represent the signal difference due to different frequency responses between a radiometer pair. For radiometers M and S of horn X,
where 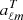 represents the average sky signal, and
represents the average sky signal, and 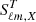 is a spurious signal map for horn X. The opposite signs are chosen so that the spurious signal will absorb the signal difference from bandpass mismatch, preventing it from leaking into polarization. We note that we do not include spurious components between horns because signal differences between horns do not contribute to polarization. We now solve for the spurious components along with the usual
is a spurious signal map for horn X. The opposite signs are chosen so that the spurious signal will absorb the signal difference from bandpass mismatch, preventing it from leaking into polarization. We note that we do not include spurious components between horns because signal differences between horns do not contribute to polarization. We now solve for the spurious components along with the usual 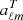 ,
, 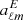 , and
, and 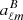 .
.
The spurious components obey the rotation properties of a temperature map. They can be distinguished from the polarization components if the sky is scanned in sufficiently different beam orientations during the mission. Unfortunately, for Planck this is true only for part of the sky due to the scanning strategy, which was optimised for temperature, not polarization. Consequently, the polarization maps we obtain from spurious fitting are very noisy compared to the usual deconvolution with three sky components. The same applies naturally to the PR3 IQUSS maps (Planck Collaboration II 2019).
Deconvolved IQUSS maps constructed from PR2 data were used for the analysis of Tau A polarization in the 2015 data release, as described in Planck Collaboration XXVI (2016). Due to the experimental nature of this method this approach was not extensively used in other Planck analyses.
The IQUSS maps could be used to construct a deconvolution-specific bandpass correction following the same procedure as the bandpass correction for undeconvolved maps; however, more analysis would be needed to implement this. At present, the best way of correcting the bandpass leakage in deconvolved maps is to apply the un-deconvolved correction maps directly.
3.5. Point sources
The 2015 Planck release included an extensive catalogue of compact sources (Planck Collaboration XXVI 2016). The catalogue is built on the PR3 (undeconvolved) frequency maps. Deconvolved maps provide valuable complementary information on the properties of sources.
In the following, we demonstrate the fidelity of the deconvolution process by showing that it efficiently reduces the asymmetry of a point source image. We take the ellipticity of the image as figure of merit. We pick the quasar 3C279 for demonstration. We consider also Tau A (the Crab Nebula), which is an important calibration source in CMB experiments. Tau A can be assumed to be point-like at the lowest LFI channels, but becomes extended at HFI channels (Planck Collaboration XXVI 2016; Ritacco et al. 2018).
We determine the ellipticity of both sources in the pixel domain by fitting a two-dimensional Gaussian shape to the source image. To reduce the contamination from background signals, we fit a constant offset along with the shape. We determine the ellipticity as the ratio of the two major axes. The ellipticity is therefore always above 1, the value corresponding to a circular source. Table 2 gives the measured ellipticies for the selected sources, for deconvolved and PR3 maps. For each source we list the ellipticity of the source, as detemined from the undeconvolved and deconvolved maps. As expected, deconvolution strongly reduces the ellipticity of the source image.
Properties of selected point sources.
4. Low-resolution analysis
Computation of the CMB angular power spectrum and subsequent cosmological analysis is complicated by noise, and a detailed description of the residual noise in the maps is therefore required. This is usually given in the form of a pixel–pixel NCVM. For reviews of power spectrum methods designed for Planck, see Gruppuso et al. (2009) and Planck Collaboration XI (2016).
A properly constructed NCVM gives a full description of noise correlation between any pair of low-resolution pixels. The 2018 Planck data release includes low-resolution maps and corresponding NCVMs at HEALPix resolution Nside = 16, This corresponds to 3°7 spatial resolution. The low-resolution maps are constructed from their high-resolution counterparts through a smoothing and downgrading process, as described in Planck Collaboration VI (2016). Each low-resolution map consists of 3072 sky pixels. Each pixel further contains estimates for the three Stokes parameters I, Q, and U. The corresponding NCVM objects contain 9 × 3072 × 3072 ≈ 8.5 × 107 numbers. Increasing the resolution to Nside = 32 would increase the matrix size further by a factor of 16, which becomes computationally prohibitive.
4.1. Low-resolution deconvolution
Deconvolution offers an alternative way of extracting the low-multipole information from CMB data. The division into low- and high-multipole regimes occurs in a natural way here, since deconvolution operates in harmonic space.
We construct deconvolved low-resolution maps from LFI data as follows. For harmonic analysis, we simply take the harmonic coefficients we have from full-resolution deconvolution, and pick the lowest multipoles for the low-resolution data set. To construct low-resolution pixel maps, we apply a FWHM = 40′ Gaussian beam to the coefficients, and construct maps at resolution Nside = 16. The smoothing width and resolution were chosen so that they correspond to the PR3 procedure as closely as possible.
We construct NCVM that describe the noise in the deconvolved low-resolution maps, both in harmonic and pixel space. The construction of the NCVM is described in detail in Keihänen et al. (2016). Required inputs are pointing, a model for the power spectral density (PSD) of noise in the time domain, and beams. The NCVM matrix essentially accounts for two aspects: the correlated residual noise that remains in the data after destriping; and the effect of the deconvolution process on it. Deconvolution modifies the noise structure, but the effect is seen mostly at high multipoles. Our harmonic NCVM describes the noise correlation between any two aslm elements up to ℓ = 50. The pixel–space NCVM describes the correlation between two Nside = 16 pixels. The noise model we use adopts the noise estimates of the official DPC (Data Processing Center) pipeline. These noise estimates are provided in the form of a PSD, as a function of frequency, up to half the sampling frequency of each channel. These estimates include one spectrum per day for each detector. The PSDs are estimated from the data, and vary strongly with frequency.
For 30 and 70 GHz, we use the raw PSDs as they are. To construct the NCVM, we need to divide each PSD into a white noise component and a correlated component. To do this, we arrange the spectrum as a function of inverse frequency, and perform a linear fit to the last ten points corresponding to the highest frequencies. We extrapolate the fit to 1/f = 0, which we take as the white noise power. We subtract this from the full spectrum to obtain the correlated component. The procedure is exact for a pure power-law spectrum with slope equal to −1.
The procedure described above works well for 30 GHz and 70 GHz, but at 44 GHz it yields unphysical negative values for the correlated power due to the large variations in the spectra. At 44 GHz, we therefore use a modified procedure, where a power-law spectrum is first fitted to the raw PSD to yield a smooth spectrum before applying the same extrapolation procedure as for 30 GHz and 70 GHz.
4.2. NCVM validation in harmonic space
The PR3 data release includes half-ring maps. These are constructed by splitting each pointing period in two, constructing two data sets from these, and applying the usual flagging and map-making procedure to both sets. The result is two half-ring (HR) maps with nearly identical signal content, but independent noise. The half-ring half-difference (HRHD) map can be constructed as the difference between the two HR maps, weighted by the actual hit count, as explained in Planck Collaboration II (2014). In an ideal situation this consists of pure noise, with structure similar to that of the noise contained in the full map. However, small differences arise because the noise correlations on the longest timescales are not tracked by the half-ring process, and the spatial sample distributions in the two halves are not identical. Despite its limitations, the HRHD maps provide the best estimate of the actual noise level in the data; these are independent of any noise modelling and are based entirely on the data.
The half-ring data sets for Planck LFI are available in the form of ring objects. This allows us to run the deconvolution process on the two HRs, and to form a HRHD harmonic vector, following a logic similar to that behind the HRHD maps. A harmonic HRHD vector is thus a set of aslm coefficients consisting of pure noise with properties similar to the noise in the actual deconvolved aslm. We validate the harmonic NCVM matrix by comparing its predictions to this HRHD noise estimate.
We readily obtain the noise bias from the diagonal of the harmonic NCVM. The noise bias is a prediction for the angular power of residual noise. As a first test we compare the noise bias with the angular power spectrum of HRHD noise, constructed directly from the deconvolved harmonic coefficients as
where X stands for T, E, or B.
Figure 6 shows the spectra and the corresponding noise bias for LFI frequencies for TT, EE, and BB. In general, the noise bias agrees well with the HRHD spectrum, but there are also differences. In particular, at 44 GHz there is an asymmetry between EE and BB spectra, the EE spectrum being above the noise bias, the BB spectrum falling below it. The same asymmetry is already present in the un-deconvolved data, as can be seen in Fig. 18 of Planck Collaboration II (2019), as well as in the 2015 data (Planck Collaboration II 2016). The 44 GHz channel is different from 30 GHz to 70 GHz as it involves the lone horn 24, which has no complementary pair with orthogonal polarization sensitivity, and which has different beam properties from the other 44 GHz horns. All these aspects are nevertheless accounted for in the NCVM and in the noise bias derived from it. The noise bias shows only a very weak asymmetry between EE and BB, as we see in the middle panel of Fig. 6. Monte Carlo simulations in Planck Collaboration II (2019) also fail to reproduce the asymmetry that in any case is well inside 1 sigma.
 |
Fig. 6. Noise bias from NCVM, and the HRHD noise estimate, for 30, 44, and 70 GHz data. Top: TT spectrum. Bottom: EE and BB spectra. |
We replot the 44 GHz polarization spectra in Fig. 7, together with the HRHD spectra derived from the LFI 25/26 horn combination, excluding the individual horn 24. With horn 24 excluded, the noise level is higher, roughly by a factor of 3/2 as expected. The asymmetry between EE and BB is reduced, suggesting that the asymmetry is related to the unusual detector combination – the horn pair plus individual horn – of the 44 GHz channel. The exact mechanism however remains unclear.
 |
Fig. 7. Noise bias from NCVM for full 44 GHz data, and HRHD noise estimate for full 44 GHz data and for 25/26 horn combination. |
It is interesting to compare the deconvolved HRHD spectra with their un-deconvolved counterparts. The structure of peaks and troughs is very similar in both. For instance, the high peak at ℓ = 10 in the 70 GHz BB spectrum is also present in Fig. 18 of Planck Collaboration II (2019).
A χ2 test provides a more stringent validation test for the NCVM. We specifically compute the measure
where N is the covariance matrix, a is the corresponding HRHD object, and Nd.o.f. is the number of degrees of freedom. Dividing by Nd.o.f. yields the reducedχ2 test. If the matrix correctly models the noise properties, we have ⟨aaT⟩=N, and the reduced χ2 test is expected to return a value close to 1. The value is not limited from below however. Therefore, a simple overestimation of the overall noise level is able to compensate for another error, and this must be kept in mind when interpreting the results. Despite its limitations, the χ2 test provides a useful measure of NCVM quality.
The χ2 results for the harmonic NCVM are given in Table 3. We compute the χ2 value between the full mission NCVM of each frequency channel and the corresponding HRHD noise object. We perform the test separately for the TT, EE, and BB blocks. The number of degrees of freedom is Nd.o.f. = (ℓmax + 1)2, which for ℓmax = 50 yields Nd.o.f. = 2601. We repeat the χ2 test for a submatrix that covers multipoles from zero to ℓ = 40 or 30.
Reduced χ2 results in harmonic space.
Consider first the 30 GHz and 70 GHz data. The NCVM appears to model the residuals rather well in polarization. The deviations from unity for EE and BB are within 2.2σ statistical variation (σ = 0.0196 for ℓ = 50). However, all the results are above unity, indicating that the NCVM may be slightly underestimating the residual noise.
At 30 GHz the results improve further when the highest multipoles are excluded. However, TT results are much poorer, especially at 30 GHz. A misestimation should affect temperature and polarization in roughly the same way, and therefore the weaker results in temperature indicate that the HRHD maps contain signal residuals. The likely source is signal variations within a sky pixel in the Galactic region where signal gradients are strong. Signal gradients distort the destriping solution, which assumes that the signal is constant within a pixel. The effect depends on the exact scanning pattern, which is different for the two HRs. However, a pair of Planck detectors sharing a horn follow very closely the same path on the sky. Since the polarization signal is determined from the signal differences of such pairs, the signal gradients tend to cancel in the polarization component of the HRHD map. The effect is not restricted to the pixels with strong gradients, but is redistributed over the sky through the destriping process. The error can be reduced with the help of a properly chosen destriping mask. The choice of the mask however is a trade-off because too wide a mask will remove too much of the data.
At 44 GHz we observe the same suspicious excess EE power that we already observed in the HRHD spectrum. The excess is insensitive to the choice of ℓmax. In contrast to 30 and 70 GHz, the χ2 results are better in temperature than polarization.
4.3. Validation in pixel space
We now proceed with the validation in pixel space. We produce low-resolution HEALPix maps as follows. We take as a starting point the harmonic coefficients that we have as deconvolution output, and smooth them with a Gaussian of a 440′ (FWHM). The same smoothing width is adopted for the PR3 pipeline. We then construct temperature and polarization maps at resolution Nside = 16 using the standard HEALPix tools. The same operations are applied to each row and column of the harmonic NCVM to obtain a pixel–pixel NCVM.
Moving to pixel space changes the number of degrees of freedom. The harmonic NCVM with ℓmax = 50 has 2601 eigenmodes, while a Nside = 16 pixel–pixel NCVM has rank 3072. Moving from harmonic to pixel space thus introduces 471 zero eigenmodes, resulting in a singular NCVM matrix. There is nothing unphysical about this. It just tells us that these eigenmodes are not present in the data. However, a χ2 test requires that the matrix be inverted. We thus need to regularize the matrix in some way.
To do this we start by constructing the eigenvalue decomposition of the pixel NCVM, and rewrite matrix N as
where ej are the eigenvectors and λj the corresponding eigenvalues. Equation (4) takes the form
where m is the HRHD noise map under consideration. In Fig. 8 we plot the eigenvalue spectrum 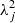 of the 30 GHz TT matrix, and the decomposition of the corresponding HRHD map,
of the 30 GHz TT matrix, and the decomposition of the corresponding HRHD map, 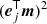 , in order of decreasing eigenvalue. The eigenvalue spectrum drops steeply at 2601, as expected, when we enter the zero eigenmode regime. The HRHD spectrum instead flattens off at around 10−4 μK2. The high-end power of the HRHD spectrum comes from the multipoles above ℓ = 50, which are not included in the NCVM. The level of the high-multipole plateau is insignificant in comparison with the general noise level; however, it will blow up in the χ2 test, which attaches equal weight to all eigenmodes regardless of their contribution to the total power.
, in order of decreasing eigenvalue. The eigenvalue spectrum drops steeply at 2601, as expected, when we enter the zero eigenmode regime. The HRHD spectrum instead flattens off at around 10−4 μK2. The high-end power of the HRHD spectrum comes from the multipoles above ℓ = 50, which are not included in the NCVM. The level of the high-multipole plateau is insignificant in comparison with the general noise level; however, it will blow up in the χ2 test, which attaches equal weight to all eigenmodes regardless of their contribution to the total power.
 |
Fig. 8. Eigenvalue spectrum of the 30 GHz TT NCVM (grey), and corresponding decomposition of the HRHD map (orange). We add a small constant of 10−6 μK2 to the NCVM for numerical stability. A larger phenomenological constant is added to the NCVM (light blue) to account for the high-end plateau. |
We add a phenomenological regularization constant 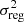 to the diagonal of the NCVM to account for the extra power. This is equivalent to assuming an additional white noise component of rms σreg. The value is chosen to match the observed level. Our procedure is different from the one applied for the PR3 maps (Planck Collaboration VI 2016), since we are not adding regularization noise to the maps themselves.
to the diagonal of the NCVM to account for the extra power. This is equivalent to assuming an additional white noise component of rms σreg. The value is chosen to match the observed level. Our procedure is different from the one applied for the PR3 maps (Planck Collaboration VI 2016), since we are not adding regularization noise to the maps themselves.
The regularization process brings along the danger of making the χ2 test results artificially good. In fact, by choosing the constant properly, one can obtain a value of exactly 1 for any matrix-map pair. To avoid any human selection bias we apply an automatic procedure where we take the regularization constant to be the mean of the HRHD power in the multipole range 2602–3072. The values of σreg are listed in Table 4, along with the rms of the HRHD noise map. The required level of regularization is in all cases very low compared with the actual noise.
Regularization constant (σreg) and rms of the HRHD map.
The χ2 results obtained with the regularized pixel–pixel NCVM are given in Table 5. We also report the TT result for cases where we have removed the Galactic region where signal gradients are large. We tried two types of mask: a simple azimuthally symmetric mask that cuts out 10% or 20% of the sky symmetrically around the Galactic equator, and the destriping mask (Planck Collaboration VI 2016) that more accurately follows the structure of Galactic emission and removes the strong point sources at high latitudes. We downgrade the destriping mask to Nside = 16 resolution and reject all pixels where any of the high-resolution subpixels are missing. This procedure leads to a lower sky coverage, especially at 30 GHz where the 78.7% sky coverage of the destriping mask at Nside = 1024 translates to 49.5% coverage at Nside = 16.
Reduced χ2 results in pixel space.
The polarization results are already very good for 30 and 70 GHz without masking. However, the mask improves the agreement in TT, indicating that at least part of the discrepancy is due to signal residuals in the HRHD temperature map.
At 44 GHz there is good agreement in temperature. In polarization, once again, we observe extra power that is not accounted for in the NCVM.
The expected 1σ statistical variation in χ2 is 0.018 for full sky, 0.019 for the 10% sky mask, and 0.020 for the 20% mask. All the 70 GHz χ2 test results, as well as 30 GHz polarization results, are well within 2σ statistical variation. This indicates that the residual noise in these map components is well described by the NCVM, and the maps along with the NCVM can be used for cosmological analysis. More caution should be taken with the 44 GHz products.
The basic χ2 test compresses a complicated noise structure into one number. It also weights all eigenmodes equally, regardless of how much they contribute to the noise, and is sensitive to the selection of the regularization constant σreg.
We obtain more information by examining how the excess χ2 builds up. The noise residuals are by nature extended structures over the sky. It is not very meaningful to look at noise amplitudes pixel by pixel. Instead, we examine them in the eigenmode space. We introduce the cumulative measure Δχ2(n), which we calculate as
Here, ej and λj are the eigenvectors and eigenvalues of the NCVM matrix in order of decreasing eigenvalue, and mj is the decomposition of the noise map under consideration. We plot Δχ2(n) in Fig. 9. The plot shows how the deviation of χ2 from unity accumulates as we add more eigenmodes, with Δχ2(3072)+1 giving the usual χ2 test. The quantity Δχ2(n) has the convenient property that the statistical variation remains the same over the plot. The cumulative Δχ2(n) in the high-eigenmode regime is insensitive to the regularization constant σreg, and thus a more reliable measure of the agreement between NCVM and data than the single χ2 value.
 |
Fig. 9. Excess χ2 in pixel space, as it builds up as a function of eigenmode. The eigenmodes are arranged in order of decreasing eigenvalue, so that the strongest noise structures are on the left. |
At both 30 and 70 GHz, the agreement in the TT block is very good for the first 500 eigenmodes, after which the excess χ2 begins to build up gradually. The strongest noise structures are therefore modelled accurately. At 44 GHz, the agreement in TT is good even further out, over 1000 eigenmodes. The excess χ2 in 44 GHz polarization is again evident, more strongly in EE than in BB.
5. Conclusions
We have produced beam-deconvolved maps from destriped Planck LFI data using the artDeco deconvolution code. The artDeco deconvolution approach corrects for all beam-related effects and yields a map with a symmetric Gaussian beam. The chosen smoothing widths are 40′ (FWHM) for 30 GHz, 30′ for 44 GHz, and 20′ for 70 GHz. These widths are sufficient to remove ringing artefacts and to suppress noise at small scales.
The release includes harmonic coefficients that form the basis of the deconvolved maps. The interested user can construct deconvolved maps at any desired resolution from those, keeping in mind that too narrow a smoothing width will result in ringing around strong point sources.
We validated the deconvolved maps though analysis of survey difference maps. Survey difference maps are insensitive to bandpass mismatch, and reveal the effects of beam mismatch particularly clearly. We demonstrate that deconvolution removes the beam residuals very well at 44 GHz. At 70 GHz the residuals are small to start with. With beam residuals cleaned away, 30 GHz survey-difference maps show traces of residual signal, which affect the maps at the 10 μK level.
Deconvolution provides a natural way of extracting the low-resolution component from Planck data. We construct low-resolution maps at HEALPix resolution Nside = 16, and corresponding NCVMs. The NCVM matrices describe the structure of residual noise in the deconvolved maps.
The effects of actual beam asymmetry are small in the low multipole regime. It is thus not surprising that the deconvolved low-resolution maps resemble the undeconvolved ones. The value of deconvolution here lies in the natural way that the low-resolution regime is separated from the high-resolution regime. Through deconvolution we avoid the complicated interplay between smoothing and pixel–space downgrading (see Planck Collaboration VI 2016).
We validate the NCVMs by comparing them against half-ring noise estimates, both in harmonic space and in pixel space. The covariance matrices model the noise well in 30 and 70 GHz polarization maps. The agreement is less good in temperature, but this is likely due to signal residuals in the HRHD estimates rather than the NCVM itself. At 44 GHz, we observe a curious asymmetry between EE and BB noise spectra. The same asymmetry can also be seen in the undeconvolved spectra.
The deconvolved maps are available through the Planck Legacy Archive. In any further analysis it should be remembered that, unlike in the case of PR3 maps, the polarization component is not corrected for bandpass mismatch, and that the residual noise is not well approximated by white noise.
Planck (http://www.esa.int/Planck) is a project of the European Space Agency (ESA) with instruments provided by two scientific consortia funded by ESA member states (in particular the lead countries France and Italy), with contributions from NASA (USA) and telescope reflectors provided by a collaboration between ESA and a scientific consortium led and funded by Denmark.
Acknowledgments
This paper was developed to support the analysis of data from the Planck satellite. The development of Planck has been sup- ported by: ESA; CNES and CNRS/INSU-IN2P3-INP (France); ASI, CNR, and INAF (Italy); NASA and DoE (USA); STFC and UKSA (UK); CSIC, MICINN, JA, and RES (Spain); Tekes, AoF, and CSC (Finland); DLR and MPG (Germany); CSA (Canada); DTU Space (Denmark); SER/SSO (Switzerland); RCN (Norway); SFI (Ireland); FCT/MCTES (Portugal); and PRACE (EU). A description of the Planck Collaboration and a list of its members, including the technical or scientific activities in which they have been involved, can be found at http://www.esa.int/Planck. Some of the results in this paper have been derived using the HEALPix (Górski et al. 2005) package. EK is supported by Academy of Finland grant 295113. This work was granted access to the HPC resources of CSC made available within the Distributed European Computing Initiative by the PRACE-2IP, receiving funding from the European Community’s Seventh Framework Programme (FP7/2007–2013) under grant agreement RI-283493. We thank CSC – the IT Center for Science Ltd. (Finland) – for computational resources. We thank the Planck review team – A. Banday, R. Keskitalo, C. Lawrence, D. Maino, D. Scott, and A. Zacchei, for helpful comments.
References
- Chon, G., Challinor, A., Prunet, S., Hivon, E., & Szapudi, I. 2004, MNRAS, 350, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Gruppuso, A., De Rosa, A., Cabella, P., et al. 2009, MNRAS, 400, 463 [NASA ADS] [CrossRef] [Google Scholar]
- Keihänen, E., & Reinecke, M. 2012, A&A, 548, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Keihänen, E., Keskitalo, R., Kurki-Suonio, H., Poutanen, T., & Sirviö, A. 2010, A&A, 510, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Keihänen, E., Kiiveri, K., Lindholm, V., Reinecke, M., & Suur-Uski, A.-S. 2016, A&A, 587, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Keihänen, E., Kiiveri, K., Kurki-Suonio, H., Reinecke, M., & Suur-Uski, A.-S. 2017, MNRAS, 466, 1348 [NASA ADS] [CrossRef] [Google Scholar]
- Mitra, S., Rocha, G., Górski, K. M., et al. 2011, ApJS, 193, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration II. 2014, A&A, 571, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration IV. 2014, A&A, 571, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration II. 2016, A&A, 594, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration IV. 2016, A&A, 594, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration VI. 2016, A&A, 594, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XI. 2016, A&A, 594, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXVI. 2016, A&A, 594, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration I. 2019, A&A, in press, https://doi.org/10.1051/0004-6361/201833880 [Google Scholar]
- Planck Collaboration II. 2019, A&A, in press, https://doi.org/10.1051/0004-6361/201833293 [Google Scholar]
- Planck Collaboration III. 2019, A&A, in press, https://doi.org/10.1051/0004-6361/201832909 [Google Scholar]
- Ritacco, A., Macas-Pérez, J. F., Ponthieu, N., et al. 2018, A&A, 616, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Deconvolution parameters by horn combination, deconvolution parameters ℓmax and kmax, polarization (T/F), and FWHM width of the smoothing kernel.
All Figures
 |
Fig. 1. From left to right: deconvolved temperature maps for 30, 44, and 70 GHz, corresponding PR3 maps, and differences between the two. The data include four years of observations for all radiometers of the respective frequency channel. The deconvolved maps are smoothed with a Gaussian beam of FWHM = 40′ (30 GHz), 30′ (44 GHz), or 20′ (70 GHz). We subtracted from the deconvolved maps the same monopole that had been subtracted from the PR3 map. The difference maps are dominated by white noise, which is suppressed in the deconvolved maps. The temperature scales of the maps are ±300 μK for temperature and ±100 μK for the difference. |
| In the text | |
 |
Fig. 2. A 10° patch around the Crab Nebula in the 30 GHz temperature map. Left: deconvolved. Right: PR3 30 GHz LFI map. |
| In the text | |
 |
Fig. 3. Half-ring cross-spectra in TT, from masked PR3 and deconvolution maps at 70 GHz, after correction for mask and beam window. |
| In the text | |
 |
Fig. 4. Survey difference T maps S1 + S3 − S2 − S4. The maps are smoothed to 1° resolution. Deconvolution reduces beam shape residuals, revealing other signal residuals. |
| In the text | |
 |
Fig. 5. Deconvolved (left) and PR3 (middle) polarization maps for LFI channels, and their differences (right). From top down: 30 GHz; 44 GHz; and 70 GHz. These maps are smoothed to 1° resolution (FWHM) to suppress noise. The maps are not corrected for bandpass leakage. |
| In the text | |
 |
Fig. 6. Noise bias from NCVM, and the HRHD noise estimate, for 30, 44, and 70 GHz data. Top: TT spectrum. Bottom: EE and BB spectra. |
| In the text | |
 |
Fig. 7. Noise bias from NCVM for full 44 GHz data, and HRHD noise estimate for full 44 GHz data and for 25/26 horn combination. |
| In the text | |
 |
Fig. 8. Eigenvalue spectrum of the 30 GHz TT NCVM (grey), and corresponding decomposition of the HRHD map (orange). We add a small constant of 10−6 μK2 to the NCVM for numerical stability. A larger phenomenological constant is added to the NCVM (light blue) to account for the high-end plateau. |
| In the text | |
 |
Fig. 9. Excess χ2 in pixel space, as it builds up as a function of eigenmode. The eigenmodes are arranged in order of decreasing eigenvalue, so that the strongest noise structures are on the left. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} W(\ell ) = {\left\{ \begin{array}{ll} \exp [-\sigma ^2\ell (\ell +1)] \quad&\mathrm{(temperature)} \\ \exp [-\sigma ^2(\ell (\ell +1)-4)] \quad&\mathrm{(polarization),} \\ \end{array}\right.} \end{aligned} $$](/articles/aa/full_html/2019/12/aa35875-19/aa35875-19-eq1.gif)
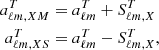
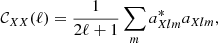
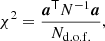
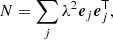
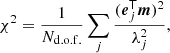
![$$ \begin{aligned} \Delta \chi ^2(n) = \frac{1}{3072} \left[ \sum _{j=1}^n\frac{1}{\lambda _j^2} (\boldsymbol{m}_j^\mathsf{T} \boldsymbol{e}_j)^2 -n \right]. \end{aligned} $$](/articles/aa/full_html/2019/12/aa35875-19/aa35875-19-eq16.gif)