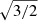| Issue |
A&A
Volume 631, November 2019
|
|
|---|---|---|
| Article Number | A130 | |
| Number of page(s) | 16 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201935974 | |
| Published online | 06 November 2019 | |
Enhanced cluster lensing models with measured galaxy kinematics
1
Dipartimento di Fisica e Astronomia “G. Galilei”, Università di Padova, Vicolo dell’Osservatorio 3, 35122 Padova, Italy
e-mail: pietro.bergamini@phd.unipd.it
2
Dipartimento di Fisica e Scienze della Terra, Università degli Studi di Ferrara, Via Saragat 1, 44122 Ferrara, Italy
3
INAF – Osservatorio Astronomico di Capodimonte, Via Moiariello 16, 80131 Napoli, Italy
4
Dipartimento di Fisica, Università degli Studi di Milano, Via Celoria 16, 20133 Milano, Italy
5
DARK, Niels-Bohr Institute, Lyngbyvej 2, 2100 Copenhagen, Denmark
6
INAF – OAS, Osservatorio di Astrofisica e Scienza dello Spazio di Bologna, Via Gobetti 93/3, 40129 Bologna, Italy
7
INFN, Sezione di Bologna, Viale Berti Pichat 6/2, 40127 Bologna, Italy
8
INAF – Osservatorio Astronomico di Trieste, Via G. B. Tiepolo 11, 34131 Trieste, Italy
9
Kapteyn Astronomical Institute, University of Groningen, Postbus 800, 9700 AV Groningen, The Netherlands
Received:
28
May
2019
Accepted:
18
September
2019
We present an improved determination of the total mass distribution of three massive clusters from the Cluster Lensing and Supernova Survey with Hubble and Hubble Frontier Fields, MACS J1206.2−0847 (z = 0.44), MACS J0416.1−2403 (z = 0.40), Abell S1063 (z = 0.35). We specifically reconstructed the sub-halo mass component with robust stellar kinematics information of cluster galaxies, in combination with precise strong lensing models based on large samples of spectroscopically identified multiple images. We used integral-field spectroscopy in the cluster cores, from the Multi Unit Spectroscopic Explorer on the Very Large Telescope, to measure the stellar velocity dispersion, σ, of 40−60 member galaxies per cluster, covering four to five magnitudes to mF160W ≃ 21.5. We verified the robustness and quantified the accuracy of the velocity dispersion measurements with extensive spectral simulations. With these data, we determined the normalization and slope of the galaxy L–σ Faber–Jackson relation in each cluster and used these parameters as a prior for the scaling relations of the sub-halo population in the mass distribution modeling. When compared to our previous lens models, the inclusion of member galaxies’ kinematics provides a similar precision in reproducing the positions of the multiple images. However, the inherent degeneracy between the central effective velocity dispersion, σ0, and truncation radius, rcut, of sub-halos is strongly reduced, thus significantly alleviating possible systematics in the measurements of sub-halo masses. The three independent determinations of the σ0 − rcut scaling relation in each cluster are found to be fully consistent, enabling a statistical determination of sub-halo sizes as a function of σ0, or halo masses. Finally, we derived the galaxy central velocity dispersion functions of the three clusters projected within 16% of their virial radius, finding that they are well in agreement with each other. We argue that such a methodology, when applied to high-quality kinematics and strong lensing data, allows the sub-halo mass functions to be determined and compared with those obtained from cosmological simulations.
Key words: gravitational lensing: strong / galaxies: clusters: general / cosmology: observations / dark matter / galaxies: kinematics and dynamics
© ESO 2019
1. Introduction
Strong gravitational lensing is a powerful technique to probe the total projected mass distribution of the inner regions of galaxy clusters and, therefore, the dark matter (DM) distribution once the baryonic mass components are independently mapped. By characterizing the substructure of cluster cores on different scales and the mass density profile of the innermost regions, one can test the ΛCDM structure formation scenario and indirectly constrain DM physical properties by comparing reconstructed mass maps with the latest cosmological simulations (e.g., Diemand & Moore 2011). In recent years, dedicated Hubble Space Telescope (HST) observational campaigns, such as the Cluster Lensing And Supernova survey with Hubble (CLASH, Postman et al. 2012), the Hubble Frontier Field campaign (HFF, Lotz et al. 2017), and the Reionization Lensing Cluster Survey (RELICS, Coe et al. 2019) have provided multi-band data with unprecedented quality on a sizable set of massive galaxy clusters. In parallel, extensive spectroscopic campaigns with highly-multiplexing multi-slit instruments (e.g., CLASH-VLT, Rosati et al., in prep.; Balestra et al. 2016), and especially with the Multi Unit Spectroscopic Explorer (MUSE) integral field spectrograph on the Very Large Telescope (VLT; Bacon et al. 2012), have secured redshifts for hundreds of multiple lensed images in cluster cores, as well identified large samples of cluster galaxies. The combination of these new imaging and spectroscopic data sets have enabled the development of new high-precision parametric strong lensing models based on 50−100 bona fide multiple images per cluster and highly complete samples of cluster members (e.g., Richard et al. 2014; Grillo et al. 2015; Jauzac et al. 2015; Limousin et al. 2016; Kawamata et al. 2016; Lagattuta et al. 2017; Caminha et al. 2016, 2017a,b, 2019; Bonamigo et al. 2018). These new lens studies typically reach a root mean square difference between the observed and predicted positions of multiple images on the lens plane of Δrms ≈ 0.5″. The latter is commonly used as a simple figure of merit for model accuracy. Nonetheless, the relatively large number of parameters used to describe the cluster mass distribution still suffer from strong internal degeneracies. The generally complex cluster mass distribution in parametric lens models is generally separated into a cluster-scale diffuse component, made of one or more large halos, and a clumpy distribution traced by cluster galaxies (Natarajan & Kneib 1997). The latter describes the sub-halo population of DM halos (De Lucia et al. 2004; Giocoli et al. 2010) and hence the inner substructure of the cluster mass distribution (Springel et al. 2001). In the effort to limit the number of free parameters, this sub-halo component is generally modeled adopting two scaling relations, which link the internal velocity dispersion and size of each halo with the luminosity of member galaxies. A fixed mass-to-light scaling is thereby assumed for all sub-halos. Since strong lensing models constrain the total projected mass within each family of multiple image positions, a certain amount of degeneracy is always present between the velocity dispersion, the size (or equivalently the profile), and the shape of each halo component of the mass distribution. Given the cross-talks among different halo components in strong lensing models, such a degeneracy can lead to systematics in the reconstruction of the substructure at different scales, for example with a transfer of mass between the clumpy and diffuse mass components. As we demonstrate in this work, such a degeneracy can be broken and significantly reduced, on the scale of the sub-halos, by using an independent measurement of the internal stellar velocity dispersion of cluster members.
A combination of lensing and kinematic measurements has long been exploited in the study of the mass density profile of field early-type galaxies. This combination has proved to be particularly effective since the two diagnostics complement each other (e.g., Treu & Koopmans 2004; Czoske et al. 2008; Barnabè et al. 2009), breaking the mass-anisotropy and mass-sheet (e.g., Falco et al. 1985; Meylan et al. 2006) degeneracies of the dynamical and lensing analyses, respectively. Joint strong lensing and stellar-dynamical studies have been used to determine the average logarithmic density slope of the total mass inside the Einstein radius (Treu & Koopmans 2004; Koopmans et al. 2009) and to decompose the total mass distribution into luminous and dark components of the lens galaxies belonging to the Lenses Structure and Dynamics (LSD) and Sloan Lens ACS (SLACS) surveys. These two surveys have measured a remarkably homogeneous total (luminous and dark) mass density profile that is consistent with an isothermal one (i.e., ρ ∝ 1/r2) out to a few hundreds of kiloparsecs (see Gavazzi et al. 2007; Bolton et al. 2008). A one-component isothermal model is fully characterized by the value of an effective velocity dispersion, approximated within ≲3% by the value of the galaxy central stellar velocity dispersion (i.e., the velocity dispersion of the stars projected within a disk of radius Re/8; see, e.g., Treu et al. 2006; Bolton et al. 2008). This result is theoretically supported by the Jeans equation for realistic stellar density distributions (e.g., Jaffe 1983; Hernquist 1990) embedded in a globally isothermal distribution (see Kochanek 1993), as observed in samples of nearby and luminous early-type galaxies (e.g., Kochanek 1994; Grillo et al. 2008).
A combination of the spatially resolved kinematics of the brightest cluster galaxy (BCG) and strong lensing modeling in the inner cores of massive clusters has also been used to constrain the central slope of their mass density profiles using simplified dynamical models (Sand et al. 2004; Newman et al. 2013). A first attempt to include cluster galaxy kinematics in cluster strong lensing models was made by Verdugo et al. (2007). A more extensive study was carried out by Monna et al. (2015) in Abell 383 at z = 0.187 with early CLASH data. They integrated the velocity dispersion measurements of 21 member galaxies, obtained with the Hectospec fiber spectrograph at the MMT, into a lens model based on the identification of nine multiply imaged systems (six of which spectroscopically confirmed). Thus, they show how typical degeneracies among lens model parameters describing the galaxy mass-to-light scaling relation can be significantly reduced. In particular, a meaningful scaling relation between galaxy halo truncation radii and velocity dispersions can be derived (see also Monna et al. 2017). Additional constraints on halo sizes can be obtained by modeling the surface brightness distribution of strong lensing features around individual member galaxies (see also Suyu & Halkola 2010; Eichner et al. 2013 who did not use galaxy kinematics).
In our work, we extend the methodology introduced by Monna et al. (2015), by using a much improved HST and spectroscopic data set on three CLASH/HFF clusters, specifically an extended set of velocity dispersion measurements obtained with the MUSE spectrograph at the VLT. A robust characterization of cluster sub-halo populations, particularly the distribution of their sizes and masses, as well as their abundance, offer a critical test of the predictions of cosmological simulations (e.g., Limousin et al. 2009; Grillo et al. 2015; Munari et al. 2016; Natarajan et al. 2009, 2017). Such a comparison can shed light on baryonic processes shaping cluster substructure, dynamical processes leading to halo stripping in different environments, and indirectly on the nature of dark matter (Despali & Vegetti 2017; Chua et al. 2017; Nipoti et al. 2018; Niemiec et al. 2019).
This work is organized as follows. In Sect. 2, we describe our imaging and spectroscopic data sets. In Sect. 3, we detail how internal velocity dispersions of member galaxies are measured, including spectral simulations to assess their robustness. Strong lensing models for the three clusters under study are described in Sect. 4, while the specific methodology to incorporate galaxy kinematics information into our lens models is discussed in Sect. 5. Results are discussed in Sect. 6 where we also present the velocity dispersion functions for the three clusters. In Sect. 7, we summarize the main conclusions of our study.
Throughout this article, we adopt a flat ΛCDM cosmology with Ωm = 0.3 and H0 = 70 km s−1 Mpc−1. With these parameters, 1″ corresponds to a physical scale of 5.68, 5.34 and 4.92 kpc at z = 0.439, 0.396, 0.348, respectively the redshift of the three clusters of this study: MACS 1206, MACS 0416 and AS1063 (see below). All magnitudes refer to the AB system.
2. Photometric and spectroscopic data
This section summarizes the photometric and spectroscopic data sets for the three clusters used in this work, namely MACS J1206.2−0847, MACS J0416.1−2403, and Abell S1063 (a.k.a. RXJ 2248.7−4431), hereafter MACS 1206, MACS 0416 and AS1063, at redshifts 0.439, 0.396 and 0.348, respectively (see Table 1). These clusters were observed with HST in 16 broad band filters, from UV to near-IR, as part of the CLASH program. HST imaging of MACS 0416 and AS1063 was significantly augmented with the HFF program by adding deep exposures in seven filters (F435, F606W, F814W, F105W, F125W, F140W, F160W). The three clusters were also part of an extensive spectroscopic campaign with the CLASH-VLT Large program (P.I. P. Rosati), using the VIMOS high-multiplexing spectrograph, which provided over 4000 redshifts in each of the three clusters, over an area of ∼25 × 25 arcmin2. These data sets yielded approximately 600 spectroscopic members for MACS 1206 (Biviano et al. 2013; Girardi et al. 2015), 900 members for MACS 0416 (Balestra et al. 2016) and over 1200 members for AS1063 (Mercurio et al., in prep.). Spectroscopic information in the cores of the three clusters has been significantly enhanced with the MUSE integral field spectrograph at the VLT, which is at the basis of the kinematic measurements presented in this work. These data, which are described in more detail below, have enabled new high-precision strong lensing models based on large samples of multiply lensed sources (see Caminha et al. 2017a,b, 2016 and Sect. 4). MUSE has a field of view of 1 arcmin2, a spatial sampling of 0.2″, a spectral resolution of ∼2.4 Å over the spectral range 4750−9350 Å, with a spectral sampling of 1.25 Å pix−1.
Most relevant parameters of three clusters of this work.
MACS 1206. MUSE data were obtained between 2015 and 20161, the redshift measurements of the member galaxies and a large sample of multiple images were presented in Caminha et al. (2017b; hereafter C17b). Three MUSE pointings cover a total area of 2.63 arcmin2, mapping the SE–NW elongation of the cluster. The exposure time is 8.5 h in the central ∼0.5 arcmin2 and 4 h in the remaining area.
MACS 0416. MUSE archival observations used in this work were presented in Caminha et al. (2017a; hereafter C17a), along with the redshift catalog, and consist of two pointings2, one of 2 h in the NE region, with a seeing of 0.5″, and a SW pointing of 11 h, with a seeing of 1″.
AS1063. MUSE data consist of two pointings, which were presented in Karman et al. (2015, 2017). The SW pointing3 has an exposure of 3.1 h and seeing ∼1.1″, the NE pointing4 has an exposure of 4.8 h and seeing of 0.9″.
3. Cluster members: spectral extraction and internal kinematics
In this section, we describe the methodology adopted to extract the spectra of the cluster members from the MUSE data-cubes and to measure their internal stellar velocity dispersions. Catalogs of cluster members for MACS 1206, MACS 0416, AS1063 were presented in C17b, C17a and Caminha et al. (2016; hereafter C16), respectively, with the main objective of identifying the sub-halos to be included in the lens models (see below). Cluster members were defined as galaxies in the redshift intervals 0.425−0.453, 0.382−0.410, and 0.335−0.362 for the three clusters respectively, lying within a rest-frame velocity of approximately ±3000 km s−1 around the median redshift of the cluster. With 114−145 spectroscopic members per cluster in the HST FoV, the extensive CLASH multi-band information was used to obtain highly (∼95%) complete and pure samples of photometric members down to mF160W = 24, following the method described in Grillo et al. (2015).
The spectra of cluster members are extracted from the MUSE data-cubes within apertures of Rap = 0.8″ radius. The latter is found to be a good compromise between the signal-to-noise of the spectra and the contamination from other sources in the field (either interlopers along the line-of-sight or close members). All the extractions are visually inspected to assess possible contamination from nearby sources and the apertures are reduced in specific cases down to 0.6″. The spectra in which the contamination from bright nearby members is too strong are discarded as the velocity dispersion of the fainter galaxy is likely biased.
We measure the stellar line-of-sight velocity distribution (hereafter LOSVD) of cluster members using the public software pPXF (penalized pixel-fitting, Cappellari & Emsellem 2004), with the latest improvements included in the 02/2018 python version (Cappellari 2017). With pPXF, we determine the best-fit LOSVD parameters (first and higher moments) by performing a cross-correlation of the observed spectrum with a set of spectral templates. The best-fit is obtained by minimizing a χ2 between the template and the observed spectrum, including an additional penalty function whose weight is regulated by a parameter λ. This bias parameter is used to suppress higher velocity moments (h3, h4), when they become unreliable in spectra with low velocity dispersion and low S/N (see Cappellari & Emsellem 2004). For each spectrum, we measure a mean signal-to-noise, ⟨S/N⟩, over the selected wavelength range. We then adopt a relation between λ and ⟨S/N⟩, as suggested in Cappellari et al. (2011), which we tested with extensive spectral simulations described in Appendix A.
To perform the pPXF spectral fits, we use a subset of 105 stellar templates of different spectral types, drawn from the National Optical Astronomy Observatory library (Valdes et al. 2004). To match the typical underlying stellar populations of early-type galaxies in the cluster cores, most of the templates are of G, K, M spectral classes. In addition, we include 10 A-stars to extend spectral fits to a non-negligible fraction of E+A galaxies in our cluster sample and a few O and B stars. The stellar templates cover a wavelength range from 3465 Å to 9469 Å, with a sampling of 0.4 Å pix−1 and have an intrinsic resolution of 1.35 Å full width at half-maximum.
In Appendix A, we describe in detail a set of simulations which reproduce our galaxy spectra with varying input LOSVD parameters, redshift and ⟨S/N⟩, to quantify the accuracy and precision of pPXF in measuring the velocity dispersions σ of member galaxies, thus optimizing pPXF input parameters. Simulated spectra are constructed from model spectra spanning the spectral type diversity of our cluster galaxy populations and by adding noise drawn from the variance map of the reduced MUSE data-cubes.
With these simulations, we check the reliability of the statistical error provided by pPXF on our data, as well as the presence of systematic errors as a function of ⟨S/N⟩ and input velocity dispersion (σin). The latter can become important especially when measuring velocity dispersions of low mass galaxies, as we approach the MUSE instrument resolution. We find that statistical errors are generally underestimated by ∼20% for ⟨S/N⟩ > 15, up to ∼25% for ⟨S/N⟩∼10, whereas a positive bias of a few km s−1 becomes evident for σ ≲ 100 km s−1 at high ⟨S/N⟩. In addition, we find that measurements become increasingly uncertain at ⟨S/N⟩ < 10. We therefore include in our galaxy kinematic sample only galaxies with ⟨S/N⟩ > 10 and σ > 80 km s−1. In all cases, we use empirical formulas (see Appendix A) to correct the measured velocity dispersions and their uncertainties in different ⟨S/N⟩ and σ regimes.
Simulations were also used to choose the optimal wavelength range for pPXF fits, for a given galaxy redshift, by excluding regions of low S/N due to the MUSE sensitivity curve, particularly on the red side of the spectrum strongly affected by sky lines residuals. The resulting selected rest-frame wavelength ranges are 3600−4900 Å, 3600−5200 Å and 3600−5300 Å for MACS 1206, MACS 0416 and AS1063, respectively. The LOSVD input velocity value (zero moment) is taken from our redshift catalogs. The measured parameters are the velocity shift (V, typically within 50 km s−1), the velocity dispersion σ, and higher moments (h3, h4), and their one-standard deviation errors. All velocity dispersions measured with pPXF are labeled in the following with the subscript “ap” to emphasize that these are line-of-sight quantities within an aperture, as opposed to σ0, and σLT, which refer to parameters inferred with the lens models (see next session). Figure 1 shows examples of pPXF spectral fitting for three cluster galaxies in MACS 1206, one in the high ⟨S/N⟩ regime, one for the median ⟨S/N⟩ of our sample (∼30), and one at the limiting ⟨S/N⟩∼10.
 |
Fig. 1. Results from line-of-sight velocity dispersion fitting of spectra of three cluster members in MACS 1206 as obtained with pPXF. Galaxy spectra are shown in black; red curves are the pPXF best-fit models, while the green points correspond to the data−model residuals. The blue shaded regions along the wavelength axis were excluded in the fitting procedure due to the presence of noisy sky subtractions around emission lines in the spectra. Corresponding residuals in these regions are marked in blue. The first from the top is a high signal-to-noise E+A galaxy. The second is a passive galaxy spectrum with a ⟨S/N⟩ = 28.1, corresponding approximately to the mean S/N of our galaxy sample. The bottom spectrum has a ⟨S/N⟩ = 10.7, close to our lower limit for reliable velocity dispersion measurements. Coordinates, measured velocity dispersion (σap), mean signal-to-noise and F160W magnitudes are indicated in each panel. Cutouts are HST RGB images, 4″ across, showing in green the apertures of 0.8″ radius used for the spectral extraction. |
In Table 1, we quote the number of uncontaminated spectra extracted in each cluster ( ), for which we can reliably measure velocity dispersions, together with the total number of spectro-photometric members and relevant cluster parameters. In Fig. 2, the data points correspond to measured velocity dispersions of member galaxies as a function of their F160W magnitude, defining the Faber–Jackson relation in the three clusters.
), for which we can reliably measure velocity dispersions, together with the total number of spectro-photometric members and relevant cluster parameters. In Fig. 2, the data points correspond to measured velocity dispersions of member galaxies as a function of their F160W magnitude, defining the Faber–Jackson relation in the three clusters.
 |
Fig. 2. Data points are measured stellar velocity dispersions of cluster members, color-coded according to their spectral ⟨S/N⟩. Green lines are 300 scaling relations randomly drawn from the posterior distributions of the σap–mag scaling relation parameters, α, |
4. Strong lensing models
Accurate strong lensing models were developed for MACS 1206, MACS 0416 and AS1063 in C17b, C17a and C16, respectively. These models were further refined in Bonamigo et al. (2018; B18 hereafter), who included the mass distribution of the hot gas component in each cluster, as derived from the Chandra X-ray data, dominating the smooth baryonic cluster component. As customary in cluster strong lensing modeling, none of these models included any kinematic information on cluster galaxies. We describe here our methodology which combines the B18 lens models with internal stellar kinematics derived from a large number of velocity dispersions measured with MUSE. For each cluster, we use the same catalogs of multiple images and cluster galaxies as in B18 and the Caminha et al. models, and likewise we employ the public software LensTool (Kneib et al. 1996; Jullo et al. 2007; Jullo & Kneib 2009).
A parametric lens model for the total mass distribution of each cluster is optimized searching for the set of parameters ξ, which minimize the χ2 defined on the lens plane as (Jullo et al. 2007):
where  identifies the number of multiple images associated to the same source j (usually called a family), Nfam is the number of families, xobs are the observed positions of the multiple images on the lens plane, xpred are their predicted positions, given the set of model parameters ξ, and Δxi, j represent the uncertainties on the observed positions. Following B18, we perform a first optimization of our lensing models assuming a positional error of 0.5″ for images identified in HST and 1″ for those only found in the MUSE data. We multiply these errors by a constant factor ensuring that the best-fit χ2 is close to the number of degree of freedom of the models. These updated errors are then used to sample the posterior distributions of the free parameters.
identifies the number of multiple images associated to the same source j (usually called a family), Nfam is the number of families, xobs are the observed positions of the multiple images on the lens plane, xpred are their predicted positions, given the set of model parameters ξ, and Δxi, j represent the uncertainties on the observed positions. Following B18, we perform a first optimization of our lensing models assuming a positional error of 0.5″ for images identified in HST and 1″ for those only found in the MUSE data. We multiply these errors by a constant factor ensuring that the best-fit χ2 is close to the number of degree of freedom of the models. These updated errors are then used to sample the posterior distributions of the free parameters.
 |
Fig. 3. Posterior probability distributions for σap–mag scaling relation parameters, obtained as described in Appendix B, from velocity dispersion measurements of 58 cluster members in MACS 1206. The 16th, 50th and 84th percentiles of the marginalized distributions for the slope (α), normalization ( |
Following the B18 modeling, the total mass distribution (or equivalently the gravitational potential ϕ) of each cluster is described as the sum of three contributions: (1) an elliptical large-scale smooth halo, which is further decomposed in a DM component and a smooth gas mass component, both described as dual pseudo-isothermal elliptical density (dPIE) profiles; the latter is obtained from deep Chandra observations, as multiple dPIE fits, as described in B18; (2) a clumpy component representing the cluster member galaxies (DM+baryons), modeled as spherical dPIE halos; (3) a shear+foreground-structure term to take into account the presence of massive structures in the outer cluster regions and line-of-sight mass distributions. Specific details on these multiple components are given below in the description of each lens model. The total cluster gravitational potential has therefore the form:
where the first sum runs over the Nh cluster-scale mass distributions, while the second on the Ng cluster member galaxies.
The general functional form for the spherical dPIE, including the relations between 3D and projected mass densities, as well as the expressions to derive aperture projected line-of-sight velocity dispersions, are given in Appendix C. Following our previous models and the general LensTool methodology, the dPIE parameters for the sub-halo population follow a scaling relation for the central velocity dispersion and the truncation radius:
where Li is the luminosity of the ith cluster member and 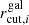 represents the corresponding truncation radius. A similar scaling relation for the core radius, rcore, is used in LensTool, however it is not relevant here since a vanishing core radius is adopted.
represents the corresponding truncation radius. A similar scaling relation for the core radius, rcore, is used in LensTool, however it is not relevant here since a vanishing core radius is adopted. 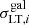 is the LensTool fiducial velocity dispersion of each member, which is related to the central velocity dispersion of the dPIE profile by
is the LensTool fiducial velocity dispersion of each member, which is related to the central velocity dispersion of the dPIE profile by 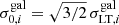 (see Appendix C). It is common practice to fix the slopes α and βcut, so that the model optimization is performed over only two free parameters, that is the normalizations of the velocity dispersion and the truncation radius corresponding to the reference luminosity L0. We measure the luminosities Li and L0 using the HST F160W Kron magnitudes, which are a good proxy of the stellar mass of the cluster members (see Grillo et al. 2015) and include members down to mF160W = 24. This leads to a minimum of 193 sub-halos to be included in the lens model (see Table 1), fixed at the galaxy positions.
(see Appendix C). It is common practice to fix the slopes α and βcut, so that the model optimization is performed over only two free parameters, that is the normalizations of the velocity dispersion and the truncation radius corresponding to the reference luminosity L0. We measure the luminosities Li and L0 using the HST F160W Kron magnitudes, which are a good proxy of the stellar mass of the cluster members (see Grillo et al. 2015) and include members down to mF160W = 24. This leads to a minimum of 193 sub-halos to be included in the lens model (see Table 1), fixed at the galaxy positions.
The total mass of a circular dPIE profile is given by (see Appendix C, Elíasdóttir et al. 2007; Limousin et al. 2005) the relation: 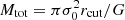 .
.
Assuming a fixed scaling between the cluster members luminosity Li (in the same band considered by Eqs. (3) and (4)) and its total mass Mtot, i, that is 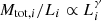 , one can obtain the following relation between the slopes of Eqs. (3) and (4):
, one can obtain the following relation between the slopes of Eqs. (3) and (4):
The main goal of this work is to use prior information for the scaling relations derived directly from measured velocity dispersions of cluster galaxies. The latter are light-weighted projected values of the 3D-velocity dispersions within the extracted spectroscopic apertures, hereafter σap. In order to compare σLT − L scaling relations with measured quantities, we need to compute the aperture-averaged line-of-sight velocity dispersion from the adopted dPIE mass models. The projection coefficients needed to transform σLT into σap are obtained with a numerical integration depending on rcut, rcore and Rap. In Appendix C we recall all the equations to perform this projection procedure.
In Fig. 2, we show the best-fit scaling relations obtained from the previous models for each cluster (red and blue curves), which did not include any prior from internal kinematics of cluster members. These curves are computed by projecting the LensTool scaling relations, using the posterior distribution of the parameters rcut and 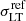 at different magnitudes, yielding the model σap as a function of mF160W. In this process, we use an aperture of 0.8″ so that the projected scaling relations can be directly compared with our kinematic measurements.
at different magnitudes, yielding the model σap as a function of mF160W. In this process, we use an aperture of 0.8″ so that the projected scaling relations can be directly compared with our kinematic measurements.
As customary in previous lens models to date, all the slopes for scaling relations α, βcut, γ (see Eq. (5)) are fixed, here instead we take advantage of the measured stellar velocity dispersions to directly fit the normalization 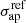 and slope α of the σ − L scaling relation. We then derive βcut by adopting γ = 0.2, which is consistent with the canonical fundamental plane (Faber et al. 1987; Bender et al. 1992), and that we verify to be appropriate using photometric and morphological data for AS1063 (see below and Mercurio et al., in prep.).
and slope α of the σ − L scaling relation. We then derive βcut by adopting γ = 0.2, which is consistent with the canonical fundamental plane (Faber et al. 1987; Bender et al. 1992), and that we verify to be appropriate using photometric and morphological data for AS1063 (see below and Mercurio et al., in prep.).
In order to fit the σ–mag relation, a Bayesian approach is used, as described in Appendix B. Thus, we derive the value of α and 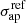 , as shown in Fig. 3, which also includes the intrinsic scatter Δσap of the measured velocity dispersions around the model (Eq. (3)). Similar behaviors for the parameters derived for the other two clusters can be found in Appendix B. The best-fit scaling relations obtained with this method are shown in Fig. 2, including the corresponding uncertainties (green curves), which are derived by sampling 300 times the posterior distributions. These best-fit parameters for each scaling relation (see Table 2) are then used as dynamical priors in our lens models, as described below. It is interesting to note that the slope that we obtain for the Faber–Jackson relation, L-σ1/α, is very similar for the three clusters (α = 0.27−0.28) and consistent with several spectro-photometric studies of cluster early-type galaxy populations in the literature (e.g., Kormendy & Bender 2013; Focardi & Malavasi 2012).
, as shown in Fig. 3, which also includes the intrinsic scatter Δσap of the measured velocity dispersions around the model (Eq. (3)). Similar behaviors for the parameters derived for the other two clusters can be found in Appendix B. The best-fit scaling relations obtained with this method are shown in Fig. 2, including the corresponding uncertainties (green curves), which are derived by sampling 300 times the posterior distributions. These best-fit parameters for each scaling relation (see Table 2) are then used as dynamical priors in our lens models, as described below. It is interesting to note that the slope that we obtain for the Faber–Jackson relation, L-σ1/α, is very similar for the three clusters (α = 0.27−0.28) and consistent with several spectro-photometric studies of cluster early-type galaxy populations in the literature (e.g., Kormendy & Bender 2013; Focardi & Malavasi 2012).
σap − L scaling relation parameters derived from measured velocity dispersions of cluster members for MACS 1206, MACS 0416 and AS1063.
We note that some galaxies deviate significantly from the best-fit scaling relations (as marked by boxes and circles in Fig. 2). This is however expected, as the Faber–Jackson relation is one of the projections of the fundamental plane relation among half-light radius Re, mean surface brightness μe within Re, and velocity dispersion: at a given luminosity, more compact galaxies tend to have higher velocity dispersion. For example, the four cluster galaxies at mF160W ∼ 19 in AS1063, with a σ significantly higher than the best-fit relation (see boxes in Fig. 2), have μe in the 16th highest percentile, however we verified that they still lie on the fundamental plane defined by Jorgensen et al. (1996) (Mercurio et al., in prep.).
On the other hand, the few galaxies lying well below the σ–mag relation (see circled data points in Fig. 2 and the spectrum in the upper panel of Fig. 1) show sign of emission lines and young stellar populations in their spectra, for which lower velocity dispersions are expected when compared to early-type galaxies with similar luminosities.
5. Combining lensing models with kinematics measurements
In Fig. 2, a comparison between the sub-halo scaling relations obtained from the lens models and those directly constrained from kinematic measurements (green curves) shows significant discrepancies in the case of MACS 0416 and AS1063, while they are consistent for MACS 1206. In the case of AS1063, the normalization of the kinematic scaling relations are found to be approximately 100 and 150 km s−1 above the values inferred from the B18 and C16 lens models, respectively. In MACS 0416, the discrepancy is significant (∼50 km s−1) for the C17a model, while it is negligible for the B18 model within the errors, albeit with a slope which deviates from the observed one (α = 0.27 against 0.35 assumed in B18). This shows how inherent degeneracies of sub-halo population parameters in strong lensing models can lead to inferred velocity dispersion normalizations which are inconsistent with kinematic measurements of cluster galaxies. Nevertheless, these lens models can reproduce the positions of the multiple images with high precision, with a root-mean square value between the observed and model-predicted images on the image plane of Δrms ≃ 0.45−0.6″ (see Table 3). It is in fact well known that parametric cluster lens models are, in general, affected by some degeneracy between the mass distribution of the macro-halo(s) and that of the sub-halos, even when a large number of constraints are available, as in our case (Meneghetti et al. 2017). Despite that, the projected total mass value within a given cluster-centric radius remains robust. In addition, a significant degeneracy exists between the central velocity dispersions and the cut-off radii of the sub-halos.
Output parameters of three lens models developed in this work.
In the following, we describe in detail our new lens models for each cluster. We start from the same parameterization and input constraints as in the B18 models, we then proceed to add critical constraints on the sub-halo scaling relation parameters, with priors from our kinematic measurements. The optimization of model parameters is obtained from MCMC chains of approximately 105 samples, excluding the burn-in phase. Model components and parameters are summarized in Table 3. As customary in the literature, no scatter in the scaling relations is assumed in our lens models, as it is currently not possible to include it in LensTool (Bergamini et al., in prep.).
5.1. MACS 1206
Following C17b and B18 models, the cluster smooth mass distribution includes three dark matter halos which can reproduce the apparent elongated asymmetry in the distribution of the cluster galaxies and intra-cluster light. The three halos are described as dPIEs profiles whose values of sky positions, ellipticities, position angles, core radii, and velocity dispersions are left free to vary with flat priors, while their truncation radii are fixed to a large value. Three dPIE gas clumps are used to model the X-ray surface brightness distribution as in B18. Thus, the cluster-scale mass components have a total of 18 free parameters. The presence of an external shear term introduces two extra free parameters in the model. Finally, the clumpy component includes 258 halos describing the cluster members and the BCG, centered on the peaks of their light emission. All these galaxies are described as circular dPIEs profiles, whose values of central velocity dispersion and truncation radius scale with their F160W magnitude, according to Eqs. (3) and (4), where the BCG magnitude is used as reference luminosity (L0). The normalization 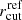 is free to vary between 1″ and 50″ (i.e. 5.67−283.9 kpc at the cluster redshift) with a flat prior. A Gaussian prior derived from our kinematic measurements is then introduced for the σ − L scaling relation. To determine this prior, we deproject the best-fit (median) normalization of the σ–mag relation (
is free to vary between 1″ and 50″ (i.e. 5.67−283.9 kpc at the cluster redshift) with a flat prior. A Gaussian prior derived from our kinematic measurements is then introduced for the σ − L scaling relation. To determine this prior, we deproject the best-fit (median) normalization of the σ–mag relation (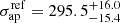 km s−1, see Fig. 3) to obtain a LensTool fiducial reference velocity dispersion,
km s−1, see Fig. 3) to obtain a LensTool fiducial reference velocity dispersion, 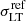 . This deprojection is achieved with an iterative procedure by computing the projection coefficient, cp(rcore, rcut, Rap) (see Appendix C), using the best-fit scaling relation parameters from a first model without kinematic prior, as
. This deprojection is achieved with an iterative procedure by computing the projection coefficient, cp(rcore, rcut, Rap) (see Appendix C), using the best-fit scaling relation parameters from a first model without kinematic prior, as 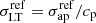 . In the case of MACS 1206, we thus obtain a Gaussian prior on
. In the case of MACS 1206, we thus obtain a Gaussian prior on 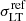 with a mean of 264 km s−1 and a standard deviation of 18 km s−1. The standard deviation also includes the uncertainty in the computation of cp, due to the allowed range of rcut. Finally, the slope α is fixed to the value obtained from the σ–mag fit (α = 0.28), while a βcut = 0.64 is obtained from Eq. (5), with γ = 0.2. The lens model is thus optimized with a total number of 22 free parameters, using the observed positions of 82 spectroscopically confirmed multiple images associated to 27 families (C17b and B18).
with a mean of 264 km s−1 and a standard deviation of 18 km s−1. The standard deviation also includes the uncertainty in the computation of cp, due to the allowed range of rcut. Finally, the slope α is fixed to the value obtained from the σ–mag fit (α = 0.28), while a βcut = 0.64 is obtained from Eq. (5), with γ = 0.2. The lens model is thus optimized with a total number of 22 free parameters, using the observed positions of 82 spectroscopically confirmed multiple images associated to 27 families (C17b and B18).
5.2. MACS 0416
Referring to Table 3, the cluster-scale mass components of this merging cluster (Balestra et al. 2016) include two massive dark matter halos, whose positions are left free to vary in areas of 30″ × 30″ and 15″ × 15″ around the northern and southern BCG, respectively (BCG,N, BCG,S); plus a third circular halo in the NW region to improve the model accuracy (Δrms) in that area. Four dPIEs with fixed parameters are used to describe the complex X-ray emitting gas distribution in MACS 0416, as done in B18. The cluster-scale component has therefore 16 free parameters. No shear is present, however an additional circular dPIE halo with free velocity dispersion and truncation radius is added to account for the presence of a foreground galaxy (Caminha et al. 2017a; Jullo et al. 2007).
The sub-halo mass component, including the BCG, comprises 193 halos in this case. The 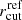 parameter is left free to vary over a wide range (1−20″, or 5.3−106.8 kpc). As described above for MACS 1206, the deprojection of the best-fit σap–mag relation provides a Gaussian prior for the normalization of
parameter is left free to vary over a wide range (1−20″, or 5.3−106.8 kpc). As described above for MACS 1206, the deprojection of the best-fit σap–mag relation provides a Gaussian prior for the normalization of 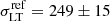 km s−1, while we use the measured slope α = 0.27 (see Fig. B.1/top), from which we derive βcut = 0.66 (from Eq. (5), with γ = 0.2). With a total number of 20 free parameters, 102 spectroscopically confirmed multiple images (associated to 37 families) are then used to constrain the lens model (as in C17a and B18).
km s−1, while we use the measured slope α = 0.27 (see Fig. B.1/top), from which we derive βcut = 0.66 (from Eq. (5), with γ = 0.2). With a total number of 20 free parameters, 102 spectroscopically confirmed multiple images (associated to 37 families) are then used to constrain the lens model (as in C17a and B18).
5.3. AS1063
The dark-matter macro-halo includes in this case an elliptical dPIE, close to the BCG position, and a circular dPIE whose position is left free to vary in an area of 150″ × 120″ centered in the north-east region of the cluster (Table 3). Three dPIEs are used to describe the gas component (B18), and no shear term is included. There are therefore nine free parameters for the cluster-scale component.
The clumpy sub-halo component is constituted by 222 cluster members, including the BCG. From our kinematic measurements and best-fit scaling relation we obtain a deprojected value of 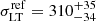 km s−1. As a result, we adopt the median value of 310 km s−1 as a Gaussian prior for the normalization of the σap − L scaling relation, while the standard deviation is reduced to 15 km s−1 to force the lens model to converge to a χ2 minimum solution compatible with our galaxy kinematics. The slope is fixed to the measured value α = 0.27 (see Fig. B.1, bottom), which implies βcut = 0.66. The lens model, which has 11 free parameters in total, is thus optimized using the positions of 55 spectroscopically confirmed multiple images, divided in 20 families, as implemented in B18.
km s−1. As a result, we adopt the median value of 310 km s−1 as a Gaussian prior for the normalization of the σap − L scaling relation, while the standard deviation is reduced to 15 km s−1 to force the lens model to converge to a χ2 minimum solution compatible with our galaxy kinematics. The slope is fixed to the measured value α = 0.27 (see Fig. B.1, bottom), which implies βcut = 0.66. The lens model, which has 11 free parameters in total, is thus optimized using the positions of 55 spectroscopically confirmed multiple images, divided in 20 families, as implemented in B18.
6. Results and discussion
The inclusion of the kinematic prior in the lens models has the main consequence of significantly reducing the intrinsic degeneracies in the scaling relation parameters. Specifically, since the projected mass of the sub-halos depends on the central velocity dispersion, σ0, and truncation radius rcut, for a vanishing core radius, there is clearly an inherent degeneracy between the normalization parameters of the σ − L and rcut − L scaling relation. This can be easily appreciated from the expression of the dPIE projected mass within a radius R, for rcore = 0 (Eq. (C.5) in Appendix C, or Jullo et al. 2007):
Therefore, several combinations of σ0 and rcut will yield similar aperture masses, which are constrained by the multiple image positions. This degeneracy, in combination with those among the parameters describing cluster-scale mass components or shear terms, can lead the lens model to predict a distribution of sub-halo masses not consistent with internal kinematics of member galaxies. This can be noticed in Fig. 2 where we display the case of MACS 0416 and AS1063. The implementation of the kinematic prior on the normalization and slopes of the scaling relation leads to models with a global precision which is similar to that of the previous lens models, as apparent from a comparison of Δrms values (see Table 3). The new values compared to the B18 models differ by 0.01″ for MACS 1206, 0.02″ for MACS 0416, and 0.04″ for AS1063, with the same number of degrees of freedom (88 for MACS 1206, 110 for MACS 0416 and 59 for AS1063). The slight increase of Δrms in the new models is expected since the freedom of model parameters is generally reduced with the Gaussian priors.
In Fig. 4, we show the posterior probability distributions for the projected values of the normalization of the σ − L and rcut − L relations, 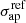 and
and 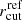 , respectively, for the new (in green) and previous models. The kinematic priors lead in general to significant smaller uncertainties for these parameters, up to factor of 10 for the truncation radius of AS1063, with respect to the B18 results.
, respectively, for the new (in green) and previous models. The kinematic priors lead in general to significant smaller uncertainties for these parameters, up to factor of 10 for the truncation radius of AS1063, with respect to the B18 results.
 |
Fig. 4. Panels a–c: posterior probability distributions for the normalization of the σap − L scaling relation, that is aperture projected velocity dispersion |
While for MACS 1206 the new solution is consistent with the kinematic data, for the other two clusters the kinematic prior moves the best-fit solution to a different region of the parameter space. In the case of MACS 0416, the B18 model had already found a different solution with a higher σ-normalization with respect to the C17a, by extending the MCMC parameter search and including the hot gas mass component. Our new lens model is consistent within 1σ with B18, further reducing parameters’ uncertainties especially on rcut. In the case of AS1063, the kinematic prior moves the 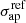 (for the BCG) to a much larger value, which is 70 km s−1 higher, and provides a much tighter constraint for
(for the BCG) to a much larger value, which is 70 km s−1 higher, and provides a much tighter constraint for 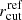 , moving the solution away from previous values of ∼190 kpc (a dPIE encircles 90% of the total projected mass within 5rcut).
, moving the solution away from previous values of ∼190 kpc (a dPIE encircles 90% of the total projected mass within 5rcut).
It is relevant to note that, despite the higher normalization of the sub-halo scaling relations for MACS 0416 and AS1063, the cluster total projected mass profile does not vary appreciably when compared to previous models. This is expected since the multiple image positions provide information about the cluster total mass projected within circles with radii equal to the average distance of the multiple images of each family. In Fig. 5, one can appreciate that the differences in the cumulative projected mass between the new and previous models are well within 10% over the radial region with multiple image constraints. Therefore, although the fraction of total mass in sub-halos differs for MACS 0416 and AS1063, the total encircled mass remains a robust measurement. This however shows that the inclusion of the kinematic prior is important to obtain a reliable estimate of the relative contribution of the diffuse and clumpy (sub-halo) mass components from strong lensing models. In general, an underestimate of the sub-halo mass component will lead to a higher contribution of the cluster-scale halos, in particular the central one.
 |
Fig. 5. Top: projected cumulative mass profiles, as a function of the projected distance from BCGs, corresponding to previous and current lens models for each cluster. The colored regions encompass the 16th and the 84th percentiles; colored solid lines are the median values. The dashed green lines correspond to the mass component associated to cluster members (i.e. sub-halos) from the new lens models with kinematic prior (16th, 50th, 84th percentiles). The multiple image projected distances from the cluster centers are marked with vertical black lines. Bottom: relative variation of the cumulative projected total masses with respect to our reference (green) model. |
6.1. Sub-halo scaling relations
The consistency of the sub-halo scaling relations, based on kinematic measurements in the three clusters, suggests a rescaling of the normalization of the σ − L and rcut − L relations to the same absolute luminosity for a meaningful comparison. To this aim, we choose as reference an absolute magnitude of 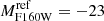 , which is close to the value of L*, estimated from the F160W luminosity function of MACS 0416 at z = 0.4 (Connor et al. 2017; Mercurio et al., in prep.). We then rescale the normalization of the scaling relations obtained from the kinematic lens models, anchored on the BCG magnitude (
, which is close to the value of L*, estimated from the F160W luminosity function of MACS 0416 at z = 0.4 (Connor et al. 2017; Mercurio et al., in prep.). We then rescale the normalization of the scaling relations obtained from the kinematic lens models, anchored on the BCG magnitude (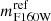 ), to the new reference
), to the new reference 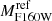 using the distance modulus μ of each cluster, as follows:
using the distance modulus μ of each cluster, as follows:
where the central reference velocity dispersion is 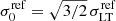 in Eq. (3), and
in Eq. (3), and
The comparison of the posterior distributions of σ0, and rcut, obtained from our lens models with kinematic prior, once renormalized to the same L* luminosity (i.e. 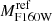 ), is shown in the bottom right panel (d) in Fig. 4. The consistency of these distributions among the three clusters is quite remarkable, particularly for rcut, and suggests an empirical relation for the truncation radius, which is generally poorly constrained by lens models without kinematic priors. By combining Eqs. (3) and (4), one obtains:
), is shown in the bottom right panel (d) in Fig. 4. The consistency of these distributions among the three clusters is quite remarkable, particularly for rcut, and suggests an empirical relation for the truncation radius, which is generally poorly constrained by lens models without kinematic priors. By combining Eqs. (3) and (4), one obtains:
where the range for each parameter represents the 16th−84th percentiles of the combined posterior distributions of 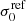 , and
, and 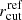 , and the slope is obtained by the distribution of βcut/α. A similar relation was derived by Monna et al. (2015) for Abell 383 (z = 0.18) incorporating the velocity dispersion measurements of 21 member galaxies. However, in that study the slopes of the σ ∝ Lα and rcut ∝ Lβcut relations are fixed, based on literature studies, assuming Mtot/L = const. In our case, the slope α is directly measured from the MUSE spectra of a cluster galaxy sample larger by more than a factor of 2, while βcut is derived assuming galaxies lying on the fundamental plane.
, and the slope is obtained by the distribution of βcut/α. A similar relation was derived by Monna et al. (2015) for Abell 383 (z = 0.18) incorporating the velocity dispersion measurements of 21 member galaxies. However, in that study the slopes of the σ ∝ Lα and rcut ∝ Lβcut relations are fixed, based on literature studies, assuming Mtot/L = const. In our case, the slope α is directly measured from the MUSE spectra of a cluster galaxy sample larger by more than a factor of 2, while βcut is derived assuming galaxies lying on the fundamental plane.
The slope βcut/α = 2.43 that we find for the rcut − σ0 relation is likewise the result of our kinematic measurements in three different clusters, whereas the slope of 1.25 quoted in Monna et al. (2015) is derived from the assumed values of α and βcut. However, the normalization of the relation in Eq. (9) turns out to be consistent with the Monna et al. (2015) result. Other attempts to constrain halo sizes of cluster galaxies have involved modeling of single strong lensing systems in clusters, with no kinematics information from spectroscopic measurements. For example, Suyu & Halkola (2010) found a 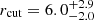 kpc for a galaxy with a lens-based velocity dispersion
kpc for a galaxy with a lens-based velocity dispersion 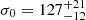 km s−1 in a group, in agreement with our results. Eichner et al. (2013) found instead a higher normalization by modeling the surface brightness distribution of the “snake arc” in MACS 1206. However, we should note that the lens model used in that work was based on a first limited sample of multiple images, when MUSE spectroscopy was not available. Limousin et al. (2007) estimated a scaling relation between halo sizes and σ0 using galaxy-galaxy weak lensing in 5 clusters at z ∼ 0.2, which is broadly consistent with our results.
km s−1 in a group, in agreement with our results. Eichner et al. (2013) found instead a higher normalization by modeling the surface brightness distribution of the “snake arc” in MACS 1206. However, we should note that the lens model used in that work was based on a first limited sample of multiple images, when MUSE spectroscopy was not available. Limousin et al. (2007) estimated a scaling relation between halo sizes and σ0 using galaxy-galaxy weak lensing in 5 clusters at z ∼ 0.2, which is broadly consistent with our results.
The consistent constraints we find on the central velocity dispersions and truncation radii of the cluster sub-halos from the independent analysis of three clusters suggest that we can combine Eqs. (C.6) and (9) to obtain an empirical relation between σ0 and the total mass of member galaxies. By propagating the uncertainties derived from the posterior distributions of σ0 and rcut, we obtain the following Mtot − σ0 relation:
where the parameter range refers to the 16th and 84th percentiles.
6.2. Sub-halo velocity dispersion function
In light of our results, we present a central velocity dispersion function of cluster members, which can be derived from the sub-halo component of the lens models. This was first presented, in the form of circular velocity function ( , see Appendix C) in Grillo et al. (2015) for MACS 0416 and later extended by B18 to the same sample of three clusters of the present study, including the hot-gas components. The new sub-halo velocity functions presented here are particularly relevant since the new lens models incorporate a prior on the σ − L scaling relation based on measured velocity dispersions of a large number of cluster members.
, see Appendix C) in Grillo et al. (2015) for MACS 0416 and later extended by B18 to the same sample of three clusters of the present study, including the hot-gas components. The new sub-halo velocity functions presented here are particularly relevant since the new lens models incorporate a prior on the σ − L scaling relation based on measured velocity dispersions of a large number of cluster members.
Each data point in Fig. 6 is obtained by extracting the central velocity dispersion of each member from 500 random realizations of the model posterior distributions, thereby computing the median number of members in each velocity bin 35 km s−1 wide. We adopt the same bin-size as in B18 to allow a direct comparison with previous results. The vertical error bars are obtained by combining the error associated to the 16th and 84th percentiles of these realizations with a Poissonian error generally appropriate for low number counts5. In order to compare the velocity functions of the three clusters, we include only member galaxies with cluster-centric distances R < 0.16 × R200c (see Table 1), which is the maximum aperture within which we have a highly complete sample of member galaxies in all three clusters.
 |
Fig. 6. Sub-halo central velocity dispersion function derived from our lens models for MACS 1206, MACS 0416 and AS1063 with kinematic prior based on measured velocity dispersions of cluster members. Previous models with no kinematic prior for AS1063 and MACS 0416 are shown for comparison. Data points correspond to median galaxy counts in 35 km s−1 bins, drawn from the posterior distributions of sub-halo model parameters. Errors also include Poissonian number statistics in each bin. Only galaxies within a cluster-centric radius of 0.16 × R200c are included (see Table 1). The top axis gives the total mass related to the central velocity dispersion by Eq. (10) (see text). |
In Fig. 6, we compare the new velocity functions with the previous determinations by Grillo et al. (2015; for MACS 0416, dashed blue line) and B18 (for AS1063, dashed green line). Not surprisingly, these previous determinations were biased low due to the lower normalization of the scaling relations in previous models, whereas the new lens models with kinematic priors produce velocity functions which are quite consistent with each other.
7. Conclusions
In this work, we have improved our previous strong lensing models of three Hubble Frontier Fields/CLASH clusters, based on a large number of spectroscopically confirmed multiple images, using robust measurements of the internal stellar velocity dispersion of large samples of clusters galaxies, thanks to MUSE integral-field spectroscopy in cluster cores. Such measurements constrain independently the normalization and slope of the Faber–Jackson σ − L relation so that the sub-halo component of the cluster mass distribution in the lens models is now bound to the kinematic measurements, thus allowing a significant improvement on the reconstruction of the cluster internal sub-structure. We summarize below the main results of our study.
Using spectra of cluster early-type galaxies with a mean S/N of 25, we measure robust velocity dispersions of 37, 49 and 58 members in AS1063, MACS 0416, MACS 1206, whose accuracy is tested with extensive spectral simulations. By obtaining kinematics measurements over 4−5 mag in each cluster, down to mF160W ≃ 21.5 which corresponds to ∼2.5 mag below L*, we sample well the Faber–Jackson relation. A maximum likelihood modeling of this relation yields well consistent normalizations and slopes for the three clusters.
The new lens models incorporating kinematics information of cluster galaxies reproduce the positions of multiple images with similar precision to previous models. While the total projected cluster mass profile remains essentially unchanged, the mass of sub-halos are now robustly constrained, thus reducing degeneracies with other mass components and parameters of the lens model.
Specifically, the inherent degeneracy of lens models between the central velocity dispersion (σ0) and truncation radius (rcut) of sub-halos is strongly reduced, thus providing robust estimates of sub-halo masses and sizes. Once normalized to the same absolute luminosity, the three σ0 − rcut scaling relations, independently derived for each cluster, are found in very good agreement. This is particularly interesting in consideration of the different dynamical states of the three systems. As a result, we obtain a statistical determination of sub-halo truncation radii with masses ranging from that of the BCG down to ∼1010 M⊙. Our findings extend the initial results derived by Monna et al. (2015) in A383 by using now a high-quality data set which includes precision lens models based on large number bona-fide multiple images and high S/N kinematic measurements of cluster members.
Interestingly, with such a robust determination of the scaling relations of the sub-halo populations, we infer fully consistent velocity dispersion functions for the three clusters, unlike in previous lens models. In addition, our new constraints on the sub-halo masses provide an empirical Mtot − σ0 relation which can be used to translate the velocity functions into sub-halo mass functions.
We plan to extend this methodology to a larger sample of CLASH clusters with strong lensing models based on MUSE observations (Caminha et al. 2019) to better explore the role of systematics in parametric lens models when constraining different mass components of galaxy clusters. Further constraints on the mass profile of cluster galaxies, including the dark matter fraction, will require the use of galaxy-scale strong lensing systems (e.g., Suyu & Halkola 2010; Grillo et al. 2014; Monna et al. 2015), in combination with the internal kinematics of the lenses to extend in dense environments the extensive work carried out in field early-type galaxies. A complementary analysis based on the statistics of galaxy-galaxy strong lensing events will also be presented in an upcoming paper (Meneghetti et al., in prep.). We defer to future papers a detailed comparison of the sub-halo mass function and halo-size distributions derived from kinematic and lensing data with results from different cosmologicalsimulations.
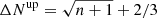 and
and 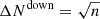 , where n is the number of objects per bin (Gehrels 1986).
, where n is the number of objects per bin (Gehrels 1986).
Acknowledgments
AA was supported by a grant from VILLUM FONDEN (project number 16599). This project is partially funded by PRIM-MIUR 2017WSCC32 “Zooming into dark matter and proto-galaxies with massive lensing clusters” and the Danish council for independent research under the project “Fundamentals of Dark Matter Structures”, DFF–6108-00470. MM acknowledges support from the Italian Space Agency (ASI) through contract “Euclid – Phase D” and from the grant MIUR PRIN 2015 “Cosmology and Fundamental Physics: illuminating the Dark Universe with Euclid”. CG acknowledges support by VILLUM FONDEN Young Investigator Programme through grant no. 10123.
References
- Agnello, A., Evans, N. W., & Romanowsky, A. J. 2014, MNRAS, 442, 3284 [NASA ADS] [CrossRef] [Google Scholar]
- Bacon, R., Accardo, M., Adjali, L., et al. 2012, The Messenger, 147, 4 [NASA ADS] [Google Scholar]
- Balestra, I., Mercurio, A., Sartoris, B., et al. 2016, ApJS, 224, 33 [Google Scholar]
- Barnabè, M., Czoske, O., Koopmans, L. V. E., et al. 2009, MNRAS, 399, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Bender, R., Burstein, D., & Faber, S. M. 1992, ApJ, 399, 462 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J., & Mamon, G. A. 1982, MNRAS, 200, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Biviano, A., Rosati, P., Balestra, I., et al. 2013, A&A, 558, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bolton, A. S., Treu, T., Koopmans, L. V. E., et al. 2008, ApJ, 684, 248 [NASA ADS] [CrossRef] [Google Scholar]
- Bonamigo, M., Grillo, C., Ettori, S., et al. 2018, ApJ, 864, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Caminha, G. B., Grillo, C., Rosati, P., et al. 2016, A&A, 587, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caminha, G. B., Grillo, C., Rosati, P., et al. 2017a, A&A, 600, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caminha, G. B., Grillo, C., Rosati, P., et al. 2017b, A&A, 607, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caminha, G. B., Rosati, P., Grillo, C., et al. 2019, A&A, in press, https://doi.org/10.1051/0004-6361/201935454 [Google Scholar]
- Cappellari, M. 2017, MNRAS, 466, 798 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., & Emsellem, E. 2004, PASP, 116, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., Emsellem, E., Krajnović, D., et al. 2011, MNRAS, 413, 813 [NASA ADS] [CrossRef] [Google Scholar]
- Chua, K. T. E., Pillepich, A., Rodriguez-Gomez, V., et al. 2017, MNRAS, 472, 4343 [NASA ADS] [CrossRef] [Google Scholar]
- Ciotti, L., & Bertin, G. 1999, A&A, 352, 447 [NASA ADS] [Google Scholar]
- Coe, D., Salmon, B., Bradac, M., et al. 2019, ApJ, 884, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Connor, T., Donahue, M., Kelson, D. D., et al. 2017, ApJ, 848, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Czoske, O., Barnabè, M., Koopmans, L. V. E., Treu, T., & Bolton, A. S. 2008, MNRAS, 384, 987 [NASA ADS] [CrossRef] [Google Scholar]
- De Lucia, G., Kauffmann, G., Springel, V., et al. 2004, MNRAS, 348, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Despali, G., & Vegetti, S. 2017, MNRAS, 469, 1997 [NASA ADS] [CrossRef] [Google Scholar]
- Diemand, J., & Moore, B. 2011, Adv. Sci. Lett., 4, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Eichner, T., Seitz, S., Suyu, S. H., et al. 2013, ApJ, 774, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Elíasdóttir, Á, Limousin, M., Richard, J., et al. 2007, ArXiv e-prints [arXiv:0710.5636] [Google Scholar]
- Faber, S. M., Dressler, A., Davies, R. L., et al. 1987, in Nearly Normal Galaxies. From the Planck Time to the Present, 175 [Google Scholar]
- Falco, E. E., Gorenstein, M. V., & Shapiro, I. I. 1985, ApJ, 289, L1 [Google Scholar]
- Focardi, P., & Malavasi, N. 2012, ApJ, 756, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Gavazzi, R., Treu, T., Rhodes, J. D., et al. 2007, ApJ, 667, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N. 1986, ApJ, 303, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Giocoli, C., Tormen, G., Sheth, R. K., & van den Bosch, F. C. 2010, MNRAS, 404, 502 [NASA ADS] [Google Scholar]
- Girardi, M., Mercurio, A., Balestra, I., et al. 2015, A&A, 579, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goodman, J., & Weare, J. 2010, Appl. Math. Comput. Sci., 5, 65 [Google Scholar]
- Grillo, C., Lombardi, M., & Bertin, G. 2008, A&A, 477, 397 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grillo, C., Gobat, R., Presotto, V., et al. 2014, ApJ, 786, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Grillo, C., Suyu, S. H., Rosati, P., et al. 2015, ApJ, 800, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Hernquist, L. 1990, ApJ, 356, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Jaffe, W. 1983, MNRAS, 202, 995 [NASA ADS] [Google Scholar]
- Jauzac, M., Richard, J., Jullo, E., et al. 2015, MNRAS, 452, 1437 [NASA ADS] [CrossRef] [Google Scholar]
- Jorgensen, I., Franx, M., & Kjaergaard, P. 1996, MNRAS, 280, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Jullo, E., & Kneib, J.-P. 2009, MNRAS, 395, 1319 [Google Scholar]
- Jullo, E., Kneib, J.-P., Limousin, M., et al. 2007, New J. Phys., 9, 447 [Google Scholar]
- Karman, W., Caputi, K. I., Grillo, C., et al. 2015, A&A, 574, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karman, W., Caputi, K. I., Caminha, G. B., et al. 2017, A&A, 599, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kassiola, A., & Kovner, I. 1993, ApJ, 417, 450 [NASA ADS] [CrossRef] [Google Scholar]
- Kawamata, R., Oguri, M., Ishigaki, M., Shimasaku, K., & Ouchi, M. 2016, ApJ, 819, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Kneib, J.-P., Ellis, R. S., Smail, I., Couch, W. J., & Sharples, R. M. 1996, ApJ, 471, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Kochanek, C. S. 1993, ApJ, 419, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Kochanek, C. S. 1994, ApJ, 436, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Koopmans, L. V. E., Bolton, A., Treu, T., et al. 2009, ApJ, 703, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J., & Bender, R. 2013, ApJ, 769, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Lagattuta, D. J., Richard, J., Clément, B., et al. 2017, MNRAS, 469, 3946 [Google Scholar]
- Limousin, M., Kneib, J.-P., & Natarajan, P. 2005, MNRAS, 356, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Limousin, M., Kneib, J. P., Bardeau, S., et al. 2007, A&A, 461, 881 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Limousin, M., Sommer-Larsen, J., Natarajan, P., & Milvang-Jensen, B. 2009, ApJ, 696, 1771 [NASA ADS] [CrossRef] [Google Scholar]
- Limousin, M., Richard, J., Jullo, E., et al. 2016, A&A, 588, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lotz, J. M., Koekemoer, A., Coe, D., et al. 2017, ApJ, 837, 97 [Google Scholar]
- Meneghetti, M., Natarajan, P., Coe, D., et al. 2017, MNRAS, 472, 3177 [Google Scholar]
- Meylan, G., Jetzer, P., North, P., et al. 2006, Gravitational Lensing: Strong, Weak and Micro (Berlin: Springer) [Google Scholar]
- Monna, A., Seitz, S., Zitrin, A., et al. 2015, MNRAS, 447, 1224 [NASA ADS] [CrossRef] [Google Scholar]
- Monna, A., Seitz, S., Geller, M. J., et al. 2017, MNRAS, 465, 4589 [NASA ADS] [CrossRef] [Google Scholar]
- Munari, E., Grillo, C., De Lucia, G., et al. 2016, ApJ, 827, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Natarajan, P., & Kneib, J.-P. 1997, MNRAS, 287, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Natarajan, P., Kneib, J.-P., Smail, I., et al. 2009, ApJ, 693, 970 [NASA ADS] [CrossRef] [Google Scholar]
- Natarajan, P., Chadayammuri, U., Jauzac, M., et al. 2017, MNRAS, 468, 1962 [NASA ADS] [CrossRef] [Google Scholar]
- Newman, A. B., Treu, T., Ellis, R. S., et al. 2013, ApJ, 765, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Niemiec, A., Jullo, E., Giocoli, C., Limousin, M., & Jauzac, M. 2019, MNRAS, 487, 653 [NASA ADS] [CrossRef] [Google Scholar]
- Nipoti, C., Giocoli, C., & Despali, G. 2018, MNRAS, 476, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2002, AJ, 124, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2010, AJ, 139, 2097 [NASA ADS] [CrossRef] [Google Scholar]
- Postman, M., Coe, D., Benítez, N., et al. 2012, ApJS, 199, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Richard, J., Jauzac, M., Limousin, M., et al. 2014, MNRAS, 444, 268 [NASA ADS] [CrossRef] [Google Scholar]
- Sand, D. J., Treu, T., Smith, G. P., & Ellis, R. S. 2004, ApJ, 604, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., White, S. D. M., Tormen, G., & Kauffmann, G. 2001, MNRAS, 328, 726 [Google Scholar]
- Suyu, S. H., & Halkola, A. 2010, A&A, 524, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Treu, T., & Koopmans, L. V. E. 2004, ApJ, 611, 739 [NASA ADS] [CrossRef] [Google Scholar]
- Treu, T., Koopmans, L. V., Bolton, A. S., Burles, S., & Moustakas, L. A. 2006, ApJ, 640, 662 [NASA ADS] [CrossRef] [Google Scholar]
- Umetsu, K., Medezinski, E., Nonino, M., et al. 2014, ApJ, 795, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Valdes, F., Gupta, R., Rose, J. A., Singh, H. P., & Bell, D. J. 2004, ApJS, 152, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Verdugo, T., de Diego, J. A., & Limousin, M. 2007, ApJ, 664, 702 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: pPXF spectral simulations
A.1. Simulated sample
We describe here our simulations of galaxy spectra to assess the robustness of the velocity dispersion measurements with the pPXF software (Cappellari 2017) which are critical in our lens model analysis. A sample of 10 000 simulated spectra of early-type galaxies were created according to the following steps:
-
(1)
From the MACS 1206 MUSE datacube we extracted all the spectra of spectroscopic members with mF160W < 24 and ⟨S/N⟩ > 20, using an aperture of R = 0.8″.
-
(2)
Using pPXF best-fit to the spectra, we determined the stellar templates and relative weights, whose linear combination reproduce our galaxy spectra, which include younger stellar populations in some cases with significant Balmer lines. From this set of template, we created rest-frame synthetic model spectra that is not yet convoluted with a LOSVD and without noise, with a dispersion of 0.4 Å per pixel and a spectral resolution of 1.35 Å FWHM.
-
(3)
Model spectra are convoluted with a LOSVD up to the 4th moment, with velocity dispersion ranging from 0 to 250 km s−1.
-
(4)
We assigned to each model spectrum a redshift so to reproduce the observed redshift distribution of cluster galaxies. The spectral resolution is then degraded to the lower MUSE instrumental resolution of 2.6 Å FWHM approximately constant over the whole considered wavelength range.
-
(6)
The spectra wavelength-range is matched to the MUSE range and re-sampled to MUSE 1.25 Å pix−1 scale. Gaussian noise, drawn from the MUSE variance spectra, is added to the spectra in such a way to reproduce a ⟨S/N⟩ from 5 to 100. In this way, the high variance due to sky subtraction around sky lines is included in the simulations.
The final set of simulations is divided into six subsets that differ for their input σ and ⟨S/N⟩ (see Table A.1). The first (Vin), third (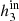 ), and fourth (
), and fourth (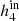 ) moments of the LOSVD are uniformly distributed within the intervals (−50.0, 50.0) km s−1, (−0.1, 0.1), and (−0.1, 0.1), respectively.
) moments of the LOSVD are uniformly distributed within the intervals (−50.0, 50.0) km s−1, (−0.1, 0.1), and (−0.1, 0.1), respectively.
Number of simulated spectra of cluster members in six bins of velocity dispersion, σin, and ⟨S/N⟩.
First, we investigated the possible presence of systematics, especially at low ⟨S/N⟩ and σ ≲ 100 km s−1, where the MUSE instrumental resolution may affect our measurements. Figure A.1 shows that an increasing bias in velocity dispersion measurements at low velocities is detectable in the high ⟨S/N⟩ regime (≫60). Using a polynomial function to fit the median values of the σ − σin distributions in seven σ bins, we found a correction for measured velocity dispersions, σ, given by:
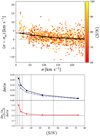 |
Fig. A.1. Top: difference between pPXF measured velocity dispersions (σ) and input velocity dispersions in simulated spectra (σin), as a function of σ. Only the galaxies with ⟨S/N⟩ > 60 are shown here. The data points are color shaded according to the spectra ⟨S/N⟩. Black triangles are the medians of the distributions in 7 different σ bins. The black polynomial line underlines the small increasing bias at low σ. Bottom: black solid (blue dashed) line shows the relative statistical error estimated from simulations (provided by pPXF), as a function of ⟨S/N⟩. The red curve corresponds to the ratio between the two; the statistical relative errors appear to be underestimated by ∼20% in our spectra. |
The increase in the σ − σin scatter at low ⟨S/N⟩ makes it difficult to detect such a small bias at lower ⟨S/N⟩. The scatter in σ − σin increases significantly below ⟨S/N⟩ = 10, with relative errors exceeding 10% and measurements become increasingly sensitive to the presence of sky lines. For this reason, we chose a limiting ⟨S/N⟩ of 10 in our analysis.
Another goal of the simulations was to quantify realistic errors on velocity dispersion measured by pPXF. In our case, we found that relative errors, δσ/σ, are systematically underestimated by ∼20% for ⟨S/N⟩≫15 and of ∼25% for ⟨S/N⟩∼10. In all our measurements, velocity dispersions are corrected for the small bias in the high ⟨S/N⟩ regime (Eq. (A.1)) and statistical errors are corrected using a polynomial fit, as shown in Fig. A.1/bottom.
Appendix B: σ–L scaling relation from kinematic measurements
Given a set of N cluster members of magnitude 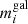 with measured velocity dispersions,
with measured velocity dispersions, 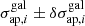 , the σ–mag scaling relation, corresponding to the σ–Lα relation in Eq. (3), can be written as:
, the σ–mag scaling relation, corresponding to the σ–Lα relation in Eq. (3), can be written as:
where 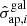 are the model predicted velocity dispersions for a cluster member with F160W magnitude
are the model predicted velocity dispersions for a cluster member with F160W magnitude 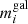 .
.
To estimate the model parameters of the scaling relation and their uncertainties, we sample the posterior distribution of 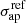 and α, including the intrinsic scatter Δσap of the measured velocities around the backbone of the scaling relation. Using Bayes’ theorem, the posterior probability function can be written as:
and α, including the intrinsic scatter Δσap of the measured velocities around the backbone of the scaling relation. Using Bayes’ theorem, the posterior probability function can be written as:
In particular, the posterior is the product of a likelihood function (B.3) and a prior (B.4):
The boundaries 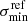 ,
, 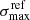 , αmin, αmax, (Δσap)min and (Δσap)max were chosen to limit the parameter space around the measured velocity dispersions.
, αmin, αmax, (Δσap)min and (Δσap)max were chosen to limit the parameter space around the measured velocity dispersions.
To sample the log-posterior in the 3D parameters space (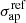 , α, Δσap), we use the Affine-Invariant Markov chain Monte Carlo (MCMC) Ensemble sampler developed by Goodman and Weare (Goodman & Weare 2010), and in particular its python implementation6 (Foreman-Mackey et al. 2013). The parameter space is explored with 100 walkers, with 5000 steps each, which are initialized in a narrow Gaussian sphere around the maximum-likelihood point. To ensure that the final distributions are independent from the initial walker positions, we remove 80 steps in the burn-in phase based on the auto-correlation time computed for each parameter.
, α, Δσap), we use the Affine-Invariant Markov chain Monte Carlo (MCMC) Ensemble sampler developed by Goodman and Weare (Goodman & Weare 2010), and in particular its python implementation6 (Foreman-Mackey et al. 2013). The parameter space is explored with 100 walkers, with 5000 steps each, which are initialized in a narrow Gaussian sphere around the maximum-likelihood point. To ensure that the final distributions are independent from the initial walker positions, we remove 80 steps in the burn-in phase based on the auto-correlation time computed for each parameter.
The posterior probability distributions of model parameters (Eq. (B.2)) obtained with this procedure are shown in Fig. 3 for MACS 1206 and Fig. B.1 for MACS 0416 and AS1063.
 |
Fig. B.1. Posterior probability distributions for scaling relation parameters in Eq. (B.1) obtained from measured velocity dispersions of cluster members in MACS 0416 and AS1063. The 16th, 50th and 84th percentiles of the marginalized distributions for the slope (α), normalization ( |
Appendix C: dPIE mass distribution
The dual pseudo-isothermal elliptical mass distribution (dPIE), described in Elíasdóttir et al. (2007) and Limousin et al. (2005), is defined by eight parameters; three for the sky position and redshift (z), two for ellipticity (e) and position angle, and three for core radius (rcore), truncation radius (rcut) and central velocity dispersion (σ0). All the halos in our lens models are described as dPIEs profiles, cluster-scale halos are generally included in the limit rcut → ∞; in this case, the dPIE reduces to a pseudo isothermal elliptical mass distribution (PIEMD), defined by Kassiola & Kovner (1993). Sub-halos associated to cluster members are instead parametrized as circular dPIEs of vanishing rcore, with rcut and σ0 following the scaling relations in Eqs. (3) and (4) (see Sect. 4).
The equations below, mostly derived in Elíasdóttir et al. (2007) and Limousin et al. (2005), refer to circular (e = 0) dPIEs. For completeness, we give the expressions for projected masses and surface-mass densities and show how the dPIE σ0 parameter can be derived from the aperture average line-of-sight (projected) velocity dispersion σap, which is associated to our kinematic measurements.
C.1. dPIE density and mass
The mass density profile for the spherical dPIE, as implemented in LensTool, is defined through the 3D-density (Limousin et al. 2005):
where r is the distance from the center of the mass distribution, while rcore and rcut are the core and truncation radii respectively (with rcut > rcore). Equation (C.1) shows a smooth separation between an isothermal behaviour, ρ ∝ r−2, where rcore < r < rcut and a steeper decrease, ρ ∝ r−4, for r > rcut.
The relation between the central density ρ0 and the 1D-central velocity dispersion, σ0, is (Limousin et al. 2005):
In the Singular Isothermal Sphere (SIS) limit, rcore → 0 and rcut → ∞, Eq. (C.1) reduces to the familiar expression 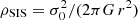 ). In LensTool, dPIEs are implemented trough a fiducial velocity dispersion σLT related to the central velocity dispersion σ0 by:
). In LensTool, dPIEs are implemented trough a fiducial velocity dispersion σLT related to the central velocity dispersion σ0 by: 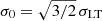 .
.
Projecting the 3D-density profile on a plane perpendicular to the line-of-sight, we obtain the projected dPIE surface-mass-density as a function of the projected distance from the center R (Elíasdóttir et al. 2007):
Integrating Eq. (C.1), we can also write the total 3D mass m(r) enclosed by a sphere of radius r:
Similarly, the total projected mass within an aperture of projected radius R, M(R), is (from Eq. (C.3)):
The dPIE profile, contrary to the SIS, has a finite total mass Mtot whose value can be obtained from Eq. (C.4) (or Eq. (C.5)) in the limit of r → ∞ (R → ∞):
In the limit rcore/rcut → 0, a sphere of radius r = rcut encloses half of the total 3D dPIE mass. While 60 (90)% of the total projected mass is included within a projected radius of R = rcut (R = 5rcut) (see Fig. C.1).
 |
Fig. C.1. Fraction of projected mass over total mass as a function of aperture radii (in units of rcut) for dPIE profiles with different rcore/rcut values. For small rcore/rcut, ∼60% of the total mass is contained within rcut, while the 90% is contained within 5rcut. |
Similarly, Elíasdóttir et al. (2007) give an expression for the half-mass radius, RMtot/2, that is enclosing half of the total projected mass, from Eq. (C.5):
Finally, from Eq. (C.4) we derive an expression for the circular velocity 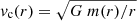 :
:
which has a maximum at 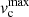 . In the SIS limit, Eq. (C.8) reduces to
. In the SIS limit, Eq. (C.8) reduces to 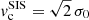 . To compare the circular velocity
. To compare the circular velocity 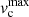 in Grillo et al. (2015) and B18 with our sigma functions in Fig. 6, we adopt
in Grillo et al. (2015) and B18 with our sigma functions in Fig. 6, we adopt 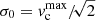 , as one can easily verify that for the full range of rcore and rcut values of our member galaxies,
, as one can easily verify that for the full range of rcore and rcut values of our member galaxies, 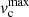 is smaller than
is smaller than 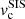 by less than the 3%.
by less than the 3%.
C.2. dPIE velocity dispersion
Assuming an isotropic mass distribution, the observed line-of-sight velocity dispersion at a projected distance R from the center is given by (Elíasdóttir et al. 2007; Agnello et al. 2014; Binney & Mamon 1982):
where ν(r) is the 3D-luminosity density of the galaxy which is related to the surface brightness profile, I(R), by:
Similarly, the average line-of-sight velocity dispersion inside an aperture radius R, σap, for an isotropic system, is given by:
where L(R) is the total projected luminosity within R:
σap is the quantity that we can directly compare to our kinematic measurements (see Sects. 4 and 5) and it can also be rewritten in terms of the measurable surface brightness of the elliptical galaxy as (Agnello et al. 2014):
The last line recasts the aperture-averaged σap in terms of the central velocity dispersion σ0 explicitly, with the projection coefficient cp(R) encompassing all other terms except the prefactor 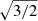 . The relation between σap and the LensTool fiducial velocity dispersion, σLT, can be written as:
. The relation between σap and the LensTool fiducial velocity dispersion, σLT, can be written as:
To compute cp(R), a surface brightness profile I(R) for cluster members is needed. For our purpose, we tested two choices for I(R) using: (1) a surface brightness profile scaling with the projected mass density Σ(R) (Eq. (C.3)) derived from the cluster lens model by B18, and (2) a Sérsic profile extracted from the HST data of MACS 0416 in the F814 band:
The Sérsic index n and the effective radius Re are determined by fitting the light profile of cluster members using the public software GALFIT (Peng et al. 2002, 2010), adopting bn = 2n − 1/3 (Ciotti & Bertin 1999).
Figure C.2 shows that for our spectral aperture radius, R = 0.8″, the differences between the σap obtained assuming a dPIE or a Sérsic surface brightness profile are within ∼5%. For this reason, in our work we always assume a dPIE surface brightness profile which makes the analysis convenient and independent from Sérsic light profile fitting.
 |
Fig. C.2. Ratio between aperture average line-of-sight velocity dispersions, computed assuming a dPIE or a Sersic surface brightness profile of 95 cluster members in MACS 0416, as a function of F160W magnitudes. The aperture radius is R = 0.8″. Red dashed lines correspond to the 16th, 50th and 84th percentiles of the entire distribution. |
Assuming I(R) = Σ(R), the projection coefficient cp(R) can be numerically computed as
In Fig. C.3, we show the projection coefficients as a function of aperture radius R, for different values of rcore and rcut. The dashed black line indicates the asynthotic value of 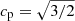 , which corresponds to the limit rcore → 0 and rcut → ∞, where the dPIE reduces to a SIS for which
, which corresponds to the limit rcore → 0 and rcut → ∞, where the dPIE reduces to a SIS for which 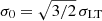 .
.
 |
Fig. C.3. Projection coefficient cp as a function of aperture radius R in arcseconds. Curves associated to the same rcore are grouped with the same color, with rcut = 5, 10, 20, 100 arcsec, from bottom to top. The thick dashed red and green lines correspond to typical values of rcore and rcut derived from our lensing+dynamics modeling of clusters. The dashed black horizontal line corresponds to |
All Tables
σap − L scaling relation parameters derived from measured velocity dispersions of cluster members for MACS 1206, MACS 0416 and AS1063.
Number of simulated spectra of cluster members in six bins of velocity dispersion, σin, and ⟨S/N⟩.
All Figures
 |
Fig. 1. Results from line-of-sight velocity dispersion fitting of spectra of three cluster members in MACS 1206 as obtained with pPXF. Galaxy spectra are shown in black; red curves are the pPXF best-fit models, while the green points correspond to the data−model residuals. The blue shaded regions along the wavelength axis were excluded in the fitting procedure due to the presence of noisy sky subtractions around emission lines in the spectra. Corresponding residuals in these regions are marked in blue. The first from the top is a high signal-to-noise E+A galaxy. The second is a passive galaxy spectrum with a ⟨S/N⟩ = 28.1, corresponding approximately to the mean S/N of our galaxy sample. The bottom spectrum has a ⟨S/N⟩ = 10.7, close to our lower limit for reliable velocity dispersion measurements. Coordinates, measured velocity dispersion (σap), mean signal-to-noise and F160W magnitudes are indicated in each panel. Cutouts are HST RGB images, 4″ across, showing in green the apertures of 0.8″ radius used for the spectral extraction. |
| In the text | |
 |
Fig. 2. Data points are measured stellar velocity dispersions of cluster members, color-coded according to their spectral ⟨S/N⟩. Green lines are 300 scaling relations randomly drawn from the posterior distributions of the σap–mag scaling relation parameters, α, |
| In the text | |
 |
Fig. 3. Posterior probability distributions for σap–mag scaling relation parameters, obtained as described in Appendix B, from velocity dispersion measurements of 58 cluster members in MACS 1206. The 16th, 50th and 84th percentiles of the marginalized distributions for the slope (α), normalization ( |
| In the text | |
 |
Fig. 4. Panels a–c: posterior probability distributions for the normalization of the σap − L scaling relation, that is aperture projected velocity dispersion |
| In the text | |
 |
Fig. 5. Top: projected cumulative mass profiles, as a function of the projected distance from BCGs, corresponding to previous and current lens models for each cluster. The colored regions encompass the 16th and the 84th percentiles; colored solid lines are the median values. The dashed green lines correspond to the mass component associated to cluster members (i.e. sub-halos) from the new lens models with kinematic prior (16th, 50th, 84th percentiles). The multiple image projected distances from the cluster centers are marked with vertical black lines. Bottom: relative variation of the cumulative projected total masses with respect to our reference (green) model. |
| In the text | |
 |
Fig. 6. Sub-halo central velocity dispersion function derived from our lens models for MACS 1206, MACS 0416 and AS1063 with kinematic prior based on measured velocity dispersions of cluster members. Previous models with no kinematic prior for AS1063 and MACS 0416 are shown for comparison. Data points correspond to median galaxy counts in 35 km s−1 bins, drawn from the posterior distributions of sub-halo model parameters. Errors also include Poissonian number statistics in each bin. Only galaxies within a cluster-centric radius of 0.16 × R200c are included (see Table 1). The top axis gives the total mass related to the central velocity dispersion by Eq. (10) (see text). |
| In the text | |
 |
Fig. A.1. Top: difference between pPXF measured velocity dispersions (σ) and input velocity dispersions in simulated spectra (σin), as a function of σ. Only the galaxies with ⟨S/N⟩ > 60 are shown here. The data points are color shaded according to the spectra ⟨S/N⟩. Black triangles are the medians of the distributions in 7 different σ bins. The black polynomial line underlines the small increasing bias at low σ. Bottom: black solid (blue dashed) line shows the relative statistical error estimated from simulations (provided by pPXF), as a function of ⟨S/N⟩. The red curve corresponds to the ratio between the two; the statistical relative errors appear to be underestimated by ∼20% in our spectra. |
| In the text | |
 |
Fig. B.1. Posterior probability distributions for scaling relation parameters in Eq. (B.1) obtained from measured velocity dispersions of cluster members in MACS 0416 and AS1063. The 16th, 50th and 84th percentiles of the marginalized distributions for the slope (α), normalization ( |
| In the text | |
 |
Fig. C.1. Fraction of projected mass over total mass as a function of aperture radii (in units of rcut) for dPIE profiles with different rcore/rcut values. For small rcore/rcut, ∼60% of the total mass is contained within rcut, while the 90% is contained within 5rcut. |
| In the text | |
 |
Fig. C.2. Ratio between aperture average line-of-sight velocity dispersions, computed assuming a dPIE or a Sersic surface brightness profile of 95 cluster members in MACS 0416, as a function of F160W magnitudes. The aperture radius is R = 0.8″. Red dashed lines correspond to the 16th, 50th and 84th percentiles of the entire distribution. |
| In the text | |
 |
Fig. C.3. Projection coefficient cp as a function of aperture radius R in arcseconds. Curves associated to the same rcore are grouped with the same color, with rcut = 5, 10, 20, 100 arcsec, from bottom to top. The thick dashed red and green lines correspond to typical values of rcore and rcut derived from our lensing+dynamics modeling of clusters. The dashed black horizontal line corresponds to |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



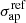
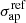
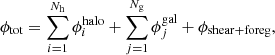
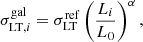
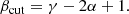
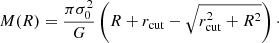
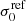
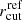
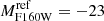
![$$ \begin{aligned} \sigma _{0}^{M} = \sigma _{0}^\mathrm{ref} 10^{0.4\, [m^\mathrm{ref}_{\rm F160W}-\mu (z_{\rm cl})-M^\mathrm{ref}_{\rm F160W}]\, \alpha }, \end{aligned} $$](/articles/aa/full_html/2019/11/aa35974-19/aa35974-19-eq118.gif)
![$$ \begin{aligned} r_{\rm cut}^{M} = r_{\rm cut}^\mathrm{ref} 10^{0.4\, [m^\mathrm{ref}_{\rm F160W}-\mu (z_{\rm cl})-M^\mathrm{ref}_{\rm F160W}]\, \beta _{\rm cut}}. \end{aligned} $$](/articles/aa/full_html/2019/11/aa35974-19/aa35974-19-eq120.gif)
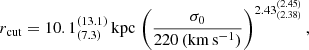
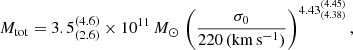
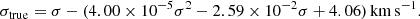
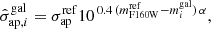
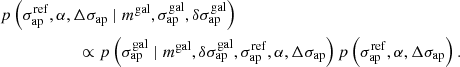
![$$ \begin{aligned}&\ln \left[p\left(\sigma _{\rm ap}^\mathrm{gal} \mid m^\mathrm{gal}, \delta \sigma _{\rm ap}^\mathrm{gal}, \sigma _{\rm ap}^\mathrm{ref}, \alpha , \Delta \sigma _{\rm ap}\right)\right]\nonumber \\&\qquad \qquad \quad = - \frac{1}{2} \sum _{i=1}^N \left\{ \frac{\left(\sigma _{\mathrm{ap},i}^\mathrm{gal}-\hat{\sigma }_{\mathrm{ap},i}^\mathrm{gal}\right)^2}{\left(\delta \sigma ^\mathrm{gal}_{\mathrm{ap},i}\right)^2 + \Delta \sigma _{\rm ap}^2} + \ln \left[2 \pi \left(\left(\delta \sigma ^\mathrm{gal}_{\mathrm{ap},i}\right)^2 + \Delta \sigma _{\rm ap}^2 \right) \right] \right\} , \end{aligned} $$](/articles/aa/full_html/2019/11/aa35974-19/aa35974-19-eq143.gif)
![$$ \begin{aligned} \ln \left[ p\left(\sigma _{\rm ap}^\mathrm{ref}, \alpha , \Delta \sigma _{\rm ap}\right)\right]= {\left\{ \begin{array}{ll} - \ln (\Delta \sigma _{\rm ap}), \scriptstyle \;\;\mathrm{if}\,\sigma _{\rm min}^\mathrm{ref}<\sigma _{\rm ap}^\mathrm{ref}<\sigma _{\rm max}^\mathrm{ref}\\ \qquad \qquad \quad \scriptstyle \mathrm{and}\,\alpha _{\rm min}<\alpha <\alpha _{\rm max} \\ \qquad \qquad \quad \scriptstyle \mathrm{and}\,\left(\Delta \sigma _{\rm ap}\right)_{\rm min}<\Delta \sigma _{\rm ap} < \left(\Delta \sigma _{\rm ap}\right)_{\rm max}\\ -\infty , \qquad \quad \;\scriptstyle \mathrm{otherwise} \end{array}\right.}. \end{aligned} $$](/articles/aa/full_html/2019/11/aa35974-19/aa35974-19-eq144.gif)
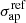
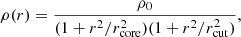
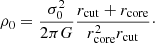
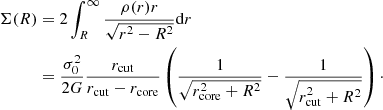
![$$ \begin{aligned} m(r)&= 4 \pi \int _{0}^{r} \rho (r^{\prime })r^{\prime 2} dr^{\prime }\nonumber \\&=\frac{2\sigma _0^2}{G}\frac{r_{\rm cut}}{r_{\rm cut}-r_{\rm core}} \left[r_{\rm cut} \arctan \left(\frac{r}{r_{\rm cut}}\right)-r_{\rm core} \arctan \left(\frac{r}{r_{\rm core}}\right)\right]. \end{aligned} $$](/articles/aa/full_html/2019/11/aa35974-19/aa35974-19-eq154.gif)
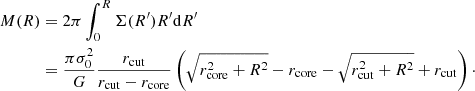
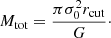
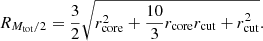
![$$ \begin{aligned} { v}_{\rm c}^2(r) = 2\sigma _0^2\frac{r^2_{\rm cut}}{r_{\rm cut}-r_{\rm core}} \frac{1}{r} \left[ \arctan \left(\frac{r}{r_{\rm cut}}\right)-\frac{r_{\rm core}}{r_{\rm cut}} \arctan \left(\frac{r}{r_{\rm core}}\right)\right], \end{aligned} $$](/articles/aa/full_html/2019/11/aa35974-19/aa35974-19-eq159.gif)
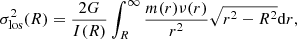
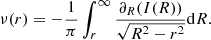
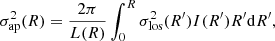
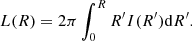
![$$ \begin{aligned} \sigma _{\rm ap}^2(R) =&\frac{4G}{3L(R)} \left[\int _{0}^{\infty }R^{\prime }I(R^{\prime })\int _{0}^{R^{\prime }}\frac{4 \pi \rho (r) r^2}{\sqrt{R^{\prime 2}-r^2}}\mathrm{d}r\mathrm{d}R^{\prime }\right. \nonumber \\&- \left. \int _{R}^{\infty }R^{\prime }I(R^{\prime })\int _{R}^{R^{\prime }}\frac{\partial _r \left(m(r)(r^2-R^2)^{3/2}/r^3\right)}{\sqrt{R^{\prime 2}-r^2}}\mathrm{d}r \mathrm{d}R^{\prime }\right]\nonumber \\& \equiv \frac{2}{3}\sigma _0^2 c_{\rm p}^2(R). \end{aligned} $$](/articles/aa/full_html/2019/11/aa35974-19/aa35974-19-eq170.gif)
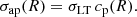
![$$ \begin{aligned} I(R)=I_{\rm e} \exp {\left\{ -b_n\left[ \left( \frac{R}{R_{\rm e}} \right)^{1/n} -1\right] \right\} }\cdot \end{aligned} $$](/articles/aa/full_html/2019/11/aa35974-19/aa35974-19-eq173.gif)