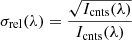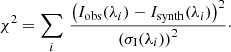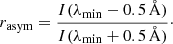| Issue |
A&A
Volume 631, November 2019
|
|
|---|---|---|
| Article Number | A146 | |
| Number of page(s) | 12 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201935358 | |
| Published online | 11 November 2019 | |
2D non-LTE modelling of a filament observed in the Hα line with the DST/IBIS spectropolarimeter
1
Astronomical Institute of Slovak Academy of Sciences, 05960 Tatranská Lomnica, Slovak Republic
e-mail: pschwartz@astro.sk
2
Astronomical Institute, The Czech Academy of Sciences, 25165 Ondřejov, Czech Republic
3
UCL-Mullard Space Science Laboratory, Holmbury St. Mary, Dorking, Surrey RH5 6NT, UK
4
Department of Physics & Astronomy, California State University, Northridge, CA 91330-8268, USA
Received:
25
February
2019
Accepted:
26
September
2019
Context. We study a fragment of a large quiescent filament observed on May 29, 2017 by the Interferometric BIdimensional Spectropolarimeter (IBIS) mounted at the Dunn Solar Telescope. We focus on its quiescent stage prior to its eruption.
Aims. We analyse the spectral observations obtained in the Hα line to derive the thermodynamic properties of the plasma of the observed fragment of the filament.
Methods. We used a 2D filament model employing radiative transfer computations under conditions that depart from the local thermodynamic equilibrium. We employed a forward modelling technique in which we used the 2D model to produce synthetic Hα line profiles that we compared with the observations. We then found the set of model input parameters, which produces synthetic spectra with the best agreement with observations.
Results. Our analysis shows that one part of the observed fragment of the filament is cooler, denser, and more dynamic than its other part that is hotter, less dense, and more quiescent. The derived temperatures in the first part range from 6000 K to 10 000 K and in the latter part from 11 000 K to 14 000 K. The gas pressure is 0.2–0.4 dyn cm−2 in the first part and around 0.15 dyn cm−2 in the latter part. The more dynamic nature of the first part is characterised by the line-of-sight velocities with absolute values of 6–7 km s−1 and microturbulent velocities of 8–9 km s−1. On the other hand, the latter part exhibits line-of-sight velocities with absolute values 0–2.5 km s−1 and microturbulent velocities of 4–6 km s−1.
Key words: Sun: filaments / prominences / radiative transfer / line: profiles / techniques: spectroscopic / methods: data analysis / methods: numerical
© ESO 2019
1. Introduction
Solar filaments, or prominences as they are referred to when observed projected above the solar limb, are an integral part of the higher solar atmosphere. The filament plasma is believed to be embedded in the coronal magnetic field in regions where the field is mostly horizontal and dipped. This type of magnetic field then supports the dense and cool filament plasma against gravity and insulates it from the hot coronal environment. Comprehensive reviews of the physics of prominences and filaments can be found in Labrosse et al. (2010) and Mackay et al. (2010), in the proceedings of the IAUS300 (Schmieder et al. 2014), in the review by Gibson (2018), or in the book “Solar Prominences” edited by Vial & Engvold (2015), for example. Filaments located within solar active regions are usually short-lived while quiescent filaments located within the quiet-Sun tend to have significantly longer life-times of up to a few months. Quiescent filaments are commonly observed in relation to filament channels (see e.g. Heinzel et al. 2001; Schmieder et al. 2003, 2004; Schwartz et al. 2004). These filament channels are best viewed using spectral lines in Extreme Ultraviolet (EUV) part of the spectrum and are able to out-live their filament counterparts. This occurs because even though filament counterparts are stable for extended periods of time, quiescent filaments can become unstable and erupt. Consequently, they frequently form the core of coronal mass ejections (CMEs, see e.g. Chen 2011). As a result, filament channels are often host to a sequence of consecutive filaments, which are most readily visible in the Hα line.
It is generally understood that the driving force of the early stage of solar eruptions (moments after the global loss of equilibrium) is due to the magnetic field through mechanisms, such as the torus instability, that is possibly triggered by the kink instability, and subsequently facilitated by the reconnection (Kliem & Török 2006; Cheng et al. 2017). However, recent studies (e.g. Jenkins et al. 2018, 2019) highlight the ability of plasma within pre-eruptive filaments to exert some influence on the stability of the host magnetic field (see also Petrie et al. 2007; Blokland & Keppens 2011; Fan 2018). In particular, Jenkins et al. (2019) underline the importance of draining the filament mass just prior to the global loss of equilibrium. It is therefore imperative to study the evolution of plasma properties within solar filaments, particularly those located within the quiet Sun (QS), in the lead up to their destabilisation, and subsequent eruption. However, in order to accurately quantify the temporal evolution of the plasma within these filaments, robust methods of deducing plasma properties in individual snapshots are first required.
In this paper we study a small part of a larger quiescent filament (hereafter referred to as the observed filament fragment), which remained stable for several days prior to its eruption. The present work focuses on the quiescent stage of this filament where we are able to assume that the filament properties do not significantly vary over timescales of hours or even a few days. For the interpretation of the Hα spectra obtained at the observed fragment of the filament, we used a 2D non-LTE radiative transfer model (non-LTE stands for departures from the LTE – Local Thermodynamical Equilibrium). This model is based on the 1D model developed by Anzer & Heinzel (1998, 1999) for the modelling of prominences. The prominence model was first generalised into 2D by Heinzel & Anzer (2001) and then used for the modelling of prominence fine structures by Heinzel et al. (2005) and Gunár et al. (2008, 2010, 2012). The 1D non-LTE radiative transfer model adapted for filaments was previously used by Molowny-Horas et al. (1999) for constructing the 2D maps of physical properties of a filament observed spectroscopically in the Hα line. Later, a similar technique was applied by Tziotziou et al. (2001) for the analysis of chromospheric cloud-like structures (including filaments) observed in the Ca II 8542 Å line. More recently, Schwartz et al. (2006, 2012) used the 1D non-LTE model to analyse filaments observed in the hydrogen Lyman series and Hα line. The 2D prominence model of Heinzel & Anzer (2001) was generalised for adoption of the filament geometry and used by Schwartz et al. (2016) to analyse Hα observations of an active region filament. These authors introduced two significant (25 km s−1) opposing line-of-sight (LOS) velocities, which were needed to reproduce the observed, very broad and symmetric profiles.
In the observed filament fragment studied in the present work, the occurrence of significantly asymmetric profiles in the observed Hα data supports the use of a single LOS-velocity value as an input parameter of the model. This approach can be applied as it was already shown by Zirker et al. (1998) that asymmetric Hα profiles in prominences are caused by systematic plasma flows. Unresolved motions of the filament plasma can then be represented by the micro-turbulent velocity as another input parameter of the model.
The paper is organised as follows. In Sect. 2 we describe the observations of the studied filament fragment together with the processes of data calibration and co-alignment. In Sect. 3 we introduce the 2D non-LTE filament model that produces the synthetic Hα spectra, which we compare with the observations. The results obtained by the modelling are presented in Sect. 4 and are subsequently discussed in Sect. 5. In this section we also discuss the influence of background radiation on the derived parameters of the observed filament plasma and we assess the uncertainties of these parameters. In Sect. 6 we offer our conclusions.
2. Observations
2.1. General information on observations
A fragment of a larger solar filament was observed on May 29, 2017. The observed filament fragment was located at the heliographic position around −24.3°, −4.85° (i.e. solar X = −400 arcsec, solar Y = −80 arcsec). This specific fragment was chosen because it was a part of the only filament on-disk on the day and its strong absorption signature and interesting shape positioned at the end of the filament made for an interesting target. The filament was initially quiescent but became activated and erupted on May 30, 2017. Exact time of the eruption cannot be stated as its progress was rather slow: According to observations taken in EUV by the EUV Imager (EUVI; Wuelser et al. 2004) instrument on board the Solar Terrestrial Relations Observatory-A (STEREO-A) satellite in the 304 Å channel, the filament seen as prominence starts to dramatically increase in height from between 10:00 and 12:00 UT. The ongoing eruption was also observed during the DST campaign from 13:47 UT and by the Atmospheric Imaging Assembly (AIA; Lemen et al. 2012) instrument on board the Solar Dynamics Observatory (SDO; Pesnell et al. 2012) in its all EUV channels. We want to emphasise here that in the present paper we focus on the quiescent stage of its evolution as observed on May 29, 2017. A study of the erupting phase of this filament will be a subject of future work.
Figure 1a shows a full-disk context image of the observed filament taken in the EUV at 193 Å by the AIA instrument. Figure 1b shows a close-up view in the same channel of the AIA instrument and Fig. 1c shows the filament in the Hα line core observed at 14:44:55 UT using the Interferometric Bidimensional Spectropolarimeter (IBIS; Cavallini 2006) mounted at the Dunn Solar Telescope (DST). IBIS is a dual Fabry-Pérot imaging spectrometer capable of taking narrow-band images in the range of 5800–8600 Å alongside broad-band images that are useful for context and alignment purposes. With a 95 arcsec diameter field of view (FOV) illuminating a 1024 × 1024 square-pixel CCD, IBIS is diffraction limited across a sub-window of 1007 × 1007 pixels, resulting in a maximum spatial sampling of ≈0.1 arcsec × 0.1 arcsec per pixel. However, due to the atmospheric seeing, the actual spatial resolution of the IBIS observation must be measured by analysing the 2D Fourier power of the IBIS line-core intensity image as a function of the spatial resolution. It was found that the Fourier power decreased with finer resolution until a value of 0.7 arcsec where the Fourier power became more-or-less constant (except for some noise). Thus, this boundary value of resolution indicates the smallest scale resolvable in the line-core image of the instrument, which is the spatial resolution of the observation. Equipped with a high-order adaptive optics system (see Rimmele 2004, for a detailed description), the DST allows IBIS to capture seeing-corrected images of the Sun with high temporal cadence. Panels d–f of the figure show the studied filament fragment in additional three AIA EUV channels – 171, 304, and 211 Å – zoomed in the same FOV as in the panel b.
 |
Fig. 1. Filament observed on May 29, 2017. Panel a: context full-disk image in the SDO/AIA 193 Å channel. Panel b: zoom-in on the box marked in the panel a. Panel c: Hα line core image of the filament taken by DST/IBIS at 14:44:55 UT. White box indicates the region from which the average quiet-Sun profile was calculated. Panel d–f: contextual SDO/AIA images in three EUV channels: 171 Å, 304 Å, and 211 Å. The images have the same zoomed-in field of view as is in panel b. |
The filament was observed at the DST for several days prior to its eruption, which occurred on the day following the snapshot shown here. Observations of the IBIS instrument made during May 29, 2017 were carried out in three blocks at the following times: 13:59:46–15:30:26, 15:30:52–15:42:12, and 20:59:00–22:18:10 UT. The snapshot shown in Fig. 1c was taken at 14:44:55 UT and represents the best seeing available within the obtained dataset. Therefore the IBIS data from this time were used in the filament modelling. The FOV of IBIS did not cover the entire filament which was approximately 660 arcsec long. The FOV in Fig. 1b and c contains what we believe to be one of the footpoints of the filament and its surroundings. The co-alignment of the Hα line core image (Fig. 1c) with the SDO/AIA 193 Å image (Fig. 1b) is only approximate.
In this paper, we use a single data segment consisting of observations of both Hα (6562.8 Å) and Ca II (8542 Å) lines. For Hα, 27 wavelength positions were selected between 6561.18 and 6564.64 Å such that there was a higher density of chosen wavelength positions in the near wings of the profile than in the farther wings and in the core. This can be seen in Fig. 2a. Another 30 wavelength positions were used to scan the Ca II line. With an exposure time for each wavelength position of 80 ms, a data segment (one full scan of both Hα and Ca II) was completed every ≈13 s. This work is devoted only to diagnostics of physical properties of the hydrogen plasma of the observed filament, thus, non-LTE modelling of the Ca II line is outside of the scope of this paper. A similar 2D slab filament model for the Ca II ion is now in preparation and is planned as the focus of our future papers.
 |
Fig. 2. Illustration of the pre-filter correction method using the Hα tables of David (1961). Panel a: average QS profile calculated from the area marked in Fig. 1c. Vertical dashed lines indicate 27 IBIS wavelength positions used. Panel b: reference David’s Hα profile at μcal = 0.91. Panel c: correction between panels a and b. Panel d: average QS profile with panel c correction applied, and panel b over-plotted in dashed-line. Panel e: residuals remaining between the corrected profile and the reference profile. |
2.2. Data reduction and co-alignment
The narrow-band (NB) and broad-band (BB) data obtained by IBIS were processed using the IBIS data processing pipeline1. The raw data were first corrected for the dark currents induced by the electronics associated with the detector. Gain tables were then calculated from flat field observations to characterise the sensitivity of the detector across its face. Detector image scale and relative rotation between NB and BB channels were determined from dot-line grid images taken during the observing run. Finally, the systematic wavelength shift induced by the collimated mounting of the Fabry-Pérot interferometer was removed from the NB data. A comparison of the observed Hα profiles with synthetic Hα profiles provided by non-LTE modelling requires the observed data to be radiometrically calibrated into the physical units. To do so, the correction for the influence of the pre-filter transmission curve on the shape of the NB line profiles needs to be taken into account. The calibration coefficient was derived by a comparison in a filament close-by QS area with the Hα reference profile constructed from the table of David (1961) for the angle between normal to the solar surface at the QS area position and the LOS of μcal = 0.91, which was measured as a length of the great arc between this position and disk centre. The QS profile (Fig. 2a) was obtained as an average from a quiet region next to the filament which is marked by a white box in Fig. 1c. Dispersion of spectral intensities of individual profiles observed inside the quiet region is only up to ±40% of the QS profile intensities. Almost 80% of profiles from the quiet region are shifted in wavelength by less than 0.1 km s−1 and the remaining profiles are shifted by less than 7 km s−1. Thus, selection of the quiet region is reliable for the QS profile as it was averaged mostly from similar profiles not influenced much by velocities. The reference Hα profile is shown in Fig. 2b. The correction for the pre-filter transmission profile takes into account the dependence of the calibration coefficient on the wavelength. The calibration coefficient as a function of wavelength (see Fig. 2c) is applied for the calibration-correction of all observed IBIS Hα profiles. Panels d and e of Fig. 2 show how well the QS profile fits the reference Hα profile after applying the calibration-correction process. The relative errors σrel(λ) of the specific intensities I(λ) calibrated to erg cm−2 s−1 sr−1 Hz−1 were calculated using the Poisson statistics:
where Icnts(λ) are the non-calibrated specific intensities in counts.
To correct the orientation and pointing of the IBIS observations we co-aligned them with the full-disk Hα data obtained by instruments of the Global High Resolution H-alpha Network belonging to the Global Oscillation Network Group (GONG; Harvey et al. 2011) of the National Solar Observatory (NSO). To do so, we used a full-disk map of intensities integrated within wavelength range Δλ = ±0.4 Å around the Hα line centre. The IBIS data were vertically flipped, rotated by 50.4° in clock-wise direction and the centre of the FOV was positioned at −389.9 arcsec in solar X and −83.0 arcsec in solar Y. The comparison of the co-aligned IBIS Hα intensity map with the corresponding cut-off from the full-disk GONG Hα image is shown in Fig. 3. To demonstrate the reliability of the co-alignment, contours of the filament in the GONG Hα image are plotted on the IBIS Hα intensity map and vice versa.
 |
Fig. 3. Co-alignment of the IBIS Hα data (top) with the full-disk Hα observations obtained by GONG (bottom). The black square in the bottom panel marks the FOV of the IBIS observations. Contours plotted in the GONG image outline the IBIS intensity map and vice versa. Any difference in contrast at the filament as seen in these two images are caused by different transmission of both instruments. |
3. 2D non-LTE filament model
At this point we should comment on the assumed 2D geometry for our filament study. Using 1D horizontal slab models, Molowny-Horas et al. (1999) and Tziotziou et al. (2001) constructed 2D maps of plasma parameters in filaments observed in the Hα and Ca II 8542 Å lines, respectively. The line of sight was intersecting a horizontally-infinite 1D slabs where the vertical extension was a free parameter. MALI1D code was used to compute a large grid of isothermal-isobaric models and then the filament parameters were derived by the least-square fitting of the observed profiles. After the grid is constructed, this method is very fast and one can make maps of parameters pixel-by-pixel. However, a disadvantage is that the 1D horizontal slab was illuminated from the solar disk only at its bottom, while in real prominences the incident radiation penetrates through filamentary structures which are then illuminated from all directions (not from corona, where Hα and Ca II radiation in not generated). Although a 2D slab model of the whole filament was introduced by Paletou et al. (1993) and Paletou (1995) (and even earlier by Vial 1982), these authors did not analyse 2D high-resolution spectra. Looking at filaments at very high resolution (e.g. in Hα), we see many fine-structure threads aligned at some angle to the filament axis. These features were modelled by Heinzel & Anzer (2006) as 2.5D magnetic dips seen against the solar disk as a filament. Their approach allowed only the lateral illumination of vertically infinite fine-structure threads to be considered. In this paper we use another 2D geometry and represent a local fine structure of the filament (i.e. at a given position of observation) by a thin (1000 km) 2D horizontal slab (see Fig. 4). This allows illumination both from the bottom and from both sides of the 2D slab, critical for the determination of the line source functions. However, we neglect possible effect of a mutual irradiation between fine structures, such effects have not been studied in case of prominences.
 |
Fig. 4. Geometrical scheme of the non-LTE 2D-slab filament model and geometry of the solar_Y–solar_Z cross-section of the 2D slab in a large scale encompassing nearly half of the Sun shown in panels a and b, respectively. In order to distinguish the coordinate system of the slab itself from the helioprojective coordinate system (Cartesian coordinate system with origin in the Sun centre and its X-axis pointing to the solar W), the first one was denoted by simple X, Y, and Z letters while for the latter these three letters are preceded by the “solar_” prefix. Panel c: same geometrical scheme in more detail. While just a schematic cartoon explaining the 2D slab-model geometry is presented in the panel a, schemes in the panels b and c are produced as a graphical output of the model code. Size of the θ angle is exaggerated in all three panels for its better recognition, in reality θ is much smaller for the studied filament fragment. |
The 2D non-LTE filament model used in this work is based on the 2D radiative transfer MALI2D code developed by Heinzel & Anzer (2001) for modelling of prominences. This code was modified here to represent the geometry of filaments. The radiative transfer is solved using the short-characteristics method (Kunasz & Auer 1988) together with the Multilevel Accelerated Lambda Iterations (MALI; Rybicki & Hummer 1991). The statistical equilibrium is calculated for a 5-level plus continuum hydrogen atom. The partial frequency redistribution (see e.g. Heinzel et al. 1987) is used in calculations of the Lyα and Lyβ lines while the complete frequency redistribution is applied for all other spectral lines of hydrogen. For the formal solution of the radiative transfer along a line of sight we used the method of Mihalas et al. (1978) and average Hα profiles from QS areas located in the close vicinity of the observed filament are used as the background radiation.
The filament was approximated by an isothermal and isobaric 2D slab placed horizontally above the solar surface. The infinite horizontal dimension was along the Y-axis and the finite dimensions (X) and (Z) formed the cross-section of the filament (see Fig. 4). The vertical, more extended dimension Z of the slab was oriented in the radial direction. The 2D slab was irradiated from the solar surface at the bottom and the sides. The dilution effect was properly taken into account. For irradiation of the slab at its bottom edge, dilution for the bottom height above the solar surface of the slab was calculated taking into account limb darkening for the spectral lines Hα – Hγ, Paschen α and β, and Bracket α. For hydrogen resonance (Lyman) lines plus continuum the limb darkening was assumed to be negligible. For irradiation from sides, irradiation from a half-plane (only half of the solar disc is seen from the slab side) was taken, and individual values of dilution factors were calculated for different heights along a side of the slab. The effect of the limb darkening was also taken into account for the same spectral lines as for irradiation from the bottom. The following QS data were used for the irradiation of the slab: the Balmer series line profiles for different values of μ from David (1961); Lyα line profiles observed by the Laboratoire de Physique Stellaire et Planetaire (LPSP) instrument (Bonnet et al. 1978) on board the Orbiting Solar Observatory 8 (OSO-8) satellite from Gouttebroze et al. (1978), Lemaire et al. (1981); the higher Lyman lines from Warren et al. (1998) observed by the Solar Ultraviolet Measurements of Emitted Radiation (SUMER) spectrograph (Wilhelm et al. 1995) on board the SOlar and Heliospheric Observatory (SoHO) satellite.
The radiation emergent from the model was computed for a LOS direction which was inclined from the radially oriented Z-axis of the slab by an angle θ, which was derived from the position of the observed filament on the solar disk as shown in the geometrical scheme in panels b and c of Fig. 4. The slab is thus seen in a projection onto the solar disk. The position along the projection of the slab is expressed in km from its south end. Size of the angle θ in the scheme is exaggerated for better understanding. The cosine of the angle θ is hereafter referred to as μ. In reality the angle θ is only around 0.20° (μ almost equal to unity) at the filament position. As it is shown further, the best fit to observed data was obtained for a vertical side of the 2D slab projected under this very small angle, not for the horizontal area on top of the 2D slab. It is necessary to note that this angle is different from μcal of 0.91 that referred previously to the position of the QS reference profile used for absolute calibration (see Sect. 2.2).
4. Results obtained by modelling
For the analysis, we chose six areas (f1–f6) located within the observed filament fragment (see Fig. 5). According to the general shape of the filament as seen in the Hα full-disc images obtained by the GONG instrument (not shown here), one can assume that in a hooked part of the observed filament fragment at the position in solar X from ≈ − 360 arcsec to −375 arcsec and in solar Y from ≈ − 65 arcsec to −78 arcsec, a footpoint or barb could occur. Assuming that the magnetic field is more vertical in a footpoint, Hα profiles from this part of the filament cannot be modelled accurately with our non-LTE model represented by a horizontal slab. Therefore the areas f1–f6 were chosen along the observed filament fragment outside the footpoint area. No special approach was used for selection of positions for the six filament areas, they were just distributed approximately along the axis of the filament fragment. Areas f1, f2, f4, and f6 were located more inside of the filament dark structure, while f3 and f5 were positioned closer to its northern edge. The average Hα profiles from these areas were fitted by the 2D non-LTE model described in the previous section. We chose also six associated QS areas (q1–q6) in the vicinity of the filament (see Fig. 5) from which the average profiles were used as the background radiation in the formal radiative transfer solution.
 |
Fig. 5. Maps of integrated intensities of the Hα line core (within Δλ = ±0.40 Å) obtained by IBIS. Marked are the six areas f1–f6 within the observed filament fragment and the six associated QS areas q1–q6 in their vicinity. The whole FOV of IBIS is shown in panel a and the zoomed area around the observed filament fragment is shown in panel b. |
For the fitting of the observed profiles from each area (f1–f6), a grid of 2D models was computed using the following ranges of input parameters: temperature from 5000 K to 19 000 K in increments of 2000 K; the gas pressure from 0.05 up to 0.80 dyn cm−2 in increments of 0.02 dyn cm−2; microturbulent velocity from 0.5 up to 14 km s−1 with the step of 0.5 km s−1; the height of the filament (Z-dimension) from 10 000 up to 60 000 km in increments of 2000 km, and the LOS component of the plasma-flow velocity vLOS from −7.5 km s−1 to +1.5 km s−1 in increments of 0.2 km s−1. Positive values of vLOS mean direction towards the observer.
Approximation of the filament by the isothermal and isobaric slab is suitable for the analysis of the Hα spectral line because Hα is predominantly formed within the cool and dense cores of prominences and filaments. Therefore the influence of the hotter prominence-corona transition region (PCTR) surrounding the cool cores is not significant and only the cool cores need to be modelled. As the modelled 2D slabs (see Fig. 4) are narrow and observed from the top, they thus represent the smaller-scale. Therefore we assumed the width of the modelled 2D slab (its X-dimension) to be 1000 km as was also adopted in modelling of the prominence fine-structure threads, for example, by Heinzel et al. (2005).
Using the described filament model we obtained synthetic Hα profiles along the extent of the projection of the 2D slab onto the solar disk. The slab was inclined from the vertical LOS by the angle θ. Hereafter, we refer to the extent of this projection as the width of the projected slab. We compared the synthetic Hα profiles obtained at all positions along the width of the projected slab with the observed Hα profiles. The best-fit profile was determined by the χ2 minimum method, where χ2 was calculated as
Here, Iobs(λi) and Isynth(λi) are intensities of the observed and the synthetic profiles, respectively. The quantity σI(λi) is the error of the observed intensity at the wavelength λi calculated as multiplication of the relative error σrel(λi) (see Eq. (1)) and the observed intensity. The position of LOS along the width of the projected slab from which the best-fit synthetic profile was obtained, measured from the slab south end, was hereafter referred to as best-fit LOS position. In this way we selected from the grid of models the one that produced synthetic profiles which had the best agreement with the observed profiles. The comparison between the observed profiles from areas (f1–f6) and their corresponding χ2-minimised synthetic profiles from the modelling is shown in Fig. 6.
 |
Fig. 6. Comparison of the best synthetic profiles (red lines) of the resulting models with observed profiles (black “+” symbols with error bars) for the six areas f1–f6. The profiles from six associated QS areas q1–q6 used as the background irradiation of the slab in the formal solution are plotted by the green asteriscs. In each plot the χ2 value of the synthetic profile fitting to the observed one is also presented. |
In Table 1 we list the input parameters of the resulting models together with their uncertainties. The uncertainties of the parameters were estimated by changing the value of each parameter in both directions from the resulting model until the best-fit synthetic profile lies within the error bars of the observed profiles. In Table 2 we present an additional list of the physical parameters of the resulting models. The 2nd and the 3rd columns are the width of the projected slab and the position of the best-fit LOS along the width of the projected slab, measured from its south end (see an example of such a LOS in Fig. 4, just the θ angle in this figure is exaggerated for better intelligibility).
Input parameters (and their uncertainties) of 2D models providing the best fit to the observed Hα profiles from the areas f1–f6.
Additional properties of the best-fit models with their uncertainties.
The sensitivity of the derived best-fit LOS position to the errors of the measured spectral intensities is rather small. This was tested by fixing the model input variables and manually varying the best-fit LOS position (such that the resulting profile remained within the error bars of the observed profiles shown in Fig. 6), we found that its uncertainties did not exceed 30% for all six filament areas. We then see that by varying the model input parameters, that were previously fixed, they have a more significant effect on the best-fit LOS position (up to ±80% of the value in the middle of each “rel. position” range). Hence, the best-fit LOS position is more sensitive to the model inputs than to errors in the observed spectral intensities. In the next three columns, values of the particle density (including free electrons, protons, neutral hydrogen, and neutral and ionised helium), plasma density, and the ionisation degree of hydrogen are listed. We would like to point out that the listed values of the densities and the ionisation degree are averaged over the entire 2D slab and variations of these quantities within the slab do not exceed 10%. The last column is the optical thickness 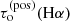 corresponding to the position of the best-fit LOS along the width of the projected slab.
corresponding to the position of the best-fit LOS along the width of the projected slab.
5. Discussion
From the results listed in Tables 1 and 2 it is clear that the observed fragment of the filament can be in general divided into two parts: region A at its SE side (areas f1–f3 from Fig. 5) and region B at its NW side (areas f4–f6 from Fig. 5). The observed Hα profiles from region A (panels f1–f3 in Fig. 6) are less deep, not too broad and significantly asymmetric. Such profiles are fitted by models with temperatures from 6000 K to 10 000 K, very high gas pressure of 0.20–0.40 dyn cm−2 and large plasma densities of the hydrogen and helium plasma (2.5–8.5 × 10−13 g cm−3). The asymmetry of these profiles results in well-defined flows directed away from an observer with derived LOS velocity components of 6–7 km s−1. In areas f1 and f3 (but not in f2) from region A we derived rather fast unresolved plasma motions represented by the micro-turbulent velocities of 8–9 km s−1. On the other hand, the Hα profiles detected in region B (areas f4–f6 in Fig. 6) are significantly deeper and broader but more symmetric. Models that fit these profiles indicate plasma with significantly higher temperatures (11 000–14 000 K), lower gas pressure (0.15 dyn cm−2) and plasma densities of 1.1–1.4 × 10−13 dyn cm−2. This part of the observed filament fragment exhibits smaller LOS velocities from 0 km s−1 to −2.4 km s−1. The derived micro-turbulent velocities are lower, 4–6 km s−1. Particle densities around 1 × 1011 cm−3 were obtained in all areas except the area f3 where a larger value of 4 × 1011 cm−3 was obtained. Values of ∼1011 cm−3 are comparable to those obtained by Schwartz et al. (2006) for another quiescent filament observed in the hydrogen Lyman series. Comparing the particle densities to plasma densities concerning the six filament areas indicates that for the areas f1 and f4–f6 there is a linear relation between the two quantities. Only for areas f2 and f3, deviations from this linear relation to larger plasma densities occur. These deviations are caused by a lower degree of ionisation of hydrogen in these two areas because there was smaller fraction of free electrons (which were included in particle density but their contribution to plasma density is negligible due to their very low mass) among other particles (protons, neutral hydrogen, and atoms and ions of helium) than in other filament areas. The deviation to larger plasma densities is remarkable mainly in the area f3 where a much lower ionisation degree of hydrogen than in other five filament areas was estimated. The observed filament fragment is in general geometrically rather extended along the Z-axis with the derived vertical size of 22 000–38 000 km. For the filament observed by the AIA instrument few days earlier as a prominence at the limb a height of approximately 20 000 km was measured what is in quite good agreement with values of the filament vertical size obtained from the modelling. In summary, the derived parameters indicate that region A was cooler, more dense, and more dynamic while in region B it was hotter, less dense, and more quiescent.
5.1. Discussion of background radiation
To support the reliability of the modelling, the influence of the selection of the background-radiation profiles used in the formal radiative transfer solution on the results should be discussed. As it was not possible to directly obtain the background radiation profiles at the surface under the filament, we approximated such a background by selecting areas outside the filament (q1–q6), which correspond to the areas f1–f6 in the filament (see Fig. 5). The areas q1–q6 were selected as close as possible to the corresponding filament areas to obtain a background radiation profile that was as realistic as possible. A good way to test the influence of the selected background-radiation areas on the modelling is to compare the results using the areas q1–q6 with results using the average QS profile used for the data calibration (see Sect. 2.2). For the QS profile an extended area with dimensions of 10 arcsec × 40 arcsec located relatively far from the filament (≈20 arcsec, see Fig. 1c) was selected to minimise any influence of plasma flows occurring in the vicinity of the filament. This way, any asymmetry or Doppler shift was eliminated from the QS profile (see panels a–d in Fig. 2).
To understand the asymmetry of an absorption profile more clearly, we can define rasym as a ratio between intensities I(λmin − 0.5 Å) and I(λmin + 0.5 Å) at wavelengths ±0.5 Å from the wavelength λmin where the intensity profile reaches the minimum:
This ratio is equal to unity for the QS profile and close to unity for profiles from areas q1–q5 (0.96–1.07). Only the background radiation profile from area q6 is more asymmetric with rasym = 1.23. The difference of the λmin positions between profiles from areas q1–q5, and the QS profile are negligible (≪0.1 Å). While the q1, q2, q4, and q5 profiles have a similar depth to the QS profile, the profiles from areas q3 and q6 are considerably deeper, with minimum intensities 12% and 6% lower, respectively.
To assess the influence of the choice of the background radiation on the modelling results, we used the model parameters derived as the best fit for each area f1–f6 and substituted only the background profiles. In areas f1, f2, and f4, only small differences in the resulting parameters occur – up to 18% for the optical thickness 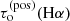 and for other quantities only up to 7%. The situation in the area f5 is different – differences for some resulting quantities are much larger, for instance, 62% in vLOS or 37% in
and for other quantities only up to 7%. The situation in the area f5 is different – differences for some resulting quantities are much larger, for instance, 62% in vLOS or 37% in 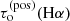 . This might be caused by f5 being located between the two regions – between the dynamic and the heated parts of the observed filament fragment which could cause numerical instability to affect the results (i.e. small changes in the modelling can cause larger changes in the results). However, it is important that the change in the plasma density is also small in area f5. Despite the fact that the q3 and q6 profiles are deeper then the QS profile, most of the properties derived in the areas f3 and f6 when the QS profile is used change by only a few %. Larger differences occur only in
. This might be caused by f5 being located between the two regions – between the dynamic and the heated parts of the observed filament fragment which could cause numerical instability to affect the results (i.e. small changes in the modelling can cause larger changes in the results). However, it is important that the change in the plasma density is also small in area f5. Despite the fact that the q3 and q6 profiles are deeper then the QS profile, most of the properties derived in the areas f3 and f6 when the QS profile is used change by only a few %. Larger differences occur only in 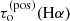 which increases by up to 63%. The most significant difference occurs in the area f6, where we obtained vLOS of −0.7 km s−1 instead of −0.1 km s−1 (difference of 85%). This is due to the significant asymmetry of the q6 profile mentioned above.
which increases by up to 63%. The most significant difference occurs in the area f6, where we obtained vLOS of −0.7 km s−1 instead of −0.1 km s−1 (difference of 85%). This is due to the significant asymmetry of the q6 profile mentioned above.
This analysis shows that the selection of the background radiation from smaller areas close to the studied areas within the filament does not significantly influence the parameters derived by the modelling. However, we would argue that in order to achieve a higher degree of accuracy, it is better to use such local background radiation profiles instead of an averaged QS profile. This may be important especially for the derivation of the LOS velocities, as can be seen in the case of the area f6.
5.2. Assessment of uncertainties of derived parameters
The temperature, gas pressure, and micro-turbulence velocity are the main parameters responsible for the width and the depth of the resulting Hα profiles. From these it is the temperature which is derived with the least uncertainty (see Table 1). When studying the influence of the temperature on the shape of the synthetic profiles we found that for low values of the gas pressure (lower than ∼0.08 dyn cm−2) and for a temperature of 7000 K our 2D model produces synthetic profiles which are deep enough but much narrower than those observed in the studied filament. With an increasing temperature, the synthetic profiles become slightly wider without changin their depth, although they do not widen enough to fit the observed profiles. Finally, when temperature is increased above 10 000 K, profiles become shallower and are no longer deep enough to match the depth of the observed profiles. On the other hand, for higher gas pressure the profile depth increases with a temperature of up to around 11 000 K, the synthetic profiles are then wide enough to accurately represent the observed profiles from the region A. Further increasing the model temperature causes a considerable broadening of the profiles resulting in both broad and deep profiles that fit those observed from the region B. It is not possible to fit these broad and deep profiles even by increasing the micro-turbulence velocity instead of the temperature while fixing the high gas pressure. This is because vMT makes profiles shallower while it broadens them. Therefore, higher temperatures are inevitable for the region B. An increase of the temperature above a critical value (e.g. 15 000 K for pressure of 0.15 g cm−2) also makes the profiles shallower. We can thus conclude that for the values of the gas pressure obtained for all six areas of the filament, the shape of all observed Hα profiles is strongly sensitive to the temperature. Therefore, the uncertainties in the derived temperature values are small (up to 11%) and the main source of these uncertainties are the errors in the measured spectral intensities.
The uncertainties of the derived gas pressure and micro-turbulence velocity values, and subsequently of the particle density and plasma density, are significantly larger than in the case of the temperature. To explain the causes of these uncertainties, we constructed two additional models for the area f6. In these models, we altered the gas pressure to be 0.08 and 0.25 dyn cm−2, respectively. These values remained within the uncertainty for the best-fit model for the area f6 (see Table 1). In Fig. 7, we show the results of these two alternative models – in the first row (panels a–c) the model with the gas pressure of 0.08 dyn cm−2 and in the second row (panels d–f) the model with the gas pressure of 0.25 dyn cm−2. The first panel in each row shows the geometric scheme of the model with the LOS (dashed line) passing through the slab embedded in the Z − Y computational domain as shown in Fig. 4. The dotted line denotes the solar surface. The second panel in each row of Fig. 7 shows the variation of the intensity (blue line) and the optical thickness (black line) at the Hα line centre. These variations are displayed along the projection of the modelled 2D slab onto the solar surface. The positions of the best fit are marked by dashed vertical lines. The third panel in each row of Fig. 7 shows the distribution of the observed intensity at the Hα line centre along a cut through the observed fragment of the filament from the solar S to the solar N. The cut passes through the centre of the area f6. The intensity is plotted with the solid black line and its errors with thin dashed black lines. The model with the lower pressure (upper row of Fig. 7) contains plasma with lower density than the higher-pressure model. Therefore, to produce the same intensity the LOS in the case of the lower-pressure model has to cover a larger distance within the modelled slab. Interestingly, even though the optical thickness values along the slab projection (see panels b and e of Fig. 7) differ significantly between the models, the τ values at the position of the best fit are similar. This means that the column mass along these two lines of sight is also similar.
 |
Fig. 7. Example of behaviour of the model and comparison of resulted synthetic intensities with observations for area f6. In the upper row we show the results of a model with the gas pressure of 0.08 dyn cm−2 and in the bottom row the results of a model with the gas pressure of 0.25 dyn cm−2. The spectral intensities I(λ) in the plots in panels b, c, e, and f are expressed in units of 10−6 erg cm−2 s−1 Hz−1. Comparing panels a–c with panels d–f one can see that for results of the modelling obtained with rather different values of gas pressure, there exist synthetic profiles for both models which agree well with the observed profile within errors of its measured spectral intensities (in panels c and f shown only for Δλ = 0 Å), although those synthetic profiles occur in radiation emergent from different positions along the projected slab. More details about the plots shown in the figure are given in the text of Sect. 5.2. |
Another interesting aspect is demonstrated by panels c and f of Fig. 7. In these plots we show in the solid blue lines the distributions of the synthetic Hα line centre intensities (the same as in panels b–e). For both models the synthetic intensity reaches values between the errors of the observed intensities within the borders of the area f6 marked by dashed red vertical lines. Panels c and f also show that the width of the projection of the modelled slab represented by the extent of the blue profiles is clearly narrower than the dip in the observed intensities which corresponds to the width of the observed fragment of the filament. This means that we would need to place multiple 2D slabs next to each other to simulate the entire extent of the filament width. We will develop such a multi-slab model in the future.
Another source of significant uncertainties which are included in the uncertainty budgets listed in Tables 1 and 2, is the fact that we cannot exactly determine the position along the width of the projected slab at which the best fit occurs. The determination of this position affects the length of the cross-section of a LOS and the modelled inclined 2D slab. This subsequently affects the derived values of the pressure, density, and ionisation degree, but also the micro-turbulent velocity. However, the column mass derived at the different positions along the width of the projected slab does not vary significantly. We want to emphasise here that the best fit between the synthetic and observed Hα profiles was obtained at all wavelengths, not only in the line centre.
An additional source of uncertainty, beyond that explicitly addressed here, lies in fact that we have only the Hα line available for this analysis. In the Hα line the filament is much less optically thick than for example in the Lyα or Lyβ lines. The optical thickness inside a filament in the Lyα line centre was shown to be of the order of 106 by Schwartz et al. (2006). On the other hand, 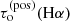 in the Hα line centre in the filament studied here was derived to be up to 4. This means that in the case of the Hα line, most of the plasma along the LOS contributes to the resulting intensity. In the Lyα case, only a very limited part of the plasma along the LOS (the plasma nearest to the observer) contributes to the resulting intensity. This can be seen for example in plots of the contribution function in Fig. 9 of Schwartz et al. (2012). Indeed, it is easier to determine the plasma conditions within a localised area than in the plasma extended along the LOS. Unfortunately we are not able to quantify the influence of this effect on uncertainties of the results of the modelling, nevertheless we want to note that these results are influenced also by this effect.
in the Hα line centre in the filament studied here was derived to be up to 4. This means that in the case of the Hα line, most of the plasma along the LOS contributes to the resulting intensity. In the Lyα case, only a very limited part of the plasma along the LOS (the plasma nearest to the observer) contributes to the resulting intensity. This can be seen for example in plots of the contribution function in Fig. 9 of Schwartz et al. (2012). Indeed, it is easier to determine the plasma conditions within a localised area than in the plasma extended along the LOS. Unfortunately we are not able to quantify the influence of this effect on uncertainties of the results of the modelling, nevertheless we want to note that these results are influenced also by this effect.
6. Conclusions
In the present paper we analysed the Hα spectral observations of a fragment of the large filament obtained by the DST/IBIS on May 29, 2017. For the analysis we used a 2D non-LTE filament model which enabled us to produce synthetic Hα spectra that were compared with the observations. Using this forward modelling technique, we derived the thermodynamic properties of plasma in selected positions within the observed filament fragment (see left panel of Fig. 8). Our analysis shows that the observed filament fragment can be broadly divided into two parts. One part marked as region A (areas f1–f3) is cooler, denser, and more dynamic. The derived temperatures range from 6000 K to 10 000 K and the gas pressure is from 0.2 dyn cm−2 to 0.4 dyn cm−2. The more dynamic nature of this region is characterised by the LOS velocities from −6 km s−1 to −7 km s−1 (negative velocities mean receding flows) and the micro-turbulent velocities of 8–9 km s−1. On the other hand, the other part marked as region B is hotter, less dense, and more quiescent. The derived temperatures are 11 000–14 000 K and the gas pressure is around 0.15 dyn cm−2. The derived LOS velocities are from −2.4 km s−1 to 0 km s−1 and the micro-turbulent velocities are 4–6 km s−1. We want to emphasise here that the broad and deep Hα profiles observed in this region cannot be reproduced by significantly lower temperatures using our 2D model. We would like to point out that higher temperatures are also found by Zhang et al. (2019) along with some mass-draining for a different prominence observed on 28 May 2014 on the NW limb during its activation phase a couple of hours before an eruption.
 |
Fig. 8. Intensity map of the observed fragment of the filament with schematically shown plasma parameters derived for individual areas f1–f6 using the forward modelling shown in the left panel. In the right panel, the intensity map overplotted with contours of the LOS magnetic field of −150, −50, −25, +25, +50, and +150 Gauss measured by the SDO/HMI instrument. |
The distinct hooked shape of the filament suggests that a barb or one of its footpoints was rooted within the FOV. To explore this, we can first assume that the motions of plasma within the filament were largely tied to the topology of the host magnetic field. Then, as the filament did not display any bulk oscillatory motions, we can assume that the observed LOS velocities correspond to motions of plasma that were aligned with the host magnetic field. Region A contained larger LOS velocities when compared with region B, this can be interpreted as the magnetic field associated with region A being more aligned with the LOS than region B. The velocities were directed away from an observer, this can be further interpreted as mass flowing into the body of the filament. For such a supposed topology of the magnetic field, this suggests a curvature in the filament towards the surface moving from region A towards region B. This is in agreement with the conclusions of Jenkins et al. (in prep.) in which the authors use the combination of a (double) Beckers Cloud Model (e.g. Tziotziou 2007), a LOS-projected HAZEL inversion from Wang et al. (in prep.), and both local and non-local thermodynamic equilibrium inversions (e.g. Beck et al. 2015, 2019) to study plasma flows and reconstruct the 3D topology of the filament footpoint.
Specifically, such a conclusion – region A contained a magnetic field more parallel to the LOS than region B that contained a magnetic field more perpendicular – is supported by the LOS-projected HAZEL inversions of spectropolarimetric observations taken in the He I infrared triplet (Asensio Ramos et al. 2008). And in the hook-shaped structure located NW from region B the field was more vertical again, also suggested by the coincidence of concentrations of the LOS surface magnetic flux at approximately (−380 arcsec in solar X, −75 arcsec in solar Y), observed by the Helioseismic and Magnetic Imager (HMI; Scherrer et al. 2012) instrument on board the SDO satellite and shown in the right panel of Fig. 8. The results of the modelling presented here are affected by several sources of uncertainties and we addressed and quantified the main contributors in Sect. 5.2. While the uncertainties in the determination of some of the parameters may be significant, these do not affect the broad conclusions stated above. To reduce the uncertainties affecting our forward modelling we plan to develop the method further to use a more sophisticated 2D model with multiple fine structures along a LOS.
Acknowledgments
P. S. acknowledges support from the project VEGA 2/0004/16 of the Science Agency. S. G. and P. H. acknowledge the support from grants 19-16890S and 19-17102S of the Czech Science Foundation (GAČR). P. S., S. G., and P. H. acknowledge support from the Joint Mobility Project SAV-AV ČR-18-03 of Academy of Sciences of the Czech Republic and Slovak Academy of Sciences. J. M. J. thanks the STFC for support via funding given in his PhD studentship. D. M. L acknowledges support from the European Commission’s H2020 Programme under the following Grant Agreements: GREST (no. 653982) and Pre-EST (no. 739500) and is grateful to the Science Technology and Facilities Council for the award of an Ernest Rutherford Fellowship (ST/R003246/1). This work utilises data obtained by the Global Oscillation Network Group (GONG) programme, managed by the National Solar Observatory, which is operated by AURA, Inc. under a cooperative agreement with the National Science Foundation. We are also thankful to anonymous referee for his/her useful comments and suggestions to the paper.
References
- Anzer, U., & Heinzel, P. 1998, Sol. Phys., 179, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Anzer, U., & Heinzel, P. 1999, A&A, 349, 974 [NASA ADS] [Google Scholar]
- Asensio Ramos, A., Trujillo Bueno, J., & Land i Degl’Innocenti, E. 2008, ApJ, 683, 542 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, C., Choudhary, D. P., Rezaei, R., & Louis, R. E. 2015, ApJ, 798, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, C., Gosain, S., & Kiessner, C. 2019, ApJ, 878, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Blokland, J. W. S., & Keppens, R. 2011, A&A, 532, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonnet, R. M., Lemaire, P., Vial, J. C., et al. 1978, ApJ, 221, 1032 [NASA ADS] [CrossRef] [Google Scholar]
- Cavallini, F. 2006, Sol. Phys., 236, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, P. F. 2011, Liv. Rev. Sol. Phys., 8, 1 [Google Scholar]
- Cheng, X., Guo, Y., & Ding, M. 2017, Sci. China Earth Sci., 60, 1383 [NASA ADS] [CrossRef] [Google Scholar]
- David, K.-H. 1961, Z. Astrophys., 53, 37 [NASA ADS] [Google Scholar]
- Fan, Y. 2018, ApJ, 862, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Gibson, S. E. 2018, Liv. Rev. Sol. Phys., 15, 7 [Google Scholar]
- Gouttebroze, P., Lemaire, P., Vial, J. C., & Artzner, G. 1978, ApJ, 225, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Gunár, S., Heinzel, P., Anzer, U., & Schmieder, B. 2008, A&A, 490, 307 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gunár, S., Schwartz, P., Schmieder, B., Heinzel, P., & Anzer, U. 2010, A&A, 514, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gunár, S., Mein, P., Schmieder, B., Heinzel, P., & Mein, N. 2012, A&A, 543, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harvey, J. W., Bolding, J., Clark, R., et al. 2011, Bull. Am. Astron. Soc., 43, 45 [Google Scholar]
- Heinzel, P., & Anzer, U. 2001, A&A, 375, 1082 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heinzel, P., & Anzer, U. 2006, ApJ, 643, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Heinzel, P., Gouttebroze, P., & Vial, J.-C. 1987, A&A, 183, 351 [NASA ADS] [Google Scholar]
- Heinzel, P., Schmieder, B., & Tziotziou, K. 2001, ApJ, 561, L223 [NASA ADS] [CrossRef] [Google Scholar]
- Heinzel, P., Anzer, U., & Gunár, S. 2005, A&A, 442, 331 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jenkins, J. M., Long, D. M., van Driel-Gesztelyi, L., & Carlyle, J. 2018, Sol. Phys., 293, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, J. M., Hopwood, M., Démoulin, P., et al. 2019, ApJ, 873, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Kliem, B., & Török, T. 2006, Phys. Rev. Lett., 96, 255002 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kunasz, P., & Auer, L. H. 1988, J. Quant. Spectrosc. Radiat. Transf., 39, 67 [Google Scholar]
- Labrosse, N., Heinzel, P., Vial, J.-C., et al. 2010, Space Sci. Rev., 151, 243 [Google Scholar]
- Lemaire, P., Gouttebroze, P., Vial, J. C., & Artzner, G. E. 1981, A&A, 103, 160 [NASA ADS] [Google Scholar]
- Lemen, J. R., Title, A. M., Akin, D. J., et al. 2012, Sol. Phys., 275, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Mackay, D. H., Karpen, J. T., Ballester, J. L., Schmieder, B., & Aulanier, G. 2010, Space Sci. Rev., 151, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Mihalas, D., Auer, L. H., & Mihalas, B. R. 1978, ApJ, 220, 1001 [NASA ADS] [CrossRef] [Google Scholar]
- Molowny-Horas, R., Heinzel, P., Mein, P., & Mein, N. 1999, A&A, 345, 618 [NASA ADS] [Google Scholar]
- Paletou, F. 1995, A&A, 302, 587 [NASA ADS] [Google Scholar]
- Paletou, F., Vial, J.-C., & Auer, L. H. 1993, A&A, 274, 571 [NASA ADS] [Google Scholar]
- Pesnell, W. D., Thompson, B. J., & Chamberlin, P. C. 2012, Sol. Phys., 275, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Petrie, G. J. D., Blokland, J. W. S., & Keppens, R. 2007, ApJ, 665, 830 [NASA ADS] [CrossRef] [Google Scholar]
- Rimmele, T. R. 2004, ApJ, 604, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Rybicki, G. B., & Hummer, D. G. 1991, A&A, 245, 171 [NASA ADS] [Google Scholar]
- Scherrer, P. H., Schou, J., Bush, R. I., et al. 2012, Sol. Phys., 275, 207 [Google Scholar]
- Schmieder, B., Tziotziou, K., & Heinzel, P. 2003, A&A, 401, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmieder, B., Lin, Y., Heinzel, P., & Schwartz, P. 2004, Sol. Phys., 221, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Schmieder, B., Malherbe, J. M., & Wu, S. T. 2014, in Nature of Prominences and Their Role in Space Weather, IAU Symp., 300, 59 [Google Scholar]
- Schwartz, P., Heinzel, P., Anzer, U., & Schmieder, B. 2004, A&A, 421, 323 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schwartz, P., Heinzel, P., Schmieder, B., & Anzer, U. 2006, A&A, 459, 651 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schwartz, P., Schmieder, B., Heinzel, P., & Kotrč, P. 2012, Sol. Phys., 281, 707 [NASA ADS] [CrossRef] [Google Scholar]
- Schwartz, P., Balthasar, H., Kuckein, C., et al. 2016, Astron. Nachr., 337, 1045 [NASA ADS] [CrossRef] [Google Scholar]
- Tziotziou, K. 2007, in The Physics of Chromospheric Plasmas, eds. P. Heinzel, I. Dorotovič, & R. J. Rutten, ASP Conf. Ser., 368, 217 [NASA ADS] [Google Scholar]
- Tziotziou, K., Heinzel, P., Mein, P., & Mein, N. 2001, A&A, 366, 686 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vial, J. C. 1982, ApJ, 254, 780 [NASA ADS] [CrossRef] [Google Scholar]
- Vial, J. C., & Engvold, O. 2015, in Solar Prominences, Astrophys. Space Sci. Lib., 415, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Warren, H. P., Mariska, J. T., & Wilhelm, K. 1998, ApJS, 119, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Wilhelm, K., Curdt, W., Marsch, E., et al. 1995, Sol. Phys., 162, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Wuelser, J. P., Lemen, J. R., Tarbell, T. D., et al. 2004, in Telescopes and Instrumentation for Solar Astrophysics, eds. S. Fineschi, & M. A. Gummin, SPIE Conf. Ser., 5171, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, P., Buchlin, É., & Vial, J. C. 2019, A&A, 624, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zirker, J. B., Engvold, O., & Martin, S. F. 1998, Nature, 396, 440 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Input parameters (and their uncertainties) of 2D models providing the best fit to the observed Hα profiles from the areas f1–f6.
All Figures
 |
Fig. 1. Filament observed on May 29, 2017. Panel a: context full-disk image in the SDO/AIA 193 Å channel. Panel b: zoom-in on the box marked in the panel a. Panel c: Hα line core image of the filament taken by DST/IBIS at 14:44:55 UT. White box indicates the region from which the average quiet-Sun profile was calculated. Panel d–f: contextual SDO/AIA images in three EUV channels: 171 Å, 304 Å, and 211 Å. The images have the same zoomed-in field of view as is in panel b. |
| In the text | |
 |
Fig. 2. Illustration of the pre-filter correction method using the Hα tables of David (1961). Panel a: average QS profile calculated from the area marked in Fig. 1c. Vertical dashed lines indicate 27 IBIS wavelength positions used. Panel b: reference David’s Hα profile at μcal = 0.91. Panel c: correction between panels a and b. Panel d: average QS profile with panel c correction applied, and panel b over-plotted in dashed-line. Panel e: residuals remaining between the corrected profile and the reference profile. |
| In the text | |
 |
Fig. 3. Co-alignment of the IBIS Hα data (top) with the full-disk Hα observations obtained by GONG (bottom). The black square in the bottom panel marks the FOV of the IBIS observations. Contours plotted in the GONG image outline the IBIS intensity map and vice versa. Any difference in contrast at the filament as seen in these two images are caused by different transmission of both instruments. |
| In the text | |
 |
Fig. 4. Geometrical scheme of the non-LTE 2D-slab filament model and geometry of the solar_Y–solar_Z cross-section of the 2D slab in a large scale encompassing nearly half of the Sun shown in panels a and b, respectively. In order to distinguish the coordinate system of the slab itself from the helioprojective coordinate system (Cartesian coordinate system with origin in the Sun centre and its X-axis pointing to the solar W), the first one was denoted by simple X, Y, and Z letters while for the latter these three letters are preceded by the “solar_” prefix. Panel c: same geometrical scheme in more detail. While just a schematic cartoon explaining the 2D slab-model geometry is presented in the panel a, schemes in the panels b and c are produced as a graphical output of the model code. Size of the θ angle is exaggerated in all three panels for its better recognition, in reality θ is much smaller for the studied filament fragment. |
| In the text | |
 |
Fig. 5. Maps of integrated intensities of the Hα line core (within Δλ = ±0.40 Å) obtained by IBIS. Marked are the six areas f1–f6 within the observed filament fragment and the six associated QS areas q1–q6 in their vicinity. The whole FOV of IBIS is shown in panel a and the zoomed area around the observed filament fragment is shown in panel b. |
| In the text | |
 |
Fig. 6. Comparison of the best synthetic profiles (red lines) of the resulting models with observed profiles (black “+” symbols with error bars) for the six areas f1–f6. The profiles from six associated QS areas q1–q6 used as the background irradiation of the slab in the formal solution are plotted by the green asteriscs. In each plot the χ2 value of the synthetic profile fitting to the observed one is also presented. |
| In the text | |
 |
Fig. 7. Example of behaviour of the model and comparison of resulted synthetic intensities with observations for area f6. In the upper row we show the results of a model with the gas pressure of 0.08 dyn cm−2 and in the bottom row the results of a model with the gas pressure of 0.25 dyn cm−2. The spectral intensities I(λ) in the plots in panels b, c, e, and f are expressed in units of 10−6 erg cm−2 s−1 Hz−1. Comparing panels a–c with panels d–f one can see that for results of the modelling obtained with rather different values of gas pressure, there exist synthetic profiles for both models which agree well with the observed profile within errors of its measured spectral intensities (in panels c and f shown only for Δλ = 0 Å), although those synthetic profiles occur in radiation emergent from different positions along the projected slab. More details about the plots shown in the figure are given in the text of Sect. 5.2. |
| In the text | |
 |
Fig. 8. Intensity map of the observed fragment of the filament with schematically shown plasma parameters derived for individual areas f1–f6 using the forward modelling shown in the left panel. In the right panel, the intensity map overplotted with contours of the LOS magnetic field of −150, −50, −25, +25, +50, and +150 Gauss measured by the SDO/HMI instrument. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.