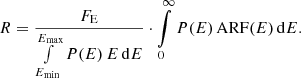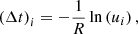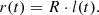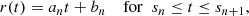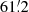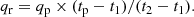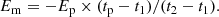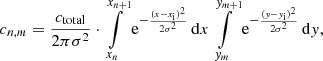| Issue |
A&A
Volume 630, October 2019
|
|
|---|---|---|
| Article Number | A66 | |
| Number of page(s) | 19 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201935978 | |
| Published online | 24 September 2019 | |
SIXTE: a generic X-ray instrument simulation toolkit⋆
1
Remeis Observatory & ECAP, Universität Erlangen-Nürnberg, Sternwartstr. 7, 96049 Bamberg, Germany
e-mail: thomas.dauser@fau.de
2
Centre National d’Etudes Spatiales, Centre Spatial de Toulouse, Toulouse Cedex 9, France
3
IRAP, Université de Toulouse, CNRS, CNES, UPS, Toulouse, France
4
Harvard-Smithsonian Center for Astrophysics, 60 Garden St., Cambridge, MA 02138, USA
Received:
29
May
2019
Accepted:
29
July
2019
We give an overview of the SImulation of X-ray TElescopes (SIXTE) software package, a generic, mission-independent Monte Carlo simulation toolkit for X-ray astronomical instrumentation. The package is based on a modular approach for the source definition, the description of the optics, and the detector type such that new missions can be easily implemented. The targets to be simulated are stored in a flexible input format called SIMPUT. Based on this source definition, a sample of photons is produced and then propagated through the optics. In order to model the detection process, the software toolkit contains modules for various detector types, ranging from proportional counter and Si-based detectors, to more complex descriptions like transition edge sensor (TES) devices. The implementation of characteristic detector effects and a detailed modeling of the read-out process allow for representative simulations and therefore enable the analysis of characteristic features, such as for example pile-up, and their impact on observations. We present an overview of the implementation of SIXTE from the input source, the imaging, and the detection process, highlighting the modular approach taken by the SIXTE software package. In order to demonstrate the capabilities of the simulation software, we present a selection of representative applications, including the all-sky survey of eROSITA and a study of pile-up effects comparing the currently operating XMM-Newton with the planned Athena-WFI instrument. A simulation of a galaxy cluster with the Athena-X-IFU shows the capability of SIXTE to predict the expected performance of an observation for a complex source with a spatially varying spectrum and our current knowledge of the future instrument.
Key words: instrumentation: detectors / X-rays: general / methods: numerical
The SIXTE code is available at https://github.com/thdauser/sixte/
© ESO 2019
1. Introduction
Simulations play an important role in the development of astronomical instrumentation and in the scientific analysis of observations with existing facilities. They provide the possibility to investigate the dependence of the scientific capabilities of the facility on various instrumental effects and allow us to test and verify whether or not the science goals of the studied future mission will be achieved by a given design choice.
In the area of X-ray astronomy a variety of existing simulation tools have been developed to address the particular needs of individual X-ray instruments. Examples include marx (Wise et al. 1997) for Chandra (Weisskopf et al. 2002), SciSim (Gabriel et al. 2005) for XMM-Newton (Jansen et al. 2001), and NuSim (Madsen et al. 2011; Zoglauer et al. 2011) for NuStar (Harrison et al. 2010). Traditionally, however, these software packages were restricted to the particular mission for which they were developed. The only exception is simx1, which enables fast simulation of observations for multiple X-ray missions, including Athena, NuSTAR, and Hitomi. Nevertheless, the latter software package does not allow detailed investigation of timing-related features and includes only a limited range of detector types and detector effects. While the simulator package is very useful to get a fast overview of the capabilities of an instrument, by design simx is not well suited for more detailed simulation studies of the scientific performance of an instrument.
SIXTE (SImulation of X-ray TElescopes) is designed to fill this gap. It strongly focuses on a detailed modeling of detector effects for any type of complex astrophysical source. Similar to simulators such as marx or SciSim its purpose is therefore to provide scientists with realistic and representative simulations of future instruments for complex astrophysical sources, while also supporting instrument development with a detailed modeling of the detector characteristics. The major difference to the aforementioned simulators is that new instruments can be easily added without changes to the software or detailed knowledge of the internal structure. In addition to the larger set of included detector types, the modularity ensures that any component can be easily replaced by a more complex and detailed description in the software.
Being able to simulate detector characteristics therefore puts SIXTE simulations far beyond a simple “fakeit” using simply the ancillary response file (ARF) and redistribution matrix file (RMF) to predict the flux in each spectral bin for a given source model. Besides the missing detector effects, fakeit is not applicable for extended sources, brighter sources which may create pile-up, or timing analysis of variable sources. On the other hand, contrary to a full simulator like marx, SIXTE does not predict the behavior of the optics, but relies on the calibration data such as vignetting, point spread function (PSF), ARF, and RMF as an input. This approach greatly eases the computational effort needed for the simulation, while keeping the flexibility to use simulated or measured calibration data of arbitrary complexity to describe the instrument under study.
SIXTE is currently the official instrument end-to-end simulator of eROSITA (Predehl et al. 2014, 2018) aboard Spektrum-Roentgen-Gamma (SRG; Pavlinsky et al. 2018) and the planned Athena satellite (Barcons et al. 2017) for both the Wide Field Imager (WFI; Meidinger et al. 2017) and the X-ray Integral Field Unit (XIFU; Barret et al. 2018) instruments. SIXTE was also used for many different assessment studies, including studies on Simbol-X (Ferrando et al. 2005), the international X-ray observatory (IXO; Barcons et al. 2011; Schmid et al. 2010, 2011), the Large Area Detector (LAD; Zane et al. 2012) and the Wide Field Monitor (WFM; Brandt et al. 2012) aboard Large Observatory For X-ray Timing (LOFT; Feroci et al. 2012; Schmid et al. 2012), the proposed Arcus grating spectrometer for the NASA medium-class explorer program (Smith et al. 2017), and the coded mask instrument Hard X-ray Imager (HXI) of the MIRAX experiment (Grindlay et al. 2011; Penacchioni et al. 2017).
This paper is structured as follows. First we present an overview of the implementation (Sect. 2), giving detailed information and assumptions on the single steps from the definition of the astrophysical source to the final output event file. A broad selection of applications is presented in Sect. 3 and a summary of the most important aspects and conclusions in Sect. 4. More detailed information on certain important aspects is given in the Appendix.
2. Implementation
2.1. Overview
The SIXTE simulator uses a Monte Carlo frame-work based on individual photons. Before any simulation is performed, the information on the astrophysical sources is collected in input files in a generic flexible image transport system (FITS)2-based format called SIMPUT3 (Sect. 2.2). This source list is then used in combination with the pointing information for the instrument to generate photons (Sect. 2.3). These photons are then propagated through a representation of the optics of the mission, resulting in a list of impact times, positions, and energies on the detector (Sect. 2.4). In the final step, these impacts are input into the detector model, which may include detection-related post processing to generate the final event list (Sect. 2.5).
Figure 1 highlights this modular approach outlined above. While the source definition does not require any mission-dependent information, an increasing level of assumptions and detector-specific details are necessary for the following steps. In order to create a list of source photons, only knowledge of the instrument effective area, the field of view (FOV), and the pointing of the instrument is required. Information on the latter two are crucial, as a SIMPUT catalog will often contain sources in an area much larger than the FOV and ensure that only photons able to hit the detector are generated. In order to process the photons through the optics, additional information is necessary, such as the vignetting and the PSF. Only in the event-detection step does a detailed description of the specific detector need to be given. Finally, regardless of the detector type, a standardized event file is produced as output of the simulation.
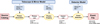 |
Fig. 1. Flow chart illustrating the three major functional blocks of the SIXTE simulation software (yellow boxes), starting from the generation of photons from a source catalog, which are then imaged and detected in the instrument and then processed to generate an event list. |
In the following sections the implementation of SIXTE is summarized. Additional background information can be found in Schmid (2012) and the SIXTE simulator manual4.
2.2. Source description: SIMPUT
Performing simulations of realistic astrophysical objects requires that the simulator be able to include any type of time variable or extended source. For this purpose we developed the SIMPUT file format (Schmid et al. 2013), which provides an instrument-independent definition of such sources. It is based on the FITS data format (Wells et al. 1981; Ponz et al. 1994; Hanisch et al. 2001; Pence et al. 2010).
The main purpose of an instrument-independent source definition is that the same input file can be used for simulations of different instruments. Depending on the knowledge or assumptions on a particular source, either basic or sophisticated models can be constructed with phenomena ranging from simple energy spectra to spatial and temporal variations of the observed spectra.
The use of the SIMPUT format is not restricted to SIXTE, but it is designed for general application. For instance, the simulation software simx implements SIMPUT as an alternative input format. In the following we give a brief summary of the basic characteristics of the format. The full formal description of the format is given in the relevant standard document5.
2.2.1. Source catalog
The core of a SIMPUT file is a source catalog specifying the properties of one or multiple X-ray sources. The file consists of a table with entries for each object defining its basic properties, such as its position and the observed flux in a particular energy band. In addition, references to other HDUs (Header and Data Unit) are given, which contain more detailed information about the energy spectrum, time variability, and spatial extent of the source. These HDUs can also be located in other SIMPUT files. While the reference to a spectrum is obligatory for each source, the specification of time variability and spatial extent are optional. The use of references to spectra and other source characteristics allows their repeated use in large source catalogs. For example, when simulating deep X-ray fields or an all sky survey with thousands to millions of sources, spectra of individual sources from a certain class of objects can be selected from a smaller set of source spectra which are representative of the class as a whole. This approach allows the memory needed in the simulation to be reduced. A schematic layout of a sample catalog is illustrated in Fig. 2.
 |
Fig. 2. Schematic layout of a SIMPUT file. The source catalog contains the main characteristics of one or multiple sources, such as their positions and observed fluxes. Additional data describing energy spectra, spatial extent, and time-variability are stored in separate Header and Data Units (HDUs) and linked in the source catalog. |
2.2.2. Energy spectrum
The most common way to define a spectrum in SIMPUT is the specification of the photon flux density Fp(E) distribution in units of photons s−1 cm−2 keV−1. Alternatively, the spectral shape can be modeled by a list of photons stored in an HDU table. The latter approach is convenient if the source model is based on input from a hydrodynamic simulation, which often provides a list of emitted photons.
As mentioned above, an individual spectral shape can be assigned to a variety of sources with different brightness. Therefore the energy spectrum given in the extension only describes the spectral shape, which is then normalized to the flux of the source under consideration which is determined by the reference flux assigned to this source in the catalog HDU.
2.2.3. Time variability
Time variability can be defined by a light curve, a power spectral density (PSD), or a photon list with time information assigned to each photon. A light curve describes the time-dependence of the flux observed from a source. If the variability is periodic, it can be defined with respect to the phase of the oscillation instead of the absolute time. Such a description is quite suitable for modeling phenomena with a typical time evolution such as type-I X-ray bursts or periodic signals from pulsars. Power spectral densities are convenient to describe random and semi-random variations such as noise or quasi periodic oscillations (QPOs). In order to obtain a proper time distribution of simulated photons, they are internally converted to light curves by the simulation software using the algorithm introduced by Timmer & König (1995). Photon lists are often convenient to use if input is available from complex three-dimensional simulations such as those used for example in cosmology. If the number of simulated photons approaches the total number of photons in the list, the same input photons might be used multiple times.
2.2.4. Source images
Sources without an image assigned are considered point sources. Extended sources are defined in the SIMPUT format by assigning an additional FITS image representing the spatial distribution of the observed flux or a photon list that includes spatial information. Both kinds of data can be obtained from an observation or a simulation of the source. As for the spectrum, such images can also be used for multiple sources as the reference point for the image, the total image flux, a scaling parameter for the source extent, and a parameter describing the image orientation are set in the source catalog.
2.3. Photon generation
Based on the definition in the SIMPUT file, a sample of photons is produced with the following three basic characteristics required for the subsequent instrument simulation: the time, the energy, and the direction of origin of each photon.
2.3.1. Source selection
A SIMPUT catalog can cover a sky area which is much larger than the part of the sky observed by the telescope. To save computational time, photons are only generated from selected sources relevant for simulation given the current pointing of the telescope. This pointing can either be fixed to one position in the sky, or optionally given as attitude in the simulation, specifying for each time step the Right Ascension (RA), Declination (Dec), and roll angle of the telescope.
Photons are therefore created for sources which have an angular separation from the optical axis that is less than a certain preset angle from the current pointing of the telescope. For typical simulations, this angle is set to 150% of the FOV of the instrument. This conservative criterion takes into account that simulations might involve a motion of the optical axis, for example, due to slews, dithering, or pointing instabilities, and ensures that the statistical properties of source light curves are not interrupted should the source move into and outside of the FOV within one simulation run. For simulations where stray light might be important, a larger angle might be required, which is set in the configuration file for a given mission.
For catalogs with a large number of X-ray sources, selecting the sources to be considered in the simulation can be computationally challenging. For instance, an all-sky catalog of active galactic nuclei (AGNs) down to a flux limit of 10−15 erg s−1 cm−2 contains several million sources. Due to the large number of sources, an efficient general search scheme for all sources within a maximum angular distance is needed.
In SIXTE, we use a general search algorithm based on k-d trees, a general data type to store data in a k-dimensional space (Bentley 1975; Friedman et al. 1977). For optimized k-d trees, the computational effort of a range search for all sources within a certain distance from a particular location scales as 𝒪(log N), where N is the number of sources in the catalog (Friedman et al. 1977; Preparata & Shamos 1985). Moore (1991) describes an algorithm based on quick sort (Hoare 1962) that allows an optimized k-d tree to be constructed from a catalog that scales as 𝒪(Nlog N). While this step is computationally more intensive, it has only to be done once at the start of the simulation, and can be precomputed if necessary. In our experience, this step is negligible compared to other steps of the simulation. Specifically, within SIXTE we construct a 3D tree based on unit vectors pointing at the catalog searches. To find all sources within a given angular distance, θ, from the pointing direction, we then use the tree to find all sources within a linear 3D distance of d = sin θ. We find that this approach scales well also to very large source catalogs and yields roughly constant search times. We note that other approaches to solve this problem which are used in astronomy, such as searching on some variant of HEALPix coordinates (Górski et al. 2005; Calabretta & Roukema 2007), are well suited for describing images, but are less well-suited for the storage of catalogs of sources which might be nonuniformly distributed on the sky.
2.3.2. Photon arrival time
The average photon rate R observed from a particular source is determined by its energy flux FE in the reference band Emin to Emax specified in the SIMPUT catalog, the shape of the photon spectrum, P(E), and the on-axis ARF of the instrument,
We model the photon generation as a Poisson process with rate R. The number N of generated photons within a certain time interval T therefore obeys a Poisson distribution with the expected value R ⋅ T. Starting at a particular point in time, the intervals (Δt)i between subsequent photons are then exponentially distributed and calculated by inversion sampling from
where ui denotes uniformly distributed random numbers ui ∈ [0,1). We note that as we include the ARF in the photon generation, the resulting photon list is specific to the observation and is therefore instrument dependent. This approach greatly speeds up the simulation.
While Eq. (2) works well for sources with a constant brightness, it is not appropriate for time-variable sources, even though we have found quite a few implementations that do so. Although the photon rate R can be determined as a function of time, a fixed value of R is used for the evaluation of Eq. (2). In other words, the determination of the arrival time ti = ti−1 + (Δt)i−1 of the ith photon requires a particular value for R, which is usually chosen as R = r(ti−1). This approach does not account for any variations of R within the interval ti−1 to ti. Particularly for rapid changes from small to large values, Eq. (2) can result in a delayed increase of the simulated photon rate, as described by Martin (2009) and illustrated in Fig. 3.
 |
Fig. 3. Comparison of different Poisson arrival process generators. The dashed black curve represents the input light curve. The red curve displays the simulated photon rate using a simple algorithm implementing Eq. (2) with R = r(ti−1). The blue curve is based on the algorithm introduced by Klein & Roberts (1984), which avoids the delay of the increasing photon rate for steeply rising profiles. |
In SIMPUT files the time-dependence of the rate function r(t) is determined by the product of the light curve l(t) of the respective source, representing the time-dependence of the relative flux variations, and the reference rate R, which is obtained according to Eq. (1) such that
The light curve is approximated by a piece-wise linear function
with the supporting points sn. We then use the Poisson arrival process generator described by Klein & Roberts (1984) to determine the photon arrival times. This algorithm is basically an extension of Eq. (2) for piece-wise linear rate functions and avoids the problems with steeply increasing photon rates.
2.3.3. Photon energy
The energies of the photons produced for a particular source are distributed according to a spectral shape obtained by multiplication of the instrument-independent spectral shape defined in the SIMPUT file with the instrument-specific energy-dependent on-axis ARF (George et al. 1998, 2007). Since the spectrum and the ARF are defined on a particular energy grid and for discrete energy bins, respectively, an interpolation of the spectrum to the energy bins of the ARF is applied. Drawing random energies with the inversion method (see Deák 1990, p. 68ff. or Gould et al. 2006, Chap. 11) reproduces the selected spectral distribution.
2.3.4. Photon direction of origin
For a point-like source, the direction of the incident photons is equivalent to the location of the target on the sky and is trivially included in the simulation. For a spatially extended source, we draw a random photon direction based on the image defined in the respective SIMPUT catalog. For this purpose the image is converted to a cumulative distribution function,
with
where N and M are the width and the height of the image, and pi, j is the normalized value of the pixel i, j such that
For each generated photon, a uniformly distributed random number r ∈ [0, 1) is selected, and the pixel indices k, l corresponding to the following relation, are determined in a two-dimensional binary search,
For a sufficiently large number of simulated photons, this method reproduces the input spatial flux distribution. Details on the definition of the coordinate systems can be found in Appendix A.
2.4. Photon imaging: Optics implementation
In the photon imaging step, the photons are processed through the optics and imaged onto the detector plane. The input consists of a photon with an arrival time t, energy E, and the direction of its origin in celestial coordinates, α and δ. The outcome of the photon projection step is photon impact with identical time t and energy E, and a position (X, Y) on the detector plane (see Appendix A.2 for a definition of the coordinate system used). If the photon does not hit the detector, it is discarded.
In the current implementation SIXTE uses pre-computed or measured calibration files to describe this imaging process. While a separate ray-tracer could be implemented, the chosen approach is computationally much faster and allows the user to include measured calibration data. The reduction in detection probability for off-axis photons compared to on-axis photons is described by a vignetting function and the imaging properties by the PSF, both of which can depend on energy, off-axis angle, θ, and azimuth, ϕ. For both components, FITS standards exist (George & Yusaf 1994, 1995). With sufficiently detailed data derived from measurement or ray-tracing, this approach mimics a full ray-trace almost entirely. Point spread function asymmetries, spatially varying vignetting, and even distortions due to single-reflection events can be captured if desired. Conversely, a simple constant Gaussian PSF can be used for missions in the early conceptual stage, giving this approach great flexibility.
Figure 4 shows an illustration of the flow of information in the imaging stage of the simulation. The individual steps are covered in the following.
 |
Fig. 4. Block diagram of the photon imaging stage of SIXTE. |
2.4.1. Vignetting correction
The vignetting function describes the reduction in detection probability for off-axis photons and has to be provided in the standard calibration file format (George & Yusaf 1994). In the simulation, vignetting is implemented as a discrete randomization progress, based on the energy, off-axis, and azimuthal angle of each photon. Depending on a probability distribution determined from these parameters, the photon is either transmitted through the optical system or is discarded.
2.4.2. Randomization of the PSF
Focusing astronomical optics such as Wolter-type telescopes (Wolter 1952) focus parallel rays of light onto the focal plane. However, as the optics are not ideal, the image of a point source, the PSF, on the detector is typically extended. Most optics are designed to optimize the image and thus the shape of the PSF inside a certain region around the optical axis. With increasing off-axis angles, the PSF usually degrades to a complex shape and grows larger in size (see, e.g., Friedrich et al. 2012a).
To randomize the impact position of the photon on the detector, for most cases SIXTE uses a pre-calculated PSF as described in standard FITS PSF calibration files (George & Yusaf 1995). The PSF is allowed to be dependent on the Energy, E, of the photon, the off-axis angle, θ, and the azimuthal angle, ϕ, that is, the angle between the intersection of the point (X, Y) = (0, 0) and the ideal impact position and the X-axis of the instrument. The randomization is calculated from the best matching entries in the calibration file, weighted by the proximity of the incident position of the photon to these entries. In order to avoid the computationally expensive 2D interpolation, this is implemented in SIXTE by first randomly drawing a single PSF – respecting the calculated weight – and then drawing the impact position of the photon from the selected PSF6.
In the case of azimuthal symmetry, the resulting PSF is optionally rotated according to the difference between the simulated azimuthal angle and the one of the PSF chosen from the calibration file. This reduces the blurring of some asymmetrical features in complex PSF-shapes. This PSF is interpreted as a spatial random distribution function for the final impact position of the photon.
In case the instrument uses a collimator instead of imaging optics, the impact positions of incident photons are randomly distributed on the detector according to the geometry of the respective collimator model. As for imaging optics, the off-axis transmission of the collimator or coded mask is defined by a vignetting function.
Apart from simple collimators, hard X-rays are often imaged using coded masks, which cast a particular shadow pattern on an imaging detector, allowing the reconstruction of the location of the illuminating sources (Cieślak et al. 2016; Caroli et al. 1987; Groeneveld 1999, and references therein). A fraction of the incident photons is absorbed by the opaque pixels of the mask. The impact positions of the transmitted photons on the detector plane are determined by geometrical considerations taking into account their angle of incidence and the positions of randomly selected transparent pixels.
2.5. Event detection: Detector implementation
2.5.1. Overview
After the photon generation and imaging described in the previous section, the simulation has generated a list of the actual impacts in the detector plane. Due to fundamentally different detector types, SIXTE provides several different tools to model the detection process. The outcome of all of these steps is a standardized list of events, the “event file”.
Currently the SIXTE simulator provides models for three different types of detectors, which will be explained in the following:
-
detectors working based on line-by-line read-outs, such as charged coupled device (CCD) or depleted field effect transistor (DEPFET) sensors (eROSITA, XMM-Newton, Athena WFI),
-
event-triggered detectors such as silicon drift detectors (SDDs), proportional counters, or cadmium-zinc-telluride detectors (Nustar),
-
TES calorimeter-type detectors (Athena X-IFU), which are a special case of event-triggered detectors, where the energy resolution of each event depends on the time intervals between the previous and the following event.
Despite the different types of sensors, the simulation of event generation follows a general structure. Mainly, this core functionality of SIXTE is broken down into two separate tasks: (1) the signal creation in the detector and the signal read out, and (2) the event reconstruction, and possible calibration. Between these two steps a RawData file is written to allow the user to investigate the raw output or to perform a separate reconstruction and calibration of the events.
The formal process of the simulation ends with the event read out. However, for many applications it is necessary to apply the reconstruction and eventual calibration in a post-processing step such that the final event file contains an estimate of the reconstructed photon energy. This process then allows for a spectral analysis of the simulated data. We note that for a calorimeter-type detector such as the Athena-X-IFU it is necessary to apply the reconstruction and notably the event grading during the simulation, as it influences the energy resolution of the events (see Peille et al. 2016).
2.5.2. Event creation
In order to convert the photon energy to a signal in the detector, SIXTE applies a randomization of the signal based on the redistribution matrix file (RMF; Popp 2000; Edgar 2011). This matrix describes the probability that a certain signal is measured for a given input photon energy. Such a description is a common element of the spectral analysis of X-ray data (George et al. 1998, 2007), and allows for a fast simulation of the detection process, while maintaining the characteristics of the specific detector and absorbing material. Most importantly, this RMF encodes the energy resolution of the detector, but might also include additional detector effects like escape peaks (see, e.g., Eggert et al. 2006, for more details).
In Si-type detectors, like CCDs or DEPFETs, the photon impact creates a charge cloud at the incident location, which is simulated in the generic approach by a 2D Gaussian (Kimmel et al. 2006; Martin 2009). For impacts close to the edge of a pixel, this electron cloud can partly drift to the adjacent pixels and create so-called split events. Details on the split model and the charge cloud size are presented in Appendix D.
For the TES-calorimeter, thermal or electrical coupling between pixels can lead to a similar effect called crosstalk. Due to this coupling, the primary impact can induce a small signal in neighboring pixels. In case of thermal crosstalk, this effect can be simply described in the instrument configuration, by specifying the strength of this coupling depending on the physical distance between pixels (Peille et al. 2018; Kirsch et al., in prep.)
For all other types of detectors, the absorption of the photon is assumed to take place in the impact location, that is, fully confined to the pixel hit by the photon.
2.6. Event read-out
The modeling of the event read-out is an important part of the overall simulation. It assigns the time te and the position (RAWX/RAWY or PIXID) to the final event. Depending on the type of read-out, this does not necessarily coincide with the arrival time and impact location.
In order to define the detector, SIXTE provides the possibility to set up a rectangular array of pixels with dimensions defined in an extensible markup language (XML) file (see Appendix C for an example). The pixel can then be uniquely identified by the RAWX, RAWY coordinate. For special detectors such as the hexagon-shaped X-IFU of Athena, such a simple identification is not possible. Instead, a unique ID (the so-called PIXID) is assigned to each pixel.
In the so-called time-triggered mode, the signals generated by incident photons are stored in the affected pixels and read out after a specific exposure time. The corresponding sequence of detector operations is defined in the configuration file. This method is used, for example, for CCD or DEPFET detectors (Boyle & Smith 1970; Amelio et al. 1970). In such cases, the frame time of the read out determines the time stamp of the event, i.e., te = tframe.
Similarly, the location (RAWX/RAWY or PIXID) assigned to the event is determined by the row in which the signal is detected. Depending on the read out type, this position might not coincide with the actual impact position. For silicon-based X-ray detectors, two distinctly different models are implemented in SIXTE which cover the majority of the currently operating X-ray telescopes.
In case of a CCD, the charge is shifted to the read-out anodes at the edge of the detector. Photons absorbed during this charge shift will be registered with incorrect spatial information (Lumb et al. 1991) and create so-called out-of-time (OOT) events. Charge loss due to charge transfer inefficiencies (CTIs), where charge is lost while it is shifted over the detector, can also be taken into account.
In a DEPFET detector, the charge is not shifted, but read out directly (see, e.g., Treberspurg et al. 2017). In such detectors, however, the detection process is more complex as the digitization of the signal from the photon happens in the pixel itself. This read-out process is modeled in the end-to-end simulator in a three-step process. First the voltage signal of the photon together with the signal baseline is measured. Then the charge is removed by a clear signal and in a second integration step the baseline is determined. In a third step, the measured signal is then determined by taking the difference between the two integrations. In case a photon hits the detector during the read-out process, the measurement will be corrupted, creating a misfit event. Depending on when exactly the photon is absorbed in the read-out process, its energy is either measured partially (first integration), split between the current and the next frame, or registered with a negative energy (second integration) and therefore discarded (see Appendix C.3 for more information).
In the event-triggered or continuous read-out mode, each absorbed photon is immediately registered as an event te = tphoton. This mode is typical for SDDs (Gatti & Rehak 1984) or proportional counters, and also for the special case of TES calorimeters. Optionally, a dead time after an event can be specified, during which the detector is insensitive to further incident photons.
In some detectors, most importantly TES-type detectors, the precision by which the signal can be measured depends on the time difference to the previous and to the following event (in the same pixel)7. Therefore, depending on these time intervals, multiple RMFs can be used in SIXTE to describe the dependence of the energy resolution on these time intervals.
2.6.1. Background
Different possibilities are provided in SIXTE to account for detector background. Events induced by interactions of cosmic-ray protons with the camera housing can be inserted from a data set obtained with GEANT4 (Geant4 Collaboration 2003; Allison et al. 2006) simulations. We note that this data set needs to be screened for particle tracks before its usage in SIXTE. For a particular exposure time, a Poisson distributed number of these events is selected and the corresponding signals are added to the detector pixels (Wille 2011). Alternatively, random background signals can be obtained from a distribution defined in a pulse height amplitude (PHA) background file (Arnaud et al. 2009), which is commonly available for many instruments. This latter method, however, does not allow to model the more complex effects that background has on event reconstruction.
We emphasize that the above description concentrates only on the background events that are created from interactions with highly energetic particles in the sensors. The X-ray background is as equally important as this particle background, but does not require special treatment in SIXTE, as it can be simulated by adding respective sources to the SIMPUT catalog for the photon generation. For instance, instead of describing the diffuse cosmic X-ray background (CXB) in a background PHA file, it can be modeled by a large number of individual AGNs (Gilli et al. 2007). Depending on the sensitivity of the simulated instrument, this model of the CXB can be partly resolved into individual sources, as with a real instrument. For the convenience of the user we provide an example of such a SIMPUT file for download8, which can be added to any simulation to model the CXB.
2.6.2. Event reconstruction
For simulations of imaging instruments, the detector coordinates assigned to the events can be projected back onto the sky in order to obtain an image of the observed region. The corresponding routine takes into account the pointing attitude of the telescope, which in general is a function of time. The use of the WCSLIB library enables the selection of different projection types (Calabretta & Greisen 2002).
If the detector model implements charge cloud splitting, the produced pattern types (“grades”) can be identified with an appropriate search algorithm. As with the measured data of real instruments, it can happen that a pattern is incorrectly identified with a single photon, although it has been created by multiple photons hitting the same or neighboring pixels during one read-out cycle of the detector. This phenomenon is called “pile-up”. Its correct modeling and elucidation is essential for understanding instrumental effects for observations of very bright sources (Popp 2000; Davis 2001; Martin 2009).
Additionally, as in real instruments an energy threshold is applied to each signal that is measured. The type and level of this threshold can again be set directly in the XML file. Such a threshold is typically applied to remove thermal noise from the measured signal. For detectors producing split events, the lower energy threshold is of special importance, as it influences the reconstructed energy. Specifically, if the fraction of charge lost to a neighboring pixel is below the lower energy threshold, it will not be detected, and therefore it will not be taken into account during the pattern recombination. This will yield a reconstructed energy smaller than the incident photon energy and will influence the detector response, as discussed in the following section.
2.6.3. Energy calibration
Effects such as the lower energy threshold will lead to reconstructed photon energies that are different9 from the energy of the incident photon. The energy can also be influenced by applying a nonzero charge transfer inefficiency (CTI), or by a photon hitting the pixel of a DEPFET-type detector while it is read out (more details in Appendix C.3). Therefore, the measured values of the signal (the so-called PHA) should never be seen as the reconstructed photon energy, but as the channel of the instrument response function in which the photon is measured. The proper assignment of the energy is only done in the reconstruction step.
It is clearly desirable for a simulator to explicitly predict such effects. When trying to analyze these simulated data however, any effect on the reconstructed energy needs to calibrated out. As the simulator predicts these effects, the task of calibration does not constitute a fundamental problem. It can also be used to produce calibration files, which mainly consist of adding these corrections to the RMF, which can then be used in standard X-ray data analysis tools (such as Xspec or ISIS) to analyze the simulated data. We emphasize that there is a danger of double counting when using a response matrix that already includes the effects of charge splitting and the lower energy threshold for modeling the detector itself.
If applicable and specified in the XML file, in SIXTE such a calibration is performed automatically. We note that in many cases it might be desirable to investigate the uncalibrated events and therefore this calibration is added as additional information in the output event file as a pulse invariant (PI) value instead of the commonly used PHA.
2.7. The software
The functionality of the simulation code is contained in the two separate software packages SIMPUT and SIXTE. All software is freely available10 and licensed under the GNU General Public License11. The software runs under Linux and Mac OSX and does not have any special dependences on other software besides standard libraries such as libgsl or libboost.
The SIMPUT package comprises the SIMPUT library, which contains basic functions to access SIMPUT files, a set of tools to handle the generation and management of these files, and functions to produce photons for the sources specified through SIMPUT files, and therefore can be used as a starting point in the development of more specialized instrument simulations. As shown in Appendix B.1, these tools allow, for example, the easy inclusion of an Xspec (Arnaud 1996) spectral model in a SIMPUT file.
The SIXTE package implements the setup and handling of instrument models, building on the SIMPUT library for the photon-generation process. SIXTE provides the simulation tools for a generic detector model and for multiple specific instrument models. An example of the usage of these tools is shown in Appendix B.2.
The majority of the code is implemented in C and can be compiled and installed using the GNU Autotools. Data are stored in FITS files using the cfitsio library (Pence 1999). In particular, as also mentioned in the previous sections, the instrument calibration files follow the standards of HEASARC12. The interface of the implemented tools is designed similarly to the ftools13 using the parameter interface library (PIL; Borkowski et al. 2002) or APE to read program parameters and other functionality of the HEAsoft package. Physical units in the FITS files are specified according to George & Angelini (1995).
The complete SIMPUT and SIXTE software package is managed by the Remeis Observatory (Bamberg, Germany), including a helpdesk reachable by email14. The software is managed under GIT version control, and official versions are released every few months and announced on the user mailing list15. The correct functionality of each release is verified by an automated test suite before it is published. Detailed information on the software including a large tutorial can be found in the simulator manual, which is constantly updated along releases and can be downloaded from the homepage.
3. SIXTE example studies
In this section we present examples of applications of the SIXTE software. Due to its generic implementation, a much wider range of different instruments than the ones listed below can be modeled. However, a comprehensive overview is not the intention of this article. In the following we highlight different aspects and use-cases for the simulator of existing and future detectors.
As SIXTE is the official end-to-end simulator of the eROSITA mission and both instruments on-board Athena, the WFI and the X-IFU, the following examples focus on these missions to illustrate simultaneously the wide range of applications and the reason for using the SIXTE simulator as a tool for science and detector simulations. The separated TES simulator included in the SIXTE software has been described in Wilms et al. (2016).
3.1. All-sky survey with eROSITA
The eROSITA experiment on SRG consists of seven co-aligned Wolter type I telescopes, each with its own p–n junction CCD (pnCCD) detector (Predehl 2012). The main objective of the mission is the performance of an all-sky survey in the X-ray band 0.5–10 keV (see Merloni et al. 2012, for more information). The imaging properties of the telescopes (Friedrich et al. 2008, 2012b) have to be well understood in order to identify the large number of discovered objects as either extended, such as galaxy clusters, or point-like, such as AGNs. This task is especially challenging for weak sources since the number of detected photons will be limited. In order to test and develop algorithms for (transient) source detection before the start of the mission, realistic simulations are crucial.
As shown in Fig. 5, the PSF strongly depends on the off-axis angle of the incident photons. Since the eROSITA all-sky survey will be performed in a slew mode (illustrated in Fig. 6), the image of an individual source is determined by a superposition of contributions from the PSF at different off-axis angles. The problem is even more complicated because the alignment of the slew motion is different for different locations in the sky, and the detectors are rotated with respect to each other. Therefore, an accurate analysis of the imaging properties has to be carried out for the position of the source in order to be able to fully exploit the observed data.
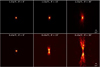 |
Fig. 5. eROSITA PSF at 1.5 keV for different off-axis angles from PANTER measurements (Burwitz et al. 2014). The on-axis PSF has a full width at half maximum (FWHM) of 16 arcsec, which deteriorates for larger off-axis angles leading to an average survey PSF of 25−30 arcsec The images are in linear scaling, and are upscaled and smoothly interpolated from the measured data by a factor of three. |
 |
Fig. 6. Detector image of multiple scanning observations over Cyg X-1 during a half-year period of the eROSITA all-sky survey. Due to the scanning motion of the spacecraft, individual passages over the source appear as stripes on the detector. Their width is relatively narrow in the center of the FOV and gets wider towards the edge according to the different quality of the PSF. In order to obtain an image of the observed target, the individual events have to be projected to the sky, taking into account the attitude of the telescope at the time of each observation. The image shows the complete FOV of eROSITA ( |
SIXTE is perfectly suited for this task because it can take into account the motion of the instrument through the appropriate attitude file as well as an energy- and angle-dependent model of the PSF. Importantly, the simulator allows the measured PSF and vignetting curve to be implemented into the simulation.
In the course of studying the overall survey performance of eROSITA, a multitude of SIXTE simulations have been performed. Whenever possible, measured calibration data (RMF, ARF, PSF, vignetting) have been used to create an output as close as possible to what eROSITA will measure. One important example is a full all-sky simulation.
Figure 7 shows a representative half-year survey of eROSITA simulated by SIXTE using the predicted attitude (Robrade, priv. comm.). The input to the simulation consists of several different SIMPUT files, including the complete ROSAT All-Sky Survey (RASS; Voges et al. 1999), the extended ROSAT soft X-ray background (Snowden et al. 1997), 589 variable bright sources from the RXTE-ASM, including their light curves, the Galactic ridge emission from unresolved sources (Türler et al. 2010), and extended objects such as M31 or the Galactic center region.
 |
Fig. 7. All-sky simulation with the full eROSITA setup for a half-year survey. Details on the simulated sources can be found in the text. Faint stripes are artifacts from the slightly inhomogeneous sampling of the extended ROSAT emission included in the simulation. We note that more counts are simulated at the poles, as the survey has a much larger exposure there and not due to differences in the sky brightness in these areas. |
This full all-sky survey of eROSITA includes a complex instrument setup containing measured calibration data, such as the PSF, combined with the predicted attitude, and a simulation input consisting of many different astrophysical objects. This simulation provided a rich data set for pre-flight studies, highlighting its capabilities and also allowing for sensitivity studies, including a test of the source detection software currently under development (Brunner et al. 2018). See Clerc et al. (2018) for further examples of SIXTE simulations for eROSITA.
3.2. The CDF-S with Athena WFI
As a second example illustrating imaging simulations, we present the result of a simulation of one snapshot of the Chandra Deep Field–South (CDFS) with the WFI large detector array, performed as part of a sensitivity study for Athena. This region has been chosen as it is mostly populated by very faint sources and has been subject to various long observations with Chandra (Giacconi et al. 2002; Lehmer et al. 2005; Luo et al. 2008; Xue et al. 2011) and XMM-Newton (Comastri et al. 2011). Therefore, rich input data exist allowing for a realistic simulation and also providing the opportunity for a detailed comparison with currently operating missions.
For the simulation, we used various types of input:
-
For the central region, we converted the catalog provided by Xue et al. (2011) from multiple observations with Chandra into a SIMPUT file. Additional sources from the extended CDFS (Lehmer et al. 2005) complement the data in the area that is not covered by the previous catalog. The spectra of the sources in both catalogs have been modeled with an absorbed power law, which is a sufficient approximation, as the main aim of this simulation is a demonstration of the imaging capabilities of the instrument.
-
As the extended CDFS still does not cover the entire FOV of the WFI, we added a sample of synthetic, randomly distributed AGNs to fill the gaps at the edge of the field. The source properties were chosen to resemble the observed log N–log S-distribution (Hasinger et al. 2001; Brandt & Hasinger 2005; Cappelluti et al. 2007, 2009; Comastri & Brusa 2008, and references therein) and the overall CXB spectrum following the distribution of spectral types according to Gilli et al. (2007) 16.
-
In addition, we compiled a catalog based on a list of galaxy groups (Finoguenov et al. 2015) and a β-model (King 1972; Jones & Forman 1999) for the radial surface brightness profile of the galaxy clusters. The spectra are modeled with apec (Smith et al. 2001).
The WFI large detector array consists of four single DEPFET chips (see Fig. 8a), with a small gap between each one (see Meidinger et al. 2017). This detector setup allows for a very large 40′ FOV, which, in combination with a 5″ PSF and the large effective area of Athena, will allow the detection of many very faint and distant objects in the early universe. As sources situated in the gaps would therefore not be observed, it is essential that Athena will be dithering during these observations. SIXTE easily allows the use of an attitude file to describe this dithering, which we have chosen to be a Lissajous-type pattern. The exposure map is shown in Fig. 8b.
 |
Fig. 8. a: detector geometry of the WFI large detector array, showing the gaps between the chips and where the read-out is located (red line). b: exposure map showing the dithering used to more homogeneously distribute the exposure despite the gaps. c: 80 ks observation of the CDFS with the WFI (40′ FOV), including dithering of the satellite. |
Finally, the simulated 80 ks observation of the CDFS is shown in Fig. 8c, which evidently shows no gaps due to the dithering over the large FOV. This simulation illustrates the outstanding sensitivity of the Athena WFI in just one snapshot, revealing a large number of distinct sources. Further studies on this simulated data set can be performed, for example to determine the limit for detecting faint sources.
3.3. Merging galaxy clusters with the Athena X-IFU
To illustrate a combination of high-resolution spectroscopy and imaging, we next show a simulation that utilizes the X-IFU instrument on Athena. This detector will be based on a large array of TES operating at 50 mK, which results in an energy resolution of 2.5 eV (Barret et al. 2018). In combination with the good imaging capabilities of Athena with a 5″ resolution over the 5′ FOV of the X-IFU, one of its main science goals are studies of the properties of galaxy clusters through spatially resolved high-resolution spectroscopy.
As an example, here we show a single simulation of the starburst galaxy M 82 based on measured Chandra data. In order to account for the change of the emitted spectrum over the cluster, we construct a complex SIMPUT from the brightness distribution and two parameter maps over the same region, giving the local absorbing column (NH) and the temperature of the collisionally ionized plasma (modeled by the apec model). All data have been taken and inferred from observations. Using the powerful simputmultispec tool (see Appendix B.1), such a SIMPUT file can be automatically created from the input data.
Figure 9 shows the result of the simulations, with two spectra extracted from the image to highlight that the X-IFU will be able to measure detailed spectra, abundances, and line ratios over the extended source. We highlight the superior signal-to-noise ratio and rich emission line spectrum, extracted from a very small region of just 3 × 3 pixels out of more than 3000 total pixels for a single 100 ks observation. Such simulations help to provide a glimpse of the data we can expect from the X-IFU, importantly also allowing us to develop methods for analyzing data sets of this kind, as Athena will routinely observe such sources.
 |
Fig. 9. Simulated 100 ksec observation of the starburst galaxy M 82 with the Athena X-IFU. The image in the center shows the inner arcminutes as simulated by SIXTE. For the two regions (indicated by green and blue) we extracted spectra, which are plotted in the left and right panels together with the input model (gray line). For each spectrum we provide a zoom into the region around 1.1 keV to highlight the difference in observed lines. |
Detailed SIXTE simulations of galaxy clusters have been performed by Roncarelli et al. (2018) and Cucchetti et al. (2018). The latter study is based on astrophysics simulations with the GADGET-3 smoothed-particle hydrodynamics code (Rasia et al. 2015; Biffi et al. 2018). Using these SPH simulations as input, the analysis of the SIXTE simulations could verify that the X-IFU is able to routinely measure the chemical abundance and also the turbulent velocity in these clusters down to a precision of 10 km s−1.
In Brand et al. (2016) we performed another study, which analyzes the capabilities of the X-IFU to detect the warm and hot intergalactic medium (WHIM) in absorption from measurements of gamma-ray bursts (GRBs). Such measurements of the baryonic matter in the universe are a core science objective of the X-IFU, but also pose strong requirements on how fast Athena has to react to alerts in order to be able to detect such short events only lasting a few hours. Extensive SIXTE simulations showed that with the currently envisaged setup Athena will be able to detect a few of these events per year.
3.4. Simulating pile-up in silicon detectors
Besides complex science observations, SIXTE is also very well suited to supporting the detector development and characterizing the detector performance.
For brighter sources, one important issue in silicon-based detectors is the increase of pile-up events in the detector. These events arise when two photons hit the detector during the same read-out frame and at the same position, and are therefore read out simultaneously. Such events can not be separated and will be mistakenly identified as only one event with the combined energy of both photons. For an increasing source flux, the likelihood of such events increases and will inevitably result in a change in spectral shape beyond a certain threshold, possibly affecting the conclusions drawn from spectral modeling. As a result, detectors will have a flux limit beyond which the fraction of pile-up events is so large that spectroscopy becomes impossible. As SIXTE is able to correctly simulate the read-out, the pile-up fraction can be predicted for any astrophysical source, since, in contrast to real observations, we know which events are piled-up in the simulation. Such simulations can be used to study the performance of currently operating detectors (such as XMM-Newton), or to predict the performance of observing bright sources for future instruments. The latter is a very crucial part of the instrument development, as will directly determine whether or not the planned science goals will be achievable with the current instrument setup17. We note that while there exist analytic studies of the pile-up effect (see Ballet 1999), simulations allow for much more detailed and realistic estimations.
In order to study the effect of pile-up in silicon-based detectors, we simulate a typical X-ray spectrum and scale it in flux. In order to ensure the same statistical quality of each simulation, we adapt the exposure time such that each obtained spectrum contains ∼106 counts. Importantly, the detailed effect that pile-up has on the spectrum is strongly dependent on the spectral shape, while its magnitude depends on the source flux. In the following we characterize the flux in units of the Crab pulsar, which we set to be Fcrab = 3.1 × 10−8 erg cm−2 s−1 in the 0.2–10 keV band for a standard Crab spectrum of an absorbed power law with photon index Γ = 2.1 and equivalent hydrogen column NH = 0.4 × 1022 cm−2. For a spectral shape deviating from this definition we require the simulated detector to measure the same count rate as for this Crab spectrum18.
To illustrate the effect pile-up has on the measured spectrum, we simulate a very soft source with a black body with a temperature of 200 eV. Figure 10 shows a simulation of such a source with the fast detector of the planned Athena-WFI instrument for an increasing flux of 0.2 Crab, 1 Crab, and 5 Crab. These flux levels yield a fraction of piled-up events among the total events of 0.15%, 0.7%, and 3.4%, respectively. Since pile-up means that two are seen as one event with the combined energy, there is a systematic shift of flux to higher energies and therefore the spectrum generally hardens with increasing pile-up.
 |
Fig. 10. Spectra from an Athena-WFI fast detector simulation of a source with a 200 eV black-body input spectrum. It can be seen that for increasing source flux the simulated spectrum starts to deviate from the input model (black line) at higher energies. |
In order to be able to quantify the effect of pile-up, we exemplarily use the above definition of the standard Crab as a typical power-law-shaped X-ray spectrum. We note that a full study of pile-up for different kinds of spectral models and source types is out of scope of this paper.
To compare the performance of a current instrument with that of a planned one, we perform simulations for the EPIC pn camera onboard XMM-Newton and for the Athena-WFI. For each instrument we simulate three different read-out modes, highlighting their different qualification to study bright sources. While in the full-frame (ff) mode of the EPIC pn one full chip is read out, in the small window (sw) mode only 63 × 64 pixels are read-out. At the cost of spatial information, the timing mode further improves the read-out speed. It uses a 200 × 64 window and using line-shifts in the CCD it combines ten rows before the read-out19. For the WFI we simulate a full-frame of one large detector chip (large), a 64-row window mode (w64) of the same chip, and the fast detector, which is the dedicated detector to observe bright sources with Athena. The fast detector is implemented 35 mm out of focus and consists of two 32 × 64 pixel chips read out simultaneously.
The results of the simulations are summarized in Fig. 11. The most basic quantity is the so-called pile-up fraction, which is the fraction of events affected by pile-up out of all detected events. Figure 11a shows that as a general trend this pile-up fraction is increasing with flux. Clearly, the important difference is that the fast read-out modes like the EPIC pn timing mode or the WFI fast detector reach a significant pile-up fraction of ∼1% only at much higher fluxes.
For a deeper understanding of how these pile-up events affect the spectral shape, we fit the simulated spectra with an absorbed power law. The flux-dependent characterization of the spectral shape (Fig. 11b) shows that for each read-out mode the obtained power-law index at low count rates agrees very well with the one of our input model (Γ = 2.1). As expected, for increasing flux there is a point for every mode where the determined Γ starts to decrease, that is, the measured spectral shape hardens. This result can be readily understood, because the energy of every pile-up event is given by the sum of at least two source photons and we are therefore artificially creating higher energetic events in the detector.
 |
Fig. 11. Simulation of a Crab-like spectrum with the EPIC pn detector on XMM-Newton and the planned Athena-WFI instrument for a selection of read-out modes with different qualification to study bright sources. Panel a: fraction of piled up events in all detected events for increasing source flux. Panel b: index of a power law fit to the simulated spectra, showing the effect of spectral distortion with increasing source flux depending on the detector and read-out mode. Panel c: obtained power-law index plotted for the determined pile-up fraction, revealing a similar and generic behavior, largely independent of the detector. |
Lastly, Fig. 11c, by plotting the photon index from the spectral fit as a function of the pile-up fraction of the respective simulated observation, illustrates how the different instruments compare in terms of their pile-up performance. The general behavior of all modes studied is similar. Most importantly, for all modes studied, the spectral shape becomes significantly distorted around 1% pile-up fraction, indicating that observations should in general strive to be below that fraction. We note that this limit only applies for sources with a similar spectrum to our chosen input model of a power law with Γ = 2.1.
4. Summary and conclusions
A detailed understanding of the instrumental features is required for the development of new X-ray missions and for the analysis and interpretation of data measured with existing instruments. This knowledge can only partly be obtained from calibration measurements. Simulations are required in order to analyze the complex phenomena arising from the assembly of the various sophisticated components making up the detection chain in an X-ray instrument. Specifically, end-to-end simulations allow a realistic description of an astrophysical source to be connected with a solid modeling of the detection and read-out process. In addition, simulated data allow comprehensive verification tests of scientific analysis software even before the launch of a new mission.
As demonstrated by the examples in Sect. 3, SIXTE provides many options for realistic simulations, covering various different instrument technologies. The supported detectors range from CCD detectors (eROSITA, XMM-Newton), to more specialized DEPFET detectors (Athena WFI), or a TES micro-calorimeter (Athena X-IFU). Additionally, the examples show that the pointing of the instrument can be easily specified to include dithering in an observation, or to simulate a full all-sky survey.
We also presented a study of the performance of a silicon-based detector for observing bright sources. Both instruments, the currently operating EPIC pn onboard XMM-Newton and the planned Athena-WFI, show very similar behavior. As a general result we conclude that above a pile-up fraction of ∼1% the spectrum becomes significantly distorted. The simulations also provide a flux limit for each read-out mode, below which sources can be observed without artificial spectral distortion from pile-up.
We have shown that the SIXTE package constitutes a universal tool for simulations of various X-ray instruments. The SIMPUT format allows for any complex source input, including time variability with light curves or power spectra, or extended sources with spectral variability. In order to ensure a reasonable simulation time, the detection process is simplified by using calibration files where possible (ARF, RMF), including a detailed representation of the optics by allowing the vignetting and the PSF to change over the FOV. A detailed implementation is given for important characteristics such as modeling the charge spread over the pixels, the detector read-out, or crosstalk in TES devices. Depending on the accuracy of the input data and instrument configuration, the simulations are therefore suitable to investigate effects which are not accessible to analytical calculations or measurements, and to connect scientific questions and goals with detector performance.
The software is designed to facilitate its use for scientific and detector development studies. After defining the source input, the simulation is run in a single step and produces an event file, which can be readily analyzed with common X-ray data-analysis tools. It already supports a large number of current and future X-ray instruments, which can be easily adjusted to add new mission configurations due to its modular concept and generic instrument model defined in an XML-like configuration file.
A study of this effect for the X-IFU is presented in Peille et al. (2018).
See https://heasarc.gsfc.nasa.gov/docs/xmm/uhb/epicmode.html for a detailed description.
Acknowledgments
We thank Andy Ptak and Mihoko Yukita for providing the data used as input for the M 82 simulation. The authors thank S. Borgani, R. Campana, M. Ceballos, B. Cobo, N. Clerc, F. Fürst, P. Friedrich, C. Großberger, I. Kreykenbohm, M. Martin, M.A. Nowak, K. Pottschmidt, M. Roncarelli, F.-W. Schwarm, P. Weber and M. Wille for helpful discussions and input. We thank the anonymous referee for valuable comments improving the paper. This work was funded by the Bundesministerium für Wirtschaft through Deutsches Zentrum für Luft- und Raumfahrt grants 50 QR 0801, 50 QR 0903, 50 QR 1103, 50 OO 1111, 50 QR 1402, and 50 QR 1603. We thank John E. Davis for the development of the SLXFIG module used to prepare the figures. This research has made use of ISIS functions (ISISscripts) provided by ECAP/Remeis observatory and MIT (http://www.sternwarte.uni-erlangen.de/isis/) and quick-look results provided by the ASM/RXTE team.
References
- Allison, J., Amako, K., Apostolakis, J., et al. 2006, IEEE Trans. Nucl. Sci., 53, 270 [Google Scholar]
- Amelio, G. F., Tompsett, M. F., & Smith, G. E. 1970, Bell Syst. Tech. J., 49, 593 [CrossRef] [Google Scholar]
- Angelini, L., Pence, W., & Tennant, A. F. 1994, The Proposed Timing FITS File Format for High Energy Astrophysics Data, OGIP/93-003, Technical report (Greenbelt, USA: GSFC) [Google Scholar]
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, eds. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [NASA ADS] [Google Scholar]
- Arnaud, K. A., George, I. M., & Tennant, A. F. 2009, The OGIP Spectral File Format, OGIP/92-007, Technical report (Greenbelt, USA: GSFC) [Google Scholar]
- Ballet, J. 1999, A&AS, 135, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barcons, X., Bregman, J., Ohashi, T., et al. 2011, IXO Assessment Study Report, Technical report (Paris: ESA) [Google Scholar]
- Barcons, X., Barret, D., Decourchelle, A., et al. 2017, Astron. Nachr., 338, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Barret, D., Trong, T. L., den Herder, J. W., et al. 2018, Space Telescopes and Instrumentation, 2018: Ultraviolet to Gamma Ray, 106991G [Google Scholar]
- Bautz, M. W., Kissel, S. E., Prigozhin, G. Y., et al. 2004, in High-Energy Detectors in Astronomy, ed. A. D. Holland, Proc. SPIE, 5501, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Bentley, J. L. 1975, Commun. ACM, 18, 509 [CrossRef] [Google Scholar]
- Biffi, V., Planelles, S., Borgani, S., et al. 2018, MNRAS, 476, 2689 [NASA ADS] [CrossRef] [Google Scholar]
- Borkowski, J., Lock, T., & Walter, R. 2002, Interface Library Users Manual (v. 1.8.5), Technical report (Versoix, Switzerland: ISDC) [Google Scholar]
- Boyle, W. S., & Smith, G. E. 1970, Bell Syst. Tech. J., 49, 587 [CrossRef] [Google Scholar]
- Brand, T., Wilms, J., Dauser, T., et al. 2016, Space Telescopes and Instrumentation 2016: Ultraviolet to Gamma Ray, 9905, 99055F [CrossRef] [Google Scholar]
- Brandt, W. N., & Hasinger, G. 2005, ARA&A, 43, 827 [Google Scholar]
- Brandt, S., Hernanz, M., Alvarez, L., et al. 2012, in Space Telescopes and Instrumentation 2012: Ultraviolet to Gamma Ray, eds. T. Takahashi, S. S. Murray, & J. W. den Herder, Proc. SPIE, 8443, 2G [Google Scholar]
- Brunner, H., Boller, T., Coutinho, D., et al. 2018, Space Telescopes and Instrumentation 2018: Ultraviolet to Gamma Ray, 106995G [Google Scholar]
- Burwitz, V., Predehl, P., Friedrich, P., et al. 2014, Space Telescopes and Instrumentation 2014: Ultraviolet to Gamma Ray, 91441X [Google Scholar]
- Calabretta, M. R., & Greisen, E. W. 2002, A&A, 395, 1077 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calabretta, M. R., & Roukema, B. F. 2007, MNRAS, 381, 865 [NASA ADS] [CrossRef] [Google Scholar]
- Cappelluti, N., Hasinger, G., Brusa, M., et al. 2007, ApJS, 172, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Cappelluti, N., Brusa, M., Hasinger, G., et al. 2009, A&A, 497, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caroli, E., Stephen, J. B., Di Cocco, G., et al. 1987, Space Sci. Rev., 45, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Cieślak, M. J., Gamage, K. A. A., & Glover, R. 2016, Radiat. Meas., 92, 59 [CrossRef] [Google Scholar]
- Clerc, N., Ramos-Ceja, M. E., Ridl, J., et al. 2018, A&A, 617, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Comastri, A., & Brusa, M. 2008, Astron. Nachr., 329, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Comastri, A., Ranalli, P., Iwasawa, K., et al. 2011, A&A, 526, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cucchetti, E., Pointecouteau, E., Peille, P., et al. 2018, A&A, 620, A173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davis, J. E. 2001, ApJ, 562, 575 [NASA ADS] [CrossRef] [Google Scholar]
- Deák, I. 1990, Random Number Generators and Simulation, Mathematical Methods of Operations Research 4 (Budapest: Akadémiai Kiadó) [Google Scholar]
- Edgar, R. J. 2011, in Handbook of X-Ray Astronomy Cambridge Observing Handbooks for Research Astronomers Detectors, eds. K. Arnaud, R. Smith, & A. Siemiginowska (Cambridge: Cambridge University Press), 23 [CrossRef] [Google Scholar]
- Eggert, T., Boslau, O., Kemmer, J., et al. 2006, Nucl. Instrum. Methods Phys. Res. Sect. A: Accel. Spectrom. Dect. Assoc. Equip., 568, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Feroci, M., Stella, L., van der Klis, M., et al. 2012, Exp. Astron., 34, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrando, P., Goldwurm, A., Laurent, P., et al. 2005, in Optics for EUV, X-Ray, and Gamma-Ray Astronomy II, Proc. SPIE, 5900, 195 [NASA ADS] [Google Scholar]
- Finoguenov, A., Tanaka, M., Cooper, M., et al. 2015, A&A, 576, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Friedman, J. H., Bentley, J. L., & Finkel, R. A. 1977, ACM Trans. Math. Softw., 3, 209 [CrossRef] [Google Scholar]
- Friedrich, P., Bräuninger, H., Budau, B., et al. 2008, in Space Telescopes and Instrumentation 2008: Ultraviolet to Gamma Ray, eds. M. J. L. Turner, & K. A. Flanagan, Proc. SPIE, 7011, 2T [Google Scholar]
- Friedrich, P., Bräuninger, H., Budau, B., et al. 2012a, Space Telescopes and Instrumentation 2012: Ultraviolet to Gamma Ray, 84431S [CrossRef] [Google Scholar]
- Friedrich, P., Bräuninger, H., Budau, B., et al. 2012b, in Space Telescopes and Instrumentation 2012: Ultraviolet to Gamma Ray, eds. T. Takahashi, S. S. Murray, & J. W. den Herder, Proc. SPIE, 8443, 1S [Google Scholar]
- Gabriel, C., Ibarra Ibaibarriaga, A., & Hoar, J. 2005, in UV, X-Ray, and Gamma-Ray Space Instrumentation for Astronomy XIV, ed. O. H. W. Siegmund, Proc. SPIE, 5898, 469 [NASA ADS] [Google Scholar]
- Gatti, E., & Rehak, P. 1984, Nucl. Instrum. Methods Phys. Res., 225, 608 [NASA ADS] [CrossRef] [Google Scholar]
- Geant4 Collaboration 2003, Nucl. Instrum. Methods Phys. Res. A, 506, 250 [Google Scholar]
- George, I. M., & Yusaf, R. 1994, The OGIP Format for “Vignetting” Functions, CAL/GEN/92-021, Technical report (Greenbelt, USA: GSFC) [Google Scholar]
- George, I. M., & Angelini, L. 1995, Specification of Physical Units within OGIP FITS Files, OGIP/93-001, Technical report (Greenbelt, USA: GSFC) [Google Scholar]
- George, I. M., & Yusaf, R. 1995, The OGIP Format for 2D (Image) Point Spread Function Datasets, CAL/GEN/92-027, Technical report (Greenbelt, USA: GSFC) [Google Scholar]
- George, I. M., Arnaud, K. A., Ruamsuwan, B. P. L., & Corcoran, M. F. 1998, The Calibration Requirements for Spectral Analysis, Technical report (Greenbelt, USA: GSFC) [Google Scholar]
- George, I. M., Arnaud, K. A., Ruamsuwan, B. P. L., & Corcoran, M. F. 2007, The Calibration Requirements for Spectral Analysis, Technical report (Greenbelt, USA: GSFC) [Google Scholar]
- Giacconi, R., Zirm, A., Wang, J., et al. 2002, ApJS, 139, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Gilli, R., Comastri, A., & Hasinger, G. 2007, A&A, 463, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Gould, H., Tobochnik, J., & Christian, W. 2006, An Introduction to Computer Simulation Methods: Applications to Physical Systems, 3rd edn. (San Francisco: Addison-Wesley) [Google Scholar]
- Greisen, E. W., & Calabretta, M. R. 2002, A&A, 395, 1061 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grindlay, J., Allen, B., Angelini, L., et al. 2011, The Hard X-Ray Imager for MIRAX, Technical report (Washington: NASA) [Google Scholar]
- Groeneveld, H. A. 1999, PhD Thesis, Eberhard-Karls-Universität Tübingen [Google Scholar]
- Hanisch, R. J., Farris, A., Greisen, E. W., et al. 2001, A&A, 376, 359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harrison, F. A., Boggs, S., Christensen, F., et al. 2010, in Space Telescopes and Instrumentation 2010: Ultraviolet to Gamma Ray, eds. M. Arnaud, S. S. Murray, & T. Takahashi, Proc. SPIE, 7732, 0S [Google Scholar]
- Hasinger, G., Altieri, B., Arnaud, M., et al. 2001, A&A, 365, L45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hoare, C. A. R. 1962, Comput. J., 5, 10 [CrossRef] [MathSciNet] [Google Scholar]
- Jansen, F., Lumb, D., Altieri, B., et al. 2001, A&A, 365, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, C., & Forman, W. 1999, ApJ, 511, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Kimmel, N., Hartmann, R., Holl, P., et al. 2006, in High Energy, Optical, and Infrared Detectors for Astronomy II, eds. D. A. Dorn, & A. D. Holland, Proc. SPIE, 6276, 0D [Google Scholar]
- King, I. R. 1972, ApJ, 174, L123 [NASA ADS] [CrossRef] [Google Scholar]
- Klein, R. W., & Roberts, S. D. 1984, Simulation, 43, 193 [CrossRef] [Google Scholar]
- Koyama, K., Tsunemi, H., Dotani, T., et al. 2007, PASJ, 59, 23 [Google Scholar]
- Lehmer, B. D., Brandt, W. N., Alexander, D. M., et al. 2005, ApJS, 161, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Lumb, D. H., Berthiaume, G. D., Burrows, D. N., et al. 1991, Exp. Astron., 2, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Luo, B., Bauer, F. E., Brandt, W. N., et al. 2008, ApJS, 179, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Madsen, K., Alexander, D., Bhalerao, V., et al. 2011, Amer. Astron. Soc., 12, 43.08 [Google Scholar]
- Martin, M. 2009, Dissertation, Eberhard-Karls-Universität Tübingen [Google Scholar]
- Meidinger, N., Andritschke, R., Elbs, J., et al. 2011, in UV, X-Ray, and Gamma-Ray Space Instrumentation for Astronomy XVII, ed. L. Tsakalakos, Proc. SPIE, 8145, 02 [Google Scholar]
- Meidinger, N., Barbera, M., Emberger, V., et al. 2017, UV, X-Ray, and Gamma-Ray Space Instrumentation for Astronomy XX, 103970V [Google Scholar]
- Merloni, A., Predehl, P., Becker, W., et al. 2012, ArXiv e-prints [arXiv:1209.3114] [Google Scholar]
- Moore, M. 1991, PhD Thesis, University of Cambridge [Google Scholar]
- Oertel, M. 2013, Diplomarbeit, Friedrich-Alexander-Universität Erlangen-Nürnberg [Google Scholar]
- Pavlinsky, M., Levin, V., Akimov, V., et al. 2018, Space Telescopes and Instrumentation 2018: Ultraviolet to Gamma Ray, 106991Y [Google Scholar]
- Peille, P., Ceballos, M. T., Cobo, B., et al. 2016, Space Telescopes and Instrumentation 2016: Ultraviolet to Gamma Ray, 9905, 99055W [CrossRef] [Google Scholar]
- Peille, P., Dauser, T., Kirsch, C., et al. 2018, J. Low Temp. Phys., 193, 940 [NASA ADS] [CrossRef] [Google Scholar]
- Penacchioni, A. V., Braga, J., D’Amico, F., et al. 2017, in The protoMIRAX Hard X-Ray Imaging Balloon Experiment, The Fourteenth Marcel Grossmann Meeting WORLD SCIENTIFIC, 3321 [Google Scholar]
- Pence, W. 1999, in Astronomical Data Analysis Software and Systems VIII, eds. D. M. Mehringer, R. L. Plante, & D. A. Roberts, ASP Conf. Ser., 172, 487 [NASA ADS] [Google Scholar]
- Pence, W. D., Chiappetti, L., Page, C. G., et al. 2010, A&A, 524, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ponz, J. D., Thompson, R. W., & Munoz, J. R. 1994, A&AS, 105, 53 [NASA ADS] [Google Scholar]
- Popp, M. 2000, PhD Thesis, Ludwig-Maximilians-Universität München [Google Scholar]
- Predehl, P. 2012, in Space Telescopes and Instrumentation 2012: Ultraviolet to Gamma Ray, eds. T. Takahashi, S. S. Murray, & J. W. den Herder, Proc. SPIE, 8443, 1R [Google Scholar]
- Predehl, P., Andritschke, R., Becker, W., et al. 2014, Space Telescopes and Instrumentation 2014: Ultraviolet to Gamma Ray, 91441T [Google Scholar]
- Predehl, P., Bornemann, W., Bräuninger, H., et al. 2018, Space Telescopes and Instrumentation 2018: Ultraviolet to Gamma Ray, 106995H [Google Scholar]
- Preparata, F. P., & Shamos, M. I. 1985, Computational Geometry. An Introduction (New York: Springer) [Google Scholar]
- Rasia, E., Borgani, S., Murante, G., et al. 2015, ApJ, 813, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Roncarelli, M., Gaspari, M., Ettori, S., et al. 2018, A&A, 618, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmid, C. 2012, PhD Thesis, Friedrich-Alexander-Universität Erlangen-Nürnberg [Google Scholar]
- Schmid, C., Martin, M., Wilms, J., et al. 2010, AIP Conf. Proc., 1248, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Schmid, C., Wilms, J., Oosterbroek, T., et al. 2011, in Fast X-Ray Timing and Spectroscopy at Extreme Count Rates, eds. D. Barret, M. Mendez, & S. Paltani, Proc. Sci. HTRS 2011, 070 [CrossRef] [Google Scholar]
- Schmid, C., Brand, T., Kuehnel, M., et al. 2012, in An INTEGRAL View of the High-Energy Sky (the First 10 Years) - 9th INTEGRAL Workshop and Celebration of the 10th Anniversary of the Launch, eds. A. Goldwurm, F. Lebrun, & C. Winkler, Proc. Sci. INTEGRAL 2012, 152 [Google Scholar]
- Schmid, C., Smith, R., & Wilms, J. 2013, SIMPUT - A File Format for Simulation Input, Technical report (Cambridge: HEASARC) [Google Scholar]
- Smith, R. K., Brickhouse, N. S., Liedahl, D. A., & Raymond, J. C. 2001, ApJ, 556, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. K., Abraham, M., Allured, R., et al. 2017, UV, X-Ray, and Gamma-Ray Space Instrumentation for Astronomy XX, 103970Q [Google Scholar]
- Snowden, S. L., Egger, R., Freyberg, M. J., et al. 1997, ApJ, 485, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Timmer, J., & König, M. 1995, A&A, 300, 707 [NASA ADS] [Google Scholar]
- Treberspurg, W., Andritschke, R., Bähr, A., et al. 2017, UV, X-Ray, and Gamma-Ray Space Instrumentation for Astronomy XX, 103970U [Google Scholar]
- Türler, M., Chernyakova, M., Courvoisier, T. J. L., et al. 2010, A&A, 512, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Voges, W., Aschenbach, B., Boller, T., et al. 1999, A&A, 349, 389 [NASA ADS] [Google Scholar]
- Weisskopf, M. C., Brinkman, B., Canizares, C., et al. 2002, PASP, 114, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Wells, D. C., Greisen, E. W., & Harten, R. H. 1981, A&AS, 44, 363 [NASA ADS] [Google Scholar]
- Wille, M. 2011, Diplomarbeit, Friedrich-Alexander-Universität Erlangen-Nürnberg [Google Scholar]
- Wilms, J., Smith, S. J., Peille, P., et al. 2016, SpaceTelescopes and Instrumentation 2016: Ultraviolet to Gamma Ray, 9905, 990564 [CrossRef] [Google Scholar]
- Wise, M. W., Huenemoerder, D. P., & Davis, J. E. 1997, in Astronomical Data Analysis Software and Systems VI, eds. G. Hunt, & H. Payne, ASP. Conf. Ser., 125, 477 [NASA ADS] [Google Scholar]
- Wolter, H. 1952, Ann. Phys., 10, 94 [Google Scholar]
- Xue, Y. Q., Luo, B., Brandt, W. N., et al. 2011, ApJS, 195, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Zane, S., Walton, D., Kennedy, T., et al. 2012, in Space Telescopes and Instrumentation 2012: Ultraviolet to Gamma Ray, eds. T. Takahashi, S. S. Murray, & J. W. den Herder, Proc. SPIE, 8443, 2F [Google Scholar]
- Zoglauer, A., Kruse-Madsen, K., Kitaguchi, T., et al. 2011, Amer. Astron. Soc., 12, 43.07 [Google Scholar]
Appendix A: Coordinate systems
A.1. Sky coordinate system
Unless specifically detailed, SIMPUT and SIXTE use an equatorial coordinate system with RA and Dec to describe position on the sky. The transformation between the sky images or coordinates and the detector plane is described by the World Coordinate System (WCS; Greisen & Calabretta 2002; Calabretta & Greisen 2002) and performed with the WCSLIB20 library. Any FITS images as source input will therefore be correctly transformed, as long as they contain a valid WCS header describing the transformation from the given image coordinates to sky coordinates.
A.2. Instrument coordinate system
The instrument coordinate system (X, Y) is defined as a planar Cartesian system located in the focal plane behind the instrument optics. Its units are in meters, with the origin being the point of intersection between the optical axis and the focal plane. If an attitude file is used which has the keyword ALIGNMEN set to MOTION, the X-axis of the instrument coordinate system points along the direction of motion of the pointing vector. In any other case, the X-axis points towards the celestial north pole. The Y-axis then points towards the west. If additionally a roll angle is defined in the attitude file, the X- and Y-axes as described before are rotated around the optical axis by this angle. The roll angle is defined clockwise, as projected onto the sky.
A.3. Detector coordinate system
To describe a detector, the detector coordinate system is introduced. Its new axes are named RAWX and RAWY, and are measured in units of pixels. The physical size of the pixels is defined via the keys xdelt and ydelt. We note that the coordinate system can be shifted with respect to the instrument system. This is done via the XML-detector description and its WCS coordinate tags. The keys xrval and yrval define a point in the (X, Y)-plane. The keys xrpix and yrpix define the respective pixel coordinates which are associated with this point. The new system can also be rotated via the rota-key using the angle from the X- to the RAWX-axis, measured clockwise when projected onto the sky (i.e., the same definition as the roll angle). Figure A.1 illustrates the coordinate systems as used by SIXTE.
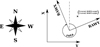 |
Fig. A.1. Coordinate systems as used by SIXTE, seen as projected onto the sky. In this figure, the X-axis points towards north. It can be realigned using an attitude file. The RAWX and RAWY axes can be rotated by the rota-key in the detector XML description. The angle is measured from the X- to the RAWX-axis clockwise when projected onto the sky. |
Appendix B: Tools and ssage
The SIMPUT and SIXTE software come with a large number of tools tailored to different purposes and to facilitate the definition of simulation input and to perform simulations. A complete overview is given in a dedicated simulator manual, which is constantly updated along with the software and can be downloaded from the SIXTE homepage21.
In the following a nonexhaustive list of important tools is given to highlight the range of possible applications of the simulator.
B.1. SIMPUT tools
As mentioned in Sect. 2, the SIMPUT software package contains a set of tools enabling the generation and handling of SIMPUT files based on the respective library routines. The following list summarizes the available programs:
-
simputfile: Generate a SIMPUT file containing a catalog with a single source, a spectrum, and optionally a light curve or a PSD and an image. A sample program call is listed below.
-
simputmerge: Merge multiple SIMPUT files.
-
simputmultipsec: Create complex SIMPUT-files where the spectrum changes over an extended region on the sky (e.g., a galaxy cluster). As input, it needs a brightness distribution, a spectral model, and one or several parameter maps, parametrizing the spatial change of the given model. The tool will then automatically create a SIMPUT, encoding the spatial change of the model (see the X-IFU simulation of M 82 in Sect. 3.3).
In order to illustrate how easily SIMPUT files can be generated with the appropriate tools of the SIMPUT software package, we show the assembly of a file with a single point-like X-ray source located at RA = 23.8°, Dec = −12.9°. The spectral model for the source is provided in the file model.xcm. With these input data, the file can be generated by the following command:
simputfile Simput=source.simput \ Src_ID=1 Src_Name=mysource \ RA=23.8 Dec=−12.9 \ XSPECFile=model.xcm Emin=2 Emax=10
Of course, SIMPUT files can also be constructed using the library routines in other programs as well as by generating the relevant FITS structure “by hand” using one of the many available libraries generating FITS such as CFITSIO or pyFITS.
B.2. SIXTE tools
The SIXTE software package contains a set of tools to perform simulations with different X-ray instruments. A selection of the most relevant tools is given below.
runsixt
-
Performs a simulation using the generic instrument model. It performs the full simulation as detailed in Sects. 2.3–2.5, from generating X-ray photons according to the source definition, imaging in a Wolter-type telescope, modeling the detection process, and performing the pattern recombination task. It outputs a standard event file. We note that there are separate tools as well, to perform the individual tasks outlined above.
xifupipeline
-
Similar to runsixt, but allows simulation of calorimeter-type detectors such as the X-IFU. Allows for a more flexible assembly of pixels (e.g., in a hexagon). The simulation includes the event grading, which depends on the separation of the events in time, and optionally also thermal and electrical crosstalk effects.
erosim
-
Derivative of runsixt specialized to the setup of the eROSITA experiment, to allow the simultaneous simulation of all seven sub-instruments.
athenawfisim
-
Derivative of runsixt specialized to the large detector array setup of the Athena WFI, consisting of four chips.
makespec
-
Produces a PHA spectrum (Arnaud et al. 2009) from the event list generated by the detector simulation.
makelc
-
Produces a light curve (Angelini et al. 1994) from the event list generated by the detector simulation.
ero_vis
-
Determines the visibility of X-ray sources at particular positions in the sky during the eROSITA all-sky survey based on the corresponding attitude file.
-
Coded mask detectors can be simulated in a threefold process (see Oertel 2013): (1) comaimg models the photon absorption and transmission process through a coded mask and determines their impact positions on the detector (2) comadet processes these impact positions and produces an event list (Oertel 2013). (3) comarecon reconstructs the positions of the illuminating sources based on the shadow pattern on the detector, which is arising from the absorption by the coded mask.
The following example of a simulation with a model of one of the seven eROSITA sub-instruments illustrates the usage of these tools:
runsixt \ XMLFile=erosita.xml \ Attitude=allskysurvey.att \ Exposure=86400.0 \ Simput=source.simput \ EvtFile=events.fits \
This program call initiates a simulation of a 1-day interval of the eROSITA all-sky survey based on the attitude specified in the FITS file allskysurvey.att. The model of the instrument is defined in the XML file erosita.xml. The observed X-ray source is described in the SIMPUT file source.simput. The output of the simulation is stored in the FITS file event.fits.
Appendix C: XML instrument configuration
One of the key features of SIXTE is the possibility to enable simulations for a wide range of different X-ray instruments. The necessary flexibility is achieved by using a generic telescope and detector module, which can be configured using a specific XML-like format. This generic approach has proven invaluable both for developing a wide coverage of various existing instruments with different operation modes and for implementations of new instrumentation in the course of several assessment studies. Especially for the latter purpose the XML format is very convenient for studying modifications of an instrument setup.
For all supported instruments, including different, relevant read-out modes, the XML configuration files, including additional instrument calibration files, are available for download on the SIXTE homepage.
Below, we illustrate the power of this concept giving examples for the setup of an eROSITA sub-instrument, the burst mode of the European Photon Imaging Camera (EPIC) pn aboard XMM-Newton, and the burst option of the X-Ray Imaging Spectrometer (XIS) aboard Suzaku. More details on this format, such as a description of the XML tags, are given in the simulator manual.
C.1. One eROSITA telescope
The XML code below represents the definition of TM1, one of the seven eROSITA sub-instruments consisting of a telescope and a detector.
<?xml version="1.0"?> <instrument telescop="eROSITA" instrume="TM1"> <telescope> <arf filename="tm1_arf_filter_000101v02.fits"/> <fov diameter="1.02"/> <focallength value="1.6"/> <vignetting filename="erosita_vig_v2.1.fits"/> <psf filename="erosita_psf_v3.1.fits"/> </telescope> <detector> <dimensions xwidth="384" ywidth="384"/> <pixelborder x="0." y="0."/> <wcs xrpix="192.5" yrpix="192.5" xrval="0." yrval="0." xdelt="75.e-6" ydelt="75.e-6" rota="90"/> <rmf filename="sixte_erormf_singles.rmf"/> <cte value="1"/> <split type="exponential" par1="0.355"/> <phabackground filename="sixte_ero_particle.pha"/> <threshold_readout_lo_keV value="50.e-3"/> <threshold_event_lo_keV value="150.0e-3"/> <threshold_pattern_up_keV value="12."/> <readout mode="time"> <wait time="0.05"/> <loop start="0" end="383" increment="1" variable="$i"> <readoutline lineindex="0" readoutindex="$i"/> <lineshift/> <wait time="0.3e-6"/> </loop> <newframe/> </readout> </detector> </instrument>
The telescope has a FOV with a diameter of 1.02 deg and a focal length of 1.6 m. The PSF and vignetting function are described in two separate files including several data sets for different energies and off-axis angles.
The detector consists of 384 × 384 pixels with an area of 75 μm × 75 μm each. The applied coordinate system is centered on the detector. Its origin coincides with the intersection of the optical axis of the telescope with the detector plane and is rotated by 90°. The pixels have no borders. The presented detector model does not include a particular framestore area as the real eROSITA charge-coupled devices (CCDs; Meidinger et al. 2011). Instead the collected charges in the sensitive part of the pixel array are read out with the same speed as the transfer time to the framestore area would require.
The combined ARF of the instrument, which takes into account the effective area of the telescope and the quantum efficiency of the detector, is stored in the file tm1_arf_filter_000101v02.fits. The energy resolution of the detector and related effects such as an escape peak are described by the RMF. A charge transfer efficiency (CTE) of 100 % is assumed and charge cloud splitting between neighboring pixels is simulated according to an exponential model model developed by Dennerl (priv. comm.). Random background events are inserted from the PHA background file sixte_ero_particle.pha.
The lower threshold for the measuring a signal is set to 50 eV. The pattern analysis algorithm selects only events with a signal of more than 150 eV as main events, which are below an upper threshold of 12 keV.
The read-out mode of the CCD is characterized by an exposure time of 50 ms followed by 384 subsequent read-outs and line shifts, which is illustrated in Fig. C.1. As mentioned above, instead of using a framestore area, for the read-out process a high line shift rate is used. A single line shift lasts 0.3 μs, that is, the read-out of the whole array takes about 115 μs and is equivalent to the transfer from the image to the framestore area.
With this XML description the essential parameters of a single eROSITA telescope and detector sub-system are defined. Similar XML definition files for various instruments can be found in the SIXTE software package.
C.2. Suzaku XIS burst option
The XIS aboard Suzaku in the normal mode provided a burst option in order to avoid pile-up for observations of bright X-ray sources. With this option, the exposure time b can be set to an arbitrary value in 1/32 s steps (Koyama et al. 2007).
Before the actual exposure takes place, the detector waits for an interval of 8 s − b. All signals collected in the 1024 × 1024 pixels of the CCD during this period are then transferred out of the imaging area and flushed without recording. In parallel, charge is injected into particular rows of the CCD according to the spaced-row charge injection mechanism, which mitigates the effects of radiation damage (Bautz et al. 2004; Koyama et al. 2007). The entire procedure results in a transfer time of 156 ms.
The signals collected during the subsequent science exposure of length b are transferred to the framestore area and read out from there. As this second transfer takes place without charge injection, it only requires 25 ms.
The described detector operation can be implemented in SIXTE with the appropriate XML tags, in this case using for an exposure b = 0.094 s:
<readout mode="time"> <wait time="7.906"/> <loop start="0" end="1023" increment="1"> <clearline lineindex="0"/> <lineshift/> <wait time="0.000152"/> </loop> <wait time="0.094"/> <loop start="0" end="1023" increment="1" variable="$i"> <readoutline lineindex="0" readoutindex="$i"/> <lineshift/> <wait time="0.0000244"/> </loop> <newframe/> </readout>
Analogous to the model of the eROSITA CCD introduced in Appendix C.1, the framestore area, which is part of the real device, is not implemented in the detector model, but the charges are directly read out from the bottom line of the CCD. Due to the different duration of the first and the second charge transfer process with and without charge injection, the images obtained from observations in burst mode exhibit an asymmetric distribution of Out Of Time (OOT) events22, as illustrated in Fig. C.2.
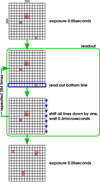 |
Fig. C.1. Schematic implementation of the read-out mode of an eROSITA CCD. For illustrative purpose not all 384 × 384 pixels are drawn. Each exposure time of 50 ms is followed by 384 subsequent read-outs and line shifts. As indicated in the text, in the simulation the transfer of signals to the framestore area, which is typical for the eROSITA CCDs, is replaced by a faster read-out with an equivalent time interval. |
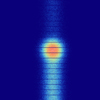 |
Fig. C.2. Simulated observation of the Crab nebula with one of the Suzaku XISs (chip width corresponds to 17 arcmin) using the burst option. The read-out direction is towards the bottom and the image is given in linear scaling. The evident asymmetric density of OOT events above and below the source is caused by the different speed of the two charge transfer processes before and after the science exposure of b = 0.094 s. |
C.3. WFI DEPFET read-out implementation
This section describes the implementation of the WFI DEPFET. The DEPFET read-out is not an instantaneous determination of the energy of the photon but it integrates first the voltage signal of the photon together with the signal baseline, and after the charge of the photon is removed by the clear, the baseline is integrated again to remove it from the measurement. In a simplified scheme, the measurement can be described with three time intervals and the corresponding integration factors, as depicted in Fig. C.3.
 |
Fig. C.3. Basic scheme of how the DEPFET read-out is implemented in SIXTE. The read-out is separated in four time steps from t0 to t4, the duration of which can be specified in the instrument description. Between the first and second integration (lower panel), the charge is removed in the clear step (upper panel) followed by a settling time. As displayed in the figure, the second integration is performed with a negative sign and therefore acts as subtraction of the baseline. |
After the initial settling, the read-out of a DEPFET begins at t0. Between t0 and t1, the signal present at the internal gate is integrated. Between t1 and t2, any charge is removed from the internal gate of the DEPFET. Between t2 and t3, the second settling occurs. Between t3 and t4, the signal is integrated again but with negative sign. The result is that the baseline signal can be subtracted from the first measurement, providing an estimate of the signal of the photon.
Misfits are photons which hit the detector during the integration time intervals. As their signal is not integrated for the full integration time, they can produce incorrect measurements. The resulting measurement Em of their true energy Ep can be described as dependent on their impact time tp:
-
tp < t0 or tp > t4: Em = Ep
-
t0 < tp < t1: Em = Ep × (t1 − tp)/(t1 − t0)
-
t2 < tp < t3: Em = −Ep
-
t3 < tp < t4: Em = −Ep × (t4 − tp)/(t4 − t3).
In the case of t3 < tp < t4, the charge is not removed in this read-out cycle and will be measured again during the next cycle, before it is cleared.
Another effect to be simulated is the limited clear speed. Instead of removing the charge instantaneously, it is cleared linearly between t1 and t2. If a photon hits the detector during this interval and causes a charge qp, it is only partially cleared and leaves a remaining charge qr, according to
The remaining charge will be measured in the second integration time and causes a negative energy measurement of the value
The charge will be measured again in the next read-out cycle. If the impact is between t2 and t3, the charge is remaining completely. If two photons impact in the same pixel during one read-out cycle, their signals add to each other.
The parameters defining the DEPFET read-out can easily be set in the XML file. In case of the full-frame read-out of on large detector of the WFI, the relevant lines are:
<detector> [...] <depfet integration="0.8e-6" clear="0.8e-6" settling="3.7e-6" type="normal"/> [...] <readout mode="time"> <loop start="0" end="511" increment="1" variable="$i"> <wait time="9.8e-6"/> <readoutline lineindex="$i" readoutindex="$i"/> </loop> <newframe/> </readout> </detector>
Appendix D: Charge cloud models
As indicated in Sect. 2.5, SIXTE needs a model to simulate the distribution of charge between neighboring pixels. The standard “Gaussian” model assumes a 2D, rotational symmetric charge cloud. We note that SIXTE also implements a specific charge cloud model, called “Exponential”, tailored specifically for eROSITA (Dennerl, priv. comm.).
In the Gaussian model, the charge fraction collected in the detector pixel with the corners (xn, ym), (xn + 1, ym), (xn + 1, ym + 1), and (xn, ym + 1) can be determined as (Popp 2000):
where (xi, yi) denotes the impact position of the photon and ctotal the total generated charge. As the charge cloud size (σ ∼ 10 μm) is typically smaller than the size of the detector pixels, Eq. (D.1) is evaluated only for the four pixels directly surrounding the impact position. By adjusting the size of the charge cloud and the lower detection threshold for split partners, the simulated pattern distribution can be adjusted to fit measurements with real detectors, as shown in Fig. D.1 for the EPIC pn camera on XMM-Newton.
 |
Fig. D.1. Comparison of the Gaussian charge cloud model (dashed lines) with the distribution of pattern types obtained with the SAS task epatplot (solid lines) for an observation of Cen A with the EPIC pn camera on XMM-Newton operated in Small Window. The simulated distribution matches very well the values expected from the instrument model. |
All Figures
 |
Fig. 1. Flow chart illustrating the three major functional blocks of the SIXTE simulation software (yellow boxes), starting from the generation of photons from a source catalog, which are then imaged and detected in the instrument and then processed to generate an event list. |
| In the text | |
 |
Fig. 2. Schematic layout of a SIMPUT file. The source catalog contains the main characteristics of one or multiple sources, such as their positions and observed fluxes. Additional data describing energy spectra, spatial extent, and time-variability are stored in separate Header and Data Units (HDUs) and linked in the source catalog. |
| In the text | |
 |
Fig. 3. Comparison of different Poisson arrival process generators. The dashed black curve represents the input light curve. The red curve displays the simulated photon rate using a simple algorithm implementing Eq. (2) with R = r(ti−1). The blue curve is based on the algorithm introduced by Klein & Roberts (1984), which avoids the delay of the increasing photon rate for steeply rising profiles. |
| In the text | |
 |
Fig. 4. Block diagram of the photon imaging stage of SIXTE. |
| In the text | |
 |
Fig. 5. eROSITA PSF at 1.5 keV for different off-axis angles from PANTER measurements (Burwitz et al. 2014). The on-axis PSF has a full width at half maximum (FWHM) of 16 arcsec, which deteriorates for larger off-axis angles leading to an average survey PSF of 25−30 arcsec The images are in linear scaling, and are upscaled and smoothly interpolated from the measured data by a factor of three. |
| In the text | |
 |
Fig. 6. Detector image of multiple scanning observations over Cyg X-1 during a half-year period of the eROSITA all-sky survey. Due to the scanning motion of the spacecraft, individual passages over the source appear as stripes on the detector. Their width is relatively narrow in the center of the FOV and gets wider towards the edge according to the different quality of the PSF. In order to obtain an image of the observed target, the individual events have to be projected to the sky, taking into account the attitude of the telescope at the time of each observation. The image shows the complete FOV of eROSITA ( |
| In the text | |
 |
Fig. 7. All-sky simulation with the full eROSITA setup for a half-year survey. Details on the simulated sources can be found in the text. Faint stripes are artifacts from the slightly inhomogeneous sampling of the extended ROSAT emission included in the simulation. We note that more counts are simulated at the poles, as the survey has a much larger exposure there and not due to differences in the sky brightness in these areas. |
| In the text | |
 |
Fig. 8. a: detector geometry of the WFI large detector array, showing the gaps between the chips and where the read-out is located (red line). b: exposure map showing the dithering used to more homogeneously distribute the exposure despite the gaps. c: 80 ks observation of the CDFS with the WFI (40′ FOV), including dithering of the satellite. |
| In the text | |
 |
Fig. 9. Simulated 100 ksec observation of the starburst galaxy M 82 with the Athena X-IFU. The image in the center shows the inner arcminutes as simulated by SIXTE. For the two regions (indicated by green and blue) we extracted spectra, which are plotted in the left and right panels together with the input model (gray line). For each spectrum we provide a zoom into the region around 1.1 keV to highlight the difference in observed lines. |
| In the text | |
 |
Fig. 10. Spectra from an Athena-WFI fast detector simulation of a source with a 200 eV black-body input spectrum. It can be seen that for increasing source flux the simulated spectrum starts to deviate from the input model (black line) at higher energies. |
| In the text | |
 |
Fig. 11. Simulation of a Crab-like spectrum with the EPIC pn detector on XMM-Newton and the planned Athena-WFI instrument for a selection of read-out modes with different qualification to study bright sources. Panel a: fraction of piled up events in all detected events for increasing source flux. Panel b: index of a power law fit to the simulated spectra, showing the effect of spectral distortion with increasing source flux depending on the detector and read-out mode. Panel c: obtained power-law index plotted for the determined pile-up fraction, revealing a similar and generic behavior, largely independent of the detector. |
| In the text | |
 |
Fig. A.1. Coordinate systems as used by SIXTE, seen as projected onto the sky. In this figure, the X-axis points towards north. It can be realigned using an attitude file. The RAWX and RAWY axes can be rotated by the rota-key in the detector XML description. The angle is measured from the X- to the RAWX-axis clockwise when projected onto the sky. |
| In the text | |
 |
Fig. C.1. Schematic implementation of the read-out mode of an eROSITA CCD. For illustrative purpose not all 384 × 384 pixels are drawn. Each exposure time of 50 ms is followed by 384 subsequent read-outs and line shifts. As indicated in the text, in the simulation the transfer of signals to the framestore area, which is typical for the eROSITA CCDs, is replaced by a faster read-out with an equivalent time interval. |
| In the text | |
 |
Fig. C.2. Simulated observation of the Crab nebula with one of the Suzaku XISs (chip width corresponds to 17 arcmin) using the burst option. The read-out direction is towards the bottom and the image is given in linear scaling. The evident asymmetric density of OOT events above and below the source is caused by the different speed of the two charge transfer processes before and after the science exposure of b = 0.094 s. |
| In the text | |
 |
Fig. C.3. Basic scheme of how the DEPFET read-out is implemented in SIXTE. The read-out is separated in four time steps from t0 to t4, the duration of which can be specified in the instrument description. Between the first and second integration (lower panel), the charge is removed in the clear step (upper panel) followed by a settling time. As displayed in the figure, the second integration is performed with a negative sign and therefore acts as subtraction of the baseline. |
| In the text | |
 |
Fig. D.1. Comparison of the Gaussian charge cloud model (dashed lines) with the distribution of pattern types obtained with the SAS task epatplot (solid lines) for an observation of Cen A with the EPIC pn camera on XMM-Newton operated in Small Window. The simulated distribution matches very well the values expected from the instrument model. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.