EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 630 (October 2019) A&A, 630 (2019) A105 Full HTML
Free Access
Issue
A&A
Volume 630, October 2019
Article Number A105
Number of page(s) 11
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/201834327
Published online 27 September 2019

© ESO 2019

1. Introduction

Be/X-ray binary systems are the most common sub-type of high-mass X-ray binaries in which magnetised neutron stars (NSs; with a magnetic field of B ∼ 1012−13 G) accrete from their massive companions (a Be-type star in our case) while moving around them in (highly) eccentric orbits. These Be/X-ray binaries show two kinds of transient X-ray behaviour (for a review of these systems see Reig 2011): type-I (normal) and type-II (giant) outbursts. The type-I outbursts, which have a short duration (a fraction of an orbital period), are caused by the accretion of matter onto the NS when the compact object passes through the decretion disk of the companion during the periastron passage. The X-ray luminosity (LX) related to these events usually peaks at LX ∼ 1036−37 erg s−1. On the contrary, the type-II outbursts normally (although not always) last for more than an orbital period and are very bright, reaching or even exceeding the Eddington limit for a NS (LX >  2 × 1038 erg s−1). The physical mechanism behind these giant, type-II outbursts remains unclear, although several studies have approached the problem by focusing on the structure of the Be-star decretion disk and its alignment with the NS orbit (Moritani et al. 2013; Martin et al. 2014; Monageng et al. 2017) or by studying the effects of perturbations in the decretion disk (Laplace et al. 2017).

The bright active episodes of Be/X-ray transients are powered by the accretion of matter onto the NS. If the accretion rate is high, the matter can overcome the magnetospheric barrier of the NS and the material is channeled toward the magnetic poles. At the end of the outbursts, when the mass accretion rate decreases, the NS spin becomes a decisive component in the accretion process. In the case of relatively fast spinning systems (with typical spin periods, Pspin <  10−100 s; depending on the exact strength of the surface magnetic field of the NS) the ram pressure of the matter in the accretion flow is unable to overcome the magnetospheric barrier. It is generally thought that this material is then expelled from the inner part of these systems through what is called the “propeller effect” (Illarionov & Sunyaev 1975; Romanova et al. 2004; D’Angelo & Spruit 2010). If the propeller effect is not very strong, the matter might also accumulate outside of the magnetosphere in what is called a “trapped” or “dead disk” (see, e.g., Syunyaev & Shakura 1977; D’Angelo & Spruit 2012; Patruno & D’Angelo 2013; D’Angelo 2014).

In the case of the very fast spinning systems (Pspin  <   10 s), the expected luminosity below which they are assumed to be in the propeller regime is LXprop ∼ 1035−36 erg s−1. Since in this regime matter is thought to no longer be accreted on the NS, these systems are expected to be very dim in quiescence. Indeed, these systems have quiescent luminosities of only ∼1032−33 erg s−1. However, it is very likely that this low-level emission of X-rays does not have a single origin. In some systems, there is strong evidence that, despite being in the propeller regime, low-level accretion onto their NS surfaces still continues. This indicates that the propeller effect might not always be completely effective although how matter exactly reaches the NS surface is still unclear (see discussions in Orlandini et al. 2004; Mukherjee & Paul 2005; Doroshenko et al. 2014). Another possible mechanism that could produce low-level emission in the propeller regime is the accretion flow at the magnetospheric boundary. This flow could produce significant radiation and might be detectable at luminosities of ∼1032−34 erg s−1 (Campana et al. 2001). However, it is unclear exactly how the emission would be generated (see Ikhsanov 2001 and Lii et al. 2014 for discussion) and likely most of the released energy will not be emitted in the X-rays but at longer wavelengths such as the ultraviolet (see discussion in Tsygankov et al. 2016).

If no matter reaches the NS surface when Be/X-ray transients are in the propeller regime, it might be possible that the NS becomes visible at LX ∼ 1032−34 erg s−1 due to thermal emission from its surface. During the outburst, matter is deposited on the NS surface and compresses the inner layers of the crust, triggering nuclear reactions that release heat deep in the crust (e.g., Haensel & Zdunik 1990, 2003, 2008; Steiner 2012; Lau et al. 2018). This release of energy heats up the crust, which can become out of thermal equilibrium with the NS core if enough energy is generated during an outburst (e.g., Rutledge et al. 2002). Once the outburst is over and the accretion has halted, the heat is conducted both inwards to the core and outwards where it is emitted as cooling emission from the surface untill the crust-core thermal equilibrium is restored again. This process has been observed in about a dozen of accreting low-magnetic field NSs in low-mass X-ray binaries (see review of Wijnands et al. 2017) and potentially could also be observed for high-magnetic field accreting NSs. Indeed, evidence for this process has been observed in two such systems (4U 0115 + 63 and V 0332 + 53; e.g., Wijnands & Degenaar 2016; Rouco Escorial et al. 2017), although it still needs to be confirmed if indeed the cooling of the accretion-heated NS crusts was the dominant emission process. The cooling-time scale of the crust in such high-magnetic field NS systems is unclear (and might be relatively short; see discussion in Rouco Escorial et al. 2017 and Tsygankov et al. 2017a), but when it is again in equilibrium with the core, thermal emission from the surface might be still observable if the NS core is hot enough. Such surface emission has been inferred for several systems (see, e.g., Campana et al. 2002; Reig et al. 2014; Elshamouty et al. 2016; Tsygankov et al. 2017a).

In order to investigate further the emission processes potentially at work in Be/X-ray transients when not in outburst, we study the behaviour of GRO J1750−27 (also known as AX J1749.1−2639) after its 2015 type-II outburst. GRO J1750−27 is a Be/X-ray transient that harbours a 4.45 s pulsar (Bildsten et al. 1997), which orbits around its companion star every 29.8 days (Scott et al. 1997). The orbit has an eccentricity of ∼0.3. The source was discovered by the Burst And Transient Source Experiment on board of the Compton Gamma Ray Observatory in 1997 (Scott et al. 1997) and studied further by Shaw et al. (2009) during its second observed outburst in 2008. It remained dormant until a new type-II outburst started at the beginning of 2015 (Finger & Wilson-Hodge 2014).

2. Observations, analysis and results

2.1. Observations and data reduction

The Neil Gehrels Swift Observatory (from now on referred to as Swift) monitored GRO J1750−27 during its giant, type-II outburst in early 2015 using the Burst Alert Telescope (BAT) and the X-ray Telescope (XRT; see Fig. 1). The Swift/BAT data were obtained from the Swift/BAT hard X-ray transient monitor web page1 (Krimm et al. 2013) and the Swift/XRT light curve from the Swift/XRT products web interface2 (Evans et al. 2009) using our updated source position (see below). Unfortunately, the BAT missed the beginning of the type-II outburst and when it started to monitor the system the quality of the data was poor (see the large error bars on the BAT points in Fig. 1). Therefore, the exact starting date of the outburst could not be obtained from the BAT and we used the date of the first good BAT point as fiducial starting point in Fig. 1. The decay of the outburst was followed using the XRT (see Fig. 1 and Table 1 for a log of the observations), but the instrument was not sensitive enough to detect the source during the final phases of the decay and its subsequent transition into quiescence (see Fig. 1).

thumbnail Fig. 1.

Swift/XRT (blue) and Swift/BAT (black) light curves during and after the 2015 type-II outburst of GRO J1750−27. All Chandra count rates have been converted to Swift/XRT count rates using the method described in Sect. 2.1. The Chandra detections (with 1σ errors) are given as red squares. The Chandra upper limits are determined in the manner explained in Sect. 2.1 and shown as red arrows. The dotted brown line and brown arrow represent the upper limit obtained in the Chandra observation 14643 taken in May 2013, i.e., almost a year and a half before the 2015 type-II outburst. The zeropoint of the light curve (the fiducial starting point of the outburst) corresponds to December 29th, 2014.

Table 1.

Log of Swift and Chandra observations for GRO J1750−27.

Once the source was no longer detected using the Swift/XRT, our multi-year Chandra monitoring campaign (PI: Wijnands) was triggered to investigate if cooling of a potential accretion-heated crust could be observed in this source. Our Chandra campaign consisted of five observations that were performed between 2015 May 20 and 2017 May 18 (see Table 1). In addition, we report on a previous Chandra observation with observation identification (ObsID) 14643 that was obtained on 2013 May 22. All our Chandra observations were performed using the ACIS-S detector using the faint and timed detector mode. Typically a 1/4 subarray was used to limit the pile-up in case the source was unexpectedly bright, except in observation 16724 during which a 1/8 subarray was used.

We reduced and analysed the data using the CIAO tools (v. 4.9)3 and the CALDB (v. 4.7.6)4. We reprocessed the data files following the standard procedures5 and inspected each observation for any possible background flares6. We did not find any period of high background, therefore all the data were used. We detected GRO J1750−27 in three of our five Chandra observations (ObsIDs 16723, 16725 and 16726; see Table 1) at a position of RA (J2000) = 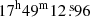and Dec (J2000) = 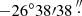6, with a 90% uncertainty radius of 0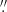9. This position was obtained using the CIAO routine WAVDETECT with default parameter values (detection threshold of sigthresh = 10−6). Our Chandra position falls well within the Swift/XRT error circle reported by Shaw et al. (2009, see left panel in our Fig. 2) obtained when the source was in outburst, demonstrating that we conclusively have detected GRO J1750−27 in quiescence.

thumbnail Fig. 2.

Close-up images (0.5–7 keV energy range) of our Chandra detections (listed by their ObsIDs; from left to right): 16723, 16725 and 16726. The blue circles indicate the source extraction regions and the dashed red annuli the background extraction regions. The green circle is the Swift/XRT error region of the source reported by Shaw et al. (2009). See Sects. 2.1 and 2.2 for more details about the detections and upper limits.

When the source was detected, we used the same source and background extraction regions as we used for our spectral analysis (see Sect. 2.3 for the details) to extract the count rates. In order to compare our Chandra count rates with the obtained Swift/XRT ones, we converted the Chandra count rates to so-called “inferred XRT count rates” (in the energy range 0.5–10 keV) using the WEBPIMMS7 tool and the spectral parameters obtained from the first Chandra detection in observation 16723 (see Sect. 2.3). When we did not detect the source, we calculated the 2σ count-rate upper limits following the method described by Gehrels (1986). The obtained Chandra upper limits were converted to XRT upper limits following the steps mentioned previously.

2.2. Light curve

As we can see from Fig. 1, the XRT count rate decreased from ∼1.6 counts s−1 at the start of the XRT observations to < 0.02 counts s−1 during the last part of the XRT monitoring. At that time, our Chandra programme had already been triggered and the first Chandra observation was taken the same day as our last Swift observation (see Table 1 for a log of our Swift and Chandra observations). Due to the better sensitivity of Chandra and the longer exposure time, the source was detected (see Fig. 2, left panel) in this first Chandra observation (ObsID 16723) with a net count rate of (9.0 ± 1.9) × 10−4 counts s−1 (24.3 ± 5.2 net source photons; for the 0.5–7 keV energy range) which resulted in an inferred XRT count rate of ∼2.6 × 10−4 counts s−1. Thus the source was almost 3 orders of magnitude fainter than when it was last detected using the XRT (see Fig. 1 and Table 1).

The next Chandra observation was obtained 68 days later and the source was not detected. We obtained an inferred XRT count rate upper limit of < 7.8 × 10−5 counts s−1 (see Table 1 for the original Chandra count-rate upper limit). After 156 days of our first observation, the source was marginally detected again in the next Chandra observation (ObsID 16725; see Fig. 2, middle panel) with a net count rate of (2.8 ± 1.2) × 10−4 counts s−1 (8.1 ± 3.3 net source photons in the 0.5–7 keV energy range) which resulted in an inferred XRT count rate of ∼7.7 × 10−5 counts s−1.

During our next Chandra observation (ObsID 16726), one year after the our first observation, the source was detected as well (see Fig. 2, right panel) with a net count rate of (5.1 ± 1.5) × 10−4 counts s−1 (14.7 ± 4.3 net source photons; 0.5–7 keV) giving an inferred XRT count rate of ∼1.5 × 10−4 counts s−1. Our last Chandra observation was obtained approximately two years later but, once again, the source was not detected resulting in an inferred XRT upper limit of < 5.7 × 10−5 counts s−1. We stacked the 2 observations were no source was detected, but this did not result in a conclusive detection8. We obtained an inferred XRT upper limit of < 3.9 × 10−5 counts s−1.

Before the 2015 outburst, Chandra observed GRO J1750−27 to determine its quiescent luminosity (PI: Wijnands). However, the exposure time was very short (∼5 ks) and consequently the source was not detected during this observation, with a count-rate upper limit of < 1.2 × 10−3 counts s−1 (see Table 1), resulting in an inferred XRT count-rate upper limit of < 3.5 × 10−4 counts s−1. This upper limit is indicated as a dotted brown line in Fig. 1. However, it is not very constraining since the count rates in the Chandra detections were lower than this pre-outburst value (as well as the upper limits obtained from the observations in which we did not detect the source).

2.3. Chandra spectral analysis

For the three Chandra observations during which GRO J1750 −27 was conclusively detected, we obtained the source spectra. The source photons were extracted using a circular region with a radius of 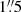centered on the new source position we previously mentioned (see Sect. 2.1). The background photons were extracted using an annulus region (centered on the same position) with an inner and outer radii of 10″ and 20″, respectively (see Fig. 2). We used the CIAO tool SPECEXTRACT to obtain the source and background spectra, as well as the response files. We grouped the spectra to 1 count per bin using GRPPHA. The spectra were fitted using XSPEC (v. 12.9.0)9 in the 0.5–10 keV energy range using W-statistics (valid for background subtracted spectra).

We fitted two main basic one-component models to the spectra: an absorbed power-law model (PEGPWRLW) and a blackbody model (BBODYRAD). In addition, we also fitted the spectra using a neutron star atmosphere model applicable for magnetised neutron stars (NSA; see Appendix B for the details and results obtained using such a model). This model could also adequately describe our Chandra spectra, however, in the rest of our paper we mainly use the results obtained when using the power-law and blackbody models in order to be able to compare our source with the other two sources (4U 0115+63 and V 0332+53), for which similar studies have been performed. However, only blackbody and power-law fit results have reported for these two sources (see Wijnands & Degenaar 2016; Rouco Escorial et al. 2017). Nevertheless, for completeness, we list our NSA model results in Appendix B.

For the absorption component, we used TBABS assuming WILM abundances (Wilms et al. 2000) and VERN cross-sections (Verner et al. 1996). Since our spectra have very few counts we could not constrain the column density from our spectral fits (see details at the end of this section) and therefore we fixed it to the expected Galactic value in the direction of GRO J1750−27 (1.03 × 1022 cm−2; Kalberla et al. 2005). In the case of the blackbody model, we left the emitting region radius and the temperature as free parameters and determined the unabsorbed 0.5–10 keV flux by using the convolution model CFLUX. For the power-law model, the energy boundaries were set to 0.5–10 keV, so that we could directly obtain the unabsorbed flux in that energy range from the model normalization. Due to the low quality of the spectra, both models could fit the data adequately and we could not determine which of the two models is preferable10. The results obtained from our spectral fits for both the power-law and the blackbody models are listed in Table 2.

Table 2.

Results of our Chandra spectral analysis.

Table 3.

Basic parameters of the systems and their type-II outbursts properties discussed in this paper.

The source distance is highly uncertain, with estimates ranging from 12 kpc to 22 kpc11 (see Shaw et al. 2009, and references therein). Unfortunately, the source is not detected with Gaia so we could not improve on the source distance ourselves (see also Appendix A). Therefore, we calculated the luminosity (for both models)12 and the radius of the emission region (for the blackbody model) using both distances. This resulted in X-ray luminosity for the source of LX ∼ 0.9−3 × 1032 erg s−1 or LX ∼ 0.3−1 × 1033 erg s−1 for the blackbody model (see Fig. 3) and LX ∼ 1.6−5.3 × 1032 erg s−1 or LX ∼ 0.5−1.8 × 1033 erg s−1 for the power-law model (see Fig. 4) assuming a distance of 12 kpc or 22 kpc, respectively. In the case of the blackbody model, there was no clear evolution in the temperature of the source (kTbb ∼ 1.1 keV; see Fig. 3); the temperatures measured for the three observations were consistent with each other. Similarly, the radii of the emission regions Rbb ∼ 26−44 m for 12 kpc and Rbb ∼ 47−80 m for 22 kpc) were consistent within the errors (see Table 2 and Fig. 3). The inferred radii are much smaller than the NS radius which would suggest that, if the blackbody model is a correct description of the spectra, the emission likely came from a small region on the NS surface, e.g., from hot spots at the magnetic poles (this conclusion also holds if we fit the spectra using a neutron star atmosphere model; see Appendix B). In the case of the power-law model, the results from the fit showed that the observed spectra are relatively hard with photon indices (Γ) of ∼0.9–1.6 (see Fig. 4 and Table 2; as also suggested by the relatively high blackbody temperatures).

thumbnail Fig. 3.

Evolution (using a blackbody model) of the spectral parameters (from the top to the bottom): the X-ray luminosity (for the energy range 0.5–10 keV), the blackbody temperature, and the associated emission radius. The orange squares are the Swift/XRT spectral results of 4U 0115+63 published by Wijnands & Degenaar (2016) and Rouco Escorial et al. (2017). The pink circles correspond to the Swift/XRT spectral results of V 0332+53 reported by Wijnands & Degenaar (2016). Luminosities and emission region radii from both sources have been recalculated using their new Gaia distances as given in Table 3. The dark stars and purple diamonds are our Chandra spectral results of GRO J1750−27 when assuming a source distance of 22 kpc or 12 kpc, respectively. Errors are 1σ. Some points of 4U 0115+63 and V 0332+53 are plotted with symbols that are larger than the corresponding error bars of these points.

thumbnail Fig. 4.

Evolution (using a power-law model) of the spectral parameters: the X-ray luminosity (for the energy range 0.5–10 keV; top panel) and the photon index (bottom panel). The colours and symbols represent the same sources as in Fig. 3. Errors are 1σ. Some points of 4U 0115+63 and V 0332+53 are plotted with symbols that are larger than the corresponding error bars of these points. The arrows indicate upper limits on the luminosity and are calculated using the method described in Sect. 2.3.

For the three Chandra observations during which the source was not detected, we converted the obtained count-rate upper limits (see Sect. 2.1 and Table 1) into flux upper limits using the WEBPIMMS tool assuming a power-law model and the spectral parameters obtained from our first Chandra detection (observation with ObsID 16723; see Table 2). We only used the power-law model because for this model we had to assume only one unknown parameter, i.e., the photon index, to obtain the flux. In the case of the blackbody model, we would have to assume values for two parameters, i.e., the radius of the emission region and its temperature (which are strongly inter-dependent) in order to determine the flux upper limits. Therefore, any upper limit determined using the blackbody model would be more affected by systematic uncertainties than one obtained using the power-law model. After obtaining the flux upper limits, we calculated the luminosity upper limits again assuming 12 and 22 kpc (see Table 2 and Fig. 4). The luminosity upper limits during the non-detection observations and the stacked one were significantly below the detection level showing that the source was fainter during these observations and indicating that the system exhibited variability in quiescence.

Since the NH is an important parameter during the spectral fitting and nothing is currently known about which exact absorption value for this parameter to be used during the quiescent state of GRO J1750−27, we tried to constrain NH from our spectral fits. For that, we assumed that the NH has always the same value for all our Chandra observations. Assuming this, we simultaneously fit the spectra of the three Chandra detections with NH tied between the spectra but it was left free during the fits. In the case of the power-law model, the obtained NH was ∼1.7 × 1022 cm−2 with a (1σ) confidence interval of [0−4.5] × 1022 cm−2 and for the blackbody model NH ∼ 1.4 × 1017 cm−2 with a confidence interval of [0−1.9] × 1022 cm−2. Therefore, the NH is not very well constrained (i.e., for the power-law model) and this is reflected in a significant increase in the errors on the other spectral parameters. However, the obtained fluxes (and thus the inferred luminosities) and their errors are not strongly affected by these uncertainties in the NH. The Galactic NH towards the source is included within the confidence-interval range obtained when we left the NH free in the fits, so we decided to fix the NH to the Galactic value. We note that any different, assumed NH in the allowed confidence interval will systematically change our spectral parameters slightly (e.g., the blackbody temperature increases by 15%–20% while the radius decreases by 20%–30% if we assume a NH close to the maximum allowed value in the blackbody model), but does not alter significantly the fluxes and inferred luminosities so the luminosity difference between GRO J1750−27 and the other two sources is robust.

3. Discussion

We present our Chandra monitoring campaign of the Be/X-ray transient GRO J1750−27 after its giant, type-II outburst in 2015. The purpose of our campaign was to determine if the crust of the NS in this system was significantly heated during this outburst and, if so, to follow its crust cooling behaviour. Such cooling of an accretion-heated crusts may have been observed for two other Be/X-ray transients (4U 0115+63 and V 0332+53) after the type-II outbursts they exhibited (Wijnands & Degenaar 2016; Rouco Escorial et al. 2017). However, contrary to what was found for these two systems, we do not see any strong evidence of such crust heating and cooling behaviour in GRO J1750−27 and, consequently, we infer that the NS crust was not significantly heated during the previous outburst (see Sect. 3.1). We do detect GRO J1750−27 in three of our five Chandra monitoring observations but the spectral parameters (the spectra are relatively hard) as well as the variability seen in quiescence (also taking into account the non-detections) argue that we likely see X-ray emission due to low-level accretion (see Sect. 3.2). Alternatively, the observed X-ray emission could potentially be originated by the companion star, which, most probably, is an early B-type star (see Lutovinov et al. 2019). Such stars are known to be (variable) X-ray emitters as well (e.g., Nazé 2009; Nazé et al. 2011). However, as discussed in detail in Tsygankov et al. (2017a, i.e., their Sect. 4.4) the X-ray luminosities of such stars are at most a few times 1031 erg s−1. This is significantly below the X-ray luminosities we detect for GRO J1750−27 and, therefore we suggest that the donor does not, or only very marginally, contribute to the observed X-ray radiation.

3.1. No heated NS crust in GRO J1750−27?

In the crust heating and cooling scenario, the difference in behaviour of GRO J1750−27 and the other two systems is unexpected if one looks at their NS parameters (i.e., spin periods and surface magnetic field strengths). For all the systems, these properties are very similar (see Table 3) and therefore one would expect, maybe naively, a similar response of the NSs to the accretion of mass. However, it might be that the outbursts of the three sources are significantly different and that might cause the NSs to react differently. As we see in Fig. 5, the outburst of GRO J1750−27 was longer than those of the other two sources and it was, at least, about equally bright (for an assumed distance of 12 kpc) or even significantly brighter than the outbursts of the other two sources (if GRO J1750−27 is located at a large distance of 22 kpc). Therefore, over the course of the outburst, GRO J1750−27 seems to have accreted more mass than the other two sources, and thus more energy was liberated in the crust of the NS in GRO J1750−27 than in that of the other two systems. This makes even more unclear why GRO J1750−27 did not show any evidence for an accretion-heated NS crust.

thumbnail Fig. 5.

Swift/BAT light curves (in the energy range 15–50 keV) of the three Be/X-ray transients discussed in the paper. The orange squares correspond to 4U 0115+63, the pink circles to V 0332+53, the dark stars to GRO J1750−27 assuming that the source is located at a distance of 22 kpc, and the purple diamonds correspond to GRO J1750−27 for an assumed distance of 12 kpc. The BAT count rates of the three sources have been normalised to a distance of 7 kpc using the best estimates for the true source distances (see Table 1). The start times of the different outbursts are listed in Table 1.

To quantify this further, we can compare the fluences of the three outbursts involved. To do this, we need the bolometric luminosities exhibited by the sources during their outbursts. Unfortunately, in the case of Be/X-ray binaries, obtaining the correct Fbol (and thus the bolometric luminosities) is complicated due to both the wide variety in intrinsic spectral shape between sources and the fast evolution of the absorption column during outburst (e.g., see Campana et al. 2001; Reig & Nespoli 2013; see Shaw et al. 2009 for the spectral evolution of GRO J1750−27 during its 2008 outburst). These combined effects make it hard to infer the correct spectral shape and therefore, the bolometric luminosities. However, since we are interested in a direct comparison between our three sources, we can get a first approximation of their fluences by comparing their BAT light curves (see Fig. 5; normalized to a distance of 7 kpc). By integrating these light curves, we obtain the BAT fluences for each outburst (the BAT fluences give the energy output not in physical energy units, but in BAT counts units). The resulting BAT fluences are listed in Table 3 (we used again two assumed distances for GRO J1750−27; 12 and 22 kpc). From these fluences it is clear that if GRO J1750−27 is located far away, it accreted the largest amount of matter of the three sources. Even if the source is located much closer, it would still have accreted significantly more matter during its outburst than 4U 0115 + 63 and only ∼35% less than V 0332 + 53.

We note that a complication in comparing the different sources with each other is the fact that a significant amount of energy injected in the crust (during outburst) might be released from the rest of the NS surface (and not only from the small emission regions inferred from the blackbody spectral fits) as was shown by Elshamouty et al. (2016). However, this radiation is unobservable because it likely has a temperature that lies below the Chandra bandpass. Therefore, it is not possible to obtain a reliable estimate for this potential, additional surface emission from any of our sources. However, if indeed the NS crust in GRO J1750−27 was heated less than in the other two sources, it remains unclear what causes this difference. Since in all three sources we have NSs with relatively high surface magnetic-field strengths of ∼1−4.5 × 1012 G (see Table 3), it might be that the magnetic field inside of the crusts plays an important role. It might be that the configuration and/or the strength of the magnetic field in the NS crust of GRO J1750−27 is such that it prohibits the crust to show up as significantly heated (see, e.g., the discussions in Rouco Escorial et al. 2017 and Wijnands et al. 2017).

Alternatively, the NS in GRO J1750−27 might have accreted significantly less matter over its lifetime than the NSs in the other two systems. As a consequence its crust might not be fully replaced yet with accreted matter (it might have a partially accreted crust; the so-called “hybrid crust”; Wijnands et al. 2013), inhibiting some or most of the deep crustal reactions that generate the heating energy (e.g., see also Fantina et al. 2018). This would result in a much less heated crust in GRO J1750−27 than in the other two systems. Finally, it is also possible that the explanation of the differences between the sources lays in, what is called, the “shallow-heating mechanism”. For the low-magnetic field NSs in low-mass X-ray binaries, it has been found that for most of them, the crust cooling curves observed after their outbursts can only be explained if during the accretion in outbursts not only the deep crustal heating reactions occur, but also another heating mechanism is active at shallow depths in the crusts (i.e., ≲150 m). It has been found that the amount of heating necessary from this mechanism can vary significantly between sources and, even within one source, between different outbursts (see Deibel et al. 2015; Parikh et al. 2017; Ootes et al. 2018). The physical mechanism behind this shallow heating process is not understood (for a detailed discussion see Deibel et al. 2015) and therefore it is quite possible that a similar process might be active during outbursts whe Be/X-ray transients are accreting as well. It might thus be possible that the shallow heating process in GRO J1750−27 was active at a much lower strength than in the other two sources (or not active at all) and, consequently, resulted in a not or hardly heated crust in GRO J1750−27.

3.2. Low-level accretion onto the magnetised NSs

The variable behaviour seen for GRO J1750−27 after its outburst cannot easily be explained using the cooling hypothesis. Therefore, it seems prudent to investigate other possibilities for the observed quiescent emission. A possible alternative scenario is one in which the observed quiescent phenomena are caused by residual, low-level accretion onto the NS. Variable levels of the accretion rate could be a natural explanation for the quiescent variability observed in GRO J1750−27. Evidence for such a low-level accretion is demonstrated by the so-called “mini type-I” outbursts seen in 4U 0115 + 63 and V 0332 + 53 (Campana et al. 2001; Wijnands & Degenaar 2016), which were observed on top of the general decay trend of their X-ray luminosities. This slowly decaying behaviour could still be due to the cooling of the NS crust, although a slowly decaying accretion rate cannot be excluded either (Wijnands & Degenaar 2016; Rouco Escorial et al. 2017). Unfortunately, how low-level accretion onto a magnetised NS would occur is currently not understood, inhibiting us from making strong conclusive statements. Our three sources are spinning rapidly enough (see Table 3) that they are expected to be in the propeller regime at the observed X-ray luminosities (see Tsygankov et al. 2016 for 4U 0115 + 63 and V 0332 + 53; GRO J1750−27 falls in the propeller-effect area of Fig. 3 in Tsygankov et al. 2017b; see also Lutovinov et al. 2019). Therefore, these systems should not exhibit any accretion emission as matter should not be able to reach the NS surface. But clearly matter still reaches the NSs in the propeller regime (as also seen for a few other sources; e.g. Orlandini et al. 2004; Mukherjee & Paul 2005), although it is unclear whether the mechanism that causes this is the same for these mini-type-I outbursts observed in 4U 0115 + 63 and V 0332 + 53, and the emission we see in GRO J1750−27 in its quiescent state.

Intriguingly, the second and third Chandra detections of GRO J1750−27 (during ObsIDs 16725 and 16726) occurred close to periastron passage (see Table 1) similar to the mini type-I outbursts in the other two sources13. This might indicate a possible link between the emission mechanisms in the different sources, although the peak luminosities at periastron vary widely between sources: LX ∼ 1034−35 erg s−1 for 4U 0115 + 63 and V 0332 + 53 (Campana 2001; Wijnands & Degenaar 2016) versus LX  ∼  1032 erg s−1 for GRO J1750−27. The large range in luminosity might be difficult to explain in any model assuming that the underlying physical mechanism is the same in all sources. In addition, the first Chandra detection of GRO J1750−27 occurred far from periastron (see Table 1). This might be explained by assuming that this Chandra observation was performed during the accretion tail from the final stage of the giant outburst (see also Lutovinov et al. 2019). Or that the accretion mechanism at work in this source is different for the first observation compared to that during the other two. In this case, it might be possible that two mechanisms are at work in GRO J1750−27, one related to the mini type-I outburst phenomenon and one that causes accretion when the source is far away from periastron. Clearly, more studies, both observational as well as theoretical, are needed to improve our understanding of low-level accretion onto magnetised NSs.

We note that if our first Chandra observation was indeed obtained during the tail of the type-II outburst, the source might not have been fully in “true” quiescence yet14. If this observation is ignored in the light curves, the detected variability during the other four Chandra observations is less significant (i.e., in the light that we only have a handful of photons detected). In order to check whether the source was indeed variable during these four Chandra observations, we fitted the observed net count rates (we used 1σ errors) with a constant model. This model could not fit the data well with a χ2 value of 12.05 for 3 degrees of freedom (leading to a p-value of 0.0072; this p-value decreases to 2.8 × 10−5 when also including our first Chandra point). This suggest that indeed the source was variable during our observations. However, even in the unlikely case that the source was not variable during the last four Chandra observations, our conclusion still holds that the neutron-star crust in GRO J1750−27 was significantly less heated (because of the very low quiescent luminosities observed from our target) during its preceding type-II outburst than the crusts in the other two sources discussed in our paper. In addition, the hard quiescent spectra we observed for our source with respect to the spectra observed for the other two sources (Figs. 3 and 4), also indicate that the emission we detected is indeed due to low-level accretion of matter on the neutron star.

8

We note that only 2.3 net photons were detected at the position of GRO J1750−27 which does not constitute a significant detection.

10

We followed the method described by Tsygankov et al. (2017a) to determine if one of the two spectral models used was preferred over the other. In our case, the difference between the values from the W-statistics (C-values) for the power-law and blackbody models was |ΔC| < 2. This difference is below the critical value indicated in Tsygankov et al. (2017a, |ΔC| = 10), therefore we could not statistically prefer one model over the other.

11

Lutovinov et al. (2019) constrained the distance towards the source to a range of 14–22 kpc, very similar to what we assume in our paper.

12

For the blackbody model, the 0.5–10 keV luminosities are close to the bolometric luminosities, however, for the power-law model the bolometric luminosity could be significantly larger than the 0.5–10 keV luminosity. We do not know the exact spectral shape above 10 keV (in the power-law model) and calculating bolometric luminosities would required additional, very uncertain assumptions about the quiescent source behaviour. Therefore, we only quote the 0.5–10 keV luminosities. This also allow for direct comparisons with 4U 0115+63 and V 0332+53 for which only the 0.5–10 keV luminosities were given (Wijnands & Degenaar 2016; Rouco Escorial et al. 2017).

13

The Chandra observation 16724 was also obtained close to periastron (see Table 1) but the source was not detected. This indicates that if the emission mechanism is linked to the periastron passage, it is not always active. This is similar to what has been found for the mini type-I outbursts in 4U 0115+63 and V 0332+53 which are not always present at periastron passages (Wijnands & Degenaar 2016; Rouco Escorial et al. 2017).

14

Even if the first Chandra observation was performed while the type-II outburst was not fully over yet, the question of how accretion onto a magnetised neutron star occurs at the very low observed accretion rate (as inferred from the very low observed X-ray luminosity during this observation) still remains.

Acknowledgments

ARE, LSO, and RW were supported by a NWO Top Grant, module 1 awarded to RW. Support for this work was provided by the National Aeronautics and Space Administration through Chandra Award Number GO5-16040X issued by the Chandra X-ray Observatory Center, which is operated by the Smithsonian Astrophysical Observatory for and on behalf of the National Aeronautics Space Administration under contract NAS8-03060. This work has benefited from support by the National Science Foundation under Grant No. PHY-1430152 (JINA Center for the Evolution of the Elements). Data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia) have been used in this project and processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement.

References

  1. Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Mantelet, G., & Andrae, R. 2018, AJ, 156, 58 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bildsten, L., Chakrabarty, D., Chiu, J., et al. 1997, ApJS, 113, 367 [NASA ADS] [CrossRef] [Google Scholar]
  3. Campana, S. 2001, in X-ray Astronomy: Stellar Endpoints, AGN, and the Diffuse X-ray Background, AIP Conf. Proc., 599, 63 [NASA ADS] [CrossRef] [Google Scholar]
  4. Campana, S., Gastaldello, F., Stella, L., et al. 2001, ApJ, 561, 924 [NASA ADS] [CrossRef] [Google Scholar]
  5. Campana, S., Stella, L., Israel, G. L., et al. 2002, ApJ, 580, 389 [NASA ADS] [CrossRef] [Google Scholar]
  6. Cominsky, L., Clark, G. W., Li, F., Mayer, W., & Rappaport, S. 1978, Nature, 273, 367 [NASA ADS] [CrossRef] [Google Scholar]
  7. D’Angelo, C. 2014, Eur. Phys. J. Web Conf., 64, 01003 [CrossRef] [EDP Sciences] [Google Scholar]
  8. D’Angelo, C. R., & Spruit, H. C. 2010, MNRAS, 406, 1208 [NASA ADS] [Google Scholar]
  9. D’Angelo, C. R., & Spruit, H. C. 2012, MNRAS, 420, 416 [NASA ADS] [CrossRef] [Google Scholar]
  10. Deibel, A., Cumming, A., Brown, E. F., & Page, D. 2015, ApJ, 809, L31 [NASA ADS] [CrossRef] [Google Scholar]
  11. Doroshenko, V., Santangelo, A., Doroshenko, R., et al. 2014, A&A, 561, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Doroshenko, V., Tsygankov, S., & Santangelo, A. 2016, A&A, 589, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Elshamouty, K. G., Heinke, C. O., & Chouinard, R. 2016, MNRAS, 463, 78 [NASA ADS] [CrossRef] [Google Scholar]
  14. Evans, P. A., Beardmore, A. P., Page, K. L., et al. 2009, MNRAS, 397, 1177 [NASA ADS] [CrossRef] [Google Scholar]
  15. Fantina, A. F., Zdunik, J. L., Chamel, N., et al. 2018, A&A, 620, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Finger, M. H., & Wilson-Hodge, C. A. 2014, ATel, 6839 [Google Scholar]
  17. Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Gehrels, N. 1986, ApJ, 303, 336 [NASA ADS] [CrossRef] [Google Scholar]
  20. Haensel, P., & Zdunik, J. L. 1990, A&A, 227, 431 [NASA ADS] [Google Scholar]
  21. Haensel, P., & Zdunik, J. L. 2003, A&A, 404, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Haensel, P., & Zdunik, J. L. 2008, A&A, 480, 459 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Ikhsanov, N. R. 2001, A&A, 375, 944 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Illarionov, A. F., & Sunyaev, R. A. 1975, A&A, 39, 185 [NASA ADS] [Google Scholar]
  25. Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Krimm, H. A., Holland, S. T., Corbet, R. H. D., et al. 2013, ApJS, 209, 14 [NASA ADS] [CrossRef] [Google Scholar]
  27. Laplace, E., Mihara, T., Moritani, Y., et al. 2017, A&A, 597, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Lau, R., Beard, M., Gupta, S. S., et al. 2018, ApJ, 859, 62 [Google Scholar]
  29. Lii, P. S., Romanova, M. M., Ustyugova, G. V., Koldoba, A. V., & Lovelace, R. V. E. 2014, MNRAS, 441, 86 [NASA ADS] [CrossRef] [Google Scholar]
  30. Lindegren, L., Hernández, J., Bombrun, A., et al. 2018, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Lutovinov, A. A., Tsygankov, S. S., Karasev, D. I., Molkov, S. V., & Doroshenko, V. 2019, MNRAS, 485, 770 [NASA ADS] [CrossRef] [Google Scholar]
  32. Makishima, K., Mihara, T., Ishida, M., et al. 1990, ApJ, 365, L59 [NASA ADS] [CrossRef] [Google Scholar]
  33. Martin, R. G., Nixon, C., Armitage, P. J., Lubow, S. H., & Price, D. J. 2014, ApJ, 790, L34 [NASA ADS] [CrossRef] [Google Scholar]
  34. Monageng, I. M., McBride, V. A., Coe, M. J., Steele, I. A., & Reig, P. 2017, MNRAS, 464, 572 [NASA ADS] [CrossRef] [Google Scholar]
  35. Moritani, Y., Nogami, D., Okazaki, A. T., et al. 2013, PASJ, 65, 83 [NASA ADS] [Google Scholar]
  36. Mukherjee, U., & Paul, B. 2005, A&A, 431, 667 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Nazé, Y. 2009, A&A, 506, 1055 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Nazé, Y., Broos, P. S., Oskinova, L., et al. 2011, ApJS, 194, 7 [NASA ADS] [CrossRef] [Google Scholar]
  39. Negueruela, I., & Okazaki, A. T. 2001, A&A, 369, 108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Negueruela, I., Roche, P., Fabregat, J., & Coe, M. J. 1999, MNRAS, 307, 695 [NASA ADS] [CrossRef] [Google Scholar]
  41. Ootes, L. S., Wijnands, R., Page, D., & Degenaar, N. 2018, MNRAS, 477, 2900 [NASA ADS] [CrossRef] [Google Scholar]
  42. Orlandini, M., Bartolini, C., Campana, S., et al. 2004, Nucl. Phys. B Proc. Suppl., 132, 476 [NASA ADS] [CrossRef] [Google Scholar]
  43. Parikh, A. S., Homan, J., Wijnands, R., et al. 2017, ApJ, 851, L28 [NASA ADS] [CrossRef] [Google Scholar]
  44. Patruno, A., & D’Angelo, C. 2013, ApJ, 771, 94 [NASA ADS] [CrossRef] [Google Scholar]
  45. Pavlov, G. G., Shibanov, Y. A., Zavlin, V. E., & Meyer, R. D. 1995, in NATO Advanced Science Institutes (ASI) Series C, eds. M. A. Alpar, U. Kiziloglu, & J. van Paradijs, 450, 71 [Google Scholar]
  46. Raguzova, N. V., & Popov, S. B. 2005, Astron. Astrophys. Trans., 24, 151 [NASA ADS] [CrossRef] [Google Scholar]
  47. Rappaport, S., Clark, G. W., Cominsky, L., Li, F., & Joss, P. C. 1978, ApJ, 224, L1 [NASA ADS] [CrossRef] [Google Scholar]
  48. Reig, P. 2011, Ap&SS, 332, 1 [NASA ADS] [CrossRef] [Google Scholar]
  49. Reig, P., & Nespoli, E. 2013, A&A, 551, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Reig, P., Doroshenko, V., & Zezas, A. 2014, MNRAS, 445, 1314 [NASA ADS] [CrossRef] [Google Scholar]
  51. Romanova, M. M., Ustyugova, G. V., Koldoba, A. V., & Lovelace, R. V. E. 2004, ApJ, 616, L151 [NASA ADS] [CrossRef] [Google Scholar]
  52. Rouco Escorial, A., Bak Nielsen, A. S., Wijnands, R., et al. 2017, MNRAS, 472, 1802 [NASA ADS] [CrossRef] [Google Scholar]
  53. Rutledge, R. E., Bildsten, L., Brown, E. F., et al. 2002, ApJ, 580, 413 [NASA ADS] [CrossRef] [Google Scholar]
  54. Rybizki, J., Demleitner, M., Fouesneau, M., et al. 2018, PASP, 130, 074101 [NASA ADS] [CrossRef] [Google Scholar]
  55. Scott, D. M., Finger, M. H., Wilson, R. B., et al. 1997, ApJ, 488, 831 [NASA ADS] [CrossRef] [Google Scholar]
  56. Shaw, S. E., Hill, A. B., Kuulkers, E., et al. 2009, MNRAS, 393, 419 [NASA ADS] [CrossRef] [Google Scholar]
  57. Steiner, A. W. 2012, Phys. Rev. C, 85, 055804 [NASA ADS] [CrossRef] [Google Scholar]
  58. Stella, L., White, N. E., Davelaar, J., et al. 1985, ApJ, 288, L45 [NASA ADS] [CrossRef] [Google Scholar]
  59. Syunyaev, R. A., & Shakura, N. I. 1977, Sov. Astron. Lett., 3, 138 [NASA ADS] [Google Scholar]
  60. Tsygankov, S. S., Lutovinov, A. A., Doroshenko, V., et al. 2016, A&A, 593, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Tsygankov, S. S., Wijnands, R., Lutovinov, A. A., Degenaar, N., & Poutanen, J. 2017a, MNRAS, 470, 126 [NASA ADS] [CrossRef] [Google Scholar]
  62. Tsygankov, S. S., Mushtukov, A. A., Suleimanov, V. F., et al. 2017b, A&A, 608, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Verner, D. A., Ferland, G. J., Korista, K. T., & Yakovlev, D. G. 1996, ApJ, 465, 487 [NASA ADS] [CrossRef] [Google Scholar]
  64. Wijnands, R., & Degenaar, N. 2016, MNRAS, 463, L46 [NASA ADS] [CrossRef] [Google Scholar]
  65. Wijnands, R., Degenaar, N., & Page, D. 2013, MNRAS, 432, 2366 [NASA ADS] [CrossRef] [Google Scholar]
  66. Wijnands, R., Degenaar, N., & Page, D. 2017, JApA, 38, 49 [Google Scholar]
  67. Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Gaia distances

Gaia did not detect the optical counterpart of GRO J1750−27 so we could not improve on the distance estimate for this source. The distances used in this paper for the other two Be/X-ray transients, 4U 0115 + 63 and V 0332 + 53, have been obtained from the second Gaia data release (GDR2; Gaia Collaboration 2016, 2018). We obtained the parallaxes of the sources from the Gaia archive15 and used the code developed by Bailer-Jones et al. (2018) 16 to determine the best distance estimates. This code computes the distance using a prior that varies depending on the Galactic longitude and latitude according to a three-dimensional model of the Galaxy (Rybizki et al. 2018). Due to the nonlinear transformation, the confidence intervals on the distances that we obtain are asymmetric. Table A.1 shows the input parameters for the code and the estimated distances. The parallaxes were corrected from the zeropoint offset in the catalogue (+0.029 mas) as determined from Gaia observations of quasars by Lindegren et al. (2018).

Table A.1.

Main parameters used for obtaining Gaia distances.

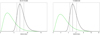thumbnail Fig. A.1.

Plots obtained using the code (Bailer-Jones et al. 2018) to determine the best Gaia distance estimates for 4U 0115 + 63 (left panel) and V 0332 + 53 (right panel). The prior is represented by the green line and the posterior is plotted in black. The black vertical line corresponds to the distance estimator, and the dashed vertical lines are the lower and upper bounds of the 68% confidence interval.

Appendix B: Spectral fit results using the neutron star atmosphere model (NSA)

We also fitted our Chandra spectra using the neutron star atmosphere (NSA) assuming a magnetised neutron star (Pavlov et al. 1995). We used the same spectral analysis set-up as the one described in Sect. 2.3, but in addition we fixed the neutron-star mass (1.4 M⊙), radius (11 km), and magnetic field strength (we used 2 × 1012 G; the results were very similar if we used 4.5 × 1012 G so we only report the first set of fit results) values. We left the normalization of the model to vary freely in order to calculate the size of the emission region for both assumed distances (12 kpc and 22 kpc). As for the blackbody model, the fluxes were obtained using the CFLUX command. The results of the fit are shown in Table B.1. Both the (unredshifted) effective temperature and the size of the emission region are fully consistent between the three Chandra observations, with the fluxes varying between these observations. We note that these inferred sizes for the emission region are much smaller than the NS radius indicative of the existence of hot spots as also was deduced from the blackbody fits (which produced slightly larger emission region sizes; see Table 2). The fluxes obtained using the neutron star atmosphere model are fully consistent with those obtained using the blackbody model.

Table B.1.

Results of the neutron star atmosphere model fitting.

All Tables

Table 1.

Log of Swift and Chandra observations for GRO J1750−27.

In the text
Table 2.

Results of our Chandra spectral analysis.

In the text
Table 3.

Basic parameters of the systems and their type-II outbursts properties discussed in this paper.

In the text
Table A.1.

Main parameters used for obtaining Gaia distances.

In the text
Table B.1.

Results of the neutron star atmosphere model fitting.

In the text

All Figures

thumbnail Fig. 1.

Swift/XRT (blue) and Swift/BAT (black) light curves during and after the 2015 type-II outburst of GRO J1750−27. All Chandra count rates have been converted to Swift/XRT count rates using the method described in Sect. 2.1. The Chandra detections (with 1σ errors) are given as red squares. The Chandra upper limits are determined in the manner explained in Sect. 2.1 and shown as red arrows. The dotted brown line and brown arrow represent the upper limit obtained in the Chandra observation 14643 taken in May 2013, i.e., almost a year and a half before the 2015 type-II outburst. The zeropoint of the light curve (the fiducial starting point of the outburst) corresponds to December 29th, 2014.
In the text
thumbnail Fig. 2.

Close-up images (0.5–7 keV energy range) of our Chandra detections (listed by their ObsIDs; from left to right): 16723, 16725 and 16726. The blue circles indicate the source extraction regions and the dashed red annuli the background extraction regions. The green circle is the Swift/XRT error region of the source reported by Shaw et al. (2009). See Sects. 2.1 and 2.2 for more details about the detections and upper limits.
In the text
thumbnail Fig. 3.

Evolution (using a blackbody model) of the spectral parameters (from the top to the bottom): the X-ray luminosity (for the energy range 0.5–10 keV), the blackbody temperature, and the associated emission radius. The orange squares are the Swift/XRT spectral results of 4U 0115+63 published by Wijnands & Degenaar (2016) and Rouco Escorial et al. (2017). The pink circles correspond to the Swift/XRT spectral results of V 0332+53 reported by Wijnands & Degenaar (2016). Luminosities and emission region radii from both sources have been recalculated using their new Gaia distances as given in Table 3. The dark stars and purple diamonds are our Chandra spectral results of GRO J1750−27 when assuming a source distance of 22 kpc or 12 kpc, respectively. Errors are 1σ. Some points of 4U 0115+63 and V 0332+53 are plotted with symbols that are larger than the corresponding error bars of these points.
In the text
thumbnail Fig. 4.

Evolution (using a power-law model) of the spectral parameters: the X-ray luminosity (for the energy range 0.5–10 keV; top panel) and the photon index (bottom panel). The colours and symbols represent the same sources as in Fig. 3. Errors are 1σ. Some points of 4U 0115+63 and V 0332+53 are plotted with symbols that are larger than the corresponding error bars of these points. The arrows indicate upper limits on the luminosity and are calculated using the method described in Sect. 2.3.
In the text
thumbnail Fig. 5.

Swift/BAT light curves (in the energy range 15–50 keV) of the three Be/X-ray transients discussed in the paper. The orange squares correspond to 4U 0115+63, the pink circles to V 0332+53, the dark stars to GRO J1750−27 assuming that the source is located at a distance of 22 kpc, and the purple diamonds correspond to GRO J1750−27 for an assumed distance of 12 kpc. The BAT count rates of the three sources have been normalised to a distance of 7 kpc using the best estimates for the true source distances (see Table 1). The start times of the different outbursts are listed in Table 1.
In the text
thumbnail Fig. A.1.

Plots obtained using the code (Bailer-Jones et al. 2018) to determine the best Gaia distance estimates for 4U 0115 + 63 (left panel) and V 0332 + 53 (right panel). The prior is represented by the green line and the posterior is plotted in black. The black vertical line corresponds to the distance estimator, and the dashed vertical lines are the lower and upper bounds of the 68% confidence interval.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.