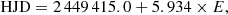EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 624 (April 2019) A&A, 624 (2019) A83 Full HTML
Free Access
Issue
A&A
Volume 624, April 2019
Article Number A83
Number of page(s) 16
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201834810
Published online 16 April 2019

© ESO 2019

1. Introduction

Undergoing the asymptotic giant branch (AGB) evolution phase, low to intermediate mass stars blow away their outer envelopes, forming planetary nebulae that will be ionized by the developing white dwarfs in their centre. However, interaction between the planetary nebula and its central progenitor is far from understood. The scheme is even more complicated when the central object is a binary star, which may be the majority of cases (e.g. De Marco et al. 2004; Jones & Boffin 2017). When the binary system is embedded in a common envelope, the components evolve together, as initially proposed by Paczyński et al. (1976). Inside the envelope the stellar cores spiral together and finally they may merge, forming a fast-rotating giant star, such as FK Comae stars (for a recent overview of binary mergers see the contribution by Ph. Podsiadlowski in González Martínez-País et al. 2014). However, if the envelope material is ejected before merging, the binary evolution may end up in a system involving a white dwarf and a main sequence companion. In this case some of the ejected nebular material is captured by the companion, yielding cataclysmic variability, while the accretion gradually spins up the accreting star. In addition, a powerful magnetic dynamo can also develop, since the common envelope is largely convective and supposed to rotate differentially (Tout & Regős 2003). However, the theory of common envelope evolution is extremely complex, involving different physical processes (e.g. ejection, accretion, spiralling, magnetic braking) on different timescales (thermal, dynamical, hydrodynamical, magneto-hydrodynamical, etc.), therefore a self-consistent, all-comprehensive treatment is still not feasible (cf. Podsiadlowski et al. 2001).

In this paper we revisit one of our former Doppler imaging targets, IN Comae (=HD 112313, Strassmeier et al. 1997a; hereafter Paper 1), the central object of the faint planetary nebula LoTr 5 (Longmore & Tritton 1980). The system consists of a white dwarf and a giant G star, which is evident from the composite spectra obtained by the International Ultraviolet Explorer (IUE; Feibelman & Kaler 1983). Actually, the central object is a long-period (Porb ≈ 2700 d, or ∼7.4 yr) binary system, consisting of a rapidly rotating magnetically active G5 giant (vsini = 67 km s−1) and a hot (Teff ≈ 150 000 K) sub-dwarf companion (cf. Jones et al. 2017, and their references). It was even suggested that the G5 component had a close companion, forming a hierarchical triple system (Jasniewicz et al. 1987; Malasan et al. 1991). However, this option has recently been disproved by Van Winckel et al. (2014), who suggested that either the white dwarf (or hot sub-dwarf) formed a close binary together with a yet undiscovered star of some 2–3 M⊙, or alternatively the orbital plane was not coplanar with the waist of the bipolar nebula. The cool star was found to be barium-rich (Thévenin & Jasniewicz 1997) as a consequence of contamination by s-process elements from the AGB progenitor envelope (cf. Bisterzo et al. 2011), supporting the presumption of spinning-up of the cool component by accreting the ejected envelope material.

Rotational and orbital period determinations of IN Com in the past yielded misinterpretations and even contradictory results. As fundamental period, 5.9 day was reported by Noskova (1989), which was attributed to rotation of the G5 giant (see Paper 1). However, Malasan et al. (1991) argued for 1.2 day as the most prominent photometric signal (i.e. the 1−f alias of 5.9 days), and also for 1.75 days, based on radial velocity measurements, as a possible orbital period of the assumed close binary. Jasniewicz et al. (1994) could not confirm this binary orbit, but they claimed that 1.2 day was indeed correct. After a revision, however, Jasniewicz et al. (1996) found the 5.9 day period to be more realistic. Oddly, Kuczawska & Mikolajewski (1993) found an even shorter period of 0.25 days, which, however, has not been confirmed since. Furthermore, the radial velocity measurements in Paper 1 did not support the close binary hypothesis. Only recently, Jones et al. (2017) have updated the first reliable orbital motion detection by Van Winckel et al. (2014) and proposed an orbital period of 2717 ± 63 days (∼7.4 yr) for the G5 star.

IN Com was observed in X-rays by XMM-Newton with all three European Photon Imaging Cameras (EPIC) on 6 June 2002, and by Chandra on 4 December 2002 (Montez et al. 2010). Spectral fitting shows that the X-ray emission is characterized by two components at about 0.65 keV (both XMM-Newton and Chandra) and at 2.27 and 3.49 keV (XMM-Newton and Chandra, respectively), while the X-ray luminosity was measured as log LX ≈ 30 erg s−1. Guerrero (2012) fitted the XMM-Newton EPIC planetary nebula spectrum with 8 × 1030 erg s−1 at 0.61 and 3.1 keV, and constructed a spectral energy distribution model from the XMM-Newton data, the available IUE spectra, and ground-based optical and near-infrared photometry. The non-local thermodynamic equilibrium (non-LTE) model showed good agreement with a contribution from a supposed G5 III companion star. It seems that the X-ray emission dominantly originates from the corona of the magnetically active late-type component of the binary (see Montez et al. 2010, for details).

Our study may contribute in moving towards a better understanding of how central binary stars in planetary nebulae evolve and how this evolution could develop fast-rotating magnetically active stars like IN Com. The paper is organized as follows. In Sect. 2 we present the photometric and spectroscopic observations. In Sect. 3 we provide updated astrophysical parameters for IN Com and present a time-series Doppler imaging study. With that we analyse the spot evolution and measure the surface differential rotation. In Sect. 4 we study the photometric and spectroscopic variability of the IN Com system, while in Sect. 5 the Hα behaviour is examined. The results are summarized and discussed in Sect. 6.

2. Observations

2.1. Photometry

Most of the photometric observations were obtained with the T6 and T7 (“Wolfgang” and “Amadeus”, respectively) 0.75 m automatic photoelectric telescopes (APTs) located at Fairborn Observatory in southern Arizona (Strassmeier et al. 1997b), operated by the Leibniz-Institute for Astrophysics Potsdam (AIP; Granzer et al. 2001). Altogether 1364 data points were observed in Johnson V (T6) and 943 in Strömgren y (T7) colours between February 1996 and June 2017 (JD 2 450 117–2 457 911). Furthermore, 643 Johnson V observations were collected with the 1 m RCC telescope of Konkoly Observatory, Budapest, located at Piszkéstető mountain station, Hungary, between January 1989–June 1993 (JD 2 447 530–2 449 141). The old photometric data from the literature completed with the new, yet unpublished V and y observations are plotted together in Sect. 4 in the top panel of Fig. 6.

2.2. Spectroscopy

Spectroscopic observations were carried out with the 1.2 m STELLA-II telescope of the STELLA robotic observatory (Strassmeier et al. 2010) located at the Izaña Observatory in Tenerife, Spain. It is equipped with the fibre-fed, fixed-format STELLA Echelle Spectrograph (SES) providing an average spectral resolution of R = 55 000. Altogether 230 high-resolution echelle spectra were recorded between 26 January and 23 June, 2017. The spectra cover the 3900–8800 Å wavelength range without gaps. Further details on the performance of the system and the data-reduction procedure can be found in Weber et al. (2008, 2012) and Weber & Strassmeier (2011). The average signal-to-noise ratio (S/N) of the spectra is 140:1. Table A.1 summarizes the division of the spectra into 12 independent subsets (dubbed S01–S12), which are used for Doppler imaging.

In addition, 20 ultra-high resolution (R = 200 000) spectra were collected during 3–15 March, 2017 with the 1.8 m Vatican Advanced Technology Telescope (VATT) fiber linked to the Potsdam Echelle Polarimetric and Spectroscopic Instrument (PEPSI) at the nearby Large Binocular Telescope (LBT). PEPSI’s characteristics and performance were described by Strassmeier et al. (2015, 2018). With cross disperser (CD) III in the blue arm and CD V in the red arm the set-up provided a wavelength coverage of 4800–5440 Å and 6280–7410 Å, respectively. The 90 min exposures gave typical S/N of 100:1 for the red and 50:1 for the blue wavelength regions. This data set is used primarily to refine some of the fundamental astrophysical parameters of IN Com (see Sect. 3.1). The log for these observations is given in Table A.2.

3. Doppler imaging

3.1. Adopted stellar parameters

The effective temperature, the surface gravity, the metallicity, and the microturbulence velocity are re-examined by applying the spectrum-synthesis code SME (Piskunov & Valenti 2017) to the ultra-high resolution PEPSI spectra. Our synthesis is based on MARCS model atmospheres (Gustafsson et al. 2008) and assuming local thermodynamic equlibrium (LTE). Atomic parameters are taken from the Vienna Atomic Line Database (VALD, Kupka et al. 1999). For the spectrum synthesis we used the 4800–5441 Å and 6278–7419 Å wavelength ranges. The SME code is applied for all single PEPSI spectra and the individual results are combined in order to estimate their error bars. This way we get Teff = 5400 ± 100 K, log g = 2.6 ± 0.1, [Fe/H] = −0.10 ± 0.05, and ξmic = 2.0 ± 0.4 km s−1 for the effective temperature, surface gravity, metallicity, and microturbulence, respectively. We note that our temperature and surface gravity values are in good agreement with the recent result by Aller et al. (2018). The radial-tangential macroturbulence dispersion of ∼7 km s−1 is estimated according to Gray (1981) and Gray & Toner (1986). SME was used to measure the Ba, Y, and Sr abundances (cf. Thévenin & Jasniewicz 1997) as well. For the abundance fits we kept all of the other redetermined astrophysical parameters fixed. We note that for the Ba line fit we take the average of 40 high quality STELLA spectra since the spectral gap between the blue and red arms of the PEPSI data significantly overlap with the 5519–6694 Å region of the 31 neutral and singly ionized barium lines taken from VALD. The new astrophysical data of IN Com are summarized in Table 1.

Table 1.

Astrophysical properties of IN Com.

The projected equatorial velocity of 67 ± 1.5 km s−1 (Paper I, but see also Van Winckel et al. 2014) and a 45 ± 15° inclination (cf. Paper I) together with the equatorial rotation period of 5.973 d (cf. Sect. 4.2) yields a stellar radius of 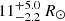. Together with Teff = 5400 ± 100 K this radius is consistent with the G5 III classification in the literature.

The new Gaia Data Release 2 (DR2) parallax of 1.977 ± 0.046 mas (Gaia Collaboration 2018) yields a distance of 506 ± 12 pc for IN Com. The brightest ever observed V magnitude of 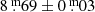(see later Fig. 7), while neglecting any interstellar and circumstellar extinction (cf. Ciardullo et al. 1999), results in an absolute magnitude 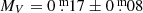. This, together with a bolometric correction for a G5 giant of taken from Flower (1996) gives a bolometric magnitude of 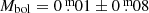, and thus a luminosity of L = 78 ± 6 L⊙ in fair agreement with the value just from the Stefan–Boltzmann law, but with a much smaller error bar. Also, taking the above radius and our measured gravity, the stellar mass is ∼1.8 ± 0.4 M⊙.

3.2. Definition of data subsets

The spectroscopic data used for the Doppler-imaging (DI) process are all from the first half of 2017 and are distributed fairly uniformly over the five-months STELLA run. In spite of the relatively short rotation period of 5.9 d, we still attained satisfactory phase coverage with between eight and 13 spectra per image for 12 subsequent intervals of typically one stellar rotation each. An additional subset can be formed from the available PEPSI spectra, with a pretty dense phase coverage. Table 2 summarizes the timely distribution of the 13 data subsets (dubbed S01–S12 and P01 for the PEPSI spectra) while Tables A.1 and A.2 record the observing logs for the STELLA and the PEPSI spectra, respectively.

Table 2.

Temporal distribution of the subsequent data sets for each individual Doppler image.

3.3. Image reconstruction with iMap

Our Doppler-imaging code iMap (Carroll et al. 2012) performs a temperature inversion for a number of photospheric line profiles simultaneously. For the inversions, 20 suitable absorption lines were selected from the 5000–6750 Å wavelength range (for the selection criteria see Künstler et al. 2015). Each spectral line is modelled individually and locally, then disc-integrated, and in the final step all disc-integrated line regions are averaged to obtain a mean theoretical profile. These mean profiles are then compared with each observed mean profile (for more details see Sect. 3 in Carroll et al. 2012). For the preparation of the observed mean profile, we proceed with a simple S/N-weighted averaging to increase the overall S/N by a factor of approximately four. The code iMap calculates the local line profiles by solving the radiative transfer with the help of an artificial neural network (Carroll et al. 2008). Atomic parameters are taken from the VALD database (Kupka et al. 1999). Model atmospheres are taken from Castelli & Kurucz (2004) and are interpolated for each desired temperature, gravity, and metallicity. Due to the high CPU demand, only LTE radiative transfer is used instead of spherical non-LTE model atmospheres.

For the surface reconstruction, iMap uses an iterative regularization based on a Landweber algorithm (Carroll et al. 2012). According to our tests (see Appendix A in Carroll et al. 2012) the iterative regularization has been proven to converge always on the same image solution. Therefore, no additional constraints are imposed for the image reconstruction. The surface element resolution is set to 5° × 5°.

3.4. Results: spot morphology and evolution

The resulting 13 time-series Doppler reconstructions of IN Com for 2017 (12 maps for the STELLA observations and one for the PEPSI spectra) are plotted in Figs. 1–3. The line-profile fits are given in Figs. A.1–A.3, respectively. The overall surface structure characteristics are reminiscent of the first and so far only Doppler image from 1994 (see Paper I), revealing a cool spot on the visible pole, cool spots at low to high latitudes, and even a few hot spots mostly at mid-latitudes. The spot temperatures range from the coolest ∼3600 K up to ∼5800 K, that is, hotter by 400 K than the unspotted photosphere of 5400 K. Hot spots are often claimed to be an artefact of the imperfect reconstruction. Lindborg et al. (2014, see their Fig. 3) have demonstrated that such artefacts are usually the result of extremely sparse phase coverage. However, regarding the reconstructions as a time series we observe that subsequent maps reveal quite similar features (cool as well as hot spots) from totally independent data. Moreover, insufficient phase sampling would introduce artificial (hot as well as cool) features at different locations from one Doppler reconstruction to the next, that is, usually around phases where the largest phase gaps appear. However, our data sets are well sampled, and their largest gaps (usually below 0.15–0.17 phase fraction, i.e. still not very large) appear randomly along the rotation phase, therefore we do not expect such artificial hot (and cool) features at similar locations over the 13 individual Doppler reconstructions. We note especially the P01 PEPSI-map shown in Fig. 3, which falls between the S04 and S05 STELLA-maps, and despite the different observing facilities and independent data the recovered surface features show remarkable resemblance. This confirms not only the reliability of the reconstructed features but also the steadiness and robustness of iMap. The polar spot seems to be the most permanent feature over the time range, while at lower latitudes the spotted surface is more variable; nevertheless, the dominant features can be tracked from one map to the next. Finally, we note that in some maps strong features are seen also below the equator, despite the fact that Doppler imaging is less powerful when reconstructing the less visible hemisphere. We assume, however, that such a feature is most likely real when it reappears on consecutive Doppler reconstructions (see S03–S04–S05 and S10–S11), although the shape, size, or contrast of these features may be inexact.

thumbnail Fig. 1.

Doppler images of IN Com for STELLA data sets S01–S06. The corresponding mid-UT dates (2017+) are indicated below the names of the maps.

thumbnail Fig. 2.

Doppler images for STELLA data sets S07–S12. The corresponding mid-UT dates (2017+) are indicated below the names of the maps.

thumbnail Fig. 3.

Doppler image for the PEPSI at VATT spectra. The corresponding mid-UT date is 11 March, 2017, which falls just between the dates of the S04 and S05 maps shown in Fig. 1.

The first reconstruction in the time series (S01) reveals an elongated polar feature of ∼4800 K together with several lower latitude nearly circular spots of ≈4000−5000 K with typically 10° diameter. The brightest feature of ∼5800 K is centred at phase ϕ = 0.4 at high (∼50°) latitude. A faint cool spot at ϕ = 0.25 becomes the most prominent cool feature for the next map (S02), while the hot spot as well as the other cool spots become less contrasted. For the next map (S03) the polar spot becomes cooler and more compact, while other cool spots shrink by ≈30−60%. The only exception is the new cool feature at the lower hemisphere, just at the border of visibility. We note that the bright spot at ϕ = 0.4 is permanently visible. For the next (S04) map, the cool spots become fainter, however, the bright spot at ϕ = 0.4 is hotter. The fifth map, S05, reveals an emerging new cool spot at ϕ ≈ 0.3, while the polar spot has become more compact and contrasted. In the next map (S06) the progeny of the new spot, as well as the other cool and bright features, become smaller and/or less contrasted. This continues in S07 map, where the hot features nearly vanish. Traces of new flux emergence are seen in S08 with a new spot at ϕ ≈ 0.2. Also, bright features appear again, in particular the well-known one at ϕ = 0.4. In the next map (S09) the polar spot becomes more prominent while the newly emerged spot at ϕ ≈ 0.2 fades and splits into two subspots. The high latitude bright spot at ϕ = 0.4 is still detectible. In the tenth map (S10) a new cool spot group emerged at ϕ ≈ 0.5, and becomes less contrasted and shifted towards the covered pole in the S11 map. Also, the formerly vanishing spot around 0.2 phase appears now strengthened. This continues during our last reconstruction (S12), where the polar spot shrinks and is displaced. Permanent rearrangements are taking place, for example the spot group in S11 at ϕ ≈ 0.9 becomes smaller in size and cooler. We note also that the high latitude warm (≈5600−5900 K) features are still present.

For each map the overall surface temperature is obtained by averaging the temperature values pixel by pixel over the stellar surface. However, tracing individual spots from one map to the next is hampered by the rapid spot rearrangements and/or the imperfect phase coverage. Instead, we split the surface into two parts above and below 65°, this way ranking the spots to be either polar or low-to-mid latitude spots. We measure the time variation of both surface partitions by deriving the spot filling factor values. In Fig. 4 we plot the time variation of the average temperature from surface integration as well as the spot filling factors. The diagrams indicate two epochs at HJD 2 457 826 (S05) and HJD 2 457 893 (S10), when the average temperature decreased by ∼50 K, simultaneously with a small drop of the filling factor at the pole, but a significant increase of ∼40% at mid-low latitudes. According to the maps, these two events may indicate significant spot rearrangements, when new fluxes emerge. On the other hand, individual spot evolutions imply that the average spot lifetime should be of the order of a month.

thumbnail Fig. 4.

Time variation of the spot filling factor (top panel) and the integrated surface temperature (bottom panel) of IN Com derived from the time-series Doppler images shown in Figs. 1–3. Upper panel: the spot filling factors are shown for the polar region and for the mid-to-low latitudes separately; see the top and the bottom curves, respectively. The different Doppler reconstructions are identified by their serial numbers.

3.5. Surface differential rotation

Tracking short-term spot migrations is among the usual methods to study stellar surface differential rotation from Doppler imaging (Donati & Collier Cameron 1997). In this paper, we apply the program ACCORD (Kővári et al. 2015, and references therein) and perform a time-series cross-correlation analysis from the 12 Doppler images obtained for the STELLA observations (for the sake of data homogeneity we excluded the P01 map from this analysis). It provides 11 consecutive cross-correlation function (ccf) maps, which are combined into an average correlation map. Its 2D correlation pattern is then fitted with a quadratic differential-rotation law in the usual (solar) form of Ω(β) = Ωeq(1 − α sin 2 β), where Ω(β) is the angular velocity at latitude β, Ωeq the angular velocity at the equator, while α = (Ωeq − Ωpole)/Ωeq is the relative angular velocity difference between the equator and the pole, that is, the surface shear coefficient.

The resulting correlation pattern for IN Com is shown in Fig. 5. It indicates anti-solar surface differential rotation in which the equator rotates slower than the polar latitudes. The most well-correlated dark regions are fitted with Gaussian curves in 5° bins. The Gaussian peaks are indicated in Fig. 5. The best fit to these peaks gave Ωeq = 60.28 ± 0.08° d−1 or an equivalent equatorial period of Peq = 5.973 ± 0.008 d with a shear coefficient of α = −0.026 ± 0.005. This yields a lap time of 230 d needed by the polar regions to lap the equator by one full rotation.

thumbnail Fig. 5.

Average cross-correlation map for IN Com showing anti-solar surface differential rotation. The best correlated dark regions are fitted by Gaussian curves in 5° bins. Gaussian peaks are indicated by dots, the corresponding Gaussian widths by horizontal lines. The best fit differential rotation law suggests an equatorial period of Peq = 5.973 d and a surface shear coefficient of α = −0.026.

4. Variability of the IN Com system

4.1. Orbital photometric modulation

Figure 6 presents photometric data of IN Com for the past 30+ years. To support a long-period search, our new photometric data are combined with the published observations from Paper I and augmented with observations from the All Sky Automated Survey (ASAS) database (Pojmanski 2002). The (binned) Super-WASP data in Aller et al. (2018) could not be used due to missing bandpass transformations but they in any case overlap with part of the ASAS data. For the period determination, we applied the Fourier-transformation-based frequency analyser code MuFrAn (Csubry & Kolláth 2004). In the top panel of Fig. 6, we show the best fit to the full photometric data set with a sinusoid of a period of 2639 d (∼7.2 yr), which has an uncertainty of about 200 d. The sine-wave fits well the first two well-observed cycles and does not contradict with the later, sparse data.

thumbnail Fig. 6.

Top: long-term photometric V and y data of IN Com. Different colours mean different sources of observations; green: data from T6 and T7 APTs, blue: observations from the Hungarian 1 m RCC telescope, red: literary data (mostly from Paper 1) that are used for seasonal period determination, grey: literary data+ASAS data that are not suitable for seasonal period determination. The sine-wave fit by black solid line represents the long-term overall brightness change with a period of 7.2 yr, which is basically the wide binary period (see Sect. 6). Bottom: independent rotational period determinations for suitable seasonal data sets. Further details can be found in the text.

The photometric cycle of 2639 d is in surprising agreement with the recently proposed orbital period of 2717 ± 63 d (Jones et al. 2017) and also with its revised value of 2689 ± 52 d by Aller et al. (2018). Orbital phase coherence of surface activity is common in comparably short period tidally-connected RS CVn binaries, but has never been seen for such long period timescales. Figure 7 shows a comparison of the orbital radial velocities with our long-term APT photometry phased with the same orbital period of 2717 days from Jones et al. (2017). Most notable is the phase coherence in the sense that the light-curve maximum coincides with a time of highest radial velocity while the light-curve minimum coincides with a time of lowest radial velocity.

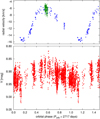thumbnail Fig. 7.

Comparing the long-term light variation with the radial velocity curve of IN Com. Top: radial velocity curve of the star taken from Jones et al. (2017) suggesting a 2717 day long orbital period. Overplotted are the radial velocities from our spectroscopic data (green circles). Bottom: long-term V + y photometric observations after folding up with the orbital period.

4.2. Rotational photometric modulation

Seasonal short period determinations are presented in the lower panel of Fig. 6. We note that the amplitude of the rotational modulation of IN Com is generally low, typically less than 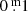in V. Therefore, seasonal rotational periods were derived only for the best quality data sets with good phase coverage and low scatter. The average value of the seasonal periods is ∼5.92 days. At this point we emphasize that any photometric period always traces the rotation period of the star at that latitude where the spot or spots occurred. Interestingly, between 1995 and 1999 the photometric period was increasing, while the overall brightness was decreasing. Such a simultaneity is explained by surface differential rotation that causes a shift of the dominant longitude usually populated by star spots (cf. Vida et al. 2014).

Our data again also demonstrate the solidity of the 5.9 day photometric period being the rotation period as opposed to for example the 1.2 day (1 − f) alias. This was already done in our Paper I but then we had not had a beautiful photometric light curve that sampled the variation with high-enough time resolution. Here we present two independent, densely sampled, and time-continuous APT data (Fig. 8) that prove without doubt that the 5.9 day period is indeed the correct one.

thumbnail Fig. 8.

Well-sampled photometric modulation indicates the solidity of the 5.9 day period. Light curves were taken during April and May 1996 (top) and April 1998 (bottom) with the T7 and T6 APTs, respectively. The light curves even show the changing amplitudes and shapes typical for star spot evolution.

The next step is to average the individual photometric period by applying a period search to the full data set. For this, we combine all the available high-precision V and y data into one single data set and analyse it with the time-frequency analysis package MuFrAn. The resulting Fourier-amplitude spectrum is obtained for the pre-whitened data, which is the data with the long-term trend and the 2639 d period removed. The resulting amplitude spectrum is shown in the top panel of Fig. 9. Its highest peak suggests a long-term average photometric period of 5.934 ± 0.001 d, which is very close to the average of the seasonal values. Consistent with the result of the differential rotation analysis in Sect. 5, this period is the apparent rotation period of the mid-latitude belt around ∼35° where spots cause the most significant light variation. Accordingly, in the bottom panel of Fig. 9 we fold the 30+ years of photometry with this period. It shows a phase coherency that is remarkable over that period of time. Thus, for future phase calculations, we suggest the use of the equation

(1)

where the reference time was taken from Paper I. This is also the ephemeris that we used to phase our Doppler images in Sect. 3.

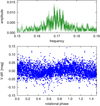thumbnail Fig. 9.

Top: Fourier-amplitude spectrum for all the combined V and y photometric data shown in Fig. 6. Bottom: V and y data folded with Prot = 5.934 days.

Another finding is the frequency splitting of the dominant Fourier peak at 0.17 d−1. The surrounding lower amplitude peaks are typical signatures of differential surface rotation of the star (see the simulations in Strassmeier et al. 2004). Its individual peaks mark the stellar latitudes where the spots preferentially occurred. The five most prominent peaks of the Fourier spectrum are listed in Table 3. Assuming that these peaks are due to surface differential rotation and the lowest and highest frequencies correspond to the polar and equatorial regions (or vice versa), we estimate a surface shear parameter of ΔP/P ≈ 0.03, albeit without any presumption on its sign. Such an estimation is usually erroneous, since the origin of the photometric signals is ambiguous (e.g. it is not known at which stellar latitudes the signaling spots are located). Nevertheless, this value is of the same order as we found from the cross-correlation analysis in Sect. 3.5 and confirms the existence of strong differential rotation on this G5 giant.

Table 3.

Five most prominent periods and their wave amplitudes from the light curve Fourier analysis.

4.3. Radial velocity modulation

The top panel of Fig. 7 also shows the STELLA SES radial velocities from 2017. We note that a systematic zero point shift of 0.503 km s−1 was added to this data (see Strassmeier et al. (2012) for its determination with respect to the CORAVEL system). At this point we caution readers that the radial velocities in the Jones et al. (2017) paper differ in their zero point to the same data re-plotted in the Aller et al. (2018) paper by ∼5 km s−1. A zero point correction of −2.6 km s−1 should be applied for the Jones et al. (2017) data to satisfactorily fit our observations.

We first remove the grossly deviant velocities by a 3-σ filter (this removed nine data points and left 214). The remaining SES velocities of IN Com have an internal precision of typically better than 2 km s−1. A Fourier analysis shows a clean peak at f ≈ 0.17, corresponding to a period of 5.95 ± 0.03 d, but with an almost as strong 1 − f alias. Its full amplitude is almost 2 km s−1 but with an rms of the sinusoidal fit of the same order (Fig. 10). Nevertheless, we can now confirm our earlier suggestion that the low-amplitude radial velocity jitter of IN Com is spot modulated. Just recently, Aller et al. (2018) arrived at the same conclusion.

thumbnail Fig. 10.

Top: rotational modulation of the disc-integrated radial velocities of IN Com. Middle: radial velocity measurements are phase folded with the rotation period and fitted with a sinusoidal. Bottom: residuals of the sinusoidal fit.

5. Characteristics of the Hα profiles

5.1. Line-profile morphology

Line-profile variation of Hα is often associated with dynamo-driven chromospheric activity, not infrequently associated with a strong inhomogeneous stellar wind, coronal mass ejections, and other violent events like flares. The most active stars have Hα in emission. Chromospheric, transition-region, and coronal activity is indeed present in the case of IN Com as amply demonstrated by for example strong Ca II H&K emission (see Paper 1), high-excitation UV lines like C IV (Modigliani et al. 1993), as well as strong X-ray emission (Montez et al. 2010). The overall Hα emission line profile appears permanently asymmetric, which suggests intense long-lived mass motions at the upper chromosphere, giving some support to an origin related to an active binary system with mass motions. Thus, one would expect some rotational modulation of it if it is related to IN Com in the first place.

A time series of 208 Hα line profiles from the first half of 2017 is shown in Fig. 11. A broad emission profile with an average full width at half-maximum (FWHM) of ∼400 km s−1 (∼8.8 Å) superimposed with a central absorption reversal of width ∼150 km s−1 appears consistently throughout the time series. The line width at continuum exceeds the expected rotational width by a factor of approximately five. The rotational period and the equatorial rotational velocity give a radius of 11 R⊙ (Table 1, adopting an inclination of 45° from Doppler imaging). If the Hα emission is bound to the star, above FWHM would then suggest an origin of at least part of the emission at an extended radius, for example due to a circumstellar environment of up to 3–4 R⋆ (assuming corotation). This would mean that the overall Hα emission is composed of two parts: a chromospheric component and a circumstellar component. This has been seen and analysed in several other (over)active stars, for example in UZ Librae (Zboril et al. 2004), FK Comae (Ramsey et al. 1981), II Pegasi (Short et al. 1998), and others, and is not a specific issue for IN Com because it is within a planetary nebula.

thumbnail Fig. 11.

Overplot of the Hα SES spectra of IN Com from the first half of 2017. Indicated are the ±300 km s−1 period-search limits imposed for the 2D FFT in Fig. 12.

All three Balmer profiles of IN Com vary slightly and consistently from one observation to the next, while its profile morphology remains basically unaltered over our entire observing season. No rotational modulation was detected so far although there are changes seen in Hα on a decade-long scale (Aller et al. 2018). The two pseudo-emission peaks frequently reverse its relative strength in our data set; at one point the blue emission is stronger, at another the red emission is stronger. At this point we note that the Hβ and Hγ profiles of IN Com look vastly different from Hα. Both are purely in absorption with an asymmetric shape but of the same average width as the central Hα absorption. We measured FWHM for Hβ of 150 km s−1 and for Hγ of 160 km s−1; however, unfortunately Hβ falls at the edge of subsequent échelle-orders, while Hγ is significantly blended with a blue line at 4337.4 Å and therefore the S/N values for both lines are significantly lower compared with Hα; we estimate errors of 10–15 km s−1. No emission above the continuum is seen either for Hβ or Hγ. We note that the width of the Hα absorption reversal is in agreement with the expected rotational broadening, and so are the absorption profiles of Hβ and Hγ.

5.2. Rotational modulation

To search for coherent temporal changes, we apply a 2D Fourier periodogram to the Hα time series. It is based on a simple fast Fourier transform (FFT) analysis to each wavelength-calibrated pixel of the Hα profile within a velocity range of ±300 km s−1 around the line centre (for a more detailed description of the technique see Strassmeier et al. 2014). We note that one SES CCD pixel disperses ∼0.06 Å at Hα. The resulting 2D periodogram is shown in Fig. 12. It reveals a clear and dominating peak at f = 0.169 d−1 (P = 5.92 ± 0.06 d), which is the expected rotation period of the giant. A second, much weaker peak is detected at 2 f and is identified as its alias.

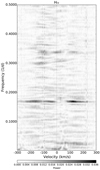thumbnail Fig. 12.

Two-dimensional Fourier periodogram of the time series Hα profile from Fig. 11. Spectral power is indicated in grey-scale. The plot’s horizontal range is ±300 km s−1 around the line core while its vertical range is from 470 d at the bottom to 2 d at the top. The dominant excess power is detected at a frequency of ∼0.17, corresponding to a period of 5.92 d.

It is puzzling though that our 2D periodogram shows a gap with zero power for the 0.169 d−1 frequency in the red part of the line core just between zero and ≈+70 km s−1 velocity. We have no ready explanation for this.

5.3. Line shape and width

We compare the IN Com Hα profiles with the chromospheric and transition-region models put forward by Zboril et al. (2004). With their model 4 (Table 3 and Fig. 4 in Zboril et al. 2004), we find the overall best match for the average IN Com profile. We note that the match is not based on a rigorous line-profile fit but only on a qualitative comparison. The enormous width of the Hα emission of >400 km s−1 had been presented as a puzzle (Aller et al. 2018) but is actually reproduced even with a normal plane-parallel atmosphere with an onset of the chromospheric temperature rise at around 5000 K at a (solar-like) mass depth of 1 g cm−2 and the assumption of complete frequency redistribution (CRD), which assumes that a photon absorbed in the wings is re-emitted in the core (see Avrett et al. 2003). The resulting Hα FWHM is of the order of 350 km s−1 with a relative intensity of the emission peak of 1.2 and a 50% central self reversal. It implies an upper chromosphere with a temperature of 10 000 K and a logarithmic column density of −2.7, as well as a transition region (to the corona) with a temperature in excess of 100 000 K and a logarithmic column density of −6.

thumbnail Fig. 13.

Relationships between rotation and differential rotation for late-type single and binary stars. The position for IN Com is in agreement with the linear fit to (effectively) single stars, represented by the dotted line, suggesting that |α| ∝ Prot[d]/200.

6. Summary and discussion

We have analysed decade-long photometric and one-season-long spectroscopic data of IN Com to derive more accurate stellar parameters and perform a time-series Doppler imaging study. From the long-term photometric observations we have confirmed a ∼5.973 day-long equatorial rotation period of the G star. Also, we have provided more accurate astrophysical parameters for IN Com. Our time-series Doppler imaging study for the first half of 2017 yielded 13 subsequent surface image reconstructions, which were used to estimate surface differential rotation. We found an anti-solar surface rotation profile with α = −0.026 shear coefficient. This value falls within the recently proposed rotation-differential rotation relationship by Kővári et al. (2017) (see Fig. 13). According to the plot, the linear fit for (effectively) single stars suggests |α| ∝ Prot[d]/200. Moreover, the derived absolute surface shear of ΔΩ = 0.027[rad d−1] would follow the general trend of 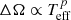where p = 5.8 ± 1.0 (see Fig. 2 in Kővári et al. 2017). Indeed, from the long-term photometric period variations we estimated the rate of the surface shear to be ΔP/P ≈ 0.03, which was in agreement with the shear coefficient derived from Doppler imaging.

The G giant star in the centre of the planetary nebula shows features originating from its evolutionary history. The giant is a barium-rich star; from our spectral synthesis (see Sect. 3.1) we estimate a [Ba/Fe] ratio of 0.85 ± 0.25, supporting the former result of 0.50 ± 0.30 by Thévenin & Jasniewicz (1997). We redetermined [Y/Fe] and [Sr/Fe] ratios as well, confirming the overabundance of these elements in the atmosphere of IN Com. The present configuration and the overabundant s-process elements of the G star in the binary could be explained if the precursor of the white dwarf had originally a higher mass and therefore evolved more quickly to the white dwarf stage, while losing mass, and afterwards the companion (now G star) was polluted by mass transfer or wind accretion (cf. Verbunt & Phinney 1995).

The parallel variation of the long-term light curve with the orbital phase suggests a connection between the orbital motion of the binary and the activity of the G giant. The star is the brightest and faintest at minimum and maximum radial velocity, respectively (see Sect. 4, Fig. 7).

We note finally that although no observational evidence has been found so far to support the existence of accreting material around the G star, its high angular momentum, the peculiar differential rotation, the Hα behaviour, and the parallel variation of the long-term brightness with the orbital phase may all be explained by the presence of an accretion disc tilted to the orbit.

Acknowledgments

We thank our anonymous referee for their valuable suggestions that have helped to improve the paper. This paper is based on data obtained with the STELLA robotic telescopes in Tenerife, an AIP facility jointly operated by AIP and IAC (https://stella.aip.de/) and by the Amadeus APT jointly operated by AIP and Fairborn Observatory in Arizona. For their continuous support, we are grateful to the ministry for research and culture of the State of Brandenburg (MWFK) and the German federal ministry for education and research (BMBF). Authors from Konkoly Observatory acknowledge support from the Austrian-Hungarian Action Foundation (OMAA). KV is grateful to the Hungarian National Research, Development and Innovation Office for OTKA grant K-113117. KV is supported by the Bolyai János Research Scholarship of the Hungarian Academy of Sciences. The authors acknowledge the support of the German Deutsche Forschungsgemeinschaft, DFG through projects KO2320/1 and STR645/1. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement.

References

  1. Aller, A., Lillo-Box, J., Vučković, M., et al. 2018, MNRAS, 476, 1140 [NASA ADS] [CrossRef] [Google Scholar]
  2. Avrett, E. H., & Loeser, R. 2003, in Modelling of Stellar Atmospheres, eds. N. Piskunov, W. W. Weiss, & D. F. Gray, IAU Symp., 210, A21 [Google Scholar]
  3. Bisterzo, S., Gallino, R., Straniero, O., Cristallo, S., & Käppeler, F. 2011, MNRAS, 418, 284 [NASA ADS] [CrossRef] [Google Scholar]
  4. Carroll, T. A., Kopf, M., & Strassmeier, K. G. 2008, A&A, 488, 781 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Carroll, T. A., Strassmeier, K. G., Rice, J. B., & Künstler, A. 2012, A&A, 548, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Castelli, F., & Kurucz, R. L. 2004, IAU Symp., 210, A20 [Google Scholar]
  7. Ciardullo, R., Bond, H. E., Sipior, M. S., et al. 1999, AJ, 118, 488 [NASA ADS] [CrossRef] [Google Scholar]
  8. Csubry, Z., & Kolláth, Z. 2004, in SOHO 14 Helio- and Asteroseismology: Towards a Golden Future, ESA Spec. Pub., 559, 396 [Google Scholar]
  9. De Marco, O., Bond, H. E., Harmer, D., & Fleming, A. J. 2004, ApJ, 602, L93 [NASA ADS] [CrossRef] [Google Scholar]
  10. Donati, J.-F., & Collier Cameron, A. 1997, MNRAS, 291, 1 [NASA ADS] [CrossRef] [Google Scholar]
  11. Feibelman, W. A., & Kaler, J. B. 1983, ApJ, 269, 592 [NASA ADS] [CrossRef] [Google Scholar]
  12. Flower, P. J. 1996, ApJ, 469, 355 [NASA ADS] [CrossRef] [Google Scholar]
  13. Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. González Martínez-País, I., Shahbaz, T., & Casares Velázquez, J. 2014, Accretion Processes in Astrophysics (Cambridge: Cambridge University Press) [Google Scholar]
  15. Granzer, T., Reegen, P., & Strassmeier, K. G. 2001, Astron. Nachr., 322, 325 [NASA ADS] [CrossRef] [Google Scholar]
  16. Gray, D. F. 1981, ApJ, 251, 155 [NASA ADS] [CrossRef] [Google Scholar]
  17. Gray, D. F., & Toner, C. G. 1986, ApJ, 310, 277 [NASA ADS] [CrossRef] [Google Scholar]
  18. Guerrero, M. A. 2012, IAU Symp., 283, 204 [NASA ADS] [Google Scholar]
  19. Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Jasniewicz, G., Acker, A., & Duquennoy, A. 1987, A&A, 180, 145 [NASA ADS] [Google Scholar]
  21. Jasniewicz, G., Acker, A., Mauron, N., Duquennoy, A., & Cuypers, J. 1994, A&A, 286, 211 [NASA ADS] [Google Scholar]
  22. Jasniewicz, G., Thevenin, F., Monier, R., & Skiff, B. A. 1996, A&A, 307, 200 [NASA ADS] [Google Scholar]
  23. Jones, D., & Boffin, H. M. J. 2017, Nat. Astron., 1, 0117 [CrossRef] [Google Scholar]
  24. Jones, D., Van Winckel, H., Aller, A., Exter, K., & De Marco, O. 2017, A&A, 600, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Kővári, Z., Kriskovics, L., Künstler, A., et al. 2015, A&A, 573, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Kővári, Zs, Oláh, K., Kriskovics, L., et al. 2017, Astron. Nachr., 338, 903 [Google Scholar]
  27. Kuczawska, E., & Mikolajewski, M. 1993, Acta Astron., 43, 445 [NASA ADS] [Google Scholar]
  28. Künstler, A., Carroll, T. A., & Strassmeier, K. G. 2015, A&A, 578, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Kupka, F., Piskunov, N., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
  30. Lindborg, M., Hackman, T., Mantere, M. J., et al. 2014, A&A, 562, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Longmore, A. J., & Tritton, S. B. 1980, MNRAS, 193, 521 [NASA ADS] [Google Scholar]
  32. Malasan, H. L., Yamasaki, A., & Kondo, M. 1991, AJ, 101, 2131 [NASA ADS] [CrossRef] [Google Scholar]
  33. Modigliani, A., Patriarchi, P., & Perinotto, M. 1993, ApJ, 415, 258 [NASA ADS] [CrossRef] [Google Scholar]
  34. Montez, Jr., R., De Marco, O., Kastner, J. H., & Chu, Y.-H. 2010, ApJ, 721, 1820 [NASA ADS] [CrossRef] [Google Scholar]
  35. Noskova, R. I. 1989, Sov. Astron. Lett., 15, 149 [NASA ADS] [Google Scholar]
  36. Paczyński, B. 1976, in Structure and Evolution of Close Binary Systems, eds. P. Eggleton, S. Mitton, & J. Whelan, IAU Symp., 73, 75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Piskunov, N., & Valenti, J. A. 2017, A&A, 597, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Podsiadlowski, P. 2001, in Evolution of Binary and Multiple Star Systems, eds. P. Podsiadlowski, S. Rappaport, A. R. King, F. D’Antona, & L. Burderi, ASP Conf. Ser., 229, 239 [NASA ADS] [Google Scholar]
  39. Pojmanski, G. 2002, Acta Astron., 52, 397 [NASA ADS] [Google Scholar]
  40. Ramsey, L. W., Nations, H. L., & Barden, S. C. 1981, ApJ, 251, L101 [NASA ADS] [CrossRef] [Google Scholar]
  41. Short, C. I., Byrne, P. B., & Panagi, P. M. 1998, A&A, 338, 191 [NASA ADS] [Google Scholar]
  42. Strassmeier, K. G., & Oláh, K. 2004, in Stellar Structure and Habitable Planet Finding, eds. F. Favata, S. Aigrain, & A. Wilson, ESA Spec. Pub., 538, 149 [NASA ADS] [Google Scholar]
  43. Strassmeier, K. G., Hubl, B., & Rice, J. B. 1997a, A&A, 322, 511 [NASA ADS] [Google Scholar]
  44. Strassmeier, K. G., Boyd, L. J., Epand, D. H., & Granzer, T. 1997b, PASP, 109, 697 [NASA ADS] [CrossRef] [Google Scholar]
  45. Strassmeier, K. G., Granzer, T., Weber, M., et al. 2010, Adv. Astron., 2010, 19 [NASA ADS] [CrossRef] [Google Scholar]
  46. Strassmeier, K. G., Weber, M., Granzer, T., & Järvinen, S. 2012, Astron. Nachr., 333, 663 [NASA ADS] [CrossRef] [Google Scholar]
  47. Strassmeier, K. G., Weber, M., Granzer, T., et al. 2014, Astron. Nachr., 335, 904 [NASA ADS] [CrossRef] [Google Scholar]
  48. Strassmeier, K. G., Ilyin, I., Järvinen, A., et al. 2015, Astron. Nachr., 336, 324 [Google Scholar]
  49. Strassmeier, K. G., Ilyin, I., & Steffen, M. 2018, A&A, 612, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Thévenin, F., & Jasniewicz, G. 1997, A&A, 320, 913 [NASA ADS] [Google Scholar]
  51. Tout, C. A., & Regős, E. 2003, in 3D Stellar Evolution, eds. S. Turcotte, S. C. Keller, & R. M. Cavallo, ASP Conf. Ser., 293, 100 [NASA ADS] [Google Scholar]
  52. Van Winckel, H., Jorissen, A., Exter, K., et al. 2014, A&A, 563, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Verbunt, F., & Phinney, E. S. 1995, A&A, 296, 709 [NASA ADS] [Google Scholar]
  54. Vida, K., Oláh, K., & Szabó, R. 2014, MNRAS, 441, 2744 [NASA ADS] [CrossRef] [Google Scholar]
  55. Weber, M., & Strassmeier, K. G. 2011, A&A, 531, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Weber, M., Granzer, T., Strassmeier, K. G., & Woche, M. 2008, SPIE Conf. Ser., 7019 [Google Scholar]
  57. Weber, M., Granzer, T., & Strassmeier, K. G. 2012, SPIE Conf. Ser., 8451 [Google Scholar]
  58. Zboril, M., Strassmeier, K. G., & Avrett, E. H. 2004, A&A, 421, 295 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

Appendix A: Log of spectroscopic data

thumbnail Fig. A.1.

Observed line profiles (thick black lines) and their model fits (thin red lines) for the Doppler reconstructions S01–S06 shown in Fig. 1. The phases of the individual observations are listed on the right side of the panels.

thumbnail Fig. A.2.

Observed line profiles (thick black lines) and their model fits (thin red lines) for the Doppler reconstructions S07–S12 shown in Fig. 2. The phases of the individual observations are listed on the right side of the panels.

Table A.1.

Observing log of STELLA-SES spectra of IN Com from 2017 used for individual Doppler reconstructions shown in Sect. 3.

Table A.2.

Observing log of PEPSI at VATT spectra of IN Com from March 2017.

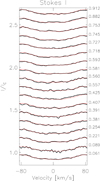thumbnail Fig. A.3.

Observed line profiles (thick black lines) and their model fits (thin red lines) for the Doppler reconstruction applied for the PEPSI at VATT spectra shown in Fig. 3. The phases of the individual observations are listed on the right side of the panel.

All Tables

Table 1.

Astrophysical properties of IN Com.

In the text
Table 2.

Temporal distribution of the subsequent data sets for each individual Doppler image.

In the text
Table 3.

Five most prominent periods and their wave amplitudes from the light curve Fourier analysis.

In the text
Table A.1.

Observing log of STELLA-SES spectra of IN Com from 2017 used for individual Doppler reconstructions shown in Sect. 3.

In the text
Table A.2.

Observing log of PEPSI at VATT spectra of IN Com from March 2017.

In the text

All Figures

thumbnail Fig. 1.

Doppler images of IN Com for STELLA data sets S01–S06. The corresponding mid-UT dates (2017+) are indicated below the names of the maps.
In the text
thumbnail Fig. 2.

Doppler images for STELLA data sets S07–S12. The corresponding mid-UT dates (2017+) are indicated below the names of the maps.
In the text
thumbnail Fig. 3.

Doppler image for the PEPSI at VATT spectra. The corresponding mid-UT date is 11 March, 2017, which falls just between the dates of the S04 and S05 maps shown in Fig. 1.
In the text
thumbnail Fig. 4.

Time variation of the spot filling factor (top panel) and the integrated surface temperature (bottom panel) of IN Com derived from the time-series Doppler images shown in Figs. 1–3. Upper panel: the spot filling factors are shown for the polar region and for the mid-to-low latitudes separately; see the top and the bottom curves, respectively. The different Doppler reconstructions are identified by their serial numbers.
In the text
thumbnail Fig. 5.

Average cross-correlation map for IN Com showing anti-solar surface differential rotation. The best correlated dark regions are fitted by Gaussian curves in 5° bins. Gaussian peaks are indicated by dots, the corresponding Gaussian widths by horizontal lines. The best fit differential rotation law suggests an equatorial period of Peq = 5.973 d and a surface shear coefficient of α = −0.026.
In the text
thumbnail Fig. 6.

Top: long-term photometric V and y data of IN Com. Different colours mean different sources of observations; green: data from T6 and T7 APTs, blue: observations from the Hungarian 1 m RCC telescope, red: literary data (mostly from Paper 1) that are used for seasonal period determination, grey: literary data+ASAS data that are not suitable for seasonal period determination. The sine-wave fit by black solid line represents the long-term overall brightness change with a period of 7.2 yr, which is basically the wide binary period (see Sect. 6). Bottom: independent rotational period determinations for suitable seasonal data sets. Further details can be found in the text.
In the text
thumbnail Fig. 7.

Comparing the long-term light variation with the radial velocity curve of IN Com. Top: radial velocity curve of the star taken from Jones et al. (2017) suggesting a 2717 day long orbital period. Overplotted are the radial velocities from our spectroscopic data (green circles). Bottom: long-term V + y photometric observations after folding up with the orbital period.
In the text
thumbnail Fig. 8.

Well-sampled photometric modulation indicates the solidity of the 5.9 day period. Light curves were taken during April and May 1996 (top) and April 1998 (bottom) with the T7 and T6 APTs, respectively. The light curves even show the changing amplitudes and shapes typical for star spot evolution.
In the text
thumbnail Fig. 9.

Top: Fourier-amplitude spectrum for all the combined V and y photometric data shown in Fig. 6. Bottom: V and y data folded with Prot = 5.934 days.
In the text
thumbnail Fig. 10.

Top: rotational modulation of the disc-integrated radial velocities of IN Com. Middle: radial velocity measurements are phase folded with the rotation period and fitted with a sinusoidal. Bottom: residuals of the sinusoidal fit.
In the text
thumbnail Fig. 11.

Overplot of the Hα SES spectra of IN Com from the first half of 2017. Indicated are the ±300 km s−1 period-search limits imposed for the 2D FFT in Fig. 12.
In the text
thumbnail Fig. 12.

Two-dimensional Fourier periodogram of the time series Hα profile from Fig. 11. Spectral power is indicated in grey-scale. The plot’s horizontal range is ±300 km s−1 around the line core while its vertical range is from 470 d at the bottom to 2 d at the top. The dominant excess power is detected at a frequency of ∼0.17, corresponding to a period of 5.92 d.
In the text
thumbnail Fig. 13.

Relationships between rotation and differential rotation for late-type single and binary stars. The position for IN Com is in agreement with the linear fit to (effectively) single stars, represented by the dotted line, suggesting that |α| ∝ Prot[d]/200.
In the text
thumbnail Fig. A.1.

Observed line profiles (thick black lines) and their model fits (thin red lines) for the Doppler reconstructions S01–S06 shown in Fig. 1. The phases of the individual observations are listed on the right side of the panels.
In the text
thumbnail Fig. A.2.

Observed line profiles (thick black lines) and their model fits (thin red lines) for the Doppler reconstructions S07–S12 shown in Fig. 2. The phases of the individual observations are listed on the right side of the panels.
In the text
thumbnail Fig. A.3.

Observed line profiles (thick black lines) and their model fits (thin red lines) for the Doppler reconstruction applied for the PEPSI at VATT spectra shown in Fig. 3. The phases of the individual observations are listed on the right side of the panel.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.