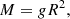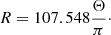| Issue |
A&A
Volume 624, April 2019
|
|
|---|---|---|
| Article Number | A35 | |
| Number of page(s) | 17 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201834514 | |
| Published online | 03 April 2019 | |
Stellar masses from granulation and oscillations of 23 bright red giants observed by BRITE-Constellation⋆
1
Institut für Astrophysik, Universität Wien, Türkenschanzstrasse 17, 1180
Vienna, Austria
e-mail: thomas.kallinger@univie.ac.at
2
Instituto de Astrofísica de Canarias, 38200
La Laguna, Tenerife, Spain
3
Departamento de Astrofísica, Universidad de La Laguna, 38206
La Laguna, Tenerife, Spain
4
Max Planck Institute for Solar System Research, Justus-von-Liebig-Weg 3, 37077
Göttingen, Germany
5
Stellar Astrophysics Centre, Department of Physics and Astronomy, Aarhus University, Ny Munkegade 120, 8000
Aarhus C, Denmark
6
Institute for Astronomy, University of Hawai‘i, 2680 Woodlawn Drive, Honolulu, HI 96822, USA
7
Institut für Kommunnikationsnetze und Satellitenkommunikation, Technical University Graz, Inffeldgasse 12, 8010
Graz, Austria
8
Institute for Machine Learning, Johannes Kepler University, Altenberger Str. 69, Computer Science Building, 4040
Linz, Austria
9
Nicolaus Copernicus Astronomical Center, ul. Bartycka 18, 00-716
Warsaw, Poland
10
Département de physique and Centre de Recherche en Astrophysique du Québec (CRAQ), Université de Montréal, CP 6128, Succ. Centre-Ville, Montréal, Québec H3C 3J7, Canada
11
Instytut Astronomiczny, Uniwersytet Wrocławski, Kopernika 11, 51-622
Wrocław, Poland
12
Institute of Automatic Control, Silesian University of Technology, Akademicka 16, 44-100
Gliwice, Poland
13
Department of Physics, Royal Military College of Canada, PO Box 17000 Station Forces, Kingston K7K 0C6, ON, Canada
14
Universität Innsbruck, Institut für Astro- und Teilchenphysik, Technikerstrasse 25, 6020
Innsbruck, Austria
Received:
26
October
2018
Accepted:
14
February
2019
Context. The study of stellar structure and evolution depends crucially on accurate stellar parameters. The photometry from space telescopes has provided superb data that enabled the asteroseismic characterisation of thousands of stars. However, typical targets of space telescopes are rather faint and complementary measurements are difficult to obtain. On the other hand, the brightest, otherwise well-studied stars, are lacking seismic characterization.
Aims. Our goal is to use the granulation and/or oscillation timescales measured from photometric time series of bright red giants (1.6 ≤ V mag ≤ 5.3) observed with BRITE-Constellation to determine stellar surface gravities and masses.
Methods. We used probabilistic methods to characterise the granulation and/or oscillation signal in the power density spectra and the autocorrelation function of the BRITE-Constellation time series.
Results. We detect a clear granulation and/or oscillation signal in 23 red giant stars and extract the corresponding timescales from the power density spectra as well as the autocorrelation function of the BRITE-Constellation time series. To account for the recently discovered non-linearity of the classical seismic scaling relations, we used parameters from a large sample of Kepler stars to re-calibrate the scalings of the high- and low-frequency components of the granulation signal. We developed a method to identify which component is measured if only one granulation component is statistically significant in the data. We then used the new scalings to determine the surface gravity of our sample stars, finding them to be consistent with those determined from the autocorrelation signal of the time series. We further used radius estimates from the literature to determine the stellar masses of our sample stars from the measured surface gravities. We also defined a statistical measure for the evolutionary stage of the stars.
Conclusions. Our sample of stars covers low-mass stars on the lower giant branch to evolved massive supergiants and even though we cannot verify our mass estimates with independent measurements from the literature, they appear to be at least good enough to separate high-mass from low-mass stars. Given the large known but usually not considered systematic uncertainties in the previous model-based mass estimates, we prefer our model-independent measurements.
Key words: stars: fundamental parameters / stars: oscillations / stars: interiors
Based on data collected by the BRITE Constellation satellite mission, designed, built, launched, operated, and supported by the Austrian Research Promotion Agency (FFG), the University of Vienna, the Technical University of Graz, the University of Innsbruck, the Canadian Space Agency (CSA), the University of Toronto Institute for Aerospace Studies (UTIAS), the Foundation for Polish Science & Technology (FNiTP MNiSW), and National Science Centre (NCN).
© ESO 2019
1. Introduction
During about the last 15 years, the seismology of red giant stars has grown into an important field in stellar astrophysics, providing a unique opportunity to probe the interior structure of stars in an eventful phase of stellar evolution (e.g., see reviews by Chaplin & Miglio 2013; Hekker & Christensen-Dalsgaard 2017). This is possible thanks to so-called solar-type oscillations that are intrinsically damped and stochastically excited by the turbulent flux of the near-surface convection. For main-sequence stars, these are pressure (p) modes that are mainly confined to the outer envelope and which produce a comb-like pattern in the frequency spectrum. The dense He cores of red giants allow for the existence of gravity (g) modes at frequencies that overlap the p-mode frequency spectrum (e.g. Dziembowski et al. 2001; Dupret et al. 2009). Resonant coupling between the g- and p-mode cavities gives rise to so-called mixed modes, which carry valuable information about the deep interior of red giants, but they can be observed on their surface.
Early attempts to observe solar-type oscillations in red giants used ground-based radial velocity measurements (e.g. Frandsen et al. 2002; De Ridder et al. 2006) and space-based photometry (WIRE: Buzasi et al. 2000; Retter et al. 2003; Stello et al. 2008; HST: Edmonds & Gilliland 1996; Kallinger et al. 2005; Stello & Gilliland 2009; Gilliland et al. 2011; SMEI: Tarrant et al. 2007, 2008; MOST: Barban et al. 2007; Kallinger et al. 2008a,b). The major breakthrough, however, came with the launch of CoRoT (Baglin et al. 2006) and Kepler (Borucki et al. 2010), which provided data of unprecedented length and quality needed to tackle various questions in stellar astrophysics, like the relation between the different seismic (e.g. Huber et al. 2011; Mosser et al. 2012a) and granulation (e.g. Mathur et al. 2011) observables, the analysis of non-radial mixed modes (e.g. Bedding et al. 2011; Beck et al. 2011; Mosser et al. 2012c) and how they are used to constrain the core-rotation rate (e.g. Beck et al. 2012; Mosser et al. 2012b; Gehan et al. 2018), and the analysis of mode amplitudes and lifetimes (e.g. Baudin et al. 2011; Vrard et al. 2018) and what they reveal about the signature of acoustic glitches (e.g. Corsaro et al. 2015; Vrard et al. 2015).
Moreover, the seismology of red giants resulted in a much more precise method for determining stellar global parameters compared to classical methods such as isochrone fitting (e.g. Lebreton & Goupil 2014). The determination of accurate stellar parameters is a fundamental and long-standing problem in astrophysics (e.g. Soderblom 2010). However, this is often only possible by means of stellar models and therefore suffers from our incomplete knowledge of the physical processes inside stars. The wealth of observations delivered by CoRoT and Kepler triggered the development of a new approach, which is founded on relations between global seismic parameters, such as the large frequency separation or the frequency of the maximum oscillation power, and stellar parameters (Ulrich 1986; Brown et al. 1991; Kjeldsen & Bedding 1995). Initially, these scaling relations were used to predict the characteristics of the oscillations. Stello et al. (2008) and Kallinger et al. (2010b) were the first to obtain seismic masses and seismic masses and radii, respectively, from global oscillation parameters. Mainly empirical, the seismic scaling relations have been shown to be accurate throughout many evolutionary stages (e.g. White et al. 2011a) and are nowadays widely used in various fields, from determining fundamental parameters of field stars (e.g. Kallinger et al. 2010a; Mosser et al. 2010), binary systems (e.g. Beck et al. 2014; Gaulme et al. 2016) and planet-hosting stars (e.g. Borucki et al. 2012) to Galactic population studies (Miglio et al. 2013).
However, the calibration of the seismic scalings still remains an issue. Several studies have shown that the extrapolation from the Sun to evolved red giants causes biases and yields masses that are too high for red giants (e.g. Miglio et al. 2012; Gaulme et al. 2016). Various model-based corrections (e.g. White et al. 2011b; Sharma et al. 2016) yield better results but suffer from known deficiencies in the models. Kallinger et al. (2018) defined revised scaling relations that account for these systematic discrepancies in a completely model-independent way.
From an observational point of view, the CoRoT and Kepler missions have contributed tremendously to the field of asteroseismology of red giants and even though they provided data of unprecedented quality, they also suffer from the fundamental problem that they are essentially limited to relatively faint stars (see Fig. 1). For such stars it is difficult to get additional constraints for example from high-resolution spectroscopy, interferometry, and other methods. (e.g. Huber et al. 2012). For bright red giants, on the other hand, apart from a few exceptions (see earlier references and e.g. Pope et al. 2016) there are effectively no photometric time-series data available that allow for detailed asteroseismic analyses. The TESS mission (Ricker et al. 2015) will change this but even though it is already in operation, it will still need several months to accumulate the necessary observing lengths. In the meantime, the satellites of the BRITE (BRIght Target Explorer)-Constellation1 mission can efficiently help to fill this gap. The BRITE satellites are designed to photometrically monitor the brightest stars in the sky for up to six months and therefore provide the time base needed for useful asteroseismic analyses of red giants. Even though the photometric quality of the BRITE instruments is likely not sufficient to clearly detect solar-type oscillations on the lower red-giant branch (with typical amplitudes of some 10 to some 100 ppm), a large fraction of the potential BRITE targets (i.e. stars brighter than about fifth magnitude) are red giants. Therefore, it was decided to monitor these stars whenever they are present in an observing field without disturbing other ongoing programmes.
 |
Fig. 1. Histrogram of magnitudes of red giant stars observed by BRITE-Constellation (red) and Kepler (grey; Huber et al. 2014). |
In this paper we report on the BRITE-Constellation observations of red giants during the first three years of the mission. During this time the BRITE satellites collected photometric time series data for 38 red giants consisting of more than two million individual measurements. We find a granulation and/or oscillation signal in 23 of the 38 stars located in nine of the 15 fields observed. This sample covers a large variety of red giants ranging from low-mass red clump stars to high-mass red supergiants. We extract the typical granulation and/or oscillation timescales of these stars from which we determine accurate surface gravities. Using radius estimates from the literature (mainly based on interferometric angular diameters and Gaia parallaxes), we can constrain the masses of these stars with typical uncertainties of 10–15%. We obtain consistent results using different methods for our measurements and mass estimations.
2. BRITE photometry
The photometric observations used in this study were collected with BRITE-Constellation. This is a fleet of five nanosatellites described in detail by Weiss et al. (2014) and Pablo et al. (2016) and consists of two Austrian satellites UniBRITE (UBr) and BRITE-Austria (BAb), one Canadian satellite, BRITE-Toronto (BTr), and two Polish satellites BRITE-Heweliusz (BHr) and BRITE-Lem (BLb). Each of the 20 × 20 × 20 cm satellites hosts an optical telescope of 3 cm aperture, feeding an uncooled CCD, and is equipped with a single filter. Three nanosats (UBr, BTr, BHr) have a red filter (550–700 nm) and two (BAb, BLb) have a blue filter (390–460 nm), which are similar to the Sloan r and Geneva B filters, respectively. The observing strategy of BRITE-Constellation is to point at least one satellite at a 20° × 24° field of the sky and simultaneously collect data for about 30 stars in this field, which are visible for about 5–30 min per 97–101 min orbit for up to six months.
A problem affecting the BRITE satellites is the sensitivity of the Kodak KAI-11002M detectors (11 million pixels with a plate scale of 27.3″ per pixel) to particle radiation, which posed a major threat to the lifetime and effectiveness of the BRITE mission. The impact of high-energy protons causes the emergence of hot and warm pixels at a rate much higher than originally expected. The affected pixels more easily generate thermal electrons and thereby significantly impair the photometric precision of the observations. An additional important problem that appeared after several months of operation was the charge transfer inefficiency, also caused by the protons. Thanks to increasing the readout time and adopting a chopping technique for data acquisition, the effect of CCD radiation damage on the photometry is now significantly reduced (Popowicz et al. 2017).
In the chopping mode, the satellite pointing is shifted slightly between consecutive exposures, so that the target point spread functions (PSF) centroids alternate by about 20 pixels between two positions on the CCD. This means that the PSF-free part of a given subraster image acts as a dark image for the subsequent exposure and subtracting consecutive exposures results in an image with one negative and one positive target PSF. The background defects are thereby almost entirely removed.
Details about data reduction are given by Popowicz et al. (2017). While in stare observing mode, bias, dark, and background corrections are necessary, they are not required for observations in chopping mode since the stellar flux is extracted from differential images. The remaining main step is to identify the optimal apertures and to extract the flux within these apertures. The light curves resulting from this pipeline reduction are deposited in the BRITE-Constellation data archive from where we extract the data.
3. Target sample
Between 2013 and 2017, BRITE-Constellation observed 24 fields. In 15 of them, a total of 38 red giant stars were observed (see Fig. 1). We carefully examined these data and found significant intrinsic variability in 23 stars observed in nine different fields. Two stars were observed in two campaigns. The sample includes a large variety of red giants with apparent magnitudes between 1.6 and 5.3 mag and spectral types ranging from G2 III to M3.5 II. For the remaining 15 stars the data sets are either too short or too noisy to detect variability.
Several stars were observed by more than one satellite. However, in this work we only show results from the data set with the best quality. A summary of the different fields observed is given in Table 1, while details about the individual stars are listed in Table 2.
Summary of the observed fields.
Overview of the 23 target stars.
McDonald et al. (2017) derived consistent estimates of the effective temperatures for all stars in our sample based on HIPPARCOS-Gaia parallaxes and a comparison between archival multi-wavelength photometry and stellar model atmospheres. Stellar luminosities are taken from the Gaia Data Release 2 (DR2) catalogue (Gaia Collaboration 2018) and from McDonald et al. (2017). For our target stars, the uncertainties are typically ±125 K for the effective temperature and 5–10% for the luminosity. Literature values for the surface gravity and metallicity are less consistent and are taken from various sources with typically much larger uncertainties.
4. BRITE data post-processing
The photometric time series as delivered by the data reduction team still includes instrumental effects and obvious outliers and therefore needs some post-processing. The BRITE-Constellation data come in different setups2 and data blocks of approximately equal length, which we treat independently. Subdivision of the data sets into blocks was required due to a limit of typically 30 000 frames for the standard data reduction software.
Adapting the recipe of Pigulski et al. (2016) and Kallinger et al. (2017), we performed the following steps for each block of each data set:
-
If the data were obtained in chopping mode, we divide the data set into two sets corresponding to the alternating PSF position on the CCD subraster.
-
Compute a 2D histogram of the X/Y positions and fit a 3D multivariate Gaussian to it. Images that were taken with the PSF centre positioned outside three times the widths of the Gaussian are eliminated from further processing. This procedure identifies most of the outliers and rejects them.
-
The procedure continues with the “cleaned” data set and applies a 4σ-clipping. Depending on the amplitude of the intrinsic signal, the σ-clipping is performed relative to the average flux of the complete data set or a running average with adaptable width.
-
Compute the correlation coefficient c between the instrumental flux and the CCD temperature and X/Y position of the PSF.
-
Build an n-dimensional correction map for all parameters with |c|> 0.1 (i.e. a 1D, 2D, or 3D map), where each axis is divided into N1/(n + 1) bins, where N is the number of data points, which results in typically 10–30 bins. All measurements in a given bin are then averaged. Finally, the correction map is divided by the average instrumental flux to produce a correction factor for each combination of instrumental parameters, which is then applied to the time series. As an example, we show in Fig. 2 the resulting 2D correction map (CCD temperature and Y position of the PSF) of a subset of the UBr observations of ε Sco, which is the star with the lowest Fourier noise in our sample. The time series has an average instrumental flux of about 1.1 × 105 ADU s−1 so that a correction factor of 0.4% corresponds to an instrumental signal of 440 ADU s−1. The rms scatter of the time series reduces from ∼6.4 ppt before the correction to ∼5.4 ppt after the correction, improving the photometric quality by about 16%.
 |
Fig. 2. Two-dimensional correction map (CCD-temperature and Y position of the PSF) for the about-30-day-long UBr time series of ε Sco obtained during observing subset 2 with the colour-coded correction factors. Right and bottom panels: correction factor as a function of the Y position of the PSF and CCD temperature, respectively, where the values of the other parameter are colour-coded (with red-green-blue symbols corresponding to low-mean-high values of the other parameter). The black dots are the actual measurements divided by the average value of the time series. |
Finally, the data subsets are combined and divided by the average value for conversion to relative flux. The 23 final light curves are between 48 and 173 d long and consist of about 15 000–136 000 individual measurements (see Table 2).
From the known fundamental parameters of our target stars, we can expect that the intrinsic variability of all stars acts on timescales not shorter than a few hours. Therefore, the typical cadences of the observations of some twenty seconds are unnecessarily short. We therefore bin the data into one measurement per BRITE orbit (97–101 min, depending on the satellite), where the standard deviation of the original measurements within a given bin (σbin) provides a good estimate for the photometric accuracy. The resulting Nyquist frequencies range from νNyq = 82.5 to 85.9 μHz, which is in any case high enough to cover the full, expected intrinsic variability of our target stars. The binned light curves consist of 481–1933 data points. The corresponding duty cycles (i.e. the actual number of data points relative to the total number of satellite orbits during the full length of the time series) range between 48 and 80%. As an example, we show the fully reduced and binned light curve of ε Sco in Fig. 3. The light curves of the other stars are illustrated in Figs. 4–6.
 |
Fig. 3. Left panel: relative instrumental flux of the approximately 161-day-long UBr binned data set of ε Sco. Middle panel: power density spectrum (in ppm2/μHz) of the binned (grey lines) and interpolated time series (black lines) along with a best global model fit (blue lines) and expected νmax (vertical red lines). Right panel: squared autocorrelation function of the binned time series (black dots) and a best fit (red line). |
 |
Fig. 6. Same as Fig. 3. For 12 Mus we correct the original light curve for the long-period variation and eclipses originating from two companions. |
In the next step we compute the unweighted Fourier spectrum of the time series and convert it to power density by dividing the spectral power by a factor that results from Parseval’s theorem. The power density spectrum (PDS) of ε Sco is shown in Fig. 3 and that of the other target stars in Figs. 4–6.
A challenge for the subsequent analysis is the relatively low duty cycle of the BRITE-Constellation observations. For stars with a strong long-periodic signal, the spectral window leaks power from the low-frequency into the high-frequency domain. If the contrast between intrinsic low-frequency and high-frequency signal is high enough, the high-frequency domain can then be dominated by this leaked power, which would significantly influence a global fit to the spectrum (see Sect. 5). To improve the situation, we fill gaps that are shorter than 0.5 d by linear interpolation at a cadence that corresponds to the BRITE orbital period (i.e. up to seven data points for a 0.5 d-long gap). Such an approach is well-tested for Kepler observations (e.g. García et al. 2014b; Kallinger et al. 2014; Stello et al. 2017) and only marginally affects the frequency range in which we are interested but significantly improves the duty cycle (see Table 2) and therefore the spectral window function. We then compute the power density spectra of the gap-filled time series. As can be seen in Fig. 3, the power density of ε Sco significantly decreases above about 20 μHz, while the low-frequency domain remains basically the same. The most severe case in our sample is ρ Per (Fig. 4) for which the “noise” at high frequencies decreases by about an order of magnitude due to gap filling in the time series (improving the duty cycle from 80 to 94%). Another effect that we find is that for several stars (e.g. NS Pup) peak amplitudes around 1 and/or 2 d−1 (∼11.6 and 23.1 μHz) are damped by gap-filling.
5. Data analysis
Brightness variations in stars with a convective envelope arise primarily from granulation and acoustic oscillations (e.g. Mathur et al. 2011; Kallinger et al. 2014), which are largely gravity-dependent. Further processes contributing to the photometric variations are dark and bright spots due to magnetic activity, which are modulated by the period of stellar rotation (e.g. García et al. 2014a; Ceillier et al. 2017; Beck et al. 2018). Rotation and magnetic activity are largely gravity-independent. While these phenomena act on different time and amplitude scales for low-luminosity red giants, it might become more difficult to disentangle them with growing luminosity. However, for an a priori unknown star it is difficult to assign which signal is due to which phenomenon.
5.1. Granulation or oscillation timescales
Kallinger et al. (2014) have shown that the power density spectrum (PDS) of a red giant (as for any other star with a convective envelope) can be globally modelled by a sequence of super-Lorentzian functions and a Gaussian. They found that the granulation signal is split into two components with their characteristic frequencies strongly tied to the frequency of maximum oscillation power (νmax, which is usually defined as the centre of the Gaussian) and approximately scale as
where νlow and νhigh are the characteristic frequency of the low-frequency (LF) and the high-frequency (HF) component, respectively.
The surface gravity g can be estimated from a measurement of νlow, νhigh, or νmax, if the effective temperature of a star is known, according to
(e.g. Brown et al. 1991; Kjeldsen & Bedding 1995).
In order to determine one (or more) of these parameters, we follow the approach of Kallinger et al. (2014) and fit the observed power density spectra with a global model
where Pn corresponds to the instrumental noise contribution and ai and νi to the rms amplitude and characteristic frequency of the ith component, respectively, and Pg, νmax, and σ are the height, central frequency, and width of the oscillation power excess, respectively. The function η(ν) accounts for the frequency-dependent damping of the signal amplitude due to averaging over the integration time (Huber et al. 2010) and is defined as
For the fit we use the Bayesian nested sampling algorithm MULTINEST (Feroz et al. 2009), which provides the posterior probability distributions for the parameter estimation and the global model evidence. The big advantage of the latter compared to other statistical tools is that it is properly normalised and evaluated over the entire parameter space and therefore allows one to reliably rate how well a given model represents a given data set compared to another model with little risk of over-fitting the data. More details are given by Kallinger et al. (2012, 2014).
Most of the stars in our sample show a strong decrease in power with increasing frequency, which is typical for the granulation signal, but no clear oscillation power excess. It is therefore difficult to decide a priori how many signal components are actually present in the data (i.e. statistically significant) and which of the measured components corresponds to granulation or something else. It can even happen that the PDS still includes some frequency-dependent instrumental signal, efor example the spectral window or instrumental drifts.
To avoid bias in the interpretation of the data, we tested various models (Eq. (3) with i = 1…n, and each of them with and without a Gaussian) and let the global evidence z, as delivered by MULTINEST, decide which model best represents the data. We start with the least complex model (i.e. one component and no Gaussian) and accept a more complex model (more components and/or a Gaussian) if its probability3pi = zi/∑jzj > 0.9. If a model is not accepted, we add another degree of complexity and stop if the probability is again below 0.9. We find that the observed PDS of our sample of stars can be best reproduced by one to three components and find strong evidence for an oscillation power excess only in two stars, 39 Cyg and σ Per. The best-fit models are shown in Figs. 3–6.
For several other targets, clear variability is detected, but the BRITE time series are not long enough to properly detect an oscillation power excess (and resolve the oscillations modes within it). The interplay between intrisic variability timescales and observing length (ΔT) is illustrated in Fig. 7, where we show the PDS of the full 1470 day-long Kepler time series of KIC 1431599 and for subsets of it. To resolve the star’s oscillation power excess (i.e. its individual oscillation modes) around νmax ≃ 2.3 μHz requires considerably longer observations than the typical oscillation periods of about 5 d. There is no clear rule for this but usually the mode pattern of a solar-type oscillator is resolved if the frequency resolution df = 1/ΔT is smaller than the frequency separation between l = 0 and 2 modes δν02. Taking into account the finite mode lifetimes and that δν02 approximately scales as 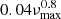 for red giants (e.g. Huber et al. 2010; Kallinger et al. 2012), we define as a rule of thumb that
for red giants (e.g. Huber et al. 2010; Kallinger et al. 2012), we define as a rule of thumb that  . In our sample of red giants only nine stars fulfil this criterion including 39 Cyg and σ Per. In the case of KIC 1431599, this means that the star needs to be observed significantly (∼3–5) longer than about 150 days to clearly detect and resolve the oscillation power excess. This is in fact shown in Fig. 7. While for the full Kepler time series the power excess is clearly detectable with its individual oscillation modes resolved (see insert in panel d), this is not the case for the two arbitrarily chosen 100-day-long subsets of the time series. Their PDSs neither reveal individual modes nor can the power excess be distinguished from the underlying granulation signal. On the other hand, the general behaviour of the granulation signal in the PDS remains unaffected from shortening the time series so that even for observations as short as ten days one still gets the typical decrease in power with increasing frequency.
. In our sample of red giants only nine stars fulfil this criterion including 39 Cyg and σ Per. In the case of KIC 1431599, this means that the star needs to be observed significantly (∼3–5) longer than about 150 days to clearly detect and resolve the oscillation power excess. This is in fact shown in Fig. 7. While for the full Kepler time series the power excess is clearly detectable with its individual oscillation modes resolved (see insert in panel d), this is not the case for the two arbitrarily chosen 100-day-long subsets of the time series. Their PDSs neither reveal individual modes nor can the power excess be distinguished from the underlying granulation signal. On the other hand, the general behaviour of the granulation signal in the PDS remains unaffected from shortening the time series so that even for observations as short as ten days one still gets the typical decrease in power with increasing frequency.
 |
Fig. 7. Full 1470-day-long Kepler time series of KIC 1431599 (grey; panel a) and 100- (red and blue) and ten- (orange) day-long subsets (panels b and c). Panel d: corresponding power density spectra along with a global fit (black line) consisting of two granulation components (dashed lines), a Gaussian, and instrumental white noise fitted to the full Kepler time series (Eq. (3)). The largest amplitude peaks in the 100 d PDS are marked with vertical arrows. The corresponding sinusoidal signal is overplotted to the respective time series. The inset shows the frequency range of the oscillation power excess with individual oscillation modes marked by their spherical degree. Panel e: autocorrelation functions of the various time series. |
Another effect of the stochastic nature of the signal is that the dominant frequency (i.e. the frequency with the largest amplitude in the spectrum) in one data set can be quite different from that of other observations of the same star. This is because the probability that frequency of the largest amplitude in a random realisation of the stellar signal follows the limiting spectrum (i.e. of an infinitely long time series) of the granulation and oscillation signal, which is well approximated by our global fit. Since the limiting spectrum is almost flat below νmax and only strongly decreases for higher frequencies, any frequency below νmax has a similar chance of being the largest amplitude peak in an arbitrary data set. In the case of KIC 1431599, this means that we can find practically any period between ΔT and about 5 d as the “dominant signal” of the time series. Or in other words, the seemingly dominant periodicity in the observations of a solar-type oscillator contain only limited information. Basically, little more can be gleaned than that the typical oscillation timescales are shorter.
In conclusion, for our sample of red giants this means that even though many of the present observations are too short to clearly detect an oscillation power excess, they are still long enough to extract valuable information from the granulation signal. Furthermore, several stars in our sample show clear variability with a seemingly dominant period when looking at their light curves. Even though these periods are of little help in our analysis, we measure them and list them in Table 3 for comparison with values found in the literature if their local (in a 10 μHz box) signal-to-noise ratio is larger than four.
Results for the target stars.
We now return to the actual analysis of the granulation signal in our sample of red giants. If we find more than one granulation component to be statistically significant in the PDS of a given star, we concentrate on the component with the smallest frequency uncertainty. To identify to which granulation component it corresponds, we compare the measured characteristic frequency and amplitude to those of a large sample of red giants observed with Kepler. As is shown in Fig. 8, the LF and HF granulation components form two populations in the amplitude-frequency diagram. To discriminate between the branches we fit a second order polynomial to the mid-point of the Kepler measurements, which is determined by the average frequency and amplitude of the two granulation components. For a pair of parameters found for our target stars, we can now identify the LF and HF component of the granulation signal. The measured characteristic granulation frequencies and νmax are listed in Table 3. We note that the amplitudes of both components are roughly the same (Kallinger et al. 2014).
 |
Fig. 8. Low- (light-red circles) and high-frequency (light-blue circles) granulation components of a sample of red giant stars observed by Kepler. The dashed line gives a fit to the midpoint of the two components. Overplotted are the stars observed by BRITE-Constellation listed in Table 2. |
With νlow and νhigh determined, we can estimate the surface gravity log g of the star. Even though we could directly define a scaling relation for log g by combining Eqs. (1) and (2), Kallinger et al. (2018) found evidence that the scaling of νmax to log g is more complex than is indicated by Eq. (2). A better way is therefore to directly relate the measured granulation frequencies of the Kepler sample with the stars’ surface gravities, determined from the new seismic scaling relations. Kallinger et al. (2018) have shown that log g, determined from a full asteroseismic analysis, is accurate to better than 0.01 (about 2% on a linear scale). The calibration is shown in Fig. 9 yielding a relation
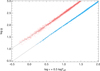 |
Fig. 9. Surface gravity as a function of the frequency of the low- (light-red circles) and high-frequency (light-blue circles) granulation components of the sample of Kepler stars. The dashed lines indicate fits to the data. |
for the HF component, and
for the LF component, with 𝒳low, high = logνlow, high + 0.5 log Teff. The scatter around those fits is 0.012 (∼2.8%) and 0.02 (∼4.5%) for Eqs. (5) and (6), respectively, reflecting the typical uncertainties of the method. We finally apply these scaling relations to our sample of stars and list the resulting log g in Table 3. In the case of 39 Cyg and σ Per, the surface gravity is determined from νmax according to Kallinger et al. (2018) as
where νmax, ⊙ = 3140 ± 5 μHz and log g⊙ = 4.438. We note that log g values determined by νlow and νhigh are consistent (but less accurate) with those based on νmax.
The uncertainties in our log g result from the combined uncertainties of the observables (νlow, high and Teff) and the calibration and range from 0.03 (∼7%) to 0.1 (∼23%), which is still quite large for a seismology-based method. Even though the log g estimates are roughly consistent with literature values, it is not guaranteed that we do not misinterpret signal from rotation, magnetic activity, or even from the instrument as granulation signal, which would seriously affect our analysis. A possibility to verify this is given by the following method.
5.2. Autocorrelation method
There are various other methods that make use of the granulation signal to estimate log g of stars in the Kepler field (Hekker et al. 2012; Bastien et al. 2016; Bugnet et al. 2018; Pande et al. 2018). They all rely on the amplitude of the brightness variations due to granulation measured in one or more given frequency bands. However, such amplitudes not only depend on the surface gravity of the star but also on other (gravity-independent) properties, like rotation and activity. Furthermore, they are calibrated to the Kepler passband and instrumental noise and can therefore not directly be applied to observations with other instruments. A more flexible and accurate approach for a log g determination has been introduced by Kallinger et al. (2016) who have shown that one can estimate log g solely from the typical timescale of the combined granulation and oscillation signal, which they derive from the autocorrelation function (ACF) of the time series. The ACF of a stochastic signal (granulation and solar-type oscillations) follows a sinc-function and its width defines a typical timescale τACF, which scales with the surface gravity of the star. The method gives good results even for short time series (see Fig. 7) and data where the oscillations are hidden in the noise. Their calibration for a large sample of Kepler stars, covering the entire region from the main sequence up to the giant branch, results in
which is accurate to about 0.017 (or about 4%).
A problem of this approach is that it is calibrated with log g values from seismology and, hence, relies on the classical  scaling. As mentioned above, Kallinger et al. (2018) found that g better scales according to Eq. (7), which also influences the τACF calibration, especially for stars with low log g. Instead of re-calibrating Eq. (8) (which is beyond the scope of this analysis), we add a correction term
scaling. As mentioned above, Kallinger et al. (2018) found that g better scales according to Eq. (7), which also influences the τACF calibration, especially for stars with low log g. Instead of re-calibrating Eq. (8) (which is beyond the scope of this analysis), we add a correction term
to Eq. (8), which accounts to first approximation for the “non-linearity” of the νmax scaling relation.
The autocorrelation functions of our target stars are shown in Figs. 3–6 along with the best-fit squared sinc-functions. The resulting τACF and log g values are given in Table 3 (see also Fig. 10), where the uncertainties for the latter cover again all error sources, from the observables to the calibration itself, and amount typically to about 0.02 (or 4.5%).
 |
Fig. 10. Hertzsprung–Russell (top) and Kiel-diagram (bottom) including the red giants observed by BRITE-Constellation (grey-filled circles). The small dots show MIST stellar evolution models for solar composition with the mass colour coded. Blue-filled circles mark stars for which solar-type oscillations have been found in the BRITE-Constellation data. |
We find generally good agreement for log g values derived with the ACF method and from granulation timescales, with the former giving more accurate results. Only for the two stars NS Pup and GZ Vel does a significant difference exist. According to Fig. 8 the observed signal is identified as the low-frequency component of the granulation signal, indicating a log g of 1.24 and 1.32 for NS Pup and GZ Vel, respectively. These values are significantly different from those based on τACF. However, if we assume the observed signal to be due to the high-frequency granulation component (i.e. using Eq. (5) instead of Eq. (6) to determine log g ), we get good agreement (see Table 3). In this case, the granulation amplitude would have been underestimated. In fact, this also happens for some Kepler stars as is indicated in Fig. 8 with blue dots below the dashed line. Possible explanations are strong magnetic fields suppressing the granulation amplitude or dilution of the observed light by another star (e.g. from a binary companion).
6. Stellar mass and evolutionary stage
Stellar masses are only known for about half of our target stars and those are often questionable as they mostly result from a comparison of spectroscopic measurements with stellar evolution models. Consequently, they are highly model dependent, so that any improvements based on actual observations are valuable for future analyses.
Given the surface gravities from above, we could directly calculate the mass as
(all in solar units) if there is a reliable estimate for the radius R available. Since all stars in our sample are bright stars that are quite close and on the giant branch (i.e. large objects), we find in fact precise measurements of the interferometric angular diameter Θ in the Catalog of High Angular Resolution Measurements (CHARM) of Richichi et al. (2005) for 11 stars in our sample. With these measurements and with the Gaia DR2 parallaxes π (Gaia Collaboration 2018), we can directly determine the radius (in solar units) as
For three stars we use the radius estimate from the Gaia DR2 catalogue. For four stars no entries in the Gaia catalogue are available yet but we find radius estimates in the literature. Only for ρ Per, σ CMa, and ε Mus are no such measurements available, so that we determine the radius according to 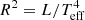 (all in solar units), with the effective temperatures and luminosities listed in Table 2. If available, we use log g from the ACF method to determine the mass.
(all in solar units), with the effective temperatures and luminosities listed in Table 2. If available, we use log g from the ACF method to determine the mass.
A special case is the star N Vel, for which the CHARM and Gaia measurements result in a radius of about 33 R⊙, which in turn would yield a mass as small as 0.5 M⊙. In fact, the interferometric radius is incompatible with the value determined from 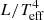 so that there seems to be a problem with the interferometric angular diameter. We therefore adopt the radius that results from the stars’ luminosity and effective temperature. The corresponding radii and resulting basically model-independent masses are listed in Table 3, with typical uncertainties of 3–9% in radius and 10–20% in mass.
so that there seems to be a problem with the interferometric angular diameter. We therefore adopt the radius that results from the stars’ luminosity and effective temperature. The corresponding radii and resulting basically model-independent masses are listed in Table 3, with typical uncertainties of 3–9% in radius and 10–20% in mass.
Another method to derive the stellar mass is to compare the log g, Teff, and R measurements with those of a grid of stellar models. We adapt a grid-modelling approach using log g, Teff, and R as input (Kallinger et al. 2010a). The model grid is extracted from the non-rotating version of the MESA4 Isochrones & Stellar Tracks (MIST5; Dotter 2016; Choi et al. 2016). The grid covers about 900 000 models from the main-sequence phase to the asymptotic giant branch with initial masses from 0.1 to 10 M⊙, and initial chemical compositions of [Fe/H] = −4.0 to 0.5. The Bayesian comparison between observed and model parameters accounts for all observational uncertainties. The solar-composition part of the grid is shown in Fig. 10. The resulting mass estimates are listed in Table 3, which are generally in good agreement with the directly determined masses.
The main reason for the grid-modelling, however, is that we can evaluate the evolutionary states of our target stars in a statistical sense. The model grid consists of isochrones with time steps of equal length. Consequently, we will find only a few grid points for parameter areas with fast stellar evolution. If we now add up the model probabilities according to their evolutionary state, we can assign each star a probability to be in a given stage of stellar evolution. In practice, we compute the probability pRGB that a star is a RGB star, or vice-versa that the star is a post-RGB star with the probability of 1 − pRGB (see also Hekker et al. 2017). In fact, with high confidence (pRGB < 9%, i.e. the odds ratio is better than about 10:1) we can only determine the evolutionary state of five stars (ρ Per, N Vel, ε Mus, α Cet, and GZ Vel) and as post-RGBs. For five more stars (η Cyg, NS Pup, g Car, σ CMa, and G Sco) the probability contrast (pRGB < 25%, i.e. the odds ratio is better than 3:1) is high enough to claim that they are post-RGBs, but for the remaining stars we can only make a tentative statement about their evolutionary state or provide no information at all if pRGB is around 50%.
Comparison with literature values. Unless a star is gravitationally bound in a binary system, reliable mass estimates are difficult to achieve and mostly rely on the comparison of some observed parameters (Teff, log g, L, etc.) with stellar evolution models. We find mass estimates in the literature for 17 stars of our sample. They are discussed in the following along with known variability timescales:
-
(A) η Cyg: Isochrone fitting by Luck (2015) yields a mass ranging from 1.10 to 2.13 M⊙.
-
(B) 23 Vul: Based on a 25.3 yr binary orbit Malkov et al. (2012) determined a dynamical mass of 2.39 ± 0.73 M⊙.
-
(D) ε Cyg: Based on model atmospheres and stellar evolutionary tracks, Fuhrmann et al. (2017) claim a mass of 1.61 M⊙, for which we expect the uncertainties to be on the order of ±0.5 M⊙.
-
(E) ρ Per: Dumm & Schild (1998) found a mass of 3.8 M⊙ from comparison of a HIPPARCOS parallax-based luminosity and spectroscopic effective temperature with a grid of stellar models. We assume an uncertainty of ±0.5 M⊙. The GCVS lists a period of 50 d, which is consistent with the dominant period of 58 d in the BRITE observations.
-
(F) σ Per: Isochrone fitting by Reffert et al. (2015) gives 1.32 ± 0.24 M⊙.
-
(G) NS Pup: Comparison of atmospheric parameters with various evolutionary models results in a median mass of 9.7 ± 0.8 M⊙ (Tetzlaff et al. 2011).
-
(I) g Car: 2.8 ± 0.5 M⊙ from Dumm & Schild (1998). The 187 d period given by Price et al. (2010) is not detectable in the 61-day-long BRITE observations, in which we find a period of about 12 d.
-
(J) N Vel: Gondoin (1999) found a mass of about 2 M⊙ based on comparison with evolutionary models, for which we expect the uncertainties to be on the order of ±0.5 M⊙.
-
(K) ε Sco: Based on model atmospheres and stellar evolutionary tracks, Fuhrmann et al. (2017) claim a mass of 1.24 M⊙, for which we expect the uncertainties to be on the order of ±0.4 M⊙.
-
(L) σ CMa: Tetzlaff et al. (2011) find a median mass of 12.3 ± 0.1 M⊙ from comparison of atmospheric parameters with different evolutionary models.
-
(M) ε Mus: 2.5 ± 0.5 M⊙ from Dumm & Schild (1998). The GCVS gives a period of 40 d and Tabur et al. (2009) list several periods between 32 and 63 d, which is consistent with the 58 d period found in the BRITE data.
-
(N) ε Cru: Jofré et al. (2015) performed a detailed analysis of high-resolution spectroscopic observations and found a mass of 1.5 ± 0.2 M⊙ based on comparison with stellar evolution models.
-
(O) γ Cru: 1.9 ± 0.5 M⊙ from Dumm & Schild (1998). Tabur et al. (2009) lists periods between 12 and 83 d, which is consistent with the 22 d period found in BRITE observations.
-
(P) G Sco: Stello et al. (2008) determined a mass of 1.4 ± 0.2 M⊙ from seismic observations with the WIRE satellite, which reduces to 1.3 ± 0.2 M⊙ when using the Gaia parallax and the non-linear scaling from Kallinger et al. (2018).
-
(R) η Sgr: 1.5 ± 0.5 M⊙ from Dumm & Schild (1998).
-
(S) HD 19349: 2.1 ± 0.5 M⊙ from Dumm & Schild (1998).
-
(T) α Cet: 2.8 ± 0.5 M⊙ from Dumm & Schild (1998).
In Fig. 11 we compare our mass estimates with those from the literature and find good agreement for several stars, especially for the stars 23 Vul (B) and G Sco (P) for which model-independent mass estimates are available in the literature. For the remaining stars, inconsistency can be explained by the mostly unconsidered systematic uncertainties in the literature values, like the degeneracy between Teff, log g, and [Fe/H]. Furthermore, the observed atmospheric parameters of a star are usually compared to those of a single set of stellar evolution models not considering the systematic errors in the models that arise from for example the insufficient physics used to produce the models. Even more, simply using models computed with similar input parameters and physics but with a different stellar evolution code can result in significantly different results. In this context, Stancliffe et al. (2016) have shown that solar-calibrated evolutionary tracks from various stellar evolution codes differ by up to 150 K when leaving the main sequence, which translates into a systematic mass uncertainty of about 5% on the main sequence and some 10% on the giant branch. On top of that, the often unknown initial hydrogen and metal abundances produce additional uncertainties as well as uncertain input physics, as do the treatment of convection, uncertain nuclear reaction rates and opacities, rotational mixing, and other factors. Furthermore, several stars in our sample are already in a luminosity regime where mass loss can play a substantial role, further complicating the mass determination via stellar models. In conclusion, the mass of a red giant determined from stellar evolution models might serve as guidance to distinguish between a high-mass star and a low-mass star but should be taken with care beyond that. We are aware that our grid-modelling approach suffers from the same deficiencies but note that the masses determined from the grid modelling are fully consistent with those from the model-independent method and should therefore be preferred over the literature values.
 |
Fig. 11. Comparison between masses determined in this work and found in the literature. |
7. Period-luminosity relation
Thanks to large ground-based microlensing surveys such as MACHO and OGLE, small-amplitude oscillations have been observed in thousands of luminous red giants (e.g. Wood et al. 1999; Wray et al. 2004; Soszynski et al. 2007; Tabur et al. 2010; Soszyński & Wood 2013, and references therein). However, the nature of these oscillations has been questioned for some time. In particular, it is debated whether they are self-excited pulsa-tions or stochastically excited modes (e.g. Bedding 2003; Christensen-Dalsgaard et al. 2001; Dziembowski & Soszyński 2010). Most of the results of the microlensing surveys are expressed as period-luminosity relations found for different sequences of oscillation modes (e.g. Soszynski et al. 2007). These sequences smoothly connect with the pattern of radial and non-radial modes observed in Kepler red giants (Mosser et al. 2013; Stello et al. 2014) with the same scaling relation that links the peak frequency to the frequency separation. It is therefore quite likely that the oscillations observed in semi-regular and even Mira-type variables are caused by stochastic excitation, similar to those found in the Sun.
Even though the limited length of our BRITE-Constellation observations did not allow us to resolve individual oscillation modes, we can still use the period-luminosity relation to verify the origin of the observed signal. This is shown in Fig. 12, where the observed PDS are sorted according to the star’s luminosity and displayed as horizontal bands with the level of power indicated by the grey scale (top panel). There is already a clear trend that for increasing luminosity the variability timescales increase. This trend is, however, smeared by stellar mass in the sense that more massive stars show their variability at lower timescales than less massive stars with the same luminosity. Such a correlation is in fact well approximated by Eq. (2), which can be written as 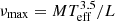 (all in solar units). If we now scale the period axis of the observed PDS with
(all in solar units). If we now scale the period axis of the observed PDS with 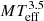 , we can expect a linear relation between the variability timescales and L, which is in fact shown in the bottom panel of Fig. 12. Practically all stars show their strongest signal above the period range at which oscillations are expected. This confirms that we do not misinterpret poorly resolved oscillations as granulation signal and that the granulation timescales in luminous red giants follow the same basic rules as in main-sequence stars. Furthermore, it confirms that the dominant periods measured in the BRITE data are basically randomly distributed so that their information content is rather limited (other than that they are longer than the typical oscillation timescales). In fact, we find only two stars (σ CMa and g Car) for which the dominant period comes close to the period range where oscillations are expected so that the visible variability in their light curves might rather be due to oscillations than to granulation.
, we can expect a linear relation between the variability timescales and L, which is in fact shown in the bottom panel of Fig. 12. Practically all stars show their strongest signal above the period range at which oscillations are expected. This confirms that we do not misinterpret poorly resolved oscillations as granulation signal and that the granulation timescales in luminous red giants follow the same basic rules as in main-sequence stars. Furthermore, it confirms that the dominant periods measured in the BRITE data are basically randomly distributed so that their information content is rather limited (other than that they are longer than the typical oscillation timescales). In fact, we find only two stars (σ CMa and g Car) for which the dominant period comes close to the period range where oscillations are expected so that the visible variability in their light curves might rather be due to oscillations than to granulation.
 |
Fig. 12. Observed power spectra as a function of period (top) and scaled period (bottom) of our sample stars. The stars are sorted according to their luminosity and displayed as an horizontal band with the level of power indicated by the grey scale. The spectrum of KIC 1431599 (from Fig. 7) is indicated by a red arrow. Open red squares correspond to the dominant periods in the BRITE data and open blue squares indicate our measurements of νmax. The period range in which to expect oscillations is marked with dashed lines. Typical spectral types and luminosity classes are given on the right-hand side. |
8. Summary and conclusion
In recent years the seismology of red giants has grown to become an important field in stellar astrophysics, providing the unique opportunity to probe the interior structure of evolved stars. Apart from this, seismic scaling relations have become a valuable method to determine the mass and radius of stars with a convective envelope. Such studies are, however, limited to relatively faint stars accessible to the long-term high-precision observations with CoRoT and Kepler with the exception of more recent observations of a few naked-eye stars in the ecliptic plane using special-aperture photometry with K2 (White et al. 2017). Bright stars, on the other hand, with plenty of additional information available (from for example spectroscopy and interferometry) are seismically less well constrained, which is even truer for red giants requiring long-term time series observations.
In this paper we present the BRITE-Constellation observations of a sample of red giant stars in which we find a clear granulation and/or oscillation signal. The sample consists of 23 stars distributed all over the sky with V magnitudes ranging between 1.6 and 5.0 and covers low-mass red clump stars to high-mass red giants. Each star has been observed almost continuously by at least one of five BRITE satellites for up to 173 d.
Even though plenty of information is available in the literature about this sample, for none of the stars is either log g or the mass sufficiently well known as one might expect for such bright stars. We therefore use the granulation and/or oscillation timescales measured from the BRITE-Constellation observations to determine model-independent estimates of log g with two different methods. Using precise radii from the literature (mostly from interferometric angular diameters and Gaia parallaxes) we can then determine the mass of the stars from our log g measurements.
We confirm that the BRITE-Constellation data are dominated by the granulation signal and that the corresponding typical timescales follow the same scalings as the typical oscillation periods even for stars high up the giant branch (G to M-type supergiants). We measure the individual timescales in Fourier space as well as in the time domain and use corresponding scaling relations to convert these timescales into surface gravities. To account for the non-linearity in the νmax − g relation recently found by Kallinger et al. (2018), we first re-calibrate the corresponding scalings using measurements from a large sample of red giants observed with Kepler.
Kallinger et al. (2014) have shown that in Fourier space the granulation signal consists of at least two components, each comprising a typical timescale and amplitude, which tightly scale with the surface gravity of the star. In noisy data, however, or in data of insufficient length or sampling, one can often detect only one component, which is then difficult to assign. Using measurements of the Kepler giants, we find an empirical relation between the granulation timescale and amplitude that allows us to evaluate whether a measured set of parameters originates from the LF or HF component of the granulation signal in order to apply the correct log g scaling. We can determine log g for all but four stars of our sample from the power density spectrum as well as from the ACF of the time series and find them to agree within the uncertainties, where the ACF method is typically more accurate.
Based on these log g measurements and stellar radii from the literature, we can then directly determine the masses of our sample stars. Comparison with parameters from a large grid of stellar models also allows us to statistically evaluate the evolutionary state of the individual stars. We find that five stars are likely and five stars are very likely post-RGB stars. For the remaining stars the probability contrast is not high enough to make more than a tentative statement.
The stellar masses presented here range from about 0.7 to more than 8 M⊙ and have formal uncertainties of about 10–20%, which covers the observational errors as well as the known uncertainties of the used scaling relations. One might question whether our simple scaling relations hold from low-mass giants with about 10 R⊙ to high-mass giants with more than 200 R⊙. Lacking independent and reliable mass estimates, this is difficult to verify. Even though there might still be some unknown systematics in the scaling relations, they appear to be at least good enough to disentangle low-mass stars from high-mass stars and given the large unknown uncertainties in the model-based masses, we prefer our model-independent estimates.
Out of the 23 stars in our sample only two (39 Cyg and σ Per) show a significant oscillation power excess, from which we can measure νmax. Even though their νmax values differ by more than a factor of two, they appear to have a very similar effective temperature of around 4200 K (i.e. spectral type of around K3). We think that this temperature represents some kind of a “sweet spot” for observing solar-type oscillations with BRITE-Constellation. For cooler stars the time base of the observations is not long enough to clearly resolve the signal and for hotter stars the oscillation amplitudes are too small to be detected by the BRITE instruments. In fact, there are two other stars (23 Vul and ε Cru) in this temperature range with no detected oscillation signal. For 23 Vul the oscillation signal seems to interfere with the instrumental 1 d−1 signal and for ε Cru there is some signal at about 4 μHz, which is, however, not statistically significant. We further note that another star in this spectral range (α Tau) shows clear solar-type oscillations in BRITE-Constellation data. The observations are, however, not yet finished, which is why the star is excluded from the present analysis. The data will be published in the near future.
“Setup” refers to a set of camera parameters but also to subraster positions on the CCD. Setups may change at the beginning of a run (during optimising of the observations) or due to adding/removing a star during the run. For each parameter change, a whole new setup is generated with a particular ID.
In probability theory p > 0.9 is considered as strong evidence (e.g. Jeffreys 1998).
Modules for Experiments in Stellar Astrophysics (Paxton et al. 2011).
Acknowledgments
TK, WW, and KZ are grateful for funding via the Austrian Space Application Programme (ASAP) of the Austrian Research Promotion Agency (FFG) and BMVIT. PGB acknowledges the support of the Spanish Ministry of Economy and Competitiveness (MINECO) under the programme Juan de la Cierva incorporation (IJCI-2015-26034). D.H. acknowledges support by the National Aeronautics and Space Administration under Grant NNX14AB92G issued through the Kepler Participating Scientist Program and support by the National Science Foundation (AST-1717000). The research leading to the presented results has received funding from the European Research Council under the European Communitys Seventh Framework Programme (FP7/2007-2013)/ERC grant agreement no 338251 (StellarAges). GH acknowledges support from the Polish National Science Centre (NCN), grant no. 2015/18/A/ST9/00578. AFJM acknowledges financial aid from NSERC (Canada) and FQRNT (Quebec). APi acknowledges support from the NCN grant 2016/21/B/ST9/01126. APo was responsible for image processing and automation of photometric routines for the data registered by BRITE-nanosatellite constellation, and was supported by NCN grant 2016/21/D/ST9/00656. GAW acknowledges Discovery Grant support from the Natural Sciences and Engineering Research Council (NSERC) of Canada.
References
- Allende Prieto, C., & Lambert, D. L. 1999, A&A, 352, 555 [NASA ADS] [Google Scholar]
- Baglin, A., Auvergne, M., & Barge, P. 2006, in The CoRoT Mission Pre-Launch Status – Stellar Seismology and Planet Finding, eds. M. Fridlund, A. Baglin, J. Lochard, & L. Conroy, ESA SP, 1306, 33 [Google Scholar]
- Barban, C., Matthews, J. M., De Ridder, J., et al. 2007, A&A, 468, 1033 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bastien, F. A., Stassun, K. G., Basri, G., & Pepper, J. 2016, ApJ, 818, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Baudin, F., Barban, C., Belkacem, K., et al. 2011, A&A, 529, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, P. G., Bedding, T. R., Mosser, B., et al. 2011, Science, 332, 205 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Beck, P. G., Montalban, J., Kallinger, T., et al. 2012, Nature, 481, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, P. G., Hambleton, K., Vos, J., et al. 2014, A&A, 564, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, P. G., Kallinger, T., Pavlovski, K., et al. 2018, A&A, 612, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bedding, T. R. 2003, Ap&SS, 284, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Bedding, T. R., Mosser, B., Huber, D., et al. 2011, Nature, 471, 608 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bordé, P., Coudé du Foresto, V., Chagnon, G., & Perrin, G. 2002, A&A, 393, 183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Borucki, W. J., Koch, D. G., Batalha, N., et al. 2012, ApJ, 745, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, T. M., Gilliland, R. L., Noyes, R. W., & Ramsey, L. W. 1991, ApJ, 368, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Bugnet, L., García, R. A., Davies, G. R., et al. 2018, A&A, 620, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buzasi, D., Catanzarite, J., Laher, R., et al. 2000, ApJ, 532, L133 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ceillier, T., Tayar, J., Mathur, S., et al. 2017, A&A, 605, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chaplin, W. J., & Miglio, A. 2013, ARA&A, 51, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Choi, J., Dotter, A., Conroy, C., et al. 2016, ApJ, 823, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen-Dalsgaard, J., Kjeldsen, H., & Mattei, J. A. 2001, ApJ, 562, L141 [NASA ADS] [CrossRef] [Google Scholar]
- Corsaro, E., De Ridder, J., & García, R. A. 2015, A&A, 578, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Ridder, J., Barban, C., Carrier, F., et al. 2006, A&A, 448, 689 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dotter, A. 2016, ApJS, 222, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Dumm, T., & Schild, H. 1998, New A, 3, 137 [Google Scholar]
- Dupret, M.-A., Belkacem, K., Samadi, R., et al. 2009, A&A, 506, 57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dziembowski, W. A., & Soszyński, I. 2010, A&A, 524, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dziembowski, W. A., Gough, D. O., Houdek, G., & Sienkiewicz, R. 2001, MNRAS, 328, 601 [NASA ADS] [CrossRef] [Google Scholar]
- Edmonds, P. D., & Gilliland, R. L. 1996, ApJ, 464, L157 [NASA ADS] [CrossRef] [Google Scholar]
- Feroz, F., Hobson, M. P., & Bridges, M. 2009, MNRAS, 398, 1601 [NASA ADS] [CrossRef] [Google Scholar]
- Frandsen, S., Carrier, F., Aerts, C., et al. 2002, A&A, 394, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuhrmann, K., Chini, R., Kaderhandt, L., & Chen, Z. 2017, ApJ, 836, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García, R. A., Ceillier, T., Salabert, D., et al. 2014a, A&A, 572, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García, R. A., Mathur, S., Pires, S., et al. 2014b, A&A, 568, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaulme, P., McKeever, J., Jackiewicz, J., et al. 2016, ApJ, 832, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Gehan, C., Mosser, B., Michel, E., Samadi, R., & Kallinger, T. 2018, A&A, 616, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gilliland, R. L., McCullough, P. R., Nelan, E. P., et al. 2011, ApJ, 726, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Gondoin, P. 1999, A&A, 352, 217 [NASA ADS] [Google Scholar]
- Hekker, S., & Christensen-Dalsgaard, J. 2017, A&ARv, 25, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hekker, S., Elsworth, Y., Mosser, B., et al. 2012, A&A, 544, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hekker, S., Elsworth, Y., Basu, S., & Bellinger, E. 2017, Eur. Phys. J. Web Conf., 160, 04006 [CrossRef] [Google Scholar]
- Huber, D., Bedding, T. R., Stello, D., et al. 2010, ApJ, 723, 1607 [NASA ADS] [CrossRef] [Google Scholar]
- Huber, D., Bedding, T. R., Stello, D., et al. 2011, ApJ, 743, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Huber, D., Ireland, M. J., Bedding, T. R., et al. 2012, ApJ, 760, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Huber, D., Silva Aguirre, V., Matthews, J. M., et al. 2014, ApJS, 211, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Ireland, M. J., Tuthill, P. G., Bedding, T. R., Robertson, J. G., & Jacob, A. P. 2004, MNRAS, 350, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffreys, H. 1998, in Theory of Probability, (New York: The Clarendon Press, Oxford University Press), Oxford Classic Texts Phys. Sci., xii+459, reprint of the 1983 edition [Google Scholar]
- Jofré, E., Petrucci, R., Saffe, C., et al. 2015, A&A, 574, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kallinger, T., Zwintz, K., Pamyatnykh, A. A., Guenther, D. B., & Weiss, W. W. 2005, A&A, 433, 267 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kallinger, T., Guenther, D. B., Matthews, J. M., et al. 2008a, A&A, 478, 497 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kallinger, T., Guenther, D. B., Weiss, W. W., et al. 2008b, Commun. Asteroseismol., 153, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Kallinger, T., Mosser, B., Hekker, S., et al. 2010a, A&A, 522, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kallinger, T., Weiss, W. W., Barban, C., et al. 2010b, A&A, 509, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kallinger, T., Hekker, S., Mosser, B., et al. 2012, A&A, 541, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kallinger, T., De Ridder, J., Hekker, S., et al. 2014, A&A, 570, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kallinger, T., Hekker, S., Garcia, R. A., Huber, D., & Matthews, J. M. 2016, Sci. Adv., 2, 1500654 [NASA ADS] [CrossRef] [Google Scholar]
- Kallinger, T., Weiss, W. W., Beck, P. G., et al. 2017, A&A, 603, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kallinger, T., Beck, P. G., Stello, D., & Garcia, R. A. 2018, A&A, 616, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kjeldsen, H., & Bedding, T. R. 1995, A&A, 293, 87 [NASA ADS] [Google Scholar]
- Lebreton, Y., & Goupil, M. J. 2014, A&A, 569, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Luck, R. E. 2015, AJ, 150, 88 [Google Scholar]
- Malkov, O. Y., Tamazian, V. S., Docobo, J. A., & Chulkov, D. A. 2012, A&A, 546, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathur, S., Hekker, S., Trampedach, R., et al. 2011, ApJ, 741, 119 [NASA ADS] [CrossRef] [Google Scholar]
- McDonald, I., Zijlstra, A. A., & Watson, R. A. 2017, MNRAS, 471, 770 [NASA ADS] [CrossRef] [Google Scholar]
- Miglio, A., Brogaard, K., Stello, D., et al. 2012, MNRAS, 419, 2077 [NASA ADS] [CrossRef] [Google Scholar]
- Miglio, A., Chiappini, C., Morel, T., et al. 2013, MNRAS, 429, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Mosser, B., Belkacem, K., Goupil, M.-J., et al. 2010, A&A, 517, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Elsworth, Y., Hekker, S., et al. 2012a, A&A, 537, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Goupil, M. J., Belkacem, K., et al. 2012b, A&A, 548, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Goupil, M. J., Belkacem, K., et al. 2012c, A&A, 540, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Dziembowski, W. A., Belkacem, K., et al. 2013, A&A, 559, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pablo, H., Whittaker, G. N., Popowicz, A., et al. 2016, PASP, 128, 125001 [NASA ADS] [CrossRef] [Google Scholar]
- Pande, D., Bedding, T. R., Huber, D., & Kjeldsen, H. 2018, MNRAS, 480, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
- Piau, L., Kervella, P., Dib, S., & Hauschildt, P. 2011, A&A, 526, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pigulski, A., Cugier, H., Popowicz, A., et al. 2016, A&A, 588, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pope, B. J. S., White, T. R., Huber, D., et al. 2016, MNRAS, 455, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Popowicz, A., Pigulski, A., Bernacki, K., et al. 2017, A&A, 605, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Price, S. D., Smith, B. J., Kuchar, T. A., Mizuno, D. R., & Kraemer, K. E. 2010, ApJS, 190, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Prugniel, P., Soubiran, C., Koleva, M., & Le Borgne, D. 2007, VizieR Online Data Catalog: III/251 [Google Scholar]
- Reffert, S., Bergmann, C., Quirrenbach, A., Trifonov, T., & Künstler, A. 2015, A&A, 574, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Retter, A., Bedding, T. R., Buzasi, D. L., Kjeldsen, H., & Kiss, L. L. 2003, ApJ, 591, L151 [NASA ADS] [CrossRef] [Google Scholar]
- Richichi, A., Percheron, I., & Khristoforova, M. 2005, A&A, 431, 773 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, Instrum. Syst., 1, 014003 [Google Scholar]
- Samus’, N. N., Kazarovets, E. V., Durlevich, O. V., Kireeva, N. N., & Pastukhova, E. N. 2017, Astron. Rep., 61, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Sharma, S., Stello, D., Bland-Hawthorn, J., Huber, D., & Bedding, T. R. 2016, ApJ, 822, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Soderblom, D. R. 2010, ARA&A, 48, 581 [NASA ADS] [CrossRef] [Google Scholar]
- Soszyński, I., & Wood, P. R. 2013, ApJ, 763, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Soszynski, I., Dziembowski, W. A., Udalski, A., et al. 2007, Acta Astron., 57, 201 [NASA ADS] [Google Scholar]
- Soubiran, C., Le Campion, J.-F., Brouillet, N., & Chemin, L. 2016, A&A, 591, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stancliffe, R. J., Fossati, L., Passy, J.-C., & Schneider, F. R. N. 2016, A&A, 586, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stello, D., & Gilliland, R. L. 2009, ApJ, 700, 949 [NASA ADS] [CrossRef] [Google Scholar]
- Stello, D., Bruntt, H., Preston, H., & Buzasi, D. 2008, ApJ, 674, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Stello, D., Compton, D. L., Bedding, T. R., et al. 2014, ApJ, 788, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Stello, D., Zinn, J., Elsworth, Y., et al. 2017, ApJ, 835, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Tabur, V., Bedding, T. R., Kiss, L. L., et al. 2009, MNRAS, 400, 1945 [NASA ADS] [CrossRef] [Google Scholar]
- Tabur, V., Bedding, T. R., Kiss, L. L., et al. 2010, MNRAS, 409, 777 [NASA ADS] [CrossRef] [Google Scholar]
- Tarrant, N. J., Chaplin, W. J., Elsworth, Y., Spreckley, S. A., & Stevens, I. R. 2007, MNRAS, 382, L48 [NASA ADS] [CrossRef] [Google Scholar]
- Tarrant, N. J., Chaplin, W. J., Elsworth, Y., Spreckley, S. A., & Stevens, I. R. 2008, A&A, 483, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tetzlaff, N., Neuhäuser, R., & Hohle, M. M. 2011, MNRAS, 410, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Ulrich, R. K. 1986, ApJ, 306, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Vrard, M., Mosser, B., Barban, C., et al. 2015, A&A, 579, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vrard, M., Kallinger, T., Mosser, B., et al. 2018, A&A, 616, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weiss, W. W., Rucinski, S. M., Moffat, A. F. J., et al. 2014, PASP, 126, 573 [NASA ADS] [CrossRef] [Google Scholar]
- White, T. R., Bedding, T. R., Stello, D., et al. 2011a, ApJ, 742, L3 [NASA ADS] [CrossRef] [Google Scholar]
- White, T. R., Bedding, T. R., Stello, D., et al. 2011b, ApJ, 743, 161 [NASA ADS] [CrossRef] [Google Scholar]
- White, T. R., Pope, B. J. S., Antoci, V., et al. 2017, MNRAS, 471, 2882 [NASA ADS] [CrossRef] [Google Scholar]
- Wittkowski, M., Aufdenberg, J. P., Driebe, T., et al. 2006, A&A, 460, 855 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wood, P. R., Alcock, C., & Allsman, R. A. 1999, in Asymptotic Giant Branch Stars, eds. T. Le Bertre, A. Lebre, & C. Waelkens, IAU Symp., 191, 151 [NASA ADS] [Google Scholar]
- Wray, J. J., Eyer, L., & Paczyński, B. 2004, MNRAS, 349, 1059 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Histrogram of magnitudes of red giant stars observed by BRITE-Constellation (red) and Kepler (grey; Huber et al. 2014). |
| In the text | |
 |
Fig. 2. Two-dimensional correction map (CCD-temperature and Y position of the PSF) for the about-30-day-long UBr time series of ε Sco obtained during observing subset 2 with the colour-coded correction factors. Right and bottom panels: correction factor as a function of the Y position of the PSF and CCD temperature, respectively, where the values of the other parameter are colour-coded (with red-green-blue symbols corresponding to low-mean-high values of the other parameter). The black dots are the actual measurements divided by the average value of the time series. |
| In the text | |
 |
Fig. 3. Left panel: relative instrumental flux of the approximately 161-day-long UBr binned data set of ε Sco. Middle panel: power density spectrum (in ppm2/μHz) of the binned (grey lines) and interpolated time series (black lines) along with a best global model fit (blue lines) and expected νmax (vertical red lines). Right panel: squared autocorrelation function of the binned time series (black dots) and a best fit (red line). |
| In the text | |
 |
Fig. 4. Same as Fig. 3 – in the cases of η Cyg, ρ Per, and β Pyx the ACF signal is not conclusive. |
| In the text | |
 |
Fig. 5. Same as Fig. 3. |
| In the text | |
 |
Fig. 6. Same as Fig. 3. For 12 Mus we correct the original light curve for the long-period variation and eclipses originating from two companions. |
| In the text | |
 |
Fig. 7. Full 1470-day-long Kepler time series of KIC 1431599 (grey; panel a) and 100- (red and blue) and ten- (orange) day-long subsets (panels b and c). Panel d: corresponding power density spectra along with a global fit (black line) consisting of two granulation components (dashed lines), a Gaussian, and instrumental white noise fitted to the full Kepler time series (Eq. (3)). The largest amplitude peaks in the 100 d PDS are marked with vertical arrows. The corresponding sinusoidal signal is overplotted to the respective time series. The inset shows the frequency range of the oscillation power excess with individual oscillation modes marked by their spherical degree. Panel e: autocorrelation functions of the various time series. |
| In the text | |
 |
Fig. 8. Low- (light-red circles) and high-frequency (light-blue circles) granulation components of a sample of red giant stars observed by Kepler. The dashed line gives a fit to the midpoint of the two components. Overplotted are the stars observed by BRITE-Constellation listed in Table 2. |
| In the text | |
 |
Fig. 9. Surface gravity as a function of the frequency of the low- (light-red circles) and high-frequency (light-blue circles) granulation components of the sample of Kepler stars. The dashed lines indicate fits to the data. |
| In the text | |
 |
Fig. 10. Hertzsprung–Russell (top) and Kiel-diagram (bottom) including the red giants observed by BRITE-Constellation (grey-filled circles). The small dots show MIST stellar evolution models for solar composition with the mass colour coded. Blue-filled circles mark stars for which solar-type oscillations have been found in the BRITE-Constellation data. |
| In the text | |
 |
Fig. 11. Comparison between masses determined in this work and found in the literature. |
| In the text | |
 |
Fig. 12. Observed power spectra as a function of period (top) and scaled period (bottom) of our sample stars. The stars are sorted according to their luminosity and displayed as an horizontal band with the level of power indicated by the grey scale. The spectrum of KIC 1431599 (from Fig. 7) is indicated by a red arrow. Open red squares correspond to the dominant periods in the BRITE data and open blue squares indicate our measurements of νmax. The period range in which to expect oscillations is marked with dashed lines. Typical spectral types and luminosity classes are given on the right-hand side. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



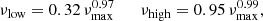
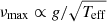
![$$ \begin{aligned} P(\nu ) = P_n + \eta (\nu )^2 \left[ \mathop \sum \limits _i \frac{2\sqrt{2}/\pi a_{i}^2/\nu _{i}}{1+(v/\nu _{i})^4} + P_{g} \exp \frac{-(\nu - \nu _\mathrm{max} )^2}{2\sigma ^2} \right], \end{aligned} $$](/articles/aa/full_html/2019/04/aa34514-18/aa34514-18-eq3.gif)
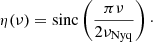
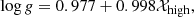


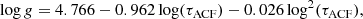
![$$ \begin{aligned} \Delta = 0.0075\pm 0.0021 [\log {g} - \log {g}_\odot - 0.5\log (T_\mathrm{eff} /5777\, \text{ K})], \end{aligned} $$](/articles/aa/full_html/2019/04/aa34514-18/aa34514-18-eq13.gif)