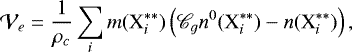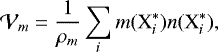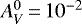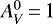| Issue |
A&A
Volume 622, February 2019
|
|
|---|---|---|
| Article Number | A100 | |
| Number of page(s) | 28 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201834248 | |
| Published online | 06 February 2019 | |
Models of irradiated molecular shocks
1
Observatoire de Paris, École normale supérieure, Université PSL, Sorbonne Université, CNRS, LERMA,
75005
Paris,
France
e-mail: benjamin.godard@obspm.fr
2
Institut d’Astrophysique Spatiale, Université Paris-Saclay,
91405
Orsay Cedex,
France
Received:
14
September
2018
Accepted:
20
November
2018
Context. The recent discovery of excited molecules in starburst galaxies observed with ALMA and the Herschel space telescope has highlighted the necessity to understand the relative contributions of radiative and mechanical energies in the formation of molecular lines and explore the conundrum of turbulent gas bred in the wake of galactic outflows.
Aims. The goal of the paper is to present a detailed study of the propagation of low velocity (5–25 km s−1) stationary molecular shocks in environments illuminated by an external ultraviolet (UV) radiation field. In particular, we intend to show how the structure, dynamics, energetics, and chemical properties of shocks are modified by UV photons and to estimate how efficiently shocks can produce line emission.
Methods. We implemented several key physico-chemical processes in the Paris-Durham shock code to improve the treatment of the radiative transfer and its impact on dust and gas particles. We propose a new integration algorithm to find the steady-state solutions of magnetohydrodynamics equations in a range of parameters in which the fluid evolves from a supersonic to a subsonic regime. We explored the resulting code over a wide range of physical conditions, which encompass diffuse interstellar clouds and hot and dense photon-dominated regions.
Results. We find that C-type shock conditions cease to exist as soon as G0 > 0.2 (nH/cm−3)1/2. Such conditions trigger the emergence of another category of stationary solutions, called C*-type and CJ-type shocks, in which the shocked gas is momentarily subsonic along its trajectory. These solutions are shown to be unique for a given set of physical conditions and correspond to dissipative structures in which the gas is heated up to temperatures comprised between those found in C-type and adiabatic J-type shocks. High temperatures combined with the ambient UV field favour the production or excitation of a few molecular species to the detriment of others, hence leading to specific spectroscopic tracers such as rovibrational lines of H2 and rotational lines of CH+. Unexpectedly, the rotational lines of CH+ may carry as much as several percent of the shock kinetic energy.
Conclusions. Ultraviolet photons are found to strongly modify the way the mechanical energy of interstellar shocks is processed and radiated away. In spite of what intuition dictates, a strong external UV radiation field boosts the efficiency of low velocity interstellar shocks in the production of several molecular lines which become evident tracers of turbulent dissipation.
Key words: shock waves / astrochemistry / ISM: kinematics and dynamics / photon-dominated region / ISM: molecules / turbulence
© ESO 2019
1. Introduction
The interstellar medium would be a nice, quiet, and somehow boring place to study if it were not constantly perturbed by strong dynamical events such as protostellar outflows, cloud collisions, supernovae, or galactic outflows. By interacting with the ambient medium, those events inject a large amount of mechanical energy in their surrounding environments at scales far larger than the diffusion length scales. A turbulent cascade therefore develops in which part of the initial kinetic energy is processed and transferred to all scales in a distribution of lower velocity dynamical structures that may carry a substantial fraction of the total kinetic energy.
The reprocessing of the initial available kinetic energy into a turbulent cascade is particularly well illustrated in the Stephan’s Quintet galaxy collisions. Colliding galaxies at relative velocities of ~ 1000 km s−1 not only trigger a large-scale initial shock clearly identified in X-rays (Trinchieri et al. 2003) but also a myriad of structures at far lower velocities (shocks, shears, and vortices). These structures carry the kinetic signature of the large-scale collision and radiate in the rovibrational lines of H2 a total power that exceeds that seen in X-rays (Appleton et al. 2006; Guillard et al. 2009). This example depicts a very generic modus operandi of the interstellar medium. Low velocity dissipative structures such as low velocity shocks allow the production of specific molecules that are usually not abundant in ambient gas. The lines of these molecules carry valuable information regarding the event driving the injection of mechanical energy and the way this energy is distributed in the gas and radiated away (Lesaffre et al. 2013; Lehmann et al. 2016).
The physics and signatures of non-irradiated molecular shocks have been the subject of numerous theoretical works, describing the dynamics and thermochemistry of gas and dust particles in shock waves (e.g. Hollenbach & McKee 1979; Draine 1980; Kaufman & Neufeld 1996; Flower & Pineau des Forêts 2003, 2010; Walmsley et al. 2005; Chapman & Wardle 2006; Guillet et al. 2007). All these works have led to valuable predictions and opened a wide observational field to study the properties and track the evolution of a great variety of galactic and extragalactic environments, including young stellar objects and molecular outflows (e.g. Gusdorf et al. 2008a,b; Flower & Pineau des Forêts 2013; Nisini et al. 2015; Tafalla et al. 2015), dense environments (e.g. Pon et al. 2016), supernovae remnants (e.g. Burton et al. 1990; Reach et al. 2005), and giant molecular clouds and filaments (e.g. Pon et al. 2012; Louvet et al. 2016; Lee et al. 2016). In many cases, the direct comparison of theoretical predictions and observations has proven to be a powerful tool to understand the nature of astrophysical sources and has given access, for instance, to their lifetimes, mass ejection rates, typical densities, and magnetization. Despite these successes, recent observations have revealed several chemical discrepancies that challenge the scope of the current models of molecular shocks. The relative emissions of oxygen-bearing species detected in the Orion H2 peak 1 (Melnick & Kaufman 2015), in the vicinity of low-mass protostars (Kristensen et al. 2013, 2017; Karska et al. 2014), in jets embedded in massive star-forming regions (Leurini et al. 2015; Gusdorf et al. 2017), or in supernovae remnants (Snell et al. 2005; Hewitt et al. 2009) all show significant disagreements with the intensity ratios predicted in non-irradiated low velocity shocks. It is usually proposed that these discrepancies could be the trace of shocks illuminated by ultraviolet photons, emitted either by an external source of radiation or by the shock itself.
Several models have been developed in the past to follow the propagation and chemistry of self-irradiated molecular shocks (e.g. Shull & McKee 1979; Neufeld & Dalgarno 1989; Hollenbach & McKee 1989). In contrast, few theoretical works have been devoted so far to shocks irradiated by an external UV field, and more generally to the formation of shock waves in photon-dominated regions (PDRs). In particular, while extensive studies of irradiated shocks have been performed both in diffuse interstellar clouds (Monteiro et al. 1988; Lesaffre et al. 2013) and dense environments (Melnick & Kaufman 2015), only low irradiation conditions were explored (up to ten times the standard interstellar radiation field).
The question of the impact of a strong UV radiation field on interstellar shocks is now magnified by the recent discovery of CH+ in submillimetre starburst galaxies at the peak of the star formation history (Falgarone et al. 2017). It is inferred that the broad line profiles seen in emission (~1000 km s−1) likely trace the turbulent gas stirred up by galactic outflows. However, the fact that broad line wings appear only in CH+ and not in other molecular tracers (e.g. CO, H2O; Swinbank et al. 2010; Omont et al. 2013) suggests that the chemistry at play in these regions of turbulent dissipation is peculiar and may be influenced by the strong radiation emitted by massive star-forming regions. The possible entwinement of radiative and mechanical energies raises the broader question of how these energies are actually processed in the interstellar medium. Building models capable of studying such environments has therefore become paramount to establish the energy budget of external galaxies and understand the relative importance of mechanical and radiative sources in the formation and excitation of molecules.
In this paper we present a detailed study of low velocity (≤ 25 km s−1) molecular shocks irradiated by an external source of ultraviolet photons. The numerical method and physical processes taken into account are described in Sect. 2. The specific dynamical, thermal, and chemical properties of irradiated shocks are presented in Sects. 3 and 4. Open questions and perspectives are addressed in Sects. 5 and 6.
2. Framework and physical ingredients
The model presented in this work is based on the Paris-Durham shock code (Flower & Pineau des Forêts 2003), a public numerical tool1 designed to compute the dynamical, thermal, and chemical evolution of interstellar matter in a steady-state plane-parallel shock wave. We further improve the version recently developed by Lesaffre et al. (2013), which is built to follow the effects of moderate ultraviolet irradiation, by including additional fundamental processes of PDR physics to study the propagation and chemistry of molecular shocks over a broad range of irradiation conditions.
 |
Fig. 1 Schematic view of the shock model geometrical assumptions in the shock frame. The positions of the ionization front and of the pre-shock are indicated as IF and PS. |
2.1. Geometry and main parameters
A schematicview of the plane-parallel geometry adopted in the model is shown in Fig. 1. Following the prescription of Lesaffre et al. (2013), we assume that a plane-parallel shock wave propagates with a speed Vs with respect to the pre-shock gas, in the direction perpendicular to the illuminated surface of the gas and to the ambient magnetic field B0. The shock wave is irradiated upstream by an isotropic flux of UV photons equal to the standard interstellar radiation field (Mathis et al. 1983) scaled with a parameter G0. A plane-parallel layer of gas and dust (hereafter designated as the “buffer”) is also assumed to stand upstream of the shock reducing the UV photon flux that reaches the pre-shock medium over a distance set by its visible extinction 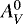 or equivalently its total hydrogen column density
or equivalently its total hydrogen column density 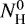 .
.
The last point of the buffer corresponds to the pre-shock medium and marks the origin of time t and distance z for the computation of the shock. The visible extinction AV and the self-shielding column densities of H2 and CO in the shock, Ns(H2) and Ns(CO), are integrated over the entire structure, including the buffer, to account correctly for the total absorption of UV photons. However, the output column density N(X) and line flux F(X) of any species X shown throughout the paper are integrated over the shock only, ignoring both the buffer and post-shock medium. Details on the computation of the timescale ts and size zs of the shock are given in Sect. 3.5.
In practice, we first compute the radiative transfer and chemical and thermal structures of the buffer with the Paris-Durham shock code by following, in a Lagrangian frame, a fluid particle moving away from the ionization front at a small and constant velocity until it reaches the position PS (see Fig. 1) where it enters the shock. Using the physical properties of the pre-shock gas as initial conditions, we then run the code in its classical configuration and compute the time-dependent dynamical, chemical, and thermal evolution of matter in the shock.
The main parameters of the model and the range of values explored in this work are given in Table 1. Compared to Table 1 of Lesaffre et al. (2013), we removed 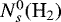 and
and 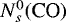 from the list of parameters because those quantities, which correspond to the column densities of H2 and CO in the buffer layer, are now self-consistently calculated by the code when computing the properties of the pre-shock gas.
from the list of parameters because those quantities, which correspond to the column densities of H2 and CO in the buffer layer, are now self-consistently calculated by the code when computing the properties of the pre-shock gas.
Main parameters of the shock code, standard model, and range of values explored in this work.
2.2. Grains and PAHs
As described in Appendix A, we assume that the grains at the ionization front (IF in Fig. 1) follow a power-law size distribution. Such distribution is subsequently modified in the buffer and in the shock as erosion, adsorption, and desorption processes take place. The initial range of sizes considered, the assumed mass densities of the grain cores and mantles, and the chemical composition of the cores are all given in Table A.1. Conversely, we model polycyclic aromatic hydrocarbons (PAHs) as single particles of size 6.4 Å and chemical composition C54 H18. To allow comparisons with the model developed by Lesaffre et al. (2013), a fixed abundance n(PAH)∕nH = 10−6 is adopted throughout the entire paper2.
2.3. Ultraviolet continuum radiative transfer
The attenuation of the UV photons flux throughout the geometry shown in Fig. 1 is solved using a simplified model of radiative transfer. We only consider absorption and neglect all emission and diffusion processes by gas and dust. Under these approximations, the specific monochromatic intensity I at a wavelength λ propagating in the cloud satisfies a reduced radiative transfer equation
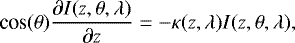 (1)
(1)
where z is the distance to the border of the cloud, θ is the angle of the propagation direction (with respect to the direction perpendicular to the cloud surface), and κ = κD + κG is the sum of the dust and gas absorption coefficients. Integrating this equation over the distance z leads to a simple relation
![\begin{equation*}I(z,\theta,\lambda) = I_0(\theta,\lambda) \,\, \textrm{exp} \left[ -\int_0^z \frac{\kappa(s,\lambda)}{\textrm{cos}(\theta)} \textrm{d}s \right] \end{equation*}](/articles/aa/full_html/2019/02/aa34248-18/aa34248-18-eq7.png) (2)
(2)
between I and I0, the specific monochromatic intensity at the border of the cloud. We define
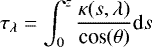 (3)
(3)
respectively, as the optical depth and the extinction along the direction θ. The monochromatic mean intensity, averaged over all directions, can be written as
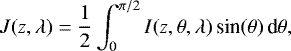 (5)
(5)
and the UV photon flux integrated between λmin = 911 Å and λmax = 2400 Å
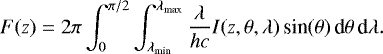 (6)
(6)
Absorption of UV photons by grain particles is calculated considering grains with density ng and a single size ag, where ng is derived from the size distribution while
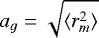 (7)
(7)
is chosen asthe size representative of the cross section of grains covered by ice mantles (see Appendix A). Within this framework, the dust attenuation coefficient at position z is therefore
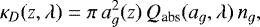 (8)
(8)
where Qabs(ag, λ) is the absorption coefficient of the grains. For simplicity, we adopt the absorption coefficients of spherical graphite grains of radius ag derived by Draine & Lee (1984) and Laor & Draine (1993). The absorption of UV photons by the gas is finally taken into account considering only continuum processes, i.e. the photodissociation and photoionization of atoms and molecules. The gas attenuation coefficients are thus
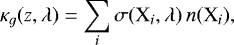 (9)
(9)
where σ(Xi, λ) is the photodissociation or photoionization cross section of species Xi. The code is written to potentially include all cross sections available in the Leiden database3 and recently updated by Heays et al. (2017). In this paper, however, and to reduce the complexity of the problem, κg (z, λ) is computed including only the photoionization of C, S, C2, CH, OH, and H2O, and the photodissociation of C2, C3, CH, OH, and H2O. We chose this approach to treat properly the ionization of the main atomic compounds and the destruction of several carbon and oxygen bearing species, which are discussed in Sect. 4. All the other photodestruction processes are implemented in the chemistry alone and not in the radiative transfer.
With these settings, the radiative transfer equation (Eq. (2)) is solved along 20 directions spread between θ = 0 and θ = π∕2. The discretization leads to an error in the calculation of the UV photon flux of about 8% for an isotropic radiation field (at the ionization front) and of less than 10% deeper in the cloud. We present in Appendix B a detailed comparison between our approach and the predictions of the Meudon PDR code (Le Petit et al. 2006) for the same environment. With the grain parameters described in Appendix A, the prescriptions adopted in this work are able to capture the physical structure and chemical transitions obtained in state-of-the art PDR codes4 (Le Petit et al. 2006; Le Bourlot et al. 2012).
2.4. Photodestruction processes
Photodestruction of atoms and molecules can involve continuum processes, i.e. occur through the absorption of photons over a continuous range of energy, or line processes, i.e. occur through the absorption of photons in atomic or molecular lines at given wavelengths (e.g. van Dishoeck 1988; van Dishoeck et al. 2006). In this work we take advantage of the computation of the radiation field spectrum to perform detailed treatments of both processes.
Following the approach of the Meudon PDR code (Le Petit et al. 2006), the continuum absorption mechanismsare treated in two different ways. If the photodestruction cross section of a species Xi is known and included in the code, the corresponding photoreaction rate is computed by direct integration over the radiation field intensity
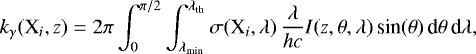 (10)
(10)
where λth is the ionization or dissociation threshold (expressed in wavelength). If not, the photoreaction rate is calculated using the analytical fits provided by Heays et al. (2017). In PDR physics, it is customary to express such rates as functions of the visual extinction AV with the form
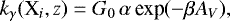 (11)
(11)
where α and β are constant coefficients. Such prescription, however, can only be applied if the visual extinction, used in this case as a proxy for the absorption of UV photons, has the same significance as the visual extinction deduced from the radiative transfer, or, in other words, if the underlying dust extinction curve used in Eq. (11) and that used in the radiative transfer are identical. To allow a coherent treatment of the photochemistry and the extinction based solely on the dust composition and size distribution chosen in input, we substitute Eq. (11) by a more versatile expression
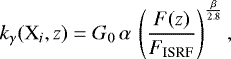 (12)
(12)
where FISRF is the UV photon flux associated with the isotropic standard interstellar radiation field (ISRF) for which the α and β coefficients are computed, and the factor 2.8 is deduced from a power-law fit of the photon flux F(z) as a function of AV for 0 ≤ AV ≤ 3 assuming a galactic extinction curve.
A different treatment is required for the photodissociations of H2 and CO that occur in lines and therefore involve self- and cross-shielding processes (Abgrall et al. 1992; Lee et al. 1996; Le Petit et al. 2002). In the previous version of the code, these aspects were taken into account using the analytical shielding expressions tabulated by Lee et al. (1996) and Draine & Bertoldi (1996) as functions of the column densities of H2 and CO at the current point (Lesaffre et al. 2013). To improve the treatment of the photodissociation of H2, we part from this approach and compute the absorption of UV photons by electronic lines of molecular hydrogen and the subsequent dissociation probabilities. This treatment is performed using the FGK approximation (Federman et al. 1979) and including all the UV lines of H2 in the Lyman and Werner bands. At each point z the code computes the central optical depth of each of those lines by integrating the abundance of H2 towards the radiation source, taking into account the thermal broadening and microturbulent motions (set with a parameter uturb, see Table 1) in the Doppler spreading of the line profiles. These optical depths are then used to attenuate the radiation field at the line central wavelengths, hence reducing the H2 dissociation rate.
Admittedly, large velocity gradients such as those found in shock waves could have an impact on the computation of optical depths and therefore on the photodissociation rate of H2 (Monteiro et al. 1988). This effect is, however, not yet included in the model.
2.5. Chemical network
The treatment of chemistry is carried out starting with the network of Flower & Pineau des Forêts (2015). This network incorporates 139 species, including gas-phase and solid-phase compounds, and about a thousand reactions. Regarding gas-phase reactions, both the sulphur and nitrogen chemistries are modified to take into account the recent updates of the reaction rates introduced in Table D.1 of Neufeld et al. (2015) and Tables B.1–B.3 of Le Gal et al. (2014). Regarding interactions with grains, we expand the network to model thermal desorption and photodesorption processes in addition to the sputtering, cosmic-ray and secondary photons desorption mechanisms already included in the previous versions.
Following Hollenbach et al. (2009), the thermal desorption rate per atom or molecule of a species 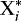 stuck on grain mantles is modelled as
stuck on grain mantles is modelled as
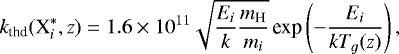 (13)
(13)
where mi is the mass of 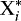 , Ei its adsorption energy taken from Hasegawa & Herbst (1993) and Aikawa et al. (1996), and Tg (z) is the grain temperature. The photodesorption rate of
, Ei its adsorption energy taken from Hasegawa & Herbst (1993) and Aikawa et al. (1996), and Tg (z) is the grain temperature. The photodesorption rate of 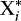 is written
is written
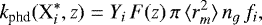 (14)
(14)
where Yi is the photodesorption yield set to 10−3 for all species (Hollenbach et al. 2009), and fi is the fraction of the surface adsorption sites occupied by 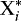 .
.
The calculation of the desorption rates by interaction with secondary photons is finally modified to be coherent with the expression used for grain ionization. Adopting the formalism of Flower & Pineau des Forêts (2003), we model the secondary photon desorption rate of species 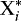 as
as
![\begin{equation*} k_{\textrm{scd}}(\textrm{X}_i^*,z) = 0.15 \, \left[ \zeta_{{\textrm{H}_2}} n({{\textrm{H}_2}}) + \zeta_{\textrm{H}} n(\textrm{H}) \right] \frac{n({{\textrm{H}_2}})}{n(\textrm{H}) + n({{\textrm{H}_2}})} \, Y_i \, f_i. \end{equation*}](/articles/aa/full_html/2019/02/aa34248-18/aa34248-18-eq25.png) (15)
(15)
The values 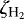 and ζH are the primary cosmic-ray ionization rates of H2 and H.
and ζH are the primary cosmic-ray ionization rates of H2 and H. ![$0.15 \, \left[ \zeta_{{\textrm{H}_2}} n({{\textrm{H}_2}}) + \zeta_{\textrm{H}} n(\textrm{H}) \right] \frac{n({{\textrm{H}_2}})}{n(\textrm{H}) + n({{\textrm{H}_2}})}$](/articles/aa/full_html/2019/02/aa34248-18/aa34248-18-eq27.png) is thus the number of secondary UV photons produced per second and per unit volume through the excitation of the Rydberg states of H2 by cosmic-ray induced electrons.
is thus the number of secondary UV photons produced per second and per unit volume through the excitation of the Rydberg states of H2 by cosmic-ray induced electrons.
Because our analysis is limited to low velocity shocks (VS ≤ 25 km s−1) and low pre-shock densities (nH ≤ 105 cm−3), we neglect, throughout this paper, the effects of grain–grain interactions, such as shattering, vaporization, and coagulation (e.g. Jones et al. 1996). This approximation is supported by recent models of grain dynamics which show that the shattering and vaporizationof large grains have a significant impact on the grain size distribution only for high velocity shocks (VS > 20 km s−1) propagating in dense media (nH > 104 cm−3; see Fig. 7 of Guillet et al. 2009 and Fig. 4 of Guillet et al. 2011). Similarly, the grain coagulation is found to marginally affect the grain size distribution in low density molecular shocks (see Fig. 14 of Guillet et al. 2011).
2.6. H2 radiative pumping
Besides the thermal and chemical evolution of the gas, the code also computes the time-dependent populations of the rovibrational levels of H2 (Flower & Pineau des Forêts 2003). In addition to inelastic collisions with H, He, H2, and H+ and the probability of exciting H2 at formation on grain surfaces, which are two processes already taken into account, we include the excitation by radiative pumping of the electronic lines of molecular hydrogen followed by fluorescence.
The radiative pumping is computed following the approach used to estimate the self-shielding and photodissociation rate (see Sect. 2.4). At each time step, the absorption of UV photons by the discrete lines of the Lyman (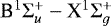 ) and Werner (
) and Werner (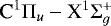 ) band systems and the subsequent cascades in the rovibrational levels of the fundamental electronic state are calculated. The line opacities, which reduce the intensity of the radiation field capable of pumping the electronic states, are integrated over the column density Ns (H2) (see Fig. 1) using the FGK approximation (Federman et al. 1979).
) band systems and the subsequent cascades in the rovibrational levels of the fundamental electronic state are calculated. The line opacities, which reduce the intensity of the radiation field capable of pumping the electronic states, are integrated over the column density Ns (H2) (see Fig. 1) using the FGK approximation (Federman et al. 1979).
2.7. Dust charge and temperature
Grains are considered to be either neutral, negatively, or positively charged. As done for the radiative transfer, the abundances of these different states are computed assuming grains with a single size ag. Photoelectric ejection, electron attachment, and charge exchange between ions and grains are modelled adopting the formalism of Bakes & Tielens (1994). The photoelectric ejection rate of a grain of charge Z is thus written
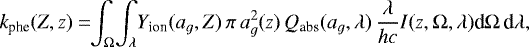 (16)
(16)
where Yion(ag, Z) is the ionization yield, and the charge attachment rate
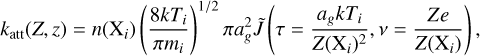 (17)
(17)
where n(X_i) and Z(X_i) are the abundance and charge of the colliding particle X_i, and Ti is the ion temperature. The function 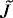 is described by Draine & Sutin (1987) and accounts for Coulomb interactions of the colliding system.
is described by Draine & Sutin (1987) and accounts for Coulomb interactions of the colliding system.
The heating rate of the gas induced by the photoelectric effect is modelled using the efficiencies deduced by Bakes & Tielens (1994) for very small graphitic grains and PAHs (Eqs. (42) and (43) of their paper).
At last, the temperature Td of grains of size ag is computed from the equilibrium between the radiative energy absorbed by the grain, the thermal exchange induced by collisions between grains and gas (at temperature Tn), and infrared radiative emission,
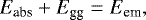 (18)
(18)
assuming that grains radiate as black-bodies with an intensity equal to the Planck function Bλ (Td). In the code, Td is computed at each time step by solving Eq. (18) using a Newton–Raphson scheme.
2.8. Cooling
Following Flower & Pineau des Forêts (2003) and Lesaffre et al. (2013), the cooling of the gas is computed taking into account the excitation of the fine structure lines and metastable lines of C, N, O, S, Si, C+, N+, O+, S+, and Si+, and the rovibrational lines of H2, OH, H2O, NH3,12 CO, and13 CO. The cooling resulting from the atomic lines and rovibrational lines of H2 is calculated in the optically thin limit. In the framework of a 1D plane-parallel geometry, this assumption is found to hold for the main coolant of the gas (namely H2, C+, and O) at alevel better than a few percent. The cooling through the rovibrational lines of OH and NH3 is calculatedanalytically using the prescription of Le Bourlot et al. (2002), while the cooling induced by the molecular lines of H2 O,12 CO, and13 CO is taken from the values tabulated by Neufeld & Kaufman (1993), which include opacity effects.
3. The models: C, C*, CJ, and J stationary shocks
The influence of the external UV field on the propagation and properties of interstellar shocks is studied through several grids of models5 − 3120 runs in total− covering a broad range of physical conditions. These include an initial pre-shock density varying between 102 and 105 cm−3, an ambient UV radiation field with a scaling factor G0 between 0 and 104, and a total hydrogen column density in the buffer between 2 × 1019 and 2 × 1022 cm−2 (see Table 1). For reasons we detail below (see Sect. 5.2), we limit our analysis to low velocity and moderately magnetized shocks, i.e. shocks with a speed comprised between 5 and 25 km s−1 and a pre-shock transverse magnetic field parameterized by b (see Table 1) varying between 0.1 and 10.
 |
Fig. 2 Temperature (top left panel), electronic fraction (i.e. n(e)∕nH,
top right panel), molecular fraction (i.e. 2n(H2)∕nH,
bottom left panel), and depletion (bottom right panel) in the pre-shock medium as functions of
G0 and |
3.1. Pre-shock conditions
The range of pre-shock conditions explored in this work are summarized in Fig. 2, which shows the temperature, electronic fraction, molecular fraction, and depletion of elements on grain surfaces in the pre-shock gas as functions of the input radiation field and size of the buffer. Since the amount of elements locked up onto grain surfaces in well-shielded environments is highly uncertain (Gibb et al. 2000), two formalisms are considered: if there is no radiation field (G0 = 0), we switch off all adsorption and desorption processes for the computation of the pre-shock conditions and adopt the chemical composition of grain mantles given in Table 2 of Flower & Pineau des Forêts (2003); conversely, if a radiation field with any strength is illuminating the gas and dust (as in Fig. 2), both adsorption and desorption processes are included. We note that this last assumption may lead to strong depletion at low radiation fields (bottom right panel of Fig. 2), which may be unrealistic compared to observations.
Figure 2 shows the well-known transition regions of PDRs discussed in many studies (i.e. Hollenbach & McKee 1979; Röllig et al. 2007). Within the FGK approximation (see Sect. 2.6), the treatment of the radiative pumping of H2 rovibrational levels has a small influence on the general properties of the gas and on the pre-shock conditions shown in Fig. 2. The most noticeable impact arises at large radiation fields (G0 ≥ 103) where the pre-shock temperature and electronic fraction increase by more than 10% when the pumping is included. While inconsequential over a wide range of parameters, this process is however paramount for shocks propagating in hot and dense PDRs (i.e. G0 = 104 and nH = 105 cm−3) in which the UV pumping strongly limits the cooling efficiency of H2 and induces a raise of the pre-shock temperature (see Fig. D.2).
As shown in Fig. 2, the range of parameters chosen in this work allows us to explore shocks propagating in a wide variety of environments, spanning atomic to molecular gas, low and high ionization conditions, and cold and hot pre-shock medium (from ~20 to ~ 1000 K). While extensive grids of shock models have been run over the entire parameter space, most of the analysis below is carried out varying one parameter at a time around two standard models defined as follows: nH = 104 cm−3, G0 = 1, VS = 10 km s−1, b = 1, and 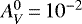 or 10−1. In order to highlight the impacts of the UV radiation field on the dynamics of the gas, a buffer visual extinction
or 10−1. In order to highlight the impacts of the UV radiation field on the dynamics of the gas, a buffer visual extinction 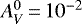 is assumed throughout all Sect. 3. Conversely, the predictions on atomic and molecular emission presented in Sect. 4 are obtained assuming
is assumed throughout all Sect. 3. Conversely, the predictions on atomic and molecular emission presented in Sect. 4 are obtained assuming 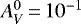 . Such choice of standard models not only opens the exploration of all the conditions shown in Fig. 2 with a limited number of runs but is also found to be sufficient to present most of our results on the physics of irradiated shocks in a synthetic manner. More exhaustive results are given in Appendix D where we lay out additional figures and predictions in a blooming potpourri.
. Such choice of standard models not only opens the exploration of all the conditions shown in Fig. 2 with a limited number of runs but is also found to be sufficient to present most of our results on the physics of irradiated shocks in a synthetic manner. More exhaustive results are given in Appendix D where we lay out additional figures and predictions in a blooming potpourri.
3.2. Stationary magnetized molecular shocks
We recall that the standard model adopted in this section is defined by a buffer visual extinction  . The physics of magnetized molecular shocks and the steady-state solutions allowed to propagate in the interstellar medium have been described in many studies (e.g. Mullan 1971; Draine 1980; Kennel et al. 1990; Dopita & Sutherland 2003). As prescribed by the Paris-Durham code, we limit our study to stationary plane-parallel shock waves where the magnetic field is assumed to be transverse to the direction of propagation. It follows that the influence of UV photons on time-dependent shocks (Chièze et al. 1998; Lesaffre et al. 2004) and on slow or intermediate steady-state shocks (Draine & McKee 1993; Lehmann & Wardle 2016) are not addressed in this work.
. The physics of magnetized molecular shocks and the steady-state solutions allowed to propagate in the interstellar medium have been described in many studies (e.g. Mullan 1971; Draine 1980; Kennel et al. 1990; Dopita & Sutherland 2003). As prescribed by the Paris-Durham code, we limit our study to stationary plane-parallel shock waves where the magnetic field is assumed to be transverse to the direction of propagation. It follows that the influence of UV photons on time-dependent shocks (Chièze et al. 1998; Lesaffre et al. 2004) and on slow or intermediate steady-state shocks (Draine & McKee 1993; Lehmann & Wardle 2016) are not addressed in this work.
A shock is a pressure-driven instability of fluid dynamics in which the kinetic energy of the flow is transferred from large scales to small scales where it dissipates primarily into heat. At steady state, a shock structure connects two thermodynamical equilibrium points: the upstream unstable state and downstream stable state. The nature of the instability, the scales involved, and the forces at play in the evolution of the fluid between these two points depend on the velocity of the flow compared to its characteristic wave speeds. Although the expressions of those speeds are different depending on the physical properties of the gas, it is customary to discuss the physics of shocks in terms of the wave speeds derived for an isothermal magnetohydrodynamic fluid in the limit of weak and strong coupling between ionized and neutral species, i.e. the sound speeds and magnetosonic speeds in the ions (ci and cims) and in the neutrals (cn and cnms)6
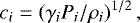 (22)
(22)
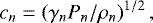 (23)
(23)
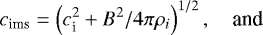 (24)
(24)
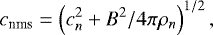 (25)
(25)
where γi, γn, Pi, Pn, ρi, and ρn are the heat capacity ratio, pressure, and mass density of the ions and the neutrals and B is the strength of the magnetic field. As we explain below (see Sect. 3.3.3), we assume that all grains are coupled with the magnetic field: it follows that ρi not only includes the mass density of ionized species but also that of dust particles. Interstellar shocks occur when the upstream flow is dynamically unstable, which happens when VS ≥ cn (resp. cnms) in the limit of weak (resp. strong) coupling between ions and neutrals.
Assuming a fixed ionization fraction, the nature of a shock can be understood by solely discussing the impact of the magnetic field and gas cooling.
In very weak magnetic field environments, ions and neutrals are fully coupled with each other. In the frame of the shock, both fluids are decelerated through the combined actions of viscous stresses and the thermal pressure gradient induced by viscous heating. The gas quickly jumps from a supersonic to a subsonic regime, with respect to the neutral sound speed, over a distance of about a few mean free paths. The resulting structure is referred to as a J-type shock. Without magnetic field, the gas pressure of the post-shock flow is only thermal, which implies that the downstream fluid is subsonic. If a magnetic field is present, magnetic pressure increases in the post-shock. In this case, the final velocity of the flow may be supersonic if the magnetic pressure is large enough to stabilize the downstream flow.
When the magnetic field is sufficiently strong such that cims > VS, a magnetic precursor can develop: the Lorentz force decelerates the ions which decouple from the neutrals in the upstream flow. In turn, this decoupling induces a drag force that slows down the neutral fluid. If the coupling between ions and neutrals is weak, the resulting effect is too small to smooth the neutral velocity gradient: the viscous stresses and thermal pressure gradient remain the dominant forces involved in the motion of the neutrals. Two characteristic lengths therefore appear: the magnetic precursor scale (Draine 1980) over which the ions decelerate continuously, and the viscous length where the neutrals velocity jumps. Such a structure is called a CJ-type shock7. While the neutral fluid necessarily becomes subsonic at the jump, the downstream flow may be supersonic (for reasons given above). In this case, the neutral fluid crosses the sonic speed twice, at the jump position and somewhere along the downstream trajectory.
Increasing the magnetic field enlarges the size of the magnetic precursor. The drag force applies for a longer time, smoothing the neutral velocity gradient and thermal pressure gradient, thus reducing the strength of viscous stresses which may become negligible over the entire trajectory. When this happens, the thermal pressure gradient and the ion-neutral friction slow down the neutrals continuously to the downstream point. Those kinds of shocks are separated into two classes. If the neutral fluid becomes subsonic along its trajectory, the structure is referred to as a C*-type shock, if not as a C-type shock. It follows that the downstream flow of a C-type shock is necessarily supersonic. It is worth noting that the differentiation between C*- and C-type shocks is one of semantics and numerics only. These two types of shocks formally and physically correspond to the same kind of structure with similar thermochemical evolutions (see Sect. 3.4).
The impact of the cooling described by Chernoff (1987) can be understood starting with a CJ-type shock. Increasing the cooling in this situation reduces the thermal pressure gradient and neutral velocity Laplacian, hence the strength of the viscous stresses. As in the previous case, if the viscous forces become small enough compared to the drag force and thermal pressure gradient, either a C*-type or a C-type structure develops.
The nature of an interstellar shock is therefore the result of a subtle interplay between the strength of the magnetic field and the ionization degree − which control the size of the magnetic precursor and its capacity to slow down and heat the neutrals − and the cooling rate. In practice single-fluid J-type shocks or bi-fluid C-type shocks are computed using a forward integration technique and starting from the pre-shock conditions (e.g. Flower & Pineau des Forêts 2015). Since this method is numerically unstable as soon as the neutral gas become subsonic, a more sophisticated algorithm is used to compute CJ-type and C*-type shocks. This algorithm, fully described in Appendix C, is based on the works of Chernoff (1987) and Roberge & Draine (1990) and combines forward integration techniques with shooting methods.
 |
Fig. 3 Neutral sound speed (dotted) and neutral (dot-dashed) and ion (solid) magnetosonic speeds as functions of the density (upper left panel), transverse magnetic field intensity (upper right panel), UV radiation field intensity (lower left panel), and visual extinction (lower right panel). All the non-varying parameters are set to their standard values (see Table 1), and the standard value of the buffer visual extinction is set to
|
3.3. Existence of J-, CJ-, C*-, and C-type shocks
The characteristic speeds cn, cims, and cnms computed in the pre-shock fluid and the domains of existence of the different kinds of stationary shocks are shown in Fig. 3 as functions of the pre-shock density, magnetic field, and irradiation conditions. Each parameter is explored around the standard model for a buffer visual extinction 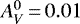 (see Table 1).
(see Table 1).
3.3.1. Critical speeds
The minimal speed required for a shock to propagate is a problem of non-ideal magnetohydrodynamic. In the limit of low coupling between ions and neutrals, a shock develops if the perturbation applied to the medium travels faster than the neutral sound speed. Conversely, in the limit of strong coupling, a shock exists only if the perturbation travels faster than the neutral magnetosonic speed. While the intermediate case has been treated in several numerical studies (e.g. Balsara 1996), no analytical formula has ever been derived. To simplify, we identify in Fig. 3 the neutral magnetosonic speed cnms as the minimal speed required to induce a shock. We do so because we found that C-type shocks below this limit (~ 2 km s−1 for the standard model) induce a relative velocity difference between the upstream and downstream flows smaller than 10%. Above this limit, the parameter space shown in Fig. 3 is divided in four different regions which set the domains of existence of J-, CJ-, C*-, and C-type shocks.
The limit between J-type and other kinds of molecular shocks is given by the ions magnetosonic speed, hence by the strength of the magnetic field and the mass density of the ionized flow in the pre-shock medium (Eq. (24)). Assuming that all grains – including the neutrals – contribute to the inertia of the charged fluid (see Guillet et al. 2007; Lesaffre et al. 2013, and Sect. 3.3.3), the mass density of the ionized flow is dominated by the grains. With an initial transverse magnetic field B0 proportional to 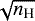 (see Table 1), cims therefore linearly depends on B0, does not depend on the gas density, and softly depends on the dust-to-gas mass ratio. Without depletion, i.e. at large radiation fields or weak extinctions (bottom panels of Fig. 2), the mass of grains lies in the cores which is set by their composition and grain size distribution (see Table A.1 and Appendix A). Conversely, if the depletion becomes important, the mantles contribute to the grain mass; in the limit of high depletion, i.e. at low radiation fields or large extinctions, the dust-to-gas mass ratio is increased by a factor of two and the ion magnetosonic speed is divided by a factor 1.4.
(see Table 1), cims therefore linearly depends on B0, does not depend on the gas density, and softly depends on the dust-to-gas mass ratio. Without depletion, i.e. at large radiation fields or weak extinctions (bottom panels of Fig. 2), the mass of grains lies in the cores which is set by their composition and grain size distribution (see Table A.1 and Appendix A). Conversely, if the depletion becomes important, the mantles contribute to the grain mass; in the limit of high depletion, i.e. at low radiation fields or large extinctions, the dust-to-gas mass ratio is increased by a factor of two and the ion magnetosonic speed is divided by a factor 1.4.
The range of existence of C-, C*-, and CJ-type shocks below the ions magnetosonic speed can be explained in the light of the driving mechanisms of molecular shocks described in Sect. 3.2. The impact of the radiation field on a C-type shock is understood by two main processes: the enhancement of the photoionization mechanisms and the increase of the photodissociation of H2. Indeed, as the electronic fraction increases, so does the coupling between the ions and the neutrals: the size of the shock therefore decreases and the compressive heating rate increases. Concurrently, the diminution of both the self-shielding and the abundance of H2 strongly reduces the cooling rate of the gas. If the cooling is insufficient to prevent the neutrals from crossing the sound speed, the structure becomes a C* shock. If the cooling is even lower, i.e. too low to repress the impact of viscous stresses, the structure becomes a CJ shock.
The role of the magnetic field is also straightforward. Low magnetic field intensities reduce the size of the magnetic precursor, hence the size of the shock, favouring the existence of C* and CJ shocks (see Sect. 3.2). Conversely, large magnetic field intensities increase the ions magnetosonic speed, hence the maximal velocity for which a magnetic precursor can develop. When cims is larger than the critical speed required to dissociate H2 by collisions (Le Bourlot et al. 2002), a domain of existence of CJ shocks appears (top right panel of Fig. 3).
3.3.2. Influence of the UV field
Figure 3 shows that the structure of interstellar stationary shocks is mostly governed by the intensity of the magnetic field and strength of the UV radiation field. The magnetic field tunes the magnitude of the coupling between ions and neutrals and therefore controls the range of velocities over which a shock can exist and a magnetic precursor can develop. Once those limits are set, the radiation field becomes the most decisive quantity: its impact on the ionization fraction and the cooling efficiency (magnified by the pumping of H2) determines the range of existence of C, C*, and CJ shocks.
Most shocks propagating in dense or low-illuminated environments (nH ≥ 104 cm−3 or G0 ≤ 1) appear to be either J or C. This ceases to be true, however, in more diffuse or illuminated media (see Figs. 3 and D.1) where the radiation field drastically reduces the domain of existence of C-type shocks in favour of C* and CJ-type structures. As a rule of thumb we find that those kinds of shocks become dominant as soon as
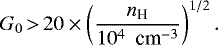 (26)
(26)
It follows that only low velocity C-type shocks (VS ≤ 5 km s−1) can propagate in prototypical PDR (nH ~ 104, G0 ~ 100) or in very diffuse clouds (nH ~ 30 cm−3, G0 ~ 1). This limit on the maximal velocity of C-type shocks is in agreement with the work of Melnick & Kaufman (2015) who found similar breakdown velocities in irradiated environments.
3.3.3. Influence of grains and PAHs
The cold neutral medium is a partially ionized environment with a very low ionization fraction. Its elemental composition in the solar neighbourhood implies that the fraction of mass contained in gas-phase ionized species is below 3 × 10−3 for diffuse and transluscent clouds and quickly drops in dark clouds. With a dust-to-gas mass ratio of about 1% and efficient ionization and recombination processes, charged dust grains are thus a dominant contributor to the inertia of the ionized flow, and therefore strongly influence its dynamics.
The impact of dust on magnetized shocks has been the subject of many studies that have successively described the effects of the dust decoupling (e.g. Ciolek & Roberge 2002; Ciolek et al. 2004), their size distribution (e.g. Chapman & Wardle 2006; Guillet et al. 2009), and the fluctuation of their charge (Guillet et al. 2007) on the structure of the shock. Two results are of particular interest in this paper. Firstly, as the ionization and recombination of grains is fast, the charge of grains rapidly fluctuates. In particular, the survival timescale of a neutral grain is found to be very small compared to its dynamical timescale (Guillet 2008), i.e. the time it needs to reach the neutral velocity. This result holds for all grain sizes and all irradiation conditions. It follows that, for a given size of grains, both neutral and charged grains can be considered as a single fluid. Secondly, whether this fluid is coupled with the neutral flow or with the ionized flow solely depends on the Hall factor Γ, which measures the ratio of the grain drag to the grain gyration timescales and depends on the grain elastic cross section σ, grain charge q, strength of the magnetic field B, mass density of the neutrals ρn, and velocity drift between grains and neutrals δv as (Guillet et al. 2007, Eqs. (9)–(11))
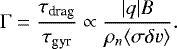 (27)
(27)
The results shown here (including Fig. 3) are obtained adopting a PAH relative abundance of ~ 10−6 and assuming that all grains are coupled to the magnetic field, i.e. Γ > 1. Large grains in irradiated environments are expected to be multiply charged (e.g. Draine 2002). Because the Hall factor is inversely proportional to the square of the grain size, we estimate that this assumption is always valid for small grains (a ≤ 0.1 μm) and holds for large grains as long as G0∕nH ≥ 10−4 cm3 and b ≥ 1. In turn, it most probably fails in dense and dark environments (G0∕nH ≤ 10−5 cm3) or in media with a very low magnetic field (b ~ 0.1), where the Hall factor computed for grains larger than 0.2 μm falls below unity, which means that a fraction of the dust mass is coupled to the neutral fluid (Guillet et al. 2007). The main impact of PAHs is to reduce the abundance of electrons in the gas phase. In irradiated environments (resp. dark clouds), where grains are dominantly positive (resp. negative), PAHs therefore lead to an increase (resp. decrease) of the Hall factor. The rather large value of PAHs abundance adopted in this work therefore strengthens our hypothesis on the coupling between grains and the magnetic field in irradiated media but weakens it in dark environments.
As a whole, the outcome of this assumption (Γ > 1) is a minimization of the ions magnetosonic velocity. This, in turn, reduces the range of existence of C, C*, and CJ shocks. In dark clouds with classical magnetization (b = 1) for instance, where it could be debated, we find that these kinds of shocks propagate at velocities necessarily smaller than ~ 25 km s−1 (see Fig. D.1); this value is significantly lower than the 40 km s−1 derived in most of the previous studies (e.g. Kaufman & Neufeld 1996; Flower & Pineau des Forêts 2003, 2010; Melnick & Kaufman 2015) and also arguable. All these results show that a detailed treatment of grains and PAHs can be critical for the nature of interstellar shocks. For the sake of simplicity, we adopt a formalism which works over most of the parameter domain and extend it to environments where it may not be justified. An accurate treatment would allow us to study magnetized shocks in dark environments at velocities larger than the maximal value we infer. In practice, such a study requires us to adopt a multi-fluid approach to treat each size of grains as a separate flow with its own momentum and thermodynamical evolution (Ciolek & Roberge 2002; Chapman & Wardle 2006; Guillet et al. 2007). This is beyond the scope of this paper.
 |
Fig. 4 Profiles of the neutral sound speed (solid black), velocity of the neutrals (solid blue) and that of the ions (solid red) in the frame of the shock, and temperature of the neutrals (dot-dashed green) computed in stationary shocks propagating in media with different densities and radiation field intensities. All the other parameters are set to their standard values (see Table 1), and the standard value of the buffer visual extinction is set to
|
3.4. Shock profiles and energetics
The main physical properties of molecular shocks are shown in Fig. 4, which shows, in the frame of the shock, the ion and neutral velocity profiles and the neutral temperature profiles computed in different environments for shocks propagating at 10 km s−1. Starting from the upstream supersonic state, a gas cell is progressively slowed down, compressed, heated up through compression, ion-neutral friction and viscosity, and eventually cooled down through line emission. The thermodynamical path followed by the cell and the final state reached downstream are simply the outcome of the mandatory conversion of the initial kinetic energy into magnetic and thermal energies and radiative losses (see Fig. 5).
In weakly magnetized J-type shocks with large compression ratios, the maximum temperature reached by the gas reduces to a simple analytical formula (Lesaffre et al. 2013)
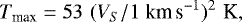 (28)
(28)
which gives 5300 K for a shock at 10 km s−1. This estimation corresponds to the extreme case where most of the initial kinetic energy is adiabatically converted into thermal energy at the shock front. In magnetized shocks or C-type shocks, part of the kinetic energy is used to compress the magnetic field, hence increase the magnetic pressure. The rest of the initial energy is converted into heat over a characteristic length controlled by both the size of the magnetic precursor and the cooling rate (see Sect. 3.2). The maximum temperature of those shocks is thus necessarily smaller than that obtained in the adiabatic case and decreases with the strength of the magnetic field and strength of the cooling. Such a behaviour has been abundantly confirmed with models of low radiation field environments or in dark clouds, where the temperature profiles of C-type shocks are found to be considerably smoother and broader than the equivalent profiles obtained in weakly magnetized J-type shocks with the same velocities (e.g. Flower 2010; Flower & Pineau des Forêts 2013; Lesaffre et al. 2013; Melnick & Kaufman 2015). For instance, these authors report typical maximal temperatures of 1000 K for 10 km s−1 C-type shocks, a value five times lower than that found in the weakly magnetized adiabatic case.
The impact of an external UV radiation field can be understood in this framework. Increasing the radiation field increases the ionization fraction of the pre-shock medium, hence the strength of the coupling between the neutrals and the ions. As the magnetic precursor shrinks, the kinetic energy is converted into heat over a smaller distance, which leads to a larger maximal temperature of C-type shocks (see Figs. 4 and D.2 and Fig. 2 of Melnick & Kaufman 2015) that eventually become C*-type shocks. As shown in Fig. D.2, this effect is moderate and appears to be stronger for low velocity shocks and low density media. In particular, the thermodynamical profiles of C-type and C*-type shocks are found to be very similar and to differ only by their size and the fact that C*-type shocks are partly subsonic. This whole picture is, however, strongly modified at large radiation fields, when the flux of UV photons is strong enough to photodissociate H2. The reduction of the cooling rate of the gas leads to larger temperatures and eventually induces an adiabatic jump along the trajectory (CJ-type shock). As the radiation field increases, the jump arises sooner, instantly8 converting a large fraction of the kinetic energy into heat and magnetic compression. Depending on the velocity and the environment considered, the maximal temperature of CJ-type shocks can be two to ten times larger than that obtained in C-type shocks and persist over a large tail set by the long cooling timescale of the gas (see Fig. D.2).
 |
Fig. 5 Kinetic, magnetic, and thermal energy fluxes compared to the integrated radiative loss in a CJ-type shock propagating at 10 km s−1 in a medium of density 104
cm−3 and illuminated by a strong radiation field G0 = 104. All the otherparameters are set to their standard values (see Table 1), and the standard value of the buffer visual extinction is set to |
3.5. Shock size and timescale
The determination of the shock size and timescale, i.e. the limit marking the beginning of the post-shock medium (see Fig. 1), is an important issue that is not only useful to interpret the physics of the shock but can also have a strong influence on the output quantities predicted by the models. Indeed, as shown for instance by Gusdorf et al. (2008a), Leurini et al. (2014), and Lehmann (2017), the inclusion of the post-shock gas (see Fig. 1) can modify by orders of magnitude the column densities of numerous species, and hence have a strong impact for the comparison with observations. Several definitions have been proposed so far, including criteria on the abundance profiles, temperature profile, or ion-neutral coupling length (Draine 1980; Wardle 1999; Lesaffre et al. 2013; Melnick & Kaufman 2015; Lehmann & Wardle 2016). Unfortunately, while these propositions may be useful to study a specific problem, they do not provide a reliable definition for comparison of shock length in different models and they cannot be applied indifferently to all kinds of shocks. In addition, any criterion based on the sole comparison of pre-shock and post-shock properties is bound to fail when strong external radiation fields are considered and if the post-shock medium conditions are nowhere near those of the pre-shock.
To overcome these issues, we adopt a definition of the shock size based on energetic considerations. As illustrated in Fig. 5, a stationary shock propagating in the interstellar medium is a structure in which the mechanical energy flux is progressively converted into magnetic and thermal energy fluxes and is partially radiated away through line emission. The transition between the shock and the post-shock medium can therefore be designated as the point at which most of the radiation induced by the shock has been emitted. In the following, we thus define the shock size zs as the distanceverifying
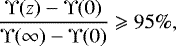 (29)
(29)
is the sum of the kinetic,
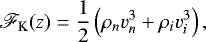 (31)
(31)
energy fluxes, and μn and μi are the mean molecular masses of the neutrals and of the ions. The shock timescale is then set as ts = t(zs), i.e. as the time required for a fluid particle to reach zs. Because they are built on a conservative quantity, these definitions have the advantage of capturing key aspects of shock physics. Moreover they offer a more universal criterion that can be applied to any kind of structures, including C-, C*-, CJ-, or J-type shocks, propagating in dark or highly illuminated environments. An example of this criterion applied to an irradiated molecular shock is shown in Fig. 5.
The values of zs and ts obtained for a 10 km s−1 shock propagating in various environments are shown in Fig. 6. To simplify, we deliberately remove from Fig. 6 the models at low radiation fields and large densities that correspond to J-type shocks propagating in a medium in which all the heavy elements are stuck onto grains. Indeed, while academically interesting, these models may be unrealistic for the study of dense and dark clouds, for which standard models usually assume a substantial fraction of heavy elements in the gas phase (e.g. Flower & Pineau des Forêts 2003, 2010; Gusdorf et al. 2008a,b; Guillet et al. 2009; Anderl et al. 2013). Because the dark clouds are not the subject of this paper, these models are not studied.
Each panel of Fig. 6 can be separated in two regions depending on G0 where the size and timescale of the shock either decrease or increase as functions of the strength of the UV field. (1) The first region, at low radiation field intensity, corresponds to the domain of existence of C-type and C*-type shocks. In this domain, the shock size is mainly given by the length of the magnetic precursor, which is inversely proportional to the electron density (see Eq. (36.44) of Draine 2011). If the UV photons are the main ionization source of the gas, i.e. at low extinction, it is easy to show that the electron density writes 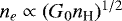 : the shock size is therefore proportional to
: the shock size is therefore proportional to 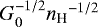 as observed on the left and middle panels of Fig. 6. Conversely, if the UV photons are a secondary ionization process, i.e. at high extinction, the dependance on G0 is progressively lost and the size of the shock becomes simply proportional to
as observed on the left and middle panels of Fig. 6. Conversely, if the UV photons are a secondary ionization process, i.e. at high extinction, the dependance on G0 is progressively lost and the size of the shock becomes simply proportional to 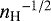 as confirmed on the right panels of Fig. 6. (2) The second region, where the size of the shock increases with the strength of the UV field, corresponds to the domain of existence of CJ-type shocks. In this domain, the ionization fraction has reached a maximum and the shock size is given by the large temperature tail induced by a reduced cooling efficiency due to the photodissociation of H2. If H2 is the major coolant of the gas, the shock size is inversely proportional to n(H2), thus directly proportionalto G0; if H2 is a secondary coolant, the dependence of zs on G0 is weak or lost. All these cases can be identified in the left and middle panels of Fig. 6.
as confirmed on the right panels of Fig. 6. (2) The second region, where the size of the shock increases with the strength of the UV field, corresponds to the domain of existence of CJ-type shocks. In this domain, the ionization fraction has reached a maximum and the shock size is given by the large temperature tail induced by a reduced cooling efficiency due to the photodissociation of H2. If H2 is the major coolant of the gas, the shock size is inversely proportional to n(H2), thus directly proportionalto G0; if H2 is a secondary coolant, the dependence of zs on G0 is weak or lost. All these cases can be identified in the left and middle panels of Fig. 6.
Overall, Fig. 6 shows that the shock sizes and timescales cover a broad range of values, spread over three orders of magnitude, depending on the medium in which they propagate. Interestingly, if J-type shocks are removed from the analysis, the size of interstellar shocks appears to be weakly dependent on the shock velocity. Exploring the entire grid of models shows that similar sizes are found for VS varying between 5 and 20 km s−1, except at very low radiation fields (G0∕nH ~ 10−5 cm3) where sizes differ by a factor of four and at large radiation fields (G0∕nH ≥ 10−1 cm3) where they differ by a factor of three.
The crossing time represented in the bottom panels of Fig. 6 can be interpreted as the time required for the shock to reach its steady-state configuration (Chièze et al. 1998; Lesaffre et al. 2004). Scaling almost exactly as the shock size, this critical dynamical timescale is found to strongly depend on the medium considered, varying from a few hundred years in dense and moderately irradiated environments to a few tens of thousand years in diffuse gas. In most cases, these values are considerablysmaller than the turnover timescales of the corresponding environment, suggesting that steady-state shocks are relevant structures for the study of interstellar medium. This is true, in particular, for diffuse and dense environments where the linewidth-size relation leads to dynamical timescales 100 times larger than the shock crossing time (e.g. Hennebelle & Falgarone 2012). This conclusion weakens, however, in outflows and jets (e.g. Gusdorf et al. 2008b) and in dense PDRsin which the photoevaporation timescale becomes comparable or smaller than the shock crossing time (Störzer & Hollenbach 1998). Comparing the results of Fig. 6 to the propagation timescale of ionization fronts (Gorti & Hollenbach 2002) shows that shocks can no longer be considered at steady state as soon as nH ≥ 105 cm−3, G0 ≥ 103 and AV ≤ 10−2, i.e. at the border of our grid of models.
 |
Fig. 6 Shocksizes (top panels) and timescales (bottom panels) as functions of the UV radiation field and different visual extinction AV computed for shocks propagating at 10 km s−1 in media of densities of 102 (empty squares), 103 (empty circles), 104 (filled squares), and 105 (filled circles) cm−3. The non-varying parameters are set to their standard values (see Table 1). J-type shocks propagating in dense and weakly irradiated clouds are deliberately removed from the figure (see main text), hence the missing points on the left side of each panel. |
4. Molecules in irradiated shocks
We recall that the standard model adopted in this section is defined by a buffer visual extinction 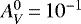 . External sources of UV radiation fields necessarily exert a major impact on the formation and excitation of molecules in space. In irradiated shocks, the role of UV photons extends far beyond the mere ionization and dissociation processes: the combined effects of radiative and mechanical energies modify the structure of shocks, leading to specific chemical and radiative tracers. To analyse such effects, the line emission of molecular shocks are derived using two different approaches depending on the molecule considered. For H2, whose level populations are self-consistently computed by the code, line emissions are calculated in the optically thin limit by summing local emissivities. The level populations of other species are computed at statistical equilibrium and their line emissions are obtained by postprocessing the output of the shock model with the Large Velocity Gradient (LVG) code of Gusdorf et al. (2008a) slightly modified to take into account self-absorption in the line radiative transfer. In all cases, both intensities and column densities are computed over the shock only, i.e. without the contribution of the post-shock region identified through Eq. (29).
. External sources of UV radiation fields necessarily exert a major impact on the formation and excitation of molecules in space. In irradiated shocks, the role of UV photons extends far beyond the mere ionization and dissociation processes: the combined effects of radiative and mechanical energies modify the structure of shocks, leading to specific chemical and radiative tracers. To analyse such effects, the line emission of molecular shocks are derived using two different approaches depending on the molecule considered. For H2, whose level populations are self-consistently computed by the code, line emissions are calculated in the optically thin limit by summing local emissivities. The level populations of other species are computed at statistical equilibrium and their line emissions are obtained by postprocessing the output of the shock model with the Large Velocity Gradient (LVG) code of Gusdorf et al. (2008a) slightly modified to take into account self-absorption in the line radiative transfer. In all cases, both intensities and column densities are computed over the shock only, i.e. without the contribution of the post-shock region identified through Eq. (29).
To discuss the results in light of a global energetic budget, this section addresses the following questions. What fraction of the input kinetic energy flux is radiated away through all the transitions of a given molecular species? How is this total intensity spread in different lines? As a first application, we focus on predictions regarding two important species: H2, whose rovibrational structure already observed in many galactic sources (e.g. Giannini et al. 2004; Gillmon et al. 2006; Neufeld et al. 2009; Habart et al. 2011) will soon be unveiled in extragalactic environments with the James Webb Space Telescope (JWST), and CH+, whose recent detection in emission in starburst galaxies at high redshift (z ~ 2–3) with ALMA may be to date the strongest signature of the combined effect of mechanical and radiative energy on interstellar chemistry (Falgarone et al. 2017). While other species are briefly discussed in Sect. 4.3, we defer detailed presentations of the impact of irradiated shocks on the rest of the chemistry to future papers, as motivated by emerging observational needs.
4.1. H2
The energy budget of molecular shocks is a complex problem that not only depends on the dynamical properties of the shock (velocity and magnetic strength) but also on the medium in which it propagates. Interestingly, all studies performed in dark and dense clouds with b = 0.1 and 1 or in environments illuminated by a moderate radiation field converge towards similar results, namely the existence of two regimes depending mostly on the velocity of the shock. At low velocity (VS ≤ 5 km s−1) most of the kinetic energy dissipates via magnetic compression and through the rotational emission of CO and H2 O (in dark environments, see Pon et al. 2012, 2016; Lehmann & Wardle 2016) or the fine structure lines of C+ and O (in media with a moderate radiation field; see Lesaffre et al. 2013). As the velocity increases, the fraction of energy spent in magnetic compression decreases and H2 becomes the dominant coolant over a wide range of shock velocities and gas densities (Figs. B.1 and B.2 of Flower & Pineau des Forêts 2015, and Fig. 8 of Lesaffre et al. 2013).
The results obtained in this work regarding H2 emission are in line with those findings, except for large UV radiation fields and in CJ-type shocks where additional processes arise. To illustrate this, in the top panels of Fig. 7 we show the total flux emitted in H2 by irradiated shocks normalized to the input flux of kinetic energy. As expected, H2 appears as a major coolant over the entire grid of models: although not necessarily dominant, the contribution of H2 to the total energy budget is never negligible, varying from about 1 to 90% of the shock initial kinetic energy flux. In concordance with Lesaffre et al. (2013), the contribution of H2 is minimal for low velocity shocks where fine structure lines of O and C+ take over, and reaches a maximum at higher velocities regardless of the density of the gas. Interestingly, a plateau of H2 emission is found over a broad range of radiation field strength, suggesting that as long as the medium is molecular, H2 always emits the same fraction of the input mechanical energy. This simple picture breaks, however, when the radiation field is strong enough to dissociate H2. At large velocities (VS≥ 10 km s−1), the combination of photodissociation and collisional dissociation in CJ-type shocks induces a strong drop in H2 abundance. The impact of this drop on H2 emission is partly compensated by the increase of the gas temperature which enhances the excitation of H2. As a result, the total flux emitted in H2 decreases by about a factor of ten only. At lower velocities (VS~ 5 km s−1), CJ-type shocks are not strong enough to dissociate H2 by collisions. In this case, the decrease of H2 abundance (solely due to photodissociation) combined with the increase of H2 excitation leads to slight variations of the total flux emitted in H2.
Two main results therefore emerge from this analysis. Firstly, whatever the physical conditions or the shock type, H2 lines systematically carry a significant amount of the shock kinetic energy. Secondly, the radiation field rarely boosts H2 emission but may reduce it while increasing its excitation.
The latter behaviour is shown in Fig. 8 which presents the normalized H2 excitation diagrams computed in different irradiation conditions. At low radiation fields, the excitation diagrams of H2 predicted in C-type shocks generally break in two parts: the low rotational levels which are mainly excited by inelastic collisions, and the remaining rovibrational levels whose populations result from a combination of inelastic collisions, chemical pumping, and UV pumping. As the radiation field increases, the temperature of the gas rises (see Figs. 4 and D.2) and the contribution of inelastic collisions to the excitation of high energy levels increases. This process, combined with the enhancement of the UV pumping, drastically changes the excitation conditions. Indeed, we find that varying the input radiation between G0 = 1 and G0 = 104 almost leads to a continuum of excitation temperatures, and amplifies the intensities of the rovibrational lines, by several orders of magnitude, for all densities and shock velocities. Interestingly, the contribution of inelastic collisions may become comparable or even larger than that of UV pumping, especially at large density or in high velocity CJ-type shocks (e.g. VS = 20 km s−1, nH > 104 cm−3) where the input mechanical energy strongly overpowers that of the UV photons (see Sect. 5.1).
The impact of shocks on the excitation of H2 in outflows has been the subject of many studies (e.g. Flower et al. 2003; Neufeld et al. 2007; Gusdorf et al. 2008b) which show that the excitation diagrams produced by stationary J-type or non-stationary CJ-type shocks are flatter than those obtained in C-type shocks with the same velocities. These studies have concluded that the comparison between observations and predictions can be a powerful tool to derive the properties of jets and the age of the associated astrophysical systems. The results obtained in this work provide a similar tool for irradiated environments. As the radiation field increases and the shock shifts from a C-type to CJ-type structure, the excitation diagram of H2 flattens. Strong degeneracies appear, implying that the sole observation of H2 excitation, although useful, is not sufficient to circumvent a unique set of physical conditions. The clear identification of irradiated shocks requires complementary data, such as the total emission of H2 and the emission and excitation diagrams of other molecules, such as CH+.
4.2. CH+
The methylidyne cation CH+ is a unique molecule and a golden goose9 for the study of dissipation of mechanical energy (e.g. Godard et al. 2014; Falgarone et al. 2017). This view stems, first and foremost, from the simplicity of its chemistry summarized in the top panel of Fig. 9. In irradiated environments, the carbon hydrogenation chain can be seen as a series of chemical cycles: a global cycle which controls the hydrogenation of C+ and C and the balance between ionized and neutral species, and subcycles which affect how the carbon is distributed over the different hydrides. Seen like this, the global production/destruction of CH+, 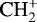 , and
, and 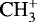 is driven by only three mechanisms: the hydrogenation of C+, the destruction of CH+ by collision with H, and the dissociative recombinations of
is driven by only three mechanisms: the hydrogenation of C+, the destruction of CH+ by collision with H, and the dissociative recombinations of 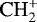 and
and 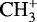 . The global production rate of CH+,
. The global production rate of CH+, 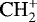 , and
, and 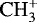 is therefore proportional to the abundances of H2 and C+, and their destruction directly proportional to the abundance of electrons. The way carbon is spread over these three hydrides then depends on the strengthof the subcycle highlighted in the top right panel of Fig. 9, hence on the electronic fraction (which favours CH+), the molecular fraction (which favours
is therefore proportional to the abundances of H2 and C+, and their destruction directly proportional to the abundance of electrons. The way carbon is spread over these three hydrides then depends on the strengthof the subcycle highlighted in the top right panel of Fig. 9, hence on the electronic fraction (which favours CH+), the molecular fraction (which favours 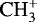 ), and the amount of UV photons (which favours CH+ through the photodissociation of
), and the amount of UV photons (which favours CH+ through the photodissociation of 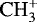 ). As a result, the density profiles of CH+ in irradiated shocks can be reduced, over the entire grid of models, to only four different categories (bottom panel of Fig. 9), driven by very few thermochemical processes whose importance mostly depends on the velocity of the shock and strength of the external radiation field.
). As a result, the density profiles of CH+ in irradiated shocks can be reduced, over the entire grid of models, to only four different categories (bottom panel of Fig. 9), driven by very few thermochemical processes whose importance mostly depends on the velocity of the shock and strength of the external radiation field.
In molecular shocks, both the ion-neutral velocity drift and the increase of temperature induced by the dissipation of mechanical energy activate the endothermic reaction
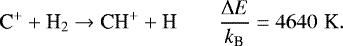 (34)
(34)
This induces a rise in the abundance of CH+ (label 1 in Fig. 9) and eventually a fall in that of C+. At a low radiation field or low velocity (schemes a and b of Fig. 9), the abundance of CH+ reaches a plateau (label 2) − somehow lower than the maximal abundance (due to the destruction of C+) − whose size is given by the cooling timescale of the gas. At a large radiation field or large velocity (schemes c and d), the collisional dissociation of H2 shuts reaction (34) off. The abundance of CH+ rises then drops (label 3) and reaches a plateau whose size is given by the formation timescale of H2 (label 4). Because of the subcycle described above and the feedback induced by the photodissociation of 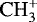 , the peak of CH+ abundances drastically increases with G0. The column density of CH+ computed across the shock therefore also increases with G0, but only as long as G0 and VS are small enough to prevent the collisional dissociation of H2, i.e. as long as the shock is either C or C*.
, the peak of CH+ abundances drastically increases with G0. The column density of CH+ computed across the shock therefore also increases with G0, but only as long as G0 and VS are small enough to prevent the collisional dissociation of H2, i.e. as long as the shock is either C or C*.
As shown in Fig. 7, this chemical result directly translates into the efficiency of shocks at producing and exciting CH+. As the surrounding UV radiation field increases by a factor of 1000, the total flux emitted in CH+ rises by several orders of magnitude − for a given input of mechanical energy − and reaches a maximum at roughly the conditions where CJ-type shocks appear. Because the critical densities of the rotational levels of CH+ are large (≥107 cm−3; Godard & Cernicharo 2013), this effect is magnified in high density media where the high production rate of CH+ is combined with high excitation rates. In these conditions, CH+ is found to radiate as much as several percent of the shock kinetic energy, a value that is almost comparable to the total flux emitted in H2. Altogether, we find that irradiated C or C*-type shocks propagating in dense media (with G0 ∕nH ~ 0.05 cm3) are the most efficient structures, in terms of energy, for the formation and excitation of CH+, hence the structures most likely to be seen in unresolved observations of interstellar environments. Large efficiencies can be obtained at all shock velocities, indicating that the sole observation of the total emission of CH+ is not sufficient to identify specific types of shocks.
This degeneracy could be solved, however, by looking at the excitation diagram of CH+. Indeed, as shown in Fig. 10, increasing the shock velocity from 5 to 10 km s−1 − hence the kinetic energy flux by a factor of 8 − drastically enhances the emission of the mid-J lines of CH+ whose intensities raise by several orders of magnitude. Observations of the total emission of CH+ and of the slope of its excitation diagram could therefore be a powerful tool to infer the type and number of shocks in a given environment, and thus deduce the total mechanical energy pervading the medium. Given the line frequencies indicated in Fig. 10, such measurements could be achieved in galactic environments using the GREAT, FIFI-LS, and HIRMES instruments on board the SOFIA telescope or in extragalactic sources at high redshift using the ALMA interferometer.
 |
Fig. 7 Total fluxes of H2 rovibrational lines (top panels) and CH+ rotational lines (bottompanels, summed up to the J = 10 → 9 transition)emerging from shocks propagating at 5 (left panels), 10 (middle panels), and 20 (right panels) km s−1 in different environments, for a buffer visual extinction |
 |
Fig. 8 H2 excitation diagrams normalized to the column density of H2 obtained for shocks propagating at 5 (top panels) and 20 (bottom panels) km s−1 in media with densities varying between 103
(left panels) and 105
(right panels) cm−3, a scaling factor of the UV radiation field of 1 (red), 10 (dark blue), 102
(light blue), 103
(green), and 104
(orange), and a buffer visual extinction |
4.3. OH, H2O, CO, and SH+
The specificity of CH+ chemistry makes irradiated shocks efficient factories of CH+. The same does not hold for all molecules, and in particular those efficiently destroyed by UV photons. Toillustrate this, we compare in Fig. 11 the column densities of CH+ computed across molecular shocks to those of CO, OH, and H2O. As already shown by Falgarone et al. (2010), the increase of the column density of CH+ with increasing values of G0 almost systematically comes with a decrease of the column densities of CO, OH, and H2 O. The associated drop can cover one to several orders of magnitude depending on the medium density and velocity of the shock. We find that the column density of CH+ linearly increases with G0 up to a maximal value, while the decrease of the column density of CO, OH, and H2 O is steeper, especially athigh G0 and large VS.
The predicted values obtained for nH = 104 cm−3 and 1 ≤ G0 ≤ 103 are reported in Table 2, along with the predictions on the total hydrogen column density NH and the column densities of H2, C+, SH+, O, and O2. The column density ratios N(H2O)∕N(OH) and N(CO)∕N(OH) appear to decrease strongly with G0, a result in line with Melnick & Kaufman (2015) who find similar behaviour in dense environments illuminated by moderate radiation fields (nH = 105 cm−3, G0 ≤ 10). Table 2 reveals that other chemical species follow CH+ and are strongly enhanced in irradiated shocks. This is the case, for instance, of the mercapto cation SH+. For a shock velocity larger than 10 km s−1, the predicted column density of SH+ is found to increase with G0, although with a power-law slope somehow shallower ( ) than that found for CH+. All these results indicate that irradiated shocks carry many specific chemical signatures that could be identified using the current observing facilities.
) than that found for CH+. All these results indicate that irradiated shocks carry many specific chemical signatures that could be identified using the current observing facilities.
 |
Fig. 9 Top panel: dominant formation and destruction pathways of the carbon hydrogenation chain in high temperature media (T ≥ 250 K) or in media irradiated by strong UV radiation field. Bottom panel: common forms of the density profile of CH+ in molecular shocks irradiated by an external radiation field of strength G0. Although the scales are arbitrary, all the density profiles are shown in log–log space. Labels highlight parts of the trajectory where the evolution of CH+ abundance is driven by a specific thermochemical process (see text). |
5. Discussion
5.1. Kinetic and radiative energies budget
Establishing the energy budget of irradiated molecular shocks is complex. In the previous sections, the results on the molecular lines emission were systematically presented with respect to the initial kinetic energy flux of the shock (see Fig. 7). The underlying interpretation was that shock radiative emission is an outcome of the reprocessing of mechanical energy only. This view could be misleading as the matter contained in irradiated shocks also reprocesses part of the input UV radiative energy.
To discuss this point, we compare in Fig. 12 the initial kinetic energy flux of shocks with the radiative energy flux contained in the ambient UV field depending on the model parameters. The grid of physical conditions explored in this work clearly covers a broad range of scenarios in which the input kinetic energy flux is either equal to, greater than, or less than the flux contained in the UV field10. In what proportion these energysources are converted into molecular lines over the duration of a shock depends on the reprocessing lengths and efficiency of energy conversion.
To simplify, we perform estimations of these quantities considering only reprocessing into thermal energy, i.e. assuming that atomic and molecular lines primarily result from the gas heating. This approach is valid as long as the radiative pumping is not the dominant excitation process of the species considered.
By definition (see Eq. (29)), the input mechanical energy is entirely reprocessed over the size of the shock, shown in Fig. 6. For shock velocity larger than 5 km s−1, and standard magnetization (b = 1), the fraction of energy spent in magnetic compression is found to be smaller than a few tens of percent (Lesaffre et al. 2013). The mechanical energy is therefore mostly converted into atomic and molecular lines with an efficiency of several tens of percent, a value that increases with the speed of the shock. In contrast, the radiative energy contained in UV photonsis reprocessed by grains over about one magnitude of extinction which corresponds to distances,
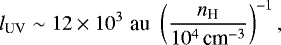 (35)
(35)
10 to 100 times larger than the shock sizes. In this case, the amount of radiative energy converted into thermal energy of the gas is given by the efficiency of the photoelectric effect which ranges between 2 and 7% (e.g. Ingalls et al. 2002). Putting together all these characteristics, we find that the amount of radiative energy reprocessed into heat dominates, on average, the amount of mechanical energy reprocessed into heat for
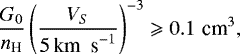 (36)
(36)
i.e. over a small fraction of our grid of models, at low density, low shock velocity, and large radiation field intensity (see Fig. 12).
This result is particularly well illustrated in Fig. D.2. The input kinetic energy fluxes of the models explored in this work are found to be always sufficient to modify the thermal state of the gas. The relative increase of the gas temperature can be, however, quite small in low velocity shocks propagating in strongly irradiated environments (e.g. VS = 5 km s−1 and G0 = 104) where the maximal temperature reached in the shock is almost identical to that found in the post-shock gas. This happens because the heating rate induced by UV photons is locally comparable to that induced by the dissipation of mechanical energy. In this case, the sole impact of the shock is to slightly compress the gas, increasing its thermal pressure and modifying its coupling with the external UV field. Except for kinematic signatures, shocks in these environments are probably undetectable because they do not impact significantly the thermochemical state of the gas.
 |
Fig. 10 Specific intensities of the first ten rotational lines of CH+ (from
J = 1 →0 to J = 10 → 9) as functions of the upper level energy expressed in Kelvin, emitted by two shocks propagating at 5 (red squares) and 10 (blue circles) km s−1 in a medium with density of 104 cm−3 and illuminated by a radiation field G0 = 102
at a visual extinction |
 |
Fig. 11 Column densities of CH+, CO, OH, and H2O calculated across shocks propagating at 5 (left panels), 10 (middle panels), and 20 (right panels) km s−1 in media of density nH = 102
(empty orange squares), 103
(empty green circles), 104
(filled green squares), and 105
(filled blue circles) cm−3, as function of the impinging radiation field G0, and for a buffer visual extinction |
 |
Fig. 12 Isocontours of the ratio of the initial kinetic energy flux contained in an interstellar shock to the radiative energy flux contained in ultraviolet photons,
|
Total hydrogen column density NH and column densities of several species computed across irradiated shocks propagating in a medium of density nH = 104 cm−3 at a visual extinction 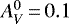 .
.
5.2. J-type shocks and self-generated UV radiation field
The model presented in this work contains all the necessary ingredients to compute the local emission and absorption of photons by gas and dust particles. It is, however, important to stress that neither the feedback of the photons produced by the shock itself on the surrounding material nor the radiative transfer of these photons within the shock are currently treated. This caveat strongly limits the upper range of J-type shocks velocities that can be studied with the Paris-Durham shock code.
The adiabatic jump conditions (Eq. (28)) imply that the temperature reached in J-type shocks are often large enough to either ionize chemical species or excite their electronic levels (Shull & McKee 1979). These mechanisms, followed by radiative recombinations and radiative decay, induce the production of high energy photons that heat, dissociate, or ionize the gas within the shock, but also in the pre-shock and post-shock media, leading to the formation of a radiative precursor (Neufeld & Dalgarno 1989; Hollenbach & McKee 1989; Draine & McKee 1993).
Without magnetic field, J-type shocks with velocities larger than 25 km s−1 emit Ly α and Ly β photons (Shull & McKee 1979). Their energies are strong enough to enhance the photoelectric effect, hence the temperature of the pre-shock gas, and the dissociation and ionization of many species. For shocks propagating at 30 km s−1 in a medium of density nH = 2 × 105 cm−3, Flower &Pineau des Forêts (2010) estimated a UV flux of 1011 photons cm−2 s−1, corresponding to an equivalent G0 = 103. Such an effect cannot be neglected.
Finding a self-consistent solution requires building an iterative procedure to compute the photon flux emitted by the shock and also to construct a radiative code capable of solving the transfer and the scattering of Ly α and Ly β photons andother optically thick lines. We deliberately chose to limit our analysis to low velocity C-, C*, and CJ-type shocks (VS ≤ 25 km s−1) where the production of high energy photons is negligible. All these developments are however in progress and will be the subject of a forthcoming paper on self-irradiated shocks.
6. Conclusions
We have built a model designed to compute the dynamics and thermochemistry of molecular shocks in environments irradiated by an external UV radiation field. The framework is that of a plane-parallel shock at steady-state propagating at a given position of a plane-parallel PDR. The steady-state solutions of magnetohydrodynamics equations are computed through a new and convoluted algorithm capable of following the evolution of the gas near and through sonic points and along subsonic trajectories of molecular shocks. The resulting code allows the simultaneous and self-consistent treatment of gas dynamics and chemistry and of the radiative transfer in a wide variety of physical conditions including diffuse clouds and dense and hot PDRs. It therefore provides a unique tool to study the combined effect of radiative and mechanical energy on the thermochemistry of interstellar matter.
Ultraviolet photons exert an impact on molecular shocks that goes far beyond ionization and dissociation: they modify the structure of the shock itself. Because of the combined effects of dynamics and photoprocesses, irradiated C-type shocks shrink with the strength of the radiation field. If the cooling is not strong enough, the gas may become subsonic along the trajectory. This induces the formation of unexplored categories of stationary shocks called C*-type or CJ-type, depending on whether the sonic point is crossed continuously or not. These types of shocks are dominant in weakly magnetized, diffuse, or irradiated environments. We find, for instance, that only low velocity C-type shocks (VS ≤ 5 km s−1) can exist in typical PDRs (nH ~ 104 cm−3, G0 ~ 100) or in very diffuse clouds (nH ~ 30 cm−3, G0 ~ 1) at low extinction and for standard magnetic field strengths (b = 1); higher velocity shocks are either C* or CJ (for 5 ≤ VS ≤ 25 km s−1), or J (for VS ≥ 25 km s−1).
The increase of the photodissociation of H2 and the diminution of the shock size with increasing UV field, lead to larger temperature which eventually triggers the collisional dissociation of H2 even at low velocity. All these processes strongly influence the energy budget of shocks but also the chemistry and excitation of atomic and molecular lines. Several molecules, such as CO, OH, and H2 O, are found to be destroyed too quickly by UV photons to be efficiently produced in irradiated shocks, while the formations of others, such as CH+ and SH+, are boosted by the entwined actions of kinetic and radiative energies.
The best diagnostics of irradiated shocks are probably the rotational lines of CH+. The combination of high production and excitation rates drastically change the efficiency of CH+ emission which can carry, at large density, as much as several percent of the shock kinetic energy. The distribution of CH+ emission over its different rotational lines is found to be highly sensitive to the shock velocity, hence providing a unique set of tracers of shock kinetic energy.
One unexpected result is the weak sensitivity of the total H2 emission to the input UV radiation field, combined with the strong sensitivity of its excitation diagram. This finding extends the results of previous studies on the excitation of H2 and offers a reliable criterion to infer the irradiation conditions of known interstellar shocks that can be tested with the impending launch of the JWST.
The analysis of the shock energy balance reveals the strong interplay of radiative and mechanical energies. In most cases, molecular line emissions result from the conversion of the shock mechanical energy while this conversion is affected by the impinging UV field. This ceases to be true, however, at low velocity, low density, or large radiation fields where the input UV radiative energy reprocessed by the shock itself becomes dominant.
The work presented in this paper sheds new light on the interpretation of line emission and provides new templates for the analysis of observations. It calls, however, for several developments. Deliberately limited to a handful of species, it would be interesting to extend our analysis to a more systematic study of the chemistry and address, for instance, the formation and excitation of other known tracers of shocks and turbulent dissipation, such as SiO, SH+, and HCO+. Similarly, it will soon be essential to broaden the exploration of the physical conditions to unveil the signatures of high velocity irradiated J-type shocks and those of shocks propagating in highly and weakly magnetized media. One of the most promising applications is the disentanglement of the contribution of stellar radiation and mechanical feedback in the emission bulk of galaxies in order to establish their energy budget and understand the nature of their chemical complexity.
Acknowledgements
The research leading to these results has received fundings from the European Research Council, under the European Community’s Seventh framework Programme, through the Advanced Grant MIST (FP7/2017-2022, No 787813). We would also like to acknowledge the support from the Programme National “Physique et Chimie du Milieu Interstellaire” (PCMI) of CNRS/INSU with INC/INP co-funded by CEA and CNES.
Appendix A: Grain size distribution
All processes involving grains are treated using a prescription similar to that proposed by Le Bourlot et al. (1995). As drawn in Fig. A.1, we assume spherical grains composed of mineral cores and surrounded by ice mantles. Shattering and coagulation processes are neglected. Erosion processes are supposed to reduce evenly the initial size of the cores by a thickness de, while adsorption and desorption mechanisms are supposed to build evenly mantles on cores over a thickness dm.
We assume that the grain cores follow a power-law size distribution from a minimal size am to a maximal size aM. At the ionization front (see Fig. 1), the initial number of cores per unit volume of gas with radii between a and a + d a, 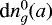 , is
, is
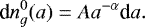 (A.1)
(A.1)
With the initial condition de = dm = 0, the integration of the grain mass over the size distribution leads to the normalization coefficient
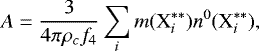 (A.2)
(A.2)
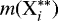 and
and 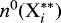 are the masses and initial densities of the chemical species
are the masses and initial densities of the chemical species 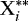 which compose the core, and ρc is the core mass density, assumed to be homogeneous and identical for all grains. The initial number of grains per unit volume of gas therefore writes
which compose the core, and ρc is the core mass density, assumed to be homogeneous and identical for all grains. The initial number of grains per unit volume of gas therefore writes
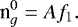 (A.4)
(A.4)
Startingfrom these initial conditions, the evolution of dust grains is computed in the buffer and in the shock taking into account several processes: i.e. adsorption, desorption, and erosion, which modify the thicknesses de and dm, and the compression induced by the shock. Defining 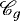 as the compression factor of the grain fluid11, the number of grains ng per unit volume of gas writes
as the compression factor of the grain fluid11, the number of grains ng per unit volume of gas writes
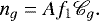 (A.5)
(A.5)
 |
Fig. A.1 Schematic view of erosion and adsorption on grains. |
If we assume that erosion, adsorption, and desorption mechanisms only depend on geometrical cross sections, the integration of the corresponding rates over the size distribution reduces to the calculation of the rate for a single grain of radius 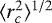 (for grain core processes) and
(for grain core processes) and 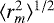 (for grain mantle processes), where
(for grain mantle processes), where
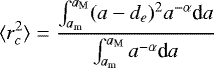 (A.6)
(A.6)
is the mean square radius of eroded grain cores and
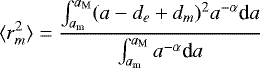 (A.7)
(A.7)
is the mean square radius of grains including mantles. The integration of those equations yields analytical expressions relating 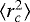 and
and 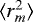 to de and dm, i.e.
to de and dm, i.e.
![\begin{equation*}\langle r_c^2 \rangle = \frac{1}{f_1} \left[ f_3 - 2 f_2 d_e + f_1 d_e^2 \right] \end{equation*}](/articles/aa/full_html/2019/02/aa34248-18/aa34248-18-eq88.png) (A.8)
(A.8)
According to the geometrical and chemical models, the volume of grain cores removed by the erosion mechanisms (per unit volume of gas) is
![\begin{equation*} \mathcal{V}_e = \mathscr{C}_{g} \int_{a_{\textrm{m}}}^{a_{\textrm{M}}} A \frac{4 \pi}{3} \left[ a^3-(a-d_e)^3 \right] a^{-\alpha} \textrm{d}a \end{equation*}](/articles/aa/full_html/2019/02/aa34248-18/aa34248-18-eq90.png) (A.10)
(A.10)
which leads to a cubic equation for de
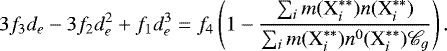 (A.12)
(A.12)
Similarly, the volume of grain mantles writes
![\begin{equation*} \mathcal{V}_m = \mathscr{C}_{g} \int_{a_{\textrm{m}}}^{a_{\textrm{M}}} A \frac{4 \pi}{3} \left[ (a-d_e+d_m)^3-(a-d_e)^3 \right] a^{-\alpha} \textrm{d}a \end{equation*}](/articles/aa/full_html/2019/02/aa34248-18/aa34248-18-eq93.png) (A.13)
(A.13)
where ρm is the mantle mass density and 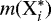 and
and 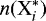 are the masses and densities (per unit volume of gas) of the chemical species
are the masses and densities (per unit volume of gas) of the chemical species 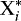 which compose the mantle. The development of those equations finally leads to a cubic expression for dm
which compose the mantle. The development of those equations finally leads to a cubic expression for dm
![\begin{eqnarray*}&&\hspace*{-4pt}3 f_3 d_m - 6 f_2 d_e d_m + 3 f_1 d_e^2 d_m + 3 f_2 d_m^2 - 3 f_1 d_e d_m^2 + f_1 d_m^3 \nonumber\\ \\[-9pt] &&\hspace*{-4pt}\quad = f_4 \frac{\rho_c}{\rho_m} \frac{\sum_i m(\textrm{X}_i^{*}) n(\textrm{X}_i^{*})}{\sum_i m(\textrm{X}_i^{**}) n^0(\textrm{X}_i^{**}) \mathscr{C}_{g}}.\nonumber \end{eqnarray*}](/articles/aa/full_html/2019/02/aa34248-18/aa34248-18-eq98.png) (A.15)
(A.15)
Parameters of the grain size distribution model and initial abundances 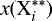 of grain core compounds.
of grain core compounds.
In the Paris-Durham shock code, Eqs. (A.12) and (A.15) are solved at each time step using a Newton-Raphson scheme. Thevalues of de and dm are then injected in Eqs. (A.8) and (A.9) to compute the mean square radii of the cores and mantlesand the subsequent erosion, adsorption, and desorption rates, which control the evolution of the 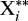 and
and 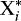 abundances over the next time step. All the parameters used in this work are given in Table A.1. The initial abundances of the grain core compounds correspond to an initial dust-to-gas mass ratio of 0.56%.
abundances over the next time step. All the parameters used in this work are given in Table A.1. The initial abundances of the grain core compounds correspond to an initial dust-to-gas mass ratio of 0.56%.
Erosionof grain mantles, adsorption, and photodesorption processes for grains of size ag and relative abundance xg occur over characteristic timescales, roughly given by (Barlow 1978; Flower et al. 2005; Hollenbach et al. 2009)
![\begin{eqnarray*} &&\mathscr{T}_{\textrm{ero}} \sim 5 \times 10^{-1} \left( \frac{10^4\,{\textrm{cm}^{-3}}}{{n_{\textrm{H}}}} \right) \left( \frac{10^{-6}\,\textrm{cm}}{a_{g}} \right)^2 \nonumber\\ &&\quad \left( \frac{10^{6}\,\textrm{cm\,\,s^{-1}}}{\Delta v} \right) \textrm{exp}\left[ 3 \left(\frac{10^{6}\,\textrm{cm\,\,s^{-1}}}{\Delta v} \right)^2 \right] \,\, \textrm{yr}, \end{eqnarray*}](/articles/aa/full_html/2019/02/aa34248-18/aa34248-18-eq101.png) (A.16)
(A.16)
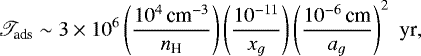 (A.17)
(A.17)
where Δv is the velocity difference between the ions and neutrals. Those values compared with the dynamical timescales given in Fig. 6 show that adsorption never occurs over the duration of a shock, while photodesorption and the erosion of grain mantles may occur within the shock depending on the density of the gas, strength of the radiation field, and ion-neutral velocity drift. It follows that the adsorption processes are important only for the computation of the equilibrium composition of the pre-shock and the post-shock gas, that the erosion processes only arise within the shock where the ions and the neutrals decouple, and that photodesorption may be important everywhere depending on the irradiation conditions.
Appendix B: Comparison with PDR models
To validate the treatment of the radiative transfer and of the multiple interactions of far-UV photons with interstellar matter, we perform comparisons of state-of-the-art PDR models with the predictions of the Paris-Durham shock code set in advection mode. In this mode, the code follows the isochoric or isobaric thermo-chemical evolution of a single fluid moving away from the ionization front with a constant velocity vadv. For simplicity, we consider a prototypical isochoric PDR of density nH = 104 cm−3, illuminated on one side by an isotropic radiation field with a scaling factor G0 = 100, and moving at a speed vadv = 0.01 km s−1. Unless indicated otherwise, all adsorption and desorption mechanisms are switched off.
 |
Fig. B.1 Ultraviolet photon flux (integrated from 911 to 2400 Å) as a function of the total hydrogen column density (bottom panel) and the visual extinction (top panel) calculated with the Meudon PDR code (a), by Tielens & Hollenbach (1985; b), and with the Paris-Durham shock model set in advection mode (c–f) for an isochoric gas of density nH = 104 cm−3 with an incident radiation field G0 = 102. The predictions of the Paris-Durham model are shown for pure graphite grains with a size distribution defined by Table A.1 (standard model, labelled c), for silicate grains with the same size distribution (d), graphite grains with a minimal radius set to 3 × 10−6 cm (e), and graphite grains with a minimal radius set to 3 × 10−6 cm where the grain absorption coefficients are scaled to impose a NH∕AV ratio of 1.87 × 1021 cm−2 (f). |
Figure B.1 shows model predictions of the photon flux (integrated between 911 and 2400 Å) as a function of the visual extinction and total hydrogen column density for different models of grains. By default, most of the existing PDR codes tune the grain absorption and scattering coefficients at all wavelengths in order to match the standard galactic extinction curve observed by Fitzpatrick & Massa (1986) and to reproduce a fixed NH ∕AV ratio of 1.87× 1021 cm−2. This is not the case in the shock model where the extinction curve and colour indices are derived from grain properties alone and may differ from one model to the next. Hence, before comparing the predictions we need to choose which of AV or NH is the best natural variable to display PDR profiles. Analysis of the absorption coefficients shows that the ratios of the visible extinction to the extinctions at other wavelengths vary considerably depending on the grain size and composition. As a result, AV is not only weakly representative of the absorption of photons over the entire UV range when the grain model is changed, but is also a poor tracer of the amount of dust in the cloud. In contrast, since the abundance of grains is considered as constant, NH is a natural proxy of the dust column density regardless of the grain size and composition. All the comparisons below will thus be discussed as functions of NH.
 |
Fig. B.2 Gasand dust (radius = 0.05 μm) temperatures (top left panel) and abundances of the main ions, atomic, and molecular compounds (other panels) as functions of the total hydrogen column density computed with the Meudon PDR code (dashed lines) and the Paris-Durham code (continuous lines) for an isochoric PDR of density nH = 104 cm−3 with an incident radiation field G0 = 102. |
The comparison of the shock results with classical PDR models, in the bottom panel of Fig. B.1 shows that almost all the prescriptions of grains adopted in this work, with the exception of pure silicate grains, give satisfactory predictions of the absorption of UV flux as a function of the depth into the cloud. This discrepancy for the pure silicate grain model is due to the absorption properties of dust at large wavelengths. While graphite and silicate have similar absorption coefficients around 1000 Å, that of silicate is up to 100 times smaller than that of graphite at 2000 Å for a grain with radius between 0.01 and 0.1 μm. The radiation field is thus absorbed over distances considerably larger when silicate grains are used. The best agreement with the Meudon PDR code is obtained for pure graphite grains with a minimal radius set to 3 × 10−6 cm and where the grain absorption coefficients are scaled homogeneously to impose a NH ∕AV ratio of 1.87× 1021 cm−2 (model f in Fig. B.1).
Keeping this last configuration, we compare the predictions of the Paris-Durham shock model with those of the Meudon PDR code regarding the main physical properties of PDRs, i.e. the temperatures of gas and dust, ionization fraction, H/H2 and C+ /C/CO transitions, and excitation of the rovibrational levels of H2. As a whole, Fig. B.2 shows a satisfactory agreement between the results of the two models. In particular, the temperature profiles, H/H2 transition, and ionization fraction are found to follow the same trends with values almost identical at the border and in the interior of the cloud. All the discrepancies observed, i.e. the difference of about a factor of five in the calculation of the S+ abundance in the environment well shielded from the radiation field and the C/CO transition that arises at distances three times larger than in the Meudon PDR code, are due to the different chemical networks and prescriptions of PAHs (e.g. size distribution, calculation of ionization, and recombination processes) used in each model. The populations of the first 200 rovibrational levels of H2 computed at the border of the cloud and shown in Fig. B.3 are found to be analogous in both models; there is a maximum discrepancy of about a factor of three for the most energetic levels. In summary, these results not only validate the treatments of the radiative processes now performed in the Paris-Durham shock code but also justify the approximation of using a single size grain in the computation of the UV radiative transfer.
 |
Fig. B.3 H2 level populations as functions of their energies computed with the Meudon PDR code (blue squares) and the Paris-Durham model (red circles) at NH = 1.87 × 1015 cm−2, in an isochoric PDR of density nH = 104 cm−3 with an incident radiation field G0 = 102. |
To check the treatments of the adsorption and desorption processes, we finally compare the solid-phase and gas-phase abundances of a few species (namely CO, CH4 and H2O) predicted by the code (when adsorption and desorption are switched on) with those obtained by Hollenbach et al. (2009; Figs. 3 and 4). In both models, mantles become the main carrier of all heavy elements at similar distances (~ 6 × 1017 cm). Comparable results are also found for gas-phase abundances. Because of the lack of efficient desorption processes in the interior of the cloud (>2 × 1018 cm), the two models converge towards a chemical equilibrium with gas-phase abundances below 10−7 for both carbon and oxygen bearing species. The fact that both models give virtually identical results is surprising in the light of the treatment of photodesorption by secondary UV photons. Indeed, according to Hollenbach et al. (2009), the secondary photon flux associated with a primary cosmic-ray ionization rate of 10−17 s−1 in a mediumwith a density of 104 cm−3 is equivalent to G0 ~ 10−3. In comparison, the treatment we propose in Sect. 2.5 leads to an equivalent radiation field of G0 ~ 10−5 for the same conditions, close to the value derived by Shen et al. (2004) and that used in Heays et al. (2017). The agreement between the gas-phase abundances computed in both models indicates that this apparent discrepancy is likely to be a typo in Hollenbach’s paper not implemented in their chemical code, which probably uses the correct value, i.e. a secondary photon flux of 2 × 103 photons cm−2 s−1 for 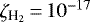 s−1 and nH = 104 cm−3.
s−1 and nH = 104 cm−3.
Appendix C: Computation of stationary solutions
The governing equations of partially ionized, plane-parallel, and magnetized molecular shocks have been derived in several papers (e.g. Draine 1980; Flower et al. 1985). Under the assumption of stationarity, they organize into a set of coupled, first-order, ordinary differential equations that fully describe the exchanges of mass, momentum, and energy that occur between the different chemical flows. Together with the initial conditions, the system thus forms an initial value problem which, in principle, may be integrated using a classical forward integration technique (e.g. DVODE, Hindmarsh 1983). As proven with the Paris-Durham shock code (e.g. Flower & Pineau des Forêts 2003, 2015), such a method is highly robust and efficient in computing the steady states of J-type shocks (single fluid) or that of C-type shocks, i.e. shocks where the neutrals and ions are decoupled and where the flow stays supersonic over its entire trajectory. In the case of C-type shocks, this method fails, however, if the cooling is not efficient enough so that the neutral flow becomes subsonic at some point along the trajectory. Indeed, these conditions trigger the emergence of another category of stationary structures, called CJ-type and C*-type shocks (Chernoff 1987; Roberge & Draine 1990). Because these structures require crossing critical points, forward integration techniques become unstable and highly sensitive to numerical errors.
The method we apply to treat CJ-type and C*-type shocks is based on the work of Roberge & Draine (1990) who thoroughly described the physics of shocks transiting from a supersonic to a subsonic regime. The trajectory of these kinds of shocks can be divided in three different parts (see Figs. 5 and 6 of Roberge & Draine 1990): (i) an upstream supersonic regime where the magnetic precursor develops inducing a decoupling between the ionized and neutral fluids; (ii) a subsonic excursion where the ions and the neutrals are still decoupled; and (iii) a downstream supersonic flow where the ions and neutrals recouple and relax down to the speed and temperature of the post-shock medium12. Downstream, the transition from the subsonic to supersonic regime (from ii to iii) can only occur continuously, passing through the downstream sonic point (labelled C’ in Fig. 1 of Roberge & Draine 1990). In contrast, the upstream transition from the supersonic to the subsonic regime (from i to ii) can potentially happen through an infinite number of trajectories, which involve either an adiabatic jump or a continuous transition via the upstream sonic point (labelled C in Fig. 1 of Roberge & Draine 1990). As shown by Chernoff (1987), most of these trajectories lead to unphysical solutions where either d vn ∕dz or d vi ∕dz change sign. For a given set of physical conditions, only one amongst all trajectories leads to the downstream sonic point, hence to a full stationary solution that satisfies all the equations of a plane-parallel molecular shock. This solution is called a CJ-type shock if it involves an upstreamadiabatic jump, and a C*-type shock if it involves a continuous upstream transition between the supersonic and subsonic regimes.
Examples of CJ and C* shocks are shown in Fig. C.1, which shows the typical evolutions of the neutral and ion velocities (vn and vi) set by the steady-state evolution equations. The initial (pre-shock) and final (post-shock) kinematic states of the gas are indicated with red points. Assuming that their initial conditions are known, both the upstream and downstream supersonic parts (i and iii in Fig. C.1) can be easily computed using the forward integration scheme of the Paris-Durham code. The real difficulty lies in calculating the subsonic excursion (part ii in Fig. C.1) connecting the two, which corresponds to a unique solution among an infinite set of trajectories and which provides theinitial conditions of the downstream flow. As shown by Roberge & Draine (1990), the solution can be found considering its two main properties: firstly, it necessarily ends at the downstream sonic point; secondly, it separates the phase diagram into two spaces where any perturbation on either the neutral or the ion velocities grows exponentially towards an unphysical solution (see Fig. C.1). In the following we define as + modes the trajectories leading to a change of sign of dvn∕dz and as − modes those leading to a change of sign of dvi∕dz.
 |
Fig. C.1 Phase diagrams of stationary shocks propagating at a speed of 10 km s−1 in a pre-shock medium with a density of 104 cm−3, located at 0.6 mpc of the ionization front illuminated by an isotropic radiation field of G0 = 102 (left panels) and 103 (right panels). All other parameters are set to their standard values (see Table 1). The coloured curves correspond to the potential trajectories computed by the algorithm described in Appendix C. The true stationary solution connects the upstream and downstream trajectories (i) and (iii). This solution is bounded in the subsonic excursion (labelled ii) by the + and − modes (see main text). Top panels: neutral and ion velocities relative to the velocity of the shock. Bottom panels: zooms of the top panels rotated to highlight the ion-neutral velocity drift. Initial and final kinematic states and potential jump conditions are indicated with red points and black circles, respectively. |
With all these considerations, we built a convoluted algorithm based on a single precision parameter ε which worksas follows:
- 1.
The upstream trajectory (i) is computed starting with the initial conditions of the flow. If the neutral fluid stays supersonic, the structure is a C-type shock and the computation is carried out as usual. If the neutral velocity gets close to the sound speed, the structure is either a CJ-type or C*-type shock and step 2 is activated.
- 2.
The upstream trajectory is scanned to identify all the possible positions of an adiabatic jump (black points in Fig. C.1), i.e. the positions where applying the Rankine–Hugoniot relations conserves the signs of dvn∕dz and dvi∕dz before and after the jump (see Roberge & Draine 1990 for more details). Potential trajectories are then computed, starting from different jump positions to find a + and a − mode. The jump positions are then refined by dichotomy such that the + and − modes converge towards the true stationary solution. This solution, identified when the relative velocities of the + and − modes differ by less than ε, is calculated as the average of the + and − trajectories. The flow then starts its subsonic excursion (ii).
- 3.
During the subsonic excursion a shooting technique is applied where both the ions and neutral velocities are perturbed in order to identify again a + and a − mode. These perturbations are done in the (vn, vi) phase space, in the direction perpendicular to the trajectory identified in step 2 as the true trajectory, with typical relative amplitudes smaller than ε. Once a + and a − modes are found, the true trajectory is computed as their average, up until the time where they differ by more than ε. At which point we start again step 3.
- 4.
The previous algorithm stops either when |vn − vi|∕VS ≤ ε or |vn − cn|∕VS ≤ ε, where cn is the sound speed and VS the shock speed. In the first case we assume that the neutrals and ions recouple; this happens for instance in the bottom right panel of Fig. C.1. In the second case, we estimate the distance d left to reach the downstream sonic point and then extrapolate all variables (dynamical, thermal, and chemical) at twice that distance to continuously jump this point (see for instance the jump between parts ii and iii in the bottom left panel of Fig. C.1). Once one of these two options is selected, the downstream trajectory (iii) is calculated by forward integration.
By default and for all the models presented in this paper, we use ε = 10−2, with the exception of Fig. C.1 where a value of 10−3 is adopted. It is worth stressing that the success or failure of the algorithm is independent of ε. Changing this parameter impacts only the precision of the results and the computational time13. Tests of thisalgorithm over the entire grid of models (see Sect. 3) shows that the procedure is stable and highly reliable with a success rate of about 97%. Most of the failures correspond to the parameter domain where stationary structures shift from C to C* shocks (i.e. at the interface between green and yellow panels in Fig. 4) and where computing the solution requires an adaptative selection of ε.
Appendix D: Exploration of the parameter space
To be exhaustive, we regroup a few additional figures and results that complement those already discussed in the main text of the paper.
 |
Fig. D.1 Neutral sound speed (dotted) and neutral (dot-dashed) and ion (solid) magnetosonic speeds as functions of the UV radiation field in a medium of density
nH = 102
cm−3 and a visible extinction |
Figure D.1 shows the domains of existence of C, C*, CJ, and J-type shocks in irradiated diffuse interstellar media (left panel) and in dense and totally shielded environments (right panel). We recall that if no radiation field is considered (G0 = 0), as it is the case in the right panel of Fig. D.1, adsorption and desorption processes are switched off for the computation of the pre-shock properties during which we adopt the chemical composition of grain mantles given in Table 2 of Flower &Pineau des Forêts (2003).
We find that the domain of existence of C-type shocks considerably reduces in diffuse environments compared with that computed in dense clouds with similar irradiation conditions (see Fig. 3). Interestingly, C-type shocks with velocity larger than 13 km s−1 do not exist in typical diffuse clouds of density nH = 102 cm−3 with mild irradiation conditions (G0 = 1), a limit that quickly drops with the strength of the radiation field. In these conditions, C-type shocks are replaced by CJ-type shocks, which clearly become a dominant dissipative structure in highly irradiated diffuse gas. The limits inferred in completely shielded environments are found to be in good agreement with those derived with the previous version of the Paris-Durham shock code (Cabrit et al. 2004), except at low magnetization where we highlight a new domain of existence of CJ-type shocks.
As a complement to Fig. 4, we represent in Fig. D.2 the temperature profiles obtained in 288 models of molecular shocks covering roughly the entire grid of parameters explored in this work. As described in the main text, the external UV radiation field reduces the size of the shock, which induces an increase of the temperature peak and reveals the entwinement of the impacts of radiative and mechanical energies on the thermal evolution of the gas. We find that low velocity shocks (VS ≤ 5 km s−1) propagating in highly illuminated environments (G0 = 104) have almost no impact on the temperature of the gas. This result unveils the limit at which the dissipation of mechanical energy is virtually undetectable compared to the amount of radiative energy locally reprocessed by interstellar matter.
In addition to Fig. 11, we finally indicate in Fig. D.3 the column densities of CH+, CO, OH, and H2 O computed across molecular shocks in well-shielded environments (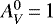 ). The results obtained in these conditions are found to be similar to those obtained at lower visual extinction for lower irradiation conditions (Fig. 11). In particular, the strong increase of CH+ column densities and the strong decrease of those of CO, OH, and H2O in highly irradiated environments is a general result that does not depend on the extinction considered.
). The results obtained in these conditions are found to be similar to those obtained at lower visual extinction for lower irradiation conditions (Fig. 11). In particular, the strong increase of CH+ column densities and the strong decrease of those of CO, OH, and H2O in highly irradiated environments is a general result that does not depend on the extinction considered.
 |
Fig. D.2 Temperature profiles of shocks from 5 to 20 km s−1 (from top to bottom panels) propagating in media with density ranging from 102
to 105 cm−3
(from left to right panels) and illuminated by a UV radiation field ranging from
10−1 to 104 (from colder to warmer pre-shock conditions on each panel), assuming a buffer visual extinction
|
References
- Abgrall, H., Le Bourlot, J., Pineau des Forêts, G., et al. 1992, A&A, 253, 525 [NASA ADS] [Google Scholar]
- Aikawa, Y., Miyama, S. M., Nakano, T., & Umebayashi, T. 1996, ApJ, 467, 684 [NASA ADS] [CrossRef] [Google Scholar]
- Anderl, S., Guillet, V., Pineau des Forêts, G., & Flower, D. R. 2013, A&A, 556, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Appleton, P. N., Xu, K. C., Reach, W., et al. 2006, ApJ, 639, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Bakes, E. L. O., & Tielens, A. G. G. M. 1994, ApJ, 427, 822 [NASA ADS] [CrossRef] [Google Scholar]
- Balsara, D. S. 1996, ApJ, 465, 775 [NASA ADS] [CrossRef] [Google Scholar]
- Barlow, M. J. 1978, MNRAS, 183, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Burton, M. G., Hollenbach, D. J., Haas, M. R., & Erickson, E. F. 1990, ApJ, 355, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Cabrit, S., Lefloch, B., Cernicharo, J., et al. 2004, in The Dense Interstellar Medium in Galaxies, eds. S. Pfalzner, C. Kramer, C. Staubmeier, & A. Heithausen (Berlin: Springer), 91, 587 [Google Scholar]
- Chapman, J. F. & Wardle, M. 2006, MNRAS, 371, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Chernoff, D. F., 1987, ApJ, 312, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Chièze, J.-P., Pineau des Forêts, G., & Flower, D. R. 1998, MNRAS, 295, 672 [NASA ADS] [CrossRef] [Google Scholar]
- Ciolek, G. E., & Roberge, W. G. 2002, ApJ, 567, 947 [NASA ADS] [CrossRef] [Google Scholar]
- Ciolek, G. E., Roberge, W. G., & Mouschovias, T. C. 2004, ApJ, 610, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Dopita, M. A., & Sutherland, R. S. 2003, Astrophysics of the Diffuse Universe (Berlin: Springer) [CrossRef] [Google Scholar]
- Draine, B. T. 1980, ApJ, 241, 1021 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2002, in The Cold Universe, Swiss Society for Astrophysics and Astronomy, Saas-Fee Advanced Course, eds. A. W. Blain, F. Combes, B. T. Draine, D. Pfenniger, & Y. Revaz (Berlin: Springer), 32 [Google Scholar]
- Draine, B. T. 2011, Physics of the Interstellar and Intergalactic Medium (Princeton: Princeton University Press) [Google Scholar]
- Draine, B. T.,& Bertoldi, F. 1996, ApJ, 468, 269 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Draine, B. T.,& Lee, H. M. 1984, ApJ, 285, 89 [Google Scholar]
- Draine, B. T.,& Li, A. 2007, ApJ, 657, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T.,& McKee, C. F. 1993, ARA&A, 31, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T.,& Sutin, B. 1987, ApJ, 320, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Falgarone, E., Ossenkopf, V., Gerin, M., et al. 2010, A&A, 518, L118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Falgarone, E., Zwaan, M. A., Godard, B., et al. 2017, Nature, 548, 430 [NASA ADS] [CrossRef] [Google Scholar]
- Federman, S. R., Glassgold, A. E., & Kwan, J. 1979, ApJ, 227, 466 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzpatrick, E. L., & Massa, D. 1986, ApJ, 307, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, D. 2010, in Lect. Notes Phys., eds. P. J. V. Garcia & J. M. Ferreira (Berlin: Springer Verlag), 793, 161 [Google Scholar]
- Flower, D. R., & Pineau des Forêts, G. 2003, MNRAS, 343, 390 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, D. R., & Pineau des Forêts, G. 2010, MNRAS, 406, 1745 [Google Scholar]
- Flower, D. R., & Pineau des Forêts, G. 2013, MNRAS, 436, 2143 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, D. R., & Pineau des Forêts, G. 2015, A&A, 578, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flower, D. R., Pineau des Forêts, G., & Hartquist, T. W. 1985, MNRAS, 216, 775 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, D. R., Le Bourlot, J., Pineau des Forêts, G., & Cabrit, S. 2003, MNRAS, 341, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, D. R., Pineau des, G., & Walmsley, C. M. 2005, A&A, 436, 933 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giannini, T., McCoey, C., Caratti o Garatti, A., et al. 2004, A&A, 419, 999 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gibb, E. L., Whittet, D. C. B., Schutte, W. A., et al. 2000, ApJ, 536, 347 [Google Scholar]
- Gillmon, K., Shull, J. M., Tumlinson, J., & Danforth, C. 2006, ApJ, 636, 891 [NASA ADS] [CrossRef] [Google Scholar]
- Godard, B., & Cernicharo, J. 2013, A&A, 550, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Godard, B., Falgarone, E., & Pineau des Forêts, G. 2014, A&A, 570, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gorti, U., & Hollenbach, D. 2002, ApJ, 573, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Guillard, P., Boulanger, F., Pineau des Forêts, G., & Appleton, P. N. 2009, A&A, 502, 515 [Google Scholar]
- Guillet, V. 2008, Ph.D. Thesis, Université Paris XI [Google Scholar]
- Guillet, V., Pineau des Forêts, G., & Jones, A. P. 2007, A&A, 476, 263 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guillet, V., Jones, A. P., & Pineau des Forêts, G. 2009, A&A, 497, 145 [Google Scholar]
- Guillet, V., Pineau des Forêts, G., & Jones, A. P. 2011, A&A, 527, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gusdorf, A., Cabrit, S., Flower, D. R., & Pineau des Forêts, G. 2008a, A&A, 482, 809 [Google Scholar]
- Gusdorf, A., Pineau des Forêts, G., Cabrit, S., & Flower, D. R. 2008b, A&A, 490, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gusdorf, A., Anderl, S., Lefloch, B., et al. 2017, A&A, 602, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Habart, E., Abergel, A., Boulanger, F., et al. 2011, A&A, 527, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hasegawa, T. I., & Herbst, E. 1993, MNRAS, 263, 589 [NASA ADS] [CrossRef] [Google Scholar]
- Heays, A. N., Bosman, A. D., & van Dishoeck E. F. 2017, A&A, 602, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hennebelle, P., & Falgarone, E. 2012, A&ARv, 20, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Hewitt, J. W., Yusef-Zadeh, F., & Wardle, M. 2009, ApJ, 706, L270 [NASA ADS] [CrossRef] [Google Scholar]
- Hily-Blant, P., Faure, A., Rist, C., Pineau des Forêts, G., & Flower, D. R. 2018, MNRAS, 477, 4454 [NASA ADS] [CrossRef] [Google Scholar]
- Hindmarsh, A. C. 1983, Scientific Computing (Amsterdam: North-Holland) [Google Scholar]
- Hollenbach, D., & McKee, C. F. 1979, ApJS, 41, 555 [NASA ADS] [CrossRef] [Google Scholar]
- Hollenbach, D., & McKee, C. F. 1989, ApJ, 342, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Hollenbach, D. J., & Tielens, A. G. G. M. 1999, Rev. Mod. Phys., 71, 173 [Google Scholar]
- Hollenbach, D., Kaufman, M. J., Bergin, E. A., & Melnick, G. J. 2009, ApJ, 690, 1497 [CrossRef] [Google Scholar]
- Ingalls, J. G., Reach, W. T., & Bania, T. M. 2002, ApJ, 579, 289 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Jones, A. P., Tielens, A. G. G. M., & Hollenbach, D. J. 1996, ApJ, 469, 740 [NASA ADS] [CrossRef] [Google Scholar]
- Karska, A., Kristensen, L. E., van Dishoeck, E. F., et al. 2014, A&A, 572, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaufman, M. J., & Neufeld, D. A. 1996, ApJ, 456, 611 [NASA ADS] [CrossRef] [Google Scholar]
- Kennel, C. F., Blandford, R. D., & Wu, C. C. 1990, Phys. Fluids B, 2, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Kristensen, L. E., van Dishoeck, E. F., Benz, A. O., et al. 2013, A&A, 557, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kristensen, L. E., van Dishoeck, E. F., Mottram, J. C., et al. 2017, A&A, 605, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Laor, A., & Draine, B. T. 1993, ApJ, 402, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Le Bourlot J., Pineau des Forêts, G., Roueff, E., & Flower, D. R. 1995, A&A, 302, 870 [NASA ADS] [Google Scholar]
- Le Bourlot J., Pineau des Forêts, G., Flower, D. R., & Cabrit, S. 2002, MNRAS, 332, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Le Bourlot, J., Le Petit, F., Pinto, C., Roueff, E., & Roy, F. 2012, A&A, 541, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Gal, R., Hily-Blant, P., Faure, A., et al. 2014, A&A, 562, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Petit, F., Roueff, E., & Le Bourlot J. 2002, A&A, 390, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Petit, F., Nehmé, C., Le Bourlot, J., & Roueff, E. 2006, ApJS, 164, 506 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, H.-H., Herbst, E., Pineau des Forêts, G., Roueff, E., & Le Bourlot, J. 1996, A&A, 311, 690 [NASA ADS] [Google Scholar]
- Lee, M.-Y., Madden, S. C., Lebouteiller, V., et al. 2016, A&A, 596, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lehmann, A. 2017, Ph.D. Thesis, Macquarie University [Google Scholar]
- Lehmann, A., & Wardle, M. 2016, MNRAS, 455, 2066 [NASA ADS] [CrossRef] [Google Scholar]
- Lehmann, A., Federrath, C., & Wardle, M. 2016, MNRAS, 463, 1026 [NASA ADS] [CrossRef] [Google Scholar]
- Lesaffre, P., Chièze, J.-P., Cabrit, S., & Pineau des Forêts, G. 2004, A&A, 427, 147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lesaffre, P., Pineau des Forêts, G., Godard, B., et al. 2013, A&A, 550, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leurini, S., Gusdorf, A., Wyrowski, F., et al. 2014, A&A, 564, L11 [Google Scholar]
- Leurini, S., Wyrowski, F., Wiesemeyer, H., et al. 2015, A&A, 584, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Louvet, F., Motte, F., Gusdorf, A., et al. 2016, A&A, 595, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., Mezger, P. G., & Panagia, N. 1983, A&A, 128, 212 [NASA ADS] [Google Scholar]
- Melnick, G. J., & Kaufman, M. J. 2015, ApJ, 806, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Monteiro, T. S., Flower, D. R., Pineau des Forêts, G., & Roueff, E. 1988, MNRAS, 234, 863 [NASA ADS] [Google Scholar]
- Mullan, D. J. 1971, MNRAS, 153, 145 [NASA ADS] [Google Scholar]
- Neufeld, D. A., & Dalgarno, A. 1989, ApJ, 340, 869 [Google Scholar]
- Neufeld, D. A., & Kaufman, M. J. 1993, ApJ, 418, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Neufeld, D. A., Hollenbach, D. J., Kaufman, M. J., et al. 2007, ApJ, 664, 890 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Neufeld, D. A., Nisini, B., Giannini, T., et al. 2009, ApJ, 706, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Neufeld, D. A., Godard, B., Gerin, M., et al. 2015, A&A, 577, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nisini, B., Santangelo, G., Giannini, T., et al. 2015, ApJ, 801, 121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Omont, A., Yang, C., Cox, P., et al. 2013, A&A, 551, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pon, A., Johnstone, D., & Kaufman, M. J. 2012, ApJ, 748, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Pon, A., Johnstone, D., Caselli, P., et al. 2016, A&A, 587, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reach, W. T., Rho, J., & Jarrett, T. H. 2005, ApJ, 618, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Roberge, W. G., & Draine, B. T. 1990, ApJ, 350, 700 [NASA ADS] [CrossRef] [Google Scholar]
- Röllig, M., Abel, N. P., Bell, T., et al. 2007, A&A, 467, 187 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shen, C. J., Greenberg, J. M., Schutte, W. A., & van Dishoeck E. F. 2004, A&A, 415, 203 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shull, J. M., & McKee, C. F. 1979, ApJ, 227, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Snell, R. L., Hollenbach, D., Howe, J. E., et al. 2005, ApJ, 620, 758 [NASA ADS] [CrossRef] [Google Scholar]
- Störzer, H., & Hollenbach, D. 1998, ApJ, 495, 853 [NASA ADS] [CrossRef] [Google Scholar]
- Swinbank, A. M., Smail, I., Longmore, S., et al. 2010, Nature, 464, 733 [Google Scholar]
- Tafalla, M., Bachiller, R., Lefloch, B., et al. 2015, A&A, 573, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tielens, A. G. G. M., & Hollenbach, D. 1985, ApJ, 291, 722 [NASA ADS] [CrossRef] [Google Scholar]
- Trinchieri, G., Sulentic, J., Breitschwerdt, D., & Pietsch, W. 2003, A&A, 401, 173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Dishoeck E. F. 1988, in Rate Coefficients in Astrochemistry, eds. T. J. Millar & D. A. Williams (Dorcrecht: Kluwer Academic Publishers), 49 [Google Scholar]
- van Dishoeck, E. F., Jonkheid, B., & van Hemert M. C. 2006, Faraday Discuss., 133, 231 [Google Scholar]
- Walmsley, M., Pineau des Forêts, G., & Flower, D. 2005, in Astrochemistry: Recent Successes and Current Challenges, eds. D. C. Lis, G. A. Blake, & E. Herbst, IAU Symp., 231, 135 [NASA ADS] [Google Scholar]
- Wardle, M. 1999, ApJ, 525, L101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Available on the ISM plateform https://ism.obspm.fr.
Draine & Li (2007) find that a PAH-to-dust mass ratio of 4.6% is required to explain the observed galactic mid-infrared emission. For a dust-to-gas mass ratio of 0.01, this corresponds to a PAH abundance of 9.7 × 10−7, which is close to the value adopted in this work.
We recall that all the shocks described in this paper are stationary structures. The CJ-type shocks explored in this work should thus not be identified to non-stationary CJ-type shocks often discussed in the literature (e.g. Chièze et al. 1998).
Amusingly, the amount of kinetic energy flux initially contained in a shock propagating at 10 km s−1 in a medium of density nH = 104 cm−3 is equivalent to that contained in UV photons in the ISRF with an amplification factor G0 = 10 (see Fig. 12).
Assuming that all grains are coupled to the magnetic field (see Sect. 3.3.3),
 is governed by the simple differential equation
is governed by the simple differential equation 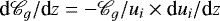 , where ui is the ion fluid velocity, and
, where ui is the ion fluid velocity, and 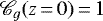 .
.
All Tables
Main parameters of the shock code, standard model, and range of values explored in this work.
Total hydrogen column density NH and column densities of several species computed across irradiated shocks propagating in a medium of density nH = 104 cm−3 at a visual extinction 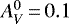 .
.
Parameters of the grain size distribution model and initial abundances 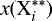 of grain core compounds.
of grain core compounds.
All Figures
 |
Fig. 1 Schematic view of the shock model geometrical assumptions in the shock frame. The positions of the ionization front and of the pre-shock are indicated as IF and PS. |
| In the text | |
 |
Fig. 2 Temperature (top left panel), electronic fraction (i.e. n(e)∕nH,
top right panel), molecular fraction (i.e. 2n(H2)∕nH,
bottom left panel), and depletion (bottom right panel) in the pre-shock medium as functions of
G0 and |
| In the text | |
 |
Fig. 3 Neutral sound speed (dotted) and neutral (dot-dashed) and ion (solid) magnetosonic speeds as functions of the density (upper left panel), transverse magnetic field intensity (upper right panel), UV radiation field intensity (lower left panel), and visual extinction (lower right panel). All the non-varying parameters are set to their standard values (see Table 1), and the standard value of the buffer visual extinction is set to
|
| In the text | |
 |
Fig. 4 Profiles of the neutral sound speed (solid black), velocity of the neutrals (solid blue) and that of the ions (solid red) in the frame of the shock, and temperature of the neutrals (dot-dashed green) computed in stationary shocks propagating in media with different densities and radiation field intensities. All the other parameters are set to their standard values (see Table 1), and the standard value of the buffer visual extinction is set to
|
| In the text | |
 |
Fig. 5 Kinetic, magnetic, and thermal energy fluxes compared to the integrated radiative loss in a CJ-type shock propagating at 10 km s−1 in a medium of density 104
cm−3 and illuminated by a strong radiation field G0 = 104. All the otherparameters are set to their standard values (see Table 1), and the standard value of the buffer visual extinction is set to |
| In the text | |
 |
Fig. 6 Shocksizes (top panels) and timescales (bottom panels) as functions of the UV radiation field and different visual extinction AV computed for shocks propagating at 10 km s−1 in media of densities of 102 (empty squares), 103 (empty circles), 104 (filled squares), and 105 (filled circles) cm−3. The non-varying parameters are set to their standard values (see Table 1). J-type shocks propagating in dense and weakly irradiated clouds are deliberately removed from the figure (see main text), hence the missing points on the left side of each panel. |
| In the text | |
 |
Fig. 7 Total fluxes of H2 rovibrational lines (top panels) and CH+ rotational lines (bottompanels, summed up to the J = 10 → 9 transition)emerging from shocks propagating at 5 (left panels), 10 (middle panels), and 20 (right panels) km s−1 in different environments, for a buffer visual extinction |
| In the text | |
 |
Fig. 8 H2 excitation diagrams normalized to the column density of H2 obtained for shocks propagating at 5 (top panels) and 20 (bottom panels) km s−1 in media with densities varying between 103
(left panels) and 105
(right panels) cm−3, a scaling factor of the UV radiation field of 1 (red), 10 (dark blue), 102
(light blue), 103
(green), and 104
(orange), and a buffer visual extinction |
| In the text | |
 |
Fig. 9 Top panel: dominant formation and destruction pathways of the carbon hydrogenation chain in high temperature media (T ≥ 250 K) or in media irradiated by strong UV radiation field. Bottom panel: common forms of the density profile of CH+ in molecular shocks irradiated by an external radiation field of strength G0. Although the scales are arbitrary, all the density profiles are shown in log–log space. Labels highlight parts of the trajectory where the evolution of CH+ abundance is driven by a specific thermochemical process (see text). |
| In the text | |
 |
Fig. 10 Specific intensities of the first ten rotational lines of CH+ (from
J = 1 →0 to J = 10 → 9) as functions of the upper level energy expressed in Kelvin, emitted by two shocks propagating at 5 (red squares) and 10 (blue circles) km s−1 in a medium with density of 104 cm−3 and illuminated by a radiation field G0 = 102
at a visual extinction |
| In the text | |
 |
Fig. 11 Column densities of CH+, CO, OH, and H2O calculated across shocks propagating at 5 (left panels), 10 (middle panels), and 20 (right panels) km s−1 in media of density nH = 102
(empty orange squares), 103
(empty green circles), 104
(filled green squares), and 105
(filled blue circles) cm−3, as function of the impinging radiation field G0, and for a buffer visual extinction |
| In the text | |
 |
Fig. 12 Isocontours of the ratio of the initial kinetic energy flux contained in an interstellar shock to the radiative energy flux contained in ultraviolet photons,
|
| In the text | |
 |
Fig. A.1 Schematic view of erosion and adsorption on grains. |
| In the text | |
 |
Fig. B.1 Ultraviolet photon flux (integrated from 911 to 2400 Å) as a function of the total hydrogen column density (bottom panel) and the visual extinction (top panel) calculated with the Meudon PDR code (a), by Tielens & Hollenbach (1985; b), and with the Paris-Durham shock model set in advection mode (c–f) for an isochoric gas of density nH = 104 cm−3 with an incident radiation field G0 = 102. The predictions of the Paris-Durham model are shown for pure graphite grains with a size distribution defined by Table A.1 (standard model, labelled c), for silicate grains with the same size distribution (d), graphite grains with a minimal radius set to 3 × 10−6 cm (e), and graphite grains with a minimal radius set to 3 × 10−6 cm where the grain absorption coefficients are scaled to impose a NH∕AV ratio of 1.87 × 1021 cm−2 (f). |
| In the text | |
 |
Fig. B.2 Gasand dust (radius = 0.05 μm) temperatures (top left panel) and abundances of the main ions, atomic, and molecular compounds (other panels) as functions of the total hydrogen column density computed with the Meudon PDR code (dashed lines) and the Paris-Durham code (continuous lines) for an isochoric PDR of density nH = 104 cm−3 with an incident radiation field G0 = 102. |
| In the text | |
 |
Fig. B.3 H2 level populations as functions of their energies computed with the Meudon PDR code (blue squares) and the Paris-Durham model (red circles) at NH = 1.87 × 1015 cm−2, in an isochoric PDR of density nH = 104 cm−3 with an incident radiation field G0 = 102. |
| In the text | |
 |
Fig. C.1 Phase diagrams of stationary shocks propagating at a speed of 10 km s−1 in a pre-shock medium with a density of 104 cm−3, located at 0.6 mpc of the ionization front illuminated by an isotropic radiation field of G0 = 102 (left panels) and 103 (right panels). All other parameters are set to their standard values (see Table 1). The coloured curves correspond to the potential trajectories computed by the algorithm described in Appendix C. The true stationary solution connects the upstream and downstream trajectories (i) and (iii). This solution is bounded in the subsonic excursion (labelled ii) by the + and − modes (see main text). Top panels: neutral and ion velocities relative to the velocity of the shock. Bottom panels: zooms of the top panels rotated to highlight the ion-neutral velocity drift. Initial and final kinematic states and potential jump conditions are indicated with red points and black circles, respectively. |
| In the text | |
 |
Fig. D.1 Neutral sound speed (dotted) and neutral (dot-dashed) and ion (solid) magnetosonic speeds as functions of the UV radiation field in a medium of density
nH = 102
cm−3 and a visible extinction |
| In the text | |
 |
Fig. D.2 Temperature profiles of shocks from 5 to 20 km s−1 (from top to bottom panels) propagating in media with density ranging from 102
to 105 cm−3
(from left to right panels) and illuminated by a UV radiation field ranging from
10−1 to 104 (from colder to warmer pre-shock conditions on each panel), assuming a buffer visual extinction
|
| In the text | |
 |
Fig. D.3 Same as Fig. 11 assuming a buffer visual extinction
|
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



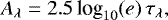
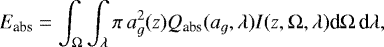
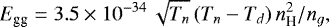
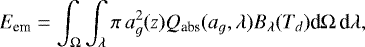
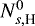
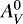
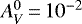
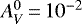
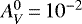
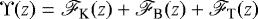
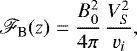
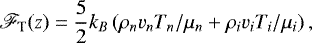
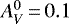
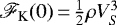
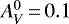
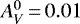
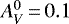
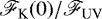
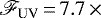
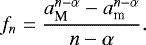
![\begin{equation*}\langle r_m^2 \rangle = \frac{1}{f_1} \left[ f_3 + 2 f_2 (d_m - d_e) - 2 f_1 d_e d_m + f_1 (d_e^2 + d_m^2) \right]. \end{equation*}](/articles/aa/full_html/2019/02/aa34248-18/aa34248-18-eq89.png)