EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 621 (January 2019) A&A, 621 (2019) A74 Full HTML
Free Access
Issue
A&A
Volume 621, January 2019
Article Number A74
Number of page(s) 11
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/201834339
Published online 10 January 2019

© ESO 2019

1 Introduction

Shortly after the discovery of the first hot Jupiter (Mayor & Queloz 1995), the theoretical basis for detecting exoplanet atmospheres through transmission spectroscopy was developed (Seager & Sasselov 2000; Brown 2001; Hubbard et al. 2001). Subsequently, Charbonneau et al. (2002) were the first to measure the transmission signal from sodium in the atmosphere of HD 290458 b using the Space Telescope Imaging Spectrograph on the Hubble Space Telescope (HST). For a long time it was thought that atmospheric exoplanet science could only be conducted from space, either with the HST or the Spitzer Space Telescope, the latter detecting the first thermal emission from exoplanets (Charbonneau et al. 2005; Deming et al. 2005a). It was not until the publications by Redfield et al. (2008) and Snellen et al. (2008) that ground-based observations started to play a role. Both studies presented detections of sodium in HD 189733 b and HD 209458 b, respectively, using high-dispersion spectrographs at 8–10 m class telescopes.

In earlier works (e.g. Charbonneau et al. 1999; Collier Cameron et al. 1999; Deming et al. 2005b; Rodler et al. 2008, 2010) it was already envisaged that ground-based high-dispersion spectroscopy could be a powerful tool to characterise exoplanet atmospheres, either in reflected light, intrinsic thermal emission, or in transmission. In the case of reflection, the light scattered from the planetary atmosphere contains a faint copy of the stellar spectrum, but Doppler-shifted depending on the changing radial component of the orbital velocity of the planet, which can be as large as 150 km s−1 or more for close-in planets. The stationary stellar component can be filtered out, after which the residual spectra contain the Doppler-shifted component reflected off the planet. In the same way molecular lines can be probed in the planetary thermal or transmission spectrum. Due to the contrast between planet and star, the technique is more efficient at infrared wavelengths, where it is used to remove the telluric absorption in a similar way as the stellar lines in the optical. A first detection was presented by Snellen et al. (2010), who measured carbon monoxide in the transmission spectrum of HD 209458 b using the Cryogenic InfraRed Échelle Spectrograph (CRIRES; Kaeufl et al. 2004) at the ESO Very Large Telescope (VLT). By measuring the radial velocity of the planet, the system could be treated as an edge-on spectroscopic binary system allowing for an assumption-free mass determination of both the star and the planet. Also, a marginally significant blue shift of 2 ± 1 km s−1 of the CO signal was interpreted as coming from the radial velocity component of a possible global wind blowing from the hot day-side to the cold night-side of the planet.

At a resolving power of 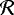= 100 000, molecular bands are resolved in tens to hundreds of individual lines (see Fig. 1). While the observing technique filters out any possible broad-band feature (and, with it, most instrumental calibration errors), the signatures of the individual lines are preserved. Because they are mostly too faint to be detected individually, cross-correlation techniques are used to optimally combine the lines to produce a joint molecular signal. The closer the model template matches the planet spectrum, the stronger the resulting cross-correlating signal should be. In principle, this can be used to constrain the temperaturestructure of the planet atmosphere and the volume mixing ratio of the targeted molecule. However, the sensitivity to these parameters is low, as there is a known degeneracy when comparing the models to the data (e.g. Brogi et al. 2014.) The technique has since thrived, with detections of both water and carbon monoxide, in the atmospheres of a handful of planets, in transmission and emission, using CRIRES at the VLT (e.g. Brogi et al. 2012, 2013, 2014, 2016; Rodler et al. 2012; Birkby et al. 2013, 2017; de Kok et al. 2013; Schwarz et al. 2015, 2016) and the near-infrared spectrograph on the Keck II Telescope (Lockwood et al. 2014; Piskorz et al. 2016, 2017).

Ground-based high-dispersion spectroscopy has recently ventured out in several different directions. Nugroho et al. (2017) detected, for the first time, titanium oxide (TiO) in the day-side thermal emission spectrum of WASP-33 b, probed in the optical wavelength regime using the High Dispersion Spectrograph on the Subaru Telescope. They showed the molecular lines to be in emission, which conclusively proved the presence of a thermal inversion. Also, improved instrumental stability and analysis techniques now allow the use of smaller telescopes. Wyttenbach et al. (2015) and Louden & Wheatley (2015) use data from HARPS (High Accuracy Radial-velocity Planet Searcher échelle spectrograph) at the ESO 3.6 m telescope (Mayor et al. 2003) to measure in detail the shape of the sodium transmission signature of HD 189733 b. Brogi et al. (2018) use GIANO at the Telescopio Nazionale Galileo to detect the presence of water in the atmosphere of HD 189733 b. Yan & Henning (2018) use the highly-stabilised high-dispersion spectrograph CARMENES (Calar Alto high-Resolution search for M dwarfs with Exoearths with near-infrared and optical Échelle Spectrographs; Quirrenbach et al. 2016) to detect atomic hydrogen absorption (Hα) during the transit of Kelt-9b. Also in this target, Hoeijmakers et al. (2018) use HARPS-North transit observations to find for the first time absorption features of atomic heavy elements (Fe, Fe+, and Ti+).

In this paper, we present transmission spectroscopy of HD 189733 b using CARMENES observations targeting its molecular water signature. The planet is one of the archetypical hot Jupiters, because it was for long the brightest known transiting system (V = 7.6 mag, J = 6.1 mag). It has been the target of many observational studies, such as of its hydrogen exosphere (Lecavelier Des Etangs et al. 2010, 2012; Bourrier et al. 2013), its transmission spectrum (e.g. Redfield et al. 2008; Sing et al. 2011; Gibson et al. 2012; McCullough et al. 2014; Brogi et al. 2016, 2018), and its emission spectrum (Deming et al. 2006; Grillmair et al. 2008; Charbonneau et al. 2008; Swain et al. 2010; Todorov et al. 2014).

Our goal is the detection of water in the atmosphere of HD 189733 b using the wavelength region covered by the CARMENES NIR channel. We have focussed mainly on the two strongest water features near 1.15 and 1.4 μm. In particular, we have attempted to detect these features individually, to confirm from the ground and with a different technique the 1.4 μm water feature as observed with the Wide Field Camera 3 (WFC3) at the HST in several planets (e.g. Sing et al. 2016). One of the striking features of the transmission spectrum of HD 189733 b is a blueward slope, most prominent in the ultraviolet and blue optical, attributed to Rayleigh scattering from haze particles high in the planet atmosphere (Lecavelier Des Etangs et al. 2008; Pont et al. 2008, 2013; Gibson et al. 2012; Sing et al. 2016; Pino et al. 2018a). The transmission spectra of a small sample of hot Jupiters observed with HST suggest that the water features in the most hazy atmospheres, like that of HD 189733 b, are partly masked. Comparison between the strength of water absorption over different bands could constrain the Rayleigh scattering ofthe high-altitude hazes in this kind of planets (Stevenson 2016). Although the known degeneracy on the models make it a complex problem (see Heng & Kitzmann 2017), the recent work of Pino et al. (2018b) suggests that ground-based high-resolution observations over multiple water bands could constrain the presence of hazes in the atmosphere of planets like HD 189733 b. In addition, the combination of low-dispersion spectroscopy from space and high-dispersion spectroscopy from the ground over multiple bands provides better constraints to the models (Brogi et al. 2017).

thumbnail Fig. 1

Top panels: CARMENES NIR spectrum of HD 189733 b taken on 2017 September 07 at 22:06:29 UT (left panel) and a zoom-in on order 40 around 1.524 μm (right panel). The major telluric absorptions by water vapour bands near 0.95, 1.14 and 1.4 μm are prominent. For this plot, the original spectrum, as provided by the CARMENES pipeline, was corrected approximately for the instrument response using an early type telluric standard star from a previous observation; so the decline of the continuum level is mainly due to the decrease of the stellar flux. The V shapes of the continuum level withineach order are instrumental effects, either due to overestimating the blaze function or the background illumination. This effect is mainly caused by the different observational conditions of the calibration star and the target, such as target altitude and background illumination. In our analysis, the instrument response was not applied, instead, we normalised each order of the spectra. The emission features observed at the reddest wavelengths (>1.5 μm) in the left and right panels are telluric emission lines. Bottom panels: atmospheric absorption model of HD 189733 b in the CARMENES NIR spectral range (left panel) and a zoom-in around 1.524 μm (right panel). The contribution of the planetary disc (i.e. opaque at all wavelengths) has been included. The most prominent features are caused by the atmospheric H2 O bands. The calculations were performed with the pressure-temperature profile of Brogi et al. (2018; see Fig. 3) and a constant H2O volume mixing ratio of 10−4. The model was computed at a very high spectral resolution ( ~ 4 × 107) and convolved with the CARMENES line spread function.
Table 1

Parameters of the exoplanet system HD 189733.

2 Observations

We used CARMENES (Quirrenbach et al. 2016) to observe the system HD 189733 (Table 1) on 7 September 20171, after two earlier attempts during which we encountered stability issues with the instrument. The two spectrograph channels of CARMENES are located in the coudé room of the 3.5 m telescope at the Calar Alto Observatory, fed by fibres connected to the front-end mounted on the telescope. One of the CARMENES spectrographs, dubbed VIS channel, covers the optical wavelength range, Δλ = 520–960 nm, through 55 orders, and the other, the NIR channel, covers the near-infrared wavelength range, Δλ = 960–1710 nm, in 28 orders. The resolving power is 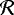= 94 600 in the VIS channel and 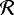= 80 400 in the NIR channel. The detector in the optical is a 4096 × 4096 pixel e2v 231-84 CCD, the near-infrared wavelength range is covered by two 2048 × 2048 pixel HAWAII-2RG infrared detectors, which results in a small gap due to the central separation between detectors. Overlap between orders is lost from the H band onwards, producing further gaps that increase from near-continuous to 15 nm wide (~30% of the order wavelength range) at the long wavelength end (Fig. 1, top left panel). Only the NIR channel data are considered in this work, since no data were taken with the VIS channel due to shutter problems during our observing night.

CARMENES offers two fibres: fibre A for the target, and fibre B for either the Fabry-Pérot etalon or the sky (Seifert et al. 2012; Stürmer et al. 2014). The Fabry-Pérot etalon is used for simultaneous wavelength calibration, in particular for high-precision radial velocity studies. An atlas of calibrated CARMENES spectra can be found in Reiners et al. (2018). However, since the wavelength-calibration requirement for transmission spectroscopy is relatively low, we opted to use the second fibre for sky measurements. These sky measurements were not used in the data calibration process, but only to visually identify sky emission lines. The observations were obtained in service mode, consisting of 46 exposures of198 s, starting at 20:14 UT and ending at 00:00 UT, corresponding to a planet orbital phase range of ϕ = −0.035 to +0.036. During the course of the observation, the relative humidity varied between 57 and 65%. The star moved from airmass 1.08 to 1.30, during which we updated the atmospheric dispersion corrector four times by reacquisition of the target (which takes about two minutes, (cf. Seifert et al. 2012). A typical continuum signal-to-noise ratio (S/N) of ≳150 was reached per spectrum.

thumbnail Fig. 2

Observed spectra matrices at different steps of the analysis for a short wavelength range in order 41. We plot wavelength along the horizontal axis and the time series of spectra along the vertical axes. Top panel: matrix of spectra as provided by the CARMENES pipeline. Upper middle panel: normalised and masked spectra ready for the telluric and stellar removal process with SYSREM. Bottom middle panel: matrix of residuals after the first iteration. At this point the telluric residuals are still visible. Bottom panel: matrix of residuals after the tenth iteration. The telluric residuals are almost completely removed.

3 Data reduction

The CARMENES data were automatically processed after the observations using the dedicated data reduction pipeline CARACAL v2.10 (Zechmeister et al. 2014; Caballero et al. 2016). The precipitable water vapour (PWV) was retrieved from the measured spectra using the ESO MOLECFIT tool (Smette et al. 2015). The PWV level during the observations was relatively high, ranging from 11.7 to 15.9 mm, compared to an average of ~7 mm at Calar Alto. This made the telluric water absorption in orders 45–42 (1.34–1.47 μm) and 54–53 (1.12–1.16 μm) too high for useful data analysis.

3.1 Outlier rejection and normalization

The spectra were processed and analysed independently per order, using very similar techniques to those developed in previous works (Birkby et al. 2017; Brogi et al. 2016, 2017, 2018). First, we removed artefacts from the data that were attributable to cosmic rays (5σ outliers) and a small number of pixels flagged as bad quality by the pipeline. The pipeline is optimised to obtain long-term radial velocity stability utilising the simultaneously obtained Fabry-Pérot data. Although we did not use this mode, we computed a night drift of ~15 m s−1 (~0.011 pixel) by measuring the radial velocity variation of telluric lines present in the observed spectra. This drift was so small that a wavelength correction was not necessary. Subsequently, we normalised the spectra using a quadratic polynomial fit to the pseudo-continuum avoiding the sky emission lines, which were present mainly in the reddest orders.

3.2 Stellar and telluric signal subtraction using sysrem

The expected water signature from the planet is several orders of magnitude smaller than the stellar and telluric absorption lines. Hence, these contaminations have to be removed before the planetary signal can be detected. Since we do not expect to retrieve any planet signal from the cores of the strongest telluric absorption lines, we masked all wavelengths that exhibit an absorption greater than 80% of the flux continuum. We also masked the wavelengths corresponding to strong sky emission lines (see Fig. 2). In total, we masked ~10% of the spectra. The remaining stellar and telluric components were removed using SYSREM (Tamuz et al. 2005; Mazeh et al. 2007), an algorithm that deploys an iterative principal component analysis allowing for unequal uncertainties for each data point. This code has already been successfully applied for the detection of planet atmospheres by Birkby et al. (2017), Nugroho et al. (2017), and Hawker et al. (2018).

We fed SYSREM with 22 matrices containing the data of each usable order and ran it, on each of these matrices individually, for 15 iterations. We show a segment of one of these matrices in the upper middle panel of Fig. 2. The rows of the matrices arecomposed of the normalised and masked spectra. Each column of the matrices is a wavelength channel (i.e. pixel column), similar to a “light curve”. SYSREM searches and subtracts iteratively common modes between the columnsof the matrix, for example, due to airmass variations. Thus, the code primarily removes the largest spectral variations, which are the quasi-static stellar and telluric signals, as shown after the first SYSREM iteration in Fig. 2. Since the planet signal is Doppler-shifted, it is preserved buried in the noise of the resulting residual matrices. However, SYSREM is also prone to remove the planet signal after a few iterations following the removal of the higher order variations. This effect is studied in detail by Birkby et al. (2017) and can start at a different iteration in each order. We find this also to be dependent on the assumed transmission spectrum model, which is further discussed in Sect. 4.3 where we defined the optimal iteration to halt the code.

4 Planet signal retrieval

After removing the main telluric and stellar contributions using SYSREM, the residual matrices contain the information of thousands of lines belonging to molecular species present in the planet atmosphere, but none of these lines are individually detectable. However, we can detect the combined signal of these numerous lines by cross-correlating the residual matrices and high-resolution absorption models of the planet atmosphere.

In the wavelength region covered by the CARMENES NIR channel, the main molecular absorption bands expected for HD 189733 b are those of water vapour (H2O, see Fig. 1). Other gases potentially contributing in this spectral region are carbon monoxide (CO) and methane (CH4). Although the expected abundance of methane is very low (Brogi et al. 2018), we tested models including only water, only methane, and a combination of water and methane in our analysis. There is a weak CO band approximately from 1.56 to 1.60 μm, which is covered by three orders of CARMENES. Based on the results of Brogi et al. (2016), who aimed for the detection of the much stronger CO band from 2.28 to 2.34 μm with CRIRES, the detection of CO alone would not be expected in our data. In addition, probing the CO band would require a dedicated correction for the stellar CO residuals left by the Rossiter–McLaughlin effect (Brogi et al. 2016, 2018). Therefore, we did not include CO in our work, but suggest doing so in a future dedicated study. The grid of used absorption models is described in the next section.

4.1 Absorption spectral models

We computed transmission spectra of HD 189733 b during its primary transit using the Karlsruhe Optimised and Precise Radiative Transfer Algorithm (KOPRA; Stiller et al. 2002). This code was originally developed for the Earth’s atmosphere and was afterwards adapted to the atmospheres of Titan and Jupiter (García-Comas et al. 2011; Montañés-Rodríguez et al. 2015). KOPRA is a well-tested general purpose line-by-line radiative transfer model that includes all the known relevant processes for studying this problem.

In particular, our models include the spectral transitions of the molecules under study. We collected the molecular spectroscopic data from the HITEMP 2010 compilation (Rothman et al. 2010) for H2 O and from the HITRAN 2012 compilation (Rothman et al. 2013) for CH4. The line shapes were modelled with a Voigt profile. We used an adaptive scheme for including or rejecting spectral lines of a given strength (see Stiller et al. 2002), which is particularly useful for calculating the transmission of very hot planet atmospheres for which the line-list of species at high temperature contains a huge number of lines (Rothman et al. 2010).

Collisions between molecular pairs of H2 –H2 and H2–He produce the so-called collision-induced absorption, resulting in ro-vibrational absorption bands. These bands are significantin a hot-Jupiter atmosphere spectrum, appearing mainly as smooth features in the 0.6–0.9, 1.0–1.4, and 2.0–2.5 μm spectral regions. We included these absorptions with the coefficients at high temperatures derived by Borysow (2002) for H2 –H2 pairs, and by Borysow et al. (1989) and Borysow & Frommhold (1989) for H2 –He. Once we computed the very high resolution (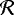 ~ 4 × 107) transmission spectra, we convolved them with the line spread function (LSF) of CARMENES.

We computed 12 synthetic transmission spectra. The first four models included only H2 O, another four models included only CH4, and the last four models included both molecules.

For the four water-only models, we used two different pressure–temperature profiles (A and B, see Fig. 3) and two constant H2 O volume mixing ratios (VMRs) of 10−5 and 10−4. Although we did not expect significant differences on the results when using these models, due to the known model degeneracy (Brogi et al. 2014), it was a robustness check of our detection. The p–T profile A was obtained from our best fit (see Sect. 5.2) to the transmission values measured with HST/WFC3 (McCullough et al. 2014). The p–T profile B was the one used by Brogi et al. (2018). This p–T profile is hotter than profile A in the lower atmosphere, below ~ 10−2 bar (cf. Fig. 3), where most of the absorption takes place. Hence, the atmosphere of the p–T B profile is more extended and, consequently, produces a larger absorption. The nominal transmission model used in the analysis was based on the p–T profile B and a constant H2O VMR of 10−4 (bottom panel of Fig. 1).

We studied the presence of CH4 in the planet atmosphere using eight models. All of them were calculated using the pressure–temperature profile B. Four of them included only methane, with CH4 VMRs ranging from 10−7 to 10−4 in increments of one order of magnitude. The other four models included water, with a VMR of 10−4, and methane with the previous range of VMRs.

During the process of removing the stellar and telluric features from the spectra (Sect. 3.2), we removed also the continuum information. Therefore, before cross-correlating the residual matrices with the computed models, we also removed the continuum information from the models by subtracting their baseline level. Thus, the analysis is sensitive only to the strength of the absorption lines.

thumbnail Fig. 3

Pressure–temperature (p–T) profiles used for computing the synthetic atmospheric absorption spectra. In dashed black, the p–T profile A, was obtained from our best fit to the HST/WFC3 data of McCullough et al. (2014). In solid red, the p–T profile B was taken from Brogi et al. (2018).

4.2 Cross correlation

The planet radial velocity changed during transit approximately from –10 to +25 km s−1 (see Fig. 4). Thus, the cross-correlation analysis was performed for each spectral order over a wide range of planet radial velocities, from −130 km s−1 to +130 km s−1, in intervals of 1.3 km s−1 set by the mean velocity step-size of the CARMENES NIR pixels. We linearly interpolated the molecular transmission templates to the corresponding Doppler-shifted wavelengths. The cross-correlation functions (CCFs) were obtained individually for each spectrum, forming a cross-correlation matrix (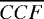) per order. The dimension of each matrix was determined by the radial velocity lags used in the cross-correlation and the number of spectra, i.e. 201 × 46. The median value from each CCF was subtracted to account for possible broad-band differences between the models and the spectra. We applied the cross-correlation process after each SYSREM iteration, obtaining 22 cross-correlation matrices, one per order used.

The cross-correlation matrices, 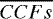, coming from the same or different iterations, should be combined before retrieving the planet signal. In a previous work, Birkby et al. (2017) injected synthetic signals in the data to find the optimal SYSREM iteration for each of their four detectors and, subsequently, they combined the cross-correlation matrices of these different optimal iterations. However, this way of finding the optimal iteration depends on the model used and the strength of injection. Hawker et al. (2018) find similar issues when optimising the iteration choice by injecting the synthetic template. This effect is more noticeable in our analysis than in that of Birkby et al. (2017), because the differences between models are more relevant the larger the studied wavelength range. We followedBrogi et al. (2018), who minimised the model dependency of the analysis and equally co-added the 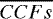that belonged to the same iteration. A side effect of this choice is that it is possible to introduce correlation noise coming from over-corrected orders (those with the least signal) or spurious signals from under-corrected ones (those with the highest telluric contamination).

Since we were most interested in studying the water bands fully covered by the CARMENES NIR channel, we chose to apply a first conservative analysis by using the useful orders from 1.06 to 1.58 μm (from bluer to redder: orders 57, 56, 55, 52, 51, 50, 49, 48, 47, 46, 41, 40, and 39; see Fig. 1). In this way, we optimised the iteration choice using the orders containing most of the signal (Sect. 4.3), while possible contaminations by noise correlations of orders with the least expected signal were removed. Later, we included all the available orders (Sect. 5) and developed a multi-band analysis of the data (Sect. 5.2).

The cross-correlation matrices, for the first, second, third and tenth SYSREM iterations are shown in Fig. 4. In the first two iterations (top panels), the cross-correlation functions are dominated by major telluric residuals around zero velocity, while for the third and tenth iterations (bottom panels), the main telluric and stellar components are removed. The atmospheric signal of the planet is expected to follow the planet radial velocity (i.e. the dashed diagonal line in Fig. 4) with positive cross-correlation values (in-transit). Therefore, each spectrum needs to be shifted to the planet rest frame and combined before obtaining the total correlation signal.

The planet atmospheric signature moves through the in-transit spectra (i.e. from 21:01 UT to 23:11 UT) due to the change in its radial velocity (vP): 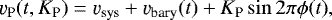(1)

where vsys is the systemic velocity of the stellar system, vbary(t) is the barycentric velocity during observation, KP is the semi-amplitude of the planet radial velocity, and ϕ(t) is the planet orbital phase.

We shifted the cross-correlation function for each spectrum to the planet rest-frame using a linear interpolation of the velocities computed by Eq. (1). Subsequently, the planet trail was vertically aligned and all the in-transit CCFs were co-added to obtain a total CCF. If a water signature is present, the peak of this CCF should be close to 0 km s−1. However, the atmospheric dynamics of the planet can lead to non-zero values, as shown in previous works (Louden & Wheatley 2015; Brogi et al. 2016, 2018). We discuss this further in Sect. 5.1.

We explored different KP values to independently provide a direct measurement of the planet KP, which depends on the stellar mass (Table 1). In a similar way, we can probe the radial component of the high altitude global atmospheric winds (vwind) to obtain a better estimate of the noise properties. We aligned the CCFs for a range of KP values from 0 to 260 km s−1 and of vwind values from –65 to +65 km s−1. For this, we included theadditive term vwind in Eq. (1).

We used this approach to study the significance of the retrieved signal and to verify that there are no significant spurious signals. In addition, the quality of our telluric removal technique can be checked by exploring possible signals at low KP, meaning in the Earth’s rest frame.

thumbnail Fig. 4

Cross-correlation values as a function of the orbital phase and planet radial velocity with respect to the Earth after one (top left panel), two (top right panel), three (bottom left panel) and ten (bottom right panel) SYSREM iterations. The first and last transit spectra are indicated with horizontal dashed lines. After the first and second iteration of SYSREM the cross correlation with the telluric residuals are visible around the zero velocity. From the third iteration onwards, the suppression of the telluric residuals increases and the planet atmospheric signature is expected along the planetary velocities, indicated with the tilted dashed lines (when vwind = 0 km s−1).

4.3 Significance of the retrieved signal

The significance of the retrieved signal was determined following similar methods to those of Birkby et al. (2017) and Brogi et al. (2018). First, we computed the S/N by measuring the peak of the CCF and dividing it by its standard deviation excluding the signal. This provided a map of the S/N as a function of KP and vwind, which revealed a pronounced signal whose position is consistent with a planetary origin (Fig. 5, left panel). However, this signal is spread over a wide range of KP values. The change in the radial velocity during the transit is very small and does not depend enough on KP to provide useful constrains. The uncertainties in KP and vwind are quoted as the limits where the S/N is one less than the peak value.

With a second method, we also used the in-transit spectra of the cross correlation matrix after alignment to the planet rest frame. The significance was obtained by performing a generalised t-test between the distribution of cross correlation values that do not carry signal (out-of-trail distribution) and the distribution of pixels that do carry signal (in-trail distribution).

The out-of-trail distributions is composed by the pixels far away from the planet radial velocity (i.e. all the pixels except for those within ±15 km s−1, making a total of 3175 pixels). This distribution should be non-correlated noise and, therefore, should be normally distributed with a zero mean. The in-trail distribution was defined as the values within ±2.6 km s−1 around zero (i.e. 5 pixel-width times 24 spectra) and its mean should be significantly different from zero in the case of a real planet signal. The differences between the distributions can be seen in Fig. 6, where we compare the two populations for the nominal transmission model at the optimal vwind and KP values. The out-of-trail population follows a normal distribution down to approximately 4σ. The null hypothesis, H0, states that both distributions have the same mean. The value of the t-statistic at which the hypothesis is rejected is then translated into a probability value (p-value) and expressed in terms of standard deviation σ. The two populations present significantly different means and, therefore, the null hypothesis is discarded on a high level of significance (σ > 7). We applied this method for the same range of vwind and KP values as in the previous method.

The results of the two methods, when using the water absorption model computed with the p–T profile B and a H2O VMR = 10−4, are shown in Fig. 5. The maximum significances in both methods are located at similar KP and vwind values, corresponding to the expected planet velocities.

We applied the S/N method to identify the iteration at which SYSREM should be halted using the conservative approach explained in Sect. 4.2. The evolution of the maximum S/N recovered for the different SYSREM iterations around the expected planet KP using the nominal transmission model is shown in Fig. 7. The signal steadily increases in the first three iterations, as SYSREM removes the major telluric and stellar contaminations. After this point, the S/N is very similar up to the 11th iteration. Beyond this iteration, SYSREM appears to mainly remove the exoplanet signal and, hence, the maximum S/N decreases. We also notice the decrease of the telluric signal observed at low KP and vwind as the number of iteration increases (i.e. the contamination is smaller at the tenth than at the third iteration; see Fig. 4). The behaviour of the S/N of the recovered CCF per iteration is similar for all the water absorption models tested in this work.

Hawker et al. (2018), who detected the H2O+CO band at 2.3 μm and the HCN band at 3.2 μm on HD 209458 b using SYSREM, found that for most orders in their dataset a few SYSREM iterations were enough to remove the contamination signals, while for heavily telluric contaminated ones, they required up to 13 iterations. We selected the tenth SYSREM iteration for providing our results, as it is the iteration for which the results are most significant.

thumbnail Fig. 5

S/N results (left panel) and t-test results (right panel, in sigma units) when cross-correlating, in a wide range of KP and vwind values, the residual matrix and the synthetic absorption model including the p–T profile B anda water vapour content of VMR = 10−4. In both panels, the strongest signals reveal at planet radial velocity semi-amplitudes (KP) compatibles with values in the literature. They also happen at the same wind velocities (vwind), indicating a cross-correlation signal blue-shifted by −3.9 ± 1.3 km s−1. No comparable signals are found close to the expected KP. Neither are there comparable signals at the Earth’s frame (low KP values), discarding the presence of significant telluric contamination.
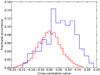thumbnail Fig. 6

Comparison between the distribution of cross-correlation values far away from the planet radial velocity (out-of-trail, red), a Gaussian distribution with the same mean and variance (dashed red line), and the distribution of the cross-correlation values near the planet radial velocities (in-trail, blue). The out-of-trail distribution follows the Gaussian distribution down to approximately 4σ. If the transmission signal of the planet were detected, both distributions would show significantly different means, as it is the case.
thumbnail Fig. 7

Retrieved S/N when cross-correlating the residual matrix after each SYSREM iteration with the H2 O absorption model including the p–T profile B anda VMR = 10−4. The values correspond to the highest S/N at the corresponding KP and vwind in the range of KP = 140–180 km s−1 and vwind = −10 to 0 km s−1. The first iteration is not shown for clarity, because it is totally dominated by telluric residuals.

5 Results and discussion

We retrieved the water vapour absorption signal of HD 189733 b in the CARMENES NIR data collected on 2017 September 7. When cross-correlating the residual matrix of this night using a conservative approach (including only useful orders from 1.06 to 1.58 μm) with the absorption model calculated with a H2O VMR of 10−4 and the pressure–temperature profile B, we measured a maximum S/N = 6.6 in the combined CCF (see Fig. 8). The generalised t-test analysis provides a p-value of 7.5σ (see Fig. 5). The results obtained with the absorption models computed with H2 O VMRs of 10−5 and 10−4 and the p–T profiles A and B are similar and compatible within 1σ.

Independently of the used water model, we recovered the maximum S/N solution at compatible KP and vwind values. From the cross correlation with the nominal model, we obtained the maximum S/N at a planet radial velocity semi-amplitude of KP = 160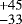 km s−1. This value is compatible with previous results found in the literature as expected for the stellar mass (e.g. KP = 152.5 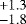km s−1; Brogi et al. 2016).

When including all the useful orders in the CARMENES NIR wavelength range, we detected the atmospheric signature at similar significances levels as when using the conservative approximation (compare CCFs in Figs. 8 and 9). This was expected since the included orders carry a significantly smaller amount of water signal (see Sect. 5.2 for more information).

We also tested our analysis when injecting the negative of the templates into the observed spectra, before the telluric removal process, at KP = 153 km s−1 and vwind = −3.9 km s−1. In this way, we found that the two models with water VMR = 10−5 were the best at cancelling the CCF signal, leaving a maximum residual of S/N ~ 2. However, the two models with VMR = 10−4 over-cancelled the signal, leaving residuals of S/N ~ −3.5 (S/N < 0 indicates negative values of the cross-correlation). These results agree with the values found by Madhusudhan et al. (2014), who re-analysed the HST/WFC3 data from McCullough et al. (2014) and constrained the water mixing ratio to be log(VMR)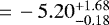. However, the presence of hazes in the atmosphere of HD 189733 b could provide similar depths of water absorption lines for higher water volume mixing ratios (e.g. Madhusudhan et al. 2014; Pino et al. 2018b). Moreover, we did not detect the signal of the exoplanet atmosphere with any model including only methane at abundances from 10−7 to 10−4. In fact, models including H2O and CH4 showed decreasing S/N with increasing CH4 abundance. Hence, we did not find any evidence of methane in the atmosphere of HD 189733 b, confirming the results of Brogi et al. (2018).

thumbnail Fig. 8

Total CCF when using the nominal model and a conservative order selection (i.e. only the orders included in the two strongest bands). The signal is blue-shifted by −3.9 ± 1.3 km s−1.
thumbnail Fig. 9

Cross-correlation functions obtained when combining all the useful orders in the CARMENES NIR wavelength range for thestudied H2O absorption models. The results are very similar for the four tested models, hence showing a degeneracy in the tested p–T profiles and H2O abundances.

5.1 Winds in the atmosphere of HD 189733 b

The total CCF (Figs. 8 and 9) shows a net blue-shifted water signal, vwind = −3.9 ± 1.3 km s−1, which is comparable with previous measurements of sodium and water signals in HD 189733 b (Louden & Wheatley 2015; Brogi et al. 2016, 2018). The model of Showman et al. (2013) predicted that the atmosphere of HD 189733 b is in the transition between two extreme regimes of wind patterns being dominated either by strong zonal jets, or by global day- to night-side winds at the terminator. These atmospheric winds are blue- and red-shifted, and the combination of their signalsduring the whole transit is expected to leave a net blue-shifted wind signature on the atmospheric signal.

In particular, the application of the Showman et al. (2013) model predicts a blue-shifted velocity with a peak near −3 km s−1 for a fractionof ~40% of the terminator at a pressure level of 10−4 bar (see their Fig. 7c). Our derived value of −3.9 ± 1.3 km s−1 agrees well with this prediction, although it is not fully comparable because it corresponds to an average of the whole terminator (i.e. blue- and red-shifted signals combined). Moreover, model contribution weighting functions (Lee et al. 2012; Blecic et al. 2017) predict that our signal, obtained mainly from the 1.15 and 1.4 μm water bands, should arise from atmospheric layers below the ~10−3 bar level (i.e. P > 10−3 bar). In addition, the velocity value quoted above from Showman et al. (2013) did not include the planetary rotation. The inclusion of rotation would slightly increase the blue-shifted velocity (see their Fig. 12).

5.2 Individual detections of the 1.15 and 1.4 μm H2 O bands

We explored the possibility of individually detecting water vapour at different bands. We were particularly interested in detecting the two strongest bands at the wavelength ranges of 1.06–1.26 μm (orders 58–50) and 1.26–1.58 μm (orders 49–40). For this analysis, we used the nominal transmission model and computed the S/N values at the optimal KP and vwind for four wavelength ranges. The results are shown in Table 2 and Fig. 10 (top panel). In order to better illustrate the spectral ranges used in the study of the different water bands, we have included (bottom panel, Fig. 10) the water transmission model that best match the data of McCullough et al. (2014). The maximum absorption reached in the high-resolution transmission spectra (in light grey) is ~550 p.p.m., which translates into ~200 p.p.m. when convolving to the WFC3 resolution. This value agrees well with the HST observations of McCullough et al. (2014). We found H2 O signals for the strongest bands at similar S/Ns, S/N1.15 = 4.9 and S/N1.4 = 4.4. Although the water band near 1.15 μm is expected to be weakerthan that at 1.4 μm, a relevant number of orders was discarded during the analysis on the later, leaving similar maximum absorptions for both bands (see high-resolution transmission model in Fig. 10). This could explain the similarity between the retrieved S/N values.

The bluest and reddest wavelength ranges do not provide a significant planet signal. The bluest orders (from 0.96 to 1.05 μm), shown in Fig. 10, cover only a fraction of a water band, while hardly any water absorption is expected in the reddest orders. In addition, the first orders are affected by the reduced efficiency of the instrument (Reiners et al. 2018).

Moreover, it is generally assumed that the 1.14 and 1.4 μm water features, as well as those at shorter wavelengths, can be suppressed by the presence of hazes (e.g. Sing et al. 2016; Pino et al. 2018a). The recent work of Pino et al. (2018b) suggested the use of the cross-correlation method in high-resolution transit spectra to detect water bands at optical and near-infrared wavelengths, which comparison could diagnose the presence of broad-band spectroscopic features, such as scattering by aerosols. According to their work, the maximum CCF contrast (in the case of a clear atmosphere and no telluric contamination) expected between the bands studied here is on the order of 100 p.p.m., i.e. ~25% of our deepest absorption lines. Therefore, it is not possible for us to derive any conclusion regarding the presence of aerosols in the atmosphere of HD 189733 b by comparing our multiple water band detections. However, the maximum CCF contrast between water features at shorter wavelengths and those studied here could be over 200 p.p.m., which makes the detection of the hazes effect more feasible. We note that these numbers were derived using slightly different techniques and therefore should be taken with caution.

In a similar way, future instrumentation with a redder wavelength coverage than CARMENES, such as CRIRES+ (Follert et al. 2014), could attempt the detection of water bands at K, L, and/or M band. These water bands are intrinsically stronger and the effects of hazes should be weaker than in J-band. Brogi et al. (2016) detected water absorption in HD189733 b using CRIRES at 2.3 μm, implying water vapour lines of up to ~1.3 × 10−3, about a factor two stronger than those at CARMENES wavelengths. This is in line with what we expect from the ratio in absorption strength. Uncertainties are currently too large to provide a constraint on the influence of hazes.

Table 2

S/N and p-values (expressed in σ values) of the CCFs for the four analysed wavelength ranges.

thumbnail Fig. 10

Top panel: S/N values of the CCFs for the four studied bands (see Table. 2). Bottom panel: water vapour absorption spectrum at the CARMENES resolution (in grey) when using the p–T profile A anda water VMR = 10−5, and the same model but Gaussian smoothed to the HST/WFC3 resolution (in blue). The lighter grey areas are the wavelength regions covered by the orders discarded during our analysis. Over-plotted in red are the HST/WFC3 measurements provided by McCullough et al. (2014). We detected the two strongest bands around 1.15 and 1.4 μm. We note that the S/Ns shown in the top panel cannot be directly compared to the HST absorption signals as shown in the bottom panel, since the former depend on the high-frequency component of the transmission spectrum, and are strongly affected by telluric absorption.

6 Conclusions

We detected the near-infrared water signature on the atmosphere of HD 189733 b using CARMENES high-resolution spectra obtained during a single transit at S/N = 6.6. The main problem for the detectability of H2 O from the ground is the telluric contamination. However, an appropriate masking of the strongest telluric lines in combination with the use of SYSREM, which performs a principal component analysis including proper error propagation, leads to an almost complete suppression of the contaminating signals even at relatively high precipitable water vapour levels. On the contrary, we did not detect methane for any of the tested planet atmosphere models.

The water signal is detected at radial velocity semi-amplitude values compatible with the one of the planet. It is slightly more blue-shifted than previous works have measured, although compatible with them. Our value, −3.9 ± 1.3 km s−1, is in good agreement with the results that Showman et al. (2013) derived using different dynamic atmospheric models for HD 189733 b. Follow-up observations aiming the detection of the water signal during the transit ingress and egress, for which our observationsdo not have enough signal, could help in deriving the blue- and red-shifted wind components and the circulation regime in the HD 189733 b middle atmosphere.

We exploited the large wavelength coverage of CARMENES to detect individually the water bands at 1.15 and 1.4 μm, only conclusively observed before from the space with the HST/WFC3. The combination of the significances at which the individual water bands are detected agrees well with the overall S/N integrated over the whole CARMENES NIR wavelength range. This confirms that the wide instantaneous wavelength range of CARMENES significantly adds to the performance of the high-dispersion spectroscopy technique. Although, these water bands have been suggested for the study of hazes in the exoplanet atmospheres, the low contrast ratio expected between them (Pino et al. 2018b) do not allow us to derive any conclusion regarding the presence of hazes in the atmosphere of HD 189733 b. As applicable with CARMENES, a simultaneous comparison between water bands at optical wavelengths and the ones presented here at higher S/N could provide an alternative way to constrain atmospheric hazes. In addition, the different water bands can be included in multi-band studies combining space and ground observations (Brogi et al. 2017), capable to better constrain the chemical composition of the planet’s atmosphere.

In general, the results presented in this paper, the ones obtained with GIANO (Brogi et al. 2018), the recent results of Yan & Henning (2018) with CARMENES and Hoeijmakers et al. (2018) with HARPS, suggest that current and upcoming highly-stabilised high-resolution spectrographs (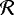 > 20 000) mounted on 4 m-class telescopes will boost the study of exoplanet atmospheres from the ground.

Acknowledgements

We thank M. Brogi and the GIANO team for providing their p– T profile and answering our questions regarding their work. We thank J. Birkby for helpful discussions regarding the use of SYSREM. We also thank J. Hoeijmakers for the kind advises regarding the analysis of the data. F.J.A.-F. and I.S. acknowledge funding from the European Research Council (ERC) under the European Union Horizon 2020 research and innovation programme under grant agreement No 694513. CARMENES is funded by the German Max-Planck-Gesellschaft (MPG), the Spanish Consejo Superior de Investigaciones Científicas (CSIC), the European Union through European Regional Fund (FEDER/ERF), the Spanish Ministry of Economy and Competitiveness, the state of Baden-Württemberg, the German Science Foundation (DFG), and the Junta de Andalucía, with additional contributions by the members of the CARMENES Consortium (Max-Planck-Institut für Astronomie, Instituto de Astrofísica de Andalucía, Landessternwarte Königstuhl, Institut de Ciències de l’Espai, Institut für Astrophysik Göttingen, Universidad Complutense de Madrid, Thüringer Landessternwarte Tautenburg, Instituto de Astrofísica de Canarias, Hamburger Sternwarte, Centro de Astrobiología, and the Centro Astronómico Hispano-Alemán). Financial support was also provided by the Universidad Complutense de Madrid, the Comunidad Autónoma de Madrid, the Spanish Ministerios de Ciencia e Innovación and of Economía y Competitividad, the Fondo Europeo de Desarrollo Regional (FEDER/ERF), the Agencia estatal de investigación, and the Fondo Social Europeo under grants ESP2014-54362-P, AYA2011-30147- C03-01, -02, and -03, AYA2012-39612-C03-01, ESP2013-48391-C4-1-R, ESP2014–54062–R, ESP 2016–76076–R, and BES–2015–074542. Based on observations collected at the Centro Astronómico Hispano Alemán (CAHA) at Calar Alto, operated jointly by the Max-Planck Institut für Astronomie and the Instituto de Astrofísica de Andalucía. We thank the anonymous referee for the insightful comments, which contributed to improve the quality of the manuscript.

References

  1. Agol, E., Cowan, N. B., Knutson, H. A., et al. 2010, ApJ, 721, 1861 [NASA ADS] [CrossRef] [Google Scholar]
  2. Birkby, J. L., de Kok, R. J., Brogi, M., et al. 2013, MNRAS, 436, L35 [NASA ADS] [CrossRef] [Google Scholar]
  3. Birkby, J. L., de Kok, R. J., Brogi, M., Schwarz, H., & Snellen, I. A. G. 2017, AJ, 153, 138 [NASA ADS] [CrossRef] [Google Scholar]
  4. Blecic, J., Dobbs-Dixon, I., & Greene, T. 2017, ApJ, 848, 127 [NASA ADS] [CrossRef] [Google Scholar]
  5. Borysow, A. 2002, A&A, 390, 779 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Borysow, A., & Frommhold, L. 1989, ApJ, 341, 549 [NASA ADS] [CrossRef] [Google Scholar]
  7. Borysow, A., Frommhold, L., & Moraldi, M. 1989, ApJ, 336, 495 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bouchy, F., Udry, S., Mayor, M., et al. 2005, A&A, 444, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Bourrier, V., Lecavelier des Etangs, A., Dupuy, H., et al. 2013, A&A, 551, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Brogi, M., Snellen, I. A. G., de Kok, R. J., et al. 2012, Nature, 486, 502 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  11. Brogi, M., Snellen, I. A. G., de Kok, R. J., et al. 2013, ApJ, 767, 27 [NASA ADS] [CrossRef] [Google Scholar]
  12. Brogi, M., de Kok, R. J., Birkby, J. L., Schwarz, H., & Snellen, I. A. G. 2014, A&A, 565, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Brogi, M., de Kok, R. J., Albrecht, S., et al. 2016, ApJ, 817, 106 [NASA ADS] [CrossRef] [Google Scholar]
  14. Brogi, M., Line, M., Bean, J., Désert, J.-M., & Schwarz, H. 2017, ApJ, 839, L2 [NASA ADS] [CrossRef] [Google Scholar]
  15. Brogi, M., Giacobbe, P., Guilluy, G., et al. 2018, A&A, 615, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Brown, T. M. 2001, ApJ, 553, 1006 [NASA ADS] [CrossRef] [Google Scholar]
  17. Caballero, J. A., Guàrdia, J., López del Fresno, M., et al. 2016, Proc. SPIE, 9910, 99100E [Google Scholar]
  18. Charbonneau, D., Noyes, R. W., Korzennik, S. G., et al. 1999, ApJ, 522, L145 [NASA ADS] [CrossRef] [Google Scholar]
  19. Charbonneau, D., Brown, T. M., Noyes, R. W., & Gilliland, R. L. 2002, ApJ, 568, 377 [NASA ADS] [CrossRef] [Google Scholar]
  20. Charbonneau, D., Allen, L. E., Megeath, S. T., et al. 2005, ApJ, 626, 523 [NASA ADS] [CrossRef] [Google Scholar]
  21. Charbonneau, D., Knutson, H. A., Barman, T., et al. 2008, ApJ, 686, 1341 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  22. Collier Cameron, A., Horne, K., Penny, A., & James, D. 1999, Nature, 402, 751 [NASA ADS] [CrossRef] [Google Scholar]
  23. Deming, D., Seager, S., Richardson, L. J., & Harrington, J. 2005a, Nature, 434, 740 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  24. Deming, D., Brown, T. M., Charbonneau, D., Harrington, J., & Richardson, L. J. 2005b, ApJ, 622, 1149 [NASA ADS] [CrossRef] [Google Scholar]
  25. Deming, D., Harrington, J., Seager, S., & Richardson, L. J. 2006, ApJ, 644, 560 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  26. de Kok, R. J., Brogi, M., Snellen, I. A. G., et al. 2013, A&A, 554, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Follert, R., Dorn, R. J., Oliva, E., et al. 2014, Proc. SPIE, 9147, 914719 [CrossRef] [Google Scholar]
  28. Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. García-Comas, M., López-Puertas, M., Funke, B., et al. 2011, Icarus, 214, 571 [NASA ADS] [CrossRef] [Google Scholar]
  30. Gibson, N. P., Aigrain, S., Pont, F., et al. 2012, MNRAS, 422, 753 [NASA ADS] [CrossRef] [Google Scholar]
  31. Grillmair, C. J., Burrows, A., Charbonneau, D., et al. 2008, Nature, 456, 767 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  32. Hawker, G. A., Madhusudhan, N., Cabot, S. H. C., & Gandhi, S. 2018, ApJ, 863, L11 [NASA ADS] [CrossRef] [Google Scholar]
  33. Heng, K., & Kitzmann, D. 2017, MNRAS, 470, 2972 [NASA ADS] [CrossRef] [Google Scholar]
  34. Hoeijmakers, H. J., Ehrenreich, D., Heng, K., et al. 2018, Nature, 560, 453 [NASA ADS] [CrossRef] [Google Scholar]
  35. Hubbard, W. B., Fortney, J. J., Lunine, J. I., et al. 2001, ApJ, 560, 413 [NASA ADS] [CrossRef] [Google Scholar]
  36. Kaeufl, H.-U., Ballester, P., Biereichel, P., et al. 2004, Proc. SPIE, 5492, 1218 [CrossRef] [Google Scholar]
  37. Koen, C., Kilkenny, D., van Wyk, F., & Marang, F. 2010, MNRAS, 403, 1949 [Google Scholar]
  38. Lecavelier Des Etangs, A., Pont, F., Vidal-Madjar, A., & Sing, D. 2008, A&A, 481, L83 [NASA ADS] [CrossRef] [Google Scholar]
  39. Lecavelier Des Etangs, A., Ehrenreich, D., Vidal-Madjar, A., et al. 2010, A&A, 514, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Lecavelier des Etangs, A., Bourrier, V., Wheatley, P. J., et al. 2012, A&A, 543, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Lee, J.-M., Fletcher, L. N., & Irwin, P. G. J. 2012, MNRAS, 420, 170 [NASA ADS] [CrossRef] [Google Scholar]
  42. Lockwood, A. C., Johnson, J. A., Bender, C. F., et al. 2014, ApJ, 783, L29 [NASA ADS] [CrossRef] [Google Scholar]
  43. Louden, T., & Wheatley, P. J. 2015, ApJ, 814, L24 [NASA ADS] [CrossRef] [Google Scholar]
  44. Madhusudhan, N., Crouzet, N., McCullough, P. R., Deming, D., & Hedges, C. 2014, ApJ, 791, L9 [Google Scholar]
  45. Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [NASA ADS] [CrossRef] [Google Scholar]
  46. Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
  47. Mazeh, T., Tamuz, O., & Zucker, S. 2007, Transiting Extrasolar Planets Workshop, ASP Conf. Ser., 366, 119 [NASA ADS] [Google Scholar]
  48. McCullough, P. R., Crouzet, N., Deming, D., & Madhusudhan, N. 2014, ApJ, 791, 55 [NASA ADS] [CrossRef] [Google Scholar]
  49. Montañés-Rodríguez, P., González-Merino, B., Palle, E., López-Puertas, M., & García-Melendo, E. 2015, ApJ, 801, L8 [NASA ADS] [CrossRef] [Google Scholar]
  50. Nugroho, S. K., Kawahara, H., Masuda, K., et al. 2017, AJ, 154, 221 [NASA ADS] [CrossRef] [Google Scholar]
  51. Pino, L., Ehrenreich, D., Wyttenbach, A., et al. 2018a, A&A, 612, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Pino, L., Ehrenreich, D., Allart, R., et al. 2018b, A&A, 619, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Piskorz, D., Benneke, B., Crockett, N. R., et al. 2016, ApJ, 832, 131 [NASA ADS] [CrossRef] [Google Scholar]
  54. Piskorz, D., Benneke, B., Crockett, N. R., et al. 2017, AJ, 154, 78 [NASA ADS] [CrossRef] [Google Scholar]
  55. Pont, F., Knutson, H., Gilliland, R. L., Moutou, C., & Charbonneau, D. 2008, MNRAS, 385, 109 [NASA ADS] [CrossRef] [Google Scholar]
  56. Pont, F., Sing, D. K., Gibson, N. P., et al. 2013, MNRAS, 432, 2917 [NASA ADS] [CrossRef] [Google Scholar]
  57. Quirrenbach, A., Amado, P. J., Caballero, J. A., et al. 2016, Proc. SPIE, 9908, 990812 [Google Scholar]
  58. Redfield, S., Endl, M., Cochran, W. D., & Koesterke, L. 2008, ApJ, 673, L87 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  59. Reiners, A., Zechmeister, M., Caballero, J. A., et al. 2018, A&A, 612, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Rodler, F., Kürster, M., & Henning, T. 2008, A&A, 485, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Rodler, F., Kürster, M., & Henning, T. 2010, A&A, 514, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Rodler, F., López-Morales, M., & Ribas, I. 2012, ApJ, 753, L25 [NASA ADS] [CrossRef] [Google Scholar]
  63. Rothman, L. S., Gordon, I. E., Barber, R. J., et al. 2010, J. Quant. Spectr. Rad. Transf., 111, 2139 [NASA ADS] [CrossRef] [Google Scholar]
  64. Rothman, L. S., Gordon, I. E., Babikov, Y., et al. 2013, J. Quant. Spectr. Rad. Transf., 130, 4 [Google Scholar]
  65. Schwarz, H., Brogi, M., de Kok, R., Birkby, J., & Snellen, I. 2015, A&A, 576, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. Schwarz, H., Ginski, C., de Kok, R. J., et al. 2016, A&A, 593, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Seager, S., & Sasselov, D. D. 2000, ApJ, 537, 916 [NASA ADS] [CrossRef] [Google Scholar]
  68. Seifert, W., Sánchez Carrasco, M. A., Xu, W., et al. 2012, Proc. SPIE, 8446, 844633 [CrossRef] [Google Scholar]
  69. Showman, A. P., Fortney, J. J., Lewis, N. K., & Shabram, M. 2013, ApJ, 762, 1 [Google Scholar]
  70. Sing, D. K., Pont, F., Aigrain, S., et al. 2011, MNRAS, 416, 1443 [NASA ADS] [CrossRef] [Google Scholar]
  71. Sing, D. K., Fortney, J. J., Nikolov, N., et al. 2016, Nature, 529, 59 [NASA ADS] [CrossRef] [Google Scholar]
  72. Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
  73. Smette, A., Sana, H., Noll, S., et al. 2015, A&A, 576, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  74. Snellen, I. A. G., Albrecht, S., de Mooij, E. J. W., & Le Poole, R. S. 2008, A&A, 487, 357 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  75. Snellen, I. A. G., de Kok, R. J., de Mooij, E. J. W., & Albrecht, S. 2010, Nature, 465, 1049 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  76. Stevenson, K. B. 2016, ApJ, 817, L16 [NASA ADS] [CrossRef] [Google Scholar]
  77. Stiller, G. P., von Clarmann, T., Funke, B., et al. 2002, J. Quant. Spectr. Rad. Transf., 72, 249 [Google Scholar]
  78. Stürmer, J., Stahl, O., Schwab, C., et al. 2014, Proc. SPIE, 9151, 915152 [CrossRef] [Google Scholar]
  79. Swain, M. R., Deroo, P., Griffith, C. A., et al. 2010, Nature, 463, 637 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  80. Tamuz, O., Mazeh, T., & Zucker, S. 2005, MNRAS, 356, 1466 [NASA ADS] [CrossRef] [Google Scholar]
  81. Todorov, K. O., Deming, D., Burrows, A., & Grillmair, C. J. 2014, ApJ, 796, 100 [NASA ADS] [CrossRef] [Google Scholar]
  82. Torres, G., Winn, J. N., & Holman, M. J. 2008, ApJ, 677, 1324 [NASA ADS] [CrossRef] [Google Scholar]
  83. Triaud, A. H. M. J., Queloz, D., Bouchy, F., et al. 2009, A&A, 506, 377 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  84. Wyttenbach, A., Ehrenreich, D., Lovis, C., Udry, S., & Pepe, F. 2015, A&A, 577, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  85. Yan, F., & Henning, T. 2018, Nat. Astron., 2, 714 [NASA ADS] [CrossRef] [Google Scholar]
  86. Zechmeister, M., Anglada-Escudé, G., & Reiners, A. 2014, A&A, 561, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
1

The reduced spectra can be downloaded from the Calar Alto archive, http://caha.sdc.cab.inta-csic.es/calto/

All Tables

Table 1

Parameters of the exoplanet system HD 189733.

In the text
Table 2

S/N and p-values (expressed in σ values) of the CCFs for the four analysed wavelength ranges.

In the text

All Figures

thumbnail Fig. 1

Top panels: CARMENES NIR spectrum of HD 189733 b taken on 2017 September 07 at 22:06:29 UT (left panel) and a zoom-in on order 40 around 1.524 μm (right panel). The major telluric absorptions by water vapour bands near 0.95, 1.14 and 1.4 μm are prominent. For this plot, the original spectrum, as provided by the CARMENES pipeline, was corrected approximately for the instrument response using an early type telluric standard star from a previous observation; so the decline of the continuum level is mainly due to the decrease of the stellar flux. The V shapes of the continuum level withineach order are instrumental effects, either due to overestimating the blaze function or the background illumination. This effect is mainly caused by the different observational conditions of the calibration star and the target, such as target altitude and background illumination. In our analysis, the instrument response was not applied, instead, we normalised each order of the spectra. The emission features observed at the reddest wavelengths (>1.5 μm) in the left and right panels are telluric emission lines. Bottom panels: atmospheric absorption model of HD 189733 b in the CARMENES NIR spectral range (left panel) and a zoom-in around 1.524 μm (right panel). The contribution of the planetary disc (i.e. opaque at all wavelengths) has been included. The most prominent features are caused by the atmospheric H2 O bands. The calculations were performed with the pressure-temperature profile of Brogi et al. (2018; see Fig. 3) and a constant H2O volume mixing ratio of 10−4. The model was computed at a very high spectral resolution ( ~ 4 × 107) and convolved with the CARMENES line spread function.
In the text
thumbnail Fig. 2

Observed spectra matrices at different steps of the analysis for a short wavelength range in order 41. We plot wavelength along the horizontal axis and the time series of spectra along the vertical axes. Top panel: matrix of spectra as provided by the CARMENES pipeline. Upper middle panel: normalised and masked spectra ready for the telluric and stellar removal process with SYSREM. Bottom middle panel: matrix of residuals after the first iteration. At this point the telluric residuals are still visible. Bottom panel: matrix of residuals after the tenth iteration. The telluric residuals are almost completely removed.
In the text
thumbnail Fig. 3

Pressure–temperature (p–T) profiles used for computing the synthetic atmospheric absorption spectra. In dashed black, the p–T profile A, was obtained from our best fit to the HST/WFC3 data of McCullough et al. (2014). In solid red, the p–T profile B was taken from Brogi et al. (2018).
In the text
thumbnail Fig. 4

Cross-correlation values as a function of the orbital phase and planet radial velocity with respect to the Earth after one (top left panel), two (top right panel), three (bottom left panel) and ten (bottom right panel) SYSREM iterations. The first and last transit spectra are indicated with horizontal dashed lines. After the first and second iteration of SYSREM the cross correlation with the telluric residuals are visible around the zero velocity. From the third iteration onwards, the suppression of the telluric residuals increases and the planet atmospheric signature is expected along the planetary velocities, indicated with the tilted dashed lines (when vwind = 0 km s−1).
In the text
thumbnail Fig. 5

S/N results (left panel) and t-test results (right panel, in sigma units) when cross-correlating, in a wide range of KP and vwind values, the residual matrix and the synthetic absorption model including the p–T profile B anda water vapour content of VMR = 10−4. In both panels, the strongest signals reveal at planet radial velocity semi-amplitudes (KP) compatibles with values in the literature. They also happen at the same wind velocities (vwind), indicating a cross-correlation signal blue-shifted by −3.9 ± 1.3 km s−1. No comparable signals are found close to the expected KP. Neither are there comparable signals at the Earth’s frame (low KP values), discarding the presence of significant telluric contamination.
In the text
thumbnail Fig. 6

Comparison between the distribution of cross-correlation values far away from the planet radial velocity (out-of-trail, red), a Gaussian distribution with the same mean and variance (dashed red line), and the distribution of the cross-correlation values near the planet radial velocities (in-trail, blue). The out-of-trail distribution follows the Gaussian distribution down to approximately 4σ. If the transmission signal of the planet were detected, both distributions would show significantly different means, as it is the case.
In the text
thumbnail Fig. 7

Retrieved S/N when cross-correlating the residual matrix after each SYSREM iteration with the H2 O absorption model including the p–T profile B anda VMR = 10−4. The values correspond to the highest S/N at the corresponding KP and vwind in the range of KP = 140–180 km s−1 and vwind = −10 to 0 km s−1. The first iteration is not shown for clarity, because it is totally dominated by telluric residuals.
In the text
thumbnail Fig. 8

Total CCF when using the nominal model and a conservative order selection (i.e. only the orders included in the two strongest bands). The signal is blue-shifted by −3.9 ± 1.3 km s−1.
In the text
thumbnail Fig. 9

Cross-correlation functions obtained when combining all the useful orders in the CARMENES NIR wavelength range for thestudied H2O absorption models. The results are very similar for the four tested models, hence showing a degeneracy in the tested p–T profiles and H2O abundances.
In the text
thumbnail Fig. 10

Top panel: S/N values of the CCFs for the four studied bands (see Table. 2). Bottom panel: water vapour absorption spectrum at the CARMENES resolution (in grey) when using the p–T profile A anda water VMR = 10−5, and the same model but Gaussian smoothed to the HST/WFC3 resolution (in blue). The lighter grey areas are the wavelength regions covered by the orders discarded during our analysis. Over-plotted in red are the HST/WFC3 measurements provided by McCullough et al. (2014). We detected the two strongest bands around 1.15 and 1.4 μm. We note that the S/Ns shown in the top panel cannot be directly compared to the HST absorption signals as shown in the bottom panel, since the former depend on the high-frequency component of the transmission spectrum, and are strongly affected by telluric absorption.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.