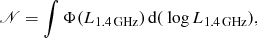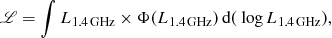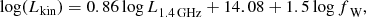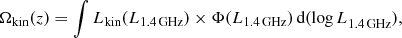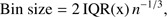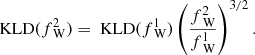| Issue |
A&A
Volume 620, December 2018
|
|
|---|---|---|
| Article Number | A192 | |
| Number of page(s) | 19 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201833935 | |
| Published online | 17 December 2018 | |
The VLA-COSMOS 3 GHz Large Project: Star formation properties and radio luminosity functions of AGN with moderate-to-high radiative luminosities out to z∼ 6
1
University of Zagreb, Physics Department, Bijenička cesta 32, 10002 Zagreb, Croatia
e-mail: lceraj@phy.hr
2
Max Planck Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
3
INAF – Osservatorio di Astrofisica e Scienza dello Spazio – Bologna, Via Piero Gobetti 93/3, 40129 Bologna, Italy
4
Argelander-Institut für Astronomie, Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
5
Astronomisches Institut, Ruhr-Universität Bochum, Universitätsstrasse 150, 44801 Bochum, Germany
6
Department of Astronomy, University of Cape Town, Private Bag X3, Rondebosch 7701, South Africa
Received:
24
July
2018
Accepted:
30
October
2018
We have studied a sample of 1604 moderate-to-high radiative luminosity active galactic nuclei (HLAGN) selected at 3 GHz within the VLA-COSMOS 3 GHz Large Project. These were classified by combining multiple AGN diagnostics: X-ray data, mid-infrared data and broadband spectral energy distribution fitting. We decomposed the total radio 1.4 GHz luminosity (L1.4 GHz, TOT) into the emission originating from star formation and AGN activity by measuring the excess in L1.4 GHz, TOT relative to the infrared-radio correlation of star-forming galaxies. To quantify the excess, for each source we calculated the AGN fraction (fAGN) defined as the fractional contribution of AGN activity to L1.4 GHz, TOT. The majority of the HLAGN, (68.0 ± 1.5)%, are dominated by star-forming processes (fAGN ≤ 0.5), while (32.0 ± 1.5)% are dominated by AGN-related radio emission (0.5 < fAGN ≤ 1). We used the AGN-related 1.4 GHz emission to derive the 1.4 GHz AGN luminosity functions of HLAGN. By assuming pure density and pure luminosity evolution models we constrained their cosmic evolution out to z ∼ 6, finding Φ*(z)∝(1 + z)(2.64 ± 0.10)+(−0.61 ± 0.04)z and L*(z)∝(1 + z)(3.97 ± 0.15)+(−0.92 ± 0.06)z. These evolutionary laws show that the number and luminosity density of HLAGN increased from higher redshifts (z ∼ 6) up to a maximum in the redshift range 1 < z < 2.5, followed by a decline toward local values. By scaling the 1.4 GHz AGN luminosity to kinetic luminosity using the standard conversion, we estimate the kinetic luminosity density as a function of redshift. We compare our result to the semi-analytic models of radio mode feedback, and find that this feedback could have played an important role in the context of AGN-host co-evolution in HLAGN which shows evidence of AGN-related radio emission (fAGN > 0).
Key words: galaxies: active / galaxies: evolution / galaxies: high-redshift / galaxies: star formation
© ESO 2018
1. Introduction
The co-evolution of the host galaxies and the active galactic nuclei (AGN) within them has been widely accepted after the discovery of scaling relations between supermassive black hole (SMBH) mass and host galaxy properties (e.g., Magorrian et al. 1998; Ferrarese & Merritt 2000). To better understand this co-evolution we need to examine how AGN and their host galaxies change through cosmic time.
Active galactic nuclei are powerful extragalactic sources visible across the entire electromagnetic spectrum, from gamma-rays and X-rays to the radio. In order to study their activity and how it changes through cosmic time, a multiwavelength approach is needed. Observations show that AGN activity occurs in at least two different flavors, resulting in two intrinsically different AGN populations (Shakura & Sunyaev 1973; Narayan & Yi 1994, 1995). This dichotomy most likely occurs due to the difference in the efficiency of the mechanism that governs the accretion onto the central SMBH (e.g., see review by Heckman & Best 2014). In the case of inefficient accretion fueled by the inflow of the hot gas at low accretion rates (below 1% of Eddington), the main energetic output is the kinetic energy transported by powerful radio jets, which can outshine the radio emission from the host galaxy. They produce a relatively small amount of radiation across the rest of the electromagnetic spectrum and are hence called low-excitation radio galaxies (LERGs) or jet-mode AGN (e.g., Best & Heckman 2012; Best et al. 2014; Pracy et al. 2016). The cold gas accretion at high rates (above 1% of Eddington) onto the central SMBH is radiatively efficient and can produce signatures that can be detected as optical emission lines. Objects containing this type of signature are referred to as high-excitation radio galaxies (HERGs) or radiative-mode AGN, some of which are found to also have strong radio jets. AGN can also be classified based on their radio power as radio-quiet (RQ) and radio-loud (RL) AGN. If this classification is based on the ratio of radio and infrared luminosities (as in, e.g., Padovani et al. 2015), most HERGs and radiative-mode AGN are found to be RQ, while LERGs/jet-mode AGN are RL due to the presence of powerful radio jets (Smolcic 2016).
The difference between the two populations is also reflected in the shape of the radio luminosity functions that are constructed from local samples of radio galaxies (Filho et al. 2006; Best & Heckman 2012; Gendre et al. 2013; Best et al. 2014; Pracy et al. 2016). The jet-mode AGN and LERGs dominate at lower radio luminosities, while radiative-mode AGN and HERGs become dominant at radio luminosities above L1.4 GHz ∼ 1026 WHz−1. However, there is substantial disagreement at L1.4 GHz < 1025 WHz−1 between luminosity functions derived from various surveys of the nearby Universe, such as Faint Images of the Radio Sky at Twenty-cm (FIRST), NRAO VLA Sky Survey (NVSS), Sloan Digital Sky Survey (SDSS), Palomar Sky Survey (Becker et al. 1994; Condon et al. 1998; York et al. 2000; Ho et al. 1997, respectively). While Filho et al. (2006; based on the Palomar Sky Survey) and Pracy et al. (2016; based on the Large Area Radio Galaxy Evolution Spectroscopic Survey – LARGESS) find substantial volume densities at luminosities L1.4 GHz ≲ 1025 WHz−1, Best & Heckman (2012; based on the SDSS survey) find up to about an order of magnitude lower volume densities at these luminosities (see Fig. 7 in Pracy et al. 2016). As argued by Pracy et al. (2016), this disagreement may be due to the different approaches they used to eliminate star-forming galaxies from the HERG sample. Best & Heckman (2012) choose a conservative approach, removing all radio galaxies where the radio emission was suspected to arise from star formation, and this may have led to an underestimation of the volume densities of their HERG population (particularly at the low-luminosity end). On the other hand, the contribution from star-forming processes may bias the low luminosity end of the luminosity functions as derived by Filho et al. (2006) and Pracy et al. (2016).
Due to the difference in the supply of cold gas needed to trigger star formation, the two different types of AGN are hosted by galaxies with different stellar populations (e.g., Smolčić et al. 2009). For radio galaxies out to redshift z ∼ 1 it has been found that HERGs have bluer colors associated with ongoing star formation, while LERGs are mostly red quiescent galaxies (e.g., Smolčić et al. 2009; Best & Heckman 2012; Ching et al. 2017). While this might not hold for the highest luminosity radio galaxies (see, e.g., Dunlop et al. 2003), a study by Bonzini et al. (2013), which, because of the small covered area, does not sample the brightest part of the radio luminosity function, found that the RQ and RL AGN with redshifts of 0.1 < z < 4 are hosted mainly in late- and early-type galaxies, respectively. To constrain the evolution of an AGN component, one first needs to infer how much of the detected radio emission arises from AGN activity and how much from star-forming processes. While the radio emission in the jet-mode AGN is expected to be dominated by radio jets, the host properties of radiative-mode AGN indicate that a significant fraction of their radio luminosity arises from ongoing star formation. Most radio sources detected in surveys such as FIRST, SDSS, Cosmic Evolution Survey (COSMOS), and the Extended Chandra Deep Field South (E-CDFS) are unresolved and morphological decomposition of radio emission into AGN and star-forming components cannot be performed. In order to study the evolution of these components separately, another approach is needed, as taken here.
Studies of the evolution of spectroscopically selected AGN show different evolutionary trends; while LERGs show little or no evolution, HERGs seem to be a strongly evolving population (e.g., Best & Heckman 2012; Pracy et al. 2016). Best et al. (2014) studied the evolution of a sample of over 200 sources spectroscopically classified as radiative- or jet-mode AGN from a combination of eight radio surveys. They found an increase in the space density of the radiative-mode AGN from the local Universe out to redshift z ∼ 0.75. For the lower luminosity (L1.4 GHz ≤ 1025 WHz−1) jet-mode AGN they find no evidence of evolution, while their higher radio luminosity counterparts showed a significant increase in space density up to z ∼ 1. Similar results were found in the study of the radio sample of 680 objects from the E-CDFS (Padovani et al. 2015), classified as RL and RQ AGN based on the ratio between 24 μm and 1.4 GHz flux densities. Their RL AGN show an increase in number density out to a peak at z ∼ 0.5, followed by a decline toward the higher redshifts. The population of RQ AGN shows a more rapid evolution, with a hint of a slower evolution at redshifts z> 1.3. As demonstrated by Rigby et al. (2015), there exists a luminosity-dependence of the redshift evolution of the radio luminosity function. Using a combination of several radio datasets they select the AGN as sources which show radio excess relative to that expected from star formation, using the so-called q parameter, defined as the ratio of the mid-infrared (24 μm) to radio (1.4 GHz) flux density. Their results indicate that the peak of the space density appears at higher redshifts for the most powerful sources (L1.4 GHz ≥ 1025.6 WHz−1), while for their lower power counterparts (L1.4 GHz < 1025.6 WHz−1) the space density appears to be constant with redshift. Their interpretation of the results is that the higher-power sources represent the cold-mode sources which were the more dominant population in the early Universe, while the plateau at lower powers corresponds to the change in dominance between the cold- and hot-mode sources toward the local Universe.
The feedback mechanism that governs the co-evolution between an AGN and the host galaxy is thought to occur in two flavors, namely radio and quasar mode feedback. The radio mode feedback was first introduced to solve the cooling flow problem arising in the earliest semi-analytical models and numerical simulations of formation of structure (e.g., Bower et al. 2006; Croton et al. 2006, 2016). It operates in massive galaxies where powerful radio jets inject energy in kinetic form into the surrounding environment, effectively heating the gas and preventing star formation. On the other hand, the quasar mode feedback is associated with periods of rapid black hole growth due to the high accretion rates triggered by galaxy mergers or disk instabilities. These episodes of rapid accretion produce quasar winds which can affect the surrounding gas blowing it out of the galaxy and hence also terminating the formation of new stars (e.g., Croton et al. 2016).
The kinetic energy injected into the environment can be estimated using one of many scaling relations between monochromatic radio luminosity and kinetic luminosity (e.g., Willott et al. 1999; Merloni & Heinz 2007; Cavagnolo et al. 2010; Godfrey & Shabala 2016). However, we note that different scaling relations can result in estimates of kinetic luminosity which differ by several orders of magnitude (see Appendix A in Smolčić et al. 2017b for details). Keeping this in mind, the estimates of the kinetic luminosity density can be further compared to models of galaxy evolution (e.g., Bower et al. 2006; Croton et al. 2006, 2016; Merloni & Heinz 2008). A recent study of the LERG and HERG evolutions by Pracy et al. (2016) out to z ∼ 0.75 found little or no evolution of the kinetic luminosity density for the most powerful LERGs, which is consistent with the result for the radio-mode AGN from the semi-analytical model of galaxy evolution by Croton et al. (2006). The local value of the kinetic luminosity density of HERGs is an order of magnitude lower than that of LERGs, but becomes comparable at z ∼ 0.75, showing that the radio mode feedback in HERGs influenced their evolution more at higher redshift than it does in the local Universe.
In this work we study the cosmic evolution of a population of AGN in the COSMOS field, detected in the VLA-COSMOS 3 GHz Large Project out to z ∼ 6. Selection of these AGN is based on a combination of X-ray and mid-infrared (MIR) criteria and broadband spectral energy distribution fitting. Using the applied selection, we aim to trace the analogs of HERGs, as these criteria are sensitive to the excess of emission likely to arise due to radiatively efficient accretion onto SMBH. We call these sources moderate-to-high radiative luminosity AGN (HLAGN; see Sect. 2.2). We develop a statistical method for decomposing the total radio luminosity into the star forming and AGN components to trace the evolution of radio emission associated only with the AGN.
The paper is structured as follows. In Sect. 2 we describe the dataset used in the analysis. In Sect. 3 we investigate star formation in the HLAGN population and describe the procedure adopted to decompose the total 1.4 GHz luminosity into contributions arising from an AGN and from processes related to star formation. AGN luminosity functions and their evolution are derived and described in Sects. 4 and 5, respectively. In Sect. 6 we discuss our results in the context of studies from the literature in order to understand what the origin of AGN-related radio emission in HLAGN is and how it may influence the properties of their host galaxies. Finally, in Sect. 7 we summarize the conclusions of our work.
Throughout this paper we assume ΛCDM cosmology with H0 = 70 km s−1 Mpc−1, Ωm = 0.3 and ΩΛ = 0.7. We assume that the synchrotron radio emission follows a simple power law spectrum of the form Sν ∝ να, where Sν is the flux density at frequency ν and α is the spectral index.
2. Data and sample
2.1. The VLA-COSMOS 3 GHz Large Project
To investigate the evolution of the radio-AGN luminosity function over cosmic time, a large sample of sources with available multiwavelength data and high-quality redshifts is needed. The VLA-COSMOS 3 GHz Large Project provides radio data from 384 hours of observations with the Karl G. Jansky Very Large Array (VLA). The 3 GHz (10 cm) observations were carried out over 2.6 deg2 centered in the COSMOS field, reaching a median 1σ sensitivity of 2.3 μJy beam−1 over the inner 2 deg2 at an angular resolution of 0.75″. The total number of radio detected sources with signal-to-noise ratios (S/N) of five or more across the entire 2 deg2 COSMOS field is 10 830. All details of the observations and the extraction of radio sources can be found in Smolčić et al. (2017a).
Smolčić et al. (2017c) cross-match the VLA-COSMOS 3 GHz Large Project radio data with the multiwavelength COSMOS2015 catalog (Laigle et al. 2016), identifying a sample of 7 729 radio sources with optical-NIR counterparts. This is 89% of all radio sources in the effective area considered (1.77 deg2). For ∼31% (∼69%) of these sources, reliable spectroscopic (photometric) redshifts are available. 33% of radio sources have also been detected in the 1.4 GHz VLA-COSMOS Large Survey (Schinnerer et al. 2007, 2010). For these sources the spectral index is calculated from the observed slope between 1.4 and 3 GHz. Otherwise, the spectral index is set to be −0.7 which is the expected value for non-thermal synchrotron radiation (e.g., Condon 1992) and corresponds to the average spectral index found for 3 GHz sources in this survey (Smolčić et al. 2017a).
2.2. Identification of moderate-to-high radiative luminosity AGN (HLAGN)
The radio sources detected in the VLA-COSMOS 3 GHz Large Project were separated into the following classes by Smolčić et al. (2017c): low-to-moderate radiative luminosity AGN (MLAGN), moderate-to-high radiative luminosity AGN (HLAGN) and star-forming galaxies (SFGs). We briefly summarize the separation method here. Firstly, HLAGN were identified using a combination of X-ray1 (LX > 1042 ergs−1) and MIR2 (color-color diagram; see Donley et al. 2012) criteria and via template fitting to the optical-to-millimeter spectral energy distributions (SED; see Delvecchio et al. 2017). The union of these three criteria yielded a sample of 1604 sources classified as HLAGN3. These objects are the main focus of this paper. The other radio sources were classified either as SFGs or MLAGN, based on optical colors, Herschel imaging and radio emission.
For every radio source, IR luminosities arising from star-forming processes were obtained from the best-fit galaxy SED, after correcting for a possible AGN-related emission (for more details see Delvecchio et al. 2017). Star formation rates (SFRs) were calculated from these luminosities, by assuming the Kennicutt (1998) scaling relation and a Chabrier (2003) initial mass function. The data products as described by Smolčić et al. (2017a) and Delvecchio et al. (2017) are available at the COSMOS IPAC/IRSA archive4.
3. Star formation properties of HLAGN
In this section we examine the star formation contribution to the radio emission of HLAGN. We present a statistical decomposition method developed to separate the total radio luminosity into contributions originating from AGN activity and star formation.
3.1. Star formation in HLAGN host galaxies
Non-thermal radio emission in extragalactic surveys arises either from AGN or star-forming processes (e.g., Condon 1992; Miller et al. 1993). Delvecchio et al. (2017) analyzed the properties of MLAGN and HLAGN (see Sect. 2.2). They find that MLAGN at redshifts z ≤ 1 show SFRs and stellar masses consistent with those of passive galaxies with little or no ongoing star formation. For the HLAGN population they find that the majority lies on the main sequence for star formation (Whitaker et al. 2012). They also argue that about 70% of HLAGN exhibit no “significant” (>3σ) radio-excess relative to their IR-based SFRs, suggesting that a large fraction of radio emission in HLAGN is of star formation origin.
Both the infrared and radio emissions can be used to trace the recent star formation in SFGs, which leads to a tight correlation between them, the so-called infrared-radio correlation (IRRC; e.g., Yun et al. 2001; Bell 2003; Magnelli et al. 2015). Delhaize et al. (2017) examined the cosmic evolution of the IRRC in the COSMOS field using a sample of 9575 SFGs. This sample was jointly selected in the far-infrared (based on Herschel fluxes) and in the radio (objects in the VLA-COSMOS 3 GHz sample) after removing HLAGN and quiescent MLAGN (as described by Smolčić et al. 2017c). They found a redshift-dependent infrared-to-1.4 GHz radio luminosity ratio, qTIR(z), with the 1σ spread of 0.35 dex. The spread around the IRRC shows the part of the IRRC parameter space in which we expect most of the radio emission to be produced in star-forming processes (e.g., Yun et al. 2001; Bell 2003).
In Fig. 1 we show the redshift evolution of the logarithm of infrared-to-total 1.4 GHz luminosity (qTOT) vs. the total 1.4 GHz luminosity (L1.4 GHz, TOT) of the HLAGN sample, overlaid with the Delhaize et al. (2017) qTIR(z) result. A significant number of HLAGN is found within and above the 1σ envelope around the IRRC at all redshifts, which is qualitatively consistent with the results by Delvecchio et al. (2017) and Smolčić et al. (2017c). This implies that star-forming processes contribute considerably to the radio emission of these HLAGN, while the excess of the radio emission in HLAGN below the IRRC envelope is mainly powered by the AGN activity. To quantify the extent to which star-forming processes and AGN activity contribute to the total 1.4 GHz luminosity, we perform a decomposition analysis as described in the next section.
 |
Fig. 1. Infrared-to-1.4 GHz radio luminosity ratio (qTOT) vs. L1.4 GHz for HLAGN (black crosses). Radio luminosity binned median values of the ratio are shown with red circles with error bars showing 16th and 84th percentiles of the distribution. The dashed magenta line corresponds to the IRRC derived by Delhaize et al. (2017) at the median redshift of the underlying HLAGN sample, along with its 1σ spread of ±0.35 dex. Blue solid lines and area show the median of the star-forming peak q̄SF,z and 1σq SF,z uncertainties calibrated on the full radio detected sample of the VLA-COSMOS 3 GHz Large Project sources with the COSMOS2015 counterparts. |
3.2. Decomposition of star formation and AGN contributions to the total radio luminosity
Most of the previous studies of luminosity functions have been conducted using surveys at 1.4 GHz (e.g., Best & Heckman 2012; Pracy et al. 2016). To compare to and complement those studies, here we derive 1.4 GHz radio luminosities. From the observed 3 GHz flux densities (S3 GHz, TOT; WHz−1 m−2) we calculated the rest frame radio luminosity at 1.4 GHz (L1.4 GHz,TOT; WHz−1) using
where DL and z are the luminosity distance (in unit m) and redshift of the source, respectively. The index TOT refers to the total 1.4 GHz radio luminosity and the 3 GHz flux density prior to decomposition. As previously discussed, we expect the radio emission in HLAGN to originate from both star-forming processes in the host galaxy and AGN activity. The total 1.4 GHz radio luminosity (L1.4 GHz, TOT) is hence the sum of star forming (L1.4 GHz, SF) and AGN (L1.4 GHz, AGN) contributions. To quantify these contributions, we performed the decomposition analysis described here.
We split our HLAGN sample into nine redshift bins, each with roughly equal number of sources, in the redshift range 0.1 < z < 6.1. We calculated the infrared-to-total 1.4 GHz luminosity ratio:
where LIR,SF is the infrared luminosity only due to star-forming processes (see Sect. 2.2). Uncertainties on qTOT, σq,TOT, are estimated by propagating the uncertainties on the luminosities. Assuming for each source a normal distribution of qTOT with root mean square scatter σq,TOT, and drawing qTOT from this distribution, in Fig. 2 we show one representation of the qTOT distribution for our HLAGN sample (2.1 < z < 3.0; gray histogram in Fig. 2).
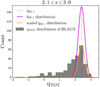 |
Fig. 2. Example of one iteration of the qTOT distribution for the HLAGN (gray histogram) overlaid with the Gaussian functional forms showing the contribution of star-forming processes in the redshift bin 2.1 < z < 3.0. Gaussian functional forms show the contribution from the star formation as derived from the full sample and after scaling it to the normalization of the HLAGN distribution at the q̄SF,z (shown with magenta and orange lines, respectively). |
We next computed the median qSF calibrated on the full radio-detected sample in each redshift bin (q̄S F,z). Here, qSF is the infrared-to-1.4 GHz radio luminosity expected to arise only from star-forming processes, with the corresponding uncertainties σSF. Appendix A describes in detail how q̄SF,z was calculated.
We have assumed that for HLAGN, the star formation contribution to the radio emission follows the same Gaussian functional form expected for the star-forming galaxy sample of radio detected sources; in other words, that it is peaked at q̄SF, z with the corresponding dispersion σSF,z. We set the normalization of the Gaussian to the value of the HLAGN qTOT distribution at the position of the q̄SF,z (see purple and orange lines in Fig. 2).
Then we find the difference in number count between the observed qTOT distribution of HLAGN (gray filled histogram in Fig. 2) and the normalized q̄SF distribution (orange line in Fig. 2) in bins of qTOT 5. This gives an estimate of the number of sources (NAGN) expected to have AGN emission contributing to the total radio emission. We randomly selected NAGN sources within each qTOT bin and calculate their AGN fractions at 1.4 GHz, fAGN, defined as
If a source within a particular qTOT bin is not selected in this process, it is given a fAGN = 0 value in this particular iteration. To account for the uncertainties, we repeated this entire procedure 1000 times using Monte Carlo simulations, constructing a new qTOT distribution each time. The result is a distribution of fAGN values for each source, which accounts for the distribution of qSF, z and the uncertainty on qTOT.
Figure 3 shows the distribution of qTOT as a function of redshift for our HLAGN sample, color-coded by the derived AGN fractions. AGN fractions range from 0 to 1, where the two extreme values correspond to situations where all radio emission is due to the star-forming processes (fAGN = 0) or AGN activity (fAGN = 1). Given the definition of fAGN in Eq. (3), AGN fractions can assume unphysical (negative) values if the source has randomly extracted qTOT value greater than the average qSF,z value calibrated on the full radio sample. In these cases we set fAGN = 0 which is equivalent to assuming that radio emission arises entirely from star formation. The distribution of the median AGN fractions is shown in Fig. 4.
 |
Fig. 3. Infrared-to-1.4 GHz radio luminosity ratio (qTOT) vs. redshift for the HLAGN. The data are color-coded by their median values of AGN fractions. The magenta dashed line is the redshift dependent analytic form calibrated by Delhaize et al. (2017) on a sample of SFGs, with ±1σ spread (magenta area). White dots show the peaks (q̄SF,z) of the underlying qTOT distribution calibrated on the star-forming galaxies in the full radio detected sample. |
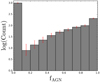 |
Fig. 4. Histogram of median AGN fractions across all redshifts, computed using Eq. (3) (see text for details). Error bars show the 16th and 84th percentile values. |
We find that the majority of HLAGN, (68.0 ± 1.5)%, have the total radio emission dominated by star-forming processes (0 ≤ fAGN ≤ 0.5), which is consistent with results by Smolčić et al. (2017c) and Delvecchio et al. (2017). On the other hand, a subsample of HLAGN is dominated by the AGN-related radio emission. We find that (9.9 ± 0.9)% of HLAGN have 1.4 GHz AGN fractions in the range 0.5 < fAGN ≤ 0.75, while (22.1 ± 0.9)% have these fractions of 0.75 < fAGN ≤ 1.
We scale the total 1.4 GHz radio luminosity and the observed 3 GHz flux density down to the AGN-related contributions:
For the (37.5 ± 2.2)% of HLAGN that show evidence for AGN-related radio emission (fAGN > 0), we estimate the 1.4 GHz AGN luminosities via the decomposition method. To test whether AGN fractions derived for this subsample evolve with redshift, we derive the median and 1σ values per redshift bin, but find no significant evidence of evolution. The median of the AGN fraction of the HLAGN sample with fAGN ≠ 0 is 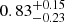 .
.
Only the radio luminosity component due to AGN (L1.4 GHz, AGN) is further used to calculate the radio AGN luminosity functions. This effectively allows us to exclude “contamination” of the AGN luminosity functions by star formation-related emission and thus derive the genuine radio AGN luminosity function.
4. Radio luminosity functions of HLAGN
In this section we describe the derivation of radio AGN luminosity functions. To ensure we have a complete sample of sources with fully observable AGN radio emission by our survey, we impose a cut in the AGN flux densities S3 GHz, AGN ≥ Slim, 3 GHz, where Slim, 3 GHz is the detection limit of the survey (Slim, 3 GHz = 5σ = 11.5 μJy). Then we construct the AGN luminosity functions using the AGN luminosities obtained with the decomposition technique for such defined sample of 575 HLAGN. To show how the decomposition affects the shape of the luminosity functions, we also calculated the total luminosity functions for the full HLAGN sample (0 ≤ fAGN ≤ 1.0), using the total 1.4 GHz luminosity which includes emission of both AGN and star-formation origin. Finally, we compared our results with those in the literature.
4.1. Derivation
To constrain the redshift evolution of the radio AGN luminosity function we calculate the comoving space density of radio sources per logarithm of luminosity in nine redshift bins (same binning as in Sect. 3.2). To find the maximum observable volume in which each of the galaxies in our sample could be observed we use the Vmax method (Schmidt 1968):
where Vmax, i is the maximum observable volume of the ith galaxy in the sample, zmin is the minimum redshift of the redshift bin under study, and zmax is the maximum redshift where the source can still be part of the sample given its radio luminosity. To take into account the area covered by the radio data and the variation of completeness of the radio catalog as a function of the observed flux, we define the completeness factor (𝒞) as
where Aobs = 1.77 deg2 is the effective unmasked area of the COSMOS optical-NIR survey, Asky is the area of the sky sphere, and 𝒞comp(S3 GHz, AGN) is the completeness of the radio catalog at the 3 GHz AGN flux density S3 GHz, AGN (for the completeness of the survey, see Fig. 16 and Table 2 in Smolčić et al. 2017a). We note that this calculation of Vmax is consistent with those by Novak et al. (2017) and Smolčić et al. (2017b).
We calculated luminosity functions, Φ(L), meaning the number of sources per comoving volume element per interval of luminosity logarithm, using
where Vmax, i is the maximum observable volume of the ith galaxy, Δlog(L) is the interval of logarithm of luminosity (here taken to be 0.8 dex), and the sum is taken over all sources within the redshift and luminosity bin under consideration. Following Marshall (1985), we calculated the errors on Φ(L) as
In the case where the number of sources used to calculate Φ(L) in a bin is less or equal to ten, we correct the values of σΦ(L) given by Eq. (9) by using the tabulated values of Poissonian uncertainty for small number statistics as given by Gehrels (1986).
To compute the AGN luminosity functions, we have to properly take into account the uncertainties on the AGN fractions (and therefore luminosities), which in some cases are significant. To do this, we used the Monte Carlo approach described in Sect. 3.2 which provides us with the distribution of the AGN fraction for each object. For each Monte Carlo iteration, we split the sample into luminosity bins and calculated luminosity functions using Eq. (8). This procedure gives us a distribution of luminosity functions per luminosity bin, from which we find the median and the corresponding 16th and 84th percentiles.
The AGN luminosity functions are tabulated in Table 1 and shown in Fig. 5. The median values of redshift quoted per redshift bin represent the median values of redshift of HLAGN that satisfy the flux density condition S3 GHz, AGN ≥ Slim, 3 GHz.
AGN luminosity functions for the HLAGN population.
 |
Fig. 5. Radio AGN luminosity function at 1.4 GHz at redshifts 0.1 < z < 6.1. AGN and total luminosity functions of HLAGN are plotted as magenta and green points, respectively. Solid and dashed magenta lines show the fit of the analytic form of the local luminosity function to our AGN luminosity function data for the pure density and pure luminosity evolutions, respectively, with shaded areas indicating 1σ confidence range. The black and red vertical dashed lines show the luminosity corresponding to the 5σ sensitivity at zmin and zmax of the redshift bin, respectively. Results from the literature are also shown, as detailed in the legend. |
As expected, based on comparison with the literature (e.g., Best et al. 2014; Pracy et al. 2016), we find that the total radio luminosity functions (without any decomposition applied) at high luminosities are dominated by AGN emission. At lower luminosities we can see the effect of the decomposition technique as the normalization of the AGN luminosity function is lower than that of the total luminosity function. This is expected given that at these luminosities the SFG luminosity function starts to significantly contribute to the total luminosity function (Novak et al. 2018).
4.2. Comparison with the literature
In Fig. 5 we compare our results with literature values of radio AGN luminosity functions at 1.4 GHz. Best & Heckman (2012) used a combined SDSS, NVSS and FIRST sample of RL AGN at redshifts z < 0.3 to study the difference between LERGs and HERGs. For both classes they constructed local luminosity functions. Their local luminosity function of HERGs is systematically lower in comparison to our data. As previously discussed by Pracy et al. (2016), this disagreement reflects the difference in the classification criteria, where Best & Heckman (2012) conservatively removed from their HERG sample all sources which showed evidence of star formation and classified them as SFGs (see also Sect. 5.1).
Pracy et al. (2016) use a sample of radio galaxies identified by matching FIRST sources with SDSS images. Based on their optical spectra, sources were classified into LERG and HERG classes (Ching et al. 2017). In Fig. 5 we show their HERG luminosity functions. As will be discussed in more detail in Sect. 5.1, 1.4 GHz luminosity functions derived by Pracy et al. (2016) for the HERG sample are dominated by the AGN emission and are in excellent agreement with our values of AGN luminosity functions.
Based on the Palomar sample of bright nearby galaxies (Ho et al. 1997) Filho et al. (2006) constructed 5 GHz radio luminosity functions of low-luminosity AGN at a median distance of 17 Mpc. The luminosity function of 37 Seyfert galaxies, scaled to 1.4 GHz luminosities, is in good agreement with our data and constrains the low-luminosity end of the local luminosity function.
Best et al. (2014) combine eight radio surveys to obtain a large source sample covering a broad range of radio luminosities. They further separated these sources into radiative-mode or jet-mode AGN based on optical emission line strengths and line flux ratios. Here we have compared our data with their luminosity functions of 123 radiative-mode AGN at redshifts 0.5 < z < 1.0. Their results are in agreement with our luminosity functions, with the Best et al. (2014) luminosity functions constraining the high-luminosity end.
Using the VLA sample of sources within the ∼0.3 deg2 of the Extended Chandra Deep Field South (E-CDFS), Padovani et al. (2015) studied the evolution out to z ∼ 4 of two radio faint populations down to the sensitivity of 5σ ∼ 32.5 μJy at 1.4 GHz. To minimize the effect of missing redshift estimation, they have applied a cut in 3.6 μm flux density, f3.6 μm > 1 μJy, yielding a sample of 680 radio detected sources. Using the scheme described in detail in Bonzini et al. (2013), these sources were classified as RL AGN, RQ AGN, or SFGs. This classification was based on the logarithm of the ratio between the observed 24 μm and 1.4 GHz flux densities, q24 obs. They define the “SFGs locus” using the SED of M 82 chosen to represent the entire population of SFGs across all studied redshifts. All sources which displayed an excess of radio emission with respect to this locus were classified as RL AGN. Sources within the SFGs locus, for which X-ray and MIR diagnostics showed evidence of AGN activity, were classified as RQ AGN. The remaining sources were classified as SFGs.
To test the evolution of their RQ AGN, Padovani et al. (2015) split their sample in six redshift bins, up to a redshift 3.66, and within each bin calculated the 1.4 GHz luminosity functions. Their RQ AGN luminosity functions agree well with our total luminosity functions in each redshift bin, possibly due to similar classification criteria (for a detailed comparison between the classifications applied in this paper and the one used by Padovani et al. 2015 see Delvecchio et al. 2017). At the low luminosity end, their luminosity functions tend to be higher than our AGN luminosity functions. This is expected since the RQ luminosity functions by Padovani et al. (2015) are based on the total 1.4 GHz luminosity which contains both star-forming and AGN contributions, while we construct HLAGN luminosity functions using only the AGN contribution to the 1.4 GHz luminosity derived with a decomposition method.
5. Cosmic evolution of the radio luminosity function out to z ∼ 6
In this section we explain the reasoning behind adopting the analytic form of the local luminosity function by Pracy et al. (2016) as an appropriate form to fit to our data. We further describe how the evolution of radio AGN luminosity function out to z ∼ 6 is constrained.
5.1. Local luminosity function
The 2 deg2 area of the COSMOS field does not sample a large enough volume at low redshift to constrain the local luminosity function over a wide range of radio luminosities below and above the break of the luminosity function (L*). Since an analytic representation of the local luminosity function over a broad luminosity range is required to constrain its cosmic evolution, in this work we have considered local luminosity functions derived on the basis of larger area surveys, such as FIRST/NVSS combined with SDSS, LARGESS and the Palomar Nearby Galaxy Survey (Becker et al. 1994; Condon et al. 1998; York et al. 2000; Ching et al. 2017; Ho et al. 1997). In these surveys, the luminosity functions were separately derived for spectroscopically selected HERGs (Filho et al. 2006; Best & Heckman 2012; Best et al. 2014; Pracy et al. 2016) which can be assumed to be the local analogs of our HLAGN (as detailed above). However, some significant disagreement exists between various local luminosity functions, being the strongest at the low luminosity end (L1.4 GHz < 1025 WHz−1). This disagreement is mainly due to the difference in the treatment of SFGs among different studies. Best & Heckman (2012) took a conservative approach removing all SFGs from the sample, which resulted in the normalization of the low luminosity end being lower by an order of magnitude than that by Filho et al. (2006) and Pracy et al. (2016). To test if the lower luminosity end of the HERG luminosity function is biased by radio emission contribution from SFGs, we independently estimated the contribution of star formation to the radio luminosity of HERGs in the LARGESS sample, used by Pracy et al. (2016) for the derivation of their luminosity function.
To the LARGESS data, we added SFR estimates provided in the MPA-JHU DR7 catalog6. In this catalog SFRs for sources classified as SFGs were derived directly from optical emission lines, while SFRs for AGN, composite, and unclassified classes were estimated on the basis of the observed spectral break at 4000 Å (D4000) and the relation existing for normal SFGs between specific SFR and D4000 (see Brinchmann et al. 2004 for details). The given SFRs are corrected for the effect of finite SDSS spectroscopic fibers as described in Salim et al. (2007).
In Fig. 6 we show the ratio of 1.4 GHz luminosity to SFR as a function of the 1.4 GHz luminosity. As seen in this figure, the radio luminosities of HERGs are systematically higher than those of SFGs and the ratio is systematically offset from that of SFGs. By subtracting this value from the fit to the median values for the HERG population, we estimate the correlation of AGN and total 1.4 GHz luminosity of HERGs (as identified in the LARGESS sample) to be
 |
Fig. 6. Distribution of the ratio of 1.4 GHz radio luminosity to SFR as a function of the 1.4 GHz radio luminosity for HERGs (blue symbols) and SFGs (yellow symbols) drawn from the LARGESS sample and cross-correlated with the MPA-JHU DR7 catalog. Median values of the ratio for HERGs and SFGs are shown by the filled black and red circles, respectively. The black solid line represents the linear fit to the median values for the HERG population. The red solid line represents the average value of the ratio of 1.4 GHz luminosity to SFR for star forming galaxies. |
We used Relation (10) to statistically decompose the total radio luminosities of the HERG sample provided in Table 1 in Pracy et al. (2016) into the luminosity components originating from an AGN and star-forming processes and then we compute the luminosity function using these estimates for the AGN radio luminosities. The results are plotted in Fig. 7 where we compare them to the original luminosity functions by Pracy et al. (2016). The decomposed radio luminosity function, as derived here, is perfectly consistent with that presented by Pracy et al. (2016). From this we conclude that the total luminosity of sources in the HERG sample is dominated by the AGN emission. The analytic form of the local HERG luminosity function as derived by Pracy et al. (2016) can hence be further used to constrain the cosmic evolution of our HLAGN sample (which is selected to trace the high redshift analogs of HERGs).
 |
Fig. 7. Local HERG luminosity function. Black circles show the total (AGN+SF) volume densities, while the gray line is the analytic fit to the data as done by Pracy et al. (2016). Magenta circles show the AGN luminosity functions derived by decomposing the total luminosity. The overlap between AGN and total volume densities confirms that the radio luminosity of sources in the HERG sample by Pracy et al. (2016) is dominated by the AGN emission. |
5.2. Cosmic evolution of the radio AGN luminosity function
The purpose of deriving the radio AGN luminosity functions of the HLAGN sample in Sect. 4.1 is to study their evolution over cosmic time. We tested their evolution with the pure density evolution (PDE) and pure luminosity evolution (PLE) models. We fit the analytic form of the local luminosity function to our data:
where αD and αL are pure density and pure luminosity evolution parameters, respectively. Φ0 is the local luminosity function as defined by Pracy et al. (2016):
where Φ* = 10−7.47 Mpc−3 dex−1 is the normalization, L* = 1026.47 WHz−1 is the knee of the luminosity function and α = −0.66 and β < 0 are the faint and bright end slopes, respectively. This analytic form was constrained using the local (0.005 < z < 0.3) sample of HERGs down to the optical apparent magnitude limit of their survey (mi < 20.5). As discussed by Pracy et al. (2016; see Sect. 3.6) due to the poor statistics they give only an upper limit for the parameter β. In our analysis, we set the bright end slope to the value of −2 as it well-matches the radiative-mode AGN luminosity functions derived by Best et al. (2014; see Fig. 5). However, to properly constrain this parameter, better statistics of bright objects are needed.
To constrain the evolution of the HLAGN sample, we used the AGN luminosity function data with luminosities above the 5σ luminosity threshold of our survey at the minimum redshift of the bin (L(zmin)). We make an exception in the first redshift bin (0.1 < z < 0.5), where our lower luminosity data are not well constrained due to the small area of the COSMOS field. In this bin, we fit the analytic form of the local luminosity function by Pracy et al. (2016) only to the data which are above the luminosity threshold of our survey at the maximum redshift of the bin (L(zmax)).
Firstly, we fit the analytic form of the local luminosity function to the data in nine redshift bins. We tested the PDE and PLE models by setting either αD = 0 or αL = 0 for the case of pure luminosity or density evolution, respectively. Evolution parameters for each redshift bin obtained with this procedure are presented in Table 2 and Fig. 8.
Best-fit evolution parameters obtained by the fitting local luminosity function to the redshift binned data assuming pure density (αD) and pure luminosity (αL) evolution.
 |
Fig. 8. Parameters obtained from fitting two different redshift evolution models to the HLAGN luminosity functions. Green and magenta circles show the evolution parameters obtained from fitting the assumed analytic form of the luminosity function in nine redshift bins assuming pure luminosity and pure density evolution scenarios, respectively (see text for details). The same color lines show the results from the continuous fit assuming that the PLE and PDE parameters evolve linearly with redshift. |
Secondly, we continuously modeled the redshift dependence of the evolution parameters following the procedure described by Novak et al. (2017). We fit a simple linear redshift-dependent evolution model to all AGN luminosity functions in all redshift bins simultaneously:
where αd, αl, βd and βl are the various evolution parameters. We again tested pure density and pure luminosity evolutions separately via a χ2 minimization procedure. The best-fit parameters obtained in the case of pure luminosity evolution (αd = βd = 0) are αl = 3.97 ± 0.15 and βl = −0.92 ± 0.06. In the case of pure density evolution (αl = βl = 0) the best-fit parameters are αd = 2.64 ± 0.10 and βd = −0.61 ± 0.04. The values of these continuous evolution parameters and their uncertainties are shown with color lines in Fig. 8.
Our results show a global decline of evolution parameters with redshift. The high parameters of evolution in the redshift bin 0.7 < z < 0.9, significantly higher than those derived with the linear redshift dependent evolution model, are likely due to the presence of a very prominent large-scale structure in the COSMOS field at z ∼ 0.73 (Guzzo et al. 2007; Iovino et al. 2016). The presence of such a structure, enhancing the normalization of the luminosity function, produces higher than expected parameters of evolution.
To test if the chosen redshift binning has a significant effect on our results, we repeated the entire analysis using the binning designed to contain roughly the same number of sources with S3 GHz, AGN ≥ Slim, 3 GHz per redshift bin. Results of the best-fit parameters of a simple linear redshift dependent evolution model obtained through this analysis are consistent within the confidence range (±1σ) with the results presented above.
6. Discussion
In this section we discuss our results in the context of galaxy evolution, also investigating the origin of the radio emission in HLAGN. We have estimated the evolution of number, luminosity, and kinetic luminosity density and compare our results to other studies of galaxy evolution.
6.1. Origin of radio emission in HLAGN
Previous studies conducted on radio samples of X-ray and mid-IR selected AGN suggest that AGN identified through these criteria are hosted mostly by star-forming systems in which the bulk of the radio emission originates from the host galaxy rather than SMBH activity (e.g., Hickox et al. 2009; Bonzini et al. 2013; Goulding et al. 2014; Padovani et al. 2015). For instance, in a comprehensive analysis performed by Delvecchio et al. (2017) on the HLAGN sample they report that only ∼30% of them display significant radio excess due to non-thermal emission originating from AGN, while the radio emission of the rest is dominated by star formation. However, this behavior does not apply to the most luminous radio sources, which are found to mostly reside in massive and passive systems (e.g., Dunlop et al. 2003).
In this work we have separated the radio emission of HLAGN into radiation originating from star formation and AGN activity using a statistical decomposition technique. By deriving AGN fractions for all galaxies within our sample, we were able to estimate the extent to which the AGN component contributes to the total radio luminosity. Based on our estimates of AGN fractions we find that the majority, (68.0 ± 1.5)%, of the HLAGN are dominated by star-forming processes (0 ≤ fAGN ≤ 0.5), while in (32.0 ± 1.5)% of HLAGN AGN activity dominates (0.5 < fAGN ≤ 1.0) in the radio regime (see Sect. 3.2). We find no significant redshift evolution of the AGN fraction for HLAGN with AGN-related radio emission.
The question that arises next is whether radio AGN emission is extended or confined to the galaxies’ nuclear regions. To answer this question, we cross-matched our 3 GHz sample of 1604 HLAGN with the Very Long Baseline Array (VLBA) 1.4 GHz radio catalog by Herrera Ruiz et al. (2017). The authors identified a sample of 468 radio AGN detected by VLBA previously targeted with the VLA-COSMOS survey at 1.4 GHz (Schinnerer et al. 2010). They find that roughly ∼70% (237/344) of the faint sources (SVLA ≤ 1 mJy) are dominated by emission originating from a compact core, while this is true for only ∼30% (6/21) of the bright population (SVLA > 10 mJy). They argue that the bulk of the radio emission of the bright population originates from structures larger than the VLBA scale. To check whether these conclusions also hold for HLAGN, we have limited our HLAGN sample to match the original VLBA selection.
To match the VLBA selection, we require a > 5.5σ VLA detection at 1.4 GHz7. Out of 619 HLAGN satisfying this condition, we find only 113 (18%) to have a VLBA counterpart within a 0.4″ radius corresponding to about half a beam size of the 3 GHz VLA-COSMOS Large Project observations. The remaining 82% of HLAGN were not detected with the VLBA either because they were not detected within the VLA-COSMOS survey at 1.4 GHz (22%) or due to their radio emission being extended to scales larger than those probed with the VLBI method8 (60%).
To study the properties of the VLBA detected HLAGN, we restricted our analysis to a luminosity-limited subsample of sources with 1.4 GHz luminosities L1.4 GHz ≥ 1024.4 WHz−1 (the lowest 1.4 GHz luminosity of the sources at redshifts z ≥ 2). This criterion yields 51 (8%) HLAGN, spanning redshifts of 0.4 < z < 3.3. By scaling the 1.4 GHz VLA fluxes by AGN fractions, we estimate the flux expected to originate from the AGN component of these sources (see Sect. 3.2). Using these fluxes we further calculate the VLBA-to-VLA AGN flux density ratios. To find the median value and the corresponding 1σ confidence range of the flux density ratios, we perform Monte Carlo simulations taking into account the measurement errors of the 1.4 GHz VLA and VLBA flux densities and AGN fractions.
For the sample of the VLBA detected HLAGN with L1.4 GHz ≥ 1024.4 WHz−1, we find the median VLBA-to-VLA AGN flux density ratio to be 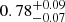 . By separating the sample in bins of the AGN luminosity (Δlog LAGN = 1), we find that the higher AGN luminosity sources tend to have lower VLBA-to-VLA AGN flux density ratios (see Fig. 9). These results suggest that the most powerful AGN are dominated by more extended radio emission. To test whether this trend changes with redshift, we separate the sample into three redshift intervals with equal number of sources (17 per bin). A trend of higher AGN luminosity sources having lower flux density ratios is present at all redshifts. Median flux density ratios of the sources with L1.4 GHz, AGN > 1026 WHz−1 at redshifts z < 1.4 and 2.15 < z < 3.3 hint that over 50% of the AGN related radio emission might arise from more extended structures (relative to scales probed by the VLBA). This is in agreement with the above-mentioned results by Herrera Ruiz et al. (2017).
. By separating the sample in bins of the AGN luminosity (Δlog LAGN = 1), we find that the higher AGN luminosity sources tend to have lower VLBA-to-VLA AGN flux density ratios (see Fig. 9). These results suggest that the most powerful AGN are dominated by more extended radio emission. To test whether this trend changes with redshift, we separate the sample into three redshift intervals with equal number of sources (17 per bin). A trend of higher AGN luminosity sources having lower flux density ratios is present at all redshifts. Median flux density ratios of the sources with L1.4 GHz, AGN > 1026 WHz−1 at redshifts z < 1.4 and 2.15 < z < 3.3 hint that over 50% of the AGN related radio emission might arise from more extended structures (relative to scales probed by the VLBA). This is in agreement with the above-mentioned results by Herrera Ruiz et al. (2017).
 |
Fig. 9. VLBA-to-VLA AGN flux density ratio vs. 1.4 GHz AGN luminosity. Yellow circles show the luminosity binned values of the ratio, while solid and dashed black lines show the median, 84th and 16th percentile values of the sample with L1.4 GHz, TOT ≥ 1024.4 WHz−1. Blue, green, and magenta circles and error bars show the data in three redshift bins as indicated in the legend. For better visibility of error bars, we introduced a small shift along the luminosity axis. |
The physical explanation for the variety of the observed radio AGN fractions in our HLAGN sample is most likely closely related to the intrinsic properties of individual AGN: the mass and spin of the central SMBH and accretion rate (e.g., King 2008). Fanidakis et al. (2011) used GALFORM, the semi-analytical simulation of formation and evolution of galaxies, to study the effect these properties might have on the appearance of an AGN. Their simulation shows that massive, rapidly spinning SMBHs are hosted by giant early-type galaxies, while lower-mass SMBHs with much lower spins are mostly found in late-type galaxies. On the basis of the Blandford-Znajek (BZ) mechanism (Blandford & Znajek 1977), the authors suggest radio-loudness to be determined by the spin of the SMBH as only a rotating SMBH can form radio jets. In this scenario, the range of AGN fractions in our HLAGN sample suggests they may have a range of spins, ranging from AGN with rapidly rotating SMBHs with prominent AGN emission to SMBHs with low spin in which faint AGN emission might be diluted by the light of the host galaxy. This is supported by the results from Falcke & Biermann (1999) who derive equations for a scaled-down AGN jet model based on equipartition assumptions and applied it to observationally well defined samples of galactic and extragalactic sources. They find that the jet powers of their studied sources were comparable to their accretion disk luminosities providing evidence for a disk-jet coupling holding from stellar mass BHs to low-luminosity AGN.
Merloni & Heinz (2008) present a synthesis model for the AGN evolution where they studied how SMBHs grow and evolve through the age of the Universe. In this model, AGN with high Eddington ratios may display either only radiative feedback (high-radiative mode, HR) or both radiative and kinetic feedback (high-kinetic mode, HK). In this context, HLAGN with low radio AGN fractions (fAGN < 0.5) would be those which display mostly radiative feedback, while those with high radio AGN fractions (fAGN ≥ 0.5) also produce kinetic feedback in the form of radio-detectable features, such as cores, jets and lobes.
Radiative feedback is expected to arise in galaxies hosting rapidly accreting SMBHs, where the energy released by the growth of the SMBH can influence the properties of the hosts (e.g., see a review by Fabian 2012). The models of galaxy evolution usually find the AGN bolometric luminosity density to increase from the local redshift out to a peak around z ∼ 2 − 3, followed by a decrease toward higher redshifts (e.g., Croton et al. 2006; Merloni & Heinz 2008). For the ∼38% of HLAGN for which we estimated a radio luminosity arising from AGN emission (Sect. 3.2) we compare the radiative luminosity density to literature expectations (e.g., Croton et al. 2006; Merloni & Heinz 2008). We binned the radiative luminosities derived from the SED-fitting decomposition (see Delvecchio et al. 2017) into nine redshift bins, finding typical values of bolometric luminosity density to be < 1% of those found from the literature for all radiatively efficient AGN. This confirms that X-ray and MIR selected AGN detected in radio are not the dominant contribution to the total bolometric output expected for radiatively efficient AGN.
In the following sections, we describe how the number and luminosity densities of HLAGN change through cosmic time. By scaling the 1.4 GHz AGN luminosity into kinetic luminosity, we calculate the kinetic luminosity density and compare it to semi-analytic model predictions.
6.2. Cosmic evolution of radio AGN
To calculate the number and luminosity density, we use
where Φ(L1.4 GHz) is the redshift evolved luminosity function, using both best-fit evolution parameters derived from the redshift binned and continuous fitting. Here we take the lower and upper limits of the integral to be L1.4 GHz = 1022 WHz−1 and L1.4 GHz = 1028 WHz−1, respectively. The normalizations of the number and luminosity density evolution curves are affected by the chosen limits of integration. For example, a decrease of the lower limit to L1.4 GHz = 1021 WHz−1 would produce a number density higher by a factor of approximately five, but it would have almost no effect on the luminosity density curve. However, a decrease of the upper limit to L1.4 GHz = 1027 WHz−1 would lower the normalization of the luminosity density by a factor of approximately two, while the number density would remain unchanged.
The evolution of the number and luminosity densities is shown in Fig. 10. We find that the number density of HLAGN increased over time, reaching a maximum of ∼9.5 × 10−5 Mpc−3 in the redshift range 1 < z < 2.5, after which it decreased by a factor of approximately five toward the local (z = 0) value. A similar trend is seen in the luminosity density evolution, with the peak at ∼1.4 × 1020 WHz−1 Mpc−3 occurring in the redshift range 1 < z < 2.5 followed by a decline of a factor ∼10 toward the local value. An outlier in redshift bin 0.7 < z < 0.9 seen in Fig. 10 most likely occurs due to a large scale structure known to exists in the COSMOS field at z ∼ 0.73, as previously discussed in Sect. 5.2.
 |
Fig. 10. Redshift evolution of the number and luminosity density of AGN in COSMOS field for the PLE model are shown in the upper and lower panels, respectively. Magenta circles show the values of number and luminosity density for the HLAGN sample calculated from the redshift binned evolution parameters. Magenta and gray lines show the continuous redshift evolution and corresponding 1σ confidence range of HLAGN and the full sample, respectively. |
In Fig. 10 we also compare our results for the HLAGN sample with the results derived for all sources containing an AGN-related radio emission in the VLA-COSMOS 3 GHz Large Project sample with COSMOS2015 counterparts (labeled full sample). The analysis of the full sample is described in Appendix A. The number and luminosity densities of the full sample flatten over the redshift range 1 < z < 2.5 at ∼2.2 × 10−4 Mpc−3 and 1.7 × 1020 WHz−1 Mpc−3, respectively. The more rapid decrease with redshift of the HLAGN number and luminosity density at z > 2 when compared to the full sample may be in part explained by the incompleteness of X-ray data used to classify sources as HLAGN (see also Discussion in Smolčić et al. 2017b). We note that the Mauch & Sadler (2007) local luminosity function used to constrain the evolution of the full sample has a different shape than the one by Pracy et al. (2016) used to constrain the evolution of HLAGN. The difference between the two local luminosity functions results in a higher normalization of the number density curve for the full sample with respect to the HLAGN curve.
6.3. Kinetic feedback of radio AGN and comparison with semi-analytic models
To get an insight into how the kinetic feedback of AGN changes through cosmic time, one of many scaling relations available in the literature (e.g., Willott et al. 1999; Merloni & Heinz 2007; Godfrey & Shabala 2016) can be used to estimate the kinetic luminosity (see, e.g., Appendix A in Smolčić et al. 2017b). Willott et al. (1999) used the minimum energy condition to estimate the energy stored in lobes from the observed monochromatic synchrotron emission, finding the relation
where Lkin is the kinetic luminosity, L1.4 GHz is the 1.4 GHz radio luminosity and fW is the factor into which all the uncertainties were combined. Using observational constraints, fW is estimated to be in the range of 1–20. In this work, the Willott et al. (1999) conversion is used to estimate the kinetic luminosity of HLAGN and the full radio detected samples. We assumed fW = 15 for which the Willott et al. (1999) relation agrees with results found from radio and X-ray observations of cavities in galaxy groups and clusters (Bîrzan et al. 2004; O’Sullivan et al. 2011).
To calculate the kinetic luminosity density at a given redshift, we use the relation
where Φ(L1.4 GHz) is the analytic form of the local luminosity function (see Eq. (12)) and Ωkin is the kinetic luminosity density (KLD; see Fig. 11). The normalization of the KLD curve is highly affected by the Willott et al. (1999) uncertainty factor fW, whose values can shift the curve both toward lower and higher values9. By assuming fW = 15, the KLD curve of HLAGN peaks at the value 2.1 × 1032 W Mpc−3 at z ∼ 1.5. The full sample KLD curve is relatively flat in the redshift range 1 < z < 2.5 at the value 3.4 × 1032 W Mpc−3.
 |
Fig. 11. Cosmic evolution of the kinetic luminosity density. Upper panel: kinetic luminosity density derived using the Willott et al. (1999) conversion between radio and kinetic luminosity for the PLE continuous and redshift binned model of HLAGN is shown by a magenta line and circles, respectively, with the corresponding 1σ uncertainties. The KLD estimate for the starburst mode of accretion based on the semi-analytic GALFORM model as calculated by Griffin et al. (in prep.) is shown by a blue dashed line. Lower panel: KLD for the PLE continuous and redshift binned models of the full sample (gray line and circles, respectively), with corresponding 1σ uncertainties. The black solid line shows the prediction of the semi-analytical model for the radio mode of BH accretion by Croton et al. (2016). Estimates of the KLD based on the GALFORM model for the starburst and hot-halo modes of accretion and their sum are shown with blue, red and black dashed lines, respectively. |
Using the calculations embedded in the GALFORM semi-analytic model of formation and evolution of galaxies (Bower et al. 2006), Fanidakis et al. (2012) studied the evolution of AGN across cosmic time. In their model, the buildup of BH mass occurs in two different modes: (i) starburst mode in which the accretion event is triggered by disk instabilities or galaxy mergers, and (ii) hot-halo mode in which the gas from a quasi-hydrostatic hot halo accretes onto the SMBH. They find that different accretion channels show different evolutionary trends, with starburst and hot-halo modes changing their dominance in the buildup of SMBH mass from higher to lower redshifts, respectively. An update of the Fanidakis et al. (2012) model, using a new version of GALFORM (Lacey et al. 2016), will be presented in Griffin et al. (in prep.). After the implementation of the Planck cosmology and using a higher resolution dark matter simulation, one of predictions by Griffin et al. is the cosmic evolution of kinetic luminosity density for the starburst and hot-halo modes of BH accretion (see Fig. 11). The kinetic luminosity density is expected to arise from AGN jets in both of these modes. In the hot halo mode gas from the hot halo slowly accretes onto the SMBH, forming an advection-dominated accretion flow (ADAF; Narayan & Yi 1994). On the other hand, in the starburst mode a merger or a disk instability causes stars to form from inflowing gas which may also accrete onto the SMBH, in the form of a standard thin disk accretion (Shakura & Sunyaev 1973).
The selection of our HLAGN sample based on X-ray and MIR criteria aims to trace the thin disk accreters and therefore should be compared to the starburst mode AGN from GALFORM. In the upper panel of Fig. 11, the HLAGN KLD curve shows a steep increasing trend similar to that predicted for the starburst mode of accretion out to a z ∼ 2. At higher redshifts the HLAGN evolutionary curve disagrees with predictions for the starburst mode of accretion. A possible reason for the disagreement could be an overly simplistic conversion between the monochromatic and kinetic luminosity. A more complex conversion dependent on various parameters, such as synchrotron age and environments (Hardcastle & Krause 2014; Kapinska et al. 2015), could alter the overall shape of the KLD curve. Another reason could be the incompleteness of the HLAGN sample at high redshifts (Delvecchio et al. 2017). If we were to exclude the highest redshift measurement and fit the evolution to the data, our results would show agreement to GALFORM prediction for the starburst mode out to a z ∼ 3 (as shown in the upper panel of Fig. 11). However, the discrepancy still remains between our results and the GALFORM prediction present at higher redshift. We note that, as detailed below, various semi-analytic models tend to disagree in this regime as well.
In the lower panel of Fig. 11 we show the comparison between the KLD curve derived for the full sample and the prediction from semi-analytic models. Despite the difference in normalizations, the KLD curve of the full sample interestingly shows a similar shape to the total KLD estimate from GALFORM, both of which contain kinetic luminosity contribution of all AGN, regardless of the assumed mode of accretion.
We also compare our results of the full sample with the semi-analytical simulation of cosmological galaxy formation by Croton et al. (2006). They examined two different modes of SMBH accretion, namely quasar and radio mode. They find that powerful outflows that occur in radio mode accretion can efficiently quench star formation in massive systems, thus offering a solution for the cooling flow problem. One of the predictions of their model is the BH accretion rate density evolution, estimated using the Bondi-Hoyle accretion model. An update to this work is presented in Croton et al. (2016) where the authors introduce the so-called radio mode efficiency factor to modulate the strength of the SMBH accretion. Using the accretion rate formula (see Eq. (16) in Croton et al. 2016), and adopting the suggested radio mode efficiency parameter value of 0.08, the SMBH luminosity can be calculated. Under the assumption that most of the accretion energy is ejected in the kinetic form, we can compare the Croton et al. (2006) SMBH luminosity to our estimate of KLD for the full sample which contains the contribution from all AGN that show evidence of AGN-related radio emission. At redshifts higher than z ∼ 1.5 the full sample KLD curve shows a decline similar to that expected from semi-analytic simulation by Croton et al. (2016) for the radio mode AGN. The observed decline toward the local value at lower redshift instead is not in agreement with the predicted radio mode curve. As discussed, the normalization of KLD curves is affected by the uncertainty on the fW factor. The normalization of the peak of the KLD curve of the full sample would agree with the Croton et al. (2016) expectations for fW = 4.
From Fig. 11 it is clear that the two compared simulations disagree in their predictions of the KLD both in normalization and overall shape. This stresses the need for more in-depth studies of the conversion between monochromatic and kinetic luminosity.
In summary, we find that our data do not completely agree with any of the predictions from the available models. However, given the significant uncertainties present both in the data and in the models, it is interesting to note that each of the features shown by the data (i.e., approximately constant maximum of KLD in the redshift range 1 < z < 2.5, with significant decreases at both lower and higher redshift), are predicted by at least one of the models. This suggests that, using somewhat different assumptions, it should be possible to generate new models of galaxy evolution which could better reproduce our data.
7. Summary and conclusions
In this work we present an analysis of a sample of 1604 X-ray and mid-IR selected AGN with moderate-to-high radiative luminosities (HLAGN) from the VLA-COSMOS 3 GHz Large Project, selected to trace analogs of local high-excitation radio galaxies (HERGs) out to z ∼ 6. Our findings are summarized as follows.
To study the origin of the radio emission in our HLAGN sample, we developed the method of statistical decomposition of the observed 3 GHz radio luminosities into contributions arising from star-forming processes and AGN activity. In agreement with other studies of X-ray and MIR selected AGN samples, we find that the majority, (68.0 ± 1.5)%, of HLAGN have radio emission dominated by star-forming processes (0 ≤ fAGN ≤ 0.5), while (32.0 ± 1.5)% of them are dominated by the AGN-related emission in the radio (0.5 < fAGN ≤ 1.0).
For all sources with fAGN > 0 we calculated the AGN luminosity by scaling the total 1.4 GHz luminosity (converted from the observed 3 GHz radio luminosity) by the derived AGN fraction. Using a complete subsample (S3 GHz, AGN ≥ Slim, 3 GHz) of HLAGN we construct the 1.4 GHz radio AGN luminosity function of HLAGN out to z ∼ 6. By assuming pure luminosity and pure density evolution models we find L*(z)∝(1 + z)(3.97 ± 0.15)+(−0.92 ± 0.06)z and Φ*(z)∝ (1 + z)(2.64 ± 0.10)+(−0.61 ± 0.04)z, respectively.
We further studied the evolution of the number and luminosity densities of the HLAGN population. We find an increasing trend from high redshifts up to a flattening at redshifts 1 < z < 2.5, followed by a significant decrease down to the value in the local Universe.
We estimated the kinetic luminosity density and find an approximately constant maximum in the redshift range 1 < z < 2.5. By comparing this behavior to expectations from semi-analytic models of galaxy formation and evolution, we find that such behavior is not entirely expected by any of the models tested here. However, given the significant uncertainties present both in the data and in the models, the similarities found show that by modifying assumptions of these models, it should be possible to better reproduce our data.
The X-ray data used to classify HLAGN are taken from the COSMOS Legacy/Chandra COSMOS surveys (see Civano et al. 2016; Marchesi et al. 2016).
The MIR data used to select HLAGN are taken from the SPLASH project (IRAC/Spitzer space telescope; see Steinhardt et al. 2014).
A justification for the use of the HLAGN nomenclature is provided in Smolčić et al. (2017c). They find that, despite the overlap between two classes, HLAGN sources classified as such on the basis of X-ray and MIR criteria, as well as SED fitting, tend to have higher (∼1 dex) radiative luminosities than MLAGN. This trend is present at all redshifts they studied (0.01 ≤ z ≤ 5.70), confirming that this naming convention is justified in a statistical sense (see also Delvecchio et al. 2017).
To minimize the effect binning might have on our results, we used Freedman-Diaconis rule (Freedman & Diaconis 1981) to choose qTOT bin widths:
where IQR(x) is the interquartile range of the data within the bin and n is the number of sources within that bin.
The average rms reported by Schinnerer et al. (2010) is 12 μJy beam−1.
Acknowledgments
The authors are grateful to the referee for comments which helped to improve the content of this article. LC is grateful to A. Griffin for useful suggestions. This research was founded by the European Union’s Seventh Frame-work program under grant agreement 337595 (ERC Starting Grant, “CoSMass”). JD acknowledges financial assistance from the South African SKA Project (SKA SA; www.ska.ac.za). EV acknowledges funding from the DFG grant BE 1837/13-1 and support of the Collaborative Research Center 956, subproject A1 and C4, funded by the Deutsche Forschungsgemeinschaft (DFG).
References
- Becker, R. H., White, R. L., & Helfand, D. J. 1994, in Astronomical Data Analysis Software and Systems III, eds. D. R. Crabtree, R. J. Hanisch, & J. Barnes, ASP Conf. Ser., 61, 165 [NASA ADS] [Google Scholar]
- Bell, E. F. 2003, ApJ, 586, 794 [Google Scholar]
- Best, P. N., & Heckman, T. M. 2012, MNRAS, 421, 1569 [NASA ADS] [CrossRef] [Google Scholar]
- Best, P. N., Ker, L. M., Simpson, C., Rigby, E. E., & Sabater, J. 2014, MNRAS, 445, 955 [NASA ADS] [CrossRef] [Google Scholar]
- Bîrzan, L., Rafferty, D. A., McNamara, B. R., Wise, M. W., & Nulsen, P. E. J. 2004, ApJ, 607, 800 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & Znajek, R. L. 1977, MNRAS, 179, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Bonzini, M., Padovani, P., Mainieri, V., et al. 2013, MNRAS, 436, 3759 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, R. G., Benson, A. J., Malbon, R., et al. 2006, MNRAS, 370, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Brinchmann, J., Charlot, S., White, S. D. M., et al. 2004, MNRAS, 351, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Capak, P., Aussel, H., Ajiki, M., et al. 2007, ApJS, 172, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Cavagnolo, K. W., McNamara, B. R., Nulsen, P. E. J., et al. 2010, ApJ, 720, 1066 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Ching, J. H. Y., Sadler, E. M., Croom, S. M., et al. 2017, MNRAS, 464, 1306 [NASA ADS] [CrossRef] [Google Scholar]
- Civano, F., Marchesi, S., Comastri, A., et al. 2016, ApJ, 819, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J. 1992, ARA&A, 30, 575 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [NASA ADS] [CrossRef] [Google Scholar]
- Croton, D. J., Springel, V., White, S. D. M., et al. 2006, MNRAS, 365, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Croton, D. J., Stevens, A. R. H., Tonini, C., et al. 2016, ApJS, 222, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Delhaize, J., Smolčić, V., Delvecchio, I., et al. 2017, A&A, 602, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delvecchio, I., Smolčić, V., Zamorani, G., et al. 2017, A&A, 602, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Donley, J. L., Koekemoer, A. M., Brusa, M., et al. 2012, ApJ, 748, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Dunlop, J. S., McLure, R. J., Kukula, M. J., et al. 2003, MNRAS, 340, 1095 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C. 2012, ARA&A, 50, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Falcke, H., & Biermann, P. L. 1999, A&A, 342, 49 [NASA ADS] [Google Scholar]
- Fanidakis, N., Baugh, C. M., Benson, A. J., et al. 2011, MNRAS, 410, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Fanidakis, N., Baugh, C. M., Benson, A. J., et al. 2012, MNRAS, 419, 2797 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrarese, L., & Merritt, D. 2000, ApJ, 539, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Filho, M. E., Barthel, P. D., & Ho, L. C. 2006, A&A, 451, 71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Freedman, D., & Diaconis, P. 1981, Probab. Theor. Relat. Fields, 57, 453 [Google Scholar]
- Gehrels, N. 1986, ApJ, 303, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Gendre, M. A., Best, P. N., Wall, J. V., & Ker, L. M. 2013, MNRAS, 430, 3086 [NASA ADS] [CrossRef] [Google Scholar]
- Godfrey, L. E. H., & Shabala, S. S. 2016, MNRAS, 456, 1172 [NASA ADS] [CrossRef] [Google Scholar]
- Goulding, A. D., Forman, W. R., Hickox, R. C., et al. 2014, ApJ, 783, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Guzzo, L., Cassata, P., Finoguenov, A., et al. 2007, ApJS, 172, 254 [NASA ADS] [CrossRef] [Google Scholar]
- Hardcastle, M. J., & Krause, M. G. H. 2014, MNRAS, 443, 1482 [NASA ADS] [CrossRef] [Google Scholar]
- Heckman, T. M., & Best, P. N. 2014, ARA&A, 52, 589 [Google Scholar]
- Herrera Ruiz, N., Middelberg, E., Deller, A., et al. 2017, A&A, 607, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hickox, R. C., Jones, C., Forman, W. R., et al. 2009, ApJ, 696, 891 [Google Scholar]
- Ho, L. C., Filippenko, A. V., & Sargent, W. L. W. 1997, ApJS, 112, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Iovino, A., Petropoulou, V., Scodeggio, M., et al. 2016, A&A, 592, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kapinska, A. D., Hardcastle, M., Jackson, C., et al. 2015, Advancing Astrophysics with the Square Kilometre Array, (AASKA14), 173 [Google Scholar]
- Kennicutt, Jr., R. C. 1998, ApJ, 498, 541 [NASA ADS] [CrossRef] [Google Scholar]
- King, A. 2008, Mem. Soc. Astron. It., 79, 1066 [NASA ADS] [Google Scholar]
- Lacey, C. G., Baugh, C. M., Frenk, C. S., et al. 2016, MNRAS, 462, 3854 [NASA ADS] [CrossRef] [Google Scholar]
- Laigle, C., McCracken, H. J., Ilbert, O., et al. 2016, ApJS, 224, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Magnelli, B., Ivison, R. J., Lutz, D., et al. 2015, A&A, 573, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magorrian, J., Tremaine, S., Richstone, D., et al. 1998, AJ, 115, 2285 [NASA ADS] [CrossRef] [Google Scholar]
- Marchesi, S., Civano, F., Elvis, M., et al. 2016, ApJ, 817, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Marshall, H. L. 1985, ApJ, 299, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Mauch, T., & Sadler, E. M. 2007, MNRAS, 375, 931 [NASA ADS] [CrossRef] [Google Scholar]
- Merloni, A., & Heinz, S. 2007, MNRAS, 381, 589 [NASA ADS] [CrossRef] [Google Scholar]
- Merloni, A., & Heinz, S. 2008, MNRAS, 388, 1011 [NASA ADS] [Google Scholar]
- Miller, P., Rawlings, S., & Saunders, R. 1993, MNRAS, 263, 425 [NASA ADS] [Google Scholar]
- Narayan, R., & Yi, I. 1994, ApJ, 428, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Narayan, R., & Yi, I. 1995, ApJ, 444, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Novak, M., Smolčić, V., Delhaize, J., et al. 2017, A&A, 602, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Novak, M., Smolcic, V., Schinnerer, E., et al. 2018, A&A, 614, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- O’Sullivan, E., Giacintucci, S., David, L. P., et al. 2011, ApJ, 735, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Padovani, P., Bonzini, M., Kellermann, K. I., et al. 2015, MNRAS, 452, 1263 [Google Scholar]
- Pracy, M. B., Ching, J. H. Y., Sadler, E. M., et al. 2016, MNRAS, 460, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Rigby, E. E., Argyle, J., Best, P. N., Rosario, D., & Röttgering, H. J. A. 2015, A&A, 581, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salim, S., Rich, R. M., Charlot, S., et al. 2007, ApJS, 173, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Sargent, M. T., Schinnerer, E., Murphy, E., et al. 2010, ApJS, 186, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Schinnerer, E., Smolčić, V., Carilli, C. L., et al. 2007, ApJS, 172, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Schinnerer, E., Sargent, M. T., Bondi, M., et al. 2010, ApJS, 188, 384 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, M. 1968, ApJ, 151, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Smolcic, V. 2016, ArXiv e-prints [arXiv:1603.05687] [Google Scholar]
- Smolčić, V., Zamorani, G., Schinnerer, E., et al. 2009, ApJ, 696, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Smolčić, V., Novak, M., Bondi, M., et al. 2017a, A&A, 602, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smolčić, V., Novak, M., Delvecchio, I., et al. 2017b, A&A, 602, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smolčić, V., Delvecchio, I., Zamorani, G., et al. 2017c, A&A, 602, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Steinhardt, C. L., Speagle, J. S., Capak, P., et al. 2014, ApJ, 791, L25 [Google Scholar]
- Whitaker, K. E., van Dokkum, P. G., Brammer, G., & Franx, M. 2012, ApJ, 754, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Willott, C. J., Rawlings, S., Blundell, K. M., & Lacy, M. 1999, MNRAS, 309, 1017 [NASA ADS] [CrossRef] [Google Scholar]
- York, D. G., Adelman, J., Anderson, Jr., J. E., et al. 2000, AJ, 120, 1579 [CrossRef] [Google Scholar]
- Yun, M. S., Reddy, N. A., & Condon, J. J. 2001, ApJ, 554, 803 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Analysis of the full radio sample in the COSMOS field
In Sect. 3.2 we introduce the method of statistically decomposing the total radio luminosity of HLAGN into the components arising from star-forming processes and from AGN activity. In this section we describe the calibration of the star formation-related infrared-to-1.4 GHz luminosity ratio, qSF, on the full sample of the radio detected sources from the VLA-COSMOS 3 GHz Large Project with COSMOS2015 counterparts. We further used the derived calibration to decompose the total radio luminosities of the full sample and constrain the evolution of its radio AGN luminosity function.
A.1. Calibration of the infrared-to-1.4 GHz luminosity ratio of the host galaxy
The full sample of the radio detected sources from the VLA-COSMOS 3 GHz Large Project with COSMOS2015 counterparts contains 7729 sources, classified as HLAGN, MLAGN or SFGs (see Sect. 2.2). We refer to this sample as the full sample. Since we aim at isolating the AGN-related radio emission, here we have used the decomposition technique to derive AGN fractions for all sources which display radio excess, assuming this excess arises from AGN activity.
By studying the sample of 9575 SFGs in the COSMOS field, Delhaize et al. (2017) found a redshift dependent IRRC. Their SFG sample contained both direct radio and far-infrared measurements and limits. On the other hand, the full sample considered here contains only radio (3 GHz) detections. For this reason, we derived a separate IRRC by binning this radio detected sample in nine redshift bins (defined as in the analysis of the HLAGN sample). For each source we calculated the infrared-to-total 1.4 GHz luminosity ratio (qTOT) as defined in Sect. 3.2, Eq. (2). The calculated values are shown in Fig. A.1.
 |
Fig. A.1. Infrared-to-1.4 GHz luminosity ratio vs. redshift, color-coded by AGN fractions. The magenta dashed line is the redshift dependent analytic form calibrated by Delhaize et al. (2017) on a sample of SFGs, with ±1σ spread (magenta area). White circles show the redshift binned peak values of the IR-to-1.4 GHz luminosity ratio calibrated on the full radio detected sample. |
To find the median and corresponding 1σ confidence range originating from the star-forming processes we locate the peak (q̄SF,z) of the qTOT distribution in each redshift bin. We then mirror the part of the qTOT distribution above the location of its peak where we are certain that all radio emission originates from the star formation (e.g., Bell 2003; Magnelli et al. 2015). By fitting a Gaussian functional form to the mirrored distribution, we find the dispersion. To account for the uncertainties on the luminosities used in the calculation of the qTOT, we used a Monte Carlo method. Derived peaks per redshift bin, q̄SF,z, are also shown in Fig. A.1 as white circles.
Derived in this way, the IRRC has slightly lower values below z ∼ 1.5 than the correlation derived by Delhaize et al. (2017) and increases toward higher redshifts. The observed trend is not in agreement with result by Delhaize et al. (2017) and most likely occurs due to differently selected samples (e.g., Sargent et al. 2010).
By following the procedure described in Sect. 3.2, we derived AGN fractions for all sources within the full sample. For (77.4 ± 1.4)% of these sources we find radio emission to be dominated by star-forming processes in the radio (0 ≤ fAGN ≤ 0.5), while the rest, (22.6 ± 1.4)%, are dominated by the AGN-related radio emission (0.5 < fAGN ≤ 1.0).
By imposing a redshift dependent threshold, Delvecchio et al. (2017) found that ∼23% of the sources in the full sample display radio excess due to the presence of AGN-related radio emission. For a comparison, with the method of statistical decomposition we effectively imposed a “lower” threshold and found evidence of AGN-related emission in ∼26% of the sample. This method enables us to retrieve information on the AGN contribution to the total radio luminosity also in sources which are not dominated by AGN activity in the radio part of the electromagnetic spectrum.
A.2. Radio AGN luminosity functions and the cosmic evolution of AGN within the full 3 GHz sample
In this section we describe luminosity functions constructed using the same methods as described in Sect. 4. The total luminosity functions were constructed from the total 1.4 GHz luminosities of all sources within the full sample. The AGN luminosity functions were calculated using the AGN luminosities of sources from the full sample which would be observable by our survey (S3 GHz, AGN ≥ Slim, 3 GHz). Both the total and AGN luminosity functions of the full sample are shown in Fig. A.2. The values of the AGN luminosity functions are listed in Table A.2.
 |
Fig. A.2. 1.4 GHz AGN luminosity function of the full VLA-COSMOS 3 GHz Large Project sample with COSMOS2015 counterparts out to z ∼ 6. The AGN and total luminosity functions are shown with black and red circles, respectively. Solid and dashed black lines show the fit of analytic local AGN luminosity function in PDE and PLE models, respectively, with shaded areas indicating 1σ confidence range. The black and red vertical dashed lines show the luminosity corresponding to the 5σ sensitivity at zmin and zmax of the redshift bin, respectively. Results from the literature are also shown, as detailed in the legend. |
Following the same procedure as in Sect. 5.2, we used the analytic form of the local luminosity function to trace the cosmic evolution of this sample, which after decomposition contains the entire radio AGN population in the COSMOS field. We used the analytic form of the local luminosity function as derived by Mauch & Sadler (2007):
with parameters Φ* = 10−5.1 Mpc−3 dex−1, L* = 1024.59 WHz−1, α = −1.27, β = −0.49. To constrain the shape of the luminosity function over six orders of magnitudes, Mauch & Sadler (2007) used a sample of 2661 spectroscopically selected RL AGN from a local (z ∼ 0.073) sample of the NVSS sources in the six-degree Field Galaxy Survey (6dFGS). We fit the Mauch & Sadler (2007) analytic form of the local luminosity function to our AGN luminosity functions. Values of evolution parameters derived as described in Sect. 5.2 are shown in Table A.1 and in Fig. A.3. Best-fit parameters obtained with a continuous fit of the analytic form are αl = 1.97 ± 0.10 and βl = −0.46 ± 0.04 in the case of pure luminosity evolution (αd = βd = 0). In the case of pure density evolution (αl = βl = 0) the best-fit parameters are αd = 1.24 ± 0.08 and βd = −0.25 ± 0.03.
Best-fit evolution parameters obtained by fitting local luminosity function to redshift binned data assuming pure density (αD) and pure luminosity (αL) evolution.
 |
Fig. A.3. Fitting parameters obtained to model the redshift evolution of the full AGN sample. Green (magenta) circles and line show the pure luminosity (density) evolution parameter values and model, respectively. |
Smolčić et al. (2017b) constructed the 1.4 GHz luminosity functions of radio AGN selected by applying a redshift dependent (>3σ) threshold in the ratio of the radio luminosity and SFRs derived from IR luminosities. This selection yielded a sample of 1814 sources in which over 80% of radio emission comes from an AGN activity. By fitting the analytical form of local luminosity function by Mauch & Sadler (2007), as done also here, they constrained the pure density and pure luminosity evolutions of the radio AGN luminosity function out to z ∼ 5.5. We show their luminosity functions for the PLE model in Fig. A.2. Their results agree well with AGN luminosity functions of the full sample. The modeling of the redshift evolution of their luminosity function is equivalent to the analysis described here. The differences found in the evolution parameters in the case of the discrete and continuous fitting of the radio luminosity function come from several factors. To ensure a complete sample, we first imposed an AGN flux density cut which reduces the number of sources used in the analysis. We calculated the maximum observable volume of each source using the AGN luminosity derived from the luminosity decomposition analysis, obtaining lower values for the volumes than would be the case if using the total luminosity of the source. Finally, to construct luminosity functions we used the AGN luminosities, which are the total luminosities scaled by AGN fraction. All of these factors result in slightly different values of evolution parameters obtained here and by Smolčić et al. (2017b). However, the results are still consistent within 2σ.
AGN luminosity functions for the full VLA-COSMOS 3 GHz Large Project sample with COSMOS2015 multiwavelength counterparts.
We also compare our results with the study done by Novak et al. (2018). Using a sample of 8035 radio detected sources from the VLA-COSMOS 3 GHz Large Project with COSMOS2015 (Laigle et al. 2016) and i-band (Capak et al. 2007) multiwavelength counterparts they constrained the evolution of the total radio luminosity function. To construct the total radio luminosity function, they combine the local luminosity functions of SFGs and of AGN from the literature. Our total (AGN+SF) luminosity functions shown in Fig. A.2 are in excellent agreement with their results.
Agreement with the results by Smolčić et al. (2017b) and Novak et al. (2018) shows that the high luminosity end of AGN luminosity function as derived here is populated by sources which are predominantly dominated by AGN activity. Sources with lower AGN fractions are more common toward the lower luminosity end of AGN luminosity function, in a regime below the luminosity threshold of our survey. In this regime, the decomposition allows us to go further in determining the true shape of the AGN luminosity function.
Using the evolution parameters as derived with the continuous fit to all data simultaneously, we further calculate the number and luminosity density evolution curves which are described in Sect. 6.2 and shown in Fig. 10. Using the Willott et al. (1999) conversion between the monochromatic 1.4 GHz luminosity and the kinetic luminosity, we estimated the kinetic luminosity density of the full sample and in Sect. 6.3 we discuss it in the context of semi-analytic models from the literature.
All Tables
Best-fit evolution parameters obtained by the fitting local luminosity function to the redshift binned data assuming pure density (αD) and pure luminosity (αL) evolution.
Best-fit evolution parameters obtained by fitting local luminosity function to redshift binned data assuming pure density (αD) and pure luminosity (αL) evolution.
AGN luminosity functions for the full VLA-COSMOS 3 GHz Large Project sample with COSMOS2015 multiwavelength counterparts.
All Figures
 |
Fig. 1. Infrared-to-1.4 GHz radio luminosity ratio (qTOT) vs. L1.4 GHz for HLAGN (black crosses). Radio luminosity binned median values of the ratio are shown with red circles with error bars showing 16th and 84th percentiles of the distribution. The dashed magenta line corresponds to the IRRC derived by Delhaize et al. (2017) at the median redshift of the underlying HLAGN sample, along with its 1σ spread of ±0.35 dex. Blue solid lines and area show the median of the star-forming peak q̄SF,z and 1σq SF,z uncertainties calibrated on the full radio detected sample of the VLA-COSMOS 3 GHz Large Project sources with the COSMOS2015 counterparts. |
| In the text | |
 |
Fig. 2. Example of one iteration of the qTOT distribution for the HLAGN (gray histogram) overlaid with the Gaussian functional forms showing the contribution of star-forming processes in the redshift bin 2.1 < z < 3.0. Gaussian functional forms show the contribution from the star formation as derived from the full sample and after scaling it to the normalization of the HLAGN distribution at the q̄SF,z (shown with magenta and orange lines, respectively). |
| In the text | |
 |
Fig. 3. Infrared-to-1.4 GHz radio luminosity ratio (qTOT) vs. redshift for the HLAGN. The data are color-coded by their median values of AGN fractions. The magenta dashed line is the redshift dependent analytic form calibrated by Delhaize et al. (2017) on a sample of SFGs, with ±1σ spread (magenta area). White dots show the peaks (q̄SF,z) of the underlying qTOT distribution calibrated on the star-forming galaxies in the full radio detected sample. |
| In the text | |
 |
Fig. 4. Histogram of median AGN fractions across all redshifts, computed using Eq. (3) (see text for details). Error bars show the 16th and 84th percentile values. |
| In the text | |
 |
Fig. 5. Radio AGN luminosity function at 1.4 GHz at redshifts 0.1 < z < 6.1. AGN and total luminosity functions of HLAGN are plotted as magenta and green points, respectively. Solid and dashed magenta lines show the fit of the analytic form of the local luminosity function to our AGN luminosity function data for the pure density and pure luminosity evolutions, respectively, with shaded areas indicating 1σ confidence range. The black and red vertical dashed lines show the luminosity corresponding to the 5σ sensitivity at zmin and zmax of the redshift bin, respectively. Results from the literature are also shown, as detailed in the legend. |
| In the text | |
 |
Fig. 6. Distribution of the ratio of 1.4 GHz radio luminosity to SFR as a function of the 1.4 GHz radio luminosity for HERGs (blue symbols) and SFGs (yellow symbols) drawn from the LARGESS sample and cross-correlated with the MPA-JHU DR7 catalog. Median values of the ratio for HERGs and SFGs are shown by the filled black and red circles, respectively. The black solid line represents the linear fit to the median values for the HERG population. The red solid line represents the average value of the ratio of 1.4 GHz luminosity to SFR for star forming galaxies. |
| In the text | |
 |
Fig. 7. Local HERG luminosity function. Black circles show the total (AGN+SF) volume densities, while the gray line is the analytic fit to the data as done by Pracy et al. (2016). Magenta circles show the AGN luminosity functions derived by decomposing the total luminosity. The overlap between AGN and total volume densities confirms that the radio luminosity of sources in the HERG sample by Pracy et al. (2016) is dominated by the AGN emission. |
| In the text | |
 |
Fig. 8. Parameters obtained from fitting two different redshift evolution models to the HLAGN luminosity functions. Green and magenta circles show the evolution parameters obtained from fitting the assumed analytic form of the luminosity function in nine redshift bins assuming pure luminosity and pure density evolution scenarios, respectively (see text for details). The same color lines show the results from the continuous fit assuming that the PLE and PDE parameters evolve linearly with redshift. |
| In the text | |
 |
Fig. 9. VLBA-to-VLA AGN flux density ratio vs. 1.4 GHz AGN luminosity. Yellow circles show the luminosity binned values of the ratio, while solid and dashed black lines show the median, 84th and 16th percentile values of the sample with L1.4 GHz, TOT ≥ 1024.4 WHz−1. Blue, green, and magenta circles and error bars show the data in three redshift bins as indicated in the legend. For better visibility of error bars, we introduced a small shift along the luminosity axis. |
| In the text | |
 |
Fig. 10. Redshift evolution of the number and luminosity density of AGN in COSMOS field for the PLE model are shown in the upper and lower panels, respectively. Magenta circles show the values of number and luminosity density for the HLAGN sample calculated from the redshift binned evolution parameters. Magenta and gray lines show the continuous redshift evolution and corresponding 1σ confidence range of HLAGN and the full sample, respectively. |
| In the text | |
 |
Fig. 11. Cosmic evolution of the kinetic luminosity density. Upper panel: kinetic luminosity density derived using the Willott et al. (1999) conversion between radio and kinetic luminosity for the PLE continuous and redshift binned model of HLAGN is shown by a magenta line and circles, respectively, with the corresponding 1σ uncertainties. The KLD estimate for the starburst mode of accretion based on the semi-analytic GALFORM model as calculated by Griffin et al. (in prep.) is shown by a blue dashed line. Lower panel: KLD for the PLE continuous and redshift binned models of the full sample (gray line and circles, respectively), with corresponding 1σ uncertainties. The black solid line shows the prediction of the semi-analytical model for the radio mode of BH accretion by Croton et al. (2016). Estimates of the KLD based on the GALFORM model for the starburst and hot-halo modes of accretion and their sum are shown with blue, red and black dashed lines, respectively. |
| In the text | |
 |
Fig. A.1. Infrared-to-1.4 GHz luminosity ratio vs. redshift, color-coded by AGN fractions. The magenta dashed line is the redshift dependent analytic form calibrated by Delhaize et al. (2017) on a sample of SFGs, with ±1σ spread (magenta area). White circles show the redshift binned peak values of the IR-to-1.4 GHz luminosity ratio calibrated on the full radio detected sample. |
| In the text | |
 |
Fig. A.2. 1.4 GHz AGN luminosity function of the full VLA-COSMOS 3 GHz Large Project sample with COSMOS2015 counterparts out to z ∼ 6. The AGN and total luminosity functions are shown with black and red circles, respectively. Solid and dashed black lines show the fit of analytic local AGN luminosity function in PDE and PLE models, respectively, with shaded areas indicating 1σ confidence range. The black and red vertical dashed lines show the luminosity corresponding to the 5σ sensitivity at zmin and zmax of the redshift bin, respectively. Results from the literature are also shown, as detailed in the legend. |
| In the text | |
 |
Fig. A.3. Fitting parameters obtained to model the redshift evolution of the full AGN sample. Green (magenta) circles and line show the pure luminosity (density) evolution parameter values and model, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



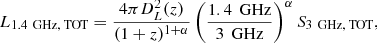
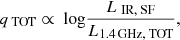
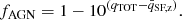
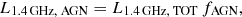
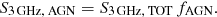
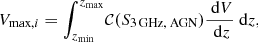
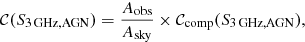
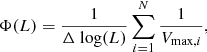
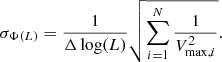
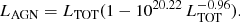
![$$ \begin{aligned} \Phi ({L,z})=(1+{z})^{\alpha _{\rm D}}\ \Phi _{0}\left[ \dfrac{L}{(1+{z})^{\alpha _{\rm L}}}\right], \end{aligned} $$](/articles/aa/full_html/2018/12/aa33935-18/aa33935-18-eq14.gif)
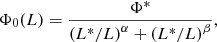
![$$ \begin{aligned} \Phi ({L,z})=(1+{z})^{\alpha _{\text{ d}}+{z}\cdot \beta _{\text{ d}}} \times \Phi _0 \left[ \dfrac{{L}}{(1+{z})^{\alpha _{\rm l}+{z}\cdot \beta _{\rm l}}} \right], \end{aligned} $$](/articles/aa/full_html/2018/12/aa33935-18/aa33935-18-eq16.gif)