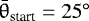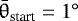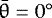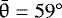| Issue |
A&A
Volume 620, December 2018
|
|
|---|---|---|
| Article Number | A201 | |
| Number of page(s) | 19 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201833596 | |
| Published online | 17 December 2018 | |
Ceres’ opposition effect observed by the Dawn framing camera
1
Deutsches Zentrum für Luft- und Raumfahrt (DLR),
12489 Berlin,
Germany
e-mail: stefanus.schroeder@dlr.de
2
Planetary Science Institute,
Tucson,
AZ 85719, USA
3
Jet Propulsion Laboratory, California Institute of Technology,
Pasadena,
CA 91109, USA
4
Institute of Geophysics and Planetary Physics, University of California,
Los Angeles,
CA 90095-1567, USA
5
Istituto di Astrofisica e Planetologia Spaziali,
Istituto Nazionale di Astrofisica,
00133 Rome, Italy
6
Goddard Space Flight Center,
Greenbelt,
MD 20771, USA
Received:
8
June
2018
Accepted:
23
October
2018
Context. The surface reflectance of planetary regoliths may increase dramatically towards zero phase angle, a phenomenon known as the opposition effect (OE). Two physical processes that are thought to be the dominant contributors to the brightness surge are shadow hiding (SH) and coherent backscatter (CB). The occurrence of shadow hiding in planetary regoliths is self-evident, but it has proved difficult to unambiguously demonstrate CB from remote sensing observations. One prediction of CB theory is the wavelength dependence of the OE angular width.
Aims. The Dawn spacecraft observed the OE on the surface of dwarf planet Ceres. We aim to characterize the OE over the resolved surface, including the bright Cerealia Facula, and to find evidence for SH and/or CB. It is presently not clear if the latter can contribute substantially to the OE for surfaces as dark as that of Ceres.
Methods. We analyze images of the Dawn framing camera by means of photometric modeling of the phase curve.
Results. We find that the OE of most of the investigated surface has very similar characteristics, with an enhancement factor of 1.4 and a full width at half maximum of 3° (“broad OE”). A notable exception are the fresh ejecta of the Azacca crater, which display a very narrow brightness enhancement that is restricted to phase angles <0.5° (“narrow OE”); suggestively, this is in the range in which CB is thought to dominate. We do not find a wavelength dependence for the width of the broad OE, and lack the data to investigate the dependence for the narrow OE. The prediction of a wavelength-dependent CB width is rather ambiguous, and we suggest that dedicated modeling of the Dawn observations with a physically based theory is necessary to better understand the Ceres OE. The zero-phase observations allow us to determine Ceres’ visible geometric albedo as pV = 0.094 ± 0.005. A comparison with other asteroids suggests that Ceres’ broad OE is typical for an asteroid of its spectral type, with characteristics that are primarily linked to surface albedo.
Conclusions. Our analysis suggests that CB may occur on the dark surface of Ceres in a highly localized fashion. While the results are inconclusive, they provide a piece to the puzzle that is the OE of planetary surfaces.
Key words: minor planets, asteroids: individual: Ceres / radiative transfer
© ESO 2018
1 Introduction
The reflectance of planetary regoliths can increase dramatically towards zero solar phase angle, a phenomenon known as the opposition effect (OE). On April 29, 2017, the framing cameras of the Dawn spacecraft captured the OE on the surface of dwarf planet Ceres in images with a spatial resolution of 1.8 km per pixel. The OE is usually observed by Earth-based telescopes, and resolved observations by spacecraft are still rare. Zero-phase images of asteroids are often acquired on approach during a flyby, as for 2867 Šteins (Schröder et al. 2010; Spjuth et al. 2012) and 21 Lutetia (Masoumzadeh et al. 2015; Schröder et al. 2015; Hasselmann et al. 2016). Sometimes, the small mass of an asteroid allows the spacecraft to slowly hover into the opposition geometry, as for 25143 Itokawa (Lee & Ishiguro 2018). In the case of Ceres, Dawn reached the opposition geometry through an ingenious scheme of orbital navigation to avoid eclipse at the other side of the asteroid (Rayman 2017). Ground-based observations of Ceres that extend to very low phase angle have been reported by Tedesco et al. (1983; minimum phase angle 1.1°) and Reddy et al. (2015; minimum 0.85°). Ceres is also the largest asteroid in the main belt and is classified as C-type in the SMASS taxonomy (Bus & Binzel 2002). This paper studies the Ceres OE as observed by the Dawn cameras in the context of observations for other rocky solar system bodies, especially asteroids and the Moon, with the aim of linking the OE characteristics to the physical properties of the regolith.
In practice, the OE as observed is not always consistently defined (Belskaya & Shevchenko 2000). In the first description of the OE for an asteroid, Gehrels (1956) wrote: “...close to opposition there is a pronounced nonlinear increase in brightness”. As he was referring to telescopic observations of 20 Massalia as an integrated point source, the OE represents a departure of the phase curve from linearity on the visual magnitude scale, which is logarithmic in intensity. The asteroid OE range typically extends from 0° to ~ 5° phase angle, whereas the “linear” part of the phase curve extends to at least 25°, but not necessarily beyond (Belskaya & Shevchenko 2000; Rosenbush et al. 2002). Two physical processes that are thought to be the dominant contributors to the OE brightness surge are shadow hiding (SH) and coherent backscatter (CB). Shadow hiding refers to the shadowscast by regolith particles and larger objects. Near phase angle zero, when the Sun is directly behind the observer, shadows arehidden, increasing the reflectance of the surface (Hapke 1984, 1986; Shkuratov et al. 1994; Shkuratov & Helfenstein 2001). While the SH opposition effect (SHOE) refers only to the contribution of SH to the OE, SH affects the phase curve over the full range of phase angles. Coherent backscatter is a form of constructive interference of light at very small phase angles, the physics of which is well understood (Tishkovets & Mishchenko 2010; Petrova & Tishkovets 2011). While originally described for media of widely separated particles in suspension (Kuga & Ishimaru 1984; Van Albada & Lagendijk 1985), CB was predicted to also play an important role in surfaces of high packing density, such as planetary regoliths (Mishchenko & Dlugach 1993; Mishchenko et al. 2009; Dlugach & Mishchenko 2013). For CB to produce an OE peak that is wide enough to be observed, the presence of grains with sizes on the order of the wavelength is required; much larger or smaller grains would produce a coherent peak that is too narrow (Mishchenko & Dlugach 1993). The scattering behavior of individual regolith particles (often described by the single particle phase function) could be considered as a third process contributing to the OE (Kaydash et al. 2013), but the balance between back- and forward scattering by a single particle can also be interpreted in terms of its ability to cast shadows (Shkuratov et al. 2012). It is generally held that the CBOE peak is narrow, at most a few degrees wide, whereas the SHOE peak can be much broader (Mishchenko & Dlugach 1993; Helfenstein et al. 1997; Hapke et al. 1998), although modeling suggests that CB may contribute to backscattering up to at least 10° phase angle (Shkuratov et al. 1999).
Given its reliance on multiple scattering, it is likely that CB is experienced by bright, atmosphereless solar system bodies like the Saturnian satellites (Helfenstein et al. 1998; Mishchenko et al. 2009) and E-type asteroids (Mishchenko & Dlugach 1993; Rosenbush et al. 2009), and not by the darkest objects (Shevchenko & Belskaya 2010). Whether CB is important for bodies of intermediate albedo is not clear. The optical properties of the lunar regolith have been studied extensively, and this particular question has been subject of a lively debate (Buratti et al. 1996; Helfenstein et al. 1997; Hapke et al. 1998, 2012; Shkuratov et al. 1999, 2012). Recent modeling suggests that CB contributes substantially to the OE of lunar maria (Muinonen et al. 2011), which are almost as dark as the surface of Ceres at visible wavelengths (Velikodsky et al. 2011). Therefore, we cannot a priori dismiss all thought of a CB contribution to the Ceres OE.
In practice, it is difficult to unambiguously demonstrate CB from remote sensing data. When both photometric and polarimetric observations are available, the latter may be more easily inferred and modeled (Mishchenko 1993; Shkuratov et al. 2002; Rosenbush et al. 2006; Muinonen et al. 2010), although quantitative interpretations of the observations in terms of sizes of particles, their refractive index, and packing density remain challenging (Petrova & Tishkovets 2011). Ceres has a very broad polarization minimum that is almost 20° wide (Muinonen et al. 2010). Polarization data are not available for very small phase angles, so it is not known if Ceres displays the so-called polarization OE, a narrow negative polarization peak, thought to be related to CB (Rosenbush et al. 2006, 2009; Dlugach & Mishchenko 2013). Dawn only acquired photometric observations of Ceres. Therefore, the challenge is to distinguish SH from CB in the absence of polarimetric data. One particular prediction of CB theory that we hope to test is that the width of the CB peak should depend on wavelength (Mishchenko 1992).
 |
Fig. 1 The locations of zero phase in clear (○) and narrow-band (□) framing camera images displayed on a map of the normal albedo in the clear filter (Schröder et al. 2017). The regions delineated by the dotted and dashed lines are two regions of interest (ROI 1 and ROI 2). |
2 Data and methods
Images that captured Ceres at zero phase were acquired by the Dawn FC1 and FC2 framing cameras (Sierks et al. 2011) as part of extended mission orbit 4 (XMO4; see Rayman 2017 for an overview of the Dawn mission phases at Ceres). The path of zero phase over the surface is indicated in Fig. 1, superposed on an albedo map. The path is situated between big, and relatively bright, Vendimia Planitia and Occator crater with the bright, enigmatic Cerealia Facula (Schenk et al. 2016; Ruesch et al. 2017). We focus our analysis on an area immediately surrounding the path: region-of-interest #1 (ROI 1, with 160° < lon < 280° and − 60° < lat < + 30°). In our study of the OE we use only FC2 images; the FC1 images are affected by residual charge (Schröder et al. 2013) and will not be considered here1. The XMO4 images (89387-89580) were acquired in the extended mission at Ceres at a relatively low spatial resolution of 1.9 km per pixel (Table 1). A total of 170 clear filter images were taken continuously in rapid succession, 155 of which captured zero phase somewhere on the surface. At four instances, a set of six narrow-band images was acquired, each set consisting of two cycles of the filter sequence F3 (effective wavelength 749 nm), F5 (964 nm), and F8 (437 nm). The footprints of only three sets are shown in Fig. 1, as the fourth one did not capture zero phase. The full width of the Ceres OE may exceed the phase angle range of the XMO4 data set (< 7°), and therefore we include RC3 images (Rayman 2017). These were acquired early in the mission at a comparable spatial resolution. The RC3 images cover a very wide phase angle range. We can distinguish three groups of RC3 images: a, b, and c (Table 1). Two of these (a and b) were acquired at very large phase angles, but cover ROI 1 in only a restricted latitude range (Li et al. 2015). The third group (c) is most relevant to our purposes, as it provides complete coverage of ROI 1 at moderate phase angles (< 50°). Figure 2 shows a few examples of images acquired at different phase angles in the two mission phases, displayed at their correct relative brightness.
All images were calibrated to reflectance as described by Schröder et al. (2013, 2014). Images through several of the narrow-band filters are affected by substantial in-field stray light (Sierks et al. 2011). For images in which the surface of Ceres fills the field-of-view (FOV) and is evenly illuminated, a satisfactory stray light correction method exists (Schröder et al. 2014). However, Ceres fills only a small fraction of the FOV in the images in this study, which invalidates the method. Nevertheless, while we did not attempt to subtract stray light from the images, we did apply a first-order correction to the data as follows. In Fig. 3, the stray light is visible as an interference pattern around the illuminated disk of Ceres. We assume that a similar amount of stray light is also present on the disk. The stray light is stronger in RC3 images than in XMO4 images because of the larger size of Ceres’ disk. For the XMO4 mission phase and one particular filter, let us consider IS,XMO4, the radiance emanating as stray light from empty space. We assume that the radiance emanating from the disk, averaged over a certain area, is IC,XMO4 = IC + IS,XMO4, with IC the true radiance of Ceres. The percentages in the top row of Fig. 3 refer to the ratio of the two: IS,XMO4∕(IC + IS,XMO4) ≈ IS,XMO4∕IC, because IS,XMO4 ≪ IC. The ratio ofthe observed radiance of Ceres in a XMO4 and RC3 image acquired at the same phase angle is therefore
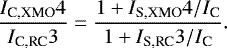 (1)
(1)
Using the numbers in Fig. 3, we find this ratio to be 0.991 for all narrow-band filters and 0.999 for the clear filter. We therefore apply a correction factor of 0.99 to all narrow-band RC3 reflectances to better match the low phase angle RC3 reflectances to the XMO4 reflectances (a 1% correction). We did not attempt to retrieve the true Ceres reflectance (IC) from the observed reflectance (IC,XMO4), as this is not necessary in light of the purpose of this paper and the uncertainties associated with the stray light. At least the two data sets will now match up better. We note that although this type of interference stray light does not affect the clear filter, the stray light in RC3 F1 images is still higher than that in XMO4 F1 images.
All images were mapped to the same equirectangular projection with a spatial resolution of 4 pixels per degree by means of the USGS Integrated Software for Imagers and Spectrometers ISIS3 (Anderson et al. 2004; Becker et al. 2012) using bi-linear interpolation. Thereby, the projected pixels on the equator have approximately the same spatial resolution as the pixels at the center of Ceres’ disk in the XMO4 images. We also used ISIS for calculating the photometricangles (incidence, emission, phase) for each image pixel. We employed the HAMO shape model described by Preusker et al. (2016), which covers about 98% of Ceres’ surface and has a vertical accuracy of about 10 m. The model is oriented in the Ceres reference frame, which is defined by crater Kait (Roatsch et al. 2016) and the Ceres rotation state derived by Preusker et al. (2016). We did not attempt to improve the projection by registering the images to the shape model (Schröder et al. 2017), as the opposition images are devoid of shading. Consequently, projected pixels associated with more extreme geometries suffer from obvious projection errors, and it was necessary to limit the incidence and emission angles of the pixels included in our analysis, typically to (ι, ϵ) < 50°.
In this paper we fit model curves to data several times. Fitting was performed using the Levenberg–Marquardt algorithm with constrained search spaces for the model parameters2 (Moré 1978; Markwardt 2009). In the fitting process we adopted the photon noise for the reflectance error, which does not account for potential projection errors. The formal error for the model parameters as reported by the fitting algorithm is often a very small fraction of the best-fit value. However, in light of the unavoidable projection errors, the true uncertainty is almost certainly larger. We estimate that the true uncertainty of the best-fit parameter values given in this paper is on the order of unity in the last digit provided.
Available FC2 image data covering ROI 1 for the RC3 and XMO4 mission phases with no restrictions on the photometric angles.
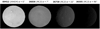 |
Fig. 2 Ceres images representing different parts of the phase curve, shown at their correct relative brightness on a linear scale. The image number, mission phase, and phase angle at the disk center are indicated. Only the Cerealia and Vinalia Faculae (the bright spots in the opposition image at far left) are not displayed at their correct brightness, as they are much brighter than the average Ceres surface (Li et al. 2016; Schröder et al. 2017). |
 |
Fig. 3 In-field stray light in full-frame FC2 images acquired with different filters (F1–F8) during the RC3 and XMO4 mission phases (image numbers indicated). The percentages refer to how the average signal in the white square compares to that in the black square in each image (for clarity, the squares are only shown for F8). Cerealia Facula is outside the black square. The images are displayed with black being zero signal and white being 5% of the average signal in the black square. The stray light in the RC3 images is about 50% stronger than in the XMO4 images. |
3 Model description
The surface reflectance of a planetary body depends on the wavelength λ and the angles of observation: the local angle of incidence ι of sunlight, the local angle of emergence ϵ, and the phase angle α. For convenience we define μ0 = cosι and μ = cosϵ. The radiance factor is defined as
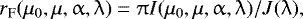 (2)
(2)
where I is the radiance in W m−2 μm−1 sr−1 and J is the normal solar irradiance in W m−2 μm−1, which depends on the distance of the planet to the Sun (Hapke 1981). The radiance factor is also known as I∕F, with F ≡ J∕π. We use the term “reflectance” for the radiance factor in the remainder of this paper.
In this paper we apply essentially two different photometric models to the surface of Ceres. In the first, the reflectance can be separated into two parts, the equigonal albedo and the disk function (Kaasalainen et al. 2001; Shkuratov et al. 2011):
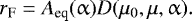 (3)
(3)
We often refer to the equigonal albedo as the “phase function”. Plotting the phase function as a function of phase angle produces the phase curve. It describes the phase dependence of the brightness (Shkuratov et al. 2011):
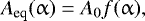 (4)
(4)
where A0 is the normal albedo3, and f(α) is the phase function normalized to unity at α = 0°. The latter depends on the choice of disk function D, which describes how the reflectance varies over the planetary disk at constant phase angle. An equigonal albedo image has no brightness trend from limb to terminator for a surface of constant albedo. The normal albedo in Eq. (4) is independent of local topography, as such brightness variations are contained in the disk function in Eq. (3). If the disk function is uniform at α = 0°, that is, D(μ0, μ, 0°) ≈ 1, then Aeq(0°) = A0 is equal to the geometric albedo of the body. This condition is met for Ceres (Schröder et al. 2017). Our strategy is to adopt the most appropriate disk function and choose a convenient form for the phase function, such that we may link spatial variations of the phase function parameters to the physical properties of the regolith.
The Akimov phase function was developed for the lunar surface (Akimov 1988b; Korokhin et al. 2007; Shkuratov et al. 2011). It also approximates the observed phase curves of asteroids with a good accuracy and is simple and convenient to use (Belskaya & Shevchenko 2000). It has the following form:
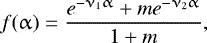 (5)
(5)
in which α is in degrees. It has three parameters: the slope ν1 of the phase curve, the OE amplitude m, and slope ν2. Occasionally, we fit Eq. (5) to data restricted to only the smallest phase angles (< 2°). In such cases we set m = 0, and ν1 plays the role of ν2 in the sense that itreally models the slope of the OE instead of that of the full phase curve. Two quantities that are often used to characterize the OE are the enhancement factor and the half-width at half-maximum (HWHM; Rosenbush et al. 2002). We use the enhancement factor ζ in the definition of Mishchenko & Dlugach (1993), as the equigonal albedo divided by the “linear” (on a logarithmic scale) part of the phase curve:
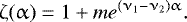 (6)
(6)
The term “enhancement factor” is also often used to denote only ζ(0°) = 1 + m. The HWHM of the enhancement factor is then
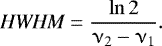 (7)
(7)
We employ two disk functions, both normalized at ι = ϵ = α = 0°. For the general Ceres surface we use the Akimov disk function (Akimov 1976, 1988a; Shkuratov et al. 1994, 2011), which has no parameters:
![\begin{equation*} D_{\textrm{A}}({\alpha, \beta, \gamma}) = \cos \frac{\alpha}{2} \cos \left[ \frac{\pi}{\pi - \alpha} \left( \gamma - \frac{\alpha}{2} \right) \right] \frac{(\cos \beta)^{\alpha / (\pi - \alpha)}}{\cos \gamma},\end{equation*}](/articles/aa/full_html/2018/12/aa33596-18/aa33596-18-eq8.png) (8)
(8)
in which α is in radians. The photometric latitude β and longitude γ depend on the incidence, emergence, and phase angles as follows:
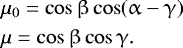 (9)
(9)
The Akimovdisk function was analytically derived for a dark, extremely rough surface with a hierarchical, self-similar structure (Shkuratov et al. 2003). It was found to provide a good match for the typical Ceres surface, although it does not perform well for Cerealia Facula, the bright central area in the Occator crater (Schröder et al. 2017; Longobardo et al. 2018). For the latter we use the combined Lambert/Lommel-Seeliger law (Buratti & Veverka 1983; McEwen 1996):
![\begin{equation*} D_{\textrm{L}}({\mu_0, \mu}, \alpha) = c_{\textrm{L}}(\alpha) \frac{2 \mu_0}{\mu_0 + \mu} + [1 - c_{\textrm{L}}(\alpha)] \mu_0,\end{equation*}](/articles/aa/full_html/2018/12/aa33596-18/aa33596-18-eq10.png) (10)
(10)
with free parameter cL, which governs the relative contribution of the Lambert and Lommel-Seeliger terms.
We also employ the Hapke (1981, 1984, 1986) model, which is not explicitly separated into a disk and phase function:
![\begin{eqnarray*} r_{\textrm{F}}(\mu_0^{\prime}, \mu^{\prime}, \alpha)\;&{=}&\;\frac{w}{4} \frac{\mu_0^{\prime}}{\mu_0^{\prime} + \mu^{\prime}} [B_{\textrm{SH}}(\alpha) P(\alpha)\nonumber\\ && + \;H(\mu_0^{\prime},w)H(\mu^{\prime},w){-}1] f(\bar{\theta}),\end{eqnarray*}](/articles/aa/full_html/2018/12/aa33596-18/aa33596-18-eq11.png) (11)
(11)
with w the so-called single scattering albedo. The H-function is given by
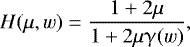 (12)
(12)
with 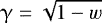 . The SHOE is described by
. The SHOE is described by
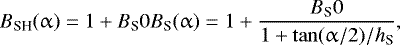 (13)
(13)
with BS0 and hS the OE amplitude and width, respectively. Hapke (2002) introduced two separate parameters for the CBOE, but we decided not to include those here for reasons of simplicity; we use Eq. (11) to merely describe the OE, which is better done with two rather than four parameters. Furthermore, Schröder et al. (2017) found that the Hapke (2002) version of the model did not perform well for the Ceres surface. The model in Eq. (11) includes 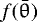 , which describes the effects of “macroscopic roughness”, a measure of the roughness of the surface on a scale up to the image resolution limit with
, which describes the effects of “macroscopic roughness”, a measure of the roughness of the surface on a scale up to the image resolution limit with  being the mean slope angle of the surface facets. The inclusion of macroscopic roughness changes μ0 and μ to
being the mean slope angle of the surface facets. The inclusion of macroscopic roughness changes μ0 and μ to 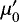 and μ′ in a way that we do not reproduce here; details can be found in Hapke (1984). The factor P(α) is the phase function of a single particle. We employ two versions of the Henyey-Greenstein function. One is the single-term version (Henyey & Greenstein 1941)
and μ′ in a way that we do not reproduce here; details can be found in Hapke (1984). The factor P(α) is the phase function of a single particle. We employ two versions of the Henyey-Greenstein function. One is the single-term version (Henyey & Greenstein 1941)
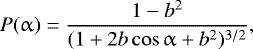 (14)
(14)
with parameter b (often written as g), with |b| < 1. This function has a single lobe, which leads to either backscattering (b < 0) or forward scattering (b > 0) behavior. Isotropic scattering corresponds to b = 0. The other version of the Henyey-Greenstein function has two terms (Shepard & Helfenstein 2007):
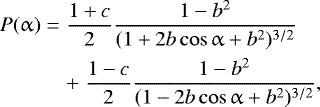 (15)
(15)
with two parameters b and c. We note that Eq. (15) reduces to Eq. (14) for c = 1. This function has two lobes, one for forward scattering, and the other for backscattering. The width of both lobes is governed by b, with 0 ≤ b < 1, and b = 0 representingisotropic scattering. The relative amplitude of the two lobes is determined by c, with |c| < 1. When b≠ 0, forward scattering dominates4 for c > 0 and backscattering dominates for c < 0, with c = 0 meaning back- and forward scattering in equal strength. Of course, abundant data in the (90°, 180°) phase angle range are required to reliably derive values for c. However, as the b parameter offers flexibility to shape the backscattering lobe, the double term Henyey-Greenstein function is always expected to improve the fit quality of the Hapke model over the single-term version.
 |
Fig. 4 Characteristics of ROI 1 (outlined in Fig. 1). Panel A: shape model with Lambert reflection and illuminationconditions from XMO4 image 89504. The green and red stars denote locations selected for detailed study. Craters of interest are indicated. Panel B: enhanced color composite with filters F5 (965 nm), F2 (555 nm), and F8 (438 nm) inthe RGB color channels (Schröder et al. 2017). ROI 2 is indicated. We note that the color and brightness of the spots in Occator cannot be displayed correctly here as they are much brighter than their surroundings, exceeding the dynamicrange of the figure. |
4 Resolved photometry
4.1 Regions of interest
ROI 1, which contains the zero-phase path in its entirety, is shown in more detail in Fig. 4. We find the Juling–Kupalo crater pair at the bottom left and Occator crater at the top right, all fresh craters with characteristic blue ejecta. The large crater at the bottom right, with a reddish interior, is named Urvara. The area close to the path of zero phase is fairly nondescript. Parts of it are slightly bluish, mostly due to the presence of Occator ejecta, but without large excursions in either albedo or color. The one exception is Azacca crater at longitude 218.4° and latitude − 6.7°, also with relatively blue and bright ejecta. This feature plays an important role in the discussion of the OE below. A second region of interest is the area between longitudes 220° and 250° and latitudes − 30° and 0°. In ROI 2 we find the results of our various photometric analyses to be most reliable, with the least artifacts.
 |
Fig. 5 Fitting the Akimov model to the average reflectance in a box of 3 × 3 pixels centered on the location of the green star in Fig. 4A. The fit, with parameters (A0, ν1, m, ν2) = (0.091, 0.023, 0.32, 0.32), was limited to data with 0.05° < α < 40° and ι, ϵ< 70°. Panel A: reflectance. Panel B: equigonal albedo (logarithmic scale), with the best-fit model from panel A drawn in red. The inset shows the enhancement factor, or the equigonal albedo divided by the “linear” part of the phase curve (dashed red line). Panel C: zooming in on the phase angle range below 1°. The solid curve accounts for the finite size of the Sun, whereas the dashed curve does not. The vertical dotted line indicates the angular radius of the Sun at Ceres. Panel D: as in panel C, but with the phase angle on a logarithmic scale. |
4.2 Model comparison
In this section, we model the phase curve at one particular location on the path of zero-phase angle to show the morphology of the phase curve, including the OE, and to illustrate the availability of data. We compare the performance of the Akimov and Hapke models below. In the following section, we extend our analysis to the entirety of ROI 1 to search for spatial variations of the model parameters.
4.2.1 Akimov model
We start our analysis by employing the Akimov model (Eqs. (3)–(8)). A known limitation of the double exponential version of this model is its failure to fit observations at high phase angles. Velikodsky et al. (2011) required a third exponential term to accurately model the lunar phase curve over a wide range of phase angles. We restrict the fit to α <50° and find that two terms suffice. We choose a location at the northern end of the path, indicated by the green star in Fig. 4A, because of the availability of observations at large phase angle in RC3 images. Figure 5A shows how the reflectance at this location compares to a fit of the Akimov model. The observed reflectance is not a smooth function of phase angle because of variations in incidence and emission angles over the surface, for which we account by dividing out the disk function (Eq. (8)) to arrive at the equigonal albedo in Fig. 5B. We display the equigonal albedo on a logarithmic scale to demonstrate the linear character of the phase curve and the departure from linearity towards zero phase that constitutes the OE (Gehrels 1956). The inset shows the enhancement factor, or the phase curve divided by the linear part, and we calculate ζ(0°) = 1.32 and HWHM = 2.3°. The Akimov model accurately describes the data at low to moderate phase angles (α < 40°). The phase angle coverage below 1° is particularly dense, and we zoom in on this region in Fig. 5C. The reflectance is well reproduced and reaches a plateau below 0.05° phase, likelydue to the finite size of the Sun (Shkuratov et al. 1999; Déau 2012). To model this phenomenon, we follow Déau (2012) and adopt the empirical limb darkening model from Hestroffer & Magnan (1998):
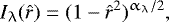 (16)
(16)
with 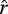 the normalized solar radius. Limb darkening parameter αλ depends on the wavelength, but the F1 filter is broadband. However, the CCD detector is most sensitive around 700 nm (Sierks et al. 2011), the Sun is brightest around 500 nm. We therefore adopt αF 1 = 0.5, valid around 570 nm5. The angular size of the Sun at the distance of Ceres during XMO4 (2.74 AU) is 0.195°. Figures 5C and D show that the finite size of the Sun has a small but significant effect on the phase curve for α < 0.05°. We therefore exclude this range from model fits to the data in the remainder of this paper. Coherent backscatter may also cause rounding of OE peak towards zero phase (Mishchenko & Dlugach 1993), but we do not have the data to distinguish such an effect from rounding due to the finite size of the Sun.
the normalized solar radius. Limb darkening parameter αλ depends on the wavelength, but the F1 filter is broadband. However, the CCD detector is most sensitive around 700 nm (Sierks et al. 2011), the Sun is brightest around 500 nm. We therefore adopt αF 1 = 0.5, valid around 570 nm5. The angular size of the Sun at the distance of Ceres during XMO4 (2.74 AU) is 0.195°. Figures 5C and D show that the finite size of the Sun has a small but significant effect on the phase curve for α < 0.05°. We therefore exclude this range from model fits to the data in the remainder of this paper. Coherent backscatter may also cause rounding of OE peak towards zero phase (Mishchenko & Dlugach 1993), but we do not have the data to distinguish such an effect from rounding due to the finite size of the Sun.
 |
Fig. 6 Fitting the Hapke model to the average reflectance in a box of 3 × 3 pixels centered on the location of the green star in Fig. 1, with α > 0.05° and ι, ϵ< 70°. The inset zooms in on the phase angle range below 1°. These four solutions, with parameters listed in Table 2, were identified by the Levenberg–Marquardt optimization algorithm. Panels A and B use the single-term Henyey–Greenstein function, whereas Panels C and D use the double-term Henyey–Greenstein function. The search start value for the photometric roughness was
|
4.2.2 Hapke model
Next, we fit the Hapke (1981, 1984, 1986) model to the same data, where we employ both the single and double termHenyey-Greenstein phase functions. As the double term version offers flexibility to shape the backscattering lobe of the particle phase function, we expect it to fit the data better. As data with phase angles > 90° are available, we can reliably derive the roughness parameter  (Helfenstein 1988). Figure 6 shows the best-fit Hapke models, with the corresponding parameters listed in Table 2. The best-fitting model overall is the double Henyey–Greenstein version with
(Helfenstein 1988). Figure 6 shows the best-fit Hapke models, with the corresponding parameters listed in Table 2. The best-fitting model overall is the double Henyey–Greenstein version with 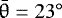 (model C inTable 2 and Fig. 6). In our trials, we found that the search algorithm converged to a local rather than the global minimum depending on the start value for the photometric roughness parameter (
(model C inTable 2 and Fig. 6). In our trials, we found that the search algorithm converged to a local rather than the global minimum depending on the start value for the photometric roughness parameter (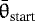 ). For
). For 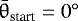 , the algorithm would converge to
, the algorithm would converge to 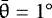 , whereas for
, whereas for 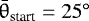 , the algorithm would converge to values around
, the algorithm would converge to values around 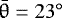 . The change in fit quality due to this difference in
. The change in fit quality due to this difference in  is partly compensated by the Henyey–Greenstein parameters. Nevertheless, the high-
is partly compensated by the Henyey–Greenstein parameters. Nevertheless, the high- models fit the data better than the low-
models fit the data better than the low- models, regardless of whether the single or double-term Henyey–Greenstein version is used. It is tempting to conclude that
models, regardless of whether the single or double-term Henyey–Greenstein version is used. It is tempting to conclude that 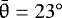 is the “correct” Hapke roughness value for these data. This would be true if the data were 100% reliable. But apart from known error sources such as photon noise, the data are affected by projection errors, which are very hard to quantify. Therefore, we may expect this kind of ambiguity when extending the Hapke model fit to other parts of the surface. Our analysis concerns primarily the OE parameters, and both BS0 and hS show considerable variation in Table 2. Moreover, the model that best fits the data in the OE range is actually model D, which comes only third out of four in the ranking of overall fit quality.
is the “correct” Hapke roughness value for these data. This would be true if the data were 100% reliable. But apart from known error sources such as photon noise, the data are affected by projection errors, which are very hard to quantify. Therefore, we may expect this kind of ambiguity when extending the Hapke model fit to other parts of the surface. Our analysis concerns primarily the OE parameters, and both BS0 and hS show considerable variation in Table 2. Moreover, the model that best fits the data in the OE range is actually model D, which comes only third out of four in the ranking of overall fit quality.
We have shown the Ceres phase curve, including the OE, for one particular location on the surface, and successfully reproduced it with both the Akimov and Hapke models. The reflectance data are densely distributed in regular fashion overthe lowest degree of phase angle. At larger phase angles, the data are mostly distributed in widely separated clumps. The distribution of data along phase angle varies over the surface. When we extend the analysis to the entirety of ROI 1, we may expect to see consequences for the model parameters in the form of artifacts (Schröder et al. 2017). The resulting ambiguities will be larger for the Hapke model, because it has more free parameters.
 |
Fig. 7 Minimum (left panel) and maximum (right panel) phase angle of observation in ROI 1 for ι, ϵ < 50°. |
4.3 Spatial photometric variations
Our next goal is to widen the photometric analysis to the entire surface in ROI 1 to identify variations in the phase curve, in particular those of the OE amplitude and slope, and correlate these to physical properties of the surface. Again, we distinguish between the Akimov and Hapke models.
4.3.1 Akimov model
First we employ the Akimov model, for which we map the distribution of the A0, ν1, ν2, and m parameters. This means that for each projected pixel in the ROI we fit the model to the observations that include that pixel. As the model fails at very large phase angles, we exclude data from RC3a and b (see Table 1) by restricting the maximum phase angle to 48°. The minimum and maximum phase angles of observation are shown in Fig. 7. In the map of the minimum phase angle we can clearly trace the path of zero phase diagonally across the center of the ROI. At the bottom of the ROI we find more extreme imaging geometries towards the limb of Ceres. Furthermore, the maximum phase angle shows a discontinuity around + 10° latitude. As the model solutions are sensitive to the imaging geometry, we initially restrict the incidence and emission angles to < 50°. Figure 8 shows maps of the model parameters. The normal albedo (A0) is reliably retrieved with little noise, and agrees nicely with the map in Fig. 1. The maps of theother parameters are much noisier and show obvious correlations with the maximum phase angle.These correlations are so strong that we can only evaluate any spatial variations within the (− 35°, +5°) latitude band. Subtle variations are associated with the relatively bright ejecta of Azacca crater. The slope of the phase curve (ν1) is anti-correlated with the normal albedo, consistent with Schröder et al. (2017) and the general trend observed for asteroids, which is linked to the role of multiple scattering in the regolith (Longobardo et al. 2016). On the other hand, the OE slope (ν2) appears to be correlated with the normal albedo, with the Azacca ejecta clearly recognizable in the ν2 map (but not them map).
We investigate the robustness of these findings by changing the maximum incidence and emission angle and minimum phase angle (Fig. 9). Including observations with incidence and emission angles up to 70° introduces additional noise in the map of m, especially in the western part of the ROI, which justifies our earlier restriction of ι, ϵ < 50°. The choice of minimum phase angle affects the visibility of the Azacca ejecta in the ν2 map. When we increase the minimum phase angle to 0.5°, the Azacca ejecta fade in with the background. In fact, we found the ejecta to disappear gradually when increasing the minimum phase angle in steps from 0.0° to 0.6°. To investigate this disappearance in more detail, we fit single exponential functions (Eq. (5) with m = 0) to the data restricted to two 0.4°-wide phase angle ranges, and map the parameters. One of these ranges is immediately below α = 0.6° and the other one above. We tried to ensure that these very narrow ranges were fully occupied with data (minimum 3 data points) by requiring the existence of at least one data point with a phase angle both below and above the range. In this way we hope to minimize bias resulting from uneven phase-angle coverage. The maps in Fig. 10 show the results as tracks over the surface, whose width and length are governed by the lower and upper limit of the phase-angle range, respectively. Where they overlap, the normal albedo (A0) tracks (A and C) have a similar appearance for both ranges, with the Azacca ejecta clearly standing out as bright. But whereas the ejecta are clearly seen in the slope (ν1) map of the lower phase-angle range (B), they are absent from the map associated with the higher phase-angle range (D). This confirms that, below 0.6° phase angle, the OE of the Azacca ejecta is steeper, and has a larger amplitude, than that of their surroundings. As the ejecta are visible in both Figs. 10A and B, it is tempting to conclude that the OE slope variations are correlated with normal albedo. But the slope map shows some distinct differences with the albedo map. We therefore suspect that the Azacca ejecta have physical properties that lead to a steeper OE slope at very low phase.
 |
Fig. 8 Maps of the Akimov model parameters (Eqs. (4) and (5)) in ROI 1, with ι, ϵ < 50°. The Azacca ejecta are encircled in the A0 map. |
 |
Fig. 9 Sensitivity analysis of the Akimov model parameter retrieval. Left panel: map of m with all phase angles included and ι, ϵ < 70°. Right panel:map of ν2 with phase angle restricted to α > 0.5° and ι, ϵ< 50°. See text for details. |
4.3.2 Hapke model
In the same way, we employ the Hapke (1981, 1984, 1986) model to map its parameters over ROI 1. Even though the Hapke model successfully models the very high phase-angle data, we again restricted the phase angle to roughly 48°, because we expect that the highly uneven coverage of the very high phase-angle observations (see Table 1) will systematically affect the parameters. With this restriction we cannot expect that the roughness parameter  is reliably derived (Helfenstein 1988), but our objective is to study the OE rather than to find the best-fit Hapke parameters for the full phase curve.We trialed both the single and double-term Henyey–Greenstein phase functions, but found that in the double-term version, w and c varied considerably over the surface in a correlated fashion. We therefore proceeded with the single-term Henyey–Greenstein function. Figure 11 shows the Hapke parameter maps. Again, the parameters exhibit considerablevariation over the surface that is associated with unequal phase-angle coverage. South of latitude − 30° the parameters are unreliable because of the more extreme illumination and observation geometries. ROI 2 appears to suffer the least artifacts. Here,
is reliably derived (Helfenstein 1988), but our objective is to study the OE rather than to find the best-fit Hapke parameters for the full phase curve.We trialed both the single and double-term Henyey–Greenstein phase functions, but found that in the double-term version, w and c varied considerably over the surface in a correlated fashion. We therefore proceeded with the single-term Henyey–Greenstein function. Figure 11 shows the Hapke parameter maps. Again, the parameters exhibit considerablevariation over the surface that is associated with unequal phase-angle coverage. South of latitude − 30° the parameters are unreliable because of the more extreme illumination and observation geometries. ROI 2 appears to suffer the least artifacts. Here,  varies between 25° and 30°, a range similar to values derived for global Ceres by Li et al. (2016; 20° ± 3°), Ciarniello et al. (2017; 29° ± 6°), and Schröder et al. (2017; 22° ± 2°). The OE width hS varies between 0.05 and 0.08, consistent with Helfenstein & Veverka (1989; 0.059 ± 0.006)6, who modeled the Tedesco et al. (1983) observations. Reddy et al. (2015) found a lower value of hS = 0.036, where we note that in both papers
varies between 25° and 30°, a range similar to values derived for global Ceres by Li et al. (2016; 20° ± 3°), Ciarniello et al. (2017; 29° ± 6°), and Schröder et al. (2017; 22° ± 2°). The OE width hS varies between 0.05 and 0.08, consistent with Helfenstein & Veverka (1989; 0.059 ± 0.006)6, who modeled the Tedesco et al. (1983) observations. Reddy et al. (2015) found a lower value of hS = 0.036, where we note that in both papers  was fixed at 20°. The OE amplitude BS0 is between 1.5 and 2.0, where Helfenstein & Veverka (1989) and Reddy et al. (2015) found 1.6 ± 0.1 and 2.0, respectively. The Henyey–Greenstein parameter b is around − 0.3, consistent with Helfenstein & Veverka (1989) and Li et al. (2016), who derived − 0.40 ± 0.01 and − 0.35 ± 0.05, respectively. In the hS map we can clearly identify the Azacca ejecta as having smaller values, which correspond to a narrower OE. The single scattering albedo w is higher here, but BS 0 is lower. As such, here the OE amplitude and width are correlated in the Hapke model, similar to what we found with the Akimov model. When we exclude data with α < 0.5° from the fit, the Azacca ejecta are no longer recognized in the hS map, just as for the ν2 map in the Akimov model.
was fixed at 20°. The OE amplitude BS0 is between 1.5 and 2.0, where Helfenstein & Veverka (1989) and Reddy et al. (2015) found 1.6 ± 0.1 and 2.0, respectively. The Henyey–Greenstein parameter b is around − 0.3, consistent with Helfenstein & Veverka (1989) and Li et al. (2016), who derived − 0.40 ± 0.01 and − 0.35 ± 0.05, respectively. In the hS map we can clearly identify the Azacca ejecta as having smaller values, which correspond to a narrower OE. The single scattering albedo w is higher here, but BS 0 is lower. As such, here the OE amplitude and width are correlated in the Hapke model, similar to what we found with the Akimov model. When we exclude data with α < 0.5° from the fit, the Azacca ejecta are no longer recognized in the hS map, just as for the ν2 map in the Akimov model.
In conclusion, we mapped the photometric parameters of the Akimov and Hapke models over ROI 1 to search for spatial variability. Interpretation of the maps is severely hindered by the uneven phase-angle coverage. Nevertheless, we identified variability associated with Azacca crater, whose relatively bright ejecta have a steeper OE slope than their surroundings, but only below 0.5° phase. It seems certain physical properties other than brightness are responsible for this phenomenon. We found the Akimov model to offer slightly more flexibility in analyzing the data than the Hapke model, and the interpretation of its parameters more straightforward. The best-fit Hapke model parameter values are consistent with the literature.
 |
Fig. 10 Maps of the OE parameters (Eq. (5) with m = 0, and ν1 the OE slope) for the clear filter, with ι, ϵ < 50°. The phase angle was restricted to 0.2° < α < 0.6° for panels A and B, and to 0.6° < α < 1.0° for panels Cand D. The Azacca ejecta are encircled. |
4.4 Opposition effect wavelength dependence
We now turn our attention to the narrow-band filters to search for wavelength-dependent variations of the OE. The analysis as performed for the clear filter in the previous section is not possible for the narrow-band filters, as their surface coverage is much more sparse. Figure 12 provides an overview of the color data available for a single location, at the red star in Fig. 4. During RC3, narrow-band images were only acquired up to about 50° phase angle.The available data for XMO4 derives from three instances when a set of narrow-band images was acquired, indicated with square symbols in Figs. 1 and 4. Each set consists of two images for each of the three narrow-band filters (F3, F5, and F8), or six images in total. The data coverage in the OE phase-angle range in this location is typical for pixels near the path of zero phase over the surface. Looking at Fig. 12B, it is clear that we can only study the wavelength dependence of the “broad OE” that extends to 10°–15° phase, and not that of the “narrow OE” (α < 0.5°) that we uncovered in the previous section. Fits of the Akimov model to the color data over the full phase angle range (Fig. 12A) reveal no obvious relation between the OE slope and wavelength at this particular location. Restricting the fit to the smallest phase angles and using a single exponential function again reveals no obvious correlation (Fig. 12B).
To evaluate the robustness of this finding, we determine the average phase curves for ROI 2. The best-fit Akimov models for the aggregated data are shown in Fig. 13 for all FC2 filters used during XMO4, with parameters in Table 4. The data are shown as a density plot, but the models were fit to the individual data points. ROI 2 was particularly frequently imaged through the clear filter during XMO4, which is represented by the high density of data points close to zero phase. For the narrow-band filters, the XMO4 coverage was more or less similar to that during RC3. We find that the normal albedo decreases with wavelength, giving this area a slightly bluish character. The geometric albedo spectrum of Ceres as reconstructed by Reddy et al. (2015) is also blue, which the authors attributed to phase reddening. Obvious correlations between the filter wavelength and the OE parameters are absent (Table 4). Restricting the phase angle to α <1° and fitting a single exponential phase curve reveals no correlations either (not shown). We also fitted the Hapke model to the aggregated ROI 2 data, and found no systematic wavelength dependence for the OE width parameter (hS, Table 5).
In a final push to uncover a correlation between OE width and wavelength, we map the OE parameters for each of the three narrow-band filters, but only using data at very small phase angles and a single exponential phase function (Eq. (5) with m = 0). As before, the retrieval of the OE parameters may be sensitive to the limits of the phase-angle range for each projected pixel. Figure 14 shows these limits (αmin and αmax) together with maps of the normal albedo (A0) and OE slope (ν1, here playing the role of ν2). We restrict the phase angle to 0.05° < α < 1.50°, but in contrast to Fig. 10, we cannot be sure that each pixel has this range fully occupied with observations. The range coversboth the narrow and broad OE, but the data are too sparse to distinguish between the two regimes. There are two “holes” in the maps where the phase angle reached zero. A third hole exists but is not visible, as we only consider data with ι, ϵ < 50°. The A0 maps appear unaffected by the uneven phase-angle distribution. This is not the case for the ν1 maps, in which the decrease of αmax towards the northwest is accompanied by an increase of ν1. Restricting the phase-angle range to a narrower 0.05° < α < 1.00° decreases the coverage but otherwise has only a minor effect on the appearance of the maps. The uneven distribution of αmin appears inconsequential for both A0 and ν1. The ejecta of Azacca crater are recognizable in all maps, meaning they are brighter and have a narrower OE than their surroundings, consistent with our findings for the clear filter. The three A0 maps appear different because of the decrease of the average A0 with wavelength. The ν1 maps appear similar, indicating that the OE slope is not correlated with wavelength. We can quantify this as follows. If we consider only projected pixels with the phase-angle range restricted to 0.2 < αmin < 0.4 and 0.7 < αmax < 0.9 (n = 3861), then the average ν1 at wavelength 437 nm is 0.0818 ± 0.0015, at 749 nm it is 0.0820 ± 0.0011 (749 nm), and at 964 nm it is 0.0819 ± 0.0010.
In conclusion, we do not find evidence for a wavelength-dependent OE width. However, due to the limited availability of narrow-band data, this conclusion applies to the regular, “broad” OE, and not to the “narrow” OE (α < 0.6°) that we uncovered in the previous section for the ejecta of the Azacca crater.
 |
Fig. 11 Hapke model parameters with the single-term Henyey-Greenstein function and ι, ϵ < 50°. The minimum and maximum phase angles are as in Fig. 7. The Azacca ejecta are encircled in the w map. |
 |
Fig. 12 Modeling the narrow-band reflectances, calculated as the average of a box of 3 × 3 pixels centered on the location of the red star in Fig. 4A, with ι, ϵ < 50°. The best-fit model parameters are listed in Table 3. Panel A: Akimov phase function (Eq. (5)). Panel B: exponential phase function (Eq. (5) with m = 0), fitted to α < 1.5°. The model curves account for the finite size of the Sun, with the vertical dotted line indicating the angular radius of the Sun at Ceres. |
 |
Fig. 13 Average phase curves of the terrain in ROI 2 (outlined in Fig. 1). The data are displayed as a density in agrid, with the colors reflecting the number of data points in each grid box. The drawn lines are best-fit Akimov phase functions, with the coefficients listed in Table 4. The fit was restricted to data with α > 0.05° and ι, ϵ< 50°. |
Best-fit Hapke parameters for the aggregated ROI 2 data, using the single-term Henyey–Greenstein function with α > 0.05° and ι, ϵ < 50°.
 |
Fig. 14 Maps of the OE parameters (Eq. (5) with m = 0, and ν1 the OE slope) for the three narrow-band filters used during XMO4. The phase angle was restricted to 0.05° < α < 1.50°, with ι, ϵ < 50°. The actual minimum and maximum phase angle of the data, αmin and αmax, are shown for filter F3 (the maps for F5 and F8 are very similar). |
4.5 Visible geometric albedo
Judging from the global albedo map in Fig. 1, ROI 2 represents a fairly typical part of the surface. We estimate Ceres’ visible geometric albedo (pV) from the average phase curve derived for this area (Fig. 13). The geometric albedo equals the normal albedo (A0) if the disk function is constant at zero phase, which is approximately true for Ceres (Schröder et al. 2017). And because Ceres’ reflectance spectrum is very flat in the visible (Reddy et al. 2015; Li et al. 2016), we can use the clear filter as a proxy for the V -band (λeff = 551 nm). We therefore determine the visible geometric albedo as pV = 0.094 ± 0.005, where we assume an error margin of 5%. This value agrees well with the pV = 0.10 ± 0.01 derived by Tedesco (1989) from IRAS observations. Tedesco et al. (2002) revised their estimate to pV = 0.113 ± 0.005, which seems a little on the high side. Our estimate is also consistent with the geometric albedo of 0.099 ± 0.003 reported by Reddy et al. (2015), who observed Ceres at phase angles as low as 0.85°, and the geometric albedo of 0.094 of Shevchenko & Tedesco (2006), who derived the diameter of Ceres from stellar occultations and accounted for the OE. Ciarniello et al. (2017) determined pV = 0.094 ± 0.007 by adopting the Hapke OE parameters from Helfenstein et al. (1997), as their data do not go below 7° phase angle.
4.6 Cerealia Facula
While Cerealia Facula was not located on the path of zero phase, it was imaged at phase angles smaller than 1°. The facula was barely resolved in XMO4 images, measuring only 2–3 pixels across. We analyze the clear filter images in combination with the RC3 images, which have a spatial resolution that is 1.5 times higher (Table 1). The area was observed up to phase angle 5.1° during XMO4 and down to8.1° during RC3. We compare our results with those of Schröder et al. (2017), who analyzed the photometric properties of Cerealia Facula using only RC3 images and found its phase curve to be unusually steep. Longobardo et al. (2018) obtained similar results using data acquired by Dawn’s visual and infrared mapping spectrometer (VIR), suggesting the steepness may be due to high surface roughness. We found that the projection of Cerealia Facula in XMO4 images was not always very accurate, and we therefore calculated the average reflectance in a relatively large box of 5 × 5 projected pixels centered on Cerealia Facula. To further minimize the influence of projection inaccuracies we restricted the photometric angles to ι, ϵ < 70°, where Schröder et al. (2017) allowed ι, ϵ < 85°. The standard deviation associated with the average reflectance was calculated by accounting for photon noise only. Of course, the true uncertainty is larger because of projection errors. We fit two photometric models to the data: (1) the combination of the Akimov phase function and Lambert/Lommel-Seeliger disk function, and (2) the Hapke model.
(1) The phase and disk function parameters were fit simultaneously. The best-fit model is shown in Figs. 15A and B, and has parameters A0 = 0.24, ν1 = 0.015, m = 0.28, and ν2 = 0.70, with cL = 0.75 − 0.0015α (with α in degrees). The disk function has a lower contribution of the Lambert term at all phase angles than found by Schröder et al. (2017), who used RC3 images only (cL = 0.23 − 0.0017α). This is expected, given that the 25 projected XMO4 pixels contain more of the surrounding terrain than the 6 projected RC3 pixels used by Schröder et al. (2017). Let us compare the best-fit Akimov model parameters with those of “Ceres average”, defined by the F1 curve in Fig. 13. Obviously, the normal albedo is much higher than average (A0 = 0.24 vs. 0.094). It is not as high as the normal albedo of 0.6 estimated by Schröder et al. (2017), because we averaged the reflectance over an area much larger than Cerealia Facula itself. The phase curve is shallower than average (ν1 = 0.015 vs. 0.022). This is also expected, as multiple scattering is more prevalent in a bright surface. The OE characteristics are clearly different from average: the OE amplitude is only slightly lower (m = 0.28 vs. 0.38), but the OE peak is substantially narrower (ν2 = 0.70 vs. 0.27). The different quality of the OE can be seen most clearly in Fig. 15B, showing the equigonal albedo. However, this figure also reveals how the XMO4 and RC3 data sets poorly match. The apparent discontinuity around 7° phase angle,most likely due to the difference in spatial resolution (Table 1), suggests that the modeling results presented here cannot be considered fully reliable. Still, this issue would mostly affect the phase curve parameters. The OE characterization for Cerealia Facula is relatively reliable, as it rests almost exclusively on XMO4 data.
(2) Thebest-fit Hapke model is shown in Fig. 15C, and has virtually the same fit quality as the model in Fig. 15A. The parameters consistently converged to w =0.62, BS 0 = 0.96, hS = 0.0069, 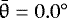 , b = 0.54, and c = 0.68, regardless of the starting values fed to the fitting algorithm. Adopting ι, ϵ < 85° as in Schröder et al. (2017) led to a worse model fit, a higher BS0, a lower hS, but similar values for the other parameters with again
, b = 0.54, and c = 0.68, regardless of the starting values fed to the fitting algorithm. Adopting ι, ϵ < 85° as in Schröder et al. (2017) led to a worse model fit, a higher BS0, a lower hS, but similar values for the other parameters with again 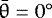 . Clearly, this result is inconsistent with the
. Clearly, this result is inconsistent with the 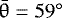 determined from only RC3 data by Schröder et al. (2017), who marked their value as unusually high for a planetary surface. When we fixed
determined from only RC3 data by Schröder et al. (2017), who marked their value as unusually high for a planetary surface. When we fixed  at 59°, we obtained the model fit in Fig. 15D, with w = 0.65, BS 0 = 10 (limit), hS = 0.00019, b = 0.15, and c = −1.0, which fails to fit the data in the OE range (inset). When we subsequently removed the limit on the OE amplitude parameter, the model converged to BS0 = 821, without noticeably improving the fit quality. We then tried to fit the XMO4 alone with
at 59°, we obtained the model fit in Fig. 15D, with w = 0.65, BS 0 = 10 (limit), hS = 0.00019, b = 0.15, and c = −1.0, which fails to fit the data in the OE range (inset). When we subsequently removed the limit on the OE amplitude parameter, the model converged to BS0 = 821, without noticeably improving the fit quality. We then tried to fit the XMO4 alone with 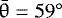 , but found that we could only achieve reasonable fits for
, but found that we could only achieve reasonable fits for 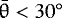 . Therefore, we conclude that the OE observations are not consistent with an unusually high value for the roughness parameter. At the same time, our results confirm that the spatial resolution of the XMO4 images is too low compared to that of the RC3 images for the two data sets to be successfully combined. The present situation is somewhat puzzling. We trust the high photometric roughness derived from the higher resolution RC3 data7, which was confirmed by Longobardo et al. (2018). Perhaps it is the consequence of large-scale topography inside Cerealia Facula, which has a dome at its center (Schenk et al. 2016). At the very minimum, the OE observations do not reinforce the notion that the high roughness value found by Schröder et al. (2017) has physical significance for the regolith properties of Cerealia Facula.
. Therefore, we conclude that the OE observations are not consistent with an unusually high value for the roughness parameter. At the same time, our results confirm that the spatial resolution of the XMO4 images is too low compared to that of the RC3 images for the two data sets to be successfully combined. The present situation is somewhat puzzling. We trust the high photometric roughness derived from the higher resolution RC3 data7, which was confirmed by Longobardo et al. (2018). Perhaps it is the consequence of large-scale topography inside Cerealia Facula, which has a dome at its center (Schenk et al. 2016). At the very minimum, the OE observations do not reinforce the notion that the high roughness value found by Schröder et al. (2017) has physical significance for the regolith properties of Cerealia Facula.
Unfortunately, an analysis of the OE wavelength dependence for Cerealia Facula using only data at small phase angles (as in Fig. 12B) is not possible, as there are only two groups of data points with the restriction of ι, ϵ < 70°, too few for a meaningful exponential model fit. We also found that the modeling of the XMO4 color data for Cerealia Facula is very sensitive to the disk function, while at the same time the cL disk function parameter is ill constrained due to the low spatial resolution and scarcity of data.
 |
Fig. 15 Fitting photometric models to the average reflectance in a 5 × 5 pixel sized box centered on Cerealia Facula in XMO4 and RC3 clear filter images, with ι, ϵ < 70° (n = 69). The insets zooms in on the smallest phase angles. Panel A: Akimov phase function with Lambert/Lommel-Seeliger disk function. Panel B: as panel A, showing the equigonal albedo. The boundary between the two data sets (XMO4 and RC3) is indicated. The best-fit model is drawn in red, while the best-fit model for Ceres average (Fig. 13), scaled to match the former at α = 0°, is drawn in green. Panle C: best-fit Hapke model, which has |
5 Ceres in context
Earlier we estimated the enhancement factor and HWHM of the average Ceres OE as 1.38 and 2.8°, respectively (Table 4). How does the Ceres OE compare to that of other asteroids? Ciarniello et al. (2017) suggest thatC-type asteroids are the closest match to Ceres’ spectrophotometric properties, so we may expect their OE to be similar. Let us consider the clear filter OE in Fig. 13 to be representative for Ceres in the visible. Published reviews of asteroid OE parameters generally consider the integrated brightness in magnitudes, whereas we consider the(resolved) surface reflectance. The integrated phase curve is steeper than the resolved one, because it includes theeffect of the diminishing size of the illuminated part of the asteroid disk with increasing phase angle. A simple geometric correction for the decreasing illuminated fraction of the disk with phase angle is the factor (1 + cosα)∕2 (Ciarniello et al. 2015; Longobardo et al. 2016). Because this factor is close to unity in the OE range (e.g., it is 0.998 for α =5°), we ignore differences between resolved and integrated phase curves.
First wecompare the Ceres OE parameters with those of the asteroids in Belskaya & Shevchenko (2000); Belskaya et al. (2003); Shevchenko et al. (2016). The authors provided two observables: the OE amplitude at 0.3° phase angle, in magnitudes, and the ratio of intensity at 0.3° and 5° phase angle. The former refers to the brightness at 0.3° phase angle relative to the extrapolated brightness of the linear part of the phase curve (on the magnitude scale) at the same phase angle. We converted this quantity to the enhancement factor ζ(0.3°). The intensity ratio is that of the observed integrated intensity, on a linear scale, at two different phase angles. We calculated both quantities for the average Ceres surface. Figure 16A shows that the enhancement factor has a maximum for asteroids of intermediate albedo: the M- and S types. The low albedo C-type asteroids have the lowest factor, whereas the high albedo E-type asteroids have a factor intermediate to that of the C- and M/S types. Belskaya & Shevchenko (2000) explain the peak at intermediate albedos as resulting from the balance between shadow hiding (SH) and coherent backscatter (CB). The former dominates at low albedos, whereas the latter dominates at high albedos. For asteroids of intermediate albedo the two mechanisms may contribute approximately equally, creating a local maximum. However, the contribution of CB as reconstructed by Belskaya & Shevchenko (2000) is the same for asteroids of both intermediate and high albedo, which is somewhat counterintuitive given that the CB amplitude should increase with increasing albedo (Hapke 1993). But, as the authors note, variations in regolith particle size from one asteroid type to another may also affect the OE amplitude. The figure shows that Ceres’ enhancement factor is typical for that of M/S types, being a little higher than that of the C types. The intensity ratio in Fig. 16B shows a similar maximum as ζ(0.3°). Here, the ratio for Ceres fits right in between the C- and M/S types, as expected for an asteroid with a geometric albedo of 0.09.
Rosenbush et al. (2002) evaluated how the HWHM and enhancement factor ζ(0°) depend on the geometric albedo for asteroids of various types, partly using the same data as the previous authors. The enhancement factor in Fig. 17A shows a similar maximum as seen earlier. The HWHM in Fig. 17B appears to be anti-correlated with albedo, although there is a lot of scatter in the data at low albedo. The location of the Ceres parameters in the two figures is consistent with its status as a C type asteroid, although its HWHM is at the high end of the C-type range. The data points in the figure lack error bars8. Ceres was also included in the Rosenbush et al. (2002) survey, with data from Tedesco et al. (1983), and its “old” location is shown as a separate data point in Fig. 17. The distance to the new location can be considered as an indication of the uncertainty of the data in the figure. Longobardo et al. (2018) found that the slope of the Ceres phase curve is close to that of other C-type asteroids. We conclude that the Ceres OE is also typical for an asteroid of its geometric albedo. We can also evaluate the enhancement factor and HWHM over the resolved surface using the Akimov model parameter maps in Fig. 8, concentrating on the area around Azacca crater where the maps are most reliable. As the enhancement factor is calculated as ζ(0°) = 1 + m (Eq. (6)), the map of the enhancement factor is essentially the map of m. We do not recognize the bright Azacca ejecta in the map of m, which implies that the enhancement factor has no clear trend with increasing albedo, where we had expected a slightly positive trend. The reason may be that the OE of the Azacca ejecta is not governed by albedo but by other physical properties, as we suggested in Sect. 4.3. The HWHM is calculated according to Eq. (7), and is about 0.5°–1.0° lower for the Azacca ejecta compared to its darker surroundings. As such, the HWHM shows a clear negative trend with increasing albedo, in line with Fig. 17B.
The figures also show the enhancement factors, full width at half maximum (FWHM), and intensity ratio for Cerealia Facula, which we calculated from the best-fit Akimov model in Fig. 15. Determining the corresponding geometric albedo is not straightforward. The Cerealia Facula phase curve was derived for an area that includes both the facula and its surroundings. However, the shape of the curve will primarily be governed by the facula because it is so much brighter. Therefore, the appropriate geometric albedo is found somewhere in the range shown, for which the lower limit is the normal albedo from the Akimov model (A0 = 0.24), and the upper limit is the geometric albedo estimate from Schröder et al. (2017; pV = 0.6). The upper part of this range overlaps the cluster of E-type asteroid data points. We conclude that the Cerealia Facula OE compares well to that of the E-type asteroids, which have a similar albedo. We infer from the comparison with other asteroids that the OE characteristics of the different Ceres terrains are primarily determined by the local albedo, rather than any other physical properties.
 |
Fig. 16 The Ceres OE compared to that of the asteroids in Belskaya & Shevchenko (2000); Belskaya et al. (2003); Shevchenko et al. (2016). Panel A: enhancement factor ζ(0.3°). Panel B: ratio of the intensities at 0.3° and 5.0°. The Ceres values are those for the clear filter in Table 4 (black star); the formal error of the enhancement factor is on the order of the plot symbol. The Cerealia Facula values are located somewhere on the horizontal line. To simplify the plot we included the F- and G types into the C type. |
 |
Fig. 17 The Ceres OE compared to that of the asteroids in Rosenbush et al. (2002). Panel A: enhancement factor ζ(0°). Panel B: the HWHM. The Ceres values are those for the clear filter in Table 4 (black star) and from Rosenbush et al. (2002; white star). The Cerealia Facula values are located somewhere on the horizontal line. To simplify the plot we included the G type into the C type. |
6 Discussion
We have characterized the OE over a strip on the surface of Ceres that is the path of zero phase as observed by the Dawn cameras. Using different photometric models, we attempted to uncover correlations between the photometric parameters to assess the relative contribution of shadow hiding (SH) and coherent backscatter (CB) to the OE. Coherent backscatter is thought to dominate the OE at very small phase angles (Mishchenko 1992; Mishchenko & Dlugach 1993; Helfenstein et al. 1997; Hapke et al. 1998). We find that the OE has very uniform characteristics over the investigated area, and has an enhancement factor of 1.4 and a FWHM of 3°. If we consider this average, “broad OE” to be representative for the Ceres OE, its characteristics are typical for an asteroid of low to moderate albedo. Azacca crater (Fig. 18) forms a notable exception. The OE of its relatively bright and blue ejecta is enhanced in a very narrow phase angle range (< 0.5°). For asteroid Itokawa, Lee & Ishiguro (2018) found a narrow (<1.4°) enhancement of the OE that correlates with the normal albedo over the surface, which they attributed to CB. Their finding is similar to ours, but the Ceres “narrow OE” is even narrower than that of Itokawa and the associated albedos are lower. The narrow Ceres OE may be highly localized. Due to the absence of a clear correlation of the OE slope with normal albedo, we suspect thatthe Azacca ejecta have physical properties that lead to the enhancement, possibly related to their emplacement. The blue color on Ceres is an indication of youth (Schmedemann et al. 2016; Schröder et al. 2017), therefore the emplacement must have been relatively recent. We note that the narrow OE on both Ceres and Itokawa is in the phase angle range of the polarization OE (a narrow, negative polarization spike) found for E-type asteroids, that Rosenbush et al. (2009) suggested to be related to CB. Although the albedo of the Azacca ejecta is much lower than that of a typical E-type asteroid surface, we speculate that the narrow OE enhancement is also due to CB. According to theory, the width of the CBOE should be substantially dependent on wavelength (Mishchenko 1992; Hapke 2002). We observed no systematic wavelength-dependent variations of the width of the regular, broad OE (FWHM = 3°) over the 0.44–0.96 μm range, which is expected if it is exclusively due to SH. Unfortunately, we do not have sufficient data to establish whether or not the width ofAzacca’s narrow OE is dependent on wavelength.
Let us look closer at the CBOE width prediction. Mishchenko (1992) gives the CBOE width (in radians) for optically thick media as follows:
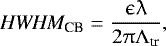 (17)
(17)
with ϵ being a constant, λ the wavelength of light, and Λtr the transport mean free path. The latter can be regarded as the average distance a photon travels before scattering changes its direction by a large angle (Hapke et al. 2012), and depends on the regolith properties as follows:
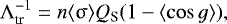 (18)
(18)
where n is the number of particles per unit volume (assumed to be well-separated), ⟨σ⟩ the mean particle geometric cross section, QS the particle scattering efficiency, and g the scattering angle. If the Ceres’ narrow OE is indeed due to CB, then we can roughly estimate the HWHM as 0.5° and find a transport mean free path of about 7 μm (with ϵ = 0.5 and λ = 732 nm, the effective wavelength of the clear filter). We note that if the HWHM is smaller, Λtr is larger. The evaluation of Eq. (17) is not straightforward. Therefore, Mishchenko (1992) provided model curves of the HWHM as a function of particle size, material refractive index (n), and filling factor (fraction of the volume occupied by the particles), assuming a size distribution of spherical particles. The HWHM in all model curves reaches a maximum for particles with a diameter near the wavelength; it approaches zero for particles much smaller or larger than the wavelength. The HWHM increases with filling factor. For refractive indices characteristic for silicates (n = 1.45-1.60), the HWHM is around 2° for the largest filling factor modeled. On the basis of his model curves, Mishchenko (1992) concluded that the HWHM should be substantially dependent on wavelength for silicate surfaces. Expanding on this work, Mishchenko & Dlugach (1993) predicted that CB contributes substantially to the OE of E-type asteroids, and should lead to wavelength-dependent changes of the angular width.
The Mishchenko (1992) prediction has driven a search for wavelength-dependent changes of the OE of rocky solar system bodies over the last few decades. Rosenbush et al. (2009) observed E-type asteroid 44 Nysa and uncovered a narrow brightness OE accompanied by a similarly narrow polarization OE, which they attributed to CB. The authors found evidence for wavelength-dependent changes of the OE width in the visible range, but their results were inconclusive due to limited data availability. For S-type asteroid 433 Eros, Clark et al. (2002) identified a decrease of the OE width parameter in the Hapke (1981, 1984, 1986) model over the 0.8–1.5 μm wavelength range, which they considered to be consistent with CB. For S-type asteroid Itokawa, Kitazato et al. (2008) derived minor, irregular variations in the OE angular width parameter in the Hapke (2002) model over the 0.85–2.1 μm wavelength range, which they considered to be suggestive of CB. However, Lee & Ishiguro (2018) reported no wavelength-dependent variations. Spjuth et al. (2012) did not report such variations either for asteroid Šteins, but may not have searched for them. Hasselmann et al. (2016) did not find evidence for such variations for asteroid Lutetia over the 0.38–0.63 μm wavelength range. Several studies failed to uncover a wavelength dependence for the OE width for the Moon (Buratti et al. 1996; Shkuratov et al. 1999; Hapke et al. 2012). However, Kaydash et al. (2013) found the slope of the lunar OE to increase with wavelength over the 0.5–3.0 μm range for most terrains under study, which they attributed to CB.
The results of the various studies are not always easy to compare because of the use of different OE definitions and the diversity of analytical methods. Nevertheless, it appears that variations of the OE HWHM with wavelength are rarely, ifever, found for planetary surfaces. Failure to find clear wavelength-dependent changes of the lunar OE width has evoked different responses in the literature. Shkuratov et al. (1999) argued that the change of wavelength in Eq. (17) is compensated for by a similar change in the transport mean free path, a structural property of the regolith they termed “quasifractal”. On the other hand, the failure led Hapke et al. (2012) to question our understanding of the CBOE. Tishkovets & Mishchenko (2010), however, argued that we fully understand the physics of CB, but that simulating light scattering by a planetary surface is an extremely complicated effort, as it requires taking into account a complex convolution of contributions from morphologically different surface types with varying albedos. They wrote: “...the only way to establish the CB nature of a laboratory or remote-sensing observation is to compare the measurement results with the results of theoretical computations”. Their argument implies that the Mishchenko (1992) and Mishchenko & Dlugach (1993) predictions were too simplistic, and that the mere absence or presence of wavelength-dependent variations of the OE width is not diagnostic for CB.
It is notobvious that CB can play a role on surfaces as dark as that of Ceres, and it seems that there are no observational photometriccriteria that are unequivocally diagnostic for CB. The Mishchenko (1992) prediction of a wavelength-dependent OE width may be physically correct, but is not necessarily valid for a complex planetary regolith. That said, the very challenging nature of the Dawn observations prevented us from even investigating the wavelength dependence of the narrow OE of the Azacca ejecta, which is our most promising candidate for CB. Perhaps our best chance of demonstrating the role of CB in the Ceres OE lies in comparing the Dawn observations with physically based simulations as described by Tishkovets & Mishchenko (2009), although these models are not easy to handle in practice. In addition, OE observations made by the on-board VIR spectrometer may help to further constrain wavelength-dependent behavior and extend the analysis to larger wavelengths.
 |
Fig. 18 Azacca crater in enhanced color (red: image 45867, 965 nm; green: image 45870, 555 nm; blue: image 45864, 438 nm). |
Acknowledgements
The authors wish to thank the editor and an anonymous referee for his/her helpful suggestions.
References
- Akimov, L. A. 1976, Sov. Astron., 19, 385 [NASA ADS] [Google Scholar]
- Akimov, L. A. 1988a, Kinematika i Fizika Nebesnykh Tel, 4, 3 [NASA ADS] [Google Scholar]
- Akimov, L. A. 1988b, Kinematika i Fizika Nebesnykh Tel, 4, 10 [NASA ADS] [Google Scholar]
- Anderson, J. A., Sides, S. C., Soltesz, D. L., Sucharski, T. L., & Becker, K. J. 2004, in Lunar and Planetary Institute Science Conference Abstracts, eds. Mackwell S. & Stansbery E., 35, 2039 [Google Scholar]
- Becker, K. J., Anderson, J. A., Barrett, J. M., Sides, S. C., & Titus, T. N. 2012, in Lunar and Planetary Institute Science Conference Abstracts, 43, 2892 [NASA ADS] [Google Scholar]
- Belskaya, I. N., & Shevchenko, V. G. 2000, Icarus, 147, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Belskaya, I. N., Shevchenko, V. G., Kiselev, N. N., et al. 2003, Icarus, 166, 276 [NASA ADS] [CrossRef] [Google Scholar]
- Buratti, B., & Veverka, J. 1983, Icarus, 55, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Buratti, B. J., Hillier, J. K., & Wang, M. 1996, Icarus, 124, 490 [NASA ADS] [CrossRef] [Google Scholar]
- Bus, S. J., & Binzel, R. P. 2002, Icarus, 158, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Ciarniello, M., Capaccioni, F., Filacchione, G., et al. 2015, A&A, 583, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ciarniello, M., De Sanctis, M. C., Ammannito, E., et al. 2017, A&A, 598, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clark, B. E., Helfenstein, P., Bell, J. F., et al. 2002, Icarus, 155, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Déau, E. 2012, J. Quant. Spectr. Rad. Transf, 113, 1476 [NASA ADS] [CrossRef] [Google Scholar]
- Dlugach, Z. M., & Mishchenko, M. I. 2013, Solar Syst. Res., 47, 454 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, T. 1956, ApJ, 123, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Hapke, B. 1981, J. Geophys. Res., 86, 3039 [Google Scholar]
- Hapke, B. 1984, Icarus, 59, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Hapke, B. 1986, Icarus, 67, 264 [NASA ADS] [CrossRef] [Google Scholar]
- Hapke, B. 1993, Theory of Reflectance and Emittance Spectroscopy (Cambridge: Cambridge University Press) [Google Scholar]
- Hapke, B. 2002, Icarus, 157, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Hapke, B., Nelson, R., & Smythe, W. 1998, Icarus, 133, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Hapke, B., Denevi, B., Sato, H., Braden, S., & Robinson, M. 2012, J. Geophy. Res., 117, E00H15 [Google Scholar]
- Hasselmann, P. H., Barucci, M. A., Fornasier, S., et al. 2016, Icarus, 267, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Helfenstein, P. 1988, Icarus, 73, 462 [NASA ADS] [CrossRef] [Google Scholar]
- Helfenstein, P., & Veverka, J. 1989, in Asteroids II, eds. R. P. Binzel, T. Gehrels, & M. S. Matthews (Tucson, AZ: University of Arizona Press), 557 [Google Scholar]
- Helfenstein, P., Veverka, J., & Hillier, J. 1997, Icarus, 128, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Helfenstein, P., Currier, N., Clark, B. E., et al. 1998, Icarus, 135, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Henyey, L. G., & Greenstein, J. L. 1941, ApJ, 93, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Hestroffer, D., & Magnan, C. 1998, A&A, 333, 338 [NASA ADS] [Google Scholar]
- Kaasalainen, M., Torppa, J., & Muinonen, K. 2001, Icarus, 153, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Kaydash, V., Pieters, C., Shkuratov, Y., & Korokhin, V. 2013, J. Geophys. Res., 118, 1221 [NASA ADS] [CrossRef] [Google Scholar]
- Kitazato, K., Clark, B. E., Abe, M., et al. 2008, Icarus, 194, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Korokhin, V. V., Velikodsky, Y. I., Shkuratov, Y. G., & Mall, U. 2007, Solar Syst. Res., 41, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Kuga, Y., & Ishimaru, A. 1984, J. Opt. Soc. Am. A, 1, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, M., & Ishiguro, M. 2018, A&A, 616, A178 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, J.-Y., Nathues, A., Mottola, S., et al. 2015, European Planetary Science Congress, Nantes, France (EPSC2015), 10 [Google Scholar]
- Li, J.-Y., Reddy, V., Nathues, A., et al. 2016, ApJ, 817, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Longobardo, A., Palomba, E., Ciarniello, M., et al. 2016, Icarus, 267, 204 [NASA ADS] [CrossRef] [Google Scholar]
- Markwardt, C. B. 2009, in Astronomical Data Analysis Software and Systems XVIII, eds. D. A. Bohlender, D. Durand, & P. Dowler, ASP Conf, Ser., 411, 251 [NASA ADS] [Google Scholar]
- Masoumzadeh, N., Boehnhardt, H., Li, J.-Y., & Vincent, J.-B. 2015, Icarus, 257, 239 [NASA ADS] [CrossRef] [Google Scholar]
- McEwen, A. S. 1996, Lunar and Planetary Institute Science Conference Abstracts, 27, 841 [NASA ADS] [Google Scholar]
- Mishchenko, M. I. 1992, Ap&SS, 194, 327 [Google Scholar]
- Mishchenko, M. I. 1993, ApJ, 411, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Mishchenko, M. I., & Dlugach, J. M. 1993, Planet. Space Sci., 41, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Mishchenko, M. I., Dlugach, J. M., Liu, L., et al. 2009, ApJ, 705, L118 [NASA ADS] [CrossRef] [Google Scholar]
- Moré, J. J. 1978, in Numerical Analysis: Proceedings of the Biennial Conference Held at Dundee, June 28–July 1, 1977, ed. G. A. Watson (Berlin, Heidelberg: Springer), 105 [Google Scholar]
- Muinonen, K., Tyynelä, J., Zubko, E., & Videen, G. 2010, in Light Scattering Reviews, ed. A. Kokhanovsky (Berlin, Heidelberg: Springer Praxis Books), 5, 375 [Google Scholar]
- Muinonen, K., Parviainen, H., Näränen, J., et al. 2011, A&A, 531, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petrova, E. V., & Tishkovets, V. P. 2011, Solar Syst. Res., 45, 304 [NASA ADS] [CrossRef] [Google Scholar]
- Preusker, F., Scholten, F., Matz, K.-D., et al. 2016, Lunar and Planetary Science Conference, 47, 1954 [NASA ADS] [Google Scholar]
- Rayman, M. 2017, 68th International Astronautical Congress (IAC), Adelaide, Australia [Google Scholar]
- Reddy, V., Li, J.-Y., Gary, B. L., et al. 2015, Icarus, 260, 332 [NASA ADS] [CrossRef] [Google Scholar]
- Roatsch, T., Kersten, E., Matz, K.-D., et al. 2016, Planet. Space Sci., 121, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenbush, V., Kiselev, N., Avramchuk, V., & Mishchenko, M. 2002, in Optics of Cosmic Dust, eds. G. Videen & M. Kocifaj (Berlin: Springer), 191 [Google Scholar]
- Rosenbush, V., Kiselev, N., & Avramchuk, V. 2006, J. Quant. Spectr. Rad. Transf., 100, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenbush, V. K., Shevchenko, V. G., Kiselev, N. N., et al. 2009, Icarus, 201, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Ruesch, O., Nathues, A., Jaumann, R., et al. 2017, in Lunar and Planetary Science Conference, 48, 2435 [NASA ADS] [Google Scholar]
- Schenk, P. M., Buczkowski, D., Scully, J. E. C., et al. 2016, in AAS/Division for Planetary Sciences Meeting Abstracts, 48, 506.04 [Google Scholar]
- Schmedemann, N., Kneissl, T., Neesemann, A., et al. 2016, Geophys. Res. Lett., 43, 11 [CrossRef] [Google Scholar]
- Schröder, S. E., Keller, H. U., Gutierrez, P., et al. 2010, Planet. Space Sci., 58, 1107 [NASA ADS] [CrossRef] [Google Scholar]
- Schröder, S. E., Maue, T., Gutiérrez Marqués, P., et al. 2013, Icarus, 226, 1304 [NASA ADS] [CrossRef] [Google Scholar]
- Schröder, S. E., Mottola, S., Matz, K.-D., & Roatsch, T. 2014, Icarus, 234, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Schröder, S. E., Keller, H. U., Mottola, S., et al. 2015, Planet. Space Sci., 117, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Schröder, S. E., Mottola, S., Carsenty, U., et al. 2017, Icarus, 288, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Shepard, M. K., & Helfenstein, P. 2007, J. Geophys. Res., 112, E03001 [NASA ADS] [Google Scholar]
- Shevchenko, V. G., & Belskaya, I. N. 2010, European Planetary Science Congress, Rome, Italy (EPSC2010), 5 [Google Scholar]
- Shevchenko, V. G., & Tedesco, E. F. 2006, Icarus, 184, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Shevchenko, V. G., Belskaya, I. N., Muinonen, K., et al. 2016, Planet. Space Sci., 123, 101 [Google Scholar]
- Shkuratov, Y. G., & Helfenstein, P. 2001, Icarus, 152, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Shkuratov, Y. G., Starukhina, L. V., Kreslavsky, M. A., et al. 1994, Icarus, 109, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Shkuratov, Y. G., Kreslavsky, M. A., Ovcharenko, A. A., et al. 1999, Icarus, 141, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Shkuratov, Y., Ovcharenko, A., Zubko, E., et al. 2002, Icarus, 159, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Shkuratov, Y., Petrov, D., & Videen, G. 2003, J. Opt. Soc. Am. A, 20, 2081 [NASA ADS] [CrossRef] [Google Scholar]
- Shkuratov, Y., Kaydash, V., Korokhin, V., et al. 2011, Planet. Space Sci., 59, 1326 [NASA ADS] [CrossRef] [Google Scholar]
- Shkuratov, Y., Kaydash, V., Korokhin, V., et al. 2012, J. Quant. Spectr. Rad. Transf., 113, 2431 [NASA ADS] [CrossRef] [Google Scholar]
- Sierks, H., Keller, H. U., Jaumann, R., et al. 2011, Space Sci. Rev., 163, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Spjuth, S., Jorda, L., Lamy, P. L., Keller, H. U., & Li, J.-Y. 2012, Icarus, 221, 1101 [NASA ADS] [CrossRef] [Google Scholar]
- Tedesco, E. F. 1989, in Asteroids II, eds. R. P. Binzel, T. Gehrels, & M. S. Matthews (Tucson, AZ: University of Arizona Press), 1090 [Google Scholar]
- Tedesco, E. F., Taylor, R. C., Drummond, J., et al. 1983, Icarus, 54, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Tedesco, E. F., Noah, P. V., Noah, M., & Price, S. D. 2002, AJ, 123, 1056 [Google Scholar]
- Tishkovets, V. P. & Mishchenko, M. I. 2009, J. Quant. Spectr. Rad. Transf., 110, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Tishkovets, V. P. & Mishchenko, M. I. 2010, J. Quant. Spectr. Rad. Transf., 111, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Van Albada, M. P., & Lagendijk, A. 1985, Phys. Rev. Lett., 55, 2692 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Velikodsky, Y. I., Opanasenko, N. V., Akimov, L. A., et al. 2011, Icarus, 214, 30 [NASA ADS] [CrossRef] [Google Scholar]
A simple fix for residual charge exists in the form of acquisition of a zero-second exposure immediately prior to the regular exposure (Schröder et al. 2013), which was, unfortunately, not implemented for XMO4.
Using the MPFITFUN library retrieved from http://cow.physics.wisc.edu/~craigm/idl/idl.html.
We note that A0 is not equal to the normal albedo of Hapke (1981), which is defined at zero phase but arbitrary incidence angle (ι = ϵ), and therefore depends on the local topography.
Shepard & Helfenstein (2007) erroneously stated the opposite.
Déau (2012) reported using βλ = αλ instead of αλ∕2 for the exponent in Eq. (16), which is not consistent with Hestroffer & Magnan (1998).
We quote this value with the caveat that Reddy et al. (2015) found Ceres’ brightness predicted by the Helfenstein & Veverka (1989) model to be off by about 20% for unknown reasons.
Schröder et al. (2017) minimized the consequences of projection errors by inspecting each projected image and removing those with large errors from their sample.
Rosenbush et al. (2002) provide the following estimated error ranges: 0.01–0.08 for ζ(0°) and 0.1°–0.7° for the HWHM.
All Tables
Available FC2 image data covering ROI 1 for the RC3 and XMO4 mission phases with no restrictions on the photometric angles.
Best-fit Hapke parameters for the aggregated ROI 2 data, using the single-term Henyey–Greenstein function with α > 0.05° and ι, ϵ < 50°.
All Figures
 |
Fig. 1 The locations of zero phase in clear (○) and narrow-band (□) framing camera images displayed on a map of the normal albedo in the clear filter (Schröder et al. 2017). The regions delineated by the dotted and dashed lines are two regions of interest (ROI 1 and ROI 2). |
| In the text | |
 |
Fig. 2 Ceres images representing different parts of the phase curve, shown at their correct relative brightness on a linear scale. The image number, mission phase, and phase angle at the disk center are indicated. Only the Cerealia and Vinalia Faculae (the bright spots in the opposition image at far left) are not displayed at their correct brightness, as they are much brighter than the average Ceres surface (Li et al. 2016; Schröder et al. 2017). |
| In the text | |
 |
Fig. 3 In-field stray light in full-frame FC2 images acquired with different filters (F1–F8) during the RC3 and XMO4 mission phases (image numbers indicated). The percentages refer to how the average signal in the white square compares to that in the black square in each image (for clarity, the squares are only shown for F8). Cerealia Facula is outside the black square. The images are displayed with black being zero signal and white being 5% of the average signal in the black square. The stray light in the RC3 images is about 50% stronger than in the XMO4 images. |
| In the text | |
 |
Fig. 4 Characteristics of ROI 1 (outlined in Fig. 1). Panel A: shape model with Lambert reflection and illuminationconditions from XMO4 image 89504. The green and red stars denote locations selected for detailed study. Craters of interest are indicated. Panel B: enhanced color composite with filters F5 (965 nm), F2 (555 nm), and F8 (438 nm) inthe RGB color channels (Schröder et al. 2017). ROI 2 is indicated. We note that the color and brightness of the spots in Occator cannot be displayed correctly here as they are much brighter than their surroundings, exceeding the dynamicrange of the figure. |
| In the text | |
 |
Fig. 5 Fitting the Akimov model to the average reflectance in a box of 3 × 3 pixels centered on the location of the green star in Fig. 4A. The fit, with parameters (A0, ν1, m, ν2) = (0.091, 0.023, 0.32, 0.32), was limited to data with 0.05° < α < 40° and ι, ϵ< 70°. Panel A: reflectance. Panel B: equigonal albedo (logarithmic scale), with the best-fit model from panel A drawn in red. The inset shows the enhancement factor, or the equigonal albedo divided by the “linear” part of the phase curve (dashed red line). Panel C: zooming in on the phase angle range below 1°. The solid curve accounts for the finite size of the Sun, whereas the dashed curve does not. The vertical dotted line indicates the angular radius of the Sun at Ceres. Panel D: as in panel C, but with the phase angle on a logarithmic scale. |
| In the text | |
 |
Fig. 6 Fitting the Hapke model to the average reflectance in a box of 3 × 3 pixels centered on the location of the green star in Fig. 1, with α > 0.05° and ι, ϵ< 70°. The inset zooms in on the phase angle range below 1°. These four solutions, with parameters listed in Table 2, were identified by the Levenberg–Marquardt optimization algorithm. Panels A and B use the single-term Henyey–Greenstein function, whereas Panels C and D use the double-term Henyey–Greenstein function. The search start value for the photometric roughness was
|
| In the text | |
 |
Fig. 7 Minimum (left panel) and maximum (right panel) phase angle of observation in ROI 1 for ι, ϵ < 50°. |
| In the text | |
 |
Fig. 8 Maps of the Akimov model parameters (Eqs. (4) and (5)) in ROI 1, with ι, ϵ < 50°. The Azacca ejecta are encircled in the A0 map. |
| In the text | |
 |
Fig. 9 Sensitivity analysis of the Akimov model parameter retrieval. Left panel: map of m with all phase angles included and ι, ϵ < 70°. Right panel:map of ν2 with phase angle restricted to α > 0.5° and ι, ϵ< 50°. See text for details. |
| In the text | |
 |
Fig. 10 Maps of the OE parameters (Eq. (5) with m = 0, and ν1 the OE slope) for the clear filter, with ι, ϵ < 50°. The phase angle was restricted to 0.2° < α < 0.6° for panels A and B, and to 0.6° < α < 1.0° for panels Cand D. The Azacca ejecta are encircled. |
| In the text | |
 |
Fig. 11 Hapke model parameters with the single-term Henyey-Greenstein function and ι, ϵ < 50°. The minimum and maximum phase angles are as in Fig. 7. The Azacca ejecta are encircled in the w map. |
| In the text | |
 |
Fig. 12 Modeling the narrow-band reflectances, calculated as the average of a box of 3 × 3 pixels centered on the location of the red star in Fig. 4A, with ι, ϵ < 50°. The best-fit model parameters are listed in Table 3. Panel A: Akimov phase function (Eq. (5)). Panel B: exponential phase function (Eq. (5) with m = 0), fitted to α < 1.5°. The model curves account for the finite size of the Sun, with the vertical dotted line indicating the angular radius of the Sun at Ceres. |
| In the text | |
 |
Fig. 13 Average phase curves of the terrain in ROI 2 (outlined in Fig. 1). The data are displayed as a density in agrid, with the colors reflecting the number of data points in each grid box. The drawn lines are best-fit Akimov phase functions, with the coefficients listed in Table 4. The fit was restricted to data with α > 0.05° and ι, ϵ< 50°. |
| In the text | |
 |
Fig. 14 Maps of the OE parameters (Eq. (5) with m = 0, and ν1 the OE slope) for the three narrow-band filters used during XMO4. The phase angle was restricted to 0.05° < α < 1.50°, with ι, ϵ < 50°. The actual minimum and maximum phase angle of the data, αmin and αmax, are shown for filter F3 (the maps for F5 and F8 are very similar). |
| In the text | |
 |
Fig. 15 Fitting photometric models to the average reflectance in a 5 × 5 pixel sized box centered on Cerealia Facula in XMO4 and RC3 clear filter images, with ι, ϵ < 70° (n = 69). The insets zooms in on the smallest phase angles. Panel A: Akimov phase function with Lambert/Lommel-Seeliger disk function. Panel B: as panel A, showing the equigonal albedo. The boundary between the two data sets (XMO4 and RC3) is indicated. The best-fit model is drawn in red, while the best-fit model for Ceres average (Fig. 13), scaled to match the former at α = 0°, is drawn in green. Panle C: best-fit Hapke model, which has |
| In the text | |
 |
Fig. 16 The Ceres OE compared to that of the asteroids in Belskaya & Shevchenko (2000); Belskaya et al. (2003); Shevchenko et al. (2016). Panel A: enhancement factor ζ(0.3°). Panel B: ratio of the intensities at 0.3° and 5.0°. The Ceres values are those for the clear filter in Table 4 (black star); the formal error of the enhancement factor is on the order of the plot symbol. The Cerealia Facula values are located somewhere on the horizontal line. To simplify the plot we included the F- and G types into the C type. |
| In the text | |
 |
Fig. 17 The Ceres OE compared to that of the asteroids in Rosenbush et al. (2002). Panel A: enhancement factor ζ(0°). Panel B: the HWHM. The Ceres values are those for the clear filter in Table 4 (black star) and from Rosenbush et al. (2002; white star). The Cerealia Facula values are located somewhere on the horizontal line. To simplify the plot we included the G type into the C type. |
| In the text | |
 |
Fig. 18 Azacca crater in enhanced color (red: image 45867, 965 nm; green: image 45870, 555 nm; blue: image 45864, 438 nm). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.