EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 665 (September 2022) A&A, 665 (2022) A15 Full HTML
Open Access
Issue
A&A
Volume 665, September 2022
Article Number A15
Number of page(s) 10
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/202143012
Published online 02 September 2022

© T. Y. Xu et al. 2022

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.

1 Introduction

Planetary photometry is a classical problem in planetary observations. It describes how the brightness of a planetary surface changes with the incidence angle (i), emission angle (e), and phase angle (g). The photometry of bodies provides essential information regarding their surface physical properties, including roughness and porosity (Hapke 1984, 2008, 2012b). Moreover, photometric models can be used for photometric correction of remote sensing data. Data can be rectified to the same observation geometry, such as (30°, 0°, 30°) in (i, e, g); hence, reflectance can be conveniently compared for different regions and various data.

Among the extraterrestrial bodies, the Moon’s photometric property is the most studied. Studies include laboratory measurements of lunar or mineral samples (e.g., McGuire & Hapke 1995; Hapke et al. 1996, 1998; Nelson et al. 1998, 2000, 2002; Shkuratov et al. 2002; Shepard & Helfenstein 2007; Johnson et al. 2013), remote measurements from Earth-based telescopes (e.g., Helfenstein & Veverka 1987; Helfenstein et al. 1997; Kieffer & Stone 2005; Saiki et al. 2008; Shkuratov et al. 2008; Goguen et al. 2010; Buratti et al. 2011; Velikodsky et al. 2016), and lunar-orbiting spacecraft (e.g., Buratti et al. 1996; Hillier et al. 1999; Shkuratov et al. 1999; Yokota et al. 2011; Boyd et al. 2012; Besse et al. 2013b; Wu et al. 2013; Sato et al. 2014; Velikodsky et al. 2016).

To a specific body, photometric parameters can be influenced by many factors, including the working wavelength (Buratti et al. 1996; Hillier et al. 1999; Shkuratov et al. 1999; Hapke et al. 2012), measuring scale or resolution (Helfenstein & Shepard 1999), and geometric angles of the measurement (Li et al. 2000). A wide range of observational angles is helpful to build an accurate model and to retrieve information on the regolith. However, Earth-based and orbiting observations often have a limited phase angle range because the observation zenith angle is mostly minimal. The phase function at large phase angles is uncertain and cannot be extrapolated in this condition. The Panoramic Camera (PCAM) on board the Chang’E-3 (CE-3) Yutu rover conducted in situ measurements of the lunar surface in three channels. The measurements included a broad phase angle range from near 0° to 160°, complementing existing measurements for the range of photometric geometry and benefiting photometric research. The in situ data by PCAM were on a millimeter-centimeter scale. In situ measurements differed from the lunar samples because the former were acquired in undisturbed lunar soil. These PCAM data provided the opportunity to study the photometric properties of pristine lunar regolith in extensive phase angles on a centimeter scale. Nevertheless, some of the measured areas were influenced by the landing of spacecraft, which caused differences between the measuring sites.

The purpose of this study is to utilize the CE-3 PCAM data for spectrophotometric analysis. We obtained phase functions of regolith in a vast phase angle range. Photometric properties were compared among different sites, where the physical properties of regolith differ because of the landing influence.

2 Background

2.1 Photometric models

Multiple photometric models have been developed over decades of studies: the Lommel-Seeliger law, Akimov disk functions (Akimov 1975, 1979; Akimov et al. 1999), Hapke photometric model (Hapke 1981, 1984, 2002, 2008, 2012b, 2021), Kaasalainen-Shkuratov model (Kaasalainen et al. 2001; Shkuratov et al. 2011; Domingue & Hapke 1989), exponential-polynomial empirical photometric model (Hillier et al. 1999; Wu et al. 2013; Besse et al. 2013a), McEwen’s disk model (McEwen et al. 1998; Yokota et al. 2011), and ROLO lunar model (Kieffer & Stone 2005). These models aim to fit the brightness changes on the lunar disk or with phase angle variations. Moreover, photometric corrections that enable one to compare the reflectance of different measurements in various geometric conditions quantitatively are often undertaken using these models (e.g., Yokota et al. 2011; Besse et al. 2013b; Wu et al. 2013; Sato et al. 2014; Domingue et al. 2016).

The opposition effect (OE) is a notable attribute in photometric measurements primarily considered in models. It denotes a rapid increase in reflectance when the phase angle is near 0°. Two mechanisms have been suggested to cause it: the shadow hiding opposition effect (SHOE) and the CBOE (Shkuratov et al. 2011; Hapke 2012b). Before, it had been widely believed that SHOE dominated the OE of the Moon (e.g., Buratti et al. 1996; Helfenstein et al. 1997; Hillier et al. 1999; Shkuratov et al. 2011). For the past few years, Hapke et al. (2012) and Hapke (2021) considered that CBOE played a primary role in lunar OE on the basis of models using Lunar Reconnaissance Orbiter Camera (LROC) Wide Angle Camera (WAC) data.

The spectra might become redder with increasing phase angle, called phase reddening. It is also a prominent phenomenon in photometric studies. In some conditions, this effect appears only at small phase angles. When the phase angle is greater, the spectra become bluer, making the entire color ratio curve similar to an arch, as determined from space observations and laboratory experiments (e.g., Kaydash et al. 2010, 2013; Johnson et al. 2013; Schröder et al. 2014). From the laboratory experiments by Schröder et al. (2014), the arch-shaped ratio curve emerged when the measured sample particles were semitransparent and smooth on the particle size scale. In other conditions, the color ratio curve keeps a monotonic phase reddening at small and large phase angles. Section 5 provides a more detailed discussion.

2.2 Landing area

The CE-3 lander arrived at (44.121° N, 19.512° W) in northern Mare Imbrium on December 14, 2013. The landing site was ~50 m east of Zi Wei, a 450 m-diameter crater. It belonged to the darkest high-Ti basalts and was young, with an age of ~2.35 Ga (Wu & Hapke 2018).

The landing area was observed as brightened by the LROC Narrow Angle Camera (NAC; Fig. 1). Among the three measurement sites circled in Fig. 1, Site 6 was the closest to the lander, and Site 8 was the furthest from it. Therefore, Site 6 was influenced by the descent exhaust more than Site 7, while Site 8 was almost not disturbed. The main effect of the exhaust disturbance was considered to be that the uppermost fine regolith was blown away. Consequently, the grain size of regolith in disturbed regions would be greater than that in undisturbed regions. Moreover, the remaining regolith in disturbed regions was less space weathered (Wu & Hapke 2018; Wang et al. 2017). Figure 2 is an example showing the regolith near the rover. The three images were in a similar relative azimuth angle of ~90°. Regions close to the rover (~3 m away) in the inner ring images have ~0.5 mm px−1 resolution. Despite the fact that millimeter-centimeter structures can be recognized in the images, this scale is still much larger than the practical grain size, which is often in micron scale. However, from the morphology of regolith, the surface of Site 8 was relatively smooth and covered by fine dust, whereas dust could hardly be recognized at Site 6. The condition at Site 7 was between those at Site 6 and Site 8.

thumbnail Fig. 1

CE-3 landing site by LROC NAC, image M1300246898L (i = 43.44°, g = 43.68°). The locations of the lander and measurement sites are indicated with arrows. The yellow dashed circles represent approximate ranges of the inner rings of Sites 6, 7, and 8.
thumbnail Fig. 2

Example images of the inner rings. The top row is the entire image, and the bottom row is the zoom of each yellow dotted box. The plotting scale represents an approximate scale at the bottom of the images. The labels of the images are 041_0006 (Site 6), 056_0007 (Site 7), and 052_0008 (Site 8).
Table 1

Channel characteristics of PCAM.

3 Observations and methodology

3.1 Instrument and measurements

The PCAM was on the top of the rover at a height of ~1.5m relative to the ground. It consisted of a pair of left and right cameras, which were of identical constructions. The field of view of the PCAM was 19.6° × 14.5°. The PCAM had two photography modes: color mode and gray mode (Ren et al. 2014). The color mode had 2352 × 1728 pixels in a Bayer CFA filter pattern (RGGB) with a red pixel at the upper left corner. There were four color channels: red, green 1, green 2, and blue. The two green channels had similar responses and were put together in the following steps. The channel effective wavelength λeff was calculated by 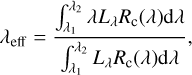λeff=∫λ1λ2λLλRc(λ)dλ∫λ1λ2LλRc(λ)dλ,${\lambda _{{\rm{eff}}}} = {{\int_{{\lambda _1}}^{{\lambda _2}} {\lambda {L_\lambda }{R_{\rm{c}}}\left( \lambda \right){\rm{d}}\lambda } } \over {\int_{{\lambda _1}}^{{\lambda _2}} {{L_\lambda }{R_{\rm{c}}}\left( \lambda \right){\rm{d}}\lambda } }},$(1)

where λ is the wavelength, Lλ is the solar irradiance spectrum at 1 AU (Thuillier et al. 2004), and Rc(λ) is the spectral response function from Ren et al. (2014). Table 1 provides the calculated effective wavelengths of the channels. The gray mode combines four-color pixels into one gray pixel with a resolution of 1176 × 864.

Color panorama photos were obtained by PCAM at three sites: 6, 7, and 8. Their positions are denoted in Fig. 1. In addition, nine pairs of images were obtained at Site 5. However, the target was the lander and a narrow range of phase angle was included. The measurement sites were to the south of the lander. There were 56 pairs of images at each site to form a panorama, in which one pair represents an image from the left camera and the other from the right camera. About an hour was needed to obtain all 56 pairs of images, during which the changes in solar illumination and solar incidence angle were negligible. The images were named from 001 to 056 in two rings at every site. Images 1–28 were the outer ring, while images 29–56 were the inner ring. Figure 3a is the mosaic of the ringed view at Site 7, depicting how the images named with serial numbers were arranged. Figures 3b–d illustrates mosaics of Sites 6, 7, and 8. The solar incidence angles for Sites 6, 7, and 8 were 73.6°, 70.0°, and 60.1 °, respectively. The inner ring had an inner radius of ~2.3–3.4 m and an outer radius of ~5–7.5 m. The outer ring extended far away near the horizon. Part of the outer ring images included a dark sky.

This study used PCAM level 2B (L2B) data, in which the digital number (DN) values had been transformed from 10-bit to 8-bit, and dark current and field distortions had been removed. Only the left camera data were used in this study because those from the left and right cameras were photometrically identical. We also used the L2B data of the CE-3 Visible-Near-Infrared Spectrometer (VNIS) for spectral correction because the phase curves for blue and green channels were found to be unusually close to each other (Sect. 3.2). The VNIS measured the regolith spectra at Sites 5, 6, 7, and 8 in a spectral range from 450 nm to 2395 nm.

thumbnail Fig. 3

Mosaic of PCAM images in a ring, including the inner and outer rings. (a) Site 7. The red numbers denote the locations of the images labeled from 1 to 56. The locations are the same among the three mosaics. (b) Site 6. The shadow of the PCAM at location 34 is the OE region, and abnormal bright regions at locations 7–12 were influenced by abnormal reflections at large phase angles. (c) Site 7. Locations 50 and 51 represent the OE region, while locations 19–22 are at large phase angles. (d) Site 8. There is no major OE region, with locations 25–28 slightly influenced by abnormal reflections.

3.2 Calibration

The radiance for each channel Lc was converted from the DN values by 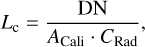Lc=DNACali · CRad,${L_{\rm{c}}} = {{{\rm{DN}}} \over {{A_{{\rm{Cali}}}}\,\cdot\,{C_{{\rm{Rad}}}}}},$(2)

where ACali is the exposure time factor, which is gain-exposure time/setting exposure time; and CRad is the radiance calibration factor of each channel in Sr m2 nm W−1, which is 5.9365 × 105 for the red channel, 5.9796 × 105 for the first green channel, 5.8939 × 105 for the second green channel, and 5.1837 × 105 for the blue channel.

This study used a radiance factor and reduced reflectance to represent reflectance. The radiance factor (RADF or I/F) is the ratio of bidirectional reflectance of a surface to that of a perfectly diffused surface illuminated at i = 0 (Hapke 2012b), calculated by 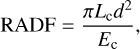RADF=πLcd2Ec,${\rm{RADF}} = {{\pi {L_{\rm{c}}}{d^2}} \over {{E_{\rm{c}}}}},$(3)

where d is the Sun-Moon distance in AU when making measurements. Furthermore, Ec is the effective solar channel irradiance at 1 AU, calculated by 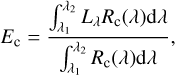Ec=∫λ1λ2LλRc(λ)dλ∫λ1λ2Rc(λ)dλ,${E_{\rm{c}}} = {{\int_{{\lambda _1}}^{{\lambda _2}} {{L_\lambda }{R_{\rm{c}}}\left( \lambda \right){\rm{d}}\lambda } } \over {\int_{{\lambda _1}}^{{\lambda _2}} {{R_{\rm{c}}}\left( \lambda \right){\rm{d}}\lambda } }},$(4)

where λ is the wavelength and Rc(λ) is the spectral response function (Ren et al. 2014). Table 1 provides the calculated results.

Reduced reflectance (denoted by rR(i, e, g)) is RADF divided by the Lommel–Seeliger function LS, which is as follows: 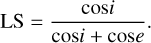LS=cosicosi+cose.${\rm{LS}} = {{\cos i} \over {\cos i + \cos e}}.$(5)

Figures 3b and c depicts large shadows of the rover camera at phase angles near 0°. Some areas were abnormally bright at large phase angles. One possible cause was the reflections off the rover. Therefore, the usable regions at large phase angles were greatly reduced and should be selected using the region of interest (ROI).

First, we removed the massive shadow and abnormal reflections by setting ROI. The craters, stones, shadows, and rover tracks were also removed using a threshold method to avoid their effects on regionally averaged reflectance. Next, pixels were binned spatially, averaging every 60 × 40 pixels (0.5° × 0.34°) into one point. Spatial binning ensured that pixels binned with similar phase angles would not differ in emission and relative azimuth angles. Finally, reflectance phase functions were collected from the binned reflectance data.

Although prominent areas affected by reflections off the rover were excluded from consideration, some residual stray light corrections were necessary for certain phase angle images. Given that most of the usable regions were near the horizon, the stray light intensity there was expected to be close to the dark sky. We employed the difference between the average radiance of dark sky regions in images influenced by stray light and in uninfluenced images. The latter exhibited an average radiance close to 0, thereby enabling an estimate of stray light intensity to be made and subtracted in the affected images. For images with no dark sky, the stray light intensity of the image at the symmetrical position at about 180° was used. The stray light intensities for different images varied remarkably. The proportion of stray light to normal light at significant phase angles varied from 5% to 74% for Site 6, 8% to 49% for Site 7, and 5% to 21% for Site 8, depending on the phase angles.

A spectral correction was necessary because we found that the PCAM spectra were abnormally concave and the spectral slopes from PCAM were different from VNIS measurements. The slope of the VNIS spectra was more accurate than that of the PCAM spectra and could match the lunar radiation better. Therefore, we used the CE-3 VNIS spectra to correct the general channel ratios of PCAM. The VNIS measurements were conducted at the same measuring sites as the PCAM measurements. The targets of the VNIS were regolith close to the rover (Wu et al. 2018). For Sites 6, 7, and 8, the solar zenith angles of VNIS measurements were 67.5°, 69.6°, and 54.0°; the view zenith angles were 47.4°, 47.0°, and 44.4°; and the phase angles were 85.6°, 86.0°, and 95.3°, respectively. The corrected ratio of the three channels based on VNIS spectra was calculated by 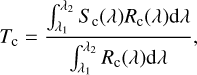Tc=∫λ1λ2Sc(λ)Rc(λ)dλ∫λ1λ2Rc(λ)dλ,${T_{\rm{c}}} = {{\int_{{\lambda _1}}^{{\lambda _2}} {{S_{\rm{c}}}\left( \lambda \right){R_{\rm{c}}}\left( \lambda \right){\rm{d}}\lambda } } \over {\int_{{\lambda _1}}^{{\lambda _2}} {{R_{\rm{c}}}\left( \lambda \right){\rm{d}}\lambda } }},$(6)

where Tc is the summation of received radiance for the channel, Sc(λ) is the CE-3 VNIS radiance spectra (Wu & Hapke 2018), and Rc(λ) is the PCAM spectral response function. The effective reflectance is Tc/Ec, corresponding to the VNIS reflectance spectra. To correct the PCAM spectra to the VNIS spectra, the reflectances of blue and red channels were multiplied by a factor to fulfill the same channel ratio as the effective reflectance. The spectra before and after correction are illustrated in Fig. 4. The slopes between the bands became more consistent than the original spectra. The correction for Site 8, which decreased the spectral slope, was opposite to those for the two other sites. The reason was that the VNIS spectrum for Site 8 had a lower slope than those for Sites 6 and 7 in this wavelength range and lacked an absorption peak near 660 nm. One possible explanation was that Site 8 was not disturbed and more space weathered.

thumbnail Fig. 4

PCAM spectra before and after spectral correction compared with VNIS spectra. The lines with markers are the PCAM spectra after correction, the dashed lines in (a) are the PCAM spectra before correction, and the lines without markers are the VNIS spectra. (a) Original spectra. (b) Spectra normalized at 555 nm for VNIS and 555.7 nm fo PCAM.

3.3 Hapke model

We employed the Hapke bidirectional reflectance distribution model (Hapke 2002, 2008, 2012b) to analyze the photometric properties of the regolith. A method developed by Hapke et al. (2012) was applied to determine the contributions of CBOE and SHOE. The Hapke model is represented by the following formulae: RADF(i,e,g)=LS(ie,ee)w4K{ p(g)[ 1+BS0BS(g) ] +M(ie,ee) }[ 1+BC0BC(g) ]S(i,e,g,θ¯),$\matrix{ {{\rm{RADF}}\left( {i,e,g} \right)} \hfill & = \hfill & {{\rm{LS}}\left( {{i_{\rm{e}}},{e_{\rm{e}}}} \right){w \over 4}K\left\{ {p\left( g \right)\left[ {1 + {B_{S0}}{B_S}\left( g \right)} \right]} \right.} \hfill \cr {} \hfill & {} \hfill & { + M\left. 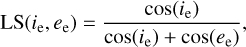{\left( {{i_{\rm{e}}},{e_{\rm{e}}}} \right)} \right\}\left[ {1 + {B_{C0}}{B_C}\left( g \right)} \right]S\left( {i,e,g,\bar \theta } \right),} \hfill \cr } $(7) LS(ie,ee)=cos(ie)cos(ie)+cos(ee)${\rm{LS}}\left( {{i_{\rm{e}}},{e_{\rm{e}}}} \right) = {{\cos \left( {{i_{\rm{e}}}} \right)} \over {\cos \left( {{i_{\rm{e}}}} \right) + \cos \left( {{e_{\rm{e}}}} \right)}}$(8) p(g)=1+c21−b2(1−2bcos(g)+b2)32+1−c21−b2(1−2bcos(g)+b2)32,$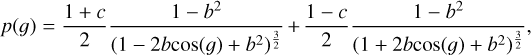p\left( g \right) = {{1 + c} \over 2}{{1 - {b^2}} \over {{{\left( {1 - 2b\cos \left( g \right) + {b^2}} \right)}^{{3 \over 2}}}}} + {{1 - c} \over 2}{{1 - {b^2}} \over {{{\left( {1 - 2b\cos \left( g \right) + {b^2}} \right)}^{{3 \over 2}}}}},$(9) BS(g)=11+tan(g2)1hS,${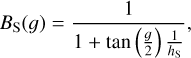B_{\rm{S}}}\left( g \right) = {1 \over {1 + \tan \left( {{g \over 2}} \right){1 \over {{h_{\rm{S}}}}}}},$(10) M(ie,ee)=H(cos(ie)K,w)H(cos(ee)K,w)−1,$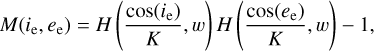M\left( {{i_{\rm{e}}},{e_{\rm{e}}}} \right) = H\left( {{{\cos \left( {{i_{\rm{e}}}} \right)} \over K},w} \right)H\left( {{{\cos \left( {{e_{\rm{e}}}} \right)} \over K},w} \right) - 1,$(11) H(x,w)={ 1−wx[ r0+(1−2r0x2)ln(1+xx) ] }−1,$H\left( {x,w} \right) = {\left\{ {1 - wx\left[ {{r_0} + \left( {{{1 - 2{r_0}x} \over 2}} \right)\ln \left( {{{1 + x} \over x}} \right)} \right]} \right\}^{ - 1}},$(12) r0=21+1−w,${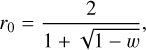r_0} = {2 \over {1 + \sqrt {1 - w} }},$(13) BC(g)=12(1+1hCtang2)2[ 1+1−exp(−1hCtang2)(1hCtang2) ],${B_{\rm{C}}}\left( g \right) = {1 \over {2{{\left( {1 + {1 \over {{h_C}}}\tan {g \over 2}} \right)}^2}}}\left[ {1 + {{1 - \exp \left( { - {1 \over {{h_{\rm{C}}}}}{\rm{tan}}{g \over 2}} \right)} \over {\left( {{1 \over {{h_{\rm{C}}}}}{\rm{tan}}{g \over 2}} \right)}}} \right],$(14) K=−ln(1−1.209ϕ23)1.209ϕ23.$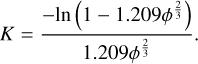K = {{ - {\rm{ln}}\left( {1 - 1.209{\phi ^{{2 \over 3}}}} \right)} \over {1.209{\phi ^{{2 \over 3}}}}}.$(15)

There are nine free parameters (w, b, c, BS0, hS, BC0, hC, 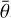θ¯$\bar \theta $, and ϕ; Table 2). We note that LS (ie, ee) is the effective Lommel–Seeliger function, p(g) is the two-parameter Henyey–Greenstein phase function, BS(g) is the SHOE function, M(ie, ee) is the isotropic multiple-scattering approximation function, H(x, w) is the Ambartsumian–Chandrasekhar H function, and BC(g) is the CBOE function. Furthermore, S (i, e, g, 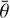θ¯$\bar \theta $) is the shadowing function. This study used the same version of S(i, e, g, 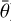θ¯$\bar \theta $) as in Sato et al. (2014). It is very complex and more details can be found in Sato et al. (2014). Meanwhile, porosity factor K is independently associated with filling factor ϕ. Hapke (2012b) and Sato et al. (2014) introduced more detailed information for the model. Table 2 lists the parameters and their initial value ranges in this paper. Considering that multiple acceptable solutions can be obtained in fitting the model, we inverted the free parameters with a Monte Carlo method (Wu et al. 2009). The Monte Carlo method is used to simulate the probability of different solutions with almost the same small root-mean-square error and to find the solution with the highest probability. We considered that the solution with the highest probability represented a reliable value, but not a local minimum. We used RADF for inversion because the photometric roughness parameter 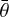θ¯$\bar \theta $ influenced LS(ie, ee), and RADF did not involve i or e in the calculation. Therefore, 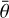θ¯$\bar \theta $ acted on RADF accurately.

We inverted the phase functions by using two independent end-member models: the CBOE-only model and the SHOE-only model. The method from Hapke et al. (2012) helps determine CBOE and SHOE amplitude simultaneously and compares the proportion of CBOE and SHOE on the basis of CBOE-only and SHOE-only parameters. Each of the CBOE-only and SHOE-only models has six free parameters: w, b, c, h, B0, and 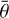θ¯$\bar \theta $. The K parameter was set to 1.25 according to Hapke & Sato (2016) because mathematical coupling of parameter K and w caused a difficulty in data inversion.

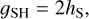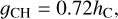The method follows these steps: parameters are inverted independently by using the two end-member models, as listed in Table 3. With the six inverted parameters, rR(0, 0, 0) and gH are calculated in the models, where gH is the half width at half maximum (HWHM) of the OE and is related to hs and he by gSH=2hS,${g_{{\rm{SH}}}} = 2{h_{\rm{S}}},$(16) gCH=0.72hC,${g_{{\rm{CH}}}} = 0.72{h_{\rm{C}}},$(17)

and rC(0, 0, 0) is the continuum reduced reflectance at a 0° phase angle by rC(i,e,g)=w4K[ p(g)+M(μ0e,μe) ]S(i,e,g,θ¯).$r\left( {i,e,g} \right) = {w \over 4}K\left[ {p\left( g \right) + M\left( {{\mu _{0e}},{\mu _e}} \right)} \right]S\left( {i,e,g,\bar \theta } \right).$(18)

The five parameters w, b, c, rR(0, 0, 0), and gH are used to anchor the two end-member models. These five parameters always have similar values when independently inverted for the two models (Hapke et al. 2012). Furthermore, BC0 and BS0 are derived from the relationship of ∆r(0, 0, 0) and rC(0, 0, 0) by 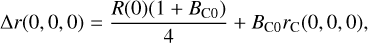Δr(0,0,0)=R(0)(1+BC0)4+BC0rC(0,0,0),${\rm{\Delta }}r\left( {0,0,0} \right) = {{R\left( 0 \right)\left( {1 + {B_{C0}}} \right)} \over 4} + {B_{C0}}{r_C}\left( {0,0,0} \right),$(19)

where ∆r(0, 0, 0) is the total height of the OE at a 0° phase angle by 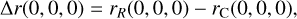Δr(0,0,0)=rR(0,0,0)−rC(0,0,0),${\rm{\Delta }}r\left( {0,0,0} \right) = {r_R}\left( {0,0,0} \right) - {r_C}\left( {0,0,0} \right),$(20)

and R(0) is the following: 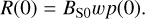R(0)=BS0wp(0).$R\left( 0 \right) = {B_{{\rm{S}}0}}wp\left( 0 \right).$(21)

By fitting the linear relationship of ∆r(0, 0, 0) and rC(0, 0, 0), comprehensively considered BS0 and BC0 were determined from the slope and intercept. That is, the two OE mechanisms combined to form the OE amplitude, rather than being considered separately in the two end-member models. To make the process clearer to understand, here, we considered the inner ring of Site 7 as an example. The values of ∆r(0, 0, 0) and rC(0, 0, 0) for the inner ring of Site 7 using the CBOE-only model, the SHOE-only model, and average values are listed in Table 3. Three bands existed; therefore, the relationship of ∆r(0, 0, 0) and rC(0, 0, 0) had three points, as plotted in Fig. 5. According to Eq. (19), BC0 is equal to the slope, and BS0 can be calculated with the vertical axis intercept. Thus, the values of comprehensively considered BS0 and BC0 were obtained, as listed in Table 3. Although the values of BS0 and BC0 differed among three conditions, the fraction of CBOE appeared robust.

Unlike other rings which include phase angles below 10°, the minimum phase angle for the outer ring of Site 8 was about 17.4°. However, OE was still considered in the inversion for the outer ring of Site 8 because the OE model includes a wide phase angle range. For SHOE, if hS = 0.05 and BS0 = 1, then BS(g) has a value of 0.25 at g = 17°. Therefore, we considered OE for Site 8 data.

Table 2

Parameters of the Hapke model and their initial value range.

Table 3

Values of parameters in the OE fraction calculation for the inner ring of Site 7.

thumbnail Fig. 5

∆r(0, 0, 0) versus rC(0, 0, 0), the linear best fit line and equation (a) for CBOE-only model parameters; (b) for SHOE-only model parameters; and (c) for averaged parameters.

4 Results

4.1 Reflectance phase functions

Figure 6 shows the moving average phase curves compared among sites and between inner and outer rings. The averaged phase curves of the inner rings almost overlap below 30°. However, the reflectances differ substantially when the phase angle is over 60°.

thumbnail Fig. 6

Moving average phase curves of the blue channel compared among sites and between inner and outer rings.

4.2 Retrieved Hapke parameters and interpretation

Mathematical coupling of parameters K and w causes a difficulty in data inversion. Therefore, we set K to 1.25 according to Hapke & Sato (2016). Thus, the filling factor ϕ, the fraction of the volume occupied by solid matter, is 0.17. If K is set to 1, the corresponding value of ϕ would correspond to a value of 0 in the K-ϕ figure (Hapke & Sato 2016), which means that the solid matter has 0 volume occupation. Table 4 lists the retrieved best-fit Hapke parameters for SHOE-only and CBOE-only models. The Monte Carlo test demonstrates that the solutions often have an uncertainty smaller than 0.1% with a given dataset. Considering the calibration error, we estimate overall errors for all the parameters as ±20% for Site 6 and ±10% for Sites 7 and 8. Table 5 compares the parameter values retrieved in this study with those from previous comparable studies, showing that the values are within the confidence interval. Fig. 7 compares a forward model calculation using retrieved parameters and a measured phase distribution function in 3D plots. Given the parameters for the blue channel (506 nm) of the CBOE-only model, the w values for the three sites are 0.16–0.20. According to Hillier et al. (1999) and Sato et al. (2014), w of 415 nm, which is the closest wavelength to this study, was around 0.13–0.20 for Maria. Given that the wavelength in this study is longer than 415 nm, the SSA ought to be greater than that in the previous studies in accordance with the spectra. The values of symmetric parameter b concentrate in the range of 0.24–0.27. Parameter c exhibits a greater value with increasing wavelength. The value range of photometric roughness 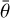θ¯$\bar \theta $ is from 15° to 22° for all three sites. The inner ring shows a wider OE width than the outer ring. In addition, gH is from 4.5° to 6.7° for the inner ring and from 2.8° to 4.3° for the outer ring. The OE amplitude B0 is slightly different in the three channels and sites. Specifically, Site 8, especially the outer ring, lacks small-phase-angle data. Consequently, the OE parameters of Site 8 are less accurate. We estimate a greater error up to ±30% for B0 and h for Site 8. Figure 8 plots the relation of b and c for the three sites, along with the results from previous studies. Compared with Sato et al. (2014), the values of b and c for Site 8 correspond to those for mare regolith. Parameter b for all three sites is almost the same, suggesting that the scattered lobe is the same. Parameter c differs among the three sites, which indicates the strongest backscattering for Site 6 compared with those for the other sites.

The derived BS0 and BC0 of the averaged parameters of the two models suggest that CBOE rather than SHOE dominates the OE, which is consistent with Hapke (2021). Table 6 provides the proportion of CBOE using averaged parameters. Site 8 is not listed because it lacks data at phase angles below 5°. For Sites 6 and 7, CBOE occupies about 80% of the total OE, while the inner ring of Site 6 has a lower CBOE proportion of about 60%. Therefore, we consider it better to use the CBOE-only parameters to represent the retrieved parameters.

Table 4

Best fitting parameter values for six rings of three sites.

Table 5

Parameter values obtained in this study as the averaged values for the blue channel of the inner ring of the three sites compared with previous mare results.

Table 6

CBOE fractions in the OE.

thumbnail Fig. 7

Phase distribution for the green channel of Site 7. (a) Calculated using the retrieved Hapke parameters for the green channel, inner ring of Site 7. The incidence angle i is 70°, the view zenith angle, or emission angle e is from 0° to 90°, and the relative azimuth angle ϕ is from 0° to 180°. The colors represent the RADF value as well as the z axis. (b) Observed. The red points are for the inner ring with i = 70.0°, and the blue ones are for the outer ring with i = 70.3°. (c) and (d) are the same plots as (a) and (b), but viewed from the phase angle versus reduced reflectance plane side.

5 Discussion

Figure 9 plots the reflectance color ratios for the three sites. The spectra become redder with increasing phase angle at small phase angles and bluer at large phase angles, forming an arch-shaped phase ratio curve. Simulations and laboratory experiments by Schröder et al. (2014) demonstrate that semitransparent samples with smooth surfaces caused arch-shaped phase curve ratios, while microscopically rough surfaces corresponded to monotonic phase reddening. Grynko & Shkuratov (2008) found that smooth particles larger than 250 µm caused phase bluing (also discussed by Fornasier et al. 2020). These results indicate that the regolith at the CE-3 landing site presents semitransparent and microscopically smooth properties. Grynko & Shkuratov (2008) suggested that the OE of semi-transparent particles are only caused by CBOE, which is in agreement with our result that CBOE dominates the OE. Johnson et al. (2021) studied the peak phase angle in the arch of phase curve ratios and suggest the influence of surface scattering as a significant control on the position of the peak phase angle. Surface scattering owing to longer optical path lengths at higher phase angles causes phase bluing at large phase angles.

The peak positions of the arched color ratio curves were estimated by fitting the curves (Fig. 9). No obvious difference in peak positions between G/B and R/B curves was found, given that the three channels (about 506, 556, and 628 nm) were close to each other. However, substantial differences in the peak positions existed among sites. The approximate peak positions of R/B curves were 19° for Site 6 inner, 32° for Site 6 outer, 48° for Site 7 inner, 65° for Site 7 outer, and 90° for Site 8 both inner and outer. As introduced in Sect. 2.2, the average grain size is considered the largest at Site 6 and the smallest at Site 8. According to the results of Johnson et al. (2021), for a specific sample, the peak arch position often increases with wavelength because greater penetration of longer-wavelength photons results in stronger internal scattering and weaker surface scattering. By contrast, for a constant wavelength, increasing particle size would result in larger surface scattering and a smaller peak arch position angle. Hence, the peak positions of the three sites differ. This theory explains why particles that are too large perform monotonic phase bluing in Grynko & Shkuratov (2008) and is consistent with the simulation results of Schröder et al. (2014) that the peak position decreases with increasing particle diameter.

We compared the difference in parameters among sites and found that parameter c for Site 6 was conspicuously greater than in other sites. Parameter B0 for Site 6 appeared slightly smaller than that for Site 7, followed by that for Site 8. As compared in Fig. 8, larger c likely represents a higher density (McGuire & Hapke 1995). A possible explanation is that the regolith density of the very surface at Site 6 increased with the removal of very fine surface dust. The regolith particles that were left were stronger, less porous, and denser. Given that photometric measurements reflect the properties of a micron-scale layer, the detected density may have been influenced. A denser surface might also produce less coherent backscattering, which reduced CBOE and the whole OE amplitude. Moreover, B0 decreased with wavelength, which was reported by Hapke et al. (2012) and Sato et al. (2014) as well. Sato et al. (2014) attribute it to that BS0 is inversely proportional to w. More observations and studies are necessary to provide further physical explanation on the influence of wavelength.

thumbnail Fig. 8

Plot of Henyey-Greenstein phase function parameters b and c. The blue curve is the hockey stick relation from Hapke (2012a). The artificial particle experimental data represented by small diamond marks and the blue reverse “J”-shaped region are from McGuire & Hapke (1995).
thumbnail Fig. 9

Phase ratios of the averaged phase curves versus phase angle for the three sites. R/B indicates the red channel divided by the blue channel, and G/B indicates the green channel divided by the blue channel. The dotted lines indicate the polynomial fitting results.

6 Conclusions

The CE-3 PCAM measured the regolith reflectance in three channels at three sites in different geologic conditions. The measuring phase angles were from 0.5° to up to 160°. We extracted phase curves of the CE-3 sites and conducted stray light correction and spectral correction. The corrected PCAM spectra matched the lunar radiation better. We retrieved the Hapke parameters from the photometric functions and compared the differences in the parameters among sites. The in situ CE-3 PCAM measurements showed that the SSA of the regolith at the measurement sites was 0.17–0.21 at 556 nm (green channel) according to the CBOE-only model. The roughness was 15–22°, and the HWHM of OE was 2.8–6.7°. The regolith presented backscattering and strong OE. The backscattering was greater with increasing wavelength. By separating the contributions of CBOE and SHOE, the model showed that CBOE accounted for a significant proportion and occupied ~80% of OE for Site 7 and the outer ring of Site 6. The photometric functions produced arch-shaped ratio curves. The peak position of the arch curves indicated that the grain size at Site 6 became greater under the influence of spacecraft exhaust. The surface density of the regolith at Site 6 might have increased because a stronger backscattering than that at other sites was detected.

Acknowledgements

We thank the whole Chang’E-3 team for making the mission a success and providing the data. This research was supported by National Key R&D Program of China (Grant No. 2020YFE0202100), the National Natural Science Foundation of China (42050202), pre-research project on Civil Aerospace Technologies by CNSA (D020201), the Macau Science and Technology Development Fund (0073/2019/A2; 0090/2020/A; 0109/2021/A2) and Minor Planet Foundation of Purple Mountain Observatory. We thank Emmanuel Lellouch for editorial help. We thank the referee, Jeffrey R. Johnson, for careful and constructive comments and suggestions which substantially improved this manuscript.

References

  1. Akimov, L. A. 1975, Sov. Astron., 19, 385 [NASA ADS] [Google Scholar]
  2. Akimov, L. A. 1979, Sov. Astron., 23, 231 [NASA ADS] [Google Scholar]
  3. Akimov, L. A., Velikodskij, Y. I., & Korokhin, V. V. 1999, Kinemat. Phys. Celest. Bodies, 15, 232 [NASA ADS] [Google Scholar]
  4. Besse, S., Sunshine, J., Staid, M., et al. 2013a, Icarus, 222, 229 [NASA ADS] [CrossRef] [Google Scholar]
  5. Besse, S., Yokota, Y., Boardman, J., et al. 2013b, Icarus, 226, 127 [CrossRef] [Google Scholar]
  6. Boyd, A. K., Robinson, M. S., & Sato, H. 2012, Lunar Planet. Sci. 43, 2795 [Google Scholar]
  7. Buratti, B. J., Hillier, J. K., & Wang, M. 1996, Icarus, 124, 490 [NASA ADS] [CrossRef] [Google Scholar]
  8. Buratti, B. J., Hicks, M. D., Nettles, J., et al. 2011, J. Geophys. Res. (Planets), 116, E00G03 [CrossRef] [Google Scholar]
  9. Domingue, D., & Hapke, B. 1989, Icarus, 78, 330 [NASA ADS] [CrossRef] [Google Scholar]
  10. Domingue, D. L., Denevi, B. W., Murchie, S. L., & Hash, C. D. 2016, Icarus, 268, 172 [NASA ADS] [CrossRef] [Google Scholar]
  11. Fornasier, S., Hasselmann, P. H., Deshapriya, J. D. P., et al. 2020, A&A, 644, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Goguen, J. D., Stone, T. C., Kieffer, H. H., & Buratti, B. J. 2010, Icarus, 208, 548 [NASA ADS] [CrossRef] [Google Scholar]
  13. Grynko, Y., & Shkuratov, Y. G. 2008, in Light Scattering Reviews 3 (Springer), 329 [CrossRef] [Google Scholar]
  14. Hapke, B. 1981, J. Geophys. Res., 86, 4571 [NASA ADS] [Google Scholar]
  15. Hapke, B. 1984, Icarus, 59, 41 [Google Scholar]
  16. Hapke, B. 2002, Icarus, 157, 523 [NASA ADS] [CrossRef] [Google Scholar]
  17. Hapke, B. 2008, Icarus, 195, 918 [Google Scholar]
  18. Hapke, B. 2012a, Icarus, 221, 1079 [NASA ADS] [CrossRef] [Google Scholar]
  19. Hapke, B. 2012b, Theory of Reflectance and Emittance Spectroscopy (Cambridge University Press) [Google Scholar]
  20. Hapke, B. 2021, Icarus, 354, 114105 [NASA ADS] [CrossRef] [Google Scholar]
  21. Hapke, B., & Sato, H. 2016, Icarus, 273, 75 [NASA ADS] [CrossRef] [Google Scholar]
  22. Hapke, B., Dimucci, D., Nelson, R., & Smythe, W. 1996, Remote Sens. Environ., 58, 63 [NASA ADS] [CrossRef] [Google Scholar]
  23. Hapke, B., Nelson, R., & Smythe, W. 1998, Icarus, 133, 89 [CrossRef] [Google Scholar]
  24. Hapke, B., Denevi, B., Sato, H., Braden, S., & Robinson, M. 2012, J. Geophys. Res. (Planets), 117, E00H15 [Google Scholar]
  25. Helfenstein, P., & Shepard, M. K. 1999, Icarus, 141, 107 [Google Scholar]
  26. Helfenstein, P., & Veverka, J. 1987, Icarus, 72, 342 [NASA ADS] [CrossRef] [Google Scholar]
  27. Helfenstein, P., Veverka, J., & Hillier, J. 1997, Icarus, 128, 2 [NASA ADS] [CrossRef] [Google Scholar]
  28. Hillier, J. K., Buratti, B. J., & Hill, K. 1999, Icarus, 141, 205 [NASA ADS] [CrossRef] [Google Scholar]
  29. Johnson, J. R., Shepard, M. K., Grundy, W. M., Paige, D. A., & Foote, E. J. 2013, Icarus, 223, 383 [NASA ADS] [CrossRef] [Google Scholar]
  30. Johnson, J. R., Grundy, W. M., Lemmon, M. T., et al. 2021, Icarus, 357, 114261 [NASA ADS] [CrossRef] [Google Scholar]
  31. Kaasalainen, M., Torppa, J., & Muinonen, K. 2001, Icarus, 153, 37 [NASA ADS] [CrossRef] [Google Scholar]
  32. Kaydash, V., Gerasimenko, S. Y., Shkuratov, Y. G., et al. 2010, Sol. Syst. Res., 44, 267 [NASA ADS] [CrossRef] [Google Scholar]
  33. Kaydash, V., Pieters, C., Shkuratov, Y., & Korokhin, V. 2013, J. Geophys. Res. (Planets), 118, 1221 [NASA ADS] [CrossRef] [Google Scholar]
  34. Kieffer, H. H., & Stone, T. C. 2005, AJ, 129, 2887 [NASA ADS] [CrossRef] [Google Scholar]
  35. Li, X., Gao, F., Wang, J., et al. 2000, Sci. China Technol. Sci., 43, 9 [CrossRef] [Google Scholar]
  36. McEwen, A., Eliason, E., Lucey, P., et al. 1998, in Lunar Planet. Sci. 29, 1466 [Google Scholar]
  37. McGuire, A. F., & Hapke, B. W. 1995, Icarus, 113, 134 [NASA ADS] [CrossRef] [Google Scholar]
  38. Nelson, R. M., Hapke, B. W., Smythe, W. D., & Horn, L. J. 1998, Icarus, 131, 223 [NASA ADS] [CrossRef] [Google Scholar]
  39. Nelson, R. M., Hapke, B. W., Smythe, W. D., & Spilker, L. J. 2000, Icarus, 147, 545 [NASA ADS] [CrossRef] [Google Scholar]
  40. Nelson, R. M., Smythe, W. D., Hapke, B. W., & Hale, A. S. 2002, Planet. Space Sci., 50, 849 [NASA ADS] [CrossRef] [Google Scholar]
  41. Ren, X., Li, C.-L., Liu, J.-J., et al. 2014, Res. Astron. Astrophys., 14, 1557 [CrossRef] [Google Scholar]
  42. Saiki, K., Saito, K., Okuno, H., et al. 2008, EPS, 60, 417 [Google Scholar]
  43. Sato, H., Robinson, M. S., Hapke, B., Denevi, B. W., & Boyd, A. K. 2014, J. Geophys. Res. (Planets), 119, 1775 [NASA ADS] [CrossRef] [Google Scholar]
  44. Schröder, S. E., Grynko, Y., Pommerol, A., et al. 2014, Icarus, 239, 201 [Google Scholar]
  45. Shepard, M. K., & Helfenstein, P. 2007, J. Geophys. Res. (Planets), 112, E03001 [CrossRef] [Google Scholar]
  46. Shkuratov, Y. G., Kreslavsky, M. A., Ovcharenko, A. A., et al. 1999, Icarus, 141, 132 [NASA ADS] [CrossRef] [Google Scholar]
  47. Shkuratov, Y., Ovcharenko, A., Zubko, E., et al. 2002, Icarus, 159, 396 [CrossRef] [Google Scholar]
  48. Shkuratov, Y., Opanasenko, N., Opanasenko, A., et al. 2008, Icarus, 198, 1 [NASA ADS] [CrossRef] [Google Scholar]
  49. Shkuratov, Y., Kaydash, V., Korokhin, V., et al. 2011, Planet. Space Sci., 59, 1326 [Google Scholar]
  50. Thuillier, G., Floyd, L., Woods, T. N., et al. 2004, Adv. Space Res., 34, 256 [NASA ADS] [CrossRef] [Google Scholar]
  51. Velikodsky, Y. I., Korokhin, V. V., Shkuratov, Y. G., Kaydash, V. G., & Videen, G. 2016, Icarus, 275, 1 [NASA ADS] [CrossRef] [Google Scholar]
  52. Wang, Z., Wu, Y., Blewett, D. T., et al. 2017, Geophys. Res. Lett., 44, 3485 [NASA ADS] [CrossRef] [Google Scholar]
  53. Wu, Y., & Hapke, B. 2018, Earth Planet. Sci. Lett., 484, 145 [CrossRef] [Google Scholar]
  54. Wu, Y., Gong, P., Liu, Q., & Chappell, A. 2009, Remote Sens. Environ., 113, 213 [NASA ADS] [CrossRef] [Google Scholar]
  55. Wu, Y., Besse, S., Li, J.-Y., et al. 2013, Icarus, 222, 283 [NASA ADS] [CrossRef] [Google Scholar]
  56. Wu, Y., Wang, Z., Cai, W., & Lu, Y. 2018, AJ, 155, 213 [NASA ADS] [CrossRef] [Google Scholar]
  57. Yokota, Y., Matsunaga, T., Ohtake, M., et al. 2011, Icarus, 215, 639 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Channel characteristics of PCAM.

In the text
Table 2

Parameters of the Hapke model and their initial value range.

In the text
Table 3

Values of parameters in the OE fraction calculation for the inner ring of Site 7.

In the text
Table 4

Best fitting parameter values for six rings of three sites.

In the text
Table 5

Parameter values obtained in this study as the averaged values for the blue channel of the inner ring of the three sites compared with previous mare results.

In the text
Table 6

CBOE fractions in the OE.

In the text

All Figures

thumbnail Fig. 1

CE-3 landing site by LROC NAC, image M1300246898L (i = 43.44°, g = 43.68°). The locations of the lander and measurement sites are indicated with arrows. The yellow dashed circles represent approximate ranges of the inner rings of Sites 6, 7, and 8.
In the text
thumbnail Fig. 2

Example images of the inner rings. The top row is the entire image, and the bottom row is the zoom of each yellow dotted box. The plotting scale represents an approximate scale at the bottom of the images. The labels of the images are 041_0006 (Site 6), 056_0007 (Site 7), and 052_0008 (Site 8).
In the text
thumbnail Fig. 3

Mosaic of PCAM images in a ring, including the inner and outer rings. (a) Site 7. The red numbers denote the locations of the images labeled from 1 to 56. The locations are the same among the three mosaics. (b) Site 6. The shadow of the PCAM at location 34 is the OE region, and abnormal bright regions at locations 7–12 were influenced by abnormal reflections at large phase angles. (c) Site 7. Locations 50 and 51 represent the OE region, while locations 19–22 are at large phase angles. (d) Site 8. There is no major OE region, with locations 25–28 slightly influenced by abnormal reflections.
In the text
thumbnail Fig. 4

PCAM spectra before and after spectral correction compared with VNIS spectra. The lines with markers are the PCAM spectra after correction, the dashed lines in (a) are the PCAM spectra before correction, and the lines without markers are the VNIS spectra. (a) Original spectra. (b) Spectra normalized at 555 nm for VNIS and 555.7 nm fo PCAM.
In the text
thumbnail Fig. 5

∆r(0, 0, 0) versus rC(0, 0, 0), the linear best fit line and equation (a) for CBOE-only model parameters; (b) for SHOE-only model parameters; and (c) for averaged parameters.
In the text
thumbnail Fig. 6

Moving average phase curves of the blue channel compared among sites and between inner and outer rings.
In the text
thumbnail Fig. 7

Phase distribution for the green channel of Site 7. (a) Calculated using the retrieved Hapke parameters for the green channel, inner ring of Site 7. The incidence angle i is 70°, the view zenith angle, or emission angle e is from 0° to 90°, and the relative azimuth angle ϕ is from 0° to 180°. The colors represent the RADF value as well as the z axis. (b) Observed. The red points are for the inner ring with i = 70.0°, and the blue ones are for the outer ring with i = 70.3°. (c) and (d) are the same plots as (a) and (b), but viewed from the phase angle versus reduced reflectance plane side.
In the text
thumbnail Fig. 8

Plot of Henyey-Greenstein phase function parameters b and c. The blue curve is the hockey stick relation from Hapke (2012a). The artificial particle experimental data represented by small diamond marks and the blue reverse “J”-shaped region are from McGuire & Hapke (1995).
In the text
thumbnail Fig. 9

Phase ratios of the averaged phase curves versus phase angle for the three sites. R/B indicates the red channel divided by the blue channel, and G/B indicates the green channel divided by the blue channel. The dotted lines indicate the polynomial fitting results.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.