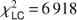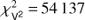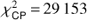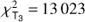| Issue |
A&A
Volume 618, October 2018
|
|
|---|---|---|
| Article Number | A112 | |
| Number of page(s) | 24 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201832952 | |
| Published online | 24 October 2018 | |
Physical properties of β Lyrae A and its opaque accretion disk⋆,⋆⋆
1
Université Côte d’Azur, OCA, CNRS, Lagrange, Parc Valrose Bât, Fizeau, 06108 Nice, France
email: denis.mourard@oca.eu
2
Astronomical Institute of the Charles University, Faculty of Mathematics and Physics, V Holešovičkách 2, 180 00 Praha 8, Czech Republic
3
Astronomical Institute, Slovak Academy of Sciences, 059 60 Tatranská Lomnica, Slovak Republic
4
The CHARA Array of Georgia State University, Mount Wilson Observatory, Mount Wilson, CA 91023, USA
5
Astronomy Department, University of Michigan (Astronomy), 500 Church St, Ann Arbor, MI 48109, USA
6
Naval Research Laboratory, Remote Sensing Division, Code 7215, 4555 Overlook Ave. SW, Washington, DC 20375, USA
7
Univ. Lyon, Univ. Lyon1, ENS de Lyon, CNRS, Centre de Recherche Astrophysique de Lyon UMR5574, 69230 Saint-Genis-Laval France
8
Hvar Observatory, Faculty of Geodesy, University of Zagreb Kačićeva 26, 10000 Zagreb, Croatia
9
Institute of Physics, The Czech Academy of Sciences, Na Slovance 1999/2, 181 21 Praha 8, Czech Republic
10
Private Observatory, Výpustky 5, 614 00 Brno, Czech Republic
11
Astronomical Institute, Czech Academy of Sciences, 251 65 Ondřejov, Czech Republic
Received:
2
March
2018
Accepted:
5
July
2018
Mass exchange and mass loss in close binaries can significantly affect their evolution, but a complete self-consistent theory of these processes is still to be developed. Processes such as radiative shielding due to a hot-spot region, or a hydrodynamical interaction of different parts of the gas stream have been studied previously. In order to test the respective predictions, it is necessary to carry out detailed observations of binaries undergoing the largescale mass exchange, especially for those that are in the rapid transfer phase. β Lyr A is an archetype of such a system, having a long and rich observational history. Our goal for this first study is to quantitatively estimate the geometry and physical properties of the optically thick components, namely the Roche-lobe filling mass-losing star, and the accretion disk surrounding the mass-gaining star of β Lyr A. A series of continuum visible and NIR spectro-interferometric observations by the NPOI, CHARA/MIRC and VEGA instruments covering the whole orbit of β Lyr A acquired during a two-week campaign in 2013 were complemented with UBVR photometric observations acquired during a three-year monitoring of the system. We included NUV and FUV observations from OAO A-2, IUE, and Voyager satellites. All these observations were compared to a complex model of the system. It is based on the simple LTE radiative transfer code SHELLSPEC, which was substantially extended to compute all interferometric observables and to perform both global and local optimization of system parameters. Several shapes of the accretion disk were successfully tested – slab, wedge, and a disk with an exponential vertical profile – and the following properties were consistently found: the radius of the outer rim is 30.0±1.0 R⊙, the semithickness of the disk 6.5±1.0 R⊙, and the binary orbital inclination i=93.5±1.0deg. The temperature profile is a power-law or a steady-disk in case of the wedge geometry. The properties of the accretion disk indicate that it cannot be in a vertical hydrostatic equilibrium, which is in accord with the ongoing mass transfer. The hot spot was also detected in the continuum but is interpreted as a hotter part of the accretion disk illuminated by the donor. As a by-product, accurate kinematic and radiative properties of β Lyr B were determined.
Key words: binaries: close / binaries: spectroscopic / binaries: eclipsing / stars: emission-line, Be / stars: individual: β Lyr A / stars: individual: β Lyr B
Based on spectro-interferometric observations obtained with the instruments CHARA/VEGA, CHARA/MIRC, and NPOI, and UBVR photometric observations from Hvar observatory.
Tables A.1 and B.1 and the individual interferometric observations are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/618/A112
© ESO 2018
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
Mass transfer between close binary components has a profound impact on their evolution. Early models of the mass transfer by Kippenhahn & Weigert (1967) have explained the Algol paradox (Crawford 1955) and demonstrated that about 80% of mass transferred during the whole process is exchanged in less than 10% of its total duration (see also De Greve 1986, for recent, more sophisticated modeling). The character and outcome of the process, that is whether the mass transfer is conservative or whether some matter and angular momentum escapes from the system and forms a common envelope around the whole system (Kuiper 1941; Paczynski 1976), depend strongly on the properties of the binary in question before the beginning of mass exchange and on the actual mechanism of the mass transfer.
Kippenhahn & Weigert (1967) introduced an initial classification of systems undergoing mass exchange, depending on whether the mass-losing component overflows the Roche limit during the core hydrogen burning (case A), or shell hydrogen burning (case B). Later, the term “case AB” was suggested to distinguish between cases when the mass exchange starts as case A close to the exhaustion of hydrogen in the core and continues as case B later during the process. All such systems are progenitors of Algols, that is systems in the later stage of the mass exchange when the mass ratio had already been reversed. Especially for the more massive Algols, the mass exchange appears to be non-conservative as found by van Rensbergen et al. (2006) from the distribution of the mass ratios among the observed Algols. The actual mechanisms of the mass and angular momentum loss from the system are not well established and modeled as yet. Bisikalo et al. (2000) proposed a purely hydrodynamical mechanism, which assumes that the gas flow, after encircling the gainer, hits the original, denser flow from the mass-losing star and is deviated above and below the orbital plane in the form of bipolar jets. On the other hand, van Rensbergen et al. (2008) and Deschamps et al. (2013) have proposed that a radiative interaction (a hot spot) between the flow, accretion disk, and the gainer may be responsible for the mass loss in the equatorial plane.
One way to discriminate between different scenarios is to carry out detailed studies of systems undergoing a phase of rapid mass exchange and deduce the true distribution and kinematics of the circumstellar gas for them. The bright, well-known binary β Lyr A (HD 174638, HR 7106, HIP 92420) with a steadily increasing orbital period of 12ḍ94, is an archetype of such systems. The history of its investigation is more than two hundred years long, and here we refer only to a subset of the more recent studies relevant to the topic of this paper. Detailed reviews of previous studies can be found in Sahade (1980) and Harmanec (2002). Unless a clear distinction is needed, we shall simply use the name β Lyr to denote β Lyr A in the rest of the text.
β Lyr is currently in a phase of rapid mass exchange, although its initial mass ratio has already been reversed and is now q = mg/md ≃ 4.50 (Harmanec & Scholz 1993), with the mass-losing component (donor) being the less massive of the two (md ≃ 4.50M⊙, and mg ≃ 13.3M⊙). Its spectral type is B6-8 II and the effective temperature Teff,d= 13 300 K (Balachandran et al. 1986). It is losing mass via a Roche-lobe overflow toward its more massive partner (gainer). The conservation of angular momentum (or equivalently, the Coriolis acceleration in the non-inertial corotating frame) forces the gas flow to encircle the gainer and to form an accretion disk around it (Huang 1963; Wilson 1974; Hubený & Plavec 1991). Being composed from hot, and mainly ionized material, it is optically (and also geometrically) thick in the continuum and because it is observed nearly edge-on, it obscures the gainer completely. It occupies almost the whole critical Roche lobe around the gainer in the equatorial plane and was found to have the temperature of its rim of 7000–9000 K (e.g., Linnell 2000; Mennickent & Djuraševć 2013). The geometry of the optically thick bodies (the donor and the disk) was reconstructed from near-infrared interferometric observations by Zhao et al. (2008). The current rate of the mass transfer between the binary components is high, ≈2.1 × 10−5 M⊙ yr−1 for a conservative transfer (Harmanec & Scholz 1993), and ≈2.9 × 10−5 M⊙ yr−1 for a non-conservative one (De Greve & Linnell 1994; van Rensbergen & De Greve 2016), as deduced from the large observed secular change of the orbital period of ≈19 s yr−1 (Harmanec & Scholz 1993; Ak et al. 2007).
The presence of a hot spot has been advocated by Lomax et al. (2012) and by Mennickent & Djuraševć (2013). The latter authors also postulated a second “bright spot” that should arise from a spiral arm that is formed within the disk. Some part of the gas flow is also deflected in the direction perpendicular to the accretion disk and forms a pair of jets, whose existence was first proposed by Harmanec et al. (1996), and was confirmed by Hoffman et al. (1998), Ak et al. (2007), Ignace et al. (2008), and Bonneau et al. (2011) via different types of observations. Observational evidence of the mass loss from the system has been presented by Umana et al. (2000, 2002), who resolved a circumbinary nebula surrounding the system in radio emission and found that it extends along the direction of the bipolar jets. An attempt to image the optically thin medium in Hα has been carried out by Schmitt et al. (2009), but their observations lacked the spatial resolution needed to separate the individual structures.
The evolution of β Lyr from the initial to the current evolutionary stage was modeled by several authors. The early conservative model of mass exchange by Ziolkowski (1976) was found unrealistic by Packet & De Greve (1979), because it would lead to a contact system. The latest evolutionary tracks by Mennickent & Djuraševć (2013) and by van Rensbergen & De Greve (2016) are in a good mutual agreement, probably thanks to the fact that the former is based on evolutionary models by van Rensbergen et al. (2008). The latter is based on improved evolutionary models including tides, and predicts that the system undergoes a case AB mass transfer and that it originated from a detached binary with initial masses of 10.35 M ⊙ (donor) and 7 M ⊙, and a period of 2.36 d and its current age is 2.63 × 107yr.
The aim of the present study is to analyze and use the very rich series of visible and infrared spectro-interferometric observations covering the whole orbit of β Lyr, complemented by series of standard UBVR, near-infrared and far-UV photometric observations. All these observations are compared to the predictions of several working models of optically thick components of the system, focusing on the size, shape and physical properties of the opaque accretion disk surrounding the gainer. To this end, we use an improved version of the modeling tool SHELLSPEC by Budaj & Richards (2004) developed for binaries embedded in a 3D moving circumstellar environment.
A continuation of this study (to be published later) will use differential spectro-interferometry and analyses of selected emission-line profiles to investigate the probable distribution and kinematics of optically thin parts of the circumstellar matter within the system.
2. Observations
Throughout this paper, reduced Julian dates RJD = HJD−2 400 000 are used. The quadratic orbital ephemeris by Ak et al. (2007):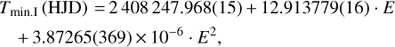 (1) is used to compute orbital phases of β Lyr A. Phase 0 corresponds to superior conjunction of the mass donor.
(1) is used to compute orbital phases of β Lyr A. Phase 0 corresponds to superior conjunction of the mass donor.
Our study is based on the following sets of dedicated spectro-interferometric observations and multicolor photometric observations (the details on the observations and their reductions being provided in Appendices A and B).
2.1 Interferometry
Three spectro-interferometric instruments took part in a twelve nights long observational campaign aimed at β Lyr in 2013. We also have at our disposal all previous interferometric observations as detailed below.
-
Navy Precision Optical Interferometer (NPOI; Armstrong et al. 1998): These observations were carried out in 16 spectral channels spread over wavelength region Δλ = 562 − 861 nm with two triplets of telescopes.
-
Michigan InfraRed Combiner (MIRC; Monnier et al. 2004, 2006): These observations were acquired with six telescopes in H-band split into eight channels. Earlier observations in four-telescope mode have already been analyzed by Zhao et al. (2008) and qualitatively compared to a working model. We note also that these observations were acquired before the instrument was equipped with photometric channels (Che et al. 2010).
-
Visible spEctroGraph and polArimeter (VEGA; Mourard et al. 2009; Mourard et al. 2011): These observations were taken in four spectral regions using medium spectral resolution R = 5000. In each of these regions two channels in continuum ≈10 − 15 nm wide were chosen. Either two or three telescopes were used.
The VEGA and MIRC instruments are mounted at Center for High Angular Resolution Astronomy (CHARA) interferometric array (Ten Brummelaar et al. 2005). On nine nights during the campaign, the MIRC and VEGA instruments were co-phased to record fringes simultaneously in the visible and infrared. Basic properties of the spectro-interferometric observations are listed in Table 1. The phase coverage of β Lyr A orbit with spectro-interferometric observations from individual instruments is shown in Fig. 1. A detailed overview of the observations is listed in Table A.1. The reduced quantities (visibilities, closure phases, and – for MIRC only – triple product amplitudes) are available at CDS in the OIFITS format (Pauls et al. 2005).
 |
Fig. 1. Phase coverage of spectro-interferometric observations of β Lyr acquired by different instruments. δ denotes the relative declination (positive toward the north), and α the relative right ascension (positive toward the east). The black line shows the size and orientation of the β Lyr orbit in the sky, the blue dots show orbital phases corresponding to NPOI observations, the magenta dots to CHARA/VEGA observations, the green dots to CHARA/MIRC observations acquired in 2013, and the red dots to CHARA/MIRC observations acquired in 2006/2007. An arbitrary vertical shift of 0.2 mas is added to separate the various orbits. |
Journal of analyzed spectro-interferometry.
2.2. Photometry
A new series of differential Johnson UBVR photometric observations were acquired at Hvar Observatory in 2013–2017, with earlier infrared photometry acquired by Jameson & Longmore (1976), and Taranova & Shenavrin (2005). Apart from that, we included NUV and FUV observations from OAO A-2, IUE, and Voyager satellites described in Kondo et al. (1994).
Moreover, there is a Johnson–Cousins differential BV(R)C photometry acquired by PS at his private observatory in Brno, Czech Republic. The latter observations were not modeled, though, because of their limited phase coverage and a relatively simple standardization procedure. Therefore these observations served only as an independent check that the Hvar UBVR measurements do not miss an important light curve feature.
Journal of photometric observations is in Table 2. The UBVR observations acquired at Hvar observatory and BV(R)C measurements collected by PS are available in Table B.1 at CDS.
Journal of analyzed photometry.
3. Choosing the initial physical properties for detailed modeling
3.1. Distance estimates
3.1.1. Trigonometric parallax
Perryman & ESA (1997) published the HIPPARCOS parallax of β Lyr 0″̣00370±0″̣00052. van Leeuwen (2007a,b) carried out a new reduction of HIPPARCOS data to obtain a more accurate value of 0″̣00339±0″̣00017. These values translate to the following distances estimates and 1 − σ ranges:
270 pc; range 237–314 pc,
295 pc; range 281–311 pc,
for the original and improved HIPPARCOS parallax, respectively.
3.1.2 Dynamical parallax from the orbital solution and spatial resolution of the orbit
Zhao et al. (2008) used two different techniques of image reconstruction and a simple model with two uniformly illuminated ellipsoids and derived three different distance estimates from the model and two methods of image reconstruction, respectively:
314 pc; range 297–331 pc,
278 pc; range 254–302 pc,
274 pc; range 240–308 pc.
It is important to realize that these distances are based on the value of the projected value of the semimajor axis a sin i = (57.87 ± 0.62) R ⊙ defined by the Kepler’s Third Law and the binary masses, which were estimated from several previous studies. In this study, we shall use a similar approach to provide an independent distance estimate based on our new models of the continuum radiation of β Lyr.
3.1.3. β Lyr B as a distance indicator of β Lyr A
β Lyr B (HD 174664, BD+33°3224, STFA 39B) is the second brightest member of the β Lyr visual system. It is a main-sequence B5 V star. A somewhat puzzling is the fact that it is also an X-ray (Berghofer & Schmitt 1994). Abt et al. (1962) measured its RV on eleven blue photographic spectra and concluded that the star is a single-line spectroscopic binary with an orbital period of 43ḍ48 and an eccentric orbit. They also studied available astrometric observations for all visual members of the β Lyrs̃ystem and concluded that β Lyr B is gravitationally bound to β Lyr A. Abt & Levy (1976) obtained new photographic RVs of β Lyr B and carried out an error analysis of newly obtained and earlier RVs to conclude that there is no evidence for duplicity of β Lyr B. From spectral classification they concluded that β Lyr B is a normal B7V star close to the zero-age main sequence.
Here, we critically re-investigate these pieces of information to see whether β Lyr B can be used to another distance estimate of β Lyr A. We first study the kinematic and radiative properties of β Lyr B. Radial velocities (RVs) were measured on Ondřejov Reticon red spectra of β Lyr B secured from 1995 to 1996, and on six Ondřejov red CCD spectra from 2003 to 2016. The linear dispersion of all these spectra was 17.2 Å mm−1, and their two-pixel resolution was 12 700. Additional details on the reduction of β Lyr B spectra are presented in Appendix C.
RVs of β Lyr B were determined using two methods:
-
An interactive comparison of direct and flipped line profiles on the computer screen until the best match is achieved in program SPEFO (Horn et al. 1996; Škoda 1996). RVs were measured independently on four spectral lines Si II 6347 Å, S II 6371 Å, Hα, and He I 6678 Å.
-
Via an automatic comparison of the observed and synthetic spectra in the PYTERPOL program (Nemravová et al. 2016)1.
The latter method produced slightly less scattered RVs, hence only these are presented here. However, the RVs obtained by both methods are listed in Table C.1. At the same time, PYTERPOL also estimated radiative properties of β Lyr A : Teff, log g, and the projected rotational velocity v sin i. The red spectra we used (Δλ ≃ 6200–6800 Å) contain numerous telluric lines, which would adversely affect the results of PYTERPOL. We handle the problem using two methods: (i) 1 Å intervals centered on each telluric spectral line were omitted from each spectrum, and (ii) telluric and stellar spectra were separated by spectral disentangling (Simon & Sturm 1994) in Fourier space by the KOREL program (Hadrava 1995, 1997). PYTERPOL was then used for both, individual observed spectra with telluric-line regions omitted, and to disentangled stellar spectrum, free of telluric lines. The synthetic spectra were taken from the BSTAR (Lanz & Hubený 2007) and AMBRE (Palacios et al. 2010) grids. The results were similar, though not exactly the same. We simply adopted their mean as a realistic estimate of radiative properties of β Lyr B, noting that both methods may introduce some systematic errors. The observed spectra still contained remnants of weaker telluric lines, while the disentangled spectra were slightly warped and had to be re-normalized. The formal errors derived from the two solutions are unrealistically small, as they do not reflect possible systematic errors. The results are summarized in Table 3 and a comparison of one observed profile, and disentangled profiles with the best-fitting synthetic spectra is shown in Fig. C.1. We assumed the solar composition in these fits guided by the results of Abt&Levy (1976) from the blue spectra since the red spectra at our disposal do not contain enough spectral lines to estimate the metallicity of β Lyr B reliably.
Kinematic and radiative properties of β Lyr B estimated via a comparison of its disentangled spectrum and all observed spectra with synthetic ones using PYTERPOL.
Do β Lyr A and β Lyr B indeed form a physical bounded system? All RV measurements of β Lyr B are plotted in Fig. 2. The rms errors are only available for Abt & Levy (1976) and for our new RVs and are shown in this plot. We explain the large scatter of the RVs from the photographic plates by the combination of four factors: moderate dispersion of the plates, variable quality of individual spectra, relatively large projected rotational velocity of β Lyr B, and line blending. It is our experience that due to blends with fainter spectral lines the apparent RVs of individual measured lines can differ systematically. Since different number of spectral lines were measured on different plates, their average RVs are then affected differently. This effect should be absent in PYTERPOL RVs, based on the comparison of whole spectral segments with interpolated synthetic spectra. Also our manual RV measurements in SPEFO should be basically free from these effects since one sees which part of the profile is measured. To check on this, we derived robust mean RVs for the four stronger lines seen in the Ondřejov spectra (using the algorithm published by Andrews 1972). They are summarized in Table 4 and confirm a very good agreement of all mean RVs of individual lines. The systemic velocity of β Lyr B based on PYTERPOL RVs is γ B = −(18.1 ± 0.5) km s−1. This number is a weighted mean of two estimates. The first one is the mean RV derived from RV measurements on individual spectra, and the latter is measured on the disentangled spectrum (both are presented in Table 3). For SPEFO RVs from individual lines one gets a 1-σ range from −17 to −21 km s−1. These estimates are to be compared to the systemic RV of β Lyr A, γ A, which was found to be in the range from about −17 to −20 km s−1, depending on the spectrograph used (see for example, solution 5 in Table 10 of Harmanec et al. 1996). From this, one can conclude that the systemic RVs of β Lyr A and β Lyr B are identical within the range of their measuring errors. In spite of their large scatter, the RVs of β Lyr B measured on old photographic spectra by Petrie & Pearce (1961) and Abt et al. (1962), Abt & Levy (1976) do not show any obvious long-term RV trend.
 |
Fig. 2. Available RVs of β Lyr B. The first three datasets are RVs measured on photographic spectra of moderate dispersion: green open circles denote the RVs measured by Petrie & Pearce (1961), the red open triangles come from Abt et al. (1962), and the black boxes are RVs from Abt & Levy (1976). The filled blue diamonds are the RVs measured on Ondřejov electronic spectra with PYTERPOL. The rms errors, available only for Abt & Levy (1976) and new RVs are also shown. We note that the most deviant RV of −45 km s−1 is based on a single line and comes probably from an underexposed spectrum. |
Robust mean RVs of individual spectral lines measured in SPEFO for Ondřejov spectra of β Lyr B.
The range of individual RVs based on our measurements with their corresponding rms errors could lead to the suspicion that β Lyr B could be a spectroscopic binary after all. To check on this, we run period searches down to 0ḍ5 for PYTERPOL RVs and also SPEFO RVs for individual lines. All the periodograms show a dense forest of comparably deep peaks but the frequencies found differ mutually, both for the individual lines and for the PYTERPOL RVs. From this, we reinforce the conclusion of Abt & Levy (1976) that β Lyr B is a single star.
The proper motions of β Lyr A and β Lyr B were also investigated. Measurements accessible through VizieR database (Ochsenbein et al. 2000) at CDS were downloaded. Only values of μα and μδ published after the HIPPARCOS mission were retained. Proper motions in the right ascension were corrected for the declination of both systems (see Appendix C.3 for details). Their weighted mean is given in Table 5. Individual measurements and the weighted average are shown in Fig. 3.
 |
Fig. 3. Proper motions of β Lyr A and β Lyr B. The black points denote proper motion measurements of β Lyr A, the black triangles proper motions of β Lyr B, the red point the mean weighted proper motion of β Lyr A, and the red triangle the mean weighted proper motion of β Lyr B. Xµ, Yµ are Cartesian coordinates of the proper motion vector given by Eqs. (C.1) and (C.2). The former is north–south oriented, and the latter east–west oriented. |
Weighted mean proper motions of β Lyr A and β Lyr B.
The close similarity of systemic RVs of β Lyr A and β Lyr B reinforce the hypothesis that the two systems formed in the same association or are even physically linked. The same cannot be said for the proper motions or for the respective tangential velocities, which differ from each other quite significantly. We conjecture that a part of this difference can be attributed to the mutual orbit – if β Lyr A and B are bound – or to the intrinsic velocity dispersion σv
of the putative stellar association. If the A − B orbit is circular and seen more or less edge on, the Keplerian velocity 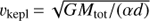 is on the order of 1.2 km s−1, assuming the mass Mtot ≃ 20 M⊙, the angular separation α ≃ 40 arcsec, and the distance d ≃ 325 pc. This should be compared with the relative tangential velocity vt = |µA – µB| d ≃ 4.2 km s−1. This value seems larger than vkepl and might be on the order of typical σv.
is on the order of 1.2 km s−1, assuming the mass Mtot ≃ 20 M⊙, the angular separation α ≃ 40 arcsec, and the distance d ≃ 325 pc. This should be compared with the relative tangential velocity vt = |µA – µB| d ≃ 4.2 km s−1. This value seems larger than vkepl and might be on the order of typical σv.
Nonetheless, the spread of proper motion measurements of β Lyr B is large and the weighed mean is dominated by the latest Gaia observation. If proper motion measurements of β Lyr B are given equal weight, the mean proper motion is: µB = 3.4 ± 2.4 mas yr−1, θB = 151 ± 43 deg, that is in agreement with measurements of β Lyr A. Therefore, we think that the proper motions of both systems do not contradict the conclusion that the systems formed within the same association. That alone allows us to use β Lyr B as a distance indicator for β Lyr A.
Gaia Collaboration (2016a) published the first parallax derived by the Gaia satellite (see Gaia Collaboration 2016b) for β Lyr B, 0″̣00310 ± 0″̣00036, which translates to a distance d = 323 pc; range 289–365 pc.
In April 2018, the second DR2 release of the Gaia catalog was made publicly available. The improved value of the β Lyr B parallax is 0″̣003006 ± 0″̣000054, which translates to a rather narrow distance range
d = 333 pc; range 327–339 pc.
We have also derived a spectroscopic distance of β Lyr B using its radiative properties (see Table 3, third Col.), and the mean all-sky UBV magnitudes based on 77 observations acquired at Hvar observatory during three seasons. The mean all-sky magnitudes: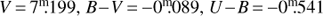 were dereddened in a standard way, which resulted in:
were dereddened in a standard way, which resulted in: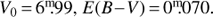 Assuming that β Lyr B is a main-sequence star, its mass and radius can be estimated from relations of Harmanec (1988) to be
Assuming that β Lyr B is a main-sequence star, its mass and radius can be estimated from relations of Harmanec (1988) to be 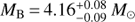 , and
, and 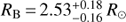 , respectively. Adopting bolometric corrections of Popper (1980), the absolute magnitude of β Lyr B is
, respectively. Adopting bolometric corrections of Popper (1980), the absolute magnitude of β Lyr B is 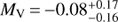 mag, and its spectroscopic distance is:
mag, and its spectroscopic distance is: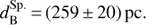 This is a significantly lower value than what Gaia obtained but it is actually in qualitative agreement with recent findings by Stassun & Torres (2016) that Gaia DR1 parallaxes are smaller than photometrical ones for well studied eclipsing binaries. Their finding was confirmed also by Graczyk et al. (2017). Since we note that in many cases the DR2 parallaxes do agree with the DR1 ones within the quoted errors (significantly smaller in DR2), the above warning might also be relevant for the DR2 parallaxes.
This is a significantly lower value than what Gaia obtained but it is actually in qualitative agreement with recent findings by Stassun & Torres (2016) that Gaia DR1 parallaxes are smaller than photometrical ones for well studied eclipsing binaries. Their finding was confirmed also by Graczyk et al. (2017). Since we note that in many cases the DR2 parallaxes do agree with the DR1 ones within the quoted errors (significantly smaller in DR2), the above warning might also be relevant for the DR2 parallaxes.
As pointed out by the anonymous referee, possible duplicity of β Lyr B could increase its observed luminosity and, therefore, its distance from us. Without a direct imaging, one cannot exclude indeed the possibility that β Lyr B is composed of two similar B7V stars seen pole on. In that case the spectroscopic distance of such an object could be as large as ∼370 pc. While it would certainly be desirable to obtain new, high-dispersion and high-S/N spectra of β Lyr B and derive its more precise RVs to check on their constancy, we do not find the duplicity of β Lyr B as too probable. Given the fact that the object was detected as an X-ray source, it is more probable that any putative secondary would be a late-type star with a chromospheric emission. However, no lines of a cool secondary have ever been detected so such an object – if present – must be much fainter than the primary. If so, its presence would not affect our spectroscopic distance estimate significantly.
3.2. The mass ratio and orbital solutions
Because the RV curve of the star hidden in the disk is only defined by a pair of fainter S II absorption lines at 6347 and 6371 Å discovered by Sahade (1966) and Skulskii (1975), one should also consider some range of plausible mass ratios. Various relevant estimates are summarized in Table 6.
Various estimates of the binary mass ratio of β Lyr.
For the purpose of our modeling, we shall use the orbital solution of Harmanec & Scholz (1993) based on Si II lines for both stars (their solution 6 of Table 10), which was basically confirmed by more extended series of spectra by Harmanec et al. (1996). In particular, we shall adopt K1 = 41.4 ± 1.3, K2 = 186.30 ± 0.35, and a sin i = 58.19 R⊙, which implies the mass ratio of 4.500.
4. Modeling the continuum radiation
Our modeling of β Lyr A and its application to spectro-interferometric and photometric observations is presented in the following section. Our models are based on the program SHELLSPEC, developed by Budaj & Richards (2004). This program was equipped with additional features that simplify modeling of binaries, computations of synthetic interferometric observables, and a solution of the inverse task.
First, we briefly outline the program and its new Python wrapper called Pyshellspec. Then, we proceed to the development of several alternative models of β Lyr in continuum and their comparison to observations.
4.1. Foundations of the model
The model is based on the existing program SHELLSPEC which was designed for the computation of synthetic light curves, spectra and images of stars and/or binaries surrounded by a moving 3D circumstellar medium by means of solving a one-dimensional LTE radiation transfer along some user-specified line-of-sight.
To provide an environment for solving the transfer, the modeled (non-stellar) objects cannot be represented with a 2D mesh covering only the photosphere of each object. Instead the grid has to sample the whole volume in 3D. The only two exceptions are models of stars, which are always opaque, hence their atmospheres form a boundary condition. In SHELLSPEC, each object is placed into an regularly sampled cuboid (divided into nx × ny × nz cells) that represents “the Universe”. All embedded objects inherit the spatial sampling of the Universe. Every object has a simple geometric shape given by several parameters. Each cell occupied by an object is assigned its density (gas, electron, and dust), temperature and velocity.
We use the following setup: LTE level populations, LTE ionisation equilibrium, the line profile is determined by thermal, microturbulent, natural, Stark, Van der Waals broadenings, and the Doppler shift. The continuum opacity is caused by HI bound-free, HI free-free, H− bound-free, and H− free-free transitions. Moreover, we account for the line opacity of Hα, He I 6678, and He I 7065, for the future spectral line analysis of the VEGA data. Abundances are assumed to be solar. We use a small grid of synthetic spectra for the stars, generated by Pyterpol (Nemravová et al. 2016) from Phoenix, BSTAR, and OSTAR grids (Husser et al. 2013; Lanz & Hubený 2007, 2003). The stars are subject to the Roche geometry, limb darkening, gravity darkening (in particular the Roche-filling donor), and the reflection effect concerning the heat redistribution over the surfaces.
On the other hand, we did not include the Thomson scattering on free electrons, the Rayleigh scattering on neutral hydrogen, because these are only implemented as optically thin (single) scattering in SHELLSPEC. It would be a much harder computational problem to account for multiple scattering in 3D moving optically thick medium, and would essentially prevent us to converge the model with many parameters. There is also neither irradiation nor reflection between the stars. As the disk is presumably hotter than the silicate condensation temperature, we account for neither Mie absorption on dust, Mie scattering, nor dust thermal emission.
The velocity field of an object is given either by a net velocity or by rotational velocity, or a combination of both. The observable quantities (flux and intensity) are computed for a line-of-sight, specified by two angles. The model is only kinematic, that is the radiation field has no effect on the state quantities of the circumstellar medium.
SHELLSPEC allows modeling of various structures, but we restrict ourselves to those that are relevant for the continuum model of β Lyr A. A very detailed description of SHELLSPEC is in Budaj & Richards (2004), and its latest improvements are described in Budaj (2011a,b).
4.2. Interface for automatic comparison and fitting
On output, SHELLSPEC computes the monochromatic flux Fv (in erg s−1 cm−2 Hz−1), and intensity Iv(x, y) (in erg s−1 cm−2 Hz−1) projected onto the plane perpendicular to the line-of-sight, where x and y are the Cartesian coordinates in this plane, but it does not carry out a comparison of these quantities to observed ones, or automatic optimization of the model parameters. Moreover, individual model components implemented in SHELLSPEC are not bound by any orbit, although some model parameters depend on orbital parameters. The components are almost independent and do not share parameters that are common. To overcome these limitations we wrapped SHELLSPEC in a Python interface2.
4.2.1. Computation of synthetic magnitudes, squared visibilities and closure phases
In our approach, the passband flux (e.g., FV) is computed from the monochromatic flux Fλ = Fvc/λ2 for a single (effective) wavelength λeff, given by the transmission curve of the respective filter. Its relation to the passband magnitude is simply mV = –2.5 log10 Fλ/Fcalib, where Fcalib denotes the calibration flux (also monochromatic), given for example by Johnson (1966), Kondo et al. (1994). This approximation is required because radiation transfer computations for many wavelengths would be very time consuming. Unfortunately, this may lead to a slight offset ΔP between the observed and synthetic light curves. The offset is thus determined by a minimization of the following formula: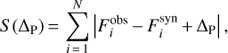 (2) where Fobs is the observed flux, and Fsyn the synthetic flux.
(2) where Fobs is the observed flux, and Fsyn the synthetic flux.
The FWHM of the passbands Δλeff of interferometric observations were as low as 20 nm in the visible and 50 nm in the infrared. Therefore the passband intensity Ip was calculated in a similar way from the monochromatic intensity Iv for the effective wavelength. This approximation is validated by the fact that the continuum does not change significantly through the narrow passbands. Images are normalized afterward, rendering any offset with respect to the emergent intensity insignificant.
The images produced by SHELLSPEC are centered on the primary component (the gainer), and their nodal line is aligned with the north–south direction. Hence, the image center has to be shifted to the system barycenter first and then rotated to a given longitude of the ascending node Ω. The complex visibility V(u, v) is computed by a two-dimensional discrete Fourier transform (DFT) of the image at spatial frequency b = (u, v) = (Bx, By)/λ, where Bx(By) denotes the projection of the baseline into east–west (north–south) direction. The triple product T3 is then computed as follows: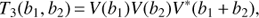 (3)where b1 and b2 denote spatial frequencies corresponding to a pair of baselines in a closing triangle. Performance of the two-dimensional fast Fourier transform (FFT) for computation of interferometric observables was also evaluated. The need for an extensive zero-padding of each image produced by SHELLSPEC to obtain a sufficient resolution, and interpolation within the two-dimensional array made it actually slower than DFT.
(3)where b1 and b2 denote spatial frequencies corresponding to a pair of baselines in a closing triangle. Performance of the two-dimensional fast Fourier transform (FFT) for computation of interferometric observables was also evaluated. The need for an extensive zero-padding of each image produced by SHELLSPEC to obtain a sufficient resolution, and interpolation within the two-dimensional array made it actually slower than DFT.
4.2.2. Interface for the solution of the inverse task
The optimization of model parameters was carried out through the minimization of the total χ2 defined as the sum of the χ2 of the different data sets. MIRC providing triple product quantities that are not totally independent from the V2 estimates, we decided to use a specific weight on the MIRC V2 and T3 data.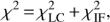 (4)where the contributions of individual types of observations are given by the following relations:
(4)where the contributions of individual types of observations are given by the following relations: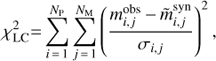 (5)
(5)
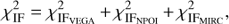 (6)with
(6)with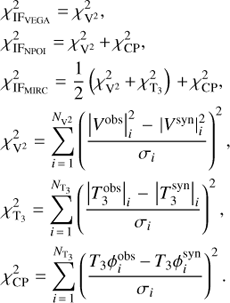 (7) where m denotes the magnitude, m̃ the magnitude corrected for the offset given by Eq. (2), NM the number of photometric observations for jth passband, Np the number of fitted passbands, |V|2 the squared visibility, |T3| the modulus of the triple product, T3ϕ ≡ arg{T3} the closure phase, NV2 the number of squared visibility observations, NT3 the number of triple product observations, and σ’s are the uncertainties of the corresponding observations. MIRC provides triple product quantities that are not entirely independent from the V2 estimates and we thus decided to use a specific weight on the MIRC V2 and T3 data. No additional weighting of the data sets is considered but a detailed analysis of the convergence process is presented in Table 8.
(7) where m denotes the magnitude, m̃ the magnitude corrected for the offset given by Eq. (2), NM the number of photometric observations for jth passband, Np the number of fitted passbands, |V|2 the squared visibility, |T3| the modulus of the triple product, T3ϕ ≡ arg{T3} the closure phase, NV2 the number of squared visibility observations, NT3 the number of triple product observations, and σ’s are the uncertainties of the corresponding observations. MIRC provides triple product quantities that are not entirely independent from the V2 estimates and we thus decided to use a specific weight on the MIRC V2 and T3 data. No additional weighting of the data sets is considered but a detailed analysis of the convergence process is presented in Table 8.
Available engines for the global minimization of Eq. (4) are the differential evolution algorithm by Storn & Price (1997), implemented within the SciPy library, and the Simplex algorithm by Nelder & Mead (1965), implemented within the NLOPT library.
As the properties of some of the objects are linked to the orbital elements, we implemented an orbit binding the objects together for the global optimization. The orbit is given by the following elements: the period P at a reference epoch, the epoch of primary minimum Tmin, the rate of the period increase Ṗ, the eccentricity e, the semimajor axis a, the mass ratio q, the inclination i, the argument of periastron ω, and the longitude of ascending node Ω. The orbit binds the two stars and supplies values of orbit-dependent parameters (the masses, Roche-lobe radii, distance between the primary and secondary, radial velocities, and the orbital phase for a given epoch). With this in hand, we then use SHELLSPEC to compute the model at different phases.
4.3. A model for β Lyr A
A model for individual components of β Lyr A is introduced here. While the model of the two binary components is straightforward, properties of the accretion disk surrounding the gainer remain uncertain. Hence several models of the accretion disk were constructed and tested.
4.3.1. A model of binary components
The two stellar components of β Lyr A were approximated with the following models:
-
The donor has a Roche geometry and is completely filling the Roche limit and its rotation is synchronized with the orbital motion. Its shape and size are driven by the semimajor axis a, and the mass ratio q. The gravity darkening (von Zeipel law, α GD = 0.25) and a linear limb darkening were assumed. Coefficients of the limb-darkening law were taken from van Hamme (1993) using the tri-linear interpolation scheme. For the interpolation, the polar temperature was used instead of the effective temperature, gravitational acceleration was approximated with that of a sphere with radius equal to the polar radius, and the solar metallicity was used. Parameters describing the donor are denoted by the index “d”.
-
The gainer is approximated with a sphere, even though it likely rotates close to its critical velocity, v crit = vkepl(Rg), because of the ongoing accretion, and should thus have an ellipsoidal shape and significant gravity darkening. Alternatively, there can be a thin transition layer (Pringle 1981), if the gainer is not (yet) rotating critically. We also checked that the accretion rate Ṁ is low enough and that the associated radial velocities within the disk are much smaller than Keplerian, vr ≪ vkepl. Nevertheless, due to the presence of the accretion disk, the only radiation that may be able to penetrate the disk is that coming from polar regions, whose radiation and shape do not depart from a spherical star so much. The component is limb-darkened using the same tables and interpolation scheme as for donor. The radius was set to a value typical for B0.5 IV–V star, R g = 6 R⊙ (Harmanec 1988), which is also in agreement with radii adopted in earlier studies (e.g., Harmanec 1992; Linnell 2000). Parameters describing the gainer are denoted by the index “g”.
4.3.2. Models of the accretion disk
SHELLSPEC allows the user to set up several models of an accretion disk. They differ in shape, radial temperature, and density profiles as presented below. In Sect. 5.2, we give more details on the preferred geometries.
The disk plane of each model lies in the orbital plane of β Lyr; z–axis is perpendicular to this plane and goes through the center of each disk. Except for the envelope-shaped disk, the z–axis is also the axis of symmetry. The radius R is measured in the disk plane from the center of the disk. The shapes of accretion disks that we tested are (see also Fig. 4):
-
Slab (panel I in Fig. 4) is limited by two spherical surfaces with radii Rin, Rout, and two surfaces z = ±H. The vertical temperature profile T(z) as well as the density ρ(z) are constant. The velocity profile v(r) is Keplerian as in all other cases.
-
Wedge (panel II) is limited by two spherical surfaces with radii Rin, Rout, and two conical surfaces z = ±R sin ϑ, where ϑ is the half-opening angle of the accretion disk. H denotes the maximal height of the disk at its outer rim.
-
Lens (panel III) is limited by a spherical surface with radius Rin and an ellipsoidal surface whose semimajor axis is equal to Rout and semiminor axis to H.
-
Envelope (panel IV) is limited by a Roche equipotential whose shape is given by the semimajor axis a of the orbit, the mass ratio q, and the filling factor ff. A synchronization between rotation and orbital motion is assumed. The vertical structure of the envelope is further limited by two surfaces z = ±H. The envelope can only be homogeneous and isothermal (ρ = const., T = const.).
-
Nebula is a standard disk with a Gaussian vertical density profile ρ(z) determined by the hydrostatic equilibrium; in other words, its scale height H is determined by the local temperature T(r). Additional parameters (hinv, tinv, hwind) can be used to account for a temperature inversion in the disk atmosphere, or a non-zero constant density in the wind region. However, in order to prevent discretization artifacts (discussed separately in Appendix D), we assume the temperature inversion is not a sudden jump from T to tinvT, and in our SHELLSPEC T(z) changes linearly between hinvH and the outer limit. In order to account also for a non-hydrostatic disks we modified SHELLSPEC to include a multiplicative factor hmul, which can be treated as a free parameter too.
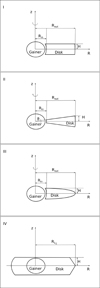 |
Fig. 4. Geometric shapes of models of accretion disks. (I) Denotes the slab, (II) the wedge, (III) the lens, and (IV) the envelope. The latter is shown as if it was filling the Roche limit, that is Rout = RL1, where Rout = RL1 denotes point radius of the Roche lobe. Here it is shown this way to emphasize the geometry of the disk, but its shape may be more symmetric depending on its filling factor. See Sect. 4.3 for the description of individual disk shapes. The Nebula is not presented here, since no simple geometrical sketch can be given. It is illustrated, however, in Fig. 5. |
Two types of radial temperature profiles T(R) were tested. The first one is a power-law: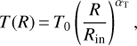 (8)where T0 is the effective temperature at the inner rim of the accretion disk Rin, and αT the exponent of the power-law. The second one corresponds to a steady accretion disk heated only by viscous dissipation (Shakura & Sunyaev 1973; Pringle 1981):
(8)where T0 is the effective temperature at the inner rim of the accretion disk Rin, and αT the exponent of the power-law. The second one corresponds to a steady accretion disk heated only by viscous dissipation (Shakura & Sunyaev 1973; Pringle 1981):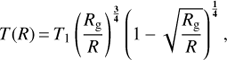 (9) where T1 is the characteristic temperature of the disk, which is actually never attained in the disk. The maximum temperature Tmax = 0.488 T1 is at the radius 49/36 Rg. The temperature along z–axis is constant.
(9) where T1 is the characteristic temperature of the disk, which is actually never attained in the disk. The maximum temperature Tmax = 0.488 T1 is at the radius 49/36 Rg. The temperature along z–axis is constant.
The radial density profile of gas ρ(R) is always approximated by a power law: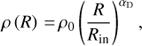 (10) where ρ0 is the gas density at the inner rim of the accretion disk. The temperature in the whole accretion disk is too high ≳7000 K for condensation of dust grains, so we assumed that the dust density is zero. The electron density was computed assuming LTE and solar chemical composition. We simply assume the disk is stable over the time span of our observations, that is 1970–2017.
(10) where ρ0 is the gas density at the inner rim of the accretion disk. The temperature in the whole accretion disk is too high ≳7000 K for condensation of dust grains, so we assumed that the dust density is zero. The electron density was computed assuming LTE and solar chemical composition. We simply assume the disk is stable over the time span of our observations, that is 1970–2017.
4.4. Realistic uncertainties of observational data
Our model represents a rather simplified view on β Lyr A, so it is no surprise that a straight preliminary comparison of the model and data gave reduced 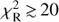 . This would mean that our model is wrong, but our model is not very different from models presented in earlier studies of the system. We attributed this mismatch to systematic errors and we tried to compensate for some of them by taking the following steps:
. This would mean that our model is wrong, but our model is not very different from models presented in earlier studies of the system. We attributed this mismatch to systematic errors and we tried to compensate for some of them by taking the following steps:
-
The observed light curves of β Lyr A, spread over more than 40 yr, exhibit small bumps (e.g., asymmetry near primary and secondary eclipses), or flickering (bottom of the primary minimum). They represent an intrinsic variability of β Lyr A that is beyond the capabilities of our model. The limited resolution of the model creates jags in the synthetic light curve. They are most pronounced at centers of both eclipses. The latter effect is higher, and the systematic signal was in general ≲0.05 mag (that is 3–5 times higher than true uncertainty of these measurements). Therefore the uncertainty of Hvar UVBR light curves was set to this value.
-
The infrared light curves lacked uncertainty estimates. They were estimated by inspecting the scatter within intervals 0.05 wide in phase. This uncertainty estimate was highly phase-dependent, but their mean was ≃0.1 mag, hence we adopted this uncertainty for all infrared light curves.
-
The squared visibility |V|2 and closure phase T3ϕ are commonly affected by systematic effects given by atmospheric fluctuation during observations. The CHARA/VEGA squared visibility observations obtained with one baseline over a short period of time (one block, ≈20 min) were frequently showing much larger spread than uncertainty of individual points. This spread is unlikely to be a product of the slow change of the projected baseline caused by the diurnal motion or produced by the intrinsic variability of β Lyr. Also our experience is that measurements of low squared visibility ≲0.05 have floor uncertainty ≈0.05. The uncertainties of all CHARA/VEGA measurements of |V|2 were adjusted according to the following formula:
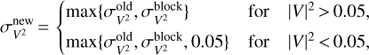 (11)where
(11)where 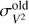 is the uncertainty estimated with the reduction pipeline (see Mourard et al. 2009, and references therein), and
is the uncertainty estimated with the reduction pipeline (see Mourard et al. 2009, and references therein), and 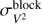 is the standard deviation of points within one block of observations (see Appendix A for details).
is the standard deviation of points within one block of observations (see Appendix A for details). -
For CHARA/MIRC observations, the uncertainty of closure phase measurements that satisfy the condition S / N|T3| ≈ 1 was adjusted following the formula by Monnier et al. (2012):
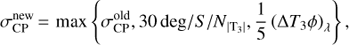 (12) where
(12) where 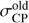 is the original value estimated by the reduction pipeline (see Monnier et al. 2004 and references therein), S / N|T3| is the signal-to-noise ratio of the corresponding triple amplitude measurement, and (ΔT3ϕ)λ is the difference between the highest and the lowest closure phase measurement in a single passband for one block of CHARA/MIRC observations (see Appendix A for details). Similarly to Zhao et al. (2011) minimal uncertainty 1 deg was adopted for all CHARA/MIRC closure phase measurements. The uncertainties on the triple product amplitudes are also corrected to account for systematic effects as described by Monnier et al. (2012): we use an additive error of 1 × 10−5 and a multiplicative factor of 10%.
is the original value estimated by the reduction pipeline (see Monnier et al. 2004 and references therein), S / N|T3| is the signal-to-noise ratio of the corresponding triple amplitude measurement, and (ΔT3ϕ)λ is the difference between the highest and the lowest closure phase measurement in a single passband for one block of CHARA/MIRC observations (see Appendix A for details). Similarly to Zhao et al. (2011) minimal uncertainty 1 deg was adopted for all CHARA/MIRC closure phase measurements. The uncertainties on the triple product amplitudes are also corrected to account for systematic effects as described by Monnier et al. (2012): we use an additive error of 1 × 10−5 and a multiplicative factor of 10%. -
A systematic offset was apparent for triple product amplitudes |T3| obtained by the NPOI instrument. While the squared visibilities |V|2 and closure phases T3ϕ can be fitted with our model, there are series of |T3| observations showing a clear trend with respect to the projected baseline B/λ, but with sudden increases of the amplitude. These are likely to be of an instrumental origin. Consequently, we decided to fit only the squared visibilities |V|2 instead. This should not affect the fitting in a negative way, because |V|2 observations should constrain the model anyway and the |T3| data do not bring important constraints due to the short baselines of NPOI observations.
4.5. Simplifications reducing the computational time
The evaluation of χ2 represented by Eqs. (4)–(6) for all available data turned out to be very demanding. The total time required for the computation of χ2 exceeded two hours even for a moderate resolution 0.6 R⊙ per pixel, and the grid size nx × ny × nz = 251 × 251 × 126. Such a long computational time prevents an extensive search of the parametric space, so three approximations were introduced: (i) low resolution. All models were computed with the grid resolution 1 R⊙ per pixel and grid size nx × ny × nz = 161 × 161 × 81; (ii) several model parameters were fixed at values determined by previous investigators of β Lyr; and (iii) a “binning” of synthetic observable quantities was introduced. The last approximation differed for the magnitudes and interferometric observables.
Synthetic magnitudes were not computed for each observation time. Instead a synthetic light curve as a function of orbital phase was sampled equidistantly with one hundred points for each passband. Synthetic magnitudes for each observation time were then obtained by a cubic-spline interpolation of the synthetic light curve.
The binning in case of the interferometry limited the number of images Iv(x, y, t, λeff) computed to derive synthetic interferometric observables. The binning was introduced into the effective wavelength λeff and the orbital phase ϕ(t). The bin size was set to 100 nm for λeff and 0.001 for ϕ. The function Iv(x, y, t, λeff) was not sampled equidistantly as it was for the photometry. Instead the following simplification scheme was adopted:
-
List pairs (λeff, ϕ) for all observations.
-
Round the lists to the bin size (precision) given in the preceding paragraph.
-
Remove repeating items.
-
Compute Iv(x, y, t, λeff) only for the remaining items.
The image defined by the pair (λeff, ϕ) that is the nearest to the observation was chosen for the computation of interferometric observables. This means that error in the effective wavelength and orbital phase introduced by this approach cannot exceed half-width of their respective bin (Δλeff = 50nm, Δϕ = 0.0005 for this particular application). We note that for computations of the spatial frequency (B/λ) the exact value of effective wavelength for a given observation is used.
Using all these steps, the computational time was reduced by a factor of ten or more, and the evaluation takes about three minutes (on a 8-core processor). The parallelization was achieved in the Python wrapper by employing the standard multiprocessing module.
4.6. Modeling strategy
Advances achieved in the previous studies of β Lyr allowed us to significantly reduce the number of optimized parameters and focus more on the properties of accretion disk. The optimized parameters were: the inclination i, the longitude of ascending node Ω, the outer radius Rout of the disk, the semi-thickness H of the disk, the radial density ρ(R) and temperature T(R) profiles, and the distance d to the system. An attempt to include the semimajor axis a and the donor temperature Teff,d among the optimized parameters has been done, but the former turned out to be completely correlated with the systemic distance, and the latter with the disk temperature. Therefore both were set to the values reported in earlier studies, even though they were likely correlated in these studies, too. Model parameters that were kept fixed during the optimization are listed in Table 7.
List of fixed parameters.
Overview of β Lyr A modeling results.
The initial set of parameters was based on models developed by Linnell (2000) and Ak et al. (2007). As a first step, photometry, visible interferometry, and infrared interferometry were each fitted independently of the remaining data. By this procedure, we established that all data are compliant with a similar model, although not exactly the same. Based on this information a generous range was selected for each optimized parameter and a search for global minimum of Eq. (4) was run over these ranges. Once the global fit converged we ran a local fit using the simplex algorithm to polish the result of the global method. This approach was repeated for each eligible combination of shape and radial temperature profiles.
Uncertainties of the optimal set of parameters were estimated from the convergence of the global fit. The resulting χ 2 was scaled down to the ideal value, that is number of degrees of freedom. All solutions had their χ 2 scaled down by the same factor as the optimal set of parameters. Solutions whose probability Pχ2(p) > 0.05, where Pχ2 is the cumulative distribution function of the χ2 probability density function, and p is the vector of optimized parameters, were accepted as possibly correct ones. The maximal differences between all accepted results and the optimal one were adopted as uncertainties.
4.7. Results
The following seven models of the accretion disk were optimized: (i) slab with power-law temperature and density, (ii) slab with steady-disk temperature and power-law density, (iii) wedge with power-law temperature and density, (iv) wedge with steady-disk temperature and power-law density, (v) lens with power-law temperature and density, (vi) envelope with homogeneous temperature and density profiles, (vii) nebula with power-law radial and exponential vertical density profiles.
Promising optimal models selected out of (i) to (vii) are shown in Fig. 5.
 |
Fig. 5. Synthetic images of β Lyr A system for five different models: slab power-law, slab steady, wedge power-law, wedge steady, and nebula. The scale of grays corresponds to the monochromatic intensity Iv (in erg s−1 cm−2 sr−1 Hz−1). The wavelength is always λ = 545 mn and the orbital phase 0.25; α goes along east–west direction, and δ along north–south direction. It is worth noting that each model converged independently, but the outcomes are remarkably similar in terms of geometry. |
 |
Fig. 6. Synthetic images of β Lyr A for the best-fit nebula model, with total (not reduced) χ 2 = 103 233, shown for four different wavelengths: λ = 155 nm (FUV), 545 nm (V band), 1630 nm (H), and 4750 nm (M). The axes correspond to the right ascension α and declination δ (in mas), while the color scale corresponds to the monochromatic intensity Iv (in erg s−1 cm−2 sr−1 Hz−1). This is a small subset of all 2392 images (per one iteration) used to derive light curves, interferometric visibilities, closure phases, and triple product amplitudes. |
 |
Fig. 7. Observed and synthetic light curves of β Lyr A, shown for all 21 datasets (see their names in the right column). The light curves are phased according to 1. Vertical offsets are arbitrary. The best-fit model is again “nebula” with χ
2 = 103 233; the individual contribution arising from light curves comparison is |
 |
Fig. 8. Similar comparison as in Fig. 7, but for squared visibilities |V|2, with a contribution |
 |
Fig. 9. Similar comparison as in Fig. 8, but for closure phases T3ϕ (left) and triple product amplitudes |T3| (right). Contributions to the total χ2 are |
The analysis led to the following findings:
-
The fit of individual data subsets (photometry, visible and infrared interferometry) converged to similar, but not identical solutions. A comparison of these particular solutions against all available data have shown clear discrepancies for data that were not fitted. For example, a model fitting the infrared interferometry did not reproduce depths of minima of the visible light curve. A detailed uncertainty analysis was not carried out though, and the relative importance of these discrepancies was not quantitatively evaluated. We report this, because it might point to a possible discrepancy in our model and/or to a systematic effect that is still affecting our data and that was not suppressed with steps described in Sect. 4.4.
-
The model with homogeneous envelope served primarily as a test whether the accretion disk around gainer could be homogeneous in temperature and density. This rather non-physical model tested our sensitivity to radial temperature and density profiles and it has shown that the sensitivity is indeed limited because the model with this profile shows only slightly higher total χ2 than the other inhomogeneous models (by approximately 5%, which is statistically significant, though). The geometric size of the disk is similar to those obtained for the remaining models (see Table 9) – filling factor
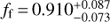 , translates into outer (point) radius
, translates into outer (point) radius 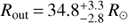 , semi-thickness
, semi-thickness 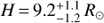 , and temperature
, and temperature 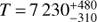 K that is reached all over the surface, because no limb-darkening is present. It also leads to a higher orbital inclination
K that is reached all over the surface, because no limb-darkening is present. It also leads to a higher orbital inclination 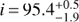 deg. Nevertheless, the geometrical configuration and higher χ2 make this model implausible.
deg. Nevertheless, the geometrical configuration and higher χ2 make this model implausible. -
The model with a lens-shaped disk has been definitively ruled out. It was tested with both temperature and density radial profiles, but the χ2 was significantly higher, by approximately 35%, than that obtained for the remaining shapes.
-
Both slab and wedge disk shapes turned out to be plausible. Nevertheless, if we carefully compare the resulting χ2 values summarized in Table 8, we can exclude the slab with a steady temperature profile, because its (not reduced) χ2 = 114 981 is well above the 3 − σ level (that is 105 669) inferred from the best-fit model. The central region of the slab seems too cold, and especially the UV light curves do not match the observations (cf. its
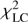 contribution). In case of the wedge, the steady profile is compensated by the central star (gainer), which is partially visible in the opening. The resulting χ2 range from 103 644 to 105 202, that is still within the 3 − σ level, or in terms of the reduced
contribution). In case of the wedge, the steady profile is compensated by the central star (gainer), which is partially visible in the opening. The resulting χ2 range from 103 644 to 105 202, that is still within the 3 − σ level, or in terms of the reduced 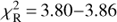 .
. -
The nebula disk model provides the best-fit, with χ2 = 103 233, which is equivalent to
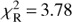 . Even though it is not significantly better on its own, if we focus on a subset of observational data, namely the light curves (
. Even though it is not significantly better on its own, if we focus on a subset of observational data, namely the light curves (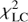 in Table 8), this fit is indeed significantly better than the others and it is thus our preferred model.
in Table 8), this fit is indeed significantly better than the others and it is thus our preferred model.
The optimal sets of parameters for the plausible models are listed in Table 9. The intervals in which the optimal solution was searched for with the global-minimization algorithm are given for each optimized parameter. Although the solutions were mostly equal from point of the total χ2, only the nebula model is plotted against the data in Figs. 6–9.
Free parameters of best-fit models of β Lyr A.
Disk-rim temperature at three wavelengths (given by the upper index in nm).
5. Discussion
This section compares our results from Sect. 4 with theoretical predictions from earlier studies of β Lyr.
5.1. Distance and inclination of β Lyr A
The distance of β Lyr A inferred from our model is d = 319.7 ± 2.7 pc, which is a bit larger distance than our preliminary expectation based on β Lyr B. The final result is essentially based on a sin i = 58.19 R⊙ value (see Table 7), which is ≲1% larger than the value accepted by Zhao et al. (2008) and is well within their uncertainty interval. Hence the choice of a slightly different s sin i cannot cause the difference between our distance and that of Zhao et al. (2008). Nevertheless, our estimate is based on a more correct physical model than that by Zhao et al. (2008), whose estimate closest to ours relied on a model with two uniform ellipses.
Our analysis reinforced the hypothesis that β Lyr A and β Lyr B share a common origin (see Sect. 3.1.3). In particular, Gaia distance d B = (333 ± 6) pc of β Lyr B is in a fair agreement with our model distance estimate of β Lyr A. The spectroscopic distance of β Lyr B derived in this study is significantly lower (259 pc), but that may result from calibration uncertainties (see the discussion at the end of Sect. 3.1.3) or from possible, still unrecognized duplicity of β Lyr B.
Concerning the inclination of β Lyr, our estimates obtained for the wedge- and slab-shaped disks do not agree with each other. This is not very surprising, because the wedge shape tends to attenuate the radiation from the hot central parts of the disk (and the gainer). Because this radiation is in fact observed, the fit converges to a lower inclination to expose central parts, and to compensate for the attenuation. The inclination of the nebula model is just in between.
5.2. Properties of the accretion disk
A critical discussion of disk parameters is presented here:
-
Radius of the accretion disk. Dense parts of the accretion disk actually fill the corresponding Roche lobe. The front, back, and side radii are Rlimit,g = 37.4 R⊙, 31.7 R⊙, and 30.3 R⊙ respectively. The disk that was obtained reaches up to the Roche limit, although the “hard” upper limit of our optimisation procedure was as high as 35 R⊙; the value is thus constrained by our observations. The tidal cutoff radius is as low as 26.3 R⊙ for the given mass ratio q, but this is not necessarily the edge of a viscous disk (Papaloizou & Pringle 1977). In earlier studies (e.g., Linnell 2000) the disk was modeled by a solid body with prescribed radiative properties. Outer radii of our disk models Rout listed in Table 9 cannot be thus directly compared to radii obtained in earlier studies, because our disks are not optically thick starting from their rim. To obtain a comparable radius, a pseudo-photosphere approximated by the optical depth τ = 2/3 has to be found. It was searched along lines of sight perpendicular to the disk rim (x, y = 0, z = 0); x ∈ [0, R out] R⊙. It was realized that the photosphere forms almost up to the geometric Rout for the slab-shaped disk,
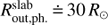 , and slightly less for the wedge-shaped disk
, and slightly less for the wedge-shaped disk 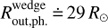 , where index “ph” stands for the photosphere. Hence, our photospheric disk radius is in excellent agreement with that obtained by Linnell (2000), R = 30 R⊙, and also with Mennickent & Djuraševć (2013), R = (2.83 ± 0.3) R⊙ (if uncertainty ≈1.5R⊙ is taken into account). This is demonstrated in Fig. 10, where the physical position of the photosphere within the accretion disk is shown for the wavelength 1630 nm.
, where index “ph” stands for the photosphere. Hence, our photospheric disk radius is in excellent agreement with that obtained by Linnell (2000), R = 30 R⊙, and also with Mennickent & Djuraševć (2013), R = (2.83 ± 0.3) R⊙ (if uncertainty ≈1.5R⊙ is taken into account). This is demonstrated in Fig. 10, where the physical position of the photosphere within the accretion disk is shown for the wavelength 1630 nm. -
Semi-thickness of the disk. For the slab-shaped model, the value of H is the same as semi-thickness of the disk photosphere. For the wedge-shaped model, we searched for the physical position of photosphere along the following lines of sight perpendicular to the disk rim: (x = 0, y = 0, z); z ∈ [0, H]. This is qualitatively demonstrated in Fig. 11. Up to a certain z the wedge is opaque; for intermediate z the ray pierces through the first lobe and the optical depth τ = 2/3 is reached in the second lobe. For high z the disk is optically thin. Hence the semi-thickness of the “opaque” wedge is about 30% smaller than the geometric semi-thickness H = Rout sin υ ≐ 7 R⊙ derived from Table 9. Our semi-thickness of the opaque disk ≃5 R ⊙ is in agreement with the result obtained by Mennickent & Djuraševć (2013), H = (5.50 ± 0.10) R⊙, and substantially lower than the value by Linnell (2000), H = 8.0 R⊙.
-
Shape of the disk. Unfortunately, it seems almost impossible to distinguish between slab, wedge and nebula shapes. Nevertheless, it is clear that their semi-thickness is so large that the disk cannot be in a vertical hydrostatic equilibrium. A hydrostatic disk with a constant vertical temperature profile, T(z) = const., would have an exponential density profile (e.g., Pringle 1981):
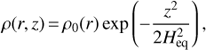 (13)with the characteristic scale Heq given by the temperature profile T(r):
(13)with the characteristic scale Heq given by the temperature profile T(r):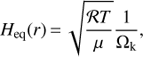 (14) where ℛ denotes the ideal-gas constant, µ the mean molecular weight, and Ωk the Keplerian angular velocity. As we also verified with SHELLSPEC (using the nebula model with h
mul = 1), the resulting Heq for our range of temperatures (30 000–7000 K) is always low, 0.2–1.2 R⊙, and the gainer would be always visible. As a consequence, H ≫ Heq is a proof that the disk is non-equilibrium, and the flow starting from the donor must have a non-negligible vertical velocities within the accretion disk. It is a matter of dynamical models (or spectro-interferometry in individual lines) to constrain the velocity field.
(14) where ℛ denotes the ideal-gas constant, µ the mean molecular weight, and Ωk the Keplerian angular velocity. As we also verified with SHELLSPEC (using the nebula model with h
mul = 1), the resulting Heq for our range of temperatures (30 000–7000 K) is always low, 0.2–1.2 R⊙, and the gainer would be always visible. As a consequence, H ≫ Heq is a proof that the disk is non-equilibrium, and the flow starting from the donor must have a non-negligible vertical velocities within the accretion disk. It is a matter of dynamical models (or spectro-interferometry in individual lines) to constrain the velocity field. -
Radial density profile and disk mass. The continuum data do not allow us to see below the pseudo-photosphere. This is evident from the high correlation between ρ0 and αD resulting from individual models, corr(ρ0, αD) ≃ 05–0.8. Hence our model does not provide the true density radial profile, but rather the minimal profile required to “produce continuum” at the correct radius and height. The disk mass given by our radial profiles is then ≃10–4–10–3 M⊙. This disk mass estimate is essentially the same as that obtained by Hubený & Plavec (1991), Hubený et al. (1994). If it was real, it would suggest a very efficient accretion, because the accretion time scale τacc = M / Ṁ ≃ 5–50 yr is much shorter than the expected duration of β Lyr A mass-transfer phase. For a steady disk (Pringle 1981), it is simply assumed the viscosity always adapts to the constant accretion rate and the viscous time scale is then equal to the accretion one, τvisc = τacc.
-
Disk-rim temperature. The rim temperature given by Eqs. (8) and (9) is not directly comparable to those obtained with solid surface models, because the photosphere does not coincide with the geometric rim. To overcome this contradiction, one can adopt the photospheric temperature, that is shown in Figs. 10 and 11. Another approach is to take the mean value of the intensity distribution over the photospheric surface 〈Idisk(x, y, λ)〉 for a given wavelength and find a temperature corresponding to the Planck law Bv(T, λ) for the mean intensity. Using this approach, we determined the following rim temperatures at three wavelengths (given by the upper index in nm; Table 10):
The rim temperature of slab-shaped models is comparable to that obtained by Mennickent & Djurašević (2013), Trim = (8200 ± 400) K. It is difficult to tell which radial temperature profile is correct. The power-law seems to give a temperature slightly above, and steady-disk gives a temperature that is slightly below the estimate by Mennickent & Djurašević (2013). Linnell (2000) generally gives larger rim temperatures. Most of the rim of his accretion disk has Trim = 9000 K, with two strips having twice higher temperature at the top and bottom of the disk. Spectroscopic studies (e.g., Harmanec & Scholz 1993; Ak et al. 2007) do not provide an accurate estimate, because spectral types from an early F-type to late A-type were attributed to rim of the accretion disk.
-
Radial temperature profile. It is almost impossible to determine the whole temperature profile, because the disk is opaque (the photosphere forms at most a few solar radii below the disk rim), and the orbital inclination is very close to 90°, which prevents us from seeing the disk face-on. The first issue manifests in itself for the power-law radial temperature profile by the extreme correlation between the inner rim temperature T0 and the exponent of the power-law ρ(T0, αT) = –0.92 for both models with slab and wedge. A comparison of models with slab and different radial temperature profiles (given by Eqs. (8) and (9)), and the temperature profile obtained by Mennickent & Djurašević (2013) is shown in Fig. 12. The radial profiles agree with each other up to ≃ 10 R⊙ below the disk rim, that is below the pseudo-photosphere. The radial profile given by Eq. (9) derived by Shakura & Sunyaev (1973) is heated only by the viscous dissipation, but the disk in β Lyr enshrouds a B0.5 V star that must considerably heat the disk, too. A problem is that asymptotically a passive irradiated disk has the same radial temperature dependence T ∼ R−3/4 as a steady disk (Friedjung 1985; Hubený 1990). Hence it is difficult to discern the two radial temperature models from their behavior in outer part of the disk. Calvet et al. (1991) modeled proto-stellar disks and found that the central regions of their disks are significantly heated by the embedded star. It is interesting to note that the temperature T0 of the power law behavior is quite close with the temperature of the central star. This is a good indication for the power law temperature behavior in the disk. From afar the proto-stellar accretion disks are very similar to that surrounding β Lyr – the accretion rate is high, and there is a star in its center. Hence there are reasons to believe that the power-law provides a better description of the radial temperature profile. Finally the best-fitting power-law αT = −0.95 is steeper than the canonical value (−3/4). This may suggest a presence of a transition layer, where the temperature falls more steeply at the outer disk rim.
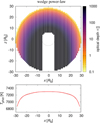 |
Fig. 10. Top panel: optical depth τ (computed for the wavelength λ = 1630 nm) of the β Lyr A disk, which is observed approximately edge-on (that is from the top). The coordinate z thus corresponds to the line of sight, while x (and y) to the sky plane. The center is empty because the gainer is a non-transparent object. In this case, the inner-rim density of the wedge power-law model is set low, ρ0 = 10−9 g cm−3, to demonstrate a separation from the outer rim. The dashed line shows the physical position of the photosphere (τ = 2/3). The lines-of-sight grid exhibits “steps” due to the limited spatial resolution of our model (1 R⊙), even though the integration of the radiation transfer (the contribution function) is internally performed on a much finer grid. Bottom panel: corresponding photospheric temperature Tphot of the disk, which varies along with the radial temperature profile T(R). |
 |
Fig. 11. Optical depth τ in the vertical (perpendicular) cross-section of the disk; other parameters are the same as in Fig. 10. The lines of sight are seemingly different from the wedge shape, but this only because they start either in the vacuum, or at the non-transparent object. |
 |
Fig. 12. Comparison of radial temperature profiles of the accretion disk surrounding the gainer. The dotted line is the profile obtained by Mennickent & Djurašević (2013), and the dashed line is mean temperature of the two-temperature model developed by Linnell (2000). The red line represents the best-fitting power-law radial temperature profile (solution slab/pl in Table 9), and the red belt all plausible solutions given by the uncertainty of the inner rim temperature and the exponent of the power-law, and the red point position of photosphere (τ = 2/3), where temperature Tph. = 7 192 K is reached. The blue line represents the best-fitting steady-disk radial temperature profile (solution slab/sd in Table 9), the blue belt all plausible solutions given by uncertainty in the inner rim temperature, and the blue point position of photosphere (τ = 2/3), where temperature Tph: = 7 192 K K is reached. The photospheric temperatures were computed for a line of sight in the plane z = 0 and piercing through center of the accretion disk |
5.3. Presence of “a hot spot”
The existence of a region heated by an interaction of the incoming flow and the accretion disk is usually required by theoretical models (e.g., Lubow & Shu 1975). For β Lyr Lomax et al. (2012) and Mennickent & Djurašević (2013) used the hot spot to explain a presence of bumps (or irregularities) in the light curve and polarized flux. We carried out an attempt to confirm their findings in continuum. A spot represented by a homogeneous sphere has been added to the slab power-law model (see Fig. 13). Parameters defining its radial position rs within the accretion disk, the position angle θ s with respect to line joining centers of both binary components, radius Rs, density ρ s, and temperature Ts were optimized using the differential evolution and simplex algorithms; the optimal values are listed in Table 11.
 |
Fig. 13. Synthetic images of slab power-law model which was further improved by a “spot” (that is a spherical structure between the primary and secondary, partly hidden inside the slab). The total (not reduced) χ2 value was decreased from 105 202 (without the spot) down to 102 005, which is a significant improvement. Four wavelengths are shown: λ = 155 nm (FUV), 545 nm (V band), 1630 nm (H), and 4750 nm (M). |
Properties of the hot spot added to slab power-law model of β Lyr A.
Detailed journal of interferometric observations.
First, only spot parameters were converged. As the spot is a substantial non-axisymmetric feature, the fit converged quickly to a location just between the primary and the disk. The spot temperature Ts about 10 000 K is logically between those of the primary and the outer rim of the disk. Second, all parameters were set free and converged again, because the original parameters might have been affected by a systematic error of the model (namely the missing spot). The procedure helped to decrease the original (not reduced) χ2 = 105 202 down to102 005, which is a statistically significant improvement and we thus may confirm the existence of the spot on the basis of continuum observations. We verified that adding a spot to other models leads to an improvement of the same order.
As illustrated by Fig. 13, the “spot” detected by our modeling is not a tiny structure corresponding to the area of interaction between the gas stream from the donor and the disk. It likely represents an illuminated part of the disk rim, where the reflection of donor light, and irradiation heating occur. We note that such lateral temperature gradient has been observationally proven for another object with an optically thick disk, ε Aur (cf., e.g., Hoard et al. 2012).
In principle, it should be possible to add a second spot to the model, and so on, and expect further improvements of the χ2, but we prefer to keep a simple model as long as possible. Otherwise, systematic uncertainties among different types of observations (light curves, squared visibilities, closure phases, etc.) might be hidden by a complex model. Moreover, there are techniques (like spectro-interferometry in lines, or Doppler tomography) better suited to pinpoint the orbital position of such non-axisymmetric features.
5.4. Comparison of SED from models and observations
Although we did not attempt to fit the spectral energy distribution (SED) of the system, it would be an important check of the model. That is why we compare synthetic SEDs to the observations of Burnashev & Skulskii (1978; see Fig. 14). It seems inevitable that SEDs exhibit some systematic offsets. Also the resolution of synthetic spectra does not match the observations. Moreover, we cannot expect that emission lines will be computed correctly, because the model is mostly focused on opaque medium and continuum flux. However, the absolute fluxes and their spread among primary minimum, secondary minimum and out of the eclipses seem to at least roughly correct. The expected systematic uncertainties of the observations (5%) might be almost of the same order, especially in UV, where the extinction is strong and variable. We thus believe it should be possible to match the observed SEDs with a future version of our model.
 |
Fig. 14. Comparison of synthetic spectral-energy distributions (thick lines) of β Lyr A and observed SED (thin lines) according to Burnashev & Skulskii (1978). The monochromatic flux Fλ (in erg s−1 cm−2 cm−1) was measured in the range of λ = 330–740 nm. The color scale correspond to the orbital phase. Observation uncertainties are on the order of 5%. The model (corresponding to a “nebula” with tinv = 4.53) was not converged with respect to these observations and the SEDs thus inevitably exhibit some systematic offsets. |
6. Conclusion and outlook
The properties of opaque bodies within β Lyr A system were studied. Our analysis was primarily targeted on the properties of the accretion disk surrounding the mass-gaining component of this close interacting binary.
For the description of interacting binary systems, we created a tool based on the SHELLSPEC code. It permitted us to significantly improve the modeling of stellar systems and the computations of radiation transfer in the co-moving circumstellar medium by Budaj & Richards (2004). Apart from improvements suitable for an optically thick medium, we can also compute interferometric observables and proceed with both local- and global-optimisation methods.
We then constructed several disk models that differed in shape, density and temperature profiles. These models were fitted to series of spectro-interferometric and photometric observations, both sampling the whole orbit. We also compared our results to those obtained by earlier investigators of the system (especially Linnell 2000; Mennickent & Djuraševć 2013) and to theoretical models of accretion disks.
Our results indicate that the opaque parts of the accretion disk have the outer radius Rout = (30.0 ± 1.0) R⊙, the semi-thickness H = (6.5 ± 1.0) R⊙ (for slab and wedge shapes), or equivalently the scale-height multiplication factor hmul = 4.3 ± 0.3 (for nebula model; see the overview in Fig. 4). But the true location of the disk pseudo-photosphere slightly depends on the wavelength. The minimum mass should be 10–4–10–3 M⊙. Given the thickness, the disk clearly cannot be in a vertical hydrostatic equilibrium. We have also determined the orbital inclination i = (9.5 ± 1.0) deg (as an average and range for admissible models), the longitude of ascending node Ω = (253.7 ± 1.0) deg, and the probable distance to the β Lyr A system d = (319.7 ± 2.7) pc.
The power-law temperature profiles (and also the steady-disk for wedge) seem compatible with the observations, but the central values remain very unconstrained, because the disk continuum is formed only a few solar radii below the disk rim.
An addition of a hot spot to our model improved the χ2, so that we can consider the existence of the spot to be confirmed in the continuum radiation, although it may be actually a compensation of missing reflection from the disk, or heating of the disk by the companion. Its position may also correspond to a flow of material from the primary (donor).
The radiative and kinematic properties of neighboring β Lyr B have been determined too. Even though we were unable to prove β Lyr A and B orbit each other, they both likely originate from the same association.
This study presents a springboard to forthcoming analyses of the optically thin circumstellar medium in β Lyr A – it is crucial to know the properties of the opaque material too. Using a series of spectroscopic and spectro-interferometric observations of strong emission lines we intend to resolve and describe the structure and kinematics of the optically thin medium within this remarkable system. Consequently, it should be possible to better determine the radial profiles of the disk atmosphere. At the same time, the mass of jets would provide an accurate estimate of the mass and angular momentum loss from the system, which would offer an invaluable test for models of mass transfer in binary systems.
The program is available at https://github.com/chrysante87/pyterpol
Available at http://sirrah.troja.mff.cuni.cz/mira/betalyr/
The tool is available at http://www.jmmc.fr/searchcal
The whole program suite with a detailed manual, examples of data, auxiliary data files, and results is available at http://astro.troja.mff.cuni.cz/ftp/hec/PHOT
The library is available through GitHub https://github.com/dfm/emcee.git and its thorough description is at http://dan.iel.fm/emcee/current/
Acknowledgments
The constructive criticism of an earlier version of this manuscript by the anonymous referee is appreciated. This research was supported by the grants P209/10/0715, GA15-2112S, and GA17-00871S of the Czech Science Foundation, by the grant no. 250015 of the Grant Agency of the Charles University in Prague. This work is based upon observations obtained with the Georgia State University Center for High Angular Resolution Astronomy Array at Mount Wilson Observatory. The CHARA Array is supported by the National Science Foundation under Grant No. AST-1211929, AST-1411654, AST-1636624, and AST-1715788. Institutional support has been provided from the GSU College of Arts and Sciences and the GSU Office of the Vice President for Research and Economic Development. We thank M. Zhao for participating in the MIRC observations, and B. Kloppenborg for his support in the earlier attempts to use the SIMTOI modeling tool. Two Reticon spectra of β Lyr B were obtained by Dr. P. Hadrava. HB acknowledges financial support from the Croatian Science Foundation under the project 6212 “Solar and Stellar Variability”. The work of JB was supported by the VEGA 2/0031/18 and APVV-15-0458 grants. We acknowledge the use of the electronic database from the CDS, Strasbourg, and the electronic bibliography maintained by the NASA/ADS system. This work has made use of data from the European Space Agency (ESA) mission Gaia (http://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, http://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular those participating in the Gaia Multilateral Agreement. In April 2012, our late friend and colleague Olivier Chesneau pointed out to some of us the publication by Lomax et al. (2012) and expressed these inspirational words: “… the hot spot… is quite extended and should show up in the interferometric observables”. This was the starting point of this study and our results are dedicated to him.
References
- Abt, H. A., &Levy, S. G. 1976, AJ, 81, 659 [NASA ADS] [CrossRef] [Google Scholar]
- Abt, H. A., Jeffers, H. M., Gibson, J., &Sandage, A. R. 1962, ApJ, 135, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Ak, H., Chadima, P., Harmanec, P., et al. 2007, A&A, 463, 233 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aller, L. H., Appenzeller, I., Baschek, B., et al.. 1982, Landolt-Börnstein: Numerical Data and Functional Relationships in Science and Technology, Group 6 Astronomy and Astrophysics, 2, 54 [Google Scholar]
- Andrews, D. F. 1972, Robust Estimates of Location (Princeton, NJ, USA: Princeton University Press) [Google Scholar]
- Armstrong, J. T., Mozurkewich, D., Rickard, L. J., et al. 1998, ApJ, 496, 550 [NASA ADS] [CrossRef] [Google Scholar]
- Balachandran, S., Lambert, D. L., Tomkin, J., &Parthasarathy, M. 1986, MNRAS, 219, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Berghofer, T. W., &Schmitt, J. H. M. M. 1994, A&A, 292, L5 [NASA ADS] [Google Scholar]
- Bisikalo, D. V., Harmanec, P., Boyarchuk, A. A., Kuznetsov, O. A., &Hadrava, P. 2000, A&A, 353, 1009 [Google Scholar]
- Boboltz, D. A., Fey, A. L., Johnston, K. J., et al. 2003, AJ, 126, 484 [NASA ADS] [CrossRef] [Google Scholar]
- Bonneau, D., Clausse, J.-M., Delfosse, X., et al. 2006, A&A, 456, 789 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonneau, D., Chesneau, O., Mourard, D., et al. 2011, A&A, 532, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Budaj, J. 2011a, A&A, 532, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Budaj, J. 2011b, AJ, 141, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Budaj, J., &Richards, M. T. 2004, Contributions of the Astronomical Observatory Skalnate Pleso, 34, 167 [NASA ADS] [Google Scholar]
- Burnashev, V. I., &Skulskii, M. Y. 1978, Bull. Crimean Astrophys. Obs., 58, 53 [NASA ADS] [Google Scholar]
- Calvet, N., Patino, A., Magris, G. C., &D’Alessio, P. 1991, ApJ, 380, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Che, X., Monnier, J. D., &Webster, S. 2010, Proc. SPIE, 7734, 77342V [NASA ADS] [CrossRef] [Google Scholar]
- Che, X., Monnier, J. D., Kraus, S., et al. 2012, Proc. SPIE, 8445, 84450Z [NASA ADS] [CrossRef] [Google Scholar]
- Crawford, J. A. 1955, ApJ, 121, 71 [NASA ADS] [CrossRef] [Google Scholar]
- De Greve, J. P. 1986, Space Sci. Rev., 43, 139 [NASA ADS] [CrossRef] [Google Scholar]
- De Greve, J. P., &Linnell, A. P. 1994, A&A, 291, 786 [NASA ADS] [Google Scholar]
- Deschamps, R., Siess, L., Davis, P. J., &Jorissen, A. 2013, A&A, 557, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drimmel, R., Cabrera-Lavers, A., &López-Corredoira, M. 2003, A&A 409, 205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., &Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Friedjung, M. 1985, A&A, 146, 366 [NASA ADS] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2016a, A&A, 595, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016b, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Graczyk, D., Konorski, P., Pietrzyński, G., et al. 2017, ApJ, 837, 7 [Google Scholar]
- Hadrava, P. 1995, A&AS, 114, 393 [NASA ADS] [Google Scholar]
- Hadrava, P. 1997, A&AS, 122, 581 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Häggkvist, L., &Oja, T. 1966, Arkiv for Astronomi, 4, 137 [NASA ADS] [Google Scholar]
- Harmanec, P. 1988, BAIC, 39, 329 [NASA ADS] [Google Scholar]
- Harmanec, P. 1990, A&A, 237, 91 [NASA ADS] [Google Scholar]
- Harmanec, P. 1992, A&A, 266, 307 [NASA ADS] [Google Scholar]
- Harmanec, P. 2002, Astron. Nachr., 323, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Harmanec, P., &Horn, J. 1998, J. Astron. Data, 4, 5 [Google Scholar]
- Harmanec, P., &Scholz, G. 1993, A&A, 279, 131 [NASA ADS] [Google Scholar]
- Harmanec, P., Grygar, J., Horn, J., et al. 1977, BAIC, 28, 133 [NASA ADS] [Google Scholar]
- Harmanec, P., Horn, J., &Juza, K. 1994, A&AS, 104, 121 [Google Scholar]
- Harmanec, P., Morand, F., Bonneau, D., et al. 1996, A&A, 312, 879 [Google Scholar]
- Hoard, D. W., Ladjal, D., Stencel, R. E., &Howell, S. B. 2012, ApJ, 748, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Hoffman, J. L., Nordsieck, K. H., &Fox, G. K. 1998, AJ, 115, 1576 [NASA ADS] [CrossRef] [Google Scholar]
- Høg, E., Kuzmin, A., Bastian, U., et al. 1998, A&A, 335, L65 [NASA ADS] [Google Scholar]
- Høg, E., Fabricius, C., Makarov, V. V., et al. 2000, A&A, 355, L27 [Google Scholar]
- Horn, J., Kubát, J., Harmanec, P., et al. 1996, A&A, 309, 521 [NASA ADS] [Google Scholar]
- Huang, S.-S. 1963, ApJ, 138, 342 [NASA ADS] [CrossRef] [Google Scholar]
- Hubený, I. 1990, ApJ, 351, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Hubený, I., &Plavec, M. J. 1991, AJ, 102, 1156 [NASA ADS] [CrossRef] [Google Scholar]
- Hubený, I., Harmanec, P., &Shore, S. N. 1994, A&A, 289, 411 [NASA ADS] [Google Scholar]
- Hummel, C. A., Benson, J. A., Hutter, D. J., et al. 2003, AJ, 125, 2630 [NASA ADS] [CrossRef] [Google Scholar]
- Husser, T.-O., Wende-von Berg, S., Dreizler, S., et al. 2013, A&A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ignace, R., Oskinova, L. M., Waldron, W. L., Hoffman, J. L., &Hamann, W.-R. 2008, A&A, 477, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jameson, R. F., &Longmore, A. J. 1976, MNRAS, 174, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, H. L. 1966, ARA&A, 4, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Kharchenko, N. V. 2001, Kinematika i Fizika Nebesnykh Tel, 17, 409 [NASA ADS] [Google Scholar]
- Kippenhahn, R., &Weigert, A. 1967, ZAp, 65, 251 [Google Scholar]
- Kondo, Y., McCluskey, G. E., Silvis, J. M. S., et al. 1994, ApJ, 421, 787 [CrossRef] [Google Scholar]
- Kuiper, G. P. 1941, ApJ, 93, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Lafrasse, S., Mella, G., Bonneau, D., et al. 2010, Proc. SPIE, 7734, 77344E [CrossRef] [Google Scholar]
- Lanz, T., &Hubený, I. 2003, ApJS, 146, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Lanz, T., &Hubený, I. 2007, ApJS, 169, 83 [CrossRef] [Google Scholar]
- Linnell, A. P. 2000, MNRAS, 319, 255 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Lomax, J. R., Hoffman, J. L., Elias, II, N. M., Bastien, F. A., & Holenstein, B. D. 2012, ApJ, 750, 59 [CrossRef] [Google Scholar]
- Lubow, S. H., &Shu, F. H. 1975, ApJ, 198, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Mennickent, R. E., &Djuraševi, G. 2013, MNRAS, 432, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Moffett, T. J., &Barnes, I. T. G. 1979, PASP, 91, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Monnier, J. D., Berger, J.-P., Millan-Gabet, R., &Ten Brummelaar, T. A. 2004, in New Frontiers in Stellar Interferometry, ed. W. A. Traub, 5491, 1370 [Google Scholar]
- Monnier, J. D., Pedretti, E., Thureau, N., et al. 2006, Proc. SPIE., 6268, 62681P [NASA ADS] [CrossRef] [Google Scholar]
- Monnier, J. D., Zhao, M., Pedretti, E., et al. 2007, Science, 317, 342 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Monnier, J. D., Anderson, M., Baron, F., et al. 2010, Proc. SPIE, 7734, 77340G [NASA ADS] [CrossRef] [Google Scholar]
- Monnier, J. D., Che, X., Zhao, M., et al. 2012, ApJ, 761, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Mourard, D., Clausse, J. M., Marcotto, A., et al. 2009, A&A, 508, 1073 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mourard, D., Bério, P., Perraut, K., et al. 2011, A&A, 531, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mozurkewich, D., Armstrong, J. T., Hindsley, R. B., et al. 2003, AJ, 126, 2502 [NASA ADS] [CrossRef] [Google Scholar]
- Nelder, J. A., &Mead, R. 1965, Comput. J., 7, 308 [Google Scholar]
- Nemravová, J. A., Harmanec, P., Brož, M., et al. 2016, A&A, 594, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ochsenbein, F., Bauer, P., &Marcout, J. 2000, A&AS, 143, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Packet, W., &De Greve, J. P. 1979, A&A, 75, 255 [NASA ADS] [Google Scholar]
- Paczynski, B. 1976, in Structure and Evolution of Close Binary Systems, eds. P. Eggleton, S. Mitton, &J. Whelan, IAU Symp., 73, 75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Palacios, A., Gebran, M., Josselin, E., et al. 2010, A&A, 516, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Papaloizou, J., &Pringle, J. E. 1977, MNRAS, 181, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Pauls, T. A., Young, J. S., Cotton, W. D., &Monnier, J. D. 2005, PASP, 117, 1255 [NASA ADS] [CrossRef] [Google Scholar]
- Perryman, M. A. C., & ESA 1997, in The HIPPARCOS and Tycho Catalogues. Astrometric and Photometric Star Catalogues Derived from the ESA HIPPARCOS Space Astrometry Mission (Noordwijk, Netherlands: ESA Publications Division), ESA SP, 1200 [Google Scholar]
- Petrie, R. M., &Pearce, J. A. 1961, Publications of the Dominion Astrophysical Observatory Victoria, 12, 1 [NASA ADS] [Google Scholar]
- Popper, D. M. 1980, ARA&A, 18, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Pringle, J. E. 1981, ARA&A, 19, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Sahade, J. 1966, Trans. Int. Astron. Union, Ser. B, 12, 494 [Google Scholar]
- Sahade, J. 1980, Space Sci. Rev., 26, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Schmitt, H. R., Pauls, T. A., Tycner, C., et al. 2009, ApJ, 691, 984 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., &Sunyaev, R. A. 1973, A&A, 24, 337 [Google Scholar]
- Simon, K. P., &Sturm, E. 1994, A&A, 281, 286 [Google Scholar]
- Škoda, P. 1996, in Astronomical Data Analysis Software and Systems V, ASP Conf. Ser., 101, 187 [Google Scholar]
- Skulskii, M. Y. 1975, AZh, 52, 710 [NASA ADS] [Google Scholar]
- Skulskii, M. Y. 1992, Sov. Astron. Lett., 18, 287 [NASA ADS] [Google Scholar]
- Skulskii, M. Y., &Topilskaya, G. P. 1991, Sov. Astron. Lett., 17, 263 [NASA ADS] [Google Scholar]
- Stassun, K. G., &Torres, G. 2016, AJ, 152, 180 [Google Scholar]
- Storn, R., &Price, K. 1997, J. Global Optim., 11, 341 [Google Scholar]
- Taranova, O. G., &Shenavrin, V. I. 2005, Astron. Lett., 31, 598 [NASA ADS] [CrossRef] [Google Scholar]
- Ten Brummelaar, T. A., McAlister, H. A., Ridgway, S. T., et al. 2005, ApJ, 628, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Touhami, Y., Gies, D. R., Schaefer, G. H., et al. 2013, AJ, 768, 128 [CrossRef] [Google Scholar]
- Umana, G., Maxted, P. F. L., Trigilio, C., et al. 2000, A&A, 358, 229 [NASA ADS] [Google Scholar]
- Umana, G., Leone, F., &Trigilio, C. 2002, A&A, 391, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Belle, G. T., Creech-Eakman, M. J., &Hart, A. 2009, MNRAS, 394, 1925 [NASA ADS] [CrossRef] [Google Scholar]
- van Hamme, W. 1993, AJ, 106, 2096 [NASA ADS] [CrossRef] [Google Scholar]
- van Leeuwen, F. 2007a, in Astrophys. Space Sci. Lib., 350 [Google Scholar]
- van Leeuwen, F. 2007b, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Rensbergen, W., &De Greve, J. P. 2016, A&A, 592, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Rensbergen, W., De Loore, C., &Jansen, K. 2006, A&A, 446, 1071 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Rensbergen, W., De Greve, J. P., De Loore, C., &Mennekens, N. 2008, A&A, 487, 1129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- von Zeipel, H. 1924, MNRAS, 84, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, R. E. 1974, ApJ, 189, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Zacharias, N., Finch, C. T., Girard, T. M., et al. 2012, VizieR Online Data Catalog: I/322 [Google Scholar]
- Zhao, M., Gies, D., Monnier, J. D., et al. 2008, ApJ, 684, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, M., Monnier, J. D., &Che, X. 2011, in Active OB Stars: Structure, Evolution, Mass Loss, and Critical Limits, eds. C. Neiner, G. Wade, G. Meynet, &G. Peters, IAU Symp., 272, 44 [NASA ADS] [Google Scholar]
- Ziolkowski, J. 1976, ApJ, 204, 512 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A:
Details on the interferometric data reductions
Additional details on the reduction process of interferometric observations are presented in this section. Detailed characteristics of all observations are presented in Table A.1. Individual interferometric observations are available in the OIFITS format through CDS. These files contain only reduced data, that is calibrated squared visibilities and closure phases. Raw data are made available upon request.
A.1. Details on the reduction of CHARA/VEGA observations
The observations were carried out during a 11 days long campaign in 2013. Both MIRC and VEGA were observing at the same time, sharing the visible and infrared photons. The majority of observations was taken in the three-telescope (3T) mode. The only two exceptions were the first (22nd Jun, 2013) and the last (1st Jul, 2013) nights. Observations from those two nights were taken in two-telescope mode. Only four CHARA telescopes (denoted E1, E2, W1, and W2) were used. The long baselines were in general east–west oriented and the short baselines north–south oriented, because the projection of β Lyr orbit on the sky is roughly east–west oriented (see Fig. A.1). The length of projected baselines ranged from ≃65 m to ≃250 m.
 |
Fig. A.1. (u, v) coverage of all interferometric observations. Colors correspond to three different instruments: NPOI (blue), CHARA/MIRC (green), CHARA/VEGA (magenta). |
 |
Fig. C.1. Comparison of an observed spectrum of β Lyr B obtained on RJD = 49866.4348 and disentangled spectra of β Lyr B with the best fitting spectra corresponding to their respective solutions listed in Table 3, that is synthetic spectra compared to observed spectrum correspond to slightly different parameters than those compared to disentangled spectra. The blue line denotes disentangled spectrum, the black line the observed spectrum, the red line best-fitting synthetic spectrum, and the yellow line fit residuals. Only principal spectral lines (Si II 6347 Å, Si II 6371 Å, Hα, He I 6678 Å) that are present within the studied spectral region Δλ ≃ 6200–6800 Å and their surroundings are plotted. |
The observations were carried out with two cameras in four passbands that were centered at following wavelengths λ C ∈ {535, 656, 706.5, 815} nm. Resolution of the recorded spectra was R = 5000. Individual frames were recorded with frequency 100 Hz, and were grouped into blocks containing 2500 frames. An observation typically contained ≃20 blocks. Within these blocks the frames were coherently summed and raw squared visibility was determined for each block. The whole passband was not used, but two narrow channels were selected in each passband. The following channels were selected: ΔCH ∈ {525–535, 535–545, 643–653, 658–667, 687–702, 709–724, 810–825, 825–840} nm. The channels avoid major spectral lines in these regions. The only exceptions are regions 643–653 nm, and 658–667 nm, which are partially affected by wings of Hα line, and 825–840 nm, which is affected by water-vapor lines. Narrow channels were chosen because of the limited coherence of the waves due to the atmospheric turbulence.
Four calibrators were observed in order to calibrate the instrumental visibilities. Due to variability of atmospheric conditions during night, a calibrator was observed before and after each observation of β Lyr. A list of calibrators and their properties are listed in Table A.2. The calibrators were chosen with help of tool SearchCal3 developed by Bonneau et al. (2006). The uniform-disk diameters of calibrators were taken from the JMMC catalog of stellar diameters by Lafrasse et al. (2010).
Journal of calibrator stars that were used to calibrate the interferometric observations of β Lyr.
List of calibrated β Lyr photometric measurement acquired at Hvar observatory.
RVs of β Lyr B.
In order to avoid modeling of highly inaccurate observations, all blocks that have instrumental visibility with S/N < 2 were removed. Also we performed simple filtering based on residual optical path delay (OPD). Correct blocks of visibility measurements have very similar OPD. Hence if OPD of one (or more) blocks deviate significantly from a mean OPD based on all blocks acquired within one measurement, this block is very likely wrong. Therefore if a block OPD differed from the mean by more than two standard deviations, it was removed.
A.2. Details on the reduction of CHARA/MIRC observations
The instrument CHARA/MIRC was used to measure squared visibilities and closure phases. MIRC performs real-time group delay tracking in the H-band. The observations come from two observational runs: (i) 2006–2007 campaign that was already analyzed by Zhao et al. (2008) and whose description can be found there, and (ii) 2013 campaign, together with VEGA, whose description follows. All observations used here were taken across the near-IR H-band.
Since 2011, MIRC can combine light from six telescopes, so it is able to record 15 squared visibilities and 20 closure phase observations. The H-band is split into eight channels with absolute wavelength accuracy ±0.25%. A more thorough description of the instrument is in studies by Monnier et al. (2010), and by Che et al. (2010), Che et al. (2012). Using Fourier transform techniques, the visibilities are measured, averaged, and corrected for biases. The bispectrum is formed using the phases and amplitudes of three baselines that form a closed triangle (Monnier et al. 2007). Amplitude calibration was performed using real-time flux estimates derived through use of a beam splitter following spatial filtering for improved performance. Lastly, observations of reference calibrators (see Table A.2) throughout the night allowed for correction of time-variable factors such as atmospheric coherence time, vibrations, differential dispersion, and birefringence in the beam train. The uncertainties of closure phase measurements were adjusted (see Sect. 4.4). MIRC and VEGA shared the same calibrators for this observing campaign.
A.3. Details on the reduction of NPOI observations
All NPOI observations were taken with the six-beam combiner. Visibilities, complex triple amplitudes, and closure phases were recorded in 16 narrow-band channels between 5500 Å and 8500 Å. The calibrators are taken from a list of single stars maintained at NPOI with diameters estimated from V and (V–K) using the surface brightness relation by Mozurkewich et al. (2003) and van Belle et al. (2009) (see Table A.2). Values of E(B–V) were derived from comparison of the observed and theoretical colors as a function of spectral type by Schmidt-Kaler in Aller et al. (1982). Values for the extinction derived from E(B–V) were compared to estimates based on the maps by Drimmel et al. (2003), and used to correct V if they agreed within 0.5 mag. Even though the surface brightness relation based on (V–K) colors is to first order independent of the reddening, we included this small correction. For these observations, only one calibrator was used: HD 176437.
NPOI data and their reductions followed the procedure described by Armstrong et al. (1998) and Hummel et al. (2003). A pipeline written in GDL4 was used for the OYSTER5 NPOI data reduction package. The pipeline automatically edits the one-second averages produced by another pipeline directly from the raw frames, based on expected performance such as the variance of fringe tracker delay, photon count rates, and narrow-angle tracker offsets. Visibility bias corrections are derived as usual from the data recorded away from the stellar fringe packet. After averaging the data over the full length of an observation, the closure phases of the calibrators were automatically unwrapped so that their variation with time, as well as that of the visibility amplitude, could be interpolated for the observations of β Lyr. For the calibration of the visibilities, the pipeline used all calibrator stars observed during a night to obtain smooth averages of the amplitude and phase-transfer functions using a Gaussian kernel of 80 min in length. The residual scatter of the calibrator visibilities and phases around the average set the level of the calibration uncertainty and was added in quadrature to the intrinsic data errors. The amplitude calibration error of typically a few percent in the red channels up to 15% in the blue channels was added in quadrature to the intrinsic error of the visibilities. The phase calibration was good to about a couple of degrees.
Appendix B:
Details on the photometric data reductions
Hvar UBVR observations are differential observations, relative to χ Lyr (HD 176437), for which the following mean Hvar all-sky values from excellent nights were adopted:
The check star v2 Lyr (HD 174602) was observed as frequently as the variable and β Lyr B was also observed as another check star on a number of nights. All Hvar UBVR observations were transformed to standard system through non-linear transformation formulæ using the HEC22 reduction program (see Harmanec et al. 1994; Harmanec & Horn 1998, for the observational strategy and data reduction)6. All observations were reduced with the latest HEC22 rel.18.2 version of the program, which allows the time variation of linear extinction coefficients to be modeled in the course of observing nights. The UBVR observations were reduced to Johnson bright standards, for which we derived robust mean UBVR values from individual observations published by Johnson (1966). The uncertainties of these observations estimated from measurements of the check star are σU,1 = 0.010 mag, σB,1 = 0.014 mag, σV,1 = 0.007 mag, and σR,1 = 0.013 mag. We underline that our R magnitudes were reduced to Johnson, not Cousins R values.
was observed as frequently as the variable and β Lyr B was also observed as another check star on a number of nights. All Hvar UBVR observations were transformed to standard system through non-linear transformation formulæ using the HEC22 reduction program (see Harmanec et al. 1994; Harmanec & Horn 1998, for the observational strategy and data reduction)6. All observations were reduced with the latest HEC22 rel.18.2 version of the program, which allows the time variation of linear extinction coefficients to be modeled in the course of observing nights. The UBVR observations were reduced to Johnson bright standards, for which we derived robust mean UBVR values from individual observations published by Johnson (1966). The uncertainties of these observations estimated from measurements of the check star are σU,1 = 0.010 mag, σB,1 = 0.014 mag, σV,1 = 0.007 mag, and σR,1 = 0.013 mag. We underline that our R magnitudes were reduced to Johnson, not Cousins R values.
Differential Johnson–Cousins BV(R)c observations were acquired at private observatory of Mr. Svoboda in Brno, Czech Republic using SBIG ST-7XME CCD camera mounted at 34 mm refractor. β Lyr and comparison star γ Lyr were observed simultaneously. The atmospheric extinction was assumed constant over the image. Seasonal transformation of the instrumental magnitudes into standard system was carried out using linear formulæ similar to Eq. (4) in Harmanec et al. (1977). Upper limit on the uncertainties of these observations are σB,2 = 0.013 mag, σV,2 = 0.013 mag, and σR,2 = 0.010 mag.
All calibrated UBVR observations acquired at Hvar observatory, and differential BV(R)c observations acquired by PS are listed in Table B.1. This table is available at CDS.
Appendix C:
Supplementary material to analysis of β Lyr B
Supplementary material to analysis of β Lyr B (see Sect. 3.1.3) is presented here.
C.1. Details on the spectroscopic observations
All 13 electronic spectrograms were obtained in the coudé focus of the 2 m reflector and have linear dispersion of 17.2 Å mm–1 and two-pixel resolution 12 600 (11–12 km s–1 per pixel). The first 7 spectra (until RJD ≃ 50 235) were taken with a Reticon 1872RF linear detector and cover a spectral region from 6300 to 6730 Å. Complete reductions (bias subtraction, flat-fielding, extraction of 1 d spectrum, wavelength calibration, normalization) of these spectrograms were carried out by PH with the program SPEFO. The remaining spectra were secured with a SITe-5800 × 2000 CCD detector and cover wavelength interval from 6260 to 6760 Å. Their initial reductions (bias subtraction, flat-fielding, extraction of 1-d spectrum, and wavelength calibration) were carried out by MŠ in IRAF7 and their normalization by PH in SPEFO. In both cases the stellar continuum was approximated by Hermite polynomials that were fitted through several (suitably chosen) continuum points.
Photometric observations of β Lyr B were obtained at Hvar observatory and their reduction procedure is described in Appendix B.
C.2. Kinematic and radiative properties of β Lyr B
Additional details on the measuring of RVs and the modeling of observed spectra with synthetic ones follow:
-
The RV measurements of β Lyr B obtained manually with SPEFO, and through comparison with synthetic spectra using PYTERPOL are listed in Table C.1. Four spectral lines were measured with the manual method on each spectrum. Instead of individual measurements, their mean and corresponding standard deviation are listed, because measurements on each spectral line did not differ systematically from RVs measured on the remaining spectral lines. The manually measured RVs give an impression that they slowly vary, but similar trend is not present in automatic measurements or RVs measured on photographic plates.
-
Uncertainties of kinematic and radiative properties of β Lyr B obtained through modeling of its observed (or disentangled) spectra with synthetic spectra (solutions 1 and 2 in Table 3) were obtained through Markov chain Monte Carlo simulation implemented within emcee8 Python library by Foreman-Mackey et al. (2013). The posterior probability distribution of for each individual optimized was fitted with a Gaussian function. Standard deviation of the function was taken for uncertainty of the optimized parameter. Only statistical part of the total uncertainty was pinpointed by this approach. The wavelength ranges fitted for observed spectra were Δλ = {6337–6410, 6530–6600, 6660–6690} Å, and for disentangled spectra Δλ = {6338–6605, 6673–6724} Å. The region Δλ = 6337–6410 Å was not modeled for observed spectra, because it contains only few weak stellar lines and is densely polluted by telluric lines.
-
Agreement between the observed (or disentangled) spectra and their best-fitting synthetic spectra (given by solutions 1 and 2 in Table 3) is demonstrated by Fig. C.1.
Only the major spectral lines and their vicinity are plotted. Only fit of one observed spectrum with high S/N is shown. Jags in the observed spectrum are remnants of telluric lines. Also we note that PYTERPOL does not require that the modeled spectra are equidistant. Hence it was not necessary to fill the gaps in spectra that emerged after the removal of telluric lines.
C.3. Proper motion of β Lyr A and B
Proper motions of β Lyr A and B were downloaded from the Vizier portal. Each 2-d vector had a component along the declination µδ
and in the perpendicular direction along the right ascension µα. The latter coordinate was corrected for declination of both systems. The following coordinates were used: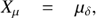 (C.1)
(C.1)
 (C.2)where δ denotes declination. For β Lyr A δ
A = 33.362667 deg, and for β Lyr B δ
B = 33.351856 deg were adopted. All studied records in coordinates given by Eqs. (C.1), and (C.2) are listed in Table C.2.
(C.2)where δ denotes declination. For β Lyr A δ
A = 33.362667 deg, and for β Lyr B δ
B = 33.351856 deg were adopted. All studied records in coordinates given by Eqs. (C.1), and (C.2) are listed in Table C.2.
Proper motion measurements of β Lyr B.
Appendix D:
A note on disk model with a vertical temperature jump
The previous version of SHELLSPEC contained a “nebula” disk model with an exponential vertical density profile ρ(z), and a possible jump in the corresponding temperature profile T(z) to mimic a hotter disk atmosphere irradiated by the star. For this model, we realized there are bright spots in FUV close to the outer rim (see Fig. D.1). They actually helped to decrease the  contribution.
contribution.
 |
Fig. D.1. Synthetic image of β Lyr A for λ = 155 nm (OAO2 band). This model is based on a “nebula” with a vertical temperature jump, T(z) profile is determined by its scale height H and multiplication factor h
mul = 5.27, together with temperature inversion scale h
inv = 5.19 and factor t
inv = 4.87. The resulting total χ
2 = 99430, with individual contributions as low as |
This is a well-known problem caused by a simple linear interpolation of both ρ and T quantities within the critical step of the optical depth, where the medium changes from thick to thin, and there is a large source Sv
(and contribution) function in the middle. When the resolution of the model is increased twice, or four times, these spots subsequently disappear and  increases again. Users should be aware of these discretization artifacts, because they sometimes appear in the course of convergence (e.g., when the orbital inclination changes). The same would be true for models with overlapping optically thick and optically thin objects, like slab + slab, or wedge + flow. Nevertheless, this problem is an indication for us that FUV radiation and corresponding light curves should be described by a more complete model of the disk atmosphere.
increases again. Users should be aware of these discretization artifacts, because they sometimes appear in the course of convergence (e.g., when the orbital inclination changes). The same would be true for models with overlapping optically thick and optically thin objects, like slab + slab, or wedge + flow. Nevertheless, this problem is an indication for us that FUV radiation and corresponding light curves should be described by a more complete model of the disk atmosphere.
All Tables
Kinematic and radiative properties of β Lyr B estimated via a comparison of its disentangled spectrum and all observed spectra with synthetic ones using PYTERPOL.
Robust mean RVs of individual spectral lines measured in SPEFO for Ondřejov spectra of β Lyr B.
Journal of calibrator stars that were used to calibrate the interferometric observations of β Lyr.
List of calibrated β Lyr photometric measurement acquired at Hvar observatory.
All Figures
 |
Fig. 1. Phase coverage of spectro-interferometric observations of β Lyr acquired by different instruments. δ denotes the relative declination (positive toward the north), and α the relative right ascension (positive toward the east). The black line shows the size and orientation of the β Lyr orbit in the sky, the blue dots show orbital phases corresponding to NPOI observations, the magenta dots to CHARA/VEGA observations, the green dots to CHARA/MIRC observations acquired in 2013, and the red dots to CHARA/MIRC observations acquired in 2006/2007. An arbitrary vertical shift of 0.2 mas is added to separate the various orbits. |
| In the text | |
 |
Fig. 2. Available RVs of β Lyr B. The first three datasets are RVs measured on photographic spectra of moderate dispersion: green open circles denote the RVs measured by Petrie & Pearce (1961), the red open triangles come from Abt et al. (1962), and the black boxes are RVs from Abt & Levy (1976). The filled blue diamonds are the RVs measured on Ondřejov electronic spectra with PYTERPOL. The rms errors, available only for Abt & Levy (1976) and new RVs are also shown. We note that the most deviant RV of −45 km s−1 is based on a single line and comes probably from an underexposed spectrum. |
| In the text | |
 |
Fig. 3. Proper motions of β Lyr A and β Lyr B. The black points denote proper motion measurements of β Lyr A, the black triangles proper motions of β Lyr B, the red point the mean weighted proper motion of β Lyr A, and the red triangle the mean weighted proper motion of β Lyr B. Xµ, Yµ are Cartesian coordinates of the proper motion vector given by Eqs. (C.1) and (C.2). The former is north–south oriented, and the latter east–west oriented. |
| In the text | |
 |
Fig. 4. Geometric shapes of models of accretion disks. (I) Denotes the slab, (II) the wedge, (III) the lens, and (IV) the envelope. The latter is shown as if it was filling the Roche limit, that is Rout = RL1, where Rout = RL1 denotes point radius of the Roche lobe. Here it is shown this way to emphasize the geometry of the disk, but its shape may be more symmetric depending on its filling factor. See Sect. 4.3 for the description of individual disk shapes. The Nebula is not presented here, since no simple geometrical sketch can be given. It is illustrated, however, in Fig. 5. |
| In the text | |
 |
Fig. 5. Synthetic images of β Lyr A system for five different models: slab power-law, slab steady, wedge power-law, wedge steady, and nebula. The scale of grays corresponds to the monochromatic intensity Iv (in erg s−1 cm−2 sr−1 Hz−1). The wavelength is always λ = 545 mn and the orbital phase 0.25; α goes along east–west direction, and δ along north–south direction. It is worth noting that each model converged independently, but the outcomes are remarkably similar in terms of geometry. |
| In the text | |
 |
Fig. 6. Synthetic images of β Lyr A for the best-fit nebula model, with total (not reduced) χ 2 = 103 233, shown for four different wavelengths: λ = 155 nm (FUV), 545 nm (V band), 1630 nm (H), and 4750 nm (M). The axes correspond to the right ascension α and declination δ (in mas), while the color scale corresponds to the monochromatic intensity Iv (in erg s−1 cm−2 sr−1 Hz−1). This is a small subset of all 2392 images (per one iteration) used to derive light curves, interferometric visibilities, closure phases, and triple product amplitudes. |
| In the text | |
 |
Fig. 7. Observed and synthetic light curves of β Lyr A, shown for all 21 datasets (see their names in the right column). The light curves are phased according to 1. Vertical offsets are arbitrary. The best-fit model is again “nebula” with χ
2 = 103 233; the individual contribution arising from light curves comparison is |
| In the text | |
 |
Fig. 8. Similar comparison as in Fig. 7, but for squared visibilities |V|2, with a contribution |
| In the text | |
 |
Fig. 9. Similar comparison as in Fig. 8, but for closure phases T3ϕ (left) and triple product amplitudes |T3| (right). Contributions to the total χ2 are |
| In the text | |
 |
Fig. 10. Top panel: optical depth τ (computed for the wavelength λ = 1630 nm) of the β Lyr A disk, which is observed approximately edge-on (that is from the top). The coordinate z thus corresponds to the line of sight, while x (and y) to the sky plane. The center is empty because the gainer is a non-transparent object. In this case, the inner-rim density of the wedge power-law model is set low, ρ0 = 10−9 g cm−3, to demonstrate a separation from the outer rim. The dashed line shows the physical position of the photosphere (τ = 2/3). The lines-of-sight grid exhibits “steps” due to the limited spatial resolution of our model (1 R⊙), even though the integration of the radiation transfer (the contribution function) is internally performed on a much finer grid. Bottom panel: corresponding photospheric temperature Tphot of the disk, which varies along with the radial temperature profile T(R). |
| In the text | |
 |
Fig. 11. Optical depth τ in the vertical (perpendicular) cross-section of the disk; other parameters are the same as in Fig. 10. The lines of sight are seemingly different from the wedge shape, but this only because they start either in the vacuum, or at the non-transparent object. |
| In the text | |
 |
Fig. 12. Comparison of radial temperature profiles of the accretion disk surrounding the gainer. The dotted line is the profile obtained by Mennickent & Djurašević (2013), and the dashed line is mean temperature of the two-temperature model developed by Linnell (2000). The red line represents the best-fitting power-law radial temperature profile (solution slab/pl in Table 9), and the red belt all plausible solutions given by the uncertainty of the inner rim temperature and the exponent of the power-law, and the red point position of photosphere (τ = 2/3), where temperature Tph. = 7 192 K is reached. The blue line represents the best-fitting steady-disk radial temperature profile (solution slab/sd in Table 9), the blue belt all plausible solutions given by uncertainty in the inner rim temperature, and the blue point position of photosphere (τ = 2/3), where temperature Tph: = 7 192 K K is reached. The photospheric temperatures were computed for a line of sight in the plane z = 0 and piercing through center of the accretion disk |
| In the text | |
 |
Fig. 13. Synthetic images of slab power-law model which was further improved by a “spot” (that is a spherical structure between the primary and secondary, partly hidden inside the slab). The total (not reduced) χ2 value was decreased from 105 202 (without the spot) down to 102 005, which is a significant improvement. Four wavelengths are shown: λ = 155 nm (FUV), 545 nm (V band), 1630 nm (H), and 4750 nm (M). |
| In the text | |
 |
Fig. 14. Comparison of synthetic spectral-energy distributions (thick lines) of β Lyr A and observed SED (thin lines) according to Burnashev & Skulskii (1978). The monochromatic flux Fλ (in erg s−1 cm−2 cm−1) was measured in the range of λ = 330–740 nm. The color scale correspond to the orbital phase. Observation uncertainties are on the order of 5%. The model (corresponding to a “nebula” with tinv = 4.53) was not converged with respect to these observations and the SEDs thus inevitably exhibit some systematic offsets. |
| In the text | |
 |
Fig. A.1. (u, v) coverage of all interferometric observations. Colors correspond to three different instruments: NPOI (blue), CHARA/MIRC (green), CHARA/VEGA (magenta). |
| In the text | |
 |
Fig. C.1. Comparison of an observed spectrum of β Lyr B obtained on RJD = 49866.4348 and disentangled spectra of β Lyr B with the best fitting spectra corresponding to their respective solutions listed in Table 3, that is synthetic spectra compared to observed spectrum correspond to slightly different parameters than those compared to disentangled spectra. The blue line denotes disentangled spectrum, the black line the observed spectrum, the red line best-fitting synthetic spectrum, and the yellow line fit residuals. Only principal spectral lines (Si II 6347 Å, Si II 6371 Å, Hα, He I 6678 Å) that are present within the studied spectral region Δλ ≃ 6200–6800 Å and their surroundings are plotted. |
| In the text | |
 |
Fig. D.1. Synthetic image of β Lyr A for λ = 155 nm (OAO2 band). This model is based on a “nebula” with a vertical temperature jump, T(z) profile is determined by its scale height H and multiplication factor h
mul = 5.27, together with temperature inversion scale h
inv = 5.19 and factor t
inv = 4.87. The resulting total χ
2 = 99430, with individual contributions as low as |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.